2023_open_source_contest_warmup_1st_issue2 finish

APP_Framework/Applications/app_test/Kconfig

@@ -243,6 +243,10 @@ menu "test app"
             menuconfig USER_TEST_HASH
                 bool "Config test hash"
                 default n
+
+            menuconfig USER_TEST_RBTREE
+                bool "Config test rbtree"
+                default n
             
         endif
 endmenu

APP_Framework/Applications/app_test/Makefile

@@ -105,5 +105,9 @@ ifeq ($(CONFIG_ADD_XIZI_FETURES),y)
         SRC_FILES += test_hash/test_hash.c
     endif 
 
+    ifeq ($(CONFIG_USER_TEST_RBTREE),y)
+        SRC_FILES += test_rbtree/test_rbtree.c
+    endif 
+
     include $(KERNEL_ROOT)/compiler.mk
 endif

APP_Framework/Applications/app_test/test_rbtree/README.md

@@ -0,0 +1,109 @@
+# **基于cortex-m4-emulator实现红黑树并测试验证**
+
+## 1. 简介
+
+基于cortex-m4-emulator实现红黑树, 实现了红黑树的插入，查找，删除的功能。设计了一些数据进行测试。
+
+## 2. 数据结构设计说明
+
+```c
+// define color of red-black tree
+enum Color {RED, BLACK};
+
+// define a node of red-black tree
+struct Node {
+    int key;
+    int value;
+    enum Color color;
+    struct Node *left, *right, *parent;
+};
+```
+
+将红黑树的红黑属性设成枚举类型。红黑树的节点分别存储key，value，color，左右子，以及父节点。
+
+## 3. 测试程序说明
+
+```c
+void TestRBTree(void)
+{   
+    struct Node *root = NULL;
+    printf("创建红黑树并且插入以下结点\n");
+    printf("key: 7, value: 7\n");
+    printf("key: 3, value: 3\n");
+    printf("key: 18, value: 18\n");
+    printf("key: 10, value: 10\n");
+    printf("key: 22, value: 22\n");
+    printf("key: 8, value: 8\n");
+    printf("key: 11, value: 11\n");
+    printf("key: 26, value: 26\n");
+    printf("key: 2, value: 2\n");
+    printf("key: 6, value: 6\n");
+    printf("key: 13, value: 13\n");
+    printf("key: 20, value: 20\n");
+    printf("key: 27, value: 27\n");
+    printf("key: 1, value: 1\n");
+    printf("key: 12, value: 12\n");
+    printf("key: 14, value: 14\n");
+    printf("key: 25, value: 25\n");
+    int values[] = {7, 3, 18, 10, 22, 8, 11, 26, 2, 6, 13, 20, 27, 1, 12, 14, 25};
+
+    for (int i = 0; i < sizeof(values) / sizeof(values[0]); i++)
+        insertNode(&root, values[i], values[i]);
+
+    printf("插入创建完毕后中序遍历红黑树结果：\n");
+    inorderTraversal(root);
+    printf("\n");
+
+    printf("查找key值为 10 的结点\n");
+    struct Node *searchResult = searchNode(root, 10);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 10);
+
+    printf("查找key值为 100 的结点\n");
+    searchResult = searchNode(root, 100);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 100);
+
+    printf("删除结点 10 和 22\n");
+    int deleteData = 10;
+    deleteNode(&root, 10);
+    deleteNode(&root, 22);
+
+    printf("查找key值为 10 的结点\n");
+    searchResult = searchNode(root, 10);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 10);
+    
+    printf("查找key值为 22 的结点\n");
+    searchResult = searchNode(root, 22);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 22);
+    
+    
+    printf("删除结点 %d 后的中序遍历结果：\n", deleteData);
+    inorderTraversal(root);
+    printf("\n");
+    printf("清空红黑树并且释放内存\n");
+    clear(root);
+}
+```
+
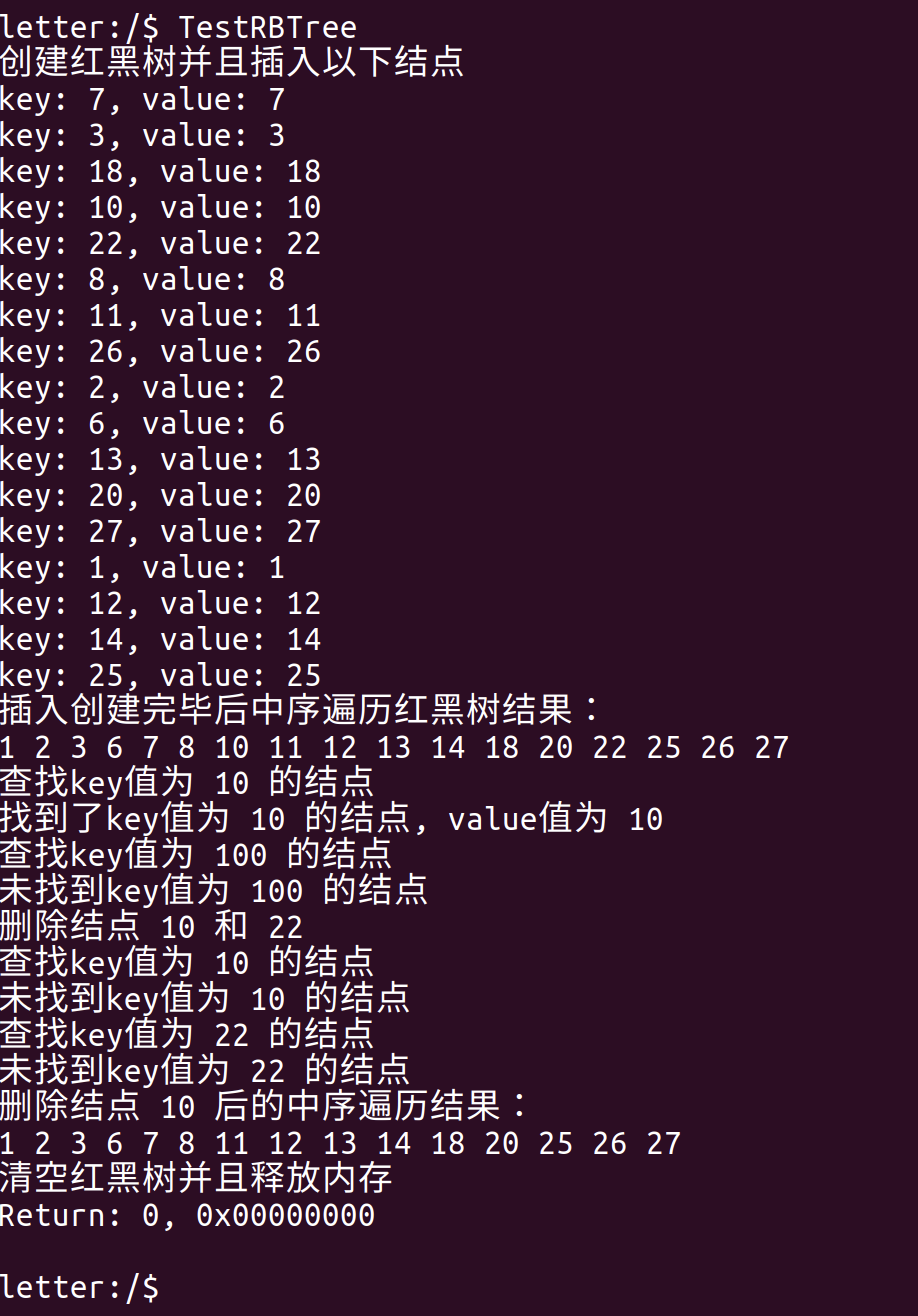
+首先先插入一些节点，然后进行中序遍历，查看是否符合预期。然后查找其中节点的值，分别是查找到了的情况和不存在的情况。然后从红黑树中删除两个节点，在此查找，不存在，再将删除后的中序遍历结果打印，最后清空红黑树并且释放内存。
+
+## 4. 运行结果（##需结合运行测试截图按步骤说明##）
+
+首先启动cortex-m4-emulator
+
+![2023_open_source_contest_warmup_1st_issue2_1](https://xubbbb-chartbed.oss-cn-shanghai.aliyuncs.com/img/markdown/2023_open_source_contest_warmup_1st_issue2_1.png)
+
+然后运行TestRBTree指令进行测试
+![2023_open_source_contest_warmup_1st_issue2_2](https://xubbbb-chartbed.oss-cn-shanghai.aliyuncs.com/img/markdown/2023_open_source_contest_warmup_1st_issue2_2.png)
+

APP_Framework/Applications/app_test/test_rbtree/test_rbtree.c

@@ -0,0 +1,100 @@
+/*
+* Copyright (c) 2020 AIIT XUOS Lab
+* XiUOS is licensed under Mulan PSL v2.
+* You can use this software according to the terms and conditions of the Mulan PSL v2.
+* You may obtain a copy of Mulan PSL v2 at:
+*        http://license.coscl.org.cn/MulanPSL2
+* THIS SOFTWARE IS PROVIDED ON AN "AS IS" BASIS, WITHOUT WARRANTIES OF ANY KIND,
+* EITHER EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO NON-INFRINGEMENT,
+* MERCHANTABILITY OR FIT FOR A PARTICULAR PURPOSE.
+* See the Mulan PSL v2 for more details.
+*/
+
+/**
+* @file:    test_rbtree.c
+* @brief:   a application to test red black tree and print result
+* @version: 1.1
+* @author:  LeviXubbbb(Bin Xu)
+* @date:    2023/06/28
+*/
+
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+#include <transform.h>
+#include "test_rbtree.h"
+#ifdef ADD_XIZI_FETURES
+
+void TestRBTree(void)
+{   
+    struct Node *root = NULL;
+    printf("创建红黑树并且插入以下结点\n");
+    printf("key: 7, value: 7\n");
+    printf("key: 3, value: 3\n");
+    printf("key: 18, value: 18\n");
+    printf("key: 10, value: 10\n");
+    printf("key: 22, value: 22\n");
+    printf("key: 8, value: 8\n");
+    printf("key: 11, value: 11\n");
+    printf("key: 26, value: 26\n");
+    printf("key: 2, value: 2\n");
+    printf("key: 6, value: 6\n");
+    printf("key: 13, value: 13\n");
+    printf("key: 20, value: 20\n");
+    printf("key: 27, value: 27\n");
+    printf("key: 1, value: 1\n");
+    printf("key: 12, value: 12\n");
+    printf("key: 14, value: 14\n");
+    printf("key: 25, value: 25\n");
+    int values[] = {7, 3, 18, 10, 22, 8, 11, 26, 2, 6, 13, 20, 27, 1, 12, 14, 25};
+
+    for (int i = 0; i < sizeof(values) / sizeof(values[0]); i++)
+        insertNode(&root, values[i], values[i]);
+
+    printf("插入创建完毕后中序遍历红黑树结果：\n");
+    inorderTraversal(root);
+    printf("\n");
+
+    printf("查找key值为 10 的结点\n");
+    struct Node *searchResult = searchNode(root, 10);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 10);
+
+    printf("查找key值为 100 的结点\n");
+    searchResult = searchNode(root, 100);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 100);
+
+    printf("删除结点 10 和 22\n");
+    int deleteData = 10;
+    deleteNode(&root, 10);
+    deleteNode(&root, 22);
+
+    printf("查找key值为 10 的结点\n");
+    searchResult = searchNode(root, 10);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 10);
+    
+    printf("查找key值为 22 的结点\n");
+    searchResult = searchNode(root, 22);
+    if (searchResult != NULL)
+        printf("找到了key值为 %d 的结点, value值为 %d \n", searchResult->key, searchResult->value);
+    else
+        printf("未找到key值为 %d 的结点\n", 22);
+    
+    
+    printf("删除结点 %d 后的中序遍历结果：\n", deleteData);
+    inorderTraversal(root);
+    printf("\n");
+    printf("清空红黑树并且释放内存\n");
+    clear(root);
+}
+
+PRIV_SHELL_CMD_FUNCTION(TestRBTree, a red black tree test sample, PRIV_SHELL_CMD_MAIN_ATTR);
+#endif

APP_Framework/Applications/app_test/test_rbtree/test_rbtree.h

@@ -0,0 +1,331 @@
+/*
+* Copyright (c) 2020 AIIT XUOS Lab
+* XiUOS is licensed under Mulan PSL v2.
+* You can use this software according to the terms and conditions of the Mulan PSL v2.
+* You may obtain a copy of Mulan PSL v2 at:
+*        http://license.coscl.org.cn/MulanPSL2
+* THIS SOFTWARE IS PROVIDED ON AN "AS IS" BASIS, WITHOUT WARRANTIES OF ANY KIND,
+* EITHER EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO NON-INFRINGEMENT,
+* MERCHANTABILITY OR FIT FOR A PARTICULAR PURPOSE.
+* See the Mulan PSL v2 for more details.
+*/
+
+/**
+* @file:    test_rbtree.h
+* @brief:   a header file to implement red black tree
+* @version: 1.1
+* @author:  LeviXubbbb(Bin Xu)
+* @date:    2023/06/28
+*/
+
+#ifndef XIUOS_TEST_RBTREE_H
+#define XIUOS_TEST_RBTREE_H
+
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+
+// define color of red-black tree
+enum Color {RED, BLACK};
+
+// define a node of red-black tree
+struct Node {
+    int key;
+    int value;
+    enum Color color;
+    struct Node *left, *right, *parent;
+};
+
+// create a new nodes
+struct Node *createNode(int key, int value) {
+    struct Node *newNode = (struct Node*)malloc(sizeof(struct Node));
+    newNode->key = key;
+    newNode->value = value;
+    newNode->color = RED;
+    newNode->left = newNode->right = newNode->parent = NULL;
+    return newNode;
+}
+
+// red-black tree left rotation
+void leftRotate(struct Node **root, struct Node *x) {
+    struct Node *y = x->right;
+    x->right = y->left;
+    if (y->left != NULL)
+        y->left->parent = x;
+    y->parent = x->parent;
+    if (x->parent == NULL)
+        *root = y;
+    else if (x == x->parent->left)
+        x->parent->left = y;
+    else
+        x->parent->right = y;
+    y->left = x;
+    x->parent = y;
+}
+
+// red-black tree right rotation
+void rightRotate(struct Node **root, struct Node *y) {
+    struct Node *x = y->left;
+    y->left = x->right;
+    if (x->right != NULL)
+        x->right->parent = y;
+    x->parent = y->parent;
+    if (y->parent == NULL)
+        *root = x;
+    else if (y == y->parent->left)
+        y->parent->left = x;
+    else
+        y->parent->right = x;
+    x->right = y;
+    y->parent = x;
+}
+
+// red-black tree fix-up
+void fixViolation(struct Node **root, struct Node *newNode) {
+    struct Node *parent = NULL;
+    struct Node *grandparent = NULL;
+
+    while ((newNode != *root) && (newNode->color != BLACK) && (newNode->parent->color == RED)) {
+        parent = newNode->parent;
+        grandparent = newNode->parent->parent;
+
+        if (parent == grandparent->left) {
+            struct Node *uncle = grandparent->right;
+
+            if (uncle != NULL && uncle->color == RED) {
+                grandparent->color = RED;
+                parent->color = BLACK;
+                uncle->color = BLACK;
+                newNode = grandparent;
+            } else {
+                if (newNode == parent->right) {
+                    leftRotate(root, parent);
+                    newNode = parent;
+                    parent = newNode->parent;
+                }
+
+                rightRotate(root, grandparent);
+                int temp = parent->color;
+                parent->color = grandparent->color;
+                grandparent->color = temp;
+                newNode = parent;
+            }
+        } else {
+            struct Node *uncle = grandparent->left;
+
+            if ((uncle != NULL) && (uncle->color == RED)) {
+                grandparent->color = RED;
+                parent->color = BLACK;
+                uncle->color = BLACK;
+                newNode = grandparent;
+            } else {
+                if (newNode == parent->left) {
+                    rightRotate(root, parent);
+                    newNode = parent;
+                    parent = newNode->parent;
+                }
+
+                leftRotate(root, grandparent);
+                int temp = parent->color;
+                parent->color = grandparent->color;
+                grandparent->color = temp;
+                newNode = parent;
+            }
+        }
+    }
+
+    (*root)->color = BLACK;
+}
+
+// insert a node into red-black tree
+void insertNode(struct Node **root, int key, int value) {
+    struct Node *newNode = createNode(key, value);
+    struct Node *current = *root;
+    struct Node *parent = NULL;
+
+    while (current != NULL) {
+        parent = current;
+        if (key < current->key)
+            current = current->left;
+        else
+            current = current->right;
+    }
+
+    newNode->parent = parent;
+    if (parent == NULL)
+        *root = newNode;
+    else if (key < parent->key)
+        parent->left = newNode;
+    else
+        parent->right = newNode;
+
+    fixViolation(root, newNode);
+}
+
+// search a node in red-black tree
+struct Node *searchNode(struct Node *root, int key) {
+    if (root == NULL || root->key == key)
+        return root;
+
+    if (root->key < key)
+        return searchNode(root->right, key);
+
+    return searchNode(root->left, key);
+}
+
+// find the minimum node in red-black tree
+struct Node *minimumNode(struct Node *node) {
+    while (node->left != NULL)
+        node = node->left;
+
+    return node;
+}
+
+// replace a node with another node
+void transplant(struct Node **root, struct Node *u, struct Node *v) {
+    if (u->parent == NULL)
+        *root = v;
+    else if (u == u->parent->left)
+        u->parent->left = v;
+    else
+        u->parent->right = v;
+
+    if (v != NULL)
+        v->parent = u->parent;
+}
+
+// fix the delete violation in red-black tree
+void fixDeleteViolation(struct Node **root, struct Node *node, struct Node *parent) {
+    struct Node *sibling = NULL;
+
+    while ((node != *root) && ((node == NULL) || (node->color == BLACK))) {
+        if (node == parent->left) {
+            sibling = parent->right;
+
+            if (sibling->color == RED) {
+                sibling->color = BLACK;
+                parent->color = RED;
+                leftRotate(root, parent);
+                sibling = parent->right;
+            }
+
+            if ((sibling->left == NULL || sibling->left->color == BLACK) &&
+                (sibling->right == NULL || sibling->right->color == BLACK)) {
+                sibling->color = RED;
+                node = parent;
+                parent = node->parent;
+            } else {
+                if (sibling->right == NULL || sibling->right->color == BLACK) {
+                    sibling->left->color = BLACK;
+                    sibling->color = RED;
+                    rightRotate(root, sibling);
+                    sibling = parent->right;
+                }
+
+                sibling->color = parent->color;
+                parent->color = BLACK;
+                sibling->right->color = BLACK;
+                leftRotate(root, parent);
+                node = *root;
+                break;
+            }
+        } else {
+            sibling = parent->left;
+
+            if (sibling->color == RED) {
+                sibling->color = BLACK;
+                parent->color = RED;
+                rightRotate(root, parent);
+                sibling = parent->left;
+            }
+
+            if ((sibling->left == NULL || sibling->left->color == BLACK) &&
+                (sibling->right == NULL || sibling->right->color == BLACK)) {
+                sibling->color = RED;
+                node = parent;
+                parent = node->parent;
+            } else {
+                if (sibling->left == NULL || sibling->left->color == BLACK) {
+                    sibling->right->color = BLACK;
+                    sibling->color = RED;
+                    leftRotate(root, sibling);
+                    sibling = parent->left;
+                }
+
+                sibling->color = parent->color;
+                parent->color = BLACK;
+                sibling->left->color = BLACK;
+                rightRotate(root, parent);
+                node = *root;
+                break;
+            }
+        }
+    }
+
+    if (node != NULL)
+        node->color = BLACK;
+}
+
+
+// delete a node from red-black tree
+void deleteNode(struct Node **root, int key) {
+    struct Node *nodeToDelete = searchNode(*root, key);
+    if (nodeToDelete == NULL)
+        return;
+
+    struct Node *child = NULL;
+    struct Node *parent = NULL;
+    enum Color originalColor = nodeToDelete->color;
+
+    if (nodeToDelete->left == NULL) {
+        child = nodeToDelete->right;
+        parent = nodeToDelete->parent;
+        transplant(root, nodeToDelete, nodeToDelete->right);
+    } else if (nodeToDelete->right == NULL) {
+        child = nodeToDelete->left;
+        parent = nodeToDelete->parent;
+        transplant(root, nodeToDelete, nodeToDelete->left);
+    } else {
+        struct Node *successor = minimumNode(nodeToDelete->right);
+        originalColor = successor->color;
+        child = successor->right;
+        parent = successor->parent;
+
+        if (successor->parent == nodeToDelete)
+            parent = successor;
+        else {
+            transplant(root, successor, successor->right);
+            successor->right = nodeToDelete->right;
+            successor->right->parent = successor;
+        }
+
+        transplant(root, nodeToDelete, successor);
+        successor->left = nodeToDelete->left;
+        successor->left->parent = successor;
+        successor->color = nodeToDelete->color;
+    }
+
+    if (originalColor == BLACK)
+        fixDeleteViolation(root, child, parent);
+    free(nodeToDelete);
+}
+
+// inorder traversal
+void inorderTraversal(struct Node *root) {
+    if (root != NULL) {
+        inorderTraversal(root->left);
+        printf("%d ", root->key);
+        inorderTraversal(root->right);
+    }
+}
+
+//clear the tree
+void clear(struct Node *root) {
+    if (root != NULL) {
+        clear(root->left);
+        clear(root->right);
+        free(root);
+    }
+}
+
+#endif //XIUOS_TEST_RBTREE_H

Ubiquitous/XiZi_IIoT/board/k210-emulator/config.mk

@@ -7,7 +7,7 @@ export APPLFLAGS := -mcmodel=medany -march=rv64imac -mabi=lp64 -nostartfiles -Wl
 
 export CXXFLAGS := -mcmodel=medany -march=rv64imac -mabi=lp64 -fno-common -ffunction-sections -fdata-sections -fstrict-volatile-bitfields -O0 -Wa,-g -ggdb -Werror
 
-export CROSS_COMPILE ?=/opt/gnu-mcu-eclipse/riscv-none-gcc/8.2.0-2.1-20190425-1021/bin/riscv-none-embed-
+export CROSS_COMPILE ?=/opt/xpack-riscv-none-embed-gcc-8.3.0-1.2/bin/riscv-none-embed-
 
 export DEFINES := -DHAVE_CCONFIG_H -DHAVE_SIGINFO