diff --git a/Blockchain/part0_Linux基础.md b/Blockchain/part0_Linux基础.md
new file mode 100644
index 0000000..5bf99d9
--- /dev/null
+++ b/Blockchain/part0_Linux基础.md
@@ -0,0 +1,384 @@
+# 新手建议
+
+## 学习Linux的注意事项
+
+* Linux严格区分大小写(命令全都是小写)—— 命令、文件名、选项等均区分大小写
+
+* Linux中**所有内容**以文件形式保存,包括硬件
+
+ * 硬盘文件是/dev/sd[a-p]
+ * 光盘文件是/dev/sr0等
+
+* Windows通过扩展名区分文件类型,还有图标可以区分;Linux不靠扩展名区分文件类型,靠文件权限区分,但也有一些约定俗成的扩展名:
+
+ * 压缩包:"*.gz", "*.bz2", "*.tar.bz2", "*.tgz"等
+ * 二进制软件包:".rpm"
+ * 网页文件:"*.sh"
+ * 配置文件:"*.conf"
+
+ 注意:这些扩展名不是必要的,即时不加扩展名也没有影响,只是便于管理而已
+
+* Linux所有存储设备都必须挂在之后用户才能使用,包括硬盘、U盘、光盘(将设备与挂载点连接的过程就是挂载)
+
+* Windows下的程序不能直接在Linux中安装和运行
+
+## 服务器管理和维护建议
+
+### 服务器管理
+
+| 目录名 | 目录作用 |
+| :----------: | :----------------------------------------------------------: |
+| /bin/ | 存放系统命令的目录,普通用户和超级用户都可以执行,不过放在/bin下的命令在单用户模式下也可以执行 |
+| /sbin/ | 保存和系统环境设置相关的命令,只有超级用户可以使用这些命令进行系统环境设置,但是有些命令可以允许普通用户查看 |
+| /usr/bin/ | 存放系统命令的目录,普通用户和超级用户都可以执行,这些命令和系统启动无关,在单用户模式下不能执行 |
+| /usr/sbin/ | 存放根文件系统不必要的系统管理命令,例如多数服务程序。只有超级用户可以使用 |
+| /boot/ | 系统启动目录,保存系统启动相关的文件,如内核文件和启动引导程序(grub)文件等 |
+| /dev/ | 设备文件保存位置,我们已经说过Linux中所有内容以文件形式保存,包括硬件,这个目录就是用来 保存所有硬件设备的 |
+| /etc/ | 配置文件保存位置,系统内所有采用默认安装方式(npm安装)的服务的配置文件全部保存在这个目录中,如用户账户和密码,服务的启动脚本,常用服务的配置文件等 |
+| /home/ | 每个用户的默认登陆位置,普通用户的home目录就是在/home下建立一个和用户名相同的目录 |
+| /lib/ | 系统调用的函数库保存位置 |
+| /lost+found/ | 当系统意外崩溃或机器意外关机时,产生的一些文件碎片放在这里,当系统启动的过程中fsck工具会对其进行检查,并修复已经损坏的文件系统。这个目录只在每个分区中出现,例如/lost+found就是根分区的备份恢复目录,/boot/lost+found就是/boot分区的备份恢复目录 |
+| /media/ | 挂载目录,系统建议是用来挂载媒体设备的,例如软盘和光盘 |
+| /mnt/ | 挂载目录,建议挂载额外设备,如U盘,移动硬盘和其他操作系统的分区 |
+| /misc/ | 挂载目录,系统建议用来挂载NFS服务的共享目录 |
+| /opt/ | 第三方安装的软件保存位置,但现在更多的是保存在/usr/local中 |
+| /proc/ | 虚拟文件系统,该目录的数据不保存到硬盘中,而是保存到内存中。主要保存系统的内核、进程、外部设备状态和网络状态灯,如/proc/cpuinfo是保存CPU信息的,/proc/devices是保存设备驱动的列表的,/proc/filesystems是保存 文件系统列表的,/proc/net/是保存网络协议信息的 |
+| /sys/ | 虚拟文件系统,主要保存内核相关信息 |
+| /root/ | 超级用户的家目录 |
+| /srv/ | 服务数据目录, 一些系统服务启动后可以在这个目录保存需要的数据 |
+| /tmp/ | 临时目录,系统存放临时文件的目录,该目录下所有用户都可以访问和写入,我们建议此目录不能保存重要数据,最好每次开机都把该目录清空 |
+| /usr/ | 系统软件资源目录,注意usr不是user的缩写,而是"Unix Software Resource"的缩写,所以不是存放用户数据,而是存放系统软件资源的目录。系统中安装的软件大多数都在这里 |
+| /var/ | 动态数据保存位置,主要保存缓存、日志以及软件运行所产生的文件 |
+
+### 服务器注意事项
+
+1. 远程服务器不允许关机,只能重启
+2. 重启时应该关闭服务
+3. 不要在服务器的访问高峰运行高负载命令
+4. 远程配置防火墙时不要把自己踢出服务器(可以设置每五分钟将防火墙规则重置一次,配置完之后再取消该设置)
+5. 指定合理的密码规范并定期更新
+6. 合理分配权限
+7. 定期备份重要数据和日志
+
+磁盘分区是用分区编辑器在磁盘上划分几个逻辑部分,碟片一旦划分成数个分区,不同类的目录和文件 可以存储进不同的分区。
+
+# 系统分区
+
+## 分区类型
+
+* 主分区:最多只能有4个
+* 扩展分区:
+ * 最多只能有1个
+ * 主分区加扩展分区最多有4个
+ * 不能写入数据,只能包含逻辑分区(这种限制是硬盘的限制)
+* 逻辑分区
+
+## 格式化
+
+硬盘经过正确分区后仍不能写入数据,我们的硬盘还必须经过格式化之后才能写入数据。格式化又称逻辑格式化,它是根据用户选定的文件系统(如FAT16、FAT32、NTFS、EXT 2、EXT3、EXT4等),在磁盘的特定区域写入特定数据,在分区中划分出一片用于存放文件分配表、目录表等用于文件管理的磁盘空间。格式化就是按照文件系统的规则将硬盘分成等大小的数据块,我们把数据块称为block。
+
+> 注:Windows可以识别的系统有FAT16、FAT32、NTFS;Linux可以识别的系统有EXT2、EXT3、EXT4
+
+## 设备文件名
+
+#### 硬盘设备文件名
+
+Windows是直接分区——>格式化——>分配盘符即可使用,Linux需要分区——>格式化——>给分区建立设备文件名——>分配盘符才能使用。
+
+| 硬件 | 设备文件名 |
+| ----------------- | ------------------- |
+| IDE硬盘 | /dev/hd[a-d] |
+| SCSI/SATA/USB硬盘 | /dev/sd[a-p] |
+| 光驱 | /dev/cdrom或dev/sr0 |
+| 软盘 | /dev/fd[0-1] |
+| 打印机(25针) | /dev/lp[0-2] |
+| 打印机(USB) | /dev/usb/lp[0-15] |
+| 鼠标 | /dev/mouse |
+
+#### 分区设备文件名
+
+分区设备文件名直接**在硬盘设备文件名后面加分区号**即可,如
+
+* IDE硬盘接口第一个分区:/dev/hda1(如今几乎看不到)
+* SCSI硬盘接口、SATA硬盘接口的第一个分区:/dev/sda1
+
+> IDE硬盘是最古老的硬盘,理论最高传输速度是133M/s
+>
+> SCSI硬盘接口与IDE硬盘同时代,更加昂贵但速度更快,理论最高传输速度可达200M/s,但这种硬盘主要用在服务器上
+>
+> 但上两种硬盘接口如今已经基本淘汰,如今使用更多的是小口的SATA串口硬盘,SATA已发展到3代,其理论传输速度最高可达500M/s,目前不管是服务器还是个人机基本使用的都是SATA硬盘接口。
+
+需要留意的是,逻辑分区永远都是从5开始的
+
+## 挂载
+
+挂载实际上就是Windows中分配盘符的过程,盘符则被相应地称为挂载点,必须分区的分区有以下两种:
+
+1. 根分区:/
+2. swap分区(交换分区):可以理解为虚拟内存,当真正内存不够用时,可以使用这部分交换分区的硬盘空间来当内存,理论上来说交换分区应该是内存的两倍,但最大不超过2GB
+
+若无这两个分区,Linux不能正常使用,但我们还推荐把/boot单独分区,这是为了防止Linux系统启动不起来,一般200MB即可。
+
+# 远程登陆管理工具
+
+## 网络连接
+
+网络连接从虚拟机设置中可以看到,一共有三种:桥接、NAT和Host-only,下面讲解其区别:
+
+* 桥接:桥接意味着虚拟机如同一个单独的主机一样访问Wifi等,也可以和其他机器通信
+* NAT:虚拟机仅能和主机通信,但若主机可以访问互联网,虚拟机也可以访问互联网
+* Host-only:虚拟机仅能和主机本机通信,不能访问互联网
+
+## 网络配置
+
+1. 首先调成Host-only模式,使得虚拟机仅与主机连接
+2. 在主机上找到VMware Network Adapter VMnet1的IP地址,我本地地址为192.168.19.1
+3. 在虚拟机上使用`ishw -c netwowrk`命令找到logical name,此即为虚拟机的网卡名称,我的虚拟网卡名称为ens33
+4. 使用命令ifconfig [不等于IP地址] logical name,例如我使用的是`ifconfig ens33 192.168.19.2`
+5. 此时再ifconfig即可看到我们设置的已生效
+6. 我们可以在主机ping这个IP地址看到生效
+7. 使用secureCRT连接即可
+
+需要注意的是,以上方法配置IP地址时不是永久生效的,也就是重新启动电脑时就失效了,若想永久生效需要改变配置文件
+
+若使用NAT模式,则步骤简单很多,只需要ifconfig获得IP地址之后直接用secureCRT连接即可
+
+## WinSCP
+
+另外推荐一个Windows主机与Linux虚拟机进行文件传输的工具——WinSCP,操作方法与上面类似,只需输入对应的IP地址即可连接。
+
+
+
+## 安装linux系统(以ubuntu为例)
+
+- 使用vmware虚拟机安装
+
+ [参考此博客:VMware安装Ubuntu18.04](https://zhuanlan.zhihu.com/p/38797088)
+
+- 使用win10子系统安装
+
+ [参考此博客:在 win10 下使用 ubuntu 子系统](https://zhuanlan.zhihu.com/p/76032647)
+
+# Linux常用命令
+
+## 一、最常用命令
+
+这是我们**使用得最多**的命令了,**Linux最基础的命令**!
+
+- 可用 `pwd`命令查看用户的当前目录
+- 可用 `cd` 命令来切换目录
+- `.`表示当前目录
+- `..` 表示当前目录的上一级目录(父目录)
+- `-`表示用 cd 命令切换目录**前**所在的目录
+- `~` 表示**用户主目录**的绝对路径名
+
+**绝对路径:**
+
+- 以斜线(/)开头 ,描述到文件位置的**完整说明** ,任何时候你想指定文件名的时候都可以使用
+
+**相对路径 :**
+
+- 不以斜线(/)开头 ,指定**相对于你的当前工作目录而言的位置** ,可以被用作指定文件名的简捷方式
+
+## 二、文件处理命令
+
+### 1. 命令格式与目录处理命令`ls`
+
+**命令格式**:`命令[-选项][-参数]`,例:`ls -la /etc`
+
+**说明**:
+
+1. 个别命令使用不遵循此格式
+2. 当有多个选项时,可以写在一起
+3. 简化选项与完整选项:`-a` 等于 `--all`
+
+`ls`命令的语法:
+
+1. `ls -a`可以显示所有文件,包括隐藏文件(以点.开头的文件是隐藏文件)
+
+2. 若希望查询的不是当前目录,可以使用`ls+其他目录`进行查询
+
+3. `ls -l`可以显示更多属性(long),属性阐述如下:
+1. 第一列分为三个部分,第一部分(如d告诉我们文件的类型是一个目录,-为二进制文件,1为软链接文件),drwx表示该文件支持读写和执行操作,r,w,x分别对应读、写、执行三个权限,三列分别对应所有者,所属组,其他人的权限
+
+2. 第二列的2、2、3等表示调用次数
+ 3. 第三列表示所有者,也就是这个文件的总负责人(拥有文件的所有权,可转让)
+4. 第四列表示所属组,也就是可以操作这个文件的人
+ 5. 第五列表示文件大小,默认单位是字节(很反Windows)
+6. 最后一个是文件的最后一次修改时间(Linux没有创建时间这个概念)
+
+4. `ls -lh`比原先的更人性化(humanitarian),它将对应的单位也显示了出来,`-h`实际上是一个通用选项,很多命令都可以加
+
+5. `-d`显示当前目录本身而不显示目录下的数据,一般与`-l`结合使用,如`ls -ld /etc`
+
+6. `ls -id`可以查看当前目录对应的文件ID
+
+### 2. 目录处理命令
+
+##### `mkdir`
+
+**语法**:`mkdir -p [目录名]`
+
+**功能描述**:创建新目录,`-p`递归创建(若一个目录本身不存在,可以在创建这个目录的同时创建子目录),也可以同时创建多个目录
+
+##### `cd`
+
+**语法**:`cd directory`
+
+**功能描述**:改变当前目录
+
+##### `pwd`
+
+**语法**:`pwd`
+
+**功能描述**:显示当前目录(print working directory)
+
+##### `rmdir`
+
+**语法**:`rmdir [目录名]`
+
+**功能描述**:删除空目录(若目录非空则不能删除)
+
+##### `cp`
+
+**语法**:`cp -rf [源文件或目录] [目标目录] -r 复制目录 -p 保留文件属性(文件创建时间等不发生变化)`
+
+**功能描述**:复制文件或目录
+
+##### `mv`
+
+**语法**:`mv [源文件或目录] [目标目录]`
+
+**功能描述**:剪切文件、改名
+
+##### `rm`
+
+**语法**:`rm -rf [文件或目录] -r 删除目录 -f 强制执行`
+
+**功能描述**:删除文件
+
+### 3. 文件处理命令
+
+##### `touch`
+
+**语法**:`touch [文件名]`
+
+**功能描述**:创建空文件
+
+##### `cat`
+
+**语法**:`cat [文件名]`
+
+**功能描述**:显示文件内容 `-n`可显示行号
+
+##### `tac`
+
+与`cat`相反,可以倒着显示
+
+##### `more`
+
+`cat`命令显示的往往过多,若希望分页显示可以使用`more`,用法与`cat`相同,使用时按空格可以一页页往后翻,使用q或Q退出
+
+##### `less`
+
+由于`more`无法向上翻,我们可以使用`less`命令,可以使用page up一页页往上翻,也可以使用上箭头一行行往上翻,其他操作与`more`相同。另外`less`还可以进行搜索,比如想要搜索关键词service,可以输入/service进行检索,页面会对这些关键词进行高亮,可以使用`n`找到其他关键词位置
+
+##### `head`
+
+若只想要看文件的前几行,可以使用`head -n`加指定行数,若不加则默认显示前10行
+
+##### `tail`
+
+与`head`类似 ,但是显示后面几行。
+
+常用搭配为:`tail -f`,该命令会动态显示文件末尾内容
+
+## 三、链接命令`ln`
+
+**语法**:`ln -s [原文件] [目标文件] -s 创建软链接`
+
+**功能描述**:生成链接文件
+
+**示例**:
+
+* `ln -s /etc/issue issue.soft`:生成软链接
+* `ln /etc/issue issue.hard`:生成硬链接
+
+**软链接和硬链接的区别**
+
+我们使用`ls -l`查看这两个文件的信息:
+
+```
+-rw-r--r-- 2 root root 26 Jul 15 2020 issue.hard
+lrwxrwxrwx 1 root root 10 Jan 31 04:55 issue.soft -> /etc/issue
+```
+
+我们会发现这两个文件的信息相差的非常多,软链接文件开头的文件类型是`l(link)`,三个权限都是`rwx`,即可读可写可执行,软链接文件就类似于Windows的快捷方式,用处是便于做管理,我们可以看到最后有一个箭头指向`/etc/issue`。另外我们看到这个文件只有31个字节,因为它只是一个符号链接。我们可以总结得出软链接的三个特点:
+
+1. 权限是`rwx`
+2. 文件很小,只是符号链接
+3. 箭头指向源文件
+
+下面我们看硬链接的特点,我们首先分别查看 这两个文件的信息:
+
+```
+ls -l issue.hard
+ls -l /etc/issue
+```
+
+我们可以看到这两个文件的所有信息一模一样,包括文件的大小,这类似于拷贝,似乎相当于`cp -p`,而硬链接和`cp -p`的最大不同就是硬链接可以实现同步更新,我们可以做一个简单的实验,我们先查看硬链接文件,然后往源文件中写入文件,可以发现硬链接文件也被同时修改了,当然软链接也会同步修改。
+
+但当我们将源文件复制到另一个位置并删除原位置文件之后,再试图打开软链接会提示“没有那个文件或目录”,而且再显示这个目录软链接会标红并一直闪,而硬链接可以正常访问,没有影响,这就是硬链接和软连接的不同之处。
+
+实际上我们可以通过命令`ls -i`来识别其`i`节点以辨别出是硬链接还是软链接,硬链接和源文件的`i`节点相同,软链接则不同。
+
+硬链接相当于一个同步文件,但可以做实时备份(一个文件删了不会影响另一个文件),硬链接有两个限制,这也是硬链接和软链接的区别:
+
+1. 不能跨分区
+2. 不能针对目录使用
+
+## 四、权限管理命令
+
+Linux用户一共分成三类,分别是所有者(U),所属组(G)和其他人(O),权限也分成三类,分别是`r`,`w`,`x`,对应读、写、执行,我们首先学习如何更改权限。
+
+#### `chmod`
+
+更改文件的人只能是文件所有者或者管理员root用户,更改文件权限有两种方式,第一种方式如下:
+
+```
+chmod [{ugoa}{+-=}{rwx}][文件或目录]
+```
+
+其中第一个花括号里`u`,`g`,`o`,`a`分别表示所有者,所属组,其他人和所有人,第二个花括号`+`和`-`分别表示增加和减少权限,`=`表示成为后面的权限。第二种方式如下:
+
+```
+chmod [mod=421][文件或目录] -R 递归修改
+```
+
+数字的意思只是将三个权限位分别用数字来表示,比如`r`用4表示,`w`用2表示,`x`用1表示,则若要表示`rwxrw-r--`则记为`764`
+
+#### `chown`
+
+命令英文原意是`change file ownership`,作用是改变文件或目录的所有者,改变文件file的所有者为user的具体用法为:
+
+```
+chown user file
+```
+
+要注意只有root和文件的所有者可以改变文件的权限
+
+#### `chgrp`
+
+命令英文原意是`change file group ownership`,作用是改变文件或目录的所属组,若具体用法和前面`chown`相同。我们可以使用`groupadd`命令添加组(使用`useradd`命令添加用户)
+
+#### `umask`
+
+命令英文原意是`the user file-creation mask`,作用是显示、设置文件的缺省权限,语法是:
+
+```shell
+umask [-S]
+```
+
+其中`-S`的作用是显示新建文件的缺省权限,但需要注意的是缺省创建文件时不可以有可执行权限的,所以当`touch`创建文件时会发现所有权限都少了`x`。
+
+当我们直接使用`umask`时,比如显示0022,第一个0是特殊权限,我们暂时不涉及,第二只第四位分别是所有者、所属组和其他人,我们的最终权限实际上是`777-022=755`,也就是`rwx r-x r-x`,当然这指的是目录,如果是文件由于没有可执行权限,文件权限应当是`rw- r-- r--`,当然缺省创建的权限可以更改,直接使用`umask 077`即可将文件缺省权限更改为`rwx --- ---`,但不推荐做这种更改
diff --git a/Blockchain/part1_基础知识介绍.md b/Blockchain/part1_基础知识介绍.md
new file mode 100644
index 0000000..8486d26
--- /dev/null
+++ b/Blockchain/part1_基础知识介绍.md
@@ -0,0 +1,537 @@
+ 注:本教程为技术教程,不谈论且不涉及炒作任何数字货币
+
+本次组队学习重点在于以太坊基础知识、以太坊客户端以及以太坊solidity编程,因此本节教程重点在于以太坊核心知识点的掌握,区块链部分的基础知识可以作为补充,请学习者量力而行。另外若学习者觉得本节内容难度太高,可以先对基本知识点有一个概览,在第二节以及第三节实战内容学习完成之后再深入学习本节内容。
+
+# 一、区块链简介 #
+
+## 1.1、区块链与区块链技术 ##
+
+在阅读本教程之前,[大家对比特币原理不太了解同学可以先阅读下此博客~](http://blog.codinglabs.org/articles/bitcoin-mechanism-make-easy.html),大家对比特币有简单了解后对于区块链会有更好的认识。
+
+**区块链**是将记录(区块)通过密码学串联并加密的链式数据结构。而**区块链技术**,是通过P2P网络和区块链来实现数据存储的**去中心化**、**不可逆**和**不可篡改**。比特币正是构建在区块链技术上的典型应用。通过区块链技术,我们可以将信息(数据、程序)保存在区块上并接入到区块链中,这样就实现了信息的去中心化存储、不可逆和不可篡改。**区块链应用**是指利用区块链技术开发的应用。
+
+## 1.2、区块链历史 ##
+
+2008年,一个网名叫中本聪(Satoshi Nakamoto)的人发表了一篇名为《比特币:一种点对点电子货币系统》的论文,论文中首次提到了“区块链”这一概念。2009年,中本聪创立了以区块链为底层技术的比特币网络,开发出了第一个区块,被称为“创世区块”。该阶段被称为“区块链1.0”。
+
+由于比特币是一个电子货币系统,所以主要功能就是记账。但随后人们发现,区块链技术作为比特币的底层技术,功能可以远远不止于记账,许多关于“未知的信任”的问题,都可以通过区块链来解决,例如电子存证、信息记录等。于是在比特币的基础上,诞生了带有智能合约的区块链系统,即允许开发者通过编写智能合约来实现特定的逻辑,这一阶段被称为“区块链2.0”。这一阶段的主要代表是以太坊。
+
+随后,人们想要提升区块链应用的性能,于是出现了EOS、ArcBlock等系统,其特点是高性能、大吞吐量,但由于引入了超级节点、云节点等特性,弱化了“去中心化”这一特点,因此受到较大的争议。这一阶段被称为“区块链3.0”。
+
+由于比特币是一款电子货币,可扩展性较低,而所谓的“区块链3.0”目前受到较大争议,且部分项目的底层算法完全不同于典型的区块链,因此学习区块链2.0中的以太坊是目前学习区块链的最佳方式。
+
+## 1.3、区块链基础技术与算法 ##
+
+区块链技术不是单独的一项技术,而是一系列技术组成的技术栈,其具有以下的特点:
+
+* 数据分布式存储
+* 存储的数据不可逆、不可篡改、可回溯
+* 数据的创建和维护由所有参与方共同参与
+
+为了实现这些特点、维护区块链应用的稳定运行,区块链技术中包含了分布式存储技术、密码学技术、共识机制以及区块链2.0提出的智能合约。
+
+
+
+### 1.3.1、区块
+
+区块链由一个个区块(block)组成。区块很像数据库的记录,每次写入数据,就是创建一个区块。
+
+
+  +
+中心化存储
+每个区块包含两个部分。
+
+> - 区块头(Head):记录当前区块的特征值
+> - 区块体(Body):实际数据
+
+区块头包含了当前区块的多项特征值。
+
+> - 生成时间
+> - 实际数据(即区块体)的哈希
+> - 上一个区块的哈希
+> - ...
+
+### 1.3.2、分布式存储技术 ###
+
+与传统的数据存储技术不同,在区块链技术中,数据并不是集中存放在某个数据中心上,也不是由某个权威机构或是大多数节点来存储,而是分散存储在区块链网络中的每一个节点上。
+
+
+
+
+中心化存储
+每个区块包含两个部分。
+
+> - 区块头(Head):记录当前区块的特征值
+> - 区块体(Body):实际数据
+
+区块头包含了当前区块的多项特征值。
+
+> - 生成时间
+> - 实际数据(即区块体)的哈希
+> - 上一个区块的哈希
+> - ...
+
+### 1.3.2、分布式存储技术 ###
+
+与传统的数据存储技术不同,在区块链技术中,数据并不是集中存放在某个数据中心上,也不是由某个权威机构或是大多数节点来存储,而是分散存储在区块链网络中的每一个节点上。
+
+
+  +
+中心化存储
+
+
+
+中心化存储
+
+  +
+分布式存储
+**节点和区块的关系是什么?**
+
+可以用共享文档来简单描述:所有可以访问共享文档的账号就叫做节点,当然全节点需要同步共享文档,也就是拥有全部的区块数据区块就是共享文档。每个人更新了,所有人都可以查看最新的文档
+
+### 1.3.3、密码学技术 ###
+
+为了实现数据的不可逆、不可篡改和可回溯,区块链技术采用了一系列密码学算法和技术,包括哈希算法、Merkle 树、非对称加密算法。
+
+##### 哈希算法 #####
+
+哈希算法是一个单向函数,可以将任意长度的输入数据转化为固定长度的输出数据(哈希值),哈希值就是这段输入数据唯一的数值表现。由于在计算上不可能找到哈希值相同而输入值不同的字符串,因此两段数据的哈希值相同,就可以认为这两段数据也是相同的,所以哈希算法常被用于对数据进行验证。
+
+在区块链中,数据存储在区块里。每个区块都有一个区块头,区块头中存储了一个将该区块所有数据经过哈希算法得到的哈希值,同时,每个区块中还存储了前一个区块的哈希值,这样就形成了区块链。如果想要篡改某一个区块A中的数据,就会导致A的哈希值发生变化,后一个区块B就无法通过哈希值正确地指向A,这样篡改者又必须篡改B中的数据......也就是说,篡改者需要篡改被篡改的区块以及后面的所有区块,才能让所有的节点都接受篡改。
+
+##### Merkle树 #####
+
+Merkle树是一种树形结构,在区块链中,Merkle树的叶子节点是区块中数据的哈希值,非叶子节点是其子结点组合后的哈希值,这样由叶子节点开始逐层往上计算,最终形成一个Merkle根,记录在区块的头部,这样就可以保证每一笔交易都无法篡改。
+
+
+
+
+分布式存储
+**节点和区块的关系是什么?**
+
+可以用共享文档来简单描述:所有可以访问共享文档的账号就叫做节点,当然全节点需要同步共享文档,也就是拥有全部的区块数据区块就是共享文档。每个人更新了,所有人都可以查看最新的文档
+
+### 1.3.3、密码学技术 ###
+
+为了实现数据的不可逆、不可篡改和可回溯,区块链技术采用了一系列密码学算法和技术,包括哈希算法、Merkle 树、非对称加密算法。
+
+##### 哈希算法 #####
+
+哈希算法是一个单向函数,可以将任意长度的输入数据转化为固定长度的输出数据(哈希值),哈希值就是这段输入数据唯一的数值表现。由于在计算上不可能找到哈希值相同而输入值不同的字符串,因此两段数据的哈希值相同,就可以认为这两段数据也是相同的,所以哈希算法常被用于对数据进行验证。
+
+在区块链中,数据存储在区块里。每个区块都有一个区块头,区块头中存储了一个将该区块所有数据经过哈希算法得到的哈希值,同时,每个区块中还存储了前一个区块的哈希值,这样就形成了区块链。如果想要篡改某一个区块A中的数据,就会导致A的哈希值发生变化,后一个区块B就无法通过哈希值正确地指向A,这样篡改者又必须篡改B中的数据......也就是说,篡改者需要篡改被篡改的区块以及后面的所有区块,才能让所有的节点都接受篡改。
+
+##### Merkle树 #####
+
+Merkle树是一种树形结构,在区块链中,Merkle树的叶子节点是区块中数据的哈希值,非叶子节点是其子结点组合后的哈希值,这样由叶子节点开始逐层往上计算,最终形成一个Merkle根,记录在区块的头部,这样就可以保证每一笔交易都无法篡改。
+
+
+  +
+Merkle 树
+##### 非对称加密技术 #####
+
+非对称加密技术使用两个非对称密钥:公钥和私钥。公钥和私钥具有两个特点:
+
+1. 通过其中一个密钥加密信息后,使用另一个密钥才能解开
+2. 公钥一般可以公开,私钥则保密
+
+在区块链中,非对称加密技术主要用于信息加密、数字签名和登录认证。在信息加密场景中,信息发送者A使用接收者B提供的公钥对信息进行加密,B收到加密的信息后再通过自己的私钥进行解密。再数字签名场景中,发送者A通过自己的私钥对信息进行加密,其他人通过A提供的公钥来对信息进行验证,证明信息确实是由A发出。在登录认证场景中,客户端使用私钥加密登录信息后进行发送,其他人通过客户端公钥来认证登录信息。
+
+- RSA 算法
+
+ RSA加密算法是最常用的非对称加密算法,CFCA在证书服务中离不了它。但是有不少新来的同事对它不太了解,恰好看到一本书中作者用实例对它进行了简化而生动的描述,使得高深的数学理论能够被容易地理解。
+ RSA是第一个比较完善的公开密钥算法,它既能用于加密,也能用于数字签名。RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名,这个算法经受住了多年深入的密码分析,虽然密码分析者既不能证明也不能否定RSA的安全性,但这恰恰说明该算法有一定的可信性,目前它已经成为最流行的公开密钥算法。
+ RSA的安全基于大数分解的难度。其公钥和私钥是一对大素数(100到200位十进制数或更大)的函数。从一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积(这是公认的数学难题)。
+
+- ECC 椭圆曲线算法
+
+ 具体可以参见此文章:[ECC椭圆曲线加密算法:介绍](https://zhuanlan.zhihu.com/p/36326221)
+
+
+
+### 1.3.4、共识机制 ###
+
+区块链系统是一个分布式系统,分布式系统要解决都首要问题就是一致性问题,也就是如何使多个孤立的节点达成共识。在中心化系统中,由于有一个中心服务器这样的“领导”来统一各个节点,因此达成一致性几乎没有问题。但在去中心化场景下,由于各个节点是相互独立的,就可能会出现许多不一致的问题,例如由于网络状况等因素部分节点可能会有延迟、故障甚至宕机,造成节点之间通信的不可靠,因此一致性问题是分布式系统中一个很令人头疼的问题。
+
+由 Eirc Brewer 提出,Lynch 等人证明的 CAP 定理为解决分布式系统中的一致性问题提供了思路。CAP 定理的描述如下:在分布式系统中,**一致性**、**可用性**和**分区容错性**三者不可兼得。这三个术语的解释如下:
+
+* 一致性(**C**onsistency):所有节点在同一时刻拥有同样的值(等同于所有节点访问同一份最新的数据副本
+* 可用性(**A**vailability):每个请求都可以在有限时间内收到确定其是否成功的响应
+* 分区容错性(**P**artition tolerance):分区是指部分节点因为网络原因无法与其他节点达成一致。分区容错性是指由网络原因导致的系统分区不影响系统的正常运行。例如,由于网络原因系统被分为 A, B, C, D 四个区,A, B 中的节点无法正常工作,但 C, D 组成的分区仍能提供正常服务。
+
+在某些场景下,对一致性、可用性和分区容错性中的某一个特性要求不高时,就可以考虑弱化该特性,来保证整个系统的容错能力。区块链中常见的共识机制的基本思路正是来自 CAP 定理,部分区块链应用中用到的共识机制如下表:
+
+| 共识机制 | 应用 |
+| -------- | ---------------------------------- |
+| PoW | 比特币、莱特币、以太坊的前三个阶段 |
+| PoS | PeerCoin、NXT、以太坊的第四个阶段 |
+| PBFT | Hyperledger Fabric |
+
+##### PoW(Proof of Work,工作量证明) #####
+
+PoW 机制的大致流程如下:
+
+1. 向所有节点广播新交易和一个数学问题
+2. 最先解决了数学问题的节点将交易打包成区块,对全网广播
+3. 其他节点验证广播区块的节点是否解决了数学问题(完成了一定的工作量),验证通过则接受该区块,并将该区块的哈希值放入下一个区块中,表示承认该区块
+
+由于在 PoW 机制中,区块的产生需要解决一个数学问题,也就是所谓的**挖矿**,这往往要消耗较大的算力和电力,因此节点们倾向于在**最长的链**的基础上添加区块,因为如果节点想在自己的链上添加新的区块,那么就需要重新计算 1 个或 $n$ 个这样的数学问题(每添加一个区块就需要计算一个)。因此在比特币中最长的链被认为是合法的链,这样节点间就形成了一套“共识”。
+
+PoW 机制的优点是完全去中心化,缺点是需要依赖数学运算,资源的消耗会比其他的共识机制高,可监管性弱,同时每次达成共识需要全网共同参与运算,性能较低。
+
+##### PoS(Proof of Stack,股权证明) #####
+
+PoS 针对 PoW 的缺点做出了改进。PoS 要求参与者预先放置一些货币在区块链上用于换取“股权”,从而成为**验证者(Validator)**,验证者具有产生区块的权利。PoS 机制会按照存放货币的量和时间给验证者分配相应的利息,同时还引入了奖惩机制,打包错误区块的验证者将失去他的股权——即投入的货币以及产生区块的权利。PoS 机制的大致流程如下:
+
+1. 加入 PoS 机制的都是持币人,称为验证者
+2. PoS 算法根据验证者持币的多少在验证者中挑选出一个给予产生区块的权利
+3. 如果一定时间内没有产生区块,PoS 就挑选下一个验证者,给予产生区块的权利
+4. 如果某个验证者打包了一份欺诈性交易,PoS 将剥夺他的股权
+
+PoS 的优点在于:
+
+1. 引入了利息,使得像比特币这样发币总数有限的通货紧缩系统在一定时间后不会“无币可发”
+2. 引入了奖惩机制使节点的运行更加可控,同时更好地防止攻击
+3. 与 PoW 相比,不需要为了生成新区块而消耗大量电力和算力
+4. 与 PoW 相比,缩短了达成共识所需的时间
+
+由于 PoS 机制需要用户已经持有一定数量的货币,没有提供在区块链应用创立初始阶段处理数字货币的方法,因此使用 PoS 机制的区块链应用会在发布时预先出售货币,或在初期采用 PoW,让矿工获得货币后再转换成 PoS,例如以太坊现阶段采用的是 PoW 机制,在第四阶段“宁静”(Serenity)中将过渡到 PoS。
+
+##### 拜占庭将军问题(Byzantine Generals Problem) #####
+
+拜占庭将军问题是分布式网络中的通信容错问题,可以描述为:
+
+> 一组拜占庭将军各领一支队伍共同围困一座城市。各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻而部分军队撤离可能会造成灾难性的后果,因此各将军决定通过投标来达成一致策略,即“共进退”。因为各将军位于城市不同方向,他们只能通过信使互相联系。在投票过程中每位将军都将自己的选择(进攻或撤退)通过信使分别通知其他所有将军,这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同投票的结果,进而做出行动。
+
+
+
+
+Merkle 树
+##### 非对称加密技术 #####
+
+非对称加密技术使用两个非对称密钥:公钥和私钥。公钥和私钥具有两个特点:
+
+1. 通过其中一个密钥加密信息后,使用另一个密钥才能解开
+2. 公钥一般可以公开,私钥则保密
+
+在区块链中,非对称加密技术主要用于信息加密、数字签名和登录认证。在信息加密场景中,信息发送者A使用接收者B提供的公钥对信息进行加密,B收到加密的信息后再通过自己的私钥进行解密。再数字签名场景中,发送者A通过自己的私钥对信息进行加密,其他人通过A提供的公钥来对信息进行验证,证明信息确实是由A发出。在登录认证场景中,客户端使用私钥加密登录信息后进行发送,其他人通过客户端公钥来认证登录信息。
+
+- RSA 算法
+
+ RSA加密算法是最常用的非对称加密算法,CFCA在证书服务中离不了它。但是有不少新来的同事对它不太了解,恰好看到一本书中作者用实例对它进行了简化而生动的描述,使得高深的数学理论能够被容易地理解。
+ RSA是第一个比较完善的公开密钥算法,它既能用于加密,也能用于数字签名。RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名,这个算法经受住了多年深入的密码分析,虽然密码分析者既不能证明也不能否定RSA的安全性,但这恰恰说明该算法有一定的可信性,目前它已经成为最流行的公开密钥算法。
+ RSA的安全基于大数分解的难度。其公钥和私钥是一对大素数(100到200位十进制数或更大)的函数。从一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积(这是公认的数学难题)。
+
+- ECC 椭圆曲线算法
+
+ 具体可以参见此文章:[ECC椭圆曲线加密算法:介绍](https://zhuanlan.zhihu.com/p/36326221)
+
+
+
+### 1.3.4、共识机制 ###
+
+区块链系统是一个分布式系统,分布式系统要解决都首要问题就是一致性问题,也就是如何使多个孤立的节点达成共识。在中心化系统中,由于有一个中心服务器这样的“领导”来统一各个节点,因此达成一致性几乎没有问题。但在去中心化场景下,由于各个节点是相互独立的,就可能会出现许多不一致的问题,例如由于网络状况等因素部分节点可能会有延迟、故障甚至宕机,造成节点之间通信的不可靠,因此一致性问题是分布式系统中一个很令人头疼的问题。
+
+由 Eirc Brewer 提出,Lynch 等人证明的 CAP 定理为解决分布式系统中的一致性问题提供了思路。CAP 定理的描述如下:在分布式系统中,**一致性**、**可用性**和**分区容错性**三者不可兼得。这三个术语的解释如下:
+
+* 一致性(**C**onsistency):所有节点在同一时刻拥有同样的值(等同于所有节点访问同一份最新的数据副本
+* 可用性(**A**vailability):每个请求都可以在有限时间内收到确定其是否成功的响应
+* 分区容错性(**P**artition tolerance):分区是指部分节点因为网络原因无法与其他节点达成一致。分区容错性是指由网络原因导致的系统分区不影响系统的正常运行。例如,由于网络原因系统被分为 A, B, C, D 四个区,A, B 中的节点无法正常工作,但 C, D 组成的分区仍能提供正常服务。
+
+在某些场景下,对一致性、可用性和分区容错性中的某一个特性要求不高时,就可以考虑弱化该特性,来保证整个系统的容错能力。区块链中常见的共识机制的基本思路正是来自 CAP 定理,部分区块链应用中用到的共识机制如下表:
+
+| 共识机制 | 应用 |
+| -------- | ---------------------------------- |
+| PoW | 比特币、莱特币、以太坊的前三个阶段 |
+| PoS | PeerCoin、NXT、以太坊的第四个阶段 |
+| PBFT | Hyperledger Fabric |
+
+##### PoW(Proof of Work,工作量证明) #####
+
+PoW 机制的大致流程如下:
+
+1. 向所有节点广播新交易和一个数学问题
+2. 最先解决了数学问题的节点将交易打包成区块,对全网广播
+3. 其他节点验证广播区块的节点是否解决了数学问题(完成了一定的工作量),验证通过则接受该区块,并将该区块的哈希值放入下一个区块中,表示承认该区块
+
+由于在 PoW 机制中,区块的产生需要解决一个数学问题,也就是所谓的**挖矿**,这往往要消耗较大的算力和电力,因此节点们倾向于在**最长的链**的基础上添加区块,因为如果节点想在自己的链上添加新的区块,那么就需要重新计算 1 个或 $n$ 个这样的数学问题(每添加一个区块就需要计算一个)。因此在比特币中最长的链被认为是合法的链,这样节点间就形成了一套“共识”。
+
+PoW 机制的优点是完全去中心化,缺点是需要依赖数学运算,资源的消耗会比其他的共识机制高,可监管性弱,同时每次达成共识需要全网共同参与运算,性能较低。
+
+##### PoS(Proof of Stack,股权证明) #####
+
+PoS 针对 PoW 的缺点做出了改进。PoS 要求参与者预先放置一些货币在区块链上用于换取“股权”,从而成为**验证者(Validator)**,验证者具有产生区块的权利。PoS 机制会按照存放货币的量和时间给验证者分配相应的利息,同时还引入了奖惩机制,打包错误区块的验证者将失去他的股权——即投入的货币以及产生区块的权利。PoS 机制的大致流程如下:
+
+1. 加入 PoS 机制的都是持币人,称为验证者
+2. PoS 算法根据验证者持币的多少在验证者中挑选出一个给予产生区块的权利
+3. 如果一定时间内没有产生区块,PoS 就挑选下一个验证者,给予产生区块的权利
+4. 如果某个验证者打包了一份欺诈性交易,PoS 将剥夺他的股权
+
+PoS 的优点在于:
+
+1. 引入了利息,使得像比特币这样发币总数有限的通货紧缩系统在一定时间后不会“无币可发”
+2. 引入了奖惩机制使节点的运行更加可控,同时更好地防止攻击
+3. 与 PoW 相比,不需要为了生成新区块而消耗大量电力和算力
+4. 与 PoW 相比,缩短了达成共识所需的时间
+
+由于 PoS 机制需要用户已经持有一定数量的货币,没有提供在区块链应用创立初始阶段处理数字货币的方法,因此使用 PoS 机制的区块链应用会在发布时预先出售货币,或在初期采用 PoW,让矿工获得货币后再转换成 PoS,例如以太坊现阶段采用的是 PoW 机制,在第四阶段“宁静”(Serenity)中将过渡到 PoS。
+
+##### 拜占庭将军问题(Byzantine Generals Problem) #####
+
+拜占庭将军问题是分布式网络中的通信容错问题,可以描述为:
+
+> 一组拜占庭将军各领一支队伍共同围困一座城市。各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻而部分军队撤离可能会造成灾难性的后果,因此各将军决定通过投标来达成一致策略,即“共进退”。因为各将军位于城市不同方向,他们只能通过信使互相联系。在投票过程中每位将军都将自己的选择(进攻或撤退)通过信使分别通知其他所有将军,这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同投票的结果,进而做出行动。
+
+
+  +
+
+
+拜占庭将军的问题在于,将军中可能出现叛徒。假设3名将军中有1名叛徒,2名忠诚将军一人投进攻票,一人投撤退票,这时叛徒可能会故意给投进攻的将军投进攻票,而给投撤退的将军投撤退票。这就导致一名将军带队发起进攻,而另外一名将军带队撤退。
+
+另外,由于将军之间通过信使进行通讯,即使所有将军都忠诚,也不能排除信使被敌人截杀,甚至信使叛变等情况。
+
+假设存在叛变将军或信使出问题等情况,如果忠诚将军仍然能够通过投票来决定他们的战略,便称系统达到了**拜占庭容错(Byzantine Fault Tolerance)**。
+
+拜占庭问题对应到区块链中,将军就是节点,信使就是网络等通信系统,要解决的是存在恶意节点、网络错误等情况下系统的一致性问题。
+
+**PBFT(Practical Byzantine Fault Tolerance)** 是第一个得到广泛应用且比较高效的拜占庭容错算法,能够在节点数量不小于 $n=3f+1$ 的情况下容忍 $f$ 个拜占庭节点(恶意节点)。
+
+
+
+# 二、以太坊介绍 #
+
+首先我们要知道我们为什么要学习以太坊,主要有以下四个原因:
+
+* 以太坊是区块链2.0的代表,学习以太坊能了解到区块链技术的所有知识
+* 引入了智能合约,拓宽了区块链的应用场景
+* 对开发者友好、对用户友好,容易编写出简单的区块链应用,学习趣味性高
+* Solidity 语法与 Javascript、Go 等语言接近,易上手
+
+## 2.1、以太坊简介 ##
+
+区块链技术常常被认为是自互联网诞生以来最具颠覆性的技术,然而,自比特币诞生后一直没有很好的区块链应用开发平台。想要在比特币基础上开发区块链应用是非常复杂繁琐的,因为比特币仅仅是一个加密数字货币系统,无法用来实现更广阔的业务需求。以太坊是目前使用最广泛的支持完备应用开发的共有区块链系统。
+
+和比特币不同,比特币只适合加密数字货币场景,不具备图灵完备性,也缺乏保存实时状态的账户概念,以及存在 PoW 机制带来的效率和资源浪费的问题,而以太坊作为区块链2.0的代表,目标是扩展智能合约和建立一个去中心化应用平台,具有图灵完备的特性、更高效的共识机制、支持智能合约等多种应用场景,使得开发者能够很方便地在以太坊上开发出基于区块链的应用。
+
+### 2.1.1、以太坊的发展 ###
+
+2014年, Vitalik Buterin 发表了文章《以太坊:一个下一代智能合约和去中心化应用平台》。同年,Buterin 在迈阿密比特币会议中宣布启动以太坊项目,并提出了多项创新性的区块链技术。2015年,以太坊CCO Stephan Tual 在官方博客上宣布以太坊系统诞生,主网上线。
+
+以太坊发展至今经历了“前沿”(Frontier)、“家园”(Homestead)以及现在所处的“大都会”(Metropolis)三个阶段。第四阶段“宁静”(Serenity)将作为以太坊的最后一个阶段,目前尚未有计划发布日期。
+
+### 2.1.2、以太坊的特点 ###
+
+以太坊团队和外界对以太坊的描述都是“世界计算机”,这代表它是一个开源的、全球的去中心化计算架构。它执行称为智能合约的程序,并使用区块链来同步和存储系统状态,以及使用名为以太币的加密数字货币来计量和约束执行操作的资源成本。同时,以太坊提供了一系列的接口,使得开发者能够通过以太坊来开发去中心化 Web 应用DApps。
+
+### 2.1.3、智能合约 ###
+
+相比比特币,以太坊最大的特点就是引入了**智能合约**。智能合约本质上就是一段编写好的程序,可以在特定的条件下被触发并执行特定的操作。由于区块链具有不可逆和不可篡改的特点,因此智能合约与区块链结合后,就成了一份“强制执行”的合约。
+
+以太坊能够作为一个去中心化应用平台和”世界计算机”,其核心就是智能合约。智能合约的引入,使得开发者能够实现许多(理论上是任何)业务逻辑。如果说比特币是通过区块链技术开发的特定计算器,那么引入了智能合约的以太坊就是基于区块链技术的通用计算机。可以简单的理解成:比特币的交易系统就是一份写死的智能合约,而以太坊则将智能合约的开发权限交给开发者。
+
+以太坊提供了对智能合约的全面支持,包括编写智能合约编程语言 **Solidity** 和运行智能合约的**以太坊虚拟机(Ethereum Virtual Machine,EVM)**。
+
+### 2.1.4、幽灵协议 ###
+
+幽灵合约的英文是“Greedy Heaviest Observed Subtree" (GHOST) protocol,在介绍幽灵协议之前,先介绍以太坊中的叔区块、叔块奖励和叔块引用奖励这三个概念。
+
+
+
+
+
+
+拜占庭将军的问题在于,将军中可能出现叛徒。假设3名将军中有1名叛徒,2名忠诚将军一人投进攻票,一人投撤退票,这时叛徒可能会故意给投进攻的将军投进攻票,而给投撤退的将军投撤退票。这就导致一名将军带队发起进攻,而另外一名将军带队撤退。
+
+另外,由于将军之间通过信使进行通讯,即使所有将军都忠诚,也不能排除信使被敌人截杀,甚至信使叛变等情况。
+
+假设存在叛变将军或信使出问题等情况,如果忠诚将军仍然能够通过投票来决定他们的战略,便称系统达到了**拜占庭容错(Byzantine Fault Tolerance)**。
+
+拜占庭问题对应到区块链中,将军就是节点,信使就是网络等通信系统,要解决的是存在恶意节点、网络错误等情况下系统的一致性问题。
+
+**PBFT(Practical Byzantine Fault Tolerance)** 是第一个得到广泛应用且比较高效的拜占庭容错算法,能够在节点数量不小于 $n=3f+1$ 的情况下容忍 $f$ 个拜占庭节点(恶意节点)。
+
+
+
+# 二、以太坊介绍 #
+
+首先我们要知道我们为什么要学习以太坊,主要有以下四个原因:
+
+* 以太坊是区块链2.0的代表,学习以太坊能了解到区块链技术的所有知识
+* 引入了智能合约,拓宽了区块链的应用场景
+* 对开发者友好、对用户友好,容易编写出简单的区块链应用,学习趣味性高
+* Solidity 语法与 Javascript、Go 等语言接近,易上手
+
+## 2.1、以太坊简介 ##
+
+区块链技术常常被认为是自互联网诞生以来最具颠覆性的技术,然而,自比特币诞生后一直没有很好的区块链应用开发平台。想要在比特币基础上开发区块链应用是非常复杂繁琐的,因为比特币仅仅是一个加密数字货币系统,无法用来实现更广阔的业务需求。以太坊是目前使用最广泛的支持完备应用开发的共有区块链系统。
+
+和比特币不同,比特币只适合加密数字货币场景,不具备图灵完备性,也缺乏保存实时状态的账户概念,以及存在 PoW 机制带来的效率和资源浪费的问题,而以太坊作为区块链2.0的代表,目标是扩展智能合约和建立一个去中心化应用平台,具有图灵完备的特性、更高效的共识机制、支持智能合约等多种应用场景,使得开发者能够很方便地在以太坊上开发出基于区块链的应用。
+
+### 2.1.1、以太坊的发展 ###
+
+2014年, Vitalik Buterin 发表了文章《以太坊:一个下一代智能合约和去中心化应用平台》。同年,Buterin 在迈阿密比特币会议中宣布启动以太坊项目,并提出了多项创新性的区块链技术。2015年,以太坊CCO Stephan Tual 在官方博客上宣布以太坊系统诞生,主网上线。
+
+以太坊发展至今经历了“前沿”(Frontier)、“家园”(Homestead)以及现在所处的“大都会”(Metropolis)三个阶段。第四阶段“宁静”(Serenity)将作为以太坊的最后一个阶段,目前尚未有计划发布日期。
+
+### 2.1.2、以太坊的特点 ###
+
+以太坊团队和外界对以太坊的描述都是“世界计算机”,这代表它是一个开源的、全球的去中心化计算架构。它执行称为智能合约的程序,并使用区块链来同步和存储系统状态,以及使用名为以太币的加密数字货币来计量和约束执行操作的资源成本。同时,以太坊提供了一系列的接口,使得开发者能够通过以太坊来开发去中心化 Web 应用DApps。
+
+### 2.1.3、智能合约 ###
+
+相比比特币,以太坊最大的特点就是引入了**智能合约**。智能合约本质上就是一段编写好的程序,可以在特定的条件下被触发并执行特定的操作。由于区块链具有不可逆和不可篡改的特点,因此智能合约与区块链结合后,就成了一份“强制执行”的合约。
+
+以太坊能够作为一个去中心化应用平台和”世界计算机”,其核心就是智能合约。智能合约的引入,使得开发者能够实现许多(理论上是任何)业务逻辑。如果说比特币是通过区块链技术开发的特定计算器,那么引入了智能合约的以太坊就是基于区块链技术的通用计算机。可以简单的理解成:比特币的交易系统就是一份写死的智能合约,而以太坊则将智能合约的开发权限交给开发者。
+
+以太坊提供了对智能合约的全面支持,包括编写智能合约编程语言 **Solidity** 和运行智能合约的**以太坊虚拟机(Ethereum Virtual Machine,EVM)**。
+
+### 2.1.4、幽灵协议 ###
+
+幽灵合约的英文是“Greedy Heaviest Observed Subtree" (GHOST) protocol,在介绍幽灵协议之前,先介绍以太坊中的叔区块、叔块奖励和叔块引用奖励这三个概念。
+
+
+  +
+
+
+假设目前以太坊区块链中的区块高度(区块链上的区块个数)为6,现在产生了一笔新的交易,矿工A先将该笔交易打包成了区块 Block 7,在矿工A将 Block 7 广播到其他节点的这段时间里,矿工B和矿工C又分别产生了 Block 8 和 Block 9。Block 7、Block 8、Block 9 都指向 Block 6,即 Block 6 是他们的父区块。由于 Block 7 是最先产生的,因此 Block 7 被认为是有效区块,Block 8 和 Block 9 就是**叔区块**(作废区块)。
+
+
+
+
+
+
+假设目前以太坊区块链中的区块高度(区块链上的区块个数)为6,现在产生了一笔新的交易,矿工A先将该笔交易打包成了区块 Block 7,在矿工A将 Block 7 广播到其他节点的这段时间里,矿工B和矿工C又分别产生了 Block 8 和 Block 9。Block 7、Block 8、Block 9 都指向 Block 6,即 Block 6 是他们的父区块。由于 Block 7 是最先产生的,因此 Block 7 被认为是有效区块,Block 8 和 Block 9 就是**叔区块**(作废区块)。
+
+
+  +
+
+
+现在链上的区块高度为7,在这基础上又产生了新的交易,并被打包成了 Block 10。在以太坊中,Block 10 除了可以引用它的父区块 Block 7 外,还可以引用叔区块 Block 8 和 Block 9。并且,Block 8 和 Block 9 的矿工会因此获得一笔奖励,称为**叔块奖励**,Block 10 的矿工除了基础奖励之外,由于引用了叔区块,还会获得一笔额外的**叔块引用奖励**。
+
+**幽灵协议**是以太坊的一大创新。由于在比特币中的出块时间被设计为10分钟,而以太坊为了提高出块速度,将出块时间设计为12秒(实际14~15秒左右),这样的高速出块意味着高速确认,高速确认会带来区块的**高作废率**和**低安全性**。因为区块需要花一定的时间才能广播至全网,如果矿工 A 挖出了一个区块,而矿工 B 碰巧在 A 的区块扩散至 B 之前挖出了另一个区块,矿工 B 的区块就会作废并且没有对区块链的网络安全做出贡献。此外,这样的高速确认还会带来**中心化**的问题:如果 A 拥有全网 30% 的算力而 B 拥有 10% 的算力,那么 A 将会在 70% 的时间内都在产生作废区块,而 B 在 90% 的时间内都在产生作废区块,这样,B 永远追不上 A,后果是 A 通过其算力份额拥有对挖矿过程实际上的控制权,出现了算力垄断,弱化了去中心化。
+
+幽灵协议正是为了解决上述问题而引入的,协议的主要内容如下:
+
+- 计算最长链时,不仅包括当前区块的父区块和祖区块,还包括祖先块的作废的后代区块(叔区块),将它们综合考虑来计算哪一个区块拥有支持其的最大工作量证明。这解决了网络安全性的问题
+- 以太坊付给以“叔区块”身份为新块确认作出贡献的废区块87.5%的奖励(叔块奖励),把它们纳入计算的“侄子区块”将获得奖励的12.5%(叔块引用奖励)。这就使得即使产生作废区块的矿工也能够参与区块链网络贡献并获得奖励,解决了中心化倾向的问题
+- 叔区块最深可以被其父母的第二代至第七代后辈区块引用。这样做是为了:
+ - 降低引用叔区块的计算复杂性
+ - 过多的叔块引用奖励会剥夺矿工在主链上挖矿的激励,使得矿工有转向公开攻击者链上挖矿的倾向(即公开攻击者可能会恶意产生大量作废区块,无限引用将会诱使矿工转移到攻击者的链上,从而抛弃合法的主链)
+ - 计算表明带有激励的五层幽灵协议即使在出块时间为15s的情况下也实现了了95%以上的效率,而拥有25%算力的矿工从中心化得到的益处小于3%
+
+### 2.1.5、以太坊的组成部分 ###
+
+在以太坊中,包括了 P2P 网络、共识机制、交易、状态机、客户端这几个组成部分。
+
+* P2P 网络:在以太坊主网上运行,可通过TCP端口30303访问,并运行称为 ÐΞVp2p 的协议。
+* 共识机制:以太坊目前使用名为 Ethash 的 POW 算法,计划在将来会过渡到称为 Casper 的 POS 算法。
+* 交易:以太坊中的交易本质上是网络消息,包括发送者、接收者、值和数据载荷(payload)。
+* 状态机:以太坊的状态转移由以太坊虚拟机(Ethereum Virtual Machine,EVM)处理,EVM 能够将智能合约编译成机器码并执行。
+* 客户端:用于用户和以太坊进行交互操作的软件实现,最突出的是 Go-Ethereum(Geth) 和 Parity。
+
+### 2.1.6、以太坊中的概念 ###
+
+* 账户:以太坊中的账户类似于银行账户、应用账户,每个账户有一个20字节的地址。账户又分为**普通账户**(又叫外部账户,External Owned Account, EOA)和**合约账户**(Contract)。普通账户是由以太坊使用者创建的账户,包含地址、余额和随机数;合约账户是创建智能合约时建立的账户,包含存储空间和合约代码
+* 状态:状态是由账户和两个账户之间价值的转移以及信息的状态转换构成的
+* 地址:地址是一个账户 ECDSA 公钥的 Keccak 散列最右边的160位,通过地址可以在以太坊上接收或发送交易。在 Etherscan 上,可以通过地址来查询一个账户的信息
+* 交易:以太坊中的交易不仅包括发送和接收以太币,还包括向合约账户发送交易来调用合约代码、向空用户发送交易来生成以交易信息为代码块的合约账户
+* Gas:Gas 是以太坊中的一种机制,用于执行智能合约或交易操作的虚拟燃料。由于以太坊是图灵完备的,为了避免开发者无意或恶意编写出死循环等浪费资源或滥用资源的情况,以太坊中的每一笔交易都需支付一定的 Gas (燃料费),即需支付一定的以太币作为 Gas。Gas 的金额通常是由交易的发起者指定并支付的
+* 挖矿:和比特币类似,以太坊同样通过挖矿来产生区块。在以太坊目前的 PoW 机制下,每当一笔交易发出并广播,就会吸引矿工来将该交易打包成区块。每产生一个区块都会有一笔**固定奖励**给矿工,目前的固定奖励是3个以太。同时,区块中所有操作所需的 Gas 也会作为奖励给矿工。与比特币不同的是,以太坊中产生叔块的矿工可能会获得叔块奖励,引用叔块的矿工会获得叔块引用奖励
+* DApp(去中心化应用):通过智能合约,开发者能够设计想要的逻辑,相当于是网站的后端。而 DApp 则相当于是一个完整的网站(前端+后端),因此 DApp = 智能合约 + Web 前端。以太坊提供了一个名为 web3.js 的 Javascript 库,通过 web3.js 可以实现 Web 与以太坊区块链的交互和与智能合约的交互,方便开发者创建 DApp
+
+## 2.2、以太坊基础 ##
+
+### 2.2.1、以太坊中的货币 ###
+
+以太坊中的货币称为 **以太币**,单位为**以太(Ether)**,也称 ETH 或符号 Ξ。以太可以被分割为更小的单位,最小的单位是 wei,1 以太 = $10^18$ wei。以太币各单位的名称及之间的关系如下表:
+
+
+
+
+
+
+
+
+现在链上的区块高度为7,在这基础上又产生了新的交易,并被打包成了 Block 10。在以太坊中,Block 10 除了可以引用它的父区块 Block 7 外,还可以引用叔区块 Block 8 和 Block 9。并且,Block 8 和 Block 9 的矿工会因此获得一笔奖励,称为**叔块奖励**,Block 10 的矿工除了基础奖励之外,由于引用了叔区块,还会获得一笔额外的**叔块引用奖励**。
+
+**幽灵协议**是以太坊的一大创新。由于在比特币中的出块时间被设计为10分钟,而以太坊为了提高出块速度,将出块时间设计为12秒(实际14~15秒左右),这样的高速出块意味着高速确认,高速确认会带来区块的**高作废率**和**低安全性**。因为区块需要花一定的时间才能广播至全网,如果矿工 A 挖出了一个区块,而矿工 B 碰巧在 A 的区块扩散至 B 之前挖出了另一个区块,矿工 B 的区块就会作废并且没有对区块链的网络安全做出贡献。此外,这样的高速确认还会带来**中心化**的问题:如果 A 拥有全网 30% 的算力而 B 拥有 10% 的算力,那么 A 将会在 70% 的时间内都在产生作废区块,而 B 在 90% 的时间内都在产生作废区块,这样,B 永远追不上 A,后果是 A 通过其算力份额拥有对挖矿过程实际上的控制权,出现了算力垄断,弱化了去中心化。
+
+幽灵协议正是为了解决上述问题而引入的,协议的主要内容如下:
+
+- 计算最长链时,不仅包括当前区块的父区块和祖区块,还包括祖先块的作废的后代区块(叔区块),将它们综合考虑来计算哪一个区块拥有支持其的最大工作量证明。这解决了网络安全性的问题
+- 以太坊付给以“叔区块”身份为新块确认作出贡献的废区块87.5%的奖励(叔块奖励),把它们纳入计算的“侄子区块”将获得奖励的12.5%(叔块引用奖励)。这就使得即使产生作废区块的矿工也能够参与区块链网络贡献并获得奖励,解决了中心化倾向的问题
+- 叔区块最深可以被其父母的第二代至第七代后辈区块引用。这样做是为了:
+ - 降低引用叔区块的计算复杂性
+ - 过多的叔块引用奖励会剥夺矿工在主链上挖矿的激励,使得矿工有转向公开攻击者链上挖矿的倾向(即公开攻击者可能会恶意产生大量作废区块,无限引用将会诱使矿工转移到攻击者的链上,从而抛弃合法的主链)
+ - 计算表明带有激励的五层幽灵协议即使在出块时间为15s的情况下也实现了了95%以上的效率,而拥有25%算力的矿工从中心化得到的益处小于3%
+
+### 2.1.5、以太坊的组成部分 ###
+
+在以太坊中,包括了 P2P 网络、共识机制、交易、状态机、客户端这几个组成部分。
+
+* P2P 网络:在以太坊主网上运行,可通过TCP端口30303访问,并运行称为 ÐΞVp2p 的协议。
+* 共识机制:以太坊目前使用名为 Ethash 的 POW 算法,计划在将来会过渡到称为 Casper 的 POS 算法。
+* 交易:以太坊中的交易本质上是网络消息,包括发送者、接收者、值和数据载荷(payload)。
+* 状态机:以太坊的状态转移由以太坊虚拟机(Ethereum Virtual Machine,EVM)处理,EVM 能够将智能合约编译成机器码并执行。
+* 客户端:用于用户和以太坊进行交互操作的软件实现,最突出的是 Go-Ethereum(Geth) 和 Parity。
+
+### 2.1.6、以太坊中的概念 ###
+
+* 账户:以太坊中的账户类似于银行账户、应用账户,每个账户有一个20字节的地址。账户又分为**普通账户**(又叫外部账户,External Owned Account, EOA)和**合约账户**(Contract)。普通账户是由以太坊使用者创建的账户,包含地址、余额和随机数;合约账户是创建智能合约时建立的账户,包含存储空间和合约代码
+* 状态:状态是由账户和两个账户之间价值的转移以及信息的状态转换构成的
+* 地址:地址是一个账户 ECDSA 公钥的 Keccak 散列最右边的160位,通过地址可以在以太坊上接收或发送交易。在 Etherscan 上,可以通过地址来查询一个账户的信息
+* 交易:以太坊中的交易不仅包括发送和接收以太币,还包括向合约账户发送交易来调用合约代码、向空用户发送交易来生成以交易信息为代码块的合约账户
+* Gas:Gas 是以太坊中的一种机制,用于执行智能合约或交易操作的虚拟燃料。由于以太坊是图灵完备的,为了避免开发者无意或恶意编写出死循环等浪费资源或滥用资源的情况,以太坊中的每一笔交易都需支付一定的 Gas (燃料费),即需支付一定的以太币作为 Gas。Gas 的金额通常是由交易的发起者指定并支付的
+* 挖矿:和比特币类似,以太坊同样通过挖矿来产生区块。在以太坊目前的 PoW 机制下,每当一笔交易发出并广播,就会吸引矿工来将该交易打包成区块。每产生一个区块都会有一笔**固定奖励**给矿工,目前的固定奖励是3个以太。同时,区块中所有操作所需的 Gas 也会作为奖励给矿工。与比特币不同的是,以太坊中产生叔块的矿工可能会获得叔块奖励,引用叔块的矿工会获得叔块引用奖励
+* DApp(去中心化应用):通过智能合约,开发者能够设计想要的逻辑,相当于是网站的后端。而 DApp 则相当于是一个完整的网站(前端+后端),因此 DApp = 智能合约 + Web 前端。以太坊提供了一个名为 web3.js 的 Javascript 库,通过 web3.js 可以实现 Web 与以太坊区块链的交互和与智能合约的交互,方便开发者创建 DApp
+
+## 2.2、以太坊基础 ##
+
+### 2.2.1、以太坊中的货币 ###
+
+以太坊中的货币称为 **以太币**,单位为**以太(Ether)**,也称 ETH 或符号 Ξ。以太可以被分割为更小的单位,最小的单位是 wei,1 以太 = $10^18$ wei。以太币各单位的名称及之间的关系如下表:
+
+
+
+
+  +
+
+
+
+
+
+### 2.2.2、以太坊钱包 ###
+
+以太坊钱包是用于创建和广播交易的应用程序,常用的钱包有
+
+* MetaMask,一款基于浏览器扩展的钱包,可以很方便地添加到 Chrome, FireFox 等支持扩展的浏览器中
+* Jaxx,一款跨平台、多币种的钱包
+* MyEtherWallet(MEW),一款基于 Web 的钱包,可以在任何浏览器中运行
+* Emerald Wallet,一款被设计来用于以太坊经典区块链的钱包,但也与其他以太坊区块链兼容
+
+#### MetaMask 基础 ####
+
+以 Chrome 为例,访问 [Google 网上应用商店](https://chrome.google.com/webstore/category/extensions),搜索 MetaMask 并添加至 Chrome
+
+
+
+
+
+
+
+
+
+### 2.2.2、以太坊钱包 ###
+
+以太坊钱包是用于创建和广播交易的应用程序,常用的钱包有
+
+* MetaMask,一款基于浏览器扩展的钱包,可以很方便地添加到 Chrome, FireFox 等支持扩展的浏览器中
+* Jaxx,一款跨平台、多币种的钱包
+* MyEtherWallet(MEW),一款基于 Web 的钱包,可以在任何浏览器中运行
+* Emerald Wallet,一款被设计来用于以太坊经典区块链的钱包,但也与其他以太坊区块链兼容
+
+#### MetaMask 基础 ####
+
+以 Chrome 为例,访问 [Google 网上应用商店](https://chrome.google.com/webstore/category/extensions),搜索 MetaMask 并添加至 Chrome
+
+
+  +
+
+
+添加完成后 Chrome 会自动打开初始化页面
+
+
+
+
+
+
+
+添加完成后 Chrome 会自动打开初始化页面
+
+
+
+  +
+
+
+
+初次使用创建钱包
+
+
+
+
+
+
+
+初次使用创建钱包
+
+
+  +
+
+
+
+为钱包设置密码
+
+
+
+
+
+
+
+为钱包设置密码
+
+
+  +
+
+
+
+
+创建密码后,MetaMask 会生成一串密语,密语是12个随机的英文单词,用于防止密码忘记。密语可以直接当成密码使用,因此需要妥善保管
+
+
+
+
+
+
+
+
+创建密码后,MetaMask 会生成一串密语,密语是12个随机的英文单词,用于防止密码忘记。密语可以直接当成密码使用,因此需要妥善保管
+
+
+  +
+
+
+
+注册完毕后就可以在 Chrome 地址栏右边的扩展程序栏点击 🦊 图标使用 MetaMask 了
+
+
+
+
+
+
+
+
+注册完毕后就可以在 Chrome 地址栏右边的扩展程序栏点击 🦊 图标使用 MetaMask 了
+
+
+
+  +
+
+
+
+
+
+
+  +
+
+#### 获取测试以太 ####
+
+除了以太坊主网以外,以太坊还提供了 Ropsten, Kovan, Rinkeby, Goerli 这几个公共测试网络,另外还支持局域网测试网络和自建测试网络。在这里我们切换到 Ropsten 测试网络
+
+
+
+
+#### 获取测试以太 ####
+
+除了以太坊主网以外,以太坊还提供了 Ropsten, Kovan, Rinkeby, Goerli 这几个公共测试网络,另外还支持局域网测试网络和自建测试网络。在这里我们切换到 Ropsten 测试网络
+
+  +
+
+
+
+
+随后点击 **Buy** 按钮,点击**测试水管**下方的获取以太
+
+
+
+
+
+
+
+
+随后点击 **Buy** 按钮,点击**测试水管**下方的获取以太
+
+
+  +
+
+
+
+
+在打开的页面中点击 request 1 ether from faucet 就可以得到1个测试以太,当然,可以多次点击。
+
+
+
+
+
+
+
+在打开的页面中点击 request 1 ether from faucet 就可以得到1个测试以太,当然,可以多次点击。
+
+  +
+
+
+
+
+
+
+
+
+  +
+
+
+测试以太仅供测试使用,除此之外没有任何价值,测试完毕后剩下的以太可以发送到水龙头账户捐赠给水龙头,以供他人测试使用。
+
+## 2.3、以太坊交易的数据结构
+
+在以太坊网络中,交易执行属于一个事务。具有原子性、一致性、隔离性、持久性特点。
+
+- 原子性: 是不可分割的最小执行单位,要么做,要么不做。
+- 一致性: 同一笔交易执行,必然是将以太坊账本从一个一致性状态变到另一个一致性状态。
+- 隔离性: 交易执行途中不会受其他交易干扰。
+- 持久性: 一旦交易提交,则对以太坊账本的改变是永久性的。后续的操作不会对其有任何影响。
+
+以太坊交易的本质是由外部拥有的账户发起的签名消息,由以太坊网络传输,并被序列化后记录在以太坊区块链上,**交易是唯一可以触发状态更改或导致合约在EVM中执行的事物**
+
+### 2.3.1、交易的数据结构
+
+以太坊的数据结构主要可以分为四部分:`nonce`、`gas`、交易目标和消息(主要部分)、交易签名
+
+
+
+
+
+
+测试以太仅供测试使用,除此之外没有任何价值,测试完毕后剩下的以太可以发送到水龙头账户捐赠给水龙头,以供他人测试使用。
+
+## 2.3、以太坊交易的数据结构
+
+在以太坊网络中,交易执行属于一个事务。具有原子性、一致性、隔离性、持久性特点。
+
+- 原子性: 是不可分割的最小执行单位,要么做,要么不做。
+- 一致性: 同一笔交易执行,必然是将以太坊账本从一个一致性状态变到另一个一致性状态。
+- 隔离性: 交易执行途中不会受其他交易干扰。
+- 持久性: 一旦交易提交,则对以太坊账本的改变是永久性的。后续的操作不会对其有任何影响。
+
+以太坊交易的本质是由外部拥有的账户发起的签名消息,由以太坊网络传输,并被序列化后记录在以太坊区块链上,**交易是唯一可以触发状态更改或导致合约在EVM中执行的事物**
+
+### 2.3.1、交易的数据结构
+
+以太坊的数据结构主要可以分为四部分:`nonce`、`gas`、交易目标和消息(主要部分)、交易签名
+
+
+  +
+
+
+
+开头是一个 uint64 类型的数字,称之为随机数。用于撤销交易、防止双花和修改以太坊账户的 Nonce 值。
+
+第二部分是关于交易执行限制的设置,gas 为愿意供以太坊虚拟机运行的燃料上限。 `gasPrice` 是愿意支付的燃料单价。`gasPrcie * gas` 则为愿意为这笔交易支付的最高手续费。
+
+第三部分是交易发送者输入以太坊虚拟机执行此交易的初始信息: 虚拟机操作对象(接收方 To)、从交易发送方转移到操作对象的资产(Value),以及虚拟机运行时入参(input)。其中 To 为空时,意味着虚拟机无可操作对象,**此时虚拟机将利用 input 内容部署一个新合约**。
+
+第四部分是交易发送方对交易的签名结果,可以利用交易内容和签名结果反向推导出签名者,即交易发送方地址。以上总结如下:
+
+* `nonce`:由发起人EOA发出的序列号,用于防止交易消息重播。
+* `gas price`:交易发起人愿意支付的gas单价(wei)。
+* `start gas`:交易发起人愿意支付的最大gas量。
+* `to`:目的以太坊地址。
+* `value`:要发送到目的地的以太数量。
+* `data`:可变长度二进制数据负载(payload)。
+* `v,r,s`:发起人EOA的ECDSA签名的三个组成部分。
+* 交易消息的结构使用递归长度前缀(RLP)编码方案进行序列化,该方案专为在以太坊中准确和字节完美的数据序列化而创建。
+
+### 2.3.2、交易中的`nonce`
+
+按以太坊黄皮书的定义, `nonce`是一个标量值,它等于从这个地址发送的交易数,或者对于关联code的帐户来说,是这个帐户创建合约的数量。因此`nonce`便有以下特征:
+
+* `nonce`不会明确存储为区块链中帐户状态的一部分。相反,它是通过计算发送地址的已确认交易的数量来动态计算的。
+* `nonce`值还用于防止错误计算账户余额。`nonce`强制来自任何地址的交易按顺序处理,没有间隔,无论节点接收它们的顺序如何。
+* 使用`nonce`确保所有节点计算相同的余额和正确的序列交易,等同于用于防止比特币“双重支付”(“重放攻击”)的机制。但是,由于以太坊跟踪账户余额并且不单独跟踪 `UTXO` ,因此只有在错误地计算账户余额时才会发生“双重支付”。`nonce`机制可以防止这种情况发生。
+
+### 2.3.3、并发和`nonce`
+
+以太坊是一个允许操作(节点,客户端,DApps)并发的系统,但强制执行单例状态。例如,出块的时候只有一个系统状态。假如我们有多个独立的钱包应用或客户端,比如 MetaMask 和 Geth,它们可以使用相同的地址生成交易。如果我们希望它们都够同时发送交易,该怎么设置交易的`nonce`呢?一般有以下两种做法:
+
+* 用一台服务器为各个应用分配`nonce`,先来先服务——可能出现单点故障,并且失败的交易会将后续交易阻塞。
+* 生成交易后不分配`nonce`,也不签名,而是把它放入一个队列等待。另起一个节点跟踪`nonce`并签名交易。同样会有单点故障的可能,而且跟踪`nonce`和签名的节点是无法实现真正并发的。
+
+### 2.3.4、交易中的`gas`
+
+Gas 中译是:瓦斯、汽油,代表一种可燃气体。 这形象地比喻以太坊的交易手续费计算模式,不同于比特币中**直接**支付比特币作为转账手续费, 以太坊视为一个去中心化的计算网络,当你发送Token、执行合约、转移以太币或者在此区块上干其他的时候,计算机在处理这笔交易时需要进行计算消耗网络资源,这样你必须支付燃油费购买燃料才能让计算机为你工作。最终燃料费作为手续费支付给矿工。
+
+> 注:可以在Etherscan上查询gas price与confirmation time的关系,如下图
+
+
+
+
+
+
+
+开头是一个 uint64 类型的数字,称之为随机数。用于撤销交易、防止双花和修改以太坊账户的 Nonce 值。
+
+第二部分是关于交易执行限制的设置,gas 为愿意供以太坊虚拟机运行的燃料上限。 `gasPrice` 是愿意支付的燃料单价。`gasPrcie * gas` 则为愿意为这笔交易支付的最高手续费。
+
+第三部分是交易发送者输入以太坊虚拟机执行此交易的初始信息: 虚拟机操作对象(接收方 To)、从交易发送方转移到操作对象的资产(Value),以及虚拟机运行时入参(input)。其中 To 为空时,意味着虚拟机无可操作对象,**此时虚拟机将利用 input 内容部署一个新合约**。
+
+第四部分是交易发送方对交易的签名结果,可以利用交易内容和签名结果反向推导出签名者,即交易发送方地址。以上总结如下:
+
+* `nonce`:由发起人EOA发出的序列号,用于防止交易消息重播。
+* `gas price`:交易发起人愿意支付的gas单价(wei)。
+* `start gas`:交易发起人愿意支付的最大gas量。
+* `to`:目的以太坊地址。
+* `value`:要发送到目的地的以太数量。
+* `data`:可变长度二进制数据负载(payload)。
+* `v,r,s`:发起人EOA的ECDSA签名的三个组成部分。
+* 交易消息的结构使用递归长度前缀(RLP)编码方案进行序列化,该方案专为在以太坊中准确和字节完美的数据序列化而创建。
+
+### 2.3.2、交易中的`nonce`
+
+按以太坊黄皮书的定义, `nonce`是一个标量值,它等于从这个地址发送的交易数,或者对于关联code的帐户来说,是这个帐户创建合约的数量。因此`nonce`便有以下特征:
+
+* `nonce`不会明确存储为区块链中帐户状态的一部分。相反,它是通过计算发送地址的已确认交易的数量来动态计算的。
+* `nonce`值还用于防止错误计算账户余额。`nonce`强制来自任何地址的交易按顺序处理,没有间隔,无论节点接收它们的顺序如何。
+* 使用`nonce`确保所有节点计算相同的余额和正确的序列交易,等同于用于防止比特币“双重支付”(“重放攻击”)的机制。但是,由于以太坊跟踪账户余额并且不单独跟踪 `UTXO` ,因此只有在错误地计算账户余额时才会发生“双重支付”。`nonce`机制可以防止这种情况发生。
+
+### 2.3.3、并发和`nonce`
+
+以太坊是一个允许操作(节点,客户端,DApps)并发的系统,但强制执行单例状态。例如,出块的时候只有一个系统状态。假如我们有多个独立的钱包应用或客户端,比如 MetaMask 和 Geth,它们可以使用相同的地址生成交易。如果我们希望它们都够同时发送交易,该怎么设置交易的`nonce`呢?一般有以下两种做法:
+
+* 用一台服务器为各个应用分配`nonce`,先来先服务——可能出现单点故障,并且失败的交易会将后续交易阻塞。
+* 生成交易后不分配`nonce`,也不签名,而是把它放入一个队列等待。另起一个节点跟踪`nonce`并签名交易。同样会有单点故障的可能,而且跟踪`nonce`和签名的节点是无法实现真正并发的。
+
+### 2.3.4、交易中的`gas`
+
+Gas 中译是:瓦斯、汽油,代表一种可燃气体。 这形象地比喻以太坊的交易手续费计算模式,不同于比特币中**直接**支付比特币作为转账手续费, 以太坊视为一个去中心化的计算网络,当你发送Token、执行合约、转移以太币或者在此区块上干其他的时候,计算机在处理这笔交易时需要进行计算消耗网络资源,这样你必须支付燃油费购买燃料才能让计算机为你工作。最终燃料费作为手续费支付给矿工。
+
+> 注:可以在Etherscan上查询gas price与confirmation time的关系,如下图
+
+
+  +
+
+
+因为手续费等于`gasPrice * gasUsed`,用户在转账,特别是执行智能合约时 gasUsed 无法提前预知。 这样存在一个风险,当用户的交易涉及一个恶意的智能合约,该合约执行将消耗无限的燃料, 这样会导致交易方的余额全部消耗(恶意的智能合约有可能是程序Bug,如合约执行陷入一个死循环)。
+
+为了避免合约中的错误引起不可预计的燃料消耗,用户需要在发送交易时设定允许消耗的燃料上限,即 gasLimit。 这样不管合约是否良好,最坏情况也只是消耗 gasLimit 量的燃料。
+
+然而,一笔交易所必须支付的燃料已经在区块中通过该交易已执行的计算量记录。 如果你不想支出太多燃料,而故意设置过低的 gasLimit 是没太多帮助的。 你必须支付足够燃料来支付本交易所必要的计算资源。如果交易尚未执行完成,而燃料已用完, 将出现一个 `Out of Gas` 的错误。特别注意的是,即使交易失败,你也必须为已占用的计算资源所支付手续费。 比如,你通过合约给 TFBOYS 投票,设置 gasPrice=2 gwei,gasLimit=40000(实现投票需要40001的燃料开销), 最终你投票失败且仍然需要支付 40000*2 gwei= 80000 gwei= 0.00008 ETH。
+
+另外,如果最终 gasUsed 低于 gasLimit,即燃料未用完。则剩余燃料(gasLimit - gasUsed )将在交易后退还给你。 比如你发送 1 Ether 到另一个账户B,设置 gas limit 为 400000,将有 400000 - 21000 返回给你。
+
+> 注意:21000 是标准转账交易的gasUsed。因此一笔标准的转账交易你可以设置 gasLimit 为21000
+
+## 2.4、以太坊账户
+
+对比比特币的UTXO余额模型,以太坊使用“账户”余额模型。 以太坊丰富了账户内容,除余额外还能自定义存放任意多数据。 并利用账户数据的可维护性,构建智能合约账户。下面我们首先将比特币的UTXO余额模型与以太坊账户进行比较,说明其各自的优缺点以及适用性。
+
+### 2.4.1、比特币UTXO和以太坊账户结构比较
+
+在当前的区块链项目中,主要有两种记录保存方式,**一种是账户/余额模型,一种是UTXO模型**。比特币采用就是UTXO模型,以太坊、EOS等则采用的是账户/余额模型。
+
+
+
+
+
+因为手续费等于`gasPrice * gasUsed`,用户在转账,特别是执行智能合约时 gasUsed 无法提前预知。 这样存在一个风险,当用户的交易涉及一个恶意的智能合约,该合约执行将消耗无限的燃料, 这样会导致交易方的余额全部消耗(恶意的智能合约有可能是程序Bug,如合约执行陷入一个死循环)。
+
+为了避免合约中的错误引起不可预计的燃料消耗,用户需要在发送交易时设定允许消耗的燃料上限,即 gasLimit。 这样不管合约是否良好,最坏情况也只是消耗 gasLimit 量的燃料。
+
+然而,一笔交易所必须支付的燃料已经在区块中通过该交易已执行的计算量记录。 如果你不想支出太多燃料,而故意设置过低的 gasLimit 是没太多帮助的。 你必须支付足够燃料来支付本交易所必要的计算资源。如果交易尚未执行完成,而燃料已用完, 将出现一个 `Out of Gas` 的错误。特别注意的是,即使交易失败,你也必须为已占用的计算资源所支付手续费。 比如,你通过合约给 TFBOYS 投票,设置 gasPrice=2 gwei,gasLimit=40000(实现投票需要40001的燃料开销), 最终你投票失败且仍然需要支付 40000*2 gwei= 80000 gwei= 0.00008 ETH。
+
+另外,如果最终 gasUsed 低于 gasLimit,即燃料未用完。则剩余燃料(gasLimit - gasUsed )将在交易后退还给你。 比如你发送 1 Ether 到另一个账户B,设置 gas limit 为 400000,将有 400000 - 21000 返回给你。
+
+> 注意:21000 是标准转账交易的gasUsed。因此一笔标准的转账交易你可以设置 gasLimit 为21000
+
+## 2.4、以太坊账户
+
+对比比特币的UTXO余额模型,以太坊使用“账户”余额模型。 以太坊丰富了账户内容,除余额外还能自定义存放任意多数据。 并利用账户数据的可维护性,构建智能合约账户。下面我们首先将比特币的UTXO余额模型与以太坊账户进行比较,说明其各自的优缺点以及适用性。
+
+### 2.4.1、比特币UTXO和以太坊账户结构比较
+
+在当前的区块链项目中,主要有两种记录保存方式,**一种是账户/余额模型,一种是UTXO模型**。比特币采用就是UTXO模型,以太坊、EOS等则采用的是账户/余额模型。
+
+ +
+### 2.4.2、比特币UTXO
+
+UTXO是 Unspent Transaction Output的缩写,意思是**未花费的输出,**可以简单理解为还没有用掉的收款。比如韩梅梅收到一笔比特币,她没有用掉,这笔比特币对她来说就是一个UTXO。关于UTXO的具体介绍大家可以查看[这篇文章](https://zhuanlan.zhihu.com/p/74050135)。
+
+**UTXO 核心设计思路是:它记录交易事件,而不记录最终状态。**要计算某个用户有多少比特币,就要对其钱包里所有的UTXO求和,得到结果就是他的持币数量。UTXO模型在转账交易时,是以UTXO为单位的,也就是说在支付时,调用的是整数倍UTXO,比如1个UTXO,3个UTXO,没有0.5个UTXO的说法。
+
+* 比特币在基于UTXO的结构中存储有关用户余额的数据,系统的整个状态就是一组UTXO的集合,每个UTXO都有一个所有者和一个面值(就像不同的硬币),而交易会花费若干个输入的UTXO,并根据规则创建若干个新的UTXO
+* 每个引用的输入必须有效并且尚未花费,对于一个交易,必须包含有每个输入的所有者匹配的签名,总输入必须大于等于总输出值。所以系统中用户的余额是用户具有私钥的UTXO的总值
+
+### 2.4.3、以太坊账户
+
+为什么以太坊不用UTXO呢?显然是因为麻烦,以太坊的做法更符合直觉,以太坊中的状态就是系统中所有账户的列表,每个账户都包含了一个余额和以太坊**特殊定义的数据**(代码和内部存储)。如果发送账户有足够多的余额来进行支付,则交易有效,在这种情况下发送账户先扣款,而收款账户将记入这笔收入。**如果接受账户有相关代码,则代码会自动运行,并且它的内部存储也可能被更改,或者代码还可能向其他账户发送额外的消息,这就会导致进一步的借贷资金关系。**
+
+### 2.4.4、优缺点比较
+
+**比特币UTXO的优点**:
+
+* 更高程度的隐私:如果用户为他们收到的每笔交易使用新地址,那么通常很难将账户互相链接。这很大程度上适用于货币,但不太适用于任何dapps,因为dapps通常涉及跟踪和用户绑定的复杂状态,可能不存在像货币那样简单的用户状态划分方案
+* 潜在的可扩展性:UTXO在理论上更符合可扩展性要求,因为我们只需要依赖拥有UTXO的那些人去维护基于Merkle树的所有权证明就够了,即使包括所有者在内的每个人都决定忘记该数据,那么也只有所有者受到对应的UTXO的损失,不影响接下来的交易。而在账户模式中,如果每个人都丢失了与账户相对应的Merkle树的部分,那将会使得和该账户有关的消息完全无法处理,包括发币给它。
+
+**以太坊账户模式的优点**:
+
+* 可以节省大量空间:不将UTXOs分开存储,而是合成一个账户;每个交易只需要一个输入、一个签名并产生一个输出
+* 更好的可替代性:货币本质上都是同质化、可替代的;UTXO的设计使得货币从来源分成了“可花费”和“不可花费”两类,这在实际应用中很难有对应模型
+* 更加简单:更容易编码和理解,特别是设计复杂脚本的时候,UTXO的脚本逻辑复杂时更令人费解
+* 便于维护持久轻节点:只要沿着特定方向扫描状态树,轻节点 可以很容易地随时访问账户相关的所有数据。而UTXO地每个交易都会使得状态引用发生改变,这对应节点来说长时间运行Dapp会有很大压力
+
+### 2.4.5、总结
+
+| | BitCoin | Ethereum |
+| ------------ | ---------------- | ---------------- |
+| **设计定位** | 现金系统 | 去中心化应用平台 |
+| **数据组成** | 交易列表(账本) | 交易和账户状态 |
+| **交易对象** | UTXO | Accounts |
+| **代码控制** | 脚本 | 智能合约 |
+
+## 2.5、以太坊账户类型
+
+以太坊作为智能合约操作平台,将账户划分为两类:外部账户(EOAs)和合约账户(contract account),下面分别做简要介绍:
+
+
+
+
+### 2.4.2、比特币UTXO
+
+UTXO是 Unspent Transaction Output的缩写,意思是**未花费的输出,**可以简单理解为还没有用掉的收款。比如韩梅梅收到一笔比特币,她没有用掉,这笔比特币对她来说就是一个UTXO。关于UTXO的具体介绍大家可以查看[这篇文章](https://zhuanlan.zhihu.com/p/74050135)。
+
+**UTXO 核心设计思路是:它记录交易事件,而不记录最终状态。**要计算某个用户有多少比特币,就要对其钱包里所有的UTXO求和,得到结果就是他的持币数量。UTXO模型在转账交易时,是以UTXO为单位的,也就是说在支付时,调用的是整数倍UTXO,比如1个UTXO,3个UTXO,没有0.5个UTXO的说法。
+
+* 比特币在基于UTXO的结构中存储有关用户余额的数据,系统的整个状态就是一组UTXO的集合,每个UTXO都有一个所有者和一个面值(就像不同的硬币),而交易会花费若干个输入的UTXO,并根据规则创建若干个新的UTXO
+* 每个引用的输入必须有效并且尚未花费,对于一个交易,必须包含有每个输入的所有者匹配的签名,总输入必须大于等于总输出值。所以系统中用户的余额是用户具有私钥的UTXO的总值
+
+### 2.4.3、以太坊账户
+
+为什么以太坊不用UTXO呢?显然是因为麻烦,以太坊的做法更符合直觉,以太坊中的状态就是系统中所有账户的列表,每个账户都包含了一个余额和以太坊**特殊定义的数据**(代码和内部存储)。如果发送账户有足够多的余额来进行支付,则交易有效,在这种情况下发送账户先扣款,而收款账户将记入这笔收入。**如果接受账户有相关代码,则代码会自动运行,并且它的内部存储也可能被更改,或者代码还可能向其他账户发送额外的消息,这就会导致进一步的借贷资金关系。**
+
+### 2.4.4、优缺点比较
+
+**比特币UTXO的优点**:
+
+* 更高程度的隐私:如果用户为他们收到的每笔交易使用新地址,那么通常很难将账户互相链接。这很大程度上适用于货币,但不太适用于任何dapps,因为dapps通常涉及跟踪和用户绑定的复杂状态,可能不存在像货币那样简单的用户状态划分方案
+* 潜在的可扩展性:UTXO在理论上更符合可扩展性要求,因为我们只需要依赖拥有UTXO的那些人去维护基于Merkle树的所有权证明就够了,即使包括所有者在内的每个人都决定忘记该数据,那么也只有所有者受到对应的UTXO的损失,不影响接下来的交易。而在账户模式中,如果每个人都丢失了与账户相对应的Merkle树的部分,那将会使得和该账户有关的消息完全无法处理,包括发币给它。
+
+**以太坊账户模式的优点**:
+
+* 可以节省大量空间:不将UTXOs分开存储,而是合成一个账户;每个交易只需要一个输入、一个签名并产生一个输出
+* 更好的可替代性:货币本质上都是同质化、可替代的;UTXO的设计使得货币从来源分成了“可花费”和“不可花费”两类,这在实际应用中很难有对应模型
+* 更加简单:更容易编码和理解,特别是设计复杂脚本的时候,UTXO的脚本逻辑复杂时更令人费解
+* 便于维护持久轻节点:只要沿着特定方向扫描状态树,轻节点 可以很容易地随时访问账户相关的所有数据。而UTXO地每个交易都会使得状态引用发生改变,这对应节点来说长时间运行Dapp会有很大压力
+
+### 2.4.5、总结
+
+| | BitCoin | Ethereum |
+| ------------ | ---------------- | ---------------- |
+| **设计定位** | 现金系统 | 去中心化应用平台 |
+| **数据组成** | 交易列表(账本) | 交易和账户状态 |
+| **交易对象** | UTXO | Accounts |
+| **代码控制** | 脚本 | 智能合约 |
+
+## 2.5、以太坊账户类型
+
+以太坊作为智能合约操作平台,将账户划分为两类:外部账户(EOAs)和合约账户(contract account),下面分别做简要介绍:
+
+
+  +
+
+
+
+### 2.5.1、外部账户(EOA)
+
+外部账户是由人来控制的,也就是常规理解的普通账户,外部账户包含以太币余额,主要作用就是发送交易(是广义的交易,包括转币和触发合约代码),是由用户私钥控制的,没有关联代码,所有在以太坊上交易的发起者都是外部账户。
+
+外部账户特点总结:
+
+1. 拥有以太余额。
+2. 能发送交易,包括转账和执行合约代码。
+3. 被私钥控制。
+4. 没有相关的可执行代码。
+
+### 2.5.2、合约账户(CA)
+
+合约账户有时也叫内部账户,有对应的以太币余额和关联代码,它是由代码控制的,可以通过交易或来自其他合约的调用消息来触发代码执行,执行代码时可以操作自己的存储空间,也可以调用其他合约
+
+合约账户特点总结:
+
+1. 拥有以太余额。
+2. 有相关的可执行代码(合约代码)。
+3. 合约代码能够被交易或者其他合约消息调用。
+4. 合约代码被执行时可再调用其他合约代码。
+5. 合约代码被执行时可执行复杂运算,可永久地改变合约内部的数据存储。
+
+
+如果大家对概念还理解不深可以先尝试学习后面部分,本教程内容有限,推荐大家有精力阅读以下读物:
+- [区块链学习的书籍](https://www.zhihu.com/question/61156867)
+- [区块链入门教程](https://www.ruanyifeng.com/blog/2017/12/blockchain-tutorial.html)
+- [IBM教程](https://developer.ibm.com/zh/technologies/blockchain/tutorials/)
+
+**参考自:**
+1. [比特币白皮书]https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system)
+2. [以太坊白皮书](https://ethfans.org/posts/ethereum-whitepaper)
+3. [超级账本白皮书](https://www.chainnode.com/doc/399)
+4. [闪电网络白皮书](https://www.chainnode.com/doc/399)
\ No newline at end of file
diff --git a/Blockchain/part2_Solidity基础.md b/Blockchain/part2_Solidity基础.md
new file mode 100644
index 0000000..1494352
--- /dev/null
+++ b/Blockchain/part2_Solidity基础.md
@@ -0,0 +1,1034 @@
+ 注:本教程为技术教程,不谈论且不涉及炒作任何数字货币
+
+# Solidity 入门教学
+
+## 1、 简介
+
+### 1.1 Solidity是什么
+- Solidity 是一门面向合约的、为实现智能合约而创建的高级编程语言。这门语言受到了 C++,Python 和 Javascript 语言的影响,设计的目的是能在以太坊虚拟机(EVM)上运行。
+- Solidity 是静态类型语言,支持继承、库和复杂的用户定义类型等特性。
+- 内含的类型除了常见编程语言中的标准类型,还包括 `address`等以太坊独有的类型,Solidity 源码文件通常以 .sol 作为扩展名
+- 目前尝试 Solidity 编程的推荐方式是使用 Remix。Remix是一个基于 Web 浏览器的 IDE,它可以让你编写 Solidity 智能合约,然后部署并运行该智能合约。
+
+### 1.2 Solidity语言特性
+
+Solidity的语法接近于JavaScript,是一种面向对象的语言。但作为一种真正意义上运行在网络上的去中心合约,它又有很多的不同:
+- 以太坊底层基于帐户,而不是 [UTXO](https://cloud.tencent.com/developer/article/1367743),所以增加了一个特殊的address 的数据类型用于定位用户和合约账户。
+- 语言内嵌框架支持支付。提供了 `payable` 等关键字,可以在语言层面直接支持支付。
+- 使用区块链进行数据存储。数据的每一个状态都可以永久存储,所以在使用时需要确定变量使用内存,还是区块链存储。
+- 运行环境是在去中心化的网络上,所以需要强调合约或函数执行的调用的方式。
+- 不同的异常机制。一旦出现异常,所有的执行都将会被回撤,这主要是为了保证合约执行的原子性,以避免中间状态出现的数据不一致。
+
+### 1.3 Solidity源码和智能合约
+
+Solidity 源代码要成为可以运行在以太坊上的智能合约需要经历如下的
+
+**步骤:**
+1. 用 Solidity 编写的智能合约源代码需要先使用编译器编译为字节码(Bytecode),编译过程中会同时产生智能合约的二进制接口规范(Application Binary Interface,简称为ABI);
+2. 通过交易(Transaction)的方式将字节码部署到以太坊网络,每次成功部署都会产生一个新的智能合约账户;
+3. 使用 Javascript 编写的 DApp 通常通过 web3.js + ABI去调用智能合约中的函数来实现数据的读取和修改。
+
+### 1.4 合约结构
+
+- 状态变量(State Variables)作为合约状态的一部分,值会永久保存在存储空间内。
+- 函数(Functions)合约中可执行的代码块。
+- 函数修饰器(Function Modifiers)在函数声明中,用来补充修饰函数的语义。
+- 事件(Events)非常方便的 EVM 日志工具接口。
+
+
+## 2、 Solidity编译器安装以及简单使用
+
+Remix 是一个开源的 IDE,是一个浏览器在线编辑器。作为 Solidity 智能合约开发环境,Solidity IDE Remix(在线浏览器编辑器)提供基本的编译、部署至本地或测试网络、执行合约等功能。
+
+### 2.1 remix安装以及使用
+
+1. **浏览器端配置**
+
+在浏览器端有俩个选择,分别为英文版与中文版(有些许差别)
+
+- Remix中文版地址:[http://remix.hubwiz.com](http://remix.hubwiz.com)
+
+- Remix英文版地址(**推荐**):[https://remix.ethereum.org/](https://remix.ethereum.org/)
+
+**PS.可能需要科学上网**
+
+
+
+
+
+
+
+### 2.5.1、外部账户(EOA)
+
+外部账户是由人来控制的,也就是常规理解的普通账户,外部账户包含以太币余额,主要作用就是发送交易(是广义的交易,包括转币和触发合约代码),是由用户私钥控制的,没有关联代码,所有在以太坊上交易的发起者都是外部账户。
+
+外部账户特点总结:
+
+1. 拥有以太余额。
+2. 能发送交易,包括转账和执行合约代码。
+3. 被私钥控制。
+4. 没有相关的可执行代码。
+
+### 2.5.2、合约账户(CA)
+
+合约账户有时也叫内部账户,有对应的以太币余额和关联代码,它是由代码控制的,可以通过交易或来自其他合约的调用消息来触发代码执行,执行代码时可以操作自己的存储空间,也可以调用其他合约
+
+合约账户特点总结:
+
+1. 拥有以太余额。
+2. 有相关的可执行代码(合约代码)。
+3. 合约代码能够被交易或者其他合约消息调用。
+4. 合约代码被执行时可再调用其他合约代码。
+5. 合约代码被执行时可执行复杂运算,可永久地改变合约内部的数据存储。
+
+
+如果大家对概念还理解不深可以先尝试学习后面部分,本教程内容有限,推荐大家有精力阅读以下读物:
+- [区块链学习的书籍](https://www.zhihu.com/question/61156867)
+- [区块链入门教程](https://www.ruanyifeng.com/blog/2017/12/blockchain-tutorial.html)
+- [IBM教程](https://developer.ibm.com/zh/technologies/blockchain/tutorials/)
+
+**参考自:**
+1. [比特币白皮书]https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system)
+2. [以太坊白皮书](https://ethfans.org/posts/ethereum-whitepaper)
+3. [超级账本白皮书](https://www.chainnode.com/doc/399)
+4. [闪电网络白皮书](https://www.chainnode.com/doc/399)
\ No newline at end of file
diff --git a/Blockchain/part2_Solidity基础.md b/Blockchain/part2_Solidity基础.md
new file mode 100644
index 0000000..1494352
--- /dev/null
+++ b/Blockchain/part2_Solidity基础.md
@@ -0,0 +1,1034 @@
+ 注:本教程为技术教程,不谈论且不涉及炒作任何数字货币
+
+# Solidity 入门教学
+
+## 1、 简介
+
+### 1.1 Solidity是什么
+- Solidity 是一门面向合约的、为实现智能合约而创建的高级编程语言。这门语言受到了 C++,Python 和 Javascript 语言的影响,设计的目的是能在以太坊虚拟机(EVM)上运行。
+- Solidity 是静态类型语言,支持继承、库和复杂的用户定义类型等特性。
+- 内含的类型除了常见编程语言中的标准类型,还包括 `address`等以太坊独有的类型,Solidity 源码文件通常以 .sol 作为扩展名
+- 目前尝试 Solidity 编程的推荐方式是使用 Remix。Remix是一个基于 Web 浏览器的 IDE,它可以让你编写 Solidity 智能合约,然后部署并运行该智能合约。
+
+### 1.2 Solidity语言特性
+
+Solidity的语法接近于JavaScript,是一种面向对象的语言。但作为一种真正意义上运行在网络上的去中心合约,它又有很多的不同:
+- 以太坊底层基于帐户,而不是 [UTXO](https://cloud.tencent.com/developer/article/1367743),所以增加了一个特殊的address 的数据类型用于定位用户和合约账户。
+- 语言内嵌框架支持支付。提供了 `payable` 等关键字,可以在语言层面直接支持支付。
+- 使用区块链进行数据存储。数据的每一个状态都可以永久存储,所以在使用时需要确定变量使用内存,还是区块链存储。
+- 运行环境是在去中心化的网络上,所以需要强调合约或函数执行的调用的方式。
+- 不同的异常机制。一旦出现异常,所有的执行都将会被回撤,这主要是为了保证合约执行的原子性,以避免中间状态出现的数据不一致。
+
+### 1.3 Solidity源码和智能合约
+
+Solidity 源代码要成为可以运行在以太坊上的智能合约需要经历如下的
+
+**步骤:**
+1. 用 Solidity 编写的智能合约源代码需要先使用编译器编译为字节码(Bytecode),编译过程中会同时产生智能合约的二进制接口规范(Application Binary Interface,简称为ABI);
+2. 通过交易(Transaction)的方式将字节码部署到以太坊网络,每次成功部署都会产生一个新的智能合约账户;
+3. 使用 Javascript 编写的 DApp 通常通过 web3.js + ABI去调用智能合约中的函数来实现数据的读取和修改。
+
+### 1.4 合约结构
+
+- 状态变量(State Variables)作为合约状态的一部分,值会永久保存在存储空间内。
+- 函数(Functions)合约中可执行的代码块。
+- 函数修饰器(Function Modifiers)在函数声明中,用来补充修饰函数的语义。
+- 事件(Events)非常方便的 EVM 日志工具接口。
+
+
+## 2、 Solidity编译器安装以及简单使用
+
+Remix 是一个开源的 IDE,是一个浏览器在线编辑器。作为 Solidity 智能合约开发环境,Solidity IDE Remix(在线浏览器编辑器)提供基本的编译、部署至本地或测试网络、执行合约等功能。
+
+### 2.1 remix安装以及使用
+
+1. **浏览器端配置**
+
+在浏览器端有俩个选择,分别为英文版与中文版(有些许差别)
+
+- Remix中文版地址:[http://remix.hubwiz.com](http://remix.hubwiz.com)
+
+- Remix英文版地址(**推荐**):[https://remix.ethereum.org/](https://remix.ethereum.org/)
+
+**PS.可能需要科学上网**
+
+
+  +
+
+ 图 1
+
+
+
+
+下面都以`英文版`为例子介绍
+
+1、**浏览器输入 [https://remix.ethereum.org/](https://remix.ethereum.org/)**
+
+如果出现加载慢,加载不完全的情况,刷新几次即可
+
+2、左侧可以看到我们所有的文件,下面是我们的remix控制台
+
+
+  +
+
+ 图 2
+
+
+
+
+上图小图标从左到右依次为:
+
+- 创建新文件
+- 创建新文件夹
+- Github代码片段分享
+- 表示打开一个本地文件
+
+控制台图片如下:
+
+
+  +
+
+ 图 3
+
+
+
+
+- 1 从左至右表示隐藏控制台、清除控制台输出、pending的交易数量
+- 2 表示监听所有交易
+- 3 表示搜索框
+- 4 表示输出区域
+- 5 表示使用JavaScript与以太坊交互的区域,可以使用Web3对象
+
+
+3、点击文件样式图标输入我们的文件名即可(以.sol为后缀)
+
+
+  +
+
+ 图 4
+
+
+
+4、安装必要的插件
+
+点击插件管理器,页面中为这个图标
+
+
+  +
+
+ 图 5
+
+
+
+
+
+- 安装compiler
+
+ 搜索关键字compiler
+
+  +
+
+ 图 6
+
+
+
+
+5、写一个简单的样例
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract SimpleStorage {
+ uint storedData;
+
+ function set(uint x) public {
+ storedData = x;
+ }
+
+ function get() public view returns (uint) {
+ return storedData;
+ }
+}
+```
+
+第一行就是告诉大家源代码使用Solidity版本0.4.0写的,并且使用0.4.0以上版本运行也没问题(最高到0.5.0,但是不包含0.5.0)。这是为了确保合约不会在新的编译器版本中突然行为异常。关键字 `pragma` 的含义是,一般来说,pragmas(编译指令)是告知编译器如何处理源代码的指令的。
+
+Solidity中合约的含义就是一组代码(它的 函数 )和数据(它的 状态 ),它们位于以太坊区块链的一个特定地址上。 代码行 `uint storedData`; 声明一个类型为 `uint` (256位无符号整数)的状态变量,叫做 `storedData` 。 你可以认为它是数据库里的一个位置,可以通过调用管理数据库代码的函数进行查询和变更。对于以太坊来说,上述的合约就是拥有合约(owning contract)。在这种情况下,函数 `set` 和 `get` 可以用来变更或取出变量的值。
+
+要访问一个状态变量,并不需要像 `this.` 这样的前缀,虽然这是其他语言常见的做法。
+
+该合约能完成的事情并不多(由于以太坊构建的基础架构的原因):它能允许任何人在合约中存储一个单独的数字,并且这个数字可以被世界上任何人访问,且没有可行的办法阻止你发布这个数字。当然,任何人都可以再次调用 `set` ,传入不同的值,覆盖你的数字,但是这个数字仍会被存储在区块链的历史记录中。
+
+
+  +
+
+ 图 7
+
+
+
+
+点击`compile test.sol`,可以看到编译按钮,建议将`Auto compile`打钩(自动编译),之后会在编译图标上看到一个以绿色为背景的对勾。
+
+编译组件说明:
+- `Compiler`可以选择Solidity的编译器版本
+- `Language`可以选择编程语言
+- `EVM Version`可以选择EVM虚拟机版本
+- `Auto compile`可以设置自动编译,修改完代码后自动执行编译操作
+- `Enable optimization`可以设置对编译进行优化
+- `Hide warnings`可以设置隐藏警告信息。
+- `Contract`选择需要编译的合约
+- `Publish on Swarm`和`Publish on Ipfs`分别将合约上传到Swarm和Ipfs这两个分布式文件系统上去
+- `Compilation Details`很重要,可以查看编译的信息,包括ABI、字节码、函数Hash等
+- `ABI`和`Bytecode`分别复制ABI和字节码。
+- 再下面的部分空白用来显示编译的Warnings和Errors。
+
+我们点击`Compilation Details`就能看到编译之后的一些信息,如下图所示(部分)
+
+
+  +
+
+ 图 8
+
+
+
+- `NAME`:合约名
+- `METADATA`:一些编译相关的信息,比如版本、所用的语言、设置等
+- `BYTECODE`:写入区块的字节码
+- `ABI`:此智能合约对应的 ABI ,也就是我们合约里面定义的一些接口
+- `WEB3DEPLOY`:智能合约编译之后的发布命令,这个就是比较重要的,之后的web3就是调用这段命令来部署合约的
+- `METADATAHASH`:数据的一个哈希值
+- `SWARMLOCATION`:Swarm网络的一个地址
+- `FUNCTIONHASHES`:合约定义的方法的hash,其实我们执行合约的时候就是通过这个hash去找到对应的方法进行执行的
+- `GASESTIMATES`:关于矿工费的一个预算,在ETH上进行合约的部署,执行等都是需要矿工费的。一般合约代码越多矿工费越高。
+
+
+点击下面的run图标,可以看到部署,以及账户信息,环境等等
+
+
+  +
+
+ 图 9
+
+
+
+
+点击deploy之后天可以看到自己的合约已经部署完成,打开之后可以看见我们写的函数`set`,`get`了,给`set`函数输入一个值,点击`get`会得到相应的值
+
+
+  +
+
+ 图 10
+
+
+
+
+- `Environment` 表示合约部署的环境。`Javascript VM`是虚拟了一个节点,而`Injected Web3`和`Web3 Provider`则真正连接一个节点。
+- `Account`代表不同的虚拟账户,每个虚拟账户每个有 100 ETH
+- `Deploy`表示合约部署按钮
+- `Deployed Contracts`表示已经部署的合约
+
+
+
+中文版界面与英文版界面有些许不一致,但都大同小异,想了解同学可以查看本博客(界面与中文版大致相同):
+[Solidity语言编辑器REMIX指导大全](https://cloud.tencent.com/developer/article/1182404)
+
+2. **本地配置:**
+ - [win下](https://cloud.tencent.com/developer/article/1374376)
+ - [ubuntu下](https://blog.csdn.net/qq_41944960/article/details/100134020)
+
+
+3. **Docker**
+
+我们为编译器提供了最新的docker构建。 stable 仓库里的是已发布的版本,nightly 仓库则是在开发分支中的带有不稳定变更的版本。
+
+```script
+docker run ethereum/solc:stable solc --version
+```
+
+目前,docker 镜像只含有 solc 的可执行程序,因此你需要额外的工作去把源代码和输出目录连接起来。
+
+## 3、Solidity基础操作
+
+**由于篇幅有限,以下只会讲解一些较基础、重要的概念(足够后面使用),有些可能会一带而过或者“忽略”,如果大家途中有没太明白地方建议先百度、Google,或者查看此教程[Solifity中文文档](https://solidity-cn.readthedocs.io/zh/develop/index.html)、[Solidity英文文档](https://remix-ide.readthedocs.io/en/latest/index.html)**
+
+### 3.1 Solidity源文件布局
+
+**源文件可以被版本杂注pragma所注解,表明要求的编译器版本**
+- 例如:
+```javascript
+pragma solidity ^0.4.0;
+```
+这样,源文件将既不允许低于 0.4.0 版本的编译器编译, 也不允许高于(包含) 0.5.0 版本的编译器编译(第二个条件因使用 ^ 被添加)。 这种做法的考虑是,编译器在 0.5.0 版本之前不会有重大变更,所以可确保源代码始终按预期被编译。 上面例子中不固定编译器的具体版本号,因此编译器的补丁版也可以使用。
+
+**import(导入其它源文件)**
+- Solidity 所支持的导入语句import,语法同 JavaScript(从ES6 起)非常类似
+
+```javascript
+import "filename";
+```
+从“filename”中导入所有的全局符号到当前全局作用域中
+```javascript
+import * as symbolName from "filename";
+```
+创建一个新的全局符号 symbolName,其成员均来自 “filename”中全局符号
+```javascript
+import {symbol1 as alias, symbol2} from "filename";
+```
+创建新的全局符号 alias 和 symbol2,分别从 "filename" 引用 symbol1 和 symbol2
+```javascript
+import "filename" as symbolName;
+```
+这条语句等同于 import * as symbolName from "filename";
+
+**注释**
+
+可以使用单行注释(//)和多行注释(/*...*/)
+
+```javascript
+// 这是一个单行注释。
+
+/*
+这是一个
+多行注释。
+*/
+```
+
+### 3.2 数据类型与运算符
+
+### 3.2.1 Solidity值类型介绍
+
+- **布尔(bool)**:
+
+
+可能的取值为字符常量值 true 或 false
+
+例子:
+```javascript
+pragma solidity ^0.4.0;
+
+contract helloworld {
+ bool boola=true; //声明一个布尔类型的值,只用一个等号
+ function booltesta() public view returns(bool){
+ return boola;
+ }
+
+ function booltestb(int a,int b) public pure returns(bool){
+ return a==b;
+ }
+}
+```
+
+  +
+
+ 图 11
+
+
+
+
+- 整型(int/uint)**:
+
+`int` / `uint` :分别表示有符号和无符号的不同位数的整型变量。 支持关键字 `uint8` 到 `uint256` (无符号,从 8 位到 256 位)以及 `int8` 到 `int256`,以 8 位为步长递增。 `uint` 和 `int` 分别是 `uint256` 和 `int256` 的别名。
+
+- **定长浮点型(fixed / ufixed)**:
+
+`fixed `/ `ufixed`:表示各种大小的有符号和无符号的定长浮点型。 在关键字 `ufixedMxN` 和 `fixedMxN` 中,`M` 表示该类型占用的位数,`N` 表示可用的小数位数。 `M `必须能整除 8,即 8 到 256 位。 `N `则可以是从 0 到 80 之间的任意数。 `ufixed` 和 `fixed` 分别是 `ufixed128x19` 和 `fixed128x19` 的别名。
+
+- **地址(address 重点,后面细讲)**:
+
+地址类型存储一个 20 字节的值(以太坊地址的大小)。 地址类型也有成员变量,并作为所有合约的基础。
+
+ **地址类型成员变量**:`balance` 和 `transfer`
+
+ 可以使用 balance 属性来查询一个地址的余额, 也可以使用 transfer 函数向一个地址发送 以太币 (以 wei 为单位):
+
+ ```javascript
+address x = 0x123;
+address myAddress = this;
+if (x.balance < 10 && myAddress.balance >= 10) x.transfer(10);
+ ```
+
+注:如果 `x` 是一个合约地址,它的代码(更具体来说是它的 fallback 函数,如果有的话)会跟 `transfer` 函数调用一起执行(这是 EVM 的一个特性,无法阻止)。 如果在执行过程中用光了 gas 或者因为任何原因执行失败,以太币 交易会被打回,当前的合约也会在终止的同时抛出异常。
+
+- **定长字节数组**:
+
+关键字有 bytes1, bytes2, bytes3, ..., bytes32
+`.length` 表示这个字节数组的长度(只读).
+
+注:可以将 `byte[]` 当作字节数组使用,但这种方式非常浪费存储空间,准确来说,是在传入调用时,每个元素会浪费 31 字节。 更好地做法是使用 `bytes`。
+
+
+- **变长字节数组**
+
+`bytes`:变长字节数组。它并不是值类型。
+
+`string`:变长 UTF-8 编码字符串类型。并不是值类型。
+
+
+- **地址字面常数(Address Literals)**
+
+比如像 `0xdCad3a6d3569DF655070DEd06cb7A1b2Ccd1D3AF` 这样的通过了地址校验和测试的十六进制字面常数属于 `address` 类型。 长度在 39 到 41 个数字的,没有通过校验和测试而产生了一个警告的十六进制字面常数视为正常的有理数字面常数。
+
+
+
+- **有理数和整数字面常数**
+
+整数字面常数由范围在 0-9 的一串数字组成,表现成十进制。 例如,69 表示数字 69。 Solidity 中是没有八进制的,因此前置 0 是无效的。
+
+十进制小数字面常数带有一个 .,至少在其一边会有一个数字。 比如:`1.,.1`,和 `1.3`。
+
+科学符号也是支持的,尽管指数必须是整数,但底数可以是小数。 比如:`2e10, -2e10, 2e-10, 2.5e1`。
+
+数值字面常数表达式本身支持任意精度,除非它们被转换成了非字面常数类型(也就是说,当它们出现在非字面常数表达式中时就会发生转换)。 这意味着在数值常量表达式中, 计算不会溢出而除法也不会截断。
+
+例如, `(2**800 + 1) - 2**800` 的结果是字面常数 1 (属于 `uint8` 类型),尽管计算的中间结果已经超过了 以太坊虚拟机 的机器字长度。 此外, `.5 * 8` 的结果是整型 4 (尽管有非整型参与了计算)
+
+- **字符串字面常数**
+
+字符串字面常数是指由双引号或单引号引起来的字符串(`"foo" `或者 `'bar'`)。 不像在 C 语言中那样带有结束符;`"foo"` 相当于 3 个字节而不是 4 个。 和整数字面常数一样,字符串字面常数的类型也可以发生改变,但它们可以隐式地转换成 `bytes1,……,bytes32`,如果合适的话,还可以转换成 `bytes` 以及 `string`。
+
+- **十六进制字面常数**
+
+十六进制字面常数以关键字 `hex` 打头,后面紧跟着用单引号或双引号引起来的字符串(例如,`hex"001122FF"`)。 字符串的内容必须是一个十六进制的字符串,它们的值将使用二进制表示。
+
+- **枚举(enum)**:
+
+一种用户可以定义类型的方法,与C语言类似,默认从0开始递增,一般用来模拟合约的状态
+
+```javascript
+pragma solidity ^0.4.16;
+
+contract test {
+ enum ActionChoices { GoLeft, GoRight, GoStraight, SitStill };
+ ActionChoices choice;
+ ActionChoices constant defaultChoice = ActionChoices.GoStraight;
+
+ function setGoStraight() public {
+ choice = ActionChoices.GoStraight;
+ }
+
+ // 由于枚举类型不属于 |ABI| 的一部分,因此对于所有来自 Solidity 外部的调用,
+ // "getChoice" 的签名会自动被改成 "getChoice() returns (uint8)"。
+ // 整数类型的大小已经足够存储所有枚举类型的值,随着值的个数增加,
+ // 可以逐渐使用 `uint16` 或更大的整数类型。
+ function getChoice() public view returns (ActionChoices) {
+ return choice;
+ }
+
+ function getDefaultChoice() public pure returns (uint) {
+ return uint(defaultChoice);
+ }
+}
+```
+
+- **函数(function)**:
+
+函数类型是一种表示函数的类型。可以将一个函数赋值给另一个函数类型的变量,也可以将一个函数作为参数进行传递,还能在函数调用中返回函数类型变量。 函数类型有两类:- 内部(`internal`) 函数和 外部(`external`) 函数:
+
+内部函数只能在当前合约内被调用(更具体来说,在当前代码块内,包括内部库函数和继承的函数中),因为它们不能在当前合约上下文的外部被执行。 调用一个内部函数是通过跳转到它的入口标签来实现的,就像在当前合约的内部调用一个函数。
+
+外部函数由一个地址和一个函数签名组成,可以通过外部函数调用传递或者返回。
+
+函数类型表示成如下的形式
+
+
+  +
+
+ 图 12
+
+
+
+
+```javascript
+function () {internal|external} [pure|constant|view|payable] [returns ()]
+```
+
+与参数类型相反,返回类型不能为空 —— 如果函数类型不需要返回,则需要删除整个 `returns ()` 部分。
+
+函数类型默认是内部函数,因此不需要声明 `internal` 关键字。 与此相反的是,合约中的函数本身默认是 `public `的,只有当它被当做类型名称时,默认才是内部函数。
+
+有两种方法可以访问当前合约中的函数:一种是直接使用它的名字,`f` ,另一种是使用 `this.f` 。 前者适用于内部函数,后者适用于外部函数。
+
+如果当函数类型的变量还没有初始化时就调用它的话会引发一个异常。 如果在一个函数被 `delete` 之后调用它也会发生相同的情况。
+
+如果外部函数类型在 Solidity 的上下文环境以外的地方使用,它们会被视为 `function` 类型。 该类型将函数地址紧跟其函数标识一起编码为一个 `bytes24` 类型。
+
+请注意,当前合约的 public 函数既可以被当作内部函数也可以被当作外部函数使用。 如果想将一个函数当作内部函数使用,就用 `f` 调用,如果想将其当作外部函数,使用 `this.f` 。
+
+**Solidity函数可见性**
+
+函数的可见性可以指定为 external,public ,internal 或者 private;对于状态变量,不能设置为 external ,默认是 internal。
+
+- external :外部函数作为合约接口的一部分,意味着我们可以从其他合约和交易中调用。 一个外部函数 f不能从内部调用(即 f 不起作用,但 this.f() 可以)。 当收到大量数据的时候,外部函数有时候会更有效率。
+- public :public 函数是合约接口的一部分,可以在内部或通过消息调用。对于 public 状态变量, 会自动生成一个 getter 函数。
+- internal :这些函数和状态变量只能是内部访问(即从当前合约内部或从它派生的合约访问),不使用 this 调用。
+- private :private 函数和状态变量仅在当前定义它们的合约中使用,并且不能被派生合约使用。
+
+**Solidity函数状态可变性**
+
+- pure:纯函数,不允许修改或访问状态
+- view:不允许修改状态
+- payable:允许从消息调用中接收以太币Ether 。
+- constant:与view相同,一般只修饰状态变量,不允许赋值(除初始化以外)
+
+**内部函数调用**
+
+当前合约中的函数可以直接(“从内部”)调用,也可以递归调用,就像下边这个荒谬的例子一样
+```javascript
+pragma solidity ^0.4.16;
+
+contract C {
+ function g(uint a) public pure returns (uint ret) { return f(); }
+ function f() internal pure returns (uint ret) { return g(7) + f(); }
+}
+```
+这些函数调用在 EVM 中被解释为简单的跳转。这样做的效果就是当前内存不会被清除,也就是说,通过内部调用在函数之间传递内存引用是非常有效的。
+
+**外部函数调用**
+
+表达式 `this.g(8)`; 和 `c.g(2)`; (其中 c 是合约实例)也是有效的函数调用,但是这种情况下,函数将会通过一个消息调用来被“外部调用”,而不是直接的跳转。 请注意,不可以在构造函数中通过 this 来调用函数,因为此时真实的合约实例还没有被创建。
+
+如果想要调用其他合约的函数,需要外部调用。对于一个外部调用,所有的函数参数都需要被复制到内存。
+
+当调用其他合约的函数时,随函数调用发送的 Wei 和 gas 的数量可以分别由特定选项 `.value()` 和 `.gas()` 指定:
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract InfoFeed {
+ function info() public payable returns (uint ret) { return 42; }
+}
+
+contract Consumer {
+ InfoFeed feed;
+ function setFeed(address addr) public { feed = InfoFeed(addr); }
+ function callFeed() public { feed.info.value(10).gas(800)(); }
+}
+```
+`payable` 修饰符要用于修饰 `info`,否则,.`value()` 选项将不可用。
+
+注意,表达式 `InfoFeed(addr)` 进行了一个的显式类型转换,说明”我们知道给定地址的合约类型是 `InfoFeed` “并且这不会执行构造函数。 显式类型转换需要谨慎处理。绝对不要在一个你不清楚类型的合约上执行函数调用。
+
+我们也可以直接使用 `function setFeed(InfoFeed _feed) { feed = _feed; }` 。 注意一个事实,`feed.info.value(10).gas(800)` 只(局部地)设置了与函数调用一起发送的 Wei 值和 gas 的数量,只有最后的圆括号执行了真正的调用。
+
+如果被调函数所在合约不存在(也就是账户中不包含代码)或者被调用合约本身抛出异常或者 gas 用完等,函数调用会抛出异常。
+
+
+### 3.2.2 引用类型介绍
+
+比起之前讨论过的值类型,在处理复杂的类型(即占用的空间超过 256 位的类型)时,我们需要更加谨慎。 由于拷贝这些类型变量的开销相当大,我们不得不考虑它的存储位置,是将它们保存在 **内存** (并不是永久存储)中, 还是 **存储** (保存状态变量的地方)中。
+
+- **数据位置**
+
+所有的复杂类型,即 **数组** 和 **结构** 类型,都有一个额外属性,“数据位置”,说明数据是保存在 **内存** 中还是 **存储** 中。 根据上下文不同,大多数时候数据有默认的位置,但也可以通过在类型名后增加关键字 `storage` 或 `memory` 进行修改。 函数参数(包括返回的参数)的数据位置默认是 `memory`, 局部变量的数据位置默认是 `storage`,状态变量的数据位置强制是 `storage`。
+
+也存在第三种数据位置, `calldata` ,这是一块只读的,且不会永久存储的位置,用来存储函数参数。 外部函数的参数(非返回参数)的数据位置被强制指定为 `calldata `,效果跟 `memory` 差不多。
+
+例子:
+```javascript
+pragma solidity ^0.4.0;
+
+contract C {
+ uint[] x; // x 的数据存储位置是 storage
+
+ // memoryArray 的数据存储位置是 memory
+ function f(uint[] memoryArray) public {
+ x = memoryArray; // 将整个数组拷贝到 storage 中,可行
+ var y = x; // 分配一个指针(其中 y 的数据存储位置是 storage),可行
+ y[7]; // 返回第 8 个元素,可行
+ y.length = 2; // 通过 y 修改 x,可行
+ delete x; // 清除数组,同时修改 y,可行
+ // 下面的就不可行了;需要在 storage 中创建新的未命名的临时数组, /
+ // 但 storage 是“静态”分配的:
+ // y = memoryArray;
+ // 下面这一行也不可行,因为这会“重置”指针,
+ // 但并没有可以让它指向的合适的存储位置。
+ // delete y;
+
+ g(x); // 调用 g 函数,同时移交对 x 的引用
+ h(x); // 调用 h 函数,同时在 memory 中创建一个独立的临时拷贝
+ }
+
+ function g(uint[] storage storageArray) internal {}
+ function h(uint[] memoryArray) public {}
+}
+```
+归纳:
+
+强制指定的数据位置:
+ 1. 外部函数的参数(不包括返回参数): calldata
+ 2. 状态变量: storage
+
+默认数据位置:
+1. 函数参数(包括返回参数): memory
+2. 所有其它局部变量: storage
+
+
+- **数组**
+
+数组可以在声明时指定长度,也可以动态调整大小。 对于 **存储** 的数组来说,元素类型可以是任意的(即元素也可以是数组类型,映射类型或者结构体)。 对于 **内存** 的数组来说,元素类型不能是映射类型,如果作为 `public` 函数的参数,它只能是 `ABI` 类型。
+
+一个元素类型为 `T`,固定长度为 `k` 的数组可以声明为 `T[k]`,而动态数组声明为 `T[]`。
+
+举个例子,一个长度为 5,元素类型为 `uint` 的动态数组的数组,应声明为 `uint[][5]` (注意这里跟其它语言比,数组长度的声明位置是反的)。 要访问第三个动态数组的第二个元素,你应该使用 `x[2][1]`(数组下标是从 0 开始的,且访问数组时的下标顺序与声明时相反,也就是说,`x[2]` 是从右边减少了一级)。。
+
+`bytes` 和 `string` 类型的变量是特殊的数组。 `bytes` 类似于 `byte[]`,但它在 `calldata` 中会被“紧打包”(译者注:将元素连续地存在一起,不会按每 32 字节一单元的方式来存放)。 `string` 与 `bytes` 相同,但(暂时)不允许用长度或索引来访问。
+
+注:
+如果想要访问以字节表示的字符串 s,请使用 `bytes(s)`.`length / bytes(s)[7] = 'x'`;。 注意这时你访问的是 `UTF-8` 形式的低级` bytes` 类型,而不是单个的字符。
+
+**成员**
+
+`length`:
+
+数组有 length 成员变量表示当前数组的长度。 动态数组可以在 **存储** (而不是 **内存** )中通过改变成员变量 .length 改变数组大小。 并不能通过访问超出当前数组长度的方式实现自动扩展数组的长度。 一经创建,**内存** 数组的大小就是固定的(但却是动态的,也就是说,它依赖于运行时的参数)。
+`push`:
+ 变长的 **存储** 数组以及 bytes 类型(而不是 string 类型)都有一个叫做 push 的成员函数,它用来附加新的元素到数组末尾。 这个函数将返回新的数组长度。
+
+例子:
+```javascript
+pragma solidity ^0.4.16;
+
+contract ArrayContract {
+ uint[2**20] m_aLotOfIntegers;
+ // 注意下面的代码并不是一对动态数组,
+ // 而是一个数组元素为一对变量的动态数组(也就是数组元素为长度为 2 的定长数组的动态数组)。
+ bool[2][] m_pairsOfFlags;
+ // newPairs 存储在 memory 中 —— 函数参数默认的存储位置
+
+ function setAllFlagPairs(bool[2][] newPairs) public {
+ // 向一个 storage 的数组赋值会替代整个数组
+ m_pairsOfFlags = newPairs;
+ }
+
+ function setFlagPair(uint index, bool flagA, bool flagB) public {
+ // 访问一个不存在的数组下标会引发一个异常
+ m_pairsOfFlags[index][0] = flagA;
+ m_pairsOfFlags[index][1] = flagB;
+ }
+
+ function changeFlagArraySize(uint newSize) public {
+ // 如果 newSize 更小,那么超出的元素会被清除
+ m_pairsOfFlags.length = newSize;
+ }
+
+ function clear() public {
+ // 这些代码会将数组全部清空
+ delete m_pairsOfFlags;
+ delete m_aLotOfIntegers;
+ // 这里也是实现同样的功能
+ m_pairsOfFlags.length = 0;
+ }
+
+ bytes m_byteData;
+
+ function byteArrays(bytes data) public {
+ // 字节的数组(语言意义中的 byte 的复数 ``bytes``)不一样,因为它们不是填充式存储的,
+ // 但可以当作和 "uint8[]" 一样对待
+ m_byteData = data;
+ m_byteData.length += 7;
+ m_byteData[3] = byte(8);
+ delete m_byteData[2];
+ }
+
+ function addFlag(bool[2] flag) public returns (uint) {
+ return m_pairsOfFlags.push(flag);
+ }
+
+ function createMemoryArray(uint size) public pure returns (bytes) {
+ // 使用 `new` 创建动态 memory 数组:
+ uint[2][] memory arrayOfPairs = new uint[2][](size);
+ // 创建一个动态字节数组:
+ bytes memory b = new bytes(200);
+ for (uint i = 0; i < b.length; i++)
+ b[i] = byte(i);
+ return b;
+ }
+}
+```
+
+- **结构体**
+
+Solidity 支持通过构造结构体的形式定义新的类型,以下是一个结构体的示例:
+```c++
+struct Funder {
+ address addr;
+ uint amount;
+}
+
+struct Campaign {
+ address beneficiary;
+ uint fundingGoal;
+ uint numFunders;
+ uint amount;
+ mapping (uint => Funder) funders;
+}
+```
+- **映射**
+映射类型在声明时的形式为 `mapping(_KeyType => _ValueType)`。 其中 `_KeyType` 可以是除了映射、变长数组、合约、枚举以及结构体以外的几乎所有类型。 `_ValueType` 可以是包括映射类型在内的任何类型。
+
+映射可以视作 哈希表 ,它们在实际的初始化过程中创建每个可能的 key, 并将其映射到字节形式全是零的值:一个类型的 默认值。然而下面是映射与哈希表不同的地方: 在映射中,实际上并不存储 key,而是存储它的 `keccak256` 哈希值,从而便于查询实际的值。
+
+正因为如此,映射是没有长度的,也没有 `key` 的集合或 `value` 的集合的概念。
+
+只有状态变量(或者在 internal 函数中的对于存储变量的引用)可以使用映射类型。。
+
+可以将映射声明为 `public`,然后来让 Solidity 创建一个 getter。` _KeyType` 将成为 getter 的必须参数,并且 getter 会返回 `_ValueType`。
+
+`_ValueType` 也可以是一个映射。这时在使用 getter 时将将需要递归地传入每个 `_KeyType `参数。
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract MappingExample {
+ mapping(address => uint) public balances;
+
+ function update(uint newBalance) public {
+ balances[msg.sender] = newBalance;
+ }
+}
+
+contract MappingUser {
+ function f() public returns (uint) {
+ MappingExample m = new MappingExample();
+ m.update(100);
+ return m.balances(this);
+ }
+}
+```
+#### 3.2.3 涉及 LValues 的运算符
+- **删除**
+
+`delete a` 的结果是将 `a` 的类型在初始化时的值赋值给 `a`。即对于整型变量来说,相当于 `a = 0`, 但 delete 也适用于数组,对于动态数组来说,是将数组的长度设为 0,而对于静态数组来说,是将数组中的所有元素重置。 如果对象是结构体,则将结构体中的所有属性重置。
+
+delete 对整个映射是无效的(因为映射的键可以是任意的,通常也是未知的)。 因此在你删除一个结构体时,结果将重置所有的非映射属性,这个过程是递归进行的,除非它们是映射。 然而,单个的键及其映射的值是可以被删除的。
+
+理解 `delete a `的效果就像是给 `a` 赋值很重要,换句话说,这相当于在 `a `中存储了一个新的对象。
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract DeleteExample {
+ uint data;
+ uint[] dataArray;
+
+ function f() public {
+ uint x = data;
+ delete x; // 将 x 设为 0,并不影响数据
+ delete data; // 将 data 设为 0,并不影响 x,因为它仍然有个副本
+ uint[] storage y = dataArray;
+ delete dataArray;
+ // 将 dataArray.length 设为 0,但由于 uint[] 是一个复杂的对象,y 也将受到影响,
+ // 因为它是一个存储位置是 storage 的对象的别名。
+ // 另一方面:"delete y" 是非法的,引用了 storage 对象的局部变量只能由已有的 storage 对象赋值。
+ }
+}
+```
+
+### 3.3 单位和全局变量
+
+
+### 3.3.1 以太币单位
+
+以太币 单位之间的换算就是在数字后边加上 `wei`、 `finney`、 `szabo` 或 `ether` 来实现的,如果后面没有单位,缺省为 `Wei`。例如 `2 ether == 2000 finney` 的逻辑判断值为 `true`。
+
+
+### 3.3.2 时间单位
+
+秒是缺省时间单位,在时间单位之间,数字后面带有 `seconds`、 `minutes`、 `hours`、 `days`、 `weeks` 和 `years` 的可以进行换算,基本换算关系与现实生活相符。
+
+### 3.3.3 特殊变量和函数
+
+在全局命名空间中已经存在了(预设了)一些特殊的变量和函数,他们主要用来提供关于区块链的信息或一些通用的工具函数。
+
+**区块和交易属性**
+
+- `block.blockhash(uint blockNumber) returns (bytes32)`:指定区块的区块哈希——仅可用于最新的 256 个区块且不包括当前区块;而 blocks 从 0.4.22 版本开始已经不推荐使用,由 `blockhash(uint blockNumber)` 代替
+- `block.coinbase (address)`: 挖出当前区块的矿工地
+- `block.difficulty (uint)`: 当前区块难度
+- `block.gaslimit (uint)`: 当前区块 `gas` 限额
+- `block.number (uint`): 当前区块号
+- `block.timestamp (uint)`: 自 `unix epoch` 起始当前区块以秒计的时间戳
+- `gasleft() returns (uint256)`:剩余的 `gas`
+- `msg.data (bytes)`: 完整的 `calldata`
+- `msg.gas (uint)`: 剩余 `gas` - 自 0.4.21 版本开始已经不推荐使用,由 gesleft() 代替
+- **`msg.sender (address)`:** 消息发送者(当前调用)
+- `msg.sig (bytes4)`: calldata 的前 4 字节(也就是函数标识符)
+- `msg.value (uint)`: 随消息发送的 wei 的数量
+- `now (uint)`: 目前区块时间戳(`block.timestamp`)
+- `tx.gasprice (uint)`: 交易的` gas` 价格
+- `tx.origin (address)`: 交易发起者(完全的调用链)
+
+**[ABI 编码函数](https://solidity-cn.readthedocs.io/zh/develop/abi-spec.html#abi)**
+
+
+- `abi.encode(...) returns (bytes)`: ABI - 对给定参数进行编码
+- `abi.encodePacked(...) returns (bytes)`:对给定参数执行 紧打包编码
+- `abi.encodeWithSelector(bytes4 selector, ...) returns (bytes):` ABI - 对给定参数进行编码,并以给定的函数选择器作为起始的 4 字节数据一起返回
+- `abi.encodeWithSignature(string signature, ...) returns (bytes)`:等价于 `abi.encodeWithSelector(bytes4(keccak256(signature), ...)`
+
+**错误处理**
+
+- `assert(bool condition)`:
+ 如果条件不满足,则使当前交易没有效果 — 用于检查内部错误。
+- `require(bool condition)`:
+ 如果条件不满足则撤销状态更改 - 用于检查由输入或者外部组件引起的错误。
+- `require(bool condition, string message)`:
+ 如果条件不满足则撤销状态更改 - 用于检查由输入或者外部组件引起的错误,可以同时提供一个错误消息。
+- `revert()`:
+ 终止运行并撤销状态更改。
+- `revert(string reason)`:
+ 终止运行并撤销状态更改,可以同时提供一个解释性的字符串。
+
+**地址相关**
+
+
+- `.balance (uint256)`:
+ 以 Wei 为单位的 地址类型 的余额。
+- `.transfer(uint256 amount)`:
+ 向 地址类型 发送数量为 amount 的 Wei,失败时抛出异常,发送 2300 gas 的矿工费,不可调节。
+- `.send(uint256 amount) returns (bool)`:
+ 向 地址类型 发送数量为 amount 的 Wei,失败时返回 false,发送 2300 gas 的矿工费用,不可调节。
+- `.call(...) returns (bool)`:
+ 发出低级函数 CALL,失败时返回 false,发送所有可用 gas,可调节。
+- `.callcode(...) returns (bool)`:
+ 发出低级函数 CALLCODE,失败时返回 false,发送所有可用 gas,可调节。
+- `.delegatecall(...) returns (bool):`
+ 发出低级函数 DELEGATECALL,失败时返回 false,发送所有可用 gas,可调节。
+
+### 3.4 表达式和控制结构(*)
+
+### 3.4.1 控制结构
+
+
+avaScript 中的大部分控制结构在 Solidity 中都是可用的,除了 `switch` 和 `goto`。 因此 Solidity 中有 `if,else,while,do,for,break,continue,return,? : `这些与在 C 或者 JavaScript 中表达相同语义的关键词。
+
+用于表示条件的括号 **不可以** 被省略,单语句体两边的花括号可以被省略。
+
+注意,与 C 和 JavaScript 不同, Solidity 中非布尔类型数值不能转换为布尔类型,因此 `if (1) { ... }` 的写法在 Solidity 中 无效 。
+
+当一个函数有多个输出参数时, `return (v0, v1, ...,vn)` 写法可以返回多个值。不过元素的个数必须与输出参数的个数相同
+
+### 3.4.2 通过 new 创建合约
+使用关键字 `new` 可以创建一个新合约。待创建合约的完整代码必须事先知道,因此递归的创建依赖是不可能的。
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract D {
+ uint x;
+ function D(uint a) public payable {
+ x = a;
+ }
+}
+
+contract C {
+ D d = new D(4); // 将作为合约 C 构造函数的一部分执行
+
+ function createD(uint arg) public {
+ D newD = new D(arg);
+ }
+
+ function createAndEndowD(uint arg, uint amount) public payable {
+ //随合约的创建发送 ether
+ D newD = (new D).value(amount)(arg);
+ }
+}
+```
+如示例中所示,使用 `.value()` 选项创建 `D` 的实例时可以转发 `Ether`,但是不可能限制 `gas` 的数量。如果创建失败(可能因为栈溢出,或没有足够的余额或其他问题),会引发异常。
+
+### 3.4.3 错误处理:Assert, Require, Revert and Exceptions
+
+`Solidity` 使用状态恢复异常来处理错误。这种异常将撤消对当前调用(及其所有子调用)中的状态所做的所有更改,并且还向调用者标记错误。 便利函数 `assert` 和 `require` 可用于检查条件并在条件不满足时抛出异常。`assert` 函数只能用于测试内部错误,并检查非变量。
+
+ `require` 函数用于确认条件有效性,例如输入变量,或合约状态变量是否满足条件,或验证外部合约调用返回的值。 如果使用得当,分析工具可以评估你的合约,并标示出那些会使 `assert` 失败的条件和函数调用。 正常工作的代码不会导致一个 `assert `语句的失败;如果这发生了,那就说明出现了一个需要你修复的 bug。
+
+还有另外两种触发异常的方法:`revert` 函数可以用来标记错误并恢复当前的调用。 `revert` 调用中包含有关错误的详细信息是可能的,这个消息会被返回给调用者。已经不推荐的关键字 `throw` 也可以用来替代 `revert()` (但无法返回错误消息)。
+
+在下例中,你可以看到如何轻松使用``require``检查输入条件以及如何使用``assert``检查内部错误,注意,你可以给 require 提供一个消息字符串,而 assert 不行。
+
+```javascript
+pragma solidity ^0.4.22;
+
+contract Sharer {
+ function sendHalf(address addr) public payable returns (uint balance) {
+ require(msg.value % 2 == 0, "Even value required.");
+ uint balanceBeforeTransfer = this.balance;
+ addr.transfer(msg.value / 2);
+ //由于转移函数在失败时抛出异常并且不能在这里回调,因此我们应该没有办法仍然有一半的钱。
+ assert(this.balance == balanceBeforeTransfer - msg.value / 2);
+ return this.balance;
+ }
+}
+```
+### 3.5 合约
+
+Solidity 合约类似于面向对象语言中的类。合约中有用于数据持久化的状态变量,和可以修改状态变量的函数。 调用另一个合约实例的函数时,会执行一个 EVM 函数调用,这个操作会切换执行时的上下文,这样,前一个合约的状态变量就不能访问了。
+
+### 3.5.1 创建合约
+
+可以通过以太坊交易“从外部”或从 Solidity 合约内部创建合约。
+创建合约时,会执行一次构造函数(与合约同名的函数)。构造函数是可选的。只允许有一个构造函数,这意味着不支持重载。
+
+在内部,构造函数参数在合约代码之后通过 `ABI` 编码 传递,但是如果你使用 `web3.js` 则不必关心这个问题。
+
+如果一个合约想要创建另一个合约,那么创建者必须知晓被创建合约的源代码(和二进制代码)。 这意味着不可能循环创建依赖项。
+
+### 3.5.2 getter 函数
+
+编译器自动为所有 `public` 状态变量创建 `getter` 函数。对于下面给出的合约,编译器会生成一个名为 `data` 的函数, 该函数不会接收任何参数并返回一个 `uint` ,即状态变量 `data` 的值。可以在声明时完成状态变量的初始化
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract C {
+ uint public data = 42;
+}
+
+contract Caller {
+ C c = new C();
+ function f() public {
+ uint local = c.data();
+ }
+}
+```
+getter 函数具有外部可见性。如果在内部访问 getter(即没有 this. ),它被认为一个状态变量。 如果它是外部访问的(即用 this. ),它被认为为一个函数。
+
+### 3.5.3 View 函数
+
+可以将函数声明为 view 类型,这种情况下要保证不修改状态。
+
+下面的语句被认为是修改状态:
+
+1. 修改状态变量。
+2. 产生事件。
+3. 创建其它合约。
+4. 使用 selfdestruct。
+5. 通过调用发送以太币。
+6. 调用任何没有标记为 view 或者 pure 的函数。
+7. 使用低级调用。
+8. 使用包含特定操作码的内联汇编。
+
+```javascript
+pragma solidity ^0.4.16;
+
+contract C {
+ function f(uint a, uint b) public view returns (uint) {
+ return a * (b + 42) + now;
+ }
+}
+```
+### 3.5.4 Pure 函数
+
+函数可以声明为 pure ,在这种情况下,承诺不读取或修改状态。
+
+除了上面解释的状态修改语句列表之外,以下被认为是从状态中读取:
+
+1. 读取状态变量。
+2. 访问 this.balance 或者 .balance。
+3. 访问 block,tx, msg 中任意成员 (除 msg.sig 和 msg.data 之外)。
+4. 调用任何未标记为 pure 的函数。
+5. 使用包含某些操作码的内联汇编。
+
+```javascript
+pragma solidity ^0.4.16;
+
+contract C {
+ function f(uint a, uint b) public pure returns (uint) {
+ return a * (b + 42);
+ }
+}
+```
+
+
+
+
+
+## 四、练习题
+
+### 4.1 将固定长度字节数组转化为`string`类型
+
+```javascript
+pragma solidity ^0.4.0;
+
+contract bytes32tostring{
+
+ bytes10 testword=0x68656c6c6f776f726c64; //为helloworld
+ function bytes32tostringF() public view returns(string){
+
+ }
+}
+```
+
+### 4.2 实现一个带有简单逻辑判断及多种数学运算的Solidity程序
+
+
+
+**参考自:**
+
+1. 黄皮书:https://github.com/yuange1024/ethereum_yellowpaper/blob/master/ethereum_yellow_paper_cn.pdf
+
+2. 白皮书:https://github.com/ethereum/wiki/wiki/White-Paper
+ [INlinKC](https://blog.csdn.net/weixin_45067603)
+ https://ethfans.org/wikis/Home
+3. 以太坊solidity学习记录: [https://blog.csdn.net/weixin_45067603/article/details/105726491](https://blog.csdn.net/weixin_45067603/article/details/105726491)
+4. [尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
diff --git a/Blockchain/part3_web3js.md b/Blockchain/part3_web3js.md
new file mode 100644
index 0000000..7176f7c
--- /dev/null
+++ b/Blockchain/part3_web3js.md
@@ -0,0 +1,1182 @@
+注:本教程为技术教程,不谈论且不涉及炒作任何数字货币
+
+## 一、以太坊客户端
+
+### 1.1、什么是以太坊客户端
+
+- 以太坊客户端是一个软件应用程序,它实现以太坊规范并通过p2p网络与其他以太坊客户端进行通信。如果不同的以太坊客户端符合参考规范和标准化通信协议,则可以进行相互操作。
+- 以太坊是一个开源项目,由“黄皮书”正式规范定义。除了各种以太坊改进提案之外,此正式规范还定义了以太坊客户端的标准行为。
+- 因为以太坊有明确的正式规范,以太网客户端有了许多独立开发的软件实现,它们之间又可以彼此交互。
+
+
+### 1.2、基于以太坊规范的网络
+
+- 存在各种基于以太坊规范的网络,这些网络基本符合以太坊“黄皮书”中定义的形式规范,但它们之间可能相互也可能不相互操作。
+- 这些基于以太坊的网络中有:以太坊,以太坊经典,Ella,Expanse,Ubiq,Musicoin等等。
+- 虽然大多数在协议级别兼容,但这些网络通常具有特殊要求,以太坊客户端软件的维护人员、需要进行微小更改、以支持每个网络的功能或属性
+
+
+### 1.3、太坊的多种客户端
+
+- [go-ethereum ( Go )](https://github.com/ethereum/go-ethereum)
+ 官方推荐,开发使用最多
+- parity ( Rust )
+ 最轻便客户端,在历次以太坊网络攻击中表现卓越
+- cpp-ethereum (C++)
+
+- pyethapp (python)
+
+- ethereumjs-lib ( javascript )
+
+- EthereumJ / Harmony ( Java )
+
+### 1.4、以太坊全节点
+
+- 全节点是整个主链的一个副本,存储并维护链上的所有数据,并随时验证新区块的合法性。
+- 区块链的健康和扩展弹性,取决于具有许多独立操作和地理上分散的全节点。每个全节点都可以帮助其他新节点获取区块数据,并提供所有交易和合约的独立验证。
+- 运行全节点将耗费巨大的成本,包括硬件资源和带宽。
+- 以太坊开发不需要在实时网络(主网)上运行的全节点。我们可以使用测试网络的节点来代替,也可以用本地私链,或者使用服务商提供的基于云的以太坊客户端;这些几乎都可以执行所有操作。
+
+### 1.5、远程客户端和轻节点
+
+- 远程客户端
+
+ 不存储区块链的本地副本或验证块和交易。这些客户端一般只提供钱包的功能,可以创建和广播交易。远程客户端可用于连接到现有网络,MetaMask 就是一个这样的客户端。
+
+- 轻节点
+
+ 不保存链上的区块历史数据,只保存区块链当前的状态。轻节点可以对块和交易进行验证。
+
+* 全节点的优缺点
+ * 优点
+ * 为以太坊网络的灵活性和抗审查性提供有力支持
+ * 权威地验证所有交易
+ * 可以直接与公众区块链上的任何合约交互
+ * 可以离线查询区块链状态(账户、合约等)
+ * 可以直接把自己的合约部署到公共区块链中
+ * 缺点
+ * 需要巨大的硬件和带宽资源,而且会不断增长
+ * 第一次下载往往需要几天才能完全同步
+ * 必须及时维护、升级并保持在线状态以同步区块
+
+ ##### 公共测试网络节点的优缺点
+
+ * 优点
+ * 一个testnet节点需要同步和存储更少的数据,大约10GB,具体取决于不同的网络
+ * 一个testnet节点一般可以在几个小时内完成同步
+ * 部署合约或进行交易只需要发送测试以太,可以从”水龙头“免费获得
+ * 测试网络是公共区块链,有许多其他用户和合约运行(区别于私链)
+ * 缺点
+ * 测试网络上使用测试以太没有价值。因此无法测试交易对手的安全性,因为没有任何利害关系
+ * 测试网络上的测试无法涵盖所有真实主网特性。例如:交易费用虽然是发送交易所必需的,但由于gas免费,因此 testnet上往往不会考虑。而且一般来说,测试网络不会像主网一样经常拥堵
+
+ ##### 本地私链的优缺点
+
+ * 优点
+ * 磁盘上几乎没有数据,也不同步别的数据,是一个完全干净的环境
+ * 无需获取测试以太,可以分配任意以太,也可以随时自己挖矿获得
+ * 没有其他用户与合约,无外部干扰
+ * 缺点
+ * 没有其他用户意味与公链的行为不同,发送的交易并不存在空间或交易顺序的竞争
+ * 除自己之外没有矿工意味着挖矿更容易预测,因此无法测试公链上发生的某些情况
+ * 没有其他合约意味着必须部署要测试的所有内容,包括所有的依赖项和合约库
+
+我们的教程主要基于本地私链的搭建,以后的交易等也主要基于我们的私链,因此以太坊客户端及私链的搭建在我们本次学习中至关重要。
+
+**JSON-RPC**
+
+- 以太坊客户端提供了API 和一组远程调用(RPC)命令,这些命令被编码为 JSON。这被称为 JSON-RPC API。本质上,JSON-RPCAPI 就是一个接口,允许我们编写的程序使用以太坊客户端作为网关,访问以太坊网络和链上数据。
+- 通常,RPC 接口作为一个 HTTP 服务,端口设定为 8545。出于安全原因,默认情况下,它仅限于接受来自localhost 的连接。
+- 要访问JSON-RPC API,我们可以使用编程语言编写的专用库,例如JavaScript的 web3.js。
+- 或者也可以手动构建HTTP请求并发送/接收JSON编码的请求,如:
+
+```javascript
+curl -X POST -H "Content-Type:application/json" --data '{"jsonrpc":"2.0","method":"web3_clientVersion","params":[],"id":1}' http://127.0.0.1:8545
+```
+
+
+## 二、用 Geth 搭建以太坊私链
+
+### 2.1安装 go
+
+大家首先输入`go version`查看自己是否配置成功go环境,若不成功参考下面博客:
+
+[go : GoLand安装及环境配置](https://blog.csdn.net/qq_44702847/article/details/108597386)
+
+若成功则如下图所示
+
+  +
+
+ 图 1
+
+
+
+
+### 2.2 安装 Geth
+
+安装 Geth 有很多种方式,这里主要就 Linux 环境给出两种方法:系统包管理器(apt-get)安装和源码安装。更加推荐大家用源码安装,在整个过程中可以看到 Geth 各组件的构建步骤。
+
+其他OS安装方法见[本教程](https://geth.ethereum.org/docs/install-and-build/installing-geth)
+
+**方法一、apt-get**
+
+```javascript
+sudo apt-get install software-properties-common
+sudo add-apt-repository -y ppa:ethereum/ethereum
+sudo apt-get update
+sudo apt-get install ethereum
+```
+
+**方法二、源码安装**
+
+1. 克隆 github 仓库我们的第一步是克隆 git 仓库,以获取源代码的副本。
+
+
+```javascript
+git clone https://github.com/ethereum/go-ethereum.git
+```
+
+2. 从源码构建 Geth要构建 Geth,切换到下载源代码的目录并使用 make 命令:
+
+
+```javascript
+cd go-ethereum
+make geth
+```
+
+如果一切顺利,我们将看到 Go 编译器构建每个组件,直到它生成 geth 可执行文件:
+
+```javascript
+build/env.sh go run build/ci.go install ./cmd/geth
+>>> /usr/local/go/bin/go install -ldflags -X
+main.gitCommit=58a1e13e6dd7f52a1d5e67bee47d23fd6cfdee5c -v ./cmd/geth
+github.com/ethereum/go-ethereum/common/hexutil
+github.com/ethereum/go-ethereum/common/math
+github.com/ethereum/go-ethereum/crypto/sha3 github.com/ethereum/go-ethereum/rlp
+github.com/ethereum/go-ethereum/crypto/secp256k1
+github.com/ethereum/go-ethereum/common [...]
+github.com/ethereum/go-ethereum/cmd/utils
+github.com/ethereum/go-ethereum/cmd/geth Done building. Run "build/bin/geth" to
+launch geth.
+```
+
+ 查看 geth version,确保在真正运行之前安装正常:
+
+
+  +
+
+ 图 2
+
+
+
+
+### 启动节点同步
+
+安装好了 Geth,现在我们可以尝试运行一下它。执行下面的命令,geth 就会开始同步区块,并存储在当前目录下。
+
+这里的 --syncmode fast 参数表示我们会以“快速”模式同步区块。在这种模式下,我们只会下载每个区块头和区块体,但不会执行验证所有的交易,直到所有区块同步完毕再去获取一个系统当前的状态。这样就节省了很多交易验证的时间。
+
+ ```javascript
+geth –datadir . --syncmode fast
+ ```
+--datadir:后面的参数是区块数据及秘钥存放目录
+
+通常,在同步以太坊区块链时,客户端会一开始就下载并验证每个块和每个交易,也就是说从创世区块开始。 毫无疑问,如果我们不加 --syncmode fast 参数,同步将花费很长时间并且具有很高的资源要求(它将需要更多的 RAM,如果你没有快速存储,则需要很长时间)。有些文章会把这个参数写成 --fast,这是以前快速同步模式的参数写法,现在已经被 –syncmode fast取代。如果我们想同步测试网络的区块,可以用下面的命令:
+
+ ```javascript
+geth --testnet --datadir . --syncmode fast
+ ```
+
+--testnet 这个参数会告诉 geth 启动并连接到最新的测试网络,也就是 Ropsten。测试网络的区块和交易数量会明显少于主网,所以会更快一点。但即使是用快速模式同步测试网络,也会需要几个小时的时间
+
+### 2.3 搭建自己的私有链
+
+因为公共网络的区块数量太多,同步耗时太长,我们为了方便快速了解 Geth,可以试着用它来搭一个只属于自己的私链。首先,我们需要创建网络的“创世”(genesis)状态,这写在一个小小的 JSON 文件里(例如,我们将其命名为 genesis.json,保存到当前目录下):
+
+ ```javascript
+{
+"config": {
+ "chainId": 15
+ },
+"difficulty": "2000",
+"gasLimit": "2100000",
+"alloc": {
+ "7df9a875a174b3bc565e6424a0050ebc1b2d1d82": { "balance": "300000" },
+ "f41c74c9ae680c1aa78f42e5647a62f353b7bdde": { "balance": "400000" }
+ }
+}
+ ```
+genesis.json介绍
+
+  +
+
+ 图 3
+
+
+
+
+要创建一条以它作为创世块的区块链,我们可以使用下面的命令:
+
+ ```javascript
+geth --datadir . init genesis.json
+ ```
+初始化完成后目录下多了geth和keystore两个文件夹:
+
+- geth:保存该链上的区块数据
+- keystore:保存该链上的账户信息
+
+**可能遇到问题**:
+- Fatal: invalid genesis file: missing 0x prefix for hex data:这个错误信息意思很明白,就是你的json文件中,对于16进制数据,需要加上0x前缀
+
+- Fatal: invalid genesis file: hex string has odd length: 从Geth 1.6版本开始,设置的十六进制数值,不能是奇数位, 比如不能是0x0,而应该是0x00。
+
+- Fatal: failed to write genesis block: genesis has no chain configuration :这个错误信息,就是说,你的配置文件中,缺少config部分。
+
+- Error: invalid sender: 这个错误虽然不会导致私有链初始化时出现失败的情况,但是会在以后的转账(web3.eth.sendTransaction),或者部署智能合约的时候产生。解决方法就是chainId 不能设置为0。 如果你完全按照Geth官方文档上给出的配置文件进行配置,就会产生这个错误。
+
+在当前目录下运行 geth,就会启动这条私链,注意要将 networked 设置为与创世块配置里的chainId 一致。
+
+ ```javascript
+// 简单开启
+(base) haobo@haobo:~/home/mnt/bitcoin/test$ geth --datadir . --networkid 150 --nodiscover console
+
+// 更一般的形式
+(base) haobo@haobo:~/home/mnt/bitcoin/test$ geth --networkid 150 --datadir "." --identity "kexin" --rpc --rpcport "8545" --rpcaddr "localhost" --port "30303" --nodiscover --allow-insecure-unlock --rpcapi "eth,net,web3,personal,admin,shh,txpool,debug,miner" console
+ ```
+参数含义:
+
+  +
+
+ 图 4
+
+
+
+
+我们可以看到节点正常启动:
+
+
+  +
+
+ 图 5
+
+
+
+启动完之后,就可以通过`admin.nodeInfo.protocols.eth`来获取到刚启动的节点的一些信息(如下),比较上文初始化的配置,相关内容是一致的。
+
+
+  +
+
+ 图 6
+
+
+
+恭喜!我们已经成功启动了一条自己的私链。
+
+## 3、Geth 控制台命令
+
+`Geth Console` 是一个交互式的 JavaScript 执行环境,其中 > 是命令提示符,里面内置了一些用来操作以太坊的 JavaScript对象,我们可以直接调用这些对象来获取区块链上的相关信息。
+
+**这些对象主要包括:**
+
+- eth:主要包含对区块链进行访问和交互相关的方法;
+- net:主要包含查看 p2p 网络状态的方法;
+- admin:主要包含与管理节点相关的方法;
+- miner:主要包含挖矿相关的一些方法;
+- personal:包含账户管理的方法;
+- txpool:包含查看交易内存池的方法;
+- web3:包含以上所有对象,还包含一些通用方法。
+
+
+
+**常用命令有:**
+
+
+- personal.newAccount():创建账户;
+- personal.unlockAccount():解锁账户;
+- eth.accounts:枚举系统中的账户;
+- eth.getBalance():查看账户余额,返回值的单位是 Wei(Wei 是以太坊中最小货币面额单位,类似比特币中的聪,1 ether = 10^18 Wei);
+- eth.blockNumber:列出区块总数;
+- eth.getTransaction():获取交易;
+- eth.getBlock():获取区块;
+- miner.start():开始挖矿;
+- miner.stop():停止挖矿;
+- web3.fromWei():Wei 换算成以太币;
+- web3.toWei():以太币换算成 Wei;
+- txpool.status:交易池中的状态;
+- admin.addPeer():连接到其他节点
+
+### 3.1 操作测试
+
+**3.1.1 创建账户**
+
+进入控制台后,可以通过使用命令来与私有链进行交互。创建一个新的账户:
+
+```javascript
+> personal.newAccount()
+Passphrase:
+Repeat passphrase:
+"0xc8248c7ecbfd7c4104923275b99fafb308bbff92"
+```
+
+输入两遍密码后,生成账户地址。以同样的方式,可创建多个账户,查看账户:
+
+```javascript
+> eth.accounts
+```
+查看账户余额
+
+```javascript
+> eth.getBalance(eth.accounts[0])
+0
+```
+
+  +
+
+ 图 7
+
+
+
+**3.1.2 挖矿**
+
+启动挖矿:
+
+```javascript
+> miner.start(1)
+```
+
+其中 `start` 的参数表示挖矿使用的线程数。第一次启动挖矿会先生成挖矿所需的 `DAG `文件,这个过程有点慢,等进度达到 100% 后,就会开始挖矿,此时屏幕会被挖矿信息刷屏。
+
+停止挖矿,在 控制台 中输入:
+
+```javascript
+> miner.stop()
+```
+
+挖到一个区块会奖励以太币,挖矿所得的奖励会进入矿工的账户,这个账户叫做 coinbase,默认情况下 coinbase 是本地账户中的第一个账户,可以通过 miner.setEtherbase() 将其他账户设置成 coinbase。
+
+可以使用以下命令,当新区块挖出后,挖矿即可结束。
+
+```javascript
+> miner.start(1);admin.sleepBlocks(1);miner.stop();
+```
+
+**3.1.3 交易**
+
+目前,账户 0 已经挖到了 3 个块的奖励,账户 1 的余额还是0:
+```javascript
+> eth.getBalance(eth.accounts[0])
+15000000000000000000
+> eth.getBalance(eth.accounts[1])
+0
+```
+
+我们要从账户 0 向账户 1 转账,先解锁账户 0,才能发起交易:
+
+```javascript
+> personal.unlockAccount(eth.accounts[0])
+Unlock account 0x3443ffb2a5ce3f4b80080791e0fde16a3fac2802
+Passphrase:
+true
+```
+发送交易,账户 0 -> 账户 1:
+
+```javascript
+> amount = web3.toWei(5,'ether')
+"5000000000000000000"
+> eth.sendTransaction({from:eth.accounts[0],to:eth.accounts[1],value:amount})
+INFO [09-12|07:38:12] Submitted transaction fullhash=0x9f5e61f3d686f793e2df6378d1633d7a9d1df8ec8c597441e1355112d102a6ce recipient=0x02bee2a1582bbf58c42bbdfe7b8db4685d4d4c62
+"0x9f5e61f3d686f793e2df6378d1633d7a9d1df8ec8c597441e1355112d102a6ce"
+```
+
+此时如果没有挖矿,用 `txpool.status` 命令可以看到本地交易池中有一个待确认的交易,可以使用 `eth.getBlock("pending", true).transactions`查看当前待确认交易。使用下面命令开始挖矿。
+
+```javascript
+>miner.start(1);admin.sleepBlocks(1);miner.stop();
+```
+
+新区块挖出后,挖矿结束,查看账户 1 的余额,已经收到了账户 0 的以太币:
+```javascript
+> web3.fromWei(eth.getBalance(eth.accounts[1]),'ether')
+5
+```
+
+**3.1.3 查看交易和区块**
+
+查看当前区块总数:
+```javascript
+> eth.blockNumber
+4
+```
+
+通过区块号查看区块:
+```javascript
+> eth.getBlock(4)
+```
+
+通过交易 Hash 查看交易(Hash 值包含在上面交易返回值中):
+
+
+```javascript
+> eth.getTransaction("0x9f5e61f3d686f793e2df6378d1633d7a9d1df8ec8c597441e1355112d102a6ce")
+```
+
+**3.1.3 其他节点加入**
+
+此时,私有链已经通过该节点创建好了,如果其他节点想加入,需要通过以太坊客户端连接到该私有区块网络,并连接该网络的节点来同步区块信息。在其他主机上安装以太坊客户端Geth,通过Geth命令进入该私有区块链,注意要指定相同的网络号。
+
+假设有两个节点:节点一和节点二,NetWorkID 都是 6666,通过下面的步骤就可以从节点一连接到节点二。
+
+首先要知道节点二的 enode 信息,在节点二的 Geth Console 中执行下面的命令查看 enode 信息:
+
+```javascript
+> admin.nodeInfo.enode
+"enode://d465bcbd5c34da7f4b8e00cbf9dd18e7e2c38fbd6642b7435f340c7d5168947ff2b822146e1dc1b07e02f7c15d5ca09249a92f1d0caa34587c9b2743172259ee@[::]:30303"
+```
+然后在节点一的 Geth Console 中执行 `admin.addPeer()`,就可以连接到节点二:
+
+```javascript
+> admin.addPeer("enode://d465bcbd5c34da7f4b8e00cbf9dd18e7e2c38fbd6642b7435f340c7d5168947ff2b822146e1dc1b07e02f7c15d5ca09249a92f1d0caa34587c9b2743172259ee@[::]:30303")
+```
+`addPeer()` 的参数就是节点二的 enode 信息,注意要把 enode 中的 `[::]` 替换成节点二的 IP 地址。连接成功后,节点二就会开始同步节点一的区块,同步完成后,任意一个节点开始挖矿,另一个节点会自动同步区块,向任意一个节点发送交易,另一个节点也会收到该笔交易。
+
+通过 `admin.peers`可以查看连接到的其他节点信息,通过 `net.peerCount`可以查看已连接到的节点数量。
+
+除了上面的方法,也可以在启动节点的时候指定`--bootnodes`选项连接到其他节点。
+
+> 如果只是自己测试开发使用,建议使用dev环境,在需要在启动时增加`–dev`参数即可,在dev模式下会监听交易,一旦有交易发送就会打包然后挖矿确认,且默认的`account[0]`开发者账户初始有一大堆以太币。
+
+## 3、智能合约操作
+
+### 3.1、创建和编译智能合约
+
+经过part2的学习大家已经基本上掌握了Solidity,接下来我们编写一个智能合约:
+
+该合约包含一个方法 multiply(),将输入的两个数相乘后输出:
+```javascript
+pragma solidity ^0.4.0;
+contract TestContract
+{
+ function multiply(uint a, uint b) returns (uint)
+ {
+ return a * b;
+ }
+}
+```
+将上面的代码复制到Remix编辑器里,程序将自动完成编译。
+
+  +
+
+ 图 8
+
+
+
+点击 run 在Environment中设选择JavaScript VM, Value可设置为1,点击Deploy,则可创建该部署智能合约的交易。
+
+因为我们要将该智能合约部署到私有链上,需要得到智能合约编译后的EVM二进制码和JSON ABI(Application Binary Interface)。将生成的交易保存到scenario.json文件,点击箭头所指按钮
+
+
+  +
+
+ 图 9
+
+
+
+
+其中38-65行为该智能合约的ABI(注意前面还有一个[符号),ABI指定了合约接口,包括可调用的合约方法、变量、事件等。
+
+
+  +
+
+ 图 10
+
+
+
+input`字段为合约EVM二进制码,可点击直接复制。
+
+在Linux下可以直接使用安装好的编译器进行编译,把合约代码保存到文件名为testContract.sol 里,通过下面两个命令分别得到EVM二进制码和JSON ABI。
+
+如果没有安装solc先执行
+
+```javascript
+sudo snap install solc
+```
+接下来执行
+```javascript
+$solc --bin testContract.sol
+$solc --abi testContract.sol
+```
+
+  +
+
+ 图 11
+
+
+
+### 3.2、部署智能合约
+
+回到 Geth 的控制台,用变量 code 和 abi 记录上面两个值:
+
+```javascript
+> code = "608060405234801561001057600080fd5b5060b88061001f6000396000f3fe6080604052348015600f57600080fd5b506004361060285760003560e01c8063165c4a1614602d575b600080fd5b606060048036036040811015604157600080fd5b8101908080359060200190929190803590602001909291905050506076565b6040518082815260200191505060405180910390f35b600081830290509291505056fea265627a7a7231582049ecffb2740a6e31f7c8fbf4a928b88d3a95f417b985dc23cd1ad4c06a9b043864736f6c63430005100032"
+> abi = [{
+ "0xd1ef8ab8f12bde83ebaee1be4183c75f45ab5835643812016a7751173bfb9dc0": [
+ {
+ "constant": true,
+ "inputs": [
+ {
+ "name": "a",
+ "type": "uint256"
+ },
+ {
+ "name": "b",
+ "type": "uint256"
+ }
+ ],
+ "name": "multiply",
+ "outputs": [
+ {
+ "name": "",
+ "type": "uint256"
+ }
+ ],
+ "payable": false,
+ "stateMutability": "view",
+ "type": "function"
+ }
+ ]
+ }]
+```
+使用账户 0 来部署合约,首先解锁账户:
+
+```javascript
+> personal.unlockAccount(eth.accounts[0])
+Unlock account 0xb51654f60dee35265558a1d2e61468fe00f12888
+Passphrase:
+true
+```
+创建合约实例,发送部署合约的交易:
+
+```javascript
+> myContract = eth.contract(abi)
+...
+> contract = myContract.new({from:eth.accounts[0],data:code,gas:1000000})
+
+```
+
+
+  +
+
+ 图 12
+
+
+此时如果没有挖矿,用 `txpool.status` 命令可以看到本地交易池中有一个待确认的交易。使用 `miner.start()` 命令开始挖矿,一段时间后交易会被确认。通过查询该交易可得到合约地址,使用命令:
+
+
+```javascript
+>eth.getTransactionReceipt("0x085b66b2591ee31c3ad58a66ca485bd19bea6c1fc8ca7550a896853ab52855a6")
+contractAddress: "0xd92845cc4bffc1d6a4b6a389933b88880d5ded24"
+```
+
+
+
+### 3.3、调用智能合约
+
+使用以下命令通过发送交易来调用合约,sendTransaction 方法的前几个参数应该与合约中 multiply 方法的输入参数对应。这种情况下,交易会通过挖矿记录到区块链中:
+
+```javascript
+>contract.multiply.sendTransaction(2, 4, {from:eth.accounts[0]})
+```
+在本地运行该方法可直接查看返回结果,不会记录到区块链中,命令如下:
+
+```javascript
+>contract.multiply.call(2,4)
+8
+```
+
+如果其他节点要调用这个已经部署好的合约,需要知道该合约的地址以及ABI。可以通过发送交易调用,也可以本地调用。我们以本地调用为例。
+创建合约实例:
+
+```javascript
+>abi = [{
+ "0xd1ef8ab8f12bde83ebaee1be4183c75f45ab5835643812016a7751173bfb9dc0": [
+ {
+ "constant": true,
+ "inputs": [
+ {
+ "name": "a",
+ "type": "uint256"
+ },
+ {
+ "name": "b",
+ "type": "uint256"
+ }
+ ],
+ "name": "multiply",
+ "outputs": [
+ {
+ "name": "",
+ "type": "uint256"
+ }
+ ],
+ "payable": false,
+ "stateMutability": "view",
+ "type": "function"
+ }
+ ]
+ }]
+>sample=eth.contract(abi)
+>samplecontract=sample.at("0xd92845cc4bffc1d6a4b6a389933b88880d5ded24")
+```
+调用合约
+
+```javascript
+>samplecontract.multiply.call(2,4)
+8
+```
+
+
+
+## 4、web3.js 简介
+
+我们除了通过Geth的JavaScript Console进行交互以外,还有许多第三方库可以使用,方便开发基于以太坊区块链的应用:
+
+
+  +
+
+ 图 13
+
+
+
+本文使用web3.js与Geth客户端交互,首先搭建开发环境。
+
+
+### 4.1 环境搭建
+
+
+**4.1.1 node.js安装**
+
+更新源
+```javascript
+sudo apt-get update
+sudo apt-get install -y python-software-properties software-properties-common
+sudo add-apt-repository ppa:chris-lea/node.js
+sudo apt-get update
+```
+
+node.js、npm安装
+```javascript
+sudo apt-get install nodejs
+sudo apt install nodejs-legacy
+sudo apt install npm
+```
+安装完后,可以通过 `node --version npm --version` 查看是否安装成功及版本号。npm 包管理工具随 node 一起安装,如果版本太低,建议升到新版本。
+
+
+**4.1.2 web3.js模块安装**
+使用npm可完成本地安装、全局安装模块。
+```javascript
+ npm install -global //全局安装
+ npm install //本地安装
+```
+
+
+我这里选择使用本地安装模块,这样方便开发的应用移植、上线等。创建一个工程文件夹etherjs。在该文件夹下初始化一个新的 package.json 文件,使用下面命令自动生成。
+```javascript
+npm init -y
+```
+
+本地安装并添加模块名到 package.json
+```javascript
+npm install --save
+或者npm install --save-dev
+```
+
+区别在于--save-dev 是你开发时候依赖的东西,--save 是你发布之后还依赖的东西。一般使用--save。
+```javascript
+npm install web3 --save
+```
+
+
+如果这样安装不成功,使用下面命令安装指定版本:
+```javascript
+npm install web3@^0.20.1 --save
+```
+
+**4.1.3 solc.js模块安装**
+solc是用来编译智能合约的模块
+```javascript
+npm install solc --save
+```
+
+**4.1.4 编译器——Visual Studio Code**
+
+这里选择Visual Studio Code,适合node.js开发,集成的终端可以很方便运行程序。
+
+安装Ubuntu Make
+```javascript
+sudo add-apt-repository ppa:ubuntu-desktop/ubuntu-make
+sudo apt-get update
+sudo apt-get install ubuntu-make
+```
+安装visual-studio-code
+```javascript
+umake web visual-studio-code
+```
+安装完成后,直接搜索Visual Studio Code应用,把图标拖拽到Unity启动器上,就可以方便使用了。
+
+
+### 4.2 web3.js 介绍
+
+web3js 的全称是Web3 JavaScript app API,它是一个JavaScript API库。要使DApper在以太坊上运行,我们可以使用web3.js库提供的web3对象。web3.js通过RPC调用与本地节点通信,它可以用于任何暴露了RPC层的以太坊节点,web3包含了eth对象 - web3.eth(专门与以太坊区块链交互)和 shh对象 - web3.shh(用于与 Whisper交互)[Whisper是以太坊生态系统的一部分,主要用来做消息传递]
+
+如果我们想要在以太坊上开发合约,目前来说最方便的方法就是调用Web3.js库,它会给我们一个Web3对象。我们进入geth控制台,直接键入web3就可以看到所有的方法。下面主要介绍如何通过web3js创建合约并调用
+
+
+**4.2.1异步回调(callback)**
+
+- web3js API 设计的最初目的,主要是为了和本地 RPC 节点共同使用,所以默认情况下发送的是同步 HTTP 请求
+- 如果要发送异步请求,可以在函数的最后一个参数位置上,传入一个回调函数。回调函数是可选(optioanl)的
+- 我们一般采用的回调风格是所谓的“错误优先”,例如:
+
+ ```javascript
+web3.eth.getBlock(48, function(error, result){
+if(!error)
+ console.log(JSON.stringify(result));
+else
+ console.error(error);
+});
+ ```
+
+**4.2.2 回调 Promise 事件(v1.0.0)**
+
+- 为了帮助 web3 集成到不同标准的所有类型项目中,1.0.0 版本提供了多种方式来处理异步函数。大多数的 web3 对象允许将一个回调函数作为最后一个函数参数传入,同时会返回一个promise 用于链式函数调用。
+- 以太坊作为一个区块链系统,一次请求具有不同的结束阶段。为了满足这样的要求,1.0.0 版本将这类函数调用的返回值包成一个“承诺事件”(promiEvent),这是一个 promise 和EventEmitter 的结合体。
+- PromiEvent 的用法就像 promise 一样,另外还加入了.on,.once 和.off方法
+
+
+ ```javascript
+web3.eth.sendTransaction({from: '0x123...', data: '0x432...'})
+.once('transactionHash', function(hash){ ... })
+.once('receipt', function(receipt){ ... })
+.on('confirmation', function(confNumber, receipt){ ... })
+.on('error', function(error){ ... })
+.then(function(receipt){ // will be fired once the receipt is mined });
+ ```
+
+**4.2.3 应用二进制接口(ABI)**
+
+- web3.js 通过以太坊智能合约的 json 接口(Application Binary Interface,ABI)创建一个 JavaScript 对象,用来在 js代码中描述\
+- 函数(functions)
+- type:函数类型,默认“function”,也可能是“constructor”
+- constant, payable, stateMutability:函数的状态可变性
+- inputs, outputs: 函数输入、输出参数描述列表
+- 事件(events)
+- type:类型,总是“event”
+- inputs:输入对象列表,包括 name、type、indexed
+
+**4.2.4 批处理请求(batch requests)**
+
+- 批处理请求允许我们将请求排序,然后一起处理它们。
+- 注意:批量请求不会更快。实际上,在某些情况下,一次性地发出许多请求会更快,因为请求是异步处理的。
+- 批处理请求主要用于确保请求的顺序,并串行处理。
+
+
+ ```javascript
+var batch = web3.createBatch();
+batch.add(web3.eth.getBalance.request('0x0000000000000000
+000000000000000000000000', 'latest', callback));
+batch.add(web3.eth.contract(abi).at(address).balance.request(a
+ddress, callback2));
+batch.execute();
+ ```
+
+**4.2.5 大数处理(big numbers)**
+
+- JavaScript 中默认的数字精度较小,所以web3.js 会自动添加一个依赖库 BigNumber,专门用于大数处理
+- 对于数值,我们应该习惯把它转换成 BigNumber 对象来处理
+
+ ```javascript
+var balance = new
+BigNumber('131242344353464564564574574567456');
+// or var balance = web3.eth.getBalance(someAddress);
+balance.plus(21).toString(10);
+//"131242344353464564564574574567477"
+ ```
+
+- BigNumber.toString(10) 对小数只保留20位浮点精度。所以推荐的做法是,我们内部总是用 wei 来表示余额(大整数),只有在需要显示给用户看的时候才转换为ether或其它单位
+
+
+### 4.3 常用 API —— 基本信息查询
+
+**4.3.1 查看 web3 版本**
+
+- v0.2x.x:web3.version.api
+- v1.0.0:web3.version
+
+查看 web3 连接到的节点版本( clientVersion )
+- 同步:web3.version.node
+- 异步:web3.version.getNode((error,result)=>{console.log(result)})
+- v1.0.0:web3.eth.getNodeInfo().then(console.log)
+
+**4.3.2 基本信息查询**
+
+获取 network id
+- 同步:web3.version.network
+- 异步:web3.version.getNetwork((err, res)=>{console.log(res)})
+- v1.0.0:web3.eth.net.getId().then(console.log)
+
+获取节点的以太坊协议版本
+- 同步:web3.version.ethereum
+- 异步:web3.version.getEthereum((err, res)=>{console.log(res)}
+- v1.0.0:web3.eth.getProtocolVersion().then(console.log)
+
+
+**4.3.3 网络状态查询**
+
+是否有节点连接 / 监听,返回 true/false
+- 同步:web3.isConnect() 或者 web3.net.listening
+- 异步:web3.net.getListening((err,res)=>console.log(res))
+- v1.0.0:web3.eth.net.isListening().then(console.log)
+
+
+查看当前连接的 peer 节点
+- 同步:web3.net.peerCount
+- 异步:web3.net.getPeerCount((err,res)=>console.log(res))
+- v1.0.0:web3.eth.net.getPeerCount().then(console.log)
+
+**4.3.4 Provider**
+
+查看当前设置的 web3 provider
+- web3.currentProvider
+
+查看浏览器环境设置的 web3 provider ( v1.0.0 )
+- web3.givenProvider
+
+设置 provider
+- web3.setProvider(provider)
+- web3.setProvider(new web3.providers.HttpProvider('http://localhost:8545'))
+
+
+### 4.4 web3 通用工具方法
+
+以太单位转换
+- web3.fromWei web3.toWei数据类型转换
+- web3.toString web3.toDecimal web3.toBigNumber字符编码转换
+- web3.toHex web3.toAscii web3.toUtf8 web3.fromUtf8地址相关
+- web3.isAddress web3.toChecksumAddress
+
+### 4.5 web3.eth
+
+**4.5.1 账户相关**
+
+coinbase 查询
+
+- 同步:web3.eth.coinbase
+- 异步:web3.eth.getCoinbase( (err, res)=>console.log(res) )
+- v1.0.0:web3.eth.getCoinbase().then(console.log)
+
+账户查询
+
+- 同步:web3.eth.accounts
+- 异步:web3.eth.getAccounts( (err, res)=>console.log(res) )
+- v1.0.0:web3.eth.getAccounts().then(console.log)
+
+**4.5.2 区块相关**
+
+区块高度查询
+- 同步:web3.eth. blockNumber
+- 异步:web3.eth.getBlockNumber( callback )
+
+gasPrice 查询
+- 同步:web3.eth.gasPrice
+- 异步:web3.eth.getGasPrice( callback )
+
+区块查询
+- 同步:web3.eth.getBlockNumber( hashStringOrBlockNumber[ ,returnTransactionObjects] )
+- 异步:web3.eth.getBlockNumber( hashStringOrBlockNumber, callback )
+
+块中交易数量查询
+- 同步:web3.eth.getBlockTransactionCount( hashStringOrBlockNumber )
+- 异步:web3.eth.getBlockTransactionCount( hashStringOrBlockNumber, callback )
+
+**4.5.3 交易相关**
+
+余额查询
+- 同步:web3.eth.getBalance(addressHexString [, defaultBlock])
+- 异步:web3.eth.getBalance(addressHexString \[, defaultBlock\]\[, callback\])
+
+交易查询
+- 同步:web3.eth.getTransaction(transactionHash)
+- 异步:web3.eth.getTransaction(transactionHash [, callback])
+
+交易执行相关
+- 交易收据查询(已进块)
+- 同步:web3.eth.getTransactionReceipt(hashString)
+- 异步:web3.eth.getTransactionReceipt(hashString [,callback])
+- 估计 gas 消耗量
+- 同步:web3.eth.estimateGas(callObject)
+- 异步:web3.eth.estimateGas(callObject [, callback])
+
+**4.5.4 发送交易**
+
+- web3.eth.sendTransaction(transactionObject [, callback])
+- 交易对象:
+- from:发送地址
+- to:接收地址,如果是创建合约交易,可不填
+- value:交易金额,以wei为单位,可选
+- gas:交易消耗 gas 上限,可选
+- gasPrice:交易 gas 单价,可选
+- data:交易携带的字串数据,可选
+- nonce:整数 nonce 值,可选
+
+**4.5.5 消息调用**
+
+- web3.eth.call(callObject [, defaultBlock] [, callback])
+- 参数:
+ - 调用对象:与交易对象相同,只是from也是可选的
+ - 默认区块:默认“latest”,可以传入指定的区块高度
+ - 回调函数,如果没有则为同步调用
+
+```javascript
+var result = web3.eth.call({ to:"0xc4abd0339eb8d57087278718986382264244252f",
+data:"0xc6888fa1000000000000000000000000000000000000000000000000000 0000000000003" });
+console.log(result);
+```
+
+**4.5.6 日志过滤(事件监听)**
+```javascript
+web3.eth.filter( filterOptions [ , callback ] )
+// filterString 可以是 'latest' or 'pending'
+var filter = web3.eth.filter(filterString);
+// 或者可以填入一个日志过滤 options
+var filter = web3.eth.filter(options);
+// 监听日志变化
+filter.watch(function(error, result){ if (!error) console.log(result); });
+// 还可以用传入回调函数的方法,立刻开始监听日志
+web3.eth.filter(options, function(error, result){
+if (!error) console.log(result);
+});
+```
+
+**4.5.7 合约相关 —— 创建合约**
+
+web3.eth.contract
+
+```javascript
+var MyContract = web3.eth.contract(abiArray);
+// 通过地址初始化合约实例
+var contractInstance = MyContract.at(address);
+// 或者部署一个新合约
+var contractInstance = MyContract.new([constructorParam1][, constructorParam2], {data: '0x12345...', from:myAccount, gas: 1000000});
+```
+
+**4.5.8 调用合约函数**
+
+可以通过已创建的合约实例,直接调用合约函数
+
+```javascript
+// 直接调用,自动按函数类型决定用 sendTransaction 还是 call
+myContractInstance.myMethod(param1 [, param2, ...] [,transactionObject] [, defaultBlock] [, callback]);
+// 显式以消息调用形式 call 该函数
+myContractInstance.myMethod.call(param1 [, param2, ...] [,transactionObject] [, defaultBlock] [, callback]);
+// 显式以发送交易形式调用该函数
+myContractInstance.myMethod.sendTransaction(param1 [,param2, ...] [, transactionObject] [, callback]);
+```
+
+**4.5.9 监听合约事件**
+
+合约的 event 类似于 filter,可以设置过滤选项来监听
+
+```javascript
+var event = myContractInstance.MyEvent({valueA: 23}[, additionalFilterObject])
+// 监听事件
+event.watch(function(error, result){
+if (!error)
+ console.log(result);
+});
+// 还可以用传入回调函数的方法,立刻开始监听事件
+var event = myContractInstance.MyEvent([{valueA: 23}][, additionalFilterObject] , function(error, result){
+ if (!error) console.log(result);
+}
+);
+```
+
+## 5、交互实现——部署智能合约
+
+通过编写一个depoly.js程序实现自动化的部署智能合约。首先要保持Geth客户端正常运行,并开启rpc。
+
+```javascript
+geth --identity "TestNode" --rpc --rpcport "8545" --datadir data0 --port "30303" --nodiscover --networkid 6666 --rpcapi admin,eth,miner,personal,txpool,eth,web3,net console
+```
+合约应该在智能合约编译器(如remix)调试好,然后将其写到test.sol文件里。
+```javascript
+pragma solidity ^0.4.0;
+contract TestContract
+{
+ function multiply(uint a, uint b) returns (uint)
+ {
+ return a * b;
+ }
+}
+```
+使用solc模块生成合约的code和abi,我将该过程自定义为一个模块test.js,方便depoly.js调用。
+```javascript
+var fs = require('fs');
+var solc = require('solc');
+//compile smart contract to get bytecode and abi
+
+var source = fs.readFileSync("./test.sol",'utf8'); //读取代码
+ //console.log("compiling contract...");
+var compiledcontract = solc.compile(source); //编译
+ //console.log('done');
+for (var contractName in compiledcontract.contracts){
+ var bytecode = compiledcontract.contracts[contractName].bytecode;
+ var abi = JSON.parse(compiledcontract.contracts[contractName].interface);
+}
+//console.log(JSON.stringify(abi, undefined, 2));
+//console.log(bytecode);
+//console.log(abi);
+
+function bytecode(){
+ console.log(bytecode);
+}
+function abi(){
+ console.log(abi);
+}
+module.exports = {bytecode:bytecode,abi:abi};
+
+```
+depoly.js通过与Geth交互部署智能合约。当合约被区块链确认后,会直接返回合约地址。
+```javascript
+var Web3 = require('web3');
+var contract = require('./test');
+var web;
+
+//connect to node
+var ethereumUri = 'http://localhost:8545';
+if (typeof web3 !== 'undefined') {
+ web3 = new Web3(web3.currentProvider);
+} else {
+ // set the provider you want from Web3.providers
+ web3 = new Web3(new Web3.providers.HttpProvider(ethereumUri));
+}
+//查询区块链中基本的账户信息
+if(!web3.isConnected()){
+ throw new Error('unable to connect to ethereum node at '+ ethereumUri);
+}else{
+ console.log('connected to etherum node at '+ ethereumUri);
+ var coinbase = web3.eth.accounts[0];
+ console.log('coinbase:' + coinbase);
+ var balance = web3.eth.getBalance(coinbase);
+ console.log('balance:' + web3.fromWei(balance, 'ether') + " ETH");
+ var accounts = web3.eth.accounts;
+ console.log(accounts);
+}
+//通过coinbase部署智能合约
+var abi = contract.abi;
+var bytecode = contract.bytecode;
+
+if (web3.personal.unlockAccount(coinbase, '123')) {
+ console.log(`${coinbase} is unlocaked`);
+}else{
+ console.log(`unlock failed, ${coinbase}`);
+}
+
+var gasEstimate = web3.eth.estimateGas({data: '0x' + bytecode}); //gas估计
+console.log('gasEstimate = ' + gasEstimate);
+var MyContract = web3.eth.contract(abi);
+console.log('deploying contract...');
+var myContractReturned = MyContract.new({
+ from: coinbase,
+ data: '0x'+ bytecode,
+ gas: gasEstimate + 50000
+}, function (err, myContract) {
+ if (!err) {
+ if (!myContract.address) {
+ console.log(`myContract.transactionHash = ${myContract.transactionHash}`); // The hash of the transaction, which deploys the contract
+ // check address on the second call (contract deployed)
+ } else {
+ console.log(`myContract.address = ${myContract.address}`); // the contract address
+ global.contractAddress = myContract.address;
+ }
+
+ } else {
+ console.log(err);
+ }
+});
+```
+
+
+**参考自:**
+
+[Go Ethereum](https://geth.ethereum.org/docs/install-and-build/installing-geth)
+
+[以太坊私有链Geth控制台操作教程](https://www.jianshu.com/p/9fa31e4cdf4d)
+
+[尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
+[web3.js 1.0中文手册](http://cw.hubwiz.com/card/c/web3.js-1.0/)
\ No newline at end of file
diff --git a/Blockchain/part4_合约编写实例补充.md b/Blockchain/part4_合约编写实例补充.md
new file mode 100644
index 0000000..5d1a5f7
--- /dev/null
+++ b/Blockchain/part4_合约编写实例补充.md
@@ -0,0 +1,402 @@
+ 注:本教程为技术教程,不谈论且不涉及炒作任何数字货币
+
+# 合约编写实战实例
+
+## 一、简单代币合约
+
+```javascript
+pragma solidity > 0.4.22;
+
+contract Coin{
+ //这里我们定义了一个address 作为key, uint做为value的hashTable balances; 我们还定义了一个address的变量minter;
+ address public minter;
+ mapping(address=>uint) balances;
+ event Sent(address from, address to, uint amount);
+ constructor(){
+ //代表创建这个合约的账户地址,被赋值给变量minter.
+ minter = msg.sender;
+ }
+
+ //添加一个挖矿合约
+ function mint(address receiver, uint amount) public{
+ require(msg.sender == minter);
+ balances[receiver] += amount;
+
+ }
+ function send(address receiver, uint amount) public{
+ require(balances[msg.sender] >= amount);
+ balances[msg.sender] -= amount;
+ balances[receiver] += amount;
+ emit Sent(msg.sender,receiver,amount);
+ }
+
+}
+```
+
+解析:
+上面实现一个简单的加密货币,币在这里可以无中生有,但只有创建合约的人才能做到,且任何人都可以给他人转币,无需注册名和密码。
+
+`address`类型是一个160位的值,不允许任何算数操作,这种类型适合存储合约地址或外部人员。
+
+`mappings`可看作是一个哈希表,它会执行虚拟初始化,以使得所有可能存在的键都映射到一个字节表示为全零的值。
+
+`event Sent(address from, address to, uint amount)`;声明了一个所谓的事件,它在send函数最后一行被发出。用户界面可以监听区块链上正在发送的事件,且不会花费太多成本,一旦它被发出,监听该事件的listener都将收到通知,而所有的事件都包含了`from`,`t`o和`amoun`t三个参数,可方便追踪事务。
+
+`msg.sender`始终是当前函数或者外部函数调用的来源地址。
+
+最后真正被用户和其他合约所调用的,用于完成本合约功能的方法是`mint`和`send`。若`mint`被合约创建者外的其他调用则说明都不会发生。
+
+`send`函数可被任何人用于向其他人发送代币,前提是发送者拥有这些代币,若使用合约发送代币给一个地址,当在区块链浏览器上查到该地址时时看不到任何相关信息的,因为,实际上发送币和更改余额的信息仅仅存在特定合约的数据存储器中。通过使用事件,可非常简单地为新币创建一个区块链浏览器来追踪交易和余额。
+
+
+  +
+
+
+
+
+
+
+## 二、水龙头合约
+
+在前面我们通过 Ropsten 测试网络的水龙头(Faucet)获取了一些以太币,并提到可以向水龙头账户发送以太币来捐赠以太币。实际上,水龙头账户是一个合约账户,水龙头就是一份合约,而整个网站就是合约+前端组成的DApp。下面我们通过 Remix 来编写一个简单的水龙头合约,借此了解如何创建、部署合约以及一些 Solidity 的基本语法。
+
+首先打开 Remix,并新建一个名为 faucet.sol 的文件,该文件就是 Solidity 的源文件
+
+
+  +
+
+
+
+
+打开 faucet.sol,并写入如下代码
+
+```javascript
+pragma solidity ^0.7.0;
+
+contract faucet {
+ function withdraw (uint amount) public {
+ require (amount <= 1e18);
+ msg.sender.transfer (amount);
+ }
+
+ receive () external payable {}
+}
+```
+
+通过这几行代码我们就实现了一个非常简单的水龙头合约。首行代码 `pragma solidity ^0.7.0 `是一个**杂注**,指定了我们的源文件使用的编译器版本不能低于 0.7.0,也不能高于 0.8.0。
+
+`contract faucet{...}` 声明了一个合约对象,合约对象类似面向对象语言中的类,对象名必须跟文件名相同。
+
+接下来通过 `function withdraw (uint amount) public {...}` 创建了一个名为 withdraw 的函数,该函数接收一个无符号整数(uint)作为参数,并且被声明为 public 函数,意为可以被其他合约调用。
+
+withdraw 函数体中的 `require` 是 Solidity 的内置函数,用来检测括号中的条件是否满足。条件满足则继续执行合约,条件不满足则合约停止执行,回撤所有执行过的操作,并抛出异常。在这里我们通过 `require (amount <= 1e18)` 来检测输入的以太币值是否小于等于1个以太。
+
+接下来的这一行 `msg.sender.transfer (amount)` 就是实际的提款操作了。`msg` 是 Solidity 中内置的对象,所有合约都可以访问,它代表触发此合约的交易。也就是说当我们调用 `withdraw` 函数的时候实际上触发了一笔交易,并用 `msg` 来表示它。`sender` 是交易 `msg` 的属性,表示了交易的发件人地址。函数 `transfer` 是一个内置函数,它接收一个参数作为以太币的数量,并将该数量的以太币从合约账户发送到调用合约的用户的地址中。
+
+最后一行是一个特殊的函数 `receive` ,这是所谓的 `fallback` 或 `default` 函数。当合约中的其他函数无法处理发送到合约中的交易信息时,就会执行该函数。在这里,我们将该函数声明为 `external` 和 `payable` ,`external` 意味着该函数可以接收来自外部账户的调用,`payable` 意味着该函数可以接收来自外部账户发送的以太币。
+
+这样,当我们调用合约中的 `withdraw` 并提供一个参数时,我们可以从这份合约中提出以太币;当我们向合约发送以太币时,就会调用 `receive` 函数往合约中捐赠以太币。
+
+代码编写完毕后,在 Remix 左侧的功能栏中选择第二项,并点击 *Compile faucet.sol* 来编译我们的 sol 文件。
+
+
+  +
+
+
+
+
+
+编译完成后会出现一个 Warning,提示我们添加 SPDX license,可以忽略。
+
+随后选择 Remix 左侧工具栏的第三项,进入合约部署界面
+
+
+  +
+
+
+
+
+
+首先将 ENVIRONMENT 选择为 Injected Web3,这样才能通过 MetaMask 钱包来发送交易。
+
+随后点击 Deploy 部署合约,MetaMask 会弹出部署合约的交易界面
+
+
+  +
+
+
+
+
+
+因为该笔交易是合约创建交易,因此我们支付的以太币为0,但仍需支付一定的 Gas 费用,可以自己设定 Gas 的价格。
+
+合约部署成功后会收到 Chrome 的消息提示,并在 Remix 的 Deployed Contracts 中也会有显示
+
+
+  +
+
+
+
+
+
+这样我们就完成了这个水龙头合约的部署。
+
+#### 水龙头测试 ####
+
+我们刚刚创建的水龙头中还没有以太坊,因此我们可以通过 MetaMask 向水龙头合约的地址中发送一些以太坊。水龙头合约的地址会显示在 Remix 中的,见上图 FAUCET AT 0X7A4...34219,可以直接复制。
+
+
+  +
+
+
+
+
+
+交易被确认后,我们的水龙头中就有了0.999726个以太币,现在我们可以通过 Remix 中合约一栏的 withdraw 按钮来提取以太币了。需要注意,这里输入的以太币个数是以 wei 为单位的。
+
+
+  +
+
+
+
+
+
+点击 withdraw 后,会弹出警告框
+
+
+  +
+
+
+
+
+
+这是因为目前我们还没有设置这笔交易的 Gas,不用担心,点击 Send Transaction 后,在弹出的 MetaMask 中设置即可。
+
+交易被确认后,我们得到了刚刚提取的0.999726个以太币
+
+
+  +
+
+
+
+
+
+若大家没有执行成功可以重新做一次、查找其他资料或者[观看此视频](https://www.bilibili.com/video/BV1sJ411D72u?p=465)
+
+## 三、投票合约的实现
+
+ +
+本次教程将以一个较复杂的投票合约作为结束,我们希望实现的功能是为每个(投票)建议建立一份合约,然后作为合约的创造者-主席,主席将赋予每个成员(地址)投票权,而成员的投票权可以选择委托给其他人也可以自己投票,结束时将返回投票最多的提案。听起来很简单一个功能实现起来却较为复杂,下面我们拆分开进行讲解
+
+注:
+
+1. 代码可直接在Remix编辑器的已有solidity文件中找到,在contract/_Ballot.sol文件里
+2. 若学习者前面部分掌握较牢固,不妨尝试直接自行阅读代码,无需阅读本节内容
+
+
+首先我们定义成员类型,我们为每个投票者定义权重、是否已投票、
+
+```javascript
+struct Voter {
+ uint weight; // weight is accumulated by delegation
+ bool voted; // if true, that person already voted
+ address delegate; // person delegated to
+ uint vote; // index of the voted proposal
+}
+```
+
+然后我们定义提案类型,包含提案名和投票总数:
+
+```javascript
+struct Proposal {
+ bytes32 name; // short name (up to 32 bytes)
+ uint voteCount; // number of accumulated votes
+}
+```
+
+定义三个变量,主席是一个公开的地址,建立投票者与地址的映射,然后定义提案动态数组:
+
+```javascript
+address public chairperson;
+mapping(address => Voter) public voters;
+Proposal[] public proposals;
+```
+
+- `address public chairperson`:投票发起人,类型为 address。
+- `mapping(address => Voter) public voters`:所有投票人,类型为 `address` 到 `Voter` 的映射。
+- `Proposal[] public proposals`:所有提案,类型为动态大小的 `Proposal` 数组。
+
+3 个状态变量都使用了 `public` 关键字,使得变量可以被外部访问(即通过消息调用)。事实上,编译器会自动为 `public `的变量创建同名的 `getter` 函数,供外部直接读取。
+
+我们还需要为每个投票赋予初始权值,并将主席的权重设置为1。我们一般使用`constructor`赋初值,这与C++等语言类似:
+
+```javascript
+constructor(bytes32[] memory proposalNames) {
+ chairperson = msg.sender;
+ voters[chairperson].weight = 1;
+
+ for (uint i = 0; i < proposalNames.length; i++) {
+ proposals.push(Proposal({
+ name: proposalNames[i],
+ voteCount: 0
+ }));
+ }
+}
+```
+
+所有提案的名称通过参数 `bytes32[] proposalNames` 传入,逐个记录到状态变量 `proposals` 中。同时用 `msg.sender` 获取当前调用消息的发送者的地址,记录为投票发起人 `chairperson`,该发起人投票权重设为 1。
+
+接下来我们需要给每个投票者赋予权重:
+
+```javascript
+function giveRightToVote(address voter) public {
+ require(
+ msg.sender == chairperson,
+ "Only chairperson can give right to vote."
+ );
+ require(
+ !voters[voter].voted,
+ "The voter already voted."
+ );
+ require(voters[voter].weight == 0);
+ voters[voter].weight = 1;
+}
+```
+
+该函数给 `address voter` 赋予投票权,即将 `voter` 的投票权重设为 1,存入 `voters` 状态变量。
+
+上面这个函数只有投票发起人 `chairperson` 可以调用。这里用到了 `require((msg.sender == chairperson) && !voters[voter].voted)` 函数。如果` require` 中表达式结果为 `false`,这次调用会中止,且回滚所有状态和以太币余额的改变到调用前。但已消耗的 `Gas` 不会返还。
+
+下面一段是整段代码的重点,其作用是委托其他人代理投票,基本思路是:
+
+1. 使用`require`判断委托人是否已投票(若投过票再委托则重复投票),并判断被委托对象是否是自己
+2. 当判断被委托人不是0地址(主席)时,被委托人代理委托人的票,【绕口警告】由于被委托人也可能委托了别人,因此这里需要一直循环直到找到最后没有委托别人的被委托人为止!
+3. 委托人找到对应的被委托人,委托人已投票(避免重复投票)
+4. 判断被委托人是否已投票,若投了票则将被委托人投的提案票数加上委托人的权重,若未投票则令被委托人的权重加上委托人的权重(以后投票自然相当于投两票)
+
+注:该函数使用了 `while` 循环,这里合约编写者需要十分谨慎,防止调用者消耗过多 `Gas`,甚至出现死循环。
+
+```javascript
+function delegate(address to) public {
+ Voter storage sender = voters[msg.sender];
+ require(!sender.voted, "You already voted.");
+ require(to != msg.sender, "Self-delegation is disallowed.");
+
+ while (voters[to].delegate != address(0)) {
+ to = voters[to].delegate;
+ require(to != msg.sender, "Found loop in delegation.");
+ }
+ sender.voted = true;
+ sender.delegate = to;
+ Voter storage delegate_ = voters[to];
+ if (delegate_.voted) {
+ proposals[delegate_.vote].voteCount += sender.weight;
+ } else {
+ delegate_.weight += sender.weight;
+ }
+}
+```
+
+投票部分仅是几个简单的条件判断:
+
+```javascript
+function vote(uint proposal) public {
+ Voter storage sender = voters[msg.sender];
+ require(sender.weight != 0, "Has no right to vote");
+ require(!sender.voted, "Already voted.");
+ sender.voted = true;
+ sender.vote = proposal;
+ proposals[proposal].voteCount += sender.weight;
+ }
+```
+
+用 `voters[msg.sender]` 获取投票人,即此次调用的发起人。接下来检查是否是重复投票,如果不是,进行投票后相关状态变量的更新。
+
+接下来是计算获胜提案:
+
+```javascript
+function winningProposal() public view
+ returns (uint winningProposal_)
+{
+ uint winningVoteCount = 0;
+ for (uint p = 0; p < proposals.length; p++) {
+ if (proposals[p].voteCount > winningVoteCount) {
+ winningVoteCount = proposals[p].voteCount;
+ winningProposal_ = p;
+ }
+ }
+}
+```
+
+`returns (uint winningProposal)` 指定了函数的返回值类型,`constant` 表示该函数不会改变合约状态变量的值。
+
+最后是查询获胜者名称:
+
+```javascript
+function winnerName() public view
+ returns (bytes32 winnerName_)
+{
+ winnerName_ = proposals[winningProposal()].name;
+}
+```
+
+这里采用内部调用 `winningProposal()` 函数的方式获得获胜提案。如果需要采用外部调用,则需要写为 `this.winningProposal()`。
+
+
+
+**参考自:**
+
+[尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
+[web3.js 1.0中文手册](http://cw.hubwiz.com/card/c/web3.js-1.0/)
+
diff --git a/Blockchain/pic/2021-02-19_110327.png b/Blockchain/pic/2021-02-19_110327.png
new file mode 100644
index 0000000..7b03f57
Binary files /dev/null and b/Blockchain/pic/2021-02-19_110327.png differ
diff --git a/Blockchain/pic/2021-02-19_120756.png b/Blockchain/pic/2021-02-19_120756.png
new file mode 100644
index 0000000..f3e64de
Binary files /dev/null and b/Blockchain/pic/2021-02-19_120756.png differ
diff --git a/Blockchain/pic/2021-02-19_125917.png b/Blockchain/pic/2021-02-19_125917.png
new file mode 100644
index 0000000..2d77359
Binary files /dev/null and b/Blockchain/pic/2021-02-19_125917.png differ
diff --git a/Blockchain/pic/2021-02-19_130053.png b/Blockchain/pic/2021-02-19_130053.png
new file mode 100644
index 0000000..35b98d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_130053.png differ
diff --git a/Blockchain/pic/2021-02-19_133508.png b/Blockchain/pic/2021-02-19_133508.png
new file mode 100644
index 0000000..78c5567
Binary files /dev/null and b/Blockchain/pic/2021-02-19_133508.png differ
diff --git a/Blockchain/pic/2021-02-19_134110.png b/Blockchain/pic/2021-02-19_134110.png
new file mode 100644
index 0000000..c7e7ba5
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134110.png differ
diff --git a/Blockchain/pic/2021-02-19_134257.png b/Blockchain/pic/2021-02-19_134257.png
new file mode 100644
index 0000000..75d426b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134257.png differ
diff --git a/Blockchain/pic/2021-02-19_134634.png b/Blockchain/pic/2021-02-19_134634.png
new file mode 100644
index 0000000..eb63545
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134634.png differ
diff --git a/Blockchain/pic/2021-02-19_135113.png b/Blockchain/pic/2021-02-19_135113.png
new file mode 100644
index 0000000..a8f69cc
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135113.png differ
diff --git a/Blockchain/pic/2021-02-19_135337.png b/Blockchain/pic/2021-02-19_135337.png
new file mode 100644
index 0000000..1b3998b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135337.png differ
diff --git a/Blockchain/pic/2021-02-19_135413.png b/Blockchain/pic/2021-02-19_135413.png
new file mode 100644
index 0000000..b24c373
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135413.png differ
diff --git a/Blockchain/pic/2021-02-19_142407.png b/Blockchain/pic/2021-02-19_142407.png
new file mode 100644
index 0000000..10704d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_142407.png differ
diff --git a/Blockchain/pic/EOA_CA.png b/Blockchain/pic/EOA_CA.png
new file mode 100644
index 0000000..9612e9b
Binary files /dev/null and b/Blockchain/pic/EOA_CA.png differ
diff --git a/Blockchain/pic/aaaaaa b/Blockchain/pic/aaaaaa
new file mode 100644
index 0000000..8b13789
--- /dev/null
+++ b/Blockchain/pic/aaaaaa
@@ -0,0 +1 @@
+
diff --git a/Blockchain/pic/bg2017122703.png b/Blockchain/pic/bg2017122703.png
new file mode 100644
index 0000000..5c91bc5
Binary files /dev/null and b/Blockchain/pic/bg2017122703.png differ
diff --git a/Blockchain/pic/gas.jpg b/Blockchain/pic/gas.jpg
new file mode 100644
index 0000000..13bd71c
Binary files /dev/null and b/Blockchain/pic/gas.jpg differ
diff --git a/Blockchain/pic/image-20210219000835894.png b/Blockchain/pic/image-20210219000835894.png
new file mode 100644
index 0000000..5fea35e
Binary files /dev/null and b/Blockchain/pic/image-20210219000835894.png differ
diff --git a/Blockchain/pic/image-20210219101124978.png b/Blockchain/pic/image-20210219101124978.png
new file mode 100644
index 0000000..28411df
Binary files /dev/null and b/Blockchain/pic/image-20210219101124978.png differ
diff --git a/Blockchain/pic/image-20210219101226095.png b/Blockchain/pic/image-20210219101226095.png
new file mode 100644
index 0000000..8ddead4
Binary files /dev/null and b/Blockchain/pic/image-20210219101226095.png differ
diff --git a/Blockchain/pic/image-20210219101300792.png b/Blockchain/pic/image-20210219101300792.png
new file mode 100644
index 0000000..2dcad74
Binary files /dev/null and b/Blockchain/pic/image-20210219101300792.png differ
diff --git a/Blockchain/pic/image-20210219101332089.png b/Blockchain/pic/image-20210219101332089.png
new file mode 100644
index 0000000..e74b090
Binary files /dev/null and b/Blockchain/pic/image-20210219101332089.png differ
diff --git a/Blockchain/pic/image-20210219102028033.png b/Blockchain/pic/image-20210219102028033.png
new file mode 100644
index 0000000..966feb4
Binary files /dev/null and b/Blockchain/pic/image-20210219102028033.png differ
diff --git a/Blockchain/pic/image-20210219102255927.png b/Blockchain/pic/image-20210219102255927.png
new file mode 100644
index 0000000..8acef84
Binary files /dev/null and b/Blockchain/pic/image-20210219102255927.png differ
diff --git a/Blockchain/pic/image-20210219102322360.png b/Blockchain/pic/image-20210219102322360.png
new file mode 100644
index 0000000..513c9de
Binary files /dev/null and b/Blockchain/pic/image-20210219102322360.png differ
diff --git a/Blockchain/pic/image-20210219102359096.png b/Blockchain/pic/image-20210219102359096.png
new file mode 100644
index 0000000..aa9a394
Binary files /dev/null and b/Blockchain/pic/image-20210219102359096.png differ
diff --git a/Blockchain/pic/image-20210219105522149.png b/Blockchain/pic/image-20210219105522149.png
new file mode 100644
index 0000000..f3e6648
Binary files /dev/null and b/Blockchain/pic/image-20210219105522149.png differ
diff --git a/Blockchain/pic/image-20210219105616335.png b/Blockchain/pic/image-20210219105616335.png
new file mode 100644
index 0000000..a23c2dd
Binary files /dev/null and b/Blockchain/pic/image-20210219105616335.png differ
diff --git a/Blockchain/pic/image-20210219105824087.png b/Blockchain/pic/image-20210219105824087.png
new file mode 100644
index 0000000..c03a2b4
Binary files /dev/null and b/Blockchain/pic/image-20210219105824087.png differ
diff --git a/Blockchain/pic/image-20210219105911910.png b/Blockchain/pic/image-20210219105911910.png
new file mode 100644
index 0000000..eff8c5c
Binary files /dev/null and b/Blockchain/pic/image-20210219105911910.png differ
diff --git a/Blockchain/pic/image1.png b/Blockchain/pic/image1.png
new file mode 100644
index 0000000..8435a7e
Binary files /dev/null and b/Blockchain/pic/image1.png differ
diff --git a/Blockchain/pic/image2.png b/Blockchain/pic/image2.png
new file mode 100644
index 0000000..5688b8c
Binary files /dev/null and b/Blockchain/pic/image2.png differ
diff --git a/Blockchain/pic/image3.png b/Blockchain/pic/image3.png
new file mode 100644
index 0000000..c3bfdca
Binary files /dev/null and b/Blockchain/pic/image3.png differ
diff --git a/Blockchain/pic/image4.png b/Blockchain/pic/image4.png
new file mode 100644
index 0000000..3ce8d94
Binary files /dev/null and b/Blockchain/pic/image4.png differ
diff --git a/Blockchain/pic/image5.png b/Blockchain/pic/image5.png
new file mode 100644
index 0000000..3038f58
Binary files /dev/null and b/Blockchain/pic/image5.png differ
diff --git a/Blockchain/pic/image6.png b/Blockchain/pic/image6.png
new file mode 100644
index 0000000..82f5ecc
Binary files /dev/null and b/Blockchain/pic/image6.png differ
diff --git a/Blockchain/pic/part2-1.png b/Blockchain/pic/part2-1.png
new file mode 100644
index 0000000..8c0da19
Binary files /dev/null and b/Blockchain/pic/part2-1.png differ
diff --git a/Blockchain/pic/part2-10.png b/Blockchain/pic/part2-10.png
new file mode 100644
index 0000000..f0b447e
Binary files /dev/null and b/Blockchain/pic/part2-10.png differ
diff --git a/Blockchain/pic/part2-11.png b/Blockchain/pic/part2-11.png
new file mode 100644
index 0000000..06cca10
Binary files /dev/null and b/Blockchain/pic/part2-11.png differ
diff --git a/Blockchain/pic/part2-12.png b/Blockchain/pic/part2-12.png
new file mode 100644
index 0000000..5eb5b8e
Binary files /dev/null and b/Blockchain/pic/part2-12.png differ
diff --git a/Blockchain/pic/part2-13.png b/Blockchain/pic/part2-13.png
new file mode 100644
index 0000000..e9433fa
Binary files /dev/null and b/Blockchain/pic/part2-13.png differ
diff --git a/Blockchain/pic/part2-14.png b/Blockchain/pic/part2-14.png
new file mode 100644
index 0000000..f87ff72
Binary files /dev/null and b/Blockchain/pic/part2-14.png differ
diff --git a/Blockchain/pic/part2-15.png b/Blockchain/pic/part2-15.png
new file mode 100644
index 0000000..abebc5d
Binary files /dev/null and b/Blockchain/pic/part2-15.png differ
diff --git a/Blockchain/pic/part2-16.png b/Blockchain/pic/part2-16.png
new file mode 100644
index 0000000..7a91692
Binary files /dev/null and b/Blockchain/pic/part2-16.png differ
diff --git a/Blockchain/pic/part2-17.png b/Blockchain/pic/part2-17.png
new file mode 100644
index 0000000..d831f99
Binary files /dev/null and b/Blockchain/pic/part2-17.png differ
diff --git a/Blockchain/pic/part2-18.png b/Blockchain/pic/part2-18.png
new file mode 100644
index 0000000..c42e156
Binary files /dev/null and b/Blockchain/pic/part2-18.png differ
diff --git a/Blockchain/pic/part2-19.png b/Blockchain/pic/part2-19.png
new file mode 100644
index 0000000..cf84b29
Binary files /dev/null and b/Blockchain/pic/part2-19.png differ
diff --git a/Blockchain/pic/part2-2.png b/Blockchain/pic/part2-2.png
new file mode 100644
index 0000000..a8ecb2c
Binary files /dev/null and b/Blockchain/pic/part2-2.png differ
diff --git a/Blockchain/pic/part2-20.png b/Blockchain/pic/part2-20.png
new file mode 100644
index 0000000..cf3cb04
Binary files /dev/null and b/Blockchain/pic/part2-20.png differ
diff --git a/Blockchain/pic/part2-21.png b/Blockchain/pic/part2-21.png
new file mode 100644
index 0000000..84896de
Binary files /dev/null and b/Blockchain/pic/part2-21.png differ
diff --git a/Blockchain/pic/part2-22.png b/Blockchain/pic/part2-22.png
new file mode 100644
index 0000000..db238cf
Binary files /dev/null and b/Blockchain/pic/part2-22.png differ
diff --git a/Blockchain/pic/part2-23.png b/Blockchain/pic/part2-23.png
new file mode 100644
index 0000000..256124b
Binary files /dev/null and b/Blockchain/pic/part2-23.png differ
diff --git a/Blockchain/pic/part2-24.png b/Blockchain/pic/part2-24.png
new file mode 100644
index 0000000..6007692
Binary files /dev/null and b/Blockchain/pic/part2-24.png differ
diff --git a/Blockchain/pic/part2-3.png b/Blockchain/pic/part2-3.png
new file mode 100644
index 0000000..1ff0dda
Binary files /dev/null and b/Blockchain/pic/part2-3.png differ
diff --git a/Blockchain/pic/part2-4.png b/Blockchain/pic/part2-4.png
new file mode 100644
index 0000000..8879b10
Binary files /dev/null and b/Blockchain/pic/part2-4.png differ
diff --git a/Blockchain/pic/part2-5.png b/Blockchain/pic/part2-5.png
new file mode 100644
index 0000000..6308a3d
Binary files /dev/null and b/Blockchain/pic/part2-5.png differ
diff --git a/Blockchain/pic/part2-6.png b/Blockchain/pic/part2-6.png
new file mode 100644
index 0000000..debad8c
Binary files /dev/null and b/Blockchain/pic/part2-6.png differ
diff --git a/Blockchain/pic/part2-7.png b/Blockchain/pic/part2-7.png
new file mode 100644
index 0000000..f9a3ea0
Binary files /dev/null and b/Blockchain/pic/part2-7.png differ
diff --git a/Blockchain/pic/part2-8.png b/Blockchain/pic/part2-8.png
new file mode 100644
index 0000000..ed642a5
Binary files /dev/null and b/Blockchain/pic/part2-8.png differ
diff --git a/Blockchain/pic/part2-9.png b/Blockchain/pic/part2-9.png
new file mode 100644
index 0000000..8c1e817
Binary files /dev/null and b/Blockchain/pic/part2-9.png differ
diff --git a/Blockchain/pic/part3-1.png b/Blockchain/pic/part3-1.png
new file mode 100644
index 0000000..094515c
Binary files /dev/null and b/Blockchain/pic/part3-1.png differ
diff --git a/Blockchain/pic/part3-10.png b/Blockchain/pic/part3-10.png
new file mode 100644
index 0000000..1c2c0c6
Binary files /dev/null and b/Blockchain/pic/part3-10.png differ
diff --git a/Blockchain/pic/part3-11.png b/Blockchain/pic/part3-11.png
new file mode 100644
index 0000000..d6f6474
Binary files /dev/null and b/Blockchain/pic/part3-11.png differ
diff --git a/Blockchain/pic/part3-12.png b/Blockchain/pic/part3-12.png
new file mode 100644
index 0000000..30c4582
Binary files /dev/null and b/Blockchain/pic/part3-12.png differ
diff --git a/Blockchain/pic/part3-13.png b/Blockchain/pic/part3-13.png
new file mode 100644
index 0000000..a1f9783
Binary files /dev/null and b/Blockchain/pic/part3-13.png differ
diff --git a/Blockchain/pic/part3-2.png b/Blockchain/pic/part3-2.png
new file mode 100644
index 0000000..2d74cd1
Binary files /dev/null and b/Blockchain/pic/part3-2.png differ
diff --git a/Blockchain/pic/part3-3.png b/Blockchain/pic/part3-3.png
new file mode 100644
index 0000000..824fd9b
Binary files /dev/null and b/Blockchain/pic/part3-3.png differ
diff --git a/Blockchain/pic/part3-4.png b/Blockchain/pic/part3-4.png
new file mode 100644
index 0000000..152a017
Binary files /dev/null and b/Blockchain/pic/part3-4.png differ
diff --git a/Blockchain/pic/part3-5.png b/Blockchain/pic/part3-5.png
new file mode 100644
index 0000000..9b62fe6
Binary files /dev/null and b/Blockchain/pic/part3-5.png differ
diff --git a/Blockchain/pic/part3-6.png b/Blockchain/pic/part3-6.png
new file mode 100644
index 0000000..00e7473
Binary files /dev/null and b/Blockchain/pic/part3-6.png differ
diff --git a/Blockchain/pic/part3-7.png b/Blockchain/pic/part3-7.png
new file mode 100644
index 0000000..f6dfe7a
Binary files /dev/null and b/Blockchain/pic/part3-7.png differ
diff --git a/Blockchain/pic/part3-8.png b/Blockchain/pic/part3-8.png
new file mode 100644
index 0000000..212eb36
Binary files /dev/null and b/Blockchain/pic/part3-8.png differ
diff --git a/Blockchain/pic/part3-9.png b/Blockchain/pic/part3-9.png
new file mode 100644
index 0000000..567481f
Binary files /dev/null and b/Blockchain/pic/part3-9.png differ
diff --git a/Blockchain/pic/picfile b/Blockchain/pic/picfile
new file mode 100644
index 0000000..ca8de66
--- /dev/null
+++ b/Blockchain/pic/picfile
@@ -0,0 +1 @@
+This folder contains some necessary picture
diff --git a/Blockchain/pic/rating.png b/Blockchain/pic/rating.png
new file mode 100644
index 0000000..204d972
Binary files /dev/null and b/Blockchain/pic/rating.png differ
diff --git a/Blockchain/pic/transaction-struct.png b/Blockchain/pic/transaction-struct.png
new file mode 100644
index 0000000..da26c42
Binary files /dev/null and b/Blockchain/pic/transaction-struct.png differ
diff --git a/Blockchain/pic/utxo_com.jpg b/Blockchain/pic/utxo_com.jpg
new file mode 100644
index 0000000..77c03d0
Binary files /dev/null and b/Blockchain/pic/utxo_com.jpg differ
diff --git a/Blockchain/readme.md b/Blockchain/readme.md
new file mode 100644
index 0000000..6fb3759
--- /dev/null
+++ b/Blockchain/readme.md
@@ -0,0 +1,46 @@
+# 1. 编程实践(区块链)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/Blockchain
+
+## 基本信息
+
+- 贡献人员:陈锴、孙子涵、李岳昆、易远哲
+- 学习周期:12天
+- 学习形式:根据教程主线进行学习
+- 人群定位:具有至少一门编程语言基础,在开展组队学习之前能够熟悉 Linux 基本操作
+- 难度系数:较难
+
+## 学习目标
+
+## 任务安排
+
+### Task00:熟悉规则并先修Linux(2天)
+
+- 组队、修改群昵称
+- 熟悉打卡规则
+- 对Linux不太熟悉的学习者先安装Linux环境(可以是虚拟机或子系统)并掌握基本命令,其他内容可以暂不了解
+
+### Task01:区块链简介与以太坊入门介绍(2天)
+
+* 学习者学习区块链基础与以太坊入门介绍,该部分以了解为主
+* 学习者可以根据教程提供的各个方面内容,对某一部分深入了解并进行打卡
+* 打卡截至时间:3月16日24:00
+
+### Task02:Solidity基础(3天)
+
+* 学习者学习Solidity在线编辑器Remix的使用以及Solidity的基础操作,该部分需要深入掌握,学习者可以根据参考链接提供的资料进一步学习
+* 打卡内容为Task02最后的Solidity练习题部分,其他内容不作硬性要求
+* 打卡截止日期:3月19日24:00
+
+### Task03:web3js基础(3天)
+
+* 学习者学习以太坊客户端的使用以及Geth控制台部署智能合约
+* 打卡内容为学习者完成一个自己编写的合约的部署,并测试函数调用等
+* 打卡截止日期:3月22日24:00
+
+### Task04:合约编写实战实例(2天)
+
+* 学习者学习编写几个Remix官网自带的合约,并回顾 Task01的教程内容重新梳理知识点
+* 打卡内容为学习者自己的学习感悟,内容不限
+* 打卡截止日期:3月23日24:00
+
diff --git a/Docker/00 开篇词.md b/Docker/00 开篇词.md
new file mode 100644
index 0000000..df37501
--- /dev/null
+++ b/Docker/00 开篇词.md
@@ -0,0 +1,24 @@
+# Chapter 0 开篇词
+
+相信大家在开发项目尤其是团队合作项目中一定会遇到下面这些场景:
+
+- 项目在我电脑上明明运行的很好呀!怎么在你这不行了呢?
+- 我这是用python 3.6写的,你电脑是python 2.7应该运行不了。
+- 项目的一些依赖包需要科学上网才能下载,你那没有的话赶紧下载一下才能运行。
+- 论文的代码已经公开到github上了,但是因为自己电脑环境和他的不一样,项目在自己电脑上死活跑不起来。
+
+以上这些问题我相信大家并不陌生,那么通过本次Docker的组队学习,希望大家能够避免卡在科研或者开发的第一步,提高自己的生产力。
+
+---
+
+通过本次docker的组队学习,我们希望你能学到以下几个方面的能力:
+
+- 了解什么是docker
+- docker镜像是怎么构建的
+- 如何运行一个docker容器
+- docker之间的网络通信是怎么样的
+- docker中的数据如何做持久化存储
+- 如何通过docker compose管理自己的项目
+- 如何将自己的个人项目打造成容器化部署的形式
+
+祝你在docker的学习上一切顺利!
\ No newline at end of file
diff --git a/Docker/04 Docker数据管理.md b/Docker/04 Docker数据管理.md
new file mode 100644
index 0000000..4283a12
--- /dev/null
+++ b/Docker/04 Docker数据管理.md
@@ -0,0 +1,176 @@
+# Chapter 4 Docker 数据管理
+
+这一章介绍如何在 Docker 内部以及容器之间管理数据,在容器中管理数据主要有两种方式:
+
+* 数据卷
+* 挂载主机目录
+
+
+## 数据卷
+
+数据卷是一个可供一个或多个容器使用的特殊目录,它绕过 UFS (UNIX File System) ,可以提供很多有用的特性:
+
+* 数据卷可以在容器之间共享和重用
+
+* 对数据卷的修改会立马生效
+
+* 对数据卷的更新,不会影响镜像
+
+* 数据卷默认会一直存在,即使容器被删除
+
+>注意:数据卷的使用,类似于 Linux 下对目录或文件进行 mount,镜像中的被指定为挂载点的目录中的文件会复制到数据卷中(仅数据卷为空时会复制)。
+
+### 创建一个数据卷
+
+```bash
+$ docker volume create datawhale
+```
+
+查看所有的数据卷
+
+```bash
+$ docker volume ls
+
+DRIVER VOLUME NAME
+local datawhale
+```
+
+在主机里使用以下命令可以查看指定数据卷的信息
+
+```bash
+$ docker volume inspect datawhale
+[
+ {
+ "Driver": "local",
+ "Labels": {},
+ "Mountpoint": "/var/lib/docker/volumes/datawhale/_data",
+ "Name": "datawhale",
+ "Options": {},
+ "Scope": "local"
+ }
+]
+```
+
+### 启动一个挂载数据卷的容器
+
+在用 `docker run` 命令的时候,使用 `--mount` 标记来将数据卷挂载到容器里。在一次 `docker run` 中可以挂载多个 `数据卷`。
+
+下面创建一个名为 `web` 的容器,并加载一个数据卷到容器的 `/usr/share/nginx/html` 目录。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount source=datawhale,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+>–-mount参数说明:
+> source :数据卷
+> target :是容器内文件系统挂载点
+
+>注意,可以不需要提前创建好数据卷,直接在运行容器的时候mount 这时如果不存在指定的数据卷,docker会自动创建,自动生成。
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`数据卷` 信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "volume",
+ "Name": "datawhale",
+ "Source": "/var/lib/docker/volumes/datawhale/_data",
+ "Destination": "/usr/share/nginx/html",
+ "Driver": "local",
+ "Mode": "",
+ "RW": true,
+ "Propagation": ""
+ }
+],
+```
+
+### 删除数据卷
+
+```bash
+$ docker volume rm datawhale #datawhale为卷名
+```
+
+数据卷是被设计用来持久化数据的,它的生命周期独立于容器,Docker 不会在容器被删除后自动删除 `数据卷`,并且也不存在垃圾回收这样的机制来处理没有任何容器引用的 `数据卷`。如果需要在删除容器的同时移除数据卷。可以在删除容器的时候使用 `docker rm -v` 这个命令。
+
+无主的数据卷可能会占据很多空间,要清理请使用以下命令
+
+```bash
+$ docker volume prune
+```
+
+## 挂载主机目录
+
+### 挂载一个主机目录作为数据卷
+
+使用 `--mount` 标记可以指定挂载一个本地主机的目录到容器中去。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+
+上面的命令加载主机的 `/src/webapp` 目录到容器的 `/usr/share/nginx/html`目录。这个功能在进行测试的时候十分方便,比如用户可以放置一些程序到本地目录中,来查看容器是否正常工作。本地目录的路径必须是绝对路径,以前使用 `-v` 参数时如果本地目录不存在 Docker 会自动为你创建一个文件夹,现在使用 `--mount` 参数时如果本地目录不存在,Docker 会报错。
+
+Docker 挂载主机目录的默认权限是 `读写`,用户也可以通过增加 `readonly` 指定为 `只读`。
+
+>注意: 如果挂载的目录不存在,创建容器时,docker 不会自动创建,此时会报错
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html,readonly \
+ nginx:alpine
+```
+
+加了 `readonly` 之后,就挂载为 `只读` 了。如果你在容器内 `/usr/share/nginx/html` 目录新建文件,会显示如下错误
+
+```bash
+/usr/share/nginx/html # touch new.txt
+touch: new.txt: Read-only file system
+```
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`挂载主机目录` 的配置信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "bind",
+ "Source": "/src/webapp",
+ "Destination": "/usr/share/nginx/html",
+ "Mode": "",
+ "RW": true,
+ "Propagation": "rprivate"
+ }
+],
+```
+
+### 挂载一个本地主机文件作为数据卷
+
+`--mount` 标记也可以从主机挂载单个文件到容器中
+
+```bash
+$ docker run --rm -it \
+ --mount type=bind,source=$HOME/.bash_history,target=/root/.bash_history \
+ ubuntu:18.04 \
+ bash
+```
diff --git a/Docker/05 Docker网络.md b/Docker/05 Docker网络.md
new file mode 100644
index 0000000..5747442
--- /dev/null
+++ b/Docker/05 Docker网络.md
@@ -0,0 +1,783 @@
+# Chapter 5 Docker 网络
+
+## 内容大纲
+
+### Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+### Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+### Docker高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+
+
+# Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+## 外部访问容器
+
+容器中可以运行一些网络应用,要让外部也可以访问这些应用,可以通过`-P`或`-p`参数来指定端口映射。
+
+当使用`-P`标记时,`Docker`会随机映射一个端口到内部容器开放的网络端口。
+使用`docker container ls`可以看到,本地主机的 32768 被映射到了容器的 80 端口。此时访问本机的 32768 端口即可访问容器内 NGINX 默认页面。
+
+```
+$ docker run -d -P nginx:alpine
+
+$ docker container ls -l
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+fae320d08268 nginx:alpine "/docker-entrypoint.…" 24 seconds ago Up 20 seconds 0.0.0.0:32768->80/tcp bold_mcnulty
+```
+
+同样的,可以通过`docker logs`命令来查看访问记录。
+
+```
+$ docker logs fa
+172.17.0.1 - - [25/Aug/2020:08:34:04 +0000] "GET / HTTP/1.1" 200 612 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:80.0) Gecko/20100101 Firefox/80.0" "-"
+```
+
+`-p`则可以指定要映射的端口,并且,在一个指定端口上只可以绑定一个容器。支持的格式有`ip:hostPort:containerPort | ip::containerPort | hostPort:containerPort`.
+
+### 映射所有接口地址
+
+使用`hostPort:containerPort`格式本地的 80 端口映射到容器的 80 端口,可以执行
+
+```
+$ docker run -d -p 80:80 nginx:alpine
+```
+
+此时默认会绑定本地所有接口上的所有地址。
+
+### 映射到指定地址的指定端口
+
+可以使用`ip:hostPort:containerPort`格式指定映射使用一个特定地址,比如`localhost`地址127.0.0.1
+
+```
+$ docker run -d -p 127.0.0.1:80:80 nginx:alpine
+```
+
+### 映射到指定地址的任意端口
+
+使用`ip::containerPort`绑定`localhost`的任意端口到容器的80端口,本地主机会自动分配一个端口。
+
+```
+$ docker run -d -p 127.0.0.1::80 nginx:alpine
+```
+
+还可以使用`udp`标记来指定`udp`端口
+
+```
+$ docker run -d -p 127.0.0.1:80:80/udp nginx:alpine
+```
+
+### 查看映射端口配置
+
+使用`docker port`来查看当前映射的端口配置,也可以查看到绑定的地址
+
+```
+$ docker port fa 80
+0.0.0.0:32768
+```
+
+**注意:**
+容器有自己的内部网络和 ip 地址(使用`docker inspect`查看,`Docker`还可以有一个可变的网络配置。)
+`-p`标记可以多次使用来绑定多个端口
+
+例如
+
+```
+$ docker run -d \
+ -p 80:80 \
+ -p 443:443 \
+ nginx:alpine
+```
+
+## 容器互联
+
+如果之前有 `Docker`使用经验,可能已经习惯了使用`--link`参数来使容器互联。
+随着 `Docker` 网络的完善,强烈建议大家将容器加入自定义的`Docker`网络来连接多个容器,而不是使用 `--link`参数。
+
+### 新建网络
+
+下面先创建一个新的 `Docker`网络。
+
+```
+$ docker network create -d bridge my-net
+```
+
+`-d`参数指定`Docker`网络类型,有`bridge overlay`,其中`overlay`网络类型用于`Swarm mode`,在本小节中你可以忽略它。
+
+### 连接容器
+
+运行一个容器并连接到新建的`my-net`网络
+
+```
+$ docker run -it --rm --name busybox1 --network my-net busybox sh
+```
+
+打开新的终端,再运行一个容器并加入到 `my-net`网络
+
+```
+$ docker run -it --rm --name busybox2 --network my-net busybox sh
+```
+
+再打开一个新的终端查看容器信息
+
+```
+$ docker container ls
+
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+b47060aca56b busybox "sh" 11 minutes ago Up 11 minutes busybox2
+8720575823ec busybox "sh" 16 minutes ago Up 16 minutes busybox1
+```
+
+下面通过 `ping`来证明`busybox1`容器和`busybox2`容器建立了互联关系。
+在`busybox1`容器输入以下命令
+
+```
+/ # ping busybox2
+PING busybox2 (172.19.0.3): 56 data bytes
+64 bytes from 172.19.0.3: seq=0 ttl=64 time=0.072 ms
+64 bytes from 172.19.0.3: seq=1 ttl=64 time=0.118 ms
+```
+
+用`ping`来测试连接`busybox2`容器,它会解析成 172.19.0.3。
+同理在`busybox2`容器执行`ping busybox1`,也会成功连接到。
+
+```
+/ # ping busybox1
+PING busybox1 (172.19.0.2): 56 data bytes
+64 bytes from 172.19.0.2: seq=0 ttl=64 time=0.064 ms
+64 bytes from 172.19.0.2: seq=1 ttl=64 time=0.143 ms
+```
+
+这样,`busybox1` 容器和 `busybox2` 容器建立了互联关系。
+
+`Docker Compose`
+如果你有多个容器之间需要互相连接,推荐使用`Docker`Compose。
+
+## 配置DNS
+
+如何自定义配置容器的主机名和 DNS 呢?秘诀就是`Docker`利用虚拟文件来挂载容器的 3个相关配置文件。
+
+在容器中使用 `mount`命令可以看到挂载信息:
+
+```
+$ mount
+/dev/disk/by-uuid/1fec...ebdf on /etc/hostname type ext4 ...
+/dev/disk/by-uuid/1fec...ebdf on /etc/hosts type ext4 ...
+tmpfs on /etc/resolv.conf type tmpfs ...
+```
+
+这种机制可以让宿主主机 DNS 信息发生更新后,所有`Docker`容器的 DNS 配置通过 `/etc/resolv.conf`文件立刻得到更新。
+
+配置全部容器的 DNS ,也可以在 `/etc/docker/daemon.json` 文件中增加以下内容来设置。
+
+```
+{
+ "dns" : [
+ "114.114.114.114",
+ "8.8.8.8"
+ ]
+}
+```
+
+这样每次启动的容器 DNS 自动配置为 114.114.114.114 和8.8.8.8。使用以下命令来证明其已经生效。
+
+```
+$ docker run -it --rm ubuntu:18.04 cat etc/resolv.conf
+
+nameserver 114.114.114.114
+nameserver 8.8.8.8
+```
+
+如果用户想要手动指定容器的配置,可以在使用`docker run`命令启动容器时加入如下参数:
+`-h HOSTNAME`或者`--hostname=HOSTNAME`设定容器的主机名,它会被写到容器内的`/etc/hostname 和 /etc/hosts`。但它在容器外部看不到,既不会在`docker container ls`中显示,也不会在其他的容器的`/etc/hosts`看到。
+
+`--dns=IP_ADDRESS`添加 DNS 服务器到容器的`/etc/resolv.conf`中,让容器用这个服务器来解析所有不在 `/etc/hosts `中的主机名。
+
+`--dns-search=DOMAIN`设定容器的搜索域,当设定搜索域为`.example.com`时,在搜索一个名为`host`的主机时,DNS 不仅搜索 `host`,还会搜索`host.example.com`。
+
+**注意:**如果在容器启动时没有指定最后两个参数,`Docker`会默认用主机上的`/etc/resolv.conf`来配置容器。
+
+# Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+可以通过`docker network ls`查看网络,默认创建三种网络。
+
+```
+[root@localhost ~]# docker network ls
+NETWORK ID NAME DRIVER SCOPE
+688d1970f72e bridge bridge local
+885da101da7d host host local
+f4f1b3cf1b7f none null local
+```
+
+常见网络的含义:
+
+| 网络模式 | 简介 |
+| :-------: | :----------------------------------------------------------: |
+| Bridge | 为每一个容器分配、设置 IP 等,并将容器连接到一个 `docker0` 虚拟网桥,默认为该模式。 |
+| Host | 容器将不会虚拟出自己的网卡,配置自己的 IP 等,而是使用宿主机的 IP 和端口。 |
+| None | 容器有独立的 Network namespace,但并没有对其进行任何网络设置,如分配 veth pair 和网桥连接,IP 等。 |
+| Container | 新创建的容器不会创建自己的网卡和配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等。 |
+
+## Bridge模式
+
+当`Docker`进程启动时,会在主机上创建一个名为`docker0`的虚拟网桥,此主机上启动的`Docker`容器会连接到这个虚拟网桥上,附加在其上的任何网卡之间都能自动转发数据包。虚拟网桥的工作方式和物理交换机类似,这样主机上的所有容器就通过交换机连在了一个二层网络中。从`docker0`子网中分配一个 IP 给容器使用,并设置 `docker0 `的 IP 地址为容器的默认网关。在主机上创建一对虚拟网卡`veth pair`设备,`Docker `将 `veth pair` 设备的一端放在新创建的容器中,并命名为`eth0`(容器的网卡),另一端放在主机中,以`vethxxx`这样类似的名字命名,并将这个网络设备加入到 `docker0` 网桥中。可以通过`brctl show`命令查看。
+
+比如运行一个基于 `busybox` 镜像构建的容器 `bbox01`,查看 `ip addr`:
+
+> busybox 被称为嵌入式 Linux 的瑞士军刀,整合了很多小的 unix 下的通用功能到一个小的可执行文件中。
+
+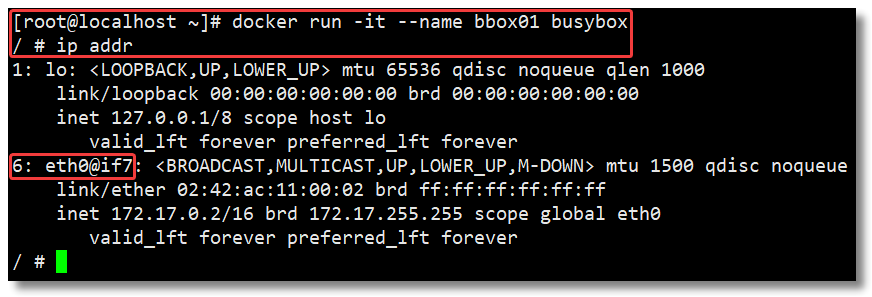
+
+然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 通过以上的比较可以发现,证实了之前所说的:守护进程会创建一对对等虚拟设备接口 `veth pair`,将其中一个接口设置为容器的 `eth0` 接口(容器的网卡),另一个接口放置在宿主机的命名空间中,以类似 `vethxxx` 这样的名字命名。
+
+ 同时,守护进程还会从网桥 `docker0` 的私有地址空间中分配一个 IP 地址和子网给该容器,并设置 docker0 的 IP 地址为容器的默认网关。也可以安装 `yum install -y bridge-utils` 以后,通过 `brctl show` 命令查看网桥信息。
+
+
+
+ 对于每个容器的 IP 地址和 Gateway 信息,可以通过 `docker inspect 容器名称|ID` 进行查看,在 `NetworkSettings` 节点中可以看到详细信息。
+
+
+
+ 可以通过 `docker network inspect bridge` 查看所有 `bridge` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+> 关于 `bridge` 网络模式的使用,只需要在创建容器时通过参数 `--net bridge` 或者 `--network bridge` 指定即可,当然这也是创建容器默认使用的网络模式,也就是说这个参数是可以省略的。
+
+
+
+
+
+bridge模式是 `docker `的默认网络模式,不写`–net`参数,就是bridge模式。使用`docker run -p`时,`docker `实际是在`iptables`做了`DNAT`规则,实现端口转发功能。可以使用`iptables -t nat -vnL`查看。`bridge`模式如下图所示:
+
+ 演示:
+
+ ```
+$ docker run -tid --net=bridge --name docker_bri1 \
+ ubuntu-base:v3
+ docker run -tid --net=bridge --name docker_bri2 \
+ ubuntu-base:v3
+
+$ brctl show
+$ docker exec -ti docker_bri1 /bin/bash
+$ ifconfig –a
+$ route –n
+ ```
+
+
+
+## Host 模式
+
+- host 网络模式需要在创建容器时通过参数 `--net host` 或者 `--network host` 指定;
+- 采用 host 网络模式的 Docker Container,可以直接使用宿主机的 IP 地址与外界进行通信,若宿主机的 eth0 是一个公有 IP,那么容器也拥有这个公有 IP。同时容器内服务的端口也可以使用宿主机的端口,无需额外进行 NAT 转换;
+- host 网络模式可以让容器共享宿主机网络栈,这样的好处是外部主机与容器直接通信,但是容器的网络缺少隔离性。
+
+
+
+
+
+ 比如基于 `host` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox02`,查看 `ip addr`:
+
+
+
+ 然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 对,你没有看错,返回信息一模一样,也可以肯定没有截错图,不信接着往下看。可以通过 `docker network inspect host` 查看所有 `host` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+如果启动容器的时候使用`host`模式,那么这个容器将不会获得一个独立的`Network Namespace`,而是和宿主机共用一个`Network Namespace`。容器将不会虚拟出自己的网卡,配置自己的`IP`等,而是使用宿主机的`IP`和端口。但是,容器的其他方面,如文件系统、进程列表等还是和宿主机隔离的。 `Host`模式如下图所示:
+
+演示:
+
+```
+$ docker run -tid --net=host --name docker_host1 ubuntu-base:v3
+$ docker run -tid --net=host --name docker_host2 ubuntu-base:v3
+
+$ docker exec -ti docker_host1 /bin/bash
+$ docker exec -ti docker_host1 /bin/bash
+
+$ ifconfig –a
+$ route –n
+```
+
+## None模式
+
+- none 网络模式是指禁用网络功能,只有 lo 接口 local 的简写,代表 127.0.0.1,即 localhost 本地环回接口。在创建容器时通过参数 `--net none` 或者 `--network none` 指定;
+- none 网络模式即不为 Docker Container 创建任何的网络环境,容器内部就只能使用 loopback 网络设备,不会再有其他的网络资源。可以说 none 模式为 Docke Container 做了极少的网络设定,但是俗话说得好“少即是多”,在没有网络配置的情况下,作为 Docker 开发者,才能在这基础做其他无限多可能的网络定制开发。这也恰巧体现了 Docker 设计理念的开放。
+
+
+
+ 比如基于 `none` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox03`,查看 `ip addr`:
+
+
+
+ 可以通过 `docker network inspect none` 查看所有 `none` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+使用`none`模式,`Docker` 容器拥有自己的 `Network Namespace`,但是,并不为`Docker` 容器进行任何网络配置。也就是说,这个 `Docker` 容器没有网卡、IP、路由等信息。需要自己为 `Docker` 容器添加网卡、配置 IP 等。 `None`模式示意图:
+
+ 演示:
+
+```
+$ docker run -tid --net=none --name \
+ docker_non1 ubuntu-base:v3
+
+$ docker exec -ti docker_non1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+## Container 模式
+
+- Container 网络模式是 Docker 中一种较为特别的网络的模式。在创建容器时通过参数 `--net container:已运行的容器名称|ID` 或者 `--network container:已运行的容器名称|ID` 指定;
+- 处于这个模式下的 Docker 容器会共享一个网络栈,这样两个容器之间可以使用 localhost 高效快速通信。
+
+
+
+ **Container 网络模式即新创建的容器不会创建自己的网卡,配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等**。同样两个容器除了网络方面相同之外,其他的如文件系统、进程列表等还是隔离的。
+
+ 比如基于容器 `bbox01` 创建了 `container` 网络模式的容器 `bbox04`,查看 `ip addr`:
+
+
+
+ 容器 `bbox01` 的 `ip addr` 信息如下:
+
+
+
+ 宿主机的 `ip addr` 信息如下:
+
+
+
+ 通过以上测试可以发现,Docker 守护进程只创建了一对对等虚拟设备接口用于连接 bbox01 容器和宿主机,而 bbox04 容器则直接使用了 bbox01 容器的网卡信息。
+
+ 这个时候如果将 bbox01 容器停止,会发现 bbox04 容器就只剩下 lo 接口了。
+
+
+
+ 然后 bbox01 容器重启以后,bbox04 容器也重启一下,就又可以获取到网卡信息了。
+
+
+
+这个模式指定新创建的容器和已经存在的一个容器共享一个`Network Namespace`,而不是和宿主机共享。新创建的容器不会创建自己的网卡,配置自己的`IP`,而是和一个指定的容器共享`IP`、端口范围等。同样,两个容器除了网络方面,其他的如文件系统、进程列表等还是隔离的。两个容器的进程可以通过lo网卡设备通信。 `Container`模式示意图:
+
+演示:
+
+```
+$ docker run -tid --net=container:docker_bri1 \
+ --name docker_con1 ubuntu-base:v3
+
+$ docker exec -ti docker_con1 /bin/bash
+$ docker exec -ti docker_bri1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+
+
+# 高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+## 快速配置指南
+
+下面是一个跟 Docker 网络相关的命令列表。
+
+其中有些命令选项只有在 Docker 服务启动的时候才能配置,而且不能马上生效。
+
+ - `-b BRIDGE` 或 `--bridge=BRIDGE` 指定容器挂载的网桥
+ - `--bip=CIDR`定制 `docker0` 的掩码
+ - `-H SOCKET...` 或 `--host=SOCKET... Docker` 服务端接收命令的通道
+ - `--icc=true|false` 是否支持容器之间进行通信
+ - `--ip-forward=true|false` 请看下文容器之间的通信
+ - `--iptables=true|false` 是否允许 Docker 添加 `iptables` 规则
+ - `--mtu=BYTES` 容器网络中的 `MTU`
+
+下面2个命令选项既可以在启动服务时指定,也可以在启动容器时指定。在 Docker服务启动的时候指定则会成为默认值,后面执行 `docker run` 时可以覆盖设置的默认值。
+
+ - `--dns=IP_ADDRESS...` 使用指定的DNS服务器
+ - `--dns-search=DOMAIN...` 指定DNS搜索域
+
+最后这些选项只有在 `docker run` 执行时使用,因为它是针对容器的特性内容。
+
+ - `-h HOSTNAME` 或 `--hostname=HOSTNAME` 配置容器主机名
+ - `--link=CONTAINER_NAME:ALIAS` 添加到另一个容器的连接
+ - `--net=bridge|none|container:NAME_or_ID|host` 配置容器的桥接模式
+ - `-p SPEC` 或 --publish=SPEC` 映射容器端口到宿主主机
+ - `-P or --publish-all=true|false` 映射容器所有端口到宿主主机
+
+
+
+
+## 容器访问控制
+
+容器的访问控制,主要通过 Linux 上的 `iptables` 防火墙来进行管理和实现。`iptables` 是 Linux 上默认的防火墙软件,在大部分发行版中都自带。
+
+### 容器访问外部网络
+
+容器要想访问外部网络,需要本地系统的转发支持。在Linux 系统中,检查转发是否打开。
+
+
+
+```
+$sysctl net.ipv4.ip_forward
+net.ipv4.ip_forward = 1
+```
+
+如果为 0,说明没有开启转发,则需要手动打开。
+
+
+
+```
+$sysctl -w net.ipv4.ip_forward=1
+```
+
+如果在启动 Docker 服务的时候设定 `--ip-forward=true`, Docker 就会自动设定系统的 `ip_forward` 参数为 1。
+
+### 容器之间访问
+
+容器之间相互访问,需要两方面的支持。
+
+- 容器的网络拓扑是否已经互联。默认情况下,所有容器都会被连接到 `docker0` 网桥上。
+- 本地系统的防火墙软件 `-- iptables` 是否允许通过。
+
+### 访问所有端口
+
+当启动 Docker 服务(即 dockerd)的时候,默认会添加一条转发策略到本地主机 iptables 的 FORWARD 链上。策略为通过(`ACCEPT`)还是禁止(`DROP`)取决于配置`--icc=true`(缺省值)还是 `--icc=false`。当然,如果手动指定 `--iptables=false` 则不会添加 `iptables` 规则。
+
+可见,默认情况下,不同容器之间是允许网络互通的。如果为了安全考虑,可以在 `/etc/docker/daemon.json` 文件中配置 `{"icc": false}` 来禁止它。
+
+### 访问指定端口
+
+在通过 `-icc=false` 关闭网络访问后,还可以通过 `--link=CONTAINER_NAME:ALIAS` 选项来访问容器的开放端口。
+
+例如,在启动 Docker 服务时,可以同时使用 `icc=false --iptables=true` 参数来关闭允许相互的网络访问,并让 Docker 可以修改系统中的 `iptables` 规则。
+
+此时,系统中的 `iptables` 规则可能是类似
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+...
+```
+
+之后,启动容器(`docker run`)时使用 `--link=CONTAINER_NAME:ALIAS` 选项。Docker 会在 `iptable` 中为 两个容器分别添加一条 `ACCEPT` 规则,允许相互访问开放的端口(取决于 `Dockerfile` 中的 `EXPOSE` 指令)。
+
+当添加了 `--link=CONTAINER_NAME:ALIAS` 选项后,添加了 `iptables` 规则。
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+ACCEPT tcp -- 172.17.0.2 172.17.0.3 tcp spt:80
+ACCEPT tcp -- 172.17.0.3 172.17.0.2 tcp dpt:80
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+```
+
+**注意**:`--link=CONTAINER_NAME:ALIAS` 中的 `CONTAINER_NAME` 目前必须是 Docker 分配的名字,或使用 `--name` 参数指定的名字。主机名则不会被识别。
+
+
+
+## 端口映射实现
+
+默认情况下,容器可以主动访问到外部网络的连接,但是外部网络无法访问到容器。
+
+### 容器访问外部实现
+
+容器所有到外部网络的连接,源地址都会被 NAT 成本地系统的 IP 地址。这是使用 `iptables` 的源地址伪装操作实现的。
+
+查看主机的 NAT 规则。
+
+
+
+```
+$ sudo iptables -t nat -nL
+...
+Chain POSTROUTING (policy ACCEPT)
+target prot opt source destination
+MASQUERADE all -- 172.17.0.0/16 !172.17.0.0/16
+...
+```
+
+其中,上述规则将所有源地址在 `172.17.0.0/16` 网段,目标地址为其他网段(外部网络)的流量动态伪装为从系统网卡发出。MASQUERADE 跟传统 SNAT 的好处是它能动态从网卡获取地址。
+
+### 外部访问容器实现
+
+容器允许外部访问,可以在 `docker run` 时候通过 `-p` 或 `-P` 参数来启用。
+
+不管用那种办法,其实也是在本地的 `iptable` 的 nat 表中添加相应的规则。
+
+使用 `-P` 时:
+
+
+
+```
+$ iptables -t nat -nL
+...
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:49153 to:172.17.0.2:80
+```
+
+使用 `-p 80:80` 时:
+
+
+
+```
+$ iptables -t nat -nL
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:80 to:172.17.0.2:80
+```
+
+**注意**:
+
+- 这里的规则映射了 `0.0.0.0`,意味着将接受主机来自所有接口的流量。用户可以通过 `-p IP:host_port:container_port` 或 `-p IP::port` 来指定允许访问容器的主机上的 IP、接口等,以制定更严格的规则。
+- 如果希望永久绑定到某个固定的 IP 地址,可以在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容。
+
+
+
+```
+{
+ "ip": "0.0.0.0"
+}
+```
+
+
+
+## 配置 docker0 网桥
+
+Docker 服务默认会创建一个 `docker0` 网桥(其上有一个 `docker0` 内部接口),它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。
+
+Docker 默认指定了 `docker0` 接口 的 IP 地址和子网掩码,让主机和容器之间可以通过网桥相互通信,它还给出了 MTU(接口允许接收的最大传输单元),通常是 1500 Bytes,或宿主主机网络路由上支持的默认值。这些值都可以在服务启动的时候进行配置。
+
+- `--bip=CIDR` IP 地址加掩码格式,例如 192.168.1.5/24
+- `--mtu=BYTES` 覆盖默认的 Docker mtu 配置
+
+也可以在配置文件中配置 DOCKER_OPTS,然后重启服务。
+
+由于目前 Docker 网桥是 Linux 网桥,用户可以使用 `brctl show` 来查看网桥和端口连接信息。
+
+
+
+```
+$ sudo brctl show
+bridge name bridge id STP enabled interfaces
+docker0 8000.3a1d7362b4ee no veth65f9
+ vethdda6
+```
+
+**注**:`brctl` 命令在 Debian、Ubuntu 中可以使用 `sudo apt-get install bridge-utils` 来安装。
+
+每次创建一个新容器的时候,Docker 从可用的地址段中选择一个空闲的 IP 地址分配给容器的 eth0 端口。使用本地主机上 `docker0` 接口的 IP 作为所有容器的默认网关。
+
+
+
+```
+$ sudo docker run -i -t --rm base /bin/bash
+$ ip addr show eth0
+24: eth0: mtu 1500 qdisc pfifo_fast state UP group default qlen 1000
+ link/ether 32:6f:e0:35:57:91 brd ff:ff:ff:ff:ff:ff
+ inet 172.17.0.3/16 scope global eth0
+ valid_lft forever preferred_lft forever
+ inet6 fe80::306f:e0ff:fe35:5791/64 scope link
+ valid_lft forever preferred_lft forever
+$ ip route
+default via 172.17.42.1 dev eth0
+172.17.0.0/16 dev eth0 proto kernel scope link src 172.17.0.3
+```
+
+
+
+## 自定义网桥
+
+除了默认的 `docker0` 网桥,用户也可以指定网桥来连接各个容器。
+
+在启动 Docker 服务的时候,使用 `-b BRIDGE`或`--bridge=BRIDGE` 来指定使用的网桥。
+
+如果服务已经运行,那需要先停止服务,并删除旧的网桥。
+
+
+
+```
+$ sudo systemctl stop docker
+$ sudo ip link set dev docker0 down
+$ sudo brctl delbr docker0
+```
+
+然后创建一个网桥 `bridge0`。
+
+
+
+```
+$ sudo brctl addbr bridge0
+$ sudo ip addr add 192.168.5.1/24 dev bridge0
+$ sudo ip link set dev bridge0 up
+```
+
+查看确认网桥创建并启动。
+
+
+
+```
+$ ip addr show bridge0
+4: bridge0: mtu 1500 qdisc noop state UP group default
+ link/ether 66:38:d0:0d:76:18 brd ff:ff:ff:ff:ff:ff
+ inet 192.168.5.1/24 scope global bridge0
+ valid_lft forever preferred_lft forever
+```
+
+在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容,即可将 Docker 默认桥接到创建的网桥上。
+
+
+
+```
+{
+ "bridge": "bridge0",
+}
+```
+
+启动 Docker 服务。
+
+新建一个容器,可以看到它已经桥接到了 `bridge0` 上。
+
+可以继续用 `brctl show` 命令查看桥接的信息。另外,在容器中可以使用 `ip addr` 和 `ip route` 命令来查看 IP 地址配置和路由信息。
+
+
+
+## 工具和示例
+
+在介绍自定义网络拓扑之前,你可能会对一些外部工具和例子感兴趣:
+
+### **pipework**
+
+Jérôme Petazzoni 编写了一个叫 [pipework](https://github.com/jpetazzo/pipework) 的 shell 脚本,可以帮助用户在比较复杂的场景中完成容器的连接。
+
+### **playground**
+
+Brandon Rhodes 创建了一个提供完整的 Docker 容器网络拓扑管理的 [Python库](https://github.com/brandon-rhodes/fopnp/tree/m/playground),包括路由、NAT 防火墙;以及一些提供 `HTTP` `SMTP` `POP` `IMAP` `Telnet` `SSH` `FTP` 的服务器。
+
+
+
+## 编辑网络配置文件
+
+Docker 1.2.0 开始支持在运行中的容器里编辑 `/etc/hosts`, `/etc/hostname` 和 `/etc/resolv.conf` 文件。
+
+但是这些修改是临时的,只在运行的容器中保留,容器终止或重启后并不会被保存下来,也不会被 `docker commit` 提交。
+
+
+
+## 实例:创建一个点到点连接
+
+默认情况下,Docker 会将所有容器连接到由 `docker0` 提供的虚拟子网中。
+
+用户有时候需要两个容器之间可以直连通信,而不用通过主机网桥进行桥接。
+
+解决办法很简单:创建一对 `peer` 接口,分别放到两个容器中,配置成点到点链路类型即可。
+
+首先启动 2 个容器:
+
+
+
+```
+$ docker run -i -t --rm --net=none base /bin/bash
+root@1f1f4c1f931a:/#
+$ docker run -i -t --rm --net=none base /bin/bash
+root@12e343489d2f:/#
+```
+
+找到进程号,然后创建网络命名空间的跟踪文件。
+
+
+
+```
+$ docker inspect -f '{{.State.Pid}}' 1f1f4c1f931a
+2989
+$ docker inspect -f '{{.State.Pid}}' 12e343489d2f
+3004
+$ sudo mkdir -p /var/run/netns
+$ sudo ln -s /proc/2989/ns/net /var/run/netns/2989
+$ sudo ln -s /proc/3004/ns/net /var/run/netns/3004
+```
+
+创建一对 `peer` 接口,然后配置路由
+
+
+
+```
+$ sudo ip link add A type veth peer name B
+
+$ sudo ip link set A netns 2989
+$ sudo ip netns exec 2989 ip addr add 10.1.1.1/32 dev A
+$ sudo ip netns exec 2989 ip link set A up
+$ sudo ip netns exec 2989 ip route add 10.1.1.2/32 dev A
+
+$ sudo ip link set B netns 3004
+$ sudo ip netns exec 3004 ip addr add 10.1.1.2/32 dev B
+$ sudo ip netns exec 3004 ip link set B up
+$ sudo ip netns exec 3004 ip route add 10.1.1.1/32 dev B
+```
+
+现在这 2 个容器就可以相互 ping 通,并成功建立连接。点到点链路不需要子网和子网掩码。
+
+此外,也可以不指定 `--net=none` 来创建点到点链路。这样容器还可以通过原先的网络来通信。
+
+利用类似的办法,可以创建一个只跟主机通信的容器。但是一般情况下,更推荐使用 `--icc=false` 来关闭容器之间的通信。
+
+### 参考文献
+
+- Docker 网络模式详解及容器间网络通信:https://juejin.cn/post/6868086876751085581
+- Docker从基础到入门:https://yeasy.gitbook.io/docker_practice/advanced_network
+- Docker网络模式:https://www.qikqiak.com/k8s-book/docs/7.Docker%E7%9A%84%E7%BD%91%E7%BB%9C%E6%A8%A1%E5%BC%8F.html
\ No newline at end of file
diff --git a/Docker/06 docker compose.md b/Docker/06 docker compose.md
new file mode 100644
index 0000000..8c44086
--- /dev/null
+++ b/Docker/06 docker compose.md
@@ -0,0 +1,605 @@
+# Chapter 6 Docker Compose
+
+相信大家学完之前的内容已经对docker的操作很熟悉了,但是有没有一种感觉,如果我一个项目要起好多个容器,每个容器之间又相互之间有一些关联,有些情况下又要修改一些容器,这种情况写起来会特别的麻烦,那么有没有一种方式能让我把项目快速的启动起来呢?
+
+答案肯定是有的,接下来就让我们学习一下docker compose。
+
+关于docker compose的安装请移步[docker compose安装与卸载](https://vuepress.mirror.docker-practice.com/compose/install/)或根据[docker官网](https://docs.docker.com/compose/install/)进行安装。
+
+> 对于docker compose的学习推荐大家多看看一些项目的docker-compose.yml文件是怎么写的,慢慢模仿着去写很多就越来越熟练清晰了。在[Compose文件夹](https://github.com/datawhalechina/team-learning-program/tree/master/Docker/Compose)下也在网上收集了一些docker-compose.yml文件,欢迎大家一起来补充。
+
+## 内容大纲
+
+- 什么是docker compose
+- 如何使用docker compose
+- docker compose基本使用
+ - 启动服务
+ - 查看服务状态
+ - 停止或删除服务
+ - 进入服务
+ - 查看服务输出日志
+- Compose模板文件
+- Compose命令
+
+## 什么是docker compose
+
+通过之前的介绍,我们知道使用一个 `Dockerfile` 模板文件,可以让用户很方便的定义一个单独的应用容器。然而,在日常工作中,经常会碰到需要多个容器相互配合来完成某项任务的情况。例如要实现一个 Web 项目,除了 Web 服务容器本身,往往还需要再加上后端的数据库服务容器,甚至还包括负载均衡容器等。
+
+`Compose`恰好满足了这样的需求。它允许用户通过一个单独的 `docker-compose.yml` 模板文件(YAML 格式)来定义一组相关联的应用容器为一个项目(project)。不理解没关系,我们先看下面这样一个文件:
+
+
+
+通过这个例子我们可以发现,这个文件里面我们好像看见了image、ports、networks这些,那么这些标签与之前docker run时候的一些指令是不是有一些关系呢?接下来就让我们继续学习。
+
+## 如何使用docker compose
+
+在`Compose` 中有两个重要的概念:
+
+- 服务 (`service`):一个应用的容器,实际上可以包括若干运行相同镜像的容器实例。
+- 项目 (`project`):由一组关联的应用容器组成的一个完整业务单元,在 `docker-compose.yml` 文件中定义。
+
+`Compose`的默认管理对象是项目,也就是通过docker-compose.yml定义的一组服务集合,通过一些命令来对项目中的一组容器进行便捷地生命周期管理。
+
+下面我们来看一个真实的场景,在该场景下我们是通过Python来写一个能够记录页面访问次数的 web 网站。完整代码:[计数器](./Compose/计数器)
+
+### web 应用
+
+新建文件夹,在该目录中编写 `app.py` 文件
+
+```python
+from flask import Flask
+from redis import Redis
+import os
+import socket
+
+app = Flask(__name__)
+redis = Redis(host=os.environ.get('REDIS_HOST', '127.0.0.1'), port=6379)
+
+
+@app.route('/')
+def hello():
+ redis.incr('hits')
+ return 'Hello Container World! I have been seen %s times and my hostname is %s.\n' % (redis.get('hits'),socket.gethostname())
+
+
+if __name__ == "__main__":
+ app.run(host="0.0.0.0", port=5000, debug=True)
+```
+
+### Dockerfile
+
+编写 `Dockerfile` 文件,内容为
+
+```docker
+FROM python:2.7
+COPY . /app
+WORKDIR /app
+RUN pip install flask redis
+EXPOSE 5000
+CMD [ "python", "app.py" ]
+```
+
+### docker-compose.yml
+
+编写 `docker-compose.yml` 文件,这个是 Compose 使用的主模板文件。
+
+```yaml
+version: "3"
+
+services:
+
+ redis:
+ image: redis
+
+ web:
+ build:
+ context: .
+ dockerfile: Dockerfile
+ environment:
+ REDIS_HOST: redis
+```
+
+### 运行 compose 项目
+
+```bash
+$ docker-compose up -d
+```
+
+此时访问本地 `5000` 端口,每次刷新页面,计数就会加 1。
+
+## docker compose基本使用
+
+### 启动服务
+
+在创建好`docker-compose.yml`文件后,可以通过下面这个命令将文件中定义的容器都启动起来,在docker compose中我们更习惯于将每一个容器叫做service。
+
+```
+docker-compose up
+```
+
+命令后会自动接一个默认值`-f docker-compose.yml`,也就是默认是使用docker-compose.yml文件的。我们也可以给文件起名为`docke-test.yml`,这样在使用时指定文件名,但是为了符合规范,还是统一为`docker-compose.yml`。
+
+```
+docker-compose up -f docer-test.yml
+```
+
+**但是直接通过这种方式的话会直接将启动时的输出打印到终端,所以我们常会加上`-d`参数。**
+
+```bash
+docker-compose up -d
+```
+
+### 查看服务状态
+
+接下来可以查看一下我们创建的service状态
+
+```
+docker-compose ps
+```
+
+要是想要查看所有service的状态可以使用-a参数:
+
+```
+docker-compose ps -a
+```
+
+### 停止或删除服务
+
+如何停止已经运行的services呢,可以使用以下两个命令
+
+```
+docker-compose stop
+docker-compose down
+```
+
+其中stop是直接停止services,而down则会停止并删除创建的service,volume和network。
+
+### 进入服务
+
+有些情况下我们还需要进入容器来执行一些命令,可以通过如下方式进入容器
+
+```
+docker-compose exec mysql bash
+```
+
+exec后面接的就是我们要进入具体的service的名字,名字后面就是我们要执行的命令。
+
+### 查看服务输出日志
+
+有些情况下一些服务可能无法正常启动,这时可以使用命令查看日志并定位发生错误的原因
+
+```
+docker-compose logs
+```
+
+以上的一些操作就能满足你在大多数情况下的场景了,但是对于一些我们个人的应用还需要详细的编写dock er-compose.yml文件才行,下面我们就更详细的学习一下。
+
+## Compose模板文件
+
+模板文件是使用 `Compose` 的核心,涉及到的指令关键字也比较多。但大家不用担心,这里面大部分指令跟 `docker run` 相关参数的含义都是类似的。
+
+*注:这里仅介绍一些较为常用的指令,更多指令请见:[Compose模板文件](https://vuepress.mirror.docker-practice.com/compose/compose_file/#cap-add-cap-drop)*
+
+默认的模板文件名称为 `docker-compose.yml`,格式为 YAML 格式。
+
+```yaml
+version: "3"
+
+services:
+ webapp:
+ image: examples/web
+ ports:
+ - "80:80"
+ volumes:
+ - "/data"
+```
+
+注意每个服务都必须通过 `image` 指令指定镜像或 `build` 指令(需要 Dockerfile)等来自动构建生成镜像。
+
+如果使用 `build` 指令,在 `Dockerfile` 中设置的选项(例如:`CMD`, `EXPOSE`, `VOLUME`, `ENV` 等) 将会自动被获取,无需在 `docker-compose.yml` 中重复设置。
+
+下面分别介绍各个指令的用法。
+
+### build
+
+指定 `Dockerfile` 所在文件夹的路径(可以是绝对路径,或者相对 docker-compose.yml 文件的路径)。 `Compose` 将会利用它自动构建这个镜像,然后使用这个镜像。
+
+```yaml
+version: '3'
+services:
+
+ webapp:
+ build: ./dir
+```
+
+你也可以使用 `context` 指令指定 `Dockerfile` 所在文件夹的路径。使用 `dockerfile` 指令指定 `Dockerfile` 文件名。使用 `arg` 指令指定构建镜像时的变量。
+
+```yaml
+version: '3'
+services:
+
+ webapp:
+ build:
+ context: ./dir
+ dockerfile: Dockerfile-alternate
+ args:
+ buildno: 1
+```
+
+使用 `cache_from` 指定构建镜像的缓存。
+
+```yaml
+build:
+ context: .
+ cache_from:
+ - alpine:latest
+ - corp/web_app:3.14
+```
+
+### depends_on
+
+解决容器的依赖、启动先后的问题。以下例子中会先启动 `redis` `db` 再启动 `web`
+
+```yaml
+version: '3'
+
+services:
+ web:
+ build: .
+ depends_on:
+ - db
+ - redis
+
+ redis:
+ image: redis
+
+ db:
+ image: postgres
+```
+
+> 注意:`web` 服务不会等待 `redis` `db` 「完全启动」之后才启动。这里需要注意,如果redis启动失败,那么web依然会正常启动。
+
+### environment
+
+设置环境变量。你可以使用数组或字典两种格式。只给定名称的变量会自动获取运行 Compose 主机上对应变量的值,可以用来防止泄露不必要的数据。
+
+```yaml
+environment:
+ RACK_ENV: development
+ SESSION_SECRET:
+
+environment:
+ - RACK_ENV=development
+ - SESSION_SECRET
+```
+
+如果变量名称或者值中用到 `true|false,yes|no` 等表达 [布尔 (opens new window)](https://yaml.org/type/bool.html)含义的词汇,最好放到引号里,避免 YAML 自动解析某些内容为对应的布尔语义。这些特定词汇,包括
+
+```bash
+y|Y|yes|Yes|YES|n|N|no|No|NO|true|True|TRUE|false|False|FALSE|on|On|ON|off|Off|OFF
+```
+
+### expose
+
+暴露端口,但不映射到宿主机,只被连接的服务访问。仅可以指定内部端口为参数
+
+```yaml
+expose:
+ - "3000"
+ - "8000"
+```
+
+### ports
+
+暴露端口信息。使用宿主端口:容器端口 `(HOST:CONTAINER)` 格式,或者仅仅指定容器的端口(宿主将会随机选择端口)都可以。
+
+```yaml
+ports:
+ - "3000"
+ - "8000:8000"
+ - "49100:22"
+ - "127.0.0.1:8001:8001"
+```
+
+*注意:当使用 `HOST:CONTAINER` 格式来映射端口时,如果你使用的容器端口小于 60 并且没放到引号里,可能会得到错误结果,因为 `YAML` 会自动解析 `xx:yy` 这种数字格式为 60 进制。为避免出现这种问题,建议数字串都采用引号包括起来的字符串格式。*
+
+### secrets
+
+存储敏感数据,例如 `mysql` 服务密码。
+
+```yaml
+version: "3.1"
+services:
+
+mysql:
+ image: mysql
+ environment:
+ MYSQL_ROOT_PASSWORD_FILE: /run/secrets/db_root_password
+ secrets:
+ - db_root_password
+ - my_other_secret
+
+secrets:
+ my_secret:
+ file: ./my_secret.txt
+ my_other_secret:
+ external: true
+```
+
+### image
+
+指定为镜像名称或镜像 ID。如果镜像在本地不存在,`Compose` 将会尝试拉取这个镜像。
+
+```yaml
+image: ubuntu
+image: orchardup/postgresql
+image: a4bc65fd
+```
+
+### labels
+
+为容器添加 Docker 元数据(metadata)信息。例如可以为容器添加辅助说明信息。
+
+```yaml
+labels:
+ com.startupteam.description: "webapp for a startup team"
+ com.startupteam.department: "devops department"
+ com.startupteam.release: "rc3 for v1.0"
+```
+
+### network_mode
+
+设置网络模式。使用和 `docker run` 的 `--network` 参数一样的值。
+
+```yaml
+network_mode: "bridge"
+network_mode: "host"
+network_mode: "none"
+network_mode: "service:[service name]"
+network_mode: "container:[container name/id]"
+```
+
+### networks
+
+配置容器连接的网络。
+
+```yaml
+version: "3"
+services:
+
+ some-service:
+ networks:
+ - some-network
+ - other-network
+
+networks:
+ some-network:
+ other-network:
+```
+
+### volumes
+
+数据卷所挂载路径设置。可以设置为宿主机路径(`HOST:CONTAINER`)或者数据卷名称(`VOLUME:CONTAINER`),并且可以设置访问模式 (`HOST:CONTAINER:ro`)。该指令中路径支持相对路径。
+
+```yaml
+volumes:
+ - /var/lib/mysql
+ - cache/:/tmp/cache
+ - ~/configs:/etc/configs/:ro
+```
+
+如果路径为数据卷名称,必须在文件中配置数据卷。
+
+```yaml
+version: "3"
+
+services:
+ my_src:
+ image: mysql:8.0
+ volumes:
+ - mysql_data:/var/lib/mysql
+
+volumes:
+ mysql_data:
+```
+
+## Compose命令
+
+之前我们已经介绍了一些命令,已经能够满足一些基本的日常使用了,下面我们再了解一些其他命令。
+
+### 命令对象与格式
+
+对于 Compose 来说,大部分命令的对象既可以是项目本身,也可以指定为项目中的服务或者容器。如果没有特别的说明,命令对象将是项目,这意味着项目中所有的服务都会受到命令影响。
+
+执行 `docker-compose [COMMAND] --help` 或者 `docker-compose help [COMMAND]` 可以查看具体某个命令的使用格式。
+
+`docker-compose` 命令的基本的使用格式是
+
+```bash
+docker-compose [-f=...] [options] [COMMAND] [ARGS...]
+```
+
+### 命令选项命令选项
+
+- `-f, --file FILE` 指定使用的 Compose 模板文件,默认为 `docker-compose.yml`,可以多次指定。
+- `-p, --project-name NAME` 指定项目名称,默认将使用所在目录名称作为项目名。
+- `--verbose` 输出更多调试信息。
+- `-v, --version` 打印版本并退出。
+
+### build
+
+格式为 `docker-compose build [options] [SERVICE...]`。
+
+构建(重新构建)项目中的服务容器。
+
+服务容器一旦构建后,将会带上一个标记名,例如对于 web 项目中的一个 db 容器,可能是 web_db。
+
+可以随时在项目目录下运行 `docker-compose build` 来重新构建服务。
+
+选项包括:
+
+- `--force-rm` 删除构建过程中的临时容器。
+- `--no-cache` 构建镜像过程中不使用 cache(这将加长构建过程)。
+- `--pull` 始终尝试通过 pull 来获取更新版本的镜像。
+
+### config
+
+验证 Compose 文件格式是否正确,若正确则显示配置,若格式错误显示错误原因。
+
+### down
+
+此命令将会停止 `up` 命令所启动的容器,并移除网络
+
+### exec
+
+进入指定的容器。
+
+### help
+
+获得一个命令的帮助。
+
+### images
+
+列出 Compose 文件中包含的镜像。
+
+### kill
+
+格式为 `docker-compose kill [options] [SERVICE...]`。
+
+通过发送 `SIGKILL` 信号来强制停止服务容器。
+
+支持通过 `-s` 参数来指定发送的信号,例如通过如下指令发送 `SIGINT` 信号。
+
+```bash
+$ docker-compose kill -s SIGINT
+```
+
+### logs
+
+格式为 `docker-compose logs [options] [SERVICE...]`。
+
+查看服务容器的输出。默认情况下,docker-compose 将对不同的服务输出使用不同的颜色来区分。可以通过 `--no-color` 来关闭颜色。
+
+该命令在调试问题的时候十分有用。
+
+### pause
+
+格式为 `docker-compose pause [SERVICE...]`。
+
+暂停一个服务容器。
+
+### port
+
+格式为 `docker-compose port [options] SERVICE PRIVATE_PORT`。
+
+打印某个容器端口所映射的公共端口。
+
+选项:
+
+- `--protocol=proto` 指定端口协议,tcp(默认值)或者 udp。
+- `--index=index` 如果同一服务存在多个容器,指定命令对象容器的序号(默认为 1)。
+
+### ps
+
+格式为 `docker-compose ps [options] [SERVICE...]`。
+
+列出项目中目前的所有容器。
+
+选项:
+
+- `-q` 只打印容器的 ID 信息。
+
+### pull
+
+格式为 `docker-compose pull [options] [SERVICE...]`。
+
+拉取服务依赖的镜像。
+
+选项:
+
+- `--ignore-pull-failures` 忽略拉取镜像过程中的错误。
+
+### push
+
+推送服务依赖的镜像到 Docker 镜像仓库。
+
+### restart
+
+格式为 `docker-compose restart [options] [SERVICE...]`。
+
+重启项目中的服务。
+
+选项:
+
+- `-t, --timeout TIMEOUT` 指定重启前停止容器的超时(默认为 10 秒)。
+
+### rm
+
+格式为 `docker-compose rm [options] [SERVICE...]`。
+
+删除所有(停止状态的)服务容器。推荐先执行 `docker-compose stop` 命令来停止容器。
+
+选项:
+
+- `-f, --force` 强制直接删除,包括非停止状态的容器。一般尽量不要使用该选项。
+- `-v` 删除容器所挂载的数据卷。
+
+### start
+
+格式为 `docker-compose start [SERVICE...]`。
+
+启动已经存在的服务容器。
+
+### stop
+
+格式为 `docker-compose stop [options] [SERVICE...]`。
+
+停止已经处于运行状态的容器,但不删除它。通过 `docker-compose start` 可以再次启动这些容器。
+
+选项:
+
+- `-t, --timeout TIMEOUT` 停止容器时候的超时(默认为 10 秒)。
+
+### top
+
+查看各个服务容器内运行的进程。
+
+### unpause
+
+格式为 `docker-compose unpause [SERVICE...]`。
+
+恢复处于暂停状态中的服务。
+
+### up
+
+格式为 `docker-compose up [options] [SERVICE...]`。
+
+该命令十分强大,它将尝试自动完成包括构建镜像,(重新)创建服务,启动服务,并关联服务相关容器的一系列操作。
+
+链接的服务都将会被自动启动,除非已经处于运行状态。
+
+可以说,大部分时候都可以直接通过该命令来启动一个项目。
+
+默认情况,`docker-compose up` 启动的容器都在前台,控制台将会同时打印所有容器的输出信息,可以很方便进行调试。
+
+当通过 `Ctrl-C` 停止命令时,所有容器将会停止。
+
+如果使用 `docker-compose up -d`,将会在后台启动并运行所有的容器。一般推荐生产环境下使用该选项。
+
+默认情况,如果服务容器已经存在,`docker-compose up` 将会尝试停止容器,然后重新创建(保持使用 `volumes-from` 挂载的卷),以保证新启动的服务匹配 `docker-compose.yml` 文件的最新内容。如果用户不希望容器被停止并重新创建,可以使用 `docker-compose up --no-recreate`。这样将只会启动处于停止状态的容器,而忽略已经运行的服务。如果用户只想重新部署某个服务,可以使用 `docker-compose up --no-deps -d ` 来重新创建服务并后台停止旧服务,启动新服务,并不会影响到其所依赖的服务。
+
+选项:
+
+- `-d` 在后台运行服务容器。
+- `--no-color` 不使用颜色来区分不同的服务的控制台输出。
+- `--no-deps` 不启动服务所链接的容器。
+- `--force-recreate` 强制重新创建容器,不能与 `--no-recreate` 同时使用。
+- `--no-recreate` 如果容器已经存在了,则不重新创建,不能与 `--force-recreate` 同时使用。
+- `--no-build` 不自动构建缺失的服务镜像。
+- `-t, --timeout TIMEOUT` 停止容器时候的超时(默认为 10 秒)。
+
+### version
+
+格式为 `docker-compose version`。
+
+打印版本信息。
\ No newline at end of file
diff --git a/Docker/07 综合实践.md b/Docker/07 综合实践.md
new file mode 100644
index 0000000..dd2ef72
--- /dev/null
+++ b/Docker/07 综合实践.md
@@ -0,0 +1,150 @@
+# Chapter 7 综合实践
+
+在本章我们希望你能通过docker的形式将您个人的项目修改为容器化部署的形式,最好可以配合上Github Action来实现CI/CD功能。
+
+在没有学习docker之前,部署项目都是直接启动文件,比如java项目就是java –jar xxxx.jar的方式,python项目就是python xxxx.py。如果采用docker的方式去部署这些项目,一般有两种方式,以jar包项目为例
+
+## 方式一 挂载部署
+
+这种方式类似于常规部署,通过数据卷的方式将宿主机的jar包挂载到容器中,然后执行jar包的jdk选择容器中的而非采用本地的。
+
+\1. 将jar包上传到服务器的指定目录,比如/root/docker/jar。
+
+
+
+2.通过docker pull openjdk:8命令获取镜像
+
+
+
+3.编写docker-compose.yml文件
+
+```yaml
+version:'3.0'
+
+services:
+
+ java:
+ image: docker.io/openjdk
+ restart:always
+ container_name: myopenjdk
+ ports:
+ - 8080:8001
+ volumes:
+ - /root/docker/jar/xxxx.jar:/root:z
+ - /etc/localtime:/etc/localtime
+ environment:
+ - TZ="Asia/Shanghai"
+ entrypoint: java -jar /root/xxxx.jar
+ mynetwork:
+ ipv4_address: 192.168.1.13
+
+networks:
+ mynetwork:
+ ipam:
+ config:
+ - subnet: 192.168.1.0/24
+```
+
+参数解释:
+
+build 指定dockerfile所在文件夹的路径 context指定dockerfile文件所在路径 dockerfile指定文件的具体名称
+
+container_name 指定容器名称
+
+volumes 挂载路径 z是用来设置selinux,或者直接在linux通过命令临时关闭或者永久关闭
+
+ports 暴露端口信息
+
+networks是用来给容器设置固定的ip
+
+3.执行命令docker-compose up –d启动jar包, 可以通过docker ps查看容器是否在运行,需要注意的是默认查看所有运行中的容器,如果想查看所有容器,需要添加参数-a
+
+
+
+\4. 注意如果容器启动失败或者状态异常,可以通过docker logs查看日志
+
+5.通过docker inspect myopenjdk查看容器详细信息,可以看到容器ip已经设置成功
+
+
+
+5.然后在虚拟机中打开浏览器输入jar包项目的访问地址,就可以看到运行的项目,需要注意访问端口是映射过的端口而非项目实际端口
+
+
+
+## 方式二 构建镜像部署
+
+1.将jar包上传到服务器的指定目录,比如/root/docker/jar。
+
+2.在该目录下创建Dockerfile文件,通过vim等编辑工具在Dockerfile中编辑以下内容
+
+```dockerfile
+FROM java:8
+MAINTAINER YHF
+LABEL description=”learn docker”
+ADD xxx.jar
+EXPOSE 8001
+ENTRYPOINT [“java”,”-jar”,”xxxx.jar”]
+```
+
+参数解释:
+
+FROM java:8 指定所创建镜像的基础镜像
+
+MAINTAINER yhf 指定作者为yhf
+
+LABEL 为生成的镜像添加元数据标签信息
+
+ADD xxxx.jar 添加内容到镜像
+
+EXPOSE 8080 声明镜像内服务监听的端口
+
+ENTRYPOINT 指定镜像的默认入口命令,支持两种格式ENTRYPOINT[“java”,”-jar”,”xxxx.jar”];ENTRYPOINT java –jar xxxx.jar。注意每个dokcerfile中只能有一个ENTRYPOINT,如果指定多个只有最后一个生效。
+
+4.Dockerfile构建完成以后可以通过命令docker build构建镜像,然后再运行容器,这里咱们用docker-compose命令直接编排构建镜像和运行容器。
+
+5.编写docker-compose.yml文件
+
+ ```yaml
+version: '3'
+
+services:
+
+ java_2:
+ restart: always
+ image: yhfopenjdk:latest
+ container_name: myopenjdk
+ ports:
+ - 8080:8001
+ volumes:
+ - /etc/localtime:/etc/localtime
+ environment:
+ - TZ="Asia/Shanghai"
+ entrypoint: java -jar /root/datawhale-admin-1.0.0.jar
+ networks:
+ mynetwork:
+ ipv4_address: 192.168.1.13
+
+networks:
+ mynetwork:
+ ipam:
+ config:
+ - subnet: 192.168.1.0/24
+ ```
+
+参数解释同方式一:
+
+6.执行docker-compose up –d直接启动基于文件构建的自定义镜像,如果镜像不存在会自动构建,如果已存在那么直接启动。如果想重新构建镜像,则执行docker-compose build。如果想在执行compose文件的时候重构,则执行docker-compose up –d –build。
+
+
+
+此使通过dockerfile文件构建的镜像已经创建
+
+
+
+通过镜像运行的容器已经正常启动,可以通过docker ps查看容器是否在运行,需要注意的是默认查看所有运行中的容器,如果想查看所有容器,需要添加参数-a
+
+
+
+7.在浏览器中输入访问路径可以看到项目已经正常运行
+
+
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml b/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml
new file mode 100644
index 0000000..823c9ce
--- /dev/null
+++ b/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml
@@ -0,0 +1,19 @@
+```yaml
+version: "3"
+
+services:
+
+ elastic:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ ports:
+ - "9200:9200"
+ - "9300:9300"
+ volumes:
+ - elastic-data:/data
+ environment:
+ - discovery.type=single-node
+
+volumes:
+ elastic-data:
+```
+
diff --git a/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml b/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml
new file mode 100644
index 0000000..8ecec99
--- /dev/null
+++ b/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml
@@ -0,0 +1,73 @@
+```yaml
+version: '2.2'
+services:
+ es01:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es01
+ environment:
+ - node.name=es01
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es02,es03
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data01:/usr/share/elasticsearch/data
+ ports:
+ - 9200:9200
+ networks:
+ - elastic
+ es02:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es02
+ environment:
+ - node.name=es02
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es01,es03
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data02:/usr/share/elasticsearch/data
+ networks:
+ - elastic
+ es03:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es03
+ environment:
+ - node.name=es03
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es01,es02
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data03:/usr/share/elasticsearch/data
+ networks:
+ - elastic
+
+volumes:
+ data01:
+ driver: local
+ data02:
+ driver: local
+ data03:
+ driver: local
+
+networks:
+ elastic:
+ driver: bridge
+```
+
diff --git a/Docker/Compose/常用服务/etcd/docker-compose.yml b/Docker/Compose/常用服务/etcd/docker-compose.yml
new file mode 100644
index 0000000..1bbbeef
--- /dev/null
+++ b/Docker/Compose/常用服务/etcd/docker-compose.yml
@@ -0,0 +1,53 @@
+```yaml
+version: '2'
+services:
+
+ etcd1:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23791:2379
+ - 23801:2380
+ environment:
+ ETCD_NAME: infra1
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd1:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd1:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd1:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd1:2379
+
+ etcd2:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23792:2379
+ - 23802:2380
+ environment:
+ ETCD_NAME: infra2
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd2:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd2:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd2:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd2:2379
+
+ etcd3:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23793:2379
+ - 23803:2380
+ environment:
+ ETCD_NAME: infra3
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd3:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd3:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd3:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd3:2379
+```
+
diff --git a/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml b/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml
new file mode 100644
index 0000000..d69fd91
--- /dev/null
+++ b/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml
@@ -0,0 +1,177 @@
+### 首先创建master结点的Dockerfile
+
+在编写之前我们先要创建一个配置master的my.cnf配置文件
+
+```
+[mysqld]
+log_bin = mysql-bin
+server_id = 10
+```
+
+之后我们创建master结点的Dockerfile
+
+```
+FROM mysql:5.7
+ADD ./master/my.cnf /etc/mysql/my.cnf
+```
+
+### 第二创建slave结点的Dockerfile
+
+在编写之前我们先要创建一个配置slave结点my.cnf配置文件
+
+```
+[mysqld]
+log_bin = mysql-bin
+server_id = 11
+relay_log = /var/lib/mysql/mysql-relay-bin
+log_slave_updates = 1
+read_only = 1
+```
+
+注意要修改server_id为不同值,否则会发生错误,之后我们创建slave结点的Dockerfile
+
+```
+FROM mysql:5.7
+ADD ./slave/my.cnf /etc/mysql/my.cnf
+```
+
+### 最终的docker-compose.yml
+
+我们创建这样一个目录结构
+
+
+
+其中master文件夹存放关于master结点的my.cnf和Dockerfile,slave文件夹存放关于slave结点的my.cnf和Dockerfile。
+
+```yaml
+version: "3"
+services:
+ db-master:
+ build:
+ context: ./
+ dockerfile: master/Dockerfile
+ restart: always
+ environment:
+ MYSQL_DATABASE: 'db'
+ # So you don't have to use root, but you can if you like
+ MYSQL_USER: 'user'
+ # You can use whatever password you like
+ MYSQL_PASSWORD: 'password'
+ # Password for root access
+ MYSQL_ROOT_PASSWORD: 'password'
+ ports:
+ # : < MySQL Port running inside container>
+ - '3306:3306'
+ # Where our data will be persisted
+ volumes:
+ - my-db-master:/var/lib/mysql
+ networks:
+ - net-mysql
+
+ db-slave:
+ build:
+ context: ./
+ dockerfile: slave/Dockerfile
+ restart: always
+ environment:
+ MYSQL_DATABASE: 'db'
+ # So you don't have to use root, but you can if you like
+ MYSQL_USER: 'user'
+ # You can use whatever password you like
+ MYSQL_PASSWORD: 'password'
+ # Password for root access
+ MYSQL_ROOT_PASSWORD: 'password'
+ ports:
+ # : < MySQL Port running inside container>
+ - '3307:3306'
+ # Where our data will be persisted
+ volumes:
+ - my-db-slave:/var/lib/mysql
+ networks:
+ - net-mysql
+
+# Names our volume
+volumes:
+ my-db-master:
+ my-db-slave:
+
+
+networks:
+ net-mysql:
+ driver: bridge
+```
+
+现在我们就可以通过docker-compose来启动这两个结点了
+
+```
+docker-compose up -d
+```
+
+接下来我们就可以看到一些镜像的构建信息,当两个结点都启动之后我们来查看一下两个结点的状态
+
+```
+docker-compose ps -a
+```
+
+
+
+可以看到两个结点的状态已经是Up了,并且主结点映射在宿主机的3306端口,从结点映射在宿主机的3307端口。我们再来查看一下这两个结点的网络信息,以便后续使用
+
+```
+docker network ls
+```
+
+
+
+这个就是我们刚才创建的网络,刚才创建的两个结点也挂载在这个网络上,我们来查看一下详细信息
+
+```
+docker inspect 62fa5033ce48
+```
+
+
+
+这样我们就差看到来两个结点的具体IP地址,因为Docker网络的配置,两个连接到同一network的容器会直接相互连通。
+
+### 主从配置
+
+启动之后进入从结点
+
+```
+docker-compose exec db-slave bash
+```
+
+进入从结点mysql中
+
+```
+mysql -u root -p
+```
+
+在从结点上配置主节点信息,然后把当前结点设置为从结点。
+
+```
+mysql> CHANGE MASTER TO MASTER_HOST='192.168.64.3', MASTER_USER='root', MASTER_PASSWORD='password', MASTER_LOG_FILE='mysql-bin.000001', MASTER_LOG_POS=0;
+Query OK, 0 rows affected, 2 warnings (0.11 sec)
+
+
+mysql> start slave;
+Query OK, 0 rows affected (0.00 sec)
+```
+
+正常情况我们应该创建一个用户然后赋予其相应的权限,而不是将root用户配置给他.现在查看一下从结点的状态
+
+```
+mysql> show slave status\G;
+```
+
+
+
+都显示为YES的话那么我们的主从配置已经成功,现在我们在主节点创建一个test_db3数据库
+
+
+
+然后切换到从结点,可以看到数据已经同步到从结点了
+
+
+
+到这里一个简单的单主节点单从结点的MySQL架构已经搭建完毕。
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/rabbitmq/docker-compose.yml b/Docker/Compose/常用服务/rabbitmq/docker-compose.yml
new file mode 100644
index 0000000..e970f80
--- /dev/null
+++ b/Docker/Compose/常用服务/rabbitmq/docker-compose.yml
@@ -0,0 +1,29 @@
+```yaml
+version: "3"
+
+services:
+
+ rabbitmq:
+ image: rabbitmq:management
+ hostname: myrabbitmq
+ ports:
+ - "5672:5672"
+ - "15672:15672"
+ volumes:
+ - rabbitmq-data:/var/lib/rabbitmq
+
+volumes:
+ rabbitmq-data:
+```
+
+查看服务状态
+
+
+
+确定服务正常启动后在浏览器输入网址[http://localhost:15672](http://localhost:15672/#/),进入RabbitMQ的登陆界面
+
+
+
+默认用户名密码都是guest。登陆之后就可以进入到主界面了
+
+
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/traefik代理/docker-compose.yml b/Docker/Compose/常用服务/traefik代理/docker-compose.yml
new file mode 100644
index 0000000..53e1c4b
--- /dev/null
+++ b/Docker/Compose/常用服务/traefik代理/docker-compose.yml
@@ -0,0 +1,32 @@
+```yaml
+version: '2'
+
+services:
+ proxy:
+ image: traefik
+ command: --api --docker --docker.domain=docker.localhost --logLevel=DEBUG
+ networks:
+ - apinetwork
+ ports:
+ - "80:80"
+ - "8080:8080"
+ volumes:
+ - /var/run/docker.sock:/var/run/docker.sock
+ - ./traefik.toml:/etc/traefik/traefik.toml
+
+networks:
+ apinetwork:
+ external:
+ name: fileserver
+```
+
+注意需要编写traefik.toml文件
+
+```
+defaultEntryPoints = ["http"]
+insecureSkipVerify = true
+[entryPoints]
+ [entryPoints.http]
+ address = ":80"
+```
+
diff --git a/Docker/Compose/计数器/Dockerfile b/Docker/Compose/计数器/Dockerfile
new file mode 100644
index 0000000..5ef98ef
--- /dev/null
+++ b/Docker/Compose/计数器/Dockerfile
@@ -0,0 +1,6 @@
+FROM python:2.7
+COPY . /app
+WORKDIR /app
+RUN pip install flask redis
+EXPOSE 5000
+CMD [ "python", "app.py" ]
\ No newline at end of file
diff --git a/Docker/Compose/计数器/app.py b/Docker/Compose/计数器/app.py
new file mode 100644
index 0000000..45d0a23
--- /dev/null
+++ b/Docker/Compose/计数器/app.py
@@ -0,0 +1,17 @@
+from flask import Flask
+from redis import Redis
+import os
+import socket
+
+app = Flask(__name__)
+redis = Redis(host=os.environ.get('REDIS_HOST', '127.0.0.1'), port=6379)
+
+
+@app.route('/')
+def hello():
+ redis.incr('hits')
+ return 'Hello Container World! I have been seen %s times and my hostname is %s.\n' % (redis.get('hits'),socket.gethostname())
+
+
+if __name__ == "__main__":
+ app.run(host="0.0.0.0", port=5000, debug=True)
\ No newline at end of file
diff --git a/Docker/Compose/计数器/docker-compose.yml b/Docker/Compose/计数器/docker-compose.yml
new file mode 100644
index 0000000..0d87d62
--- /dev/null
+++ b/Docker/Compose/计数器/docker-compose.yml
@@ -0,0 +1,13 @@
+version: "3"
+
+services:
+
+ redis:
+ image: redis
+
+ redis-web:
+ build:
+ context: .
+ dockerfile: Dockerfile
+ environment:
+ REDIS_HOST: redis
\ No newline at end of file
diff --git a/Docker/readme.md b/Docker/readme.md
new file mode 100644
index 0000000..8246e93
--- /dev/null
+++ b/Docker/readme.md
@@ -0,0 +1,89 @@
+# Docker组队学习
+
+## 简介
+
+该目录用于存储Docker组队学习教程,该教程是与《[docker从入门到实践](https://vuepress.mirror.docker-practice.com/)》的合作项目,在经得作者同意的前提下,我们在原项目的基础上进行了整理与重构使得内容更适合与我们本期的Docker组队学习。
+
+## 目录
+
+0. 开篇词
+
+1. docker简介
+
+2. docker安装
+
+3. docker容器与镜像
+
+4. docker数据管理
+
+5. docker网络
+ 5.1. Docker 基础网络介绍
+ - 外部访问容器
+ - 容器互联
+ - 配置DNS
+
+ 5.2. Docker的网络模式
+ - Bridge 模式
+ - Host 模式
+ - None 模式
+ - Container 模式
+
+ 5.3. Docker高级网络配置
+ - 快速配置指南
+ - 容器访问控制
+ - 端口映射实现
+ - 配置docker0网桥
+ - 自定义网桥
+ - 工具和示例
+ - 编辑网络配置文件
+ - 实例:创建一个点到点连接
+
+6. docker compose
+ 6.1. 什么是docker compose
+ 6.2. 如何使用docker compose
+ 6.3. docker compose基本使用
+ 6.4. Compose模板文件
+ 6.5. Compose命令
+ 6.6. [常见服务的docker-compose.yml集合]()
+
+7. 综合实践
+
+## 贡献人员
+感谢以下Datawhale成员对项目推进作出的贡献(排名不分先后):
+
+
+
+本次教程将以一个较复杂的投票合约作为结束,我们希望实现的功能是为每个(投票)建议建立一份合约,然后作为合约的创造者-主席,主席将赋予每个成员(地址)投票权,而成员的投票权可以选择委托给其他人也可以自己投票,结束时将返回投票最多的提案。听起来很简单一个功能实现起来却较为复杂,下面我们拆分开进行讲解
+
+注:
+
+1. 代码可直接在Remix编辑器的已有solidity文件中找到,在contract/_Ballot.sol文件里
+2. 若学习者前面部分掌握较牢固,不妨尝试直接自行阅读代码,无需阅读本节内容
+
+
+首先我们定义成员类型,我们为每个投票者定义权重、是否已投票、
+
+```javascript
+struct Voter {
+ uint weight; // weight is accumulated by delegation
+ bool voted; // if true, that person already voted
+ address delegate; // person delegated to
+ uint vote; // index of the voted proposal
+}
+```
+
+然后我们定义提案类型,包含提案名和投票总数:
+
+```javascript
+struct Proposal {
+ bytes32 name; // short name (up to 32 bytes)
+ uint voteCount; // number of accumulated votes
+}
+```
+
+定义三个变量,主席是一个公开的地址,建立投票者与地址的映射,然后定义提案动态数组:
+
+```javascript
+address public chairperson;
+mapping(address => Voter) public voters;
+Proposal[] public proposals;
+```
+
+- `address public chairperson`:投票发起人,类型为 address。
+- `mapping(address => Voter) public voters`:所有投票人,类型为 `address` 到 `Voter` 的映射。
+- `Proposal[] public proposals`:所有提案,类型为动态大小的 `Proposal` 数组。
+
+3 个状态变量都使用了 `public` 关键字,使得变量可以被外部访问(即通过消息调用)。事实上,编译器会自动为 `public `的变量创建同名的 `getter` 函数,供外部直接读取。
+
+我们还需要为每个投票赋予初始权值,并将主席的权重设置为1。我们一般使用`constructor`赋初值,这与C++等语言类似:
+
+```javascript
+constructor(bytes32[] memory proposalNames) {
+ chairperson = msg.sender;
+ voters[chairperson].weight = 1;
+
+ for (uint i = 0; i < proposalNames.length; i++) {
+ proposals.push(Proposal({
+ name: proposalNames[i],
+ voteCount: 0
+ }));
+ }
+}
+```
+
+所有提案的名称通过参数 `bytes32[] proposalNames` 传入,逐个记录到状态变量 `proposals` 中。同时用 `msg.sender` 获取当前调用消息的发送者的地址,记录为投票发起人 `chairperson`,该发起人投票权重设为 1。
+
+接下来我们需要给每个投票者赋予权重:
+
+```javascript
+function giveRightToVote(address voter) public {
+ require(
+ msg.sender == chairperson,
+ "Only chairperson can give right to vote."
+ );
+ require(
+ !voters[voter].voted,
+ "The voter already voted."
+ );
+ require(voters[voter].weight == 0);
+ voters[voter].weight = 1;
+}
+```
+
+该函数给 `address voter` 赋予投票权,即将 `voter` 的投票权重设为 1,存入 `voters` 状态变量。
+
+上面这个函数只有投票发起人 `chairperson` 可以调用。这里用到了 `require((msg.sender == chairperson) && !voters[voter].voted)` 函数。如果` require` 中表达式结果为 `false`,这次调用会中止,且回滚所有状态和以太币余额的改变到调用前。但已消耗的 `Gas` 不会返还。
+
+下面一段是整段代码的重点,其作用是委托其他人代理投票,基本思路是:
+
+1. 使用`require`判断委托人是否已投票(若投过票再委托则重复投票),并判断被委托对象是否是自己
+2. 当判断被委托人不是0地址(主席)时,被委托人代理委托人的票,【绕口警告】由于被委托人也可能委托了别人,因此这里需要一直循环直到找到最后没有委托别人的被委托人为止!
+3. 委托人找到对应的被委托人,委托人已投票(避免重复投票)
+4. 判断被委托人是否已投票,若投了票则将被委托人投的提案票数加上委托人的权重,若未投票则令被委托人的权重加上委托人的权重(以后投票自然相当于投两票)
+
+注:该函数使用了 `while` 循环,这里合约编写者需要十分谨慎,防止调用者消耗过多 `Gas`,甚至出现死循环。
+
+```javascript
+function delegate(address to) public {
+ Voter storage sender = voters[msg.sender];
+ require(!sender.voted, "You already voted.");
+ require(to != msg.sender, "Self-delegation is disallowed.");
+
+ while (voters[to].delegate != address(0)) {
+ to = voters[to].delegate;
+ require(to != msg.sender, "Found loop in delegation.");
+ }
+ sender.voted = true;
+ sender.delegate = to;
+ Voter storage delegate_ = voters[to];
+ if (delegate_.voted) {
+ proposals[delegate_.vote].voteCount += sender.weight;
+ } else {
+ delegate_.weight += sender.weight;
+ }
+}
+```
+
+投票部分仅是几个简单的条件判断:
+
+```javascript
+function vote(uint proposal) public {
+ Voter storage sender = voters[msg.sender];
+ require(sender.weight != 0, "Has no right to vote");
+ require(!sender.voted, "Already voted.");
+ sender.voted = true;
+ sender.vote = proposal;
+ proposals[proposal].voteCount += sender.weight;
+ }
+```
+
+用 `voters[msg.sender]` 获取投票人,即此次调用的发起人。接下来检查是否是重复投票,如果不是,进行投票后相关状态变量的更新。
+
+接下来是计算获胜提案:
+
+```javascript
+function winningProposal() public view
+ returns (uint winningProposal_)
+{
+ uint winningVoteCount = 0;
+ for (uint p = 0; p < proposals.length; p++) {
+ if (proposals[p].voteCount > winningVoteCount) {
+ winningVoteCount = proposals[p].voteCount;
+ winningProposal_ = p;
+ }
+ }
+}
+```
+
+`returns (uint winningProposal)` 指定了函数的返回值类型,`constant` 表示该函数不会改变合约状态变量的值。
+
+最后是查询获胜者名称:
+
+```javascript
+function winnerName() public view
+ returns (bytes32 winnerName_)
+{
+ winnerName_ = proposals[winningProposal()].name;
+}
+```
+
+这里采用内部调用 `winningProposal()` 函数的方式获得获胜提案。如果需要采用外部调用,则需要写为 `this.winningProposal()`。
+
+
+
+**参考自:**
+
+[尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
+[web3.js 1.0中文手册](http://cw.hubwiz.com/card/c/web3.js-1.0/)
+
diff --git a/Blockchain/pic/2021-02-19_110327.png b/Blockchain/pic/2021-02-19_110327.png
new file mode 100644
index 0000000..7b03f57
Binary files /dev/null and b/Blockchain/pic/2021-02-19_110327.png differ
diff --git a/Blockchain/pic/2021-02-19_120756.png b/Blockchain/pic/2021-02-19_120756.png
new file mode 100644
index 0000000..f3e64de
Binary files /dev/null and b/Blockchain/pic/2021-02-19_120756.png differ
diff --git a/Blockchain/pic/2021-02-19_125917.png b/Blockchain/pic/2021-02-19_125917.png
new file mode 100644
index 0000000..2d77359
Binary files /dev/null and b/Blockchain/pic/2021-02-19_125917.png differ
diff --git a/Blockchain/pic/2021-02-19_130053.png b/Blockchain/pic/2021-02-19_130053.png
new file mode 100644
index 0000000..35b98d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_130053.png differ
diff --git a/Blockchain/pic/2021-02-19_133508.png b/Blockchain/pic/2021-02-19_133508.png
new file mode 100644
index 0000000..78c5567
Binary files /dev/null and b/Blockchain/pic/2021-02-19_133508.png differ
diff --git a/Blockchain/pic/2021-02-19_134110.png b/Blockchain/pic/2021-02-19_134110.png
new file mode 100644
index 0000000..c7e7ba5
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134110.png differ
diff --git a/Blockchain/pic/2021-02-19_134257.png b/Blockchain/pic/2021-02-19_134257.png
new file mode 100644
index 0000000..75d426b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134257.png differ
diff --git a/Blockchain/pic/2021-02-19_134634.png b/Blockchain/pic/2021-02-19_134634.png
new file mode 100644
index 0000000..eb63545
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134634.png differ
diff --git a/Blockchain/pic/2021-02-19_135113.png b/Blockchain/pic/2021-02-19_135113.png
new file mode 100644
index 0000000..a8f69cc
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135113.png differ
diff --git a/Blockchain/pic/2021-02-19_135337.png b/Blockchain/pic/2021-02-19_135337.png
new file mode 100644
index 0000000..1b3998b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135337.png differ
diff --git a/Blockchain/pic/2021-02-19_135413.png b/Blockchain/pic/2021-02-19_135413.png
new file mode 100644
index 0000000..b24c373
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135413.png differ
diff --git a/Blockchain/pic/2021-02-19_142407.png b/Blockchain/pic/2021-02-19_142407.png
new file mode 100644
index 0000000..10704d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_142407.png differ
diff --git a/Blockchain/pic/EOA_CA.png b/Blockchain/pic/EOA_CA.png
new file mode 100644
index 0000000..9612e9b
Binary files /dev/null and b/Blockchain/pic/EOA_CA.png differ
diff --git a/Blockchain/pic/aaaaaa b/Blockchain/pic/aaaaaa
new file mode 100644
index 0000000..8b13789
--- /dev/null
+++ b/Blockchain/pic/aaaaaa
@@ -0,0 +1 @@
+
diff --git a/Blockchain/pic/bg2017122703.png b/Blockchain/pic/bg2017122703.png
new file mode 100644
index 0000000..5c91bc5
Binary files /dev/null and b/Blockchain/pic/bg2017122703.png differ
diff --git a/Blockchain/pic/gas.jpg b/Blockchain/pic/gas.jpg
new file mode 100644
index 0000000..13bd71c
Binary files /dev/null and b/Blockchain/pic/gas.jpg differ
diff --git a/Blockchain/pic/image-20210219000835894.png b/Blockchain/pic/image-20210219000835894.png
new file mode 100644
index 0000000..5fea35e
Binary files /dev/null and b/Blockchain/pic/image-20210219000835894.png differ
diff --git a/Blockchain/pic/image-20210219101124978.png b/Blockchain/pic/image-20210219101124978.png
new file mode 100644
index 0000000..28411df
Binary files /dev/null and b/Blockchain/pic/image-20210219101124978.png differ
diff --git a/Blockchain/pic/image-20210219101226095.png b/Blockchain/pic/image-20210219101226095.png
new file mode 100644
index 0000000..8ddead4
Binary files /dev/null and b/Blockchain/pic/image-20210219101226095.png differ
diff --git a/Blockchain/pic/image-20210219101300792.png b/Blockchain/pic/image-20210219101300792.png
new file mode 100644
index 0000000..2dcad74
Binary files /dev/null and b/Blockchain/pic/image-20210219101300792.png differ
diff --git a/Blockchain/pic/image-20210219101332089.png b/Blockchain/pic/image-20210219101332089.png
new file mode 100644
index 0000000..e74b090
Binary files /dev/null and b/Blockchain/pic/image-20210219101332089.png differ
diff --git a/Blockchain/pic/image-20210219102028033.png b/Blockchain/pic/image-20210219102028033.png
new file mode 100644
index 0000000..966feb4
Binary files /dev/null and b/Blockchain/pic/image-20210219102028033.png differ
diff --git a/Blockchain/pic/image-20210219102255927.png b/Blockchain/pic/image-20210219102255927.png
new file mode 100644
index 0000000..8acef84
Binary files /dev/null and b/Blockchain/pic/image-20210219102255927.png differ
diff --git a/Blockchain/pic/image-20210219102322360.png b/Blockchain/pic/image-20210219102322360.png
new file mode 100644
index 0000000..513c9de
Binary files /dev/null and b/Blockchain/pic/image-20210219102322360.png differ
diff --git a/Blockchain/pic/image-20210219102359096.png b/Blockchain/pic/image-20210219102359096.png
new file mode 100644
index 0000000..aa9a394
Binary files /dev/null and b/Blockchain/pic/image-20210219102359096.png differ
diff --git a/Blockchain/pic/image-20210219105522149.png b/Blockchain/pic/image-20210219105522149.png
new file mode 100644
index 0000000..f3e6648
Binary files /dev/null and b/Blockchain/pic/image-20210219105522149.png differ
diff --git a/Blockchain/pic/image-20210219105616335.png b/Blockchain/pic/image-20210219105616335.png
new file mode 100644
index 0000000..a23c2dd
Binary files /dev/null and b/Blockchain/pic/image-20210219105616335.png differ
diff --git a/Blockchain/pic/image-20210219105824087.png b/Blockchain/pic/image-20210219105824087.png
new file mode 100644
index 0000000..c03a2b4
Binary files /dev/null and b/Blockchain/pic/image-20210219105824087.png differ
diff --git a/Blockchain/pic/image-20210219105911910.png b/Blockchain/pic/image-20210219105911910.png
new file mode 100644
index 0000000..eff8c5c
Binary files /dev/null and b/Blockchain/pic/image-20210219105911910.png differ
diff --git a/Blockchain/pic/image1.png b/Blockchain/pic/image1.png
new file mode 100644
index 0000000..8435a7e
Binary files /dev/null and b/Blockchain/pic/image1.png differ
diff --git a/Blockchain/pic/image2.png b/Blockchain/pic/image2.png
new file mode 100644
index 0000000..5688b8c
Binary files /dev/null and b/Blockchain/pic/image2.png differ
diff --git a/Blockchain/pic/image3.png b/Blockchain/pic/image3.png
new file mode 100644
index 0000000..c3bfdca
Binary files /dev/null and b/Blockchain/pic/image3.png differ
diff --git a/Blockchain/pic/image4.png b/Blockchain/pic/image4.png
new file mode 100644
index 0000000..3ce8d94
Binary files /dev/null and b/Blockchain/pic/image4.png differ
diff --git a/Blockchain/pic/image5.png b/Blockchain/pic/image5.png
new file mode 100644
index 0000000..3038f58
Binary files /dev/null and b/Blockchain/pic/image5.png differ
diff --git a/Blockchain/pic/image6.png b/Blockchain/pic/image6.png
new file mode 100644
index 0000000..82f5ecc
Binary files /dev/null and b/Blockchain/pic/image6.png differ
diff --git a/Blockchain/pic/part2-1.png b/Blockchain/pic/part2-1.png
new file mode 100644
index 0000000..8c0da19
Binary files /dev/null and b/Blockchain/pic/part2-1.png differ
diff --git a/Blockchain/pic/part2-10.png b/Blockchain/pic/part2-10.png
new file mode 100644
index 0000000..f0b447e
Binary files /dev/null and b/Blockchain/pic/part2-10.png differ
diff --git a/Blockchain/pic/part2-11.png b/Blockchain/pic/part2-11.png
new file mode 100644
index 0000000..06cca10
Binary files /dev/null and b/Blockchain/pic/part2-11.png differ
diff --git a/Blockchain/pic/part2-12.png b/Blockchain/pic/part2-12.png
new file mode 100644
index 0000000..5eb5b8e
Binary files /dev/null and b/Blockchain/pic/part2-12.png differ
diff --git a/Blockchain/pic/part2-13.png b/Blockchain/pic/part2-13.png
new file mode 100644
index 0000000..e9433fa
Binary files /dev/null and b/Blockchain/pic/part2-13.png differ
diff --git a/Blockchain/pic/part2-14.png b/Blockchain/pic/part2-14.png
new file mode 100644
index 0000000..f87ff72
Binary files /dev/null and b/Blockchain/pic/part2-14.png differ
diff --git a/Blockchain/pic/part2-15.png b/Blockchain/pic/part2-15.png
new file mode 100644
index 0000000..abebc5d
Binary files /dev/null and b/Blockchain/pic/part2-15.png differ
diff --git a/Blockchain/pic/part2-16.png b/Blockchain/pic/part2-16.png
new file mode 100644
index 0000000..7a91692
Binary files /dev/null and b/Blockchain/pic/part2-16.png differ
diff --git a/Blockchain/pic/part2-17.png b/Blockchain/pic/part2-17.png
new file mode 100644
index 0000000..d831f99
Binary files /dev/null and b/Blockchain/pic/part2-17.png differ
diff --git a/Blockchain/pic/part2-18.png b/Blockchain/pic/part2-18.png
new file mode 100644
index 0000000..c42e156
Binary files /dev/null and b/Blockchain/pic/part2-18.png differ
diff --git a/Blockchain/pic/part2-19.png b/Blockchain/pic/part2-19.png
new file mode 100644
index 0000000..cf84b29
Binary files /dev/null and b/Blockchain/pic/part2-19.png differ
diff --git a/Blockchain/pic/part2-2.png b/Blockchain/pic/part2-2.png
new file mode 100644
index 0000000..a8ecb2c
Binary files /dev/null and b/Blockchain/pic/part2-2.png differ
diff --git a/Blockchain/pic/part2-20.png b/Blockchain/pic/part2-20.png
new file mode 100644
index 0000000..cf3cb04
Binary files /dev/null and b/Blockchain/pic/part2-20.png differ
diff --git a/Blockchain/pic/part2-21.png b/Blockchain/pic/part2-21.png
new file mode 100644
index 0000000..84896de
Binary files /dev/null and b/Blockchain/pic/part2-21.png differ
diff --git a/Blockchain/pic/part2-22.png b/Blockchain/pic/part2-22.png
new file mode 100644
index 0000000..db238cf
Binary files /dev/null and b/Blockchain/pic/part2-22.png differ
diff --git a/Blockchain/pic/part2-23.png b/Blockchain/pic/part2-23.png
new file mode 100644
index 0000000..256124b
Binary files /dev/null and b/Blockchain/pic/part2-23.png differ
diff --git a/Blockchain/pic/part2-24.png b/Blockchain/pic/part2-24.png
new file mode 100644
index 0000000..6007692
Binary files /dev/null and b/Blockchain/pic/part2-24.png differ
diff --git a/Blockchain/pic/part2-3.png b/Blockchain/pic/part2-3.png
new file mode 100644
index 0000000..1ff0dda
Binary files /dev/null and b/Blockchain/pic/part2-3.png differ
diff --git a/Blockchain/pic/part2-4.png b/Blockchain/pic/part2-4.png
new file mode 100644
index 0000000..8879b10
Binary files /dev/null and b/Blockchain/pic/part2-4.png differ
diff --git a/Blockchain/pic/part2-5.png b/Blockchain/pic/part2-5.png
new file mode 100644
index 0000000..6308a3d
Binary files /dev/null and b/Blockchain/pic/part2-5.png differ
diff --git a/Blockchain/pic/part2-6.png b/Blockchain/pic/part2-6.png
new file mode 100644
index 0000000..debad8c
Binary files /dev/null and b/Blockchain/pic/part2-6.png differ
diff --git a/Blockchain/pic/part2-7.png b/Blockchain/pic/part2-7.png
new file mode 100644
index 0000000..f9a3ea0
Binary files /dev/null and b/Blockchain/pic/part2-7.png differ
diff --git a/Blockchain/pic/part2-8.png b/Blockchain/pic/part2-8.png
new file mode 100644
index 0000000..ed642a5
Binary files /dev/null and b/Blockchain/pic/part2-8.png differ
diff --git a/Blockchain/pic/part2-9.png b/Blockchain/pic/part2-9.png
new file mode 100644
index 0000000..8c1e817
Binary files /dev/null and b/Blockchain/pic/part2-9.png differ
diff --git a/Blockchain/pic/part3-1.png b/Blockchain/pic/part3-1.png
new file mode 100644
index 0000000..094515c
Binary files /dev/null and b/Blockchain/pic/part3-1.png differ
diff --git a/Blockchain/pic/part3-10.png b/Blockchain/pic/part3-10.png
new file mode 100644
index 0000000..1c2c0c6
Binary files /dev/null and b/Blockchain/pic/part3-10.png differ
diff --git a/Blockchain/pic/part3-11.png b/Blockchain/pic/part3-11.png
new file mode 100644
index 0000000..d6f6474
Binary files /dev/null and b/Blockchain/pic/part3-11.png differ
diff --git a/Blockchain/pic/part3-12.png b/Blockchain/pic/part3-12.png
new file mode 100644
index 0000000..30c4582
Binary files /dev/null and b/Blockchain/pic/part3-12.png differ
diff --git a/Blockchain/pic/part3-13.png b/Blockchain/pic/part3-13.png
new file mode 100644
index 0000000..a1f9783
Binary files /dev/null and b/Blockchain/pic/part3-13.png differ
diff --git a/Blockchain/pic/part3-2.png b/Blockchain/pic/part3-2.png
new file mode 100644
index 0000000..2d74cd1
Binary files /dev/null and b/Blockchain/pic/part3-2.png differ
diff --git a/Blockchain/pic/part3-3.png b/Blockchain/pic/part3-3.png
new file mode 100644
index 0000000..824fd9b
Binary files /dev/null and b/Blockchain/pic/part3-3.png differ
diff --git a/Blockchain/pic/part3-4.png b/Blockchain/pic/part3-4.png
new file mode 100644
index 0000000..152a017
Binary files /dev/null and b/Blockchain/pic/part3-4.png differ
diff --git a/Blockchain/pic/part3-5.png b/Blockchain/pic/part3-5.png
new file mode 100644
index 0000000..9b62fe6
Binary files /dev/null and b/Blockchain/pic/part3-5.png differ
diff --git a/Blockchain/pic/part3-6.png b/Blockchain/pic/part3-6.png
new file mode 100644
index 0000000..00e7473
Binary files /dev/null and b/Blockchain/pic/part3-6.png differ
diff --git a/Blockchain/pic/part3-7.png b/Blockchain/pic/part3-7.png
new file mode 100644
index 0000000..f6dfe7a
Binary files /dev/null and b/Blockchain/pic/part3-7.png differ
diff --git a/Blockchain/pic/part3-8.png b/Blockchain/pic/part3-8.png
new file mode 100644
index 0000000..212eb36
Binary files /dev/null and b/Blockchain/pic/part3-8.png differ
diff --git a/Blockchain/pic/part3-9.png b/Blockchain/pic/part3-9.png
new file mode 100644
index 0000000..567481f
Binary files /dev/null and b/Blockchain/pic/part3-9.png differ
diff --git a/Blockchain/pic/picfile b/Blockchain/pic/picfile
new file mode 100644
index 0000000..ca8de66
--- /dev/null
+++ b/Blockchain/pic/picfile
@@ -0,0 +1 @@
+This folder contains some necessary picture
diff --git a/Blockchain/pic/rating.png b/Blockchain/pic/rating.png
new file mode 100644
index 0000000..204d972
Binary files /dev/null and b/Blockchain/pic/rating.png differ
diff --git a/Blockchain/pic/transaction-struct.png b/Blockchain/pic/transaction-struct.png
new file mode 100644
index 0000000..da26c42
Binary files /dev/null and b/Blockchain/pic/transaction-struct.png differ
diff --git a/Blockchain/pic/utxo_com.jpg b/Blockchain/pic/utxo_com.jpg
new file mode 100644
index 0000000..77c03d0
Binary files /dev/null and b/Blockchain/pic/utxo_com.jpg differ
diff --git a/Blockchain/readme.md b/Blockchain/readme.md
new file mode 100644
index 0000000..6fb3759
--- /dev/null
+++ b/Blockchain/readme.md
@@ -0,0 +1,46 @@
+# 1. 编程实践(区块链)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/Blockchain
+
+## 基本信息
+
+- 贡献人员:陈锴、孙子涵、李岳昆、易远哲
+- 学习周期:12天
+- 学习形式:根据教程主线进行学习
+- 人群定位:具有至少一门编程语言基础,在开展组队学习之前能够熟悉 Linux 基本操作
+- 难度系数:较难
+
+## 学习目标
+
+## 任务安排
+
+### Task00:熟悉规则并先修Linux(2天)
+
+- 组队、修改群昵称
+- 熟悉打卡规则
+- 对Linux不太熟悉的学习者先安装Linux环境(可以是虚拟机或子系统)并掌握基本命令,其他内容可以暂不了解
+
+### Task01:区块链简介与以太坊入门介绍(2天)
+
+* 学习者学习区块链基础与以太坊入门介绍,该部分以了解为主
+* 学习者可以根据教程提供的各个方面内容,对某一部分深入了解并进行打卡
+* 打卡截至时间:3月16日24:00
+
+### Task02:Solidity基础(3天)
+
+* 学习者学习Solidity在线编辑器Remix的使用以及Solidity的基础操作,该部分需要深入掌握,学习者可以根据参考链接提供的资料进一步学习
+* 打卡内容为Task02最后的Solidity练习题部分,其他内容不作硬性要求
+* 打卡截止日期:3月19日24:00
+
+### Task03:web3js基础(3天)
+
+* 学习者学习以太坊客户端的使用以及Geth控制台部署智能合约
+* 打卡内容为学习者完成一个自己编写的合约的部署,并测试函数调用等
+* 打卡截止日期:3月22日24:00
+
+### Task04:合约编写实战实例(2天)
+
+* 学习者学习编写几个Remix官网自带的合约,并回顾 Task01的教程内容重新梳理知识点
+* 打卡内容为学习者自己的学习感悟,内容不限
+* 打卡截止日期:3月23日24:00
+
diff --git a/Docker/00 开篇词.md b/Docker/00 开篇词.md
new file mode 100644
index 0000000..df37501
--- /dev/null
+++ b/Docker/00 开篇词.md
@@ -0,0 +1,24 @@
+# Chapter 0 开篇词
+
+相信大家在开发项目尤其是团队合作项目中一定会遇到下面这些场景:
+
+- 项目在我电脑上明明运行的很好呀!怎么在你这不行了呢?
+- 我这是用python 3.6写的,你电脑是python 2.7应该运行不了。
+- 项目的一些依赖包需要科学上网才能下载,你那没有的话赶紧下载一下才能运行。
+- 论文的代码已经公开到github上了,但是因为自己电脑环境和他的不一样,项目在自己电脑上死活跑不起来。
+
+以上这些问题我相信大家并不陌生,那么通过本次Docker的组队学习,希望大家能够避免卡在科研或者开发的第一步,提高自己的生产力。
+
+---
+
+通过本次docker的组队学习,我们希望你能学到以下几个方面的能力:
+
+- 了解什么是docker
+- docker镜像是怎么构建的
+- 如何运行一个docker容器
+- docker之间的网络通信是怎么样的
+- docker中的数据如何做持久化存储
+- 如何通过docker compose管理自己的项目
+- 如何将自己的个人项目打造成容器化部署的形式
+
+祝你在docker的学习上一切顺利!
\ No newline at end of file
diff --git a/Docker/04 Docker数据管理.md b/Docker/04 Docker数据管理.md
new file mode 100644
index 0000000..4283a12
--- /dev/null
+++ b/Docker/04 Docker数据管理.md
@@ -0,0 +1,176 @@
+# Chapter 4 Docker 数据管理
+
+这一章介绍如何在 Docker 内部以及容器之间管理数据,在容器中管理数据主要有两种方式:
+
+* 数据卷
+* 挂载主机目录
+
+
+## 数据卷
+
+数据卷是一个可供一个或多个容器使用的特殊目录,它绕过 UFS (UNIX File System) ,可以提供很多有用的特性:
+
+* 数据卷可以在容器之间共享和重用
+
+* 对数据卷的修改会立马生效
+
+* 对数据卷的更新,不会影响镜像
+
+* 数据卷默认会一直存在,即使容器被删除
+
+>注意:数据卷的使用,类似于 Linux 下对目录或文件进行 mount,镜像中的被指定为挂载点的目录中的文件会复制到数据卷中(仅数据卷为空时会复制)。
+
+### 创建一个数据卷
+
+```bash
+$ docker volume create datawhale
+```
+
+查看所有的数据卷
+
+```bash
+$ docker volume ls
+
+DRIVER VOLUME NAME
+local datawhale
+```
+
+在主机里使用以下命令可以查看指定数据卷的信息
+
+```bash
+$ docker volume inspect datawhale
+[
+ {
+ "Driver": "local",
+ "Labels": {},
+ "Mountpoint": "/var/lib/docker/volumes/datawhale/_data",
+ "Name": "datawhale",
+ "Options": {},
+ "Scope": "local"
+ }
+]
+```
+
+### 启动一个挂载数据卷的容器
+
+在用 `docker run` 命令的时候,使用 `--mount` 标记来将数据卷挂载到容器里。在一次 `docker run` 中可以挂载多个 `数据卷`。
+
+下面创建一个名为 `web` 的容器,并加载一个数据卷到容器的 `/usr/share/nginx/html` 目录。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount source=datawhale,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+>–-mount参数说明:
+> source :数据卷
+> target :是容器内文件系统挂载点
+
+>注意,可以不需要提前创建好数据卷,直接在运行容器的时候mount 这时如果不存在指定的数据卷,docker会自动创建,自动生成。
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`数据卷` 信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "volume",
+ "Name": "datawhale",
+ "Source": "/var/lib/docker/volumes/datawhale/_data",
+ "Destination": "/usr/share/nginx/html",
+ "Driver": "local",
+ "Mode": "",
+ "RW": true,
+ "Propagation": ""
+ }
+],
+```
+
+### 删除数据卷
+
+```bash
+$ docker volume rm datawhale #datawhale为卷名
+```
+
+数据卷是被设计用来持久化数据的,它的生命周期独立于容器,Docker 不会在容器被删除后自动删除 `数据卷`,并且也不存在垃圾回收这样的机制来处理没有任何容器引用的 `数据卷`。如果需要在删除容器的同时移除数据卷。可以在删除容器的时候使用 `docker rm -v` 这个命令。
+
+无主的数据卷可能会占据很多空间,要清理请使用以下命令
+
+```bash
+$ docker volume prune
+```
+
+## 挂载主机目录
+
+### 挂载一个主机目录作为数据卷
+
+使用 `--mount` 标记可以指定挂载一个本地主机的目录到容器中去。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+
+上面的命令加载主机的 `/src/webapp` 目录到容器的 `/usr/share/nginx/html`目录。这个功能在进行测试的时候十分方便,比如用户可以放置一些程序到本地目录中,来查看容器是否正常工作。本地目录的路径必须是绝对路径,以前使用 `-v` 参数时如果本地目录不存在 Docker 会自动为你创建一个文件夹,现在使用 `--mount` 参数时如果本地目录不存在,Docker 会报错。
+
+Docker 挂载主机目录的默认权限是 `读写`,用户也可以通过增加 `readonly` 指定为 `只读`。
+
+>注意: 如果挂载的目录不存在,创建容器时,docker 不会自动创建,此时会报错
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html,readonly \
+ nginx:alpine
+```
+
+加了 `readonly` 之后,就挂载为 `只读` 了。如果你在容器内 `/usr/share/nginx/html` 目录新建文件,会显示如下错误
+
+```bash
+/usr/share/nginx/html # touch new.txt
+touch: new.txt: Read-only file system
+```
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`挂载主机目录` 的配置信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "bind",
+ "Source": "/src/webapp",
+ "Destination": "/usr/share/nginx/html",
+ "Mode": "",
+ "RW": true,
+ "Propagation": "rprivate"
+ }
+],
+```
+
+### 挂载一个本地主机文件作为数据卷
+
+`--mount` 标记也可以从主机挂载单个文件到容器中
+
+```bash
+$ docker run --rm -it \
+ --mount type=bind,source=$HOME/.bash_history,target=/root/.bash_history \
+ ubuntu:18.04 \
+ bash
+```
diff --git a/Docker/05 Docker网络.md b/Docker/05 Docker网络.md
new file mode 100644
index 0000000..5747442
--- /dev/null
+++ b/Docker/05 Docker网络.md
@@ -0,0 +1,783 @@
+# Chapter 5 Docker 网络
+
+## 内容大纲
+
+### Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+### Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+### Docker高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+
+
+# Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+## 外部访问容器
+
+容器中可以运行一些网络应用,要让外部也可以访问这些应用,可以通过`-P`或`-p`参数来指定端口映射。
+
+当使用`-P`标记时,`Docker`会随机映射一个端口到内部容器开放的网络端口。
+使用`docker container ls`可以看到,本地主机的 32768 被映射到了容器的 80 端口。此时访问本机的 32768 端口即可访问容器内 NGINX 默认页面。
+
+```
+$ docker run -d -P nginx:alpine
+
+$ docker container ls -l
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+fae320d08268 nginx:alpine "/docker-entrypoint.…" 24 seconds ago Up 20 seconds 0.0.0.0:32768->80/tcp bold_mcnulty
+```
+
+同样的,可以通过`docker logs`命令来查看访问记录。
+
+```
+$ docker logs fa
+172.17.0.1 - - [25/Aug/2020:08:34:04 +0000] "GET / HTTP/1.1" 200 612 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:80.0) Gecko/20100101 Firefox/80.0" "-"
+```
+
+`-p`则可以指定要映射的端口,并且,在一个指定端口上只可以绑定一个容器。支持的格式有`ip:hostPort:containerPort | ip::containerPort | hostPort:containerPort`.
+
+### 映射所有接口地址
+
+使用`hostPort:containerPort`格式本地的 80 端口映射到容器的 80 端口,可以执行
+
+```
+$ docker run -d -p 80:80 nginx:alpine
+```
+
+此时默认会绑定本地所有接口上的所有地址。
+
+### 映射到指定地址的指定端口
+
+可以使用`ip:hostPort:containerPort`格式指定映射使用一个特定地址,比如`localhost`地址127.0.0.1
+
+```
+$ docker run -d -p 127.0.0.1:80:80 nginx:alpine
+```
+
+### 映射到指定地址的任意端口
+
+使用`ip::containerPort`绑定`localhost`的任意端口到容器的80端口,本地主机会自动分配一个端口。
+
+```
+$ docker run -d -p 127.0.0.1::80 nginx:alpine
+```
+
+还可以使用`udp`标记来指定`udp`端口
+
+```
+$ docker run -d -p 127.0.0.1:80:80/udp nginx:alpine
+```
+
+### 查看映射端口配置
+
+使用`docker port`来查看当前映射的端口配置,也可以查看到绑定的地址
+
+```
+$ docker port fa 80
+0.0.0.0:32768
+```
+
+**注意:**
+容器有自己的内部网络和 ip 地址(使用`docker inspect`查看,`Docker`还可以有一个可变的网络配置。)
+`-p`标记可以多次使用来绑定多个端口
+
+例如
+
+```
+$ docker run -d \
+ -p 80:80 \
+ -p 443:443 \
+ nginx:alpine
+```
+
+## 容器互联
+
+如果之前有 `Docker`使用经验,可能已经习惯了使用`--link`参数来使容器互联。
+随着 `Docker` 网络的完善,强烈建议大家将容器加入自定义的`Docker`网络来连接多个容器,而不是使用 `--link`参数。
+
+### 新建网络
+
+下面先创建一个新的 `Docker`网络。
+
+```
+$ docker network create -d bridge my-net
+```
+
+`-d`参数指定`Docker`网络类型,有`bridge overlay`,其中`overlay`网络类型用于`Swarm mode`,在本小节中你可以忽略它。
+
+### 连接容器
+
+运行一个容器并连接到新建的`my-net`网络
+
+```
+$ docker run -it --rm --name busybox1 --network my-net busybox sh
+```
+
+打开新的终端,再运行一个容器并加入到 `my-net`网络
+
+```
+$ docker run -it --rm --name busybox2 --network my-net busybox sh
+```
+
+再打开一个新的终端查看容器信息
+
+```
+$ docker container ls
+
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+b47060aca56b busybox "sh" 11 minutes ago Up 11 minutes busybox2
+8720575823ec busybox "sh" 16 minutes ago Up 16 minutes busybox1
+```
+
+下面通过 `ping`来证明`busybox1`容器和`busybox2`容器建立了互联关系。
+在`busybox1`容器输入以下命令
+
+```
+/ # ping busybox2
+PING busybox2 (172.19.0.3): 56 data bytes
+64 bytes from 172.19.0.3: seq=0 ttl=64 time=0.072 ms
+64 bytes from 172.19.0.3: seq=1 ttl=64 time=0.118 ms
+```
+
+用`ping`来测试连接`busybox2`容器,它会解析成 172.19.0.3。
+同理在`busybox2`容器执行`ping busybox1`,也会成功连接到。
+
+```
+/ # ping busybox1
+PING busybox1 (172.19.0.2): 56 data bytes
+64 bytes from 172.19.0.2: seq=0 ttl=64 time=0.064 ms
+64 bytes from 172.19.0.2: seq=1 ttl=64 time=0.143 ms
+```
+
+这样,`busybox1` 容器和 `busybox2` 容器建立了互联关系。
+
+`Docker Compose`
+如果你有多个容器之间需要互相连接,推荐使用`Docker`Compose。
+
+## 配置DNS
+
+如何自定义配置容器的主机名和 DNS 呢?秘诀就是`Docker`利用虚拟文件来挂载容器的 3个相关配置文件。
+
+在容器中使用 `mount`命令可以看到挂载信息:
+
+```
+$ mount
+/dev/disk/by-uuid/1fec...ebdf on /etc/hostname type ext4 ...
+/dev/disk/by-uuid/1fec...ebdf on /etc/hosts type ext4 ...
+tmpfs on /etc/resolv.conf type tmpfs ...
+```
+
+这种机制可以让宿主主机 DNS 信息发生更新后,所有`Docker`容器的 DNS 配置通过 `/etc/resolv.conf`文件立刻得到更新。
+
+配置全部容器的 DNS ,也可以在 `/etc/docker/daemon.json` 文件中增加以下内容来设置。
+
+```
+{
+ "dns" : [
+ "114.114.114.114",
+ "8.8.8.8"
+ ]
+}
+```
+
+这样每次启动的容器 DNS 自动配置为 114.114.114.114 和8.8.8.8。使用以下命令来证明其已经生效。
+
+```
+$ docker run -it --rm ubuntu:18.04 cat etc/resolv.conf
+
+nameserver 114.114.114.114
+nameserver 8.8.8.8
+```
+
+如果用户想要手动指定容器的配置,可以在使用`docker run`命令启动容器时加入如下参数:
+`-h HOSTNAME`或者`--hostname=HOSTNAME`设定容器的主机名,它会被写到容器内的`/etc/hostname 和 /etc/hosts`。但它在容器外部看不到,既不会在`docker container ls`中显示,也不会在其他的容器的`/etc/hosts`看到。
+
+`--dns=IP_ADDRESS`添加 DNS 服务器到容器的`/etc/resolv.conf`中,让容器用这个服务器来解析所有不在 `/etc/hosts `中的主机名。
+
+`--dns-search=DOMAIN`设定容器的搜索域,当设定搜索域为`.example.com`时,在搜索一个名为`host`的主机时,DNS 不仅搜索 `host`,还会搜索`host.example.com`。
+
+**注意:**如果在容器启动时没有指定最后两个参数,`Docker`会默认用主机上的`/etc/resolv.conf`来配置容器。
+
+# Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+可以通过`docker network ls`查看网络,默认创建三种网络。
+
+```
+[root@localhost ~]# docker network ls
+NETWORK ID NAME DRIVER SCOPE
+688d1970f72e bridge bridge local
+885da101da7d host host local
+f4f1b3cf1b7f none null local
+```
+
+常见网络的含义:
+
+| 网络模式 | 简介 |
+| :-------: | :----------------------------------------------------------: |
+| Bridge | 为每一个容器分配、设置 IP 等,并将容器连接到一个 `docker0` 虚拟网桥,默认为该模式。 |
+| Host | 容器将不会虚拟出自己的网卡,配置自己的 IP 等,而是使用宿主机的 IP 和端口。 |
+| None | 容器有独立的 Network namespace,但并没有对其进行任何网络设置,如分配 veth pair 和网桥连接,IP 等。 |
+| Container | 新创建的容器不会创建自己的网卡和配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等。 |
+
+## Bridge模式
+
+当`Docker`进程启动时,会在主机上创建一个名为`docker0`的虚拟网桥,此主机上启动的`Docker`容器会连接到这个虚拟网桥上,附加在其上的任何网卡之间都能自动转发数据包。虚拟网桥的工作方式和物理交换机类似,这样主机上的所有容器就通过交换机连在了一个二层网络中。从`docker0`子网中分配一个 IP 给容器使用,并设置 `docker0 `的 IP 地址为容器的默认网关。在主机上创建一对虚拟网卡`veth pair`设备,`Docker `将 `veth pair` 设备的一端放在新创建的容器中,并命名为`eth0`(容器的网卡),另一端放在主机中,以`vethxxx`这样类似的名字命名,并将这个网络设备加入到 `docker0` 网桥中。可以通过`brctl show`命令查看。
+
+比如运行一个基于 `busybox` 镜像构建的容器 `bbox01`,查看 `ip addr`:
+
+> busybox 被称为嵌入式 Linux 的瑞士军刀,整合了很多小的 unix 下的通用功能到一个小的可执行文件中。
+
+
+
+然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 通过以上的比较可以发现,证实了之前所说的:守护进程会创建一对对等虚拟设备接口 `veth pair`,将其中一个接口设置为容器的 `eth0` 接口(容器的网卡),另一个接口放置在宿主机的命名空间中,以类似 `vethxxx` 这样的名字命名。
+
+ 同时,守护进程还会从网桥 `docker0` 的私有地址空间中分配一个 IP 地址和子网给该容器,并设置 docker0 的 IP 地址为容器的默认网关。也可以安装 `yum install -y bridge-utils` 以后,通过 `brctl show` 命令查看网桥信息。
+
+
+
+ 对于每个容器的 IP 地址和 Gateway 信息,可以通过 `docker inspect 容器名称|ID` 进行查看,在 `NetworkSettings` 节点中可以看到详细信息。
+
+
+
+ 可以通过 `docker network inspect bridge` 查看所有 `bridge` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+> 关于 `bridge` 网络模式的使用,只需要在创建容器时通过参数 `--net bridge` 或者 `--network bridge` 指定即可,当然这也是创建容器默认使用的网络模式,也就是说这个参数是可以省略的。
+
+
+
+
+
+bridge模式是 `docker `的默认网络模式,不写`–net`参数,就是bridge模式。使用`docker run -p`时,`docker `实际是在`iptables`做了`DNAT`规则,实现端口转发功能。可以使用`iptables -t nat -vnL`查看。`bridge`模式如下图所示:
+
+ 演示:
+
+ ```
+$ docker run -tid --net=bridge --name docker_bri1 \
+ ubuntu-base:v3
+ docker run -tid --net=bridge --name docker_bri2 \
+ ubuntu-base:v3
+
+$ brctl show
+$ docker exec -ti docker_bri1 /bin/bash
+$ ifconfig –a
+$ route –n
+ ```
+
+
+
+## Host 模式
+
+- host 网络模式需要在创建容器时通过参数 `--net host` 或者 `--network host` 指定;
+- 采用 host 网络模式的 Docker Container,可以直接使用宿主机的 IP 地址与外界进行通信,若宿主机的 eth0 是一个公有 IP,那么容器也拥有这个公有 IP。同时容器内服务的端口也可以使用宿主机的端口,无需额外进行 NAT 转换;
+- host 网络模式可以让容器共享宿主机网络栈,这样的好处是外部主机与容器直接通信,但是容器的网络缺少隔离性。
+
+
+
+
+
+ 比如基于 `host` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox02`,查看 `ip addr`:
+
+
+
+ 然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 对,你没有看错,返回信息一模一样,也可以肯定没有截错图,不信接着往下看。可以通过 `docker network inspect host` 查看所有 `host` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+如果启动容器的时候使用`host`模式,那么这个容器将不会获得一个独立的`Network Namespace`,而是和宿主机共用一个`Network Namespace`。容器将不会虚拟出自己的网卡,配置自己的`IP`等,而是使用宿主机的`IP`和端口。但是,容器的其他方面,如文件系统、进程列表等还是和宿主机隔离的。 `Host`模式如下图所示:
+
+演示:
+
+```
+$ docker run -tid --net=host --name docker_host1 ubuntu-base:v3
+$ docker run -tid --net=host --name docker_host2 ubuntu-base:v3
+
+$ docker exec -ti docker_host1 /bin/bash
+$ docker exec -ti docker_host1 /bin/bash
+
+$ ifconfig –a
+$ route –n
+```
+
+## None模式
+
+- none 网络模式是指禁用网络功能,只有 lo 接口 local 的简写,代表 127.0.0.1,即 localhost 本地环回接口。在创建容器时通过参数 `--net none` 或者 `--network none` 指定;
+- none 网络模式即不为 Docker Container 创建任何的网络环境,容器内部就只能使用 loopback 网络设备,不会再有其他的网络资源。可以说 none 模式为 Docke Container 做了极少的网络设定,但是俗话说得好“少即是多”,在没有网络配置的情况下,作为 Docker 开发者,才能在这基础做其他无限多可能的网络定制开发。这也恰巧体现了 Docker 设计理念的开放。
+
+
+
+ 比如基于 `none` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox03`,查看 `ip addr`:
+
+
+
+ 可以通过 `docker network inspect none` 查看所有 `none` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+使用`none`模式,`Docker` 容器拥有自己的 `Network Namespace`,但是,并不为`Docker` 容器进行任何网络配置。也就是说,这个 `Docker` 容器没有网卡、IP、路由等信息。需要自己为 `Docker` 容器添加网卡、配置 IP 等。 `None`模式示意图:
+
+ 演示:
+
+```
+$ docker run -tid --net=none --name \
+ docker_non1 ubuntu-base:v3
+
+$ docker exec -ti docker_non1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+## Container 模式
+
+- Container 网络模式是 Docker 中一种较为特别的网络的模式。在创建容器时通过参数 `--net container:已运行的容器名称|ID` 或者 `--network container:已运行的容器名称|ID` 指定;
+- 处于这个模式下的 Docker 容器会共享一个网络栈,这样两个容器之间可以使用 localhost 高效快速通信。
+
+
+
+ **Container 网络模式即新创建的容器不会创建自己的网卡,配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等**。同样两个容器除了网络方面相同之外,其他的如文件系统、进程列表等还是隔离的。
+
+ 比如基于容器 `bbox01` 创建了 `container` 网络模式的容器 `bbox04`,查看 `ip addr`:
+
+
+
+ 容器 `bbox01` 的 `ip addr` 信息如下:
+
+
+
+ 宿主机的 `ip addr` 信息如下:
+
+
+
+ 通过以上测试可以发现,Docker 守护进程只创建了一对对等虚拟设备接口用于连接 bbox01 容器和宿主机,而 bbox04 容器则直接使用了 bbox01 容器的网卡信息。
+
+ 这个时候如果将 bbox01 容器停止,会发现 bbox04 容器就只剩下 lo 接口了。
+
+
+
+ 然后 bbox01 容器重启以后,bbox04 容器也重启一下,就又可以获取到网卡信息了。
+
+
+
+这个模式指定新创建的容器和已经存在的一个容器共享一个`Network Namespace`,而不是和宿主机共享。新创建的容器不会创建自己的网卡,配置自己的`IP`,而是和一个指定的容器共享`IP`、端口范围等。同样,两个容器除了网络方面,其他的如文件系统、进程列表等还是隔离的。两个容器的进程可以通过lo网卡设备通信。 `Container`模式示意图:
+
+演示:
+
+```
+$ docker run -tid --net=container:docker_bri1 \
+ --name docker_con1 ubuntu-base:v3
+
+$ docker exec -ti docker_con1 /bin/bash
+$ docker exec -ti docker_bri1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+
+
+# 高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+## 快速配置指南
+
+下面是一个跟 Docker 网络相关的命令列表。
+
+其中有些命令选项只有在 Docker 服务启动的时候才能配置,而且不能马上生效。
+
+ - `-b BRIDGE` 或 `--bridge=BRIDGE` 指定容器挂载的网桥
+ - `--bip=CIDR`定制 `docker0` 的掩码
+ - `-H SOCKET...` 或 `--host=SOCKET... Docker` 服务端接收命令的通道
+ - `--icc=true|false` 是否支持容器之间进行通信
+ - `--ip-forward=true|false` 请看下文容器之间的通信
+ - `--iptables=true|false` 是否允许 Docker 添加 `iptables` 规则
+ - `--mtu=BYTES` 容器网络中的 `MTU`
+
+下面2个命令选项既可以在启动服务时指定,也可以在启动容器时指定。在 Docker服务启动的时候指定则会成为默认值,后面执行 `docker run` 时可以覆盖设置的默认值。
+
+ - `--dns=IP_ADDRESS...` 使用指定的DNS服务器
+ - `--dns-search=DOMAIN...` 指定DNS搜索域
+
+最后这些选项只有在 `docker run` 执行时使用,因为它是针对容器的特性内容。
+
+ - `-h HOSTNAME` 或 `--hostname=HOSTNAME` 配置容器主机名
+ - `--link=CONTAINER_NAME:ALIAS` 添加到另一个容器的连接
+ - `--net=bridge|none|container:NAME_or_ID|host` 配置容器的桥接模式
+ - `-p SPEC` 或 --publish=SPEC` 映射容器端口到宿主主机
+ - `-P or --publish-all=true|false` 映射容器所有端口到宿主主机
+
+
+
+
+## 容器访问控制
+
+容器的访问控制,主要通过 Linux 上的 `iptables` 防火墙来进行管理和实现。`iptables` 是 Linux 上默认的防火墙软件,在大部分发行版中都自带。
+
+### 容器访问外部网络
+
+容器要想访问外部网络,需要本地系统的转发支持。在Linux 系统中,检查转发是否打开。
+
+
+
+```
+$sysctl net.ipv4.ip_forward
+net.ipv4.ip_forward = 1
+```
+
+如果为 0,说明没有开启转发,则需要手动打开。
+
+
+
+```
+$sysctl -w net.ipv4.ip_forward=1
+```
+
+如果在启动 Docker 服务的时候设定 `--ip-forward=true`, Docker 就会自动设定系统的 `ip_forward` 参数为 1。
+
+### 容器之间访问
+
+容器之间相互访问,需要两方面的支持。
+
+- 容器的网络拓扑是否已经互联。默认情况下,所有容器都会被连接到 `docker0` 网桥上。
+- 本地系统的防火墙软件 `-- iptables` 是否允许通过。
+
+### 访问所有端口
+
+当启动 Docker 服务(即 dockerd)的时候,默认会添加一条转发策略到本地主机 iptables 的 FORWARD 链上。策略为通过(`ACCEPT`)还是禁止(`DROP`)取决于配置`--icc=true`(缺省值)还是 `--icc=false`。当然,如果手动指定 `--iptables=false` 则不会添加 `iptables` 规则。
+
+可见,默认情况下,不同容器之间是允许网络互通的。如果为了安全考虑,可以在 `/etc/docker/daemon.json` 文件中配置 `{"icc": false}` 来禁止它。
+
+### 访问指定端口
+
+在通过 `-icc=false` 关闭网络访问后,还可以通过 `--link=CONTAINER_NAME:ALIAS` 选项来访问容器的开放端口。
+
+例如,在启动 Docker 服务时,可以同时使用 `icc=false --iptables=true` 参数来关闭允许相互的网络访问,并让 Docker 可以修改系统中的 `iptables` 规则。
+
+此时,系统中的 `iptables` 规则可能是类似
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+...
+```
+
+之后,启动容器(`docker run`)时使用 `--link=CONTAINER_NAME:ALIAS` 选项。Docker 会在 `iptable` 中为 两个容器分别添加一条 `ACCEPT` 规则,允许相互访问开放的端口(取决于 `Dockerfile` 中的 `EXPOSE` 指令)。
+
+当添加了 `--link=CONTAINER_NAME:ALIAS` 选项后,添加了 `iptables` 规则。
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+ACCEPT tcp -- 172.17.0.2 172.17.0.3 tcp spt:80
+ACCEPT tcp -- 172.17.0.3 172.17.0.2 tcp dpt:80
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+```
+
+**注意**:`--link=CONTAINER_NAME:ALIAS` 中的 `CONTAINER_NAME` 目前必须是 Docker 分配的名字,或使用 `--name` 参数指定的名字。主机名则不会被识别。
+
+
+
+## 端口映射实现
+
+默认情况下,容器可以主动访问到外部网络的连接,但是外部网络无法访问到容器。
+
+### 容器访问外部实现
+
+容器所有到外部网络的连接,源地址都会被 NAT 成本地系统的 IP 地址。这是使用 `iptables` 的源地址伪装操作实现的。
+
+查看主机的 NAT 规则。
+
+
+
+```
+$ sudo iptables -t nat -nL
+...
+Chain POSTROUTING (policy ACCEPT)
+target prot opt source destination
+MASQUERADE all -- 172.17.0.0/16 !172.17.0.0/16
+...
+```
+
+其中,上述规则将所有源地址在 `172.17.0.0/16` 网段,目标地址为其他网段(外部网络)的流量动态伪装为从系统网卡发出。MASQUERADE 跟传统 SNAT 的好处是它能动态从网卡获取地址。
+
+### 外部访问容器实现
+
+容器允许外部访问,可以在 `docker run` 时候通过 `-p` 或 `-P` 参数来启用。
+
+不管用那种办法,其实也是在本地的 `iptable` 的 nat 表中添加相应的规则。
+
+使用 `-P` 时:
+
+
+
+```
+$ iptables -t nat -nL
+...
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:49153 to:172.17.0.2:80
+```
+
+使用 `-p 80:80` 时:
+
+
+
+```
+$ iptables -t nat -nL
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:80 to:172.17.0.2:80
+```
+
+**注意**:
+
+- 这里的规则映射了 `0.0.0.0`,意味着将接受主机来自所有接口的流量。用户可以通过 `-p IP:host_port:container_port` 或 `-p IP::port` 来指定允许访问容器的主机上的 IP、接口等,以制定更严格的规则。
+- 如果希望永久绑定到某个固定的 IP 地址,可以在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容。
+
+
+
+```
+{
+ "ip": "0.0.0.0"
+}
+```
+
+
+
+## 配置 docker0 网桥
+
+Docker 服务默认会创建一个 `docker0` 网桥(其上有一个 `docker0` 内部接口),它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。
+
+Docker 默认指定了 `docker0` 接口 的 IP 地址和子网掩码,让主机和容器之间可以通过网桥相互通信,它还给出了 MTU(接口允许接收的最大传输单元),通常是 1500 Bytes,或宿主主机网络路由上支持的默认值。这些值都可以在服务启动的时候进行配置。
+
+- `--bip=CIDR` IP 地址加掩码格式,例如 192.168.1.5/24
+- `--mtu=BYTES` 覆盖默认的 Docker mtu 配置
+
+也可以在配置文件中配置 DOCKER_OPTS,然后重启服务。
+
+由于目前 Docker 网桥是 Linux 网桥,用户可以使用 `brctl show` 来查看网桥和端口连接信息。
+
+
+
+```
+$ sudo brctl show
+bridge name bridge id STP enabled interfaces
+docker0 8000.3a1d7362b4ee no veth65f9
+ vethdda6
+```
+
+**注**:`brctl` 命令在 Debian、Ubuntu 中可以使用 `sudo apt-get install bridge-utils` 来安装。
+
+每次创建一个新容器的时候,Docker 从可用的地址段中选择一个空闲的 IP 地址分配给容器的 eth0 端口。使用本地主机上 `docker0` 接口的 IP 作为所有容器的默认网关。
+
+
+
+```
+$ sudo docker run -i -t --rm base /bin/bash
+$ ip addr show eth0
+24: eth0: mtu 1500 qdisc pfifo_fast state UP group default qlen 1000
+ link/ether 32:6f:e0:35:57:91 brd ff:ff:ff:ff:ff:ff
+ inet 172.17.0.3/16 scope global eth0
+ valid_lft forever preferred_lft forever
+ inet6 fe80::306f:e0ff:fe35:5791/64 scope link
+ valid_lft forever preferred_lft forever
+$ ip route
+default via 172.17.42.1 dev eth0
+172.17.0.0/16 dev eth0 proto kernel scope link src 172.17.0.3
+```
+
+
+
+## 自定义网桥
+
+除了默认的 `docker0` 网桥,用户也可以指定网桥来连接各个容器。
+
+在启动 Docker 服务的时候,使用 `-b BRIDGE`或`--bridge=BRIDGE` 来指定使用的网桥。
+
+如果服务已经运行,那需要先停止服务,并删除旧的网桥。
+
+
+
+```
+$ sudo systemctl stop docker
+$ sudo ip link set dev docker0 down
+$ sudo brctl delbr docker0
+```
+
+然后创建一个网桥 `bridge0`。
+
+
+
+```
+$ sudo brctl addbr bridge0
+$ sudo ip addr add 192.168.5.1/24 dev bridge0
+$ sudo ip link set dev bridge0 up
+```
+
+查看确认网桥创建并启动。
+
+
+
+```
+$ ip addr show bridge0
+4: bridge0: mtu 1500 qdisc noop state UP group default
+ link/ether 66:38:d0:0d:76:18 brd ff:ff:ff:ff:ff:ff
+ inet 192.168.5.1/24 scope global bridge0
+ valid_lft forever preferred_lft forever
+```
+
+在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容,即可将 Docker 默认桥接到创建的网桥上。
+
+
+
+```
+{
+ "bridge": "bridge0",
+}
+```
+
+启动 Docker 服务。
+
+新建一个容器,可以看到它已经桥接到了 `bridge0` 上。
+
+可以继续用 `brctl show` 命令查看桥接的信息。另外,在容器中可以使用 `ip addr` 和 `ip route` 命令来查看 IP 地址配置和路由信息。
+
+
+
+## 工具和示例
+
+在介绍自定义网络拓扑之前,你可能会对一些外部工具和例子感兴趣:
+
+### **pipework**
+
+Jérôme Petazzoni 编写了一个叫 [pipework](https://github.com/jpetazzo/pipework) 的 shell 脚本,可以帮助用户在比较复杂的场景中完成容器的连接。
+
+### **playground**
+
+Brandon Rhodes 创建了一个提供完整的 Docker 容器网络拓扑管理的 [Python库](https://github.com/brandon-rhodes/fopnp/tree/m/playground),包括路由、NAT 防火墙;以及一些提供 `HTTP` `SMTP` `POP` `IMAP` `Telnet` `SSH` `FTP` 的服务器。
+
+
+
+## 编辑网络配置文件
+
+Docker 1.2.0 开始支持在运行中的容器里编辑 `/etc/hosts`, `/etc/hostname` 和 `/etc/resolv.conf` 文件。
+
+但是这些修改是临时的,只在运行的容器中保留,容器终止或重启后并不会被保存下来,也不会被 `docker commit` 提交。
+
+
+
+## 实例:创建一个点到点连接
+
+默认情况下,Docker 会将所有容器连接到由 `docker0` 提供的虚拟子网中。
+
+用户有时候需要两个容器之间可以直连通信,而不用通过主机网桥进行桥接。
+
+解决办法很简单:创建一对 `peer` 接口,分别放到两个容器中,配置成点到点链路类型即可。
+
+首先启动 2 个容器:
+
+
+
+```
+$ docker run -i -t --rm --net=none base /bin/bash
+root@1f1f4c1f931a:/#
+$ docker run -i -t --rm --net=none base /bin/bash
+root@12e343489d2f:/#
+```
+
+找到进程号,然后创建网络命名空间的跟踪文件。
+
+
+
+```
+$ docker inspect -f '{{.State.Pid}}' 1f1f4c1f931a
+2989
+$ docker inspect -f '{{.State.Pid}}' 12e343489d2f
+3004
+$ sudo mkdir -p /var/run/netns
+$ sudo ln -s /proc/2989/ns/net /var/run/netns/2989
+$ sudo ln -s /proc/3004/ns/net /var/run/netns/3004
+```
+
+创建一对 `peer` 接口,然后配置路由
+
+
+
+```
+$ sudo ip link add A type veth peer name B
+
+$ sudo ip link set A netns 2989
+$ sudo ip netns exec 2989 ip addr add 10.1.1.1/32 dev A
+$ sudo ip netns exec 2989 ip link set A up
+$ sudo ip netns exec 2989 ip route add 10.1.1.2/32 dev A
+
+$ sudo ip link set B netns 3004
+$ sudo ip netns exec 3004 ip addr add 10.1.1.2/32 dev B
+$ sudo ip netns exec 3004 ip link set B up
+$ sudo ip netns exec 3004 ip route add 10.1.1.1/32 dev B
+```
+
+现在这 2 个容器就可以相互 ping 通,并成功建立连接。点到点链路不需要子网和子网掩码。
+
+此外,也可以不指定 `--net=none` 来创建点到点链路。这样容器还可以通过原先的网络来通信。
+
+利用类似的办法,可以创建一个只跟主机通信的容器。但是一般情况下,更推荐使用 `--icc=false` 来关闭容器之间的通信。
+
+### 参考文献
+
+- Docker 网络模式详解及容器间网络通信:https://juejin.cn/post/6868086876751085581
+- Docker从基础到入门:https://yeasy.gitbook.io/docker_practice/advanced_network
+- Docker网络模式:https://www.qikqiak.com/k8s-book/docs/7.Docker%E7%9A%84%E7%BD%91%E7%BB%9C%E6%A8%A1%E5%BC%8F.html
\ No newline at end of file
diff --git a/Docker/06 docker compose.md b/Docker/06 docker compose.md
new file mode 100644
index 0000000..8c44086
--- /dev/null
+++ b/Docker/06 docker compose.md
@@ -0,0 +1,605 @@
+# Chapter 6 Docker Compose
+
+相信大家学完之前的内容已经对docker的操作很熟悉了,但是有没有一种感觉,如果我一个项目要起好多个容器,每个容器之间又相互之间有一些关联,有些情况下又要修改一些容器,这种情况写起来会特别的麻烦,那么有没有一种方式能让我把项目快速的启动起来呢?
+
+答案肯定是有的,接下来就让我们学习一下docker compose。
+
+关于docker compose的安装请移步[docker compose安装与卸载](https://vuepress.mirror.docker-practice.com/compose/install/)或根据[docker官网](https://docs.docker.com/compose/install/)进行安装。
+
+> 对于docker compose的学习推荐大家多看看一些项目的docker-compose.yml文件是怎么写的,慢慢模仿着去写很多就越来越熟练清晰了。在[Compose文件夹](https://github.com/datawhalechina/team-learning-program/tree/master/Docker/Compose)下也在网上收集了一些docker-compose.yml文件,欢迎大家一起来补充。
+
+## 内容大纲
+
+- 什么是docker compose
+- 如何使用docker compose
+- docker compose基本使用
+ - 启动服务
+ - 查看服务状态
+ - 停止或删除服务
+ - 进入服务
+ - 查看服务输出日志
+- Compose模板文件
+- Compose命令
+
+## 什么是docker compose
+
+通过之前的介绍,我们知道使用一个 `Dockerfile` 模板文件,可以让用户很方便的定义一个单独的应用容器。然而,在日常工作中,经常会碰到需要多个容器相互配合来完成某项任务的情况。例如要实现一个 Web 项目,除了 Web 服务容器本身,往往还需要再加上后端的数据库服务容器,甚至还包括负载均衡容器等。
+
+`Compose`恰好满足了这样的需求。它允许用户通过一个单独的 `docker-compose.yml` 模板文件(YAML 格式)来定义一组相关联的应用容器为一个项目(project)。不理解没关系,我们先看下面这样一个文件:
+
+
+
+通过这个例子我们可以发现,这个文件里面我们好像看见了image、ports、networks这些,那么这些标签与之前docker run时候的一些指令是不是有一些关系呢?接下来就让我们继续学习。
+
+## 如何使用docker compose
+
+在`Compose` 中有两个重要的概念:
+
+- 服务 (`service`):一个应用的容器,实际上可以包括若干运行相同镜像的容器实例。
+- 项目 (`project`):由一组关联的应用容器组成的一个完整业务单元,在 `docker-compose.yml` 文件中定义。
+
+`Compose`的默认管理对象是项目,也就是通过docker-compose.yml定义的一组服务集合,通过一些命令来对项目中的一组容器进行便捷地生命周期管理。
+
+下面我们来看一个真实的场景,在该场景下我们是通过Python来写一个能够记录页面访问次数的 web 网站。完整代码:[计数器](./Compose/计数器)
+
+### web 应用
+
+新建文件夹,在该目录中编写 `app.py` 文件
+
+```python
+from flask import Flask
+from redis import Redis
+import os
+import socket
+
+app = Flask(__name__)
+redis = Redis(host=os.environ.get('REDIS_HOST', '127.0.0.1'), port=6379)
+
+
+@app.route('/')
+def hello():
+ redis.incr('hits')
+ return 'Hello Container World! I have been seen %s times and my hostname is %s.\n' % (redis.get('hits'),socket.gethostname())
+
+
+if __name__ == "__main__":
+ app.run(host="0.0.0.0", port=5000, debug=True)
+```
+
+### Dockerfile
+
+编写 `Dockerfile` 文件,内容为
+
+```docker
+FROM python:2.7
+COPY . /app
+WORKDIR /app
+RUN pip install flask redis
+EXPOSE 5000
+CMD [ "python", "app.py" ]
+```
+
+### docker-compose.yml
+
+编写 `docker-compose.yml` 文件,这个是 Compose 使用的主模板文件。
+
+```yaml
+version: "3"
+
+services:
+
+ redis:
+ image: redis
+
+ web:
+ build:
+ context: .
+ dockerfile: Dockerfile
+ environment:
+ REDIS_HOST: redis
+```
+
+### 运行 compose 项目
+
+```bash
+$ docker-compose up -d
+```
+
+此时访问本地 `5000` 端口,每次刷新页面,计数就会加 1。
+
+## docker compose基本使用
+
+### 启动服务
+
+在创建好`docker-compose.yml`文件后,可以通过下面这个命令将文件中定义的容器都启动起来,在docker compose中我们更习惯于将每一个容器叫做service。
+
+```
+docker-compose up
+```
+
+命令后会自动接一个默认值`-f docker-compose.yml`,也就是默认是使用docker-compose.yml文件的。我们也可以给文件起名为`docke-test.yml`,这样在使用时指定文件名,但是为了符合规范,还是统一为`docker-compose.yml`。
+
+```
+docker-compose up -f docer-test.yml
+```
+
+**但是直接通过这种方式的话会直接将启动时的输出打印到终端,所以我们常会加上`-d`参数。**
+
+```bash
+docker-compose up -d
+```
+
+### 查看服务状态
+
+接下来可以查看一下我们创建的service状态
+
+```
+docker-compose ps
+```
+
+要是想要查看所有service的状态可以使用-a参数:
+
+```
+docker-compose ps -a
+```
+
+### 停止或删除服务
+
+如何停止已经运行的services呢,可以使用以下两个命令
+
+```
+docker-compose stop
+docker-compose down
+```
+
+其中stop是直接停止services,而down则会停止并删除创建的service,volume和network。
+
+### 进入服务
+
+有些情况下我们还需要进入容器来执行一些命令,可以通过如下方式进入容器
+
+```
+docker-compose exec mysql bash
+```
+
+exec后面接的就是我们要进入具体的service的名字,名字后面就是我们要执行的命令。
+
+### 查看服务输出日志
+
+有些情况下一些服务可能无法正常启动,这时可以使用命令查看日志并定位发生错误的原因
+
+```
+docker-compose logs
+```
+
+以上的一些操作就能满足你在大多数情况下的场景了,但是对于一些我们个人的应用还需要详细的编写dock er-compose.yml文件才行,下面我们就更详细的学习一下。
+
+## Compose模板文件
+
+模板文件是使用 `Compose` 的核心,涉及到的指令关键字也比较多。但大家不用担心,这里面大部分指令跟 `docker run` 相关参数的含义都是类似的。
+
+*注:这里仅介绍一些较为常用的指令,更多指令请见:[Compose模板文件](https://vuepress.mirror.docker-practice.com/compose/compose_file/#cap-add-cap-drop)*
+
+默认的模板文件名称为 `docker-compose.yml`,格式为 YAML 格式。
+
+```yaml
+version: "3"
+
+services:
+ webapp:
+ image: examples/web
+ ports:
+ - "80:80"
+ volumes:
+ - "/data"
+```
+
+注意每个服务都必须通过 `image` 指令指定镜像或 `build` 指令(需要 Dockerfile)等来自动构建生成镜像。
+
+如果使用 `build` 指令,在 `Dockerfile` 中设置的选项(例如:`CMD`, `EXPOSE`, `VOLUME`, `ENV` 等) 将会自动被获取,无需在 `docker-compose.yml` 中重复设置。
+
+下面分别介绍各个指令的用法。
+
+### build
+
+指定 `Dockerfile` 所在文件夹的路径(可以是绝对路径,或者相对 docker-compose.yml 文件的路径)。 `Compose` 将会利用它自动构建这个镜像,然后使用这个镜像。
+
+```yaml
+version: '3'
+services:
+
+ webapp:
+ build: ./dir
+```
+
+你也可以使用 `context` 指令指定 `Dockerfile` 所在文件夹的路径。使用 `dockerfile` 指令指定 `Dockerfile` 文件名。使用 `arg` 指令指定构建镜像时的变量。
+
+```yaml
+version: '3'
+services:
+
+ webapp:
+ build:
+ context: ./dir
+ dockerfile: Dockerfile-alternate
+ args:
+ buildno: 1
+```
+
+使用 `cache_from` 指定构建镜像的缓存。
+
+```yaml
+build:
+ context: .
+ cache_from:
+ - alpine:latest
+ - corp/web_app:3.14
+```
+
+### depends_on
+
+解决容器的依赖、启动先后的问题。以下例子中会先启动 `redis` `db` 再启动 `web`
+
+```yaml
+version: '3'
+
+services:
+ web:
+ build: .
+ depends_on:
+ - db
+ - redis
+
+ redis:
+ image: redis
+
+ db:
+ image: postgres
+```
+
+> 注意:`web` 服务不会等待 `redis` `db` 「完全启动」之后才启动。这里需要注意,如果redis启动失败,那么web依然会正常启动。
+
+### environment
+
+设置环境变量。你可以使用数组或字典两种格式。只给定名称的变量会自动获取运行 Compose 主机上对应变量的值,可以用来防止泄露不必要的数据。
+
+```yaml
+environment:
+ RACK_ENV: development
+ SESSION_SECRET:
+
+environment:
+ - RACK_ENV=development
+ - SESSION_SECRET
+```
+
+如果变量名称或者值中用到 `true|false,yes|no` 等表达 [布尔 (opens new window)](https://yaml.org/type/bool.html)含义的词汇,最好放到引号里,避免 YAML 自动解析某些内容为对应的布尔语义。这些特定词汇,包括
+
+```bash
+y|Y|yes|Yes|YES|n|N|no|No|NO|true|True|TRUE|false|False|FALSE|on|On|ON|off|Off|OFF
+```
+
+### expose
+
+暴露端口,但不映射到宿主机,只被连接的服务访问。仅可以指定内部端口为参数
+
+```yaml
+expose:
+ - "3000"
+ - "8000"
+```
+
+### ports
+
+暴露端口信息。使用宿主端口:容器端口 `(HOST:CONTAINER)` 格式,或者仅仅指定容器的端口(宿主将会随机选择端口)都可以。
+
+```yaml
+ports:
+ - "3000"
+ - "8000:8000"
+ - "49100:22"
+ - "127.0.0.1:8001:8001"
+```
+
+*注意:当使用 `HOST:CONTAINER` 格式来映射端口时,如果你使用的容器端口小于 60 并且没放到引号里,可能会得到错误结果,因为 `YAML` 会自动解析 `xx:yy` 这种数字格式为 60 进制。为避免出现这种问题,建议数字串都采用引号包括起来的字符串格式。*
+
+### secrets
+
+存储敏感数据,例如 `mysql` 服务密码。
+
+```yaml
+version: "3.1"
+services:
+
+mysql:
+ image: mysql
+ environment:
+ MYSQL_ROOT_PASSWORD_FILE: /run/secrets/db_root_password
+ secrets:
+ - db_root_password
+ - my_other_secret
+
+secrets:
+ my_secret:
+ file: ./my_secret.txt
+ my_other_secret:
+ external: true
+```
+
+### image
+
+指定为镜像名称或镜像 ID。如果镜像在本地不存在,`Compose` 将会尝试拉取这个镜像。
+
+```yaml
+image: ubuntu
+image: orchardup/postgresql
+image: a4bc65fd
+```
+
+### labels
+
+为容器添加 Docker 元数据(metadata)信息。例如可以为容器添加辅助说明信息。
+
+```yaml
+labels:
+ com.startupteam.description: "webapp for a startup team"
+ com.startupteam.department: "devops department"
+ com.startupteam.release: "rc3 for v1.0"
+```
+
+### network_mode
+
+设置网络模式。使用和 `docker run` 的 `--network` 参数一样的值。
+
+```yaml
+network_mode: "bridge"
+network_mode: "host"
+network_mode: "none"
+network_mode: "service:[service name]"
+network_mode: "container:[container name/id]"
+```
+
+### networks
+
+配置容器连接的网络。
+
+```yaml
+version: "3"
+services:
+
+ some-service:
+ networks:
+ - some-network
+ - other-network
+
+networks:
+ some-network:
+ other-network:
+```
+
+### volumes
+
+数据卷所挂载路径设置。可以设置为宿主机路径(`HOST:CONTAINER`)或者数据卷名称(`VOLUME:CONTAINER`),并且可以设置访问模式 (`HOST:CONTAINER:ro`)。该指令中路径支持相对路径。
+
+```yaml
+volumes:
+ - /var/lib/mysql
+ - cache/:/tmp/cache
+ - ~/configs:/etc/configs/:ro
+```
+
+如果路径为数据卷名称,必须在文件中配置数据卷。
+
+```yaml
+version: "3"
+
+services:
+ my_src:
+ image: mysql:8.0
+ volumes:
+ - mysql_data:/var/lib/mysql
+
+volumes:
+ mysql_data:
+```
+
+## Compose命令
+
+之前我们已经介绍了一些命令,已经能够满足一些基本的日常使用了,下面我们再了解一些其他命令。
+
+### 命令对象与格式
+
+对于 Compose 来说,大部分命令的对象既可以是项目本身,也可以指定为项目中的服务或者容器。如果没有特别的说明,命令对象将是项目,这意味着项目中所有的服务都会受到命令影响。
+
+执行 `docker-compose [COMMAND] --help` 或者 `docker-compose help [COMMAND]` 可以查看具体某个命令的使用格式。
+
+`docker-compose` 命令的基本的使用格式是
+
+```bash
+docker-compose [-f=...] [options] [COMMAND] [ARGS...]
+```
+
+### 命令选项命令选项
+
+- `-f, --file FILE` 指定使用的 Compose 模板文件,默认为 `docker-compose.yml`,可以多次指定。
+- `-p, --project-name NAME` 指定项目名称,默认将使用所在目录名称作为项目名。
+- `--verbose` 输出更多调试信息。
+- `-v, --version` 打印版本并退出。
+
+### build
+
+格式为 `docker-compose build [options] [SERVICE...]`。
+
+构建(重新构建)项目中的服务容器。
+
+服务容器一旦构建后,将会带上一个标记名,例如对于 web 项目中的一个 db 容器,可能是 web_db。
+
+可以随时在项目目录下运行 `docker-compose build` 来重新构建服务。
+
+选项包括:
+
+- `--force-rm` 删除构建过程中的临时容器。
+- `--no-cache` 构建镜像过程中不使用 cache(这将加长构建过程)。
+- `--pull` 始终尝试通过 pull 来获取更新版本的镜像。
+
+### config
+
+验证 Compose 文件格式是否正确,若正确则显示配置,若格式错误显示错误原因。
+
+### down
+
+此命令将会停止 `up` 命令所启动的容器,并移除网络
+
+### exec
+
+进入指定的容器。
+
+### help
+
+获得一个命令的帮助。
+
+### images
+
+列出 Compose 文件中包含的镜像。
+
+### kill
+
+格式为 `docker-compose kill [options] [SERVICE...]`。
+
+通过发送 `SIGKILL` 信号来强制停止服务容器。
+
+支持通过 `-s` 参数来指定发送的信号,例如通过如下指令发送 `SIGINT` 信号。
+
+```bash
+$ docker-compose kill -s SIGINT
+```
+
+### logs
+
+格式为 `docker-compose logs [options] [SERVICE...]`。
+
+查看服务容器的输出。默认情况下,docker-compose 将对不同的服务输出使用不同的颜色来区分。可以通过 `--no-color` 来关闭颜色。
+
+该命令在调试问题的时候十分有用。
+
+### pause
+
+格式为 `docker-compose pause [SERVICE...]`。
+
+暂停一个服务容器。
+
+### port
+
+格式为 `docker-compose port [options] SERVICE PRIVATE_PORT`。
+
+打印某个容器端口所映射的公共端口。
+
+选项:
+
+- `--protocol=proto` 指定端口协议,tcp(默认值)或者 udp。
+- `--index=index` 如果同一服务存在多个容器,指定命令对象容器的序号(默认为 1)。
+
+### ps
+
+格式为 `docker-compose ps [options] [SERVICE...]`。
+
+列出项目中目前的所有容器。
+
+选项:
+
+- `-q` 只打印容器的 ID 信息。
+
+### pull
+
+格式为 `docker-compose pull [options] [SERVICE...]`。
+
+拉取服务依赖的镜像。
+
+选项:
+
+- `--ignore-pull-failures` 忽略拉取镜像过程中的错误。
+
+### push
+
+推送服务依赖的镜像到 Docker 镜像仓库。
+
+### restart
+
+格式为 `docker-compose restart [options] [SERVICE...]`。
+
+重启项目中的服务。
+
+选项:
+
+- `-t, --timeout TIMEOUT` 指定重启前停止容器的超时(默认为 10 秒)。
+
+### rm
+
+格式为 `docker-compose rm [options] [SERVICE...]`。
+
+删除所有(停止状态的)服务容器。推荐先执行 `docker-compose stop` 命令来停止容器。
+
+选项:
+
+- `-f, --force` 强制直接删除,包括非停止状态的容器。一般尽量不要使用该选项。
+- `-v` 删除容器所挂载的数据卷。
+
+### start
+
+格式为 `docker-compose start [SERVICE...]`。
+
+启动已经存在的服务容器。
+
+### stop
+
+格式为 `docker-compose stop [options] [SERVICE...]`。
+
+停止已经处于运行状态的容器,但不删除它。通过 `docker-compose start` 可以再次启动这些容器。
+
+选项:
+
+- `-t, --timeout TIMEOUT` 停止容器时候的超时(默认为 10 秒)。
+
+### top
+
+查看各个服务容器内运行的进程。
+
+### unpause
+
+格式为 `docker-compose unpause [SERVICE...]`。
+
+恢复处于暂停状态中的服务。
+
+### up
+
+格式为 `docker-compose up [options] [SERVICE...]`。
+
+该命令十分强大,它将尝试自动完成包括构建镜像,(重新)创建服务,启动服务,并关联服务相关容器的一系列操作。
+
+链接的服务都将会被自动启动,除非已经处于运行状态。
+
+可以说,大部分时候都可以直接通过该命令来启动一个项目。
+
+默认情况,`docker-compose up` 启动的容器都在前台,控制台将会同时打印所有容器的输出信息,可以很方便进行调试。
+
+当通过 `Ctrl-C` 停止命令时,所有容器将会停止。
+
+如果使用 `docker-compose up -d`,将会在后台启动并运行所有的容器。一般推荐生产环境下使用该选项。
+
+默认情况,如果服务容器已经存在,`docker-compose up` 将会尝试停止容器,然后重新创建(保持使用 `volumes-from` 挂载的卷),以保证新启动的服务匹配 `docker-compose.yml` 文件的最新内容。如果用户不希望容器被停止并重新创建,可以使用 `docker-compose up --no-recreate`。这样将只会启动处于停止状态的容器,而忽略已经运行的服务。如果用户只想重新部署某个服务,可以使用 `docker-compose up --no-deps -d ` 来重新创建服务并后台停止旧服务,启动新服务,并不会影响到其所依赖的服务。
+
+选项:
+
+- `-d` 在后台运行服务容器。
+- `--no-color` 不使用颜色来区分不同的服务的控制台输出。
+- `--no-deps` 不启动服务所链接的容器。
+- `--force-recreate` 强制重新创建容器,不能与 `--no-recreate` 同时使用。
+- `--no-recreate` 如果容器已经存在了,则不重新创建,不能与 `--force-recreate` 同时使用。
+- `--no-build` 不自动构建缺失的服务镜像。
+- `-t, --timeout TIMEOUT` 停止容器时候的超时(默认为 10 秒)。
+
+### version
+
+格式为 `docker-compose version`。
+
+打印版本信息。
\ No newline at end of file
diff --git a/Docker/07 综合实践.md b/Docker/07 综合实践.md
new file mode 100644
index 0000000..dd2ef72
--- /dev/null
+++ b/Docker/07 综合实践.md
@@ -0,0 +1,150 @@
+# Chapter 7 综合实践
+
+在本章我们希望你能通过docker的形式将您个人的项目修改为容器化部署的形式,最好可以配合上Github Action来实现CI/CD功能。
+
+在没有学习docker之前,部署项目都是直接启动文件,比如java项目就是java –jar xxxx.jar的方式,python项目就是python xxxx.py。如果采用docker的方式去部署这些项目,一般有两种方式,以jar包项目为例
+
+## 方式一 挂载部署
+
+这种方式类似于常规部署,通过数据卷的方式将宿主机的jar包挂载到容器中,然后执行jar包的jdk选择容器中的而非采用本地的。
+
+\1. 将jar包上传到服务器的指定目录,比如/root/docker/jar。
+
+
+
+2.通过docker pull openjdk:8命令获取镜像
+
+
+
+3.编写docker-compose.yml文件
+
+```yaml
+version:'3.0'
+
+services:
+
+ java:
+ image: docker.io/openjdk
+ restart:always
+ container_name: myopenjdk
+ ports:
+ - 8080:8001
+ volumes:
+ - /root/docker/jar/xxxx.jar:/root:z
+ - /etc/localtime:/etc/localtime
+ environment:
+ - TZ="Asia/Shanghai"
+ entrypoint: java -jar /root/xxxx.jar
+ mynetwork:
+ ipv4_address: 192.168.1.13
+
+networks:
+ mynetwork:
+ ipam:
+ config:
+ - subnet: 192.168.1.0/24
+```
+
+参数解释:
+
+build 指定dockerfile所在文件夹的路径 context指定dockerfile文件所在路径 dockerfile指定文件的具体名称
+
+container_name 指定容器名称
+
+volumes 挂载路径 z是用来设置selinux,或者直接在linux通过命令临时关闭或者永久关闭
+
+ports 暴露端口信息
+
+networks是用来给容器设置固定的ip
+
+3.执行命令docker-compose up –d启动jar包, 可以通过docker ps查看容器是否在运行,需要注意的是默认查看所有运行中的容器,如果想查看所有容器,需要添加参数-a
+
+
+
+\4. 注意如果容器启动失败或者状态异常,可以通过docker logs查看日志
+
+5.通过docker inspect myopenjdk查看容器详细信息,可以看到容器ip已经设置成功
+
+
+
+5.然后在虚拟机中打开浏览器输入jar包项目的访问地址,就可以看到运行的项目,需要注意访问端口是映射过的端口而非项目实际端口
+
+
+
+## 方式二 构建镜像部署
+
+1.将jar包上传到服务器的指定目录,比如/root/docker/jar。
+
+2.在该目录下创建Dockerfile文件,通过vim等编辑工具在Dockerfile中编辑以下内容
+
+```dockerfile
+FROM java:8
+MAINTAINER YHF
+LABEL description=”learn docker”
+ADD xxx.jar
+EXPOSE 8001
+ENTRYPOINT [“java”,”-jar”,”xxxx.jar”]
+```
+
+参数解释:
+
+FROM java:8 指定所创建镜像的基础镜像
+
+MAINTAINER yhf 指定作者为yhf
+
+LABEL 为生成的镜像添加元数据标签信息
+
+ADD xxxx.jar 添加内容到镜像
+
+EXPOSE 8080 声明镜像内服务监听的端口
+
+ENTRYPOINT 指定镜像的默认入口命令,支持两种格式ENTRYPOINT[“java”,”-jar”,”xxxx.jar”];ENTRYPOINT java –jar xxxx.jar。注意每个dokcerfile中只能有一个ENTRYPOINT,如果指定多个只有最后一个生效。
+
+4.Dockerfile构建完成以后可以通过命令docker build构建镜像,然后再运行容器,这里咱们用docker-compose命令直接编排构建镜像和运行容器。
+
+5.编写docker-compose.yml文件
+
+ ```yaml
+version: '3'
+
+services:
+
+ java_2:
+ restart: always
+ image: yhfopenjdk:latest
+ container_name: myopenjdk
+ ports:
+ - 8080:8001
+ volumes:
+ - /etc/localtime:/etc/localtime
+ environment:
+ - TZ="Asia/Shanghai"
+ entrypoint: java -jar /root/datawhale-admin-1.0.0.jar
+ networks:
+ mynetwork:
+ ipv4_address: 192.168.1.13
+
+networks:
+ mynetwork:
+ ipam:
+ config:
+ - subnet: 192.168.1.0/24
+ ```
+
+参数解释同方式一:
+
+6.执行docker-compose up –d直接启动基于文件构建的自定义镜像,如果镜像不存在会自动构建,如果已存在那么直接启动。如果想重新构建镜像,则执行docker-compose build。如果想在执行compose文件的时候重构,则执行docker-compose up –d –build。
+
+
+
+此使通过dockerfile文件构建的镜像已经创建
+
+
+
+通过镜像运行的容器已经正常启动,可以通过docker ps查看容器是否在运行,需要注意的是默认查看所有运行中的容器,如果想查看所有容器,需要添加参数-a
+
+
+
+7.在浏览器中输入访问路径可以看到项目已经正常运行
+
+
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml b/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml
new file mode 100644
index 0000000..823c9ce
--- /dev/null
+++ b/Docker/Compose/常用服务/elasticSearch-单点模式/docker-compose.yml
@@ -0,0 +1,19 @@
+```yaml
+version: "3"
+
+services:
+
+ elastic:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ ports:
+ - "9200:9200"
+ - "9300:9300"
+ volumes:
+ - elastic-data:/data
+ environment:
+ - discovery.type=single-node
+
+volumes:
+ elastic-data:
+```
+
diff --git a/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml b/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml
new file mode 100644
index 0000000..8ecec99
--- /dev/null
+++ b/Docker/Compose/常用服务/elasticSearch-集群模式/docker-compose.yml
@@ -0,0 +1,73 @@
+```yaml
+version: '2.2'
+services:
+ es01:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es01
+ environment:
+ - node.name=es01
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es02,es03
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data01:/usr/share/elasticsearch/data
+ ports:
+ - 9200:9200
+ networks:
+ - elastic
+ es02:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es02
+ environment:
+ - node.name=es02
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es01,es03
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data02:/usr/share/elasticsearch/data
+ networks:
+ - elastic
+ es03:
+ image: docker.elastic.co/elasticsearch/elasticsearch:7.6.2
+ container_name: es03
+ environment:
+ - node.name=es03
+ - cluster.name=es-docker-cluster
+ - discovery.seed_hosts=es01,es02
+ - cluster.initial_master_nodes=es01,es02,es03
+ - bootstrap.memory_lock=true
+ - "ES_JAVA_OPTS=-Xms512m -Xmx512m"
+ ulimits:
+ memlock:
+ soft: -1
+ hard: -1
+ volumes:
+ - data03:/usr/share/elasticsearch/data
+ networks:
+ - elastic
+
+volumes:
+ data01:
+ driver: local
+ data02:
+ driver: local
+ data03:
+ driver: local
+
+networks:
+ elastic:
+ driver: bridge
+```
+
diff --git a/Docker/Compose/常用服务/etcd/docker-compose.yml b/Docker/Compose/常用服务/etcd/docker-compose.yml
new file mode 100644
index 0000000..1bbbeef
--- /dev/null
+++ b/Docker/Compose/常用服务/etcd/docker-compose.yml
@@ -0,0 +1,53 @@
+```yaml
+version: '2'
+services:
+
+ etcd1:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23791:2379
+ - 23801:2380
+ environment:
+ ETCD_NAME: infra1
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd1:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd1:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd1:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd1:2379
+
+ etcd2:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23792:2379
+ - 23802:2380
+ environment:
+ ETCD_NAME: infra2
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd2:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd2:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd2:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd2:2379
+
+ etcd3:
+ image: quay.io/coreos/etcd:v3.1.13
+ restart: always
+ ports:
+ - 23793:2379
+ - 23803:2380
+ environment:
+ ETCD_NAME: infra3
+ ETCD_INITIAL_ADVERTISE_PEER_URLS: http://etcd3:2380
+ ETCD_INITIAL_CLUSTER: infra3=http://etcd3:2380,infra1=http://etcd1:2380,infra2=http://etcd2:2380
+ ETCD_INITIAL_CLUSTER_STATE: new
+ ETCD_INITIAL_CLUSTER_TOKEN: etcd-tasting-01
+ ETCD_LISTEN_CLIENT_URLS: http://etcd3:2379,http://localhost:2379
+ ETCD_LISTEN_PEER_URLS: http://etcd3:2380
+ ETCD_ADVERTISE_CLIENT_URLS: http://etcd3:2379
+```
+
diff --git a/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml b/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml
new file mode 100644
index 0000000..d69fd91
--- /dev/null
+++ b/Docker/Compose/常用服务/mysql主从复置集群/docker-compose.yml
@@ -0,0 +1,177 @@
+### 首先创建master结点的Dockerfile
+
+在编写之前我们先要创建一个配置master的my.cnf配置文件
+
+```
+[mysqld]
+log_bin = mysql-bin
+server_id = 10
+```
+
+之后我们创建master结点的Dockerfile
+
+```
+FROM mysql:5.7
+ADD ./master/my.cnf /etc/mysql/my.cnf
+```
+
+### 第二创建slave结点的Dockerfile
+
+在编写之前我们先要创建一个配置slave结点my.cnf配置文件
+
+```
+[mysqld]
+log_bin = mysql-bin
+server_id = 11
+relay_log = /var/lib/mysql/mysql-relay-bin
+log_slave_updates = 1
+read_only = 1
+```
+
+注意要修改server_id为不同值,否则会发生错误,之后我们创建slave结点的Dockerfile
+
+```
+FROM mysql:5.7
+ADD ./slave/my.cnf /etc/mysql/my.cnf
+```
+
+### 最终的docker-compose.yml
+
+我们创建这样一个目录结构
+
+
+
+其中master文件夹存放关于master结点的my.cnf和Dockerfile,slave文件夹存放关于slave结点的my.cnf和Dockerfile。
+
+```yaml
+version: "3"
+services:
+ db-master:
+ build:
+ context: ./
+ dockerfile: master/Dockerfile
+ restart: always
+ environment:
+ MYSQL_DATABASE: 'db'
+ # So you don't have to use root, but you can if you like
+ MYSQL_USER: 'user'
+ # You can use whatever password you like
+ MYSQL_PASSWORD: 'password'
+ # Password for root access
+ MYSQL_ROOT_PASSWORD: 'password'
+ ports:
+ # : < MySQL Port running inside container>
+ - '3306:3306'
+ # Where our data will be persisted
+ volumes:
+ - my-db-master:/var/lib/mysql
+ networks:
+ - net-mysql
+
+ db-slave:
+ build:
+ context: ./
+ dockerfile: slave/Dockerfile
+ restart: always
+ environment:
+ MYSQL_DATABASE: 'db'
+ # So you don't have to use root, but you can if you like
+ MYSQL_USER: 'user'
+ # You can use whatever password you like
+ MYSQL_PASSWORD: 'password'
+ # Password for root access
+ MYSQL_ROOT_PASSWORD: 'password'
+ ports:
+ # : < MySQL Port running inside container>
+ - '3307:3306'
+ # Where our data will be persisted
+ volumes:
+ - my-db-slave:/var/lib/mysql
+ networks:
+ - net-mysql
+
+# Names our volume
+volumes:
+ my-db-master:
+ my-db-slave:
+
+
+networks:
+ net-mysql:
+ driver: bridge
+```
+
+现在我们就可以通过docker-compose来启动这两个结点了
+
+```
+docker-compose up -d
+```
+
+接下来我们就可以看到一些镜像的构建信息,当两个结点都启动之后我们来查看一下两个结点的状态
+
+```
+docker-compose ps -a
+```
+
+
+
+可以看到两个结点的状态已经是Up了,并且主结点映射在宿主机的3306端口,从结点映射在宿主机的3307端口。我们再来查看一下这两个结点的网络信息,以便后续使用
+
+```
+docker network ls
+```
+
+
+
+这个就是我们刚才创建的网络,刚才创建的两个结点也挂载在这个网络上,我们来查看一下详细信息
+
+```
+docker inspect 62fa5033ce48
+```
+
+
+
+这样我们就差看到来两个结点的具体IP地址,因为Docker网络的配置,两个连接到同一network的容器会直接相互连通。
+
+### 主从配置
+
+启动之后进入从结点
+
+```
+docker-compose exec db-slave bash
+```
+
+进入从结点mysql中
+
+```
+mysql -u root -p
+```
+
+在从结点上配置主节点信息,然后把当前结点设置为从结点。
+
+```
+mysql> CHANGE MASTER TO MASTER_HOST='192.168.64.3', MASTER_USER='root', MASTER_PASSWORD='password', MASTER_LOG_FILE='mysql-bin.000001', MASTER_LOG_POS=0;
+Query OK, 0 rows affected, 2 warnings (0.11 sec)
+
+
+mysql> start slave;
+Query OK, 0 rows affected (0.00 sec)
+```
+
+正常情况我们应该创建一个用户然后赋予其相应的权限,而不是将root用户配置给他.现在查看一下从结点的状态
+
+```
+mysql> show slave status\G;
+```
+
+
+
+都显示为YES的话那么我们的主从配置已经成功,现在我们在主节点创建一个test_db3数据库
+
+
+
+然后切换到从结点,可以看到数据已经同步到从结点了
+
+
+
+到这里一个简单的单主节点单从结点的MySQL架构已经搭建完毕。
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/rabbitmq/docker-compose.yml b/Docker/Compose/常用服务/rabbitmq/docker-compose.yml
new file mode 100644
index 0000000..e970f80
--- /dev/null
+++ b/Docker/Compose/常用服务/rabbitmq/docker-compose.yml
@@ -0,0 +1,29 @@
+```yaml
+version: "3"
+
+services:
+
+ rabbitmq:
+ image: rabbitmq:management
+ hostname: myrabbitmq
+ ports:
+ - "5672:5672"
+ - "15672:15672"
+ volumes:
+ - rabbitmq-data:/var/lib/rabbitmq
+
+volumes:
+ rabbitmq-data:
+```
+
+查看服务状态
+
+
+
+确定服务正常启动后在浏览器输入网址[http://localhost:15672](http://localhost:15672/#/),进入RabbitMQ的登陆界面
+
+
+
+默认用户名密码都是guest。登陆之后就可以进入到主界面了
+
+
\ No newline at end of file
diff --git a/Docker/Compose/常用服务/traefik代理/docker-compose.yml b/Docker/Compose/常用服务/traefik代理/docker-compose.yml
new file mode 100644
index 0000000..53e1c4b
--- /dev/null
+++ b/Docker/Compose/常用服务/traefik代理/docker-compose.yml
@@ -0,0 +1,32 @@
+```yaml
+version: '2'
+
+services:
+ proxy:
+ image: traefik
+ command: --api --docker --docker.domain=docker.localhost --logLevel=DEBUG
+ networks:
+ - apinetwork
+ ports:
+ - "80:80"
+ - "8080:8080"
+ volumes:
+ - /var/run/docker.sock:/var/run/docker.sock
+ - ./traefik.toml:/etc/traefik/traefik.toml
+
+networks:
+ apinetwork:
+ external:
+ name: fileserver
+```
+
+注意需要编写traefik.toml文件
+
+```
+defaultEntryPoints = ["http"]
+insecureSkipVerify = true
+[entryPoints]
+ [entryPoints.http]
+ address = ":80"
+```
+
diff --git a/Docker/Compose/计数器/Dockerfile b/Docker/Compose/计数器/Dockerfile
new file mode 100644
index 0000000..5ef98ef
--- /dev/null
+++ b/Docker/Compose/计数器/Dockerfile
@@ -0,0 +1,6 @@
+FROM python:2.7
+COPY . /app
+WORKDIR /app
+RUN pip install flask redis
+EXPOSE 5000
+CMD [ "python", "app.py" ]
\ No newline at end of file
diff --git a/Docker/Compose/计数器/app.py b/Docker/Compose/计数器/app.py
new file mode 100644
index 0000000..45d0a23
--- /dev/null
+++ b/Docker/Compose/计数器/app.py
@@ -0,0 +1,17 @@
+from flask import Flask
+from redis import Redis
+import os
+import socket
+
+app = Flask(__name__)
+redis = Redis(host=os.environ.get('REDIS_HOST', '127.0.0.1'), port=6379)
+
+
+@app.route('/')
+def hello():
+ redis.incr('hits')
+ return 'Hello Container World! I have been seen %s times and my hostname is %s.\n' % (redis.get('hits'),socket.gethostname())
+
+
+if __name__ == "__main__":
+ app.run(host="0.0.0.0", port=5000, debug=True)
\ No newline at end of file
diff --git a/Docker/Compose/计数器/docker-compose.yml b/Docker/Compose/计数器/docker-compose.yml
new file mode 100644
index 0000000..0d87d62
--- /dev/null
+++ b/Docker/Compose/计数器/docker-compose.yml
@@ -0,0 +1,13 @@
+version: "3"
+
+services:
+
+ redis:
+ image: redis
+
+ redis-web:
+ build:
+ context: .
+ dockerfile: Dockerfile
+ environment:
+ REDIS_HOST: redis
\ No newline at end of file
diff --git a/Docker/readme.md b/Docker/readme.md
new file mode 100644
index 0000000..8246e93
--- /dev/null
+++ b/Docker/readme.md
@@ -0,0 +1,89 @@
+# Docker组队学习
+
+## 简介
+
+该目录用于存储Docker组队学习教程,该教程是与《[docker从入门到实践](https://vuepress.mirror.docker-practice.com/)》的合作项目,在经得作者同意的前提下,我们在原项目的基础上进行了整理与重构使得内容更适合与我们本期的Docker组队学习。
+
+## 目录
+
+0. 开篇词
+
+1. docker简介
+
+2. docker安装
+
+3. docker容器与镜像
+
+4. docker数据管理
+
+5. docker网络
+ 5.1. Docker 基础网络介绍
+ - 外部访问容器
+ - 容器互联
+ - 配置DNS
+
+ 5.2. Docker的网络模式
+ - Bridge 模式
+ - Host 模式
+ - None 模式
+ - Container 模式
+
+ 5.3. Docker高级网络配置
+ - 快速配置指南
+ - 容器访问控制
+ - 端口映射实现
+ - 配置docker0网桥
+ - 自定义网桥
+ - 工具和示例
+ - 编辑网络配置文件
+ - 实例:创建一个点到点连接
+
+6. docker compose
+ 6.1. 什么是docker compose
+ 6.2. 如何使用docker compose
+ 6.3. docker compose基本使用
+ 6.4. Compose模板文件
+ 6.5. Compose命令
+ 6.6. [常见服务的docker-compose.yml集合]()
+
+7. 综合实践
+
+## 贡献人员
+感谢以下Datawhale成员对项目推进作出的贡献(排名不分先后):
+
+
+ 贡献者名单
+
+
+ | 成员 |
+ 个人简介及贡献 |
+ 个人主页 |
+
+
+
+
+ | 苏鹏 |
+ 东北大学硕士,Datawhale成员 |
+ Github |
+
+
+
+## 项目贡献情况
+
+- 项目构建与整合:苏鹏
+- 第一章:陈安东(校对:乔石)
+- 第二章:陈安东(校对:乔石)
+- 第三章:陈长沙,乔石(校对:于鸿飞,苏鹏)
+- 第四章:丁一超(校对:陈长沙)
+- 第五章:刘雯静(校对:丁一超)
+- 第六章:苏鹏(校对:刘雯静)
+- 第七章:于鸿飞(校对:苏鹏)
+
+## 特别鸣谢
+特别鸣谢《docker从入门到实践》的作者[Baohua Yang](https://github.com/yeasy)对本次组队学习的支持,希望大家未来也能将自己的内容进行整理并开源出来帮助更多的人。
+
+## 关注我们
+
+> "Datawhale是一个专注AI领域的开源组织,以“for the learner,和学习者一起成长”为愿景,构建对学习者最有价值的开源学习社区。关注我们,一起学习成长。"
+
+ \ No newline at end of file
diff --git a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
index 0e789f1..d48f2af 100644
--- a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
+++ b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
@@ -1,38 +1,7 @@
{
"cells": [
{
- "attachments": {
- "image.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAgAElEQVR4Ae19B3yc1ZX9biBslk02CSH7DyGEABsgoQVMhxgCpkMgYBuDscHgXrCNewM3MO699ypZ7l2y3G1ZVrcs2yq21aVR1/T2zcz5/85939gOS/DIK8xGvPFvLGnmK+877737zj3vvvv+BfqlEdAIaAQ0AhoBjYBGQCPQYAT+pcFn6BM0AhoBjYBGQCOgEdAIaASgSZRuBBoBjYBGQCOgEdAIaAQuAwFNoi4DNH2KRkAjoBHQCGgENAIaAU2idBvQCGgENAIaAY2ARkAjcBkIaBJ1GaDpUzQCGgGNgEZAI6AR0AhoEqXbgEZAI6AR0AhoBDQCGoHLQECTqMsATZ+iEdAIaAQ0AhoBjYBGQJMo3QY0AhoBjYBGQCOgEdAIXAYCmkRdBmj6FI2ARkAjoBHQCGgENAKaROk2oBHQCGgENAIaAY2ARuAyENAk6jJA06doBDQCGgGNgEZAI6AR0CRKtwGNgEZAI6AR0AhoBDQCl4GAJlGXAZo+RSOgEdAIaAQ0AhoBjYAmUboNaAQ0AhoBjYBGQCOgEbgMBDSJugzQ9CkaAY2ARkAjoBHQCGgENInSbUAjoBHQCGgENAIaAY3AZSCgSdRlgKZP0QhoBDQCGgGNgEZAI6BJlG4DGgGNgEZAI6AR0AhoBC4DAU2iLgM0fYpGQCOgEdAIaAQ0AhoBTaJ0G2jCCIQQCpnvJvyU+tE0AhoBjYBG4LtBoEmQqBCxCwGBUBAGDED+DyIUBBCUrxDkASEvgua/EL8MyNcIIoBQiH9wwFWf8ac6OcjLISTn8xp+BENe+NQtG7fWeO/z9w8hwMKzmKEAgixfwLypKqo8E5+DjxkIuREI+eQc/i0XatzSNeBqARB8hSVL44IPfhjnKyOEYDByBHkdVR+qCCRGX30Fg8QhgFDAQCgQgOGtgztnA6b37IoRczZg6zkHCCGrkWVjewiQYJ0HXFV3MBSCX4D+6h303xqBxkFANTlaFNM4mc1SPpe2baj+SxvFRhuiTeNPdoRwG+afvAJtl3IUguxz0nYNsRdsy+x9Hp4i12UHEEso96Y1lD4QYl8wgIDv7zta4zzu+T7HZ2B5wv1XHsd8XrGvjXW/8HWIX5B2iKB5lB2l5Q75lO03bYHUBI8JKntrFtLE3Dhvds9fVkaYgDkmyAOdP9YcPcKHfuNP9fyqPqWIYutpf0IwWDb+x7qV2uIHARnT5Fg2Bw4J/FgMvjzMN95Pf/ntINAkSFSQzS7IBhaEGBL56Ucg/DeH7xCHcP4MIRAMwWDro40KkSOFwK7CY3idAD+hAQqGEAiojsW/eQUam1DQUI23keuEnSJIkhYkEeD9WSYaQvVcNHiq04QU2TI7GMuvzlPHi0ESxtDIBYz4cn74Q0H4xAYQZD8CJDahgBBdPkSIhkxGhEtfVIzGVw5T9RMEyRN/V+8gggF+FkLQcMOoOIUNw15A64790WdFGipMkkyyHSZQbC9+OZ/l5LVkWIq0aF8plf5TI3BpBNiexYkTAqTaHP9WbZjnq7aoRkySHvUOt/XzRIqUiXbv/Lm8MEfiIELSD9iW2e94bdo02kg6Dux6qg+IzQvRntHOKWLA4bgxXzK8y/Vpf8kNWCraKvOZ4Y/YFjSoXHJ9ZTsBtxBOsakBjg3EQxE64seyECfyFhkazhNU5ZbLM9AemxgRLz6SOleeRsYOuWjEhWTdiYeuCJPBa9JGGjD4OcEyyybUV34nlaJ99cEf5IjEsnsRChFDYVMR310f2DgINAkSFYBPlA2SGxoJDqKhkFc6BVUcwCeDthApIVGAQXJEYiUdJySDPjsWgn4E5fggbREM6ShhsqVIgDJEjd9gSQACVMuCPoR4Y1NdCZtRQ8rO+4a9TzXW83sxpOcNJLt845cv4iYXMlgj8CkrJYMD3TnWBY0+rVQw6I3YcHJwCb/4e3gwEfXpvKepHlkIMg1RwBCDV7KzFzq3egdv9lqGBCuNNkkzDY9JooMheIWE8rvwgMRrXbhn+N76p0agURCQEVkpTKrfcvBUJCfM3qk8h0mVKFRso9LW2U7Vm2WRPmA6EdK4aQPopPAtThiVczVYS/smQ6CwRdWFY3TYwaS5YJcwBa9GeU7zImqgZ79XSgodLJIE2mPKKVTPxKlpzJvK49C5JNHks/rFiAuXE0eZipRSpIVqCnGhm63gYanC5RYnVXANIBhQTq6QKJJVwZjnKVX7IlN1yadRbrlf6hOGUtB5PbYFcaT5DMSH44CMaSyRSaLOa/uKRIlzH6FTesmC6QMahEATIVHsLIpIqYGVWoxX1CXxsERZIkEyiZVYD8rXLhii/FBxUsQqFCSjVw1bdUA//B4rKkqtcLh80llIvNjIwwavQYh/w8FUwKgoBYJUbsKeiCJ6SoWil6nKF/TZYLVZUWHzmg4Ly3zB0/wuKYASoM3/w6RHiB6NOQ1REH7Do4zHN+AR/koGj4sUJ6paXyVWPJYGkt6kL+iD3++Cn2S4aDOmtm+Dt/86ALNT3KJCsmSGxwp7bTnKSspQWFCI4qJSFBcXorCsDGV1HoSMb2E0CT+Q/vn9RkAIPAkEB3ZlRmh3qCYo1Yl+hiL6QqCE7IQP5ee0ESQBynGgfaqtLkNRURlKSypR5zXgFYWKBIqqhlJX5dr8nA6aoQiGTBSK4GE6YpSP6Xc24kuRFL+QKLIAOoM+Vy2sVQUoLS5A8bla1HrpeDXui/CQQBkkKIp9KJ4pyh5pj1LpGGgQYF2IjREXVdlUEjDRr2izSEzJ+YII+n1CYYIcK0zlW0iU6XtFSqQIs3LofAiJ26nqXEIM6GgKiVKqIkMUZLYhDBEJr6h6wqoE00autvCd9M9LINAkSJS0bpnrJvEge2f3MafzpOGbipJ8ym/YAKn0eFVL5DEya6em9digRRGiUXOXwpq1FsM/jsHulFLU0cLQg/o2Xuw1LIc4i9LFAX8Q8BlCqhirQ+k2AC+8ebHYuHU9hm45DSdPM3goDRGlZYiyRhS+ixdRVICS1LFENDGUxZU65VeudQOKxmk6A0ESG/OlvHI1jcePzv8t9c87ESe2hULsGfM+Pnz5dTw/IxleepKhEGpOb8COFZ+gd98e6PbSX9Hlg07o+H5rvNN7ELquyYKfA41+aQS+DQSEtPgQDLiUYCxtlv3WgJ/Tbufvyd8uMCh2GzoAKiyBVkx9bT0VheipPfFO657o0XMSNuZUochnwBMyIH2Nxk0MHFUZRic6pT/6Q354wooxnTbDJXaPlqdRX+ZjyIMxZCHgQ3nqKsRM/Qgd23fEuy0WYGd2BaovevJGub+o3iSmyiYygsAfAFRkLEmTKTuJ3Q2qL+lMUyUjoaJ4JmWiPTNZiznT4eZVqHDxMgbnQhh5FhQ7TKgjegkuqhBSrwE6gIpOKT3M5MlyT5bEJ2RJrs9z2SDOh5so7Syi++qDGhWBJkGiJKZFyI1iIJRD6VVUJS3Hmuld0bHDm2j9VAu0ePodtPmwC7r17Y0+vbuhZ5dWeL5le/SYugE7T1rgFO+P88sqtsawn8WZvdGY8PbnmB+bjZwaB/wijZuxSY1aFWanqMtB6rYp+Kx3O7T6aBpWJVaj1KokXZH3g/TrDARcNcg+uAbzJg5Cj0WnUFznFZWFc/b0qkin2DGv/Iuy9hmc3DwL4/r0wd/6Tsas5HJU230S8E0FT3nHNG6Rlu/vpzDUNMcFAsVn5GdCmsQgKoPDekSgHulLPkTPVx7DXa1XIdnwwek8gZ3LNmLBjM2IT9iIVe//F57u1B1vt2yBtu+1wotzklFvKOn8yuOn79jUEVDjsVIWRAFnW7toqs7UQkRdpxMic2w0bRJLyF5DFUmdwy5kS5mNVctGofvSw8g9WYQqhwduIwB7xRmkx67CqD6fYcb08fh01FRMXhaHhFKHDMBUPIxgEH6JHeU1aTck3Lxxq0DijAIgaSNx4U+3vRSVRUdwdNMKjPj559idWobKxr2rqHkkjaGgCwzXBn8PuVFfno4ja0ajR4t30O+zTdibWgE3JyaomosQZ8Zr0XwQc57LYCkhu+o4xiSpqTcGgYfgo62hk9eA+VAxVcKD5Q4qlpP39FTDmReHDRMGY+rUSRg3ZhwmjJ+HefHnUO0LCF3jGMDngd+viG8D7tvIMH/vL9ckSBTjYBhvI7I1GzNdiCBgy09A4rZJGNvtNTx09X/gR7e3x4cjp2NB1GpErV6JlctmYsLobni/9Xto12cGZsTnwR5ymwHmTlSnrMX28f3RuX8sksqssAdIsOilcMCO1N1oQBsjp3BaUJi2Bgs/ewfNf/UYnh+xC7tyauAx5X2ShfD8uLMsGQnRn6NT6wFYlVyKEgcD7DmtSS9JKEUDbt54hwaDFpRkbMCiIR3w0qPP4KHuW3GoyAqHGDSvzPFTJ4qYRCkdXXnTtGXm1B5LrPBQ5oj/S/UL0aQC5kbx4VVYNqY12vzlQTzxwPuYm+ODxVaAjKQcJCadQdGZnVj61A/x0tAZ+GLRcmzfug5RqSVwmwGkjYeKvpJGQCGgnAA6Q1zUQJWcg3dYDqcRkGUuQmpkAYY4heE4JyWK8ChR00NB1B+djtVrJmNwfJmaiqMtLE3BgaUzMbDTcIyesxnbYrdh89JJmDhkGIaMWIrkEsDh4ZhvBktT5RISQSWskW2biDjmohxOLXKKjX00aIElfScmXDUc8ceKURHpPFiEDSkcdkGbKC6WLNjxw1VbhOy9yzDhrT/i8cffwYC58cioJXGisETnSak6LI7Ev5JESYyZwoj4SO2JTVaES0JsaZdkmjUyJS88VIm2KKu+fQj5LShJWYdV/dui16iZWLpuO3ZsWYPF00ei98e9MXpPLvJqqRia078G5yV8ZvuJ1CmNEEB9WEQINAkSRfZPEiUBi6JuKPmakzpGVRoOzfkYD/zHz/Grd5ZiTXoZHBKoF4Qv4IS/fAOmvNQMf7rxGTzZKxrZXh98jDlwZCNhwSiM69QTY5IdqPGI8K1WzIlHGFlHiagWzIOUYaQ8XIozB2ei7y3X4hePDsXEnadR7qcRoiJjKI9UgiWtqDi1E0vbPIa20/Yj7kwtvBIbRq/ru+tQanioQs7OCRjd4jb84DfdMTOxBEVekjxOs3LBceSmmue4HFbUVFehqrISlV95V1RUoKqqApV1Trg8jG/wweMqR1naTqz+oh/GfD4IfT56Cx/d/0e8taQAWVU2uAJ+eDwVKEtagcG//Bm6TI9HfCHTRARgfCXItyF1qI/VCFwaARVEzmllmeSWwZeOH9UFDuBsw1Q4GIBNksOgY6Wuy8BrzvDJii0EYE2chjUmiRJiBTssceMwpl1rPPLiROyrBGx+H4KWeGwb/SHevPtFdN9YhcI6M4BZArzpnJlELmKF+NJPKkeIYWPsjkkWA0FZ2OMLlaMsYzsmXTUMu48VooIP15gv5VGZcVDq/owHCxoh+OqKcW7tm3jmztvxl66TsSizXpxThkyowH0q3eKlSX2Eia8ZGIWQ4RciKPUjTjuJlVLzGPcZyUt4s6QxIBHzyNtfcQjxM3vgpdsfQseNZ3GqmtO+1cg7PBuf/+1m3P7+Mmw5XgoH7ajEl3LdoVrwpAocyZ31MY2JQJMgUWqZqGlZpOWzQXN9WBC+/F3Y8MVruObn1+Pxz/fhUL5d+RGUlEN2hAKJWPvWn/HsVXfggWdHYUcN4AwasGWtxoxPhuDd9guRHAzBHfDKVJ6s1hNb8+2QFEZb+eCFJXcXojv+DL++7nn0mHUAaXXmihzDZ64kFEkGnqpMZK1qhbteG49pO7NhMSjPE4vGD3yPtOEJMiGg+sR6rB54P/7t6lvx0bIMJFs4IFDOl6izyJWogB+lxflIT0tCYmICkpKSkJCQiISEo0hMTMSxY4nyeeKJEpTWOeD1WGDJ2oaorm+i27DliEk+jYw9szH5zdvxwzbLsfNEDsoqLKjIy0Dmhql47d/vxdjV6TheVg+bvRalThXF9e3UcKQo6uOaLgJ0cvwI+b3weypQX2FBbWUd6urqYLVXod5WA1u9DTUOD6x+U2EPeCUQnSu1RCFR47tEFTtTpmBNzAT0iS+CIdNMZ7Dv8zfw9gsv4uEhe1DPLEmS0qAIqSuGott9d+KHXeOQVGJX2dskbUsQgQAXezR+qxcCQsfTCMHgMn7DkBQDvlAZStJ3YcpVIxGfVICKxlbATIzIpZTuTZtIBcdA0FMH49QC9Hj097ivRU98vOY0OOknY4mscjYVf/4u0ZzqJxcDsPyhujLUVFhgqbWh3u1DgIuWJGY1Yn1dykSizPATg6uyA37UJizA7E4v45e39sD8HAfKfKJTwZ6zDQcG3Yf/d20HjNuciTwfSRxjZRnjRZ+ZNr/x667p9sHGe7ImQaIowcrqCPE8VPwQBVxK5FVJ8zG3y+249rob8EFUITKrlLTLph4KuhGqicOklx/Bff/aDI88Pwv7nCG4Qi7krumM/gN6ovXsVLglD5VaEksnjZ6Kwc8a2WNjF6DszFU6vopMnFv1Nm676Zd4ss8CrDpuM3O5hGN/FIkKestQlzsPXf/wBkZP2oNjFZzJ5DHfVUwUezQxCiBQcQzpSzrhjquuwfXdVmJ5epXoT4yJ4iqXiOGjOuR3w+d1wefzwOfznX97vV54PPzMA5+fqQ1qUZq0Fkv6dMBdH0Uj5kQRKr0e2HLjsGvsm/jhT3th0uTe6NSmC1q/2BmffdYd//H/PsCk+NPIPLwCuzfPxbhUK4wGpGBovO6or/R9QEAUi6AfnvoC5CbOw7gBH2Nw33EYM34upi+ZjTmL5mDxnIWI3nIYaWerRLXlQK6GS+Uc0U8yJN45COvRaVgVNRn99pWruJy6g5jz3nNo9lBLPDEjU6iJmuquRfbWsRjx3K245v7ZWJdThRpZEaycG6rX38YwTGvJhTqBAG0SzYMfASOAoFGDyvT9mHLVEOxKKkB5I5MokhqDyp5fQrLVGMESEAy/GzCSsey9P+HJG1/BK502IZMqvp+KkDmhR1Iiij6VQ6VMUSH0eG0wsqMxdUA3DBw1H6sOFaDar0iQpJNoAIokbQw7IDK+UCVORfXGkD/fg1/fOha7qxywcooVIbgKjyB18qu47sd3o/OCwzhWaQaVS4yuUsG+ndr7PvTI/90zNgkSpWKETCZu5kzxSKCxFWc2f4qRLW7Cf/5XS4xPqkChS8yJDOAhjx32xNFo9+TtuOWelmg/8RBKA6RHuYjt9yo+6dQfw2PVwK/yqqh7GK4qVJ3eieWzZmL+pNGYMH0RJq/cjoQDszBj7jR8+dnnWBS9G8cqAgj5vHCfWIUZg3uj+6eLMP9YrepiJBnSQWgJL2TQFSmZHoa3HLacZeh6229wd/N+GByVhXo+G42CLG1lHBg7Uh089Tsw89m70WvkSkSfUoZKlkiLweKy2Yu8V7YXxdak5TSk45n0TXk8okUrwiZdWJL5qcR0TEUjHq23AiWJSzH03h/gV7f3xsioTJTIUl1zVaRYbJbAA4f1DE5sm4G5EydhztSxmDR9NsYtSkChB7JiRQU7XVTwi9q98p5p8CgRemA5l4W9G9Zj/dEClNndEvRpOCpQmrkfUyetxJYVn6Bj+3fxVIu30aHTu2je7GX0H/0lRn05A3NXb0dynRteYiah6hfHqjAwlZ+bGErYmfx1UWn0r//cCLA+TdX3ogfx1ecj79hGzJo4HbMnjcSo2euwdN1WxG9bgNGTJ+PLYeMQFX8c2bXsf+wRYRmElzMHY/YLfhy0oixlK3bNGY3xm/ZiX0IKMjJycDr7LHLP5eF0/jnkn8tDSbkF9Q7GaCq7IylMZPWeWngv7T4UQp2QqEkYtKdUBRvnr8TYvz2KWx9qhccXHFdrkmX6vxa5O8Zi5NO/wjU/64U5SSUo8asFGsqmsHxs7+qz8/3afKKgqxK1J+MRPW0AerzTEm++8z66fDoTy+Kyke8OwiunBhHyOWAvyML+xaMwqN8n6NOnP/qPmIwxy/Yiz08nVYUmBAMVqEqNw7SrRyCWJIo5+gJMJan6l4Rby24NVK/VUn5iEanNEuJD7GUaUZEgPqcYUCqBQRuyFrbD24/8AQ+8+gkW5/jhNRyylo+hIJIeR3w93tGc5pNgcz+C9mLknkhH8v447Fw5HzNGj8Ko9QlIK66F06fiq9Q6S7PgEj9FGkw67Jc8XtJI5HnCxxfg6JyO6HzHHfj1bWOxp8YOq/m07qIEJE97Htf95Gd4/fPNiDvL2FIKBVwEpZ7touaqf72CCDQREqXkTLJ6qjjiaJCkGGdwZHp3dPj9Hbj+wXHYWFCPGuYYYgfx2+EoOYpN/Z7FX556Ga/1n4eY4xZ4ODftOIR5rVqg1wcjMD/NE7Z8KsjQW4nS7MNYPn0JFq1Zh/Vrp2Jc/554++UP0GHYp5g4vidaPtMcLT78FKOOlCPotaN+zyB89Oc/4a7nPsbHm86pdbUBJp5k12QHohysbK10fDEyLnisWYhqcy8e+uOraPPpRmTalXEX7iRBoOw8LnjdqdjU4Ra07jcZ4/dXi41QZIz24yskKixVC4HjcCHmPqImx2PF0yJZkURz7MRmRxZSSJmef5tBjyEP6guOIv7jO/Dfv3wY7b7YhINV4SR7anAJGtUoOxWHzfPGoPvgcZi9YCU2bFiDxbNHYsTQjzHthAMV7gjLKCQqAKfDgfJSC+xen0wfCIkMGvC77SgtPoPC03HYunUdFq5Yi5h1UYhZtBibt25FzK6jOJRZBKeYOU4ByBMrL1SC1V2ywlAET5HhVVxCpEY9IpD1Qd8xAhz02N4uanOeMpw+EoeVsxZiScx6bIr+Av3bd1QpBUZ8igmff4Tn7nsArw5fhhUnatTqXgnLZH81CYmQGNXbnIXx2LduKibOWIrNJyyocbH/q+kjBlxLpn8JcaaCYyaoNa+jSLxoWYrsBIOoT5yCNVGTMHi3BZK76OR89H7tQfz0wTZ4fO4pZW+EyNmQu30cRjW/Dldf8zYm7y1EgStsU0gaeElVZhmcZSWtyj1nhJyozj6KpMVTMWPuTEwY+RkG93oPH7z9Ft56vS+6D1+L/Xm1qLWWI//oFqz+cgRGjZuAz6fNwqx5C7Bw4ULMWbQSM1amIrvaLkQqFCpHZdoOTL5qOGKTilBOB0tIFO0M7aFaAUfopGwMG6PycnHdfFNrIWZmvJniobS17LPm3EUQsKdNw4i3muHuR97EO2sL4DCUEiWLh8zYWZ7LmiM2imCyjqgg+eGqL8aZlL3YvnIplm7ago3RS7BuayziMopR5lIr98Ln8ZlIsVmnTIaqFpRT9VK7N/iRg31j30f7n92B39w6DnE1dtSRRIUAV9FhJMx6Ctf/5Ed4ZuhabDrtUG2DJZMVnA1Q9r8JM/1dgxFoEiRKgjCF4TO/k0dEIwYABuv2YvWAVnj0urtxw8sTsfpAMpJOZOD48TSkpxzEoV0LMazV6+g4aAGWH8xHnRGA33AgVLgeQ194FR07TcTGsyrnkUxBMbt1RRKSd81Hr2G7kV7thM2Vhi2jOuCVm+7HrR2jsG/LF+j17it4ssNwfLL7HIJ+B6yp8zC1b1d0GTwDc47kyx5+TIVO48DOyQgcEenFgNGAsKMF4XPXIGXSU2jxxz/g0Xe/wOKTDpF26SUp75T8jgHSRTj46e/xfJch6Ls2z1RumPdFbQtBw0MXWEx40AVbVSlKC/NxrqAI+QUFKIjgXVhYiKIqF2xeM6M6SYW5UlGMTDgLsUzTkXh6JIjcVZmLM8v/irtv/imadZyI2Ul14o2xPIwFsJfEY9vUzni3+Qt4dNQhpJQ64Ap6cXb/PCwf8CTe31WLfCvRieDFgtDAivGkxxcyg/BpiPg5r6OSlyryF1b2OMGg3qLuCRFU+1eFVTWqAMyqE5CtGXg95pvySM1pEhVB3fzTHCJShZJCzDJ7i3Zj+4oVGDftMIoCXhi2/Zj9ZnM8cfdreG7wEpyMHYY3//wYmg9ahDkpleYKUfoZbGt0k1SQOPtqADbkrJuIpXNmY8axarXlkKn+kLgwhYqEJcvWUmpLIk5JsQOzeV/8Vn0oAFviZERFTcbA3VUw6CRmLECHV5vhB83a4PFZ2aJlcAAPBR3I3T4eo58miWqJiTvzcc5GkmZuNUXeaKoaVLyZ2Jd0jYqHr/40jseuwdIJi7H7rBNWpxv1ObHYMbEL2t57H37+r0/io6kbELN5MRaO6Ya273TEl7tycMbqgY/2x1mCsuTNGNp+GNal56PIQ4fXgsr0HZhw1RDEJpWgXGaoFFZ8YpWeQK20VlONdNC4QloQumSLYr+k3SaxFHXQTOHAJLwq514IKNuBBR++gj/d3By/77UO+TaDafmE5HB3BZ5PkyL4CRqcQWAOLvZ/xskasjND0O+Ep/AY9iweiynTpmL6mh3YdyQVCceLUVLrhMevlCypXWJLZzbAJM/Updwis/mRjT2D26Ptv9yJm26ZgJ21DtTSlhG+osM4PPcp/PI/f4QnB0ch5qRVSJzYK074ioDAtqtfVxqBJkGimCuDHhwD7JibUvRgei+n5mDkR4/g339xE25r8S46dOyBbt17oXunTujeuS96jIzC8kP5yKv3wCtGJoSA145Q5iy0f/oDtO25EgerSD0Y6q1k09rMbUjYMB4LU1ywuX0Ilu/G0oGt8dhdz+CVBTk4m7IFO9etwtrYNGRYlIilNHylCvlZOJHkqdbQuyHBoX/CDsCF/361t5Thg6e2CIfHv4Tn7r4Ov2jeHm+vyJYdoDw0ASQF5AU0cJ56pMy7E8992B2dF6WiRliNJD5RSUPp/4i6RYTKcHr/RmyaNwcLZi/CwtkLMW/uPMydO/cb3/Pmzcey3eeQW1EPQ7QaYsJnIHDkLswK7LkQiRXwI+Rzw27JROrK13H/bT/Fvz3WFe8vSUOlWfZA0IHsmN7o+/y9uPnenpiT60JhnQP2+rNIXj0P097tifknDJ5DSMwAACAASURBVFS5IzMOLIv46KYHSozCxVP4KoVB0u9JmRV+JEdq6oCYSeQ74KfxFOapVkyZdSTnkp4xlQSPiaxoV7pf6/s1IgKWI/MRu3091mXRvvgQLNiI4a89ij+/0BF9ojJgzdqCqMVrselYAXK5AET5L5Ixn0Ok0iyoOjPnUyrW95mABZ9GI9nmhsvlgcfthMfthsdth9tTB6fbDbfTA6/HrwKx2cbYFCWVi0y4iRYTbnpcnbcqahI+iS8TJQdpC9HplQfww4fexGNz0sTesN36Q/XI3vEFRj99Pa65uh0m7MhHnp0OHK0bA6NJmEz+yLABbkgs7kUA7pRliF0/H2MOVAvJCwUVmfFWH0dGVB88f+01+M/bH8ad99+CZ999F51jciWWVNKR8FrBANyWbGTNeBAjtqfiQAmn06pQkRKPiVcNRXxSMcpN+81pQT6vIelaLpAolYCShCMyp0pxQjqrPP7C5uy0EbTDvoAHzrztmPfBy3jwmlvwm//ujugcN6pdzLtpyM4HQk5YGDEkikB5RVVkhbCQLI5y0GhjJGdp/Tmc3TMPc3q+jTe6LcKS/enILq+CzemCJ+REKOAWeyxqn5A0PjBLexb7hnyId35wB264ZRx21DpQx3sEAE9hApJmP4+fX3cNHh+yEutP1qnVnLy/xHBRNw+3iEZs/PpSl0SgSZAoBi2GfFw1wXwZ9KrYsAyU7OyP3q/ehBvvexrto84i55wFxRWVKK0oQyXf1XbUujkPTiavCEHI54I3YwFaPd0RLXutwr5q+pEkNlxdEoThtsPhqEOtRykx/uMLMe7D5/CHh1ph7FEfamxWOG31sNs9cPsY7aNWopDscCUGuzI7JFfQSTnp+XFzXtIPJr7jd/DCVnoMB6e/jlc7tsTLd92CZr97Bn/uHI2TCMIt5k5dh0Yv4HUga+G9eLFzd3RYcgylNBoyzcauqabblPdGg2TA43LAVl+P+vp6WPm28m295Nvm9EnwtlohpJQeWccmnhVNsNfMWcJnDaCu5AjiV/bDk891wEvNr8Nvb2mO13qswjG7SuUVqkvF2q6v47kbbsONj3XA4Nkr8MWoQRjUrxdGfDEfMfGFsHq5+zor9NIvc6xRpoRGT1gmoaAXrwyMOkYlMFRcTpnU8Hwq78RVxyq5HjEW/c4cSjgc+mAEPcpL5jUjK9qlC6+P+I4QMNvJP6xIblFSD5vDBit3DjAcsB0eg7ZPNcPTbUZgUboXPrcD9dZa2F1eeP2ckqLKotQM9ntpZ+LwGEBlLGb26IfO7T7ByKXzsGjpEixbvByLl6zAkiVLsXzxQqxYuAhLlq3E+h3JOHG2VhwTtck6M5wznpAER63qIjmoTZqIVTETMHifRcUFnlqFYa89ghuavYXHZmeIgyblgQPZ28dj5BP/hR//sAtmHipGkZvXCqdWcKkcbKIyc8pK5T1imy9cNx27lszCukL1bNIvqJgHXKg/dxA7+92D3//2Olxz+1/xxuj1SLTT8pmkzNzSJmAvhfdAfzw7dw+WpFUDgUpUZMRi/DWczsuHhTZY0osIMxF7KHZMsqozLYKKA1UO0aWbi1L5leqjVHnlCIva5rMhVHAAczp0RJcXWuDJh+7Fz3/3J7TbXIZTtezn/CfRSyqLvGzRI9YOblGHzOSddBYlRITfMUCf9twPn8uK+vIClGUdxsZJH6JbryHos/AoTjJHlihp5nQelW0iJVhmI3Fie3T+zR349e+/xN5auwSW0zX0FB9GyswXcd1PfoxnPt2GLaeZaNOc56RNkhmNS2Oij2h8BJoEiZINg7lURfZUM/caQh2SZr+F9x6+DXc17415mX44PBzcmadI7XlEPsN93GSeXY2ogM+FQPpcvPnUB3izxwrst4h/oabbhPAoWV28QgRQFDsQfV9/Fn96eiQ2VHthNZRKRNJCYiadkcqTJJdTGx2TPYk8TNXDjC0KBzL6gx7U5e1H3PxhePmdjzEmJhaLx7TDe80fwB+f7YvVxSFYvSRGfCueEPA4kDbvLrz00cfosDgdBeazhP0bqlDKG+P9VHyBOHtCLBrAAsKkgafQWIjDqGRpSdrHyS2JwTJgOxuPjTOH48N2/TBsdSK2TmmJVx++G83eGITZGXYlkxduxJjWf8Y9dz+DF0ZtQOLpPKQmH0PikQSknMhFfi2nBU23NIK2L+W5iDDxXDWNZ9aZKZqJd2l6k6JdES/T2ZQEiBy2ZCCk2seBRE2fqmNpKE1jTyIsS88bgGEEz6EPuZIIfBOJ4neq71JRoUoc8NbhzKrX8XKzZ/F698XYV0dnSMXLCFkX0qTaE/snnSK1jF2RK1h3Y/6AKRg7bCV2nz6F7Jxs5ObkIDsnB6f5Mzsbeaez5fNzRWWosTnFhqjAZjpkKpaS9oekgu1bxURNxOA9phJVEosprZ7GXQ+1xGNzMiU1gpqsrkL2zjEY+Zcb8aPrR2JJRglKDcaOmqqKOSUkA7qUm52CVMSG40u+xIaZ07CzjP2Ryj9DBThd6YffWYaapMnodNdNuPEnv8Of2n6KGSfqZFin2qL6VFCOQ+IIvDp3L5anV4NJeS0Z2/Hlj0ZgV3IxysWRVXjTLpoijIr9EYKl1LiwQ3SpVkILJeu2qSKLz2mSOlcVajK3YNYHb6LjJ5MwZ8kMzBnSBo9dfwtu7r0He87VmCq7ibcZVC42j7izRkTlDsd+ctpPZX+nbeHNgl4rrAWJODSrP4b16otBX0Yh5mgx6oinBLoru6LsKJ+VWBbj+KKu6POnu/Hr2yZid00d6gX/ENxFh5E6pQV+8eNfoNXEeOwtVOerPf9YHq1EXao9fFvfNwkSJUKtNEIGYpIo+AF3FjZ0fwrP3/YwHmk9DwdrQ/CI0WFMD1eBqEBOdlYaOdUpuFmlE6HsJejx7Hvo0G0R4kuUFE1TQK/SY7Wg/NxxnEg/gzKnBQdntEa7Z17EY+3WID3ggSNkoDYvHedys5Fv59QdaRQHXRUDxQBSWY3HXk3SJ14fiQ3NpBvVOfuwae5ofNxrIDpN2Y+0MhcKE2di7AeP49a7X0KrDVUosbLTKhGEndfrqUPqtDvxUpe+6LryBKrF7TQ9YFndQk9HIjOAkB1VBTnITktFemoGMlLTkZaWdul3ejoyCmpQ4+SqEIWFNEp2csYOmPEDQb8b9rP7sHnGUPTvPhB9x+9Aeq0Be9ZcjHzjQTzwcEu8uygLVpqivBUY8tajuK/52+i64axEKvilXpRRYdJTzuRFSlEuJlFiaMXQKWPDuhPohf9x0FPqlPpJTqiIksSw0OiKQedzeuB21KLKUgWrmwPXBWVLYhokGzLvrF//nAj8IxLFz0kYvHBW5iM/+wQyc3NR5jiD2IH34slH2+K9L+KQTSIRcKAqMx45xSUoc6t2RbWI9ENCmNnX5Tiu1j2F7Z9PxdJp65Fsk7kY5YpIWzUdI+E0nGbjP16HA6xa1yVkzmzLzBHEfmc/OgNRq6dgwO4SITYh+wms+/hVPNf8r3ho/FHUcw89Lt9HMU5EDcfg+2/Df/5lObadqUIdY/08DjhqLSiqtMNjiKUzF5AoRTsQcuF09EisnjUGi046Jf6Ge7ypRJMeeOpzcW7LQHzw5D34w49/jFt+/wxeH7YVeTYn3IFw4tAQvHVnUbv+XfSIPoJtZ5iyxYLy9J2YdM0wxCWXwGJO+wUMP7z1pSivtsHKkAnaLklEqtR68f0iaGzKDNKRYn8WFwghRymKj67Fss+6oE3b/pi8JQ2nSk4ha+NI9Ln3Blxz76dYePgcLH61ebNaDX2RvRB7TYsethl8Pr4VwfO5ilGYsQ8HtsRg7cYYrF8+E4tXx2FPShEqrCpNDmc0eF0SJ1k4IIody2lH4c6xGPv6E/jV74ZifUE9qg1+HoDjzC4cGnMfrvuvx9F7VQLS69XnzBUlkxtC5LUdiqBZNPohTYJEcetHtV8cZ7q5S7kHwbJt+PK5B3H3717F00N2IZ95OERVUFN+VH4YJ8DOJVsQSIM24A24ECzbhMkvvol+naZh0zkGOEhEAYIhN0pPbMfW2cMwZOhK7D9zAPM7/wUtnnwDT4/dj8qQDz5nOY6umI2YmC3YX8H4CC/cdTnIOZ6E41nnUFhHs+pWREqkXYhszsBEa0EStk3ugw8/7IGWY7bhjBXgwrSAZS/Wf9YKj9x2H378URySS5wSzCgaWciA01OGlJG349U+AzFg82lZ6SPUQ0J81POKERFJuhLnkuOxJyYK66I3YH3UesSsjcHatWu/+R2zDuuT8pFfSxWJ1zRn4MUYqLDsgNcK+7kE7J7SGR+17oYeYzfhWA0JloGQNx1b+ryGV+98DHd/tBInvEG4irZgyvtP4/kX26LnlkJmQxFZOhjwwF1TgtKzp5FlNeCmhYrgRTwUKVJKHdUlmc40V9mQcPJ7MXhiBC+oCCqIVBmmsDfJKWGvPRdZyVuwbEk0Yo5Vw2Kj2qbUPBJxmeaNoGz6kP+rCHwTiWK/dyF/71IsGz8Wo2etxKGSeIx75mbc9UJfdF2djsqADf7aLGybOgAxBxORSQeHdiZA0uJVCoEow2paKRB0Inf1RKyZMQ3zj5XCIW1JRmBxqMLKKQkKaROjGMXJk/3fmHBTKTV0Cti+qaoLiVozFf13lwjtCoWqcXxBN3T/22t4oEsU0ryAkwkiXSdweNIn+Oimh/HwuGRkVLjggxM1Z5OQELUYM5buQEapDTY/B/nwXnNUOUKoSpyKmMWfYVhULur8QXhkNioAj70YeUdWYMp7j+K1Lu+j5XOPo8WNf8Afb3sPY9cfQ1apDU5vEAGPFTXZ+7F92IuYfPA4Umv5dBWwZMRjytUDEZ9UBAudSvZ9ayFObJiNZSs242BmAWq9ql8GA07BMzJrIBENakU1yRmpqKcKZcdWY/mI9/HGK20wMLYcBbWc2nehKmMl1nS5Ddf+8DH0WpaM5BouUmKd0VCQDtN2KIfRH5ToNgnHoN3w+11w11eg9PQJZGTEYcvSiZgyejQ+Xb4bSdUuWGW3CVUeke/FeSauHK/8olaKIhUAHNkbsGpYa/zxd29h8qFqFNvogNthyViOld1vwA1PDMesI9koZc4t2uDz3rRw8f+rnaxJl6tJkCg2dPHKOGfOAEaXFfaUeWjz5N34j8fb4eXF6fBQtpbO5BUSQMNEBUsNmFRtaPhImHyA9TDmvvYE+rQbiiWZKiaKod8GipG6vA96PXALfnpnfyzePAudWjyK2554By8sTITH64A3fRFGjFmC8etSUcb4LLcTZbHd0f6J3+KRV3tjZHydpFGQJa5mDLM35IJhP459g17H0w+9jL8OXoI9VT5Z+MrQzmCoEtlrh2J4sxtx7U96YXmKBRXmag8qJYb7FGI734G2Q8ZiwqFCNXVnRreqlAPCJqT/Kpmc8/f0b+nERKrzmPH6ooubwfF09dRuFEJJHZY0HJ38HB767RN4b+h67DrHJHISBSZKX250Jwx89re4/d6uWJTvQYX7LPZ8+Ta6tW2JVkuz4GEGZ8MHw1qGU5vmYX7vdpiQWA+Lk4pAhC+ZTqHJJHDKBrKYJH0Gt0oI+GXLCSqP4nNzypUxceLJqfgEWZGjnHCUp8zE+O534d+uvxU/eHMDtp6qBVONETdZ5uxX8QwRlk4f9n8OAQ7JbF9hVShcQLYF9noHDg5viTZ33Y8/vTAAG3bPwxs3/xq/emM4+m3PkYSZ9QlT0KbnGmxILIad7chQ8TE+OCR4OUDjJJyHV3QhWLIHq2bNwtt9ViPJa8Dp96os2FTIZXtZP7wSRG4OjDKQq3KJukVnTRRQ9X190lSsjpqEgbEV8hS0bL7T0VjYpzMee6QfFp8zUEXyf2It1vRpj+ebdcGcbKDaSX6QhyPzB+H9f/sZrr36NvReexLHazgdSZtIddzckN11HAlrlmJM+4XYW+VEtccHj78eZ46swIzur+HGp6YgOrUCRVnrED3wJdx/zQ24+gdvYMiyTGSWOGA/dxRHl4/Fsy8twMZcCyqFllRJTNQXP+qLuKR8lIlVKkNZ5nIM+PdrcOPVN+BvQ5djR5GaEpSFQ6LvRUijZDaedk6toPOd3YDZ3Z5Fi6dfxrsL01BiuOALucWyByqTcWJlW1x/7TW4p180VmfWm3n4FMYynSqqjyJWLAFjobi4xFNVhMK9SzH1vRboMHwG5h/IQYErADdJjhm3RMdLcl2Zhkk0RiFlgE+aBzPGhxD05eL4xhH4+J7b0HLOcaTl18PrOYeUXePQ48mb8cSUY0gscCoCJ43KEMMcqToXbt36Z+Mh0DRIlEzFAMGqkzi+bTo+aNcS7Z+9BTdf/yP84Prf4bePtUav3rOxu8iOar+SoQ16dCJJ8G+aURIDenrMcHsG24a8gF49emLorjK115I4JDaUHF6Ahf1eQbMXPkSH93rh81HD0LdTD7R58X0MG/kpug2Yh/nbM3Cywi4ehihMB0ag28v/jRsfeQsvTTiKKhmAmcFXbcYZdBbDnjIDbzz9OtoOXYGY5FKV44jUhNMAQR+sx2Owvl9z/Oba3+H95ceRUsEAU7IwK3z1uzGj2X3oNmw1VmWHV/qZMQXnpyrFjquAVxIN5ciKhxZpc5KOKh6waD5mAjqqPtxGoRCF+xej101/QKuB0diYXCarF0laxOCEAGf2Wiwf/CIevv8RPLP8DHKr7bDnxGHLrMH48P2O6D9+JT4fPxKffj4dM5bFIiGrCJXcgoX3jOQlHr+S3sMkikOjKrLodueXAkvGdBncLsRgiKepIjlM9hWAvywFKRu/xIAO7fHEL8ZgbSL3+FJL17k4QNpQhMWL5BH0Md8FAqzAryNR3C+zHic3D8Hwbq/jz690Rc8PhmHqF8PwQauP8GGbrhg2bAy6DlmA6KNFKLByvaqaFuaCLZl6E9sUnkpniFFQcsfV5CRg9/Ip6Nr9M6w+mIf8OtlGVrk2QujJYyQaXTVg81fptxIPqWwHO1d94gysjpqCgXvKpD+LQ+CuQ3HSLsSMG4KuHwzBqC+GY3D/fhjEQX5zJqocARgMewjWozRtN9YN7YoOz9+Ldxcdxt5Cl/QZOiEyDc4+EXTBWpqFlI3zMLrTB+jWoQPebvUe2nUejDHzt+HQqXKUOf2yurDuXBISo6ZjaKtX8MJTzfBgs0fxzGsfofekGGxJq4bFQVJDpCyozNiLyVcPxq6kYpSJA+SGozILB8cPxLC3nsL7oxdgbppVCI0E0zeELcjsAtMZUPWqw7Epr6Nj+zZoP34D0qqdss+ohDnQufZaUH5iDT5pfhPubD4Cn63LQikNh0GHjLFPVKADMmvAqUwqZrbcPdg8ayyGDx2DMev34+jpXOSVVqLG7oFP4p7IjpSXKbFhMi1JGmxOS5K7y3EkiWpj9lDAC3fZCWRvnoDR/TpgwKgxGDpkBIb1H4IhM1bhUHE9rB4qUGwWDBWh2qnsuRja76L7fM/v2TRIFKVWegauKlTkJWPrlg3YGr0YK5YuwIKly7Eiegvi4lKRb/PBJY4Ejw/LFOZ4KdoFWzU9MAdOremBvv37oOXMNFSTq3DaKuiHs+oM8tLisTV2P+J3HcKJrEykHz2K/Zt2Yv+hg9h18DTyym1wkZnxakE//OXJSFg/Ej2Gfo53JyTAIX2Hq7yojjHDbz08lmRs3hSHg5nFKLdTBhEBWU2bccrRWozi9J2IWrIMsacrYHGa29A4y+E6Phtt72mN4XP3IrFe7bUlnqR6GkHn78Z5ASvc8v/um/CHX//z787jIUJVlOE2bLAVn8TehdHYn1mOchtJqQq4lYtRDXKUID8jHls2rpcluvVurt2tgSUvDYd2x2LP0SwcOXoIBxNSkZ5TjhrO0zboRWaonkf+VwLcRbaFn6oyy3FCztTxilWGyaE5VcIB0V0NW8FhHIqZi3cfno3YjBLUymoaFczZEJveoEfRB19hBMx2cP6u/JvkxwtrWTrSk/dge9wh7I89htzck0jcux/7d8ThwMGj2HU4B6U2HzwcXE1bFG5avAo/u9DupFsg6KpGbX4q4nbEYk9CEvYdPIi98XHYExeH+Lh47InfgyOpp5FvsYozxsFeBmT+ZI+j42eo6Wlb4gysiZqCQbvLpP1zUCWB89sssGQnYu+OfTicsBfx+w/hcGoO8qsd51fkMT7TU1+BgoQt2DDoQfSPycBhph8gDqrwF57Jb4fNchrHdm5D7LZt2LhhC7bvPoq0M9VwB7iy2HxKww13dQFOHdmFrTHLsHTJUqxcF4u96UUo9zB9AG0s45zKUZkRh4lXj5JkmxbTCTI8dtTlZWHPpLcwZtFSLD3hVNNytKlSsPOVdIlfaEOpGRMzD8pStmDvvv04lG1RK+xoC+QZeV0vPLYSHI+NRszGY0jKq4adnVsOMacDZWuWkGw/Zc/dh4T4OGzdshPb9x5GQl4pqv1++GXBiomdXJwXCLcLVV8sk7I3F477u8/8Lvhq8nDiyE4cSDiC/fsP4/ChJKSctcDB7XIuqhel0YWvcwk49NffCgJNhEQ1Mjb07rKWYtKng9CyxzIk2gAvN80UVccMSJeWHOF9QwZcuVFYvnYZBqw5LV2aRlGmlEiiJAiVoYqRWQh6IBJsyZgdywnkLW2PZ1tOwoLdp1FhGGaMV2TXivAJvpeHyVRowA9/9XGc3j8bbfvtRXJ+DTwyAKhpXtp9/dIINAQBGZulD3Ma2Y7y4mykHzuIA3Qk4nYjfvce7I6Px4HU08irsKkUB8xKze2hqGaYygOFVDoqtsSpWLNmEgbGl8nYTMdMVh2HN7YNk36ZIuSgroKaVXAgvUo7as8cwbper2DeobM4xR2LG/ElK4lFZeLqZLqvSkULBKlE7cT4q0cijjFR55U3H2BYsHtiNyxctwnx5WqvTSpsIsFEaCcb8RHkUuzxsgDI44Q9Zy+S03JwqswGG4lNgNG4SqFm/ejX9wcBTaK+pq7pNwTcp7F39hgMf6c3JiXaUONRy/c5BadWV3zNiV/3ETuUpx6ntk/G/OhFmHW8RrhSWKoXeZ/Tig3peLR7dJKMelRkbsWyLo+j/bzDOJhnkw1IaUAZ1qq78tdVSAM+o+frccKSFYtNiwei85YynKk1t37hChsG6kuG9gZcUx/6vUeA/ZLpAYwApVbzzfxPEtipTAGJEPf/lD1AOSVocPqeU89UcUwBRZAMoD5hElavmYCB+8pEZ2VMFgmSJCDmKlOJa1JTzzI9J84gVxUqRchny0X2geUY2HoM4vPKUd0QBzGC2pTymvdi4ameMAeVL2RBRcYOjL96MGKZbFOmPg0EfDVwFG3A1L5TEL0tBYV+RQolRk0Wx3xXnouprNPx9bvAkBCiSwWOb9YrZx5ENYwAF31I00BAk6j/UY/sCiqMvD5rPaKn98Y9PXcis8YlyfmZQI6z+VSRInoFvAjmrcW4scswOSoNJcJ+eC5X6HFlBme1VaB2pEqUspTMVZeMlJjxeObZaVh3vAaVskzRkKSjfpkOjKiE+qB/gIAEk9YkYPf6JegwYAvyPAacEmehYhIkJk0GwQjbwj+4j/74+4UALQzVGS50UbFYErl3nhnJYCy6NFUnrs5i7JIKPxBCYg7Yyk0KwHZsMqKjJ2LoHk7nMSklV5GpOBm2TIn2kpuSW3HajRue+0QVYkrM/ITt2Dq2P6YcrpNl+CRajf4S+c107OTyfLZiWDK2YNy1w7AjqQTFTNcS8qO2NAd7+7fCnC0ZSC9yIsR0AxIt5lJhGI1euAgvKBWjEKVKHWIMrZBhRYWVH8w61fYgQkSbxGGaRH1NNapgwxB8zhqcSd2M+aPfxpCtZ5FpYRAf80pFTHeU/OyqQnGRBSVVdiFilHslWFGm8igRc61G5AaCfdkwipG5YwUWDhyLGfvLcNbmg/f80lkVC9CAUn4NCvojqoMBnw2VVRacPFcFDzeHlSQa3J+RW3LQXGrFT7eUhiEgY7HYkHCsTDhHWTiGnCEDjMFksLEaqCU2R9Qck2sJCVPxNvWJMzFnfA+8+MksbIjZheRKK+rESKmpOwmjCrgBUUm4LpcrlJkoltwsALe1ElVFeSipN+BlnFXDHueSR0u2LEmLonY5oHPiyE/D8fj5mD9+GN65+jNsSCpCGRdscKNwjwt1+SdRXuWAzcMcV5woY7mUEtfoBbzkE5gHkBsJwVRT+VTU1NSqmqIUa0Cb3pBZhUjvrY/7P4uAJlFfUzWMUZKtFUIhuOpLkH9sJXallKK4zgsmN+MA2pCOzC4nMi/leFGI2PkYF8DYBNXpJPNspBelU+ovR+HJJCTEJiLPZsBtJr/jhpgqv4n2hr6mahv2EQcaM3OzLADg7xKoqjKWs5motBmNPew0rJj66H8yBIRFKRPCAHDScI7NHHvVV7QJtBVqVVh4/k5CgiRImaRLDeA8wVOehrSjOxG14wgy0rJQ5HDAQTvF6THmohOuFU4gqzJqy70Y38xl+rQZ/Be2R40MJ0mTxHEGw6pYEK7qQhTlJCDx4F5smnIUueW1cEpSTAacq1gvgkKSx1VxVNNUDIMijo1cxMguF64jKSD3ORUaJTGtkoVX6lEpgJFdUB/VFBDQJOrralGkc3qCAUkxYDBxntMJnwRt0xtigOfXnfj1n9H3k21XzD2qaEpoVFSCUP6kgWgA6aFiHHDBb7jh4WQ8ryuDPaV6kijK/19fFv1pAxAwVxeqwFjThnMQkylZtdJGCHVDGkMDbq8PbcoIhNuPUjKFPEnAuFKPFN1QDpYIG+EBnLYk3McJj5xohgOQdFCNDjFRpFpgwrgoCT+Q88xEoLQNskSeZeDx5iKX8IKVb6E9k3eo5LR0QpWdoq2S6Ul5DtpURhiRcJkPS+dTysRnlsWSaoXid2jcWDROlSpUSYBVAk4mexJVShSzptxu9bN9FQFNor6KiPAZNVD6ggZcQW7uyMBBbgOgOjNXaDQoEJz3oG0UJ5CyRKkJAgAABb5JREFUtOwhjkDIp4ITeT0SoUiNl9yeZWTWR1oX81TZR5Q+pfht6nP9/+UjIPWsBhlmJpe9yoTA0qCzHjkARr6q8vILos9sWgiwzyomE5764U86bZJXzYyVks84aLO/h/mSkCFz/8/wZST9gVJwmCtYksVS4ZIdEcR6SRpLkhMeKnvlMRhatBQqXiQzarWKrBiO1A5FWil0RmTvUMZrucXJo40S5Ut2LVF9iTaVNpbBDcpghvuYqT7xh6xt/m48RKkDqQvmFhT9UNkAYVbcjFkRqUhh0cc1DQQ0ifpKPbLb+uAx5XKTK4XjP8l1GJjJzLXS0dmtInhxnlyyqfMs3oEyfQiG4UIg4BE+1hAhypwAEOPHZc/iTQpLYyc2t5v4buxMBGD88xwiMRjhJeUckDiQscrDG0fL9F44uek/z3Ppkn63CNAC8N/5l/zK/0yJiL+Z0/zC4+UbBqJfFG9jni7Tgcx0LuqUukQwyNQJJEckHSRn5oAvCqry5mh/ZP83yVlEmYj39siKPlF9zhfuf/+LlEUSe6ryXKzA8znB8tIhkWJwiiw8pacW+JA4sS+KifvfF+eyr0DIVb2xhMoWMMs4A/mViqZmBC77BvrEf0oENIn6mmoTA2ZuuyBp58QRUkZO5GV6eTKafs3J/+AjiQkQYyAXk50mJB5BtnpQBu8fnPo/PhaTaOZdoYGRsEvGNki5eP2LjO3/OFt/EDEC9IxNvYneOqdIZFAyJX0SY+UZmyNaxBfWB36fEVBUScXbCQ4yOl8gUPxTDdLsyxK4JO2MxOciSUocMcY/ihMlU4Gc/iIB8ytVS+IkqT5xet+cPpQ4K49ch7Hn5zdfD4bgY9iCuaqvMetHKWq0mSoo6sLm3jRVXFhDK8u+pY4hWQx7lspBNJ3W83N/jVm6yK+lykeCp7AkqSN/kh0VTFshqWsuJsiRX14f+U+KgCZR/6jiTBmdxky9FIm6IDOHP4/sZ3g4FusVvhRtosjCF+4SydXE5sq5PFq6tniSNFbC7XiA7siRQHnJYwRrwZJ0SpYIqL+Iv7jsAvYlr6MP0AiEEVBtij304rYT/lT1XPUX/w+TK/40X+ahPF/ZlQvkSn1FJ0o5emy1ioipo6UNM2bSvLJkNzcJGOOnGugbhkt0yZ/hksrjCDG8UOawss5nVYTr/AOacUZhDPj5d/cSBMNEziS04ZIJzFI0s+zfXTH1na8wAppEXWHA9e00AhoBjYBGQCOgEWgaCGgS1TTqUT+FRkAjoBHQCGgENAJXGAFNoq4w4Pp2GgGNgEZAI6AR0Ag0DQQ0iWoa9aifQiOgEdAIaAQ0AhqBK4yAJlFXGHB9O42ARkAjoBHQCGgEmgYCmkQ1jXrUT6ER0AhoBDQCGgGNwBVGQJOoKwy4vp1GQCOgEdAIaAQ0Ak0DAU2imkY96qfQCGgENAIaAY2ARuAKI6BJ1BUGXN9OI6AR0AhoBDQCGoGmgYAmUU2jHvVTaAQ0AhoBjYBGQCNwhRHQJOoKA65vpxHQCGgENAIaAY1A00BAk6imUY/6KTQCGgGNgEZAI6ARuMIIaBJ1hQHXt9MIaAQ0AhoBjYBGoGkgoElU06hH/RQaAY2ARkAjoBHQCFxhBDSJusKA69tpBDQCGgGNgEZAI9A0ENAkqmnUo34KjYBGQCOgEdAIaASuMAKaRF1hwPXtNAIaAY2ARkAjoBFoGghoEtU06lE/hUZAI6AR0AhoBDQCVxgBTaKuMOD6dhoBjYBGQCOgEdAINA0ENIlqGvWon0IjoBHQCGgENAIagSuMgCZRVxhwfTuNgEZAI6AR0AhoBJoGAppENY161E+hEdAIaAQ0AhoBjcAVRkCTqCsMuL6dRkAjoBHQCGgENAJNAwFNoppGPeqn0AhoBDQCGgGNgEbgCiOgSdQVBlzfTiOgEdAIaAQ0AhqBpoGAJlFNox71U2gENAIaAY2ARkAjcIUR+P+dZ+PsniJUywAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E6%8A%95%E7%A1%AC%E5%B8%81.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAFdCAYAAADL1o0TAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAEzwSURBVHhe7Z35m1XVmajvP9HdP/a9T/c16Sl2YjtEYxCixJg4RDSKMw4YJ6TDIDhPOIAoKGA7gqCioiDKpEgLBEQBEQcmERwQcQAaUBAkuu591z47lmVVcXTVrn2O532fZz9Vdc6uc/a41ru/tda3/lcQERERqSOUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlJcqWbVqVRgyZEj4r//6r3DXXXe5uLi4uLh0+HLrrbeGefPmVWqmxkV5qZJp06aFH/3oR+H8888PvXv3dnFxcXFx6fBl//33D0OHDq3UTI2L8lIl//3f/x1+97vfhf/5n/+pvCIiItKx/Od//mdsAWh0lJcqUV5ERKRslJcM5aVKlBcRESkb5SVDeakS5UVERMpGeclQXqpEeRERkbJRXjKUlypRXkREpGyUlwzlpUqUFxERKRvlJUN5qRLlRUREykZ5yahrefniiy/Cyy+/HMaNGxeX8ePHh/fffz989dVXlTW+htfefPPNMGzYsHD//feH0aNHh/nz54ctW7ZU1mgb5UVERMpGecmoa3l59913o4iQdXDgwIHhpJNOCjNnzgxbt26trPE1O3bsCFOmTAmdOnUKffr0ietPnDgxfPTRR5U12kZ5ERGRslFeMupaXhCVyZMnhzfeeCNs3rw5Ssl9990XIyzNee+998KECRPCFVdcEd555524/ueff15599sQqdm+fXvYtGlT+Pjjj8OkSZPCEUccobyIiEhpKC8ZdS0vyAcRFZqPNm7cGM4+++zw0EMPhXXr1lXW+JpFixbFaMu+++4bDj/88HDuueeGZ555Jnz55ZeVNb7JZ599FmWnR48ecf2DDjooLkiPiIhIGSgvGT+IDruffvppWLBgQejWrVt4/vnnW4yorF69Ok6u+OSTT4Y5c+aEyy67LIwcOTLOFt0Su3fvjhK0cOHCMHfu3HD77beHrl27GnkR+Z6Mmf92OHPMoppbeo5dHNZt3lHZSpHaRnnJqHt5IeqydOnScNVVV4XbbrstNgm1BB1zN2zYECMqNAnRvHTLLbeEWbNmVdZoG/u8iKTR//FXw99fMqXmln+8dFpYuWFbZStFahvlJaOu5QUJIaJy7733hgsvvDCsWbMm7Nq1q/LuN6HPC31jtm3bFpuK6Og7ePDg8Oyzz1bWaBvlRSQN5UUkHeUlo67lhSjKiBEjwhlnnBGmTp0aPvjggxhhQVDoC9MURhYRnZk3b14cTt23b99w4403hmXLllXWaBvlRSQN5UUkHeUlo67lhdFG3bt3D3vttVcUi2OPPTZcfvnlYciQIeGJJ56orJVB5OWee+4Jv/zlL0Pnzp1Dz549Y4ddmp2qQXkRSUN5EUlHecmoa3khRwujiJ577rmYcI7l9ddfDytXrozRlabs3LkzCszs2bPjQj8ZRihVi/IikobyIpKO8pJR9x12OwrlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJaOu5eWrr74K27dvDxs3bozLpk2bwq5duyrvfpsvvvgiyscnn3wStmzZ0ua6zVFeRNJQXkTSUV4y6lpeEJcHH3wwnHTSSaF79+6hR48eYcmSJeEvf/lLZY1v8tprr4VevXqFo48+OlxxxRXhpZdeqryzZ5QXkTSUF5F0lJeMupaXBQsWRHkZP358mDlzZjj//PPDY489FtatW1dZ42vefffd8NBDD4ULL7wwrnv99deHCRMmxGhNNSgvImkoLyLpKC8ZdS0vq1atCq+//nrYsGFDlJALLrggPPDAA2Ht2rWVNb5m3rx54ZZbboknnYgNwsO6r776amWNb0KT0tKlS+N6d911V+jXr1/o0qVL2Lx5c2UNEfkuKC8i6SgvGT+IDrv0ZXnrrbfCKaecEiZPnhz7vzTnqaeeitGW+fPnx/WRGeRlxowZlTW+yY4dO8KsWbPi//Tu3TuceOKJoVOnTsqLyPdEeRFJR3nJKF1eEIndu3dX/vomX375ZXyfjrmtwXtEXh5//PFw8sknxz4vLTFp0qQwaNCgsGzZsvh9ixcvDvfff3944oknKmu0jc1GImkoLyLpKC8ZpcoLcoJsrFmzpvLKN0EUaNZBYFrj888/D88880w49thjYzRl27aWC6EpU6aEwYMHx+/j84jA0ByE9FSD8iKShvIiko7yklGqvBA1ueyyy8I555wThg4dGptxZs+eHT788MPYwXbixInh0ksvbVVIGFU0ffr0cOWVV4b77rsv9ntpbaQRnXtHjhwZHn300Sg8SMuIESNi591qUF5E0lBeRNJRXjJKkRciLjt37ozyQifb8847L44Eevjhh8O4cePCsGHDopBcc8018XX6n7TEypUrQ//+/cOvfvWrcPXVV4d77703TJs2LYoGw6KbwggkOt+ee+654cknnwwXX3xxGD58eFi9enVljbZRXkTSUF5E0lFeMkqRFzrUzp07NzbdnH322WHIkCHhlVdeiZ1tb7755vCHP/whCknfvn3D+vXrW42mLFq0KNxwww3hzDPPDAMHDowLTUEMnyaC0xSail588cUoS4gOP4nsIFHVoLyIpKG8iKSjvGSUIi+ICgnl6KdywAEHhNNOOy0KBRJyxhlnhDvuuCMOa2akD6OBqhWMPYHA0CRFU9Obb74Zh0xXi/IikobyIpKO8pJRirxs3bo1dsSl8yxRF0SmW7duUV54neHI5GqhDwxiQ1+WtkYcVQufQRSHPi+MOPoun6m8iKShvIiko7xklCIv+dDmW2+9NVx++eXhrLPOiieE4cxEXq666qpw7bXXhhtvvDFGXpCNslFeRNJQXkTSUV4ySpGXFStWhAEDBsSkcscff3xsPqLj7XPPPRcOOeSQeHKIwtCplmYeOviWjfIikobyIpKO8pJRirwwSoiJEYm4HHjggeGwww6L8kLSuK5du8ZoDJ11eY1kcm3leekolBeRNJQXkXSUl4xS5GXLli1x5M+oUaPCoYceGqMvdNClGWmvvfaKr9EXhqHTSE5reV46EuVFJA3lRSQd5SWjFHkho+5tt90WhzUjJzQP3XTTTTFT7lFHHRUlhgkXFy5cGCdERBjao8NuCsqLSBrKi0g6yktGKfLy2WefxeRwjChirqGXX345jjJ65513wtSpU+Ns0ayDKOxpeoCOQnkRSUN5EUlHeckoRV6ASApSwrJr166Yy4VRRcgBryEv77//fnj77bdbTVLXkSgvImkoLyLpKC8ZpckLssJ8Q0ym+MYbb4RPPvmk8k4mNkRcmPGZ95GbslFeRNJQXkTSUV4ySpMXZOW4446LfVwYXdQ0nT8ddOkP06tXr9jvxWYjkfpHeRFJR3nJKFVeyO9CYjomUST3C5DT5Z577omzTTORIlGXsjvrgvIikobyIpKO8pJRqrwwJQBSwASNd999d8zzQmbd22+/PcycOTNm4q0VlBeRNJQXkXSUl4wOlxfmKVq6dGmYMGFCTE5HVl36tQwbNixOC0AzEsOnX3rppZqIuOQoLyJpKC8i6SgvGR0uL4wgmjJlSmwW6ty5c4y4IDDTpk2LHXSZSZroC01GzPxcKygvImkoLyLpKC8ZHS4vzOa8bt268Nhjj4XzzjsvnH766fFEkPMln8PohRdeCNddd124+eabw/bt2+3zIvIDQHkRSUd5ySilzwt5W5CSzZs3h1deeSU2IU2cODFs3LgxCgyddJ966qlw5ZVXRsnZsWNH5T/LQ3kRSUN5EUlHeckorcMu8vL444+HwYMHR3Eh58vIkSNjkxG/M/qICMzcuXPN8yLyA0B5EUlHeckoRV4+/vjjOA3AoEGDwujRo8Py5cvja/R7QWCY92js2LHhz3/+cxxxlDcnlYnyIpKG8iKSjvKSUYq8vPfee1FOHnnkkbB+/frKq1lzErJCJ17EZvLkyZV3ykd5EUlDeRFJR3nJKK3ZiE64LGTPZaoAmob4nQ69/ERwHG0k8sNBeRFJR3nJKFVemIiRnC80D5HXhfmMmFH63XffDR988EHYsmVLZe3yUV5E0lBeRNJRXjJKkxeaiMj5QvMQSemYEoD5jO68884wYsSI2JH36quvjsOlP/3008p/lYfyIpKG8iKSjvKSUYq8EHWhmWj16tWhX79+UVDIsjtr1qwoMYxCYs6jG264IRxxxBExEkNzUpkoLyJpKC8i6SgvGaXIC/ldmM+IIdJ9+vSJssJoI2aWpiMvUkO/l0WLFoWePXuGt956q/Th0sqLSBrKi0g6yktGKfJCP5ezzjorTszIzNKMLmLKAP6+/PLLw5IlS2J/GJLWkfNl27ZtpQ+XVl5E0lBeRNJRXjJKkReiKh999FFYuHBhnMvonHPOCTfddFMcYYQcEGWhaSnPtsvvZaO8iKShvIiko7xklNZhFyH57LPPwi233BJOPPHE0KNHjzB06NA4u/Tw4cPjQsfdhx56yOkBRH4AKC8i6SgvGaXIC01CDIVGSpi/iJPByKLjjz8+jjgaM2ZM6N+/f5y48emnn47rl43yIpKG8iKSjvKSUYq80Dn32WefDXPmzIl9X+64447Y5+XII4+MieloUiIC86c//SnKgtMDiNQ/yotIOspLRinywtBn8rlceOGFcSj0qFGjwvTp08Pvf//7OLKIjro0GfXt2zeOTFJeROof5UUkHeUloxR5IUEdiecQEyIvhxxySPjtb38b9tlnn3DccceFE044IXTp0iUceOCBsemoFjLtKi8iaSgvIukoLxmlddjNYUqAuXPnxrwv5Hl54YUX4vBopgzg9ZdffjmOTiob5UUkDeVFJB3lJaMUeSFbLpEXOuzmy/bt2+PCe4xEou8LwrB8+fLSs+uC8iKShvIiko7yklGKvKxfvz5m1aXDLhGWPMpC9IXOvERa+J3cL0OGDHFuI5EfAMqLSDrKS0Yp8jJz5szw4x//OPZnueiii2LH3V69eoXLLrssvPjii3EY9dq1a+Owafq9fPLJJ5X/LA/lRSQN5UUkHeUloxR5IarCtABvv/12eOmll2I/F5qJmGWaiAwSc+6554ZjjjkmHHzwwcqLyA8A5UUkHeUloxR5QVbIqstoIyZnJMsu2XVvvPHGcPrpp8cRSLfeemuYOnVqeP7550uflBGUF5E0lBeRdJSXjFLkhf4thx9+ePw5evToKC3XXXddzLKLxNx+++0xcd2TTz4Ztm7d6txGIj8AlBeRdJSXjFLkhQkZibxwAsaOHRsefPDBMG7cuPDoo4+GNWvWxOHTSM3gwYNjp14jLyL1j/Iiko7yklGKvGzYsCH2bSGz7oQJE+Lv48ePj1l2161bF955550oMcxr1LNnz5oQBuVFJA3lRSQd5SWjFHkhw+57770XunfvHodJM3P0DTfcECdg5D2akYjGrFy5MjzxxBNx9umym46UF5E0lBeRdJSXjFLkBYi+7LfffjGywpQATAdw7bXXxoX+MJdccklsXmKSRoSmLcgLw3xJ11xzTRSe1qD5ibmTLrjggjjp48CBA2Pz1LZt2/YoR8qLSBrKi0g6yktGKfKCKJDL5Ze//GUUDoZFH3300eHhhx+OC8npBgwYEMViT5B9d9WqVbGjb6dOneJIptZgdBM5Zs4888yY/I7PZ3ZrMvwqLyLForyIpKO8ZJQmL8wcTT6XN954I0ybNi3cfffdlXdD+PDDD8OYMWPiiKM9QVMTERoiKQcddFDMIdMa9KXhpPO99LNZvHhx7GPTEkgR7/HZjIpiBFTXrl2VF5HvifIiko7yklGavNCEg0wwnxHDoZGZnC+//DJGU5iUcU/wOTT70MH3qKOOihl6W4N5kvr37x+OOOKIKCKnnnpquP/++1ucO4l+NnQm7tGjR2zGQoxYiN6IyHdHeRFJR3nJKK3PCwKTT8KIrLA0hfeqGSLN/7MQraHpqS15YR2ajVavXh3nVyKy06dPn/h38341fCZitWnTpjjf0qRJk6L0GHkR+X4oLyLpKC8ZpcgLUkKTDJEN+rgw2ohRRbNmzQpXXXVVuPTSS6NUXHzxxXHkUTUTM9Kxl+kE2pIXmphYj+9HlvjOK664IsyePXuPomSfF5E0lBeRdJSXjFLkZefOnXGoNOJCkrrLL788SsTSpUvjEGn6u5x//vnhD3/4Q0xcR4faPVGNvNBMxXcyVxLb8MADD0RJYn4lRiy1hfIikobyIpKO8pJRirzQREM/lRUrVoRly5bFHC99+/atvJtBXxQ61lZLU3mhuYeh2AhS0+agJUuWxNmrSYjHvElEefgO1m3ebNUc5UUkDeVFJB3lJaMUeaE/C/KSL3feeWfo16/ft14jD0u1EE2hcy2CQs6XGTNmxKgNTUU59F9BWuiA27lz5zhCiaaqalBeRNJQXkTSUV4ySpEXOsiSZ4XcLCzMc3TooYfGmaRZ8tf++Mc/Vv5jzxA5QU7ou0K0BWkhAkPH2xzW4XU64BKpQUSayk1bKC8iaSgvIukoLxmlyAsjfYiK0GGW5cILLwzdunX7698sZMG96KKLKv9RPsqLSBrKi0g6yktGKfJCRIS8LG+//XZciMIgK/nf+WvkZKkVlBeRNJQXkXSUl4zSOuySBI6+Kbmo0OelKd+1w27RKC8iaSgvIukoLxmlyAv9TOj3ct9994VRo0aFc845J+Z0yZPCkW135MiRyovIDwjlRSQd5SWjFHkhxwpJ6p588sk4xxBJ6saNGxf7wZxyyimx/wsjgr7LaKOiUV5E0lBeRNJRXjJKkZd81A/p+smxwgzTdOIlLwsJ45gZmgkWmYuoVlBeRNJQXkTSUV4ySpGXekR5EUlDeRFJR3nJKF1eXnvttfD888/H+YX4yUJH3mrzr3QUyotIGsqLSDrKS0bp8sIcRvvvv3/o0qVL6NSpU9h7773jnEM0KdUSyotIGsqLSDrKS0bp8sIM0ow4IuvtypUrw+9///swb968b8xJVAsoLyJpKC8i6SgvGaXLCzNKM9IImJ+ImaTbmhm6LJQXkTSUF5F0lJeMUuQFSUEG5syZE04//fQoMHPnzg1PP/10bD6666674t+8z8gj5isqG+VFJA3lRSQd5SWjFHkhQd3NN98cJ2Hs2rVrOPXUU8Pw4cPDoEGDwk9/+tM42/OwYcPiBI0kqyMbb9koLyJpKC8i6SgvGaXIC3ldSE43efLkcMIJJ4Q+ffqEqVOnhocffjgcfPDBUWqmTJkSJk2aFNephZFHyotIGsqLSDrKS0Yp8kJn3B07dsTlkksuidMEICjvv/9+OO6442KTUf4+y1dffVX5z/JQXkTSUF5E0lFeMkrvsDtgwIC/jjZasWJFOProo+NoI7Lw1hLKi0gayotIOspLRunywuSLvXr1iifjtttui4Iwffr08Omnn1bWqA2UF5E0lBeRdJSXjNLlhX4u1157bbj++uvjwu/Ma7Rly5bKGrVBe8rL6o8+Dc8t/7Aml83byx/ZJT9MlBeRdJSXjNLlhf4vzZuIvvjii7B79+6a6OuS057yctP0FS0WorWwvPDWxspWirQvyosUya7dX4YPt35ek8unO3dXtjId5SWjdHlhJmn6uzTl9ddfD2vWrIkSUysoLyJpKC9SJC+u3RT2G/RcTS7/NXtNZSvTUV4ySpUXIit33nlnmDZtWvybCAwJ7EhaxwikWupforyIpKG8SJHMffPjFs9vLSy3PLOqspXpKC8ZpcsLcxsxESNRlvXr14cRI0aEHj16hLFjx4bt27dX1iwf5UUkDeVFikR5aSxKbzYaOHBgTEr3yiuvhEcffTTOMn3eeefFEUe1hPIikobyIkWivDQWpcgLnXG3bdsWlwsuuCCcdNJJoXfv3jHb7owZM8I555wT5zfifYZM/9CS1Ckv0ogoL1IkyktjUYq8MLfR4MGD49xFP/nJT8I//uM/hmOPPTY2Id1www3h0EMPjULD/Ed33HHHD25uI+VFGhHlRYpEeWksSpGXdevWhXHjxoXx48eHffbZJ/z93/996N69e+ykS96Xbt26xYgM60yYMOEHN7eR8iKNiPIiRaK8NBalyAtNQatWrYoRGKTlqKOOinMcEXmh38vJJ58cIzNvvvlmHDJNLpiyUV5E0lBepEiUl8ai9A67TA9w0003haeeeirKC1MEMNrokUceqaxRGygvImkoL1IkyktjUbq8kNOF5iFyvJCs7oorrgh9+vSJuV927txZWat8lBeRNJQXKRLlpbEoVV4QFiIvyEv+N3MaXX311VFi5s6dG1+vBZQXkTSUFykS5aWxKFVeGAK9YsWK2IG3KeR8eemll+LUAbWC8iKShvIiRaK8NBalyQtRlk2bNsVlx44dYdeuXWHz5s3x9YULF4bly5fH12oF5UUkDeVFikR5aSxKkRek5IMPPgiLFy8OL7/8cvz9/fffD1OnTo3DokeNGvXX+Y5qBeVFJA3lRYpEeWksSpGXDRs2hEmTJoV77rkn5nVZunRpmDVrVszvwnsMmx49enSUHBYz7HbcorxIUSgvUiTKS2PR4fJCzpZXX301XHzxxeGAAw6IPxkWfffdd4fDDjssPPvss+GMM86InXZfeOGFsGjRojhpY9koLyJpKC9SJMpLY9Hh8kIUhb4tjCRimDQTMebDo8m2y5QAv/71r8Npp50WpwYgAlMLs0srLyJpKC9SJMpLY1GKvLz77rvh/vvvD0OGDAmDBg0KDzzwQBSVzp07x2R1ZNglYd3s2bPDggULaqLjrvIikobyIkWivDQWpcjLypUr4wSMw4cPDxMnTozTANBxt1+/frHz7oABA/6a+6VWUF5E0lBepEiUl8ailA67QD8W+r7MmzcvrF27Nqxfvz5MmTIlLFmyJFxzzTVh8uTJlTVrA+VFJA3lRYpEeWksSpMXIjAIDP1dHnrooRh5Ofvss+PvRGLI/VJLKC8iaSgvUiTKS2NRiry88cYboW/fvrHD7n777Rd+8YtfxJml995773DqqafG5iPeGzhwYOwTwyzUZaO8iKShvEiRKC+NRSnyQofde++9N3bUPfzww8MRRxwRzjzzzNhhl4WRRyNGjIgjjRhGXQtRGOVFJA3lRYpEeWksSms2yqHTLiOP6Pty++23x7wvEyZM+NZ8R23BlALbtm2L8yExDLstyOBLE9X8+fPD66+/Hj755JPKO22jvIikobxIkSgvjUXp8rJs2bKwZs2asHPnzigWb731VnjxxRfDO++8U1mjbeg7g7iQ0I4oDkOrW4M+Nnw+OWSOPvroGOFhGgI+Y08oLyJpKC9SJMpLY1G6vCAUzCyNHPATgSGvC5l4q4H1yQfD1AL77rtvjKi0BqOaRo4cGfvTkLmX6QnoU0MSvD0JjPIikobyIkWivDQWpcsL0jB+/PjQv3//OEz6u04FgLwQpSFfTNeuXduMvNBcdMEFF8Qh2Rs3bgzTp0+PzVY0H+3evbuyVgb9bJhv6frrrw+9e/cOJ554YujUqdMem6WqQXmRRkR5kSJRXhqLmmg2IvrBZIwkqKs24pKDdNDkRB8ZmoJocmoNojInnXRSWL58eZQe/ib6MnPmzG9l8eVvJoxErO666644AqpLly7Ki8j3RHmRIlFeGovS5AVJYQbpUaNGheuuuy5OC5DCRx99FI455pg25YVOwd27d4+RGiI8rIu8kBAPAWoLm41E0lBepEiUl8aiFHkhqkFGXaIaTMw4ZsyYGNGg423zhRwv1XSorUZeGI1EIjyiPURe5syZE0c4IU7KS7YoL1IUyosUifLSWHS4vNDMQ2fZnj17hvPOOy88+uijUWKYpPHWW2/96zJ06NAwePDgmO/ls88+q/x361QjL0jLtddeG5544om4Pv1kmIoAqdlTXxvlRSQN5UWKRHlpLDpcXpCExYsXR3GhjwpJ6GbMmBEnYkRimi5MFUDOF6Ike6KpvNAcxc/nnnvuG31Z6KTL0Gj6vdDPhs679LUh6kOumLZQXkTSUF6kSJSXxqLD5SXv6zJ16tQYWSESgqQw0mj16tXfWJjjiBww1XTiJTqD8Lz//vtRRhh2/corr3wjosLvdOwdNmxY/O7bbrstjjwyz8vXi/IiRaG8SJEoL41FaR12aT4iYRxDkW+88caYZG5P0Y/2gO9AbhCbPDleNSgvImkoL1IkyktjUZq85BBhQWDIdrtly5YOEZjvg/IikobyIkWivDQWpcsLEZinn346ziDNqCOy3dYiyotIGsqLFIny0liULi9APxVGIL3xxhvfynRbKygvImkoL1IkyktjUbq8fPjhh2HhwoUx+vL444/HnCuIAp11qxki3VEoLyJpKC9SJMpLY1GavDDyhxFBzC9EcxHJ4hgBdMMNN4Rbbrkl3HvvvXHCReYYqmY0UNEoLyJpKC9SJMpLY1GavCABzBfEUGmSxTE5IqN/aDpiGDU5WMiGy0zQ33W+oyJQXkTSUF6kSJSXxqI0efn444/DkUceGRPJEV0hEkN/F36SlI4suFdddVV49tlnqx7OXCTKi0gayosUifLSWJQaeenfv39cmLUZiSEr7p///OeYtI4TdOmll8Y5kIy8dNyivEhRKC9SJMpLY1GavBBNmT9/fhQX5jIaOXJknOGZvi68dvfdd8eoSy2ICygvImkoL1IkyktjUZq85KxcuTJOzshcQ5dffnm47rrrwoMPPhj7wNRCc1GO8iKShvIiRaK8NBalyQuZdLdu3RqbikaPHh1ndybLLieGTrwMm2b6ACMvHbsoL1IUyosUifLSWJQmL4gLcxoxNQB9XGhCevnll8O8efPiTNOMNurVq5d9Xjp4UV6kKJQXKRLlpbEoTV4++eSTcMIJJ8Rh0mTYZV6jTz/9NErNBx98EO67774wYMCA2IF3165dlf8qD+VFJA3lRYpEeWksSpMXZnY+77zzYkK6adOmxVme6f9CnhdEIe8DQyK7WpgyQHkRSUN5kSJRXhqL0uSFCRjJ5XLllVfG/i6MMKKj7tixY+PoI16nL0ytzHWkvIikobxIkSgvjUVp8pKzevXq2Dn35ptvjh11hwwZEiZNmlRTnXVBeRFJQ3mRIlFeGovS5eW1116LERYS0tFJ9/zzz4/DpZ955pmwcWPtVKTKi0gayosUifLSWJQmL8wYTRMRyenGjRsXpkyZEidpfPLJJ6PMXHbZZXGiRjr2Mqy6bJQXkTSUFykS5aWxKE1eNm3aFHr06BFFhegLI4yItGzYsCEsX748duTlJC1evDjOd1Q2yotIGsqLFIny0liUJi+IyimnnBKjL2TTfe+998KHH34Y87ow6oiTQ6fdhQsXKi8duCgvUhTKixSJ8tJYlCYv5HQZNWpUOOuss0Lfvn1jXhdGH40fPz72eTnzzDNjAjtyvHz11VeV/yoP5UUkDeVFikR5aSxKkxeEBIFZsmRJFJahQ4fGPi633357HG1ENIbEdbUgLqC8iKShvEiRKC+NRWnykkNSOpqOaCLipPzpT3+KeV7mzp0b5aVWUF5E0lBepEiUl8aiNHn5/PPPw3PPPRcefvjhKC+MOBozZky455574ggk8r0w5xHTBdhs1HGL8iJFobxIkSgvjUVp8sL0AOR1GT58eJg9e3ZMSsccR2vXro2TNDI1AO8vW7bM6QE6cFFepCiUFykS5aWxKE1ePv7443D00UeHGTNmxOYhpgsgGrNjx46wbdu2mHWXaQNmzZoVdu7cWfmv8lBeRNJQXqRIlJfGojR5oTmI0UTkerniiivCo48+GrPqPvXUU7HJ6LTTTguXXHJJFBmbjTpuUV6kKJQXKRLlpbEoTV6IpsyZMydMmDAhTsp42223xSYk+rsgNQ888EBMVlcL2XVBeRFJQ3mRIlFeGovS5IVh0ojKokWLwsSJE0O/fv1Cnz594pDp3r17R5Eh826toLyIpKG8SJEoL41FafLCnEXdunULCxYsCI899lg499xz/5rjhWajiy++OMpNraC8iKShvEiRKC+NRanycswxx8Th0nfccUfM75I3ETEdAJGXXr16xb9rAeVFJA3lRYpEeWksSpMX5jHab7/9wh//+MfQvXv3GHlhskYEhnmOrr76auWlhEV5kaJQXqRIlJfGotQOu+R3mTZtWmweIvrChIwMlyZZHR14n3/++cra5aO8iKShvEiRKC+NRWnyAgyBJtqCtDCXEdEYmoyYGoDZpJ0eoOMX5UWKQnmRIlFeGotS5aWeUF5E0lBepEiUl8ZCeakS5UUkDeVFikR5aSyUlypRXkTSUF6kSJSXxkJ5qRLlRSQN5UWKRHlpLJSXKlFeRNJQXqRIlJfGQnmpEuVFJA3lRYpEeWks6l5eyAuzefPmsHHjxjgD9e7duyvvfBvWZTg22X1ZmF/pL3/5S+XdtlFeRNJQXqRIlJfGou7lZfr06aFnz57huOOOC4MHDw5vv/125Z1vQuZepiI44IAD4rQEzKt05513hnXr1lXWaBvlRSQN5UWKRHlpLOpaXpYvXx4nc7zqqqvCM888E2elJsEdEZjmEJl56qmn4nQEs2bNCvPnzw9vvfVW2LFjR2WNtlFeRNJQXqRIlJfGoq7lZeLEiXEGamai3rp1a5xS4PHHHw9r166trPE1K1asiKLDPEojRoyIM1mT2Zcsvy2xa9eusHTp0jB+/Phw1113hX79+oUuXbrEJqpUlBdpRJQXKRLlpbGoa3lhTiRE5LXXXosRlClTpoT77rsvLF68uLLG17z66qth2LBh4eyzz44n/5xzzgkPPfRQnJ6gJfg8IjTXX3996N27dzjxxBNDp06dlBeR74nyIkWivDQWdS0vyMjdd98dIy10xqVpB6GZN29eZY2v+eCDD2L0hY669H+59dZbw8033xwWLFhQWaNtbDYSSUN5kSJRXhqLupYXOtzec889YdWqVTFSMnXq1DB8+PAW5YVmINZBXIDmJQTm6aefjn/vCeVFJA3lRYpEeWks6lpeJk+eHAWGUUR00h01alT8e8mSJZU1vmbOnDlh7Nix4b333oszV994441h0KBBRl6aLcqLFIXyIkWivDQWdS0vRFyItAwcODA88cQT4ZRTTol9XpAZ+sE05cUXXwxDhw4N11xzTey4e9FFF4UxY8bEvC/VoLyIpKG8SJEoL41FXcvLzp07o7TQofbKK6+MnXFnzpwZZs+eHZemIB1IzYUXXhiXO+6441uC0xbKi0gayosUifLSWNS1vAAddcnXMmPGjLB+/frYt6UIlBeRNJQXKRLlpbGoe3khTwtTAiAxpPpvLW9LKsqLSBrKixSJ8tJY1L28dBTKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0ljUvbysWLEiPPbYY2HMmDFRMDZt2lR559t88MEHYeLEieG+++4L06ZNC++++27lnT2jvIikobxIkSgvjUVdywuiMnbs2HDuueeGvn37hgEDBoRXX301fPHFF5U1vmbbtm3hueeeC2eddVb405/+FC655JLwzDPPhM8//7yyRtsoLyJpKC9SJMpLY1HX8jJ79uxwww03hDvvvDNs3rw59OvXL0ydOjV8/PHHlTW+Bqm54447wsCBA8Onn34afyda895771XW+CZfffVV2L59exQkPo+ITdeuXcNbb70V/05ZrnxkfvjfFz8c/k/v8TW3TF+0qsVtbrp8+OGHLb5eD8tHH30Ul5beq4elno99r9Gza/K636vPI2HBsrUtbnPzpZ6vnXq/9ve07U+/tLLF81sLy7UTFrTbsT/vvPNindfo1LW83HvvvWH48OHhhRdeCJ999ll45JFHwrhx48Lrr79eWeNrpk+fHgYNGhSbi3bu3BlmzpwZozZz5syprPFN+LwJEyaEHj16hMMPPzzst99+4e/+7u/Cr371q/h3yvKz/Q8M//cn/xF+euAhNbd0ObRri9ucL4cddljYf//92+U4lLEcfPDB4Re/+EWL79X6cuihh8brkJ8tvV/ry97/cUDYa+/9Wrzuylx+9v+XQw9r+7pn+fWvfx1+/vOfh86dO7f4fq0vhxxySDjwwANbfK/WFx4cDzjggNClS5cW32fp/P/LrpbOby0s+xxwUDjooINa3O7vuuy1115h8ODBlZqqcalrebn99ttj+GzVqlVhx44d4dlnnw133XVXePHFFytrfM2TTz4Zrr/++rBkyZLYrPTSSy/FyMtTTz1VWeOb7N69O6xbty4sXLgwzJ07NzYbIUDIDn+nLH369AmnnXZai+/V+vL444+HfffdN4pjS+/X+nLRRReFs88+u8X3an15+OGHw9577x2lu6X3a32heff8889v8b16WCgDEBgqjpber/XlqquuCscee2yL79X6QtmLNA4bNqzF92t9IeJ/4okntvjed1148F69enWlpmpc6lpeRowYEe65557YlJPLC81B8+bNq6zxNZMnTw433nhjeO2116KYIDhUwFTGHQ3bSJ+beoROzkQvFi9eXHmlvhgyZEgsxOsRJB1xfOONNyqv1BfXXXddvAfrlV27doU//OEP4emnn668Ul8Qle7Zs2flr/pi69at4aijjooVdz1CPdWrV6/KX9Ie1LW8cDPefffdsSKlmWf8+PFRDFqKvNBZ97bbbotPTxRCiM6oUaNajbwUifJSHspLeSgv5aK8lIfy0v7UtbwQQhs5cmR48MEHYxPP1VdfHS8SmoaIxDSFfjAMkUZgNmzYEJubaHZasGBBZY2Og+++8sorK3/VF3RwJnT+yiuvVF6pL+gjRd+neoRQMf0Wli9fXnmlvrj55pvD0KFDK3/VHzQ3n3766bEJox6hT2C9VqDIywknnBCef/75yiv1BV0UGFAi7UddywvDlm+99dZo5EQy6NA1evTo8Oijj4YnnniislYGkRmajij8L7300lgB0366ZcuWyhodx5///OcwZcqUyl/1BaO6aK5DFusRCr8ZM2ZU/qovGGnANYt81yM8Nc+aNavyV/3xl7/8JfY3WrZsWeWV+uLll1+OgxDqEVJa3H///eHNN9+svFJf0BowadKkyl/SHtS1vFCYkKSOG5KIC/1X1q5dG95///24NOXLL7+MryEwNDXxFMITLJ/R0SBdn3zySeWv+oKnT6Iv1ebHqTUY+r5xY33msqHZgmY7ftYjHPe2kkjWOqRPINElD0L1CNELhtrXI3n5TfqKeoSHZIZKS/tR1/ICdL6lUFy5cmW8QNqSEd4jWR3Cw1NsvVYCIiIijUzdy4uIiIg0FspLO0JTCn1CiAQR4WkrCkTzC+vSfETEKI8CER7lbz6D5qWOap75Lt9L+JwQdN4MwP/xGrDfhEfZLxY+h88uGjpo501Cezr2rNt0G2kGYH22k//lMzg3zTt9FwXfzTHf07Fn+9hW9jPfdhb+hwgk56SMY8+551ixHXuCbWI/2T4yXbPdwM98v9iPjoqKsu0cf843yStbg/XYxvz+ZlvZfuAYs+/5sed97u/8nigSvpumFO7BtmA9trf59ZHvF9vPa3xOW8ehPan22OfXdn7dEDXn9/z6Ydt5jfc4L7xW9LHn8/OygoVtaKvM4Vjn5T3/xzYC10nTY29rQPUoL+0IUxMwFPH444+PQ3Lbmvhx6dKlMWHa0UcfHa644oqwaNGi+Do3wmWXXRaHZPbu3Tt+ZkfAzUNHZr6XuTPIRNwSFILcfIzs6t69ezj55JNjAqb8hmQ0SadOnUK3bt3iwudQoBQNneFIPkciKLZh/fr1lXe+CdtPvycypZKwi22kIyB9GTgGdADnM/isjurcyLYyN9dxxx0Xf7Y2HJTjSIdR5udiu4888sjYWZ1RDO+8804cRUWH9PzY8zkUjEXDuae/GdveFhTupCjgmuG6J1XBmjVr4jmhIyaJG3//+9/H/cjvh6Kh8qAD9AUXXNBmZ2IqFY7xhRdeGM/TmWeeGTuus+1cN+x7fuy5fsgn1RESwLEneSFlRltwHXC8ybCbXx+MmkJ8yJNFWcP9wPxwjOLsCDj2lJHnnHNOi7m5cjjuDLE/6aST4naTZZZzwKhNtp1ylAR2vMc1REqBIiUAcUGcSFaYl4EXX3xx7E/E9dASXPckaeQY33TTTfG6B/pd8r/HHHNMPIdki5fqUF7aCUYgMBKESp3RLEz+yA2ZP501hRuW4d3cdOSfIf8FhT9DYflfLnJGTFE4svC01NpN0R5Q+FKQUYgwQzd5aCjo+N7mTzDsDyOlqPDJkUPuCAo+CjxuRLb3mmuuCfPnz48LFUPRTxMMg7/llltiBmW2jeGgZFBuqWMlT2hICceebWYb6eTNvnK+qHg49hSMdOymL1WRT3F8L3lDmIaC+bO4hvhetrM5eQVKxc5200mdjLVcO8zdRRoAKv782FOYFn3sqfzo/H7KKafEiqMtSGGQXx+MuEO6uP45xg888ECUZs4fhTujBouu/Kk8+e7+/ftH8WgrfwvXMdm7EQWkkP1ge6mE2BeEmXuG4076BZ6ii7xnuSY59tx/VOp7yt9C+cT1wlxw+fXBPtH5nuuHe59jT4WMIPMQVSRclwge2cbJG9VW/hb2k36KjNhhuxlyz/w+HGdGD7LNnBve475H6Io89mw7MsLwZx6aKDO5D9mHlh7UuMa4XnhIZR2ue+blo7zk3mFfKPc5N+Qq64iHvR8Cyks7QQFAtIVpCCi4KMwYrv32229X1vgaKk0qWyopwokPPfRQLDD4DP6Pm5FKiidBJuDipszDjEXAzZV/L2JFhcL38hTQPBTK9jLkkv/haY51eBrl5qPw4+mBG5mcOtzYVMJFVv5AAcCxzyflpPLju1uadBPRYV9PPfXUKCiIDE9vnCcqUKSGColpIfgboSiyIMzFi2NP9AeJ5LqgEG7ruHEemBWdaBmjMDhnpAtg+xFLrkMKwaKPPTLLdUolhIC1BRU/BTTbyjFFNrnmWdgPzgXXFPcCIsA9UCTIEeeaiu83v/lNvH5bg3uaBJekCODYs81EwHjK51qnQuLap0JjvaJHJHFeqaS5BnhypwJsC+5PKk+Ei+uL6wy5Jdkk1x/STLMG9w37wz1eJBx7jh15upi3iGuiGrimqeC5x3noYlu59tg3rhumb+H8FAllMZFzhIrt4cEBeSSi29JDB69zjLlmuC7INcW1TrnP6xwDziUSxPXDZ8ueUV7aiTxaQWXEkwJPcdxYPG02h4qFJ2Qqfp7+eHKjouSGpBCkoOGm4LO4wFmKfAqlAOPpk4KQAownIr6TQoLtaw36OdAsRCHODcxNSuTpj3/8YyxQqcxaiz61J8gIFRBPl7SNUwAz9QP70Zy8sOZJk4Kc5iEKlfzpmXNGNCR/IiWa0VZbdipcAzS7UXiz7ST/IypH4daWeCBcnCO2j/W4Zkh8SCVG5Ilj31r0qT2houB6Z3uJGLYFhTbygmyxzVQ2CA3ixnYTAeOplusQASs6gSSVENuOmHyX5HMIFpEhtpnKiohGLo75QjNYW/dOe5Afe66XPSWfQ8yo4HnQYF22nYqe18k4TSSAz+KaIZrDvVwkHBu+j3uNaGe1yed4kOMe5aGC/UfEKLs45uwbEW+kt+hjn8M2cOyIfhEZaqmsyxOiIiWU4zxkcX0Tgbz22mtj2cPrlAXcE6012cs3UV7aCfpKUGHyBE+lztMooUIuyOZQKdKGS2VLxUgzABczT27cfNwEmDhPJggEUZAinyYosHh64Sc3H1EVvhchaK3ZgcqHJw/2kUKD7aPZiydZKgNC0kRgKNiLnkQM6eOJhagR209Il8KipX4TPDmzf4TF2QcqU6SF40/0hkIRceSplMgZhUuRUS8KLio+nnQpzLkmkBIK6LbkhWsoLxCBa4XKHwHiOCBl7BOvdQRUdnuSlzy6x7XNviE8SDvSxf8iBdwPVAZsO+exI6CiQ/aqkZd8+2i6IFpBBIkHlDz3ERJ/xBFHdFhfL6CZc0/ywvXBQtnEPXLGGWfEY8zC8c/76LD9VKBcgx0B20K/kWrkhWsGWUcGuD+5L3kYQYbZdqKl9KXiQYBrqWjYHso2BIrrh0hQS1BGss2UjZSnXD886PKgSvnCQyrXINcR5RgRGNkzyks7QeiPCocnLiohnmgo3HhSaA4FPRUlT9ncgEQnuLh5MuIpnGYlBIA5bLiYudCLlBcqTsL2VKRUftxMfC/S1Jq8UOiwf3RURGIoxCkYKUT4nYKbJ20Km6JD0HwH20s0gu3n+PIahVlz2D6OZd4UxJM/4sn6bC/SRiGE5PA7kaQi5YXoApUHkssxRUaoUBDh1uSF1xEBBDg/Pxx7fme/eJrlffappehTEVQjL8gWUS+uDfaBJ3z2kydQKt+8QkJauB+IJnUE1coL20zTHg8ZRE7ZXiC6xbHnfa5B9oVoSEvNlkVQjbxwzbOwjfyk0swjAjTfIfq8zj3DOWH7O4Jq5YXtZl2iRGwfEslrHHvOH79TDhFN5b5trcN+e8J35/3OKKtbi/YgNzwI8tBE+cN1xnGnrOcepnzk+qEsYF3Op+wZ5aWdoCmIwoCICxUoMkPl31L7JULD+xg2FzNPoLmd0/zEzcnNh8RQoXIxs15R8ESWfy+FM08GfC/b1/yGpJCggmHfKMAJgVLoAQUeNyaVJ09DVAjsU9EpvTl+fA9hcCIqSBV/tzSBIRUjhRtyQgFIYchTNE1NHGdEgkoHsaQg4biwXlEQaeHcI740QfDUSMFGBIhj3RJUkAgX/5NDMwb7xmcQbSGMzfmspcgLx5friooSySJixjayH1Sm9BWhguKpH/lqST6LoBp54RrgaR6ZZduIjvIa9wLngnuViBIV0WGHHRabjYvu9JpTjbxwzROt46GI/WCEDBUv542yiGgL7/HQxTXfUaMcq5UXzhH3N8c6l1oeErmGqPQ59jwAEPXKm7+LhPPOAxODLbhXeXho7X7lmFJesl1sMyLD3ywcex6gECHqEMoC1pM9o7y0E1g1lSZPZVSmVB48QVMZEcloCpUjBTTtzozYoeChwqKwpjc6IX9uDAp0Po+n5yIrUApZbhiGfxLG50mYpgy2BRlrWhDkT2cMaWWiNCp+CkbCzcgLhQlNMTxhE5qmQqJQLBJ67fN9iAfbwnZRGHPskYOm5J2lObYU0jw1UXhQyVMIMlScY88+UFFRqOZRmiJANqgoGKnD8SP6xjnPjz0i3BwqHAq5ps0qiCZPcSw0zfB5eSStI2gqL4gr10PzzuoIIdvN/uX7zH1Ahc/5Yrgyna9pwuQ6oumxI2gqLxwvZJ5rnAoph2gRlRRpALg/c8FEJIlwEb0gmorQ8z7iXOQDR1NyeeE6Rcp5YKLpsCmIC9c89ysCQAdTrjG2n/1g/7mG6D/COpRnHUFTeaGc4Hu5HpofO84F202Zmj+U8FrTY49IUKbysNRaxLg94HqhiQcBpBykrMjLG8o7moeawvZw3VOm8pDEdU+ZwzXGMaf/HeeALgPsY9EPez8UlJd2Io+gMGyYSpQCjIuZm5InhqZw8fOUQGFNBUkFinVj5YgNoU8KeH5SwbZl9e0BYkRhRydbvpd94OmSip+bLA+PA08IiA7rst2EPik82E8KfSp++sDQnEQ0oOn/FgVCRSXI8br88stjB2KOOce/ebMdlRAVJ9vI8efJh3Azx5eoE4V33rGRKEHeN6YoeIKj3ZxjybZzXKkYEV6aVVp6emf7qWipeHKo6HmSZrvZBwrTjnryByIRHEug8OV6aN5kxdMxsk6Hbq57rjPOD9c9FRbnjeZLrh0kpkhpbArXPw8ebANNhlQq9Flhe3OIJhIhonLkHHHdU9FwnthPKlHOIddO8/8tGiSVKCHHi8qfCrS5tFOucE2w/Rx3hIfoLtcf28/rlFt0fEWi82hq0fA9iAfbgMjT747ICtdEU1iPfcyjq8B5497l/zn2XFOUTU2lswgQI44x9xnXMtcC550HP45d82g7dQPlO9cNkV5khQcl9pE+O2w7r1Me5dF42TPKSzvCDUZFxA1EwdCW/SMwVDgUdBT2+c1KAcTTHxECboKOenLOv5fCoSO/t72gwEKeeJrkuHJ8vytICueQyoCKrKMqfwphnjrzCr8jK76Ohusc6UJikMX8POX3A8LJeeyoylMygUbquXeIYhINkfYFISG6y0MH0bFcUDj2SBt1BuLJw6FUh/LSjlD5cTFS8FIhtfXEznusw7r8T9N1EQkubgr0jnr6hLK+tz34Lse+Lfg/jgHi6bFvf/LzhGw2PU/8bO1+kOLhmuPYc/157Nuf/LpvXj7xMz/2XvffDeVFRERE6grlRUREROoK5UVERETqCuVFpGBo46YPDf0J2ou8rbzWaKnN/ru047Mux6ve+v2wvfRZaM9zLCKto7yIFAx5Txh+y0iO9oIRIYxQosKsFRCP5p0O89eo3KuRGEYjMeqI0S8dQS5LTTtRtkS+Xmv7weg8RlG15zkWkdZRXkQSobIljwP5Gkj2RQZN8n8w5JmKmwRu5Mshp0NTSKhHLhcqQyIzJJ0jvwk5OPg9ryT5mS85TCnBek0/k4q1aeVKJlWyeOa5KJouJDUjpwp5Tb6PALG9DPkk1wm5gUhsSL4NMhuTKI/PZ+F1cljkeTwYhk4COpK58R7/S1I68oyccsopMcEg20vSrhz2h+1EaFiYc4ph5a3lEGJ9jkNb5McKCSRHDbmKBgwYEI8N+YKYLJCkYflr/GRhXYbQkyitaZJA8jZxLlvL0ov4kHWXVAQkHyQfCPvIMeE8krtnT9ssIl+jvIgkQv4GEsSRmJAMrFTIZDQl4RQVE5Uy2YapIJEY0uNTaVKBU7EjD4gOv5MdlwynVJR5ZUaFTeVI0j8SYZEMjmRifC4VLEnt8kn2yBuEVACVLImvfvSjH8XtarrsvffeoXPnzjEq9H2aOthmKl4qYRLjMckc+5bPjk7m0WOOOSYmPiPzKblbkCmS0uVZgJEdEncxozPix36zIH8kK8th+xBAxI7jQDIyfm+eRTaH84HgcLxY8mkeOE75a4gjGX8Zokp+DT6P48d7bO+//uu/xm3M188X1iXKQpIyMqvmn4G0sR+cj3xdjg35gpApIkp5Snj2m0RxSBE5lch8yz6zXr6ISNsoLyKJkAafypAKiCkWqKCoDIk8kDUWUfjVr34V04mTQp9Kkqd2IgwIDxU1wkHmTSSIipBpCnJ5IZkb2ZtJ6X7ccceFX//61+HII48M3bp1i4Jw6KGHxtl0+X++G1EAZIHMn126dInf3XT57W9/G6Mc3zehH1DJ0kzCNhNFIDpCdIHfkSsWjguyxXusj/CQWp0MsCR05H2yOfM/rVXayEEuRWSJJTJCkju2vSWI8hARyqMmHLff/e53oWvXrn+NoiCOCAjwvZxDRAO5IoJy4IEHxm1ClliIcLFOnniSfWCaCUSE4414Hn/88VFKyLyayyXnGtFj/zk3XBOnnnpqfA+xRPh4DckjMSXXxZ4SXIqI8iKSDJUa0xMQNUBGiBLQPEKzDPLAEzlRF57GmYiQpgUqsH/4h3+IURGiDlSc/CRyQsXM+7m8ULkiN3wun8P3UCkiNHwvFSiVH+JAhU4TBU/6RCYQC7aBuVWaLlTeLAgEUR/+57vCdpEyn8gGzTj060EU+FwqZ0SO7f35z3/+V6FCRIgIUZmzsE+IBpV4/hrvN800ytxazBdDcwuig3zRTEcfE9ZHiNhvKvxcgNgf+gTxkxTyecSqJViH6QFo8kPqfvGLX4R///d/j8KDJLJwDpkugu8DhAQBQzzYdvYBEUM8iJTxHnLDa2zXO++8EyNOHIt/+qd/it9DcxnXy29+85somCw//vGP43ksemJBkXpHeRFJBHnhaZ2nbypsmjWowHmyHjVqVHwap4Jj3ieiLVSAzDRL5IMndP6mKYI5fRCb5vJCRU4TFK/R5ESEJ5cXmiaQFyISfBbRCeaxYX2+i+9gklAmg2u6IBe8zqR4+Tw33wUkgUqZSBCV/UEHHRQOOOCAGFk6/PDDwz//8z+Hf/u3fwuHHHJIFLR8rh3SoBMxQgxoWvrlL38Zfvazn8VIx7HHHhtFgc9k/4BjgASw77zH+n/zN38TI1n8P59F5f8v//IvsT9KnnadY4DQITUtyQufmx9fRIRjz3FANpA9ZIvPI1qCnDGhHk1jTaM9RKw4d4gPERPkKo+6ISAIFs1CHCe2hyYlrgkEjz41CNHBBx8c57TK16cJjnXzbRORllFeRBLJm43yvihUYPxOM87s2bNjZYXYMKssTQv0d+Epnuaeww47LEZCqARpzqASbC4vpNKnbwX9aJAcohVUpogAEkTFTF8M/iYCguwQqSGKQ6VMRIGmDMSK32l2IcrD3wgQEQy+g4XoCZJA5KitOW5okmI72Qc+mwqYZhmEiUkKiSjwHewnfWzymXLZXuSJiprOq+w7xwUBo8mGfUP2ctFAkhAJmtZYn8gVUoQM0mk5b+ZBXmguyiNIyBLbRsQGeaF/StNmIz4/7+yMvORNUUgEnYf5m/PGtiGIHFsiJTTh5fA720+zEtEftg9xJRpFRIvJHDmGubzwGRwbFkSJBflCaoig8d0ch46aU0uknlFeRBJBXqiIaBZiBA2VF80I9HfhyZsK6qijjgpHHHFErFCpnKgcaUKg/woV66uvvhoFAPloLi9UrjQBMSIFMUKQiALwXfwPwkBlzEy1NFnkTSd0XGU9voOnfCIi/E60hagFEQ5GzSAtQNSCUVI8/dOnI58stCUQJCITrEvlTlSJ5hyatIg2se/IC7KBDFB5A/tA9AG5InKB3BHZoOIGIkA0NfEZzaFzMRElpIJjTJQKsUHs9t133782TQHHk4gOryEvnA+Oad6ZFolCMKAleaEjMfLZmrwgkcgKx55zw7li34ho0VzYdCQUx5Ht4dwhjESniMzx2ew7HbyJ9nAMkbof8sScIu2F8iKSSB55ocKlEqJCom9GLi958wwCQ9MK0Q0iADR3UMETbaEypU8EQtBcXoCneCIp9LGgiQb5QGKoYOmfQYVOBCAXF6CfBd+DMLE+ssT3I1EsNClRsdMPBfg+IgW8RgXa9PtbgvfpXMzCfvN5VPJUyogSFTUREqI7RGpgT/KCoLQkL2wjM04TwaKCJ6LDKB2iUURg2K9cRgBZ2GeffWLEp6Vmo6Y0lxe2n866CBJNVs3lhf1GmBi9RBQFGUVWkCKOAfJDRAjBgVxeOHdEoRBIRI8mMLaZ7WI0GvuDbBGpEZG2UV5EEkFeqOB4mqbCZpgulSrNI/RRoaJFUKjcEAkqaypKohYMy6Xyox8LT940//AeT/BUYlTaVK6AmNAsQqSG5gr6WFDZ0hTF9+QSkkO0g74jRGfo/4FAUbnSlETzBlESmozyfiJ8NttCRIFmrPx7W4PtIZrAfiIPVMoIE5U0fVqIdhDVaSpBCBj7nQ/RzuWFfeZvKnkiSnQ0zuF1RjUhCnw228XCvtPcgszQJEQTUc73kRcElM9DUmbMmBH/5hixj5zTXF4QPPoYEUGhuYjOtQga+0ukiXPJPiBVrMtxZWE7ibJwPrgmkCQiTUTtODdExzgXTQVURFpGeRFJhOYZKj0qLp6k6dRJBUYnVCosKjHWoUmGSpGoBpU6skMlh0AQlaHJiPfo98FQaf5n5syZUY6agpQQUaFyZtQKssFTfvNKj+8iyoEwMZLlJz/5SVzoJEplT0SIiA+jcoCKlgjD3/7t38btzqMlrcH3kT+FDqqIFxETmpNoquL7qIyp9GnKyvuisI9ET4gkIQ38zbGiAqfPCiKGoDQdxkyUA7lgn5E7XmPhGCJLbCuRqrz5hu8i4tWWvORCwefk8kJ0is7H5HjJh1bTHIWYMSQ9lxea1BBRIjNEkBBQmpk4Duw/x41jQTSMfcubkIjAcD5Zl3NAsx19eRAkIlWcD45BcwkVkW+jvIgkgnzQaZQKjSdxoixUaDSlECUh0sFCpUzUAdEhwkEFx9M7TSm8TpMBFSoCkedt4QmdjqVUcjzZU/EjPDQx0bmTRGo8yfP5eaI4oiZsEx1TqXSJiDA656c//WlcaK7gNSpomrbIL5JPNUBFSxSEiAARjz3BtiFsCBVNJTSXESFBWtgvIj8cC4aCI2bsN/uZRxiIHiEVRKrYBj6DqAnCw/awL0SN+EyOQV6x879ERuhzQtMbx58ICJ9NVISmG5rXOOY0rxHJIrqBALFwrIiWsT18D0LBqCGEj21iO5BO5AqZZBvpSIy8ICfsL1KEOCIoSEneHwaBQpryJjOOD/9DNInzxk+OMUJF9AUBpC8P8sv+sP95PyQRaRnlRSQRKlqe9IkQ8ORN5UMFSIWNyFDJUqEiN/ykQiRSQpMJlTxP26yf95HIIzlUilSOVJR8JiLA/xOloHMugsKoGipI3qOfCOLD51CRMiKJSp3P4ifNMyxESXiNypsKlEqY7f4+5FEkpAt54DsRGo4Jf3MMqJjZ1pYqZJp6kJJ8TiAqfsQE+Ez2hf4nHN+m/886HD/62yAJRGBoZkO6iNpwPDjerS1ETfJIF99JcxZRnZb6mxAxQUDoIMz6OWwPskSn55aiVERl2G8EjOPLdyB0+fEmUsS5pMkP6WVdtivfFxFpHeVFpAbIK+zWoLIjKtLWelSyLFKbNBUz4PeWXhORPaO8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEgdEcL/A7Fjxw5bpmCxAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E9%A2%91%E6%95%B0%E5%9B%BE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApIAAAFYCAYAAADgExwpAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAE6cSURBVHhe7b0Hl1Vltq///wrnA5xxbv9Hn3u6b5/DUdvQ2mZRaRVBERBoRFHJ6ZBDk3NqMk2QLEmQnCTnnKPknHPOzNvP3Hvb6KWpWmXhYr/r94wxR1WtndbeVbvqqRne9/8zIYQQQggh8oBEUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHlCIimEEEIIIfKERFIIIYQQQuQJiaQQQgghhMgTEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIYQQQog8IZEUQgghhBB5QiIphBBCCCHyhERSCCGEEELkCYmkEEIIIYTIExJJIYQQQgiRJySSCWDq1KnWvXt369+/v0KhUCgUsUSPHj3s22+/Tf9lEqEgkUwA1atXt9dff91q1aqlUCgUCkUs8dZbb1n58uXTf5lEKEgkE8Bf/vIX++tf/5r+SgghhPjl+dvf/mb/8z//k/5KhIJEMgFIJIUQQsSNRDJMJJL5wI0bN2zevHnWrFkzjzZt2tjWrVtt1apV1rFjR2vYsKENHz7cDh8+7Nc/ePCgdevWzY/zxtq0aZMf536GDh3q99GlSxdbsGCBH4eZM2f6/bZs2dJ7TC5dupS+JGckkkIIIeJGIhkmEsl8YPv27TZixAjr1KmTDRo0yL788ksbM2aMDRgwwN80NBk3aNDAli5daocOHbIZM2bYF198Yb1797YWLVrYuHHj7Pjx47Zhwwa/focOHTx69uxpp0+ftp07d7qQNmnSxJuVGzVqZLt377abN2+mz+DhSCSFEELEjUQyTCSS+cC6dets0aJFtmfPHrt8+bLVq1fPGjdubM2bN7fBgwfb1atXXQzJJE6ZMsVlsFWrVnb27Fn7+uuv7auvvrK5c+dav379rGnTprZ582ZbuHChde7c2ZYtW+ZZSrKRCCiPgVBy/TNnzqTP4MdcvHjR5XPx4sUeNDcjuUIIIURcSCTDRCKZj9y9e9flsEKFCvbuu++6FK5Zs8Yzh9OmTXMhbNu2rWchEcFr1665KJLNpNTNGwzZJDu5Y8cOGzlypGcz69Sp40L6/fff28mTJz3byddI5YMgQ0ppvFChQh4FChSw1q1bpy8VQgghfnkkkmEikcxHyASSASxevLiVKFHCevXq5SXoW7dueYaRjCMlbkSSvkh6Iiln0z9J9rJKlSreF3nu3Dnbt2+fl7zbt29vlSpVsrFjx9qRI0c8Czl9+nRfFxJhfBA8Hj2Up06d8kBEu3btmr5UCCGE+OWRSIaJRDKfIOu4evVq748cNWqUD8XwpiGLyGVz5szxnkj6GylTUw5HJMlY0lfJgA3rbDG0Q1YTASUjyXVr1KjhIkl/JT2TEyZM8Izjtm3b0o/+cNQjKYQQIm4kkmEikcwHKGmvXbvWZY3M4oEDB1z8eNPQO4kwUr7u06ePl7DpkZw4caJduXLFvvvuOz/OMfoY6ZlEGNevX+/HkU8GbZDNjRs3elaS48SuXbvSZ/BwJJJCCCHiRiIZJhLJfICeRgZj3n//fe9ppDxNryMCyHEkk/LykCFDbPbs2Z5prF+/vq1YscKvQ9mZjCV9lGQsGcgZNmyYD9VwHNlkWAeZZBmgypUru4ieOHEifQYPRyIphBAibiSSYSKRzAcQx4oVK9rTTz9txYoV80AOWSeyaNGiLpFvvPGGT13Tu7hkyRJ78803vZRdpEgR73fkOEJaunRpL4+XKVPGqlat6scJSt9cxuNwW4Zx6IXMDRJJIYQQcSORDBOJZD5A6ZoBGTKE9DASyB8T1vRAjh492nsiL1y4YPfu3fOSNiLIMA1rSyKQlMdv375t+/fvd+Ekc8nnHOc2XIcy+aRJk3zI5vr16348N0gkhRBCxI1EMkwkko8QJBBpPHbsmK8lydeAADKAg3ginAhkBj5nMhsxvT/jeOfOHRdRprAR19xKJOSXSN66c9eaTtpi5Yeueeyi1dTcDR4JIYSIB4lkmEgkE0B+ieSN23ftzb8usn9rMO2xi/d6LkmfpRBCiMcRiWSYSCQTQBJE8uVO823u9hOPXRw6ezX96gkhRLKRSIaJRDIBJEEkH9cYsmx/+tUTQohkI5EME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZD5y7949u337tp09e9Zu3rzpceHCBTt9+rTHqVOn7Ny5c3b16lW/XuYYH7ne3bt3/X6uXLni90Fcvnz5h+M3btzw23P9ixcv+n3kBolkfCGRFEKIFBLJMJFI5iOI4/79++3zzz+35cuX28qVK13iihUr5lGwYEH78ssvbezYsbZ792575513rFChQn5ZkyZNXBzv3Lljw4YNs88++8w++eQT69u3r50/f97vf8GCBVapUiUrWrSotWvXzr7//ns/nhMSyfhCIimEECkkkmEikcwnkMhNmzZZ7dq17aWXXrJ58+a5GG7ZssWWLVvmUatWLWvdurV/PmvWLJdHpJKvuR6ZynXr1lmrVq1c/MaPH+/3t3XrVtu4caO/CRs1amTz58+3hg0b2pw5czwzmRMSyfhCIimEECkkkmEikcwnKDuTIezdu7dnHpG9DJSmT5w4YV26dLGRI0fajh07XOyqVKli7du3d5lcv36938egQYOsc+fOtnDhQs9ucvm0adP8OLcfM2aMX49MJbfbtWtX+lH+AY9F9rJ///4eZDA7dOiQvjTvSCSjh0RSCCFSSCTDRCKZT9y6dcszisePH7cSJUrYokWL0pekspXIYL9+/Wzp0qV24MAB69ixo2coq1evblWrVnVJPHnypGcPKW1T+ubrcePG2YABAzwT2b17dxdOHouM5uDBg72E/lMQ0FGjRvn9E6+88oqXwn8uEsnoIZEUQogUEskwkUjmM5SaS5Ys+SORvHTpktWoUcOmTp3qwzL0PK5YseKHoZzRo0db5cqV/RilbOTx6NGjdubMGZs+fbpnL2vWrGl9+vRxwWTIZvHixS6mlNBzQqXt+EIiKYQQKSSSYSKRzGd+KpJIH1JYtmxZL1dT5maghmlsPjLpTa9js2bNvCeyfv36XrI+ePCgT3RzjFJ3vXr1vJy9fft2v8/Zs2dbr169bO7cuf44D0MiGV9IJIUQIoVEMkwkkvnMT0WSrCKZyJYtW/pADdDX2Lx5c9u3b5+Xw4cPH+7T3GQkM32Nq1evdpns2rWrf002kjfhjBkzPItJzyRiuWrVKr/PhyGRjC8kkkIIkUIiGSYSyXzmpyJJKbpFixY+JHPkyBE/tmfPHhfJtm3buuA1btzY2rRp4z2R9EAinQzZ0ANZunRpzz4ilrwJ69ata1OmTLHy5ct7L+WhQ4f8Ph+GRDK+kEgKIUQKiWSYSCTzGTKMnTp1+iH7yOBLjx49bPPmzb7QOFDWXrNmjZexGbQh68iak5S5r1+//oMwMmDDZDfDOdwv/ZL0WiKmFSpUcFklO5kTEsn4QiIphBApJJJhIpF8DEEaEVF6KtnFhl5KYNkfpBKhpOyNdOYGiWR8IZEUQogUEskwkUg+hpCZZIkfxDGzPSJktmBEIDODOrlBIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJL5yJ07d+zs2bM2ZswY279/v928edO2b9/uEjdo0CAbMmSIrVixwq5fv263bt2yOXPm2PDhw+3bb7+1TZs2pe/FbM2aNTZ69GgbOXKkLVu2zK5du+bHd+/ebePGjbPBgwfb3Llz7eTJk348JySS8YVEUgghUkgkw0QimU/cvXvXjh8/bhMmTLA//elPtmDBAjt16pSLX8GCBf3N06hRI5s8ebKdO3fO9u7da3Xq1LEaNWpY/fr1rX///nb58mU7ceKES1+VKlWsXr161qJFCzt8+LCdPn3axo4daxUqVLC6detaw4YNbdWqVS6rOSGRjC8kkkIIkUIiGSYSyXyCLCPZw+LFi9tzzz1n8+bN82zk0KFDrWfPnrZv3z47f/683bhxw4WTTGStWrVs3bp19t1331nbtm09K0l2smnTpv7x+++/d9HkfmfMmGGdOnWybt26+WM1a9bMpZX7+ilkOy9duuQiSyCsXbt2TV+adySS0UMiKYQQKSSSYSKRzCcQxDNnztiWLVvsww8/tIULF3qQWXzppZfszTff9DcQmcqdO3dagwYNvHR95MgRv82wYcM8Gjdu7NnJzZs327Fjx1xER4wYYW3atHEZXLx4sYsiEslxRPSnILBdunSxQoUKeRQoUMBat26dvjTvSCSjh0RSCCFSSCTDRCKZT1Davn37tvdIlihRwhYtWuRCN378eM84zp8/30vVvXv39s+rVavmPZJcf8+ePfbNN99Y586drWrVqt4fefDgQS9nUwrv1auXZxXJbHKfPA73MXDgQH+cn3Lx4kWXVaSTKF++vGczfy4SyeghkRRCiBQSyTCRSOYzSFzJkiVd8OiFpL+RPkZEk7J0hw4dXBRr1qzpMsh1EEmOkXVEMJHKTF/kpEmTPLtYu3Zt69OnjwtiRiT79u3rJfScUI9kfCGRFEKIFBLJMJFI5jP3iyRZxQ0bNnjZG/nr3r27iyRDMy1btvTyNOVrythkF5E9hmvon9yxY4dfxoR2jx49vDTNm3DlypVe2qaHkuwmGceckEjGFxJJIYRIIZEME4lkPnO/SJJZ5E2zdetWXw6IwRmyjuvXr7dRo0ZZ+/btbe3atTZz5kw/Thmc25C5nD59um3cuNEnveml5DhvQsSSARpum+mlzAmJZHwhkRRCiBQSyTCRSOYz94vkrl27PJv4xz/+0V599VV/A1GSZl1Ilv8pUqSIVapUycqUKeN9jCz9w9qQ9EOWKlXK+yVffPFFz2pyvF+/fvbOO+9YkyZN/DiZTZYMygmJZHwhkRRCiBQSyTCRSOYzlLDJMjLBjTCSiUQemeAmM0lP5L179/wyjjOpTSmbEjW3zdyenkmyj1OmTLELFy74cRYkp6RNJpIM5YEDB7z3MickkvGFRFIIIVJIJMNEIhkTyCS9k4jmoUOHfti9BhjOYX1IhnCuXLnygywik4gok9usScnXuUEiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkmnOnj1rly5dSn/1Y27duuXbFOZmO8LHEYlkfCGRFEKIFBLJMJFI/h22K5wxY4ZNmzbNduzY4XtYI5YIJNsYslXh1KlT7erVq+lbZBcSyfhCIimEECkkkmEikfw7iOTnn39u7777rrVu3doGDhxo8+fPt3379tnWrVvtq6++slKlStmpU6fSt8guJJLxhURSCCFSSCTDJPEiiURCgwYNrFWrVrZ8+XKbPHmyde3a1cqUKWNvvfWW1axZ07Zv3+4ZymxEIhlfSCSFECKFRDJMEi2SO3futObNm1u7du2scOHC1rBhQ5syZYpLJBnKL774wkqXLm116tSx77//XiIpkYwcEkkhhEghkQyTRIvkoUOHvGzdp08fK1++vJUrV86zj9WqVbNBgwbZzJkz7dtvv7XevXtbz5497eLFi+lbZhcSyfhCIimEECkkkmGSaJFkSnvjxo0+aENZu2TJklakSBFr1KiRl7fXrVtny5Yts8GDB3vpmwGcbEQiGV9IJIUQIoVEMkwSLZJMY7dp08YqVapkNWrUsMqVK1uLFi1s4cKF9swzz9inn37q5W2ylFu2bLGbN2+mb5ldSCTjC4mkEEKkkEiGSeJ7JBs3bmwVK1a0999/37ORSBciWaJECe+drFq1qlWoUMGzl1pHUiIZNSSSQgiRQiIZJokWyWPHjtmoUaOsZcuW9vzzz9vbb79tzZo1s06dOtlzzz1nn3zyiYtmhw4dbMyYMXblypX0LbMLiWR8IZEUQogUEskwSbRIHj582IdtOnfu7OtEfvzxxz7FTU/kSy+95GXtkSNH+mLk9evXV4+kRDJySCSFECKFRDJMEi2SR48edVEcN26cDRkyxLp16+YSuWnTJhdHju3atct7Kbt37+7bJGYjEsn4QiIphBApJJJhkmiRBBYkv3btmp05c8ZOnjzpceTIEVu/fr2dP3/e+yKvX79u586dU4+kRDJySCSFECKFRDJMEi+SgEwiiZm4c+eOT2jzOWtHslUigzlakFwiGTUkkkIIkUIiGSaJF0kGaHr16uV9kiw+Thn7fpjg7tKli82ZM8czlw/j9u3bPsDDtDfLBV29etXWrFnj61IytMNjsC4lkkp/Zu3ata1WrVp+ef/+/V1akVfWtWRZIta25JwuX77s98+6lgwCsablsGHD7ODBg348JySS8YVEUgghUkgkwyTxIknJumzZsr5+5OjRo138MiCDPXr08Mt27Njx0IwkEpnppXzjjTds/vz5vq3i119/7SLKTjmsRzlgwADbv3+/LVq0yJcdYiKcXkzkEWGkJ5NjyB+PjWTu3r3bs6JDhw518UQ62c5x8eLFLqs5IZGMLySSQgiRQiIZJokXSSaxixcvbhMmTLAVK1bYvHnzXPTokRw4cKALGJKXE/RRcpt69erZyy+/7CKJiE6bNs17LhFNhBRJ5HEQyqZNm9rYsWNdXskukqlkmSGykWzPiEA2adLE5s6da998841nNDmnGzdueGaSIaEHZSXJbFKKRzQJtn/k+j8XiWT0kEgKIUQKiWSYJFYk6YNEyCgxf/TRR7ZgwQJbu3atixpZxdKlS7voLV++PH2Lh4MEsmg50oiYknHMQA8moklJGhnMlLsLFy5sb731lpUpU8bfYAhgZvkhRPDEiRMulnxNVpGp8tWrV3tmdPr06Z6hXLVqVfpR/sH27ds9C1qoUCGPAgUKWOvWrdOX5h2JZPSQSAohRAqJZJgkViRZ+ofsY+/eve3NN9+0WbNmeRaxbdu2/oP++uuvu/iRPcwNyCLBpDd7dt8vkkgmPZaUoymfnzp1yr777juXRcSTtSyrVatmGzZssDp16nj2keNMkpPRRGwpaXOulL7JbpJppMSNAP8URBOp5XEI7rNr167pS/OORDJ6SCSFECKFRDJMEiuS9EaSbaSMzOLjSOPkyZNt48aNXpJmKAbB69mzp5eZcwtZxftFkqzn3r17rUqVKj4gc+DAAT9GtpGPmeEaMpRTpkzx0jgieejQIZdASu5kF+vWrWt9+/b1Xk1EknJ3nz59XIZzQj2S8YVEUgghUkgkwySxIkmWkAlrprIRRqRsxIgRtnLlSi97AyVi5I0pbAZncrP8z/0iifCRdezYsaMLKwudc4xsI1J5/Phxl0nEsXr16p4RvX9RdMrunBeBTPImJAPJubOQOscR3pyQSMYXEkkhhEghkQyTxA/bII2UudkGkelpltthmR0ykwziLFmyxLOSXJ6bCen7RRJR5T6feeYZF1LK22QUkVUylIgrvY6U0yk/MziDKDKQg0ySCa1cubJNnDjRZs+e7W9CpJShHjKUTIJT6s4JiWR8IZEUQogUEskwSbRIkh2kfEx2kHUe6UdE9JA6luqhj5ElfbZu3epiyMBMTtCbWKlSJe+tJFtIpvGpp56y999/34oVK+YiSEmd0nSRIkXstdde8+vQo0mPJetaMuTDsA/LAzGMQzaU+x0+fLjfhvMrWLCgl8LJaOaERDK+kEgKIUQKiWSYJFokWZuRZXFq1KjhmUBkjfI1ckkGsGrVqv5DT9YQYUP0coLr0H9J+Znb8Dn9kKdPn/bgMbgMKeVrtmTkOhlJ5fZkMhHXSZMmeXk989hcj8nyUaNGedaUwZ7cnJNEMr6QSAohRAqJZJgkWiSROnoRKWNn9tUGPlLWZpkeZI7exV8Syu0XLlxwob1fYDkvyuuIJh8zvZw5IZGMLySSQgiRQiIZJokWScSMDCQf6W0k48dHJI3jBNnE3G5F+LgikYwvJJJCCJFCIhkmiR+2IdtHZpKeRZb/ocTNgA09jiz+zWAMwZJAlKSzEYlkfCGRFEKIFBLJMEm8SDJww0DNF1984TvSsJ4jwyxMS3/55Zf25z//2Y8z+EKpOTc9iY8bEsn4QiIphBApJJJhIpFMi2TLli3t66+/9t5EdpShP5LFw/mcYZsXX3zRJ7pzs5bk44ZEMr6QSAohRAqJZJgkWiQRSBYbZx9qluxhX+tt27ZZq1atfDkg9rG+du2ar9XI9eiVlEhKJKOERFIIIVJIJMMk0SLJQuRkIdmHmtJ28+bNfWmdfv36+UdEk75Ieijpkbx8+fIPk93ZhEQyvpBICiFEColkmCRaJOl3ZP1GlgBiEfBPPvnEPy5dutTXb2R7Q4KM5P79+70Mno1IJOMLiaQQQqSQSIZJ4kUysxbj0KFDfQFyStyUtSllt2/f3lq0aOExcOBAz0xmIxLJ+EIiKYQQKSSSYZJokSQbyeLeyGT9+vU9evTo4dsPjh8/3rdIbNKkiX366ae+HFButiN8HJFIxhcSSSGESCGRDJNEiyTDM/xgM1zzwQcfWM+ePV0e33vvPd/fmoltLmffbaa5s7E/EiSS8YVEUgghUkgkwyTRIokozpkzxwdrihQp8sPAzTPPPGO9e/e24cOHe6m7cOHCNm7cOLty5Ur6ltmFRDK+kEgKIUQKiWSYJFok76dLly5WpUoVX4ycoRsWJkfAqlWr5oLZsWNHz0pmIxLJ+EIiKYQQKSSSYSKRTMPgzYN2rWH5HzKR9Edm4642IJGMLySSQgiRQiIZJhLJHFi3bp2vNclONxq2kUhGDYmkEEKkkEiGSaJFcuPGjfbZZ59Zs2bNfOCGYKvEDh06+ALkV69e9aGbXr16+eT26dOn07fMLiSS8YVEUgghUkgkwyTRIrl48WJ7/vnnrX///r5O5KBBgzz7OHr0aJs3b54HQzYNGjSwp59+2nfCyUYkkvGFRFIIIVJIJMMk0SK5cuVKK1GihGcaKWEvWLDA99dmzUiykAgYGUomuZneZso7G5FIxhcSSSGESCGRDJPEi+RHH33kmcbu3btb2bJlrUyZMlauXDkrVKiQT2uzDNCyZcv8OpldcLINiWR8IZEUQogUEskwSbRIsqf2G2+8YTNnzvT1JKdPn+4xa9YsW79+vY0ZM8a3S6Rn8vLly1qQXCIZOSSSQgiRQiIZJokWya1bt1rt2rX9h/urr776Idh3e/v27XbgwAGXTXon2Trx4sWL6VtmFxLJ+EIiKYQQKSSSYZJokTx79qxviVi3bl375ptvXCARLkreJ06c8MsWLlzoQzlMdHP9bFxLUiIZX0gkhRAihUQyTBItksCgTdGiRX07RPok2dlmw4YNHux007VrV9u2bZvNnj3by9sPE0lK3yxezpqTDOZw3fPnz/sAD5lNlhLia7h165YvP7R8+XLbvHmznTx50o9zm927d/vAz9q1a+3w4cN2+/ZtP37s2DGXXHo29+7d68sT5QaJZHwhkRRCiBQSyTBJvEgicOytzfT222+/7Z/XrFnTatSoYX/605/8I1nJnED0EE3k7/333/cJ8OvXr7tAfvDBB36sadOmLo5I5JEjR6xChQq+xzePN2nSJBdRyuft2rVzuWXtSpYlQj4RVJYl4viHH35onTp1sp07dz5UbDNIJOMLiaQQQqSQSIZJokUSCTt16pRLHutFst92xYoVbf/+/bZv3z5fR7Jt27a+z3ZOsOsNmcLixYvbc88957dlYIcsJ2XxPXv2WJs2bbzfkoxj3759fSF0bsPalUjmuXPnbOTIkX69CRMm2JIlS3yKnOwjA0HII29EspQsR8SAEFs45oREMr6QSAohRAqJZJgkXiTJACJyiB7ZRCa2yRgiaPRETps2zcveOYFIHjp0yKZOnWrvvvuuZyS5baNGjTyjee3aNb+fwYMHe/aRbOTEiRO9F5PrIrGUs8lOIpu7du1y4WRqfNGiRZ6lRCRZ75JMJ5Pk3J7MZk5IJOMLiaQQQqSQSIZJ4kUSaSTDR7/hpUuXfrQNIqVmLtuxY0f6yD+HNSaRSTKclMmRP5YPYiqcNSjpc0QsGeghG0l5mowlgklPJbvrjB8/3m9LNvLChQsupj179vSvq1Wr5jLI/SO53A+lbvo3f0pGTrlPgnI44vlzkUhGD4mkEEKkkEiGSaJFElFE5BA9hBFx4yNfr1692jOEmUD2EMWcIMNZsmRJF0lEj+Edehx5LLKdZBvJPtI3iaAihQjlgAEDXA6LFSvma1kitpwL0knGlJI7UonschtK4FyfoaCfQml+1KhRVqtWLY9XXnnFM5o/F4lk9JBICiFEColkmCRaJBEy5BHhGzZsmGfvWEdy8uTJ9tlnn7kQ0j/J0A273Nyfrfxn3C+SZBIpTSOEZCQpRfNGYk1KdtFBIBFGJrE5NmLECN9Vh8dHPlnHknI2IokQsssOw0GcN+eKlDL5nRMqbccXEkkhhEghkQyTxIskkjd27FiXOCa0q1ev7hPSlJApEfODj8QhkbnZIvF+kSQQQQZlEEayi926dXOhZP9u1q4k+zljxgyXvcxwz5AhQ7xkzaLoDNVQEkciM9s1kkWl9xL5ZRAnJySS8YVEUgghUkgkwyTxpW0GVzKlbbKC9DTSO5kJBmTq16/vn+eG+0WS+ySbSN8j09uffPKJP8bBgwdt7ty5vrxPy5YtXVSRWLKNrDnZoEEDPw+mvRnc2bJli23atMkllMxonz59PFPK0A7SmxMSyfhCIimEECkkkmGSaJFE+ugxpDxMsOwOJe3M1wQZQiapcwt9lCwlRFmaz5FABl06d+7sMsm6kgz4II0IIRnLTJYys44kmUqWHGIx9H79+vmyQAgj098cp8cSIWWB89wIrkQyvpBICiFEColkmCRaJOmPpM+QoRWCJXnIAFIyJjLHiLyCNFImpw+SpXoopwMCSB8kmUaW+iEzmoGFzVlsHJGlJJ6RRa7DObOoOUsT0XeZGySS8YVEUgghUkgkwyTRIklJm+lmeiTJArLEDkvl8HkmOEafYjYjkYwvJJJCCJFCIhkmiRZJhmfI+GWCiW2W6/npsXr16qVvkZ1IJOMLiaQQQqSQSIZJokWS0jAlYpbhYd1IBl8YerkfprkZfslmJJLxhURSCCFSSCTDJNEiyTAMQzHsQENPZIsWLXxZHgZwWPCbZXiqVq3qSwJlMxLJ+EIiKYQQKSSSYZJokWTwJbOOI4uAMznNXtkszUN2krUaWZqHHWWyGYlkfCGRFEKIFBLJMEm0SCYFiWR8IZEUQogUEskwkUgmAIlkfCGRFEKIFBLJMJFIpmG/bcrZrVu39h1l+HzJkiW+1mO2I5GMLySSQgiRQiIZJhLJNE2bNvU1I/lBZ6eZwoULe7/kpUuX0tfIXiSS8YVEUgghUkgkw0QimaZx48Y+VMMuNOwq8+GHH/qWhGxbmO1IJOMLiaQQQqSQSIZJokUysyD5tWvXXCQHDBjgnx87dsxKlixp8+fP968zkZt9rR9HJJLxxeMoknfu3rNTl27YiYvXH7s4f/VW+iyFEKEhkQyTRIskS//QGzl+/HgrUaKErxc5YcIEGz58uL388svWvn17/5rLWRoI6cxGJJLxxeMokofPXbPXuyy0Z9vOfeyi7riN6bMUQoSGRDJMEi2Se/futc6dO1v37t2tUKFCVrZsWevdu7d16tTJnn76aatdu7b16tXLeyYpe1+8eDF9y+xCIhlfPI4iuf/MFfuvFt898Hzjji+GrUmfpRAiNCSSYZJokWR7xEWLFtnSpUvts88+c+Favny5fffdd/bmm29a//79bdmyZT69zXWuX7+evmV2IZGMLySS0UIiKUS4SCTDRMM2aZo1a+ZbIsK5c+esVKlSLpEhIJGMLySS0UIiKUS4SCTDRCKZBtmirM3U9u7du6148eI+tc1ATrYjkYwvJJLRQiIpRLhIJMNEIpmGQZs//OEPVrBgQXvjjTfsySeftMGDB9vx48fT18heJJLxhUQyWkgkhQgXiWSYSCTTbN682TOQ9EwSfH7gwIGs7Yu8H4lkfCGRjBYSSSHCRSIZJhLJNAjjzZs301+lYHvEy5cvp7/KXiSS8YVEMlpIJIUIF4lkmEgk/w4Lja9du9Z27dr1w9e3bt3y6W2muLM9KymRjC8kktFCIilEuEgkw0Qi+XfYBpGdbQYNGuRfI5H79++38uXLW6tWrbK+T1IiGV9IJKOFRFKIcJFIholEMk3Tpk19+Z/bt2/b4cOH7YsvvrBq1arZzJkzs35yWyIZX0gko4VEUohwkUiGiUQyDbLVsmVL3w6xQYMG1rVrV/vyyy9t1KhR6WtkLxLJ+EIiGS0kkkKEi0QyTBItkmx5uH79etuwYYOVLFnSt0msWbOmB/ttly5d2lq0aOHX2bhx4/8zjJMTx44dswULFnimkxgwYICNGDHC9/dm20VK6RxnSpxF0MmGrlixwuWVWLlyZfqezLZt2+b7fg8dOtR7N69cuZK+JGckkvGFRDJaSCSFCBeJZJgkWiQPHjzocofQsW7kv/7rv/pC5H369PFjRYsWtc8//9yvg/BFneDes2ePjRw50ho1auTx0UcfWbly5XzNyhdffNFq1arlx8eOHWtHjhzxXkx22EFkebP16NHDTp8+7dPjbNdYo0YNP07GdOfOnXbjxo30Iz0ciWR8IZGMFhJJIcJFIhkmiRZJeiFZdJzs43PPPWf//u//7llIpGvgwIEukpS3kUiEMEoW8Kcw0IOQsnvOt99+6zLIlDiZyGvXrrkszp8/38qUKWOLFy/2zGSvXr1sxowZvtd3vXr1XG4ZAurUqZNnJ48ePZq+9x/DsNClS5d8lx6iTp06Xqr/uUgko4dEMlpIJIUIF4lkmCRaJBmiQQ4Jfrg//fRTa9iwoX344Yc2efJkH7ghO8nlV69e9WWB8gISidC1a9fOBZKs4+9//3t76623XFSnTJnii58jjkjs999/b4cOHbJJkyZZ27ZtPTNJKZwSOMI5b948F8OtW7emH+HHbN++3bp06eKleqJAgQLWunXr9KV5RyIZPSSS0UIiKUS4SCTDRMM2aZjaRtaQMySyfv36VrVqVZe8nwslaHoeySiOGzfOJ8EnTpzo/ZP0YPK4ZB7bt2/vPZRIJCVteiEpc7ME0VdffeV9mkgtPZuc77p169KP8GPo/aT0TWaTYBkjspg/F4lk9JBIRguJpBDhIpEME4nk3yHTSB8hZW6ylJSbv/nmG6tdu7b/4NNL+XOgzEx/I1JKaZohHPotyVR+/fXX1rFjR++BRPYYxKHkjkgil5UqVfJsIuV1tnFEJBFIRHf16tXpR3g46pGMLySS0UIiKUS4SCTDJPEiiUTSo0j/IuLG10xP02eI4JElZKo7rzDpjTyWLVvWex0ZqkEIkUukld7LDh06eE8mGcu+ffva7t27XV6RWd50vPn69etny5Ytc8mdPXu2L6D+zzKSP0UiGV9IJKOFRFKIcJFIhkmiRRJppOyMtCF79B8ilWQEkUnKz8jlmTNn0reIDredNm2a90UikNOnT7cmTZp4yZkSNpJHeRvJpAeSwRguQxrpjSQogSO0SCf9kz179vRyOJ/nBolkfCGRjBYSSSHCRSIZJokWScrEO3bs8J5Iys4Mqaxatcp7ChFASsrDhg3zEnReYQkg7ofJcMSRjCT3+fLLL9trr73mywvx2Agt5eyPP/7Yy9lMj5PF5PzIXiKiTHRXqVLF/vjHP/rAzYULF9KP8nAkkvGFRDJaSCSFCBeJZJgkViQpKzNYQ69hiRIlvIy9dOlSH4R5//33XeDq1q3rGcGTJ0/61HVetkpEVskcIpDXr1/3UjefL1y40IOyOfcNlNOXL1/umUd6IufMmeMZUkSWc2XZIIZuKHlHOR+JZHwhkYwWEkkhwkUiGSaJFUnkjBI22UGyfExoUz5u3ry5Pfvss74UD+tIsgQQ1xkzZoxL4aOGkjqZS8rtZCIzII0ILf2TlOCjZEklkvGFRDJaSCSFCBeJZJgkurTN4ApZQXoO2WWGNST5IX/iiSesTZs29vbbb3uJmawkwzj3i102IZGMLySS0UIiKUS4SCTDJLEiyaDN2rVr7c9//rMvEk7WMdMjSW8i2T8EjEnqbEciGV9IJKOFRFKIcJFIhkmiM5L0K7K/NcvpsD3h3r17fXqbHkV2miFLyfqO2Y5EMr6QSEYLiaQQ4SKRDJNEiyTQa3j27FkXRgZttm3b5iVueiLnzp3rQpntSCTjC4lktJBIChEuEskwSbRIMtTCFDRl7Y8++sgqVKjg2xG++eabVrlyZe+N5DImqMlS/hLDNo8CiWR8IZGMFhJJIcJFIhkmiRZJeiJZ4gfReuGFF3x9xiJFitjTTz9thQoVsooVK3r/ZKNGjVwwmZbORiSS8YVEMlpIJIUIF4lkmCS+tJ0B2aKkTYm7XLlyvig5u9pQ9s52JJLxhUQyWkgkhQgXiWSYSCTTzJo1yxcDv3z5sg/g0C85fvx427JlS/oa2YtEMr6QSEYLiaQQ4SKRDBOJZBq2RLx48aJ/nhnAOXr06A/HshmJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSCUAiGV9IJKOFRFKIcJFIholE8hFy794927x5s33++edWv359a9SokY0dO9Y2btxow4YNs4YNG1qnTp1sxYoVfv2bN2/a5MmTrVWrVh5Tpkzx47B06VLr2rWrNWnSxAYNGmQXLlxIX5IzEsn4QiIZLSSSQoSLRDJMJJKPkEuXLtns2bOtaNGi1rt3bxsyZIhNnz7dZfGLL76wHj16WMuWLW3kyJG2f/9+27t3r9WuXdvatWtnHTp0sO7du/uxI0eOuAg2btzYjyGT69evt8uXL6cf6eFIJOMLiWS0kEgKES4SyTCRSD5CkMMRI0ZYhQoVXCDXrFljy5Ytc6Hk2MmTJ23WrFk2ePBg+/bbb23q1KlWqVIlz1AiigMGDLBvvvnGZs6c6fI4atQoO3z4sPXt29c/P3jwYPqRfszFixdt586dtnjxYo/y5ct75vPnIpGMHhLJaCGRFCJcJJJhIpF8hGzYsMEzji+//LIVKlTISpcubXXr1rUuXbq4TCJ8u3fv9oxkixYtvHSNJO7Zs8eOHTvm8tm0aVOXQDKaCCa3QUbbt29vmzZtSj/Sj9m+fbs/Bo9JFChQwFq3bp2+NO9IJKOHRDJaSCSFCBeJZJhIJB8hZA9XrVpl27Zts+PHj7vc1ahRw4WR7OOVK1e8bP31119brVq1vKQ9evRoP3b27Fkvi1etWtWaN2/u4rllyxa7evWqCyT9lmQ4H8StW7e8rH7q1CmPOnXq+GP+XCSS0UMiGS0kkkKEi0QyTCSSjxCk79y5c3bjxg0fvBk3bpy1bdvWeyMnTpzoInngwAGXxJo1a7pokp08dOiQCyAZSUrd3IbrIJD0RSKQ9erVs9WrV6cf6eGoRzK+kEhGC4mkEOEikQwTieQjhEwkPZD0Qt6+fdt7Hhs0aOBlaWTy/Pnz3gvZr18/n9Km75HM4Y4dO3zIBqlksnvo0KHWq1cvW7BggZ05c8anuZs1a+al89wgkYwvJJLRQiIpRLhIJMNEIvkIWbRokWcTWeqHMjVZRCave/bs6VPbLOmDRJKJZNhm7dq1Vr16dc9cMmTTpk0bH9bhOPeDTM6dO9fFECndt29f+pEejkQyvpBIRguJpBDhIpEME4nkI4TsISXs119/3YM3EFlFspAsCUQ5+7333vMMJVlL+hq//PJLq1ixopUqVco/p8+S9SUZuClXrpwf477ovaR0nhskkvGFRDJaSCSFCBeJZJhIJB8hd+/etWvXrv0w9EIpm37J69ev+9JAZCHnz5/vy/jcuXPHr89QDtnLGTNmeImb4/RXIqVMbSOm69atc4nkeG6QSMYXEsloIZEUIlwkkmEikYwBBJCeSbKQ7FDDlHUGZJKJbQLhzMDxzCR2FIkEiWR8IZGMFhJJIcJFIhkmEskEIJGMLySS0UIiKUS4SCTDRCKZACSS8YVEMlpIJIUIF4lkmEgkE4BEMr6QSEYLiaQQ4SKRDBOJZAKQSMYXEsloIZEUIlwkkmEikUwAEsn4QiIZLSSSQoSLRDJMJJIJQCIZX0gko4VEUohwkUiGiUQyAUgk4wuJZLSQSAoRLhLJMJFIJgCJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSj5C7d+/a2bNnbeXKlbZixQpbtWqVHTp0yE6fPm1z5861pUuX2rJly2zXrl129epVv/7evXv9esS+ffvS92R27NgxW79+vS1fvty2bdtmN2/eTF+SMxLJ+EIiGS0kkkKEi0QyTCSSj5ArV67YggUL7KOPPrKSJUv6x4EDB9rMmTPtt7/9rRUuXNiKFStm3bt3twMHDtilS5esU6dO9vHHH1upUqWsR48eduPGDbt165aNHDnSypcvbx9++KHVrVvXjhw54uKZGySS8YVEMlpIJIUIF4lkmEgkHyGbNm2yESNG2NSpU138evbsaQ0bNrS2bdtavXr1bPfu3Z6dRCDPnz/vWcgyZcr49WfNmuWCuWTJEtuwYYM1aNDAb09WsmXLln75qVOn0o/0cCSS8YVEMlpIJIUIF4lkmEgkHyEXLlzwUvaZM2fszp07LobVq1e32rVrW8GCBa1q1arWvn17l0VEc/DgwS6JW7ZscckcO3asZyU53qFDB5dHxHPSpEnWp08f27lzZ/qRfsz+/ftt1KhRVqtWLY9XXnnF2rVrl74070gko4dEMlpIJIUIF4lkmEgkfwEoQdPjSGawfv36NmTIEOvYsaP169fP6tSp42+uRYsW+TEuo8x98uRJF0fK2GQw+/fvb+vWrbPLly/bmjVrrEWLFp6dfBAnTpzwkjq3IYoWLeoi+nORSEYPiWS0kEgKES4SyTCRSD5i7t275/JHhrB58+Y2bNgwH6KhlI1gDho0yLOSfET2xowZ49lJspiIZKVKlTxLOXToUM9U0ndJqRshXb16dfpRHo5K2/GFRDJaSCSFCBeJZJhIJB8xTGPTK1m8eHGbMGGCHT161Ce5b9++7ZJJmbpr165ewu7du7dnJClNk8GcOHGil7+5/KuvvrK1a9faxYsXvRSOSJKZzA0SyfhCIhktHleRvHDtlp24eP2xi5OXbtjtu/fSZynE441EMkwkko8Q+iKRv9KlS3smkn7J6dOnW5s2bWzHjh12/fp1L1sjemQfmeZu0qSJZxy3bt1qAwYM8MunTZtmnTt3tilTptjx48f9vshikqHMDRLJ+EIiGS0eV5FsMH6TPdt27mMXr3ReYAf+/v0UIhuQSIaJRPIRwsAMAvjrX//ap7EZsiGTyMBNuXLlrHLlyh4s7cMQzcGDB/14s2bNfKq7SpUqvm4kWUx6ImvUqOFi+cEHH7hUamr78Q+JZLR4XEWy0oi1DzzfuOO3TWfZnlOX02cpxOONRDJMJJKPEMrTZBoZoqE0Tdma8jYZxr59+3pQ2kY4gTUj6aVkupuMI9Pa9FKS2ZwzZ4716tXL15nkMsrfuV2UXCIZX0gko4VEMlpIJEU2IZEME4nkYwaLj2/fvt1L2/RSZqCnkowlk9tMdCOXuUUiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFr9pOtNW7TtrJy5ef6zi0vXb6VdOiH8gkQwTiWQCkEjGFxLJaCGRjBb/q+E0e6r1bHu27dzHKjrO/D79ygnxDySSYSKRTAASyfhCIhktJJJhxF8mbkm/ckL8A4lkmEgks4jdu3fbuHHjbPDgwTZ37lw7efJk+pKHI5GMLySS0UIiGUZIJMWDkEiGiUQySzh//ryNHTvWKlSoYHXr1rWGDRvaqlWr7ObNm+lr/HMkkvGFRDJaSCTDiMdZJL8/fsnmbj/xWMXyPWfszt176TMMF4lkmEgks4Rly5ZZp06drFu3bnb9+nVr1qyZTZgwwY4fP56+xj+4deuWXbp0yU6dOuVRu3Zta9Wq1Q9f5zWOHDthr7WebP+r5ij7Va3RiYx/qzHy7x9z//x7z1j3wNcyzli/86AVaDjugef7sOD7nnr+D748P6Jc37kPPOe447O+cxL/cx/l+dcdseSBr+PjEPX+fm4POueHRdT3fdR49e+/Vw8ePf7A830cgurXg45HjS5duljNmjXTf6lEKEgks4QRI0ZY165dbfHixS6KSCTH1q1bl77GP9i+fbu/YQsVKuTx61//2n7729/+8HVe462337b//V9P2f/5/fP25AuvJi4KPPeS/dtvCth/PfviAy9/ULz8esEHvpZxxptvvW1P/fG1B57vw+J3T79gv/o/T9gTz7/ywMvzI/7w8usPPOe44z+fetZ+8+RzDzzn4OP5V+3//92Tkd73L7z6xgNfx8chOLcHnfM/i9T7/r8jve+jxtMvvmZv//3364PON+54/fXX7Q9/+IO99dZbD7w8Svz3f/+3ffLJJ+m/VCIUJJJZwoABA6xnz54uibdv37b58+fbwIEDbdGiRelr/IOLFy/azp07XTqJ2bNn25w5c374Oq8xb948/2VCZvRBl4ceo0ePtieeeMKGDRv2wMtDjx49etirr75qM2fOfODlIUfZsmW9peRBl4Ue/K5BcpL6vh8zZow9+eSTNnTo0AdeHnrwd+eVV16x6dOnP/DyKMHfkPXr16f/UolQkEhmCV999ZX16dPHBTEjkn379vU35i8F/ZjFixe3qVOnpo8ki127dtlzzz1nmzdvTh9JFgx4FS5c2C5cuJA+khzq1atnvXv3Tn+VLKiAlCxZMrHv+z179tjzzz9vmzZtSh9JFvytee+99+zcuXPpI0L8GIlklvDNN994o/LKlSv9F/u3337rf9j4L++XQiIpkZRIJg+JpERSIikehkQyS1ixYoWLJEv/0LTcvn1769+//y8qNYgk/S2UNpMIf1Bee+0127p1a/pIsliwYIGVKFHCWyeSBisf0F6SRBDJcuXK2YwZM9JHksW+ffvsjTfesC1bkrmkEe1TJBBYOUSIByGRzBLIAvXr18/eeecda9Kkib344ou+HNDly7/cPruU1IcPH27btm1LH0kWp0+f9j7BY8eOpY8kCzKygwYN8lUDkgbZuKVLl6a/ShZ37txJ9Pv+zJkz3ieY1Pc96xfTWnXt2rX0ESF+jEQyS+CXOW9oStpkIil1HzhwwO7evZu+xqPn3r17dvToUbty5Ur6SLIgI3vw4EG7ceNG+kiyuHr1qh05cuQX/Zl7XKAKkNSMDO97JOqX/Kf1cYKMrN73R/xvkBAPQiKZRZARpE+FyW3+qPG1EEIIIURcSCSFEOIhkJHiHzd6Q/XPmxBC/BiJpMgV/AHljyn9QvRrJq3MQ3kPoeD5J0kmeN4IFM+b4GcgSaVtvtf79+/3gQN2lzp06FAiS/s8Z34OklTeZncwdnShN5qgNzhp33ueM68Dv+/5XSDEg5BIilzB5CJ7pBYrVswaNGjgE7xJgl+oGzZs8Of//fffp4+GDX80+SPSunVrK1WqlJUpU8aXwaG9Igl/VJDIw4cP+8Qyz5t97tnejeefNKHgOfNz0KtXr/SRsKEfsGPHjr4QN+954rvvvkvcEjizZs36YUc1esSFeBASSZEjNNqzJePnn39uU6ZM8e0X2eWB/9KTAP+NM7FbtWpVe/bZZxOzjiRN9iz5wpJTkydPtpEjR1qNGjX8n4gkrCVJBm716tU+sbx8+XIbMmSINW7c2NasWZOojDxSxS5arCXYpk2b9NGw4R8IJrWRZzLRxPHjxxMlUwxz8o9Du3bt/Hd9EjPxIndIJEWOsKUV8vjXv/7Vf6EgkywHwR/UJMCyFxs3bvQt4l544YXErCeHLPG9JwNLSRupqly5sm+Vdvbs2fS1woXvO39MkQqmdjMiyetBm0MS4GeA1SKoQhQsWNCzdEmADFyjRo2sWrVq/o/UpEmTvLUjKeVdpJF1U6tUqeJrFrOGrqa2xT9DIilyhJ0NmjZt6pkolv5BIEeMGGETJ05MXyNsyEKQnWMhchYmTuKC5EgVpT3KvMhl0paAWrJkictU7dq1vU8wCdkZpIlqBBshsH4q+4137949fWnY8LPevHlzq1SpkrczfPbZZ74pRBJ+7mnp4B8oKlC0c7B+8ejRo317Xq0lKR6ERFLkyJw5c3xnD7YIo1eQ0i4iSckvSfBfeRJFEqEgC8fe7vxhpW8ySfD8v/76a6tYsaL/Q5WUgSPe62zJWqRIEc/Ct2rVKjEiiTTRF057A2so8r2nCsPvgNDh/U32nWzsqFGjbNWqVd7S0LlzZ39NhPgpEkmRIwsXLvQ/IpQ2+Y907dq1vsPJsGHD0tdIBkkVSTJw7DPNsBVrmCaxxJXpF6XMx0e+Dh2Gy8hE8j6nlYFeuaSIJL/nqETwDwPtPN26dfPgNQkdvtfsnoY4837na6pSZGVp8RHip0gkRY7wywORYMCGbAx7bdOETa9kkkiaSJKJo8zFTkpkJPh+k6VKSp/YiRMnfCcpMvLsbMNHhi8oeyahxEcvLHssf/rpp1a3bl179dVXPTvJrlqhgzzzfeb7Tn/sJ5984j2DSchIMkjHpDYlbapQtDewHW/16tUT2dYjckYiKXKEP6g0m9Mfxy+Uhg0benaC/1aTRNJEkkEL+mE/+ugjF4oOHTp4qYt/LJKwniDDFcgU2RkycW3btvVhE8p7SRi24f3NoAllToKfA7JSDKKEzvjx4/3nnQw0JV1+91GZScJqBfyzyJQ6w4UEQ5b8I8GqDUyuC/FTJJIiR8hKbdu2zSd26RHjP1P+Y+cXTpLglyhSQYYiCZB1IwtHSZvvPVOstDjMmzcvEevpUcInI4VI8Nz552nq1KmJycj+lHHjxvkyUEmA9zoSTZ8ga4jy+46fhSTAzze/2/mnkYGj+vXr+/uexfiTslqBiIZEUuQKZBJ5mDt3rktlkna4EEIIIcSDkUiKXEPjOf+p8l9pUrMyQgghhPgHEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIR45mTUpWVIoP3eF4b5C6tflueTm+XAdpspZNDuk5y+EyD4kkkKIRw57FLPNIvu1sz5jfoBEcl/sMhPCbjs8H8QQ2c4JnjPLsbDLVNKW4RJCPF5IJIUQ+QK7YPTs2dO+/PJLq1q1qs2ePdsOHz7s61Hu3bvX1+VjLUIWuM/ATkkNGjTwvZyRwQMHDtiYMWM82EGFpaYyZLJ1mQwcMsUiydOmTbP9+/f7MeB+MplKxIzLWA+wVq1avh7k/VGhQgXfM549lfMT9mfm+fK8eC5sMZeT8LGkFq8Zt7sfMrlII69H5jx37Njh+3/z/P/ZItksKj1r1ixbvny5P0duv3v3bl9QfODAgfmaGRZCJBeJpBAiXyDbyFaK7IDCDkCIDuLIbkjskPHuu++6zCGb7BiD1LDwM9ddtGiRZ+KQn4oVK/p2nFyXLQoBOURK2aaRy9gHuEuXLlaqVCn7/PPPrVmzZta3b19fOJp94FetWuV7BHOf7ERUoEAB+/3vf2+vvPLKj+LXv/61LzKfX1nSDIgeC7nzmowYMcKFjx2BkDe2nGOhd841I9cI9MmTJ/26f/nLX9L3koLnzv2xMDb3x/Niv2+27eO14nmz8wy3ZbF4YImuCRMm+F7Zffr0sZo1a/ruJJnH5b7uF/OMnAshRFQkkkKIfIFMF5LCLhjsz8yWcmwpyK44hQsXtv/4j/+wEiVKWOnSpX2HJDJk7JTy3HPPuQwhfIjihx9+6CXb8uXL+36/QFZu586dLqRsV8eez2+++aZ98MEHVqxYMZfUQoUK+VaOSBM70CCpZCR37dplb731lr3//vtWpkyZHwX7R7Nzzc/ZqefSpUu2fv16z/ytWLHCVq5c6VnIkiVLusQhvZw3e5aTRWWrTWSY14jzZhs+zpc97Fu2bGlffPGFCzWvJ7soIcNINFvV8XryGIjje++9ZzVq1HAp5DmzfSGvK1JI5hJB5TJeL4SbTPHf/vY3l30eY+nSpZ4B5fXhvIQQIi9IJIUQ+QLigyw1btzYS8mUdymhkmEjO4fQkIEbMGCAjR492nr37m0vv/yy/cu//It/JFPJcYQIsatdu7ZLWAayeRs2bHAJY7tCxAphQ5h4HI4hSVwHuUMiuZ/Nmzf7ObF3Mo95f5CNJHOKqCFsecnMIcBkBxFVRBZR5vMnn3zSRRXpLVq0qGcET58+/UM/JxlEWgB4XLKoPO9nn33Wfve737kgv/jii/560QrAc+e5IJq8xkSvXr38vMmmIoO8Lggrz4HsJveJbP7qV7+y1157zR+rUqVKft9kY5HY3/72t9atWze/HyGEyAsSSSFEvoBIImd16tTxbCJZRgSSLBlZN8RwzZo1/hFBolzLdf7zP//TJk6c6CVbsphky+idvF8kMyLFvr8I4XffffeDSJLZRCR5bDJ1iBsl3HXr1nlpl8zgxx9/bH/+859d+O4PspJk68jcLVmyJE+DK4gkgkZ2jxI1Yoe8InXIHeVozpfL7+9LzIgk4scwEplKni8ZXSSc147XBfkEbkumkTI5z5vXEvlGhMnsks2lRYD74zZdu3b1HlCknkwwIk8Wl2Pjx4/358vryceM3AohRFQkkkKIfAGRROTIClavXt1LtfQ5UjomO4bMIEpkxCj5Ug5Gcn7zm9+4PHJ9pKtKlSoPFEkkit5KSruUuRkgYZgESUOMuIzBGo7Tf5nJRvI1skgZOFMCpq+yYcOGLpNkTOktzGQLGV5BdJEsMnWU1R8GA0GIM/eJGDZv3txLyKNGjfLsK+V5nj9yez8ZkcyAhJKRJdvIgBKvIYNEZFeBDCu3QUgZvuE1YGCI15JWADKXPGdEks8RRO6LTC3iyWtEmwHnyXnxWiPaDAQJIURekUgKIfIFRJJsGSVXZIoMGVKIrCCYzzzzjPcFPvXUU97rh7y98847PghDtiyTWSM7iDTeL5LIESKFfDK8Q4aTnj8eh3IvZWOkChFDIun54zZMQtO7SCYOkSU7+fbbb9uf/vQnlz8Gfbg9EpcBcSMTSEYPIcspW4eIIaetW7f2+0JA27Zt69lVPucyXgPKz/eDFPL6cP9kQhE/BJYhGc6f2yHXPG8uJ4PL/fF8EGsElueErPO6ZOAyHovvBeJMqZ3sKK8P55HJDvPaks2lD1MIIfKKRFIIkS8gkpRymaZmihoZIwOGvJAVpA+SDOQTTzzh4kdvY9myZe2Pf/yjl6WRJq6HZCKA94tkBtaiJJuGHD399NOeyUSWyHIWLFjQRY5sZgZKxkxwI44M/DCQ8/zzz9sLL7zg0+X0DiJ9ZPgyIHb0GCKXSBxC+jCYxqZETvaTzxFEMoGUqimz0zeJsCF43BeiSuaUEj2XMZyDJPIaIOFIIedNOZ5sK+fD+XE5crt9+3bPPJKNZdAIIea15pyBx+GxyUQizfRaIt28/mQ4MxPfZEMZ6sksKSSEEHlBIimEyBcQSUq6ZM3ItO3bt8+FEbGk7MxHBAf5Y9kaMpAI1uuvv+4TxKtXr/ZeR0qwlHYRSaSRpWzIyGWEjo8M1FCqZnkgMnkMjCCR9CciUhkQMta35DKC7B2ChvjxNUM4ZDFZkicDj8e6l0gh5/EwkeQyRJWpcASPHkXK2NwnIoq0kjXlvpBjJJKeSsrdlNtfeuklfy3I2PK6IN2cM+V1JBGR5Llzv8gw90MvKWVphBvR5jUjy0gmEylEPDkvXhdkktcRsaWUz7lynJ5OpuU555wyrkII8TAkkkKIfIFSLsv/kPGi35CBEUrJZL7o62P45dSpU17SRgQRJjJtSBgSSiaP8it9icgNAoR8kunLCFUGbot4clumo5EkSsz3SyQcPXrUxY5sJNcl+0kpnawoGUxK3sgkgpWBc2/RooVPNVMiRiz/GWQsWWz8D3/4g2dYGWQhQ4rc8ZGljBBFBoMoyfMcee7chl5PXiPOkbI4MphZJxL5pexPlhb5Rkx5LcjIIoVINPLM60DwHJFDzpvXlHNmGpzeSe6b8+P5IOn0bpIp5bXge0V2Uwgh8opEUgiRLyCIiCSSRGaMiWJK3GT+yMqRDWQXG2QLuUEe6UFkKRrkiGwmU9yZcjK3IXtIhpN+P4SLDCQlYYSJ+yArh2BRnkZCkU8eA8nk+ogY09pk8yjzkgFEPOnTRCI5RombASGykJn9wOk/JEtKFvGncno/ZPTILvKYCO+kSZP8PHiOlKLJ/nHfLP9DFpQeUErQyCL3jVhTlmayfe7cuZ7FpNzMfdDXiDhyPeQaoczsUkP2kYxvBuSRtSjpseTckUPuFzkly4kwIpBMhHMMqUUqkV0uU3lbCJFXJJJCiHwhUw5GcCgJIyj0/yFGDN4gQATZM0SIEi+ShPwgXMgfmbgMmZ5LJo7J4iFH3CdlYMQSUUKaeFweA1FCSOkz5Diyhtwht1yf4P4olxOU1jlGlpDeQRYwj1rmReAoOyN4lK2RRLKnGaFDinkNOKfu3bv7ud6f4UTguBwJR6p53ZjGpuRPhjUzsQ0ILb2V3C/n+lPIpCKe3A9ZSl4TxJVlgpBjboNYZx6L1weh5LXVguRCiLwikRRCZA3I0j/bWxqQLeTsYeXo/ITHI4t5v4Aig/cLICDMnPsvCed2fzaVLC9f39/zef/nQgiRFySSQgghhBAiT0gkhRBCCCFEnpBICiGEEEKIPCGRFEIIIYQQeUIiKYQQQggh8oREUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHnA7P8CjgKyVQ7kIWEAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E5%9D%87%E5%8C%80%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E8%A1%A8%E7%A4%BA%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAACRCAYAAAC7bsHuAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAACIsSURBVHhe7d2Fsy3Ftcfx9zelQhWSQAgSFyJEiUGUKHF3IS7ElSRECHEXIhB3IO7u7j6vPp35UevN2+fcc849+95zuetb1TUzPT09/tur1+qe/T9T0zRNM2hBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJo18p///Gek5fxeYLNjse5f//rXvLR1bPfvf//78rrNSxXrklDLb4T1KbfdbbdDC2LTrJG8yKG+zLv5Iu8PGx1PPdbtULcx7/w3E65lvuVlXrZf1rUst7+0IDbNGln1cofN1h1IHEOE5g9/+MP0+9//fvr73/9++bqdHGO2yfbbqaeWXW6b4wzJ3y1aEJtmjdSXGVlOXl13sCB+v/zlL6fvfe970xe+8IXpwx/+8Ehf+9rXpr/97W9zqe0R0Vqea03JW0Utp65aPqku7xYtiE1zAPDSerGJD5H55z//eXn+wcT+ieF73vOe6aUvfen0qle9anrYwx423fjGN54e9KAHTT/60Y+27EuMOEnOz3Y5P1PnLy8CJ6VMFT3I/+tf/zqul3z1Zf2q8rtFC2LTHAC8vH/605+mr3zlK0Nk8lIfTByD9OUvf3k688wzp/e+973j2L773e8OYTzhhBOm1772tdNPf/rTeYvNSX1/+ctfRh0//vGPx3zO1bRSl7Nt8ojhxz72senzn//8WK7rTNd17VoQm2bNsHZ+9atfTS984QsvFx0v9MEWxKCZfKMb3Wh6yUteMn3/+98fVtnFF188Xe1qV5se97jHTV//+tfnklvjhz/84XTOOeeMJjdBRMQs570UN9OaXLM3velN0yte8YrxIyIv5WvabVoQm2aNeGlZWG984xunxz/+8dMnPvGJEbhY50u9VbL/n/zkJ9N55503ffzjH59+/etfj+bpJz/5yenqV7/69MQnPnH6xje+MW+xbwjgZz/72emss86avv3tb0//+Mc/xj7SBCZumuevf/3rp/PPP3963/veNyxUgZwcj4RPf/rT40fk+c9//riGqWuZdpMWxKZZI5rJF1100XSve91riOLPfvazec1/2e0XejvYd7XWYJ5P8a1vfet0/etff4jWVpvM0Ey27SMe8Yjp5z//+eX7IHif+cxnhsVHZB/84AdP9773vUd6ylOeMprHv/3tb0cdOZ4//vGP0zvf+c7hyyTYv/nNby5fZ1rTbtGC2DRrwovKunrRi1403fGOdxxNyVg5YTdf5p2wFBSW3Kc+9akhWqw8vsAEgLYCn9/znve8IaSx+tSp+Xyf+9xnevSjHz194AMfmL70pS9N73rXu0beVa961ekBD3jAsJ6JJ3JMmvAve9nLppNOOmn66le/OuoKKbubtCA2e46lSGzlwc82psvtUfNXWUXLad2n+Swvt11S65C89KwhEVwWT912s3pWsSyfZccUoVhV//KYcy6QLyWPALHinvSkJw1rL1HeyqprkGXddZ72tKdd7osEi/Mtb3nLdN3rXnc0kflT/TCwnr/1rW9NN7zhDaerXOUqY5/WVZzXF7/4xWGtvuY1rxnHFHLsu0kLYrPn2eihry9mLZMXZbndRvmrUCb1L1PWr5oPlvnjnvOc5wzr8MILLxw+tKyLAC232xe2WwqS+aSN1oeNypnnS3zDG94wve51rxsWHEFjIfJ5ItvWlHxo0mouO2ddi1Lmm9/85sg75phjpnvc4x7T5z73uZFvn0TxDne4w3TUUUeNdazTkO31j/Sj8tjHPna65JJLLl+3PM/doAWx2dPkpagkL8nLx8912WWXDWvCC1j9TZpu/FMZhWEqeeFZKsmzjXICA142gvaDH/xgvJAiw5aJmjLyBA3M58VcJsfzyEc+cvjJ1LMMCiDTraCsfUlhWZdkP87FMfPjpQ+fc5S3PBbzzu3tb3/79OpXv3r6yEc+Mso5v3e84x2jqV/rr/M179JLLx1NZaIYrHNvCO21rnWt0USOIMK++RtPPvnkIYx8hqjXlIXJh+iHhQUa6nXYLVoQmz1LXoi8PKHmefGJ4Jvf/Obx0px77rmjyefF8uJ7abzYnPaar8ppvr3tbW8b3UkIBgGw7KXV1eOjH/3oaJqxVvTHe+5znzvq5fsSibWeUOijJ1Bi/8RmebzK3Pe+9x3RZXn1Ja9pqyibOupyFQbi953vfGf64Ac/OI5NRJdvji9T1Na5Ez6BHs1TdRAc18uxau46Z0l09wUveMFo1oa676QsE0LNWv7CimNSx1Of+tTp3e9+9/8JLBFE+7ze9a43nXHGGeN41VXP07V1/3QWJ7isyrrv3aQFsdmT5IHPQ79cBsvwQx/60HDUa25p6l1wwQXDCrnZzW42Xug///nPo1uHJtstb3nL0bfuiCOOGF1KXvnKV44+eA996EOHY//4448ffq773//+w9dFYG9/+9uPpp5Oyve85z1H3U9/+tOnF7/4xcP6Uw/LRTeVNImDLiNeckJQcQ4RsvribwU+tQQ5sm2SZc1eVt7DH/7w0cx8whOeMN30pjcd/Qmf/OQnTw95yEOGr+6a17zmEHjb6Apz+umnDwvOeTonyTLRV2f2sQr5zl3fQz9Grnnyk+ynBkQgj3VuZIzjEVhhZcoPts091FeSePohW+Uz3Q1aEJs9SV6ksFwGa41Vc+c733k0pbxcXh6dir34hIB1yKJgZbBS9H8jfkZmsJJ+8YtfDOvwlFNOGdFM4qAZ7AW3jeY3wSUQd7vb3YalwqoUIFHWC2qd47DOMeaFtk4zkIWJ5fFvl1XXIHmSc3/mM585REmz1Hlo7vohuMENbjCOhxVHwI899thhDTsP5VjJrqEfGMm860MMXYtV+83UDxPfnh8AFuCy7BLrJfvVUd2x3eY2txkWLYtxiR8AVuypp546mtcZvbIOWhCbPUlemrBcJjrPeMYzhpCx6Ly48pTx8rD+TjzxxGHhpD8cn6HmZMRS/zfNx2c/+9mjiUj86stvql5N3mtf+9qjK4rmXiw0vkbNZevsi9VIlGO9POYxjxmC+PKXv3zUlbQ/OMdqQQXnRvxYhISMmBMqzdc0R50r64pougb6BRIg5/O73/3u/yXn4npUy65em8zbj65FrqFgTC2TaU2wT8fmh0RT2DXitwy1rKlrzepnTer4nfzc892iBbHZk9QXAvXBNyUAOjtrAnvZ+f/4xySWD/EiVKyi+BIlLxbf4F3ucpfp1re+9WhWepkJpRc79Sd5SUU3iYomYfxXgfje6U53Gt1G1CWQkm01xR0bqzR5y/NgobHIlNlX4j8z5Rowzz0QESEwAiPEkGjbD1GzfI1rXGN61KMeNcTb/jRL+RPjQ6zHUxPq8WLVevtRP+swwaxaBjXPsfJpssj9YLAsCXV+aELdxv0+7bTTxjXWMqjrpN2iBbHZkywf9LrMYiFMxOboo48ewsZH+KxnPWtYe+YJIVEkGprFXlzb5QXXeVj/N34pTUxCGaxPuaUgapbmWCQCoEmt47AmtWBG6jDCwjE6hqDe1G1qe4EIx7qdxA/Iwl0Oq8txqZt1y2pjvRIdPwzWVVK+pn1Ry7EgHQMrWjO9nttGsGQJuh8M1zQfgVAX4atkX/Jve9vbTg984AOHSyT72W1aEJs9SV6EkHlTwsbSYZkJeLBO5K0qv0S+F4/fkICxIo3IYOmtahp6WQUkCCKxrQEDLyXr6Oyzzx4BCE13zdDAmvESC3Ionzqz7WaisYrNRCD1awLnWhCq+93vftNxxx03rGbNaHVYX5vCymZ+uY/Mm9b5lGNl8kv6UeGjzbqw3M5+lSfmxDrHpJ58ISdla3LdNZldU9atvJznbtKCeJBxU/MwbkQePsl8feCw3YdiX+V3+yFbB46RBaapqp9fmn+rqPksDRFLIsqqYd1pUmqGamoqK+UaVwsxgpgyEBhIHfxbfGjZlhXHQjRKZRX1uLZL3db+PEOanAkKWS+CzgrmoxPwUY5bgOUoaLIcV71Vcv4SV4OIto7nflRyXFmf+exbOS4KXZLqPRMoYSkT7lw/WM965G90HvyyAjjZTtnM7wYtiAcRN7Km+ouXvMxnWpOHoT482yX1ZD7U/L0MfyELTNcYfqX4oBw7y82LI4rpxYPrS+BYfESKL1H3GhFOQRZ94IgJcg1iIeo4rJsNyzSwdogr31Y+nxVRkPjIdNVJlBlZJ+3vvQvmHTd/oe5Hgjuar/oWiqjL4zeEa+E8NePT4Xq75PidP2tNlF9AinW6PK+UdXzcCaLEmu+EkQjya+qy5BpxeWgOZ5tAEAm9aDRrfLufI9sOLYgHkXrTzedBygNRU1jm26au3y7ZdlnP/tR5oOAT44MiiKwUIsBf6EVnARE9L5hyXlj97vgXr3Od6wyLkKXkgwEsuyOPPHJYmoIzrDyR6Qgoq0Q3FYEYL6/ghRecBSbSzXJhbRKH+MBcP81y/RZFfoP8ZdoOy23Mu3esPX45TXfHJKIsmmzZcTs2I0ZcD8IjkJMfin1R91nnNXEFefxQuO7I+ppcK/sVUWZpc3Vo+op0s/Jd91vc4hbDN8riXG6vWW179839W+UL3S1aEPcAufF1frkcvHAGzvvVjIjV9dtBYMKDbPtqnWKndR5InD9REkDRsVhTjMXHMtLtxugSliKLgjh54UQ1ddVhIRERLzVRvfnNbz5eSo5+XXVYLyzOCCI/HEuI38tIFdYYwWV9sSBZm17cijrUp8Ox5uKqa7rd6+ycpYplwRnHdPe7331YqvyWrovO2ASHWLIMXReWK1FZBjC2guNNMgKG+Lq21XJGLed5tV9WuI7v/LamPthAIC3HJVGj1Hm+PaN8lDe5yU3GDxmBTZndpgXxIOOmEiMvjBeKj2rZ/QDKaZJ4uDzwrCAPdB6a7WIbnZZ1lWDx1H1at3zp9jKEzctumBnRM0KFRaFJ55oRJs1rI0/4qYgFn5oXjeCxCq2TLxFL623LimThaa4JBBBbwss/SHB0JlbPqnvmR0tTkEjZT5qUO7lfyH3Z6J57hgxPZBlqlhIsefxyjp14OX4/Evtzf23rXN7//vePUTuukfPPuS2PzXo/VCzTJOJXE8uPBR9hrXUZN+6HhbXthyfrs8/dpAXxIOPh4nfy8HqRPdBeHiKZh9ZNN8+P4kHnR9H8yQNj3U4eDPvxQouOphmiruz3UMG18kPiZdKZ2DRRVOfkh8N6FrGpRCisz7bW1fW2dx00nQkii4YlyYJRjqiwVOwr9dTrlntDgI2KEURQZ10nbffeZTvUbU0dAxH2w+q4co7OR15G8uzk/tb9mrounh2Cbx9Zp27LkGeZcDl3x5SU48lyji31BPeOK4R16fpzfezk+LdKC+JBxM1n6fHD8GOxUvh79Nr3q1gfDlE2TUBiKFjgwbe+pu2gvDr4y3Q70UxkfaaudT50u4VjzHnX6XK+LtfzyrplnuXkEUDXnP+KNRRBkbI96nIEQoqfUbM5llnKZrodUm+dr8uZLvNg3j4jWNsh2+aYWWqa4YIjQX5SqHmb7bduV7fJl3JEy1n9hDTlUOd3gxbEg4ibqdkhIMAXxSel+0Y63OZm+6UnmiwVzR/LeTB3+kBkW1YO60WHV81OIomdvKwHmpxDUs0L5uu1yksdki9l2XqWCWvEC6+ppnMzX5yXkuOfVaNstYaSsg/zrq9Itz6PLB0vdNZJ26Vut1EdyV+uS149/61Q68u58eX5Aa8/okl1m2A+511ZLiPbapYTXu4JrhAtmtSR6art94cWxIMIa4O/x2B7N5zvirVG9BLskPj69IXzYGjaIuv254GwreaM4/Cya5Kkc+3+1HugcaxekMyHnId19WWs8yFlkzTxRGK5MQiirjWavvyUiTQrt/QdZvu6D4EbI2N0hxHgqT9o2yX1I5ZoJcspV9cvy26VWpfEZ6up7EfadZJXz6cu15R1dX6jewFiS3Q9+7oN1VbRTq/fvmhBPEi4mYSOEPkaiYfLTdaEZkUEeZqzhFJTGvVByAOyXZbbqVsfMc2T5Uu+V1med10279qFVcsh86aZZyHqY8hCZEH7jqImoimBI2qrqPtJfa6nwILuKazw/NjV49kJts/xos6vIseT+e2gvP05F/0JtWZEtXMOOZa6D9TlZf5yW5gSeknXIe4GAbGsS1oXLYhrYHnDslxvqIdAJJN1KAqpnxg0E+rDZV6EzRAsEUJ5q0h+tst8pS4vy2ma+FiC5rv+aXlYK8mr226XVduqt+5v1fqwP/veDvbhXhA+VhDrhCVtShS2egzKOX7bsKx8qWXpH97rONYcL6HiztERftWHY7dKrssS+a6VZ1DUWRcn171StzW/3X1vRgvimqg3ys1L88bNFqUUWdbFw/hMTTJdQzwE1gdWCovRSArNBg76zR4A5flZWJ7VChER9BImL2Q9lEnXBtsvyyXV5d1iX3WvWrcss5fJsXoGEk3FoXYOSY7fs8qPmnXbJXUFz6GUfD88nteN+hwqu50fpq3SgrgGcgNrys3mkOcj1JdQRFkQxfAz/jtRZNHkvDCazn6J9YHTT4s4VlI3K4bgaVpo8mp+a2bblh9Mvrp1KmahEOS6PVhDvuzMT2aUR/JTppbFqrztkm1rPblOIetqmUOF5XnUF76mQ4V6rM5leT77Q60vy5mv+6gpRsZu0oK4BpY3s8IvpS+hIIrPpvtslBEQIsu6dRAsVoTtOO75rHT5IGjyK8oQMuNtjQQwKoHoKasbj6FS/FYCN5rCt7rVrUakmj+roh7JcTkWowLqOcC8vIp9+xXXP9KY1J0kza9YAcix1OXlsRwqLM/DC5xzqfmHEstj383zSH21XmS5Xru6fjdpQTxA1Bspseruete7jm/56cKQMplKmtXEyXhUVl915KcMK5Iv0tA143I1I1iSgiRXutKVRjNY1x7LhkgpJyhQ8aBJhnT5Ogthrb++pktRMq/JxMdjHC/x3W7SN8+oBcJY66/CsSTHkmT5UEruT87vUDx+yTnUY9/JeeT8k2q+61OvUZ7Fut1yfrdoQVwTuWG5WfXmsayIlt73+qdxHqdMphLLjyVplIRIpwdj+TBqKltn1EC6gug/Jzp35StfeQiqZSNg9HUUKdXZOKQe6OIgyONzVva1ETk+2xFplisrbyvJviXzOipL6qjHESznxciy8+dfIsYZXbKXkx8siRvEMZsm37kfCufhGHMemc9xm+70PHJNVqVcp5QzlV+Pw3O32XO6E1oQ10Be7lUJbqahega36xCtX1tdn3l9DnWF8Wkp3TWSn3LwsIheCooIqlinA7DheL4VyB/owdG0NSpFWYIcUhfR4dvkQ/QlkvqgKVNFKSnL+0OtT4rQmma+rhN8cm7Efa8nvQdMfQLM1I9f8pZl9nKq52G+prp+qynlc11qfUlZV8tnXbaV9IfkdtktWhDXSF7ikBebhUR8NGFZcvnkUS0DEWPRZYKYfzNbplDzBFIEavRvTDO6rk+qWOav9JDxPxLElDFdilOo81tlWc+q+ewvJF/QSTPbhxUEgfZy4hd2nPVY5UnmD4VzkOrxcqfknORbXpbf35RrlP0mr5aRHIOx4ksX0P7QgrhG8mLXecn4TFFjQRX+Q82BUIVAOYKpyeyz67X5mHKmmpz5Yo15zWeRaV+F1uxWjlXIMtVUNS8v+wma0359NdOriIYsJymj+wXLk1W61SRwlCTI5Aciddb91Pkss4Kd66GQXJuanKcp37Dpqm32YqrnoKURt0c9F2nVtjtJqU/dlu0r81lvOfuuvvX9pQVxTdSXGBEwiUWoE7RgCcsv1PLmNW91z9E1Z6OgCjHVZOAjJHasSp9TIrb1C84eHMELTU7NbMcTcYUyItWazLav62B9yLb2rUO3SLbm4L6SIJKpfWTZtwb9D8mq48k+q7V6KJJjd36H8nlUluexk/OyTbbL/Gb1bLZut2hBXDP1Juel1+zLf13kX9pCypr6ZfQdOR/P1K9QMKGiDDExisWfpfsKjj8cF8HlnxRd5vBWjmVG6FhkRl5UAcrUOF1fMxaRTt5mqJfFxkcZq2G7ybbqaP57PV1301XIT1qy0TY7RX1beQauaLQgron64GZe0lzVVMyfIxGqlMk0iUXIPyIaTaQ0F6qIKUNQfUJfJ29jS3Wdud3tbjf8jvwrgi1EU7SZBShCt8qnSJh8+Vk9fJDymgNPrnvuS1guI3l13WaCuhm1jszvpJ5DnRbENeFhysNZE+HxOagjjjhidJjebJic7TVvCR4HMstyWSeLj+Wnq4wvs+iYbeA9p7NO2IYHEkN+RR2o6z4yr07H4T8uWJu66WR9c2BYXu96j7DqfqTMvsptRq1jWY+0U4E9VGlBXBN5oJIIG+uQj4+ldvTRR48hdXx8lboNPJAizf6Mh58weYEfTyRZcMbnpViDrEJCyYdILEW06/cVK/L46FiFugARUr7I5sBS7/nyPmVZUCwBB60Fz44gR4ILmW432W65rR/uPBvL47ki04K4ZoiXpi+B0hlbUIO1p8uNpjN/XvDg5eHLvMQvqP+V7TR3qyBCmeSZSqkn1DKpN8lDTzj1P2RJLutv1s+q+5N598ePKfeKLx75LJYfR8kfPEny9ETQSV+yvK+knPpMU0eScfCH43PQgrgGIkiSoEY+82U8sf5UhqyJMut4XcsuSZ7gg/5eusPkv0+w0XaVff3CE1gWJd+hLj4+YNqCeGDJfaz3yX3LsyHoxF3Cx2uo56mnnjr8yub9U6AvJkn+ObDO7yupQ1n9VdVjWb48fVFZivE3Hy60IK6BPECmmp8CHyLFmqS6mQimiAALcCiTVKn5HkpWor6LgiuhlpGS50WKqNV1oZYhtrr06DpjCKGm/aptmvVRr3emEUNwi/inP/deNy1dnYxuMtrJ1HLyMr+VVMsv69K3NN2zDidaENeMJrGABcHhn/Ng60JTf323kviK8t/CeVjr+qUA1gfZciVliDXrVSDFKBX+zZRdbtMcGOr1l7hb8vxkGGbWV+vfdCfile2Wz0/yTQ8nWhDXSB4mD5Zghz6FvoytibrqQdvoIbQsif4SU5FjddSHOPNLVtUVdOlRn2i0+do8Wm7XHBiW190PIZ8eH2+N/rvfrHtfreafFlhzD1mThHKrqKc+R0l1+XCiBXFNeJA8aJs9XPt62FZtw7IkiIbkbTQEb5m30TLLw0cjat/ErG8OHLkfSwgbsdPLQHM21qF8YqhngHHdPvHGP000/eB6RrYiisv9Lp/X7QjrFYUWxEMMD63msod11Uu0HYhgRq0066GKThUc1HWo8zB0UwRY/1CWYu6TT74RP//C6AeNP9rHhY18MsxTP9T8PWhY1r0VdrLNoU4LYtMcIAiMRNiq9ZX8CFCEk7XH58y/G58xVwlfsi+bc8Hw+7II+ZWNUjr++ONHFJorhOVf66v7qNN6PLXM4UgLYtOsiVXiEgGSsrwsZx0B1M/Q/znrahWXhm5RrEOWoBFICYQJvlin64xhob6jya9o3VIQk2C6PJ66nG0PF1oQm2ZNRFyqoJhPqstLBEv8YZhUywis8Bsec8wxo3cAH2PgY/T5tuOOO2505NdVK9tm+7rMB81lIhHUHKtpLMYWxKZpdo0qLhGWiE5dTpLPGjSsU/9QTWHIlwRT9EXUKZulWMfCG9rnG5isR59XE3SB7YifCLQhf/yREtFVf5JAHb+ldcTVdocbLYhNs0YichGXCF+owTFTwmWIpyAJUUxPgqxXj8/A8SUuewcQMSOiWI/+X1tXL1gvEKNjt//4Pvnkk8c/ORJO85LPxxlO6hudvpRkVEx3zG6aZi0QrvQTrBCrJBA744t9AMS4d/mrAh6ZwnxGRPm6OkHjX2RN2u9ll102rEkfCOFb9GUkI6f8XYQO34aR+sK6dYSQGDsG+21BbJpmV2HJsdZ8nMPwyHTMr+ImER8RY3/rqjO2/89OfsrUlG2JnoCKYaGEzZh0vkXrCKyvHgnO+OqR0S4XXHDB+Fo5/6RlX0k666yzxqilSy+9dARjsu/s53ChBbFp1ojPavlyjEDIiSeeOJqyF1988RC5pfXFB+gLSD6sYGxx/UJ6FcAqVKb+e0fXHM1hokjUNLWhDtZi/jqCGBNCliC/IR+kT8cZVsqiTN05vuzncKEFsWnWiD/y94Ujo01OOOGE6dhjjx19C0V1UYXNf+2cc8454zNeRG4pRpaXeSLEOmfnz/91yI7fcVXSbNck1nnbvP/ZYT36O0/N7qUIHm6i2ILYNGtEoEPkVhOUVSZowZdHiCo+8cUq1F1G1xqCWYUsolTn4evrfIJEN8M5iSRfpWmwjTrt47TTThvbiTiLRItMGw7qWGvddf5woQWxadYE64p/T3CCUGmi+jsIfwDm7x6sD0RQ01XwozZdl6Jk2XbEzvhmlp7t/D1EgiCazPogxo+YJHotWOMPzvgcHdOFF144PgzMSqxfSs9+Mz1caEFsmjVRxYhYsdDOPvvsEQnWgZr/jmBGmIiSr2KnOY0qSKkrQRrBE/5BVp8mNiHlsySQhvEpo3yavcr5CMQZZ5wxfInQp1GfRVYmi7GWPxxpQWyaNUNc0nVGU9VfvZ5yyinTeeedNwIdhuaZF+0lhsouBcmypLzmtua3pq/vY7L6jF3WkdtU4Iaf0Fe2QeA0hzWLTz/99PHnZrEGDQ/0L41EMv7HCOLyGA4HWhCbZk2sEhSWnK/UCK74QAP/ou4w/hNbP0LbpOlbSV06WOtGI0BjzPJRRx01kj8tO/LII8e8KZ8iizFoUotAi0SLemtyq1PQRz/Ek046aUS4CS5yHIcbLYhNcwAhMueff/7wI+qGI0KcoMaqKG+QJ/n3RM1knarPPPPMEYRJkidpjotUV2G1Hb+ljwGzFuPb1Gw/99xzR7NZ1JmFuhTjw4kWxKZZM9XaMs+35xuHrDkdpI0WYR1qrlq/kShC9FhwpI5BFjyp8xLLUx1J+jiyLo1fdizJ10/RF3MuueSSMb/c92bHckWkBbFp1gxBidVlXuBD52jfLtRUNcaY/66WSQqZr+tqquvCMn+5HpbtN/uuZN1ymysyLYhNc4AhMMYXa94KjIj+asLKX6ZQ86pIJS9strxcB8sbieGy7OFAC2LTrInNREXA46KLLhpRYVFmRJzSpF2yrG+z+aQqdsnbjLrt4UgLYtMcBAiVAIaobvyLzcGnBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmYwTf8L0KzWV25D8RQAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAENASURBVHhe7X0HYJ3Fle57CWGzbLJJCNkXQggBNkBCx3SIIWA6BAK2McU2BveCbdwbuIFx771XybLlXiTL3ZZlSZZkWbZVbKv33m7TvVffO9+ZK8ouu8iKwBvvfNLc+5cpZ2bOOfPN/OX+H1hYWFhYWFhYWFw0LImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImyuIxRj/r6QAgcsbCwsLCwaC5cFiRKB0j58NX74ZU/6Kcfsgv50vOyJxtu+TZ/9Tzp09MSfLLPHQ645hi/dYvxJEsdhnmwvk6iueFhHEZpTrBsBm5KWT5uyb9PZPNTPvnXQo2ocorysjaM45Tg0TTc1wiXDCKgyGXaktI4pL3qtE9UfpHN7298C2qzfyUq2+Y/wu9nSdKPPq8EH7zucjhTQjGzd3eMmheKbRdq5LhEZFJtM2lfyaf+iwZnJhStXiRlRAuL7wZf2C4VLqDKqn48rrotDoc79D1U2nr6NH7zWCAyN2Xf+C76AdmmzanuiqWpz9AS4GJ0ptVzjMPkftAbqg1I8LEMn9ikxmtmaIGURD1aQBZTlNkWm9VIzQyWKX7BlOGSOrJ81lGCNAWbmHG0JxhH4qqARkj5MG3PVvuqdNzmUZWZO1+JG0gs4dvBZJq04VuSsj/q5ICX+/yQfZVP85QyJY7GZXESfIF0mokGi+8blwWJ8lPt/FQwGRxpFPotQ2HDvjoVDuH8Foch1uOl9gUUkiZMo2Ac5iNDsBwXxZV4Pp9E0niaizqber/E/g70lUZBuf2Sf70U4BdZjCM09aCBGaOh0fPLGBjlN+lMfP4ZxnCpUIc6kddDMdTqpS9IbEQmEl1Wop6OjHI2AlKl/wTTP9IuErhtguxLf7Hf/F4nvIVnEDriObTtPBD9VsWhUI4zL8rQQKDYrnWBtHJAv+keGymahcVFgzqo+kZNC+icCUY/jcP5MoiWamjQddVNjUdf1pAH0/KcpBEbqFc7oC7T7niePo0+knrPpMYG1OdJULtkXvrXvFBxNX/6X3IDSkVfFZBb/IWJ1czQ/KUdWDac0oJSJn2kj2MD60252G4mDtuJvEWHBraNxGfbkBpROo4NTE+J2V7M1qTV2uh5zbTRMPlr5izYa/LgGOPlcTaW5i+BkXSbqehfZVrK9uSfTOrrxceq3lh877gsSJRPZhdc2SC50YGRjkIUi0bB2QfkPAdtJVKi5ORFXn7oPg1HzJhxJT38QkY0PvdVr2XbBBItYzySvzio5gYJgI+rZawLCyZJMOapgXKSGBrjYx1FLqaTT8r7pYM0Ry8ZpF2ltYVEmYZT566zJmk/OholiG5GNPG/BZo+AG43DCZfJVEKqbISZDoin/StfOfs6oOubd7C631WILKScdmPdDyyIfHZZuKCVA90kNFv5vVlmRYWzQqqFv2S2ImxWwZDcsxJqt+XNk5VlBgBXf8yaDzagMaTSIHInIBpEP3XyZXmZfLncWUFko5F6dSQfpDZMTnFku/mBL2YWUmX8qUc+lqSBJbLdhCvJi5B5A3Eby4wR+PvWVchGSxDNukXOGZwR9tVyydx4TTbNA+lapBbWk7SsE0NAeMkV8cB8demjZmOeUu4iEqYaXmdpBGhvJKDtg8D+4M5UmTuixyaNyWibEKiRH6ztk8Z3Sq/xNB8Lb5fXCYkisZiiJQZWKlOQqLUOKh2omA0WBm4lVhR2bjvc8g+jUIMTWycxKpeSBRXUlRh1QBFYV2VKMytRI3Do8aiMwMSrmZWWpqrWUHjyg3lNXKyPLMKJXURI6Z8fk8VKqtEriohXYwmab4607yU5sTW/+JP5Fbnr9sinwSSxTqvS9u4MdD0DHSCbAc6G/luQMM2s2P/ekQP6uoc6mjqs7Zgeod2ePOvgzA31qkki39e6dPqsnzk5eQhMyMT2Vm5yM7ORGZeHvLKRTbvdzCaWFgQ1Cv6Dx3YuS//ar8SZFDkIdo6/Q9tW+3bRNPzxkeQBMgB0Xn6p7KSPGRl5SE3pwjlbi/cHIzp2wLkgD5P8+ZxTtC8zJvDOMti+bQtOc/lY3K5ZoQhKVJXOlktuh4eRxkqizOQm52B7AtlKBOZuTbdnGDzkEB5SVDoagImLS0o5+jJzSodyYjKpz6G0Uy7q68x0ovPkvZhevFd/jqPUhg/xwruS+QGCmPSsfRvB5tZaZCMXdIiKpcSYmYi5VFk7ROOSyRw7E9NKZAojKaX/SQjnWCbMxbfMy6PG8up3TRBJUpUPGoWHY0opSq+KBmP61ETSExIqlQTGYe7EoPEiwqtK0KitPXOXFQmrcfID0OwJzYX5RqZruc7AC2EctA4RAqSKtTJAY9IJaRKaiTnZNYhBNGdFoZN2zZi+NazqGUyjUpHRJOXbRof87wEUNesDSptKc7ezOXMfWpcnapjBVnXRoP9KKlJbAIws3I6flPLL/YlXxJm3vHB2PX1mdg7riPef/FVPDsrBm7OJCVe6dlQ7Fz1Efr274UeL/wV3d7rgs4d2+KtvkPQfV2SkLyLEtDCovEQlaVd+GUSp3agOku7FRsX3f3SbrnFyOaLZsOhmuse9E0KOVZ5JgjB03vjrba90av3FGxKKUaW+AyX5KW2pkYhQbZJvurEY9Ae6yQPl+SmK8actHkd6veafTiW7L8IkrXf50H+iTUImf4BOnfojLdbLcKu5EKUaIRmBJ2/2Dvro75Ahog62TB3xpI0yUG6cu0D+eBJ+ddVMvoT3aVM9GfyrX5L2l+Ck7loGjkkfsmjd55JvgHX1ygwa41sKBgnlx7Jm3TKCGaisDxzGVEm8QEfZ07Ih6RhdJ2gajqL7xuXBYnSe1qo/QFHweVQ0ToUR6/Eupnd0bnT62j7RCu0evIttHu/G3r074t+fXugd7c2eLZ1B/SaHopdpwtQK+nN9WUO2uKqqs/j3L5gTHrzUywMS0ZKaY2UJcoq5XH21uygUZSn4MT2afikb3u0+WAG1kSVILeSZKSBJHBmJKTKUYrkQ+uwYPIQ9FpyBtnlQhoCxsZZFekUW+X7B2U8h9Nb5mBCv374W/+pmBOTj5JqkYezKekbMzumc2usfKy7CUQDeWJogPYJvxkl4HA0vq8C8cveR++XHsHtbdcgxutBbe0p7FqxCYtmbUFE5Cas6fhveLJLT7zZuhXeebcNnp8XgwohUdYlWXwXoNryMpGuKHHQpq6pfTfouBkQdYWCK04kA3JYV0Oo9zwr8XQQl7yqYudizYox6Ln8CFJPZ6G4xgWnDOzVhecQH7YGY/p9glkzJ+LjMdMxdUU4InNrKIDkLVRK8qiTYFa96DdIMWhJzQiRkZfySdpYD347q3NRlHUUxzavwqhffIo9J/JQFIjeXOBqHkljvd8hIrBs+gQnKvLjcXTdWPRq9RYGfLIZ+04USnsxPtuArc++kb4QWX1sc6blkg+bW+vC2z+YL/2ytKHsexiZkzz2FSM1ApJCQ6AE6U/6b8nfVYLatHCEThqK6dOnYMK4CZg0cQEWRFxAicendE0n2NSNOtEhjlkXUa5F8+LyuJwnykcj1WVrKrNsUzur0iMRtX0Kxvd4BQ9c8S/48S0d8P7omVgUtBZBa1dj9YrZmDS2Bzq2fRft+83CrIg0VIuRcZCv99eiJHY9dkwciK4DwxCdV4lqHwkWZykcsKn+zQzaQG0BMuPWYfEnb6Hlrx/Bs6N2Y3dKqcwqjaOjE2X5dLa1eTGIDP4UXdoOwpqYXOTUCDERw+L9RiRTJsPvH35/AXISQrFkWCe88PBTeKDnNhzOqkSNOjQavFknovNoFNifGti3zJ+DjUlr2oN9Ie3DfUaRfc4NfTJfzD6yBivGtUW7v9yPx+7riPkpHhRUZSAhOgVR0eeQdW4Xlj/xI7wwfBY+W7ISO7ZtQNCJHDjpIC9R+1lc3lAiJIpKH1InKubl4Nmg37LNVQie05VwLp/opFDScECnfksUxtLVdAkVx2Zi7bqpGBqRx9FVjokvzI3FweWzMbjLSIydtwXbw7Zjy/IpmDxsBIaNWo6YHEC4loz5UhJ1nXnSluj7mtu3Sd7mlgTJm99inyRvPvETBfG7MOmHIxFxPBuFFKIZYYgmfbn4HTYMt311cJRlIXnfCkx640949NG3MGh+BBLKSJy4sEQ/YkistgnbnRTni7bnvomj+Utba920K0i8eEWEnfDt0PzY7ZKb3lZCYlYnvjN2A9YMfAd9xszG8g07sHPrOiydORp9P+yLsXtTkVbGFUPqhgQhbnxW3OhP87afReNweVzOEydgZjpc6KYiGefCizre4jgcnvch7vuXX+DXby3Huvg8GcxpXH54fLWoyw/FtBda4J7rnsLjfYKR7PbIrELYfU0yIheNwYQuvTEupgalLl34VodjZoSNM5SLgUouH35vLs4dmo3+N16FXz48HJN3nUV+nRiq1ElJnBo061iJwjNCAto9gndmHED4uTK4xRD1Wr0640sDdTAoRsquSRjb6mb84Lc9MTsqB1lukjxeZuUDx4131UzjqKlEaUkxiouKUPQfQmFhIYqLC1FUXguHi/c3eOBy5CMvbhfWfjYA4z4dgn4fvIEP7v0T3liWgaTiKjjEmbpchciLXoWhv/o5us2MQEQmXxMhAxCdrfbvpWtDi8sZRr/MPUmBS0ec9ChZ4gBOHeYKBwdXiaeDv1ld14FX1JKaKXvy6UNl1AysC5AoJVaoRkH4BIxr3xYPPT8Z+4tkQlknfqEgAtvHvo/X73gePTcVI7OcZVMWyVsy1YmXpm9mvTfCKhHRwZ6r/BI89WKjCTsw5YcjsOd4ppCoxnqERkIbiz7TFM/yeT+Y31sPT3k2Lqx/HU/ddgv+0n0qliRWSP1Jl0gomYY+nnmQNLGNuM/82EYSx1unRFD7h8dkm/1hiK/sNwKaFVe4NA8ZXyTUFR5GxOxeeOGWB9B503mcKZF+85Ug7chcfPq3G3BLxxXYejJXxjCuQEk6yUO8lmxTtmbuN4tG4bIgUQ1OQI1VFYkKLcrHz/TdCP3sFVz5i2vw6Kf7cTi9Wo+TyTvrq0V/o7D+jT/j6R/eivueHoOdpUCtOJaqpLWY9dEwvN1hMWLEuJw+t5A0DrBSBJX/OyIpUhOR3I2C1N0I7vxz/ObqZ9FrzkHEldOwpXCvR8kiV99ouK7iRCStaYPbX5mIGbuSUSACmvsgmNN3I+O3QUuVj5JTG7F28L34pytuwgcrEhBTwAHBXH7lOhHdU6MghCc3Ox3xcdGIiopEdHQ0IiOjJByT/SgcPx6lx6NO5SC3vAZul8xwk7YjqPvr6DFiJUJiziJh71xMff0W/KjdSuw6lYK8wgIUpiUgMXQ6XvnnuzB+bTxO5lWgqroMubVcLG+0dBYWFwlOcmSwrROfIkS+QnSxrKgc5eXlqKwuRkVVKaoqqlBa40JlXWCFXfwPb0TX1Q5RTOqmGTN9qI2dhnUhk9AvIkvicrX3HPZ/+hrefO55PDhsLyokFleyffVZOLFqOHrcfRt+1D0c0TnVIokQKa4QSb4+Hx/2aH6tVwKiBEboiPineq+QRPGxnvo85MTvxrQfjkZEdAYKxS83N7StJFvjbegTSXKkzq5yeM8sQq+H/4C7W/XGh+vOghf9dCwR/0n/riv+DGyjhvS6+iPtVZ6HUum3grIqVDjFm/GhJSlFrxaYor8VSpdFON5+4uU9uOLnyiIXYW6XF/Grm3phYUoN8jycbHpRnbIdB4fcjf93VSdM2JKINA9JnJQoYxGfc2a5WlmL7x2Xxz1RqmaivLQWYTh0CFzA5QyhOHoh5ne7BVddfS3eC8pEYrFZ2qWq1/udqC8Nx5QXH8Ld/7cFHnp2DvbX1sNR70Dquq4YOKg32s49IUyfzovLtMyfusry5Bh3mhHMTWUTQ/UUJuLCmjdx8/W/wuP9FmHNySoz2xCj5jxHSZzU0+/OQ3nqAnT/42sYO2UvjhfKYc2F9bxERsVmkrb3FR5H/LIuuPWHV+KaHquxMr5YJBKZ6bR1/TsQ/9sgeXnrnPC4HfB4XBI8XwS32w2Xi8ckyIDj8wkJil6PZf064fYPghFyKgtFbheqUsOxe/zr+NHP+mDK1L7o0q4b2j7fFZ980hP/8v/ew5SIs0g8sgp7tszHhBOV4qAa/woGC4uLAe2Tq8WuigykRi3AhEEfYmj/CRg3cT5mLpuLeUvmYem8xQjeegRx54t11dYQAOqkmRzR/GUsV19UeWwG1gRNxYD9+XJQvEP5Icx79xm0eKA1HpuVSHPUUO8vQ/K28Rj1zE248t652JBSjFLJTy9JaaTvxmPQW/K+HZ+PPon7dfCJnH5vKYriDwiJGobdQqLyVcrmA0kNX3dSX6e3ZMsf6ycSsBjxJ/DGYMW79+Dx617CS102I5Gr+HVcERJCKfGUmLChmZLkSDa5QuhyV8GbHIzpg3pg8JiFWHM4AyVCiPX1Bxx/WEYjQdLG2w7YMp76IpwJ6othf74Tv7lpPPYU16BSyqO+ODKP4sTUl3H1T+5A10VHcLyIwkhFWJ7Ia0he48u1aD5cFiTK3CMkChQI3HZJ8KES57Z8jNGtrse//ltrTIwuRKaDFsR48u+qRnXUWLR//BbceGdrdJh8GLn6FFwqwga8jI+6DMTIMDPwq5cJ5O91FKP47C6snDMbC6eMxaSZSzB19Q5EHpyDWfNn4PNPPsWS4D1CaETBPW44T63BrKF90fPjJVh4vMyoOkmG5EUH89U36NIgODPxufNRlbIC3W/+Le5oOQBDg5JQIfH1ZkaJx5sZmR6+cnHGOzH76TvQZ/RqBJ8xjoqEizXlJ50Co/I4w5cb/ApsNAIB+ib/DLItXzog8JPESAJdvEw6ZVs+3IXIiVqO4Xf9AL++pS9GByUiRx/VDTwVKf/8kN5CTeU5nNo+C/MnT8G86eMxZeZcTFgSiUwX9IkVQ2CZQBN9DVoWj+vlCBcKLiRhX+hGbDyWgbxqcVCS1ltTiNzEA5g+ZTW2rvoInTu8jSdavYlOXd5GyxYvYuDYzzHmcyl/7Q7ElDvhZptpfZkn+59lSNvqcVOcaQ7ds7hswP6kPtN6voSnIh1pxzdhzuSZmDtlNMbM3YDlG7YhYvsijJ06FZ+PmICgiJNILqP9GdtT3dDs5COg79yt91ciL3Ybds8bi4mb92F/ZCwSElJwNvk8Ui+k4Wz6BaTLd05+ASpqeI8mE9Kv0fZJBcSGJDT4vHIlUVMwZG+ulCO+JH01xv/tYdz0QBs8uuiklMiVL9pPGVJ3jsfoJ3+NK3/eB/Oic5AjBIP5MCu9sqT6bo59Ydfyp37EUYSy0xEInjEIvd5qjdff6ohuH8/GivBkpDv9cGtSSeOpQXVGEg4sHYMhAz5Cv34DMXDUVIxbsQ9pUp5D4qh/8hWi+EQ4ZlwxCmEkUUIseY+WSEtB5F+2pM5sOt47RtHMSg93vh1aLybWy4isE4/pCcmIE+MqJC1ujzcf+iPue/kjLE2pg9tbI8VwJdrIKF9aHtvF+GbJjmSpOhupp+IRcyAcu1YvxKyxYzBmYyTisstQ6zEys+WYusGH8BiffdQJOJ0klYRyyXkTPwPH5nVG11tvxW9uHo+9pdUygvE84MyKRMyMZ3H1T3+OVz/dgvDzvLeU9WI7mrpZXBpcJiQqYFw6kHNdikYnpuA9h6Mze6LTH27FNfdPwKaMCpSKkdIl+OqqUZNzDJsHPI2/PPEiXhm4ACEnC4R8yUyk5jAWtGmFPu+NwsI4GcWpoGpAUoa7CLnJR7By5jIsWbcBG9dPx4SBvfHmi++h04iPMXlib7R+qiVavf8xxhyVuZW7GhV7h+CDP9+D25/5EB9uviCZCdUQOfSGeDUgLgezDrQp1oMG7ICrMglB7e7CA396Ge0+3oTEauPcaTBKwDSuA27nCWzudCPaDpiKiQdK9PwXBi8fXyNRrIMaH1uBdszPxoFxdaZFsiICf5GPlkFSKORPj4mT0OBCRcYxRHx4K/79Vw+i/WebcajYXD5QYRjXW4K8M+HYsmAceg6dgLmLViM0dB2Wzh2NUcM/xIxTNSgUB90oKInyobamBvm5Bah2y/yT90BoW4jrclYjN/scMs+GY9u2DVi8aj1CNgQhZMlSbNm2DSG7j+FwYhZq1c3R9WmNpR5sMw5bDsme9W9oX3Nfgpw15VtcBlDFDIQAXHk4ezQcq+csxrKQjdgc/BkGduhsXikw6mNM+vQDPHP3fXh55AqsOlWquqGcRT6MPYuemwOaa21mBPZvmI7Js5Zjy6kClDpo/4wjA6zE0zf9iwaaFRz6CWUngbwkT+okcwroZUXUNKwTEjV0T4HkIZp7eiH6vnI/fnZ/Ozw6/4yUKPYmeUNIQ+qOCRjT8mpcceWbmLovExkyqTQ+hT6HWRqZ1abFZoy987JTLUqSjyF66XSZKM7GpNGfYGifd/Hem2/gjVf7o+fI9TiQVoayynykH9uKtZ+PwpgJk/DpjDmYs2ARFi9ejHlLVmPW6hNILqlWIlVfn4+iuJ2Y+sORQqKykM8JlpIoKZvi6qVJOSZVVdmURBn/3SgE2qdh4mnuQ6PNmrYVEVAdNwOj3miBOx56HW+tz0CN16xEsS/0FTlMT1nkj22jecq3h75OJHVUZONc7D7sWL0cyzdvxabgZdiwLQzhCdnIc7DdTHymY51IsdVnsELKrehXhPhqj6dg//iO6PDzW/HbmyYgXEhUuRxn+Y6sI4ic8wSu+emP8dTw9dh8Vsie5KM+isSZjSTxLL5/XBYkSm/CFA3StySRBNHGaDDl+7B2UBs8fPUduPbFyVh7MAbRpxJw8mQc4mMP4fDuxRjR5lV0HrIIKw+lo9wrZiEzkfrMjRj+3Mvo3GUyNp3ngE+jptHVw10YjZjdC9FnxB7El9SiyhGHrWM64aXr78VNnYOwf+tn6PP2S3i800h8tOeCTHhqUHliAab3745uQ2dh3tF0yc8tfo3Kb4yT8x6u4BgHxrJoaGKozlLETnkCrf70Rzz89mdYerqGpixxTRwaDU3P5crCoY//gGe7DUP/9WmBlRvJUaaWdMB0PIzLsmQ6iariXORmpuNCRhbSMzKQ0YiQmZmJrGJJ6+aTf3RudLoiiZRFUeh49P0qusRM4umSOOJkilJxbuVfcccNP0OLzpMxN7pcZ2P6L066OicC26d3xdstn8PDYw4jNrcGDr8b5w8swMpBj6Pj7jKkV7J1GgEKwjrKtzp+KcTchN/gyJgPBwbTfgzGwfICgwm6uifxeY4zczOwMD1dpkuIOZ0y9yW21LHhIoHF5QL2ZUMwcGftwY5VqzBhxhFk+dzwVh3A3Ndb4rE7XsEzQ5fhdNgIvP7nR9ByyBLMiy0S/ZDUEnjfj04uJC+990U0yIcqpGyYjOXz5mLW8RK9P5BTKVEoiSs6qPEFXI3WfUlLEiWxZPNrgSJSf6uipiIoaCoG7ymGlyQ/YRE6vdwCP2ghJGpOMlNSpSVujZCoiRj7JElUa0zeJT6giiRNdFnKo8xUeM2fZXLFhaklsafiLE6GrcPySUux53wtKmudqEgJw87J3fDOXXfjF//3cXwwPRQhW5Zi8bgeeOetzvh8dwrOVbqEcEhetTnIi9mC4R1GYEN8OrJcUl59AYrid2LSD4cJicpBvpRLMqn3gFEU9TOyRbloc1oPPiHNs98OE58+irde0ObNKxzM277pF6XAvJ1Y9P5LuOeGlvhDnw1Ir5JRhC5f2sH4TtmR8rX9tDWkveSYS+2f98ny3i45U1cLV+Zx7F06HtNmTMfMdTux/+gJRJ7MRk6ZnKszfkZ7V+sk0rEMvfLhFGnpX5Kxd2gHvPN/bsP1N07CrrIalEne2nxCoo7MfwK/+tcf4/GhMvE7Xakp1F/xgq/IQT9l8f3jsiBRfFcGZ3C8Y4DvphTdUsX3nZmH0R88hH/+5fW4udXb6NS5F3r07IOeXbqgZ9f+6DU6CCsPpyOtwgU3jUQU2+euRn3iHHR48j2803s1DhWTevBWb/kWpS9L3I7I0IlYHCuEwumBP38Plg9ui0dufwovLUrB+dit2LVhDdaHxSGhgIYn4IcEdYoUjgov34Y0iYVwxqWR+OC/1IWO1OuBqywLRya+gGfuuBq/bNkBb65KFnPzi8nQeGjZklRk9rgqELvgNjzzfk90XXICpTQmcYp0iPrSUM5/aMAkb5BZ9YFN2LxgHhbNXYLFcxdjwfwFmD9//n8bFixYiBVCClMLK8QRca2GbcI6SFkUXZ2wOMxATfQldx4nqgsScWL1q7j35p/hnx7pjo7L4lAUkN0nTj05pC/6P3sXbrirN+alOpBZXoPqivOIWbsAM97ujYWnvCh2ao7fCp1BS+mGHLG+bF8jnpFKCpVAlypNo7tsP5IjfirJIgnktYM6Ok/51iR0gKZmmpbESRy8n3GYj8VljYKjCxG2YyM2JNG/SL9nbMLIVx7Gn5/rjH5BCahM2oqgpeux+XgGUvkAiKgFCTgHaw6RZs2CesMVgxPY2G8SFn0cjJgqJxwOF1xOGWSdTgnVcLrKUSvbzlrxSS5JS9JOHaMq0j/JDikE1bJB9fh0Hi/nfcSn84REIW4xurx0H370wOt4ZF6c6jXLr6uvQPLOz4REXYMrr2iPSTvF91VzGkAfwRujaTeSITOmzvMHiSUlh35n7AqEbVyIcQdLtHx9VYn4KXfJSSQE9cOzV12Jf73lQdx27414+u230TUkVe8lbXjykMFZkIykWfdj1I4TOJgjEvmLURgbgck/HI6I6GzkszQpn5cFKYOXba2Eg/JQKGlYJRz8/nYwGX0ACSLXgHTVRo/TjqV3fC7Upu3AgvdexP1X3ojf/ntPBKc4UeIQOYTc8JcPGi5nGkdiCJSbs1/uUyZmLX1kfLr0Dfu+4gLO712Aeb3fxGs9lmDZgXgk5xejqtYh5KtWsnFKcpI6BknAOqpk57F/2Pt46we34tobJ2CnkKhyliGnXZmRiJ77LH5x9ZV4dNhqbDxdLklYmCSTfEjOWC+L7x+XyUqUGLRHjFKIB2cb1HEqdc6ugej78vW47u4n0SHoPFIuFCC7sAi5hXkoYiipRpmT18HJ5CW9GEa9xwG3zOTaPNkZrfuswf4ScQBicLosK8biFUdXU1OOMhcHaXFOJxdjwvvP4I8PtMH4Yx6UVlWitqoC1dUuOD2824eXuDjomhkWTZkGyCfoVE4ZzXmJiKSEAz9nniIRqnKP49DMV/Fy59Z48fYb0eL3T+HPXYNxWkzFKbHVlVImycPnrkHS4rvwfNee6LTsOHJpXHKO9kfDorGa2ZsEOedy1KCqogIVEioZKhkqvzVU1Xr05m1dIpf8jRSsm8mXP7Vj3lnCuvpQnnMUEasH4PFnOuGFllfjdze2xCu91uB4tYhH8ctPYH33V/HMtTfjukc6YejcVfhszBAMGdAHoz5biJCITFS6+evrbKhvB11IQ2D91THJl/ar7jec52DGejCGcalKntgncp4DoH6wXhKJx8xQwuFQBkYhizpLZp48afEPDHY2O/G/6kjRFkcFqmqqUMlfDvCK7RwZh3eeaIEn243CknjReGcNKirLUO0Q/Rf74Nv1qRr6RJrolOqZBK68oigMs3sNQNf2H2H08gVYsnwZVixdiaXLVmHZsuVYuXQxVi2WgXeFDJQ7Y3DqfBk9g0hH0sE3nPN+QhIc0VvmJ2fLoidjTcgkDN0vszbq7Jk1GPHKQ7i2xRt4ZG6CpKb+syYyadkxEaMf+zf85EfdMPtwNrKczEvyYZ5wiJzM10xAeC8hJwvU+cwNM7F72RxsyDR1kxNq5z6fAxUXDmHXgDvxh99djStv+SteG7sRUeL/6BFYd73/SPyrrzoX7oMD8fT8vVgWVyI2V4TChDBMvJKX89JRQB9MP0JioX6Fjca6G1n4o/EkkfxrDJjOrPxIfF2VlyOcPbFfPFWozziIeZ06o9tzrfD4A3fhF7+/B+235OFMGe2cfw3kkzJxkqXeDk7KIJNEfXknJ4tc/dPY0vfsbznmcVSiIj8DeUlHsGnK++jRZxj6LT6G0yIDfSN7Q6LrmKKeVNsyGVGTO6Drb2/Fb/7wOfaVVeuN5WwBV/YRxM5+Hlf/9Cd46uPt2HpWfBgZJ+tDn6R1tbgUuDzuiaKb4aMqVGYaPh0MyoW5v4F3H7wZt7fsiwWJdahxcXAXY+Z9Axw0aV/yrdfZae00eCFRvvj5eP2J9/B6r1U4UEAlpoHQhmggEkRvdVYof1lhg9H/1adxz5OjEVriRqXXrBKRtKjj4B+NkI5J0vD1BPSotGt9Qk2dIc3IOK46GaDL0w4gfOEIvPjWhxgXEoal49rj3Zb34U9P98fa7HohFiRGDFp5+Fw1iFtwO1744EN0WhqPjEBdaFTypXUzszFzUP2IHg9k0FhoxeVbA9tFDvFPMtSX9kktSBQ5u6o6H4FNs0fi/fYDMGJtFLZNa42XH7wDLV4bgrkJ1RoHmZswru2fcecdT+G5MaGIOpuGEzHHEXU0ErGnUpFexsuCKqmEb4fKQ6ej9eJOoF/1mIociPOlg6aDMnF0V9qFwxWdIx2bHJd4jKurWxqXjjLg7CVDvz56zgax+McENYL99019yHNGV0gu9PKJuxzn1ryKF1s8jVd7LsX+ctEB6ojogOoe7UL2mZT6ppfjeE5ICskVKvdg4aBpGD9iNfacPYPklGSkpqTIdwrO8js5GWlnk/X4haw8mZTVSrlmkKbe8hLTF/dPqS9quCdqMobuDaxE5YRhWpsncfsDrfHIvESRhVMAhmIk7xqH0X+5Dj++ZjSWJeQg1yv56YRBAu2CdZCgt0hIoG77UYWTyz5H6OwZ2JVHe+TKv8QRG+Ckta5W5Iyeii63y4T1p7/HPe98jFmnyiWd1FnSG5uSIPEQNQovz9+HlfElUocCFCTswOc/HoXdMdnIl7y+sE31y8ZP6b0/PCeHze0DcqIRkJhSKutEe5Z91o3d7ChGaeJWzHnvdXT+aArmLZuFecPa4ZFrbsQNffdi74VSmQwaWbS9te1ZONPTV1Me9jfjMLCeclz1QPqY+26ZeGZE4fCcgRjRpz+GfB6EkGPZKJd0JHI6sWU9madISX/or8/GySXd0e+eO/CbmydjT2k5KhhfYjizjuDEtFb45U9+iTaTI7Av06Rnu0iG2kaMZ/H947IgUbpQq0oo6k1l5yzBmYTQnk/g2ZsfxENtF+BQWT1c6nR4T4+YNBVZrZQzA0NgaCheby3qk5eh19PvolOPJYjIEQOiA6QhSXxXZQHyL5zEqfhzyKstwKFZbdH+qefxSPt1iPe5UCMylKXF40JqMtKrzexFF/NF4Y1voGOSWQStmqRPDYGOgm7SiZKU/dg8fyw+7DMYXaYdQFyeA5lRszH+vUdx0x0voE1oMXIqWV+xHak7jdftKseJGbfhhW790X31KZTQyQQcBgki20VJnZg/6qtRnCHOOu4E4k8kIOFEPOLi4r49xMcjIaMUpbV8KsS0hUIK0ReQMrAP6pyoPr8fW2YNx8CeQjAn7kS8zOyqk+Zj9Gv3474HW+PtJUmopCtKW4VhbzyMu1u+ie6h56UfxSFrvxinwpee8koe69kYUKKGQUAdbaBP2cZKeHhI4piVuS/jMapZWmccOiRxugHnyEuUzpoyFBcUo1KE4RPkX6QTWXVFyjqvf2CoRgTCV8HjHMLdqC1KR3ryKSSmpiKv5hzCBt+Fxx9+B+9+Fo5kEglfDYoTI5CSnYM80RHqBgc2Dn8kD7ryoPFEnzxnsOPT6Vg+YyNiqjixYTlMY3RSzYrJRf/NH/Ohb+OdhPJNfxHQZfIl2l31sVkIWjsNg/bkyDmx9epT2PDhy3im5V/xwMRjMhB7hcx5JJ9snAoaiaH33ox//ctKbD9XLIO6eCeZhNWUFSCrqBour3o6tQNd6RKZ+JDL2eDRWDtnHJacFv9I2xQBzIsmXXBVpOLC1sF47/E78cef/AQ3/uEpvDpiG9KEADqFODYQMnf5eZRtfBu9go9K2Xxli/jS+F2YcuUIhMfkoED9itifTETdFbnIL6kSm+PKdkAW2hptmW3UCDCemczSnqVObOeaXGQfW48Vn3RDu3cGYurWOJzJOYOkTaPR765rceVdH2PxkQsoqJOek3qqr/uqv1B/TY/OPjJ+ipNk+nCOJx5HNjIT9uPg1hCs3xSCjStnY+nacOyNzUJhJf2+5MXVJ+qHpuP4wHxZTjUyd43H+Fcfw69/PxwbMypQIg6Hdag5txuHx92Nq//tUfRdE4n4CnOc74qimpp2aWTDWDQrLgsS5ZJARs7FV6791PMJi7zt+PyZ+3HH71/Gk8N2I10U1aODqbnkJ+5I4hrD0J8gCBiD2+eQtJsx9fnXMaDLDGy+IEoqRs1LPv56J3JP7cC2uSMwbPhqHDh3EAu7/gWtHn8NT44/gCIxVk9tPo6tmouQkK04UEiDccNZnoKUk9E4mXQBmeV0q07Rel5SooMVEkhjrKuVmUs0tk/th/ff74XW47bjXKVwQfHtvoJ92PhJGzx08934yQfhiMmp1ZsZ+UeZa115iB19C17uNxiDtpw1RE1KkUrqIM/6qhORb9QX4UJMBPaGBGFDcCg2Bm1EyHox+PXr//sQsgEbo2UwKeMqEvOUurHx1RmwTpylV6L6QiT2TOuKD9r2QK/xm3G8VM7TsbvjsbXfK3j5tkdwxwerccrthyNrK6Z1fBLPPv8Oem/NlPwc2i9+IaPOUpklnz+LpEqvOOLGOQdtEbaL1lXSyD+lVFLGEDinDk/iK2miTkhdGm7AN06Xgwc9k+hDdSqSYrZixbJghBwvQYEMfOwzzUM+9DKvKd7iHxLsvf+KRNHuHUjftxwrJo7H2DmrcTgnAhOeugG3PycTlrXxKPJVoa4sCdunD0LIoSgkcoJDnfKRtLhFT6hXkrfol2yIntUide1krJs1AwuP58qki7pEZZI0AV2UDyUopE28i1Enefr7b1z15MDOuJKGaWVCqCRq3XQMFBJF2lVfX4KTi3qg599ewX3dghAnyWr5gkjHKRyZ8hE+uP5BPDghBgmFDpm41KL0fDQig5Zi1vKdSMitQlUd8+cKB8kHJxX1KI6ajpCln2BEUCrK5byLZcufqzobaUdXYdq7D+OVbh3R+plH0eq6P+JPN7+L8RuPI0nyqxVb97kqUZp8ADtGPI+ph07iRBlrV4iChAhMu2IwIqKzUECSSduvzMSp0LlYsWoLDiVmoMxt7NLvq9X2lKIbBTYr20kJivSG11WMvONrsXJUR7z2UjsMDstHRhn9sAPFCauxrtvNuOpHj6DPihjElPIhJfaZZCTtLS0i+dGPCIGSIKl4WP1GXZ0DzopC5J49hYSEcGxdPhnTxo7Fxyv3ILrEgUppL/oLyqPC6+SZ7crxSv60/yV/Ka4mORRrRrTFn37/BqYeLkF2leigv1raaSVW97wW1z42EnOOJiOX79wSeVQPVMZA3hbfOy6PG8upzNR30VQqtdMhg3nsArR7/A78y6Pt8eLSeJlhidLKOToikoCG+5PMgElDE4XkcrtXzKPyCOa/8hj6tR+OZYlMoxd4xD1l48TKfuhz34342W0DsXTLHHRp9TBufuwtPLc4Ci53DdzxSzBq3DJM3HACeSQXzlrkhfVEh8d+h4de7ovREeX6GgWuYlBu3sPslpmet/ok9g95FU8+8CL+OnQZ9hYLIZOqqbEK8UlePxwjW1yHq37aBytjC1AYeNqDKyVe5xmEdb0V7wwbj0mHM8W4WSfWhe0RIBRSltpY4PIlyYrEkBag9TUOZvZFckEyRmctOUomdCYkUTUFcTg29Rk88LvH8O7wjdh9gS+R07vAxGH4kRrcBYOf/h1uuas7lqS7UOg8j72fv4ke77RGm+VJcPENztL+3so8nNm8AAv7tsekqAoU1DKHRkKdJl0mt/Wf3SuHpb4yMPAdL/zJCcojn3JOjvGeOPY/25Mto21n0uXHzsbEnrfjn665CT94PRTbzpSBrxpju+ljznWBdrD4BwX7jvpFa/hqP1IXaPU1ODSyNdrdfi/ueW4QQvcswGs3/Aa/fm0kBuxI0RdmVkROQ7ve6xAalY1q6pH4GtEMSV2jNy/76Jwka9FMOSaTtJy9WDNnDt7stxbRbpkEid7rW7C5Qq5Twjq4RYfpIphOlVgVml9iaZys6QqoQD4qoqdjbdAUIQWFWgt6Ns/ZYCzu1xWPPDQAS2UiWEzyf2o91vXrgGdbdMO8ZKCkVuL603B04RB0/Kef46orbkbf9adxslQKE52mHSmVo604TiJy3XKM67AY+4prUeLyiL1W4JwQqFk9X8F1T0xD8IlCZCVtQPDgF3Dvldfiih+8hmErEpGYUyOTq2M4tnI8nn5hETalFqBIpBRqpvdEffbj/giXCVoebU8+8xJXYtA/X4nrrrgWfxu+EjuzaKmBB4fkmykbBakGCS2JJSednvOhmNvjabR68kW8vTgOOV4hkTIxps37imJwavU7uOaqK3HngGCsTayQ9pdyqBryxZbQ1TAdaEy36A+qi/27irOQKUR7+rut0GnkLCw8mIIMh4xD9CeB+5Y48dJ3XWk/GpnUB8m+R9VD6ijx/J5UnNw0Ch/eeTNazzuJuPQKuF0XELt7Ano9fgMem3YcURm1mo4jk/p5umPmbXFJcHmQKCqjKJG/WBzA9pl4r31rdHj6RtxwzY/xg2t+j9890hZ9+s7FnqxqlIgmc5bHx/ENkTEKrgu0fHpNztXXncP2Yc+hT6/eGL47D/pbS1KM31+FnCOLsHjAS2jx3Pvo9G4ffDpmBPp36YV2z3fEiNEfo8cgGfx3JOB0YbXOMHSF6eAo9Hjx33HdQ2/ghUnHxHVwAOYbfMVwxBr8teJ8Y2fhtSdfxTvDVyEkJte840ji1Ynh8pUClSdDsHFAS/z2qt+j48qTiC0UWWlJdZXwVOzBrBZ3o8eItViTTOdKizJtQkM1lyqlamwqfsuJL/YlXmOhhspMZcP8kYRIDtKWflcmMg8sRZ/r/4g2g4OxKSZPn14kadFy5KM2eT1WDn0eD977EJ5aeQ6pJdWoTpGZ25yheL9jZwycuBqfThyNjz+diVkrwhCZlIUi/gQLy2wMpJ5sE5WJ+/Khg4qK3CCvIT3mfjR6Lw5e3GY6OmjjsDUD0YW6vFjEbvocgzp1wGO/HIf1UfyNLxItzkiZDzNnYRb/uGAHfhOJcslnBU5vGYaRPV7Fn1/qjt7vjcD0z0bgvTYf4P123TFixDh0H7YIwceykFHJO2lod+JTqEKiVzpQ0qcwf6oK7d1djdKUSOxZOQ3de36CtYfSkF6uj2TIn8RTHZa41GfVadkJbJrjtDnjO5hnRdQsIVHTMHhvnuxKWqZ3liM7ejdCJgxD9/eGYcxnIzF04AAM4SC/JRHFNWJXvO3BX4HcuD3YMLw7Oj17F95ecgT7MoXoSb6mTObIshyozE0SW1iAsV3eQ49OnfBmm3fRvutQjFu4HYfP5COvtk6fLiy/EI2ooJkY3uYlPPdEC9zf4mE89coH6DslBFvjSlBQYy7V+yFkKmEfpl4xFLujs5FHe/I7UVOUhEMTB2PEG0+g49hFmB9XKe1obJZ1bzTETnlpng/q8B7Z49NeRecO7dBhYijihEHyd0Z15ZmTa3cB8k+tw0ctr8dtLUfhkw1JyGUjiO/XaxaSF8cNXjXgpUyumFWl7sWWOeMxcvg4jNt4AMfOpiIttwil1S4hRuwj41/Yn9pfWhZbU8plH5GgaTz6HJFRj7nhzDuF5C2TMHZAJwwaMw7Dh43CiIHDMGzWGhzOrkCli31MteBaIFc7RR42y0U0jUXz4fIgUaI9qkMOmdmkxWDb1lBsC16KVcsXYdHylVgVvBXh4SeQXiXzQJ1IMD61UJMGvvhJrZZz/hqcWdcL/Qf2Q+vZcSiRU1zC5b1UtcXnkBYXgW1hBxCx+zBOJSUi/tgxHNi8CwcOH8LuQ2eRll8FB5kZc5M0dfkxiNw4Gr2Gf4q3J0XK/JS2w6e8uDom0ngq4CqIwZbN4TiUmI38ajrcgJT8FgvxVmYjO34XgpatQNjZQhTUCq2jJdXmw3FyLt65sy1Gzt+HqAoSRDlOwzK1Cfx9BeZEAF8789/ja+kIthkPiYzeKlRln8a+xcE4kJiP/CqSUspu4jCdvyYH6QkR2Lppoz6iW+GU9naVoiAtDof3hGHvsSQcPXYYhyJPID4lH6WclF8UpJCAk9VPltmwreBWgzw8yf3AWe5rmwVaS/5JpvzOElRlHMHhkPl4+8G5CEvIQZkMdOYyB0mZSW7xj47/2JHcJ/lxozIvHvExe7Ej/DAOhB1HauppRO07gAM7w3Hw0DHsPpKCXPEtLg6u+velapkvPSJBd9Rs/Y4SlKWfQPhO0fvIaOw/dAj7IsKxNzwcEeER2BuxF0dPnEV6QaVOxqhvOiDryEu/INKJj6FvqBIStU5I1JA9eXKKK1hyXvxKXVUBCpKjsG/nfhyJ3IeIA4dx5EQK0ktqJBsO7sxT5K4oREbkVoQOuR8DQxJwhK8fCMiq8uqfRK+rRlXBWRzftR1h27djU+hW7NhzDHHnSuAUgsOVFq2l1wlnSQbOHN2NbSErsHzZcqzeEIZ98VnIF5vmfY9KXPz5QqLCMfmKMfqyzQJtGKGRrmqUpyVh75Q3MG7Jciw/VStxJQ19KgVpNOhDacVsMxfyYrdi3/4DOJxcYJ6wo7TMT7Y5gXZV5eBkWDBCNh1HdFoJqnlco1APSG9lMi3H+PNT1an7ESn9tW3rLuzYdwSRabkyQRdfL/KbPFk+P7hvWlD/dJvtzjK/jPe1Y3UOeErTcOroLhyMPIoDB47gyOFoxJ4vQI1X6hNIx1Ssm5Rg0llcElwmJKqZIQpZkbQcUz4egta9ViCqCnB7zfKrcVASQTW5kRDn50gNwsr1KzBo3Vk1aTMIyyBNEkWCxpWwRloCZyA6u5V83QWnkLa8A55uPQWL9pxFochp7vGyVvX3Qi+Fymy9ruQkzh4QojpgH2LSS2Ww5ABAx8r7FQKRLSwaCZqmsWFeRq5GfnYy4o8fwkFOJML3IGLPXuyJiMBBIVFphVVctxA/wUkTA+2eg7HopzoSv5Co6Vi3bgoGR+SZ42L/+tSxn6snfAdUgPSLPtPnMA+9ZK0r8ZKJyFB27ig29HkJCw6fxxn+YnEzwtx7KDJL0NV5Dv30UX6uRO3CxCtGI7yBRDGwrt4C7JncA4s3bEZEvsjPVSglKDS4S+PbaPH0qz5XLapTxBfEpeBMnkweSWzET/AirvHLl0Y+i0sDS6K+ATovcJ7FvrnjMPKtvpgiLKrURYckhk9j1qcrApG/DTQoVwXO7JiKhcFLMOdkqfqAhqV6Xd7VS0IXYXj0exLd761AYeI2rOj2KDosOIJDacL21KC5YCx5B6JbNBGc+YrDLEgKw+alg9F1ax7OlQV++oU6wHvDpK1tQ1tcDKgufIrO6+NSayDw/U8N99tIBJIM/v6n/gao+Am/l5fveemZZMTkYdTOh4rIKVi7bhIG789jctFNyUd8ir6AWHSUq2lKvHQFSEiMZMAHUuh3OBnwVKUi+eBKDG47DhFp+Sihc2lGqLyBsrgjpZvLYvUFKEzYKSRqKML4sk2eE7l8nlLUZIViev9pCN4ei8w6+kj6M15+Myvclwa0eSlb2rW+ziHuoeE9UtCgfeLnpT+pp8X/GlgS9Z9AU+Dcz4uKpI0IntkXd/behcRSR+Bdufqcnjq2RsEnM8G09ZgwfgWmBsUhR9kP0/IJPT6ZwavadAwyM9SyGwEml6i8GTI2ZCKeenoGNgg5K6I/5vuNvB7J15KovxcyfKG+NBJ7Ni5Dp0FbkSZEupZOnm3LPtB+ZKM3UhcsLAS0S67O8EEXehQTRId4QkLgSwJXNbjaKf6BusYoDIE4xsJ9qDo+FcHBkzF8Ly/n+fXBCfM+JU2iuXObO9Rd3pguTEW+zcuA0yN3YNv4gZh2pFwfwyfRanaoMAGfpB+sWzYKErZiwlUjsDM6B9kSh6SvLDcF+wa2wbytCYjPqhU3aW4n9/K3K7VGlwiUWw1ffIC2ryG25Kz0AtrGUi/T6hb/W2BJ1DeAMwk6Ek9tKc6d2IKFY9/EsG3nkVjAm/jEmMVY1F4aAxqdoxjZWQXIKa5WIsZZod6sSKci5XBWeDEOgmV7vdlI3LkKiwePx6wDeThf5YGbKyTimHWQV2NutJQW3wTpJ5+nCkXFBTh9oRgu6S/zq1v8fcY66QO6y8DAYGHRSFBfOODKMBz44woMV4hEnxh4ROzYz59W0TeUq6IFVnMa0pOEcaceFVGzMW9iLzz/0RyEhuxGTFElytVJaSL+y9gunkdXSbySFZ9QljLkOMtxVhahOCsNORVeuCUd829O0NeZ16Jwasr8fahJj8PJiIVYOHEE3rriE4RGZyGPskld61wOlKefRn5xDapk4sKJpklnVuKaXcDGgu6Z5ZMAmqm09oPx53pS5Jfek32L/z2wJOoboMvOEmgMjoocpB9fjd2xucgud4MvN+MAejGGTJPTZV4uxwcIDr/Nu4mM0embZxubqdirvy4fmaejERkWhbQqL5xi3Hx6hD9RYN5vQqO2+LtA5yiB74LSBwC4LX1nCDAvh0jfUk8uRhksLKguEvjFQVdJE/cDxzgkm6dIDekRZdMThjNR20i6jH/icVd+HOKO7ULQzqNIiEtCVk0Naqifko7580lB88LJhvyYVr8k0AdRq3nPVMAfUcZmBP2d3gMmcphVMT8cJZnISolE1KF92DztGFLzy1CrMopsdF38kEYhydOnqZkRG8k0Ave+f7DNNFBA/s6p0igRVRqSy1GyTX9xqcSzuDSwJOqbQEOlQ5HAVwx4+eK82lp49KZtzoZ4g2cgbiPAuZ++u6nhiRgeEcdgXhDKbznEMhsLZuFzoM7rhIsX45mvWC7v2TIkisv/JqrF3wFpTzpMnbVTJaSp1UmaDTnH4xdBfi0svkCD/hjSooG6xQGa7EZpA/UvMChL4LekENUL2Dih5zipo2+Rs1yNFjKiq9uSN4NZMzHEyzzIImlUn5k345vVaz3Pfc20ecEyzctpOQk1fkp/k47V1Qj0qULyKKlWVCumsikZ5K7yFNMulwoUi5dKTasG/ujTPWxHttx30XoW/5NhSdQ3oOFJEo8QH4cQJpptnRh4gzHrk29q5BcBOgtyHS7JiwHy9Z36mgN1JsyUpTQyTy2eMkqmysDMMQpKJxqYt1n8vdB+NoMMV6P0t8qUwDKwHzkAWhJlcbGgvpAIGJKkR+Sbg7G+Vy0w0dJjcpqBsUygD6qD/v4nDzAbKiX1VLb5rmB98k58g65CKekwv9CgpEmi6m/lyT8vTPNOI131YplSkJIpzbgZIXnSV3E11+tzShnmSTZd+RLxDG2jg2R9KRFlNvs83nBOv9T4ZOMSgK1CMSgVJ6wNsmkfsu2UwDZz21n8j4clUf8BNBAP73mhU6LB0CaMT1Mr0hszafkNBxoDcR4kT3yQS9yV/HFZXQzR6xDDc2kZEqXRMG6OxisyNCyBy746UtnXn5u4NH7msoL0kGlb6SAOAtrjqg/SuHxaiH2oDyE0Ug8sLATUl6/pjG7yg0ZrDFcvq1Hv5LA5Q/9hjikCXyRK+lug4gt0PiXJ/X6+OoG6a8oyq10SlJFJBJImOUn6zzUqkhw9ztvMmV8g7+aCyqIv9jTyfHUFnvUE5VX5KAYlEpujOPRt6jHp38T6NP2lA8s2/UYJZVs2+ZZx3shvVtHojy+lhBaXApZEfQPUgemsjLM1+aCNqHHQicnsSR3NxRmLLpWrM9DMaIfiWJgXl4WNw2ss1CWKfJSRDoazOpMX5WL+lPPi5LP4BkgbaltLIGHlJRK2uBmLZEsUhO0vEU18C4tGQCzU6FWDjfJLWQOD2TWDNG1ZHYXqmdq0xjWB++aFr+acCZILV825qiU6qr/tqATGnDe/o+nS9FyQ0te20F/IeQ9vW9B4kn8zwpQb8E3KMyiDyMzqSXkkVYYsmTgNN8yLMCYeE2lCHjd5XgoY+Si3aUt2l06MZZ/yGj8hBy6lkBbfOyyJ+q9AG5FAZ2ZAw6CB0JDFWPRY42FMLGBgDVlxU4zODMSNB5PThhm4J6Yt+dHhBBxg4LjF3w/TnPw0/cRt3ZMPOlPbzhYXiwat+boX+VKXvn4+4HM0BBCIYHRRh+6vHGOgL+CAb84aImZiGzLGNSiTo748WP2GUBX1IXqq2cGSVRYWGpCHu+YQz5g6GsIVOMF/2W44ZxJcOmj7NRC5gPwNknHbSKcndcvifwcsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwuGgA/x+dZ+PsC4OU5gAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%A0%B7%E6%9C%AC%E6%A0%87%E5%87%86%E5%B7%AE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcIAAAEbCAYAAABJKYSiAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADmqSURBVHhe7Z0HlBRF/sd9/n2nHmIA9ZAznSRzYM0B04liThgQRRTz7Yo5Zz1B0GEBUQxnVgzorCKKIpwKqBjWwYAonDmgaw6Y69/f31TN9vR0z3RP2O2Z+n7eq7fb1WGqm6U+86uusJgihBBCLIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJCQif/75p9pxxx3VxRdfzGRRIrULRUhIRO6++27Vs2dPteWWWzJZlEjtQhESEpErrrhCXXPNNXqLEFLtUISEROTggw9Wd911l94i1cwff/yRScReKEJCIoD3g7169VJPPfWUzgnHl19+qV577bVMpTtv3jz19ttvy/UqDT5v1KhR6ocfftA5tc/rr7+ujjrqqLyC+/jjjyW633///dVNN92kPv/8c72H2AZFSEgEfvzxR7XYYoupX375RecUZuHCheqCCy5Q3bt3V+eff77aZ5991Pjx49Xee+8tgqokEO3AgQPVlVdeaVXUg/vu3bu3PHe/Lxt4Ftttt52aPXu2fKnZYYcd1CabbKK+//57fQSxCYqQkAjMnDlTbbHFFpEiuT322ENNnTpVnXzyyerAAw/MnHvqqadKNFIp8DmjR4+Wjh6//fabzrUHRHwrr7yyGjt2bM6/15133qk6deqkmpubZbupqUm+4LDJ204oQkIiMG7cOBFYFKZPn65+//13tfbaa6sbbrhB8lAxb7/99urmm2+W7Uowf/58teaaa6oJEybonOoGURyeY6Hk5oEHHlBdu3ZVH3zwgc5J8+ijj0oUiH8bgPMgwpEjR8o2sQuKkJAIHH/88WrixIl6KzwzZsyQinbOnDmy/emnn6qOHTtKs+kbb7wheeUE0jjuuOOkebBWmkRxH4ceeqiM4fRLO+20k/r111/10WlwTrdu3dSFF16YN4rHFxL8+zz++OM6h9gERUhISFCR4r0SOrpE5fTTT1ebb755pjIeM2aMWnfddSUSwbvCcvPuu++q5ZZbTp1xxhk6p/qB1KZNm5Y3eUUITjrpJIkK8X7XD1wX0SFkWStfGkg0KEJCQoJKEu+VvM1vhTDNoKhoDUOGDFH33HOPuvbaa9XTTz+tc8vHLbfcIhHOK6+8onNywf3gXvDTCNq7HTdQLpQRyZTRnefHiy++KM8CPUm94F779+8vTaX4ndgJRUhISN5//315z1dMhYkpuj766CO9la6A8e7O++6qXDQ0NKillloqsKzIP+CAA+QdIqKlQw45RDqOYBvSqK+vDxRLe4EyDx48WG200UZqxRVXlI5HP//8s9wHvmhguMRbb72lj24F5+FZTJ48WeekQT568Q4YMEB+/+yzz6SXKbEPipCQkEyaNEntu+++sY2WDKjUIYYuXbrI716QB6GMGDFCfsf4RshvvfXWU5dddpm6/PLLZfu2227TZ7Q/eOboAQtxLViwQMqNMkKGSLgXbCcSCX1GKzgWz+L666/P+re7+uqrRXxPPvmkDKFAxD5o0CC9l9gERUhISIYPH67OOeccvRVfMFSiT58+MvDfT9pTpkxR2267bWYf3qtBIogKIQ28L8P2Cy+8IPsNLS0tmV6WbQ2i00033VTKB/BzpZVWUmussUZWme+44w7Z7wb3iWeB97TmfDRL43hvijpRAqkNKEJCQoDKFFOr+VW0cQOVPSLCoPGOiJ7cFT4iP0gAERPA+Rj36AWyOfHEE/VWfh5++OGCCTIyCROZ+5XV8Oyzz8q7PAOalFFmNGvivG+++UYiOyM6N9iPZ7Hffvtl9uP+/RI63BD7oAgJCQEq03XWWUeaEQ0YEoHmtEqnqIPhUdmjCTfswP9jjz1WpPLOO+/oHH/Q2eSTTz7RW/lBk+Oll14qM9qgCRLNmhAtpjILSmHKajCdgTCusxBGhPhy4CdKQihCQkKACtTb+QSSQmVsEiImvMOCBPKlM888U+Rz0EEHqV133VVtttlmaq211pLhDu7rmQSZRAFlPO2006RjTyG5oMlxq622kt6w7nvznod97v3tCcp2yimnyLNxD2UJulfk41mgudjGGXZIYShCQkLw6quvqg033DCrsoUYMG+oW1po5sMx+RLOc/80vyOh5yJmn9lrr70y10QnFuwLC66HacXQG9TvvJdfflmkjeZPRHjLLLNM1hhHnIPPNeei2RLXQlQVpRzlBMJGp5hkMim///Of/5Teo6Y8+ImmU7+mTexD+RERmnskxA1FSEgI8B4Ns5p4mTt3bmbIARIW7H3vvff03uJBhY2xbYhkcF3MhRkFHN+hQ4ccceG6prwvvfSSDOzH7xguYcB7QPQqxbGQTo8ePTIdalKplD6q7UA5MO4Sn49eoc8995z87hbbsGHDJLpGeb3gGeBZYEgJIX5QhISEADO04F2XH4iYUDGbdPjhh+cIqFjQlIcmWDSjRrkmxgSiLN5xihAHJgFHRAh5QLQQH3qMIkJEpIWmWiMU9BJFlIVhFTivXPcVFfT4RESKuUCXXnppaYJGlIfxmUceeaTca9DMMRj/if3/+c9/dA4h2VCEhBQA8ujXr1/g0AHsP/vsszMiRPJb8aBYICXMozlr1iydU5ivvvpKygGJesH0a2jChUwQ4UFuZhsz0XijKtwHmoXRLNleQOi4F0SEjz32mJTxwQcflDzMzJPv3R/+bSDNSk1eQKqfWIuwpTmlWvTvrbSoZH2DSi7Um4VoTqiG+kTO8S1NDSrRmFKhGnqca9TVRfjM0OBeEroMKZWoT/rcrz9S/vQKMrksTKqGurrg/SQSEAXGrOVb2BbHQJZGhJ07d5Z3ceUC0Ro62oQF8kJzIt79+UVxUSSNz1522WVFPri3cgk+KsV8Ls7BnK4QZntFsyT+xDsilArdiEIjeQ2qoSncuwoIo84RnpegfF8gQvexWjR1gSm7zC1NuSIW9HUamrT+RLie+81DqtH5LB95Rro3UpAPP/xQenUWqojRoQaRh5Fh0DurtgID4lGOqO8XvVx00UXSEQURMSawriYQNTIaJIWIfdOoVPauSj1vJJRDcPSI62QEVAivCCPjRHuO8DLldiJdXC1XWDguvAj9j48WWZLCoEkQIggTkdx6660ZESKdddZZ7RaJoLxYO3HPPfcsqQw4F/eP+6mmqAoRPGajQTRYTDRJ7CH+7wjRtJkRllPJRxFSHoG1rQidkruit5QjQiPphnoTRaYjQ5Gj3paUJTWc49rnPqZAlBr6XkkOqEgx/2YYIAozxs0kTK7dXhUxyrP77rvLKhc2geeNd54HHnhgVcmbtA8xFWGuJIJSvugQ8knvT0dk5pyMcByBJCEo175W8WSf405FScUI3RFWEmWCXJ1rucsfSc5uIMEsYZJygQoVERWmBAsLhhqYuS+R0Kz69ttv671tDzqSYJHeapgerlzce++98uzbs2maVA+xFmHezimFKv9MhJTb1GiirobGRFpKhShDRGhoaUpKeVKNadFHF2GuoBucZ+Xezk6V6OQTDMSBVdcxnRYiKSR08jC/I1UTiCaKeceEsW7LL798RoaMTAiJLzUrQogm2eRuVjWkr52AiJpSzjGFBZf1njIj2NYEmckxWfl+5ddNu841Ek65WiPWNMVGhN7rtBeo6CE6jPMyAvAmDObOJwREL/gWHzVVCqwhiLXvokoMXwjQHOm+93//+9/t1kRKCAmmNkWoRZNpjnSjozsjncAenRlQFi23gM8LLSLnsxPNzvUa09fJlac3hYnmECHm72DTstD3KZUVI0FU+Hifhg4m1113nQyCRp5Z8w2Dm/PJALO3uOURNuHalQD3gTF8xQgMUj/66KOzyllqD05CSPmJsQhbhZBoyo3CJPmKyRGDyc8RYatgW6MvHaUFYSJAHAOJ+nxmOBHisx1hNSczcosaEfqJM9GYftdYMAV9aSgTd911l1T0V1xxRZY0zBI/8+fP1zn5gVCDEiI/9zY+x6RKAbkPHTpUb0UHc4diMLoR4eqrry6zvpQbDPHAYHim8idS+1RFRJhyKvscVZmoz4sT/WRyvSLU0SBwSyefyEwTa/q8bMmaiM2c71tOnGNk5BFuVBH6ka/s+cBnlUuQixYtkg4hGHTuneYKM4FAAN5FXqsFTKpd6tRciIbdzcUHHHCA3lM+IEJzfabypd12200/YVLLxFSEXtIyyZZEixNdFajCs0TokphDlnQk6guQmIkEsySWjlhzRZr9Ga1kH2/AeVlRm0/ynpNFTrnCkxFhkee7QY9IVBrHH3+8zkmDSG3vvfdWXbp0yTsFlht3xBclVQKU/x//+EfJUQHKh8Vw8Yz69u1bkfJ+/vnnTBVKpPaJoQjRgaVVMJmKWmSV/c5MKvN8EY1LhBLZec51SyYtpWwZZt4feoWDsrg+1x2VBZXJfYzBm+ctU34g3YSTWqUpn2uacjPJT/DlBauHo5L3LpKKVRjQcxKDusN2aMGacebbeJQU9R0h3tUVKtN3330n1w4r8SAgPkzEvcYaa8jitoSQeBE7EUIGRg7ZotDv2MyWnodUxBNU2WsRmuvgZ6sgPCkjFSPMViF7ReiVanY5/aNXRIRu6YHiRZj9LDJ4BN1WoDl0ySWXVPfff7/OSYN3a1FF4n0PGDZFAZEemjw//vhjneMPJnfGzCSlvIPEuViIF8/B+3wIIfEgXiL0RH1eUbhJNZkKPy0e3+NEhEmV8tkXKfpyi9D5PYzQspsc/ctYnAhxrWwRZ4ggQny2fAHIKmdxQF4HH3yw+te//iVRIMR04403yorrWBmgFJFUgv/+978ipkmTJukcfy655BJ1wgkn6K3o4L6xdBM+q7GxUecSQuJGjESYjprczYrBIvREh3qQeg46IvSjKBFCND7iyCnnwpRKZYkqWIQ5kWlOckV+8kUhIPoFEUQossb1yyBCgKV99t13X6n0sfICokH0mIybBBGdHnHEEVJOrG2Xj/3226+kjjJmnUL0PI3bcyCEtBLrzjKZyjogFRRZOUXoFYxIqbUs/sLOT7Do/XBkasqA8rg+O1QKKchSQGVvmjbjWvE/8cQTmYVcjz32WJ2bC8rfrVu3ot/p4Z0lImJKkJD4E2sRlkwlRWjAviKjKv/hFqRSQEg777yzDPSHCLFMUpCkIPOOHTtGfv8IIM+ePXvKkkWldrQhhFSe2hYhIS7uu+8+GcOHdfUgwrXXXjtQdBgSsuOOO0YW4RdffKG23357kWwxEg3ioYceUtOmTdNbhJByQhESa5g7d650kMG7S4hwqaWWChxCgZly0NszSrMmxIdOQ5hJptDQjCjgWhtssIF65JFHdA4hpJxQhMQ6ICwMlIcM582bp3OzOe2009QDDzygtwoDYdbX16u//e1vZZfgMccco9Zff/2qbWbF88Z9mC8V+GlSOaNmQoqFIiTWgQoYM7xAhH5j+7B/vfXWkwnCw4DjL7vsMrneJ598onNLA9fEUk5oZsV1MYdrNfL111+rrbbaStZnRLM0ZI4hJb169ZL7Qs9cTMhASHtCERIrwZhHVMTo1ekFUQqWXgob2Y0fP16u9fzzz4vAghKui+Texk98Dn7HOo4zZ85Ul156qdpss83kmia99dZb+tOqC6xFecMNN6gHH3xQ7gMyRJPzV199JfsxLR/yyhlFExIVipBYyZgxY6RixthHyMjNL7/8orbeemuRUyGwTBPeNSJyi5ownRx+YqmqTp06ZYnPnTDxc5iyxA3I7a9//auU3axCgqnmzPPGT4gQ+exdS9oTipBYydSpU6UCxlhBr2RmzJihBg8enCNIL4jeMH+oEValEqKpagTPD1848HPAgAFyL+4JzPHcTeRbjaIntQNFSKzE9BxFwnssN1g6atiwYXorGIwXxAD9KGnKlCm++ViqyZ0gapOqvdkQkkPEi45EbuHhvvH8DznkkIJfOgipJBQhsRJUyKussopUxM8884zOTXPYYYdJkycpDxA7njOeq5uGhgbJN8+aUSFpLyhCYiWIQPB+DhXx2LFjdW46HwPtq7VzShwZPny4PGfM6GOA9DbaaCNZqxKrl9x0000yEw8jQ9IeUITEWkxHDfeco6igl1hiCUYnZQJiQ9MnnvPs2bN1rlIvv/yy5B166KHyrDH13Z133qn3EtK2UITEWkzPUYxzM5HIhx9+KGMIi41MzjjjDNW/f3+9FY2JEyfKNGpXXXWVRKu1EB3h/eaaa66punfvnvXl4vvvv5f5WAcNGqQGDhyoevfuzS8fpN2gCIm1mHdXyyyzTKYSRg9NRDDFcvHFF6s77rhDb0UDYxpNqhURAtzP/Pnz9VYr6EGKjkm10CGIVDcUIbGWlpYWESGSeSd47rnnyswn7UmtiTAfNtwjiT8UIbEWRIFmHOCECROkUt5ll11kVf2ovPbaa+qggw6SGWtKrdxtEiEhcYAiJNYC0ey1114iQkSCEOOSSy6pFi1apI8IB87D7DCYkQbXwqK8AHLFFGPudP755+fk3XvvvXK8wYiQ78wIaRsoQmI15513nshrjz32kPdU6NIfVUDo4HLRRReppqYmGTj+7bffSj5Ei2u5E6YS8+Z5Iz9GhIS0LRQhsRpEYxAhljmaNWuWOvroo4sSEIS25557ylRi5nz8DJvcUISEtC0UIbEarEcIEXbu3FmNGjVKjR49Wu+JhrkOosKbb75Z8iA05BVKjY2NcryBIiSkbaEIidWgqbJDhw4iJAybQFf+YrjxxhtVjx491K+//irXAhCZtxnULxnh4SeS+x0hZUhI5aEIidVANJtuuqnIa/XVV1effvqp3hONBQsWqK5du0qnmTlz5ujcaECAZmkmlAcrYCCPEFJZKEJiNRDhEUccIeJZaaWVJAorFlyr1PO9yXS8IYRUDoqQWM+IESNEhHwvR4idUITEep599lkRIQbDE0LsgyIk1mM6uIwfP17nEEJsgiIk1oP3eiuuuKJMAk0IsQ+KkFgP3gsWO2yCEFL9UISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkKK4M8//1QnnXSSuvjii5ksS6T2oAgJKYI//vhDrbvuumqLLbZQW265JZNFidQeFCEhRfD777+rDTfcUIRICKluKEJCiuCll15Sm2yyiTSRkuoHX2hMIvZBERJSBGPHjlUXXnih3goHosinnnpKKlv8jjRnzhz1448/6iMqB4R99913W1fRv/7662rw4MF573vGjBnqrLPOUvvvv7+66aab1Oeff673EFugCAmJCKQycOBAddttt+mcwuCcxRZbTPXr10/1799fnX/++dLxYsiQIWqvvfaqqKDw2ZA2Pr9aRfjbb7/lpEWLFqmffvpJfvrtx30j9e7dW+4fv3v54osv1JFHHqneeust+ZKyww47SKT//fff6yOIDVCEhEQEFermm28u0VxYJkyYICKaOHGidLJ57bXXJL+pqUl17ty5ooK67rrrRAaQQ7Vy1113qRNPPDErDRo0SB177LHq8MMPz9k3bty4jPg+/vhjtfLKK0sU7wVfZvDv8v7778s2/j2wjc8j9kAREhIRSGv11VePJK/p06dLU+iAAQPUYYcdpnOVRCqo0P2ilXKAMkKCt99+u86pTnAf3gSx//LLL/LTb7/7mT7wwAOqa9eu6oMPPtA5aSZNmiRRII4HCxYsEBGOHDlStokdUISEROTDDz+UqC6qvFBhd+rUSV177bWyDTHusssu6t5775XtcoPy3XDDDapnz57yWTYD0XXr1i2widQwZswYEeFjjz2mc4gNUISERCSZTGZFdWEx0QZ+gueff16233vvPflZ7qgQ8tt5550lCiVKJkBAVBjUOQlfcNZbbz2RpYkQiR1QhIRE5KKLLlKXXHKJ3grPPffco7bffvuM8O644w7pOHPggQeqCy64QPLKybx580SwiAqDQFkQqUKaplyQALbjLANTRhPpouzIy1fmF198UZ4HepJ6wfn4t3j00Udjfd+kMlCEhEQAFSbENWXKFJ0THogPPRMNqHCnTp2aGVJRbu6//36p+F9++WWdkw0+89BDD5Vjll9+ebkvvHM74IADJO+YY46R3pRxI5VKqW222UatuOKKMqkBhoWYLxnoeBT0pQLSXGqppdTkyZN1Tho8B9wzmqzx+2effVaRLyYkvlCEhEQAFWW1zCiDsXEQWktLi85pBUK/7LLLpML/9ttvpRcrjoUMkRobG2U7kUjoM+IBZLbZZpup++67T+4B5Uc5kSDxbbfdVq222mqZSNEN/s26dOmirr/+ejkX4Oe5554r18EXEiTTgYnYA0VISARQwXbs2DFTkcYVVPoYSI5Iz0/aGPqx1VZbZfbhviCTNdZYQ/LQkxLbiGLdQKroAdse4JkfdNBB6rjjjtM5So0ePVrKefXVV0t0jd8x/6ufCHF+r1691Omnn565b0SSOMeb3JE7qX0oQkIi8Nxzz6k999wz9iJE+XbffXe10UYb+YoQPVUhAQOGFUAApmPN119/rZ588smc+4QgMQA9DA8//HDBhDKYhCbOQs8V7/HM/eDYhoYGKffs2bMlD82mSH7geEhyv/32y1zDRIHeVKgcpLagCAmJAGaDQRd7AypMNKVFSWiG88vPl6JGYSgXoqeNN97YV4RezLABDL7PB64b5noAs+dceuml6sorr5SIDdEbmiUxjVlQiiIglAMR3tprrx2qTLg2RIgvCGHvgdgBRUhISFCR4h2UW0qIHkxzGtKyyy4rQxYQNaIDxiGHHKKOOOII6XiC7vunnHKKvLuDDOvr62VWFBy79dZby3g/dABxX8+kvn37RpIEjsU7wDCz1uBYREn4nDfeeEPnpvPdYDtOApk2bZqUGc/VTdBzQj6kiSbjap5lh5QfipCQkEACK6ywQs48lIh83NLadddd5VhUvEHJ7Hf/NOnXX39VDz74oDRBusVopmULA66Ja+A8dIbx8vbbb0szJ94Bfvrpp3JfiJZwHkA50GkGPwGmiOvevbuqq6vL5LU1+FxMk3bqqafK76ajDGaNMaDJF188/MA5GEd49tlnZ+6TEEAREhISTPC86qqr5ogA25g42wgLqRwrmaOynjt3rkSMuCaaSKNU4Bgvh/O84+ZwjYMPPlj2XXPNNZlm0aFDh+ojlBo2bJgIHcei4wkk+PPPP8txUYRcTt588035fMgMPUQx+B3b6CQD8O+AYRVBq0dgf4cOHWRYCSFuKEJCQoJ5KXfbbTdfGaGSxvyjqJhNeuKJJ/Te0kAFjuECmCLsm2++0bmFQfMfIj13xGRAz0lEgGeccYY0FyKqRW9YDJtAJIrym56XX375pURaw4cPlxXa/XpktgWIxCG/W2+9VcYMnnDCCZmZYPBuc4MNNlBXXHFFzhcVAybWxn3FcWwkaV8oQlIxIAxUSniPNn/+/EwFhXy/2T3iDkRw3nnn6a1csGKBW4QQzQ8//KD3lgaeGVZVgKjCgueNd4/oWenF9ArFIHL0soQ0IUxI5emnn855h4bPx3AL7G9PML0dmj4xiTiEjLLfeOONasSIETK0w+9LigFNoogY20vkJL7EU4TNCdXQmFKtw4BTKtWsf3XjHJfwy89DS1ODc06LalmoM8LgfE5dXYNKRjknFC0qWZ9w7g6kVKI+6brn/KTvQ294WZhUDXV1kZ9NOUFFim/pWNsNnUCWW245WboIkxljkDY6clQb6PyC925BoBI+88wzs2R48skn562co4AKHO/FsDp+WPBvsP766/tW/lHKtXDhQrXMMsuod999V6aYK9c9FUMxn40vBZgo/aqrrgqMGIm9xFaEdR4ppBrrVJ0jRzeSV2dEEg4IJOo5Uh73Z2vRoOOAf8q+fktTwl+i+joNTfpORbjhyyb37yNPuUfPs2pLUOmiN+Qee+wh67uh4kLlgw4XECIEgW/21QTuAe8Hvcv4eMF94t2aW4Z+TZNtBf4t8DdZ6vNGVI8xfOjIE9QZJc7gCwzeLZp1BwlxE18R5lTkTsTklga2I0RQBkii9Roh8S1PFNJlz0RozU6E6/zIFRaOiyJpv+OLey7lAiJA1IKB3H5Te6Fpbemll666FcBxX34dZfxobm6WqbyMCIOeRVuB8Xt4p1bKkAGUHyLEMJAwzyBOoHl60003jdzZiNhDFYkwW2KBUVYB2keEjp5c0VvKEaFTEpWsd8pS3xpJolwiR70tKUtqOMe1z31MgSg18j0XCSKQfLOPPPTQQ1UxM4sX9JTE+6Ww5b7llluyokK8p2svgeBz0ayLLyjVJrFSwb8XOgJhKIhf8zAhIEYiTEdNUmk7gvBW5K0JEVDrsSa5K/ocmZjkyCy9z5FowDGt18n9jNxjIuDIVM5zhJVEZAi5Otdyv8crStIAEmzHKNCN6ZkXtF4fvpW3d4eLYkDnjLBTiwFUwGb6L5PQbb+9vgBAgJijE02cNoHernj2lCDJRywjQpFVYATm1xwYEi2fhiZHRlGEU4aI0NDifDaulGpMR4PRRejzJSDvF4dKdPIJBr34TMWPqbWwBhya5IwAUCG3lwxKAcMNRo4cqbfCsWjRIrXddttlngc6Df3vf//TewkhcSGWIvTrGNNKsSJMNytCGpBNS7O7V2p+ssrj0wQJmaU77riTn4CcsuM6zjUSThlwTjkiQu912hO8jzEDnU3C+zJEgVHeUeEbfDGpEkDcGDA/a9YsnROeGTNmSG9L8yww5ZptzZOExJ0YitAV8ZjmPh3JBacQYsQ1nOuljGy0jArjei8X0PwYWkROGTB0I9mYvk6uPL0pTDRX+ItBy8Iw91k+Xn31Vemc4ZYhEsahoRt+IU477TSZr7NPnz4ygBsdHbAG4DrrrCMznGCpoFVWWUXm0cTcnlhs9f/+7//kHVglgLjw+cWIFueatf1MwqDvaoyKCalV4idCIz0ncpIm0hz5FBMRpmUGWbmjrlRjiOuYCBCRnJapVyvhRIgyOJ/XnMzILWpE6CfOhHMP3jzfFCDxSgEBQIhYUQBL+xgJ3HbbbfqI/OB8v4So0r0NobhTJcCQAZQdn1cMOG/gwIGZZ4CEd46V4JVXXmGqUCK1S+xEiHdnySancpemSEd6ZRChWzBZsgnRySSwPCLsdMRmhOYvVpRXy0iu0UpUEfoRTsK54LPKLcggUSDfTJCMSLHaoqEXXnhBZmgppdyIhDGhgBEhBndXYnYdRMnmM5jKl44++mj9hEktEjMROtIwkZeWRqbCLpgC5OiJ4ryykesHyiC3PGn0+0Z9nVYZuUSZRfbxBr8Iz5vyijGnXOHJPNciz/cC2aGix6oGfmA6L1QomNsyDLhe1FRM02WYdf7GjRsnzbWlYp4BBnZXKsLAhNNMlUmkdomVCE2PyvwVPCKskBGhT8TnFaGRlJ9IM2MVveXxXNcdlQWJ1S9y8+blli0fkG7CSS5x4nNNU24mRYuei+Wrr75Sf/nLXwI7xGCVA0gA0VUhsHKD+SYeJUV9RwhxQk75QBR41FFHlTw7DK6D6b1QTsxJSgiJD/ERoVOBZzqvlEOEuIYjBnSOaZVCQGpMahkimQ4qqdYhFp7ySHOpq89HttBQPm8k1/qO0k3xItTvG/VWhhBNvZVi9uzZUsnjnaAXCAedXzAEAZFbGLzRXtgUBUyKPWXKFL3lD67Zu3dvWbOvFO6++255PpzdhJD4Eb/OMqBEEUIwQefnk01g70p3eZzfwwgt+/PTciyPCHGtbBFniCBCeUbyJSDfkwwPoh00+WHoxPPPPy/yQ4UPkWDVhIMOOqikKb7KDcqFHqiIVPOB4yCwqJJ1g9UcsBzSkCFDKEFCYkgNijBgpQpNtOZHjSkPRONTLq/Q1EKnDFmiChZhVmTqm1z3Ks2eee49gghF1rh+GUSIyr1v377qmWeekSVx1lxzTZlmDR1jVl55ZXXOOefESoIA829CcPvuu29eOWGlB0SExQpswYIFsvoDppUrRaaEkMpRkxFhPnKjtRCgPF7BiJRaheWVXBhyBJoX575NGVAe12eHShVuMkWnE8gC6ccff5QekZjOC7/HTQAoj+nBWWgi7fHjx0skVwxYRR0rUeALASVYOdD6cM8997DZmRQNRRgGPxEa8pY1P6HGMZKy88gjj6hRo0aJCJE+++wzvSeXY489Vtb0iwrEh042vXr1il00XAvg+WIybUwmjgkX8O9IEZJiiacICakQqEC33XZbGSSPaBAV6OOPP673ZoNKFc2iUYc64Dz0YMWsN8UM6Qjiu+++a9eJu+OEEeHUqVPlJ0VISoEiJFaBihIVJipS9GRFBTps2DC9Nxscg/34GRZc//rrr5fzyrkGIcqA6LQaV/avNPj3pAhJKVCExFrQmxUVKJaM8qtAEQni/WqUynXSpElqiSWWUM8995zOKR18/ogRI6Ss6JHblkDASO7mXUS5yDM9g9sbipCUCkVIrGXMmDFSgW6wwQa+FSjGRGJF9rBgZXpMCD5hwoSyVMi4xjvvvCPvGlHO/fffP1J0Wir4fHQUQs9aDItBhxQIHtvoGYzndtJJJ5W1+bcYKEJSKhQhsRb0akUFiuQnGESMY8eO1Vv5+eKLL2Q+0kQiIddChYwU9Ls3Dz8hFLwHhFAxrVu/fv0y5UMKO2F5uZg5c6bMiTpv3rxMGbC+IiZPABAj8jC5entiRIj3sniWhESFIiTW8uWXX6rFF19cKlHIxw0qVCwbhfUECwGB9e/fPzN2stj097//PSMcb+rUqVObR17ohHLrrbeq+fPnSxmwrqK7yffOO++U/KB3rG0FI0JSKhQhsRZEYVjjEJUoKnw32LfkkkvKQsP5wHFDhw6Va1QyITpt60oeYnnxxRczwhs+fLjek+bkk0+WfPTczAfKjWgN14uSwoJjUQ78pAhJMVCExFpQaeK9GypRzIPqZs6cOapnz54iukJgvtInnngidPIej4m/vQlycad3331Xf1rbc8opp8gzmjx5ss5JPzssmoxFkTFpQj7wDClCEmcoQmI1phLFwGx3JXrLLbfI/Ki2V6yQWJ8+feQZffLJJzpXZZpLMXUcmmzDfGGoFBQhKRWKkFgNlldCJbrxxhtnVaL19fXq8ssv11v2Asl17NgxJzpGj1o8t2QyKcfg97Z+h2mgCEmpUITEakxkg1lgTEWPynSbbbaRMYHtSRwq9TfffFOej7vpGOXaZ599MvLDbDdHHnlkm0eFKAeSW4QoQxyeG6kuKEJiNag4sUQSKlIz5yjyll56afXRRx/JdlQwjhDXK6ZCnjZtmpx/xx13qLXXXrvN5eLFRH5YSsoNxIh8vOPEXJ/ogduW4LmgyRa9bdFbF2XBWEfTc7dQBx5C3FCExGpMhYqKFOPmAFbOwFCGYiWE8Yk333yz3ooGKnBENviJMrW3CCHla6+9NqccEN9DDz2kBg0aJGMo2xqUx69TERLy8W9ASFgoQmI1iNowewqkgzlCwe2336723nvvdm1iM4P921uEhNgARUisBwPCIR0zVg/j4y699FK9NzyQ1gknnBA4d2kUENlQhIS0DRQhsZ6JEyeKdNBBBgLDNGKPPfaY3hsevKOaNWuWvKdC8yZ44403ZAydO2HGFm+eOd5gRMi1DAmpPBQhsR68E4R0MIUYekF26NAh8hJKECiu8cEHH0gPVLdIEdW5Ez7Dm4fkhhEhIW0HRUisB1EXpIMEKfbo0aNoASGy6969e9aYOkgyTHJDERLSdlCExHogobXWWkvEgxUeMMtMMQLCdbBEEeYefe2110Sq06dPz0g2Xzr00EP1VdJQhIS0HRQhIQ5mgDg6yuCdnTdCCwPWDsQ1MEh/+eWXVy+99JLkQ2ZhEjDRoREhIstiykIICQ9FSIjDyJEjRTzo6IJ19ooBMttiiy1U165dZfxdMWDYBDrdIKE8e+yxh5SJMiSkclCEhDggeoN4MK9mKpXSudGBDEuVlokKzbUoQUIqC0VIiAM6zGD9QdMcSQixB4qQEAdEX926dVMbbLBB5n0dIcQOKEJCHCA/zDlajllhCCHVBUVIiAZLCY0aNUpvEUJsgSIkRIMem2wWJcQ+KEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJMThzz//lPTkk0+qqVOnSnL//tRTT+kjCSG1BkVIrOePP/5QQ4cOVSuttJJabLHFfNNee+2ljyaE1BoUIbEaSHD77bdXq6++ukokEhL5DRkyRHXq1EltscUW6qabbpLI8PPPP9dnEEJqDYqQWAuaQkeNGiURX1NTk85NM2DAANWlSxf1+++/6xxCSK1CERJrmTJlikhwt912EykaECUOGjRILbvssuq3337TuYSQWoUiJNZy4403iggRFbr54YcfJBrs27cvI0JCLIAiJNZy+eWXiwhTqZTOSfPggw9K/oUXXijRISGktqEIibVMnjxZhPfpp5/qnPR7wz59+qhddtmF0SAhlkAREmvB+7+11lpLjRkzRiI/pDPOOEOtu+66fDdIiEVQhMRqZs+erfbcc0+JDHv06CHNoYwECbELipBYD8SHZGaXIYTYBUVICCHEaihCQgghVhNPETYnVF1dg0ou1Ntlo0Ul6xMq3Vk+pRL1SSenbWlpalCJZr3hZWFSNdTVBe8nhBBSduIrwkbX2C4tiLrAZOSWpqUp4S9RfZ2GJq0/EW72uTk45yS9YnLyEvUNnjKYVFjgqUbnOB8JQ5JZ993GoNekeV+GhJ6T7m1CCKlFqkOEkXGiPUdKmciqOSWyyxUNjisgQgeIKyNPAKH6li9slOn3ue0ToQJ0EJkwYYI65JBDZLJp9KD0S+XqSGI6pURNhBBSCWpUhGl5magr5Ygw3SzaoBrqW6M3yE3kmInmWs/Jwhs5RhYhPtv1Ge7P0lFqzj6dsgRcASCYe+65R0S35pprqmOOOUZWY+jYsaPaYYcd1AUXXCBDCu67776yyQjXLyZRhoSQShAjESJKKqMMHHnJeaZpU2SW/f4NEgx3badsbvGVHBFqcJ0ox1cATC+GKPCAAw7INH9COEcddZRaeuml1a+//ip55cQsdOuXnnnmGfX888+rl19+Wc2dO1d98MEHqqWlRf3000/6bEIIKS81GxEaWpqSEsmlGtPRYHEi9JAvigsUW67oGwLfMyJVorNQNngniOWGEA3OmzdP56ZBFIh8rMVXTQwbNkytscYa7ZogcEJI9RBLEUqzphGhj3QgMzkmK99PHDqSc66RcISHc8KL0NucGaZptEW1RJCXtzxtzSeffCKywzJEXrAMEfZ99dVXOqd8IOIsJoUBC+m2d6IICakuYihCl4ACoqvQAnEiy0Szc73G9HVy5elNAVGYaWYFXjFDiLrZteB1skCEmL+jTsvCIEmXB0wvBtmNHDlS56RBb1G8L9xyyy1zVl/A+8RZs2ZJMyr2nXDCCWrGjBk5x+Xj+OOPV8cdd1xWOvDAAwumKJ9BCCFhiZ8IjWiMYHxkGE6EEKojmuZkRkrRIkIXbhF6QRl9o8NW/AScaPTKMyBV8B3i+++/LyKcNm2azkkzYsQIyX/22Wd1TpqHHnpIygRJoun0/PPPl/d6EOakSZP0UYXBObg23gW+9NJLodKLL76ozyaEkPISOxHiXV6yycjF1flEoq50pGWElnJkkqsg17s4j6AqIcJi3zOGk3ku+LxyCRIR1k477SQ9QwGaHyGc1VZbzXctPsjxiy++UJ07d5ahFjgex/Ts2VNdddVV+ihCCKkuYiZC/U4vJ8pKN5ca4bRKxCXKLLKPN/hFZt7kKzUjQidaTTZlN41KhxenDEnvtfOJKkQUGURGhEWe7yWZTKru3burbt26yRCFrbbaSt15552+zZAQH3pxQogLFiyQPBNVIsojhJBqJFYizMwI4xUFmktdYnFHUyIGH+n4RVzevOgRYev7RoNc05FjzuwzgUDeCSd5pOl99xhioH+5+PHHH9WcOXNEaoXew2HoA8pnjhs3bpxaaaWV1Ndff13w3GoDTcEvvPBCpEQIqT5iJMKUE21pxXhEKM2lrs4n2UJLN4VmCy0dEZZbhN5ytAo6V5D+oFw+gvOIPs6cfvrp0qPU9OREFInOL+h4M3HiRH1U9TNq1Ci1/PLLS7QbNmHoBCGk+ohfZxngFqHzexihZTcVpuVYThEiCsp7PS3LYFCmgN6kEUSIz5SIsUxNo1Ew4nO/D+zfv7+M3cPitosWLdK51Q0i2969e6uZM2eqb7/9NlIihFQf8RYhBOFT4XuFphamVCpLMMEibG16DEq5EVuuaP3zcH1fGUqzZ56mzggilM9FOdtBhADvAr/77ju9pdRnn30mzaXmnWEtgLGA2267rYifEFL7xFeEXjGITFqF5ZVcGHIEWhT+HXHSpPdlCxXvBPW96MgyUqqSJtNaAdFgv379ZKo3QogdVI8IDSZaLAL/4RbhSUdjAc2bLlJNlFe1gskC1l13XUaDhFhEPEVISDsA+WHu1UcffVTnpEGUiGTkiJ/Yxgw8+EkIqW4oQkI0jzzyiAwFccsN70AxtrJr167SWxarcaCXLJap6tChgxo4cKC6//779dGEkGqEIiTEAVEeesRiLlUDhHj44YfLXKpmNY4+ffqou+66S6JBJDSjQoxsSiWkeqEICXHAXKmbbLJJVjSIuVB79eoleWY1juHDh+u9SiYehwghULOWIyGk+qAIifUgmsM0c7feeqvOSXPvvfeqCRMmiAgxn+oKK6yQJTxEhJAjROgWKCGkuqAISU0DQWGZKayUEdR8iWgQQyaCojpMHwfhYfIA9zXwThH5o0eP1jmEkGqEIiQ1CyK2IUOGqC5duoiwXn31Vb2nFYhtnXXWkYnGg8Aq/Th//PjxOid9Hq6NadiwwDG2g0RLCIk3FCGpWTBNGjq5nH322SKyM888U+9pxe/doBvIzZz/5ptv6lylWlpaJG+fffaRYxoaGtRtt92m9xJCqgmKkNQsJkJ766231OKLLy7vAd3Nn5Af1mO8+uqrdU4uOAYz/Ky66qpZssRUcxBhIpGQfPyOJaoIIdUHRUhqHghx8ODBIiusv2iYPHmyWmWVVWRsYBCQKM7DQHt30+fcuXMlH+8JN910UzVmzJjAqJIQEm8oQmIF06dPF3FhlQwjLMgNnWjyAflhBX9vRxrkT5s2TV188cWyqj8lSEj1QhESK0DHGUjQRIXz5s2T3xcuLDBxLCGk5qEIiTXcfffdIj80ZeLd3kknnaT3EEJshiIk1oDmS3R8gQwxZALv/wghhCIkVjFu3DgR4dChQ3UOIcR2KEJiFej0AhG+8sorOocQYjsUIbEO9Ph0D4UghNgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqYizCFpWsr1N1jSm93b60NDWoRLPe8LIwqRrq6oL3x5g2va/mhKqra1DJhXq7bOBvJaHSfykplahPOjnhKNv9B95bumzJhWFLRAhpa2IuwvJWmqj0ShFrqtERs08lW+p1S6Vq7guycF9Pi6YuMBm5pWlpglD0hht9nYYmfQcipexz81GO+8exmc93E1KmUoase08nXFPK4bPPr8x+lP3fkZAaI8YidL7ZVyB6kEohQsSQDcrkrWCjRSCVoiruyyvCyKCcLqk0p6TMuRW93/3ko9T7d0ek2aBsvoIMSannG0r7+yCktom5CH2+BQek0M13+IYeqYLz+TycXyCaKUflFYlquK+SRej8Vbiit5QjwvS9OLJw3Y9vFJX1bMp1/wHXcVL67zH4b9j3OTrPx/t3nCtCfc2ozzHS3wchdhFzEUb5Vm8oUPlIs5n//nQKEYW2S6VSrfcVUQaFcO5TznPKmoQ09H27BVJ0FBX5/tMSznquuIaRlCmrG+zP83ctondJznsvInhfCbbB3wchNUp8RVigwiiG4EokH7kVTINT+bm3s1PbVyhVc1+ojCOX05+WpqT8baQa09FgdBGW4/7zidC5vp9UC/5dp8tl7ifrXnBuEV9Uivv7IMQe4i3CMkcn4SrIwuBbu7cJqz1pr/sK6uCRSZ5/v6xoR4SQfTw+O/eafgJyZIHrONdIOPftLXexzyPq/TufFCjCVGOA7OS+83/Bg9zNNVvvJUCsISjX3wchtUpsRViwknWnkBWE7zWdigwVcviKAt/Y81dkLW3cVb697uvjadeqa6/Lk+5Pqe/0sWlpmLL5/3uFFpETWSaanes1pq9T+G/FT6Zeivl3DRKhUy7J85EX9rvzRIx+ZQ6b8pcZlOfvg5DaJdbvCJMh/pOGrjz9Ki2Q5xu6XwWScL7pe/N8U5Hf3qNTJfdlKnxEcmgi9blOuH9L3K9zX83JzD17zysUAZXv/lEWn2NczZAoS1azpFeEBSg9mov+90GIbcRYhGFIV0ThRBjQtBSxYgpXWeciFWJORVoO2ve+wiLNfU3mHaGrzNKJI11RmzL4NysiYssVDYgqQj+Ku38fyeC5e8XnFk7Ef5fSRVievw9CapkaEKHPt10/nArXt0KJ0oEjyrEeMiIs8vxA2vG+II9MFOSXMhWtUxnj+jmfk/4iY8rfKqOAyttzvKFgOZyUVyZF/7uGEKEI3HVMW4uwHH8fhNQ4MRJhupLzq8R8k/wn9lQygeDa/s1AIqhQFQIq54STXGVAhSbf+F15bdrc1L73FfYdYWZGGG/l65GCOyqT8vsIwy9y8+ZFk0cp/64BIvSUOz3eUYNn4HNfQZQmwlL+Plz/HyOUl5BqpMojQogwhHiCvhU7oBItXNEEVCg+lV6bUhX35XrX6xGhu3ckyBYa/m2995CunMsnwlLvH+cXFmEWbSnCUv4+nHMzz9T9OyE1SHWLMFSFhW/8Qcf4V6zZoEIOiDojCAMVj3y7DhWlhSEe9xUJtwh9Klc/oWU/r7Qcw5xXWB7luP8iRRjhb6B4EZb490EREouoahGKXPJWKqjssr/xZ3eBz1MZAlRq+SLOCMKQSr1sIozPfUXCSADX93kOXqGphSmVyroH3Je/CFubMIOS637Ldv9poeR8Vp5zo4oN9xZdhCX+fQiue6vE3wIhMaK6RCgVmKvCyfefGZWuT2WXEZJJgf/JncrC7JNruc4JkypVeVTzfeHzvOd7/k2LiTxyBJqXct5/uIjQK+oo9xhZhCX/fRBiH9UZEUrlGSxBqXgKRF5yTJVVBlV/X34iNGBfkdFy4CwuFccRoR7UX5h0hFVcM2c4avXvnpBKU+WdZQghhJDSoAgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiNVQhIQQQqyGIiSEEGI1FCEhhBCroQgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiMUo9f+ovebP0qnL/QAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83-%E5%85%AC%E5%BC%8F%E5%B0%8F.jpg": {
- "image/jpeg": "/9j/4AAQSkZJRgABAQEAYABgAAD/4TnWRXhpZgAATU0AKgAAAAgABgALAAIAAAAmAAAIYgESAAMAAAABAAEAAAExAAIAAAAmAAAIiAEyAAIAAAAUAAAIrodpAAQAAAABAAAIwuocAAcAAAgMAAAAVgAAEUYc6gAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdpbmRvd3MgUGhvdG8gRWRpdG9yIDEwLjAuMTAwMTEuMTYzODQAV2luZG93cyBQaG90byBFZGl0b3IgMTAuMC4xMDAxMS4xNjM4NAAyMDIwOjA5OjAzIDE1OjAyOjUxAAAGkAMAAgAAABQAABEckAQAAgAAABQAABEwkpEAAgAAAAMyMgAAkpIAAgAAAAMyMgAAoAEAAwAAAAEAAQAA6hwABwAACAwAAAkQAAAAABzqAAAACAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMjAyMDowOTowMyAxNDo1ODo1NQAyMDIwOjA5OjAzIDE0OjU4OjU1AAAAAAYBAwADAAAAAQAGAAABGgAFAAAAAQAAEZQBGwAFAAAAAQAAEZwBKAADAAAAAQACAAACAQAEAAAAAQAAEaQCAgAEAAAAAQAAKCkAAAAAAAAAYAAAAAEAAABgAAAAAf/Y/9sAQwAIBgYHBgUIBwcHCQkICgwUDQwLCwwZEhMPFB0aHx4dGhwcICQuJyAiLCMcHCg3KSwwMTQ0NB8nOT04MjwuMzQy/9sAQwEJCQkMCwwYDQ0YMiEcITIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIy/8AAEQgAvgEAAwEhAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A9/ooAKw9She91uG3iuZIJYIDPGVPBO7HzDuKARtru2jdjdjnHTNLQAUUAFFACZHrWXKLn/hJLZkEn2XyGDkN8u7PGR60hl+W4ji++4AHqcU9JFdA6kFTyCDmhO4WEklWJC7nCjqSelQQahbXEmyKaN2PICsDmlcdjP1xknu9LsH3AT3G/joQg3EH61iWWqax/wAJHe2w8zUFtQyQAFIlk55Lk45XhflHvimIi1DXNQuNVu9NthcNcrPa5jt1LeUpGZMsB0zWsum2N1r1xaJEJrNR5s0bDKRTZ4Kn+FsckCgDpFUIiqowqjAFLTEFFABketFABTGmiUZaRAN23JYdfT60ARNfWiTxwPcxLLL9xC4y30HerFABRQAUUAIzBVLHoBmuYttW+1eNCEsbxEWwYeZLDtU4cHg+lIZC/iy8Fvav9hQNfv5doQ+QGyQQ/p061r6jeXenXVnKWSS3mkWCSLHIZujKf6UAa9Z93cajFdIltYxzQnG6RrgIV/DBzTBGhWZry2Y0uW5vbR7mK3Bk8uMAtx6ZIoEc3Hcw3MUckHhLWDEyh0bdGuQeRj95W5aaTZX9mst3p00TOMNDdPuYD3wSP1pIZDH4T8Jzzs6aRpk0sTYY+UrFD7+hrSv7i20XR5bgqsNtbRltqgAAeg7UAtzE0nVNRm1O3t9QNnNHeQtKsVuCWtx6OckMCOM4HPHNdDDp9lbSeZb2dvFJj7yRhT+YFCBsw79tRvkMFz4emkQPlXhvUUgjowYMrKfpRZXd7NlLGwsGntv3TC61EvKg9Cyq5/M0IHYy5vEep6dPeL9i02IRsXuJYnuJlDY5ywhAz7ZrprD+1ZWhnnubRrZ03bI4WVuRxyT/AEpgadFAhruscbSOwVVGST0ArJvr29l3QWemyTW80Xy3ayoFGR1xnJ/CgDlNIn8Raff2k2oJeT2zo4jiVc4VV6P/ALWRkH0rpNGnbUtPuZnuybmfkxRtgwccKM9D6n1pWAqWdjr32C9ibUQ98XVVlYHasfoP9vHU+tRah4fvdV0O0sohLpxiuVeVRKHLjPLbvXvTAr6b8PV066tp/wC0pZmiuRM3mKCWCkkAHt15x1rt6ACigAooAa7BEZ26KMmsOzuY9Q8UNc2z74I7Ly2bBHzFwcc+woAv3WjWN3am3kgAj7bOCOc8HtzVmS1hmnimkQM8RyhP8J9aAJqz7nRNMvJzPcWcckp6s2aAL6qERVUYVRgD0FY/irULfTvDl5NclgjoY1CqWJZuAAB70AcjPJrD2DW6DVbeJLNDC7EIqyBR0KHdtxnO41fg1+TUPB14lndJJcQFYnmiczMqMAd5wSSeT+VJDOg8MDboNuvkLEFyo2xlAwB4bB55681Z1vTRq+jXVgXCecmAxGQD15HpTEUdKt7+2n2nRtNsUP8ArZbeTPmfRdo6+54963aAEOcHBAOOCRXO22g6r/wkceq32qWU6xxsiRQWBhPPcuZGJ+nT2oAi0Xw7KtpeWOswpcWrT+bEkhV/mySSCAD6deRXTgAAAdBQAtFACMqupVlDKRggjINCqFUKoAUDAAHSgBajEESzNMIkErDaXC8kemaAJKKACigAooAKKACkwO3egBaKACkZ1XG5gMnAyepoAWq91ZW96IhcRhxFIJUB7MOhoAnwMYwMelMjjhj3LGiL6hQBRcCSigAooAKKACigAooAKKACigAooAKKACigCtfWYvYPL8+aBgcrJE2GBrmLfUL648WQ6Tc3hEdoC5mhG1bl8ZEbehAySB6CkM6XU7m4tdPlmtLZrmcDCRL3P+FZ0Oo6hp93DBrAt/LuDtjnhztV/wC62fXsaOodDTsr6G/jkkg3GNZCgYjhsdSPUf4VgeKLm9W8tI7C5Mb2wN5PGBnzY1wNv4kihgi5okv2/U9T1FXcwl0ghBPylVUNuH13fpSakyXHibTbUu3+jxyXbJ2YAbR+RYGgCTRvElprU7wQRypIkYkYOMcFmX+amtS4mS3geWRgqIpZiewFKT0C2pyL63qut6FPf6RauVV/9GEUg8xyGH31bACkc4znBFaOsx/YrYa9Dm3vY0XzUzxMP7jDueePSiKsgZ0VFUIKKACigAooAKKACigAooAKKACigAooAKzP7CsxbJCvmLtuftO8P8xfdnk+nb6cUAadQ3Vpb31u1vdRLLE3VWoAfDDHbwrFCipGgwqqMACqg0q3GoXV6QWmuIlibccgKM8D0znn6CgCHw9pLaHokOntIJPKZ8MB2LkgfgCB+FVtUsriPW4dVt4Wm/0WS0kRSMgMVYMM9eVA/GgB3h3w5aaFbbo0Ju5UHnyu25mPXGfQEnAq5/Z4aO7iubiW4S5JyrnARcYwuKmQyPRdFh0S3lhhmll8x9xaU5PAAA/ICrdxZxXUsLzDesTb1Q9N3Y/hVCLFFABRQAUUAFFABRQAUUAFFABRQAUUAFFAHA22uNe6hp5ttXvpLiSaENHJAIoZo2ySyqRk/Krcg131JDZ53P8AEU2mqa1CU81LcH7MpGA23CkZ6kljgY9DXaaPfTahZmeWONfnIVo2yrgHqM8j8aEwZoUUxGJpMmoXF5cXUt6r2ZmkjWAxgFNpAGD36Hr61qrd27TGFZ4jKDtKBxkHGcY9cc0DYs1xDbhTNKkYdgil2xlj0H1qrqWp2ul2zXN3IUiUgZ2kkknAAA5JJ7CpkOKH6bqdrqtr9otHLIG2sGQoyt6FWAIPI6+tXKokKKACigAooAKKACigAooAKKACigAooAKKAPHdP8LeJrXxLDeNok5srZWEJW8jE3IUYyzHC/L2Pc16jp9zqF5bzm+05rFgcIhmVywx1yvApDObtvB9rbxgT6QLuSYea0hkCtEyr8q5zySxY5Hc5q3pd14gs9XtdPurNpNPlXK3LsGeP5SSjEcEggDPegDqqrX0P2i0eM3MluDj95G20j8aYjl9M8OxzyJPFf3UsMN1MHSWcujhlIJHbOW6+xqSDwtPpelwWNiyyul6JkupGw6LwWLH+InkfQgdqSG2beu2015pE1vbwxSyyYRfNGVXJxuI746/hVC88PiHw7Y2NmnnvYSwzRCV+XMbhuT74P50AW9Fs54JNQurmMRPeXPmiMNnaoVVGT6/LmtamIKKACigAooAKKACigApCSBxQAisW7U6gbEAxS0CCigAooAqTX3k6hb2rQSlZw22VVyoIGcH04zVoMpJAIJHUZ6UALRQBy2oeMVtJ7xVt18i2mS1M7ygDzmAO3b1IAZST7+1R6B4x0/xfK1kLORFaNiyzEZLLt3Lj23de+DUpjsbVzqWm6IILaTEKspKIkZICjGTwOnI59606oRWv7+30y0a6un2QqQGbGcZOB/OrOaAEzUF7ewafZTXd0/lwQqXdsZwB9KVwLFFMApksscETyyuqRoCzOxwFA7k0AVrDVLLUxL9juFlMTbXAyCM8g4PYjkHoRyM1Ld3K2dpLcukjrEpYrGhdiB6Ack+woAybLxZpd/gwz7leQRwlRnzuQCVA5KgnBOMZB9KZofiu213U7myhgkRoFcsWI/hleLt6lCfpSQ2jey27oMfWmNcwrdR2zOBNIpdU7kDGT+o/Oi4EtFMQUUAFFABRQAUUAcpr16bDXoLa5vGa0v7afEDHaAyKp4YcjjNZ3gDVrZtOuJ5Io7OOdllJku95DGNCV+Y5wCTip6j6HcxyxzRrJE6ujchlOQafVCOOt00Yz+J/wC0vs8lvDqIuWEmDt228Jzj221a8M6r4d1SZhpFqIZIw7gtEEJDNl8f8CPP1FIZV1d9bj8Y20tqlnNElpMPK2sZGj8yHf3xu6Y7VZsLvxHDpKNfW6zagt4kUscajZ5R2gsp46A5J9cjpQBmeNo76+uJLBBdyRu1sVt4Y8rJH5hMxJ6ZCjI57DHWtnS59Tk8V6lHeSSCyRP9CUpgOON5OPQlQPqaAF124kNykK/2vAFGTLZxqyvntzz+lWPFIU+G7pG+64VDnvlgP60AbNQXNytsItySOZJFjURoWwSep9AOpPtTET1jeJtIGs6TJbskky4z9nV1VZD/ALW4EHHXB4PegA8LWM+n+G7K3u2ne5SPEhuFQODk8YQlQB2AJ4xzWhex3MsIS2kiQk4fzFJyuO2CMGgDmITdaTcjR9Gt4BGhVpxBbl0h3HALEyA5OMkDJ7nrWjoPh59Gup5SNO2y7mJt7MxyFmbcSzlyTz2oAfaWF6niGa7ltYUgbO2Rb+Z2Pp+6I2D8KoXekLb+LrK78rUbpXjl5EjbI3MkbDOMALgHg8HGOaAOq3ru27huxnGeaWgAooAKKACigAooArXWnWV88bXdpBO0edhljDbc9cZqAaFpA6aVYj6W6f4UAXYYYreJYoY0jjXhURQAPoBRI6Rxu8hCooJYnsKAOVXWfCOm6Y00YgWCM7ZB5eWUMpbLZ5IKgnJ7Cr3h9dF1Qrr+nWYhmaNrZjt2sFDDKkDjqo/DFLQZqJp9nHqL6gsCC7dPLaXuV44/QflS/b4v7Raxw/mrCJi2PlAJwOfXg/lTDUsg5HFLQIyNd1iXSBZeTbLcNcTtGUMmzCrE8hIJ4zhO/wCYrAg8fW0+jQahc2rRRTXKxFZgYxCrNgFywxuA+Ygfn3pDRLpviLVdcudFltYYIra7t0vXXzc/uWUBlPyn5lZh0K5/AiuwJCjJOAO5piFpM80ABYAVDZ3kF/AZraTfGHeMnBHzIxRh+DKR+FK+oGFc2dl4c1C81qGK4ub7UXEYgVkXewXoCducKhPzE4AOMZINLRfH9pr2qWVtZQEQ3CDJlbZKjmNpMbO6hVHzAkZYYzzhjOwJxUctxFCuXkVeM/McUmwOG0K8uNZ8ZS3kt5CYoJZYoVtGLhl2R4DnaOMhyMnqTXW63qY0jSbi+MZk8lchB/EScAfmaANDeu/ZuG4DJGecUtMQUUAFFABRQAUUAFY3i7I8Ha0QxUixmOR2+Q80Ma3IL7wz4fN1JqF5BGjP5Rcu2FPlFnXj8Tn2q9osWlR2LNo3k/ZZZWkzCcqWPXH5UgMK61u5j1G4iTU7HyYpShX7NK7qeuCV4zzV77BeOH1GXVo7fzIlBkSFQNgyRnf0+8aSQ7k+m6feC4ivH8QS3tuQSsYijCPkcHKjmsqw8Q3uoTRSwtvjnvWhFuLdxthDMu/fjG7jd1xjgDPNMRNrHhed7WBdHuY4LiKbzvOuw85B2shwN3OVZgQfX1rDlttQuLSK6S/0RkivxKIE0yYM9wybQpRpQc4cHnGOD0oA3PDz3dzql2LsxW93auqSpFAF86LZlMk5wAWPAJ5U8mqvxD1KZPDesWFrDHM50yaS4LTeX5MbAqG6HcSd2BxnaeRQwNt9cZfEUGjLZTea4aUyOQq+So5kU87sOUTbwfmz06t1HWbe31W20+PVtKt7l3UPBcyjzXBIACpuByecHnnHBoAp+KXv7Mw3Npe3g3tsMKmJYYwqs7OzGF3HC44zyR05NYGga3qVxq50uxlsVjtpI5roLulGyZt+RJtRSX3EjGfpRYL6HX6uqnU9BJAyL58f+A81Pd9E0OJI2+xWSQo8qLhU2L1ZgO3Xn60xGb4g1Ca60vTX0pZLyG+nCkW0qo0kflu+FYkAZ2AE5zgnHNSaNpKpNJJd2WxAyyWsN1IJ5YCANxDZbAztPU8/hQMTSdC1TT9XmvZtStZI58ebDDaeUDjdz94/MSwye+Kx/F9481vqG67MMVte2lqIMjEm5ondm7/dfj02k0AaFkLhfiDqM891AsZ0+2CoF+8pln24J75xn8K6qgQUUAFFABRQAUUAFZmuaZNrGnTWKXf2eG4ieGb92GLKwwcZ6HGfzoAqa74Xg13TpbOa7uY1kZTlXztA4IHplSyn61Jo+gweGdMu7bTFYxNI00MDdI/lACD2yP1pWHc4KPTPGt3HJqaQT6YlzfR3N1ZQ3GJCAQsgXtyq8fnXQavB4j1Lw9pMywsLqFmkmg2rl5ACsRZTxtz8xHbgjpQgO1RFRFRFCqBgBRgCufbTk0ZQX1ie305rncsARdql33bdwGQpY+vQ46UxG9cQrcW8kLPIiyKVLRuVYZ9COQfcVzb+AtHNr9nia7jX7ULvJuGciUBhvG4nDfMeRzkA9QKAOnwM5xz61k6v4Z0vXJN9/A8m6PypFWVkWVM5CuAQGAJJGc4JOOtAE8ui2M+pWuoSRs11aLthkLtlRgg9+4Y59ePStDFAGLeaE+oavPcXV/dCye1WBLWCZogG3FmfcpDBj8oyCOMg5qmngbSre4jeylurSNTbF4YmUrL9nIMW4urNwFA4YZAoAv6pp2oX15aS293b262kvnRl4DISTG6EEbl4w5PWq114bbUrzTrjUriGf7MHE6JBsSf5laPILHG0qCOTz9aAL8mh2Emnx2PlOsMbmSMrIwdHJJ3Bs5z8x79CR0NSWmmW9nKZU8ySYjb5krl2A44Geg4HTrgUAXaqS6XYTztPNZwySOu1i6A5GCvP4Ej6EigB7WNo8kUjW8ZaIAIdv3QCCB+BAI+lWKACigAooAKKAEyMZzx61kP4gt7WW4F48KRIwEUkcgffnOBtHIPBoAu6bqNtq1hHe2jl4JCQpIx0JB/UVboAyj4i0sX62Rux9oZioj2NkkEA9vUj861aVxmXrmoXNhaw/Y4lluJ5liRW6YwWY47narY98VyVn4z8SXGrQQDw9O9vhBctsxszIYyV56ZBPOSNvuKAO3vdRs9OjWS8uY4FbOC7YzgZP5DmuG12cav4y0UIsl7pLLJBKFCGFnLRsOTkkjbnseOO9MEdnrmoNpOh32oIgdrW2knCHo2xS2P0pNP1UXtw9s0MiTR28Uzkj5fn3cA+o2nP1FLqHQ0aQbstuIIzxgdBTELRQAUUAFFK4CY55NLTAKKACigAooAKKACigDF8L6fcabocdndIyvGSuGlMhI7HcfasXXfDVxLcXaaVYQxwTw2xcxSeSXaOYsUyuDyjMM0ug+pf0e11W1urGBLGOx0u3hkR4fOEhZiVKnPqMN1/vVvW6urTl4ym6QkZfORgc+30pgcze+JNKTxZYsbr5Iba5jkby3wrFocDp/sn8q1NSt7PV47WSS0luoCu+N42K4zjtxSAg1SS0srvQrYSqghut20t9xBDIuSewyQMn1qtJ40tB4hi0u0t2lj80RzXIBCKzDKhTjDHJ55HXvTAZr2nR32uyJfm4WxmsVgDRpuByz+YnAJUkFOR2Fa50fTdRSzuJrHabc7oUcYMZ6ZwO+KBHPeOtIu9XjubZNMkvlnsmgtNrgJBO24GR8ngAFcEAngjvVq0SLStUk1C5sriNJIlaS7ubkGO3XABTG44O4dAMY78UDN+61exsWjW6uFh8xWZWfhSFGTz06c49AT2NXAQyhlIIIyCKBC0UAFISAMmgBAw6Z5p1JAICD0IP0paYENzcx2sDzSsFRBkn0rC0XxZb61rVzY24V4kTzIpkJwyg4Ocj1zjHUUD6HR0UCE5z1paACigAooAKKACigCCGe1u9/lPHJsba4HJU+hqcAAYAwKAOW8Q+JYNHvcy2CT2qPFFczYyULnjgA8AYJ+oqLQte1DUtamtX0IW+nxPIguAvDOjYBHTAx7UhiXvj2DT973FhOIR5pRlyxdY3Cs2AMAdTyenpWr4c18+ILSadrKW0MUgTZLnPKhu4HrjjPTrTCxO/iHSlikkjvY7gROEkFqDOyNzwVTJHT0rzLXdL1nUAjyWUk+kyyqzuqFmJ3zknymTqfMThhgbaARd8LeFL26/e6mhv8W6GyvbxIpAj7EVmABPOFG36HJOa7+yure0v00GNZC9vaJKHboVJZQPr8poAn1TUodJsXu51do0KghACeSB/WrgO5QR3GaAAkDrXP69bJqt4unTRSz24tZJWt45jF5zHCqNwI/2u+OQe1IRzeiaJremagt69jdJMVigVPtQkRY9yFydzHtkDqflFaNzpWo67HHqFpdS2l5/aEis6XDAJAu9BheVJ4VsEYzmmBs+HtKuNGguILmWFleQGNkZvm+UAkhuhJBJAJ5yc81bfWrBdPN6k4lh3mNTEN5dwcFVA6nIPSgCp/aF9fQSTWcCxWrQ+bDdSsPm4B5XqO456YrM8Da3YXmmtYW04/0FREYyPuqvG7dnkH1oGXtO8Rxal4ju7W3uIZLGK0hkWRf+ejSSKRn/AIAKPEPiK2s/C93fW1zmR7aY2zRjdllRjkewx1oEWI9ftlvbSwcSvNKq7pFTKKxUsAT2JAJ/KtGW8tbeRY5rmGN2+6ryAE/QGgCpf69pumT+TeXHlSFN4Gxjke2ByfajSNf03Xo5JNNufPSMgMwRlxkZHUDtQBpUUAZ2jzXNxBNJcyhyJ5EXCbcKrED9BWjQNhXGeKYtPuNVst4uZXS6X7QqM+1Ywjdce+2kwRtaPpFjaXFzqNlJcf6a3mSK7nazYAzg+wAqTSp76aWb7WJQo+6GhCD8DnmgDDbUotL1LxZOVjuZInin+zFwGKrDHnj2wTV/w54vsPEU0ttbxTQzxRrKyyJhWVs8of4hx1oAzYfF2haP4cs3vriN85hZUw7KTngjtnHetq7nbXfCV1JpLFZLm2dYiflYMRjHse1AFLwzaxw3BkCXAla3WJla3ESxBSSAcdW+Y8jI4rc1LTodVsmtLh51if73kzNExHTGVIOPamIZZ2CaPpht7MSyJEp8qOSQseBwoJ7Vw1vJrf8Absl9bw6hcTizgWUSwbNzLIxkjQsAvRhjnHXBoGN1i08TXfhbSoJ7W9mu/ID3KQuod5Q6EKzbgAMbvY/lXTaHDqk+oy3OqRugtw8duJEUMVdt3VSQcKI1+qnrQA9Uc66znRtaA80/6Q2oKYP97y/P+77bPwqC+1ZLLxWgME05FuI9sQBOWLEDkjJwpOBzjtS6gdFbXMV3bRXMD74pVDI3qDXNaTr1np1j5d67o0l9cRx7YmYECfYMkDjll/OmI1fElg+paBd28KbrgxkwENtKyY4IPY1natp80c+jNCLiK2tY5EZbWMMUYhQpxg9AGGQOM0AbWloItNgiFu9usa7FjcgkKOBnFLqVs13pd1bRbQ8sLIuehyMYPtQBy39jajqb6wlxp8dkbywS3t33hhGV3YJ29wW3DHbHeres6FeTwLa2MUO1rB7JZGOBAGwGbHfIA49hQBX0vwteReIW1C+W3J8xJvMiduWWFY9oB7cMcn1FadzpeoXOq/aHg0l4lcbHkjZpAoP5ZoAW60vVLvW4rp7q3FpBnyYgh3AkYLE/3sEgUy30C7025ddNvI4rSV42kR48sNqquFPuF7+tAHQUUAFFABRQAmaXqKAKdvpVhaBhBaRJvzuO3JOeuT1pW0yxYAG1iwI/KGFx8n936UANTSNOjiiiWxtxHEQUXyx8pAI/kTTtO0610qySzs4/LgQkquc4ycmgC3TWbHagEKDkdMUtAGRc+I7G3u2tvKvppFO0m3spZUB7jeqlcjvzxWpDKJ4ElCuocZ2upVh9QelAD6oXOi2F3C8UkJXfL5xeN2R9+MbgykEHBx16cUAWktoY7QWsa+XCqbFVCRgexHSs+Xw5pc62yyWxYW0hkj/eMPmJDEnB+bJAPOeRQBq0UAFFABRQAUUAFFABRQBhaF4hbWLu6t3tjC0ABPzZ65x+nNbtJO6G1ZlIHURZHcLdrreMbSdpXd798frVt13xsu4ruGNw6imI5qzsrmLxjJEdTvpbaKzSTy5JcqXLMDnj0A4revYJ7iDZb3bWsgYHzFUN+GDQMwLfXNSi0TWtSnSGa3s1ka0kUFTOEXJJHQDIwMdqZ4Y+0Q6nPA9zNPG1nDPIZW3YmbO76cbTikB1dQ3N1FaRiSYsFLBRtQtyfYA0xDd0VnFulmIV3zulboWPAyeg7AU3UVtG0+cXwDWu3MgIJGPwoA5nwPNp0Fvd29pbyxebezyR/wCiSIpj3nb8xUDGMY5rUtprm1nubm6GqNAEdyJhDsQLzwEO4k9uvSgDkIpvE+pWd4dGt9RsLeV7idXeOFXLmTKqAzE8gnOQO3Ndhod3qM08sVza3SW6xIUluVVW34wy8Ek9M598dqBm3RQIKKACigAooAKKACigAooAKKAK0Gn2ltMZYYESQjBZepHv61ZoAgktUkvILks4eFWVQGwp3Yzkd+lOuYPtNtJD5kke8Y3xthh9DQBhR+D7WK5kuF1PVfNlADt9qPzY6dql1nxDo+k25t725b5o3DCM7mAGAc46HkD6mge5b0yXTtV0GE2qK9hPDtVCOCpGCCKmsNMs9KiaOzhEasctjknjA/SgRyGu67fSeNrHTbG6toIrcrJM0lwR5m4kFMA4JwO9d3SQ2IyK67XUMPQijAIwRxTEGVXjgUZBFK4C0UwCigBB1paACigAooAKKACigAooAKKAMzTddtNVmkjgEgKMRlkwDjvWnQncbVhrlgjFRuYDgZ6mmQNIIY1uCnnEfMFPGfagQ+QkRsV6gHFctoGj6fqvhzSbq4i8yRAZN56uSTnd6j29qQzegtbTRdOlW1gEcCb5TGg79TgVyWkabdas9vd6jZbTcFnuJTcbllU/dQL6dPpigDXm8KQf2lZXFmYrOO1OQsUQLP6gk9qo+LfEMlhe2EVqlw7Q3iecIsYYFGIQjPPY0wN3QtVfU9Cg1C5ha2Z0LOHAXGO/U8U2x1dNQvnjtr7Tp4kySIJg747ZAPFAHGan4otn12/K3rzW6stvDEt89sBKFyRxyQfXn9a2vC3iJJ9OtEmgliknuZYSsly0zIyngEv83PNIDr6KYgooAKKACigAooAKKACigAooAKKAM+z0a0sZ0lgUqVj8vHHPOcnjJNaFA27kbQxvMkrA70BCnJ70rRRtKkrKC6AhW9M9aBEd5cfZbWSbyJp9o/1cK7mP0FcpYWPiK18HR2dnHFBOkJMYdvnVt2cHt0pDRf8ADNt4hgmuv7emSbeFKMjfLnuAvb+tWbDSdMs9QeG3lmZ4f3gt3lZkiz3UdBQBtVz82g6HeeJPt0jiS+jw/k+dkK2MB9meuOM0xGpY6Xa6crpbB1jbojOSqj0UHoPYVZSKKM5SNFz/AHVAoA5XVdVj8O6g1tZ6RHOJIvNZkPz7ySBxjkADk5GBWXrOv21hqkFwnhtXvGgWVLxrNjtcttOSASqgc5JFK47HTeFb3VdQ0WO51WOBZJCWjMTE7kzxuGBg/StumIKKAKcmoxJqEdmd3mSIXHHGB15qyr7jwOKVyrFa61SxspViubuGGRgCFdwCc8Cn2WoWmowmayuYp4wxQtG2QCOopklmud1TxFPb63b6bp1ul1McNOm/aUUnGeaAOiHTpiigAooAKKACigCsl/aSXBgSdGlHBQHkVZoAgubkwNEqxPI0j7QF7epPtU9AGDdvc3XihbKO4eGOKzM42Hq5YqN3qB6VS0bTfFkOtpc6vqkFxa7WVo4l2j/Z+X19TSGW73xfZWGoSWUtpfmWMZOyHcCPUc9KhtfEVnJJcX0GlaodwAlkaAKAAP8AaYUXCxqaRrMOsxSSQ29zEqEDM8e3d7jnkVysXh2TxJZx3qajPYyNPMZzB1kBPCn24oA6nSreTRfD8MN9dee1rEfMnIxkDJz+VYula/B4p1AxQyvD5cYmRrW8Dhkzj5wPun254pgU9S0e1i124ktvDFvPEIJHeWS0QgyY+XawO45PXg1V8MeDBc3J1XVLGzEU8Hlm0ktRuDZzuB+UAdsbAcdaANXxfqkelaGLDTTJFcGWGGNbdWHlguOMgYXgHgnpW7ba5p13qLWFtcrNcoCZETJ8vBx83pz60AO1DUl09498F3Krf8+9u8uPrtBouftl7Yxvp1ylq7kNuubVmO302FkIP1/KgDk7R/Et9qN5Ii2x+yyNbeaZvJV8ck42SH9a3dITXBfMbyewe02YKwyM8gb67VGPwpWG2Rz6ZY69qOr2Oo2yzQqYeD3G3OPpmtXTNKtdIt3gtFdY2cvhmLYz2Ge1MRh2fia41a6KWItRbvI8MchctIGXqSmPu/jWLrapp/iSylvNVvmuZHVZBA5REUnIwNpGM9cmgDc8X66NO0e5jg883Hkh98SE+WCQNxParHhzxLaa209vbzLK1sFUsM5bjk9PWgRpnUAL0W32S7OTjzRF8g/Go7a5nl1i+gZl8iER7BjnJGTQBoUUAFFAGXZ6RHb3012JpWeR9xy3U4xz7VqUkNkVus6oRcSK7bjgquAB2ohM3lkziPdk48vOMduvemI5X+2mk1yW9tbdSABanzWweuSeAartH4ofXI7l9Wg+xx3wj8hFK7o++eOTSGUZTqviXWdUawmisPskgj8xXffIq9jjp+tQxf2vqGmalocl8XMEYkaWSQlmO7puxnFAzs31I6L4ZjvL8GZool3+SByfbOK4nS/Ft03hH7bpCIk51AxulyvyEuTgcHOKBHUeGtQu/EGj39vqZj85JZLd2hGBjHb860NH0q600bJr4TxKgRFEKocDoSQOTTA1qKBHO3vheW6vHkj1WeCF51uTGsalhIvTDEfd9iD+FXLfQY7bWn1VLmZriYbZ9x4kXHyjA4GPpnnk0AWNQ0uLUfL8ye7hMZyDb3DxZ+u0jP406e1ddKe1hnl3lNgldzvGe+71oA5yDwffKgjn1SGaIuxm32xLXAI4DneAfpg5qr4V8HX/AITm+zWKaetibqSZ5FZlkkVhwCoXHHb5qBk2qWviW3XWbyBNNVbhFIP2mQMgQY4wnU/WrXhObVhdXVrql79qKxxyo3HAYdOg/rSA0tN0y800pAlxC9ohO0tH+8AJJ25/HrWvTEc9q3hubUri68vUGt4LoRmVQm45Tpj0HrVvTtNvLC+uD9pje1mkaYrsw+9sZ/DigCyun7bnz/td0TuzsMny/TGOlSQ2ghvbm5DkmfblcdNoxQBZooAKKAP/2QD/4THoaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdG9yVG9vbD5XaW5kb3dzIFBob3RvIEVkaXRvciAxMC4wLjEwMDExLjE2Mzg0PC94bXA6Q3JlYXRvclRvb2w+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMDktMDNUMTQ6NTg6NTUuMjIxPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICA8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwADAgIDAgIDAwMDBAMDBAUIBQUEBAUKBwcGCAwKDAwLCgsLDQ4SEA0OEQ4LCxAWEBETFBUVFQwPFxgWFBgSFBUU/9sAQwEDBAQFBAUJBQUJFA0LDRQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQU/8AAEQgFWQc6AwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A/VOiiigAooooAKKKKACiiigAooooAKKKKACo/M/e7Mds5qSk2jcD3oAWiiigAooooAKKKKACiiigApKWkoAMcV5N+0r8dtP/AGefhpe+Lb8ecsB2x2+cGVuy5r1gtxX5Y/8ABZb4lXtrD4R8HpLshk3Xc6I/3sdOMVnI1pxTd2ZvgP8A4LTaoPGT/wDCXeCoP+EZmkwrabMTcW656kHhj7ZFfo/8Fvj14L+P3haLXfBusQ6lblQZoAw863Yj7sidVNfGv7JP/BPb4f8Ai79lPSR400dZ9e16E339oxp5dzbBwfLCtk5xwe2a+d/Ffg/x7/wSf+Mlpr2iX3/CV+Bdc/duLgeQLgDkpIAW2uueD3osKy6H7K0Vx/wl+Jem/F74eaH4t0p0a01O3WYKjbtjEcrn1B4rsKtO5GwUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFITgZoAWikznGKWgAooooAKKKKACiiigAooooAKKKKACk60MwWloAaqhelOoooAKKKKACiiigAooooAKKKKACik3D1paACiiigApKWigCGS4EcirtJ3elStypFGKYzLuCbsGsgMjXL5ND0fULtkkZYYmk2wj5jgE4HvXwD8L/8Agqpb698eYvBGq+HprfRrq8GnW14W/eiYuEXcPTJr9E22yRsGAK989K/n7+PVraeGf26r6PQkW3jh8VW8sKRDCq/nqePxotrc1v7rP6CFO9QRTqq6ZI8mn2zSjEjRKW+pAzVqtE7mQUUUUwCiikoAGxgk9qRWDrkVFOxWM80jI2MoQox07VPMVYl5VThs/WlVgehzVKWJHVFZnQ5BPlkjP1xVqMpu2rjIo5g5SWiiiqJCiikPQ0ALRTV+7TqACiiigApsjbEZj0AzTqRvumgCja3YuVdhyAf4uKs+ZgAgZzUaxxsxIXFTRgdqyNHYkoooq+YzCiiiqAKY/UUvme1OoAKKKb5ntU8wDqKKKoAopDyDSIu0VPMA6o5KJI93NRSTCEqDzk4olKxSVwnuIrS2lnkYJFEhd2PQADJNfhb+zjoEv7Q//BQS1vNQDXEC63capNIBkBYmJjz+IWv1N/b7+Kl18Jf2Y/FmpWKh727gNgmeyygox/I18Uf8EW/h/PceKvHPjSYsY4YY9OjYj7xJ3H+lTHUo/WBFEahVGAKiluI4iwz81WWGVI9q+CP2nP8AgpjpXwJ+Ll94Im8H3WppYFDNdbwmSR1UHrilLQI6n3VZyiaNvr0qyFXbxXkn7Ovxr0L45eB7HxJo0ckCXkeXilcEoR2Nem3s5tbVwhw2OD6e9A7GH4k8cWOgtJHdTw20YGDJO4RR9SeKq6Dq41y4tLj7RDdWZ/1clvIHTPbkHFfkT/wUi/a7ufiD49uPBuhTPDpemN5V5JC+BM44I4r7b/4Ja/DfxX4R+Acep+KLuaWPVZPPsLSckmGHt19amzL5kkfZ0c26VlPapqb5a+lLnitznDcPUUtQbA+COKkrPmfYdjE8WeI9M8MaY9/q1/babZpy1xdzLEg7/eYgVb0DXLDxFpNvqGl3kOoWM67ori3kEiOPUMDg18If8Fjtcn034FeHbWG9ktftWqbXWNsb128g/nXXf8EmvEt74g/ZZtory6a5NjfzW0W5slEByB7UjTpY+0ea8i/ae/aA8Pfs3/DC88Ua6yyS8xWVnvCtczY4Ue3TPoK9gr8x/wDgthrEg8K/D7SQf3ctzNOfqABV8pFz6n/Yp/ayg/aw8F6rq6aGugXOnXX2ea2STeCSMg19INnHAzX5x/8ABFqylj+Fnjm7aJ1im1ZQkhU7WxGAcHvX6O0com7n5xf8FD/+CdUfxDhvfiP8NNMK+J0DS6lo9shY3wxktGgBzJ7Ac14B+wh+35r/AMCfEUPw6+KV3dReFIpPs0bahEVn02Qtt2uWwUQHru6c1+zlfE37cn/BOzQP2gtPu/FXhKKHQ/HdvGz/ALtAsV/gE7XAH3j0B96LDuz7D8M+JtJ8X6Pbatomp22q6ZcrviurSVZY3HqGUkGq3jzwrD468F634enuZLSHU7OWzaeLlkEiFNwHtmvxf/Y//bI8V/sY+PJ/h/8AECzuf+EXW6MN5bXIYTWTk43oG/hHX6V+z3gnxtofxE8O2eveHdTt9W0i7UPDdWrh1YemR39qXMFj8xtZ/wCCJd951w+l/Ei2ZWJKLeWLZPoGIJ/SuZvv+CYv7THguMQeGviDFeWUP+qt9P1y4tVA9Ar4Ar9gKKsOZn5EfDT9in9rbT/iXoM+ta3qlpotvfQzXc48TrKPKDqXwNx3cZ4xzX64WsLW9vHEztIY1C+Y5yW46mp6KCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGqu3OO9OoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApglBbb3p9JjnNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAw1+MX7aun3/AMbP+Ciek+Cr1THZx3lrZpk7w0WQzHHHUAiv2db5a/HPR9Ql8ef8FavMkZrkWuvyQqoXG1I4zzUS3RtDZn6/aHpNtoOjWWm2cSwWlpCsEUajAVVGAP0ryr9q/wCAun/tFfBnWvC91bpLfeW0+nyMBmO4VTswe2TgGvZNtG33qzLqflV/wS5+PmrfC/4iat8A/GkctrcCaQ6esxP7qZSd8WMdCBkHNfqtXw3+1h+w9feJPjJ4T+LHw3V7fxRHrFu+qxK4RHgDDe498A8V9wW28QIJPv45qYqw5O5LRRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UANKAkHJGPSnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1kDcmnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA3aPSnUUUAFFFFABRRSUALTSi7t2OfWjdULO29txKqOhFZDsO2gBlI4NfgL+0JajRf29r+OWMBV8V2khU9189DX77SHzoZCrbTjAIr+fb9rbWjH+2Z4h1CWd5GttahcyMeQEdT/Sn1SLXws/oLsZFltYXThGQEfTFWKxvBt9HqfhPRryJt8c9nDIreoKA1sU47EMWiikp8whaQ0xmOetJIxC9cVLnYqwMoYYPI9KOMYHFUpl3fclb8GoZn+WNCS2Ouaz5jXkLTId644FJH99ztw2cD3FU0mmt5VSVt2R3NP8AOlMmBtPbPpVXDlZpUVRXzTMDv+VeCM1O8jR8nkHitOYzcbE9FMBOKM1RA+imZpnDg9etTzDsTUVHg+tAJxRzDsSUhqL69KGJEY2c0uYVgaIPg9KevWomxIpXOKdH8i4PNSUTUVQmvQs3ld6IZvLMgPPNA+Rl7NN8yqEl633dmM8ZpyN8hUvnaKrmH7PuW/MqvHdO1wUMZVB0k7GqtrdB0UJyCTUozkVhzMvkNGm8D5vWq3lyAZ30i3IjUiRxurQy5S7RUCSfuwaZFOH3j0NXzC5S1RUNNk2IN/eouKxO33TVEOJJCCnC80vm7uKIIUEhwOaJPmNEuU/N/wD4LIfFD+y/BHhvwXb4El9P9rfnnC19H/8ABOr4Pr8If2Z/D0T5N5rA/tOcn1k5H6V+bP8AwUO8RSfGf9tSDwnbFmhtbm30ZWXnG+QBj+GTX7W+DvDyeEvCej6LE2+PT7SK1DHvsULn9KqGwpaGvXxh/wAFAv2F7X9o/wAOv4k8M28cPjuxj/d4+UXaD+An19K+0KSqauSnY/B39kf9orxD+xp8Xrjw140tr2y0VrgQ39jLkeQ+7G8DuB1r9Xf2lf2i9C8G/sxa1470XV4Jo7uxK6dcQuCWkdcLj3BNeL/8FOv2P7f4xeAZfHfh+0RPFeixGSfy0+a6twMkHHUgCvyO1D4w+Kdc+Gel/DqWd5NIsboywQnqGJxj86gvc9b/AGFPgPdftOftJWC6zaPe6JZztqesyt91xnIQn1Zu31r9+9O0+20fT7eys4Vt7S3jEcUSDCooGABXy1/wTr/Zvt/gH8C7C5uYseIdeRby9kI5AIyqfgK+htW8baXo7XDX2p2VjDD95rq4SMfqarmIsdJ5gb0oaRI1+8APrXzz4u/bG+Evgoi41L4haU0AJ3xW83mMD6ALmvAPjh/wVQ8AaT4A1CbwLqEOseIGPlw28sTKMHjdk9xS5n2NPZrufoEtxG7FVdWYdQDyKkr4P/4Jqftd6l8fLPX9C8VsG8Rac/2lZEHEkLHgfhX3lT5iJaH5kf8ABa6+k/4RP4f2Kn5ZLmaTb3yAK7T/AIIz3E8n7P3iOKWNljj1ptjEcH5BnH415j/wWu1OH7R8ObFZF+0KJ5iuRuC+uPSvo/8A4JXeED4X/ZP0a5dSkmqXM12wYY6tjNSPofYdflR/wWw1BP7U+HFmGXeI55CuecZ64r9V6/ED/grf8Tj4w/aUTQ4mR7bQLNIAyMGBZjuatTM+2P8Agj9arb/suzSKhUzarMzEjqa+56+Mv+CTVvHF+yTpjoys0l/cMwB6Hd3r7NoAKSlpKAPlz9tr9jfwn+0R8OdYv006Cw8YWNtJc2upW8I82ZkQt5b4HzZxj15r4n/4JD/HHxD4f+J2pfC3U5Jp9IvIpJ7eKZjm3mjOHCg9vWv1l8VajBpHhjV766dY7a2tJZpWcgKFVCTk/QV+O/8AwS50WXxR+2ZrmuWkTDTbGC9n3AZVRJJ8oz2z2qbFrY/Z+iiiqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBrNge9JHu2/N1pWUnFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu4U6k/KloAKKKKACiiigAooooAimcRxszcBRk1+Sv7GNtD4u/4KbeOdaCKY4DfzhcZ2sWC5z68frX6teJpWg0G/lX7yQOw/AGvyb/AOCXN5/aH7ZvxGuJhuuJIbtt3p++IqJG0fhZ+vNFFFWYhSUtFABRRRQAUUUlK6AKWmqu3vmnUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopvPrS9Oc0AB/Km7iu1fvGmxyiRc5FJ/y0+9g1PMOxNRUR3+YCD8vcUk0jLExU8ilzICaiqTTSssbrn5uq1czQpKQNWFopvNHNVcB1JRQ2cGi4iLeWkKlePWnbRt244qFZJEkw+3Zjr3pRcFpMAcVkaWZHfTJpul3M5HyxRtIfwBNfzi/GLV0+Kn7Seu3EW6KLVtfMK/7KtKEr+kC5tku7eWCVd0cilGX1BGDX5q33/BK250z9qbSfFNlcw3vgCTUv7QuLUvsmt2Dbwo9Ruqno7jjZpo/RbwRo6eHfB2iaUn3bKyhtx/wFAv9K2h3oVQqgAYFFUlZGbeotJTMnvxTfMHIzzWdwsEmdpI6jmq7O0kPzjbmms7ru2MWJHTPSq0kjRwhJbgbvcVjKXMbKLJYbdV6HioUm+zSO33xnvTftULL5YlwfY1Vkmht1MDyfe5DE81NzflNL91P+9fHTjNZUc3mXEgWVgM8YNWLcpNAFRtwPFVruG20uNmaTDZ655rRS5h8ps2kiKNhOW75q7uDLgjNYOl3EeoYdGwfat+PpWpz1EFRtMq8ZqSolgCtn731rUxVhHbarbWNETcdanbAU8VTEIZvNVm3f3c8VlLQtalnJ9KZvJxtXimtcKvBpc42fSgBGZ/tGCP3eKZNN8yAHHFSlw2D2xmmbo9y/Lk9qmwD1XbGNx3H1FNWR9zZG5exFEkg4HaobxzbW7bOlUOxXa4G4M8XlYJ5amx3yyDfHJHKD/dNRSXSTAHeCMViXUv9mIJNiCKTkYpXOrlOiMm4Yfg1G2YVYb+SKw7nUo5o4yruZMf6v0qGNrlo5Aaz5kFma8P+oO3/W5p9w88OpJ/d2DNYLSSww9cH1qbTb6VmbLxzHHXNZcyK5GdJGyyOWkfKjkUTTIv7wdT0rIsJpGl8mWTlua2LGKfzH3f6rPFXzomVo6ktp/x7l5OrGriwovQVGv+uNP8yq5jlZJUckYPNLH92nN901e5GzK1Murr+zNPu7yZ90cMbSn6AE/0qaHoc1zXxQmFv8MPFMoHEel3L/lGxpR94tn42fsuL/wuj/go5DrJGbf+27rVD7CPKiv3Cr8Wv+CQdvBqn7UmvX8uPNXS55Ygf9p/8K/aRulaLTQU9xaSlorQzPP/AI6fEjQ/hT8LPEPiHxDcpb6fb2sikOeXYqQFA7k5r+cG5u7mfxXeeIbCxmlsYL83YZYyUQeZuAYgYH41+kH/AAWA+PEHiDVdB+FmkyGWe2mW6u/LOcueFTjv7V9DfsT/ALF2jeFf2WbrQ/Fumw3GoeLoDPfLKnzRKy/IvPQrnNZGm2523wX/AGih+0z+zDqd/wCAXW38XWumtafZCwDRXIjwMexPQ1+dv/Dvv9qX4uapcy+Jma2aZ90k2qaodh57KKg/Z78Ra1+wn+2vJ4R1a6ktfD93qP8AZ95G4+SS3c/uph27jmv22jkWRFdGDowyGU5BHqKvlE3Y/KfwH/wRUv54Vl8X+PUtpc8w6Xb7v/HmrrdS/wCCKfht43+w/EPVIWwdvm20bDPbPFfphRVE3Z8d/sT/ALAf/DJvibWtduPFB8QXeoQC3CrB5aooOc9ea+w6WoL26FlZz3DDKwxtIR9Bmp5Qbufit/wWC8cL4g/aMstDjQ/8SfTUiY+7ndX6r/sq+H4PCv7O3gCxgG2NNJgkP1ZQx/nX4P8A7TPxVl+Ln7SniPxNqh8u2fU/KwozthifaOPoDX6KfET/AIKreAvhx8JdK0X4crNrmvw2MdvG9zCY4YSFAyc9celSWfcvxs+M3h34H/D7UvFHiC+S2tbeImJFYGSaTHyqi9WJOOlfzjfEjxZc/ELxxrfiS5M0s+o38szSTE8BmJVfqB2r6PbTv2kf2+vE2lxanZa1qWkSS7ku5bV7fTYlzyyuVCHA7A19W/tofsI/8IT+yz4W034deFH1rX9HuI31B9NtXmu7piuGYIgLNzWhNj2f/gkiW/4ZQtgQQF1O4AOOvNfa1fL3/BN34c6z8M/2V/D+m+INNu9I1aaea5ms72BoZY9zcBkYAg/UV9Q0EiZozTa8I/an/a08J/s1+Br+/u9Rs7zxDsKWejx3CGd5CPlJjzu2g47UDPM/+CnHx90v4V/s96x4cj1MweJvEkZtLS3t3HmhD99yM5C44z714/8A8Ebfg/daH4H8SfEC+SSNtYkW1tt6EBo0PLA9xmvj/wCE/gL4m/8ABRT4/wAGq+KDqF1oa3Ia/wBRWJ/stlEDnyVbGFJHGOtfuJ4D8C6L8NfCem+G/D1kmn6Rp8QiggTsB3J7k+tBWysdFRRRQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUgCiikZgoJqeZgLRUcUvmrkKy/WpKsAooooAKKKKACiiigAooooAKKjkmEZAxnNSUAFFFJQAtJUbSFVzimu5ZcnjFA7Ml3f5zS/hVNrxV6R7vxqaOTzBnpWd2PlZLuo3U3HvSLllyePatBD91AbNN2j0oAxQBJRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAyPFriPw1qjEZAtpD/wCOmvyP/wCCWF5G37ZXjlWUxyzW96VTr/y2J61+uuu5bRb4MgkPkP8AL0zwa/Kv/glbb2d5+1p8V52t1W6t1ujE2c7VNyVIrOWuxtH4T9Z6KKK0MQooooAKKKKACim7qTcfSo5WA+iiiqugCiiimAUU1mxQrbqBjqKKKBBRRRQAUUUUAFFFFABRRTWbbQAnl/7TU+iigAoopKAFoqIM/qPyqQ1Nxi0VGsm4n2p9UGwtFFFAgooooAKKKKACiiigApKWigCNmCjJNVJNUjJKRhnb6VcaMMvIr4e/bo/ba1n9lXxVpOm6b4KbVhfx+aNRvboxW2c8qpXv9awk3E2pRi9z7YWaJmWMr5b9QrDFLsSbOQc/3s1+SVp/wWi8TwyEz/D3TZj0H/EyI/XbWun/AAWx1WNVU/CyyC99utk/+0qYWP1UkkaGIBCpHqxqKa6niVAId+fvc9K/LMf8FpjcSILr4dsIO8cN+p/pXS6X/wAFoPCu5/tHgHWEXoNtyjAUtexeh+lM2oQwxbwcj/ZpLXUBfJujKj/er84V/wCCyXgSOXevgvVtx6/Ov+NOvP8AgtF4ORSLXwLqbcdTIq0o3QnGPQ/R64upII93y577jgU231RJlLNhB7mvzEk/4LEeF75g03gjWpiPS7QCpv8Ah8X4TdcH4f6swHY3SVNpFcsOp+mkOoGVmwV2Doat+Z5ikA4avzCH/BZ7w78sa/D2+ijzzi6Xj3ruNB/4K7fCmcG41CHWbOT/AJ4pbBh/Oi0iLRPvi4hY7JMcrwTSeY8JyGDe+K+ILH/gr78Iry8eK5tNXtIccO1vkGq+pf8ABYD4T2cMgtrHVL1wDgJBgGq1C7Pu61uhtw8oYtyKtq4bnrX5e3v/AAWc0aOQ/Y/ANxKg+6ZJcEVUX/gtAkLN5XgOR1xxunxVp9wcV0P1QqOTO0kNgV+VNn/wW0uxIftPw5hMXYx3hB/lXJeLv+CzHjnWJJYtB8J6dpcbjA86RpWxVc3kZ8p+vcdxHIOJEf8AGqd9qUVixldlw3yrz3r8Urv/AIKk/GG6t0XT4dItMHJeGGRifxqx/wAPPPjXcRhZtJ0u7UHI/wBDmOPeubkqdja8O5+zLahHuWZphCSOecLUN9uvIo1VgQ/STdz+dfhx4m/4KGfH/wAYXggs9WewiBwtrY6ch/DlCaq6p+1N+1BNaxRS6t4qtEbhGg054z+GFo9mzbnj2P3JbS0s1LGZtuPvyOCa5rVNcskuY7V76KFxxukkQt+TNX4vaa37XvxOwmnn4l6jF6q1zaqP/HgKfN+wn+1H4w1ZLrUfCGvXV2zAfbNS1NSw56lmfNV7Ey9sux+yGoePvDvhm3P9peKLHTo1Gd8t2AfxAbivHfGX7Ynwk8Mwyy3XxC0q/lzzFBfmb8hXwrY/8Eg/jvrV5HJq954dttzASSvqUk7AZ5PTmvoTwn/wRO8KQ2oPiX4g6peXPcabaRwp+BbJq407dQ9sux20f/BUn4LeHUKw6tf3g/6Z2R/wr6c/Z3/aY8EftKeHbjVfBt5NcR2rBLiO4iKPGxHQ5r5U/wCHLPwjUHHi3xdntme3x/6Kr6m/Zj/Zl8M/st+Am8M+HJJb0SztPPf3SKJpmPQMQOg7VpymMpcx67RTqDVmYN9056VUcJGg2AmneZJ5hGOKWVf3YOMt6LWUtTRKwTRrJHnHvSqymMnPFJ5wx04qGaZlQNGoKt7VNwLG5fVaNqVSVH+1HjirHlmmVyjvyqG4/wCPd/Wmc+tRzTfMkdM05R8OnB1WSYAnH3QK8J/bK+MGnfs9/CSXxVcW01wfNWCGGL+8RxXvkJ9TxWZ4y8EaD8RNBn0bxFpdrrOlTj57a6jDoffmnymfPJdT8wPh1/wV00W1iWPxD4ZvYpMf6y2mBFdZD/wV68C2/n7PD2rM2flHH+NfS+uf8E2f2etekLy+ALa1Y/8APnM8P/oJFYY/4JV/s4jr4Ouz/wBxa5/+Lp8kRe0kfP2lf8FevBE9xcPq3hbVE3dNpH+NWrz/AIK4fDprQLb+H9fLLyMFR/WveB/wSr/Zu7+CrtvrrV5/8cp6/wDBK/8AZsX/AJkW4b661e//AB2p9nEr2rPjjxZ/wVwgvdRil0zwZNcICM/brrDY9sd6/Sv9mv4nL8Y/g7oPitdNuNJF9GW+z3Em9hz1z6V5J/w67/Ztx/yT9s+v9rXn/wAdr6J+HvgDRfhf4R07wz4dtTZ6RYR+XBCXL7R9Sc0/ZxIlPmOgpu35s1LRVcqIuMops33fwqrH+64rKTsVGNyWTfuH1qHV9Pj1nSb6wlGYrqF4GB9GUqf505Zv31WlPzGiKSHqfgn8MfFVx+xh+29N9sgaCwsdVks7hfW2kbAP0AIr949L1O21vT7a/s5VntbiNZYpEOQysMg1+af/AAVQ/Y41rxhqEHxQ8Gaabue3h26pDB98gdHA749q479hr/gpBN4Oh034e/Ex2t7GALBZ37oQyjoFbNUD94/Wmo7lnW3lMYy4QlQPXHFc94d8daN4mtkutL1C3vbWRA6yRSqev40XnxH8L6dcm2uvEGm283QxyXUan8ia1J5Wfk38Cf2WfFnxz/bg8Q+JPGOi3lv4d0zV5b24kvIyglKP+7VSRzyB0r9hVRY1VEXCDoKS1nhuYVlt3WSJxlXQ5BHqDU1TyhJ8x+OX/BZSzg0/46eE761CpfS6Uxdh1+V/lNfpP+x98RG+Kn7NvgTxA5Zp5dOjhmZhyXjGwn9K8y/bc/YN079rSTR9Ug1dtD17TgYvP27lkiP8JHrXu3wJ+FVr8E/hP4c8F2konj0m2ELTAY8xsklsfU1Qrne0UUUCCuC+PPihPBXwY8a627+WLLSriQMOoOwgfqa72vAP29rqS0/ZE+JskTbX/smQD8cUAfi/+x7+ze/7XHxkk8N3mpy6VF9nlv7q+jTe+c54B9Sa/Un4Sf8ABKD4N/Dq6jvdZhvPGV9GwcHVHHlBgcg7FAH518p/8EWfC9xcfFfxlrjxSCC000W4lKnbuZxxnpn2r9gqmxXMUdL0iy0OxistOtIbGziG2OC3jCIo9AB0q3T6KokKKKKAPNfj94H8b/EL4d3mj+AfGh8Ca/KRs1QW4lwvdfVfqOa+E9D/AOCQfiHxj4l/tr4sfFu48RTlg0i20Mk8kozyDJMwK59hX6bUUDucZ8KvhF4U+CvhG18N+ENIh0nS7cYCxr88h/vO3Vj7muwp9FAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKTcKG+6aqzS8qPun0oKSuWtw257UAg9KbIW2fKMmlQFRzQSOoopnzUAPpGYKMnpS1Gzbmx2oAkoopKADcOuaNwppjG3FM8pvLAzzWd5ASbxSeYpOM800x+lQw2hSctjj60+YuyLdFFFWQNLgZJNMW5RwCp3A9xXhP7WHjj4rfD3wVFr/wAMdCtvENxZS+ZfWMwy7Q99g7mvGP2dv+Clngf4o6iNF8aQt4H8TxNsljucrBu9Cx6Go5mXyn2/5i4zTFuY3DYPQVnrqMGpW8M9tMs0E67opIzkSD1B7037N5Mg+YnPYVPMyuVDob8GZvn+XtS/2iysoKkZ9apXDR2ymZImkRcltmPlx61Ws/EVhrUoW3lWVl6qjKSPyNHMzX3TpPO+UEZI9qk8we9VrOaKaH9ywcDipRHzT5mYWRNkU1pAqkmnbajeENR7xBFHdGXkDH1pzT4GRlh6inbUUHjbXmHxG/aI+Hfwz8VaD4U8ReIodO1rWpVis7UAsxJ4BbH3QTxzWFmXZHpK3xdioU59abbiVZGZ+V7Cp7e38tBkDd3NPK4rWKb3D3egRyBl+6V+tP3U2mJMkmdjq3+6c1sSS7qN1Rt8qkk8UK27tUczHYlorD8ZeNNE+H/h2713xDqMOlaVarvmuLhgqqP6mvOPgr+1p8Nv2gtY1XTvA+syavLpqB52Fu6Lg+mRzVknsdFFJQAm4UnmYbG3j1qLcXUtjaBXgP7U37ZHg39l/wAMzy6pc/bvEU0ZNlpEDAyyMRwT6AH1rO7Lsdv8cP2ivAv7Pnh86r4x1eGx3AmC2zmWYgdFX+tRfs5ftCaH+0p8OY/GGg2l1Y2TzvB5N1jeCp65HUGvx58C/Cf4wf8ABSb4sXfiLU7h7bRllBmvrkMLS3jzzHEO5x6V+0nwh+FOi/Bf4f6T4R0CLytO0+LYGIw0jd2b3NaCaR2m6jd2703adxOeKj2vvzjigLHzH+2Z+3Fof7JK6Na3ug3XiDUdUVnjt7e4EOxV4ySVNdh+yz8frX9pb4VxeLdNtnsfMlaKSylkDtER6sAM/lXx/wD8FqPDlufCHgLXguLy3u5LZSOpVhn+ld3/AMEcbCWH9nbWbqRiUn1Z/LU9FULQHM0fZfjDxhovwz8I3/iTxLqEen6PZR+ZPcSDhBVH4V/GLwV8YtHGpeDfEVnrtr/F5DEMv1U8iviT/gsl4+8Q+H/hn4Z8PWTCDQNYuWW+kHJYqMquPSvhD9mjRfjT8M/Ctz8YvhzDNdaFp115F/b28pJIHJzGO2PypWQczP6BMV8C/wDBQ7/goSfgT5vgLwHNHN40mjzd32cjT0I7AjlyPcYrR+Dn/BWb4YeMfCdxc+L/ADfC2t2sRaS1IMySEDorADkn2r4R/Z38Br+2/wDtuX2r6pBc3Ph6bUJdUvP9i3Rsxxk++AKZJi+GL79r74qaONd0a7+Ims6S6mQXsFzKkRAGSQ2efwrtv2TP+CiHxF+CvxIt9B+Iep6p4i8MXV0tte2+syPJd2TMQN6ljkYPUV+2em6ZZ6PYw2Vhaw2dnCuyOCBAiIvoAOAK/Hv/AILJfD/SPC/xa8Ja5pVlDZXusWMz3bwx7TI6MuGOO/NA7s/YbT7+DVLG3vLWRZra4jWWORTkMpGQfyqxXjH7GviOfxX+y/8ADnUrmIwzyaVGjKZN5OwlM5wOu3Nez0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKbtPy89KfRQBi+MJJYfC+qPEVWVbaQgscD7p71+T/8AwSmvvs/7YHxMtmYM9xb3R6+lxur9VPiTHdy+BNdSxljhujZyBHkTcAdp7ZFfk9/wSZ0+4X9rbxybgq00FhdGR8clvP2n9ay62NPsn7D0UUVqZhRSbqaXoAfRUUjyD7qqR7morPUIrxpVQ5MZ2t9aV0OxMTjNRqxYb1yQf4aQxbW3F+PepVYMMjpWXMyiSms3YfepGb5c186/tJftmfDn9n24g03xJfXMWqTDckNtHuYD1NHWwlFvY+i13Y+bGfanVwXwR+LPh/41fDvTPFPhq9a/026BUO4w6sOqsPUV3tap3JMDxbrkXhfQr3VbqYpb2sZlbA7AZP8AKuS+Bvx+8H/H/wAKrrnhTUo7qLcUkt2YebGR6rXb+IPDtv4k0u5sLwl7a4jaNkwOhBH9a/Ef4seF/iX/AME6f2gJNU8Pm6h8K3Fz5llMS32W4jJ5R8d8VHvXua3jy2P3Nor5t/ZJ/be8I/tUaS8dqo0bxHbj9/pczjJ9SnqK+kc1adzNqwtFFFMQUUUUAFFFFABSMu6looAKKaWNQySSZQJjJ65qeZDsWKQ9DUFxO0ceRgVSbftkYSGRWGVANO5Si2WofOaQlnTZ2CjmrEjbVqpBGLWHcE5PULUktwvALLzU2G1dhb43MQcg1ZXpWZa3Ijd1I+UdMVoB84weKtajnFpklFFFBkFFFFABRRRQAUUUUAFFFFABXJfEL4TeDvixp8Nj4x8N6b4js4X3xw6hAJAreozXW0lJpPcNeh4Prn7CPwC8RWYtbz4XaIIR0+yrJbt/31Gyn9a5lf8Agmb+zWv/ADTSP8dZ1E/+3FfT9FA7nzCv/BM/9mleR8L7b/waX/8A8fqKb/gmX+zfK2U+HUUI9I9Su/6ymvqL8aRV28DgfSlzCPle6/4Ji/s8XC4TwXLbn1j1G4/q5p0f/BMj9nlLXyf+ELdmxjzWv593/oWP0r6mzRmqsPU+TLb/AIJd/s92y4/4RGeU/wB6S+kz+hFZ+tf8Epf2ftYxs0LU9OH/AE5aiy/zBr7EaozKisFLAMegpcpV2z4oH/BH/wDZ+3EmDxKfb+1v/sKeP+CQf7Py5ItvEm71Orn/AOIr7XGaj87dIVVc46mlzEI+I/8Ahz/8Cv4m8Qt9dRP+FWof+CQ/wBj62evP9dUcf0r7YpKodz5F0f8A4JWfs86O+4eGr+89rzUpJBXT2v8AwTp/Z9tMY+HtjLj/AJ6szfzNfSlFAHgtv+wj8AIeR8KvDch9ZLNWrpfD/wCyn8HvCtwlxpHw28N6fOn3ZIdPjBH6V6rRQBkxeEdDgULHo9gijoFtkH9KmXw/pi/d061H0gX/AAq/RSsBUXRtPjOVsbZT7QqP6VN9jg/54R/98CpqKYhqqq/dUD6CnUUUAFFFFABRRRQAUlLTFXZ1OaAI5F/dkjqKzobyaZH3QlBV2aRFVyT0rNh1RLiQhCyezCsjojG4SaknnJHtNSf2ioV/QVnzQINx2YIfruqnJqItLWZ3ZTxhfepsa2Q++8TQ2d4saM7GTpxUkOssi+WfMMnevCPi58fvB/wx0uS/v/EVhb6hCnyWrSgyflXyZqX/AAVb0W08Q2xgs7q6hTiW4VeD+FLUeh+nUmZLUGMk1Wt4g02zcSR718x/AX9vT4a/Fq+tdPt9eXTL+VseTqBCbj6CvrHZHIEkiVXj/vJVk3LcanywD1p6/dpdnvRH0rU5Lj6KKKBBRRRQAUUUUAFFIvSq80wjqeYaVx00g6VnTTZPlxUkkKTTZ8zJpZIaxkrnXGKRLCXA60q3LRq7t61F89Z0li8s26WTMXasyuVM6GGQTJmvlj9pf/gnb8Of2h7yTWFjfwz4lfltRsFx5h/21719N2syRLgVPFMzdxW1zn5WflXL/wAEi/iz4SSSLwj8Xbe1tGOfLWW5tv0Tiu1+D/8AwSINp4kGv/FPxf8A8JLcK4f7Pbb33kHPzM/Jr9Kd1V3vlXpzV8xPvMbpOl22iabbafZQpbWdrGsUMSDAVVGAKuVD9oHqKbJI2Mg8UcxPKyfNG4Dqaq+dynNK7Pt+Uq31FHMPlLOR60bh61TkuhCUDMAD14p3nqVygwPXFWLlLRYDvXOePPAekfEvwbqvhnXIPtGl6lA1vPHnqp/rWzJ++UMpwBzk09SzdOB7igLHlX7O/wCzH4L/AGY/Dt5pPhCCZIruXzZ5rh98jntk165mm1R+1kyMv8C9W7UCSuX96+oo8xScbhn0rJjvogsmZVH4imWupW8kLs12gjH8RIBoL5V3NrNGR61lTa3p1ja/brjUoYbT/npLIqp+ZrKn+J3hG3k2y+JdLjPo15GP5mgix1WR601pUVcl1A9Sa4y8+M3gCwVjP418PRADJ3apAOP++683k/bc+CcM0yTfErwuFXhR/bFt/wDF1HMPlPe1lRlyHUj1Bp24eteFWP7afwNuJBBD8T/DbsxwMarAf5NXzV+0p/wVS0r4NfFL/hGvD2l2PjDS4Y0aa+tbtWCMeoBUkZAo5h8p+hdFcZ8Hvijonxm+G+h+MPD05uNL1KASIW+8rDhlb3BBBrs6sgKKKKACiiigAooooAKKKKACiiigAooooAQ1WELNNuZcDtVqigadhKWiigQUUUUAFJtHpS0UAFFFFABRRRQAnPpRz6Um4HpzRuqeUB1JS0jMF60uYCGWSOOGR5SFiUEuz9MY5P0r8y/23/2KfC/xq0/UPiN8FZ7HUfEdm5k1TTtNnVxOO7ADowr9APjdoeteJvhF4t0zw3dix1u602aO0nI+65Q4r8gf+CZvxjl+CP7SFx4W8Q/aI49fP9nTxSkjybkHjcD0Ge9SaI77/gn/APt0a34G8R2nwq+JEzppYPkWt1fErLZMOiNntX6t6fqEWoAXUTh9oyy55A9fpXwh/wAFH/2EY/iDo9x8T/ANmLbxRpsZuLyytkCm7VedwA/jGK+R/Bn/AAU48YeE/hfc+G7rT/tGvpbG0g1aSQhgOQSw9RRYnmZ9A/8ABRz9ve+8N6rP8NPhvqKpMUxqWo2nLBm/5ZqR3r4S8G/G740/Au+g1iG/1zTLeY4V9SjlEUvsCwr6t/4Js/sSX/xY8UJ8WfiBFJLodvcedZW10MnUJuu9gRygPfvX3T/wUG+CunfFP9l/xZEljH/aGj2zanZGJACHjBJAwO4zxQK52/7I/wAXI/jh8BvDXiz92Ly6i23aRn7sqnDCvZNtfl7/AMEVfHlzPa+O/B8txJLawRw6lbo3RMnY/wBOSK/USr5UFwpobcKdXF/GD4qaL8Fvh3rPi/XpvK07TYWlZVxukb+FVBIyScDrVCOZ/aU/aA8O/s4/DLU/E+uXqQzrCy2Nsu1pZ5sfKFQkbucZr8l/2Pfh/wCOv21P2rLbx74pluL3S9Ou1v8AUb9VKQoV5WGPjAOQOBXC/ED4ifEX/got+0FpmnQRlFnnENnpuWNvYxZ+ZnODg45ziv2x/Z5+A+gfs5/DDTPBugKJIrVd094yBZLmU9XbHelYd2elUEUtFMR5H+094K8eeO/hLq2l/DvxL/wjPiKSM+XcbfvjHKbgCVJ6ZA71+MU3i39qD9kfVhdardeJtAjLgN/aO6e2k56ZORzX78Vl+JvCuj+MtJm0zXNNttVsJgVe3uow6nIx3oHc+Df2Of8Agp9ZfGzWrbwd44s7fRPEM4xb3qOFt7g+nJ4avvTXde0/wzo11qupXcVpYW0ZllnkYBQoGetfkn+3T/wTdn+D73HxJ+FHmroVm32m40sMWksiDndGf7o+ua+cviF+3j8Uvix8Jbb4datdrNa+YqyXceRNNg8KaVkFz0D9t79sHX/2v/iNbeD/AAUl4/hKCby7KygB36hJn/WEDt6Zr9JP2Af2TYf2afhbFNqK7vFutRpcai2T+7yARH06jvXlf/BOT9gzT/hPoOmfEjxbD9p8XX8HnWtpIo2WKN04/vEV990xC0jEKpLHAxyTRu49K/Nb/gpH/wAFBJ/AtxcfDP4d30cmrSxtFqmoW7Za2J/5ZoR/FQB6D+2l/wAFJfD3wRs7jw34FuLfXvGZYwuykNDZH1f1PsK+QP2Y/wBjv4ifto/EgfEL4pS3kXhqeUXMt5dblkuhniOIfwj+ldf+wT/wTlb4qx23xH+KK3H9jvMLiy0uUnzL05zvlJ52/wA6/W/TdMtNFsILKxto7S0gUJHDCoVUUdgBSsh3MnwV4F0H4deH7bRPDel2+kaXbrtjt7ZAqj39zW2zBVyaUsF6nFBAdcdqYCr8y5r5x/aL/b0+GX7NWvroPiKe8vdcaMSmysYt5VT0yc8V9Hqu1QK/HH9rj9g741fFP9qjxJqGk6b/AGpp2qSC4ttSeXbFFFjHlknuKBHG/wDBQb9ujw3+1ZpXhfTPDGlX9hBpc73Fw18VG/IwAAK9I/Yj/wCCjHw0/Zt+B1v4R1zSdZutUinkmeSziQo5boMlhXjH7SH/AATr179mP4I2fjjxF4htbzUZbxLeXTbWM7YwwOPnJ5PHpXqP7E//AATI8MftIfB218d+KvFGs6b9ruJI4LPTViUbUIBLF1bOfbFAHnf7ZP7bmqftoJp2i6H4PmsdN0uWS6ESN9qldQPvthRtGOa+pv8Agi7q8OpfDvx9oE7LNHFdxymBvmVldSDkfp+NfTPw1/YN+GnwT8G+JtP8IadJHqmr6fLZvqd23nTgMpxgnpz6V+TX7P37Rnin9gX4oeONH/sgalcMHsJbOZ/JxIp+SXkHIHBx+tAHp/8AwVc+Hvwi+HfxC0qy8EWUel+LZkM2qWNhhbdEP3SUxgMfQYrjP2F/2sn/AGNvFl4nibwjcSaV4gjjaS4WIx3CxDo0YI+cd+orT/Y3+COu/tvftLah4x8ZB7/Q7e7/ALQ1e4+6skvVIk9s4GPSv1d/aI/ZB+Hf7R/hFNH1/SIrS7tYvL0/UrJFjmtPQKQPu/7PSgDovgf+0Z4C/aI0OXU/BOtx6kkLbZrdhsmiP+0h5x71+c3/AAWz2/8ACV/Dcggt9hvAw7j5kxXzn8Qvhf8AGP8A4Jx/FhdY0e4lisySLXVreNmtbpP7si54+hNcP8Vvjd49/bX+LHh+XX0hutWlaOws7PS7Zo49rMN+FLH19aAP2Y/4J2/bh+x78PF1CFoJltXCBjklPMYqfxBr6Rrm/h34Uh8BeA/D3hy3RUh0qwhtBsGAdiBScdskE/jXSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJmmiTnGDnGT6UAPoqtNfw26u0jqgXrzzWPqnxA8OaLGz3mtWUKr13Tr/jU8y7lKLeyIfHkc0ng/V/nAH2dyCq84weOtflZ/wSkDL+2F8Sckk/Ybzd9ftYr9DPGf7V3wp0/Rb9ZPGekyt5TIUW4B6ivyV/ZD/an8H/sz/tN+M/E+rrdapoOrLcW8VzYoGKq8wlD4zz6frWSa5rl2ajZn7rnPYUtfMHwN/wCCg/ws+OnjC18LaJqc39t3eTb28lvIocAZPLKMGvpzzPatrkcrQ6vmr9qP9tbwf+zhHDbahdLc6lIwDW0B3SIPXFfSuOMV+CX7cWm/8Jf+3Br2jRebum1G3tArPuA3YyQD061nK5UT638D/tZ/H79rrx4+lfDKzHhXwmu7drlza7wQPc4ANfOviv8Aaa/aG/ZP/aBmi8Z69qWpRQ3Hz290oFvexZ5ZcDHT0r9kvhT8LdA+DfgbTPCnhy1FtpthGEX+857sx7k1wf7Uf7KfhP8Aal8Dy6JriCx1KMZstXhiDTWze2cZHtRyD5/I6D4K/HDwv8fvh7ZeKPD1z51tcJuktmI86Fh1Vlr0JldV+Vs/hX4Y+JvDPxk/4JpfFi2msr2SbR5v9Xcruazu0zyrDopr9Nv2Tf29PA/7T1mbJCPD/iiBV87TLpwA7H/nkx+8Kkk928eeOrLwD4W1HWtRljgtrSMsWkbGTX4JeP7nxZ+2p+1FeWekBtQvtUvGisxn5I4Afve3FfXP/BXL9o2T+3tO+GuhXMsUkKCfUJIZOGDdF4r2L/gl3+x2nwl8HxfEjxBGsniPXLcNZxso/wBGt2GfruIoWruW3ZaH1Z+zj8FdN/Z9+Euh+DtPVC9pEpup14E0xHzv+deo03aKdWkU0YhXE/Fv4O+Fvjd4Nu/DPizTItR02ccblG6JuzKexFdtRVgfh1+0x+yP8RP2FfiEnjT4fXuoTeGA2+21W2G6S16fLNgYx79K+6/2C/8AgoFp37Qmkx+GPGN3a6f48t/lHREvVH8S8/e9q+x/EPhzTfFWi3mk6raRXun3kbRzQTKGVlIwcg1+GH7bn7Lt/wDsY/F7Tda8K3FxH4evpvtGl3O/EkMi8mLIxwPzxUS0Lj725+8Jz/jS15n+zh8SJfi38DfBviy4MRu9T0+OW4WHOxZMYYDJJ4I7mvS81SdyWrC0UUUxBRRRQAUUUUAQqzlmyuB25pJANysc5FSKq8kUmD6VHKyror3GTGwZSR2xXAeIvih4d8N6klre6xa6fcIMNDcSqhH5mvR1XcOa/Nb9rD/gmn8TfjV8XtY8W6B4zso7G+bdHZ3c0iGL2GBionGUtjWM1Hc+2r743eDrO182XxVpVuzcYa7Uiq1r8VvBd1EHXxhpE5UcbL1R/Wvyu8Sf8El/j1Z2m6DU9N1kj/lmuoMG/wDHq5mP/gll+0gqjbp1nCPQauo/rS9m+4/arsfqlrH7WXw08H3Swap4u0u2Mhx+8nUnJ+ma9q8O6pZa9pNrqOn3cV7ZzrvingcOjA+hFfihpf8AwSb+POrahGt7Dp9nFkBppr0Pgd6/XP8AZn+B6fs8fB/R/BK6rPrLWW53u5zyWY5IUdl9BWkU0KdTm2PUqWiirMAooooAKKKKACiiigAooooAKKKSgBm4UyO4jkOFbJrD8beLtP8AA/h+51XVbyGwsrdd0lzcOqIPxNfM11/wUU+D1q2bbxppkv8AwI1nKol0N4w5lc+s5boQ/ebr0p3n/u1b1r5RuP8Agod8GpbVbmfxjpwK8iNWJNcJ4k/4K8fB3RVEdjb6rrMnpbW+F/M1HMHIfcktwY1wp3N71WtdUEzuPMBx/e4r8z/EP/BZrQJdRiNh4G1XyR18yeMZ/CnXf/BZXw7Lny/BF8M/7aii8irKx+mtxcTMR5AVl9Say7uQTMskZxMn3sdK/LXxF/wWOlktVg0LwZNBJ3+03Ix+lYyf8Fi/GUcYSPwPo5Q9WN0xz+OKLyHG0T9dbHU47pAoLbsfxDmp4LVIizKTluTz1r8iof8AgsZ4gk1C3mvPBltFGPvra3WA35iu1m/4LLWQjKx+Er8P7yIKd32IcV0P0+m1C3t5BG8gDn+HvU+6vxU8df8ABWv4ka/q0Vz4e0iw0mGNuftEfnM3sa/Sf9h/4++J/wBo74Mp4q8VaKmj3/2uSBPKQrHOi4w6g/XFaKV+hLirH0RRSUtUZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSHpS0UAZd3CZJ4yvAXr71FNDGuSHAf0FaUzKqnAGfpWTagNITIBn6VkdUGyt9laSHLS7PZh1r5N/bK/ai0r4DWLRyPuvJExDZRuN2fevYf2mvjbp3wZ+HeoeIbm52yQQ/Kn+12r8ZfAvg/x9+35+0MI2aeZbibfd3HLQ2Nvnv6cfrQNy5RPh/8Ffih+3Z8TtU1DSrXEckpaa9uGb7Lbf7Ib+lfaXhT/ginpi6SR4h+IFwdQYdNOtgIgf8AgXJr9CPg58HfDfwN8DWPhbwxZJaWFsuCwUB5W/vMR1NdvWpzczPwF/ap/YV8e/sl3EOtyXA1jw95gEOsWmUMTZ4DDsa+9f8Agmb+2hdfGexk+H3iV/8AieafbeZb3RPMyjr+NfbfxM+HehfFbwTqnhjxFYRajpd9C0ckMoyOnBHoQa/CD4K6XqPwB/bs8OaCbmW2OmeLItPkKNgSQeftwfUEYqLDu2f0E02PpT6KsgKKKKACiiigAooooAQfdrM1zULfSdNuL25ZUhiQsWboBWpXjf7V3wRv/j58EfEng/TdQGn6heRBraRvu715APsazsyk7HKaZ+2R8K3upLUeO/Dz3cb4MMOoR13ej/GXQNftvtcWoWk9senlTV+N+p/8Erv2i7OZgPBNvfgniS11uyA/8eYGr+nf8E7f2qtMt/stn4YvLO3HPlx+IrQD9JKOU29qux+yNx4605Y4n+2wRNL/AMsfOrW03XIbiDlhj61+MM37Bv7WJKyPpWuMw5/5GWMkf+RKlb9mv9tDTbfEcHjJh6R6yW/TfWPKy/aLsfs3ea1Y2bRjzV/OlOq2lrJuLKF9Sa/FAfBj9s64QSf2f42+pnb/ABrZ/wCGef21tYtRDcReKli/uS3u3+tXZi9oux+zM3i2y2h0nXHfkUy38Q6bcTFEuEAH+0K/GX/hjP8Aa9k4Nv4j5/va83/xVWI/2Ef2tW6HWF/3vELf/FVrymftF2P1x8UfFnwr4VlhjuddsojI/O+dBj9aoeKf2jPhx4P0Vr2/8ZaTbxH+IXaN+gNfk9df8Ev/ANpPxM+/U7O0lf8Av3evK5rc0T/gjv8AGHVbqIa1rui2Vrn5mNw0zAfSjlD2nkffurf8FEPgPo+Qvjywmb0jDHP6V5V4i/4K6fCrRzJBbxX2oEcBoIcD9a4G3/4IoaGMfaPiNfyf7lmgrttC/wCCNXwosY1Oo65reoy55O9VFHKRzHnGt/8ABYnwrI/+i+DL1yOR5k2KxNV/4LOSTxeXa+AlQD+9c19kaB/wTh+AWg2qwr4It7wjrJdSM7H862V/YF/Z/Xp8MND/ABg/+vVC5j4Duf8AgtL4nls2gj8B6ap6ZaZiPyrJk/4LMfENUxb+EvD8B/2vMP8AWv0Y/wCGD/gF/wBEv0D/AMBhSf8ADB3wC/6Jd4fP1tRQFz8vvEP/AAVy+MetHEEOi6b/ANc4WP8AWuUT/gpf8ftUWeG11tJDIfuwWu5vwwK/afwf8Dfhx8NbMQeH/B2h6ND0/cWca5/HHNdbF4d0mPmPTLJPdbdB/SgfMfhbbftS/tWXyh7b/hJZ1PRodFmYfpHUt94p/bK+JkbB9O8eNH/saXNAD+OwV+7CWcEa4SCNR6KgFUtd17SPBujXGp6vf2ej6XbjdNdXkqwxRj1ZmIA/Ggk/Dux/ZP8A2uviFELO70XxY8B5K6lrK28f4h3Fdf4V/wCCQ3xy8T5Ovah4f0ADobu/luW/KMEfrX7A+B/ip4Q+JVsbjwv4l0vXox1/s+8jnx9djGuqoHzH5CR/8ETPHUjK03xL0FT322dwx/U1vQ/8ESdVX5n+KdsG/wBnS2P83r9XaKnlDmPykb/giTqWdw+KUDN/2DGX/wBnrG8Rf8EUPFdtp80ukfEHTNQvM5SC4tHjDf8AA8nmv10oo5Q5jzr9nn4TwfA/4M+FPBUJV30uySOeROjzHmRh9WJr0WiiqJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKAFpD0NAIPSloArqnlxnaffmqyrLIm5W3D2Nfn7/wUX/b28TfBPXp/h34Q0x7TU5rVJn1qQHagbsg7mvibRv+Cjn7QGmnbHrq3K9v9EJqOZmqP3lt5GWFRJ9/HNZfibxfo/hHR59T1q/h0ywhyXnuWCLx9a/FJv8Agop+01fKDGlwQf8AnnpT/wCFP1uP9rb9sy207SNQ0TVpdEmYMJXtzawY9WY4qLMVkfsr8N/il4Y+LmhnWfCesWuuaXvMZntX3BW9D6GvyD/4Ke/CqX4H/tPaT460NBaWuuFLtTGcbbhD835gA1+lv7Gv7KNj+yf8OZdCh1OXVdQv5Fub6ZuI/NxjCDsK+Zf+C0fh03fwm8EaukSlrfWPs5kPUb42I/D5a05URc+xP+F2aHpv7Odp8SNZuI4tKk0OO/mZjwxaIEp7ktxX4JaJ8GPHv7R2t+MPE/gjwdcX2nQ3VxfTR2YGyBXcsIxkjOAeg9K9h+IP7VOs/F74D/Dv4EeEIZ7hUjitb5th3yyqfuqO6jOc1+uv7I/7Odl+zX8FdL8I4huNSYGbUriNRiWZuoz3A6CnYR8d/wDBPv8A4KLeG5PDuhfC7xwsOgXmnxLZWF/jZDKq8ASE/dav0d1y0tte8OX1s4S4tbu2dD3VlZSPywa/Kr/gpF+wBF4NXUPiv8PLd1s3m87VtJhX/U5/5axADgZ6j3r0n/gmL+29cfEmA/CzxteRpqen2YGl3czbWuEXhkYk/eApcqA8W/4JXapF4B/bG8beEzJsiubW9sIl9TDPuH6LX7EV+K/7Nenp4Y/4KmXljbOTEPEGpqCDkMjbyOe/Wv2nzVARXl5Bp9rLc3UyW9vEpeSWRgqqo5JJr8Wv24P2kNZ/bK+OemfDX4fXM2o+F4btbOygtztTULknBkPPKDsf0r2H/gqd+2deW+pS/BrwddPDI4X+17y3OXJJ4hTBzn16V6P/AME1/wBgm2+EOi6f8TPGtmX8a30JazsbheNOjPR8EAiQjr6ZoA+iv2T/ANknwp+zD4EsbDT7C2m8SyQr/aWrBdzzSY+baxGQvoK95oooAKKKKACkZgqkk4A5Jpa+Mv2zf2qfEFnqg+Dfwcs5td+J+qr5Vy1vEWTTIGXl2bGA2D+FAHkv/BQD9uZfEDX3wR+FcL+INf1QNZajd2oDrGG4MaEHlvXjHvXzH8QP+CWPxA+F/wABNR+IGsatZJremJ9qm0K1BkaOIcn94OCw9Bke9foT+x1/wT78J/s4JaeJtYP/AAkPxAkjBm1CZi8dtIfveVkAn/eIzX1B4006DVvB+t2V1GJbeeymjdGGQQUPFAHyF/wS3/aVv/jh8G59B1yZrnW/DLLbfaGxmWAjCE98jGK+16/G7/gjH4gms/jp4m0mN2Fre6N5zJ23Iy8/qa/ZGgDI8WWd7qHhnVbbTZFhv5rWSOCRs/K5UgH86/nt8efs5/GP4L+MxrnirwhqN1dw3H2l7yaFrmKZ853ORnINf0U1FcW0N3EYp4kmjbqkihgfwNAH5U/Av/gsV/YMMejfEjwn5UMKhIbnRU2hVHYxn+lfZPwp/wCChHwT+Lt3HZab4pXTL6QcW+rRm2J9gW4Na/xY/YZ+DHxkmFxrvg20gvB/y9aaPs0n/jvH6V8c/tAf8EdbAWMmqfCnXJor+Eb10zVZC4k/2UfsfrQB+mqyR3kYkgdZ0PR0YFfzFWlXHevw/wBJuv2wP2S7gxw23iBtMhOWhkVr232/qa9N8J/8FiPiZqes2WkXPw/0rUbqaQRtDbGYTn6J2oHc/XSlrO8PX1zqeh2N3eWzWVzcQrLJbuctESM7Se5FaNAj80P+C1XjSSz8E+AvCys4h1C7mvJgp6rEoAH5v+lfQ/8AwTHTb+xr4JfG0SG4IGPSVh/Sua/4KIfsW+Iv2soPCNx4Y1WxsL7RXmjljvtwDxy7eQw6bdvTHNfR/wABfhXD8EfhD4X8EQ3CXY0e0Fu1zHHsEr5JZ9uTjJJ70Ad9XxR+2N/wTX8P/tKeIrfxLoeox+FvEDP/AKdP5BlW5XjqAy4OO9fa9IR+dAHn3wL+B/hr9n/4e6f4T8M2qxW1sg824KjzLh+7ue5r0KiigDB8beCdH+IHhu90TW7C31Gxuo2RormMOoJGAee4r4d/Y6/4Jn337PXx21Lxt4k1fS9Z06yEg0K3tRIZI2c/6x9ygKQMjALfWv0AooAbt5yOD3p1FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADG71+b37X3/BRf4kfs6/G6Xw5aeFLKLQfs4e2bUAVe47FwwHA/Ov0jxXE+O/gn4E+J2padqHivwppfiC808k2s2oWyymLPpmolG5cJct9D8cfFf7b37Sn7Snm2PhfQ7yO3k4x4b02V2x/10FXPBH/AATj/ag+KEP2jWbw+GYWOCuv6vIsn/fEYc1+0+i+G9J8N232fSdMtNMt858qzgWJfyUCtHHvS9nEp1JdGfknP/wRN8SpYyyP8UdNkn27jH/ZsmM+m7zP6V53+xL+wv4R+OHxC+I3hnxnqeopN4Zc26CxKwliW27yCDj6V+1lx/q2x6Gvy/8A+CePiqbWv28vjoot/sEVwLovbB9wzDdLGDnA68np3pWWw07q7PqD4B/8E6PhX+z/AOKLbxNpf9qaz4jtWJt7/VLneYgRjAVQBX1HtpefWjn1p2ZldhX4h/td+EU0/wD4KQwWkl55P27VNPne4/557ypxiv28NfiB/wAFJdLvPBX7bq69eO8kVybO7hkI2gCPA2A/gOaqRcD9wKKr2d9DqFnBdW0izW8yLJHIhyGUjII/Cpt1O6Iscn8Svhb4X+L3hmfQPFmkW+r6bN1jmXJU+qnsa/FT9uD9lW9/Yr+JGk6/4N1K8i0S/cvY3AbbJbOuPkyOv41+4HiLxNY+GLT7TfXEdvCD8zSNjAr8m/20vjPqP7b/AMYtC+DPgnSoHGmag7DUt5YuduDkdABUXjsaKL3PHf2Efgncftg/tGPqHjbUjqtlpUa3+ox3MhMlyoICoPbJFfurY2UGm2cFpaxLBbQoI440GFVQMAD8K/C4eEPiH/wTL+PnhjV72WG9F1FidbVz5NzG3DRN9P6V+4PhHxVp/jjwvpWv6TOtzpupW6XNvKpyGRhkVUbITNqiiiqMwoopKACvzS/4LOeL9Lb4e+DtA3RtrTagbqMfxLGFIz9Dmv0kvNQgsLWS5uZkgt4xl5JDgKPU1+IP7cPiOX9qb9ty28JeG5ku4EuINDs3gJZS5OJHH0J/SokaRR+l/wDwTl8N6l4Z/ZA8CQaocz3EMl3GPSKRyUH/AHzj86+l/wCGuc+HPguD4c/D/wAN+FbWWS4ttF0+DT45Zcb3SKMIGbAA3ELk4A5NdJRFaEyd2LRRRVkhRRRQAUUUUANVAvSnUUUAIq7elLVBNSH2gxMMGpvtiO3lq+HPTip5kVyss0VC1wvIVl3e5pyMeSzA+mKOZCsySioI5mZmDLjHepQwNNO4NWHUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAcB8bfg7oXx5+HOqeDfEaTHTb9Cplgcq8TfwsPXHoa/HL9sT/gnBrf7MXhm78YWfiG01/wmlzHEN8flXkYbjlfunn0NfuVtHPAzXxp/wAFYYZG/ZA1cg5KX9qWOO2/B/nUSS3NIt7H5wfsQfsJ6h+1wdY1SfV10HQNLdIHuI4w7yyEZwoPtX3h4b/4I1/CTR9Shub7xB4i1WFPvW7yxxK/1KrmqH/BGGNE+Bfi9lGGOt7T9BGMfzNfoXSVmDbR8or/AMEvf2dFGP8AhCJPqdQn/wDiqcv/AATC/Z6X/mT5j9dQm/8Aiq+rKK0IufMOn/8ABNf9njT5hIvgCCYg52zXUrD/ANCr1Cw/Zj+E+mWotrb4eeH44R/D9hRv1Ir03mjmkFzyPUv2SPg5q0PlXXw50CSP0FqF/liuVX/gn3+z4sm//hV+jH2IkP8A7NX0Lg0bTTA8c0v9jn4KaKoFn8NdBhAOR/o+f5mvWdN0qz0WyistPtYrO0hXbHDAgRFHoAKt0tJKwgooopgFFFFABRTdwHesfUtfh0rz3vZobO3QZ8+aVUX9TQNJs2qK+J/il/wUr+G/hOOay0TxPHr+sZxHHYWzyIx9OBXjvhn/AIKIfGzXviHYJYfDC91zQ58CSCzsZwwz3BI7Vnz+RpGnzdT9OqKp6XfNqOn2tzJbzWjyxq5hmwGQkdDjvVytDIKKKKACiiigAooooArzQrtL5qBrJPMaTJ+lWZNqRNnpjvVe7uAulzzf6sCJm57cVHKaqTR+O/8AwVS/aTfxp45Hw40j9zYaS269deCzdgfWvtX/AIJj/AfTfhT+zzpXiJYs634qiW/upWA3BCTsT6d6/FD4neLj4q+KXiXXpJpL2K81Se4DyMSXQyEgfTGK/c79mn9tP4S/ED4a6JDY6zY+HLi0tY7dtLu5Fh8oqAMDOBjipHJ8x9RUVwtv8ZvBlxbCZfEmmsv+xdI36g1X1T4zeENPUTP4k01YvVrtF/mavmI5TttS1GDSbGa7uZBFDEu5mNfht42uLTxf/wAFLrZ7EiaC88Y6eylfcpmvqv8Abi/4KLeH9I8Har4K8FXw1LxJcELJfQEPBEvfBFcF/wAEu/2P9a8SeNrf41+NbR0sYP32kLc533M5xi457DnFUVZI/WeikpaDIKKKKACiiigAooooAbuo3U6igAooooAZRT6KBjKKfRQAUhOBk8ClrhvjZ4d8VeKvhjrul+C9Wi0TxHcQFbW8mTcqN/8AXoEdwGDDIIIo3A8g5FfiNq37SX7Vv7J+vmz8Xzag1q3JOo2/mxsPUOOK9++Hv/BZHRpmt7XxR4WubIjgvbtvoL5fM/Tykrwb4KftkfDv43ZTRdbgNxnC28jBJD/wE8mvdI5BIu4UE2ZNRRRQIKZNMlvC8kjrHGgLMzHAAHcmnZzyORXwX/wVO/aql+EvgG38DeHdQ+z+JtcGZWgkG+CDPVucrn3oA8m/bo/4KUavpfih/A/wqv4Ha3by73VIQJcydNsRGcn6V4/8Mvhf+2x8UGOu6bqvifSVb/lrq2oNa5+kbYP6V3P/AAS//YhPjnU4Pi546sRNokDn+yLK6j/4+5Af9e4I5UdvU1+uKRrGqqq7EXoBQVzH4OfE74nftafs665Fc+MNd8VaQwfYl1JI0lpIf7ofBQn2r9KT8NdQ/by/Ys8KR+KNUuvD2q6rZpdG4sm+WRlJALr3U46V9PeNvAPh34j6K+k+JtHtNa05juMF3EHUEdxnoazdQ1zwZ8DvAtsLu8sPDPhrTYBFbrLKscaIo4Vcnk+1AXPw++Ln7G/x5/ZAvJ9csItSl0e3ZtuveG5XdFjH8Uyryg/3uK+0f+CVn7WHxJ+M3iDxB4S8ZXMuv6fp9klzDqjIS0LFgAjuOORnAPpXhn7e3/BSJ/jZpt58P/h0rw+ELj91fajImJbzn7ijP3f519g/8Etf2bdR+BnwSn1nxDYSWHiHxNIt09vcRNHPBABhEdWAKnqcGgk+1KKKKACiiigAooooAKKKKACiiigApM460tNkBI4oAarlunNSU1VCinUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMkTd3xT68g/aw+OA/Z5+BXiTxpHEs97ZxBLSFwcPMxwoP8AP8KAPTrHXLC+1C8sILqOW7s9vnwq2Wj3DIz9a0a/ND/glT8VPF3xo+Lnxb8XeIZJJ4tQt7ZmZc+THMDjavpxX6XL0oKkrHM+Jvhl4T8aTLNr3hrStYmUYEl7aRytj0yRmmW/wr8GWePI8IaFD/uabCP/AGWuqoqeVCuVI9JsYhhLO3QeixKP6VaVQqgKAAOABS0VQgr5K/4KffDHVPid+ytrEGjWT39/pdzDqKwxDL7UJ3FR3OCa+taZJGk0bRyKHRgVZWGQQexoA/Hv/gkT+zfd+JPiXefEzWbAro2hwm309pUwJrhuNwBHIUEnNfsPWfofh/TfDOnx2Gk2Fvp1lH92C2jCIPwFaFAEN5Zwahay211Ck9vKpV45FDKwPYg1+Kf/AAUK/Y5179nH4h3PxH8FmWDwlqFybhJLMlZNOnOSV4HCHsc1+2VZHizwnpHjnw/eaJrtjDqWl3aGOa3nUMrCgD8Mv+CaUOoeMf21fC2p3Usl9eYub+5mkJJPyNlj+NfuB8SP+EhbwJrq+E0tX8StZyLp4vJCkPnFTt3MASBn2NeEfs9fsD+BP2bvixrfjXwxNdE31t9mt7GY7ktVJBfaepzivplc45oA/nN1y2+Jn7Ovxug8U+N/Ds7eJLO9F/I2tW3nQ3T5zy3Qg1+qHwY/4K2fCPx5FZWHi1b7wRrbIBO11CJLJW9FkVi2PqtfYvi7wD4d8faXJp3iLRbLWbOQYaK8hWQfqK+I/jp/wSF+GnjbT3m8ATSeCdVUZRCzz27n0IY5H4UAfdHh/wAS6T4s0uLUdF1G11Swl5S4tJRIh/EVoq24n5SB68YNfhk3wh/a2/Yj1eV9Ci1l9NQAvdaCGv7Jh6FNuR+KivqD4C/8FkdE1ZodO+Knh+TR3GEfWtJHmwhvWSIkMo/3QfpQB+l9Fcp8Pfip4S+K2kDU/CWv2Ou2mFLPZyhymRwGHUH611dABWbZ+G9J0/U7rUbXTLS31C6x591FAqyy4/vMBk1pUUAN2n1yaz/Ek8Vt4d1SWeRYoUtZWd3OAo2HJJrSr57/AG8PD/xB8Vfs1+JdK+G8TT67dKqSxREiV7fP7xY8fxEfpmgD89v+CLXhG8vPjR4t19SosrDSPIcnOWaR1wBxjjBzX7G18a/8EwP2c9d+AvwX1KbxTpo0zX9cvftLW7j97FCFAVW9DnJxX2VQAUUUUAFJgccUtFADZI0mQpIqujcFWGQa82s/2bfhppvj1fGln4O0u28SKCBexwAHnvjpmvS6KAEpaKKAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK99Mbe0mlVN5RGbbnGcDpX5N/8E29Rk1b/AIKCfFu8MP2QXEGqTNBu3bc3yDGcDP5V+r2tM0ek3jL94QuR+Rr8kv8Aglncy6h+2r8StTEbNHc2d9k9k8y6WTr+GPxrL7Rol7p+vdFFFamYjdK+I/8Agp1+yjq/x8+GtlrnhGwS98T6JL5rQLxJPBg5VT3I9K+3KQpmgpOzPgP/AIJo/tkaR4v8B6X8KPF2oGx8c6KGtbSO83K13ACSnLD76g7dvXAFffdeQ3P7IfwguvGsXi5vAumx+JIrv7cuoQ+ZG/nf3sKwH4YxXsG2s+Vjuj4l/wCCg2o/E64sbbwr4K8J3Orxa/tto9Tt2/495P8AaHYV0n7Df7Ddh+zRoMus+IXi1jx5ftvuL0jcLcH+BG7/AFr60MatjcA2DkZHSnUo01FtlOo5RSPhr/grl8O9L8Rfs0yeI5o9mqaJewvBMoG4qxKspPpzWL/wR7+Mtz44+COseDdQnM1z4YuwLbexLC2kGQv0VgcfWvSv+CoWm6rqv7I+v22k6XPq0z3dv5sVupZ0i3Es4A9OPzr5V/4Im6PqC+JPiXqnkumlNaWttvYEAyhicfXGaqxNz9YKKKKsgQniq8l0sbAMyqfc1P8Aw15z8cbjxNZ+Cbp/CVp9r1kkCMYHApmtKKnLlZ81/wDBRX9rLR/hZ8K7/wAH6fJJd+LPEVs0FrDH1hDHG84OcjPFeZf8Et/2K73we/8Awt3xrasmq3kTLpVlcrl4gx5nbIyHPIH1Ndp+zz/wT5mvvHl58R/jTcf8JLrksnmWGmSOXhtRycnPccYGa+8I40hjSONQiKMKqjAA9KhJ9R1LR0RJtAzjilooqjEKKKKACiiigAooooAKKKKAPkr9uv8Aa81P9knTdDv9O8OQ67LqsjRI80xjSIqM5bAr4gk/4LEePTcFl8JaSFfrsuGbH04r9cvGfw88NfETTf7P8TaJY65ZA7hDfQrIAfUZ6Vwlt+yP8G7PHlfDjw+mOn+iA1nymvN5n5p3P/BYbx3cLgeBdF+ou5GP/oNUNQ/4Kz/FHULd4YPB+m26+sUspP8AKv1Vh/Z3+GNv/q/AXh9fpYR/4VuW/wAMPB1qCIvCmixg9dunxf8AxNL2aH7Q/G64/wCCqHxpbPl2+moT627f41Hp3/BVT9oS61q1srBtGkWWVI1tV0wO7EnoDmv2VHww8HDp4T0P/wAF0P8A8TUVv8JfBNreR3cPhLRYrqNtyTJYRKyn1BC1UYqIpVLmx4ZutSvPD+nTaxbR2WqyW8b3VvE25IpCPmUHvg5rUpMUtWZBRRRQAUUUUAFFFFABRRRQAUUUUAFfJn/BUK3juf2QPFYkXcEeFx9Q2Qf0r6yr5h/4KSBf+GQfHDPjCwqRke9RL4S4fEeEf8EWbhpPg147i3ZWPW0IHpmL/wCtX6LV+Z//AARHuZH+H/xMgLZiTU7VwvoTE2f5Cv0Z8U+KdM8G6NNqmr3kVjYw/fmmYKB7c0o6BLV2NXcN2O9OrxzwZ+034D8c6glrpniOzu7g/wAMMox+terWOrW+oKfJk3Y5IpqSkOUHEkur6Kyj8yZtif3qqQ+ItPkcRJdI7/WvJf2wPH2ufC/4BeJ/E3h7TRqupWUQdIGBIAzjdgc8V+Nmn/8ABSD41aXP5kWq6e7/AN6SyB/9mqrlKMban76SapDBDvkdc+gNTLeR8BmCsV3Fc9BX4laD/wAFX/ippqM19pGj6gOxZWX+tJ4g/wCCrnxd152/s2w0uxmZdjSRxmTj0ouFodz9u45FkXcjBh6g06vzS/4Je/tHfGH41/EPxHp/ijUV1TwpZ2huZJJotrxSswCRocdOv5V+lWaZk9B9FFFAgpD0NB6Vj+ItYj0XT5Z5ZNgVCc5oGlc8++Kfxm034XaPNf6hcxxpGPlSVwpavxU/aF/ak+JP7WHxCl0vT5bt9OefyrLSdL37HUnALhev1q78bviV42/bi/aK/wCEd8IvdXdhcT/Z9NsUkITy16yv29ya/V/9jf8AYn8M/ss+D0R4rbWPF9z897q7RAsDjGyMkZVf50G8pLocD+wn/wAE/wDRfgH4YTX/ABlp1pq3jm+G+QTRrLHZDPCx5HB9SK+z4bOGEARQxxgcDaoFT0tBhcQKFyQOT1paKKBBRRRQAUUUUAFFFFAERXcMHkVheO5mt/Auvyrw6afO49iIya6GvLv2o/Elx4P/AGc/iRrVp/x8WWg3cyfURNQO5+Lf/BPH9mPRv2oPi1qOk+JYrhtB0/Tmnme3baQ5IC8/U19Z+Pv+CK9mzSSeC/HstvkZEGqQZyf95a53/giNj/hKfidxyLGzx+LNn+VfrJU8pXMfjLJ/wSG+N1jHssPE+mBP7ovXQfkKzLT/AIJP/HvVbs299qGmxW4/5aTXzMPwGa/a2iixB+df7P8A/wAEgfCnhGZNU+JOqt4q1Dr9it8x24Puepr9CdN0210ixgsrKBLW0t1CRwxqFVVHYAcAVcoqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvXvC+j+KrFrPWdLs9VtG6w3kCyr+TA186/Ev8A4Jx/A34lKXfwquhXXafSHMJH4dK+ndwo3D1oA/H345f8EqfHvwikn8TfCjX59ehtjvFkrGK9Re+GHWvRv+CY/wC25r/i7xdc/DH4hahNeapcAvptzdcPuUfNE2ec4/lX3J8cf2jfB/wD8F6jr3iO/hR7dT5dirjz5j2AXrX5HfsN6NefHD9v6z8W6Lpr6dpFvqd34hmUZKwQsTiMt0ySwGPeouaep+5VFFFWZnP+PfG2l/DfwbrHibW7lbPStLtnuZ5n6Kqj+vSvwt+GPh3X/wDgoN+2Qs+rrK9nf3h1C/JYkWunowxGvpwQAPev0R/4K4fFf/hBf2a/+EcgljF54ou1sjGXAbyl+dzj04HNfnT+wL+1hov7Jvi7xPrOtaJNqj6lYLaxSRHDRYcHB9AcCgD95vD/AIf0/wAK6JZaRpNpHY6bZRLDb28K4WNB0AFaNfKv7L3/AAUO+H/7THiL/hHLRJdC19kLw2t66gXGOSsZ7sB2619VUAcl8WfH0fwt+G/iPxZJZzagukWUl39lt1LSS7RkKAOSSa/n1/aP/at8bftKeLr3U9e1K4ttMkf/AEXRbeUiCFRwBjP86/oxnhjuoWiljEsUgwysoIYHsQa51fhf4PViw8LaOG9fsMf/AMTQB/P/APss/Fb4a/B3xUPEnjbwVe+Ndds5lk0+1Nwq2+fV1YEZHuDX70/Af4wWXx4+Feh+OdO0q+0aw1ZGkhtdRVVl2hiobgkEHGQa8/8AjN+wv8HfjlbomueFYLG4Q5W60gC1l/NR/SvVvhf8OdI+Efw/0PwfoKSJpGkW4trcStubaCTknuck0AdTRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8e/wDBSr4G/Ej9oL4ZeGvC3w/s1vYm1QTaojXUUAWIKdrfOw3YJ6DJr7CpOeO9AHh/7H/7Ndj+y/8ABvTvCsJjn1aQ/adTvIxjzpyOfwUcCvcBS0UDbuFFFFAgooooAKKKKACiiigAooooAKKKKACiiigBGUOpDAMD1Br4+/aY/wCCZvw0+Ozvq+hRr4C8WF951HS4h5U3HSSHIU9uRg/WvsKigD8tP+Cdf7Fvxi+CH7RWtX/ic3GgeGNGjkgcxTs1trDtkKYhjDKBySwUjj6V+pdFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1mC4ycU6mSRCTG7tT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMjxZqlpovhnU76+mWC0gt5Hkkc4AGK/J3/gkjeDUv2n/iLdWuY7KTT2lEedwG6UHGfbFfpd+0b4fXxZ8F/FejNcNaveWTokq8lT64yM/nX5x/8EUNHZvGvxL1AplYrK2g83H8TOzEf+O/rWLV5G0dIn6z0UUVsYhRRRQAUUUUAFFFFAEc9vHdQvFNGssTjDI4BBHoRXOeBPhr4Z+Gdjc2fhjRrXRra4l86WO1QKGbGM109FABRRRQA3HFJt3dRmnYo20wEwKDS7aMUC1FooopDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5p/4KLQ2tx+yL49W7JCC03Lj+8OQfzr6VOa+Z/8Ago4W/wCGQPHu04P2YdvespP3S4fEfNv/AARJii/4Vz8TXUfvTq1spbPbymxX2j+01+z/AGX7SXwzuPB9/rN7okMsiy/aLLG7I6Ag9RXx/wD8EVbKCH4O+PZ402zS62iu2TyFiG0fhk/nX6M4oFfW5+MHif8A4JJfG/wLeGfwnrun62i8h7K9a0k/JsVyk3xg/au/Y51C3j8QHVEsbdfLj/ta2+0Wu09PnAyfxav3J21yHxYn8N2PgTVLzxZZ2d9o0ERaWO+iV4/yak0hqb6nz9+xj+254a/a/wDDt5omrWVvp3iyGJmvNHf545oc43LnqOele0yfs2/CqT73w88N/hpsQ/8AZa/I7/gmeba4/b1d/DDPFoPkalIqYOBbYxGpz2BK1+1Ov6tHoWhajqUxCw2dtJcO3oqKWP6CmLU/Kz9sr9qbwB8EPipeeAPA/wAK/CerNZogubqS1U4mPJjAA6isz9gb9pjTviR8d9I8AT/DTwlYadeJcu1xHYqZRtUsoywPpXy78O7VP2hv2wvtieYINS1x74jG4iIMSB+WK9h/4Jv6TG3/AAUFmiWNfLsF1YqoHCgZRcfTdQa8zsfsvaaT4a8AWM89tZaZ4ftGOZZIoo7dCT6kAVrWOoW2qWsd1Z3Ed1bSDKTQuGVh7EV82f8ABSPw7Pr37IfjWS2d45tPjS+DRsVICMM9PrXln/BH34lS+MP2d9W0G9vJbu+0HVnQec5ZkhkVWRRnsCGq+Yytpc+8aKKKokaWFfA//BUv9qab4SeBLTwl4cvPs/iXVuWubeTEttGO4I6Zr7xnkW3tZpZDhUVmLegHNfgf8TtUn/bM/bZttHsrl5LDVNWj0+3kdiwSBT87+2QCaDSOhP8A8E5Pjp4H/Z7+NV/4m8bSyw250yS2gkhj37HJGTj3Ax+Nftt8M/jh4E+MGnRXnhHxPp2tLIu7yYJ185fXdHncPyr5U8T/APBIT4KapoL2mkHWNFvjyt2t602D7q5INfnX8WPgL8YP+CfnxEsNas9Rns7fzsWPiPTWYQSjuki/zU0C0Z+/dFfP37E37UUH7VXwdi8QzW8djr+nznT9WtIz8qzqqneo/usGBH4+lfQNBAUUUUAFFFFABRRRQAUUUUAFc58RvBtp8RPAXiDwxfLutNXsZrOQezoV/rXR0UAfgr/wT7+Ok37LX7TRsfE8jaPo2oB9K1pLgECF1JKMfTDD9a/d/TdStNasIL2yuI7uyuIxJDcQuGSRWGQQR2r86P8AgoV/wTnf4hXWpfEv4cW2/wAQSHz9U0Vel50y8Y7N6jvXjf8AwT3/AOCgEXwNhb4ZfEyS6g0SKfy7G8mBLWHrG+ei5/Kgqx+w1FYvhvxhovi/R4tU0XVbXUtOlGUubeUMh/EVpi6iZNwlUr65oJJ6KzLjXrC2Db7mMY96+Yv2n/2+PA/wR8Paja294mpeIh+7jsYGBbJ70Dsz6nt9Rt7qRkikDMvWrNfk5/wTe8O/GX4zfHKb4sa3r2o2fhWMN5wmZvK1EkYCopOMDqSK/WOgQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNS1G30nTri9u5BDbW8ZllkPACgcmvlyT/AIKc/AOK7kgbxavycb/LODX0Z8RPB0XxC8B+IPDE9xJaQ6vYzWTzwnDoJEKkj86/OqT/AIIo6Sfu/Eu7H105P/iqAPozUf8AgpR8ANL06W5HjeG8k7RW8TsSfQCvkP8AaG/4K5yalHd6X8MNPkttzYTVr/t9FrpIf+CJ9sv+s+JUp/3bBR/WrT/8ETdGP3fiPej/ALck/wAaC+byPhz4Q/CX4lftsfEKJbvVri9tvtObzVNQuMpbIxycAn+Vfsv8FfBPwd/ZM0Wz8HaNqemWOp3Cjzbi4njFzdsTwTzk+wFfGWp/8EgfHfhLTZU8D/FZ45Jf9ZC6vbq31KmuU+G//BLn4yWvxu8Jal4z1G1v9C0+9huLnUY9QaWURRnOxQ3OeKnlFzH6+0UgG0AUtUSfjb/wWo8SXV/8dfCGhlj9i0/QBcqvYvLPIGP1wi193/B//gn98HfBvw107SbzwvbazdT2sZu728G6SViASc9uTXwR/wAFntNmi/aF8LXfkyeVceHkjWTadrMs0uVB7nkce4r9M/2T/jxpP7QHwX8O+ILK6hbUfskcd/aI4LwTBQGDDORkjNA7aH5Eftpfs3av+w78ddH8QeCLm8ttDuj9q0jUEB3W0wyDEW6bvQdxX7Mfs9fGCz+PHwb8MeOLMLGuq2oklhVgTFKCQ6HHQgg8V8+f8FWvA9t4r/ZJ1jUXjzeaHeQX1vIBynzbG/MNXn//AARl8d3OvfATxJ4bnRvK0HVswuRwVmXeRn2Kn86Atpc/QmiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFUNY1RtK0y6vFtpbswoXEEIy747AetfO3wl/wCChnwc+LGuLoMety+GvEG7YdO1+E2rbv7oY/KT+NK6K5WfTFFQwXUV1GJIZEljPRo2DA/iKk3UxHiH7ZsurWP7PXjO/wBFuY7S+ttNmkWaRsAYGa+Uf+CK+hpa/DH4h6pu3Pd6xHDnbj5Y4+x/4Ga90/4KQfEaDwL+zT4nhlmtg2qWr2SQSvh2ZxgEfSud/wCCTfhldB/ZH0m88jypdUvri6ZscuN+0H8lrJO8rov7J9m0UUVqZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFQ3CSyQkRSeU/rgGnxhlQB23NQBFcXC265bgetfOn7eWnz+Jf2VfiBHbODFb6bLNIuRk7eRWR+3N+1dF+zb8PZpofLl1y9Hlabb5BMjd3Ix0FflbqH/AAUR+J3ibwj4t8N+IZ7bVbLX7SW1kdYxE0SsOgAAB/LNc7vJWR0pKK13PuX/AIIu7o/g/wCOgTlTrYwP+2Qr79vvGGi6ZcS291qlpBcRLueGSZVYD6E18Uf8EefD9vYfsy3+qIpE+oazOZGJPIQKq18r/tcfsb/tFa18dPFOs6JYar4h0jUrx5LO40+6f5IeqqQGGMDjnPSrM9Ln6J/FP9uH4V/CWNk1nxTaTznotiwkP6Zr8zf2qf8AgoX41/ams5/AXgbR7mx8NzzYZYUMl1dp/Cr8fKPpXmcv/BO79oiZvNk8C6hM/rIysf1NXfg7/wAL1/ZP1LUdQ074Y3TmbCyyalpLuRg8YOOPwoKsj9Hv+Cdv7Dtv+zv4di8ZeI0MnjvVLXY8Z4FjExDGMY6kkAnPpX0N+1Hrh8N/s4/EvUl+9D4fvcfjCy/1r8u9F/4KpfH7U/EFhpEHhrT7q9ku122CWMgmlQ/wdenvX3x+294qvbX9iPxpqF/b/wBm399pSQzW7HOxpCoZP50ibH50/wDBIbwVD4m/aJ1TW7mMNbaJpbS/MOAzEDNaP/BMqVL39vjxDdJ91rXUmH1Mq816t/wRq8Mx2Xgr4o+LZYlVP3dmGPXCRF3/AFIryD/gkfGLz9rnWriQ75U0q6fceuTKmTVAfq9+094TvPHX7PfxC0DT4ftF/qGiXUNvH6yGMlfxyBX5Vf8ABI74wD4b/H3V/A2rMbeHxLB5KCT5dt1CThSPUjcK/aE/NweRX4RftmeFrz9lP9tqfXdCia3iS+h8Q2JXgYY5cD6ncDTsStrH7wUVxHwV+KWm/Gj4X+HfGWlH/RNWtUnCE5KMR8yn3BzXb1ZBwfxyvtR0n4K+O73SMtqlroV7PagdTIkDsuPfIFfi1/wS00OLXP2y/DzXAD/YLS8uRuH8YUgH82r9z9c0sa3ot/p7sUW6gkgLDsGUr/WvwX+AniST9jH9tyCPxG5gg0nUbjS9QkA/5YPkb/fsaC0fvvXiP7aHgnw147/Zu8b2Xib7LFbxafLNbXV0FP2e4Cny3Uno2cD8a9lt9Stbqzhu4riJ7aZQ6ShxtYEZBBr82f8Agrt+0rb2PhWy+FWi3KS3l8y3OotG2fLjX7qnFBKOZ/4IkLIuq/FNdzGFYrDC543Hzcn6nA/Kv1Yr4O/4JE/B278A/AnU/FGpWgtr3xRdi4jLJhvs6LtjH05Yge5r7xoEFFFFABRRRQAUUUUAFFFFABRRRQAyviH9sX/gmf4a+P8AeT+JfCUsHhfxXKwa42piC69yo6N719wUUDPw5v8A9i/9q34HzPaeHI9budOHT/hH7wvF/wB8E4/Sp7Kw/bZ2+VGvjbH+0FFft/RQPmPxK0/9n39tPx1IRO3iO3jlPzyX16sQH5V9H/AD/gkfaabq8Gv/ABe10+J7teTpkLsYs9tznk1+k9FAcxlaD4e07wno9tpek2MNhp1unlxW9uoREX6CtWkpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPDf2sv2WfD/AO1J8OZ9E1ONLbWbdWfTNT25e2kP9Djmvyhh/Zq/ag/Y18RNrfhfTNRJ3FRc6E5uIZl9HiH+FfuhTHUSfKy7hQVc/GT4vftFftU/Hb4bXfgLWPhtqkFnfKi3VxHosys4BzjO31r7T/4Jg/AXxb8C/gvq8PjDTo9L1DV9SN5Haj/WJHsCgP6cg8V9k49h+VOoC4UUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMAoooo5mAUUUUczAKKKKsAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopu75iMUAOooooAKKKKACiiigAooooAKKKKACiiigBuyvkz9rz/gnp4Q/acaPWbG5Twh4ujwDq1taeb5ijs0YdMn3zX1pz60c+tZ2Y7s/GzUfgr+2l+ylaznw7qWpa/pLHh9Jna9IX1MZG4VyPh//AIKv/H3wTNbWGtDTdVNu/wC+TULIxTSD0LcY+uK/cDbXLeJvhP4K8aSiXX/CWh61L/z0v9Ohmb82Umnylcx+Ff7Tv7bmv/tReH7XTdZ0C2sJobkXAuI75XXaARs2bV/PNfsp+xj4Jvfh3+zD8PNB1GHyL610yMzR4xhm+Y/zrrY/2f8A4YxY2fDnwkuOmNDtf/jdd3HGsaqqgKqjAVRgAelNRsEncfRRRVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANVs06kC7aWgAooooAKKKKACiiigAooooAKKKKACm7Ru3d6Wua+JXih/BXgPXNcjAaSxtXmUMCRkDjgUm7K40rux+KP/BU/x2/jH9p68023u2vItIhSzWNWyqyd8Ad+lfN/xA+BPjn4W6ZpWp+KfD15pNnqi77OadPllHuc8VveG9Wufix+09oN5qbq0mu+KLVZd3PyvcqpB/A4r9/vi78BfB/xu8CP4U8U6TFeWPk+VDIo2yW5xgMh7EYrKN47Gsnc+cf+CSNvdW/7JFj9pt2gV9TuXiLfxoWGGFfadcZ8HfhXpXwU+HGieDdGeSXTtLgEUcs2N7nJJY49Sa7XAq+UzuG0HikaNZFKsoZT1DDINLgUbRRykmDD8P8Awxb6rHqcXh3So9RjGEu0soxKo9mC5ri/2mPgpF+0F8Gdf8EvdfYnv0UxT9ldTlc+1ep0VVhnzl+yH+ylF+zL8FtQ8HXF8upXWoyzT3dxGMBi67cD8ABX5G/sK/HrRP2b/wBpiTXfEDyR6NcxXFhPJGMlMv8AKT+Kiv3+2ivzy+IH/BGrwD4n1q4v9F8W6poS3DmR7cwpKuScnBJpcpXMe7Q/8FFfgNKAT43tl+qGvgL/AIKmfGL4V/HS38IeIPBmuQaprlmr2s/loQxizuAP0JP517B/w5J8Of8ARSdU/wDAKP8Axqyv/BEvwh/F8RdZPfi1iFUK6MD/AIIy/Gq8vF8VfDfUdQlnt7VFv9NglbKxoThwg9yQa/Uuvlr9lX/gn74L/ZX8SXfiDS9Tvtb1i4h+zi4vAo8uPjgAfSvqWgkZX51/8FHv+Cfuq/GTWYviD8OdPhuPETDZqenAiM3QA4kB7t61+i1GB6UDPwP8N/Ej9q3wfoP/AAhNhF40jtbQbIbX+zpZTEB2VscCvdf2bP8Agnb8Rvjd8Qx4z+Oi30GksuWhvrovd3XorZyQv1r9ePs8QbcI03eu0Zp+B6UD5ijoOhaf4Z0e00rSrSGw060jEUFtboESNQMAADpV+iigkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilyoAoooo5UAUUUUWQBRRRTAKKYisvU5p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFN2/MTnrSeZ+8CYP1p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtZWvR6lItqdNdFZZQZQ/dfSgDVopFzgZ60tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5B+1wuuSfs7+Nl8OW013q7WDiGKDlzx2Hf6V7BTWUOpDDIPY1MldWKi7NM/A7/gnP8GZPi5+1NogulY2ugv8A2veBkI2yRvlB1H8ePy71++GB6VzPhn4W+D/Ber6hqugeGdK0bUdQO66ubG0SJ5j/ALRUCuowKXKNyFoooqyAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiio5mAmRRkUzdVZmO/HNTzMpIu0VB5Mn9+pq1JFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqOMSDO8gj2qSigAooooATHfvS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNDgkjI4oAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlN3H0oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUmayAZtqNiPNHGakZgvU0ir82aVix21vWn0UVsQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSZo3U3AoAczbaWmN8wx0pd1Ax1FN3CjdQIdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gBc4yTwKYqJ95QDuokXzI2UnAIxmkhi8iMICWA7mgCWim7jRuoAdRSUmTSbsA6ik5paYBRRRQAUUUUAFFFFABTMsu4nkdqduqNpAG27gDQBIKWq9vO8jMHTYAcAnvU+eKSdxtWFooopiCiiigAooooAKKKKACiiigAoooqeZAFFJRzRcBaKZuOKNxqfaIdh9FNyaMmmpJhYdRTdxo3UcyEOopm73pdxqrodh1FQmRvSjzOm5tv41n7RBYmopu6kzWidwH0UUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADJASKdS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTdgpQ26lrICN4Q1O206igdwooorUQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAReYN2CcH0qhdrNdXAEUrxImVbbjr6185/tlftraR+ynZ2NreaFqmr3+poxgktQqxR4/vOxGK4/4Af8ABTf4RfFaGPTtW1CXwjrBAVo9Y2okrYwSrqSPzIrLmZrGPKrn2PB5iqBIQ2BjIqasnw74p0bxVYR3WjapaapakYWW1mWRT+INafzc9KzXNHzJFVSKNx3Y2n61RutU8mFXCtnftxVqGVnXkc1cZOO5Ti1qycsVxxnNKx20xl37ecYqlq+sQaTZy3E5CxxjczMcAD61pzJamaTk7I0KWvFvDf7Ynwi8U+MP+EWsfGentrYYp9nd9oLDgqGPGc17NHKsiqynIYZBHII+tNNPYGmtx9FFFMQUUUUAFFFJu4JxQAtN3dKA4PGeajZn3KFVSvru/wDrUroBWLeZjb8v97NKrBs45qGWY+ZtCblPU56U1JY7dmUnA65NY85pysuUVVa4ClD1RujCpy+3HFa3RFmPoooqhBRRRQAUUUUAFFFFABRRRQAUVE0xEwTYcEZ3dqczHBx1oAKYju2dyY/Gm7WJDs2Mdh0pJp/LXIx+NJuxSjcfvfuF+nenox289a4Tx3r8mj6XPJFcFZkRpC6D7oAz+dfGXwm/4KRJ44/aCsfAMGm3H2GSV7eW8upBuMikj5QO2RXP7T37G/sWfoPtoZguM0kbeZGrYxkZpTg9a35kYW7j+1Vbi+S3YhzirDHg4Irl/GGpR6Lp82oPHJJ5Y5AHy1E3oXTim9SzY+KLS5uWWS5jhjdtsJdgpc9wM9a39/y8dcV+BH7Un7Q/jP8AaF/aCuNK8P6neW9lFqH9naVZ2Urw/Pu27jg8ndnmv3M+FWi6j4b+G/hjS9Xne51O106CK5eQ7mMgjUNk9+c0oXXxDqKP2TrqKQUtbGIUUUUAJmgsB1qKTKKTgsfQUuQ6jORQOxXu5H5GDtx1r5N/bO/assPgP4Ea6SWZtVuJcWsKttbcPX1FfUet6pDpdncTXEohijUn5v4sCvw+/ac8e6l+13+1hZ+ELAtDp41BdPtlJzt+bDsfXvXJL947M6oe5C/U/RP/AIJ0ftHeP/2hvCOt3njLStllaz5sdTCbBMpP3cd8etfZH8NcZ8Ifhjpnwj+Hei+FdLhWK0063WIbf42A5Y+pJrtOK6Ixsc0nd3Clpu75gMfjTqskKKKKACiiigAooooAKKKKnmQBRTcmjJqADdRuqIyc9KbHIzMcmuf2rL5Sam5psm8r8pwaa0m1RnrUuaAk3UbjVWRhCqszFsn0p32hNwXccms41LFWLG7b1NGarsxbqc1yXiL4teF/CfiCz0fVdYtbC6uU3Is8gXP51XOwsztNv+1QjHnnNRwzRXkEc0MiyROAyuhyCD0IqVVCjFdHKxFZZm891xxXlH7TnxQuvg38LNS8Xw232tdPUO0ePevYBAOTn5j3rA8deBdK+JHhHU/DeuW4utL1CFoJo2GDgjGR7ijlHzLsfJH7HP8AwUg0D9oLUJfDviK3j8PeIFY+QXcCKZc8AE9DivtVZBIoZWDKeQwOQa/FL49f8Exfij8GdcvNb8AiTxFokLmaGSzcrdxLkkDHcgY6V2n7Hf8AwUs134T6wvgn4xPez6RGxiXUbtWa6tmBxhweSo6VrH3RH6/DoKWsHwb400b4geHbPXNA1CLUtLu0DxXELZBBH6Gtv8a0Mx9FJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMBqrtzTqKKdkAUUUVABRRRWoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBzHj34a+GPihocuj+KtEs9c06QYMN3GGx7g9QfpX5/ftGf8EfdB8RO2pfCjUY/D9zjL6XqTtJAx/2WwSPxr9KKaVPQHA+manlRXMz8Ibz4W/tM/sL6lFr8dvqGn6VbyZL2lx9ps3H+0qk4B9xX3n+yn/wVG8FfFqPTfD/AI4x4V8XTFYBJIP9FuX6Aq38JPocV9wapo9nrVhNY39rDe2cy7ZIJ0DIw9CDX5t/tc/8EoINbmuvFPwdddO1J3aafQ5pCI3YkkmFv4Tk9KmzHdH6UKIrmNJEKSxsNyspyD6EU6GLy8kmvxj+E/7aHxt/Y18TWnhH4maZf3vh+CVYZItSQmWOMcfupOhAHvX6z/CL4zeE/jd4Ttte8K6tBqNrMgZ40ceZExHKsvUEdKfNfcbv3O4kkEcbNjoM1+X3/BTv9rHVPDulJ4F0G9e1uL8k3TxMVdEB6Z96/QP44+Oo/hv8N9X12S8itBaws4aU/e46CvxQ+F/w78S/t+ftPyHVLiT+y3uWe6vFU7Y7dWOFHuRis5K87dC4+7Hm6mP+xz+x/wCLP2qPFj3GnXjaToenzBrzV8kSAnnCnu1fvh4P8Pf8In4W0rRvtUt6LG2jthcTHLuEULk+5xXP/CP4M+FPgf4Sg8PeEtMi02xjA3lR88rAY3Me5NdxWkbmUncWiiirJCiiigApu07gc8U6o5JCikgZoArzNH5jDzFDHtmmxL9nj2sFOOc5qldXltbbppdm4ckHqK8m+MH7S/g74L6Pc6nr2u2Fr5aFxZSTD7S47bY+Sc1kdipNq5684mkYOJ1tx2jcA5/HNWGhE0Z3KCCOWzxX40/Gb/grN4y1zxE7eBdMg0axibCS6gPOaRex2YGPzNYfhH/grz8bNB1C1XUoPD+vacjZktfsbQvID2EgY7fyNc9NS1cokfM/bS13lNu0IgGF7/jU+0/Lk8ivln9mL/gob8NP2htPtrO4vrfwl4rI2yaLfTjlv+mchChx+tfUihZAsituUjIIPBrcyJqWmMWCjaAT9aNp7nBrW6Mx9FFFMAopKKAFooooAKKKKAI9v5UdtvTincZ60i8k0DGbtyADnsc1HJGuMkAipjGMYBxis/UlbgrNtx/DXPO5pDV2R82ftsfEq5+EfwX1/X454SqxGGCNupmbge/Ffhn4P+Jmr+EPiRY+M7dxJqdrei8OeAzbskH2NfoX/wAFYPGkupXXhnwNa3Uhu5rozS2qn5WJOFzXinx4/wCCbXiP4R/BXSfH9nqJ1WN7ZLnULZsZgDKG4wO2e9RStZuW501G01Y/YT9m34uD46fBPwr42+z/AGWTVLXfLCBgK4JVsc9MivSua/P3/gkJ8cLfxZ8I73wBcTEah4ffzII27wOSePxNfoLtrZanK9GRnbGpZuPWvnz9sb4qT/Db4L+JNUjby1FrJFH672GBX0Mw3KQeRX5k/wDBYj4gNo/hPRvDFreFZL+4Es8IP8KjoKUk3ZFQt1Pl/wD4Jl/B2b4wftQ2et3aO9hoJbVLqTghpskqM4PUmv3V2/ga+F/+CQvwri8I/s5z+KZrcJqHiO+kkEmOTAnyqOnru/KvuvbV8rIbClooqyAoopGOBQA1qbI21SafjNVL6T92VX/WdvSk3YqKuzyn9pTxhp/gn4U+INUvZQfLtn2c9G28V+XP/BKvwFa/Ez9qjWPFd9C1xHpEMt9GxPAmdyFJ9eDX1Z/wVU8dN4a+Av2NXWO91G6WIcfeXHNcj/wRb8BvY+A/GfiqSPaL65S0ibuVUZP61zQWrZ0TdopH6VelJsFOqFpirbcc10t23Oa1wjjcKwZsg/nUo4AFRR3CyZGckUjTnztgBxjrjii+lws9ieimjNLzTELRRRQAUUUUAFFFNas2rAJRS0zcal2Q7AahiheNiWfcD2xT5pNi5qrJM6jIavPlLl3NYpvYnMxyahWYXGU2sretUGacsT5h/IVahhK4Z3+fHBzU86NnFRJtrbWjY7j2b0pjL5Kb3+dx3qtcal5LbY2V+xLMAK5rVvij4e0BdmsatbacM4LXLLGPwJPNRo9iOU621LyMSTwa/NX/AIK8/BLW7i38P/ELQ/tc8VnugvFt937peobjoK/SPw7rGn+ILRL3TbyG8tWHyvBIHB9+Kf4l8Oaf4u0O90fV7WO90y9haGeCUZVlI5Fd1GC6kczPzv8A+Caf7dQ8XWsfw28eahHFq1rGq6dfzuB56AABCfUDFfpIMNhhyDyCK/DL9vL9je9/ZN8YWHibwrdzf8IxfXDPaSxjD2cuchM+npn0r9Ov2Bf2ih+0R8CNOvbtgNc0cLp98pbLMyKAHP8AvAZrpSvsS+59LUdKKWnymYxucg8ivjD9uD/gn3oH7QGl3nibwvaw6T47hiJV4VCJeY6LJ7+9faNFHKVc/Dz9kv8Aa+8dfsafEI+AfG8E0fhg3nkXVldg/wCifPhpIx6cfiK/avwr4s0nxtoNprOh30Oo6bdIJIp4HDKQRnt39q+Tf29P2DtF/aO8P3HiXRIk03xvYQs6TQoP9NVQSI39/Q18Z/8ABOH9sO/+A/jp/hR43W4TRb29+ywtOTmxud20qQeik8VQ9z9lqWkVgygg5BGQRS0yAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopWQBRRRTAKbvFOpmw1kA+ikpa1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBFbdS01VK5zTqACiiigAooooAKKKKAPOfjh8CfCfx+8F3nhzxTp0VzDMhEVzsHm2744dD2Ir8gPHvw3+L3/AATG+KMOuaFqP27w3dysIrtAxt7pMkiKVT0bGMn16V+4e2vLP2kvDvhPxP8ACvVtP8Y2ttc6XLGVzcKCYyR95T2IrKXu6s0jduyPzM/ak/b80/8AaT/Z7S0sbX+xtYiKpf2EsgJkYgBmTH8Oc4zX0x/wSN+FaeE/2f5vEt1ZrFf61dsySsuH8peB+Br8fPihoekeFfiFrum6HdjUNJtbtktpieWTdwp+g4/Cv3f/AGAfif4W+In7Ovhu38PXUDXWlWyWt9ZoQHhlAAOR6HsamEeVt33He0bH0nS0lLW5kFFFFABRRRQAlRuwC81JXJ/EjxUng3wxf6pMHFvawSTyPGu4hVUk8fhRexcI8zsj5W/bg/bFsv2ePC9zBpNib7xFfhoYPMk2CPsXxtOQPwr83P2d/wBl34jft3ePL3Vb7U7ix0jzS154gu4mmWLJzsjQuufYA8VyXxn+Ll3+1d+0RBdXck0GnX+oRWlnbySZEUTMFz0HJHP41++fwn+HOifCvwFo/hvQLCDT7Kzto4ysKgb2CgM59SSM5rGK7nRUqSkrdD52+Cv/AATD+C3wntoZdR0X/hNdYVQJLzWhvjLY5Kw/dUZ7HNdt8Rf2Cfgb8SdFksLvwFpmkuwwt3osK2kqH1BQY/MV9CKp2jJyaNtVZnNc/Fr9rH/glz4o+B9jP4o8A6jceK/D0G6eVGiEV5YgcjBDHzB74Few/wDBO3/gojHIunfC74k3Uovd4t9M1q6kPz/wrC4K8EcDJNfqFLAk8bRyKskbDDKwyCPQivyR/wCCqf7IaeBdWtfir4G0j+z9MfjVkslCLBLuyJlA+6STzinZjufrgMMMg8HuKdXwP/wS1/a2h+Knw8PgbxNrPn+LNKbFt9qkzLc2+OOT1K4r733VJNhaKTdSMwXGTg1rsIiuLgwx7htPPPNPhk8xQa+Sf21/24/D37NWmixt1j1fxXPExtbFZPlQ9Nz+mK6f9gnxV42+InwNt/GXji9Nxe67cyXVvAY9ggi3EAD1BxWV5OWmxrypRu9z6TopKWtTIKKKKAGNHukDZPHalVduadRQBF8+09M9q5nUbSewE8wZpmJyit057VuX2pLYqAwYljhTjjNcZ8VvF8fhf4beI9XuZltnsLOWYSfw7gpI/WsJ6ux1Um4vm6H5F/Ef7b+0N/wUdstFdVmitdUjtwsJyAkZBbrnuDX7G+MvAth4t+H+o+F7mEPYXNm1rswPu7cDqMZr8nf+CUHh8fFD9qbxh471FGluLOKe9D9V82aQjv6bjiv2LqopIynLmZ+GnwP1rUP2Nf28G8OW8v8AxL59UXTZRdZw9tKRg/LjkZwO3FfuVX4y/wDBVT4e6h4B/aE0z4gWkDR2d0Iisg4xLG24H8a/WT4J+Ov+FlfCPwh4nZ43l1TS7e5m8n7okaMFwMk9GyOacWhSXU62a8igL+Y4UAZr8N/+ClHjGb4mftaT+H7PfMtk8NnCuDzI+P6Gv3B1m8tdH0u8vrx1S2hjaSR26BQMmvxL8B28f7UH/BSgXmkwSS6Q+vC9kdVBCQW4ALdOh2frR1Q1tc/Y34H+Brb4a/CDwf4ZtYjFHpumQQspxnfsBcnAHO4tXcUlLWhkFFFFABSEbqWigBKq3JTcFb5Qe+KtVla1fGzt5TkZ2kqp65qJ7GkE27I/LH/gst4utri48IaBA+97cvLIQfWvsb/gm/4IbwP+yR4Mjltfs1zfxvfSZ6tvY7T/AN8gV+Z37dk194+/a+0zw9PcpfGSW3gWGMcKzuMgj6Gv218FeGbXwb4Q0XQrFDHaabZxWsSk5IVECgfpUQWhdTsbVY99ffZ45mAcKmSWIrXqhrqr/Y95ubaPLbn04q57GcdzkfDvjDSr2+aBtWtI5/M2+RLMqyknoAua7ny8rjJ/Ov5wvip8VvFWi/tBeJ9atdbuvt2na/ctbMZDtTy52CDbnGMAcV+9/wCzD8Tb/wCMnwB8E+MtUiEOo6rYLLcKowDIrMjMB2yVJx70qd7WZpUld6Hpcl3DZxgzzRxL0DSMB/OpVlVlDKQQeQQeDX5g/wDBYb4p+IfC9x4L8PaTezafb3gknla3kKMxBwBkV1H/AASF+NHjL4keH/F+heJdauNYsNHWA2X2o75I92QRvPJHHSruiGlY/RmikFLTMwooooAKa1BakrOTuA12IHFJSyAlTTVB2jmuKbNClM5kYDccKeeO1Vri4IZQo4zWr5fX368VTnjjH8PSsJxN6cl2GLCrRO5XAA9a+Zf2r/2stG/Z20Vbprn7bqJ+7ZqwzXf/ALRX7RGl/A74c6nrVyBNNDGwjhJA3N2r8VtQbx7+3T8dAun2U0k97OqLGoLQ2kZP3mP61rTpxmrmnNyRfMjtfG37e3xt+NHitbLwjdXWjpNIVg03SLdZ5ZsnjO5Tz9Kn8Ufsh/tYfFi1j1LxFoGtakdgdIruRUYgjP3Riv1T/ZH/AGLfCP7LvhSOKC3h1bxPOA93q80QL7scqn90A+lfReBXbGmo/Cjj5mfkJ/wTd0z41/Cf9pCHwf4h03XdO8Py28ov7PUY28hdqna6sfTjGDiv1yuLyC1iMk0qxIBkljip/JjMgcou8DG7HOPrX5g/8FRviz8Zvhr49sYfDNxfaZ4NurMYvLGLeDLnkMcHFVaXQVz1j/gp98YvAS/s+6t4Yu7621DWrza9rbxsGZGB+97Vx/8AwRd8NyWfwj8Z63NEU+3alFFE3qqIc/qRX5J+JNc13xhqT3mr3l1qd2xO53JY5zk8dq+ov2Q/2+fGf7MOlnwwmnWuteH7i7WRorglJIMkBiMD09aqKsF9D94qWsnwpr8XirwxpOswDbFqFpFdKuc4DoGA/WtaqJCiiigBhr8h/wDgrH+zQfh74usPi14YtxZ2eoTBL9bZNgjuBysvHc+tfr0a+Sv+CoNzpsH7IviddRjDtJJCtvxkrJvGCPegqO53n7D/AMaYvjp+zf4T1xpmm1O1tl0+/wDMbc/nxAKSx9WADfjXvVfAn/BGtXH7OuvOwO19achj/F8g5r77oJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKVkAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaAGTTLBG8jkKijcSegFflz/AMFLP2ubmz0FfCOkXMUqX5dWaFwSig4ycV9wftVfGbQ/hP8ACfXrrVL4Ws01pJHAqsAzMVIAFfjL+yb+zX4g/bM+MEi3dxMPD1nIZ7++nLMFTORGD6msWuZ26G8VyrmPof8AYP8A+CcnhT4+fCceO/Hd3qBF/O62lvbP5fyqcFmPfmvN/GS+JP8Agmd+1oR4cuLyXwtPtdVuc+XeWzHlG7Er0z7V+0nw/wDA2k/DXwZpHhjQ7dbbS9Mt0toYwOyjGT7nqfrXzn/wUY/Zttfj58B9RuLa3U+I9BRr6xlVcsQoy6fQiqsRzH0N8M/H2mfFDwHofinSJ47ix1S1juUaNshSyglfqDkfhXT1+Vf/AASF/aR/su/1f4QeI71oWkb7To0NwcbZAT5sPse4HtX6pbq0IHUUUUCCk3D1paTaPSgAB61U1DT4NUt5ILmJJoZUaOSORchlIwRire2k2+9TJXHdp6H58eIP+CQ/hv8A4WXD4r8KeNtQ8PquoC/NnJbJOiHfv2JyuB2Gc4FfoDY27WtrDE8hmeNFQyN1YgYz+NTbe3alC4qbMfM7WFooorQkKwfHXgjSPiP4T1Pw3r1qt7pWoQmGeFu4Pf6it6igD8Ef2mPgn4l/YI/aL0/V/DdxMNM84Xmj3x+RWAOWiOCenSv2N/ZZ/aC0n9pD4Q6P4q0+aP7c0SRajao2TBcBRvGPTOcVxv7dX7Lcf7Unwhl0q0aODxHpzG602eRc/PjlM54DdM1+Wf7Cv7QV/wDsg/tEXnh3xZcTWXh+4uZNL1e36pFMrFBJ9Aw6+lRZmtro/d1jtGa47xp4psPD2j3erarepp1lZRvLJNI2Bhc8D1NXNW+Ifh3R/CLeJbvV7WLRRALgXhlGwoRkEH3Br8df28f2yL79pTxpZ+Afh291JoUNx9nAtyc3szHBxjquaiTvogjE5a40fU/2/v20rkWFu8miNdeXLMn3Us43I357Fl5/Gv3B8IeFNN8C+FtK8PaRALbTNMto7W3iH8KIoA/Hivnj9g/9k3T/ANmf4WWJu4Ffxdq0EdxqEzoBJEWUMYfopJH4V9P7auKsRKVxaKKKskKKKKACiiigChqDK0ZV9uPevib/AIKnfEr/AIQv9m640y1n8q51icWw2nDFCctX2Zq2p2yJKH+ZkOMCvyZ/4K7eMP7d8c+B/BVsc3CRm6dM8DzG2oD+tc3O3I7ErQue7f8ABG/4Snwz8HNc8bTM/m69dm3hU4x5UR69M8t/Kv0MrzX9m34cQfCb4FeCfC8CBHstLg88gAbpmQNIf++ia9KrWzOM+Lv+Co3wtk+IH7PuoX8UG+XR/wDSlcDkY6/hXNf8EfPig/i79n/UfDN1dCW68P3xWKNiSwhcZH4ZyK+yPix4Vi8afDXxNocqqy3+nzQDcOAWQgH86/HD/gnP8X4f2X/2oNX8K+KZV0/StWMmlT3M5KpHLG/yP6YLL19DUxVjW94n6lftg+LIfCfwT8Vz3V01pA2mzKGU43OVwBXw3/wRZ+H6zal488aTW7ErFFp9vcOASCx3vgkdeB+tejf8FWvjZ4R1b4Ax6HpPiW0vNRvLtQkNo+8uqn5gSO1et/8ABMD4ap4A/ZR8PXbFjd668moy9MAFiEA4/ugdc01qO9o2PraiiitTEKKKKACiiigBB3rnvF80Nvptw8jBT5bDce3Fb0hWPknArzP9oDxIvhv4fX955DTqsEjHZ1ACE1nN2izal8aPyT/Z70Oy+Lv/AAUiZtRke8httXnuCc/xQswUfT5RX7d1+Mn/AASkhtfF37YXibWZoz5n2K8v4efus8wHP4Ma/ZynFWRM3diHtUV4qSW0iyDKFSCPapap6w7Lp8204Ow8/hRL4WTHdH85n7Q2mQa9+1R4102wjWKO48RzWyKo4yZip/XNf0G/B7wbB8PfhX4T8N28Qgi0zTLe22D+8EG4/i2T+NfgJqFqPEn7aWoW44Fx43mQsD1H2xhmv6J2ZLe3JY4RF5PsBSjoXI/IP/gtBrKz/EvwNarxJBZTO/f+MYr2f/gi54PSx+EvjHxHJGwuL/UEt0kycGNFzjH1NfEf/BSn4tW3xT/aY1dNPk8zT9HX+z0zz86kiT9RX29/wRl+I39s/CnxR4Rki2yaTeLco4UAFZBzk9zkUAz9GaWkpa0MgooooAa3WmswUUrd6iaMt1rCTsNaj2b5M1H+dG44x2qBJnk4wVw2M1w1DVImLD5lH3scVwXxI+IWnfDvTft+q3sNpZqpMs87BUTFd5GuZCT16Zr4K/4K9WkMP7P8N2L9re4fUY4xCrkCRcZIx3pfFZGtNqL1PhP9vj9rBPjp44l0rw3cufDFkxDMp+WeQHBYd8Zr0v8A4JuftffDX9njSdU07xhEbK8vZsjUEi3ED3PpWF/wTn/Yd8L/ALU1r4k1jxi2r2ulaW8cELafMkazSMMspJQ9B6V7h+1l/wAEnfC/hD4a6n4m+Ftxqzajp8Znl0y/mWdZI1GW2EIDnHau9QjGPKjJu71P008H+LtI8eeGtP13Qr2PUNLvoUngnibIKsoI+hwRxWyOABnNflN/wSB/aE/svV9d+Fmv6k6NOVuNKguGxtkAxJGueR9Pav1ZrVMyasLVPU9HsNatzBqFjb38B/5Z3MSyL+TA1coqhHKQ/CXwPbsWi8G+H42PJZdLgBP47KB8JvBCyNIPB2gb25Lf2ZBk/wDjtdXRQBFbWsNnAkMESQwoNqxxjCqB0AHYVLRRQAUUUUAJX5j/APBZL40W0HhfQPhxZzN9tuZxe3Ko3Gxfug/jX6DfF/4lWHwl+HOveKdQkRItNtXmCu2NzAfKv4mvxG+Hui+N/wDgoh+1Pa32oq9zaees97IQfJsrRWyE9sjA9yanmLj3P1Y/4J4fDGf4W/sp+DrO9tooNQ1CE6lM0a4ZxMd6FvU7CtfSlVNJ0u10PSrPTbGFbeys4Ut4IUGFSNFCqo9gABVuqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAG+tZviLWLfQdFu765uI7aKGMsZZGwo4rTr44/4KdeGfiZ4i+B2PAFvNd20MnmalFZsfP8AKA6qo6j6VEuboVFK+p+ff/BQb9oZvjt8QrDwjoE0l9FYzmI+WcrPMz7dq4681+pH7Ef7O+n/ALPHwP0fTY7TyNc1CCK81WRh8xnKAlfopJFfm/8A8E6/2HfGfjP4taJ8QPF2iTaZ4S0uX7YjagpSS8kxlAqnkjOCSa/aPFEVYucr7BTZoUuIXilQPG4KsrDIIPUU+irMj8W/+Ch3wXH7KP7R3hv4h+D5WsbTWrr7cscIK/Z542UuAfRgen1r9Xv2f/jBp/x4+EPhrxtp21U1O1V5oVYN5MwGJIyR3DZr5R/4LCeA5fEn7OtjrkFt58mi6gsjOo5RH4Y/TiuS/wCCLPiTUtQ+Gfj3RZWlm0XT9Qt5bOR+FV5I281QPqqmgrofpBS0UUEhRRRQAUUUUAFFFFABRRRQAUUUUANK5z6V+bX/AAUc/wCCe178Q7q5+Jvw6svP1tYwNS0S3TDXQH/LVP8AaHcY561+k9FA7s/n60n9m/8Aad8U6LF4atvDPjOTQ5AALW+SRIVXt944Ax2r9J/2Ef8AgnnonwD0my8WeMbaHVPiBMgkVXG6PT1IGEA7uO57V9vUlKyHzMTb706iimSFFFFABRRRQAUUUUAfI37bn7TVp+zX4bk1JIvtep3EqpbW7Z2OepzjmvzZ8M+MLz9uD9tTwNeDSmtXnktVu4Y8tGkUJ8yR+c8Z3fpX1r/wWU8F3118N/DGuxwtPaWd+yzOo4XcDjNef/8ABFv4bxX/AIw8ceOJovMFhaRabaSMB8ryHdJj3wuPxNc0Va7Z0Sk7K2x+tKgKoAGABgAUtJS10nOMlUPGysNytwQa/Fb/AIK3fA4/Dz4xaZ4u021SDR9dg27YRtVLhTzjHcjBr9q25FfDv/BW34ZP42/Ztj1mBZGufDt6t4BHjlSCrZ46YPbuBUWLj2PyD+Geg6j8XPFfhrwTD5lzc32pRxxF3ztRj83X2r+jf4X+B7b4afDvw54Vs+bfSbGK0VjjnaoBPQdTk1+Cn/BO9I5v2xPhrG8auhv2+9/1zYiv6E6cVYJO4UUUVRAUUUUAFFFFAEW3ceQD9a4L46aWt/8ACrxSGBcpp07Iqjv5Zrv9veuZ+JVrcXvgnWIreRY3NrJkuMjbsOaznFyTSNYfErH5Jf8ABGuAt+0h4maUFZY/DszFemD9pjB/nX7LV+Mf/BLbV18P/tt+J9N82NUvLXULRc/xBZt4x+KV+za9KtbESTT1FrE8W6kuleHdTupOEhgkc/QITW1XG/GCTy/hd4qcfeXTbjH/AH7alJXVgjufgd8CdnjP9tLQJ8F477xY9zkcZDTlxX7M/tpftNaR+zz8LtRmmmU6xeQtFaxAgkMRgHFfgZ4G8Zav4C8caZ4i0Jj/AGvptytzbsU3/MvqvevsaPwL8cv+CknjzSNT1nS5NJ8OxCOKfUWh8qFQANzKvc/41Ni2fM2q/B74heMvCd38UR4fvNR0PUruaWbULeMuBKXJbIHQZNfp9/wRp8Dz+HvhT4y1a90+4s7m+1CNI3uIym+NUJBAPbJr7X+Efwe0L4R/CnQvA2n2sMunadaJBJvQETyBQHkYHuzZP412Wn6XZ6TbiCytorWEdI4UCr+Qp2ZPMWaWiirICiimsTSbsrgI3f0rmI/iLoS6hNY3N8tlPFKIR9rIjEjHoFyea4b44ftH+Ffgpo9zdavq9nHNEpJt/MG/ODjivxf8UfGLx3+0l+1Bp93oFzf37vq0MtjZRuxiVRICGK9AMY7e1cbnKb0N4011P3/2j0puBVfTVuv7NtfthUXflJ52zG3fgbgPbOas7huI79aJJMz1I1IVj8tfnB/wWkTy/hj4H2xtifVWEkuTgYjJGR0r9IYyT1ry/wDaP/Z58O/tJ/De78K6+hjbPnWd4n3racAhXA79ehpwje0uxV9T5J/4I2eLtNvPgl4i0FbiL+1LXVWmeLIDsjKMNj04r9CJFDxsrDIIwRX8+cx+LX/BP346XwtFudLurO5MUc0tuDa6nbKxVWyQfldRnjkZr7d8G/8ABaXw/Jp8aeK/BN7a36qBJJp8qyRM2PmK55xnOK3EfJvxVsG+CP8AwUSupdIVlW38Vw3UMUXBIuHEjqPxdhX7y1+FvhPxZa/tf/8ABRjQvEGhWEmnaXfavbXQjnG4xxQqCxbr94qfoTxX7p1cVYUncKKKKogKKKKACiiigAqO4uEtYJJpGCoilixOAAKivryOxt3nlcJGoyWY4FfJf7SPx71rxlDcfDP4aKt94t1M+Q1xCcpbRk4Ziw6YrKdRQ0NYU5T1Wx8o/t0ftBeKP2mvisPgf8O4JLm0a4S3vJYMsGYNhgxH8INfcf7GX7JOj/so/DxtOhdb3X9Q2y6hfbAGLYHyA/3Qc1B+yP8Asb6B+zfor6ldbNa8c6kol1LWZlDSGRhl1Rjzt3E19HYqrEzd9EFLRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJuHrS1GsKhiakoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEVQqhVACgYAHQUtFFABRRRQBieNPBmkfELwxf+H9es0v9KvozFPBIOGU1hfCP4M+Evgf4ZOheD9Ji0qwZ/NkWMcu2MZJ78V3FFABRRRQAUUUUAFFN2+9LQAtFFIWAIBPNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHJfFD4XeHfjB4PvfDPiexS/0u7XDRt1U9mHuK5f9nf8AZw8Kfs0eD7rw74USX7Lc3b3cks+C7E9FJA6KOBXqtFKyHdhRRRTEJXiP7aGqW2j/ALMfj65vLRr22GnOrxIu488A/gcV7fVDXNCsfEmj3ml6lbR3lheRNDPBKuVdWGCCKBp2Z/Oh+yD4+tvhX+0t8PfEt8m6ytNVhWfB6LKNmfw3Z/Cv6PEkEihlIKtyCDkEeor8EP28f2PL79mf4q3F1o9veT+DdTke6sbuKMsbZmdmETEAAbcgD2FfsP8Asa6n4g1n9l34a6h4nl+0axc6PDK0u0gtER+5YgkncYvLY+5PQcAHyvc9pVtygjoaWkXoKWgkKKKKACiiigBrdqg1C3W+s57d1DLIjIQ3QgjGKsYo20BqndH4R+Fb7/hmX/gpKG1EfZ9Pt/FM0cm3/n3uJG2/gN4/Kv3bQhlyDkGvy7/4K/8A7OtjY2Wi/F/Q7aaPVjeJY6p5AyCuC0cowOGBUgn3Few/8E4P23o/jt4TXwV4w1G1TxzpSLHb7V8v7bbKqqrjJ5fAyfXOaDSXvan3JXkf7V3iaXwj+z1441OH/WRabKBxnquP6161uOORiua+JPgvSviL4F1rw1rZZdL1O2a2nZG2sqkdQexFBMdGfj7/AMEhvhTpfxA+NHiPVdY0yDUrLR9PV1S4QOgkc4Bwepr9ndN0uz0e0S1sbWGztk+7FAgRR+Ar48/YP/Zz8Lfst+KvG2hWnjXTvEOqaxIj29vDKPNSCMvgFc9RkZr7P2igG7sKWiigkKKKKACqWrNPHpt09tH5s6xsUjzje204HtzV2kqWrqwH4k+Nv2Jf2jf2jPjFr13rGiy6VZ3WozuLvUJdkCx+Y20qo6jGMYr9Fv2MP2G/Df7Knh1rmRo9b8ZXqL9s1RlOI+ATHEDwFBzzgE19QbaMdKyiraFczIyAUA6j60xVDNuPXpT29KQYXrxUcuow+7nFOU0cHmlxiqhv5Acv8QPhn4X+Knh+60XxVolnrWn3CbHjuo8nGc8MPmX8CK+SvEH/AASF+BetajJdW7+I9HikYt9jstQQwpk5wu+NmAHQZJr7f2ijaK15RXPnn9m39hf4Zfsv6hdan4Xtr2+1e4XZ9v1SVZZUX0XCqB+VfQ9FFWSFFFFABRRRQAUUUUAcX8XvB+o+PfAOq6LpN/8A2Zf3Me2K5/uGuB/Zp/Zn074E6D5126at4quhuvdWdcuzHlgD6bs17lRWbpxcuZ7miqSUeVbCCloorQzCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopN1NeTauQpc+i4oAfRSVE8jbTtXBzj5qAJqKaudoz1xzTqACiiigAooooAKKKKACiiigAooooAKKKKACiiigApCoJBI5paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6lpFlrNube/tIL23JyYriMOv5EVNbWkVnbxW9vEkEEShI4o1CqigYAAHQAVNRQAUUUUAFFFFABRRRQAUUUUAZniDw7pvirSbnS9XsodQsLhSklvcIHVgRjoa/I/wDau/4J1eMP2fNfvPid8IL26udJs5zdLaWzsL2yBOcLj76Lx+FfsFtprRrIpVgGVhgqRkEUDTsfkP8ABn/gsB4m8D6GdH+IPhlvEN9bbYo7qBvImIUY/eKf4jjk+tM8b/8ABRT4uftIarH4d+F3hK6sbi5DQKsKmYFW4yx6KcH8K/TDxH+zH8KfF2pPqGr+AdDvr13LtNJaKGZicknGMnNdZ4V+HfhjwPapbeH9A0/R4UGFWztkjP5gZoKuj43/AGEf2AdR+CevxfEzx/rNxqXji7tiyWIlYx2ZlXMqyf33BOM9Mg191UUUEBRRRQAUUUUAFFFFTzIAopuTTdx9azAUgZpjR7up4pJHKjg1FuB5MmDUcyLSY+NjuK54HFTVX2lYyynnsaWOYrGCx3GsE3F6jtpcs0tIKWvQMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKTcPWgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKYWbP3c/jThQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIx20DkZoYbhQOABQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbvVSQJbzGcK7vJhML2q5tNG2gYbht681DcKzKu045zUMlwVuljRee5NMnVruZQpZPLPJ5plxTuXo5N3BBUj1p9R44BPLCnK3AyOaRA6iiigQUUUUAFFFFABRRRQAUUm6gtRsAtFRNPsx8rH6UfaFDBT8pPIzUcyY7MeW5AxTqjV9yn604NxVgM+0L53lnhu1S0zjduxz60u6gQ6im7qN1ADqKKKACiikY7RQAtFIDkA0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNY4FGTUZZvMwfu4rOSsOwu47Qe+aKbuG7aRwOacrKy5HSoGVLi62kjYTimMyyQjaNkjd6syMvpVZpEJ+dHIB4wKxNktCbzGjt9pGWUYJqKzkLsQYSBnOc/rT45Dcn5TsRTyCOtWFxtGOBUtXaZLfKrE1LVcoc9alXIUCu3mRlYVWJJp1IAOtLVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSloAKbtFOooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIvOTzNn8X+6f51DfanaaXbvcXdzDbQL96SZwqj8TX4O65/wUW/aM+JOsm20vxDNbTXD7orLRbQM3J4UBQT+dXW+FP7Y/wC0FMLW90fxxd20p3F9WVtPt2z3DyFFI+hxWfv9jS0O5+v3jz9rT4SfDeKSTXvHGj2jKu4RrcK7t7AKTzXzR4y/4LGfCHQL5bfSNK13xGM4aS2hSJQfrI65HuK+XvBf/BGv4s699mvPEviPw54eSUBprdp5bu6jJ6g7Y/LYj1DkV774K/4Is+B7BGfxV431jWJ26DToY7RU+hO/P5Cndj902fDv/BZf4T6lqUdrqnhrxLpEbNg3UkcEkae52Slj+Ar6t+F/7UXww+MVvBJ4W8XWF/JMiuLdpPLlGR0KNgg+1fFvxH/4Iu+Er3S5W8GeNdVstRX/AFSa0FmiPsWRQR+Ar88fjt8CfGn7I/xA/sbUtXgh1HZ5kd1pFyRvXPDYOGGfcUubYVrn9GqMHUMpDKRkEHINOrwP9ha/1vUf2Vfh9ea/c3F5fTabHIZrk5coR8uT1PFe91oZi0UUUAFFFFABRRRQBHJlQSOfaq/2hpoWKqUccYbvVrbWfdLNFI8kYWQZ6dxxisJ8xcUie1uBMoUn59oP1qRoVkYFhlhxX4+f8FBfD/xs+B/jq48U2PjnWbjw5qkzzobWRoktdxyI8Z5x0rm/2Of+Cifxi0fxp4f8FXit48sNRulgjhvGJuUBOCVk5wByeRRB6XLa1sftQV6KOMUpcKMsQv41HBI8kCSPHsdlBKZ6H0ql5qTOy3CmPa+VyetOU3F2YuW5p0VSTVEa68kKSuPvAE/h0qaYSSNEUAwGycnHH5VrFqWxHK09SekbODgZNMYtvABUA+vWnIrLnLbufSi6Cw9CWUEjBx0p1JS0yQpv3sjpTqQLgk0AAGABS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAITj6UA55FIF65JIPrSgbQAKAILi8S3wXZY1zg7q4S++PfgfR9Wh03UfEWn2N1J0Wa4VRn0PPFef/tbfFIfCH4b63r80c8qxwMsRQ/KrkYFfjD8I/gL8S/21fiFrE/h5o5ZVka4uLrUrh0hi3HOAcH8qxUm2buCirs/oT0vXNN1uFZdOv7W+iYZD20yyDH1Bq5uG7aDz7ivwh+IP7MP7Rn7FN9b+I9Our6O1VN76l4duXlhjYdRIGz+o/Kvuf/gnT+3xffH5pPAvjdhJ4utIvMgv449i3cajksM/f7nGB7Vpcy5WffA6dMUtFFUSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADKa+ByetSYpjxq3UVE9ikxFAZQcdqrnbDuG/g/w1L5m2NsD7vFVo7pF5ZGJ78VjzIpIi87aWByw/hHtS8tt3ZAI6ZpI7iC4uG2ZLg9DU8rKPvrnFZm4JGxPDYXtVhRtUCqUUxDnj5e1WoZgzENxzxQtTOaZKW2jpmlU5ANJuA+lOGK6VEyHUtFFaEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANX7xp1FJ060ALRTQ6t0INOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDzT4O/s4/Dr4E6PBYeDPCthpJRAr3nlB7mUgY3PKfmJP1r0umhqZNcxW67pZFjHqxxS23AdtG4sBz05py/dHes2+8RaZp1uLi61C2tYOvmTShFP4k07R/EWl+IIWl0vULXUIlOC9rKsgB+oNF0Ow7WNQj0rS7u8mYJFbxtKzH0AJr8BPj346vP2r/ANr1TbR4jvdUTTrRe5iWTGTjPbNfup8YNWh0n4da/POgeNbOUlW7jaa/Gf8A4Jw/D2D4i/tkC/lh22mkSTXwT0O47f1rLeVjZaRP2z8FeHLfwn4R0bRbVNltY2kVsiegVQK26SlrUwCiiimAUUUUAFFFFAEM1wIVJIY844FN84bCV5H86ex3Eg9DXOeINS/4RXStQ1CaVTHFDJKN3GNqkiuebdrmsUnofl7/AMFdv2gZLvVtO+HWnsVSNPtF2pGcE9q6f/gkr+yTZQ6Gnxj11POvrhni0m3kjx5SA4Muc87u3FfBvxe+Iq/tAftFXWreJb9dJ0+7vxA91KC6wwB8E8deK/UK4/4KD/Aj9nf4U6d4Y8FaqNek0mzW3tra1jZVZgvXcR3NEXyqzKlufeHPA6Cqt9ZpdR88MOhr8NvjZ/wVI+LPxNklg0K/bwhphPyx2Lfvtvu4A/PFfo7/AME39a8Z+KP2WtO1nxbq9/qeo393O9vLqTmSTyd5C/MeSD1qk9LyRMVruZn7YX7dH/DJc2h21v4VXxHJqDv5jy3ZgEO046bW3fpT/Cf7bF1+0R8BfEuvfC62WPxxpNiLifSJEMpjfGSqk43dPSuG/wCCp3gPw1qPwWute1bEerWLLHZybsbmPUYrwP8A4It20s3xR8bXWJDAumxIWXhN248EevvWEfej2N5yXNscN8O/+Crvxq+HPi+7h8YwWfiCy+1H7Xp17A0M8HPKoQflx6EGv1L/AGbf2s/An7TnhwX/AIZvxHqEar9p0y5IWaJiORjuPcVy/wC1J+wt8PP2lNFma40+20DxRy0GuWduBJvPP7wKRvBPc81+THjz9lf49/sY+II/F/2C6tLSyn3Ra3pE4nhYA/KZApyoPowrptoYL3tj9+dwHfmm+Y27G3t618nf8E/v2yG/am8Ay2us2skHizR1SO+lVCYbjjiRTgAE/wB3t6mvrWtDMRTuUHGKWiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUw7+2MU+igBu4hcnrTqQrnijnnOPagD4O/4KxeJLjR/gPPYQTYjvp1EgbqMHtVL/gjh4VtrH9n/AFfX1i23mo6nJHJISTlY+Bgdq47/AIK/arDD8PdOtjMftMt4f3eeNor2j/gk3Ypa/sb6BMud89/es/pxMwH6VhE6qjtFI+vNU0uz1zTrmwv7aO7s7hDHLBMoZXU9QRX40ftlfBO//Yh/aK8PeO/h48un6TqFybmLAPlwsZPmgIXHyY7da/aLFYfirwPoHjizjtPEGj2Ws20biRIr2BZVVh0IBHBrTlZjCVnqSeDdabxF4S0fVHAV7y0inYL0yygmtmo4IY7aFIokWONFCqqjAAHQCpKsh7hRRRQIKKKKACiiigAooooAKKKKACiiigAopuTmlzSAWmHNDMRTM7sE9azmykiOZyuQKrxxpKzBmPTpnFWXAY8jNQsWjyUUVzmq12IlVY/ugfXHNSbvMG081V84ozF2yOu3HSo4b5HyVyp9cVldG/Ky+22NVGMdqZNMm7B6KKzLzVltot0pJGfvCqzahJfIJIU2qTwx7ihVFEqNJ9TW+2OR6ir9rIXiUms+zgeaNR9w45q9DG8R2nkDvXXTu9TGpy7ItUtNVgeO9OrW5yhRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJD8pp9NZQwoAq/MoUqpPPpVsdKbGu3Ip9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfk/4L/4LKT+HvhPptrrHhRtc8aQR+S8yT7IZNowHfjIJ9s188/F7/gpX8ZPjLcS2ljcR+HrSZyYrPSVLugPRQ2Mk/WtD9jP/AIJ0a5+1J4Zg8Y3HiOw0nwsLw209upk+1uEPzYHllee3zV+tnwc/ZC+FXwL023g8O+E7E3kSBW1G7iE08hH8RZs4P0xUJKT1Luz8E/GzfFm+0tdV8U/8JadJmOftOpLcLA2fTOFx9K+6f+CL41ubxt4yl3XT+H0s0QF2bylmz0APHSvrL9rz4D+If2tobLwhp2t3HhzQLaXfcSLAHSUj1+YcV6/+zT+zr4f/AGZ/hva+F9EIuJB893fNGEa4k7sR2+maLFPTc5b9uDxvH4D/AGf/ABbfTNkSWTwxqv3tzcZ5r4U/4It+F3v/AB94+8SFgY7e2jt/mzks7EnFep/8FjPH2oeH/h94Y0W0XFpqk0izS5BAx2PetP8A4I06HaWnwJ8QalHsN3daoySMvXaowBSjuVLZH6E0tN3Uu6tDnFooooGFFFFABRRRQAwq27jGK+Sf+CjXxV/4Vf8AAvVJ47xYb+9/cQwq2GIPBNfWVxeR2+3ecbjgV+JP/BVD40P8RfjofDNjctNpukIItkb5V5T2x61hPWyRvTXU84/Zz/YI+JX7T2lxeIdGFnpnh+ado5NRu5CTkHkhO9fYd3/wSB8E+BvAOpa14p+IWsvNY2jzyfYlihhDKucDcrHGfevkv4Q/tjfGz9kfQbfw/a2q2ujn95Bb6nakx885B71L8bP+ClHxX+OHgO88Jaw2mWem3bfvpLCExsw9M56UWk+ojgv2Z/gK/wAfPj/p/hbTba6m8Pi+3XdxJhnS3U87mGByB6DrX9B3hrwrp3gzw1p2h6Rbx2WmafCsMMSDARVFfif/AME6f2pfh3+y7q3iXVvGQ1ie5volitotOsVl4HU7mkXr9K+r/Gn/AAWI+Ht5p8sOj+F/EnmMrBTcLHFk446Fqp7NCW54z/wVk+PlxrWvWfw6g2yW1nIbqWZRjcOgGP8A69fSH/BI/wCD0/gX4J3nie/WNLvX5/MjRR8yRDpmvyM+MHxJvvi58RtU8TXUbeZezmSO3djI0a54XoM19H2n/BQ/43Q/DfRvBnhKzi0Wz0+BbdZ9NsHM7ADAJIBwayjFxikVu3c/djqOtVdU0my1zT57HUbWG+s51KSwXCB0cHsQeDX89msftOftF3F0Rd+M/F8Ezn/Vjzk59htr9SP+CYP/AAtfUPhbqmu/EzVdZ1KPUplfTP7YnZ2EQHVVblQTWyk+pDjbVM+s/BPw38L/AA2sJbLwtoNhoNrK5keKxgEYZj3OK6Skpa0MwooooAKKKKACiiigAooooAKKKKACiiildAFFFFF0AUU0tSbjuxii6HYfSMu5SM4qKSV1wVXcO9LHMZFyV2+1F0Fj8o/+CyOlmF/C9z5shEk7rsJG369OtfT3/BKFSv7GXhwFg3+n32Mdv3x4r5u/4LJagbi18NW/2dlaK4Yq/Zq+gP8Agkjeed+x/pkOAPJ1W9U/jJmsoam1TVo+1KKazbetG6tbmA6io/M+bb1NNWY7vm49Kew7E1FJSM23JPAFK9hC0tfP/wAav2yfh38BdSSLxJrMYLjmK3YSSA+hUdK7D4EftFeDP2jfDMuteC9R+2QQt5c0cilXib0YUuZFuLR6hRXxF+1F/wAFANa/ZT+J+m+Hdd8LQaxpV6ol/tCGVozGhOOmCCQK+o/g38ZPDPxz8D2Xijwtfx31hcKCyqfniburDsRVBKLjud1RRRQQFFFFABRRRQBDJMI+O5PTNPzu9q+Fv+CjHxg+KX7P2k2/ibwobf8AsS5cQ/aHG9reX1Kngg1lfsO/8FKLD4vtbeEPiJJb6R4pVQsF8xCRXh+nRTWMZScndG0oLlTTPvuRsDjk1BFMWkZSOlWI5ElRXjZXRhkMpyD9KTysMWB5PtSkmyE1sU1mkJYtwoJ/EVXkvI0Vmlc5/u+lWrmzMwYhsHGOtRR2oaNvNUM3risrHRFxKceoRtEXU8dBVd75vtCxiMLEw+9U8mmIFOBjJyeaz7qxaJXZW8kAZLHnj8awaZ0xs9ipr2vaTocEr3t3GiIN7FzgAV81fEX/AIKSfBjwDeTae+uTXt9a5V7ext2fDj+EnpXzx/wUp/ai/wCEQuE8EeGbvzNTni3Xd0uCY1PVMYrwr9h//gn3qP7Uyy+KfEWqTaR4QEjRm5s2AuppB127lIx71pTp9WZ1KjWiPoHVf+C0lla6g6aZ4EuLmzRsLNLOqM6+u3tXtHwX/wCCsnwp+IEUdv4nkn8H6m8gRUuVLxHPT5xVQf8ABG34Gtgy6t4yd8ckajbgE/8AgP8A1r57/av/AOCS8ngfw/P4h+F+o3WqWFlGZLjT9SdWnVVGSwZQA34AfSuyMeU5ZSUuh+sPh/WtO8TaVbatpV5Ff6fdoJIZ4WDI6noQRWlX5H/8Eiv2iNU0vx7qfwu1zU7ibT7qIyabb3D7hDKh+ZVzyMjt0r9cBRymTVhaKKKsQUUUUAFFFFADVPzGnVEG/eMBxinZoAfRURkCnBNODZGQaB2H0UgpaBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTWO0E06mt94UAKrblBpaKKACimr9406gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoprMF60KwbpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/PT/AII/ePrBPgHqHh+RZFms9SmlkuG2rCqtyBuJBz+FfQ3xm/bt+DXwVjni1nxbbXupx7gNN0z/AEiZiO3HA/Eivw/8Rn4p/A3VtV+GE97f6NcC4EUtjZ7lE7dPkIALA5rpde/Yp+K/hX4eXXj7xXpCeH9BCrIZNSnBnnVucqAGIJ98VknbcvqfUfjv/gsn4hW8vbfwX4NtLSyZ28m51FiJ2XsWRcgH8a+e/GH/AAUe+OnimaUp4pk0mNst5Vqu0L7Cvs7/AIJ4+D/2XfjJo6afpnw/kn8ZaXao1/N4ixL57/xPGolYY+qj6Vif8Fbv2cfC/g7wB4b8W+FPD2n6IsF2be7Wyi8veGHHAGMVpccmz4C8U+KvH/xo8I3Wta/r+peJIdMuMyLMWkEZfuPQV+uv/BJ3wLJ4R/Zftr6V0dtYu5LtQucqvTBBHHSvmX/gjW+k6xffEPw/q1la38FxFFN5VzErgAHng9q+pfjl+2R8I/2RftGn6RIdRv5kKroOilCkTf3vvALUx0Y+lj7IyKU1+T/7K/8AwUe+IvxQ/aM0jwxJYQ3Hh7Wbloxatlpbdezbvav1g28VoZySWwopaSlpCCiiigApCcUtIw3CgDj/AIjeIrXwn4P8Q63cIzRWFlJOTnHIU8D3r8If2dvDLfGv9p+bWtXhku9ItruXV9QcqX2xKxYZ/Kv0w/4KgfHi3+GHwQvfD1lfbNa1p/I8lT8wjPUn2riP+CRvwG0/T/gzrHjfU7Tzb3xHLJaL5g4NsvHH1JNcyjzXsdPwrU4zx7/wUy+B2vLLo+r/AAik8QQWLm3gaTysFV4BGUzjivjSfw5pH7YX7TNppXw88LL4L0zVJVVre3Uv5KD70pGcA+wr64/4KEfsd/Bb4BfDfUPF+m2F7Fr+pXfl29ql6VjRmOSwXHQeldZ/wRz+A9vp/g/WPiXfwZvryVrOyMkfKxjq4OehrSCsZvud34R/4I8fB7R7eI61qGua7dADezXIiRj34Uf1r5V/4KNfs6/Av9nHw9pmk+DLG6XxleS72U3zyiGP/aUk8n0r9avi9qfirRfAGr3fgvTI9Y8QxwsbazklEe9scYJBGa/JT4HfsZ/Fn9pz9pO/8T/FnT9R0Oxs70Xd/JqVuwW4YMD5MXOCOByOKqzuI+eP2efHz/s4eONJ8WeLfh4+s6BOAF+32xjWQd2R2Uhq/cT9nr42fC343eFrXU/AFxpq7og0umxxpFcW3qrxjkY/Kp/jv+zp4Z+OPwhvfAl7aW9pAYBHY3PkBvscgGFdQCOn1Ffit4++G3xU/wCCevxosNSWaa2e3l3WerWoP2e/iB+645wT3BJxRZiuj9/mtYnYMYkJXoSo4qXaa+c/2Ov20PC/7V3g1J4PK0fxVaoFv9FkuA8gbHLpwCyH1xxX0Zx6VVxai0tN3UbqLoVh1FN3c0oOaYhaKKKACiiigAooooAKKKKACms4UgGnUmAeoqOVgLTWYIuT0p1IRnrUgR+YGUsASKGz5ZxwcUSDbG2Dt+lef/ED4x6B8LrIXviLU4NOsS2zzp2x81TKSjubQi5bHdwRt5IUs27ue9SxoY1wWLe5rwm8/bS+EWm2P2qbx5ohQjK4uBn8q8y1z/gqV8FtBu5YX1pr4RnG6ziZwfoe9LmTK9nI+Zv+CxVnqFxcaNP5ebKGTG4Hua+mP+CUOjxaX+x/ockbszXV/dTOG/hJfpXwf/wUI/bB8C/tD6bZWnhE3sn7wSytcrtAPoBiu9/Yb/4KO+C/2evgTa+DPFGmX1zdWl3I9udPj3Flc5O7Jx19KKacd+4pe89D9dpjlcZxXHfEfxvB8P8Awxf61qUyw2NpE0jMvB4FfnV8Wv8AgszH9mWP4feCjNcD702uF9ifVUKn9a8A+K3/AAVC8b/Gr4V6l4Q8R+GtHgmuyR9u0czQqq+hV3c/rSndr3QjaO57L4R/b4+Lvx4/ac0Hw18PpIIdC+3eXKptdwkgB5Zznpj6V+gn7THjzX/hb8FfEPiTSYDcXVjZPJI0C/OjY4dQewNfBX/BF34bwT3XjPxrPE0k0YSxt5MDYO7YyM5/Gv1K1bSrXW9MutPvoEubO6jaGaGRQVdSMEEGteW6sKUtT4I/Y1/4KiaF8VGt/C3xHmt9C8SYWKC/AKQXZ6c5J2t+lfRf7VX7Rnh34I/C++1a91KNZ5o2S1jhkBaRiOCMdq+A/wBs7/gl3J4L+3eMfhXcyy2MZa6udKuZl82HuTEQo+Uelfn3qPirxN4ym07Rdb1u6uYLdxbQpfTkxw845z6U7c2iElZ3Z6J4R8B+Mv2wfjZcQaNb3F7fapdNNJcTFmjt0J53HtgV+537LP7M/h39mD4cW/h/RkZ76YLLqN27bjNNjkjgYHoK8+/4J4fs8aT8DvgRpksc9pqms6tm7udQtyHX5uiK2OgFfU+2jlIlK54R+1x+yroP7Unw2utGvUjtdchUyadqW35oZB0B9VNflJ+zj8UPG3/BP/8AaUPhfxk1xp3h55/I1G0cExSxk4WaMdPQ5FfultxXyL/wUS/ZM0n4/fCq+8QWln/xWWg27TWVxHwZEHLRsMfMMdKsV31Pqrw94g0/xVollq+lXUd7p95Es0E8TZV1IyCK0a/I3/gl3+2Nf+EfFKfCDxheiLSJmZNMkuvvwTZ5iLHsewr9cVOaAasLRRRQIKKKKAOW+JHw70H4qeENR8M+JbBNS0i+jMcsLcEZ/iU9iPUV+UPx7/4JG+NPBd/c6x8MdUXXNPjLTR2c7+XdQgchUb+LFfsK3WkqXZlxfKfg18Kf25vjp+yr4g/sHW7m9v7C1k8ubQ9fQswA7I7DI/A19+/Cn/grh8JvGy2Fn4jgvvCupzKBO0yBrdH74cHOPrX058YfgH8Nvi9od3D438OadewbCXvJUEcsYx1Egww/OvwK/ae8B+Ffhz8aPEOgeB9YXW/D1tLi3cZcR5/5ZgnO4j1qLA31P6FPh/8AFLwf8TrNrrwp4j03XYQMt9jnDsoPqM5FdRJA5ZdrYHevz2/4JBfAfU/A/wAPdb8a67YTWN3rEojs0nDI3kqOW2nsT61+iNP2cSbmZfL5b56g9q5X4i6jLp/gzUrpd0ccEJbIGTgDJrt5LaOQlmXJ+prO1/Q49e8OahpzAYuoHi59SCBXO6eptGpY/m7/AGhfHEvxA+L3iTVmlMsT3LRxMRztBwK/dD/gn74QvPBP7JvgKyv12XMtmLgpjoHJI/Svw1/aI+Eut/Bf4veIvDmuWzQzQ3UjxyMMCaItkMv51/QT+zRfrqv7P/w/uhG8Yk0a3wsgwwwgHP5V0xtYid3qek1Fd2sd9azW8q7opkaN19VIwR+tT4FG0VZmfglMyfs6/wDBQ+aK1JitNK8U+SFXj9zIw6e3zV+9NrMtxbxyp9yRQ4+hGa/D3/gpVotv4Z/bYe7sFEM929pduV5y+4c8/Sv2v8HyNN4T0WRzl3soGJ9zGtBcuhsUUUUEBRRRQAU1pApAPenU1kViCRkjpQA0r8xpACvAHFSUUDuRsinkqM1FJJGq9QDVnA9KY1vE3VFP4UDuMhYyKP7vY1NQqhFCqMAdqWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmthgRnFOpMe1ADIxt461JSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMaTaQME0NIFGTUF1ciM4H3qgW6M+V2kEdT2rLmZai92TSyF84qWHKoM+lNiUMgz1qXpWonYdS0i9KWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPBJPFH7OnxT8aWWpvrXgfX/E0BH2eY3sDzg9sfNya7H4+fDTRPi18JNe0DV7WO8tJbV3iXj5XC5UivyP+J3/BI344eCdUaTwj/ZXjWyRwYLiwvEsrke7JMVCnPo7fWmR/Br9t/wCH3h+60tLDxRHpaxFJY476G5VExzgrI2ePTNKUUzSxxf7Ffji2/Zz/AGvIl1vU49J0y3mlsruRyQhTPA/lX6hft06XpPx1/Y98S3/h++tdVtYoRe29xC+5W2nJxjvX4Pa+NR/tq/Grec+opKftH2kYk35wcj619KeJP2zPElr+z1oHwv8ACdr/AGNYLb+ZqV3CxaSckkYOenFQM8n+BfxM8f8Aw08S3svgBrv+1by1a2eO1iZ3ZDweBX0v+zd/wTd+Jfx+8TJ4h8fQ3HhvQJpBcz3F+GFzeAnkIMcfjis//glL4otNC/amtbS6hjuv7StJIVlkwfLc85Ge/wBK/cqkB498Hf2R/hX8DZre78KeFbW01OGPyxqEmXnPqdx7mvZKaDS5rRGQtFRNMVbG35f72a8y+Kv7S3gH4L3WkQeLNZj01tUn+z27EbgW98dBT2KUXLY9SoqGzvIdQtIbm3kWWCZBIjqchlIyCPwqagkKQ8AmlpP5UAflb/wU2/Z9+J3xq+L2l6l4X8JXuraPa2flFrfBBbd97Ga+7/hfqHhz4DfAvwrp+ttD4VtNN0uITx3BCiJ9uXBx3zmvQNc8d6B4Zmjj1TVLPTmkcIguJlQsT6A15p+1R+znY/tNfCW98Mpqb6ZPKRPb3kBypcdN2OqmudLSyZ1SkpWUlY/K39tb42RftiftC+HfC3g7UZdQ0V7pbS3wDsZ2bBbHoOa/Yr4K/DSy+EHwv8PeErFESLTbVImMa7Qz4+ZvxOa/Of8AYN/4J5+NPhh+0Jc+J/H9hBBYeHy62GwhluZDwsi+gA5r9Tq0joYz7A360iqqjiikrQzFCjJPeuS+KHwq8NfGHwleeHvFGl2+p2FwhXEyBjGSOGU9QR7V1u6jdQB+G/7QH7DXxd/ZN8eXPirwCupahoFnN59lrWjlkmgTOdsiKxOB06819D/stf8ABXiC9uLfw78ZbJLGUEQx+I7NG2lumJogDt92B/Cv0+mhjuI3jlRZI3G1kcZBHoRXwB+1t/wS18JfE681PxZ4Jv4/CGtzbp7m22j7LO+Oy5UJn64rN+ZotdD7u8N+JtJ8YaNa6tomo22q6bcoJIbq1kEkbqe4IrTr8D/hr+0F8av2DPEs2hIFk0hZszWF1+/tplB58uQEhcj0r9Tv2X/+CgXw7/aO0yOA3kPhvxMqjzdKvpguW/2HONwpBY+nxIGkK4OR7cVItfFnjr9t688BftoaF8MZ20+XwxqMaRzSICZYrh+g3ZwR07d6+1FrRO6FJWFooopkBRRRQAUUUUAFFFFABRRRQAVDcSOsbGJd7jsampixhXZh1brUWYEUjFl2HhmHPtXzD+3V+yxrv7Svwrj0bwzqUFhqttL5yx3PyxzexYAkV9RmMFt3ehY9rEhj+dHLfctScVofixoH/BHH416i0Z1LWvCumQE/MDcyyuB9BFjP419C+Ff+CKvgqPSbZvEXjrXn1Qp+/wD7NW3SEN/s74mOPrX6SdKP1o5RczPx3/bN/wCCZ/gn9nP4O3/jPQPFWuX97byqot9UeDYwJ5+5Epz+Ndj+wT/wT2+EPx2+A+keOPFsWranqlzcTRTW8V8YrddhAAAVQ2ef71e0f8FbNUs7H9nueCSQi5nuolVVPXJ71e/4I/3zT/snGAnKwa3dhc9eQhxU+hq9I3N+b/glD+zpIxI8L6lF6BdYuCB+bH9a+Y/22v8AgmL4B+Evwp1rx74H1bU9ObTUV5NO1CdZYWXOPlIQNn6k1+r2M815D+1p8On+KX7PPjXw9FvM9xYO8Sp1LKNwHT2rSyMrnyT/AMEYPENvdfBzxbpKYE9tqgmP94qy9/xr9E26V+JH/BMP9o7Tv2evjDq3hXxc66bpmvlbZ7y5ygtp0OBuJ4ANftLo+vaV4r037XpWoWuqWMmVE9nMsiH1G5TTB73Py/8A2/P2l/Efjf4uJ8Kvhqszatu+y3FzasWbJ4I46DnnNc34o/4JCa3Z/Bt/EUXiRrnxott9rudP2bkduSVU4zmv0V+G/wCyV8NPhZ421Xxfomhk+ItTlaWe+u5jK4LHJ254Ar2HaKhRsy5STtY/I3/gmb+2FqXw08YR/BbxwJYbK4uWgsJbkEPaT/8APNsn7p7cV+uY6etfiF/wVGsY/hz+2NHrmiQQ6fcm1ttRZofl3zAn5yB3+UV+xfwX8WS+OvhL4Q8QTjE+o6Xb3En+8UGf1zVmR2dMkjWWNkdQyMMMrDIIp9Z+va5Y+G9Hu9T1K4S1sbWMySzSHAVQOaAPxH/4KJfD+3+Bn7YFnr2iWa2VjeNBqsaw8KGVxvxjp0r9qPh9ryeKPA2gaxGSUvrCC4Gf9pAf61+HX7eHxo0/9pP9oaytPCMr6jZwgadbsoz5jO4DEe1ftn8G/Dtz4R+FPhLRrs5ubHTLeCT6qgGKC5O52VFFFBAUUUUANbrUUkwhUs3AqRm68V518aPi1pfwd8C6p4i1u7htrS3RggcgFmI4A/Gsm9bGkVc+Hf8AgqB+2Ung3SX+G/hi9kGt3g3Xl1EwxBGeqY9a8X/4Js/sMD4wahZ/FDxmpl8OWlyWtbGZT/psg6SE5+6DXi3wh+FviD9uz9qLUZpmdtNurxrq+u2UhUt1bhMjpkDtX7sfD3wDo3wx8GaT4Y0G0Wz0nTYBBBCpJwB1OScnJz1qrBKXQ3re3itLeOGCNYoY1CqijAAHQVIBjiloqzMKRVCjA6UtFRygfin/AMFebeOP9prTT5jOJNMQsrLgKQ3TPev1u+Ad1De/BPwPNbhRC2kWwXZ04jA/pX58/wDBaH4cR/2f4P8AG8FqWmR2sLmcAn5DyoPpzX0l/wAEyfixF8TP2VfDtsZHe+0AtplxvABO0koeO20gfhSWho9UfWVIzbVJ9BmiuA+PPjhPh18I/FOvNc/ZZLWwlaKTjIfacYz71XMiFqfjz+1ZqU/7QP8AwUIGjaZbmRo9SttMVV5/1bAu30r9u9Jsxp2m2lov3YIUiH/AVA/pX4wf8Eq/CNx8VP2sdS8ZaoXvTpMM9888h5M0hwrH86/amqKk+gtFFFBAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTXzt+UZNOooAamdo3cGnUUUAFFFFABRRRQAUUUUAFJuFLUTsFUk9KY0SbhRurPfV7eOTZ5gLf3e9TJceYMqRjrU3RXKy1S1m3WpeSmRUVlqktzk7MqKhTTY/Zs1t1G6oI5w6ZPB7im/aM5IPAq7oXKyzS0yKQOop9MgKKKKACiiigAooooAKZIrt90gU+igDMa3aa4IPY1cjthGDU20Ak45panlRo5tqxGsZWnbadRVGYlLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfE2vf8FdPgNpMCPaza9q7t/yztLFAR9S8iiufvP8Agsx8FYbbdHoPi+4mI5hWyt+PbPn4/KtC3/4I6/BKKRWk1zxxcqP+WcurQbf0twf1rUj/AOCRfwEE2+SLxLOveOTVvlP5ID+tZ63Luj8tv2kPjl4F+MfxrtfG+heGLjTbKS5Wa/tLuNF84BuchGYcgV9vWX7dn7Kdn4DFnZ/DjbqMtn5Txf2EjgPtx989RnnrXvo/4JQ/s8rNC48Pal+7/h/tSQhvrWz/AMOw/wBnUyBz4Fyf+whcAfkHp2HdH4j6D4+ufA/xbh8Y6FE9p9l1I3cCW6FF8vfkKAenHGK/Q/U/+C0gGk+TZ+BbpNQVVAlnlQKxwMkgE45r7E03/gnb+zxpaoI/hpp8rL/FPcXDk/XMmK6eD9jP4JW1ukMfw10JY0GAvkE/qTSswuj867r/AILSeMpIIxb+BdLE38Re8bn8NtU2/wCCznxIZsp4I0QL6NPJn+VfpPa/sg/Bizk3w/Dbw+r/AN42gJ/Wt63/AGefhlbRqkfgLw8FXgZ06I/qVrQpzVrfofmBJ/wWZ+IMsJRvAehjcME/a5M/+g18l/tDftJ65+0X4sstV1iyj0v7Ku2G1tZGePcSPm5r99m/Z/8Ahq/XwH4eP/cOi/8Aiax7/wDZT+EepXAnn+HugvKDkEWir+gqZahGfKa37Pc3n/A3wLIWLFtHtiWY5OfLGf1r0Kqul6ba6Np9vY2UCW1pboI4oYxhUUDAAHpVqmtjJu7uFMl/1bfSn0UxH5Tf8FhfCV3px8J+KIZ7m3bzGtf3bkLjqG4PXNfUv/BMPxtf+Nv2UNCk1K+lv7ixuZ7PzZiWfapBAJPX71eg/tVfsp6J+1R4Nh0LVtRuNKaCQSRXFsoJU/Q10f7OfwB0T9m34Z2Xg3Qrm4vLWB2le5useZK7dWOOP/1Vkou50SkpRXc9Nz6V4z+1xr3jzwz8D9d1P4dKzeIrePzE8tQzBR1IBBya9o202SJZoyjAMpGCCODVWMIuzuz8lv2df+Ct+v8Ag+aXQvjFpF9rjxttW+sIVW5j55DxnG4/iK+vvg9/wUk+FHxu8f6f4O0Cx8UQavfEiH7fpipHx3JWRiB+FdL8Qv8Agn/8Dfidr11rWueC4X1O6bfNPazyQFzgDPyMPStL4L/sR/CD4BeIzr3g7wx9i1jYY1u7i6luHVT1C72OPwqipNPU9M+J1x4ltPAGuzeD4refxLHaSNYR3RxG0oHANfj/AKb/AMFWPj98NPGU+k+MbPStQayuil9p93Y+TMuDgqrKRjjpwa/anbXj/wAZv2R/hV8eY5G8XeErK7vn5/tGBPJuQcYz5i4JP1zTEmeYfs//APBSb4SfHjVNO0KO8ufDvia7wi2GpR7UaT+6knQ/jiuH/wCCkn7NHxb+OGj2eo+Atd8zStPhZrrw+s7xSTkc5TaMMf8AZNUfhd/wSN8E/Df4vWvi6TxVe6zo9jP9osdEmtdhhYHK5mEnzAH/AGRX3qqBVAHAFTvuVdLY/nu+GXx5vvhE1z4B+JPhdtV8Oq+2503VISl1a+oTcpI659816F/wxbZ/HVZvF3wE1+GW2IMx0C8n8i9tcD7owSc5Bx9RX6q/tFfsWfDH9pKGSbxLoy22umMpDrFn+7nRscFsffxxwa/KP4z/ALIvxr/Yn8cNr3hS61XUtEQmS313R43YhRj/AF6AnZ+JIxU8r6D5kdL+yn+wn8ZPEHx+8P674s0PUNJ0zRbxLq41DV3LGTYchVJOWzX7ZL0r8rv2OP8Agqp4k8R+LtK8EfErTV1ifUJ47W01fT49kgdiABJHjB+oxX6o04p9SZO4tFFFWQFFFFABRRRQAUUUUroAooopgFFFFABRRRQAUUUUAfBf/BWLwk2ufBG5vY3iAs3jlbd97IPFL/wRyl3/ALMOpLnO3XZz+apXTf8ABUbQhcfs269eB2QLt3bTwea4f/gjHdNN+z94ntyFCQ62SuP9qMZ/lWcd2bSfun6CL0oZQylWAKkYIPQ0UtaGJ8ffHP8A4Jg/CP44eOJvFFw2qeHb64/4+YdHkjihmf8A56FWjb5voce1ex/s2/sz+Ff2XfBc/hrwpc6nd2lxP9olm1SdZZGfGONqqAPoK9d20baB3BelLSUtAj5L/au/4J3eEf2pvHVh4u1HXtQ0XVLeGO2lWCJZYpYlJONpIIPJ5yfpX054O8L2fgjwppHh/TwRZaZax2kO7rtRQoJ9+K2KKAOK+MHxNtvhD4B1XxReWs97DYxl/It13Mxr8e/j5+258Wv2wtUbwR4N0K6sNKvJPLSztUYyyL6Oe1ftndWkF9bvBcwx3ELjDRyqGVh7g1k6P4G8OeHrhrjS9B03Tp2OTLa2kcbn8QM0Afnx+wR/wTRm+GurWfj74mwoddhIkstIUhlgb+9Ie59q/SLpwKWigAooooAKKKKAI5W8uN3J4AzzX4wf8FUP2lJ/HnxFbwBptyp0nSSpvEjHJmxkAnvwRX7RMoYEEZBr42+O3/BMP4d/G74rp45k1C+0W5nlSXUbO2IaK7K4HflcgAfLis3G7uaRkkO/4Jd/Am2+Ff7OeleIJrdo9c8TL9tuDIMFI8kIo9BgZ/GvsiqOh6NaeHdFsdKsIhBZWUCW8EY/hRFCqPyFXq0MwooooAKKKKAPKf2mvgjYftAfB/XvCV4FWeeBntJ2BPlTAfK2B15r8RPgN+0V8QP2G/ixq9jb2xnjhuGtNR0S63JHPtbG4ZBwe4Ir+hDFeS/GL9lH4U/HlYz408G2OqXEZ3LdR7refPvJEVY/iTU2KTPjaH/gtb4JWyiM3gLXPtW0eYqSxbA3cAk5x+FfLP7XX/BR3xN+01aHw14a0+Tw34Zk+WS2fbLPck8bTgHH4V+iK/8ABK39nXzt58I3ZXP+r/tS42/+h5/WvS/hv+xX8E/hNcJc+G/h9plvdpyLi6Ml0+fX96zYP0pcoRdnc8e/4Jf/ALNP/Ck/gnH4j1W0a38UeJ1E9wsgZXhhBOyMjOO27pnmvs+moixqFUBVUYAAwBTqsTCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACMwUZPAoVgygjkUEbuDQqhRgdKAFooooAKKKKACiiigAooooAazBRk1Xl/fx/KeDUsnzZFRbdoAqOY0j3Mh9Dg+0GY7g5OSauLlWVY13ADBzUrQM8zfMQKezR2aFmYDHUtWVjVy7EH9nmZiWGFParVvbpbxhV6VjX3iZA0awnIY4Jq+sjELkkgiqTtsHLN7kzAKzE9D6VBHtYSKCSc1JIwAwTg+9NtbZlm3joetS9WF7Fy1XEantjvU9IvSlrdbHO9wooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu3rnkHsaZcWsN5bSW88STQSKUeORQVZT1BB6ipaKAPniP9gv4O2fxc034i6d4d/snXbGf7SkVjJ5ds8nZjGBj34r6HoooAKKKKACmTSGNNwGafSUACsWUEjFLRSA0rgLRTSaMmoYh1FIKWrQwooopgFFJXlf7RXxwH7P/wAOdV8WzaVJrUdnCWSztyQ8jfXBwKmUlHcqMXJ2R6rSEhRknAr8s7X/AILabpovtfw2WGFvvNFf72/LaKxvGH/BZ7VJNUmPh/wdGtjs/dreTgHdgdQBnrnvS5vIfIz6s/4KTK2vfs1+JdOW8s7AeX5ifaZQHm2noozXmf8AwRhtWh/Z/wDFMxR1WTWyo3d8RLnH518A3Ft8dP2/PiJdXWn6dqOrRXDhjGrNFp1kvC/eY4xxnrnJNfsh+xr+zvL+zH8D9J8HXN1HfamHe6v7iP7jTOeicD5QAo5zznmiKBvSx7pRRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJtGc45paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiip5gCikpadwCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSZGcd6WgAooooAKKKKACiiigAooooAa2c9KjWMiRmPfpU1FTyodxkgbadvJrH1DR7rUCN0oVP7tbdFHKhqTicvJ4Vm3ho3Xg5ANbNrYyLzM2T7VfopcqLdWT0KVzZhyGbPy9MU+BtzYAP5VZowB0FPlRHMwFLRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUroAoooouA1mC9aRT82KR8lgABj1NNjkRnIVgxHUCs29RjpZBGASM84p/FQXTyDb5YBycEnt71HtaSBo/N+f+9T8x8uly5RUKMY9sedxA5NSbqq6FYdRTN9Lup3QWHVXvbG31G3eC5gjuIZBtaORQykHqCDU9FDSYbHgHir9gr4DeNNSnv8AVPhzpbXU7b5Htw0GTjHRCKZov7AXwA0Fomtfhno7PH91rhWlPXPJYnP419BYox70BdmX4b8K6N4O0uLTdD0u00mwiGEt7OFYkUfRR71q0UUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4BRTWbaM4zQrblBpgOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKY4Y4wanmAfRUZB3HBqNmPPzYqeYaVyfcB1Io3D1qrDIs0nDBwvcGpuxz0pXuPlI3ky528j2qVGJUU1VCrlRSZc8jioCxMKKhDherZPoKAu/JywHp0rWMr6BYnopF4UCirJFooooAKKKKACiiigAooooASjNRthmIzzSqu1cZzUcxViSikXpS1ZIUUUUAFFFFABRRRQAUUU103Y5xUcwCBTuJ7U+iirAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKhurpLO3eaTOxBltoJ49a+evDv/BQL4HeJvG8vhO18YpHrKXDW3l3NrNEjSKxUgOyheo9alySdmUouSukfRdFNSRZFDKwZTyCOQaXNUSLRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUySTZ2zTBcKULDnFZPcdmDXARmDYUDuT1psl4kSl2ZRGOrE9KxtfvIYLV5rgME4247Hpivhn9sb9uxPgNfPoEds+o63cWhe3t1OIlyxAZmHNcrqS5uVI6fZLl5mz7/wB/m7XVg0Z/u85qGG3EHmSqmGY/dr8QfB3/AAVi+NPhPVLdrn+y9U0hG5sJLfb8pPQSA5z17V92fs8/8FUfh98ZNes/D+uWE/hHV7gAK91IrQM57Bv8a6NbXZh6H154m1SXQtNuL8OBHAplkXGTtA5rxr4K/tmfDf4469qOgadrUdjrlpK0f2O6YRtJtODtz15Fe7yRxaxbnbJFPZzJglcMGBH8q/Nj/goB+w9JoMsPxN+F1q+marZtvnisflyRzu479al3urbG94uNup+l7yJa7N2fmO0HGakjJwQxBIPavgX9g/8A4KJaZ8UrfTPh74/l/s7xpCrQx3twwEV2VYgLk9HxgfUV96SFLQvK0gRWI+90HFabmVuhY79KQ7u2MV8+/tAftleDP2dbGObXrg3bykhIbRgXznuK8D8I/wDBYr4ZatqVvZaroWr6ZFJMI/tzBWiAJ4JHXioUk9inBx3P0BXO0Z606szw34i03xbodnq+kXkV/pt2nmQ3ELbldfY/XP5Vp1utjFhRRRTEFFFFABRVa6ujBwqFmJwvHWpgxwM9aAH0VFNN5UZbG7HYU2G4Eyg/dPoaV0OxPRSL0paYgooooAKKKKACiiigAooooAKKKKAGtnacdaI920butI2d3Bo5rJ7gPopm40bm+taLYB9FMWQsxUjFPpgFFFFABRRRQAUUnNLQAUUxmPToabJMIsZGc+gqOZDJaKQcilp8wgopjMV6VFNMUhLd81Q7FiioFnyoOKPPGcc5qeYfKyeioBcLu2k4NSMTtPNUKw+ioY5GOeM0sZZuScUCJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKO5qGaTZmp5hpXJs02TJQ4PNUi8r5ZWwv8AKljmLKRvVm9jWdy+UfMzIu7dWbdXk+VRIWfcfmakI82Ykz52nBXPAq2u55Dg446fpUJ3Zulyoms4VtYN2NvqtVmuLm4n+UKluOv95qxta8feE9L1608Oat4k02x1q6AeHT57yOOdwTgYQsGOT04roJ4I4YzIsbEg4wPyq7GSab1J4x8gw2B708g7fvc0yOIbRtOBShTGxZj8tIl2voJFHhyx5NTUxX3HjketO3c4FVH3RDx0pv8Ay0NfEP7VX/BUTwx+zh8RNW8CWnhW98R+I9MMQuW89YLdTJCkqgNgk/LIueODmvev2Tvj9J+018GdM8eSaONBkup7i3ayS4E6AxyFQQ4AzkD04ORVcwrHs9FfnZ+1X/wVbk+B/wAX9Y8DeFvCdrr50VvJvb68ujGpm2qzIgA6qSVIPcGvtj4F/E7/AIXN8IfCvjb7A2mf21ZLdG1dtxjySOvccZHsRVknd0UUUAJmikOM1BPeR23LkKPU0NpAk2Ts6r1OKa8iiMsWAHrXPatqrLIhh+dWPVafJJczWrIqsT6YrP2iOhUtL3NCTUrWKQIZAZD0HrSQapFNMQrj6ZrANtcSSISu0rxk1bsdLlW8ZtodOu/1rLmZq6cIrc6VTuUGnVHEAqhe9SVqpHGFFFFPmEFFFJRzALRRSA5o5gFooop2uAUUUVQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEc0SzRup6MCDjrivxw/b3/wCCe3iHwD4qvfG/w9sr3VtEu5XurmGNi81vIzbiVwOmSTX7JZpjqsilGAIYYKnkEVnKN3c0jNx0Pxp/Y+/4KceI/gn9k8G/E+3vNc8OoVhgu2GLuz553FyN6gk9TkYr9cvAPxJ8NfFDQbfWPDGsWur2MyBw9vIGIGSOR1HIPX0r86v+CsHwZ8L6tB4avdCsIrfxldXIsrSwsIAHvixGThRjjvn0r2z/AIJz/sW6r+zH4cvtd8Rar9p8Qa9bIkmnwlvJtUDFlHOPmxjPHrWUJ3ehdSm0k31PtClpF46nJpC2K6LmA6k3fNik3Un8RNF0MfRSbqWi4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUU3eN2O9G72pXQ7DqKaGz2pjyurYVMj1zRdBYJ28uNmxu9qqr5hjbBVEIyGp9w05mjKsFQcsMZzVGa6+3WcyRrs5Ow+vr+uax+1c2jFtHn/wAXfFU/g3wPq2tThXjtIHk2sflO0Eg1+Fmi6P4v/bS/aOXToZJLrU9YuSpmzlbW2VuWHsq1+mf/AAUq+LWr/Dv4I39naoJotQlFkHLFSoZRlunOCTXk3/BFb4W2048cfEGaFXmilXSLaRhynyrI5H1DAfjUU4py5jas7aH2l4D/AGFPgv4I8EWvh1vA+l6qFhVLi8vYt8s7Y5YtnjnPTpXgv7S3/BKrwP4w8Pvf/C+1Twl4ktz5kcaOfJlwOF5PynivvgkDjPNNVldioYEjqM8it9DkWmp+CXin4yftIfsa+KJvCeqeJNQsZ441ES3DefEykB8qT/vV+oP7BPx38TftPfAG81nxrbWlxdCZ7TdEuFnUblJI7HjtXg3/AAWZt/Dv/Cu/Dcsluh8QC92JMoG8R7c4Nehf8EhbuOb9lkW6qqTQ6jcKxHUgyOQT+dQaM/KL9p3wwfhd+0Z4u03Smntfsd8txbyA7GTeiy5BHozn8q+7f2Q/+Cn2lSeBbXwT8X7ueC6tkZLbxEoMjTLuYr5g7FQQox2Arjf+CunwPg8J+JtC8cWyHztR3Wt48YG0kL8jH3wAK+WvGHwFSH9nnwz8U9MmQW1xI1hqNqGzskV2QMv1Cgn3NK6aswTlGV0dVdeD9e/bW/avvtA8Oas9/ZX1w0kF3Pu8qK3RQC+3t0NfRPx+/wCCScfwt+E934j0PxjeatqVlGJLi1u40WJj327RmvFf+CdX7U3g/wDZh+IWoXvizR2ng1aIWyatF80lqueRt9D371+zV34w8MfG74S3uoeGdQt/Eel31szJ9lcMTgkEEdQQQRj2qnaEROTnK7Pzi/4JD/tJatb+OLz4R65qElzZ3EMk+mRzMT5LRgs6L7H5jj1r9aK/Cr9nfT7f4Z/8FHvCdtF5lrZSay0UbMNmfNhIK/TexFfupu6VcZKSuRJWY6ikpaokKQ8ClpOtK6ApTPJ525Qzbe3YVy/jj4veE/hnpE2p+KNcttIs4SA8twcDn09a6HXb4aZZvIDg9BX4of8ABS/42ar8RPjZ/wAIRYTSzaXpqxQ/ZISf3tw4DAe/3l49c1lzPmsjqULw5nsfqlY/tsfAzUtQSxg+JmgG5cgCN7kJ16dcV7BouuaZ4k0+K/0q+ttSspc7Li1lWSNsHBwwODyCPwr8h/ht/wAEc/F3jD4ef2zrviiz8P61dQeda6V9mMmwkZAkfPGePpXl1l4i/aG/4JsePLG11Hz10ZyTHY3Dm4028jLZbaQRtbk9+CTTMra2R+7S9KWvNf2ffjpoH7Q3wv0nxj4fmDQ3aFZ7cn54JlJV0Yf7wOPUYNek81otjN6PUWikFLTEFFFFABRRRQAUUUUAFI3SlpKAIJN7DIr5+/ak/a80L9lXTrC81+CW6a+3C2t4hzIwHrX0Pt2jivyt/wCC1Vx50/w0ULugVrgM2ON3GB+tYta7msXpsfbn7Iv7V2hftaeAb3xBpNlNpd3p919kvbKY5MbEbkIPcFcGvda/K7/giTeSs3xKg8xvI/0Z/LzxuwQT+lfqjjNaohir92nVGXCYBOKXd70xDi2Kasgboc1UaZvthjY/Ieg/CpoIwp6c1gpOTshtWJ6Wm5xRurW5IyabyyBmpFbdUMkIkbJp6/LgVnd31GRXBfcNhANSJuCjccmo2txJMXYk+2al4UUD6D16UtMVuKXdTFYjkYhjVaZvmAxuLHkelWmx1PFMWFS28dT3paloazCOREOTTjjccLz61MqjAzyaXaOuKvlFcriEbt7KC1PVt7MMcetO3BmZfSgKAMdqsVyDaQ5AkOPTNc/41+IWi/DrTl1DX7+303T94R7q6mCKufrXR+WolXHHtXwF/wAFmNan034A+F7G3meE6hrYjkCHG9FiY7T6jO38qXMXofc/g/x14e8f6X/aPhvWbPW7HdtNxZSiRM+mRW9X5sf8ES7yab4YfESB5XeKLV4NischcwnOPTmv0manuQ1Z2FooooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKQjcCKWigCBVaBcDkCnI7SLnGKhvrpLGCa4lUmOJDIdi7m4BJwPoK+Kfgz/wAFQvBHxZ/aCuPAgsZtH0e72waTql8uyS5ueAUdf4cncB9BnvU3KsfXPjzx34d+G2hSa14o1+x0HS0dY2udSmWOHcegJPetrRdb07xFpsF/pV9b6jYzqHiuLWVZI3X1DA4Irwn9uL9nG5/af+A994U024S21iC5jv7J5PutIgYbD7EMa/Ib9nv4/wDj/wDYL+N15pusWV0LFLkxa54d3AC4+XiRfRgCCD/+qmFj9/aK8q/Z7/aU8EftLeDY9f8AB2pLPt+W6sZsLcWr5I2yJ26ZB7gg16rTJCiiigAooooAKKKKAGf8tBVO8kAZhsZjtPSrjd6iCjcTms3uXHTU8j/ac+Luo/A74G+JfG2j6Q2sXulW6uLXsuSB5jDuBkE18k/sDf8ABRS/+M/jDXPDnxN1HTNNvrjZJpMiKsKHPDR5PfpX6CeI/D2neKtA1HR9Vtku9Nv7d7a5hcZDxsCCPyJr8Zv20v8AgnDrv7PcjeNvh893rfhfz95ht0ZrrTjnKH5eWX37VJVz9kpbWL7Z9pjkUxH5mVTnPvXlv7SX7QGn/s5/B3XvF2pzxLdRo0Wm2shAee4YfIoB5IB5OK+CP2Nf+CoH9lW1p4S+LnmTW8EIit9ZRcuSCdok/DA/CvAv2vf2gNf/AG5Pj/o2geF7O5bS45hp+k2Iywdy+1pmA/E57AUlGzuXzaWOY+BXhH4j/ttftL2N/c6he3OotdLeX+tZbZZQodwUHovTAFfvTpBurexht2EjJDGqb5uWYgYJJ9zXif7H37J+g/sgfDO4tlnF9rl1H9p1fU9uN7KCdq+iqDj3xmvk/wCIn/BZ6z0vWNRs/DXgCS5toJDFBeX13t8wjgkoBwMg9+lUSml0P0vt5Wa28w/KTnj8axNe8VWPh/SrrUdVvLWz0y1UtcXd5IscUI/2mJwOo6+tfkfqX/BZb4oXUkhs/Dfhm0jb7qzxyyMPqQ2DXiPx+/b9+Kn7RXhz/hHdavLXTNF+9PZ6PC0ST+m4E5I+tFiouKd2j9y/hb8TdA+Kmmzar4Z1mx13SlkaH7Tp8qyRh1OCpwTg+x7EHvXc18J/8EefA+peG/2YrvW7uZWs/EOrzXVnCpz5aR4gb83iavuyq5TOT1P50f23vFkPjr9rP4paxbbmgbWpbVdw5IgAgz9P3WfxFfs//wAE6/DFv4U/Y1+GltAjIbmykvpN4IYvNNJISf8AvoD6AV+Ffxyme4+Nnj5xjMmv6gR+M71/QL8BLe2+FX7Lfgo6jOsNro/hq3uLiSVggULAHbJPTHPWnYGfiT/wUPs0sf20vinEieWjagsuMd2tomJ/Ekn8a/Z/9hJpH/Y/+FDSoyOdEiOGGDtJbafoRg/jX4HfGT4k3/xk+LnivxlqJVrvWL2Wc9lVSCqD8FCj8K/oc/Zi0ltC/Zw+FunvF5Mlt4Y02J48YwwtYw3HrnNUQz02iiigQmKz9R08ahtUhgFOfrWjRUyjzFKTRn2+mwoMFOB0B7VY8pYVOBk1KeppOKiyWhXM2Vo4QzcpgVaVBGvApF+9x0qSgmUmyNU3MWPFP9qWm4O8mr5SRaa7bSDn8KVutN9agYyOV2b5l2iia6SHO87VA3FjwoA7k1Ev7ydhu4r4r/4KsfHDXfg38D9JsPDl6bG98R3zWkkyNh1jVMtj06ikOx9oac0dxm4hu1uYn6eW4ZfzFX81+ev/AARw1jxP4k+EfjO/1nWrjVdKg1cWVmtw5cxusayScnkf61T+NfoRTCw+ikXpS1otiQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFQ2AUUUVYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGqu94kd4luwYOy7gccfTNZuTQ7XLPeqOqeetuxthmbBCk9B9auZoyPrRKLkrXHF8rvY860X4S2V5r1j4i8QRQ6jrNi7taMy7lgLcErkdcV6MvyjHpQpArI8VeIofC+i3ep3bJDaW0TSSSSOFC4HeotGjFtmjcqsrGn9oXzgg5NScGvyp+L/8AwVx1zwb4s1DS9B8J2d39nk2i6nuiFlUgEFQoPY14j4u/4KnfHDxZI40b7LpEMwGy3s4zM6cYPOM8nn8aUZuSUkipU1F2uftjr3iTSvC9hJe6vqNtptpGMtNcyBFA+prxjUv27PgPpN/LZ3HxK0UTRHDbZtw/MV+HPxb+K/xg+IVqdQ8c6j4gnspiAPtJkit84xwuMdqtfs1fsq+OP2nvEEul+FLaNLW2/wCPnUbo4hg4yNxA6mrM7W3P6Afhn8aPBPxk06S+8GeI7HxBbRnEjWkgYpyRyOo5FdvXyL+wP+xDdfsmaPrV1rerw6r4h1Zgsn2PcIY41PygZ6n3r66qopozCiiirAKKKKACiiigAooooAKKKKACiiigBjKNxPekNP202SMsjKG2kjGcdKizKuNjztGRg015QrBSevtSoPLVULbmAxnpmnYB6ipGVbjcJI2jGc8HJqq1n9nVpl+/zzngfhWrsVsEimfZxhhnKt2NHKy4zsflZ/wV28Yt/wAI/pegkCQSXazBhxjCDtXq/wDwRctwn7Nfiqb+KTxVPkfS1tqx/wDgrV4B0S1+FsviG4gY6h50aW7L0GcKfpW3/wAEX2/4xp8UJ/c8Uzjg9f8ARbas6el0+5VWSk7o+7tchuptNuFsn8u52Hyzj+LHAr8iv2qP2qP2k/Bvj3V/DFtp95oMCyBUubO1aR5VKgg7wMdD2r9hetVbjSbK8kD3FpBcOOjSxKxH5itrERnyqx/NZ8UvG3xH8Zxwy+OrzWL4I5ZJNTRx8x44JHpXefBf4f8A7Qb+E21T4cWfia20Od2Jl06RkjlYcHAzzyDX3T/wWX36X4Q8J21rYRR2FxMxkmhgVSrDtuA9q7r/AII4+NNW8T/APxBpmoTNJZ6Pq5gs93Xa6LI3/jzGlZil0Z8i6X8JfjN8Rf2ZPibffEN9Ta10WOK5sl1okzeYr5kAJ9q+VdF+IGua34JsvhtHIW0y41NJ44yT/rGbGPpk5r+j3x94NtPG3gnW/D1xEhg1K1kgORxllIBP44r8Kvhv+yX4w8P/ALYnhzwFrWjX1uLXWY5JLxLdmiMCkSK+7GMFcZ+tPlLTufdfjX/gk74I8e/B/R20Jm8MeNEs0lknjO6G4lK9HBBwO3FfAetWPx2/YG8a3dhHeah4bEnyC6tyXs7pSA3y5474+ua/oIgjEUKIOAqhRXK/En4T+E/i74fl0TxbotrrWnSDmO4TJX3U9QfpVW0szJOzPwC8JfGbWviF+0t8PfFetRxDUrfV7JJHt/l83Eq/MR6kGv6J4m3Rxn1ANfDln/wST+FmjfFPTPFmkapq9jZ2N1HdLo+9Hh3IQQMspbBI9a+44YVhjVFGFXgCpjHlHJpoevSlpKWrICims22jdUWu9BnP+Opobbw/c3EzqiwqXO72FfiN8C20/wCKn/BSHR59SgW6tJ/EEx8thlW8mMlOD7oK/af4sLFN4H1mOUcfZJGz3GAa/Eb9h1Um/b88Kkk4/tm+YY/65SVml+8Ol39kkfvTyqgDpXK/E74Z+Hfi54Pv/DviXS7fVdPuomTZcICUYjhlPVSD3FdaOlG2tbHLqndHwd+wf+zH8SP2Zfi5420i/O7wBeAy2h37suGwh9M7eDxzX3ivSjFG2q6Gk5ubuxaKbnFKTQZi0UgpaACiiigAooooAKKazBepwKTcTn07GlfoArfdNfmL/wAFooreDwJ4DCgCYalKxz1I8uv05JO05r8sf+C1c5kt/h7EpPlGSctkfxDioe5pHZnIf8EVfEpsvif440NpBsu9NjuFXA5ZXA6/Qmv1+Ar8WP8AgjbZST/tGa1cRqfKh0dg57csBX7UVUeopdBjKGGCMigKFGAKdSU76EFaa3LSFwPmHQ1MuVAz170x1Ls4DY/Onxx/KAXLEdcjmstd0aS2H5zTWk2nGKeoGKXaKNTNEO0vz0ojDBzk8DpU20UjLxxwaViriVHIewPNNjmPmMjdu9R7is7Hgg9DT+Q46ljYvpSMD0U4oj3bRmmeXJ5pbfhfSgAaPdHgnLetLGwVQvekmkWHDFtpY05GVj8vPuKBky9KWmKTuxT61WxmR7QHZu5oB3c4p9FMZA2POXrmvzh/4LXXTR/DL4ewquAdWmcv6YjFfpJgbs4r8tv+C2F5KX+Gdj5rG2ZL2Zoc/KWCqA2PUc1n1LWrPVv+COvw8l8Lfs23viKU5/4SXVJbiPjnZF+5/LcjV95tXhn7Dei22hfslfC62toUhRtEgnYRjALyLvdvqWYk+5r3WrRMnqFFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAprosilT3prL8x9K+Ef28P+CjWmfAyxvfB3gS5g1Pxw4Mc1wp3R6fnufVsGpuVY639tz9v/wAL/s46be+GdK8jX/HUsflvpZYgWqugKtJgd1YED0NfjJ4B8C+Kfjt8TIbDw7p09zquq324tag7bbe+5jnsBkn8K9i+E37Efxs/a40vUfiHp1tava6hLLImparcrGL2RXZXCcEjDKVyQBxWvp/7B37VHwvkm1TQfCOt6XcwHP2rRNZgMj47qkT+YfypWKP27+FvhW+8D/D3QNB1LVZtbvrC0SCW+uAN8hA749On4V5l+1B+x34D/ai8Nzwa7p8dn4jSLZZa9bpi4gI5AJ/iX2Nflt4P/wCChX7Sv7OuvrpHjiK+1ZISBNpfjGykgucEZ4kYB+QcgnPBHav1u/Zm+NUn7QnwX0Dx3Noknh2XUvOVtPll8wxmOZ487sDIbZuHHQiqJd1qfkT4Z/Zd/aH/AGU/2iNGstAstcjtLjULe3fXNBgea0u4DIpO84xjafmB6HNfuPDv8mPzDl9o3HGOcU5elLTJCiiigAooooAKKKKAGt1pu0HnFJNIU6DNKOlZvcsRlPGOKZc2sV5byW88azQyKUeNxlWB4IIqWvHf2rv2iNM/Zn+D+p+Lb3bNe/8AHvp9qx5nuGB2jHoOp+lID8yP+Cq/wz+DfgPxZpw8GSRad42kkDappVhgwRwleHYDhXz2968T/YZ+PWk/s3/Hiw1fxLosd1ZXKLbSXUkf72zVv+Wq59Qcn616N+xT8EdT/bc/aT1vxt41a4k0fT7salfzKAyz3G4GOAk8YwBkeg969m/4LFeE/Avh208BjR9MtbDxncGbzPsiLHutAqrmTHoeAT6GmUfqNo2saZ4y8O22o6fcQ6lpOowCSKaJg8csbj1HBBBr5juP+CYXwDvPE15rM/haWVrmUytam6cQKT1woPAzXoH7EPgSX4cfsrfDrRZtQk1OQaat150nUCZjMEHsgfaPZRXuVPlIueO+Hf2P/gr4XsYbWy+GfhsrFnbJcafHNJySeXcEnr3Neg6H8P8Awx4ZsUstJ8O6ZptomdsNraRxoMkk4AHqSfxroaKfKSQW9rFZwrFBEkMS9EjUKBnnoKS6uY7K1muJmEcMKNI7McAKBkkn6VYryn9qvxtJ8Ov2cviH4hiIEtnpEwTP95x5Y/V6oD+eL4oanBqXxY8V6hDMDaXGs3MyyRkMCpnYgg9+Oa/SX9tL9tzwbqf7Knh34b+APE6614l1ixsoLw6dJuEEQjUPFIy8B2OBtz2r4s/ZP/ZL1n9rnWvE+laDr1jomu6TbpdomqLIsUoZyGDOisw/KvuH9nz/AII93vh3xpa638UfEmnaja6fKs1vpugtK8UjK2RueVVbH4e3I5oKufmp8Tvg/wCKfg/ren6Z4n09rC/u7SO8gibrsdQ65/A1+yv/AATN/aq8VftHeCdX03XtAt7G08Kw2thDqVsxxcNsOVIPAYKq9PUeterftM/sTfD39qW107/hJkvLC/02Iw2l9prqjovoQVIYV0H7MX7MPhb9lbwHL4Y8LyXF3HcXLXVzeXmPNmcgAZwAOAAB9KCT2CiiigApMjOO9LXPePvFkHgPwbrniO6jeS10qzlvZUj+84RScD8qAN3duY46etVp45ZCApxg5z61+Ul7/wAFqNe/tGf7J8P7U2e8+X5t0Q+3tnAqtN/wWs8VLIwj+HWmlezPevn9FrN7miP1tiOE+bil59cV+M3jb/gsV8U/EWmNDoPh/SPDspBBmDNM/wDwHNfVv/BLX4zfFH43+GfGmueO9VbVtNjvkgtJpY9jLLsDOo9gGX86diWj7uHT1paRelGOvNWSRhgzEg5FNkuEjbDHH41Q1zXNN8K6Peanq15DYadZxtNNcTttVFAySTXg9j/wUC/Z91TUvsUXxG0wzZwC0cir/wB9FayZdj6AtW3zMcEZ9q/Kz/gthrQXxR8NNN8zIhtLm6MRzjLOFU/mh/Kv0Am/a2+DVrbm4f4j6CsSjccXIJx9MZr8if8AgqF8evDHx2+OWkX3g/WYta0bS9IjtluIQwQy+a7MvzAf3hQM/Rn/AIJa/CeX4W/sn6PPO+648TXL6864xtEkcaIP++IkP419dA57Yr8vdI/4Ks+EfhX+zn4L8O+HtLutV8YWOiW1m++LZawSpEqkEnlsY5wMZz1ry74O/wDBRT9o/wCMnxn8NeGtK1XTZhql9GJLC30u32RwAjzDvI3cKCTzV2Qan7LL0paZDu8pN/38fNj1p9UZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUrIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANavL/2jvjppf7OvwzvvGmrWM+o2tq6obe1KiRtx7biB+teokVyXxS+Fvh74xeDb/wx4nslvtKvF2umcMp7Mp7GspJuI476nwtpv/BaH4bTXIW58I+JLaNudzJA2PxEpqzq3/BZ/wCFlqdtv4R8VXfGVkjjtwp/OYH9K6H/AIc8fBn7YZf7X8Uxwk5FtDfRqi+wzGT+tY3xV/4JS/CLw58Odd1Dw9ba1caxbWkkkJur3zCzAZycKB+lZyajq0aKx61+yT+354X/AGtPFer6Bo3h/VtGvdOtRdu2oCLa6FtuF2uxz+FfTOvaDY+JtNm0/U7eO8sZ12y28oyrj0NfjB/wSTkudG/ay1CwAdFOl3EE6k55Vxj+VftfWu+j2E3Z3Wh4z4g/Y3+C/ieQSaj8PNGlmAUeYsJQ4AwBwfQCup8LfAn4ceA7OOLRfBWh6dHCPldbGMuOc/eIJ/WuvvtatNMs7i7vJltbW3UvLNKQqoAM5JrB8J/FDwf8REdNB8Q6fq5wd0dtcK7DnHQGp0WiDXdnxF/wV41yz039n/SbOwtbcJeX4UyRxKNoXPGe1ZH/AARRsPL+FPj67EissmspEI8crthU9ffdXa/8FWPCdrdfs63swgZjaXUc0e3+EHg/rVT/AII2+G4dK/Zr1TVUfdNqetTO6+gRVQf+g1MdByWiPvhcgc0tJuo3Ct7oyFooopgFFIeKFbcM0ALRRRQAUUUUAFFFFABRRRQAUUUUAQtCrSb8fNT6dtpNtQ0yrir0paSlqyT4a/4Kx6fqt5+znqEkFotxZxXMRZ8couQSfzriP+CJ+uxzfBrx9o4IMtv4g+19edslvEo4+sZr6I/4KFXEdl+y34znliW4T7NsELcDJP3s+1fIP/BEZZI2+KEm4mKY2QEfYFfMyfx3fpWC3Zo/hR+qNLSUtbmZ5d+0T8C9E/aF+GuqeEtZjRGuYz9muygZreTswrC/ZD/Zpsf2WfhLB4Rtr3+1LpriS6ur0xhDI7HgYHYDA/CvbNvzZpcYoHfSwEVAbC3a6FyYIjcAYEuwb/z61YooEJS0UUAIeaAMUtFABRRRQBDcK7fcKg/7VEfmfx7fwpWlUSFc5P06VnXfijRdPLC61aytiv3hNcIuPzNY+6nqy9exzPxcQyeDdXVVd5HtHRAvckEV+Kv7DWmyx/t/eGrd1ZXg1a+LA9RiKTNftL4o+JXhCHRbqaXxNowVEZlEl7GwOBzwDmvxn+A/xN8LeBf+ChFp4nl1O1t/DrapdeZfXEgWJPMjZSc9gCeKSfv3Oi94ryP3YXpQzBVLHgAZNfOniz/goJ8BvCETmb4h6XfOv/LPT3M5PsCvH618/Wf/AAVgsvH3xp8P+CvAfhKbVbDUryO2N9dHYZFb7xVe2DkZPpWvMjn5Wz7B8dftHfDn4ZtGvijxbpuiySNtSK4mAf8AFeorv9L1a01rTbbULG4jurO5jWWGaJsq6EZBB9CK/ND/AIKr/shT+IbRPiz4Y06ea+ijWPWLZX3KI1UKrquOMAc1y/7G/wDwU70H4f8Awft/BPjqKW2v9Ht3istQUFhMuSUVh2IGB+FHMkVyqx93ftEftjfD79mN9Oi8ZXF1Hc34LQQW0BkdlBwW+ldn8Efjp4U/aA8FQ+KPCF615pkjtGfMQo6MpIIIPuK/GSHR/iL/AMFLf2imeOaRdHgby3uypNvYW44z/vMBnHqa/Z/4I/Bjw78Cfh/pvhTw5aJbWlpGBJIo+aaQ8s7e5OTVXuKSSR3y0m4buvtivIf2p/DHxC8UfCHU4fhfr02g+L4SsttLDt/eAdU+YHk9q/Mfwr/wUY/aC/Z08UponxW0ybXLWKXbOmqWwiuZPUpKAAR6YFK5CVz9l1O4UteUfs+ftKeCv2kfCa614R1FZnTAurGX5Z7dvRl/r3r1XcaYh1FJnimTTLDGzscAUgPFf2pv2iNI/Z1+H954h1VncrxbwqBiWTbxHn3POa/KY/tJ/tXftTa9c3fgW71610+2LeXDoebeKIZ6FxjceO9dF/wVQ+NV98R/jbpfgO1mc2WmmNZLRT8rTSEYJ99pAr9Uf2ZvhVpHwg+C3hfQNK09LBY7RJJlAy7SONzlj1JyTWEbt3RtJKKsflz8Hf8Agox8Yv2dfG0fhj4y22o65YJII7ldSXF9CCc7w/V+D0Pauy/4KlfF7wP8cvgv4C8T+EdWi1GNr1xjo6Dacqw7HNfb/wC2N+yZ4W/aP+HOqrPpkKeK7W3eXTdTjBSRZAvCsR94HGMGv5//ABJHqnh+9u/Dt8ZIfsFwyPbtkASL8pOPfFaEx2P0m/4Im6Dbyaz8QdZKn7THHDag84Cn5v5iv1jr8+/+CN3hG30v9n/VtfSHbc6rqUiySc/MIyVFfoEveqirCkfKnxh/4KI/D34D/Fj/AIQvxdZ6tbMyJIdQigDwoGAx6E+/pX01o/iKx8QaDa6xptwl3p93AtxBMh4dCMg/lXwT/wAFSv2PtW+LGi2PxC8H2n2vWdGt2ivbFMlp4Mk5UZ6jJ6c18r/sjf8ABQ3VfgT8O9f8D+K57y7jt4JF0gzfes3wcpzycMTwanbQdk7HuH/BQr9v/wAU+APEEXg7wHfR6Tfhd9zeqVkkizyBtYEdPavdP+CYvxo+JPxn+D99qPj62lu4YbpksPEEyLG18uTuG1QFwjZXIHavzL/ZV+D+sftoftNwS+JRdappMlw19rV5IGwYl6RFlxjPAGMV+9nhrwzpfg3QbLRdFsodO0yzjEUFtAuFRR/nr3oUQkzUXpS0i9KWnymYUUUUcoEEkW5iema87+Od34t0f4Z6/f8AgyO3bXLS2aWAXGSGIGTgV6VSMiupDAMCMEHvU8nmaRm4n43Wv/BYL4uaDILPU/DGgzSW58uXzS8chIOCTWv/AMPovG8kWU8EaOD/ALV038sV+l/ij9mX4U+NLqS61rwBoV9cSHLytaKrMfUlcVTsP2Tfg5plsLe2+HHh9IhnhrNWPJz1OTT5RXR+UvxE/wCCunxZ8XWb2uj2OkeHVI5kjQyuOOxP+FfXP/BKv4xfFX4zeHfGGq+OtVm1fRIbhIrC4uIwpEmCXCEAZXkfjX1nZ/s3/CzTxiD4feHUHXnTom/mK7fRPD+l+GbBbHSNOtdLslJK29nCsUYJ6naoAo5RXL4HfvS0UVoSFFFFACdzX5V/8FrstrHwyQbRm3vTn+L+H9K/VP8Air8hf+Czl5O/xl8B2zOwt00hmVc8AtMQx/EACoa6lR3ufpJ+ybbR2f7MvwuiiBCL4csevX/ULmvWK474OWkFh8KfCNtbRrFbxaVbJGiDCqojXAFdjVLYUtwooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+Dv8AgpF+3XN8BdNHgXwPfIvjy8Cm4nTlrCJgGU4P8TAgj2NeB/sef8EztR+LzwfEn40zXK2l/I10miuxE95kkiSZh0U5yAOSD2r9H/FH7Nfwy8Z/EKLxxrngzS9U8UxbNmpXMIeQbAAnXjgAAV6Q0S+SYl/drt2jZxjjtU2KufLmtft6fs4fAmRvBQ8VRWP9hgWf9n6bp88yQbRjYCqEEjoeeteYeLv+CyHwd0W+MGiaR4g8SRcYuIbcW6txzgSENweOnaszxZ/wRx8C+LvHWreIJ/HWvQW+oXL3LWccMRKsxyw8w5J5J7VwH7T37Dv7Pv7I3wG1bxBqNnrPiPX7kG00yS+v2GJm5yFQBQB7imPQT4nf8Fd/h54r0+NY/g5L4kmtzvj/ALeMJjhbscbG/Svon9gP9rzxT+1PZ+IJdS8C2PhjQ9L2R213pshMMjnrGAR1C46V+W37FP7H+oftb/EC9sZLybQ/DOmxrJe3kSluCeI1JPJPPWv3M+CfwS8L/ADwDY+EPCVrJa6ValmDSvveRmYszMfUkk0xPsd8vSlpFz39aWgkKKKKACiiigAooooAY3eojIVJGCcVMc54r5h/ak/b28Efss+JdP0PXbG+1XULqITmOw2ny1z/ABe+Oaze5cddD6ViYyyFlOVr5T/b0/Y48Q/tcWfhW00nxNDolppMksktvcRF1kdgMNweoxj8aqeC/wDgqZ8BPE1upudduNAl6mK+tiMfiK6o/wDBRz9nhevxGsf+/Mv/AMTSGdb+yb+zTpP7Lfwns/CdhIt7fMxnv9QCbTczHvj0AwB7Csr9pD9i34fftPa5oOreLILkX2k4jWS2lKedDu3GNx3Gc/nWfb/8FEv2dZ495+KGlxf7Lwz5/SOhf+Cin7ObMVHxS0vI/wCne5/+NUCPoHQdHs/Dui2OlWESwWVlClvBEv8AAigBR+Qq9mvmLUP+Ck37OmnxyMvxFtbxkGdlvaXBZvYZjA/WvNNS/wCCw3wMs7qSKC28TXqKcCWKwjCt9MyZrRbCsz7ozRmvgpv+CyXwXH3dE8WP9LKH/wCO1nXX/BZz4VRyMLfwj4qnj7M0UKH8t5pisz9Bs15j+0z8KZ/jh8CfGPgi0uEtrzVrPyoJZCQokVldc+2VFfIMP/Bab4VFgsvg7xYp/wCmaW7fzkFTXX/BZ34VR25ktvB3i6c9laGBM/j5hFAWZ2n/AATh/Yv8QfstaT4q1DxmLCTxLq86RxvZyeZst0HALe7EmvtOvzA1b/gt9pMN46aZ8Jry5thjZJea5HC545yghYDn3rHm/wCC4Vwsh2fCFAn+1r+f18igR+q9Ffkd4g/4LbeKri3zovw00uxY8CS+1GSdR+Coma+m/wDgnv8AtteNv2sbrxHbeJvC9jZW2lorLq+lLItuzsT+6KuThgMd6APtaiiigAqtqWm2usafc2N7BHdWdzG0U0MgyrowwVI9CDVmigD5n1T/AIJy/AHVNQmu38CQRPK24pDM6oPoM8VFH/wTd/Z/j/5kaFv96Zz/AFr6doqbDueJeFP2L/gr4NjUad8PNH3qSfNnh81/zavVfDvhTR/CGnmx0TTLXSbMsXMFnEI03HqcDvxWxRVAIucc0tFFAj5q/b0+BHjj9ob4Mp4V8C39vY30l8ktz9qnMSSQhSCuQPUg4r8+tL/4Iy/FS7VZL/xD4f0+QnmOJ3lA/HAr9mqKVirn5D2P/BFvxxIyC78eaNFH32WTM357ua+ZP2vP2R5/2UPHWh+HLnxNb67cahafbS8FuYjChk8vJGT3B6HtX9CdfjF/wVd1BPE37Yui6Pbv501tptjYPGvVZJJRIF/FZAfxpcoczPtv9nn/AIJtfBn4c+GLG8v9Cj8ZapdQJJJd60omT5hn5Yz8qjn07V9A+DfgD8OPh7q41Tw14I0PQ9RA2i6sbGOKQAjBAYDPSuw8OW32Pw/pkH/PO2jT8lFaNUK4gpaKKBBRRRQAUUUUAFMfd/CM0+igBse7aN3WnUUUAFFFFACUA5obkUijatRcB1FFFWAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5t+0B4hg8L/CvxFqNxdtZ+TZytGyn752dCK9JPUV598fLGLUPhB4rjltY7vGnTERyD/YPT3rCv8DLjuflh/wAEjpY9f/ag8X6i8RMp0+WdWA4XdL/9ev2PWvxP/wCCTfiq38MftUavZzyJaxX2m3EREhxysgYD8s1+0Gja9Za7bmeynS4QcHYQcH0pxkloxyu9TzL9qDw7c+J/gx4t020aRJJ9OlRDGcfOV4HHNfgX8IvHHif4QfGTRZtIvbjS9RtdSjtpoxIQrZkCsGHpX9EHxM1RtP8AA+tXZhx5Ns8ib8YLBSRn2r+deCe48XfHy2uAAbq88QI5VRxnzgePahF/Zsfsd/wUa8daLoP7NN3Dr7hrnWLRIbdEH/LXG7PPavzv/ZI/4KGan+y38N9T8K2+hDVllme4tZCwCozcndn39K+t/wDgrXfaddfAXwtbXW6PULe4jMSnqcxjNeB/sA/8E9fC/wC0x8Ob7xh4s1q6itftT2kFnYna6MvVmJ45pKMWN/Cdn4D/AOC1WvWMTJ4t8C2+o4+7Lp0/lt+IbivuP9jz9sfR/wBrrw5q2oadot3oV1pkwint7hw4ORlSGHtXjH/DnP4OeUE/tLW8/wB7zVr3n9mP9jrwh+yqusr4UvNQuE1QoZkvJNygqMAgVXL2MtD3lc7eaWkoz7VoQDfdNNjbtSn6U1V280XQElFJS0wCiiigAooooAKKKKACk5paQru60AC5xzS0iqFGBS0AFFFFAHgX7b2gx+KP2e/E+myyeWkls77sZPygnpXwX/wRZ1qaDx/8Q9GA/wBHNrFPnP8AEHZa/SP9pCOL/hTPiqaSETmKwlIVv901+Xf/AAR11h7b9ovxhp4iUpeaW8jPnGzZLwAP+BfpUaXubP4UfsiKWkWlqzEKSk3HnivAv2tP2hNa/Z28FjxHp3h+bxBEGw0UWcL7nHah6Fxg5uyPf6K+Sf2Z/wDgo18Pvj80Ol3cw8NeJGHzWV22EY5xhWPWvoH4jfFfQPhn4butY1fUrW1ghj8wCWQLv4yMVPMg5Hex2tFfmF4r/wCC0ltpGv3NnpXgJNUsoX2i6a88vePYYr6l/ZT/AG8fAv7UkZsrBZND8SRruk0m6cMxHqjcZp3QuVn0xRRRTJCiiigD5o/bk+G/xN+IXwruovhnrMthrEDiT7NbOYpJ0xyobPWvyhh/Yo/af8a6oY5vCPiWGaRv3l1ql+FjJ7nJbpX76YoxUcqvc39q+VRaPw8n/wCCTP7Q/kRTiPSJpSPnjOsAOPbPSvKfhj+xb4w8dftES/CTUZrTw9rVuhkuppXFwkagbgRt68EV/QTr10LPSbubcybImOV69K/HH9i7xhc6r/wUm1C4ndppLya+hLSHJwucfoKltp2CMbxbN7xh/wAEW/GWk6TNe6T480nVLiFC5t2s3hL454OSK+ef2LdLtPBH7anhHTPEkiobDU5LV2jYBfNUEJ/49X9AToJAVIypGCD0r8N/25PgNr37Mv7TX/Cd2ulyf8Ivd6nHqdlcwNlS4YO6E/wnORg09SYpM/ZL4y/ELwp8Ofh5q+reMLu3t9G8hkkWcjEoIxtAPXNfzffEK4stU8ba9qGixNHo017K9uyqQuwsSo/Kv2blh+Dn/BTfwnoVkPFuowXeixxz32j2DiJwT1DhlORnIyK9v079jH4RaX8PpPCEHg+xbTniaMzSxK0+SPvb8daFzC0W54Z/wSX8Q+CdY/Z6a38O6dHpviC0umj1hc5eR8ko5PcFSMelfca1+Imtr4m/4Jj/ALW0MVjfyXfg+6dZ5I+Slzav1BXI+dOgPtX7N/D/AMcaX8SPBuleJdFnFxpupQLcQuPQjOD7itBSOh7mvKv2iP2d/Cn7RfgO+8P+ItPgluXiYWd+yDzbWQjhlbr1xxXqnRq5Pxp8UvCnw9tZrjxHr1hpMcSGRhc3Cq2B6KTms3uJdz8KfhP8QPFH7Cv7VE9pNJMbbTr77BqUBBC3NuXwHx3+XkGv300TVoNe0ey1K1bdbXcKTxn1VgCP51+E/wDwUA+N3g39oD4+WOpeCLQ3Bj8u2lvIlx9rIYAcD8s1+3nwnt5Lf4ZeFopozFKmmwKyH+E7BxVrYcnc6r+GkmQSJgjOORmnUjAspAODjg0En4F3Fk/ir/goh9j8Rq1yJ/F22RScZRZPkH0wBX75W8axQRoowqqAB7V+E37U9vN8Av2/JNafcyW+q2uoh3XKuG2s+M+mTX7i+GfEFt4m8O6bqtpKJLa8gSaN1ORhgDWcfd3NJvm2NZq/Bz/gqV4e8N6D+1NqjeHYUhF1aQzXaxsSvnkfMcduMV+2Xxa+IFj8Mvh7rXiHUZhDFaW7spPGWwcY/Gv5yPi9441P4sfEDXvFN40lyJ5z++28Ko4UHHTin1Ej9nf+CTcKw/se6FtB+a/vGOfeZq+y1r8zv+CSv7U+m6n4bg+D95aPFqlr5tzaTxqAjx5yQffnrX6YrWnQUhk23y234KbfmDdMV/Pl+39Z+CbX9pbxGnglBFZ5V7pFctF55GX2ZJPXt65r9ef2+P2mov2bvgrf3VpME8R6sjWenKArFWIwXwQRgD1r81P2Ff2H7r9ri81zxl4ukeLw6jSxiQl1e7umBO4MpGArHnFZ9R7K59z/APBJvwr4O0f9m2HVfDsv2nV9RuGbVpXJDiVTjZtJ4UdBjr1r7cavxk/YR+Imv/spftdal8KtfmltdF1a8eykgmAx5wJ8mQZ5GR6Eda/Zv7y1V0TJdQXpS0i9KWqJCiiigAorxT4+ftffDf8AZvurK08Z6tJaXd2u+KCGFpGK+vArzC0/4Kmfs/XSbj4puIefuyWUgP8AKlcrlZ9dUV8q6f8A8FNv2fNQuPK/4TVbf0ee2kVfzIr03wl+1p8IfHFuJdI+IGiXCnjDXSo35GmKzPXaK811v9pH4YeHbczah460OBB63iE/kDXVeC/Heg/ETQIdb8NarbazpMzMqXVq4ZGKnDDPsRQB0FFIvSloEFFFFADT1r8iv+C008EnxS+H0UeBcrprhyOuDMSBX66nrX48f8Fko0l+P3hBd3zHQ1+X0bzzz9cVLfQqKP1U+ChY/CPwcWOW/sq3yT/1zFdrXJ/Ce3Fr8MfC0IOQmm24z/2zFdZTWwnuFFFFMQUUUUAFFFFABRRRQAUUUUAFFNPWvkX9tb9vaL9krxF4d0e38OL4ku9Rhe4nj+0+UYYwcDsck1Nx2PryiuD+BnxWtvjd8K/D/jS0s5dPg1W3Ewt5jlkPcZ7iu8qhBRRRQAUUUUAFFFFABRRRQAUUUUANbrWf4g12y8MaJfatqM3kWFlC088mCdqKMk4rSqC9s4NRs57S5jWa3nRopI26MpGCD+BoA+PfC/8AwVa+A/iLxRPo9xqmpaMiyeXFf39mVgl5xnKkkfiK+Jv22Pi1c/twftUeFPh38PNRj1fw/bstnY3EIIRpJFDXE3PZVBHP92vob42f8EcfDHirUNQ1TwB4ruvDd1dStKbG/XzrYEnOAR8wGfrXxZ8Wv2Lfjn+xnqNl44hjjmttOkEkfiLw45YWzA8GRSAQD7jHvQVc/af4F/A7wz8AfAOneGvDWn29pHDCi3NykYWS6kCgGSRurHjv0r0aPO0Z5PTpX4z/AA//AOCxfxX0ebSIfEui6DrthG6i7khgkju3iGAzcNtB79K/XT4a+PtP+KHgTRPFelLKmn6rbJdRLOhRwGGcEGgk6aiiigAooooAKKKKACiiigBP4q+Nf2uf+Cb3h39pzxa3iuHXrnQfEEiJHNJjzImVFCr8vY4FfZdFTyjTsflTa/8ABE26eUtd/ElCuePLsjyO3etyH/gijo3ljzfiHe7+/l2q4/Wv06oo5R8zPy01b/giejSZ034lSonHy3FkCffkEVCv/BE2Vsb/AImsPXbYD/4qv1Roo5Q5j819B/4Ir+FYLdBq/wAQ9aupcnd9lhjjXGeMZBNdnpf/AARx+Dlrs+3ax4l1LHVXu0QH/vlRX3mxC/MTgAZr4h/az/4KfeE/gLq8nhrwpZw+MfE0Y/f+XcD7LbkjIBdScsO69uhqhXZeH/BJT4BhQv8AZmrH3/tB81Ys/wDgk78ALVstompXHtJqEn9DXwZY/wDBTr9pjx5rc0Xhm7WeSRt0em6T4eivGjB6AfIWNa91/wAFGv2pvhTq+n33jmwuo7CZxustb8NnT/OUdQhMa849CaAuz7Q1n/gkb8AtWnMkVjremjAGy01Ehen+0DUWm/8ABIf4A2aqZbTXr7vum1Ruf++VAr2H9kr9rbwz+1h4Ik1fSojpus2Mnk3+kzMGlt27OPVWHQ/hXvK9O/rzQF2fJ+nf8Et/2cLJV83wLLeuOr3Gq3WT+CyKP0rpbP8A4J3/ALOljbrFH8LdKdR/FNNcSN/300hNfRlFAj5ruv8AgnD+zjdzmV/hfYK3/TO8ukH/AHyJQP0r2L4XfB3wZ8FfD7aJ4J8PWvh7TGkMrQWu5tzHqSzEsfxNdlRQAUUUUAFfKX/BQr9pDxx+zf8ADHTdX8E6St5c3Vz5U99NA0sVquOCwHqa+rapavoun+ILGSy1Oxt9Qs5Bh7e6iWRG+qkYoA/FCP8A4Ky/H26xFA2izyAYJh0uRifw3USf8FLP2m72TdFCAG6CHRJMfyr9idD+C/gHw3I0ml+DNCsZGOS8OnxA/ntrqIdIsbdQsVlbxqOipEoH8qAPw78Qf8FDf2o77TpoXuLrTkI+aaLSGjYD6kV91/8ABLHxd8V/iH8Nde8TfEDWbrVdIu7wx6Y18v7wlCVkIP8Ad3AjHtX2vc6Hp16hS40+1nQ9VkhVgfzFO0vSLHQ7MWunWcFjaqxYQ20YjQEnJOAMcmgC3RRRQAUUUUANZiq5Aya/Gz9pbSIfil/wVe0/TLJ1uov7R02KYL/C8EEZkXnuuw/lX7K1+Htx4t0vwH/wVS1nWdcv49N0u18aXhlu7gkRxqwZQSewyRQB+38aCGNEHRQAPwpl1eQWNvJcXM8dvbxjc8srBVUepJ4ArzDxd+1N8JPBOhPrGq/EPw+tkozm1vo7h246BIyzZ/CvzN/aK/am+IP7fXxGtPhv8FbPVrbwzHlZ3in8lbsEgGWc5AVFGcKTk+mam5SR+vGi6/pniSyF5pOo2mqWhYqLiynWaPI4I3KSMir9eNfstfs56N+zZ8L9M8O6bFu1B4kfU7rzGfz7jHzMMngZ9K9lqiQooprMEUljgVHMA6imrIsgypyKdRzAFFJS1YBRRRQAUUUUAFFNK570o4pWAWmswXANOpjRhjk1N7APoooqwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAa33hXnHx81j+x/hj4hd+IpbCaMsOxKGvSCORXlv7TcKzfAvxiWwPL0+VgfQ4rCt8DNabXMrn862m+JNX8KeNbi+0O9ltdQE8kcc0JwSGYjFfvh+w74B134e/APSJPE2q/wBqarqK/bHkyx2q/KqcgHIBr8A9FvYtN8ZWd3dc28F8sknGflD5P6V+93gH9uH4Df8ACFaPC3xE0WzKWkatbXE4R0wo4INPlV0x8y5bHrvjuYah4R1+31OAJbfY5mXaeoCGvxf/AGC/g+nxV/bELxiNdM0W6lv3WUE5CudoGO+a/QT9pD9v74ON8MddsNB8Y2up6tcWskMAszvG5lIHNfnN+wB+0x4f/Zx+NF/r/iuW4j0XUoGhklhiMjbi2d2B2oFdWPrr/gsxZL/whvheZY2Xbc4z24GBXQ/8EX7ueT4N+L7eRyY4dX+Re3MYJxXl3/BQL9tb4QftB/CkeHvDl5dX2qxzCWKdrVkUD05Fec/8E5f20PDH7MfhnxTpnixpmt7udbmCOCPLEhcEVKLeqP2spNx9K/OzxH/wWc8BabMg03wZrWqRkAl/MSLB78GsS/8A+Czvhry1kt/CV8rn/l3d1J/766VfMjPlP0rknEbKCGwTjNIszGTaUIHrmvy3vP8AgtH5jA2fw9uAPSW7jxXGt/wWb8cQ30zN4P04wEny4zIcgds4NK77MXKu5+vkgZ1YL17URKyqFbk+vavyN0X/AILReL47h21XwPp81ufuraTMrD6k5FesfCL/AILA6X8QfiBovhvVPA02kR6ncJbLefbQyxsxxkjb0pjt5n6PUtMhcSRq6ncrDIPtT60MwooopgFFFFABRSbqTzBnFK6GLRkVGzfNjpTwvvUczb0EOopKWtACiko3DnmgDzf9oyYQfBTxex286fKBuOBnFflB/wAEj782n7WGrwmPcbjS7lSw/hxIDX1X/wAFRP2ptO8E/DGXwZo12JNd1I7JPLkGY0xzkda+UP8AglT8RPA3wn8beL/FHjbXbPRnNqsEE12+CcnLY+tZGtnZH7VrS14HY/t1/AzUIRJB8RNJKE4+aXFOuP25vghbSpG3xA0sljgFZMiruiOVnudzcCFSSM+gHrXxl44/4KGfBvVPH178MvEFhfTSPdHT55HjHlB87TX1h4T8c6B8RtBGr+GtXtdW09sqt1auHUMO31FfiZ/wUs+Hsfwr/ae/tOwwp1CKPUfMjwA0gPP54rOTvoaRSSv1Oy/bk/Yi/wCGe0T4peAtSmbQpbpZY40xm33cggjtmvAbP4gfFv8Aa+17RPAj6y+r3kmI4EkcRrtH976CvavjZ+2Nrf7TPgHwn8JfBGmXEtxLHHFdeYPmlkAAwvtmuF8S/sG/Hz4A+H7fx+umG2+xHzmfSrnfc2wHcgClHbUTlqfb/wAGv+CPvgDTfBKf8LCu77VvEVwmZPss5iitmI6Ljrj3r4g8YeGdQ/YN/bG0w2dw15pum3kUsUzsf3tq5G5WIxkhTj8K+2P2J/8Agp5pnja20/wX8ULlNN8RLiCDVWBWO47ASZ6N715p/wAFjPhrY2t94O8c20oljvhJbOI1ypGMqQw+tUVHzP1T8M+ILXxV4d03WbGQS2l9bpcROvQqwBFadfNf/BO3XTr37IfgOczyXDxW7QM0pyQysQR9BX0nnitEYvQWikFLTEFFQ3V0lnC80rrHEoyWbgCsrRfGmheI7ie30zV7G/uITiWG3nV3T6qDkVLkk7MrlbV7Ffx85j8K6mynDrbuy+mdp61+L37CEkkn/BRCF3VS7XN8XIHAyD0r9lfinerZeBdWkchV+zuC3p8pr8gv+Cbeirrn7c2rXwLstit3MGBHdsc8VL3OmP8ADS9T9qc1heN/Afh/4j+H7jRPEuk2us6VcDEltdIGU+49D7it4L3pafKzki2eM/A/9kn4b/s86xq2qeDNIksr3U+JpJZN+1c5CLwMCvZKdto21Y3qfBf/AAVM/ZT1v45eEdI8VeFbFtQ1zQ1aKS1iHzywsc8DuQa9U/4Jw+F/Fvgv9lzQdI8Y6fPpmo29xcCO1uRiRYjISmfwr6f20uKB30sI1fNf7Tv7Bnw+/agvDqmtS6hpXiARCJNQspuMDpujPDY/CvpXbRtqLMLnxN+z1/wSz+H/AMFPGK+JNU1a88Y39uR9jF5CkUUeO7IMhuehr7XjjWFAijCjgDsB6U6lqyQooooA/Pn/AIKlfsi618YdDsvG3hGw+36xpURS5toh+8ki65A7kV8SfA//AIKIfGD9mjQ/+EQmt7bU7C13LFZa3AyzQMT/AHhhiPav3gZQwIIyD1ridc+CHw/8Tai1/qvg7Rr+9brPPZozH8cVNi+Y/E74jftofHr9rd28GxxR3lrqDCNNJ0jTh39ZMbgPqa/QX9lv/gnH4T8G/AS60Lx/pUeoeI9dQvfyLKwMII+RVweCoxnHU19eeG/hj4S8H3LXGieG9M0qdhgyWtsiNj6gV020UuUOY+CP2TP+Cbup/s1/tAXHjQ+Jba/0KK2lgs7VIyJsOQfnJ44Ar72Wl2iirE3c/MX/AIKu/BTx78VPip8P4vDWi6lrWlT25t5DbQ74reYyYLHHT5cda+8P2d/g1pXwE+EOgeD9HjZIbSLfM0hyzzP80jH/AIETXpLIrHJGaXFRyg3dWPxQ/wCCpng3xF8N/wBrCPxrbboINUit7vTrtVAxNCihvbOVr9Zv2bviI3xX+BfgvxVLJ5txqWmxSzNtC5k24bgcda5P9rj9k3Qf2sfAVvoOqX02kX9jN59lqUC72iYjDAqSNwIrvfgj8K7P4J/Czw74KsLmS9ttItVtxcSgBpCOrY7UcoN6WO4XpS0UVZIUUUUAeEftNfsc+AP2pNNiXxNbS22sWybLXVrZ28yBe4C7tpz7ivkmb/giX4UeZmi+JurQxnon9mRsR+PmD+VfpZgGjaPSpsPmZ+YGrf8ABEvSxCy6b8Srp5Oqm6sAFz7gMa8+1D/gir4+hvnNh490JoONrtHMjfkFr9gMCjaKY+Zn413/APwRr+KqyLEnijQr2LIzNvkBH4EV+kP7Gn7P97+zT8C9K8EalfQ6lf209xPJcwAhT5khcDn0zivc9oo2imK7BelLRRQIKKKKAGN1r8Uf+CrGrSeJP2w7DSY5BJ9ls7S1Cg52l2Bx+Zr9r261/Pv+3BqeqW/7bfjq5/eXN3a65mzikBbcEZfLQD09KmxcT97PAdk2m+CdBtX+9DYwofwQVvVxnwb13VPE3wr8LanrWnvpeqXOnwyXFpIMGNtoyMdq7OqICiiigAooooAKKKKACiiigAooooA8I/as/az8Kfst+D5NQ1mb7RrNxG39n6an35n7Z9Bmvyj+Hvwd+LH/AAUY+Mk/inWvPttBknDXGoTljBBFniKIHgHHGBX66fGj9k/4Z/tA6zpmqeONBOr3enLtgP2h0UDOcEA816L4Q8F6F4B0K30bw7pNpo+mW67Y7aziEaj3OOp9zzU2KuR+A/B9j4A8G6P4d02NY7LTbZLaJVUKMKMZwK3qKKokKKKKACiiigAooooAKKKKACiiigAooooAKYwJ74/Cn0UAfNXx2/YD+F3x48Taf4lvLB9B8RWtzHO9/paiM3GxgQsing9OvWvo+ztVsrSC3T7kKLGufQDFTUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZ+v69Y+F9EvtX1O4S00+yhaeeaQgKiKMk5NAHzr/wUB/aNi/Z7+A+qz2V9Hb+JtUQ2unxBx5gzw0gXOcAd6/P/wDYS/4J63f7QrQfEr4kTSJ4XuLl5UsHBWXUGDHLMTghM9x1FeN/tNfHub9r/wDaaiku9QFl4TS+S0sFuZAkUFqGAaQ57sASa/af4F/ET4b6z4b0/wAL+BfE+j6umjWsdubawuUdlVVAztBzjPfFBVjtfCHw98NeA9KttO8P6JY6VZ26CONLaFVwo98ZNc78dvgj4e+Pvw51Twp4gtYZY7qJlguXjDPbSY+WRM9CDXoa9KWgk+bf2I/2PbT9kXwTq2mHUY9Z1fU7szT36RlN0Y4jTB9B+tfSVFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfnF+27/wS+1j43fEnU/H/gHV9Ps9S1La91pWoKY43kCgNIHAPLHnpX6O0UAfjd8O/wDgjf8AE7Vr+3j8Z6/oujaUr/vRp8rXE7LnnBKAV+kn7NP7I/gb9lvQ7mz8KwTz3t5tN1qN64eaXHQZ6AD0Fe20UrDuIKWiipvYQmaZIqSqUbmklUtnBxVb7VDb+Y0sqosal3djhUUdST0A+tQ2VYsxqsXyrwtP4bnNcj4f+LXgjxZI0ejeLtE1SVZDEY7TUIpG3g4K4DZzmuswCOKYWI+FnJ5JxU0biRcj9aqM3lvnOWzjmrSuNo7U+YbjZCs4RcnpVeO6FxMVjyQOvGKnBJ4xlfWlVQvQYp8zIHUUUUcwCUZFRyBmbg4FCLtXBO6jmKsSZoyKZuxTd3zYqQsTUU1fu06tFsSFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8++P3g/UPH3wb8XaBpTbdRvtPlit8nGXxwPxr0GmlaTipaMa0Z+Dfwn/4Jh/Gb4qa9qVjeWVv4OS0G43euiRY5snomxWzXvPh3/gij4sVlGs/EPRYYu4sbWSU/m6LX62LwKWpswe5+Yo/4Il6VIgMnxRu0fuE0iMj894qwv8AwRF8M9T8U9V6c40iL/45X6ZUU7CPzy0X/gi/8NbG0WPUPGGvahOCSZY0SEEdhtBNdNbf8EfvgrHt8671+Yjri8C5/SvueijlRXMz4tt/+CSfwHhVfMttenYHkvqbc+3Sux8O/wDBNX9n/wAOKNnglL9v79/O0pNfUNFHKg5meC2/7CXwEgXH/CsNCc+rwkn+dWZP2IfgU9u0A+GWgpG3922wfzr3GiqJPkjXv+CXH7PuualJd/8ACLXFjvAHk2V9JFEPcKDWdoP/AASt+Cfhnxpp3iLTbbVYZLCVJ4rWS8aSLcvOTnnrX2PtpNtQ0yrjYYxDCkajCqNqj2HSpKSlqyQooooAKKKKAGt1qKeBJ1AYZxyOcVK3WkrN7lkUMm9SD1XipxUQWPzD2c9alpxRItFFFWI83/aG8ReLPCnwi8Rat4Jsv7Q8SWsBe2t9m4se+B3NfkFr/wC39+0/eW91o01vNbXTEpKU0mRJl9sg9q/cWqraVZNMZTZ25lJyXMS7vzxUcpalY/Ff9nH9gH4l/tba9/wmPxH1K+0XQZJSslzeKftc+04KojdB719reIP+CSfwY1HwcujWDatp16p3f2q04mlJ9wQBivtvGOnAoYZ74pqIuZn5HeKf+CKvixdal/4R3x5o82lYHltqltIs3vkJkfrWTcf8EVfiNsBXxx4bY/3VgmH6kV+w+Pejn1pNMOZngH7Gv7KsX7Kfwzk8ONrk2u3d1N9ouJXG2NGIxtRfT3rl/wBsb9hHw3+1BobXMEx0jxZbRkWd91T/AHWHpX1RRVWFdnxP+xj/AME4NA/Z4mt/EfiiSPXvG8LMVuoWYW8Sk/LtU98d6+0L6xg1KyntLmJZbedDHJGwyGUjBFT0tFkI/Jf9vn/gm3c+Hbj/AITn4S6PLcWe4y6hptu5adG67489R7V8ReKP2i/ibefD8fDbxDqc13otrIWSz1S3DTQNnkBmG4V/SIyhgQRkHqK+Qv2zv+Ce/hz9pjTY7/Q2tfDHiyFs/bUgGycekgHP40rDuzlP+CRPxDi8Vfs1tojyL9u0S/ljeNABhHO5SRX3Q3Svj/8A4J9fsZ+Iv2R9P8WW+v6zZ6s2rTRvF9jVgqhRjnNfYFUJ6gvSlpKWgCrqFjDqVnNbXEaywyrtZG6EGvyv/aw/Y1+K/wAEPidL8TvgZJq91aXT+bc2GlSlriBhyxK4+ZD6YJFfqztpNtTyxbuzRVJRXKj8UfGf/BUD4oal8O73wP418LQJrBRoZNQy9lcDPA3wkNyPXjPoK6D/AII22E9/8ePFmqvFJIg00q0x5AZnzgn1r9VvHfwM+H/xOfzPFfg7Rtem6edeWaPLjsN+N361H8K/gP4D+CUN9D4I8N2nh+G9fzJktQfmP1JJx7UmtdDT2i5bHeilpKWrOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnFNVw3APNJIu4Y3YNRxgQxksfm/vVPMOxPQTjk1TS7VpOH49KladGO0vz6U7j5WSBg3Ir54+Of7C/w1+O3i608Vaja3GkeJbeaOc6npj+XJKyEY3+vTrX0ImBwvSphS5g2INPtRY2NvbK7SLDGsYaQ5Y4GMk+tWKQUtUSFFNJpu/5iO9TzDsLtO7O7j0p9eC/tCftpfDX9mXVdN03xrfXkV7fqZI4bK2MxVAfvNyMCuw+FP7RXw5+NVjDceD/ABbpurSSIH+xrOq3KZ/vRE7h+VHMOx6Qc9iKFBA5OTTPJBk8zc2fTPFS1RIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Zf8FXPidcfD/wDZbu7CzuDb3Wv3kdhlTgmP7zgfhivs2vzZ/wCC1WiatefDrwFqVvC02kWd/MLnbnCMyAKTQB4H+xb/AME0LD9pL4RL441/xFeaPBdzywWVvBF82EO3ec9QT0xXmfxz/Z1+J3/BPv4k6Rr+lanM9gZQ9hrVnuVJSpz5Uo6Zx2PWvs/9hf8A4KCfCDwT8BPDvgzxhrB8J6xolv5Lie2kaKcZJDKUB5PuK8F/b8/bUt/2sdS0j4a/DjS5tW0JbxJFumhInvLj7qiNeoUE9fzoLVz9RP2XfirffGv4D+EfGWpwJb6hqdoJJ1j+7vHBI9jXqteTfso/DvU/hT+zv4E8K6yqx6rpumxxXManIV+SV/DNes0EhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEzRuAqGSHdJu3H6UySTYpGCMVjKWpSjcbeMxAKE+/pXF/Fn4dt8V/hn4g8KwazdaHNqls0S31lJtkQkY5/wBn19q0/HHi5PBPgrXfEElsZ49Ns5Lsop5k2qSBX52fsRft6fFX4+ftQP4f167s5fC99FPLHp8duiG2VT8uHwCT+Jo31LtbQ+ZPiB/wTR/aG+Fes6jfaLoZ1zTrBfOTW9C1OFHcDnPlNIspYd8L+dd1+xT+398S/CPxS0TwP431S88Q6PeXS2DLqCs91bOTgDoSQDX6Gftk/tm+Fv2XfBdwJbqG/wDF93GUsdIjcNJkj77j+FR79a/M/wD4J9+JfAWoftF6z8S/if4p0fQXt2ku7eHUpFjV5pDkkZ44pgftx9l87DnLZ5GeKtIiqAuK4H4X/H74e/Gia9i8EeK9P8SPZKGuPsMu/wAsE4BP413/APFntQQ22KOKWiir5SQoopjMc8VACOwzg01SFGM0yZgrZY9aXYfX9aDRLQf97ocUqrnnNQNlWwc4qxHgDFAPRDhS0i9KWtFsZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQHNLQAUUUmegoAWikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAYxGaar7u1J5Kicy/xEYpWyMkDJ9Kza6ljlRd27HPrT6amSoyMGnVSasSFFITimtKq/eIFO6AfRUH2kOgaPD59DUoY45HNAWHUUlLTEFFNZsHFLu4pXAWikBpaYBRSE0m6gB1FIKWgBKKWigAooooAKKKKACiiigAooooAKKKKACik5o5oAWik5paACikJppY0APopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA055waYtzE0vleahlxkx7hu/Ksrxpfy6X4T1i8hkMUtvaSzI46qVQkH9K/Dn9nL9sLxPoX7XFp4r8aeMr5tIubqSC9kupS0ZhLEAbPugfQVNyrH7wUxpAvWuO+Hnxi8G/FbS01Dwr4isdYtmJA+zzAsCOoK9a6PU5MxNsLB164ockgjFydh1xdM0hVMhf71QSbpo22vuWvk39t39syP8AZt8C+RpZS58S6mrR2cbHJjPdzXzF/wAE5v2ifjp8avj1PFrPiO61nwlFE8l/b3WDDDnpswOuazvzanTy8uh+pUNsIwGao7jE0n7jO/1HSppGZuFXKdt1Nt5PIkxgKD2Fc3tLuxor7k9usscIaRvmz0FaEL+ZGCRivI/j5+0J4b/Zz8Hy+JPE/nNaL8sUMIBaVj2FYH7L/wC2Z4C/amS/i8MPcWuo2Sh5rG8ADhT/ABD1FdMdTmme/ClrmviF40sfh74P1nxHqTMmn6XbNczbepCjOBXwn+zp/wAFVI/i98dY/B2r+HxpujarN5Gk3UZJkzn5d/1rS9jOx99+IPFGj+FrdbjWNTtNLhZtqyXcyxgn0GTV+3niuoUngkSWKRQyyIQQwPQg18Cf8FePhf4m8YfC7w5r/h+2u7+30e7Y3trZhi2xhw5A6gGvPP8AgnT/AMFC9Os9G0v4XfEi+NrdQnytM1m6ckMpOFilYngjpmpGfY/7U37G/gv9qjR7ePXDNpWs2oIttYsVXzkB/hOfvL7Zr8xf2iv+CbPxF/ZdsP8AhNfB3iiTWdOsf3jXtgrWl3a46NlT+oNfsZ40+KXhH4daRHqfiTxFp+j2Mo3RTXM6qJBjPy/3vwr8rP27P+CljfFGxu/h/wDCt7iDRLgmHUNWVGEt0OnlxgHhT+tIZ9Bf8E2/279S+O8UXw88XWk9x4o0608xNXDGT7TEvGZCSTv9SetfftfFP/BMr9k+x+CHwpt/GGpwibxb4khWZ5JI03W0B5WNTyQT1PNfa1aEPcKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQmhhmgBaKRRiloAKKKKACiiigAoopKnmAWkpitimsy5560uYdiWlqHIyuKcCOfrUe0AkoplFaxfMFh9FItLTEFFFFABXK/Er4Y+G/i94TuvDfirTY9V0i5x5kEnqOhB7GuqooA/Ovxh/wRl8A6z4gmu9F8W6voenSNuFiqrKE9QGYZxXvX7Nf7APwy/Zrul1TTLKTW/EYzt1bUsPJGD2QdF+oGa+mqKB3Yi0ZpGprLu7kVPMFhxkVTgsAfrSeanTcM/Wqk1i0hJVzmoLfT5luDIz/AC46UuYvlXc1Nw9aAwboQaqXKtHHlTT7ddowTk9TVk2LGaM18C/8FEv2+9c/Z112z8D+B4rU+Jbi3W6uLu4AkFvG2dvy56nB615n+zz/AMFjIZlttK+LeiC3kJC/23pA3J6AyRZyPqD+FArM/UeisHwR440L4i+G7TXvDmp2+raVdLviubaQOp46cdD7VvUCCiiigAooooAKKKKACiiikAlGRTSwPQ0ZqeZDHZozTc0UcwDtwpPMX1phYHvULSKpwTg1m6juUohcXBWTA6VQmvD5m3eFLcBT97P0qeVt0oIP8PykjvX55/tq/wDBTLXPgD8T9S8DeEPDVrJqVisfnanqaswJYZwq8ZHTmsI+/J3NfhR9nftEyJZ/AHx29w6xKNIuMsf901+XX/BHj4fS+Ivjlrnil42e00SxaNZAQAJJDjGM5PHtXAfE7/gqR8Xfil4H1PwtqcPh+2sdTgMU0trblX2nryWNeT/s6/Fv45eC4dS0T4PT67LJeENcQ6FphupPrwjEV02toRufb37Tf/BLb4pfF748a94q0nxTol3pGrTeYlxq88qz2q4+5tCEEL2wazbX/gibrLaMTcfE3T/7SAOIY9NZos9sylt3/jtfOPiQ/to+Jrx73UNN+Ms0rKFaRdOv7dMD/YRAPxr9Of8AgnD8M/iT4E+D99qHxP1PXrjXtXu/Nj0/XZ2kktYVXCkbjuUtkkg4Ix0q7EXZj/sAfsKaz+yLP4o1DxDrWnazqmrqtvH/AGYZDEkKnIJLqp3HuMfjX2Yq7VAp1FHKSFFFFK9gEzTWmVVzmiQ4BJ9KqSLls54qGy4x5hfNG8uwBpjTIzHa1O/drHyM0kEcbln2nHpSNNELG/nLtVunWrCjy8ZOfeviT9rD/gpd4f8A2Z/iYPBtl4ek8RahAiPfMsvlrFu5AB7nFfVPwh+J1r8Xvh/oniuxtJrSz1S2W4SOcYZc9qol6nbilpq9KdWi2MgopGzjjrTY9235+vtTAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACCgnFNjLFfm605huFAC01lDMD6UtGaAADbS01WDZwc84p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANao5CQwO7AHbHWnshZs7sD0pdoPXmplqhkBuJVuAiw7oz/wAtN39MVZpBxS1PKxDWprKG6gGnNUU0jRrlV3Gk9NykOjUR5UIqoOmKcX7KQW9K86+MXxIT4d+FL7VzFNILaMuwj7ACvy3+KX/BXL4gTahNbeCdJ06wELFDe3imWWTB6eXxge+aSnd2Rq6TSUn1P2Po53e1flL+zn/wWB1OTWLDRfiro9ssE0mx9csmZNuSAMxYwAPXNfqN4f16w8VaRZ6vpV7HeabdxrLDNEcq6kZBzWt+5jY02xmsbX/FWn+GbWS71O5jtLGNSzzyNhUA7k1rSbN3PXFecfFaLwrrfhHVNK8Sz29vp11GY5xdSbEK+hPasJycdUXCKbOn8L/Ejwv4040LX9P1Vtu7ba3CucfQGuhklEaM7YCqM1+Lnxi/Z98Y/sw+Jx8UPg1qV5c+GY387ZCxdUXPK4HVPeu+0X/gsHqGveD7vTPEvhuLTtYWBliurKRikrBcDeDyDn0pqTtcpwsfY3xa/wCCg3w0+DV9La65fC4uY2Km1szulHPcV0v7NX7aHgD9qD7dF4amms9QtW+axvgFkZf7w9RX5Kfsw/sjeJv24PHmu6/qdzc6Poe5ppNQC7gXJ4Rd3UVneNPBviH9gb9rPTNK07WGu2tZbe4W43FVuIJGxtkA9MGtumpFl0P35WlqhoOpJrWiWGoRlSl1BHOCpyPmUHj86v0yAooopXQBRRRRdAFFITSbqYDqKjEnzEHGRTt1K6HYdRSA1HJIV4XGaXMgFeZY2wc5+lORxIuR0qKNpG5bA+lSltq+tHMgFZgOpxWH4u8baL4F0eTVNd1GHTbCM4aedgFrUmX7RtxuXmvgv/grla3Fn+z+t3De3UY+3QxGJZMIytnORiobZpGKZ9UeAf2nPhp8UfFD+H/C/iqz1fVkQyG3gbJ2jqa9SQnvX5H/APBF74f6drHjTxl4tuEk/tDS4I7W3KthMSZ3ZGOTx61+uO3bWl9NRSSVrA1R87uvy0rkdCcVHgIu7fk0yUhk1y0cqqFyvfipI7mOViqsNw7d6QyBuVXdSW9rGGaTy9rk9TSukVZW1LK0tN+70oyaZmOopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAU0tjtQ7beScUtK+tgOL+M94bP4T+L5w2wppdwQf+2Zr+f79mf4AX37TPxig8HWd6th50cs0l0ybhGq5OSK/dv9q3W4PDn7Pfj3UJ22rHpM6g57lSBX5yf8EV/CJ1D4ieO/EkiBlsrOO2RmHIaRs8fgDUPc02R8//ABW/Zy+Nf7EPjCLVLGbUIdNt5M2+uaUWMMg/2l7H1zX098Ef+Cuenw6DFa/EzSruXV41Mf27T/8AVyqMbd6n+Lrmv1J1jRNP8Q6fNY6nZQX1nKCrw3EYdWH0Nfi7/wAFWPhD8N/hR8QPD9r4I0mDRdQvYGnvba1YiIDJw20k4JOfypOKkHPbY8m8Zaj4p/bv/aeNjoSySRahN5NkkmSltbg8sfTiv2p/Zl/Zv8Pfs1/DOx8N6PbxG82772+C4e4lIG4k+melfiz+wn+0hY/st/FeHxBr2jPc6TqEZtpbsxnfEh/ijJ61+i37ZH7dmt+CfhP4e8U/CVrfVbLWzt+3tH5nkccgqOh+tL4dAu2fcX2M7WJOWzWdN5FnL5813GkQ42ysFHvya/D1/wBsT9q/4myKuia74lZ2+QLo1kyq34hcZ5qn4k+F37XfxWto5PEGn+NNXReEF5MVAJ74yKhUtbj52tD7h/4LC6pp8v7P+iJC8VxJJqS+XJGwbC45wRXg/wDwRd8M3V98WPF2ug/6NZ2Ahf3Lniqn7ZHw01H4PfsP/DXQ/FE11J4nuLzzZIrqTe8XGSmfYV63/wAET/DNxb+EPiFr0iAW9zdwWsTf7qksP1FbKNiXK6PrT9vXXk8N/sn/ABBu36GwaIfVjivyO/4Jn+HIvEH7XPg+OeCOdLES3LLIoIyFyp+or75/4K8fGaz8J/A2LwPFJu1TxDMuY1PIiU5JNfOv/BF/4fwa58U/F/i6cLJJpNklvCGGSGkPUenANOwk7H693NvFd28kM0SzRSKVaNxlWB4INflF/wAFBf8AgnFb+EbPWvin8Nljs9OhBu9S0RR8sXdpIvQZ5x2r9YzxWb4m0Gz8T+H9R0m/tobyzvYHglguEDo6sCMMDwRS5QUj8SP2ffg74w/4KEeGo/D2pfEiGxu/BsASyt9QiedpYm6ZO7+Hp3xXY+I/+CMPxX09ZJNI8W+GdXMY+SN3mgkb80Kj8683/Z8vtW/Zu/4KBW+hW9xPBDHrz6Zc28DlElhdvlVgOCuCOPav3ho5R8x+Mn7Pv/BOv9o3wH8bfD17PH/wjWn2V2k93q9nrHyvEDkoAjZbI7Y71+zUalY1UtuIGC3r706irICiiigAooooAKKaxqJrqOOQIzgMe1TzDsyeimqwYZBzTqOYQUUUVQBRRRQAUUUUAFFNfdj5aWp5gKeoXq2qnd0xVXS9QF580ZymcVfurZLpdriiKFIQFQYAqeVvW5tFxUbWJl6U6mUVoYj6KRaWgAoooqeYApDSNTGUZDelQMjaTa2KNxbmmpbr8x7sc0x5WhPB4rJyL9B23bIW74qJZC8m2nLctIoJHGcV5L+1F+0Vpn7Mfw3bxhqek3Gq2yzpAIrc4OW460kuZlN2R6788bhR0qwpJHPWvnr9kH9sPQf2ttH1260fSLzRptGmSKWG6IbIcEqQR9DX0Csm12G3GWrXl5dbkbk60tNU0vWtE7kC0UgpaoAooooAKKKKAGtXxX/wUX/bYvf2a/D9h4e8JS27eMtWUlWbDNax9A+31J6fSvtC6mW2gkmc4SNS7H2Aya/GvwD4af8Ab4/4KDa5fazP53hfRbp5ngLDm2gbZGij0Zu/TmpsWjzaH4t/to6iw1mxT4l3EFwPPW4tdEumhZTzlSIsEY7jitX4X/8ABT747/CnxQU8W6i/im0hcx3eka3CIpo8EZAbaGDe1fuJb29vptnHBCiW9rAgRUUBVRQOB7ACvxP/AOCiPjD4M/Fb9pHT7fwpczWF3HKNP8Qa7aQpJaNhiMxoD87KSdzDr+FFhbn6qfs3ftSeCf2oPBser+HL6OPUE+S90eeRVurZwBkmPO7Zzw2MGu9+I3j/AEX4V+CdV8T6/fQ6fpenQNLJNcSKikgcLliBkngCvxh8ffs0/Gf9grxFpfxC+Hurz+IPDU0Uc8WsabbvsdGG7ZcQjOFxj5icHNcx+1B/wUD8b/tUeBtF8JajplrocEUqtdmxlbZeP0UkE9M9ulMdit4R0XW/28/2zPMvILq/03UL/wA66ba3+jWCHhSw+6uOh96+vv2wP+CUvh+HwjdeJfhBbz2ep2MW+bQ3dpVuUA52E87vavo7/gn9+yloP7PHwj0/U1jW78V69bpdX2oOPmVWAKwr/sj9c19QakvmafdKRkNEw/Q0wvqfjV/wSp+P+q/Dr42p8Otb1CS30LWDJbxWVzJ8sN4DwoB6EkYx7V+0FfhP+yL8OZfGv/BQaO0hYwxaXrt3qD4HQRSMa/digl7hRRRQIKKKKACkpahkYt9w5pN2Q0rhLJt4XlvSo1nKnMg2L6mo/wB4rbjgDpzUrL54AI461hvqVyibd7fK1PVSoweaXaEXijce/FLlGLigsFXk4pNxHbNMfMi8ClzWAbvXrmmGWP61G7CPhjg+lNhjMmDjK5qdDVJW1HNB50oIZlXrwOPcVyPiz4D/AA7+IGoLqHifwRoOvX4AX7TqGnxTSkDoCzAk4o+J/wAcPAfwW00X3jXxRY6BAR8q3DkyN7hFBY/gK850P9v79n/xAq/ZfiXpiFuguYZ4M+/zxiqhHW5m3c+ZP+CrXhX4dfCn9n/S7HQvBfh3SNX1PUUjt5LPSo4nVVBZiGRRjgd69m/4JkfBOD4U/s06NqVxZwxa34iLajPOEXzDG3+rTcCeABnHvXxj/wAFbP2hPBvxcvvBeheEtftPEFrpyy3dxPYOZI1dhhVLYxnrx2719KfB/wD4Kafs/eAfhN4O8P6h4lvlv9P0m2t7iO30q4kVJFjAZd2wZIIPTj3rZi6H3mtLkV8CfEz/AILFfCPw7pDt4PstW8Vamy/u0e1a1iU9ixfBI+gr5a8I/wDBYr4q6b4oub7XNL0XWdEmclNMjiMEkC54Af8AiNWtibM/aClryX9l/wCOk37RXwntPGc3hq88K/aJ5IUsr45ZlULiRTgZVs8fSvWqZIUUU0rnvSsAyZdyketQvGVAHXip2XtVe7uDGpCjJxWT3Li3cgkm8n72NtWLSQTZKjjsapWsLXTF5l+UcVbuGFrpl08IwUjZh9QDQXJn87/7cU0lx+1l8Si0nmY1ZgpJzgBV4r9zf2RYHh/Zn+HCPt3jR4c7enev5+/i3ql34v8Ajh4rvL85urzWpVkOf+mxX+QFf0XfBPw6PCfwh8H6QvS00u3Tj/cB/rWljK7O0Vdox+NOooqhDGkCsFPWn1HJHuwR1p4zjnrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWQYOOcdacp3DNIFxmloAWkpaKAGRxrFkKMZOafSZpN4zQA6ikpaAEoLYBNNcOVbaVBx8ufWmLHL5ahnG/+IgcUAPik8xSdpXnHNPpKWgAooooAKKazbe2aRJN65xigB9FIKWgAooooAKKKKACiiigAooooAQ9KzdVmK25w+wd2B5rRb09aw75GjDh3Hl54YisZnRRinLU+G/8Agph8X9Q8G/Bu6sdGMjf2lIttLdBsFC3QAY54zVv/AIJk/s5+Eb79mnR/E/ibwbpOpatq1zPcRX19brPI8O4KPvDgZVq+T/8AgqH8Qr7xZ8bNH8AadclrGFIpGih/5aTO7KpI9QAfzr9XvgP4BT4S/Anwh4Xs90/9laXGmCuGdyu9hj/eY1FNW1NK07uy2PlL9ur/AIJ86R8WfD8WreAdL0/RtesVJFnYwJCkw9wMc18ueH/iV+0P+xx+z9e2l/b3FvaRX4itmuUMgiUjnB7DjpXQ/tDfty/tH+C/irq1vp/hU+G7G3crFHc6bJdGRASA+/A4Pp2xXzJ8dv2zPjR8bvDZ0fxjdhdIOd8UFgYEY/j3rRxuzLmtofqb/wAE3/2lvEv7Snwt1e48WzwT6pp92YPMhXbmMgFSR69a8v8A+CsGla9pXwbjuLCaaO1a8U3DRMeYx0yRXwN+x9+1p8QP2ctauLfwjpia5p166m509oSxfkDO4civ1v8Ajlp978eP2Qdcn8Q6V/ZV9daZ9sS3UbmjYLkDmsJe67Mq2t0eIf8ABJn4uQfE74L6/wCCNfZNSudGl4W4AbdauPlXB64O786/Pz9vjw54a0P9pTW7PwhbxQ6b5cZMFuBgSlm3AAd+BXC/AH46eIP2c/HTazo1zKgZHt7m3VsLJkEYP0PNfcP/AATl/ZGtPj1rGqfGTx/FJqFo2oSfYbO4GVmfOSxz2GePpXRr0Jew3/gnD+3p4f8Ahvo9l8L/ABpZrpUTTFbXVlGBuJ+7L6fWqP8AwVo+Ff2zXtH+KWjyrd6PKi2stxG4YbuqsPbpXQf8FDv+CdcOj2lz8RPhlp0p2uZtR0u2GSo/vxgV8OXH7S3jWT4V6h8OdauTqehSAeXFdrmW0ZTwAT9KUuYSkftx+wP8Sj8UP2WvBeoy/wDH1a232GfnJLRnGfxGK+ha+C/+CN921x+zPqsbSu4g1uVAjHhcxoeK+9a0jojJ7hRRRUPcQUlBNRO3ze1S9B2Ekm2SYOMY9aiSZmk5Tj1HSory0W6cHuB602EiNdsR4HVc81PObqKsTtIeXVec7TuHapo3Vl44FVLeYMzfMZBnPTv6Ui3ZWZlICp196fMhcrLjybcVD537xuDxUM9wrYwxBpikLIAzn5hRzIpR0Ln2gLjPFRteIG2hsGqn2hJLlkzlVHWp18gyBNpJIzmqDlS6EyTHI53AnsK+Hf8AgrovmfsxysASF1O3z+Zr7jVRG4RWwOtfDn/BWe8W3/Zlvbe5dd8uoW5i9eCaTegR3Z5V/wAESx/xI/iSwHBuLfn8Gr9Nry4MKjg49RX5q/8ABFCzKeDfHtzsYLJdRJv/AIcgHj681+k2oTLCMtk54xjNVfRkR1kiOSbyoRIjBo8/Nmqy3Qt7jDZMZ5XvVXVrTzrUwo0irJgnacUsaLarBG6NIFUANmou+h0qCLE2uvbwyNFbmTaegqex1k3gUmJkJGSDUQkHlsOME/dA5q/DNGkYPl7D0qjOaivslhG3Lk8U6o2VZ0GDSbHzjORWq2OayJ16UtV2m8tguCfepkbcuaVxNWHUUlLTEFFMkkCdTzUSyOZiN2VxUuSWhVrliioZJhG2C2KfCxZSSd3NFxW6j6KaTSM+0Ek8VQh9FVLjVbOzwLi6hgJ6CRwp/Ws/UfHHh7SFDX2t6faKeczXKL/M0rjszXmUMBmnjoK8w8S/tLfC/wAJszar470O2QLu2/a0J+vBq/8AC/4+eAfjQLv/AIQvxPY68bU4mW1k3FPqPSoW9wszwb/gqRr15of7I/iX7JK0RupYbeTbjlGYZFeH/wDBE3w9PafDn4i6xKP3d5qNtBH/AMAjfd/6EK9i/wCCrUE837I+ttDE0oW6gZ8D7q7xzXln/BF7xrZ33wl8Y+GU4vLLU1vG90kQL/NDQy+h+iGoXCWttJI77ECklicYHc1+G/x6jm/a6/b3Ph+wkaexa+TTI2jO4LBGcsw9jlvyr9oPiZ4JvfHWg3FhZavNpLyQSR+ZCOpZSBmviP8AYj/4J4+KfgL8etX8a+Lb61v7aGKRbFojuaV3Y/OfQgfzpDVrHqf7TX7Bngb4j/Ae10DSNOh0nU/DlqX0+6tYwHYqvKt67sV8h/8ABJn4mRW3xG174SeIrOPUbeQTT2iXkayLFJGfnADA4yBX6K/tWfHSz/Z4+DOs+LLy1kuwi/Z4407u/Az+NfkX/wAEy/EE2sft2aJfEFRfLqMzJ6boXb/Cq0EfuTp+h6dpaBbLT7WzUHhbeFUH6Cr1ItLVmZ+Uf/BbHxLLJqfw+0JABGkc90eepOAP61X/AOCdf7Xvw6/Zx/Ze8RR+KdYij1ldVmuINMjUmecFE2/gSD9Oa8a/4KseOp/iB+1bPoNvP5tno9rBYxKw+VJnyWGfxWvS/g1/wRz8U64ul6n4y8VWOnaXcRpObbTVLzFWUEAseO9AHyr+1h+0d4j/AGsPiRL4xudOms9Ms4Vtra1twzxwRhm+cnoGbPP0Fet/8E4/2xvC37KeoeJoPFWnX1xZ64IRHcWQDlGQkcqSP71frj8H/wBlr4e/Bf4byeC9I0K3utLuNzXbXsayvcswAYuSOenSvC5v+CU/wdHxTg8XWsd9aWSSid9BR1azds5xggkL0+XpxQB9e+HdetfFOgadrFl5n2O/t0uYfMXa2x1DDI7HBp/iDWLfw/od/qd1IsNtaQPPJI3RVVSST+VTAWmjacB+6tLK1iwOipGij9AAK/OH9vb/AIKTeDV8B+IPh38Or6TWte1BTZ3OpwAi2gQkhwrZyzYBHAxzQB8wfsu2Z/aQ/wCCikfiGdpLq0bVrjV3ZRkeXF/qyfbgCv3Hr86/+CRf7NmsfD3whq3xD8S6b9hutcjSDTI7iMectuDkuCeVDE9Pav0UoGFFFFAgooooAKKSoJpdr4pXGlclkqr9jSaTzG5PSlM3ydajhIkmw27HbnisHLU0s4q5Rv8AxRomi6pHZ32sWdjcuBst57lEZ88DCk5rdVgygqcqRkEV+CH/AAUn1nW7f9s7xVLd6j589mLYWEkZ/wBRGFDKvsQS351+uP7B/j7VviZ+yr4G17W5PO1Ga3kjklPV9kjKD+QrRK6uZvc9/ooorQQUUUUAFI2e1LRU8wEcbM2cjinrnnNNZsUBqgdhH+9QvSq18y/IGLA5/hqaMBFwMn61XMVbQe2dvHWo2MoYYAK96kDdqXGKsWwbgF5OKWNty5znmk4704Y7VPMSLUb/AHqkoqAIainuBCMlse1SzSbaoyNubNZuSuawjfUR5m25WTrUawrGpLtknnJqCTcbnjpinyMvST5g3G2sm9Tr5SeNlWZVXla+Sf8AgrFEsn7IOtM38F7akf8AfwV9XwK0nloEEaq/AFfJv/BWhQ37IWrZ6rfWpH/fwVpS1ZzVNHY8W/4Ij6fIvg/4oX5BEUt9ZxrkcEhJCf6V+mONrN7mvin/AIJG+ER4d/ZVGoO2ZdV1We4PptCoB/WvsqS4dpsAYWtZyViIq7LnmYbbUiVQZtrZzk1Nb3DMvK96zjJLqOUOpcopqtuHpTq6FqjIKKKKYBRRRQB5r+0h44Hw4+BfjfxHzusdKnkTH97YQP1Nfnx/wRX8Jx6hqnxP8ZXKML4G3skZgcESF5Hwe/KD86+mP+CpHjSbwj+yP4jigxv1WWLT/fDtzj8BXD/8EddBn079mPUtSuLVoDqOtzGOR0KmVEjjUMCeq53DI7g0FdD7m1GzGpafc2pdkWeJoyy9RuBGR+dfzoftafAnXv2efjhr3h/VIphBJO93p97Ip23MDsSHDYwSCcH0r+jla/Nv/gtJ8OItR+G/gzxnDADc6fqDWM8qpz5MiEjcew3KOvrQJOxheG/+Ckfg7Rf2HrLTtSuo9V8fJp7aMdFdfMJCjasr8YClSOp/hr4j/Z3/AGL/AIlftUafret+ELWytbKxkJM95K0Mckh+by4yAQSMj6ZFc9+y1+zZ4g/aa+KFh4W0SJ0sgwk1LUsHyreDqxLAEBsZAB6mv6CfhH8IfDvwR8AaZ4Q8L2gs9KsYwucDzJm/idz3Y+tA+Y/FXR/2iv2nf2JvEEeha5PrSWVudiab4ihkmtJEzjMTuPunHBU19GaT/wAFrUm0Ge21v4dOmptAVWexvwYt5BGdpXOM+9fqBrfhvSfFNm1rrOlWeqWrAgw3tusq4PswNfNnxI/4Jn/AP4j3TXb+FH8PXbdZdBuDbDPPO3BXPPpQFz8+v+CV9xq/jL9su98RCFnhmtb27vJApIi8wnAY9skgDNftZXiH7N37IHgP9ltdWPhH+0bm51IKs93qtwJpti8hAwVcLnnGK9voJCiiigApGOBxS0yQnbgDmk3ZAIrfLzxTDGBkg0yIFVO485pk0nUK3oPzrKU1YtIWGNjkueAaesxbOFxim24Kg72xjnBrx34vfti/CL4Ihk8TeMLFL1eljaN58xPptXofqalJtDZ7FNI20cU/azAEivjvw7/wVa+AfiLUPs0+rappSFtolv8ATysec9dwJr6g8E/FDwj8RtPivPDPiLTtZgkUMv2W4Vmx7rnI/EVVgOl3LGuGPPpXKeIvi74E8H3xsdd8ZaDo96Bk299qUMMgB6EqzA9q6XULEahaTw+a8DSRtGJozh0yMZB9a/K345f8EifHvi74halrHh3xxa6rZXchlEuvyObhSSSVJAOQM8VWnYD9G4/j78LLmQKnxG8JPIei/wBt22fy31esvjJ8P77VoNKs/Gnh+71G45itbfUoZJH+gVjX5Qt/wRk+Kf2Qsnirw4LnP3P3gH/fQWuq+CP/AAST+JnhX4o+HdY8UeJdEtdH026W6lk0m5le5k2kEINyADOPWjQR9J/t6/8ABP68/aq1HT/EnhrXotK8S2kS2zQ6izG0kiXJHCgkNk9cGvm7wv8A8EV9eXR1n8S/FDStHulJMkdppH2uJR6+Y8kZ/DbX6zRrtUAdBxXgX7bHwN8VftAfBa68NeDtYXRtYM6TLI8zxLIo6oSvr71aFc+EvEn/AARd1fUNN+0eEvitoutTg7St3pn2aHI7b4nk5/Cm+Df+CJfia42HxX8R9KsV3fPFo9lJcHHs8mz8sV5Cf2R/2xvgPNJceHrDxJFbwuZFn8Oays6SN3byFkLknA6r6V1/g7/go5+0l+z7qtjafFXQ77VLGQn/AETxHpTafeMo43CRkXI689+aLBzM+qvA/wDwRz+DXh0K+u6p4h8Tyr/DLcpbxH/gKLn/AMersb7/AIJS/s+3Xl+T4f1GxMbBgYNRfqPXdmvX/wBmH9qLwl+1L4DXxB4blNvdQv5V7plwQJreQAE8fxL8www4Nex0xXZmeGfDtl4S8P6fo2nReTYWMK28CE5IRRgVp0UUCCiiigBjMB1qAyLJNsAzx6U+WQbiO/0psfy5OOaye5aXUCCm4KvGKr3Em/SLssMYjf8A9BNSSSS7WwlMuDv0y4XGD5TA/kaBvY/mo8aA3Xxu11YxzJr0gUf9vBr+k7wahh8H6HG/3lsIFP1Ea1/OB4gsX/4aI1O243/8JLImM/8ATwa/pH0KPytD09P7tvGPyUVaethWNDdRuptNEgMhTuBmmtiDz34z/tCeBP2f9IttR8b63HpEF0xSBSpZ5SOu0D0rW+F3xc8K/GbwxF4g8IarHq+lSMU86MEYYdVIPQjI/OvyG/4LH+I9Sn/aa0nR3vJH0u00G2uIbQt8iSvJMGbHqQq/lX35/wAEyPB8fhP9kLwm625gk1N5r+QseXLPt3fkgplW0Pq2lpFpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAE3Ddihm2jOM0m07s0ySRlcKFz70ASK24Zxj60tJS0ARuDnIP+FNRW6tjPtRPJtUgH5yOBRbpIsf7xgze1AyVaWkFLQIKKKKACiiigApAwbODnFJIGZflIB96RIxGuB35NAEclwFYLglvSpKjaFtwZSAfcVLtoGKtLSDiloEFFFFABRRRQAUUUUAFFFFAEbbt3A4+tcp40vv7N0u4uZo3KxI0m1ehwM9a6uZTtyK4D4yWs174PvwkrW6LbSs8gPQBDXPUhfU6KL94/EmHxH/AMLl/bu0O4ltiUk8RQQ+QzbvkSQ8Zx0r99o1CooAwBwBX4M/sD+HIfFf7dWhl5i0dnqFxdhiN3mFCxH0r951HFVFaWInuytPY215kT28U4x/y0QN/Ovjj/gplouh+Hf2frzWH0rTo4428kkWyq5Z+FAIHrX2htrhfjN8FfC3x68E3HhbxdZveaVMwcrG5RlYdGB9RV2ZKep+eH/BGXTfDOtaH49t7rRrefXbSaGT7VNEHIhkBwoyOMFc/jX6V+L/AA7/AMJB4R1TSIgi/arZ4FyOBlcV57+zh+yt4I/Ze0XUtP8ACEFwX1GUS3N1dyb5XwMKuf7o9PevYaFHe4uZn85Pxn+AetfD34+Xvgm8tpWubjUFS22xnDpI+A3H41/QD8G/h5p/wq+GPhzwvpkC29tp9nHEVAwS+0bifcnNa2r/AA/8Na9q1vqmo6FYXuo25BiuprdWkQjphsZrf21SVlYHK5HLEk0bRyIrowwysMgj0r87/wBsj/glhZfFbWLvxd8OLy30PWZFL3GlyJiC4bkllI6MenpX6KbaNtMV7Hxz/wAEyf2e/G37PXwl17TPGkEdnc3+pefDaK+4qoQLuyPX09q+xlORRt6+lCrt4HSgQtFFMZW3bgx6fd7Vm9wG+ZuztHI9arLdLMzoeHX0qwSWz2PtVSQLayB9ud3BJrOb0NIq4jQhU3vKyD2qL7OsjeZGuGx/rB1rz34iftHfDX4W6kll4u8Xabod2yCQW15JhihJAbHoSD+VJ4L/AGoPhD4+mNtoHxE0C9m/55repG34B8VjH3tEbaxWp363SNvBdlZfXFRNHJdbfmBX1FLDfaPqkb/Y761vT1PkTox/Q1UuPEeg6X8s2s2Nvt6ia8RCKrRaM0UotXLEjNCoVueTz/KqrXn7wKwbeFzxXL6z8dPhrot0bTUPHGi20zAPsa8RjjnnIPsapr+0d8I4S0z+PdB54Ja9Qfpmp91vc0U7LY9FtLWNUMy7ju67qleZvLBRQBnGSK8nuv2yPghpbeVP8SfD8TYzt+2J/jWVdft2/AK3cI/xK0Vu/wC7m3D9K6FT03Od1NdUezLI4nU5ZyPSviP/AIKs+BfEHj74KWr6PZXN+1neI8lvbxliR68V6n4g/wCCk/7PvhtlX/hNoL5iN2LKF5P1Ark9S/4Kufs/xxsv9o6heg8lE092B/MUcrtYaqWexT/4JQ/CrW/hr+z3qEmuadPpV9qmpvOkFyu1vLCIFbB9ea+wru4mVioUu2eTjiviO8/4LE/ByzmMVtpeuTRKvystsEGfTBrgdc/4LVeGorl007wDfXMP8LzTqhP4U+V2aIjPld2j9FPt007FTbk4HDGp7a0uGIlkGD2XtX5oXH/Ba2zMeIfhtIzHjD3YA/lXK6z/AMFrvFYkK6Z8PNLii7Nc3cjMPyGKVmXzvofrCtqWk7DueKufZlYfNz9K/FjW/wDgr/8AGPWGl/szT9E01mXCRwwGUqfXnrXIXf8AwUY/ae8QQvHFqtwqyjaTZaNg/gQKqxlKV+p+6awOk+Qw8rH3e+akkmjhQtI6oo6sxAFfzzaj4y/aK8emS6ubzx3eiRsEw21yV9cDaOOvSs6L4b/H/VoWaHRvHl1CxwxaO4UE+mGotIzufuL46/bA+E/w38TW2geIfFdtp+qXBUJCQX6kgElc4GQa9mtbiO7t4p4XEkMqh0dejKRkH8q/nv8Ahn+xz8a/HXjjSEm8Fa1BELuJpbzVI2VUUMCclq/oJ0ey/s3SbKzOCbeBIjt6fKoH9KfKwbXQtjvTdxbO08dKVqpvdC2IAUkMe1VsgUW9iS4aVWG1dw7mqkN1Kt0YjCSOu6n6hq0Gm2sl3dTLb2kQ3SzSsFVB6k18b/Gz/gqt8JvhTqV7pmjx3njHVrc7GWy2pBuyRjeeT+VZS953L+FWZ9nyRmSQFhhfSrK8LX5j6D/wWw0aS8H9ufDPULaxJwJrK9V2H4MoH619FfBT/gph8FPjRqY0yLWLjwvqbHCW+vxrAsnT7sgYqfoSOlMnVo+rjVXU4ribT7lLORYbto2WKRxkKxHBP41PbzR3UKTROssUihkkQ5VgeQQR1FSbRWi2JPyB+OX7Bn7WPjr4k6pq0uvf8JLHdSGSO8t9bFrGqZO1BGSu3Ax0GOa41/8Aglf+0f4gtUOqTaaWDbdl9rPnOB65BIx7V+2FLSsVzs/Gqx/4Iw/FW9tle68WeG7OTvDJJM5H4qhFfZ37Av7Ct5+yX/wkeo+IdWsda13U9kUUmn7xFFCuSR8wGSSfTtX2NRtFLlYcx5x+0N8L4vjJ8G/FPhKVtjahZusTYziQDKn8wK/Fb9iX476l+yL+0TLp2tB7XSLyc6bq0Ew24KsQsn4Hmv3vavh/9tr/AIJu6R+0Tdt4o8IS23h/xfj/AEguCIrzGcbvRuetIaPs7w/4g07xRo9tqek3kV9YXKiSKeBwysD7itBpgnWvyT+Ev7Hf7Y/g4L4Y0nxm3hLw9GWXzheq8QU9Sq4JzX6UfAf4aaz8LPhxZaF4h8U3vi/WFdprnU705ZnYAFV/2Rjj6mi7FZFr41fB/wAPfHr4d6p4P8SQGbTr1PvKcNE45Vx7g818l/sd/wDBNiT9m34z3HjjU/EMOs/ZYpbfTo4oyrKrjbub32kivut4lyX25bGKr/2taR7vOnjtiD0mcKfryaQF5aCcDJqgNc03GRqFrj/ruv8AjTTr2mMCDqNqQf8Apuv+NaLYk/n6/aevk1f9uPxhMW8yJvE0acnIIBRf6V/QbpUaQ6XZxxqFRIUVVHQAKMCvz0+Jn/BMmHxl+1VpPxB0PUrOfwhd6imoavZytucOp3MEIPIbA4r9CG1CystsL3UEJUYCNIAQPpmmBdoryL4iftZfCT4U3xsfE/jrS9OvQgk+z7zI+0kgHCA+hrzu4/4KVfs9wHH/AAnkcvvHayn/ANloCzPpDxBoNn4o0O+0nUI2lsb2FoJo1coWRhgjIORx6V80+GP+CZf7PnhXxBa6zbeC3ubu2lE6LfahcXERcHOTG7lTz2IrN1D/AIKm/s96e20eKLy54zmCwcj6c4rita/4LEfBewujHYab4l1aHGfOhtEQZ9MM+f8A9dAWZ91wwx28KRRIscSKFVEGAoHQAU+vzp17/gtN8ObOzkOmeCvEV3d4/dx3DRQrnsScnivjjxp/wVQ+PfiDxNc6npXiePw/pjSf6NpdvYQPEig5AZ2UsxweeaB8rP3dorxn9jz4ra78bf2dPB/jPxIkS6xqUDtO0ChUkKyMm4KOBnb0r2agkKKKSgCOZsVRlkG7k81NNIzSmLtjOaoXEUbSAFznPrXLL4jppxXUmWdhIqgZTuasWfzSMQflGRj8qzmhNvDIUYnnpmrmlPJImWTaMdfWoWrKnFJXPwL/AOCkFraWP7Y3j1LSZ51lkieQuxO2QxLkD2HFfsj+w3oEHhv9lH4cWtv91tMWZv8AeZiTX4xf8FDGc/tlfEoOMAXkOPp5MVftv+ybj/hmv4cYGB/YsHA/3a647HPJdT1yimZozVED6KgmkWPBY4qk2pw3BKIx4ODU8xSjc0T/AKynHHeq6IFUc+/WjydzZz8tQPlJzg9KY1OjUIuBT6BXsVW/134UyL/XVNNjd9zPFQSTNDxHFlqC76E+8KWHvSNcKrbe9Qqr7sAbd3JqdY9vWq5haEsbblzTqj9KctPlvqQx1IRu4paz9dgvptJvhpckUWpNA62zTA+WJMHaWxzgGjlETNJAjFHmRX9NwBqJYYjMZFnUjGMAivwb+MHwO/arf4qa5c6v4b8ca1rTXDbtV0a3upYJRuO3yni+XZjoB0rLtfhF+17Gg+z6B8WYFB+6BqCfpmpsuxor9z99fscfmF1YHPHWq0+jyMxaJ9pPWvwdb4Y/tlLx/ZXxeH+7LqA/k1dN4Zb9tbwRp7wwQ/E2GLeZCt7bS3ByQBnMoLY46ZxWTp3dzTnl3P3GsbE2y4c5714p+278C9X/AGifgBrHg3QpYIdUuZ7eWJ7jhfklVjz9Aa/KXWvj7+2L4RjW81K+8ZWca/8APxpgA/EbauaR/wAFGP2otJhUNLc6kq87rrRHz9MhRWsYcqMZNyep+tn7L3wVT9n34L6F4GW9F9Lp6MZ5gMAyMdzY9ua9EuIpkmKIeDzX4x6d/wAFfPjfo9/jU9N0S62fK8E1m0T/AInORXoOlf8ABarxJGFOpfD7T527tb3TAH8xWUqbY1Kx+rEVrdLKPlBT+93rQ8p1AwSa/MXT/wDgthatD/pPw3lR8/8ALK8BH61px/8ABazQtv7z4e3wP+zcrQqKsVKdz9L7cFY/m65qWvyZ8ef8FptbnuIf+EQ8EWtvb7f3n9pTF33ZOcbeMYx+tfZf7CP7Wmpftb/D3WNc1Pw+uiXOmXi2hkhJaGfKbjtJ7juO2RXQlZWMj6bopKWmAUUUUAfn/wD8FktQli+BPhKyQgR3XiCPeO5xFIR+tev/APBNPTRp/wCxd8PCH3/aIrifjtm4kXH/AI7Xzr/wWq1qWz8E/DazRSY5NUmuGOOMpHgD/wAer6l/4J92a6f+xz8L4V6f2a7/APfU8jf1oLex9CrWH408C+HviNoM+ieJ9Hs9c0mf/WWl7EJI2x3wa3aKCDmfAnw18K/C/Rf7J8JeH9P8O6bu3m3063WJWbgZOByeByfSulXOORilooAKKKKACiiigAooooAKYzYODTtw9aimYetTLYa1Yu5ccc1BNcQ2sMlxPIsUMal3ZzgKB1JNMVhvzuGBzivhb/grR8fb/wCGvwj0zwjoGoNZax4lkczeS22UWkYBc+wOQKyglc0t0PFP26f+Ckl/4j1O7+HPwfubhV837Pd65ZZaS4PIMcWBnGe9ea/Av/gld8S/jZZW/iDxpfjwjYXR8z/TFMl7MDg7yCeM57+lfQH/AASp/Y2sdM8Lx/F7xfp0dzqWpE/2Nb3SBxDCMf6QM92JYf8AAa/SwDAwBgVuRc/LXxR/wRQj+zr/AMI/8RJA46x6haBlJ/4Ca+Xfjd+yx8Zv2HdW0/xDBq0yacXxHrWiSOqI2chHTPHSv3trn/HfgnSfiH4V1HQdasor6xvIWieOVQ2MgjIz0IpWDmZ8q/8ABPj9uAftPeHZvD3iCIWvjTR7dGmkByt7H0Mo9DnqPevsjaa/nt8H+JNf/Yv/AGvLq0s55LY6LrH2G4hY/wCttmbIzjrlGB/Gv6Eo2LxqxUoSMlT1HtS5RXDaaNpp1FHKguIKWkJCgk8CvAfHX7e3wE+G/iS50HX/AIiWltqttxLDb2V3dBDkjBeGJ1zweM5qhHv1cT8WPg74S+NfhO98P+LNIt9Ts7mJow8kYMkWR95G6givCtY/4Kf/ALOOm2MtxB46n1KVFytra6JfiST2BeFV/Mivz3/ah/4KofEL4rXV1pHgN7nwJ4WJK+fAMX06gnlpP4ARjgUDSuT/ALNfhnxF+zv/AMFFB8PvAuqHUdL/ALRaxu2zuU2gAdhIOxUH8+lftZkV+Z3/AASv+CNj4Rhv/i74x8U6bN4l1xHhtbaXUYZZVibaTK7BiQzfMMHnivsr4yfthfCH4BXGmQeNvGMGmzakrvbR29tNeFlTG4nyUfaPmGN2M84zg0A0ez0tc54B+Ifhz4n+GbPxB4W1a31rR7tQ8V1bHI5AOGHVWwR8pwRmuizQIWkpaKAIwuOornPHnxG8MfDDQ31jxXrdloWmocG4vZQik+gz1NbupX0Gl2NxeXUiw21vG0skjHAVQMkn8K/Ev4lf8J7/AMFJv2r9b0jwpeTf8IrYSeXD58zJa21tGxBlKHjexJPqeKmxSP050f8Ab4+Auu6ilja/EXSftDvsVZH2gn6mvbrXWtP17R5LvTL23v7Z4iVlt5A6nI9RX5veIv8Agivo8mgxjRviBdRav5Y803VopheTuRjkCvmm91r47/8ABNfx0mmXV6l1pWpRnyg0rTWky5K5GT8r4HT6UcpR4bJpNzrf7VU1pEv+k3Pi0xorHHLXJxX9G9lCbezgiPWONVP4DFfzqfs7atL4z/as8D6hcr/pep+KLaeYdvMeck49ua/oxppdRSGtIEHJxVa3vYZ5SEOWHBp1xNaqxWaaNGx0ZwDVOGXTLGR5ftduhPUtKowPzphpY/GD/grRavrf7ZtjZRqWlk0SwgVR3LTTD+tfsL8HvBkHw++FfhTw5bLti03TYIMe4Qbv1Jr8qf2uNV0Txx/wU48ErBd215p0cul2tzIsqlFKzSF8tnHAPrX6K/Gr9tP4R/AbSjd6/wCKLe+myFGn6M6XVye33AwA6dzQS2e5Clry79n79o7wb+0v4Nl8S+DJruSwhuGtpEvYBFKkiqrEFQT2Yd+9eo0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEGe9LRRQA3YN+7HzYxTqKKACiiigAooooAKKKKAEpqyBmwOaSSRVYIwPIpIo1HzLwD2oAkparXFq81xBIshQRkkqP4qs0AFFFFABRRRQAUU0t82ByadQAUUU3b85bPbGKAHUU1V255zk5oZSd3OMjFACnHSvOPjfYXN94D1tY5dsP2GXcg4/gPeu9nm+yqgwXbpmuG+L0c2oeA9bhgcxtJZzKW/u/IecVnN+6b0ou9z8av8AgmaTa/ttaWgXcG+2LnPT73P6V+7C1+Hn/BLPS/O/bVUOQ5t7a+bcepK5Ga/cJacVrciQ6iiirMwooooAKKKKACiiigAooooAKKKKze4DGHNRT2sdwoDjcB0qfbTJNwXCY3f7VDSsNXufBn7fX/BO3Wv2lPE1l4w8Ha3a2ms29mllLp+oDEUiIzsCrgZDZkPXjivz+1X/AIJn/tEabqElungVrryjhbizvYNj+4ORX73m5WJgshG7GeKct1GwB3DkZqVZLQt8zWp+DOl/sE/tRaGxGneEda08sPmNrq8cYP1w/WnSf8E7f2nNSYvceFtQct977Rq8bE+5+ev3oVwwz1FIsyNnBBwcU9BK5+EOn/8ABLH9oXWJ0Evhmzs9zYMl1qcWB7n5ia7iP/gjV8ZZkRv7d8LwEj5o5bqXIP4RkfrX7TeYN2Kdn2qkmFz8Yof+CMvxh2/N4m8JL/21mP8A7Sqdf+CMPxbb7/izwov0ab/41X7LAZpdtWLmPx80v/giz8RpGH27x54at488iKOZ2+v+rArudP8A+CJqyRK2ofE9op88ra6cGX8yw/lX6lbaQKBmgOZn56+Ff+CMfwy0+Ff+Eh8Va9rkwbO6EpbDHHGPm9/zrrV/4JAfAH/lpH4mkP8A2FQP/ZK+3ttG2gV2fFMP/BIj9n6F1Y2fiKUKc7X1YkH6/JXdaZ/wTd/Z+02NFbwHb3pUbd13K7k/XkV9OUtMLs8m8F/so/CL4f25h0P4f6HZLvL5+yh2yQB1bPoK9CtPB+hWEYS20XT4EXoI7VB/SteikIhhs7e3XbFBHEvXaiAD9Kk2KOigfhTqKAEwB0FLRRQA1qrSrtzsYBsZC+9WWryz9oz4sQ/BX4T+JPFsirM2n2byLDu2ktj5efrUTdkXE/O7/gqN+2JqE2pRfDHwnrQtbVkZtaa0IYnBwIt3VTkE8Edq5b9gT/gmvD8aNNXx18VbC8t/C8hH9n6V5jQSagpGTI7KQ4TngggnBrwP9lv4Qal+2T+1FGL5dtlcXTavq0mNypEGyVz6sePxr+gDTdPt9H0+1sbOJYLS2iWGGJeiIoAUD6ACp2Kk+ZaHy1N/wS1/ZnkiZR8O5I2IIDrruo5X3GbjGfqK+Tf2lP8Agj2+g6Xda38ItVu9VMOZToOqujSEDJ2xSKFJ4xgHn3r9X6KCUfi3+xF+3x4w+APjy2+HvxIub6+8KvcGyMF6F83TJ8heHI3lBgDaTgZJHXNftHb3Ed1bxzwuJIpFDo69GUjII/Cvw7/4KseF9M8GftZSzaXFDGNV022vbmOMDPn+Y4LH0JAFftF8NZDJ8OfCrnILaVannr/qVrRCZ01FItLTJCmyN5cbMckKM8U6igD8k/2uv+CoXxR8I/FnUvC/gzTrfwzp2mSmEyanaF5rhgT84yRhTxjjsa8n0/8A4KfftIa1b/6NNZyk8BrfSHf9QSK/ZXxT8H/A3ji+jvfEHhDRNZvI+FuL2wilkA9NxXOOTx71o6T4B8M6DbiDTPDulafCDkR2tlHGufXCqPSpsVdH4mSftWfth/ES/wD+JRqvidWYbPJ0vSxHH1z/ABITnn19K6K10/8Abu1aDzi3juQN3RY1H8hX7Tw2cFrxBBHCP+maBf5VNzRyhzH4i3/wn/bc8UN9nu4PHBVhgmW5WMY+oIqxpf8AwTp/am8UWpuLy+uLRmcgx6jr0gk6DnAJ45/nX7Z49aKXKPmPxYb/AIJf/tL7hH/a1oUxnd/b0uBSyf8ABLX9pCMAf2zYycZ41uXvX7TUVQuY/Ey9/wCCaf7Ttim2G+ScYzth1uUCo9N/4Jk/tL63I015cW1nJuwWutblZj78Z4r9t6KYcx+Ouif8Eb/ijrX7zxB4w0OyYtg7RJcvj13HHvxXayf8EadI8NaDc6n4k+K76dbWqGWe4FkoijQDkksa/Rrxl8dPh58PtQFj4k8Z6Lot60YmFveXiI+wkgNjPTKkfhXG+I/Fnwp/as8G674B03xzp+qLqNuYpk0i/UTqPVcHJoC7Pz3+D/7BH7MnxB8UJp9t8dZfFNzGSDYQslq0hH91mXn8K+p9P/4JLfs+Wu03OjatqBH/AD21aZcj0+Rlr4m/ao/4Jh+I/wBnDwZfePfCvixdb0TSCss8cqC2uoEL4DKwOGIJHPB59q+z/wDglD8XPGXxZ/Z/1KTxZfTaumj6s+nWl/dMWmZBFE+xmPLY8zqfUUA2dSv/AAS5/ZqVQD8PpHx/e1u//pPWzov/AATh/Zz0GdJrf4Z2Uzo24fbby6uRn6SSsMe1fS2KKBXZm+G/DmleEdDs9G0TTrXSNJs08u3srKFYoYl64VVAAGST+NadFFAgoopKAKF5OY5wqoMEfexUC2qzliSCeNo6HP1rQMYkbJGa8p/aa+Nem/s9/CbXPGF7NClxawMtjbyHHnTkHC479q55Ruzbm0shfix+0d8M/gaq/wDCZ+LLHR5mw32dm8yUqeB8gycEg847VzPgX9uz4FePNSGnaP4+04XUmWWO6Jgz0/vgV+SHwc+AnxI/4KH/ABe1rxBf3rWEEjtLc6xco8kEHIIgT0xuztH97PevTPjB/wAEhfiN4B0ObVPDetWni3yfne2hjMcuBkkgGtIxsZ3fU81/4KYTadfftfeIbnTJoLi3ura1dpYHV1ZsAE5Hfge9ftp8DdEj8OfBvwRpsXKW+jWqj/v0p/rX81dzZ3tv4ga21BZEvo7jyZ1lJLB1cAg59On4V/Th4Ai8nwJ4cjx93TbZfyiWtAk7m5UcxYIdtfOv7dH7VF9+yh8LrXxDpmiprOoX10LSJZmKxRHBO5sV88/sy/8ABWzSPiJ4ptPDPxG0iDwzd3cqwwapayFrXeez5+6M96AXc/Qa3aSTcCM0yT7Npdrc3d3JHb26KWkkchVVRzkmrdrNDdQJPbyJNDKA6SRsGVgRwQR2r4N/4KyftKXPwu+GNn4E0S5EeteJVP2nacPHajI3D6kEfhU2K5uh9neCfil4P+ITXMXhnxHpuuSWvEyWU6yNH25A6V1nFfjd/wAEi/gl421T4tH4i200+m+D7GOa3mkbOL5yAPLx3xuBzX7I0uUh7hTWkCyBe9PpKOUQjV83/tl/tiWf7I/hzTNSuPDl5rs+pSGGDy22QIwBPzN619Hn/WCsbxh4H8PfELRpNI8TaJYa/pcnL2eo26zRE+u1gRRyjufjN44/4K//ABp1y9lbQk0fwxbMcJFDZJcso9zJnn8Kxbb9s39rv4paXKdD1bxRqkDZjMmg+HUGDjOBJCmQcEe/Ir9e/Dn7K/wd8I6kuoaL8MfCmm3inK3FtpECOv0IXivT4bWG3ULFFHGo6BFAFPlHzH8/Hh6f9o2H4qeFL/XpPiBZ+IZNShSzu9cS6Vhl/m/1wzt5+nWv6BLGOWK1hSZ/NmWNQ8mMbmxyfzqYopOSoJ+lOqgcrhRRRQSFFFNbC5Yjt1oAjubiO1heaaRIolGWeRgFA9Sa4HU/2gvhnod79jv/AB3oFnddfJm1CMN6Zxn2Nflz+0d+0x8Qf2uP2lL34JeEvEUfhnwvNqUmkQNlk+1OnytvYc4JB4qgv/BGP4qKSD4l8MuM8HzJc/8AoNTqWfrdpfxS8H61D5lh4p0i5j/vx3kZH55q1N438MujI/iDSdp4O69ix+W6vyAvv+CNfxbhXNtr3h6dsfcWZ1H6isKT/gkF8c1m2BdCdMf6xdQUD8jzTFZH65TeHfg/ql5LNPpvgm8u5m3SSSQWbyOfUkgk1jat+zR8D/GFyJbrwN4XvJSuweTDGnHJ6IQO9flha/8ABIX452kqSwXei28g53x6hgj8RWxN/wAE0P2ndFYTWfiBJmUcfZ9fkjI9utMLI/RnUv2A/wBn/VAfM+GWjpkYzErr/wCzVxGuf8Esf2etavBcDwvdafhAnk2N+8cfBJzj15/QV8KSfsT/ALYWksLm01PVBNGchk8RvIf++S1WJ/D/AO3h4bhMJXxnNFHxvt5YnGPqTmgOU+zpv+CS/wCz/JGyx6Tq0RI6/wBpOTX0R8BvgJ4T/Zx8Cnwn4NtprbSmunvHE8pkZpWVVZsn2Rfyr8gY/C/7YfizxvoE2qyeNrGV7uO0F1dSFVjVm5JC8YHPJr9tPD9rPp+h2Fpd3Bu7u3t44pp2HMjhQC34nmgk0KKKKACiiigD8x/+C3CSHwf8MioJH2+6HA7+WuP619dfsEyCT9j/AOFrKcj+ycce0jivlj/gtdCf+FbfDeYcbNalG70zCf8ACvpr/gnju/4Yy+F27r/Z0nX0+0S4/Sgt/Cj6LooooICiiigAooooAKKTNGR60ALSUBg3Q5paAGKvXNNkhDVLRSauNaFJbRUk3Htjk1+Lf7VEmoftff8ABQ628DRXP/EttL2PQ4ZIm3IsSfPM/sfmIP8Au1+tn7RHjx/hh8D/ABx4piBM+l6TcXEW3rvCHb+uK/GX9gv9oz4f/BH4s+JvHvxKa8vdanti1nLbw+a3myNukb64OKlRsWnfU/cfwj4Z0/wV4Y0vQNLhW307TbaO1giUYCoigD+Va+RX5E/tgf8ABU22+KPw/g0X4WT6t4cvpLoi7upY9jvAF42sOhzn8q8M+A//AAUm+LPwT0O50xLyPxPZyTtcbtZdpZVJCjAb0+XOPc1ZPKfvTkUbh61+LF9/wV++NmpSRx6bpOjQvIMKkdmZXJ9hVe7+On7Zn7T1u+k6PpmvQ2cijzP7NsvsKMue8jbR+RoDlOP/AOCjlvpeuftxaovhd49SlumskmW0+bN0BsZPdvlX86/d5WEiqw6MMjjFfmn+xb/wTJ8TfD/4paf8RPipeWdzeWLG5ttNhma4Z52AIklZh94EngZ5FfpdQSFFFFAFbUrFdT065s3do0njaIshwwBGMj3r8vvEX/BFOfU/EV9d2fxRWKyuJnlC3ekiaYbmJ5bzBnrX6lUUAflpD/wRFZFx/wALejT1B8MpJ+puBTp/+CIamENH8XwbkHjd4ZRY8fQXHX3r9SaKB3Z+Smrf8EUfF0KkaZ8T9HuwB8q3WnS2y/QhGb86898Yf8Eevjdodm9zpV34X8SyxYKWljfyRPJk8j9+qKP++q/a2igfMz5l/YH/AGX7z9mP4LW2naxLcp4n1Rvteq2j3KywW82SAsewlfu7ckE5xX0yvSlooJCk3DcB3NLSMNykGgD4s/4KnftDT/Br4EjQdKl8rW/FbPZxsCcpAoBlYe+CB+NQf8Em/g3/AMK7/ZtXxBe2Sx6v4mvHvRcsBva12osan23CQ/jXyB/wUs1af42ftyeGfAWmXBmWxt7LS/srZCi4lldn68co8fPtX7B+EfDdp4O8L6ToVjGsVnptrHaxKowNqKFzj8KB3NTvjvXzT+35+zfY/tEfAnUoHk+zavoaPqdjNxjciHcpPoRX0uVO4GuW+LEbTfC/xai/ebSboD/v01AH4CfsO6PLq37W3wwtfleRfEFvK2Txtibc36Cv6IZlfyn2ffwdufXtX4Af8E6rWS4/bN+Hahcst5LI2e2Fcn9BX9AZGeD0oC9z8Mf2kPh5+1P4r+NmvyajoviW7uGnZbdtJkcW3k728sKVIHQ1R0L9iP8Aat8SW5kXTNasVYAf6dqpQkfTca/dtqSgD+bu2+APj29+PMXwvki2+ODefZnE05KpLgNuLjJIxzX3Pa/8EUvEF+sEmq/E/Tw7KrTLDpbs6tgFgHL8855xWb8LmXXP+CxmvtHErJDqV5uzxjy7XBP13Cv1yoEeW/s5/s9+G/2avhraeEPDUWIlf7Rd3TffubgqqtIfTIRePavUqKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilcAoooougEx8wPaikZtuOKXd7UDFoopkkgj9z6UxD6KYm5m3HgYxilVSu7Jzk5oAdRRRQA0rzkcGnUUUAFFFFABRSE02SQqhIGSO1ACsuea87+NAmh8Ea7PA+1k064YKB1IQ16Gr7lDYx7VyHxS0mbU/BetrEy5+wzrtbvlDWVRe6b0naWp+Of8AwSesDqX7ZD3ckjRywaffSlQfvEnBH61+3i1+DH/BOfxg/gj9t/w5D8uzUbm60uTLYH7wMB+oH51+84rSOxM99B1FJu9qM+1MyFopMn0qGa7SAEsQFGMnPC+59qV7DsT0lcX4/wDF+oeH/Bur6xplob2azheaKOPlZtoyMEV8pfBX/gqd4E8aawNA8cWNx4H1pFYSSXoxBuDEYBPI/Gk5Jbl8jtc+4dwzjPPpQTt618E/tVf8FR9C+ETWun+BLSz8WandRmRbjzswouSBnHPUGvC/g/8A8FlNe/4SaO3+IHh6x/seaUbrrT9++JTgEYJwcdfxpKSauRZn61LnvS1ieDPF2l+PPDGneINFukvdK1CFbi2nToyEfzrbqk7q4PTQKKKKloQxmKsOVA/Wq890Yc5TK5xuzip5I1kIJHI6VSv9NW+ZRI/yD+Dt9azlfY0jbqZ8hl1K4KhRBtHVmyceoFWLPSp7c7DcFowvGBznPrivlr/goT8YvF3wC+C93rXgvVU03UmeKLzTEHZFLEZXPevyR1D9sX4++PdShJ+Jnim51GTEUdrptw8W4DkHZFtB5J7Z4pR1R0Sk7JJn9ESwNkB23LjGc8/yoUQ2cblnVE+8WZgAK/BVfjL+19r2mJp8Wp/Eu4hhbaWhtLiQlsDgyBc9COM1JpvwP/a++MkZElh4+vbVpPKeTVruW2QHAOCJHHGCPatOVnNfufug/jrw1FIUfXtMVxwVN3HkfrV7T9f0zVYzJZaha3canaWhmVwD6cGvxT03/glD+0TqUPn3Mek6fIxyY59Y3Ofc7Sf8isbXP+CfX7UfwxWWewsL+aGNTK0mhazuHfPyhsk4Hp6VaFofuktzF/z1T/voVIGDDIORX84k2s/HPTdX/sifVPHcGrFtiWi3FypJzgHrzzn8q/cP9iPwL4v8A/s7+HrPxzq97q/iG6BvZWv5WklgV1XbES3PG3P/AAKmSe80UUUAFJS1HIx5wdtADlbdmnVAHZXPA2Yz71598Sf2ifh38I4428WeK9O0l5ACsMkoMhBJGdo9wfypXHY9Ior5vt/+ChnwEur9LRPH9kJGOAzKwT88V9C6XqdtrOn299ZTx3VncRrLDNGcq6EZBBphZot0UUUCCiiigBp+9ivhD/grv40j8M/s7ppWxvtGtXiW6ODj5V+Zh+VfdzD5s98V+cv/AAWrVm+Evw92puLa3Iu7+7+6qJLmLi7M5v8A4IyXHhDRfB3jq+vNV0+z8Uz38dqYbidY5GtljQqQCem9m6elfpta6ha3yk21zDcAdTFIG/lX4Wfst/8ABOHx/wDtIfDlfG+j+ItN8OaXczSQ2/2oSGV2jbBI29Fzx+Fd34g/4JnftP8Aw7ZJ/CniFNWdRvL6RrUls+cntIV54HQ9xRyi2P2grgvjD8bPCfwR8K32teJ9XtrBYIGljgkkAklIBwFXryRjNfjxffAf9uOxmETyfEaUqvH2fxM7p1PHEuK3fh//AME3/wBov9oDVIrn4l6rqGg6dCxjN14m1J726wAGASMs3y5Y4Pruo5QujifgH4D1v9vz9si51fXvtF/oRu21HVZnO0RWanEcYxjbu2hRjHev3WsbKDTbG3tLaPyra3jWKKMEnaqgADn0Arx39lf9lLwj+yn4FbRPD0bXWpXhWXU9Vmz5l1IBgHGcIo7KuB1Peva9oqhN3BaWkpaYgooooAKKKKAGs2Gx7Zr51+OH7fHwi+APiSTw94j1qaTW4wrSWVnA0rRhieWI4HSvomRVdSGGQeDXxL+1n/wTF8P/ALSvxCufG1l4on8M6xPaJBLbx2yyQzSKznzWOc5IZV4HRBQPQ+j/AIO/tJ/Dv47aQdQ8H+JbTUFVtjwM4jlRsKcFDz/EK9Nr8SvGX/BLf4/fCu7N54RvINZjhXes+j3bQS9TwVJGTgA/jUHgf9ub9o79lXUP7H8Z2moavbEqFtPEsTfIoJH7uQDodp7+tK47H7e0V4J+xf8AtMTftWfCA+M7jRf7Bmj1CXT3tlcurGNI23qT2PmY/A173TJGtjGScAc9cV+Z3/BQD/goHqMHiC5+EPwhmmufEM0wsNR1CzyzFmAxFblej5OCw+le8/8ABRj9q+b9m34R/Z9FljPijxCWsrIZ+a3Xad834A4HvXzN/wAEp/2OW1qaH45eNFmlnW4kGh2l0p/eNj5rps9eWIX3XNAHYfs//wDBJvQ9V8Ex6r8aLzUNU8Y3jmVore9bZBEyqQjHu4YyZPTkVf0L/glSPhh+0V4N8XeAPFU+m+E9Nmjub22upGa6Z0diUVhgbWXauD71+idDDKnHWgdz4G/4K7/HHS/CfwFb4dQzJL4g8TzQsY1cboLeKVJC7DsG2FfpmvXf+Cb/AMJ0+E/7JnhKIukl3r6nX7howMbrhE2DI64jWMfhX5v/ALWX7Fv7SHjf44eINbv9AvPGCXcjPaX9ncK6Lbb3EcfzEFSB29CK8x8aWv7VPwP8L2una7f/ABF8O+HYYEgihjvbn7DFCo2qm6NyigBcBewAoEf0FA56dKWvyh/4I+/FT4h+JviR4o0XV9X1nXPCH9nvcLJePJNbw3YeIHDt0Ypjj0I9a/V6gAooooAKKKKAI2BLMOi44Ir8af8AgqJ8btU+Nn7Q2mfCjw6GuLLQ5lsBbox/f385AbI6HaNgB7HNfr9448SReDfBuva/PjyNK0+e+fPTbFGzn9Fr8W/+CcOi2nx2/ben8S+JA19Pb/bNeQTfMTMW/d5z/d3Aj6CptqWj9bv2Zfgvp/wD+C/hzwjZW8cNzBbRy6hIigGe6KKJJGI6n5QM+iivUaFqC/u00+xuLqU4jgjaVj7KCTVEn4AftYeH7XT/ANvbxbpcEEcVs/ii2CwogCAP5ZIwOO9f0A2dutnaQQIAqRIqAKMAADFfzpeIfHTfE79sRvFEhMg1PxZDKpY5yonCr+GFFf0Z0COT+Jnwv8M/F7wnd+G/FmlQ6vpF0uHhmHI91PUH3Ffmj+0//wAEi00PR9U8S/CjUp7o26mceHbr5mZRklY37kDGAa/Vmgigdz8eP+Cfv/BQa++E2qWvwy+JVzNLoJnMFtfXTEyac33fLYnqoK/hmvDv2sfF2p/tafto6jY+G7r+14bq+j0TRni5QwDjI/FmNfVX/BVj9jXStH0qT4w+ELKPT284DXreEBUYNgLKqjgHOAa8d/4I7aH4f1L9pfU7vVpUGsWOkSS6VA+DvdmCyEZ7qnNIvzP1q/Z3+D1l8Bfg74a8EWLCRdMt9sswGDLKxLOx9eT+QFej0i0tMzCiiigAorwn9r79qXS/2TfhzF4n1DTpdXuLy4FpaWcbhAz4JJJ9MV8Qw/8ABbO4WPEvwxiMuTnbqe0D81NA7H6qUV+VM3/BbS7/AOWXwxt1/wB/VM/+y1nXX/BbbXNp8j4bacj9g987j8xigfKz9Z6K/Oj9kL/gp54t/aP+PGleB9Q8B2NlY38MrG40+d2a32KW3tu6rxg/hX6L0EhRRRQAVW1K6Sx0+6uJOI4Ymkb6AEmrNcd8Zbw6f8IfG90v3odEvXH4QOaAPxL/AGGLGTx9+314fvhlo11i+1Y4H8OXPP6V+2vxG+LHg74R6TFqfjLxHp/hyxlfZHNqE6xh24yBnr1FfmD/AMESfC1vqnjv4n+J5oA13YWdpaxSH+Hz3lZsf9+RX1z/AMFCP2ONX/ay8J+HJPDurQadr/hxrp7aC6H7q5E6xhkJ/hP7tefc0DPpvw34v0TxjpsF/oerWeq2c6CSOa0mWRWU9+DWvX4Fal8D/wBpT9jea41+007XfDlrBgvfaU/nWrdsNjI525+mK++/+CfH/BRQ/H28j8BePfLtvGpDNY3kS7Yr5FQFlPpJwx9CMUBbS5n/ALR//BV6P4G/GPXvBFn4FbVI9GmFtcXVxdeU7yYBJVcfdwVwe9cof+C1+hCzRv8AhXl99oYfd+0rt/OvsP46/stfCD4lR6z4r8ZeFNOudSjsmM2qPmN9qISCxBAOB3PoK/A/wj4Hj8WXXi6+hjdtJ0jTbnUE25IRQ5WME9s5oKVmfcPjb/gsl8Qde1S2g8HeE9P0dGKKIrzM8krlsYH1BFfq38MtY1nxB8PfDmp+IrWOx1y8sYZ7y3iztjkZQSoz9a/NL/gkB8AfBPjzwT4t8a+JNDt9Z1iz1eOwtDeLvWARwxyblH97Mg59hX6p9OBQJjlpa8h8A/tVfDn4kfFXX/h3omuLP4o0ZnSa1Zdocpw4Q/xbSDn6GvXqCQooooAKKKKAPzi/4LXZPwh8AqOWbW3AHc/uTX0t/wAE+JFl/Y0+FjIwdf7MYZU55E8gI/MGvnP/AILRQs3wj+HEoRiF8R4LAcDMLYBPvj9K93/4JozCb9iD4YEMGxb3inBzjF9cDFA76WPpyiiigQUnWkbODj04pI9wUbuvtQA7Ipa8Q/ab8YfF7wfotncfCPwdpPirUWbF22pXYiMMeCRtXcu7JHrXyj4Z/wCCr2p/DvXh4b+Ofwz1Lwjq0T7J7izUkKOzeU3zEHnlSQe1BVtLn6MydaVcYwa8U+Cn7Y3wn/aFvLiy8G+KoL2+gXe9jdRPbT7cc4SQAsB6gY7djXin/BQD9vG3/Zx0g+F/CNzb3Pj+5hScRyRl0t4GLDeSON3yng/1qbgkfZGoa9peiyQxXuoWtnJMwSNJ5lQux6AAnmr6urKGUhlIyCDwa/nQ1LS/jl+0Na6t48uofE/iez0kNNdanmQw2yg7sIegCg5wOma+/v8Aglf+2vrXjy/k+FHjrUn1DUY4DNol9ckCR40UBoCf4iMFgTz19KYcp+mdFItLTJPDP24rKbUP2SfipFApaT+wrhvl9FGSfyBr8hv2Df2KLf8AbA1DxUb/AMQy6JYeHhaGRbeIO8hmD4HPTiJvyr9lP2somn/Zk+KUaKXd/Dl8qqBkkmFgBX53f8ESvGOm6Z4s+J/hy5uo4tS1a1025s4WPzTLALkSbR32+aM0DuewSf8ABGH4Wm3jSPxNryupyzkp834V2mi/8Ek/gXp+nx295aatqUyHJuJL1kLDjghePX86+1aKAuzxj4U/sf8Awl+DUIHhvwbYxzq/mC6u0E8wOAOGbJA46e5r2GG2jt1CRRrEg6KgAH5CpqKBCLS0mcdaWgAooooAKKKKACiiigAooooAKKKKACiiigD8Y7ZLbxl/wWJmeD/SYIPFRVt/GGt4FV+D6PG1fs3kV+GfiTxFL8B/+Cp+t6vf4VF8ZSzyLnd+5un3oePVJV+mcV+5KsJFVlOVYZBoGO3CvnL/AIKA/GyL4H/syeKNSSYR6pqcf9l2CdS0soIP4BdxzX0Xjg9vevxn/wCCgnxM8R/thftL2fws8B2kmpWXhwzW8Nur/LcXSrummPooXCjPofWgdjgP+CUOljWP2ytBkmO5rWwvLoZ9fL/xav3br8Av+Cfnj60+Av7YXh2bxSX0uAtc6RcmZCDFJIuwBh2wwH51+/UcqTRq8bB0YAqynIYEZBB9KBMcRSbadRQI/Eez8cy/Az/gqtrusa0hjjk8V3cUhXnNvckiIjP+y6/rX7b7hX41f8FgPBx8I/tOeFfFltCtvb6po9vK0sX3muLeebzCffYYcHvg+lfrT8KvFdn45+GfhbxBp9yLy01LTLe5SZT97dGpP45zmgp9zrKWkWue8dfEPw18MtBl1rxVrVnoWlxfeubyTav0Hcn6UEnRUVk+E/Fek+OPDmn69oV9FqWkahEJ7a7hOUlQ9CK1qACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikbOOOtNjDqDvIJz2oAfRRRQAUUUVDTuAUUUhpWYFW6Z4WM2792q8r3NTW8wnhWQdGGaBCSpDEMDT1jCDC8ChRd7lX0HU1lDfWnUVoSIKWiigAooooAKKKKACkY7RS0jDcMUANbmk9utONJt70DG7l5TOCBmqmqfZ73T7m3k2ypJGyMm7G7jpn8amvLUXdu8RYoGGMjqKzL7T00/R51UkmOMsH7kiplsXFRb3P5+rq2f4G/tsQjDRDSfFKSrzjCtKDjP0bFf0N28yXEEcsbbo5FDKw7gjIr+eT9rC+m1D9rjxVdTwNbTPrMJRT6DaM/pX70nXr/w78I7bVLHTZdXvrXS4pUsofvykRjge9JSSWo5LWyO3U0Buufwr8mfGn/BYzx34Z8XXNifhrZ2cNsTE9nqFzIk24Mec7OOMce1Mt/8AgtZ4nnt2LfDLTVkzgbNSkI/9Ap8y3FyM/Wk55x6V8Mf8FLj8RbX4S3Y8IXs9jaRlrm/nt3KyNAozgEdBnNfMesf8Fh/id4iktNP0DwTpen3lxOqptmeeR+RlQpA61+kXirSNQ+Mf7P13DrGnLpt/q2iP9ohPLRu0ecAGolqzSHuX8z4I/wCCQ3x98T+KPFviT4fa/rFzrOktZG9to71zI0TAhWUMecEZ4rtf+CpH7Pvwt0/4a3/jT7Omk+MY9sVqbchRMuSdrL9WPPvXyn+wL4lHwG/ayv8ARNSk+xyXEclgsj9Qd3H516V/wVa8Tah40+MnhL4eWErXl08EDoEbiR5HdQCB9BS5m35By2urnyX+yl8M/CHxZ+LWm6P431waLonDSymXYXH90E9K+v8A9ub9gjwP8O/gnZ+NPhUsl3Zaa4N863Hnl43J+cn24rI+LX/BKPXPh38BY/Fml6tJqXiaxg+1XunqmAq4BYKRySK+Zfhl+1t40+HXhfVvCd7cNq/hzUYJLWexvGY7MqAMc9QRUyUr3iyIW6n6w/8ABKL4lW/jr9lbT9ME3mX3h27k0+4Q/wAIwHT81b+dfZlflj/wRG8RJt+K+jbsFnsb2JM9v36sf0Wv1NFbRtsRLe4tFFFUSNakpxGaTbS0GfI3/BTTwrba9+zL4juJ42P2WNZA69QVJI/Dmvzm/wCCUPi610T9qjTdIvNOtLyHVrSWOOaaHfJDIqFlKHPHPWv1a/bb0mLWv2bvHFnNuEX9myyll6gqMivx5/4J2/ErwR8If2h7LxF40vhp9rDA8UFxIMojOMEmsVu0bPZH7/r0pa5PwD8VPCXxQ09r7wn4hsNetVOGezmDFTgHkdR1HbvXB/tCftZeA/2bdAk1LxVeyGXd5cNnaxl5JZMZ2jsDWtzKzPaKK/Na6/4LZeEo5WWD4ba5KnZmuolz+FYWs/8ABbyzhljGmfCm4nQj5je6uISD7BYmBHTvTuHKz9PX020kuBcPawtcL0laMFh+OM1Zr4t/Y5/4KKS/tYeNL7w8Ph3eaH9li85763uxdQRqeBvOxdpJz619og0xNNC0UUUCErkvih8QtI+FvgnVPEmtXCQWFlGXYu2MnHA+tdXLIsMbOxCqoySe1fjp/wAFP/2mtQ+I3xGX4WeFruWTTLWRI7qOF9wubhmICgD0G386VzSMb6nFfGb9u/4y/tLfEVfD/wAOLnUNNsXcw2tjo4Imm+Y/OzDnBBH5V9D/AAt/4JDv4x0Ky1v4t+ONYuNeukEsunwsHEBYZ2l2JOck5xxX0F+wf+w1on7MvhVNc1Fv7V8aanEsk1zIgAtEZVPkoOxB3ZbvmvrjbU2YOR+ey/8ABGP4XjUIpH8Va/JZq2Xtf3Y3D03dRX3j4N8LWXgjwvpegad5n2HTbdLaHzW3NtUYGT3NbO0UVfQlu4tFFFBIUUUUANavzp/4LURzt8GfAkka/uY9bdpGx9391gH9TX6L4r5z/b3+B9x8dP2d9e0qwCtqNihvoEKbi7IM4HoeKBrc8Q/4I2/Eo+KP2edb8JylTP4Y1ZlQL/zwnXzFP/fYmr78r8Qf+CWPx6b4F/Hi68H6tbCCw8ZPFp07zEIbe5hMhjJz0H71gf8AeHoMft3u96AY+im5NJuoEOJpNx59e1cF8ZvixpnwZ8C6t4o1aZVtLC3eZlZgMlRkKO5LHAr4O/YQ+OPxc/a0/ac1vxvq2r3mmfD3SLaUR6LbkizLycRxdPnYffJOT0GcYFTfWxfK7XP0vBz70tItLVEBRRRQAUUUyRiuWwSAOg70AOxznvQzBVJJwBySa/PP9tj/AIKa6x8BviBc+BvB3hkSatZ/8fGoauhWFuM/ux/EPevhH4n/APBSL46fFTTW0+48UpotlIMSR6ND9nZ19CeT+IoA/X/46fts/Cv4AyLB4h15J74nAs7IiWTv1x06V+U/7XP7VXif9urx5pPhbwd4dmTR4JtlnaxR7prhmJAkcgcDBHHbmvkK8vLvVLo3N3eSXczknzbmYs2T6k19Sfs5ftuH9mvQ4IPD3w68O3Wqrnz9Yumc3EjEAfe7DAH61Nirn7Hfsl/Bo/AX4A+EvB0yr/aFnah711H3p3+Z/wAs4/CvX6/HDVv+CyvxQmA+xeF/D9oO7N5jj36/hX6AfsJ/tGeJv2nfg3c+L/E+ixaLcrqclnbiAMEniWONvMGe25nH/AaYPuflD/wUB+OVp8ZP2uNQ+1yTXHhPw9dR6VHBCdxaKJyZmVemWZn/ACFfo/8AB/8A4KVfs/X0mgeDNKvL3w7AsUVnaC+sxDAmAAFyCQB71+ZX7EvgTwl8av2tLbSPiOwu9PvJLudo7iUoLm45IVj3ySfrX1D/AMFH/wBgfwF8H/hTJ8RfAVrJov2O8hjudNWQvCwkO3cufu4OOKYWP1dtbqG9t457eVJ4JFDJJGwZWB6EEdRUtfEX/BIv4geIfHn7MeoJ4h1GbUn0fX5tNs5Z3LstutvbuqZPYNI+K+3aCQpkkKTLtkRZF9GGRT6KAI4beK3BEUSRj/YUCpKKKACiiigAooooA5L4t6IviX4W+MNJcZW+0e7tyPXdC4/rX42f8EktQj0X9r46fNIEefS7u3XJxuZcHH5Cv26urdLq3lglXdHIhRh6gjBFfgJ8fPAPjb9i39qi91bSvM0hor6TUNHvNpWG4hZ2wuR2OCCtBcex/QAtfPH7efxztPgP+zh4m1Nptmr6nbvpemRg8tNKpBP4Lk/hXyT4I/4LUaQug2ieK/At8NWVNtxJp0qmJmHcBsECvlL44fGT4mf8FD/jHaaXoGlX1xpUUmNL0mIEx2qM2POlI4zyfmPpQLlPlPT7240/UrW9gZxcW8onDA4IZDuyD9a/pb+BHj2L4ofBvwd4qhJK6ppkFwSTn5igDfqDX5a/t0fsJ2vwJ/Zx8Aat4bsJLu+0hjF4iuoE3GQui7pCeu3cCPSvVf8Agjb8etV8SeH/ABJ8L9Q869stDAv9PvHyRFC5CmD2AIJH1NBJ+mNFFFAH56/8Flvii/hz4J+HPBNs5E/iW+aeZVOD5NsFY59izr+Vfm7aeAfiX+y3N8NPi3FEbGHVnW+0q6hbiTGGMbf7ynp6V61/wVR+N3/C0/2mb7Q4ZGj0nwlG2kKAfvzKxaVvxZtv/ARX6lat8BfC37Qn7JvhXwzqWno0P9gWsunPja1vN9nXYw9OcZoKudx+zZ8eNG/aP+EejeNtGxELpTHd2m7LWtwvDxt7jgj2YV6hX4Y/sLfHXWP2R/2ln8GeI5J4NDvr59J1a0YkrFcbiscwHQc7R7gV+5qsGUMOQRkUEi0UUUAeYfHv9nPwR+0l4cs9E8cadJqFlZzfaIBFO8TI5GCcqR2rw/Tf+CVP7O1hMskvhO8vWU5xPqtxtP1AcCvr+igdzwXSf2FfgHo9qkEXwr8OTqvRryzWd/pufJrTT9jX4Fxq6r8JfCA3DBb+x4M/gduRXs9FAXZ4b8F/2Nfhl8AfiFrfjDwXo76Vf6pai0e3WUmCFN5c+Wv8OTt/BR717lRRQIKKKKACvLP2qDj9mv4of9i3f/8Aoh68T/4KXftLeJf2cPg/pNz4PvI9P1/WNQ+yR3TRrIYkVSzMA3HoOlfKXwd/4KNSfFj9n34meA/ixrUVr4nn0a8Gma0sIjS7UxbViKqMb927njINBVj0H/giVpMMPw7+Jmpgfv7jVLO2Y/7McBZf1lav0rr87f8AgitFGPgT45lVCsjeJCpPqBaQY/mfzrwH9uj/AIKAfGXTfix4k8DaJJL4I0fTbhrNTbxEXNxtdv3okPQEEDA9KAsfpb+0x+0h4H/Z7+Heoav4rure6MkbQ2+k7g0l5IVOI9voeck1+VH/AATf8EXvxf8A2z4/HGl6PFpfh/SZrrU7iC3BENt5iusUKn1BIOPSvj7xFdeLvHGpNqmsNq+t3sgwbq7EkznknGTnHUnHvX0n+zR+2R8XPhbZ+Gfhl8PdE0qyku79Q6yWJae8kZgCZDwfu4HsBSKsfqV/wUk8XSeD/wBjfx/LDJ5c19DDp6HOCfNlVWA99u6vzE+EXwtn8Mf8E8/jD8R5w0NzrF/Z6RbKQRugSWPcw+pkYf8AATX2P/wV+1vWY/2ZfBGn3duy3t5rEU979mBaJJI4HyM+m5zj6VgftHaDL4N/4JF+DtOW3+zyPZ6TJNGFwQZCJGJHrk80xLY9A/4I5eHZNJ/Za1W/mQo2reJLq5RsdUEMEfH4xtX3dXyr/wAEw/EGi61+x14Mt9IkVn083FrdoCNyzec7Nn3IZT+NfVtBLPxJ8I3r/AT/AIKw3KzPtgn8WXFvI7cfur3cQfp+9Br9ta/GH/grh8Obz4cftPaH8QbFPIt/EFtDdLcIcMLu1wjAf8AEJ/Gv1u+D3ji1+JPwt8LeJ7OXzoNU06G5DZydxQbgfcHI/CgR2NFFFABRRSUAfA//AAWQh8z9n7we+M7PFNuT+MMor0v/AIJbyCT9h/4eqCCUbUFIz0/0+4P9a88/4LENt/Zx8Pcc/wDCSW3/AKLlruP+CVq+X+xX4Nyc5uL8/wDk3LQVbS59cUnmL/eH51XuJTuAVhjHrUKfKDk55oGo31L3mL/eH50nmIWwGGfTNU1Xc+dwHHrUsMOxiTyc9aBuKXU+S/2+P22NW/ZKXwtBovhmDXrrWDI0kl8zxQRqvQCQDG7OflznFWvhPrfws/4KSfANdS8T+GrKW+DfY9St4yPtNjcKAfklxuCkNkZ45PpXY/twfs7WX7RnwG1vRmiX+27CNr7TLjblklQZKj2YAj8q/O7/AII6+Przwv8AH/xL4MuDKsGs6a0pgJIWOeB+SR6lSw/CgW6NP9sL/gmTL8A/Dd18Q/hn4puE0XSoDJe2+qXghuLf5jhoZF27hyoC9c565r4q+Gvj3RF+Lmka/wDFOz1Dxho0U4a+glnJllII6k8kDA+XPNfe3/BWj47XPxC8feGPgd4Qmnu7qO5jOoxWchYT3UzBIbdlXqV4OD3avqj9nz/gnn8N/BPwF0nwl438K6X4j12QPcajfSJlzM/UI4wQFAUDtxSsK9ix8G/29v2dPGmk2+haR4g07wvb+WLePS9WhFmpGANgDDDccd881+bnjK+8P/ssf8FGItX8J3trc+FYtXhuo5LeUPFHBcqvmpuHGFZ3H4V9W/Gf/gjP4Z126lvfhz4ouPDg2grpuoKZo/MyTkSDkDBAxg9OtfDPxe/YT+Mfwj+IGm6Zf+GbrWlvJ4xb6ho8Tzwznd03f38DJB6ZFAXP6B7WdLq3jmiYPHIodWXoQRkGpazfDdvJZ+HdMglUrLFbRoyt1BCgGtKmSVdV0y21rTLvT72JZ7O6iaCaJhw6MCGB/A1+FPxj8E+IP+CeP7YlrqehGZdKhlGo6dIwIF1ZyEh4vfbhgR7V+8FfNX7b37Hdj+1t4HsbaO+/srxJo7SS6ddkfKxYDKP/ALOQKAPavhf8S9B+LXgnSvE3h7UbbUbC+t0mDW8gfYWUEq3oQeMGurr8FvDOu/tCf8E+fHGoWcGm3lpaNuMqzQvLp90oYgSqQCBnbjseK+ofBv8AwWysLXw/bJ4q+Hl5d6xj95Npl4kcLe+1gSDnP6UAfqRRX5uWv/BbLwRMpMvw61uHnH/H9E3/ALLTLj/gth4O83Za/DfWpywwv+nRg7vTAXmgD9HdS1C10qymu726hsrSJS0lxcSBI0HqWPAH1r8xv2o/21viJ8a/jdafCX9nbUZp7GRFtbzWNPh3F5izCR1kH3YlXHzccg4NefazaftI/wDBSbXgsMVz4N+G63DKFuyYIYwMNyBhpWww7beOtfoT+yf+x/4Q/ZR8JSWGjL/aOt3hD3+sToPMlbaBtX+4nGQo7k+tAHT/ALNfwXl+A/wtsfDd3rl94i1R3N3f6jfztK8tw6qH27jwvygAf416nRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH5H/8FfP2c7zQPiFpPxj0KJ/s2pJHa6m0KEmC5hAEcxx2KBB/wCu1/ZT/AOCtnhjT/Advofxe+2WmrafGsMGq2Nq1wl3GqhQWC5IfIPPTpX6VeIPDumeLNHudK1mwt9T065QxzWtzGHR1IwQQa+MvFH/BIz4KeINcur+1Or6PFM2/7Ja3A8tCeTtyMgUDueGftaf8FU7bxl4ftfDHwQe+a+1FjFc6lNaPFKgPG2NCMknPWvRf+CWf7J/iH4aw6/8AErx5pstn4k1keTZLdnM3kt87TEHlWYttwey17n8A/wDgnr8JP2f9Yl1jS9Lk1rVycxXerESmAcfcGMD6+9fTNAXPzE/4KDf8E2Nf+IHjS7+I/wAK7dbvUL9hLqeiq4jYyjJM0R7k/KNvtmuB/Z/s/wBunwhrmjaDbaRq8Gih44t3iFE8iOFTzuYkkccV+vNJtAYnuetAiO2837PF5+3zto37em7HOPxqWiigD4h/4Ktfs+6j8YPgjp2v+H9PfUNf8M3Zn8mFNzy2zqRKvvjCnH1r4q/YR/4KIT/sz6XdeD/HVtqWs+Ew+bRbcbp9OYHDIFbGRwPlyMV+2LqsisrAMrDBUjIIr5i+In/BN/4F/EzxJPrmpeF3tb64OZf7PuXgR2ySWKqcZ56+woHc8K+J3/BZTwHp+iIPAHhnWdb1qVtqRatbi2jGe/yuzGvJfhT8A/jb+3p8UrTxX8aF1HSfhvby/ak0+4JhSVScrDFH124xliBwa+8PhV+wn8FPg7dC70LwVZy3yvvW71HNzKhwPus+cDjt6mvfEjWNFVFCKowAowBQIy/CfhXSvA/hvTtA0Oyj07SNPhW3trWEYSNB0ArWpkalQQcAZ4xT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBD1qrcapaWsgjmuYYXPRZHAJ/OrLLur4s/bU/YI8T/tM+MLPxP4d+If8Awjl3aWK2aafNHKsT4kd9xdH4Pz4+72qHfoXFRd7s+zGv7aOJpXuIljUZLFxgfjXmHjr9qT4TfD1pIfEHjvRLKZYjKYGu0ZyuSOFB9Qa/Ntf+CWv7S0NnNYJ8TdMFi5yYv7bvNj8YyV8r0FQ+Gf8Agi78RdWvi3inx5oVjBnmWzWa6lP4Oq/zpu7QlZHh/wAZ/FehftQftpaRc+BLO4ubLUdTt4FXysM+yUlnA/u7T19jX70afbrZ2FvAq7VjjVAPQAYr5X/ZR/4J1+Bf2X9XbXkvpvFXiUJsi1G8gEQgB+9sQMcZ9c19YbaSj3CUjzLxr+zJ8LPiPrR1bxL4G0fVtS2eX9pmgwxXJODgjPJP51y91+wr8BLyQPL8MNEZgMDCSLx+DV7tS1XKhXZ4r4a/Yz+Cng3WYNV0f4daPZX8BzFMsbMUPqNzHmvW9Us5LjSbm2tysbvEUXI4GRir1G2iwXZ/Pb+254a1z4W/tMapeSMbC/uHF9btCcbRuKAg/VD+dekfsCrqf7Rn7ZWh6z4slfVZtMtvtLPN8wXyx8g59/51+nH7Vn7C/gf9qWxFxqTS6P4jhj8u31W2UMwALMFYHqNzH865v9h/9guw/ZN/tPVrzWf7d8SainlSSLEFjhjByFQ9TnvmoUWlY0ck22fWVxBHcQvDKiyROpVkYZBB6g1+Tv8AwUk/YCnsbub4i/DvRli0yKAtqen2oACtvZjKo9wQPwr9ZmGar32n2+p2c9pdxLcW0ylJIpBlWU9QRTsyEz8Of+CUnxOHw5/agt9LuGaOz8TWr6cVP/PRTvTPvkH86/c5a+T/AAz/AME4Phx4N/aAtfino17qFjc207XMWixrH9kWRhjcPl3D86+sKEne45NMWiikqyBGz2pPmxWH4q8Uf8I3ptxemFpktk82VVGTs56e/Ffm/wCH/wDgsbcp8WpND8QeErKDwt/aDWovbXzFuIo921Xbc5UnueBWejdjX2cuXmPsT9sXUbhPgh4rsIoleW802aJeD3HPevxS/ZU/ZC8TftZeKvEGiaBqen6TJo8Annl1DeVO5iqqNoJzlTX7WftR67YzfArVPFdtOl3p66dJJG6fMjq6cGvgT/gkX8X/AAT4B1P4lx+I7630a7uTFdLqN7MEjMILDy/rkk/jWcdGyn8KPBvG/wCzL+0P+wrqyeKrE3Vhbx5/4nvhy4aWELn7soxwODwR3619sfsp/EDwr/wUc+Fet+Evif4eW48SaSFeXVIRtLllC+dH12txjBz0ryL9vz/gpFF8QIb/AOHHwzeK50eVvKvNY2nM3YrHk42+5Fe9f8Ep/wBm3W/hL8Or/wAV61cW6v4mVJYbWJw5WLAwWx0Oc960Yr6H5eftdfBGx/Z7+OGt+D9MvJb/AEy2Ie2muHDSlDn7xAAJyD0Aq1+xh8PND+K/7Rfg3wr4ksv7Q0PULl1uLfzHTICE5BUjByBWz+3/AK7P4i/ax8dPMqKILz7OgjyFCqB7n3rrP+CXXh6DXP2xPDC3DSBbOC4uk8sgfOqcZ46c0CP0e+MHgXSv+CfPwb1nxl8FPCdskr3kLara3k0kweEZBIJbIwPfHtXtn7LP7Tfhr9qT4djxJ4fZop7eQWt/ZyDDQT7Fcr7jDDBrd/aE+HcHxT+Dfivw3cKzreWMiqqHB3AEjFfjt/wTz+NWo/s4ftQDwfqVx9m0TWLptNvop87VlBIRxzgHOAT6VSYnqj90aa0gXqefShWDqGHIPIpdoLAkc1RmeG/tc/HG3+C3wQ8T6zIwgvGtZLe0395GXAOPxr8UP2SPjF4N+HPx4g8cfEm0uNegt1kuI8jzGNwfuuQepHavtz/gtb4ovLbTfh/oUUjx2d21xcXGAdrFNoQfq36Vi/sA/wDBPj4U/HT4JaV468WnUNS1O4nmje1trvy4UKyEAFcdcY71NjW9krHrtp/wWW+E/mIs+h65HGTjcsQOPwr6E+AP7cHwr/aO1J9L8L6y8esLkjT76PypXAAJKg9ev6V5z4p/4JU/ATxJbsItF1HTJRHtRrO+ZF3Y4YjBzX5g/s5eHZ/hj+3r4V8O2dy0Y07xM1iZQ3Lxhiu0nvkCmQ9Xof0B0Ui0tMkKKKKACiiigApDyCCMilooA/E//gqL+zhN8E/jZB4+0H/RtC8RSfaQ0Klfsd2pOQMdBwG/Gvaf2Zf+Cu2heH/AOm6F8WbDVLjWbP8Acf23psKSpcRAAK7rlcNnIIAxgDvmv0e+I3ww8L/Frw5PoXizR7fWtLmBDQzg5GRglWGCp9wRXyl40/4JE/ADxRDEml2Wu+EigwW0rVHlLck8/aRL69sUFXVjUh/4Kufs7TQiT/hJdRT1R9KmDD9K5zxV/wAFgPgZocLtpcPiTxFKE3L9k08RJu5+UtI64/I9axov+CLvwbU/vPGHj6QDov2+zAx/4C11vhf/AIJIfs++H1K6hpmveKstu3arrEiEcDj/AEfyhjv0zyeaA0Pg3xz8Svi9/wAFN/irBoHhnTW03w3CxdbTePs9om7madx958YG0kjgYHJNfrZ+zJ8BdN/Zu+D+i+C7CVbqW1TfdXioFNxM3LOf5DPYCuo+Gfwh8GfBzQE0XwV4a0/w5py8mKyiCtIcY3O5yztgDliTxXXYqUtbg3cBS0lLVEhRRRQAUUUUAeXfFz9mf4afHW+srnxv4TsddurMYimnUhguT8u5SCR1qDwT+yj8H/h2ki6B8OtBshIxdt9oJjkgD/lpuxwBXrFFAHKL8JvA69PBvh8fTS4P/iKc/wAK/BckZQ+EdD2HqBpsI/8AZa6migDzPxN+zV8LPF1uLfVvAWg3kGP9W1kgH6AV1/g7wZonw/8ADlloHhzTLfR9Gs12W9laptjjXOcAVuUUDPxt/aq/4Jq/EL4XePtR8a/CuCTWNEa6N5a29hIUvLF2YttVR1APQivNviR8bv2oviF8M5vhh4t0bxBrFjcPHuF3oL/aHKNkAy7ckdOTX7t0xreJ2DNGjN/eKgmgfMfKv/BNb4A69+z3+zqmmeJEEGrazqD6xLa87oN8USBG9wIxn619XUUUEhRRRQAUUUUAFFFFABRRRQA1q5D4jfCXwb8XNJGm+MfDen+IbRc7FvYQ7R57o3VT9CK7CigD5O1P/gl7+zzqUm9fCFxZHuLa/lAPP+0TXtnwf+APgL4EaQ2n+C/DtppCPxJcLGDPJwBhpMbiOBxnFei0UDuUtX0Ww8RaXc6bqdnDf2FyhjmtrhA8cinqCD1rlvhh8FfA3wZ0+4s/Bfhmw8Pw3EhkmNrFh5GPqxySPbOBXb0UCCmk/MBnAx0p1JQB88/Ez9gv4NfFvx83jHX/AAwG1x5VlnktZTGk7g53SKOCT3PfFe/2FjBpdjb2drEsFtbxrFFGgwFUDAA9sVYooA+CviN/wThufGH7aWnfFeHU7X/hFpNQi1XUdPlHzmaIAhVHTBIH6196KAoAHSlooAKKKKACiiigAooooAKKKKACkpaKAPyK/wCC1/jtNQ+IHw78KxfONN0+41F8dN00vl4P/gP+tfJ/xC/Y28ceAfgb4S+KpgF/4Z1y1juHMHMlrvXcN47AjvR+17He3n7YHxCg1r/Wv4mljkx08kzEDH4V+/Wm+EdH1n4Y2nhq5t1u9DuNMSzeB+jwmMLj8qCuY+H/APgixCF/Z28YyGPa7eKZdp7Ffslr0/HNfc3iT4c+E/GdzFceIPC+ja7cQgLHLqWnxXDoASQFLqSBknp61n/CD4P+GPgb4JtvCvhKx+waRbu8ixlixLMxLEnuea7WgVzFtfCGhWMKw22iadbxLwscVpGqj6ACs6H4W+DrfxBDrsPhXR4dZhyY7+OxiWZc8HDhc11dFAjL17w5pXiiwNjrOm2mq2ZYObe8hWVNwOQcMCMivIf2xvgjN8dv2cPFHgzTF2X7wpPYxR4RTLEQyJ9DjGK9yooGfzs+CNa+P37P91qOj+Fh4s8OlblmubbT7KQxNKAFLfcIPCqM+1eiab+0d+1/JEb631bxzPHE20lrB8Z64xs561+8VFAj+eb42eP/AI/ftFwaBB490DxJrCaK8xtn/saZWHm+WHBwncRrX6//APBNzSdZ0P8AY28BWOv2lzY6lELzdb3kTRyohu5jGGVgCPkK9a+mqKACiimSSeXG7Bd7KM7R1PtQA+mH74r4J1f/AIK3eGPBPi/UNB8afDnxJ4dltJ3iEjlWZ1ViA2xgpwcVzfi7/gtV4DsVKeG/BOsavMR8rXk6W6Z9wAxoA7f/AIK+WbXX7M2mOgLGDX7aQ4GcLskBY+wyOa1P+CW/jDQNP/Y38K2t1rmm29zDc3qywy3cavGTcyMAyk5BKkHnsQe9fnT8e/2pvi9+3x4k03wzpmgzDTVkXydB0aGSVNxY/vJnAJ6EDPA4rstJ/wCCSvx7ktY2WTw/YLKA7QyalKvlk9sIpBoKvpY/Ya8+K3gTS8i78Y+Hrbv+/wBUgT+b1h3f7SXwf099l18UvBNs+M7ZvEVmp/WSvyq/4dA/HVlC/wBteE2DcnzNTuxj24jNV5v+COnxyjYBNW8HOCMnbqV0B+sNBOp+rFn+038G9SvorSz+Kvgi7upWVI4bfxFZyMzE4CgCTJJPavTlxtBXkHnIr8afh5/wSd+Lnhz4veDJPEtvot34ajv47i+vtK1B3eJEO7BDqp6qMYGOetfsrDGIYUjXJVFCjPXjigAkVWUq4BVhgg96/n4m+LWqfsk/ti+Ntf8ADtrG91pupahZfZ5h8qq7sMEeoNf0FHAGTwBX8/8A/wAFJPCsPhf9tTx/aWaeZ9ruLe+EarndJcQJKwx/vPQNOx7/AP8ABL34V3H7QPx+8WfGLxxHNqs2jzJJBPNGWil1CRi2VboTEoQ4zxvU1+wNfOP7AnwFj+AH7OPh/SpY9usaov8AauoswwfOlVfl55+VQq/hX0cM4560CFpjRqzAlQSOmRnFPooASloooAKRvbrS0UAZ2s+H9N8R6fNY6rYW9/ZzDa8NxGHVh7g145ffsO/AjUbmSef4ZaE0shyxEGP617pRQB883H/BP/4B3Egf/hXOlxYGNsSlR+Wa3vCn7GvwX8F3C3Gl/D3RY7hW3rNJbh2U+xNe0UUAQWtjb2ESxW0EcEajCpEoUAfQVNS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTWUt3pVGKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooATijigjNJtoELS0g4paBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGJ4ltGktAUCvlgrRuMq454PtzX86n7WmiR+E/wBonx3ptughgXUZG8teANx3Y+mTX9GWvxzSWeIEZ3Vg2F68V+EPx6/Zz+J3xk/as8aW2j+Ctal+1axLGl09m6wLGGwHZyMdOetY/budN700jK+FP7Z2s+Hfgrrvw08QXN1e6PdQslpLvLmHKgBcE9OO3rXC/Bj9lf4n/H6O5m8DeF7rVbBZfKkvZJFhtwwwcEkjPBFdZ+0V+wl8S/2a7Sxv9X059W0qeATTajpsbPFatuI2SHscDP41+gX/AARi1yW++CvizTzbEQ2esEJdZJ37okJHPTGadtbom/u2PjiH/gk3+0RJw3h/SQqcDOrwqfWvav2b/wBhf9q74aeM9Nul1y18P6RYylzBdauZ4X4xjy0J4+mOlfrd1o2iqszO5+BP7Rn7Hfxzh+Luu3uueFpr6e+llvTqNh+8tmjyfmBySOnQ81o/8ExfEmkeBf2stMn8QahBpiG1uLcS3DhEEhGMEn6V+72oWKahY3NrISEnjaJvowIP86/Fv4/f8EsPiv4f+IF4/gnTF8VaLdSPcxXUU6xvFuc/I4OOQMHI45osw5j9m7XXNM1C3E1vf2txCw4dJVZSPrmvwl/4KIeAz8Hf2sb+/wBNaMx6g0etWxhYfLhyOx45U1Zt/wBgf9qXT4vKttD1q3ixjy4dWwPyD1k6x/wT/wD2ktX1W2/tPwbqt/PIBGt1cXQmEa56Ekk4o5Quj9t/2f8A4i2nxY+DfhLxVZv5kWoWEUhOc/PtAYfmDXoVeV/sv/CVvgf8CfCXg2Uk3On2gE+WziRjucZ9Mk16pVEnxt/wU1/Zv1v48/Bu2uPDVtHdavoMzXghI/eSR7fmVT+HSvgL/gn5+2pL+yz4ou/CPjATReD765ZrhWQl7GfhScenAzX7iMocEEZB4I9a+Jv2xP8Agmn4a+P0kmveEntfC/ijGZNsWIbk5J+bHQnPWmNM+mNN+O3gbxF4IuvE+j+J9NvtMitmuPNjuF4wuQCM8H2r8Zv2P/DEnxq/b+tNUjdzb22r3GrySBv4VZivPucVBqX/AATp/aP8MTXelaf4buriykbYz2N7iCUZ4bGeK/QH/gnL+xBqf7NOm6x4k8ZQ2/8AwmGpYiiSCTeILfap2n/a3bs0BdI+4F6U6kXvS0EhRRRQAUUUUAFFFFABRRRQAUlI1GTQA6im5NGTQA6ikWloAKKKKVwCims2KTdRcdh9FNzS0r62ELRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQB8+fGL9hH4PfHLxxF4u8T+H5W11SplubO5aHz9vTeBwTwOevFe96fYw6XY29nbLst7eNYo1JJwoGAMmrFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNb0p1FAHD+NPgl4B+JFz9p8U+D9H1652hPO1CzSV8DtkiszQP2afhR4Wk36T8PPDmnvnO6DTolOfXpXpdFAGfp2gaZo+PsOn2tnxj9xCqfyFX6WigAooooAKKKKAE61w3ib4F/Dzxp4gOu6/4K0LWdaOwG/vrCOWY7AAvzMCeMDFd1RQAyGFLeJIokWONAFVFGAAOgAp9FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIGzkelAC0UUUAFFFFACU0RqrEhVBPU4p2KNtKwGdr+g6f4n0i70rVrSLUNOu4zFPbTqGR1PUEVy3wo+Cvgv4H6Pe6X4I0K30DT7y4N1Nb25O1pCAN3JPYCu620baYAtLSUtABRRRQAUUUUAFFFFABRRRQAUlLRQAijaMZz9aWiigAooooAKKKKACiiigAoprGmTSFIyQQD70rjsPasrVrq9tYZBa7DOUcxeYhZSwGQCBzzVibVI7aN5ZjiNF3Flya8xuv2pvhbY+MLbw7deL7CDWrlxBHaNKCS2eAcdDS5kUovsflb8Tv+ClP7SHh34lXsk9zZ6Dp2n3kkA0v+xQtvMquQAzyKZM47hhX2J+xP8A8FLNM/aE1ODwj4ytLXQfGUrFbf7KW+z3QAzxno3XjNfUvxuXwKnw91i88dWem3ehR2zPIL5EO/AJAUnnP05r8df2H/Aum/Fr9uKzv/Cunf2T4Y0i8l1RIkZjsjXKquSScE+9HMPc/c9aWkWlqjMKSlorN7gQnLd8Uo+Udc05lHpTSo2nis2mV5FaTUBHdJDsZi3O4DgVdpqRqOgp1VHTcTFooorYQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGpKAHZozUbSKvGaa0yqcE4NA7MmyKMiofMywA5qSgLDqWkWloEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJu+bFLSbfmBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARc4GetLRRQAUUUUAFFFFABRRRQAUUhNG6gBaKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopCaTdQA6im7qN1ADqKrtclZthAAxnNTBwwyORSumOw6im7qNxphYbIpZ1+bAp9N7g04Gp5lewhaKKKoAooooAKKa27tj8aVc9/wBKAFooooAKKKKACik5paACio235OCv5U7caAHUVBcXUdrG0ksixxqMlmOAPfNZ+j+KtJ8QSyx6dqdpfSRffS3mVyv1ANK47O1zXopBmlpiCiiigAooooAKKKKACimsaQMTQA+io2UNyaRWCqcA0rjHSNtqlNIJAAx43Y6UXFy7ZVRj3NVft0FrG0l1JHbQqctLMdq/99E4FQ9zbkaVzkvjpqk/h74W+JNSglMMdrp08jFexCHB/Ovw5/Yz8DXPx4/a08PW9/vukXUH1K7nJILKpzgkYxzjpX67/tlfHDwZofwB8ZWI8V6O2oXlhJBHbx3aSOxIxjCk81+cv/BKn4pfDj4R+PvFmveO/FFj4euHtFgsftiNhlLZYhgD7DFOwuZ2PX/+Cm3w5+PnxK+IkGj+GPC+vav4Bt7WP7PFodmbiN2HUyMvzbvY8V8mfCf4W/tQ/ALxBJrvgXwT4w8PanNH5Ek/9g79y5ztKyowx74r9oPA/wC2B8GviR4mt/D3hv4gaTq+s3BKxWcLsHcjrjIFex7RRZkcx5F+yn4s8e+NPgnoWp/EnR5tG8VupW5huIxG74OA5QAbc+mBXr1JS1RIUUUjZwccmoe4hGpjMN3JqFrhuQ67T2pjEsuTzWbkaRjfUthwFznNOByM1mbmVsA4XvV+3bctNSvoKUXElopCaj85d2M81pzW0JJaKQUtWIKKKKACiiigAooooAKKKKACiiigAopGpM0AOopFpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQmmRuW3ZGMGlbO8elIuBnnk0rjFdgtRMwdThsU25kVcDcKrrIA23PWolNI0jHS7HAfvMA7jUzxArubgimmN1TMYy1MW1lkYGV+PSkpN9A0BZhHIBjIIq3GxfJxikjgVccZqWtFtqQ2ItLRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKTIFLSYBqG3cAzS0mMUtUgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJ+FAC0UUUAFFFFABRRSUAMaRVcKQSTTtwb7pyPavlv9vvxV8TfCvwnOo/DW4kgvUfbOsMReUr6rgV+c/7Of/BR/wCJX7P/AImnsvHwvvE+kXk++5h1Albi3PTMZPb2rPmd7G/snyKR+3i06vGPgV+118M/2hLYDwrr8MmorGHl0+Y7Jo8jkYPXHtXsysG5HSqujCzQtFJmjPtVALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4DWqB0VmDsvK+9TtUUi+ZwGxRdFIGkPy7Bu5wfalkZlU4GabH+7BGO+KZNcCNsE5GMk1MpLYpK7siRWVmxgE4phmK4CruFQx3iTbmi5PQ0xWkt4ZHbjniue7K5WWWmbcMJkVJG24Hr+NV7ZpGj8xn4PQCrUbCTkc0o3uQ9NB2KXpRRXQrIgKWkpau6AKKKKLoAooopgFFFFABSUjNggUkjBRzQBm6xrkGixma5cLCEZi3QDAycmvyr/aD/wCCv3jXRfHmoaR8OdH0WPSLOVrc3erW8kzyOpwSpWVRj8K+jf8AgpJ+0TJ8K/hNf6XZFRfasPssMkRO5M9T19K+Tf8AgmD+xboPxubVPiJ49szqmjWc/kWWmzf6u4l6s7+oHp61kpcz0OicFGKvuY/h3/gsJ8adK1S1n17RvDupaYxDSRxWMsEjL3CMZSP0NfpX+yv+2B4N/ao8NyXehu2n6xabVvdJuiBLExGcr/eX3FTfGv8AY/8Aht8YPh3L4cl8MabYSQQGOwubSBYntmxxggdM1+Py6F4g/YF/ag0C5k1Uzw29yGufIY/Pb79rKw78UnJp2MktD9zfH3g5fG3hm+0uWd4vtEbR742K9a/Fv4paP8VP+CfPx1k8UaHczf2ZcTt5bzu0sEyk8pIMjJx0r9ltU+JFufhXL4z0eE6patp/2+3jiP8ArFKbgM1+dfw9/aEsP+CgPiTXvhh4w8OQ6VdTxSGym3btjLkbvZhTWptFvlaPtH9l39rbwn+0d8PbHWbfULXT9Z2AXumyyqrxOByQCeldT4j/AGnPhV4R1NNO1fx9odjescCGS8XdnOK/CP8AaM+AXjL9kD4jNo1zfzwJOhktb+1kZBNHnpkd69J/Z9/4J9+N/wBp34Z3njXSfEumw/vHAs7xmknlYDPLds+9aXtoZ8q6n7o6L4i03xJp8d9pOoW2o2kgBSa3lDqQenIrSVt1fiB+xP8AtJeKP2RfjrN4C8ZtdR6HeXa2N5ZTksLeUHasi56D+lft1b3CXVvHNEweKRQ6sO4IyDTM2rE1FItLQIKKKKAGSNtUnBOPSo4ZDJk7So9GqSTO044NRx7iuCee5oK6Dt7buOneobicx4xxUoUAnB+tQXFsJmC7yD2qbFxtfUpSSC4BVz9McV8l/wDBQH4E/Ef41fC2Cy+H95cvd282ZdNinEInT1JOP519hwWcUPQbm7k1PtA6DFLlZpKotkfzxfED9hv43/Dnwzf+IPEvgq40/R7NPNuLqS9hdV7Z4c12P7H3/BPrxN+1hoeo65b63Z+HNCtZ/s/2m4iaaSRwMnaoIGPrX6G/8FaNc1fRf2abiC1uJBY6jfQ29xGqKV2ZycnGRz3rwT/gl9+178Lfgz8L9S8HeM/EY0DVJtSe5ie5icwMhH95QcfjVGR71+yX/wAEvfD/AOzr4+j8Za14kbxZrFpn7Ci232eKBiOXI3Esfrx7V9yV8nfFb/gpj8EPhtoq3tj4jXxdO52ra6KN7A/7ROMV9FfDPx1bfEzwHofimzt5rS11a1S6jhuBh0VhkA0yWnudPRRRQSFJS0x85wOBjrUSXUCGaMSfMeoqqobcfn+X0qWSUN8vf1qqrBiyjj1rme51QTsK17BCJHeRFjjGXZjgKPUmuF039pX4V6l4ui8L2XjnRrjXZn8pLGG5DSM/oPeuA/bZ1C78K/s3+OdRsbl7KcaeVEsZwwycV+If7L+oXcX7Rfw+njlYzNrMDF+5y3PNVDW7Imtj+klulQxxISSRzRdTGOLI65qJWM2B90HjPfNaPchLQuKQRxTqpxXEKziE3EYlPSPeNx/CrS9xnJFarYgdRRRTEFFFFABRRRQAUUUUAFFFFADWrL8SeJdP8J6Rc6nqc4t7O3QvJIecD6VrVm614dsPEEPk39utxF3jflT9R3qZXtoONr+8Yvw5+J2gfFLR5dS8PXTXVrG/lszRshB/EV1lUdJ0Ww0G1Ftp1nDZQD/lnCgRfyFXqI3S97ccrX93YKKKKokKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKSpcgFoqDzG8wc4HoamVg3SlzALRRRRzAFFFFHMAUUUVQBRRRScgCmtnacdadSUuYCH55OSdgHrVW81D7MuI0aZz0Va0KaI1U5CjNDXMUnY5/ydS1GQGSJLaI++WrXsbBLVMZaQ+rVbpaSgkVKbkrCLS0UVoZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0maWoyytk4zipbAfS01cY4GKdTQBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooorN7gFFFFWtgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbfuG3GO+acM96N1LQAUUUUAFFFFABRSZpFbdQBHPbxXClJY1kQ9VYAivn74/fsM/DD9oFWm1rShYamEKJfWACOueenQ19CmlyKnTqUpOJ+WGrf8ABIvxh4F8UWmqfDb4iLZ+W+RLch45UXPTK9Riv0y8EaXqOi+ENIsNWu1vtTtraOK4uUziRwMFhn1rYmmS3Qu5wvSvFf2kP2sfCn7Mej22oeKLTUZLe6JSF7WHcGfGQpOe9S7GnvVNEj21fl607Ir8m/G3/BajXFv0/wCEY8AWaWQyH/tS5YueeCNnTiuI17/grt8aPFVq0OheGNL05mGPMsoJZ2GenXoaOZk+ztofs3urC1nx14d8Oso1PW9PsCxwBcXKIc/QmvwV1j49ftMfEC+l1F9U8XMznGy1glSIAnpgDArx/WfEnijUfGUVp4t1bVXuUukW4S6lbemWGeCaLsfIf0x29zHdwpNC6ywuAySI2QwPcVLXIfCKOzh+F/hVLCRpbNdNgEcj9WGwcmuvq1sZvcKKKKYgooooAazFVyBmlU7hnGKKKAFooooAKKKKhp3Aa1QrEyyFg2QanavIv2ivjvL8B/B8uuR+HL7xCUUsYbMDjHqazlG2rNYRc3aJ6w3TOMmqs0EnzOi7i3VTX5nWf/BaaBruRLj4Z3gjVtp2Xilh9QRW4v8AwWj8Lxsgl+Hes7T1KzxcfmaFFNXC7i7H6Jww+VtATaT1qw0bOrKwytfnVcf8Fp/BUHX4ea+Sfukzwj/2aoT/AMFrfB8nEPw61xjj+K6hH9arkQ25Nn6NoiwqIwDzU6LtHTFfmyv/AAWr8LGPJ+HGsb8fd+1xfzr6W/Y//bLtP2tLTWri08OzeH001kUpPcJKz7gT/D06UK0WQ4vc+kqWmr3p1DICikJpN1ADqKr3N19nUMRnJxUS3LybSQFDexpXRXK2XaKjjYHODmpK1WxIUU1pApANLTACu7mquoRrJEQV3MRgDvVuq91hVLkdFPPpxSKjufkR/wAFari3tdQ8PadHOGuLmZpBCzZKqOOfxNfd/wCxj4Z0/wCCX7JvhManPb6dbCz+33M7ttVd/wAxJJr8wf8Ago9qUfi79ry20wSPJbolvCBnld7jJHvX6/3vwh0zxj8CbXwJPNNBp8+kRWfncNIg8sDd2BNYRWh0VHeVmeN+Mv8Agp98A/B2qy6dJ4ml1KWI7WfT7Z5UB9N2MV+Uf7d3x68K/H74uJ4g8I/aW09YmjZrqIxkknPT0r7isf8AgiX4RS+eS9+JOrXFqWJEMOmxxsB6bzIc/lXxn+25+y34S/Z0+NHh3wT4T1e+1GO+gRrltRZC0Ts4UfdA4xk9K15btM59dkeufCT/AIKkyfDr9nu1+H0/hCTVtTtLRrOK7afEewggZHXjNfMn7O/xqn+Gv7R2geOB5WnRHUM3SICUWNz8w6+hr9ZvhP8A8Eu/gXpPgLSk1vw9N4j1Oe3jnmvLu8fO5lBIUJtAXnvn618Rf8FQP2WfAX7O994VufBGlS6TDqRkSaHzmkQkDIxnkH8adik2Uf2/fjRD+1v8aPD2geBbZtYNuv2eBIR8zuxH6Vwfh/xR8ev+Ce/iy2Sa0utHtLoiV7O6UvaXI7+wPavbP+COfwgsPFfxQ8Q+M78NI+gxLFbJtyvmP/ET6gCv1a+Knwh8LfGbwpd+H/FWlQalY3CFA0iAvET/ABIexpWYXPwP/an/AGjNJ/aF8TWPim28N/8ACPeJsD7bJE3ySsMEN9eK/bP9ivxtdfEP9lz4ea5fS+fez6aqTSYxlkYr/ICvhj4g/wDBFe6k8TxHwd42ij0GZi0qanCfNgGeFXb97jPWv0V+APwhtvgV8I/Dnga0umvYdIt/J+0MMFySST+ZNUiWz0BadSUtMkKKa5IXjrVOC6mmaTIwV4wRx9aVx2LMkojUs3QU1ds8eRnBrO17xFp3hm0e71O+ttPtEQs811KsaAD3Jr5l8bf8FNPgP4JvLm2bxPLq1zbnY6abbF0LezHGaYz6njTEjpu+X0qRhtwcZwK+avgP/wAFAvhP+0Brk+kaPqcuj6kmDHDqYWLzx/snpXuXi74n+EvAPkDxH4k0zRDMpeIX1ykZdR3GTyKBm/8AavkJ8tt3OFA61+Vn7an/AAUl+LfgL4lXnhHwhaQ+CbawZo3vryyW4e65+8vmIygfQV+g8n7VXwfjbDfEjw4D0x9vT/Gt3S7T4d/E5X1Owi8P+KASC1xEsN1tz0yecUC+R+GHxU/bN+Ov7Q/g0eG/EVy2saOf9YtroyATN2bKRZB+hFeFR/DXxfMpMXhfW5OxMenTH/2Wv3X/AG0f2mE/Yx+Huk6p4a8HWGo3OpXn2YQlPIt4/lJ3MUxzXy98Pf8AgtbbeY0fjv4eGFfMCi48PXiyBR3JSQ5b8DSKPzJPgPxXpDxS3HhjVYMOCvn2Eqhj6crzX77fsEa74w8Q/sy+FbnxraCy1NUaKGPyvKbyF4jyuBjisr4W/wDBQr4D/Gi+tNMsfFEdjqVyQIrHW7c27lz/AAgtlSfoa+moyrRqyEFSMgr0xTE3pYfRSLS0EBTJPu05qjk5HXBqZPoUihcKVkUhsccVQVmS4OG6nmrd35qnLqpAHBzVCHzGZ2KqOeMGuV7nfTty3Z8//wDBRS6Mf7J/jT5vvWyj/wAeFfjH+yPateftIfD2EDLf2vCT9Ac1+yH/AAUqzF+yJ4qYfKzKgOPTcK/LL/gmnodt4h/a88HR3sC3MUJknCv0DKpIP4VpTWjOWUk2rH773EYMLYHvWP4mlnt/DN7LbO0cqwSMGXqCFOK38BuCMis/X4l/sHUEx8pt5P8A0E1bWpmmfz9eD/jL400v9quy1E+JtVeb/hIlidmu3IKGcKVwTjBHFf0KowZQwGMjNfz1fBH4e3PxM/bO0rQ7dd4bxE88vpsjlLHP5V/Qso2qAOgrRbCluLRRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmNIFkVT3p9JQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANZiO1KrZpaSs3uAjKrEEjmlHtTWYetOXpSW4C0UUVfKAUUUVDASjIqKWQH5c9e9RQeYGZWO4djVcxVtC3RTVp1SSNbPam7W3DPNO8xem4Z+tKrBuhzQAtFFFaLYAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUjLuXFLRQAyNSoweaXbtzgZNOopWAQUtFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooqG9QCiiiqQBRRRUtu4BRRRTtcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA5eb4neFYPEC6HJr9gmrs2wWTTqJSfTbXTK2a/Cn4ifGzwhrH7d1h488N6tdaj4dmv4XaRgU2nPIAJ6V+kXxQ/4KYfBv4YQiNtTu9b1VVUvpum2zNKpIzjLFV/WoUlbXc6HS/lPraivPfgX8ZNO+O3w/svFml6dqGlWl19231OJY5R7kKzDH416FVJ31RhKLi7MKKKKYiG4uEt4ZJZDsjjXczHoAK+cfiD/AMFCvgd8MdcfSda8W5vk4aO0tnn2n0JUcfjX0XdWa3lvNDJykiFCPYjFfmz8Wv8AgjmvjbXNa13RfH/2TUb65edLe+tS0ShjkAspyMfSpbdzWPLZ3PqOz/4KCfAXULWKeL4g6cokXdskJVl9mB6GvGPjN/wVr+GngHzbbwrBP4zvhwHtjshX3LGvna0/4In+PJJALz4geHEj/iaGGdm/VBXVW/8AwRPnbyvtXxITYB84is+/tmlZisuh5fqX/BVb4ufFTx1oOkaNa6b4esbi9jhMMMZlaQM4A3E9D9K/U34mfADwh8fPAun6J4+03+1oljSQsrmN0k2jJUjpzX4r/F/4E2XwD/bB8N+B/C15PqkltcWLG4mAzJMzZYgDoOK/fC0My6ZAXXE/lLuX/awM/rU76oqXMtEfNfgf/gm98BPAl2Li28If2nOrb1bVrhrnb7AHtXumi/Cnwb4cjCaZ4X0myUdobOMf0r5H/bi/b41b9mCaw0nR9Hhvtdv1d45LjmKJVIzkd+or5Htf+CyvxZWI7/Dvh+cj+Iq6/pmmmrbDlGUd2fsTJpNla28oisbdF2k4WJQP5V+A3xs0NvHf7bmqaZCqq174hjtwmAwALDnAr648O/8ABat00Mxa/wDDiS71Ergy2F6EjPvhga+df2V5I/2iP29dK15LUWEV3qD6kbfdv8oKM4JwMmgSP3L8L6RHoHh3TdNiRUjtLaOEKowBtUCtSmrxSNJtBq+hluxWYL1oVg3SovtSsDs+dv7oPWpgc0XTCwtFFFMQUU1mCLknA968I8fftxfBn4YeMLrwx4n8Y2+lavbbTJFLG5UBs9wD6VLkluNRb2PeaK53wH8QfDvxO8N23iDwtq1vrWjXOfKvLVso2Ov0/GuiqhBRRRQA1qpalo9lrVu0F9aQ3cLAq0cyBgQe2DV6hV20Arp3R4Tr37DPwI8TX0l3qHw00eW4kJLSIJI8k98KwFYsv/BO39nwj5Ph1YxDHOyWX+rGvpDHOaa1Ry9hrc/HH/gpF+xr4C+Bfh+08ReCLZtLzOIpbPeWX5uh55r0f/gnP+w/8J/i58E18YeLNLfX9Turlo9krlUgC8YAHXOe/pXS/wDBYqP7J8M9HZTzcXiBq9V/4JMNG37JenlWzINQuFcenIxUJu9mdEvhudFqH/BMH9n3UJkkbwjLBt/ggu3VW+or2b4N/s8+AvgHptzZeCNCh0eK5KmZlJZ5CBgEk9etejL3p1a2Rz3YlLRRU8ohrUlOPauO+K3xS0L4OeC7/wAT+IZ2g060Us2xSzMfQAVL93VjSvojrJYvNAB6VEIZYyAp3L/tV+Znib/gtbp1nqUyaH8PJL6wVyqT3N9sZx64C8VVX/gtmrR8/C3a/wD2GFIP/jnFTyqWpfLJaH6ixqVzk5Jp9flh/wAPtLhJl3fCyFou+3WgG/8ARZrSt/8AgtxpYmAu/hXdRRf3odaSQ/8AoritE1FWJ5T9PMA9etLXzV+yP+2dpv7Xq67No/hq90KHR2iSV7i4WQMXDEYwo/umvpSqJFqG5UNDID0KkGpagvD/AKLLnptOaBrc/Br9sy5Vf23JivzCK8tEH0Div3c0HnQ9OP8A07x/+givwl/a5tftn7cM8CRsWlv7MLj/AK6Cv3g0uA2+m2kRGDHCikfRQKxjqjer8RYr8u/28v2Cfip8aP2g08Z+D7S3v7C+giSRmuEiNq0ZAGcnnOc8elfqNto21sYXOW+F+g3/AIV+HfhzR9VnNzqNjYQ29xMW3bnVQDz3rxz9tT9key/ay+H9rpQvY9L1rT5vPs7yRSygkYKkDsa+iwoHSl20wPDP2Pf2Y7D9ln4Tw+GIZ47/AFOaU3F9fIuPOc9B9AOle50dKWgQUUUUAFFFFADGb5gMV5n8fPjt4Y/Z/wDAd34l8TXYgtk+SONeXmkxwgHvXo17cLbwvI7iNEUuzN0AHWvw7/b0+OGt/tHfH4eBdDuGvNHtL1bOytYhnfMxALHHXHvWb3NEtLnNeMfiJ8XP+Cg3xok03QxdTwyMyWumrKYra2gHQyEcZ7819dfDP/gi34ePh62m8deNdWGtEbng0bylhTI5GXRifrxX1v8Ase/sqeHv2Y/hva2NnaK/iK9iSXVL5iWaSXHQE9AMngV79VkuR+AX7aX7Lt7+x78VLGDQ7+/uNFnjWex1Kd1EocHkHaBjBr6g+Jf/AAT5+Jn7U3hHwB410fxtY3Zu9DhaePW5ZEMchAzs2K3B7/Ss7/gtXr7t428A6RFdI0S2U9xLAMFg4ZQpPccE8V+iP7ILPJ+zH8NWlUq50aEkH6Ux8x+Xw/4I2/GXy9j694Qzn7yXNwWHv/qhX2d+wr+wPqf7KepahrmueL5dc1O7gEK2FiWjs489WIb7zehI4r7S2ijgcmgXMZHiLwnofi60Frruj2Gs2wORDqFsk6A/RwRXiXxb/ZN/Z7m8F6zqfiT4ZeF7HTrO1knnu7DTks5Y1VSSQ8IVgfxryD9qn/gqV4N+BOtXPhrwrpv/AAmfie2dormPzDHb27rj5WYck89vSvzu/aU/4KMfFX9ozSZtBu7qz8MeGZxifSNIClZuR9+VvnOP7oIBzyKBHR/8E+Pghovxk/a6e70+zZ/Bnh+5m1GOO4VmBjVz5KFs5yeDye1fugqhUAUYAGAB0FfhR+xx+3zb/sk+C9R0Wy+H9nr2oX9x50+pPqQgdlAwqkYYYHtj8a+wP2fv+Covi/8AaA+NHhvwVpfw1sLW2v5T9rnTVPPeGIfefhQBj3oBu5+i606kpaBEczFYyRVeSQtCAVzmrZAYYNZ+r6lBo9s9zcSLBbQxtLNI5wqIBkkmokupSHTW63UIjyQgHIU81VsdFhty21sgnkZzzX5Tftdf8FIPGHj7xovgf4GXV1a26zGKS/0+ESXN2+cYjyDhevavGtMn/bR8CRz6lbt46tizfaZXljMqnPfDA4+gqVZmqbSsfo9/wVAV4f2RfEoiJChow30zX55f8EidHt9U/anjnmVTJZ6ZPNHns2AOKqfE7/goX8QPH/wP174a/EfRUutVutqR3skBhlXB5LjjJzjpXR/8EcbQSftMarIU/wBTokxBPYllB/nTWhn1P2sHasXxxfDTPB+t3bZ2w2UznHXhDVrXvEOmeF9Ll1HV7+302xhGZLi5kCIv1Jr5h+OX7fHwY0PwD4ltLHxpp+saqbOWGO1tSZNzlSAM4p2vqJbn55/8EyNJuPGH7cE+qxMRFZpeXku7uCSB+pFft5X4CfsQ/tU6D+zH8UPEnjHWdJutS+3WUsFva2hC4LOGA56CvU/i9/wV2+KXjaaWz8H2Vr4QspPljaMebck9vmPT8KobV2ftRRXjn7Ies+MPEX7PHg7U/HVxLdeJLu186eWcYkYEkqW98Yr2OmQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNZwvWgB1Jx0pgkD9O1HfNZvcdhuA0jDGNtSiqkNw0lwV2MAvGSKuU1HqAUUUVYgprNtHQn6CnUVNgGYDKDtxRtx2p9FHKO4i0E4HTNLRRyiGLGOTjk04ADoKRmI6DNKpJ6jFHKAtFFFUAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlGRTZG20inIzQMfS01adQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKarBs47U6gAooorN7gFFFFWtgCiiiiwBRRRTAKKKKACiiigAooooAKKKTNAC0U1pFTqcUzzA/3TmgCWimp3p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH4tXXhX9nfwf+2tZwpcQWfhSzfdNavMPISfIwNxIGPbNfeWtfG79k6bV7GLUbzwNcakHSO3CwQTTAkgDOwEjt1Nc38Hf2Rv2dfjn4P0bxjH4bs9SuSqyT7Lnd8/pIAeenevW9W+DX7Ofw6A13UPCPgbRmtSHF5PaW6spXockZyPzrmppu0rnfNq9ktT2/SIbO30+BbCKKGz2AxJCoVApGRgDtV2uJ+GXxg8FfFqxuLjwZ4gsddtrUiOU2UgYR5zgEduh/Ku2rpOKV09QooooJCiiigApjfdIP3cHJp9NPyrSA/Gv4/Wthaf8FQfDIt5zKhv7EyNIDgEseK/ZJvukHpX40ft93g8G/wDBQjwzrK2rCLfp9wPLGDJtcg49/wDGv2P0+8XUtPtblVKCeJZQrdRuAOP1rOm9NTWpdH5p/wDBYT4W2zeCdD8UofLltLnyyxGSwfAIz9cVwH/BKn9l/wAFfFzw14u1vxx4Rg1yG3uUt7O5vASn3TvCj8q+sP8AgqR4bXxF+y/rzPIENgY7pflz0cVw/wDwRx8QHUP2fdf0w4YWesO4x1AdRgH/AL5NLRaIbvKNz0zx5/wTF+BHjdUeHwy2gTKhUNpczRA57kdCRWT+zT/wTb8Lfs2/Fn/hNdM1y71No4Xigtrgf6vcMZz3r7Ho20zNMK5j4ia1caL4S1K7sUEt3FCzxqRkbgDiumPpWR4k01r7S54o03lkI25xnirfwl07c6ufkJ+yL+0p8RPGv7clhaeJfE98dPku7m3fTWl2wqCCqgL09DX7JrX8+n7Qun6n+zr+1tdalaySQXNvfx6jHKo2YUtll96/dz4S/ECw+J3w58P+J9NuVu7bULSOUyJ/f2jcPqDms49yqm7sdjRSUtbGBBeQ/aIGj/vDr6V+a/7dP/BOTxx8cPicvi/wM2llriNYLuC4l8liB/Hk5z34r9LivOaQKF6VnKF3c0jNxTR4/wDsm/AqT9nP4IaF4Jnv11K6tA0s86JtXzHOWA5PA6Zr2KkpataaEN31CiiimIKKKKACmtTqQrQB+c//AAWOs2m+EWjTsuBDeoQR35AP8677/gkfdWs37LIigbMsOqzrKPThSKq/8FZtHXUP2b7u4deba4iZTj/bA/rWZ/wRxC/8M569g8rrsiH8EX/GsftfM6ZfBfyPvZadSUtbHMFFFFABVDWtD0/xFp8tjqdlBf2cow8FwgdGHuDV4mmNJtIB70rXGfN/ij/gnT8APF2rNqN94Bto7hiWYWc8kCMT6qjAVfs/+Cf/AMArOBIl+G+lSqowDOpkP5k19BZ5NLmp5ew7s8DP7B3wFGAPhnoY/wC2FYPiL/gm5+zv4m2m4+HlrbMoIDWNzPbHn18txn8a+mutLtqrCuzyX4A/stfDv9ma11eDwBpE2lR6q8b3fnXk1xvKBguPMZsfePSvW6TGKWmIQ9qgu2C2spboEOanNRXEYmt5E6blIpPYa3Pwg/ai1Ka5/bpiuIFjSWPUbMR5B2nEgxnmv3gtS7QoZMeYVBbHTOOcV+Bv7Zuj3nhT9se8M1zDJP8Aa7aZDDn5R5gxmv3p0OQy6LYSMcs9vGxPuVFZQTsbVWmy9RRRWxgFFFFABRSE0m6gB1FIDS0AFFFFAHz/APtw/EyT4Wfs8+K9Wt5Whu2s3hgdR0duBX5n/wDBKn4f6d4o+MXiH4ieJ3hk0/wxavdvJMeRM+Tv98AE19W/8Fh/HE+i/A/TNCidQmpXyCRe5UZJH8qs/wDBJv4T+H/+GW7/AFeaBbi58SXU1te7u8aDaFH4MazW7Nr+6eiXX/BUT9n+0m8pvE1277mU7LJjgg4PevLPiZ/wWN+HGh2M0fg7QtS8R6jnbG1xi3hHuTyam8Xf8Ea/hh4h167vtO8UeINDtbhzJ9jtzFIqknJwzqTitz4e/wDBIT4LeD7sXGty6x4wKsGSPULnykUjttiChge+7PStDPQ+Bvh78OfiF/wUq/aH1DXdSZrbS0lVry/Vf3VpCD8sS44yRn8q/cbwX4UsvAvhLR/D2nKUsdMtY7WEMSTtRQBkn6VR8AfDHwr8LdJOmeFNBsdBsmwWisYVjDkdC2Op9zXUUCCmtgqQRnI6U6igR8c/ED/glj8F/iR8TJ/F9/Hrlm11Obm+0y1vytvduxy24kGRc/7DLXq/hb9iH4C+D7CKzsPhR4Znhi+4dUsVv3H/AAO43sfzr26loA8zi/Zh+DkCssXwm8DxK3Xy/Dlmufyjq74D+APw3+F+sXOreEvBGieHdRuF2SXOn2aROV9BgcD6Yrv6KACiiigBGOK+LP8AgqV8fNS+DvwNj0jSPLW/8USNp3mbsNFHtJZh+HH419oyZyCD07etfjd/wVz8VXHjP9o7wp4IRjHHp1mjk5+XdcOFzj22frUy7FRPXf8Agkt+ydb6foB+MHiK1ZtRui0OjwyDCpGPvTY9SeB+NfpnwcgiuM+Cfgc/Df4SeEfC7EM+labDbOQMfMFGf1zXbbR1xU8o29T8rf8Agsp8LYrPT/C/izTNEhhj81ory+gj2nJxtDY9T/KuO/4IraXb3Hxa8c3zqxuLfSFRCeg3Srn+VfTn/BX/AMSadpX7Ly6Xcvi91HU4Ftk7kqdzH8hXiX/BEPSlml+Kmpbfmi+xW+7uA/mtj/xz9Kqwrn2N+3p8CfE/7QnwHuvDPhO7W21UXEdwI3fasyr1Qn3r8wPDf/BLX4tX3hvxDrHihbPwpa6NC8yxzkO1wFUklcdB8vf1r9zcV5r+0pqq6H8AfH963HlaLdEfXyzimCZ+OH/BOn9kXRv2ofiDrr+KnlPh/QYkaaO3faZpCxCgn+6QDmv1n0n9iH4EaJJbS2nwt8OpPblWSZrUM+4dGyepr4o/4Ii5e0+KcmwHLWGW9M+f/h+lfqTTBsitbeK0t44IY1ihjUIiKMBVAwABU1FFBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMu6gBaKRV20tABRRRQAUUUUAFFFFABRRRQAUUUUAFNIywNDUlS5DsIcKx2jHrQBupeO9OVQOlQO4irtp1FFaLYkKKKTNJyAWikoYkdBmlzALRTVbseDTqOYAoooqgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRntTXcL1qssuyRm3ZBqWylFstMPfFNZjHwOe9RRXGd5fgDpTWukkchSWKjkAU7hyu5NDMJQT0p5b0qnZzxMzxrLG0gPKq4JH4Vbpg9ypcK8jACrMUZjQDvTN2yQe9WKBPsItLRRQIKKKKACiiigAooooAKKKKACiiigAoopPwzQAtFJ+GKWgBM0Zoaq9zN5a4z1FJ7DSu7Cy3ISQKOSfShbgbsZrMiyGY5zT4LjyZG8zv0rNSZu6ehrKAuSB1oL47VWhvo5l4z+VTqwbpT5mY2H0itnPGKYxdenIp0bMc5FIkfRRRWi2AKKKKYBRRRQAhOKTd7U2SQJjIJ+gqHzndwFQge9ZylylJFkHNLTUz3p1aEkckwixkE/QVGt15jYRCR3zxU9HFAxjKzdG2/hmk8ndy7bvTtUgpaBDQgHalwB0GKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/JXwf4B8DfsvfEGPwrcfEu98O+IYZDiJi8dvdkjCBlGQSD/6FXKeBf2F/i5+0h8aL7U/GUWpW3w/e/aSS9vbsRCePPHlR7iTkdwPxFfaP7Wn7IM/7Q/hBNV1xIo/FumQltMuNHixLHI2CRIf4xlVx6c18b+Gv26P2i/2SryPw3498OjxRotiTDHJfwNAzL0XEyqf1U1wxpqMtz0ZSbjaJ+nfwO/Zt8B/s8aXNYeCdJ/s2OcL9odpC7zFQQGYnqeT+deodK8C/Y1/aY1L9qT4b3XinUfCp8KGK5NvHB57TLIAOWDFF46dq9+rsjtocEr394KKKKokKKKKACorhtsZzx2/PipCcVDcNiNiFLkD7vrQNbn4vf8ABVhdU8J/Hbwjq8syPcfZ5HgbGceW6Yz+de3/APBOP9q74rftD/GqXTdeuxJ4X0nSm8yONMKrcCPJ9Tg145/wV8i1Fvid4S+12gisYre6jgus8SFihYf8B4/Ovpj/AII6/Cv/AIRX4I654vuIMXfiK9VY5D18mEEAfmxrmULpHXV+Js9z/wCCh0aH9kD4jFomkb+zztKrnadw5r8qv2A/22ov2SdS1yDV9Im1jw3rLRGf7NIBLA6AgMAeoO48e1ft98Svh9pfxW8D6z4U1pWbS9Ut2t5xGcNg9x9K+E9U/wCCKvw2vL1pbPxt4i0+AkkQLHC4GfdhW0Y2OXm0sdzF/wAFfPgC0al5fEkbEAlf7LBAPpnfzW7pP/BVT9n7VIWkfX9QsAMYW7sSpb6YJ/ya8cm/4Im+A/JVYviH4j3fxF4IMH/x2su7/wCCJvh6Nk+w/EbU1X+P7Raxk+2NoHvTa10HG1tT3+4/4Kkfs+Q28ko8UXU2zqkdk24/TJFcjqH/AAV++B8O77JZ+Kb4KfvJpyKp+h8yuI0//giv4E8tRf8Aj3xEXH3vsiQqG+u5DXW+H/8Agjr8F9J8w3+peI9aLY2/aLtY9vXP+rVevv6UK+wtEfAP/BQb9o7wF+01408P694K0nVNPuIIJIr+S/gWPfkrsxtJz0NfWn/BGj4wa1r2i+K/AV9M1zpmkpHd2THJEQZmDp07kg/8Br22D/gkz+z/AB436Lqc2P72pSj+Rr3v4J/s0/Dz9nm0vYPAnh+LRvtwQXUquzvNsztyzEn+I1HLokh8x6eo2iloorUgjmlEKlmOFAyTXgPxc/bn+E3wS8cWPhLxPrVxDrd35ZENtbtKsQc4Uuw+6K931CzN5C6ByhZSufrX5vfHj/glD4q+M3xY1DxYfiTYwQXrjMd1pzs8KKflVSJDu79dtS+a+htGMWtT9JbK8iv7WG5t5FlgmRZI5FOQykZBH1FT1y3ww8Fj4dfD/QPDK3Ul6NKs47U3MhJaQqMFufU11NNX6mT30CiiimIKKKT8KAFopCcUjSBeaVwPjr/gqZcWw/Za1+KZtsu6Mx8dSHXivN/+CMGrG4+CnjKxK48jWhMGz13x4/8AZf1r1L/gphDYy/sueKZtUUKoVVhIPO7euK8T/wCCLek31v8AD/x7qDHOmXGpRRwjPQqjZP47h+VZ3946X8CR+lNFN3dRRurU5h1FN3UbqAEbO4ccUnJxmquqXz2NpJMkLTsiltidTjtX5W/thf8ABQz44eCPiRc6P4Osm8MaNaZXzpdKFw1yTjklwQuMduu6o5lzcvU05Xy8x+rm3DEgdetLX4Y6V/wVK/aP0m+iurvWLXUoMH/R7rRYo0f8VUH9a7K2/wCCzXxjtFxc+FfCsx7NNb3Kf+gyirIP2dWnV+Oem/8ABar4oSvIs/gjwjIduI1hS6BLdusxzX6pfBDx1qXxL+EvhTxTrFgml6nq1hHdXFnGrKsTMPugMScfU0D5Xa53VFJS0EjWpG/1bU6mv8qmkHU/CX/gpFAuh/ti3snlgEW9nNhe58w/4V+4fgm8OoeDdBuiNpnsLeUj03Rqf61+IH7feq23ib9tR4pCs2GtLWbZ93Al7e/Jr9y9HtY9P0ixtYRiGCCOJAf7qqAP0FTHY0qfFcvUUgNI2fwqzMWgHt3r5z/bo+LHxF+Dfwb/AOEk+G9haX2pW95H9r+2QmVUt8NuO0MvOcc5r52+A/8AwV68J+JvDOqJ8RrI+HNcsoPMhkt1LxXZAOQB/Cc7eD1zU8yK5Xa59D/tj/tlaB+yn4TS5mji1TxFdfLZ6WZNrSerH2GRn618YfCX/gsjrmpeOLK08beF7G28P3VwsD3Fi5DwZONxz1x/SvmWDR/Hv/BQ79pS5Nstxc2U93n7TJnydPtCe/YEhf0r2X9ub/gm9H8EfAUHjLwQ0l5pthGseowucsOg8388/nRcasfsRpOpW2s6ba39nKs9pdRLNDIvRkYAg/kat18hf8EvvjVcfF79mXT7bUZxPqvhyb+zJTjnygoMRPvjPPtX17VEhRRRQI/Nr/gs9olxJ8OvB+pJbs9tFqJSefGRGChwPxNex/8ABKe4tJP2PtAS1ZWkjvbrz1DZKuXHUduMVuf8FJvhzrPxN/Zb8Q6dodmLy7tSl+yYy2yI7mC++K+Af+CVP7UWmfB3x5rfg7xfqy6V4f1hVktmuMhYbtW2hfbcGP5VGzZpvGx+0YoIzTVkDqGUhlYZBHQ0uTVGYvSlpu6ue8b/ABF8M/DXRpNV8U65Y6Fp8YJM97MIxx1wDyeo6UwOjorh/hT8bPBXxu0q71LwTr1vr1naS+TNJb7sI3OAcgdcGu4oAKKKKACiiigAooooAa3UV+EH7emuTX/7c2sPdymSK1urSHLY+VFkBAz+NfvBX5Hf8FGP2EPiJqHxR1z4meELV/Emkagonube2H+kWpXB+7/EM88elS1dplJn606fMlxZwzRuJUkRXEgP3sgc1YIyRzivxc/Zu/4KmeOfgqsXh34hWEnibR4nWLe6eVe2qrkEEYAbt/3z719SfEr/AIK9fC6H4cX9z4QXUrzxRNCUtbK4tzH5chGAzE8YHtVCPnX/AILHfG5PE3xP0H4e2bRva6DB9suXX5iZ5OAue2FB/wC+q9E/4If3kQ0v4t2xdVnefTZVjzyVC3Azj2yPzr5g/Z1/ZA8e/t1614x8aX2p/YV3vK9/dgnzrlslUX2GDn04rmLdfjL/AME8fi5HO1u2halIjIS3zWmoQgrnnoe3uM0CP6DK8w/aesU1H9nn4iQOgdTod2dp9omNfM37BX7eXjH9qzx9qvh/WfDFlZWOm6YbubUrJ2K+b5iKienzAsf+AmvsD4paK3iT4beKNKSIzNe6ZcW4jXqxaNhj9aAPzL/4Ii6tIuqfEzTNpMMttZ3BPYFXlUf+hmv1cr+cv4M/GLx5+x/8UZNV0hJtO1C3ZrS802+jZI7mMNna/ryOK+w/FH/BZrxf4g8NrY+F/A1rpviGY7BcvIbhQf8AYj7n60DsfoJ+0h+114C/Zm0eObxFem81a4O210eyIe4mOQOnbqOtemfD/wAWnx34L0jxAdPuNKGo263AtLoYkjDDIDV+av7H/wCxD44+MvxKg+NHx1aadXZb6x029kLyXDkkqZEP3EGBhe9fqLHCkKgRqEAUKAowAB0FAE1FR+YPWmSXKRDJNTcLMnoqv9qG0Ec1XmuJW+4CKXMWoNl8ttpplUEAnGazbeeXcd5Jb+Fc9afMXMiFxt9qOYbp2drmjS1HDnbUlWZsKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUm5fUfnQANUcuPvHIx6U/erdGB+hpjSKMjOamxSuRwmNSWLlt396rIIPSs2ZZbzasJCbGG7I6itAcfSpSu2hyQ6lppIFIHU9CDT5kiB1I2D1oyKa3bFJtAOGF70uajp0fepWrsAPzgDr604UtFacoBRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSU1pFXqf0pAR3RHHNUfNXcRnmluSWlVnB2jjNUL66UwuYYizA43DoKzk9TqhsSX8xSPKk8VmySXt1uSLekcw8pnT7ygg/N68VCr3USmSQFwOcY/wA5qn8QfiloHwf8A6p4w8RXiWWkafAZZm6szfwqo7k+gqbXLk1yn40fH24+Of7H/wC0RrGrLrWtQWsl7Jd2V7LNJNaXMLNkAgnb3AI7V+gn7Gf/AAUe8N/tCSW3hjxLEvhzxj5arH5jDyL5sHcY26AjA+U9d3FeM/BP/goBF+11+0B/wrjxd4G0u88D64rwWVvcx+ZNGVBIZif7wxnGMYFeRf8ABRb9iWD9mm80v4l/DmS4sPD8t4EngiY50+bgxsh67ThvoQB3q07aHNufsqIlLFsc0+vk7/gmv+0Pq37QXwD+0eIbh73xDot0bG7unx+9GMo31x1r6yq0QwooopiCiiigAooooAKKKKACiiigBGbbTTIB2NPpNo4oAaxbGVH51EJ5WJCxbsdcnFWKSgBkTO2d6bPTnNSUlLQAnNNaNZPvAGn0UAQfZI+yinrbovRF/KpKKnlQ7sZ5YHQBfoKXbTqKfKgEFLRRRyoQUUUUwCiiigAooooAQjNJtp1FACAYpaKKAEIzSbadRQAgGKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGdc5rO1jwzo/iGHytU0yz1GPrtuoFkHH+8DWkFPejbSDVFfTdLs9HtVtrC1hsrZfuw28YjQfQAYq1SDilpgFFFFABRRRQA1qNu6lo5oA83+Kv7PfgH41Np58Y+HrfWTYOzwecPulsbunrtH5V2PhXwnpHgnQbTRdC0+DS9KtF2Q2tuu1EHsK1ttLjigpybAY7UtIBiloJCiiigAooooAKKKKACiiigBGptPpKYhFp1FFIYUUUUAFcv44+Jfhr4b6VLqXiTWLXSLOMZMlxIFz9B3rpZORivlb9sr9jK//ap0/T7S18Vf8I+lvIxkWSEyK4bb6EdNv61nLm05TWCTvzFPWP8AgqN8AdJvEgbxNLdZZlL21s7quMckgcdf0r0Hwb+258FPH0QbS/HmmDgZW6k8lhnpw30Nfn7a/wDBFPxnJqdzHcePdFg05TiGWOGUyOPVlxgH8aivP+CJ3jqO5JsfiF4fMQ+600M6v+imq5SEtT0//gqh8bPC/ir4KjTfD/izTdWa4uo1a1s5w5AVgcnH0rC/4I1/FPS9L8L+PfDmpaja6dHHcxX0Yup1jzuUqQuTyAF5+tee3H/BFv4nqVC+OPDtz3PyzcfmtFv/AMEbfivphd7bxhofmOpX900ideuanlNHJbM/VaT42eAIiVfxnoasODuvox/Wom+O3w6Tg+N9BH/b/H/jX5Q/8Oc/jD85bxHoEh6jdK5rndU/4JH/AB6tJwlsNBvE/wCeiX2wfqK0M9D9gofjj8Pbi4igi8aaHJNK21EW/jJYnsOa7dWDqGUhlIyCOhr8WvAP/BKT452PjfQLjVhpFnp8F7FNPPDfb2RFYFuMelftDY2a2NnBbqcrDGsYPsoxQLQlxmszUPC+j6pu+2aXZ3W773nQq2fzFau2jbU2V7i6WObPw18KOm1vDmlsvobRP8Kpz/BvwJdf67wfokn+9Yxn+ldgBilqgOFi+Bfw7t7pLiHwP4fjnT7si6dEGH0O2u1gt0t4kjiRY40AVUUYAA6ACpOtLQO7CimsxFeU/tI/tGaD+zH8OZfGPiOx1DULBJ0txFpsSu5djgZLEAClcLXPWK4n4xfEzTvhH8P9X8Taoyi1sYHkK7wpYgcAZ98V+enjf/gthZLp86eEfhtK90wIhutY1NNi9MFoY1LHvxuFfKHijxZ+0z+3ZrwglsNa1TTpJAqWdjavBp1srkZPPb5AeWP3altbFqLvqcv8HfDfiD9sD9rKyMEe2bUdSF9cSLnEFuj7yec4OBX9CcaCONUHRRgV8NfC/wCC9p/wTq/Zr1XxJaeHm8XfESaLzbgQRtIS2OI0KqSEXPPPPrXyTqn/AAVV/aO1IyGHQdA0lGOEWLRbtmXk8ZaQgn8KcdhS3P2eWqWtTXcOmzvZRrJcqhKBumcV+McX/BVv9ovRo0a70rQLyNTlmm0a5RiPqJAP0rtrf/gtB47bTYYpPh1pEuoDiR1vnAc+ybc/qab2JRy/h39vrx1p/wC1ddWPxO1gXPgiO/n0290doB9nEJYqrbfUADkmvIf2/bH4YzfGK2u/hYsH2K8txJPbWnMYf5du1AO+W/IV0v8AwUA+Fut29n4L+J2peFoPDcviq2N3qENq+5UmkCsgx243fnXsn/BKP9j2bxNrX/C3fF1kkukWitBpFneRhxcS8hpSG7Lxj6+1QosuUk0eZfsE/tsab+yPJe+G/FXhKWOw1i6ie51VUK3EKgHGVI+ZfmPA6c1+lPxF+Lnwy/ah+BHi7w94Y8c6TdNq2lyxqouAsiZUnlTyDxWx+0t+xb8O/wBpTwvJZ6ppNvpeuQxsLHWLGMRywMccHA+ZcgZB/Cvyn+LH/BNH43fBObUNU0S2/wCEg0m1UuL3SZispQdyg5/Cnykqx79/wRj14+G/HvxY8E3VynnMltPHEDw5geVGZfwkBP4V+rFfg1/wTHh8Tx/tleG47FJ43UXH9q+YpyINmXDA9DuA61+8tUhPcKKKKYiK5gjuoXhlRZIpFKsjDIIPUGvyj/bf/wCCYWqWOq6p4/8AhSkuoLcStdXegrw8TZB3Q46/xcewr9YKNoqWtSkz8Lfhh+3Z+0n8C9NXSLr7XqWnwvgReItPeRl28Mqybd2OnevUE/4LFfFxYwg8E+GZXxgt5N3kH6Bq/XWXQtNn/wBZp9rJ/vQqf6VB/wAInonH/EnsRj/p2T/Cmguj8if+Hi/7VHxdxY+CfCcMNxna76Lo0k23d93c0oYL0OOneul8K/sFftCftT+JrLWPjz4vvNO0SNfMW2knEsoz1SOEfJHnaM8enBr9XbXTbSxyLa1ht/8ArlGF/lVmmPm7HBfBf4KeE/gL4KtvDHhDTY9O06L5nYD55pD1dz3JrvaKKCQooooEFFFFABRRRQAUlLRQB4r8XP2NvhB8bZGuPFHgyymvyCBfWmbeYZxk5TAJ4HUGvnHWv+CN/wAIb64SSw1zxFp6b9zRtMkoI9ASoxX3xRQBxXwf+D/hf4GeBbLwn4R09dO0m1y20ElpJD952J7k1t+IvBfh/wAYJEmu6Hp2srFkR/b7VJtmcZxuBxnA6egraooAx/D/AIP0HwkkiaHomn6OsmBILC1SHfjOM7QM4yevrWxTJZBGpZiFUDJJPArmPC/xS8JeNdUvNN0LxFp+rX9pnz7e1nV3jwcHIHvQMzPiB8Cfh78UrfyPFfg/SdbiJyRdWykk+5HNc94L/ZL+Dnw71qPV/Dnw50DStTjGEuobQb1+mc167RxQAxVCKFUBVAwAOgrjNW+Nfw/0HV5dK1LxpoNhqMRAe1udRijkUnsQWrf8QpHe6RdRf2iNPV0eI3G4LsYggHJ6EE1+QnxW/wCCTfxe1TxhqOpaL4h03xXa3sjXI1C7uWjlbcxOD1yce9TcaR+wGl6xpmv24n0y/tdQhI4ltJllX81Jpt5EVjDPztPavwT8D/F34yfsH/FabRpr6fdDIsVxoslyZLa4wTg7c4yMnH+9X7teEdVufE3g/R9Xv7X7Dc31nFcS2qtkIWUNj9almsXZl2O425Kg7cd6ntboTSBEOW789KiWNFRmViy9CDUun24t5JQF5wCfepWrNZtWPkj9qj/gpB4O/Zh8eQ+FJPDOoeKNYiiEt00E6wRwKxGMFgdxPPbjFezfs5/tSeA/2n/Ccer+FtQjS9RR9q0i4dftVqxzwy9xweR6Vxn7T/7Bfw3/AGnLN7rULMaB4oVCsOu6fGolySP9YOPMAxwCeMnHU1+THxv+A/xR/wCCfvxc0zWrLULkQeaX0zxBYs0Ud2E2lo3CtkfeXKnr707dDl3P3p8SeI9K8I6TPqusajbaVp1upaW6upQkafXJxXn/AML/ANqT4XfGbxNqnh/wd4wsNb1TTgpmhhYjeDnmPON4G0525xxXBfCbxd4e/b3/AGS0k1y2j8rW7WSw1KGNQfs90owzJnoQSGH1r8i/GXgnxt/wTr/ag0m4lJul0y4+12F5GCkd/bEjcPc4IDCqTDlP6BqK4v4O/FTRPjV8OdF8YeH7hbjTtSgWQbTkxvj50PupyK7SrJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKlsCOVwuAe9QTKMfL3qeRA2M9qbtHfoKyerLTKsKC3LH+9UUd0lxcOoyu3r71cmUKmQu6q9xcWml2Ut7eTQ2VtEu+WaZwiIo6lmPAH1osy+Zblq1jEanGTn1qQ1keHvF+g+LYpZNC1vTtajhIWR9Pu45whPQEoTj8a1ZFLLgHFWnZWI3dyKQbj1wKhnmEW3YM884qfydygE5IpGtVxknFY8rLTRWutQ8kDJChuMmrMbExrng1Xn0xbpVDHKhgw/Cru3LfSnySBtdATPNSCkWnVrGNtzJhRRRWggooprNjA6mpcgHUUxZB3IHanA55HNLmAWiio5biKHHmSLHnpuYDNHMBJRSBg2MHORkUtUAUUUUwCiiigAooooAKKKKACiiigBKMikakoAXcBTfOTdjPNV7y4WFQSf0qrb7p5Fckgdveg0UdLlnULwQQkqfm+lRWlyzQhnHLdKsModwXX7vT3qNlbzCQny+lZSWpStaxw3xw+JOm/CX4Z614x1jzv7L0mEzzRwEBn5wAM18feDf+CwXwl1a9gtdc8MeI/D9nIcfb7iCOeFeep2OW/Ja+3PiF4B0j4p+DtU8KeIbRbrRdUt2guIyeecYx6HrXxfff8EbvhHcef8AZ9f8R2ivzHGsyMifUFcn86ajoHNbQ+tfhz8bvhz8VrWKXwl4r0nWhIgk8m3uVMqg5+8hO5eh4I7V+XX/AAVg/aVfx78QLL4SeG3WXSNFcSX3kkn7Rdk4WPA67f5tXCftSf8ABP8A+IH7HmlT+PfDXib7b4Ys5AkmoWk32a6tvMdEjVlzl8l/4cgY7Vgf8E4vg/e/Gz9qzS9Qvof7S07w+51jUZbw+YWKsFQMT94l+n0NVYW593/sb/sa/Dv9mf4b+HPiv49drHxsln9vubjUbgJFY71PyKvrtI9818zf8FC/+Ci2lfG7Qb34b+A4TN4aaVTe6xOhU3G1gQqKeQMg89812X7b37I/7THxx+N3iK70qGXVvBE8y/2bZnV4o4FjCgDMZcYORnkV5N4D/wCCP/xq8QXEieIBonhWJcETT3i3O/rwqxE4xjnPqKOUz2PpT/gl58b/AIQ/Db4c6X8Pz4ohPjzxJfyXs9t5TBA7AKkIk+6SFX82r9I6/Pb9mn/glFB8Efil4c8a6v4yTWptHk88WMVpiOSTBAOW5ABNfoTVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopXAKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAI1Np9JQIbRTqKYWBaWiikMKKKKACiiigAooooAKKKKACiiigBOtZfiTwrovjLSZdL17SbLWtNl5ez1C3SeJsdMqwINalGPeoaA860X9m/4U+G9QF9pXw28KadeD/lvbaNbo/wCYSvQoreOCNY4kWONRhVQAAD0Ap9LTsO7GqoUYHSkWGNVCiNQvoAMU+iqEUdQ0PTdWi8u+0+1vY/7lxCsg568EVyH/AAoT4bf2l/aH/CB+Hftmc+d/ZsO4H2+Xiu8JpN1AjnfGHw38LfEDTYtP8SaBp+tWMRDR295AsiIR0wD0xWvo+i2Hh3TYNP0uyg0+xgXbFb20YREHsBVwGloGFIyhlIIyDwQaWigDl9B+GHhLwt4gvdd0jw7p2m6xertuLy2t1SSQZzgke9dRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNJoA+Tf+CmPx61b4E/s5TSeH7g2mveIL1NHt7hThoUdHaSQH1AXH/Aq8B/4JE/s06lo9hqfxo8QS3AuNYje10iF5CBJEWPmzOvfcVXafY1wP/BZH4nyeJviZ4I+GlldEx2Nubu5gUgg3E7osRPuqK3/fZr9S/hz4Xs/BfgLw7oNhax2Vpp1hBbR28QwqBUAwBQW9FY84/bI+Md38Bv2e/FXjGwfZqFrB5FrwOJpGCI34E188f8Eq/j38Tfjx4Z8fXXxB1OTWbTTLmzg067mQBi7CczrkdcDyfzrB/wCCzHxQ/wCEd+DfhfwZHnzPEGpfapQD96K3AJU+26RT+Ar17/gmH8OYPAP7Ivha6UKbvxC0msXEgHLGQ4XP0VVFAaWPkj/gs18QNS0vxl4F8N6Xq15Y2n2W5u7m0t52jR3ZogjMAeTw1fMXgX/gof8AGX4dfCqPwLoviFltIZJDDqEw8y6jQhcIjnlQuDj/AHq9U/4LG3Rb9qrS4my8cXh+2YJnjmSXP54H5V9N/wDBLf8AZz+HfiL9mWPxP4l8K6TrOq6hqFwJLrULdZCI0OEXJ7DJ/Opa1H0Pyfk8eaj4g8dWvinxPd3GuX/26O4uprx/MaUBskHP0r94vgf+3R8H/i7feGPCuheIF/4SLUbYJFprW7Jhkj3MmcYGADj6VB8Vv2N/gHrHgfxDqKeAPDdtdW2n3EiXdhDHE6uIyQdy98gYzX5j/wDBLHT7Ff2y9Omv0jSKzsb14pJmAEb7dqnJ74LDiiwLufo9/wAFHfjxr37Pv7PtxqXhfzrTV9Uvo9Oiv4R/x67kZi+ex44965P/AIJW/tBeJ/jp8MvFcXjDWLrXtb0TUUjF7dHLtDKmUG7vzG/6103/AAUo03w/46/ZS8X2K6xZHVbSOPU7SBZ1ZnMMi7sAHrtcjPvXh/8AwRP0zb4F+JurF8G71K1hEK/dQRpIRgfWQ1OzLcro8H/4KVfHz4q+A/2r9e0nRPH/AIh0HS7W0tpLS00rVp7eKJXjBLBUYAMT1r59/aB/ay+J3xy8K+EvCnja6eO30CAbDIHWa7cqu2ednyXYheG9ye9esftqWS/GD/goxf8Ah20DTG41Wx0d1XknbsDj+dfshrHwJ+HHiOa1m1nwF4b1i4t4Ft4p9Q0mCd1jUAKoZ0JwAOlVvqRsfhH+zj+258V/2c9LTQ/B2q2kuiyXQc6Nd2aS+ZJIRuKEDdk7QMk9xX6oft6fAY/tLfso2/iEadFD4z0PT11q1YwjzVHlB7iAEjIVgM4zjKDPSvfLf9mT4R2erJqdv8MPBsF/GQyXMegWgkQjoVby8it74teJtL8E/C3xVrWsyRw6VY6ZPJOZR8m3yyNp+pIH40uUVz8zv+CMfxxv18U+KfhXePNPYXFmdbsVLEpaukgSZFXOFDeah4HVa/WKvxz/AOCM3hKXWv2gvG/iuLcllpeitat6M1zcKyfpA35V+xlUiXuFFFFMQUUUUAFFFFABRRTG6igB9FFFTcAoqHLbuOnenL92jmHYkopkbbs0+mAUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtRc5NZvcB7MByTXK/Er4leG/hN4RvfE3irUodM0azXdJNKeSewUdz7CulcDaSxCqOWz0xX4jftpfGLxf+2d+0nN4B8CPd6z4fsrg2em6fb/6mR0wss7Y6jcBgngUikj628W/8Fl/hromqSW2k+Fda1q2Tj7VvSEH6Bhmvnj9tL/gpVpX7RnwVj8K+ELLVPDk9xeo2oxzSDM1uFbKBl7Zxkd+K+rf2f/8Aglh8LvA/hSyk8bac3ijxLNApumuJD5UTkcqgHp/Svlr9tj/glzqPw5h1Lxt8LUk1Tw7GGmu9EGWuLZAMlo/76jHTr0qrFaFr/glR+1Z8PPg3a674K8WyHQtU17UVuINWuH/0dlCBVic/wYO7n/ar9F/2ovjhf/Bj4B61498L6fH4luLVFaBIMzRlWOPMymcqOpPSvx8/Zh/YeP7Vnwq8Ta1oms/2J4j8O3HkzW92h8i6BUsG3H7pGCDXsn/BKP4h+M9U+POv/DXWdXm1vwj/AGJdC8026cTwAxSpGCmei/vCOODuFHKBo+D/APgtN4usbV4/EXgfS9UuDtKTWc7Q4HOQwOfbp71s63/wWt1JtLmSw+HVvb37LiKWW93Kh9SMc12H/BVb4L/DX4YfAPT9R8OeC9J0bXtU16C1F3ZW6xkIY5GfOOv3V/OviGfwr4X0P9gmw8QS6dA/i7XvF72qXkg/eC1hjJYL6DcRmnewrX1Pv7/gnD+1Z8Xf2qvin4vu/Ft/af8ACJ6Jpyj7Fa2ixBLmaUeUCwGThIpe/wDOv0Kr4e/4JAeEV0H9lN9TktliutZ1q4uTNtw0sahETJ7gFXx9TX1h4i+MngTwl4li0HXfGGh6LrMoUx2WoalDBM244XCOwY5I445qhbHZLTqRenr70tBIVneIPEWmeFNFvNX1m/t9M0yzjMtxd3UgSONB1JY9KvswGMnGeBX43ftvfFrxx+2N+1OvwV8BXch0TTrt9NjtY7gRw3cygGeWQ5wyrtOM9ADQNK59EfEj/gsx8OPC/iK40/wx4Y1TxdZQMUbUVmS1jcg4+QMCzDrzgV1XwJ/4KzfCv4teIo9F8QWt14BubhlS2uNWlQ2sjHOQ0o4TnaBuxndXo37P3/BP74TfBfwPZaZfeFdL8Va75am91bVbVZ3lk5yFDAhVGTjA+vt41+2h/wAEv/B/xE8NXXiT4Z2dl4O8S2SSTy2cY8u0vFABII6Iw2kgjj5jU2EfVOk/tSfC/XPidP4As/GGnv4piVW+xNJs8zcCQI2OBIcDPyk44z1FerD19RX8y/w38E+LviN4+stC8KW15qPiaRmliNtIRcBkBBKODk4x2r9Bf2RP+CmniH4Z65B8NfjlFMtrYO9o2vXasLq1ZTgLcKRkgdN3X1zRygfqR448X2HgDwbrfiXVJPK07SbOW9nb/YRSx/lX4cfHz9qb4vftkfEm5uPBNtr1vo+mRs1ppWhvIJIosKWlkCHnO0HJ6V9B/wDBQb9uC1+O02i/B74O6sNWtdXuEi1LUbMnZcMxQRwoR1XJbd9BX2p+xH+yTpf7Kfwtj00+XeeJ9S2z6tfBRlnxxGp/urkijlA+B/2JP+CmHiH4f+JLLwP8XLuW+8PyFLWHVbkET2L5IzKTyynIyT0xX6/Wd5DqFpDdW0qz28yLJHIhyrqRkEH0INfmd/wVw/ZLsbzwnZfFjwnpENne6a5i1z7JHt82JigjlIHA2kNk/wC0K9v/AOCV/wAarn4tfsz21hqmotf634bum0+cyNlxD1hyf93I/wCA1QH2RRRRQAUUUUAFFFFABRRRQAUUUUANamPnHFPamswUZPAoGUZlc/Ns3be1TW4Pytsx6j0pbiaQRkwrvbsPWks1m2s83DNj5fSg0cnYmcFqjOBwTU5qCRTuBwT9Kze4kxGVgykfzqfcOPU8U3Zu60qqqn3q1sJn5wf8Fnvi4dH+HXhD4cWk2LjXbptRvEXPEMOBGD/vSMf++K0v+CMPw7GjfBLxV4yntwl1rmqi0hmJBL29uuR9P3ksg/4CK8F/4LEfDrxXefHrw/4lh0y8ufD9zoyWNrPEhdftEcjmRcDkcSx89Dnjoa/Qz9hL4a3Pwp/Za8D6Jex+VfNa/a7iPj5XkJYjj2Iph0Pflpabt3Uowpxnk0EDqKKKACiiigAoopu4bsUAOooooAKKKKACiiigAooooAKKKKACimu+wHgngnj2rwr4sftu/B74I+NI/C3i7xUmnaw2N0SQSTCLP98op29R1/oaAPd6Kz/D+v2HinQ7HWNKuUvNNvoVuLe4j+7IjDII/CtCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCLzGRV8wfOf7vIqWkwD2paACiiioadwCiiiqWwBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnH0oBzz2oZQy4PShVCrgdKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsT2oAdRXI/Ev4reFvg/4VuvEXi7WLfRtKt1y0s7csf7qr1Y+wr4Y8cf8Fovh/o2pNb+GfBmseJrZWwbp5ltVI9QCpNJuw7M/RWivn79l39tb4f8A7VGlt/YN0dN8QQpvutDvGAniBJGQejjg8ivf91F0Fhc0zzk8wx7hvAztzzj1pWztJHWvyn/bV/aQ8Zfs2/tZaP4v0XxG2pWUsHk3XhyVyUSNcZyoI5O44PtRdFKLaufq1mlrx39m/wDae8H/ALSngm01vw9fRR3rRg3WlySDz7ZumGHpkHBr55/4KSfttap+zrodn4V8IvCPFOsI5N0rBmsYxtwSvq244/3TSuibM+6KSvwP8H/tt/tI/C6+sfF2pa9rGo6NcShNusW+61uAOSq8DBwTyDX7Vfs9/GrSv2gPhNoPjbScJFqEIM0G7JglHDofcHNO4+VrU9HooopkhRTWOO+KpaprdhocBn1G+t7GHBPmXEqxjjryTSuBforzqX9or4YwSvHJ480FXU4Km+Tj9a6Xwz8QPDXjRXOg69p+r7ACws7hZCuc4yAfY/lS5kOzOgopOvQ0c+tHMhC0UhqK4uorOCSeeVYYYxueSQgKoHcmjmQyaivkj4nf8FPPgr8L/GB0C81HUNUliYpPc6XbiaKIjsSWGfw9K96+EHxw8G/HXwtHr/g3WodUsWHzopAlhPPDpnKng9fSmFmd7RTVzk06mIKKKKACiiigAooooAKKKKACmSAt0OORStSUDPxA+OOiH4zf8FQ5tEUi6ik8S21uxc5Ajh2ll+mFxX7fKu1QPQYr8K5vGtp8Gf8AgpVe+JPEazWlha+KZ5Lh5FxthkJCt9Buz+FfuPouuaf4j02DUNLvIb+ymUOk1u4dWBGeooKkfkh/wWo8YR6h8VvAvhtE/faZpM10W9fPlVf5Q/rX6SfsneHZPCf7Nfw30qVdr2+iWwK+mUDAfrX5a/8ABYSwkT9qnQ7mRl8mTQrUDn7oWaTOfzr9cfBms6foPwl0TU7ieO30200eGZ5SQFWNYgSfyFAPY/Gv/grnr0GuftbzQWrI7afo9taykdQ43uQfwcV9H/An4K+Ovir/AMExdL8PeCdV/s7XLu/lu49kpjMsXmHMZYdM1+cn7R3xGPxU+OnjXxS0zTpqGpzSxSOc/ugSEA9sACv2V/4JWQ3sP7H3hz7aJAGubhod/wDzzL/Lj2pDeiPy48Yfsc/tG+CtL1abUfDmsR6fZxSS3c8F6XiaNQNxxu5GM9q8k+C3wt8YfGbx7b+GPBMEkuuTI8ilZDHsQfey3Yc1/Q3+0RouoeIvgT480zSld9Ru9HuIYFj+8WKEYHvX5Wf8Ep/hz4x8K/tUNcan4V1Gw0+HSbqC4u7q3ZUSQshXDEdTyOKYuY7T4P8A/BN/xz4E+Hvxd1j4jS2rXMnhi6i0mK3uDMVl2M7McjjGxAMeprG/4JO/G3T/AIT+Bvjfca5crDpukWtpqsSMxAaQLOrKB6sVSv1R+Lkcknwr8YrCcSnRrwLj18h6/mr03xZrPh+x1zSbC7ktrbVAsN5ApP78KzFVI78saloa1Psr/gm34G1j9oL9tC5+IerCa8tdFln1q7up2L5uJNywqSepyxI/3K/bWvkz/gmr+z//AMKP/Z6srjUNOW08R+IGF9eysB5joR+6Vj6AE4H+0a+s6aJe4V+V3/BVD9rWbxdqdr8Dfh9dTX87z+Xry2QLG4lJQw26FTk4O/evQkr6V6d+3F+2d8TtH8cXvwn+Cfhy81DXBAi3uuWls8stu8mcJCMbQcZ+Y5wRxU3/AAT/AP2A734W6tP8Svip5WrePL3bd2lldMZJNNkcuZJZDkhpH+Xnqu085JpiWh6x/wAE7P2Ybr9mn4Hpb67awQ+LtblF5qTxj51UA+VCx/2AzcdizV9UUUUCCiiigAooooAKKKKACkpaKACmtnjFLTWYL1PFTy3Aa77VORikjZWX5Tmqt1drGvHei1mLLwOtQ9Dbl0Ly06mrnvTq0WxkFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRSVLYC0m4DvUEjyMwCcDvUnlBsE81AHzb/AMFDPjhN8C/2ZPEOo6fM0Gt6uRpFg8Z+ZJJQ25x9EDfjivmX/gjV8FdMh8G+KfihdwtPq9xqD6RYTSL9y2RUZ2X/AH3cg/7lcl/wWm+In9peJPh38P7Cd/tVmk2rXEQ6F5WSOH8Rsk/76r9Av2UfhDB8Df2f/B3hGLDTWlkslzIB9+aT55D/AN9MapIdz1ikZA6lWXcrDBBGQakqpq2rWeg6bc6hqFzFZ2NtGZZriZwqIo6kk9KsR4f+1F4l8Nfs9fsz/EDVbK1s9C+0afcW9tHaxrEZruaNkTAGMtk5+gNfFH/BFj4WTrffEL4iXkBXKRaLZy44bJ824578rB+RrzD9tj9obVf26vjd4a+F3w18+88OW915cBVDiecnDTOB/AoHBPQE+tfqX+zP8C9M/Z1+DuheDNOAZ7aPzLyb/ntcMAZH/E/oBQV0Ph//AILYeNHtPC3w08LwFGa5u7vU5gSMqIljVD+Jkf8AKvlr9rjwna+Af2Tf2ZdJtVkjn1HTb7WbxXBGXlEDA4/4E1d7/wAFldWm1H9pbwxpZlP2a38PQIF7Kz3ErE/lt/Km/wDBVbT30HR/gJogRoksfCwiCsMYPyKQf++BUPcpH6N/8E/tJh0f9j34YQwgASaUs7e7OzOf1avg3/gsv4Lfwz8Yvh/47syy3N/YtEDjjzLWVGXHviYflX6L/sh6MPD/AOzL8NbEHd5eiWxyPeMH+tfLX/BZ3wrbal8AfCWuyFUu9O8QLaROTjCzwuW/9Er+VFyd2fZPwH8Y/wDCwPgx4J8RGRZX1LSLa4dlYMCzRqW5Hvmu8r5U/wCCY/jCDxZ+x74LjjmWWfSll06ZVcEoySMVBHb5Cp57EV9V1QnozyX9qr4wJ8DPgP4s8WCQLf29o0OnpnDPdSArEF9SCd2P9k1+ev8AwR8+Clz4t8deLfjPr8c0s1u7WWnXEgOJp5dxuZM9CQNq8f3mrpP+Cznxuhj0Pwt8LtOlaS/klOr6lGhIESqAsH1JLP8Ap619g/sH/Ddfhb+yr4B0hrSWzvJrBb+7iniMUgmm/eMGUgEEbsc+lMLnvy1keMI2m8I63GilnaxnVVAySTG2BWxTXUSKysNysMEHuKBH4k/8EmUjt/2zJ7e6j/fx6NfqgYfNHIJUB/8AHS3519Nf8FcPhP8ACjTfhl/wl13Yxad8RLufbYvZAI92AV81pFH3goK/N7+9fLf7JPxA8JfAX9tL4leLPE2pQ6Xoui2ur/Z/NkCm5n81dkCZ+87APhRzxW94Bk8T/wDBTb9ryO88QLcx+ANFlW4e12ny7W3BykXoGlKn67T6UAfM/wAE/EXjH9nHx14W+KUvhKa70tJt0Et7Zt9nuEGNxjfGMgHr7iv2s/Zz/b0+Fv7RVmkVhrMOh69uCHR9UlWKdjjOUBPzL7ivZfEfwv8ADHivwHN4O1DSbeTw9Jb/AGX7IiBVRMY+Xj5SPUV+Uf7Qn/BI/wAaeAn1TxF8MNVXX9Ohd54dKVmivYk44U/xEdsHtQB+qHxs8DJ8Ufg/4w8LZUjWNKntkbGRuZDtP/fWK/LX/gjjr+o+Ef2g/HvgWdXhiutIee6ikyMXNrcrGAB67bhs/SsT4A/8FT/HvwF0NPBnxA8OzeJf7Nb7NHNcymK8iCnG18j5scDPsa1f+CXOsP8AED9uDxv4vs7CSx0y70u+maEtuELS3EDBSfU7T+R9KAP2HooooAKKKKACiiigAooooAKKKKAGtUNxs2fMcCpiQahkjMmBjjNA0LHEFUY5qQ/L1pVxVW61Kyt28ue7gibH3ZJFU/qalsZHcatBAypvDM3pk0+EPI6OWwM5Az14I/qKzP7Y8OQtJIdS08bfvsblOPrzUGi/Ejwl4i1qXRdJ8TaRqWrQxmWSxs72KWZEBALFFYkDJHOO9QVp0PzA/wCCjn7UXx++Hfx5v/DXhe/1bwx4UWCL+zpLC0U/bMxqZH8wqTkMSMDp+NfOXhPxl+2N4pm/tbQZ/iRrZUgtJb21xOgz0yApAB5+uK/e5kRsblDY6ZGa8w+OX7TXw4/Zx0+xu/H/AIhTRUvmZbaJYJJ5ZMYyRHGrNgZHOMVa2Fc/JDU9W/bl1xVjvdB+IUsakFQdCdhn/gUdbkPj79vtVCjSPHoVVCKv9gDgD/tnX6tfCv8AaT+GfxotYpfB/jLS9XkkQP8AZVmCXCg5xuibDL0PUdq9MDBhkHIqhXZ+K03i/wDb4m+c6X4+G3J50YKP/QK6H9kfUv2pfHH7UHh218Ta14r03T7WYz6qNVgKQC3Xlo8EYy2ABjmv2JpPegkRc85p1FFABRRSFgOpxQAMQBzUEagybs5FNu59q8DNLayLJHwMY60Dtpc+B/2wv+CoF1+zj8bZvAeieE7bW10yOFtTuL6R423SRrIqxbTggIw5Pevsn4I/FSy+Nvwq8N+ONPtpbS01q1W5SCb7yZJBB/EGvxE/4KiMrftsePD0Bisv0s4h/Ov19/YY086X+yT8L7c440aF+P8AaG7+tAHu1FFFAgooooAKKKKACikJx2zTPM3NgAr9aAJK/n0/4KK3Bn/bH+JSzbvkuQq/NgcIuDX9BEZ3DNfz8/8ABSSMD9sj4iEf8/EbH/vhKAP2k/Y2bd+yz8Lz66Da547+WM17LXk37J+mvo/7NXw0tJMF49BtM7enMSmvWaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBryCMZIJ+lJHJ5gzgj60+mKrb2JbK9h6UAPooooAKKKarbiRQA6iiigAooooAKKKKVwCikNJuougHUUmaTdTAdRTGycYbaO9KqkdWzQA6iiigAooooAKKKKACiiigAooooAKKKKACq2oXiWFrJcSnEUY3OfRRViuB+O3iN/Cfwq8S6ouwC3sZWJkzjO3jvUSbS0Gtz8d/wBtz4oeJ/2tv2nLTwB4Zlk1G0tbo2Wm2aMQpdsb2bnHG0Hp2r64+C3/AASF8A6N8P4ZfiE11r3jSeEtKsN2Y7O3fnCoEUMccZJJ6cV8hf8ABNDQW+I37bEOs3Uc7pYx3epGa34VZCQqhsg/Kdze/HWv3J6Uox93U0lufzv/ABt+G/jf9jH41SyaVeyeHryKeQ6ddWFwS4jBHBOemCOvWvT/AIT/ALd/x5+KXxr8E6RP42uY4LzUra0eytYkSORCwDluCSSPev0B/a0/Yl+GP7SHiH+2NS8br4d1yINxFcxbG6Z3q2T27etfnz4X+Gfgb9mr9sDwy83j/TL3SNHvEnW7jcT/ADr2fbjHWs4tpWluNK5+6Sb47MZJd1Tv1JxX4t/8Fbfh1e6T8ZdP8YiMrYaraiEsoPySJyQfru/Q1+gfjP8A4KVfAjwZcWVs3iv+157ptgXS7d5th4xu44zn9DXjv/BVbR9K8cfsz6Z4ts2lRFuIriJmXaHVgMAjHoTVocXZNM/OjRfgb8XPhb8I7b4x+H7640bQ5TH/AKVpt2yS89N4B+vX3qH9nzxfoHxE/aO0HVfjfrt5qejs+bi8vJi7FwB5YYnPy561Npf7SHiLXPgNbfBhPliu9RhjExycoWwo69if1r7W8Gf8EdtL1f4SQy6n4hntfGM6eckiMDbcjKhlxn9e9MR9TftFeGfhp8cP2Z9d0XQL3QbuC3sGn00QyxhYXVcgrjocDFfJP/BGP4nalaeKvHPw2vLndYQ266haW+chZFkKzEfXdH+VfLnxq/Yv+OH7OPns9tqF9oJLr9t0iR3iKDGdyjoOe9er/wDBH3w3q8H7T+pak1ndJZR6DcQzTSQsq7mliIBJ7/IaEtbie1j9p6Kbuo3VoZHLfEbxpZeBPDN7rF9KsdvaRNLJuPBUda/D74+fHP4i/tu/H46F4ZuLy5tZbg2WkaXauY4hGPvO+D7AkntX6Vf8FRPF0Hgz9l/VpRM0V/qMy2NvtPXfyw/IV8tf8Ea/gra6nrnif4m30RL2JGn6eSeFLAmQ47n7oqOpq7ci7mp4B/4IwXV74Xjm8W+PJrHXJF3NBYQrJHGfQs3J/CvIPjN+wj8Yf2O7V/HPhXxTNqOnWcwbzNOd0lRV5BkUHBH/ANev2ulmSCMySuscajLOxwB9TXk/xq+KvgS3+HPiWzvvFOhb5LGZBDLeRtlthwNoPrSJUmfK/wDwT5/4KGa/+0R4qh+HvirR0fXINPkuzrFuwUSKjKp3J6/MvStP/goD+058ef2c72G/8I6ZpC+DpQCNUaDz5Y2BAKurcDORg/Wvkv8A4JOpoOm/tIeMPEer+INN0aOwsHt4Bd3McC3HnS5OzcRnHlDp6iv0k/aI8afBfx18Ntb8O+LfGvh37Ld2rjaNRjkZWAyCArE5zilcrS+p8hfs9f8ABYmxuoZLH4v6U1ncb18nUtIgyhU5yXTPHbpWH/wUI/4KAWPxC8K6B4L+EWtSXK6wT/aF1Cu12VtojiHcEknOOa+Z/wBkn9nHwL8cfiP478PanrrLZ6dA0umXCuUWfG/35wAv514SNH1fwD8ULpPDyS6lfeH7wzwyQW/ngGJ8q7LgggY7jFKLUpOKHY+9/gz/AMEetc8V+C5tX8ceLX0HVb6JZ7WxsY/MKEgnE5fr26dMmvDP2Q/Guv8A7Jv7Zdp4ZvLqeGxn1E6NqMKkhJlZsIzKeODgj619z/su/wDBVrwN8QNNstF+JMqeD/EiIsZvWUmyuWwcncB+7PAyDx83FfM3/BTiDwtoPxy+H/xU8E6tY39vrHl3U8+nzpMhmglDbyBnBKsvX0q7iP2TjYMoYdCM0+ud+HviJPFngbQdajbcl/Yw3AP+8gP9a6KrMgooooAKKKKACiiigAoqnq+qW+i6bc395KIbW2jaWWRuiqBkmvzu8b/8FkfDHh/xxc6ZpPg+91bRrWQxvqHmhC+DjIX0oKUWz9GpM7eOtNBO3JHNfCOlf8Fifg3eW6teWOuWc2BuT7NuAP1FWbr/AIK/fBWGMNFBrU7f3fs23+dAWZvft1fsDWn7TNrb674Yaz0bxlBu864lTAvEIUBHPtt/WvhLwNeftZ/sT3V9pum6Lql3o8c3mSWz25vLRwM/Mh/hznt7elfUevf8Fn/h/bsi6L4O1rU2OQVkZI/m42geuea+6vhj4yPxL+Huh+I59Jm0n+1LRLhrC7ALxbhna1AX7n89X7TXx28XftDfEJvE3jSBLDU0gW1SzWMxiJFJONpHqTRe/tOfGLxB4Ni8KSeONbuNDWE232JJmKNCQBsIA5GBX9DWofC/wfq1z9ovfC2j3U//AD0lsY2b89tWYfAPhi2wIvDmkxY6bLGIf+y0D5j+Ye60m6tiBc28tuOitMjKD9Mivs/4J/8ABUL4h/Bj4d6L4N0zRdAvdO0uEQwtNHIHK5J/h6mv1p+OPxJ+E/wD8O22s+PIdL02xuJTFBusEkaRhgkKAvbI/OvKdD/a2/ZT8XCBhrPhm3eXhFvdPER/H5OPxpBc+StJ/wCC2Gv2sJTV/h7plzJgAG0upE+uQ2a39F/4LW2UbSm6+FWM42m11RI/XOdyHPavtGP4Qfs6/FxYrpPDHgXxN/EjLb28rDd7dRnH6VfT9jD4Dx/d+EXg7/wTwn/2WmSfF15/wWn0HULSa1ufhLdT206NFLG2uxYZWGCCPK5yCa+Cbv4hfDC6+Mx8WH4eXUHh77YLsaFDrMQT72dv+r6e1fufH+x18DFBA+EXg3B4P/Ektz/7LTh+x78CwoH/AAp/wSQOgOg2x/8AZKBp2Phb/h9Zpen2cVrYfCSSFYUEcStrqMoUDAHEIxXvf7En7fGq/tdeNvEOjT+CYfD9lpdml19st777R8zOQEfgYzg4+hr07XP2Cv2fvEkcsV18LfD8KuMEWEH2Ur9DEVI/Cux+CP7M/wANf2c7K/tvh94Xt9AF+VN1Mssk0020kqGkkZmIXc2BnAyaAuj01e9KFC5wMZ5NLRQSFFJRj3qbgBxwT25r8po/+ConxG/4acTwudP0yTwl/wAJANJaNF/eFTJsyGz171+q8i7kKnoRiv5q7y4Om/tBrcNKyeT4kDlgTnIuev14o5hpXP6VY38yNWxjcAadVPSJhcaXaSK25WhRg3rlRVyqEFFFFABRRSd6AEYgdao3U6Hv0qW5LeYAenaq10o2rxT6G9NLcrK0d/MsQUnByWHYV8EfFz/gq5YfDf49P4P07wzHqPhrTb77Df6h5h80tkAmMDjg5r9AbGMGTcONvP8AOv50P2noDbftJeP1xtA164xj/rqKy3Km9bH9G2j6lDrWlWd/b7vIuolmj3DB2sARn86uVy/wuYv8OfDLE5J023/9Fiuoq1scwUUUUwCiiigAooooAKKKKACimtSUDH0UyjIoAfSZqNjQtYSlrYdiSjIHU0i0MobBIzimtST8WP2+LWXx7/wUqsvD0h3QfatFsFA5+R44nb9WNftHaRCC1hjHARFX8hX45/tGCOP/AIK5aL5hCL/bOknLHA/1MeP1xX7JVqtgCvxq/wCCkn7WnxQ8T/EjxP8ACmxs7zSPCVvcm2WOG3dZL8L1bOPmUn04r9lG/TvWXdeF9J1C9W8vdMs7y8UbVnnt0dwvoCRTA/nd+BWv/GD4H+KpPEPgbw5rEWqtAYhN/Yss5VTngZTivoWL4m/th/tWzWXgVk1+wtrhw01y2mPpsQUdTJLtGQPTPNftTFp1pBgx2sMfb5YwKmjjEYwAAPYYoKufzt/tJfDnXPA/7QB8B6v4hufF2qaa1tYLcuWdixRSIlByxIZse5r6n/4LNTRr40+FkEjhXTQ2Z4/4gplx0/A/lX1347/4J26J41/a0074yS63IkEV1Ff3GktECJJ48bCG9MgH8Kz/ANvv9gG//a18ReGvEega/baJrOl2hsJFvY2eKSLzC6Yx0ILv+YqbBzHoP7Nv7Vvwg1j4LeEY18f+HtJmtNMt7eW01TUoLWWNljCkFXYdxXjP/BT74mfDP4mfsp6pYaT4/wDDOsarZ6jbXtrZ6bq9vcTSOpZCAiOSflkbtXjGm/8ABE3W5ohJf/E6xt7lvvrFo/mp+GZBitKP/giTPn978VoNuOieH1HPb/lrRyivrc1/+CJuuao/hf4laJNFMuk293a3cDsD5fmurpIoPTIESEj3HrX6cV86/sYfsixfsjeD9a0VfEX/AAkkup3n2p7j7Ettt4wFwCSfxNfRVMG7u5+H/wC1dND8cP8AgpRFoSSm/s5NcsNHcwnzF8tGUOvGeAAc+mDX7c2VrHY2cFtEoSKFFjVR0AAwBX4kfBGzh1T/AIKqWkd3zH/wlWoSYJ/iSGZlP5gV+31MQUUUUAfit+07/wAE+PiLrH7WWqad4M8L6lf+HNcuReLrbWrmxtvNJMm+XG0EfWv1L/Zp/Zr8L/sz/Duy8O+H7OP7WUVr6/YZluZepJbrjJOB2r16igBF4/nS0UUAeD/Hr9in4WftA6fe/wBt+Hrey1qdCE1qxQR3EbcYbjhunesD9jX9iXQf2RtN177LqT67rWsSKJ9RlTYfJQsUQDtjcc+tfS9FACDpS0UUAFFFFABRUdxcRWsLyzyJDEg3NJIwVVHqSelc1oHxS8HeKtYm0rRvE+k6pqUIzJa2l4kki/gDQB1NFFFABRRXzx+13+2Z4V/ZT8MxvelNU8UXqn7Bo6PgvjGWduiryOuM9qAPe7u3uJWTyZfKAPzcdashTgZ5Nfil4m/4K3fHjXi17odtpmiWEbn5YNLFwCPR3cEDHtXpfwA/4LHeIZvEun6X8UdC0+50q5kSFtW0lGilhJOC7R5IYcjgAUAfcv7bvw5+I3xN+BeoaT8MdUfTvEazJP5cMohkuUXOY1kLAKT79cV+PHwp/ZB+OP7QHinXdOs4Eg1XSbk22qNr2seTLBJnkmPeZGX/AGgpU9jX7/abqEGrafbXtq/m21xGssb4I3KRkHn2rkLf4M+ErH4qXXxFttLWDxZd2a2FxeRyMoliByNy5wWHrilYrm0sfkvff8EfvjtZ2sjwa14PvXC5EcOqXayMfQbogufqa9n/AOCbf7Dfxb+APx21fxd4+0S20bT00mWwhYX8Fy1y8kkbZXypGK7RF/EB94Y71+nFLRYVyJQwOCvHJzn3r52/au/Yd8GftZNpl3rt9f6PrOnRtFb39iwbCE5wyNwefTHWvo6imFz8e/ih/wAEj/ir8O7621H4VeJk8RSK3GLhdNuohxzvLAH/AL67V58Pif8AtefsZ68ZPEa+ILjTIWAddXZr+zkH91ZgWHfqDX7f3VzFZwPNPKkMMYLNJIQFUDqSa/Pf9tj/AIKbeEvAtre+DPAtrYeMddLGK7mvYfNsYBj8nbk9OmKB7nffsf8A/BSfwh+0NPpvhjxDGfDnj26LKlmEZrefaCco+MA8dDzX2fuFfjt/wTX/AGRvFPxB+Klj8ZddtI9G8N2dzJd2kfl7DcyknhF7ID3r9O/j1+0R4L/Zv8JQ+IfGmotZWc84toUhjaWWVyMnai8nA6ntkUBY9Opa4b4P/Gbwl8cvB9t4l8H6oupabcDPIKSRn0dDyp9jXc0EiUjBWxkZpk0yQgFzjNOBzzQAybaUwwwKSHbs+WnsoYYNCqFGAKB9D8Dv+CoikftqeOc947Q/+S0VfsX+xa/mfsr/AAxP/UDth/44K/Hv/gp9Cb79tTxisZxvjtEH1EEa/wA6/aP9mvwjc+A/gJ4D0G8KG6sdIt4pfLbcu4IM4NAM9LooooENdxGpY9BUNtex3W7YG+X+8MVM1eX/ABs/aU+HP7PFnYz+O/EUOi/bmK28PlvJJJjqQqgnAz1oGeo5pa5P4Y/FLwv8YfCdt4l8IatHrOi3BIjuo0ZQSOoIYAgj6V1lAgppB3Zp1fH/AO2V/wAFGPC/7K+rWvh3T9KXxj4rlRnnsorxYI7McbfNbDctk8AcYoA+vo1Krg1/Pt/wUe3f8NjfEcsMf6SoHI6bEr6usP8AguBftcRrefCW3WIsA7Q66SQM9RmDB496+Ff2pvjPZ/tBfG7xN450/TZtIttSKstrcuHdcBRyRx2oA/oA/ZwV4/gF8PVkOWGhWecf9cVr0evOf2cZBN8A/h64OQdDs/8A0UteikkYwM0ALXEfEn42eBvhDZi68YeJ9P0KNvurdThWb6L1NeM/t1ftlWv7JHgfTpbfTzqviXWzJFp0BI8tCgXLyc5x8w6V+Tvwj+Hvjz/gop+0JdDW9bltjMkl3c6hLG8kFuikDy0HQE54HtQB+yfhP9tD4L+N9UtNO0bx/pN3eXT7IYhMAWY9BzXtSsHUMDkHkEd6/Db9sD/gnV4k/ZS0Cy8Y6JrzeINChlUTXccJhms5Mjaxx2J9+1fop/wTU/aEufjp8A4odXvftniDQJvsF1IzZeVQAUk9cEcc+lAH1vRRRQAUUUUAFFIzbVzjNIrblzjFADqKKKACiiigAorO8Q+ItM8J6PdarrF9Bp2nWyF5rm4cIiAepNfK7f8ABVD9nuHUryzl8S30ZtpPLM39nu0cnOMoVzkUAfXNFeT/AA9/at+EXxSW1Xw18QNDvri5IEVo92sM7N/d8t8Nn8K9X9MdKAForG1vxloHhl1TV9c07S3YZVb27jhJHsGIrlNU/aM+FeikC/8AiP4Vs92QPO1i3XOOuMvQB6JRXjGrftmfA3RQhuPip4WbfnAt9TimPHrsJxXn/iv/AIKa/s8+FYyT45j1WUZ/dabayznj3C4/WgD6nor4f8K/8FdPg34s8Z2OgQaf4itUvJ0t4tQubRFh3scDOHLAfUV9uwyrPEkiHcjgMD6g0APooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0ZoAWikzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTVXaSadRQAUUUUAFFJmjt6UALRUaLtZiTnNK0gXrgD3NZvcYSOFxk4zSNzXIfET4seEvhlotxqviPWrLT7a3QyETTqHbHZVzya+JNc/4LN/DXS9auLWz8J6/qllGxVbq3ES78d8Mw4qS1F2ufoMfMKtjCnHFfFX7dX7SPxP8Ag9ov2LwX4W1G7nljMj61FEXitQPUAc55/KvJr7/gtfob3JGmfDm+ltlBLPd3qRsPThQ3X619mfs0fHLT/wBqr4RWni59Dk0uG6Z4JtOusSKcHHcfMKFaTsXF8utj8yvg/wD8FeviX4T1J4PHWn2vimwO1d8KfZ5ocE7jjndnj06V+jP7P37c3wt/aEhgg0bW47LW3QNJpd4fLkU+gz1qD4ufsc/APWNJv9Y8R+DtI0tI43klvIT9mxxySRxn8K/En4oafoXhn4yz2fwrvLyW2S62Wc1vIWbdnGFI5Ip3a0JSUtT+kGORZFDKQynkEHINOrg/gXa39j8IfCUOpvLJqC6bD57Tff37BnNd1uq46ohqzHUUgNLVEhRRRQAUUhbFAYGgBaKKKACiiigBO4r5d/4KPfEm3+Hv7Lfigs6i71BVsoVYE5L9eh7CvqJuBmvz6/4K8akJfgXaWzDa39qQc98ENn+VRLYuKb1PNf8Agif4J+X4i+LpCSZDb6dEOMfLudj0/wBod+1fpZ490G+8TeFdS07T702Vxc20kKuOOWXA57V8X/8ABHPS47f9mvVb0KRNd61MXb12gKP5V957aLKQSep+Inij/gln+0RJr2p3NvZ2N9HJLJIl1/bC+Y654zz1x2xXyH8Sfh/rPws8Zap4U8SWwttZ0+Ux3Cbw204HcDmv6d9tfCn7SH/BLPQv2hPjFdeOT41vNF/tCVXv7IWay7wMAiNsjaeOpDVRNzx79lf/AIJSeBvGXgXwv428T+LtQ1VdQhivktNKCwxq2d21mYNkdAeB0NfRX/BSfwwsf7IGraRpWnyTJbGERrGpby409cfzr6X+Fvw00j4RfD/RfCGhmdtL0q3W3ha4cNIQO7EADP4V0l3Y29/ayW1zDHcW8i7XilUMrD0IPWlZjTPwK/4J4/Aq++L37THhr7Tp8z6JpDf2jdyyxHy/3eNqk+7EflX79JGsaKijaqjAA7Csrw/4P0PwrG6aNpFlpav977JAsefrgVr496VmJsiuLeK5haKaNZonGGjkUMpHoQapaV4d0vQtw07TbSw3fe+zQrHn64FaWKNtUhDaKdtpAKYH51f8Fm/EFpH8IPBmkmQNcTa0ZvLHUBI+f/Q69H/4JM+Hl0j9krTroxbX1C/ubgt/eG8qD+Sivmz/AILSatp/9ueAdNtp9+qR/aZ54M/dV1jVTj3wa+7f2H/Bv/CCfsueAdKKGNv7PWdgTnmT5z/OoWruavRG7+1D8PPE/wAT/g1rnh/whfrp2uXUe2GWRyq+4JFfj18R/wDgmz8a/h74P1jxP4gm0v8AszTYmubiY37OxA9iK/d3vXPfELwHo3xN8Hap4Y8QWxu9H1KEwXESsVYqfQjkGnbqRfofz3/su/sp+Mv2p/Emr6Z4RmsbU6XFHLdTXczIqK5YLjaMnJU19HN/wR1+NEl0Q+t+Gnjz/rGupT+myv03/Zt/ZF8A/stw6yngy0uYpNVZTcTXU7SsVUnaoJPQZP517W3Q4644qvUL22P5n/FGmeI/2f8A4mazo0WqLb6tpkj2s01ixCt2IHsa/Vj/AIJN/s4f8Ir8M9Y+IHiOz83VvFJCRpeR7itupbnn+8WOfXFexfGf/gnT8J/jl8TLTxprNne2l8JPMvbexmMUd4eMb/TGP4cE5r6a0TR7Pw/pNpplhAttZWkSwwxL0VFGAPyoslqhNn50ftj/APBKiDx5q0/iv4SNa6NqExaW80K4YrbzScYaLqEJ5yDx0r8v/it8I/Gvwb1htD8Z6FfaNdJuSJZ1YwvyCTG3Q/ge9f0yVzXjj4Z+FfiVYx2fijQbHW7eNt8a3kIfY2Qcqeo6DpU2K5jk/wBl5J4/2e/h+lwnlyro1spXOekYr1KoLKyg020htbWFLe3hQJHFGMKqgYAA9KnpokKKT0rM8TeI7Hwlod7rGpzpbafZxNNNM5wFUDNFxEmva/p3hjS7jUtWvYNPsLdS8txcOERQO5Jr40+KH/BWr4OfD/XX0vS49U8XSRMVluNKiXyVx6MzDPfp6V8GftsftseJf2rvGkHhLwet5F4Yhna3trC35a+kYgZbAyRwOM96+mP2Vf8AgkX4aj8N6dr3xea6v9WnUSnQLeXyoYlPQSMvzE+wIpjasdLH/wAFpPhs0oB8FeJvL7sFhyPw3179+zn+358Lf2ltYfR9Au7rS9aVN62OqxiJ5fUIckMR7GsfVv8AgmL+zveaTc2tn4Ej024lQql5Fe3DvEexAeQjj3FflH+1p+zlrf7EvxmsBompXosGK3el6uvyPuBBIyO44yKASuf0A3VpDfW7w3EUc8LjDRyKGVh6EHrXhnxC/YZ+CHxMvnvdZ8Bael84w1xY7rZj+CEL+leh/BXxYfHXwl8Ja+0/2h9Q0yCd5T1ZigyfzrtqAPjPU/8Agkx+z/qDhhpmtWg/u22pFR+qmqK/8Eh/2f8AkG38SMf9rVzx/wCOV9s0bRQF2fG3g/8A4JS/A7wb4t0zXrS11a7lsJhOltfXnnROwORuGBnBr7HhhS3hSKJFjjQBVVRgADoBTqWgQUUUUAeIftafsv6P+1V8O4PDWp3r6XNbXIube/ijDvEf4gM+oA/KvhzVv+CJ1xNcSHT/AIoJHC55W60ze2B0wQ4r9UqaxVVLMQABkk9qB3Pxi8cf8Enfjb8PGS88G6/Z+IvLJYfZbh7WZdvIIDEjP0NZ/wADP+Cgnxx/Z98bR+BfGcF34sVLuOxOla0c3cLFtuEl6nr0ORwK+0v23v8Agox4b+BGj3PhvwTf2mueO5t0LGNt8On8D53I4Y8nAB7V8p/sE/s5eO/2kvjtbfGb4k28+o+HbWVrmO81Rc/2hOMhNqt1VTznGOBQPm7n6+aPeS6hpdpdT27Wk00SyPAxBMZIyVJHpV2kVQihVGABgAUtBIUUUUAFFFFADWbFVZJ3WUDHFWXYDAPfpUDRFpie2OKlouNuo+GQyKc1/Nx420c6h+0tqumQ/KJvE7Qpt4xm4xX9I6RjauexzX84vj5W0f8Aas1XDEND4qLAg8j/AEgUrFddD+i7wzZjT/D2m2oYsIbaNMnqcKBWnVHRW36RZN13QRn/AMdFXqoyCikam5pgPpKbk1Wubpo8gCpuUouWiHTyB+B2rK1CQpHnNZ+sa9Jp8RcRl8ntVb+0v7YsyJoGRWHBHrUOp0sdcYcq1N3TbrzliA6hufyNfz3/ALYzhv2qviIQMD+2JOB/viv6D/D0Jjt1V4yjIOM9wa/A79v7Rf7B/bB+IMAGEkvBOv8AwLaaUXcxk7s/eT4WnPw48Mn/AKh1v/6LFdMn3jXIfBtt3wp8In10u3/9FiuyrVbGLGOu5kPpQzHzFA/GmXDOqgqM+tRopuMmQfLjGPrTC3UsrnHPWlr8nP2oP27vi14W/bAvfA/gbxHDZaNBqFvpyWsltG6MxKhySw9zX6raK1y2j2RvJFluzChldBgM2BkgfWgRdooooAKKa1Qt5uTjBHapuOxM1QSSHIwdo71GIJmYktxTms2YYLcHrWb1LVluQ3cnnRFIzuJ6n0pkMLQ5Hm7zjp6VY+wiNcRttb1qG1094yxlbcxNTaXQ0UlYIw37zNWbf7tPCbelOWp5X1Ik7jlp1Qp95qlB4rSPYzZ+Ln7bzfYf+CpmgzDp/a3h9z7f8e/+FftGrblBHQ81+K37edvJcf8ABTK2giO2aa70PYffyoq/aOyVks4Fb7wjUH8q2ET0UUUAFFFFABRRRQAUUUUAFFFFAH4ifBb9z/wVYtM8Y8T34P4wy1+3dfiJ4Ojk8O/8FXoI7hGhP/CVXGRINpG+OTB59civ27oAKKKKACiiigAooooAKKKKACiivz9/4KNftgfFv9m3xl4cj8IaVFa+GXjLy6lcW5lju5eMxE/wbRj67qAP0Ab3OKQFVxz14FfFv7Gv/BSHw7+0heW/hfxBbJ4b8YtGPLQv+5u25yI89+M4969c/bT+PJ/Z3+AGv+JrZ4/7YkQWlgjnGZn4BA74GTQM+Af+Cl37a2u+MPHEnwv+G+r3D6PahoNSfSdxkupjgNEcDOFIxx610H/BI39m3xDo/jrxH4+8ZeGNT0g29pFFo9xfIYvNZy/nEqTknATqO9R/8Ep/2XY/Hmq6l8bPGMEl1P8AamXS1m+7JKSTJMR3GSAPcGv1aVQihVAUDoAKAYtFFISFBJOAKBHlv7Snx90X9m/4Val4w1n94YyILO1X71xcMDsQccdCSenFfkF+z/8ACHxp/wAFC/2jrzxP4wF1e+Gornz9VvBKBHDHk+XbpnGehHy5x3rtP29Pjpqn7YX7Rmi/CXwb5k+i6XqP2CHyT/x8XDECWYg4+VQvGfQ+tfqd+zl8CdE/Z3+FOjeDtFTK2sYNxcMoDzynlmYj3oA2vCPwb8E+BPDceg6L4Z02y0tYxEYFtlIcAfxZHzfjX5af8Fe/gd4Q+G/iTwJ4m8MaXb6PeawbiG6t7ONY4j5RjKuFAABO8/lX6+tX5Cf8FX/EU3jz9qTwD4Ht7hZ7eyjt42hBxslnlGQc8crtoGtT9S/g1I83wn8IPJ99tKty2fXyxXZVkeEdJTQvC+k6dGMJa2sUIH+6oFa9AgooooAK89+P/jzV/hj8H/FHijQdL/tjV9Ns3mt7TkhmHcgdQOtehU2SNZEZHUOjDBVhkEehoA/nv+JX7Wn7QH7RF1Jpt7retT2945jGj6NbNFEc/wAGEGW/GrXh/wD4Jx/tC+IrCO8h8A3cMcuJFF5PHA/PchiDX766T4Y0bQWdtM0mx05nOWNpbJEWPqdoGa06B3Pwab4Dftg+C4YtBtdF+ICWdou2KHR7qYwIPYxnFVx+x3+1R8aby3sdb8NeKphbEvC/im8dYkLcEqZTgHgZx7V+9tNZQ2M0D5mfN37Bf7OE37OXwQsNK1nRoNK8X3JZtWaC5E6ysGO0hgcYwe3rX0nSUtBJHLGsmNyhsetfFP7fv7e9r+zlpp8J+FGF148ukDZ2bo7RD0JP94+lfW3xG8baf8N/A+t+J9VmWCw0u0kupGb/AGVyB9ScD8a/FH9ln4Rah+3F+1bq3iPxB5174ehu31HUJpCSAhYmOIH8OlBSNnRfCv7aPxY0k+MdOu/E8ttcZmi8u6EAdTzlUJ6V1HwH/wCCjHxS/Zv8ZXPhb43WmpanZKFjaO9TF1a4JJYf3sg+vav2F0jTLbRdNtrCyhW3tLaNYookGAqgYAFea/HH9mX4f/tBaLJZeLNBtrqfafKvlQLNGxHUMOTQFz8Nv2pvino/7RH7Umo+J/C0c0enazdW8dt9sXY5OUXLDJxyK/oJ8J2z2fhfSIJMeZHaRI2OmQgr+cvXvh8vw5/aXbwpby+dHpniKK1jYnqomAFf0f6QCuk2QPXyE/8AQRQSWicUbq8x/aWu/G1j8FfE0/w8ilm8XLbk2SQhS5bPO3JAzivxzs/2nP2rvghrk2v+IbnxhDF5wFxDr1pK1lJg8gbl2j/gNA0rn7rySLGpZjtUclicAD1NfiJ+0ZL4n/by/bg1Dwr4RnhWCxd9Psri4ZvIhgiyHlbaG6kn68V9L/Fr/gqR4e8Rfslz3+hh7Tx5rMb6W9lgD7MxXEk33s7cE7T+la//AASD+BEXhv4a6r8TdSt92seIpTDazPyfsysTnkcFmJ6dQBSKWh9W/sm/s/r+zT8GNJ8EnU/7XuLctLPdBNqtI5ywUegNeyU1adTIPPvj38XtM+BXwl8ReNNVcLDptszRRkgGWYjEaDJHJbFfh/8AsyfBfXv24v2k7yXVZTJYvdHVtbupixKxF+IweeTyAPrX2x/wWW+NVrpvgfw38NLWYvfahcjUr6MY+WJOIx1zkkt27V61/wAEu/2d1+EHwIt/EWpWqxeI/E/+lzSc7hBkmJTkDnB/WgD0Txx+wH8E/F/gSTw7H4F0vTHWErb3tnF5UySbcBiw5POOua/B/wCM3w1vvg38S/Eng7URm40u5kt1YA/MoYFWBIHBFf011+I3/BX7QrPTP2o4rm3RInvNIilmCjq/Iyfc4oA/VX9jvUf7U/Zh+G1xz82i2459kAr2SvBP2EZGk/ZL+GxYEEaVGOfYV7tdXCWlrNPIcJEhdj7AZNAH4af8FLvjNJ8cP2mToGmCVbXQnXSYIpMHMxbDuuCeCcflX6wfshfs/wCifAL4NeH9KsbKFNUktElvrxU/eSyMNxyeuMmvwx8VfEyGx/ac1bxm2nDUY4fEEt79nbkuiydPTPFfsD8Jv+Cn/wADPHug276h4hPhLUEjUSWWsRmPB6YVxlW6djQB7d+034DtviX8A/HPh+5jSQXGlzvH5g4WRELqfzWvyx/4I7eOrnwv+0N4g8I/M9trOmu7qD8qPbvgHHqd5r9BfHH7eXwHHhHV41+IelXTzWc0axwSb2YlCAMD61+eX/BJjw3N4j/a217xFZYbTbCwuCzEEcSyDbj/AL5NAH7SUtFFABRSE4r4m/4KPftWeP8A4Aad4e0rwBpd19v1MSPPqYszNGijACrj+LqT9RQB9tUxpEiXLMqD/aOK/Cuz+Pn7YfxVnmi0jUPGF6ZANyWlsYkAPTqBitLT/wBkX9sbx8XuL6PXIC3zbtS1gx7s+gDGgD9sNQ8WaJpChr7WdPslPQ3F0kYP5msTT/jF4G1bWItJsvF2jXepSnEdrDexvIx9AAea/HKb/gmH+0vrkZN41mxHOLnWpG/oa9N/ZQ/4Jp/Fv4efH7wt4n8ZQ6ba6LpM/wBqeS3v2mdmA+UYwO5oA/XCiiigDmfiR8O9F+K3gvVPC3iG3+1aTqMRimQHDY9Qexr4c8Uf8EY/hpeWcy+HvGfijRbpiTF9okhuYIyf9jYrH/vqv0JooA/HL4rf8Eg/H/wz0OTX/Bfja38VahZlrh4xYnTpo1UZDRsJX3N1446V7D/wTB/bS8U+PPEM3wn8d3E2p39ratJp+ozqTNmNiJI5GJ+bAK4PHev0a8RalbaPoV/fXzpHY29vJLO8hwFjVSWP5V+K3/BPfT4fGv7fU2o6VcXNrpkLX9/G0R4dN+Ap6YB3fpQUjt/2qf8Agnf+0j8SvjJrGuWT23jDTdQu5Hguf7WjtxbRE/KrRyupHH93d07V5L8Xv+CZ/wARPgF8GdU+IHirV9FxZ+Xv02xJuJBuYL8zsAo6/wAOa/dvJBr4A/4LKeNpdD+A/hvw/FcPF/beqnzEQ/6xIlBII+rD8qCT5N/Y1/4Jz+HP2tfhw/i3/hY9zpL2t21pdabDoqMY3ADY8zzhnII/hrnf28P2KfC37Ho8F/2b4iv9dOuSzC7+0wCMwxx7MMm1jknc3X0FfbH/AARl0P8As39nDxBe5Y/2hr0kuGHTbGifj92vAP8AgtV4knm+K3gbRHIW0t9HkuU9d7yMD+iigD2/9lP/AIJy/A3xR4M8GfEiy1HxFrNxIsV9Gs92iweapzgoI84B/wBqv0Khj8lAgPyjhRjoPSvnr/gnzAtv+yH8OgqeWGsA236kmvomgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBuKNtfKt5/wUa+Gdv4guNHTTvExurcMZGk0somB6HdzXikn/BZnwV/wmr6XH4I1g6Rv8ldQknjWTfnGTHzgfjWMa0XomdEqFSHxKx+ih+WlVs1+d3j/APbl+OXxOt7i0+EHwd1JLXGV1e7PmFvQquAMfjX1t+zB4s+IHjD4T6Zf/EvQxoPinJSe3A27gOjEdia1jJSV0KdGUFdnrtFJS0zAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBK+UP+CgX7R3j79nzwDpdz4B0Vr/U9Qmkje7FubgWwVVIJQKRzuPX0r6vIpNoPUZqWrjTsz8I779un9rDxxMlvZavrAnzjytJ0bY3PriOrdn4Z/ba+L8jqrfEKcKAxNzcPYx4b03FAelfueI1T7qhfoKdtqeVluVz+ff4ofsa/tCeGtLuNd8eaJfPZQo0r3GoamlxjAycYkPNZH7Gn7Lk/7VPxSHhyS/fS9Ito/OvbmIBnjXsFUnuRX66f8FH7qy/4Zn8SCWULPHESm0884GPxr50/4Is+EdMXwn458Q+Vu1U3kdn5h/hjCbsD8TUpvmsXb3T2jwL/AMEm/gT4NkgnvbLVvElzGVYnUrweUSP9hFHB9CTXV/tQftKeG/2Jfh3Z22i+E3LSL5Vha2MAS3UgD7zDp1FfUeOawvF/gHw94+08WPiLR7TWbRTkRXcQcA+o9KuSfQzT6M/n8/aE/bU+Jv7Q8rLretyWOjrI3k6XZsUQAgcNj73Qdad+xv8AHDwV8AfiBceJfGPg248WSJGoslgdMQPk5chj1xiv2nvP2GPgbfNOZPh1pIMxyxVGGPpzxXKXn/BNH9n28Lk+Cli3dfKuXH9aOXSxV4nz7ff8FpPCCQ7dN+HmtSSgcLNPEqn6YNfV/wCyn+1t4Y/at8KXOp6HBNp9/ZkLeWFxgtETnHI6jg1xUf8AwTE/Z8jheP8A4Q5iG/iN2+R9K9k+C37PXgT9n7RZ9M8EaLHpUE7bpn3FpJD23MetGt9Cbo9GWnU37tDMR0GRVkDqKimuY7eN5JXWKNBlndgAPqa4/VvjV4B0OTy7/wAZ6Dayf3X1CLP5bqVx2O1ory+6/ae+E9ljzviH4eTPT/T0P8jUMP7VXwhuJBHH8RfD7OegF6tLmQWZ6tRVDQ9e0/xLpsOo6VewajYzDdHcW0gdHHsRV+mncQUUUUwGt92vzS/4LLeKLex8D+FdFWBjNeXhlkkHHCL8oH/fVfpa/wB09jX5b/8ABY+BLnQPC0sl0rXMFyQEXjhhj+lZya0RtDZn0F/wSh0MaT+yPo8+STe3lxOQe3zkf0r7Ir43/wCCUWqS6h+yTo8UgULa3c8KFQckbj15r7Iqo7GT3CkpaKoQUUUUAFFFFABRRRQAUg+7RSZ4FID8V/8AgsBpd5aftCaZdTuogfTFMBHXhu9fqv8Asu6l/a37Pfw/ufMEhfRrfLAY52CvzI/4LNa9YzfFnwppUcH+lw6c0ktx/eVmwB+GK/RP9hy4kuP2U/h1JJ97+y4xwMVEXZG0tj3UfeNLSL9406tDETaN2cc0MobrS0UAFFFFABRRRQAUUUUAJ3FfBv8AwVs+OTfD34OWHg6xl8vU/E0hTKtgpCp+Yn2OcV95NX4of8FhPHkHib9o7TdHtpS/9h6UttKp52uzlzgevNQ9yo7nqn/BIH9me01WTU/izrtmlx9mk+yaOrgnY4z5kmOhzwAT6V+rQzn8K/Nf9jH/AIKGfAj4U/Azw54M1nUL/wAP3+mWwE7S2MkiSyEncQ0YOfXmvoGL/gp1+znIpI8egezafcg/rHVIJbn1O1flN/wWy8RWVxffDrRUZWvrZLm5kXPKq+wL/wCgmvpjxT/wVU+AWj6Tcz6f4ln1a9WNjDbw2Mw3sBwCSoA5r8xdSb4mf8FFv2hn1G006S6DSJEGCYhsrTdwCcemetMSP2Q/YrsJ9N/Za+HEFwCJBpEJ59CMivbawvAvheDwV4N0TQbZQkOnWcVsqr0+VQK3aACiiigQUUUUAFFFFAH5z/tYf8FUdX+BPxi1bwT4c8I6fqcelkRz3epSyKWcjnaFI4+tfIfx2/4KlfF34xeHm0Wza18G6dIT57aGZFmmQ/wGRjkD6etfrt4//ZJ+EHxQ8QS654m8AaNq2rzHM15PbgyS+m496p6f+xX8CtMwbf4VeF0YfxHT0J/UUAfz+fDTxP4c0Tx7Zax420m48T6ZHMJprETbTOc5wxIOc1+rvgX/AIK9fBzRdFstJHgzXdAtLSJYo7SzijlSJQMADBXivrfVP2TfgzrSqt/8MfC92q9BNpkTf0rh/Gn/AATv+AXjTT2tZPh7pukAncJNHj+yOD9Uxn8aAOE03/grR8Ab541n1DXNOVuDJdaYdi/UqxP6V9QfDP4p+F/jD4Vt/EfhDVY9Y0efhLiNGQZ7jDAHNfCnjb/gi38PdXuml8N+L9Y0CIn/AFMypdKPoWwf1r7g+C/wssPgv8NNC8H6dJ58GmW6wm48tUMzDq5A7mgDt6KKKACikam5oAZdTQ2sLTTyJFFGCzSSMFCj1Jrx/Wf2xPgp4f1h9Kvvib4bh1BG2NB/aEbFT6HB4r88P+Cj/wC0z4r+Mvxei+B/gG5mfT47hLW5hsSQ97cMcFGI/hX0rrPhb/wRdsLrw3DP488aXVvrEqBzZ6VCpSHPYs3U/Sgq3c/R7w38SvCnjWOKXQfEWm6vGRu3WV5HJge4Br+fr41Ko/a614ADyz4pzwOP9cK+99b/AOCNU2hyLc+Bfitf6bdAk7rmAxMOOMNE2a+BvA/w7uND/ay0Pwbq93Hqt3beJIba5uslxMwlG4nd1zjvSKR/RBofzaHp3Ug28fT/AHRVfVvGOh+H7y3tdT1ezsLm4IWGG4nVGkJOBtBOTWpbwi3gjiUYVFCjHoBivw7/AG+PiFf6x+3hNJ5zyR6HqVnaW6FiVGGXOB260rk2P3IJyARyK8e/ao/aH079mX4UXnjK+s21F43WG3s1bb5rt2z2r1PQZTPoenSN957eNj+Kivz3/wCC1Vxfw/BvwPFbswsJNWm+1KDjJEa7M/iTRzCW59CfsX/tl6T+1v4a1OePTv7E17SpAt3p2/eFRs7HB98H8q+i7lo9pDDJNflr/wAES9Nh874makWLXLLa2x9No3MD9ck1+pN0wVRxyaVr6l6JmfeRwPGi+UWYHjAz+dcZ8Wvix4T+Bfgq48R+Lb23sraJGaKBnCyTsBnagPU816AzJb2rzSsscSqWdm6BQMk1+KX7XHjzWv25P2t7XwL4OmM+l2kxsLI7j5YxxJKR+H6UcpblfRHdfED/AILLeM5PEFwfBvhnS7XRVfbD9vDPK4Hc46V8VfH3476v+0F8RrnxnrVnZ2upXCqHSzUqvy9zX7UfB/8A4J9/DT4S/C290aTQLXXddvbBoby+ukDtJJtP3M/d5Pavw5+JHhG88CfEHXdBvbKTT5LK6kjW3lHKrv4+tOxCP6I/2YdUfWf2f/Ad3Ihjd9Jt8g+yAV6hXnn7P2P+FI+BtoAH9kW/A/3BX5a/8FR/i58SfBH7T2lJa67cadpunW0d5pMMLlUB/iJA6kkd6ZO7P2KkXdiqmralBoulXmoXLbLa1heeRvRVBJ/QV5F+x38a2+PvwB8MeK7l1fU5YPJvdoxiZeG/PrXPft8fGyx+Cf7N/iW6ny+o6xA+l2EQ6tJIME/gCTTF5H5m/sy+FLP9qz/goVqer3Ku2jw6jca42043eVIPLB9s4/Kv29VQqhQMADAr81/+CNPwim0rwT4r+Id/C27VrhbCydh1iiJLH/vtiPwr9J1/XrQDHUUUUCM3xFqDaRol9fpbvdvaQSTrBG2GkKqTtH1xX4/fEH/grv8AGCTxFfQ+H/DWh6HaQzPEI7i1kmnOCR853AZ+gr9kmGevTuMVUXSrOO489LWFZv76oAamxSZ+LGkf8FLv2o/Hdy1j4fs4Lq84Ij03QjMwz7ZOK10/aS/bp1SdzHp3i2Ju62vhSMj/AMejr9mh15xmlo5Quux+M918X/27ryAhrXx4kZ5Zv+EXhjx9D5dfUP8AwTzj/aT17xLq2v8Axc1TVI/DPkNFb2Gr2yxyyyluGUAAqBg/nX3xSHpT2QhvHTPNFI3Sq8kjRyLjoTzWDlqOxYbPamwr8vzcnNRvPHHk5570lreLcSMq/wANEZahy6H41ft2fL/wVE8Ont9v0An8DFX7QV+LH7eTFf8AgppoLZwBf6Gf/Ho6/aeugkKKKKACiiigAooooAKKKKACiiigD8ZPF0KTf8Fcl8ohwPESklTkA+XyK/ZuvxP+LV1L8M/+Cpp1C5z5beI4JfnGCUmAAI9ua/a5WDqGU5DDIoAdRRRQAUUUUAFFFFABRRRQAlcz8Qfhr4a+Knhu60HxTpFvq+l3K7XhuEz+IPY/SunooA/HP9tD/gnVq37PH2z4n/DDUpIvDul7bmSFpStxZndjKkdVBIrwv4uftMePv20bz4aeBZ4WkktzHaJDCebqckK0jepwP0r9uf2jtDs/EfwH8e6ffhTay6Nclt3TKxlh+oFfjX/wS08MaVrv7XuhjUTHItjZXN1bK/I84ABQPflqC1sftX8I/ANh8L/hzoHhjTrZLW30+0jiKIoGWCjcT7k5rsKatOoICvD/ANtH4vR/BP8AZx8YeIRP5F61q1nZsOvnSAquPoMn8K9wr83v+C12tXdn8Lfh5p0MxS1vdVuDPHnh9kSlc/iTQB4F/wAEfvC9r4u/aO8QeIb+IXl3pWmNIkz84klfBfnvwRX7O5Ffzl/AX/hefw61D/hLPhhoPiiP7RGFN1pWmTzRTKCeDtQhhnNfRiftZ/txXOLeLQvFoZjtH/FIOP8Ax8w8UFWP2I8eePND+G/he+8QeIdQi07TLKJpZZpSegHQAZJPsBX48fBfw/qX7dX7el745S0dPDWm36X9xMGG2OJGIhXBOTkr26d6ms/2Wf2uf2sPE1jH8SbjWtJ0Ine11rF0ixRK33gsCvkEgdNtfqh+z7+z34U/Zz8BWfhvwxYRQbEBurvb+9uZO7Mep5oHsenRqsahR0AwKfkVDLII1/2j0p0ZLKCRg1LYrElLTVp1NEhRRRTAKKKKACiiigAooooA+Bv+Cvnxrj8DfA/T/Bdv8194muP3m1sFIY8E5+pOPwrr/wDglj8Hm+Gf7M9jqV1Ei6h4imbUHYD5vLPCKT9K+Mv+CzHnp+0F4ZE0rNaNoqvHGT8qkSEE+1fqj+zo1i3wK8CnTWRrL+yLfyynT7g/rQO56Iq7Sfem3Ewt7eSVvuxqWP0AzUlY3jLVrbQvCes6heTLb2ttaSySSOcBQENAj+fVrwfET9taOeHkaj4uBTzOOBPxn8q/odtIzDawxnqiKv5Cv53P2dox4l/bC8HvanzBJ4k89T2K+azZ/Kv6KaAEIzWN4s8H6T440C90bWrKG/0+8iaGWGZAwIYYJ571tVy3xS8aWfw7+HPiPxJfyNFa6bYy3DMoBbhTjGT1zigD+cj4r+B7bw78afEfhPSXM1tb6vJYWo9MyYX+df0R/ArwPF8Ofg/4Q8OQxxxrp+mwxMI+hbYMn86/B/8AZb0Ob41ftieF2kia7W91ttRuFcdUDF8n9K/objjWONUUYVRgD0FA7igYpaKx/GWqDRPCOtagSVFrZTTZXr8qE/0oEfir8ctUh/aw/wCCjlvormZdJXV49MVXUZEUP3s4J4JB/Ov230nS7fRNLtNPtIxFbWsSwxoowAqjAr8Uv+CY/k+Mv27bnUr6NbmZrTUb5XkGSsgdcH64Y1+3FABX4U/8FYtZfWv2tNVg37hY2MMOD2AGcfrX7qswVSScAckmv51/23fHEfj/APai+IWrQ7mg+2vAjHHRCF4wenFAH7p/sqaGnh39nP4e2CbT5ej2+SvTJQE1oftGa/N4X+A/jzVbdzHPa6PcOjDsdhA/nVX9mHVYNa/Z7+H93bNuik0e3x+CAEVz/wC23dPafsp/EuSMMW/slx8vXBIFAH5Qf8E2P2dfB37TfxK8ZWPjvTrjVLO1sY7mOSC4aIxyO7ZJI6//AFq+vfEn/BGbwLqGoNJoXjrWNDs8nFrNZxXYGfQswxXEf8ETNBt7e3+JWohle5L29s3HIUAsP51+pNAH5V/Fr/gkL4a+Hvwz8S+Jz8StRupNJsZLtYpNLijV2UZAJD9+laf/AART8GiLTfiL4qZG3XM0Ngr4wpCbm4/76rtv+Csn7SzeD/Atn8MPD1yx13XWBvlhILJbngIec5Yn9K95/wCCffwTm+B/7NPh3TL2PytU1AHULtcYIaTkA+4GKAPpEZ70tFFACHP0qveabaakqrd2sN0q8gTRh8fTIqzRQBXtbC2sci3t4bdSMYiQL/KrFFFABRRUf2iITeUZUEuM7Nw3flQBJRRRQAUUV8Y/8FAv26NJ/Z78I33hXw7eJdfEG/i8uOKPDCzRhgu57HHQUAed/wDBUj9tSD4e+F7j4U+FZFudf1mArqN1G4ItYGx8gxnLNyCMgir3/BKH9lO5+F/gm7+I/iK1e21zxFGq2VvKPmgtOoJ92PPT0r51/YL/AGC/Efxn8a2XxT+JEE8XhqKcXkEOofNPqcuchuuVQHB5zmv2Ih8i0WK2j8uIKu2OJSBgDsBQO5KBivye/wCC23jS1n1j4c+F0Ob20iuL9yD0WTCAYx/sZ/Gv1ir8gP8AgpT8CPit8Vv2rrX+zPCuoatot1awW2nXdpAXiVeN5ZhwCDng0CPuD/gm74JTwX+yX4OTyWgnvojeSq3Xcx618D/8FqIy3x68IseFGgce/wC+ev1s+FfhuXwb8N/DOiTRLDNYWENu8a9FZUANfmz/AMFrvBM003w/8VR2ryQrHPYTTImQnIdSx7daAPuj9jOyTT/2X/hzCmAo0iE/L7rXtNfmh/wTx/4KEeD7PwFoPwx8cXJ0TV9PQW9pqFww+zzpngFv4SK/SHS9c0/XLVLnT763vrdxlZbeQOpH1BoAuSSLGjO7BVUZLHoBVTS9asNatzPp97BewgkF4JA4yOvSma9Hb3Gj3tvczJBBPC8TyOwAUFSCf1r8Nv2X/wBqLXv2bP2m7zSYtSm1HwhfazJY3Vm0hdMNKVV164POfegD92aKitp1ureKZPuSIHX6EZFS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGLqHhfTL6ZZJ9Pt5WwQWMSEkHqDkdK/Jr9rj4B+DvDf7cnhRYptP0zR9UmgnuNMtwd7Nu/u4xz9a/XxslcV+OP/BTqO78H/tgeE/EaqMFbd4xvBPyuM5Hasai093c6acm92fr9oOlWel6PZ2tjAkFpHEqxxooUBcccCtHbtrH8G6g2qeFdIu2G0z2kUmPqgNbPNapuxhK93cRadSc0tMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0E0AB7UkjbVJwT9KTJPal59KNhnxL/AMFThHZ/s4avcImyaUqh+bqMjtXln/BFa83eC/iBb4OBfxSfmmP6V3v/AAVU8y4+BuqRIJWbKZ2rlcA/pXJ/8EW7VR8KfGd35TB5NSVTJt4OE6ZrH7VzeT0P0d/ipabz1pc1sc4tFJS0AFFFFABUcu7bhfSnkUjcc5x60AfD37aXw4/aQ+MH2nQPAs9jpPhtIsv9nnMct3njazV8QeG/+CUHx88RXS/2qNL0pWPzTXd4ZT9eBX7fvIkaF3YIgGSzHAFZk3irRLeTZLrFhE/Xa90gP86iW5o5cz2PyVj/AOCLPj+Tbv8AH2hx5+9/ocjY/wDHq2LT/giT4jZozc/FPTohn51h0l8474PmV+p7+MvD8Slm1zTVUdSbuMD+dchrn7R/wv8ADbOmo+O9CtnT7y/bUYj8iaNEtSbsl+AfwftPgR8K9E8F2d5JqEWmxbDdSKFaQ9zivQ65/wAE+PPD/wARtFTV/Deq2+sac52rc2rblJHaugqlZrQQUUUUxCN0r82v+CyPhmK4+HXhrV0ixLBfrG7L0YNnGfyr9I5H2gcE59K+Fv8AgrZpouP2cpZtjsYL+CYMBwACc59uaxnuma0+pqf8Ej2U/spwgNkrqdwCPT5q+2K/Pv8A4I2+Ko9R+BXiDRcYlsdVeU89nGa/QStI7ES3Ciq9/NNb2rvb2/2mUD5YtwXP4nivyN/a28bftW6p8ULu0uNfl8B6CbhhptraarDZq0fZmYMGc49TijmSHGLlqj9eqTd82McetfiY37RH7XP7M2k2Ov6xrMviHw9cHEVxqDJf27AdcshDD6k19qfsnf8ABTzwZ8bfs2g+L1h8I+LHIRFc4trpj3Rj0z6H86OZC5WfcFFMhlWaNXRg6MMhlOQRSMjtIDuHl45XHP51RI+lpAoWloAQ0xiQBTmphPTjPP5UmM/Gb/gsRp3nfGPw5qscUiW8mmmLcw4LK2Tj86/Tb9ja0jsf2YPh1FEMJ/ZEJ5Oeor84v+CzF7P/AMLG8H2JXbCtm8g9Mk4r9DP2GdUbV/2U/h5OzBiNNSPIHpxWK2NZnu6/eNOpgYbjzUGoXi2NnNcOzBIUaRioycAZNaJmRaor5Z+HX/BRz4QfEDxndeFm1O50HV4blrZU1SLy0lYNjhs/zr6ht7iO6hSWJ1licbldDkEeoNO6G4tEtFJzmjn1o5kSLRSUtUAUUUUANavwP/b2tYdc/bi8SW+oxS2lrdX9vC7q4Vgh2ruGRX73TAshA6npk4r8mv8AgsB+zxe2PiTR/inpNnmwmiFrqk8e4tHKD8kh54GOOKl73Lie+xf8Ei/gZr2k2FzBd+KdPaS2jZmtNTjKyMVBLHdE3X2wK47xD/wRT8CXjIdG+IfiDTeSWF3bx3OR6ZBTFd5/wS1/aaf4xfCGTwnrd8LjxL4axFmQ/PLbdEY/TpX2/k00S9z8/fDX/BGT4V2FuE1zxT4j1iUEHfbvHbA88gjD8GvsT4N/AfwR8A/DSaJ4K0ODSbXAEko+aaYju7nk/wAq72lyaYh1FcR4w+NHgvwBr+kaJr/iGz0/VtWlENnZySDzJWPYCu260ALRRRQAUUUUAFFFFABRRRQAUm0ZzjmlooAKKKKACiiigBrVzHxN8YW/gD4e+IfEd0xSDTbGW4ZgcdFOP1xXU18xf8FIPGEXg/8AZB8cs0hjl1CFLCIqcHc7DofoDQNbn57/APBMnwjP8a/2vtd8cXjG4i0jztSlNwPM3vM5CEk55HrX7RV+Yf8AwRN0eBtD+JWriKNZ2ube1LbRu2hN2M+me1fp9QOW5FNIIYnc9FUt+VfzxeFdTlvv2ztMvTK7PJ4w3b2Yk/8AHyR1+lfut+0n8TrT4P8AwT8WeKLqUQi1spFibOP3jAquPfJr8Df2Z7p9c/ak8C3Vz+9Nxr8crCQZyWctk0Dif0dr90fSvwV/aisSn/BQLWoJvnD+JrdiG5zl1NfvXX4g/wDBTSyuPhz+2s3iNbVBHMtpqMSgY8woRn8SRUtBE/bbSVC6XZgDAESAf98ivzP/AOC13jOFfDnw+8LRXC/aZLme9mgB5CbQqkj6g19c/C39sj4ceMPgnp/ji58RWGmQpag3VpPOolikVeU25znI4r8Y/wBt/wDaTf8Aaa+NF34ggg+zaXZL9isU3ZLRqfvfjU9QS1Pur/gibpoXwX8R74YGdRghx34iBr9LpIxJjPavzq/4It6zp8nwl8ZaXFEU1GHU1mmYj7ylMLzX6MN2q1sKT1PFf2zPHj/Df9mfx3rMJKzrp7wRspwQzjbn9a/OT/gjb8Nl8RfFjxb41vrVpX0iyWG0mY8edIx3/jgCvs3/AIKoXL2/7H/iJUJAlureI492rzr/AII16Kln8APEWo7R5t5rDAtjnCqBilfWw+lz2rxZ8SvjPoP7Uem6Dp3hNdV+Gl5BGJdQQYMD9WbP9K/Jj/goxqNjqf7X3jI2LKYYpUiYL/fAG79a/fDWNSi0fSry+mOIraF5nJ9FBJ/lX80vxs8WSeOfi14t8QHLf2jqU7oO+3eQP5UwR/RV8C1Efwa8FKOg0m2/9FivgH/gtV4CFx4c8A+LrezDSW9xNZXVyo+YRkBlB9sk19R/8E+/jNpHxc/Zx8NpYSf6ZolumnXcLH5lZBgH8asf8FB/hxH8S/2UvGlm2BPYQjUoWxyHiOf5E0xbM8p/4I/6t/aH7LssHOLTVJoxn86+Zf8Agq98bI/jN8WPCnwn8KFdTn0m4ZZVj73kuE2fgAKyv+Cfn7bHg/8AZ2+BfxA0DxBdTQ6r5rXmlIqZ852j27fY7uao/wDBMb4I3vx5/aP1j4m+IFkfT9BuGvszDImu5GJVf+Ag5oE9z9Pv2Qfg/N8C/wBn3wl4Su1C6hbWwkuwDnEr/Mwz9TXstFFAgooooAKZJIsYyxxXB/Gj43+D/gJ4TPiPxpqn9maaG2IVRneRvRVHU14Vpn/BUb9nXUpFQ+NZbP3udOuFH5hDU3HY+rPtiM2AcVIJAehzXzTN/wAFHP2d4irH4kWTKegW1nJ/9Aqjdf8ABTf9nGzxu+ICyZ4/c6ddP/KOp36jsfUytmlbpXyPe/8ABUj9naNFaLxzMeeQNIumJ/8AHBXb/Av9t74VftFeKrrw94L1a61DU7aD7Q6z2MsC7c44LgZ+lHSwWPfs7l45qtcMIwWPapooxGo2rsB52ioLiTZJym5e/tXPLQpGcrLPJvI+XPNXrONVuXKcLVO8WE7HWRtgPKrV7TxG37xCxU9mpU3dlP4T8ZP+ChDKv/BSfRCg48/RSx98pmv2mgYeTHz/AAj+Vfi1+3Cya5/wUm02G0dbgrdaXG3knf8AMCMjjuK/aG1Xy7WFT/Cij9K7DEsUU1adTAKKKKACiiigAooooAKKKKAPxS/bzUWf/BSCxkc7FNzpTlm4GMrzX7S2DBrG2IOQY1II+gr8ZP8AgpZAln+31o85YKskWluWJwOGAr9ldDYNomnsDkG3jII/3RQBeooooAKKKKACiiigAooooAKKKKAPKP2rPEUXhX9nP4h6pMwWODR58lunzDaP1Nfjp/wSw0241T9sfQJICf3Fpc3Eij+7tGf5iv1j/b4Xd+x78UxnH/Eob/0Na/PH/giv4fhvvjZ421WSEPLY6PGIZSPu75MNj6gCgdz9jFpaKKBCV+d3/BZ/wZqGufBvwbrltGr2Oj6rILot281Aqn81NfolXzp/wUI8Kjxd+yH8QrZYvNnt7IXcKgZO9GB/lmgDy7/gkp8RR4z/AGYxo7yB7rw7fPZOO4U/MnOPQ19rs6rkk4r8j/8AgjH8XLLQfFnirwHf3CW8mrJHeWStnM0q8Mo9wvrX60Xlu83IYgY+7QVGzepH/akQkK5y3rjAqaK5FwWUcHFZg0UsxJJIP4Vj+PPiJ4T+Evh2XVvFmtWui6dCCxkuH+Z8c4VRlmPsAaDeUYJaHXR7QgzubnGSpqTntX5PeAf2jfjp+1f+15c33wo1uSDwVotwGe2vZjFZ/ZS23c6EAsWx0AJHtX6t2bTtBH9pRUm2jfsOV3d8e31rN7mJYXPOadTVp1WtiWFFFFMQUUUUAFFFFABRRRQB+c//AAWM+CX/AAknw20P4i2S4utDk+x3eBndBIcj8mr1j/gl98YrL4kfsz6RowlH9q+G82FxFnnYOUYeoIr6U+Knw90z4rfD/W/CurwrPZalbPCysOhI4Ye4OK/Dy4s/jF/wTc+ND3UUT21nJKQg3GSzvrfcSFYjjOPxFBSVz97t1fCf/BWD9oaP4a/BVfBenT/8TrxKxikEbfNFAMEk88Z6VzGk/wDBZXwDN4JW6vvDGrReJfKObKEBoTIB/fz0/CvmH4C+B/EX/BRz9qi78V+L0m/4RixP2m5AJEccYP7uFOME560Bbueef8E2vBo8RftieErW4BQ6eJbwqwwSETP581++m6vxH+M2qSfsRf8ABQyXXbC1FvoiTR3KxxLu/wBDlUBlA9QBX6z/AAY/aT+Hvx70eG/8IeIba8eRctZSOqXKf70ec0A12PUc189/t+WtxefsmeP4rZJHlNnnbECTgMCa+g1qtqul2muabc6ff26XVncxmKWGQZV1IwQRQSfiB/wSY0O61T9rTT7uK3MlvY6XcPNIoyseQAu70Oc1+5VeP/BD9lH4c/s96zrmq+C9G/s691g/6TIzlvlyWCrnoMmvYKACuU+K+m3GsfDHxVY2pUXE+mXEce4kDJjb0rq6ZLGssbI67kYFWX1BoA/Dr/glbcNoP7atvBcjEjWOoWjAY4ckeuP7pr9x91fid+2R+xj8VfgB8Xta+JHgWxupPDU1017b6hokheWzLHLLImAy/gCPeuTj/wCCjP7SHjbw9H4N0zWjc3c6i1EtjpoN7LkYK7wuQ3vQVa598ft9f8FBdJ+BekXPg3wfLFqvja7Ro5WXDQ2cZGCWbP3ueBivyjvv2Z/ihqvwyf4q3Hhm9uPDlzcSGW6CNvGfmMhU87CT1r7O/ZH/AOCXPjDxl4tsvG3xoBtdGLC5bRrq4dr66kzkeaMYVe/3sn0r9Yv+Eb0v+wRon9n2/wDZAhFsLLyx5XlgY27emMUCZ+Qv7Kf/AAVVX4J/DjTfB/irwvPrWn6XEIre60plWTbn7rByOa+9fjn8QrX40fsL+MPFOkWN3b2ur6C88VtdIBKg4OGAJHbsa5u6/wCCXvwSuviUfFzaXdRjzhP/AGTHIFtN2c/dx09q+o7rwppk3hWbw8llDFpT2zWgtVQCNYyuNuPSgR+Yv/BE/wAR2P2j4laOWKXzfZ7sBiACnK4HOc5FfoZ8evjp4a/Z9+Hep+K/Ed2sUNtGfJtww8yeTHyoo7kmvxZ+MH7K/wAcv2V/ihf6x4Z03V7Wzku5GstV0He6OhYsqnaOwPcVofCv9m39oD9tbxtBD4v1DXLfSbciWfU/EDSLDGmcERoRgsfYUAdN+zN4F8Sft6/tdT+O/EsE0nhywuhf3UrDEaorZihB6E5AyK/bKCNIYY44xtjRQqj0AHFeffAb4F+Gf2e/h3p/hLwzarDa265mnI/eXEh+87HuSa9EoAWiikOe3WgD5G/b+/bL139lHRvDf/COaJbarqOrSyKz3u7y41UAjGOpr4sP/BYz4uXEeyHwhoPnYwNqysSfYV+vGueFdG8TrEusaTZaosRJjF5brKEJ643A4rOt/hj4PtZA8PhbR43HRlsIgf8A0GgD8iJf+Cin7WXih/tOkeHJIbduQtr4feVcfUrUf/Dcn7Z0n3dC1P8A4D4Wb/4iv2ZttPtbNdtvbQwL02xxhR+lT7R6D8qAPxZuP2y/20NSheBtG11TIMK0Phpo2H0ISrP7JvwZ/aM+Kn7Rmm694ru/FXhq0gk+2XmoakskaSKpyIgpI61+zu0eg/KloAjhV0RVZt2FAz3J9a5H4weObz4a/DTxB4lsNKk1q8021aeKxjzmVgOnHOK7GkZVkUqyhlIwQRkGgD8NvGP/AAU4/aL8cazdxaRef2LHIxRNP03TcyRZ427tpYn3NeQ2v7Mv7QHxu1i81j/hAvFGt3103nS3moRGLzCe++UqD9B0r+g+x8F+H9NunubTRNPtriQ5aWK2RWY+pIFbKqFGFAUewoA/Dq1/Y5/bSttFt7W10/xFb2UMexLVfE1ugVfQKJhge1c3Z/sZ/teadrSaha+EfE1vqsTblvotai35/wB43GMV+9VFAHyB+wTB+01psetaf8ebZl0mG2j/ALKuLq4t5rp5dx3h2ikYkbcfeFfX9FFABXNfED4c+Hfil4Xu/D3inSrfWNHuhiS3nXj6g9QfcV0tIV3daAPyV/aW/wCCQOuL4iuNW+EN3bXWjSkuNFvZvLktz6K5PzfpXz3F+y5+1n8K5G0/R9E8b2sJ/wCgFcytEf8AvhsV+99FAH4QWPwB/bH8ayf2bcWXj/y3GP8Aia3kscXPu7YrufhF/wAEpPjdb/EDRdU8Qw6Xpmn295Fd3Ej3yTO21gxGFJ5r9pqKAILG3NrZwxMQTHGqcdOBip6KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDN0XUm1bTba7MMkInQSLHKAHUHpkAnB/Gvyg/4LAaDaWvxc8A30FoYru4Co9xu4cBwQMdq/Uvx74mm8D+D9S1i20u51me1hZ47CzTLysBwB6V+LP7THx2+Jf7Y3xX8LaFd/DyfQrjTb4Ja2MVrK07ZYAl2K9MfhWU1qrHTDdvoftB8KZPN+G/hlj1OnQf+gCusrnfh9pU+h+CtD0+6UJc21nFFIo7MFGRXRVqYS3YUUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANbHc4qve6jaabaPc3d1Da2yDLTTOERR6kk4FLqFvJdWkscb+W7KQG96/Nr9vT9kr9on41+JtKn8JzRa5oUcBjfToNRitBC2epErqGyPSs5Sadi1FNXufbkn7UnwihvJrVviR4Z+0wnEkY1OIlfr81U9Q/a6+DWlKjXPxJ8Oxhzhf9PQ5P4Gvx70j/glL+0ZqF55Nz4R0/TUP/Le81m1dP/IUjH9K77T/APgjJ8Zrry/tOveDbFWPz/6XcOyj6CEg/nT1YtFue4/8FIv2tvhx4w+D1zong7xjpviHU72RYpbeyO8on97NZH/BLH9pL4d/Cf4M6vo3i/xXpnh+5k1Bpo0vZRGWGMd+tctb/wDBEfxaZl8/4k6Kse35mjs5SQfYccVY1D/giT4kht86f8StKmn9LmwkRfzBb+VLk63KurWPv63/AG1PgZcsQvxQ8Nrgfx36L/M1aj/bC+Ccwby/if4YfaMnGpR/41+Zg/4Iw/F1JXC+LvCGzPDM0+T+Hk0+T/gjL8XPL/5G3wm59FaYf+0hT1Ija+p+qvwz+O3gP4w3OoweDfE2n+IJNPx9p+wyhxHnpkiu+r5i/YT/AGQbj9kzwLqthqmqWusa1qtws881rFtWMAYCBiMsO9fTtUr9Rytf3QooopkhSUtFAHx//wAFCvh38ZfiR4LsNM+GHmNH5jPcC0uTDNjGME55Ffn7pP8AwTe/ab8XKLu8jWynxg/2jq7qzflmv3CoqGi1Kx+J03/BK/8AaRkjAOoaWQeqnWZT/wCy03Sf+CQPxy1K6YalqOgWcZH+sa+kl/QKK/bIjNG2qtoHMeJ/sf8AwBm/Zu+C2meD7y9S/v4WaS4nj+4WJ7e1e20mMUtCViQooopiEr4z/wCCpmsDT/2XdeUY3TSxQfMm4YLdR6GvstmxivjX/gq1a3Fx+yhq7wEBI7qF5RtyWUN0z2rOXYuOh59/wRo8Ow2fwY8T6yqMJ77UtjsXBXCLgADGR+Jr9Da/Nr/gjd4u0Sz+E3imwuNVhtryPUPNe3uJ1QAMOCAa/QuXxp4fhXdJrmnIvq10gH86cdEEtWbDV+XH/BXv4P8AiDxC2meMtO0lprDTU8u5njXPynoSPrX6g2d9balAs9rPHcwt0kicMp/EVx/xo8LweMfhj4i0WeHz0vrSSHZgE5IOCPelLuEW1ofFn/BMjXfD/wAfP2Yb7wJ4n061v/7ImNvJDJEu54m5BJ/Svn7/AIKH/sQ+C/2ftDh8YeBry60yX7SJHsZ5xtUH/njwDkHtk189/AX47eIP2L/j9qBD3P8AZVvdvb6jp6kfvowxxn3r0r4wfETxf/wUu/aG03QPCyT2vh6BQILeYEx2oIw0r479s0irNbnn/gv/AIKNfHXwH4NTw3pnipXtoxiO5u4BNcIvZQ7HoPpWja/tZftT3mljxZH4t8QXmjQvve4SCM249m2p0r6S+LX/AAR/j8H/AAbn1Pw5rVzrnjKzTzpYMfupwByqLjP618Z/CP8AaM8VfAa31jwnfW/2vQ7l2ivdIul+63IPB6Ua9A0P1z/4J5ftkXP7UHgO7svEnkp4y0chbswrsWdD0kC5OPevryvwu/4Jc+Lriz/bGsYbJ2tbHVorlZLdT8pUAsq/hX7oVafciSsMmBKHHWmxR7ecnJp5OcihvlXin5gn0Pxn/wCCyPiBb743eGrEDMdvpxPTnJav0F/4J0xTw/sg+AlnyG+zMRn03HFfnR/wWBsxbfHvQpG5Mmllsf8AA6+2/wBjP9qz4U+F/wBmLwRY65420fR7+0s/JmtbiXa6sCe2KyWxrPsfZqxgMT60skaNGysAVIwQ3TFfNWrf8FG/2ftJkkR/H1rO6dRbxO+fpxXnWo/8Fa/gnJff2fZDWtRMziFJI7UKrFjjjJ96DJJ3PCv24f2ffgt8QPGV23gnxppuh/ExGLtpvnbYp2B+5nojZ9K4L9jL/goN4h/Z+8USfDz4rXEt34dgk8hbqX55bJgefm6steJftjfC1/hL+0VbanK8/wBg8QTxazbmdh5ixu4O3I5GM17t/wAFKtG+Ev8AwrPwJrugC0HjO+giZ2s2BMkewZ8wdOtM1l2PWP2sv+Csdvogt9D+CzQare3UeX1qaHzBC3ZUjIIJ+oNfPXgf/gpl+0L8PfGWl6n4/kudT8PTMPPsrrSIrZZYz/EjiMEEdeDXin7FPxa8A/Br40WXiLx7oX9saei7IXHItZCf9Zs6Nx61+s/7X3wz8M/tW/sq3Wr+G5ba4SG3/tLT7yNeflGSvHtxg0EK3U+kfhr8QdJ+KfgfR/FOiXC3Om6nbrcRMpBxkcqfcHiunr80v+CN/wAZJNS8OeKfhnemRrjS5DqFszNlVjZtrIB2+bmv0srRbEPcWiiimIRq5P4o/DfR/i34D1fwpr1utzpupQmKRWzwezDB6g11lG0UAfg38Wfgj8Xv+Cf/AMWZPEXhd7630qOU/Y9ct4PMhkj6+XKCCMY9RX1l8Cf+CyGg3unwWPxS0K40y/UBTqmlp5sMh9SnVT61+keuaFp3iPTZ9O1Wxt9RsZ1KSW91GHRx6EGvjj4r/wDBJv4OfEC8mvdC+3+CLuZizjTZDJCSf+mbnj6A0FX7nouh/wDBQ/4Aa9p63cfxD0+1U9Y7sNE4PphhXk/x4/4KufC7wV4fuoPA13J4w8QupjgFrGRBG2OGZiOR9K80tf8AgiP4dS6D3HxS1GSEn5oo9HjBI9N3m8flXvfwV/4Jg/Bn4N61BrH2K88UapEBsfWpQ8SMDncsagDP+9kUC0PmT9iH9m/4iftBfGqL46fFsXT6fDJ9p06DUBgzNn5Sq8bVXtxX6q1FbW8NrCkNvGkMMY2rHGoVVA7ADoKloBhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAK8B/bk+Ct/8AHr9nPxH4X0mKObV/ku7RZADmSM5AHua9+prLuFAz8Ev2Qf2svEf7EPxG1fSdb0ieTRryVYtX0yRCkkDoceYg9ccfSv1N8B/8FKPgF47tRInjSLR5woZrfVYXgce2SMH8DXafGr9jf4S/H4SS+KPClqNSc7jqmnxrbXZbGMtKo3N9GyK+G/jB/wAEXbma+N18OfGVt9mY82fiBXDp/uyIDn8QKAbuzkf+Cmv7Z+j/ABvh0X4dfDjVxrOkGcS3s9juK3MnRIvcA818meA9C1P9m39o7wbJ49tH0d7G5tr+dZBkxwtyCR9K/S39k3/glLpHwh8RWPinx/rEPibVrM+Zb6ZBF/okUgP3m3ff+mBXeftif8E49D/ae8S2/ifTddbwv4iWNYJ5DD5sM0ajCgrkYIoGnY7Xwz/wUK+CnjTxzpPhPQvEz6nqupSCKEQW0hQMR0LYrY/ay/ZH8L/tS+DTZajFHZa/aqzWOqRoBIjY4Vmxkr7Vw/7KP/BO3wJ+zPPFrc7DxL4tVdo1G5TEcR9Y0PQ+9fWasGGaBeh+Id1/wSZ+Otlq0mm21vpNzp7S/Lem+ATb2Yrnr+Fep/Gz/gmrZ/Az9kDW9bikXWfHNm0V3e3CrmNIVb51jHtnrX61VDfWNtqVpLa3lvFd2sy7JIZ0Do6+hU8EfWpaHzH53/8ABGn4bX+hfDHxX4uuiyW2s3aw2sbKRlYxy351+i9U9J0bT9BsUstMsbbTrOP7lvaQrFGv0VQAKuU0Jnhv7Z3wLvf2iPgHrnhDTJ47fVJSlxbPIfl3ocgH61+OPw6+N3xr/YG8W6jov2WbTFuJP3unanETbzbT99Pr6iv6AKwfEvgLw34yVRrug6fq+0YBvLZJCPoSM0ra3HfSx+Knxg/4KsfE74ueAdQ8LHTdO0SG9Typ7qzDeaUPUDnjNWfgJ/wTJ8X/ABi+B+seNLppdK1i4USaFZTnb9oHUs3oD2r9aY/2Ufg/DqUeoR/Dnw8t5G25ZvsS5B9a9StbWGxt47e3iSCCNQqRxqFVQOgAHSqC5+Evw/8A2D/2nfD/AIsS10TQtS8O3cMof+0U1BYrdefvfK3zflX7OeBfAurv8G7Hwr471BfEGqS6f9k1G6xxKWXDfX616HSNyMUBc/nV/a7/AGd9S/Zt+MmoeGrtQ+n3DtdaW6tnfCzfKD7gmv2b/wCCfvwYb4K/sz+GtPucHUtSj/tK6OP4pBkD8Bivcda8D+H/ABJqVrf6po1nqF3aHMMtzArtGfVcjit1FVFCqAqgYCgYAFAh1FFFAgpDjqaWigD51/bJ/Y70/wDa+8NaFpV74km8NHSbl7lJ4bNLnzCybcEMy4H0NfJMP/BEfTlwJPivOw/2dAj/APj1fqBRSsVc/NjS/wDgij4Pt3Y3/wASNYu1I4Fvp0UGD/322a11/wCCL/w24z408Qsf9yOv0QopcqDmZ+cevf8ABFrwHc2IXSfG+s2l2DnzLiBJFP4AjFew/sW/sEwfsj+JPEmr/wDCTf8ACRyavbpbBWthF5QV92c5OTX13RRyhzEY7+lV7iFpFI4Aq2aqXiv5LEde1RKK2Y4lJbBYcFD8x61YkuV03TLi6lI2QxtKcnAwoJP8qqWlrPlZJJAqk4Ix2r5K/wCCi37Xmk/Ar4Xah4T0q8hl8aa1btbxW0bbmt4mGGdvTg8VCilsXLsj8+v2fdQn+K//AAUTfXoNOGrv/a15qMNruwH8rdt5/Kvavih4b/bP/ae8ZXlqdJ1TwZ4cjuXFtH532WJF3Fc7lO5uK6j/AII5/s+tawa38V9XgJnmVtP03zFIKjOZHXPr0r6K/wCCif7X2ofst/D7TYfD1usvibXXeK2lf7tuqjJf3Pat0Z7HyZN/wTH/AGirDTRd2fxO87U1XcIP7VuRz7EtivHPE3ib9rb9kfXLHWPEd34iFjaTYE1zKbqwkHcMRnAI7nFfe3/BL3x/8TPi18O/EXjDx9r9xrFre3mywSbGEA+9t46V9c+PvA+j/EfwjqXh3XrSO90u/iaKWGUZHI4P1FMk8B/Yu/bi8OftWaC9oyLpHjGxiD3mmuwxIOnmR+oz2HSvp+vwf0Pw/rv7FP7dWm2CI0VnHqixxBWIElrK+0D3HNfu7HIJY0cdGAI/GgB9FFFABRRRQAUUUUAfi5/wVKjb/ht7Q8KSWtNPxgdfnr9kPC+R4Z0kEYP2SHIP+4K/G3/gpZqSX37fWi2+QyRQaZHwc87zkfXpX7MaKhj0exQgqVgjBB6j5RQBZuLiK1heaeRYYkG5nkYBVHqSa+Ef2qf+Cqnhb4L6+fDvgfT7Xx3q8RIubiK9UWsBx03KG3NnqOMV9WfHv4L2nx6+Hd54SvtZ1LQre6ILXWly7JMDt7ivyE+D83gX4M/tqD4eaN4U0/x9o8+prpD3XiSATTJLu+aSMAY3dR0xQUlc0/FH/BWD4/6/m60my0fRLVTu8u202WXA/wBp3JBH0xX1F+wz/wAFNJ/jh4ysvAXj+xttO8QXi7LDULc4ju5h/wAsyvZsdK+85fCOi3GjnSH0qz/svyzGLMW6CIKRjhcYHFfiT8M/B9r8Pv8AgqNoOiWMP2eztvF2Iox0RGDED9aCT9z6KKKACiiigAooooA82/aQ+Gt58YvgX418F2EscF7rWnvawyS/dDEgjP5V4F/wTd/ZN179mbwT4kl8WRW6eIdZu1P7nqkKDaFz6E819jUUAFFFFABWf4g0Kz8T6Hf6TqEK3FjewtBNGwyGVhgitCigD8Rv2qP2IfiL+yd4+PjX4bDU73w9HObq2v8AT/8AW2LdSrAHJHvirOgf8FcPjhoGh22mXOlabqV5AgRru8tHMzkd2wRzX7WTRJNGUkRZEPVWGQazB4V0YSFxpNiHPVvs6ZP6UDPxp/4bc/a5/aKmj0Pwda3VtPMTj+wNNEDYPHzTPgKPckV1vgj/AIJa/HP4yarBqfxg8YrpVoz+ZLHNqD399z1AHMa8dwx+lfrtb2NtacQW8UI/6ZoF/lUrSBe9A/Q8q/Z3/Zp8F/sy+Dl8P+ELOQK7b7i+uiHuJ29WbA49hXq3TrUckhVQccd6fncARWb3GPWnU1adVR2JYUUUVQgooooAKKKKACiiigBGrm/G3w58N/EjS207xLotnrFoQQEuog+3IwSCehrpaKAPkPUv+CWHwA1K+luf+EdvLZpG3FIL51Qc84FfQvwm+DPhL4I+FofD3g7SIdJ02Pnagy7n1ZupNdvRQO58sftjfsFeG/2sJLHVH1F/D/iWzjMSahGm8SJ2V17gGvlbwX/wR38Z+E/ElrqFr8WLfTVhlV/N06ykjlKg5xnf3r9UKKAuyhoenPpGj2NlJcPdyW8CRNPJ96QqoBY+5xV+iigQUUUUAFMkUtjGCPQ0+igCOSFZo2R0V1YYZWGQfrWPp/gjw9pF615Y6Dpdldty1xb2ccch+rBc1uUUAIBS0UUAFFFFACUBQFAAAHpS0UAIM96WiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM4paZIu7FAD6Kj5xjFKgIoAfRRRQAUUUUAFFFFABRRRQAUUUUAIeagFhbLcm4FvEJyMGXYN/wBM4zU5pMH1oAULilpBmloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqTJp1JQIRadRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGpjSBFLMwVRySTwKc/Svj39sL9kf4p/tJeIrb+wfip/wiXhi3iwNLjgk+eQ8FmKOueKV0XFX3PcPiV+1B8LPhLps134l8c6LZtHn/AEWO8SW4ZgM7RGpLZ/Cvya/bY/b/ANT/AGpJG8D+C7C4t/CckyhU8pjc37g8LgHAHfGM165o/wDwRO1i81JJNe+Ktv8AZ92ZTaaUzyv64Ly4B98Gvsv9nP8AYB+E/wCzeyX2k6XLrniLbhta1hxLN1z8igBE57hc+9TvqPRH5SfDD/gmv+0D8QNLbU7Tw6vh21kAaNdYvfszyDsQo5/MV1c3/BKX9o6ORVFvpUqk43LrowPcg4NfuDjFLRyi5j5i/YG/Zx8X/s3/AAputF8Z6smo6rc3RmEcNy00cK4+6CR/KvpmaNZFG7oDmpKQjNO2lib63Pwf/wCCm3wbu/hz+0XqmrLbyJo2usLmK4ONpcjLKOK+u/8AgjT8H00XwJ4k+IVwjrd6rJ9gh3DgwoQ2R+Nfbnxo/Z48DfH7Rf7L8Z6QupQKP3Tg7ZIT/eRscHFdF8NfhroPwl8G6d4X8N2n2LSbBNkUecsfdjjkn1qVF2Kk00dK33TxX58f8FJP2HtE8ceBdR8f+ENJhsfE2n5uLtbVdv2pMfMSAOT3zX6E4qtqOnxalp9zaTKrRTxtG6sMggjHSnZiWh/Px/wT38TxeDP2t/BFzdRsoe5a1wezONpr+hD0r89fC/8AwSjh8H/tB6d4+07xeg0i11D7eNOe3O8Nu3bQemM1+hdHKwk7jNwDHPFc54s+JXhbwRZ/adf1/T9KgyRuubhVyQM46184ftrfs1/FP42NYXPw78d3HhxoQRLZi4aFH49Vr40X/gkn8avGDxv4o+IFm+58v9ouZbggeoyetV0sGh5R/wAFFvjB4b/aM+PWmHwJNNrX2WEaenlKcTOW6L61o6P/AMElfjLrXg221of2bbXkyCVdNnmIkCkZAJ9a+5v2Wv8Agl34T+AXjCHxTrWtSeLdUt0BtoJIFjgglyDvA6k445r7e2gYwMVPKx8x+THwp/4Iz6trnh5Lnx14wk0PUGPFnp8Sy7fqxFe0/DH/AII9/DzwL4u03WtU8Sar4jhs5PNFlMqRI7jlSSoBwD2r7/20VVtCbu5+aX/BYz4PWMnw38MeOLZVhuNJnXT22r8zRMMKM+gOK+Gf2OP2fdZ/ay+MWk6HqMtxceHNLVZdQuGYnyoAfuA+54r9zP2gPgToH7RXw11DwZ4iaaKxuyria3IEkTqcqwz71wf7In7Gnhj9kXQ9Zs9F1G71m91WZZLi+vQofaowqAKAAOaViuY8O/bS/wCCdPhrxt8I7Nvhp4esdJ8RaDCfJS3j2NdxgcoxH3m9zXxf+x7+2xrX7Luoan8O/iDYXV14VlLWs9pMMPYueGIB6jFfuJtFfk1/wWB/ZpsdBudK+Kmh2zxyajcfY9VSNTsGFJWU+nTFLlDmPOv+CZusQTft8agNDuJBod9BqTqqnarx4Lxgj2r9qsV+H/8AwSD0W7vv2skvYI99vp+k3TXDAcAOuxT+ZFfuDVEsKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACiiigAooooAKT3paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioWkZmKp1pYo3ViWOaAJaKKKAGtSY3cU+svxRbXt54c1O302TydQltpEt5M42yFSFOfripauB5v+01+0Bo/7Nfwr1Lxdqqi5eL93bWgYBppT0UfzNfll+z3+zX4s/4KIfGLWvih41lbT/Ccl3umlUYabaflgj9gO9dUP+Cbf7Q3xU8babF8S9ba48PyXrS3V1PrJujEm7qkWcKSOMj1r9U/hb8MtC+D/gXSvCfhy1W00vT4hGigcse7N6kmjlK5jR8G+ENK8B+G7DQdEs47HTLGJYYYYxgAAY/Ovzs/4LZaC0vgH4d6uiMXj1OW13AcLuiLc/lX6XV5D+1V8A7L9pD4M614PuSkV3Mnm2Vywz5M68qw9PSmtCTyL/glprmlan+yP4etNPlQ3FjNNHdQhgXRy2fmHbIr65YDqTwOtfhv8DfiZ44/4Js/tBXuieN7OZdGu41F9bwjek8Wflmj9W7fjX1T+0H/AMFaPh7rfwl1nTPh2dXl8WahCbe3aa28oQlhgsDk5I9qYHhn/BSTxtovjL9tLwdZaBNHc3mmNa213JCQwMpmUhcjqQK/YnSVZdLsw/3xCgP12ivzV/4Ju/sKXSXMPxh+KFs13q90ftGk2d5lmG7nz5Af4vQH61+mtABRRRQAUUUUAFJmvnP9rT9q7U/2V/7A1i48EXfiPwheSNFf6lZSEPZsBkEjaQBjPJwKwvAP/BTP4C+PNNuLk+K/+Efmt4TK9vrURti2P4UY/K59gaAPzh/4KAX0etf8FBo0sHW9aG80+FhbsJCHDqSpx3HpX7h2v/HtF/uD+Vfhj8F5rT9pr/go7ba1YRvc6Rda42o5kXJ8qPkNj0wBX7pUAJIpZSAcZ71+Dnh3Qbrwj/wUusbfUN0Tp4xMjGUbSFaQkE56ZBr95a/E7/gqJ8IvEXwk/aST4jWCzDTtYkjuLfUI42CQXKDOwtjG7C5x6UDTsftfkLyeBX4uaYr+JP8AgrdYy6ahvUi8TpK5txvCxonzucdh3NUtT/4KofGv4h+BbPwXoWkWkWu3Uf2VtS09GkuZhjb8qdmPrXtn/BNX9iT4g+E/ijH8XfiDbXGkSCGYQ2WooyXkksgwXdWGQMEnNAj9RqKKKACiiigAooooAKKKKACiiigAqPDMxzwKkooAYV96acrknpUjUxl3KQaBjImLsT2pWVg2QuaevHA6U+gdyKRC6EYpyqQoFOJA60jMFxmlYVwUU6kpaBBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAT9aB9MU12O07QC3bdwKbG77f3oUN/sHIoAlopM0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlpDzQAA56dKWkA29OlLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACGkwPWlo20AAxS0mKWgAooooAKKKKACiiigAooooAKKKKAEo4oo20CDNLSYpaBhRRRQAUUUUAFcz8R/h1oHxW8H6j4X8TWK6ho+oRmOaFiVJHqCOQfcV01FAHh37Nf7Hvw/8A2WRrDeDba7NzqjDz7q+n82QIDkRrwMKK9xoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqOV9qj1PFMQlc7mNTcqxPRUC3Cu21WyR1qamLYWiiimIKKKKACiiigAooooAKKKKACiiipbsAUU122j603fhtvtmjmHYkopqtmnUcwgoprsFHNMYnjFHMOxLRTBTXcJjNHMFiWimIwbpT6a1EFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPHvj/APsn/Dn9pS1tk8aaN9qurVWFvewuY5o8jGNw6j2rwz4Tf8Ep/hR8LvHFt4iku9S8RpaP5ttp2pbDBG4OQxwMtj3r7UooAZFEkMaxxqEjUbVVRgADtT6KKACiiigAooooAyfFPhXSPG2g3mi67p8GqaVeIY57W5QMjqexFfF/xG/4JB/BfxdcTXOgy6t4OncHathP5kSHPUI+fyzX3NRQB8x/sn/sD+CP2T9UvNb0rUtR8QeJLyA2suo6jtAWMsGwiAfKeOuelfTSn5iOh/SnUUAIaxvE/g3QfG2nvYa/o9lrNk4IaC+t1lTnjow4PuK2qKAPPfBH7Pfw0+G901z4Y8DaHo1yf+W9tZIJOueGIyK9CoooAKKKKACiiigAooooAKKKKAEo3CgnFNbLY4oAfRSUtACNTBu3HI4qSigBqimqX8w5GF7VJRQA1wWxilpaZIpZcCgBonXcVPFSA56VDHb7W3E5qegAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAjZtq5wT9KRm4HBo38DjBPrT9tA9gWnUgFLQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQ00vigB9FN3UbqAHU1m24o3UjfNilcY+ikWgnFF0IWiolmLOVC/nUlF0AtIx2qTS03lsg/pTAVTlQaWkAwMUtABRRSE45oAWimqwYZFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopGpuTSvYY+kpqt83Jqo8jmQ7G3YPSlzDUbkhmRlIY/Mpp25JEBLcVUkUq5JRTmq8nmS/IgCfSok9TVQLaxpHITGRuxzUqSOOWbj2qtaWSQtlpHZ8c7jxTVmEsjxqCNvOanVsLF4XS5xmpwdwyKz47cs1XVG1QK2Wi1M5LUkoqOMMM7mzUlMgKKKKV7AFFI1M3Hd1qeYCSikWlqlqAUUUVEtwEbpUbLuxUjUxsgcCpGhyjFOqBmbqcjHPAzmuW8T/FLwb4Hu0tdf8UaZo1043iG8ukjcg+xNA9zrJpFjTLVB5yogYHOTiuDl/aG+GAVWfx74fCk8f8TCP/Gmv+0T8LY49zePfDoX/sIR/wCNUlcex6EsysOTioVU/aM/w15F4h/a7+Cnhu1+0X/xI0OKPdt/c3XmHOM9EB9K4W+/4KPfs9abFJKnjyO+MfJjghkY/UZAp8oz6dt4tjM3rU9fDHiT/grp8EtPjM2nr4h1R487Y47MRpKcEYLFq9i/Y9/a+0v9rbw7rmp6ZoF5oiaTcrbv9oYMj5GRgjvgdKpEM+haKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTTQA7IpDIq9TTN3rxSLtf3qWyrEhb5cgZoRiw5XFC06mtSQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBD5J3hsnP6VNTFlVnZQcsvWn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJnrRTVUqzEnOaAH0UUUAFFFFABRRRQAUUUUAFFFFABRSGk3UAK1Q7P3u7PbpSpMJWwPu+tDusasxOcccUrlaj6Oc+1Mmb5cBhk+9U5dQW3KqWDHp1pcyHGDlsXWkVNoJxuOBS7ucd6r28n2pdzLjacimedIt95ZX5CMhql6j5baFhJG3EMoHpip6iReuWzUtFiGFJt5JpajmDNGQpwfajlYgkHmAx5K5H3hTo18tFUktgYyaSLPljPJp9WgCiiimAUUUUAJjHSlopqsGJwwOOuKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADWpu4etObJHFN8lScsM1nLcaKs3mNIcEhaj+WLc2OcVfYBV6VGY0bhlFI1jJGXHIZ5CSx2+lWY7Yrl1OT71P9giwAgCjOeKnEKhQvaqTXUqVRdCpDMJnzyG6Fe1IbdlYsvBJqwwih7qMckk9PesfWfHfhrw3b+dqviHS9MhzjzLu9jiGeuMsw54P5UJXdyObsauyRV461JHGVUbiWPvXl+rftVfB7Q4XlvPiX4YjVeoTU4pGH4KSa820f8A4KMfA7xJ8RtJ8HaT4luNS1PUrpLO3lgtG+ztI52rlzjjJ9Ksl3Z9PLTqatOoICiiipauAjVHt+Yn2p7DIpjNt96h6D3HrTqqC4fzAAufWrWfzqlIBaKKKT1EFFIelNzTTGK3avy+/ah/4JffEn42fGbxJ4ys/FthcWupXPmW9veM26CPHCD0A9q8f/4KBftM/Eiw/ax1TQbHxDfaRougXFskFpaytErggNubBG7O7vX7E+D76TUvCWiXkzb5rixgldvVmjUk/maW7K2PyCs/+CM/xRklIn8S6DDHjhm3Pz6YFa1v/wAEXPHjkCXxroUSnqVtnP8AWv1/WnVdhcx+WnhX/gijHDKza/8AEQvGUxs0+z2HdkdSxPGM12tj/wAEW/hysiG98Za/MqnLLEI13e3K1+i1FMLs+EvEX/BH34M6p4ejstLuda0jUkYN/aC3ZkZhgjBRvl754Havpn9m79nnw9+zN8Nbbwf4dkmubdJGnmurnHmzSN1JwK9UooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGqORSy4HFSN904602NmZcsMGgBkcbKxzzT9vtT6KVh3GqKdRRRsIKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWNVdmAwzdTT6TNLQAUUUm6gBaKQNmloAKKKKACiiigAooooAKKKKACikooAWiiigAopKN1AC0UjNtGaRW3Ur9AHUUUUwCiiigBGphzT2qOVhFGXboOaBieWONuAM5NQ3EMu0iJl5Pf0r4H/a9/4Kbaj+z78QpvCvh/whFq8kcQLXl9O8SKx9AFOenrXyVd/wDBXr473U0v2W28PRI7ZSNLB5GQemd/P5Vn8WqNHGUdGftkttGJPMx85GDTJreDerOFUg5yeK/Edv27P2sPjE39m6C95DMP35Gh6QVk2j5eS24bcsPxxWD4gt/2x9btZ73VJ/Gvkwr5js5MYA6dFA9ar4VqCvfc/dNtSsIAQ13boe+ZVH9axNc+JHhPw3Gs2q+I9LsUJ2hprtBzjOOvtX83+qfEj4g3Wqz2V74l1xtREvlNBJeSby+cbcZ65r334df8E9/2gfjFb2t7Pp9xYWVwcrca1csBj+9gnPeluSftr4R+Mngbxxqb6d4e8VaVrF+qs5trS5V3wOpwDXa5O7pxXwn+wn/wTkuf2ZvGD+NPFGuW+qeIPs8ttDbWSERRhyvzFjyTgEfjX3ZVIlg2e3WkXd3AxTqKYhKWiigAoqC7uVtYTK7BUXliR2r8+/i9/wAFfPDPw/8AHF94f0jwfeaxHptw0F5dyShB8pwdgH49anmsUotq5+hdFeA/B39ub4O/Ge0tRpfjCw07VJow7aZqcwglQ8AjLYVuTjg/hXvFvdR3UKTQyJNE4yskbBlYeoI60cyFZk1QwWqW5crkljkk1KDRzTuhC0UnNLTAKKKQmgAbPGPXmvnz9qr9tLwV+ynoVvPrnm6lrV2+220i1I85htY72z0XK4z/ALQrvvj78XrH4HfCfxD4x1AFotOt2dFXqXIwv64r8Sfgp8O/F/8AwUS/aUvLXXNek3Nbyane3U2W+zWayovlxjsSZVApXsVyu1z6mh/4LeXEmpfN8K4103P+sGrEy4z/AHfLx+tfoH+zz+0d4P8A2lPBEXiLwpeiULhLq0fiW3kxkqw/rXzx4+/4JT/B+++FN9oXhbSJdN8TLEGttZmunaRpQP4wTtwT6Adua/Mn4PeNPFv7Ef7VVrZX17NYJpOqpY6xaRs3lXVuxAclScHjkHsQKLoVrn9CFFVdL1CDVtOtb22cSW1zEk0TjujAEH8iKtUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIaz9a8R6V4chSbVdRtdOikbYj3Uyxhm9ASetX2zjivyL/AOCmereJf2iv2mfDfwq8HWOp6g2kqsDxIjCD7TIwJkzj+FcjJ96VylG5+uUE8d1Ck0MiyxOAyuhyGB7g1JXHfB/wTJ8N/hh4X8MSzNcS6Xp8VtJKxzucKNxz6bs12NAgooopiCiiigAopDUEkxU/Kcn0rOW40rk7dKgk3sQMcetL5jNKinpjNTChK49iBwyL8r4Y9M9K/LX9ur9sH9oTQfiZe+EfCOgaz4O0WEslvfWVoZpr4A4MqyKDtHPSv1RKhsZFQTWFtcOry28UrrwGdASPzp8o+ZdT8KtN+FH7Yf7Q2mgTt4y1TTWbeG1zUGiRj0yA7A9Ce3eqPxH/AOCdvx88A/D/AFLxVrtvDNY2EXmzwQ6g00wQdTt6YH1r96VjWMAKoUDoAK8p/axke3/Zh+K00TmOWLwxqMiOvBVlt3II9wRVIOY/Ab9nH4Ca/wDtLfFCz8F+HjDHdTRNNNcXTEJBCpAaQ45OCw496/Ur4B/8Ek9D+Evjjwv4w1Xxtd6xrGjXcd4LWG0SO2ZkyQOcnrg5z2r45/4JCawmm/tgWds67m1HRb62Q+hCpLn8oz+dfuZQJsRadTVp1MkKKKKV7AI3So3zxjrXmv7Q3x00n9nz4a6t4v1e3muILGPMcMfHnSHO1M9s8/lX51n/AILaax9sl2/DGzNqeYlbVir49SfLx+FZN3ZSR+sCL3wM06vyem/4LZ6z5eY/hjZK2f8AoLl/0EYriPE3/BZz4oak/wDxJvDOgaPEDn98XnYjB46j2/Kr5RM/ZmivBf2I/i140+OH7Pui+MfHNlbWWrahLMYhaoUWSANhH2nOM4P5V71RyiGSjMbUi8KKkpKOUdz8PP8AgqlBHH+2heKiqplsNPZ9oxuPAyffFftR4LXy/B+hKBgCwgH/AJDWvxt/4K3W4t/2xNMlAAMuj2THHfErD+lfsr4YkSHwnpLuwRFsoSWY4AHlijl1uVfQ1NpZsVIBiq9vPDeIk0LrKhB2vG2RXzN+3F+2nbfsheH/AA9JBpMWua5rM8ghs55TGghjX55MjuGaMY/2jVk7n1FRX47+J/8Ags98RLy0VdI8JeH9Kl3Z3s8kzYweMMcen5VyD/8ABUr9o7xJY3F9psFpHZWw3zTWekCREHT5jg4HI5qbj5T9t6K/Ay8/aw/aV/adujoWma7rmpPIdos/D8JiToQS5QcDB7+1ftn8BdB1jwv8FfBGk+ICTrlnpFvFe5cufNEY3ZJ6nPWmJqx6BRXkeuftUfDXwv8AGI/DHWfEMeleKzbx3CQ3a7InEmNiK54LHOcexr1tWDqGUhlIyCOhpiFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopNwJwCCfSgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBn41BeX1tp8fmXVxFbJ/elcKPzNef/AAA0fxdofwj8O2njfXP7f8Si2Vrq9ZApZiM4PTOPevhr/gsNJ40h8O+Dv7Mmu00EOxu5rV2RVlJwu4r2wT+YrNy0uaqld2ufpTb3EV1Ck0EqTRMMq8bAqR6g1LXyD4J8D+OvCf7FXhzT/B/iSabxB9jjnS8kYueRuI3EZwcY+prW/ZN/aU8SeOGvfDfxMgttC8VQSlbSBmCPdRjA34z1yR09ay9suZRa3Nfq8nBziz6opaapzzTq6TlCiiigAooooAKKKKACiiigDz/41fGbRfgd8N9a8Z62skun6WgZoofvyMTgKvua+YPgP/wVb+HHxi8aR+HNW0m88EzXT7LK61C5SWCY88MwA2HjvX1t4/8ABGmeONAk0rVNNttUsJj+9tblNyN15Ir8sP2tv+CW2t6TqFx4k+FsDXVvNKZZdHzt8heSSjeg4GPf2rOUrOx0xjFxu9z9c7e4iu4I5oJEmhkUMkkbBlYHoQR1FS1+PH7G/wC2v40/Za8Tr4E+MkOqN4PlIggu7xWY6a46ENg7kwCNo56HtX68aFrll4l0ey1XTbhbqwvIVngnTo6MMgj8DTjK5hKLRepGIXk8UpNQXE2z5duQerelUxJXdj5C/b7/AG2r/wDZh8KabD4b0Zb/AF3VpHSG8uz+5tgmSW2jlycYxkdc17p+zJ8YJPj18DPCPjqezWwudWtPMnt0bcqSKxRsHHQlc+2cV+R//BTr4sWfxE+Mlh4T0C4/tBNGMluTCc+bPIwGzHbGcV+rf7HPw7vvhX+zP8P/AAzqcfk6hZaavnx91Z2LkH3+asad3qzaolHRHs1FFFbmAUUUUAI1J7Up5o20AcR4q+CvgTxzefavEPhPSdZuOvmXlqshyO/I61R0v9nf4YaLcC4svAPh63mAwGXToj3z3HtXou2k20bbDbbKOnaHp2jriw0+1shjbi3hWPj04FY/xL1KPSPAeuXUrBVjtJCM+u01022vOf2hIxJ8I/ERaTyo1tnLv/dG0jP61E/hsVHdH4FeAbqTxt+1p4dm8hZm1DxVChiA3DaZ1BOO+Bz+Ff0cooRFVQFUDAAGAK/ED/glb8NrXx1+1lLqt3bi8tNAtZr+NmHCTmVVjb8t5r9wdtOOwpaMFp1IBilqiQooooAKKKKAIrq3S6geGRd0bgqw9jXxd8Uv+CUfwi+I+qalqcM2raDqN/cm5lms5wRk5yArAjknP4V9qnmjFGhSk1oj8kPi1/wRp8RaLIlx8OPFqavDwGttXRYpwcHkSJgY4HbvXjE0P7Wv7F908Nnc+ILWwZfLDQp9utWGQcBWVgPudQPXnmv3W20yW3jnUrIiyKeMMAalrsVzH43eDf8Agsb8W/DFxbWnivwzoOsxR4WYtazWl0R65EmzP/AO9fXXwt/4K2/Bbx1BHHr76j4K1A/ei1CHzYRyBxKnHfuBX0Z8Rf2avhn8UtPe08ReDNIv1Y7t7Wqq4bBGdy4OeTX5Of8ABRj9lf4Ufs6tp3/CL30lr4k1BwRokcu6OOLDEyEMCQOAOo+8Kkasz9efBHxw8A/Ejyv+Ea8XaTq7yjKR29yu9vopwe/pXc1+HH/BLv8AZl1T4tfG7TvGt1bTweE/DEv2prpWZBNcrjZGCOo5JPsCK/cVTlRVrYiW+g6mNnIx+NOrN8SaxH4f0S+1OUZhs4Xnde5CqTgflRe2olqfnf8A8FhvjNpWn/DzS/h3Z6iy69qF3Fc3Vsh4W1UOct9W28Vtf8EgfgQnhP4Wan8TNQtGt9Y8TObe2zgKLJCMFRjPzOuev8Ir8wvj98VNS/aH+Omta9eljNqV6La2jJJEab9qgDsK/oQ+CvhG38A/Cbwh4ftY/Kg0/S7e3CccERjP45zSavqaSeh2jV+L3/BYPwCNH+Oem+Jrawkih1K08qe6VMRvMvQZ/vYDflX7RHtX5xf8FmfD15dfC/wrq6XafY7XUVRrVhzvKOA+fTDEfjU7ExPpj9gX4mS/FT9lXwNql1Ms99a2g0+4Zf70PyDPvtC19DV8J/8ABHaORf2XLx2dmjOuXKxqegUBf6k192VS2Je4UUUVQgooooAKKKKACiiigAooooAKKKKACiikbO0460ALRTIt+35/vU+gBKpx6Lp8V898ljbJev8AeuViUSH6tjNXKNoqWrgFLSYpaa0AKKKKYBRRSNntQAN0qLykJzt5qRQe9LUtXHcjWMeZn24qWkpaa0BhRRRTEFcz8TvD9v4s+G/irRbuNZrbUNLurWSNxlWV4mUgj05rpWqnqyiTS7xG5VoXBB/3TQB+If8AwSZ0tYv20reN1V2sdJ1DaxHIb5U3D3wxH41+5Ffit/wSvhSH9uTWkVQAmm6oAAOg86HFftVSGxq06iimIKKKKlq4GJ4z8F6F8QvDd5oPiTS7bWdHvE8uezuk3I4/ofcc14Po/wDwTp/Z20OYywfDWymkznN3d3M4+gV5SAPwr6Sam0KI7nlul/sr/BzSVC2/wu8I4AwPN0aCX/0NTWl/wzr8KOv/AArHwbn/ALAFp/8AG69BWlx702wK2l6VZaHp8Fhp1nb6fY267IbW1iWKKNfRVUAAfSrVJS0LUQUUjU3NMD8Vf+CxTEftWaOV4P8AYVsP/Ijmv0E/bw+B/j34+fBHQdJ+HGptpOr2uoR3kwjumt/Nt/IkUx5UjPzMnHtXwB/wVoP2j9sLSocbv+JRYrz7ymv2W0FSuh6eDyRbxg/98igrZH4Xa9+zL+1Z8HZodVW08SSDT3Eyy2OoyTIMc5KbsEcV7R+z3+0tof7Y3xE0P4W/tF+FLPXNVVmi0rV1jMVwtwMfuXA7MN5J9UFfqJ8YPit4b+C/gPUfFXiq9jstJtFOQ+MzvtYiJR3Y4PHtX5NfsTXF3+0t/wAFFrj4k2ukpYaNZTXmqtFGgVLdDC8MSYAxkmVT/wABNTexW57B/wAFJv2T/hH8Ef2a5Ne8K+F7XRNZm1W2s0uoyS7KUkYpz2OwH8K+e/g/4pm8Pf8ABMv4vSCGNZrjxBBpyzBRv2ShNwz1xkV9Tf8ABa6/8v4KeA7IE5m155doPB2QMP8A2evnTV/BJ8F/8Ej7O8dcTeI/FEV4T6qPNC/+i6ncOh7Z/wAEStCjg8K/FLVHVWnkv7K0DY5URxyE4+u8fkK/Tavgn/gjf4TfSf2c9c1+Thtc1uWUD/ZjVUz+YNffNUtiZbn5x/8ABWT9ku88eaDF8XvDKFtV0K08jV4IzhpLNCzCVf8AaQn8j7Vof8EtP2zLr4paCvwp8VSGTxBoNiJdOvj/AMvVmpRArf7S71H0r9AtU0+DVtNurG6jEttcxNDKjDhlYEEfka/ADwTrjfsl/t0+dMWtrLw/4knsrlVPBti5Qj6YYH8KoLXP6B8nI4xTqrafeQ6jZwXVu4kgnjWSNx0KkZB/KrNBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTBGFYsOtPooAKKTIpaACiiigAopGJHQZpFYnqMUAOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPzP0P9qz4kftAftYalpvwylW78B6Lw16dy24VSqlsgHOd3THNef8A/BRj9qrxdq3hm4+HN74RvdOtRMjvrt3bbYpQMgmMgngkjqAeOlfenwX+Ffw+/ZR+HP8AYOlx2VhIlv8AaL6SSTMk8gA5Jxkivjz9uP4tfED4zfDGXw74Q+GWqX2hSN++8QS2f7sKCTtiJ5wfU46V581G61PT1lG1vmev/sM6j48+MX7KelQ6i/8AZlgim2tZ2ys8qLwGXjBU84JNcb4+/ZA8KWvxs0XxP4x+LNx4e1G1ZJbWGa6jRyFOcH5uM/rXO/sE+Jvi38RP2d9b8Ov4l/4Re00FxZ2dxBbIblF5yvzLgHqc+1Q/D39mH4JfHb47az4Y8U/EbxP8TvFtjZPc3UdzOUhi2uithgvUFwMZ7mnpKSS6BCbimnsfpbo1xBd6XaTWtyt7bPEpjuFYMJFxw2Rwc1drE8F+EtO8B+F9M8PaREYNN06BbeCNmLEKowMk9TW3Xcea9wooopiCiiigAooooAKKKaWC9SBQAtNIDEqRkY5FPpu35s0gOZ8Q/DHwl4qiEeseHNM1OPdu23Vqj89jyPc10FjZwadaw2trClvbQoI44o12qigYAA7DFTtTam2tx9B1RXFsLi2khckB1KkrweRipQaKpiPmbwf/AME8/g/4X+IT+NZNHl1XX2umvPMvpi8ayE53BOnBr6ZACgADAoApaUVZDbb1YUUUVQgooooAKKRiQOBmmq5bquPxpXGPopAaWmIRq8g/aoaab4H+L7QP9nhm02bdcjqhClhx+FeuyvsUcZycV4P+3Jr6eG/2WPiFdyDAbTXhRh1VnwoP60naxcd7nwP/AMEV72Kz+J3xKsHjVrmbTraQP/dVJHHH18wf98iv1y96/JD/AIIp2K3PxA+It+Y8vHp9rCJPqzEj9K/XClEc9woooqjMKKKKACiiigAooooAKKKQnFAHlv7THx00/wDZ1+D+teNb6NbhrVfLtbdjgTTsDsTqPQ/lX4TpN48/bo/aStIL2Uy634gusHy9xisrfqcDJ2qq+vtX1N/wVS/aCl+LvxJ0b4UeHLtbuwsbtPMgTO2S7OUXJB7bzX2h+wT+xLpH7MXgmHVtVt4rzx/qUOb2+4byEbB8mM44HAz15FRvqi/h3PdPgT8GdD+Anwy0bwZoEe20sIgHmYLvmkP3nYgDJJ9vSvQaTGKWqRIjV51+0R4hTwr8E/GeqSBWEGmTHDdOVI/rXorV8sf8FI49a/4ZX8WzaS7Axxp5qp3jJw36Gpl8LKjufh18LLm2n+L3hNrzCWp1mBpWP90zLnmv6ZbPb9lg2Y2bF246YxX8/f7Ff7HuuftYeKtUGmatBodhopglubmZSz8tkBQO52nn2r9+PDelyaHoGnafLP8AaZLW3SFpiMbyqgZ/HFWtgexpN1Ffmf8A8Fn/ABksHgvwj4aVo/8ASLprqRcfPhVfAz6ZIr9L2Y/jX4pf8FaPE7+Lv2ktO8O2Uq3cljbrBHDHyRLIw+U/jUPcI9T7p/4JP6Q+lfsf6GzRGL7Xe3VwMj7wL4z+lfY9eYfsy/D8fC/4C+B/DXleTLZaXCJk9JWUM/8A48TXp9UtiAooopgFFFFABSE4xmlpGUNjPY5oAM8470tJtG7d3xiloAKKKKACiiigAopDWN4u1x/DXhvUtWS3mvGsoHn+zwDLSbVJ20D3NqivyPu/+Cxvjmz+JoN54P02z8J2c/k3WnAt9sZN2C4Zj1HpjHIr6x8J/wDBVL4AeJltEm8SXei3ExAaLUbGRBGT6sAVx+NK43Fo+v6KzfD3iLTfFWkW2qaRew6jp1ygkhuLdwyOp7gitKgkKKKKYBRSV8d/tU/Hb4i/s5/HLwTrEVxHqXwz16WPTryyePBtJiQDIGA7jJ59aTdiox5nY+xaKitZ1ureKZGDJIoYEHIIIzUtMkKRs9uKWigBqg9zmnUUUAFFNf7vUjntXB/GP40+FPgV4TbxH4v1RdM04P5aYG55WwTtVe/AoA71qy/EsjQ+HNVkUkMlpKwI9kNfAXj7/gs18PNItR/wi3hjVtduPM2k3RWCPbg5OeTnOK8c8cf8FoPEGteH72x0bwDp9hLcxtCLi6uml2BlIJ2jHPNBVmcn/wAEj9HuNT/a88Tam5Yi20e8LOepZriGv2g9q/nw/Y//AGurv9lv4p6x4rXQIPEMGq2r289qs/2YRlpFfKsQRxtxj39q+3YP+C2nh8q/nfC7UFcDGYtWjfn6eX096AlufpnRX5Y6p/wW1kUk2HwtPl54N1qJX+SVR8I/8FePid8UviFoXhvwr8NNGaXULuODyTNNPIVLAMflIxgHrigk/Vyio7dne3jaVQkhUFlHQHHIqSgD8xf+Cln7ZHxZ+FfxVs/B3w91G50HTY7WOSa7g08SSTzNn5Vd1Ixg9B6V85+Ff2gf22PEUMb6Vq3jS/ikXcpg0GCYn35izj3r9wJ7SC6KGaGOUocr5iBsH1Galx7UFJn45Qt/wUE8WQjY3iuFG5/0m1tbM/8AoINcj8SvBf7b/g7wrc614k1XxemmRnEr2epB3QYJ3ERNuAAB56V+3eB6VHPbRXUMkM0SSwyKUeORQyspGCCD1BFS0NSXY/ET/gnnrnxj+Kn7Tng+a58V+MNY8L6fcyXGpPeancyWoCxPhHDOVOWK8Gv3ArH8NeDdA8GWstt4f0PTdCtpX8ySHTbSO3R2PViEABPvWxTRLd2UNe1SPRdEv9QmZUitYJJ2ZugCqSc/lX8+OqftlfEyP46SePn8V6nNLb6o1yNNS9kW0MatgJ5W7bjHtX7X/tteKv8AhDP2UPidqgcxsujyW6spwQ0xWEEH6yCvwb+BPwF8T/tFeJNT0XwzB517Y6a+otH3dUKpge5LUNlRPeP2uv2gPDX7S/7Qfwz8SeH7VxdtHYwaghGf3nnKdvvjmvrL9r7/AIKgeJPgj45ufBfhXwkkV1aQoHvNVUgElQcqo6gZr80PhLZyeAf2gPCFv4htpLA6frtqLyC4XDJiUA5Br+inXvhf4N8cNb3mt+GdJ1aYINs11aRyOQQP4iMnpQDP55vi58f/AImftL68JPEurX+vSswMWn2it5KY4BES9xnGcd60vgrpPxq+HPj2wvvA2i+JdP12R1MUcdlKizAEcPkAFfr6V/QXonwr8GeG5RJpXhTRtPlUYElvYxKw/ELmulFrCJFcQxh1+620ZH0pWDmPzD/4LEprV58H/g5e6rZyJIs9x/aTwj93FM0MJ259SQ+P9015Jpvwh+I3iL/gllqL3aOdPsdei1yxt5Dl/sKRyI5A9N0gI+hr9gfF3gvQvHujnS/EOlWusaeXWT7PeRB03DocHvVmPw/pyaKdHFlbjSvKMH2MRAReWRjbt6YxRyi5j8af2Af+CiWn/s2+F7nwN4ysLm+8M+a91ZXVmoaWBnK7kYd16n61996b/wAFPf2etQsUuZPGL2e7rFcWcm8H0wAaxvHf/BKf4E+NL64vINKvtBuJ2LudPumC5PJwpyBzXmE3/BFj4cySME8a+I4rfdkRr5Jx+JSmJnst/wD8FQv2eLOEunjGa7Yf8s7ewlLdCe4A7etflf8At/fHH4dftCfGJPF/gW31CBZrRYr5rqBYvNkUYV8An2zmv0H0P/gjV8HNPkDX2s+I9TXGCj3KRgn1yiA/rXsXw1/4Jz/Ab4Xara6pp3gqK/1G25iuNUnkutrZB3BXJXPHXGaYJ2NH9gOXxLP+yf4Ck8VyM+ptaNs8wfOId7eUG99m2voao4YUt41jjUJGowqqAAo9BUlAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCJgd3SpKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEY4pFYntTqKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD5u8O/sw+CvAa2Op+O/FN94u1e2hWP7drVzsRgMD/AFYOOuK9l1z+ypfD8tnC8cenm1Y7oceWse0+nQYr5Q8HfBGx/Zy+GI1j4z+Nr7xdqiyedN9su5J1MnJCRgjLd8ZxXGaxY/FP9sn+y9K8H2198Mvho0kiXut5MVzeQZAEaJz1Hrgcda8/mSfJY9NxulNzPjW8/ak8a+F/HXiv4a/Di6tLKy1nWDDFft1DEsvX05PPtX6b/sc/st6V+yj8OL/Vta1KLU/FGqj7drOsyfdHGSqsRnaOvua80+IH/BKv4Zr8M0svB8F9Z+MLGPzLfWJLk+bNNjO5+3X0r4T+Nvir9qf4J+CrrwV411fWP+EYvT9mWaX955i84RZB8wBA6H0rblUHYxdqmtz9xPDniKw8VaRBqemzLc2U4zFMvRxnGRWpXyh/wTT+IGp+NP2Z9FtNV0m80650cmyEt1GUE6joy569a+r66VscklyyaCiiimSFFFJQAtFFFACGoPsaFTuyx65zViigBkcYjXAOfrQsmZNu3HvT6SgBG4XNRLMDGXwcDt3qZqguLhbaNmYZCgmga1JY23AHpkd6fX58/tg/8FLdd/Z3+KCeEtI8KWd5EIo5nvLuZslWPOFA4r7i+HHjGD4geBdC8RW7RtHqVpHc/uzlQWUEj8DS5kxyi47nSUUUUyQooooAKKKKAEao3YqOBuNSHmmiP5sk5qGhoVadTGdUPLAH0Jpd1NaAEjBVyTgDvXyT/wAFH9QuP+GZfGlsWT7NLZqVO7gkSJgfXGa+rtRJNlNhN+FJ2k4B4r8OP+ChHxY+KWrfETVdE8Q3klr4RaXFpaQN+7dV6ZNS3qaRR9Z/8EW/A7aX8K/GPieWHYdU1BbeKQjqsS84/FjX6PV8bf8ABKLw7eeH/wBknR2ulZRe3lxdRBhj5GbivsfdVR2IluOopN1Q3V7b2UfmXE0cEecbpWCj8zVEk9FUtN1qw1hZGsL2C8WNtjmCQOFPocGrtABRRRQAUUUlAC14L+2R8fLD4B/CPVdWuLlYb2aB47KMNh5JiCFAGfqfwr3O8vIdPtZbm5lSGCJS8kjnCqoGSSfSvxX/AG1/ixJ+2r+1R4e8A+DJHawt7kaZbzM52SOT88uBkYADVLfQpLqW/wDgmn+zxqP7QHx0vvil4otJbjQdJma5imk+5PfFwVHzA7lUbs++Oa/aMfLgAYGK4L4G/B/RvgT8MND8G6HHstdOgVHkwA00nV3bA5JOTXfUR2CTuwoooqiRG6V4b+2ZpF34j/Z68XaVYsFuZ7N/vdCApyK9yasrxJodt4i0W90+5iWWO4heLDD1Uj+tTJXjYpH4y/8ABJf4oXPw/wD2lNR8JXTRxWfiCzMEgbP+uhOY8c9SGfPWv2tr+fb49fDnxP8Asa/tJR6rYSbZ7e8/tDTp2JCkbidrYx61+kP7P/8AwVc+GfxA0Qw+Opf+EI1y1iBlFxl4JyAMsjD37HmhaLUbR9c/Fr4iaZ8Kfh5rnijV7lba00+1km3McbmAO0D3JxX4Yfs76RrP7VP7aukX1xFJdi41gavesQT5dtG+7rzgfdH419E/8FBv+ChHhX4zeFJPAPgBZNV06dla51JkZQ5BOEQdcng59q+gP+CUX7M9x8L/AIcXnjzX7MQ694jRBbrImHgtl6D23dT9BRuO9lY+9Y0Eaqg6KMCn0m35s5paaMwooopgFFI3SkGaVwHUUxZQzEDtShg2CDilzIdh1FN3ccGm+Z8wXnkZ6UcyCxJRTVNOpiCiiimAhprKGU5GR3Bp1FAHjHxP/Y6+DfxilafxT4C0u8um63NurW0p6/xxFT3rzmD/AIJgfs421zFMngNmMZBCy6reOvHsZq+rdoo2ipauVzGV4Z8NaX4Q0W00jRrGPTtNtIxHDbwjCqo6D3rWpNo3Z7/WlprQQUUUUxCNXhX7a3hq18S/s0eOIp7GW+ngsWntvIj3yRSryrqPavdSM02WGOeJ4pEWSNwVZWGQQeoIqZK5Sdj8rf2N/wDgqpp/hnwzYeDfi0tystiv2eDXETcWUEBVlUdCB39q/UDwv4n0zxloFjrWjXcd9pl7GJYLiI5V1PevkX4rf8Epvg58TNeu9Yh/tLw7e3cplmXT5R5TE8n5COOfSvpL4H/B/S/gR8N9J8GaNdXV5p+nIUjlvH3OcnNUJ6s72iiigQUUUUAI1fM/7av7Gtv+19oOh2cniGbQLnR3lkgZE3xuXCg7lyM/dH619MMoYYIyKKBn5P6f/wAET9WaQC++Jdqsf/THTSTj8Xr1nwF/wRp+FuhsH8T65q/iU7CDGkn2ZN2Rz8nPr371+g9FA+ZnyNo//BK79nXSbpJz4Qurxl6Jdarcun1K78V6FY/sJ/ALTwAnwr8OS8Y/0iyWXP8A31nn3r3eloJPFP8Ahin4D7SP+FSeEef+oRDn89tafw1/ZT+E3wh8TTeIfCPgfS9F1mRGj+2QxkvGjYyqbidgOBwuK9YooAKKKKACiiigAooooAKKKKAPJf2qfgtcftBfA3xJ4GtL5NOutRRPKmlBKblYMAwHbI/lXy1+wN+wT46/Zb+LOteJPEOs6XdaXc6c9ksFmCXdi6MHyRwBtbj3r7/pKlq47nwl+0v/AME4JPjR+0hovxH0nU9O03TRNay6np8kRDTGJgSwI4ywFfdNvCtvbxxLwsahR+AxUtFNaAFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFIWA6nFIxwOarGdZpfLA981LdhpXLVLTV4p1NaiCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXqnhvTdaZDqFnDfLGQyR3EauqkdwCOtX44VhjVI1WNFGFVRgAemKkGaDSHd7DV9Koax4b0rxFFHFqum2mpRxuJES7gWUKw6EBgcHmtEZpaPUWxFb20VpCsUESQxKMKkahVH0AqWiimAUUUUAFRqsnmZJGzHTvUlNZio4GaAHUUlLQAUUUUAFFFFACN0qORdx9umKkpkkZdSFbafWgaPyU/4K7fA3V7jxtovjrS7E3thNb/ZrmO2BZ42XoSB2r7F/wCCZ+rXeo/sl+FYb0XIms/Mt/8ASoyjYDHGM9sV9G6p4M0nXFYajY294Dn/AFiA9evWtLS9Js9Fs47SxtorS2jGFihQKo/AVlFO5rOSlsW6KKK1MQooooAKKKKAI5txT5Tg14v+1B8RPGvw5+FWpap4K0Y6xri4SKNRkoCDl8YOcYH517WwzTDCGXDAMMYORUuNzSMktz8EPEHxO/av+IevyXclz4y+1qSRHYQSRogz2CitrR/G37aNqohs7rx1kDgvalzj/gSmv3ShsoLfPlQxxZ67EA/lUu2lYHJM/EKPxt+3IFJafxs6MNpDWMfOf+AV5v4++FP7TXxMgRPFXhvxRrEaPvUXFkOG554HvX9AwGKWml3J5j8JfCuqftjeBvD1loWgxeMdM0yzXZBbw2i7UHpytbS+KP249Q+UXfjb14hVf/Za/b880m2nYOY/EN4f24rpf3k3jaRfRio/pWJq/wAEf2wviA3l6pp/jC/jHz+XJdbF479R61+7G2jFMfMfHX/BNb9nvxp8C/hprDePPtEGt6rd+cLO4nMpiQDA5z1NfY1N2gHIp1BLdwooooEFFFFAHzv+274J+J/xE+Dt74f+GDRLql9IsVx5k3kkwENvG4n1218wfsDf8E3fFfwW+J9r8QPiHeWi3ljFKlppduwlIkcAeYz9OBnp61+k1G3nNTbW5V9LC0UUVRIUUUUAI1Np1G2gDzH4zfs7+CPjto0tj4p0a3vHZdqXDIDJHx1B7V+dPxM/4Ix6y2uGXwN4ns101mz5OqElk+hC8/lX6ybaNtS0ykz4M/ZZ/wCCVXhb4N69beJvGupp4v16DJitViC2cZOMEqRliMe1feFvbxWsKQwxrDDGAqRxqAqgdAAKfilpoTCiiimIKKQ0m40rjFqN5Ap29PemSM6nLH5PYc1BdPkJsbvk5FQy4xuwjmQP5YOGzmvnv9vDTvH2q/APVV+HV7dWmswss7GyOJXjUEMqkc5ORXvc1wY5lYeWFXl2Y4wvc18/yft4/Cab4vW3w2XUnl1a4m+zCfA8kSZ+6W9SaRs1ytH4/wCh/tEftA/A3X7bU5tb8TWZgkDGLWFkeF/VSGGCDX318Bf+CwXhnxNb2WlfEHQbzTtdlkSBbjS0EsUpJAB25BHJ7V9TftQfEL4T/DX4fX9z8QIdLvUaFjDp8yo0szY4CjqPrX49/sh+DND+MH7Xen6oJNL0DwxZ6g2om01CdYkMSklUGT1yR+VMybTP3y0++i1Kzt7qHd5U8YkTcMHBGRkdqtVnaPrGlarFjTL60vY4wAfssyyBR2+6TitGqjsZhRRRVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTScUAK+GXnmq7Rjd8owafJllwpwaWFiyfN1qWrl7IWPduwalpq06mtCQooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKa8ixrlmCj1NADqKQHPI5FLQAUUUn60ALRRRQAUUhz2pAD3NK4AEw27Jp1FFMAooooAKKKKACiimSP5a5xmgB9FIrblBxiloAKKKKACiiilcAopCcU0SZYjHSlzIB9FIDS073AKKKKYBRRRQAUUUUAFFFFABRRRQAUUhzRnmlcBaKjeZI2Ad1TPTccZp+RRdALRTN5XcSy8fhiuJ1b44fD/Qdch0bUPGmhWmrSnalnJfxiUn025yPxpgdzRUcMyTxq8bK8bDKspyCPUGpKACiiigAooooAKKKKACiiigAoqOaRo0yqFznGBSqxZQSMe1ACTbto2cHNId2Bg0rMd2O1NaRV53AVnLcpCTZ8s4ODis+2t3uELF23dORVld8zM+/930UAVieOPGlh8OfCN/4g1aVktLKMySbRk4+lTc1i3FWRNrmiPNpdyitzJG6MSemVPNfzs6pYapaftK3VlprGfWI/EDLbndjdIJDt5+tfXX7Sf/BWD4ha34g1HSfh9BB4e0H5oBNdWglnnBGCw3D5fwr4P8P+L9fsPHFt4i064d/EC3QuYpVTezTE5HHfmmPmb+I+z/iR+wH+1J8avEk2ueILa1u2mbdELrURtRccALjA4rFs/wDglL8Y9NUTarqPh3Qoxy7vqJ3AevQVrXetftyeO9LivoT4uW2ugrxtZkW5Ax2AIwKyLP8AZl/a5+KWr2eneIh4pFlcTL50+qaiTGi55JG70qrMSstz9HP2BP2T7z9mbwjqz6l4jXxFfa0ySeZC5aJEUcBcmvq+uQ+Evgj/AIVz8O9A8OGZriTT7RIXlZixZgOTk+9dfVLQyk7sKKKKZIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFI1NzQA+imfe4zilXC/LuyfegB1FFJ+NK4C0U1unBpfxpcwC0UnQU3NHMMfRTVp1PcQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqifNStUcjFVyBk0DW5Hg06PIbmnRt5ig4xUTXGbgRAHpnNS3YvcsLTqatOprUzCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJoUuIzG6hlbgg0+igCK3t0tYljTO1em45qWiigApkmfLbGc47U+kbPbr70ARWpPlDdnPvU1FFACMwUZPAoznGORSOodSD0pI08tAvpUNAPoooqlsAUUUUwCiiigApKWigBKWiigAooooAKKKKhoBKNopaKfL3ASlooqgCiiigAooooAKKKKACiiigAoorgvi58b/AAf8E/Ds2seLNat9MgQZWN3HmSH0VepoHud4xxVXULxNNsbi6k/1cKF2x6AZr8ufih/wVW8c+JtUnt/hJ4Ol1DS4n/5CE9rJIxwegC8YNfTX7Of7VGqfHL4W30Xi7RJvC/iGGMxym6TyYZyR/Du7VhOajqzZUnufnh+2T+1f4z+PXxxHhjw1qV9pmnWd19jt4bSV4wz7sbm2nmu90z4zftJ/sHx2MnimU+L/AApcKrmK+dnCbumHzkGvIvAevaT4J/b/AIZLyyt7jT5NWNqyud8YLsAHyD1Br9kfjd4F8P8AibwXf3etQQ3WmwW5eSGZFZDGBnuKorS9mfnd8VP+CxB8XfDK+03w94VudA8R3UflC5kuVkiUHgkcAivjHw5+z78SPir4N1b4lxK1zYRyPI95K7eYzjklf/11jfErw7ZeOPjHqul/DvRZJbaSRhBZ2ozjHUivqz9kP9uK0+DOly/C/wCJ+ht/Yit9n8toyBAehLAmjXoCtex7V/wSn/a+1zxlrVz8KfFtzJeXdvbNNp1zMzGTan3kYk8+2AK/Tevwy8O+LPDPwu/by8N+IvBGqwTaDqF+sY8g8RRyHDKcV+5MUyzRpIp3IwDA+oNXHYymtSSiiiqMwooooAKKQ0m6lcY6imB93QigtilzILDm6VGzhQCTgU7du3LSeWOO+Klt9BjHdQRu6HvUUtnFJGQBwPQ0jWPmXG9mYqOig8VOsQjztz+NTr1KI4QuPKHGwCs/xP4WsfF2j3GmajEJ7OddkkbDIIq/BDIkzMzglj2FfI37Wn/BR7wx+zP4mi8M22kTeJPEIG+4t1kESQL2yT3NXdbMavfQ9h179mD4Z3Gl3Ek/hHS5ZYYH2SPbrlflPOcV+Tn/AAT9+E2meMf23Ly2vrWCbStHlvJ1gYZUsj/Jge1e3eJP+Czz6v4f1Cytfh81tc3EDxJM16CELAjOPxr84tB+IviTwz4tuvEWgavd6Hqk0ryG4s5WRl3HJGRTaDV7n9NF5fWWi2ZmuriCxtYxgyTOI0X8TxS6bqdprFnHd2NzFeWsgyk0Lh1b6EV/Nt4w+PvxP8eWL2et+Ntc1a1cgtby3cjIcd9te8fAv/gpV8VvgT4FsfClha6Xq2lWIKwC+t2LKCc8sME/iaETyn7tr1p1fkn8BP8AgpZ8b/jN8evCXhw2emx6PqF4sVzZ2NhlvL/ibewJAH1r9bKokKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSE4oNNbJpN2GDSKBzTd2e+BSMm4YYjFNaMY+9+tZSbKVgZvJUdXJNG8ZLntUVwfLmiOf1plzIWyFOOR0palWLHnhj8uTS+Ye4xVaSXykGOtQtcOwxyKzbdy1C5Za4ZX2MPfNTLN8tU4JNylpDnHrzT5HVo1dTx0q47A4paFlptnWhZC3bAqvbWzMp3sTnpk1bSFU960SuZuyHLTqSlq1oZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkzQ3SmH8qAHNUcj7V96dzVaThutBSQ5pJNvyLz9KkhjZVBfl/WpI+gp9K1wuNWnUUUbEhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRjgdM0UALRRRQAUUUUAFFFFK4CM20ZoHNDLuGKBwMUwFooooAKKKKACiiigAooooAKKKKACikNJuNAHNfEbxpD4B8I6lrdwVEdpA8pMhwowCea/FHwBpvir/got+1w1l4i1WaLR42ku3xlo4LaM5CKvTLdBmvuj/grT8UP+EP8AgSui22ofZ7/VpVj8hGwzx5+b9K5//gjv8JrPQ/g/q/je4siusavdtbx3Ug58hOgHtms73ZslaNz7U8E/B3wl8P8AwtBoOh6LZ2VlHEIm8uFQz4GMk4618uftG/8ABPnU/jR4ug1DTviBqHh/R1wJLCAEqAOuMHrX21jb70jcU+VSJjN7H4N/tzfs/wCnfss/Efwo/h17xi0S3D3V0+ZJZUIJb26V96/Fz9po61+wDaeLoZY1vNR05bVlZjgyY2kHnNZn/BV74S3PjL4Y2+t6Xow1DU9NlVvOjTMiRZ+cZ9MV+UEfxI8W+JfCGk/DpLq4fSI7nEFmpPMjHABHoDU2exs9Hdn6hf8ABI/9n/Q2+Gd98StVsPtWt6hePFbvOqsscanqvGck+9Vf+Ck37Ct14+uofG3gHSozqaoxv7WBMGUDncMd6+z/ANk/4Wf8Kb/Z/wDB3hdt32i3s1kn3Yz5jjcw4HvXrTRq/UZppXMlKzP5fLX+0vAniyGW4tXtNR024WRreYFWRkbOCPwr+jX9mn4oR/GL4I+FPFKKsb3dmglRM4WRRhgMk+nrXyr/AMFAP+Ces/x0mtfE3w602xtvFSti5jd1gS4XuWOOtex/8E//AII+NfgJ8CIPDHjgwpqUdy8kcEE4lWJD23DirRLtayPpiiiimQFIy7hjOKKaX29aVxjcbWGCSO9OqGbzFU+VgsefmrnPiL8QLD4Y+B9U8TawwistPgaaTkDOBwo9zUNlJC+PviF4c+Ffhu813xHqcGmafbIXeSZwCfYDuTXw/wCJP+CzHwy0/Umg0rw1reqWqttN0VSNevUAnNfC/wAXvjT8Q/8AgoB8c7fw/o0czadcz+XY6ZDuCJGD/rJBnBwOc19w/Dv/AII1/Dmz8Kxr4y1vV9R8QOuZJdNnWGGM+gUqSfzpFW7nrHwd/wCCm3wd+LmsWGjpqFzoOq3jbEh1CLapb03dK+tBNHJCssbq6MNwYHII9a/GH9oz/glV40+FVxca38PrxvEmlw/vUi3bbuHHIx6ke1ep/sH/APBQK4tXtPhF8UvtEF15n2Oy1SUkSIenlyE988A0D5NLnqv7VH/BVDT/AIE/EC88JeGvDUPim8siFup5rkxxxt3XgcmvFbL/AILba20+Lr4aWAjA5EN8+79RX2T40/4J5/B/4i+KT4i1zRDfX0vzS7ZSiTE92A6mq2rf8E0f2f8AU9Pa2j8Fx2MjDHn28zBx9CTTSuRotj5m0/8A4LYaa237V8ObrdjlIbxfzyan+DXi/wCEf/BQr4vahPrnwxljvvI3XF7cS53BegyvSvXtL/4JG/AzS9Zhv/I1i7SNt32We9JjP146V9ZeB/hn4X+G+lQ6f4b0Sy0m3iUIPs0Kox+pAyaHEaklqeGWH/BOr9n/AEnMjeArKdFBOLhmdQPpmvEP+Gsv2QPhH4xm8L2XhGztmspWtpr2DSUaNGBwQSeT9a/QW4gFxbyRE4DqVJHuMV+dHjz/AII56D4t8U61rNv491GxGo3Elz9n+zoyqzEnr171qJan1X8OvG/wH+LVjFJ4Zn8K6iJBkW4ihSUexQjOa9BHwl8E+WUHhTR9h5x9ijx/KvyI+M3/AAS8+JHwP0ebxD4O1xtajskaWQ2rGGYKOcjHtX0p/wAEqv2r/FHxUs9X+Hfi9rjUb7RYvOttSm5fZnBic+o7E0hyjbqfeOjfD/wz4fu0udM0DTbC4XIWW3tURh+IFdFSYpaDMKKKKAGvnbkAk+gxUc1zHa27zXMqQRRrud3YKqj1JNSt71+eH/BYS68U/wDCl9Ol0/UXsNBt9SRL2CJ8G43DCZ9gaVyoxctj9BdM1ax1q1Fzp95b31uTgTW0qyIfxBIq3X5Bf8EZ/iLrkfxO8QeDpNQlfQpNON2lmxBVZQ33hxkce+K/X2mJqwUUUUCCiiigAooooAKKKKACimGQbtvejcc0APopm6kV9wz0oGSUU1W5p1AhrttWm06Tlaj27hjpWctylsI6eZghj+FU7jz0mO1Ny1D4m8Raf4P0G81fU7hbSws42mlkboFAya/PbxR/wWc8MaPr19Z6L8Pb/XLC3kMa3smpJbrJg9RlGwKktNrU/RIJLcYDx7fRqGs3IOG5+tfmhP8A8FtLPafK+E0gPq3iGM/yhrNvv+C3Eqwt9n+FMSv2aTXA4/IRA/rRYOZ9D9PpbOf5CrBiOuagaG73MBGp9K/ILXP+Cz3xT1K6L6R4Y8L6RB2juEnuG/MMKzX/AOCwXxv8sg2HhNc/xLp1wD+r1Ljcrmkfspa2sq/LKODU8luI4z8yoPfpX4jXX/BQH9q/4mTl9Bvb21tuqjQtBjkH5vGx/WuF8VfGj9qvxVqENlqmuePhcTN+7htFmtCzduIgtNK2gXb3P38i2qoI6e9Sbgehr57/AGL9P8eWHwA8My/ELVLy912SBmliv8tOATxvZjuJx6177bYMSsBg+9ax2M5IsUU0dadVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIelNK5p9FAEbL0NNaENyRU1FA7jVGMU6iigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJmgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEo5oakwaBDqKQnFG4UDFopu78KXdQAtFJupaACiiigAooooAKKKKACiiigApMHdnPFLRQAUUUUAFFFFABSZx1oNed/Hb4waT8E/hrrPijVJokFnCTDFI+3zJTwig4PU45xWctNxpN7HbS69pkGpR6fJqNrHfyDKWrTqJWHsucmr9fkF+xP8Odc/be/aG1v4o+ONV1A6JoNyJraGCdkVpScpGpHYd/Wv18VQihQMADAqo7ALRRRVCCiiigAooooAKKKKACikNRGRw5yAE/vZpXGFzcLbRl2yRnHFQTakkMPmtkL9Oak3qzgZ3Z/KqGuW7NaySxuBtU5FYy5r6bGkEm7SPx4/4K4eNZPE3xc8OaOE3W9vAXWTnJLHGMdK/UT9lDwlbeCf2ePAelWsflrHpkUj8AFmYbiT781+PH/BQDUjqX7VFvpzzGW2tfITeep3OM1+3/w7tI7HwH4ct4jmOPTrcKfby1poup2Oi7ihhmilrVaHOc5428FWPjrw3f6LqBkS1vIzHI0Rw2CMcGvnr4Z/8E2/gt8MvFlp4ksdGur7VraQyxyX1y0i7j32fd/Svqfb1oC7aTVyuZ2EChdoAwBwAKdSUtNaEhRRRTAKKKRhuFACMeKY/Ip2z1NDL7ZFQ0MYu7A3EEewr8xf+CvH7SktpYWfwj0aSN2vgl1qLRk+YArZVAQeCT1GOlfob8WPGkHw7+Hut69cHEdjbPNwcdATX4ffsw+FNQ/a8/bOsp9Xne5tpr2XU7iSYlgIYyXVOc8EADHvWd9TVLqfol/wTJ/ZFsfg38NrTxxrFqT4t16ASqZMH7NAw4VRjKkjrzX3DtqK1tYrK2iggQRwxKERFGAqgYAFSbvatFbqZvUrXlnFIvmMMMv8Qr8Ef2xNPtfDf7cGrrpC/Zw2rW8xA6by6kmv3r1a4MOm3MnGEQt+Qr8LPHmgn48f8FDBpdoDdQ32uwoWt2yRChBds+2DS06GsfhP3Q8OM0nh/TGc5drWIk++wVoVDZWq2VnBbpny4UWNc9cAYFT1UdjAKQDFLRVAcj8RPi34O+E+nx33i/xFY6BayHaj3km3cfYdTXi2tf8ABRv9n/RQ+7x5b3TL/Dawu5P04Feb/tzfsIeMP2rvE2l3+m+MbbTLOyQoltdQllXPU/KRmvmew/4Im+MHmQXvxF0pYP4vJsXJ/DLUD0Kv7ZH/AAVUuviFpd74T+F0cmnaNcoYbnVbiMebMp6hAfugjv1rh/2Bf2zfhr+yn4V8S3Gv6Jq2peK9SkG6e1YFJIxyFyTwc96+jfC3/BFHwnazQyeIPHuq6iq/fhtYUiVvbOCRXon/AA57+B4mRhLr3lrgmP7ccN9eKAR6b+xz+29o37Xk3iGLTfD91ocmkbGYXEokDqxwOgHNfTdeT/AD9mLwF+zTol1pngfTJLKO7fzLiaedppJCPVmJ49q9YoB26BRSE4qpLqUSEqG+YcYoBJvYtsM18P8A/BXDTjffstXMiqzNBqFvJhR0Abk19mjUJfOVcF1buBXzp/wUA0b+1v2VvHkRRpTFaGbBGSCCDkVne5so8j1PzU/4JG64un/tbWdrlh9t0u5iHvhC39K/chm2rn+Vfgn/AMEtpWT9svwkV53QXSk+3kNX70zSeXE7+g7VVzORn6z4o0jw3HFJq+qWmmJMwSM3cyx7mPQDJ5NacciTRq6MHRhlWU5BHrX4df8ABTf4ueKvEX7UlzoM99Ouk6IYfsFpwqxscHdwOTn1zX7G/A8XX/Cn/Bhvsm7OlW7SE9dxQEn9aOYVjuqKaDTqe5IUUUUwCiikagBpRc7sc+tNbO4Yryz9pj472f7O/wAI9a8aXUC3hsQix2zNgO7sFUE+mTXwR4Z/4LXFf+Ri+Haqrco2n3mTj3DUFWZ+pEnmbhtAxTdsrcEhR7V8CR/8FmPhU2mCZ/DevC7xzbqqkZ/3q868Zf8ABahRDIPCnw+3tkBZtVuCEAzzkJzSuPU/UZF24HWn18e/sB/tbePP2qrfxJqHibw7p+kaVYuq2tzZrIBKx6qC3BxX19I+089KLk9Rz8LzUCzLJJhajmMkmfLJJ9GPFLHGFHzRbT3K1ne5drGT4u8L2fjbw7eaTqVtDdWVyhjkgnUMjqeoINfgv+3n8FfD/wABvjtceHfD8eLd4VuXgj+VItx4CgdBX9AylcYAx+FfhL/wVSuvP/a610Ic7bO3Vh68cD86B36H29+wP+yN8IfiF+zD4S8QeJfAWka3q915jzXV/apJI5DYGTjkV9LW/wCxj8CbVsp8JPB5P+3o8D/oVNYX7AXhe48I/sl+ALO5G2WWzNyVPUB2JH6V7/NEJuDwem4HBH0NBKPPtJ/Zu+EugyLJp3ww8HWMqjAkg0G1Rh+IjzXQWvww8G2Ugkt/CWhwSDgNFpsKkfiFqj8V/ix4R+CvhCfxL411qLRNHidUNxIWyzk4VVC8kn0H418leI/+Cw3wT0uOYaTY+JtckjbaDFYLFG3OM7mfP6UAfbtroun2aeXb2FtBH12xQqo/ICrbW8TurtEjMv3WKjI+lfmt4i/4LW+FYdPlOifDvWLi8GNn264jii98kZP6V5T4i/4LU+P7y326H4G0HTpG+7LeTS3GPbau3+dUgsz9gWUHqAfwpOnA4FeRfsr/ABE8V/Ff4H+GPFfjSyt7DXdTiaZ4bSF4owhPyEKxJ5HfNeu1XQkVetOpq06hO4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACNxSKxPbFOooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASm+WN4bGDT6KACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSk5qW7AOopBmlpp3AKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFJtpaKAEb6ZrzH9oT456R+z38OL7xjrdjeahp9myiSKyVWk5YDIDMB39a8z8Q/8FJP2ePC+vXejaj4+EV7auY5fK0y7mQMOo3JERXgX7bf7bXwf+IvwC13Q9M1e81GbVrUpZp/Z00YaTOVOZFUAVk6iWxtTg73aPrT9mf8Aae8M/tSeE73xB4XstSsrOznFtIupxxoxYjPGx2GPxr2PcK/NT/gk38cvBehfCLUfBpuJz4lhuHvp4Y7ZyrIQAMNjGRg169+0J/wUq8H/AALuorR/D+razdSqSscKCNQR03OxGB9AarnXUbpuWq2Ps1WDDIORS14P+x/+0w37U3w1k8V/8I/L4eWO5a3EMkokD4/iBx0r3iqunsZNcrsFFFFMkKKKKACiiigAooooARm2jNFDLuGKBwKAFooooAKKKKAIbsyLCTEu5+wNfnj+2Z8Evix+078btA8CQ2dxpHgJtr3mrqd8QUHcTt4544GetfomeaTYM5xWU4czTN6dX2aasec/AT4E+GP2efh/Z+E/CsDR2UPzyTSnMk0hHzOx+v5V6RSKu36UtaGLdwopKTdTEOopN1LQAUUUUAFFFFADW+7TOG4IyKkPNJt96lopCKoGMDFZ2uWpudPuI0Yxs6Fcj3FaWMVBef6hzjJ6AVLTsVF+8j8C/wBvPR9R8P8A7U179viMZZoTC/ZgG6mv3Q+E94dQ+GfhS4JBMml27cdP9Wtfjh/wVa+X416Zc5fzTAd2VwMg9jX6pfsZ+JJfFn7MXw71GbHmvpccbYOfu5X+QpLdGlRWue1UUUVqc4UUUUAFFFFABRRRQAUhz2pabJII13HpQBFMSCAThfWnfeTCtTsLIoPakEYQYFBXQ+F/+Cq3xiX4f/BD+xLaY/2jrcn2ZEDY/d/xn8q/KL4B/EX4i/BXxNH478CWk4ls0MUtx9laWAqeCrY9a+vf+Cy2ovP8XPCenCZmgj055PLzwGLda+//ANif4V+HfD/7K/gqzTSbaVNR05bm686JWMrP1ycciudG89Ldj40+GH/BaK8t7NIPHngN7y4U4a50SQLn/gDn+tenSf8ABZ34XLalh4S8TLc44ikSIAn6h69i8a/8E1/gX421S5v38LnS7q4OWbT5iignqQpyK8+tv+CPnwSt9SW6kuvEVxEG3G1a8RUPtwmcVra5nJx6HyF8ZP8AgpF8XP2kNcfwv8NNKvNB064HlpaafF515L9WHAB7+1fTH/BNP9h/W/hTqN18TviHaGDxTdo6WVpcczW4bId392Br7H+FP7O/w8+CtosXhDwrp+kS4Aa5jiDTP7lzzXo1HKyXLohN1OpNvelqloQFFFFMAooooAKKKKACiiigCG6DtCQhwayJLOSWf7mVx29a2Z0MkTKOD2rw39qz9om2/Zc+DOq+LZ7X+0dRVhBZWrNtEkrkKuf9kE5PtUt9DaEuVEfx8/bC+F/7MEMcPi3WGbVpE3x6VYJ51ww9cZ+UfU18S/Hj/grp4L+Ifwx8ReGNE8Daws+r2cloLrUXiEShgRnCkkmvnv8AZ1/Zf8df8FA/i1rPi7xLfy2Ph5rvzNW1ccn5jkQ224EZAGPQd/f7W/aY/wCCdPwT8Efs5a7qWmaRd2mqeHdMlng1JrpmllZRndIBhSfoAPapSJvrqfn/AP8ABNcTv+2R4EETbCZJQ/OMr5TZH5V+/wBIu+Nhkr7iv5iPhv8AETXfhV4403xR4ZuzZa1p8vm207IGw3TlcEHivraH/gqZ+0fdRlY7vT2GNpYaOC3TrkLj9KdgZc/4Kh+AdQ039rzTryeFmi1qK3MEkfO8hwp6d6/ZrwTAun+CdAgb92IdPt0+bjGI1FfzlfFL49/En4peMLHxJ4y8Q3d/rll81pcSQpD5IByAqqgHX1zXvGk65+2V+0F4PMun3njLWtAcKyyWoW2VgMYw0aoSOOxosB+7EciycowYeqnNSV8T/wDBOL4D/F/4W6Dqmp/E/wAQ6o632Ps2hahdNO0J7uxYkg+2a+2KpEMKKKKYgqMurMVzkjqKe33arrbrGxbJ3NQNHLePvhronxK0mbSdcsodR0ycbZraZdysPpXzz4s/4Je/AnxNFtt/Dj6IT959OlKE/nmvquONoZsqWK+lWgxPtUuKZbkz4aH/AAR9+CIYEza9t7qL0jNeheFv+CavwC8L2SwN4Mi1dh1l1KRpmP1ya+pBS4HpRy9ieY57wL4B8O/DXw/BofhfR7XQ9Jhz5dpZxhEGepwK6BlBHSlpadtBFVmEaneKTzuPlqeaJZUIYVwvxa+L3g74G+FZNf8AF+rRaVYIcJvOXlb+6q9SaztymiaOytrrzm2lGVvpxX4RftqWM3jv9vrV9GaTd9q1S1s18zkAHaMfTmv10/Z5/bG+Gn7Swu4fCeqlNQtn2tYXoEUzjruUZ+YfSvyr+PVk9v8A8FP44rqDaZPE1gyhuQylk5ph1PsL9v8A+N3xn/ZT8F+Fbf4bpZ6P4SgtIbO41WGwimMMqgAKFkUqobHp3r5L+Ev/AAVu+M3g/VjL4rlsvHultkyW89rHazJ7q8Sgce4NftH4m8J6L400mXS9f0qz1rTZcF7S+gWaJsdMqwINeW+Mf2f/AIHeGfAeqf234E8J6Z4ZgiMt0rafDBCAOcnCjnPT3oSuK58W6h+098HP+ClVjpXwy8W2es+AvED3Im0658xJYjLg8A8D5hxyO9eS/Fr/AII6eOvBtlfan4U8T6Vr+nW8TyvDdhobgKozxxtJx715Z+yb4V0H4mft/aCvhfSfs/hS21qS+trVcypHbxFnUknjHyjH1FfuD8TLpbL4eeJbhjtWLT53J9MIaNgPwM/YX+F+jfEn9qbwt4W8SWa3mns9x9qtZUV0JjjZsEHIIyvetjRfh5oOsft/2/hO1sbeHw8nioWws2iUwmNZPubMYwcYxivRv+CV/h9fFn7WtxrU0gMlhp13eITyzF8rnP8AwKvOvA88i/8ABRXS2LMrHxyqk55P+kYoKP34sbC20y0gtbO3itbaBBHFDCgRI1HAVQOAB6Cp6d6UGqWxkfmf8Uv26PFnwj/4KCp4a1jU8/D5Wis5bBUwF8xcCTPqGIP4V+l0UqTRpJGwZHAZWHQg9DX4s/8ABXbwM/hL9ovR/EcAwmr2aSDbx88bfzr9V/2Y/HyfE74A+BvEaSrK13pkQkKnPzoNjA++VqYuyKaPUqKaOtOq07kBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPyI/4JS/s/aR418QeLfFniOwsdSFhN9lt/OVpHWbOWLK3y4Izg5JzX03/wUO+E3gu/+EN7f6ra2emy2VtI9qYowo3KMgbRjvXmH/BNDWI/BvxU+Lnh64JtbV9VY28LDGW3HH9KZ/wUCtfFH7UHxi8PfCH4emZ7uziebVpTn7NACOBI65I6elcOk46PU9HlkpPTQ6H/AIJJ+A/CGi/COfW47uxm8T6q7R3EYkBlEYOQMHnpXq3/AAUM+GHh7Vf2afFl7Npdu11Z2pmjnWMCTcp3Dn8K+b/j9+wDe/BX4L6N4h+H1xdWnjTRYFkv7zTrqUK7ADcUXAyDz1xxXFeAv24PEf7Q3wR8a/Drxtp0lxqdpo08o1G2jwCqRniTJzuyOwo5mo+8iYxu1Z6H1z/wSvt1i/ZR0dx5eXuZchOuQR1r7Dr4n/4JMyCb9mYNGZPJW/kRRJ6gDOPbmvtiuuGxy1FyzaCiiirMgooooAKKKKACiiigAooooAKKSk3UgHUUzzPmIwacDTAWikzS0AFFFFACNSBh6YpT0r4r/wCCiv7Wnjn9nHwzp6+CtPt1nupNs+rXCGQW6noAmMH8TSukUouWx9qcUtfnj/wT5/4KDeN/2hvH0XgLxj4fguLv7FJef29ZHYoVRkB4wMDPTO7rX6HUCtYKKKKYgooooATPalpmz5s5pd3zYpXAVvu1Xum8m3kcc7RVhulQXXzQuuM5FHQa3R+Rv/BYrTLa31rwTLFCq3EwkLy45bivt/8A4JwXct5+x/4EaYAFIpUXH90SNivjL/gs5E39teA1jX90Ff8AeDrnHSvrb/gl7fG9/Y68I5bd5ctzH+Uh/wAayidNU+sqKbu6U6tjlCiik3DdjIz6UALRSGk3UAOopoanUAFIRnqM0tFABTXOFzTqQ80Afjh/wV38B6zH8QND8YTR/wDEplR7ONvRgd3NfoF+wL8UNM+Jn7MvhE2Mqm40u0SxuYl6oy9PzH8q5P8A4KQfBRPix8BL8JC0l/pga9t/J4+dRnB4OQQDXxD/AMEifjhD4L+Ld/4G1W++yWWswt9njnbAFwgLEc+oUjHqax20ZvKSlqj9lRTqKWtI7GIUUjZxwcV8Nf8ABQr9vq//AGa5NP8AC/glbC98XXQWWZrhfNW0TcOGQEZLDIHPencLXPuXnPtS15L+yt4w8X/ED4D+E/EnjkW6+I9UtvtUy20PkoqsxKDZk4O3FetUCCiiimAUUUUAFFFFABRRRQA187TjrX45/wDBYD4wT+JPi7o/gS2uGaw0e382eFD8plk4BP4Gv2JuHMcDsOqgmv56filrs3xa/bUvn8QH7ZDeeJo7KVG/d5hEwXb8uMcDqOah7mkUftv+yH8P9P8Ahp+zj4E0fT7JbENpkN1Oi5+aaRA7scnqSa8v/wCCnHxIT4e/sp+I48B5tYK6aiZwSJDg4+gz0r6n0vTrfR9NtLCzTyrS1hSCFMk7UVQqjJ5PAFflj/wWq+IrvdeB/BcM+ETzNQmiGOSQUXP609hbs8H/AOCUfgDRPHf7UiJr9hbanDp2l3FzHbXaB0MgAQNtPBxu7+lft3a+E9EsVxbaNp9uOmIrVF/kK/Dv/glT4utfC37Wekrdzpbpf2NxZq8jADcRnGT9K/dmmhSPxm/4Kyppkf7TXhTTLS1hhQWkTTxQoFVi0ncD2r9ePh3o9loHgPw/p+nWyWllBYwrFDH0UbAa/Iz/AILDeGX8OftFeGPEiKfLv9LQh8nAkikPH5Yr9RP2afilpvxe+CnhPxBYXEczy6fClxGjAmKVUAZWHY8Z/GmD2PUV606oyM45I57U1pxEN0jqijqW4H50Ek1FNVt2CDkU6gBsjBVJY4HrXxD8e/8AgqV4N+BvxO1bwXN4X1XWbvTJFSee3dEXJXJxu+tfb0kayKVYblPY18z/ABw/4J4/B/47a5d63q+kXGna1eOHub7T52R5SMcnOR2x0oGjyXRf+CxXwb1CENe6Zr+ny94/swkx+Kmum0v/AIKxfAbUJkSbUNXsVbrJPYNtHHfmueT/AII6fBVJCwv/ABDj+79sA/pXMeIv+CLnw+1CYnSvGmuabEf4JFSXH50D0PbrT/gpn+z5dKCvjTYf7sls4Nbnw/8A2/fgv8UPHmn+D/D/AInN1rGoSeVbK0LIrvjOAT3r5Wuv+CJPhoW7m1+I2qfaMfIZrSPZn3xzXQfs1/8ABKF/gz8Y9F8Z654vg1u00e5NxBZRWpRpXCny2Zs8bW2t+FBJ+itFMTOcEc+vbrT6AEbpX5Lf8FsNVvP+Es+HenCeQ2X2W4m+z7js37lG7HTOO9frPnrX5ff8FsNFgbSPhtqQhT7U13Pb+bj5tuwHbn0ziol0LifnF4PvPHvwr/sj4k6EdQ0SOOYxWmrQFlDOBgrkdQRkH617h+z/AOPtU/ac/bq+HeueLxC+o3Gp2zXDW67fMMPzAn67QDX21+yZ8E9C/aQ/4Ju2vhi/s4JLoTXZtp2QM8Vwj7lYHqOw+lfEX7Cfg/xF4R/bm8JaINLku9R0jUZ47uEqQsSrG+5yT0wMnn0osWfuJ8Qvix4P+FOltqHi3xDYaFbAbgbuYKzf7q9T+Ar8iP8AgoN/wUH/AOF/RzeBfAEkyeC4yDfXRyjXxDAgYBzsBAOO9fUP7eX/AAT38f8A7TfxQs/FPhnxTp62K2iWx0vWZpljgIJy0ewNjPGcAZIrxbQf+CJfime1Vta+JWl2s4HENnYyTIvtudh/KqtYjYzv+Cf3xi/Z3/ZZ0tvEfiPx/cX/AI1123EM9tDpUvladGDnZuC8kkDJH5V98/tRfFTS9S/Yw8e+MvDepG60+88PzvY3tsCMl0KqexHJFfJfgH/gizZ6P4t0298TfEAazotu++ewtrDyml4OF3FiAM4zxyM1+jkfgHw5H4Oj8KNoenT+Gktxaf2VNaxvbNEBjYYiNpHtik1cVz8g/wDgjz4G17VvjnrniW3UroFnpclvc3G3arSOV2ov48keleRroj+B/wDgo5Fa6hLtFr45jZpCf784dT+RFfuv4P8Ah94W+HtjJZeFvDWkeGrOR/Me30ewitI2b+8VjUAn3r8kv20P2C/jXq37QXi7x54O0GfWdOv7pb+2udOu8XEbgAAqMhgVI7enFHKPmP2M7ihulfgNL8a/2sPhPavbah4i8fad5DYLajA9wo5xjzJQ2a6Lw/8A8FKP2ltLjWGXWW1JlGA13pKn89iDNFhJXPqj/gtJ4Be98E+CPFtvbSSNZ3r2U8y/dRXUlM+nzAD8a7//AIJCfE4eKv2e73wvMQLvw7fMgXv5b/MP1z+dfnv8cP27PjN8ZPAF94U8Y/YDo93teRV0to3BRgysrN0IIHNfTf8AwRLaZvEHxLG5ntvs1sQx6Ftxz+NLlKbtofq4vWnUlLVJWICiiimIKKKKACkPNLRQA0LjvTqKKACiiigAooooAKKKKACiiigAoqORAzBicCl81d4XPJoAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfi/8AsmaX4+1b9q7xl4Q0PXbddXmEs02rXMRlghC/eJGM5IOBx1Ir9U/g/wDAPw38Hzf32n26z+INUw2p6tJnzLphz0JOBntXzD+yH+xj48+F37SHi34n+LNSsbO0uxNb2+l6exczhjwzkqAFA5GDnNfdO6ualT5Vqddapd2i9CO6tYbq3khmjWSF1KujjKsD1BFfJ/xw+Hvwc8JeAfiF/YL+G/D3iG80ueG5MU6LNuZTgbBk5J4/Gvq28hS4t5I3GVYc5r8wv2m/+CV/jbx78QtY8W+DfGVndtq0/mvaaiZIWjBwMBlVhgde3etJx5laxNKy1bPcf+CUK6fa/s4z2dhqkWpeRqcgm8oH905AODkV9q14R+xr+zRD+y38G7Lws1xHeavNIbvUrmEko87AAhcgHaAABkV7vVQjyqxFWSnNyQUUUVZiFFFFABRRRQAUUUUAFFFFABVW+naG1lZBukCnYucZbsPzqyaY0CSffUMM5waloaep+QvxYtf22vFPxT1ObTh4m0/SmvnFgtlcrHbpGG+XOD0x6jvX3Z+x14P+OugeHJ7r40eK4tWvZuINOSNXeEeryjGT7Yr6Q2DsMUoGKXKaOd1sHNLSYpapKxkFFFFMBG6Vx/xI+FPhf4taLJo/ijSYdUsJPvRyDn867CjbRZPcabTPA/2dP2K/h7+zD4n8Q634NjvEn1hFhaO6m8xYYw27avHrj8q99pAMUtAgooooAKQ9PSlprruXGcUAAXB60u35s0jLllOelOqWrgI3So5ovMjYA4JGKkoz1o6Aflr/AMFhtJew8N+GLuTMrrc7FbHAXrmvVP8Agjv46j139nW+8OkoJ9G1GQ7QfmKyfNk/jXUf8FRvhrH44/Z31W8MeJdLia8SbjIKENt+hxj8a+ev+CJgLX/xOZZT5SxWeIuwLbiT+mKzWx0TfMk/I/VH+JafTKXdVpmIrdKqLHHJP5wzvXirLNxzXlv7RXx00r9nf4Yar4x1WB7mCzVcQxfedmdUX/x5hVXW44xvoehy65ZQ3y2Ml7bJeMAVt2mUOc+ik5q/X4T6h4v+JX7Yni7xh8SvDeqzaJrvh/y57bS7OWQboi2ARyfm/Svdv2P/APgqF4j8M+LJfCXx4vJnsHXZb6tNbBJraQA5EuANynAHTIJqVJN2G49EfrFz2rzn4j/tIfDL4Q3y2XjHxvo+gXrLv+zXVwPNC+pQZIH1FfJ/7aH/AAUv8L/D34fHTvhVrlp4g8XaooWG8tx5kNkm4b2YcfNt3Y9Dg1+dXw5/Zd+Mf7Wsev8Aj1xNewRs0l1rGrE752AzhAfvfh0pSkCj3P3e+G/xe8G/F/S5NR8GeI7HxFZRsFeayk3BSegI6iuwr8Of+CaPxU8Q/B/9rbTvATX6R6JrlxNY39s6nYZFikMZXng7wo71+4o5FOMrikrC0UlLVkGX4l0aPxBol3YShSs8bR/MMjkYr8Fv2vP2Z/F37MfxWm1+1WSKxmvGu7K7tsjyjuyOR2zX7+Mu4YrkfiR8J/C3xb8Oz6H4r0mHVtPmGCko5HIPDDkcis3F3ujSMklZn5y/BP8A4LGWOj+BdKsPiD4a1LVddhXypLvSUUCZQMK2HbrxzzXokn/BZb4bhWCeCPFW/GRvWAD9Hrvov+CWvwTj1SeY+HFNox+SMXEu4c+pbFaKf8Et/wBn0ahFdSeGLqYL1ga9bym47gAH9aeoe6fI/wAXv+CyXiTxJp0mmfDjwgujXsx8v7bqJ8+Rcn+GNTjOPfvVD9kn9gvxz+0L46t/ir8ZJruHTHnF0IL1iLm/IyUBBHyoG2nB6gYr9HfBP7Ifwc+Hc8U+g/D7R7O4jIZZmhMrgjocuTXrojVVCgYUcADpRZiuuhDZWsNjbxW9vEkFtEgSOOMYVVAwAB6YqzSBcUtUtCQooopiCiiigAooooAKKKKAIbtS9vIobYSpG70r+fL9sr4beIPgv+0pr+ovZyWMU2of2jY3W0lGbO4HP1/nX9CLjK4rzr4tfAfwf8atDm0rxRo9tqFvImzdIgLr6EHrkGp5Xe5rFq1j5r/Zd/4KYfDX4ifDiFPG+tW/hHxRpVqqXsN+21LkquN8ZxznH3euTX5m/tZfF65/bI/aekvvDttcPY3LxaZpNts3O0anBcADoTluegr3Px5/wR++J6eOL+LwnNos3htpz9lmvboq8cZPGRyWx719n/sS/wDBOnQv2XruTxJr95b+KfGbx+XDdeSRFYqR8wiz3P8Aexmm0T8J+eXxq/4Jz/Fr4M3Wk6t4Z0W+1yBoI3M2lbnuILg47Kcg5/TNfq5+xT4g+ImvfAfRV+JugXmheI7MfZv9O4luI1+7Iy9QcY6173tFG0ULQTdz5L/4KA/sYz/tYeCtNk0S8js/FWiuWs1uDiGZGIDox7cZI9wK/MLwd4k/aK/4J/8Aiq7ig0++0yy3kz2t5aGfT7oYKgkgZHXIKsOcZzX747RVTUtHsNZtzb6hZW99A3WK5iWRT+BBFMEz8mdJ/wCC03i9bVVv/h/pM9yBhmjvWhBb2UgnGaqeCfiR+0H/AMFGfiJb6Z9tuvBHw8hmSS8Glq6Qoq8n98AGZjjGM4ya/Tcfs4fCn7c14fhx4We6Y7jK+kQMcn6rXb6PoOmeHbMWmlada6Zar0gs4FiQf8BUAUBdDtH02PR9LsrCJneK1hSBGkYsxCqACSep4q7SYpaCQooooAKKKKACiiigBNo9PeloooAaw4r86f8Ags94Y1PWPhH4N1WysmmtNL1VmurgLnyw8ZVfzYiv0YqrqWl2esWrW19aw3luxyYp0DqcexqZK407HwR/wRruryb9nzxJaXBnEFvrbCBZMgKGjUkKD2zX21o/wx8JaB4mvfEWm+HNLsdevjm61K3tES4nP+24GW/E1t6bpFjotuYLCzgsoSdxjgjCLn1wKuVQNiYpaKKBBSUtFABRRRQAyaFLiMpIiyIeqsMg1R/4R3SyCDptoQev7hOf0rRooA5jXvhj4R8T2clrq/hfR9Tt5OGjurGKQHnPdaPBPwy8JfDeCWHwv4d0zQEmOZP7PtUhMmP7xUDP4109FABRSGvm/wDa8/bU0P8AZJj8P/2tot9q76tIQPs2AsaA/MST39qTdh2ufSNFeKfBP9sH4XfHy1gPhfxLbPqEg/5Bt04iuAcEkbT1wAenpXtK9sHPc5oTuA6iiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkyPWhmwKZuDcVLdgH5ozTWYKcYpN/tS5gH0tMVuRxT6pO4BRRRTARjtGcZpqybmxgj8KfTP4xQA+iiigAooooAKKKRmCjJOBQAtFIrBuhzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIzbVzgn6UALRSdaWgAopu8ZA9eB706gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKi88eaEA696AJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAroiW+TtVB0zntTvMGcAFvcUy6tlu4jE+QrEdPY5p0Maw/ulzgetBQy6KC3Yu2xe5qGyZmZtm3ysAKRVxog4wwB+tKsYUYAAHtQO+lh2AOgpaKKCAooooAKKKKACikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiko3AYB6mgBaKQ0hYgZoAdTGbaCaFct2pex4qboNz5g/4KG+HdR8S/s3+LLfTZyky2ErGMHG5QAW/QGvjH/gibq23xz8StPEbDzNOtZd2PlBV2HP1ya+qP+CmHiu98C/s5+JbnT5c3d/CLb74HlK8iIxA6nKsRXyx/wAET7aRfiB8S5R/qV0y1jJ/2i5J/lWaNnsj9UfF3jTQvAWiyat4j1a00bTYyoe6vJRGgJIUDJ9yB+Nef/8ADWnwc3bf+Fj+Hy390XYJrxn9vr9j3xh+1fH4btfD3iaHRrPTg5uLW6DGKZichiAeSMCvjZv+CL/xJ2nZ400EN2/cOD+eaCbH6Oal+2t8DtKjZrj4k6INvVUlZj+QFcj+0Fomm/tSfAfUp/B2p2ms6Vq1nJFbz5yhcfdwMdcjv7V8SeG/+CLfi7+2LNtd8aaadN8wfaRaI4kKdwpPGa/TX4R/Azwx8E/h3Z+DfDdvJFpFsMfvnLs7E5LE+uae60LjJRZ+P3/BNu9vPhv+1pP4L1m323WoBtNlgkPy+YgYgn1HBP5V7d/wV3+Fvgzwn4S8O67p1nDaeIZ79oWaFFVpcpuO8Y5AXJGMcgV5F/wUi0e7+Av7WOi+JvD0Z0e5ls47uG6tTtaSRJDuYn1I4/GvMviH8VviP/wUJ+L3hbw+liTMoS3hhtwxCjHzzSHkZ2gnPFZxi+a5TkeO/AfV/CWg/GLwtfeObRr7wlBdq2oW8ROXQA4/JtpPsK/oK+DPxs+F3xL8M2tv4H1jTDp4j8uLT4ykTKvTATP8q8C8Rf8ABMn4at8AI/COnaVCviS3t1P9tEDzpZsgsScdOuOK/Kr4kfBT4rfsoeI5Lx49Q0uC3fEGqWjMIwN4ALducgfjVS10IsraHqHivS3+Fv8AwUssS9odPhi8VW80CuPldWlUAjHY5r92l+6K/mw0/wCKXiP4kfHDwf4h8SX0mpahFq1iDMxzkCZCMflX9JsbB41YdGGeaqKaJlK6sOXpS0nfFLWpmFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUmzFOooATbS0hIHJ4ooAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKTdgCquqalBo+mXd/dP5drawvPK/91FUsx/IGrNfPv7fHjCbwT+yF8TNRt5DHPJpZskcHBBndYcg+v7ylzDtcZ+zT+3B8P/2pfFHiHQPCiahBqOjoZ3W9iVVmg3hPMQgnjJHHuK+hq/mm+B9z8U7fxRLd/CmbxDBr1valZZvDssiTCDIZlbYRlMrnaeCRX1l8J/8AgqN8a/gvry6b8SNOuPF2nsMNBqcBtbxMA5Kvt5P1BouPlP2mr5F/4KK/teax+yv4B8Ov4V+xzeKdX1DCQ3YDBbWNC8rFfc7Vz7ml+D//AAVA+B/xTh8u812TwfqSoXa01qMqpwCSFkUFWwAfSvzh/am+Imrft9ftiad4f8GBrrTFk/sjSATkeSuXlnIPABCs3/ARUvVhyn7Bfst/FLVvjV8A/B3jbW7WGy1LWbP7RLDACEHzsoxn6V6tXMfDXwPY/DT4f+HvCumosdlo9jFZxhFwDsUAtj1JyfxrpM0J2FYfXzL+0T/wUH+Ff7N+vXHh/Wrm91fxHbqjS6XpcIeRA2DliSFGBz17V9L5r+fX/goUJI/2zPiUHdm3alGPmOflManb9Paq5h2P3H+Afxs0f9ob4W6X440G3ubTTr9nCQ3ahZFKNgg4JHauF/bS/agX9lH4RweKItMGsaleahFptnZu5VWdlZ2JPskbVwf/AASrhaH9i7wjuJO+5vXH0+0P/hXzd/wW11qSOH4Z6X50ghMlxdtDuOwsMKGI6ZAJGfc1L1Gkey/D/wD4KYw+KP2dNf8AiZd+C7rzdBvYbS+srSTeMPIibwfYPnHtXbQ+IPgh/wAFHvhfPYm7EzBFLQSMI7yyYEPkA+6847Zrxv8A4JW/B3SfF37Hnim11eMXFl4n1CeCdcZICKqgj3BwfqK/P39ob4VeMf2Ifjdquj6Vqt1p8E8cv9n6hbOVaW2cFfzwxU/U0itOhwHxW8HwfCX42a94d8JeIJL2HS71rW21S1lMbNzt4ZSOxwfxr+hP4e+LtC8M/DbwfZav4l0+K9j0mzidry+jEjuIVBJ3NkkkGvxS8Hf8E2PjX8RfBdr4t07TrO5tNRhW8t994vmTb2HP15J/Crmof8E3/wBpK6niN5oc12FIRXm1DzNnYEZPGM1SYmrn7wwzx3MKSwyLLE4yrowKsPUEVJXmH7NHgjWfhp8CfBHhbxDKJta0vTkt7lg5f5hnuevUCvT6pO5AUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUmaG6U2gB1LTOe1JuK9SMVLdhjLhtqk1VaYkYDYPapZGEmQp3cdqoybgqEIX/ANkVDZ0QiralhboH5fMUv7EVIrOGBZvlqpp9qOWeHy2J4yasSFjCFIPB9Km4O2yJ7WYyMcjGOlWqoxbscHaakVnWNt7bvp1q1IyktSySFGScCmrKj/ddW+hqm7453kj+6abHIsaNtGT320+YahdF2SQKhOT/AMBGTUcLZyxlYj+6wxWe1m8rH98yqxyasxrGzEIzE+ueDS5tR8i7l7NLVaOBluN+/wCX+7VmtDEKKKKACkOG4PNLScVLdgEGOgFG4ZxnmkU4zUbMqnJOCelLmGlcmo3CmLIOOaa7nPtRzBZkuaWmqwKinVSdxBRRRTAKKKKACiiigAooooAKKKKACiiigApMihulM3AcZoAczccVHJKFhd3fy41UlmPGB60M+Oc4FfOf/BRLxbrHgf8AY5+IesaDfyaZqUMVpGlzEcMqyXkEbgfVHZfxoKscR+29+194u+BvhfR7z4aaNb+I7e53NPqyqbqC22sMq6pyM9Pqa8A+FX/BZ+JY4bT4i+DpUnLgTXukONsak4JMbc5HpWX/AMEZdQ1LxDq/xK03U7qXUtDjtrdls7w+dGJGckn5sjkCtH/gpzpf7PHg3wPqNloui6OnxPurhBGumAiSHa6mQyBeBlcjn1qWx2R+jnwx+Knhj4weF7bxB4U1WHVNNmUMGjPzx5GQrr1U+xrr6/Kn/gkb8R/APwv8G+LG8SeOdN0nVdVu4/K0u6utu1EU4YA9+TX6h+HfE2k+LdMTUdF1G21SxckLcWsgdCR1GRTRL0NOiiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASk2KDnHNOooAKKKKACiiigAooooAKKKKlsAooopoAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQrKjMuGBycCpNvzE0irj060+gYUUUm4ZxnmgQtFFFABRRRQAUh54paZtO4HPFAChQKdSA5paACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEYFlIBwfWk2/dzyVp1NZsHGKAFNMZgBz0pQxPGKUqMUAfDX/AAUe+Mnxk+E8GgXfw2kkt9OzuvGt7fzXY5GBjHSvnSL/AILNeNdI8Lw2d58PrGXxDGgjae4llRWYdWK+vtX6yX2jWepxxrdQR3AT7vmKGxxjvXEar+zv8NtcuDPf+DNHu5i28ySWik5/Ks1FnRzQaWh+JHiG++P37fXjY3H9m6jq8MjeVFHAjQ2VqOuDnjAA71+p37Af7Grfsm+BdR/ta+XUPFGtskl6Yh+7hCg4jQ9T1yc96+m9B8M6V4XsVs9I062021UYEVrEsa/kBWltp2Zk5XEWloxS00iRKGpaSmI+Of27P2Fb39ra48OXen+IIdFvdLRoBJPD5ilGOSWAwSfoRS/sP/8ABPmz/ZM1bVvEGp+IU8T+Ir6IW6TR2vkxQRg5+UFmO49Cc9K+xdtG2oUWXzDDyK87+NHwV0f41+ENQ8Pa3H51hewNBIoVdwz0ZSRwVOGHuBXo+2kCAc96pRXUnmaeh+aPhP8A4Ix6f4X+I2ma+nxJml0jT7yK7i02XSw8z7HDANMJAvbtHz7da/S5eFA/KlxSbcYwTQkDdw/ip1J70tUIKKKaxIUkdaAHU2SRIly7Kg9WOKFzt5r8WP8AgoL+2N4/1b436j4H0HW7nStD0G8CILNzFJMxx99gfmHNK+tilFtXP2pormvhvqF5qvw/8N3mokG+uNPglnI7uYwT+tdLTEFFFFAgooooAKKKKACiiigAopDQTgUr2AWiqy3JkUsPlAPU1jeM/iB4d+Heiy6x4n1qy0LTI+txfTCNeoHGep5HApcyK5WdBIgkQqehpscZjwN3HpXxV4t/4K5fAvwzrMunW0uua35b7Gu7GzUwdeSGLgkY9BX1P8Kfit4a+Mvgux8UeFNTXVNJuxlJeAynurDsR6UcwrM7KiommCtjPNLu5A9auwWZJRTRmnUhBRRRQAUUUUAFFFFABRRRQAUUUUAFFIelNzQA4nFIGBpPrSbvmwBUSHYeelfJH/BUxZT+xZ422cp5tiHX1H2uHH6jP4V9a5rxf9sL4aSfFj9njxnoEKebM+nyTxR5xukjHmJ+O5BUlI+KP+CJ/hG1Gg/EXxN5YM7XMFgrMvIULvIz9SK+7vjP+zd8OPjpYhPG3hyx1IwxsEu5I1EsIx1WQjK49q/Nf/gjf8UpPDfxR8WfDy+umSDVLUXsFu/AW5iO1xg9yv8A6DX3v+3JpHxF8SfADXNF+GUbSeIb8JGywuY5niDqXWNgRglc555GR3oH1Pxh/bM+Hvw3+GPxiu/C3w01KfWbG0KrLI03nRiQjmNSOuDxxXpP/BNP4v8Ag74B/tCTt4+0z7BJfWjW9rq12u3+zH8tnO4EZG8DYMc/MO1fUv7AP/BNW+8C+ILb4g/Fmxt5dRi/eafoVxiURSEEGSZSCrEAkgdjg9q+c/8AgoJ4c8N3X7dltp/hiVZru6ubJdQRcFEnaRFZMew7Uxn1542/4LI/DbQdQ1Cy0Lwl4g8RNau0a3CiKGCTBxncWJA64+WvLNQ/4LZXu2U2vwwEY/5ZtPqBI/HCV9O3H/BL34C69dx6lqfhu5lvJEUyrb3rwQs2Bk7Ex1Nbf/DtX9nceX/xb2E7Bt5vbgZyMc4fmkLQ4H/gn9+2t4z/AGtPGHjeLX9I03S9I0yKJ7NbIsWDMxBBYnnjBz71+XP7ePiKLxF+1n8Rr63O6P8AtJo8+6jaPyr9yvA3wa+Hn7Lfw810+DdBtvD+nQQS3lxIGZ5JNqk/NIxLHpwM1/Pb4rm1T4r/ABI8Q6lYWc+oXV/d3F8Y4gWby9xOfwpgfvH+wmlh4c/Y2+HErGGytItI8+eU4RR8zM7sfzJJr8kv+CjX7SEf7Q3x+ul0y4S58NaADp+nSxtlZRnLyfi2fyrl/CPxO+P/AMUvB+l/CLw9qOuXWi24McemWURiwhb7kjqASnsTivY/jB/wS/8AFXwj/Zzl+IN1qX27X7QJPf6PbxFjFGzBeD3K7sn6UDPvj/glNCsP7HHhwBVBa8u2O3uTKeT714T/AMFrtLsv+EV+H2ofZ0/tA3U8An2jd5YjJ2k+ma+ev+CW8vxOuv2iPDVppl7raeBIDcNq0Jkf7EqmCQp8h+UEybOler/8FqvFUd54o+HvhmCYyXNvazXcsIP3d7BFJ9zg0Afff7F7Fv2VvhiT1/sS3z/3zXtNee/s7eEZvAXwJ8AeHbj/AI+NN0S0tpP95YlBz75r0ShK5Fxq/ep9FFWlYQUUUUN2EFFFFCdwCiiimAUUUUAFFFFABRRRQAUUUUAFFRSSfNtqRfuigBaKKKACiiigAooooARulMboaezBVyelVZ2MnAbavqKluxUVcd5hjC7uneopbgdhmlaYJtXG/wB6qzSvuzsyvdahs3jHUQF4ZlcFfL74r5L/AOCnnxt8T/A/9neyuvC90dP1HWNSj097yJsPAuxpMr9dmPxr6muI0DcMwZv4M18Rf8FmLbzP2bPDbAZMevxn/wAgyiluaTWqON/4JGfHbxz8UPEnjrR/FXiK916zsrWG5gN45fy3ZiCAT7Cv0pdWXBJ4zX5N/wDBE7P/AAnXxH44+w2//obV+sGoQyyY8tttVy3RhF8z1EkmESluuO1RLf8AmHbtIz7VDtmC7Dhx/s81XmZfLYNzjqB1rG1zpjGJZkkdmwgy2alXcjMC6gN71mWYlFwzBQkX95m5rR+ymZchs1SQNJdRrNIZNq/MD6VJFbzQGPaGPPPFSW2InUH/AL6rR7itFHqYzlyuyGx5wM9afRRWhzBRRRQAjfdqvIrMc7toqwxwpJrnvG3jrw/8PfDd7r3iXVLbSNGs9v2i7um2xpkgDJ9yR+dRIuJpIz/OFfeVIyBSTxyHDYJxX5VfFD9uz43fGr41a74a+AjLe+HbBt0V3YWvm74wPvsx6AnivUPg7+3Z8S/g9fQaT+0p4XvNC026fZbeJGtisZO0nBA69qk05mfoJbylxleedv4+lSySNGhZhgCvLfhZ+1F8JvjNrDaf4O8Z6Zq+pqnmGzjcrJj1AOM160yqy4Zdw9KpK4nIjtp/O5AOOlWMivgP9s7/AIKcWHwI17U/BHgixi1rxTbxpv1B3D28EhYZUgfeOMj6kV8jfB//AIKjfFmy+MGg3vjnXln8IzXYF9Y/ZlRFhfKFgQM4UsG4/u1WxDVz9tc0tUdF1a01/SrLU7CZbiyvIVngmXOHRgCpGfUGr1MgKKKKACiiigAooooAKKKKACiiigBG6VDJgfMxwvrUzdKyPFV9eaX4b1O70+yfUL6C3eSC1jIDSOASACTjrQNGkqL1/nXyZ/wVO1MWP7FfjS2P3r2exgX6i7if/wBkr83vEn7fX7SOl/FLUyms3tjci5kRNFuLMMqAZAXbjn8PSvPP2iP2tvjH8bNKttA8f30lrYxnzxZmDyFkI6EjvzUtl2P0H/4Iv+C00n4K+LfEboom1XVhCr5G7ZEgH4csa8a+KX/BKX4o+N/iz4m1l/FWjLY6lqE1zDqF5OS/lsSwDKOR2FfPn7OPwP8A2lPF2gyr8Nl1/StEk/fsUuzaQyEj7y7iAfwruPiB+yv+2BoOk/bdVfxJqsUnHlWOq/aJB9VVsijcZ1N9/wAEafirbx+bY+JfD9+Qu5BG7puPbk1+gf7Av7PGu/szfBpvC/iS8+16xcXsl5OscnmRQ7gBtVvT5RXp/wCzboeteG/gT4H0zxGLhdct9LhS8W6ffIJNo3Bj3Oa9KxVGbFooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSsAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZ5a7w/en03eu7GRn0oAdRRRQAjMFUknA9aM55HSmXEC3MLRvna3XFLHH5aqoPCjFADutJtA6U6igBkalVwTmn0UUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU3b82aU1GZH8zAUY9c0AP3fMBRIu9SM4pshCrvJAC8kk4Arxnxj+2X8HPAOrTaZrfjvS7W+hGZI1l37fbjvSugPaFXauM5p1cN8Lfjb4K+NGlyah4N1+01y2jO1zbv8yn3HUV3HNMewtFFFAgoppfGT0A71yNx8X/BFnqw0ubxdoseoltotmvo9+fTG6lcZ2FFRxzLNGskbK6MMqynII9Qadu7UAOopoanUxBRRRQAUUUUAFFFFABRRRQA1m2qSegr8B/+ChNjbp+2V4lt9Jtwk811BsUdGkbHX8SK/fW5k8u3kb+6pP6V+GP7VNvb+KP+Ci1nbR8xza9p0cn/AH8jz+lZv4jeHwM/b7wzYx6d4d0q1jB8uC2jjXccnAUCtWobWMR28SjoqAfpU1aGAUUUUAFFFFABRRRQAUUUUAI3Sq97FLMqCOTYmfnGOoqxTAwfPHSpaDqcn8R/HFj8Lfh54g8T3uBaaNZS3bB2wGKqSqZ9zgfjX4bT6h8Zf+CjXxo+xRzz6kskrS+Xu8uy0u23HAbAC5A6E8k4r7C/4LAftCPp+gaV8LdJnkS5vpBcaikZ/wBbHwUQ/wDAsGvoP/gmz+zm3wE/Z/s5dSt44/EXiFhqN4653KrD93Gf91f5mkldXLbsfNvxU/4JP+GfA3wbmm0i/wBW1HxJZ27XN3eQBm80gZ2LEG2nn/Zzjmu8/wCCQvgvxn4N+GXiZNe0680zSri/3WsF9A0T5AwWAYdDW1/wUe+Lnxf+ENrZeJfAHiu30LQ9NQG9tHhR2uCzBcEMpyMt2rxD4O/8Fnr6zaz0/wCIvg+GeHhH1PSJtrAY+8YiPXsKiLuzTVI/VGO1fd5jtuYHI9KkeSRtpRcf71eT+Df2sfhd43+HcvjSy8WWEOjwQtNOLmZY5YsDJBUnOfpX5W/Hb/goF8av2iPiRfaV8KbnWtF8OIGFrp+gQCS8ljVv9czqvmAn0UjArTm7E6vc/a+HKjBfe3c1LX4AeFf2uv2iv2dfFFrc65rniQxM5eTTvEaswnGCMEygsOueD2r9lv2S/wBoi0/aY+EOneLYIltrosYLu3U58uVeoo5u5Lj1PaaKT0pae5AUUUUwCiiigAoprZ2nBwagDPDCS53Ee9Juw7Fmiq0Fx5iqW4Zh0qNdTtZGKLdwu+cbVkBP5ZoWoWLh6VFJIItuecnFOzlev5Uzy89TuIOQT2qZXGiNRO0jBtoj7etebfGP9pX4b/s+rZJ448SwaNNeKWt4HVpJJFBwWAUE4z3r04puKkkgj0PFfDX7bX/BPHXv2pvHdt4msPGEGnPb2wt47S7gLoBnPBB4HWoKJvil/wAFcPg74O01z4Y+3eMdRxlIYYzBFnI6uw9M9u1c18BP+Ctfhf4q+KpdG8ZaFZ+C9OkBAv7q/wB0QXB+/le/T8a8Gl/4Is+PVjLJ440R2HRfsz1bs/8Agir4wmUNdePtJic9dlo7VSVw0PFP2vNF0P4N/H6b4i/Bzx1oj6feXIu7NND1E/aLOQ8uu1eik5796+yP2cf+Cu3g7XNNt9I+LFrL4U1O3iCtq0aSXNvPgfeKopcE47A9a8xj/wCCKPiPd8/xK04A9cacx/8AZq3tN/4IlxlV+3/FKZCDnFtpYwPoC9Ow9GfUs3/BTT9m37PIV+JcO8KcD+yb4nOP+uI/mK/Ob4V+MPgR4f8A2un+KHiz4nzeJLD7ZPqMME+g3LhpXVwodpN33dwYEg4KjGOK+nNL/wCCJ/gaNl/tL4jeIrtf4vs1tDCfwzux+RrWj/4Ir/CdSd3jTxi2eT++tR/7Ro5RaI9Puv8Agql+zzZkBfFF5P8A9ctOmP8A7LUS/wDBVz9n1v8AmYL8fXTpf8K8+j/4Iw/CVWBbxh4yYf8AXzbj/wBo1I//AARn+EmMx+K/Fwft5lzAw/ECIfzp2YvdPSpv+Ch37NvxK8P6ho+peNIYLC9haCeK9gli3IRg8leK4X9n/wAX/sX/AAGF9e+EvFvh8XszEvf6nMsk8YbgojOMqpB6DrXw9+3F/wAE99T/AGa5otc8KPeeIfBlx8rzbN0tpJxxJtHQ5614P+zX8D4P2gPiRb+DpfEmn+GLq5jY20+oqxSWQfwDHeizHp0P3j8G/tBfA3UpDceG/GPhFZrjhms7iCN3784wT+Ndkfid4E1uFrRvEuh3sU42NC91E6uD2IJwRX5R6h/wRd+Jlrbs1n4s8M3smSAmZkyM8HJWvP8AUf8Agkz8ftH1BY7XTtNvkJyJrXUURR75JyKXKI/WH4+eCZdS+B/iPRfhlqumeCvEU0cclleaeYbZVZZFYgkYABUMMn1r8tvhb+yL8QPi9+0Fot18U/Gmk3Nta3Mcl5dXWtw3M00aNuESLu6EgDHuarax/wAE5f2pf7PaN47m6hChTCPEHmAj027uR7VxVv8A8E2v2iLXWLXHg6aGXzV23kdyuIjn7xIOeKOUObSx++NvEkEEUcf+rRQq49AOKlrnfhzo9/4d8BeHtL1Wb7RqVnYQwXMuc75FQBjnvyK6KqSsQFFIelMbOOOtMAGefmzTz1Fcz438Waf8P/COq69fuy2thbvcy4POFGcficCviD9m7/gqVH8cfjxpvgC78Ix6TZapNLHYX0U7M2UR3y4PqEP51EiuU/QamR/dpF+Yj0zkVJTjsIa+SpA602GEQRhF6U8nAzSBsnFUIdRRRQAUUUUAFFFFABUUn1x70STbWC45pu8+1BSVx/DKo3U7cAQKprMk0zqhwR1NWU4GM5oBxsS1ArFrg7T8q8NU9FBIUUUUAFFFFACNjacjIqnKSzcABatthlqncxkKcHBqWjSG5A0/7yJAecnPtxUMyv5gIOR7VEpAncH7x6GpbyQwRfIetYOR1ddCs0SNdRMfmKnOAea+O/8Agr7qlpYfsrwQT2/nT3WsQQwSf8822OxP5Lj8a+v4Waa5Qxjac4Oa+Kf+Cyl/Hafs3+H7d1DST69Ht9RiJyT+tVF3FUeqOM/4IqeDBb+BvHfimSJxJeXsdnHIVIBREyQD35av0fv2mM6KnCd6+MP+CQtukH7KCMhBaTVrlmx9RX2rcMzMVAOcdcVr0MIaMqrDJB8wbd6gUKsfKsuWb2plwXghZy+3HcnFJGxkj4yz9iKwubrXVsf9lVWDZwvpVGbXobW9W08xBI3AUsM9PSpLxpFtZWLMAoySozisYyQ3sHnDD3HG0lfm60uZ3skaqN0dPZ5EIB+dmPbnFaY6CsOxkkiAJOOK2o38xAa6I7HHV+IfRRRVGIUUUUANkYLGxY4UDJNfmF/wWY+Nf9n6D4V+G2nXjLNeMdR1CONvvRjiNWH1ya/T2T7pB6V+Inx6jk/ai/4KTf8ACNSSf6EusppSA84igBeTj6I351Ei4n6M/wDBPP8AZ/034J/s9eHrj7HGviDW7ZL6+umQCQ7xuVM9cAEcVyX/AAUi/Zl8UfHj4Y3mo6V4oa20/wAP20upNokkQKTNHGSSG65wDX2Jpenw6TptrZWyLHb28SxRqo4CqMACsb4lQ/aPhz4qi2eZ5mlXS7fXMLDFCVwufzh/CHw7471bxHcX3w9tr99a0eJr5pdNz5sSDhunbBP4Zr6Wm/4KrfGQ/DW48Ju9ompSRfZl1kLi5QAjJ+uARn3rzv8AZc/alb9l29+IDLoialc65ZyWMDt1hbJHPtg1618O/wDgl346+LXwWf4iJqMNlrmpxtfWejSx4MqMcgZ7EjJH4VRR7T+w3/wTht/FFppvxO+Kb/2tLqDC9tdPZxIH3AndKcnIPXH0rif+Cwfwf8PeA/EXw91Hw/pFrotpd2dzbvHaRBFdoyG7ezD86zv2Rf29PEn7Id1J8Lvito14dB06R1XKZu7E5Py4J+Zc46HjNdD/AMFTPjx8Pf2gvhf8O9V8D+IrPWZLW8u/OhUlZoVeOPAZSP8AZP5UC1ufod+x34mfxd+zH8N9Tc5eTRrdG+qIF/pXstfPn7AtmdP/AGR/htCTu/4lqsD7Ekj+dfQdMh7hRRRQIKKKKACiik6UALRSUtABRRRQA1mA6nFNYB1xnj2ptxF5iEHpSIUhQjcAF65PSgZzmofC/wAI6triazeeGtLudVQYW8ktUMv/AH1ivyj/AOCsraZqX7THw+8M2WnWsBS2t0n8qMIXMs3AOPYiv17t9QtbosIbmGYqcERyBsflX47/APBWLwvrfgv9qHQfiBLbLPok8FqbVhKpLSQkFlK5yOnek0VE/XLwHoFv4X8F6LpVrClvDaWkUSxxgYGFA7VvV8qfs8/8FD/hH8XvCtqbzxBa+Ftat4VW5sNUfydrAY+Rjww47Vh+FP8AgpN4N8aftQ23wr0mzNzpdyXgh19ZB5TzKhcjHZcKeaNhan2QvWnVz8njzw3b6pFp0mvaal/L9y3a6Te30Ga3+vIpki0UUUAFFFFACUm4Chjha8X/AGtP2irf9mL4Q33jObTv7WmjkSC2s920SyMejN2AGTn2FS2NI9oVt3bFOr5I/YX/AG6k/a5/t6wvtCTQda0oJMY4Zd8ckT5wQTzkY5r63poGFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtgFFFFNAFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmeWpYNj5hT6KACiiigAooooAKKKKACiiigAooooAYilc5OafRRQAUUUUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAhpjHbT6ztYd47WR0ODt4NTJ2RcVzOx8mf8FHf2jrj4MfBG5g0eeS21zWM2lu68FBkb2/75DD8a+FP2H/APgnrfftIWZ8beNpZoPClxI3l4cie665YN2Gau/8FWvGX9vfFHw/4dtb2S6e3iBe1/hV2OB+dfrP8DfB1p4B+EPhLQbKEQwWenQptAx82wEn8zWUU5K5tO0Hofnd8SP2Y/H/AOxT8WvD2t/AG31PVtL1DAu9PncyoxB5Vh6YzX6MaR46uNL+GEPifxjbLoc8Fl9qv4ByISBkgV2LRK2CQCR046Vx/wAW7GPVvh34j057f7SLrT54xGVyCShA/Wny2Iv7RpHgPw1/4KZfBf4leMm8OwatcaTOWKRXOpR+VDKRngN26d6+prHUrXVLOO7tLmK5tZF3JNE4ZWHqCK/mg034e6pr3xQ/4RC0jEOpyXr26Cb5NpyT17dK9g8TfHb47fs3wal8OrjxXe2Vm0XlhFfd8mR9xuorSPYTikffH/BQj/gohb/DOyvfAPw8vYrrxLIhivdRjbctmpxkLjgt1H41+V8Pgb4ieKI5PEcOg6/qAkYznUYreVgxzktuH9K90/YH/Zks/wBqn4vS3HifVsaZp0guruCSQGe8bJO3nsTjNfudp/g7SfDvhcaNpWm21rYw25hit44wFA24AqWw0R+Nf7E/7e3xO8J/FTwf4G8Qa0+r+F9Qvo9Okhvo8y2+47FCt1HzFa/bFfujnNfzwJpdx4R/bX0+G5tmjlh8YQSLCoyCPtSkV/Q9A3mQo/QsAaqJMth69adTVp1UQFFFFABRSGm7/SgB9FRRu5zvUL6c0/dQA6im7vXijf8AMAAT70ARX3/HrIMbtw24HvxX56+G/wDgnTrvij9qi7+KvirVoYNOt9VW+tbKEHfJs+5k88ZAz64r9D2UOuDyKFQLUta3NYz5Y2EjG0Aegp9Qnd5q4XC5qaqMgooooAKKaW+YCnUAFFFFABRRRQAUxyAjk8DHNONY3jPVl0HwlrOoswQWtpLLuY4AIU4/Wk2HU/C74u6rqH7QX7f9vptz/plvL4kg01UYYxbpMCy5HP3VbnrX7x2FpHYWMFtCoSKGNY1UdgBgCvw4/YA0ofE79vaz1i7/AHv2W7vNUOOhbDKDx/v1+51TG5pM+VP+Ck3w1bx5+y/4puLSMHUdNiW5jbcQdqupbp7A1+cX/BNv9nHwP+0VrfjbTvG1p59nbWSurK5R4jnJdXByOQO/av2o+IPhW28beCNc0G7jMtvqNnLbOinBO5SOtfzk+IpfEnwd+IfizwvoWp32mTGeTT51tJP3k0Yf5U+XnOQOnNLlsVHVFv8AaE8I6N8M/ihrvg/wX4hudf8ADtvOyxPu+83cEL1xX1T/AMEwf2n/AIefALxBqfh7xrYJouoawy7PEdyn3AAcRMTyq/Tqa96/4Jy/8E/rLRdDtviZ8S9Ie48Q3h87T9MvOUgjOcSOp5LNnoSa7j9sz/gmb4f+NjXvirwa8eg+KRHk2qLi3uCMcbc4XjPQCq5RaM6z/gol8P8Awx8W/wBlPxL4q0+LT9S1HT7SO7sNQjVHYr5secP1xtzXg/8AwRT8aJJ4d8eeFZZH8+G5jvY4z0CsuDj8RX55ePm+KvwTkv8AwPr+o6vp1l80MljJKzW8i9Plzxj6V9if8EWbhv8AhbnjZAcI2lx5H0filyg9rH7C9xS00dadVJWMgooopgFFIajZm7HFJuw7EjdKgaNZupOPSnru3DJyKk2j0qfiHscZ8VV1k+A9YtfDoCarPaSxW8h6IxUgGvxA8efsiftJeHfEcwl07X9VkuWMouLK8kKkkk5OG4r98toxjHFG0elLlY+Y/BPSvh7+154Ftz/ZVv43sEXkLb3UjH8BmqXijxT+13rVq2ja/qHxFubecbGtZjNsfHOCRx2r9+cD0pjW8Uhy0SMfdQadmHMfFH/BLn4N+Pvhr8L9X1Lx5PqMNzq9wJLbTL6VmMEYHXaTwSa+2qAAvAGBS1SRLYhrxb4mfthfCX4QeNLbwr4q8WW+na1MVBh2swi3dC5Awtezy7vLOzG7tmvzl/bj/wCCZ2o/FjVNV8feBdTlu/Fd03mXWm383yTjj5Y2P3SP6UxpX3P0O0fWbDxBptvqGmXkN/Y3C74ri2kDo6+oI61d/OvwX+Ef7Unx4/Yh1xfDOo299Fo1vN+80HW4maFlGdwhY/d9cqa/W/8AZh/bI8BftQaBHNoN8tnrsaD7Vo10wWaJu5A/iX3FA3Gx7zSU5ulfO/7dX7REn7OHwB1nXtLv7ez8VXJS20hbhPMDSlgWO3uAm78SKCCL9q79uDwL+yrp0cWqO2s+JLhSbfR7N13/AFkP8A/DmvzV8c/8FI/2ivjc+oWfg2yl0TSbomOOPQrB5bhVzniYAkHHcYrL/ZV/ZH8f/tvfEqXx147ur7/hFZrnztQ1S7djLeDk+XCW6jOPYCv2d+Gvwr8LfCHwzbaF4T0a10ewhQLtt4lVpMfxOQMsfc0F6I+R/wDgmb8M/iPo/wANvFGofFtNYmbVrkPbweIruSdni2/MzJITgGvjI6f4Z8a/8FSNKtfAVpBbaGmvRts02IRQr5KEybQoAAJU59c17r+37/wUm13wT4m8RfDDwFZSaZfWhNpfa1OoLAkfN5S9uM8mvzo+C/x98UfAn4gN4x8OSWsmslXUyX8IlBLDlhnoeTyPWgZ/Smvan18df8E+f22NY/aw03XbPxBo0Gnatoyx7ri0JMU+4HJwehyP1r7FoICiiigQUUUUANY4XJqJkC72BwSKmbpUEkwDYPIoGrnzZ/wUW8VT+Df2R/G19aDFzPHFaq3p5jhSfyzX4yfsWalLp37VnwynjJMo1mKMY/usGVv0Y1+t/wDwVc1a30z9j3XoJpAj3l7bQRL/AHm3Fv5Ka/If9i+Ty/2qvhkx/wCgzF/Wk0VeyP6PV606iihKxIUUh6VFv2yBfWmImopnnLvC55NPoAKKKKACiimS7tp29e1AEN0rctnis/59rhPvdqsTXLop3CoGZpCxT72KzluddNWQWgbdh+tX0bbKVqiu9UyRl6uw3BlyNuCKqOwqnkWqKqfanWZUI4NWPMHfiqOUfRTdwI4NJQA+mthlIzSV8Yf8FNvjd8Rfg18M9Fk8AfarSTUblobnULOMvLBjBGMA4z0z71LdhpXPtBVCjFMkjV+vSvwa8M/GD9rnx9MBpGs+Ob4ydFEToG+hKgfrXR3Hgf8AbW8URtbSW3juYTfKUa6VFP8A48KVy1HzP26bT4WbPSq9wNPt1JnuoY17+ZIo/nX4lWP7Dv7WutTK91Z6xGW5JvNaZMfXa5raj/4Jr/tN6mQbi4gjz1E2uSkVKSHd9z9gNW+IHgvwqvm6r4p0TS0X+K81CGIen8TCvzz/AOCu3xg8D+NvhL4T0vw74u0nXdRi1UzmLSb6K4KLsIyxRjjrXkcf/BIf43a+Y/7X8S6FGrfeMt7POUH0I5rq9I/4In6/JtOqfEGyiH8S2tmT+RJqrJ7A31bNT/gmf+2F8Mfgn8EdR0Dx54wj0a7XUXmhhlt5pPlYDkFFPpX1jP8A8FOv2b7fP/FwlkI7Jpl2f/aVfO+n/wDBFHwqtqBd+P8AU2uMffht0AH51ftf+CK/gqORTN8QvEDx9xHFEpP44NUK6Pa5v+CpX7OMcZK+NZ5mHRE0q5yfzQD9azX/AOCsX7O0bEf8JDqpx3XSZT/SvPY/+CMfwyVfn8a+LGPqJYB/7Tpkv/BGH4ZyAgeOPFi/70kBH/ouotYND2Hwt/wUo/Z38dXQtIvHkOjv1J1qzltY29t7DaPzrutP/am+BV/cRw2nxb8GtIx2pH/btuufbBevkTWP+CJfhCaKQ6Z8Stctp8fJ9qsoplB98FSfzry7xV/wRW8ZaXvfQPiN4fu4/XVreW1xz3ZA+PwpaFqTWzP1b0TxN4c8SWyz6TrmnanBjIls7qOVT+Kk1tw3dszCOOeN27Krgmvw+1//AIJL/G/RfNlsn8La9EqFjJZ6rtBwO3mBDT/+CadhH4G/bTtdJ8V6rHol/Z211BHazTqY5bnKqIlYvgsRuIAyTitEQ9ep+4tLTV606mZhRRRQBDd3C2lrNO/3I0Lt9AM1+NX7BdtB8UP+Ci/iLxJcoM28mo6nCD/eL+Xn8nNfsN4qvrfTfDGr3l3KsFrb2c0ssrnCoioSzE+gANfkd/wSc0OTWP2sPG2u22ZrGzsLhXkj5VTLONmT7hDj6Umi1sfsHj2qG+s01CyuLWQfu5o2jb6EYP8AOrNFCViT8mJ/+CQfim++O0txNrVkvgSa+a6e4X/XiMsW2BfXoPoa/VfQ9Gt/D+jWOmWibLWzhSCNR2VQAP5VoUUwvc8D/aO/Yr+G37S1m7+ItKFrrQQrFq1nhJlPv/e/GvzWvv8Agj38VYfiA2l2eo6a/hhnO3VnmO5Yz/sY+92r9paKAuzjPg78Obf4SfDLw54QtZfPh0mzjtvNxjeVHJ/E12dFFAgooooAKTcKSRgqknpUDXAAzjigpJsn3Comd/MwB8nrUSXSTEMrDYDgkHinZM33QducHII/nUt9h8vcsKRtFLkVEo2dTT6adyWOyKRm4rzX9ob4oaz8G/hTrXi7RPDMniy602MSnTopfLZl3AE5wTxnPAPSvzmk/wCC2XiFXIPwpsU+Yja2stuGPUeTxTCx+sLbmUjFebftEfDvX/ij8HfEvhrwvrj+Hddv4QLe/jJG1gwbbkcjIGM+9fnK3/BbLxEVO34W6cG7Z1lv/jVLZ/8ABa/xD9qi+1fDHT/s+75/J1Vi+PbMfWgdmeNL+xh+1z4L1qa00608RJJK5Et3Ya3mKUZ4O4PgfjU3iD/gnf8AtY/EL7K3iK0l1Yxg+T/aevxyGP8A76c4r9bv2bfj9pv7SPwzs/GGmabeaTFMxje1vUwyuOuD3HvXceMvHHh/4e6HLrPiXWLPQ9KhID3d9KI41JOAMmgd2fiH/wAOmf2iW5bw/pKn1OswHP60W3/BLH9o3SbpJ7bRbGC4jO5JLfV4w4PsQa/bLwb8TPCnxEs/tfhnxFp2uW+ceZY3CyD9DXTUC5mfhPD+wR+0rpPj7RLzU9D1CWVr2ENqUF753krvGWLA8cZr9y9BtH07RdPtJpWmmhgSN3Y5LEKASau9aFj2gAYGDQJu4+iiigQU0uB3pT06ZqrMx7rgVLdioq42ScyTBFPtXw7/AMFhrwW37L9jGRnztahT6fI5/pX27bBBNuJ5zXwV/wAFnLgp+z54bhB/1mtKxH0jb/GhalyXK7I+X/8AgjbHfN+0ZrZgkxZLozG4XJ5O8bP61+09fjn/AMEWYSfjL4ykGNq6UgPry9fsWTiqM2LRVe61C30+3e4upo7W3QZeWZwir9STgVX0bxDpfiK3afStRtdShVtrSWkyyqD6EqTzQI0KKKKACiiigAooooAKKKTNAC0UUUAFFFFACVjeLvGWieA9Dn1nxDqdvpGlwY8y6un2IuegzWy3Svib/grlpd1f/snyXEFw0MVpq9vLOgPEiFXGD+JFAz7A8JeNND8eaPFqvh7VLXWNOl+5c2kgdD+Irar8pf8Agi78RNWm1rxp4Oa4eXQ4YUvYI5Dny3JwcfWv1aoB6BRRRQIKKKKACiiigAooooAKKKKACiiipbAa+dpwcGoVWcTAHBj7nNTkbuDS0LXcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaACigniotr+Zu3/L/dxQBNRTd1LuoAWikzS0AFJu+bFLTSvzA0AOooooAKKKKACiiigAooooAQ0yaZYY2kd1RFGWZjgAepNOdwi5bgV8af8FDv2xtM+BHw/uvDOms1x4t1qCSCBFGVhBGCzfgTxS5knYqMbs958J/tPfDLxx46n8H6H4u0/UvEMLMrWcEm4kr94A98V6mOa/Pn/glz+yQPAfhNvid4psYm8TazmSx86I+ZawtyTncclvoOK/QYcDFMcklsLRRRQQFFFFABRRRQAUitnNLSBdtABVLVpI49PuGk4RY2JP4VdrL8SeX/AGJfCVxHH5LbnboBjrUT+EqO6PwV+MGpXXxU/bgs7KOPz2bXre1Vc53osyk/oDX762EP2ext4sY2RquPoMV+Fn7NelDxt/wUS064tCs8Ftrc917Mqbh/XP4V+7Sqcc0U9I2LqPUcagvIfOt3UDOR09fapzzRim0Zp2dz8Kf24Pgr4+8F/tIav4l0Pw1qFnb3E3n2t1p0LOA3qMV5d4U+APxq/aS8ZW8DaLrWoXEp8ptR1OB444uM/MzDpxX9Dt1pdreMhngjmKHKl0Bx9KmgtYbUEQxJED12KB/Kkk7lykpH4t3n/BMn4+fCax/tzwfqu7VFTc8enXJilz0wpH1NeTeNvHP7U/wySWy8R6141sokGH8yeR48fWv6AdtZ+reHdM163eDUbC3vYXGGSeMMCPxFFmLmP53f2Zb3WfEn7UfgW/u7e48Qan/a8c0qTKzMSCSS306/hX9F1uxaBCRtJAJX0rifDHwM8B+DdXbVNG8LabYaix3faYoFDg+xxxXdBcYqlsDd1YFpaSimQLRXgH7X37X2i/skeC7XWdR0a41++vXMdpYQzCBZGGM7pCrbRjP8Jr41j/4LjWrSL5nwbmWL+Jl8TKzD6D7KM/nU8yK5WfqPJnadvX3pq7tvzYz7V+Y8H/BcDQ5J0WX4S6jHET8zx62jsPophGfzFdjpX/BZn4bXdv5l54M8TWj/ANyJI5f13CndDUWfoM33hxzTZmdYyUALds18RaN/wV7+B9/t/tCLxHo7d/tOnbgPxRmrSuv+Ctn7P0MbNFqusXLjpHHpcuW+mQBRdBytH2eOcZA96dj8K+Epv+Cw3wZjkYR6V4nkQfx/YVA/V6jj/wCCxnwZaRRJpniOKPu5s1OPyai6Fys+8qK+HZf+CwHwKRRsbXJGI+6NPYVSuP8AgsX8Fo42MNh4huZP4Y1tAC34k0roOVn3fRX5v+I/+C0vg21glbRvAWt3rqPlNzJHGuffBJrze+/4LceIo5WNt8L9LMJ+75upybvxwlULY/WiivyLk/4LaeMp12xfDPRYSf8Alo2oSsF/8dqOT/gtF46ZPk8CaEp/vfapCP5Urglc/XfaM5pa/Hab/gst8TpGzD4R0BE/3pD+tMX/AILKfFIuMeE/DrDuuZeaB2P2Mor8aH/4LGfF681KGG18OeHkaRwiwBJGLEnAHJzX63fC/XNZ8TfD/QdV8QWcOn6xeWkc9zbQElI2ZQcDPNCdwasdTRRRTJEb7teG/twas+i/sp/Ee5iuDayjTCqyr1BLqK9yr5r/AOCilvLefsifEC3hRnkezGNvtIhP6A1Eioq7sfC//BF/w3HqHxS8Za88Yd7LTktklJ5BkfLfngV+vtfkf/wRV1byvHXjzTlO1JbSGbb9CRX64VS2HIRuleZaB+zn8O9B8Zah4qh8I6QfEF3cm6bUGtVaVXIxkE9DyelenUmKZNxPYcCl7UbRRigR5B8fP2X/AAR+0R4fm07xLpsbSlCsV3Gu2WNuuQQQT+Neb/sf/sG6D+yXrOu6tY65c63e6moiDTRhBFGDnHB5NfU+0UbRQPmfURetOpMUtAgooooARvumq8uIo2Z3IHrUs5xEeC3sPrXkH7VnxisvgV8EfEfiu5mX7Ta25+yW7MAZpSQAo9eufwqJFIyv2hv2xvh9+zbp8beJdQNzqUv+r06xIaZvw7V8w3X/AAWi8BrMy2ngPXriJf8Alo08S/p1r4M+Dvwh+IP7e3xsnmuZLiW2mm87UdTmyYrWEn7qn17Yr9LbH/gkf8EYfD8FjcxatPeIQz3y3ZVyccgYHApXsNpdzqPgb/wUw+EHxmuoLCXUH8LatNJ5cdpqpC7m/wB7pX1hb3EV1Ck0MiyxSDckiEFWB7g1+P37YH/BLuT4Y2LeIPhpLdXel28bTXEF1IXkQAZJDV65/wAEjf2mdW8YWGrfC/xHez393pUf2mxmuZCzLCDgxjPYGq5rhy6XP0poooqiAoopGoAKNteNftGftXeAf2YdFt77xhfTfabo4ttOsYxJcTY6kKSAB7k18afEX/gtV4Zs9OuI/BfgbUb3UCuIZ9YlWKJT6lEyT+YoK5WfaH7TXw8+F/iz4aazefE6ysP7GtLV2e/uUXzIBjrGxGQ2emO9flX/AMExtFh1L9tq6uPDH2iXw3ZW13LHJcHLeRuCx7/9rnj8a8Q/aH/bQ+KH7TH7rxNrZi0VW3DR9LDxWq+hdc4Y+5zX2P8A8ES4LZ9b+JUpt1NzHb2oWYqMhSWyAe2aB3srH6uN0r8Sf+CsPx6b4mfHNfB9jNnSPCyeS2G+SSc8sfT2r9tJpBDC8jfdUFj+Ffgx8N/C+ifHD/goiNH8SW/23QtV8S3Rns3YqJVUOwU4PTKik2Ee56p8M/8Agrb4g+F/wz0HwrpPwx0+SPTLVYBcm6dEbA+9sVO/1r6b/Y//AOCo2n/HrxxF4P8AGei2nhXWb1gmnyW1w0kVw+CdnI4OB619Xa74C+Ffw38E3D6l4c8N6N4cs4f3oms4Y4goHQ5HOfQ9a/FX4E+H4vi5+3ppU3grSDbeH/8AhI2v44rGLEVtbo5bdwMKvA46c0Jj0Z+ufxS/YP8Agz8ZfHFz4s8U+GHvNZuQBPJDdyQrKQMZZUIyfeuWb/gmD+zqykDwOyZ4yuo3Gf8A0OvqoU6mRdnA/B/4F+B/gToH9jeCdAttFtGO6RoxullPq7n5m/E139JS0CCiiigApKR2CqSeBVR7otjCnDcA0m7FJXJLmbCnFU4ZPNlVT3NSX2ntfW5TzCjMOoqDT7CeFgr8Kvf1pcxvDlUXd6nw5/wWUvEh/Zp0i3ON82txED6I3+NfmF+xDp51T9rL4Y246tq6N/3yrN/SvvX/AILXM6eH/h7Erts82Y7NxweBzivkL/gmh4bk1z9snwIw6afJNet9FiZf/Z6d7mLR/QBSHim0HmmQI0mFPFZ63n+lmE/6/r+FTyptO70qrHIbi7Yr95RxQbRjpcuHH8X3qsp90V83/G/9u74U/s++MLTwt4pvbqXWJsefDp1t5ot1PRn5FfQXh/WLPxFodhqensXsbyFZoWK7cowyOO1BnI0KKKKCQqGdioJHWpqhmXzPlPQ0DW5nzxyS5NV4GeO4YHpV2QMsxEhyvbkj+VeJ/GT9sj4RfAvXk0Dxp4pXTNWKCVreGKWUqp6E7ATUSOlSsrHs0037s0W8pyOxr5f/AOHln7N67X/4T3cPT+zron/0Guv8K/t0fAPxcAbD4j6QjngR3sxgb/vl8GknYOdWtY99TaxBZtzUy5xdJtU8g1zWm/FjwNqluk9n4q0WeJuVeO9jIP61qWPjXw5qd0lvZ65pt1cOcJFDdRs5PsAc1adzG/kadrG0bMD0qVYtrbtxNSjrTqZLYyqeoaTZazAsN7aw3kIbcI5kDLkexq/RSauK5Bb2sNqoSGFIUHAWNQoH5VNn2paKXKIo65rNr4f0e91O+k8mztImmlkPZVGTX5x+IP8Ags54e03xBqVpY+BbrUNOt5WiiuvtSoXwcZII6V+kd9Zw6hZz2tzEs1vMhjkjcZDKRgg/hX5Zf8FKv2L/AIUfCH4T3XjjwzpzaJrVxfIghWZjFIWySAp6etHKVE05P+C2Omo2F+HE5HvfD/4moz/wW0sB/wA02mI/7CA/+Jr5E/4Jz/B3SvjN+0rpGja/o8et+H4rSa5vreeMtEVUAKG9Mk8fSv2CX9gv4Ap0+F+g/wDgMKaGz4P8Vf8ABa7xHcW8ieH/AIf6dZOw+We8unl28+gxXmur/wDBXz45apE8diug6V5nCzQad5rrz2DkqfxFfrx4N+APw5+H6Rr4f8GaNphjOVaGzTcPxxmuzXRdPX7thbD6Qr/hTFc/Fmw/bo/bI8XWofSI9e1CGT7smm+DUkz9CkJ/Srtr8dv29fFMgs7XSfHMLzfKsjeFvsoHf77wgL9Sa/aJbeKNdqxIq+iqBTwNvAAApWDmPxouvhL+378SUji1G68XQwyHB3+ILexUe5CupH5VG3/BMf8Aai8WWcz6/wCILGVpB80GqeI57hz7fLlT+Jr9nKKXKHMfh/q3/BJ39oWx0u4aCz0XUiq5Fvb6vh5PYByq5+pq3+zP/wAE1/jJH8cvCc3jXwvc+GfD2nXaX13frdwscIdwVWjY8kgDHoTX7a0U7BzEcMYiREGcKMDNSUUUyQooooA82/aTkeP9n/4itG/lv/YN4A2cdYWFfm5/wRFYf8Jv8VgTuf8As+xJP/bSWv0B/bS1KbSf2VfiZdQZ81dIkUY9GIU/oTX5/f8ABEm3ePx18UpAh8htOs0EnYsJJDj8jS6lr4WfrZRSdzS0yAooooAKKKKACiiigAooooAjuOYWqqjDYx6hRzVyRdyEHisa6uoNItLy8vJBFZ26NJLI5woVRknP4VnJGkXoeC/tiftcaH+yj4IXUJohqXiG+G3TdK5VWPd39AOa/KLxZ+0N+03+1Pq01zpMnjC702Rz9nsfDNpP9nTn7uYhycfWtj4xeJtU/b7/AGzodJ0oyrpTXX2G2IyyQ28ZO6UjgDIH6iv2q+Ffw30b4T+A9I8M6FaR2ljYwLGBGoXewHLH3JpxiNs/ELS/gf8Atjabbvq8OkfEq2S3XzN0dzMJh2+WIuHY+wFd18C/2/vjZ+zb44sdC+KiaxqGhzzp9rt/E0Esd7BETguhcBuM5xznFfthXwj/AMFZ/gTp/jb4EyeOLXT7Ua34fmjee8IxK1sx2lc98EiqsTc+1PCfijSPiF4V0/XNInj1DR9Tt1mhk2na6MO4I/QiuQv/ANmj4UanJNJc/Dnw1LJMd0kn9mRBmOc5JC5r5p/4JF+NLrxN+zI+n3c7zNo+oyWse8k7U6gD86+4qZOx5Mn7KPwejYFfhv4dB/68Up//AAyr8IfMV/8AhXPh7cpyD9hSvVqKAuzP0fQ9P8PWEdjpdjb6fZxjCQW0axov0AryH9rb9mXT/wBqX4Vy+Frq+bTL2GUXNjeclIpBx8y/xDGa9upGXcMUCPxD1/8A4J0/tK/A3VLi98GPc6haxOWhutA1LZI/v5QIP5itjwj/AMFDf2h/2c9RtdG+Imjy6haxMEeHWrdopyvT5X7mv2dvLqCwt5Li5ljt4I1LNJI21VA6kk1+Wv8AwUu/bR+HPjXwzf8Aw38L2Vp4o1p2WObVlhDC1YMDiKTHJ4xx60i07n3r+zP+0h4a/ac+H0fifw6ZEEb/AGe7t5kKtDMBkrz1HvXrtfEn/BKT4L658KfgLd3uv2kljd69efbIoJDyIdoCnHbNfbdMl7hRRSUCBjtUnGarSyF8gDBxnpU8jLsYscKBkseBXxJ+1r/wU68J/ADUH8P+FrKPxh4mUZk/eYtYOejMpyT7DFJoqJ9m29n+9Dt65xX5xf8ABarUJ4/h74KsgrfZ5Lx5C3bcFxXlWl/8FpPiHHrUJ1LwLoR04uDJFEZll2d9pLdfwqT/AIKLftS/Dn9pn4C+DtR8NamTrkN5uuNLlG2aAFecj0z3qdti9Xqxf+CLNuf+FpeOJOMLp0a/+PGv18Y4U4GfpX5K/wDBFPT5m8aeP7rbmKO2hjZx0ySeK/WvdziqRmz4q/4K367e6D+yZILK6ltvtes2tvP5bYMkRDkqSPcLXk3/AARbvr+48HePbdp9+nwX0exXyWyVycHNb3/BZ/xYlj8FfCvh8FvNvtU+0EY42xqf6mtD/gjj4Ev/AA38BNa129g8mLWtRMluzAgyIqhc8jpmmI/QGiiigAooooASjdQ3SuP+I3xa8H/CPS4tR8X+ILHQLOV/LSS8lCBm9BQB1+6mooUk14L/AMN3fAYuEHxL0TP/AF3p0n7dnwHiUk/ErRDjss4JoHZnve6jdXyd4v8A+CnvwA8JSCP/AISt9Vk7jTrV5QPxAxWz+zf+3p4E/ae8b6j4a8K6fq8U9nB9oNzeQBY3XOPXI/GgLM+mN1LTV606gQjdK+MP+Cs2rWth+yTqFrcZ8y91K2iiIPAYEnJ/Cvs9ulfAv/BZK+jh/Zw0S2YgPPrUZUHvtRs/zoGtzyv/AIIqeBZVj8deLDKohZ47FI9p3HA3E59Oa/U+vkb/AIJf+FNO0H9lPw7fWNp9mm1NmnuGPV2BxmvrmgHuFFFFAgooooAKKKKACiiigAooooAKY8m3tmnHimfeYcVEgHKxYZIxTqKKcdgCiiiqAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCldapaWODPcww5GR5kirx68msO4+KHhC18zzPE2kAx/fH22PK/UbuK8n+P37F/g39pLxLp2qeMNQ1k29knliwsLwwROv+1iuT0j/gm78EPCLi40nQbm1kj+bfPqEsob/eDHmom2tjrpxotpTke9zfGLwRa2Ul3N4q0mO3jXc0jXkeAPzrjl/a8+D01re3EHjvS7qKzBaf7PIZCoHsoJNfm3/wUi8M+DPCz+HfC3hiKO21me5VJWt3IUITjnnP6V9rfslfsW/Df4X/AAz0q7TSbbV9Z1C2WW7vpXMgLEchcjgfhWEJzlo9GVWp0oStFtog8Zf8FQfgP4d025l0/X7zxFfRozJY6fYTb5GH8ILqqj8TXr37NHxwg/aE+Glt4xtdLvdIhu5GC218oDgA+xIx+NF9+y58N7i8a8g8LadZ3hTZ58MC5Hv0616RoGh2nhzSLbTrGGOC2t0CIkaBR+Qrojfqc8uXl0NDBzTqaOtOqzK9xCcc0Ag9KGG4YoVQvApALRRRQAUUUUAFFFFABRRRQBxHxg8aS+A/Auqazb2F1qU9rCzpb2sRkdj2wB1r8yv2Xf2U/FP7WPxv1b4k/Fy01CHw9Z3TPbadqUTIbj5iVXBxhRxX61ModSGGR6GkjjWNcIoUf7IxUuN3cpSsrEOm6fbaTY29lZwrb2tugjiiQYVVAwAKs0m2lqiQooooAKKKKACiiilcAoooougENcP8WvENtpPgrXN4ErLaSZjzj+E13DfdNeSftKXjaX8K9fuI7dZJvskp3+mEJrKo9DSnrI/Jn/gma0F9+23BNJGFLxX0iL1wd1fuDivw6/4JWsNQ/bOsyVztsb+XI7HIP9a/catI7CnqwoooqiAooooAKKKKACiiigAprjcpAOPcU6koA85+M/wL8J/Hfw2dD8YaSmr2Gcqpcxuhz1V1IKn6GvnPUP8AglT+zlp9jdXV5ot5Zwopdp21i5VYwOSTukIr7RZfl461w3xd8CyfELwHq+iSSKq3Vu8Y2kjGRjNZWsaJ30PzV1r4Y/8ABPzw9rR0lvEl3c38bbHeO9ungDZwQWwB+tdXc/Af9gHTY4J7rxFbYlGVVtYust+APFfmP8TPBL+DvidrPhdZPNNpfNbIxALHLYGcAZr9FPB3/BGm38VeCdD1a68e3NlqN5axzzQtah0jLAHAHB/M0XtqO+ti5qHwo/4J8wSFx4p2bedkep3BX9Rn9azr7wb/AME+tAi+1y6vcaiFG4QwXly5b2wOTW+v/BEnTVjbPxKuDLjj/iXLt/8AQq2NF/4Ip+FLe3f+1PHeqXM/8P2WCOJf1DGlcrTueY3Wu/8ABPUfOmk6wWXoIxd8/mapHxb+wA2V/wCEf17Hricf1r2i1/4Iu+BvtaG48X62bbPzIjx7yPY7OPyrfuP+CM/wiGw2+v8AigYHzCW7iOfyiqlqLTufNWseKP2DvsrSWHh3X5LgL8sSeaNx/E1p/sx/BX4A/tZeJ9R0fQPBmqaRDZ/NJcyzM25PY54NfRen/wDBG34NxSIbvVvFE8YOWRL+Nc/+Qq+qvgd+zj4D/Z30A6V4L0gWMbD97cStvml/3mwM/lUuF3cOex43pP8AwTL+Bmj+S0PhnzZ4eVkuJWfJ9SOh/Kty9/4J6fA7VmhbUPBlrctF02lkH4hSK+lNtGPer5URzs8E0H9hX4G+HJUlsvh7pYkQ5VpVaTH4E4rrv+GevhVptpJv8D+H4LdRl2ks4wAPckV32ua5YeG9JudS1O7isbG3QvLPO4VFA7kmvyC/bo/4KBa58btYf4bfC17mHRXn8ia4swfOv3B4VCOdv0o5ewXbPqT4y/tRfsqfBHUm0iTw5pGvagh2y2+j6fHL5ePVsYrxnxR/wUW/Zrt9JnGgfClLu/ZfkWawiiUH3OKq/so/8EmF8QaXb+J/i9e3SC8USjRbWQpIQef3j9QfavtbQ/2BfgNoOmLZQfDzTJlVdvnXCmSU8ddx71VtLBfU+Uf2Of2hvg7+0X8UrTw9P8H9N0jxCFa4ivFiR0BU5B6cGv0vRVjVVUBVUYAHQCvDfg3+xX8JvgL4wuPE3g7w++n6vPG0RkkuGkVVJyQqngV7pSirBKXMwoooqiBK8U/bLU/8M0+P3VA7R6ZKwBGe1e115x+0LaQal8GvFllcxGaC5sJY2UZ7qfSolsXD4kflt/wRh1a2h+OXi20mIW5udJUwLnGdrnd/MV+yNfhV/wAEy7xtA/bS0e1DGHzEu7RkPcHoP0r91apbBLcKKKKZAUUUUAFFFFABRRRQAUUUjdOuKABulfj1/wAFPvi9ffG34/6D8JfDVyZrbT5FgljVvkkuXPf6Cv1h+JHiYeDfAev60W2/YrKacH0KoSP5V/Ofot145+LHxlutT8LLfan4vvL2S/he2G6bcGJDDjsKh7lxP3o/ZF/Z5039m34OaT4atUje/dBPfXSrhpZWGTk+3SvbOPWvxDl8Xft2abD81/45WGMdFiQ4H/fNOh+L37b+h2sstzceM7iIr96a3BK+/C00h8tz9f8A46+ItO8LfB/xhqWpyxx2cOmTl/MIAPyEAc+pIr8q/wDgj/4LuvEn7QnifxakbJpum2ckZZeF3yPlR+Qry7X/AAX+2F+0PYRab4gg8Xazps0nEGoN5cIz3I44r9Sv2Cf2YW/Zl+DMGm6pbW6eKdRf7TqU8I+Yn+FCe+0cUW1uHwqx9L0UUVRmFNanUUAfOH7WH7Evg/8AawjsJNaurnSdUs12RahZhfMCnnHIwfxryPwj/wAEfPgjoluF1mTXPEU3dpr0wg/hGFx+dfdWBRQVzM+V9B/4Jlfs76FG6DwIt/vGC19fTzEfQl8ivZvhD+z/APD74D2NzaeBPC9j4fS6I+0SW6kyzY6B3YliB2BNehUtBJHcR+dbyR5xuUrn6ivwb+MnwI+NHwI/aU1TxV4a8Oa0LuLU5r7S9U0uxacLuJGQoBB4Y8H1r96KSk0UnY/Cpfhr+1T+234qtdK8Tr4judOgdfMn1mD7DZWv+35eFVjj0BNfqt+yX+x74S/ZW8Hx2emxJqXiKdB9u1qaNfOc90U9VTPbNe/0UJWBsRetOpKWmSFFFFABRRSHpQBVab98Yzzu4qlq2oWeg6VeajqNytpY2sbTTTMcBFAyTWjLEdpKhS/vX5F/8FFP2s/Ffj/4qXnwW8JStaaRBdR2VxJbsRJcSMQCpIPI56VEi4nU/FX/AIK4eLF+IGqaT8MfCNrreiWchSK6kjklkmA4LYUdM1y+n/8ABWL47NcMtx8M7W5TvGtlcKf5V+gf7J/7N+h/An4OaBobabZ3GqrCJbq8kt0MrO3JBbGcCvZRoOmKxI060B9fIX/ChK47rsfgR+15+2r4q/asi0i08RaHYaD/AGQzFYLYvvLHruDV6z/wR78LDWP2lr7VZf8AmF6PI6Y9ZGA/pXcf8Fmfh3pfhrxR4K17S7K3s5NQglgnS3iVAxU5zwOtd1/wRV8BtDoPjjxdNHg3E0dlExHYDJFVYnY/TsnAzX5rfHH/AIKy6z8J/jdrXhW38F2N7oGlz+TJPNLIlxKB1K84z+FfpVINykGvlD9qD/gnz4H/AGjPM1HZ/YniRsn+0oBy3puHemOKXU9F/Z1/ak8D/tN+Eo9Q8OXkMeooga40ieQGaBvcdx70n7VXx4tv2c/g3rniqVVa9iiMVojceZMwwoH0zn8K/G740/so/Fr9jHxNba8CxsLWfzrbXNNkIHB4346f/Xqp+1B+2T4o/a0j8IaPd2K2I0+NIPKjcn7ROcKHP1NBSLX7LPwC179uL9oC8udcv5jYiY3+s3zN8+0sSET36V+93h/RbfwzoWn6Valvs1lAlvHuOSVVQBn8q+d/2B/2Zof2cPgpYW93GD4m1dVvdTlzn5yMhR7AV9M0GbCiiigQUyX7pp9Mk+7QNblKSNZpijZ2kc4ODXwP+0V/wS2h+Pnxg1PxfD47bTIr0qZLeS281l46A5FffrKXyvrSws/KntStc2Z+abf8ET/Dxtxj4j332gDr9gQLn/vquX8Q/wDBE/UIraV9E+IltNOB8kd5ZlQx9yCcV+rAc57VIHzS5TPmaPxF8Z/8EhvjP4Zh8zSZNJ8Qr/dtp9rfk2K2v2U/+CcXxs0X41aBrWt2Ung7TdJvI7ie989d7qpyVQDrnp+NftFRTsLmI412qoJ3EDGT3qSiimSFFFFABSZobpTaAHMeK/P3/gstfJF+z34etsjzJtZUqvc4Q9Pzr7/4YY9a/NX/AILXX5h8AfDq0HRtRnc49oxigpbnP/8ABFHwVC0Pj7xVJGTcq8VhG5HRcbiK/U6vjz/gln8NYPAf7LOk6griS51+ZtQmYds8AfkK+wt1AnuLRSbqNwoELSZrC8XePPDXgHTW1DxNr+m+H7Fetxqd3Hbp+bkV5z/w2N8DPNEZ+LPhFW/2tXhA/Pdik3YD2OjNeI6/+238BfDdk91dfFjwrNGoyVsdRjupD9EiLMT7AV5VqH/BV79nezklSHxHql8yHH7jSJwGPsXVR+eKnmHY+w6Wvnf9mX9tjwd+1RrmtWPhPStZt4tLAZ7rUIFjRs9OjHBr6IqlqD0CiiimIKKKKAPF/wBsyyl1D9ln4lwQxtLI2jykKoyeCCf0FfB3/BE2SJdU+JUW9ftHkWreX325Iz+dfon+0cFb4C+Pw/3Tot0P/IZr81/+CJiuPiB8THbhW022UfUStUvctfCz9baWiiqICiiigAooooAKKKKACiiigBG6V+WH/BXj48+NPCXijRvA2jatcaVoF/p5mu0hbaLjJwVJr9T26V+Rv/Bar7A/jzwIsUitqS2Uplj2kHZu4Oen61DLicr/AMErfjF8HPg7rfiC/wDH2uw6H4r1Ara6fc3sUpiEOMkb1UqmT3Yiv2B8L+MtA8baet94f1qw1qzYAiawuUmXn1Kk4r8n/hp/wSRj+KnwF8OeLLDxrLpvibVrUXXlXUIe22t91SV+YVxMv7A/7Vn7Nuqf2v4Eu57sQEuJvCmq4dvc28hXzP8AdwfpTQ2rn7X18V/8FWPjNp/gH9m/UPCjMsmq+KStrFFg5WNWDM/THVQK+KdP/at/bj8M+fZy6N4tvnUGMtfeEWkZT6hhFjP51e+Cv7HXx7/a8+KGm+MPi+dW0/QbeZZZ7rxChhmkVWz5cEBAK9McqBVCtY+3v+CXHwq1L4Y/sw6dJq1m1ld63O2pBJCCxjYfKeDxkdjX2DVTS9Pg0nT7WxtkEdvbxLFGijACqMAfpVugkKKKTrxQI+Sf+CiH7VHi39l/4f6DqPhCwtrm81S8ktpLi8RmSAKoIOB61+d95/wVo+O95ayxRXWj27MMCSKyO5fcZNftb4r8F6D460ltM8Q6TaaxYNybe8iEi/XnpXC2v7K/wismJh+HmgoTyf8ARFP86APwX+IH7WHxf+KDXI1/xvq0kE4Kva28pihIPUFR2rl/hD8Qv+FU+ObPxJP4fsfEv2X5ls9SUmJm7E1/Q4P2b/haOngHQB/24p/hSS/s2/C2aJo38A6CUYYI+xJ/hQO5+Wl1/wAFlviM1vbwaT4O0GwSAAFAXcFR2A4xX6Tfse/tDSftNfBXTvGVzpy6XeySPBcW6HKB1OMqfQ1zPjn/AIJ2/Afx1HN5/gm30yaQYE2muYWX3GK9M+AvwE8M/s6eBx4V8KLcLpgmaf8A0qUyNubrzQI9IpG+6aWmSMEUsxCqBkk9qAPkT/go5+1BZfAf4NahoVleTW3i7xFbNBpzwjiEZG5yc8cZA+tfD/8AwT8/YNvvjhrlr8RvHIJ8NRT+ekEzEyXr88MpH3c85zWB8ZNUuP2zv+Cg1n4Sublm0NNU/syLyiSscMeSzD6kV+0Hgnwfp/gLwrpug6XCsFlYwrCiqAM4GMn3oLfu7HmXxO/Y8+E3xY8NjR9a8H6ekaR+XDcWcQhmi9CrLg1+QP7fP7E1l+yZrmjT6Pq8upaHrLSeTHcAebEV/hJ7j3r9526V+X3/AAWytzJofw6cFeJ51wTzyBSEmeK/8E7f2xvhz+yn4F8Uv4pi1K51XUbqMpDp1ursUA7lnXFfXNv/AMFl/gjJnfonjIEf3NPt2H63Ar5V/wCCcv7C/hP9pLwT4l8Q+OFuHsUnFnafY5zG6sv3j0r6z8Nf8Ef/AIJ6PqElxqM+ua3BuzHbXF5sRR6EoAT+dCG7Hw//AMFEv2zPCn7WF54SXwdp+tW1jpSuZl1S3SGR2Y/w7HcdK91/Zh/4Kp/Dj4P/AAh8PeDtb8FeIoH0mHyWk0sRToQP4v3joc+1fO37Rn7Kvhnwp+29pPwr8NRyWWh6nPaqEeViY1k5IDHJ6A1+j+n/APBK/wDZ7tdNSCbwnc3U+BvuJNTnD5xyRhsfpTDQ4vwB/wAFfvhl48+IemeGx4V8S6Za6jcpbQajcrBtR2OAZFWQ4GcdC3WvvJWDqGU5UjINfGui/wDBKz4M+FfG+j+J9AGsadeaZcpdRW8l350LMpyAVYdPxr7KA2gCgl26C0UUUCEr5i/bS/Yi0r9rbR9Oc6xLoWvabkW1wQXhZT2dP6ivp6igD8n9J/4In66wb+0viVp0Zz8v2XT2fj33Yretf+CJ8G5ftHxPfHcx6Uuf1av1CooKuz80NE/4In+GoZpTq3xE1C6Vvu/Z7FE/Mbq97/ZH/YB0z9k3xxreu6X4ouNbg1C3ECw3NuEdBnPUE19aUUCuxoFOoooEI3SvzY/4LZed/wAKx+HISTbC2q3AdPU+UpFfpO3Svzb/AOC17/8AFsfhwv8A1Frj/wBEigpbn0/+wFbJa/smfD5UGA1iG/Ek19DV88fsAsW/ZK+Hm45P2EfzNfQ9AnuFFFFAgooooAKKKKACiiigAooooAKKKKVgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAh6V4/+078eNF+AXwx1LX9TuY45xEwtYGxmaTHCjJr0Pxl400rwH4Y1LXtbuFsdMsIGuJppWCgKBnHJ61+aq2/iv/gp98SUS6s7rw78G9CuGmhmkgxJfEHG0Nkjn2NZya2N6cU9WfG3jDwb8Rv2iLPXPjDqkP2fSLa6RUMgZCVZhjZxjj61+znwTv5vh58B/DhTT7nVRFYJLIIWDSH5cnGev5181/8ABSaDQPhP+yba+B9Dh/sqGOW3jto7cAGQr/fx9OtfSH7HdxJ4i/Zl8CXM8jeedPVJCDndgYrBXUtDZtWvJDvhL+2b8MPi/rB0bS9djtNcRikmnX37qVXBxtwep+le6rX5D/8ABQT9lHWPAvjRvib4Okuo7yS6ErW9rDsaHHO/K9a+2/8Agn38XvGvxe+B1tf+NrBrW+tJPssU7qVadFGNxB71tTk5LUyqQW8dj6d/ip1N7g06tTmCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtXAKKKKnlYDW+6c15H+1JqkOkfA/xbc3Cs8a6fNgKMnlCK9drwT9tiaeH9njxg9vN5L/AGKRTkZyNtROL5Wa0/iPzS/4I96F9u/ac1PVQW2WejTHp3kYDH6V+1Nfj1/wRfkH/C3vGIYZZtLVg3/A+lfsLWyIYUUUUyQopCQoJPAryXxD+1d8KfCnjUeFNX8a6Zp+t5Cm3nl2hSezN0H40DSb2PW6KyND8WaN4os/tWjapZ6rBjIks51kH6Gvn/8AbA/bU8M/sx+DLlhc2+peK50ZbLT4nDYfsX54FK6Cx9L0V+BN18fP2nv2hNWutf0nVfE1zZwu0qrppaK2hUc7RjAOK+o/2Ff+CjnjG8+IOm/DP4qO1/LdzC0t9RuE23EUp4CyHoR+GaLorlZ+qdFNDZp1MgQ9KhvP+PWUkZGw/wAqmPSqmpvImnzmMAvsOA3Spa0KW5/Pv8XPDMvij9tu90fT4lNze+IYlRe2TICf5V+/9pLB4f8AD1ub6eK1gtLdFlmmcIiBVAySeBX4fagqab/wUs0pm5UeJISce5Nfpb/wUV+Evjf4xfAG40rwK97NqKzq82nWsgUXcP8AEjcZP50k0kkXKPvNM+mNI1rTdetRdaZfW2oW2cedayrImfTKkinaxr2n+HdPkvtUvbfTrKPl7i6lEaL9SeK/AHwR8Xf2hv2L5Xs7H+0/DdgJSz6fqFoJbZm75yOPwIrpNU+NHx3/AOCjHjTRvA093bskYaT7FYRNb2y4HMsvzEk/jj2p3I5baI/YTXP2xPgv4dujbX3xH0CKYHGFvEYfmDWPP+3h8B7fOfiXojH+6k+4/kK/Iv8AaL/4J8eL/wBmv4ZweLtc1G0nV5hFJDFg7SfrXzl4c8E6p4o0XV9Ttos2WlxebcSbQAB6ZxTui1DWx+/Vj+318CdQ1O1sLf4gafJdXMqwxJhvmZjgDOPU19BI6yIrKdysMgjuK/GD/gmr+wvafGnUrf4j+KTNH4e0u8V7OzB/4+pEORu4+6Div2dXZDGB8qIowOwApmb3JKKbu3DKnI7Vn+INct/Dej3epXbhLa2iaV29gM0m7CWp+Z3/AAWG+P1/ZLoXww0O9eP7UPtWoxwHDOM4RCR29q7T/gmt+wpa/DfRbH4meMbZbnxFfwrLp9nMnFkp6Pg/xkd6/Nf9or4ra18c/wBo7XPEllDLe3M98YrCBELEojYUBe/Svqz4ef8ABUn4sfCPUNI0T4geFo5tNgCxTK8BhmCAYG36Ci6NFtY/Yqlrz34J/HLwr8fPBdv4j8KahHe2jgLLGD88L45Vh616FRuQFFFFMQUUUUAJWL4vsE1Lwvqls6CRXgf5T34NbVUdakWHR72R/upEzH6AVMtrDjuj8EfgbrF34Z/b/wBBnsE+wSDxK1uY8A4VmIPB9RX7+1+AfhfVotY/4KGaXd2gAjk8VqE2jjG81+/lEdip/EwoooqiAopOfXj6UtABRRRQAUUUUAFIeRilooA8J/bZ1O80T9mvxpe2PLxWUm5ezKRgj9a/Nf8A4I42NheftAa5cTwxvdwaSzW7MOY8tg4/Cv1t+MPg+Lx98L/E2gSxrKt9YyxBW7nacV+D/wCzL8Vbj9k/9qfT77VxPYabb3z2eqxFMN9n3EcD8qh7lx2P6DWUOu0jINK0Ksu1lDL6EZFYPgfx1ofxE8PWet+H9Rg1HT7pBIkkLhsZGcH0NdBV3uSxFUKAAMAdhTqTNeU/Eb9p74cfCvxRpHh3xB4jhg1nVJ1t7e0h/ePvY4G4D7vPrQI9XopgNPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDH8Y+IIfCfhPWNZuHEcNhaS3LM3QbVJ/pX4xfsBeFx+0N+29qPivVo/tNtZy3GssJPmBYsRHnNfrL+1A88f7PPxBa2jMs40ecqi9T8tfkV/wAEr/jH4b+FHx8vYvEl4unRa3ai0gnmbbGkhbIDE9BUSLjsfuAqhQAOFAwBTqjt7iK8gjmhkWWGRQySIchgehBp0siwxvI52ogLMfQCnHYln5af8FsJofM+G8Yb/SP37bf9nI5r3f8A4JG2Qtv2UIZcAGbVblicdcEV+cP/AAUY/aD/AOF8ftBagbCTdougk6faejFT87fnX33/AMEgPidpGufAO48HpdRjWtKvZZ3tv4vLkIIb86obWh99mk60lcn8TviboHwf8Faj4p8TXn2PSbFN8sgGSfYDuaCTyH9vH4r+GfhX+z14jn1+3tL+7vrd7bT7G6AImmYYHX06/hX4J6PpfiCzeHxfZ6Pdvp1jdrL9sjtmNvG6sGClgMCvp74zfFLxj/wUa/aW0zQvDsE1vpPmmDTLZsgQQ5+ad/w5r9X/AAJ+yP4T8H/s3L8KJIVnsZrRkubhgNzzMOXz9aRpsVP2L/2rNC/ad+GlpdWzpa+JNOiSLU9Nyd0TAYDD/ZNfQ9fhNoN94r/4Js/tcJFdjztImmAnjU8XNkzdvf8Awr9w/CviSz8X+HNN1vT5PNsdQt0uYW9VYAimS0a1FN/ip1BIU1s44606igCpMrLhhz9axfEninQvB9j9u13WbTSLVuk99dCFfzJxXRsAVORkV8Bf8FOf2U/id+0VceE7rwNaLq9np6yLPp7XMcW1j0YbiAaDTmufbWieOPC2tQpNpuvaXfI3SSC6jfP4g10EV1BOAY5o5B/ssDX4NW3/AATL/aLt5kli8Em3kU5WRNVtwy+4IbNdPB+xz+194YgCWMPieOJBxHY+IWXH0w9AWT6n7hZpa/ETTPhj+3J4T3SWq+OiqchWumuj/wCPE5rlNU+OX7W3gXxRa2mrar4wtNRaVVjhu7MlWYnABAXGKBcp+81Fcb8H28RSfDHwy/iyVZvEb2MT3zqu3MhGTxXZUEBRRRQA1/untWB4s8YaL4F0g6hr2sWWjWKnDXF9MsafmTyfpW+yhlIPSvx9/wCCxvxeu9W+KGh+A7a7kTTdNtPtNxCp+VpXPGR9KTZSP1i8H+OfDvj/AE/+0fDet2Wt2anYZrGdZEDehweDX5w/8FspD/YPw5QHBa4n5/4CK+Uf2Ef2oNc/Zh+Lun6dqkd1b+FtbkjivrO5DIqBjxMoP86+jf8Ags54kj12b4ZWdn++tJYZbuO4XlJA2AMHoTzU3Ktqdx8QLj44fC/9h/4Ut8KVvIpI7ESaiNMgZ7oIwyu1QCe/pXy7dfFL9tfwhYpq8934+8ib5/30Mk4H1Tadv4iv2S+Cdqbf4N+CYHXldGtAQw/6ZLXZtEkgwyKw9CKOYLn4zeDf+Co/x/8Ahh9mh8baBDq9sHw39sWElnM/sHwozX33+x/+3h4Y/aw+1abbadNoniSzi86eykO9CvTcrelW/wDgoF4g8IeD/wBmPxdc+IrCzu5ri3NvYQyRqXe4bhdvfjrkV8T/APBF/wAB6nP498Y+L3tGh0mOxWzimZCFdy+cKehwKfMx6G/+3l+x/wDtC/H745XV9oumLrHhDYsdlnU4oYoeOS0bNu/IGvlD9oD/AIJ++Pf2bfhjF4w8Y6jpKiW6S1Sys5XlfJ99uK/f6vzM/wCC03xBjt/CPgrwbHPEZbu5e+liVwXUKMKSOoBqb3DmPg3wr+zVp+q/sz658XtU8XR6bBY3v9n22lramV55j0Ut0XPvUv7NP7FXxH/akM954Ts7aDRLOYQXOqXkqxohPovVjjsK+gPiT4Fj8Af8EsfCbhXE2v65Ffy7hjuQD+lfTP8AwRgtpI/gR4rlZWCPrOFJHBwnOKaVxOR71+xp+xnof7JHhm9hs9Qn1bW9UCNf3UnCblH3UHpW38Pf2uPCnjT4y+I/hdfJLoHi/SZikdreHC3admjbufavdK/Jv/gpxpGq/AP9pTwV8YfCtvPaXM203F0iHymlQ/dY9Mle1VsTufrJS1w3wV+Jmn/GD4X+HfFunTRzQ6lapK/luG2SYG9TjoQc8V3NMkKKKKAPEP23NUl0X9k74oXkDbZYtGl2n6kD+tfDH/BE2O3XUviQTIpu/KtsLn5tmTz9M19tft5RNN+x/wDFZFGWOiS4H0KmvhH/AIIn/L40+IgJ66bbj8fMqJFrY/WmlplPqk7knyX+2H+2J4l/ZT8aeFrifwmuq+Ab4Fb/AFKMnzYmz0UdM49a9s+B/wC0D4K/aE8Jx694P1aO+h6TW5OJoG/uuvatr4p/Cvw58Y/BmoeGPFGnx6hpl5GY2Vh8yZ/iU9iK/GDxdYePP+CZv7Sz3WiSXE3hm5bMLTAmG7tieUPbcPWk2NK5+5mRRkV454J/ao+H/ir4O2XxCm8QWNhpklt5syTTqHjcD5k29Sc+1fml8d/+CqHxP8XfEC8tfhWp07w/auY4tlr50s2D99jg8UuYOU/ZDIpa/L39h3/gpd4l8cfE6LwZ8VtQtdt+y29heJbiJvPJ4R8Dv71+oVUmJqwUUUUxCHpX49/8FnrV1+MHg+YjCNpL4P0fmv2Er8x/+C0Xw5urzw/4L8a28G63s5XsLmXcoC7+UGCc9fSk1cqJ9i/sS6nHq37K/wAOZopPMVdLjjJweoyCOa9y2+1fF/8AwSj+JUHjb9mOz0fz0e+0C5a1ljGdyqeV/wAivtKhCe43aaNpp1FMQ0A06iigAooooAKKKKACiiigAooooAK4f43+IpPCfwg8Y6xCcS2elXEqE9jsOK7evM/2lLE6l8AfH9sP+Wmj3A4/3CaBn5e/8Ef9JtPE37Q3inXdQiWfUINOM8TsN2HdzubPrX7H1+NP/BGzXrWw+PHiDTZZQk95pGIVbgvsbJx+FfsrQOW4HpX5Df8ABZX4nWOu/EHwp4NtmWSbSrd7id88Kznhfriv1Q+KHxI0P4TeB9W8T+Ib6Ow06wgaVpJDyxA4UDuSe1fzi/G74lXnxg+KniPxXeySSDUbt5It45VMnYvtxQET9if+CR+kPp/7KkVyybRd6pcMD64IGa+2K+Z/+CccdlH+yD4GFj9wxOZP+um47q+mKBPc/J344SR6x/wV28FWyDOy8sY2z0yI2NfrHtr8ctS8RJff8FgLOa4DbI/EcVtGOMjEWAevTmv2PoGxuKXdS1WuL61tJYYp7iKGSY7Y0kcKXPoAepoJLG6ik47c0tAB68UzzkH8S/nXk/7VWi+O/EHwK8UWPw3vJLLxZJbH7I0D7JWOeVRv4WI6GvyHX4E/toahfXCvB49eYtiRm1eRQf8Ax7FA0rn7nPeQRqWeaNQOpZgKyLzx14d0+YRXOuafBKeAklygP86/F2D9jP8AbI8SQtFNF4jWOTgpfeJgike4aSrdn/wSr/aN1hfO1Keztp+uLjXBI35qTQOyP2gt/FOjXjKsGq2crN0CXCEn9aupfW8jBVnjZj0CuCa/GW+/4JX/ALRXh+1jvdK120vL1eVgtdaeJ0PszYH61sfCP9jH9rDwZ8VPC2q6rNqK6ZZ6hFNcyDxAJ1EYb5vl3Hdx2oCyP2I3UtRI33fXvUtBIh6V+cX/AAWq0+Wb4R+AbpVzHBrEoc+m6Hiv0dr4G/4LH6tZ2f7OWjWc0Ze6utZj8hgR8u1SW/McUDW57d/wT6kEn7JHw+I7WeP/AB419GV80/8ABOrP/DIfgIE5It2H/jxr6WoB7hRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+VP2k/gr4o/aS+JfhrwhdTXGm/DLT/wDS9bZXKNqLH7sS4zlfXOPoa+jfDPgvSPBfhmy0DQ7OPTNKs4hFDb26hQoA68d61FVnyHB68dKLpmht3IZV44LVCir3ZvKXNZHxF/wVe02xb9nmSVrZJL37VEY7iQfcA9D613P/AATJ8RP4h/ZJ8Ll23yWrSQEn2NdV+138ED8fvhXH4WN00aT3MZaaNcsozyRxXX/s4/AnS/2e/htZeFdFubi4soiZM3QG/cevT3rGMXztlzS5FrqejalotjrEPl31pDdx/wByZAw/I07TdLtNJtUtbK2itLdPuxQoFUfgKt4NLXQko7HNzO1gpaKKYgooooAKKKKACiiigCK5uEtbeWaQ4jjUux9ABk18Y+I/+CsXwX8NeItQ0maHxDdPZSmF5rSxDoWBwcZYV9lahZx6lZT2kwJinQxvg44Iwa+Obv8A4JVfBzUfEl3q11a3kpubgzvCLl1Xk5IwDUu/Q0jy/aNXwb/wVG+BfjTWLXTLbU9Xs7u5dY41vbDYCxOAOGNfWtrcLdW8c6cxyKHU+oIyDXz18Pf2A/gt8M/E9vr2j+Ebf+0LchoXuGMoRh0YBu9fRKqFUADAHAFNX6ilb7ItFFFMgKKKazYXNADqK/PT/gph8SPjV4L1bwovwzu/EWnrJvaZtDUupx2YBTn8a8N/Z0/bb/ai8I+OtPsPGfhTxH4+0S4dYXt7jSzBcJuON6yLHyR6Ggvkkfr7RVezumurWCZongaRFcxSDDJkZ2n3FWKCAooooAKKKSgBa8E/bOtlv/gf4hs3Yp59rINy84whNe87q+Y/+CgnjWLwV+zv4iuXkjE8tu8cKO20sxGMD3qJbGtPc+M/+CKugCbxj4/1ZmKm1tIrdVxw2WPNfrVX5Yf8EeY4/BfgL4neNNUnMOjRhNzsMALGCzNXYeKv+C0HhDS9TuLfSPAuqalbxSGNbl540V8HGQM5pp6ClFn6P0V+aFn/AMFsPDZVvtXw21ZWAyBHeRY/WvR/h3/wV6+D/i+aCDWbPV/C00rBN11EJYwT6svandE8rPszxvqr6L4R1e+jTzZbe1kkRB/EQpIFfzneIdUvfjH+0Bc/25ut7jVtUMEuxctENxAAzX9F0F5Y+OfDlteWkoudM1CEOjYwHjYdfyr8bv8Agod+zbc/AL4lwfETw0n2eynulkKqAUhlzlSPr71nK99DeC921ziPjV8EfiD+yP4d0jxNoPj67h0rVJdsFnBcNHMMDqyg4I/CvmuTxTP4u8YWuqeLr+81OB51N1K7lpGTPIBPGcV6t4g+LPj/APbA8ReB/Bt9El/eRTra262seHO4gMTjjgV+wOjf8E//AIZaT8HoPBkOhWvmtb4udQmhVriWQryS2OOfSkrpakytfTY3v2a/Gnws8b/CPSNI8BXFlaW0Nqii1XYkgfbzkD7xz1r8of21Ph7qHwQ/a2stQEDaZHd3UF9FNGcA/vBuIrJ+P37PHxS/Yz8ZTajpdzqFjov2gyWl9ZSNtUA5G7HFeJ/E343+NfjJd2154w1qfXbq1GIricgui+g9qFvdBeyP6T/Cmoxav4Z0m9hk86K4tYpVkBzuBQHNa9eJ/sY+Jm8W/sx/D+/kOZP7NjiY+pQYz+le11rdGItQXUfnW8iFtoYY3eleP/tafHyH9nX4K654sISS/jiMdlC5wJJiPlFfhNq37W3xW8Q+NP8AhIdS8aa5O32nzzZpqEq24wc7Qm7G3HrRcaWt2fQ+peF20v8A4Kl6VZMWuIl8RwzM8nPydewr9sbi5hs4XlnlSGJBlnkYKqj1JNfgD4Z+Pl/8T/2rfB3ibT7RdL1GS4htRKzEuX6byc9c16v8Vf2bv2wPi14o1mbULPxHrGl3ExMUUmrNHaNGegEZkGRiszSVviR9Qf8ABSj9rz4deHPBV54JsrbT/FvibUImik8tldLRSPvFh1PoAa4v/gjf4G0jRfDXjDx3fz2UFzdTLZW7TTKJI4xyfpmvmWz/AOCVn7Q+qW0l5caBYxOF/wBVdalH5h9utaGi/wDBMn9pXT1FrZ2kem20z5dItVCJn1IBo2Fufan/AAVi8UaJ4g/ZZmXTdUtr+aLVrdNtrKr4JPIOD6V8cfCfSdD03/gn38Q9RgRZtTvN0UrEfMmMfpWV8dPgT4//AGZ/2dtU8N+Pfs0k+ranbz2ckVwZW+U/N82a9gj8J2vhv/gmbqUosI7ZrmIz/aIpA3mN6Gi9zWNos+iv+CQfi6TxB+zVdadJtA0nUnhQKMHDDPNcb/wVy+N3i34caT4R0nwxrl5of26SRrh7N9jOAOBn0qz/AMEYIbpfg34wmcxi0l1VTGo+9nac59qX/gsH8ILvxd8NdD8WWMUs0uiysJFQcCNhyTVJma0Z9G/sFfELUfib+y/4P1jVr46jqXlNBPcMcsxU4598V6Z8bNNn1j4X+I7O1dUuJrKVY2k+6DtPWvh7/gjT8TItV+FfiPwdNcL9s068+0Qwnr5bDn9a/QXxHosXiPRbzTp9wiuYmjYqcHBGKdubYX2rn4kf8E0/DulX37ZCWevtbl7IXJgjmAYSTBjgL719+/8ABRj9mfQfiR8INT16009YfENgvnRTQjbuIHfHavzn/a2+B+vfsgfHiHXvCz3lra+ebu0vMklHzk5b0r660X/grb8PNW+Ca2HizSNQv/FLWPkXFokQEVxJjGd3YGlYLWZ4r/wSH+Lt94U+N194DljY2OuQyOEV+I5YhknFfsxX4q/8ExdLl8eftp3PirS9Ea00S1hu7hwCSlt5inaufXJ6V+1VUiJBRRRTJCiim7qAFrE8ZyCHwjrMhxhbSQnJwMbTWxIzeW2zbu7bulfNH7fX7QmjfBH4A+JYptQSLxDq9o9nptqjAymRxgMV/uj1qWrjjvc/IT9nG3bxF+3B4TNpEcS+Jy6KCW2qJDk5r+hVc7Rnk96/F/8A4JK/A3VPHHxsk+IV1Fs0fw+H2ysv+tuH6YPtX7QU0VLcK+TP+CjPxo8b/BP4M/2x4J8R2Ph2/eURtJNHHJO69xEkisCfwr60r88P+CwnwpvvE3ws0fxVYrJLHo8xNygYkBCPvY6VMrhHc+Xfhf8A8FRP2gvA+m2mr+I4rPxl4Ye5Mck95pwhkOOqrJEFUH6g1+ifwC/4KCfC340+F0vbrXrLw3qsabrqwv5hH5frgnGRXyb/AMEs/D/hX40/Avxj4D8R2Ed19ivftL+bn7ki4GCCMdO1fEX7ZXhjwT4R+Puv6B8O43Gj2LCBtshbzJf4wOTkA1OpWh+p37RX/BVL4a/C3Tb6w8HXK+MvEwjYW4txm0STt5j5HH0r4Rm/4KnftBN4oXXpNUtodFZwRo8OnotuRn7okZC+f+BV4/8AsfwfDi1+OWhw/Fm3YaBJKFKXKssAY9DLgg7a/Yj43fsq/Dr40fAmbTvC1pY2unpaNPpx08DyywXKkEc0aodkdp+yT+09o/7UHwytvEFl5dtqkWIr+xDZaKT1+hr3Gvxr/wCCSOq6h4R/ag8Q+Eby4e1R7GeOSzbgSSxt97Hriv2Uq4mclYKKKKokQ9DXwR+3b/wT7j+NH23xT4NsYIPEqxl9kY2mdvQ/WvvimtGrqVIyDUtFJ2P57Phf8evjT+xl4m1DSrGe5017eXZcaVqELPA5Hfn+le62v/BYz4twrtudG0KeTH8EJXn6V+vPiD4YeEfFc3nax4b0zUpe73Nqjk/UkVhy/s7/AAymJL+BNBYkYJ+wx5/lTK5kfj34i/4KDftM/Gq3ay0KW5sbeRthXw7pxR8Ht5gFe2/sRfsG+M/GHxGh+KHxiF9DLZzrdWlteSbpZ5ByC4Pav088O+AvDfhO0Fro2hafpkAOfLtrdUH6Ct3A9KYuZdBiDaAMk47mpKTFLQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1HT7fVbC4s7uJZ7adDHJG4yGUjBBr8rf2xv8AglXqUmsXfiv4ShZYpiZZtFY7WRuuYz/Sv1bpMUmhp2Pwc+Hn7aXx+/ZJuf8AhF9TkuJILcFF0rxFExCY7qx5IroPiN/wVJ+NHxm0VfCmjWlpotxqA+zOdJjZp5t3G1SeRn2r9n/Enw38K+MLlJ9b8O6Zqky8CS7tUkb6ZIzVTTfg74F0a8iurHwhotpcwsHjlhsY1ZWHQg44NFh8x+X37Hv/AATEuviB4E1/X/ihbT6VqOpxPFp9vdIfNhkPPnMO/PavO/En/BPf9ob9n/4kG++Gy6jqcMJ82DVtCuVt5cdlwSOfrX7aUtMOY+Cf2L/DP7W0PjuO6+KutXEPhGJTvtNXkjnuJvYFeh96+mv2pPgXH+0X8Gdc8FG8GnXF4gNvdMu5Y5AcgkdxXrlFArnyd+xP+wfpP7J8N/ql3qf/AAkHiu+TypL7ZtSOP+6gr6up9JQI/J3/AILUSN/wkfgJG0UJD5MrHVlX5nOf9Xn2619hf8E2f7a/4ZI8H/23nzsSeTu6+Vu+XNfSeqaPY6xGI722iuUH8Mqhh+tWLW3htYEhgjSKJBhUjGAKB30sSfxU6iigQUUUUAJTafRQAynbRS0UANKjFRyQpIylkDFTkH0qaigYzpin0UUCCiiigBK/DD/go5Yt44/bm1DRbb97LM1lZKIzk5YgHp6A1+5zfdNfhz40uY/F3/BUy2AZZ428W29v8h3A4KjtUsuJ9Q/8FF/2MbOP9n7R/FXhuwU634TsoIb1olJe4gRApY46kda/Ny4+L3iD4qXXw68N+IbprnTdDnhtLUSZYhGkUZOa/o717RbTxJot9pV/Es9leQtBNGw4ZWBBFfhx8YP2DPHnwz/ak07w94c8P6hq/h281OK403UILd5IYofMViJXAwhXnqaSQ0z9fviJ8d/h/wDs5+C9Nk8X+ILbTI4bSNYLUMGuJVVQuUjzkgcc186+Jv8Agrz8DtJs7n+zP7d1i+VD5MUdiqI7Y4BYvwPfBrp/22v2FB+1nY+G7i11xNB1vR4TAsskXmRujYyCMj0rxn4c/wDBFvwTo7QT+LvF+pa5IpDSW9mi28Teq92x+NPlJufnz+0l+1F4o/ag+IY1PxXc3NloEco8jS7Vsx28OeoBOC+PWvv/APZ7/wCChv7M3wD+G+l+EvD1t4kto4UV55W0yPdLMQNxYrJzzntXrkf/AASZ+AKDB0fUn/3tQk/xrn/EH/BHb4J6nDL/AGdeeIdHmYfK0N6HUH6Mpz+dHKHMfTHwH/aV8BftIaLdal4H1V7+K1YJcQzwtFLET03Ka/KX/grz4mXxL+05pWiWmJJ9P0+OAqp3He7cDH5cV+qf7Nv7NvhX9l/4exeF/DSyTbn8y5v7gDzrlz3bAr57/aG/4Jt2/wAdv2hrL4jv4q+wWReBr3TDbktKIyDhXB4zj0o5Rpo8m/bs8IzeD/8Agm/8OdIuoWgubB7BXjdSrKxGSCD0616J/wAEc1K/s3audpUNrMhBI4PA6V2X/BTL4Ra/8RP2V7nTPCthNqc+kzw3bWdvG0s0kUfUIqgljj0r8sv2df23vin+yZ5uh6KLaXRhcGW40XVrUj5u4zwyfhR8I7c2x/QdXyd/wU4+GF/8Tv2UPEEWlWv2rUNLmi1FVWPe/lxtmTbjvtr4qtf+C1vxG+2xG58CeGntd37xIZJ1cj0DFiAfqK1dZ/4LMa94i0W/0wfDHTpftcDwlZL5pEwwI5XbyOaaYuVo7f8A4I5/tAQ3Wh6v8KNTuMXtszahpweQfNGfvoo9R1r9Oq/m+/Z58Ya54Y/aN8Ja/olncWd42sxn7LYo3KO+GjA7rg9K/o/jYMoIPB6Uwkuo7NGa+bv277r4paP8HF1z4UXFxHruk3aXk8FtH5jzQL95duDu+lfHvh3/AILOX2i+GxY+J/h5NN4mtk8uSRJ/KjkkHByCMrzSbFY+4v24IJrr9kv4pxwI0kp0OfaqjJPAr4M/4IlwhvE3xHmJyy2luo+m+vIfjV+3H8bf2vIbrQPCWhXunaHLAyXWmaMjTtLGeodsdK8X+Avx4+K/7LGtawvhKylsb/UEFvcwXdg8h+U5GBjrmo3Ktof0UU7NfhZL+3P+1f421CO0sL3VoZZ22JFYaWVYk+mVra+3ftx+MI9qL47ZJRjd5SRj+lCdhWPuP/gqP4+8ffDH4T6H4i8Fa9Jokdvfqt00Jw7Z+7+FRfD9/C//AAUO/Y0im8ZRRtrVrA0VzfhQJLe5jXPmqewOM4r86PiZ8E/2tfF2gsPGnh/xfqWkwDz3ivGDRrt53Ebq4P4aftSeLfg78J/GXgTR55LGLxA675EYhoOocD0Joeo7HlviZLjw7rmq6JaapNc2NldyRRtHK2xgGIyBX7Df8Eq/Bfwt1j4GHU9I0y3u/EqytDqrXih5FbsAD0GK4L9i3/gnj4P+JX7ME2rePtJZvEPibfcWl+T++toz9x19yea+V9Qh+LH/AATL+Oo8l5jok0+5H/5dtTtw3Q+hx+NIZ6X/AMFQfgDp/wAB/ix4b+IHhOJdNi1afc1vFhVE6ENlfTgV+tvwu18+Kvhr4W1hjue+0y2nc5z8zRqW/XNfkt/wUZ/az+Hn7TvwN8AzeG9Vj/4SO21AzXulOjiW2BhIJzt2kbjjg1+kP7EtxLdfsr/DiSW5+1udLQeZ9CRj8KuOxEj3CiiiqJEryv8Aaa+Bmn/tEfBvX/Bd9+7ku4S1rcYBMM68owz716rRQB+EP7PPxy8Zf8E5/jdreieKtCuZ9Omby9Q0zequ6KflkjbO0nHoe9fpH8OP+CpnwE8d29qL/wAQ3nhO/nYL9m1bT59isfWaNGjUe7MBXr3x1/ZT+Gv7RlmkXjXw/He3MYxFfQMYriP6OP65r5M8Vf8ABF/4aak8r6D4v17Qic7ElSO6RT2yDjI/GgvR7n3B4X+MXgXxtbxT6B4w0TV45Pu/Y7+KQn8A2azfiJ8f/h98LdJub/xH4s0uwWCNn8g3KtM+BnCxqSxP0Ffm7e/8ET/EUdxN9i+KGnGHpH5mmyRE/wC8Fb+Vbnhf/gidGt1FL4j+KJmhBBkgsNJ5YdwJHlyv1waAtHue7fsqf8FANT/am+Nmr+G9J8HR6f4RsYHkGqSXBeViDhcgDHzelfaVeZfBH9nnwP8As++HYtH8HaLFYKEVZrsjM1wR1Z27mvTaCXboFFFFAgooooAKKKKACiiigBKy/E2gxeJvDup6ROcQ31tJbufQMpH9a1aKAP585LjxD+wj+10Z1Rp30C+Zo4pFKi7tWJ4z3ypr9L9R/wCCtHwaj+Hv9r2lxqE+uvB8mlfZsETY+6SW+7nvXsP7T/7GfgT9qLSQuvW32HW4UK2+r2qgTR/X1H1r5s8B/wDBGnwBoPiCO98ReKdU8R2ETh0sCqxK2D0YgZIoHc+KvGPxV+Of/BRLx7a6DYW1zJo7zqFs7ZWSztlJxvkbGOB9a+l/2p/+Cab+Fv2YPDi+BrNdR8SeHQ11qqou6a+3L8+zAySD0FfpX4K+Hvhz4d6Pb6X4c0e00mzhQRqltEF4AxyR1roCueCAR6UBc/Br4KftVftB/CHwrH8J/CVtdWUkt0Y7OK500m5hZz0QsvHNftD+z9a+N7b4SeH1+Il3Fe+LTAGvJYhgZPIB4HIHXiu3/sHTPtguv7PtftI6TeSu4fjir9AXPxy/4KifCrV/gj+0boPxc8MxTWsWpSx3BvI8lY7yMjg4HGQK+xv2Zf8Agpd8MPi/4dsLPxVrVt4M8XIix3NvqjiGCV+m5JScYPX5sYr6U+Lnwi8MfG/wPqHhPxbp66hpN4m1lzteM9mRuqsPUV+dXjT/AIIprNrk03hL4jrY6Y7FkttW0wXLxDsu4OMj8KClbqfaXxY/ba+Dnwl8O3Go3/jnR9SuBEz29jpV3HdTXDAcKoRsD8SK+AfgR4k+L/7cH7Uej+PtTbUdK8D+H7z7TbLbK8Vt5atwo7MxGM/zrovA/wDwRWvbXxJZ3Pin4h2N7pUU6vNa2GmsjzIDkqCW+XPrzX6c+EfCOleBfDdhoWi2cNjptlEsUUMKBRgDGTjuaBaLY1Yx8qn+fWnnOOOtFLQSJg4560m2nUUAN20badRQA3bQVzTqKAGbcYp9FFABX5tf8FqLHU7z4b+BXtbOaeyt9RkknmjQsqExkAHHSv0lrO1zw9pnifT3sdWsLfUrN/vQXMYdD+BoGfKf/BLPX7rWv2S9BgurWS3NjcTW6NIMeYucgj2r69rO0Tw/p3huxjsdLsoNPsov9Xb28YRF+gFaNAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAx7q1nhuVlW5IjEeCrHv60yS6+0fu2XzbYjBcdc1cvv8AVn/cNZul/wDHiP8ArpUSOyOqux9hHLpszxmZGtzgQx87h654rcR96g4xVWb/AFkdWk+7Tic83fUdRRRVGYxJN7MMEYp9MX77U+gAooooAKKKKACkPSlooAQdKWiigAooooAKKKKACkIpaKAK0tnHNLHI6KzR/dJAOKl8sbs7Rn1xUlFMd2N206iikIKKKKAGTSCONmJwAK8Y+JH7Xnwo+EHiB9F8W+L7LSdSSLzTA5LNj6DvXsV5/q6/B7/gpl/yc9rv/XGP+tZSfvHRTipJ3P0D+Mn/AAVo+E3gvw7cyeDZpPGWt7CYLdYpIYC3YPJt4H4V+efxA+LXxm/4KBfEK00uDT7qTTpbhfI06xRmtrQE4yzkDIHqa+bdO/482/3a/a7/AIJp/wDJO4/+vdf6U7kv3Hoenfs5/si6L8FvgOPAFxcPqP2+PdqMzIFLsw+ZMA9ByK4KP/glj8EYrye4Gj3DmXJKPKSASc8elfYtMoUUyPaNHxxd/wDBKr4I3t4J/wCyrqAYxsjmI/Gtjwb/AMEwfgP4N1a31GLw9c6jPBIJUTULppY9wOfu9MV9X0+hqwnNyK9rYwWFnFa2sS29vCgjjjjGFRQMAAV85ftlfsw3P7Snwx1Dw3a37WV+zLPbTEDYZU5VX9FPfFfStRj7xpFxm43PhP8AYA/4J6Tfs46tf+LPGj2uoeJ2/c2aQjdHbp3cE87jX3ftpq96fVpGfM2c/wCNvAWg/ETQbnRvEWmW+q6dcIUkhuEDAg9celfDHxM/4I8/DbxRrx1HQ9a1rQo55cy2lu8Pkxqeu0GMn9a/QekpPQak0cN8FvhXYfBX4baH4N0y5nvLPS4fKSe52+Y/fJ2gD9K7n+Gmt94U7+GpFe7Pyc/4LMfF+31DWPDPw8tJmeSzBv7xFPAJGFB/nXnvwD/4Jnt8Zv2Vb7x42pzW/i68DTaTaLt8kxp/Cw25y31riP8AgqR/yd5rn/XpD/6DX6x/sR/8mxeB/wDryWmauKtc/EL9nWxk8E/tNeE9N16wkhmi1aO0uIJ12OhL7Sygj8q/owtdn2WHy/8AV7Rt+mOK/GP9pr/lI34S/wCwvbf+ja/Zuy/484P9xf5UglHliT/40hQNjrx70v8AjS1SRkeCftJfsXeAv2p7rS5/Gd3rkX9nZ8mPS7xIUOeu4NG2f0rhP2nv2ctN8L/sU+JvA3gnT5ZYdPsHa2ikYPM5A7nAyfwr61rM8Rf8gPUP+uDfyNEikz+fL9nv9sL4n/sk/wBsaX4WWxVLyT/SbXVrV5VRxxlQHXBruviT/wAFLPjX8W/BuoeGNaj0FtM1BDHKLXTnEmD2B8w/yrqfj1/yUDUf+vtv510Hw9+9Y/8AXRf51Jocl/wSt1zX/Df7U2mW9vbTix1KCW2vC8LbNuMg56A571+5O2vlD9lP/kaZvrL/ACr6xq4mcjkfiF8KfCvxU0l9N8U6Na6vaOpUrOgJwfQ18rXv/BI/4CXmoy3QtNchSR97QRakQg56DjgV9qt9001elUTqee/Bf4A+B/gDoLaR4K0aPTLeTb5spO6WbAwC79TXo1Mp9AgooooAQnAJr49+OH/BTb4dfAvxxqPhbVdE1u81GzXloYlWN29AWP619gyfdNfjd/wU8/5KFqn+6azlJxaRtTgpbl/4w/8ABY7x34iWSz+Hnh+z8KqW+S+ugt5MV/3CCoP4V8MePvip4j+L3jmTxD491a81q7mlDXDFghC55VFxhRjsABXtX7JX/Hre/jWL+0d/yGo/9+o52ypRUdj7E+Dv/BT74MfAH4c2XhPwf8Odahit49zA3SESzYGWZ2JPJ/Ktfw//AMFoJNa8Uabp7/DIJZ3dykBkh1PzJgrMBkIE5PPSvynj/wCQm/1Netfsjf8AJxngr/sJxf8AoYp3Ykkz+jWzuhfWcFwgZFmjWQBhyMjPNcb8avAKfE74a674dl27L22eM7hnqDXbQ/6uP6Clk7/SjdGezP5w28c/EH9mDxZ4u8JaHrN14eM8xguvJjTfJGCQuGZSw49CK+7f+CV37Itl4mjvfi5450hL+V5iml2+oxM43dWmw3DfjmvlL/goV/yd54h/34v51+3n7Pv/ACRPwX/2DIf5VXRD7nz1+19/wT38EfGjwzqGqeHNEh0jxiqFobi2Z1RjjpsDbf0r8ztT8aftOfsw2U/h+PVtd0XRbEtGrR20csO0d8ujYFfvvXzv+17/AMk38Qf9er/+gmpGj8cv2PfjlqPhf9rzwf4u1zUFdr/U0g1K7eNVzHK21zhQAOvYV/QuGDAEcg1/M78Jv+S4eGv+w3B/6NFf0xVpEmQtFFFUQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMmTzInT+8CK/O3wH/AME0PE/hj9re3+Kc3iaxOi22vHV0tBGTK67twU+h561+itFJq5SdlYQ02n0UJWJG06iimAUUUUAFJS0UAIVB4xXI+I/g/wCBvF4kGt+ENE1USAh/tdhFJuB6g5Xn8a6+ik1cd2eRn9kf4J7w/wDwqjwfuHI/4k0H/wATWxpH7PHwu0C4SfTvhx4Vsp0OVkh0a3VlPqDsyDXolFCVguznYfh/4Ys7hLmDw3pMNzGdyTR2ESupHcELkGt6P5R0PPepKKYDGXdwRkGvP9Y/Z8+Guv3kt3qPgXQb25lbe8s1hGzM3qeK9DopNXC5zHhL4a+FfASSJ4c8O6book+/9itkjLfUgVek8IaHNeC7k0XT3ugciZrVC/54zWzRS5QuUo9IsYWDR2VvGw6MsSg/yq1j8KfRRyhcq31mmoWU9tIoZJY2jO4Z4IxX4Bab+y7r3ib9tKf4bXel3dvaS+IpPNmaIgLaGYsJM9MbTX9A9eBw/wDJ0L/9ev8ASjlHc9n8NeHbPwn4f07RtPiWCxsIEt4Y1GAFUYFcd8bvgH4P/aC8IzeHvF+lx3tswPlTAYlgb+8jdjXo1FHKK5+DP7bn7B2rfst6tFqWlvPrPgi8ciO7ZMtbMeivj271+pH/AATavbi9/Y+8Dtchg6JLGoYYO0OcV3X7V/8AySHUvwrW/Zt/5Ir4X/69/wCpphe56dRRRTEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH//Z"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83-%E6%AF%8F%E5%8D%81%E5%88%86%E9%92%9F%E6%8E%A5%E5%88%B0%E8%AE%A2%E7%A5%A8%E7%94%B5%E8%AF%9D%E7%9A%84%E6%AC%A1%E6%95%B0.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApkAAAFaCAYAAABVO0bVAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAFdnSURBVHhe7b2HtxVllr//+y9m1sys/nbP6plpv/NttZ22bbW7MTQYuhtBmiAoKCBRwhAEYQiSY5MZcs5BMkrOGUGS5CRBco4C7p/P7lN6ZV3lnnteOKeKz7PWXtxbp6pOnaq61HP2++73/f9MCCGEEEKIwEgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRHEmmEEIIIYQIjiRTCCGEEEIER5IphBBCCCGCI8kUQgghhBDBkWQKIYQQQojgSDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMnOIWbNmWc+ePW3gwIEKhUKhUGQlevXqZVOnTk09mYQoPJLMHKJOnTr2wgsvWP369RUKhUKhyEoUK1bMKleunHoyCVF4JJk5xP/8z//Y3/72t9RvQgghxIPnf//3f+2///u/U78JUXgkmTmEJFMIIUS2kWSKUEgycwhJphBCiGwjyRShkGTmEJJMIYQQ2UaSKUIhycwhJJlCCCGyjSRThEKSmUNIMoUQQmQbSaYIhSQzh5BkCiGEyDaSTBEKSWYOIckUQgiRbSSZIhSSzBxCkimEECLbSDJFKCSZOYQkUwghRLaRZIpQPJSS+fXXX9utW7fs7NmzdvPmzdTSv8Pyixcv2tWrV/33O3fu2Pnz5+3MmTN24cIFu3Hjhi+Hy5cv+/Jz587ZtWvXfL/Azywnrly5Yrdv3/bl90KSKYQQIttIMkUoHkrJRCwPHjxoVapUsdWrV6eWmsvg/v377cMPP7Rx48a5NCKWDRs2tFKlSlmTJk1s8eLFvi4y2qdPHytbtqy9++67NmXKFJdO9jFr1iwrX768bzNo0CA7dOiQb3MvJJlCCCGyjSRThOKhk0wEc8uWLdagQQP7/e9/b4sWLUq9Yp51bNOmjZUoUcLl8OTJkzZp0iRr2rSpTZgwwfr372+dO3f2TOcnn3xi7du392WsU7t2bTt8+LCtWbPGevXq5a8hpPXr17cVK1bYV199lXqXH0aSKfJy8tINe2/cJqs8YkPORZ9Fe1NHKYRIGpJMEYqHTjJp7t61a5f17dvX/vjHP36bmUQcyWqStfzzn/9sAwcO9PX4Qxs1apQdOXLE5s2bZx06dHBJRQgRTH7euXOn1atXz9auXWu9e/d2EV26dKldv37dWrZsaTNmzLBTp075++TlxIkTtmTJEn8vArnt1KlT6lXxsHPwzBX7Zet59n+azM65qDpyQ+oohRBJQ5IpQvHQSSYZRfpbfvnll1amTBlbtmyZN3EjlO3atbMxY8ZY5cqVXfo2bdrkTd7r16/3LCf/DhgwwKZPn25vvPGGN5HTr5MMZo8ePVwmkc3u3bvb8ePHPWs6dOhQz4Ky/7uhyZ5mebKdRJEiRVxihQBJphAiG0gyRSgeyj6ZQOaS/pRIJoU9H3/8sVWoUMGOHj1qLVq0cMncuHGjvfbaay6IyOnmzZttyJAhNnLkSCtZsqTNmTPHi3zYhvXHjh3r/TPJZtI/E8kcP368Z0LZ9l6ouVzkRZIphMgGkkwRCknmN5K5cOFCzyDSdI000sSNNCKGrLNt2zZv+t6wYYM3s48YMcIzmbNnz3aZJJPZs2dPl0n6ZrIOFedI5vDhwz2bSVb0XkgyRV4kmUKIbCDJFKGQZH4jmWQmixYtajVr1vQK8meffdbefPNN69evn/9OtThFQAsWLPDKc7KeCCFN63v37rXdu3f7HyTN6F27dnXJRCoRU9ZHSvfs2ZN65x9GkinyIskUQmQDSaYIhSTzG8kkQ0kRD1lHonjx4lanTh2bP3++97ts1KiRZyPps8kfHsMcIZpUoiOFVKK//vrrvh/2R3V5VPAT9d0ks3kvJJnZY8muU9Zjwe6cilYzttu/N5+br+RlOySZQiQXSaYIxUMrmRT/dOnSxZvC74a+lQxRRHM3Y1wime+//75nNRkbk0IhBlqniZyCnebNm1vjxo0928m4mkhlrVq1rFWrVl4IhHxGA7X/GJLM7IHQ5SdTivxDkilEcpFkilA8tJJZUJjx5/Tp07Zy5UrvoxnNBAQUDLFs+fLldunSJV8XqESneZzCIIYpKsgYmSDJzB6SzPRCkilEcpFkilBIMgsA8sj4mshi3owky1nGa3mX8zMzAtEnk6xnQbKYIMnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGQZOYQkszsIclMLySZQiQXSaYIhSQzh5BkZg9JZnohyRQiuUgyRSgkmTmEJDN7SDLTC0mmEMlFkilCIcnMISSZ2UOSmV5IMoVILpJMEQpJZg4hycweksz0QpIpRHKRZIpQSDJzCElm9pBkpheSTCGSiyRThEKSmUNIMrOHJDO9kGQKkVwkmSIUkswcQpKZPSSZ6YUkU4jkIskUoZBk5hCSzOwhyUwvJJlCJBdJpgiFJDOHkGRmD0lmeiHJFCK5SDJFKCSZOYQkM3tIMtMLSaYQyUWSKUIhycwhJJnZQ5KZXkgyhUgukkwRCklmDiHJzB6SzPRCkilEcpFkilBIMnMISWb2kGSmF5JMIZKLJFOEQpKZQ0gys4ckM72QZAqRXCSZIhSSzBxCkpk9JJnphSRTiOQiyRShkGTmEJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4TioZTMW7du2fHjx61Dhw62bds2u3r1qm3YsME++OADa9asmXXt2tVWrVplX3/9tV2+fNl69+7tr/Xr188+/fRT38ft27dt8uTJLoYdO3a0xYsX+37u3LljK1eutFatWvk206dPty+//NK3uReSzOwhyUwvJJlCJBdJpgjFQyeZCOa+ffusZ8+e9uKLL7oc7tq1y8aMGWPdunWzoUOHWr169WzQoEF24MABW7RokTVo0MC6dOlinTt3tv79+38rpe3bt3eZREKbN2/u4vr555/bwIEDrVGjRr4PRHP9+vX+vvdCkpk9JJnphSRTiOQiyRSheOgk8/r167Zp0yZr3Lix/eEPf3DJJJs5e/ZsO3r0qMtg69atrVOnTv4a4kcGc//+/TZr1iyXSiSV1xHCtWvX2vbt261q1aq2efNmGzZsmL/GuteuXbOGDRv6vs+fP586gu+4ePGi7d6925YvX+5RuXJll1nx4JFkpheSTCGSiyRThOKhk8ybN2/apUuXXChLly5ty5YtS71i3jyOhDZp0sSbzJFM1qHpnG0QSjKZc+bMsQoVKtjEiRPt1KlTdujQIc+CspysJz9/8cUX/l5kMydNmmR79uxJvct3kPVk3Zdfftnj0UcftbZt26ZeFQ8SSWZ6IckUIrlIMkUoHjrJRCQJMotly5b9nmQihQsWLLCmTZva+PHjvZm7ePHitnPnTn+NTOWQIUNs9OjRVrJkSc9Q0nSOsA4YMMC3qVatmvXq1cullG3GjRvn63/22Wepd/mOr776ytdDVAmynt27d0+9Kh4kksz0QpIpRHKRZIpQPJSFP0BTdV7JvHHjhjeJ16pVy0aOHOnZSZrVyWTu2LHDX9+4caNnMkeMGOHbIplXrlzxrCX9MpFJtu/Tp49LLJLJvmhCZ1/3Qn0ys4ckM72QZAqRXCSZIhSSzG8kk36Y9I2ksKddu3a2ZcsWX0Zzdt26dW3hwoV29uxZW7JkiVekUzFOs/iECRNcMPfu3esFPlOmTLE2bdpY3759PftJ0zv7HD58uP9+LySZ2UOSmV5IMoVILpJMEQpJ5jeSSVU4Ivjkk096ppImc6SQoHmcQp558+b5Hx5V41u3brWxY8d60zb9MmfMmGFvvPGGrVixwn8mq0mFOZlPCoKQ0RMnTqTe+YeRZGYPSWZ6IckUIrlIMkUoHlrJpC9kjRo1bM2aNV7YU6dOHXviiSe8D2apUqU8A0kTN8Mb8TuV35UqVfKiILKcjH1JhXqZMmV8P6+//rodOXLEzpw543+gf/rTnzzbyf4YBol+oPdCkpk9JJnphSRTiOQiyRSheGglE+k7d+6c95ukvyU/k208ffq0R1S4QyCaDElEtTlZT2Awdvpt0pQ+c+ZMO3jwoBfyMBj7yZMnbfXq1V70Q39OBnQvCJLM7CHJTC8kmUIkF0mmCMVDK5kFBRlFQhFPinmQywikkmW8RnYzylbyM2KJkNIvE/EsCJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGInWQyNiXjUOYH41HyekFm18lFJJnZQ5KZXkgyhUgukkwRilhJJhK5efNm27dvX2rJ97lw4YK/ziw9cUSSmT0kmemFJFOI5CLJFKGIlWSSoWzRooVVrVrVunXrZiNHjrQlS5b4POJffPGFTZ8+3ecWZ4rIOCLJzB6SzPRCkilEcpFkilDEQjLJYDK1I5JZp04dq169uo0dO9bnBh89erT17NnTWrVqZa1bt/bfCzpXeK4hycweksz0QpIpRHKRZIpQxEIyz549a8uXL7dVq1ZZtWrVrHPnzt4sPmPGDOvSpYuVK1fOXnzxRatfv74dPXr0e/OLxwlJZvaQZKYXkkwhkoskU4QiFpK5ZcsWe+edd+z111+3p59+2t58803PWlauXNnefvtt6927t3Xv3t3atGljc+fOtatXr6a2jBeSzOwhyUwvJJlCJBdJpghFLCTz0qVLLpqbNm3yvpgIZ6lSpVwwWUYfzIMHD9qYMWOsfPnyduLEiVhWmEsys4ckM72QZAqRXCSZIhSxkEykcerUqS5giBiFP/Xq1fPmcrKZLVu2tLZt21qHDh2UyRSFQpKZXkgyhUgukkwRilhI5q5du6xp06b21ltvWenSpb3ZvFGjRrZ48WLvi4lwIp61a9d2IVWfTJEuksz0QpIpRHKRZIpQxEIy9+zZ8+3QRc8++6z98Y9/dMkcMWKEvfzyy9asWTN7//33fdn69eu9Ej2OSDKzhyQzvZBkCpFcJJkiFLGQzIsXL9q6dev8xi9atKj3x+zatasPXfTII494NpOK8wkTJtgHH3ygcTJF2kgy0wtJphDJRZIpQhELyTxw4ID16NHDBg4c6P0vaR7v2LGjLViwwEqWLOnCGRUG8Ydx+vRpFf6ItJBkpheSTCGSiyRThCIWknnlyhXbu3evy+aOHTvs008/dak8fPiwF/rQZ5N1mFbys88+U3O5SBtJZnohyRQiuUgyRShiIZlAZvKrr77yYG5yRPL69et2/vx5X4ZkHjt2zEX01q1bqa3ihSQze0gy0wtJphDJRZIpQhEbyUQs165daytXrrTt27d7k3gEArpt2zYf5mjFihUun3FEkpk9JJnphSRTiOQiyRShiI1kMrVk2bJlrXjx4ta8eXMfviiCwdqHDh3qQxhRIKTmcpEuksz0QpIpRHKRZIpQxEoyGSOTbOXWrVvt888/9+V37tyxYcOG+TBGzPhDxjOORT8gycweksz0QpIpRHKRZIpQxEoyy5QpYwsXLrTVq1fboEGDbPjw4T5fea9evWz+/Pl2/Pjx1NrxRJKZPSSZ6YUkU4jkIskUoch5yUQuqSQng/nSSy+5TK5atcrHyGzdurW99tpr3nyOeMY1gxkhycweksz0QpIpRHKRZIpQ5LxkUjE+Z84cF7AXXnjBBgwYYIsWLfKhiz766CNr3769ZzPHjh1ru3fvTm3149DETjX6hg0b7MyZMy6nVKnTn5PCIoZE4negcp1hkZBYmulPnjzpy9mGYZXWrFljGzdutCNHjnhVO8vJqFKkhAzv37+/wHOpSzKzhyQzvZBkCpFcJJkiFDkvmYjb0aNHbfLkyV7YU6lSJevfv78PVYQsAkKHbBII3Y9lNHnt8uXLLoYUES1ZssSr0ZFLBnZnGVNYIpUIJu9drVo1z5gyCPz06dP9fZmFqEOHDlaiRAl7++23bfDgwS6myOv48eN9OXOsd+nSxeX3x44pQpKZPSSZ6YUkU4jkIskUoYhFn8zbt2/btWvXfLrIzZs325QpU7z5nGGMED6Kfch2IodMLYno/RBUnpNhpIjoqaee8qwoMwXR/E5GdN++fdauXTuvVidTidAyyxDbUFjEe3AcZE5Zj2wqwyZVqFDBs5Yff/yxiyV/pGQ3a9So4TMTcYz3QpKZPSSZ6YUkU4jkIskUoYhN4Q+SiVgicEgm2ct+/fq5GCKANHGTfVy6dOmPjpOJZH7xxRc2a9Ys+9Of/uSZzNmzZ/uc52zL+4waNcor1slaksWcNm2anThxwtft1q2bN5GT1URE9+zZ4zJKdfuyZcs8u8kxMisRx9GpUyffnozo3Rw8eNDGjRtn9evX9yhSpIhvLx48ksz0QpIpRHKRZIpQxEIyyVjSBxMBo6KcqSWjZWQamdd85MiRtnz5cvvyyy898/lD8BqieerUKa9WRwzJfjZo0MD7f9I8j3SOGDHC902TN5lO5JM+nMyfjuSyLVlMprJEWnv37u2/v/fee56NZP9kL9kPzecc891E4so+CZrYkVLx4JFkpheSTCGSiyRThCIWkkmzM9lFZC1vRpCmcqRyyJAh3h+TjGFBoU8lg7sjmey3YcOG3qeSfX7yySeepSRrST/NnTt3ujAimwydhDiWKlXKm+jpA8rxIaQ0p1evXt2FkwHi2YZmddanmf9eqLk8e0gy0wtJphDJRZIpQhGb5nIKZwiKcchEInD8TOaRfxG9glaXQ17JJANJc3dUIY6s8kfG+JtvvfWWyyUySRM9y0aPHu0FSDNmzHAxPXTokDeRI5k0e/ft29er0DlGMpQIKxXq90KSmT0kmemFJFOI5CLJFKGIlWTSx5ExMym0YbghfkYsDx8+7MMGRcMOFYS8kkkgiRTtIJNREzyy2apVK5s0aZI3pdM8jwhSLETmNGq6Z/YhCnxoZkcwCfqJ0sROX0+a8ikKuheSzOwhyUwvJJlCJBdJpghFbCSTvpQ0ldMvExljyCCyhPwxIHVdu3b1wdl5vSCymVcyyWCShaSfJVXmFStW9Iwl8soMQwxR9OGHH3qWsm7dup6lRHKbNGnifTkpPqKIaNu2bS6+CGrVqlW9MIkhkSgg+rGK9whJZvaQZKYXkkwhkoskU4QiFpJJFpOmZ4YXQuw6duzo41ouXrzY+2MyhiZZR4pmihUr5tXeNHv/GDS5sx1N3fyMILI9soposn+a4RFKZJFMZ5TdjMbJJMPZuXNn6969uw8Sz9BGyCRV6iynTyeySuW7xsnMbSSZ6YUkU4jkIskUoYiFZJKZpPmZvpONGjWyiRMnenU5WUj6RzKMEEJIcU3lypVd6hDHdGB7KsLpd0nGFKkF5JD3J0PJ++QdHolB3Wmup79l3kHgWYeKc4ZUYlrMewlvhCQze0gy0wtJphDJRZIpQhELyWQ6xypVqnhFN0MKkTWkfyQ/M285s/fQ/xGhQ+zIMv7YMEa5iiQze0gy0wtJphDJRZIpQhELyYyyjOvXr/eCm3fffdf7XpItJMtI1pEsYjT7D//GEUlm9pBkpheSTCGSiyRThCI2hT9IJP0dkbBy5cp5MQ59Iek/Sb9Hok+fPt58TjN2HJFkZg9JZnohyRQiuUgyRShiIZn0cWSIIprEqSCnyptq77/+9a/+x8Bg502bNvWB0Bm7kv6RcUSSmT0kmemFJFOI5CLJFKGIhWTSVD5v3jwv9KGpnOwlY1q++uqrPkYlFeAMY8TwQlR4q7lcpIskM72QZAqRXCSZIhSxkEz6XlLsU6dOHR+Pkmbx+fPn+xiUVJKfOXPGXyfDKckUhUGSmV5IMoVILpJMEYpYSCaV4vSzpMinWrVqVqRIEZfNJ554wivOGVT9xRdftKefftoznQxvFEckmdlDkpleSDKFSC6STBGK2BT+RDCc0fLly33cTAY9Z8iiNWvW+FSTNKcznFG6Y2TmCpLM7CHJTC8kmUIkF0mmCEUsJJPBzMlkUvgTBcU9BK9Rec4sP8wpzlziDHkURySZ2UOSmV5IMoVILpJMEYpYSCaV5VOmTPHMJRlLgmwmUz9S9INUMlMPUzkyNeSFCxdSW8YLSWb2kGSmF5JMIZKLJFOEIhaSSYbyP/7jP6xGjRpe/PPee+95JfkHH3zgzeXHjh2zAwcO2NChQ+3JJ5/03+OIJDN7SDLTC0mmEMlFkilCEQvJpM9liRIlbN++fT7rD/0xmTMcmZw6daq1aNHCx8hkmsmnnnpKkinSRpKZXkgyhUgukkwRilhIJk3hZcqU8arxadOmWbdu3Xy2n44dO/rMP8xrzrI5c+Z41pPB2+OIJDN7SDLTC0mmEMlFkilCEQvJJHNZrFgxW7Jkic/uQ7/Ltm3b+uw/yGbv3r197EyymhcvXtQ4mSJtJJnphSRTiOQiyRShiIVkMiwRY2Fy448aNcrGjBnjc5RPmDDBm9AZ1mjkyJFe+IOIKpMp0kWSmV5IMoVILpJMEYpYSOaJEye8upwbf9KkSf7z+PHjbe7cuXb48GE7dOiQ7d+/33+vXLmyBmMXaSPJTC/eGrrOTly8nnNx41Y8WzGEyCUkmSIUsZBMZvw5evSovfnmmz7gOhnMdu3aecaS17p06eKZzD179tjkyZPt0qVLPnZm3JBkZg9JZnrx783n2m/aL8y5WLzzZOqKCiEKiyRThCIWkgmnTp36dtrI0qVL23PPPWdt2rTxeOWVV6xRo0a2bt06HzeTAdrjiCQze0gykxFzt32ZuqJCiMIiyRShiIVkkpVEHp9//nkv9qlZs6b95S9/sXHjxnnQF7Np06Y2ZMiQ1BbxRJKZPSSZyQhJphCZI8kUoYiNZJ49e9bHw6TI55NPPrEBAwakXv17n00Kgnr27JlaEk8kmdlDkpmMkGQKkTmSTBGK2EjmzZs3vcDnypUr3ufyzJkzqVfNhyyiP+aGDfGueJVkZg9JZjJCkilE5kgyRShi0ycT0aTIh3+Ju8fCpB8mIhpnJJnZQ5KZjJBkCpE5kkwRilhIJvJIdTlDF9EHc+zYsT7wOmNifvjhh9asWTNr2LCh1atXz6vOz58/n9oyXkgys4ckMxkhyRQicySZIhSxkcwjR4740EX0vaRvZvPmzW3Lli0unMwCVKdOHfvrX//q42fSpB5HJJnZQ5KZjJBkCpE5kkwRilhIJs3k9MPcuXOn7dixw6eVrF+/furVv8MMQE2aNEn9Fk8kmdlDkpmMkGQKkTmSTBGKWEgm/S2RzCgGDRpkDRo0+N6ywYMHW+PGjVNbpEdUWEQxEbMFnTt3zgd6531pemfZhQsX7MaNG9+uzxzprM+6165d8+Vw9epVr4QnLl++nNY86pLM7CHJTEZIMoXIHEmmCEUsJJMpI7t27Wrdu3f3KF++vL344osuZES0rEqVKqkt0gN5XLNmje/j1VdfterVq/sUlbt37/Z+niVLlrQPPvjAVqxY4esjle3bt7c33njDateu7f1DI2jOf+edd6xixYrWv3//tPqHSjKzhyQzGSHJFCJzJJkiFLGQzOPHj9vEiRNd5oi6deu6+EW/R8tq1KiR2iI9du3a5c3tyOr8+fOtZcuWPpMQY3FWq1bNhZMm+jFjxrjwUnDE+yGUZFARYPqMrl+/3tq2bev7oUiJbOv27du/l+n8MSSZ2UOSmYyQZAqROZJMEYpYSCZN0MjdwYMHPRAxZv2Jfid69OhR6D+KzZs3+x9Vv379fGYhRPHtt9/2AqPevXt7NhKRHTZsmE2fPt0lkvnSkdPVq1dbnz59bN68eda3b18XTiSUY+rYsaPNnj3bB4vPD5az7sCBAz1KlCjhMisePJLMZIQkU4jMkWSKUMRCMunXSMX44cOHv5VMsoR5yaTwB4Fle/p0Ll++3OdBL1OmjGc0ly1b5pnItWvXeuYSiaQJfebMmS6kNKlT0Y5gUoxEpfvevXt9rvXJkyd7/1F+zw8+C0MysR1RpEgR69ChQ+pV8SCRZCYjJJlCZI4kU4QiFpJJEc6+ffs8k0g/R5qw33vvvW+LbCjAIRNYWMlECGkSp38l86Ajm/SrpB8m01hSFES2c+TIkZ7drFWrli1dutQznAcOHHCZpI8mzfWTJk2yY8eO+XHNmTPHhZiK+IKg5vLsIclMRkgyhcgcSaYIRSwkMxonc8aMGd7XkbExyTwidBTYlCpVyl5++WXPQBYG+mEid7wHVeRII30+X3jhBdu4caMXBq1bt877X7Zq1cqzqAsWLHC5ZTpLjoVB4MlG0neUjCviyrGS+ZRk5j6SzGSEJFOIzJFkilDEprmcbCZ9GL/88ksvBCJbiBQif/SLXLVqVYFl7m6mTZvmWVC2530o+KlcubIP8E6xD0Mk0TxO30sypvTTRDjJYlLs07NnT/89ep1liCZ9N/mdLGxBkGRmD0lmMkKSKUTmSDJFKGIhmfcbRJUinaZNm3pVeaVKlTxjSf9KhkUiI0kTOllJBJJ+mzStI5A0r5PZZDn7YXv6VdK0z5BIFATRdF4QJJnZQ5KZjJBkCpE5kkwRithJJn0kqcimTyTBz4cOHfIMZGFBAmn+pmK9bNmyXthDf0r6YbKMAiD6gFKkQz9QmsmZ1pI+m8yZTkU4ywmyoDTb81pUAc+g7gVBkpk9JJnJCEmmEJkjyRShiJ1kInu/+c1vvL/kc889Z48//rgNHTrUm9FDgxwilPTZZEpLZvABZvyhCZ0B3Dds2PC9AdcRzW3btrkAM1MQU2IWFElm9pBkJiMkmUJkjiRThCJ2komI0feRwhqKbkqXLu1Cl47MpUPUH/Srr75yuYyIpqIk8k4dyXLWpVgonSklQZKZPSSZyQhJphCZI8kUoYidZNJ0TV9JYN5w+j1S9JMEJJnZQ5KZjJBkCpE5kkwRilhIJk3Wixcv9oHRmYmnWbNmXnxDv8miRYv62Jn8zusrV67MqH9mNpFkZg9JZjJCkilE5kgyRShiIZkMAUQVNwL20ksvWYUKFaxXr15eEf7rX//ax6dkGCGGDGJ4oYsXL6a2jBeSzOwhyUxGSDKFyBxJpghFLCSToh6GEWIw9nLlyvnNTxaTgc+ZipGhhZgjnHnFGfOS4ps4IsnMHpLMZIQkU4jMkWSKUMRCMinqYf5wgqGBmA+cJnEGZWfIIZrSo9eJvAU6cUKSmT0kmckISaYQmSPJFKGIXeEP/THzVpczpSTV5elWcucikszsIclMRkgyhcgcSaYIRewks0WLFj7dI4Oe0w+zePHi3lTOuJVxJ+mSufXoBeuxYHdOxmt9V+YrLYp4hSRTiMyRZIpQxE4yx48f71M3tmvXzoOfV6xY8b0B0eNK0iVz7NrD+YqBQhEqJJlCZI4kU4QidpJJ/8y7m8YZ/JzZeeLaFzNCkqlQZBaSTCEyR5IpQhE7yfziiy+8P2Zetm/f7sMcIZtxRpKpUGQWkkwhMkeSKUIRK8kkUzlw4EDvgwlkNJkfvFWrVr487k3mkkyFIrOQZAqROZJMEYrYSSYiNnz4cG8eZ/xMZvupXLmyDRs2LLbjY0ZIMhWKzEKSKUTmSDJFKGLXXN68eXPr1q2bbd682SZPnmy1a9e2mjVr2qxZs1JrxBdJpkKRWUgyhcgcSaYIRSwkk6wlQxQRdevW9Vl/mEqydOnSNnfuXKtevbr169fv23XiOmamJFOhyCwkmUJkjiRThCIWkrl//37r0qWLMTf5448/bj//+c/t9ddf94HZO3ToYMWKFXPxZB3GztTc5bmJJFNxv0OSKUTmSDJFKGIhmUePHrXRo0f7GJlPPvmk/eQnP/HpJIcMGWLjxo3zjGaNGjV8HeYzv3LlSmrLeCHJVCgyC0mmEJkjyRShiIVkIo27d++2vXv32ptvvml//vOfrUmTJj6P+YQJE+ytt97yjCbTTMZ5KCNJpkKRWUgyhcgcSaYIRewKf5hWEqGk0IfmcqSsSpUqNmbMmNQa8UWSqVBkFpJMITJHkilCETvJbNmypY0YMcKLe86cOWOtW7e2hg0bunTeuHEjtVY8kWQqFJmFJFOIzJFkilDESjIRy0gyo98p8mnbtq0PbbR06VJfHlckmQpFZiHJFCJzJJkiFLGSTAZj37Vrl08tmZctW7bY2rVr7fDhw6kl8USSqVBkFpJMITJHkilCERvJJGt57tw5O3v2rF27ds1u3rzpv7N8w4YNPn85y+KMJFOhyCwkmUJkjiRThCIWkok8MoXkp59+ahs3brRjx4550A8T4WTecs34k/tIMhX3OySZQmSOJFOEIhaSeeLECZs2bZoNHjzYx8VkSkn6X5YoUcLH0KQ/5qBBg1xGCZrV44gkU6HILCSZQmSOJFOEIucl8/bt27Zt2zafRvLpp5/2aSUZlJ2B2F944QX7+OOPfQgjBG3NmjW2fv362FaZSzIVisxCkilE5kgyRShyXjLJStL3csWKFV5ZXqtWLZexRo0a2RNPPGEdO3a0V155xQdp79Onjw0dOtTnLy8MyCnjbX7yySdeXEQhUY8ePaxp06b+R0eBUbQeFe4cT7du3WzJkiW+HJDedu3a2YcffmhTp05N61gkmQpFZiHJFCJzJJkiFLGQTIRv+PDhLnQMxI7g9evXz4oUKWLTp0+3ihUr2vvvv+9N6KtWrSpUJvP69eu2c+dOz5SyT36eO3euVa1a1fr27evjcU6ePNn7htJczx9gp06dPHr37m2nT5/2WYk6d+7szfe9evXyGYmYpaigBUmSTIUis5BkCpE5kkwRilhIJtNFIpc9e/b07CAy99lnn/kg7EeOHHGpQ0ILC+9x6NAhz1pWrlzZ5s2b55lTRLFNmzZe0U6Gkyb6hQsX2oABA3zmoa1bt7rYdu3a1eUW+SWLiZwyvSXHxfoMGl8QJJkKRWYhyRQicySZIhSxKPwB5iNH6lauXGn79++348eP2+zZs23Tpk0+GDvyWVjIfC5YsMB+9atfWYMGDVwmyUiSiUQSqWBHIkePHu0iyh8f70dWk4zn2LFjvcId6R02bJiP5Xny5EmfV53fEc784DPRnH7q1CkPtu/evXvq1eQhyVTc75BkCpE5kkwRithIJtlGpIxm61GjRnmTNVlHxI/MJiJYWHbs2OFyV7ZsWVu3bp2L4auvvmrPP/+898NEQnk/3rdVq1beL5R+mPQVPXDggDej0ze0Ro0aNnHiRK94J3s5Z84cz75+/vnnqXf6PiynC8DLL7/s8eijj7owJxVJpuJ+hyRTiMyRZIpQxEIykTEKfWhOfuqpp+yZZ56x1157zaWMgp/GjRv7a2Qead4+f/58asuCQZM329HkTt9KsqMU+5QrV87H5kQyGfCdoiKKfah0X7RokTej0+eSTCbN5PTnRDLpQ8p+PvroI5dIJDY/mBITQV6+fLkH0tylS5fUq8lDkqm43yHJFCJzJJkiFLGQTKSNJuyRI0d6hpFqcoYtItNI0MRNcQ6SiPBduXIltWXBQPAo4JkyZYpvS7N8s2bNrGTJkj4+J8vop0mxEf00EUH6aHJcCCnLeX+a2BFR+ouSzWQ5QZ/SgqA+mQpFZiHJFCJzJJkiFLFpLo9gmCKEkz6SVHWTVYyyh4WFPpQILMVFUWFPvXr1rFKlSl61zvibCCRN6vTdpC8oWdOZM2f6dhT4sBwRRVYRTYYyqlmzpksqg8kXBEmmQpFZSDKFyBxJpghF7CSTpnMKf2jCZtghfqYf5cGDB1NrpA9DDNEsznBFpUqVsuLFi7vMMl5m0aJFXWRpnqd/JYU6FPyUL1/e3n33XatQoYLVrl3blxM0p/Na9erVfVsKg+hLWhAkmQpFZiHJFCJzJJkiFLGTTISNzOPixYtd4Cj4QRJv3bqVWiN9KCpiH/SxpGCH/pSXL1/24D0o7KGqHbm8c+eOvxdSy1BF8+fP959Zzn5YZ9myZT7WJkKMCLO8IEgyFYrMQpIpROZIMkUoYieZCNukSZO8EIjsY0EHOi8MkXzS3E2WMq/I8jNCSoV53kwl02BeuHDBhyQi21pQwQRJpkKRWUgyhcgcSaYIRSybyxkuCMk8duyYS11SkGQqFJmFJFOIzJFkilDERjJpjqYpmqIcxpKkOTppSDIVisxCkilE5kgyRShiIZk0WTPDDzPoUGTDYOk0U0fFNnmDfpQIaRyRZCoUmYUkU4jMkWSKUOS8ZNL3kb6X1apV8yGBEE2C+cIRsigYXojxKxnHkkHO44gkU6HILCSZQmSOJFOEIuclk6IaJBPBZBihcePG+dBCTCc5fvz47wUDsTNmZrqDsecKkkyFIrOQZAqROZJMEYqcl0yavqnuZrggspdM/8hsO8y0w5SOeYOZdfbt21fgcSlzDUmmQpFZSDKFyBxJpghFbAp/aDZn4PX27dv7zDzM+BPXvpc/hCRTocgsJJlCZI4kU4QiNpIZQaYSyWQWnvPnzydKNCWZCkVmIckUInMkmSIUsZNMMppz5szxucOHDx/u1eRJQZKpUGQWkkwhMkeSKUIRO8kEBmHfsGGDbd++Pbb9L/NDkqlQZBaSTCEyR5IpQhE7yaQICMGcPXu2TZkyxWbOnOnzmO/evTu2VeURkkyFIrOQZAqROZJMEYpYFf7s2rXLPv74Yxs5cqT16dPHq82ZYrJbt242ePBgW7JkiV27di2t+cJzCUmmQpFZSDKFyBxJpghFbCSTAdabNGniQxhNnTrVtm7d6tXmNJkzvFHdunXt7bff9mUIaRyRZCoUmYUkU4jMkWSKUMRGMs+ePWslSpSw+fPne7aSvpjIJP9ev37dZsyYYS1atLB58+b563FEkqlQZBaSTCEyR5IpQhGrTCYV5e+//74NHDjQFi5caOvWrbOVK1f6LEANGzb0144ePWq3b99ObRUvJJkKRWYhyRQicySZIhSxkcybN2/a6tWrXTCZp7xfv37eD3PIkCG+bNCgQT7dZFwFEySZCkVmIckUInMkmSIUsZHMCKrIJ02a5DP/IGX00WQec/po3rhxI7VWPJFkKhSZhSRTiMyRZIpQxEYyqRi/dOmSN5EzCPuHH37oTeT8ISCaiCfzlyuTmbtIMhX3OySZQmSOJFOEIjaSycw+nTt3tnbt2tmYMWN87vJPP/3U/504caLVqVPHatWq5QO1q09mbiLJVNzvkGQKkTmSTBGK2EjmuXPnrHz58j4AO8U9Fy5c8MHXKQj68ssvbcSIEV74s3z5cq82jyOSTIUis5BkCpE5kkwRithI5vnz5+29997zAdgZF3Pz5s0+OPuOHTt8EHYGZaf6/PPPP4/tVJOSTIUis5BkCpE5kkwRithIJtnJadOmWcuWLa1169ZeUU6z+ahRo6xHjx7WqlUrrzRn7EzN+JObSDIV9zskmUJkjiRThCI2khlBcQ8z/tA/k4IfMpsfffRR7It+QJKpUGQWkkwhMkeSKUIRO8lkqCL6XzZr1sxq167txT7IJnOanz59OrVWPJFkKhSZhSRTiMyRZIpQxEYyr1696uNhMgg7/86ePdvFcvr06T6kEYLWoUMHF01Vl+cmkkzF/Q5JphCZI8kUoYhV4U/VqlVt2LBhns08fvy4nTlzxivLKfahX2bdunVtw4YNsR2UXZKpUGQWtcd+aj0W7M656Lt4r529cjP1lyBEbiPJFKGIjWQyhFGlSpVs5MiRtm3bNvviiy/sxIkTPi4mswAxxSSSxmDtmUgm01ey/wMHDvjg71SxMxYnYhs1x5MpRWzXrFljmzZtsiNHjvhyOHTokK1fv96PY9++fWlVuksyFYpkxiMtPrF9py6n/hKEyG0kmSIUsZFMxsQcMGCAZzOZ6Wfo0KFeADR+/HgfoL1KlSpedY4kFra6HHk8ePCgVa9e3ZgfHcF8++237bXXXrN69erZvHnzXBrPnj3rY3KWKlXKj4c+olS1UwFPc365cuXsjTfe8Ob7kydPFvh4JJkKRTJDkinihCRThCI2komoMesP4jdhwgSXwC5dulivXr28unzLli0+QHsmwxfR77NFixb2hz/8wQuKaJqvWbOmj8fJ+yC2ZDnpB0rR0cKFC110kVyq2xcsWODb00d07dq1vs7GjRv9uAuCJFOhSGZIMkWckGSKUMRGMiMYfJ3CH8bL5I+gQYMGLpxLly71fpuFJZoXnf0VK1bMZxdigHfG4eQ1BoAnY8l7U83OH+H+/ft9astBgwa5bLJ+7969fT80offt2/fbGYryg6zpuHHjrH79+h5FihTx7GdSkWQqHtaQZIo4IckUoYiNZNLPcvHixS5l9MtE9pA++mLSRN2tWzdfRjbzzp07qa0KBtnPPXv2uDyOHTvWKleubK+//ro3v9PvkmZw+lkinIgk86QjnfTRJINJZrVnz55eeMQx0J+T18iw8sdKn9H8oE8psxUxsDxRokQJ69SpU+rV5CHJVDysIckUcUKSKUIRG8lEHpE7ZA4xo6iGDCFCt3r1ap/xh76U27dv936Z6YAQzpkzx5vIDx8+7GNwlixZ0qWTZngElwIfpJYMKtNbcgwUI5HNnDhxojeZs/2kSZP8uKh8nzVrlmdZyb4WBDWXKxTJDEmmiBOSTBGK2EgmxTZkF8kgIpz0nyTDeO3aNW/OZspJRJN+kSxLB5rakUSymFStN2rUyIt92B+V5bwP/5JtbNu2rTVt2tSP49SpU7Zz506XTzKcFAORaUU8KfjhZySTSvSCIMlUKJIZkkwRJySZIhSxkUxEkv6K77zzjjVv3tyzh1R7ky2kqZzhjag6Z710m8upUKcf5quvvuoZzF/84hf2k5/8xIoWLeoV7UgtfSsp/oma6Pv06eNN7GRRmdqSJnwKg2i6X7Fihfe3RFxZxs8FQZKpUCQzJJkiTkgyRShiI5k0gS9fvtwmT57sGUUGX0f6kDpkjopumsrTFUygSIdMZRSILE3z/fv394wm78NQRvSXpH/lZ599ZhUrVvQ+mxQK0UzOcgIBZrij9u3bu7SuXLnSxbcgSDIVimSGJFPECUmmCEVsJJNxMrnxKcBhCKHGjRt75pIsJn8MSCf9J0NAf0sqxCnqQfpo8u7cubMPWUT/zIsXL9qQIUO+HUaJZnaWEzNnzvRtOC7+ZUaigk5zKclUKJIZkkwRJySZIhSx6pNZpkwZzwzSdF2tWjUfLoi+mAgdQwCRcQwJckhTOcLJTD5RX0+q0ekTypiZ9MnMOw4m/Tfpk0mhEEMqpZNZlWQqFMkMSaaIE5JMEYpYSSYz7MyfP9+bsWmSjgSOWXhYRrN1nJFkKhTJDEmmiBOSTBGK2EgmldzPPPOMD1PEQOlM58gwQYgmFeHREEJxRpKpUCQzJJkiTkgyRShiI5n0d1y2bJkPHUTWkqZxpnukCZsB0JGzRYsWpdaOJ5JMhSKZIckUcUKSKUIRG8kE+kIyADpV3Fu3bvUZc6g6p58m/SbpPxlnJJkKRTJDkinihCRThCJWkpl0JJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzh5BkKhTJDEmmiBOSTBEKSWYOIclUKJIZkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGZJMESckmSIUkswcQpKpUCQzJJkiTkgyRSgkmd/w9ddf282bN+3MmTMeZ8+etatXr9pXX31l58+ft9OnT9uFCxfsxo0b365/8eJFX/fcuXN27do1Xw5sx/bE5cuX7c6dO6lX7o0kU6FIZkgyRZyQZIpQSDK/AcFcu3atlS9f3sqVK2eVKlWyiRMn2o4dO6xevXpWsmRJ++CDD2zFihW+PlLZvn17e+ONN6x27do2depUXw6jRo2yd955xypWrGj9+/d3SS0okkyFIpkhyRRxQpIpQiHJ/IY9e/bYpEmTbPDgwbZs2TJr06aNde3a1UaPHm3VqlWzuXPnWqdOnWzMmDG2f/9+W7JkidWtW9eFkm1Y98iRI7Z+/Xpr27atde/e3aZMmWINGjSw7du3fy/T+WNIMhWKZIYkU8QJSaYIhSTzG44fP26bN2+2gwcP2q1bt6x3795Wo0YNz17yM9lIspXDhg2z6dOnu0R26dLFdu3aZatXr7Y+ffrYvHnzrG/fvi6cSCj76tixo82ePdtOnDiReqfvw3LWHThwoEeJEiVcZpOKJFPxsIYkU8QJSaYIhSQzD/S1pO8lmczixYvbe++955lNMpE0p5O5RCJpQp85c6adPHnSdu/ebePHj3fBrF+/vo0YMcL27t1rp06dssmTJ9ugQYP89/xARMeNG+fbEUWKFLEOHTqkXk0ekkzFwxqSTBEnJJkiFJLMFAgmhT1Lly61hg0bev/M1q1b29atW73PJpnOkSNHWosWLaxWrVq+HhnOAwcOuEzSR5PsJ83ux44d88KfOXPmePM3fTsLgprLFYpkhiRTxAlJpgiFJDMFzeT0q6TwB5kkEMeNGze6fK5bt877X7Zq1cr7Wi5YsMCry+nPSd/Ndu3aeTaSgqHDhw97JpN+mWQ+JZl/R5KpeFhDkinihCRThEKS+Q0MM/T5559bkyZNvs08rlmzxvr16+fFPpcuXfLmcfpe0neSfpoIJ1lMin169uzpv0evswzRpO8mv+/bty/1Tj+OJFOhSGZIMkWckGSKUEgyv4Hm7SFDhthjjz3mWUr6V9K3EuGrUqWKZyQbN27sWUkEcvny5T50EQLZuXNn34blZDvpz0m/SoqEaHKnIIim84IgyVQokhmSTBEnJJkiFJLMbyDTiGQihcgkVeUIJEU5NWvWtJYtW3oREL8z2DrN5M2bN/f16L9JRTjLiQEDBlijRo38NbaNKtYLgiRToUhmSDJFnJBkilBIMn8E5BChnD9/vu3cudNn8AGKhGhCp0l9w4YN3xtwHdHctm2bFwYxU9Dt27dTr9wbSaZCkcyQZIo4IckUoZBk3gP6a16/ft2nmEQuI/iZqnMi79SRLGddioXSmVISJJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzhwglmbfufG2jVh+yHgt251RUHrE+3wewQpH0kGSKOCHJFKGQZOYQoSTzxq07VvRvy/J92CkUigcfkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGb9o8bGtO3DWTly8nlNx6fqt1P8aQnyHJFOEQpKZQ0gyFYpkxk+bzrYn2s6337RfmFPR+eNdqf81hPgOSaYIhSQzh5BkKhSKBxn/M21b6n8NIb5DkilCIcnMISSZCoXiQYYkU+SHJFOEQpKZQ0gyFQrFgwxJpsgPSaYIhSQzh5BkKhSKBxmSTJEfkkwRCklmDiHJVCgUDzIkmSI/JJkiFJLMHEKSqVAoHmRIMkV+SDJFKCSZ94G9e/fa5MmTbdiwYbZw4UI7efJk6pUfR5KpUCgeZEgyRX5IMkUoJJmBOX/+vE2cONGqVatmjRo1sqZNm9q6devs5s2bqTV+GEmmQqF4kPH2sPW28PMTORlHzl1L/Y8mHjSSTBEKSWZgVq1aZV26dLEePXrY9evXrWXLlvbRRx/Zl19+mVrjO7766iu7dOmSnTp1yqNBgwbWpk2bb38vbBw9fsKebzvDflpvnP2s/nhFwOCc6ryGj5/WH2f/p+7YfF9TZB5xvG/7f7wp3//fci1oqcpveZyjW7duVq9evdSTSojCI8kMzOjRo6179+62fPlyl0gEk2Wffvppao3v+Pzzz/2P+eWXX/b4+c9/bo888si3vxc2ir30kv37L5+w//tfT9uvnnlOETD+4/Hf2L89+mS+rykKH//vyWftZ//3cXvst3/I93VFZvHvjz1p//HYb/J9LVfjDy8Uzff/t1yK559/3n7729/aS9/8n5vf63GNxx57zCpWrJh6UglReCSZgRk0aJD17t3bBfLWrVu2ePFiGzx4sC1btiy1xndcvHjRdu/e7UJKzJ8/3xYsWPDt74WNRYsWWbFixTyjmt/risJH3bp1rXLlyvm+pih89O/f35555hmbMWNGvq8rMot3333Xateune9risIHCYUXX3zR/+/O7/W4Bs+QTZs2pZ5UQhQeSWZghgwZYv369XN5jCSTByh/tA8K+n+WLl3aZs2alVoiQkHmmb6zIiwrVqywokWLFrhITqRH69atrVOnTqnfRCg+/vhjK1mypF29ejW1RAiRF0lmYCZNmuSdpteuXevN5VOnTrW+ffv6t8MHhSTz/iHJvD9IMu8vksz7gyRTiB9HkhmYNWvWuGQyfBEdqDt27GgDBw60rVu3pta4/yCZ9KfhP0ARFrpCtG3bNvWbCMXq1avttdde878ZER7+HwoxcoX4PnRvKl++vCRTiB9AkhmYCxcu2IABA+zVV1+15s2b2+9+9zsf0ujy5cupNe4/NNOPGjXKduzYkVoiQrF06VLJ+33gwIED/mXsQf6dPEzMmzfPu+6IsOzcudOGDx9eoCHqhHgYkWQG5vbt2z4YO83kPDRpPj906JDduXMntcb95+uvv7Zjx47ZlStXUktEKM6dO2enT59O/SZCce3aNTty5Ij//YjwnDlzxs6ePZv6TYSC/2P5v/ZB/v8uRJyQZN4HyCQiI1SYMzg7vwshhBBCPExIMoUQQgghRHAkmQmDrCnZU5rH6B9648aN1CsiU2hupDCF5nIy1YweQNcEUThoYmSs2Khogt9172YO9yTnlHMInFd+pnKfe5fzq3s3PThXzODGuYu6HvA7fTGjLjScY/XNFOL7SDITBgUUzDlbqlQpa9KkiS1ZsiT1iigsPGDoK1ilShUfZodzW6NGDduyZYuqSgsJ4sODulWrVjZu3Dg/xzy8mcqO8/vBBx94kZVIH6aqpdiQv39AgPj5ueee83PL8GafffaZJD4NOFcLFy70SvJy5cpZpUqVbM6cObZ+/Xp77733rHjx4j6FcH4zuwnxMCPJTBDHjx/3aSyRoZkzZ/qYjiNGjFChSoaQndi3b581a9bMh6difvqNGzd65kKFKulDtv3EiRPWrl07e+WVV3w0Bub2nzBhgr3//vsuSIwty/1LtkgZt4LDlx6kvUKFCvbOO+/4uVu3bp0PX8Q55d5luCgyxipWKTjbtm3z+5NKcs4h/xf06dPHZ3PjixGV+23atPH/f8lsCiH+jiQzQTANGA9mHiiIJaLJDEQbNmxIrSEKA5mh2bNnW/Xq1f3hwvBQzOBEk6NIH84bkjlmzBgrW7asT8W6fft2a9Cggc/zf/ToUc8SMXg4IzWocK7gcK8ydiPnsmrVqi6SY8eOtcaNG/u9y5dO7l0NFZUeX3zxhbdc8C/ntEOHDlazZk0fpg7R5Iso9y6BkAoh/o4kM0HwbbpFixbeRM7QGsgl/+lNmzYttYYoDGQsyWLw4Gb+Z5rHyLgdPHhQfbAKAdlfMm4EzbhDhw71ZkeEk+ZG7l0mNWAIMISIbKYoGJwrziv3a61atVyIEMumTZtanTp1PFi+a9cufUkqBNy7ZIH5+6eJHHnnXmX5smXLbOTIkS75Qoi/I8lMEPznxpSHfOPmYcMsQ0gmmTdReDiXURaDBzgPlbp16/oYqOqKkBlk15BMpmGlvyDdEpAfZJMsPM2PnHORHpw3ZJLm8s2bN9vhw4f9PiZj/NJLL3lmnj6wouBwLskUz58/379svvnmm9a5c2cfqg6Z54sS9/KMGTNSWwghJJkJgkIJ+gXxnx2DW9NvkP/0+HYtCg8PELJrUUUuDxW6JfTs2dObdkXhiSSTrDv9CJlBhSILpLNfv34+qYEkM30iyQTuXTLu3Ltk38lm8uUT8RQFh3OIpDOb25QpUzzT3r17dy+iIpPJ/Pv0L54+fXpqCyGEJDNB8J8dnftpHqNJh+kP6ZxO30xReMhWdu3a1QsoOK/Lly+3atWqeYGKMpmZEUkm4k6TLn0xGSaKe5c54mmCVHN5+kSSifz06NHDv4CSheP/iBdeeMGzbbp3Cw5fNPkixP3Kl8v9+/d7t6T+/fu7cPIFNCpY0/SdQnyHJDNBUEzBt2iG1+A/PB7adFDnAS4KD0PtkKGgGhrZbN26tffPpF+bBCgzIsnk3qX7AeeVCt4PP/zQGjVqpKkmC0leyUSEEHbuXf4/oOqcrjQawqjgMDUwsv6b3/zGh9finPJlnuZyzvOsWbM8Q4xkIqBCiL8jyUwQVOHu2LHDqx4pAOI/PZrKJUKZQZaCpkWqnSn6YWxHMkGqes4c+gvTl5imSB7OjPFKMRCFFTzIySCJ9GGYIobbool8z549nn1DhuizTbaYQfBFweGLOgL51ltv+f2JaA4bNsy/EPF/Al+KOL+0GknehfgOSWbCQHwYp42BgxFODVUi4gJCSVM5fds00L2IA3wBZYxXxJ3htnTPCvF9JJkJhIc12cuoUEWIuMC9SyZI966IA9yjdEng/1u+4OueFeL7SDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQaUCfQfoLhpxOkn5c7DdX+nNxHEnsW8ZnCjUcUnTNxHd/EzofQoi7kWQKkQYMYE3lczRfcQgodGEszmhWlmxC8QIjElDIkDRp4DwzHufd143PSaRz7jlH3AsF3Yb17rUur3Ns6RxHtuF+OXnypA/yzsgAQgiRF0mmEHlgCj5m9GE8wSpVqvgg1kzTybBQSCDjDzK2I/MX5x0nk3UYKy+qjGZKzwkTJvig+AwynvcBfLdwMF83AzsvWrTIZxSCu4WDoVEYloqBtKNx+qJo3LixD8C/atUqn040Ew4cOODjKzKlI7PtMGh33mAebIZsyY9jx47552WsQGTux+BcMlQR03IyJzxzlbN/zl1eOAeMUcqYhHfPpMKUk/nNwc3MNps2bbLBgwf7eJCcO5YxYwtjGTKwNpLIubpw4YJfKwYpZz56xuls3ry5tWzZ0saMGePHBlwjlrEtx4hUcZ54D4au4fii7bh3GGSe3xnAm2Pks/EeTJBQr149nzGKf999910/Jgah5zWuJ8fJ8d4NU0Eyu8wPwb3CtsyWxPFxLzNGJueWsUjHjh3rM4AxsUDec4Yss28+B+cE4eZzd+zY8XvXkeW8Hg3XA3w5Yr+Mx7t7925fdjesy7XiyxnHP378eJ82lCkuGXOW98r79yCESA6STCHygHQghQ0bNrRXXnnFpY4HJMsQKCSkTJkyLhFDhgzx6fp4EPPgLVGihD/YkRpEFGFAQhjAmTFLgdcZ2JnXEUvmP0ZK2CeD6DPg+6BBg3yQZx7ezCrEgx3p4EH+L//yL/a73/3OihQp8m0888wz9s///M9+nPnJSUHhs3/yySf+mRFmxGPatGnfC84D8zfnB0LD8TNoNQLxQyBpzOSDLCN4iCbnj3n3kZ+8wsFn53O/+eabfj6Rk+h8MAPT3/72N39ffkdICaQJqULcEF+m/xs3bpyv+6c//cmPj3PLlwmkEQni2v71r3+1119/3dq3b+/XB6lduXKlyxNC/PLLL/vc6hw/n4/jevvtt326UUSS68n1ZkYo5LFLly5+zng9klTO7UsvvWS//vWv/d//+q//8utZvHhx3xeD0G/bts0/I/cJ++ReIP7yl79Y6dKlv/2d4P7gMwPnjWPlnuJe4LwiynzZ4b0ROj7n3YOxMwh+5cqV/X35khSNs1uuXDn/UsH55PzypYrXmTmIfSL/fCnh2rA9UsoxcV4QSQSUbRBfzgXLuYbRrE58YeMz8Rk49iiEEMlBkilEHnj48oBmqkOEkoczwsIUh2Sffv/739uTTz5pFSpUsPLly3umiinlunXrZs8//7w/nBEKHsRkpsgG/va3v/UHLSByZBzr169vb7zxhksPMluqVCkPRIZliCmyQoaUrBtyynGxLx7+vH8UCCrT3ZHBYr3CQPM4XQCQgapVq/p7k8XNG0gg0vJDGSs+N+eBmXqQtx+C5tXJkyf7+yCZvDeyzvlEciPRZDkCQqaP4P2RP84f69euXduljPNC9pT9IlbICyKJ/CCJiBrZXjKH3bt39/POlwiyasguGTpEimV8eeA8EIgVssSxclyvvvqqf8Yow8zPCGne6UXJRHMPMN0g2csIMrecF+4Xjrls2bJ+fyCNCCkCyKw8ZJCRM0AIEVHEjODee/HFF/1nBJ37hpmn8vYP5rNwrHPnznX5JmsZnWve4/jx4/65kFgEEFFE+IoVK+biSAaY4+fLAueP881xIORsB9wDkUAj/dz3fAbOHwJZvXp1v5c5P3zh4npFgs015l/OG9lfPh9fXMjik3HVTERCJAtJphB54CHHvM+9evXy5lP+JdMTNYPyAOVBSpYPaeBBywP/8ccft3/4h3/wbCYPfh7SCBcPcR7CPEABOUEaya717t3bsz/sBxEgaM5EpsiIkSVCBBAYsqVIJA9ytkOiokBcOCYybzTL393kXBBoAkdw+HzsDwn685//7MJLlo0s3x//+EfvJoA4IFp8DoQQQSMQaTKgCEiUASNYh3XZJmomR/SQc14Hmkx5f+R63rx5LuMIIJJDtwWkiXWQdjK+SD9ihMxwzJxjhIcvBFyrF154wR599FGXSqQTkSLzyeckY8j1Y/+cK8Sca877kO3k/YsWLfqtdJNZJvsXSSafn+Pj2DnfUSYRfkgyuYY1atTwbB5ZVKZ9Ra5oUuce4/0RWtYh+wpI2Guvvebnj+A+i7K9yCLncPr06f4ZkEuOi9c4Bj4nmVAkHnHkSw1yy88s44sCn4EvU//6r//qGVzOGQIYSSLHwt8AX3w439EXBz4L14V7nGNGetkvks814h5BOlmfY0F6Obf/+I//aE899ZRVrFjRp2JEOJ999lmXZTK6bBNlNYUQyUCSKUQeIslEEqK+ckgAD0mEAylAXJBEhBKBIVPDA/y555779sFKkyWydrdk0txIsyTNhFETfCSZ/I5kIpj03yOThHAgLUgJ4odY8JDOG4gZD2xeQ5LYf7pwXIgJoooc8/noc8hx0NSMXCEdiBxSw+fiuMmilixZ0qWErNQvf/lLF27EhGW8RraO84HUcR4Qa84tohQJGv8i0mRQ2SefA0lDSJEZBI/PT6YR0UY2kRuuDVlMMnWILU29vA+iz9z9nAsydBw725Nh/tWvfuXvzzqIGNeP7DRCjVSRsUZ66OeKdCGZSG4kmUgowsf6fE7EKuKHJJPzy+fmWiHt7AuBRLCQeX7merNO1H+XLCQCyPkg/vM//9Mee+wx/xnp/+lPf+qyzPVAeMkwcq75DFwbhJbrxz55H+45fmYZ9x3XkHudpm62R9C5vzkOvlDxuZBWPj9fAMgSAxKI0HINOP98GeK9EHmyynQd4F+uBX9PiDBiz3Uj887++dvh/HH83Gtcb7bP289ZCBF/JJlC5CGSTB6sNGfSTEyzKg9vsjZIEFkYHq6ICZLJ+ggMAsDDGblAFBHGuyUTIUCCeCgjLAgOD3yyP2R8eA/2yfr8TAYQ+WI95I/j4LiQJgQIWUJwETrejywVGSqkDVlBhvgseQuP8gMh4HMiHGS02D9iQIYLgaW5mX6EvCfHThEHxx9JNoEkc27IeiEZ0XLWIRuMVJLFQ9hZj2PnPcicISBIIcKFJCFMCCLbcG7oIsA2nFf2TzcCrgUihhyR3UQyadLluBBkPgfnEBki88b6yBLSidjQvxKx5hqxnC8RSCxCzz7JUiOyd0smx8Q15jyQ8SyIZCJPSC2CxzXhGuYNlpFpRZijZmmyjOyf80cg0pwbfqb5GknjPHNPIbFRP9G8EklmkOD6IZDR79yDiCKSx3XlGLgWnEe+HHEvRM3r7JMvCVHWGWje5osR+yI7zd8D9ycCzv1KVpPPzPmgCIkvKvxtIJJsx98VoskXNs4ty8kWCyGShSRTiDxEkomUIAo8cHlAkmmieRcZQF4Qr5/97GcuFAgKy+gXST9OBIVMEkJ0t2TSrIkEIjn0FURqkCuaQWlqRiKQBJrG82b6eGjzIH7mmWdcBDkeModkCsm40QyJWEQiwPsgjpEw8POPQZMxzcMcAzJFMzyiSRMm8oO0UWSEqCEYUZNuXhCwH+uTyXvQpI5kIFw04ZKRQzDZhvdBnKJ+nwggx826rMfxsB7niz59fHbEiGtCpo59IzSIJRloMoacM64D74Go0i+T5nQymrwPmVnOLSLFZ+PckskkG0d/Tq7L3ZIZXROkluwgwhaRn2QijYgh78lxIMt8Bv7NG9w7ZBq5f/hSwLGTtYzg+JAyQOz47Egpkglcc+Sba4Ww8bkoTqPZnS8HXEvuOT53dD9wrugGwXshlYgg9wtfVpBAzin3ApIZyS8ZTZaxL84FmU2+6HB92DYv3Cfcy+yba4vAc/65x7mWnGv6ovLlg/cUQiQLSaYQeYgkEzFBeniok+1B6nig8xAm24aM/NM//ZPLCVkcMoks5+GOkCCeZPbulkygTxsyEEkVgkoRC5LBuggV75m3bxrSgfhSiUw2k/UoAmJb3vvpp5/2BzzNm8C2UbN2lFUqCDzoETEkhOPnPCBI7JfPzOs/1GfuXpKZF4STLCTZV84Fv3OOEJVINhAYjoNzimyRyeO8cg0QVLonIH4IFEKE9JE5RapYB9GkQIgMJRlBmsCROzJ3NFvTRIsQcn7IGiL8dDngvfgMSCYZNwQrb5/MvJLJNScjSvaOLw/5SSaFPNw7LONLBOcXKeO4CcST7CzLkXzEj+wogkihT5QRJgPM8fMz2VmOEwGPCn8iyUTaEGOynBQL8Z7sn2B7mvjJLAPbc+9xTRFKrglfphBJZJBlXFOWky3lPiITzJcXMszcyxQYsV/OKdcz77XniwICSUacTD/N5ZxHzivHwDZcV74gsa4QIllIMoXIQySZyCXZJUQkyljx0Eb0yASR9UPykAIyc4gMD32aIHlwIy30J4wkk4c/MhAJASAFbMs+aConq4YY8VDmOPJChpJ1aNYkC0RWiswcTc1k9ZAWhCrKUCENSAGZPcSInwsCUsHnRhTYjs+KZCESCAJZNoQwPwoqmUgaGS6kCaEiY4uIsW+adO/uU8p5QgA5TzQTI3xsT9YP+UHmEHv2w/lF9MgUc07YL0MUcVw0zyNniB3Xhv0SiBJShRzS/zMSIDKUZOz4IvFDmUyyydwXSCRdCDj/yFdeyeRaRE3HXEOOgWPi2JF4tiPYDpnnywHbkClEzPgSQTzyyCPe5xVhi5bxvuyX68tn4R7iHCJvZDrJUiLv7JfgCwNfTPgcQJcArkPUJ5OiMiSTY0Cc2S/iyDVlWfRlg+w+P5Nx5nxFY4by98L6nHeuBZ+De4cvB9yzyCnZYa4755djJUPOPV/QL0JCiPggyRQiD2SjyODRfMj4hmS5EJJf/OIXniFCXigWIdOEXCCRiCUPezKQCBjNt0gm2Udki4wbksID/u4mQR7uSAzZNYSC7BX7RhjygtCQ+SSzhdjQH5TqaZro+R2ZQAQieeCBjTjRZMyDPCrauBdIKeKKwPJ52B7BJpP7k5/8xH/ms+YH4kSTMELxY+Nk8vlYhwIQZB1p4/g4D8ggUhLBeUCiyDCSleMaIIVsE2XYEM5oGVKD4CCMXAd+5lxw7skU/9u//ZtfDzJnSBISxfEg6OybY6JqHdFGbDk+rilfEjjPyGd0bbg/kD4yg3xZ4FoiZhS6IKuRZCJbnA8ylgRfYpBKpJnjpzKb5nnOO19UuAZ8Hu5F7i/2S9CvkmZn7sloGWKIoHH8HBcCzjWjGZpjIntLlpf9EnQxyCuZ3Oc///nPv60uZzskk/MYnU++QCGPXAe+QCGKvB/3dJSZRTY5TxSOkRlFRDl39ClGTjnHSCiZX7LKnB9e57qSnefcs44QIllIMoXIAw92sixkkRhAnYHHyRwiakgehSBkG2l6JFOELFH8gCQgekholJnk4Uq2howTVeBsT2EEwkHmhwwQ/ezIRPIgJ3vK72Tg2D8P4qgwhWwikoDoEPTBpEqabGq0jEwjmVYyesgBYyHStMpn4OeCQAYVAUIAEDO2R0SQS0SEptL8+mMCcsi5Ihv2Q5JJJhJR4jxyrsj8kblEMsiocX4QwwjECXHj/HCuEdmISGjzCjSfky8JZC05x4gecoNw8r50QyCiIhS+MPAlgswjwbFzDpEozgP3AzKJHCK5fC7OLeKKeCJtdFPgOvNefA66M7CP6Lj4DPRn5LORaeQ8kc1EenkfvoxwnXmNLy7IYyR4kdACGULuOe4/jp97kr7BNGtzr7I+ld4INO9FVhqBY59cS4LrR+aQ88j6nCuOl+uM5HMPcu9yHyDq3Iu8B/cf9zPXnnNAdpQsKF0TuH7R/cW1o5sBXwDYJ/ci5497mfucY0F+kVYknowoy8hu8iWJzy6ESA6STCHyQAYJWSBzyMOf7ArZIbJLCAFCgUDwQEZeKGpAMMjkRA/cqJkckAseomQ2EVHW40HN9gRCSzaKhz4Pbx7w7B9BQnR5aJO5iiqkyVoR7I9+d/wbLeN1HvB5JS1TEBGysYgZ54Fz8kOQGUQikSWyXvmBuCEWfE4yX9H+2TdN85wbZCaC1zmHnP+7xRWJQWDydi0ga4hMcS64jlwHMm7IFceGNCJ0XAuyblw7zj1SxnVD1hAjstOR4HFNOc9cb7YHJJBjJWuJKLMu9wr75dohr+wjgtdZj8wpQkZGlM+MQEfNxHxurh37zg8ynpw7rnt0//BenMvouNg/9wvvxb/cQ/wcwfVDrnkfzi1fkDg/wLFE3SvIQHIeEVvua/4e8sK69EWNMqJ54fNxzji3HBfvwd8A0so9QnCPIJuIOMfHtaC7wN3dRIQQ8UaSKURgeHj/GFFTNkL7QyAcPHDvta8HAdKDOIQ4Fj57Xom8H3CckSDyL5HJsXOdEN1cuBYPCq45osk9mLcfcWHIez0i8lsmhEgekkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMoUQQgghRHAkmUIIIYQQIjiSTCGEEEIIERxJphBCCCGECI4kUwghhBBCBEeSKYQQQgghgiPJFEIIIYQQwZFkCiGEEEKI4EgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRGLP/H2S5DyniM30hAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F%E8%A1%A8%E7%A4%BA.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWgAAAByCAYAAAB+30ucAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADDmSURBVHhe7d2HlyZF1Qbw738SEyYUwQyKCRXMGFCMoKKomLMYEbOoKEbELIqYMQdMmHPOOft+59eeZ71b9js7C7NMz859zqnT1dWVurr7qVu3blX/36rRaDQai0QTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3Sj0WgsFE3QjUajsVA0QTcajcZC0QTdaDQaC0UTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3SjsWD8+9//nlzFvs4ravqN4s0haWseQc7r8V//+tfkh5omx2DuvKbdatS6BDXsQJZ9edEE3WgsHCETRDISTZBwx3/+85+TH/aVbh1qmuQR1Lzm/I41HJyP9Rj9Y5qtRMoP6vmBLPfyogm60dgBGAls7jxHBF3Pa7zNQppKqCO5VqSM0QVJO3ctWBd+eVHLXEfQS0YTdKOxYKwjrUo84zk3kk/i7Q/ksb/kOsbhTx5z5zAXtlVI3nNlHojythpN0I3GDsI6YhEWIoIQUnWXBWPaeh5/DasQlvqMcSLlV1cl/61EbReoZS4dTdCNxg5GJZqRdHJewzYLZBmSHyGsEl5FSDakmPSOcUH1HygoY1/1WHcvS0ATdKOxcIRk5ogmmAuPv55vFuKmzKDWIe63v/3t6pe//OXkfvOb3+xVRuL84x//mI5/+MMfVr/4xS9Wv/71ryf3t7/9bU8c7kCg5j+WsS58SWiCbjQWjjkiqef1etzcRGHON4sxDX8IWv7I+eMf//jqnHPOWZ1xxhmrs846a/XjH/94It7EjyQu/C1vecvqWc961uoVr3jF6p3vfOfqpz/96Z56xh0IjB1LcCDL3Co0QTcaCwaJ81e/+tXqL3/5yx4yGUklRJPwv//976uf/OQnE4FWKXV/UOOTgH/+859P+f31r3+dyE4YKfhjH/vY6nGPe9zqqKOOWt3ylrdcffazn1398Y9/3FOmeOrziU98YvWQhzxkddvb3nb1+Mc/fnXeeedNdYx0Dftbx81AfdX797///XRey0gdD0S5W4Um6EZjgUCCf/7zn1fvfe97VxdffPEkbQqDOWKp/j/96U9TGqRIcq3S9P5CWh0EifeLX/ziRHbySl0Q7Pnnn7+65z3vubr97W+/+vCHP7wXGbr+s5/9bEr/wAc+cCLpz33uc1N44lzWum0G6v6FL3xhqruOIvWumAtbCpqgG41twhw5OUcYiPDCCy+cVAKOo353I4RUH/OYx0zkKW0IEdaVOxf2u9/9bvWpT31qdcopp6wuueSSSSLNNfjhD3+4ev3rX786+eSTV3e7291Wr3nNayapH8RB1u973/tW73jHO1b3uc99Vg9+8IMnyTmk6Bi/+PxjPdahpq2o+Ti+7nWvWz396U9fffvb394Tf13apaEJutFYCBAKR0Xw6U9/enWve91rImcSKIIVTqWAdL/5zW9OE3MkZaT4gQ98YJKypUfQ4r///e9fPe1pT1u98pWv3CPVjkiZ3AgqjHe9612rRz3qUauLLrpoIn35htikUU/k+7znPW910kknrV74whdOUrtryPx73/veRODnnnvuJD0jyqhdQpIpPy55j/4a9o1vfGMaXWgP9+b8bW972+qtb33rJC0H4murs88+e/Wwhz1s9a1vfWuPukjZ2mrJaIJuNLYRlXRyvPTSSyfCQ2gIBYmQZL/0pS+t3v72t0+ESbJGRh/96Ecnkn7Sk540kTm1SMgHgZu4e/SjHz0RrHxSBqTsuTD4yEc+snrqU5+6evKTnzzlhZzrdUedhbwR+SMf+chJv4yUgaT8wQ9+cPWZz3xmIu5TTz116ixgJOf4g4THH6Qt5PvSl750aicd1Ic+9KEp7EUvetHqJS95yUTKqS9Cdu1+97vf6rnPfe7q+9///p7yUo+logm60dgGhIBCEgFpkLXDiSeeOJEeVQdQJSDgT37yk5Okeu9733v18pe/fPWDH/xgkkhPOOGE1Qte8IKJFCFkTLI2icfJO+FxFTWctPz85z9/9fCHP3wiN+mCmpZFhk7i85///ETm973vfSdyZFJHknUP/E984hOnjuKCCy6Y0oYg6YVdV17M7+KnmuESbgThXhFsyPi0005bnX766ZNeWzqk/dCHPnS6XidIpdFet7jFLSbLE9J97iF1WSKaoBuNbULII+BHNKRhBIxQQ97UBogFUdHlIkMSNSmRhcXxxx8/hZG45VPTIS3Xv/rVr07SJNQ4MNbFZB+9M+k5UnnAr1wEiKB1GlQMpNPb3e52qy9/+curr3zlKxNJOopngvCZz3zm6mtf+9qecuXjfqRl/SEfzuSmI8mbCoWfHty9qct3v/vdyU9SJrWzCFEfTielLHk4D/nqYL7+9a+vjjjiiEndUvXgS0YTdKOxjUAelSgQHosIZIZgQozisM5AZkzVSI8kRlIlVcQd7nCH1Wtf+9qJwGp+/O95z3sm4qQOiJ46DubOlX//+99/9epXv3o6R3DyShykiyTVV6eC8BDfkUceOZEjSZn0rD7f+c53Vne84x0ndYs6Q8rTuSBiemzqG2ni5/hZgJhoRPapC5UL/bqRBl27tiIlU/886EEPmjqmtEPKMnlp4pQumkpkJ6AJutHYBlSyC5AnAkE61Bkj0SI30uLd7373aUIMSSJGUiNJEhE7N6lYVRkIkD772GOPnaRIYTVvSFzhSF8ngciQf+pa49ADm6RDqKwj1E3517jGNSZJ2uQdkjQKQLJUMG9+85snIq2InTLy5BAvl/MaThUSGA0gY/cdCxdlPuIRj1g94QlPmNJQ/2RCkJMe6d/5znee1B3uAVxbKpqgG41tQEijwlCe+oIESI+bOHHIlxrDZBu9L6IkNZJ0X/ziF09ESCUwSo8IlD750EMP/R/9az1yrpFUkTkJlfSbOAECZ3JH/WGiEhGS7uV99atffZK+5SGvH/3oR6tnPOMZk24aoaecIOdx6QzmrlWn43jsYx+7OvPMM6dz6UjwOjj3SiXC/hkpJ40OTbtS9yBxoxHhS0YTdKOxTQhxBMzRLPYgBZLucj1xELSJNhYRJEjhwkiRVA1veMMbJuLKYpKA9Gni8ZBDDlm98Y1vnKTLoBI5RyfMKuJmN7vZpONNPRLHpB7VBnWKjoGqxQSheMjvrne966SSQNocUjbRSJ+tbIRdSbhCWK7ty8lXO5DgpTFieNOb3jRJ7+pNUkbA0bmDeFQu7LXVnZoj+S0VTdCNxjYBYXABG2FLpkl3MBIHNcLLXvayaSiPdIHkSvJG0EiJxAs1X6TEFO+qV73qNAEZXS7UeMJYi5hkO+yww1avetWrJqkzcVynslAeIoyj2kC8pFV+JK+uJhpdp/vmEKqJQ6h5jvfp3PWEJ07OXdMG8jI6CNy7UYTOw/1WdUrSAvtyOnsSN9Q2WBqaoBuNhYDkfPOb33yycQ5pjESFMOuSZWGkR2HVaqESkmukXARN1UAVUVHjknrpn1k7kHiDWp5y1IOjxki5HH/K5yfBJi6X60Hi7i/kk3JBHvzulYsOfoQwKiQdoXa+LGVfkWiCbjS2CcghDiyDtuEQSbNeqy6o5zV8DoiLSgRB3+Me95jUIElf0/IzYaN/vvGNbzwtQhmxLt14HozXthI1b/eY87nyajiVkI6Qjn3paIJuNLYJlVA41hu3vvWtJ3WF85BOjTuHdeGB6/Sx17rWtVZ3uctdpsUrY345pyawmAOBUZmsi5ew8Ryqf4Rr9b5gTL8ZjPlsJo9ct2jG/TnCvtJtJ5qgG41tBoIw/DfBxsbZ/sqVcKofqr9io3gm9m54wxtOulc2xSOSlk73Bje4wdRRvPvd755IkKuo5cRfw2DuPMc5gh7L2BekqXkENXyMEz/VBoJmpgc1ztLQBN1obDOQE9M1izmoF0xyjcQSAuNfRyjjtUqEiBcp6QAsIqmoaUjabJnVY47IRyTtWHbO59yIdeH7g+ThntNWVQ9dy7BgxiiBdQkkfIlogm40tgkhDQ6ZWMxRrQvmIG6IN/4QUVwwEjTTuSpB51pNw1Tu8MMPnwiaKVvFmD+/skOIQS23QlwuyHnizqVZB3HHcuqkIdR8a7znPOc50/2xaFk6mqAbjW1CJQ5Hi1SoFpjSwUh8iWvlnP0uLBaxVLrmEX+QMMR7netcZy8ddEXi2YnOsnCTlXTQIUHHkRDBOfUMszppOfWri2HA6kYWIq5bXMP0L+Sc/Me8NwJzP7v+WYzCFrzmxaUjqGE5t+Oee3z2s5+9J3ypaIJuNLYRCCLkZDEHKTfEUcmjxmNpYRN68SxAEZ44NQ04R6DM7K5ylatMNsBsiINKjI7Ik6WHelhWnutxc2D/bOc6+3ZYSGO1oxWNScvUjuWIFX4m5thXKyckvlHe64DomQHSJ1ugwrQukFcIGsYy7IB3q1vdqgm60WjMI8TgGCJ7ylOeMulGHUfiqPEs5ba0mz2vpc7CE2eEMNImqfnKV77y1AnYmyPXRsnTghN7cJhQ1AnkesV4brEMaV5dbnOb26yud73rTaaCViyqG2nZ4hbLsO3JbMUjaRpB555gzHcjZJc+bWAxjE4okE/aBHKe/KU55phjpg5j6WiCbuxo7M9HvSRUwggssTZRSDc6SoQ1rrTiklatnBuvQz1HlCTtq13tahP5Uw0EiZc8rFC0+RJLDuZ+pN+RROMqqFps8GTFIOmbTbeVhInnfqwytMkTzOU31ybrIC6iZ9Ps3uif16GWgchtNkUXrwNaOg5qgp572DWMdJCXwjEYz7cSKX8zZYiT+JDzhNVrwRg2F2cpULeN2sA1rt7v6EYJL+FLx1hnsHTZKj4bzltyPd5L/CRWiyzsUEe1kPAav7YrHS3TPSoOpEQfXFHbmLRtL42jjz562mcjO8VBjkHKEM76A2FSv9jn4rjjjpsIPqDS0JnYGjTPFaTlan2DGp54gTag3iANk97nJP0gaXUS7LzVzapN26TOlbskHHQEPT5ISNhceEWNN147EEgZjl6Ueh43Yu7aXBiM59sF9cj9OdZ7DZzH5aOpccb4wZjvTkLuNyCF0o/azIc0OnfP7pFNMxtee3bYGAkpklaZz9nEP0j+SInK4drXvva0VzMpUnhtr8RFYtQPITG6ZOE1TlwNI5WT6qkz7HCnoyHdkshdp4MmPdOFO0/ZSZ8wxzkkTvzu2W52RhE2atIBaAO22ykjceOQOv07U0M77lGTJN5ScVASdI618XM+F56XZXxBqn+rMVePufISvj9xg5zPxb0iUesxuo2uB/wjmTjP86r+nQT1rQ452jDpTne6016LVbgaH8n4hZVJLn8oQUr2N0bYdf+MwN9KbFFKfZL9oDdyCNyqRvt22C0ucC2I31G9kSKJWVrkqX7+CqNupFvStQ6ENJ904zPjr24dXEP4yrCVKemdjt3/Dm2BapQw5sXZxImeXOfD1jw73anHUnHQqjg8kLkXwMvEJIjkwV8/7uqP22rUvOfKqGGOY32qG1HD40/67UIte/TnfKxjveY491yc0zsakrMi2EgHuVTU+4lDZCbSkO14zxzYltREHmsJ+0IjKxYXyCc66QAJIVmrFC3QqH9UgfjrOZhAU48sO69wrm4BNYgNmNQLQZv808GwBiHhCkOe6lktNzwzaZE2adYxzjln0pLzzbqXpGUrThVEX68NTELaO8Q9zum5dRKkbJI9/Xj9o0q9l6XhoNdB5yUHD8kwUm9r8xgfNrieuF4CQyHHDAW3EuoQp4PwwqajSB3iF4c/yHmuSRc3xk0+2w11jUt9HNU3LvcPNV7uMwsQHLncq7azAIP05qMOSUu3E5B2iR9Ig4bf/vqBvNwrJK57JCXadJ4OGvka4tNZU2WYEKx5kmbtj0yapRqpJDdCmHZ1JJkjV2oEkmeNL07qBfKlP0fSeXb8VupZEKJuTPBI8ikjz0850vozuO+SH3lyzumsXWPvTHeetGecccY0IqCDZq+tjghYXaJjV1bqbaUm9Y7VlNpDW+0EHJQEnQeTh+OBeqG8yB48yYChf17WPHQP0QN2zYvDjzy2GjoAujmkQqJxpLurUJ/UH6rfR0py9OJH0jAikAaSlguZbTfSzuD+dY7uwYflgxrbOXX3jDwX8R3FJU1loQM/oiJRjZNfS0Z9vrnXtBFrBxIvSRBJB547AcOKQ3/2ZjKXeNqh5pm2JlEzbyNZpgMLxK11iB/4mbGZ8KM2Ub8RiU9PbXWi9zD5eD7S+UchNQTLEJN5FerInln6OH9C4fgRuok8ZoG+R9+MengXfMPUMNqASsgIIvru1AvEV46FOszxSNCEs4RDjkvEQa3iqA+KNKw3Niw0FIp04uFwruuJbVbOltPDNyxD6lsNH6CPxsvC3MdfNEyo1GFXhfvIS4SI8186q6FMKKmzj8lLXO97bIPtROqizVke+FhIdSRBUpbhcBZQJJ6jSS+6Vm0krvZCSqRI8RE76Yr5GKuDUdrbCUjbBEjr7LPPntoFqblH13VQ2oN0TfWAxEz+aQ8EJJ0RRdqO9IwcLQ4Zdc/gmLgBv3fNUV6kTWRIiPCN5BrE77vSEbie/Bxtmu8Zs6n2fqoPJL0jKdp9VZfOm0tnjvC1gzK8594XdUPinrvvwURlpOhAGTovnZiVmiYwQ+Q7AQftJCHwxyEFUoQXlk6LNFGvO9ezethIgCE7IvRybDW8YCZMDNOuec1rTv9xs8S32mWmXj6C+hF56Q07b3KTm0x2rYbD7EB9rKSrfDTVCdtu1PqQdJGrZ2HIaXMebeD5eDZjXDpGJlW2yyQtmxAz/PXBi0PKRlj0tpvZ4GcpyD1WOEdGiJh06H1EPJ6hzplKw7A+EiudtVVxLBgM4XVW3hfERw/MLlncqtqYc0ENQ4akWZ2hjgBJ55r6yJN6SQeKLBFq3jVxPB8LaiwxV2/1F16R/Ko/bu5d9j26H3pkeRqB+k4JKzoKumhtUPMjgVs+r5Mw6tQ2woPqXxoOaoIG5x4IicSsrz8L58FXOOc8ZLPXZno9aGm3EinHy0y35uOyOTrjfi9R6lVfTh8cRzKgyyMxIzbpdDx54eZc8tpu1Po46hCZkpFqjFaQr+E04k2cOPeOsLSRj9Pop14HQ2EkrvMidS3hnveFWv96P+ru/aCPRX4m15Ch+9aJ2+wHMSI8HZ3JMhIivS+pV1wStQ7PhkckxpSRozLGNqp1SFwjEuXbv4IAg7Rd884hYBOD2lzbj3bFpGES7gMe8IApbYSiYCxr3Xn1G9ESSHQ8Og/nSNkIFFETYLRB4quD94y6JaMLdRzzXSoO6klC8DBIZV7i008/ffofG6x7MBla2rPAhIsHupVIuXpywy12rzawMQz04Y16QhCfVEVKJMmQHuj2DB9JUfWFg5SxVGhT5EKlxNbWUWfDkcQMZfOhuw+Ea4RgGGsYH7iWe0cY9NA6Vp0WktpJGEkj949wdE7aC2nroAgR3mkQRpIUZuJLOyAtpIrAjKqg5p1j/FDPlV3rg+RI6CR5eQv3TEimOgbkh6ipOcb3Vzyqu0jPyRNqGSPm4nK+AyMqLqMt9dMRaQNCTAQWIGHrOPLdV4xlLBE7iqDHBo3f0cML8jBBj29lFF0tvacXZh3kYzhHvUFiAPmsK/eyQnokQhom0dPx2eKRHtULOObvpScFqRMCQ+rIjHqDfm2zqO0Cubc5CE/cjeJdFsiLmsf9M+cipRlJXOlKV5oWYIRUAp0ZIvBs5iYCUz8jEhK5kZLhuPDcAyTeRveSazXeRmmEj+WMaXMcwzaDmg7Gc9hs2OXBRmVUN4d14ZcVc2Xtq/x11yrGeDkfw69I7BiC9gHoGRGVj7Q2GFITTuIdh1EI2fDLMCvqDchHlcbn1yPT79FBk6RrPiQH5SZNkPSbReKTSHQYpCO6aCoLE4eRjGo5CEvddTSGuO4FoVkEsL868pSf/HVgpBskCQnXjvJOm9b68G8WKa/Cufs3CWvC1HM1eUuvru3pVRMPSG70qSRtz2EO4hrq0lHbcIi5Wuoctw7j9Y3iwhi3umA8b+wMeGbr3u/teJ47gqA1jCGr4Z6tCqkCSF6kMMMn0pXhrUknxGoYnA8EySDdk08+ec8G5LlWnWG1IaFhNJ0oacxQ3LARiSAIS1n5DamCpN8sxJWevszsOmI0kWL/XTpYJJM8vSiuG96bGKNDy4Y6iMywDbltFskzR52ayUptqU3ViV6RLhNJ0ombpEKkdJrSJZ/NQtzqEqYs+YZI6VuZjxlJUHtUqI/RgvutqouaJ8jLfZhw1I6JW+MEtS71+hg+dz3n47X6YddrafMaFxLWbhkuWBe+HdgRBI0oEQRyRsIM4K9//etPkrGP3MduT1gqAsSFsE2o+DCoAMzwImhkrsHzIdWHQApHSkzs5E8FgZxJqYbihs300pbMkirH9JuFuKRkHYlVUCRY0nFMzegY80GTXNWDfo9+jaRrcoS0bSgfU8HNQp7JWzp5mkiiMlE2MzadhWWw7lmngKB1COqQyab9gbKqU77O0P0rQwcq3CjBHIH9IpRnPwjx1FOnSPUx3m/yDIxw1JOqxHMTfw6pR/zKMpmlI4gjDHD1vF6vYToOHelYn/jVOe0+Xm+3HFexLvyKxo4gaFIiAibFIjDDfCZmJoSQjI/cx2zCzEw/MmU/iuDYRd7oRjeahr4+Jg1eP844eZBok94Ha7YYefoAkZUdvlhQRA9a89ospLEQxoQfMlRvky2kR9I7MsrHjBBNAJFkDe2RGOlSHS/v73p0DHS67s/kDpL2W342tUYaJp/Eca+ke+UaYVwWpI05z8R9mew06hGWNtQm1BPuD3kjPZ2SDpilANS8RiBk92LfY++ICaIRc+lNOFkmrT108nHULnaNc9Tewpxz9br7YGcMY72cV3Le3/elccWiPqc8t+3EjiBoKgEfKBMs5EaqY5ZFWgpZgo/5pje96UR0hu6GuPSXdJsh7bkGF4YApaPbRVYIgiQpnB7bB08FgUCRV/Jx3N+HaIadtM5EyktgEkzeyIlEG8Q8iLkfYkOQWdyibvuDWl9lIl8SKylQu+ogjjjiiIngIikbVTCPUi8r13SGl/WlTbmOOj8ry1ixCAuEM5c69NBDV0cdddQ0atI5es71R6qOYx2ce/6ezyGHHDJ1aiTjYKN6e77u2cSi0Q1i19nzezac8zGMM5pSrg4exnJyf8L46/02lgXPxmgno7Q8yzy77cCOUXHQv1JXkHYY8DN+Ry75MJAJ8kbQzNZInj48JjYkaBNx0aPmQ4lfB4CIsmgCOegQSEWILFIfadzHWIes+wtpEA6pywfunKRIBUNCpw8Whiyoauhm1Y+kjaypa5Cle98fjPV1ziSJ1GnyzRaMVqi5Z2WBzgkpaz+LQJDlZYFyU7Zy3RcVhxFN4Ho6QuorC3hI8p6j9vLcR0jjWSRv74DJRyMBErF3Jkicilonz9h9c0ZsnnvON3LSxQXyjYO8L+BZmlMgBOhs2y3DUfE5muvwXXj+9Z3hzzO8IrEjCBp8AF50H7dlv3TFdMT5MEgyCMzHTVdM+szHgGAMX0Mw9QPiECQyYFtMOmUlYWKRNMdygpQuXsDvYXH86rUZiEv6NpFFQifhC/My2JiG6RxJ3zlSQo4ktsQxnNYB+bj3d7MXeeSYFw3BIGjSpnxJ1KTH3Jey6fy1H12/Tir57A+kidNWRkCW2+vw6nUwqvD8bC5v603PLROkUONC/WgQtNEJCZqu3odW444Y8wpq+Do/pJ0g1+JcS93iF4781ct8ijq2W4ZjUcVRpTIy8G3U5wk5XpHYMQQNXm4fKwnXdosZigPCokP2PzQTSobLCJBkjPiYsGUJaJDGN3SlEz3ssMMmEkTKzuleWXSwCEAsSLKa8uXD2yxBi4tokE6G7HHKVU+rGHUkVpBZLaYs6Uiz6mJBi9EAor8sSL3jZwnDvhpB6zQQtnD3ZERiwo50rQNTB53ZKF1sBikXiXpOOh8Ss/Dk5Yi0LclFsiZObYRDV5/7lUfS1HSc0ZR8TRLqBLIUPHFyHP3eHRK6+Q0dO8cf595zjJ+jRnNulDZOEjrWdo4T5r3U+SGCdstx3hfPxbuWZ+cY/3ZgRxE06Y5UZRKJrpa6AZAJ8iV50SEjGg0tXBqETkJF2vlQIH7DehIzEy8Tgz506hASNFWKiTTERSVhCI1kQDzkTsLeDEkjWxIi8tUJpHwvAJ0sFYuRgckyEmZUIJG6qEAsosnk2hyEe8F0JAg1L1fKqg4QjU6B6kRHhDTB6IOpoU7LKkxtpw4kVPm6X0Sjk3T/6jj3IqccQOzuSQeKEGs9gJ/kgvB0tEia/tvkcK7nWD+cnFOB0aFLZwSSSULX6/NJPgEdvPfKRKjRCcef8/hZ98z5I+HLd8wb1G0uvLF8jO/ZFY3FEXQaob7s8TM588EgKh9t9M8IA+H50SUVAakQpEFW2S2OzjONDWl8hCBPkiIClc4H5+Nj9oXwEZRJrVhUAPUJUz9DIxIUpK4g75zzIyg6VgRrgUrCwaQhqxRqFhJmTPlA3oiHqoF5HSmxImVwiAixkiBJd1GjBMqLWgi0o3JJ59ozdTbB5l7pc9WZdKGjMnIJ8ZOwqT4MEdkg67hqWRXCdXLqZgTBciVx65FTtg5V56DzINGmnUD96z0kHSsXQ1QErSPJ/SROwF/z282o7QI5z3sQpL0c17XdmFeQNPX6XNx16XczFkHQHkx9OEhm7mEhCEPe6173upPEi8R8lPTSiBsJI1vSX8AvLr0y29iUlRcG2SA/lgMkRaQj3CQdYmYBQpolaZLaERGiJTkjJlK3OCTvqqvOEUhyJEbkQWVgDw1SctWr5j9uJjhJsshOfixPTJRRgZAqLQuXj2G5dHHJhwSMRHU4yM29jRAvHxlp3k56CLF+eJWgdSic+6fnjzRKFUHil96knOdR6xRHyqa2yfOLXbUy6rMKEKv2isljOjNu/Ngd876Q8NUDsUsTEq9xgurfbUgbQm0HYXm24FocuJa2r+kqci151Xhz6RI2hjf+g20n6PHh1Ac2vkjIhArDRB47VNIr0mD5gPCoOXzweYkcER0JlxkZwhWe/IB0ilyRH8sCQ3Dp5IMcWVeQaH34iFG4D59kjvCRICJRh0qaFaRFk20sQ9gZI2gTcux7Ez97c6gDSdPLbftI92VmmVrASIA5HgmUxB1VQ/JQb6oGbaIMjv4WxjpJ5x7US57yq4i0q9PQOVDBGKVoH5AfCxP3gXR1gJnQzPU4nSZJ3TOjhjJjTu8tv7qFZaB9qSt0NKM9c55tTRO/EY120smN+uc5stitcO9xOc9xbN9cA89XR2tuxNyOb8ezqvHi9/yoDj1735FnmNEcp5zEr/7G3lgEQQd5ePF7cHlhEC2VAzUEgqKKsHEQUjOUp9aYS0unSRpDCgg++uMA4XrhSMOkZ9Kb9CEwkrPl1SRRZXghUyfkwkSN5K0u6whaOgSYXb8cObrPxEe20pMC5Q/qw66XdE2KJ8UmvWF/VA0gj9yzdDoTk4mk3Fyv9RIv9+felFuh3YwSSO86MHU1kRLIi2RMlcAqBUGLn3qkPM79e0buwb2ov/bwXHzIiRfwy4Mqhx37qDpJ/IQ5ei7aSqfkWRpZ1XiJC+P5bsL4bGDOX13gWRAqvFd09uZjvIPiyDd5+4Y8O+8FIcq76v3yrSVPcSHnNazxXyxGB10fFFfDkKXhMP2rXemQYn2Y69LF+cCpP0jCo2pAPnPSVVxF4iecH2mRrknTkQaD5JGwes7lHmqeEH8NS9yKMU1N54PQTkgxSJwaL/6NMKaDnFPDIHnSMb96ak8Ocm8cfz3napwgcRNW4wY1TFzqFZN1bLkt6KkjqYqkG8N3CzyX+gxgbGuSLum4SrzgXTfCs6DLhDaizqiJi/CiQ7by0oS2bzYSNOc5zVkBOZ97Xrsd207Q48sCeYk4fsN2vbWPj7Qa87Oahr+GSVvPSWz53VWQMmrauIoa5pg0nCFfXsIqnbs2fgwhrZxXJKzGS/qgxglyD+ImHSBN6gFtVdM41nyTvmIsgzQtjrAa17mhrolCI4hIrUHSjEiZueaoTvUc5u4/4M81R+oY8xDej6iIxKlpaplQ/bsJ2qG2KyTMt0ZSpn4y35I2TNsZUVFrGc3al7xuogXiSSuOURX1IkL2PAgx7L8JSeP3VvNo/BeLkaDBwx0fnOESCwr6W3bCdJgkQz1x4kqXD5I/zjk4sq+lJ/YBk/RiiD7Grajp566T6g3Z6WgjPcK6vBKurqkvjOXPpYeN4vHH0ROT6ql/Yl0SJM6cP/UfUctNPEfDW/dPn0y68iEmjvurSLoxr/hh7nqOwuMfHUmPKofURuVS27ZiDJuLsxuhvbSvUYdvDfGa//DtBXkuSJaKkbBDnYSg89wIKNJTXflezd/oOPM8fLO+XeRtEjcmndDPYh6LmSSMy4cIzpGNXhcJ6JERrEUkhrHjpENeoriAX1xmdojLx8yGeow7ptkIXjqTIPSeXkr5B8lzjihqPYP4Hes9JKy6Me0YX5kkIDpAE486MUjaGr+6mm/C5pBrHJ2zcuio67DVUX7xB0kXjOep34jEqy4Qn1SHNMwVkJ4TXuM1/gvtUtvH0Xvim7Kkn/UO1YWwPA9xzBcgWN+fOFQYsXoS15yE78HEoMlaBB37cPBuGnGaI7BwDEmT2CFxGntjEQTtJciLAHlYjnrdrO4y0WT45OhBI4W8aMknaStyzcfrJWSRgFwz+ZQ08dewYAzzstGpkSCySKPGcawEneO6OoLwuXzq+Ziev4bxI07qhqpygZr36FwLangwF+aDZS1RLTuC+Mc0kLDx2kZh8Qf8SMEIAVlYmYksgqSraRr/gTYZ3yOjQaoqJqnmL/JO570QV4fPpFWHbBLaIi6WU655DvwslghCVCCk6CqFg4lpoxyrRE146wign9M8FqHi8HDiYHx5Rn89H1+i8fro94LQm+rlEbawpIekH9PVsHqtYqx3UNNCzmv4eD5iDK/nc2nW5QO5tq90oz8u2Nd5UMPjr/FG/7rzMdyohWrFPt/50OdQ84DxfDdh7r6p+1jykJ7NJej4xvbybhupZMToyEaeaSPVCIGJ8MSPwK20jIlnhbwIEDoCtvds/hM+V7fdjkXpoBuNxoHHSIbmT5Czvc6RL4KGMR7CZW5JyCEt+3ONka2JaEcT+UaNzOuoOEjbc6RLqqbLtp6BFF2FrMbeaIJuNHYZKiEiUJIxcjbZnQ2sKnJu0RT1BRJm4WHFJr2/9NQWiFtc0jOzS6PUQHjyUbYJZpORJnbFc62qBBv/QRN0o7GLEKKsjkUGU1GT8c4Biea6uR5qCRI0lYQwcw9W9dI1M2HNPuKk8fxBn9qp5hPk3CIWliB1MVVjbzRBNxq7CJUsSazmYZAknTDb+VyPNGui2UQ4k00LvSzvN4HIbNWCFb+So49G4OKx8rA3i0UsSLxa9wQpIz9Apouei9dogm40dh1CkMiX/tiGV3TG9MoQqRdYA1FhIHCrcZEx6x2SMlM5UjdiRtDI2RJw2yog6EwgriNeemjSNlUHi6hWcfwvmqAbjV2EEKAj0zg7DNov3a6BrJsqxCEpI17OoiQqDuSM3JndIXDSL1NLVhwIHKFzTO5MCIbwHbnAdRt1kcQtbkHQjb3RBN1o7DIgS456gxWF7XJN6mX720Ac5Gvyz6QeZxIxC1iQdOyl6Z9dtwAs8cUNITvKL3BuwtH2uXZDROhN0P+LJuhGYxch5AwWgVnV5zdqjiTjXB/dSLAwXk+ceh4Iq3BOArfa0Da6djiMeV/jv2iCbjR2EUKUjvS+Jv6OOOKIafk2lYfwObcvgl7nRtQwVh503/79yZKDFN7YG03QjcYuBKK0PS7dsz/h+0Va/vEZEh1JNuc1vBJ3Da9Yd1159tihA7dXexP0/6IJutHYZQhRkqBZYiBoi1DolIVXawrHqCqSLhj9VaURJM4YlzOxyDIEQVt9eEUSdOpQ6wXO6/1WzI0iYDNhSRu3WTRBNxq7CJUgWGDYBZCKA0HXHRlhM2SSOOviCV9HTuykLXSJisOE47p8Lg/GcqGG1Wv8mays10c/Vwk7YfHnOBe2juhhzLMJutHYRQhBcLYHtbOjfdbpoOvvx0YSid+ud+yb/XLOohUrCFltAGJjGWI/D9cvvvjiaRk3yVx+kPw59tOnnnrq9Bs7i1YOpARdy8152gHiH+Osc7kejNeCdWH1GCQul/o0QTcauwwhAGRqm1YqBgtLkG8liPjjwMSeFYdUEmyY/QSD/bTrrDCQte2AhdMrs5+ma64mdMkPudvf/bjjjpt20zvQVhzKDPGlDvzqZkFNleDn7j+uYl/Xkk9Fwus1xznXBN1o7CLkwwe2yuyPjz766MmaA2FCriduzoGUa/WhvZ79zd4qRCQsPCRsz3V/i7cRkgUoFquMBA027LdC0Z/ubbZ0IAh6rD9/JUeOrbdOJCoeYeo7pst50oOwmlfOOXm4J04Z8jea0Bkoz4ilLnFP+oom6EZjFyFkAhaSINBsekQ1EYRoKmEkzE9h6Yw5JE1NQl0SuG4ZNxWHNHN5AFI+8cQTp6XhSD3hW4lafq2HskLCSJI/hJrORhwuYQknaVd9vetJLy8dkrYVDyEzX2Qx41+MFgPpCLW1rVtdq5BH6qnsJuhGY5chxINM/D2FBEuS9fuyEJrr8YcwAnt2IGULXag5pLXEWxpAPMiZlUiQ/CqoNfxj1D8KxwnKrUK9h7EOzqlk6NIRJfLUaXB+AkEFZFtV7SKOzkyYNvP3npCyPE24GhHoaJCvUYaFP4g5v59DzCZGLZ9H1n42UaX2sc25JuhGYxehfvwIgaRnNzn/+7QvR1DjcQkjRZokZDdNcqRrPuGEE6aj6/Kk1/bTWR1A0o0O/KpMubYxreFbiZonfyVpEi4CNaFJ5UCXzk/PbvMn9fenGMTsnJNGmDZAzvIDRIukka+jEQXpmSmh0YTOTGdAvYHkhWv7EHzqBrWOTdCNxi5CPvyKc845ZyJKUjHSrajx+RENEjv//PMncrF5ks3+7UhHQhTmt1lVvTHmgYCQE7WKzf3rNqcHGiFBQJgsSUjEyLQSbyDMpk6pH0d6JiknXsK1nXyqzj2Tqjo2cVxDzsoUP2njIH55NEE3GrsIlQgCKgtESZKmlhivB8IRliG7NMiO5Mha4/jjj1+dddZZkyTq57OITvxKiAEpFMnZalRaw/51ZW4F5D2XP4KmanBEhiHjStDq6V5yH2mDMYwf4ep4kG+2WUXQ2is6bGoN6o8QdNKnfjkCsm+CbjR2ESoZBM5JvaeccsrqggsumMimEkYlWcN9uuNK5IbwNv1n0UFypo/OznhjWcB6gbRus/+LLrpoD7kdCCh/7l5qOPBfeumlE3nWOMiYTrnGrVI15OgeqDbo4KlOnDvSXyNn0rO0dNU6gZonOE84RxXSBN1o7EKEDAISsV9fnXTSSROZzEEaZHzeeedN5BMioXc988wzV4cffviktqACQS6uQQhPeaRnqpBjjjlmdfbZZ09pIXG3GqnjmL86pV6OrtM5GxFU8ow6o5I2XTWC1gZJm2vSIuK0T4iZX5j8ucTlah6Qc+qkJuhGYxcCAcSBYb4N9+mSkXB2tqtALK6RoHPNUbjN/I888sjVscceO5F9CCpkE78hvlWDpPWsMgyS51ZDuRykLhw7cFYaOoxYcVBdIGSTnDoZBI2Ma3oETarOvUkrD/GqFQfpGckK5+Qdl3PqHeqQCnlCE3SjsQsRgooL0SAL5HnaaadN5EmfCqRAE1sWtfjRq/8TGsonPSAlpOsfg1QFUPPmqEWoPyxicYyUXd1WQ57qUAk25bg/HYb7pjtHsoiZGoJZnE4rBJ00jiHoSNqIXj7Sie+6NkCwVmdqN/m5njgcP8sQ9Uj+Fa3iaDR2IZBBHIRESb0mzexwh0CjZ0YgrDX8dYUKg77aYhQEFTAtu/DCC6cl4Mg8eTsmf5K1DuDcc8/dMzEXJP5WI2XDujLUQyeEUN1zVDziI9EQdFxUHOIlz1yLP9AWlr5T7QSu1w6Dv54H2r0JutHYZVhHCPz0sEjKUB25iCeMOVpdiEFijBojJIOwLM4IwUGuAwnV0D8WDtG/QuIcCNQ6BGMYaVWnQV9sdKBe6kcS1rGIm7pW0obkVfMD8bUhK47onefiBcKlSRzlN0E3GrsII0HEn3AOMSCUELBzEiBHZ8yNOubkITxhjlyuIXp5JCxwTRkHGqknjPWjgiAZGwlQdyBs9eWnY651RtD0xwlzrHnnnKtmdpDwEQnTDvHLpwm60dhlqAQx+qsL6vl4vZ4nrBIU57yS2EbXDgRSRkXK1qEw+/MDWxI+CRohk/RJ1Dojqg/WJqRpkjPCDUHXewn4ES2Cp99mSsi/Lu7ceVwTdKOxyzASQkUlhxE1vF5PeL1Wz0cCrte5SnRbjeTP5TxH5ExCRsbUNlQ7wmKvTBUTtY3rpOxM7kXPHhcoRzqTg/T0l1xyyZR/Rhxjmpq2hsU1QTcauwiVEDaLpJkj2nVwbV/XA/4x761C6pG8Q9RAjYNoLa4hIZOWxSP9xpYZkDhSJklnYjD5jZA/9UjUIPT20tVyYUzvvMZJGU3QjUbjoAbiC/mFGB0RMqmZmVzIeGlogm40Ggc9IpGGoIGkTIoepdsloQm60Wgc9BjJGZwvmZxXq9Xq/wEjtQIr3CFknAAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E7%8B%97%E7%9A%84%E6%95%B0%E9%87%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAsEAAAF5CAYAAAB+wPfxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAGB3SURBVHhe7Z0HmJRllrY3/htm07W7s3nChgmOo6OOedQxATKKiSAgIiAISBpylJxzZoiD5JyRnHPOOUrOUZKg5/c+VjHdPQ3ddDkW71fPfV3n6u6v0lfddHPXqec97x+ZEEIIIYQQKYYkWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIYQQQgiRckiChRBCCCFEyiEJFkIIIYQQKYckWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIcQt+fTTT+38+fN25cqV2JFwuHjxoi1atMj27NnjzyNKXL9+3U6ePGknTpywy5cvx44KIYS4EyTBQohbgkSOGzfONm3aFDvyFTdu3LCrV6/aZ5995kJ2q/r888/tiy++iN3q90Guz507Z6dPn75tXbhwwR8ru/CYe/futZIlS1qbNm1s/fr1fnvO507hNtm5HTKKlB49evTm9TmP48eP24oVK/x7eOnSJT+eKHw/pkyZYv369fOf0dmzZ2OXCCGEyC6SYCHELXn//fft5z//uXXt2jV25CsQU6Ru27ZttmvXLtu9e3emhRAiy7eC68ybN88mTpx421q2bJl3PrMLj7lw4UL71re+Zf/93/9tPXv2tE8++cQOHDhgR44c8fPKTnFdbsNj307mYefOnTZ27Fj76KOPvAuNCPNi4eOPP7aXX37ZSpcu7d+rrO4nO3BO77zzjv3rv/6r/4zWrl0bu0QIIUR2kQQLIW7JBx98YE888YT16tUrduQrhg8fbv/7v/9r//7v/27/8R//ccsqXry4rVu3Lnar3+c3v/mN/fKXv7Rvf/vbt613333Xli5dGrtV1iCJXbp0sT/90z+1WrVqWe/eva18+fJ+Tv/5n/95R8VtKleunGXsYMiQIfbCCy/YI4884p3neNcXyUeCeR7Tpk1LOJqBWG/YsMG+//3ve/HcbvdCQwghROZIgoUQDp1LOpXEHyZPnmxTp061fPny2b333muVKlWySZMm+WV0f5cvX25t27a1Vq1a2VNPPeWy+OKLL1qHDh28ypQpYz/4wQ/szTfftC1btsQe4ffp1q2bPfDAA3b//fe7rLZo0eJmNWzY0Ludf/RHf2RFixa1JUuWxG6VNfPnz/fH5rwQz40bN/q5t27d2jp37mzdu3e3Hj16ZFpVq1b17jcd5Lp16/rzpBt9uzgGXWNE+Z577rESJUp4pxxZhYMHD/r9/vVf/7XHM+hqZwW3j3ejiVjQiT516pTX5s2b/Tlwf6+//rr/XNJeHi+OUcQx4l1txSaEEOJ3SIKFEA6SN378ePvVr35lb7zxhhUoUMD+7//+zzuYDz30kL366quWN29e7wIjdvv27fPc7WuvvebSiLQePnzYDh06ZAMHDvQO8ltvveUxhFtBTIH7Rrbp9HJ/8SJu0b9/f/vjP/5j7wQj3tmBjDEd5h/+8If23HPP2datW70re+zYMT8XhBAxjMtlxkIqef4PP/ywLViwwLvKXPd2MYahQ4fa008/7UUkIm2GmC4tcQXO5ac//ak1b97cF+vdjpEjR9qHH35ov/71r61atWpWvXr1m/Xee+/ZL37xC/uTP/kT/77TbU97ecbi9txP/fr1XeaFEEJ8hSRYCOEgwUgSUluwYEErVKiQi+S//Mu/+Fv8dFYR4VGjRrloXrt2zQWRTjBv9yNucbgOx+nk0pW8FcQskODChQu7WKeFxV90pJFgOqgsLssOXA9R/Md//EcXxKyEMyOIL+fz+OOPe9f1dvA92L9/v3+vfvKTn1iVKlVcpDMK85kzZ+y3v/2tSzAyjKRndr04ZLA5h1y5clnu3LktT548XnTN/+mf/sn+6q/+yiWd+EX8sqyqSJEiNmDAgNgjCCGEkAQLIW6ClKUVM6QOaaMjG7+MotNJR5U8KrEB4hLkVIHLEb7HHnvMZfR2WVpkkG4mwkcHOS1pJbhUqVLZkmBEnvgC8o4sppVgJlEgnnSE0xZdYeIHTLOA7Eowz5PvAY9HNpcOOp30zOC6PD6L44hoPPPMM94xji+gywgvMnjxgDwzoo7r8ZGfA7fl+U2fPv1mXIIXI8QduB6Z48yKn8PtIh1CCJFqSIKFEA6ChKhR5FkRt7gEM4qLy4kVUAgaUw/+53/+x7O/gwYN8rf9uQ235a38++67z+WYY7ciLsF0KYlSpCUnEsx1iDLQKf2v//qvdBLMfSHmHE9bRD5eeukl2759u18vuxKMcM6ePdu++93vuth26tTJpfVW8H0gm0y045//+Z/9+8OLCCQ8I4hx2uK2PA9eVLAgEZnm+8P3mm46cRIiD/Gfwe1KCCHEV0iChRAOmVxyva+88orHHigkF2HjbXhEi9gDEodcMtXhH/7hHzzjumPHDl8Ax0xeFmvRqSQfi+TdDhaMEYdAgulkpuVOJBgZ5PoVK1b0LDKxA+ICaSV4zJgxLp5PPvmkNW3a1B8byed6yHFceLMjwcQgEGCe61/8xV949pbcb2Zd3bTQjWVaBGPNGG/GeSKvc+fO9fPPDMQVueX7/LOf/cyjDdxH/LFYiMhz4nukKRFCCJF9JMFCCIexXixUY8oBExJYUIX40uml+8gxpBFRpsOLJPM1MQi6xyxAIxqApCHK3FdWmVqyrwj222+//Xsd0TuRYKSURW90rRHqcuXKuaRzHnEJZjoEsstjrV692qMRxBd4juSX41MsspJgHgtpZQIG49OQeKZkcK7MJs6q6KDzfaL7zO3pRPN45Kgzk1iiEVyG3DNFo06dOv6cOH8KOeZcixUr5t30+PG0xf1mJehCCJFqSIKFEE48M4tIkZFlnBYxBxbKMRWCr7mcKMSaNWs898tCK0aQzZkzx4WS2bx0Y/nI10jk7bqT7du39+4sC+gyRgnuVILJxdJVZV4v2dmMEsz5MFWB+2L6BCCzLPjjukg8ZCXBTMXgBQEvDujMIqWcP/KNiPJ5VsX3qFGjRv6R+6AaN27s2d208D2fOXOmPf/88/Z3f/d3fj1egNBhjxeL8jgXOu90t9NeFi828lCXWAgh0iMJFkLchK4ju7ghwkjT6NGjLX/+/N4thXiulLf1EUg2yyATy+I4usXxYqEYOVk6shljDmlp0qSJ/fjHP3YxRcLTcicSHIfz536YcpGZBNPxzSjBPL87kWCknxcGdGabNWvm85T5nCkaTKRgfi+zjf/+7//ejxF7iBfRkr/8y7/0ecLMQkZ66YZTGZ8f32MEmMgF98nGH//v//0/v9+09/m3f/u3fpwcdNrH47H+5m/+xr9/gwcP9hc2QgghfockWAhxE7Km8c7iokWLXJ7iEszb6YgxXVfkbdasWfZnf/ZnnqllHjDxgHiRK0aO6YzeToLp3JIfpiOacdFWTiQ4vojsVhKcWSf4TiUYOV21apVnqOPTG+gO8zhEHcghI6wsWCNiQYc6XjwHOs8PPvigLwpkIgW3p9J2ajlOhpkMNkJLdOI73/mOnydd9rT3SQeZc2VDEV7AxI/z82MDkj//8z/32c7aKEMIIdIjCRZC3ASJI1dLR5HcLLN/Gf31b//2b979RIbZrYz8MAKJoLIdMbLK5IN49enT52ZOlRFet4J5xHRFyRlnJCcSHCczCSYTTMc2owTfaRwCeBHAdAiEG/FmYR4fEWNeENCZZeEcLxjSghTzIoPzIOfL7dLC13Sz+R4zA/hHP/qRd4I5J7rY5K2Je6SF63L+LLZL+3gIMd1mzoWOPqIthBDid0iChRA3QR6RLaYWIIV0I5FgYg/IIiKMdCG6iBmCSieS6RBpoUvMNsp0RTN7G55xa0QukMFHH33UF9Fl5OuWYObysrCMkWws+mNCBJtwkLO9k4Vxt4PZvdwXXVu6xRm722z9zAsJXmggyRkXq/E1z5ucMefPIr4pU6b494tcdk4lOD6TWAghxO+QBAshbkLnl2kNCCBSSAeRTiQxAuSQBXCIIQvkeLs9OxKc2excjiHYjGBjygSil5GsJJj4QMZOapzMJJjHo7NKV5sd8FhIRiyB6Add123btvn1cirBZJHZLppMNLIa7yynhU473xeE9lYj1TjG+Xfr1s3zx/HrSIKFEOLrRRIshHDoWjLtga4vskinkq/ZfCK+MC4Oncl4J7hmzZoeA2DEWbyQZ3Y2YxJCxm2TeRwEjS4ni7eYsRvfqCItWUkw98Euc2zekbHjmpkEkwlmni5iPn/+fJ+YwP3TFSbSQa4XcirBnA8dXDK8bBaScRtoGDZsmHeK6aqz3XLG874dOZFgxqdJgoUQInMkwUIIh5wrGy+wkIpNMOj+IsC8dZ9Rgul60u1lCgKjuxBnIgDx+va3v+1TEFislXFhHNlU5JPbMScX0c6YnYWsJJhFddw/+eOMedfMJHjXrl02YsQIl3siGog8i9zoSiPqd7ptckZ4HswhZqHf8uXLf2/cGbBYjjgG583zuxNy587tlV0JprNdr149/3mSh5YECyFEeiTBQgiHSANdUbYSZvQXUx8QWr5m2kNaEEY2p+At+9vVjBkz0skg4hnfaQ25ZZLEypUrY5emJ60EI7OIJdA9JQZBZ5TRbHRfM87AnTBhgndc0+4Yh/AeO3bMpTcuvJmREwnmNiyIY9wbWxsziSGzqAbxBHLJXOdWUY5bwaxgohRZSfCyZcs8Y83WyjwWnWB+Dpm90BBCiFRGEiyEcBBO3qanm0nXtHXr1r5ojY4tMsW4NKZCIHjkVJEqJj/crph0wPUQPmILjGArW7asizWbZNCxvdX82vicXCSY82BXNjK1zOVlEw86rhTnmTFWQPSBRXfEMeISnBWcJ8KOQCObWUkwj0l3lV3g6FTfe++9nm9mcVzGrC9f8/y5HqLMZht3CqKLCGeU4E6dOnn0hBcUvBggt83z5gUCeWcWM7KQMeM5CSFEqiMJFkK4oNGlRIB5qx6OHj3qO7ohWGx+wYI55I3FX3Rz6TgyRm3dunVeLPTi6/gMXXK3dCDpktLVJT7BNAYWjiGMyCuPcSvo1nJ/iC7ZYRaxMTeXaRVEChjjRscW6cwIGVgWv8Vn52YHOs0sniNmQSaaGEhmi9sAuSduwOMwBo7vD9fv169fuq40MQ2ux/eBRYdsscw0inbt2sWukX3o0pO/RnLTQoSF6ArdZR6b50snv0CBAsacYB5bM4KFEOL3kQQLIXyRFt1DJJjOYhw6nUgUsQKmKrBbGZ1hNsKgU8omDkQb6DYiqCzcoluJ7H3ve9/zbDByyAI2usyIK1KLzNF5zWphGIvskDy6uuxAx/2x8IzHZ7oD3enMpk8wg5fuNTN56WpnBySS+/6TP/kTf5y0eeK00FFF8pFlzuNb3/qWfy+GDh36e7lbOrDENbg/dnTjusxGZurDncL3izhJxo4uQs3PjfNFgvme8gLidpEPIYQQkmAhxJcgV0QT+vbt653cOAgXsQQWt3GcnC+yiNjSzWVhG1sFs3UvW/tSbNXL18gykYf69et7HIKFbQghsQbuLysBBm5H15XrswsaOWSKzzmGdGb2Nj9CSscZOWcKRHbo0aOHyzvPB6FfvHhxpovJOCd2YMuVK5fHOipVquTPja5vxnNhAeFHH33kskwnnesSCaHzfqfw/crse8b3k/suUqTIzS70ra4rhBDid0iChRAuTGR46dhmtrMYcofQMfaL7iabPhBvYL4v8kwGlwkEfCRTy7FJkyb5jmzx8WcIJYvv2K3tTheF3SlIMh1sIhuZiWxmEH0gF83ziEttZufJ94rOOflkBJd5ypmNaQOO8T0jsoH8cl2k/uuE7ykRCRYYZvaCQAghROZIgoUQ4kvootL1piueFchtfLyaEEKIMJEECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAcKq9e7du1q/fv3V6lUKpUqKcVoQSbCCBEikuBA6d69u++gVbFiRZVKpVKpklJsMc5OkEKEiCQ4UH7729/aBx98EPtKCCGE+Ob5zW9+47snChEikuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLkRiXr92ws5c+C7IuXLkeexZCJBdJsAgZSXCgSIKFSIwOM3fYU23mBlnv9Fth165/HnsmQiQPSbAIGUlwoEiChUiMBuM32fdqTwmycnVcYFclweIuQBIsQkYSHOPGjRt2+vRpGzt2rB04cMA++eQTmzlzpg0dOtSrf//+Nn78eNu0aZOdOHHCJXTgwIF+2ezZs+3y5cv2xRdf2Jo1a2zMmDFeK1eutKtXr/r979692yZMmGBDhgyxBQsW2KlTp/z4yZMnbcqUKX58xowZ/rjZQRIsRGJIgoVIHEmwCBlJ8Jd8/vnndvz4cZs4caK99NJLLqkbNmyw7t27W/Xq1b3y5MljZcuWdRFevny5vfrqq1ayZEm/rGfPnnb27FmX4w4dOvj1qlatas2bN7cjR464XI8YMcLKlCljVapUsTp16rgsc5tFixZZqVKlrGLFilarVi2bOnXqTXG+HZJgIRJDEixE4kiCRchIgr/kypUrLr6vv/66PfroozZv3rzYJV9Bl7ht27bWt29f27Jliw0fPty6du1qGzdutIsXL7q0UpMnT7b69eu7KG/evNmFF2GeNm2atW7d2jp37uzXR4InTZpk8+fPd4HmDwidYf6Y8BiZdYMRdc7zwoULdv78eb9d+fLlY5cKIe4USbAQiSMJFiEjCf4SBJYu7qpVq+y1116zhQsXxi4xu379um3dutXatWvnneJt27ZZ7dq1LXfu3N41rlChgo0ePdo+/fRTa9mypfXu3dsjE4cOHbIBAwZ4XKJFixbWqVMnF21EduTIkTZ48GA/RreYmAS3nzNnjg0aNMjmzp0be/TfcfToUY9fFC1a1LvQTzzxhL3zzjuxS4UQd4okWIjEkQSLkJEEfwld1s8++8wjEQUKFPCIQhzktGPHjjZs2DDbuXOnxxvoBCPEdHhbtWrl3V9EuUaNGh57IFOMVCO33bp188gE0QoE+tq1a54h7tOnj9+uSZMmLt+I+OrVq12CySVnhMzxrl27vHs8a9Ys7yYTrxBC5AxJsBCJIwkWISMJTsOZM2esYMGCNyU4nhUuXbq0i+elS5dcilnkxkdiEggr8jt9+nSrVq2aL4ijCxyX4Pbt23s+mD8USDQSTMe3R48eLrLNmjWz9evX+3EkmO4xkp0VygQLkRiSYCESRxIsQkYSnIaMEozorlu3zhe6MekBWMxG55ZsL1EJRBeZJQ+M0DLlAdlFhBFVcsB0e/lDEe/4Isp0holJIMnx6RJkkXv16pVpJzgjkmAhEkMSLETiSIJFyEiC05BRgg8ePOgL1RDWPXv2+DFElsgEC964HMllSgRxCOSWr+kas2iuQYMGLsV0dlnIxucsgCNCQRyC6ASj15goQeb3o48+8tuTHc4KSbAQiSEJFiJxJMEiZCTBacgowYgsC9+YF8yYMzh27JjLbL58+SxXrlyeyyUvTIeX6ATRh+LFi1ulSpXs+eef96gDOWJEmkV3DRs2tKefftqFmePkip999lnPB7PgrU2bNjcf63ZIgoVIDEmwEIkjCRYhIwlOA7ncpUuX+gYWEI8+kO9l4RxwncOHD3uEgRzwihUr/GsgHsHtWdxGB3ncuHF27tw5v218tBpxByZG7Nu3z49zW4SYqRJ0gteuXev3kxWSYCESQxIsROJIgkXISIK/ZpBk8sDkgskNs7gOEFuiEMwPpuMcF10W13E94hREIugoZwdJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOFAkwUIkhiRYiMSRBIuQkQQHiiRYiMSQBAuROJJgETKS4ECRBAuRGJJgIRJHEixCRhIcKJJgIRJDEixE4kiCRchIggNFEixEYkiChUgcSbAIGUlwoEiChUgMSbAQiSMJFiEjCQ4USbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjEkAQLkTiSYBEykuBAkQQLkRiSYCESRxIsQkYSHCiSYCESQxIsROJIgkXISIIDRRIsRGJIgoVIHEmwCBlJcKBIgoVIDEmwEIkjCRYhIwkOFEmwEIkhCRYicSTBImQkwYEiCRYiMSTBQiSOJFiEjCQ4UCTBQiSGJFiIxJEEi5CRBAeKJFiIxJAEC5E4kmARMpLgQJEEC5EYkmAhEkcSLEJGEhwokmAhEkMSLETiSIJFyEiCA0USLERiSIKFSBxJsAgZSXCgSIKFSAxJsBCJIwkWISMJDhRJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOMbnn39uly5dsk2bNtm5c+fsxo0bduLECVu2bJmtXbvW1q1bZ4cOHbLr16/7Zbt377YNGzbY1q1b7fjx47F7Mb8O90EdPHjQrw+nTp2yLVu2+P3s3bvXHws+/fRT27Ztmx/fuXOnnT171o9nhSRYiMSQBAuROJJgETKS4BhIKVL76quv2sKFC12ER40aZT/4wQ/sxRdftLx581qvXr38+JkzZ6xGjRr2yiuvWMmSJW3IkCEu0Qhvt27dLH/+/FagQAFr166dXxdpnjhxohUpUsTy5Mlj9erVcyHm+Pr16+3dd9+13LlzW6VKlWz27Nn2xRdfxM7q1kiChUgMSbAQiSMJFiEjCf6Sq1evese3WLFi9vjjj9u8efNs165dNnz4cBdZOrUHDhxwoaXrO2nSJBfQ6dOn29ChQ61169a2Z88emzt3rjVo0MAGDBjgn/OHAbFeunSpdezY0Zo1a+b3VbNmTb/tmjVr7KOPPrLy5cv79bjOwIED7dixY7EzuzWSYCESQxIsROJIgkXISIK/BAnet2+fd35feuklW7BggS1ZssQ7toULF3Zp7d27t23cuNFjEC1atLAePXp4rGH58uV+2fjx461NmzbWpUsXW7Fihd8fn3Oc7nCHDh1sypQpdvnyZevXr58LNh+5DUJ74cIFmzx5sksw95mR06dPuzgj0vXr17c333zTSpQoEbtUCHGnSIKFSBxJsAgZSfCXEGO4cuWKHTlyxGMMixYtstWrV1vXrl1dUtu3b2+VK1e2wYMHuxzzCz9t2jQ7efKkbd++3YW2c+fOHmegM4wA0zEeO3asRyhq1arlIoxEX7t2zWbMmGH9+/e3Ro0aWZMmTbxTzOMjz4MGDfLoREaIYXBePXv2tE6dOlnx4sWtVKlSsUuFEHeKJFiIxJEEi5CRBKeBuEPBggVdNhFiBJfOLdnd5s2be+xhzJgxLsR0i1nERmd45MiRfjmxBi4/fPiwL6ojNoFA8wcCGSZigQQTt0Bma9eubU2bNvUoBMdZgEdXGKnOCsUhhEgMSbAQiSMJFiEjCU5DWgmmM3vx4kVfpEYRXSDSwMc6derYzJkzfeID0yHI9RKRqF69ugvx/v377ejRozZixAjPFCO7RCY2b97s0YupU6d6l5n8MGJNB5jjdIS5niRYiD88kmAhEkcSLEJGEpyGtBJMlpfuLpEHJkcguEQX6AAjqmSCWQy3ePFil2OyvH369PEOL4vsuKxVq1Yee+jbt693gukMc1/du3f3r7mMPyCINZlg4hPIMYKdFZJgIRJDEixE4kiCRchIgtOQVoLpzrZs2dIqVqzoAswv+bhx4zzry2WMNSMvTN63SpUqPvKMYjEdnWIuY/EaksxxxPf999934eU43V6OT5gwwR8TsS5Tpox3jj/55JPYGd0aSbAQiSEJFiJxJMEiZCTBaaBLS7SBqQ9MY0CG6ea2bdvWF6sRc2AeMJcx+YEoA91ihJT4BEUcgtsg0Hxk3BnH58+f75EJ5JgFcWyOwXFGpnEfHKfTzII78sFZIQkWIjEkwUIkjiRYhIwkOAeQEWanN0SWbi5RhjgspNuxY4etWrXKO8tIMyC27CbHRhzkheOiy2QKrsfUCeSb22cHSbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjECFmCf9poulUcttaqDF8XZM3dfjz2UxChIwkWISMJDhRJsBCJEbIEh159Fu6J/RRE6EiCRchEQoJZmHarBWUsPOPy+AK1qCAJFiIxJMHJK0lwdJAEi5AJXoKRWyYrbNy40ScufPbZZy6+THDgMja7YCc2dmSLEpJgIRJDEpy8kgRHB0mwCJlIdIIrVapk+fLls5o1a1rHjh1t8uTJdvDgQdu9e7cNHjzYypUr57N9o4QkWIjEkAQnryTB0UESLEImWAm+ceOGRyDo+FatWtVq167t2w2zNfGgQYOsfv36vkMbO7hxnI0pooQkWIjEkAQnryTB0UESLEImWAk+cuSIjRkzxqto0aK+29qCBQtcgNmRrWTJkvbaa69ZjRo1fBMKIhJRQhIsRGJIgpNXkuDoIAkWIROsBG/dutUFt2zZspYnTx4rXry41a1b10qVKmXVq1d3Ge7bt69vbTx8+HDf4S1KSIKFSAxJcPJKEhwdJMEiZIKV4EuXLnnmd+fOndajRw+X39dff93KlClj27Zts4sXL3oueOjQoVaoUCE7fvy4RyeigiRYiMSQBCevJMHRQRIsQiZYCT58+LAvemvYsKHngUuXLm21atWy+fPnW968eT0PXKVKFWvcuLGtWrVK0yGEEOmQBCevJMHRQRIsQiZYCd6yZYv/4hUpUsReffVVnw5RrVo1mz59uscjWBBHVKJ8+fLeBWYhXZSQBAuRGJLg5JUkODpIgkXIBCvBLHbr0KGDVa5c2X7xi1+4+JIJJgf87LPP+nE6xHSKZ82apekQQoh0SIKTV5Lg6CAJFiETrAQz93fevHnWq1cv7wTTEW7Xrp317NnT7r//fp8Mwefjxo1zOT5z5kzsltFAEixEYkiCk1eS4OggCRYhE6wEsyiuffv21q9fP2vTpo13fdu2betj0hiZxi8m19m0aZNnhZFmLYwTQsSRBCevJMHRQRIsQiZYCWaLZLZEPnXqlC+SIx6xf/9+O3r0qC1fvtyPcR021GBKhOYECyHSIglOXkmCo4MkWIRMsBIMdHYRXQSX+uyzz/xrxqPx9fnz512OGZnGZVFCEixEYkiCk1eS4OggCRYhE7QEs9iNbZJHjx7tMYgDBw7ELvlKkFesWOGyuGjRIo1IE0KkQxKcvJIERwdJsAiZoCWYnC8bYbBbHHlgZDfOoUOHfGFczZo1bcOGDd4hjhKSYCESQxKcvJIERwdJsAiZoCWYPHCBAgVs5syZvgiO2AMxCLq+Xbt29akQ48ePj107WkiChUgMSXDyShIcHSTBImSCl+CCBQva3LlzPQ7RsWNHnxhRoUIF69Kliy1btsxzwVFEEixEYkiCk1eS4OggCRYhE6QEHzt2zBYvXuwbY7zwwgveCUZ4e/ToYc2aNfMZwYxFIx4RpbFoaZEEC5EYkuDklSQ4OkiCRcgEKcFsgzxnzhwX3ty5c3v3d+rUqd4R5jhyTFcYUVy5cmXsVtFCEixEYkiCk1eS4OggCRYhE6QE37hxw+cBT5s2zRo3bmxVq1a1Pn362NatW30UGt3f9evXuxy3aNHCpZnbRAlJsBCJIQlOXkmCo4MkWIRM0JlgYCHczp07fXvkESNG+CYZjE5DemfNmuWSPHDgQPv0009jt7g1yDMS/fnnn/vXfGSqBJX2ONeLH6c4h3jsgsdNezwOt43PMU57/fhjcjztY2SFJFiIxJAEJ68kwdFBEixCJmgJRmwHDBhg9erVs7Fjx9ratWutZcuWVrFiRRfgPXv2+LbJ5IWzmhOMhO7bt88qV65sa9as8Q035s+fbyVKlLCSJUt6xpioBfeDdDOa7a233vLLW7dubWfPnnWBHT58uD8+9dFHH/n9AAv3qlevbu+++64v2mMTD9i1a5efP8ebN2/us42zgyRYiMSQBCevJMHRQRIsQiZYCT5y5IgNGzbM4w50gdky+dy5c75lMh1hxLRTp042Y8YMnyd8uw4rHVhkuUGDBvbMM8+4/DJbmA4yRd4YgeWXffv27b4Qj68R0enTp3vuGCHnNk2bNrU2bdq4ANepU8d27Nhhmzdv9tvy9YQJE1yoeYx4B/v999/3DT94Lpz7mTNnYmd2ayTBQiSGJDh5JQmODpJgETLBSjATIiZPnuwSSuY3DrLL6DTkks0yyA1nBfEJRBVxfu6557xri6AuXLjQTpw44REHBJkNOZYuXeqdXH7pu3fv7oJMFvny5cveleY+5s2b5x1eOrucHyLdrl07l/ZLly65nCO9o0aN8gV8HTp0cIEfOXKk3wcynRE6yuSc6XjHu83vvfde7FIhxJ0iCU5eSYKjgyRYhEzQcQjytEgvgohEMhOYzxFNpPTgwYMeicgKOsF0crl+/vz50+08x/3TmWXnOTbgIHJBt7dUqVIeYShTpowfR8Tr16/vHWA27mDhHpLLpAo27UCcuS1xCsSZTi7TLZo0aeJdYUQcwR40aJBfnhHuH3FmBjLxjBdffNF3yhNC5AxJcPJKEhwdJMEiZIKXYISXHC0RBTq3RBM2btzonVikFoFFcuML0W4H12XzjbQSjEyz6xxRBj4SrWBGMd1mcsRIa/ny5T13XKVKFe/UEtU4efKkyyxdXnLGvXr1ciHnNnSa+ZpYBBJMFIPj69atc4kmEpEVikMIkRiS4OSVJDg6SIJFyAQtwcQUPvnkE++0MiaNeELnzp19NBoL5DhO55Rf0OzkbDNKMN1Zog5FihTxri5ii1CzCC4+4eHjjz+2Dz/80OW3Ro0a3q1FvuncjhkzxiMUHOcPBXliZJeccrdu3fz8OE8W4tEhRubpHBN3yApJsBCJIQlOXkmCo4MkWIRMsBKMgCKORA+YrkAkgY7q6tWrbfDgwS6adIbJBRMdIOOLwN6OtBLMdcng0gFGWLk90s3jkeNFdOkS0wlGRrkNO9YhscQeWKiHkPMHgigEnV8mVnCb/v37+3kh7dw3nV9iHFOmTLmZM84KSbAQiSEJTl5JgqODJFiETLASTKd14sSJLp0sEkMkDxw44B3b3r17eweXritiTCc2HkW4HWklmBFmyOtDDz1krVq1sqFDh/rkCaIQiDGX9evXz7vAzCImAkEkgrwwl3F9csMsjOM2CHLDhg09tsE0COSZ4yyGQ2ZZwEemmPjEli1bYmd0ayTBQiSGJDh5JQmODpJgETLBSjDRAmSUhWlFixZ18WQiRLly5VwkkV/iDEQX6MzSab3dmDS4cOGCiygd4FWrVrncvvrqqy6tCCe70nFfdJjjj4v0Is3xfDJTILgu8QxmCNMRZtEdsss0B7rWhQsX9gkSHCcC8fbbb3s0gusjt5x3VkiChUgMSXDyShIcHSTBImSCzgTHd4tDPJmU0KhRI58QQZSBy+JFjOGbArFFlGfPnu3d6vhjI7ZEKZgTjBjHRZdz5XqMe2NMG7KeHSTBQiSGJDh5JQmODpJgETJBS3A8F0xGl93b6KjSySWiEC+6ueRu6fJ+E9BtJveLzMYXzwEfiWMg6XxMe5zrcRwxzqpbHUcSLERiSIKTV5Lg6CAJFiETrAQTPYhHDdjIonbt2j4V4o033vA8Lh1XjjO+jOhBdiIGISEJFiIxJMHJK0lwdJAEi5AJVoLZMW7SpEkuu2xawVQFJkK88sorPiOYeb5MYCCbS5c1ux3WUJAEC5EYkuDklSQ4OkiCRcgEK8FMY2AbYjabeO2113y7Yhafvfzyy7ZkyRKfsMCMXjrBO3bsyHI8WmhIgoVIDElw8koSHB0kwSJkgs4Ex2FDjCeeeMKee+45H2mWO3due+mll+ypp56yRx991De7YKOLKCEJFiIxJMHJK0lwdJAEi5CJhAQfOnTIIxBMX2BaBDOBKY7xNbvKsfgsSkiChUgMSXDyShIcHSTBImSClWCk9ty5cz6FgcVxFJ8zBYLoA1MXNm7c6LOD2UUuq40yQkMSLERiSIKTV5Lg6CAJFiETrATv27fPd2EbP368L5CL18cff2yHDx926V2zZo1vnMHYNDbNiBKSYCESQxKcvJIERwdJsAiZYCV47ty5dt999/lOa+zCxke2JW7Tpo3v4Ma2yUhw586d7bHHHrOjR4/GbhkNJMFCJIYkOHklCY4OkmARMsFK8LJly6xQoUK+4I2d1tatW+cdYDq+I0aMsCpVqviCOKZFPP300z5SLUpIgoVIDElw8koSHB0kwSJkgpXg5cuX+y5xSDDSy6g0OsE1a9a0/PnzW8mSJX1OMLKMJGtEmhAiLZLg5JUkODpIgkXIBCvBRB5eeOEFzwAPHDjQs7/MBSYOgSAOGDDAOnXqZIMGDfIFdNosQwiRFklw8koSHB0kwSJkgpVg4g9lypTxX8DBgwf7VskUG2YwHo1M8JgxYzwTzIQItlmOEpJgIRJDEpy8kgRHB0mwCJlgJfjEiRM2ZcoU69ixo0vu6NGjves7b948302OCAS7xs2cOdMqV67s2yhHCUmwEIkhCU5eSYKjgyRYhEywEswcYPLA5H+JRgwZMsQzwTdu3PD68MMPrXfv3rZ3716PTDBHmNtEBUmwEIkhCU5eSYKjgyRYhEywEgzHjx+3hx9+2AoWLGh58uTxLZLp+laqVMmeffZZnxCxdOlSO3/+vDLBQoh0SIKTV5Lg6CAJFiETdCeYsWe5cuXy3G+NGjV8WgTxB6pfv37WoEED31AjikiChUgMSXDyShIcHSTBImSClmBmArdv3962b99u8+fPt2HDhsUuNTt16pSNGjXKIxFRRBIsRGJIgpNXkuDoIAkWIRO0BDP799ChQ3b58mW7ePGinTlzJnapefyBrZU3btwYOxItJMFCJIYkOHklCY4OkmARMkFnggEZppDetJ9nrKghCRYiMSTByStJcHSQBIuQCVaCr1696p1eZJBfQnaHY9MMxqZVrFjRSpcubcWKFbPChQtb1apV03WJo4AkWIjEkAQnryTB0UESLEImWAm+du2aHT582GcEs0EGI9Hq1q1ru3btshkzZtjUqVOtTp069s4779isWbPsypUrsVtGA0mwEIkhCU5eSYKjgyRYhEywEkzEgdm/7A63e/dua9eunVWrVi126Vd89NFHLsJRRBIsRGJIgpNXkuDoIAkWIROsBNPZZVFcvBiTRgwi7bEuXbr46LQoIgkWIjEkwckrSXB0kASLkAlWgnfs2OE7xDVp0sTrjTfesKefftqaNm3qxbE333zTSpUqFbtFtJAEC5EYkuDklSQ4OkiCRcgEK8FHjx61CRMm2OTJk30xHIvf2DmOz+NFPKJChQqxW0QLSbAQiSEJTl5JgqODJFiETNBxCBbGHTlyxIvoA9slx7+munbtmu04xPXr130Huu7du9vOnTt91NrevXv9flu3bu3CvX//fj/OTOIBAwZY27ZtbciQIbZ582a/jxs3brh8d+jQwf8wLF++3KdYkF9esWKFderUyTf3mD17tm/mwX0x4SLjY2QHSbAQiSEJTl5JgqODJFiETLASjHCeO3fOtm3bZps2bbIWLVp4Nzgt2V0Yx3198skn1r9/f3vxxRdtwYIF3mkeP368j1rjvhs3bmzTp0+306dP2+LFi124mUjRrFkzF1I27OA8mjdvbjVr1rSWLVv67U6cOOEL99i5jsxymzZt/HYbNmxwic/4GNOmTXMhzwpJsBCJIQlOXkmCo4MkWIRM0J1gJkMwGxjBrFy5snd9T5486Z1c5JiObHYkmPuia1umTBl78sknfQtmRBgx7dOnj3d+mT7Rr18/W7lypeeN6eoit2PHjrVGjRp5R5cuL9dbunSprVu3zvPIW7dudRmn04vwXrhwweUVof74449dmjn/8+fP+/n27ds305nGjISjU83z2rJli0t22bJlY5cKIe4USXDyShIcHSTBImSClWCkkAkQxA+IETAvePTo0S6c+fLls+eee86effZZq1WrVuwWt4bIAhJKFCF//vy2aNEiGzFihEs1C/DYnhnZHTRokMcgihQpYkuWLHGh5WOvXr18LnHRokVt1KhRdvz4cRd0pJjOLh3qjh07ereZjjEbe4wZM8bFuHr16rZ9+3Z/DJ4D579+/frYmf2OgwcPWrdu3ez555+3Rx55xH7yk5/Y22+/HbtUiOTwOTs0Blr1JcFJK0lwdJAEi5AJVoLJ0yKORCLOnj3rRQeVrC0dWrrBCCyinBXcF5EIusgFChRwCSbriwRzf2R6kVm6zsgsUyfoyCLiq1ev9g7x4MGD7fXXX3cZZn4xwoscs5EHHWayxpwrXWdkmvuvV6+eL97jMXh8usM8xsKFC2Nn9jt4rkQr4l1uBFqdYJFMdh67aC93XRRsPdh0ZqaCpvrDlyQ4OkiCRcgEK8F/CJBoJkwgwcOGDbPatWvflGA6zkQViDu89dZb3r1FgolHILt0iBFoZBkJpqtM5xY5Rla5DhJMJ5g8L4UE06mOSzACzWPMnTs3dka3RplgkWw2HDybqeCoVFmVJDg6SIJFyERCgumc0nElisBHiiwuMnonpJVgRq+R/WWxG11YOrc9evRwSWWBG4+J1M6bN8+nRBDF4DgxByZT0LElK8zxBg0auATTob506ZJfn44vcQkeY+PGjS7UQ4cO9cdYtmxZ7IxujSRYJBtJsCqnJQmODpJgETKRkGAmNbzwwgveoSXT+/DDD3vkgPjAnZBWgletWuWdXH7B6fqyAQejzJBeog18zmI6OsAsvuP6CDJj2Yg1zJw500qUKOEL7IYPH+73xUeiDO+//75njukucxxB5jiTJtj5jjxxVkiCRbKRBKtyWpLg6CAJFiETCQlm5BgLyoARZoULF/YFa3dKWgmmy0tX98EHH/Q4Q548ebxLS3eZ8WYsumOBHPlgJJxuMYvXyP++/PLLVrx4ccuVK5dnklkox2g0drRDXJ966imbNWuW55hZDPfAAw+4GPMYCDbxi6yQBItkIwlW5bQkwdFBEixCJhISzPbJcQlGZJFgxpTdKeRy2SCDkWh8jrzOmTPH75uPCC2CiggTWSB2QTc3vrkGIkx8gmkVRDMYk8bkCeb+cr/khbkvzo3zjD8GGWA612yikZ2FfCAJFslGEqzKaUmCo4MkWIRMsBLMzNyJEye6hDKajFFjLCxDTOnSMnOXr7l8xowZPpXhTkFSEWJmANMZ5mtAeFnghrASuUi7uQXSi9iyEQZSzHWBzxFf7ovbxru98cdgIV3ax8gKSbBINpJgVU5LEhwdJMEiZIKVYHKziC4Z3Lx583r8gLgCi87IBCPF8ewuc3mZ6RslJMEi2UiCVTktSXB0kASLkAlWgum20ullAVqxYsV8cRqRBaIIbJSBHBMvYJFaTjvBdzOSYJFsJMGqnJYkODpIgkXIRG5hHJEDFqzlJBMcEpJgkWwkwaqcliQ4OkiCRchEQoLr1q3rnd+jR4/6fGB2bps/f362piyEiiRYJBtJsCqnJQmODpJgETKR6QQzxow8MLN28+XLZ5MmTfKFZlFFEiySjSRYldOSBEcHSbAImUhIMLu7sekEC+MoFsSxeUXUFsOlRRIsko0kWJXTkgRHB0mwCJlISDBbDjOCLC1sT8xiuPiIsqghCRbJRhKsymlJgqODJFiETCQkmNm7zA1OCxtVsN0xghxFJMEi2UiCVTktSXB0kASLkAlegun0durUybcfBhbDIcTMCWaxHNMioogkWCQbSbAqpyUJjg6SYBEykZDgBg0a2MCBAz0SceDAAWvZsqW99957NnTo0MjNB44jCRbJRhKsymlJgqODJFiETCTiEPXq1bNWrVrZwoULbcCAAVarVi0rX768b6scVSTBItlIglU5LUlwdJAEi5AJVoLp8B45csTr/ffft/z581ulSpWsaNGiLr90golJHD582OcH37hxI3bLaCAJFslGEqzKaUmCo4MkWIRMsBK8Y8cOa9iwoTVu3Nh+/OMf23e/+1179dVXbx5j6+Q33njDZwi3aNEicjODJcEi2UiCVTktSXB0kASLkAlWgunwjhgxwsaMGWOPPvqoSzDbJbN98ujRo+2tt96yihUr2siRI238+PE+Mi1KSIJFspEEq3JakuDoIAkWIROsBF++fNn279/vC+FKlixphQoV8gVyVatWtWHDhlmxYsWsXbt29sknn9jBgwcVhxDia0YSrMppSYKjgyRYhEwkFsYReWDL5Dlz5libNm3889KlS3unOKpIgkWykQSrclqS4OggCRYhE7wEMyKNHDAxCGYEMxe4ffv2VrNmTRs7dqydP38+ds1oIQkWyUYSrMppSYKjgyRYhEzwEkzMgU4wEhwHMW7evLmL8MyZM2NHo4UkWCQbSbAqpyUJjg6SYBEykegEHzp0yE6dOhU78hW7du2yzZs3+3i0KCIJFslGEqzKaUmCo4MkWIRM0BJM/OHEiRN2/Phx+/TTT+3q1at28uRJP7548WJbv3697yIXRSTBItlIglU5LUlwdJAEi5AJVoLZLIPJD8uXL/diAgRfDx8+3Meh9ejRQzvGCfEHRBKsymlJgqODJFiETJASTAQiPie4c+fONnDgQFu1apXNmjXLXnvtNR+dVrt2bf/lvHjxoneJuU2UkASLZCMJVuW0JMHRQRIsQiZICWYxHFGH8uXL23333WflypWzwYMH+y8jO8VNnjzZSpQoYfXq1bMFCxbYkiVLPCoRJSTBItlIglU5LUlwdJAEi5AJthN84cIFW7t2rbVu3dplkM5vlSpV7IEHHrBmzZpZ7ty5fQe5jh073uwIRwlJsEg2kmBVTksSHB0kwSJkgpXgvXv3WpcuXVyC2Rxj1KhR1r9/f3vhhRc8FvHee+/5/GBiEnSNr127Frt1NJAEi2QjCVbltCTB0UESLEImaAnu3r27/wKyAI6RaBs3bvSZwWylTBQi7ezgO4UpE2vWrLGpU6d68RjTp093wR45cqRHLjiOYNOVvn79um3atMnnEnOdrVu3xu7JbM+ePTZv3jz7+OOPbeXKlTejGYxvI6oxadIkW7Ro0e+NebsdkmCRbCTBqpyWJDg6SIJFyAQpwXEQT2Rz9uzZtm3bNp8QMXr0aFuxYoXvGod05pQtW7ZYz549vaNM5cmTx9566y0rWbKkPfTQQ/bOO+/4cbrPSDfS3LRpUytVqpRv2dytWzePYDCpguuULVvW3n33XatTp45fn8V606ZNs4oVK9rbb7/tH5ctW5bt7LIkWCQbSbAqpyUJjg6SYBEyQUsw0BUmD4xorl692nPACCJCnMhECG7LvOF49e7d23/ZJ0yYYE2aNLHTp0/7ca537tw5X4CXP39+mz9/vhdRjTlz5ngcg6xyv379bMeOHb6THR1khLddu3ZWq1Yt7yR36tTJp13s3r07dga3RxIsko0kWJXTkgRHB0mwCJlgJZgYAp1YOqg/+9nPvH75y1/aPffcYwULFvTOK5cxQaJGjRp25syZ2C3vDESXmEKrVq2sQYMGvujumWeesWLFilndunVt7ty5PpINSW7ZsqV3pIk/0JGmG81xZJc4BN3iKVOmuCDTZUZ8hw4d6ht6INF9+vSxhQsXxh45PWwIQgyD50NH+fnnn7fixYvHLhXim0cSrMppSYKjgyRYhEywEnzkyBEbO3asZ3XfeOMN78LScSW2wJg0MsGDBg3yzi2d18uXL8dueWewKcf48eP9F50xbGPGjHFZRUjpQCOzZIDbtGnjGWSiDggrUYxq1ap557dv3743s8NkgpHpRo0a+YYeSDQj35BnZh4jyZlBtILMM88Hwa5cubLHLoRIFpJgVU5LEhwdJMEiZIKPQwBSSkeVOAQxASQTQWYHuUQ5f/68yyyyTZyB++QYHeIBAwa4/CK5TKggzsAmHnR8EW+6tnSO2cxj8+bNLrKcI51pzpEuMQvikOCdO3f6fSDc2UFxCJFsJMGqnJYkODpIgkXIREKCEUiytHRaWXC2b98+n+xAVzYRWHhHtrhQoUIuq+SAuU+6w0gwY9mIOtDR5Q8BMsxjxxfo0Znu2rWrH0d+z5496zlhcsDIM/LO4jgeh8sZ95bdrZ4lwSLZSIJVOS1JcHSQBIuQiYQEsziNKRGMMGNMGTOBOUYlAtLLyDMmOmzYsMHGjRvnMQu6uogw49jo6DKdYsaMGS63xB64bq9evVx0OU6emJFqhw4d8gV8yC6dav54INBMhECaO3To4Nnh7CAJFslGEqzKaUmCo4MkWIRMZCSYvG6lSpW8A/x1bYzBAjciCogrMQi+pntLBrlw4cK++A6ZZToEHWImUyDCbOPMZexox6K6+vXr+9fI9Msvv+xijRATp+A2SHLevHn9a45nB0mwSDaSYFVOSxIcHSTBImQiIcHr1q3zBWh0aVmURsb264D4AjOHiVsQs2BxHbng4cOHexFtiEcu6Ayz6QU5X6Y/sICOeAaxCaIUiDTH+YNBbpiJEMwiZjEdxykWvmlOsAgFSbAqpyUJjg6SYBEyQUswskuHFoFkPBnRg2SC2CLMFN3hOPFsMTEKOsNxSecjkQu610y7yK4AgyRYJBtJsCqnJQmODpJgETJBSjDxB3ZioyvLGLSqVav6BAZE89ixY+mKrYm/zu7w3YIkWCQbSbAqpyUJjg6SYBEyQUowndXly5d7npZtilmwxngydnJjJFm82Ma4cePGvhCNsWZRQhIsko0kWJXTkgRHB0mwCJkgJZjYAYvO2BEuX758NmzYMF9sRk6XLG68mLjAphZIMp3jKCEJFslGEqzKaUmCo4MkWIRMkBLMYjM2pGCrYXZsY0wZcQjGo5ERTltsacziNbrHUUISLJKNJFiV05IERwdJsAiZ4BfGIbkdO3b0hXHM60WQUwFJsEg2kmBVTksSHB0kwSJkgpbgOHv37vV5vmxvzEK4qC2CywxJsEg2kmBVTksSHB0kwSJkIiHBTItgtzjmBLNT28WLF2OXRBdJsEg2kmBVTksSHB0kwSJkIiHBwBg05vDu2rUrcvnfzJAEi2QjCVbltCTB0UESLEImEhLMVsOLFy+2UaNG+Q5sTIuYMmWKL5Rj17YoIgkWyUYSrMppSYKjgyRYhEzQEsyoNHZbmzBhgssvWxZ369bNOnXq5NWjRw+XYbY8JjIRJSTBItlIglU5LUlwdJAEi5AJWoLZmrh69erWqlUrl92tW7f6tIjt27f7pAguK126tG9jrBFpQny9SIJVOS1JcHSQBIuQCVqCmRX88ssv2/z58300Gt3eePH1xx9/7DvG8fHy5cuxW0UDSbBINpJgVU5LEhwdJMEiZIKWYLZC/vDDD61y5co+K3jq1Km2aNEimzNnjvXr188qVKhgtWrV8kVzURubJgkWyUYSrMppSYKjgyRYhEzwmWC2Tx48eLB17drVunfv7r+Qffr0sf79+9vQoUNdiqM4N1gSLJKNJFiV05IERwdJsAiZoCU4DhngESNGWPPmzX1WMBEIJHHdunWRi0HEkQSLZCMJVuW0JMHRQRIsQiZoCSb3e+zYMVu4cKFLIQvk6tevb3Xq1LEWLVp4J3jDhg3eMdZ0CCG+XiTBqpyWJDg6SIJFyASfCW7UqJE1bNjQhXfVqlU+IWL16tU2ZswYK1u2rJUsWdIOHjyoTLAQXzOSYFVOSxIcHSTBImSCluBTp05ZwYIFbdKkST4pgnnAxB/4ePr0aRfjunXr2rx58+zKlSuxW0UDSbBINpJgVU5LEhwdJMEiZIKW4LNnz/ovH1lgOr/Lly/3XeJYLMdYNLrESHAUt1KWBItkIwlW5bQkwdFBEixCJmgJpruL7LZu3dozwPwysnPcwIEDfVoEx4cPHx45AQZJsEg2kmBVTksSHB0kwSJkgpbgOOwIN3r0aJdeJkPwcdSoUT41IooCDJJgkWwkwaqcliQ4OkiCRchEQoKZAIEUEn0oX768L4gjCsFWyidOnIhdK1pIgkWykQSrclqS4OggCRYhE7QEswCOjTE6derkG2bMnDnTF8FNmzbNBg0a5LvFMTlCO8YJ8fUjCVbltCTB0UESLEImaAk+c+aMvfvuuy7ARB/o+rJYjo+7d+/2HeSqVavmC+auXr0au1U0kASLZCMJVuW0JMHRQRIsQiZ4CS5VqpR3g1esWOHie+DAAdu/f7+tX7/eunXrZg0aNPBpEdeuXYvdKhpIgkWykQSrclqS4OggCRYhE7QEX7p0yWWwYsWKvktcv379fEEc84FZHMfxtm3b5njHOOIWLLrbu3ev7du3z2cRX7x40Xep4xibcFy4cMGvy+51zC3+5JNPvJhTHOfcuXN+Xe6D28ajGZz/kSNH/L4OHz58R7OMJcEi2UiCVTktSXB0kASLkAl+YRzTH4hCMCe4ffv2vnVy586dfQMNOsMIcE5AaufOnWs/+tGP7LnnnrNcuXK5UM+ePdu7yy+88IIVL17cpk6d6tdHaLt06WJvvPGG5c+f33r16uXHATEvUaKE5c2b1+rVq+cdbFi0aJFVrlzZnnnmGStXrpx3r7OLJFgkG0mwKqclCY4OkmARMsFLMGzevNkXwn344YdWpUoV/4VEWOfMmXNTOO8UurrMIK5QoYItWbLENm7c6JKK0L799ts2f/5869Gjhz/uunXrbM2aNS66w4YN80KI2b6ZbZyR5g4dOviCvSZNmtiCBQv8nBHl6tWre2aZOccTJ060Q4cOxc7g9kiCRbKRBKtyWpLg6CAJFiETtAQTH6ATywYZyOiIESO8+JxfzJYtW3pemMVydHbvhG3btt3s7CKoAwYMcLlFXJFt5Hrx4sX+2P3797chQ4Z4JINxbVu2bPGveWxu06xZMz/Po0eP+uYdHGcxX8eOHf08WbQ3efJkfwyyzZnBc0CeyTm3a9fOihUrZiVLloxdKsQ3jyRYldOSBEcHSbAImaAlGDFkLjAd2aVLl/qCOESTTO6qVatcPunkIqZ3ujAOkY3/ciO9dF2ZNEFHF5ElL7xnzx6X2fr167uYkkmOnwPSW7t2bY9ncD90is+fP2/Lli3zDT04N4SWsW5EOugMs8sd3eLMIGPMdRF7xr4VKFDAO89CJAtJsCqnJQmODpJgETJBSzCRhYIFC9qECRNcPJFiFqohm4xJoyvMphlEF+5k0RkwW3jHjh3+GHSRe/bs6dEFZhIjuJcvX/boAp1gIhjILlEJFrhxG2QWQUd4uQ5SjTgzqaJGjRqeDeaPB1ELFsqRX0akx48fHzuD26M4hEg2kmBVTksSHB0kwSJkgpZghJfsb9GiRb1LSwyCXeLGjh3rndbChQu7cCKsdzodgu4s3eP47Ygr0AWme4uoshCOTnDfvn39DwCL8YhAMAUCIUfMWezWpk0bF1a60cg50su5IsfEIhD0eCcYkR43bpw/XlZIgkWykQSrclqS4OggCRYhE7QEI6nECxBUcrlIKjlbRLV58+YeW2D8WE7Go7HzHPlfbs/jILNEK1jYRkaYrjOZYDbk4HGRXsQWmWUxHOfTtGlTl1qmVsyYMcPlOJ4RJkbBHw9ywNw/8s71Zs2aFTuD2yMJFslGEqzKaT3VZq7l77U0yPpgyBq7ePV67LdASIJFyAQtwczsJZ7AYjK6s3RYq1at6jLJ6DHElWxwTmDiAwvj2HoZ6a1UqZJndplBTIeZrnPNmjW9e8uoMxbSsVCN8yG3y2UILd1iIhnkiolUsLkH49yIRyDKiCyyXqZMGevdu7dHMLKDJFgkG0mwKhULgT97KWejN6OIJFiETCQywUQMyOOWLVvWF6cx2ixthjcnxKMLdevW9SL2sGnTJpdUpJZuLsKNwLIZBkJOR5juLwvi+JzzI+rAdeggMyqNc2IDDjLKTHuge8xt2NiDaAS54ewgCRbJRhKsSsWSBKdHEixCJngJfv311z1KQCaXBWrx3dgYO0YsggjD1wmL5MgiI6x0cxFgIHLBYzIFgmJ3uThs2IE8E59g4Vz8HBFkdoxjAw46xmSXs4skWCQbSbAqFUsSnB5JsAiZoCWYCQ6PPfaYxxDoCJcuXdrlE1FlVBkd1q9bggHhRWR5nIx5Y47d6ji3yXg87X3dCZJgkWwkwapULElweiTBImSClmA6rHRd2d6YuAIRCBal0VElb0sUgkhDFJEEi2QjCValYkmC0yMJFiETtAQDnVQiCcQJtm/f7p1g5JgFcWxzTHQhikiCRbKRBKtSsSTB6ZEEi5AJXoJTFUmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4Fvw2Wef2fr1661WrVpWo0YNq1evns2cOdNWr15tRYoUsUqVKvkv/tChQ+3o0aN25coVGzVqlNWtW9fq169v48ePj92T2dy5c6158+ZWvXp16927t124cMGPb9iwwTp16mQVKlSwdu3a2a5du/x4dpAEi2QjCValYkmC0yMJFiEjCb4F+/bts3HjxlmbNm1s+PDhLsN8jsQWLFjQ+vfvbyNGjLDly5fbsWPHbPv27S7G7du3tw4dOljXrl1dag8cOGCtW7e2hg0bWs+ePf3j2rVrbf/+/TZ48GD/44HQNmjQwGbMmGGnTp2KncHtkQSLZCMJVqViSYLTIwkWISMJvgV79uyxBQsW2NatW70r3K1bN6tatarVrl3bSpcu7YK8aNEil9zjx49757d8+fK2atUqW7NmjfXr18/lecqUKd4ZHj16tF+3T58+NmTIEJs4caLLMh1gush0lAcNGuTd58y4dOmS7dixw+bMmWPTp093KS9TpkzsUiG+eSTBqlQsSXB6JMEiZCTBWfDFF1/Y1atXrUWLFlalShWPReTOndveeOMNe+edd1x0N2/e7ELbq1cv27t3rx0+fNgmT57s3V26xz169LCVK1fauXPnXJyJRrRs2dK7xVOnTrXr16+7/Hbv3t0jF5lB5AJJLlasmL3++uv25JNP+uOLsDl58artO/lpkDVt09FMJUGlinJJgtMjCRYhIwnOArrA69at86hDs2bNPBOM6J4/f97Fl6gDIozUjhw50gWYSAPRBuIKjRo1soEDB9qWLVvs008/9fuii4tM88djyZIlduPGDe88E6WYMGFC7JHT8/nnn9u1a9e8I8z9cFs6zyJs6o/fZPc2nB5k3fPhtEwlQaWKckmC0yMJFiEjCb4NdGgPHTrkMkuMgYVsdHORUTrERBwQVzq6CPGwYcP8+mSEJ02a5JKKHCPBGzdu9AVxZIirVavmcky+mMgFEkzsAqFOu6DudigTHA2qj1qf6X+0KpXq7ixJcHokwSJkJMG3gM4r3dmOHTu6sNIBXrFihccckFwEmYVuxCToBFPke1kgx4I4ogtkgVn8hiTPnz/fTpw44ZLL4jgEmGJxHVJN1rdt27Y2bdq02BncHklwNJAEq1RhlSQ4PZJgETKS4Ftw8uRJF9QnnnjCRRd5RWYZc0ZXmIVtfM6xTZs2+YI4Or/cBvFt2rSpf07Wl8+7dOni+d86derYgAEDPAbRt29fj0UsW7bMGjdu7Jlg4hLZQRIcDSTBKlVYJQlOjyRYhIwk+BYgtixge/TRR61QoUL29ttve5aXLu7LL7/shdAuXrzYr3/27FmX4IoVK/qCtcqVK3s+mEwxHWImOZQrV87y5cvnoku2d+zYsfbuu++6TOfJk8cnThC3yA6S4GggCVapwipJcHokwSJkJMG3gJwuo8tYAHfx4kVfjHb58mUvvqb4nFgEEJ84ffq0xxpmz57ti+c4BtwHnWKiFGR/mTZBphgRJj5Btpixaog0x7ODJDgaSIJVqrBKEpweSbAIGUnw1wjSSyc3vnguDseRZiQZsY6LLh/5mqwwQox4ZxdJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVW3ddohjWZtMVaT9sWbI1dcyj2FyhxJMEiZCTBgSIJjgaSYJVK9U1XmY9Wxf4CJY4kWISMJDhQJMHRQBKsUqm+6ZIEC/EVkuBAkQRHA0mwSqX6pksSLMRXSIKTzL59+6xdu3ZWrVo169atm61fvz52ye2RBEcDSbBKpfqmSxIsxFdIgpPIiRMnbMqUL/8glSljvXv3tiZNmtjo0aPt/PnzsWvcGknwVxw4fcnaTNsWbOXptCDT/6RUKpXqD1WSYCG+QhKcRNauXWudO3e2Fi1a2NmzZ23IkCHWv39/27p1a+wat0YS/BXL957O9I+8SqVSqTIvSbAQXyEJTiIzZszw7u/cuXPt8uXLtmTJEhs8eLB9/PHHsWv8jhs3bniH+OjRo3b48GHr1KmTlShRwo4cOZJwHTp0yCuzy+72mrp8i/1PlSG3rO9XGuSV2WWh1n9XHmLfqzjoy4+DM7089PrqZxat58bP6nsVP4rkzyyqz+2r58XvWeaXh1zFu023gwcP+v8lmf1dvZNq27atVa5cOfY/lRBhIQlOIlOnTnUJ3rhxo127ds3WrVtnH330kY0cOTJ2jd/BH6s+ffrYq6++as8//7z95Cc/se985zv+eaL16KOP2uOPP57pZXd7PfPsc/bQ40/fsn740wftR/c/lOllodaDjz9l/3PPfXbvg49menno9b/33G8/efCRTC8Lte5/5An73g9/Yvc9/Himl4dcP3vkSfv+D++1+34ered270OP2n//+D574LFfZHp5yPXgl/8eH3roIXv22Wcz/bt6J/XTn/7UihUrFvufSoiwkAQnkenTp3sUYs2aNXb16lVbuXKl9evXz4YPHx67xu+4cuWKffLJJ36dpUuX2oIFC2zevHn+eaJVsmRJq1mzZqaXhV6lS5e2qlWrZnpZqLVo0SLLmzevtW/fPtPLQ698+fJZmzZtMr0s1BozZow9+OCDHnnK7PKQa/z48fbII4/4C/jMLg+1unfv7pI3e/bsTC8PuXr16mXPPPOMvxuZ2eV3UgsXLrQNGzbE/qcSIiwkwUlk2bJl1qVLFxs3bpx9+umnNm3aNOvRo4dNnjw5do1vhjp16ljXrl1jX0WLBg0aWIcOHWJfRYPr169b4cKFbdKkSbEj0YKu0tixY2NfRYNdu3b5uy286xM19u/fb08//bS/mI8Ss2bN8nfesrNQOTRooPBC+vTp07EjQqQmkuAkwni0oUOHWo0aNWzx4sXWsmVL69ixo8civkkkwWEhCQ4PSXB4SIKFiD6S4CRCDjj+1jZv2b/55pv+FtylS5di1/hmaNy4sa/wjSLNmzf372mUQIJLlSqV6QLKKPD+++9HTvD37NljL774om3evDl2JDocOHDAXnrppWzPOA8FRLFIkSJ24cKF2JHowP87BQoUsDNnzsSOCJGaSIKTyBdffOHCS5eIzCDxCGYHc/ybBJmiEx1FyLyRWYsSn3/+ub+DsGXLltiRaEEmftOmTbGvosGpU6f8xRjTXaIGItWzZ0+fMBMldu7caQMHDvT1GlGDF2WM4/ymGy5C3G1IgpMMwktHGPm9ePGij0L7puE/6HPnzsW+iha83ccM5ijBv5ljx455jjyKRPG5ffbZZz6Sit/1qME7Ewhw1GSRsZWMAONFZ9SIP7dk/H8jxN2EJFgIkXQQKV6I8a4IL1r4WgghhPhDIgkWkYWuGxnM3bt3x46EDR0p3nomukIxnmjv3r3Bd6roRvE8Jk6c6DOyWRTHW9FREmG69/ExiHSEQ4fnw86WM2fO9HGNFLPMo9Tp5sUYCxl5XqF3ufldYgEj//74Wc2fP983aVq9enUkF/4JkV0kwSkM/5Hxh/748eN28uTJyLwFzfPijz5dxWrVqvkYuijAzwfxLVSokBUtWtQ/MlKPGE3IsPAI+WURUrdu3XyRFXnFKMVYkKjt27f7YqRhw4bFjoYLz6dZs2Y+8YJ/hxRzz6MybYC/H6zRYMEyayZCf15kf0ePHm0VK1b0n9Urr7ziEz0qVaqUrW36hYgqkuAUhlwY/5EVLFjQypUr538kowD/gSH2/IFnIDybSkQBFsKxIQGTE8hgsoNg69at/T/rkKFTT2eK58F/1myUwaYx27Zti10jfPh5VahQwXdnZGv00OFnxr8/fk68WKEQ46jkZ9mYiEVx5cuX93dfQn9eNAbYcImuLz8rtuhH8Onka0KESGUkwSkKfwh5O4w939nFiv/M2AOexRKhvw3N+fOHffny5S4eUZmBTMeUt9JZyEiEgLF2jIBbu3Zt7BphQoebnxeLQ5kKUbZsWZ9+EZWuIs9jzpw5PvqNHchGjRoVuyRcmKHLi8zXX3/dqlev7rO4EUdkK3T43Ro0aJC/28JOmrxAi9LCYV5oMv6NrjB/T0L/ey9EIkiCUxTyYXRIKd6m5W123ormjyMd4pCha0NXimrSpEnk5gQjGozaoovfrl07l8coQPeenxVv17KLIj+/0OHfIrlLtkdnDCKbnERhIxAy6bxw5gUmPzPmVhOH4AVa6PAORKNGjey9997zd8cY/8aoxaiMgOMdJSSfF9EakSZSHUlwisIf+ipVqvhb68jHjh07fD4rWcwoLZSI2mYZ8bc1ydAi+MhiVEDmeYudt6DplpJTDx3eWRkxYoTVr1/ff6/ockdBgtkgAymki8/fD3a9RKqiEGFBfBs2bGh9+/b1Til/E/k7EpV54xMmTLBWrVr5z0pdYJHqSIJTFBZDfPDBB/5WH9EIVufzx59tm/k6KkRNgunS87MrXry4v2iJws8KqSfqEX8HgsV+vXr18g5q6PAiE+Hgd4vufYkSJTxrGvoiVF6gEBFAooh7EIfo1KlT8NEc4N8f74rx749pF0R0atWqZePHj49dI1x4d4UXK/Xq1YtEdEWIRJEEpyhEIMjyke3jLUw6wSzY4T+zKC2UiJIE89Y6I9/YXnvAgAG2b9++SPxHRjadrhuLdICIR+/evSOxaxxxgVy5cvnW6K+99pp9//vf9+kXZJ5DhsWLLNKkI0wWmGww8Qj+TYYOL1j4ufHvkckrxFg+/PBD/1sZOryA5gUmv19CCElwysJ/XnQ7kA+6wCtWrLDOnTt7VkxxiLsTBIP/nBEpcrMsaqRrFXr3jbeceQFGBpO31Vmww1gqusOhw8+MBZrxyp8/v7/bEvqs4EWLFnkch842k2V4V4nOaejrCQCp5+8ii2p//etfe46bsXah/8yA+BR/D+MvOIVIdSTBKQqiy39k/OdFZ4C3bJmpu27dukgsSIrDc1y1alXsq7AhM0vXlMWMdIJ5wTJt2jR/ERMybClMh4opJfERcIhIFOHnFYXcLDEcJl7QUfztb3/rn0clRsW/x/Xr13uWm3+PPD9mjkdhI5ANGzb438OoLPITIlEkwSkKY4DI8rEAhEU7jAJiRBqrhZUVE0IIIUTUkQSnMMgubzmzSQFvZUZpQZwQQgghxO2QBKc4iDBv/1FR2e1JCCGEECIrJMFCCCGEECLlkAQLIYQQQoiUQxIshAgCojsUsR02m1B8RwghRCJIgoUQdy3xHckYT8WmLhSLOZlrzZi/zESYWbVIMhNQAHFm0wMqI9wv98dYQD5yn9yejDwj6fiYER6TDWXYEpktg9PWsWPH/CPnzeMKIYS4e5EECyHuSpDY3bt3W6VKlXxDEGZZU2w68cwzz/gMaEb6ZWT69Ok2cuRI36YYEFK2Kmbea0aYm8rmAdwXm8ewYyKzfJlbXKRIEd9JMaPMsmVw3bp17cknn/Sd0tLWCy+8YK+++qrPOY7CXFkhhIgykmAhxF0J8slQ/6ZNm7qQsnUtG4R06tTJvvvd71rx4sV96+9atWq5HK9Zs8almN2+ENv47mVsNc3l3I5dvyguo/vLxgHMx2bnvfhudb/5zW9s4cKFLrVsL855xAvoTLNb3w9/+EP75S9/ma4eeOABe/rpp23//v2SYCGEuMuRBAsh7kqINDC/+v3337f777/fmjVrZv369bMyZcpYixYt/HN29GrTpo3vdshOc2xJjByXKlXKZXjWrFnWrl07K1++vAszcswGMXSAiTsgu0j0Sy+95B1ctgFu1KiR3+bZZ5+11q1b+3bio0eP9qgDInzu3Dm/vGDBgi7Daevdd9/17Z8PHz6caZRCCCHE3YMkWAhxV0K2lmjCr3/9axdUhJQqWrSoRx4WLFjgndr58+d7jGHcuHHehY3LKULKbekiI8mIa5MmTTxKwe3p1nL/CDMdXKT3nXfecckuVKiQV9myZe3ll192gWbr3AMHDrg40z2mc9yyZct0xe6LderU8ftnO+vM4hpCCCHuDiTBQoi7Ejq169at83wtnV+qffv2vsX3r371Ky+O0fGlGzxlyhQX18GDB9umTZs8A/z22297xIEuMYvqiEJUqFDBli5d6lGLqVOn2gcffODdYT6WK1fOJTpv3rze/V25cqXf/4gRI3xHxTFjxty8zltvvWXFihVzyaZ4LASdcyhcuLANHz7cH0MIIcTdiSRYCHFXwhQGsrsscCOuQKQBIY3HICgWvBFXQIaJPjzxxBNeSCy3qVevns2bN8/lmdvRyaXTS8yCyMLOnTtt9uzZ1qBBA5s4caJ3eYlMvPnmmx6/GD9+vD/OjBkzbp7Pxo0bvaNM7KFx48Z+f6VLl/YOcNWqVf1zJJsJEvEJFUIIIe4+JMFCiLsSBHLPnj0eRShZsqRLJhMckFK6tNSQIUM8CsHiOeIRyCuxh8mTJ1uXLl0838uECW7H4jjklMwwIstxOrzEIR5//HGXV+IQdIXpHPN58+bNvaNLZzkOMQdkl+kQb7zxhv3iF7/wz+lMv/jiiy7f69evVxRCCCHuciTBQoi7EuILc+fO9ZwtEks3l4VvdGqJLtAZJiNMPhdxXbZsmQsuAssMX0SYTi2RhMWLF3s3lw4wMYZt27b5/ROhoKNLTphRbIgvUySIYBB7IN6AKNPVjUOkAqEm9oCc58qVy0ejEYGIZ4q5/ytXrsRuIYQQ4m5EEiyEuCshBrFkyRKfCzxq1Cjr2bOnxyHoBCOuLFpDjun4khNmlnCBAgU8H0y0AZmlE4wEM2mCzTLo/ubLl8/n/wJCy0xhus2INB/JEsc70Iw942tuH4fFeF27dvXFd1WqVLHXXnvN7xP5pUOMtJNlVidYCCHubiTBQoi7FsaMIcNMXmCWL5ta0KWl04vUMuGhf//+3hVmegMTHognMNGBikswM3sZbcZOc3Rt6dQy7oxuLcI7YMAAF2imUJAvpmtMlxe5JV7BrGE23eB8iGEQoUCQn3rqKbv33nvtnnvusccee8wfn4gEos45amtnIYS4e5EECyHuWvbt2+cRA+IPLGCju0pWmEIwiUeQxa1du7YLLTOFhw0b5t1aFrXRFUZGiUGw2QbiyiQHOsIscmMxHdMiWBjHxhlcjy4vnWaiGHSXEWkKWSZLTEwiPp0id+7c9vDDD9vPf/5zF+D48VdeecVjGewuJ4QQ4u5EEiyEuGtBehlThnyS4Y3v2haH7i9Z4HhnlwVsbGrBbnAIKLLL53STuR4j0RDbuExzXXaa4/ZEHigWviHDjETjegg12yhzGd1kFr0R0eC8+Eh3muL+OUa3mc+Rbx5bCCHE3YkkWAgReYgx0PnNuFgNcc4YWeBYRtkWQggRPSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAshhBBCiJRDEiyEEEIIIVIOSbAQQgghhEg5JMFCCCGEECLlkAQLIYQQQoiUQxIshBBCCCFSDkmwEEIIIYRIOSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUgyz/w+pIh3FACiA0gAAAABJRU5ErkJggg=="
- }
- },
+ "attachments": {},
"cell_type": "markdown",
"metadata": {},
"source": [
@@ -49,15 +18,17 @@
"在对数据进行预处理时,经常加入新的操作或改变处理策略,此时如果伴随着随机操作,最好还是指定唯一的随机种子,避免由于随机的差异对结果产生影响。\n",
"\n",
"---\n",
- "# 离散型随机变量\n",
- "## 二项分布\n",
+ "\n",
+ "## 离散型随机变量\n",
+ "\n",
+ "### 二项分布\n",
+ "\n",
"二项分布可以用于只有一次实验只有两种结果,各结果对应的概率相等的多次实验的概率问题。比如处理猜10次拳赢6次的概率等类似的问题。\n",
"\n",
"二项分布概率函数的代码表示:binom.pmf(k) = choose(n, k) p\\*\\*k (1-p)\\*\\*(n-k)\n",
"\n",
"二项分布概率函数的数学表示:\n",
- "\n",
- "\n",
+ "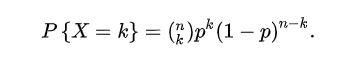\n",
"\n",
"\n",
"- `numpy.random.binomial(n, p, size=None)` Draw samples from a binomial distribution.\n",
@@ -65,6 +36,7 @@
"表示对一个二项分布进行采样,`size`表示采样的次数,`n`表示做了`n`重伯努利试验,`p`表示成功的概率,函数的返回值表示`n`中成功的次数。\n",
"\n",
"【例】野外正在进行9(n=9)口石油勘探井的发掘工作,每一口井能够开发出油的概率是0.1(p=0.1)。请问,最终所有的勘探井都勘探失败的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -90,10 +62,12 @@
"print(np.around(s, 3))\n",
"# [0.387 0.387 0.172 0.045 0.007 0.001 0. 0. 0. 0. ]\n",
"```\n",
- "\n",
+ "\n",
+ "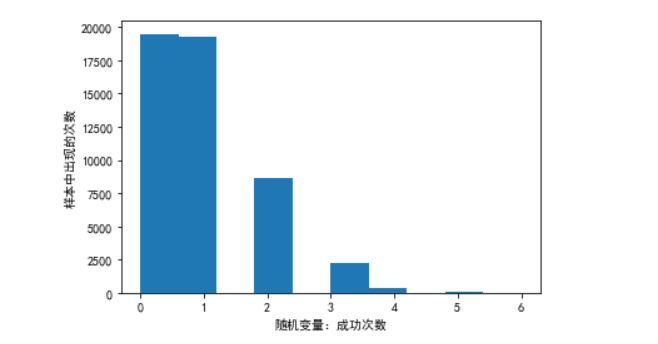\n",
"\n",
"\n",
"【例】模拟投硬币,投2次,请问两次都为正面的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"from scipy import stats\n",
@@ -112,7 +86,7 @@
"print(np.sum(x == 1) / size) # 0.49874\n",
"print(np.sum(x == 2) / size) # 0.24972\n",
"\n",
- "plt.hist(x, density=True)\n",
+ "plt.hist(x)\n",
"plt.xlabel('随机变量:硬币为正面次数')\n",
"plt.ylabel('50000个样本中出现的次数')\n",
"plt.show()\n",
@@ -121,7 +95,8 @@
"print(np.around(s, 3))\n",
"# [0.25 0.5 0.25]\n",
"```\n",
- "\n",
+ "\n",
+ "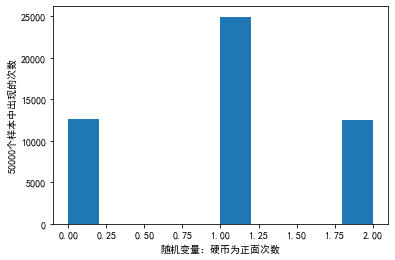\n",
"\n",
"```\n",
"#计算期望和方差\n",
@@ -132,14 +107,16 @@
"moments参数中:m为期望,v为方差\n",
"'''\n",
"```\n",
- "## 泊松分布\n",
+ "\n",
+ "### 泊松分布\n",
+ "\n",
"泊松分布主要用于估计某个时间段某事件发生的概率。\n",
"\n",
"泊松概率函数的代码表示:poisson.pmf(k) = exp(-lam) lam\\*k / k!\n",
"\n",
"泊松概率函数的数学表示:\n",
"\n",
- "\n",
+ "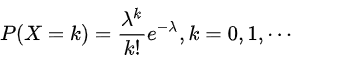\n",
"\n",
"- `numpy.random.poisson(lam=1.0, size=None)` Draw samples from a Poisson distribution.\n",
"\n",
@@ -171,13 +148,14 @@
"print(x) # 0.14900277967433773\n",
"```\n",
"\n",
- "\n",
+ "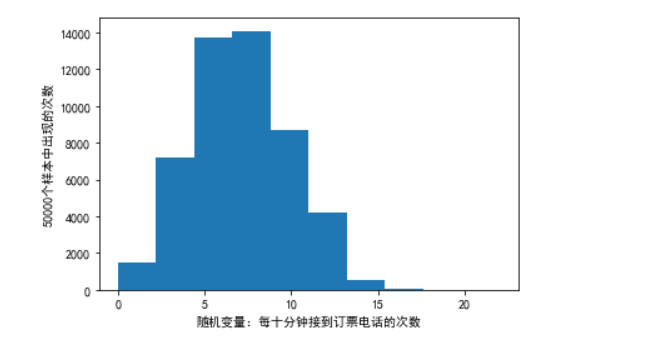\n",
"\n",
"\n",
- "## 超几何分布\n",
+ "### 超几何分布\n",
"\n",
"在超几何分布中,各次实验不是独立的,各次实验成功的概率也不等。\n",
- "超几何分布概率函数的数学表示:\n",
+ "超几何分布概率函数的数学表示:\n",
+ "\n",
"\n",
"\n",
"- `numpy.random.hypergeometric(ngood, nbad, nsample, size=None)` Draw samples from a Hypergeometric distribution.\n",
@@ -219,7 +197,8 @@
"# [0. 0.004 0.048 0.199 0.358 0.286 0.095 0.01 ]\n",
"```\n",
"\n",
- "\n",
+ "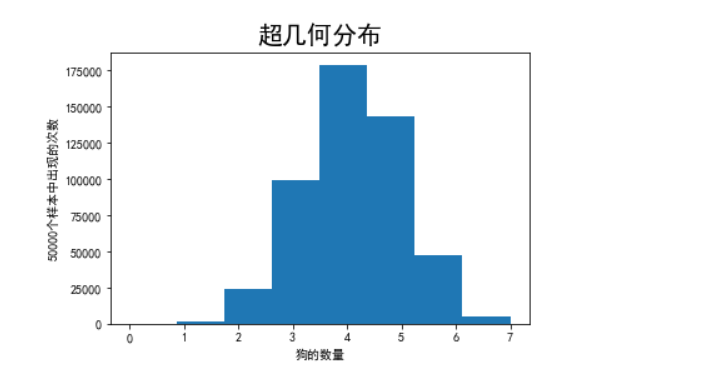\n",
+ "\n",
"```\n",
"'''\n",
"超几何分布的均值与方差\n",
@@ -233,15 +212,17 @@
"```\n",
"\n",
"---\n",
- "# 连续型随机变量\n",
"\n",
- "## 均匀分布\n",
+ "## 连续型随机变量\n",
+ "\n",
+ "### 均匀分布\n",
"\n",
"- `numpy.random.uniform(low=0.0, high=1.0, size=None)` Draw samples from a uniform distribution.\n",
"\n",
"Samples are uniformly distributed over the half-open interval `[low, high)` (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by `uniform`.\n",
"\n",
"【例】在low到high范围内,创建大小为size的均匀分布的随机数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -265,7 +246,8 @@
"print(b - a) # 0.4\n",
"```\n",
"\n",
- "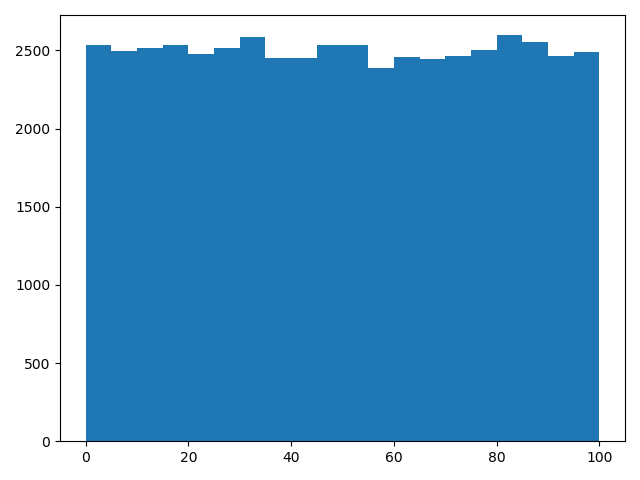\n",
+ "\n",
+ "\n",
"\n",
"作为`uniform()`的特列,可以得到`[0,1)`之间的均匀分布的随机数。\n",
"\n",
@@ -315,6 +297,7 @@
"\n",
"\n",
"【例】若`high`不为`None`时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -340,10 +323,10 @@
"```\n",
"\n",
"\n",
- "## 正态分布\n",
+ "### 正态分布\n",
"\n",
"标准正态分布数学表示:\n",
- "\n",
+ "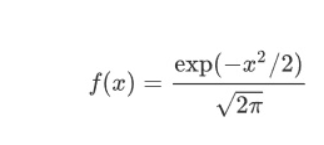\n",
"\n",
"- `numpy.random.randn(d0, d1, ..., dn)` Return a sample (or samples) from the \"standard normal\" distribution.\n",
"\n",
@@ -377,7 +360,7 @@
"print(y3) # 0.9973002039367398\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"还可以指定分布以及所需参数来进行随机,例如高斯分布中的mu和sigma。\n",
@@ -385,13 +368,14 @@
"- `numpy.random.normal(loc=0.0, scale=1.0, size=None)` Draw random samples from a normal (Gaussian) distribution.\n",
"\n",
"`normal()`为创建均值为 loc(mu),标准差为 scale(sigma),大小为 size 的数组。\n",
- "\n",
+ "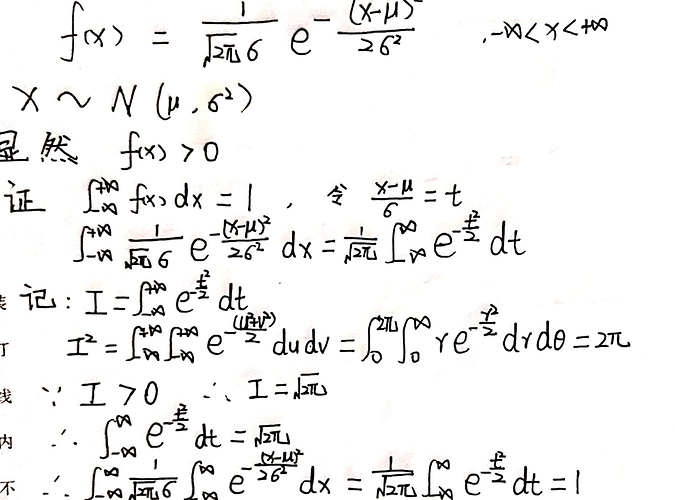\n",
"\n",
"```python\n",
"sigma * np.random.randn(...) + mu\n",
"```\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -424,22 +408,27 @@
"Means Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.\n",
"'''\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
+ "\n",
"```\n",
"plt.hist(x, bins=20)\n",
"plt.show()\n",
"```\n",
"\n",
- "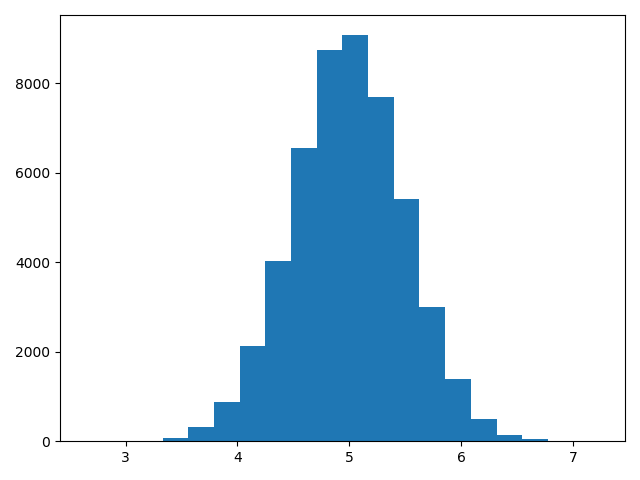\n",
+ "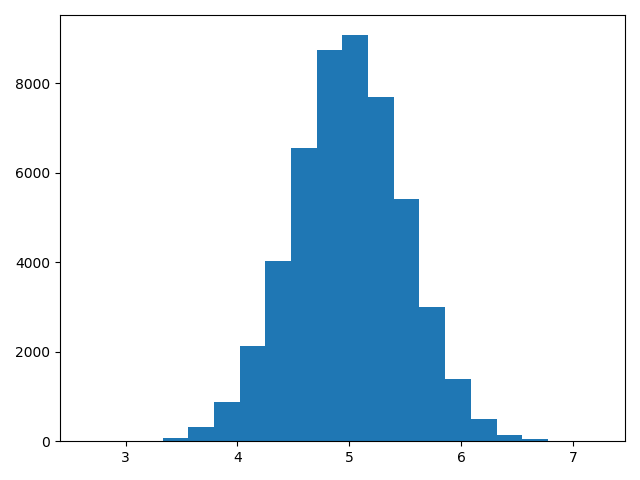\n",
+ "\n",
+ "### 指数分布\n",
"\n",
- "## 指数分布\n",
"指数分布描述时间发生的时间长度间隔。\n",
"\n",
- "指数分布的数学表示:\n",
+ "指数分布的数学表示:\n",
+ "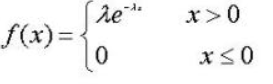\n",
"\n",
"- `numpy.random.exponential(scale=1.0, size=None)` Draw samples from an exponential distribution.\n",
"\n",
"【例】`scale = 1/lambda`\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -470,18 +459,21 @@
"print(y3) # 0.950212931632136\n",
"```\n",
"\n",
- "\n",
+ "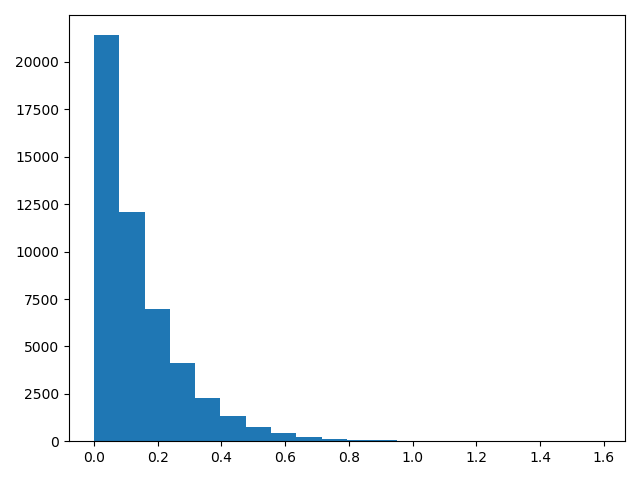\n",
"\n",
"\n",
"---\n",
- "# 其它随机函数\n",
"\n",
- "## 随机从序列中获取元素\n",
+ "## 其它随机函数\n",
+ "\n",
+ "### 随机从序列中获取元素\n",
+ "\n",
"- `numpy.random.choice(a, size=None, replace=True, p=None)` Generates a random sample from a given 1-D array.\n",
"\n",
"从序列中获取元素,若`a`为整数,元素取值从`np.range(a)`中随机获取;若`a`为数组,取值从`a`数组元素中随机获取。该函数还可以控制生成数组中的元素是否重复`replace`,以及选取元素的概率`p`。\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -503,7 +495,8 @@
"x = np.random.randint(0, 10, 3)\n",
"print(x) # [2 0 1]\n",
"```\n",
- "## 对数据集进行洗牌操作\n",
+ "\n",
+ "### 对数据集进行洗牌操作\n",
"\n",
"数据一般都是按照采集顺序排列的,但是在机器学习中很多算法都要求数据之间相互独立,所以需要先对数据集进行洗牌操作。\n",
"\n",
@@ -514,6 +507,7 @@
"对`x`进行重排序,如果`x`为多维数组,只沿第 0 轴洗牌,改变原来的数组,输出为None。\n",
"\n",
"【例】洗牌,改变自身内容,打乱顺序。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -584,71 +578,17 @@
"\n",
"\n",
"---\n",
+ "\n",
"**参考文献**\n",
- "- https://www.jianshu.com/p/63434ad5ea64\n",
- "\n"
+ "\n",
+ "- https://www.jianshu.com/p/63434ad5ea64"
]
},
{
"cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:02.029113Z",
- "start_time": "2020-09-15T01:02:02.026084Z"
- }
- },
+ "execution_count": null,
+ "metadata": {},
"outputs": [],
- "source": [
- "dic={1:('I','V'),2:('X','L'),3:('C','D'),4:'M'}"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:09.390007Z",
- "start_time": "2020-09-15T01:02:09.379035Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'M'"
- ]
- },
- "execution_count": 2,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "dic[4]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:29.206128Z",
- "start_time": "2020-09-15T01:02:29.201134Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'I'"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
"source": []
}
],
diff --git a/LanQiao/readme.md b/LanQiao/readme.md
new file mode 100644
index 0000000..1ba4e99
--- /dev/null
+++ b/LanQiao/readme.md
@@ -0,0 +1,52 @@
+# 编程实践(蓝桥刷题94道)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/LanQiao
+
+## 基本信息
+
+- 学习周期:14天,每天平均花费时间2小时-5小时不等,根据个人学习接受能力强弱有所浮动。
+- 学习形式:练习
+- 人群定位:有一定编程基础,对学习算法有需求的学员。
+- 先修内容:[Python编程语言](https://github.com/datawhalechina/team-learning-program/tree/master/PythonLanguage)、[数据结构与算法](https://github.com/datawhalechina/team-learning-program/tree/master/DataStructureAndAlgorithm)、[编程实践(LeetCode 分类练习)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeClassification)
+- 难度系数:中
+
+## 学习目标
+
+每天刷三道题,利用14天对于蓝桥杯这个比赛有一个初步的了解,掌握基本的蓝桥杯赛题解法。
+
+
+
+## 任务安排
+
+### Task00:熟悉规则(1天)
+- 组队、修改群昵称
+- 熟悉打卡规则
+
+### Task01:热身练习(2天)
+- 完成热身练习文件夹中的7道题目
+- 熟悉基本输入输出及蓝桥杯的练习系统的使用方法。
+
+### Task02:基础练习(3天)
+- 完成基础练习文件夹中的7道题目
+
+### Task03:基础练习2(3天)
+- 完成基础练习2文件夹中的8道题目
+
+### Task04:真题练习(3天)
+- 完成真题练习文件夹中的10道题目
+
+### Task05:真题练习2(3天)
+- 完成真题练习文件夹中的7道题目
+
+
+## 开源贡献者
+
+韩绘锦:华北电力大学
+
+- CSDN:https://blog.csdn.net/weixin_45569785
+
+黄建国:华北电力大学
+
+荆宝加:华北电力大学
+
+吴丹飞:华北电力大学
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/01字串.md b/LanQiao/task1热身练习/01字串.md
new file mode 100644
index 0000000..d1587cf
--- /dev/null
+++ b/LanQiao/task1热身练习/01字串.md
@@ -0,0 +1,79 @@
+## 01字串
+
+**问题描述**
+
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
diff --git a/LanQiao/task1热身练习/1083、Hello,world.md b/LanQiao/task1热身练习/1083、Hello,world.md
new file mode 100644
index 0000000..c031a2d
--- /dev/null
+++ b/LanQiao/task1热身练习/1083、Hello,world.md
@@ -0,0 +1,53 @@
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1083.html
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
diff --git a/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
new file mode 100644
index 0000000..442dd80
--- /dev/null
+++ b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
@@ -0,0 +1,218 @@
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1084.html
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/1095、3n+1问题.md b/LanQiao/task1热身练习/1095、3n+1问题.md
new file mode 100644
index 0000000..2f8c997
--- /dev/null
+++ b/LanQiao/task1热身练习/1095、3n+1问题.md
@@ -0,0 +1,72 @@
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/2080、十六进制转八进制.md b/LanQiao/task1热身练习/2080、十六进制转八进制.md
new file mode 100644
index 0000000..a80f5b6
--- /dev/null
+++ b/LanQiao/task1热身练习/2080、十六进制转八进制.md
@@ -0,0 +1,168 @@
+## 十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2080.html
+
+**题目描述**
+
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+
+**输入**
+
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+
+**输出**
+
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+
+**样例输入**
+
+```
+2
+39
+123ABC
+```
+
+**样例输出**
+
+```
+71
+4435274
+```
+
+
+```
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
diff --git a/LanQiao/task1热身练习/2082、十六进制转十进制.md b/LanQiao/task1热身练习/2082、十六进制转十进制.md
new file mode 100644
index 0000000..9edf75a
--- /dev/null
+++ b/LanQiao/task1热身练习/2082、十六进制转十进制.md
@@ -0,0 +1,47 @@
+## 十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2082.html
+
+**题目描述**
+
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+
+**输入**
+
+```
+一个十六进制数
+
+```
+
+**输出**
+
+```
+对应得十进制
+```
+
+**样例输入**
+
+```
+FFFF
+```
+
+**样例输出**
+
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
diff --git a/LanQiao/task1热身练习/2083、十进制转十六进制.md b/LanQiao/task1热身练习/2083、十进制转十六进制.md
new file mode 100644
index 0000000..c0ba52b
--- /dev/null
+++ b/LanQiao/task1热身练习/2083、十进制转十六进制.md
@@ -0,0 +1,76 @@
+## 十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2083.html
+
+**题目描述**
+
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+
+**输入**
+
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+
+**输出**
+
+```
+输出这个整数的16进制表示
+```
+
+**样例输入**
+
+```
+30
+```
+
+**样例输出**
+
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
diff --git a/LanQiao/task2基础练习/1460、2n皇后问题.md b/LanQiao/task2基础练习/1460、2n皇后问题.md
new file mode 100644
index 0000000..e34c4b2
--- /dev/null
+++ b/LanQiao/task2基础练习/1460、2n皇后问题.md
@@ -0,0 +1,114 @@
+# 2n皇后问题
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1460.html
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
diff --git a/LanQiao/task2基础练习/1462、Huffuman树.md b/LanQiao/task2基础练习/1462、Huffuman树.md
new file mode 100644
index 0000000..0852108
--- /dev/null
+++ b/LanQiao/task2基础练习/1462、Huffuman树.md
@@ -0,0 +1,82 @@
+# Huffuman树
+
+
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1316 解决: 750
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1462.html
+
+**题目描述**
+
+```
+Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
+
+给出一列数{pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
+
+1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
+
+2. 重复步骤1,直到{pi}中只剩下一个数。
+
+在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
+
+本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
+
+
+
+例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
+
+1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
+
+2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
+
+3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
+
+4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
+
+5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。
+
+```
+**输入**
+```
+输入的第一行包含一个正整数n(n< =100)。
+
+接下来是n个正整数,表示p0, p1, …, pn-1,每个数不超过1000。
+
+```
+**输出**
+```
+输出用这些数构造Huffman树的总费用。
+
+```
+**样例输入**
+```
+5
+5 3 8 2 9
+```
+**样例输出**
+```
+59
+```
+
+
+```
+n=int(input())
+list_=list(map(int,input().split()))
+res=[]
+while len(list_)>1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1463、Sine之舞.md b/LanQiao/task2基础练习/1463、Sine之舞.md
new file mode 100644
index 0000000..6a86bd8
--- /dev/null
+++ b/LanQiao/task2基础练习/1463、Sine之舞.md
@@ -0,0 +1,92 @@
+# Sine之舞
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1463.html
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
diff --git a/LanQiao/task2基础练习/1467、完美的代价.md b/LanQiao/task2基础练习/1467、完美的代价.md
new file mode 100644
index 0000000..6bd8b98
--- /dev/null
+++ b/LanQiao/task2基础练习/1467、完美的代价.md
@@ -0,0 +1,143 @@
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1467.html
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1470、时间转换.md b/LanQiao/task2基础练习/1470、时间转换.md
new file mode 100644
index 0000000..91c6951
--- /dev/null
+++ b/LanQiao/task2基础练习/1470、时间转换.md
@@ -0,0 +1,58 @@
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1470.html
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1475、高精度加法.md b/LanQiao/task2基础练习/1475、高精度加法.md
new file mode 100644
index 0000000..f7182a1
--- /dev/null
+++ b/LanQiao/task2基础练习/1475、高精度加法.md
@@ -0,0 +1,92 @@
+## 高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1475.html
+
+**题目描述**
+
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+
+- 输出一行,表示a + b的值。
+
+**样例输入**
+
+```
+20100122201001221234567890
+2010012220100122
+```
+
+**样例输出**
+
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_pointxl and y_up>y_down:
+ cross+=(xr-xl)*(y_up-y_down)
+ count+=1
+ return (count,cross)
+
+
+
+n=int(input())
+for i in range(n):
+ n=int(input())
+ matrixs=[]
+ for j in range(n):
+ matrixs.append(list(map(int,input().strip().split())))
+ for k in range(n):
+ target=matrixs[k]
+ count,cross=Area_cross(target,matrixs,k)
+ print(count,cross)
+
+```
+
+ 1
+ 3
+ 0 0 2 6
+ 1 1 4 4
+ 1 3 3 9
+ 2 6
+ 2 5
+ 2 5
+
+
+
+
+## 试题 基础练习 矩形面积交
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+问题描述
+
+ 平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
+
+输入格式
+
+ 输入仅包含两行,每行描述一个矩形。
+
+ 在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
+
+输出格式
+
+ 输出仅包含一个实数,为交的面积,保留到小数后两位。
+
+样例输入
+
+```
+1 1 3 3
+2 2 4 4
+```
+样例输出
+
+```
+1.00
+```
+
+参考答案
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+x1=[min(x1i[0],x1i[2]),min(x1i[1],x1i[3]),max(x1i[0],x1i[2]),max(x1i[1],x1i[3])]
+x2=[min(x2i[0],x2i[2]),min(x2i[1],x2i[3]),max(x2i[0],x2i[2]),max(x2i[1],x2i[3])]
+xl=max(x1[0],x2[0])
+xr=min(x1[2],x2[2])
+yup=min(x1[3],x2[3])
+ydown=max(x1[1],x2[1])
+x=xr-xl
+y=yup-ydown
+if xr>xl and yup>ydown:
+ print('{:.2f}'.format(x*y))
+else:
+ print('{:.2f}'.format(0))
+```
+
+ 1 1 4 5
+ 1 1 4 5
+ 12.00
diff --git a/LanQiao/task3基础练习2/1097、蛇形矩阵.md b/LanQiao/task3基础练习2/1097、蛇形矩阵.md
new file mode 100644
index 0000000..4a10e0b
--- /dev/null
+++ b/LanQiao/task3基础练习2/1097、蛇形矩阵.md
@@ -0,0 +1,73 @@
+## 题目 1097: 蛇行矩阵
+
+时间限制: 1Sec 内存限制: 64MB 提交: 7484 解决: 5014
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem.php?id=1097
+
+**题目描述**
+蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。
+**输入**
+
+> 本题有多组数据,每组数据由一个正整数N组成。(N不大于100)
+
+**输出**
+
+> 对于每一组数据,输出一个N行的蛇形矩阵。两组输出之间不要额外的空行。矩阵三角中同一行的数字用一个空格分开。行尾不要多余的空格。
+
+**样例输入**
+
+```python
+5
+```
+
+**样例输出**
+
+```python
+1 3 6 10 15
+2 5 9 14
+4 8 13
+7 12
+11
+
+```
+
+参考答案:
+
+
+```
+n=int(input())
+temp=[[] for i in range(n)]
+num=1
+grade=0
+while grade 只有1行,为两个正整数,用一个空格隔开: k w
+
+**输出**
+
+> 1行,是一个正整数,为所求的计算结果,即满足条件的不同的r的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
+> (提示:作为结果的正整数可能很大,但不会超过200位)
+
+**样例输入**
+
+```python
+3 7
+```
+
+**样例输出**
+
+```python
+36
+```
+
+参考答案:
+
+
+```
+k,w=map(int,input().strip().split())
+Digits=w//k # 可以有完整k位的位数
+remainder=w%k # 最高位余下的位数
+def f (count,Digit):
+ if Digit>count:
+ return 0
+ re=1
+ for i in range(1,Digit+1):
+ re*=(count-i+1)/i
+ return re
+s0=sum([f(2**k-1,i) for i in range(2,Digits+1)]) #不考虑最高位或者说是只考虑所有的位数都有完整k位的情况。那么对于每一个位数的可能数就是从2**k-1中选取位数个数字的所有可能性
+
+s1=sum([f(2**k-1-i,Digits) for i in range(1,2**remainder)])# 依次计算最高位取每一个可能的数字时所有的可能性。
+print(int(s0+s1))
+```
+
+ 3 7
+ 36
+
+
+
+
+
+
+
diff --git a/LanQiao/task3基础练习2/1117、K-进制数.md b/LanQiao/task3基础练习2/1117、K-进制数.md
new file mode 100644
index 0000000..1bf2eb1
--- /dev/null
+++ b/LanQiao/task3基础练习2/1117、K-进制数.md
@@ -0,0 +1,75 @@
+## 题目 1117: K-进制数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2458 解决: 959
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1117.html
+
+**题目描述**
+
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+>
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+
+**例:**
+
+1010230 是有效的7位数
+1000198 无效
+0001235 不是7位数, 而是4位数.
+
+给定两个数N和K, 要求计算包含N位数字的有效K-进制数的总数.
+
+假设2 <= K <= 10; 2 <= N; 4 <= N+K <= 18.
+
+**输入**
+
+> 两个十进制整数N和K
+
+**输出**
+
+> 十进制表示的结果
+
+**样例输入**
+
+```python
+2
+10
+```
+
+**样例输出**
+
+```python
+90
+```
+## 提示
+
+> 从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+> 令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+> 前提:n 最小是 2*k-1.
+>
+> 组合 [(h+1)*h*(h-1)*```````(h+1-k)] /[k*(k-1)*(k-2)*``````1]
+>
+> 排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+参考答案:
+
+```
+N=int(input())
+K=int(input())
+re1=(K-1)**N
+def f (n,k):
+ h=n-k
+ re=1
+ for i in range(1,k+1):
+ re*=(h+1-i+1)/i
+ return re*((K-1)**(n-k+1))## n-k+1中+1是加上了首位
+
+
+re2=sum([f(N-1,k) for k in range(1,int(((N-1)+1)/2)+1)])# 因为首位不能为零,所以从其他位置选取为零的点
+print(int(re1+re2))
+```
+
+ 2
+ 10
+ 90
\ No newline at end of file
diff --git a/LanQiao/task3基础练习2/1465、回形取数.md b/LanQiao/task3基础练习2/1465、回形取数.md
new file mode 100644
index 0000000..7c18103
--- /dev/null
+++ b/LanQiao/task3基础练习2/1465、回形取数.md
@@ -0,0 +1,136 @@
+# 回形取数
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1831 解决: 590
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1465.html
+
+**题目描述**
+
+- 回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
+
+**输入**
+
+- 输入第一行是两个不超过200的正整数m, n,表示矩阵的行和列。接下来m行每行n个整数,表示这个矩阵。
+
+**输出**
+
+- 输出只有一行,共mn个数,为输入矩阵回形取数得到的结果。数之间用一个空格分隔,行末不要有多余的空格。
+
+**样例输入**
+```
+3 3
+1 2 3
+4 5 6
+7 8 9
+```
+**样例输出**
+```
+1 4 7 8 9 6 3 2 5
+```
+
+### 思路一
+
+
+```
+m,n=map(int,input().split())
+nn=[]
+for i in range(m):
+ nn.append(input().split())
+dir=[[1,0],[0,1],[-1,0],[0,-1]]
+re=[]
+x=0
+y=0
+state=0
+n_left=0
+m_left=0
+m_right=m-1
+n_right=n-1
+while len(re)m_right):
+ state=(state+1)%4
+ n_left+=1
+ elif((tx+x)n_right):
+ state=(state+1)%4
+ m_right-=1
+ elif ((ty+y) 程序首先读入一个整数N(2< N< 100),表示小朋友的人数。 接着是一行用空格分开的N个偶数(每个偶数不大于1000,不小于2)
+
+**输出**
+
+> 要求程序输出一个整数,表示老师需要补发的糖果数。
+
+**样例输入**
+
+```python
+3
+2 2 4
+```
+
+**样例输出**
+
+```python
+4
+```
+
+参考答案:
+
+
+```
+n=int(input())
+num=list(map(int,input().strip().split()))
+re=0
+def b(num):
+ temp=num[0]
+ for i in num:
+ if i!=temp:
+ return False
+ return True
+while not b(num):
+ temp=num.copy()
+ for i in range(len(temp)):
+ temp[i]=int(temp[i]/2)
+ for i in range(len(num)):
+ num[i]=int(num[i]/2)+temp[(i+1)%len(temp)]
+ if num[i]%2!=0:
+ num[i]+=1
+ re+=1
+print(re)
+
+```
+
+ 3
+ 2 2 4
+ 4
diff --git a/LanQiao/task4真题练习/试题 B 合并检测.md b/LanQiao/task4真题练习/试题 B 合并检测.md
new file mode 100644
index 0000000..6f38276
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 B 合并检测.md
@@ -0,0 +1,143 @@
+## 试题 B: 合并检测
+
+
+本题总分:5 分
+
+**【问题描述】**
+
+新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准备给大量民众进病毒核酸检测。
+然而,用于检测的试剂盒紧缺。
+为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看,如果检测前 k − 1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用了 k + 1 个试剂盒完成了 k 个人的检测。
+A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能最节省试剂盒?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+lis=[]
+for k in range(1,101):
+ temp=100+k*k
+ lis.append([temp/k,k])
+lis.sort(key=lambda x :x[0])
+lis[0][1]
+```
+
+
+
+
+ 10
+
+
+
+
+```
+lis
+```
+
+
+
+
+ [[20.0, 10],
+ [20.09090909090909, 11],
+ [20.11111111111111, 9],
+ [20.333333333333332, 12],
+ [20.5, 8],
+ [20.692307692307693, 13],
+ [21.142857142857142, 14],
+ [21.285714285714285, 7],
+ [21.666666666666668, 15],
+ [22.25, 16],
+ [22.666666666666668, 6],
+ [22.88235294117647, 17],
+ [23.555555555555557, 18],
+ [24.263157894736842, 19],
+ [25.0, 5],
+ [25.0, 20],
+ [25.761904761904763, 21],
+ [26.545454545454547, 22],
+ [27.347826086956523, 23],
+ [28.166666666666668, 24],
+ [29.0, 4],
+ [29.0, 25],
+ [29.846153846153847, 26],
+ [30.703703703703702, 27],
+ [31.571428571428573, 28],
+ [32.44827586206897, 29],
+ [33.333333333333336, 30],
+ [34.225806451612904, 31],
+ [35.125, 32],
+ [36.03030303030303, 33],
+ [36.333333333333336, 3],
+ [36.94117647058823, 34],
+ [37.857142857142854, 35],
+ [38.77777777777778, 36],
+ [39.7027027027027, 37],
+ [40.63157894736842, 38],
+ [41.56410256410256, 39],
+ [42.5, 40],
+ [43.4390243902439, 41],
+ [44.38095238095238, 42],
+ [45.325581395348834, 43],
+ [46.27272727272727, 44],
+ [47.22222222222222, 45],
+ [48.17391304347826, 46],
+ [49.12765957446808, 47],
+ [50.083333333333336, 48],
+ [51.04081632653061, 49],
+ [52.0, 2],
+ [52.0, 50],
+ [52.96078431372549, 51],
+ [53.92307692307692, 52],
+ [54.886792452830186, 53],
+ [55.851851851851855, 54],
+ [56.81818181818182, 55],
+ [57.785714285714285, 56],
+ [58.75438596491228, 57],
+ [59.724137931034484, 58],
+ [60.69491525423729, 59],
+ [61.666666666666664, 60],
+ [62.63934426229508, 61],
+ [63.61290322580645, 62],
+ [64.58730158730158, 63],
+ [65.5625, 64],
+ [66.53846153846153, 65],
+ [67.51515151515152, 66],
+ [68.49253731343283, 67],
+ [69.47058823529412, 68],
+ [70.44927536231884, 69],
+ [71.42857142857143, 70],
+ [72.40845070422536, 71],
+ [73.38888888888889, 72],
+ [74.36986301369863, 73],
+ [75.35135135135135, 74],
+ [76.33333333333333, 75],
+ [77.3157894736842, 76],
+ [78.2987012987013, 77],
+ [79.28205128205128, 78],
+ [80.26582278481013, 79],
+ [81.25, 80],
+ [82.23456790123457, 81],
+ [83.21951219512195, 82],
+ [84.20481927710843, 83],
+ [85.19047619047619, 84],
+ [86.17647058823529, 85],
+ [87.16279069767442, 86],
+ [88.14942528735632, 87],
+ [89.13636363636364, 88],
+ [90.12359550561797, 89],
+ [91.11111111111111, 90],
+ [92.0989010989011, 91],
+ [93.08695652173913, 92],
+ [94.0752688172043, 93],
+ [95.06382978723404, 94],
+ [96.05263157894737, 95],
+ [97.04166666666667, 96],
+ [98.03092783505154, 97],
+ [99.0204081632653, 98],
+ [100.01010101010101, 99],
+ [101.0, 1],
+ [101.0, 100]]
\ No newline at end of file
diff --git a/LanQiao/task4真题练习/试题 C 分配口罩.md b/LanQiao/task4真题练习/试题 C 分配口罩.md
new file mode 100644
index 0000000..72e882d
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 C 分配口罩.md
@@ -0,0 +1,64 @@
+## 试题 C: 分配口罩
+
+本题总分:10 分
+
+**【问题描述】**
+
+某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文
+字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目
+录下有一个文件 mask.txt,内容与下面的文本相同)
+
+```python
+9090400
+8499400
+5926800
+8547000
+4958200
+4422600
+5751200
+4175600
+6309600
+5865200
+6604400
+4635000
+10663400
+8087200
+4554000
+```
+
+
+ 现在市长要把口罩分配给市内的2所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+
+```
+def main():
+ f=open('mask.txt','r')
+ #string=f.readlines()
+ num_lis=[]
+ for i in f:
+ #print(i)
+ num_lis.append(int(i))
+ print(num_lis)
+ re=[abs(num_lis[0]-num_lis[1])]
+ def dfs(num1,num2,num_lis):
+ #global re
+ if not num_lis:
+ re[0]=min(re[0],abs(num1-num2))
+ return
+ dfs(num1+num_lis[0],num2,num_lis[1:])
+ dfs(num1,num2+num_lis[0],num_lis[1:])
+ dfs(0,0,num_lis)
+ print(re[0])
+ return
+main()
+```
+
+ [9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, 6604400, 4635000, 10663400, 8087200, 4554000]
+ 2400
\ No newline at end of file
diff --git a/LanQiao/task4真题练习/试题 F 解码.md b/LanQiao/task4真题练习/试题 F 解码.md
new file mode 100644
index 0000000..dbc5c8c
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 F 解码.md
@@ -0,0 +1,54 @@
+## 试题 F: 解码
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+
+**【问题描述】**
+小明有一串很长的英文字母,可能包含大写和小写。
+在这串字母中,有很多连续的是重复的。小明想了一个办法将这串字母表
+达得更短:将连续的几个相同字母写成字母 + 出现次数的形式。
+例如,连续的 5 个 a,即 aaaaa,小明可以简写成 a5(也可能简写成 a4a、
+aa3a 等)。对于这个例子:HHHellllloo,小明可以简写成 H3el5o2。为了方便表
+达,小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串,请帮助小明还原成原来的串。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出一个字符串,表示还原后的串。
+
+**【样例输入】**
+
+```python
+H3el5o2
+```
+
+**【样例输出】**
+
+```python
+HHHellllloo
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由大小写英文字母和数字组成,长度不超过100。
+请注意原来的串长度可能超过 100。
+
+参考答案:
+
+```
+num_set={'0','1','2','3','4','5','6','7','8','9'}
+string=input()
+re=[]
+for i in string :
+ if i in num_set:
+ for i in range(int(i)-1):
+ re.append(re[-1])
+ else:
+ re.append(i)
+print(''.join(re))
+```
+
+ H3el5o2
+ HHHellllloo
diff --git a/LanQiao/task4真题练习/试题 G 走方格.md b/LanQiao/task4真题练习/试题 G 走方格.md
new file mode 100644
index 0000000..1f61a7f
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 G 走方格.md
@@ -0,0 +1,110 @@
+## 试题 G: 走方格
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+在平面上有一些二维的点阵。
+这些点的编号就像二维数组的编号一样,从上到下依次为第 1 至第 n 行,
+从左到右依次为第 1 至第 m 列,每一个点可以用行号和列号来表示。
+现在有个人站在第 1 行第 1 列,要走到第 n 行第 m 列。只能向右或者向下
+走。
+注意,如果行号和列数都是偶数,不能走入这一格中。
+问有多少种方案。
+
+**【输入格式】**
+
+> 输入一行包含两个整数 n, m。
+
+**【输出格式】**
+
+> 输出一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+3 4
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【样例输入】**
+
+```python
+6 6
+```
+
+参考答案:
+
+
+```
+n,m=map(int,input().strip().split())
+def main():
+ re=[0]
+ def dfs(x,y):
+ if x==n-1 and y==m-1:
+ re[0]+=1
+ if 0<=x+1<=(n-1) and not ((x+1)%2==0 and (y)%2==0):
+ dfs(x+1,y)
+ if 0<=y+1<=(m-1) and not ((x)%2==0 and (y+1)%2==0):
+ dfs(x,y+1)
+ dfs(0,0)
+ print(re[0])
+main()
+```
+
+ 3 4
+ 2
+
+
+### bfs
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ queue=[(0,0)]
+ re=0
+ while queue:
+ x,y=queue.pop(0)
+ if x==n-1 and y==m-1:
+ re+=1
+ if 0<=x+1 第一行包含 2 个整数 n 和 K。
+> 第二行包含 n 个整数 A1, A2, · · · , An。
+
+**【输出格式】**
+
+> 一个整数代表答案。
+
+**【样例输入】**
+
+```python
+4 33
+1 2 3 4
+```
+
+**【样例输出】**
+
+```python
+8
+```
+
+**【评测用例规模与约定】**
+对于 30% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ K ≤ 108, 1 ≤ Ai ≤ 104。
+对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ K ≤ 1010,1 ≤ Ai ≤ 109.
+
+参考答案:
+
+```
+n,K=map(int,input().strip().split())
+num_lis=list(map(int,input().strip().split()))
+re=0
+for i in range(n):
+ for j in range(i+1,n):
+ if (num_lis[i]*10+num_lis[j])<=K:
+# print( num_lis[i]*10+num_lis[j])
+ re+=1
+ if (num_lis[j]*10+num_lis[i])<=K:
+# print(num_lis[j]*10+num_lis[i])
+ re+=1
+print(re)
+
+
+```
+
+ 4 33
+ 1 2 3 4
+ 8
diff --git a/LanQiao/task4真题练习/试题 I BST 插入节点问题.md b/LanQiao/task4真题练习/试题 I BST 插入节点问题.md
new file mode 100644
index 0000000..a0fa6a2
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 I BST 插入节点问题.md
@@ -0,0 +1,102 @@
+## 试题 I: BST 插入节点问题
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分
+
+**【问题描述】**
+
+给定一棵包含 N 个节点的二叉树,节点编号是 1 ∼ N。其中 i 号节点具有
+权值 Wi,并且这些节点的权值恰好形成了一棵排序二叉树 (BST)。
+现在给定一个节点编号 K,小明想知道,在这 N 个权值以外,有多少个整
+数 X (即 X 不等于任何 Wi ) 满足:给编号为 K 的节点增加一个权值为 X 的子
+节点,仍可以得到一棵 BST。
+例如在下图中,括号外的数字表示编号、括号内的数字表示权值。即编号
+1 ∼ 4 的节点权值依次是 0、10、20、30。
+
+如果 K = 1,那么答案为 0。因为 1 号节点已经有左右子节点,不能再增
+加子节点了。
+如果 K = 2,那么答案为无穷多。因为任何一个负数都可以作为 2 的左子
+节点。
+如果 K = 3,那么答案为 9。因为 X = 11, 12, · · · , 19 都可以作为 3 的左子
+节点。
+
+**【输入格式】**
+
+> 第一行包含 2 个整数 N 和 K。
+>
+> 以下 N 行每行包含 2 个整数,其中第 i 行是编号为 i 的节点的父节点编号
+>
+> Pi 和权值 Wi 。注意 Pi = 0 表示 i 是根节点。
+>
+> 输入保证是一棵 BST。
+
+**【输出格式】**
+
+> 一个整数代表答案。如果答案是无穷多,输出 −1。
+
+**【样例输入】**
+
+```python
+4 3
+0 10
+1 0
+1 20
+3 30
+```
+
+**【样例输出】**
+
+```python
+9
+```
+
+**【评测用例规模与约定】**
+
+> 对于 60% 的评测用例,1 ≤ K ≤ N ≤ 100,0 ≤ Wi ≤ 200,且 Wi 各不相同。
+>
+> 对于所有评测用例,1 ≤ K ≤ N ≤ 10000,0 ≤ Wi ≤ 100000000,且 Wi 各不 相同。
+
+参考答案:
+
+```
+class TreeNode:
+ def __init__(self,x):
+ self.val=x
+ self.left=None
+ self.right=None
+ self.parent=None
+N,K=map(int,input().strip().split())
+map_=[]
+map_node=[]
+for i in range(N):
+ p,w=map(int,input().strip().split())
+ map_.append([p,w])
+ map_node.append(TreeNode(w))
+ if p==0:
+ root_index=i
+for i in range(N):
+ if map_node[map_[i][0]-1].val 输入的第一行包含一个整数 n,表示初始时的石子数量。
+>
+> 第二行包含 n 个整数 w1,w2, · · · ,wn,依次表示每颗石子的重量。
+
+**【输出格式】**
+
+> 输出一行包含一个整数,表示最少需要的胶水数。
+
+**【样例输入】**
+
+```python
+3
+3 4 5
+```
+
+**【样例输出】**
+
+```python
+47
+```
+
+**【样例输入】**
+
+```python
+8
+1 5 2 6 3 7 4 8
+```
+
+**【样例输出】**
+
+```python
+546
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 15。
+>
+> 对于 60% 的评测用例,1 ≤ n ≤ 100。
+>
+> 对于 80% 的评测用例,1 ≤ n ≤ 1000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 100000,1 ≤ wi ≤ 1000。
+
+参考答案:
+
+
+```
+n=int(input())
+num_lis=list(map(int,input().strip().split()))
+def f(num_lis):
+ re=num_lis[0]*num_lis[1]
+ re_index=0
+ for i in range(len(num_lis)-1):
+ if num_lis[i]*num_lis[i+1] - 输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从 1 至 n 编号。
+> 接下来 m 行,每行三个整数,表示一个操作。
+> 如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。
+> 如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
+
+**【输出格式】**
+
+> 输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+**【样例输入】**
+
+```python
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+
+**【样例输出】**
+
+```python
+13 13 5 3
+```
+
+**【评测用例规模与约定】**
+
+> 对于 30% 的评测用例,1 ≤ n ≤ 20,1 ≤ m ≤ 100。
+>
+> 对于 50% 的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000。
+>
+> 对于 70% 的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ t ≤ 100。
+
+参考答案:
+
+```
+n,m=map(int,input().strip().split())
+message1=[]
+for i in range(m):
+
+ or1_2,a,b=input().strip().split()
+ message1.append([or1_2,a,b])
+
+
+map_=[[0 for i in range(n)]for i in range(n)]
+for i in range(n):
+ map_[i][i]=1
+
+re=[0 for i in range(n)]
+
+def f(map_,a,b,re,visited):
+ for i in range(n):
+ if map_[a-1][i]==1:
+ if i not in visited:
+ f(map_,i+1,b,re,visited|{i})
+ else:
+ if re[i]==0:
+ re[i]+=b
+
+
+
+for or1_2,a,b in message1:
+ a=int(a)
+ b=int(b)
+ if or1_2=='1':
+ map_[a-1][b-1]=1
+ map_[b-1][a-1]=1
+ else:
+ temp=[0 for i in range(n)]
+ f(map_,a,b,temp,{a-1})
+
+ for i in range(len(re)):
+ re[i]+=temp[i]
+
+for i in re:
+ print(i)
+
+```
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题A解密.md b/LanQiao/task5真题练习2/试题A解密.md
new file mode 100644
index 0000000..b4ef62c
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题A解密.md
@@ -0,0 +1,40 @@
+## 试题 A: 解密
+
+本题总分:5 分
+
+**【问题描述】**
+
+小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的
+字符 Tc。下表给出了字符变换的规则:
+
+
+例如,将字符串 YeRi 加密可得字符串 EaFn。
+小明有一个随机的字符串,加密后为
+EaFnjISplhFviDhwFbEjRjfIBBkRyY
+(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
+(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容
+是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符
+串,后面 52 行依次为表格中的内容。)
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+只包含 30 个大小写英文字母的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
+
+
+
+```
+f=open('str.txt','r')
+strings=f.readlines()
+j=0
+dic_={}
+target=strings[0]
+for string in strings[1:]:
+ a,b=string.strip().split()
+ dic_[b]=a
+for i in target[:-2]:
+ print(dic_[i],end='')
+
+```
+
+ YeRikGSunlRzgDlvRwYkXkrGWWhXa
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题B数列求值.md b/LanQiao/task5真题练习2/试题B数列求值.md
new file mode 100644
index 0000000..8c4264a
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题B数列求值.md
@@ -0,0 +1,29 @@
+## 试题 B: 数列求值
+
+本题总分:5 分
+
+**【问题描述】**
+
+给定数列 1, 1, 1, 3, 5, 9, 17, …,从第 4 项开始,每项都是前 3 项的和。求
+第 20190324 项的最后 4 位数字。
+
+**【答案提交】**
+
+这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
+个 4 位整数(提示:答案的千位不为 0),在提交答案时只填写这个整数,填写
+多余的内容将无法得分。
+
+
+```
+n=20190324#int(input())
+re=[1,1,1]
+next_num=3
+for i in range(4,n+1):
+ pop_num=re.pop(0)
+ re.append(next_num)
+ next_num=(2*next_num-pop_num)%10000
+print(str(re[-1])[-4:])
+
+```
+
+ 4659
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题B纪念日.md b/LanQiao/task5真题练习2/试题B纪念日.md
new file mode 100644
index 0000000..ebfa263
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题B纪念日.md
@@ -0,0 +1,41 @@
+## 试题 B: 纪念日
+
+本题总分:5 分
+
+**【问题描述】**
+
+2020 年 7 月 1 日是中国共产党成立 99 周年纪念日。
+中国共产党成立于 1921 年 7 月 23 日。
+请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包
+含多少分钟?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+```
+import datetime
+end=datetime.datetime(year=2020,month=7,day=1,hour=12)
+start=datetime.datetime(year=1921,month=7,day=23,hour=12)
+re=end-start
+re
+```
+
+
+
+
+ datetime.timedelta(36138)
+
+
+
+
+```
+36128*24*60
+```
+
+
+
+
+ 52024320
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题D矩阵.md b/LanQiao/task5真题练习2/试题D矩阵.md
new file mode 100644
index 0000000..03cc003
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题D矩阵.md
@@ -0,0 +1,31 @@
+## 试题 D: 矩阵
+
+本题总分:10 分
+
+**【问题描述】**
+
+把 1 ∼ 2020 放在 2 × 1010 的矩阵里。要求同一行中右边的比左边大,同一
+列中下边的比上边的大。一共有多少种方案?
+答案很大,你只需要给出方案数除以 2020 的余数即可。
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+f=[[ 0 for i in range(1011)]for i in range(1011)]
+f[0][0]=1
+for i in range(1011):
+ for j in range(1011):
+ if i>j:
+ f[i][j]+=f[i-1][j]
+ if j!=0:
+ f[i][j]+=f[i][j-1]
+ f[i][j]%=2020
+print(f[-1][-1])
+```
+
+ 1340
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题F分类计数.md b/LanQiao/task5真题练习2/试题F分类计数.md
new file mode 100644
index 0000000..54affbf
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题F分类计数.md
@@ -0,0 +1,63 @@
+## 试题 F: 分类计数
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
+
+**【问题描述】**
+
+输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字
+母,多少个数字。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
+
+**【样例输入】**
+
+```python
+1+a=Aab
+```
+
+**【样例输出】**
+
+```python
+1
+3
+1
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由可见字符组成,长度不超过 100。
+
+参考答案:
+
+
+```
+string=input()
+num_set=set()
+for i in range(10):
+ num_set.add(str(i))
+# print(num_set)
+num_len=0
+h_len=0
+l_len=0
+for i in string:
+ if i in num_set:
+ num_len+=1
+ elif 'A'<=i<='Z':
+ h_len+=1
+ elif 'a'<=i<='z':
+ l_len+=1
+print(h_len)
+print(l_len)
+print(num_len)
+
+```
+
+ 1+a=Aab
+ 1
+ 3
+ 1
diff --git a/LanQiao/task5真题练习2/试题G八次求和.md b/LanQiao/task5真题练习2/试题G八次求和.md
new file mode 100644
index 0000000..9244ef7
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题G八次求和.md
@@ -0,0 +1,68 @@
+## 试题 G: 八次求和
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+给定正整数 n, 求 1
+8 + 28 + · · · + n
+8 mod 123456789 。其中 mod 表示取
+余。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n。
+
+**【输出格式】**
+
+> 输出一行,包含一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+2
+```
+
+**【样例输出】**
+
+```python
+257
+```
+
+**【样例输入】**
+
+```python
+987654
+```
+
+**【样例输出】**
+
+```python
+43636805
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 20。
+> 对于 60% 的评测用例,1 ≤ n ≤ 1000。
+> 对于所有评测用例,1 ≤ n ≤ 1000000。
+
+参考答案:
+
+```
+def f(x):
+ re=1
+ for i in range(8):
+ re*=x
+ re%=123456789
+ return re
+n=int(input())
+res=0
+for i in range(1,n+1):
+ res+=f(i)
+ res%=123456789
+print(res)
+```
+
+ 987654
+ 43636805
diff --git a/LanQiao/task5真题练习2/试题H字符串编码.md b/LanQiao/task5真题练习2/试题H字符串编码.md
new file mode 100644
index 0000000..5bc0154
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题H字符串编码.md
@@ -0,0 +1,64 @@
+## 试题 H: 字符串编码
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大
+写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, ... Z →
+26。
+这样一个字符串就能被转化成一个数字序列:
+比如 ABCXYZ → 123242526。
+现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样
+的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字
+符串。
+
+**【输入格式】**
+
+
+> 一个数字序列。
+
+**【输出格式】**
+
+> 一个只包含大写字母的字符串,代表答案
+
+**【样例输入】**
+
+```python
+123242526
+```
+
+**【样例输出】**
+
+```python
+LCXYZ
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,输入的长度不超过 20。
+> 对于所有评测用例,输入的长度不超过 200000。
+
+参考答案:
+
+
+```
+dic_={}
+for i in range(1,27):
+ dic_[str(i)]=chr(i+64)
+
+string=input()
+point=0
+while point 输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0 对于每个测试实例,输出在第n年的时候母牛的数量。 每个输出占一行。
+
+**样例输入**
+
+```python
+2
+4
+5
+0
+```
+
+**样例输出**
+
+```python
+2
+4
+6
+```
+
+
+```
+def f(n,l4,l3,l2,l1):
+ if n==1:
+ return l2+l3+l4+l1
+ l4+=l3
+ l3=l2
+ l2=l1
+ l1=l4
+ return f(n-1,l4,l3,l2,l1)
+while True:
+ n=int(input())
+ if n==0:
+ break
+ else:
+ print(f(n,1,0,0,0))
+```
+
+ 2
+ 2
+ 4
+ 4
+ 5
+ 6
+ 0
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md b/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md
new file mode 100644
index 0000000..cf5f8b3
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md
@@ -0,0 +1,83 @@
+## 题目 1094: 字符串的输入输出处理
+
+时间限制: 1Sec 内存限制: 64MB 提交: 14661 解决: 5300
+
+**题目描述**
+
+字符串的输入输出处理。
+
+**输入**
+
+> 第一行是一个正整数N,最大为100。之后是多行字符串(行数大于N), 每一行字符串可能含有空格,字符数不超过1000。
+
+**输出**
+
+> 先将输入中的前N行字符串(可能含有空格)原样输出,再将余下的字符串(不含有空格)以空格或回车分割依次按行输出。每行输出之间输出一个空行。
+
+**样例输入**
+
+```python
+2
+www.dotcpp.com DOTCPP
+A C M
+D O T CPP
+```
+
+**样例输出**
+
+```python
+www.dotcpp.com DOTCPP
+
+A C M
+
+D
+
+O
+
+T
+
+CPP
+```
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ print(temp)
+ print()
+while True:
+ li=input().strip().split()
+ for i in li:
+ print(i)
+ print()
+```
+
+ 2
+ www.dotcpp.com DOTCPP
+ www.dotcpp.com DOTCPP
+
+ A C M
+ A C M
+
+ D O T CPP
+ D
+
+ O
+
+ T
+
+ CPP
+
+
+
+
+
+```
+print(1,sep='\n\n')
+# print('\n')
+print(3)
+```
+
+ 1
+ 3
diff --git a/LanQiao/蓝桥杯习题/1096、扫雷.md b/LanQiao/蓝桥杯习题/1096、扫雷.md
new file mode 100644
index 0000000..b2095ae
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1096、扫雷.md
@@ -0,0 +1,113 @@
+## 译文1096:扫雷
+
+时间限制:1秒内存限制:64MB提交:3446解决:1442
+
+**译文描述**
+```
+
+扫雷你玩过扫雷吗?这个可爱的小游戏带有一定的操作系统,我们不记得它的名字。游戏的目标是找到所有地雷在M x N字段中的位置。游戏在一个正方形中显示一个数字,告诉您该正方形附近有多少个地雷。每个方格最多具有八个相邻方格。左侧的4 x 4字段包含两个地雷,每个地雷由一个``*''字符表示。如果我们通过上述提示号表示同一字段,那么我们将在右侧显示该字段:* ... ....。* .. .... * 100 2210 1 * 10 1110
+```
+**输入**
+```
+输入将包含任意数量的字段。每个字段的第一行包含两个整数n和m(0 =0 and (index[0]-1)=0 and (index[0]+1)=0 and (index[0]-1)=0 and (index[1]-1)=0 and (index[0]+1)=0 and (index[1]-1)=0 and (index[1]-1)=0 and (index[0]-1)=0 and (index[1]+1)=0 and (index[0]+1)=0 and (index[1]+1)=0 and (index[1]+1) 输入包含多组测试数据。第一个整数N(N<=15),N表示组数,每组数据包含两个整数a,b。a表示一个单位的DNA串的行数,a为奇数且
+> 3<=a<=39。b表示重复度(1<=b<=20)。
+
+**输出**
+
+> 输出DNA的形状,每组输出间有一空行。
+
+**样例输入**
+
+```python
+2
+3 1
+5 4
+```
+
+**样例输出**
+
+```python
+X X
+ X
+X X
+
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+```
+
+
+```
+n =int(input())
+for i in range(n):
+ a,b=map(int,input().strip().split())
+ temp=[' ']*a
+ start=0
+ end=a-1
+ count=1
+ while count<=b:
+ temp2=temp[:]
+ temp2[start]='X'
+ temp2[end]='X'
+ print(''.join(temp2))
+ if end==0:
+ start,end=end,start
+ count+=1
+ start+=1
+ end-=1
+ print()
+```
+
+ 2
+ 3 1
+ X X
+ X
+ X X
+
+ 5 4
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+
+
+
+
+
+```
+num="1.2.3.4".split('.')#[0].isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+'2'.isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+num=input()
+```
+
+ 1.2.3.4
+
+
+
+```
+num.split()
+```
+
+
+
+
+ ['1.2.3.4']
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1116、IP判断.md b/LanQiao/蓝桥杯习题/1116、IP判断.md
new file mode 100644
index 0000000..e10ec3f
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1116、IP判断.md
@@ -0,0 +1,81 @@
+## 题目 1116: IP判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6196 解决: 2532
+
+**题目描述**
+```
+在基于Internet的程序中,我们常常需要判断一个IP字符串的合法性。
+合法的IP是这样的形式:
+A.B.C.D
+其中A、B、C、D均为位于[0, 255]中的整数。为了简单起见,我们规定这四个整数中不允许有前导零存在,如001这种情况。
+现在,请你来完成这个判断程序吧^_^
+```
+**输入**
+
+> 输入由多行组成,每行是一个字符串,输入由“End of file”结束。 字符串长度最大为30,且不含空格和不可见字符
+
+**输出**
+
+> 对于每一个输入,单独输出一行 如果该字符串是合法的IP,输出Y,否则,输出N
+
+**样例输入**
+
+```python
+1.2.3.4
+a.b.c.d
+267.43.64.12
+12.34.56.bb
+210.43.64.129
+-123.4.5.6
+```
+
+**样例输出**
+
+```python
+Y
+N
+N
+N
+Y
+N
+```
+
+
+```
+while True :
+ str=input()
+ if str=="End of file":
+ break
+ num=str.split('.')
+ i=0
+ while i1)) or( not num[i].isdecimal()):
+# print(not num[i])
+# print( num[i][0]=='0'and len(num[i]>1))
+# print(not num[i].isdecimal())
+# print(num[i])
+# print(i)
+ break
+ if int(num[i])<0 or int(num[i])>255:
+# print(2)
+ break
+ i+=1
+ if i==len(num):
+ print('Y')
+ else:
+ print('N')
+```
+
+ 1.2.3.4
+ Y
+ a.b.c.d
+ N
+ 267.43.64.12
+ N
+ 12.34.56.bb
+ N
+ 210.43.64.129
+ Y
+ -123.4.5.6
+ N
+ End of file
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1118、Tom数.md b/LanQiao/蓝桥杯习题/1118、Tom数.md
new file mode 100644
index 0000000..0bdd71e
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1118、Tom数.md
@@ -0,0 +1,45 @@
+## 题目 1118: Tom数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 8198 解决: 3197
+
+**题目描述**
+
+正整数的各位数字之和被Tom称为Tom数。求输入数(<2^32)的Tom数!
+
+**输入**
+
+> 每行一个整数(<2^32).
+
+**输出**
+
+> 每行一个输出,对应该数的各位数之和.
+
+**样例输入**
+
+```python
+12345
+56123
+82
+```
+
+**样例输出**
+
+```python
+15
+17
+10
+```
+
+
+```
+while True :
+ num=map(int,list(input()))
+ print(sum(num))
+```
+
+ 12345
+ 15
+ 56123
+ 17
+ 82
+ 10
diff --git a/LanQiao/蓝桥杯习题/1231、杨辉三角.md b/LanQiao/蓝桥杯习题/1231、杨辉三角.md
new file mode 100644
index 0000000..b3061b6
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1231、杨辉三角.md
@@ -0,0 +1,71 @@
+## 杨辉三角
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1796 解决: 633
+
+**题目描述**
+
+```
+还记得中学时候学过的杨辉三角吗?具体的定义这里不再描述,你可以参考以下的图形:
+1
+1 1
+1 2 1
+1 3 3 1
+1 4 6 4 1
+1 5 10 10 5 1
+```
+
+**输入**
+
+- 输入数据包含多个测试实例,每个测试实例的输入只包含一个正整数n(1<=n<=30),表示将要输出的杨辉三角的层数。
+
+**输出**
+
+- 对应于每一个输入,请输出相应层数的杨辉三角,每一层的整数之间用一个空格隔开,每一个杨辉三角后面加一个空行。
+
+**样例输入**
+
+```
+2 3
+```
+
+**样例输出**
+
+```
+1
+1 1
+
+1
+1 1
+1 2 1
+```
+
+
+```
+num=map(int,input().strip().split())
+for n in num:
+# n=int(input())
+ temp=[1]
+ for i in range(n):
+ print(' '.join(list(map(str,temp))))
+ n1=len(temp)
+ t1=[1]
+ j=0
+ while j+1=0 and next_x<3 and next_y>=0 and next_y<3:
+ str2=str1[:]
+ str2[x*3+y],str2[next_x*3+next_y]=str2[next_x*3+next_y],str2[x*3+y]
+
+ if ''.join(str2) not in dic:
+ dic[''.join(str2)]=dic[''.join(str1)]+1
+
+ if str2==last:
+ return dic[''.join(str2)]
+# break
+ else:
+ queue.append(str2)
+ return -1
+first=list(input().strip())
+last=list(input().strip())
+print(main())
+
+```
+
+ 12345678.
+ 123.46758
+ 3
+
+
+### 提示
+对于每个状态当前能有的可能就是4种可能,所以我们要做的就是从first开始利用队列层序的遍历所有的可能,用dic记录其走的步数,直到其转化为last的状态。
+
+
diff --git a/LanQiao/蓝桥杯习题/1427、买不到数目.md b/LanQiao/蓝桥杯习题/1427、买不到数目.md
new file mode 100644
index 0000000..39772b7
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1427、买不到数目.md
@@ -0,0 +1,65 @@
+## 题目 1427: [蓝桥杯][2013年第四届真题]买不到的数目
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4243 解决: 2207
+
+**题目描述**
+小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。
+小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
+你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。
+本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
+**输入**
+
+> 两个正整数,表示每种包装中糖的颗数(都不多于1000)
+
+
+
+**输出**
+
+> 一个正整数,表示最大不能买到的糖数
+
+**样例输入**
+
+```python
+4 7
+```
+
+**样例输出**
+
+```python
+17
+```
+
+
+```
+a,b=map(int,input().strip().split())
+max_=max(a,b)
+min_=min(a,b)
+map=[]
+for i in range(1,min_):
+ map.append(i)
+multiple=1
+re=min_-1
+while map:
+ temp=max_*multiple
+ del_map=[]
+ for i in range(len(map)):
+ if (temp+map[i])%min_==0:
+ del_map.append(map[i])
+ else:
+ re=temp+map[i]
+ for i in del_map:
+ map.remove(i)
+ multiple+=1
+print(re)
+```
+
+ 4 7
+ 17
+
+
+### 提示
+- 首先将两个数字分出大数跟小数,我们以大数为基础来思考,首先我们知道可以在大数的倍数的基础上加上无限的小数来表示其他的数字,那么可能不能表示的数字就存在于大数的倍数加上1~min_之间的数字产生的数字,这些数字中可能存在不能表示的数字。
+- 受到题目中启发,大于某个数字的数全都能被这两个数字表示,那么我们深入考虑其中的原因无非就是其中一些大数被小数的倍数给补上了,从而补上了那个差
+
+#### 策略
+- 那我们就首先把所有的1~min_之间的数字全部都存到map_中,然后分别对于不同倍数的大数加上这之间的数字看能不能被小数给整除,假如能整除的的话说明这个数能被表示就可以把从map中删除掉,直到map为空,那么最后记录的数字就是最大不能组合的数字。
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1428、公式求值.md b/LanQiao/蓝桥杯习题/1428、公式求值.md
new file mode 100644
index 0000000..fca8d94
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1428、公式求值.md
@@ -0,0 +1,240 @@
+## 题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1441 解决: 25
+
+题目描述
+输入n, m, k,输出下面公式的值。
+
+[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TBIJDDFR-1609161353087)(attachment:image.png)]
+
+
+其中C_n^m是组合数,表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如下:
+
+
+
+
+
+
+[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BPbYZL5z-1609161353089)(attachment:image.png)]
+数据规模和约定
+
+对于100%的数据,n在十进制下不超过1000位,即1≤n< 10^1000,1≤k≤1000,同时0≤m≤n,k≤n。
+
+提示
+
+999101是一个质数;
+当n位数比较多时,绝大多数情况下答案都是0,但评测的时候会选取一些答案不是0的数据;
+
+**输入**
+
+输入的第一行包含一个整数n;第二行包含一个整数m,第三行包含一个整数k。
+
+**输出**
+
+计算上面公式的值,由于答案非常大,请输出这个值除以999101的余数。
+
+**样例输入**
+
+3
+
+1
+
+3
+
+**样例输出**
+
+162
+
+
+```
+import decimal
+n=int(input())
+m=int(input())
+k=int(input())
+def C(n,m):
+ re=1
+ if m>(n-m):
+ m=n-m
+ for i in range(1,m+1):
+ re*=((n-i+1)%999101)/i
+# re%=999101
+ return re
+def f(i,k):
+ re=1
+ for j in range(k):
+ re*=i
+ re%=999101
+ return re
+res=0
+cnm=C(n,m)
+cni=1
+for i in range(1,n+1):
+ cni*=((n-i+1)%999101)/i
+ res+=cni*(f(i,k))
+ res%=999101
+# print(res)
+# print(res)
+print((int(cnm*res%999101)))
+```
+
+ 990
+ 300
+ 5
+
+
+
+ ---------------------------------------------------------------------------
+
+ InvalidOperation Traceback (most recent call last)
+
+ in
+ 23 cni*=(decimal.Decimal(n-i+1)%999101)/i
+ 24 res+=cni*(f(i,k))
+ ---> 25 res%=999101
+ 26 # print(res)
+ 27 # print(res)
+
+
+ InvalidOperation: []
+
+
+
+```
+import java.math.*;
+import java.util.*;
+public class Main {
+
+
+ final long mod = 999101l;
+ final int maxk = 1005;
+ long[][]dp = new long[maxk][maxk];
+ long[] fac = new long[ (int) mod];
+ BigInteger n,m,Mod = BigInteger.valueOf(mod);
+ int k;
+ long ans;
+ Main()
+ {
+ Scanner jin = new Scanner(System.in);
+ n = jin.nextBigInteger();
+ m = jin.nextBigInteger();
+ k = jin.nextInt();
+ if(n.equals(new BigInteger("7349813")) && m.equals(new BigInteger("3590741")) && k == 9)//原题第四个数据貌似输出有误,正确应该输出为0
+ {
+ System.out.println(591101);
+ return;
+ }
+ getfac();
+ long lc = lucas(n,m);
+ if(lc == 0l)
+ {
+ System.out.println(0);
+ return;
+ }
+ getdp();
+ ans = 0l;
+ int i;
+ long p = qpow(2l,n.subtract(BigInteger.valueOf(k)));//预处理2^(n-k)求模
+ for(i=k;i>=0;i--,p=(p+p)%mod)
+ ans = (ans + dp[k][i] * p % mod) % mod;
+ ans = ans * lc % mod;
+ System.out.println(ans);
+ }
+ void getdp()//计算系数求模
+ {
+ int i,j;
+ dp[0][0] = 1l;
+ long N = n.mod(Mod).longValue();
+ for(i=0;i0l;b>>=1l,a=a*a%mod)
+ if((b&1l) == 1l)
+ ans = ans * a % mod;
+ return ans;
+ }
+ void getfac()//预处理[0,mod-1]的阶乘求模
+ {
+ int i;
+ fac[0] = 1l;
+ for(i=1;i 程序先读入两个整数 m n 用空格分割 (m,n< 10)。 表示表格的宽度和高度。
+> 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。
+
+**输出**
+
+> 输出一个整数,表示在所有解中,包含左上角的分割区可能包含的最小的格子数目。
+
+**样例输入**
+
+```python
+3 3
+10 1 52
+20 30 1
+1 2 3
+```
+
+**样例输出**
+
+```python
+3
+```
+
+### 思路一
+
+
+```
+def main():
+ m,n=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ all_sum=0
+ for i in range(n):
+ for j in range(m):
+ all_sum+=map_[i][j]
+ if all_sum%2!=0:
+ print(0)
+ return
+ visited=set()
+ temp_sum=0
+ res=[]
+ temp=[]
+ def helper(visited,row,col,temp_sum,temp):
+ '''
+ visited:记录已经遍历过的点
+ row:当前横坐标
+ col:当前纵坐标
+ temp_sum:已经遍历过的点的值的和
+ temp:储存了当前遍历的点的坐标
+ '''
+ if temp_sum==all_sum/2:
+ res.append(temp)
+ return
+ if temp_sum>all_sum/2:
+ return
+ if (row-1,col) not in visited and 0<=(row-1) 输入数据第一行包含2个整数n(2 < = n < = 1000), m(0 < = m < =
+> 2000),分别代表站点数,通道数; 接下来m行,每行两个整数 u,v (1 < = u, v < = n; u !=
+> v)代表一条通道; 最后1行,两个数u,v,代表询问两点之间的危险系数DF(u, v)。
+
+
+
+**输出**
+
+> 一个整数,如果询问的两点不连通则输出-1.
+
+**样例输入**
+
+```python
+7 6
+1 3
+2 3
+3 4
+3 5
+4 5
+5 6
+1 6
+```
+
+**样例输出**
+
+```python
+2
+```
+
+### 思路一
+
+
+```
+def main():
+
+ n,m=map(int,input().strip().split())
+ map_={}
+ for i in range(1,n+1):
+ map_[i]=[]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1].append(temp2)
+ map_[temp2].append(temp1)
+ visited=set()
+ start,end=map(int,input().strip().split())
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in map_[start]:
+ if i not in visited:
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+# print(res)
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+#### 提示
+我们发现其实关键点就是所有的从start到end的路径上都需要经过的点,那么我们记录下来从start到end的所有的可能的路径,然后取交即可求得这些关键点。
+
+### 思路二
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ map_=[[0 for i in range(n)]for j in range(n)]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1-1][temp2-1]=1
+ map_[temp2-1][temp1-1]=1
+ visited=set()
+ start,end=map(int,input().strip().split())
+ start-=1
+ end-=1
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in range(n):
+ if (map_[start][i]==1) and (i not in visited):
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
diff --git a/LanQiao/蓝桥杯习题/1434、回文数字.md b/LanQiao/蓝桥杯习题/1434、回文数字.md
new file mode 100644
index 0000000..7224646
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1434、回文数字.md
@@ -0,0 +1,183 @@
+## 题目 1434: [蓝桥杯][历届试题]回文数字
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7799 解决: 3232
+
+**题目描述**
+
+观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
+
+本题要求你找到一些5位或6位的十进制数字。满足如下要求:
+该数字的各个数位之和等于输入的整数。
+
+**输入**
+
+> 一个正整数 n (10< n< 100), 表示要求满足的数位和。
+
+**输出**
+
+> 若干行,每行包含一个满足要求的5位或6位整数。
+> 数字按从小到大的顺序排列。
+> 如果没有满足条件的,输出:-1
+
+**样例输入**
+
+```python
+44
+```
+
+**样例输出**
+
+```python
+99899
+499994
+589985
+598895
+679976
+688886
+697796
+769967
+778877
+787787
+796697
+859958
+868868
+877778
+886688
+895598
+949949
+958859
+967769
+976679
+985589
+994499
+```
+
+
+```
+n=int(input())
+res=set()
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (2*i+2*j+k)==n:
+ res.add(i*10000+i+j*1000+j*10+k*100)
+ if (2*(i+j+k))==n:
+ res.add(i*100000+i+j*10000+j*10+k*1000+k*100)
+res=sorted(list(res))
+for i in res:
+ print(i)
+if not res:
+ print(-1)
+```
+
+ 44
+ 99899
+ 499994
+ 589985
+ 598895
+ 679976
+ 688886
+ 697796
+ 769967
+ 778877
+ 787787
+ 796697
+ 859958
+ 868868
+ 877778
+ 886688
+ 895598
+ 949949
+ 958859
+ 967769
+ 976679
+ 985589
+ 994499
+
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+def main():
+ n,m,k=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ x=0
+ y=0
+ res=[]
+ def helper(x,y,temp):
+ if (x==n-1) and (y==m-1):
+# print(temp)
+ if len(temp)>=k:
+ res.append(temp)
+ if (n>(x+1)>=0) and (m>y>=0):
+# if map_[x+1][y]>temp[-1]:
+# helper(x+1,y,temp+[map_[x+1][y]])
+# else:
+ helper(x+1,y,temp+[map_[x+1][y]])
+ if (n>(x)>=0) and (m>(y+1)>=0):
+# if map_[x][y+1]>temp[-1]:
+# helper(x,y+1,temp+[map_[x][y+1]])
+# else:
+ helper(x,y+1,temp+[map_[x][y+1]])
+
+ helper(0,0,[map_[0][0]])
+ print(len(res))
+ print(res[0])
+ temps=[]
+ def f (x,k,temp):
+ if len(x)+len(temp)20 and int(h)<30:
+ str1='twenty'+' '+map_[str(int(h)%10)]
+if m=='0':
+ str2='o\'clock'
+elif (int(m))>20 and int(m)<30:
+ str2='twenty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==3:
+ str2='thirty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==4:
+ str2='forty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==5:
+ str2='fifty'+' '+map_[str(int(m)%10)]
+else:
+ str2=map_[m]
+print(str1,end=' ')
+print(str2,end='')
+```
+
+ 20 21
+ twenty twenty one
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1469、数的读法.md b/LanQiao/蓝桥杯习题/1469、数的读法.md
new file mode 100644
index 0000000..644b5e0
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1469、数的读法.md
@@ -0,0 +1,206 @@
+数的读法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1037 解决: 350
+
+**题目描述**
+```
+Tom教授正在给研究生讲授一门关于基因的课程,有一件事情让他颇为头疼:一条染色体上有成千上万个碱基对,它们从0开始编号,到几百万,几千万,甚至上亿。
+
+比如说,在对学生讲解第1234567009号位置上的碱基时,光看着数字是很难准确的念出来的。
+
+所以,他迫切地需要一个系统,然后当他输入12 3456 7009时,会给出相应的念法:
+
+十二亿三千四百五十六万七千零九
+
+用汉语拼音表示为
+
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+这样他只需要照着念就可以了。
+
+你的任务是帮他设计这样一个系统:给定一个阿拉伯数字串,你帮他按照中文读写的规范转为汉语拼音字串,相邻的两个音节用一个空格符格开。
+
+注意必须严格按照规范,比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”,“100000”读作“shi wan”而不是“yi shi wan”,“2000”读作“er qian”而不是“liang qian”。
+```
+**输入**
+
+- 有一个数字串,数值大小不超过2,000,000,000。
+
+**输出**
+
+- 是一个由小写英文字母,逗号和空格组成的字符串,表示该数的英文读法。
+
+**样例输入**
+```
+1234567009
+
+```
+**样例输出**
+```
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+```
+
+### 思路一
+
+
+```
+import math
+num=input().strip()
+map1={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=[None,'shi','bai','qian']
+num_lis=[]
+
+'''
+输入按照单位分开
+'''
+while num:
+ if len(num)//4>0:
+ num_lis.append(num[-4:])
+ num=num[:-4]
+# print(num)
+ else:
+ num_lis.append(num)
+ num=None
+# print(num_lis)
+
+
+'''
+对每一个单位进行操作的操作函数
+'''
+def op(s):
+ j=0
+ res=[]
+ for i in s[::-1]:
+ if i=='0':
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map1[i])
+ j+=1
+ continue
+ else:
+ res.append(map2[j])
+ res.append(map1[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res[::-1]
+# print(num_lis)
+
+
+'''
+输出结果
+'''
+re=[]
+m=[None,'wan','yi','wanyi']
+for i in range(len(num_lis))[::-1]:
+ if op(num_lis[i]):
+ re+=op(num_lis[i])
+ re.append(m[i])
+# print(re)
+for i in re:
+ if i :
+ print(i,end=' ')
+# print(' '.join(re))
+
+
+
+```
+
+ 1234567009
+ ['7009', '3456', '12']
+ shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+### 思路二
+
+
+```
+s=input()
+map_={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=['','shi','bai','qian']
+s1=''
+s2=''
+s3=''
+n=len(s)
+nl=[0]*4
+for i in range(4):
+ if n<=0:
+ break
+ nl[i]=4 if n>=4 else n
+ n-=4
+s1=s[0:nl[3]]
+s2=s[nl[3]:nl[3]+nl[2]]
+s3=s[nl[3]+nl[2]:nl[2]+nl[1]+nl[3]]
+s4=s[nl[2]+nl[1]+nl[3]:nl[2]+nl[1]+nl[3]+nl[0]]
+res=[]
+
+
+
+def op(s,res,map_,map2):
+ j=0
+ res=[]
+# print(s1,s2,s3)
+ for i in s[::-1]:
+ if i=='0':
+
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map_[i])
+ j+=1
+ continue
+ res.append(map2[j])
+ res.append(map_[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res
+
+
+
+
+
+r4=op(s4,res,map_,map2)
+res+=r4
+
+if nl[1]>0:
+ res.append('wan')
+ r3=op(s3,res,map_,map2)
+ if r3:
+ res+=r3
+ else:
+ res.pop(-1)
+
+
+if nl[2]>0:
+ res.append('yi')
+ r2=op(s2,res,map_,map2)
+ if r2:
+ res+=r2
+ else:
+ res.pop(-1)
+
+
+if nl[3]>0:
+ res.append('wan yi')
+ r1=op(s1,res,map_,map2)
+ if r1:
+ res+=r1
+ else:
+ res.pop(-1)
+
+res=reversed(res)
+a=' '.join(res).split()
+print(' '.join(a))
+```
+
+ 2000000000000
+ er wan yi
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1473、芯片测试.md b/LanQiao/蓝桥杯习题/1473、芯片测试.md
new file mode 100644
index 0000000..7c8b02a
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1473、芯片测试.md
@@ -0,0 +1,150 @@
+
+
+芯片测试
+
+时间限制: 1Sec 内存限制: 128MB 提交: 981 解决: 503
+
+**题目描述**
+```
+有n(2≤n≤20)块芯片,有好有坏,已知好芯片比坏芯片多。
+
+每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时,能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时,会随机给出好或是坏的测试结果(即此结果与被测试芯片实际的好坏无关)。
+
+给出所有芯片的测试结果,问哪些芯片是好芯片。
+```
+**输入**
+```
+输入数据第一行为一个整数n,表示芯片个数。
+
+第二行到第n+1行为n*n的一张表,每行n个数据。表中的每个数据为0或1,在这n行中的第i行第j列(1≤i, j≤n)的数据表示用第i块芯片测试第j块芯片时得到的测试结果,1表示好,0表示坏,i=j时一律为1(并不表示该芯片对本身的测试结果。芯片不能对本 身进行测试)。
+```
+
+**输出**
+```
+按从小到大的顺序输出所有好芯片的编号
+```
+**样例输入**
+```
+3
+1 0 1
+0 1 0
+1 0 1
+```
+**样例输出**
+```
+1 3
+```
+
+
+```
+n=int(input())
+map_=[]
+dic={}
+for i in range(n):
+ temp=input().split()
+ map_.append(temp)
+ dic[tuple(temp)]=dic.get(tuple(temp),0)+1
+a=max(dic,key=dic.get)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+```
+
+ 3
+ 1 0 1
+ 0 1 0
+ 1 0 1
+ 1 3
+
+
+```
+n=int(input())
+map_=[]
+dt={}
+for i in range(n):
+ temp=list(map(int ,input().split()))
+ map_.append(temp)
+ dt[tuple(temp)]=dt.get(tuple(temp),0)+1
+
+a=max(dt,key=dt.get)
+# b=max(dt.values())#,key=dt.values()
+# print(b)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+
+```
+
+ 3
+ 1 1 1
+ 1 1 1
+ 1 11
+ 2
+ 1 2
+
+**python 字典获取最大和最小的value**
+
+
+```
+my_dict = {'x':500, 'y':5874, 'z': 560}
+
+key_max = max(my_dict.keys(), key=(lambda k: my_dict[k]))
+key_min = min(my_dict.keys(), key=(lambda k: my_dict[k]))
+
+print('Maximum Value: ',my_dict[key_max])
+print('Minimum Value: ',my_dict[key_min])
+```
+
+可以用max(dict,key=dict.get)方法获得字典dict中value的最大值所对应的键的方法,max(dict, key)方法首先遍历迭代器,并将返回值作为参数传递给key对应的函数,然后将函数的执行结果传给key,并以此时key值为标准进行大小判断,返回最大值
+
+**sorted函数使用**
+
+
+```
+a=[1,2,3]
+sorted(a)
+```
+
+
+
+
+ [1, 2, 3]
+
+
+
+
+```
+L=[('b',2),('a',1),('c',3),('d',4)]
+
+sorted(L, key=lambda x:x[1])
+```
+
+
+
+
+ [('a', 1), ('b', 2), ('c', 3), ('d', 4)]
+
+
+
+
+```
+from operator import itemgetter, attrgetter
+L=[('b',2,2),('a',1,1),('c',3,3),('d',4,4),('e',4,3)]
+print(sorted(L, key=lambda x:(x[1],x[2]) ))
+
+```
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+```
+sorted(L, key=itemgetter(1,2))
+```
+
+
+
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md b/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md
new file mode 100644
index 0000000..274fb2a
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md
@@ -0,0 +1,177 @@
+龟兔赛跑预测
+
+时间限制: 1Sec 内存限制: 128MB 提交: 3055 解决: 818
+
+**题目描述**
+```
+话说这个世界上有各种各样的兔子和乌龟,但是 研究发现,所有的兔子和乌龟都有一个共同的特点——喜欢赛跑。于是世界上各个角落都不断在发生着乌龟和兔子的比赛,小华对此很感兴趣,于是决定研究不同兔 子和乌龟的赛跑。他发现,兔子虽然跑比乌龟快,但它们有众所周知的毛病——骄傲且懒惰,于是在与乌龟的比赛中,一旦任一秒结束后兔子发现自己领先t米或以 上,它们就会停下来休息s秒。对于不同的兔子,t,s的数值是不同的,但是所有的乌龟却是一致——它们不到终点决不停止。
+
+然而有些比赛相当漫长,全程观看会耗费大量时间,而小华发现只要在每场比赛开始后记录下兔子和乌龟的数据——兔子的速度v1(表示每秒兔子能跑v1 米),乌龟的速度v2,以及兔子对应的t,s值,以及赛道的长度l——就能预测出比赛的结果。但是小华很懒,不想通过手工计算推测出比赛的结果,于是他找 到了你——清华大学计算机系的高才生——请求帮助,请你写一个程序,对于输入的一场比赛的数据v1,v2,t,s,l,预测该场比赛的结果。
+```
+**输入**
+
+- 输入只有一行,包含用空格隔开的五个正整数v1,v2,t,s,l,其中(v1,v2< =100;t< =300;s< =10;l< =10000且为v1,v2的公倍数)
+
+**输出**
+
+- 输出包含两行,第一行输出比赛结果——一个大写字母“T”或“R”或“D”,分别表示乌龟获胜,兔子获胜,或者两者同时到达终点。
+
+- 第二行输出一个正整数,表示获胜者(或者双方同时)到达终点所耗费的时间(秒数)。
+
+**样例输入**
+```
+10 5 5 2 20
+```
+**样例输出**
+```
+D
+4
+```
+
+
+```
+# v1,v2,t,s,l=map(int ,input().split())
+
+# l1=0
+# l2=0
+# l1time=0
+# l2time=0
+# while True:
+# dettime=(t-l1+l2)/(v1-v2)
+# #print('dettime',dettime)
+# detl1=dettime*v1
+# #print('detl1',detl1)
+# detl2=dettime*v2
+# #print('detl2',detl2)
+# if l1+detl1>=l or l2+detl2>=l:
+# l1time+=(l-l1)/v1
+# l2time+=(l-l2)/v2
+# if l1time>l2time:
+# print('T')
+# print(int(l2time))
+# print('l2',l2)
+# break
+# elif l1time==l2time:
+# print('D')
+# print(int(l1time))
+# break
+# else:
+# print('R')
+# print(int(l1time))
+# break
+# else:
+# l1+=detl1
+# if l2+detl2+s*v2>l:
+# print('T')
+# l2time+=dettime+(l-(l2+detl2))/v2
+# #print(int(l2time))
+# l2+=detl2+s*v2
+# l1time+=dettime+s
+# l2time+=dettime+s
+
+```
+
+ 25 10 20 3 100
+ dettime 1.3333333333333333
+ detl1 33.33333333333333
+ detl2 13.333333333333332
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ R
+ 9
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int,input().split())
+l1=0
+l2=0
+l1_time=0
+l2_time=0
+while True:
+ if l1-l2>=t:
+ l2+=v2*s
+ l1_time+=s
+ l2_time+=s
+ dt1=l1_time+(l-l1)/v1
+ dt2=l2_time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1_time+=1
+ l2_time+=1
+ if l1>=l or l2>=l:
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt2))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+```
+
+ 10 5 5 2 20
+ D
+ 4
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int ,input().split())
+l1=0
+l2=0
+l1time=0
+l2time=0
+while True:
+ if l1-l2>=t:
+ l2+=s*v2
+ l1time+=s
+ l2time+=s
+ dt1=l1time+(l-l1)/v1
+ dt2=l2time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1time+=1
+ l2time+=1
+ if l1>=l or l2>=l:
+# if l1>l2:
+# print('R')
+# print(l1time)
+# break
+# elif l1==l2:
+# print('D')
+# print(l1time)
+# break
+# else:
+# print('T')
+# print(l2time)
+# break
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ #print('l2',l2)
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt1))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+
+```
+
+ 83 37 193 8 9213
+ R
+ 247
diff --git a/LanQiao/蓝桥杯习题/三角形面积.md b/LanQiao/蓝桥杯习题/三角形面积.md
new file mode 100644
index 0000000..3664db0
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/三角形面积.md
@@ -0,0 +1,28 @@
+# 三角形面积
+
+已知三角形三个顶点在直角坐标系下的坐标分别为:
+
+(2.3, 2.5)
+
+(6.4, 3.1)
+
+(5.1, 7.2)
+
+求该三角形的面积。
+
+注意,要提交的是一个小数形式表示的浮点数。
+要求精确到小数后3位,如不足3位,需要补零。
+
+
+```
+a=(2.3,2.5)
+b=(6.4, 3.1)
+c=(5.1, 7.2)
+di=((a[0]-b[0])**2+(a[1]-b[1])**2)**(1/2)
+k=(a[1]-b[1])/(a[0]-b[0])
+b_=a[1]-k*a[0]
+h=(c[1]-c[0]*k-b_)/(1+k**2)**(1/2)
+print((h*di)/2)
+```
+
+ 8.795000000000002
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/只出现一次的数II.md b/LanQiao/蓝桥杯习题/只出现一次的数II.md
new file mode 100644
index 0000000..527887c
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/只出现一次的数II.md
@@ -0,0 +1,34 @@
+## 只出现一次的数字||
+
+
+```
+def singleNumber( nums) -> int:
+ one=0
+ two=0
+ three=0
+ for num in nums:
+ two|=one&num
+ one=one^num
+ three|=one&two
+ print(three)
+ print('{:b}'.format(three))
+ one=one&~three
+ two=two&~three
+ return one
+singleNumber([2,2,3,2])
+```
+
+ 0
+ 0
+ 0
+ 0
+ 2
+ 10
+ 2
+ 10
+
+
+
+
+
+ 1
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/回文数.md b/LanQiao/蓝桥杯习题/回文数.md
new file mode 100644
index 0000000..f30a490
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/回文数.md
@@ -0,0 +1,13 @@
+## 回文数
+
+
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ print(i*1000+i+j*100+j*10)
+```
+
+
+
diff --git a/LanQiao/蓝桥杯习题/子母图形.md b/LanQiao/蓝桥杯习题/子母图形.md
new file mode 100644
index 0000000..74232fc
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/子母图形.md
@@ -0,0 +1,201 @@
+## 子母图形
+
+**问题描述**
+
+```
+利用字母可以组成一些美丽的图形,下面给出了一个例子:
+
+ABCDEFG
+
+BABCDEF
+
+CBABCDE
+
+DCBABCD
+
+EDCBABC
+
+这是一个5行7列的图形,请找出这个图形的规律,并输出一个n行m列的图形。
+```
+
+**输入格式**
+
+```
+输入一行,包含两个整数n和m,分别表示你要输出的图形的行数的列数。
+```
+
+**输出格式**
+
+```
+输出n行,每个m个字符,为你的图形。
+```
+
+**样例输入**
+
+```
+5 7
+```
+
+**样例输出**
+
+```
+ABCDEFG
+BABCDEF
+CBABCDE
+DCBABCD
+EDCBABC
+```
+
+**数据规模与约定**
+
+```
+1 <= n, m <= 26。
+```
+
+
+```
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'
+]
+t1=q[0:mn[1]]
+print(''.join(t1))
+#print('t1',t1[1],type(t1[1]))
+
+for i in range(1,mn[0]):
+ if i==1:
+ print( ''.join(list(t1[1])+t1[0:-i]))
+ else:
+ t2[:]=reversed(t1[1:i+1])
+ print(''.join(t2+t1[0:-i]))
+```
+
+
+```
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'
+]
+t1=q[0:mn[1]]
+print(''.join(t1))
+#print('t1',t1[1],type(t1[1]))
+j=1
+start=0
+for i in range(1,mn[0]):
+ if j==1:
+ print( ''.join(list(t1[1])+t1[start:-j]))
+ else:
+ t2[:]=reversed(t1[start+1:j+1])
+ print(''.join(t2+t1[start:-j]))
+ j=j+1
+ if j>=mn[0]:
+ j=j-mn[0]
+ start+=1
+```
+
+**上面的思路错了,下面的是对的**
+
+
+```
+def op1(mn,t1):
+ print(''.join(t1[0:mn[1]]))
+ #print('t1',t1[1],type(t1[1]))
+ re=[]
+ for i in range(1,mn[0]):
+ if i==1:
+ re=list(t1[1])+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+ else:
+ t2=[]
+ t2[:]=reversed(t1[1:i+1])
+ re=t2+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+
+
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
+op1(mn,q)
+
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+```
+a=[1,2,3,3.3]
+for i in a:
+ print(i,end='')
+```
+
+ 1122333.33.3
+
+
+```
+print(chr(65))
+```
+
+ A
+
+
+
+```
+m,n=map(int,input().split())
+s=0
+for i in range(m):
+ k=65+i
+ for j in range(n):
+ print(chr(k), end='')
+ if k==65:
+ s=1
+ if s==0:
+ k=k-1
+ else:
+ k=k+1
+ s=0
+ print()
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+##
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/序列求和.md b/LanQiao/蓝桥杯习题/序列求和.md
new file mode 100644
index 0000000..7136b28
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/序列求和.md
@@ -0,0 +1,56 @@
+## 序列求和
+
+**问题描述**
+
+```
+求1+2+3+…+n的值。
+```
+
+**输入格式**
+
+- 输入包括一个整数n。
+
+**输出格式**
+
+- 输出一行,包括一个整数,表示1+2+3+…+n的值。
+
+**样例输入**
+
+```
+4
+```
+
+**样例输出**
+
+```
+10
+```
+
+**样例输入**
+
+```
+100
+```
+
+**样例输出**
+
+```
+5050
+```
+
+**数据规模与约定**
+
+```
+1 <= n <= 1,000,000,000。
+```
+
+
+```
+a=int(input())
+res=0
+for i in range(1,a+1):
+ res+=i
+print(int(((1+a)/2)*a))
+```
+
+##
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/找假币.md b/LanQiao/蓝桥杯习题/找假币.md
new file mode 100644
index 0000000..f74a75b
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/找假币.md
@@ -0,0 +1,96 @@
+# 找假币
+
+
+
+
+```
+
+标题:找假币
+
+在8枚硬币中,有1枚假币,假币外观与真币一模一样,只是重量略轻或略重一点。
+给你一架天平,要求最多称3次,就找出假币,并且知道它是重一些还是轻一些。
+下面的代码给出一个解决方案,仔细分析逻辑,填写划线位置缺少的代码。
+
+#include
+
+int balance(int a, int b)
+{
+ if(ab) return 1;
+ return 0;
+}
+
+void judge(char* data, int a, int b, int std)
+{
+ switch(balance(data[a],data[std])){
+ case -1:
+ printf("%d light\n", a);
+ break;
+ case 0:
+ printf("%d heavy\n", b);
+ break;
+ case 1:
+ printf("err!\n", b);
+ }
+}
+
+// data 中8个元素,有一个假币,或轻或重
+void f(char* data)
+{
+ switch(balace(data[0]+data[2]+data[1],data[5]+data[4],data[3]) ____________________________________ ){ // 填空
+ case -1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,0,3,1);
+ break;
+ case 0:
+ judge(data,2,5,0);
+ break;
+ case 1:
+ judge(data,1,4,0);
+ }
+ break;
+ case 0:
+ judge(data,6,7,0);
+ break;
+ case 1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,4,1,0);
+ break;
+ case 0:
+ judge(data,5,2,0);
+ break;
+ case 1:
+ judge(data,3,0,1);
+ }
+ break;
+ }
+}
+
+int main()
+{
+ int n;
+ char buf[100];
+
+ scanf("%d", &n);
+ gets(buf);
+
+ int i;
+ for(i=0; ia[2i]。
+ 小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
+```
+**输入格式**
+
+ 输入一行包含两个整数 m,n。
+
+**输出格式**
+
+输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
+
+**样例输入**
+
+3 4
+
+**样例输出**
+
+14
+
+**样例说明**
+
+```
+ 以下是符合要求的摆动序列:
+ 2 1 2
+ 2 1 3
+ 2 1 4
+ 3 1 2
+ 3 1 3
+ 3 1 4
+ 3 2 3
+ 3 2 4
+ 4 1 2
+ 4 1 3
+ 4 1 4
+ 4 2 3
+ 4 2 4
+ 4 3 4
+```
+**评测用例规模与约定**
+```
+ 对于 20% 的评测用例,1 <= n, m <= 5;
+ 对于 50% 的评测用例,1 <= n, m <= 10;
+ 对于 80% 的评测用例,1 <= n, m <= 100;
+ 对于所有评测用例,1 <= n, m <= 1000。
+```
+
+
+```
+a=[1,2]+[3]
+print(a)
+```
+
+ [1, 2, 3]
+
+
+
+```
+m,n=map(int,input().split())
+res=[]
+for k in range(1,n+1):
+ res.append([k])
+while len(res[0]) in
+ 1 p=2
+ 2 a='%.{0}f'.format(p)
+ ----> 3 b='{2}{0}.{1}f{3}}'.format(':',p,'{','}')
+ 4 print(b.format(t1+t2+t3))
+ 5 print(a%(t1+t2+t3))
+
+
+ ValueError: Single '}' encountered in format string
+
+
+
+```
+chr(115)
+```
+
+
+
+
+ 's'
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md b/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md
new file mode 100644
index 0000000..27572e4
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md
@@ -0,0 +1,141 @@
+## 试题 算法训练 Sereja and Squares
+
+提交此题
+资源限制
+时间限制:4.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ Sereja在平面上画了n个点,点i在坐标(i,0)。然后,Sereja给每个点标上了一个小写或大写英文字母。Sereja不喜欢字母"x",所以他不用它标记点。Sereja认为这些点是漂亮的,当且仅当:
+ ·所有的点可以被分成若干对,使得每个点恰好属于一一对之中。
+ ·在每对点中,横坐标较小的会被标上小写字母,较大的会被标上对应的大写字母。
+ ·如果我们在每对点上画一个正方形,其中已知的一对点会作为正方形的相对的顶点,它们间的线段会成为正方形的对角线,那么在所有画出的正方形中不会有相交或触碰的情况。
+ 小Petya擦掉了一些小写字母和所有大写字母,现在Sereja想知道有多少种方法来还原每个点上的字母,使得还原后这些点是漂亮的。
+```
+**输入格式**
+```
+ 第一行是一个整数n,表示点的个数。
+ 第二行是一个长度为n的字符串,包含小写字母和问号"?",是按照横坐标递增的顺序的每个点的描述。问号表示这个点的字母被Petya擦掉了。保证输入串不含字母"x"。
+```
+**输出格式**
+```
+ 输出答案对4294967296取模的值。如果没有可行的方案,输出0。
+```
+
+**样例输入**
+
+```
+4
+a???
+```
+
+**样例输出**
+
+```
+50
+```
+
+**样例输入**
+
+```
+4
+abc?
+```
+
+**样例输出**
+
+```
+0
+```
+
+**样例输入**
+
+```
+6
+abc???
+
+```
+
+**样例输出**
+
+```
+1
+
+```
+
+**数据规模和约定**
+
+```
+ 20个测试点的n分别为:
+ 5,10,20,50,100,
+ 200,500,1000,2000,5000,
+ 10000,20000,30000,40000,50000,
+ 60000,70000,80000,90000,100000.
+```
+
+
+```
+# print('a'>'b')
+# print(ord('a'))
+# print(ord('A'))
+# print(ord('a')-ord('A'))
+# print(ord('b')-ord('B'))
+n=int(input())
+s=list(input())
+len_=0
+re=1
+label=0
+temp2=26
+for j in s:
+ if j=='?':
+ len_+=1
+for i in range(n):
+ if s[i]>='a'and s[i]<='z':
+ temp2-=1
+ if chr(ord(s[i])+32)in s[i:]:
+ s.remove(chr(ord(s[i])+32))
+ else:
+ if len_<=0:
+ label=1
+ break
+# re*=len_
+ len_-=1
+# print(re,len_)
+
+# print('test1',re)
+if len_%2!=0:
+ label=1
+else:
+ temp=len_//2
+ for i in range(temp):
+ re*=temp2
+ temp2-=1
+# temp-=1
+print('test2',re)
+if label ==1:
+ print(0)
+else:
+ if len_==0:
+ print(1)
+ else:
+ print(re*(2**temp))
+```
+
+ 10
+ ??????????
+ test2 7893600
+ 252595200
+
+
+
+```
+410156250/(25**5)
+# 410156250/252595200
+# 4294967296
+5*4*3*2
+```
+
+
+
+
+ 120
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md b/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md
new file mode 100644
index 0000000..6036ba5
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md
@@ -0,0 +1,65 @@
+## 试题 算法训练 Yaroslav and Algorithm
+
+提交此题
+资源限制
+时间限制:100ms 内存限制:128.0MB
+
+**问题描述**
+```
+ (这道题的数据和SPJ已完工,尽情来虐吧!)
+
+ Yaroslav喜欢算法。我们将描述一个他最喜欢的算法。
+
+ 1.这个算法接受一个字符串作为输入。我们设这个输入字符串为a。
+ 2.这个算法由一些命令组成。i号命令的形式为"s[i]>>w[i]"或"s[i]<>w[i]",其中s[i]和w[i]是长度不超过7的字符串(可以为空),由数字或字符"?"组成。
+ 3.这个算法每次寻找一个编号最小的命令i,使得s[i]是a的子串。如果没有找到这样的命令,那么整个算法终止。
+ 4.设找到的命令编号为k。在字符串a中,s[k]第一次出现的位置会被w[k]替换。如果这个命令形如"s[k]>>w[k]",那么这个算法继续执行(译注:回到第3步)。否则,算法终止。
+ 5.算法的输出就是算法终止时字符串a的值。
+
+ Yaroslav有一个n个正整数的集合,他需要一个这样的算法,且能够使每一个数加1。更正式地,如果我们把每个数看成一个十进制表示的字符串,那么对于每个字符串独立地运行这个算法,这个算法需要输出一个输入串对应的数+1的字符串。
+ 帮帮他吧!
+
+```
+**输入格式**
+
+ - 第一行包含一个整数n(集合中数的个数),接下来n行,每行包含一个正整数。
+
+**输出格式**
+```
+ 输出一个符合题意的算法(能够分别将每个数增加1)。第i行输出这个算法的第i个命令,不包含空格。
+ 你的算法将会对于每个输入运行一遍。你的输出会被认为是正确的,当且仅当:
+ ·每行都是一个合法的命令(格式见题目描述)
+ ·命令的条数不能超过50。
+ ·算法需要对每个给出的数+1。
+ ·为了得到结果,算法必须对于每个输入都执行不超过200步。
+```
+**样例输入**
+```
+2
+10
+79
+```
+**样例输出**
+```
+10<>11
+79<>80
+
+```
+**数据规模和约定**
+
+ 1≤每个数≤10^25。共有20个测试点,对于第i个测试点,n=5i。
+
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=int(input())
+ print(str(temp)+'<>'+str(temp+1))
+```
+
+ 2
+ 10
+ 10<>11
+ 79
+ 79<>80
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/约瑟夫环.md b/LanQiao/蓝桥杯习题/约瑟夫环.md
new file mode 100644
index 0000000..e4c377b
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/约瑟夫环.md
@@ -0,0 +1,58 @@
+## 约瑟夫环
+```
+n 个人的编号是 1~n,如果他们依编号按顺时针排成一个圆圈,从编号是1的人开始顺时针报数。
+(报数是从1报起)当报到 k 的时候,这个人就退出游戏圈。下一个人重新从1开始报数。
+求最后剩下的人的编号。这就是著名的约瑟夫环问题。
+
+本题目就是已知 n,k 的情况下,求最后剩下的人的编号。
+
+题目的输入是一行,2个空格分开的整数n, k
+要求输出一个整数,表示最后剩下的人的编号。
+
+约定:0 < n,k < 1百万
+```
+**例如输入:**
+```
+10 3
+```
+**程序应该输出:**
+```
+4
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+```
+
+- 请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+
+```
+
+
+```
+n,k=map(int,input().strip().split())
+re=[i for i in range(1,n+1)]
+start=0
+while len(re)!=1:
+
+ for i in range(k-1):
+ start=(start+1)%len(re)
+ re.pop(start)
+ start=start%len(re)
+# print(re)
+print(re[0])
+```
+
+ 10 3
+ 4
diff --git a/LanQiao/蓝桥杯习题/自描述序列.md b/LanQiao/蓝桥杯习题/自描述序列.md
new file mode 100644
index 0000000..35b6073
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/自描述序列.md
@@ -0,0 +1,75 @@
+## 自描述序列
+```
+小明在研究一个序列,叫Golomb自描述序列,不妨将其记作{G(n)}。这个序列有2个很有趣的性质:
+
+1. 对于任意正整数n,n在整个序列中恰好出现G(n)次。
+2. 这个序列是不下降的。
+
+以下是{G(n)}的前几项:
+
+n 1 2 3 4 5 6 7 8 9 10 11 12 13
+G(n)1 2 2 3 3 4 4 4 5 5 5 6 6
+
+给定一个整数n,你能帮小明算出G(n)的值吗?
+```
+**输入**
+```
+----
+一个整数n。
+
+对于30%的数据,1 <= n <= 1000000
+对于70%的数据,1 <= n <= 1000000000
+对于100%的数据,1 <= n <= 2000000000000000
+```
+**输出**
+```
+----
+一个整数G(n)
+
+```
+**【样例输入】**
+```
+13
+```
+**【样例输出】**
+```
+6
+```
+
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+
+```
+n=int(input())
+dic_={1:1,2:2}
+num=1
+i=1
+while num<=n:
+# print(dic_)
+ for j in range(dic_[i]):
+ dic_[num]=i
+ num+=1
+ i+=1
+print(dic_[n])
+
+```
+
+ 13
+ 6
diff --git a/LanQiao/蓝桥杯习题/蓝桥杯 (2).md b/LanQiao/蓝桥杯习题/蓝桥杯 (2).md
new file mode 100644
index 0000000..1b1c1f4
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/蓝桥杯 (2).md
@@ -0,0 +1,10066 @@
+## 题目 1669: 求圆的面积
+
+时间限制: 1Sec 内存限制: 128MB 提交: 13903 解决: 6011
+
+**题目描述**
+```
+题目很简单,已知半径r,求一个圆的面积是多大。
+
+公式不用提了吧~~
+```
+**输入**
+
+- 输入一个半径,浮点类型~
+
+**输出**
+
+- 输出它对应的面积大小,保留两位小数哦!
+
+**样例输入**
+```
+2
+```
+**样例输出**
+```
+12.57
+```
+
+
+```
+import math
+PI=3.14159265358979323
+r=float(input())
+from decimal import *
+a=PI*r*r
+print ('%.7f'%a)
+```
+
+ 2
+ 12.5663706
+
+
+
+```
+import math
+math.pi
+```
+
+
+
+
+ 3.141592653589793
+
+
+
+
+```
+a=int(input())
+
+temp1=1
+temp2=1
+res=0
+t=0
+for i in range(3,a+1):
+ res=(temp1+temp2)%10007
+ temp1=temp2%10007
+ temp2=res%10007
+# if res >10007:
+# print(res%10007)
+# t=1
+# break
+if a<=2: #t==0 and
+ print(1)
+elif a>2: #t==0 and
+ print(res%10007)
+
+```
+
+## 序列求和
+
+**问题描述**
+```
+求1+2+3+…+n的值。
+```
+**输入格式**
+
+- 输入包括一个整数n。
+
+**输出格式**
+
+- 输出一行,包括一个整数,表示1+2+3+…+n的值。
+
+**样例输入**
+```
+4
+```
+**样例输出**
+```
+10
+```
+**样例输入**
+```
+100
+```
+**样例输出**
+```
+5050
+```
+**数据规模与约定**
+```
+1 <= n <= 1,000,000,000。
+```
+
+
+```
+a=int(input())
+res=0
+for i in range(1,a+1):
+ res+=i
+print(int(((1+a)/2)*a))
+```
+
+## 题目 1853: [蓝桥杯][基础练习]数列排序
+
+时间限制: 1Sec 内存限制: 128MB 提交: 982 解决: 628
+
+**题目描述**
+
+- 给定一个长度为n的数列,将这个数列按从小到大的顺序排列。1<=n<=200
+
+**输入**
+```
+第一行为一个整数n。
+第二行包含n个整数,为待排序的数,每个整数的绝对值小于10000。
+```
+**输出**
+
+- 输出一行,按从小到大的顺序输出排序后的数列。
+
+**样例输入**
+```
+5
+8 3 6 4 9
+
+```
+**样例输出**
+```
+3 4 6 8 9
+```
+
+
+```
+a=int(input())
+num=sorted(list(map(int,input().strip().split())))
+for i in num:
+ print(i,end=' ')
+```
+
+ 5
+ 8 3 6 4 9
+ 3 4 6 8 9
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+## 进制转换
+
+ASCII码转换为int:ord('A') 65
+
+int转为ASCII码:chr(65) 'A'
+
+在日常生活中我们频繁使用到数学的进制,如季度逢三进一,星期逢七进一;×××、小时使用12进制,每天使用24进制,每月使用30进制,分秒使用60进制,一年使用360进制等等;在编程过程中我们经常需要转换进制,虽然Python已经内置了常用进制转换函数,如int,bin,hex,oct;但是如果我们需要转换成其他进制怎么办呢?
+
+ 我们知道,十进制转换成二进制时,使用“除2取余,逆序排列”即可。二进制转换成十进制时按权展开,即可得到十进制。类似地可以实现十进制转换成任意进制,任意进制也可以转换成十进制;通过十进制进行中转,即可实现任意进制数之间的转换了。
+
+
+
+```
+#将十进制数转换成任意进制20进制以内,任意进制只需添加不同的符号即可
+def decimalToAny(num,n):
+ if num==0:
+ return 0
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+97)
+ print(baseStr)
+ new_num_str = ""
+ while num != 0:
+ remainder = num % n
+ if remainder > 9:
+ remainder_string = baseStr[remainder]
+ else:
+ remainder_string = str(remainder)
+ new_num_str = remainder_string+new_num_str
+ num = num // n
+ return new_num_str
+decimalToAny(58,30)
+```
+
+ {10: 'a', 11: 'b', 12: 'c', 13: 'd', 14: 'e', 15: 'f', 16: 'g', 17: 'h', 18: 'i', 19: 'j', 20: 'k', 21: 'l', 22: 'm', 23: 'n', 24: 'o', 25: 'p', 26: 'q', 27: 'r', 28: 's', 29: 't'}
+
+
+
+
+
+ '1s'
+
+
+
+
+```
+#将任意进制数转换成十进制
+def anyToDecimal(num,n):
+ baseStr={}
+ for i in range(10):
+ baseStr[str(i)]=i
+ for i in range(10,n):
+ baseStr[chr(i-10+97)]=i
+ print(baseStr)
+ new_num = 0
+ for i in range(len(num)):
+ new_num+=baseStr[num[len(num)-1-i]]*(n**i)
+ return new_num
+anyToDecimal('1s',30)
+```
+
+ {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9, 'a': 10, 'b': 11, 'c': 12, 'd': 13, 'e': 14, 'f': 15, 'g': 16, 'h': 17, 'i': 18, 'j': 19, 'k': 20, 'l': 21, 'm': 22, 'n': 23, 'o': 24, 'p': 25, 'q': 26, 'r': 27, 's': 28, 't': 29}
+
+
+
+
+
+ 58
+
+
+
+
+```
+print('{0}xxxxxxxx{1}'.format('这是0要传入的东西','这是1要传入的东西'))
+```
+test={'nan':'werty'}
+print("ghjk{nan}gbhnjmk".format(**test))
+test
+进制转化,b o d x 分别表示二、八、十、十六进制
+
+
+```
+print('{:b}'.format(250))
+print('{:o}'.format(250))
+print('{:d}'.format(250))
+print('{:x}'.format(250))
+#千分位分隔符,这种情况只针对与数字
+print('{:,}'.format(100000000))
+print('{:,}'.format(235445.234235))
+```
+
+ 11111010
+ 372
+ 250
+ fa
+ 100,000,000
+ 235,445.234235
+
+
+精度和类型f精度常和f一起使用
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+ 4.2
+ 4.1000
+
+
+## 题目 2080: [蓝桥杯][基础练习]十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+**题目描述**
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+**输入**
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+**输出**
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+**样例输入**
+```
+2
+39
+123ABC
+```
+**样例输出**
+```
+71
+4435274
+```
+
+
+```
+
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
+
+
+## 题目 2082: [蓝桥杯][基础练习]十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+**题目描述**
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+**输入**
+```
+一个十六进制数
+
+```
+**输出**
+```
+对应得十进制
+```
+**样例输入**
+```
+FFFF
+```
+**样例输出**
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
+## 题目 2083: [蓝桥杯][基础练习]十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+**题目描述**
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+**输入**
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+**输出**
+```
+输出这个整数的16进制表示
+```
+**样例输入**
+```
+30
+```
+**样例输出**
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
+
+## 题目 2084: [蓝桥杯][基础练习]特殊回文数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 663 解决: 312
+
+**题目描述**
+```
+123321是一个非常特殊的数,它从左边读和从右边读是一样的。
+输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。
+
+```
+**输入**
+```
+输入一行,包含一个正整数n。
+```
+
+**数据规模和约定**
+```
+1<=n<=54。
+```
+**输出**
+
+- 按从小到大的顺序输出满足条件的整数,每个整数占一行。
+
+**样例输入**
+```
+52
+```
+**样例输出**
+```
+899998
+989989
+998899
+```
+
+
+```
+n=int(input())
+list_=[]
+for i in range(1,10):
+ for j in range(0,10):
+ for k in range(0,10):
+ if 2*(i+j+k)==n:
+ list_.append(i*100000+i+j*10000+j*10+k*1000+k*100)
+ if (2*i+2*j+k)==n:
+ list_.append(i*10000+i+j*1000+j*10+k*100)
+a=list(set(list_))
+a.sort()
+for i in range(len(a)):
+ print(a[i])
+```
+
+## 回文数
+
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ print(i*1000+i+j*100+j*10)
+```
+
+## 特殊的数字
+**资源限制**
+时间限制:1.0s 内存限制:512.0MB
+
+**问题描述**
+- 153是一个非常特殊的数,它等于它的每位数字的立方和,即153=111+555+333。编程求所有满足这种条件的三位十进制数。
+
+**输出格式**
+- 按从小到大的顺序输出满足条件的三位十进制数,每个数占一行。
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (i*i*i+j*j*j+k*k*k)==(i*100+j*10+k):
+ print(i*100+j*10+k)
+```
+
+## 杨辉三角形
+
+
+
+```
+n=int(input())
+temp=[1]
+for i in range(n):
+ print(' '.join(list(map(str,temp))))
+ n1=len(temp)
+ t1=[1]
+ j=0
+ while j+1=mn[0]:
+ j=j-mn[0]
+ start+=1
+```
+
+**上面的思路错了,下面的是对的**
+
+
+```
+def op1(mn,t1):
+ print(''.join(t1[0:mn[1]]))
+ #print('t1',t1[1],type(t1[1]))
+ re=[]
+ for i in range(1,mn[0]):
+ if i==1:
+ re=list(t1[1])+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+ else:
+ t2=[]
+ t2[:]=reversed(t1[1:i+1])
+ re=t2+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+
+
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
+op1(mn,q)
+
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+```
+a=[1,2,3,3.3]
+for i in a:
+ print(i,end='')
+```
+
+ 1122333.33.3
+
+
+```
+print(chr(65))
+```
+
+ A
+
+
+
+```
+m,n=map(int,input().split())
+s=0
+for i in range(m):
+ k=65+i
+ for j in range(n):
+ print(chr(k), end='')
+ if k==65:
+ s=1
+ if s==0:
+ k=k-1
+ else:
+ k=k+1
+ s=0
+ print()
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+## 01字串
+
+**问题描述**
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
+## 闰年判断
+
+
+```
+a=int(input())
+if (a%4==0 and a//4!=0) and not(a%100==0and a//100!=0) or(a%400==0and a//400!=0):
+ print('yes')
+else:
+ print('no')
+
+```
+
+ 5
+ no
+
+
+## 题目 1039: [编程入门]宏定义之闰年判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6412 解决: 4348
+
+**题目描述**
+```
+给年份year,定义一个宏,以判别该年份是否闰年。提示:宏名可以定义为LEAP_YEAR,形参为y,既定义宏的形式为 #define LEAP_YEAR(y) (读者设计的字符串)
+
+```
+**输入**
+
+- 一个年份
+
+**输出**
+
+- 根据是否闰年输出,是输出"L",否输出"N"
+
+**样例输入**
+```
+2000
+```
+**样例输出**
+```
+L
+```
+
+
+```
+a=int(input())
+if (a%4==0 and a//4!=0) and not(a%100==0and a//100!=0) or(a%400==0and a//400!=0):
+ print('L')
+else:
+ print('N')
+```
+
+ 2000
+ L
+
+
+## 题目 1474: [蓝桥杯][基础练习VIP]阶乘计算
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1948 解决: 858
+
+**题目描述**
+```
+输入一个正整数n,输出n!的值。
+
+其中n!=1*2*3*…*n。
+
+算法描述
+
+n!可能很大,而计算机能表示的整数范围有限,需要使用高精度计算的方法。使用一个数组A来表示一个大整数a,A[0]表示a的个位,A[1]表示a的十位,依次类推。
+
+将a乘以一个整数k变为将数组A的每一个元素都乘以k,请注意处理相应的进位。
+
+首先将a设为1,然后乘2,乘3,当乘到n时,即得到了n!的值。
+
+```
+**输入**
+```
+输入包含一个正整数n,n< =1000。
+
+```
+**输出**
+```
+输出n!的准确值。
+
+```
+**样例输入**
+```
+10
+```
+**样例输出**
+```
+3628800
+```
+
+
+```
+n=int(input())
+res=1
+for i in range(1,n+1):
+ res*=i
+print(res)
+```
+
+ 10
+ 3628800
+
+
+
+```
+n=int(input())
+def op (res,k):
+ carry=0
+ for i in range(len(res)):
+ temp=res[i]*k+carry
+ res[i]=temp%10
+ carry=temp//10
+ while carry!=0:
+ res.append(carry%10)
+ carry//=10
+ return res
+res=[1]
+for i in range(1,n+1):
+ res=op(res,i)
+for i in res[::-1]:
+ print(i,end='')
+```
+
+ 10
+ 3628800
+
+
+```
+def op (k,res):
+ n=len(res)
+ temp=0
+ for i in range(n):
+ t=res[i]*k+temp
+ res[i]=(t%10)
+ temp=t//10
+ while temp!=0:
+ res.append(temp%10)
+ temp=temp//10
+ return res
+n=int(input())
+res=[1]
+for i in range(1,n+1):
+ res=op(i,res)
+p=res[::-1]
+print(''.join(map(str,p)))
+```
+
+ 10
+ 3628800
+
+
+## 题目 1475: [蓝桥杯][基础练习VIP]高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+**题目描述**
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+- 输出一行,表示a + b的值。
+
+**样例输入**
+```
+20100122201001221234567890
+2010012220100122
+```
+**样例输出**
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_point1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
+
+
+## 题目 1460: [蓝桥杯][基础练习VIP]2n皇后问题
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
+
+
+## 题目 1468: [蓝桥杯][基础练习VIP]报时助手
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2238 解决: 867
+
+**题目描述**
+```
+给定当前的时间,请用英文的读法将它读出来。
+
+时间用时h和分m表示,在英文的读法中,读一个时间的方法是:
+
+如果m为0,则将时读出来,然后加上“o'clock”,如3:00读作“three o'clock”。
+
+如果m不为0,则将时读出来,然后将分读出来,如5:30读作“five thirty”。
+
+时和分的读法使用的是英文数字的读法,其中0~20读作:
+
+0:zero, 1: one, 2:two, 3:three, 4:four, 5:five, 6:six, 7:seven, 8:eight, 9:nine, 10:ten, 11:eleven, 12:twelve, 13:thirteen, 14:fourteen, 15:fifteen, 16:sixteen, 17:seventeen, 18:eighteen, 19:nineteen, 20:twenty。
+
+30读作thirty,40读作forty,50读作fifty。
+
+对于大于20小于60的数字,首先读整十的数,然后再加上个位数。如31首先读30再加1的读法,读作“thirty one”。
+
+按上面的规则21:54读作“twenty one fifty four”,9:07读作“nine seven”,0:15读作“zero fifteen”。
+```
+**输入**
+
+- 输入包含两个非负整数h和m,表示时间的时和分。非零的数字前没有前导0。h小于24,m小于60。
+
+**输出**
+
+- 输出时间时刻的英文。
+
+**样例输入**
+```
+0 15
+```
+**样例输出**
+```
+zero fifteen
+```
+
+
+```
+h,m=input().split()
+m=str(int(m))
+h=str(int(h))
+map_={'0':'zero', '1': 'one', '2':'two', '3':'three', '4':'four', '5':'five', '6':'six', '7':'seven', '8':'eight', '9':'nine', '10':'ten', '11':'eleven', '12':'twelve', '13':'thirteen', '14':'fourteen', '15':'fifteen', '16':'sixteen', '17':'seventeen', '18':'eighteen', '19':'nineteen', '20':'twenty'}
+if int(h)<=20:
+ str1=map_[h]
+elif (int(h))>20 and int(h)<30:
+ str1='twenty'+' '+map_[str(int(h)%10)]
+if m=='0':
+ str2='o\'clock'
+elif (int(m))>20 and int(m)<30:
+ str2='twenty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==3:
+ str2='thirty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==4:
+ str2='forty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==5:
+ str2='fifty'+' '+map_[str(int(m)%10)]
+else:
+ str2=map_[m]
+print(str1,end=' ')
+print(str2,end='')
+```
+
+ 20 21
+ twenty twenty one
+
+## 题目 1465: [蓝桥杯][基础练习VIP]回形取数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1831 解决: 590
+
+**题目描述**
+
+- 回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
+
+**输入**
+
+- 输入第一行是两个不超过200的正整数m, n,表示矩阵的行和列。接下来m行每行n个整数,表示这个矩阵。
+
+**输出**
+
+- 输出只有一行,共mn个数,为输入矩阵回形取数得到的结果。数之间用一个空格分隔,行末不要有多余的空格。
+
+**样例输入**
+```
+3 3
+1 2 3
+4 5 6
+7 8 9
+```
+**样例输出**
+```
+1 4 7 8 9 6 3 2 5
+```
+
+### 思路一
+
+
+```
+m,n=map(int,input().split())
+nn=[]
+for i in range(m):
+ nn.append(input().split())
+dir=[[1,0],[0,1],[-1,0],[0,-1]]
+re=[]
+x=0
+y=0
+state=0
+n_left=0
+m_left=0
+m_right=m-1
+n_right=n-1
+while len(re)m_right):
+ state=(state+1)%4
+ n_left+=1
+ elif((tx+x)n_right):
+ state=(state+1)%4
+ m_right-=1
+ elif ((ty+y)=l or l2+detl2>=l:
+# l1time+=(l-l1)/v1
+# l2time+=(l-l2)/v2
+# if l1time>l2time:
+# print('T')
+# print(int(l2time))
+# print('l2',l2)
+# break
+# elif l1time==l2time:
+# print('D')
+# print(int(l1time))
+# break
+# else:
+# print('R')
+# print(int(l1time))
+# break
+# else:
+# l1+=detl1
+# if l2+detl2+s*v2>l:
+# print('T')
+# l2time+=dettime+(l-(l2+detl2))/v2
+# #print(int(l2time))
+# l2+=detl2+s*v2
+# l1time+=dettime+s
+# l2time+=dettime+s
+
+```
+
+ 25 10 20 3 100
+ dettime 1.3333333333333333
+ detl1 33.33333333333333
+ detl2 13.333333333333332
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ R
+ 9
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int,input().split())
+l1=0
+l2=0
+l1_time=0
+l2_time=0
+while True:
+ if l1-l2>=t:
+ l2+=v2*s
+ l1_time+=s
+ l2_time+=s
+ dt1=l1_time+(l-l1)/v1
+ dt2=l2_time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1_time+=1
+ l2_time+=1
+ if l1>=l or l2>=l:
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt2))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+```
+
+ 10 5 5 2 20
+ D
+ 4
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int ,input().split())
+l1=0
+l2=0
+l1time=0
+l2time=0
+while True:
+ if l1-l2>=t:
+ l2+=s*v2
+ l1time+=s
+ l2time+=s
+ dt1=l1time+(l-l1)/v1
+ dt2=l2time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1time+=1
+ l2time+=1
+ if l1>=l or l2>=l:
+# if l1>l2:
+# print('R')
+# print(l1time)
+# break
+# elif l1==l2:
+# print('D')
+# print(l1time)
+# break
+# else:
+# print('T')
+# print(l2time)
+# break
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ #print('l2',l2)
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt1))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+
+```
+
+ 83 37 193 8 9213
+ R
+ 247
+
+
+## 题目 1473: [蓝桥杯][基础练习VIP]芯片测试
+
+时间限制: 1Sec 内存限制: 128MB 提交: 981 解决: 503
+
+**题目描述**
+```
+有n(2≤n≤20)块芯片,有好有坏,已知好芯片比坏芯片多。
+
+每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时,能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时,会随机给出好或是坏的测试结果(即此结果与被测试芯片实际的好坏无关)。
+
+给出所有芯片的测试结果,问哪些芯片是好芯片。
+```
+**输入**
+```
+输入数据第一行为一个整数n,表示芯片个数。
+
+第二行到第n+1行为n*n的一张表,每行n个数据。表中的每个数据为0或1,在这n行中的第i行第j列(1≤i, j≤n)的数据表示用第i块芯片测试第j块芯片时得到的测试结果,1表示好,0表示坏,i=j时一律为1(并不表示该芯片对本身的测试结果。芯片不能对本 身进行测试)。
+```
+
+**输出**
+```
+按从小到大的顺序输出所有好芯片的编号
+```
+**样例输入**
+```
+3
+1 0 1
+0 1 0
+1 0 1
+```
+**样例输出**
+```
+1 3
+```
+
+
+```
+n=int(input())
+map_=[]
+dic={}
+for i in range(n):
+ temp=input().split()
+ map_.append(temp)
+ dic[tuple(temp)]=dic.get(tuple(temp),0)+1
+a=max(dic,key=dic.get)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+```
+
+ 3
+ 1 0 1
+ 0 1 0
+ 1 0 1
+ 1 3
+
+
+```
+n=int(input())
+map_=[]
+dt={}
+for i in range(n):
+ temp=list(map(int ,input().split()))
+ map_.append(temp)
+ dt[tuple(temp)]=dt.get(tuple(temp),0)+1
+
+a=max(dt,key=dt.get)
+# b=max(dt.values())#,key=dt.values()
+# print(b)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+
+```
+
+ 3
+ 1 1 1
+ 1 1 1
+ 1 11
+ 2
+ 1 2
+
+**python 字典获取最大和最小的value**
+
+
+```
+my_dict = {'x':500, 'y':5874, 'z': 560}
+
+key_max = max(my_dict.keys(), key=(lambda k: my_dict[k]))
+key_min = min(my_dict.keys(), key=(lambda k: my_dict[k]))
+
+print('Maximum Value: ',my_dict[key_max])
+print('Minimum Value: ',my_dict[key_min])
+```
+
+可以用max(dict,key=dict.get)方法获得字典dict中value的最大值所对应的键的方法,max(dict, key)方法首先遍历迭代器,并将返回值作为参数传递给key对应的函数,然后将函数的执行结果传给key,并以此时key值为标准进行大小判断,返回最大值
+
+**sorted函数使用**
+
+
+```
+a=[1,2,3]
+sorted(a)
+```
+
+
+
+
+ [1, 2, 3]
+
+
+
+
+```
+L=[('b',2),('a',1),('c',3),('d',4)]
+
+sorted(L, key=lambda x:x[1])
+```
+
+
+
+
+ [('a', 1), ('b', 2), ('c', 3), ('d', 4)]
+
+
+
+
+```
+from operator import itemgetter, attrgetter
+L=[('b',2,2),('a',1,1),('c',3,3),('d',4,4),('e',4,3)]
+print(sorted(L, key=lambda x:(x[1],x[2]) ))
+
+```
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+```
+sorted(L, key=itemgetter(1,2))
+```
+
+
+
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+
+## 试题 基础练习 FJ的字符串
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+**问题描述**
+```
+ FJ在沙盘上写了这样一些字符串:
+ A1 = “A”
+ A2 = “ABA”
+ A3 = “ABACABA”
+ A4 = “ABACABADABACABA”
+ … …
+ 你能找出其中的规律并写所有的数列AN吗?
+ ```
+**输入格式**
+
+- 仅有一个数:N ≤ 26。
+
+**输出格式**
+
+- 请输出相应的字符串AN,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+ABACABA
+```
+
+
+```
+chr(65)
+```
+
+
+
+
+ 'A'
+
+
+
+
+```
+N=int(input())
+def op(n,s):
+ if n==N+65-1:
+ print (s+chr(n)+s)
+ return
+ op(n+1,s+chr(n)+s)
+op(65,"")
+```
+
+ 3
+ ABACABA
+
+
+## 题目 1463: [蓝桥杯][基础练习VIP]Sine之舞
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
+
+
+## 题目 1469: [蓝桥杯][基础练习VIP]数的读法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1037 解决: 350
+
+**题目描述**
+```
+Tom教授正在给研究生讲授一门关于基因的课程,有一件事情让他颇为头疼:一条染色体上有成千上万个碱基对,它们从0开始编号,到几百万,几千万,甚至上亿。
+
+比如说,在对学生讲解第1234567009号位置上的碱基时,光看着数字是很难准确的念出来的。
+
+所以,他迫切地需要一个系统,然后当他输入12 3456 7009时,会给出相应的念法:
+
+十二亿三千四百五十六万七千零九
+
+用汉语拼音表示为
+
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+这样他只需要照着念就可以了。
+
+你的任务是帮他设计这样一个系统:给定一个阿拉伯数字串,你帮他按照中文读写的规范转为汉语拼音字串,相邻的两个音节用一个空格符格开。
+
+注意必须严格按照规范,比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”,“100000”读作“shi wan”而不是“yi shi wan”,“2000”读作“er qian”而不是“liang qian”。
+```
+**输入**
+
+- 有一个数字串,数值大小不超过2,000,000,000。
+
+**输出**
+
+- 是一个由小写英文字母,逗号和空格组成的字符串,表示该数的英文读法。
+
+**样例输入**
+```
+1234567009
+
+```
+**样例输出**
+```
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+```
+
+### 思路一
+
+
+```
+import math
+num=input().strip()
+map1={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=[None,'shi','bai','qian']
+num_lis=[]
+
+'''
+输入按照单位分开
+'''
+while num:
+ if len(num)//4>0:
+ num_lis.append(num[-4:])
+ num=num[:-4]
+# print(num)
+ else:
+ num_lis.append(num)
+ num=None
+# print(num_lis)
+
+
+'''
+对每一个单位进行操作的操作函数
+'''
+def op(s):
+ j=0
+ res=[]
+ for i in s[::-1]:
+ if i=='0':
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map1[i])
+ j+=1
+ continue
+ else:
+ res.append(map2[j])
+ res.append(map1[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res[::-1]
+# print(num_lis)
+
+
+'''
+输出结果
+'''
+re=[]
+m=[None,'wan','yi','wanyi']
+for i in range(len(num_lis))[::-1]:
+ if op(num_lis[i]):
+ re+=op(num_lis[i])
+ re.append(m[i])
+# print(re)
+for i in re:
+ if i :
+ print(i,end=' ')
+# print(' '.join(re))
+
+
+
+```
+
+ 1234567009
+ ['7009', '3456', '12']
+ shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+### 思路二
+
+
+```
+s=input()
+map_={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=['','shi','bai','qian']
+s1=''
+s2=''
+s3=''
+n=len(s)
+nl=[0]*4
+for i in range(4):
+ if n<=0:
+ break
+ nl[i]=4 if n>=4 else n
+ n-=4
+s1=s[0:nl[3]]
+s2=s[nl[3]:nl[3]+nl[2]]
+s3=s[nl[3]+nl[2]:nl[2]+nl[1]+nl[3]]
+s4=s[nl[2]+nl[1]+nl[3]:nl[2]+nl[1]+nl[3]+nl[0]]
+res=[]
+
+
+
+def op(s,res,map_,map2):
+ j=0
+ res=[]
+# print(s1,s2,s3)
+ for i in s[::-1]:
+ if i=='0':
+
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map_[i])
+ j+=1
+ continue
+ res.append(map2[j])
+ res.append(map_[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res
+
+
+
+
+
+r4=op(s4,res,map_,map2)
+res+=r4
+
+if nl[1]>0:
+ res.append('wan')
+ r3=op(s3,res,map_,map2)
+ if r3:
+ res+=r3
+ else:
+ res.pop(-1)
+
+
+if nl[2]>0:
+ res.append('yi')
+ r2=op(s2,res,map_,map2)
+ if r2:
+ res+=r2
+ else:
+ res.pop(-1)
+
+
+if nl[3]>0:
+ res.append('wan yi')
+ r1=op(s1,res,map_,map2)
+ if r1:
+ res+=r1
+ else:
+ res.pop(-1)
+
+res=reversed(res)
+a=' '.join(res).split()
+print(' '.join(a))
+```
+
+ 2000000000000
+ er wan yi
+
+
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
+
+
+## 题目 2101: 矩阵面积相交
+
+题目 2101: 矩阵面积相交
+
+时间限制: 1Sec 内存限制: 128MB 提交: 20 解决: 9
+
+**题目描述**
+
+
+
+
+
+
+
+**输入**
+
+输入包含多组测试数据,输入的第一行包含一个正整数 T,表示测试数据的组数。
+
+接下来依次描述每组测试数据,对于每组测试数据:
+
+第一行包含一个正整数 n,表示矩形的数量。
+
+
+
+**输出**
+
+对于每组测试数据,输出 n 行,其中第 i 行包含两个非负整数,用恰好一个空格隔开,这里第 i 行的第一个整数表示与输入给出的第 i个矩形严格有交集的矩
+
+形数量(不含第 i 个矩形),第二个整数表示这些矩形分别与第 i 个矩形的交集面积之和。
+
+
+**数据范围:**
+
+T <= 10 , 所有坐标均为不超过 5000 的非负整数。
+
+**样例输入**
+
+```
+2
+2
+0 0 1 1
+1 1 2 2
+3
+0 0 2 6
+1 1 4 4
+1 3 3 9
+```
+**样例输出**
+
+```
+
+0 0
+0 0
+2 6
+2 5
+2 5
+```
+
+
+```
+def Area_cross(target,matrixs,target_index):
+ count=0
+ cross=0
+ for i in range(len(matrixs)):
+ if i!=target_index:
+ xr=min(target[2],matrixs[i][2])
+ xl=max(target[0],matrixs[i][0])
+ y_up=min(target[3],matrixs[i][3])
+ y_down=max(target[1],matrixs[i][1])
+ if xr>xl and y_up>y_down:
+ cross+=(xr-xl)*(y_up-y_down)
+ count+=1
+ return (count,cross)
+
+
+
+n=int(input())
+for i in range(n):
+ n=int(input())
+ matrixs=[]
+ for j in range(n):
+ matrixs.append(list(map(int,input().strip().split())))
+ for k in range(n):
+ target=matrixs[k]
+ count,cross=Area_cross(target,matrixs,k)
+ print(count,cross)
+
+```
+
+ 1
+ 3
+ 0 0 2 6
+ 1 1 4 4
+ 1 3 3 9
+ 2 6
+ 2 5
+ 2 5
+
+
+
+
+## 试题 基础练习 矩形面积交
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+问题描述
+
+ 平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
+
+输入格式
+
+ 输入仅包含两行,每行描述一个矩形。
+
+ 在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
+
+输出格式
+
+ 输出仅包含一个实数,为交的面积,保留到小数后两位。
+
+样例输入
+
+```
+1 1 3 3
+2 2 4 4
+```
+样例输出
+
+```
+1.00
+```
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+# if x1[2]=0:
+ print('{:.2f}'.format(res))
+ else:
+ print(1)
+ print('{:.2f}'.format(0))
+if (x1[0]>=x2[0]and x1[0]<=x2[2]and x1[1]>=x2[1]and x1[1]<=x2[3])or(x1[2]>=x2[0]and x1[2]<=x2[2]and x1[3]>=x2[1]and x1[3]<=x2[3]):
+ print('zhen')
+ s(x1,x2)
+elif (x1[2]>=x2[0]and x1[2]<=x2[2]and x1[1]>=x2[1]and x1[1]<=x2[3])or (x1[0]>=x2[0]and x1[0]<=x2[2] and x1[3]>=x2[1]and x1[3]<=x2[3]):
+ print('dao')
+ s([x1[2],x1[1],x1[0],x1[3]],[x2[2],x2[1],x2[0],x2[3]])
+else:
+ print(2)
+ print('{:.2f}'.format(0))
+# else:
+# s([x1[0],x1[3],x1[2],x1[1]],[x2[0],x2[3],x2[2],x2[1]])
+```
+
+ 283323.2393 2938832.3994 29838432.38288 983723.828
+ 27783.84384 8793002.2 3995852.3884 2928344.2
+ dao
+ 312660026120.76
+
+
+## 这道题刚开始思路错了下面是正确的
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+x1=[min(x1i[0],x1i[2]),min(x1i[1],x1i[3]),max(x1i[0],x1i[2]),max(x1i[1],x1i[3])]
+x2=[min(x2i[0],x2i[2]),min(x2i[1],x2i[3]),max(x2i[0],x2i[2]),max(x2i[1],x2i[3])]
+xl=max(x1[0],x2[0])
+xr=min(x1[2],x2[2])
+yup=min(x1[3],x2[3])
+ydown=max(x1[1],x2[1])
+x=xr-xl
+y=yup-ydown
+if xr>xl and yup>ydown:
+ print('{:.2f}'.format(x*y))
+else:
+ print('{:.2f}'.format(0))
+```
+
+ 1 1 4 5
+ 1 1 4 5
+ 12.00
+
+
+## 题目 1472: [蓝桥杯][基础练习VIP]矩阵乘法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1972 解决: 594
+
+**题目描述**
+
+```
+给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
+
+例如:
+
+A =
+
+1 2
+
+3 4
+
+A的2次幂
+
+7 10
+
+15 22
+```
+**输入**
+```
+第一行是一个正整数N、M(1< =N< =30, 0< =M< =5),表示矩阵A的阶数和要求的幂数
+
+接下来N行,每行N个绝对值不超过10的非负整数,描述矩阵A的值
+输出
+输出共N行,每行N个整数,表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
+```
+
+**样例输入**
+```
+2 2
+1 2
+3 4
+```
+**样例输出**
+```
+7 10
+15 22
+```
+
+### 思路一
+
+
+```
+N,M=map(int,input().strip().split())
+A=[]
+for i in range(N):
+ A.append(list(map(int,input().split())))
+def f(A,B,i,j,N):
+ re=0
+ for k in range(N):
+ re+=A[i][k]*B[k][j]
+ return re
+
+
+def op(A,M):
+ temp=[[0]*N for i in range(N)]
+ for i in range(N):
+ for j in range(N):
+ if i==j:
+ temp[i][j]=1
+ temp_next=[i.copy() for i in A]
+ for i in range(M):
+ for i in range(N):
+ for j in range(N):
+ temp_next[i][j]=f(temp,A,i,j,N)
+ temp=[i.copy() for i in temp_next]
+# print(temp)
+# print()
+ for i in temp:
+ print(' '.join(list(map(str,i))))
+ return temp
+op(A,M)
+
+
+
+
+```
+
+ 2 2
+ 1 2
+ 3 4
+ 7 10
+ 15 22
+
+
+
+
+
+ [[7, 10], [15, 22]]
+
+
+
+### 思路二
+
+
+```
+N,M=map(int,input().split())
+A=[]
+for i in range(N):
+ A.append(list(map(int ,input().split())))
+def op(A,B,N):
+ re=[[0]*N for _ in range(N)]
+ for i in range(N):
+# temp=A[i]
+ for j in range(N):
+ for k in range(N):
+ re[i][j]+=B[i][k]*A[k][j]
+ return re
+B=[[0 for j in range(len(A[0]))] for i in range(len(A))]
+for i in range(N):
+ B[i][i]=1
+for i in range(M):
+ B=op(A,B,N)
+for i in range(N):
+ print(' '.join(map(str,B[i])))
+```
+
+ 2 2
+ 1 2
+ 3 4
+ 7 10
+ 15 22
+
+
+## 题目 1464: [蓝桥杯][基础练习VIP]分解质因数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2156 解决: 1312
+
+**题目描述**
+```
+求出区间[a,b]中所有整数的质因数分解。
+
+提示
+
+
+先筛出所有素数,然后再分解。
+
+数据规模和约定
+
+2< =a< =b< =10000
+
+```
+
+
+
+**输入**
+
+- 输入两个整数a,b。
+
+**输出**
+
+- 每行输出一个数的分解,形如k=a1*a2*a3...(a1< =a2< =a3...,k也是从小到大的)(具体可看样例)
+
+**样例输入**
+```
+3 10
+```
+**样例输出**
+```
+3=3
+4=2*2
+5=5
+6=2*3
+7=7
+8=2*2*2
+9=3*3
+10=2*5
+```
+
+
+```
+a,b=map(int,input().split())
+map_={1:'1',2:'2'}
+def op(k,map_):
+ for i in range(2,k):
+ if k%i==0:
+ map_[k]=map_[i]+'*'+map_[k//i]
+# print(k,map_[k])
+ return
+ map_[k]=str(k)
+# print(k,map_[k])
+for i in range(1,b+1):
+ op(i,map_)
+# print(map_)
+for i in range(a,b+1):
+ print(str(i)+'='+map_[i])
+
+
+
+```
+
+ 3 10
+ 3=3
+ 4=2*2
+ 5=5
+ 6=2*3
+ 7=7
+ 8=2*2*2
+ 9=3*3
+ 10=2*5
+
+
+
+```
+a,b=map(int,(input().split()))
+map_={1:'1',2:'2'}
+def op(k,map_):
+ for i in range(2,k):
+ if k%i==0:
+ map_[k]=map_[i]+'*'+map_[k//i]
+ return
+ map_[k]=str(k)
+for i in range(1,b+1):
+ op(i,map_)
+for i in range(a,b+1):
+ print(str(i)+'='+map_[i])
+```
+
+ 3 10
+ 3=3
+ 4=2*2
+ 5=5
+ 6=2*3
+ 7=7
+ 8=2*2*2
+ 9=3*3
+ 10=2*5
+
+
+
+
+## 题目 1466: [蓝桥杯][基础练习VIP]字符串对比
+
+时间限制: 1Sec 内存限制: 512MB 提交: 4380 解决: 2608
+
+**题目描述**
+```
+给定两个仅由大写字母或小写字母组成的字符串(长度介于1到10之间),它们之间的关系是以下4中情况之一:
+
+1:两个字符串长度不等。比如 Beijing 和 Hebei
+
+2:两个字符串不仅长度相等,而且相应位置上的字符完全一致(区分大小写),比如 Beijing 和 Beijing
+
+3:两个字符串长度相等,相应位置上的字符仅在不区分大小写的前提下才能达到完全一致(也就是说,它并不满足情况2)。比如 beijing 和 BEIjing
+
+4:两个字符串长度相等,但是即使是不区分大小写也不能使这两个字符串一致。比如 Beijing 和 Nanjing
+
+编程判断输入的两个字符串之间的关系属于这四类中的哪一类,给出所属的类的编号。
+```
+**输入**
+
+- 包括两行,每行都是一个字符串
+
+**输出**
+
+- 仅有一个数字,表明这两个字符串的关系编号
+
+**样例输入**
+```
+BEIjing
+beiJing
+```
+**样例输出**
+```
+3
+```
+
+
+```
+'S'.lower()
+```
+
+
+
+
+ 's'
+
+
+
+
+```
+str1=input()
+str2=input()
+def main(str1,str2):
+
+ if len(str1)!=len(str2):
+ print(1)
+ return
+ elif str1==str2:
+ print(2)
+ return
+ elif str1.lower()==str2.lower():
+ print(3)
+ return
+ else:
+ print(4)
+ return
+main(str1,str2)
+```
+
+ MSN
+ MQN
+ 4
+
+
+
+```
+s1=input()
+s2=input()
+if len(s1)!=len(s2):
+ print(1)
+elif s1==s2:
+ print(2)
+elif s1.lower()==s2.lower():
+ print(3)
+else:
+ print(4)
+```
+
+ BEIjing
+ beiJing
+ 3
+
+
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
+
+
+## 只出现一次的数字||
+
+
+```
+def singleNumber( nums) -> int:
+ one=0
+ two=0
+ three=0
+ for num in nums:
+ two|=one&num
+ one=one^num
+ three|=one&two
+ print(three)
+ print('{:b}'.format(three))
+ one=one&~three
+ two=two&~three
+ return one
+singleNumber([2,2,3,2])
+```
+
+ 0
+ 0
+ 0
+ 0
+ 2
+ 10
+ 2
+ 10
+
+
+
+
+
+ 1
+
+
+
+
+## 试题 算法训练 猴子吃包子
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ 从前,有一只吃包子很厉害的猴子,它可以吃无数个包子,但是,它吃不同的包子速度也不同;肉包每秒钟吃x个;韭菜包每秒钟吃y个;没有馅的包子每秒钟吃z个;现在有x1个肉包,y1个韭菜包,z1个没有馅的包子;问:猴子吃完这些包子要多久?结果保留p位小数。
+ ```
+**输入格式**
+
+- 输入1行,包含7个整数,分别表示吃不同包子的速度和不同包子的个数和保留的位数。
+
+**输出格式**
+
+- 输出一行,包含1个实数,表示吃完所有包子的时间。
+
+**样例输入**
+```
+4 3 2 20 30 15 2
+
+```
+**样例输出**
+```
+22.50
+```
+
+**数据规模和约定**
+```
+ 0 in
+ 1 p=2
+ 2 a='%.{0}f'.format(p)
+ ----> 3 b='{2}{0}.{1}f{3}}'.format(':',p,'{','}')
+ 4 print(b.format(t1+t2+t3))
+ 5 print(a%(t1+t2+t3))
+
+
+ ValueError: Single '}' encountered in format string
+
+
+
+```
+chr(115)
+```
+
+
+
+
+ 's'
+
+
+
+
+## 试题 算法训练 Yaroslav and Algorithm
+
+提交此题
+资源限制
+时间限制:100ms 内存限制:128.0MB
+
+**问题描述**
+```
+ (这道题的数据和SPJ已完工,尽情来虐吧!)
+
+ Yaroslav喜欢算法。我们将描述一个他最喜欢的算法。
+
+ 1.这个算法接受一个字符串作为输入。我们设这个输入字符串为a。
+ 2.这个算法由一些命令组成。i号命令的形式为"s[i]>>w[i]"或"s[i]<>w[i]",其中s[i]和w[i]是长度不超过7的字符串(可以为空),由数字或字符"?"组成。
+ 3.这个算法每次寻找一个编号最小的命令i,使得s[i]是a的子串。如果没有找到这样的命令,那么整个算法终止。
+ 4.设找到的命令编号为k。在字符串a中,s[k]第一次出现的位置会被w[k]替换。如果这个命令形如"s[k]>>w[k]",那么这个算法继续执行(译注:回到第3步)。否则,算法终止。
+ 5.算法的输出就是算法终止时字符串a的值。
+
+ Yaroslav有一个n个正整数的集合,他需要一个这样的算法,且能够使每一个数加1。更正式地,如果我们把每个数看成一个十进制表示的字符串,那么对于每个字符串独立地运行这个算法,这个算法需要输出一个输入串对应的数+1的字符串。
+ 帮帮他吧!
+
+```
+**输入格式**
+
+ - 第一行包含一个整数n(集合中数的个数),接下来n行,每行包含一个正整数。
+
+**输出格式**
+```
+ 输出一个符合题意的算法(能够分别将每个数增加1)。第i行输出这个算法的第i个命令,不包含空格。
+ 你的算法将会对于每个输入运行一遍。你的输出会被认为是正确的,当且仅当:
+ ·每行都是一个合法的命令(格式见题目描述)
+ ·命令的条数不能超过50。
+ ·算法需要对每个给出的数+1。
+ ·为了得到结果,算法必须对于每个输入都执行不超过200步。
+```
+**样例输入**
+```
+2
+10
+79
+```
+**样例输出**
+```
+10<>11
+79<>80
+
+```
+**数据规模和约定**
+
+ 1≤每个数≤10^25。共有20个测试点,对于第i个测试点,n=5i。
+
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=int(input())
+ print(str(temp)+'<>'+str(temp+1))
+```
+
+ 2
+ 10
+ 10<>11
+ 79
+ 79<>80
+
+
+
+## 试题 算法训练 Sereja and Squares
+
+提交此题
+资源限制
+时间限制:4.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ Sereja在平面上画了n个点,点i在坐标(i,0)。然后,Sereja给每个点标上了一个小写或大写英文字母。Sereja不喜欢字母"x",所以他不用它标记点。Sereja认为这些点是漂亮的,当且仅当:
+ ·所有的点可以被分成若干对,使得每个点恰好属于一一对之中。
+ ·在每对点中,横坐标较小的会被标上小写字母,较大的会被标上对应的大写字母。
+ ·如果我们在每对点上画一个正方形,其中已知的一对点会作为正方形的相对的顶点,它们间的线段会成为正方形的对角线,那么在所有画出的正方形中不会有相交或触碰的情况。
+ 小Petya擦掉了一些小写字母和所有大写字母,现在Sereja想知道有多少种方法来还原每个点上的字母,使得还原后这些点是漂亮的。
+ ```
+**输入格式**
+```
+ 第一行是一个整数n,表示点的个数。
+ 第二行是一个长度为n的字符串,包含小写字母和问号"?",是按照横坐标递增的顺序的每个点的描述。问号表示这个点的字母被Petya擦掉了。保证输入串不含字母"x"。
+```
+**输出格式**
+```
+ 输出答案对4294967296取模的值。如果没有可行的方案,输出0。
+```
+
+**样例输入**
+
+```
+4
+a???
+```
+
+**样例输出**
+
+```
+50
+```
+
+**样例输入**
+
+```
+4
+abc?
+```
+
+**样例输出**
+
+```
+0
+```
+
+**样例输入**
+
+```
+6
+abc???
+
+```
+
+**样例输出**
+
+```
+1
+
+```
+
+**数据规模和约定**
+
+```
+ 20个测试点的n分别为:
+ 5,10,20,50,100,
+ 200,500,1000,2000,5000,
+ 10000,20000,30000,40000,50000,
+ 60000,70000,80000,90000,100000.
+```
+
+
+```
+# print('a'>'b')
+# print(ord('a'))
+# print(ord('A'))
+# print(ord('a')-ord('A'))
+# print(ord('b')-ord('B'))
+n=int(input())
+s=list(input())
+len_=0
+re=1
+label=0
+temp2=26
+for j in s:
+ if j=='?':
+ len_+=1
+for i in range(n):
+ if s[i]>='a'and s[i]<='z':
+ temp2-=1
+ if chr(ord(s[i])+32)in s[i:]:
+ s.remove(chr(ord(s[i])+32))
+ else:
+ if len_<=0:
+ label=1
+ break
+# re*=len_
+ len_-=1
+# print(re,len_)
+
+# print('test1',re)
+if len_%2!=0:
+ label=1
+else:
+ temp=len_//2
+ for i in range(temp):
+ re*=temp2
+ temp2-=1
+# temp-=1
+print('test2',re)
+if label ==1:
+ print(0)
+else:
+ if len_==0:
+ print(1)
+ else:
+ print(re*(2**temp))
+```
+
+ 10
+ ??????????
+ test2 7893600
+ 252595200
+
+
+
+```
+410156250/(25**5)
+# 410156250/252595200
+# 4294967296
+5*4*3*2
+```
+
+
+
+
+ 120
+
+
+
+## 上面这道题没做出来,没理解题目的意思
+
+
+```
+n=int(input())
+s=list(input())
+dp=[[0for i in range(n)] for j in range(2)]
+m=0
+n2=n//2
+now=0
+dp[0][0]=1
+for i in range(n):
+ if s[i]=='?':
+ now^=1
+ for j in range((i+1)//2+1):
+ #print(now,j)
+ dp[now][j]=dp[now^1][j]+dp[now^1][j-1]
+ #print(dp[now])
+ else:
+ m+=1
+if (n2>1
+#print (n2)
+for i in range(n):
+ if s[i]=='?':
+ j=(i+1)//2 #(i+1)>>1
+ while j>=1:#max(1,(i+1)-n2)
+ f[j]+=f[j-1]
+ j-=1
+ print(f)
+ else:
+ m+=1
+print(f)
+if (n20:
+ f[n2]*=25
+ f[n2]= f[n2]%4294967296
+ i-=1
+ print(f[n2])
+```
+
+ 10
+ ??????????
+ [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 2, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 3, 2, 0, 0, 0, 0, 0, 0, 0]
+ [1, 4, 5, 0, 0, 0, 0, 0, 0, 0]
+ [1, 5, 9, 5, 0, 0, 0, 0, 0, 0]
+ [1, 6, 14, 14, 0, 0, 0, 0, 0, 0]
+ [1, 7, 20, 28, 14, 0, 0, 0, 0, 0]
+ [1, 8, 27, 48, 42, 0, 0, 0, 0, 0]
+ [1, 9, 35, 75, 90, 42, 0, 0, 0, 0]
+ [1, 9, 35, 75, 90, 42, 0, 0, 0, 0]
+ 410156250
+
+
+
+```
+1855780572/16796
+```
+
+
+
+
+ 110489.4362943558
+
+
+
+## 试题 算法训练 Rotatable Number
+
+
+```
+
+```
+
+## 试题 算法训练 Playing with String
+
+
+```
+s=list(input())
+n=len(s)
+index=[]
+i=0
+while i=0 and c+j+1=1:
+ index.append(i+1)
+ i+=1
+ else:
+ i+=1
+print(index)
+if len(index)%2==0:
+ print('Second')
+else:
+ print('First')
+ print(index[0])
+
+```
+
+ ccccccc
+ [2, 3, 4, 5, 6]
+ First
+ 2
+
+
+
+```
+a=(6**7)/2
+print(a)
+print(12.5*1024)
+```
+
+ 139968.0
+ 12800.0
+
+
+
+```
+
+```
+
+
+## 模拟题1
+**问题描述**
+```
+ 将LANQIAO中的字母重新排列,可以得到不同的单词,如LANQIAO、AAILNOQ等,注意这7个字母都要被用上,单词不一定有具体的英文意义。
+ 请问,总共能排列如多少个不同的单词。
+答案提交
+ 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+ ```
+
+
+```
+res=1
+for i in range(1,8):
+ res*=i
+print(res/2)
+```
+
+## 模拟题2
+问题描述
+```
+ 给定三个整数 a, b, c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。
+ 请问在 1 至 n 中有多少个反倍数。
+```
+**输入格式**
+```
+ 输入的第一行包含一个整数 n。
+ 第二行包含三个整数 a, b, c,相邻两个数之间用一个空格分隔。
+
+```
+**输出格式**
+ - 输出一行包含一个整数,表示答案。
+
+**样例输入**
+```
+30
+2 3 6
+```
+**样例输出**
+
+- 10
+
+**样例说明**
+```
+以下这些数满足要求:1, 5, 7, 11, 13, 17, 19, 23, 25, 29。
+评测用例规模与约定
+ 对于 40% 的评测用例,1 <= n <= 10000。
+ 对于 80% 的评测用例,1 <= n <= 100000。
+ 对于所有评测用例,1 <= n <= 1000000,1 <= a <= n,1 <= b <= n,1 <= c <= n。
+```
+
+
+```
+n=int(input())
+a,b,c=map(int,input().split())
+res=0
+for i in range(1,n+1):
+ if i%a!=0and i%b!=0 and i%c!=0:
+# print(i)
+ res+=1
+print(res)
+```
+
+ 30
+ 2 3 6
+ 1
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 25
+ 29
+ 10
+
+
+## 模拟题3
+**问题描述**
+```
+ 给定一个单词,请使用凯撒密码将这个单词加密。
+ 凯撒密码是一种替换加密的技术,单词中的所有字母都在字母表上向后偏移3位后被替换成密文。即a变为d,b变为e,...,w变为z,x变为a,y变为b,z变为c。
+ 例如,lanqiao会变成odqtldr。
+```
+
+**输入格式**
+
+输入一行,包含一个单词,单词中只包含小写英文字母。
+
+**输出格式**
+
+输出一行,表示加密后的密文。
+
+**样例输入**
+
+lanqiao
+
+**样例输出**
+
+odqtldr
+
+**评测用例规模与约定**
+ 对于所有评测用例,单词中的字母个数不超过100。
+
+
+```
+# ord('a')
+s=input()
+res=''
+for i in s:
+ temp=chr((ord(i)-97+3)%26+97)
+ res+=temp
+print(res)
+```
+
+ lanqiao
+ odqtldr
+
+
+## 模拟题4
+**问题描述**
+```
+ 对于一个 n 行 m 列的表格,我们可以使用螺旋的方式给表格依次填上正整数,我们称填好的表格为一个螺旋矩阵。
+ 例如,一个 4 行 5 列的螺旋矩阵如下:
+ 1 2 3 4 5
+ 14 15 16 17 6
+ 13 20 19 18 7
+ 12 11 10 9 8
+```
+**输入格式**
+```
+ 输入的第一行包含两个整数 n, m,分别表示螺旋矩阵的行数和列数。
+ 第二行包含两个整数 r, c,表示要求的行号和列号。
+```
+**输出格式**
+```
+ 输出一个整数,表示螺旋矩阵中第 r 行第 c 列的元素的值。
+
+```
+**样例输入**
+```
+4 5
+2 2
+```
+**样例输出**
+```
+15
+```
+**评测用例规模与约定**
+```
+ 对于 30% 的评测用例,2 <= n, m <= 20。
+ 对于 70% 的评测用例,2 <= n, m <= 100。
+ 对于所有评测用例,2 <= n, m <= 1000,1 <= r <= n,1 <= c <= m。
+ ```
+
+
+```
+a,b=[1,2]
+print(a)
+```
+
+ 1
+
+
+
+```
+n,m=map(int,input().split())
+r,c=map(int,input().split())
+nn=[[0]*m for i in range(n)]
+i=0
+j=0
+num=1
+n_status=['=','+','=','-']
+m_status=['+','=','-','=']
+n_s=0
+m_s=0
+def op1(n_status,m_status,n_s,m_s,i,j):
+ if n_status[n_s]=='+':
+ i+=1
+ elif n_status[n_s]=='-':
+ i-=1
+ if m_status[m_s]=='+':
+ j+=1
+ elif m_status[m_s]=='-':
+ j-=1
+ return [i,j]
+def op2(n_status,m_status,n_s,m_s,i,j):
+ if n_status[n_s]=='+':
+ i-=1
+ elif n_status[n_s]=='-':
+ i+=1
+ if m_status[m_s]=='+':
+ j-=1
+ elif m_status[m_s]=='-':
+ j+=1
+ return [i,j]
+while True :
+ if (i+1)==r and (j+1)==c:
+ print(num)
+ break
+ if ia[2i]。
+ 小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
+ ```
+**输入格式**
+
+ 输入一行包含两个整数 m,n。
+
+**输出格式**
+
+输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
+
+**样例输入**
+
+3 4
+
+**样例输出**
+
+14
+
+**样例说明**
+
+```
+ 以下是符合要求的摆动序列:
+ 2 1 2
+ 2 1 3
+ 2 1 4
+ 3 1 2
+ 3 1 3
+ 3 1 4
+ 3 2 3
+ 3 2 4
+ 4 1 2
+ 4 1 3
+ 4 1 4
+ 4 2 3
+ 4 2 4
+ 4 3 4
+ ```
+**评测用例规模与约定**
+```
+ 对于 20% 的评测用例,1 <= n, m <= 5;
+ 对于 50% 的评测用例,1 <= n, m <= 10;
+ 对于 80% 的评测用例,1 <= n, m <= 100;
+ 对于所有评测用例,1 <= n, m <= 1000。
+ ```
+
+
+```
+a=[1,2]+[3]
+print(a)
+```
+
+ [1, 2, 3]
+
+
+
+```
+m,n=map(int,input().split())
+res=[]
+for k in range(1,n+1):
+ res.append([k])
+while len(res[0]) 输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0 对于每个测试实例,输出在第n年的时候母牛的数量。 每个输出占一行。
+
+**样例输入**
+
+```python
+2
+4
+5
+0
+```
+
+**样例输出**
+
+```python
+2
+4
+6
+```
+
+
+```
+def f(n,l4,l3,l2,l1):
+ if n==1:
+ return l2+l3+l4+l1
+ l4+=l3
+ l3=l2
+ l2=l1
+ l1=l4
+ return f(n-1,l4,l3,l2,l1)
+while True:
+ n=int(input())
+ if n==0:
+ break
+ else:
+ print(f(n,1,0,0,0))
+```
+
+ 2
+ 2
+ 4
+ 4
+ 5
+ 6
+ 0
+
+
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
+
+
+
+## 题目 1094: 字符串的输入输出处理
+
+时间限制: 1Sec 内存限制: 64MB 提交: 14661 解决: 5300
+
+**题目描述**
+
+字符串的输入输出处理。
+
+**输入**
+
+> 第一行是一个正整数N,最大为100。之后是多行字符串(行数大于N), 每一行字符串可能含有空格,字符数不超过1000。
+
+**输出**
+
+> 先将输入中的前N行字符串(可能含有空格)原样输出,再将余下的字符串(不含有空格)以空格或回车分割依次按行输出。每行输出之间输出一个空行。
+
+**样例输入**
+
+```python
+2
+www.dotcpp.com DOTCPP
+A C M
+D O T CPP
+```
+
+**样例输出**
+
+```python
+www.dotcpp.com DOTCPP
+
+A C M
+
+D
+
+O
+
+T
+
+CPP
+```
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ print(temp)
+ print()
+while True:
+ li=input().strip().split()
+ for i in li:
+ print(i)
+ print()
+```
+
+ 2
+ www.dotcpp.com DOTCPP
+ www.dotcpp.com DOTCPP
+
+ A C M
+ A C M
+
+ D O T CPP
+ D
+
+ O
+
+ T
+
+ CPP
+
+
+
+
+```
+print(1,sep='\n\n')
+# print('\n')
+print(3)
+```
+
+ 1
+ 3
+
+
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
+
+
+## 题目 1431: [蓝桥杯][2014年第五届真题]分糖果
+
+时间限制: 1Sec 内存限制: 128MB 提交: 5807 解决: 2969
+
+**题目描述**
+**问题描述**
+
+有n个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果,然后进行下面的游戏:
+
+每个小朋友都把自己的糖果分一半给左手边的孩子。
+
+一轮分糖后,拥有奇数颗糖的孩子由老师补给1个糖果,从而变成偶数。
+
+反复进行这个游戏,直到所有小朋友的糖果数都相同为止。
+
+你的任务是预测在已知的初始糖果情形下,老师一共需要补发多少个糖果。
+
+**输入**
+
+> 程序首先读入一个整数N(2< N< 100),表示小朋友的人数。 接着是一行用空格分开的N个偶数(每个偶数不大于1000,不小于2)
+
+**输出**
+
+> 要求程序输出一个整数,表示老师需要补发的糖果数。
+
+**样例输入**
+
+```python
+3
+2 2 4
+```
+
+**样例输出**
+
+```python
+4
+```
+
+
+```
+n=int(input())
+num=list(map(int,input().strip().split()))
+re=0
+def b(num):
+ temp=num[0]
+ for i in num:
+ if i!=temp:
+ return False
+ return True
+while not b(num):
+ temp=num.copy()
+ for i in range(len(temp)):
+ temp[i]=int(temp[i]/2)
+ for i in range(len(num)):
+ num[i]=int(num[i]/2)+temp[(i+1)%len(temp)]
+ if num[i]%2!=0:
+ num[i]+=1
+ re+=1
+print(re)
+
+```
+
+ 3
+ 2 2 4
+ 4
+
+
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
+
+
+
+
+
+## 译文1096:扫雷
+
+时间限制:1秒内存限制:64MB提交:3446解决:1442
+
+**译文描述**
+```
+
+扫雷你玩过扫雷吗?这个可爱的小游戏带有一定的操作系统,我们不记得它的名字。游戏的目标是找到所有地雷在M x N字段中的位置。游戏在一个正方形中显示一个数字,告诉您该正方形附近有多少个地雷。每个方格最多具有八个相邻方格。左侧的4 x 4字段包含两个地雷,每个地雷由一个``*''字符表示。如果我们通过上述提示号表示同一字段,那么我们将在右侧显示该字段:* ... ....。* .. .... * 100 2210 1 * 10 1110
+```
+**输入**
+```
+输入将包含任意数量的字段。每个字段的第一行包含两个整数n和m(0 =0 and (index[0]-1)=0 and (index[0]+1)=0 and (index[0]-1)=0 and (index[1]-1)=0 and (index[0]+1)=0 and (index[1]-1)=0 and (index[1]-1)=0 and (index[0]-1)=0 and (index[1]+1)=0 and (index[0]+1)=0 and (index[1]+1)=0 and (index[1]+1) 本题有多组数据,每组数据由一个正整数N组成。(N不大于100)
+
+**输出**
+
+> 对于每一组数据,输出一个N行的蛇形矩阵。两组输出之间不要额外的空行。矩阵三角中同一行的数字用一个空格分开。行尾不要多余的空格。
+
+**样例输入**
+
+```python
+5
+```
+
+**样例输出**
+
+```python
+1 3 6 10 15
+2 5 9 14
+4 8 13
+7 12
+11
+```
+
+
+```
+n=int(input())
+temp=[[] for i in range(n)]
+num=1
+grade=0
+while grade 只有1行,为两个正整数,用一个空格隔开: k w
+
+**输出**
+
+> 1行,是一个正整数,为所求的计算结果,即满足条件的不同的r的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
+> (提示:作为结果的正整数可能很大,但不会超过200位)
+
+**样例输入**
+
+```python
+3 7
+```
+
+**样例输出**
+
+```python
+36
+```
+
+
+```
+k,w=map(int,input().strip().split())
+Digits=w//k # 可以有完整k位的位数
+remainder=w%k # 最高位余下的位数
+def f (count,Digit):
+ if Digit>count:
+ return 0
+ re=1
+ for i in range(1,Digit+1):
+ re*=(count-i+1)/i
+ return re
+s0=sum([f(2**k-1,i) for i in range(2,Digits+1)]) #不考虑最高位或者说是只考虑所有的位数都有完整k位的情况。那么对于每一个位数的可能数就是从2**k-1中选取位数个数字的所有可能性
+
+s1=sum([f(2**k-1-i,Digits) for i in range(1,2**remainder)])# 依次计算最高位取每一个可能的数字时所有的可能性。
+print(int(s0+s1))
+```
+
+ 3 7
+ 36
+
+
+
+```
+[' ']*2
+```
+
+
+
+
+ [' ', ' ']
+
+
+
+## 题目 1115: DNA
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7279 解决: 2538
+
+**题目描述**
+
+小强从小就喜欢生命科学,他总是好奇花草鸟兽从哪里来的。终于, 小强上中学了,接触到了神圣的名词--DNA.它有一个双螺旋的结构。这让一根筋的小强抓破头皮,“要是能画出来就好了” 小强喊道。现在就请你帮助他吧
+
+**输入**
+
+> 输入包含多组测试数据。第一个整数N(N<=15),N表示组数,每组数据包含两个整数a,b。a表示一个单位的DNA串的行数,a为奇数且
+> 3<=a<=39。b表示重复度(1<=b<=20)。
+
+**输出**
+
+> 输出DNA的形状,每组输出间有一空行。
+
+**样例输入**
+
+```python
+2
+3 1
+5 4
+```
+
+**样例输出**
+
+```python
+X X
+ X
+X X
+
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+```
+
+
+```
+n =int(input())
+for i in range(n):
+ a,b=map(int,input().strip().split())
+ temp=[' ']*a
+ start=0
+ end=a-1
+ count=1
+ while count<=b:
+ temp2=temp[:]
+ temp2[start]='X'
+ temp2[end]='X'
+ print(''.join(temp2))
+ if end==0:
+ start,end=end,start
+ count+=1
+ start+=1
+ end-=1
+ print()
+```
+
+ 2
+ 3 1
+ X X
+ X
+ X X
+
+ 5 4
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+
+
+
+
+```
+num="1.2.3.4".split('.')#[0].isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+'2'.isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+num=input()
+```
+
+ 1.2.3.4
+
+
+
+```
+num.split()
+```
+
+
+
+
+ ['1.2.3.4']
+
+
+
+## 题目 1116: IP判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6196 解决: 2532
+
+**题目描述**
+```
+在基于Internet的程序中,我们常常需要判断一个IP字符串的合法性。
+合法的IP是这样的形式:
+A.B.C.D
+其中A、B、C、D均为位于[0, 255]中的整数。为了简单起见,我们规定这四个整数中不允许有前导零存在,如001这种情况。
+现在,请你来完成这个判断程序吧^_^
+```
+**输入**
+
+> 输入由多行组成,每行是一个字符串,输入由“End of file”结束。 字符串长度最大为30,且不含空格和不可见字符
+
+**输出**
+
+> 对于每一个输入,单独输出一行 如果该字符串是合法的IP,输出Y,否则,输出N
+
+**样例输入**
+
+```python
+1.2.3.4
+a.b.c.d
+267.43.64.12
+12.34.56.bb
+210.43.64.129
+-123.4.5.6
+```
+
+**样例输出**
+
+```python
+Y
+N
+N
+N
+Y
+N
+```
+
+
+```
+while True :
+ str=input()
+ if str=="End of file":
+ break
+ num=str.split('.')
+ i=0
+ while i1)) or( not num[i].isdecimal()):
+# print(not num[i])
+# print( num[i][0]=='0'and len(num[i]>1))
+# print(not num[i].isdecimal())
+# print(num[i])
+# print(i)
+ break
+ if int(num[i])<0 or int(num[i])>255:
+# print(2)
+ break
+ i+=1
+ if i==len(num):
+ print('Y')
+ else:
+ print('N')
+```
+
+ 1.2.3.4
+ Y
+ a.b.c.d
+ N
+ 267.43.64.12
+ N
+ 12.34.56.bb
+ N
+ 210.43.64.129
+ Y
+ -123.4.5.6
+ N
+ End of file
+
+
+## 题目 1117: K-进制数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2458 解决: 959
+
+**题目描述**
+
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+>
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+
+**例:**
+
+1010230 是有效的7位数
+1000198 无效
+0001235 不是7位数, 而是4位数.
+
+给定两个数N和K, 要求计算包含N位数字的有效K-进制数的总数.
+
+假设2 <= K <= 10; 2 <= N; 4 <= N+K <= 18.
+
+**输入**
+
+> 两个十进制整数N和K
+
+**输出**
+
+> 十进制表示的结果
+
+**样例输入**
+
+```python
+2
+10
+```
+
+**样例输出**
+
+```python
+90
+```
+## 提示
+
+> 从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+> 令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+> 前提:n 最小是 2*k-1.
+>
+> 组合 [(h+1)*h*(h-1)*```````(h+1-k)] /[k*(k-1)*(k-2)*``````1]
+>
+> 排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+### 提示
+从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+
+令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+前提:n 最小是 2*k-1.
+组合 [(h+1)*h*(h-1)*```````(h+1-k)] / [k*(k-1)*(k-2)*``````1]
+排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+```
+N=int(input())
+K=int(input())
+re1=(K-1)**N
+def f (n,k):
+ h=n-k
+ re=1
+ for i in range(1,k+1):
+ re*=(h+1-i+1)/i
+ return re*((K-1)**(n-k+1))## n-k+1中+1是加上了首位
+
+
+re2=sum([f(N-1,k) for k in range(1,int(((N-1)+1)/2)+1)])# 因为首位不能为零,所以从其他位置选取为零的点
+print(int(re1+re2))
+```
+
+ 2
+ 10
+ 90
+
+
+## 题目 1118: Tom数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 8198 解决: 3197
+
+**题目描述**
+
+正整数的各位数字之和被Tom称为Tom数。求输入数(<2^32)的Tom数!
+
+**输入**
+
+> 每行一个整数(<2^32).
+
+**输出**
+
+> 每行一个输出,对应该数的各位数之和.
+
+**样例输入**
+
+```python
+12345
+56123
+82
+```
+
+**样例输出**
+
+```python
+15
+17
+10
+```
+
+
+```
+while True :
+ num=map(int,list(input()))
+ print(sum(num))
+```
+
+ 12345
+ 15
+ 56123
+ 17
+ 82
+ 10
+
+
+## 题目 1426: [蓝桥杯][历届试题]九宫重排
+
+题目 1426: [蓝桥杯][历届试题]九宫重排
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2574 解决: 767
+
+题目描述
+
+如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
+
+
+
+
+我们把第一个图的局面记为:12345678.
+
+把第二个图的局面记为:123.46758
+
+显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
+
+本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
+
+**输入**
+
+输入第一行包含九宫的初态,第二行包含九宫的终态。
+
+**输出**
+
+输出最少的步数,如果不存在方案,则输出-1。
+
+**样例输入**
+
+12345678.
+
+123.46758
+
+**样例输出**
+
+3
+
+
+```
+
+def main():
+ def find(str):##(找到空格的点的x,y坐标并返回。)
+ for i in range(3):
+ for j in range(3):
+ if str1[i*3+j]=='.':
+ x=i
+ y=j
+ return (x,y)
+ if first==last:
+ return 0
+ queue=[first]
+ dir=[[0,1],[0,-1],[1,0],[-1,0]]## 空格点可以移动的方向
+
+
+ dic={}
+ dic[''.join(first)]=0
+ count=0
+ while queue:
+ str1=queue.pop(0)
+ x,y=find(str1)
+ for i in range(4):
+ next_x=x+dir[i][0]
+ next_y=y+dir[i][1]
+ if next_x>=0 and next_x<3 and next_y>=0 and next_y<3:
+ str2=str1[:]
+ str2[x*3+y],str2[next_x*3+next_y]=str2[next_x*3+next_y],str2[x*3+y]
+
+ if ''.join(str2) not in dic:
+ dic[''.join(str2)]=dic[''.join(str1)]+1
+
+ if str2==last:
+ return dic[''.join(str2)]
+# break
+ else:
+ queue.append(str2)
+ return -1
+first=list(input().strip())
+last=list(input().strip())
+print(main())
+
+```
+
+ 12345678.
+ 123.46758
+ 3
+
+
+### 提示
+对于每个状态当前能有的可能就是4种可能,所以我们要做的就是从first开始利用队列层序的遍历所有的可能,用dic记录其走的步数,直到其转化为last的状态。
+
+
+
+
+## 题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1441 解决: 25
+
+题目描述
+输入n, m, k,输出下面公式的值。
+
+
+
+
+其中C_n^m是组合数,表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如下:
+
+
+
+
+
+
+
+数据规模和约定
+
+对于100%的数据,n在十进制下不超过1000位,即1≤n< 10^1000,1≤k≤1000,同时0≤m≤n,k≤n。
+
+提示
+
+999101是一个质数;
+当n位数比较多时,绝大多数情况下答案都是0,但评测的时候会选取一些答案不是0的数据;
+
+**输入**
+
+输入的第一行包含一个整数n;第二行包含一个整数m,第三行包含一个整数k。
+
+**输出**
+
+计算上面公式的值,由于答案非常大,请输出这个值除以999101的余数。
+
+**样例输入**
+
+3
+
+1
+
+3
+
+**样例输出**
+
+162
+
+
+```
+import decimal
+n=int(input())
+m=int(input())
+k=int(input())
+def C(n,m):
+ re=1
+ if m>(n-m):
+ m=n-m
+ for i in range(1,m+1):
+ re*=((n-i+1)%999101)/i
+# re%=999101
+ return re
+def f(i,k):
+ re=1
+ for j in range(k):
+ re*=i
+ re%=999101
+ return re
+res=0
+cnm=C(n,m)
+cni=1
+for i in range(1,n+1):
+ cni*=((n-i+1)%999101)/i
+ res+=cni*(f(i,k))
+ res%=999101
+# print(res)
+# print(res)
+print((int(cnm*res%999101)))
+```
+
+ 990
+ 300
+ 5
+
+
+
+ ---------------------------------------------------------------------------
+
+ InvalidOperation Traceback (most recent call last)
+
+ in
+ 23 cni*=(decimal.Decimal(n-i+1)%999101)/i
+ 24 res+=cni*(f(i,k))
+ ---> 25 res%=999101
+ 26 # print(res)
+ 27 # print(res)
+
+
+ InvalidOperation: []
+
+
+
+```
+import java.math.*;
+import java.util.*;
+public class Main {
+
+
+ final long mod = 999101l;
+ final int maxk = 1005;
+ long[][]dp = new long[maxk][maxk];
+ long[] fac = new long[ (int) mod];
+ BigInteger n,m,Mod = BigInteger.valueOf(mod);
+ int k;
+ long ans;
+ Main()
+ {
+ Scanner jin = new Scanner(System.in);
+ n = jin.nextBigInteger();
+ m = jin.nextBigInteger();
+ k = jin.nextInt();
+ if(n.equals(new BigInteger("7349813")) && m.equals(new BigInteger("3590741")) && k == 9)//原题第四个数据貌似输出有误,正确应该输出为0
+ {
+ System.out.println(591101);
+ return;
+ }
+ getfac();
+ long lc = lucas(n,m);
+ if(lc == 0l)
+ {
+ System.out.println(0);
+ return;
+ }
+ getdp();
+ ans = 0l;
+ int i;
+ long p = qpow(2l,n.subtract(BigInteger.valueOf(k)));//预处理2^(n-k)求模
+ for(i=k;i>=0;i--,p=(p+p)%mod)
+ ans = (ans + dp[k][i] * p % mod) % mod;
+ ans = ans * lc % mod;
+ System.out.println(ans);
+ }
+ void getdp()//计算系数求模
+ {
+ int i,j;
+ dp[0][0] = 1l;
+ long N = n.mod(Mod).longValue();
+ for(i=0;i0l;b>>=1l,a=a*a%mod)
+ if((b&1l) == 1l)
+ ans = ans * a % mod;
+ return ans;
+ }
+ void getfac()//预处理[0,mod-1]的阶乘求模
+ {
+ int i;
+ fac[0] = 1l;
+ for(i=1;i 两个正整数,表示每种包装中糖的颗数(都不多于1000)
+
+
+
+**输出**
+
+> 一个正整数,表示最大不能买到的糖数
+
+**样例输入**
+
+```python
+4 7
+```
+
+**样例输出**
+
+```python
+17
+```
+
+
+```
+a,b=map(int,input().strip().split())
+max_=max(a,b)
+min_=min(a,b)
+map=[]
+for i in range(1,min_):
+ map.append(i)
+multiple=1
+re=min_-1
+while map:
+ temp=max_*multiple
+ del_map=[]
+ for i in range(len(map)):
+ if (temp+map[i])%min_==0:
+ del_map.append(map[i])
+ else:
+ re=temp+map[i]
+ for i in del_map:
+ map.remove(i)
+ multiple+=1
+print(re)
+```
+
+ 4 7
+ 17
+
+
+### 提示
+- 首先将两个数字分出大数跟小数,我们以大数为基础来思考,首先我们知道可以在大数的倍数的基础上加上无限的小数来表示其他的数字,那么可能不能表示的数字就存在于大数的倍数加上1~min_之间的数字产生的数字,这些数字中可能存在不能表示的数字。
+- 受到题目中启发,大于某个数字的数全都能被这两个数字表示,那么我们深入考虑其中的原因无非就是其中一些大数被小数的倍数给补上了,从而补上了那个差
+
+#### 策略
+- 那我们就首先把所有的1~min_之间的数字全部都存到map_中,然后分别对于不同倍数的大数加上这之间的数字看能不能被小数给整除,假如能整除的的话说明这个数能被表示就可以把从map中删除掉,直到map为空,那么最后记录的数字就是最大不能组合的数字。
+
+## 题目 1429: [蓝桥杯][2014年第五届真题]兰顿蚂蚁
+
+题目 1429: [蓝桥杯][2014年第五届真题]兰顿蚂蚁
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2854 解决: 1304
+
+**题目描述**
+
+
+兰顿蚂蚁,是于1986年,由克里斯·兰顿提出来的,属于细胞自动机的一种。
+
+
+平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只“蚂蚁”。
+蚂蚁的头部朝向为:上下左右其中一方。
+
+蚂蚁的移动规则十分简单:
+
+若蚂蚁在黑格,右转90度,将该格改为白格,并向前移一格;
+
+若蚂蚁在白格,左转90度,将该格改为黑格,并向前移一格。
+
+规则虽然简单,蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称,像是会重复,但不论起始状态如何,蚂蚁经过漫长的混乱活动后,会开辟出一条规则的“高速公路”。
+
+蚂蚁的路线是很难事先预测的。
+
+你的任务是根据初始状态,用计算机模拟兰顿蚂蚁在第n步行走后所处的位置。
+
+**输入**
+
+输入数据的第一行是 m n 两个整数(3 < m, n < 100),表示正方形格子的行数和列数。
+接下来是 m 行数据。
+
+每行数据为 n 个被空格分开的数字。0 表示白格,1 表示黑格。
+
+接下来是一行数据:x y s k, 其中x y为整数,表示蚂蚁所在行号和列号(行号从上到下增长,列号从左到右增长,都是从0开始编号)。s 是一个大写字母,表示蚂蚁头的朝向,我们约定:上下左右分别用:UDLR表示。k 表示蚂蚁走的步数。
+
+**输出**
+
+输出数据为一个空格分开的整数 p q, 分别表示蚂蚁在k步后,所处格子的行号和列号。
+
+**样例输入**
+'''
+5 6
+0 0 0 0 0 0
+0 0 0 0 0 0
+0 0 1 0 0 0
+0 0 0 0 0 0
+0 0 0 0 0 0
+2 3 L 5
+'''
+
+样例输出
+'''
+1 3
+'''
+
+
+
+```
+dir_dic={'U':0,'D':2,'L':3,'R':1}
+direction=[[-1,0],[0,1],[1,0],[0,-1]]
+dic_1={0:1,1:2,2:3,3:0}
+dic_0={0:3,3:2,2:1,1:0}
+m,n=map(int,input().strip().split())
+map_=[]
+for i in range(m):
+ map_.append(input().strip().split())
+x,y,s,k=input().strip().split()
+x=int(x)
+y=int(y)
+s=dir_dic[s]
+k=int(k)
+
+for i in range(k):
+ if map_[x][y]=='1':
+ map_[x][y]='0'
+ s=dic_1[s]
+ tx,ty=direction[s]
+ x+=tx
+ y+=ty
+
+# for k in map_:
+# print(k)
+# print(x,y)
+# print(tx,ty)
+# print()
+ elif map_[x][y]=='0':
+ map_[x][y]='1'
+ s=dic_0[s]
+ tx,ty=direction[s]
+ x+=tx
+ y+=ty
+# for k in map_:
+# print(k)
+# print(x,y)
+# print(tx,ty)
+# print()
+print(x,y)
+
+```
+
+ 5 6
+ 0 0 0 0 0 0
+ 0 0 0 0 0 0
+ 0 0 1 0 0 0
+ 0 0 0 0 0 0
+ 0 0 0 0 0 0
+ 2 3 L 5
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 3 3
+ 1 0
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '1', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 3 4
+ 0 1
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 2 4
+ -1 0
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '1', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 2 3
+ 0 -1
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '0', '1', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 1 3
+ -1 0
+
+ 1 3
+
+
+
+```
+import numpy as np
+np.sum([[1,1,1],[2,2,2]])
+```
+
+
+
+
+ 9
+
+
+
+
+```
+a=[[1,2],[5]]
+max(a,key=len)
+```
+
+
+
+
+ [1, 2]
+
+
+
+
+```
+m,n=map()
+```
+
+## 题目 1432: [蓝桥杯][2013年第四届真题]剪格子
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2448 解决: 858
+
+**题目描述**
+历届试题 剪格子
+时间限制:1.0s 内存限制:256.0MB
+
+**问题描述**
+如下图所示,3 x 3 的格子中填写了一些整数。
+```
++--*--+--+
+|10* 1|52|
++--****--+
+|20|30* 1|
+*******--+
+| 1| 2| 3|
++--+--+--+
+```
+我们沿着图中的星号线剪开,得到两个部分,每个部分的数字和都是60。
+本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
+如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
+如果无法分割,则输出 0。
+**输入**
+
+> 程序先读入两个整数 m n 用空格分割 (m,n< 10)。 表示表格的宽度和高度。
+> 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。
+
+**输出**
+
+> 输出一个整数,表示在所有解中,包含左上角的分割区可能包含的最小的格子数目。
+
+**样例输入**
+
+```python
+3 3
+10 1 52
+20 30 1
+1 2 3
+```
+
+**样例输出**
+
+```python
+3
+```
+
+### 思路一
+
+
+```
+def main():
+ m,n=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ all_sum=0
+ for i in range(n):
+ for j in range(m):
+ all_sum+=map_[i][j]
+ if all_sum%2!=0:
+ print(0)
+ return
+ visited=set()
+ temp_sum=0
+ res=[]
+ temp=[]
+ def helper(visited,row,col,temp_sum,temp):
+ '''
+ visited:记录已经遍历过的点
+ row:当前横坐标
+ col:当前纵坐标
+ temp_sum:已经遍历过的点的值的和
+ temp:储存了当前遍历的点的坐标
+ '''
+ if temp_sum==all_sum/2:
+ res.append(temp)
+ return
+ if temp_sum>all_sum/2:
+ return
+ if (row-1,col) not in visited and 0<=(row-1) 输入数据第一行包含2个整数n(2 < = n < = 1000), m(0 < = m < =
+> 2000),分别代表站点数,通道数; 接下来m行,每行两个整数 u,v (1 < = u, v < = n; u !=
+> v)代表一条通道; 最后1行,两个数u,v,代表询问两点之间的危险系数DF(u, v)。
+
+
+
+**输出**
+
+> 一个整数,如果询问的两点不连通则输出-1.
+
+**样例输入**
+
+```python
+7 6
+1 3
+2 3
+3 4
+3 5
+4 5
+5 6
+1 6
+```
+
+**样例输出**
+
+```python
+2
+```
+
+### 思路一
+
+
+```
+def main():
+
+ n,m=map(int,input().strip().split())
+ map_={}
+ for i in range(1,n+1):
+ map_[i]=[]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1].append(temp2)
+ map_[temp2].append(temp1)
+ visited=set()
+ start,end=map(int,input().strip().split())
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in map_[start]:
+ if i not in visited:
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+# print(res)
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+#### 提示
+我们发现其实关键点就是所有的从start到end的路径上都需要经过的点,那么我们记录下来从start到end的所有的可能的路径,然后取交即可求得这些关键点。
+
+### 思路二
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ map_=[[0 for i in range(n)]for j in range(n)]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1-1][temp2-1]=1
+ map_[temp2-1][temp1-1]=1
+ visited=set()
+ start,end=map(int,input().strip().split())
+ start-=1
+ end-=1
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in range(n):
+ if (map_[start][i]==1) and (i not in visited):
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+## 题目 1434: [蓝桥杯][历届试题]回文数字
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7799 解决: 3232
+
+**题目描述**
+
+观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
+
+本题要求你找到一些5位或6位的十进制数字。满足如下要求:
+该数字的各个数位之和等于输入的整数。
+
+**输入**
+
+> 一个正整数 n (10< n< 100), 表示要求满足的数位和。
+
+**输出**
+
+> 若干行,每行包含一个满足要求的5位或6位整数。
+> 数字按从小到大的顺序排列。
+> 如果没有满足条件的,输出:-1
+
+**样例输入**
+
+```python
+44
+```
+
+**样例输出**
+
+```python
+99899
+499994
+589985
+598895
+679976
+688886
+697796
+769967
+778877
+787787
+796697
+859958
+868868
+877778
+886688
+895598
+949949
+958859
+967769
+976679
+985589
+994499
+```
+
+
+```
+n=int(input())
+res=set()
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (2*i+2*j+k)==n:
+ res.add(i*10000+i+j*1000+j*10+k*100)
+ if (2*(i+j+k))==n:
+ res.add(i*100000+i+j*10000+j*10+k*1000+k*100)
+res=sorted(list(res))
+for i in res:
+ print(i)
+if not res:
+ print(-1)
+```
+
+ 44
+ 99899
+ 499994
+ 589985
+ 598895
+ 679976
+ 688886
+ 697796
+ 769967
+ 778877
+ 787787
+ 796697
+ 859958
+ 868868
+ 877778
+ 886688
+ 895598
+ 949949
+ 958859
+ 967769
+ 976679
+ 985589
+ 994499
+
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+def main():
+ n,m,k=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ x=0
+ y=0
+ res=[]
+ def helper(x,y,temp):
+ if (x==n-1) and (y==m-1):
+# print(temp)
+ if len(temp)>=k:
+ res.append(temp)
+ if (n>(x+1)>=0) and (m>y>=0):
+# if map_[x+1][y]>temp[-1]:
+# helper(x+1,y,temp+[map_[x+1][y]])
+# else:
+ helper(x+1,y,temp+[map_[x+1][y]])
+ if (n>(x)>=0) and (m>(y+1)>=0):
+# if map_[x][y+1]>temp[-1]:
+# helper(x,y+1,temp+[map_[x][y+1]])
+# else:
+ helper(x,y+1,temp+[map_[x][y+1]])
+
+ helper(0,0,[map_[0][0]])
+ print(len(res))
+ print(res[0])
+ temps=[]
+ def f (x,k,temp):
+ if len(x)+len(temp)min_len[0]:
+ return
+ if (x==n-1)and (y==m-1):
+ res.append(temp)
+ min_len[0]=len(temp)
+ return
+
+ if (0<=(x+1)0:
+ if b&1:
+ re*=a
+ a=a**2
+ b>>=1
+ return re
+
+```
+
+
+```
+p=891234941
+q=1123984201
+n=1001733993063167141
+c=20190324
+d=212353
+for i in range(1,500000): #枚举因子 d*e%((p-1)*(q-1))=1 (((q-1)*(p-1))*yz+1) %d =0
+ if(((p-1)*(q-1)*i+1)%d==0):
+ e=((p-1)*(q-1)*i+1)//212353
+ print(((p-1)*(q-1)*i+1)//d)
+ break
+def quick_mod(a,b,c):
+ a=a%c
+ ans=1
+ while b!=0:
+ if b&1:
+ ans=(ans*a)%c
+ b>>=1
+ a=(a*a)%c
+ return ans
+x=quick_mod(c,e,n) #x=c^e%n 579706994112328949
+print(x)
+print(quick_mod(x,d,n)) #c=x^d%n
+```
+
+ 823816093931522017
+ 579706994112328949
+ 20190324
+
+
+## 试题 F: 完全二叉树的权值
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+**【问题描述】**
+给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从
+上到下、从左到右的顺序依次是 A1, A2, · · · AN,如下图所示:
+现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点
+权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
+注:根的深度是 1。
+**【输入格式】**
+
+> 第一行包含一个整数 N。
+> 第二行包含 N 个整数 A1, A2, · · · AN 。
+
+**【输出格式】**
+
+> 输出一个整数代表答案。
+
+**【样例输入】**
+
+```python
+7
+1 6 5 4 3 2 1
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【评测用例规模与约定】**
+
+> 对于所有评测用例,1 ≤ N ≤ 100000,−100000 ≤ Ai ≤ 100000。
+
+
+```
+N=int(input())
+node_list=list(map(int,input().split()))
+queue=[node_list.pop(0)]
+# print(queue)
+max_sum=0
+max_depth=0
+depth=1
+while queue:
+ temp=0
+ for i in range(len(queue)):
+ temp+=queue.pop(0)
+ if node_list:
+ queue.append(node_list.pop(0))
+ if node_list:
+ queue.append(node_list.pop(0))
+ if temp>max_sum:
+ max_sum=temp
+ max_depth=depth
+
+ depth+=1
+print(max_depth)
+```
+
+ 7
+ 1 6 5 4 3 2 1
+ [1]
+ 2
+
+
+## 试题 G: 外卖店优先级
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+
+“饱了么”外卖系统中维护着 N 家外卖店,编号 1 ∼ N。每家外卖店都有
+一个优先级,初始时 (0 时刻) 优先级都为 0。
+每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减
+到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
+如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果
+优先级小于等于 3,则会被清除出优先缓存。
+给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优
+先缓存中。
+
+**【输入格式】**
+
+第一行包含 3 个整数 N、M 和 T。
+以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到
+一个订单。
+
+**【输出格式】**
+
+输出一个整数代表答案。
+
+
+**【样例输入】**
+```
+2 6 6
+1 1
+5 2
+3 1
+6 2
+2 1
+6 2
+```
+**【样例输出】**
+```
+1
+```
+**【样例解释】**
+
+6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,
+加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。
+
+**【评测用例规模与约定】**
+
+对于 80% 的评测用例,1 ≤ N, M, T ≤ 10000。
+对于所有评测用例,1 ≤ N, M, T ≤ 100000,1 ≤ ts ≤ T,1 ≤ id ≤ N。
+
+
+```
+N,M,T=map(int,input().strip().split())
+shop=[0 for i in range(N)]
+message=[[] for i in range(T)]
+
+for i in range(M):
+ ts,id=map(int,input().strip().split())
+ message[ts-1].append(id)
+# message.sort(key=lambda x:x[0])
+first=set()
+for i in range(len(message)):
+ for id in message[i]:
+ shop[id-1]+=3
+ for id in range(1,len(shop)):
+ shop[id-1]-=1
+ if shop[id-1]>5:
+ first.add(shop[id-1])
+ if shop[id-1]<=3:
+ first=first-{shop[id-1]}
+print(len(first))
+
+
+
+```
+
+ 2 6 6
+ 1 1
+ 5 2
+ 3 1
+ 6 2
+ 2 1
+ 6 2
+ 1
+
+
+## 试题 H: 修改数组
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+
+**【问题描述】**
+
+给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现
+的整数。
+现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
+A2, A3, · · · , AN。
+当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则
+小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直
+到 Ai 没有在 A1 ∼ Ai−1 中出现过。
+当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
+现在给定初始的 A 数组,请你计算出最终的 A 数组。
+
+**【输入格式】**
+
+第一行包含一个整数 N。
+第二行包含 N 个整数 A1, A2, · · · , AN 。
+
+**【输出格式】**
+
+输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
+
+**【样例输入】**
+
+- 5
+- 2 1 1 3 4
+
+**【样例输出】**
+
+- 2 1 3 4 5
+
+**【评测用例规模与约定】**
+
+- 对于 80% 的评测用例,1 ≤ N ≤ 10000。
+- 对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
+
+
+```
+N=int(input())
+nums=list(map(int,input().strip().split()))
+visited=set()
+for i in range(len(nums)):
+ while nums[i] in visited:
+ nums[i]+=1
+ visited.add(nums[i])
+nums=list(map(str,nums))
+print(' '.join(nums))
+```
+
+ 5
+ 2 1 1 3 4
+ 2 1 3 4 5
+
+
+
+```
+a=[{2},{3},set(),set()]
+a.remove(set())
+print(a)
+```
+
+ [{2}, {3}, set()]
+
+
+
+```
+help(list.remove)
+```
+
+ Help on method_descriptor:
+
+ remove(...)
+ L.remove(value) -> None -- remove first occurrence of value.
+ Raises ValueError if the value is not present.
+
+
+
+
+```
+[{3}-{3},set(),{4}].remove({4})
+# a=[{3}-{3},set(),{4}].remove({3}-{3})
+# print(a)
+```
+
+
+```
+N,M,k=map(int,input().strip().split())
+queue=[]
+for i in range(N):
+ candy1,candy2,candy3=map(int,input().strip().split())
+ queue.append({candy1,candy2,candy3})
+re={}
+all=set([ i for i in range(1,M+1)])
+
+while all!=re and queue:
+ temp=max(queue,key=len)
+ re|=temp
+# queue.remove()
+ remove_count=0
+ for i in queue:
+
+
+
+
+```
+
+## 试题 A: 解密
+
+本题总分:5 分
+
+**【问题描述】**
+
+小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的
+字符 Tc。下表给出了字符变换的规则:
+
+
+例如,将字符串 YeRi 加密可得字符串 EaFn。
+小明有一个随机的字符串,加密后为
+EaFnjISplhFviDhwFbEjRjfIBBkRyY
+(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
+(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容
+是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符
+串,后面 52 行依次为表格中的内容。)
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+只包含 30 个大小写英文字母的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
+
+
+
+```
+f=open('str.txt','r')
+strings=f.readlines()
+j=0
+dic_={}
+target=strings[0]
+for string in strings[1:]:
+ a,b=string.strip().split()
+ dic_[b]=a
+for i in target[:-2]:
+ print(dic_[i],end='')
+
+```
+
+ YeRikGSunlRzgDlvRwYkXkrGWWhXa
+
+## 试题 B: 纪念日
+
+本题总分:5 分
+
+**【问题描述】**
+
+2020 年 7 月 1 日是中国共产党成立 99 周年纪念日。
+中国共产党成立于 1921 年 7 月 23 日。
+请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包
+含多少分钟?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+```
+import datetime
+end=datetime.datetime(year=2020,month=7,day=1,hour=12)
+start=datetime.datetime(year=1921,month=7,day=23,hour=12)
+re=end-start
+re
+```
+
+
+
+
+ datetime.timedelta(36138)
+
+
+
+
+```
+36128*24*60
+```
+
+
+
+
+ 52024320
+
+
+
+## 试题 C: REPEAT 程序
+
+本题总分:10 分
+
+**【问题描述】**
+
+附件 prog.txt 中是一个用某种语言写的程序。
+其中 REPEAT k 表示一个次数为 k 的循环。循环控制的范围由缩进表达,
+从次行开始连续的缩进比该行多的(前面的空白更长的)为循环包含的内容。
+例如如下片段:
+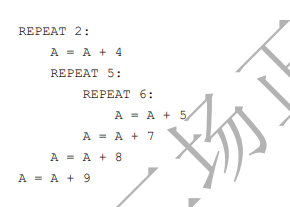
+
+
+该片段中从 A = A + 4 所在的行到 A = A + 8 所在的行都在第一行的
+循环两次中。
+
+ REPEAT 6: 所在的行到 A = A + 7 所在的行都在 REPEAT 5: 循环中。
+ A = A + 5 实际总共的循环次数是 2 × 5 × 6 = 60 次。
+ 请问该程序执行完毕之后,A 的值是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+### 在txt里面对循环哪里简单做个替换就ok了
+
+
+
+```
+A = 0
+for i in range( 2):
+ A = A + 4
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 7
+ for i in range( 6):
+ A = A + 7
+ for i in range( 4):
+ A = A + 2
+ A = A + 7
+ A = A + 2
+ for i in range( 7):
+ for i in range( 4):
+ A = A + 8
+ A = A + 7
+ A = A + 4
+ A = A + 5
+ A = A + 8
+ for i in range( 8):
+ A = A + 5
+ for i in range( 1):
+ A = A + 2
+ for i in range( 7):
+ A = A + 5
+ A = A + 5
+ for i in range( 2):
+ for i in range( 3):
+ A = A + 1
+ A = A + 1
+ for i in range( 5):
+ A = A + 1
+ for i in range( 9):
+ for i in range( 6):
+ A = A + 5
+ A = A + 1
+ for i in range( 6):
+ A = A + 2
+ A = A + 8
+ A = A + 3
+ for i in range( 2):
+ A = A + 5
+ for i in range( 3):
+ A = A + 9
+ for i in range( 1):
+ A = A + 4
+ for i in range( 2):
+ A = A + 9
+ for i in range( 1):
+ A = A + 6
+ A = A + 6
+ A = A + 4
+ for i in range( 3):
+ A = A + 7
+ A = A + 1
+ for i in range( 2):
+ A = A + 3
+ for i in range( 5):
+ A = A + 2
+ A = A + 5
+ A = A + 2
+ A = A + 4
+ A = A + 3
+for i in range( 4):
+ A = A + 4
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ for i in range( 4):
+ A = A + 5
+ A = A + 7
+ for i in range( 5):
+ A = A + 3
+ for i in range( 3):
+ A = A + 3
+ A = A + 1
+ A = A + 8
+ A = A + 2
+ for i in range( 9):
+ A = A + 5
+ for i in range( 1):
+ A = A + 5
+ A = A + 2
+ A = A + 8
+A = A + 6
+for i in range( 3):
+ for i in range( 4):
+ A = A + 9
+ for i in range( 5):
+ A = A + 2
+ A = A + 1
+ for i in range( 9):
+ A = A + 9
+ A = A + 2
+ for i in range( 1):
+ A = A + 6
+ A = A + 8
+ for i in range( 2):
+ A = A + 9
+ A = A + 4
+ A = A + 7
+ for i in range( 2):
+ for i in range( 7):
+ A = A + 3
+ A = A + 5
+ for i in range( 3):
+ A = A + 5
+ A = A + 3
+ A = A + 6
+ A = A + 4
+ for i in range( 9):
+ A = A + 2
+ A = A + 8
+ A = A + 2
+ A = A + 3
+ for i in range( 2):
+ for i in range( 8):
+ A = A + 5
+ A = A + 1
+ A = A + 6
+ A = A + 1
+ A = A + 2
+ for i in range( 6):
+ for i in range( 1):
+ A = A + 3
+ for i in range( 1):
+ A = A + 2
+ for i in range( 4):
+ A = A + 7
+ A = A + 1
+ A = A + 8
+ for i in range( 6):
+ A = A + 5
+ for i in range( 6):
+ A = A + 3
+ for i in range( 2):
+ A = A + 2
+ A = A + 9
+ A = A + 7
+ for i in range( 9):
+ A = A + 8
+ for i in range( 9):
+ A = A + 8
+ A = A + 9
+ A = A + 3
+ A = A + 2
+ for i in range( 6):
+ A = A + 3
+ for i in range( 9):
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ for i in range( 2):
+ A = A + 4
+ A = A + 9
+ A = A + 8
+ for i in range( 5):
+ A = A + 6
+ A = A + 9
+ A = A + 1
+ for i in range( 1):
+ A = A + 4
+ A = A + 2
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 4
+ for i in range( 7):
+ A = A + 8
+ A = A + 3
+ for i in range( 5):
+ A = A + 9
+ for i in range( 8):
+ A = A + 9
+ A = A + 8
+ for i in range( 4):
+ A = A + 7
+ A = A + 7
+ A = A + 3
+A = A + 5
+for i in range( 6):
+ A = A + 7
+for i in range( 7):
+ A = A + 2
+ A = A + 2
+A = A + 1
+for i in range( 8):
+ for i in range( 1):
+ for i in range( 4):
+ A = A + 6
+ A = A + 6
+ A = A + 2
+ for i in range( 5):
+ A = A + 4
+ A = A + 8
+ A = A + 4
+ for i in range( 1):
+ A = A + 5
+ for i in range( 7):
+ A = A + 8
+ for i in range( 6):
+ A = A + 4
+ A = A + 4
+ A = A + 8
+ for i in range( 4):
+ A = A + 2
+ for i in range( 2):
+ A = A + 4
+ for i in range( 2):
+ A = A + 3
+ for i in range( 1):
+ A = A + 2
+ A = A + 8
+ for i in range( 2):
+ A = A + 7
+ for i in range( 8):
+ A = A + 6
+ A = A + 1
+ A = A + 7
+ for i in range( 8):
+ A = A + 2
+ for i in range( 8):
+ for i in range( 6):
+ A = A + 1
+ A = A + 6
+ for i in range( 2):
+ A = A + 4
+ A = A + 1
+ A = A + 7
+ A = A + 4
+for i in range( 4):
+ for i in range( 9):
+ A = A + 2
+ for i in range( 1):
+ A = A + 2
+ A = A + 5
+for i in range( 8):
+ for i in range( 6):
+ A = A + 3
+ for i in range( 4):
+ A = A + 1
+ A = A + 6
+ A = A + 1
+ for i in range( 7):
+ A = A + 7
+ for i in range( 7):
+ A = A + 3
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ for i in range( 3):
+ A = A + 5
+ A = A + 5
+ A = A + 6
+ A = A + 2
+ for i in range( 1):
+ A = A + 4
+ for i in range( 2):
+ A = A + 7
+ for i in range( 1):
+ A = A + 7
+ for i in range( 4):
+ A = A + 7
+ A = A + 2
+ for i in range( 5):
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ A = A + 9
+ for i in range( 5):
+ A = A + 5
+ for i in range( 1):
+ A = A + 6
+ for i in range( 2):
+ A = A + 3
+ A = A + 2
+ A = A + 6
+ A = A + 8
+ A = A + 8
+ A = A + 7
+ A = A + 5
+ A = A + 5
+for i in range( 2):
+ A = A + 1
+ A = A + 7
+A = A + 3
+for i in range( 2):
+ A = A + 7
+A = A + 1
+A = A + 4
+for i in range( 1):
+ for i in range( 7):
+ for i in range( 2):
+ A = A + 3
+ A = A + 5
+ A = A + 2
+ A = A + 6
+ A = A + 1
+A = A + 2
+A = A + 4
+A = A + 9
+for i in range( 1):
+ A = A + 8
+for i in range( 8):
+ for i in range( 4):
+ for i in range( 8):
+ A = A + 4
+ for i in range( 3):
+ A = A + 1
+ A = A + 8
+ for i in range( 7):
+ A = A + 8
+ for i in range( 7):
+ A = A + 7
+ A = A + 7
+ for i in range( 7):
+ A = A + 6
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 4):
+ A = A + 5
+ A = A + 5
+ A = A + 4
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 4
+ A = A + 3
+ A = A + 6
+ for i in range( 1):
+ A = A + 3
+ A = A + 3
+ A = A + 6
+ for i in range( 6):
+ A = A + 7
+ A = A + 7
+ A = A + 5
+ A = A + 5
+ A = A + 1
+ A = A + 2
+ A = A + 6
+ A = A + 6
+ for i in range( 9):
+ A = A + 6
+ for i in range( 1):
+ for i in range( 2):
+ A = A + 4
+ A = A + 7
+ for i in range( 3):
+ A = A + 6
+ for i in range( 5):
+ A = A + 3
+ A = A + 6
+ for i in range( 9):
+ A = A + 3
+ A = A + 6
+ for i in range( 5):
+ A = A + 8
+ A = A + 8
+ for i in range( 3):
+ A = A + 7
+ A = A + 9
+ A = A + 8
+ A = A + 3
+ A = A + 3
+ A = A + 9
+for i in range( 6):
+ A = A + 9
+A = A + 1
+for i in range( 4):
+ for i in range( 1):
+ A = A + 7
+ for i in range( 9):
+ A = A + 2
+ A = A + 9
+ A = A + 1
+A = A + 2
+A = A + 8
+A = A + 7
+A = A + 9
+A = A + 6
+for i in range( 4):
+ for i in range( 2):
+ A = A + 3
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+for i in range( 6):
+ A = A + 6
+A = A + 1
+A = A + 5
+A = A + 8
+for i in range( 2):
+ A = A + 6
+ for i in range( 1):
+ for i in range( 2):
+ A = A + 2
+ for i in range( 3):
+ A = A + 1
+ for i in range( 1):
+ A = A + 8
+ A = A + 7
+ A = A + 4
+ A = A + 2
+ A = A + 8
+ A = A + 4
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 8
+ for i in range( 9):
+ A = A + 5
+ A = A + 5
+ for i in range( 5):
+ A = A + 5
+ for i in range( 3):
+ for i in range( 5):
+ A = A + 4
+ for i in range( 4):
+ A = A + 6
+ A = A + 3
+ for i in range( 7):
+ A = A + 3
+ A = A + 3
+ A = A + 1
+ A = A + 7
+ A = A + 7
+ A = A + 6
+ A = A + 5
+ A = A + 5
+ A = A + 6
+ for i in range( 1):
+ A = A + 9
+ A = A + 3
+ for i in range( 1):
+ for i in range( 1):
+ A = A + 1
+ for i in range( 8):
+ A = A + 5
+ for i in range( 8):
+ A = A + 6
+ for i in range( 4):
+ A = A + 9
+ A = A + 4
+ for i in range( 2):
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ A = A + 7
+ A = A + 5
+ A = A + 8
+ A = A + 7
+ A = A + 8
+ A = A + 5
+ for i in range( 2):
+ A = A + 5
+ A = A + 7
+ A = A + 8
+A = A + 5
+A = A + 9
+for i in range( 2):
+ for i in range( 6):
+ A = A + 9
+ A = A + 1
+ A = A + 8
+ A = A + 7
+ A = A + 1
+ A = A + 5
+ for i in range( 3):
+ A = A + 3
+ A = A + 9
+ A = A + 7
+ for i in range( 3):
+ A = A + 9
+ A = A + 1
+ for i in range( 6):
+ A = A + 1
+ for i in range( 9):
+ for i in range( 7):
+ A = A + 3
+ for i in range( 5):
+ A = A + 5
+ A = A + 8
+ A = A + 8
+ A = A + 1
+ A = A + 2
+ for i in range( 4):
+ A = A + 6
+ for i in range( 3):
+ A = A + 3
+ A = A + 7
+ for i in range( 8):
+ for i in range( 1):
+ A = A + 7
+ A = A + 8
+ A = A + 3
+ A = A + 1
+A = A + 2
+A = A + 4
+A = A + 7
+for i in range( 1):
+ for i in range( 1):
+ for i in range( 1):
+ A = A + 4
+ A = A + 6
+ for i in range( 1):
+ A = A + 3
+ A = A + 9
+ A = A + 6
+ for i in range( 9):
+ A = A + 1
+ A = A + 6
+ for i in range( 5):
+ A = A + 3
+ A = A + 9
+ A = A + 5
+ A = A + 5
+ A = A + 7
+ A = A + 2
+ for i in range( 2):
+ A = A + 7
+ A = A + 7
+ for i in range( 7):
+ for i in range( 4):
+ A = A + 6
+ A = A + 8
+ for i in range( 6):
+ A = A + 6
+ for i in range( 2):
+ A = A + 1
+ A = A + 7
+ A = A + 6
+ A = A + 7
+ for i in range( 4):
+ for i in range( 7):
+ A = A + 1
+ for i in range( 2):
+ A = A + 2
+ A = A + 5
+ A = A + 8
+ A = A + 2
+A = A + 1
+A = A + 4
+for i in range( 8):
+ A = A + 5
+A = A + 6
+for i in range( 7):
+ for i in range( 6):
+ for i in range( 9):
+ A = A + 7
+ A = A + 8
+ for i in range( 4):
+ A = A + 6
+ A = A + 4
+ A = A + 3
+ A = A + 6
+ for i in range( 9):
+ A = A + 3
+ for i in range( 9):
+ A = A + 2
+ A = A + 7
+ A = A + 5
+ A = A + 2
+for i in range( 7):
+ for i in range( 8):
+ for i in range( 6):
+ A = A + 4
+ A = A + 9
+ A = A + 5
+ A = A + 3
+ A = A + 9
+ for i in range( 4):
+ for i in range( 1):
+ A = A + 6
+ A = A + 8
+ for i in range( 1):
+ A = A + 6
+ A = A + 4
+ A = A + 6
+ for i in range( 3):
+ A = A + 7
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+ A = A + 2
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ A = A + 6
+ A = A + 5
+ for i in range( 1):
+ for i in range( 8):
+ A = A + 5
+ for i in range( 3):
+ A = A + 6
+ for i in range( 9):
+ A = A + 4
+ A = A + 3
+ for i in range( 6):
+ for i in range( 2):
+ A = A + 1
+ A = A + 5
+ A = A + 2
+A = A + 2
+A = A + 7
+for i in range( 4):
+ A = A + 7
+A = A + 9
+A = A + 2
+for i in range( 8):
+ A = A + 9
+ for i in range( 9):
+ for i in range( 2):
+ A = A + 3
+ A = A + 2
+ A = A + 1
+ A = A + 5
+ for i in range( 9):
+ A = A + 1
+ A = A + 3
+ A = A + 9
+ for i in range( 7):
+ A = A + 2
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 2):
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ for i in range( 5):
+ A = A + 5
+ A = A + 4
+ A = A + 2
+ A = A + 4
+ for i in range( 6):
+ A = A + 2
+ for i in range( 5):
+ A = A + 7
+ A = A + 7
+ A = A + 8
+ A = A + 3
+ for i in range( 8):
+ A = A + 2
+ A = A + 5
+ for i in range( 1):
+ A = A + 8
+ A = A + 5
+ A = A + 1
+ A = A + 1
+ A = A + 5
+ for i in range( 2):
+ A = A + 6
+ for i in range( 6):
+ A = A + 9
+ A = A + 2
+ A = A + 5
+ for i in range( 4):
+ A = A + 7
+ A = A + 1
+ for i in range( 6):
+ A = A + 8
+ A = A + 4
+ for i in range( 3):
+ for i in range( 2):
+ A = A + 1
+ A = A + 5
+ for i in range( 2):
+ A = A + 7
+ for i in range( 9):
+ A = A + 6
+ A = A + 8
+ A = A + 9
+ A = A + 5
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 7
+ A = A + 7
+ A = A + 9
+ A = A + 7
+ for i in range( 5):
+ A = A + 7
+ A = A + 2
+ A = A + 1
+ A = A + 8
+ A = A + 3
+ A = A + 5
+A = A + 1
+for i in range( 8):
+ A = A + 4
+A = A + 2
+A = A + 2
+A = A + 8
+for i in range( 4):
+ for i in range( 4):
+ A = A + 8
+ for i in range( 7):
+ A = A + 5
+ A = A + 2
+ for i in range( 2):
+ A = A + 6
+ for i in range( 4):
+ A = A + 8
+ A = A + 6
+ A = A + 1
+ A = A + 3
+A = A + 2
+A = A + 7
+A = A + 4
+for i in range( 8):
+ A = A + 2
+ A = A + 4
+for i in range( 5):
+ for i in range( 3):
+ for i in range( 6):
+ A = A + 8
+ A = A + 1
+ A = A + 6
+ A = A + 5
+ A = A + 9
+for i in range( 8):
+ A = A + 7
+for i in range( 6):
+ A = A + 4
+A = A + 5
+for i in range( 3):
+ A = A + 1
+ for i in range( 1):
+ for i in range( 5):
+ A = A + 6
+ A = A + 2
+ for i in range( 9):
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 9):
+ A = A + 9
+ A = A + 8
+ for i in range( 8):
+ for i in range( 5):
+ A = A + 9
+ A = A + 4
+ for i in range( 9):
+ A = A + 3
+ A = A + 4
+ A = A + 5
+for i in range( 9):
+ for i in range( 7):
+ A = A + 5
+ for i in range( 3):
+ A = A + 7
+ for i in range( 9):
+ for i in range( 6):
+ A = A + 4
+ A = A + 6
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 3
+ A = A + 3
+ A = A + 3
+ A = A + 5
+ for i in range( 7):
+ A = A + 5
+ for i in range( 2):
+ A = A + 5
+ A = A + 6
+ for i in range( 2):
+ A = A + 2
+ A = A + 5
+ A = A + 3
+A = A + 5
+A = A + 5
+for i in range( 4):
+ A = A + 2
+ A = A + 1
+ for i in range( 9):
+ A = A + 9
+ A = A + 5
+ A = A + 6
+ A = A + 2
+ A = A + 2
+ A = A + 5
+ for i in range( 9):
+ A = A + 5
+ A = A + 4
+ for i in range( 4):
+ for i in range( 4):
+ A = A + 1
+ A = A + 2
+ for i in range( 6):
+ A = A + 9
+ A = A + 3
+ for i in range( 2):
+ A = A + 5
+ A = A + 1
+ A = A + 1
+ A = A + 3
+ A = A + 8
+ for i in range( 7):
+ A = A + 4
+ for i in range( 6):
+ A = A + 9
+ for i in range( 5):
+ A = A + 9
+ A = A + 8
+ A = A + 3
+ A = A + 9
+ A = A + 4
+ A = A + 6
+for i in range( 7):
+ A = A + 9
+for i in range( 9):
+ A = A + 4
+ A = A + 9
+ A = A + 1
+ A = A + 3
+ for i in range( 5):
+ for i in range( 1):
+ A = A + 4
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ A = A + 6
+ A = A + 2
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+ for i in range( 3):
+ A = A + 5
+ A = A + 2
+ A = A + 8
+ A = A + 3
+ A = A + 6
+ A = A + 4
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ A = A + 3
+ for i in range( 3):
+ A = A + 2
+ A = A + 5
+ A = A + 8
+ A = A + 2
+ A = A + 5
+ for i in range( 8):
+ for i in range( 2):
+ A = A + 6
+ A = A + 7
+ A = A + 6
+ A = A + 9
+ A = A + 2
+for i in range( 2):
+ A = A + 3
+ for i in range( 8):
+ A = A + 7
+ A = A + 2
+ A = A + 1
+ A = A + 4
+ A = A + 1
+ A = A + 5
+ A = A + 2
+ A = A + 1
+ for i in range( 1):
+ A = A + 1
+ for i in range( 6):
+ A = A + 4
+ A = A + 3
+ A = A + 3
+ for i in range( 5):
+ A = A + 3
+ for i in range( 6):
+ for i in range( 1):
+ A = A + 5
+ A = A + 7
+ A = A + 7
+ A = A + 7
+ for i in range( 5):
+ A = A + 9
+ A = A + 7
+ for i in range( 5):
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 8
+ for i in range( 1):
+ A = A + 2
+ for i in range( 5):
+ A = A + 8
+ for i in range( 3):
+ A = A + 2
+ A = A + 9
+ A = A + 6
+ A = A + 3
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 5
+ for i in range( 4):
+ A = A + 5
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ A = A + 1
+ for i in range( 8):
+ A = A + 8
+ A = A + 1
+ A = A + 4
+ for i in range( 6):
+ A = A + 6
+ for i in range( 2):
+ A = A + 3
+ A = A + 9
+ A = A + 6
+ A = A + 9
+ for i in range( 1):
+ A = A + 4
+ for i in range( 3):
+ A = A + 3
+ A = A + 4
+ A = A + 2
+ A = A + 8
+ for i in range( 2):
+ A = A + 4
+ A = A + 1
+ for i in range( 9):
+ A = A + 2
+ A = A + 9
+ A = A + 7
+for i in range( 7):
+ for i in range( 7):
+ for i in range( 5):
+ A = A + 7
+ for i in range( 5):
+ A = A + 1
+ A = A + 1
+ for i in range( 5):
+ A = A + 6
+ for i in range( 1):
+ A = A + 4
+ for i in range( 9):
+ A = A + 4
+ A = A + 1
+ for i in range( 6):
+ A = A + 8
+ A = A + 5
+ for i in range( 1):
+ A = A + 4
+ for i in range( 5):
+ A = A + 8
+ A = A + 7
+ A = A + 2
+ for i in range( 3):
+ A = A + 3
+ for i in range( 8):
+ for i in range( 8):
+ A = A + 4
+ A = A + 7
+ for i in range( 5):
+ A = A + 1
+ for i in range( 8):
+ A = A + 7
+ A = A + 8
+ A = A + 4
+ A = A + 7
+ A = A + 6
+ A = A + 9
+ A = A + 5
+for i in range( 3):
+ A = A + 5
+ for i in range( 9):
+ A = A + 1
+ A = A + 7
+for i in range( 1):
+ A = A + 8
+A = A + 4
+for i in range( 8):
+ for i in range( 7):
+ A = A + 2
+ for i in range( 4):
+ A = A + 6
+ A = A + 6
+ for i in range( 1):
+ A = A + 7
+ A = A + 1
+for i in range( 9):
+ for i in range( 5):
+ A = A + 6
+ A = A + 5
+ for i in range( 7):
+ A = A + 3
+ A = A + 6
+ A = A + 8
+ for i in range( 2):
+ A = A + 7
+ A = A + 1
+ A = A + 9
+ for i in range( 3):
+ for i in range( 3):
+ A = A + 5
+print(A)
+```
+
+ 241830
+
+
+## 试题 D: 矩阵
+
+本题总分:10 分
+
+**【问题描述】**
+
+把 1 ∼ 2020 放在 2 × 1010 的矩阵里。要求同一行中右边的比左边大,同一
+列中下边的比上边的大。一共有多少种方案?
+答案很大,你只需要给出方案数除以 2020 的余数即可。
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+f=[[ 0 for i in range(1011)]for i in range(1011)]
+f[0][0]=1
+for i in range(1011):
+ for j in range(1011):
+ if i>j:
+ f[i][j]+=f[i-1][j]
+ if j!=0:
+ f[i][j]+=f[i][j-1]
+ f[i][j]%=2020
+print(f[-1][-1])
+```
+
+ 1340
+
+
+## 试题 E: 完美平方数
+本题总分:15 分
+
+**【问题描述】**
+
+如果整个整数 X 本身是完全平方数,同时它的每一位数字也都是完全平方
+数,我们就称 X 是完美平方数。
+前几个完美平方数是 0、1、4、9、49、100、144……
+即第 1 个完美平方数是 0,第 2 个是 1,第 3 个是 4,……
+请你计算第 2020 个完美平方数是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+visited={0}
+def f(string):
+ for i in string:
+ if i not in {'0','1','4','9'}:
+ return False
+ return True
+num=1
+while True :
+ if f(str(num**2)):
+ visited.add(num**2)
+ print(len(visited))
+ if len(visited)==2020:
+ print(num**2)
+ break
+ num+=1
+# 491499994440019919104
+```
+
+
+```
+# def f (x):
+# for i in range(int(x**(0.5))+1):
+# if i**2==x:
+# return True
+# # return False
+
+# import math
+# def is_sqr(n):
+# a = int(math.sqrt(n))
+# return a * a == n
+# # Squares=set()
+# # for i in range(20200000):
+# # Squares.add(i**2)
+# visited={0,1,4,9}
+# #num=50
+# len_=1
+# queue=[1,4,9]
+# while queue:
+# num=queue.pop(0)
+# queue.append(int(str(num)+'0'))
+# queue.append(int(str(num)+'1'))
+# queue.append(int(str(num)+'4'))
+# queue.append(int(str(num)+'9'))
+# # label=1
+# # for i in str(num):
+# # if int(i) not in visited :
+# # label=-1
+# # if label==1:
+# if is_sqr(num) :
+# visited.add(num)
+# len_+=1
+# print(len(visited))
+# if len(visited)==2020:
+# print(num)
+# break
+```
+
+## 试题 F: 分类计数
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
+
+**【问题描述】**
+
+输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字
+母,多少个数字。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
+
+**【样例输入】**
+
+```python
+1+a=Aab
+```
+
+**【样例输出】**
+
+```python
+1
+3
+1
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由可见字符组成,长度不超过 100。
+
+
+```
+string=input()
+num_set=set()
+for i in range(10):
+ num_set.add(str(i))
+# print(num_set)
+num_len=0
+h_len=0
+l_len=0
+for i in string:
+ if i in num_set:
+ num_len+=1
+ elif 'A'<=i<='Z':
+ h_len+=1
+ elif 'a'<=i<='z':
+ l_len+=1
+print(h_len)
+print(l_len)
+print(num_len)
+
+```
+
+ 1+a=Aab
+ 1
+ 3
+ 1
+
+
+
+
+## 试题 G: 八次求和
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+给定正整数 n, 求 1
+8 + 28 + · · · + n
+8 mod 123456789 。其中 mod 表示取
+余。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n。
+
+**【输出格式】**
+
+> 输出一行,包含一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+2
+```
+
+**【样例输出】**
+
+```python
+257
+```
+
+**【样例输入】**
+
+```python
+987654
+```
+
+**【样例输出】**
+
+```python
+43636805
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 20。
+> 对于 60% 的评测用例,1 ≤ n ≤ 1000。
+> 对于所有评测用例,1 ≤ n ≤ 1000000。
+
+
+
+```
+def f(x):
+ re=1
+ for i in range(8):
+ re*=x
+ re%=123456789
+ return re
+n=int(input())
+res=0
+for i in range(1,n+1):
+ res+=f(i)
+ res%=123456789
+print(res)
+```
+
+ 987654
+ 43636805
+
+
+## 试题 H: 字符串编码
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大
+写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, ... Z →
+26。
+这样一个字符串就能被转化成一个数字序列:
+比如 ABCXYZ → 123242526。
+现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样
+的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字
+符串。
+
+**【输入格式】**
+
+
+> 一个数字序列。
+
+**【输出格式】**
+
+> 一个只包含大写字母的字符串,代表答案
+
+**【样例输入】**
+
+```python
+123242526
+```
+
+**【样例输出】**
+
+```python
+LCXYZ
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,输入的长度不超过 20。
+> 对于所有评测用例,输入的长度不超过 200000。
+
+
+```
+dic_={}
+for i in range(1,27):
+ dic_[str(i)]=chr(i+64)
+
+string=input()
+point=0
+while point 第一行包含 2 个整数 N 和 K。
+>
+> 以下 N 行每行包含 2 个整数,其中第 i 行是编号为 i 的节点的父节点编号
+>
+> Pi 和权值 Wi 。注意 Pi = 0 表示 i 是根节点。
+>
+> 输入保证是一棵 BST。
+
+**【输出格式】**
+
+> 一个整数代表答案。如果答案是无穷多,输出 −1。
+
+**【样例输入】**
+
+```python
+4 3
+0 10
+1 0
+1 20
+3 30
+```
+
+**【样例输出】**
+
+```python
+9
+```
+
+**【评测用例规模与约定】**
+
+> 对于 60% 的评测用例,1 ≤ K ≤ N ≤ 100,0 ≤ Wi ≤ 200,且 Wi 各不相同。
+>
+> 对于所有评测用例,1 ≤ K ≤ N ≤ 10000,0 ≤ Wi ≤ 100000000,且 Wi 各不 相同。
+
+
+
+```
+class TreeNode:
+ def __init__(self,x):
+ self.val=x
+ self.left=None
+ self.right=None
+ self.parent=None
+N,K=map(int,input().strip().split())
+map_=[]
+map_node=[]
+for i in range(N):
+ p,w=map(int,input().strip().split())
+ map_.append([p,w])
+ map_node.append(TreeNode(w))
+ if p==0:
+ root_index=i
+for i in range(N):
+ if map_node[map_[i][0]-1].val - 输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从 1 至 n 编号。
+> 接下来 m 行,每行三个整数,表示一个操作。
+> 如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。
+> 如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
+
+**【输出格式】**
+
+> 输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+**【样例输入】**
+
+```python
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+
+**【样例输出】**
+
+```python
+13 13 5 3
+```
+
+**【评测用例规模与约定】**
+
+> 对于 30% 的评测用例,1 ≤ n ≤ 20,1 ≤ m ≤ 100。
+>
+> 对于 50% 的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000。
+>
+> 对于 70% 的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ t ≤ 100。
+
+
+
+```
+n,m=map(int,input().strip().split())
+message1=[]
+for i in range(m):
+
+ or1_2,a,b=input().strip().split()
+ message1.append([or1_2,a,b])
+
+
+map_=[[0 for i in range(n)]for i in range(n)]
+for i in range(n):
+ map_[i][i]=1
+
+re=[0 for i in range(n)]
+
+def f(map_,a,b,re,visited):
+ for i in range(n):
+ if map_[a-1][i]==1:
+## print(visited)
+ if i not in visited:
+ f(map_,i+1,b,re,visited|{i})
+ else:
+ if re[i]==0:
+ re[i]+=b
+
+
+
+for or1_2,a,b in message1:
+ a=int(a)
+ b=int(b)
+ if or1_2=='1':
+ map_[a-1][b-1]=1
+ map_[b-1][a-1]=1
+## print('a',a,'b',b)
+## print('map',map_)
+ else:
+ temp=[0 for i in range(n)]
+ f(map_,a,b,temp,{a-1})
+
+ for i in range(len(re)):
+ re[i]+=temp[i]
+## print('re',re)
+
+for i in re:
+ print(i)
+
+```
+
+## 试题 B: 合并检测
+
+
+本题总分:5 分
+
+**【问题描述】**
+
+新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准备给大量民众进病毒核酸检测。
+然而,用于检测的试剂盒紧缺。
+为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看,如果检测前 k − 1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用了 k + 1 个试剂盒完成了 k 个人的检测。
+A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能最节省试剂盒?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+lis=[]
+for k in range(1,101):
+ temp=100+k*k
+ lis.append([temp/k,k])
+lis.sort(key=lambda x :x[0])
+lis[0][1]
+```
+
+
+
+
+ 10
+
+
+
+
+```
+lis
+```
+
+
+
+
+ [[20.0, 10],
+ [20.09090909090909, 11],
+ [20.11111111111111, 9],
+ [20.333333333333332, 12],
+ [20.5, 8],
+ [20.692307692307693, 13],
+ [21.142857142857142, 14],
+ [21.285714285714285, 7],
+ [21.666666666666668, 15],
+ [22.25, 16],
+ [22.666666666666668, 6],
+ [22.88235294117647, 17],
+ [23.555555555555557, 18],
+ [24.263157894736842, 19],
+ [25.0, 5],
+ [25.0, 20],
+ [25.761904761904763, 21],
+ [26.545454545454547, 22],
+ [27.347826086956523, 23],
+ [28.166666666666668, 24],
+ [29.0, 4],
+ [29.0, 25],
+ [29.846153846153847, 26],
+ [30.703703703703702, 27],
+ [31.571428571428573, 28],
+ [32.44827586206897, 29],
+ [33.333333333333336, 30],
+ [34.225806451612904, 31],
+ [35.125, 32],
+ [36.03030303030303, 33],
+ [36.333333333333336, 3],
+ [36.94117647058823, 34],
+ [37.857142857142854, 35],
+ [38.77777777777778, 36],
+ [39.7027027027027, 37],
+ [40.63157894736842, 38],
+ [41.56410256410256, 39],
+ [42.5, 40],
+ [43.4390243902439, 41],
+ [44.38095238095238, 42],
+ [45.325581395348834, 43],
+ [46.27272727272727, 44],
+ [47.22222222222222, 45],
+ [48.17391304347826, 46],
+ [49.12765957446808, 47],
+ [50.083333333333336, 48],
+ [51.04081632653061, 49],
+ [52.0, 2],
+ [52.0, 50],
+ [52.96078431372549, 51],
+ [53.92307692307692, 52],
+ [54.886792452830186, 53],
+ [55.851851851851855, 54],
+ [56.81818181818182, 55],
+ [57.785714285714285, 56],
+ [58.75438596491228, 57],
+ [59.724137931034484, 58],
+ [60.69491525423729, 59],
+ [61.666666666666664, 60],
+ [62.63934426229508, 61],
+ [63.61290322580645, 62],
+ [64.58730158730158, 63],
+ [65.5625, 64],
+ [66.53846153846153, 65],
+ [67.51515151515152, 66],
+ [68.49253731343283, 67],
+ [69.47058823529412, 68],
+ [70.44927536231884, 69],
+ [71.42857142857143, 70],
+ [72.40845070422536, 71],
+ [73.38888888888889, 72],
+ [74.36986301369863, 73],
+ [75.35135135135135, 74],
+ [76.33333333333333, 75],
+ [77.3157894736842, 76],
+ [78.2987012987013, 77],
+ [79.28205128205128, 78],
+ [80.26582278481013, 79],
+ [81.25, 80],
+ [82.23456790123457, 81],
+ [83.21951219512195, 82],
+ [84.20481927710843, 83],
+ [85.19047619047619, 84],
+ [86.17647058823529, 85],
+ [87.16279069767442, 86],
+ [88.14942528735632, 87],
+ [89.13636363636364, 88],
+ [90.12359550561797, 89],
+ [91.11111111111111, 90],
+ [92.0989010989011, 91],
+ [93.08695652173913, 92],
+ [94.0752688172043, 93],
+ [95.06382978723404, 94],
+ [96.05263157894737, 95],
+ [97.04166666666667, 96],
+ [98.03092783505154, 97],
+ [99.0204081632653, 98],
+ [100.01010101010101, 99],
+ [101.0, 1],
+ [101.0, 100]]
+
+
+
+## 试题 C: 分配口罩
+
+本题总分:10 分
+
+**【问题描述】**
+
+某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文
+字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目
+录下有一个文件 mask.txt,内容与下面的文本相同)
+
+```python
+9090400
+8499400
+5926800
+8547000
+4958200
+4422600
+5751200
+4175600
+6309600
+5865200
+6604400
+4635000
+10663400
+8087200
+4554000
+```
+
+
+ 现在市长要把口罩分配给市内的2所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+
+```
+def main():
+ f=open('mask.txt','r')
+ #string=f.readlines()
+ num_lis=[]
+ for i in f:
+ #print(i)
+ num_lis.append(int(i))
+ print(num_lis)
+ re=[abs(num_lis[0]-num_lis[1])]
+ def dfs(num1,num2,num_lis):
+ #global re
+ if not num_lis:
+ re[0]=min(re[0],abs(num1-num2))
+ return
+ dfs(num1+num_lis[0],num2,num_lis[1:])
+ dfs(num1,num2+num_lis[0],num_lis[1:])
+ dfs(0,0,num_lis)
+ print(re[0])
+ return
+main()
+```
+
+ [9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, 6604400, 4635000, 10663400, 8087200, 4554000]
+ 2400
+
+
+## 试题 F: 解码
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+
+**【问题描述】**
+小明有一串很长的英文字母,可能包含大写和小写。
+在这串字母中,有很多连续的是重复的。小明想了一个办法将这串字母表
+达得更短:将连续的几个相同字母写成字母 + 出现次数的形式。
+例如,连续的 5 个 a,即 aaaaa,小明可以简写成 a5(也可能简写成 a4a、
+aa3a 等)。对于这个例子:HHHellllloo,小明可以简写成 H3el5o2。为了方便表
+达,小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串,请帮助小明还原成原来的串。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出一个字符串,表示还原后的串。
+
+**【样例输入】**
+
+```python
+H3el5o2
+```
+
+**【样例输出】**
+
+```python
+HHHellllloo
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由大小写英文字母和数字组成,长度不超过100。
+请注意原来的串长度可能超过 100。
+
+
+
+```
+num_set={'0','1','2','3','4','5','6','7','8','9'}
+string=input()
+re=[]
+for i in string :
+ if i in num_set:
+ for i in range(int(i)-1):
+ re.append(re[-1])
+ else:
+ re.append(i)
+print(''.join(re))
+```
+
+ H3el5o2
+ HHHellllloo
+
+
+## 试题 G: 走方格
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+在平面上有一些二维的点阵。
+这些点的编号就像二维数组的编号一样,从上到下依次为第 1 至第 n 行,
+从左到右依次为第 1 至第 m 列,每一个点可以用行号和列号来表示。
+现在有个人站在第 1 行第 1 列,要走到第 n 行第 m 列。只能向右或者向下
+走。
+注意,如果行号和列数都是偶数,不能走入这一格中。
+问有多少种方案。
+
+**【输入格式】**
+
+> 输入一行包含两个整数 n, m。
+
+**【输出格式】**
+
+> 输出一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+3 4
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【样例输入】**
+
+```python
+6 6
+```
+
+
+
+
+```
+n,m=map(int,input().strip().split())
+def main():
+ re=[0]
+ def dfs(x,y):
+ if x==n-1 and y==m-1:
+ re[0]+=1
+ if 0<=x+1<=(n-1) and not ((x+1)%2==0 and (y)%2==0):
+ dfs(x+1,y)
+ if 0<=y+1<=(m-1) and not ((x)%2==0 and (y+1)%2==0):
+ dfs(x,y+1)
+ dfs(0,0)
+ print(re[0])
+main()
+```
+
+ 3 4
+ 2
+
+
+### bfs
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ queue=[(0,0)]
+ re=0
+ while queue:
+ x,y=queue.pop(0)
+ if x==n-1 and y==m-1:
+ re+=1
+ if 0<=x+1 第一行包含 2 个整数 n 和 K。
+> 第二行包含 n 个整数 A1, A2, · · · , An。
+
+**【输出格式】**
+
+> 一个整数代表答案。
+
+**【样例输入】**
+
+```python
+4 33
+1 2 3 4
+```
+
+**【样例输出】**
+
+```python
+8
+```
+
+**【评测用例规模与约定】**
+对于 30% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ K ≤ 108, 1 ≤ Ai ≤ 104。
+对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ K ≤ 1010,1 ≤ Ai ≤ 109.
+
+
+
+```
+n,K=map(int,input().strip().split())
+num_lis=list(map(int,input().strip().split()))
+re=0
+for i in range(n):
+ for j in range(i+1,n):
+ if (num_lis[i]*10+num_lis[j])<=K:
+# print( num_lis[i]*10+num_lis[j])
+ re+=1
+ if (num_lis[j]*10+num_lis[i])<=K:
+# print(num_lis[j]*10+num_lis[i])
+ re+=1
+print(re)
+
+
+```
+
+ 4 33
+ 1 2 3 4
+ 8
+
+
+## 试题 I: 超级胶水
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:25 分
+
+**【问题描述】**
+
+小明有 n 颗石子,按顺序摆成一排。他准备用胶水将这些石子粘在一起。
+每颗石子有自己的重量,如果将两颗石子粘在一起,将合并成一颗新的石
+子,重量是这两颗石子的重量之和。
+为了保证石子粘贴牢固,粘贴两颗石子所需要的胶水与两颗石子的重量乘
+积成正比,本题不考虑物理单位,认为所需要的胶水在数值上等于两颗石子重
+量的乘积。
+每次合并,小明只能合并位置相邻的两颗石子,并将合并出的新石子放在
+原来的位置。
+现在,小明想用最少的胶水将所有石子粘在一起,请帮助小明计算最少需
+要多少胶水。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n,表示初始时的石子数量。
+>
+> 第二行包含 n 个整数 w1,w2, · · · ,wn,依次表示每颗石子的重量。
+
+**【输出格式】**
+
+> 输出一行包含一个整数,表示最少需要的胶水数。
+
+**【样例输入】**
+
+```python
+3
+3 4 5
+```
+
+**【样例输出】**
+
+```python
+47
+```
+
+**【样例输入】**
+
+```python
+8
+1 5 2 6 3 7 4 8
+```
+
+**【样例输出】**
+
+```python
+546
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 15。
+>
+> 对于 60% 的评测用例,1 ≤ n ≤ 100。
+>
+> 对于 80% 的评测用例,1 ≤ n ≤ 1000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 100000,1 ≤ wi ≤ 1000。
+
+
+```
+n=int(input())
+num_lis=list(map(int,input().strip().split()))
+def f(num_lis):
+ re=num_lis[0]*num_lis[1]
+ re_index=0
+ for i in range(len(num_lis)-1):
+ if num_lis[i]*num_lis[i+1]
+
+int balance(int a, int b)
+{
+ if(ab) return 1;
+ return 0;
+}
+
+void judge(char* data, int a, int b, int std)
+{
+ switch(balance(data[a],data[std])){
+ case -1:
+ printf("%d light\n", a);
+ break;
+ case 0:
+ printf("%d heavy\n", b);
+ break;
+ case 1:
+ printf("err!\n", b);
+ }
+}
+
+// data 中8个元素,有一个假币,或轻或重
+void f(char* data)
+{
+ switch(balace(data[0]+data[2]+data[1],data[5]+data[4],data[3]) ____________________________________ ){ // 填空
+ case -1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,0,3,1);
+ break;
+ case 0:
+ judge(data,2,5,0);
+ break;
+ case 1:
+ judge(data,1,4,0);
+ }
+ break;
+ case 0:
+ judge(data,6,7,0);
+ break;
+ case 1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,4,1,0);
+ break;
+ case 0:
+ judge(data,5,2,0);
+ break;
+ case 1:
+ judge(data,3,0,1);
+ }
+ break;
+ }
+}
+
+int main()
+{
+ int n;
+ char buf[100];
+
+ scanf("%d", &n);
+ gets(buf);
+
+ int i;
+ for(i=0; i
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+
+```
+
+
+```
+n,k=map(int,input().strip().split())
+re=[i for i in range(1,n+1)]
+start=0
+while len(re)!=1:
+
+ for i in range(k-1):
+ start=(start+1)%len(re)
+ re.pop(start)
+ start=start%len(re)
+# print(re)
+print(re[0])
+```
+
+ 10 3
+ 4
+
+
+
+## 标题:自描述序列
+```
+小明在研究一个序列,叫Golomb自描述序列,不妨将其记作{G(n)}。这个序列有2个很有趣的性质:
+
+1. 对于任意正整数n,n在整个序列中恰好出现G(n)次。
+2. 这个序列是不下降的。
+
+以下是{G(n)}的前几项:
+
+n 1 2 3 4 5 6 7 8 9 10 11 12 13
+G(n)1 2 2 3 3 4 4 4 5 5 5 6 6
+
+给定一个整数n,你能帮小明算出G(n)的值吗?
+```
+**输入**
+```
+----
+一个整数n。
+
+对于30%的数据,1 <= n <= 1000000
+对于70%的数据,1 <= n <= 1000000000
+对于100%的数据,1 <= n <= 2000000000000000
+```
+**输出**
+```
+----
+一个整数G(n)
+
+```
+**【样例输入】**
+```
+13
+```
+**【样例输出】**
+```
+6
+```
+
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+
+```
+n=int(input())
+dic_={1:1,2:2}
+num=1
+i=1
+while num<=n:
+# print(dic_)
+ for j in range(dic_[i]):
+ dic_[num]=i
+ num+=1
+ i+=1
+print(dic_[n])
+
+```
+
+ 13
+ 6
+
+
+
+## 标题:采油
+```
+LQ公司是世界著名的石油公司,为世界供应优质石油。
+最近,LQ公司又在森林里发现了一大片区域的油田,可以在这个油田中开采n个油井。
+LQ公司在这n个油井之间修建了n-1条道路,每条道路连接两个油井,路径中间不会路过任何油井,而且这些道路将所有油井连通。
+建立油井的时候需要使用一台大型设备,运输起来非常麻烦,LQ公司准备在其中的一个油井位置建立一个空运站,先将设备空运到空运站,之后每次经过他们建立的道路来运输这个大型设备以建立不同的油井,当油井建立完毕后再从空运站将大型设备运走。
+为了减少运输的麻烦,公司要求大型设备在道路上运输的总路程是最短的。
+
+在建立油井和采油的过程中需要花费一些人力,第i个油井需要花费Bi个人,而一旦油井建成,就需要Si个人一直坚守在油井上进行维护。
+当然,如果一个人参与了油井的建设,他可以直接留下来维护油井,或者参与下一个油井的建设,但是在维护油井的人不能再参加后续油井的建设了。
+
+现在LQ公司想知道,大型设备运输的总路径长度最短是多少?在保证总路径长度最短的情况下,LQ公司至少需要花费多少人力才能完成所有油井的建立与维护。
+```
+**【输入格式】**
+```
+ 输入的第一行包含一个整数n,表示油井的数量。油井由1到n依次标号。
+ 第二行包含n个整数,依次表示B1, B2, …, Bn,相邻的整数之间用一个空格分隔。
+ 第三行包含n个整数,依次表示S1, S2, …, Sn,相邻的整数之间用一个空格分隔。
+ 接下来n-1行描述油井之间的道路,其中的第i行包含两个整数a,b,用一个空格分隔,表示一条道路的起点为i+1、终点为a,长度为b,道路是双向的,设备可以从任意一端运送到另一端,每条道路都可以经过任意多次。数据保证任意两个油井之间都可以通过道路连接。
+```
+**【输出格式】**
+```
+ 输出包含两个整数,用一个空格分隔,表示最优情况下大型设备需要运输的总路程,以及在总路程最短的情况下最少需要花费的人力数量。
+```
+**【样例输入】**
+```
+2
+10 20
+15 15
+1 8
+```
+**【样例输出】**
+```
+16 30
+```
+**【样例说明】**
+```
+ 有两种方案达到最优。
+ 方案一:在油井2建立空运站,先建立油井2,再将大型设备运输到油井1建立油井1,最后将大型设备运回油井2。
+ 方案二:在油井1建立空运站,先将大型设备运输到油井2建立油井2,再将大型设备运送到油井1建立油井1。
+```
+**【样例输入】**
+```
+6
+3 10 20 7 15 9
+2 6 10 4 8 7
+1 9
+1 2
+2 5
+3 4
+3 7
+```
+**【样例输出】**
+```
+54 38
+```
+**【数据规模和约定】**
+```
+ 对于20%的数据:n不超过10;
+ 另外20%的数据:每个油井最多和两个油井之间有道路直接连接;
+ 另外10%的数据:有n-1个油井只有一条道路与其他油井连接;
+ 对于100%的数据:n不超过100000,B、S、c均为不超过10000的正整数。
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+```
+n=int(input())
+B_lis=map(int,input().strip().split())
+S_lis=map(int,input().strip().split())
+map_=[[0 for j in range(n)]for j in range(n) ]
+for i in range(1,n):
+ a,b=map(int,input().strip().split())
+ map_[i][a-1]=b
+print(map_)
+```
+
+ 2
+ 10 20
+ 15 15
+ 1 8
+ [[0, 0], [8, 0]]
+
+
+
+```
+int n,l=0,num=0,b,s;
+
+int main(){
+
+ cin>>n;
+
+ for(int i=1;i<=n;i++)
+
+ cin>>b;
+
+ for(int i=1;i<=n;i++){
+
+ cin>>s;
+
+ num+=s;
+
+ }
+
+ for(int i=2;i<=n;i++){
+
+ int a1,a2;
+
+ cin>>a1>>a2;
+
+ l+=a2;
+
+ }
+
+ cout<min_len[0]:
+ return
+ if (x==n-1)and (y==m-1):
+ res.append(temp)
+ min_len[0]=len(temp)
+ return
+
+ if (0<=(x+1)0:
+ if b&1:
+ re*=a
+ a=a**2
+ b>>=1
+ return re
+
+```
+
+
+```
+p=891234941
+q=1123984201
+n=1001733993063167141
+c=20190324
+d=212353
+for i in range(1,500000): #枚举因子 d*e%((p-1)*(q-1))=1 (((q-1)*(p-1))*yz+1) %d =0
+ if(((p-1)*(q-1)*i+1)%d==0):
+ e=((p-1)*(q-1)*i+1)//212353
+ print(((p-1)*(q-1)*i+1)//d)
+ break
+def quick_mod(a,b,c):
+ a=a%c
+ ans=1
+ while b!=0:
+ if b&1:
+ ans=(ans*a)%c
+ b>>=1
+ a=(a*a)%c
+ return ans
+x=quick_mod(c,e,n) #x=c^e%n 579706994112328949
+print(x)
+print(quick_mod(x,d,n)) #c=x^d%n
+```
+
+ 823816093931522017
+ 579706994112328949
+ 20190324
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题E、完美平方数.md b/LanQiao/蓝桥杯习题/试题E、完美平方数.md
new file mode 100644
index 0000000..50514a1
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题E、完美平方数.md
@@ -0,0 +1,75 @@
+## 试题 E: 完美平方数
+本题总分:15 分
+
+**【问题描述】**
+
+如果整个整数 X 本身是完全平方数,同时它的每一位数字也都是完全平方
+数,我们就称 X 是完美平方数。
+前几个完美平方数是 0、1、4、9、49、100、144……
+即第 1 个完美平方数是 0,第 2 个是 1,第 3 个是 4,……
+请你计算第 2020 个完美平方数是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+visited={0}
+def f(string):
+ for i in string:
+ if i not in {'0','1','4','9'}:
+ return False
+ return True
+num=1
+while True :
+ if f(str(num**2)):
+ visited.add(num**2)
+ print(len(visited))
+ if len(visited)==2020:
+ print(num**2)
+ break
+ num+=1
+# 491499994440019919104
+```
+
+
+```
+# def f (x):
+# for i in range(int(x**(0.5))+1):
+# if i**2==x:
+# return True
+# # return False
+
+# import math
+# def is_sqr(n):
+# a = int(math.sqrt(n))
+# return a * a == n
+# # Squares=set()
+# # for i in range(20200000):
+# # Squares.add(i**2)
+# visited={0,1,4,9}
+# #num=50
+# len_=1
+# queue=[1,4,9]
+# while queue:
+# num=queue.pop(0)
+# queue.append(int(str(num)+'0'))
+# queue.append(int(str(num)+'1'))
+# queue.append(int(str(num)+'4'))
+# queue.append(int(str(num)+'9'))
+# # label=1
+# # for i in str(num):
+# # if int(i) not in visited :
+# # label=-1
+# # if label==1:
+# if is_sqr(num) :
+# visited.add(num)
+# len_+=1
+# print(len(visited))
+# if len(visited)==2020:
+# print(num)
+# break
+```
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md b/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md
new file mode 100644
index 0000000..fdf42c9
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md
@@ -0,0 +1,83 @@
+## 试题 G: 外卖店优先级
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+
+“饱了么”外卖系统中维护着 N 家外卖店,编号 1 ∼ N。每家外卖店都有
+一个优先级,初始时 (0 时刻) 优先级都为 0。
+每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减
+到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
+如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果
+优先级小于等于 3,则会被清除出优先缓存。
+给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优
+先缓存中。
+
+**【输入格式】**
+
+第一行包含 3 个整数 N、M 和 T。
+以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到
+一个订单。
+
+**【输出格式】**
+
+输出一个整数代表答案。
+
+
+**【样例输入】**
+```
+2 6 6
+1 1
+5 2
+3 1
+6 2
+2 1
+6 2
+```
+**【样例输出】**
+```
+1
+```
+**【样例解释】**
+
+6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,
+加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。
+
+**【评测用例规模与约定】**
+
+对于 80% 的评测用例,1 ≤ N, M, T ≤ 10000。
+对于所有评测用例,1 ≤ N, M, T ≤ 100000,1 ≤ ts ≤ T,1 ≤ id ≤ N。
+
+
+```
+N,M,T=map(int,input().strip().split())
+shop=[0 for i in range(N)]
+message=[[] for i in range(T)]
+
+for i in range(M):
+ ts,id=map(int,input().strip().split())
+ message[ts-1].append(id)
+# message.sort(key=lambda x:x[0])
+first=set()
+for i in range(len(message)):
+ for id in message[i]:
+ shop[id-1]+=3
+ for id in range(1,len(shop)):
+ shop[id-1]-=1
+ if shop[id-1]>5:
+ first.add(shop[id-1])
+ if shop[id-1]<=3:
+ first=first-{shop[id-1]}
+print(len(first))
+
+
+
+```
+
+ 2 6 6
+ 1 1
+ 5 2
+ 3 1
+ 6 2
+ 2 1
+ 6 2
+ 1
diff --git a/LanQiao/蓝桥杯习题/试题G外卖店优先级.md b/LanQiao/蓝桥杯习题/试题G外卖店优先级.md
new file mode 100644
index 0000000..f09ba00
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题G外卖店优先级.md
@@ -0,0 +1,39 @@
+## 题目 1853: [蓝桥杯][基础练习]数列排序
+
+时间限制: 1Sec 内存限制: 128MB 提交: 982 解决: 628
+
+**题目描述**
+
+- 给定一个长度为n的数列,将这个数列按从小到大的顺序排列。1<=n<=200
+
+**输入**
+```
+第一行为一个整数n。
+第二行包含n个整数,为待排序的数,每个整数的绝对值小于10000。
+```
+**输出**
+
+- 输出一行,按从小到大的顺序输出排序后的数列。
+
+**样例输入**
+```
+5
+8 3 6 4 9
+
+```
+**样例输出**
+```
+3 4 6 8 9
+```
+
+
+```
+a=int(input())
+num=sorted(list(map(int,input().strip().split())))
+for i in num:
+ print(i,end=' ')
+```
+
+ 5
+ 8 3 6 4 9
+ 3 4 6 8 9
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题H修改数组.md b/LanQiao/蓝桥杯习题/试题H修改数组.md
new file mode 100644
index 0000000..ad384a1
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题H修改数组.md
@@ -0,0 +1,107 @@
+## 试题 H: 修改数组
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+
+**【问题描述】**
+
+给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现
+的整数。
+现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
+A2, A3, · · · , AN。
+当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则
+小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直
+到 Ai 没有在 A1 ∼ Ai−1 中出现过。
+当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
+现在给定初始的 A 数组,请你计算出最终的 A 数组。
+
+**【输入格式】**
+
+第一行包含一个整数 N。
+第二行包含 N 个整数 A1, A2, · · · , AN 。
+
+**【输出格式】**
+
+输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
+
+**【样例输入】**
+
+- 5
+- 2 1 1 3 4
+
+**【样例输出】**
+
+- 2 1 3 4 5
+
+**【评测用例规模与约定】**
+
+- 对于 80% 的评测用例,1 ≤ N ≤ 10000。
+- 对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
+
+
+```
+N=int(input())
+nums=list(map(int,input().strip().split()))
+visited=set()
+for i in range(len(nums)):
+ while nums[i] in visited:
+ nums[i]+=1
+ visited.add(nums[i])
+nums=list(map(str,nums))
+print(' '.join(nums))
+```
+
+ 5
+ 2 1 1 3 4
+ 2 1 3 4 5
+
+
+
+```
+a=[{2},{3},set(),set()]
+a.remove(set())
+print(a)
+```
+
+ [{2}, {3}, set()]
+
+
+
+```
+help(list.remove)
+```
+
+ Help on method_descriptor:
+
+ remove(...)
+ L.remove(value) -> None -- remove first occurrence of value.
+ Raises ValueError if the value is not present.
+
+
+
+
+
+```
+[{3}-{3},set(),{4}].remove({4})
+# a=[{3}-{3},set(),{4}].remove({3}-{3})
+# print(a)
+```
+
+
+```
+N,M,k=map(int,input().strip().split())
+queue=[]
+for i in range(N):
+ candy1,candy2,candy3=map(int,input().strip().split())
+ queue.append({candy1,candy2,candy3})
+re={}
+all=set([ i for i in range(1,M+1)])
+
+while all!=re and queue:
+ temp=max(queue,key=len)
+ re|=temp
+# queue.remove()
+ remove_count=0
+ for i in queue:
+
+```
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/进制转换知识整理.md b/LanQiao/蓝桥杯习题/进制转换知识整理.md
new file mode 100644
index 0000000..59f9e7e
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/进制转换知识整理.md
@@ -0,0 +1,109 @@
+## 进制转换
+
+ASCII码转换为int:ord('A') 65
+
+int转为ASCII码:chr(65) 'A'
+
+在日常生活中我们频繁使用到数学的进制,如季度逢三进一,星期逢七进一;×××、小时使用12进制,每天使用24进制,每月使用30进制,分秒使用60进制,一年使用360进制等等;在编程过程中我们经常需要转换进制,虽然Python已经内置了常用进制转换函数,如int,bin,hex,oct;但是如果我们需要转换成其他进制怎么办呢?
+
+ 我们知道,十进制转换成二进制时,使用“除2取余,逆序排列”即可。二进制转换成十进制时按权展开,即可得到十进制。类似地可以实现十进制转换成任意进制,任意进制也可以转换成十进制;通过十进制进行中转,即可实现任意进制数之间的转换了。
+
+
+
+```
+#将十进制数转换成任意进制20进制以内,任意进制只需添加不同的符号即可
+def decimalToAny(num,n):
+ if num==0:
+ return 0
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+97)
+ print(baseStr)
+ new_num_str = ""
+ while num != 0:
+ remainder = num % n
+ if remainder > 9:
+ remainder_string = baseStr[remainder]
+ else:
+ remainder_string = str(remainder)
+ new_num_str = remainder_string+new_num_str
+ num = num // n
+ return new_num_str
+decimalToAny(58,30)
+```
+
+ {10: 'a', 11: 'b', 12: 'c', 13: 'd', 14: 'e', 15: 'f', 16: 'g', 17: 'h', 18: 'i', 19: 'j', 20: 'k', 21: 'l', 22: 'm', 23: 'n', 24: 'o', 25: 'p', 26: 'q', 27: 'r', 28: 's', 29: 't'}
+
+
+
+
+
+ '1s'
+
+
+
+
+```
+#将任意进制数转换成十进制
+def anyToDecimal(num,n):
+ baseStr={}
+ for i in range(10):
+ baseStr[str(i)]=i
+ for i in range(10,n):
+ baseStr[chr(i-10+97)]=i
+ print(baseStr)
+ new_num = 0
+ for i in range(len(num)):
+ new_num+=baseStr[num[len(num)-1-i]]*(n**i)
+ return new_num
+anyToDecimal('1s',30)
+```
+
+ {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9, 'a': 10, 'b': 11, 'c': 12, 'd': 13, 'e': 14, 'f': 15, 'g': 16, 'h': 17, 'i': 18, 'j': 19, 'k': 20, 'l': 21, 'm': 22, 'n': 23, 'o': 24, 'p': 25, 'q': 26, 'r': 27, 's': 28, 't': 29}
+
+
+
+
+
+ 58
+
+
+
+
+```
+print('{0}xxxxxxxx{1}'.format('这是0要传入的东西','这是1要传入的东西'))
+```
+test={'nan':'werty'}
+print("ghjk{nan}gbhnjmk".format(**test))
+test
+进制转化,b o d x 分别表示二、八、十、十六进制
+
+
+```
+print('{:b}'.format(250))
+print('{:o}'.format(250))
+print('{:d}'.format(250))
+print('{:x}'.format(250))
+#千分位分隔符,这种情况只针对与数字
+print('{:,}'.format(100000000))
+print('{:,}'.format(235445.234235))
+```
+
+ 11111010
+ 372
+ 250
+ fa
+ 100,000,000
+ 235,445.234235
+
+
+精度和类型f精度常和f一起使用
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+ 4.2
+ 4.1000
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/采油.md b/LanQiao/蓝桥杯习题/采油.md
new file mode 100644
index 0000000..72022de
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/采油.md
@@ -0,0 +1,138 @@
+## 采油
+```
+LQ公司是世界著名的石油公司,为世界供应优质石油。
+最近,LQ公司又在森林里发现了一大片区域的油田,可以在这个油田中开采n个油井。
+LQ公司在这n个油井之间修建了n-1条道路,每条道路连接两个油井,路径中间不会路过任何油井,而且这些道路将所有油井连通。
+建立油井的时候需要使用一台大型设备,运输起来非常麻烦,LQ公司准备在其中的一个油井位置建立一个空运站,先将设备空运到空运站,之后每次经过他们建立的道路来运输这个大型设备以建立不同的油井,当油井建立完毕后再从空运站将大型设备运走。
+为了减少运输的麻烦,公司要求大型设备在道路上运输的总路程是最短的。
+
+在建立油井和采油的过程中需要花费一些人力,第i个油井需要花费Bi个人,而一旦油井建成,就需要Si个人一直坚守在油井上进行维护。
+当然,如果一个人参与了油井的建设,他可以直接留下来维护油井,或者参与下一个油井的建设,但是在维护油井的人不能再参加后续油井的建设了。
+
+现在LQ公司想知道,大型设备运输的总路径长度最短是多少?在保证总路径长度最短的情况下,LQ公司至少需要花费多少人力才能完成所有油井的建立与维护。
+```
+**【输入格式】**
+```
+ 输入的第一行包含一个整数n,表示油井的数量。油井由1到n依次标号。
+ 第二行包含n个整数,依次表示B1, B2, …, Bn,相邻的整数之间用一个空格分隔。
+ 第三行包含n个整数,依次表示S1, S2, …, Sn,相邻的整数之间用一个空格分隔。
+ 接下来n-1行描述油井之间的道路,其中的第i行包含两个整数a,b,用一个空格分隔,表示一条道路的起点为i+1、终点为a,长度为b,道路是双向的,设备可以从任意一端运送到另一端,每条道路都可以经过任意多次。数据保证任意两个油井之间都可以通过道路连接。
+```
+**【输出格式】**
+```
+ 输出包含两个整数,用一个空格分隔,表示最优情况下大型设备需要运输的总路程,以及在总路程最短的情况下最少需要花费的人力数量。
+```
+**【样例输入】**
+```
+2
+10 20
+15 15
+1 8
+```
+**【样例输出】**
+```
+16 30
+```
+**【样例说明】**
+```
+ 有两种方案达到最优。
+ 方案一:在油井2建立空运站,先建立油井2,再将大型设备运输到油井1建立油井1,最后将大型设备运回油井2。
+ 方案二:在油井1建立空运站,先将大型设备运输到油井2建立油井2,再将大型设备运送到油井1建立油井1。
+```
+**【样例输入】**
+```
+6
+3 10 20 7 15 9
+2 6 10 4 8 7
+1 9
+1 2
+2 5
+3 4
+3 7
+```
+**【样例输出】**
+```
+54 38
+```
+**【数据规模和约定】**
+```
+ 对于20%的数据:n不超过10;
+ 另外20%的数据:每个油井最多和两个油井之间有道路直接连接;
+ 另外10%的数据:有n-1个油井只有一条道路与其他油井连接;
+ 对于100%的数据:n不超过100000,B、S、c均为不超过10000的正整数。
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+```
+n=int(input())
+B_lis=map(int,input().strip().split())
+S_lis=map(int,input().strip().split())
+map_=[[0 for j in range(n)]for j in range(n) ]
+for i in range(1,n):
+ a,b=map(int,input().strip().split())
+ map_[i][a-1]=b
+print(map_)
+```
+
+ 2
+ 10 20
+ 15 15
+ 1 8
+ [[0, 0], [8, 0]]
+
+
+
+```
+int n,l=0,num=0,b,s;
+
+int main(){
+
+ cin>>n;
+
+ for(int i=1;i<=n;i++)
+
+ cin>>b;
+
+ for(int i=1;i<=n;i++){
+
+ cin>>s;
+
+ num+=s;
+
+ }
+
+ for(int i=2;i<=n;i++){
+
+ int a1,a2;
+
+ cin>>a1>>a2;
+
+ l+=a2;
+
+ }
+
+ cout<微信公众号:LSGO软件技术团队|华北电力大学
+马燕鹏|CSDN:https://lsgogroup.blog.csdn.net/
\ No newline at end of file
diff --git a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
index 0e789f1..d48f2af 100644
--- a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
+++ b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
@@ -1,38 +1,7 @@
{
"cells": [
{
- "attachments": {
- "image.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAgAElEQVR4Ae19B3yc1ZX9biBslk02CSH7DyGEABsgoQVMhxgCpkMgYBuDscHgXrCNewM3MO699ypZ7l2y3G1ZVrcs2yq21aVR1/T2zcz5/85939gOS/DIK8xGvPFvLGnmK+877737zj3vvvv+BfqlEdAIaAQ0AhoBjYBGQCPQYAT+pcFn6BM0AhoBjYBGQCOgEdAIaASgSZRuBBoBjYBGQCOgEdAIaAQuAwFNoi4DNH2KRkAjoBHQCGgENAIaAU2idBvQCGgENAIaAY2ARkAjcBkIaBJ1GaDpUzQCGgGNgEZAI6AR0AhoEqXbgEZAI6AR0AhoBDQCGoHLQECTqMsATZ+iEdAIaAQ0AhoBjYBGQJMo3QY0AhoBjYBGQCOgEdAIXAYCmkRdBmj6FI2ARkAjoBHQCGgENAKaROk2oBHQCGgENAIaAY2ARuAyENAk6jJA06doBDQCGgGNgEZAI6AR0CRKtwGNgEZAI6AR0AhoBDQCl4GAJlGXAZo+RSOgEdAIaAQ0AhoBjYAmUboNaAQ0AhoBjYBGQCOgEbgMBDSJugzQ9CkaAY2ARkAjoBHQCGgENInSbUAjoBHQCGgENAIaAY3AZSCgSdRlgKZP0QhoBDQCGgGNgEZAI6BJlG4DGgGNgEZAI6AR0AhoBC4DAU2iLgM0fYpGQCOgEdAIaAQ0AhoBTaJ0G2jCCIQQCpnvJvyU+tE0AhoBjYBG4LtBoEmQqBCxCwGBUBAGDED+DyIUBBCUrxDkASEvgua/EL8MyNcIIoBQiH9wwFWf8ac6OcjLISTn8xp+BENe+NQtG7fWeO/z9w8hwMKzmKEAgixfwLypKqo8E5+DjxkIuREI+eQc/i0XatzSNeBqARB8hSVL44IPfhjnKyOEYDByBHkdVR+qCCRGX30Fg8QhgFDAQCgQgOGtgztnA6b37IoRczZg6zkHCCGrkWVjewiQYJ0HXFV3MBSCX4D+6h303xqBxkFANTlaFNM4mc1SPpe2baj+SxvFRhuiTeNPdoRwG+afvAJtl3IUguxz0nYNsRdsy+x9Hp4i12UHEEso96Y1lD4QYl8wgIDv7zta4zzu+T7HZ2B5wv1XHsd8XrGvjXW/8HWIX5B2iKB5lB2l5Q75lO03bYHUBI8JKntrFtLE3Dhvds9fVkaYgDkmyAOdP9YcPcKHfuNP9fyqPqWIYutpf0IwWDb+x7qV2uIHARnT5Fg2Bw4J/FgMvjzMN95Pf/ntINAkSFSQzS7IBhaEGBL56Ucg/DeH7xCHcP4MIRAMwWDro40KkSOFwK7CY3idAD+hAQqGEAiojsW/eQUam1DQUI23keuEnSJIkhYkEeD9WSYaQvVcNHiq04QU2TI7GMuvzlPHi0ESxtDIBYz4cn74Q0H4xAYQZD8CJDahgBBdPkSIhkxGhEtfVIzGVw5T9RMEyRN/V+8gggF+FkLQcMOoOIUNw15A64790WdFGipMkkyyHSZQbC9+OZ/l5LVkWIq0aF8plf5TI3BpBNiexYkTAqTaHP9WbZjnq7aoRkySHvUOt/XzRIqUiXbv/Lm8MEfiIELSD9iW2e94bdo02kg6Dux6qg+IzQvRntHOKWLA4bgxXzK8y/Vpf8kNWCraKvOZ4Y/YFjSoXHJ9ZTsBtxBOsakBjg3EQxE64seyECfyFhkazhNU5ZbLM9AemxgRLz6SOleeRsYOuWjEhWTdiYeuCJPBa9JGGjD4OcEyyybUV34nlaJ99cEf5IjEsnsRChFDYVMR310f2DgINAkSFYBPlA2SGxoJDqKhkFc6BVUcwCeDthApIVGAQXJEYiUdJySDPjsWgn4E5fggbREM6ShhsqVIgDJEjd9gSQACVMuCPoR4Y1NdCZtRQ8rO+4a9TzXW83sxpOcNJLt845cv4iYXMlgj8CkrJYMD3TnWBY0+rVQw6I3YcHJwCb/4e3gwEfXpvKepHlkIMg1RwBCDV7KzFzq3egdv9lqGBCuNNkkzDY9JooMheIWE8rvwgMRrXbhn+N76p0agURCQEVkpTKrfcvBUJCfM3qk8h0mVKFRso9LW2U7Vm2WRPmA6EdK4aQPopPAtThiVczVYS/smQ6CwRdWFY3TYwaS5YJcwBa9GeU7zImqgZ79XSgodLJIE2mPKKVTPxKlpzJvK49C5JNHks/rFiAuXE0eZipRSpIVqCnGhm63gYanC5RYnVXANIBhQTq6QKJJVwZjnKVX7IlN1yadRbrlf6hOGUtB5PbYFcaT5DMSH44CMaSyRSaLOa/uKRIlzH6FTesmC6QMahEATIVHsLIpIqYGVWoxX1CXxsERZIkEyiZVYD8rXLhii/FBxUsQqFCSjVw1bdUA//B4rKkqtcLh80llIvNjIwwavQYh/w8FUwKgoBYJUbsKeiCJ6SoWil6nKF/TZYLVZUWHzmg4Ly3zB0/wuKYASoM3/w6RHiB6NOQ1REH7Do4zHN+AR/koGj4sUJ6paXyVWPJYGkt6kL+iD3++Cn2S4aDOmtm+Dt/86ALNT3KJCsmSGxwp7bTnKSspQWFCI4qJSFBcXorCsDGV1HoSMb2E0CT+Q/vn9RkAIPAkEB3ZlRmh3qCYo1Yl+hiL6QqCE7IQP5ee0ESQBynGgfaqtLkNRURlKSypR5zXgFYWKBIqqhlJX5dr8nA6aoQiGTBSK4GE6YpSP6Xc24kuRFL+QKLIAOoM+Vy2sVQUoLS5A8bla1HrpeDXui/CQQBkkKIp9KJ4pyh5pj1LpGGgQYF2IjREXVdlUEjDRr2izSEzJ+YII+n1CYYIcK0zlW0iU6XtFSqQIs3LofAiJ26nqXEIM6GgKiVKqIkMUZLYhDBEJr6h6wqoE00autvCd9M9LINAkSJS0bpnrJvEge2f3MafzpOGbipJ8ym/YAKn0eFVL5DEya6em9digRRGiUXOXwpq1FsM/jsHulFLU0cLQg/o2Xuw1LIc4i9LFAX8Q8BlCqhirQ+k2AC+8ebHYuHU9hm45DSdPM3goDRGlZYiyRhS+ixdRVICS1LFENDGUxZU65VeudQOKxmk6A0ESG/OlvHI1jcePzv8t9c87ESe2hULsGfM+Pnz5dTw/IxleepKhEGpOb8COFZ+gd98e6PbSX9Hlg07o+H5rvNN7ELquyYKfA41+aQS+DQSEtPgQDLiUYCxtlv3WgJ/Tbufvyd8uMCh2GzoAKiyBVkx9bT0VheipPfFO657o0XMSNuZUochnwBMyIH2Nxk0MHFUZRic6pT/6Q354wooxnTbDJXaPlqdRX+ZjyIMxZCHgQ3nqKsRM/Qgd23fEuy0WYGd2BaovevJGub+o3iSmyiYygsAfAFRkLEmTKTuJ3Q2qL+lMUyUjoaJ4JmWiPTNZiznT4eZVqHDxMgbnQhh5FhQ7TKgjegkuqhBSrwE6gIpOKT3M5MlyT5bEJ2RJrs9z2SDOh5so7Syi++qDGhWBJkGiJKZFyI1iIJRD6VVUJS3Hmuld0bHDm2j9VAu0ePodtPmwC7r17Y0+vbuhZ5dWeL5le/SYugE7T1rgFO+P88sqtsawn8WZvdGY8PbnmB+bjZwaB/wijZuxSY1aFWanqMtB6rYp+Kx3O7T6aBpWJVaj1KokXZH3g/TrDARcNcg+uAbzJg5Cj0WnUFznFZWFc/b0qkin2DGv/Iuy9hmc3DwL4/r0wd/6Tsas5HJU230S8E0FT3nHNG6Rlu/vpzDUNMcFAsVn5GdCmsQgKoPDekSgHulLPkTPVx7DXa1XIdnwwek8gZ3LNmLBjM2IT9iIVe//F57u1B1vt2yBtu+1wotzklFvKOn8yuOn79jUEVDjsVIWRAFnW7toqs7UQkRdpxMic2w0bRJLyF5DFUmdwy5kS5mNVctGofvSw8g9WYQqhwduIwB7xRmkx67CqD6fYcb08fh01FRMXhaHhFKHDMBUPIxgEH6JHeU1aTck3Lxxq0DijAIgaSNx4U+3vRSVRUdwdNMKjPj559idWobKxr2rqHkkjaGgCwzXBn8PuVFfno4ja0ajR4t30O+zTdibWgE3JyaomosQZ8Zr0XwQc57LYCkhu+o4xiSpqTcGgYfgo62hk9eA+VAxVcKD5Q4qlpP39FTDmReHDRMGY+rUSRg3ZhwmjJ+HefHnUO0LCF3jGMDngd+viG8D7tvIMH/vL9ckSBTjYBhvI7I1GzNdiCBgy09A4rZJGNvtNTx09X/gR7e3x4cjp2NB1GpErV6JlctmYsLobni/9Xto12cGZsTnwR5ymwHmTlSnrMX28f3RuX8sksqssAdIsOilcMCO1N1oQBsjp3BaUJi2Bgs/ewfNf/UYnh+xC7tyauAx5X2ShfD8uLMsGQnRn6NT6wFYlVyKEgcD7DmtSS9JKEUDbt54hwaDFpRkbMCiIR3w0qPP4KHuW3GoyAqHGDSvzPFTJ4qYRCkdXXnTtGXm1B5LrPBQ5oj/S/UL0aQC5kbx4VVYNqY12vzlQTzxwPuYm+ODxVaAjKQcJCadQdGZnVj61A/x0tAZ+GLRcmzfug5RqSVwmwGkjYeKvpJGQCGgnAA6Q1zUQJWcg3dYDqcRkGUuQmpkAYY4heE4JyWK8ChR00NB1B+djtVrJmNwfJmaiqMtLE3BgaUzMbDTcIyesxnbYrdh89JJmDhkGIaMWIrkEsDh4ZhvBktT5RISQSWskW2biDjmohxOLXKKjX00aIElfScmXDUc8ceKURHpPFiEDSkcdkGbKC6WLNjxw1VbhOy9yzDhrT/i8cffwYC58cioJXGisETnSak6LI7Ev5JESYyZwoj4SO2JTVaES0JsaZdkmjUyJS88VIm2KKu+fQj5LShJWYdV/dui16iZWLpuO3ZsWYPF00ei98e9MXpPLvJqqRia078G5yV8ZvuJ1CmNEEB9WEQINAkSRfZPEiUBi6JuKPmakzpGVRoOzfkYD/zHz/Grd5ZiTXoZHBKoF4Qv4IS/fAOmvNQMf7rxGTzZKxrZXh98jDlwZCNhwSiM69QTY5IdqPGI8K1WzIlHGFlHiagWzIOUYaQ8XIozB2ei7y3X4hePDsXEnadR7qcRoiJjKI9UgiWtqDi1E0vbPIa20/Yj7kwtvBIbRq/ru+tQanioQs7OCRjd4jb84DfdMTOxBEVekjxOs3LBceSmmue4HFbUVFehqrISlV95V1RUoKqqApV1Trg8jG/wweMqR1naTqz+oh/GfD4IfT56Cx/d/0e8taQAWVU2uAJ+eDwVKEtagcG//Bm6TI9HfCHTRARgfCXItyF1qI/VCFwaARVEzmllmeSWwZeOH9UFDuBsw1Q4GIBNksOgY6Wuy8BrzvDJii0EYE2chjUmiRJiBTssceMwpl1rPPLiROyrBGx+H4KWeGwb/SHevPtFdN9YhcI6M4BZArzpnJlELmKF+NJPKkeIYWPsjkkWA0FZ2OMLlaMsYzsmXTUMu48VooIP15gv5VGZcVDq/owHCxoh+OqKcW7tm3jmztvxl66TsSizXpxThkyowH0q3eKlSX2Eia8ZGIWQ4RciKPUjTjuJlVLzGPcZyUt4s6QxIBHzyNtfcQjxM3vgpdsfQseNZ3GqmtO+1cg7PBuf/+1m3P7+Mmw5XgoH7ajEl3LdoVrwpAocyZ31MY2JQJMgUWqZqGlZpOWzQXN9WBC+/F3Y8MVruObn1+Pxz/fhUL5d+RGUlEN2hAKJWPvWn/HsVXfggWdHYUcN4AwasGWtxoxPhuDd9guRHAzBHfDKVJ6s1hNb8+2QFEZb+eCFJXcXojv+DL++7nn0mHUAaXXmihzDZ64kFEkGnqpMZK1qhbteG49pO7NhMSjPE4vGD3yPtOEJMiGg+sR6rB54P/7t6lvx0bIMJFs4IFDOl6izyJWogB+lxflIT0tCYmICkpKSkJCQiISEo0hMTMSxY4nyeeKJEpTWOeD1WGDJ2oaorm+i27DliEk+jYw9szH5zdvxwzbLsfNEDsoqLKjIy0Dmhql47d/vxdjV6TheVg+bvRalThXF9e3UcKQo6uOaLgJ0cvwI+b3weypQX2FBbWUd6urqYLVXod5WA1u9DTUOD6x+U2EPeCUQnSu1RCFR47tEFTtTpmBNzAT0iS+CIdNMZ7Dv8zfw9gsv4uEhe1DPLEmS0qAIqSuGott9d+KHXeOQVGJX2dskbUsQgQAXezR+qxcCQsfTCMHgMn7DkBQDvlAZStJ3YcpVIxGfVICKxlbATIzIpZTuTZtIBcdA0FMH49QC9Hj097ivRU98vOY0OOknY4mscjYVf/4u0ZzqJxcDsPyhujLUVFhgqbWh3u1DgIuWJGY1Yn1dykSizPATg6uyA37UJizA7E4v45e39sD8HAfKfKJTwZ6zDQcG3Yf/d20HjNuciTwfSRxjZRnjRZ+ZNr/x667p9sHGe7ImQaIowcrqCPE8VPwQBVxK5FVJ8zG3y+249rob8EFUITKrlLTLph4KuhGqicOklx/Bff/aDI88Pwv7nCG4Qi7krumM/gN6ovXsVLglD5VaEksnjZ6Kwc8a2WNjF6DszFU6vopMnFv1Nm676Zd4ss8CrDpuM3O5hGN/FIkKestQlzsPXf/wBkZP2oNjFZzJ5DHfVUwUezQxCiBQcQzpSzrhjquuwfXdVmJ5epXoT4yJ4iqXiOGjOuR3w+d1wefzwOfznX97vV54PPzMA5+fqQ1qUZq0Fkv6dMBdH0Uj5kQRKr0e2HLjsGvsm/jhT3th0uTe6NSmC1q/2BmffdYd//H/PsCk+NPIPLwCuzfPxbhUK4wGpGBovO6or/R9QEAUi6AfnvoC5CbOw7gBH2Nw33EYM34upi+ZjTmL5mDxnIWI3nIYaWerRLXlQK6GS+Uc0U8yJN45COvRaVgVNRn99pWruJy6g5jz3nNo9lBLPDEjU6iJmuquRfbWsRjx3K245v7ZWJdThRpZEaycG6rX38YwTGvJhTqBAG0SzYMfASOAoFGDyvT9mHLVEOxKKkB5I5MokhqDyp5fQrLVGMESEAy/GzCSsey9P+HJG1/BK502IZMqvp+KkDmhR1Iiij6VQ6VMUSH0eG0wsqMxdUA3DBw1H6sOFaDar0iQpJNoAIokbQw7IDK+UCVORfXGkD/fg1/fOha7qxywcooVIbgKjyB18qu47sd3o/OCwzhWaQaVS4yuUsG+ndr7PvTI/90zNgkSpWKETCZu5kzxSKCxFWc2f4qRLW7Cf/5XS4xPqkChS8yJDOAhjx32xNFo9+TtuOWelmg/8RBKA6RHuYjt9yo+6dQfw2PVwK/yqqh7GK4qVJ3eieWzZmL+pNGYMH0RJq/cjoQDszBj7jR8+dnnWBS9G8cqAgj5vHCfWIUZg3uj+6eLMP9YrepiJBnSQWgJL2TQFSmZHoa3HLacZeh6229wd/N+GByVhXo+G42CLG1lHBg7Uh089Tsw89m70WvkSkSfUoZKlkiLweKy2Yu8V7YXxdak5TSk45n0TXk8okUrwiZdWJL5qcR0TEUjHq23AiWJSzH03h/gV7f3xsioTJTIUl1zVaRYbJbAA4f1DE5sm4G5EydhztSxmDR9NsYtSkChB7JiRQU7XVTwi9q98p5p8CgRemA5l4W9G9Zj/dEClNndEvRpOCpQmrkfUyetxJYVn6Bj+3fxVIu30aHTu2je7GX0H/0lRn05A3NXb0dynRteYiah6hfHqjAwlZ+bGErYmfx1UWn0r//cCLA+TdX3ogfx1ecj79hGzJo4HbMnjcSo2euwdN1WxG9bgNGTJ+PLYeMQFX8c2bXsf+wRYRmElzMHY/YLfhy0oixlK3bNGY3xm/ZiX0IKMjJycDr7LHLP5eF0/jnkn8tDSbkF9Q7GaCq7IylMZPWeWngv7T4UQp2QqEkYtKdUBRvnr8TYvz2KWx9qhccXHFdrkmX6vxa5O8Zi5NO/wjU/64U5SSUo8asFGsqmsHxs7+qz8/3afKKgqxK1J+MRPW0AerzTEm++8z66fDoTy+Kyke8OwiunBhHyOWAvyML+xaMwqN8n6NOnP/qPmIwxy/Yiz08nVYUmBAMVqEqNw7SrRyCWJIo5+gJMJan6l4Rby24NVK/VUn5iEanNEuJD7GUaUZEgPqcYUCqBQRuyFrbD24/8AQ+8+gkW5/jhNRyylo+hIJIeR3w93tGc5pNgcz+C9mLknkhH8v447Fw5HzNGj8Ko9QlIK66F06fiq9Q6S7PgEj9FGkw67Jc8XtJI5HnCxxfg6JyO6HzHHfj1bWOxp8YOq/m07qIEJE97Htf95Gd4/fPNiDvL2FIKBVwEpZ7touaqf72CCDQREqXkTLJ6qjjiaJCkGGdwZHp3dPj9Hbj+wXHYWFCPGuYYYgfx2+EoOYpN/Z7FX556Ga/1n4eY4xZ4ODftOIR5rVqg1wcjMD/NE7Z8KsjQW4nS7MNYPn0JFq1Zh/Vrp2Jc/554++UP0GHYp5g4vidaPtMcLT78FKOOlCPotaN+zyB89Oc/4a7nPsbHm86pdbUBJp5k12QHohysbK10fDEyLnisWYhqcy8e+uOraPPpRmTalXEX7iRBoOw8LnjdqdjU4Ra07jcZ4/dXi41QZIz24yskKixVC4HjcCHmPqImx2PF0yJZkURz7MRmRxZSSJmef5tBjyEP6guOIv7jO/Dfv3wY7b7YhINV4SR7anAJGtUoOxWHzfPGoPvgcZi9YCU2bFiDxbNHYsTQjzHthAMV7gjLKCQqAKfDgfJSC+xen0wfCIkMGvC77SgtPoPC03HYunUdFq5Yi5h1UYhZtBibt25FzK6jOJRZBKeYOU4ByBMrL1SC1V2ywlAET5HhVVxCpEY9IpD1Qd8xAhz02N4uanOeMpw+EoeVsxZiScx6bIr+Av3bd1QpBUZ8igmff4Tn7nsArw5fhhUnatTqXgnLZH81CYmQGNXbnIXx2LduKibOWIrNJyyocbH/q+kjBlxLpn8JcaaCYyaoNa+jSLxoWYrsBIOoT5yCNVGTMHi3BZK76OR89H7tQfz0wTZ4fO4pZW+EyNmQu30cRjW/Dldf8zYm7y1EgStsU0gaeElVZhmcZSWtyj1nhJyozj6KpMVTMWPuTEwY+RkG93oPH7z9Ft56vS+6D1+L/Xm1qLWWI//oFqz+cgRGjZuAz6fNwqx5C7Bw4ULMWbQSM1amIrvaLkQqFCpHZdoOTL5qOGKTilBOB0tIFO0M7aFaAUfopGwMG6PycnHdfFNrIWZmvJniobS17LPm3EUQsKdNw4i3muHuR97EO2sL4DCUEiWLh8zYWZ7LmiM2imCyjqgg+eGqL8aZlL3YvnIplm7ago3RS7BuayziMopR5lIr98Ln8ZlIsVmnTIaqFpRT9VK7N/iRg31j30f7n92B39w6DnE1dtSRRIUAV9FhJMx6Ctf/5Ed4ZuhabDrtUG2DJZMVnA1Q9r8JM/1dgxFoEiRKgjCF4TO/k0dEIwYABuv2YvWAVnj0urtxw8sTsfpAMpJOZOD48TSkpxzEoV0LMazV6+g4aAGWH8xHnRGA33AgVLgeQ194FR07TcTGsyrnkUxBMbt1RRKSd81Hr2G7kV7thM2Vhi2jOuCVm+7HrR2jsG/LF+j17it4ssNwfLL7HIJ+B6yp8zC1b1d0GTwDc47kyx5+TIVO48DOyQgcEenFgNGAsKMF4XPXIGXSU2jxxz/g0Xe/wOKTDpF26SUp75T8jgHSRTj46e/xfJch6Ls2z1RumPdFbQtBw0MXWEx40AVbVSlKC/NxrqAI+QUFKIjgXVhYiKIqF2xeM6M6SYW5UlGMTDgLsUzTkXh6JIjcVZmLM8v/irtv/imadZyI2Ul14o2xPIwFsJfEY9vUzni3+Qt4dNQhpJQ64Ap6cXb/PCwf8CTe31WLfCvRieDFgtDAivGkxxcyg/BpiPg5r6OSlyryF1b2OMGg3qLuCRFU+1eFVTWqAMyqE5CtGXg95pvySM1pEhVB3fzTHCJShZJCzDJ7i3Zj+4oVGDftMIoCXhi2/Zj9ZnM8cfdreG7wEpyMHYY3//wYmg9ahDkpleYKUfoZbGt0k1SQOPtqADbkrJuIpXNmY8axarXlkKn+kLgwhYqEJcvWUmpLIk5JsQOzeV/8Vn0oAFviZERFTcbA3VUw6CRmLECHV5vhB83a4PFZ2aJlcAAPBR3I3T4eo58miWqJiTvzcc5GkmZuNUXeaKoaVLyZ2Jd0jYqHr/40jseuwdIJi7H7rBNWpxv1ObHYMbEL2t57H37+r0/io6kbELN5MRaO6Ya273TEl7tycMbqgY/2x1mCsuTNGNp+GNal56PIQ4fXgsr0HZhw1RDEJpWgXGaoFFZ8YpWeQK20VlONdNC4QloQumSLYr+k3SaxFHXQTOHAJLwq514IKNuBBR++gj/d3By/77UO+TaDafmE5HB3BZ5PkyL4CRqcQWAOLvZ/xskasjND0O+Ep/AY9iweiynTpmL6mh3YdyQVCceLUVLrhMevlCypXWJLZzbAJM/Updwis/mRjT2D26Ptv9yJm26ZgJ21DtTSlhG+osM4PPcp/PI/f4QnB0ch5qRVSJzYK074ioDAtqtfVxqBJkGimCuDHhwD7JibUvRgei+n5mDkR4/g339xE25r8S46dOyBbt17oXunTujeuS96jIzC8kP5yKv3wCtGJoSA145Q5iy0f/oDtO25EgerSD0Y6q1k09rMbUjYMB4LU1ywuX0Ilu/G0oGt8dhdz+CVBTk4m7IFO9etwtrYNGRYlIilNHylCvlZOJHkqdbQuyHBoX/CDsCF/361t5Thg6e2CIfHv4Tn7r4Ov2jeHm+vyJYdoDw0ASQF5AU0cJ56pMy7E8992B2dF6WiRliNJD5RSUPp/4i6RYTKcHr/RmyaNwcLZi/CwtkLMW/uPMydO/cb3/Pmzcey3eeQW1EPQ7QaYsJnIHDkLswK7LkQiRXwI+Rzw27JROrK13H/bT/Fvz3WFe8vSUOlWfZA0IHsmN7o+/y9uPnenpiT60JhnQP2+rNIXj0P097tifknDJ5DSMwAACAASURBVFS5IzMOLIv46KYHSozCxVP4KoVB0u9JmRV+JEdq6oCYSeQ74KfxFOapVkyZdSTnkp4xlQSPiaxoV7pf6/s1IgKWI/MRu3091mXRvvgQLNiI4a89ij+/0BF9ojJgzdqCqMVrselYAXK5AET5L5Ixn0Ok0iyoOjPnUyrW95mABZ9GI9nmhsvlgcfthMfthsdth9tTB6fbDbfTA6/HrwKx2cbYFCWVi0y4iRYTbnpcnbcqahI+iS8TJQdpC9HplQfww4fexGNz0sTesN36Q/XI3vEFRj99Pa65uh0m7MhHnp0OHK0bA6NJmEz+yLABbkgs7kUA7pRliF0/H2MOVAvJCwUVmfFWH0dGVB88f+01+M/bH8ad99+CZ999F51jciWWVNKR8FrBANyWbGTNeBAjtqfiQAmn06pQkRKPiVcNRXxSMcpN+81pQT6vIelaLpAolYCShCMyp0pxQjqrPP7C5uy0EbTDvoAHzrztmPfBy3jwmlvwm//ujugcN6pdzLtpyM4HQk5YGDEkikB5RVVkhbCQLI5y0GhjJGdp/Tmc3TMPc3q+jTe6LcKS/enILq+CzemCJ+REKOAWeyxqn5A0PjBLexb7hnyId35wB264ZRx21DpQx3sEAE9hApJmP4+fX3cNHh+yEutP1qnVnLy/xHBRNw+3iEZs/PpSl0SgSZAoBi2GfFw1wXwZ9KrYsAyU7OyP3q/ehBvvexrto84i55wFxRWVKK0oQyXf1XbUujkPTiavCEHI54I3YwFaPd0RLXutwr5q+pEkNlxdEoThtsPhqEOtRykx/uMLMe7D5/CHh1ph7FEfamxWOG31sNs9cPsY7aNWopDscCUGuzI7JFfQSTnp+XFzXtIPJr7jd/DCVnoMB6e/jlc7tsTLd92CZr97Bn/uHI2TCMIt5k5dh0Yv4HUga+G9eLFzd3RYcgylNBoyzcauqabblPdGg2TA43LAVl+P+vp6WPm28m295Nvm9EnwtlohpJQeWccmnhVNsNfMWcJnDaCu5AjiV/bDk891wEvNr8Nvb2mO13qswjG7SuUVqkvF2q6v47kbbsONj3XA4Nkr8MWoQRjUrxdGfDEfMfGFsHq5+zor9NIvc6xRpoRGT1gmoaAXrwyMOkYlMFRcTpnU8Hwq78RVxyq5HjEW/c4cSjgc+mAEPcpL5jUjK9qlC6+P+I4QMNvJP6xIblFSD5vDBit3DjAcsB0eg7ZPNcPTbUZgUboXPrcD9dZa2F1eeP2ckqLKotQM9ntpZ+LwGEBlLGb26IfO7T7ByKXzsGjpEixbvByLl6zAkiVLsXzxQqxYuAhLlq3E+h3JOHG2VhwTtck6M5wznpAER63qIjmoTZqIVTETMHifRcUFnlqFYa89ghuavYXHZmeIgyblgQPZ28dj5BP/hR//sAtmHipGkZvXCqdWcKkcbKIyc8pK5T1imy9cNx27lszCukL1bNIvqJgHXKg/dxA7+92D3//2Olxz+1/xxuj1SLTT8pmkzNzSJmAvhfdAfzw7dw+WpFUDgUpUZMRi/DWczsuHhTZY0osIMxF7KHZMsqozLYKKA1UO0aWbi1L5leqjVHnlCIva5rMhVHAAczp0RJcXWuDJh+7Fz3/3J7TbXIZTtezn/CfRSyqLvGzRI9YOblGHzOSddBYlRITfMUCf9twPn8uK+vIClGUdxsZJH6JbryHos/AoTjJHlihp5nQelW0iJVhmI3Fie3T+zR349e+/xN5auwSW0zX0FB9GyswXcd1PfoxnPt2GLaeZaNOc56RNkhmNS2Oij2h8BJoEiZINg7lURfZUM/caQh2SZr+F9x6+DXc17415mX44PBzcmadI7XlEPsN93GSeXY2ogM+FQPpcvPnUB3izxwrst4h/oabbhPAoWV28QgRQFDsQfV9/Fn96eiQ2VHthNZRKRNJCYiadkcqTJJdTGx2TPYk8TNXDjC0KBzL6gx7U5e1H3PxhePmdjzEmJhaLx7TDe80fwB+f7YvVxSFYvSRGfCueEPA4kDbvLrz00cfosDgdBeazhP0bqlDKG+P9VHyBOHtCLBrAAsKkgafQWIjDqGRpSdrHyS2JwTJgOxuPjTOH48N2/TBsdSK2TmmJVx++G83eGITZGXYlkxduxJjWf8Y9dz+DF0ZtQOLpPKQmH0PikQSknMhFfi2nBU23NIK2L+W5iDDxXDWNZ9aZKZqJd2l6k6JdES/T2ZQEiBy2ZCCk2seBRE2fqmNpKE1jTyIsS88bgGEEz6EPuZIIfBOJ4neq71JRoUoc8NbhzKrX8XKzZ/F698XYV0dnSMXLCFkX0qTaE/snnSK1jF2RK1h3Y/6AKRg7bCV2nz6F7Jxs5ObkIDsnB6f5Mzsbeaez5fNzRWWosTnFhqjAZjpkKpaS9oekgu1bxURNxOA9phJVEosprZ7GXQ+1xGNzMiU1gpqsrkL2zjEY+Zcb8aPrR2JJRglKDcaOmqqKOSUkA7qUm52CVMSG40u+xIaZ07CzjP2Ryj9DBThd6YffWYaapMnodNdNuPEnv8Of2n6KGSfqZFin2qL6VFCOQ+IIvDp3L5anV4NJeS0Z2/Hlj0ZgV3IxysWRVXjTLpoijIr9EYKl1LiwQ3SpVkILJeu2qSKLz2mSOlcVajK3YNYHb6LjJ5MwZ8kMzBnSBo9dfwtu7r0He87VmCq7ibcZVC42j7izRkTlDsd+ctpPZX+nbeHNgl4rrAWJODSrP4b16otBX0Yh5mgx6oinBLoru6LsKJ+VWBbj+KKu6POnu/Hr2yZid00d6gX/ENxFh5E6pQV+8eNfoNXEeOwtVOerPf9YHq1EXao9fFvfNwkSJUKtNEIGYpIo+AF3FjZ0fwrP3/YwHmk9DwdrQ/CI0WFMD1eBqEBOdlYaOdUpuFmlE6HsJejx7Hvo0G0R4kuUFE1TQK/SY7Wg/NxxnEg/gzKnBQdntEa7Z17EY+3WID3ggSNkoDYvHedys5Fv59QdaRQHXRUDxQBSWY3HXk3SJ14fiQ3NpBvVOfuwae5ofNxrIDpN2Y+0MhcKE2di7AeP49a7X0KrDVUosbLTKhGEndfrqUPqtDvxUpe+6LryBKrF7TQ9YFndQk9HIjOAkB1VBTnITktFemoGMlLTkZaWdul3ejoyCmpQ4+SqEIWFNEp2csYOmPEDQb8b9rP7sHnGUPTvPhB9x+9Aeq0Be9ZcjHzjQTzwcEu8uygLVpqivBUY8tajuK/52+i64axEKvilXpRRYdJTzuRFSlEuJlFiaMXQKWPDuhPohf9x0FPqlPpJTqiIksSw0OiKQedzeuB21KLKUgWrmwPXBWVLYhokGzLvrF//nAj8IxLFz0kYvHBW5iM/+wQyc3NR5jiD2IH34slH2+K9L+KQTSIRcKAqMx45xSUoc6t2RbWI9ENCmNnX5Tiu1j2F7Z9PxdJp65Fsk7kY5YpIWzUdI+E0nGbjP16HA6xa1yVkzmzLzBHEfmc/OgNRq6dgwO4SITYh+wms+/hVPNf8r3ho/FHUcw89Lt9HMU5EDcfg+2/Df/5lObadqUIdY/08DjhqLSiqtMNjiKUzF5AoRTsQcuF09EisnjUGi046Jf6Ge7ypRJMeeOpzcW7LQHzw5D34w49/jFt+/wxeH7YVeTYn3IFw4tAQvHVnUbv+XfSIPoJtZ5iyxYLy9J2YdM0wxCWXwGJO+wUMP7z1pSivtsHKkAnaLklEqtR68f0iaGzKDNKRYn8WFwghRymKj67Fss+6oE3b/pi8JQ2nSk4ha+NI9Ln3Blxz76dYePgcLH61ebNaDX2RvRB7TYsethl8Pr4VwfO5ilGYsQ8HtsRg7cYYrF8+E4tXx2FPShEqrCpNDmc0eF0SJ1k4IIody2lH4c6xGPv6E/jV74ZifUE9qg1+HoDjzC4cGnMfrvuvx9F7VQLS69XnzBUlkxtC5LUdiqBZNPohTYJEcetHtV8cZ7q5S7kHwbJt+PK5B3H3717F00N2IZ95OERVUFN+VH4YJ8DOJVsQSIM24A24ECzbhMkvvol+naZh0zkGOEhEAYIhN0pPbMfW2cMwZOhK7D9zAPM7/wUtnnwDT4/dj8qQDz5nOY6umI2YmC3YX8H4CC/cdTnIOZ6E41nnUFhHs+pWREqkXYhszsBEa0EStk3ugw8/7IGWY7bhjBXgwrSAZS/Wf9YKj9x2H378URySS5wSzCgaWciA01OGlJG349U+AzFg82lZ6SPUQ0J81POKERFJuhLnkuOxJyYK66I3YH3UesSsjcHatWu/+R2zDuuT8pFfSxWJ1zRn4MUYqLDsgNcK+7kE7J7SGR+17oYeYzfhWA0JloGQNx1b+ryGV+98DHd/tBInvEG4irZgyvtP4/kX26LnlkJmQxFZOhjwwF1TgtKzp5FlNeCmhYrgRTwUKVJKHdUlmc40V9mQcPJ7MXhiBC+oCCqIVBmmsDfJKWGvPRdZyVuwbEk0Yo5Vw2Kj2qbUPBJxmeaNoGz6kP+rCHwTiWK/dyF/71IsGz8Wo2etxKGSeIx75mbc9UJfdF2djsqADf7aLGybOgAxBxORSQeHdiZA0uJVCoEow2paKRB0Inf1RKyZMQ3zj5XCIW1JRmBxqMLKKQkKaROjGMXJk/3fmHBTKTV0Cti+qaoLiVozFf13lwjtCoWqcXxBN3T/22t4oEsU0ryAkwkiXSdweNIn+Oimh/HwuGRkVLjggxM1Z5OQELUYM5buQEapDTY/B/nwXnNUOUKoSpyKmMWfYVhULur8QXhkNioAj70YeUdWYMp7j+K1Lu+j5XOPo8WNf8Afb3sPY9cfQ1apDU5vEAGPFTXZ+7F92IuYfPA4Umv5dBWwZMRjytUDEZ9UBAudSvZ9ayFObJiNZSs242BmAWq9ql8GA07BMzJrIBENakU1yRmpqKcKZcdWY/mI9/HGK20wMLYcBbWc2nehKmMl1nS5Ddf+8DH0WpaM5BouUmKd0VCQDtN2KIfRH5ToNgnHoN3w+11w11eg9PQJZGTEYcvSiZgyejQ+Xb4bSdUuWGW3CVUeke/FeSauHK/8olaKIhUAHNkbsGpYa/zxd29h8qFqFNvogNthyViOld1vwA1PDMesI9koZc4t2uDz3rRw8f+rnaxJl6tJkCg2dPHKOGfOAEaXFfaUeWjz5N34j8fb4eXF6fBQtpbO5BUSQMNEBUsNmFRtaPhImHyA9TDmvvYE+rQbiiWZKiaKod8GipG6vA96PXALfnpnfyzePAudWjyK2554By8sTITH64A3fRFGjFmC8etSUcb4LLcTZbHd0f6J3+KRV3tjZHydpFGQJa5mDLM35IJhP459g17H0w+9jL8OXoI9VT5Z+MrQzmCoEtlrh2J4sxtx7U96YXmKBRXmag8qJYb7FGI734G2Q8ZiwqFCNXVnRreqlAPCJqT/Kpmc8/f0b+nERKrzmPH6ooubwfF09dRuFEJJHZY0HJ38HB767RN4b+h67DrHJHISBSZKX250Jwx89re4/d6uWJTvQYX7LPZ8+Ta6tW2JVkuz4GEGZ8MHw1qGU5vmYX7vdpiQWA+Lk4pAhC+ZTqHJJHDKBrKYJH0Gt0oI+GXLCSqP4nNzypUxceLJqfgEWZGjnHCUp8zE+O534d+uvxU/eHMDtp6qBVONETdZ5uxX8QwRlk4f9n8OAQ7JbF9hVShcQLYF9noHDg5viTZ33Y8/vTAAG3bPwxs3/xq/emM4+m3PkYSZ9QlT0KbnGmxILIad7chQ8TE+OCR4OUDjJJyHV3QhWLIHq2bNwtt9ViPJa8Dp96os2FTIZXtZP7wSRG4OjDKQq3KJukVnTRRQ9X190lSsjpqEgbEV8hS0bL7T0VjYpzMee6QfFp8zUEXyf2It1vRpj+ebdcGcbKDaSX6QhyPzB+H9f/sZrr36NvReexLHazgdSZtIddzckN11HAlrlmJM+4XYW+VEtccHj78eZ46swIzur+HGp6YgOrUCRVnrED3wJdx/zQ24+gdvYMiyTGSWOGA/dxRHl4/Fsy8twMZcCyqFllRJTNQXP+qLuKR8lIlVKkNZ5nIM+PdrcOPVN+BvQ5djR5GaEpSFQ6LvRUijZDaedk6toPOd3YDZ3Z5Fi6dfxrsL01BiuOALucWyByqTcWJlW1x/7TW4p180VmfWm3n4FMYynSqqjyJWLAFjobi4xFNVhMK9SzH1vRboMHwG5h/IQYErADdJjhm3RMdLcl2Zhkk0RiFlgE+aBzPGhxD05eL4xhH4+J7b0HLOcaTl18PrOYeUXePQ48mb8cSUY0gscCoCJ43KEMMcqToXbt36Z+Mh0DRIlEzFAMGqkzi+bTo+aNcS7Z+9BTdf/yP84Prf4bePtUav3rOxu8iOar+SoQ16dCJJ8G+aURIDenrMcHsG24a8gF49emLorjK115I4JDaUHF6Ahf1eQbMXPkSH93rh81HD0LdTD7R58X0MG/kpug2Yh/nbM3Cywi4ehihMB0ag28v/jRsfeQsvTTiKKhmAmcFXbcYZdBbDnjIDbzz9OtoOXYGY5FKV44jUhNMAQR+sx2Owvl9z/Oba3+H95ceRUsEAU7IwK3z1uzGj2X3oNmw1VmWHV/qZMQXnpyrFjquAVxIN5ciKhxZpc5KOKh6waD5mAjqqPtxGoRCF+xej101/QKuB0diYXCarF0laxOCEAGf2Wiwf/CIevv8RPLP8DHKr7bDnxGHLrMH48P2O6D9+JT4fPxKffj4dM5bFIiGrCJXcgoX3jOQlHr+S3sMkikOjKrLodueXAkvGdBncLsRgiKepIjlM9hWAvywFKRu/xIAO7fHEL8ZgbSL3+FJL17k4QNpQhMWL5BH0Md8FAqzAryNR3C+zHic3D8Hwbq/jz690Rc8PhmHqF8PwQauP8GGbrhg2bAy6DlmA6KNFKLByvaqaFuaCLZl6E9sUnkpniFFQcsfV5CRg9/Ip6Nr9M6w+mIf8OtlGVrk2QujJYyQaXTVg81fptxIPqWwHO1d94gysjpqCgXvKpD+LQ+CuQ3HSLsSMG4KuHwzBqC+GY3D/fhjEQX5zJqocARgMewjWozRtN9YN7YoOz9+Ldxcdxt5Cl/QZOiEyDc4+EXTBWpqFlI3zMLrTB+jWoQPebvUe2nUejDHzt+HQqXKUOf2yurDuXBISo6ZjaKtX8MJTzfBgs0fxzGsfofekGGxJq4bFQVJDpCyozNiLyVcPxq6kYpSJA+SGozILB8cPxLC3nsL7oxdgbppVCI0E0zeELcjsAtMZUPWqw7Epr6Nj+zZoP34D0qqdss+ohDnQufZaUH5iDT5pfhPubD4Cn63LQikNh0GHjLFPVKADMmvAqUwqZrbcPdg8ayyGDx2DMev34+jpXOSVVqLG7oFP4p7IjpSXKbFhMi1JGmxOS5K7y3EkiWpj9lDAC3fZCWRvnoDR/TpgwKgxGDpkBIb1H4IhM1bhUHE9rB4qUGwWDBWh2qnsuRja76L7fM/v2TRIFKVWegauKlTkJWPrlg3YGr0YK5YuwIKly7Eiegvi4lKRb/PBJY4Ejw/LFOZ4KdoFWzU9MAdOremBvv37oOXMNFSTq3DaKuiHs+oM8tLisTV2P+J3HcKJrEykHz2K/Zt2Yv+hg9h18DTyym1wkZnxakE//OXJSFg/Ej2Gfo53JyTAIX2Hq7yojjHDbz08lmRs3hSHg5nFKLdTBhEBWU2bccrRWozi9J2IWrIMsacrYHGa29A4y+E6Phtt72mN4XP3IrFe7bUlnqR6GkHn78Z5ASvc8v/um/CHX//z787jIUJVlOE2bLAVn8TehdHYn1mOchtJqQq4lYtRDXKUID8jHls2rpcluvVurt2tgSUvDYd2x2LP0SwcOXoIBxNSkZ5TjhrO0zboRWaonkf+VwLcRbaFn6oyy3FCztTxilWGyaE5VcIB0V0NW8FhHIqZi3cfno3YjBLUymoaFczZEJveoEfRB19hBMx2cP6u/JvkxwtrWTrSk/dge9wh7I89htzck0jcux/7d8ThwMGj2HU4B6U2HzwcXE1bFG5avAo/u9DupFsg6KpGbX4q4nbEYk9CEvYdPIi98XHYExeH+Lh47InfgyOpp5FvsYozxsFeBmT+ZI+j42eo6Wlb4gysiZqCQbvLpP1zUCWB89sssGQnYu+OfTicsBfx+w/hcGoO8qsd51fkMT7TU1+BgoQt2DDoQfSPycBhph8gDqrwF57Jb4fNchrHdm5D7LZt2LhhC7bvPoq0M9VwB7iy2HxKww13dQFOHdmFrTHLsHTJUqxcF4u96UUo9zB9AG0s45zKUZkRh4lXj5JkmxbTCTI8dtTlZWHPpLcwZtFSLD3hVNNytKlSsPOVdIlfaEOpGRMzD8pStmDvvv04lG1RK+xoC+QZeV0vPLYSHI+NRszGY0jKq4adnVsOMacDZWuWkGw/Zc/dh4T4OGzdshPb9x5GQl4pqv1++GXBiomdXJwXCLcLVV8sk7I3F477u8/8Lvhq8nDiyE4cSDiC/fsP4/ChJKSctcDB7XIuqhel0YWvcwk49NffCgJNhEQ1Mjb07rKWYtKng9CyxzIk2gAvN80UVccMSJeWHOF9QwZcuVFYvnYZBqw5LV2aRlGmlEiiJAiVoYqRWQh6IBJsyZgdywnkLW2PZ1tOwoLdp1FhGGaMV2TXivAJvpeHyVRowA9/9XGc3j8bbfvtRXJ+DTwyAKhpXtp9/dIINAQBGZulD3Ma2Y7y4mykHzuIA3Qk4nYjfvce7I6Px4HU08irsKkUB8xKze2hqGaYygOFVDoqtsSpWLNmEgbGl8nYTMdMVh2HN7YNk36ZIuSgroKaVXAgvUo7as8cwbper2DeobM4xR2LG/ElK4lFZeLqZLqvSkULBKlE7cT4q0cijjFR55U3H2BYsHtiNyxctwnx5WqvTSpsIsFEaCcb8RHkUuzxsgDI44Q9Zy+S03JwqswGG4lNgNG4SqFm/ejX9wcBTaK+pq7pNwTcp7F39hgMf6c3JiXaUONRy/c5BadWV3zNiV/3ETuUpx6ntk/G/OhFmHW8RrhSWKoXeZ/Tig3peLR7dJKMelRkbsWyLo+j/bzDOJhnkw1IaUAZ1qq78tdVSAM+o+frccKSFYtNiwei85YynKk1t37hChsG6kuG9gZcUx/6vUeA/ZLpAYwApVbzzfxPEtipTAGJEPf/lD1AOSVocPqeU89UcUwBRZAMoD5hElavmYCB+8pEZ2VMFgmSJCDmKlOJa1JTzzI9J84gVxUqRchny0X2geUY2HoM4vPKUd0QBzGC2pTymvdi4ameMAeVL2RBRcYOjL96MGKZbFOmPg0EfDVwFG3A1L5TEL0tBYV+RQolRk0Wx3xXnouprNPx9bvAkBCiSwWOb9YrZx5ENYwAF31I00BAk6j/UY/sCiqMvD5rPaKn98Y9PXcis8YlyfmZQI6z+VSRInoFvAjmrcW4scswOSoNJcJ+eC5X6HFlBme1VaB2pEqUspTMVZeMlJjxeObZaVh3vAaVskzRkKSjfpkOjKiE+qB/gIAEk9YkYPf6JegwYAvyPAacEmehYhIkJk0GwQjbwj+4j/74+4UALQzVGS50UbFYErl3nhnJYCy6NFUnrs5i7JIKPxBCYg7Yyk0KwHZsMqKjJ2LoHk7nMSklV5GpOBm2TIn2kpuSW3HajRue+0QVYkrM/ITt2Dq2P6YcrpNl+CRajf4S+c107OTyfLZiWDK2YNy1w7AjqQTFTNcS8qO2NAd7+7fCnC0ZSC9yIsR0AxIt5lJhGI1euAgvKBWjEKVKHWIMrZBhRYWVH8w61fYgQkSbxGGaRH1NNapgwxB8zhqcSd2M+aPfxpCtZ5FpYRAf80pFTHeU/OyqQnGRBSVVdiFilHslWFGm8igRc61G5AaCfdkwipG5YwUWDhyLGfvLcNbmg/f80lkVC9CAUn4NCvojqoMBnw2VVRacPFcFDzeHlSQa3J+RW3LQXGrFT7eUhiEgY7HYkHCsTDhHWTiGnCEDjMFksLEaqCU2R9Qck2sJCVPxNvWJMzFnfA+8+MksbIjZheRKK+rESKmpOwmjCrgBUUm4LpcrlJkoltwsALe1ElVFeSipN+BlnFXDHueSR0u2LEmLonY5oHPiyE/D8fj5mD9+GN65+jNsSCpCGRdscKNwjwt1+SdRXuWAzcMcV5woY7mUEtfoBbzkE5gHkBsJwVRT+VTU1NSqmqIUa0Cb3pBZhUjvrY/7P4uAJlFfUzWMUZKtFUIhuOpLkH9sJXallKK4zgsmN+MA2pCOzC4nMi/leFGI2PkYF8DYBNXpJPNspBelU+ovR+HJJCTEJiLPZsBtJr/jhpgqv4n2hr6mahv2EQcaM3OzLADg7xKoqjKWs5motBmNPew0rJj66H8yBIRFKRPCAHDScI7NHHvVV7QJtBVqVVh4/k5CgiRImaRLDeA8wVOehrSjOxG14wgy0rJQ5HDAQTvF6THmohOuFU4gqzJqy70Y38xl+rQZ/Be2R40MJ0mTxHEGw6pYEK7qQhTlJCDx4F5smnIUueW1cEpSTAacq1gvgkKSx1VxVNNUDIMijo1cxMguF64jKSD3ORUaJTGtkoVX6lEpgJFdUB/VFBDQJOrralGkc3qCAUkxYDBxntMJnwRt0xtigOfXnfj1n9H3k21XzD2qaEpoVFSCUP6kgWgA6aFiHHDBb7jh4WQ8ryuDPaV6kijK/19fFv1pAxAwVxeqwFjThnMQkylZtdJGCHVDGkMDbq8PbcoIhNuPUjKFPEnAuFKPFN1QDpYIG+EBnLYk3McJj5xohgOQdFCNDjFRpFpgwrgoCT+Q88xEoLQNskSeZeDx5iKX8IKVb6E9k3eo5LR0QpWdoq2S6Ul5DtpURhiRcJkPS+dTysRnlsWSaoXid2jcWDROlSpUSYBVAk4mexJVShSzptxu9bN9FQFNor6KiPAZNVD6ggZcQW7uyMBBbgOgOjNXaDQoEJz3oG0UJ5CyRKkJAgAABb5JREFUtOwhjkDIp4ITeT0SoUiNl9yeZWTWR1oX81TZR5Q+pfht6nP9/+UjIPWsBhlmJpe9yoTA0qCzHjkARr6q8vILos9sWgiwzyomE5764U86bZJXzYyVks84aLO/h/mSkCFz/8/wZST9gVJwmCtYksVS4ZIdEcR6SRpLkhMeKnvlMRhatBQqXiQzarWKrBiO1A5FWil0RmTvUMZrucXJo40S5Ut2LVF9iTaVNpbBDcpghvuYqT7xh6xt/m48RKkDqQvmFhT9UNkAYVbcjFkRqUhh0cc1DQQ0ifpKPbLb+uAx5XKTK4XjP8l1GJjJzLXS0dmtInhxnlyyqfMs3oEyfQiG4UIg4BE+1hAhypwAEOPHZc/iTQpLYyc2t5v4buxMBGD88xwiMRjhJeUckDiQscrDG0fL9F44uek/z3Ppkn63CNAC8N/5l/zK/0yJiL+Z0/zC4+UbBqJfFG9jni7Tgcx0LuqUukQwyNQJJEckHSRn5oAvCqry5mh/ZP83yVlEmYj39siKPlF9zhfuf/+LlEUSe6ryXKzA8znB8tIhkWJwiiw8pacW+JA4sS+KifvfF+eyr0DIVb2xhMoWMMs4A/mViqZmBC77BvrEf0oENIn6mmoTA2ZuuyBp58QRUkZO5GV6eTKafs3J/+AjiQkQYyAXk50mJB5BtnpQBu8fnPo/PhaTaOZdoYGRsEvGNki5eP2LjO3/OFt/EDEC9IxNvYneOqdIZFAyJX0SY+UZmyNaxBfWB36fEVBUScXbCQ4yOl8gUPxTDdLsyxK4JO2MxOciSUocMcY/ihMlU4Gc/iIB8ytVS+IkqT5xet+cPpQ4K49ch7Hn5zdfD4bgY9iCuaqvMetHKWq0mSoo6sLm3jRVXFhDK8u+pY4hWQx7lspBNJ3W83N/jVm6yK+lykeCp7AkqSN/kh0VTFshqWsuJsiRX14f+U+KgCZR/6jiTBmdxky9FIm6IDOHP4/sZ3g4FusVvhRtosjCF+4SydXE5sq5PFq6tniSNFbC7XiA7siRQHnJYwRrwZJ0SpYIqL+Iv7jsAvYlr6MP0AiEEVBtij304rYT/lT1XPUX/w+TK/40X+ahPF/ZlQvkSn1FJ0o5emy1ioipo6UNM2bSvLJkNzcJGOOnGugbhkt0yZ/hksrjCDG8UOawss5nVYTr/AOacUZhDPj5d/cSBMNEziS04ZIJzFI0s+zfXTH1na8wAppEXWHA9e00AhoBjYBGQCOgEWgaCGgS1TTqUT+FRkAjoBHQCGgENAJXGAFNoq4w4Pp2GgGNgEZAI6AR0Ag0DQQ0iWoa9aifQiOgEdAIaAQ0AhqBK4yAJlFXGHB9O42ARkAjoBHQCGgEmgYCmkQ1jXrUT6ER0AhoBDQCGgGNwBVGQJOoKwy4vp1GQCOgEdAIaAQ0Ak0DAU2imkY96qfQCGgENAIaAY2ARuAKI6BJ1BUGXN9OI6AR0AhoBDQCGoGmgYAmUU2jHvVTaAQ0AhoBjYBGQCNwhRHQJOoKA65vpxHQCGgENAIaAY1A00BAk6imUY/6KTQCGgGNgEZAI6ARuMIIaBJ1hQHXt9MIaAQ0AhoBjYBGoGkgoElU06hH/RQaAY2ARkAjoBHQCFxhBDSJusKA69tpBDQCGgGNgEZAI9A0ENAkqmnUo34KjYBGQCOgEdAIaASuMAKaRF1hwPXtNAIaAY2ARkAjoBFoGghoEtU06lE/hUZAI6AR0AhoBDQCVxgBTaKuMOD6dhoBjYBGQCOgEdAINA0ENIlqGvWon0IjoBHQCGgENAIagSuMgCZRVxhwfTuNgEZAI6AR0AhoBJoGAppENY161E+hEdAIaAQ0AhoBjcAVRkCTqCsMuL6dRkAjoBHQCGgENAJNAwFNoppGPeqn0AhoBDQCGgGNgEbgCiOgSdQVBlzfTiOgEdAIaAQ0AhqBpoGAJlFNox71U2gENAIaAY2ARkAjcIUR+P+dZ+PsniJUywAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E6%8A%95%E7%A1%AC%E5%B8%81.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAFdCAYAAADL1o0TAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAEzwSURBVHhe7Z35m1XVmajvP9HdP/a9T/c16Sl2YjtEYxCixJg4RDSKMw4YJ6TDIDhPOIAoKGA7gqCioiDKpEgLBEQBEQcmERwQcQAaUBAkuu591z47lmVVcXTVrn2O532fZz9Vdc6uc/a41ru/tda3/lcQERERqSOUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlJcqWbVqVRgyZEj4r//6r3DXXXe5uLi4uLh0+HLrrbeGefPmVWqmxkV5qZJp06aFH/3oR+H8888PvXv3dnFxcXFx6fBl//33D0OHDq3UTI2L8lIl//3f/x1+97vfhf/5n/+pvCIiItKx/Od//mdsAWh0lJcqUV5ERKRslJcM5aVKlBcRESkb5SVDeakS5UVERMpGeclQXqpEeRERkbJRXjKUlypRXkREpGyUlwzlpUqUFxERKRvlJUN5qRLlRUREykZ5yahrefniiy/Cyy+/HMaNGxeX8ePHh/fffz989dVXlTW+htfefPPNMGzYsHD//feH0aNHh/nz54ctW7ZU1mgb5UVERMpGecmoa3l59913o4iQdXDgwIHhpJNOCjNnzgxbt26trPE1O3bsCFOmTAmdOnUKffr0ietPnDgxfPTRR5U12kZ5ERGRslFeMupaXhCVyZMnhzfeeCNs3rw5Ssl9990XIyzNee+998KECRPCFVdcEd555524/ueff15599sQqdm+fXvYtGlT+Pjjj8OkSZPCEUccobyIiEhpKC8ZdS0vyAcRFZqPNm7cGM4+++zw0EMPhXXr1lXW+JpFixbFaMu+++4bDj/88HDuueeGZ555Jnz55ZeVNb7JZ599FmWnR48ecf2DDjooLkiPiIhIGSgvGT+IDruffvppWLBgQejWrVt4/vnnW4yorF69Ok6u+OSTT4Y5c+aEyy67LIwcOTLOFt0Su3fvjhK0cOHCMHfu3HD77beHrl27GnkR+Z6Mmf92OHPMoppbeo5dHNZt3lHZSpHaRnnJqHt5IeqydOnScNVVV4XbbrstNgm1BB1zN2zYECMqNAnRvHTLLbeEWbNmVdZoG/u8iKTR//FXw99fMqXmln+8dFpYuWFbZStFahvlJaOu5QUJIaJy7733hgsvvDCsWbMm7Nq1q/LuN6HPC31jtm3bFpuK6Og7ePDg8Oyzz1bWaBvlRSQN5UUkHeUlo67lhSjKiBEjwhlnnBGmTp0aPvjggxhhQVDoC9MURhYRnZk3b14cTt23b99w4403hmXLllXWaBvlRSQN5UUkHeUlo67lhdFG3bt3D3vttVcUi2OPPTZcfvnlYciQIeGJJ56orJVB5OWee+4Jv/zlL0Pnzp1Dz549Y4ddmp2qQXkRSUN5EUlHecmoa3khRwujiJ577rmYcI7l9ddfDytXrozRlabs3LkzCszs2bPjQj8ZRihVi/IikobyIpKO8pJR9x12OwrlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJaOu5eWrr74K27dvDxs3bozLpk2bwq5duyrvfpsvvvgiyscnn3wStmzZ0ua6zVFeRNJQXkTSUV4y6lpeEJcHH3wwnHTSSaF79+6hR48eYcmSJeEvf/lLZY1v8tprr4VevXqFo48+OlxxxRXhpZdeqryzZ5QXkTSUF5F0lJeMupaXBQsWRHkZP358mDlzZjj//PPDY489FtatW1dZ42vefffd8NBDD4ULL7wwrnv99deHCRMmxGhNNSgvImkoLyLpKC8ZdS0vq1atCq+//nrYsGFDlJALLrggPPDAA2Ht2rWVNb5m3rx54ZZbboknnYgNwsO6r776amWNb0KT0tKlS+N6d911V+jXr1/o0qVL2Lx5c2UNEfkuKC8i6SgvGT+IDrv0ZXnrrbfCKaecEiZPnhz7vzTnqaeeitGW+fPnx/WRGeRlxowZlTW+yY4dO8KsWbPi//Tu3TuceOKJoVOnTsqLyPdEeRFJR3nJKF1eEIndu3dX/vomX375ZXyfjrmtwXtEXh5//PFw8sknxz4vLTFp0qQwaNCgsGzZsvh9ixcvDvfff3944oknKmu0jc1GImkoLyLpKC8ZpcoLcoJsrFmzpvLKN0EUaNZBYFrj888/D88880w49thjYzRl27aWC6EpU6aEwYMHx+/j84jA0ByE9FSD8iKShvIiko7yklGqvBA1ueyyy8I555wThg4dGptxZs+eHT788MPYwXbixInh0ksvbVVIGFU0ffr0cOWVV4b77rsv9ntpbaQRnXtHjhwZHn300Sg8SMuIESNi591qUF5E0lBeRNJRXjJKkRciLjt37ozyQifb8847L44Eevjhh8O4cePCsGHDopBcc8018XX6n7TEypUrQ//+/cOvfvWrcPXVV4d77703TJs2LYoGw6KbwggkOt+ee+654cknnwwXX3xxGD58eFi9enVljbZRXkTSUF5E0lFeMkqRFzrUzp07NzbdnH322WHIkCHhlVdeiZ1tb7755vCHP/whCknfvn3D+vXrW42mLFq0KNxwww3hzDPPDAMHDowLTUEMnyaC0xSail588cUoS4gOP4nsIFHVoLyIpKG8iKSjvGSUIi+ICgnl6KdywAEHhNNOOy0KBRJyxhlnhDvuuCMOa2akD6OBqhWMPYHA0CRFU9Obb74Zh0xXi/IikobyIpKO8pJRirxs3bo1dsSl8yxRF0SmW7duUV54neHI5GqhDwxiQ1+WtkYcVQufQRSHPi+MOPoun6m8iKShvIiko7xklCIv+dDmW2+9NVx++eXhrLPOiieE4cxEXq666qpw7bXXhhtvvDFGXpCNslFeRNJQXkTSUV4ySpGXFStWhAEDBsSkcscff3xsPqLj7XPPPRcOOeSQeHKIwtCplmYeOviWjfIikobyIpKO8pJRirwwSoiJEYm4HHjggeGwww6L8kLSuK5du8ZoDJ11eY1kcm3leekolBeRNJQXkXSUl4xS5GXLli1x5M+oUaPCoYceGqMvdNClGWmvvfaKr9EXhqHTSE5reV46EuVFJA3lRSQd5SWjFHkho+5tt90WhzUjJzQP3XTTTTFT7lFHHRUlhgkXFy5cGCdERBjao8NuCsqLSBrKi0g6yktGKfLy2WefxeRwjChirqGXX345jjJ65513wtSpU+Ns0ayDKOxpeoCOQnkRSUN5EUlHeckoRV6ASApSwrJr166Yy4VRRcgBryEv77//fnj77bdbTVLXkSgvImkoLyLpKC8ZpckLssJ8Q0ym+MYbb4RPPvmk8k4mNkRcmPGZ95GbslFeRNJQXkTSUV4ySpMXZOW4446LfVwYXdQ0nT8ddOkP06tXr9jvxWYjkfpHeRFJR3nJKFVeyO9CYjomUST3C5DT5Z577omzTTORIlGXsjvrgvIikobyIpKO8pJRqrwwJQBSwASNd999d8zzQmbd22+/PcycOTNm4q0VlBeRNJQXkXSUl4wOlxfmKVq6dGmYMGFCTE5HVl36tQwbNixOC0AzEsOnX3rppZqIuOQoLyJpKC8i6SgvGR0uL4wgmjJlSmwW6ty5c4y4IDDTpk2LHXSZSZroC01GzPxcKygvImkoLyLpKC8ZHS4vzOa8bt268Nhjj4XzzjsvnH766fFEkPMln8PohRdeCNddd124+eabw/bt2+3zIvIDQHkRSUd5ySilzwt5W5CSzZs3h1deeSU2IU2cODFs3LgxCgyddJ966qlw5ZVXRsnZsWNH5T/LQ3kRSUN5EUlHeckorcMu8vL444+HwYMHR3Eh58vIkSNjkxG/M/qICMzcuXPN8yLyA0B5EUlHeckoRV4+/vjjOA3AoEGDwujRo8Py5cvja/R7QWCY92js2LHhz3/+cxxxlDcnlYnyIpKG8iKSjvKSUYq8vPfee1FOHnnkkbB+/frKq1lzErJCJ17EZvLkyZV3ykd5EUlDeRFJR3nJKK3ZiE64LGTPZaoAmob4nQ69/ERwHG0k8sNBeRFJR3nJKFVemIiRnC80D5HXhfmMmFH63XffDR988EHYsmVLZe3yUV5E0lBeRNJRXjJKkxeaiMj5QvMQSemYEoD5jO68884wYsSI2JH36quvjsOlP/3008p/lYfyIpKG8iKSjvKSUYq8EHWhmWj16tWhX79+UVDIsjtr1qwoMYxCYs6jG264IRxxxBExEkNzUpkoLyJpKC8i6SgvGaXIC/ldmM+IIdJ9+vSJssJoI2aWpiMvUkO/l0WLFoWePXuGt956q/Th0sqLSBrKi0g6yktGKfJCP5ezzjorTszIzNKMLmLKAP6+/PLLw5IlS2J/GJLWkfNl27ZtpQ+XVl5E0lBeRNJRXjJKkReiKh999FFYuHBhnMvonHPOCTfddFMcYYQcEGWhaSnPtsvvZaO8iKShvIiko7xklNZhFyH57LPPwi233BJOPPHE0KNHjzB06NA4u/Tw4cPjQsfdhx56yOkBRH4AKC8i6SgvGaXIC01CDIVGSpi/iJPByKLjjz8+jjgaM2ZM6N+/f5y48emnn47rl43yIpKG8iKSjvKSUYq80Dn32WefDXPmzIl9X+64447Y5+XII4+MieloUiIC86c//SnKgtMDiNQ/yotIOspLRinywtBn8rlceOGFcSj0qFGjwvTp08Pvf//7OLKIjro0GfXt2zeOTFJeROof5UUkHeUloxR5IUEdiecQEyIvhxxySPjtb38b9tlnn3DccceFE044IXTp0iUceOCBsemoFjLtKi8iaSgvIukoLxmlddjNYUqAuXPnxrwv5Hl54YUX4vBopgzg9ZdffjmOTiob5UUkDeVFJB3lJaMUeSFbLpEXOuzmy/bt2+PCe4xEou8LwrB8+fLSs+uC8iKShvIiko7yklGKvKxfvz5m1aXDLhGWPMpC9IXOvERa+J3cL0OGDHFuI5EfAMqLSDrKS0Yp8jJz5szw4x//OPZnueiii2LH3V69eoXLLrssvPjii3EY9dq1a+Owafq9fPLJJ5X/LA/lRSQN5UUkHeUloxR5IarCtABvv/12eOmll2I/F5qJmGWaiAwSc+6554ZjjjkmHHzwwcqLyA8A5UUkHeUloxR5QVbIqstoIyZnJMsu2XVvvPHGcPrpp8cRSLfeemuYOnVqeP7550uflBGUF5E0lBeRdJSXjFLkhf4thx9+ePw5evToKC3XXXddzLKLxNx+++0xcd2TTz4Ztm7d6txGIj8AlBeRdJSXjFLkhQkZibxwAsaOHRsefPDBMG7cuPDoo4+GNWvWxOHTSM3gwYNjp14jLyL1j/Iiko7yklGKvGzYsCH2bSGz7oQJE+Lv48ePj1l2161bF955550oMcxr1LNnz5oQBuVFJA3lRSQd5SWjFHkhw+57770XunfvHodJM3P0DTfcECdg5D2akYjGrFy5MjzxxBNx9umym46UF5E0lBeRdJSXjFLkBYi+7LfffjGywpQATAdw7bXXxoX+MJdccklsXmKSRoSmLcgLw3xJ11xzTRSe1qD5ibmTLrjggjjp48CBA2Pz1LZt2/YoR8qLSBrKi0g6yktGKfKCKJDL5Ze//GUUDoZFH3300eHhhx+OC8npBgwYEMViT5B9d9WqVbGjb6dOneJIptZgdBM5Zs4888yY/I7PZ3ZrMvwqLyLForyIpKO8ZJQmL8wcTT6XN954I0ybNi3cfffdlXdD+PDDD8OYMWPiiKM9QVMTERoiKQcddFDMIdMa9KXhpPO99LNZvHhx7GPTEkgR7/HZjIpiBFTXrl2VF5HvifIiko7yklGavNCEg0wwnxHDoZGZnC+//DJGU5iUcU/wOTT70MH3qKOOihl6W4N5kvr37x+OOOKIKCKnnnpquP/++1ucO4l+NnQm7tGjR2zGQoxYiN6IyHdHeRFJR3nJKK3PCwKTT8KIrLA0hfeqGSLN/7MQraHpqS15YR2ajVavXh3nVyKy06dPn/h38341fCZitWnTpjjf0qRJk6L0GHkR+X4oLyLpKC8ZpcgLUkKTDJEN+rgw2ohRRbNmzQpXXXVVuPTSS6NUXHzxxXHkUTUTM9Kxl+kE2pIXmphYj+9HlvjOK664IsyePXuPomSfF5E0lBeRdJSXjFLkZefOnXGoNOJCkrrLL788SsTSpUvjEGn6u5x//vnhD3/4Q0xcR4faPVGNvNBMxXcyVxLb8MADD0RJYn4lRiy1hfIikobyIpKO8pJRirzQREM/lRUrVoRly5bFHC99+/atvJtBXxQ61lZLU3mhuYeh2AhS0+agJUuWxNmrSYjHvElEefgO1m3ebNUc5UUkDeVFJB3lJaMUeaE/C/KSL3feeWfo16/ft14jD0u1EE2hcy2CQs6XGTNmxKgNTUU59F9BWuiA27lz5zhCiaaqalBeRNJQXkTSUV4ySpEXOsiSZ4XcLCzMc3TooYfGmaRZ8tf++Mc/Vv5jzxA5QU7ou0K0BWkhAkPH2xzW4XU64BKpQUSayk1bKC8iaSgvIukoLxmlyAsjfYiK0GGW5cILLwzdunX7698sZMG96KKLKv9RPsqLSBrKi0g6yktGKfJCRIS8LG+//XZciMIgK/nf+WvkZKkVlBeRNJQXkXSUl4zSOuySBI6+Kbmo0OelKd+1w27RKC8iaSgvIukoLxmlyAv9TOj3ct9994VRo0aFc845J+Z0yZPCkW135MiRyovIDwjlRSQd5SWjFHkhxwpJ6p588sk4xxBJ6saNGxf7wZxyyimx/wsjgr7LaKOiUV5E0lBeRNJRXjJKkZd81A/p+smxwgzTdOIlLwsJ45gZmgkWmYuoVlBeRNJQXkTSUV4ySpGXekR5EUlDeRFJR3nJKF1eXnvttfD888/H+YX4yUJH3mrzr3QUyotIGsqLSDrKS0bp8sIcRvvvv3/o0qVL6NSpU9h7773jnEM0KdUSyotIGsqLSDrKS0bp8sIM0ow4IuvtypUrw+9///swb968b8xJVAsoLyJpKC8i6SgvGaXLCzNKM9IImJ+ImaTbmhm6LJQXkTSUF5F0lJeMUuQFSUEG5syZE04//fQoMHPnzg1PP/10bD6666674t+8z8gj5isqG+VFJA3lRSQd5SWjFHkhQd3NN98cJ2Hs2rVrOPXUU8Pw4cPDoEGDwk9/+tM42/OwYcPiBI0kqyMbb9koLyJpKC8i6SgvGaXIC3ldSE43efLkcMIJJ4Q+ffqEqVOnhocffjgcfPDBUWqmTJkSJk2aFNephZFHyotIGsqLSDrKS0Yp8kJn3B07dsTlkksuidMEICjvv/9+OO6442KTUf4+y1dffVX5z/JQXkTSUF5E0lFeMkrvsDtgwIC/jjZasWJFOProo+NoI7Lw1hLKi0gayotIOspLRunywuSLvXr1iifjtttui4Iwffr08Omnn1bWqA2UF5E0lBeRdJSXjNLlhX4u1157bbj++uvjwu/Ma7Rly5bKGrVBe8rL6o8+Dc8t/7Aml83byx/ZJT9MlBeRdJSXjNLlhf4vzZuIvvjii7B79+6a6OuS057yctP0FS0WorWwvPDWxspWirQvyosUya7dX4YPt35ek8unO3dXtjId5SWjdHlhJmn6uzTl9ddfD2vWrIkSUysoLyJpKC9SJC+u3RT2G/RcTS7/NXtNZSvTUV4ySpUXIit33nlnmDZtWvybCAwJ7EhaxwikWupforyIpKG8SJHMffPjFs9vLSy3PLOqspXpKC8ZpcsLcxsxESNRlvXr14cRI0aEHj16hLFjx4bt27dX1iwf5UUkDeVFikR5aSxKbzYaOHBgTEr3yiuvhEcffTTOMn3eeefFEUe1hPIikobyIkWivDQWpcgLnXG3bdsWlwsuuCCcdNJJoXfv3jHb7owZM8I555wT5zfifYZM/9CS1Ckv0ogoL1IkyktjUYq8MLfR4MGD49xFP/nJT8I//uM/hmOPPTY2Id1www3h0EMPjULD/Ed33HHHD25uI+VFGhHlRYpEeWksSpGXdevWhXHjxoXx48eHffbZJ/z93/996N69e+ykS96Xbt26xYgM60yYMOEHN7eR8iKNiPIiRaK8NBalyAtNQatWrYoRGKTlqKOOinMcEXmh38vJJ58cIzNvvvlmHDJNLpiyUV5E0lBepEiUl8ai9A67TA9w0003haeeeirKC1MEMNrokUceqaxRGygvImkoL1IkyktjUbq8kNOF5iFyvJCs7oorrgh9+vSJuV927txZWat8lBeRNJQXKRLlpbEoVV4QFiIvyEv+N3MaXX311VFi5s6dG1+vBZQXkTSUFykS5aWxKFVeGAK9YsWK2IG3KeR8eemll+LUAbWC8iKShvIiRaK8NBalyQtRlk2bNsVlx44dYdeuXWHz5s3x9YULF4bly5fH12oF5UUkDeVFikR5aSxKkRek5IMPPgiLFy8OL7/8cvz9/fffD1OnTo3DokeNGvXX+Y5qBeVFJA3lRYpEeWksSpGXDRs2hEmTJoV77rkn5nVZunRpmDVrVszvwnsMmx49enSUHBYz7HbcorxIUSgvUiTKS2PR4fJCzpZXX301XHzxxeGAAw6IPxkWfffdd4fDDjssPPvss+GMM86InXZfeOGFsGjRojhpY9koLyJpKC9SJMpLY9Hh8kIUhb4tjCRimDQTMebDo8m2y5QAv/71r8Npp50WpwYgAlMLs0srLyJpKC9SJMpLY1GKvLz77rvh/vvvD0OGDAmDBg0KDzzwQBSVzp07x2R1ZNglYd3s2bPDggULaqLjrvIikobyIkWivDQWpcjLypUr4wSMw4cPDxMnTozTANBxt1+/frHz7oABA/6a+6VWUF5E0lBepEiUl8ailA67QD8W+r7MmzcvrF27Nqxfvz5MmTIlLFmyJFxzzTVh8uTJlTVrA+VFJA3lRYpEeWksSpMXIjAIDP1dHnrooRh5Ofvss+PvRGLI/VJLKC8iaSgvUiTKS2NRiry88cYboW/fvrHD7n777Rd+8YtfxJml995773DqqafG5iPeGzhwYOwTwyzUZaO8iKShvEiRKC+NRSnyQofde++9N3bUPfzww8MRRxwRzjzzzNhhl4WRRyNGjIgjjRhGXQtRGOVFJA3lRYpEeWksSms2yqHTLiOP6Pty++23x7wvEyZM+NZ8R23BlALbtm2L8yExDLstyOBLE9X8+fPD66+/Hj755JPKO22jvIikobxIkSgvjUXp8rJs2bKwZs2asHPnzigWb731VnjxxRfDO++8U1mjbeg7g7iQ0I4oDkOrW4M+Nnw+OWSOPvroGOFhGgI+Y08oLyJpKC9SJMpLY1G6vCAUzCyNHPATgSGvC5l4q4H1yQfD1AL77rtvjKi0BqOaRo4cGfvTkLmX6QnoU0MSvD0JjPIikobyIkWivDQWpcsL0jB+/PjQv3//OEz6u04FgLwQpSFfTNeuXduMvNBcdMEFF8Qh2Rs3bgzTp0+PzVY0H+3evbuyVgb9bJhv6frrrw+9e/cOJ554YujUqdMem6WqQXmRRkR5kSJRXhqLmmg2IvrBZIwkqKs24pKDdNDkRB8ZmoJocmoNojInnXRSWL58eZQe/ib6MnPmzG9l8eVvJoxErO666644AqpLly7Ki8j3RHmRIlFeGovS5AVJYQbpUaNGheuuuy5OC5DCRx99FI455pg25YVOwd27d4+RGiI8rIu8kBAPAWoLm41E0lBepEiUl8aiFHkhqkFGXaIaTMw4ZsyYGNGg423zhRwv1XSorUZeGI1EIjyiPURe5syZE0c4IU7KS7YoL1IUyosUifLSWHS4vNDMQ2fZnj17hvPOOy88+uijUWKYpPHWW2/96zJ06NAwePDgmO/ls88+q/x361QjL0jLtddeG5544om4Pv1kmIoAqdlTXxvlRSQN5UWKRHlpLDpcXpCExYsXR3GhjwpJ6GbMmBEnYkRimi5MFUDOF6Ike6KpvNAcxc/nnnvuG31Z6KTL0Gj6vdDPhs679LUh6kOumLZQXkTSUF6kSJSXxqLD5SXv6zJ16tQYWSESgqQw0mj16tXfWJjjiBww1XTiJTqD8Lz//vtRRhh2/corr3wjosLvdOwdNmxY/O7bbrstjjwyz8vXi/IiRaG8SJEoL41FaR12aT4iYRxDkW+88caYZG5P0Y/2gO9AbhCbPDleNSgvImkoL1IkyktjUZq85BBhQWDIdrtly5YOEZjvg/IikobyIkWivDQWpcsLEZinn346ziDNqCOy3dYiyotIGsqLFIny0liULi9APxVGIL3xxhvfynRbKygvImkoL1IkyktjUbq8fPjhh2HhwoUx+vL444/HnCuIAp11qxki3VEoLyJpKC9SJMpLY1GavDDyhxFBzC9EcxHJ4hgBdMMNN4Rbbrkl3HvvvXHCReYYqmY0UNEoLyJpKC9SJMpLY1GavCABzBfEUGmSxTE5IqN/aDpiGDU5WMiGy0zQ33W+oyJQXkTSUF6kSJSXxqI0efn444/DkUceGRPJEV0hEkN/F36SlI4suFdddVV49tlnqx7OXCTKi0gayosUifLSWJQaeenfv39cmLUZiSEr7p///OeYtI4TdOmll8Y5kIy8dNyivEhRKC9SJMpLY1GavBBNmT9/fhQX5jIaOXJknOGZvi68dvfdd8eoSy2ICygvImkoL1IkyktjUZq85KxcuTJOzshcQ5dffnm47rrrwoMPPhj7wNRCc1GO8iKShvIiRaK8NBalyQuZdLdu3RqbikaPHh1ndybLLieGTrwMm2b6ACMvHbsoL1IUyosUifLSWJQmL4gLcxoxNQB9XGhCevnll8O8efPiTNOMNurVq5d9Xjp4UV6kKJQXKRLlpbEoTV4++eSTcMIJJ8Rh0mTYZV6jTz/9NErNBx98EO67774wYMCA2IF3165dlf8qD+VFJA3lRYpEeWksSpMXZnY+77zzYkK6adOmxVme6f9CnhdEIe8DQyK7WpgyQHkRSUN5kSJRXhqL0uSFCRjJ5XLllVfG/i6MMKKj7tixY+PoI16nL0ytzHWkvIikobxIkSgvjUVp8pKzevXq2Dn35ptvjh11hwwZEiZNmlRTnXVBeRFJQ3mRIlFeGovS5eW1116LERYS0tFJ9/zzz4/DpZ955pmwcWPtVKTKi0gayosUifLSWJQmL8wYTRMRyenGjRsXpkyZEidpfPLJJ6PMXHbZZXGiRjr2Mqy6bJQXkTSUFykS5aWxKE1eNm3aFHr06BFFhegLI4yItGzYsCEsX748duTlJC1evDjOd1Q2yotIGsqLFIny0liUJi+IyimnnBKjL2TTfe+998KHH34Y87ow6oiTQ6fdhQsXKi8duCgvUhTKixSJ8tJYlCYv5HQZNWpUOOuss0Lfvn1jXhdGH40fPz72eTnzzDNjAjtyvHz11VeV/yoP5UUkDeVFikR5aSxKkxeEBIFZsmRJFJahQ4fGPi633357HG1ENIbEdbUgLqC8iKShvEiRKC+NRWnykkNSOpqOaCLipPzpT3+KeV7mzp0b5aVWUF5E0lBepEiUl8aiNHn5/PPPw3PPPRcefvjhKC+MOBozZky455574ggk8r0w5xHTBdhs1HGL8iJFobxIkSgvjUVp8sL0AOR1GT58eJg9e3ZMSsccR2vXro2TNDI1AO8vW7bM6QE6cFFepCiUFykS5aWxKE1ePv7443D00UeHGTNmxOYhpgsgGrNjx46wbdu2mHWXaQNmzZoVdu7cWfmv8lBeRNJQXqRIlJfGojR5oTmI0UTkerniiivCo48+GrPqPvXUU7HJ6LTTTguXXHJJFBmbjTpuUV6kKJQXKRLlpbEoTV6IpsyZMydMmDAhTsp42223xSYk+rsgNQ888EBMVlcL2XVBeRFJQ3mRIlFeGovS5IVh0ojKokWLwsSJE0O/fv1Cnz594pDp3r17R5Eh826toLyIpKG8SJEoL41FafLCnEXdunULCxYsCI899lg499xz/5rjhWajiy++OMpNraC8iKShvEiRKC+NRanycswxx8Th0nfccUfM75I3ETEdAJGXXr16xb9rAeVFJA3lRYpEeWksSpMX5jHab7/9wh//+MfQvXv3GHlhskYEhnmOrr76auWlhEV5kaJQXqRIlJfGotQOu+R3mTZtWmweIvrChIwMlyZZHR14n3/++cra5aO8iKShvEiRKC+NRWnyAgyBJtqCtDCXEdEYmoyYGoDZpJ0eoOMX5UWKQnmRIlFeGotS5aWeUF5E0lBepEiUl8ZCeakS5UUkDeVFikR5aSyUlypRXkTSUF6kSJSXxkJ5qRLlRSQN5UWKRHlpLJSXKlFeRNJQXqRIlJfGQnmpEuVFJA3lRYpEeWks6l5eyAuzefPmsHHjxjgD9e7duyvvfBvWZTg22X1ZmF/pL3/5S+XdtlFeRNJQXqRIlJfGou7lZfr06aFnz57huOOOC4MHDw5vv/125Z1vQuZepiI44IAD4rQEzKt05513hnXr1lXWaBvlRSQN5UWKRHlpLOpaXpYvXx4nc7zqqqvCM888E2elJsEdEZjmEJl56qmn4nQEs2bNCvPnzw9vvfVW2LFjR2WNtlFeRNJQXqRIlJfGoq7lZeLEiXEGamai3rp1a5xS4PHHHw9r166trPE1K1asiKLDPEojRoyIM1mT2Zcsvy2xa9eusHTp0jB+/Phw1113hX79+oUuXbrEJqpUlBdpRJQXKRLlpbGoa3lhTiRE5LXXXosRlClTpoT77rsvLF68uLLG17z66qth2LBh4eyzz44n/5xzzgkPPfRQnJ6gJfg8IjTXX3996N27dzjxxBNDp06dlBeR74nyIkWivDQWdS0vyMjdd98dIy10xqVpB6GZN29eZY2v+eCDD2L0hY669H+59dZbw8033xwWLFhQWaNtbDYSSUN5kSJRXhqLupYXOtzec889YdWqVTFSMnXq1DB8+PAW5YVmINZBXIDmJQTm6aefjn/vCeVFJA3lRYpEeWks6lpeJk+eHAWGUUR00h01alT8e8mSJZU1vmbOnDlh7Nix4b333oszV994441h0KBBRl6aLcqLFIXyIkWivDQWdS0vRFyItAwcODA88cQT4ZRTTol9XpAZ+sE05cUXXwxDhw4N11xzTey4e9FFF4UxY8bEvC/VoLyIpKG8SJEoL41FXcvLzp07o7TQofbKK6+MnXFnzpwZZs+eHZemIB1IzYUXXhiXO+6441uC0xbKi0gayosUifLSWNS1vAAddcnXMmPGjLB+/frYt6UIlBeRNJQXKRLlpbGoe3khTwtTAiAxpPpvLW9LKsqLSBrKixSJ8tJY1L28dBTKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0ljUvbysWLEiPPbYY2HMmDFRMDZt2lR559t88MEHYeLEieG+++4L06ZNC++++27lnT2jvIikobxIkSgvjUVdywuiMnbs2HDuueeGvn37hgEDBoRXX301fPHFF5U1vmbbtm3hueeeC2eddVb405/+FC655JLwzDPPhM8//7yyRtsoLyJpKC9SJMpLY1HX8jJ79uxwww03hDvvvDNs3rw59OvXL0ydOjV8/PHHlTW+Bqm54447wsCBA8Onn34afyda895771XW+CZfffVV2L59exQkPo+ITdeuXcNbb70V/05ZrnxkfvjfFz8c/k/v8TW3TF+0qsVtbrp8+OGHLb5eD8tHH30Ul5beq4elno99r9Gza/K636vPI2HBsrUtbnPzpZ6vnXq/9ve07U+/tLLF81sLy7UTFrTbsT/vvPNindfo1LW83HvvvWH48OHhhRdeCJ999ll45JFHwrhx48Lrr79eWeNrpk+fHgYNGhSbi3bu3BlmzpwZozZz5syprPFN+LwJEyaEHj16hMMPPzzst99+4e/+7u/Cr371q/h3yvKz/Q8M//cn/xF+euAhNbd0ObRri9ucL4cddljYf//92+U4lLEcfPDB4Re/+EWL79X6cuihh8brkJ8tvV/ry97/cUDYa+/9Wrzuylx+9v+XQw9r+7pn+fWvfx1+/vOfh86dO7f4fq0vhxxySDjwwANbfK/WFx4cDzjggNClS5cW32fp/P/LrpbOby0s+xxwUDjooINa3O7vuuy1115h8ODBlZqqcalrebn99ttj+GzVqlVhx44d4dlnnw133XVXePHFFytrfM2TTz4Zrr/++rBkyZLYrPTSSy/FyMtTTz1VWeOb7N69O6xbty4sXLgwzJ07NzYbIUDIDn+nLH369AmnnXZai+/V+vL444+HfffdN4pjS+/X+nLRRReFs88+u8X3an15+OGHw9577x2lu6X3a32heff8889v8b16WCgDEBgqjpber/XlqquuCscee2yL79X6QtmLNA4bNqzF92t9IeJ/4okntvjed1148F69enWlpmpc6lpeRowYEe65557YlJPLC81B8+bNq6zxNZMnTw433nhjeO2116KYIDhUwFTGHQ3bSJ+beoROzkQvFi9eXHmlvhgyZEgsxOsRJB1xfOONNyqv1BfXXXddvAfrlV27doU//OEP4emnn668Ul8Qle7Zs2flr/pi69at4aijjooVdz1CPdWrV6/KX9Ie1LW8cDPefffdsSKlmWf8+PFRDFqKvNBZ97bbbotPTxRCiM6oUaNajbwUifJSHspLeSgv5aK8lIfy0v7UtbwQQhs5cmR48MEHYxPP1VdfHS8SmoaIxDSFfjAMkUZgNmzYEJubaHZasGBBZY2Og+++8sorK3/VF3RwJnT+yiuvVF6pL+gjRd+neoRQMf0Wli9fXnmlvrj55pvD0KFDK3/VHzQ3n3766bEJox6hT2C9VqDIywknnBCef/75yiv1BV0UGFAi7UddywvDlm+99dZo5EQy6NA1evTo8Oijj4YnnniislYGkRmajij8L7300lgB0366ZcuWyhodx5///OcwZcqUyl/1BaO6aK5DFusRCr8ZM2ZU/qovGGnANYt81yM8Nc+aNavyV/3xl7/8JfY3WrZsWeWV+uLll1+OgxDqEVJa3H///eHNN9+svFJf0BowadKkyl/SHtS1vFCYkKSOG5KIC/1X1q5dG95///24NOXLL7+MryEwNDXxFMITLJ/R0SBdn3zySeWv+oKnT6Iv1ebHqTUY+r5xY33msqHZgmY7ftYjHPe2kkjWOqRPINElD0L1CNELhtrXI3n5TfqKeoSHZIZKS/tR1/ICdL6lUFy5cmW8QNqSEd4jWR3Cw1NsvVYCIiIijUzdy4uIiIg0FspLO0JTCn1CiAQR4WkrCkTzC+vSfETEKI8CER7lbz6D5qWOap75Lt9L+JwQdN4MwP/xGrDfhEfZLxY+h88uGjpo501Cezr2rNt0G2kGYH22k//lMzg3zTt9FwXfzTHf07Fn+9hW9jPfdhb+hwgk56SMY8+551ixHXuCbWI/2T4yXbPdwM98v9iPjoqKsu0cf843yStbg/XYxvz+ZlvZfuAYs+/5sed97u/8nigSvpumFO7BtmA9trf59ZHvF9vPa3xOW8ehPan22OfXdn7dEDXn9/z6Ydt5jfc4L7xW9LHn8/OygoVtaKvM4Vjn5T3/xzYC10nTY29rQPUoL+0IUxMwFPH444+PQ3Lbmvhx6dKlMWHa0UcfHa644oqwaNGi+Do3wmWXXRaHZPbu3Tt+ZkfAzUNHZr6XuTPIRNwSFILcfIzs6t69ezj55JNjAqb8hmQ0SadOnUK3bt3iwudQoBQNneFIPkciKLZh/fr1lXe+CdtPvycypZKwi22kIyB9GTgGdADnM/isjurcyLYyN9dxxx0Xf7Y2HJTjSIdR5udiu4888sjYWZ1RDO+8804cRUWH9PzY8zkUjEXDuae/GdveFhTupCjgmuG6J1XBmjVr4jmhIyaJG3//+9/H/cjvh6Kh8qAD9AUXXNBmZ2IqFY7xhRdeGM/TmWeeGTuus+1cN+x7fuy5fsgn1RESwLEneSFlRltwHXC8ybCbXx+MmkJ8yJNFWcP9wPxwjOLsCDj2lJHnnHNOi7m5cjjuDLE/6aST4naTZZZzwKhNtp1ylAR2vMc1REqBIiUAcUGcSFaYl4EXX3xx7E/E9dASXPckaeQY33TTTfG6B/pd8r/HHHNMPIdki5fqUF7aCUYgMBKESp3RLEz+yA2ZP501hRuW4d3cdOSfIf8FhT9DYflfLnJGTFE4svC01NpN0R5Q+FKQUYgwQzd5aCjo+N7mTzDsDyOlqPDJkUPuCAo+CjxuRLb3mmuuCfPnz48LFUPRTxMMg7/llltiBmW2jeGgZFBuqWMlT2hICceebWYb6eTNvnK+qHg49hSMdOymL1WRT3F8L3lDmIaC+bO4hvhetrM5eQVKxc5200mdjLVcO8zdRRoAKv782FOYFn3sqfzo/H7KKafEiqMtSGGQXx+MuEO6uP45xg888ECUZs4fhTujBouu/Kk8+e7+/ftH8WgrfwvXMdm7EQWkkP1ge6mE2BeEmXuG4076BZ6ii7xnuSY59tx/VOp7yt9C+cT1wlxw+fXBPtH5nuuHe59jT4WMIPMQVSRclwge2cbJG9VW/hb2k36KjNhhuxlyz/w+HGdGD7LNnBve475H6Io89mw7MsLwZx6aKDO5D9mHlh7UuMa4XnhIZR2ue+blo7zk3mFfKPc5N+Qq64iHvR8Cyks7QQFAtIVpCCi4KMwYrv32229X1vgaKk0qWyopwokPPfRQLDD4DP6Pm5FKiidBJuDipszDjEXAzZV/L2JFhcL38hTQPBTK9jLkkv/haY51eBrl5qPw4+mBG5mcOtzYVMJFVv5AAcCxzyflpPLju1uadBPRYV9PPfXUKCiIDE9vnCcqUKSGColpIfgboSiyIMzFi2NP9AeJ5LqgEG7ruHEemBWdaBmjMDhnpAtg+xFLrkMKwaKPPTLLdUolhIC1BRU/BTTbyjFFNrnmWdgPzgXXFPcCIsA9UCTIEeeaiu83v/lNvH5bg3uaBJekCODYs81EwHjK51qnQuLap0JjvaJHJHFeqaS5BnhypwJsC+5PKk+Ei+uL6wy5Jdkk1x/STLMG9w37wz1eJBx7jh15upi3iGuiGrimqeC5x3noYlu59tg3rhumb+H8FAllMZFzhIrt4cEBeSSi29JDB69zjLlmuC7INcW1TrnP6xwDziUSxPXDZ8ueUV7aiTxaQWXEkwJPcdxYPG02h4qFJ2Qqfp7+eHKjouSGpBCkoOGm4LO4wFmKfAqlAOPpk4KQAownIr6TQoLtaw36OdAsRCHODcxNSuTpj3/8YyxQqcxaiz61J8gIFRBPl7SNUwAz9QP70Zy8sOZJk4Kc5iEKlfzpmXNGNCR/IiWa0VZbdipcAzS7UXiz7ST/IypH4daWeCBcnCO2j/W4Zkh8SCVG5Ilj31r0qT2houB6Z3uJGLYFhTbygmyxzVQ2CA3ixnYTAeOplusQASs6gSSVENuOmHyX5HMIFpEhtpnKiohGLo75QjNYW/dOe5Afe66XPSWfQ8yo4HnQYF22nYqe18k4TSSAz+KaIZrDvVwkHBu+j3uNaGe1yed4kOMe5aGC/UfEKLs45uwbEW+kt+hjn8M2cOyIfhEZaqmsyxOiIiWU4zxkcX0Tgbz22mtj2cPrlAXcE6012cs3UV7aCfpKUGHyBE+lztMooUIuyOZQKdKGS2VLxUgzABczT27cfNwEmDhPJggEUZAinyYosHh64Sc3H1EVvhchaK3ZgcqHJw/2kUKD7aPZiydZKgNC0kRgKNiLnkQM6eOJhagR209Il8KipX4TPDmzf4TF2QcqU6SF40/0hkIRceSplMgZhUuRUS8KLio+nnQpzLkmkBIK6LbkhWsoLxCBa4XKHwHiOCBl7BOvdQRUdnuSlzy6x7XNviE8SDvSxf8iBdwPVAZsO+exI6CiQ/aqkZd8+2i6IFpBBIkHlDz3ERJ/xBFHdFhfL6CZc0/ywvXBQtnEPXLGGWfEY8zC8c/76LD9VKBcgx0B20K/kWrkhWsGWUcGuD+5L3kYQYbZdqKl9KXiQYBrqWjYHso2BIrrh0hQS1BGss2UjZSnXD886PKgSvnCQyrXINcR5RgRGNkzyks7QeiPCocnLiohnmgo3HhSaA4FPRUlT9ncgEQnuLh5MuIpnGYlBIA5bLiYudCLlBcqTsL2VKRUftxMfC/S1Jq8UOiwf3RURGIoxCkYKUT4nYKbJ20Km6JD0HwH20s0gu3n+PIahVlz2D6OZd4UxJM/4sn6bC/SRiGE5PA7kaQi5YXoApUHkssxRUaoUBDh1uSF1xEBBDg/Pxx7fme/eJrlffappehTEVQjL8gWUS+uDfaBJ3z2kydQKt+8QkJauB+IJnUE1coL20zTHg8ZRE7ZXiC6xbHnfa5B9oVoSEvNlkVQjbxwzbOwjfyk0swjAjTfIfq8zj3DOWH7O4Jq5YXtZl2iRGwfEslrHHvOH79TDhFN5b5trcN+e8J35/3OKKtbi/YgNzwI8tBE+cN1xnGnrOcepnzk+qEsYF3Op+wZ5aWdoCmIwoCICxUoMkPl31L7JULD+xg2FzNPoLmd0/zEzcnNh8RQoXIxs15R8ESWfy+FM08GfC/b1/yGpJCggmHfKMAJgVLoAQUeNyaVJ09DVAjsU9EpvTl+fA9hcCIqSBV/tzSBIRUjhRtyQgFIYchTNE1NHGdEgkoHsaQg4biwXlEQaeHcI740QfDUSMFGBIhj3RJUkAgX/5NDMwb7xmcQbSGMzfmspcgLx5friooSySJixjayH1Sm9BWhguKpH/lqST6LoBp54RrgaR6ZZduIjvIa9wLngnuViBIV0WGHHRabjYvu9JpTjbxwzROt46GI/WCEDBUv542yiGgL7/HQxTXfUaMcq5UXzhH3N8c6l1oeErmGqPQ59jwAEPXKm7+LhPPOAxODLbhXeXho7X7lmFJesl1sMyLD3ywcex6gECHqEMoC1pM9o7y0E1g1lSZPZVSmVB48QVMZEcloCpUjBTTtzozYoeChwqKwpjc6IX9uDAp0Po+n5yIrUApZbhiGfxLG50mYpgy2BRlrWhDkT2cMaWWiNCp+CkbCzcgLhQlNMTxhE5qmQqJQLBJ67fN9iAfbwnZRGHPskYOm5J2lObYU0jw1UXhQyVMIMlScY88+UFFRqOZRmiJANqgoGKnD8SP6xjnPjz0i3BwqHAq5ps0qiCZPcSw0zfB5eSStI2gqL4gr10PzzuoIIdvN/uX7zH1Ahc/5Yrgyna9pwuQ6oumxI2gqLxwvZJ5rnAoph2gRlRRpALg/c8FEJIlwEb0gmorQ8z7iXOQDR1NyeeE6Rcp5YKLpsCmIC9c89ysCQAdTrjG2n/1g/7mG6D/COpRnHUFTeaGc4Hu5HpofO84F202Zmj+U8FrTY49IUKbysNRaxLg94HqhiQcBpBykrMjLG8o7moeawvZw3VOm8pDEdU+ZwzXGMaf/HeeALgPsY9EPez8UlJd2Io+gMGyYSpQCjIuZm5InhqZw8fOUQGFNBUkFinVj5YgNoU8KeH5SwbZl9e0BYkRhRydbvpd94OmSip+bLA+PA08IiA7rst2EPik82E8KfSp++sDQnEQ0oOn/FgVCRSXI8br88stjB2KOOce/ebMdlRAVJ9vI8efJh3Azx5eoE4V33rGRKEHeN6YoeIKj3ZxjybZzXKkYEV6aVVp6emf7qWipeHKo6HmSZrvZBwrTjnryByIRHEug8OV6aN5kxdMxsk6Hbq57rjPOD9c9FRbnjeZLrh0kpkhpbArXPw8ebANNhlQq9Flhe3OIJhIhonLkHHHdU9FwnthPKlHOIddO8/8tGiSVKCHHi8qfCrS5tFOucE2w/Rx3hIfoLtcf28/rlFt0fEWi82hq0fA9iAfbgMjT747ICtdEU1iPfcyjq8B5497l/zn2XFOUTU2lswgQI44x9xnXMtcC550HP45d82g7dQPlO9cNkV5khQcl9pE+O2w7r1Me5dF42TPKSzvCDUZFxA1EwdCW/SMwVDgUdBT2+c1KAcTTHxECboKOenLOv5fCoSO/t72gwEKeeJrkuHJ8vytICueQyoCKrKMqfwphnjrzCr8jK76Ohusc6UJikMX8POX3A8LJeeyoylMygUbquXeIYhINkfYFISG6y0MH0bFcUDj2SBt1BuLJw6FUh/LSjlD5cTFS8FIhtfXEznusw7r8T9N1EQkubgr0jnr6hLK+tz34Lse+Lfg/jgHi6bFvf/LzhGw2PU/8bO1+kOLhmuPYc/157Nuf/LpvXj7xMz/2XvffDeVFRERE6grlRUREROoK5UVERETqCuVFpGBo46YPDf0J2ou8rbzWaKnN/ru047Mux6ve+v2wvfRZaM9zLCKto7yIFAx5Txh+y0iO9oIRIYxQosKsFRCP5p0O89eo3KuRGEYjMeqI0S8dQS5LTTtRtkS+Xmv7weg8RlG15zkWkdZRXkQSobIljwP5Gkj2RQZN8n8w5JmKmwRu5Mshp0NTSKhHLhcqQyIzJJ0jvwk5OPg9ryT5mS85TCnBek0/k4q1aeVKJlWyeOa5KJouJDUjpwp5Tb6PALG9DPkk1wm5gUhsSL4NMhuTKI/PZ+F1cljkeTwYhk4COpK58R7/S1I68oyccsopMcEg20vSrhz2h+1EaFiYc4ph5a3lEGJ9jkNb5McKCSRHDbmKBgwYEI8N+YKYLJCkYflr/GRhXYbQkyitaZJA8jZxLlvL0ov4kHWXVAQkHyQfCPvIMeE8krtnT9ssIl+jvIgkQv4GEsSRmJAMrFTIZDQl4RQVE5Uy2YapIJEY0uNTaVKBU7EjD4gOv5MdlwynVJR5ZUaFTeVI0j8SYZEMjmRifC4VLEnt8kn2yBuEVACVLImvfvSjH8XtarrsvffeoXPnzjEq9H2aOthmKl4qYRLjMckc+5bPjk7m0WOOOSYmPiPzKblbkCmS0uVZgJEdEncxozPix36zIH8kK8th+xBAxI7jQDIyfm+eRTaH84HgcLxY8mkeOE75a4gjGX8Zokp+DT6P48d7bO+//uu/xm3M188X1iXKQpIyMqvmn4G0sR+cj3xdjg35gpApIkp5Snj2m0RxSBE5lch8yz6zXr6ISNsoLyKJkAafypAKiCkWqKCoDIk8kDUWUfjVr34V04mTQp9Kkqd2IgwIDxU1wkHmTSSIipBpCnJ5IZkb2ZtJ6X7ccceFX//61+HII48M3bp1i4Jw6KGHxtl0+X++G1EAZIHMn126dInf3XT57W9/G6Mc3zehH1DJ0kzCNhNFIDpCdIHfkSsWjguyxXusj/CQWp0MsCR05H2yOfM/rVXayEEuRWSJJTJCkju2vSWI8hARyqMmHLff/e53oWvXrn+NoiCOCAjwvZxDRAO5IoJy4IEHxm1ClliIcLFOnniSfWCaCUSE4414Hn/88VFKyLyayyXnGtFj/zk3XBOnnnpqfA+xRPh4DckjMSXXxZ4SXIqI8iKSDJUa0xMQNUBGiBLQPEKzDPLAEzlRF57GmYiQpgUqsH/4h3+IURGiDlSc/CRyQsXM+7m8ULkiN3wun8P3UCkiNHwvFSiVH+JAhU4TBU/6RCYQC7aBuVWaLlTeLAgEUR/+57vCdpEyn8gGzTj060EU+FwqZ0SO7f35z3/+V6FCRIgIUZmzsE+IBpV4/hrvN800ytxazBdDcwuig3zRTEcfE9ZHiNhvKvxcgNgf+gTxkxTyecSqJViH6QFo8kPqfvGLX4R///d/j8KDJLJwDpkugu8DhAQBQzzYdvYBEUM8iJTxHnLDa2zXO++8EyNOHIt/+qd/it9DcxnXy29+85somCw//vGP43ksemJBkXpHeRFJBHnhaZ2nbypsmjWowHmyHjVqVHwap4Jj3ieiLVSAzDRL5IMndP6mKYI5fRCb5vJCRU4TFK/R5ESEJ5cXmiaQFyISfBbRCeaxYX2+i+9gklAmg2u6IBe8zqR4+Tw33wUkgUqZSBCV/UEHHRQOOOCAGFk6/PDDwz//8z+Hf/u3fwuHHHJIFLR8rh3SoBMxQgxoWvrlL38Zfvazn8VIx7HHHhtFgc9k/4BjgASw77zH+n/zN38TI1n8P59F5f8v//IvsT9KnnadY4DQITUtyQufmx9fRIRjz3FANpA9ZIvPI1qCnDGhHk1jTaM9RKw4d4gPERPkKo+6ISAIFs1CHCe2hyYlrgkEjz41CNHBBx8c57TK16cJjnXzbRORllFeRBLJm43yvihUYPxOM87s2bNjZYXYMKssTQv0d+Epnuaeww47LEZCqARpzqASbC4vpNKnbwX9aJAcohVUpogAEkTFTF8M/iYCguwQqSGKQ6VMRIGmDMSK32l2IcrD3wgQEQy+g4XoCZJA5KitOW5okmI72Qc+mwqYZhmEiUkKiSjwHewnfWzymXLZXuSJiprOq+w7xwUBo8mGfUP2ctFAkhAJmtZYn8gVUoQM0mk5b+ZBXmguyiNIyBLbRsQGeaF/StNmIz4/7+yMvORNUUgEnYf5m/PGtiGIHFsiJTTh5fA720+zEtEftg9xJRpFRIvJHDmGubzwGRwbFkSJBflCaoig8d0ch46aU0uknlFeRBJBXqiIaBZiBA2VF80I9HfhyZsK6qijjgpHHHFErFCpnKgcaUKg/woV66uvvhoFAPloLi9UrjQBMSIFMUKQiALwXfwPwkBlzEy1NFnkTSd0XGU9voOnfCIi/E60hagFEQ5GzSAtQNSCUVI8/dOnI58stCUQJCITrEvlTlSJ5hyatIg2se/IC7KBDFB5A/tA9AG5InKB3BHZoOIGIkA0NfEZzaFzMRElpIJjTJQKsUHs9t133782TQHHk4gOryEvnA+Oad6ZFolCMKAleaEjMfLZmrwgkcgKx55zw7li34ho0VzYdCQUx5Ht4dwhjESniMzx2ew7HbyJ9nAMkbof8sScIu2F8iKSSB55ocKlEqJCom9GLi958wwCQ9MK0Q0iADR3UMETbaEypU8EQtBcXoCneCIp9LGgiQb5QGKoYOmfQYVOBCAXF6CfBd+DMLE+ssT3I1EsNClRsdMPBfg+IgW8RgXa9PtbgvfpXMzCfvN5VPJUyogSFTUREqI7RGpgT/KCoLQkL2wjM04TwaKCJ6LDKB2iUURg2K9cRgBZ2GeffWLEp6Vmo6Y0lxe2n866CBJNVs3lhf1GmBi9RBQFGUVWkCKOAfJDRAjBgVxeOHdEoRBIRI8mMLaZ7WI0GvuDbBGpEZG2UV5EEkFeqOB4mqbCZpgulSrNI/RRoaJFUKjcEAkqaypKohYMy6Xyox8LT940//AeT/BUYlTaVK6AmNAsQqSG5gr6WFDZ0hTF9+QSkkO0g74jRGfo/4FAUbnSlETzBlESmozyfiJ8NttCRIFmrPx7W4PtIZrAfiIPVMoIE5U0fVqIdhDVaSpBCBj7nQ/RzuWFfeZvKnkiSnQ0zuF1RjUhCnw228XCvtPcgszQJEQTUc73kRcElM9DUmbMmBH/5hixj5zTXF4QPPoYEUGhuYjOtQga+0ukiXPJPiBVrMtxZWE7ibJwPrgmkCQiTUTtODdExzgXTQVURFpGeRFJhOYZKj0qLp6k6dRJBUYnVCosKjHWoUmGSpGoBpU6skMlh0AQlaHJiPfo98FQaf5n5syZUY6agpQQUaFyZtQKssFTfvNKj+8iyoEwMZLlJz/5SVzoJEplT0SIiA+jcoCKlgjD3/7t38btzqMlrcH3kT+FDqqIFxETmpNoquL7qIyp9GnKyvuisI9ET4gkIQ38zbGiAqfPCiKGoDQdxkyUA7lgn5E7XmPhGCJLbCuRqrz5hu8i4tWWvORCwefk8kJ0is7H5HjJh1bTHIWYMSQ9lxea1BBRIjNEkBBQmpk4Duw/x41jQTSMfcubkIjAcD5Zl3NAsx19eRAkIlWcD45BcwkVkW+jvIgkgnzQaZQKjSdxoixUaDSlECUh0sFCpUzUAdEhwkEFx9M7TSm8TpMBFSoCkedt4QmdjqVUcjzZU/EjPDQx0bmTRGo8yfP5eaI4oiZsEx1TqXSJiDA656c//WlcaK7gNSpomrbIL5JPNUBFSxSEiAARjz3BtiFsCBVNJTSXESFBWtgvIj8cC4aCI2bsN/uZRxiIHiEVRKrYBj6DqAnCw/awL0SN+EyOQV6x879ERuhzQtMbx58ICJ9NVISmG5rXOOY0rxHJIrqBALFwrIiWsT18D0LBqCGEj21iO5BO5AqZZBvpSIy8ICfsL1KEOCIoSEneHwaBQpryJjOOD/9DNInzxk+OMUJF9AUBpC8P8sv+sP95PyQRaRnlRSQRKlqe9IkQ8ORN5UMFSIWNyFDJUqEiN/ykQiRSQpMJlTxP26yf95HIIzlUilSOVJR8JiLA/xOloHMugsKoGipI3qOfCOLD51CRMiKJSp3P4ifNMyxESXiNypsKlEqY7f4+5FEkpAt54DsRGo4Jf3MMqJjZ1pYqZJp6kJJ8TiAqfsQE+Ez2hf4nHN+m/886HD/62yAJRGBoZkO6iNpwPDjerS1ETfJIF99JcxZRnZb6mxAxQUDoIMz6OWwPskSn55aiVERl2G8EjOPLdyB0+fEmUsS5pMkP6WVdtivfFxFpHeVFpAbIK+zWoLIjKtLWelSyLFKbNBUz4PeWXhORPaO8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEgdEcL/A7Fjxw5bpmCxAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E9%A2%91%E6%95%B0%E5%9B%BE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApIAAAFYCAYAAADgExwpAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAE6cSURBVHhe7b0Hl1Vltq///wrnA5xxbv9Hn3u6b5/DUdvQ2mZRaRVBERBoRFHJ6ZBDk3NqMk2QLEmQnCTnnKPknHPOzNvP3Hvb6KWpWmXhYr/r94wxR1WtndbeVbvqqRne9/8zIYQQQggh8oBEUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHlCIimEEEIIIfKERFIIIYQQQuQJiaQQQgghhMgTEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIYQQQog8IZEUQgghhBB5QiIphBBCCCHyhERSCCGEEELkCYmkEEIIIYTIExJJIYQQQgiRJySSCWDq1KnWvXt369+/v0KhUCgUsUSPHj3s22+/Tf9lEqEgkUwA1atXt9dff91q1aqlUCgUCkUs8dZbb1n58uXTf5lEKEgkE8Bf/vIX++tf/5r+SgghhPjl+dvf/mb/8z//k/5KhIJEMgFIJIUQQsSNRDJMJJL5wI0bN2zevHnWrFkzjzZt2tjWrVtt1apV1rFjR2vYsKENHz7cDh8+7Nc/ePCgdevWzY/zxtq0aZMf536GDh3q99GlSxdbsGCBH4eZM2f6/bZs2dJ7TC5dupS+JGckkkIIIeJGIhkmEsl8YPv27TZixAjr1KmTDRo0yL788ksbM2aMDRgwwN80NBk3aNDAli5daocOHbIZM2bYF198Yb1797YWLVrYuHHj7Pjx47Zhwwa/focOHTx69uxpp0+ftp07d7qQNmnSxJuVGzVqZLt377abN2+mz+DhSCSFEELEjUQyTCSS+cC6dets0aJFtmfPHrt8+bLVq1fPGjdubM2bN7fBgwfb1atXXQzJJE6ZMsVlsFWrVnb27Fn7+uuv7auvvrK5c+dav379rGnTprZ582ZbuHChde7c2ZYtW+ZZSrKRCCiPgVBy/TNnzqTP4MdcvHjR5XPx4sUeNDcjuUIIIURcSCTDRCKZj9y9e9flsEKFCvbuu++6FK5Zs8Yzh9OmTXMhbNu2rWchEcFr1665KJLNpNTNGwzZJDu5Y8cOGzlypGcz69Sp40L6/fff28mTJz3byddI5YMgQ0ppvFChQh4FChSw1q1bpy8VQgghfnkkkmEikcxHyASSASxevLiVKFHCevXq5SXoW7dueYaRjCMlbkSSvkh6Iiln0z9J9rJKlSreF3nu3Dnbt2+fl7zbt29vlSpVsrFjx9qRI0c8Czl9+nRfFxJhfBA8Hj2Up06d8kBEu3btmr5UCCGE+OWRSIaJRDKfIOu4evVq748cNWqUD8XwpiGLyGVz5szxnkj6GylTUw5HJMlY0lfJgA3rbDG0Q1YTASUjyXVr1KjhIkl/JT2TEyZM8Izjtm3b0o/+cNQjKYQQIm4kkmEikcwHKGmvXbvWZY3M4oEDB1z8eNPQO4kwUr7u06ePl7DpkZw4caJduXLFvvvuOz/OMfoY6ZlEGNevX+/HkU8GbZDNjRs3elaS48SuXbvSZ/BwJJJCCCHiRiIZJhLJfICeRgZj3n//fe9ppDxNryMCyHEkk/LykCFDbPbs2Z5prF+/vq1YscKvQ9mZjCV9lGQsGcgZNmyYD9VwHNlkWAeZZBmgypUru4ieOHEifQYPRyIphBAibiSSYSKRzAcQx4oVK9rTTz9txYoV80AOWSeyaNGiLpFvvPGGT13Tu7hkyRJ78803vZRdpEgR73fkOEJaunRpL4+XKVPGqlat6scJSt9cxuNwW4Zx6IXMDRJJIYQQcSORDBOJZD5A6ZoBGTKE9DASyB8T1vRAjh492nsiL1y4YPfu3fOSNiLIMA1rSyKQlMdv375t+/fvd+Ekc8nnHOc2XIcy+aRJk3zI5vr16348N0gkhRBCxI1EMkwkko8QJBBpPHbsmK8lydeAADKAg3ginAhkBj5nMhsxvT/jeOfOHRdRprAR19xKJOSXSN66c9eaTtpi5Yeueeyi1dTcDR4JIYSIB4lkmEgkE0B+ieSN23ftzb8usn9rMO2xi/d6LkmfpRBCiMcRiWSYSCQTQBJE8uVO823u9hOPXRw6ezX96gkhRLKRSIaJRDIBJEEkH9cYsmx/+tUTQohkI5EME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZD5y7949u337tp09e9Zu3rzpceHCBTt9+rTHqVOn7Ny5c3b16lW/XuYYH7ne3bt3/X6uXLni90Fcvnz5h+M3btzw23P9ixcv+n3kBolkfCGRFEKIFBLJMJFI5iOI4/79++3zzz+35cuX28qVK13iihUr5lGwYEH78ssvbezYsbZ792575513rFChQn5ZkyZNXBzv3Lljw4YNs88++8w++eQT69u3r50/f97vf8GCBVapUiUrWrSotWvXzr7//ns/nhMSyfhCIimEECkkkmEikcwnkMhNmzZZ7dq17aWXXrJ58+a5GG7ZssWWLVvmUatWLWvdurV/PmvWLJdHpJKvuR6ZynXr1lmrVq1c/MaPH+/3t3XrVtu4caO/CRs1amTz58+3hg0b2pw5czwzmRMSyfhCIimEECkkkmEikcwnKDuTIezdu7dnHpG9DJSmT5w4YV26dLGRI0fajh07XOyqVKli7du3d5lcv36938egQYOsc+fOtnDhQs9ucvm0adP8OLcfM2aMX49MJbfbtWtX+lH+AY9F9rJ///4eZDA7dOiQvjTvSCSjh0RSCCFSSCTDRCKZT9y6dcszisePH7cSJUrYokWL0pekspXIYL9+/Wzp0qV24MAB69ixo2coq1evblWrVnVJPHnypGcPKW1T+ubrcePG2YABAzwT2b17dxdOHouM5uDBg72E/lMQ0FGjRvn9E6+88oqXwn8uEsnoIZEUQogUEskwkUjmM5SaS5Ys+SORvHTpktWoUcOmTp3qwzL0PK5YseKHoZzRo0db5cqV/RilbOTx6NGjdubMGZs+fbpnL2vWrGl9+vRxwWTIZvHixS6mlNBzQqXt+EIiKYQQKSSSYSKRzGd+KpJIH1JYtmxZL1dT5maghmlsPjLpTa9js2bNvCeyfv36XrI+ePCgT3RzjFJ3vXr1vJy9fft2v8/Zs2dbr169bO7cuf44D0MiGV9IJIUQIoVEMkwkkvnMT0WSrCKZyJYtW/pADdDX2Lx5c9u3b5+Xw4cPH+7T3GQkM32Nq1evdpns2rWrf002kjfhjBkzPItJzyRiuWrVKr/PhyGRjC8kkkIIkUIiGSYSyXzmpyJJKbpFixY+JHPkyBE/tmfPHhfJtm3buuA1btzY2rRp4z2R9EAinQzZ0ANZunRpzz4ilrwJ69ata1OmTLHy5ct7L+WhQ4f8Ph+GRDK+kEgKIUQKiWSYSCTzGTKMnTp1+iH7yOBLjx49bPPmzb7QOFDWXrNmjZexGbQh68iak5S5r1+//oMwMmDDZDfDOdwv/ZL0WiKmFSpUcFklO5kTEsn4QiIphBApJJJhIpF8DEEaEVF6KtnFhl5KYNkfpBKhpOyNdOYGiWR8IZEUQogUEskwkUg+hpCZZIkfxDGzPSJktmBEIDODOrlBIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJL5yJ07d+zs2bM2ZswY279/v928edO2b9/uEjdo0CAbMmSIrVixwq5fv263bt2yOXPm2PDhw+3bb7+1TZs2pe/FbM2aNTZ69GgbOXKkLVu2zK5du+bHd+/ebePGjbPBgwfb3Llz7eTJk348JySS8YVEUgghUkgkw0QimU/cvXvXjh8/bhMmTLA//elPtmDBAjt16pSLX8GCBf3N06hRI5s8ebKdO3fO9u7da3Xq1LEaNWpY/fr1rX///nb58mU7ceKES1+VKlWsXr161qJFCzt8+LCdPn3axo4daxUqVLC6detaw4YNbdWqVS6rOSGRjC8kkkIIkUIiGSYSyXyCLCPZw+LFi9tzzz1n8+bN82zk0KFDrWfPnrZv3z47f/683bhxw4WTTGStWrVs3bp19t1331nbtm09K0l2smnTpv7x+++/d9HkfmfMmGGdOnWybt26+WM1a9bMpZX7+ilkOy9duuQiSyCsXbt2TV+adySS0UMiKYQQKSSSYSKRzCcQxDNnztiWLVvsww8/tIULF3qQWXzppZfszTff9DcQmcqdO3dagwYNvHR95MgRv82wYcM8Gjdu7NnJzZs327Fjx1xER4wYYW3atHEZXLx4sYsiEslxRPSnILBdunSxQoUKeRQoUMBat26dvjTvSCSjh0RSCCFSSCTDRCKZT1Davn37tvdIlihRwhYtWuRCN378eM84zp8/30vVvXv39s+rVavmPZJcf8+ePfbNN99Y586drWrVqt4fefDgQS9nUwrv1auXZxXJbHKfPA73MXDgQH+cn3Lx4kWXVaSTKF++vGczfy4SyeghkRRCiBQSyTCRSOYzSFzJkiVd8OiFpL+RPkZEk7J0hw4dXBRr1qzpMsh1EEmOkXVEMJHKTF/kpEmTPLtYu3Zt69OnjwtiRiT79u3rJfScUI9kfCGRFEKIFBLJMJFI5jP3iyRZxQ0bNnjZG/nr3r27iyRDMy1btvTyNOVrythkF5E9hmvon9yxY4dfxoR2jx49vDTNm3DlypVe2qaHkuwmGceckEjGFxJJIYRIIZEME4lkPnO/SJJZ5E2zdetWXw6IwRmyjuvXr7dRo0ZZ+/btbe3atTZz5kw/Thmc25C5nD59um3cuNEnveml5DhvQsSSARpum+mlzAmJZHwhkRRCiBQSyTCRSOYz94vkrl27PJv4xz/+0V599VV/A1GSZl1Ilv8pUqSIVapUycqUKeN9jCz9w9qQ9EOWKlXK+yVffPFFz2pyvF+/fvbOO+9YkyZN/DiZTZYMygmJZHwhkRRCiBQSyTCRSOYzlLDJMjLBjTCSiUQemeAmM0lP5L179/wyjjOpTSmbEjW3zdyenkmyj1OmTLELFy74cRYkp6RNJpIM5YEDB7z3MickkvGFRFIIIVJIJMNEIhkTyCS9k4jmoUOHfti9BhjOYX1IhnCuXLnygywik4gok9usScnXuUEiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkmnOnj1rly5dSn/1Y27duuXbFOZmO8LHEYlkfCGRFEKIFBLJMJFI/h22K5wxY4ZNmzbNduzY4XtYI5YIJNsYslXh1KlT7erVq+lbZBcSyfhCIimEECkkkmEikfw7iOTnn39u7777rrVu3doGDhxo8+fPt3379tnWrVvtq6++slKlStmpU6fSt8guJJLxhURSCCFSSCTDJPEiiURCgwYNrFWrVrZ8+XKbPHmyde3a1cqUKWNvvfWW1axZ07Zv3+4ZymxEIhlfSCSFECKFRDJMEi2SO3futObNm1u7du2scOHC1rBhQ5syZYpLJBnKL774wkqXLm116tSx77//XiIpkYwcEkkhhEghkQyTRIvkoUOHvGzdp08fK1++vJUrV86zj9WqVbNBgwbZzJkz7dtvv7XevXtbz5497eLFi+lbZhcSyfhCIimEECkkkmGSaJFkSnvjxo0+aENZu2TJklakSBFr1KiRl7fXrVtny5Yts8GDB3vpmwGcbEQiGV9IJIUQIoVEMkwSLZJMY7dp08YqVapkNWrUsMqVK1uLFi1s4cKF9swzz9inn37q5W2ylFu2bLGbN2+mb5ldSCTjC4mkEEKkkEiGSeJ7JBs3bmwVK1a0999/37ORSBciWaJECe+drFq1qlWoUMGzl1pHUiIZNSSSQgiRQiIZJokWyWPHjtmoUaOsZcuW9vzzz9vbb79tzZo1s06dOtlzzz1nn3zyiYtmhw4dbMyYMXblypX0LbMLiWR8IZEUQogUEskwSbRIHj582IdtOnfu7OtEfvzxxz7FTU/kSy+95GXtkSNH+mLk9evXV4+kRDJySCSFECKFRDJMEi2SR48edVEcN26cDRkyxLp16+YSuWnTJhdHju3atct7Kbt37+7bJGYjEsn4QiIphBApJJJhkmiRBBYkv3btmp05c8ZOnjzpceTIEVu/fr2dP3/e+yKvX79u586dU4+kRDJySCSFECKFRDJMEi+SgEwiiZm4c+eOT2jzOWtHslUigzlakFwiGTUkkkIIkUIiGSaJF0kGaHr16uV9kiw+Thn7fpjg7tKli82ZM8czlw/j9u3bPsDDtDfLBV29etXWrFnj61IytMNjsC4lkkp/Zu3ata1WrVp+ef/+/V1akVfWtWRZIta25JwuX77s98+6lgwCsablsGHD7ODBg348JySS8YVEUgghUkgkwyTxIknJumzZsr5+5OjRo138MiCDPXr08Mt27Njx0IwkEpnppXzjjTds/vz5vq3i119/7SLKTjmsRzlgwADbv3+/LVq0yJcdYiKcXkzkEWGkJ5NjyB+PjWTu3r3bs6JDhw518UQ62c5x8eLFLqs5IZGMLySSQgiRQiIZJokXSSaxixcvbhMmTLAVK1bYvHnzXPTokRw4cKALGJKXE/RRcpt69erZyy+/7CKJiE6bNs17LhFNhBRJ5HEQyqZNm9rYsWNdXskukqlkmSGykWzPiEA2adLE5s6da998841nNDmnGzdueGaSIaEHZSXJbFKKRzQJtn/k+j8XiWT0kEgKIUQKiWSYJFYk6YNEyCgxf/TRR7ZgwQJbu3atixpZxdKlS7voLV++PH2Lh4MEsmg50oiYknHMQA8moklJGhnMlLsLFy5sb731lpUpU8bfYAhgZvkhRPDEiRMulnxNVpGp8tWrV3tmdPr06Z6hXLVqVfpR/sH27ds9C1qoUCGPAgUKWOvWrdOX5h2JZPSQSAohRAqJZJgkViRZ+ofsY+/eve3NN9+0WbNmeRaxbdu2/oP++uuvu/iRPcwNyCLBpDd7dt8vkkgmPZaUoymfnzp1yr777juXRcSTtSyrVatmGzZssDp16nj2keNMkpPRRGwpaXOulL7JbpJppMSNAP8URBOp5XEI7rNr167pS/OORDJ6SCSFECKFRDJMEiuS9EaSbaSMzOLjSOPkyZNt48aNXpJmKAbB69mzp5eZcwtZxftFkqzn3r17rUqVKj4gc+DAAT9GtpGPmeEaMpRTpkzx0jgieejQIZdASu5kF+vWrWt9+/b1Xk1EknJ3nz59XIZzQj2S8YVEUgghUkgkwySxIkmWkAlrprIRRqRsxIgRtnLlSi97AyVi5I0pbAZncrP8z/0iifCRdezYsaMLKwudc4xsI1J5/Phxl0nEsXr16p4RvX9RdMrunBeBTPImJAPJubOQOscR3pyQSMYXEkkhhEghkQyTxA/bII2UudkGkelpltthmR0ykwziLFmyxLOSXJ6bCen7RRJR5T6feeYZF1LK22QUkVUylIgrvY6U0yk/MziDKDKQg0ySCa1cubJNnDjRZs+e7W9CpJShHjKUTIJT6s4JiWR8IZEUQogUEskwSbRIkh2kfEx2kHUe6UdE9JA6luqhj5ElfbZu3epiyMBMTtCbWKlSJe+tJFtIpvGpp56y999/34oVK+YiSEmd0nSRIkXstdde8+vQo0mPJetaMuTDsA/LAzGMQzaU+x0+fLjfhvMrWLCgl8LJaOaERDK+kEgKIUQKiWSYJFokWZuRZXFq1KjhmUBkjfI1ckkGsGrVqv5DT9YQYUP0coLr0H9J+Znb8Dn9kKdPn/bgMbgMKeVrtmTkOhlJ5fZkMhHXSZMmeXk989hcj8nyUaNGedaUwZ7cnJNEMr6QSAohRAqJZJgkWiSROnoRKWNn9tUGPlLWZpkeZI7exV8Syu0XLlxwob1fYDkvyuuIJh8zvZw5IZGMLySSQgiRQiIZJokWScSMDCQf6W0k48dHJI3jBNnE3G5F+LgikYwvJJJCCJFCIhkmiR+2IdtHZpKeRZb/ocTNgA09jiz+zWAMwZJAlKSzEYlkfCGRFEKIFBLJMEm8SDJww0DNF1984TvSsJ4jwyxMS3/55Zf25z//2Y8z+EKpOTc9iY8bEsn4QiIphBApJJJhIpFMi2TLli3t66+/9t5EdpShP5LFw/mcYZsXX3zRJ7pzs5bk44ZEMr6QSAohRAqJZJgkWiQRSBYbZx9qluxhX+tt27ZZq1atfDkg9rG+du2ar9XI9eiVlEhKJKOERFIIIVJIJMMk0SLJQuRkIdmHmtJ28+bNfWmdfv36+UdEk75Ieijpkbx8+fIPk93ZhEQyvpBICiFEColkmCRaJOl3ZP1GlgBiEfBPPvnEPy5dutTXb2R7Q4KM5P79+70Mno1IJOMLiaQQQqSQSIZJ4kUysxbj0KFDfQFyStyUtSllt2/f3lq0aOExcOBAz0xmIxLJ+EIiKYQQKSSSYZJokSQbyeLeyGT9+vU9evTo4dsPjh8/3rdIbNKkiX366ae+HFButiN8HJFIxhcSSSGESCGRDJNEiyTDM/xgM1zzwQcfWM+ePV0e33vvPd/fmoltLmffbaa5s7E/EiSS8YVEUgghUkgkwyTRIokozpkzxwdrihQp8sPAzTPPPGO9e/e24cOHe6m7cOHCNm7cOLty5Ur6ltmFRDK+kEgKIUQKiWSYJFok76dLly5WpUoVX4ycoRsWJkfAqlWr5oLZsWNHz0pmIxLJ+EIiKYQQKSSSYSKRTMPgzYN2rWH5HzKR9Edm4642IJGMLySSQgiRQiIZJhLJHFi3bp2vNclONxq2kUhGDYmkEEKkkEiGSaJFcuPGjfbZZ59Zs2bNfOCGYKvEDh06+ALkV69e9aGbXr16+eT26dOn07fMLiSS8YVEUgghUkgkwyTRIrl48WJ7/vnnrX///r5O5KBBgzz7OHr0aJs3b54HQzYNGjSwp59+2nfCyUYkkvGFRFIIIVJIJMMk0SK5cuVKK1GihGcaKWEvWLDA99dmzUiykAgYGUomuZneZso7G5FIxhcSSSGESCGRDJPEi+RHH33kmcbu3btb2bJlrUyZMlauXDkrVKiQT2uzDNCyZcv8OpldcLINiWR8IZEUQogUEskwSbRIsqf2G2+8YTNnzvT1JKdPn+4xa9YsW79+vY0ZM8a3S6Rn8vLly1qQXCIZOSSSQgiRQiIZJokWya1bt1rt2rX9h/urr776Idh3e/v27XbgwAGXTXon2Trx4sWL6VtmFxLJ+EIiKYQQKSSSYZJokTx79qxviVi3bl375ptvXCARLkreJ06c8MsWLlzoQzlMdHP9bFxLUiIZX0gkhRAihUQyTBItksCgTdGiRX07RPok2dlmw4YNHux007VrV9u2bZvNnj3by9sPE0lK3yxezpqTDOZw3fPnz/sAD5lNlhLia7h165YvP7R8+XLbvHmznTx50o9zm927d/vAz9q1a+3w4cN2+/ZtP37s2DGXXHo29+7d68sT5QaJZHwhkRRCiBQSyTBJvEgicOytzfT222+/7Z/XrFnTatSoYX/605/8I1nJnED0EE3k7/333/cJ8OvXr7tAfvDBB36sadOmLo5I5JEjR6xChQq+xzePN2nSJBdRyuft2rVzuWXtSpYlQj4RVJYl4viHH35onTp1sp07dz5UbDNIJOMLiaQQQqSQSIZJokUSCTt16pRLHutFst92xYoVbf/+/bZv3z5fR7Jt27a+z3ZOsOsNmcLixYvbc88957dlYIcsJ2XxPXv2WJs2bbzfkoxj3759fSF0bsPalUjmuXPnbOTIkX69CRMm2JIlS3yKnOwjA0HII29EspQsR8SAEFs45oREMr6QSAohRAqJZJgkXiTJACJyiB7ZRCa2yRgiaPRETps2zcveOYFIHjp0yKZOnWrvvvuuZyS5baNGjTyjee3aNb+fwYMHe/aRbOTEiRO9F5PrIrGUs8lOIpu7du1y4WRqfNGiRZ6lRCRZ75JMJ5Pk3J7MZk5IJOMLiaQQQqSQSIZJ4kUSaSTDR7/hpUuXfrQNIqVmLtuxY0f6yD+HNSaRSTKclMmRP5YPYiqcNSjpc0QsGeghG0l5mowlgklPJbvrjB8/3m9LNvLChQsupj179vSvq1Wr5jLI/SO53A+lbvo3f0pGTrlPgnI44vlzkUhGD4mkEEKkkEiGSaJFElFE5BA9hBFx4yNfr1692jOEmUD2EMWcIMNZsmRJF0lEj+Edehx5LLKdZBvJPtI3iaAihQjlgAEDXA6LFSvma1kitpwL0knGlJI7UonschtK4FyfoaCfQml+1KhRVqtWLY9XXnnFM5o/F4lk9JBICiFEColkmCRaJBEy5BHhGzZsmGfvWEdy8uTJ9tlnn7kQ0j/J0A273Nyfrfxn3C+SZBIpTSOEZCQpRfNGYk1KdtFBIBFGJrE5NmLECN9Vh8dHPlnHknI2IokQsssOw0GcN+eKlDL5nRMqbccXEkkhhEghkQyTxIskkjd27FiXOCa0q1ev7hPSlJApEfODj8QhkbnZIvF+kSQQQQZlEEayi926dXOhZP9u1q4k+zljxgyXvcxwz5AhQ7xkzaLoDNVQEkciM9s1kkWl9xL5ZRAnJySS8YVEUgghUkgkwyTxpW0GVzKlbbKC9DTSO5kJBmTq16/vn+eG+0WS+ySbSN8j09uffPKJP8bBgwdt7ty5vrxPy5YtXVSRWLKNrDnZoEEDPw+mvRnc2bJli23atMkllMxonz59PFPK0A7SmxMSyfhCIimEECkkkmGSaJFE+ugxpDxMsOwOJe3M1wQZQiapcwt9lCwlRFmaz5FABl06d+7sMsm6kgz4II0IIRnLTJYys44kmUqWHGIx9H79+vmyQAgj098cp8cSIWWB89wIrkQyvpBICiFEColkmCRaJOmPpM+QoRWCJXnIAFIyJjLHiLyCNFImpw+SpXoopwMCSB8kmUaW+iEzmoGFzVlsHJGlJJ6RRa7DObOoOUsT0XeZGySS8YVEUgghUkgkwyTRIklJm+lmeiTJArLEDkvl8HkmOEafYjYjkYwvJJJCCJFCIhkmiRZJhmfI+GWCiW2W6/npsXr16qVvkZ1IJOMLiaQQQqSQSIZJokWS0jAlYpbhYd1IBl8YerkfprkZfslmJJLxhURSCCFSSCTDJNEiyTAMQzHsQENPZIsWLXxZHgZwWPCbZXiqVq3qSwJlMxLJ+EIiKYQQKSSSYZJokWTwJbOOI4uAMznNXtkszUN2krUaWZqHHWWyGYlkfCGRFEKIFBLJMEm0SCYFiWR8IZEUQogUEskwkUgmAIlkfCGRFEKIFBLJMJFIpmG/bcrZrVu39h1l+HzJkiW+1mO2I5GMLySSQgiRQiIZJhLJNE2bNvU1I/lBZ6eZwoULe7/kpUuX0tfIXiSS8YVEUgghUkgkw0QimaZx48Y+VMMuNOwq8+GHH/qWhGxbmO1IJOMLiaQQQqSQSIZJokUysyD5tWvXXCQHDBjgnx87dsxKlixp8+fP968zkZt9rR9HJJLxxeMoknfu3rNTl27YiYvXH7s4f/VW+iyFEKEhkQyTRIskS//QGzl+/HgrUaKErxc5YcIEGz58uL388svWvn17/5rLWRoI6cxGJJLxxeMokofPXbPXuyy0Z9vOfeyi7riN6bMUQoSGRDJMEi2Se/futc6dO1v37t2tUKFCVrZsWevdu7d16tTJnn76aatdu7b16tXLeyYpe1+8eDF9y+xCIhlfPI4iuf/MFfuvFt898Hzjji+GrUmfpRAiNCSSYZJokWR7xEWLFtnSpUvts88+c+Favny5fffdd/bmm29a//79bdmyZT69zXWuX7+evmV2IZGMLySS0UIiKUS4SCTDRMM2aZo1a+ZbIsK5c+esVKlSLpEhIJGMLySS0UIiKUS4SCTDRCKZBtmirM3U9u7du6148eI+tc1ATrYjkYwvJJLRQiIpRLhIJMNEIpmGQZs//OEPVrBgQXvjjTfsySeftMGDB9vx48fT18heJJLxhUQyWkgkhQgXiWSYSCTTbN682TOQ9EwSfH7gwIGs7Yu8H4lkfCGRjBYSSSHCRSIZJhLJNAjjzZs301+lYHvEy5cvp7/KXiSS8YVEMlpIJIUIF4lkmEgk/w4Lja9du9Z27dr1w9e3bt3y6W2muLM9KymRjC8kktFCIilEuEgkw0Qi+XfYBpGdbQYNGuRfI5H79++38uXLW6tWrbK+T1IiGV9IJKOFRFKIcJFIholEMk3Tpk19+Z/bt2/b4cOH7YsvvrBq1arZzJkzs35yWyIZX0gko4VEUohwkUiGiUQyDbLVsmVL3w6xQYMG1rVrV/vyyy9t1KhR6WtkLxLJ+EIiGS0kkkKEi0QyTBItkmx5uH79etuwYYOVLFnSt0msWbOmB/ttly5d2lq0aOHX2bhx4/8zjJMTx44dswULFnimkxgwYICNGDHC9/dm20VK6RxnSpxF0MmGrlixwuWVWLlyZfqezLZt2+b7fg8dOtR7N69cuZK+JGckkvGFRDJaSCSFCBeJZJgkWiQPHjzocofQsW7kv/7rv/pC5H369PFjRYsWtc8//9yvg/BFneDes2ePjRw50ho1auTx0UcfWbly5XzNyhdffNFq1arlx8eOHWtHjhzxXkx22EFkebP16NHDTp8+7dPjbNdYo0YNP07GdOfOnXbjxo30Iz0ciWR8IZGMFhJJIcJFIhkmiRZJeiFZdJzs43PPPWf//u//7llIpGvgwIEukpS3kUiEMEoW8Kcw0IOQsnvOt99+6zLIlDiZyGvXrrkszp8/38qUKWOLFy/2zGSvXr1sxowZvtd3vXr1XG4ZAurUqZNnJ48ePZq+9x/DsNClS5d8lx6iTp06Xqr/uUgko4dEMlpIJIUIF4lkmCRaJBmiQQ4Jfrg//fRTa9iwoX344Yc2efJkH7ghO8nlV69e9WWB8gISidC1a9fOBZKs4+9//3t76623XFSnTJnii58jjkjs999/b4cOHbJJkyZZ27ZtPTNJKZwSOMI5b948F8OtW7emH+HHbN++3bp06eKleqJAgQLWunXr9KV5RyIZPSSS0UIiKUS4SCTDRMM2aZjaRtaQMySyfv36VrVqVZe8nwslaHoeySiOGzfOJ8EnTpzo/ZP0YPK4ZB7bt2/vPZRIJCVteiEpc7ME0VdffeV9mkgtPZuc77p169KP8GPo/aT0TWaTYBkjspg/F4lk9JBIRguJpBDhIpEME4nk3yHTSB8hZW6ylJSbv/nmG6tdu7b/4NNL+XOgzEx/I1JKaZohHPotyVR+/fXX1rFjR++BRPYYxKHkjkgil5UqVfJsIuV1tnFEJBFIRHf16tXpR3g46pGMLySS0UIiKUS4SCTDJPEiiUTSo0j/IuLG10xP02eI4JElZKo7rzDpjTyWLVvWex0ZqkEIkUukld7LDh06eE8mGcu+ffva7t27XV6RWd50vPn69etny5Ytc8mdPXu2L6D+zzKSP0UiGV9IJKOFRFKIcJFIhkmiRRJppOyMtCF79B8ilWQEkUnKz8jlmTNn0reIDredNm2a90UikNOnT7cmTZp4yZkSNpJHeRvJpAeSwRguQxrpjSQogSO0SCf9kz179vRyOJ/nBolkfCGRjBYSSSHCRSIZJokWScrEO3bs8J5Iys4Mqaxatcp7ChFASsrDhg3zEnReYQkg7ofJcMSRjCT3+fLLL9trr73mywvx2Agt5eyPP/7Yy9lMj5PF5PzIXiKiTHRXqVLF/vjHP/rAzYULF9KP8nAkkvGFRDJaSCSFCBeJZJgkViQpKzNYQ69hiRIlvIy9dOlSH4R5//33XeDq1q3rGcGTJ0/61HVetkpEVskcIpDXr1/3UjefL1y40IOyOfcNlNOXL1/umUd6IufMmeMZUkSWc2XZIIZuKHlHOR+JZHwhkYwWEkkhwkUiGSaJFUnkjBI22UGyfExoUz5u3ry5Pfvss74UD+tIsgQQ1xkzZoxL4aOGkjqZS8rtZCIzII0ILf2TlOCjZEklkvGFRDJaSCSFCBeJZJgkurTN4ApZQXoO2WWGNST5IX/iiSesTZs29vbbb3uJmawkwzj3i102IZGMLySS0UIiKUS4SCTDJLEiyaDN2rVr7c9//rMvEk7WMdMjSW8i2T8EjEnqbEciGV9IJKOFRFKIcJFIhkmiM5L0K7K/NcvpsD3h3r17fXqbHkV2miFLyfqO2Y5EMr6QSEYLiaQQ4SKRDJNEiyTQa3j27FkXRgZttm3b5iVueiLnzp3rQpntSCTjC4lktJBIChEuEskwSbRIMtTCFDRl7Y8++sgqVKjg2xG++eabVrlyZe+N5DImqMlS/hLDNo8CiWR8IZGMFhJJIcJFIhkmiRZJeiJZ4gfReuGFF3x9xiJFitjTTz9thQoVsooVK3r/ZKNGjVwwmZbORiSS8YVEMlpIJIUIF4lkmCS+tJ0B2aKkTYm7XLlyvig5u9pQ9s52JJLxhUQyWkgkhQgXiWSYSCTTzJo1yxcDv3z5sg/g0C85fvx427JlS/oa2YtEMr6QSEYLiaQQ4SKRDBOJZBq2RLx48aJ/nhnAOXr06A/HshmJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSCUAiGV9IJKOFRFKIcJFIholE8hFy794927x5s33++edWv359a9SokY0dO9Y2btxow4YNs4YNG1qnTp1sxYoVfv2bN2/a5MmTrVWrVh5Tpkzx47B06VLr2rWrNWnSxAYNGmQXLlxIX5IzEsn4QiIZLSSSQoSLRDJMJJKPkEuXLtns2bOtaNGi1rt3bxsyZIhNnz7dZfGLL76wHj16WMuWLW3kyJG2f/9+27t3r9WuXdvatWtnHTp0sO7du/uxI0eOuAg2btzYjyGT69evt8uXL6cf6eFIJOMLiWS0kEgKES4SyTCRSD5CkMMRI0ZYhQoVXCDXrFljy5Ytc6Hk2MmTJ23WrFk2ePBg+/bbb23q1KlWqVIlz1AiigMGDLBvvvnGZs6c6fI4atQoO3z4sPXt29c/P3jwYPqRfszFixdt586dtnjxYo/y5ct75vPnIpGMHhLJaCGRFCJcJJJhIpF8hGzYsMEzji+//LIVKlTISpcubXXr1rUuXbq4TCJ8u3fv9oxkixYtvHSNJO7Zs8eOHTvm8tm0aVOXQDKaCCa3QUbbt29vmzZtSj/Sj9m+fbs/Bo9JFChQwFq3bp2+NO9IJKOHRDJaSCSFCBeJZJhIJB8hZA9XrVpl27Zts+PHj7vc1ahRw4WR7OOVK1e8bP31119brVq1vKQ9evRoP3b27Fkvi1etWtWaN2/u4rllyxa7evWqCyT9lmQ4H8StW7e8rH7q1CmPOnXq+GP+XCSS0UMiGS0kkkKEi0QyTCSSjxCk79y5c3bjxg0fvBk3bpy1bdvWeyMnTpzoInngwAGXxJo1a7pokp08dOiQCyAZSUrd3IbrIJD0RSKQ9erVs9WrV6cf6eGoRzK+kEhGC4mkEOEikQwTieQjhEwkPZD0Qt6+fdt7Hhs0aOBlaWTy/Pnz3gvZr18/n9Km75HM4Y4dO3zIBqlksnvo0KHWq1cvW7BggZ05c8anuZs1a+al89wgkYwvJJLRQiIpRLhIJMNEIvkIWbRokWcTWeqHMjVZRCave/bs6VPbLOmDRJKJZNhm7dq1Vr16dc9cMmTTpk0bH9bhOPeDTM6dO9fFECndt29f+pEejkQyvpBIRguJpBDhIpEME4nkI4TsISXs119/3YM3EFlFspAsCUQ5+7333vMMJVlL+hq//PJLq1ixopUqVco/p8+S9SUZuClXrpwf477ovaR0nhskkvGFRDJaSCSFCBeJZJhIJB8hd+/etWvXrv0w9EIpm37J69ev+9JAZCHnz5/vy/jcuXPHr89QDtnLGTNmeImb4/RXIqVMbSOm69atc4nkeG6QSMYXEsloIZEUIlwkkmEikYwBBJCeSbKQ7FDDlHUGZJKJbQLhzMDxzCR2FIkEiWR8IZGMFhJJIcJFIhkmEskEIJGMLySS0UIiKUS4SCTDRCKZACSS8YVEMlpIJIUIF4lkmEgkE4BEMr6QSEYLiaQQ4SKRDBOJZAKQSMYXEsloIZEUIlwkkmEikUwAEsn4QiIZLSSSQoSLRDJMJJIJQCIZX0gko4VEUohwkUiGiUQyAUgk4wuJZLSQSAoRLhLJMJFIJgCJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSj5C7d+/a2bNnbeXKlbZixQpbtWqVHTp0yE6fPm1z5861pUuX2rJly2zXrl129epVv/7evXv9esS+ffvS92R27NgxW79+vS1fvty2bdtmN2/eTF+SMxLJ+EIiGS0kkkKEi0QyTCSSj5ArV67YggUL7KOPPrKSJUv6x4EDB9rMmTPtt7/9rRUuXNiKFStm3bt3twMHDtilS5esU6dO9vHHH1upUqWsR48eduPGDbt165aNHDnSypcvbx9++KHVrVvXjhw54uKZGySS8YVEMlpIJIUIF4lkmEgkHyGbNm2yESNG2NSpU138evbsaQ0bNrS2bdtavXr1bPfu3Z6dRCDPnz/vWcgyZcr49WfNmuWCuWTJEtuwYYM1aNDAb09WsmXLln75qVOn0o/0cCSS8YVEMlpIJIUIF4lkmEgkHyEXLlzwUvaZM2fszp07LobVq1e32rVrW8GCBa1q1arWvn17l0VEc/DgwS6JW7ZscckcO3asZyU53qFDB5dHxHPSpEnWp08f27lzZ/qRfsz+/ftt1KhRVqtWLY9XXnnF2rVrl74070gko4dEMlpIJIUIF4lkmEgkfwEoQdPjSGawfv36NmTIEOvYsaP169fP6tSp42+uRYsW+TEuo8x98uRJF0fK2GQw+/fvb+vWrbPLly/bmjVrrEWLFp6dfBAnTpzwkjq3IYoWLeoi+nORSEYPiWS0kEgKES4SyTCRSD5i7t275/JHhrB58+Y2bNgwH6KhlI1gDho0yLOSfET2xowZ49lJspiIZKVKlTxLOXToUM9U0ndJqRshXb16dfpRHo5K2/GFRDJaSCSFCBeJZJhIJB8xTGPTK1m8eHGbMGGCHT161Ce5b9++7ZJJmbpr165ewu7du7dnJClNk8GcOHGil7+5/KuvvrK1a9faxYsXvRSOSJKZzA0SyfhCIhktHleRvHDtlp24eP2xi5OXbtjtu/fSZynE441EMkwkko8Q+iKRv9KlS3smkn7J6dOnW5s2bWzHjh12/fp1L1sjemQfmeZu0qSJZxy3bt1qAwYM8MunTZtmnTt3tilTptjx48f9vshikqHMDRLJ+EIiGS0eV5FsMH6TPdt27mMXr3ReYAf+/v0UIhuQSIaJRPIRwsAMAvjrX//ap7EZsiGTyMBNuXLlrHLlyh4s7cMQzcGDB/14s2bNfKq7SpUqvm4kWUx6ImvUqOFi+cEHH7hUamr78Q+JZLR4XEWy0oi1DzzfuOO3TWfZnlOX02cpxOONRDJMJJKPEMrTZBoZoqE0Tdma8jYZxr59+3pQ2kY4gTUj6aVkupuMI9Pa9FKS2ZwzZ4716tXL15nkMsrfuV2UXCIZX0gko4VEMlpIJEU2IZEME4nkYwaLj2/fvt1L2/RSZqCnkowlk9tMdCOXuUUiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFr9pOtNW7TtrJy5ef6zi0vXb6VdOiH8gkQwTiWQCkEjGFxLJaCGRjBb/q+E0e6r1bHu27dzHKjrO/D79ygnxDySSYSKRTAASyfhCIhktJJJhxF8mbkm/ckL8A4lkmEgks4jdu3fbuHHjbPDgwTZ37lw7efJk+pKHI5GMLySS0UIiGUZIJMWDkEiGiUQySzh//ryNHTvWKlSoYHXr1rWGDRvaqlWr7ObNm+lr/HMkkvGFRDJaSCTDiMdZJL8/fsnmbj/xWMXyPWfszt176TMMF4lkmEgks4Rly5ZZp06drFu3bnb9+nVr1qyZTZgwwY4fP56+xj+4deuWXbp0yU6dOuVRu3Zta9Wq1Q9f5zWOHDthr7WebP+r5ij7Va3RiYx/qzHy7x9z//x7z1j3wNcyzli/86AVaDjugef7sOD7nnr+D748P6Jc37kPPOe447O+cxL/cx/l+dcdseSBr+PjEPX+fm4POueHRdT3fdR49e+/Vw8ePf7A830cgurXg45HjS5duljNmjXTf6lEKEgks4QRI0ZY165dbfHixS6KSCTH1q1bl77GP9i+fbu/YQsVKuTx61//2n7729/+8HVe462337b//V9P2f/5/fP25AuvJi4KPPeS/dtvCth/PfviAy9/ULz8esEHvpZxxptvvW1P/fG1B57vw+J3T79gv/o/T9gTz7/ywMvzI/7w8usPPOe44z+fetZ+8+RzDzzn4OP5V+3//92Tkd73L7z6xgNfx8chOLcHnfM/i9T7/r8jve+jxtMvvmZv//3364PON+54/fXX7Q9/+IO99dZbD7w8Svz3f/+3ffLJJ+m/VCIUJJJZwoABA6xnz54uibdv37b58+fbwIEDbdGiRelr/IOLFy/azp07XTqJ2bNn25w5c374Oq8xb948/2VCZvRBl4ceo0ePtieeeMKGDRv2wMtDjx49etirr75qM2fOfODlIUfZsmW9peRBl4Ue/K5BcpL6vh8zZow9+eSTNnTo0AdeHnrwd+eVV16x6dOnP/DyKMHfkPXr16f/UolQkEhmCV999ZX16dPHBTEjkn379vU35i8F/ZjFixe3qVOnpo8ki127dtlzzz1nmzdvTh9JFgx4FS5c2C5cuJA+khzq1atnvXv3Tn+VLKiAlCxZMrHv+z179tjzzz9vmzZtSh9JFvytee+99+zcuXPpI0L8GIlklvDNN994o/LKlSv9F/u3337rf9j4L++XQiIpkZRIJg+JpERSIikehkQyS1ixYoWLJEv/0LTcvn1769+//y8qNYgk/S2UNpMIf1Bee+0127p1a/pIsliwYIGVKFHCWyeSBisf0F6SRBDJcuXK2YwZM9JHksW+ffvsjTfesC1bkrmkEe1TJBBYOUSIByGRzBLIAvXr18/eeecda9Kkib344ou+HNDly7/cPruU1IcPH27btm1LH0kWp0+f9j7BY8eOpY8kCzKygwYN8lUDkgbZuKVLl6a/ShZ37txJ9Pv+zJkz3ieY1Pc96xfTWnXt2rX0ESF+jEQyS+CXOW9oStpkIil1HzhwwO7evZu+xqPn3r17dvToUbty5Ur6SLIgI3vw4EG7ceNG+kiyuHr1qh05cuQX/Zl7XKAKkNSMDO97JOqX/Kf1cYKMrN73R/xvkBAPQiKZRZARpE+FyW3+qPG1EEIIIURcSCSFEOIhkJHiHzd6Q/XPmxBC/BiJpMgV/AHljyn9QvRrJq3MQ3kPoeD5J0kmeN4IFM+b4GcgSaVtvtf79+/3gQN2lzp06FAiS/s8Z34OklTeZncwdnShN5qgNzhp33ueM68Dv+/5XSDEg5BIilzB5CJ7pBYrVswaNGjgE7xJgl+oGzZs8Of//fffp4+GDX80+SPSunVrK1WqlJUpU8aXwaG9Igl/VJDIw4cP+8Qyz5t97tnejeefNKHgOfNz0KtXr/SRsKEfsGPHjr4QN+954rvvvkvcEjizZs36YUc1esSFeBASSZEjNNqzJePnn39uU6ZM8e0X2eWB/9KTAP+NM7FbtWpVe/bZZxOzjiRN9iz5wpJTkydPtpEjR1qNGjX8n4gkrCVJBm716tU+sbx8+XIbMmSINW7c2NasWZOojDxSxS5arCXYpk2b9NGw4R8IJrWRZzLRxPHjxxMlUwxz8o9Du3bt/Hd9EjPxIndIJEWOsKUV8vjXv/7Vf6EgkywHwR/UJMCyFxs3bvQt4l544YXErCeHLPG9JwNLSRupqly5sm+Vdvbs2fS1woXvO39MkQqmdjMiyetBm0MS4GeA1SKoQhQsWNCzdEmADFyjRo2sWrVq/o/UpEmTvLUjKeVdpJF1U6tUqeJrFrOGrqa2xT9DIilyhJ0NmjZt6pkolv5BIEeMGGETJ05MXyNsyEKQnWMhchYmTuKC5EgVpT3KvMhl0paAWrJkictU7dq1vU8wCdkZpIlqBBshsH4q+4137949fWnY8LPevHlzq1SpkrczfPbZZ74pRBJ+7mnp4B8oKlC0c7B+8ejRo317Xq0lKR6ERFLkyJw5c3xnD7YIo1eQ0i4iSckvSfBfeRJFEqEgC8fe7vxhpW8ySfD8v/76a6tYsaL/Q5WUgSPe62zJWqRIEc/Ct2rVKjEiiTTRF057A2so8r2nCsPvgNDh/U32nWzsqFGjbNWqVd7S0LlzZ39NhPgpEkmRIwsXLvQ/IpQ2+Y907dq1vsPJsGHD0tdIBkkVSTJw7DPNsBVrmCaxxJXpF6XMx0e+Dh2Gy8hE8j6nlYFeuaSIJL/nqETwDwPtPN26dfPgNQkdvtfsnoY4837na6pSZGVp8RHip0gkRY7wywORYMCGbAx7bdOETa9kkkiaSJKJo8zFTkpkJPh+k6VKSp/YiRMnfCcpMvLsbMNHhi8oeyahxEcvLHssf/rpp1a3bl179dVXPTvJrlqhgzzzfeb7Tn/sJ5984j2DSchIMkjHpDYlbapQtDewHW/16tUT2dYjckYiKXKEP6g0m9Mfxy+Uhg0benaC/1aTRNJEkkEL+mE/+ugjF4oOHTp4qYt/LJKwniDDFcgU2RkycW3btvVhE8p7SRi24f3NoAllToKfA7JSDKKEzvjx4/3nnQw0JV1+91GZScJqBfyzyJQ6w4UEQ5b8I8GqDUyuC/FTJJIiR8hKbdu2zSd26RHjP1P+Y+cXTpLglyhSQYYiCZB1IwtHSZvvPVOstDjMmzcvEevpUcInI4VI8Nz552nq1KmJycj+lHHjxvkyUEmA9zoSTZ8ga4jy+46fhSTAzze/2/mnkYGj+vXr+/uexfiTslqBiIZEUuQKZBJ5mDt3rktlkna4EEIIIcSDkUiKXEPjOf+p8l9pUrMyQgghhPgHEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIR45mTUpWVIoP3eF4b5C6tflueTm+XAdpspZNDuk5y+EyD4kkkKIRw57FLPNIvu1sz5jfoBEcl/sMhPCbjs8H8QQ2c4JnjPLsbDLVNKW4RJCPF5IJIUQ+QK7YPTs2dO+/PJLq1q1qs2ePdsOHz7s61Hu3bvX1+VjLUIWuM/ATkkNGjTwvZyRwQMHDtiYMWM82EGFpaYyZLJ1mQwcMsUiydOmTbP9+/f7MeB+MplKxIzLWA+wVq1avh7k/VGhQgXfM549lfMT9mfm+fK8eC5sMZeT8LGkFq8Zt7sfMrlII69H5jx37Njh+3/z/P/ZItksKj1r1ixbvny5P0duv3v3bl9QfODAgfmaGRZCJBeJpBAiXyDbyFaK7IDCDkCIDuLIbkjskPHuu++6zCGb7BiD1LDwM9ddtGiRZ+KQn4oVK/p2nFyXLQoBOURK2aaRy9gHuEuXLlaqVCn7/PPPrVmzZta3b19fOJp94FetWuV7BHOf7ERUoEAB+/3vf2+vvPLKj+LXv/61LzKfX1nSDIgeC7nzmowYMcKFjx2BkDe2nGOhd841I9cI9MmTJ/26f/nLX9L3koLnzv2xMDb3x/Niv2+27eO14nmz8wy3ZbF4YImuCRMm+F7Zffr0sZo1a/ruJJnH5b7uF/OMnAshRFQkkkKIfIFMF5LCLhjsz8yWcmwpyK44hQsXtv/4j/+wEiVKWOnSpX2HJDJk7JTy3HPPuQwhfIjihx9+6CXb8uXL+36/QFZu586dLqRsV8eez2+++aZ98MEHVqxYMZfUQoUK+VaOSBM70CCpZCR37dplb731lr3//vtWpkyZHwX7R7Nzzc/ZqefSpUu2fv16z/ytWLHCVq5c6VnIkiVLusQhvZw3e5aTRWWrTWSY14jzZhs+zpc97Fu2bGlffPGFCzWvJ7soIcNINFvV8XryGIjje++9ZzVq1HAp5DmzfSGvK1JI5hJB5TJeL4SbTPHf/vY3l30eY+nSpZ4B5fXhvIQQIi9IJIUQ+QLigyw1btzYS8mUdymhkmEjO4fQkIEbMGCAjR492nr37m0vv/yy/cu//It/JFPJcYQIsatdu7ZLWAayeRs2bHAJY7tCxAphQ5h4HI4hSVwHuUMiuZ/Nmzf7ObF3Mo95f5CNJHOKqCFsecnMIcBkBxFVRBZR5vMnn3zSRRXpLVq0qGcET58+/UM/JxlEWgB4XLKoPO9nn33Wfve737kgv/jii/560QrAc+e5IJq8xkSvXr38vMmmIoO8Lggrz4HsJveJbP7qV7+y1157zR+rUqVKft9kY5HY3/72t9atWze/HyGEyAsSSSFEvoBIImd16tTxbCJZRgSSLBlZN8RwzZo1/hFBolzLdf7zP//TJk6c6CVbsphky+idvF8kMyLFvr8I4XffffeDSJLZRCR5bDJ1iBsl3HXr1nlpl8zgxx9/bH/+859d+O4PspJk68jcLVmyJE+DK4gkgkZ2jxI1Yoe8InXIHeVozpfL7+9LzIgk4scwEplKni8ZXSSc147XBfkEbkumkTI5z5vXEvlGhMnsks2lRYD74zZdu3b1HlCknkwwIk8Wl2Pjx4/358vryceM3AohRFQkkkKIfAGRROTIClavXt1LtfQ5UjomO4bMIEpkxCj5Ug5Gcn7zm9+4PHJ9pKtKlSoPFEkkit5KSruUuRkgYZgESUOMuIzBGo7Tf5nJRvI1skgZOFMCpq+yYcOGLpNkTOktzGQLGV5BdJEsMnWU1R8GA0GIM/eJGDZv3txLyKNGjfLsK+V5nj9yez8ZkcyAhJKRJdvIgBKvIYNEZFeBDCu3QUgZvuE1YGCI15JWADKXPGdEks8RRO6LTC3iyWtEmwHnyXnxWiPaDAQJIURekUgKIfIFRJJsGSVXZIoMGVKIrCCYzzzzjPcFPvXUU97rh7y98847PghDtiyTWSM7iDTeL5LIESKFfDK8Q4aTnj8eh3IvZWOkChFDIun54zZMQtO7SCYOkSU7+fbbb9uf/vQnlz8Gfbg9EpcBcSMTSEYPIcspW4eIIaetW7f2+0JA27Zt69lVPucyXgPKz/eDFPL6cP9kQhE/BJYhGc6f2yHXPG8uJ4PL/fF8EGsElueErPO6ZOAyHovvBeJMqZ3sKK8P55HJDvPaks2lD1MIIfKKRFIIkS8gkpRymaZmihoZIwOGvJAVpA+SDOQTTzzh4kdvY9myZe2Pf/yjl6WRJq6HZCKA94tkBtaiJJuGHD399NOeyUSWyHIWLFjQRY5sZgZKxkxwI44M/DCQ8/zzz9sLL7zg0+X0DiJ9ZPgyIHb0GCKXSBxC+jCYxqZETvaTzxFEMoGUqimz0zeJsCF43BeiSuaUEj2XMZyDJPIaIOFIIedNOZ5sK+fD+XE5crt9+3bPPJKNZdAIIea15pyBx+GxyUQizfRaIt28/mQ4MxPfZEMZ6sksKSSEEHlBIimEyBcQSUq6ZM3ItO3bt8+FEbGk7MxHBAf5Y9kaMpAI1uuvv+4TxKtXr/ZeR0qwlHYRSaSRpWzIyGWEjo8M1FCqZnkgMnkMjCCR9CciUhkQMta35DKC7B2ChvjxNUM4ZDFZkicDj8e6l0gh5/EwkeQyRJWpcASPHkXK2NwnIoq0kjXlvpBjJJKeSsrdlNtfeuklfy3I2PK6IN2cM+V1JBGR5Llzv8gw90MvKWVphBvR5jUjy0gmEylEPDkvXhdkktcRsaWUz7lynJ5OpuU555wyrkII8TAkkkKIfIFSLsv/kPGi35CBEUrJZL7o62P45dSpU17SRgQRJjJtSBgSSiaP8it9icgNAoR8kunLCFUGbot4clumo5EkSsz3SyQcPXrUxY5sJNcl+0kpnawoGUxK3sgkgpWBc2/RooVPNVMiRiz/GWQsWWz8D3/4g2dYGWQhQ4rc8ZGljBBFBoMoyfMcee7chl5PXiPOkbI4MphZJxL5pexPlhb5Rkx5LcjIIoVINPLM60DwHJFDzpvXlHNmGpzeSe6b8+P5IOn0bpIp5bXge0V2Uwgh8opEUgiRLyCIiCSSRGaMiWJK3GT+yMqRDWQXG2QLuUEe6UFkKRrkiGwmU9yZcjK3IXtIhpN+P4SLDCQlYYSJ+yArh2BRnkZCkU8eA8nk+ogY09pk8yjzkgFEPOnTRCI5RombASGykJn9wOk/JEtKFvGncno/ZPTILvKYCO+kSZP8PHiOlKLJ/nHfLP9DFpQeUErQyCL3jVhTlmayfe7cuZ7FpNzMfdDXiDhyPeQaoczsUkP2kYxvBuSRtSjpseTckUPuFzkly4kwIpBMhHMMqUUqkV0uU3lbCJFXJJJCiHwhUw5GcCgJIyj0/yFGDN4gQATZM0SIEi+ShPwgXMgfmbgMmZ5LJo7J4iFH3CdlYMQSUUKaeFweA1FCSOkz5Diyhtwht1yf4P4olxOU1jlGlpDeQRYwj1rmReAoOyN4lK2RRLKnGaFDinkNOKfu3bv7ud6f4UTguBwJR6p53ZjGpuRPhjUzsQ0ILb2V3C/n+lPIpCKe3A9ZSl4TxJVlgpBjboNYZx6L1weh5LXVguRCiLwikRRCZA3I0j/bWxqQLeTsYeXo/ITHI4t5v4Aig/cLICDMnPsvCed2fzaVLC9f39/zef/nQgiRFySSQgghhBAiT0gkhRBCCCFEnpBICiGEEEKIPCGRFEIIIYQQeUIiKYQQQggh8oREUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHnA7P8CjgKyVQ7kIWEAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E5%9D%87%E5%8C%80%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E8%A1%A8%E7%A4%BA%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAACRCAYAAAC7bsHuAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAACIsSURBVHhe7d2Fsy3Ftcfx9zelQhWSQAgSFyJEiUGUKHF3IS7ElSRECHEXIhB3IO7u7j6vPp35UevN2+fcc849+95zuetb1TUzPT09/tur1+qe/T9T0zRNM2hBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJo18p///Gek5fxeYLNjse5f//rXvLR1bPfvf//78rrNSxXrklDLb4T1KbfdbbdDC2LTrJG8yKG+zLv5Iu8PGx1PPdbtULcx7/w3E65lvuVlXrZf1rUst7+0IDbNGln1cofN1h1IHEOE5g9/+MP0+9//fvr73/9++bqdHGO2yfbbqaeWXW6b4wzJ3y1aEJtmjdSXGVlOXl13sCB+v/zlL6fvfe970xe+8IXpwx/+8Ehf+9rXpr/97W9zqe0R0Vqea03JW0Utp65aPqku7xYtiE1zAPDSerGJD5H55z//eXn+wcT+ieF73vOe6aUvfen0qle9anrYwx423fjGN54e9KAHTT/60Y+27EuMOEnOz3Y5P1PnLy8CJ6VMFT3I/+tf/zqul3z1Zf2q8rtFC2LTHAC8vH/605+mr3zlK0Nk8lIfTByD9OUvf3k688wzp/e+973j2L773e8OYTzhhBOm1772tdNPf/rTeYvNSX1/+ctfRh0//vGPx3zO1bRSl7Nt8ojhxz72senzn//8WK7rTNd17VoQm2bNsHZ+9atfTS984QsvFx0v9MEWxKCZfKMb3Wh6yUteMn3/+98fVtnFF188Xe1qV5se97jHTV//+tfnklvjhz/84XTOOeeMJjdBRMQs570UN9OaXLM3velN0yte8YrxIyIv5WvabVoQm2aNeGlZWG984xunxz/+8dMnPvGJEbhY50u9VbL/n/zkJ9N55503ffzjH59+/etfj+bpJz/5yenqV7/69MQnPnH6xje+MW+xbwjgZz/72emss86avv3tb0//+Mc/xj7SBCZumuevf/3rp/PPP3963/veNyxUgZwcj4RPf/rT40fk+c9//riGqWuZdpMWxKZZI5rJF1100XSve91riOLPfvazec1/2e0XejvYd7XWYJ5P8a1vfet0/etff4jWVpvM0Ey27SMe8Yjp5z//+eX7IHif+cxnhsVHZB/84AdP9773vUd6ylOeMprHv/3tb0cdOZ4//vGP0zvf+c7hyyTYv/nNby5fZ1rTbtGC2DRrwovKunrRi1403fGOdxxNyVg5YTdf5p2wFBSW3Kc+9akhWqw8vsAEgLYCn9/znve8IaSx+tSp+Xyf+9xnevSjHz194AMfmL70pS9N73rXu0beVa961ekBD3jAsJ6JJ3JMmvAve9nLppNOOmn66le/OuoKKbubtCA2e46lSGzlwc82psvtUfNXWUXLad2n+Swvt11S65C89KwhEVwWT912s3pWsSyfZccUoVhV//KYcy6QLyWPALHinvSkJw1rL1HeyqprkGXddZ72tKdd7osEi/Mtb3nLdN3rXnc0kflT/TCwnr/1rW9NN7zhDaerXOUqY5/WVZzXF7/4xWGtvuY1rxnHFHLsu0kLYrPn2eihry9mLZMXZbndRvmrUCb1L1PWr5oPlvnjnvOc5wzr8MILLxw+tKyLAC232xe2WwqS+aSN1oeNypnnS3zDG94wve51rxsWHEFjIfJ5ItvWlHxo0mouO2ddi1Lmm9/85sg75phjpnvc4x7T5z73uZFvn0TxDne4w3TUUUeNdazTkO31j/Sj8tjHPna65JJLLl+3PM/doAWx2dPkpagkL8nLx8912WWXDWvCC1j9TZpu/FMZhWEqeeFZKsmzjXICA142gvaDH/xgvJAiw5aJmjLyBA3M58VcJsfzyEc+cvjJ1LMMCiDTraCsfUlhWZdkP87FMfPjpQ+fc5S3PBbzzu3tb3/79OpXv3r6yEc+Mso5v3e84x2jqV/rr/M179JLLx1NZaIYrHNvCO21rnWt0USOIMK++RtPPvnkIYx8hqjXlIXJh+iHhQUa6nXYLVoQmz1LXoi8PKHmefGJ4Jvf/Obx0px77rmjyefF8uJ7abzYnPaar8ppvr3tbW8b3UkIBgGw7KXV1eOjH/3oaJqxVvTHe+5znzvq5fsSibWeUOijJ1Bi/8RmebzK3Pe+9x3RZXn1Ja9pqyibOupyFQbi953vfGf64Ac/OI5NRJdvji9T1Na5Ez6BHs1TdRAc18uxau46Z0l09wUveMFo1oa676QsE0LNWv7CimNSx1Of+tTp3e9+9/8JLBFE+7ze9a43nXHGGeN41VXP07V1/3QWJ7isyrrv3aQFsdmT5IHPQ79cBsvwQx/60HDUa25p6l1wwQXDCrnZzW42Xug///nPo1uHJtstb3nL0bfuiCOOGF1KXvnKV44+eA996EOHY//4448ffq773//+w9dFYG9/+9uPpp5Oyve85z1H3U9/+tOnF7/4xcP6Uw/LRTeVNImDLiNeckJQcQ4RsvribwU+tQQ5sm2SZc1eVt7DH/7w0cx8whOeMN30pjcd/Qmf/OQnTw95yEOGr+6a17zmEHjb6Apz+umnDwvOeTonyTLRV2f2sQr5zl3fQz9Grnnyk+ynBkQgj3VuZIzjEVhhZcoPts091FeSePohW+Uz3Q1aEJs9SV6ksFwGa41Vc+c733k0pbxcXh6dir34hIB1yKJgZbBS9H8jfkZmsJJ+8YtfDOvwlFNOGdFM4qAZ7AW3jeY3wSUQd7vb3YalwqoUIFHWC2qd47DOMeaFtk4zkIWJ5fFvl1XXIHmSc3/mM585REmz1Hlo7vohuMENbjCOhxVHwI899thhDTsP5VjJrqEfGMm860MMXYtV+83UDxPfnh8AFuCy7BLrJfvVUd2x3eY2txkWLYtxiR8AVuypp546mtcZvbIOWhCbPUlemrBcJjrPeMYzhpCx6Ly48pTx8rD+TjzxxGHhpD8cn6HmZMRS/zfNx2c/+9mjiUj86stvql5N3mtf+9qjK4rmXiw0vkbNZevsi9VIlGO9POYxjxmC+PKXv3zUlbQ/OMdqQQXnRvxYhISMmBMqzdc0R50r64pougb6BRIg5/O73/3u/yXn4npUy65em8zbj65FrqFgTC2TaU2wT8fmh0RT2DXitwy1rKlrzepnTer4nfzc892iBbHZk9QXAvXBNyUAOjtrAnvZ+f/4xySWD/EiVKyi+BIlLxbf4F3ucpfp1re+9WhWepkJpRc79Sd5SUU3iYomYfxXgfje6U53Gt1G1CWQkm01xR0bqzR5y/NgobHIlNlX4j8z5Rowzz0QESEwAiPEkGjbD1GzfI1rXGN61KMeNcTb/jRL+RPjQ6zHUxPq8WLVevtRP+swwaxaBjXPsfJpssj9YLAsCXV+aELdxv0+7bTTxjXWMqjrpN2iBbHZkywf9LrMYiFMxOboo48ewsZH+KxnPWtYe+YJIVEkGprFXlzb5QXXeVj/N34pTUxCGaxPuaUgapbmWCQCoEmt47AmtWBG6jDCwjE6hqDe1G1qe4EIx7qdxA/Iwl0Oq8txqZt1y2pjvRIdPwzWVVK+pn1Ry7EgHQMrWjO9nttGsGQJuh8M1zQfgVAX4atkX/Jve9vbTg984AOHSyT72W1aEJs9SV6EkHlTwsbSYZkJeLBO5K0qv0S+F4/fkICxIo3IYOmtahp6WQUkCCKxrQEDLyXr6Oyzzx4BCE13zdDAmvESC3Ionzqz7WaisYrNRCD1awLnWhCq+93vftNxxx03rGbNaHVYX5vCymZ+uY/Mm9b5lGNl8kv6UeGjzbqw3M5+lSfmxDrHpJ58ISdla3LdNZldU9atvJznbtKCeJBxU/MwbkQePsl8feCw3YdiX+V3+yFbB46RBaapqp9fmn+rqPksDRFLIsqqYd1pUmqGamoqK+UaVwsxgpgyEBhIHfxbfGjZlhXHQjRKZRX1uLZL3db+PEOanAkKWS+CzgrmoxPwUY5bgOUoaLIcV71Vcv4SV4OIto7nflRyXFmf+exbOS4KXZLqPRMoYSkT7lw/WM965G90HvyyAjjZTtnM7wYtiAcRN7Km+ouXvMxnWpOHoT482yX1ZD7U/L0MfyELTNcYfqX4oBw7y82LI4rpxYPrS+BYfESKL1H3GhFOQRZ94IgJcg1iIeo4rJsNyzSwdogr31Y+nxVRkPjIdNVJlBlZJ+3vvQvmHTd/oe5Hgjuar/oWiqjL4zeEa+E8NePT4Xq75PidP2tNlF9AinW6PK+UdXzcCaLEmu+EkQjya+qy5BpxeWgOZ5tAEAm9aDRrfLufI9sOLYgHkXrTzedBygNRU1jm26au3y7ZdlnP/tR5oOAT44MiiKwUIsBf6EVnARE9L5hyXlj97vgXr3Od6wyLkKXkgwEsuyOPPHJYmoIzrDyR6Qgoq0Q3FYEYL6/ghRecBSbSzXJhbRKH+MBcP81y/RZFfoP8ZdoOy23Mu3esPX45TXfHJKIsmmzZcTs2I0ZcD8IjkJMfin1R91nnNXEFefxQuO7I+ppcK/sVUWZpc3Vo+op0s/Jd91vc4hbDN8riXG6vWW179839W+UL3S1aEPcAufF1frkcvHAGzvvVjIjV9dtBYMKDbPtqnWKndR5InD9REkDRsVhTjMXHMtLtxugSliKLgjh54UQ1ddVhIRERLzVRvfnNbz5eSo5+XXVYLyzOCCI/HEuI38tIFdYYwWV9sSBZm17cijrUp8Ox5uKqa7rd6+ycpYplwRnHdPe7331YqvyWrovO2ASHWLIMXReWK1FZBjC2guNNMgKG+Lq21XJGLed5tV9WuI7v/LamPthAIC3HJVGj1Hm+PaN8lDe5yU3GDxmBTZndpgXxIOOmEiMvjBeKj2rZ/QDKaZJ4uDzwrCAPdB6a7WIbnZZ1lWDx1H1at3zp9jKEzctumBnRM0KFRaFJ55oRJs1rI0/4qYgFn5oXjeCxCq2TLxFL623LimThaa4JBBBbwss/SHB0JlbPqnvmR0tTkEjZT5qUO7lfyH3Z6J57hgxPZBlqlhIsefxyjp14OX4/Evtzf23rXN7//vePUTuukfPPuS2PzXo/VCzTJOJXE8uPBR9hrXUZN+6HhbXthyfrs8/dpAXxIOPh4nfy8HqRPdBeHiKZh9ZNN8+P4kHnR9H8yQNj3U4eDPvxQouOphmiruz3UMG18kPiZdKZ2DRRVOfkh8N6FrGpRCisz7bW1fW2dx00nQkii4YlyYJRjqiwVOwr9dTrlntDgI2KEURQZ10nbffeZTvUbU0dAxH2w+q4co7OR15G8uzk/tb9mrounh2Cbx9Zp27LkGeZcDl3x5SU48lyji31BPeOK4R16fpzfezk+LdKC+JBxM1n6fHD8GOxUvh79Nr3q1gfDlE2TUBiKFjgwbe+pu2gvDr4y3Q70UxkfaaudT50u4VjzHnX6XK+LtfzyrplnuXkEUDXnP+KNRRBkbI96nIEQoqfUbM5llnKZrodUm+dr8uZLvNg3j4jWNsh2+aYWWqa4YIjQX5SqHmb7bduV7fJl3JEy1n9hDTlUOd3gxbEg4ibqdkhIMAXxSel+0Y63OZm+6UnmiwVzR/LeTB3+kBkW1YO60WHV81OIomdvKwHmpxDUs0L5uu1yksdki9l2XqWCWvEC6+ppnMzX5yXkuOfVaNstYaSsg/zrq9Itz6PLB0vdNZJ26Vut1EdyV+uS149/61Q68u58eX5Aa8/okl1m2A+511ZLiPbapYTXu4JrhAtmtSR6art94cWxIMIa4O/x2B7N5zvirVG9BLskPj69IXzYGjaIuv254GwreaM4/Cya5Kkc+3+1HugcaxekMyHnId19WWs8yFlkzTxRGK5MQiirjWavvyUiTQrt/QdZvu6D4EbI2N0hxHgqT9o2yX1I5ZoJcspV9cvy26VWpfEZ6up7EfadZJXz6cu15R1dX6jewFiS3Q9+7oN1VbRTq/fvmhBPEi4mYSOEPkaiYfLTdaEZkUEeZqzhFJTGvVByAOyXZbbqVsfMc2T5Uu+V1med10279qFVcsh86aZZyHqY8hCZEH7jqImoimBI2qrqPtJfa6nwILuKazw/NjV49kJts/xos6vIseT+e2gvP05F/0JtWZEtXMOOZa6D9TlZf5yW5gSeknXIe4GAbGsS1oXLYhrYHnDslxvqIdAJJN1KAqpnxg0E+rDZV6EzRAsEUJ5q0h+tst8pS4vy2ma+FiC5rv+aXlYK8mr226XVduqt+5v1fqwP/veDvbhXhA+VhDrhCVtShS2egzKOX7bsKx8qWXpH97rONYcL6HiztERftWHY7dKrssS+a6VZ1DUWRcn171StzW/3X1vRgvimqg3ys1L88bNFqUUWdbFw/hMTTJdQzwE1gdWCovRSArNBg76zR4A5flZWJ7VChER9BImL2Q9lEnXBtsvyyXV5d1iX3WvWrcss5fJsXoGEk3FoXYOSY7fs8qPmnXbJXUFz6GUfD88nteN+hwqu50fpq3SgrgGcgNrys3mkOcj1JdQRFkQxfAz/jtRZNHkvDCazn6J9YHTT4s4VlI3K4bgaVpo8mp+a2bblh9Mvrp1KmahEOS6PVhDvuzMT2aUR/JTppbFqrztkm1rPblOIetqmUOF5XnUF76mQ4V6rM5leT77Q60vy5mv+6gpRsZu0oK4BpY3s8IvpS+hIIrPpvtslBEQIsu6dRAsVoTtOO75rHT5IGjyK8oQMuNtjQQwKoHoKasbj6FS/FYCN5rCt7rVrUakmj+roh7JcTkWowLqOcC8vIp9+xXXP9KY1J0kza9YAcix1OXlsRwqLM/DC5xzqfmHEstj383zSH21XmS5Xru6fjdpQTxA1Bspseruete7jm/56cKQMplKmtXEyXhUVl915KcMK5Iv0tA143I1I1iSgiRXutKVRjNY1x7LhkgpJyhQ8aBJhnT5Ogthrb++pktRMq/JxMdjHC/x3W7SN8+oBcJY66/CsSTHkmT5UEruT87vUDx+yTnUY9/JeeT8k2q+61OvUZ7Fut1yfrdoQVwTuWG5WfXmsayIlt73+qdxHqdMphLLjyVplIRIpwdj+TBqKltn1EC6gug/Jzp35StfeQiqZSNg9HUUKdXZOKQe6OIgyONzVva1ETk+2xFplisrbyvJviXzOipL6qjHESznxciy8+dfIsYZXbKXkx8siRvEMZsm37kfCufhGHMemc9xm+70PHJNVqVcp5QzlV+Pw3O32XO6E1oQ10Be7lUJbqahega36xCtX1tdn3l9DnWF8Wkp3TWSn3LwsIheCooIqlinA7DheL4VyB/owdG0NSpFWYIcUhfR4dvkQ/QlkvqgKVNFKSnL+0OtT4rQmma+rhN8cm7Efa8nvQdMfQLM1I9f8pZl9nKq52G+prp+qynlc11qfUlZV8tnXbaV9IfkdtktWhDXSF7ikBebhUR8NGFZcvnkUS0DEWPRZYKYfzNbplDzBFIEavRvTDO6rk+qWOav9JDxPxLElDFdilOo81tlWc+q+ewvJF/QSTPbhxUEgfZy4hd2nPVY5UnmD4VzkOrxcqfknORbXpbf35RrlP0mr5aRHIOx4ksX0P7QgrhG8mLXecn4TFFjQRX+Q82BUIVAOYKpyeyz67X5mHKmmpz5Yo15zWeRaV+F1uxWjlXIMtVUNS8v+wma0359NdOriIYsJymj+wXLk1W61SRwlCTI5Aciddb91Pkss4Kd66GQXJuanKcp37Dpqm32YqrnoKURt0c9F2nVtjtJqU/dlu0r81lvOfuuvvX9pQVxTdSXGBEwiUWoE7RgCcsv1PLmNW91z9E1Z6OgCjHVZOAjJHasSp9TIrb1C84eHMELTU7NbMcTcYUyItWazLav62B9yLb2rUO3SLbm4L6SIJKpfWTZtwb9D8mq48k+q7V6KJJjd36H8nlUluexk/OyTbbL/Gb1bLZut2hBXDP1Juel1+zLf13kX9pCypr6ZfQdOR/P1K9QMKGiDDExisWfpfsKjj8cF8HlnxRd5vBWjmVG6FhkRl5UAcrUOF1fMxaRTt5mqJfFxkcZq2G7ybbqaP57PV1301XIT1qy0TY7RX1beQauaLQgron64GZe0lzVVMyfIxGqlMk0iUXIPyIaTaQ0F6qIKUNQfUJfJ29jS3Wdud3tbjf8jvwrgi1EU7SZBShCt8qnSJh8+Vk9fJDymgNPrnvuS1guI3l13WaCuhm1jszvpJ5DnRbENeFhysNZE+HxOagjjjhidJjebJic7TVvCR4HMstyWSeLj+Wnq4wvs+iYbeA9p7NO2IYHEkN+RR2o6z4yr07H4T8uWJu66WR9c2BYXu96j7DqfqTMvsptRq1jWY+0U4E9VGlBXBN5oJIIG+uQj4+ldvTRR48hdXx8lboNPJAizf6Mh58weYEfTyRZcMbnpViDrEJCyYdILEW06/cVK/L46FiFugARUr7I5sBS7/nyPmVZUCwBB60Fz44gR4ILmW432W65rR/uPBvL47ki04K4ZoiXpi+B0hlbUIO1p8uNpjN/XvDg5eHLvMQvqP+V7TR3qyBCmeSZSqkn1DKpN8lDTzj1P2RJLutv1s+q+5N598ePKfeKLx75LJYfR8kfPEny9ETQSV+yvK+knPpMU0eScfCH43PQgrgGIkiSoEY+82U8sf5UhqyJMut4XcsuSZ7gg/5eusPkv0+w0XaVff3CE1gWJd+hLj4+YNqCeGDJfaz3yX3LsyHoxF3Cx2uo56mnnjr8yub9U6AvJkn+ObDO7yupQ1n9VdVjWb48fVFZivE3Hy60IK6BPECmmp8CHyLFmqS6mQimiAALcCiTVKn5HkpWor6LgiuhlpGS50WKqNV1oZYhtrr06DpjCKGm/aptmvVRr3emEUNwi/inP/deNy1dnYxuMtrJ1HLyMr+VVMsv69K3NN2zDidaENeMJrGABcHhn/Ng60JTf323kviK8t/CeVjr+qUA1gfZciVliDXrVSDFKBX+zZRdbtMcGOr1l7hb8vxkGGbWV+vfdCfile2Wz0/yTQ8nWhDXSB4mD5Zghz6FvoytibrqQdvoIbQsif4SU5FjddSHOPNLVtUVdOlRn2i0+do8Wm7XHBiW190PIZ8eH2+N/rvfrHtfreafFlhzD1mThHKrqKc+R0l1+XCiBXFNeJA8aJs9XPt62FZtw7IkiIbkbTQEb5m30TLLw0cjat/ErG8OHLkfSwgbsdPLQHM21qF8YqhngHHdPvHGP000/eB6RrYiisv9Lp/X7QjrFYUWxEMMD63msod11Uu0HYhgRq0066GKThUc1HWo8zB0UwRY/1CWYu6TT74RP//C6AeNP9rHhY18MsxTP9T8PWhY1r0VdrLNoU4LYtMcIAiMRNiq9ZX8CFCEk7XH58y/G58xVwlfsi+bc8Hw+7II+ZWNUjr++ONHFJorhOVf66v7qNN6PLXM4UgLYtOsiVXiEgGSsrwsZx0B1M/Q/znrahWXhm5RrEOWoBFICYQJvlin64xhob6jya9o3VIQk2C6PJ66nG0PF1oQm2ZNRFyqoJhPqstLBEv8YZhUywis8Bsec8wxo3cAH2PgY/T5tuOOO2505NdVK9tm+7rMB81lIhHUHKtpLMYWxKZpdo0qLhGWiE5dTpLPGjSsU/9QTWHIlwRT9EXUKZulWMfCG9rnG5isR59XE3SB7YifCLQhf/yREtFVf5JAHb+ldcTVdocbLYhNs0YichGXCF+owTFTwmWIpyAJUUxPgqxXj8/A8SUuewcQMSOiWI/+X1tXL1gvEKNjt//4Pvnkk8c/ORJO85LPxxlO6hudvpRkVEx3zG6aZi0QrvQTrBCrJBA744t9AMS4d/mrAh6ZwnxGRPm6OkHjX2RN2u9ll102rEkfCOFb9GUkI6f8XYQO34aR+sK6dYSQGDsG+21BbJpmV2HJsdZ8nMPwyHTMr+ImER8RY3/rqjO2/89OfsrUlG2JnoCKYaGEzZh0vkXrCKyvHgnO+OqR0S4XXHDB+Fo5/6RlX0k666yzxqilSy+9dARjsu/s53ChBbFp1ojPavlyjEDIiSeeOJqyF1988RC5pfXFB+gLSD6sYGxx/UJ6FcAqVKb+e0fXHM1hokjUNLWhDtZi/jqCGBNCliC/IR+kT8cZVsqiTN05vuzncKEFsWnWiD/y94Ujo01OOOGE6dhjjx19C0V1UYXNf+2cc8454zNeRG4pRpaXeSLEOmfnz/91yI7fcVXSbNck1nnbvP/ZYT36O0/N7qUIHm6i2ILYNGtEoEPkVhOUVSZowZdHiCo+8cUq1F1G1xqCWYUsolTn4evrfIJEN8M5iSRfpWmwjTrt47TTThvbiTiLRItMGw7qWGvddf5woQWxadYE64p/T3CCUGmi+jsIfwDm7x6sD0RQ01XwozZdl6Jk2XbEzvhmlp7t/D1EgiCazPogxo+YJHotWOMPzvgcHdOFF144PgzMSqxfSs9+Mz1caEFsmjVRxYhYsdDOPvvsEQnWgZr/jmBGmIiSr2KnOY0qSKkrQRrBE/5BVp8mNiHlsySQhvEpo3yavcr5CMQZZ5wxfInQp1GfRVYmi7GWPxxpQWyaNUNc0nVGU9VfvZ5yyinTeeedNwIdhuaZF+0lhsouBcmypLzmtua3pq/vY7L6jF3WkdtU4Iaf0Fe2QeA0hzWLTz/99PHnZrEGDQ/0L41EMv7HCOLyGA4HWhCbZk2sEhSWnK/UCK74QAP/ou4w/hNbP0LbpOlbSV06WOtGI0BjzPJRRx01kj8tO/LII8e8KZ8iizFoUotAi0SLemtyq1PQRz/Ek046aUS4CS5yHIcbLYhNcwAhMueff/7wI+qGI0KcoMaqKG+QJ/n3RM1knarPPPPMEYRJkidpjotUV2G1Hb+ljwGzFuPb1Gw/99xzR7NZ1JmFuhTjw4kWxKZZM9XaMs+35xuHrDkdpI0WYR1qrlq/kShC9FhwpI5BFjyp8xLLUx1J+jiyLo1fdizJ10/RF3MuueSSMb/c92bHckWkBbFp1gxBidVlXuBD52jfLtRUNcaY/66WSQqZr+tqquvCMn+5HpbtN/uuZN1ymysyLYhNc4AhMMYXa94KjIj+asLKX6ZQ86pIJS9strxcB8sbieGy7OFAC2LTrInNREXA46KLLhpRYVFmRJzSpF2yrG+z+aQqdsnbjLrt4UgLYtMcBAiVAIaobvyLzcGnBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmYwTf8L0KzWV25D8RQAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAENASURBVHhe7X0HYJ3Fle57CWGzbLJJCNkXQggBNkBCx3SIIWA6BAK2McU2BveCbdwbuIFx771XybLlXiTL3ZZlSZZkWbZVbKv33m7TvVffO9+ZK8ouu8iKwBvvfNLc+5cpZ2bOOfPN/OX+H1hYWFhYWFhYWFw0LImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImyuIxRj/r6QAgcsbCwsLCwaC5cFiRKB0j58NX74ZU/6Kcfsgv50vOyJxtu+TZ/9Tzp09MSfLLPHQ645hi/dYvxJEsdhnmwvk6iueFhHEZpTrBsBm5KWT5uyb9PZPNTPvnXQo2ocorysjaM45Tg0TTc1wiXDCKgyGXaktI4pL3qtE9UfpHN7298C2qzfyUq2+Y/wu9nSdKPPq8EH7zucjhTQjGzd3eMmheKbRdq5LhEZFJtM2lfyaf+iwZnJhStXiRlRAuL7wZf2C4VLqDKqn48rrotDoc79D1U2nr6NH7zWCAyN2Xf+C76AdmmzanuiqWpz9AS4GJ0ptVzjMPkftAbqg1I8LEMn9ikxmtmaIGURD1aQBZTlNkWm9VIzQyWKX7BlOGSOrJ81lGCNAWbmHG0JxhH4qqARkj5MG3PVvuqdNzmUZWZO1+JG0gs4dvBZJq04VuSsj/q5ICX+/yQfZVP85QyJY7GZXESfIF0mokGi+8blwWJ8lPt/FQwGRxpFPotQ2HDvjoVDuH8Foch1uOl9gUUkiZMo2Ac5iNDsBwXxZV4Pp9E0niaizqber/E/g70lUZBuf2Sf70U4BdZjCM09aCBGaOh0fPLGBjlN+lMfP4ZxnCpUIc6kddDMdTqpS9IbEQmEl1Wop6OjHI2AlKl/wTTP9IuErhtguxLf7Hf/F4nvIVnEDriObTtPBD9VsWhUI4zL8rQQKDYrnWBtHJAv+keGymahcVFgzqo+kZNC+icCUY/jcP5MoiWamjQddVNjUdf1pAH0/KcpBEbqFc7oC7T7niePo0+knrPpMYG1OdJULtkXvrXvFBxNX/6X3IDSkVfFZBb/IWJ1czQ/KUdWDac0oJSJn2kj2MD60252G4mDtuJvEWHBraNxGfbkBpROo4NTE+J2V7M1qTV2uh5zbTRMPlr5izYa/LgGOPlcTaW5i+BkXSbqehfZVrK9uSfTOrrxceq3lh877gsSJRPZhdc2SC50YGRjkIUi0bB2QfkPAdtJVKi5ORFXn7oPg1HzJhxJT38QkY0PvdVr2XbBBItYzySvzio5gYJgI+rZawLCyZJMOapgXKSGBrjYx1FLqaTT8r7pYM0Ry8ZpF2ltYVEmYZT566zJmk/OholiG5GNPG/BZo+AG43DCZfJVEKqbISZDoin/StfOfs6oOubd7C631WILKScdmPdDyyIfHZZuKCVA90kNFv5vVlmRYWzQqqFv2S2ImxWwZDcsxJqt+XNk5VlBgBXf8yaDzagMaTSIHInIBpEP3XyZXmZfLncWUFko5F6dSQfpDZMTnFku/mBL2YWUmX8qUc+lqSBJbLdhCvJi5B5A3Eby4wR+PvWVchGSxDNukXOGZwR9tVyydx4TTbNA+lapBbWk7SsE0NAeMkV8cB8demjZmOeUu4iEqYaXmdpBGhvJKDtg8D+4M5UmTuixyaNyWibEKiRH6ztk8Z3Sq/xNB8Lb5fXCYkisZiiJQZWKlOQqLUOKh2omA0WBm4lVhR2bjvc8g+jUIMTWycxKpeSBRXUlRh1QBFYV2VKMytRI3Do8aiMwMSrmZWWpqrWUHjyg3lNXKyPLMKJXURI6Z8fk8VKqtEriohXYwmab4607yU5sTW/+JP5Fbnr9sinwSSxTqvS9u4MdD0DHSCbAc6G/luQMM2s2P/ekQP6uoc6mjqs7Zgeod2ePOvgzA31qkki39e6dPqsnzk5eQhMyMT2Vm5yM7ORGZeHvLKRTbvdzCaWFgQ1Cv6Dx3YuS//ar8SZFDkIdo6/Q9tW+3bRNPzxkeQBMgB0Xn6p7KSPGRl5SE3pwjlbi/cHIzp2wLkgD5P8+ZxTtC8zJvDOMti+bQtOc/lY3K5ZoQhKVJXOlktuh4eRxkqizOQm52B7AtlKBOZuTbdnGDzkEB5SVDoagImLS0o5+jJzSodyYjKpz6G0Uy7q68x0ovPkvZhevFd/jqPUhg/xwruS+QGCmPSsfRvB5tZaZCMXdIiKpcSYmYi5VFk7ROOSyRw7E9NKZAojKaX/SQjnWCbMxbfMy6PG8up3TRBJUpUPGoWHY0opSq+KBmP61ETSExIqlQTGYe7EoPEiwqtK0KitPXOXFQmrcfID0OwJzYX5RqZruc7AC2EctA4RAqSKtTJAY9IJaRKaiTnZNYhBNGdFoZN2zZi+NazqGUyjUpHRJOXbRof87wEUNesDSptKc7ezOXMfWpcnapjBVnXRoP9KKlJbAIws3I6flPLL/YlXxJm3vHB2PX1mdg7riPef/FVPDsrBm7OJCVe6dlQ7Fz1Efr274UeL/wV3d7rgs4d2+KtvkPQfV2SkLyLEtDCovEQlaVd+GUSp3agOku7FRsX3f3SbrnFyOaLZsOhmuse9E0KOVZ5JgjB03vjrba90av3FGxKKUaW+AyX5KW2pkYhQbZJvurEY9Ae6yQPl+SmK8actHkd6veafTiW7L8IkrXf50H+iTUImf4BOnfojLdbLcKu5EKUaIRmBJ2/2Dvro75Ahog62TB3xpI0yUG6cu0D+eBJ+ddVMvoT3aVM9GfyrX5L2l+Ck7loGjkkfsmjd55JvgHX1ygwa41sKBgnlx7Jm3TKCGaisDxzGVEm8QEfZ07Ih6RhdJ2gajqL7xuXBYnSe1qo/QFHweVQ0ToUR6/Eupnd0bnT62j7RCu0evIttHu/G3r074t+fXugd7c2eLZ1B/SaHopdpwtQK+nN9WUO2uKqqs/j3L5gTHrzUywMS0ZKaY2UJcoq5XH21uygUZSn4MT2afikb3u0+WAG1kSVILeSZKSBJHBmJKTKUYrkQ+uwYPIQ9FpyBtnlQhoCxsZZFekUW+X7B2U8h9Nb5mBCv374W/+pmBOTj5JqkYezKekbMzumc2usfKy7CUQDeWJogPYJvxkl4HA0vq8C8cveR++XHsHtbdcgxutBbe0p7FqxCYtmbUFE5Cas6fhveLJLT7zZuhXeebcNnp8XgwohUdYlWXwXoNryMpGuKHHQpq6pfTfouBkQdYWCK04kA3JYV0Oo9zwr8XQQl7yqYudizYox6Ln8CFJPZ6G4xgWnDOzVhecQH7YGY/p9glkzJ+LjMdMxdUU4InNrKIDkLVRK8qiTYFa96DdIMWhJzQiRkZfySdpYD347q3NRlHUUxzavwqhffIo9J/JQFIjeXOBqHkljvd8hIrBs+gQnKvLjcXTdWPRq9RYGfLIZ+04USnsxPtuArc++kb4QWX1sc6blkg+bW+vC2z+YL/2ytKHsexiZkzz2FSM1ApJCQ6AE6U/6b8nfVYLatHCEThqK6dOnYMK4CZg0cQEWRFxAicendE0n2NSNOtEhjlkXUa5F8+LyuJwnykcj1WVrKrNsUzur0iMRtX0Kxvd4BQ9c8S/48S0d8P7omVgUtBZBa1dj9YrZmDS2Bzq2fRft+83CrIg0VIuRcZCv99eiJHY9dkwciK4DwxCdV4lqHwkWZykcsKn+zQzaQG0BMuPWYfEnb6Hlrx/Bs6N2Y3dKqcwqjaOjE2X5dLa1eTGIDP4UXdoOwpqYXOTUCDERw+L9RiRTJsPvH35/AXISQrFkWCe88PBTeKDnNhzOqkSNOjQavFknovNoFNifGti3zJ+DjUlr2oN9Ie3DfUaRfc4NfTJfzD6yBivGtUW7v9yPx+7riPkpHhRUZSAhOgVR0eeQdW4Xlj/xI7wwfBY+W7ISO7ZtQNCJHDjpIC9R+1lc3lAiJIpKH1InKubl4Nmg37LNVQie05VwLp/opFDScECnfksUxtLVdAkVx2Zi7bqpGBqRx9FVjokvzI3FweWzMbjLSIydtwXbw7Zjy/IpmDxsBIaNWo6YHEC4loz5UhJ1nXnSluj7mtu3Sd7mlgTJm99inyRvPvETBfG7MOmHIxFxPBuFFKIZYYgmfbn4HTYMt311cJRlIXnfCkx640949NG3MGh+BBLKSJy4sEQ/YkistgnbnRTni7bnvomj+Utba920K0i8eEWEnfDt0PzY7ZKb3lZCYlYnvjN2A9YMfAd9xszG8g07sHPrOiydORp9P+yLsXtTkVbGFUPqhgQhbnxW3OhP87afReNweVzOEydgZjpc6KYiGefCizre4jgcnvch7vuXX+DXby3Huvg8GcxpXH54fLWoyw/FtBda4J7rnsLjfYKR7PbIrELYfU0yIheNwYQuvTEupgalLl34VodjZoSNM5SLgUouH35vLs4dmo3+N16FXz48HJN3nUV+nRiq1ElJnBo061iJwjNCAto9gndmHED4uTK4xRD1Wr0640sDdTAoRsquSRjb6mb84Lc9MTsqB1lukjxeZuUDx4131UzjqKlEaUkxiouKUPQfQmFhIYqLC1FUXguHi/c3eOBy5CMvbhfWfjYA4z4dgn4fvIEP7v0T3liWgaTiKjjEmbpchciLXoWhv/o5us2MQEQmXxMhAxCdrfbvpWtDi8sZRr/MPUmBS0ec9ChZ4gBOHeYKBwdXiaeDv1ld14FX1JKaKXvy6UNl1AysC5AoJVaoRkH4BIxr3xYPPT8Z+4tkQlknfqEgAtvHvo/X73gePTcVI7OcZVMWyVsy1YmXpm9mvTfCKhHRwZ6r/BI89WKjCTsw5YcjsOd4ppCoxnqERkIbiz7TFM/yeT+Y31sPT3k2Lqx/HU/ddgv+0n0qliRWSP1Jl0gomYY+nnmQNLGNuM/82EYSx1unRFD7h8dkm/1hiK/sNwKaFVe4NA8ZXyTUFR5GxOxeeOGWB9B503mcKZF+85Ug7chcfPq3G3BLxxXYejJXxjCuQEk6yUO8lmxTtmbuN4tG4bIgUQ1OQI1VFYkKLcrHz/TdCP3sFVz5i2vw6Kf7cTi9Wo+TyTvrq0V/o7D+jT/j6R/eivueHoOdpUCtOJaqpLWY9dEwvN1hMWLEuJw+t5A0DrBSBJX/OyIpUhOR3I2C1N0I7vxz/ObqZ9FrzkHEldOwpXCvR8kiV99ouK7iRCStaYPbX5mIGbuSUSACmvsgmNN3I+O3QUuVj5JTG7F28L34pytuwgcrEhBTwAHBXH7lOhHdU6MghCc3Ox3xcdGIiopEdHQ0IiOjJByT/SgcPx6lx6NO5SC3vAZul8xwk7YjqPvr6DFiJUJiziJh71xMff0W/KjdSuw6lYK8wgIUpiUgMXQ6XvnnuzB+bTxO5lWgqroMubVcLG+0dBYWFwlOcmSwrROfIkS+QnSxrKgc5eXlqKwuRkVVKaoqqlBa40JlXWCFXfwPb0TX1Q5RTOqmGTN9qI2dhnUhk9AvIkvicrX3HPZ/+hrefO55PDhsLyokFleyffVZOLFqOHrcfRt+1D0c0TnVIokQKa4QSb4+Hx/2aH6tVwKiBEboiPineq+QRPGxnvo85MTvxrQfjkZEdAYKxS83N7StJFvjbegTSXKkzq5yeM8sQq+H/4C7W/XGh+vOghf9dCwR/0n/riv+DGyjhvS6+iPtVZ6HUum3grIqVDjFm/GhJSlFrxaYor8VSpdFON5+4uU9uOLnyiIXYW6XF/Grm3phYUoN8jycbHpRnbIdB4fcjf93VSdM2JKINA9JnJQoYxGfc2a5WlmL7x2Xxz1RqmaivLQWYTh0CFzA5QyhOHoh5ne7BVddfS3eC8pEYrFZ2qWq1/udqC8Nx5QXH8Ld/7cFHnp2DvbX1sNR70Dquq4YOKg32s49IUyfzovLtMyfusry5Bh3mhHMTWUTQ/UUJuLCmjdx8/W/wuP9FmHNySoz2xCj5jxHSZzU0+/OQ3nqAnT/42sYO2UvjhfKYc2F9bxERsVmkrb3FR5H/LIuuPWHV+KaHquxMr5YJBKZ6bR1/TsQ/9sgeXnrnPC4HfB4XBI8XwS32w2Xi8ckyIDj8wkJil6PZf064fYPghFyKgtFbheqUsOxe/zr+NHP+mDK1L7o0q4b2j7fFZ980hP/8v/ew5SIs0g8sgp7tszHhBOV4qAa/woGC4uLAe2Tq8WuigykRi3AhEEfYmj/CRg3cT5mLpuLeUvmYem8xQjeegRx54t11dYQAOqkmRzR/GUsV19UeWwG1gRNxYD9+XJQvEP5Icx79xm0eKA1HpuVSHPUUO8vQ/K28Rj1zE248t652JBSjFLJTy9JaaTvxmPQW/K+HZ+PPon7dfCJnH5vKYriDwiJGobdQqLyVcrmA0kNX3dSX6e3ZMsf6ycSsBjxJ/DGYMW79+Dx617CS102I5Gr+HVcERJCKfGUmLChmZLkSDa5QuhyV8GbHIzpg3pg8JiFWHM4AyVCiPX1Bxx/WEYjQdLG2w7YMp76IpwJ6othf74Tv7lpPPYU16BSyqO+ODKP4sTUl3H1T+5A10VHcLyIwkhFWJ7Ia0he48u1aD5cFiTK3CMkChQI3HZJ8KES57Z8jNGtrse//ltrTIwuRKaDFsR48u+qRnXUWLR//BbceGdrdJh8GLn6FFwqwga8jI+6DMTIMDPwq5cJ5O91FKP47C6snDMbC6eMxaSZSzB19Q5EHpyDWfNn4PNPPsWS4D1CaETBPW44T63BrKF90fPjJVh4vMyoOkmG5EUH89U36NIgODPxufNRlbIC3W/+Le5oOQBDg5JQIfH1ZkaJx5sZmR6+cnHGOzH76TvQZ/RqBJ8xjoqEizXlJ50Co/I4w5cb/ApsNAIB+ib/DLItXzog8JPESAJdvEw6ZVs+3IXIiVqO4Xf9AL++pS9GByUiRx/VDTwVKf/8kN5CTeU5nNo+C/MnT8G86eMxZeZcTFgSiUwX9IkVQ2CZQBN9DVoWj+vlCBcKLiRhX+hGbDyWgbxqcVCS1ltTiNzEA5g+ZTW2rvoInTu8jSdavYlOXd5GyxYvYuDYzzHmcyl/7Q7ElDvhZptpfZkn+59lSNvqcVOcaQ7ds7hswP6kPtN6voSnIh1pxzdhzuSZmDtlNMbM3YDlG7YhYvsijJ06FZ+PmICgiJNILqP9GdtT3dDs5COg79yt91ciL3Ybds8bi4mb92F/ZCwSElJwNvk8Ui+k4Wz6BaTLd05+ASpqeI8mE9Kv0fZJBcSGJDT4vHIlUVMwZG+ulCO+JH01xv/tYdz0QBs8uuiklMiVL9pPGVJ3jsfoJ3+NK3/eB/Oic5AjBIP5MCu9sqT6bo59Ydfyp37EUYSy0xEInjEIvd5qjdff6ohuH8/GivBkpDv9cGtSSeOpQXVGEg4sHYMhAz5Cv34DMXDUVIxbsQ9pUp5D4qh/8hWi+EQ4ZlwxCmEkUUIseY+WSEtB5F+2pM5sOt47RtHMSg93vh1aLybWy4isE4/pCcmIE+MqJC1ujzcf+iPue/kjLE2pg9tbI8VwJdrIKF9aHtvF+GbJjmSpOhupp+IRcyAcu1YvxKyxYzBmYyTisstQ6zEys+WYusGH8BiffdQJOJ0klYRyyXkTPwPH5nVG11tvxW9uHo+9pdUygvE84MyKRMyMZ3H1T3+OVz/dgvDzvLeU9WI7mrpZXBpcJiQqYFw6kHNdikYnpuA9h6Mze6LTH27FNfdPwKaMCpSKkdIl+OqqUZNzDJsHPI2/PPEiXhm4ACEnC4R8yUyk5jAWtGmFPu+NwsI4GcWpoGpAUoa7CLnJR7By5jIsWbcBG9dPx4SBvfHmi++h04iPMXlib7R+qiVavf8xxhyVuZW7GhV7h+CDP9+D25/5EB9uviCZCdUQOfSGeDUgLgezDrQp1oMG7ICrMglB7e7CA396Ge0+3oTEauPcaTBKwDSuA27nCWzudCPaDpiKiQdK9PwXBi8fXyNRrIMaH1uBdszPxoFxdaZFsiICf5GPlkFSKORPj4mT0OBCRcYxRHx4K/79Vw+i/WebcajYXD5QYRjXW4K8M+HYsmAceg6dgLmLViM0dB2Wzh2NUcM/xIxTNSgUB90oKInyobamBvm5Bah2y/yT90BoW4jrclYjN/scMs+GY9u2DVi8aj1CNgQhZMlSbNm2DSG7j+FwYhZq1c3R9WmNpR5sMw5bDsme9W9oX3Nfgpw15VtcBlDFDIQAXHk4ezQcq+csxrKQjdgc/BkGduhsXikw6mNM+vQDPHP3fXh55AqsOlWquqGcRT6MPYuemwOaa21mBPZvmI7Js5Zjy6kClDpo/4wjA6zE0zf9iwaaFRz6CWUngbwkT+okcwroZUXUNKwTEjV0T4HkIZp7eiH6vnI/fnZ/Ozw6/4yUKPYmeUNIQ+qOCRjT8mpcceWbmLovExkyqTQ+hT6HWRqZ1abFZoy987JTLUqSjyF66XSZKM7GpNGfYGifd/Hem2/gjVf7o+fI9TiQVoayynykH9uKtZ+PwpgJk/DpjDmYs2ARFi9ejHlLVmPW6hNILqlWIlVfn4+iuJ2Y+sORQqKykM8JlpIoKZvi6qVJOSZVVdmURBn/3SgE2qdh4mnuQ6PNmrYVEVAdNwOj3miBOx56HW+tz0CN16xEsS/0FTlMT1nkj22jecq3h75OJHVUZONc7D7sWL0cyzdvxabgZdiwLQzhCdnIc7DdTHymY51IsdVnsELKrehXhPhqj6dg//iO6PDzW/HbmyYgXEhUuRxn+Y6sI4ic8wSu+emP8dTw9dh8Vsie5KM+isSZjSTxLL5/XBYkSm/CFA3StySRBNHGaDDl+7B2UBs8fPUduPbFyVh7MAbRpxJw8mQc4mMP4fDuxRjR5lV0HrIIKw+lo9wrZiEzkfrMjRj+3Mvo3GUyNp3ngE+jptHVw10YjZjdC9FnxB7El9SiyhGHrWM64aXr78VNnYOwf+tn6PP2S3i800h8tOeCTHhqUHliAab3745uQ2dh3tF0yc8tfo3Kb4yT8x6u4BgHxrJoaGKozlLETnkCrf70Rzz89mdYerqGpixxTRwaDU3P5crCoY//gGe7DUP/9WmBlRvJUaaWdMB0PIzLsmQ6iariXORmpuNCRhbSMzKQ0YiQmZmJrGJJ6+aTf3RudLoiiZRFUeh49P0qusRM4umSOOJkilJxbuVfcccNP0OLzpMxN7pcZ2P6L066OicC26d3xdstn8PDYw4jNrcGDr8b5w8swMpBj6Pj7jKkV7J1GgEKwjrKtzp+KcTchN/gyJgPBwbTfgzGwfICgwm6uifxeY4zczOwMD1dpkuIOZ0y9yW21LHhIoHF5QL2ZUMwcGftwY5VqzBhxhFk+dzwVh3A3Ndb4rE7XsEzQ5fhdNgIvP7nR9ByyBLMiy0S/ZDUEnjfj04uJC+990U0yIcqpGyYjOXz5mLW8RK9P5BTKVEoiSs6qPEFXI3WfUlLEiWxZPNrgSJSf6uipiIoaCoG7ymGlyQ/YRE6vdwCP2ghJGpOMlNSpSVujZCoiRj7JElUa0zeJT6giiRNdFnKo8xUeM2fZXLFhaklsafiLE6GrcPySUux53wtKmudqEgJw87J3fDOXXfjF//3cXwwPRQhW5Zi8bgeeOetzvh8dwrOVbqEcEhetTnIi9mC4R1GYEN8OrJcUl59AYrid2LSD4cJicpBvpRLMqn3gFEU9TOyRbloc1oPPiHNs98OE58+irde0ObNKxzM277pF6XAvJ1Y9P5LuOeGlvhDnw1Ir5JRhC5f2sH4TtmR8rX9tDWkveSYS+2f98ny3i45U1cLV+Zx7F06HtNmTMfMdTux/+gJRJ7MRk6ZnKszfkZ7V+sk0rEMvfLhFGnpX5Kxd2gHvPN/bsP1N07CrrIalEne2nxCoo7MfwK/+tcf4/GhMvE7Xakp1F/xgq/IQT9l8f3jsiBRfFcGZ3C8Y4DvphTdUsX3nZmH0R88hH/+5fW4udXb6NS5F3r07IOeXbqgZ9f+6DU6CCsPpyOtwgU3jUQU2+euRn3iHHR48j2803s1DhWTevBWb/kWpS9L3I7I0IlYHCuEwumBP38Plg9ui0dufwovLUrB+dit2LVhDdaHxSGhgIYn4IcEdYoUjgov34Y0iYVwxqWR+OC/1IWO1OuBqywLRya+gGfuuBq/bNkBb65KFnPzi8nQeGjZklRk9rgqELvgNjzzfk90XXICpTQmcYp0iPrSUM5/aMAkb5BZ9YFN2LxgHhbNXYLFcxdjwfwFmD9//n8bFixYiBVCClMLK8QRca2GbcI6SFkUXZ2wOMxATfQldx4nqgsScWL1q7j35p/hnx7pjo7L4lAUkN0nTj05pC/6P3sXbrirN+alOpBZXoPqivOIWbsAM97ujYWnvCh2ao7fCp1BS+mGHLG+bF8jnpFKCpVAlypNo7tsP5IjfirJIgnktYM6Ok/51iR0gKZmmpbESRy8n3GYj8VljYKjCxG2YyM2JNG/SL9nbMLIVx7Gn5/rjH5BCahM2oqgpeux+XgGUvkAiKgFCTgHaw6RZs2CesMVgxPY2G8SFn0cjJgqJxwOF1xOGWSdTgnVcLrKUSvbzlrxSS5JS9JOHaMq0j/JDikE1bJB9fh0Hi/nfcSn84REIW4xurx0H370wOt4ZF6c6jXLr6uvQPLOz4REXYMrr2iPSTvF91VzGkAfwRujaTeSITOmzvMHiSUlh35n7AqEbVyIcQdLtHx9VYn4KXfJSSQE9cOzV12Jf73lQdx27414+u230TUkVe8lbXjykMFZkIykWfdj1I4TOJgjEvmLURgbgck/HI6I6GzkszQpn5cFKYOXba2Eg/JQKGlYJRz8/nYwGX0ACSLXgHTVRo/TjqV3fC7Upu3AgvdexP1X3ojf/ntPBKc4UeIQOYTc8JcPGi5nGkdiCJSbs1/uUyZmLX1kfLr0Dfu+4gLO712Aeb3fxGs9lmDZgXgk5xejqtYh5KtWsnFKcpI6BknAOqpk57F/2Pt46we34tobJ2CnkKhyliGnXZmRiJ77LH5x9ZV4dNhqbDxdLklYmCSTfEjOWC+L7x+XyUqUGLRHjFKIB2cb1HEqdc6ugej78vW47u4n0SHoPFIuFCC7sAi5hXkoYiipRpmT18HJ5CW9GEa9xwG3zOTaPNkZrfuswf4ScQBicLosK8biFUdXU1OOMhcHaXFOJxdjwvvP4I8PtMH4Yx6UVlWitqoC1dUuOD2824eXuDjomhkWTZkGyCfoVE4ZzXmJiKSEAz9nniIRqnKP49DMV/Fy59Z48fYb0eL3T+HPXYNxWkzFKbHVlVImycPnrkHS4rvwfNee6LTsOHJpXHKO9kfDorGa2ZsEOedy1KCqogIVEioZKhkqvzVU1Xr05m1dIpf8jRSsm8mXP7Vj3lnCuvpQnnMUEasH4PFnOuGFllfjdze2xCu91uB4tYhH8ctPYH33V/HMtTfjukc6YejcVfhszBAMGdAHoz5biJCITFS6+evrbKhvB11IQ2D91THJl/ar7jec52DGejCGcalKntgncp4DoH6wXhKJx8xQwuFQBkYhizpLZp48afEPDHY2O/G/6kjRFkcFqmqqUMlfDvCK7RwZh3eeaIEn243CknjReGcNKirLUO0Q/Rf74Nv1qRr6RJrolOqZBK68oigMs3sNQNf2H2H08gVYsnwZVixdiaXLVmHZsuVYuXQxVi2WgXeFDJQ7Y3DqfBk9g0hH0sE3nPN+QhIc0VvmJ2fLoidjTcgkDN0vszbq7Jk1GPHKQ7i2xRt4ZG6CpKb+syYyadkxEaMf+zf85EfdMPtwNrKczEvyYZ5wiJzM10xAeC8hJwvU+cwNM7F72RxsyDR1kxNq5z6fAxUXDmHXgDvxh99djStv+SteG7sRUeL/6BFYd73/SPyrrzoX7oMD8fT8vVgWVyI2V4TChDBMvJKX89JRQB9MP0JioX6Fjca6G1n4o/EkkfxrDJjOrPxIfF2VlyOcPbFfPFWozziIeZ06o9tzrfD4A3fhF7+/B+235OFMGe2cfw3kkzJxkqXeDk7KIJNEfXknJ4tc/dPY0vfsbznmcVSiIj8DeUlHsGnK++jRZxj6LT6G0yIDfSN7Q6LrmKKeVNsyGVGTO6Drb2/Fb/7wOfaVVeuN5WwBV/YRxM5+Hlf/9Cd46uPt2HpWfBgZJ+tDn6R1tbgUuDzuiaKb4aMqVGYaPh0MyoW5v4F3H7wZt7fsiwWJdahxcXAXY+Z9Axw0aV/yrdfZae00eCFRvvj5eP2J9/B6r1U4UEAlpoHQhmggEkRvdVYof1lhg9H/1adxz5OjEVriRqXXrBKRtKjj4B+NkI5J0vD1BPSotGt9Qk2dIc3IOK46GaDL0w4gfOEIvPjWhxgXEoal49rj3Zb34U9P98fa7HohFiRGDFp5+Fw1iFtwO1744EN0WhqPjEBdaFTypXUzszFzUP2IHg9k0FhoxeVbA9tFDvFPMtSX9kktSBQ5u6o6H4FNs0fi/fYDMGJtFLZNa42XH7wDLV4bgrkJ1RoHmZswru2fcecdT+G5MaGIOpuGEzHHEXU0ErGnUpFexsuCKqmEb4fKQ6ej9eJOoF/1mIociPOlg6aDMnF0V9qFwxWdIx2bHJd4jKurWxqXjjLg7CVDvz56zgax+McENYL99019yHNGV0gu9PKJuxzn1ryKF1s8jVd7LsX+ctEB6ojogOoe7UL2mZT6ppfjeE5ICskVKvdg4aBpGD9iNfacPYPklGSkpqTIdwrO8js5GWlnk/X4haw8mZTVSrlmkKbe8hLTF/dPqS9quCdqMobuDaxE5YRhWpsncfsDrfHIvESRhVMAhmIk7xqH0X+5Dj++ZjSWJeQg1yv56YRBAu2CdZCgt0hIoG77UYWTyz5H6OwZ2JVHe+TKv8QRG+Ckta5W5Iyeii63y4T1p7/HPe98jFmnyiWd1FnSG5uSIPEQNQovz9+HlfElUocCFCTswOc/HoXdMdnIl7y+sE31y8ZP6b0/PCeHze0DcqIRkJhSKutEe5Z91o3d7ChGaeJWzHnvdXT+aArmLZuFecPa4ZFrbsQNffdi74VSmQwaWbS9te1ZONPTV1Me9jfjMLCeclz1QPqY+26ZeGZE4fCcgRjRpz+GfB6EkGPZKJd0JHI6sWU9madISX/or8/GySXd0e+eO/CbmydjT2k5KhhfYjizjuDEtFb45U9+iTaTI7Av06Rnu0iG2kaMZ/H947IgUbpQq0oo6k1l5yzBmYTQnk/g2ZsfxENtF+BQWT1c6nR4T4+YNBVZrZQzA0NgaCheby3qk5eh19PvolOPJYjIEQOiA6QhSXxXZQHyL5zEqfhzyKstwKFZbdH+qefxSPt1iPe5UCMylKXF40JqMtKrzexFF/NF4Y1voGOSWQStmqRPDYGOgm7SiZKU/dg8fyw+7DMYXaYdQFyeA5lRszH+vUdx0x0voE1oMXIqWV+xHak7jdftKseJGbfhhW790X31KZTQyQQcBgki20VJnZg/6qtRnCHOOu4E4k8kIOFEPOLi4r49xMcjIaMUpbV8KsS0hUIK0ReQMrAP6pyoPr8fW2YNx8CeQjAn7kS8zOyqk+Zj9Gv3474HW+PtJUmopCtKW4VhbzyMu1u+ie6h56UfxSFrvxinwpee8koe69kYUKKGQUAdbaBP2cZKeHhI4piVuS/jMapZWmccOiRxugHnyEuUzpoyFBcUo1KE4RPkX6QTWXVFyjqvf2CoRgTCV8HjHMLdqC1KR3ryKSSmpiKv5hzCBt+Fxx9+B+9+Fo5kEglfDYoTI5CSnYM80RHqBgc2Dn8kD7ryoPFEnzxnsOPT6Vg+YyNiqjixYTlMY3RSzYrJRf/NH/Ohb+OdhPJNfxHQZfIl2l31sVkIWjsNg/bkyDmx9epT2PDhy3im5V/xwMRjMhB7hcx5JJ9snAoaiaH33ox//ctKbD9XLIO6eCeZhNWUFSCrqBour3o6tQNd6RKZ+JDL2eDRWDtnHJacFv9I2xQBzIsmXXBVpOLC1sF47/E78cef/AQ3/uEpvDpiG9KEADqFODYQMnf5eZRtfBu9go9K2Xxli/jS+F2YcuUIhMfkoED9itifTETdFbnIL6kSm+PKdkAW2hptmW3UCDCemczSnqVObOeaXGQfW48Vn3RDu3cGYurWOJzJOYOkTaPR765rceVdH2PxkQsoqJOek3qqr/uqv1B/TY/OPjJ+ipNk+nCOJx5HNjIT9uPg1hCs3xSCjStnY+nacOyNzUJhJf2+5MXVJ+qHpuP4wHxZTjUyd43H+Fcfw69/PxwbMypQIg6Hdag5txuHx92Nq//tUfRdE4n4CnOc74qimpp2aWTDWDQrLgsS5ZJARs7FV6791PMJi7zt+PyZ+3HH71/Gk8N2I10U1aODqbnkJ+5I4hrD0J8gCBiD2+eQtJsx9fnXMaDLDGy+IEoqRs1LPv56J3JP7cC2uSMwbPhqHDh3EAu7/gWtHn8NT44/gCIxVk9tPo6tmouQkK04UEiDccNZnoKUk9E4mXQBmeV0q07Rel5SooMVEkhjrKuVmUs0tk/th/ff74XW47bjXKVwQfHtvoJ92PhJGzx08934yQfhiMmp1ZsZ+UeZa115iB19C17uNxiDtpw1RE1KkUrqIM/6qhORb9QX4UJMBPaGBGFDcCg2Bm1EyHox+PXr//sQsgEbo2UwKeMqEvOUurHx1RmwTpylV6L6QiT2TOuKD9r2QK/xm3G8VM7TsbvjsbXfK3j5tkdwxwerccrthyNrK6Z1fBLPPv8Oem/NlPwc2i9+IaPOUpklnz+LpEqvOOLGOQdtEbaL1lXSyD+lVFLGEDinDk/iK2miTkhdGm7AN06Xgwc9k+hDdSqSYrZixbJghBwvQYEMfOwzzUM+9DKvKd7iHxLsvf+KRNHuHUjftxwrJo7H2DmrcTgnAhOeugG3PycTlrXxKPJVoa4sCdunD0LIoSgkcoJDnfKRtLhFT6hXkrfol2yIntUide1krJs1AwuP58qki7pEZZI0AV2UDyUopE28i1Enefr7b1z15MDOuJKGaWVCqCRq3XQMFBJF2lVfX4KTi3qg599ewX3dghAnyWr5gkjHKRyZ8hE+uP5BPDghBgmFDpm41KL0fDQig5Zi1vKdSMitQlUd8+cKB8kHJxX1KI6ajpCln2BEUCrK5byLZcufqzobaUdXYdq7D+OVbh3R+plH0eq6P+JPN7+L8RuPI0nyqxVb97kqUZp8ADtGPI+ph07iRBlrV4iChAhMu2IwIqKzUECSSduvzMSp0LlYsWoLDiVmoMxt7NLvq9X2lKIbBTYr20kJivSG11WMvONrsXJUR7z2UjsMDstHRhn9sAPFCauxrtvNuOpHj6DPihjElPIhJfaZZCTtLS0i+dGPCIGSIKl4WP1GXZ0DzopC5J49hYSEcGxdPhnTxo7Fxyv3ILrEgUppL/oLyqPC6+SZ7crxSv60/yV/Ka4mORRrRrTFn37/BqYeLkF2leigv1raaSVW97wW1z42EnOOJiOX79wSeVQPVMZA3hbfOy6PG8upzNR30VQqtdMhg3nsArR7/A78y6Pt8eLSeJlhidLKOToikoCG+5PMgElDE4XkcrtXzKPyCOa/8hj6tR+OZYlMoxd4xD1l48TKfuhz34342W0DsXTLHHRp9TBufuwtPLc4Ci53DdzxSzBq3DJM3HACeSQXzlrkhfVEh8d+h4de7ovREeX6GgWuYlBu3sPslpmet/ok9g95FU8+8CL+OnQZ9hYLIZOqqbEK8UlePxwjW1yHq37aBytjC1AYeNqDKyVe5xmEdb0V7wwbj0mHM8W4WSfWhe0RIBRSltpY4PIlyYrEkBag9TUOZvZFckEyRmctOUomdCYkUTUFcTg29Rk88LvH8O7wjdh9gS+R07vAxGH4kRrcBYOf/h1uuas7lqS7UOg8j72fv4ke77RGm+VJcPENztL+3so8nNm8AAv7tsekqAoU1DKHRkKdJl0mt/Wf3SuHpb4yMPAdL/zJCcojn3JOjvGeOPY/25Mto21n0uXHzsbEnrfjn665CT94PRTbzpSBrxpju+ljznWBdrD4BwX7jvpFa/hqP1IXaPU1ODSyNdrdfi/ueW4QQvcswGs3/Aa/fm0kBuxI0RdmVkROQ7ve6xAalY1q6pH4GtEMSV2jNy/76Jwka9FMOSaTtJy9WDNnDt7stxbRbpkEid7rW7C5Qq5Twjq4RYfpIphOlVgVml9iaZys6QqoQD4qoqdjbdAUIQWFWgt6Ns/ZYCzu1xWPPDQAS2UiWEzyf2o91vXrgGdbdMO8ZKCkVuL603B04RB0/Kef46orbkbf9adxslQKE52mHSmVo604TiJy3XKM67AY+4prUeLyiL1W4JwQqFk9X8F1T0xD8IlCZCVtQPDgF3Dvldfiih+8hmErEpGYUyOTq2M4tnI8nn5hETalFqBIpBRqpvdEffbj/giXCVoebU8+8xJXYtA/X4nrrrgWfxu+EjuzaKmBB4fkmykbBakGCS2JJSednvOhmNvjabR68kW8vTgOOV4hkTIxps37imJwavU7uOaqK3HngGCsTayQ9pdyqBryxZbQ1TAdaEy36A+qi/27irOQKUR7+rut0GnkLCw8mIIMh4xD9CeB+5Y48dJ3XWk/GpnUB8m+R9VD6ijx/J5UnNw0Ch/eeTNazzuJuPQKuF0XELt7Ano9fgMem3YcURm1mo4jk/p5umPmbXFJcHmQKCqjKJG/WBzA9pl4r31rdHj6RtxwzY/xg2t+j9890hZ9+s7FnqxqlIgmc5bHx/ENkTEKrgu0fHpNztXXncP2Yc+hT6/eGL47D/pbS1KM31+FnCOLsHjAS2jx3Pvo9G4ffDpmBPp36YV2z3fEiNEfo8cgGfx3JOB0YbXOMHSF6eAo9Hjx33HdQ2/ghUnHxHVwAOYbfMVwxBr8teJ8Y2fhtSdfxTvDVyEkJte840ji1Ynh8pUClSdDsHFAS/z2qt+j48qTiC0UWWlJdZXwVOzBrBZ3o8eItViTTOdKizJtQkM1lyqlamwqfsuJL/YlXmOhhspMZcP8kYRIDtKWflcmMg8sRZ/r/4g2g4OxKSZPn14kadFy5KM2eT1WDn0eD977EJ5aeQ6pJdWoTpGZ25yheL9jZwycuBqfThyNjz+diVkrwhCZlIUi/gQLy2wMpJ5sE5WJ+/Khg4qK3CCvIT3mfjR6Lw5e3GY6OmjjsDUD0YW6vFjEbvocgzp1wGO/HIf1UfyNLxItzkiZDzNnYRb/uGAHfhOJcslnBU5vGYaRPV7Fn1/qjt7vjcD0z0bgvTYf4P123TFixDh0H7YIwceykFHJO2lod+JTqEKiVzpQ0qcwf6oK7d1djdKUSOxZOQ3de36CtYfSkF6uj2TIn8RTHZa41GfVadkJbJrjtDnjO5hnRdQsIVHTMHhvnuxKWqZ3liM7ejdCJgxD9/eGYcxnIzF04AAM4SC/JRHFNWJXvO3BX4HcuD3YMLw7Oj17F95ecgT7MoXoSb6mTObIshyozE0SW1iAsV3eQ49OnfBmm3fRvutQjFu4HYfP5COvtk6fLiy/EI2ooJkY3uYlPPdEC9zf4mE89coH6DslBFvjSlBQYy7V+yFkKmEfpl4xFLujs5FHe/I7UVOUhEMTB2PEG0+g49hFmB9XKe1obJZ1bzTETnlpng/q8B7Z49NeRecO7dBhYijihEHyd0Z15ZmTa3cB8k+tw0ctr8dtLUfhkw1JyGUjiO/XaxaSF8cNXjXgpUyumFWl7sWWOeMxcvg4jNt4AMfOpiIttwil1S4hRuwj41/Yn9pfWhZbU8plH5GgaTz6HJFRj7nhzDuF5C2TMHZAJwwaMw7Dh43CiIHDMGzWGhzOrkCli31MteBaIFc7RR42y0U0jUXz4fIgUaI9qkMOmdmkxWDb1lBsC16KVcsXYdHylVgVvBXh4SeQXiXzQJ1IMD61UJMGvvhJrZZz/hqcWdcL/Qf2Q+vZcSiRU1zC5b1UtcXnkBYXgW1hBxCx+zBOJSUi/tgxHNi8CwcOH8LuQ2eRll8FB5kZc5M0dfkxiNw4Gr2Gf4q3J0XK/JS2w6e8uDom0ngq4CqIwZbN4TiUmI38ajrcgJT8FgvxVmYjO34XgpatQNjZQhTUCq2jJdXmw3FyLt65sy1Gzt+HqAoSRDlOwzK1Cfx9BeZEAF8789/ja+kIthkPiYzeKlRln8a+xcE4kJiP/CqSUspu4jCdvyYH6QkR2Lppoz6iW+GU9naVoiAtDof3hGHvsSQcPXYYhyJPID4lH6WclF8UpJCAk9VPltmwreBWgzw8yf3AWe5rmwVaS/5JpvzOElRlHMHhkPl4+8G5CEvIQZkMdOYyB0mZSW7xj47/2JHcJ/lxozIvHvExe7Ej/DAOhB1HauppRO07gAM7w3Hw0DHsPpKCXPEtLg6u+velapkvPSJBd9Rs/Y4SlKWfQPhO0fvIaOw/dAj7IsKxNzwcEeER2BuxF0dPnEV6QaVOxqhvOiDryEu/INKJj6FvqBIStU5I1JA9eXKKK1hyXvxKXVUBCpKjsG/nfhyJ3IeIA4dx5EQK0ktqJBsO7sxT5K4oREbkVoQOuR8DQxJwhK8fCMiq8uqfRK+rRlXBWRzftR1h27djU+hW7NhzDHHnSuAUgsOVFq2l1wlnSQbOHN2NbSErsHzZcqzeEIZ98VnIF5vmfY9KXPz5QqLCMfmKMfqyzQJtGKGRrmqUpyVh75Q3MG7Jciw/VStxJQ19KgVpNOhDacVsMxfyYrdi3/4DOJxcYJ6wo7TMT7Y5gXZV5eBkWDBCNh1HdFoJqnlco1APSG9lMi3H+PNT1an7ESn9tW3rLuzYdwSRabkyQRdfL/KbPFk+P7hvWlD/dJvtzjK/jPe1Y3UOeErTcOroLhyMPIoDB47gyOFoxJ4vQI1X6hNIx1Ssm5Rg0llcElwmJKqZIQpZkbQcUz4egta9ViCqCnB7zfKrcVASQTW5kRDn50gNwsr1KzBo3Vk1aTMIyyBNEkWCxpWwRloCZyA6u5V83QWnkLa8A55uPQWL9pxFochp7vGyVvX3Qi+Fymy9ruQkzh4QojpgH2LSS2Ww5ABAx8r7FQKRLSwaCZqmsWFeRq5GfnYy4o8fwkFOJML3IGLPXuyJiMBBIVFphVVctxA/wUkTA+2eg7HopzoSv5Co6Vi3bgoGR+SZ42L/+tSxn6snfAdUgPSLPtPnMA+9ZK0r8ZKJyFB27ig29HkJCw6fxxn+YnEzwtx7KDJL0NV5Dv30UX6uRO3CxCtGI7yBRDGwrt4C7JncA4s3bEZEvsjPVSglKDS4S+PbaPH0qz5XLapTxBfEpeBMnkweSWzET/AirvHLl0Y+i0sDS6K+ATovcJ7FvrnjMPKtvpgiLKrURYckhk9j1qcrApG/DTQoVwXO7JiKhcFLMOdkqfqAhqV6Xd7VS0IXYXj0exLd761AYeI2rOj2KDosOIJDacL21KC5YCx5B6JbNBGc+YrDLEgKw+alg9F1ax7OlQV++oU6wHvDpK1tQ1tcDKgufIrO6+NSayDw/U8N99tIBJIM/v6n/gao+Am/l5fveemZZMTkYdTOh4rIKVi7bhIG789jctFNyUd8ir6AWHSUq2lKvHQFSEiMZMAHUuh3OBnwVKUi+eBKDG47DhFp+Sihc2lGqLyBsrgjpZvLYvUFKEzYKSRqKML4sk2eE7l8nlLUZIViev9pCN4ei8w6+kj6M15+Myvclwa0eSlb2rW+ziHuoeE9UtCgfeLnpT+pp8X/GlgS9Z9AU+Dcz4uKpI0IntkXd/behcRSR+Bdufqcnjq2RsEnM8G09ZgwfgWmBsUhR9kP0/IJPT6ZwavadAwyM9SyGwEml6i8GTI2ZCKeenoGNgg5K6I/5vuNvB7J15KovxcyfKG+NBJ7Ni5Dp0FbkSZEupZOnm3LPtB+ZKM3UhcsLAS0S67O8EEXehQTRId4QkLgSwJXNbjaKf6BusYoDIE4xsJ9qDo+FcHBkzF8Ly/n+fXBCfM+JU2iuXObO9Rd3pguTEW+zcuA0yN3YNv4gZh2pFwfwyfRanaoMAGfpB+sWzYKErZiwlUjsDM6B9kSh6SvLDcF+wa2wbytCYjPqhU3aW4n9/K3K7VGlwiUWw1ffIC2ryG25Kz0AtrGUi/T6hb/W2BJ1DeAMwk6Ek9tKc6d2IKFY9/EsG3nkVjAm/jEmMVY1F4aAxqdoxjZWQXIKa5WIsZZod6sSKci5XBWeDEOgmV7vdlI3LkKiwePx6wDeThf5YGbKyTimHWQV2NutJQW3wTpJ5+nCkXFBTh9oRgu6S/zq1v8fcY66QO6y8DAYGHRSFBfOODKMBz44woMV4hEnxh4ROzYz59W0TeUq6IFVnMa0pOEcaceFVGzMW9iLzz/0RyEhuxGTFElytVJaSL+y9gunkdXSbySFZ9QljLkOMtxVhahOCsNORVeuCUd829O0NeZ16Jwasr8fahJj8PJiIVYOHEE3rriE4RGZyGPskld61wOlKefRn5xDapk4sKJpklnVuKaXcDGgu6Z5ZMAmqm09oPx53pS5Jfek32L/z2wJOoboMvOEmgMjoocpB9fjd2xucgud4MvN+MAejGGTJPTZV4uxwcIDr/Nu4mM0embZxubqdirvy4fmaejERkWhbQqL5xi3Hx6hD9RYN5vQqO2+LtA5yiB74LSBwC4LX1nCDAvh0jfUk8uRhksLKguEvjFQVdJE/cDxzgkm6dIDekRZdMThjNR20i6jH/icVd+HOKO7ULQzqNIiEtCVk0Naqifko7580lB88LJhvyYVr8k0AdRq3nPVMAfUcZmBP2d3gMmcphVMT8cJZnISolE1KF92DztGFLzy1CrMopsdF38kEYhydOnqZkRG8k0Ave+f7DNNFBA/s6p0igRVRqSy1GyTX9xqcSzuDSwJOqbQEOlQ5HAVwx4+eK82lp49KZtzoZ4g2cgbiPAuZ++u6nhiRgeEcdgXhDKbznEMhsLZuFzoM7rhIsX45mvWC7v2TIkisv/JqrF3wFpTzpMnbVTJaSp1UmaDTnH4xdBfi0svkCD/hjSooG6xQGa7EZpA/UvMChL4LekENUL2Dih5zipo2+Rs1yNFjKiq9uSN4NZMzHEyzzIImlUn5k345vVaz3Pfc20ecEyzctpOQk1fkp/k47V1Qj0qULyKKlWVCumsikZ5K7yFNMulwoUi5dKTasG/ujTPWxHttx30XoW/5NhSdQ3oOFJEo8QH4cQJpptnRh4gzHrk29q5BcBOgtyHS7JiwHy9Z36mgN1JsyUpTQyTy2eMkqmysDMMQpKJxqYt1n8vdB+NoMMV6P0t8qUwDKwHzkAWhJlcbGgvpAIGJKkR+Sbg7G+Vy0w0dJjcpqBsUygD6qD/v4nDzAbKiX1VLb5rmB98k58g65CKekwv9CgpEmi6m/lyT8vTPNOI131YplSkJIpzbgZIXnSV3E11+tzShnmSTZd+RLxDG2jg2R9KRFlNvs83nBOv9T4ZOMSgK1CMSgVJ6wNsmkfsu2UwDZz21n8j4clUf8BNBAP73mhU6LB0CaMT1Mr0hszafkNBxoDcR4kT3yQS9yV/HFZXQzR6xDDc2kZEqXRMG6OxisyNCyBy746UtnXn5u4NH7msoL0kGlb6SAOAtrjqg/SuHxaiH2oDyE0Ug8sLATUl6/pjG7yg0ZrDFcvq1Hv5LA5Q/9hjikCXyRK+lug4gt0PiXJ/X6+OoG6a8oyq10SlJFJBJImOUn6zzUqkhw9ztvMmV8g7+aCyqIv9jTyfHUFnvUE5VX5KAYlEpujOPRt6jHp38T6NP2lA8s2/UYJZVs2+ZZx3shvVtHojy+lhBaXApZEfQPUgemsjLM1+aCNqHHQicnsSR3NxRmLLpWrM9DMaIfiWJgXl4WNw2ss1CWKfJSRDoazOpMX5WL+lPPi5LP4BkgbaltLIGHlJRK2uBmLZEsUhO0vEU18C4tGQCzU6FWDjfJLWQOD2TWDNG1ZHYXqmdq0xjWB++aFr+acCZILV825qiU6qr/tqATGnDe/o+nS9FyQ0te20F/IeQ9vW9B4kn8zwpQb8E3KMyiDyMzqSXkkVYYsmTgNN8yLMCYeE2lCHjd5XgoY+Si3aUt2l06MZZ/yGj8hBy6lkBbfOyyJ+q9AG5FAZ2ZAw6CB0JDFWPRY42FMLGBgDVlxU4zODMSNB5PThhm4J6Yt+dHhBBxg4LjF3w/TnPw0/cRt3ZMPOlPbzhYXiwat+boX+VKXvn4+4HM0BBCIYHRRh+6vHGOgL+CAb84aImZiGzLGNSiTo748WP2GUBX1IXqq2cGSVRYWGpCHu+YQz5g6GsIVOMF/2W44ZxJcOmj7NRC5gPwNknHbSKcndcvifwcsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwuGgA/x+dZ+PsC4OU5gAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%A0%B7%E6%9C%AC%E6%A0%87%E5%87%86%E5%B7%AE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcIAAAEbCAYAAABJKYSiAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADmqSURBVHhe7Z0HlBRF/sd9/n2nHmIA9ZAznSRzYM0B04liThgQRRTz7Yo5Zz1B0GEBUQxnVgzorCKKIpwKqBjWwYAonDmgaw6Y69/f31TN9vR0z3RP2O2Z+n7eq7fb1WGqm6U+86uusJgihBBCLIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJCQif/75p9pxxx3VxRdfzGRRIrULRUhIRO6++27Vs2dPteWWWzJZlEjtQhESEpErrrhCXXPNNXqLEFLtUISEROTggw9Wd911l94i1cwff/yRScReKEJCIoD3g7169VJPPfWUzgnHl19+qV577bVMpTtv3jz19ttvy/UqDT5v1KhR6ocfftA5tc/rr7+ujjrqqLyC+/jjjyW633///dVNN92kPv/8c72H2AZFSEgEfvzxR7XYYoupX375RecUZuHCheqCCy5Q3bt3V+eff77aZ5991Pjx49Xee+8tgqokEO3AgQPVlVdeaVXUg/vu3bu3PHe/Lxt4Ftttt52aPXu2fKnZYYcd1CabbKK+//57fQSxCYqQkAjMnDlTbbHFFpEiuT322ENNnTpVnXzyyerAAw/MnHvqqadKNFIp8DmjR4+Wjh6//fabzrUHRHwrr7yyGjt2bM6/15133qk6deqkmpubZbupqUm+4LDJ204oQkIiMG7cOBFYFKZPn65+//13tfbaa6sbbrhB8lAxb7/99urmm2+W7Uowf/58teaaa6oJEybonOoGURyeY6Hk5oEHHlBdu3ZVH3zwgc5J8+ijj0oUiH8bgPMgwpEjR8o2sQuKkJAIHH/88WrixIl6KzwzZsyQinbOnDmy/emnn6qOHTtKs+kbb7wheeUE0jjuuOOkebBWmkRxH4ceeqiM4fRLO+20k/r111/10WlwTrdu3dSFF16YN4rHFxL8+zz++OM6h9gERUhISFCR4r0SOrpE5fTTT1ebb755pjIeM2aMWnfddSUSwbvCcvPuu++q5ZZbTp1xxhk6p/qB1KZNm5Y3eUUITjrpJIkK8X7XD1wX0SFkWStfGkg0KEJCQoJKEu+VvM1vhTDNoKhoDUOGDFH33HOPuvbaa9XTTz+tc8vHLbfcIhHOK6+8onNywf3gXvDTCNq7HTdQLpQRyZTRnefHiy++KM8CPUm94F779+8vTaX4ndgJRUhISN5//315z1dMhYkpuj766CO9la6A8e7O++6qXDQ0NKillloqsKzIP+CAA+QdIqKlQw45RDqOYBvSqK+vDxRLe4EyDx48WG200UZqxRVXlI5HP//8s9wHvmhguMRbb72lj24F5+FZTJ48WeekQT568Q4YMEB+/+yzz6SXKbEPipCQkEyaNEntu+++sY2WDKjUIYYuXbrI716QB6GMGDFCfsf4RshvvfXWU5dddpm6/PLLZfu2227TZ7Q/eOboAQtxLViwQMqNMkKGSLgXbCcSCX1GKzgWz+L666/P+re7+uqrRXxPPvmkDKFAxD5o0CC9l9gERUhISIYPH67OOeccvRVfMFSiT58+MvDfT9pTpkxR2267bWYf3qtBIogKIQ28L8P2Cy+8IPsNLS0tmV6WbQ2i00033VTKB/BzpZVWUmussUZWme+44w7Z7wb3iWeB97TmfDRL43hvijpRAqkNKEJCQoDKFFOr+VW0cQOVPSLCoPGOiJ7cFT4iP0gAERPA+Rj36AWyOfHEE/VWfh5++OGCCTIyCROZ+5XV8Oyzz8q7PAOalFFmNGvivG+++UYiOyM6N9iPZ7Hffvtl9uP+/RI63BD7oAgJCQEq03XWWUeaEQ0YEoHmtEqnqIPhUdmjCTfswP9jjz1WpPLOO+/oHH/Q2eSTTz7RW/lBk+Oll14qM9qgCRLNmhAtpjILSmHKajCdgTCusxBGhPhy4CdKQihCQkKACtTb+QSSQmVsEiImvMOCBPKlM888U+Rz0EEHqV133VVtttlmaq211pLhDu7rmQSZRAFlPO2006RjTyG5oMlxq622kt6w7nvznod97v3tCcp2yimnyLNxD2UJulfk41mgudjGGXZIYShCQkLw6quvqg033DCrsoUYMG+oW1po5sMx+RLOc/80vyOh5yJmn9lrr70y10QnFuwLC66HacXQG9TvvJdfflmkjeZPRHjLLLNM1hhHnIPPNeei2RLXQlQVpRzlBMJGp5hkMim///Of/5Teo6Y8+ImmU7+mTexD+RERmnskxA1FSEgI8B4Ns5p4mTt3bmbIARIW7H3vvff03uJBhY2xbYhkcF3MhRkFHN+hQ4ccceG6prwvvfSSDOzH7xguYcB7QPQqxbGQTo8ePTIdalKplD6q7UA5MO4Sn49eoc8995z87hbbsGHDJLpGeb3gGeBZYEgJIX5QhISEADO04F2XH4iYUDGbdPjhh+cIqFjQlIcmWDSjRrkmxgSiLN5xihAHJgFHRAh5QLQQH3qMIkJEpIWmWiMU9BJFlIVhFTivXPcVFfT4RESKuUCXXnppaYJGlIfxmUceeaTca9DMMRj/if3/+c9/dA4h2VCEhBQA8ujXr1/g0AHsP/vsszMiRPJb8aBYICXMozlr1iydU5ivvvpKygGJesH0a2jChUwQ4UFuZhsz0XijKtwHmoXRLNleQOi4F0SEjz32mJTxwQcflDzMzJPv3R/+bSDNSk1eQKqfWIuwpTmlWvTvrbSoZH2DSi7Um4VoTqiG+kTO8S1NDSrRmFKhGnqca9TVRfjM0OBeEroMKZWoT/rcrz9S/vQKMrksTKqGurrg/SQSEAXGrOVb2BbHQJZGhJ07d5Z3ceUC0Ro62oQF8kJzIt79+UVxUSSNz1522WVFPri3cgk+KsV8Ls7BnK4QZntFsyT+xDsilArdiEIjeQ2qoSncuwoIo84RnpegfF8gQvexWjR1gSm7zC1NuSIW9HUamrT+RLie+81DqtH5LB95Rro3UpAPP/xQenUWqojRoQaRh5Fh0DurtgID4lGOqO8XvVx00UXSEQURMSawriYQNTIaJIWIfdOoVPauSj1vJJRDcPSI62QEVAivCCPjRHuO8DLldiJdXC1XWDguvAj9j48WWZLCoEkQIggTkdx6660ZESKdddZZ7RaJoLxYO3HPPfcsqQw4F/eP+6mmqAoRPGajQTRYTDRJ7CH+7wjRtJkRllPJRxFSHoG1rQidkruit5QjQiPphnoTRaYjQ5Gj3paUJTWc49rnPqZAlBr6XkkOqEgx/2YYIAozxs0kTK7dXhUxyrP77rvLKhc2geeNd54HHnhgVcmbtA8xFWGuJIJSvugQ8knvT0dk5pyMcByBJCEo175W8WSf405FScUI3RFWEmWCXJ1rucsfSc5uIMEsYZJygQoVERWmBAsLhhqYuS+R0Kz69ttv671tDzqSYJHeapgerlzce++98uzbs2maVA+xFmHezimFKv9MhJTb1GiirobGRFpKhShDRGhoaUpKeVKNadFHF2GuoBucZ+Xezk6V6OQTDMSBVdcxnRYiKSR08jC/I1UTiCaKeceEsW7LL798RoaMTAiJLzUrQogm2eRuVjWkr52AiJpSzjGFBZf1njIj2NYEmckxWfl+5ddNu841Ek65WiPWNMVGhN7rtBeo6CE6jPMyAvAmDObOJwREL/gWHzVVCqwhiLXvokoMXwjQHOm+93//+9/t1kRKCAmmNkWoRZNpjnSjozsjncAenRlQFi23gM8LLSLnsxPNzvUa09fJlac3hYnmECHm72DTstD3KZUVI0FU+Hifhg4m1113nQyCRp5Z8w2Dm/PJALO3uOURNuHalQD3gTF8xQgMUj/66KOzyllqD05CSPmJsQhbhZBoyo3CJPmKyRGDyc8RYatgW6MvHaUFYSJAHAOJ+nxmOBHisx1hNSczcosaEfqJM9GYftdYMAV9aSgTd911l1T0V1xxRZY0zBI/8+fP1zn5gVCDEiI/9zY+x6RKAbkPHTpUb0UHc4diMLoR4eqrry6zvpQbDPHAYHim8idS+1RFRJhyKvscVZmoz4sT/WRyvSLU0SBwSyefyEwTa/q8bMmaiM2c71tOnGNk5BFuVBH6ka/s+cBnlUuQixYtkg4hGHTuneYKM4FAAN5FXqsFTKpd6tRciIbdzcUHHHCA3lM+IEJzfabypd12200/YVLLxFSEXtIyyZZEixNdFajCs0TokphDlnQk6guQmIkEsySWjlhzRZr9Ga1kH2/AeVlRm0/ynpNFTrnCkxFhkee7QY9IVBrHH3+8zkmDSG3vvfdWXbp0yTsFlht3xBclVQKU/x//+EfJUQHKh8Vw8Yz69u1bkfJ+/vnnTBVKpPaJoQjRgaVVMJmKWmSV/c5MKvN8EY1LhBLZec51SyYtpWwZZt4feoWDsrg+1x2VBZXJfYzBm+ctU34g3YSTWqUpn2uacjPJT/DlBauHo5L3LpKKVRjQcxKDusN2aMGacebbeJQU9R0h3tUVKtN3330n1w4r8SAgPkzEvcYaa8jitoSQeBE7EUIGRg7ZotDv2MyWnodUxBNU2WsRmuvgZ6sgPCkjFSPMViF7ReiVanY5/aNXRIRu6YHiRZj9LDJ4BN1WoDl0ySWXVPfff7/OSYN3a1FF4n0PGDZFAZEemjw//vhjneMPJnfGzCSlvIPEuViIF8/B+3wIIfEgXiL0RH1eUbhJNZkKPy0e3+NEhEmV8tkXKfpyi9D5PYzQspsc/ctYnAhxrWwRZ4ggQny2fAHIKmdxQF4HH3yw+te//iVRIMR04403yorrWBmgFJFUgv/+978ipkmTJukcfy655BJ1wgkn6K3o4L6xdBM+q7GxUecSQuJGjESYjprczYrBIvREh3qQeg46IvSjKBFCND7iyCnnwpRKZYkqWIQ5kWlOckV+8kUhIPoFEUQossb1yyBCgKV99t13X6n0sfICokH0mIybBBGdHnHEEVJOrG2Xj/3226+kjjJmnUL0PI3bcyCEtBLrzjKZyjogFRRZOUXoFYxIqbUs/sLOT7Do/XBkasqA8rg+O1QKKchSQGVvmjbjWvE/8cQTmYVcjz32WJ2bC8rfrVu3ot/p4Z0lImJKkJD4E2sRlkwlRWjAviKjKv/hFqRSQEg777yzDPSHCLFMUpCkIPOOHTtGfv8IIM+ePXvKkkWldrQhhFSe2hYhIS7uu+8+GcOHdfUgwrXXXjtQdBgSsuOOO0YW4RdffKG23357kWwxEg3ioYceUtOmTdNbhJByQhESa5g7d650kMG7S4hwqaWWChxCgZly0NszSrMmxIdOQ5hJptDQjCjgWhtssIF65JFHdA4hpJxQhMQ6ICwMlIcM582bp3OzOe2009QDDzygtwoDYdbX16u//e1vZZfgMccco9Zff/2qbWbF88Z9mC8V+GlSOaNmQoqFIiTWgQoYM7xAhH5j+7B/vfXWkwnCw4DjL7vsMrneJ598onNLA9fEUk5oZsV1MYdrNfL111+rrbbaStZnRLM0ZI4hJb169ZL7Qs9cTMhASHtCERIrwZhHVMTo1ekFUQqWXgob2Y0fP16u9fzzz4vAghKui+Texk98Dn7HOo4zZ85Ul156qdpss83kmia99dZb+tOqC6xFecMNN6gHH3xQ7gMyRJPzV199JfsxLR/yyhlFExIVipBYyZgxY6RixthHyMjNL7/8orbeemuRUyGwTBPeNSJyi5ownRx+YqmqTp06ZYnPnTDxc5iyxA3I7a9//auU3axCgqnmzPPGT4gQ+exdS9oTipBYydSpU6UCxlhBr2RmzJihBg8enCNIL4jeMH+oEValEqKpagTPD1848HPAgAFyL+4JzPHcTeRbjaIntQNFSKzE9BxFwnssN1g6atiwYXorGIwXxAD9KGnKlCm++ViqyZ0gapOqvdkQkkPEi45EbuHhvvH8DznkkIJfOgipJBQhsRJUyKussopUxM8884zOTXPYYYdJkycpDxA7njOeq5uGhgbJN8+aUSFpLyhCYiWIQPB+DhXx2LFjdW46HwPtq7VzShwZPny4PGfM6GOA9DbaaCNZqxKrl9x0000yEw8jQ9IeUITEWkxHDfeco6igl1hiCUYnZQJiQ9MnnvPs2bN1rlIvv/yy5B166KHyrDH13Z133qn3EtK2UITEWkzPUYxzM5HIhx9+KGMIi41MzjjjDNW/f3+9FY2JEyfKNGpXXXWVRKu1EB3h/eaaa66punfvnvXl4vvvv5f5WAcNGqQGDhyoevfuzS8fpN2gCIm1mHdXyyyzTKYSRg9NRDDFcvHFF6s77rhDb0UDYxpNqhURAtzP/Pnz9VYr6EGKjkm10CGIVDcUIbGWlpYWESGSeSd47rnnyswn7UmtiTAfNtwjiT8UIbEWRIFmHOCECROkUt5ll11kVf2ovPbaa+qggw6SGWtKrdxtEiEhcYAiJNYC0ey1114iQkSCEOOSSy6pFi1apI8IB87D7DCYkQbXwqK8AHLFFGPudP755+fk3XvvvXK8wYiQ78wIaRsoQmI15513nshrjz32kPdU6NIfVUDo4HLRRReppqYmGTj+7bffSj5Ei2u5E6YS8+Z5Iz9GhIS0LRQhsRpEYxAhljmaNWuWOvroo4sSEIS25557ylRi5nz8DJvcUISEtC0UIbEarEcIEXbu3FmNGjVKjR49Wu+JhrkOosKbb75Z8iA05BVKjY2NcryBIiSkbaEIidWgqbJDhw4iJAybQFf+YrjxxhtVjx491K+//irXAhCZtxnULxnh4SeS+x0hZUhI5aEIidVANJtuuqnIa/XVV1effvqp3hONBQsWqK5du0qnmTlz5ujcaECAZmkmlAcrYCCPEFJZKEJiNRDhEUccIeJZaaWVJAorFlyr1PO9yXS8IYRUDoqQWM+IESNEhHwvR4idUITEep599lkRIQbDE0LsgyIk1mM6uIwfP17nEEJsgiIk1oP3eiuuuKJMAk0IsQ+KkFgP3gsWO2yCEFL9UISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkKK4M8//1QnnXSSuvjii5ksS6T2oAgJKYI//vhDrbvuumqLLbZQW265JZNFidQeFCEhRfD777+rDTfcUIRICKluKEJCiuCll15Sm2yyiTSRkuoHX2hMIvZBERJSBGPHjlUXXnih3goHosinnnpKKlv8jjRnzhz1448/6iMqB4R99913W1fRv/7662rw4MF573vGjBnqrLPOUvvvv7+66aab1Oeff673EFugCAmJCKQycOBAddttt+mcwuCcxRZbTPXr10/1799fnX/++dLxYsiQIWqvvfaqqKDw2ZA2Pr9aRfjbb7/lpEWLFqmffvpJfvrtx30j9e7dW+4fv3v54osv1JFHHqneeust+ZKyww47SKT//fff6yOIDVCEhEQEFermm28u0VxYJkyYICKaOHGidLJ57bXXJL+pqUl17ty5ooK67rrrRAaQQ7Vy1113qRNPPDErDRo0SB177LHq8MMPz9k3bty4jPg+/vhjtfLKK0sU7wVfZvDv8v7778s2/j2wjc8j9kAREhIRSGv11VePJK/p06dLU+iAAQPUYYcdpnOVRCqo0P2ilXKAMkKCt99+u86pTnAf3gSx//LLL/LTb7/7mT7wwAOqa9eu6oMPPtA5aSZNmiRRII4HCxYsEBGOHDlStokdUISEROTDDz+UqC6qvFBhd+rUSV177bWyDTHusssu6t5775XtcoPy3XDDDapnz57yWTYD0XXr1i2widQwZswYEeFjjz2mc4gNUISERCSZTGZFdWEx0QZ+gueff16233vvPflZ7qgQ8tt5550lCiVKJkBAVBjUOQlfcNZbbz2RpYkQiR1QhIRE5KKLLlKXXHKJ3grPPffco7bffvuM8O644w7pOHPggQeqCy64QPLKybx580SwiAqDQFkQqUKaplyQALbjLANTRhPpouzIy1fmF198UZ4HepJ6wfn4t3j00Udjfd+kMlCEhEQAFSbENWXKFJ0THogPPRMNqHCnTp2aGVJRbu6//36p+F9++WWdkw0+89BDD5Vjll9+ebkvvHM74IADJO+YY46R3pRxI5VKqW222UatuOKKMqkBhoWYLxnoeBT0pQLSXGqppdTkyZN1Tho8B9wzmqzx+2effVaRLyYkvlCEhEQAFWW1zCiDsXEQWktLi85pBUK/7LLLpML/9ttvpRcrjoUMkRobG2U7kUjoM+IBZLbZZpup++67T+4B5Uc5kSDxbbfdVq222mqZSNEN/s26dOmirr/+ejkX4Oe5554r18EXEiTTgYnYA0VISARQwXbs2DFTkcYVVPoYSI5Iz0/aGPqx1VZbZfbhviCTNdZYQ/LQkxLbiGLdQKroAdse4JkfdNBB6rjjjtM5So0ePVrKefXVV0t0jd8x/6ufCHF+r1691Omnn565b0SSOMeb3JE7qX0oQkIi8Nxzz6k999wz9iJE+XbffXe10UYb+YoQPVUhAQOGFUAApmPN119/rZ588smc+4QgMQA9DA8//HDBhDKYhCbOQs8V7/HM/eDYhoYGKffs2bMlD82mSH7geEhyv/32y1zDRIHeVKgcpLagCAmJAGaDQRd7AypMNKVFSWiG88vPl6JGYSgXoqeNN97YV4RezLABDL7PB64b5noAs+dceuml6sorr5SIDdEbmiUxjVlQiiIglAMR3tprrx2qTLg2RIgvCGHvgdgBRUhISFCR4h2UW0qIHkxzGtKyyy4rQxYQNaIDxiGHHKKOOOII6XiC7vunnHKKvLuDDOvr62VWFBy79dZby3g/dABxX8+kvn37RpIEjsU7wDCz1uBYREn4nDfeeEPnpvPdYDtOApk2bZqUGc/VTdBzQj6kiSbjap5lh5QfipCQkEACK6ywQs48lIh83NLadddd5VhUvEHJ7Hf/NOnXX39VDz74oDRBusVopmULA66Ja+A8dIbx8vbbb0szJ94Bfvrpp3JfiJZwHkA50GkGPwGmiOvevbuqq6vL5LU1+FxMk3bqqafK76ajDGaNMaDJF188/MA5GEd49tlnZ+6TEEAREhISTPC86qqr5ogA25g42wgLqRwrmaOynjt3rkSMuCaaSKNU4Bgvh/O84+ZwjYMPPlj2XXPNNZlm0aFDh+ojlBo2bJgIHcei4wkk+PPPP8txUYRcTt588035fMgMPUQx+B3b6CQD8O+AYRVBq0dgf4cOHWRYCSFuKEJCQoJ5KXfbbTdfGaGSxvyjqJhNeuKJJ/Te0kAFjuECmCLsm2++0bmFQfMfIj13xGRAz0lEgGeccYY0FyKqRW9YDJtAJIrym56XX375pURaw4cPlxXa/XpktgWIxCG/W2+9VcYMnnDCCZmZYPBuc4MNNlBXXHFFzhcVAybWxn3FcWwkaV8oQlIxIAxUSniPNn/+/EwFhXy/2T3iDkRw3nnn6a1csGKBW4QQzQ8//KD3lgaeGVZVgKjCgueNd4/oWenF9ArFIHL0soQ0IUxI5emnn855h4bPx3AL7G9PML0dmj4xiTiEjLLfeOONasSIETK0w+9LigFNoogY20vkJL7EU4TNCdXQmFKtw4BTKtWsf3XjHJfwy89DS1ODc06LalmoM8LgfE5dXYNKRjknFC0qWZ9w7g6kVKI+6brn/KTvQ294WZhUDXV1kZ9NOUFFim/pWNsNnUCWW245WboIkxljkDY6clQb6PyC925BoBI+88wzs2R48skn562co4AKHO/FsDp+WPBvsP766/tW/lHKtXDhQrXMMsuod999V6aYK9c9FUMxn40vBZgo/aqrrgqMGIm9xFaEdR4ppBrrVJ0jRzeSV2dEEg4IJOo5Uh73Z2vRoOOAf8q+fktTwl+i+joNTfpORbjhyyb37yNPuUfPs2pLUOmiN+Qee+wh67uh4kLlgw4XECIEgW/21QTuAe8Hvcv4eMF94t2aW4Z+TZNtBf4t8DdZ6vNGVI8xfOjIE9QZJc7gCwzeLZp1BwlxE18R5lTkTsTklga2I0RQBkii9Roh8S1PFNJlz0RozU6E6/zIFRaOiyJpv+OLey7lAiJA1IKB3H5Te6Fpbemll666FcBxX34dZfxobm6WqbyMCIOeRVuB8Xt4p1bKkAGUHyLEMJAwzyBOoHl60003jdzZiNhDFYkwW2KBUVYB2keEjp5c0VvKEaFTEpWsd8pS3xpJolwiR70tKUtqOMe1z31MgSg18j0XCSKQfLOPPPTQQ1UxM4sX9JTE+6Ww5b7llluyokK8p2svgeBz0ayLLyjVJrFSwb8XOgJhKIhf8zAhIEYiTEdNUmk7gvBW5K0JEVDrsSa5K/ocmZjkyCy9z5FowDGt18n9jNxjIuDIVM5zhJVEZAi5Otdyv8crStIAEmzHKNCN6ZkXtF4fvpW3d4eLYkDnjLBTiwFUwGb6L5PQbb+9vgBAgJijE02cNoHernj2lCDJRywjQpFVYATm1xwYEi2fhiZHRlGEU4aI0NDifDaulGpMR4PRRejzJSDvF4dKdPIJBr34TMWPqbWwBhya5IwAUCG3lwxKAcMNRo4cqbfCsWjRIrXddttlngc6Df3vf//TewkhcSGWIvTrGNNKsSJMNytCGpBNS7O7V2p+ssrj0wQJmaU77riTn4CcsuM6zjUSThlwTjkiQu912hO8jzEDnU3C+zJEgVHeUeEbfDGpEkDcGDA/a9YsnROeGTNmSG9L8yww5ZptzZOExJ0YitAV8ZjmPh3JBacQYsQ1nOuljGy0jArjei8X0PwYWkROGTB0I9mYvk6uPL0pTDRX+ItBy8Iw91k+Xn31Vemc4ZYhEsahoRt+IU477TSZr7NPnz4ygBsdHbAG4DrrrCMznGCpoFVWWUXm0cTcnlhs9f/+7//kHVglgLjw+cWIFueatf1MwqDvaoyKCalV4idCIz0ncpIm0hz5FBMRpmUGWbmjrlRjiOuYCBCRnJapVyvhRIgyOJ/XnMzILWpE6CfOhHMP3jzfFCDxSgEBQIhYUQBL+xgJ3HbbbfqI/OB8v4So0r0NobhTJcCQAZQdn1cMOG/gwIGZZ4CEd46V4JVXXmGqUCK1S+xEiHdnySancpemSEd6ZRChWzBZsgnRySSwPCLsdMRmhOYvVpRXy0iu0UpUEfoRTsK54LPKLcggUSDfTJCMSLHaoqEXXnhBZmgppdyIhDGhgBEhBndXYnYdRMnmM5jKl44++mj9hEktEjMROtIwkZeWRqbCLpgC5OiJ4ryykesHyiC3PGn0+0Z9nVYZuUSZRfbxBr8Iz5vyijGnXOHJPNciz/cC2aGix6oGfmA6L1QomNsyDLhe1FRM02WYdf7GjRsnzbWlYp4BBnZXKsLAhNNMlUmkdomVCE2PyvwVPCKskBGhT8TnFaGRlJ9IM2MVveXxXNcdlQWJ1S9y8+blli0fkG7CSS5x4nNNU24mRYuei+Wrr75Sf/nLXwI7xGCVA0gA0VUhsHKD+SYeJUV9RwhxQk75QBR41FFHlTw7DK6D6b1QTsxJSgiJD/ERoVOBZzqvlEOEuIYjBnSOaZVCQGpMahkimQ4qqdYhFp7ySHOpq89HttBQPm8k1/qO0k3xItTvG/VWhhBNvZVi9uzZUsnjnaAXCAedXzAEAZFbGLzRXtgUBUyKPWXKFL3lD67Zu3dvWbOvFO6++255PpzdhJD4Eb/OMqBEEUIwQefnk01g70p3eZzfwwgt+/PTciyPCHGtbBFniCBCeUbyJSDfkwwPoh00+WHoxPPPPy/yQ4UPkWDVhIMOOqikKb7KDcqFHqiIVPOB4yCwqJJ1g9UcsBzSkCFDKEFCYkgNijBgpQpNtOZHjSkPRONTLq/Q1EKnDFmiChZhVmTqm1z3Ks2eee49gghF1rh+GUSIyr1v377qmWeekSVx1lxzTZlmDR1jVl55ZXXOOefESoIA829CcPvuu29eOWGlB0SExQpswYIFsvoDppUrRaaEkMpRkxFhPnKjtRCgPF7BiJRaheWVXBhyBJoX575NGVAe12eHShVuMkWnE8gC6ccff5QekZjOC7/HTQAoj+nBWWgi7fHjx0skVwxYRR0rUeALASVYOdD6cM8997DZmRQNRRgGPxEa8pY1P6HGMZKy88gjj6hRo0aJCJE+++wzvSeXY489Vtb0iwrEh042vXr1il00XAvg+WIybUwmjgkX8O9IEZJiiacICakQqEC33XZbGSSPaBAV6OOPP673ZoNKFc2iUYc64Dz0YMWsN8UM6Qjiu+++a9eJu+OEEeHUqVPlJ0VISoEiJFaBihIVJipS9GRFBTps2DC9Nxscg/34GRZc//rrr5fzyrkGIcqA6LQaV/avNPj3pAhJKVCExFrQmxUVKJaM8qtAEQni/WqUynXSpElqiSWWUM8995zOKR18/ogRI6Ss6JHblkDASO7mXUS5yDM9g9sbipCUCkVIrGXMmDFSgW6wwQa+FSjGRGJF9rBgZXpMCD5hwoSyVMi4xjvvvCPvGlHO/fffP1J0Wir4fHQUQs9aDItBhxQIHtvoGYzndtJJJ5W1+bcYKEJSKhQhsRb0akUFiuQnGESMY8eO1Vv5+eKLL2Q+0kQiIddChYwU9Ls3Dz8hFLwHhFAxrVu/fv0y5UMKO2F5uZg5c6bMiTpv3rxMGbC+IiZPABAj8jC5entiRIj3sniWhESFIiTW8uWXX6rFF19cKlHIxw0qVCwbhfUECwGB9e/fPzN2stj097//PSMcb+rUqVObR17ohHLrrbeq+fPnSxmwrqK7yffOO++U/KB3rG0FI0JSKhQhsRZEYVjjEJUoKnw32LfkkkvKQsP5wHFDhw6Va1QyITpt60oeYnnxxRczwhs+fLjek+bkk0+WfPTczAfKjWgN14uSwoJjUQ78pAhJMVCExFpQaeK9GypRzIPqZs6cOapnz54iukJgvtInnngidPIej4m/vQlycad3331Xf1rbc8opp8gzmjx5ss5JPzssmoxFkTFpQj7wDClCEmcoQmI1phLFwGx3JXrLLbfI/Ki2V6yQWJ8+feQZffLJJzpXZZpLMXUcmmzDfGGoFBQhKRWKkFgNlldCJbrxxhtnVaL19fXq8ssv11v2Asl17NgxJzpGj1o8t2QyKcfg97Z+h2mgCEmpUITEakxkg1lgTEWPynSbbbaRMYHtSRwq9TfffFOej7vpGOXaZ599MvLDbDdHHnlkm0eFKAeSW4QoQxyeG6kuKEJiNag4sUQSKlIz5yjyll56afXRRx/JdlQwjhDXK6ZCnjZtmpx/xx13qLXXXrvN5eLFRH5YSsoNxIh8vOPEXJ/ogduW4LmgyRa9bdFbF2XBWEfTc7dQBx5C3FCExGpMhYqKFOPmAFbOwFCGYiWE8Yk333yz3ooGKnBENviJMrW3CCHla6+9NqccEN9DDz2kBg0aJGMo2xqUx69TERLy8W9ASFgoQmI1iNowewqkgzlCwe2336723nvvdm1iM4P921uEhNgARUisBwPCIR0zVg/j4y699FK9NzyQ1gknnBA4d2kUENlQhIS0DRQhsZ6JEyeKdNBBBgLDNGKPPfaY3hsevKOaNWuWvKdC8yZ44403ZAydO2HGFm+eOd5gRMi1DAmpPBQhsR68E4R0MIUYekF26NAh8hJKECiu8cEHH0gPVLdIEdW5Ez7Dm4fkhhEhIW0HRUisB1EXpIMEKfbo0aNoASGy6969e9aYOkgyTHJDERLSdlCExHogobXWWkvEgxUeMMtMMQLCdbBEEeYefe2110Sq06dPz0g2Xzr00EP1VdJQhIS0HRQhIQ5mgDg6yuCdnTdCCwPWDsQ1MEh/+eWXVy+99JLkQ2ZhEjDRoREhIstiykIICQ9FSIjDyJEjRTzo6IJ19ooBMttiiy1U165dZfxdMWDYBDrdIKE8e+yxh5SJMiSkclCEhDggeoN4MK9mKpXSudGBDEuVlokKzbUoQUIqC0VIiAM6zGD9QdMcSQixB4qQEAdEX926dVMbbLBB5n0dIcQOKEJCHCA/zDlajllhCCHVBUVIiAZLCY0aNUpvEUJsgSIkRIMem2wWJcQ+KEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJMThzz//lPTkk0+qqVOnSnL//tRTT+kjCSG1BkVIrOePP/5QQ4cOVSuttJJabLHFfNNee+2ljyaE1BoUIbEaSHD77bdXq6++ukokEhL5DRkyRHXq1EltscUW6qabbpLI8PPPP9dnEEJqDYqQWAuaQkeNGiURX1NTk85NM2DAANWlSxf1+++/6xxCSK1CERJrmTJlikhwt912EykaECUOGjRILbvssuq3337TuYSQWoUiJNZy4403iggRFbr54YcfJBrs27cvI0JCLIAiJNZy+eWXiwhTqZTOSfPggw9K/oUXXijRISGktqEIibVMnjxZhPfpp5/qnPR7wz59+qhddtmF0SAhlkAREmvB+7+11lpLjRkzRiI/pDPOOEOtu+66fDdIiEVQhMRqZs+erfbcc0+JDHv06CHNoYwECbELipBYD8SHZGaXIYTYBUVICCHEaihCQgghVhNPETYnVF1dg0ou1Ntlo0Ul6xMq3Vk+pRL1SSenbWlpalCJZr3hZWFSNdTVBe8nhBBSduIrwkbX2C4tiLrAZOSWpqUp4S9RfZ2GJq0/EW72uTk45yS9YnLyEvUNnjKYVFjgqUbnOB8JQ5JZ993GoNekeV+GhJ6T7m1CCKlFqkOEkXGiPUdKmciqOSWyyxUNjisgQgeIKyNPAKH6li9slOn3ue0ToQJ0EJkwYYI65JBDZLJp9KD0S+XqSGI6pURNhBBSCWpUhGl5magr5Ygw3SzaoBrqW6M3yE3kmInmWs/Jwhs5RhYhPtv1Ge7P0lFqzj6dsgRcASCYe+65R0S35pprqmOOOUZWY+jYsaPaYYcd1AUXXCBDCu67776yyQjXLyZRhoSQShAjESJKKqMMHHnJeaZpU2SW/f4NEgx3badsbvGVHBFqcJ0ox1cATC+GKPCAAw7INH9COEcddZRaeuml1a+//ip55cQsdOuXnnnmGfX888+rl19+Wc2dO1d98MEHqqWlRf3000/6bEIIKS81GxEaWpqSEsmlGtPRYHEi9JAvigsUW67oGwLfMyJVorNQNngniOWGEA3OmzdP56ZBFIh8rMVXTQwbNkytscYa7ZogcEJI9RBLEUqzphGhj3QgMzkmK99PHDqSc66RcISHc8KL0NucGaZptEW1RJCXtzxtzSeffCKywzJEXrAMEfZ99dVXOqd8IOIsJoUBC+m2d6IICakuYihCl4ACoqvQAnEiy0Szc73G9HVy5elNAVGYaWYFXjFDiLrZteB1skCEmL+jTsvCIEmXB0wvBtmNHDlS56RBb1G8L9xyyy1zVl/A+8RZs2ZJMyr2nXDCCWrGjBk5x+Xj+OOPV8cdd1xWOvDAAwumKJ9BCCFhiZ8IjWiMYHxkGE6EEKojmuZkRkrRIkIXbhF6QRl9o8NW/AScaPTKMyBV8B3i+++/LyKcNm2azkkzYsQIyX/22Wd1TpqHHnpIygRJoun0/PPPl/d6EOakSZP0UYXBObg23gW+9NJLodKLL76ozyaEkPISOxHiXV6yycjF1flEoq50pGWElnJkkqsg17s4j6AqIcJi3zOGk3ku+LxyCRIR1k477SQ9QwGaHyGc1VZbzXctPsjxiy++UJ07d5ahFjgex/Ts2VNdddVV+ihCCKkuYiZC/U4vJ8pKN5ca4bRKxCXKLLKPN/hFZt7kKzUjQidaTTZlN41KhxenDEnvtfOJKkQUGURGhEWe7yWZTKru3burbt26yRCFrbbaSt15552+zZAQH3pxQogLFiyQPBNVIsojhJBqJFYizMwI4xUFmktdYnFHUyIGH+n4RVzevOgRYev7RoNc05FjzuwzgUDeCSd5pOl99xhioH+5+PHHH9WcOXNEaoXew2HoA8pnjhs3bpxaaaWV1Ndff13w3GoDTcEvvPBCpEQIqT5iJMKUE21pxXhEKM2lrs4n2UJLN4VmCy0dEZZbhN5ytAo6V5D+oFw+gvOIPs6cfvrp0qPU9OREFInOL+h4M3HiRH1U9TNq1Ci1/PLLS7QbNmHoBCGk+ohfZxngFqHzexihZTcVpuVYThEiCsp7PS3LYFCmgN6kEUSIz5SIsUxNo1Ew4nO/D+zfv7+M3cPitosWLdK51Q0i2969e6uZM2eqb7/9NlIihFQf8RYhBOFT4XuFphamVCpLMMEibG16DEq5EVuuaP3zcH1fGUqzZ56mzggilM9FOdtBhADvAr/77ju9pdRnn30mzaXmnWEtgLGA2267rYifEFL7xFeEXjGITFqF5ZVcGHIEWhT+HXHSpPdlCxXvBPW96MgyUqqSJtNaAdFgv379ZKo3QogdVI8IDSZaLAL/4RbhSUdjAc2bLlJNlFe1gskC1l13XUaDhFhEPEVISDsA+WHu1UcffVTnpEGUiGTkiJ/Yxgw8+EkIqW4oQkI0jzzyiAwFccsN70AxtrJr167SWxarcaCXLJap6tChgxo4cKC6//779dGEkGqEIiTEAVEeesRiLlUDhHj44YfLXKpmNY4+ffqou+66S6JBJDSjQoxsSiWkeqEICXHAXKmbbLJJVjSIuVB79eoleWY1juHDh+u9SiYehwghULOWIyGk+qAIifUgmsM0c7feeqvOSXPvvfeqCRMmiAgxn+oKK6yQJTxEhJAjROgWKCGkuqAISU0DQWGZKayUEdR8iWgQQyaCojpMHwfhYfIA9zXwThH5o0eP1jmEkGqEIiQ1CyK2IUOGqC5duoiwXn31Vb2nFYhtnXXWkYnGg8Aq/Th//PjxOid9Hq6NadiwwDG2g0RLCIk3FCGpWTBNGjq5nH322SKyM888U+9pxe/doBvIzZz/5ptv6lylWlpaJG+fffaRYxoaGtRtt92m9xJCqgmKkNQsJkJ766231OKLLy7vAd3Nn5Af1mO8+uqrdU4uOAYz/Ky66qpZssRUcxBhIpGQfPyOJaoIIdUHRUhqHghx8ODBIiusv2iYPHmyWmWVVWRsYBCQKM7DQHt30+fcuXMlH+8JN910UzVmzJjAqJIQEm8oQmIF06dPF3FhlQwjLMgNnWjyAflhBX9vRxrkT5s2TV188cWyqj8lSEj1QhESK0DHGUjQRIXz5s2T3xcuLDBxLCGk5qEIiTXcfffdIj80ZeLd3kknnaT3EEJshiIk1oDmS3R8gQwxZALv/wghhCIkVjFu3DgR4dChQ3UOIcR2KEJiFej0AhG+8sorOocQYjsUIbEO9Ph0D4UghNgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqYizCFpWsr1N1jSm93b60NDWoRLPe8LIwqRrq6oL3x5g2va/mhKqra1DJhXq7bOBvJaHSfykplahPOjnhKNv9B95bumzJhWFLRAhpa2IuwvJWmqj0ShFrqtERs08lW+p1S6Vq7guycF9Pi6YuMBm5pWlpglD0hht9nYYmfQcipexz81GO+8exmc93E1KmUoase08nXFPK4bPPr8x+lP3fkZAaI8YidL7ZVyB6kEohQsSQDcrkrWCjRSCVoiruyyvCyKCcLqk0p6TMuRW93/3ko9T7d0ek2aBsvoIMSannG0r7+yCktom5CH2+BQek0M13+IYeqYLz+TycXyCaKUflFYlquK+SRej8Vbiit5QjwvS9OLJw3Y9vFJX1bMp1/wHXcVL67zH4b9j3OTrPx/t3nCtCfc2ozzHS3wchdhFzEUb5Vm8oUPlIs5n//nQKEYW2S6VSrfcVUQaFcO5TznPKmoQ09H27BVJ0FBX5/tMSznquuIaRlCmrG+zP83ctondJznsvInhfCbbB3wchNUp8RVigwiiG4EokH7kVTINT+bm3s1PbVyhVc1+ojCOX05+WpqT8baQa09FgdBGW4/7zidC5vp9UC/5dp8tl7ifrXnBuEV9Uivv7IMQe4i3CMkcn4SrIwuBbu7cJqz1pr/sK6uCRSZ5/v6xoR4SQfTw+O/eafgJyZIHrONdIOPftLXexzyPq/TufFCjCVGOA7OS+83/Bg9zNNVvvJUCsISjX3wchtUpsRViwknWnkBWE7zWdigwVcviKAt/Y81dkLW3cVb697uvjadeqa6/Lk+5Pqe/0sWlpmLL5/3uFFpETWSaanes1pq9T+G/FT6Zeivl3DRKhUy7J85EX9rvzRIx+ZQ6b8pcZlOfvg5DaJdbvCJMh/pOGrjz9Ki2Q5xu6XwWScL7pe/N8U5Hf3qNTJfdlKnxEcmgi9blOuH9L3K9zX83JzD17zysUAZXv/lEWn2NczZAoS1azpFeEBSg9mov+90GIbcRYhGFIV0ThRBjQtBSxYgpXWeciFWJORVoO2ve+wiLNfU3mHaGrzNKJI11RmzL4NysiYssVDYgqQj+Ku38fyeC5e8XnFk7Ef5fSRVievw9CapkaEKHPt10/nArXt0KJ0oEjyrEeMiIs8vxA2vG+II9MFOSXMhWtUxnj+jmfk/4iY8rfKqOAyttzvKFgOZyUVyZF/7uGEKEI3HVMW4uwHH8fhNQ4MRJhupLzq8R8k/wn9lQygeDa/s1AIqhQFQIq54STXGVAhSbf+F15bdrc1L73FfYdYWZGGG/l65GCOyqT8vsIwy9y8+ZFk0cp/64BIvSUOz3eUYNn4HNfQZQmwlL+Plz/HyOUl5BqpMojQogwhHiCvhU7oBItXNEEVCg+lV6bUhX35XrX6xGhu3ckyBYa/m2995CunMsnwlLvH+cXFmEWbSnCUv4+nHMzz9T9OyE1SHWLMFSFhW/8Qcf4V6zZoEIOiDojCAMVj3y7DhWlhSEe9xUJtwh9Klc/oWU/r7Qcw5xXWB7luP8iRRjhb6B4EZb490EREouoahGKXPJWKqjssr/xZ3eBz1MZAlRq+SLOCMKQSr1sIozPfUXCSADX93kOXqGphSmVyroH3Je/CFubMIOS637Ldv9poeR8Vp5zo4oN9xZdhCX+fQiue6vE3wIhMaK6RCgVmKvCyfefGZWuT2WXEZJJgf/JncrC7JNruc4JkypVeVTzfeHzvOd7/k2LiTxyBJqXct5/uIjQK+oo9xhZhCX/fRBiH9UZEUrlGSxBqXgKRF5yTJVVBlV/X34iNGBfkdFy4CwuFccRoR7UX5h0hFVcM2c4avXvnpBKU+WdZQghhJDSoAgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiNVQhIQQQqyGIiSEEGI1FCEhhBCroQgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiMUo9f+ovebP0qnL/QAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83-%E5%85%AC%E5%BC%8F%E5%B0%8F.jpg": {
- "image/jpeg": "/9j/4AAQSkZJRgABAQEAYABgAAD/4TnWRXhpZgAATU0AKgAAAAgABgALAAIAAAAmAAAIYgESAAMAAAABAAEAAAExAAIAAAAmAAAIiAEyAAIAAAAUAAAIrodpAAQAAAABAAAIwuocAAcAAAgMAAAAVgAAEUYc6gAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdpbmRvd3MgUGhvdG8gRWRpdG9yIDEwLjAuMTAwMTEuMTYzODQAV2luZG93cyBQaG90byBFZGl0b3IgMTAuMC4xMDAxMS4xNjM4NAAyMDIwOjA5OjAzIDE1OjAyOjUxAAAGkAMAAgAAABQAABEckAQAAgAAABQAABEwkpEAAgAAAAMyMgAAkpIAAgAAAAMyMgAAoAEAAwAAAAEAAQAA6hwABwAACAwAAAkQAAAAABzqAAAACAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMjAyMDowOTowMyAxNDo1ODo1NQAyMDIwOjA5OjAzIDE0OjU4OjU1AAAAAAYBAwADAAAAAQAGAAABGgAFAAAAAQAAEZQBGwAFAAAAAQAAEZwBKAADAAAAAQACAAACAQAEAAAAAQAAEaQCAgAEAAAAAQAAKCkAAAAAAAAAYAAAAAEAAABgAAAAAf/Y/9sAQwAIBgYHBgUIBwcHCQkICgwUDQwLCwwZEhMPFB0aHx4dGhwcICQuJyAiLCMcHCg3KSwwMTQ0NB8nOT04MjwuMzQy/9sAQwEJCQkMCwwYDQ0YMiEcITIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIy/8AAEQgAvgEAAwEhAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A9/ooAKw9She91uG3iuZIJYIDPGVPBO7HzDuKARtru2jdjdjnHTNLQAUUAFFACZHrWXKLn/hJLZkEn2XyGDkN8u7PGR60hl+W4ji++4AHqcU9JFdA6kFTyCDmhO4WEklWJC7nCjqSelQQahbXEmyKaN2PICsDmlcdjP1xknu9LsH3AT3G/joQg3EH61iWWqax/wAJHe2w8zUFtQyQAFIlk55Lk45XhflHvimIi1DXNQuNVu9NthcNcrPa5jt1LeUpGZMsB0zWsum2N1r1xaJEJrNR5s0bDKRTZ4Kn+FsckCgDpFUIiqowqjAFLTEFFABketFABTGmiUZaRAN23JYdfT60ARNfWiTxwPcxLLL9xC4y30HerFABRQAUUAIzBVLHoBmuYttW+1eNCEsbxEWwYeZLDtU4cHg+lIZC/iy8Fvav9hQNfv5doQ+QGyQQ/p061r6jeXenXVnKWSS3mkWCSLHIZujKf6UAa9Z93cajFdIltYxzQnG6RrgIV/DBzTBGhWZry2Y0uW5vbR7mK3Bk8uMAtx6ZIoEc3Hcw3MUckHhLWDEyh0bdGuQeRj95W5aaTZX9mst3p00TOMNDdPuYD3wSP1pIZDH4T8Jzzs6aRpk0sTYY+UrFD7+hrSv7i20XR5bgqsNtbRltqgAAeg7UAtzE0nVNRm1O3t9QNnNHeQtKsVuCWtx6OckMCOM4HPHNdDDp9lbSeZb2dvFJj7yRhT+YFCBsw79tRvkMFz4emkQPlXhvUUgjowYMrKfpRZXd7NlLGwsGntv3TC61EvKg9Cyq5/M0IHYy5vEep6dPeL9i02IRsXuJYnuJlDY5ywhAz7ZrprD+1ZWhnnubRrZ03bI4WVuRxyT/AEpgadFAhruscbSOwVVGST0ArJvr29l3QWemyTW80Xy3ayoFGR1xnJ/CgDlNIn8Raff2k2oJeT2zo4jiVc4VV6P/ALWRkH0rpNGnbUtPuZnuybmfkxRtgwccKM9D6n1pWAqWdjr32C9ibUQ98XVVlYHasfoP9vHU+tRah4fvdV0O0sohLpxiuVeVRKHLjPLbvXvTAr6b8PV066tp/wC0pZmiuRM3mKCWCkkAHt15x1rt6ACigAooAa7BEZ26KMmsOzuY9Q8UNc2z74I7Ly2bBHzFwcc+woAv3WjWN3am3kgAj7bOCOc8HtzVmS1hmnimkQM8RyhP8J9aAJqz7nRNMvJzPcWcckp6s2aAL6qERVUYVRgD0FY/irULfTvDl5NclgjoY1CqWJZuAAB70AcjPJrD2DW6DVbeJLNDC7EIqyBR0KHdtxnO41fg1+TUPB14lndJJcQFYnmiczMqMAd5wSSeT+VJDOg8MDboNuvkLEFyo2xlAwB4bB55681Z1vTRq+jXVgXCecmAxGQD15HpTEUdKt7+2n2nRtNsUP8ArZbeTPmfRdo6+54963aAEOcHBAOOCRXO22g6r/wkceq32qWU6xxsiRQWBhPPcuZGJ+nT2oAi0Xw7KtpeWOswpcWrT+bEkhV/mySSCAD6deRXTgAAAdBQAtFACMqupVlDKRggjINCqFUKoAUDAAHSgBajEESzNMIkErDaXC8kemaAJKKACigAooAKKACkwO3egBaKACkZ1XG5gMnAyepoAWq91ZW96IhcRhxFIJUB7MOhoAnwMYwMelMjjhj3LGiL6hQBRcCSigAooAKKACigAooAKKACigAooAKKACigCtfWYvYPL8+aBgcrJE2GBrmLfUL648WQ6Tc3hEdoC5mhG1bl8ZEbehAySB6CkM6XU7m4tdPlmtLZrmcDCRL3P+FZ0Oo6hp93DBrAt/LuDtjnhztV/wC62fXsaOodDTsr6G/jkkg3GNZCgYjhsdSPUf4VgeKLm9W8tI7C5Mb2wN5PGBnzY1wNv4kihgi5okv2/U9T1FXcwl0ghBPylVUNuH13fpSakyXHibTbUu3+jxyXbJ2YAbR+RYGgCTRvElprU7wQRypIkYkYOMcFmX+amtS4mS3geWRgqIpZiewFKT0C2pyL63qut6FPf6RauVV/9GEUg8xyGH31bACkc4znBFaOsx/YrYa9Dm3vY0XzUzxMP7jDueePSiKsgZ0VFUIKKACigAooAKKACigAooAKKACigAooAKzP7CsxbJCvmLtuftO8P8xfdnk+nb6cUAadQ3Vpb31u1vdRLLE3VWoAfDDHbwrFCipGgwqqMACqg0q3GoXV6QWmuIlibccgKM8D0znn6CgCHw9pLaHokOntIJPKZ8MB2LkgfgCB+FVtUsriPW4dVt4Wm/0WS0kRSMgMVYMM9eVA/GgB3h3w5aaFbbo0Ju5UHnyu25mPXGfQEnAq5/Z4aO7iubiW4S5JyrnARcYwuKmQyPRdFh0S3lhhmll8x9xaU5PAAA/ICrdxZxXUsLzDesTb1Q9N3Y/hVCLFFABRQAUUAFFABRQAUUAFFABRQAUUAFFAHA22uNe6hp5ttXvpLiSaENHJAIoZo2ySyqRk/Krcg131JDZ53P8AEU2mqa1CU81LcH7MpGA23CkZ6kljgY9DXaaPfTahZmeWONfnIVo2yrgHqM8j8aEwZoUUxGJpMmoXF5cXUt6r2ZmkjWAxgFNpAGD36Hr61qrd27TGFZ4jKDtKBxkHGcY9cc0DYs1xDbhTNKkYdgil2xlj0H1qrqWp2ul2zXN3IUiUgZ2kkknAAA5JJ7CpkOKH6bqdrqtr9otHLIG2sGQoyt6FWAIPI6+tXKokKKACigAooAKKACigAooAKKACigAooAKKAPHdP8LeJrXxLDeNok5srZWEJW8jE3IUYyzHC/L2Pc16jp9zqF5bzm+05rFgcIhmVywx1yvApDObtvB9rbxgT6QLuSYea0hkCtEyr8q5zySxY5Hc5q3pd14gs9XtdPurNpNPlXK3LsGeP5SSjEcEggDPegDqqrX0P2i0eM3MluDj95G20j8aYjl9M8OxzyJPFf3UsMN1MHSWcujhlIJHbOW6+xqSDwtPpelwWNiyyul6JkupGw6LwWLH+InkfQgdqSG2beu2015pE1vbwxSyyYRfNGVXJxuI746/hVC88PiHw7Y2NmnnvYSwzRCV+XMbhuT74P50AW9Fs54JNQurmMRPeXPmiMNnaoVVGT6/LmtamIKKACigAooAKKACigApCSBxQAisW7U6gbEAxS0CCigAooAqTX3k6hb2rQSlZw22VVyoIGcH04zVoMpJAIJHUZ6UALRQBy2oeMVtJ7xVt18i2mS1M7ygDzmAO3b1IAZST7+1R6B4x0/xfK1kLORFaNiyzEZLLt3Lj23de+DUpjsbVzqWm6IILaTEKspKIkZICjGTwOnI59606oRWv7+30y0a6un2QqQGbGcZOB/OrOaAEzUF7ewafZTXd0/lwQqXdsZwB9KVwLFFMApksscETyyuqRoCzOxwFA7k0AVrDVLLUxL9juFlMTbXAyCM8g4PYjkHoRyM1Ld3K2dpLcukjrEpYrGhdiB6Ack+woAybLxZpd/gwz7leQRwlRnzuQCVA5KgnBOMZB9KZofiu213U7myhgkRoFcsWI/hleLt6lCfpSQ2jey27oMfWmNcwrdR2zOBNIpdU7kDGT+o/Oi4EtFMQUUAFFABRQAUUAcpr16bDXoLa5vGa0v7afEDHaAyKp4YcjjNZ3gDVrZtOuJ5Io7OOdllJku95DGNCV+Y5wCTip6j6HcxyxzRrJE6ujchlOQafVCOOt00Yz+J/wC0vs8lvDqIuWEmDt228Jzj221a8M6r4d1SZhpFqIZIw7gtEEJDNl8f8CPP1FIZV1d9bj8Y20tqlnNElpMPK2sZGj8yHf3xu6Y7VZsLvxHDpKNfW6zagt4kUscajZ5R2gsp46A5J9cjpQBmeNo76+uJLBBdyRu1sVt4Y8rJH5hMxJ6ZCjI57DHWtnS59Tk8V6lHeSSCyRP9CUpgOON5OPQlQPqaAF124kNykK/2vAFGTLZxqyvntzz+lWPFIU+G7pG+64VDnvlgP60AbNQXNytsItySOZJFjURoWwSep9AOpPtTET1jeJtIGs6TJbskky4z9nV1VZD/ALW4EHHXB4PegA8LWM+n+G7K3u2ne5SPEhuFQODk8YQlQB2AJ4xzWhex3MsIS2kiQk4fzFJyuO2CMGgDmITdaTcjR9Gt4BGhVpxBbl0h3HALEyA5OMkDJ7nrWjoPh59Gup5SNO2y7mJt7MxyFmbcSzlyTz2oAfaWF6niGa7ltYUgbO2Rb+Z2Pp+6I2D8KoXekLb+LrK78rUbpXjl5EjbI3MkbDOMALgHg8HGOaAOq3ru27huxnGeaWgAooAKKACigAooArXWnWV88bXdpBO0edhljDbc9cZqAaFpA6aVYj6W6f4UAXYYYreJYoY0jjXhURQAPoBRI6Rxu8hCooJYnsKAOVXWfCOm6Y00YgWCM7ZB5eWUMpbLZ5IKgnJ7Cr3h9dF1Qrr+nWYhmaNrZjt2sFDDKkDjqo/DFLQZqJp9nHqL6gsCC7dPLaXuV44/QflS/b4v7Raxw/mrCJi2PlAJwOfXg/lTDUsg5HFLQIyNd1iXSBZeTbLcNcTtGUMmzCrE8hIJ4zhO/wCYrAg8fW0+jQahc2rRRTXKxFZgYxCrNgFywxuA+Ygfn3pDRLpviLVdcudFltYYIra7t0vXXzc/uWUBlPyn5lZh0K5/AiuwJCjJOAO5piFpM80ABYAVDZ3kF/AZraTfGHeMnBHzIxRh+DKR+FK+oGFc2dl4c1C81qGK4ub7UXEYgVkXewXoCducKhPzE4AOMZINLRfH9pr2qWVtZQEQ3CDJlbZKjmNpMbO6hVHzAkZYYzzhjOwJxUctxFCuXkVeM/McUmwOG0K8uNZ8ZS3kt5CYoJZYoVtGLhl2R4DnaOMhyMnqTXW63qY0jSbi+MZk8lchB/EScAfmaANDeu/ZuG4DJGecUtMQUUAFFABRQAUUAFY3i7I8Ha0QxUixmOR2+Q80Ma3IL7wz4fN1JqF5BGjP5Rcu2FPlFnXj8Tn2q9osWlR2LNo3k/ZZZWkzCcqWPXH5UgMK61u5j1G4iTU7HyYpShX7NK7qeuCV4zzV77BeOH1GXVo7fzIlBkSFQNgyRnf0+8aSQ7k+m6feC4ivH8QS3tuQSsYijCPkcHKjmsqw8Q3uoTRSwtvjnvWhFuLdxthDMu/fjG7jd1xjgDPNMRNrHhed7WBdHuY4LiKbzvOuw85B2shwN3OVZgQfX1rDlttQuLSK6S/0RkivxKIE0yYM9wybQpRpQc4cHnGOD0oA3PDz3dzql2LsxW93auqSpFAF86LZlMk5wAWPAJ5U8mqvxD1KZPDesWFrDHM50yaS4LTeX5MbAqG6HcSd2BxnaeRQwNt9cZfEUGjLZTea4aUyOQq+So5kU87sOUTbwfmz06t1HWbe31W20+PVtKt7l3UPBcyjzXBIACpuByecHnnHBoAp+KXv7Mw3Npe3g3tsMKmJYYwqs7OzGF3HC44zyR05NYGga3qVxq50uxlsVjtpI5roLulGyZt+RJtRSX3EjGfpRYL6HX6uqnU9BJAyL58f+A81Pd9E0OJI2+xWSQo8qLhU2L1ZgO3Xn60xGb4g1Ca60vTX0pZLyG+nCkW0qo0kflu+FYkAZ2AE5zgnHNSaNpKpNJJd2WxAyyWsN1IJ5YCANxDZbAztPU8/hQMTSdC1TT9XmvZtStZI58ebDDaeUDjdz94/MSwye+Kx/F9481vqG67MMVte2lqIMjEm5ondm7/dfj02k0AaFkLhfiDqM891AsZ0+2CoF+8pln24J75xn8K6qgQUUAFFABRQAUUAFZmuaZNrGnTWKXf2eG4ieGb92GLKwwcZ6HGfzoAqa74Xg13TpbOa7uY1kZTlXztA4IHplSyn61Jo+gweGdMu7bTFYxNI00MDdI/lACD2yP1pWHc4KPTPGt3HJqaQT6YlzfR3N1ZQ3GJCAQsgXtyq8fnXQavB4j1Lw9pMywsLqFmkmg2rl5ACsRZTxtz8xHbgjpQgO1RFRFRFCqBgBRgCufbTk0ZQX1ie305rncsARdql33bdwGQpY+vQ46UxG9cQrcW8kLPIiyKVLRuVYZ9COQfcVzb+AtHNr9nia7jX7ULvJuGciUBhvG4nDfMeRzkA9QKAOnwM5xz61k6v4Z0vXJN9/A8m6PypFWVkWVM5CuAQGAJJGc4JOOtAE8ui2M+pWuoSRs11aLthkLtlRgg9+4Y59ePStDFAGLeaE+oavPcXV/dCye1WBLWCZogG3FmfcpDBj8oyCOMg5qmngbSre4jeylurSNTbF4YmUrL9nIMW4urNwFA4YZAoAv6pp2oX15aS293b262kvnRl4DISTG6EEbl4w5PWq114bbUrzTrjUriGf7MHE6JBsSf5laPILHG0qCOTz9aAL8mh2Emnx2PlOsMbmSMrIwdHJJ3Bs5z8x79CR0NSWmmW9nKZU8ySYjb5krl2A44Geg4HTrgUAXaqS6XYTztPNZwySOu1i6A5GCvP4Ej6EigB7WNo8kUjW8ZaIAIdv3QCCB+BAI+lWKACigAooAKKAEyMZzx61kP4gt7WW4F48KRIwEUkcgffnOBtHIPBoAu6bqNtq1hHe2jl4JCQpIx0JB/UVboAyj4i0sX62Rux9oZioj2NkkEA9vUj861aVxmXrmoXNhaw/Y4lluJ5liRW6YwWY47narY98VyVn4z8SXGrQQDw9O9vhBctsxszIYyV56ZBPOSNvuKAO3vdRs9OjWS8uY4FbOC7YzgZP5DmuG12cav4y0UIsl7pLLJBKFCGFnLRsOTkkjbnseOO9MEdnrmoNpOh32oIgdrW2knCHo2xS2P0pNP1UXtw9s0MiTR28Uzkj5fn3cA+o2nP1FLqHQ0aQbstuIIzxgdBTELRQAUUAFFK4CY55NLTAKKACigAooAKKACigDF8L6fcabocdndIyvGSuGlMhI7HcfasXXfDVxLcXaaVYQxwTw2xcxSeSXaOYsUyuDyjMM0ug+pf0e11W1urGBLGOx0u3hkR4fOEhZiVKnPqMN1/vVvW6urTl4ym6QkZfORgc+30pgcze+JNKTxZYsbr5Iba5jkby3wrFocDp/sn8q1NSt7PV47WSS0luoCu+N42K4zjtxSAg1SS0srvQrYSqghut20t9xBDIuSewyQMn1qtJ40tB4hi0u0t2lj80RzXIBCKzDKhTjDHJ55HXvTAZr2nR32uyJfm4WxmsVgDRpuByz+YnAJUkFOR2Fa50fTdRSzuJrHabc7oUcYMZ6ZwO+KBHPeOtIu9XjubZNMkvlnsmgtNrgJBO24GR8ngAFcEAngjvVq0SLStUk1C5sriNJIlaS7ubkGO3XABTG44O4dAMY78UDN+61exsWjW6uFh8xWZWfhSFGTz06c49AT2NXAQyhlIIIyCKBC0UAFISAMmgBAw6Z5p1JAICD0IP0paYENzcx2sDzSsFRBkn0rC0XxZb61rVzY24V4kTzIpkJwyg4Ocj1zjHUUD6HR0UCE5z1paACigAooAKKACigCCGe1u9/lPHJsba4HJU+hqcAAYAwKAOW8Q+JYNHvcy2CT2qPFFczYyULnjgA8AYJ+oqLQte1DUtamtX0IW+nxPIguAvDOjYBHTAx7UhiXvj2DT973FhOIR5pRlyxdY3Cs2AMAdTyenpWr4c18+ILSadrKW0MUgTZLnPKhu4HrjjPTrTCxO/iHSlikkjvY7gROEkFqDOyNzwVTJHT0rzLXdL1nUAjyWUk+kyyqzuqFmJ3zknymTqfMThhgbaARd8LeFL26/e6mhv8W6GyvbxIpAj7EVmABPOFG36HJOa7+yure0v00GNZC9vaJKHboVJZQPr8poAn1TUodJsXu51do0KghACeSB/WrgO5QR3GaAAkDrXP69bJqt4unTRSz24tZJWt45jF5zHCqNwI/2u+OQe1IRzeiaJremagt69jdJMVigVPtQkRY9yFydzHtkDqflFaNzpWo67HHqFpdS2l5/aEis6XDAJAu9BheVJ4VsEYzmmBs+HtKuNGguILmWFleQGNkZvm+UAkhuhJBJAJ5yc81bfWrBdPN6k4lh3mNTEN5dwcFVA6nIPSgCp/aF9fQSTWcCxWrQ+bDdSsPm4B5XqO456YrM8Da3YXmmtYW04/0FREYyPuqvG7dnkH1oGXtO8Rxal4ju7W3uIZLGK0hkWRf+ejSSKRn/AIAKPEPiK2s/C93fW1zmR7aY2zRjdllRjkewx1oEWI9ftlvbSwcSvNKq7pFTKKxUsAT2JAJ/KtGW8tbeRY5rmGN2+6ryAE/QGgCpf69pumT+TeXHlSFN4Gxjke2ByfajSNf03Xo5JNNufPSMgMwRlxkZHUDtQBpUUAZ2jzXNxBNJcyhyJ5EXCbcKrED9BWjQNhXGeKYtPuNVst4uZXS6X7QqM+1Ywjdce+2kwRtaPpFjaXFzqNlJcf6a3mSK7nazYAzg+wAqTSp76aWb7WJQo+6GhCD8DnmgDDbUotL1LxZOVjuZInin+zFwGKrDHnj2wTV/w54vsPEU0ttbxTQzxRrKyyJhWVs8of4hx1oAzYfF2haP4cs3vriN85hZUw7KTngjtnHetq7nbXfCV1JpLFZLm2dYiflYMRjHse1AFLwzaxw3BkCXAla3WJla3ESxBSSAcdW+Y8jI4rc1LTodVsmtLh51if73kzNExHTGVIOPamIZZ2CaPpht7MSyJEp8qOSQseBwoJ7Vw1vJrf8Absl9bw6hcTizgWUSwbNzLIxkjQsAvRhjnHXBoGN1i08TXfhbSoJ7W9mu/ID3KQuod5Q6EKzbgAMbvY/lXTaHDqk+oy3OqRugtw8duJEUMVdt3VSQcKI1+qnrQA9Uc66znRtaA80/6Q2oKYP97y/P+77bPwqC+1ZLLxWgME05FuI9sQBOWLEDkjJwpOBzjtS6gdFbXMV3bRXMD74pVDI3qDXNaTr1np1j5d67o0l9cRx7YmYECfYMkDjll/OmI1fElg+paBd28KbrgxkwENtKyY4IPY1natp80c+jNCLiK2tY5EZbWMMUYhQpxg9AGGQOM0AbWloItNgiFu9usa7FjcgkKOBnFLqVs13pd1bRbQ8sLIuehyMYPtQBy39jajqb6wlxp8dkbywS3t33hhGV3YJ29wW3DHbHeres6FeTwLa2MUO1rB7JZGOBAGwGbHfIA49hQBX0vwteReIW1C+W3J8xJvMiduWWFY9oB7cMcn1FadzpeoXOq/aHg0l4lcbHkjZpAoP5ZoAW60vVLvW4rp7q3FpBnyYgh3AkYLE/3sEgUy30C7025ddNvI4rSV42kR48sNqquFPuF7+tAHQUUAFFABRQAmaXqKAKdvpVhaBhBaRJvzuO3JOeuT1pW0yxYAG1iwI/KGFx8n936UANTSNOjiiiWxtxHEQUXyx8pAI/kTTtO0610qySzs4/LgQkquc4ycmgC3TWbHagEKDkdMUtAGRc+I7G3u2tvKvppFO0m3spZUB7jeqlcjvzxWpDKJ4ElCuocZ2upVh9QelAD6oXOi2F3C8UkJXfL5xeN2R9+MbgykEHBx16cUAWktoY7QWsa+XCqbFVCRgexHSs+Xw5pc62yyWxYW0hkj/eMPmJDEnB+bJAPOeRQBq0UAFFABRQAUUAFFABRQBhaF4hbWLu6t3tjC0ABPzZ65x+nNbtJO6G1ZlIHURZHcLdrreMbSdpXd798frVt13xsu4ruGNw6imI5qzsrmLxjJEdTvpbaKzSTy5JcqXLMDnj0A4revYJ7iDZb3bWsgYHzFUN+GDQMwLfXNSi0TWtSnSGa3s1ka0kUFTOEXJJHQDIwMdqZ4Y+0Q6nPA9zNPG1nDPIZW3YmbO76cbTikB1dQ3N1FaRiSYsFLBRtQtyfYA0xDd0VnFulmIV3zulboWPAyeg7AU3UVtG0+cXwDWu3MgIJGPwoA5nwPNp0Fvd29pbyxebezyR/wCiSIpj3nb8xUDGMY5rUtprm1nubm6GqNAEdyJhDsQLzwEO4k9uvSgDkIpvE+pWd4dGt9RsLeV7idXeOFXLmTKqAzE8gnOQO3Ndhod3qM08sVza3SW6xIUluVVW34wy8Ek9M598dqBm3RQIKKACigAooAKKACigAooAKKAK0Gn2ltMZYYESQjBZepHv61ZoAgktUkvILks4eFWVQGwp3Yzkd+lOuYPtNtJD5kke8Y3xthh9DQBhR+D7WK5kuF1PVfNlADt9qPzY6dql1nxDo+k25t725b5o3DCM7mAGAc46HkD6mge5b0yXTtV0GE2qK9hPDtVCOCpGCCKmsNMs9KiaOzhEasctjknjA/SgRyGu67fSeNrHTbG6toIrcrJM0lwR5m4kFMA4JwO9d3SQ2IyK67XUMPQijAIwRxTEGVXjgUZBFK4C0UwCigBB1paACigAooAKKACigAooAKKAMzTddtNVmkjgEgKMRlkwDjvWnQncbVhrlgjFRuYDgZ6mmQNIIY1uCnnEfMFPGfagQ+QkRsV6gHFctoGj6fqvhzSbq4i8yRAZN56uSTnd6j29qQzegtbTRdOlW1gEcCb5TGg79TgVyWkabdas9vd6jZbTcFnuJTcbllU/dQL6dPpigDXm8KQf2lZXFmYrOO1OQsUQLP6gk9qo+LfEMlhe2EVqlw7Q3iecIsYYFGIQjPPY0wN3QtVfU9Cg1C5ha2Z0LOHAXGO/U8U2x1dNQvnjtr7Tp4kySIJg747ZAPFAHGan4otn12/K3rzW6stvDEt89sBKFyRxyQfXn9a2vC3iJJ9OtEmgliknuZYSsly0zIyngEv83PNIDr6KYgooAKKACigAooAKKACigAooAKKAM+z0a0sZ0lgUqVj8vHHPOcnjJNaFA27kbQxvMkrA70BCnJ70rRRtKkrKC6AhW9M9aBEd5cfZbWSbyJp9o/1cK7mP0FcpYWPiK18HR2dnHFBOkJMYdvnVt2cHt0pDRf8ADNt4hgmuv7emSbeFKMjfLnuAvb+tWbDSdMs9QeG3lmZ4f3gt3lZkiz3UdBQBtVz82g6HeeJPt0jiS+jw/k+dkK2MB9meuOM0xGpY6Xa6crpbB1jbojOSqj0UHoPYVZSKKM5SNFz/AHVAoA5XVdVj8O6g1tZ6RHOJIvNZkPz7ySBxjkADk5GBWXrOv21hqkFwnhtXvGgWVLxrNjtcttOSASqgc5JFK47HTeFb3VdQ0WO51WOBZJCWjMTE7kzxuGBg/StumIKKAKcmoxJqEdmd3mSIXHHGB15qyr7jwOKVyrFa61SxspViubuGGRgCFdwCc8Cn2WoWmowmayuYp4wxQtG2QCOopklmud1TxFPb63b6bp1ul1McNOm/aUUnGeaAOiHTpiigAooAKKACigCsl/aSXBgSdGlHBQHkVZoAgubkwNEqxPI0j7QF7epPtU9AGDdvc3XihbKO4eGOKzM42Hq5YqN3qB6VS0bTfFkOtpc6vqkFxa7WVo4l2j/Z+X19TSGW73xfZWGoSWUtpfmWMZOyHcCPUc9KhtfEVnJJcX0GlaodwAlkaAKAAP8AaYUXCxqaRrMOsxSSQ29zEqEDM8e3d7jnkVysXh2TxJZx3qajPYyNPMZzB1kBPCn24oA6nSreTRfD8MN9dee1rEfMnIxkDJz+VYula/B4p1AxQyvD5cYmRrW8Dhkzj5wPun254pgU9S0e1i124ktvDFvPEIJHeWS0QgyY+XawO45PXg1V8MeDBc3J1XVLGzEU8Hlm0ktRuDZzuB+UAdsbAcdaANXxfqkelaGLDTTJFcGWGGNbdWHlguOMgYXgHgnpW7ba5p13qLWFtcrNcoCZETJ8vBx83pz60AO1DUl09498F3Krf8+9u8uPrtBouftl7Yxvp1ylq7kNuubVmO302FkIP1/KgDk7R/Et9qN5Ii2x+yyNbeaZvJV8ck42SH9a3dITXBfMbyewe02YKwyM8gb67VGPwpWG2Rz6ZY69qOr2Oo2yzQqYeD3G3OPpmtXTNKtdIt3gtFdY2cvhmLYz2Ge1MRh2fia41a6KWItRbvI8MchctIGXqSmPu/jWLrapp/iSylvNVvmuZHVZBA5REUnIwNpGM9cmgDc8X66NO0e5jg883Hkh98SE+WCQNxParHhzxLaa209vbzLK1sFUsM5bjk9PWgRpnUAL0W32S7OTjzRF8g/Go7a5nl1i+gZl8iER7BjnJGTQBoUUAFFAGXZ6RHb3012JpWeR9xy3U4xz7VqUkNkVus6oRcSK7bjgquAB2ohM3lkziPdk48vOMduvemI5X+2mk1yW9tbdSABanzWweuSeAartH4ofXI7l9Wg+xx3wj8hFK7o++eOTSGUZTqviXWdUawmisPskgj8xXffIq9jjp+tQxf2vqGmalocl8XMEYkaWSQlmO7puxnFAzs31I6L4ZjvL8GZool3+SByfbOK4nS/Ft03hH7bpCIk51AxulyvyEuTgcHOKBHUeGtQu/EGj39vqZj85JZLd2hGBjHb860NH0q600bJr4TxKgRFEKocDoSQOTTA1qKBHO3vheW6vHkj1WeCF51uTGsalhIvTDEfd9iD+FXLfQY7bWn1VLmZriYbZ9x4kXHyjA4GPpnnk0AWNQ0uLUfL8ye7hMZyDb3DxZ+u0jP406e1ddKe1hnl3lNgldzvGe+71oA5yDwffKgjn1SGaIuxm32xLXAI4DneAfpg5qr4V8HX/AITm+zWKaetibqSZ5FZlkkVhwCoXHHb5qBk2qWviW3XWbyBNNVbhFIP2mQMgQY4wnU/WrXhObVhdXVrql79qKxxyo3HAYdOg/rSA0tN0y800pAlxC9ohO0tH+8AJJ25/HrWvTEc9q3hubUri68vUGt4LoRmVQm45Tpj0HrVvTtNvLC+uD9pje1mkaYrsw+9sZ/DigCyun7bnz/td0TuzsMny/TGOlSQ2ghvbm5DkmfblcdNoxQBZooAKKAP/2QD/4THoaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdG9yVG9vbD5XaW5kb3dzIFBob3RvIEVkaXRvciAxMC4wLjEwMDExLjE2Mzg0PC94bXA6Q3JlYXRvclRvb2w+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMDktMDNUMTQ6NTg6NTUuMjIxPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICA8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwADAgIDAgIDAwMDBAMDBAUIBQUEBAUKBwcGCAwKDAwLCgsLDQ4SEA0OEQ4LCxAWEBETFBUVFQwPFxgWFBgSFBUU/9sAQwEDBAQFBAUJBQUJFA0LDRQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQU/8AAEQgFWQc6AwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A/VOiiigAooooAKKKKACiiigAooooAKKKKACo/M/e7Mds5qSk2jcD3oAWiiigAooooAKKKKACiiigApKWkoAMcV5N+0r8dtP/AGefhpe+Lb8ecsB2x2+cGVuy5r1gtxX5Y/8ABZb4lXtrD4R8HpLshk3Xc6I/3sdOMVnI1pxTd2ZvgP8A4LTaoPGT/wDCXeCoP+EZmkwrabMTcW656kHhj7ZFfo/8Fvj14L+P3haLXfBusQ6lblQZoAw863Yj7sidVNfGv7JP/BPb4f8Ai79lPSR400dZ9e16E339oxp5dzbBwfLCtk5xwe2a+d/Ffg/x7/wSf+Mlpr2iX3/CV+Bdc/duLgeQLgDkpIAW2uueD3osKy6H7K0Vx/wl+Jem/F74eaH4t0p0a01O3WYKjbtjEcrn1B4rsKtO5GwUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFITgZoAWikznGKWgAooooAKKKKACiiigAooooAKKKKACk60MwWloAaqhelOoooAKKKKACiiigAooooAKKKKACik3D1paACiiigApKWigCGS4EcirtJ3elStypFGKYzLuCbsGsgMjXL5ND0fULtkkZYYmk2wj5jgE4HvXwD8L/8Agqpb698eYvBGq+HprfRrq8GnW14W/eiYuEXcPTJr9E22yRsGAK989K/n7+PVraeGf26r6PQkW3jh8VW8sKRDCq/nqePxotrc1v7rP6CFO9QRTqq6ZI8mn2zSjEjRKW+pAzVqtE7mQUUUUwCiikoAGxgk9qRWDrkVFOxWM80jI2MoQox07VPMVYl5VThs/WlVgehzVKWJHVFZnQ5BPlkjP1xVqMpu2rjIo5g5SWiiiqJCiikPQ0ALRTV+7TqACiiigApsjbEZj0AzTqRvumgCja3YuVdhyAf4uKs+ZgAgZzUaxxsxIXFTRgdqyNHYkoooq+YzCiiiqAKY/UUvme1OoAKKKb5ntU8wDqKKKoAopDyDSIu0VPMA6o5KJI93NRSTCEqDzk4olKxSVwnuIrS2lnkYJFEhd2PQADJNfhb+zjoEv7Q//BQS1vNQDXEC63capNIBkBYmJjz+IWv1N/b7+Kl18Jf2Y/FmpWKh727gNgmeyygox/I18Uf8EW/h/PceKvHPjSYsY4YY9OjYj7xJ3H+lTHUo/WBFEahVGAKiluI4iwz81WWGVI9q+CP2nP8AgpjpXwJ+Ll94Im8H3WppYFDNdbwmSR1UHrilLQI6n3VZyiaNvr0qyFXbxXkn7Ovxr0L45eB7HxJo0ckCXkeXilcEoR2Nem3s5tbVwhw2OD6e9A7GH4k8cWOgtJHdTw20YGDJO4RR9SeKq6Dq41y4tLj7RDdWZ/1clvIHTPbkHFfkT/wUi/a7ufiD49uPBuhTPDpemN5V5JC+BM44I4r7b/4Ja/DfxX4R+Acep+KLuaWPVZPPsLSckmGHt19amzL5kkfZ0c26VlPapqb5a+lLnitznDcPUUtQbA+COKkrPmfYdjE8WeI9M8MaY9/q1/babZpy1xdzLEg7/eYgVb0DXLDxFpNvqGl3kOoWM67ori3kEiOPUMDg18If8Fjtcn034FeHbWG9ktftWqbXWNsb128g/nXXf8EmvEt74g/ZZtory6a5NjfzW0W5slEByB7UjTpY+0ea8i/ae/aA8Pfs3/DC88Ua6yyS8xWVnvCtczY4Ue3TPoK9gr8x/wDgthrEg8K/D7SQf3ctzNOfqABV8pFz6n/Yp/ayg/aw8F6rq6aGugXOnXX2ea2STeCSMg19INnHAzX5x/8ABFqylj+Fnjm7aJ1im1ZQkhU7WxGAcHvX6O0com7n5xf8FD/+CdUfxDhvfiP8NNMK+J0DS6lo9shY3wxktGgBzJ7Ac14B+wh+35r/AMCfEUPw6+KV3dReFIpPs0bahEVn02Qtt2uWwUQHru6c1+zlfE37cn/BOzQP2gtPu/FXhKKHQ/HdvGz/ALtAsV/gE7XAH3j0B96LDuz7D8M+JtJ8X6Pbatomp22q6ZcrviurSVZY3HqGUkGq3jzwrD468F634enuZLSHU7OWzaeLlkEiFNwHtmvxf/Y//bI8V/sY+PJ/h/8AECzuf+EXW6MN5bXIYTWTk43oG/hHX6V+z3gnxtofxE8O2eveHdTt9W0i7UPDdWrh1YemR39qXMFj8xtZ/wCCJd951w+l/Ei2ZWJKLeWLZPoGIJ/SuZvv+CYv7THguMQeGviDFeWUP+qt9P1y4tVA9Ar4Ar9gKKsOZn5EfDT9in9rbT/iXoM+ta3qlpotvfQzXc48TrKPKDqXwNx3cZ4xzX64WsLW9vHEztIY1C+Y5yW46mp6KCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGqu3OO9OoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApglBbb3p9JjnNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAw1+MX7aun3/AMbP+Ciek+Cr1THZx3lrZpk7w0WQzHHHUAiv2db5a/HPR9Ql8ef8FavMkZrkWuvyQqoXG1I4zzUS3RtDZn6/aHpNtoOjWWm2cSwWlpCsEUajAVVGAP0ryr9q/wCAun/tFfBnWvC91bpLfeW0+nyMBmO4VTswe2TgGvZNtG33qzLqflV/wS5+PmrfC/4iat8A/GkctrcCaQ6esxP7qZSd8WMdCBkHNfqtXw3+1h+w9feJPjJ4T+LHw3V7fxRHrFu+qxK4RHgDDe498A8V9wW28QIJPv45qYqw5O5LRRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UANKAkHJGPSnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1kDcmnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA3aPSnUUUAFFFFABRRSUALTSi7t2OfWjdULO29txKqOhFZDsO2gBlI4NfgL+0JajRf29r+OWMBV8V2khU9189DX77SHzoZCrbTjAIr+fb9rbWjH+2Z4h1CWd5GttahcyMeQEdT/Sn1SLXws/oLsZFltYXThGQEfTFWKxvBt9HqfhPRryJt8c9nDIreoKA1sU47EMWiikp8whaQ0xmOetJIxC9cVLnYqwMoYYPI9KOMYHFUpl3fclb8GoZn+WNCS2Ouaz5jXkLTId644FJH99ztw2cD3FU0mmt5VSVt2R3NP8AOlMmBtPbPpVXDlZpUVRXzTMDv+VeCM1O8jR8nkHitOYzcbE9FMBOKM1RA+imZpnDg9etTzDsTUVHg+tAJxRzDsSUhqL69KGJEY2c0uYVgaIPg9KevWomxIpXOKdH8i4PNSUTUVQmvQs3ld6IZvLMgPPNA+Rl7NN8yqEl633dmM8ZpyN8hUvnaKrmH7PuW/MqvHdO1wUMZVB0k7GqtrdB0UJyCTUozkVhzMvkNGm8D5vWq3lyAZ30i3IjUiRxurQy5S7RUCSfuwaZFOH3j0NXzC5S1RUNNk2IN/eouKxO33TVEOJJCCnC80vm7uKIIUEhwOaJPmNEuU/N/wD4LIfFD+y/BHhvwXb4El9P9rfnnC19H/8ABOr4Pr8If2Z/D0T5N5rA/tOcn1k5H6V+bP8AwUO8RSfGf9tSDwnbFmhtbm30ZWXnG+QBj+GTX7W+DvDyeEvCej6LE2+PT7SK1DHvsULn9KqGwpaGvXxh/wAFAv2F7X9o/wAOv4k8M28cPjuxj/d4+UXaD+An19K+0KSqauSnY/B39kf9orxD+xp8Xrjw140tr2y0VrgQ39jLkeQ+7G8DuB1r9Xf2lf2i9C8G/sxa1470XV4Jo7uxK6dcQuCWkdcLj3BNeL/8FOv2P7f4xeAZfHfh+0RPFeixGSfy0+a6twMkHHUgCvyO1D4w+Kdc+Gel/DqWd5NIsboywQnqGJxj86gvc9b/AGFPgPdftOftJWC6zaPe6JZztqesyt91xnIQn1Zu31r9+9O0+20fT7eys4Vt7S3jEcUSDCooGABXy1/wTr/Zvt/gH8C7C5uYseIdeRby9kI5AIyqfgK+htW8baXo7XDX2p2VjDD95rq4SMfqarmIsdJ5gb0oaRI1+8APrXzz4u/bG+Evgoi41L4haU0AJ3xW83mMD6ALmvAPjh/wVQ8AaT4A1CbwLqEOseIGPlw28sTKMHjdk9xS5n2NPZrufoEtxG7FVdWYdQDyKkr4P/4Jqftd6l8fLPX9C8VsG8Rac/2lZEHEkLHgfhX3lT5iJaH5kf8ABa6+k/4RP4f2Kn5ZLmaTb3yAK7T/AIIz3E8n7P3iOKWNljj1ptjEcH5BnH415j/wWu1OH7R8ObFZF+0KJ5iuRuC+uPSvo/8A4JXeED4X/ZP0a5dSkmqXM12wYY6tjNSPofYdflR/wWw1BP7U+HFmGXeI55CuecZ64r9V6/ED/grf8Tj4w/aUTQ4mR7bQLNIAyMGBZjuatTM+2P8Agj9arb/suzSKhUzarMzEjqa+56+Mv+CTVvHF+yTpjoys0l/cMwB6Hd3r7NoAKSlpKAPlz9tr9jfwn+0R8OdYv006Cw8YWNtJc2upW8I82ZkQt5b4HzZxj15r4n/4JD/HHxD4f+J2pfC3U5Jp9IvIpJ7eKZjm3mjOHCg9vWv1l8VajBpHhjV766dY7a2tJZpWcgKFVCTk/QV+O/8AwS50WXxR+2ZrmuWkTDTbGC9n3AZVRJJ8oz2z2qbFrY/Z+iiiqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBrNge9JHu2/N1pWUnFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu4U6k/KloAKKKKACiiigAooooAimcRxszcBRk1+Sv7GNtD4u/4KbeOdaCKY4DfzhcZ2sWC5z68frX6teJpWg0G/lX7yQOw/AGvyb/AOCXN5/aH7ZvxGuJhuuJIbtt3p++IqJG0fhZ+vNFFFWYhSUtFABRRRQAUUUlK6AKWmqu3vmnUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopvPrS9Oc0AB/Km7iu1fvGmxyiRc5FJ/y0+9g1PMOxNRUR3+YCD8vcUk0jLExU8ilzICaiqTTSssbrn5uq1czQpKQNWFopvNHNVcB1JRQ2cGi4iLeWkKlePWnbRt244qFZJEkw+3Zjr3pRcFpMAcVkaWZHfTJpul3M5HyxRtIfwBNfzi/GLV0+Kn7Seu3EW6KLVtfMK/7KtKEr+kC5tku7eWCVd0cilGX1BGDX5q33/BK250z9qbSfFNlcw3vgCTUv7QuLUvsmt2Dbwo9Ruqno7jjZpo/RbwRo6eHfB2iaUn3bKyhtx/wFAv9K2h3oVQqgAYFFUlZGbeotJTMnvxTfMHIzzWdwsEmdpI6jmq7O0kPzjbmms7ru2MWJHTPSq0kjRwhJbgbvcVjKXMbKLJYbdV6HioUm+zSO33xnvTftULL5YlwfY1Vkmht1MDyfe5DE81NzflNL91P+9fHTjNZUc3mXEgWVgM8YNWLcpNAFRtwPFVruG20uNmaTDZ655rRS5h8ps2kiKNhOW75q7uDLgjNYOl3EeoYdGwfat+PpWpz1EFRtMq8ZqSolgCtn731rUxVhHbarbWNETcdanbAU8VTEIZvNVm3f3c8VlLQtalnJ9KZvJxtXimtcKvBpc42fSgBGZ/tGCP3eKZNN8yAHHFSlw2D2xmmbo9y/Lk9qmwD1XbGNx3H1FNWR9zZG5exFEkg4HaobxzbW7bOlUOxXa4G4M8XlYJ5amx3yyDfHJHKD/dNRSXSTAHeCMViXUv9mIJNiCKTkYpXOrlOiMm4Yfg1G2YVYb+SKw7nUo5o4yruZMf6v0qGNrlo5Aaz5kFma8P+oO3/W5p9w88OpJ/d2DNYLSSww9cH1qbTb6VmbLxzHHXNZcyK5GdJGyyOWkfKjkUTTIv7wdT0rIsJpGl8mWTlua2LGKfzH3f6rPFXzomVo6ktp/x7l5OrGriwovQVGv+uNP8yq5jlZJUckYPNLH92nN901e5GzK1Murr+zNPu7yZ90cMbSn6AE/0qaHoc1zXxQmFv8MPFMoHEel3L/lGxpR94tn42fsuL/wuj/go5DrJGbf+27rVD7CPKiv3Cr8Wv+CQdvBqn7UmvX8uPNXS55Ygf9p/8K/aRulaLTQU9xaSlorQzPP/AI6fEjQ/hT8LPEPiHxDcpb6fb2sikOeXYqQFA7k5r+cG5u7mfxXeeIbCxmlsYL83YZYyUQeZuAYgYH41+kH/AAWA+PEHiDVdB+FmkyGWe2mW6u/LOcueFTjv7V9DfsT/ALF2jeFf2WbrQ/Fumw3GoeLoDPfLKnzRKy/IvPQrnNZGm2523wX/AGih+0z+zDqd/wCAXW38XWumtafZCwDRXIjwMexPQ1+dv/Dvv9qX4uapcy+Jma2aZ90k2qaodh57KKg/Z78Ra1+wn+2vJ4R1a6ktfD93qP8AZ95G4+SS3c/uph27jmv22jkWRFdGDowyGU5BHqKvlE3Y/KfwH/wRUv54Vl8X+PUtpc8w6Xb7v/HmrrdS/wCCKfht43+w/EPVIWwdvm20bDPbPFfphRVE3Z8d/sT/ALAf/DJvibWtduPFB8QXeoQC3CrB5aooOc9ea+w6WoL26FlZz3DDKwxtIR9Bmp5Qbufit/wWC8cL4g/aMstDjQ/8SfTUiY+7ndX6r/sq+H4PCv7O3gCxgG2NNJgkP1ZQx/nX4P8A7TPxVl+Ln7SniPxNqh8u2fU/KwozthifaOPoDX6KfET/AIKreAvhx8JdK0X4crNrmvw2MdvG9zCY4YSFAyc9celSWfcvxs+M3h34H/D7UvFHiC+S2tbeImJFYGSaTHyqi9WJOOlfzjfEjxZc/ELxxrfiS5M0s+o38szSTE8BmJVfqB2r6PbTv2kf2+vE2lxanZa1qWkSS7ku5bV7fTYlzyyuVCHA7A19W/tofsI/8IT+yz4W034deFH1rX9HuI31B9NtXmu7piuGYIgLNzWhNj2f/gkiW/4ZQtgQQF1O4AOOvNfa1fL3/BN34c6z8M/2V/D+m+INNu9I1aaea5ms72BoZY9zcBkYAg/UV9Q0EiZozTa8I/an/a08J/s1+Br+/u9Rs7zxDsKWejx3CGd5CPlJjzu2g47UDPM/+CnHx90v4V/s96x4cj1MweJvEkZtLS3t3HmhD99yM5C44z714/8A8Ebfg/daH4H8SfEC+SSNtYkW1tt6EBo0PLA9xmvj/wCE/gL4m/8ABRT4/wAGq+KDqF1oa3Ia/wBRWJ/stlEDnyVbGFJHGOtfuJ4D8C6L8NfCem+G/D1kmn6Rp8QiggTsB3J7k+tBWysdFRRRQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUgCiikZgoJqeZgLRUcUvmrkKy/WpKsAooooAKKKKACiiigAooooAKKjkmEZAxnNSUAFFFJQAtJUbSFVzimu5ZcnjFA7Ml3f5zS/hVNrxV6R7vxqaOTzBnpWd2PlZLuo3U3HvSLllyePatBD91AbNN2j0oAxQBJRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAyPFriPw1qjEZAtpD/wCOmvyP/wCCWF5G37ZXjlWUxyzW96VTr/y2J61+uuu5bRb4MgkPkP8AL0zwa/Kv/glbb2d5+1p8V52t1W6t1ujE2c7VNyVIrOWuxtH4T9Z6KKK0MQooooAKKKKACim7qTcfSo5WA+iiiqugCiiimAUU1mxQrbqBjqKKKBBRRRQAUUUUAFFFFABRRTWbbQAnl/7TU+iigAoopKAFoqIM/qPyqQ1Nxi0VGsm4n2p9UGwtFFFAgooooAKKKKACiiigApKWigCNmCjJNVJNUjJKRhnb6VcaMMvIr4e/bo/ba1n9lXxVpOm6b4KbVhfx+aNRvboxW2c8qpXv9awk3E2pRi9z7YWaJmWMr5b9QrDFLsSbOQc/3s1+SVp/wWi8TwyEz/D3TZj0H/EyI/XbWun/AAWx1WNVU/CyyC99utk/+0qYWP1UkkaGIBCpHqxqKa6niVAId+fvc9K/LMf8FpjcSILr4dsIO8cN+p/pXS6X/wAFoPCu5/tHgHWEXoNtyjAUtexeh+lM2oQwxbwcj/ZpLXUBfJujKj/er84V/wCCyXgSOXevgvVtx6/Ov+NOvP8AgtF4ORSLXwLqbcdTIq0o3QnGPQ/R64upII93y577jgU231RJlLNhB7mvzEk/4LEeF75g03gjWpiPS7QCpv8Ah8X4TdcH4f6swHY3SVNpFcsOp+mkOoGVmwV2Doat+Z5ikA4avzCH/BZ7w78sa/D2+ijzzi6Xj3ruNB/4K7fCmcG41CHWbOT/AJ4pbBh/Oi0iLRPvi4hY7JMcrwTSeY8JyGDe+K+ILH/gr78Iry8eK5tNXtIccO1vkGq+pf8ABYD4T2cMgtrHVL1wDgJBgGq1C7Pu61uhtw8oYtyKtq4bnrX5e3v/AAWc0aOQ/Y/ANxKg+6ZJcEVUX/gtAkLN5XgOR1xxunxVp9wcV0P1QqOTO0kNgV+VNn/wW0uxIftPw5hMXYx3hB/lXJeLv+CzHjnWJJYtB8J6dpcbjA86RpWxVc3kZ8p+vcdxHIOJEf8AGqd9qUVixldlw3yrz3r8Urv/AIKk/GG6t0XT4dItMHJeGGRifxqx/wAPPPjXcRhZtJ0u7UHI/wBDmOPeubkqdja8O5+zLahHuWZphCSOecLUN9uvIo1VgQ/STdz+dfhx4m/4KGfH/wAYXggs9WewiBwtrY6ch/DlCaq6p+1N+1BNaxRS6t4qtEbhGg054z+GFo9mzbnj2P3JbS0s1LGZtuPvyOCa5rVNcskuY7V76KFxxukkQt+TNX4vaa37XvxOwmnn4l6jF6q1zaqP/HgKfN+wn+1H4w1ZLrUfCGvXV2zAfbNS1NSw56lmfNV7Ey9sux+yGoePvDvhm3P9peKLHTo1Gd8t2AfxAbivHfGX7Ynwk8Mwyy3XxC0q/lzzFBfmb8hXwrY/8Eg/jvrV5HJq954dttzASSvqUk7AZ5PTmvoTwn/wRO8KQ2oPiX4g6peXPcabaRwp+BbJq407dQ9sux20f/BUn4LeHUKw6tf3g/6Z2R/wr6c/Z3/aY8EftKeHbjVfBt5NcR2rBLiO4iKPGxHQ5r5U/wCHLPwjUHHi3xdntme3x/6Kr6m/Zj/Zl8M/st+Am8M+HJJb0SztPPf3SKJpmPQMQOg7VpymMpcx67RTqDVmYN9056VUcJGg2AmneZJ5hGOKWVf3YOMt6LWUtTRKwTRrJHnHvSqymMnPFJ5wx04qGaZlQNGoKt7VNwLG5fVaNqVSVH+1HjirHlmmVyjvyqG4/wCPd/Wmc+tRzTfMkdM05R8OnB1WSYAnH3QK8J/bK+MGnfs9/CSXxVcW01wfNWCGGL+8RxXvkJ9TxWZ4y8EaD8RNBn0bxFpdrrOlTj57a6jDoffmnymfPJdT8wPh1/wV00W1iWPxD4ZvYpMf6y2mBFdZD/wV68C2/n7PD2rM2flHH+NfS+uf8E2f2etekLy+ALa1Y/8APnM8P/oJFYY/4JV/s4jr4Ouz/wBxa5/+Lp8kRe0kfP2lf8FevBE9xcPq3hbVE3dNpH+NWrz/AIK4fDprQLb+H9fLLyMFR/WveB/wSr/Zu7+CrtvrrV5/8cp6/wDBK/8AZsX/AJkW4b661e//AB2p9nEr2rPjjxZ/wVwgvdRil0zwZNcICM/brrDY9sd6/Sv9mv4nL8Y/g7oPitdNuNJF9GW+z3Em9hz1z6V5J/w67/Ztx/yT9s+v9rXn/wAdr6J+HvgDRfhf4R07wz4dtTZ6RYR+XBCXL7R9Sc0/ZxIlPmOgpu35s1LRVcqIuMops33fwqrH+64rKTsVGNyWTfuH1qHV9Pj1nSb6wlGYrqF4GB9GUqf505Zv31WlPzGiKSHqfgn8MfFVx+xh+29N9sgaCwsdVks7hfW2kbAP0AIr949L1O21vT7a/s5VntbiNZYpEOQysMg1+af/AAVQ/Y41rxhqEHxQ8Gaabue3h26pDB98gdHA749q479hr/gpBN4Oh034e/Ex2t7GALBZ37oQyjoFbNUD94/Wmo7lnW3lMYy4QlQPXHFc94d8daN4mtkutL1C3vbWRA6yRSqev40XnxH8L6dcm2uvEGm283QxyXUan8ia1J5Wfk38Cf2WfFnxz/bg8Q+JPGOi3lv4d0zV5b24kvIyglKP+7VSRzyB0r9hVRY1VEXCDoKS1nhuYVlt3WSJxlXQ5BHqDU1TyhJ8x+OX/BZSzg0/46eE761CpfS6Uxdh1+V/lNfpP+x98RG+Kn7NvgTxA5Zp5dOjhmZhyXjGwn9K8y/bc/YN079rSTR9Ug1dtD17TgYvP27lkiP8JHrXu3wJ+FVr8E/hP4c8F2konj0m2ELTAY8xsklsfU1Qrne0UUUCCuC+PPihPBXwY8a627+WLLSriQMOoOwgfqa72vAP29rqS0/ZE+JskTbX/smQD8cUAfi/+x7+ze/7XHxkk8N3mpy6VF9nlv7q+jTe+c54B9Sa/Un4Sf8ABKD4N/Dq6jvdZhvPGV9GwcHVHHlBgcg7FAH518p/8EWfC9xcfFfxlrjxSCC000W4lKnbuZxxnpn2r9gqmxXMUdL0iy0OxistOtIbGziG2OC3jCIo9AB0q3T6KokKKKKAPNfj94H8b/EL4d3mj+AfGh8Ca/KRs1QW4lwvdfVfqOa+E9D/AOCQfiHxj4l/tr4sfFu48RTlg0i20Mk8kozyDJMwK59hX6bUUDucZ8KvhF4U+CvhG18N+ENIh0nS7cYCxr88h/vO3Vj7muwp9FAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKTcKG+6aqzS8qPun0oKSuWtw257UAg9KbIW2fKMmlQFRzQSOoopnzUAPpGYKMnpS1Gzbmx2oAkoopKADcOuaNwppjG3FM8pvLAzzWd5ASbxSeYpOM800x+lQw2hSctjj60+YuyLdFFFWQNLgZJNMW5RwCp3A9xXhP7WHjj4rfD3wVFr/wAMdCtvENxZS+ZfWMwy7Q99g7mvGP2dv+Clngf4o6iNF8aQt4H8TxNsljucrBu9Cx6Go5mXyn2/5i4zTFuY3DYPQVnrqMGpW8M9tMs0E67opIzkSD1B7037N5Mg+YnPYVPMyuVDob8GZvn+XtS/2iysoKkZ9apXDR2ymZImkRcltmPlx61Ws/EVhrUoW3lWVl6qjKSPyNHMzX3TpPO+UEZI9qk8we9VrOaKaH9ywcDipRHzT5mYWRNkU1pAqkmnbajeENR7xBFHdGXkDH1pzT4GRlh6inbUUHjbXmHxG/aI+Hfwz8VaD4U8ReIodO1rWpVis7UAsxJ4BbH3QTxzWFmXZHpK3xdioU59abbiVZGZ+V7Cp7e38tBkDd3NPK4rWKb3D3egRyBl+6V+tP3U2mJMkmdjq3+6c1sSS7qN1Rt8qkk8UK27tUczHYlorD8ZeNNE+H/h2713xDqMOlaVarvmuLhgqqP6mvOPgr+1p8Nv2gtY1XTvA+syavLpqB52Fu6Lg+mRzVknsdFFJQAm4UnmYbG3j1qLcXUtjaBXgP7U37ZHg39l/wAMzy6pc/bvEU0ZNlpEDAyyMRwT6AH1rO7Lsdv8cP2ivAv7Pnh86r4x1eGx3AmC2zmWYgdFX+tRfs5ftCaH+0p8OY/GGg2l1Y2TzvB5N1jeCp65HUGvx58C/Cf4wf8ABSb4sXfiLU7h7bRllBmvrkMLS3jzzHEO5x6V+0nwh+FOi/Bf4f6T4R0CLytO0+LYGIw0jd2b3NaCaR2m6jd2703adxOeKj2vvzjigLHzH+2Z+3Fof7JK6Na3ug3XiDUdUVnjt7e4EOxV4ySVNdh+yz8frX9pb4VxeLdNtnsfMlaKSylkDtER6sAM/lXx/wD8FqPDlufCHgLXguLy3u5LZSOpVhn+ld3/AMEcbCWH9nbWbqRiUn1Z/LU9FULQHM0fZfjDxhovwz8I3/iTxLqEen6PZR+ZPcSDhBVH4V/GLwV8YtHGpeDfEVnrtr/F5DEMv1U8iviT/gsl4+8Q+H/hn4Z8PWTCDQNYuWW+kHJYqMquPSvhD9mjRfjT8M/Ctz8YvhzDNdaFp115F/b28pJIHJzGO2PypWQczP6BMV8C/wDBQ7/goSfgT5vgLwHNHN40mjzd32cjT0I7AjlyPcYrR+Dn/BWb4YeMfCdxc+L/ADfC2t2sRaS1IMySEDorADkn2r4R/Z38Br+2/wDtuX2r6pBc3Ph6bUJdUvP9i3Rsxxk++AKZJi+GL79r74qaONd0a7+Ims6S6mQXsFzKkRAGSQ2efwrtv2TP+CiHxF+CvxIt9B+Iep6p4i8MXV0tte2+syPJd2TMQN6ljkYPUV+2em6ZZ6PYw2Vhaw2dnCuyOCBAiIvoAOAK/Hv/AILJfD/SPC/xa8Ja5pVlDZXusWMz3bwx7TI6MuGOO/NA7s/YbT7+DVLG3vLWRZra4jWWORTkMpGQfyqxXjH7GviOfxX+y/8ADnUrmIwzyaVGjKZN5OwlM5wOu3Nez0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKbtPy89KfRQBi+MJJYfC+qPEVWVbaQgscD7p71+T/8AwSmvvs/7YHxMtmYM9xb3R6+lxur9VPiTHdy+BNdSxljhujZyBHkTcAdp7ZFfk9/wSZ0+4X9rbxybgq00FhdGR8clvP2n9ay62NPsn7D0UUVqZhRSbqaXoAfRUUjyD7qqR7morPUIrxpVQ5MZ2t9aV0OxMTjNRqxYb1yQf4aQxbW3F+PepVYMMjpWXMyiSms3YfepGb5c186/tJftmfDn9n24g03xJfXMWqTDckNtHuYD1NHWwlFvY+i13Y+bGfanVwXwR+LPh/41fDvTPFPhq9a/026BUO4w6sOqsPUV3tap3JMDxbrkXhfQr3VbqYpb2sZlbA7AZP8AKuS+Bvx+8H/H/wAKrrnhTUo7qLcUkt2YebGR6rXb+IPDtv4k0u5sLwl7a4jaNkwOhBH9a/Ef4seF/iX/AME6f2gJNU8Pm6h8K3Fz5llMS32W4jJ5R8d8VHvXua3jy2P3Nor5t/ZJ/be8I/tUaS8dqo0bxHbj9/pczjJ9SnqK+kc1adzNqwtFFFMQUUUUAFFFFABSMu6looAKKaWNQySSZQJjJ65qeZDsWKQ9DUFxO0ceRgVSbftkYSGRWGVANO5Si2WofOaQlnTZ2CjmrEjbVqpBGLWHcE5PULUktwvALLzU2G1dhb43MQcg1ZXpWZa3Ijd1I+UdMVoB84weKtajnFpklFFFBkFFFFABRRRQAUUUUAFFFFABXJfEL4TeDvixp8Nj4x8N6b4js4X3xw6hAJAreozXW0lJpPcNeh4Prn7CPwC8RWYtbz4XaIIR0+yrJbt/31Gyn9a5lf8Agmb+zWv/ADTSP8dZ1E/+3FfT9FA7nzCv/BM/9mleR8L7b/waX/8A8fqKb/gmX+zfK2U+HUUI9I9Su/6ymvqL8aRV28DgfSlzCPle6/4Ji/s8XC4TwXLbn1j1G4/q5p0f/BMj9nlLXyf+ELdmxjzWv593/oWP0r6mzRmqsPU+TLb/AIJd/s92y4/4RGeU/wB6S+kz+hFZ+tf8Epf2ftYxs0LU9OH/AE5aiy/zBr7EaozKisFLAMegpcpV2z4oH/BH/wDZ+3EmDxKfb+1v/sKeP+CQf7Py5ItvEm71Orn/AOIr7XGaj87dIVVc46mlzEI+I/8Ahz/8Cv4m8Qt9dRP+FWof+CQ/wBj62evP9dUcf0r7YpKodz5F0f8A4JWfs86O+4eGr+89rzUpJBXT2v8AwTp/Z9tMY+HtjLj/AJ6szfzNfSlFAHgtv+wj8AIeR8KvDch9ZLNWrpfD/wCyn8HvCtwlxpHw28N6fOn3ZIdPjBH6V6rRQBkxeEdDgULHo9gijoFtkH9KmXw/pi/d061H0gX/AAq/RSsBUXRtPjOVsbZT7QqP6VN9jg/54R/98CpqKYhqqq/dUD6CnUUUAFFFFABRRRQAUlLTFXZ1OaAI5F/dkjqKzobyaZH3QlBV2aRFVyT0rNh1RLiQhCyezCsjojG4SaknnJHtNSf2ioV/QVnzQINx2YIfruqnJqItLWZ3ZTxhfepsa2Q++8TQ2d4saM7GTpxUkOssi+WfMMnevCPi58fvB/wx0uS/v/EVhb6hCnyWrSgyflXyZqX/AAVb0W08Q2xgs7q6hTiW4VeD+FLUeh+nUmZLUGMk1Wt4g02zcSR718x/AX9vT4a/Fq+tdPt9eXTL+VseTqBCbj6CvrHZHIEkiVXj/vJVk3LcanywD1p6/dpdnvRH0rU5Lj6KKKBBRRRQAUUUUAFFIvSq80wjqeYaVx00g6VnTTZPlxUkkKTTZ8zJpZIaxkrnXGKRLCXA60q3LRq7t61F89Z0li8s26WTMXasyuVM6GGQTJmvlj9pf/gnb8Of2h7yTWFjfwz4lfltRsFx5h/21719N2syRLgVPFMzdxW1zn5WflXL/wAEi/iz4SSSLwj8Xbe1tGOfLWW5tv0Tiu1+D/8AwSINp4kGv/FPxf8A8JLcK4f7Pbb33kHPzM/Jr9Kd1V3vlXpzV8xPvMbpOl22iabbafZQpbWdrGsUMSDAVVGAKuVD9oHqKbJI2Mg8UcxPKyfNG4Dqaq+dynNK7Pt+Uq31FHMPlLOR60bh61TkuhCUDMAD14p3nqVygwPXFWLlLRYDvXOePPAekfEvwbqvhnXIPtGl6lA1vPHnqp/rWzJ++UMpwBzk09SzdOB7igLHlX7O/wCzH4L/AGY/Dt5pPhCCZIruXzZ5rh98jntk165mm1R+1kyMv8C9W7UCSuX96+oo8xScbhn0rJjvogsmZVH4imWupW8kLs12gjH8RIBoL5V3NrNGR61lTa3p1ja/brjUoYbT/npLIqp+ZrKn+J3hG3k2y+JdLjPo15GP5mgix1WR601pUVcl1A9Sa4y8+M3gCwVjP418PRADJ3apAOP++683k/bc+CcM0yTfErwuFXhR/bFt/wDF1HMPlPe1lRlyHUj1Bp24eteFWP7afwNuJBBD8T/DbsxwMarAf5NXzV+0p/wVS0r4NfFL/hGvD2l2PjDS4Y0aa+tbtWCMeoBUkZAo5h8p+hdFcZ8Hvijonxm+G+h+MPD05uNL1KASIW+8rDhlb3BBBrs6sgKKKKACiiigAooooAKKKKACiiigAooooAQ1WELNNuZcDtVqigadhKWiigQUUUUAFJtHpS0UAFFFFABRRRQAnPpRz6Um4HpzRuqeUB1JS0jMF60uYCGWSOOGR5SFiUEuz9MY5P0r8y/23/2KfC/xq0/UPiN8FZ7HUfEdm5k1TTtNnVxOO7ADowr9APjdoeteJvhF4t0zw3dix1u602aO0nI+65Q4r8gf+CZvxjl+CP7SFx4W8Q/aI49fP9nTxSkjybkHjcD0Ge9SaI77/gn/APt0a34G8R2nwq+JEzppYPkWt1fErLZMOiNntX6t6fqEWoAXUTh9oyy55A9fpXwh/wAFH/2EY/iDo9x8T/ANmLbxRpsZuLyytkCm7VedwA/jGK+R/Bn/AAU48YeE/hfc+G7rT/tGvpbG0g1aSQhgOQSw9RRYnmZ9A/8ABRz9ve+8N6rP8NPhvqKpMUxqWo2nLBm/5ZqR3r4S8G/G740/Au+g1iG/1zTLeY4V9SjlEUvsCwr6t/4Js/sSX/xY8UJ8WfiBFJLodvcedZW10MnUJuu9gRygPfvX3T/wUG+CunfFP9l/xZEljH/aGj2zanZGJACHjBJAwO4zxQK52/7I/wAXI/jh8BvDXiz92Ly6i23aRn7sqnDCvZNtfl7/AMEVfHlzPa+O/B8txJLawRw6lbo3RMnY/wBOSK/USr5UFwpobcKdXF/GD4qaL8Fvh3rPi/XpvK07TYWlZVxukb+FVBIyScDrVCOZ/aU/aA8O/s4/DLU/E+uXqQzrCy2Nsu1pZ5sfKFQkbucZr8l/2Pfh/wCOv21P2rLbx74pluL3S9Ou1v8AUb9VKQoV5WGPjAOQOBXC/ED4ifEX/got+0FpmnQRlFnnENnpuWNvYxZ+ZnODg45ziv2x/Z5+A+gfs5/DDTPBugKJIrVd094yBZLmU9XbHelYd2elUEUtFMR5H+094K8eeO/hLq2l/DvxL/wjPiKSM+XcbfvjHKbgCVJ6ZA71+MU3i39qD9kfVhdardeJtAjLgN/aO6e2k56ZORzX78Vl+JvCuj+MtJm0zXNNttVsJgVe3uow6nIx3oHc+Df2Of8Agp9ZfGzWrbwd44s7fRPEM4xb3qOFt7g+nJ4avvTXde0/wzo11qupXcVpYW0ZllnkYBQoGetfkn+3T/wTdn+D73HxJ+FHmroVm32m40sMWksiDndGf7o+ua+cviF+3j8Uvix8Jbb4datdrNa+YqyXceRNNg8KaVkFz0D9t79sHX/2v/iNbeD/AAUl4/hKCby7KygB36hJn/WEDt6Zr9JP2Af2TYf2afhbFNqK7vFutRpcai2T+7yARH06jvXlf/BOT9gzT/hPoOmfEjxbD9p8XX8HnWtpIo2WKN04/vEV990xC0jEKpLHAxyTRu49K/Nb/gpH/wAFBJ/AtxcfDP4d30cmrSxtFqmoW7Za2J/5ZoR/FQB6D+2l/wAFJfD3wRs7jw34FuLfXvGZYwuykNDZH1f1PsK+QP2Y/wBjv4ifto/EgfEL4pS3kXhqeUXMt5dblkuhniOIfwj+ldf+wT/wTlb4qx23xH+KK3H9jvMLiy0uUnzL05zvlJ52/wA6/W/TdMtNFsILKxto7S0gUJHDCoVUUdgBSsh3MnwV4F0H4deH7bRPDel2+kaXbrtjt7ZAqj39zW2zBVyaUsF6nFBAdcdqYCr8y5r5x/aL/b0+GX7NWvroPiKe8vdcaMSmysYt5VT0yc8V9Hqu1QK/HH9rj9g741fFP9qjxJqGk6b/AGpp2qSC4ttSeXbFFFjHlknuKBHG/wDBQb9ujw3+1ZpXhfTPDGlX9hBpc73Fw18VG/IwAAK9I/Yj/wCCjHw0/Zt+B1v4R1zSdZutUinkmeSziQo5boMlhXjH7SH/AATr179mP4I2fjjxF4htbzUZbxLeXTbWM7YwwOPnJ5PHpXqP7E//AATI8MftIfB218d+KvFGs6b9ruJI4LPTViUbUIBLF1bOfbFAHnf7ZP7bmqftoJp2i6H4PmsdN0uWS6ESN9qldQPvthRtGOa+pv8Agi7q8OpfDvx9oE7LNHFdxymBvmVldSDkfp+NfTPw1/YN+GnwT8G+JtP8IadJHqmr6fLZvqd23nTgMpxgnpz6V+TX7P37Rnin9gX4oeONH/sgalcMHsJbOZ/JxIp+SXkHIHBx+tAHp/8AwVc+Hvwi+HfxC0qy8EWUel+LZkM2qWNhhbdEP3SUxgMfQYrjP2F/2sn/AGNvFl4nibwjcSaV4gjjaS4WIx3CxDo0YI+cd+orT/Y3+COu/tvftLah4x8ZB7/Q7e7/ALQ1e4+6skvVIk9s4GPSv1d/aI/ZB+Hf7R/hFNH1/SIrS7tYvL0/UrJFjmtPQKQPu/7PSgDovgf+0Z4C/aI0OXU/BOtx6kkLbZrdhsmiP+0h5x71+c3/AAWz2/8ACV/Dcggt9hvAw7j5kxXzn8Qvhf8AGP8A4Jx/FhdY0e4lisySLXVreNmtbpP7si54+hNcP8Vvjd49/bX+LHh+XX0hutWlaOws7PS7Zo49rMN+FLH19aAP2Y/4J2/bh+x78PF1CFoJltXCBjklPMYqfxBr6Rrm/h34Uh8BeA/D3hy3RUh0qwhtBsGAdiBScdskE/jXSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJmmiTnGDnGT6UAPoqtNfw26u0jqgXrzzWPqnxA8OaLGz3mtWUKr13Tr/jU8y7lKLeyIfHkc0ng/V/nAH2dyCq84weOtflZ/wSkDL+2F8Sckk/Ybzd9ftYr9DPGf7V3wp0/Rb9ZPGekyt5TIUW4B6ivyV/ZD/an8H/sz/tN+M/E+rrdapoOrLcW8VzYoGKq8wlD4zz6frWSa5rl2ajZn7rnPYUtfMHwN/wCCg/ws+OnjC18LaJqc39t3eTb28lvIocAZPLKMGvpzzPatrkcrQ6vmr9qP9tbwf+zhHDbahdLc6lIwDW0B3SIPXFfSuOMV+CX7cWm/8Jf+3Br2jRebum1G3tArPuA3YyQD061nK5UT638D/tZ/H79rrx4+lfDKzHhXwmu7drlza7wQPc4ANfOviv8Aaa/aG/ZP/aBmi8Z69qWpRQ3Hz290oFvexZ5ZcDHT0r9kvhT8LdA+DfgbTPCnhy1FtpthGEX+857sx7k1wf7Uf7KfhP8Aal8Dy6JriCx1KMZstXhiDTWze2cZHtRyD5/I6D4K/HDwv8fvh7ZeKPD1z51tcJuktmI86Fh1Vlr0JldV+Vs/hX4Y+JvDPxk/4JpfFi2msr2SbR5v9Xcruazu0zyrDopr9Nv2Tf29PA/7T1mbJCPD/iiBV87TLpwA7H/nkx+8Kkk928eeOrLwD4W1HWtRljgtrSMsWkbGTX4JeP7nxZ+2p+1FeWekBtQvtUvGisxn5I4Afve3FfXP/BXL9o2T+3tO+GuhXMsUkKCfUJIZOGDdF4r2L/gl3+x2nwl8HxfEjxBGsniPXLcNZxso/wBGt2GfruIoWruW3ZaH1Z+zj8FdN/Z9+Euh+DtPVC9pEpup14E0xHzv+deo03aKdWkU0YhXE/Fv4O+Fvjd4Nu/DPizTItR02ccblG6JuzKexFdtRVgfh1+0x+yP8RP2FfiEnjT4fXuoTeGA2+21W2G6S16fLNgYx79K+6/2C/8AgoFp37Qmkx+GPGN3a6f48t/lHREvVH8S8/e9q+x/EPhzTfFWi3mk6raRXun3kbRzQTKGVlIwcg1+GH7bn7Lt/wDsY/F7Tda8K3FxH4evpvtGl3O/EkMi8mLIxwPzxUS0Lj725+8Jz/jS15n+zh8SJfi38DfBviy4MRu9T0+OW4WHOxZMYYDJJ4I7mvS81SdyWrC0UUUxBRRRQAUUUUAQqzlmyuB25pJANysc5FSKq8kUmD6VHKyror3GTGwZSR2xXAeIvih4d8N6klre6xa6fcIMNDcSqhH5mvR1XcOa/Nb9rD/gmn8TfjV8XtY8W6B4zso7G+bdHZ3c0iGL2GBionGUtjWM1Hc+2r743eDrO182XxVpVuzcYa7Uiq1r8VvBd1EHXxhpE5UcbL1R/Wvyu8Sf8El/j1Z2m6DU9N1kj/lmuoMG/wDHq5mP/gll+0gqjbp1nCPQauo/rS9m+4/arsfqlrH7WXw08H3Swap4u0u2Mhx+8nUnJ+ma9q8O6pZa9pNrqOn3cV7ZzrvingcOjA+hFfihpf8AwSb+POrahGt7Dp9nFkBppr0Pgd6/XP8AZn+B6fs8fB/R/BK6rPrLWW53u5zyWY5IUdl9BWkU0KdTm2PUqWiirMAooooAKKKKACiiigAooooAKKKSgBm4UyO4jkOFbJrD8beLtP8AA/h+51XVbyGwsrdd0lzcOqIPxNfM11/wUU+D1q2bbxppkv8AwI1nKol0N4w5lc+s5boQ/ebr0p3n/u1b1r5RuP8Agod8GpbVbmfxjpwK8iNWJNcJ4k/4K8fB3RVEdjb6rrMnpbW+F/M1HMHIfcktwY1wp3N71WtdUEzuPMBx/e4r8z/EP/BZrQJdRiNh4G1XyR18yeMZ/CnXf/BZXw7Lny/BF8M/7aii8irKx+mtxcTMR5AVl9Say7uQTMskZxMn3sdK/LXxF/wWOlktVg0LwZNBJ3+03Ix+lYyf8Fi/GUcYSPwPo5Q9WN0xz+OKLyHG0T9dbHU47pAoLbsfxDmp4LVIizKTluTz1r8iof8AgsZ4gk1C3mvPBltFGPvra3WA35iu1m/4LLWQjKx+Er8P7yIKd32IcV0P0+m1C3t5BG8gDn+HvU+6vxU8df8ABWv4ka/q0Vz4e0iw0mGNuftEfnM3sa/Sf9h/4++J/wBo74Mp4q8VaKmj3/2uSBPKQrHOi4w6g/XFaKV+hLirH0RRSUtUZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSHpS0UAZd3CZJ4yvAXr71FNDGuSHAf0FaUzKqnAGfpWTagNITIBn6VkdUGyt9laSHLS7PZh1r5N/bK/ai0r4DWLRyPuvJExDZRuN2fevYf2mvjbp3wZ+HeoeIbm52yQQ/Kn+12r8ZfAvg/x9+35+0MI2aeZbibfd3HLQ2Nvnv6cfrQNy5RPh/8Ffih+3Z8TtU1DSrXEckpaa9uGb7Lbf7Ib+lfaXhT/ginpi6SR4h+IFwdQYdNOtgIgf8AgXJr9CPg58HfDfwN8DWPhbwxZJaWFsuCwUB5W/vMR1NdvWpzczPwF/ap/YV8e/sl3EOtyXA1jw95gEOsWmUMTZ4DDsa+9f8Agmb+2hdfGexk+H3iV/8AieafbeZb3RPMyjr+NfbfxM+HehfFbwTqnhjxFYRajpd9C0ckMoyOnBHoQa/CD4K6XqPwB/bs8OaCbmW2OmeLItPkKNgSQeftwfUEYqLDu2f0E02PpT6KsgKKKKACiiigAooooAQfdrM1zULfSdNuL25ZUhiQsWboBWpXjf7V3wRv/j58EfEng/TdQGn6heRBraRvu715APsazsyk7HKaZ+2R8K3upLUeO/Dz3cb4MMOoR13ej/GXQNftvtcWoWk9senlTV+N+p/8Erv2i7OZgPBNvfgniS11uyA/8eYGr+nf8E7f2qtMt/stn4YvLO3HPlx+IrQD9JKOU29qux+yNx4605Y4n+2wRNL/AMsfOrW03XIbiDlhj61+MM37Bv7WJKyPpWuMw5/5GWMkf+RKlb9mv9tDTbfEcHjJh6R6yW/TfWPKy/aLsfs3ea1Y2bRjzV/OlOq2lrJuLKF9Sa/FAfBj9s64QSf2f42+pnb/ABrZ/wCGef21tYtRDcReKli/uS3u3+tXZi9oux+zM3i2y2h0nXHfkUy38Q6bcTFEuEAH+0K/GX/hjP8Aa9k4Nv4j5/va83/xVWI/2Ef2tW6HWF/3vELf/FVrymftF2P1x8UfFnwr4VlhjuddsojI/O+dBj9aoeKf2jPhx4P0Vr2/8ZaTbxH+IXaN+gNfk9df8Ev/ANpPxM+/U7O0lf8Av3evK5rc0T/gjv8AGHVbqIa1rui2Vrn5mNw0zAfSjlD2nkffurf8FEPgPo+Qvjywmb0jDHP6V5V4i/4K6fCrRzJBbxX2oEcBoIcD9a4G3/4IoaGMfaPiNfyf7lmgrttC/wCCNXwosY1Oo65reoy55O9VFHKRzHnGt/8ABYnwrI/+i+DL1yOR5k2KxNV/4LOSTxeXa+AlQD+9c19kaB/wTh+AWg2qwr4It7wjrJdSM7H862V/YF/Z/Xp8MND/ABg/+vVC5j4Duf8AgtL4nls2gj8B6ap6ZaZiPyrJk/4LMfENUxb+EvD8B/2vMP8AWv0Y/wCGD/gF/wBEv0D/AMBhSf8ADB3wC/6Jd4fP1tRQFz8vvEP/AAVy+MetHEEOi6b/ANc4WP8AWuUT/gpf8ftUWeG11tJDIfuwWu5vwwK/afwf8Dfhx8NbMQeH/B2h6ND0/cWca5/HHNdbF4d0mPmPTLJPdbdB/SgfMfhbbftS/tWXyh7b/hJZ1PRodFmYfpHUt94p/bK+JkbB9O8eNH/saXNAD+OwV+7CWcEa4SCNR6KgFUtd17SPBujXGp6vf2ej6XbjdNdXkqwxRj1ZmIA/Ggk/Dux/ZP8A2uviFELO70XxY8B5K6lrK28f4h3Fdf4V/wCCQ3xy8T5Ovah4f0ADobu/luW/KMEfrX7A+B/ip4Q+JVsbjwv4l0vXox1/s+8jnx9djGuqoHzH5CR/8ETPHUjK03xL0FT322dwx/U1vQ/8ESdVX5n+KdsG/wBnS2P83r9XaKnlDmPykb/giTqWdw+KUDN/2DGX/wBnrG8Rf8EUPFdtp80ukfEHTNQvM5SC4tHjDf8AA8nmv10oo5Q5jzr9nn4TwfA/4M+FPBUJV30uySOeROjzHmRh9WJr0WiiqJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKAFpD0NAIPSloArqnlxnaffmqyrLIm5W3D2Nfn7/wUX/b28TfBPXp/h34Q0x7TU5rVJn1qQHagbsg7mvibRv+Cjn7QGmnbHrq3K9v9EJqOZmqP3lt5GWFRJ9/HNZfibxfo/hHR59T1q/h0ywhyXnuWCLx9a/FJv8Agop+01fKDGlwQf8AnnpT/wCFP1uP9rb9sy207SNQ0TVpdEmYMJXtzawY9WY4qLMVkfsr8N/il4Y+LmhnWfCesWuuaXvMZntX3BW9D6GvyD/4Ke/CqX4H/tPaT460NBaWuuFLtTGcbbhD835gA1+lv7Gv7KNj+yf8OZdCh1OXVdQv5Fub6ZuI/NxjCDsK+Zf+C0fh03fwm8EaukSlrfWPs5kPUb42I/D5a05URc+xP+F2aHpv7Odp8SNZuI4tKk0OO/mZjwxaIEp7ktxX4JaJ8GPHv7R2t+MPE/gjwdcX2nQ3VxfTR2YGyBXcsIxkjOAeg9K9h+IP7VOs/F74D/Dv4EeEIZ7hUjitb5th3yyqfuqO6jOc1+uv7I/7Odl+zX8FdL8I4huNSYGbUriNRiWZuoz3A6CnYR8d/wDBPv8A4KLeG5PDuhfC7xwsOgXmnxLZWF/jZDKq8ASE/dav0d1y0tte8OX1s4S4tbu2dD3VlZSPywa/Kr/gpF+wBF4NXUPiv8PLd1s3m87VtJhX/U5/5axADgZ6j3r0n/gmL+29cfEmA/CzxteRpqen2YGl3czbWuEXhkYk/eApcqA8W/4JXapF4B/bG8beEzJsiubW9sIl9TDPuH6LX7EV+K/7Nenp4Y/4KmXljbOTEPEGpqCDkMjbyOe/Wv2nzVARXl5Bp9rLc3UyW9vEpeSWRgqqo5JJr8Wv24P2kNZ/bK+OemfDX4fXM2o+F4btbOygtztTULknBkPPKDsf0r2H/gqd+2deW+pS/BrwddPDI4X+17y3OXJJ4hTBzn16V6P/AME1/wBgm2+EOi6f8TPGtmX8a30JazsbheNOjPR8EAiQjr6ZoA+iv2T/ANknwp+zD4EsbDT7C2m8SyQr/aWrBdzzSY+baxGQvoK95oooAKKKKACkZgqkk4A5Jpa+Mv2zf2qfEFnqg+Dfwcs5td+J+qr5Vy1vEWTTIGXl2bGA2D+FAHkv/BQD9uZfEDX3wR+FcL+INf1QNZajd2oDrGG4MaEHlvXjHvXzH8QP+CWPxA+F/wABNR+IGsatZJremJ9qm0K1BkaOIcn94OCw9Bke9foT+x1/wT78J/s4JaeJtYP/AAkPxAkjBm1CZi8dtIfveVkAn/eIzX1B4006DVvB+t2V1GJbeeymjdGGQQUPFAHyF/wS3/aVv/jh8G59B1yZrnW/DLLbfaGxmWAjCE98jGK+16/G7/gjH4gms/jp4m0mN2Fre6N5zJ23Iy8/qa/ZGgDI8WWd7qHhnVbbTZFhv5rWSOCRs/K5UgH86/nt8efs5/GP4L+MxrnirwhqN1dw3H2l7yaFrmKZ853ORnINf0U1FcW0N3EYp4kmjbqkihgfwNAH5U/Av/gsV/YMMejfEjwn5UMKhIbnRU2hVHYxn+lfZPwp/wCChHwT+Lt3HZab4pXTL6QcW+rRm2J9gW4Na/xY/YZ+DHxkmFxrvg20gvB/y9aaPs0n/jvH6V8c/tAf8EdbAWMmqfCnXJor+Eb10zVZC4k/2UfsfrQB+mqyR3kYkgdZ0PR0YFfzFWlXHevw/wBJuv2wP2S7gxw23iBtMhOWhkVr232/qa9N8J/8FiPiZqes2WkXPw/0rUbqaQRtDbGYTn6J2oHc/XSlrO8PX1zqeh2N3eWzWVzcQrLJbuctESM7Se5FaNAj80P+C1XjSSz8E+AvCys4h1C7mvJgp6rEoAH5v+lfQ/8AwTHTb+xr4JfG0SG4IGPSVh/Sua/4KIfsW+Iv2soPCNx4Y1WxsL7RXmjljvtwDxy7eQw6bdvTHNfR/wABfhXD8EfhD4X8EQ3CXY0e0Fu1zHHsEr5JZ9uTjJJ70Ad9XxR+2N/wTX8P/tKeIrfxLoeox+FvEDP/AKdP5BlW5XjqAy4OO9fa9IR+dAHn3wL+B/hr9n/4e6f4T8M2qxW1sg824KjzLh+7ue5r0KiigDB8beCdH+IHhu90TW7C31Gxuo2RormMOoJGAee4r4d/Y6/4Jn337PXx21Lxt4k1fS9Z06yEg0K3tRIZI2c/6x9ygKQMjALfWv0AooAbt5yOD3p1FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADG71+b37X3/BRf4kfs6/G6Xw5aeFLKLQfs4e2bUAVe47FwwHA/Ov0jxXE+O/gn4E+J2padqHivwppfiC808k2s2oWyymLPpmolG5cJct9D8cfFf7b37Sn7Snm2PhfQ7yO3k4x4b02V2x/10FXPBH/AATj/ag+KEP2jWbw+GYWOCuv6vIsn/fEYc1+0+i+G9J8N232fSdMtNMt858qzgWJfyUCtHHvS9nEp1JdGfknP/wRN8SpYyyP8UdNkn27jH/ZsmM+m7zP6V53+xL+wv4R+OHxC+I3hnxnqeopN4Zc26CxKwliW27yCDj6V+1lx/q2x6Gvy/8A+CePiqbWv28vjoot/sEVwLovbB9wzDdLGDnA68np3pWWw07q7PqD4B/8E6PhX+z/AOKLbxNpf9qaz4jtWJt7/VLneYgRjAVQBX1HtpefWjn1p2ZldhX4h/td+EU0/wD4KQwWkl55P27VNPne4/557ypxiv28NfiB/wAFJdLvPBX7bq69eO8kVybO7hkI2gCPA2A/gOaqRcD9wKKr2d9DqFnBdW0izW8yLJHIhyGUjII/Cpt1O6Iscn8Svhb4X+L3hmfQPFmkW+r6bN1jmXJU+qnsa/FT9uD9lW9/Yr+JGk6/4N1K8i0S/cvY3AbbJbOuPkyOv41+4HiLxNY+GLT7TfXEdvCD8zSNjAr8m/20vjPqP7b/AMYtC+DPgnSoHGmag7DUt5YuduDkdABUXjsaKL3PHf2Efgncftg/tGPqHjbUjqtlpUa3+ox3MhMlyoICoPbJFfurY2UGm2cFpaxLBbQoI440GFVQMAD8K/C4eEPiH/wTL+PnhjV72WG9F1FidbVz5NzG3DRN9P6V+4PhHxVp/jjwvpWv6TOtzpupW6XNvKpyGRhkVUbITNqiiiqMwoopKACvzS/4LOeL9Lb4e+DtA3RtrTagbqMfxLGFIz9Dmv0kvNQgsLWS5uZkgt4xl5JDgKPU1+IP7cPiOX9qb9ty28JeG5ku4EuINDs3gJZS5OJHH0J/SokaRR+l/wDwTl8N6l4Z/ZA8CQaocz3EMl3GPSKRyUH/AHzj86+l/wCGuc+HPguD4c/D/wAN+FbWWS4ttF0+DT45Zcb3SKMIGbAA3ELk4A5NdJRFaEyd2LRRRVkhRRRQAUUUUANVAvSnUUUAIq7elLVBNSH2gxMMGpvtiO3lq+HPTip5kVyss0VC1wvIVl3e5pyMeSzA+mKOZCsySioI5mZmDLjHepQwNNO4NWHUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAcB8bfg7oXx5+HOqeDfEaTHTb9Cplgcq8TfwsPXHoa/HL9sT/gnBrf7MXhm78YWfiG01/wmlzHEN8flXkYbjlfunn0NfuVtHPAzXxp/wAFYYZG/ZA1cg5KX9qWOO2/B/nUSS3NIt7H5wfsQfsJ6h+1wdY1SfV10HQNLdIHuI4w7yyEZwoPtX3h4b/4I1/CTR9Shub7xB4i1WFPvW7yxxK/1KrmqH/BGGNE+Bfi9lGGOt7T9BGMfzNfoXSVmDbR8or/AMEvf2dFGP8AhCJPqdQn/wDiqcv/AATC/Z6X/mT5j9dQm/8Aiq+rKK0IufMOn/8ABNf9njT5hIvgCCYg52zXUrD/ANCr1Cw/Zj+E+mWotrb4eeH44R/D9hRv1Ir03mjmkFzyPUv2SPg5q0PlXXw50CSP0FqF/liuVX/gn3+z4sm//hV+jH2IkP8A7NX0Lg0bTTA8c0v9jn4KaKoFn8NdBhAOR/o+f5mvWdN0qz0WyistPtYrO0hXbHDAgRFHoAKt0tJKwgooopgFFFFABRTdwHesfUtfh0rz3vZobO3QZ8+aVUX9TQNJs2qK+J/il/wUr+G/hOOay0TxPHr+sZxHHYWzyIx9OBXjvhn/AIKIfGzXviHYJYfDC91zQ58CSCzsZwwz3BI7Vnz+RpGnzdT9OqKp6XfNqOn2tzJbzWjyxq5hmwGQkdDjvVytDIKKKKACiiigAooooArzQrtL5qBrJPMaTJ+lWZNqRNnpjvVe7uAulzzf6sCJm57cVHKaqTR+O/8AwVS/aTfxp45Hw40j9zYaS269deCzdgfWvtX/AIJj/AfTfhT+zzpXiJYs634qiW/upWA3BCTsT6d6/FD4neLj4q+KXiXXpJpL2K81Se4DyMSXQyEgfTGK/c79mn9tP4S/ED4a6JDY6zY+HLi0tY7dtLu5Fh8oqAMDOBjipHJ8x9RUVwtv8ZvBlxbCZfEmmsv+xdI36g1X1T4zeENPUTP4k01YvVrtF/mavmI5TttS1GDSbGa7uZBFDEu5mNfht42uLTxf/wAFLrZ7EiaC88Y6eylfcpmvqv8Abi/4KLeH9I8Har4K8FXw1LxJcELJfQEPBEvfBFcF/wAEu/2P9a8SeNrf41+NbR0sYP32kLc533M5xi457DnFUVZI/WeikpaDIKKKKACiiigAooooAbuo3U6igAooooAZRT6KBjKKfRQAUhOBk8ClrhvjZ4d8VeKvhjrul+C9Wi0TxHcQFbW8mTcqN/8AXoEdwGDDIIIo3A8g5FfiNq37SX7Vv7J+vmz8Xzag1q3JOo2/mxsPUOOK9++Hv/BZHRpmt7XxR4WubIjgvbtvoL5fM/Tykrwb4KftkfDv43ZTRdbgNxnC28jBJD/wE8mvdI5BIu4UE2ZNRRRQIKZNMlvC8kjrHGgLMzHAAHcmnZzyORXwX/wVO/aql+EvgG38DeHdQ+z+JtcGZWgkG+CDPVucrn3oA8m/bo/4KUavpfih/A/wqv4Ha3by73VIQJcydNsRGcn6V4/8Mvhf+2x8UGOu6bqvifSVb/lrq2oNa5+kbYP6V3P/AAS//YhPjnU4Pi546sRNokDn+yLK6j/4+5Af9e4I5UdvU1+uKRrGqqq7EXoBQVzH4OfE74nftafs665Fc+MNd8VaQwfYl1JI0lpIf7ofBQn2r9KT8NdQ/by/Ys8KR+KNUuvD2q6rZpdG4sm+WRlJALr3U46V9PeNvAPh34j6K+k+JtHtNa05juMF3EHUEdxnoazdQ1zwZ8DvAtsLu8sPDPhrTYBFbrLKscaIo4Vcnk+1AXPw++Ln7G/x5/ZAvJ9csItSl0e3ZtuveG5XdFjH8Uyryg/3uK+0f+CVn7WHxJ+M3iDxB4S8ZXMuv6fp9klzDqjIS0LFgAjuOORnAPpXhn7e3/BSJ/jZpt58P/h0rw+ELj91fajImJbzn7ijP3f519g/8Etf2bdR+BnwSn1nxDYSWHiHxNIt09vcRNHPBABhEdWAKnqcGgk+1KKKKACiiigAooooAKKKKACiiigApM460tNkBI4oAarlunNSU1VCinUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMkTd3xT68g/aw+OA/Z5+BXiTxpHEs97ZxBLSFwcPMxwoP8AP8KAPTrHXLC+1C8sILqOW7s9vnwq2Wj3DIz9a0a/ND/glT8VPF3xo+Lnxb8XeIZJJ4tQt7ZmZc+THMDjavpxX6XL0oKkrHM+Jvhl4T8aTLNr3hrStYmUYEl7aRytj0yRmmW/wr8GWePI8IaFD/uabCP/AGWuqoqeVCuVI9JsYhhLO3QeixKP6VaVQqgKAAOABS0VQgr5K/4KffDHVPid+ytrEGjWT39/pdzDqKwxDL7UJ3FR3OCa+taZJGk0bRyKHRgVZWGQQexoA/Hv/gkT+zfd+JPiXefEzWbAro2hwm309pUwJrhuNwBHIUEnNfsPWfofh/TfDOnx2Gk2Fvp1lH92C2jCIPwFaFAEN5Zwahay211Ck9vKpV45FDKwPYg1+Kf/AAUK/Y5179nH4h3PxH8FmWDwlqFybhJLMlZNOnOSV4HCHsc1+2VZHizwnpHjnw/eaJrtjDqWl3aGOa3nUMrCgD8Mv+CaUOoeMf21fC2p3Usl9eYub+5mkJJPyNlj+NfuB8SP+EhbwJrq+E0tX8StZyLp4vJCkPnFTt3MASBn2NeEfs9fsD+BP2bvixrfjXwxNdE31t9mt7GY7ktVJBfaepzivplc45oA/nN1y2+Jn7Ovxug8U+N/Ds7eJLO9F/I2tW3nQ3T5zy3Qg1+qHwY/4K2fCPx5FZWHi1b7wRrbIBO11CJLJW9FkVi2PqtfYvi7wD4d8faXJp3iLRbLWbOQYaK8hWQfqK+I/jp/wSF+GnjbT3m8ATSeCdVUZRCzz27n0IY5H4UAfdHh/wAS6T4s0uLUdF1G11Swl5S4tJRIh/EVoq24n5SB68YNfhk3wh/a2/Yj1eV9Ci1l9NQAvdaCGv7Jh6FNuR+KivqD4C/8FkdE1ZodO+Knh+TR3GEfWtJHmwhvWSIkMo/3QfpQB+l9Fcp8Pfip4S+K2kDU/CWv2Ou2mFLPZyhymRwGHUH611dABWbZ+G9J0/U7rUbXTLS31C6x591FAqyy4/vMBk1pUUAN2n1yaz/Ek8Vt4d1SWeRYoUtZWd3OAo2HJJrSr57/AG8PD/xB8Vfs1+JdK+G8TT67dKqSxREiV7fP7xY8fxEfpmgD89v+CLXhG8vPjR4t19SosrDSPIcnOWaR1wBxjjBzX7G18a/8EwP2c9d+AvwX1KbxTpo0zX9cvftLW7j97FCFAVW9DnJxX2VQAUUUUAFJgccUtFADZI0mQpIqujcFWGQa82s/2bfhppvj1fGln4O0u28SKCBexwAHnvjpmvS6KAEpaKKAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK99Mbe0mlVN5RGbbnGcDpX5N/8E29Rk1b/AIKCfFu8MP2QXEGqTNBu3bc3yDGcDP5V+r2tM0ek3jL94QuR+Rr8kv8Aglncy6h+2r8StTEbNHc2d9k9k8y6WTr+GPxrL7Rol7p+vdFFFamYjdK+I/8Agp1+yjq/x8+GtlrnhGwS98T6JL5rQLxJPBg5VT3I9K+3KQpmgpOzPgP/AIJo/tkaR4v8B6X8KPF2oGx8c6KGtbSO83K13ACSnLD76g7dvXAFffdeQ3P7IfwguvGsXi5vAumx+JIrv7cuoQ+ZG/nf3sKwH4YxXsG2s+Vjuj4l/wCCg2o/E64sbbwr4K8J3Orxa/tto9Tt2/495P8AaHYV0n7Df7Ddh+zRoMus+IXi1jx5ftvuL0jcLcH+BG7/AFr60MatjcA2DkZHSnUo01FtlOo5RSPhr/grl8O9L8Rfs0yeI5o9mqaJewvBMoG4qxKspPpzWL/wR7+Mtz44+COseDdQnM1z4YuwLbexLC2kGQv0VgcfWvSv+CoWm6rqv7I+v22k6XPq0z3dv5sVupZ0i3Es4A9OPzr5V/4Im6PqC+JPiXqnkumlNaWttvYEAyhicfXGaqxNz9YKKKKsgQniq8l0sbAMyqfc1P8Aw15z8cbjxNZ+Cbp/CVp9r1kkCMYHApmtKKnLlZ81/wDBRX9rLR/hZ8K7/wAH6fJJd+LPEVs0FrDH1hDHG84OcjPFeZf8Et/2K73we/8Awt3xrasmq3kTLpVlcrl4gx5nbIyHPIH1Ndp+zz/wT5mvvHl58R/jTcf8JLrksnmWGmSOXhtRycnPccYGa+8I40hjSONQiKMKqjAA9KhJ9R1LR0RJtAzjilooqjEKKKKACiiigAooooAKKKKAPkr9uv8Aa81P9knTdDv9O8OQ67LqsjRI80xjSIqM5bAr4gk/4LEePTcFl8JaSFfrsuGbH04r9cvGfw88NfETTf7P8TaJY65ZA7hDfQrIAfUZ6Vwlt+yP8G7PHlfDjw+mOn+iA1nymvN5n5p3P/BYbx3cLgeBdF+ou5GP/oNUNQ/4Kz/FHULd4YPB+m26+sUspP8AKv1Vh/Z3+GNv/q/AXh9fpYR/4VuW/wAMPB1qCIvCmixg9dunxf8AxNL2aH7Q/G64/wCCqHxpbPl2+moT627f41Hp3/BVT9oS61q1srBtGkWWVI1tV0wO7EnoDmv2VHww8HDp4T0P/wAF0P8A8TUVv8JfBNreR3cPhLRYrqNtyTJYRKyn1BC1UYqIpVLmx4ZutSvPD+nTaxbR2WqyW8b3VvE25IpCPmUHvg5rUpMUtWZBRRRQAUUUUAFFFFABRRRQAUUUUAFfJn/BUK3juf2QPFYkXcEeFx9Q2Qf0r6yr5h/4KSBf+GQfHDPjCwqRke9RL4S4fEeEf8EWbhpPg147i3ZWPW0IHpmL/wCtX6LV+Z//AARHuZH+H/xMgLZiTU7VwvoTE2f5Cv0Z8U+KdM8G6NNqmr3kVjYw/fmmYKB7c0o6BLV2NXcN2O9OrxzwZ+034D8c6glrpniOzu7g/wAMMox+terWOrW+oKfJk3Y5IpqSkOUHEkur6Kyj8yZtif3qqQ+ItPkcRJdI7/WvJf2wPH2ufC/4BeJ/E3h7TRqupWUQdIGBIAzjdgc8V+Nmn/8ABSD41aXP5kWq6e7/AN6SyB/9mqrlKMban76SapDBDvkdc+gNTLeR8BmCsV3Fc9BX4laD/wAFX/ippqM19pGj6gOxZWX+tJ4g/wCCrnxd152/s2w0uxmZdjSRxmTj0ouFodz9u45FkXcjBh6g06vzS/4Je/tHfGH41/EPxHp/ijUV1TwpZ2huZJJotrxSswCRocdOv5V+lWaZk9B9FFFAgpD0NB6Vj+ItYj0XT5Z5ZNgVCc5oGlc8++Kfxm034XaPNf6hcxxpGPlSVwpavxU/aF/ak+JP7WHxCl0vT5bt9OefyrLSdL37HUnALhev1q78bviV42/bi/aK/wCEd8IvdXdhcT/Z9NsUkITy16yv29ya/V/9jf8AYn8M/ss+D0R4rbWPF9z897q7RAsDjGyMkZVf50G8pLocD+wn/wAE/wDRfgH4YTX/ABlp1pq3jm+G+QTRrLHZDPCx5HB9SK+z4bOGEARQxxgcDaoFT0tBhcQKFyQOT1paKKBBRRRQAUUUUAFFFFAERXcMHkVheO5mt/Auvyrw6afO49iIya6GvLv2o/Elx4P/AGc/iRrVp/x8WWg3cyfURNQO5+Lf/BPH9mPRv2oPi1qOk+JYrhtB0/Tmnme3baQ5IC8/U19Z+Pv+CK9mzSSeC/HstvkZEGqQZyf95a53/giNj/hKfidxyLGzx+LNn+VfrJU8pXMfjLJ/wSG+N1jHssPE+mBP7ovXQfkKzLT/AIJP/HvVbs299qGmxW4/5aTXzMPwGa/a2iixB+df7P8A/wAEgfCnhGZNU+JOqt4q1Dr9it8x24Puepr9CdN0210ixgsrKBLW0t1CRwxqFVVHYAcAVcoqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvXvC+j+KrFrPWdLs9VtG6w3kCyr+TA186/Ev8A4Jx/A34lKXfwquhXXafSHMJH4dK+ndwo3D1oA/H345f8EqfHvwikn8TfCjX59ehtjvFkrGK9Re+GHWvRv+CY/wC25r/i7xdc/DH4hahNeapcAvptzdcPuUfNE2ec4/lX3J8cf2jfB/wD8F6jr3iO/hR7dT5dirjz5j2AXrX5HfsN6NefHD9v6z8W6Lpr6dpFvqd34hmUZKwQsTiMt0ySwGPeouaep+5VFFFWZnP+PfG2l/DfwbrHibW7lbPStLtnuZ5n6Kqj+vSvwt+GPh3X/wDgoN+2Qs+rrK9nf3h1C/JYkWunowxGvpwQAPev0R/4K4fFf/hBf2a/+EcgljF54ou1sjGXAbyl+dzj04HNfnT+wL+1hov7Jvi7xPrOtaJNqj6lYLaxSRHDRYcHB9AcCgD95vD/AIf0/wAK6JZaRpNpHY6bZRLDb28K4WNB0AFaNfKv7L3/AAUO+H/7THiL/hHLRJdC19kLw2t66gXGOSsZ7sB2619VUAcl8WfH0fwt+G/iPxZJZzagukWUl39lt1LSS7RkKAOSSa/n1/aP/at8bftKeLr3U9e1K4ttMkf/AEXRbeUiCFRwBjP86/oxnhjuoWiljEsUgwysoIYHsQa51fhf4PViw8LaOG9fsMf/AMTQB/P/APss/Fb4a/B3xUPEnjbwVe+Ndds5lk0+1Nwq2+fV1YEZHuDX70/Af4wWXx4+Feh+OdO0q+0aw1ZGkhtdRVVl2hiobgkEHGQa8/8AjN+wv8HfjlbomueFYLG4Q5W60gC1l/NR/SvVvhf8OdI+Efw/0PwfoKSJpGkW4trcStubaCTknuck0AdTRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8e/wDBSr4G/Ej9oL4ZeGvC3w/s1vYm1QTaojXUUAWIKdrfOw3YJ6DJr7CpOeO9AHh/7H/7Ndj+y/8ABvTvCsJjn1aQ/adTvIxjzpyOfwUcCvcBS0UDbuFFFFAgooooAKKKKACiiigAooooAKKKKACiiigBGUOpDAMD1Br4+/aY/wCCZvw0+Ozvq+hRr4C8WF951HS4h5U3HSSHIU9uRg/WvsKigD8tP+Cdf7Fvxi+CH7RWtX/ic3GgeGNGjkgcxTs1trDtkKYhjDKBySwUjj6V+pdFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1mC4ycU6mSRCTG7tT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMjxZqlpovhnU76+mWC0gt5Hkkc4AGK/J3/gkjeDUv2n/iLdWuY7KTT2lEedwG6UHGfbFfpd+0b4fXxZ8F/FejNcNaveWTokq8lT64yM/nX5x/8EUNHZvGvxL1AplYrK2g83H8TOzEf+O/rWLV5G0dIn6z0UUVsYhRRRQAUUUUAFFFFAEc9vHdQvFNGssTjDI4BBHoRXOeBPhr4Z+Gdjc2fhjRrXRra4l86WO1QKGbGM109FABRRRQA3HFJt3dRmnYo20wEwKDS7aMUC1FooopDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5p/4KLQ2tx+yL49W7JCC03Lj+8OQfzr6VOa+Z/8Ago4W/wCGQPHu04P2YdvespP3S4fEfNv/AARJii/4Vz8TXUfvTq1spbPbymxX2j+01+z/AGX7SXwzuPB9/rN7okMsiy/aLLG7I6Ag9RXx/wD8EVbKCH4O+PZ402zS62iu2TyFiG0fhk/nX6M4oFfW5+MHif8A4JJfG/wLeGfwnrun62i8h7K9a0k/JsVyk3xg/au/Y51C3j8QHVEsbdfLj/ta2+0Wu09PnAyfxav3J21yHxYn8N2PgTVLzxZZ2d9o0ERaWO+iV4/yak0hqb6nz9+xj+254a/a/wDDt5omrWVvp3iyGJmvNHf545oc43LnqOele0yfs2/CqT73w88N/hpsQ/8AZa/I7/gmeba4/b1d/DDPFoPkalIqYOBbYxGpz2BK1+1Ov6tHoWhajqUxCw2dtJcO3oqKWP6CmLU/Kz9sr9qbwB8EPipeeAPA/wAK/CerNZogubqS1U4mPJjAA6isz9gb9pjTviR8d9I8AT/DTwlYadeJcu1xHYqZRtUsoywPpXy78O7VP2hv2wvtieYINS1x74jG4iIMSB+WK9h/4Jv6TG3/AAUFmiWNfLsF1YqoHCgZRcfTdQa8zsfsvaaT4a8AWM89tZaZ4ftGOZZIoo7dCT6kAVrWOoW2qWsd1Z3Ed1bSDKTQuGVh7EV82f8ABSPw7Pr37IfjWS2d45tPjS+DRsVICMM9PrXln/BH34lS+MP2d9W0G9vJbu+0HVnQec5ZkhkVWRRnsCGq+Yytpc+8aKKKokaWFfA//BUv9qab4SeBLTwl4cvPs/iXVuWubeTEttGO4I6Zr7xnkW3tZpZDhUVmLegHNfgf8TtUn/bM/bZttHsrl5LDVNWj0+3kdiwSBT87+2QCaDSOhP8A8E5Pjp4H/Z7+NV/4m8bSyw250yS2gkhj37HJGTj3Ax+Nftt8M/jh4E+MGnRXnhHxPp2tLIu7yYJ185fXdHncPyr5U8T/APBIT4KapoL2mkHWNFvjyt2t602D7q5INfnX8WPgL8YP+CfnxEsNas9Rns7fzsWPiPTWYQSjuki/zU0C0Z+/dFfP37E37UUH7VXwdi8QzW8djr+nznT9WtIz8qzqqneo/usGBH4+lfQNBAUUUUAFFFFABRRRQAUUUUAFc58RvBtp8RPAXiDwxfLutNXsZrOQezoV/rXR0UAfgr/wT7+Ok37LX7TRsfE8jaPo2oB9K1pLgECF1JKMfTDD9a/d/TdStNasIL2yuI7uyuIxJDcQuGSRWGQQR2r86P8AgoV/wTnf4hXWpfEv4cW2/wAQSHz9U0Vel50y8Y7N6jvXjf8AwT3/AOCgEXwNhb4ZfEyS6g0SKfy7G8mBLWHrG+ei5/Kgqx+w1FYvhvxhovi/R4tU0XVbXUtOlGUubeUMh/EVpi6iZNwlUr65oJJ6KzLjXrC2Db7mMY96+Yv2n/2+PA/wR8Paja294mpeIh+7jsYGBbJ70Dsz6nt9Rt7qRkikDMvWrNfk5/wTe8O/GX4zfHKb4sa3r2o2fhWMN5wmZvK1EkYCopOMDqSK/WOgQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNS1G30nTri9u5BDbW8ZllkPACgcmvlyT/AIKc/AOK7kgbxavycb/LODX0Z8RPB0XxC8B+IPDE9xJaQ6vYzWTzwnDoJEKkj86/OqT/AIIo6Sfu/Eu7H105P/iqAPozUf8AgpR8ANL06W5HjeG8k7RW8TsSfQCvkP8AaG/4K5yalHd6X8MNPkttzYTVr/t9FrpIf+CJ9sv+s+JUp/3bBR/WrT/8ETdGP3fiPej/ALck/wAaC+byPhz4Q/CX4lftsfEKJbvVri9tvtObzVNQuMpbIxycAn+Vfsv8FfBPwd/ZM0Wz8HaNqemWOp3Cjzbi4njFzdsTwTzk+wFfGWp/8EgfHfhLTZU8D/FZ45Jf9ZC6vbq31KmuU+G//BLn4yWvxu8Jal4z1G1v9C0+9huLnUY9QaWURRnOxQ3OeKnlFzH6+0UgG0AUtUSfjb/wWo8SXV/8dfCGhlj9i0/QBcqvYvLPIGP1wi193/B//gn98HfBvw107SbzwvbazdT2sZu728G6SViASc9uTXwR/wAFntNmi/aF8LXfkyeVceHkjWTadrMs0uVB7nkce4r9M/2T/jxpP7QHwX8O+ILK6hbUfskcd/aI4LwTBQGDDORkjNA7aH5Eftpfs3av+w78ddH8QeCLm8ttDuj9q0jUEB3W0wyDEW6bvQdxX7Mfs9fGCz+PHwb8MeOLMLGuq2oklhVgTFKCQ6HHQgg8V8+f8FWvA9t4r/ZJ1jUXjzeaHeQX1vIBynzbG/MNXn//AARl8d3OvfATxJ4bnRvK0HVswuRwVmXeRn2Kn86Atpc/QmiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFUNY1RtK0y6vFtpbswoXEEIy747AetfO3wl/wCChnwc+LGuLoMety+GvEG7YdO1+E2rbv7oY/KT+NK6K5WfTFFQwXUV1GJIZEljPRo2DA/iKk3UxHiH7ZsurWP7PXjO/wBFuY7S+ttNmkWaRsAYGa+Uf+CK+hpa/DH4h6pu3Pd6xHDnbj5Y4+x/4Ga90/4KQfEaDwL+zT4nhlmtg2qWr2SQSvh2ZxgEfSud/wCCTfhldB/ZH0m88jypdUvri6ZscuN+0H8lrJO8rov7J9m0UUVqZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFQ3CSyQkRSeU/rgGnxhlQB23NQBFcXC265bgetfOn7eWnz+Jf2VfiBHbODFb6bLNIuRk7eRWR+3N+1dF+zb8PZpofLl1y9Hlabb5BMjd3Ix0FflbqH/AAUR+J3ibwj4t8N+IZ7bVbLX7SW1kdYxE0SsOgAAB/LNc7vJWR0pKK13PuX/AIIu7o/g/wCOgTlTrYwP+2Qr79vvGGi6ZcS291qlpBcRLueGSZVYD6E18Uf8EefD9vYfsy3+qIpE+oazOZGJPIQKq18r/tcfsb/tFa18dPFOs6JYar4h0jUrx5LO40+6f5IeqqQGGMDjnPSrM9Ln6J/FP9uH4V/CWNk1nxTaTznotiwkP6Zr8zf2qf8AgoX41/ams5/AXgbR7mx8NzzYZYUMl1dp/Cr8fKPpXmcv/BO79oiZvNk8C6hM/rIysf1NXfg7/wAL1/ZP1LUdQ074Y3TmbCyyalpLuRg8YOOPwoKsj9Hv+Cdv7Dtv+zv4di8ZeI0MnjvVLXY8Z4FjExDGMY6kkAnPpX0N+1Hrh8N/s4/EvUl+9D4fvcfjCy/1r8u9F/4KpfH7U/EFhpEHhrT7q9ku122CWMgmlQ/wdenvX3x+294qvbX9iPxpqF/b/wBm399pSQzW7HOxpCoZP50ibH50/wDBIbwVD4m/aJ1TW7mMNbaJpbS/MOAzEDNaP/BMqVL39vjxDdJ91rXUmH1Mq816t/wRq8Mx2Xgr4o+LZYlVP3dmGPXCRF3/AFIryD/gkfGLz9rnWriQ75U0q6fceuTKmTVAfq9+094TvPHX7PfxC0DT4ftF/qGiXUNvH6yGMlfxyBX5Vf8ABI74wD4b/H3V/A2rMbeHxLB5KCT5dt1CThSPUjcK/aE/NweRX4RftmeFrz9lP9tqfXdCia3iS+h8Q2JXgYY5cD6ncDTsStrH7wUVxHwV+KWm/Gj4X+HfGWlH/RNWtUnCE5KMR8yn3BzXb1ZBwfxyvtR0n4K+O73SMtqlroV7PagdTIkDsuPfIFfi1/wS00OLXP2y/DzXAD/YLS8uRuH8YUgH82r9z9c0sa3ot/p7sUW6gkgLDsGUr/WvwX+AniST9jH9tyCPxG5gg0nUbjS9QkA/5YPkb/fsaC0fvvXiP7aHgnw147/Zu8b2Xib7LFbxafLNbXV0FP2e4Cny3Uno2cD8a9lt9Stbqzhu4riJ7aZQ6ShxtYEZBBr82f8Agrt+0rb2PhWy+FWi3KS3l8y3OotG2fLjX7qnFBKOZ/4IkLIuq/FNdzGFYrDC543Hzcn6nA/Kv1Yr4O/4JE/B278A/AnU/FGpWgtr3xRdi4jLJhvs6LtjH05Yge5r7xoEFFFFABRRRQAUUUUAFFFFABRRRQAyviH9sX/gmf4a+P8AeT+JfCUsHhfxXKwa42piC69yo6N719wUUDPw5v8A9i/9q34HzPaeHI9budOHT/hH7wvF/wB8E4/Sp7Kw/bZ2+VGvjbH+0FFft/RQPmPxK0/9n39tPx1IRO3iO3jlPzyX16sQH5V9H/AD/gkfaabq8Gv/ABe10+J7teTpkLsYs9tznk1+k9FAcxlaD4e07wno9tpek2MNhp1unlxW9uoREX6CtWkpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPDf2sv2WfD/AO1J8OZ9E1ONLbWbdWfTNT25e2kP9Djmvyhh/Zq/ag/Y18RNrfhfTNRJ3FRc6E5uIZl9HiH+FfuhTHUSfKy7hQVc/GT4vftFftU/Hb4bXfgLWPhtqkFnfKi3VxHosys4BzjO31r7T/4Jg/AXxb8C/gvq8PjDTo9L1DV9SN5Haj/WJHsCgP6cg8V9k49h+VOoC4UUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMAoooo5mAUUUUczAKKKKsAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopu75iMUAOooooAKKKKACiiigAooooAKKKKACiiigBuyvkz9rz/gnp4Q/acaPWbG5Twh4ujwDq1taeb5ijs0YdMn3zX1pz60c+tZ2Y7s/GzUfgr+2l+ylaznw7qWpa/pLHh9Jna9IX1MZG4VyPh//AIKv/H3wTNbWGtDTdVNu/wC+TULIxTSD0LcY+uK/cDbXLeJvhP4K8aSiXX/CWh61L/z0v9Ohmb82Umnylcx+Ff7Tv7bmv/tReH7XTdZ0C2sJobkXAuI75XXaARs2bV/PNfsp+xj4Jvfh3+zD8PNB1GHyL610yMzR4xhm+Y/zrrY/2f8A4YxY2fDnwkuOmNDtf/jdd3HGsaqqgKqjAVRgAelNRsEncfRRRVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANVs06kC7aWgAooooAKKKKACiiigAooooAKKKKACm7Ru3d6Wua+JXih/BXgPXNcjAaSxtXmUMCRkDjgUm7K40rux+KP/BU/x2/jH9p68023u2vItIhSzWNWyqyd8Ad+lfN/xA+BPjn4W6ZpWp+KfD15pNnqi77OadPllHuc8VveG9Wufix+09oN5qbq0mu+KLVZd3PyvcqpB/A4r9/vi78BfB/xu8CP4U8U6TFeWPk+VDIo2yW5xgMh7EYrKN47Gsnc+cf+CSNvdW/7JFj9pt2gV9TuXiLfxoWGGFfadcZ8HfhXpXwU+HGieDdGeSXTtLgEUcs2N7nJJY49Sa7XAq+UzuG0HikaNZFKsoZT1DDINLgUbRRykmDD8P8Awxb6rHqcXh3So9RjGEu0soxKo9mC5ri/2mPgpF+0F8Gdf8EvdfYnv0UxT9ldTlc+1ep0VVhnzl+yH+ylF+zL8FtQ8HXF8upXWoyzT3dxGMBi67cD8ABX5G/sK/HrRP2b/wBpiTXfEDyR6NcxXFhPJGMlMv8AKT+Kiv3+2ivzy+IH/BGrwD4n1q4v9F8W6poS3DmR7cwpKuScnBJpcpXMe7Q/8FFfgNKAT43tl+qGvgL/AIKmfGL4V/HS38IeIPBmuQaprlmr2s/loQxizuAP0JP517B/w5J8Of8ARSdU/wDAKP8Axqyv/BEvwh/F8RdZPfi1iFUK6MD/AIIy/Gq8vF8VfDfUdQlnt7VFv9NglbKxoThwg9yQa/Uuvlr9lX/gn74L/ZX8SXfiDS9Tvtb1i4h+zi4vAo8uPjgAfSvqWgkZX51/8FHv+Cfuq/GTWYviD8OdPhuPETDZqenAiM3QA4kB7t61+i1GB6UDPwP8N/Ej9q3wfoP/AAhNhF40jtbQbIbX+zpZTEB2VscCvdf2bP8Agnb8Rvjd8Qx4z+Oi30GksuWhvrovd3XorZyQv1r9ePs8QbcI03eu0Zp+B6UD5ijoOhaf4Z0e00rSrSGw060jEUFtboESNQMAADpV+iigkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilyoAoooo5UAUUUUWQBRRRTAKKYisvU5p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFN2/MTnrSeZ+8CYP1p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtZWvR6lItqdNdFZZQZQ/dfSgDVopFzgZ60tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5B+1wuuSfs7+Nl8OW013q7WDiGKDlzx2Hf6V7BTWUOpDDIPY1MldWKi7NM/A7/gnP8GZPi5+1NogulY2ugv8A2veBkI2yRvlB1H8ePy71++GB6VzPhn4W+D/Ber6hqugeGdK0bUdQO66ubG0SJ5j/ALRUCuowKXKNyFoooqyAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiio5mAmRRkUzdVZmO/HNTzMpIu0VB5Mn9+pq1JFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqOMSDO8gj2qSigAooooATHfvS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNDgkjI4oAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlN3H0oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUmayAZtqNiPNHGakZgvU0ir82aVix21vWn0UVsQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSZo3U3AoAczbaWmN8wx0pd1Ax1FN3CjdQIdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gBc4yTwKYqJ95QDuokXzI2UnAIxmkhi8iMICWA7mgCWim7jRuoAdRSUmTSbsA6ik5paYBRRRQAUUUUAFFFFABTMsu4nkdqduqNpAG27gDQBIKWq9vO8jMHTYAcAnvU+eKSdxtWFooopiCiiigAooooAKKKKACiiigAoooqeZAFFJRzRcBaKZuOKNxqfaIdh9FNyaMmmpJhYdRTdxo3UcyEOopm73pdxqrodh1FQmRvSjzOm5tv41n7RBYmopu6kzWidwH0UUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADJASKdS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTdgpQ26lrICN4Q1O206igdwooorUQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAReYN2CcH0qhdrNdXAEUrxImVbbjr6185/tlftraR+ynZ2NreaFqmr3+poxgktQqxR4/vOxGK4/4Af8ABTf4RfFaGPTtW1CXwjrBAVo9Y2okrYwSrqSPzIrLmZrGPKrn2PB5iqBIQ2BjIqasnw74p0bxVYR3WjapaapakYWW1mWRT+INafzc9KzXNHzJFVSKNx3Y2n61RutU8mFXCtnftxVqGVnXkc1cZOO5Ti1qycsVxxnNKx20xl37ecYqlq+sQaTZy3E5CxxjczMcAD61pzJamaTk7I0KWvFvDf7Ynwi8U+MP+EWsfGentrYYp9nd9oLDgqGPGc17NHKsiqynIYZBHII+tNNPYGmtx9FFFMQUUUUAFFFJu4JxQAtN3dKA4PGeajZn3KFVSvru/wDrUroBWLeZjb8v97NKrBs45qGWY+ZtCblPU56U1JY7dmUnA65NY85pysuUVVa4ClD1RujCpy+3HFa3RFmPoooqhBRRRQAUUUUAFFFFABRRRQAUVE0xEwTYcEZ3dqczHBx1oAKYju2dyY/Gm7WJDs2Mdh0pJp/LXIx+NJuxSjcfvfuF+nenox289a4Tx3r8mj6XPJFcFZkRpC6D7oAz+dfGXwm/4KRJ44/aCsfAMGm3H2GSV7eW8upBuMikj5QO2RXP7T37G/sWfoPtoZguM0kbeZGrYxkZpTg9a35kYW7j+1Vbi+S3YhzirDHg4Irl/GGpR6Lp82oPHJJ5Y5AHy1E3oXTim9SzY+KLS5uWWS5jhjdtsJdgpc9wM9a39/y8dcV+BH7Un7Q/jP8AaF/aCuNK8P6neW9lFqH9naVZ2Urw/Pu27jg8ndnmv3M+FWi6j4b+G/hjS9Xne51O106CK5eQ7mMgjUNk9+c0oXXxDqKP2TrqKQUtbGIUUUUAJmgsB1qKTKKTgsfQUuQ6jORQOxXu5H5GDtx1r5N/bO/assPgP4Ea6SWZtVuJcWsKttbcPX1FfUet6pDpdncTXEohijUn5v4sCvw+/ac8e6l+13+1hZ+ELAtDp41BdPtlJzt+bDsfXvXJL947M6oe5C/U/RP/AIJ0ftHeP/2hvCOt3njLStllaz5sdTCbBMpP3cd8etfZH8NcZ8Ifhjpnwj+Hei+FdLhWK0063WIbf42A5Y+pJrtOK6Ixsc0nd3Clpu75gMfjTqskKKKKACiiigAooooAKKKKnmQBRTcmjJqADdRuqIyc9KbHIzMcmuf2rL5Sam5psm8r8pwaa0m1RnrUuaAk3UbjVWRhCqszFsn0p32hNwXccms41LFWLG7b1NGarsxbqc1yXiL4teF/CfiCz0fVdYtbC6uU3Is8gXP51XOwsztNv+1QjHnnNRwzRXkEc0MiyROAyuhyCD0IqVVCjFdHKxFZZm891xxXlH7TnxQuvg38LNS8Xw232tdPUO0ePevYBAOTn5j3rA8deBdK+JHhHU/DeuW4utL1CFoJo2GDgjGR7ijlHzLsfJH7HP8AwUg0D9oLUJfDviK3j8PeIFY+QXcCKZc8AE9DivtVZBIoZWDKeQwOQa/FL49f8Exfij8GdcvNb8AiTxFokLmaGSzcrdxLkkDHcgY6V2n7Hf8AwUs134T6wvgn4xPez6RGxiXUbtWa6tmBxhweSo6VrH3RH6/DoKWsHwb400b4geHbPXNA1CLUtLu0DxXELZBBH6Gtv8a0Mx9FJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMBqrtzTqKKdkAUUUVABRRRWoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBzHj34a+GPihocuj+KtEs9c06QYMN3GGx7g9QfpX5/ftGf8EfdB8RO2pfCjUY/D9zjL6XqTtJAx/2WwSPxr9KKaVPQHA+manlRXMz8Ibz4W/tM/sL6lFr8dvqGn6VbyZL2lx9ps3H+0qk4B9xX3n+yn/wVG8FfFqPTfD/AI4x4V8XTFYBJIP9FuX6Aq38JPocV9wapo9nrVhNY39rDe2cy7ZIJ0DIw9CDX5t/tc/8EoINbmuvFPwdddO1J3aafQ5pCI3YkkmFv4Tk9KmzHdH6UKIrmNJEKSxsNyspyD6EU6GLy8kmvxj+E/7aHxt/Y18TWnhH4maZf3vh+CVYZItSQmWOMcfupOhAHvX6z/CL4zeE/jd4Ttte8K6tBqNrMgZ40ceZExHKsvUEdKfNfcbv3O4kkEcbNjoM1+X3/BTv9rHVPDulJ4F0G9e1uL8k3TxMVdEB6Z96/QP44+Oo/hv8N9X12S8itBaws4aU/e46CvxQ+F/w78S/t+ftPyHVLiT+y3uWe6vFU7Y7dWOFHuRis5K87dC4+7Hm6mP+xz+x/wCLP2qPFj3GnXjaToenzBrzV8kSAnnCnu1fvh4P8Pf8In4W0rRvtUt6LG2jthcTHLuEULk+5xXP/CP4M+FPgf4Sg8PeEtMi02xjA3lR88rAY3Me5NdxWkbmUncWiiirJCiiigApu07gc8U6o5JCikgZoArzNH5jDzFDHtmmxL9nj2sFOOc5qldXltbbppdm4ckHqK8m+MH7S/g74L6Pc6nr2u2Fr5aFxZSTD7S47bY+Sc1kdipNq5684mkYOJ1tx2jcA5/HNWGhE0Z3KCCOWzxX40/Gb/grN4y1zxE7eBdMg0axibCS6gPOaRex2YGPzNYfhH/grz8bNB1C1XUoPD+vacjZktfsbQvID2EgY7fyNc9NS1cokfM/bS13lNu0IgGF7/jU+0/Lk8ivln9mL/gob8NP2htPtrO4vrfwl4rI2yaLfTjlv+mchChx+tfUihZAsituUjIIPBrcyJqWmMWCjaAT9aNp7nBrW6Mx9FFFMAopKKAFooooAKKKKAI9v5UdtvTincZ60i8k0DGbtyADnsc1HJGuMkAipjGMYBxis/UlbgrNtx/DXPO5pDV2R82ftsfEq5+EfwX1/X454SqxGGCNupmbge/Ffhn4P+Jmr+EPiRY+M7dxJqdrei8OeAzbskH2NfoX/wAFYPGkupXXhnwNa3Uhu5rozS2qn5WJOFzXinx4/wCCbXiP4R/BXSfH9nqJ1WN7ZLnULZsZgDKG4wO2e9RStZuW501G01Y/YT9m34uD46fBPwr42+z/AGWTVLXfLCBgK4JVsc9MivSua/P3/gkJ8cLfxZ8I73wBcTEah4ffzII27wOSePxNfoLtrZanK9GRnbGpZuPWvnz9sb4qT/Db4L+JNUjby1FrJFH672GBX0Mw3KQeRX5k/wDBYj4gNo/hPRvDFreFZL+4Es8IP8KjoKUk3ZFQt1Pl/wD4Jl/B2b4wftQ2et3aO9hoJbVLqTghpskqM4PUmv3V2/ga+F/+CQvwri8I/s5z+KZrcJqHiO+kkEmOTAnyqOnru/KvuvbV8rIbClooqyAoopGOBQA1qbI21SafjNVL6T92VX/WdvSk3YqKuzyn9pTxhp/gn4U+INUvZQfLtn2c9G28V+XP/BKvwFa/Ez9qjWPFd9C1xHpEMt9GxPAmdyFJ9eDX1Z/wVU8dN4a+Av2NXWO91G6WIcfeXHNcj/wRb8BvY+A/GfiqSPaL65S0ibuVUZP61zQWrZ0TdopH6VelJsFOqFpirbcc10t23Oa1wjjcKwZsg/nUo4AFRR3CyZGckUjTnztgBxjrjii+lws9ieimjNLzTELRRRQAUUUUAFFFNas2rAJRS0zcal2Q7AahiheNiWfcD2xT5pNi5qrJM6jIavPlLl3NYpvYnMxyahWYXGU2sretUGacsT5h/IVahhK4Z3+fHBzU86NnFRJtrbWjY7j2b0pjL5Kb3+dx3qtcal5LbY2V+xLMAK5rVvij4e0BdmsatbacM4LXLLGPwJPNRo9iOU621LyMSTwa/NX/AIK8/BLW7i38P/ELQ/tc8VnugvFt937peobjoK/SPw7rGn+ILRL3TbyG8tWHyvBIHB9+Kf4l8Oaf4u0O90fV7WO90y9haGeCUZVlI5Fd1GC6kczPzv8A+Caf7dQ8XWsfw28eahHFq1rGq6dfzuB56AABCfUDFfpIMNhhyDyCK/DL9vL9je9/ZN8YWHibwrdzf8IxfXDPaSxjD2cuchM+npn0r9Ov2Bf2ih+0R8CNOvbtgNc0cLp98pbLMyKAHP8AvAZrpSvsS+59LUdKKWnymYxucg8ivjD9uD/gn3oH7QGl3nibwvaw6T47hiJV4VCJeY6LJ7+9faNFHKVc/Dz9kv8Aa+8dfsafEI+AfG8E0fhg3nkXVldg/wCifPhpIx6cfiK/avwr4s0nxtoNprOh30Oo6bdIJIp4HDKQRnt39q+Tf29P2DtF/aO8P3HiXRIk03xvYQs6TQoP9NVQSI39/Q18Z/8ABOH9sO/+A/jp/hR43W4TRb29+ywtOTmxud20qQeik8VQ9z9lqWkVgygg5BGQRS0yAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopWQBRRRTAKbvFOpmw1kA+ikpa1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBFbdS01VK5zTqACiiigAooooAKKKKAPOfjh8CfCfx+8F3nhzxTp0VzDMhEVzsHm2744dD2Ir8gPHvw3+L3/AATG+KMOuaFqP27w3dysIrtAxt7pMkiKVT0bGMn16V+4e2vLP2kvDvhPxP8ACvVtP8Y2ttc6XLGVzcKCYyR95T2IrKXu6s0jduyPzM/ak/b80/8AaT/Z7S0sbX+xtYiKpf2EsgJkYgBmTH8Oc4zX0x/wSN+FaeE/2f5vEt1ZrFf61dsySsuH8peB+Br8fPihoekeFfiFrum6HdjUNJtbtktpieWTdwp+g4/Cv3f/AGAfif4W+In7Ovhu38PXUDXWlWyWt9ZoQHhlAAOR6HsamEeVt33He0bH0nS0lLW5kFFFFABRRRQAlRuwC81JXJ/EjxUng3wxf6pMHFvawSTyPGu4hVUk8fhRexcI8zsj5W/bg/bFsv2ePC9zBpNib7xFfhoYPMk2CPsXxtOQPwr83P2d/wBl34jft3ePL3Vb7U7ix0jzS154gu4mmWLJzsjQuufYA8VyXxn+Ll3+1d+0RBdXck0GnX+oRWlnbySZEUTMFz0HJHP41++fwn+HOifCvwFo/hvQLCDT7Kzto4ysKgb2CgM59SSM5rGK7nRUqSkrdD52+Cv/AATD+C3wntoZdR0X/hNdYVQJLzWhvjLY5Kw/dUZ7HNdt8Rf2Cfgb8SdFksLvwFpmkuwwt3osK2kqH1BQY/MV9CKp2jJyaNtVZnNc/Fr9rH/glz4o+B9jP4o8A6jceK/D0G6eVGiEV5YgcjBDHzB74Few/wDBO3/gojHIunfC74k3Uovd4t9M1q6kPz/wrC4K8EcDJNfqFLAk8bRyKskbDDKwyCPQivyR/wCCqf7IaeBdWtfir4G0j+z9MfjVkslCLBLuyJlA+6STzinZjufrgMMMg8HuKdXwP/wS1/a2h+Knw8PgbxNrPn+LNKbFt9qkzLc2+OOT1K4r733VJNhaKTdSMwXGTg1rsIiuLgwx7htPPPNPhk8xQa+Sf21/24/D37NWmixt1j1fxXPExtbFZPlQ9Nz+mK6f9gnxV42+InwNt/GXji9Nxe67cyXVvAY9ggi3EAD1BxWV5OWmxrypRu9z6TopKWtTIKKKKAGNHukDZPHalVduadRQBF8+09M9q5nUbSewE8wZpmJyit057VuX2pLYqAwYljhTjjNcZ8VvF8fhf4beI9XuZltnsLOWYSfw7gpI/WsJ6ux1Um4vm6H5F/Ef7b+0N/wUdstFdVmitdUjtwsJyAkZBbrnuDX7G+MvAth4t+H+o+F7mEPYXNm1rswPu7cDqMZr8nf+CUHh8fFD9qbxh471FGluLOKe9D9V82aQjv6bjiv2LqopIynLmZ+GnwP1rUP2Nf28G8OW8v8AxL59UXTZRdZw9tKRg/LjkZwO3FfuVX4y/wDBVT4e6h4B/aE0z4gWkDR2d0Iisg4xLG24H8a/WT4J+Ov+FlfCPwh4nZ43l1TS7e5m8n7okaMFwMk9GyOacWhSXU62a8igL+Y4UAZr8N/+ClHjGb4mftaT+H7PfMtk8NnCuDzI+P6Gv3B1m8tdH0u8vrx1S2hjaSR26BQMmvxL8B28f7UH/BSgXmkwSS6Q+vC9kdVBCQW4ALdOh2frR1Q1tc/Y34H+Brb4a/CDwf4ZtYjFHpumQQspxnfsBcnAHO4tXcUlLWhkFFFFABSEbqWigBKq3JTcFb5Qe+KtVla1fGzt5TkZ2kqp65qJ7GkE27I/LH/gst4utri48IaBA+97cvLIQfWvsb/gm/4IbwP+yR4Mjltfs1zfxvfSZ6tvY7T/AN8gV+Z37dk194+/a+0zw9PcpfGSW3gWGMcKzuMgj6Gv218FeGbXwb4Q0XQrFDHaabZxWsSk5IVECgfpUQWhdTsbVY99ffZ45mAcKmSWIrXqhrqr/Y95ubaPLbn04q57GcdzkfDvjDSr2+aBtWtI5/M2+RLMqyknoAua7ny8rjJ/Ov5wvip8VvFWi/tBeJ9atdbuvt2na/ctbMZDtTy52CDbnGMAcV+9/wCzD8Tb/wCMnwB8E+MtUiEOo6rYLLcKowDIrMjMB2yVJx70qd7WZpUld6Hpcl3DZxgzzRxL0DSMB/OpVlVlDKQQeQQeDX5g/wDBYb4p+IfC9x4L8PaTezafb3gknla3kKMxBwBkV1H/AASF+NHjL4keH/F+heJdauNYsNHWA2X2o75I92QRvPJHHSruiGlY/RmikFLTMwooooAKa1BakrOTuA12IHFJSyAlTTVB2jmuKbNClM5kYDccKeeO1Vri4IZQo4zWr5fX368VTnjjH8PSsJxN6cl2GLCrRO5XAA9a+Zf2r/2stG/Z20Vbprn7bqJ+7ZqwzXf/ALRX7RGl/A74c6nrVyBNNDGwjhJA3N2r8VtQbx7+3T8dAun2U0k97OqLGoLQ2kZP3mP61rTpxmrmnNyRfMjtfG37e3xt+NHitbLwjdXWjpNIVg03SLdZ5ZsnjO5Tz9Kn8Ufsh/tYfFi1j1LxFoGtakdgdIruRUYgjP3Riv1T/ZH/AGLfCP7LvhSOKC3h1bxPOA93q80QL7scqn90A+lfReBXbGmo/Cjj5mfkJ/wTd0z41/Cf9pCHwf4h03XdO8Py28ov7PUY28hdqna6sfTjGDiv1yuLyC1iMk0qxIBkljip/JjMgcou8DG7HOPrX5g/8FRviz8Zvhr49sYfDNxfaZ4NurMYvLGLeDLnkMcHFVaXQVz1j/gp98YvAS/s+6t4Yu7621DWrza9rbxsGZGB+97Vx/8AwRd8NyWfwj8Z63NEU+3alFFE3qqIc/qRX5J+JNc13xhqT3mr3l1qd2xO53JY5zk8dq+ov2Q/2+fGf7MOlnwwmnWuteH7i7WRorglJIMkBiMD09aqKsF9D94qWsnwpr8XirwxpOswDbFqFpFdKuc4DoGA/WtaqJCiiigBhr8h/wDgrH+zQfh74usPi14YtxZ2eoTBL9bZNgjuBysvHc+tfr0a+Sv+CoNzpsH7IviddRjDtJJCtvxkrJvGCPegqO53n7D/AMaYvjp+zf4T1xpmm1O1tl0+/wDMbc/nxAKSx9WADfjXvVfAn/BGtXH7OuvOwO19achj/F8g5r77oJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKVkAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaAGTTLBG8jkKijcSegFflz/AMFLP2ubmz0FfCOkXMUqX5dWaFwSig4ycV9wftVfGbQ/hP8ACfXrrVL4Ws01pJHAqsAzMVIAFfjL+yb+zX4g/bM+MEi3dxMPD1nIZ7++nLMFTORGD6msWuZ26G8VyrmPof8AYP8A+CcnhT4+fCceO/Hd3qBF/O62lvbP5fyqcFmPfmvN/GS+JP8Agmd+1oR4cuLyXwtPtdVuc+XeWzHlG7Er0z7V+0nw/wDA2k/DXwZpHhjQ7dbbS9Mt0toYwOyjGT7nqfrXzn/wUY/Zttfj58B9RuLa3U+I9BRr6xlVcsQoy6fQiqsRzH0N8M/H2mfFDwHofinSJ47ix1S1juUaNshSyglfqDkfhXT1+Vf/AASF/aR/su/1f4QeI71oWkb7To0NwcbZAT5sPse4HtX6pbq0IHUUUUCCk3D1paTaPSgAB61U1DT4NUt5ILmJJoZUaOSORchlIwRire2k2+9TJXHdp6H58eIP+CQ/hv8A4WXD4r8KeNtQ8PquoC/NnJbJOiHfv2JyuB2Gc4FfoDY27WtrDE8hmeNFQyN1YgYz+NTbe3alC4qbMfM7WFooorQkKwfHXgjSPiP4T1Pw3r1qt7pWoQmGeFu4Pf6it6igD8Ef2mPgn4l/YI/aL0/V/DdxMNM84Xmj3x+RWAOWiOCenSv2N/ZZ/aC0n9pD4Q6P4q0+aP7c0SRajao2TBcBRvGPTOcVxv7dX7Lcf7Unwhl0q0aODxHpzG602eRc/PjlM54DdM1+Wf7Cv7QV/wDsg/tEXnh3xZcTWXh+4uZNL1e36pFMrFBJ9Aw6+lRZmtro/d1jtGa47xp4psPD2j3erarepp1lZRvLJNI2Bhc8D1NXNW+Ifh3R/CLeJbvV7WLRRALgXhlGwoRkEH3Br8df28f2yL79pTxpZ+Afh291JoUNx9nAtyc3szHBxjquaiTvogjE5a40fU/2/v20rkWFu8miNdeXLMn3Us43I357Fl5/Gv3B8IeFNN8C+FtK8PaRALbTNMto7W3iH8KIoA/Hivnj9g/9k3T/ANmf4WWJu4Ffxdq0EdxqEzoBJEWUMYfopJH4V9P7auKsRKVxaKKKskKKKKACiiigChqDK0ZV9uPevib/AIKnfEr/AIQv9m640y1n8q51icWw2nDFCctX2Zq2p2yJKH+ZkOMCvyZ/4K7eMP7d8c+B/BVsc3CRm6dM8DzG2oD+tc3O3I7ErQue7f8ABG/4Snwz8HNc8bTM/m69dm3hU4x5UR69M8t/Kv0MrzX9m34cQfCb4FeCfC8CBHstLg88gAbpmQNIf++ia9KrWzOM+Lv+Co3wtk+IH7PuoX8UG+XR/wDSlcDkY6/hXNf8EfPig/i79n/UfDN1dCW68P3xWKNiSwhcZH4ZyK+yPix4Vi8afDXxNocqqy3+nzQDcOAWQgH86/HD/gnP8X4f2X/2oNX8K+KZV0/StWMmlT3M5KpHLG/yP6YLL19DUxVjW94n6lftg+LIfCfwT8Vz3V01pA2mzKGU43OVwBXw3/wRZ+H6zal488aTW7ErFFp9vcOASCx3vgkdeB+tejf8FWvjZ4R1b4Ax6HpPiW0vNRvLtQkNo+8uqn5gSO1et/8ABMD4ap4A/ZR8PXbFjd668moy9MAFiEA4/ugdc01qO9o2PraiiitTEKKKKACiiigBB3rnvF80Nvptw8jBT5bDce3Fb0hWPknArzP9oDxIvhv4fX955DTqsEjHZ1ACE1nN2izal8aPyT/Z70Oy+Lv/AAUiZtRke8httXnuCc/xQswUfT5RX7d1+Mn/AASkhtfF37YXibWZoz5n2K8v4efus8wHP4Ma/ZynFWRM3diHtUV4qSW0iyDKFSCPapap6w7Lp8204Ow8/hRL4WTHdH85n7Q2mQa9+1R4102wjWKO48RzWyKo4yZip/XNf0G/B7wbB8PfhX4T8N28Qgi0zTLe22D+8EG4/i2T+NfgJqFqPEn7aWoW44Fx43mQsD1H2xhmv6J2ZLe3JY4RF5PsBSjoXI/IP/gtBrKz/EvwNarxJBZTO/f+MYr2f/gi54PSx+EvjHxHJGwuL/UEt0kycGNFzjH1NfEf/BSn4tW3xT/aY1dNPk8zT9HX+z0zz86kiT9RX29/wRl+I39s/CnxR4Rki2yaTeLco4UAFZBzk9zkUAz9GaWkpa0MgooooAa3WmswUUrd6iaMt1rCTsNaj2b5M1H+dG44x2qBJnk4wVw2M1w1DVImLD5lH3scVwXxI+IWnfDvTft+q3sNpZqpMs87BUTFd5GuZCT16Zr4K/4K9WkMP7P8N2L9re4fUY4xCrkCRcZIx3pfFZGtNqL1PhP9vj9rBPjp44l0rw3cufDFkxDMp+WeQHBYd8Zr0v8A4JuftffDX9njSdU07xhEbK8vZsjUEi3ED3PpWF/wTn/Yd8L/ALU1r4k1jxi2r2ulaW8cELafMkazSMMspJQ9B6V7h+1l/wAEnfC/hD4a6n4m+Ftxqzajp8Znl0y/mWdZI1GW2EIDnHau9QjGPKjJu71P008H+LtI8eeGtP13Qr2PUNLvoUngnibIKsoI+hwRxWyOABnNflN/wSB/aE/svV9d+Fmv6k6NOVuNKguGxtkAxJGueR9Pav1ZrVMyasLVPU9HsNatzBqFjb38B/5Z3MSyL+TA1coqhHKQ/CXwPbsWi8G+H42PJZdLgBP47KB8JvBCyNIPB2gb25Lf2ZBk/wDjtdXRQBFbWsNnAkMESQwoNqxxjCqB0AHYVLRRQAUUUUAJX5j/APBZL40W0HhfQPhxZzN9tuZxe3Ko3Gxfug/jX6DfF/4lWHwl+HOveKdQkRItNtXmCu2NzAfKv4mvxG+Hui+N/wDgoh+1Pa32oq9zaees97IQfJsrRWyE9sjA9yanmLj3P1Y/4J4fDGf4W/sp+DrO9tooNQ1CE6lM0a4ZxMd6FvU7CtfSlVNJ0u10PSrPTbGFbeys4Ut4IUGFSNFCqo9gABVuqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAG+tZviLWLfQdFu765uI7aKGMsZZGwo4rTr44/4KdeGfiZ4i+B2PAFvNd20MnmalFZsfP8AKA6qo6j6VEuboVFK+p+ff/BQb9oZvjt8QrDwjoE0l9FYzmI+WcrPMz7dq4681+pH7Ef7O+n/ALPHwP0fTY7TyNc1CCK81WRh8xnKAlfopJFfm/8A8E6/2HfGfjP4taJ8QPF2iTaZ4S0uX7YjagpSS8kxlAqnkjOCSa/aPFEVYucr7BTZoUuIXilQPG4KsrDIIPUU+irMj8W/+Ch3wXH7KP7R3hv4h+D5WsbTWrr7cscIK/Z542UuAfRgen1r9Xv2f/jBp/x4+EPhrxtp21U1O1V5oVYN5MwGJIyR3DZr5R/4LCeA5fEn7OtjrkFt58mi6gsjOo5RH4Y/TiuS/wCCLPiTUtQ+Gfj3RZWlm0XT9Qt5bOR+FV5I281QPqqmgrofpBS0UUEhRRRQAUUUUAFFFFABRRRQAUUUUANK5z6V+bX/AAUc/wCCe178Q7q5+Jvw6svP1tYwNS0S3TDXQH/LVP8AaHcY561+k9FA7s/n60n9m/8Aad8U6LF4atvDPjOTQ5AALW+SRIVXt944Ax2r9J/2Ef8AgnnonwD0my8WeMbaHVPiBMgkVXG6PT1IGEA7uO57V9vUlKyHzMTb706iimSFFFFABRRRQAUUUUAfI37bn7TVp+zX4bk1JIvtep3EqpbW7Z2OepzjmvzZ8M+MLz9uD9tTwNeDSmtXnktVu4Y8tGkUJ8yR+c8Z3fpX1r/wWU8F3118N/DGuxwtPaWd+yzOo4XcDjNef/8ABFv4bxX/AIw8ceOJovMFhaRabaSMB8ryHdJj3wuPxNc0Va7Z0Sk7K2x+tKgKoAGABgAUtJS10nOMlUPGysNytwQa/Fb/AIK3fA4/Dz4xaZ4u021SDR9dg27YRtVLhTzjHcjBr9q25FfDv/BW34ZP42/Ztj1mBZGufDt6t4BHjlSCrZ46YPbuBUWLj2PyD+Geg6j8XPFfhrwTD5lzc32pRxxF3ztRj83X2r+jf4X+B7b4afDvw54Vs+bfSbGK0VjjnaoBPQdTk1+Cn/BO9I5v2xPhrG8auhv2+9/1zYiv6E6cVYJO4UUUVRAUUUUAFFFFAEW3ceQD9a4L46aWt/8ACrxSGBcpp07Iqjv5Zrv9veuZ+JVrcXvgnWIreRY3NrJkuMjbsOaznFyTSNYfErH5Jf8ABGuAt+0h4maUFZY/DszFemD9pjB/nX7LV+Mf/BLbV18P/tt+J9N82NUvLXULRc/xBZt4x+KV+za9KtbESTT1FrE8W6kuleHdTupOEhgkc/QITW1XG/GCTy/hd4qcfeXTbjH/AH7alJXVgjufgd8CdnjP9tLQJ8F477xY9zkcZDTlxX7M/tpftNaR+zz8LtRmmmU6xeQtFaxAgkMRgHFfgZ4G8Zav4C8caZ4i0Jj/AGvptytzbsU3/MvqvevsaPwL8cv+CknjzSNT1nS5NJ8OxCOKfUWh8qFQANzKvc/41Ni2fM2q/B74heMvCd38UR4fvNR0PUruaWbULeMuBKXJbIHQZNfp9/wRp8Dz+HvhT4y1a90+4s7m+1CNI3uIym+NUJBAPbJr7X+Efwe0L4R/CnQvA2n2sMunadaJBJvQETyBQHkYHuzZP412Wn6XZ6TbiCytorWEdI4UCr+Qp2ZPMWaWiirICiimsTSbsrgI3f0rmI/iLoS6hNY3N8tlPFKIR9rIjEjHoFyea4b44ftH+Ffgpo9zdavq9nHNEpJt/MG/ODjivxf8UfGLx3+0l+1Bp93oFzf37vq0MtjZRuxiVRICGK9AMY7e1cbnKb0N4011P3/2j0puBVfTVuv7NtfthUXflJ52zG3fgbgPbOas7huI79aJJMz1I1IVj8tfnB/wWkTy/hj4H2xtifVWEkuTgYjJGR0r9IYyT1ry/wDaP/Z58O/tJ/De78K6+hjbPnWd4n3racAhXA79ehpwje0uxV9T5J/4I2eLtNvPgl4i0FbiL+1LXVWmeLIDsjKMNj04r9CJFDxsrDIIwRX8+cx+LX/BP346XwtFudLurO5MUc0tuDa6nbKxVWyQfldRnjkZr7d8G/8ABaXw/Jp8aeK/BN7a36qBJJp8qyRM2PmK55xnOK3EfJvxVsG+CP8AwUSupdIVlW38Vw3UMUXBIuHEjqPxdhX7y1+FvhPxZa/tf/8ABRjQvEGhWEmnaXfavbXQjnG4xxQqCxbr94qfoTxX7p1cVYUncKKKKogKKKKACiiigAqO4uEtYJJpGCoilixOAAKivryOxt3nlcJGoyWY4FfJf7SPx71rxlDcfDP4aKt94t1M+Q1xCcpbRk4Ziw6YrKdRQ0NYU5T1Wx8o/t0ftBeKP2mvisPgf8O4JLm0a4S3vJYMsGYNhgxH8INfcf7GX7JOj/so/DxtOhdb3X9Q2y6hfbAGLYHyA/3Qc1B+yP8Asb6B+zfor6ldbNa8c6kol1LWZlDSGRhl1Rjzt3E19HYqrEzd9EFLRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJuHrS1GsKhiakoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEVQqhVACgYAHQUtFFABRRRQBieNPBmkfELwxf+H9es0v9KvozFPBIOGU1hfCP4M+Evgf4ZOheD9Ji0qwZ/NkWMcu2MZJ78V3FFABRRRQAUUUUAFFN2+9LQAtFFIWAIBPNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHJfFD4XeHfjB4PvfDPiexS/0u7XDRt1U9mHuK5f9nf8AZw8Kfs0eD7rw74USX7Lc3b3cks+C7E9FJA6KOBXqtFKyHdhRRRTEJXiP7aGqW2j/ALMfj65vLRr22GnOrxIu488A/gcV7fVDXNCsfEmj3ml6lbR3lheRNDPBKuVdWGCCKBp2Z/Oh+yD4+tvhX+0t8PfEt8m6ytNVhWfB6LKNmfw3Z/Cv6PEkEihlIKtyCDkEeor8EP28f2PL79mf4q3F1o9veT+DdTke6sbuKMsbZmdmETEAAbcgD2FfsP8Asa6n4g1n9l34a6h4nl+0axc6PDK0u0gtER+5YgkncYvLY+5PQcAHyvc9pVtygjoaWkXoKWgkKKKKACiiigBrdqg1C3W+s57d1DLIjIQ3QgjGKsYo20BqndH4R+Fb7/hmX/gpKG1EfZ9Pt/FM0cm3/n3uJG2/gN4/Kv3bQhlyDkGvy7/4K/8A7OtjY2Wi/F/Q7aaPVjeJY6p5AyCuC0cowOGBUgn3Few/8E4P23o/jt4TXwV4w1G1TxzpSLHb7V8v7bbKqqrjJ5fAyfXOaDSXvan3JXkf7V3iaXwj+z1441OH/WRabKBxnquP6161uOORiua+JPgvSviL4F1rw1rZZdL1O2a2nZG2sqkdQexFBMdGfj7/AMEhvhTpfxA+NHiPVdY0yDUrLR9PV1S4QOgkc4Bwepr9ndN0uz0e0S1sbWGztk+7FAgRR+Ar48/YP/Zz8Lfst+KvG2hWnjXTvEOqaxIj29vDKPNSCMvgFc9RkZr7P2igG7sKWiigkKKKKACqWrNPHpt09tH5s6xsUjzje204HtzV2kqWrqwH4k+Nv2Jf2jf2jPjFr13rGiy6VZ3WozuLvUJdkCx+Y20qo6jGMYr9Fv2MP2G/Df7Knh1rmRo9b8ZXqL9s1RlOI+ATHEDwFBzzgE19QbaMdKyiraFczIyAUA6j60xVDNuPXpT29KQYXrxUcuow+7nFOU0cHmlxiqhv5Acv8QPhn4X+Knh+60XxVolnrWn3CbHjuo8nGc8MPmX8CK+SvEH/AASF+BetajJdW7+I9HikYt9jstQQwpk5wu+NmAHQZJr7f2ijaK15RXPnn9m39hf4Zfsv6hdan4Xtr2+1e4XZ9v1SVZZUX0XCqB+VfQ9FFWSFFFFABRRRQAUUUUAcX8XvB+o+PfAOq6LpN/8A2Zf3Me2K5/uGuB/Zp/Zn074E6D5126at4quhuvdWdcuzHlgD6bs17lRWbpxcuZ7miqSUeVbCCloorQzCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopN1NeTauQpc+i4oAfRSVE8jbTtXBzj5qAJqKaudoz1xzTqACiiigAooooAKKKKACiiigAooooAKKKKACiiigApCoJBI5paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6lpFlrNube/tIL23JyYriMOv5EVNbWkVnbxW9vEkEEShI4o1CqigYAAHQAVNRQAUUUUAFFFFABRRRQAUUUUAZniDw7pvirSbnS9XsodQsLhSklvcIHVgRjoa/I/wDau/4J1eMP2fNfvPid8IL26udJs5zdLaWzsL2yBOcLj76Lx+FfsFtprRrIpVgGVhgqRkEUDTsfkP8ABn/gsB4m8D6GdH+IPhlvEN9bbYo7qBvImIUY/eKf4jjk+tM8b/8ABRT4uftIarH4d+F3hK6sbi5DQKsKmYFW4yx6KcH8K/TDxH+zH8KfF2pPqGr+AdDvr13LtNJaKGZicknGMnNdZ4V+HfhjwPapbeH9A0/R4UGFWztkjP5gZoKuj43/AGEf2AdR+CevxfEzx/rNxqXji7tiyWIlYx2ZlXMqyf33BOM9Mg191UUUEBRRRQAUUUUAFFFFTzIAopuTTdx9azAUgZpjR7up4pJHKjg1FuB5MmDUcyLSY+NjuK54HFTVX2lYyynnsaWOYrGCx3GsE3F6jtpcs0tIKWvQMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKTcPWgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKYWbP3c/jThQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIx20DkZoYbhQOABQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbvVSQJbzGcK7vJhML2q5tNG2gYbht681DcKzKu045zUMlwVuljRee5NMnVruZQpZPLPJ5plxTuXo5N3BBUj1p9R44BPLCnK3AyOaRA6iiigQUUUUAFFFFABRRRQAUUm6gtRsAtFRNPsx8rH6UfaFDBT8pPIzUcyY7MeW5AxTqjV9yn604NxVgM+0L53lnhu1S0zjduxz60u6gQ6im7qN1ADqKKKACiikY7RQAtFIDkA0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNY4FGTUZZvMwfu4rOSsOwu47Qe+aKbuG7aRwOacrKy5HSoGVLi62kjYTimMyyQjaNkjd6syMvpVZpEJ+dHIB4wKxNktCbzGjt9pGWUYJqKzkLsQYSBnOc/rT45Dcn5TsRTyCOtWFxtGOBUtXaZLfKrE1LVcoc9alXIUCu3mRlYVWJJp1IAOtLVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSloAKbtFOooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIvOTzNn8X+6f51DfanaaXbvcXdzDbQL96SZwqj8TX4O65/wUW/aM+JOsm20vxDNbTXD7orLRbQM3J4UBQT+dXW+FP7Y/wC0FMLW90fxxd20p3F9WVtPt2z3DyFFI+hxWfv9jS0O5+v3jz9rT4SfDeKSTXvHGj2jKu4RrcK7t7AKTzXzR4y/4LGfCHQL5bfSNK13xGM4aS2hSJQfrI65HuK+XvBf/BGv4s699mvPEviPw54eSUBprdp5bu6jJ6g7Y/LYj1DkV774K/4Is+B7BGfxV431jWJ26DToY7RU+hO/P5Cndj902fDv/BZf4T6lqUdrqnhrxLpEbNg3UkcEkae52Slj+Ar6t+F/7UXww+MVvBJ4W8XWF/JMiuLdpPLlGR0KNgg+1fFvxH/4Iu+Er3S5W8GeNdVstRX/AFSa0FmiPsWRQR+Ar88fjt8CfGn7I/xA/sbUtXgh1HZ5kd1pFyRvXPDYOGGfcUubYVrn9GqMHUMpDKRkEHINOrwP9ha/1vUf2Vfh9ea/c3F5fTabHIZrk5coR8uT1PFe91oZi0UUUAFFFFABRRRQBHJlQSOfaq/2hpoWKqUccYbvVrbWfdLNFI8kYWQZ6dxxisJ8xcUie1uBMoUn59oP1qRoVkYFhlhxX4+f8FBfD/xs+B/jq48U2PjnWbjw5qkzzobWRoktdxyI8Z5x0rm/2Of+Cifxi0fxp4f8FXit48sNRulgjhvGJuUBOCVk5wByeRRB6XLa1sftQV6KOMUpcKMsQv41HBI8kCSPHsdlBKZ6H0ql5qTOy3CmPa+VyetOU3F2YuW5p0VSTVEa68kKSuPvAE/h0qaYSSNEUAwGycnHH5VrFqWxHK09SekbODgZNMYtvABUA+vWnIrLnLbufSi6Cw9CWUEjBx0p1JS0yQpv3sjpTqQLgk0AAGABS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAITj6UA55FIF65JIPrSgbQAKAILi8S3wXZY1zg7q4S++PfgfR9Wh03UfEWn2N1J0Wa4VRn0PPFef/tbfFIfCH4b63r80c8qxwMsRQ/KrkYFfjD8I/gL8S/21fiFrE/h5o5ZVka4uLrUrh0hi3HOAcH8qxUm2buCirs/oT0vXNN1uFZdOv7W+iYZD20yyDH1Bq5uG7aDz7ivwh+IP7MP7Rn7FN9b+I9Our6O1VN76l4duXlhjYdRIGz+o/Kvuf/gnT+3xffH5pPAvjdhJ4utIvMgv449i3cajksM/f7nGB7Vpcy5WffA6dMUtFFUSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADKa+ByetSYpjxq3UVE9ikxFAZQcdqrnbDuG/g/w1L5m2NsD7vFVo7pF5ZGJ78VjzIpIi87aWByw/hHtS8tt3ZAI6ZpI7iC4uG2ZLg9DU8rKPvrnFZm4JGxPDYXtVhRtUCqUUxDnj5e1WoZgzENxzxQtTOaZKW2jpmlU5ANJuA+lOGK6VEyHUtFFaEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANX7xp1FJ060ALRTQ6t0INOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDzT4O/s4/Dr4E6PBYeDPCthpJRAr3nlB7mUgY3PKfmJP1r0umhqZNcxW67pZFjHqxxS23AdtG4sBz05py/dHes2+8RaZp1uLi61C2tYOvmTShFP4k07R/EWl+IIWl0vULXUIlOC9rKsgB+oNF0Ow7WNQj0rS7u8mYJFbxtKzH0AJr8BPj346vP2r/ANr1TbR4jvdUTTrRe5iWTGTjPbNfup8YNWh0n4da/POgeNbOUlW7jaa/Gf8A4Jw/D2D4i/tkC/lh22mkSTXwT0O47f1rLeVjZaRP2z8FeHLfwn4R0bRbVNltY2kVsiegVQK26SlrUwCiiimAUUUUAFFFFAEM1wIVJIY844FN84bCV5H86ex3Eg9DXOeINS/4RXStQ1CaVTHFDJKN3GNqkiuebdrmsUnofl7/AMFdv2gZLvVtO+HWnsVSNPtF2pGcE9q6f/gkr+yTZQ6Gnxj11POvrhni0m3kjx5SA4Muc87u3FfBvxe+Iq/tAftFXWreJb9dJ0+7vxA91KC6wwB8E8deK/UK4/4KD/Aj9nf4U6d4Y8FaqNek0mzW3tra1jZVZgvXcR3NEXyqzKlufeHPA6Cqt9ZpdR88MOhr8NvjZ/wVI+LPxNklg0K/bwhphPyx2Lfvtvu4A/PFfo7/AME39a8Z+KP2WtO1nxbq9/qeo393O9vLqTmSTyd5C/MeSD1qk9LyRMVruZn7YX7dH/DJc2h21v4VXxHJqDv5jy3ZgEO046bW3fpT/Cf7bF1+0R8BfEuvfC62WPxxpNiLifSJEMpjfGSqk43dPSuG/wCCp3gPw1qPwWute1bEerWLLHZybsbmPUYrwP8A4It20s3xR8bXWJDAumxIWXhN248EevvWEfej2N5yXNscN8O/+Crvxq+HPi+7h8YwWfiCy+1H7Xp17A0M8HPKoQflx6EGv1L/AGbf2s/An7TnhwX/AIZvxHqEar9p0y5IWaJiORjuPcVy/wC1J+wt8PP2lNFma40+20DxRy0GuWduBJvPP7wKRvBPc81+THjz9lf49/sY+II/F/2C6tLSyn3Ra3pE4nhYA/KZApyoPowrptoYL3tj9+dwHfmm+Y27G3t618nf8E/v2yG/am8Ay2us2skHizR1SO+lVCYbjjiRTgAE/wB3t6mvrWtDMRTuUHGKWiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUw7+2MU+igBu4hcnrTqQrnijnnOPagD4O/4KxeJLjR/gPPYQTYjvp1EgbqMHtVL/gjh4VtrH9n/AFfX1i23mo6nJHJISTlY+Bgdq47/AIK/arDD8PdOtjMftMt4f3eeNor2j/gk3Ypa/sb6BMud89/es/pxMwH6VhE6qjtFI+vNU0uz1zTrmwv7aO7s7hDHLBMoZXU9QRX40ftlfBO//Yh/aK8PeO/h48un6TqFybmLAPlwsZPmgIXHyY7da/aLFYfirwPoHjizjtPEGj2Ws20biRIr2BZVVh0IBHBrTlZjCVnqSeDdabxF4S0fVHAV7y0inYL0yygmtmo4IY7aFIokWONFCqqjAAHQCpKsh7hRRRQIKKKKACiiigAooooAKKKKACiiigAopuTmlzSAWmHNDMRTM7sE9azmykiOZyuQKrxxpKzBmPTpnFWXAY8jNQsWjyUUVzmq12IlVY/ugfXHNSbvMG081V84ozF2yOu3HSo4b5HyVyp9cVldG/Ky+22NVGMdqZNMm7B6KKzLzVltot0pJGfvCqzahJfIJIU2qTwx7ihVFEqNJ9TW+2OR6ir9rIXiUms+zgeaNR9w45q9DG8R2nkDvXXTu9TGpy7ItUtNVgeO9OrW5yhRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJD8pp9NZQwoAq/MoUqpPPpVsdKbGu3Ip9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfk/4L/4LKT+HvhPptrrHhRtc8aQR+S8yT7IZNowHfjIJ9s188/F7/gpX8ZPjLcS2ljcR+HrSZyYrPSVLugPRQ2Mk/WtD9jP/AIJ0a5+1J4Zg8Y3HiOw0nwsLw209upk+1uEPzYHllee3zV+tnwc/ZC+FXwL023g8O+E7E3kSBW1G7iE08hH8RZs4P0xUJKT1Luz8E/GzfFm+0tdV8U/8JadJmOftOpLcLA2fTOFx9K+6f+CL41ubxt4yl3XT+H0s0QF2bylmz0APHSvrL9rz4D+If2tobLwhp2t3HhzQLaXfcSLAHSUj1+YcV6/+zT+zr4f/AGZ/hva+F9EIuJB893fNGEa4k7sR2+maLFPTc5b9uDxvH4D/AGf/ABbfTNkSWTwxqv3tzcZ5r4U/4It+F3v/AB94+8SFgY7e2jt/mzks7EnFep/8FjPH2oeH/h94Y0W0XFpqk0izS5BAx2PetP8A4I06HaWnwJ8QalHsN3daoySMvXaowBSjuVLZH6E0tN3Uu6tDnFooooGFFFFABRRRQAwq27jGK+Sf+CjXxV/4Vf8AAvVJ47xYb+9/cQwq2GIPBNfWVxeR2+3ecbjgV+JP/BVD40P8RfjofDNjctNpukIItkb5V5T2x61hPWyRvTXU84/Zz/YI+JX7T2lxeIdGFnpnh+ado5NRu5CTkHkhO9fYd3/wSB8E+BvAOpa14p+IWsvNY2jzyfYlihhDKucDcrHGfevkv4Q/tjfGz9kfQbfw/a2q2ujn95Bb6nakx885B71L8bP+ClHxX+OHgO88Jaw2mWem3bfvpLCExsw9M56UWk+ojgv2Z/gK/wAfPj/p/hbTba6m8Pi+3XdxJhnS3U87mGByB6DrX9B3hrwrp3gzw1p2h6Rbx2WmafCsMMSDARVFfif/AME6f2pfh3+y7q3iXVvGQ1ie5volitotOsVl4HU7mkXr9K+r/Gn/AAWI+Ht5p8sOj+F/EnmMrBTcLHFk446Fqp7NCW54z/wVk+PlxrWvWfw6g2yW1nIbqWZRjcOgGP8A69fSH/BI/wCD0/gX4J3nie/WNLvX5/MjRR8yRDpmvyM+MHxJvvi58RtU8TXUbeZezmSO3djI0a54XoM19H2n/BQ/43Q/DfRvBnhKzi0Wz0+BbdZ9NsHM7ADAJIBwayjFxikVu3c/djqOtVdU0my1zT57HUbWG+s51KSwXCB0cHsQeDX89msftOftF3F0Rd+M/F8Ezn/Vjzk59htr9SP+CYP/AAtfUPhbqmu/EzVdZ1KPUplfTP7YnZ2EQHVVblQTWyk+pDjbVM+s/BPw38L/AA2sJbLwtoNhoNrK5keKxgEYZj3OK6Skpa0MwooooAKKKKACiiigAooooAKKKKACiiildAFFFFF0AUU0tSbjuxii6HYfSMu5SM4qKSV1wVXcO9LHMZFyV2+1F0Fj8o/+CyOlmF/C9z5shEk7rsJG369OtfT3/BKFSv7GXhwFg3+n32Mdv3x4r5u/4LJagbi18NW/2dlaK4Yq/Zq+gP8Agkjeed+x/pkOAPJ1W9U/jJmsoam1TVo+1KKazbetG6tbmA6io/M+bb1NNWY7vm49Kew7E1FJSM23JPAFK9hC0tfP/wAav2yfh38BdSSLxJrMYLjmK3YSSA+hUdK7D4EftFeDP2jfDMuteC9R+2QQt5c0cilXib0YUuZFuLR6hRXxF+1F/wAFANa/ZT+J+m+Hdd8LQaxpV6ol/tCGVozGhOOmCCQK+o/g38ZPDPxz8D2Xijwtfx31hcKCyqfniburDsRVBKLjud1RRRQQFFFFABRRRQBDJMI+O5PTNPzu9q+Fv+CjHxg+KX7P2k2/ibwobf8AsS5cQ/aHG9reX1Kngg1lfsO/8FKLD4vtbeEPiJJb6R4pVQsF8xCRXh+nRTWMZScndG0oLlTTPvuRsDjk1BFMWkZSOlWI5ElRXjZXRhkMpyD9KTysMWB5PtSkmyE1sU1mkJYtwoJ/EVXkvI0Vmlc5/u+lWrmzMwYhsHGOtRR2oaNvNUM3risrHRFxKceoRtEXU8dBVd75vtCxiMLEw+9U8mmIFOBjJyeaz7qxaJXZW8kAZLHnj8awaZ0xs9ipr2vaTocEr3t3GiIN7FzgAV81fEX/AIKSfBjwDeTae+uTXt9a5V7ext2fDj+EnpXzx/wUp/ai/wCEQuE8EeGbvzNTni3Xd0uCY1PVMYrwr9h//gn3qP7Uyy+KfEWqTaR4QEjRm5s2AuppB127lIx71pTp9WZ1KjWiPoHVf+C0lla6g6aZ4EuLmzRsLNLOqM6+u3tXtHwX/wCCsnwp+IEUdv4nkn8H6m8gRUuVLxHPT5xVQf8ABG34Gtgy6t4yd8ckajbgE/8AgP8A1r57/av/AOCS8ngfw/P4h+F+o3WqWFlGZLjT9SdWnVVGSwZQA34AfSuyMeU5ZSUuh+sPh/WtO8TaVbatpV5Ff6fdoJIZ4WDI6noQRWlX5H/8Eiv2iNU0vx7qfwu1zU7ibT7qIyabb3D7hDKh+ZVzyMjt0r9cBRymTVhaKKKsQUUUUAFFFFADVPzGnVEG/eMBxinZoAfRURkCnBNODZGQaB2H0UgpaBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTWO0E06mt94UAKrblBpaKKACimr9406gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoprMF60KwbpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/PT/AII/ePrBPgHqHh+RZFms9SmlkuG2rCqtyBuJBz+FfQ3xm/bt+DXwVjni1nxbbXupx7gNN0z/AEiZiO3HA/Eivw/8Rn4p/A3VtV+GE97f6NcC4EUtjZ7lE7dPkIALA5rpde/Yp+K/hX4eXXj7xXpCeH9BCrIZNSnBnnVucqAGIJ98VknbcvqfUfjv/gsn4hW8vbfwX4NtLSyZ28m51FiJ2XsWRcgH8a+e/GH/AAUe+OnimaUp4pk0mNst5Vqu0L7Cvs7/AIJ4+D/2XfjJo6afpnw/kn8ZaXao1/N4ixL57/xPGolYY+qj6Vif8Fbv2cfC/g7wB4b8W+FPD2n6IsF2be7Wyi8veGHHAGMVpccmz4C8U+KvH/xo8I3Wta/r+peJIdMuMyLMWkEZfuPQV+uv/BJ3wLJ4R/Zftr6V0dtYu5LtQucqvTBBHHSvmX/gjW+k6xffEPw/q1la38FxFFN5VzErgAHng9q+pfjl+2R8I/2RftGn6RIdRv5kKroOilCkTf3vvALUx0Y+lj7IyKU1+T/7K/8AwUe+IvxQ/aM0jwxJYQ3Hh7Wbloxatlpbdezbvav1g28VoZySWwopaSlpCCiiigApCcUtIw3CgDj/AIjeIrXwn4P8Q63cIzRWFlJOTnHIU8D3r8If2dvDLfGv9p+bWtXhku9ItruXV9QcqX2xKxYZ/Kv0w/4KgfHi3+GHwQvfD1lfbNa1p/I8lT8wjPUn2riP+CRvwG0/T/gzrHjfU7Tzb3xHLJaL5g4NsvHH1JNcyjzXsdPwrU4zx7/wUy+B2vLLo+r/AAik8QQWLm3gaTysFV4BGUzjivjSfw5pH7YX7TNppXw88LL4L0zVJVVre3Uv5KD70pGcA+wr64/4KEfsd/Bb4BfDfUPF+m2F7Fr+pXfl29ql6VjRmOSwXHQeldZ/wRz+A9vp/g/WPiXfwZvryVrOyMkfKxjq4OehrSCsZvud34R/4I8fB7R7eI61qGua7dADezXIiRj34Uf1r5V/4KNfs6/Av9nHw9pmk+DLG6XxleS72U3zyiGP/aUk8n0r9avi9qfirRfAGr3fgvTI9Y8QxwsbazklEe9scYJBGa/JT4HfsZ/Fn9pz9pO/8T/FnT9R0Oxs70Xd/JqVuwW4YMD5MXOCOByOKqzuI+eP2efHz/s4eONJ8WeLfh4+s6BOAF+32xjWQd2R2Uhq/cT9nr42fC343eFrXU/AFxpq7og0umxxpFcW3qrxjkY/Kp/jv+zp4Z+OPwhvfAl7aW9pAYBHY3PkBvscgGFdQCOn1Ffit4++G3xU/wCCevxosNSWaa2e3l3WerWoP2e/iB+645wT3BJxRZiuj9/mtYnYMYkJXoSo4qXaa+c/2Ov20PC/7V3g1J4PK0fxVaoFv9FkuA8gbHLpwCyH1xxX0Zx6VVxai0tN3UbqLoVh1FN3c0oOaYhaKKKACiiigAooooAKKKKACms4UgGnUmAeoqOVgLTWYIuT0p1IRnrUgR+YGUsASKGz5ZxwcUSDbG2Dt+lef/ED4x6B8LrIXviLU4NOsS2zzp2x81TKSjubQi5bHdwRt5IUs27ue9SxoY1wWLe5rwm8/bS+EWm2P2qbx5ohQjK4uBn8q8y1z/gqV8FtBu5YX1pr4RnG6ziZwfoe9LmTK9nI+Zv+CxVnqFxcaNP5ebKGTG4Hua+mP+CUOjxaX+x/ockbszXV/dTOG/hJfpXwf/wUI/bB8C/tD6bZWnhE3sn7wSytcrtAPoBiu9/Yb/4KO+C/2evgTa+DPFGmX1zdWl3I9udPj3Flc5O7Jx19KKacd+4pe89D9dpjlcZxXHfEfxvB8P8Awxf61qUyw2NpE0jMvB4FfnV8Wv8AgszH9mWP4feCjNcD702uF9ifVUKn9a8A+K3/AAVC8b/Gr4V6l4Q8R+GtHgmuyR9u0czQqq+hV3c/rSndr3QjaO57L4R/b4+Lvx4/ac0Hw18PpIIdC+3eXKptdwkgB5Zznpj6V+gn7THjzX/hb8FfEPiTSYDcXVjZPJI0C/OjY4dQewNfBX/BF34bwT3XjPxrPE0k0YSxt5MDYO7YyM5/Gv1K1bSrXW9MutPvoEubO6jaGaGRQVdSMEEGteW6sKUtT4I/Y1/4KiaF8VGt/C3xHmt9C8SYWKC/AKQXZ6c5J2t+lfRf7VX7Rnh34I/C++1a91KNZ5o2S1jhkBaRiOCMdq+A/wBs7/gl3J4L+3eMfhXcyy2MZa6udKuZl82HuTEQo+Uelfn3qPirxN4ym07Rdb1u6uYLdxbQpfTkxw845z6U7c2iElZ3Z6J4R8B+Mv2wfjZcQaNb3F7fapdNNJcTFmjt0J53HtgV+537LP7M/h39mD4cW/h/RkZ76YLLqN27bjNNjkjgYHoK8+/4J4fs8aT8DvgRpksc9pqms6tm7udQtyHX5uiK2OgFfU+2jlIlK54R+1x+yroP7Unw2utGvUjtdchUyadqW35oZB0B9VNflJ+zj8UPG3/BP/8AaUPhfxk1xp3h55/I1G0cExSxk4WaMdPQ5FfultxXyL/wUS/ZM0n4/fCq+8QWln/xWWg27TWVxHwZEHLRsMfMMdKsV31Pqrw94g0/xVollq+lXUd7p95Es0E8TZV1IyCK0a/I3/gl3+2Nf+EfFKfCDxheiLSJmZNMkuvvwTZ5iLHsewr9cVOaAasLRRRQIKKKKAOW+JHw70H4qeENR8M+JbBNS0i+jMcsLcEZ/iU9iPUV+UPx7/4JG+NPBd/c6x8MdUXXNPjLTR2c7+XdQgchUb+LFfsK3WkqXZlxfKfg18Kf25vjp+yr4g/sHW7m9v7C1k8ubQ9fQswA7I7DI/A19+/Cn/grh8JvGy2Fn4jgvvCupzKBO0yBrdH74cHOPrX058YfgH8Nvi9od3D438OadewbCXvJUEcsYx1Egww/OvwK/ae8B+Ffhz8aPEOgeB9YXW/D1tLi3cZcR5/5ZgnO4j1qLA31P6FPh/8AFLwf8TrNrrwp4j03XYQMt9jnDsoPqM5FdRJA5ZdrYHevz2/4JBfAfU/A/wAPdb8a67YTWN3rEojs0nDI3kqOW2nsT61+iNP2cSbmZfL5b56g9q5X4i6jLp/gzUrpd0ccEJbIGTgDJrt5LaOQlmXJ+prO1/Q49e8OahpzAYuoHi59SCBXO6eptGpY/m7/AGhfHEvxA+L3iTVmlMsT3LRxMRztBwK/dD/gn74QvPBP7JvgKyv12XMtmLgpjoHJI/Svw1/aI+Eut/Bf4veIvDmuWzQzQ3UjxyMMCaItkMv51/QT+zRfrqv7P/w/uhG8Yk0a3wsgwwwgHP5V0xtYid3qek1Fd2sd9azW8q7opkaN19VIwR+tT4FG0VZmfglMyfs6/wDBQ+aK1JitNK8U+SFXj9zIw6e3zV+9NrMtxbxyp9yRQ4+hGa/D3/gpVotv4Z/bYe7sFEM929pduV5y+4c8/Sv2v8HyNN4T0WRzl3soGJ9zGtBcuhsUUUUEBRRRQAU1pApAPenU1kViCRkjpQA0r8xpACvAHFSUUDuRsinkqM1FJJGq9QDVnA9KY1vE3VFP4UDuMhYyKP7vY1NQqhFCqMAdqWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmthgRnFOpMe1ADIxt461JSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMaTaQME0NIFGTUF1ciM4H3qgW6M+V2kEdT2rLmZai92TSyF84qWHKoM+lNiUMgz1qXpWonYdS0i9KWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPBJPFH7OnxT8aWWpvrXgfX/E0BH2eY3sDzg9sfNya7H4+fDTRPi18JNe0DV7WO8tJbV3iXj5XC5UivyP+J3/BI344eCdUaTwj/ZXjWyRwYLiwvEsrke7JMVCnPo7fWmR/Br9t/wCH3h+60tLDxRHpaxFJY476G5VExzgrI2ePTNKUUzSxxf7Ffji2/Zz/AGvIl1vU49J0y3mlsruRyQhTPA/lX6hft06XpPx1/Y98S3/h++tdVtYoRe29xC+5W2nJxjvX4Pa+NR/tq/Grec+opKftH2kYk35wcj619KeJP2zPElr+z1oHwv8ACdr/AGNYLb+ZqV3CxaSckkYOenFQM8n+BfxM8f8Aw08S3svgBrv+1by1a2eO1iZ3ZDweBX0v+zd/wTd+Jfx+8TJ4h8fQ3HhvQJpBcz3F+GFzeAnkIMcfjis//glL4otNC/amtbS6hjuv7StJIVlkwfLc85Ge/wBK/cqkB498Hf2R/hX8DZre78KeFbW01OGPyxqEmXnPqdx7mvZKaDS5rRGQtFRNMVbG35f72a8y+Kv7S3gH4L3WkQeLNZj01tUn+z27EbgW98dBT2KUXLY9SoqGzvIdQtIbm3kWWCZBIjqchlIyCPwqagkKQ8AmlpP5UAflb/wU2/Z9+J3xq+L2l6l4X8JXuraPa2flFrfBBbd97Ga+7/hfqHhz4DfAvwrp+ttD4VtNN0uITx3BCiJ9uXBx3zmvQNc8d6B4Zmjj1TVLPTmkcIguJlQsT6A15p+1R+znY/tNfCW98Mpqb6ZPKRPb3kBypcdN2OqmudLSyZ1SkpWUlY/K39tb42RftiftC+HfC3g7UZdQ0V7pbS3wDsZ2bBbHoOa/Yr4K/DSy+EHwv8PeErFESLTbVImMa7Qz4+ZvxOa/Of8AYN/4J5+NPhh+0Jc+J/H9hBBYeHy62GwhluZDwsi+gA5r9Tq0joYz7A360iqqjiikrQzFCjJPeuS+KHwq8NfGHwleeHvFGl2+p2FwhXEyBjGSOGU9QR7V1u6jdQB+G/7QH7DXxd/ZN8eXPirwCupahoFnN59lrWjlkmgTOdsiKxOB06819D/stf8ABXiC9uLfw78ZbJLGUEQx+I7NG2lumJogDt92B/Cv0+mhjuI3jlRZI3G1kcZBHoRXwB+1t/wS18JfE681PxZ4Jv4/CGtzbp7m22j7LO+Oy5UJn64rN+ZotdD7u8N+JtJ8YaNa6tomo22q6bcoJIbq1kEkbqe4IrTr8D/hr+0F8av2DPEs2hIFk0hZszWF1+/tplB58uQEhcj0r9Tv2X/+CgXw7/aO0yOA3kPhvxMqjzdKvpguW/2HONwpBY+nxIGkK4OR7cVItfFnjr9t688BftoaF8MZ20+XwxqMaRzSICZYrh+g3ZwR07d6+1FrRO6FJWFooopkBRRRQAUUUUAFFFFABRRRQAVDcSOsbGJd7jsampixhXZh1brUWYEUjFl2HhmHPtXzD+3V+yxrv7Svwrj0bwzqUFhqttL5yx3PyxzexYAkV9RmMFt3ehY9rEhj+dHLfctScVofixoH/BHH416i0Z1LWvCumQE/MDcyyuB9BFjP419C+Ff+CKvgqPSbZvEXjrXn1Qp+/wD7NW3SEN/s74mOPrX6SdKP1o5RczPx3/bN/wCCZ/gn9nP4O3/jPQPFWuX97byqot9UeDYwJ5+5Epz+Ndj+wT/wT2+EPx2+A+keOPFsWranqlzcTRTW8V8YrddhAAAVQ2ef71e0f8FbNUs7H9nueCSQi5nuolVVPXJ71e/4I/3zT/snGAnKwa3dhc9eQhxU+hq9I3N+b/glD+zpIxI8L6lF6BdYuCB+bH9a+Y/22v8AgmL4B+Evwp1rx74H1bU9ObTUV5NO1CdZYWXOPlIQNn6k1+r2M815D+1p8On+KX7PPjXw9FvM9xYO8Sp1LKNwHT2rSyMrnyT/AMEYPENvdfBzxbpKYE9tqgmP94qy9/xr9E26V+JH/BMP9o7Tv2evjDq3hXxc66bpmvlbZ7y5ygtp0OBuJ4ANftLo+vaV4r037XpWoWuqWMmVE9nMsiH1G5TTB73Py/8A2/P2l/Efjf4uJ8Kvhqszatu+y3FzasWbJ4I46DnnNc34o/4JCa3Z/Bt/EUXiRrnxott9rudP2bkduSVU4zmv0V+G/wCyV8NPhZ421Xxfomhk+ItTlaWe+u5jK4LHJ254Ar2HaKhRsy5STtY/I3/gmb+2FqXw08YR/BbxwJYbK4uWgsJbkEPaT/8APNsn7p7cV+uY6etfiF/wVGsY/hz+2NHrmiQQ6fcm1ttRZofl3zAn5yB3+UV+xfwX8WS+OvhL4Q8QTjE+o6Xb3En+8UGf1zVmR2dMkjWWNkdQyMMMrDIIp9Z+va5Y+G9Hu9T1K4S1sbWMySzSHAVQOaAPxH/4KJfD+3+Bn7YFnr2iWa2VjeNBqsaw8KGVxvxjp0r9qPh9ryeKPA2gaxGSUvrCC4Gf9pAf61+HX7eHxo0/9pP9oaytPCMr6jZwgadbsoz5jO4DEe1ftn8G/Dtz4R+FPhLRrs5ubHTLeCT6qgGKC5O52VFFFBAUUUUANbrUUkwhUs3AqRm68V518aPi1pfwd8C6p4i1u7htrS3RggcgFmI4A/Gsm9bGkVc+Hf8AgqB+2Ung3SX+G/hi9kGt3g3Xl1EwxBGeqY9a8X/4Js/sMD4wahZ/FDxmpl8OWlyWtbGZT/psg6SE5+6DXi3wh+FviD9uz9qLUZpmdtNurxrq+u2UhUt1bhMjpkDtX7sfD3wDo3wx8GaT4Y0G0Wz0nTYBBBCpJwB1OScnJz1qrBKXQ3re3itLeOGCNYoY1CqijAAHQVIBjiloqzMKRVCjA6UtFRygfin/AMFebeOP9prTT5jOJNMQsrLgKQ3TPev1u+Ad1De/BPwPNbhRC2kWwXZ04jA/pX58/wDBaH4cR/2f4P8AG8FqWmR2sLmcAn5DyoPpzX0l/wAEyfixF8TP2VfDtsZHe+0AtplxvABO0koeO20gfhSWho9UfWVIzbVJ9BmiuA+PPjhPh18I/FOvNc/ZZLWwlaKTjIfacYz71XMiFqfjz+1ZqU/7QP8AwUIGjaZbmRo9SttMVV5/1bAu30r9u9Jsxp2m2lov3YIUiH/AVA/pX4wf8Eq/CNx8VP2sdS8ZaoXvTpMM9888h5M0hwrH86/amqKk+gtFFFBAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTXzt+UZNOooAamdo3cGnUUUAFFFFABRRRQAUUUUAFJuFLUTsFUk9KY0SbhRurPfV7eOTZ5gLf3e9TJceYMqRjrU3RXKy1S1m3WpeSmRUVlqktzk7MqKhTTY/Zs1t1G6oI5w6ZPB7im/aM5IPAq7oXKyzS0yKQOop9MgKKKKACiiigAooooAKZIrt90gU+igDMa3aa4IPY1cjthGDU20Ak45panlRo5tqxGsZWnbadRVGYlLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfE2vf8FdPgNpMCPaza9q7t/yztLFAR9S8iiufvP8Agsx8FYbbdHoPi+4mI5hWyt+PbPn4/KtC3/4I6/BKKRWk1zxxcqP+WcurQbf0twf1rUj/AOCRfwEE2+SLxLOveOTVvlP5ID+tZ63Luj8tv2kPjl4F+MfxrtfG+heGLjTbKS5Wa/tLuNF84BuchGYcgV9vWX7dn7Kdn4DFnZ/DjbqMtn5Txf2EjgPtx989RnnrXvo/4JQ/s8rNC48Pal+7/h/tSQhvrWz/AMOw/wBnUyBz4Fyf+whcAfkHp2HdH4j6D4+ufA/xbh8Y6FE9p9l1I3cCW6FF8vfkKAenHGK/Q/U/+C0gGk+TZ+BbpNQVVAlnlQKxwMkgE45r7E03/gnb+zxpaoI/hpp8rL/FPcXDk/XMmK6eD9jP4JW1ukMfw10JY0GAvkE/qTSswuj867r/AILSeMpIIxb+BdLE38Re8bn8NtU2/wCCznxIZsp4I0QL6NPJn+VfpPa/sg/Bizk3w/Dbw+r/AN42gJ/Wt63/AGefhlbRqkfgLw8FXgZ06I/qVrQpzVrfofmBJ/wWZ+IMsJRvAehjcME/a5M/+g18l/tDftJ65+0X4sstV1iyj0v7Ku2G1tZGePcSPm5r99m/Z/8Ahq/XwH4eP/cOi/8Aiax7/wDZT+EepXAnn+HugvKDkEWir+gqZahGfKa37Pc3n/A3wLIWLFtHtiWY5OfLGf1r0Kqul6ba6Np9vY2UCW1pboI4oYxhUUDAAHpVqmtjJu7uFMl/1bfSn0UxH5Tf8FhfCV3px8J+KIZ7m3bzGtf3bkLjqG4PXNfUv/BMPxtf+Nv2UNCk1K+lv7ixuZ7PzZiWfapBAJPX71eg/tVfsp6J+1R4Nh0LVtRuNKaCQSRXFsoJU/Q10f7OfwB0T9m34Z2Xg3Qrm4vLWB2le5useZK7dWOOP/1Vkou50SkpRXc9Nz6V4z+1xr3jzwz8D9d1P4dKzeIrePzE8tQzBR1IBBya9o202SJZoyjAMpGCCODVWMIuzuz8lv2df+Ct+v8Ag+aXQvjFpF9rjxttW+sIVW5j55DxnG4/iK+vvg9/wUk+FHxu8f6f4O0Cx8UQavfEiH7fpipHx3JWRiB+FdL8Qv8Agn/8Dfidr11rWueC4X1O6bfNPazyQFzgDPyMPStL4L/sR/CD4BeIzr3g7wx9i1jYY1u7i6luHVT1C72OPwqipNPU9M+J1x4ltPAGuzeD4refxLHaSNYR3RxG0oHANfj/AKb/AMFWPj98NPGU+k+MbPStQayuil9p93Y+TMuDgqrKRjjpwa/anbXj/wAZv2R/hV8eY5G8XeErK7vn5/tGBPJuQcYz5i4JP1zTEmeYfs//APBSb4SfHjVNO0KO8ufDvia7wi2GpR7UaT+6knQ/jiuH/wCCkn7NHxb+OGj2eo+Atd8zStPhZrrw+s7xSTkc5TaMMf8AZNUfhd/wSN8E/Df4vWvi6TxVe6zo9jP9osdEmtdhhYHK5mEnzAH/AGRX3qqBVAHAFTvuVdLY/nu+GXx5vvhE1z4B+JPhdtV8Oq+2503VISl1a+oTcpI659816F/wxbZ/HVZvF3wE1+GW2IMx0C8n8i9tcD7owSc5Bx9RX6q/tFfsWfDH9pKGSbxLoy22umMpDrFn+7nRscFsffxxwa/KP4z/ALIvxr/Yn8cNr3hS61XUtEQmS313R43YhRj/AF6AnZ+JIxU8r6D5kdL+yn+wn8ZPEHx+8P674s0PUNJ0zRbxLq41DV3LGTYchVJOWzX7ZL0r8rv2OP8Agqp4k8R+LtK8EfErTV1ifUJ47W01fT49kgdiABJHjB+oxX6o04p9SZO4tFFFWQFFFFABRRRQAUUUUroAooopgFFFFABRRRQAUUUUAfBf/BWLwk2ufBG5vY3iAs3jlbd97IPFL/wRyl3/ALMOpLnO3XZz+apXTf8ABUbQhcfs269eB2QLt3bTwea4f/gjHdNN+z94ntyFCQ62SuP9qMZ/lWcd2bSfun6CL0oZQylWAKkYIPQ0UtaGJ8ffHP8A4Jg/CP44eOJvFFw2qeHb64/4+YdHkjihmf8A56FWjb5voce1ex/s2/sz+Ff2XfBc/hrwpc6nd2lxP9olm1SdZZGfGONqqAPoK9d20baB3BelLSUtAj5L/au/4J3eEf2pvHVh4u1HXtQ0XVLeGO2lWCJZYpYlJONpIIPJ5yfpX054O8L2fgjwppHh/TwRZaZax2kO7rtRQoJ9+K2KKAOK+MHxNtvhD4B1XxReWs97DYxl/It13Mxr8e/j5+258Wv2wtUbwR4N0K6sNKvJPLSztUYyyL6Oe1ftndWkF9bvBcwx3ELjDRyqGVh7g1k6P4G8OeHrhrjS9B03Tp2OTLa2kcbn8QM0Afnx+wR/wTRm+GurWfj74mwoddhIkstIUhlgb+9Ie59q/SLpwKWigAooooAKKKKAI5W8uN3J4AzzX4wf8FUP2lJ/HnxFbwBptyp0nSSpvEjHJmxkAnvwRX7RMoYEEZBr42+O3/BMP4d/G74rp45k1C+0W5nlSXUbO2IaK7K4HflcgAfLis3G7uaRkkO/4Jd/Am2+Ff7OeleIJrdo9c8TL9tuDIMFI8kIo9BgZ/GvsiqOh6NaeHdFsdKsIhBZWUCW8EY/hRFCqPyFXq0MwooooAKKKKAPKf2mvgjYftAfB/XvCV4FWeeBntJ2BPlTAfK2B15r8RPgN+0V8QP2G/ixq9jb2xnjhuGtNR0S63JHPtbG4ZBwe4Ir+hDFeS/GL9lH4U/HlYz408G2OqXEZ3LdR7refPvJEVY/iTU2KTPjaH/gtb4JWyiM3gLXPtW0eYqSxbA3cAk5x+FfLP7XX/BR3xN+01aHw14a0+Tw34Zk+WS2fbLPck8bTgHH4V+iK/8ABK39nXzt58I3ZXP+r/tS42/+h5/WvS/hv+xX8E/hNcJc+G/h9plvdpyLi6Ml0+fX96zYP0pcoRdnc8e/4Jf/ALNP/Ck/gnH4j1W0a38UeJ1E9wsgZXhhBOyMjOO27pnmvs+moixqFUBVUYAAwBTqsTCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACMwUZPAoVgygjkUEbuDQqhRgdKAFooooAKKKKACiiigAooooAazBRk1Xl/fx/KeDUsnzZFRbdoAqOY0j3Mh9Dg+0GY7g5OSauLlWVY13ADBzUrQM8zfMQKezR2aFmYDHUtWVjVy7EH9nmZiWGFParVvbpbxhV6VjX3iZA0awnIY4Jq+sjELkkgiqTtsHLN7kzAKzE9D6VBHtYSKCSc1JIwAwTg+9NtbZlm3joetS9WF7Fy1XEantjvU9IvSlrdbHO9wooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu3rnkHsaZcWsN5bSW88STQSKUeORQVZT1BB6ipaKAPniP9gv4O2fxc034i6d4d/snXbGf7SkVjJ5ds8nZjGBj34r6HoooAKKKKACmTSGNNwGafSUACsWUEjFLRSA0rgLRTSaMmoYh1FIKWrQwooopgFFJXlf7RXxwH7P/wAOdV8WzaVJrUdnCWSztyQ8jfXBwKmUlHcqMXJ2R6rSEhRknAr8s7X/AILabpovtfw2WGFvvNFf72/LaKxvGH/BZ7VJNUmPh/wdGtjs/dreTgHdgdQBnrnvS5vIfIz6s/4KTK2vfs1+JdOW8s7AeX5ifaZQHm2noozXmf8AwRhtWh/Z/wDFMxR1WTWyo3d8RLnH518A3Ft8dP2/PiJdXWn6dqOrRXDhjGrNFp1kvC/eY4xxnrnJNfsh+xr+zvL+zH8D9J8HXN1HfamHe6v7iP7jTOeicD5QAo5zznmiKBvSx7pRRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJtGc45paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiip5gCikpadwCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSZGcd6WgAooooAKKKKACiiigAooooAa2c9KjWMiRmPfpU1FTyodxkgbadvJrH1DR7rUCN0oVP7tbdFHKhqTicvJ4Vm3ho3Xg5ANbNrYyLzM2T7VfopcqLdWT0KVzZhyGbPy9MU+BtzYAP5VZowB0FPlRHMwFLRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUroAoooouA1mC9aRT82KR8lgABj1NNjkRnIVgxHUCs29RjpZBGASM84p/FQXTyDb5YBycEnt71HtaSBo/N+f+9T8x8uly5RUKMY9sedxA5NSbqq6FYdRTN9Lup3QWHVXvbG31G3eC5gjuIZBtaORQykHqCDU9FDSYbHgHir9gr4DeNNSnv8AVPhzpbXU7b5Htw0GTjHRCKZov7AXwA0Fomtfhno7PH91rhWlPXPJYnP419BYox70BdmX4b8K6N4O0uLTdD0u00mwiGEt7OFYkUfRR71q0UUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4BRTWbaM4zQrblBpgOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKY4Y4wanmAfRUZB3HBqNmPPzYqeYaVyfcB1Io3D1qrDIs0nDBwvcGpuxz0pXuPlI3ky528j2qVGJUU1VCrlRSZc8jioCxMKKhDherZPoKAu/JywHp0rWMr6BYnopF4UCirJFooooAKKKKACiiigAooooASjNRthmIzzSqu1cZzUcxViSikXpS1ZIUUUUAFFFFABRRRQAUUU103Y5xUcwCBTuJ7U+iirAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKhurpLO3eaTOxBltoJ49a+evDv/BQL4HeJvG8vhO18YpHrKXDW3l3NrNEjSKxUgOyheo9alySdmUouSukfRdFNSRZFDKwZTyCOQaXNUSLRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUySTZ2zTBcKULDnFZPcdmDXARmDYUDuT1psl4kSl2ZRGOrE9KxtfvIYLV5rgME4247Hpivhn9sb9uxPgNfPoEds+o63cWhe3t1OIlyxAZmHNcrqS5uVI6fZLl5mz7/wB/m7XVg0Z/u85qGG3EHmSqmGY/dr8QfB3/AAVi+NPhPVLdrn+y9U0hG5sJLfb8pPQSA5z17V92fs8/8FUfh98ZNes/D+uWE/hHV7gAK91IrQM57Bv8a6NbXZh6H154m1SXQtNuL8OBHAplkXGTtA5rxr4K/tmfDf4469qOgadrUdjrlpK0f2O6YRtJtODtz15Fe7yRxaxbnbJFPZzJglcMGBH8q/Nj/goB+w9JoMsPxN+F1q+marZtvnisflyRzu479al3urbG94uNup+l7yJa7N2fmO0HGakjJwQxBIPavgX9g/8A4KJaZ8UrfTPh74/l/s7xpCrQx3twwEV2VYgLk9HxgfUV96SFLQvK0gRWI+90HFabmVuhY79KQ7u2MV8+/tAftleDP2dbGObXrg3bykhIbRgXznuK8D8I/wDBYr4ZatqVvZaroWr6ZFJMI/tzBWiAJ4JHXioUk9inBx3P0BXO0Z606szw34i03xbodnq+kXkV/pt2nmQ3ELbldfY/XP5Vp1utjFhRRRTEFFFFABRVa6ujBwqFmJwvHWpgxwM9aAH0VFNN5UZbG7HYU2G4Eyg/dPoaV0OxPRSL0paYgooooAKKKKACiiigAooooAKKKKAGtnacdaI920butI2d3Bo5rJ7gPopm40bm+taLYB9FMWQsxUjFPpgFFFFABRRRQAUUnNLQAUUxmPToabJMIsZGc+gqOZDJaKQcilp8wgopjMV6VFNMUhLd81Q7FiioFnyoOKPPGcc5qeYfKyeioBcLu2k4NSMTtPNUKw+ioY5GOeM0sZZuScUCJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKO5qGaTZmp5hpXJs02TJQ4PNUi8r5ZWwv8AKljmLKRvVm9jWdy+UfMzIu7dWbdXk+VRIWfcfmakI82Ykz52nBXPAq2u55Dg446fpUJ3Zulyoms4VtYN2NvqtVmuLm4n+UKluOv95qxta8feE9L1608Oat4k02x1q6AeHT57yOOdwTgYQsGOT04roJ4I4YzIsbEg4wPyq7GSab1J4x8gw2B708g7fvc0yOIbRtOBShTGxZj8tIl2voJFHhyx5NTUxX3HjketO3c4FVH3RDx0pv8Ay0NfEP7VX/BUTwx+zh8RNW8CWnhW98R+I9MMQuW89YLdTJCkqgNgk/LIueODmvev2Tvj9J+018GdM8eSaONBkup7i3ayS4E6AxyFQQ4AzkD04ORVcwrHs9FfnZ+1X/wVbk+B/wAX9Y8DeFvCdrr50VvJvb68ujGpm2qzIgA6qSVIPcGvtj4F/E7/AIXN8IfCvjb7A2mf21ZLdG1dtxjySOvccZHsRVknd0UUUAJmikOM1BPeR23LkKPU0NpAk2Ts6r1OKa8iiMsWAHrXPatqrLIhh+dWPVafJJczWrIqsT6YrP2iOhUtL3NCTUrWKQIZAZD0HrSQapFNMQrj6ZrANtcSSISu0rxk1bsdLlW8ZtodOu/1rLmZq6cIrc6VTuUGnVHEAqhe9SVqpHGFFFFPmEFFFJRzALRRSA5o5gFooop2uAUUUVQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEc0SzRup6MCDjrivxw/b3/wCCe3iHwD4qvfG/w9sr3VtEu5XurmGNi81vIzbiVwOmSTX7JZpjqsilGAIYYKnkEVnKN3c0jNx0Pxp/Y+/4KceI/gn9k8G/E+3vNc8OoVhgu2GLuz553FyN6gk9TkYr9cvAPxJ8NfFDQbfWPDGsWur2MyBw9vIGIGSOR1HIPX0r86v+CsHwZ8L6tB4avdCsIrfxldXIsrSwsIAHvixGThRjjvn0r2z/AIJz/sW6r+zH4cvtd8Rar9p8Qa9bIkmnwlvJtUDFlHOPmxjPHrWUJ3ehdSm0k31PtClpF46nJpC2K6LmA6k3fNik3Un8RNF0MfRSbqWi4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUU3eN2O9G72pXQ7DqKaGz2pjyurYVMj1zRdBYJ28uNmxu9qqr5hjbBVEIyGp9w05mjKsFQcsMZzVGa6+3WcyRrs5Ow+vr+uax+1c2jFtHn/wAXfFU/g3wPq2tThXjtIHk2sflO0Eg1+Fmi6P4v/bS/aOXToZJLrU9YuSpmzlbW2VuWHsq1+mf/AAUq+LWr/Dv4I39naoJotQlFkHLFSoZRlunOCTXk3/BFb4W2048cfEGaFXmilXSLaRhynyrI5H1DAfjUU4py5jas7aH2l4D/AGFPgv4I8EWvh1vA+l6qFhVLi8vYt8s7Y5YtnjnPTpXgv7S3/BKrwP4w8Pvf/C+1Twl4ktz5kcaOfJlwOF5PynivvgkDjPNNVldioYEjqM8it9DkWmp+CXin4yftIfsa+KJvCeqeJNQsZ441ES3DefEykB8qT/vV+oP7BPx38TftPfAG81nxrbWlxdCZ7TdEuFnUblJI7HjtXg3/AAWZt/Dv/Cu/Dcsluh8QC92JMoG8R7c4Nehf8EhbuOb9lkW6qqTQ6jcKxHUgyOQT+dQaM/KL9p3wwfhd+0Z4u03Smntfsd8txbyA7GTeiy5BHozn8q+7f2Q/+Cn2lSeBbXwT8X7ueC6tkZLbxEoMjTLuYr5g7FQQox2Arjf+CunwPg8J+JtC8cWyHztR3Wt48YG0kL8jH3wAK+WvGHwFSH9nnwz8U9MmQW1xI1hqNqGzskV2QMv1Cgn3NK6aswTlGV0dVdeD9e/bW/avvtA8Oas9/ZX1w0kF3Pu8qK3RQC+3t0NfRPx+/wCCScfwt+E934j0PxjeatqVlGJLi1u40WJj327RmvFf+CdX7U3g/wDZh+IWoXvizR2ng1aIWyatF80lqueRt9D371+zV34w8MfG74S3uoeGdQt/Eel31szJ9lcMTgkEEdQQQRj2qnaEROTnK7Pzi/4JD/tJatb+OLz4R65qElzZ3EMk+mRzMT5LRgs6L7H5jj1r9aK/Cr9nfT7f4Z/8FHvCdtF5lrZSay0UbMNmfNhIK/TexFfupu6VcZKSuRJWY6ikpaokKQ8ClpOtK6ApTPJ525Qzbe3YVy/jj4veE/hnpE2p+KNcttIs4SA8twcDn09a6HXb4aZZvIDg9BX4of8ABS/42ar8RPjZ/wAIRYTSzaXpqxQ/ZISf3tw4DAe/3l49c1lzPmsjqULw5nsfqlY/tsfAzUtQSxg+JmgG5cgCN7kJ16dcV7BouuaZ4k0+K/0q+ttSspc7Li1lWSNsHBwwODyCPwr8h/ht/wAEc/F3jD4ef2zrviiz8P61dQeda6V9mMmwkZAkfPGePpXl1l4i/aG/4JsePLG11Hz10ZyTHY3Dm4028jLZbaQRtbk9+CTTMra2R+7S9KWvNf2ffjpoH7Q3wv0nxj4fmDQ3aFZ7cn54JlJV0Yf7wOPUYNek81otjN6PUWikFLTEFFFFABRRRQAUUUUAFI3SlpKAIJN7DIr5+/ak/a80L9lXTrC81+CW6a+3C2t4hzIwHrX0Pt2jivyt/wCC1Vx50/w0ULugVrgM2ON3GB+tYta7msXpsfbn7Iv7V2hftaeAb3xBpNlNpd3p919kvbKY5MbEbkIPcFcGvda/K7/giTeSs3xKg8xvI/0Z/LzxuwQT+lfqjjNaohir92nVGXCYBOKXd70xDi2Kasgboc1UaZvthjY/Ieg/CpoIwp6c1gpOTshtWJ6Wm5xRurW5IyabyyBmpFbdUMkIkbJp6/LgVnd31GRXBfcNhANSJuCjccmo2txJMXYk+2al4UUD6D16UtMVuKXdTFYjkYhjVaZvmAxuLHkelWmx1PFMWFS28dT3paloazCOREOTTjjccLz61MqjAzyaXaOuKvlFcriEbt7KC1PVt7MMcetO3BmZfSgKAMdqsVyDaQ5AkOPTNc/41+IWi/DrTl1DX7+303T94R7q6mCKufrXR+WolXHHtXwF/wAFmNan034A+F7G3meE6hrYjkCHG9FiY7T6jO38qXMXofc/g/x14e8f6X/aPhvWbPW7HdtNxZSiRM+mRW9X5sf8ES7yab4YfESB5XeKLV4NischcwnOPTmv0manuQ1Z2FooooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKQjcCKWigCBVaBcDkCnI7SLnGKhvrpLGCa4lUmOJDIdi7m4BJwPoK+Kfgz/wAFQvBHxZ/aCuPAgsZtH0e72waTql8uyS5ueAUdf4cncB9BnvU3KsfXPjzx34d+G2hSa14o1+x0HS0dY2udSmWOHcegJPetrRdb07xFpsF/pV9b6jYzqHiuLWVZI3X1DA4Irwn9uL9nG5/af+A994U024S21iC5jv7J5PutIgYbD7EMa/Ib9nv4/wDj/wDYL+N15pusWV0LFLkxa54d3AC4+XiRfRgCCD/+qmFj9/aK8q/Z7/aU8EftLeDY9f8AB2pLPt+W6sZsLcWr5I2yJ26ZB7gg16rTJCiiigAooooAKKKKAGf8tBVO8kAZhsZjtPSrjd6iCjcTms3uXHTU8j/ac+Luo/A74G+JfG2j6Q2sXulW6uLXsuSB5jDuBkE18k/sDf8ABRS/+M/jDXPDnxN1HTNNvrjZJpMiKsKHPDR5PfpX6CeI/D2neKtA1HR9Vtku9Nv7d7a5hcZDxsCCPyJr8Zv20v8AgnDrv7PcjeNvh893rfhfz95ht0ZrrTjnKH5eWX37VJVz9kpbWL7Z9pjkUxH5mVTnPvXlv7SX7QGn/s5/B3XvF2pzxLdRo0Wm2shAee4YfIoB5IB5OK+CP2Nf+CoH9lW1p4S+LnmTW8EIit9ZRcuSCdok/DA/CvAv2vf2gNf/AG5Pj/o2geF7O5bS45hp+k2Iywdy+1pmA/E57AUlGzuXzaWOY+BXhH4j/ttftL2N/c6he3OotdLeX+tZbZZQodwUHovTAFfvTpBurexht2EjJDGqb5uWYgYJJ9zXif7H37J+g/sgfDO4tlnF9rl1H9p1fU9uN7KCdq+iqDj3xmvk/wCIn/BZ6z0vWNRs/DXgCS5toJDFBeX13t8wjgkoBwMg9+lUSml0P0vt5Wa28w/KTnj8axNe8VWPh/SrrUdVvLWz0y1UtcXd5IscUI/2mJwOo6+tfkfqX/BZb4oXUkhs/Dfhm0jb7qzxyyMPqQ2DXiPx+/b9+Kn7RXhz/hHdavLXTNF+9PZ6PC0ST+m4E5I+tFiouKd2j9y/hb8TdA+Kmmzar4Z1mx13SlkaH7Tp8qyRh1OCpwTg+x7EHvXc18J/8EefA+peG/2YrvW7uZWs/EOrzXVnCpz5aR4gb83iavuyq5TOT1P50f23vFkPjr9rP4paxbbmgbWpbVdw5IgAgz9P3WfxFfs//wAE6/DFv4U/Y1+GltAjIbmykvpN4IYvNNJISf8AvoD6AV+Ffxyme4+Nnj5xjMmv6gR+M71/QL8BLe2+FX7Lfgo6jOsNro/hq3uLiSVggULAHbJPTHPWnYGfiT/wUPs0sf20vinEieWjagsuMd2tomJ/Ekn8a/Z/9hJpH/Y/+FDSoyOdEiOGGDtJbafoRg/jX4HfGT4k3/xk+LnivxlqJVrvWL2Wc9lVSCqD8FCj8K/oc/Zi0ltC/Zw+FunvF5Mlt4Y02J48YwwtYw3HrnNUQz02iiigQmKz9R08ahtUhgFOfrWjRUyjzFKTRn2+mwoMFOB0B7VY8pYVOBk1KeppOKiyWhXM2Vo4QzcpgVaVBGvApF+9x0qSgmUmyNU3MWPFP9qWm4O8mr5SRaa7bSDn8KVutN9agYyOV2b5l2iia6SHO87VA3FjwoA7k1Ev7ydhu4r4r/4KsfHDXfg38D9JsPDl6bG98R3zWkkyNh1jVMtj06ikOx9oac0dxm4hu1uYn6eW4ZfzFX81+ev/AARw1jxP4k+EfjO/1nWrjVdKg1cWVmtw5cxusayScnkf61T+NfoRTCw+ikXpS1otiQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFQ2AUUUVYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGqu94kd4luwYOy7gccfTNZuTQ7XLPeqOqeetuxthmbBCk9B9auZoyPrRKLkrXHF8rvY860X4S2V5r1j4i8QRQ6jrNi7taMy7lgLcErkdcV6MvyjHpQpArI8VeIofC+i3ep3bJDaW0TSSSSOFC4HeotGjFtmjcqsrGn9oXzgg5NScGvyp+L/8AwVx1zwb4s1DS9B8J2d39nk2i6nuiFlUgEFQoPY14j4u/4KnfHDxZI40b7LpEMwGy3s4zM6cYPOM8nn8aUZuSUkipU1F2uftjr3iTSvC9hJe6vqNtptpGMtNcyBFA+prxjUv27PgPpN/LZ3HxK0UTRHDbZtw/MV+HPxb+K/xg+IVqdQ8c6j4gnspiAPtJkit84xwuMdqtfs1fsq+OP2nvEEul+FLaNLW2/wCPnUbo4hg4yNxA6mrM7W3P6Afhn8aPBPxk06S+8GeI7HxBbRnEjWkgYpyRyOo5FdvXyL+wP+xDdfsmaPrV1rerw6r4h1Zgsn2PcIY41PygZ6n3r66qopozCiiirAKKKKACiiigAooooAKKKKACiiigBjKNxPekNP202SMsjKG2kjGcdKizKuNjztGRg015QrBSevtSoPLVULbmAxnpmnYB6ipGVbjcJI2jGc8HJqq1n9nVpl+/zzngfhWrsVsEimfZxhhnKt2NHKy4zsflZ/wV28Yt/wAI/pegkCQSXazBhxjCDtXq/wDwRctwn7Nfiqb+KTxVPkfS1tqx/wDgrV4B0S1+FsviG4gY6h50aW7L0GcKfpW3/wAEX2/4xp8UJ/c8Uzjg9f8ARbas6el0+5VWSk7o+7tchuptNuFsn8u52Hyzj+LHAr8iv2qP2qP2k/Bvj3V/DFtp95oMCyBUubO1aR5VKgg7wMdD2r9hetVbjSbK8kD3FpBcOOjSxKxH5itrERnyqx/NZ8UvG3xH8Zxwy+OrzWL4I5ZJNTRx8x44JHpXefBf4f8A7Qb+E21T4cWfia20Od2Jl06RkjlYcHAzzyDX3T/wWX36X4Q8J21rYRR2FxMxkmhgVSrDtuA9q7r/AII4+NNW8T/APxBpmoTNJZ6Pq5gs93Xa6LI3/jzGlZil0Z8i6X8JfjN8Rf2ZPibffEN9Ta10WOK5sl1okzeYr5kAJ9q+VdF+IGua34JsvhtHIW0y41NJ44yT/rGbGPpk5r+j3x94NtPG3gnW/D1xEhg1K1kgORxllIBP44r8Kvhv+yX4w8P/ALYnhzwFrWjX1uLXWY5JLxLdmiMCkSK+7GMFcZ+tPlLTufdfjX/gk74I8e/B/R20Jm8MeNEs0lknjO6G4lK9HBBwO3FfAetWPx2/YG8a3dhHeah4bEnyC6tyXs7pSA3y5474+ua/oIgjEUKIOAqhRXK/En4T+E/i74fl0TxbotrrWnSDmO4TJX3U9QfpVW0szJOzPwC8JfGbWviF+0t8PfFetRxDUrfV7JJHt/l83Eq/MR6kGv6J4m3Rxn1ANfDln/wST+FmjfFPTPFmkapq9jZ2N1HdLo+9Hh3IQQMspbBI9a+44YVhjVFGFXgCpjHlHJpoevSlpKWrICims22jdUWu9BnP+Opobbw/c3EzqiwqXO72FfiN8C20/wCKn/BSHR59SgW6tJ/EEx8thlW8mMlOD7oK/af4sLFN4H1mOUcfZJGz3GAa/Eb9h1Um/b88Kkk4/tm+YY/65SVml+8Ol39kkfvTyqgDpXK/E74Z+Hfi54Pv/DviXS7fVdPuomTZcICUYjhlPVSD3FdaOlG2tbHLqndHwd+wf+zH8SP2Zfi5420i/O7wBeAy2h37suGwh9M7eDxzX3ivSjFG2q6Gk5ubuxaKbnFKTQZi0UgpaACiiigAooooAKKazBepwKTcTn07GlfoArfdNfmL/wAFooreDwJ4DCgCYalKxz1I8uv05JO05r8sf+C1c5kt/h7EpPlGSctkfxDioe5pHZnIf8EVfEpsvif440NpBsu9NjuFXA5ZXA6/Qmv1+Ar8WP8AgjbZST/tGa1cRqfKh0dg57csBX7UVUeopdBjKGGCMigKFGAKdSU76EFaa3LSFwPmHQ1MuVAz170x1Ls4DY/Onxx/KAXLEdcjmstd0aS2H5zTWk2nGKeoGKXaKNTNEO0vz0ojDBzk8DpU20UjLxxwaViriVHIewPNNjmPmMjdu9R7is7Hgg9DT+Q46ljYvpSMD0U4oj3bRmmeXJ5pbfhfSgAaPdHgnLetLGwVQvekmkWHDFtpY05GVj8vPuKBky9KWmKTuxT61WxmR7QHZu5oB3c4p9FMZA2POXrmvzh/4LXXTR/DL4ewquAdWmcv6YjFfpJgbs4r8tv+C2F5KX+Gdj5rG2ZL2Zoc/KWCqA2PUc1n1LWrPVv+COvw8l8Lfs23viKU5/4SXVJbiPjnZF+5/LcjV95tXhn7Dei22hfslfC62toUhRtEgnYRjALyLvdvqWYk+5r3WrRMnqFFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAprosilT3prL8x9K+Ef28P+CjWmfAyxvfB3gS5g1Pxw4Mc1wp3R6fnufVsGpuVY639tz9v/wAL/s46be+GdK8jX/HUsflvpZYgWqugKtJgd1YED0NfjJ4B8C+Kfjt8TIbDw7p09zquq324tag7bbe+5jnsBkn8K9i+E37Efxs/a40vUfiHp1tava6hLLImparcrGL2RXZXCcEjDKVyQBxWvp/7B37VHwvkm1TQfCOt6XcwHP2rRNZgMj47qkT+YfypWKP27+FvhW+8D/D3QNB1LVZtbvrC0SCW+uAN8hA749On4V5l+1B+x34D/ai8Nzwa7p8dn4jSLZZa9bpi4gI5AJ/iX2Nflt4P/wCChX7Sv7OuvrpHjiK+1ZISBNpfjGykgucEZ4kYB+QcgnPBHav1u/Zm+NUn7QnwX0Dx3Noknh2XUvOVtPll8wxmOZ487sDIbZuHHQiqJd1qfkT4Z/Zd/aH/AGU/2iNGstAstcjtLjULe3fXNBgea0u4DIpO84xjafmB6HNfuPDv8mPzDl9o3HGOcU5elLTJCiiigAooooAKKKKAGt1pu0HnFJNIU6DNKOlZvcsRlPGOKZc2sV5byW88azQyKUeNxlWB4IIqWvHf2rv2iNM/Zn+D+p+Lb3bNe/8AHvp9qx5nuGB2jHoOp+lID8yP+Cq/wz+DfgPxZpw8GSRad42kkDappVhgwRwleHYDhXz2968T/YZ+PWk/s3/Hiw1fxLosd1ZXKLbSXUkf72zVv+Wq59Qcn616N+xT8EdT/bc/aT1vxt41a4k0fT7salfzKAyz3G4GOAk8YwBkeg969m/4LFeE/Avh208BjR9MtbDxncGbzPsiLHutAqrmTHoeAT6GmUfqNo2saZ4y8O22o6fcQ6lpOowCSKaJg8csbj1HBBBr5juP+CYXwDvPE15rM/haWVrmUytam6cQKT1woPAzXoH7EPgSX4cfsrfDrRZtQk1OQaat150nUCZjMEHsgfaPZRXuVPlIueO+Hf2P/gr4XsYbWy+GfhsrFnbJcafHNJySeXcEnr3Neg6H8P8Awx4ZsUstJ8O6ZptomdsNraRxoMkk4AHqSfxroaKfKSQW9rFZwrFBEkMS9EjUKBnnoKS6uY7K1muJmEcMKNI7McAKBkkn6VYryn9qvxtJ8Ov2cviH4hiIEtnpEwTP95x5Y/V6oD+eL4oanBqXxY8V6hDMDaXGs3MyyRkMCpnYgg9+Oa/SX9tL9tzwbqf7Knh34b+APE6614l1ixsoLw6dJuEEQjUPFIy8B2OBtz2r4s/ZP/ZL1n9rnWvE+laDr1jomu6TbpdomqLIsUoZyGDOisw/KvuH9nz/AII93vh3xpa638UfEmnaja6fKs1vpugtK8UjK2RueVVbH4e3I5oKufmp8Tvg/wCKfg/ren6Z4n09rC/u7SO8gibrsdQ65/A1+yv/AATN/aq8VftHeCdX03XtAt7G08Kw2thDqVsxxcNsOVIPAYKq9PUeterftM/sTfD39qW107/hJkvLC/02Iw2l9prqjovoQVIYV0H7MX7MPhb9lbwHL4Y8LyXF3HcXLXVzeXmPNmcgAZwAOAAB9KCT2CiiigApMjOO9LXPePvFkHgPwbrniO6jeS10qzlvZUj+84RScD8qAN3duY46etVp45ZCApxg5z61+Ul7/wAFqNe/tGf7J8P7U2e8+X5t0Q+3tnAqtN/wWs8VLIwj+HWmlezPevn9FrN7miP1tiOE+bil59cV+M3jb/gsV8U/EWmNDoPh/SPDspBBmDNM/wDwHNfVv/BLX4zfFH43+GfGmueO9VbVtNjvkgtJpY9jLLsDOo9gGX86diWj7uHT1paRelGOvNWSRhgzEg5FNkuEjbDHH41Q1zXNN8K6Peanq15DYadZxtNNcTttVFAySTXg9j/wUC/Z91TUvsUXxG0wzZwC0cir/wB9FayZdj6AtW3zMcEZ9q/Kz/gthrQXxR8NNN8zIhtLm6MRzjLOFU/mh/Kv0Am/a2+DVrbm4f4j6CsSjccXIJx9MZr8if8AgqF8evDHx2+OWkX3g/WYta0bS9IjtluIQwQy+a7MvzAf3hQM/Rn/AIJa/CeX4W/sn6PPO+648TXL6864xtEkcaIP++IkP419dA57Yr8vdI/4Ks+EfhX+zn4L8O+HtLutV8YWOiW1m++LZawSpEqkEnlsY5wMZz1ry74O/wDBRT9o/wCMnxn8NeGtK1XTZhql9GJLC30u32RwAjzDvI3cKCTzV2Qan7LL0paZDu8pN/38fNj1p9UZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUrIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANavL/2jvjppf7OvwzvvGmrWM+o2tq6obe1KiRtx7biB+teokVyXxS+Fvh74xeDb/wx4nslvtKvF2umcMp7Mp7GspJuI476nwtpv/BaH4bTXIW58I+JLaNudzJA2PxEpqzq3/BZ/wCFlqdtv4R8VXfGVkjjtwp/OYH9K6H/AIc8fBn7YZf7X8Uxwk5FtDfRqi+wzGT+tY3xV/4JS/CLw58Odd1Dw9ba1caxbWkkkJur3zCzAZycKB+lZyajq0aKx61+yT+354X/AGtPFer6Bo3h/VtGvdOtRdu2oCLa6FtuF2uxz+FfTOvaDY+JtNm0/U7eO8sZ12y28oyrj0NfjB/wSTkudG/ay1CwAdFOl3EE6k55Vxj+VftfWu+j2E3Z3Wh4z4g/Y3+C/ieQSaj8PNGlmAUeYsJQ4AwBwfQCup8LfAn4ceA7OOLRfBWh6dHCPldbGMuOc/eIJ/WuvvtatNMs7i7vJltbW3UvLNKQqoAM5JrB8J/FDwf8REdNB8Q6fq5wd0dtcK7DnHQGp0WiDXdnxF/wV41yz039n/SbOwtbcJeX4UyRxKNoXPGe1ZH/AARRsPL+FPj67EissmspEI8crthU9ffdXa/8FWPCdrdfs63swgZjaXUc0e3+EHg/rVT/AII2+G4dK/Zr1TVUfdNqetTO6+gRVQf+g1MdByWiPvhcgc0tJuo3Ct7oyFooopgFFIeKFbcM0ALRRRQAUUUUAFFFFABRRRQAUUUUAQtCrSb8fNT6dtpNtQ0yrir0paSlqyT4a/4Kx6fqt5+znqEkFotxZxXMRZ8couQSfzriP+CJ+uxzfBrx9o4IMtv4g+19edslvEo4+sZr6I/4KFXEdl+y34znliW4T7NsELcDJP3s+1fIP/BEZZI2+KEm4mKY2QEfYFfMyfx3fpWC3Zo/hR+qNLSUtbmZ5d+0T8C9E/aF+GuqeEtZjRGuYz9muygZreTswrC/ZD/Zpsf2WfhLB4Rtr3+1LpriS6ur0xhDI7HgYHYDA/CvbNvzZpcYoHfSwEVAbC3a6FyYIjcAYEuwb/z61YooEJS0UUAIeaAMUtFABRRRQBDcK7fcKg/7VEfmfx7fwpWlUSFc5P06VnXfijRdPLC61aytiv3hNcIuPzNY+6nqy9exzPxcQyeDdXVVd5HtHRAvckEV+Kv7DWmyx/t/eGrd1ZXg1a+LA9RiKTNftL4o+JXhCHRbqaXxNowVEZlEl7GwOBzwDmvxn+A/xN8LeBf+ChFp4nl1O1t/DrapdeZfXEgWJPMjZSc9gCeKSfv3Oi94ryP3YXpQzBVLHgAZNfOniz/goJ8BvCETmb4h6XfOv/LPT3M5PsCvH618/Wf/AAVgsvH3xp8P+CvAfhKbVbDUryO2N9dHYZFb7xVe2DkZPpWvMjn5Wz7B8dftHfDn4ZtGvijxbpuiySNtSK4mAf8AFeorv9L1a01rTbbULG4jurO5jWWGaJsq6EZBB9CK/ND/AIKr/shT+IbRPiz4Y06ea+ijWPWLZX3KI1UKrquOMAc1y/7G/wDwU70H4f8Awft/BPjqKW2v9Ht3istQUFhMuSUVh2IGB+FHMkVyqx93ftEftjfD79mN9Oi8ZXF1Hc34LQQW0BkdlBwW+ldn8Efjp4U/aA8FQ+KPCF615pkjtGfMQo6MpIIIPuK/GSHR/iL/AMFLf2imeOaRdHgby3uypNvYW44z/vMBnHqa/Z/4I/Bjw78Cfh/pvhTw5aJbWlpGBJIo+aaQ8s7e5OTVXuKSSR3y0m4buvtivIf2p/DHxC8UfCHU4fhfr02g+L4SsttLDt/eAdU+YHk9q/Mfwr/wUY/aC/Z08UponxW0ybXLWKXbOmqWwiuZPUpKAAR6YFK5CVz9l1O4UteUfs+ftKeCv2kfCa614R1FZnTAurGX5Z7dvRl/r3r1XcaYh1FJnimTTLDGzscAUgPFf2pv2iNI/Z1+H954h1VncrxbwqBiWTbxHn3POa/KY/tJ/tXftTa9c3fgW71610+2LeXDoebeKIZ6FxjceO9dF/wVQ+NV98R/jbpfgO1mc2WmmNZLRT8rTSEYJ99pAr9Uf2ZvhVpHwg+C3hfQNK09LBY7RJJlAy7SONzlj1JyTWEbt3RtJKKsflz8Hf8Agox8Yv2dfG0fhj4y22o65YJII7ldSXF9CCc7w/V+D0Pauy/4KlfF7wP8cvgv4C8T+EdWi1GNr1xjo6Dacqw7HNfb/wC2N+yZ4W/aP+HOqrPpkKeK7W3eXTdTjBSRZAvCsR94HGMGv5//ABJHqnh+9u/Dt8ZIfsFwyPbtkASL8pOPfFaEx2P0m/4Im6Dbyaz8QdZKn7THHDag84Cn5v5iv1jr8+/+CN3hG30v9n/VtfSHbc6rqUiySc/MIyVFfoEveqirCkfKnxh/4KI/D34D/Fj/AIQvxdZ6tbMyJIdQigDwoGAx6E+/pX01o/iKx8QaDa6xptwl3p93AtxBMh4dCMg/lXwT/wAFSv2PtW+LGi2PxC8H2n2vWdGt2ivbFMlp4Mk5UZ6jJ6c18r/sjf8ABQ3VfgT8O9f8D+K57y7jt4JF0gzfes3wcpzycMTwanbQdk7HuH/BQr9v/wAU+APEEXg7wHfR6Tfhd9zeqVkkizyBtYEdPavdP+CYvxo+JPxn+D99qPj62lu4YbpksPEEyLG18uTuG1QFwjZXIHavzL/ZV+D+sftoftNwS+JRdappMlw19rV5IGwYl6RFlxjPAGMV+9nhrwzpfg3QbLRdFsodO0yzjEUFtAuFRR/nr3oUQkzUXpS0i9KWnymYUUUUcoEEkW5iema87+Od34t0f4Z6/f8AgyO3bXLS2aWAXGSGIGTgV6VSMiupDAMCMEHvU8nmaRm4n43Wv/BYL4uaDILPU/DGgzSW58uXzS8chIOCTWv/AMPovG8kWU8EaOD/ALV038sV+l/ij9mX4U+NLqS61rwBoV9cSHLytaKrMfUlcVTsP2Tfg5plsLe2+HHh9IhnhrNWPJz1OTT5RXR+UvxE/wCCunxZ8XWb2uj2OkeHVI5kjQyuOOxP+FfXP/BKv4xfFX4zeHfGGq+OtVm1fRIbhIrC4uIwpEmCXCEAZXkfjX1nZ/s3/CzTxiD4feHUHXnTom/mK7fRPD+l+GbBbHSNOtdLslJK29nCsUYJ6naoAo5RXL4HfvS0UVoSFFFFACdzX5V/8FrstrHwyQbRm3vTn+L+H9K/VP8Air8hf+Czl5O/xl8B2zOwt00hmVc8AtMQx/EACoa6lR3ufpJ+ybbR2f7MvwuiiBCL4csevX/ULmvWK474OWkFh8KfCNtbRrFbxaVbJGiDCqojXAFdjVLYUtwooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+Dv8AgpF+3XN8BdNHgXwPfIvjy8Cm4nTlrCJgGU4P8TAgj2NeB/sef8EztR+LzwfEn40zXK2l/I10miuxE95kkiSZh0U5yAOSD2r9H/FH7Nfwy8Z/EKLxxrngzS9U8UxbNmpXMIeQbAAnXjgAAV6Q0S+SYl/drt2jZxjjtU2KufLmtft6fs4fAmRvBQ8VRWP9hgWf9n6bp88yQbRjYCqEEjoeeteYeLv+CyHwd0W+MGiaR4g8SRcYuIbcW6txzgSENweOnaszxZ/wRx8C+LvHWreIJ/HWvQW+oXL3LWccMRKsxyw8w5J5J7VwH7T37Dv7Pv7I3wG1bxBqNnrPiPX7kG00yS+v2GJm5yFQBQB7imPQT4nf8Fd/h54r0+NY/g5L4kmtzvj/ALeMJjhbscbG/Svon9gP9rzxT+1PZ+IJdS8C2PhjQ9L2R213pshMMjnrGAR1C46V+W37FP7H+oftb/EC9sZLybQ/DOmxrJe3kSluCeI1JPJPPWv3M+CfwS8L/ADwDY+EPCVrJa6ValmDSvveRmYszMfUkk0xPsd8vSlpFz39aWgkKKKKACiiigAooooAY3eojIVJGCcVMc54r5h/ak/b28Efss+JdP0PXbG+1XULqITmOw2ny1z/ABe+Oaze5cddD6ViYyyFlOVr5T/b0/Y48Q/tcWfhW00nxNDolppMksktvcRF1kdgMNweoxj8aqeC/wDgqZ8BPE1upudduNAl6mK+tiMfiK6o/wDBRz9nhevxGsf+/Mv/AMTSGdb+yb+zTpP7Lfwns/CdhIt7fMxnv9QCbTczHvj0AwB7Csr9pD9i34fftPa5oOreLILkX2k4jWS2lKedDu3GNx3Gc/nWfb/8FEv2dZ495+KGlxf7Lwz5/SOhf+Cin7ObMVHxS0vI/wCne5/+NUCPoHQdHs/Dui2OlWESwWVlClvBEv8AAigBR+Qq9mvmLUP+Ck37OmnxyMvxFtbxkGdlvaXBZvYZjA/WvNNS/wCCw3wMs7qSKC28TXqKcCWKwjCt9MyZrRbCsz7ozRmvgpv+CyXwXH3dE8WP9LKH/wCO1nXX/BZz4VRyMLfwj4qnj7M0UKH8t5pisz9Bs15j+0z8KZ/jh8CfGPgi0uEtrzVrPyoJZCQokVldc+2VFfIMP/Bab4VFgsvg7xYp/wCmaW7fzkFTXX/BZ34VR25ktvB3i6c9laGBM/j5hFAWZ2n/AATh/Yv8QfstaT4q1DxmLCTxLq86RxvZyeZst0HALe7EmvtOvzA1b/gt9pMN46aZ8Jry5thjZJea5HC545yghYDn3rHm/wCC4Vwsh2fCFAn+1r+f18igR+q9Ffkd4g/4LbeKri3zovw00uxY8CS+1GSdR+Coma+m/wDgnv8AtteNv2sbrxHbeJvC9jZW2lorLq+lLItuzsT+6KuThgMd6APtaiiigAqtqWm2usafc2N7BHdWdzG0U0MgyrowwVI9CDVmigD5n1T/AIJy/AHVNQmu38CQRPK24pDM6oPoM8VFH/wTd/Z/j/5kaFv96Zz/AFr6doqbDueJeFP2L/gr4NjUad8PNH3qSfNnh81/zavVfDvhTR/CGnmx0TTLXSbMsXMFnEI03HqcDvxWxRVAIucc0tFFAj5q/b0+BHjj9ob4Mp4V8C39vY30l8ktz9qnMSSQhSCuQPUg4r8+tL/4Iy/FS7VZL/xD4f0+QnmOJ3lA/HAr9mqKVirn5D2P/BFvxxIyC78eaNFH32WTM357ua+ZP2vP2R5/2UPHWh+HLnxNb67cahafbS8FuYjChk8vJGT3B6HtX9CdfjF/wVd1BPE37Yui6Pbv501tptjYPGvVZJJRIF/FZAfxpcoczPtv9nn/AIJtfBn4c+GLG8v9Cj8ZapdQJJJd60omT5hn5Yz8qjn07V9A+DfgD8OPh7q41Tw14I0PQ9RA2i6sbGOKQAjBAYDPSuw8OW32Pw/pkH/PO2jT8lFaNUK4gpaKKBBRRRQAUUUUAFMfd/CM0+igBse7aN3WnUUUAFFFFACUA5obkUijatRcB1FFFWAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5t+0B4hg8L/CvxFqNxdtZ+TZytGyn752dCK9JPUV598fLGLUPhB4rjltY7vGnTERyD/YPT3rCv8DLjuflh/wAEjpY9f/ag8X6i8RMp0+WdWA4XdL/9ev2PWvxP/wCCTfiq38MftUavZzyJaxX2m3EREhxysgYD8s1+0Gja9Za7bmeynS4QcHYQcH0pxkloxyu9TzL9qDw7c+J/gx4t020aRJJ9OlRDGcfOV4HHNfgX8IvHHif4QfGTRZtIvbjS9RtdSjtpoxIQrZkCsGHpX9EHxM1RtP8AA+tXZhx5Ns8ib8YLBSRn2r+deCe48XfHy2uAAbq88QI5VRxnzgePahF/Zsfsd/wUa8daLoP7NN3Dr7hrnWLRIbdEH/LXG7PPavzv/ZI/4KGan+y38N9T8K2+hDVllme4tZCwCozcndn39K+t/wDgrXfaddfAXwtbXW6PULe4jMSnqcxjNeB/sA/8E9fC/wC0x8Ob7xh4s1q6itftT2kFnYna6MvVmJ45pKMWN/Cdn4D/AOC1WvWMTJ4t8C2+o4+7Lp0/lt+IbivuP9jz9sfR/wBrrw5q2oadot3oV1pkwint7hw4ORlSGHtXjH/DnP4OeUE/tLW8/wB7zVr3n9mP9jrwh+yqusr4UvNQuE1QoZkvJNygqMAgVXL2MtD3lc7eaWkoz7VoQDfdNNjbtSn6U1V280XQElFJS0wCiiigAooooAKKKKACk5paQru60AC5xzS0iqFGBS0AFFFFAHgX7b2gx+KP2e/E+myyeWkls77sZPygnpXwX/wRZ1qaDx/8Q9GA/wBHNrFPnP8AEHZa/SP9pCOL/hTPiqaSETmKwlIVv901+Xf/AAR11h7b9ovxhp4iUpeaW8jPnGzZLwAP+BfpUaXubP4UfsiKWkWlqzEKSk3HnivAv2tP2hNa/Z28FjxHp3h+bxBEGw0UWcL7nHah6Fxg5uyPf6K+Sf2Z/wDgo18Pvj80Ol3cw8NeJGHzWV22EY5xhWPWvoH4jfFfQPhn4butY1fUrW1ghj8wCWQLv4yMVPMg5Hex2tFfmF4r/wCC0ltpGv3NnpXgJNUsoX2i6a88vePYYr6l/ZT/AG8fAv7UkZsrBZND8SRruk0m6cMxHqjcZp3QuVn0xRRRTJCiiigD5o/bk+G/xN+IXwruovhnrMthrEDiT7NbOYpJ0xyobPWvyhh/Yo/af8a6oY5vCPiWGaRv3l1ql+FjJ7nJbpX76YoxUcqvc39q+VRaPw8n/wCCTP7Q/kRTiPSJpSPnjOsAOPbPSvKfhj+xb4w8dftES/CTUZrTw9rVuhkuppXFwkagbgRt68EV/QTr10LPSbubcybImOV69K/HH9i7xhc6r/wUm1C4ndppLya+hLSHJwucfoKltp2CMbxbN7xh/wAEW/GWk6TNe6T480nVLiFC5t2s3hL454OSK+ef2LdLtPBH7anhHTPEkiobDU5LV2jYBfNUEJ/49X9AToJAVIypGCD0r8N/25PgNr37Mv7TX/Cd2ulyf8Ivd6nHqdlcwNlS4YO6E/wnORg09SYpM/ZL4y/ELwp8Ofh5q+reMLu3t9G8hkkWcjEoIxtAPXNfzffEK4stU8ba9qGixNHo017K9uyqQuwsSo/Kv2blh+Dn/BTfwnoVkPFuowXeixxz32j2DiJwT1DhlORnIyK9v079jH4RaX8PpPCEHg+xbTniaMzSxK0+SPvb8daFzC0W54Z/wSX8Q+CdY/Z6a38O6dHpviC0umj1hc5eR8ko5PcFSMelfca1+Imtr4m/4Jj/ALW0MVjfyXfg+6dZ5I+Slzav1BXI+dOgPtX7N/D/AMcaX8SPBuleJdFnFxpupQLcQuPQjOD7itBSOh7mvKv2iP2d/Cn7RfgO+8P+ItPgluXiYWd+yDzbWQjhlbr1xxXqnRq5Pxp8UvCnw9tZrjxHr1hpMcSGRhc3Cq2B6KTms3uJdz8KfhP8QPFH7Cv7VE9pNJMbbTr77BqUBBC3NuXwHx3+XkGv300TVoNe0ey1K1bdbXcKTxn1VgCP51+E/wDwUA+N3g39oD4+WOpeCLQ3Bj8u2lvIlx9rIYAcD8s1+3nwnt5Lf4ZeFopozFKmmwKyH+E7BxVrYcnc6r+GkmQSJgjOORmnUjAspAODjg0En4F3Fk/ir/goh9j8Rq1yJ/F22RScZRZPkH0wBX75W8axQRoowqqAB7V+E37U9vN8Av2/JNafcyW+q2uoh3XKuG2s+M+mTX7i+GfEFt4m8O6bqtpKJLa8gSaN1ORhgDWcfd3NJvm2NZq/Bz/gqV4e8N6D+1NqjeHYUhF1aQzXaxsSvnkfMcduMV+2Xxa+IFj8Mvh7rXiHUZhDFaW7spPGWwcY/Gv5yPi9441P4sfEDXvFN40lyJ5z++28Ko4UHHTin1Ej9nf+CTcKw/se6FtB+a/vGOfeZq+y1r8zv+CSv7U+m6n4bg+D95aPFqlr5tzaTxqAjx5yQffnrX6YrWnQUhk23y234KbfmDdMV/Pl+39Z+CbX9pbxGnglBFZ5V7pFctF55GX2ZJPXt65r9ef2+P2mov2bvgrf3VpME8R6sjWenKArFWIwXwQRgD1r81P2Ff2H7r9ri81zxl4ukeLw6jSxiQl1e7umBO4MpGArHnFZ9R7K59z/APBJvwr4O0f9m2HVfDsv2nV9RuGbVpXJDiVTjZtJ4UdBjr1r7cavxk/YR+Imv/spftdal8KtfmltdF1a8eykgmAx5wJ8mQZ5GR6Eda/Zv7y1V0TJdQXpS0i9KWqJCiiigAorxT4+ftffDf8AZvurK08Z6tJaXd2u+KCGFpGK+vArzC0/4Kmfs/XSbj4puIefuyWUgP8AKlcrlZ9dUV8q6f8A8FNv2fNQuPK/4TVbf0ee2kVfzIr03wl+1p8IfHFuJdI+IGiXCnjDXSo35GmKzPXaK811v9pH4YeHbczah460OBB63iE/kDXVeC/Heg/ETQIdb8NarbazpMzMqXVq4ZGKnDDPsRQB0FFIvSloEFFFFADT1r8iv+C008EnxS+H0UeBcrprhyOuDMSBX66nrX48f8Fko0l+P3hBd3zHQ1+X0bzzz9cVLfQqKP1U+ChY/CPwcWOW/sq3yT/1zFdrXJ/Ce3Fr8MfC0IOQmm24z/2zFdZTWwnuFFFFMQUUUUAFFFFABRRRQAUUUUAFFNPWvkX9tb9vaL9krxF4d0e38OL4ku9Rhe4nj+0+UYYwcDsck1Nx2PryiuD+BnxWtvjd8K/D/jS0s5dPg1W3Ewt5jlkPcZ7iu8qhBRRRQAUUUUAFFFFABRRRQAUUUUANbrWf4g12y8MaJfatqM3kWFlC088mCdqKMk4rSqC9s4NRs57S5jWa3nRopI26MpGCD+BoA+PfC/8AwVa+A/iLxRPo9xqmpaMiyeXFf39mVgl5xnKkkfiK+Jv22Pi1c/twftUeFPh38PNRj1fw/bstnY3EIIRpJFDXE3PZVBHP92vob42f8EcfDHirUNQ1TwB4ruvDd1dStKbG/XzrYEnOAR8wGfrXxZ8Wv2Lfjn+xnqNl44hjjmttOkEkfiLw45YWzA8GRSAQD7jHvQVc/af4F/A7wz8AfAOneGvDWn29pHDCi3NykYWS6kCgGSRurHjv0r0aPO0Z5PTpX4z/AA//AOCxfxX0ebSIfEui6DrthG6i7khgkju3iGAzcNtB79K/XT4a+PtP+KHgTRPFelLKmn6rbJdRLOhRwGGcEGgk6aiiigAooooAKKKKACiiigBP4q+Nf2uf+Cb3h39pzxa3iuHXrnQfEEiJHNJjzImVFCr8vY4FfZdFTyjTsflTa/8ABE26eUtd/ElCuePLsjyO3etyH/gijo3ljzfiHe7+/l2q4/Wv06oo5R8zPy01b/giejSZ034lSonHy3FkCffkEVCv/BE2Vsb/AImsPXbYD/4qv1Roo5Q5j819B/4Ir+FYLdBq/wAQ9aupcnd9lhjjXGeMZBNdnpf/AARx+Dlrs+3ax4l1LHVXu0QH/vlRX3mxC/MTgAZr4h/az/4KfeE/gLq8nhrwpZw+MfE0Y/f+XcD7LbkjIBdScsO69uhqhXZeH/BJT4BhQv8AZmrH3/tB81Ys/wDgk78ALVstompXHtJqEn9DXwZY/wDBTr9pjx5rc0Xhm7WeSRt0em6T4eivGjB6AfIWNa91/wAFGv2pvhTq+n33jmwuo7CZxustb8NnT/OUdQhMa849CaAuz7Q1n/gkb8AtWnMkVjremjAGy01Ehen+0DUWm/8ABIf4A2aqZbTXr7vum1Ruf++VAr2H9kr9rbwz+1h4Ik1fSojpus2Mnk3+kzMGlt27OPVWHQ/hXvK9O/rzQF2fJ+nf8Et/2cLJV83wLLeuOr3Gq3WT+CyKP0rpbP8A4J3/ALOljbrFH8LdKdR/FNNcSN/300hNfRlFAj5ruv8AgnD+zjdzmV/hfYK3/TO8ukH/AHyJQP0r2L4XfB3wZ8FfD7aJ4J8PWvh7TGkMrQWu5tzHqSzEsfxNdlRQAUUUUAFfKX/BQr9pDxx+zf8ADHTdX8E6St5c3Vz5U99NA0sVquOCwHqa+rapavoun+ILGSy1Oxt9Qs5Bh7e6iWRG+qkYoA/FCP8A4Ky/H26xFA2izyAYJh0uRifw3USf8FLP2m72TdFCAG6CHRJMfyr9idD+C/gHw3I0ml+DNCsZGOS8OnxA/ntrqIdIsbdQsVlbxqOipEoH8qAPw78Qf8FDf2o77TpoXuLrTkI+aaLSGjYD6kV91/8ABLHxd8V/iH8Nde8TfEDWbrVdIu7wx6Y18v7wlCVkIP8Ad3AjHtX2vc6Hp16hS40+1nQ9VkhVgfzFO0vSLHQ7MWunWcFjaqxYQ20YjQEnJOAMcmgC3RRRQAUUUUANZiq5Aya/Gz9pbSIfil/wVe0/TLJ1uov7R02KYL/C8EEZkXnuuw/lX7K1+Htx4t0vwH/wVS1nWdcv49N0u18aXhlu7gkRxqwZQSewyRQB+38aCGNEHRQAPwpl1eQWNvJcXM8dvbxjc8srBVUepJ4ArzDxd+1N8JPBOhPrGq/EPw+tkozm1vo7h246BIyzZ/CvzN/aK/am+IP7fXxGtPhv8FbPVrbwzHlZ3in8lbsEgGWc5AVFGcKTk+mam5SR+vGi6/pniSyF5pOo2mqWhYqLiynWaPI4I3KSMir9eNfstfs56N+zZ8L9M8O6bFu1B4kfU7rzGfz7jHzMMngZ9K9lqiQooprMEUljgVHMA6imrIsgypyKdRzAFFJS1YBRRRQAUUUUAFFNK570o4pWAWmswXANOpjRhjk1N7APoooqwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAa33hXnHx81j+x/hj4hd+IpbCaMsOxKGvSCORXlv7TcKzfAvxiWwPL0+VgfQ4rCt8DNabXMrn862m+JNX8KeNbi+0O9ltdQE8kcc0JwSGYjFfvh+w74B134e/APSJPE2q/wBqarqK/bHkyx2q/KqcgHIBr8A9FvYtN8ZWd3dc28F8sknGflD5P6V+93gH9uH4Df8ACFaPC3xE0WzKWkatbXE4R0wo4INPlV0x8y5bHrvjuYah4R1+31OAJbfY5mXaeoCGvxf/AGC/g+nxV/bELxiNdM0W6lv3WUE5CudoGO+a/QT9pD9v74ON8MddsNB8Y2up6tcWskMAszvG5lIHNfnN+wB+0x4f/Zx+NF/r/iuW4j0XUoGhklhiMjbi2d2B2oFdWPrr/gsxZL/whvheZY2Xbc4z24GBXQ/8EX7ueT4N+L7eRyY4dX+Re3MYJxXl3/BQL9tb4QftB/CkeHvDl5dX2qxzCWKdrVkUD05Fec/8E5f20PDH7MfhnxTpnixpmt7udbmCOCPLEhcEVKLeqP2spNx9K/OzxH/wWc8BabMg03wZrWqRkAl/MSLB78GsS/8A+Czvhry1kt/CV8rn/l3d1J/766VfMjPlP0rknEbKCGwTjNIszGTaUIHrmvy3vP8AgtH5jA2fw9uAPSW7jxXGt/wWb8cQ30zN4P04wEny4zIcgds4NK77MXKu5+vkgZ1YL17URKyqFbk+vavyN0X/AILReL47h21XwPp81ufuraTMrD6k5FesfCL/AILA6X8QfiBovhvVPA02kR6ncJbLefbQyxsxxkjb0pjt5n6PUtMhcSRq6ncrDIPtT60MwooopgFFFFABRSbqTzBnFK6GLRkVGzfNjpTwvvUczb0EOopKWtACiko3DnmgDzf9oyYQfBTxex286fKBuOBnFflB/wAEj782n7WGrwmPcbjS7lSw/hxIDX1X/wAFRP2ptO8E/DGXwZo12JNd1I7JPLkGY0xzkda+UP8AglT8RPA3wn8beL/FHjbXbPRnNqsEE12+CcnLY+tZGtnZH7VrS14HY/t1/AzUIRJB8RNJKE4+aXFOuP25vghbSpG3xA0sljgFZMiruiOVnudzcCFSSM+gHrXxl44/4KGfBvVPH178MvEFhfTSPdHT55HjHlB87TX1h4T8c6B8RtBGr+GtXtdW09sqt1auHUMO31FfiZ/wUs+Hsfwr/ae/tOwwp1CKPUfMjwA0gPP54rOTvoaRSSv1Oy/bk/Yi/wCGe0T4peAtSmbQpbpZY40xm33cggjtmvAbP4gfFv8Aa+17RPAj6y+r3kmI4EkcRrtH976CvavjZ+2Nrf7TPgHwn8JfBGmXEtxLHHFdeYPmlkAAwvtmuF8S/sG/Hz4A+H7fx+umG2+xHzmfSrnfc2wHcgClHbUTlqfb/wAGv+CPvgDTfBKf8LCu77VvEVwmZPss5iitmI6Ljrj3r4g8YeGdQ/YN/bG0w2dw15pum3kUsUzsf3tq5G5WIxkhTj8K+2P2J/8Agp5pnja20/wX8ULlNN8RLiCDVWBWO47ASZ6N715p/wAFjPhrY2t94O8c20oljvhJbOI1ypGMqQw+tUVHzP1T8M+ILXxV4d03WbGQS2l9bpcROvQqwBFadfNf/BO3XTr37IfgOczyXDxW7QM0pyQysQR9BX0nnitEYvQWikFLTEFFQ3V0lnC80rrHEoyWbgCsrRfGmheI7ie30zV7G/uITiWG3nV3T6qDkVLkk7MrlbV7Ffx85j8K6mynDrbuy+mdp61+L37CEkkn/BRCF3VS7XN8XIHAyD0r9lfinerZeBdWkchV+zuC3p8pr8gv+Cbeirrn7c2rXwLstit3MGBHdsc8VL3OmP8ADS9T9qc1heN/Afh/4j+H7jRPEuk2us6VcDEltdIGU+49D7it4L3pafKzki2eM/A/9kn4b/s86xq2qeDNIksr3U+JpJZN+1c5CLwMCvZKdto21Y3qfBf/AAVM/ZT1v45eEdI8VeFbFtQ1zQ1aKS1iHzywsc8DuQa9U/4Jw+F/Fvgv9lzQdI8Y6fPpmo29xcCO1uRiRYjISmfwr6f20uKB30sI1fNf7Tv7Bnw+/agvDqmtS6hpXiARCJNQspuMDpujPDY/CvpXbRtqLMLnxN+z1/wSz+H/AMFPGK+JNU1a88Y39uR9jF5CkUUeO7IMhuehr7XjjWFAijCjgDsB6U6lqyQooooA/Pn/AIKlfsi618YdDsvG3hGw+36xpURS5toh+8ki65A7kV8SfA//AIKIfGD9mjQ/+EQmt7bU7C13LFZa3AyzQMT/AHhhiPav3gZQwIIyD1ridc+CHw/8Tai1/qvg7Rr+9brPPZozH8cVNi+Y/E74jftofHr9rd28GxxR3lrqDCNNJ0jTh39ZMbgPqa/QX9lv/gnH4T8G/AS60Lx/pUeoeI9dQvfyLKwMII+RVweCoxnHU19eeG/hj4S8H3LXGieG9M0qdhgyWtsiNj6gV020UuUOY+CP2TP+Cbup/s1/tAXHjQ+Jba/0KK2lgs7VIyJsOQfnJ44Ar72Wl2iirE3c/MX/AIKu/BTx78VPip8P4vDWi6lrWlT25t5DbQ74reYyYLHHT5cda+8P2d/g1pXwE+EOgeD9HjZIbSLfM0hyzzP80jH/AIETXpLIrHJGaXFRyg3dWPxQ/wCCpng3xF8N/wBrCPxrbboINUit7vTrtVAxNCihvbOVr9Zv2bviI3xX+BfgvxVLJ5txqWmxSzNtC5k24bgcda5P9rj9k3Qf2sfAVvoOqX02kX9jN59lqUC72iYjDAqSNwIrvfgj8K7P4J/Czw74KsLmS9ttItVtxcSgBpCOrY7UcoN6WO4XpS0UVZIUUUUAeEftNfsc+AP2pNNiXxNbS22sWybLXVrZ28yBe4C7tpz7ivkmb/giX4UeZmi+JurQxnon9mRsR+PmD+VfpZgGjaPSpsPmZ+YGrf8ABEvSxCy6b8Srp5Oqm6sAFz7gMa8+1D/gir4+hvnNh490JoONrtHMjfkFr9gMCjaKY+Zn413/APwRr+KqyLEnijQr2LIzNvkBH4EV+kP7Gn7P97+zT8C9K8EalfQ6lf209xPJcwAhT5khcDn0zivc9oo2imK7BelLRRQIKKKKAGN1r8Uf+CrGrSeJP2w7DSY5BJ9ls7S1Cg52l2Bx+Zr9r261/Pv+3BqeqW/7bfjq5/eXN3a65mzikBbcEZfLQD09KmxcT97PAdk2m+CdBtX+9DYwofwQVvVxnwb13VPE3wr8LanrWnvpeqXOnwyXFpIMGNtoyMdq7OqICiiigAooooAKKKKACiiigAooooA8I/as/az8Kfst+D5NQ1mb7RrNxG39n6an35n7Z9Bmvyj+Hvwd+LH/AAUY+Mk/inWvPttBknDXGoTljBBFniKIHgHHGBX66fGj9k/4Z/tA6zpmqeONBOr3enLtgP2h0UDOcEA816L4Q8F6F4B0K30bw7pNpo+mW67Y7aziEaj3OOp9zzU2KuR+A/B9j4A8G6P4d02NY7LTbZLaJVUKMKMZwK3qKKokKKKKACiiigAooooAKKKKACiiigAooooAKYwJ74/Cn0UAfNXx2/YD+F3x48Taf4lvLB9B8RWtzHO9/paiM3GxgQsing9OvWvo+ztVsrSC3T7kKLGufQDFTUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZ+v69Y+F9EvtX1O4S00+yhaeeaQgKiKMk5NAHzr/wUB/aNi/Z7+A+qz2V9Hb+JtUQ2unxBx5gzw0gXOcAd6/P/wDYS/4J63f7QrQfEr4kTSJ4XuLl5UsHBWXUGDHLMTghM9x1FeN/tNfHub9r/wDaaiku9QFl4TS+S0sFuZAkUFqGAaQ57sASa/af4F/ET4b6z4b0/wAL+BfE+j6umjWsdubawuUdlVVAztBzjPfFBVjtfCHw98NeA9KttO8P6JY6VZ26CONLaFVwo98ZNc78dvgj4e+Pvw51Twp4gtYZY7qJlguXjDPbSY+WRM9CDXoa9KWgk+bf2I/2PbT9kXwTq2mHUY9Z1fU7szT36RlN0Y4jTB9B+tfSVFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfnF+27/wS+1j43fEnU/H/gHV9Ps9S1La91pWoKY43kCgNIHAPLHnpX6O0UAfjd8O/wDgjf8AE7Vr+3j8Z6/oujaUr/vRp8rXE7LnnBKAV+kn7NP7I/gb9lvQ7mz8KwTz3t5tN1qN64eaXHQZ6AD0Fe20UrDuIKWiipvYQmaZIqSqUbmklUtnBxVb7VDb+Y0sqosal3djhUUdST0A+tQ2VYsxqsXyrwtP4bnNcj4f+LXgjxZI0ejeLtE1SVZDEY7TUIpG3g4K4DZzmuswCOKYWI+FnJ5JxU0biRcj9aqM3lvnOWzjmrSuNo7U+YbjZCs4RcnpVeO6FxMVjyQOvGKnBJ4xlfWlVQvQYp8zIHUUUUcwCUZFRyBmbg4FCLtXBO6jmKsSZoyKZuxTd3zYqQsTUU1fu06tFsSFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8++P3g/UPH3wb8XaBpTbdRvtPlit8nGXxwPxr0GmlaTipaMa0Z+Dfwn/4Jh/Gb4qa9qVjeWVv4OS0G43euiRY5snomxWzXvPh3/gij4sVlGs/EPRYYu4sbWSU/m6LX62LwKWpswe5+Yo/4Il6VIgMnxRu0fuE0iMj894qwv8AwRF8M9T8U9V6c40iL/45X6ZUU7CPzy0X/gi/8NbG0WPUPGGvahOCSZY0SEEdhtBNdNbf8EfvgrHt8671+Yjri8C5/SvueijlRXMz4tt/+CSfwHhVfMttenYHkvqbc+3Sux8O/wDBNX9n/wAOKNnglL9v79/O0pNfUNFHKg5meC2/7CXwEgXH/CsNCc+rwkn+dWZP2IfgU9u0A+GWgpG3922wfzr3GiqJPkjXv+CXH7PuualJd/8ACLXFjvAHk2V9JFEPcKDWdoP/AASt+Cfhnxpp3iLTbbVYZLCVJ4rWS8aSLcvOTnnrX2PtpNtQ0yrjYYxDCkajCqNqj2HSpKSlqyQooooAKKKKAGt1qKeBJ1AYZxyOcVK3WkrN7lkUMm9SD1XipxUQWPzD2c9alpxRItFFFWI83/aG8ReLPCnwi8Rat4Jsv7Q8SWsBe2t9m4se+B3NfkFr/wC39+0/eW91o01vNbXTEpKU0mRJl9sg9q/cWqraVZNMZTZ25lJyXMS7vzxUcpalY/Ff9nH9gH4l/tba9/wmPxH1K+0XQZJSslzeKftc+04KojdB719reIP+CSfwY1HwcujWDatp16p3f2q04mlJ9wQBivtvGOnAoYZ74pqIuZn5HeKf+CKvixdal/4R3x5o82lYHltqltIs3vkJkfrWTcf8EVfiNsBXxx4bY/3VgmH6kV+w+Pejn1pNMOZngH7Gv7KsX7Kfwzk8ONrk2u3d1N9ouJXG2NGIxtRfT3rl/wBsb9hHw3+1BobXMEx0jxZbRkWd91T/AHWHpX1RRVWFdnxP+xj/AME4NA/Z4mt/EfiiSPXvG8LMVuoWYW8Sk/LtU98d6+0L6xg1KyntLmJZbedDHJGwyGUjBFT0tFkI/Jf9vn/gm3c+Hbj/AITn4S6PLcWe4y6hptu5adG67489R7V8ReKP2i/ibefD8fDbxDqc13otrIWSz1S3DTQNnkBmG4V/SIyhgQRkHqK+Qv2zv+Ce/hz9pjTY7/Q2tfDHiyFs/bUgGycekgHP40rDuzlP+CRPxDi8Vfs1tojyL9u0S/ljeNABhHO5SRX3Q3Svj/8A4J9fsZ+Iv2R9P8WW+v6zZ6s2rTRvF9jVgqhRjnNfYFUJ6gvSlpKWgCrqFjDqVnNbXEaywyrtZG6EGvyv/aw/Y1+K/wAEPidL8TvgZJq91aXT+bc2GlSlriBhyxK4+ZD6YJFfqztpNtTyxbuzRVJRXKj8UfGf/BUD4oal8O73wP418LQJrBRoZNQy9lcDPA3wkNyPXjPoK6D/AII22E9/8ePFmqvFJIg00q0x5AZnzgn1r9VvHfwM+H/xOfzPFfg7Rtem6edeWaPLjsN+N361H8K/gP4D+CUN9D4I8N2nh+G9fzJktQfmP1JJx7UmtdDT2i5bHeilpKWrOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnFNVw3APNJIu4Y3YNRxgQxksfm/vVPMOxPQTjk1TS7VpOH49KladGO0vz6U7j5WSBg3Ir54+Of7C/w1+O3i608Vaja3GkeJbeaOc6npj+XJKyEY3+vTrX0ImBwvSphS5g2INPtRY2NvbK7SLDGsYaQ5Y4GMk+tWKQUtUSFFNJpu/5iO9TzDsLtO7O7j0p9eC/tCftpfDX9mXVdN03xrfXkV7fqZI4bK2MxVAfvNyMCuw+FP7RXw5+NVjDceD/ABbpurSSIH+xrOq3KZ/vRE7h+VHMOx6Qc9iKFBA5OTTPJBk8zc2fTPFS1RIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Zf8FXPidcfD/wDZbu7CzuDb3Wv3kdhlTgmP7zgfhivs2vzZ/wCC1WiatefDrwFqVvC02kWd/MLnbnCMyAKTQB4H+xb/AME0LD9pL4RL441/xFeaPBdzywWVvBF82EO3ec9QT0xXmfxz/Z1+J3/BPv4k6Rr+lanM9gZQ9hrVnuVJSpz5Uo6Zx2PWvs/9hf8A4KCfCDwT8BPDvgzxhrB8J6xolv5Lie2kaKcZJDKUB5PuK8F/b8/bUt/2sdS0j4a/DjS5tW0JbxJFumhInvLj7qiNeoUE9fzoLVz9RP2XfirffGv4D+EfGWpwJb6hqdoJJ1j+7vHBI9jXqteTfso/DvU/hT+zv4E8K6yqx6rpumxxXManIV+SV/DNes0EhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEzRuAqGSHdJu3H6UySTYpGCMVjKWpSjcbeMxAKE+/pXF/Fn4dt8V/hn4g8KwazdaHNqls0S31lJtkQkY5/wBn19q0/HHi5PBPgrXfEElsZ49Ns5Lsop5k2qSBX52fsRft6fFX4+ftQP4f167s5fC99FPLHp8duiG2VT8uHwCT+Jo31LtbQ+ZPiB/wTR/aG+Fes6jfaLoZ1zTrBfOTW9C1OFHcDnPlNIspYd8L+dd1+xT+398S/CPxS0TwP431S88Q6PeXS2DLqCs91bOTgDoSQDX6Gftk/tm+Fv2XfBdwJbqG/wDF93GUsdIjcNJkj77j+FR79a/M/wD4J9+JfAWoftF6z8S/if4p0fQXt2ku7eHUpFjV5pDkkZ44pgftx9l87DnLZ5GeKtIiqAuK4H4X/H74e/Gia9i8EeK9P8SPZKGuPsMu/wAsE4BP413/APFntQQ22KOKWiir5SQoopjMc8VACOwzg01SFGM0yZgrZY9aXYfX9aDRLQf97ocUqrnnNQNlWwc4qxHgDFAPRDhS0i9KWtFsZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQHNLQAUUUmegoAWikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAYxGaar7u1J5Kicy/xEYpWyMkDJ9Kza6ljlRd27HPrT6amSoyMGnVSasSFFITimtKq/eIFO6AfRUH2kOgaPD59DUoY45HNAWHUUlLTEFFNZsHFLu4pXAWikBpaYBRSE0m6gB1FIKWgBKKWigAooooAKKKKACiiigAooooAKKKKACik5o5oAWik5paACikJppY0APopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA055waYtzE0vleahlxkx7hu/Ksrxpfy6X4T1i8hkMUtvaSzI46qVQkH9K/Dn9nL9sLxPoX7XFp4r8aeMr5tIubqSC9kupS0ZhLEAbPugfQVNyrH7wUxpAvWuO+Hnxi8G/FbS01Dwr4isdYtmJA+zzAsCOoK9a6PU5MxNsLB164ockgjFydh1xdM0hVMhf71QSbpo22vuWvk39t39syP8AZt8C+RpZS58S6mrR2cbHJjPdzXzF/wAE5v2ifjp8avj1PFrPiO61nwlFE8l/b3WDDDnpswOuazvzanTy8uh+pUNsIwGao7jE0n7jO/1HSppGZuFXKdt1Nt5PIkxgKD2Fc3tLuxor7k9usscIaRvmz0FaEL+ZGCRivI/j5+0J4b/Zz8Hy+JPE/nNaL8sUMIBaVj2FYH7L/wC2Z4C/amS/i8MPcWuo2Sh5rG8ADhT/ABD1FdMdTmme/ClrmviF40sfh74P1nxHqTMmn6XbNczbepCjOBXwn+zp/wAFVI/i98dY/B2r+HxpujarN5Gk3UZJkzn5d/1rS9jOx99+IPFGj+FrdbjWNTtNLhZtqyXcyxgn0GTV+3niuoUngkSWKRQyyIQQwPQg18Cf8FePhf4m8YfC7w5r/h+2u7+30e7Y3trZhi2xhw5A6gGvPP8AgnT/AMFC9Os9G0v4XfEi+NrdQnytM1m6ckMpOFilYngjpmpGfY/7U37G/gv9qjR7ePXDNpWs2oIttYsVXzkB/hOfvL7Zr8xf2iv+CbPxF/ZdsP8AhNfB3iiTWdOsf3jXtgrWl3a46NlT+oNfsZ40+KXhH4daRHqfiTxFp+j2Mo3RTXM6qJBjPy/3vwr8rP27P+CljfFGxu/h/wDCt7iDRLgmHUNWVGEt0OnlxgHhT+tIZ9Bf8E2/279S+O8UXw88XWk9x4o0608xNXDGT7TEvGZCSTv9SetfftfFP/BMr9k+x+CHwpt/GGpwibxb4khWZ5JI03W0B5WNTyQT1PNfa1aEPcKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQmhhmgBaKRRiloAKKKKACiiigAoopKnmAWkpitimsy5560uYdiWlqHIyuKcCOfrUe0AkoplFaxfMFh9FItLTEFFFFABXK/Er4Y+G/i94TuvDfirTY9V0i5x5kEnqOhB7GuqooA/Ovxh/wRl8A6z4gmu9F8W6voenSNuFiqrKE9QGYZxXvX7Nf7APwy/Zrul1TTLKTW/EYzt1bUsPJGD2QdF+oGa+mqKB3Yi0ZpGprLu7kVPMFhxkVTgsAfrSeanTcM/Wqk1i0hJVzmoLfT5luDIz/AC46UuYvlXc1Nw9aAwboQaqXKtHHlTT7ddowTk9TVk2LGaM18C/8FEv2+9c/Z112z8D+B4rU+Jbi3W6uLu4AkFvG2dvy56nB615n+zz/AMFjIZlttK+LeiC3kJC/23pA3J6AyRZyPqD+FArM/UeisHwR440L4i+G7TXvDmp2+raVdLviubaQOp46cdD7VvUCCiiigAooooAKKKKACiiikAlGRTSwPQ0ZqeZDHZozTc0UcwDtwpPMX1phYHvULSKpwTg1m6juUohcXBWTA6VQmvD5m3eFLcBT97P0qeVt0oIP8PykjvX55/tq/wDBTLXPgD8T9S8DeEPDVrJqVisfnanqaswJYZwq8ZHTmsI+/J3NfhR9nftEyJZ/AHx29w6xKNIuMsf901+XX/BHj4fS+Ivjlrnil42e00SxaNZAQAJJDjGM5PHtXAfE7/gqR8Xfil4H1PwtqcPh+2sdTgMU0trblX2nryWNeT/s6/Fv45eC4dS0T4PT67LJeENcQ6FphupPrwjEV02toRufb37Tf/BLb4pfF748a94q0nxTol3pGrTeYlxq88qz2q4+5tCEEL2wazbX/gibrLaMTcfE3T/7SAOIY9NZos9sylt3/jtfOPiQ/to+Jrx73UNN+Ms0rKFaRdOv7dMD/YRAPxr9Of8AgnD8M/iT4E+D99qHxP1PXrjXtXu/Nj0/XZ2kktYVXCkbjuUtkkg4Ix0q7EXZj/sAfsKaz+yLP4o1DxDrWnazqmrqtvH/AGYZDEkKnIJLqp3HuMfjX2Yq7VAp1FHKSFFFFK9gEzTWmVVzmiQ4BJ9KqSLls54qGy4x5hfNG8uwBpjTIzHa1O/drHyM0kEcbln2nHpSNNELG/nLtVunWrCjy8ZOfeviT9rD/gpd4f8A2Z/iYPBtl4ek8RahAiPfMsvlrFu5AB7nFfVPwh+J1r8Xvh/oniuxtJrSz1S2W4SOcYZc9qol6nbilpq9KdWi2MgopGzjjrTY9235+vtTAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACCgnFNjLFfm605huFAC01lDMD6UtGaAADbS01WDZwc84p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANao5CQwO7AHbHWnshZs7sD0pdoPXmplqhkBuJVuAiw7oz/wAtN39MVZpBxS1PKxDWprKG6gGnNUU0jRrlV3Gk9NykOjUR5UIqoOmKcX7KQW9K86+MXxIT4d+FL7VzFNILaMuwj7ACvy3+KX/BXL4gTahNbeCdJ06wELFDe3imWWTB6eXxge+aSnd2Rq6TSUn1P2Po53e1flL+zn/wWB1OTWLDRfiro9ssE0mx9csmZNuSAMxYwAPXNfqN4f16w8VaRZ6vpV7HeabdxrLDNEcq6kZBzWt+5jY02xmsbX/FWn+GbWS71O5jtLGNSzzyNhUA7k1rSbN3PXFecfFaLwrrfhHVNK8Sz29vp11GY5xdSbEK+hPasJycdUXCKbOn8L/Ejwv4040LX9P1Vtu7ba3CucfQGuhklEaM7YCqM1+Lnxi/Z98Y/sw+Jx8UPg1qV5c+GY387ZCxdUXPK4HVPeu+0X/gsHqGveD7vTPEvhuLTtYWBliurKRikrBcDeDyDn0pqTtcpwsfY3xa/wCCg3w0+DV9La65fC4uY2Km1szulHPcV0v7NX7aHgD9qD7dF4amms9QtW+axvgFkZf7w9RX5Kfsw/sjeJv24PHmu6/qdzc6Poe5ppNQC7gXJ4Rd3UVneNPBviH9gb9rPTNK07WGu2tZbe4W43FVuIJGxtkA9MGtumpFl0P35WlqhoOpJrWiWGoRlSl1BHOCpyPmUHj86v0yAooopXQBRRRRdAFFITSbqYDqKjEnzEHGRTt1K6HYdRSA1HJIV4XGaXMgFeZY2wc5+lORxIuR0qKNpG5bA+lSltq+tHMgFZgOpxWH4u8baL4F0eTVNd1GHTbCM4aedgFrUmX7RtxuXmvgv/grla3Fn+z+t3De3UY+3QxGJZMIytnORiobZpGKZ9UeAf2nPhp8UfFD+H/C/iqz1fVkQyG3gbJ2jqa9SQnvX5H/APBF74f6drHjTxl4tuEk/tDS4I7W3KthMSZ3ZGOTx61+uO3bWl9NRSSVrA1R87uvy0rkdCcVHgIu7fk0yUhk1y0cqqFyvfipI7mOViqsNw7d6QyBuVXdSW9rGGaTy9rk9TSukVZW1LK0tN+70oyaZmOopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAU0tjtQ7beScUtK+tgOL+M94bP4T+L5w2wppdwQf+2Zr+f79mf4AX37TPxig8HWd6th50cs0l0ybhGq5OSK/dv9q3W4PDn7Pfj3UJ22rHpM6g57lSBX5yf8EV/CJ1D4ieO/EkiBlsrOO2RmHIaRs8fgDUPc02R8//ABW/Zy+Nf7EPjCLVLGbUIdNt5M2+uaUWMMg/2l7H1zX098Ef+Cuenw6DFa/EzSruXV41Mf27T/8AVyqMbd6n+Lrmv1J1jRNP8Q6fNY6nZQX1nKCrw3EYdWH0Nfi7/wAFWPhD8N/hR8QPD9r4I0mDRdQvYGnvba1YiIDJw20k4JOfypOKkHPbY8m8Zaj4p/bv/aeNjoSySRahN5NkkmSltbg8sfTiv2p/Zl/Zv8Pfs1/DOx8N6PbxG82772+C4e4lIG4k+melfiz+wn+0hY/st/FeHxBr2jPc6TqEZtpbsxnfEh/ijJ61+i37ZH7dmt+CfhP4e8U/CVrfVbLWzt+3tH5nkccgqOh+tL4dAu2fcX2M7WJOWzWdN5FnL5813GkQ42ysFHvya/D1/wBsT9q/4myKuia74lZ2+QLo1kyq34hcZ5qn4k+F37XfxWto5PEGn+NNXReEF5MVAJ74yKhUtbj52tD7h/4LC6pp8v7P+iJC8VxJJqS+XJGwbC45wRXg/wDwRd8M3V98WPF2ug/6NZ2Ahf3Lniqn7ZHw01H4PfsP/DXQ/FE11J4nuLzzZIrqTe8XGSmfYV63/wAET/DNxb+EPiFr0iAW9zdwWsTf7qksP1FbKNiXK6PrT9vXXk8N/sn/ABBu36GwaIfVjivyO/4Jn+HIvEH7XPg+OeCOdLES3LLIoIyFyp+or75/4K8fGaz8J/A2LwPFJu1TxDMuY1PIiU5JNfOv/BF/4fwa58U/F/i6cLJJpNklvCGGSGkPUenANOwk7H693NvFd28kM0SzRSKVaNxlWB4INflF/wAFBf8AgnFb+EbPWvin8Nljs9OhBu9S0RR8sXdpIvQZ5x2r9YzxWb4m0Gz8T+H9R0m/tobyzvYHglguEDo6sCMMDwRS5QUj8SP2ffg74w/4KEeGo/D2pfEiGxu/BsASyt9QiedpYm6ZO7+Hp3xXY+I/+CMPxX09ZJNI8W+GdXMY+SN3mgkb80Kj8683/Z8vtW/Zu/4KBW+hW9xPBDHrz6Zc28DlElhdvlVgOCuCOPav3ho5R8x+Mn7Pv/BOv9o3wH8bfD17PH/wjWn2V2k93q9nrHyvEDkoAjZbI7Y71+zUalY1UtuIGC3r706irICiiigAooooAKKaxqJrqOOQIzgMe1TzDsyeimqwYZBzTqOYQUUUVQBRRRQAUUUUAFFNfdj5aWp5gKeoXq2qnd0xVXS9QF580ZymcVfurZLpdriiKFIQFQYAqeVvW5tFxUbWJl6U6mUVoYj6KRaWgAoooqeYApDSNTGUZDelQMjaTa2KNxbmmpbr8x7sc0x5WhPB4rJyL9B23bIW74qJZC8m2nLctIoJHGcV5L+1F+0Vpn7Mfw3bxhqek3Gq2yzpAIrc4OW460kuZlN2R6788bhR0qwpJHPWvnr9kH9sPQf2ttH1260fSLzRptGmSKWG6IbIcEqQR9DX0Csm12G3GWrXl5dbkbk60tNU0vWtE7kC0UgpaoAooooAKKKKAGtXxX/wUX/bYvf2a/D9h4e8JS27eMtWUlWbDNax9A+31J6fSvtC6mW2gkmc4SNS7H2Aya/GvwD4af8Ab4/4KDa5fazP53hfRbp5ngLDm2gbZGij0Zu/TmpsWjzaH4t/to6iw1mxT4l3EFwPPW4tdEumhZTzlSIsEY7jitX4X/8ABT747/CnxQU8W6i/im0hcx3eka3CIpo8EZAbaGDe1fuJb29vptnHBCiW9rAgRUUBVRQOB7ACvxP/AOCiPjD4M/Fb9pHT7fwpczWF3HKNP8Qa7aQpJaNhiMxoD87KSdzDr+FFhbn6qfs3ftSeCf2oPBser+HL6OPUE+S90eeRVurZwBkmPO7Zzw2MGu9+I3j/AEX4V+CdV8T6/fQ6fpenQNLJNcSKikgcLliBkngCvxh8ffs0/Gf9grxFpfxC+Hurz+IPDU0Uc8WsabbvsdGG7ZcQjOFxj5icHNcx+1B/wUD8b/tUeBtF8JajplrocEUqtdmxlbZeP0UkE9M9ulMdit4R0XW/28/2zPMvILq/03UL/wA66ba3+jWCHhSw+6uOh96+vv2wP+CUvh+HwjdeJfhBbz2ep2MW+bQ3dpVuUA52E87vavo7/gn9+yloP7PHwj0/U1jW78V69bpdX2oOPmVWAKwr/sj9c19QakvmafdKRkNEw/Q0wvqfjV/wSp+P+q/Dr42p8Otb1CS30LWDJbxWVzJ8sN4DwoB6EkYx7V+0FfhP+yL8OZfGv/BQaO0hYwxaXrt3qD4HQRSMa/digl7hRRRQIKKKKACkpahkYt9w5pN2Q0rhLJt4XlvSo1nKnMg2L6mo/wB4rbjgDpzUrL54AI461hvqVyibd7fK1PVSoweaXaEXijce/FLlGLigsFXk4pNxHbNMfMi8ClzWAbvXrmmGWP61G7CPhjg+lNhjMmDjK5qdDVJW1HNB50oIZlXrwOPcVyPiz4D/AA7+IGoLqHifwRoOvX4AX7TqGnxTSkDoCzAk4o+J/wAcPAfwW00X3jXxRY6BAR8q3DkyN7hFBY/gK850P9v79n/xAq/ZfiXpiFuguYZ4M+/zxiqhHW5m3c+ZP+CrXhX4dfCn9n/S7HQvBfh3SNX1PUUjt5LPSo4nVVBZiGRRjgd69m/4JkfBOD4U/s06NqVxZwxa34iLajPOEXzDG3+rTcCeABnHvXxj/wAFbP2hPBvxcvvBeheEtftPEFrpyy3dxPYOZI1dhhVLYxnrx2719KfB/wD4Kafs/eAfhN4O8P6h4lvlv9P0m2t7iO30q4kVJFjAZd2wZIIPTj3rZi6H3mtLkV8CfEz/AILFfCPw7pDt4PstW8Vamy/u0e1a1iU9ixfBI+gr5a8I/wDBYr4q6b4oub7XNL0XWdEmclNMjiMEkC54Af8AiNWtibM/aClryX9l/wCOk37RXwntPGc3hq88K/aJ5IUsr45ZlULiRTgZVs8fSvWqZIUUU0rnvSsAyZdyketQvGVAHXip2XtVe7uDGpCjJxWT3Li3cgkm8n72NtWLSQTZKjjsapWsLXTF5l+UcVbuGFrpl08IwUjZh9QDQXJn87/7cU0lx+1l8Si0nmY1ZgpJzgBV4r9zf2RYHh/Zn+HCPt3jR4c7enev5+/i3ql34v8Ajh4rvL85urzWpVkOf+mxX+QFf0XfBPw6PCfwh8H6QvS00u3Tj/cB/rWljK7O0Vdox+NOooqhDGkCsFPWn1HJHuwR1p4zjnrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWQYOOcdacp3DNIFxmloAWkpaKAGRxrFkKMZOafSZpN4zQA6ikpaAEoLYBNNcOVbaVBx8ufWmLHL5ahnG/+IgcUAPik8xSdpXnHNPpKWgAooooAKKazbe2aRJN65xigB9FIKWgAooooAKKKKACiiigAooooAQ9KzdVmK25w+wd2B5rRb09aw75GjDh3Hl54YisZnRRinLU+G/8Agph8X9Q8G/Bu6sdGMjf2lIttLdBsFC3QAY54zVv/AIJk/s5+Eb79mnR/E/ibwbpOpatq1zPcRX19brPI8O4KPvDgZVq+T/8AgqH8Qr7xZ8bNH8AadclrGFIpGih/5aTO7KpI9QAfzr9XvgP4BT4S/Anwh4Xs90/9laXGmCuGdyu9hj/eY1FNW1NK07uy2PlL9ur/AIJ86R8WfD8WreAdL0/RtesVJFnYwJCkw9wMc18ueH/iV+0P+xx+z9e2l/b3FvaRX4itmuUMgiUjnB7DjpXQ/tDfty/tH+C/irq1vp/hU+G7G3crFHc6bJdGRASA+/A4Pp2xXzJ8dv2zPjR8bvDZ0fxjdhdIOd8UFgYEY/j3rRxuzLmtofqb/wAE3/2lvEv7Snwt1e48WzwT6pp92YPMhXbmMgFSR69a8v8A+CsGla9pXwbjuLCaaO1a8U3DRMeYx0yRXwN+x9+1p8QP2ctauLfwjpia5p166m509oSxfkDO4civ1v8Ajlp978eP2Qdcn8Q6V/ZV9daZ9sS3UbmjYLkDmsJe67Mq2t0eIf8ABJn4uQfE74L6/wCCNfZNSudGl4W4AbdauPlXB64O786/Pz9vjw54a0P9pTW7PwhbxQ6b5cZMFuBgSlm3AAd+BXC/AH46eIP2c/HTazo1zKgZHt7m3VsLJkEYP0PNfcP/AATl/ZGtPj1rGqfGTx/FJqFo2oSfYbO4GVmfOSxz2GePpXRr0Jew3/gnD+3p4f8Ahvo9l8L/ABpZrpUTTFbXVlGBuJ+7L6fWqP8AwVo+Ff2zXtH+KWjyrd6PKi2stxG4YbuqsPbpXQf8FDv+CdcOj2lz8RPhlp0p2uZtR0u2GSo/vxgV8OXH7S3jWT4V6h8OdauTqehSAeXFdrmW0ZTwAT9KUuYSkftx+wP8Sj8UP2WvBeoy/wDH1a232GfnJLRnGfxGK+ha+C/+CN921x+zPqsbSu4g1uVAjHhcxoeK+9a0jojJ7hRRRUPcQUlBNRO3ze1S9B2Ekm2SYOMY9aiSZmk5Tj1HSory0W6cHuB602EiNdsR4HVc81PObqKsTtIeXVec7TuHapo3Vl44FVLeYMzfMZBnPTv6Ui3ZWZlICp196fMhcrLjybcVD537xuDxUM9wrYwxBpikLIAzn5hRzIpR0Ln2gLjPFRteIG2hsGqn2hJLlkzlVHWp18gyBNpJIzmqDlS6EyTHI53AnsK+Hf8AgrovmfsxysASF1O3z+Zr7jVRG4RWwOtfDn/BWe8W3/Zlvbe5dd8uoW5i9eCaTegR3Z5V/wAESx/xI/iSwHBuLfn8Gr9Nry4MKjg49RX5q/8ABFCzKeDfHtzsYLJdRJv/AIcgHj681+k2oTLCMtk54xjNVfRkR1kiOSbyoRIjBo8/Nmqy3Qt7jDZMZ5XvVXVrTzrUwo0irJgnacUsaLarBG6NIFUANmou+h0qCLE2uvbwyNFbmTaegqex1k3gUmJkJGSDUQkHlsOME/dA5q/DNGkYPl7D0qjOaivslhG3Lk8U6o2VZ0GDSbHzjORWq2OayJ16UtV2m8tguCfepkbcuaVxNWHUUlLTEFFMkkCdTzUSyOZiN2VxUuSWhVrliioZJhG2C2KfCxZSSd3NFxW6j6KaTSM+0Ek8VQh9FVLjVbOzwLi6hgJ6CRwp/Ws/UfHHh7SFDX2t6faKeczXKL/M0rjszXmUMBmnjoK8w8S/tLfC/wAJszar470O2QLu2/a0J+vBq/8AC/4+eAfjQLv/AIQvxPY68bU4mW1k3FPqPSoW9wszwb/gqRr15of7I/iX7JK0RupYbeTbjlGYZFeH/wDBE3w9PafDn4i6xKP3d5qNtBH/AMAjfd/6EK9i/wCCrUE837I+ttDE0oW6gZ8D7q7xzXln/BF7xrZ33wl8Y+GU4vLLU1vG90kQL/NDQy+h+iGoXCWttJI77ECklicYHc1+G/x6jm/a6/b3Ph+wkaexa+TTI2jO4LBGcsw9jlvyr9oPiZ4JvfHWg3FhZavNpLyQSR+ZCOpZSBmviP8AYj/4J4+KfgL8etX8a+Lb61v7aGKRbFojuaV3Y/OfQgfzpDVrHqf7TX7Bngb4j/Ae10DSNOh0nU/DlqX0+6tYwHYqvKt67sV8h/8ABJn4mRW3xG174SeIrOPUbeQTT2iXkayLFJGfnADA4yBX6K/tWfHSz/Z4+DOs+LLy1kuwi/Z4407u/Az+NfkX/wAEy/EE2sft2aJfEFRfLqMzJ6boXb/Cq0EfuTp+h6dpaBbLT7WzUHhbeFUH6Cr1ItLVmZ+Uf/BbHxLLJqfw+0JABGkc90eepOAP61X/AOCdf7Xvw6/Zx/Ze8RR+KdYij1ldVmuINMjUmecFE2/gSD9Oa8a/4KseOp/iB+1bPoNvP5tno9rBYxKw+VJnyWGfxWvS/g1/wRz8U64ul6n4y8VWOnaXcRpObbTVLzFWUEAseO9AHyr+1h+0d4j/AGsPiRL4xudOms9Ms4Vtra1twzxwRhm+cnoGbPP0Fet/8E4/2xvC37KeoeJoPFWnX1xZ64IRHcWQDlGQkcqSP71frj8H/wBlr4e/Bf4byeC9I0K3utLuNzXbXsayvcswAYuSOenSvC5v+CU/wdHxTg8XWsd9aWSSid9BR1azds5xggkL0+XpxQB9e+HdetfFOgadrFl5n2O/t0uYfMXa2x1DDI7HBp/iDWLfw/od/qd1IsNtaQPPJI3RVVSST+VTAWmjacB+6tLK1iwOipGij9AAK/OH9vb/AIKTeDV8B+IPh38Or6TWte1BTZ3OpwAi2gQkhwrZyzYBHAxzQB8wfsu2Z/aQ/wCCikfiGdpLq0bVrjV3ZRkeXF/qyfbgCv3Hr86/+CRf7NmsfD3whq3xD8S6b9hutcjSDTI7iMectuDkuCeVDE9Pav0UoGFFFFAgooooAKKSoJpdr4pXGlclkqr9jSaTzG5PSlM3ydajhIkmw27HbnisHLU0s4q5Rv8AxRomi6pHZ32sWdjcuBst57lEZ88DCk5rdVgygqcqRkEV+CH/AAUn1nW7f9s7xVLd6j589mLYWEkZ/wBRGFDKvsQS351+uP7B/j7VviZ+yr4G17W5PO1Ga3kjklPV9kjKD+QrRK6uZvc9/ooorQQUUUUAFI2e1LRU8wEcbM2cjinrnnNNZsUBqgdhH+9QvSq18y/IGLA5/hqaMBFwMn61XMVbQe2dvHWo2MoYYAK96kDdqXGKsWwbgF5OKWNty5znmk4704Y7VPMSLUb/AHqkoqAIainuBCMlse1SzSbaoyNubNZuSuawjfUR5m25WTrUawrGpLtknnJqCTcbnjpinyMvST5g3G2sm9Tr5SeNlWZVXla+Sf8AgrFEsn7IOtM38F7akf8AfwV9XwK0nloEEaq/AFfJv/BWhQ37IWrZ6rfWpH/fwVpS1ZzVNHY8W/4Ij6fIvg/4oX5BEUt9ZxrkcEhJCf6V+mONrN7mvin/AIJG+ER4d/ZVGoO2ZdV1We4PptCoB/WvsqS4dpsAYWtZyViIq7LnmYbbUiVQZtrZzk1Nb3DMvK96zjJLqOUOpcopqtuHpTq6FqjIKKKKYBRRRQB5r+0h44Hw4+BfjfxHzusdKnkTH97YQP1Nfnx/wRX8Jx6hqnxP8ZXKML4G3skZgcESF5Hwe/KD86+mP+CpHjSbwj+yP4jigxv1WWLT/fDtzj8BXD/8EddBn079mPUtSuLVoDqOtzGOR0KmVEjjUMCeq53DI7g0FdD7m1GzGpafc2pdkWeJoyy9RuBGR+dfzoftafAnXv2efjhr3h/VIphBJO93p97Ip23MDsSHDYwSCcH0r+jla/Nv/gtJ8OItR+G/gzxnDADc6fqDWM8qpz5MiEjcew3KOvrQJOxheG/+Ckfg7Rf2HrLTtSuo9V8fJp7aMdFdfMJCjasr8YClSOp/hr4j/Z3/AGL/AIlftUafret+ELWytbKxkJM95K0Mckh+by4yAQSMj6ZFc9+y1+zZ4g/aa+KFh4W0SJ0sgwk1LUsHyreDqxLAEBsZAB6mv6CfhH8IfDvwR8AaZ4Q8L2gs9KsYwucDzJm/idz3Y+tA+Y/FXR/2iv2nf2JvEEeha5PrSWVudiab4ihkmtJEzjMTuPunHBU19GaT/wAFrUm0Ge21v4dOmptAVWexvwYt5BGdpXOM+9fqBrfhvSfFNm1rrOlWeqWrAgw3tusq4PswNfNnxI/4Jn/AP4j3TXb+FH8PXbdZdBuDbDPPO3BXPPpQFz8+v+CV9xq/jL9su98RCFnhmtb27vJApIi8wnAY9skgDNftZXiH7N37IHgP9ltdWPhH+0bm51IKs93qtwJpti8hAwVcLnnGK9voJCiiigApGOBxS0yQnbgDmk3ZAIrfLzxTDGBkg0yIFVO485pk0nUK3oPzrKU1YtIWGNjkueAaesxbOFxim24Kg72xjnBrx34vfti/CL4Ihk8TeMLFL1eljaN58xPptXofqalJtDZ7FNI20cU/azAEivjvw7/wVa+AfiLUPs0+rappSFtolv8ATysec9dwJr6g8E/FDwj8RtPivPDPiLTtZgkUMv2W4Vmx7rnI/EVVgOl3LGuGPPpXKeIvi74E8H3xsdd8ZaDo96Bk299qUMMgB6EqzA9q6XULEahaTw+a8DSRtGJozh0yMZB9a/K345f8EifHvi74halrHh3xxa6rZXchlEuvyObhSSSVJAOQM8VWnYD9G4/j78LLmQKnxG8JPIei/wBt22fy31esvjJ8P77VoNKs/Gnh+71G45itbfUoZJH+gVjX5Qt/wRk+Kf2Qsnirw4LnP3P3gH/fQWuq+CP/AAST+JnhX4o+HdY8UeJdEtdH026W6lk0m5le5k2kEINyADOPWjQR9J/t6/8ABP68/aq1HT/EnhrXotK8S2kS2zQ6izG0kiXJHCgkNk9cGvm7wv8A8EV9eXR1n8S/FDStHulJMkdppH2uJR6+Y8kZ/DbX6zRrtUAdBxXgX7bHwN8VftAfBa68NeDtYXRtYM6TLI8zxLIo6oSvr71aFc+EvEn/AARd1fUNN+0eEvitoutTg7St3pn2aHI7b4nk5/Cm+Df+CJfia42HxX8R9KsV3fPFo9lJcHHs8mz8sV5Cf2R/2xvgPNJceHrDxJFbwuZFn8Oays6SN3byFkLknA6r6V1/g7/go5+0l+z7qtjafFXQ77VLGQn/AETxHpTafeMo43CRkXI689+aLBzM+qvA/wDwRz+DXh0K+u6p4h8Tyr/DLcpbxH/gKLn/AMersb7/AIJS/s+3Xl+T4f1GxMbBgYNRfqPXdmvX/wBmH9qLwl+1L4DXxB4blNvdQv5V7plwQJreQAE8fxL8www4Nex0xXZmeGfDtl4S8P6fo2nReTYWMK28CE5IRRgVp0UUCCiiigBjMB1qAyLJNsAzx6U+WQbiO/0psfy5OOaye5aXUCCm4KvGKr3Em/SLssMYjf8A9BNSSSS7WwlMuDv0y4XGD5TA/kaBvY/mo8aA3Xxu11YxzJr0gUf9vBr+k7wahh8H6HG/3lsIFP1Ea1/OB4gsX/4aI1O243/8JLImM/8ATwa/pH0KPytD09P7tvGPyUVaethWNDdRuptNEgMhTuBmmtiDz34z/tCeBP2f9IttR8b63HpEF0xSBSpZ5SOu0D0rW+F3xc8K/GbwxF4g8IarHq+lSMU86MEYYdVIPQjI/OvyG/4LH+I9Sn/aa0nR3vJH0u00G2uIbQt8iSvJMGbHqQq/lX35/wAEyPB8fhP9kLwm625gk1N5r+QseXLPt3fkgplW0Pq2lpFpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAE3Ddihm2jOM0m07s0ySRlcKFz70ASK24Zxj60tJS0ARuDnIP+FNRW6tjPtRPJtUgH5yOBRbpIsf7xgze1AyVaWkFLQIKKKKACiiigApAwbODnFJIGZflIB96RIxGuB35NAEclwFYLglvSpKjaFtwZSAfcVLtoGKtLSDiloEFFFFABRRRQAUUUUAFFFFAEbbt3A4+tcp40vv7N0u4uZo3KxI0m1ehwM9a6uZTtyK4D4yWs174PvwkrW6LbSs8gPQBDXPUhfU6KL94/EmHxH/AMLl/bu0O4ltiUk8RQQ+QzbvkSQ8Zx0r99o1CooAwBwBX4M/sD+HIfFf7dWhl5i0dnqFxdhiN3mFCxH0r951HFVFaWInuytPY215kT28U4x/y0QN/Ovjj/gplouh+Hf2frzWH0rTo4428kkWyq5Z+FAIHrX2htrhfjN8FfC3x68E3HhbxdZveaVMwcrG5RlYdGB9RV2ZKep+eH/BGXTfDOtaH49t7rRrefXbSaGT7VNEHIhkBwoyOMFc/jX6V+L/AA7/AMJB4R1TSIgi/arZ4FyOBlcV57+zh+yt4I/Ze0XUtP8ACEFwX1GUS3N1dyb5XwMKuf7o9PevYaFHe4uZn85Pxn+AetfD34+Xvgm8tpWubjUFS22xnDpI+A3H41/QD8G/h5p/wq+GPhzwvpkC29tp9nHEVAwS+0bifcnNa2r/AA/8Na9q1vqmo6FYXuo25BiuprdWkQjphsZrf21SVlYHK5HLEk0bRyIrowwysMgj0r87/wBsj/glhZfFbWLvxd8OLy30PWZFL3GlyJiC4bkllI6MenpX6KbaNtMV7Hxz/wAEyf2e/G37PXwl17TPGkEdnc3+pefDaK+4qoQLuyPX09q+xlORRt6+lCrt4HSgQtFFMZW3bgx6fd7Vm9wG+ZuztHI9arLdLMzoeHX0qwSWz2PtVSQLayB9ud3BJrOb0NIq4jQhU3vKyD2qL7OsjeZGuGx/rB1rz34iftHfDX4W6kll4u8Xabod2yCQW15JhihJAbHoSD+VJ4L/AGoPhD4+mNtoHxE0C9m/55repG34B8VjH3tEbaxWp363SNvBdlZfXFRNHJdbfmBX1FLDfaPqkb/Y761vT1PkTox/Q1UuPEeg6X8s2s2Nvt6ia8RCKrRaM0UotXLEjNCoVueTz/KqrXn7wKwbeFzxXL6z8dPhrot0bTUPHGi20zAPsa8RjjnnIPsapr+0d8I4S0z+PdB54Ja9Qfpmp91vc0U7LY9FtLWNUMy7ju67qleZvLBRQBnGSK8nuv2yPghpbeVP8SfD8TYzt+2J/jWVdft2/AK3cI/xK0Vu/wC7m3D9K6FT03Od1NdUezLI4nU5ZyPSviP/AIKs+BfEHj74KWr6PZXN+1neI8lvbxliR68V6n4g/wCCk/7PvhtlX/hNoL5iN2LKF5P1Ark9S/4Kufs/xxsv9o6heg8lE092B/MUcrtYaqWexT/4JQ/CrW/hr+z3qEmuadPpV9qmpvOkFyu1vLCIFbB9ea+wru4mVioUu2eTjiviO8/4LE/ByzmMVtpeuTRKvystsEGfTBrgdc/4LVeGorl007wDfXMP8LzTqhP4U+V2aIjPld2j9FPt007FTbk4HDGp7a0uGIlkGD2XtX5oXH/Ba2zMeIfhtIzHjD3YA/lXK6z/AMFrvFYkK6Z8PNLii7Nc3cjMPyGKVmXzvofrCtqWk7DueKufZlYfNz9K/FjW/wDgr/8AGPWGl/szT9E01mXCRwwGUqfXnrXIXf8AwUY/ae8QQvHFqtwqyjaTZaNg/gQKqxlKV+p+6awOk+Qw8rH3e+akkmjhQtI6oo6sxAFfzzaj4y/aK8emS6ubzx3eiRsEw21yV9cDaOOvSs6L4b/H/VoWaHRvHl1CxwxaO4UE+mGotIzufuL46/bA+E/w38TW2geIfFdtp+qXBUJCQX6kgElc4GQa9mtbiO7t4p4XEkMqh0dejKRkH8q/nv8Ahn+xz8a/HXjjSEm8Fa1BELuJpbzVI2VUUMCclq/oJ0ey/s3SbKzOCbeBIjt6fKoH9KfKwbXQtjvTdxbO08dKVqpvdC2IAUkMe1VsgUW9iS4aVWG1dw7mqkN1Kt0YjCSOu6n6hq0Gm2sl3dTLb2kQ3SzSsFVB6k18b/Gz/gqt8JvhTqV7pmjx3njHVrc7GWy2pBuyRjeeT+VZS953L+FWZ9nyRmSQFhhfSrK8LX5j6D/wWw0aS8H9ufDPULaxJwJrK9V2H4MoH619FfBT/gph8FPjRqY0yLWLjwvqbHCW+vxrAsnT7sgYqfoSOlMnVo+rjVXU4ribT7lLORYbto2WKRxkKxHBP41PbzR3UKTROssUihkkQ5VgeQQR1FSbRWi2JPyB+OX7Bn7WPjr4k6pq0uvf8JLHdSGSO8t9bFrGqZO1BGSu3Ax0GOa41/8Aglf+0f4gtUOqTaaWDbdl9rPnOB65BIx7V+2FLSsVzs/Gqx/4Iw/FW9tle68WeG7OTvDJJM5H4qhFfZ37Av7Ct5+yX/wkeo+IdWsda13U9kUUmn7xFFCuSR8wGSSfTtX2NRtFLlYcx5x+0N8L4vjJ8G/FPhKVtjahZusTYziQDKn8wK/Fb9iX476l+yL+0TLp2tB7XSLyc6bq0Ew24KsQsn4Hmv3vavh/9tr/AIJu6R+0Tdt4o8IS23h/xfj/AEguCIrzGcbvRuetIaPs7w/4g07xRo9tqek3kV9YXKiSKeBwysD7itBpgnWvyT+Ev7Hf7Y/g4L4Y0nxm3hLw9GWXzheq8QU9Sq4JzX6UfAf4aaz8LPhxZaF4h8U3vi/WFdprnU705ZnYAFV/2Rjj6mi7FZFr41fB/wAPfHr4d6p4P8SQGbTr1PvKcNE45Vx7g818l/sd/wDBNiT9m34z3HjjU/EMOs/ZYpbfTo4oyrKrjbub32kivut4lyX25bGKr/2taR7vOnjtiD0mcKfryaQF5aCcDJqgNc03GRqFrj/ruv8AjTTr2mMCDqNqQf8Apuv+NaLYk/n6/aevk1f9uPxhMW8yJvE0acnIIBRf6V/QbpUaQ6XZxxqFRIUVVHQAKMCvz0+Jn/BMmHxl+1VpPxB0PUrOfwhd6imoavZytucOp3MEIPIbA4r9CG1CystsL3UEJUYCNIAQPpmmBdoryL4iftZfCT4U3xsfE/jrS9OvQgk+z7zI+0kgHCA+hrzu4/4KVfs9wHH/AAnkcvvHayn/ANloCzPpDxBoNn4o0O+0nUI2lsb2FoJo1coWRhgjIORx6V80+GP+CZf7PnhXxBa6zbeC3ubu2lE6LfahcXERcHOTG7lTz2IrN1D/AIKm/s96e20eKLy54zmCwcj6c4rita/4LEfBewujHYab4l1aHGfOhtEQZ9MM+f8A9dAWZ91wwx28KRRIscSKFVEGAoHQAU+vzp17/gtN8ObOzkOmeCvEV3d4/dx3DRQrnsScnivjjxp/wVQ+PfiDxNc6npXiePw/pjSf6NpdvYQPEig5AZ2UsxweeaB8rP3dorxn9jz4ra78bf2dPB/jPxIkS6xqUDtO0ChUkKyMm4KOBnb0r2agkKKKSgCOZsVRlkG7k81NNIzSmLtjOaoXEUbSAFznPrXLL4jppxXUmWdhIqgZTuasWfzSMQflGRj8qzmhNvDIUYnnpmrmlPJImWTaMdfWoWrKnFJXPwL/AOCkFraWP7Y3j1LSZ51lkieQuxO2QxLkD2HFfsj+w3oEHhv9lH4cWtv91tMWZv8AeZiTX4xf8FDGc/tlfEoOMAXkOPp5MVftv+ybj/hmv4cYGB/YsHA/3a647HPJdT1yimZozVED6KgmkWPBY4qk2pw3BKIx4ODU8xSjc0T/AKynHHeq6IFUc+/WjydzZz8tQPlJzg9KY1OjUIuBT6BXsVW/134UyL/XVNNjd9zPFQSTNDxHFlqC76E+8KWHvSNcKrbe9Qqr7sAbd3JqdY9vWq5haEsbblzTqj9KctPlvqQx1IRu4paz9dgvptJvhpckUWpNA62zTA+WJMHaWxzgGjlETNJAjFHmRX9NwBqJYYjMZFnUjGMAivwb+MHwO/arf4qa5c6v4b8ca1rTXDbtV0a3upYJRuO3yni+XZjoB0rLtfhF+17Gg+z6B8WYFB+6BqCfpmpsuxor9z99fscfmF1YHPHWq0+jyMxaJ9pPWvwdb4Y/tlLx/ZXxeH+7LqA/k1dN4Zb9tbwRp7wwQ/E2GLeZCt7bS3ByQBnMoLY46ZxWTp3dzTnl3P3GsbE2y4c5714p+278C9X/AGifgBrHg3QpYIdUuZ7eWJ7jhfklVjz9Aa/KXWvj7+2L4RjW81K+8ZWca/8APxpgA/EbauaR/wAFGP2otJhUNLc6kq87rrRHz9MhRWsYcqMZNyep+tn7L3wVT9n34L6F4GW9F9Lp6MZ5gMAyMdzY9ua9EuIpkmKIeDzX4x6d/wAFfPjfo9/jU9N0S62fK8E1m0T/AInORXoOlf8ABarxJGFOpfD7T527tb3TAH8xWUqbY1Kx+rEVrdLKPlBT+93rQ8p1AwSa/MXT/wDgthatD/pPw3lR8/8ALK8BH61px/8ABazQtv7z4e3wP+zcrQqKsVKdz9L7cFY/m65qWvyZ8ef8FptbnuIf+EQ8EWtvb7f3n9pTF33ZOcbeMYx+tfZf7CP7Wmpftb/D3WNc1Pw+uiXOmXi2hkhJaGfKbjtJ7juO2RXQlZWMj6bopKWmAUUUUAfn/wD8FktQli+BPhKyQgR3XiCPeO5xFIR+tev/APBNPTRp/wCxd8PCH3/aIrifjtm4kXH/AI7Xzr/wWq1qWz8E/DazRSY5NUmuGOOMpHgD/wAer6l/4J92a6f+xz8L4V6f2a7/APfU8jf1oLex9CrWH408C+HviNoM+ieJ9Hs9c0mf/WWl7EJI2x3wa3aKCDmfAnw18K/C/Rf7J8JeH9P8O6bu3m3063WJWbgZOByeByfSulXOORilooAKKKKACiiigAooooAKYzYODTtw9aimYetTLYa1Yu5ccc1BNcQ2sMlxPIsUMal3ZzgKB1JNMVhvzuGBzivhb/grR8fb/wCGvwj0zwjoGoNZax4lkczeS22UWkYBc+wOQKyglc0t0PFP26f+Ckl/4j1O7+HPwfubhV837Pd65ZZaS4PIMcWBnGe9ea/Av/gld8S/jZZW/iDxpfjwjYXR8z/TFMl7MDg7yCeM57+lfQH/AASp/Y2sdM8Lx/F7xfp0dzqWpE/2Nb3SBxDCMf6QM92JYf8AAa/SwDAwBgVuRc/LXxR/wRQj+zr/AMI/8RJA46x6haBlJ/4Ca+Xfjd+yx8Zv2HdW0/xDBq0yacXxHrWiSOqI2chHTPHSv3trn/HfgnSfiH4V1HQdasor6xvIWieOVQ2MgjIz0IpWDmZ8q/8ABPj9uAftPeHZvD3iCIWvjTR7dGmkByt7H0Mo9DnqPevsjaa/nt8H+JNf/Yv/AGvLq0s55LY6LrH2G4hY/wCttmbIzjrlGB/Gv6Eo2LxqxUoSMlT1HtS5RXDaaNpp1FHKguIKWkJCgk8CvAfHX7e3wE+G/iS50HX/AIiWltqttxLDb2V3dBDkjBeGJ1zweM5qhHv1cT8WPg74S+NfhO98P+LNIt9Ts7mJow8kYMkWR95G6givCtY/4Kf/ALOOm2MtxB46n1KVFytra6JfiST2BeFV/Mivz3/ah/4KofEL4rXV1pHgN7nwJ4WJK+fAMX06gnlpP4ARjgUDSuT/ALNfhnxF+zv/AMFFB8PvAuqHUdL/ALRaxu2zuU2gAdhIOxUH8+lftZkV+Z3/AASv+CNj4Rhv/i74x8U6bN4l1xHhtbaXUYZZVibaTK7BiQzfMMHnivsr4yfthfCH4BXGmQeNvGMGmzakrvbR29tNeFlTG4nyUfaPmGN2M84zg0A0ez0tc54B+Ifhz4n+GbPxB4W1a31rR7tQ8V1bHI5AOGHVWwR8pwRmuizQIWkpaKAIwuOornPHnxG8MfDDQ31jxXrdloWmocG4vZQik+gz1NbupX0Gl2NxeXUiw21vG0skjHAVQMkn8K/Ev4lf8J7/AMFJv2r9b0jwpeTf8IrYSeXD58zJa21tGxBlKHjexJPqeKmxSP050f8Ab4+Auu6ilja/EXSftDvsVZH2gn6mvbrXWtP17R5LvTL23v7Z4iVlt5A6nI9RX5veIv8Agivo8mgxjRviBdRav5Y803VopheTuRjkCvmm91r47/8ABNfx0mmXV6l1pWpRnyg0rTWky5K5GT8r4HT6UcpR4bJpNzrf7VU1pEv+k3Pi0xorHHLXJxX9G9lCbezgiPWONVP4DFfzqfs7atL4z/as8D6hcr/pep+KLaeYdvMeck49ua/oxppdRSGtIEHJxVa3vYZ5SEOWHBp1xNaqxWaaNGx0ZwDVOGXTLGR5ftduhPUtKowPzphpY/GD/grRavrf7ZtjZRqWlk0SwgVR3LTTD+tfsL8HvBkHw++FfhTw5bLti03TYIMe4Qbv1Jr8qf2uNV0Txx/wU48ErBd215p0cul2tzIsqlFKzSF8tnHAPrX6K/Gr9tP4R/AbSjd6/wCKLe+myFGn6M6XVye33AwA6dzQS2e5Clry79n79o7wb+0v4Nl8S+DJruSwhuGtpEvYBFKkiqrEFQT2Yd+9eo0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEGe9LRRQA3YN+7HzYxTqKKACiiigAooooAKKKKAEpqyBmwOaSSRVYIwPIpIo1HzLwD2oAkparXFq81xBIshQRkkqP4qs0AFFFFABRRRQAUU0t82ByadQAUUU3b85bPbGKAHUU1V255zk5oZSd3OMjFACnHSvOPjfYXN94D1tY5dsP2GXcg4/gPeu9nm+yqgwXbpmuG+L0c2oeA9bhgcxtJZzKW/u/IecVnN+6b0ou9z8av8AgmaTa/ttaWgXcG+2LnPT73P6V+7C1+Hn/BLPS/O/bVUOQ5t7a+bcepK5Ga/cJacVrciQ6iiirMwooooAKKKKACiiigAooooAKKKKze4DGHNRT2sdwoDjcB0qfbTJNwXCY3f7VDSsNXufBn7fX/BO3Wv2lPE1l4w8Ha3a2ms29mllLp+oDEUiIzsCrgZDZkPXjivz+1X/AIJn/tEabqElungVrryjhbizvYNj+4ORX73m5WJgshG7GeKct1GwB3DkZqVZLQt8zWp+DOl/sE/tRaGxGneEda08sPmNrq8cYP1w/WnSf8E7f2nNSYvceFtQct977Rq8bE+5+ev3oVwwz1FIsyNnBBwcU9BK5+EOn/8ABLH9oXWJ0Evhmzs9zYMl1qcWB7n5ia7iP/gjV8ZZkRv7d8LwEj5o5bqXIP4RkfrX7TeYN2Kdn2qkmFz8Yof+CMvxh2/N4m8JL/21mP8A7Sqdf+CMPxbb7/izwov0ab/41X7LAZpdtWLmPx80v/giz8RpGH27x54at488iKOZ2+v+rArudP8A+CJqyRK2ofE9op88ra6cGX8yw/lX6lbaQKBmgOZn56+Ff+CMfwy0+Ff+Eh8Va9rkwbO6EpbDHHGPm9/zrrV/4JAfAH/lpH4mkP8A2FQP/ZK+3ttG2gV2fFMP/BIj9n6F1Y2fiKUKc7X1YkH6/JXdaZ/wTd/Z+02NFbwHb3pUbd13K7k/XkV9OUtMLs8m8F/so/CL4f25h0P4f6HZLvL5+yh2yQB1bPoK9CtPB+hWEYS20XT4EXoI7VB/SteikIhhs7e3XbFBHEvXaiAD9Kk2KOigfhTqKAEwB0FLRRQA1qrSrtzsYBsZC+9WWryz9oz4sQ/BX4T+JPFsirM2n2byLDu2ktj5efrUTdkXE/O7/gqN+2JqE2pRfDHwnrQtbVkZtaa0IYnBwIt3VTkE8Edq5b9gT/gmvD8aNNXx18VbC8t/C8hH9n6V5jQSagpGTI7KQ4TngggnBrwP9lv4Qal+2T+1FGL5dtlcXTavq0mNypEGyVz6sePxr+gDTdPt9H0+1sbOJYLS2iWGGJeiIoAUD6ACp2Kk+ZaHy1N/wS1/ZnkiZR8O5I2IIDrruo5X3GbjGfqK+Tf2lP8Agj2+g6Xda38ItVu9VMOZToOqujSEDJ2xSKFJ4xgHn3r9X6KCUfi3+xF+3x4w+APjy2+HvxIub6+8KvcGyMF6F83TJ8heHI3lBgDaTgZJHXNftHb3Ed1bxzwuJIpFDo69GUjII/Cvw7/4KseF9M8GftZSzaXFDGNV022vbmOMDPn+Y4LH0JAFftF8NZDJ8OfCrnILaVannr/qVrRCZ01FItLTJCmyN5cbMckKM8U6igD8k/2uv+CoXxR8I/FnUvC/gzTrfwzp2mSmEyanaF5rhgT84yRhTxjjsa8n0/8A4KfftIa1b/6NNZyk8BrfSHf9QSK/ZXxT8H/A3ji+jvfEHhDRNZvI+FuL2wilkA9NxXOOTx71o6T4B8M6DbiDTPDulafCDkR2tlHGufXCqPSpsVdH4mSftWfth/ES/wD+JRqvidWYbPJ0vSxHH1z/ABITnn19K6K10/8Abu1aDzi3juQN3RY1H8hX7Tw2cFrxBBHCP+maBf5VNzRyhzH4i3/wn/bc8UN9nu4PHBVhgmW5WMY+oIqxpf8AwTp/am8UWpuLy+uLRmcgx6jr0gk6DnAJ45/nX7Z49aKXKPmPxYb/AIJf/tL7hH/a1oUxnd/b0uBSyf8ABLX9pCMAf2zYycZ41uXvX7TUVQuY/Ey9/wCCaf7Ttim2G+ScYzth1uUCo9N/4Jk/tL63I015cW1nJuwWutblZj78Z4r9t6KYcx+Ouif8Eb/ijrX7zxB4w0OyYtg7RJcvj13HHvxXayf8EadI8NaDc6n4k+K76dbWqGWe4FkoijQDkksa/Rrxl8dPh58PtQFj4k8Z6Lot60YmFveXiI+wkgNjPTKkfhXG+I/Fnwp/as8G674B03xzp+qLqNuYpk0i/UTqPVcHJoC7Pz3+D/7BH7MnxB8UJp9t8dZfFNzGSDYQslq0hH91mXn8K+p9P/4JLfs+Wu03OjatqBH/AD21aZcj0+Rlr4m/ao/4Jh+I/wBnDwZfePfCvixdb0TSCss8cqC2uoEL4DKwOGIJHPB59q+z/wDglD8XPGXxZ/Z/1KTxZfTaumj6s+nWl/dMWmZBFE+xmPLY8zqfUUA2dSv/AAS5/ZqVQD8PpHx/e1u//pPWzov/AATh/Zz0GdJrf4Z2Uzo24fbby6uRn6SSsMe1fS2KKBXZm+G/DmleEdDs9G0TTrXSNJs08u3srKFYoYl64VVAAGST+NadFFAgoopKAKF5OY5wqoMEfexUC2qzliSCeNo6HP1rQMYkbJGa8p/aa+Nem/s9/CbXPGF7NClxawMtjbyHHnTkHC479q55Ruzbm0shfix+0d8M/gaq/wDCZ+LLHR5mw32dm8yUqeB8gycEg847VzPgX9uz4FePNSGnaP4+04XUmWWO6Jgz0/vgV+SHwc+AnxI/4KH/ABe1rxBf3rWEEjtLc6xco8kEHIIgT0xuztH97PevTPjB/wAEhfiN4B0ObVPDetWni3yfne2hjMcuBkkgGtIxsZ3fU81/4KYTadfftfeIbnTJoLi3ura1dpYHV1ZsAE5Hfge9ftp8DdEj8OfBvwRpsXKW+jWqj/v0p/rX81dzZ3tv4ga21BZEvo7jyZ1lJLB1cAg59On4V/Th4Ai8nwJ4cjx93TbZfyiWtAk7m5UcxYIdtfOv7dH7VF9+yh8LrXxDpmiprOoX10LSJZmKxRHBO5sV88/sy/8ABWzSPiJ4ptPDPxG0iDwzd3cqwwapayFrXeez5+6M96AXc/Qa3aSTcCM0yT7Npdrc3d3JHb26KWkkchVVRzkmrdrNDdQJPbyJNDKA6SRsGVgRwQR2r4N/4KyftKXPwu+GNn4E0S5EeteJVP2nacPHajI3D6kEfhU2K5uh9neCfil4P+ITXMXhnxHpuuSWvEyWU6yNH25A6V1nFfjd/wAEi/gl421T4tH4i200+m+D7GOa3mkbOL5yAPLx3xuBzX7I0uUh7hTWkCyBe9PpKOUQjV83/tl/tiWf7I/hzTNSuPDl5rs+pSGGDy22QIwBPzN619Hn/WCsbxh4H8PfELRpNI8TaJYa/pcnL2eo26zRE+u1gRRyjufjN44/4K//ABp1y9lbQk0fwxbMcJFDZJcso9zJnn8Kxbb9s39rv4paXKdD1bxRqkDZjMmg+HUGDjOBJCmQcEe/Ir9e/Dn7K/wd8I6kuoaL8MfCmm3inK3FtpECOv0IXivT4bWG3ULFFHGo6BFAFPlHzH8/Hh6f9o2H4qeFL/XpPiBZ+IZNShSzu9cS6Vhl/m/1wzt5+nWv6BLGOWK1hSZ/NmWNQ8mMbmxyfzqYopOSoJ+lOqgcrhRRRQSFFFNbC5Yjt1oAjubiO1heaaRIolGWeRgFA9Sa4HU/2gvhnod79jv/AB3oFnddfJm1CMN6Zxn2Nflz+0d+0x8Qf2uP2lL34JeEvEUfhnwvNqUmkQNlk+1OnytvYc4JB4qgv/BGP4qKSD4l8MuM8HzJc/8AoNTqWfrdpfxS8H61D5lh4p0i5j/vx3kZH55q1N438MujI/iDSdp4O69ix+W6vyAvv+CNfxbhXNtr3h6dsfcWZ1H6isKT/gkF8c1m2BdCdMf6xdQUD8jzTFZH65TeHfg/ql5LNPpvgm8u5m3SSSQWbyOfUkgk1jat+zR8D/GFyJbrwN4XvJSuweTDGnHJ6IQO9flha/8ABIX452kqSwXei28g53x6hgj8RWxN/wAE0P2ndFYTWfiBJmUcfZ9fkjI9utMLI/RnUv2A/wBn/VAfM+GWjpkYzErr/wCzVxGuf8Esf2etavBcDwvdafhAnk2N+8cfBJzj15/QV8KSfsT/ALYWksLm01PVBNGchk8RvIf++S1WJ/D/AO3h4bhMJXxnNFHxvt5YnGPqTmgOU+zpv+CS/wCz/JGyx6Tq0RI6/wBpOTX0R8BvgJ4T/Zx8Cnwn4NtprbSmunvHE8pkZpWVVZsn2Rfyr8gY/C/7YfizxvoE2qyeNrGV7uO0F1dSFVjVm5JC8YHPJr9tPD9rPp+h2Fpd3Bu7u3t44pp2HMjhQC34nmgk0KKKKACiiigD8x/+C3CSHwf8MioJH2+6HA7+WuP619dfsEyCT9j/AOFrKcj+ycce0jivlj/gtdCf+FbfDeYcbNalG70zCf8ACvpr/gnju/4Yy+F27r/Z0nX0+0S4/Sgt/Cj6LooooICiiigAooooAKKTNGR60ALSUBg3Q5paAGKvXNNkhDVLRSauNaFJbRUk3Htjk1+Lf7VEmoftff8ABQ628DRXP/EttL2PQ4ZIm3IsSfPM/sfmIP8Au1+tn7RHjx/hh8D/ABx4piBM+l6TcXEW3rvCHb+uK/GX9gv9oz4f/BH4s+JvHvxKa8vdanti1nLbw+a3myNukb64OKlRsWnfU/cfwj4Z0/wV4Y0vQNLhW307TbaO1giUYCoigD+Va+RX5E/tgf8ABU22+KPw/g0X4WT6t4cvpLoi7upY9jvAF42sOhzn8q8M+A//AAUm+LPwT0O50xLyPxPZyTtcbtZdpZVJCjAb0+XOPc1ZPKfvTkUbh61+LF9/wV++NmpSRx6bpOjQvIMKkdmZXJ9hVe7+On7Zn7T1u+k6PpmvQ2cijzP7NsvsKMue8jbR+RoDlOP/AOCjlvpeuftxaovhd49SlumskmW0+bN0BsZPdvlX86/d5WEiqw6MMjjFfmn+xb/wTJ8TfD/4paf8RPipeWdzeWLG5ttNhma4Z52AIklZh94EngZ5FfpdQSFFFFAFbUrFdT065s3do0njaIshwwBGMj3r8vvEX/BFOfU/EV9d2fxRWKyuJnlC3ekiaYbmJ5bzBnrX6lUUAflpD/wRFZFx/wALejT1B8MpJ+puBTp/+CIamENH8XwbkHjd4ZRY8fQXHX3r9SaKB3Z+Smrf8EUfF0KkaZ8T9HuwB8q3WnS2y/QhGb86898Yf8Eevjdodm9zpV34X8SyxYKWljfyRPJk8j9+qKP++q/a2igfMz5l/YH/AGX7z9mP4LW2naxLcp4n1Rvteq2j3KywW82SAsewlfu7ckE5xX0yvSlooJCk3DcB3NLSMNykGgD4s/4KnftDT/Br4EjQdKl8rW/FbPZxsCcpAoBlYe+CB+NQf8Em/g3/AMK7/ZtXxBe2Sx6v4mvHvRcsBva12osan23CQ/jXyB/wUs1af42ftyeGfAWmXBmWxt7LS/srZCi4lldn68co8fPtX7B+EfDdp4O8L6ToVjGsVnptrHaxKowNqKFzj8KB3NTvjvXzT+35+zfY/tEfAnUoHk+zavoaPqdjNxjciHcpPoRX0uVO4GuW+LEbTfC/xai/ebSboD/v01AH4CfsO6PLq37W3wwtfleRfEFvK2Txtibc36Cv6IZlfyn2ffwdufXtX4Af8E6rWS4/bN+Hahcst5LI2e2Fcn9BX9AZGeD0oC9z8Mf2kPh5+1P4r+NmvyajoviW7uGnZbdtJkcW3k728sKVIHQ1R0L9iP8Aat8SW5kXTNasVYAf6dqpQkfTca/dtqSgD+bu2+APj29+PMXwvki2+ODefZnE05KpLgNuLjJIxzX3Pa/8EUvEF+sEmq/E/Tw7KrTLDpbs6tgFgHL8855xWb8LmXXP+CxmvtHErJDqV5uzxjy7XBP13Cv1yoEeW/s5/s9+G/2avhraeEPDUWIlf7Rd3TffubgqqtIfTIRePavUqKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilcAoooougEx8wPaikZtuOKXd7UDFoopkkgj9z6UxD6KYm5m3HgYxilVSu7Jzk5oAdRRRQA0rzkcGnUUUAFFFFABRSE02SQqhIGSO1ACsuea87+NAmh8Ea7PA+1k064YKB1IQ16Gr7lDYx7VyHxS0mbU/BetrEy5+wzrtbvlDWVRe6b0naWp+Of8AwSesDqX7ZD3ckjRywaffSlQfvEnBH61+3i1+DH/BOfxg/gj9t/w5D8uzUbm60uTLYH7wMB+oH51+84rSOxM99B1FJu9qM+1MyFopMn0qGa7SAEsQFGMnPC+59qV7DsT0lcX4/wDF+oeH/Bur6xplob2azheaKOPlZtoyMEV8pfBX/gqd4E8aawNA8cWNx4H1pFYSSXoxBuDEYBPI/Gk5Jbl8jtc+4dwzjPPpQTt618E/tVf8FR9C+ETWun+BLSz8WandRmRbjzswouSBnHPUGvC/g/8A8FlNe/4SaO3+IHh6x/seaUbrrT9++JTgEYJwcdfxpKSauRZn61LnvS1ieDPF2l+PPDGneINFukvdK1CFbi2nToyEfzrbqk7q4PTQKKKKloQxmKsOVA/Wq890Yc5TK5xuzip5I1kIJHI6VSv9NW+ZRI/yD+Dt9azlfY0jbqZ8hl1K4KhRBtHVmyceoFWLPSp7c7DcFowvGBznPrivlr/goT8YvF3wC+C93rXgvVU03UmeKLzTEHZFLEZXPevyR1D9sX4++PdShJ+Jnim51GTEUdrptw8W4DkHZFtB5J7Z4pR1R0Sk7JJn9ESwNkB23LjGc8/yoUQ2cblnVE+8WZgAK/BVfjL+19r2mJp8Wp/Eu4hhbaWhtLiQlsDgyBc9COM1JpvwP/a++MkZElh4+vbVpPKeTVruW2QHAOCJHHGCPatOVnNfufug/jrw1FIUfXtMVxwVN3HkfrV7T9f0zVYzJZaha3canaWhmVwD6cGvxT03/glD+0TqUPn3Mek6fIxyY59Y3Ofc7Sf8isbXP+CfX7UfwxWWewsL+aGNTK0mhazuHfPyhsk4Hp6VaFofuktzF/z1T/voVIGDDIORX84k2s/HPTdX/sifVPHcGrFtiWi3FypJzgHrzzn8q/cP9iPwL4v8A/s7+HrPxzq97q/iG6BvZWv5WklgV1XbES3PG3P/AAKmSe80UUUAFJS1HIx5wdtADlbdmnVAHZXPA2Yz71598Sf2ifh38I4428WeK9O0l5ACsMkoMhBJGdo9wfypXHY9Ior5vt/+ChnwEur9LRPH9kJGOAzKwT88V9C6XqdtrOn299ZTx3VncRrLDNGcq6EZBBphZot0UUUCCiiigBp+9ivhD/grv40j8M/s7ppWxvtGtXiW6ODj5V+Zh+VfdzD5s98V+cv/AAWrVm+Evw92puLa3Iu7+7+6qJLmLi7M5v8A4IyXHhDRfB3jq+vNV0+z8Uz38dqYbidY5GtljQqQCem9m6elfpta6ha3yk21zDcAdTFIG/lX4Wfst/8ABOHx/wDtIfDlfG+j+ItN8OaXczSQ2/2oSGV2jbBI29Fzx+Fd34g/4JnftP8Aw7ZJ/CniFNWdRvL6RrUls+cntIV54HQ9xRyi2P2grgvjD8bPCfwR8K32teJ9XtrBYIGljgkkAklIBwFXryRjNfjxffAf9uOxmETyfEaUqvH2fxM7p1PHEuK3fh//AME3/wBov9oDVIrn4l6rqGg6dCxjN14m1J726wAGASMs3y5Y4Pruo5QujifgH4D1v9vz9si51fXvtF/oRu21HVZnO0RWanEcYxjbu2hRjHev3WsbKDTbG3tLaPyra3jWKKMEnaqgADn0Arx39lf9lLwj+yn4FbRPD0bXWpXhWXU9Vmz5l1IBgHGcIo7KuB1Peva9oqhN3BaWkpaYgooooAKKKKAGs2Gx7Zr51+OH7fHwi+APiSTw94j1qaTW4wrSWVnA0rRhieWI4HSvomRVdSGGQeDXxL+1n/wTF8P/ALSvxCufG1l4on8M6xPaJBLbx2yyQzSKznzWOc5IZV4HRBQPQ+j/AIO/tJ/Dv47aQdQ8H+JbTUFVtjwM4jlRsKcFDz/EK9Nr8SvGX/BLf4/fCu7N54RvINZjhXes+j3bQS9TwVJGTgA/jUHgf9ub9o79lXUP7H8Z2moavbEqFtPEsTfIoJH7uQDodp7+tK47H7e0V4J+xf8AtMTftWfCA+M7jRf7Bmj1CXT3tlcurGNI23qT2PmY/A173TJGtjGScAc9cV+Z3/BQD/goHqMHiC5+EPwhmmufEM0wsNR1CzyzFmAxFblej5OCw+le8/8ABRj9q+b9m34R/Z9FljPijxCWsrIZ+a3Xad834A4HvXzN/wAEp/2OW1qaH45eNFmlnW4kGh2l0p/eNj5rps9eWIX3XNAHYfs//wDBJvQ9V8Ex6r8aLzUNU8Y3jmVore9bZBEyqQjHu4YyZPTkVf0L/glSPhh+0V4N8XeAPFU+m+E9Nmjub22upGa6Z0diUVhgbWXauD71+idDDKnHWgdz4G/4K7/HHS/CfwFb4dQzJL4g8TzQsY1cboLeKVJC7DsG2FfpmvXf+Cb/AMJ0+E/7JnhKIukl3r6nX7howMbrhE2DI64jWMfhX5v/ALWX7Fv7SHjf44eINbv9AvPGCXcjPaX9ncK6Lbb3EcfzEFSB29CK8x8aWv7VPwP8L2una7f/ABF8O+HYYEgihjvbn7DFCo2qm6NyigBcBewAoEf0FA56dKWvyh/4I+/FT4h+JviR4o0XV9X1nXPCH9nvcLJePJNbw3YeIHDt0Ypjj0I9a/V6gAooooAKKKKAI2BLMOi44Ir8af8AgqJ8btU+Nn7Q2mfCjw6GuLLQ5lsBbox/f385AbI6HaNgB7HNfr9448SReDfBuva/PjyNK0+e+fPTbFGzn9Fr8W/+CcOi2nx2/ben8S+JA19Pb/bNeQTfMTMW/d5z/d3Aj6CptqWj9bv2Zfgvp/wD+C/hzwjZW8cNzBbRy6hIigGe6KKJJGI6n5QM+iivUaFqC/u00+xuLqU4jgjaVj7KCTVEn4AftYeH7XT/ANvbxbpcEEcVs/ii2CwogCAP5ZIwOO9f0A2dutnaQQIAqRIqAKMAADFfzpeIfHTfE79sRvFEhMg1PxZDKpY5yonCr+GFFf0Z0COT+Jnwv8M/F7wnd+G/FmlQ6vpF0uHhmHI91PUH3Ffmj+0//wAEi00PR9U8S/CjUp7o26mceHbr5mZRklY37kDGAa/Vmgigdz8eP+Cfv/BQa++E2qWvwy+JVzNLoJnMFtfXTEyac33fLYnqoK/hmvDv2sfF2p/tafto6jY+G7r+14bq+j0TRni5QwDjI/FmNfVX/BVj9jXStH0qT4w+ELKPT284DXreEBUYNgLKqjgHOAa8d/4I7aH4f1L9pfU7vVpUGsWOkSS6VA+DvdmCyEZ7qnNIvzP1q/Z3+D1l8Bfg74a8EWLCRdMt9sswGDLKxLOx9eT+QFej0i0tMzCiiigAorwn9r79qXS/2TfhzF4n1DTpdXuLy4FpaWcbhAz4JJJ9MV8Qw/8ABbO4WPEvwxiMuTnbqe0D81NA7H6qUV+VM3/BbS7/AOWXwxt1/wB/VM/+y1nXX/BbbXNp8j4bacj9g987j8xigfKz9Z6K/Oj9kL/gp54t/aP+PGleB9Q8B2NlY38MrG40+d2a32KW3tu6rxg/hX6L0EhRRRQAVW1K6Sx0+6uJOI4Ymkb6AEmrNcd8Zbw6f8IfG90v3odEvXH4QOaAPxL/AGGLGTx9+314fvhlo11i+1Y4H8OXPP6V+2vxG+LHg74R6TFqfjLxHp/hyxlfZHNqE6xh24yBnr1FfmD/AMESfC1vqnjv4n+J5oA13YWdpaxSH+Hz3lZsf9+RX1z/AMFCP2ONX/ay8J+HJPDurQadr/hxrp7aC6H7q5E6xhkJ/hP7tefc0DPpvw34v0TxjpsF/oerWeq2c6CSOa0mWRWU9+DWvX4Fal8D/wBpT9jea41+007XfDlrBgvfaU/nWrdsNjI525+mK++/+CfH/BRQ/H28j8BePfLtvGpDNY3kS7Yr5FQFlPpJwx9CMUBbS5n/ALR//BV6P4G/GPXvBFn4FbVI9GmFtcXVxdeU7yYBJVcfdwVwe9cof+C1+hCzRv8AhXl99oYfd+0rt/OvsP46/stfCD4lR6z4r8ZeFNOudSjsmM2qPmN9qISCxBAOB3PoK/A/wj4Hj8WXXi6+hjdtJ0jTbnUE25IRQ5WME9s5oKVmfcPjb/gsl8Qde1S2g8HeE9P0dGKKIrzM8krlsYH1BFfq38MtY1nxB8PfDmp+IrWOx1y8sYZ7y3iztjkZQSoz9a/NL/gkB8AfBPjzwT4t8a+JNDt9Z1iz1eOwtDeLvWARwxyblH97Mg59hX6p9OBQJjlpa8h8A/tVfDn4kfFXX/h3omuLP4o0ZnSa1Zdocpw4Q/xbSDn6GvXqCQooooAKKKKAPzi/4LXZPwh8AqOWbW3AHc/uTX0t/wAE+JFl/Y0+FjIwdf7MYZU55E8gI/MGvnP/AILRQs3wj+HEoRiF8R4LAcDMLYBPvj9K93/4JozCb9iD4YEMGxb3inBzjF9cDFA76WPpyiiigQUnWkbODj04pI9wUbuvtQA7Ipa8Q/ab8YfF7wfotncfCPwdpPirUWbF22pXYiMMeCRtXcu7JHrXyj4Z/wCCr2p/DvXh4b+Ofwz1Lwjq0T7J7izUkKOzeU3zEHnlSQe1BVtLn6MydaVcYwa8U+Cn7Y3wn/aFvLiy8G+KoL2+gXe9jdRPbT7cc4SQAsB6gY7djXin/BQD9vG3/Zx0g+F/CNzb3Pj+5hScRyRl0t4GLDeSON3yng/1qbgkfZGoa9peiyQxXuoWtnJMwSNJ5lQux6AAnmr6urKGUhlIyCDwa/nQ1LS/jl+0Na6t48uofE/iez0kNNdanmQw2yg7sIegCg5wOma+/v8Aglf+2vrXjy/k+FHjrUn1DUY4DNol9ckCR40UBoCf4iMFgTz19KYcp+mdFItLTJPDP24rKbUP2SfipFApaT+wrhvl9FGSfyBr8hv2Df2KLf8AbA1DxUb/AMQy6JYeHhaGRbeIO8hmD4HPTiJvyr9lP2somn/Zk+KUaKXd/Dl8qqBkkmFgBX53f8ESvGOm6Z4s+J/hy5uo4tS1a1025s4WPzTLALkSbR32+aM0DuewSf8ABGH4Wm3jSPxNryupyzkp834V2mi/8Ek/gXp+nx295aatqUyHJuJL1kLDjghePX86+1aKAuzxj4U/sf8Awl+DUIHhvwbYxzq/mC6u0E8wOAOGbJA46e5r2GG2jt1CRRrEg6KgAH5CpqKBCLS0mcdaWgAooooAKKKKACiiigAooooAKKKKACiiigD8Y7ZLbxl/wWJmeD/SYIPFRVt/GGt4FV+D6PG1fs3kV+GfiTxFL8B/+Cp+t6vf4VF8ZSzyLnd+5un3oePVJV+mcV+5KsJFVlOVYZBoGO3CvnL/AIKA/GyL4H/syeKNSSYR6pqcf9l2CdS0soIP4BdxzX0Xjg9vevxn/wCCgnxM8R/thftL2fws8B2kmpWXhwzW8Nur/LcXSrummPooXCjPofWgdjgP+CUOljWP2ytBkmO5rWwvLoZ9fL/xav3br8Av+Cfnj60+Av7YXh2bxSX0uAtc6RcmZCDFJIuwBh2wwH51+/UcqTRq8bB0YAqynIYEZBB9KBMcRSbadRQI/Eez8cy/Az/gqtrusa0hjjk8V3cUhXnNvckiIjP+y6/rX7b7hX41f8FgPBx8I/tOeFfFltCtvb6po9vK0sX3muLeebzCffYYcHvg+lfrT8KvFdn45+GfhbxBp9yLy01LTLe5SZT97dGpP45zmgp9zrKWkWue8dfEPw18MtBl1rxVrVnoWlxfeubyTav0Hcn6UEnRUVk+E/Fek+OPDmn69oV9FqWkahEJ7a7hOUlQ9CK1qACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikbOOOtNjDqDvIJz2oAfRRRQAUUUVDTuAUUUhpWYFW6Z4WM2792q8r3NTW8wnhWQdGGaBCSpDEMDT1jCDC8ChRd7lX0HU1lDfWnUVoSIKWiigAooooAKKKKACkY7RS0jDcMUANbmk9utONJt70DG7l5TOCBmqmqfZ73T7m3k2ypJGyMm7G7jpn8amvLUXdu8RYoGGMjqKzL7T00/R51UkmOMsH7kiplsXFRb3P5+rq2f4G/tsQjDRDSfFKSrzjCtKDjP0bFf0N28yXEEcsbbo5FDKw7gjIr+eT9rC+m1D9rjxVdTwNbTPrMJRT6DaM/pX70nXr/w78I7bVLHTZdXvrXS4pUsofvykRjge9JSSWo5LWyO3U0Buufwr8mfGn/BYzx34Z8XXNifhrZ2cNsTE9nqFzIk24Mec7OOMce1Mt/8AgtZ4nnt2LfDLTVkzgbNSkI/9Ap8y3FyM/Wk55x6V8Mf8FLj8RbX4S3Y8IXs9jaRlrm/nt3KyNAozgEdBnNfMesf8Fh/id4iktNP0DwTpen3lxOqptmeeR+RlQpA61+kXirSNQ+Mf7P13DrGnLpt/q2iP9ohPLRu0ecAGolqzSHuX8z4I/wCCQ3x98T+KPFviT4fa/rFzrOktZG9to71zI0TAhWUMecEZ4rtf+CpH7Pvwt0/4a3/jT7Omk+MY9sVqbchRMuSdrL9WPPvXyn+wL4lHwG/ayv8ARNSk+xyXEclgsj9Qd3H516V/wVa8Tah40+MnhL4eWErXl08EDoEbiR5HdQCB9BS5m35By2urnyX+yl8M/CHxZ+LWm6P431waLonDSymXYXH90E9K+v8A9ub9gjwP8O/gnZ+NPhUsl3Zaa4N863Hnl43J+cn24rI+LX/BKPXPh38BY/Fml6tJqXiaxg+1XunqmAq4BYKRySK+Zfhl+1t40+HXhfVvCd7cNq/hzUYJLWexvGY7MqAMc9QRUyUr3iyIW6n6w/8ABKL4lW/jr9lbT9ME3mX3h27k0+4Q/wAIwHT81b+dfZlflj/wRG8RJt+K+jbsFnsb2JM9v36sf0Wv1NFbRtsRLe4tFFFUSNakpxGaTbS0GfI3/BTTwrba9+zL4juJ42P2WNZA69QVJI/Dmvzm/wCCUPi610T9qjTdIvNOtLyHVrSWOOaaHfJDIqFlKHPHPWv1a/bb0mLWv2bvHFnNuEX9myyll6gqMivx5/4J2/ErwR8If2h7LxF40vhp9rDA8UFxIMojOMEmsVu0bPZH7/r0pa5PwD8VPCXxQ09r7wn4hsNetVOGezmDFTgHkdR1HbvXB/tCftZeA/2bdAk1LxVeyGXd5cNnaxl5JZMZ2jsDWtzKzPaKK/Na6/4LZeEo5WWD4ba5KnZmuolz+FYWs/8ABbyzhljGmfCm4nQj5je6uISD7BYmBHTvTuHKz9PX020kuBcPawtcL0laMFh+OM1Zr4t/Y5/4KKS/tYeNL7w8Ph3eaH9li85763uxdQRqeBvOxdpJz619og0xNNC0UUUCErkvih8QtI+FvgnVPEmtXCQWFlGXYu2MnHA+tdXLIsMbOxCqoySe1fjp/wAFP/2mtQ+I3xGX4WeFruWTTLWRI7qOF9wubhmICgD0G386VzSMb6nFfGb9u/4y/tLfEVfD/wAOLnUNNsXcw2tjo4Imm+Y/OzDnBBH5V9D/AAt/4JDv4x0Ky1v4t+ONYuNeukEsunwsHEBYZ2l2JOck5xxX0F+wf+w1on7MvhVNc1Fv7V8aanEsk1zIgAtEZVPkoOxB3ZbvmvrjbU2YOR+ey/8ABGP4XjUIpH8Va/JZq2Xtf3Y3D03dRX3j4N8LWXgjwvpegad5n2HTbdLaHzW3NtUYGT3NbO0UVfQlu4tFFFBIUUUUANavzp/4LURzt8GfAkka/uY9bdpGx9391gH9TX6L4r5z/b3+B9x8dP2d9e0qwCtqNihvoEKbi7IM4HoeKBrc8Q/4I2/Eo+KP2edb8JylTP4Y1ZlQL/zwnXzFP/fYmr78r8Qf+CWPx6b4F/Hi68H6tbCCw8ZPFp07zEIbe5hMhjJz0H71gf8AeHoMft3u96AY+im5NJuoEOJpNx59e1cF8ZvixpnwZ8C6t4o1aZVtLC3eZlZgMlRkKO5LHAr4O/YQ+OPxc/a0/ac1vxvq2r3mmfD3SLaUR6LbkizLycRxdPnYffJOT0GcYFTfWxfK7XP0vBz70tItLVEBRRRQAUUUyRiuWwSAOg70AOxznvQzBVJJwBySa/PP9tj/AIKa6x8BviBc+BvB3hkSatZ/8fGoauhWFuM/ux/EPevhH4n/APBSL46fFTTW0+48UpotlIMSR6ND9nZ19CeT+IoA/X/46fts/Cv4AyLB4h15J74nAs7IiWTv1x06V+U/7XP7VXif9urx5pPhbwd4dmTR4JtlnaxR7prhmJAkcgcDBHHbmvkK8vLvVLo3N3eSXczknzbmYs2T6k19Sfs5ftuH9mvQ4IPD3w68O3Wqrnz9Yumc3EjEAfe7DAH61Nirn7Hfsl/Bo/AX4A+EvB0yr/aFnah711H3p3+Z/wAs4/CvX6/HDVv+CyvxQmA+xeF/D9oO7N5jj36/hX6AfsJ/tGeJv2nfg3c+L/E+ixaLcrqclnbiAMEniWONvMGe25nH/AaYPuflD/wUB+OVp8ZP2uNQ+1yTXHhPw9dR6VHBCdxaKJyZmVemWZn/ACFfo/8AB/8A4KVfs/X0mgeDNKvL3w7AsUVnaC+sxDAmAAFyCQB71+ZX7EvgTwl8av2tLbSPiOwu9PvJLudo7iUoLm45IVj3ySfrX1D/AMFH/wBgfwF8H/hTJ8RfAVrJov2O8hjudNWQvCwkO3cufu4OOKYWP1dtbqG9t457eVJ4JFDJJGwZWB6EEdRUtfEX/BIv4geIfHn7MeoJ4h1GbUn0fX5tNs5Z3LstutvbuqZPYNI+K+3aCQpkkKTLtkRZF9GGRT6KAI4beK3BEUSRj/YUCpKKKACiiigAooooA5L4t6IviX4W+MNJcZW+0e7tyPXdC4/rX42f8EktQj0X9r46fNIEefS7u3XJxuZcHH5Cv26urdLq3lglXdHIhRh6gjBFfgJ8fPAPjb9i39qi91bSvM0hor6TUNHvNpWG4hZ2wuR2OCCtBcex/QAtfPH7efxztPgP+zh4m1Nptmr6nbvpemRg8tNKpBP4Lk/hXyT4I/4LUaQug2ieK/At8NWVNtxJp0qmJmHcBsECvlL44fGT4mf8FD/jHaaXoGlX1xpUUmNL0mIEx2qM2POlI4zyfmPpQLlPlPT7240/UrW9gZxcW8onDA4IZDuyD9a/pb+BHj2L4ofBvwd4qhJK6ppkFwSTn5igDfqDX5a/t0fsJ2vwJ/Zx8Aat4bsJLu+0hjF4iuoE3GQui7pCeu3cCPSvVf8Agjb8etV8SeH/ABJ8L9Q869stDAv9PvHyRFC5CmD2AIJH1NBJ+mNFFFAH56/8Flvii/hz4J+HPBNs5E/iW+aeZVOD5NsFY59izr+Vfm7aeAfiX+y3N8NPi3FEbGHVnW+0q6hbiTGGMbf7ynp6V61/wVR+N3/C0/2mb7Q4ZGj0nwlG2kKAfvzKxaVvxZtv/ARX6lat8BfC37Qn7JvhXwzqWno0P9gWsunPja1vN9nXYw9OcZoKudx+zZ8eNG/aP+EejeNtGxELpTHd2m7LWtwvDxt7jgj2YV6hX4Y/sLfHXWP2R/2ln8GeI5J4NDvr59J1a0YkrFcbiscwHQc7R7gV+5qsGUMOQRkUEi0UUUAeYfHv9nPwR+0l4cs9E8cadJqFlZzfaIBFO8TI5GCcqR2rw/Tf+CVP7O1hMskvhO8vWU5xPqtxtP1AcCvr+igdzwXSf2FfgHo9qkEXwr8OTqvRryzWd/pufJrTT9jX4Fxq6r8JfCA3DBb+x4M/gduRXs9FAXZ4b8F/2Nfhl8AfiFrfjDwXo76Vf6pai0e3WUmCFN5c+Wv8OTt/BR717lRRQIKKKKACvLP2qDj9mv4of9i3f/8Aoh68T/4KXftLeJf2cPg/pNz4PvI9P1/WNQ+yR3TRrIYkVSzMA3HoOlfKXwd/4KNSfFj9n34meA/ixrUVr4nn0a8Gma0sIjS7UxbViKqMb927njINBVj0H/giVpMMPw7+Jmpgfv7jVLO2Y/7McBZf1lav0rr87f8AgitFGPgT45lVCsjeJCpPqBaQY/mfzrwH9uj/AIKAfGXTfix4k8DaJJL4I0fTbhrNTbxEXNxtdv3okPQEEDA9KAsfpb+0x+0h4H/Z7+Heoav4rure6MkbQ2+k7g0l5IVOI9voeck1+VH/AATf8EXvxf8A2z4/HGl6PFpfh/SZrrU7iC3BENt5iusUKn1BIOPSvj7xFdeLvHGpNqmsNq+t3sgwbq7EkznknGTnHUnHvX0n+zR+2R8XPhbZ+Gfhl8PdE0qyku79Q6yWJae8kZgCZDwfu4HsBSKsfqV/wUk8XSeD/wBjfx/LDJ5c19DDp6HOCfNlVWA99u6vzE+EXwtn8Mf8E8/jD8R5w0NzrF/Z6RbKQRugSWPcw+pkYf8AATX2P/wV+1vWY/2ZfBGn3duy3t5rEU979mBaJJI4HyM+m5zj6VgftHaDL4N/4JF+DtOW3+zyPZ6TJNGFwQZCJGJHrk80xLY9A/4I5eHZNJ/Za1W/mQo2reJLq5RsdUEMEfH4xtX3dXyr/wAEw/EGi61+x14Mt9IkVn083FrdoCNyzec7Nn3IZT+NfVtBLPxJ8I3r/AT/AIKw3KzPtgn8WXFvI7cfur3cQfp+9Br9ta/GH/grh8Obz4cftPaH8QbFPIt/EFtDdLcIcMLu1wjAf8AEJ/Gv1u+D3ji1+JPwt8LeJ7OXzoNU06G5DZydxQbgfcHI/CgR2NFFFABRRSUAfA//AAWQh8z9n7we+M7PFNuT+MMor0v/AIJbyCT9h/4eqCCUbUFIz0/0+4P9a88/4LENt/Zx8Pcc/wDCSW3/AKLlruP+CVq+X+xX4Nyc5uL8/wDk3LQVbS59cUnmL/eH51XuJTuAVhjHrUKfKDk55oGo31L3mL/eH50nmIWwGGfTNU1Xc+dwHHrUsMOxiTyc9aBuKXU+S/2+P22NW/ZKXwtBovhmDXrrWDI0kl8zxQRqvQCQDG7OflznFWvhPrfws/4KSfANdS8T+GrKW+DfY9St4yPtNjcKAfklxuCkNkZ45PpXY/twfs7WX7RnwG1vRmiX+27CNr7TLjblklQZKj2YAj8q/O7/AII6+Przwv8AH/xL4MuDKsGs6a0pgJIWOeB+SR6lSw/CgW6NP9sL/gmTL8A/Dd18Q/hn4puE0XSoDJe2+qXghuLf5jhoZF27hyoC9c565r4q+Gvj3RF+Lmka/wDFOz1Dxho0U4a+glnJllII6k8kDA+XPNfe3/BWj47XPxC8feGPgd4Qmnu7qO5jOoxWchYT3UzBIbdlXqV4OD3avqj9nz/gnn8N/BPwF0nwl438K6X4j12QPcajfSJlzM/UI4wQFAUDtxSsK9ix8G/29v2dPGmk2+haR4g07wvb+WLePS9WhFmpGANgDDDccd881+bnjK+8P/ssf8FGItX8J3trc+FYtXhuo5LeUPFHBcqvmpuHGFZ3H4V9W/Gf/gjP4Z126lvfhz4ouPDg2grpuoKZo/MyTkSDkDBAxg9OtfDPxe/YT+Mfwj+IGm6Zf+GbrWlvJ4xb6ho8Tzwznd03f38DJB6ZFAXP6B7WdLq3jmiYPHIodWXoQRkGpazfDdvJZ+HdMglUrLFbRoyt1BCgGtKmSVdV0y21rTLvT72JZ7O6iaCaJhw6MCGB/A1+FPxj8E+IP+CeP7YlrqehGZdKhlGo6dIwIF1ZyEh4vfbhgR7V+8FfNX7b37Hdj+1t4HsbaO+/srxJo7SS6ddkfKxYDKP/ALOQKAPavhf8S9B+LXgnSvE3h7UbbUbC+t0mDW8gfYWUEq3oQeMGurr8FvDOu/tCf8E+fHGoWcGm3lpaNuMqzQvLp90oYgSqQCBnbjseK+ofBv8AwWysLXw/bJ4q+Hl5d6xj95Npl4kcLe+1gSDnP6UAfqRRX5uWv/BbLwRMpMvw61uHnH/H9E3/ALLTLj/gth4O83Za/DfWpywwv+nRg7vTAXmgD9HdS1C10qymu726hsrSJS0lxcSBI0HqWPAH1r8xv2o/21viJ8a/jdafCX9nbUZp7GRFtbzWNPh3F5izCR1kH3YlXHzccg4NefazaftI/wDBSbXgsMVz4N+G63DKFuyYIYwMNyBhpWww7beOtfoT+yf+x/4Q/ZR8JSWGjL/aOt3hD3+sToPMlbaBtX+4nGQo7k+tAHT/ALNfwXl+A/wtsfDd3rl94i1R3N3f6jfztK8tw6qH27jwvygAf416nRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH5H/8FfP2c7zQPiFpPxj0KJ/s2pJHa6m0KEmC5hAEcxx2KBB/wCu1/ZT/AOCtnhjT/Advofxe+2WmrafGsMGq2Nq1wl3GqhQWC5IfIPPTpX6VeIPDumeLNHudK1mwt9T065QxzWtzGHR1IwQQa+MvFH/BIz4KeINcur+1Or6PFM2/7Ja3A8tCeTtyMgUDueGftaf8FU7bxl4ftfDHwQe+a+1FjFc6lNaPFKgPG2NCMknPWvRf+CWf7J/iH4aw6/8AErx5pstn4k1keTZLdnM3kt87TEHlWYttwey17n8A/wDgnr8JP2f9Yl1jS9Lk1rVycxXerESmAcfcGMD6+9fTNAXPzE/4KDf8E2Nf+IHjS7+I/wAK7dbvUL9hLqeiq4jYyjJM0R7k/KNvtmuB/Z/s/wBunwhrmjaDbaRq8Gih44t3iFE8iOFTzuYkkccV+vNJtAYnuetAiO2837PF5+3zto37em7HOPxqWiigD4h/4Ktfs+6j8YPgjp2v+H9PfUNf8M3Zn8mFNzy2zqRKvvjCnH1r4q/YR/4KIT/sz6XdeD/HVtqWs+Ew+bRbcbp9OYHDIFbGRwPlyMV+2LqsisrAMrDBUjIIr5i+In/BN/4F/EzxJPrmpeF3tb64OZf7PuXgR2ySWKqcZ56+woHc8K+J3/BZTwHp+iIPAHhnWdb1qVtqRatbi2jGe/yuzGvJfhT8A/jb+3p8UrTxX8aF1HSfhvby/ak0+4JhSVScrDFH124xliBwa+8PhV+wn8FPg7dC70LwVZy3yvvW71HNzKhwPus+cDjt6mvfEjWNFVFCKowAowBQIy/CfhXSvA/hvTtA0Oyj07SNPhW3trWEYSNB0ArWpkalQQcAZ4xT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBD1qrcapaWsgjmuYYXPRZHAJ/OrLLur4s/bU/YI8T/tM+MLPxP4d+If8Awjl3aWK2aafNHKsT4kd9xdH4Pz4+72qHfoXFRd7s+zGv7aOJpXuIljUZLFxgfjXmHjr9qT4TfD1pIfEHjvRLKZYjKYGu0ZyuSOFB9Qa/Ntf+CWv7S0NnNYJ8TdMFi5yYv7bvNj8YyV8r0FQ+Gf8Agi78RdWvi3inx5oVjBnmWzWa6lP4Oq/zpu7QlZHh/wAZ/FehftQftpaRc+BLO4ubLUdTt4FXysM+yUlnA/u7T19jX70afbrZ2FvAq7VjjVAPQAYr5X/ZR/4J1+Bf2X9XbXkvpvFXiUJsi1G8gEQgB+9sQMcZ9c19YbaSj3CUjzLxr+zJ8LPiPrR1bxL4G0fVtS2eX9pmgwxXJODgjPJP51y91+wr8BLyQPL8MNEZgMDCSLx+DV7tS1XKhXZ4r4a/Yz+Cng3WYNV0f4daPZX8BzFMsbMUPqNzHmvW9Us5LjSbm2tysbvEUXI4GRir1G2iwXZ/Pb+254a1z4W/tMapeSMbC/uHF9btCcbRuKAg/VD+dekfsCrqf7Rn7ZWh6z4slfVZtMtvtLPN8wXyx8g59/51+nH7Vn7C/gf9qWxFxqTS6P4jhj8u31W2UMwALMFYHqNzH865v9h/9guw/ZN/tPVrzWf7d8SainlSSLEFjhjByFQ9TnvmoUWlY0ck22fWVxBHcQvDKiyROpVkYZBB6g1+Tv8AwUk/YCnsbub4i/DvRli0yKAtqen2oACtvZjKo9wQPwr9ZmGar32n2+p2c9pdxLcW0ylJIpBlWU9QRTsyEz8Of+CUnxOHw5/agt9LuGaOz8TWr6cVP/PRTvTPvkH86/c5a+T/AAz/AME4Phx4N/aAtfino17qFjc207XMWixrH9kWRhjcPl3D86+sKEne45NMWiikqyBGz2pPmxWH4q8Uf8I3ptxemFpktk82VVGTs56e/Ffm/wCH/wDgsbcp8WpND8QeErKDwt/aDWovbXzFuIo921Xbc5UnueBWejdjX2cuXmPsT9sXUbhPgh4rsIoleW802aJeD3HPevxS/ZU/ZC8TftZeKvEGiaBqen6TJo8Annl1DeVO5iqqNoJzlTX7WftR67YzfArVPFdtOl3p66dJJG6fMjq6cGvgT/gkX8X/AAT4B1P4lx+I7630a7uTFdLqN7MEjMILDy/rkk/jWcdGyn8KPBvG/wCzL+0P+wrqyeKrE3Vhbx5/4nvhy4aWELn7soxwODwR3619sfsp/EDwr/wUc+Fet+Evif4eW48SaSFeXVIRtLllC+dH12txjBz0ryL9vz/gpFF8QIb/AOHHwzeK50eVvKvNY2nM3YrHk42+5Fe9f8Ep/wBm3W/hL8Or/wAV61cW6v4mVJYbWJw5WLAwWx0Oc960Yr6H5eftdfBGx/Z7+OGt+D9MvJb/AEy2Ie2muHDSlDn7xAAJyD0Aq1+xh8PND+K/7Rfg3wr4ksv7Q0PULl1uLfzHTICE5BUjByBWz+3/AK7P4i/ax8dPMqKILz7OgjyFCqB7n3rrP+CXXh6DXP2xPDC3DSBbOC4uk8sgfOqcZ46c0CP0e+MHgXSv+CfPwb1nxl8FPCdskr3kLara3k0kweEZBIJbIwPfHtXtn7LP7Tfhr9qT4djxJ4fZop7eQWt/ZyDDQT7Fcr7jDDBrd/aE+HcHxT+Dfivw3cKzreWMiqqHB3AEjFfjt/wTz+NWo/s4ftQDwfqVx9m0TWLptNvop87VlBIRxzgHOAT6VSYnqj90aa0gXqefShWDqGHIPIpdoLAkc1RmeG/tc/HG3+C3wQ8T6zIwgvGtZLe0395GXAOPxr8UP2SPjF4N+HPx4g8cfEm0uNegt1kuI8jzGNwfuuQepHavtz/gtb4ovLbTfh/oUUjx2d21xcXGAdrFNoQfq36Vi/sA/wDBPj4U/HT4JaV468WnUNS1O4nmje1trvy4UKyEAFcdcY71NjW9krHrtp/wWW+E/mIs+h65HGTjcsQOPwr6E+AP7cHwr/aO1J9L8L6y8esLkjT76PypXAAJKg9ev6V5z4p/4JU/ATxJbsItF1HTJRHtRrO+ZF3Y4YjBzX5g/s5eHZ/hj+3r4V8O2dy0Y07xM1iZQ3Lxhiu0nvkCmQ9Xof0B0Ui0tMkKKKKACiiigApDyCCMilooA/E//gqL+zhN8E/jZB4+0H/RtC8RSfaQ0Klfsd2pOQMdBwG/Gvaf2Zf+Cu2heH/AOm6F8WbDVLjWbP8Acf23psKSpcRAAK7rlcNnIIAxgDvmv0e+I3ww8L/Frw5PoXizR7fWtLmBDQzg5GRglWGCp9wRXyl40/4JE/ADxRDEml2Wu+EigwW0rVHlLck8/aRL69sUFXVjUh/4Kufs7TQiT/hJdRT1R9KmDD9K5zxV/wAFgPgZocLtpcPiTxFKE3L9k08RJu5+UtI64/I9axov+CLvwbU/vPGHj6QDov2+zAx/4C11vhf/AIJIfs++H1K6hpmveKstu3arrEiEcDj/AEfyhjv0zyeaA0Pg3xz8Svi9/wAFN/irBoHhnTW03w3CxdbTePs9om7madx958YG0kjgYHJNfrZ+zJ8BdN/Zu+D+i+C7CVbqW1TfdXioFNxM3LOf5DPYCuo+Gfwh8GfBzQE0XwV4a0/w5py8mKyiCtIcY3O5yztgDliTxXXYqUtbg3cBS0lLVEhRRRQAUUUUAeXfFz9mf4afHW+srnxv4TsddurMYimnUhguT8u5SCR1qDwT+yj8H/h2ki6B8OtBshIxdt9oJjkgD/lpuxwBXrFFAHKL8JvA69PBvh8fTS4P/iKc/wAK/BckZQ+EdD2HqBpsI/8AZa6migDzPxN+zV8LPF1uLfVvAWg3kGP9W1kgH6AV1/g7wZonw/8ADlloHhzTLfR9Gs12W9laptjjXOcAVuUUDPxt/aq/4Jq/EL4XePtR8a/CuCTWNEa6N5a29hIUvLF2YttVR1APQivNviR8bv2oviF8M5vhh4t0bxBrFjcPHuF3oL/aHKNkAy7ckdOTX7t0xreJ2DNGjN/eKgmgfMfKv/BNb4A69+z3+zqmmeJEEGrazqD6xLa87oN8USBG9wIxn619XUUUEhRRRQAUUUUAFFFFABRRRQA1q5D4jfCXwb8XNJGm+MfDen+IbRc7FvYQ7R57o3VT9CK7CigD5O1P/gl7+zzqUm9fCFxZHuLa/lAPP+0TXtnwf+APgL4EaQ2n+C/DtppCPxJcLGDPJwBhpMbiOBxnFei0UDuUtX0Ww8RaXc6bqdnDf2FyhjmtrhA8cinqCD1rlvhh8FfA3wZ0+4s/Bfhmw8Pw3EhkmNrFh5GPqxySPbOBXb0UCCmk/MBnAx0p1JQB88/Ez9gv4NfFvx83jHX/AAwG1x5VlnktZTGk7g53SKOCT3PfFe/2FjBpdjb2drEsFtbxrFFGgwFUDAA9sVYooA+CviN/wThufGH7aWnfFeHU7X/hFpNQi1XUdPlHzmaIAhVHTBIH6196KAoAHSlooAKKKKACiiigAooooAKKKKACkpaKAPyK/wCC1/jtNQ+IHw78KxfONN0+41F8dN00vl4P/gP+tfJ/xC/Y28ceAfgb4S+KpgF/4Z1y1juHMHMlrvXcN47AjvR+17He3n7YHxCg1r/Wv4mljkx08kzEDH4V+/Wm+EdH1n4Y2nhq5t1u9DuNMSzeB+jwmMLj8qCuY+H/APgixCF/Z28YyGPa7eKZdp7Ffslr0/HNfc3iT4c+E/GdzFceIPC+ja7cQgLHLqWnxXDoASQFLqSBknp61n/CD4P+GPgb4JtvCvhKx+waRbu8ixlixLMxLEnuea7WgVzFtfCGhWMKw22iadbxLwscVpGqj6ACs6H4W+DrfxBDrsPhXR4dZhyY7+OxiWZc8HDhc11dFAjL17w5pXiiwNjrOm2mq2ZYObe8hWVNwOQcMCMivIf2xvgjN8dv2cPFHgzTF2X7wpPYxR4RTLEQyJ9DjGK9yooGfzs+CNa+P37P91qOj+Fh4s8OlblmubbT7KQxNKAFLfcIPCqM+1eiab+0d+1/JEb631bxzPHE20lrB8Z64xs561+8VFAj+eb42eP/AI/ftFwaBB490DxJrCaK8xtn/saZWHm+WHBwncRrX6//APBNzSdZ0P8AY28BWOv2lzY6lELzdb3kTRyohu5jGGVgCPkK9a+mqKACiimSSeXG7Bd7KM7R1PtQA+mH74r4J1f/AIK3eGPBPi/UNB8afDnxJ4dltJ3iEjlWZ1ViA2xgpwcVzfi7/gtV4DsVKeG/BOsavMR8rXk6W6Z9wAxoA7f/AIK+WbXX7M2mOgLGDX7aQ4GcLskBY+wyOa1P+CW/jDQNP/Y38K2t1rmm29zDc3qywy3cavGTcyMAyk5BKkHnsQe9fnT8e/2pvi9+3x4k03wzpmgzDTVkXydB0aGSVNxY/vJnAJ6EDPA4rstJ/wCCSvx7ktY2WTw/YLKA7QyalKvlk9sIpBoKvpY/Ya8+K3gTS8i78Y+Hrbv+/wBUgT+b1h3f7SXwf099l18UvBNs+M7ZvEVmp/WSvyq/4dA/HVlC/wBteE2DcnzNTuxj24jNV5v+COnxyjYBNW8HOCMnbqV0B+sNBOp+rFn+038G9SvorSz+Kvgi7upWVI4bfxFZyMzE4CgCTJJPavTlxtBXkHnIr8afh5/wSd+Lnhz4veDJPEtvot34ajv47i+vtK1B3eJEO7BDqp6qMYGOetfsrDGIYUjXJVFCjPXjigAkVWUq4BVhgg96/n4m+LWqfsk/ti+Ntf8ADtrG91pupahZfZ5h8qq7sMEeoNf0FHAGTwBX8/8A/wAFJPCsPhf9tTx/aWaeZ9ruLe+EarndJcQJKwx/vPQNOx7/AP8ABL34V3H7QPx+8WfGLxxHNqs2jzJJBPNGWil1CRi2VboTEoQ4zxvU1+wNfOP7AnwFj+AH7OPh/SpY9usaov8AauoswwfOlVfl55+VQq/hX0cM4560CFpjRqzAlQSOmRnFPooASloooAKRvbrS0UAZ2s+H9N8R6fNY6rYW9/ZzDa8NxGHVh7g145ffsO/AjUbmSef4ZaE0shyxEGP617pRQB883H/BP/4B3Egf/hXOlxYGNsSlR+Wa3vCn7GvwX8F3C3Gl/D3RY7hW3rNJbh2U+xNe0UUAQWtjb2ESxW0EcEajCpEoUAfQVNS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTWUt3pVGKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooATijigjNJtoELS0g4paBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGJ4ltGktAUCvlgrRuMq454PtzX86n7WmiR+E/wBonx3ptughgXUZG8teANx3Y+mTX9GWvxzSWeIEZ3Vg2F68V+EPx6/Zz+J3xk/as8aW2j+Ctal+1axLGl09m6wLGGwHZyMdOetY/budN700jK+FP7Z2s+Hfgrrvw08QXN1e6PdQslpLvLmHKgBcE9OO3rXC/Bj9lf4n/H6O5m8DeF7rVbBZfKkvZJFhtwwwcEkjPBFdZ+0V+wl8S/2a7Sxv9X059W0qeATTajpsbPFatuI2SHscDP41+gX/AARi1yW++CvizTzbEQ2esEJdZJ37okJHPTGadtbom/u2PjiH/gk3+0RJw3h/SQqcDOrwqfWvav2b/wBhf9q74aeM9Nul1y18P6RYylzBdauZ4X4xjy0J4+mOlfrd1o2iqszO5+BP7Rn7Hfxzh+Luu3uueFpr6e+llvTqNh+8tmjyfmBySOnQ81o/8ExfEmkeBf2stMn8QahBpiG1uLcS3DhEEhGMEn6V+72oWKahY3NrISEnjaJvowIP86/Fv4/f8EsPiv4f+IF4/gnTF8VaLdSPcxXUU6xvFuc/I4OOQMHI45osw5j9m7XXNM1C3E1vf2txCw4dJVZSPrmvwl/4KIeAz8Hf2sb+/wBNaMx6g0etWxhYfLhyOx45U1Zt/wBgf9qXT4vKttD1q3ixjy4dWwPyD1k6x/wT/wD2ktX1W2/tPwbqt/PIBGt1cXQmEa56Ekk4o5Quj9t/2f8A4i2nxY+DfhLxVZv5kWoWEUhOc/PtAYfmDXoVeV/sv/CVvgf8CfCXg2Uk3On2gE+WziRjucZ9Mk16pVEnxt/wU1/Zv1v48/Bu2uPDVtHdavoMzXghI/eSR7fmVT+HSvgL/gn5+2pL+yz4ou/CPjATReD765ZrhWQl7GfhScenAzX7iMocEEZB4I9a+Jv2xP8Agmn4a+P0kmveEntfC/ijGZNsWIbk5J+bHQnPWmNM+mNN+O3gbxF4IuvE+j+J9NvtMitmuPNjuF4wuQCM8H2r8Zv2P/DEnxq/b+tNUjdzb22r3GrySBv4VZivPucVBqX/AATp/aP8MTXelaf4buriykbYz2N7iCUZ4bGeK/QH/gnL+xBqf7NOm6x4k8ZQ2/8AwmGpYiiSCTeILfap2n/a3bs0BdI+4F6U6kXvS0EhRRRQAUUUUAFFFFABRRRQAUlI1GTQA6im5NGTQA6ikWloAKKKKVwCims2KTdRcdh9FNzS0r62ELRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQB8+fGL9hH4PfHLxxF4u8T+H5W11SplubO5aHz9vTeBwTwOevFe96fYw6XY29nbLst7eNYo1JJwoGAMmrFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNb0p1FAHD+NPgl4B+JFz9p8U+D9H1652hPO1CzSV8DtkiszQP2afhR4Wk36T8PPDmnvnO6DTolOfXpXpdFAGfp2gaZo+PsOn2tnxj9xCqfyFX6WigAooooAKKKKAE61w3ib4F/Dzxp4gOu6/4K0LWdaOwG/vrCOWY7AAvzMCeMDFd1RQAyGFLeJIokWONAFVFGAAOgAp9FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIGzkelAC0UUUAFFFFACU0RqrEhVBPU4p2KNtKwGdr+g6f4n0i70rVrSLUNOu4zFPbTqGR1PUEVy3wo+Cvgv4H6Pe6X4I0K30DT7y4N1Nb25O1pCAN3JPYCu620baYAtLSUtABRRRQAUUUUAFFFFABRRRQAUlLRQAijaMZz9aWiigAooooAKKKKACiiigAoprGmTSFIyQQD70rjsPasrVrq9tYZBa7DOUcxeYhZSwGQCBzzVibVI7aN5ZjiNF3Flya8xuv2pvhbY+MLbw7deL7CDWrlxBHaNKCS2eAcdDS5kUovsflb8Tv+ClP7SHh34lXsk9zZ6Dp2n3kkA0v+xQtvMquQAzyKZM47hhX2J+xP8A8FLNM/aE1ODwj4ytLXQfGUrFbf7KW+z3QAzxno3XjNfUvxuXwKnw91i88dWem3ehR2zPIL5EO/AJAUnnP05r8df2H/Aum/Fr9uKzv/Cunf2T4Y0i8l1RIkZjsjXKquSScE+9HMPc/c9aWkWlqjMKSlorN7gQnLd8Uo+Udc05lHpTSo2nis2mV5FaTUBHdJDsZi3O4DgVdpqRqOgp1VHTcTFooorYQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGpKAHZozUbSKvGaa0yqcE4NA7MmyKMiofMywA5qSgLDqWkWloEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJu+bFLSbfmBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARc4GetLRRQAUUUUAFFFFABRRRQAUUhNG6gBaKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopCaTdQA6im7qN1ADqKrtclZthAAxnNTBwwyORSumOw6im7qNxphYbIpZ1+bAp9N7g04Gp5lewhaKKKoAooooAKKa27tj8aVc9/wBKAFooooAKKKKACik5paACio235OCv5U7caAHUVBcXUdrG0ksixxqMlmOAPfNZ+j+KtJ8QSyx6dqdpfSRffS3mVyv1ANK47O1zXopBmlpiCiiigAooooAKKKKACimsaQMTQA+io2UNyaRWCqcA0rjHSNtqlNIJAAx43Y6UXFy7ZVRj3NVft0FrG0l1JHbQqctLMdq/99E4FQ9zbkaVzkvjpqk/h74W+JNSglMMdrp08jFexCHB/Ovw5/Yz8DXPx4/a08PW9/vukXUH1K7nJILKpzgkYxzjpX67/tlfHDwZofwB8ZWI8V6O2oXlhJBHbx3aSOxIxjCk81+cv/BKn4pfDj4R+PvFmveO/FFj4euHtFgsftiNhlLZYhgD7DFOwuZ2PX/+Cm3w5+PnxK+IkGj+GPC+vav4Bt7WP7PFodmbiN2HUyMvzbvY8V8mfCf4W/tQ/ALxBJrvgXwT4w8PanNH5Ek/9g79y5ztKyowx74r9oPA/wC2B8GviR4mt/D3hv4gaTq+s3BKxWcLsHcjrjIFex7RRZkcx5F+yn4s8e+NPgnoWp/EnR5tG8VupW5huIxG74OA5QAbc+mBXr1JS1RIUUUjZwccmoe4hGpjMN3JqFrhuQ67T2pjEsuTzWbkaRjfUthwFznNOByM1mbmVsA4XvV+3bctNSvoKUXElopCaj85d2M81pzW0JJaKQUtWIKKKKACiiigAooooAKKKKACiiigAopGpM0AOopFpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQmmRuW3ZGMGlbO8elIuBnnk0rjFdgtRMwdThsU25kVcDcKrrIA23PWolNI0jHS7HAfvMA7jUzxArubgimmN1TMYy1MW1lkYGV+PSkpN9A0BZhHIBjIIq3GxfJxikjgVccZqWtFtqQ2ItLRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKTIFLSYBqG3cAzS0mMUtUgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJ+FAC0UUUAFFFFABRRSUAMaRVcKQSTTtwb7pyPavlv9vvxV8TfCvwnOo/DW4kgvUfbOsMReUr6rgV+c/7Of/BR/wCJX7P/AImnsvHwvvE+kXk++5h1Albi3PTMZPb2rPmd7G/snyKR+3i06vGPgV+118M/2hLYDwrr8MmorGHl0+Y7Jo8jkYPXHtXsysG5HSqujCzQtFJmjPtVALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4DWqB0VmDsvK+9TtUUi+ZwGxRdFIGkPy7Bu5wfalkZlU4GabH+7BGO+KZNcCNsE5GMk1MpLYpK7siRWVmxgE4phmK4CruFQx3iTbmi5PQ0xWkt4ZHbjniue7K5WWWmbcMJkVJG24Hr+NV7ZpGj8xn4PQCrUbCTkc0o3uQ9NB2KXpRRXQrIgKWkpau6AKKKKLoAooopgFFFFABSUjNggUkjBRzQBm6xrkGixma5cLCEZi3QDAycmvyr/aD/wCCv3jXRfHmoaR8OdH0WPSLOVrc3erW8kzyOpwSpWVRj8K+jf8AgpJ+0TJ8K/hNf6XZFRfasPssMkRO5M9T19K+Tf8AgmD+xboPxubVPiJ49szqmjWc/kWWmzf6u4l6s7+oHp61kpcz0OicFGKvuY/h3/gsJ8adK1S1n17RvDupaYxDSRxWMsEjL3CMZSP0NfpX+yv+2B4N/ao8NyXehu2n6xabVvdJuiBLExGcr/eX3FTfGv8AY/8Aht8YPh3L4cl8MabYSQQGOwubSBYntmxxggdM1+Py6F4g/YF/ag0C5k1Uzw29yGufIY/Pb79rKw78UnJp2MktD9zfH3g5fG3hm+0uWd4vtEbR742K9a/Fv4paP8VP+CfPx1k8UaHczf2ZcTt5bzu0sEyk8pIMjJx0r9ltU+JFufhXL4z0eE6patp/2+3jiP8ArFKbgM1+dfw9/aEsP+CgPiTXvhh4w8OQ6VdTxSGym3btjLkbvZhTWptFvlaPtH9l39rbwn+0d8PbHWbfULXT9Z2AXumyyqrxOByQCeldT4j/AGnPhV4R1NNO1fx9odjescCGS8XdnOK/CP8AaM+AXjL9kD4jNo1zfzwJOhktb+1kZBNHnpkd69J/Z9/4J9+N/wBp34Z3njXSfEumw/vHAs7xmknlYDPLds+9aXtoZ8q6n7o6L4i03xJp8d9pOoW2o2kgBSa3lDqQenIrSVt1fiB+xP8AtJeKP2RfjrN4C8ZtdR6HeXa2N5ZTksLeUHasi56D+lft1b3CXVvHNEweKRQ6sO4IyDTM2rE1FItLQIKKKKAGSNtUnBOPSo4ZDJk7So9GqSTO044NRx7iuCee5oK6Dt7buOneobicx4xxUoUAnB+tQXFsJmC7yD2qbFxtfUpSSC4BVz9McV8l/wDBQH4E/Ef41fC2Cy+H95cvd282ZdNinEInT1JOP519hwWcUPQbm7k1PtA6DFLlZpKotkfzxfED9hv43/Dnwzf+IPEvgq40/R7NPNuLqS9hdV7Z4c12P7H3/BPrxN+1hoeo65b63Z+HNCtZ/s/2m4iaaSRwMnaoIGPrX6G/8FaNc1fRf2abiC1uJBY6jfQ29xGqKV2ZycnGRz3rwT/gl9+178Lfgz8L9S8HeM/EY0DVJtSe5ie5icwMhH95QcfjVGR71+yX/wAEvfD/AOzr4+j8Za14kbxZrFpn7Ci232eKBiOXI3Esfrx7V9yV8nfFb/gpj8EPhtoq3tj4jXxdO52ra6KN7A/7ROMV9FfDPx1bfEzwHofimzt5rS11a1S6jhuBh0VhkA0yWnudPRRRQSFJS0x85wOBjrUSXUCGaMSfMeoqqobcfn+X0qWSUN8vf1qqrBiyjj1rme51QTsK17BCJHeRFjjGXZjgKPUmuF039pX4V6l4ui8L2XjnRrjXZn8pLGG5DSM/oPeuA/bZ1C78K/s3+OdRsbl7KcaeVEsZwwycV+If7L+oXcX7Rfw+njlYzNrMDF+5y3PNVDW7Imtj+klulQxxISSRzRdTGOLI65qJWM2B90HjPfNaPchLQuKQRxTqpxXEKziE3EYlPSPeNx/CrS9xnJFarYgdRRRTEFFFFABRRRQAUUUUAFFFFADWrL8SeJdP8J6Rc6nqc4t7O3QvJIecD6VrVm614dsPEEPk39utxF3jflT9R3qZXtoONr+8Yvw5+J2gfFLR5dS8PXTXVrG/lszRshB/EV1lUdJ0Ww0G1Ftp1nDZQD/lnCgRfyFXqI3S97ccrX93YKKKKokKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKSpcgFoqDzG8wc4HoamVg3SlzALRRRRzAFFFFHMAUUUVQBRRRScgCmtnacdadSUuYCH55OSdgHrVW81D7MuI0aZz0Va0KaI1U5CjNDXMUnY5/ydS1GQGSJLaI++WrXsbBLVMZaQ+rVbpaSgkVKbkrCLS0UVoZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0maWoyytk4zipbAfS01cY4GKdTQBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooorN7gFFFFWtgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbfuG3GO+acM96N1LQAUUUUAFFFFABRSZpFbdQBHPbxXClJY1kQ9VYAivn74/fsM/DD9oFWm1rShYamEKJfWACOueenQ19CmlyKnTqUpOJ+WGrf8ABIvxh4F8UWmqfDb4iLZ+W+RLch45UXPTK9Riv0y8EaXqOi+ENIsNWu1vtTtraOK4uUziRwMFhn1rYmmS3Qu5wvSvFf2kP2sfCn7Mej22oeKLTUZLe6JSF7WHcGfGQpOe9S7GnvVNEj21fl607Ir8m/G3/BajXFv0/wCEY8AWaWQyH/tS5YueeCNnTiuI17/grt8aPFVq0OheGNL05mGPMsoJZ2GenXoaOZk+ztofs3urC1nx14d8Oso1PW9PsCxwBcXKIc/QmvwV1j49ftMfEC+l1F9U8XMznGy1glSIAnpgDArx/WfEnijUfGUVp4t1bVXuUukW4S6lbemWGeCaLsfIf0x29zHdwpNC6ywuAySI2QwPcVLXIfCKOzh+F/hVLCRpbNdNgEcj9WGwcmuvq1sZvcKKKKYgooooAazFVyBmlU7hnGKKKAFooooAKKKKhp3Aa1QrEyyFg2QanavIv2ivjvL8B/B8uuR+HL7xCUUsYbMDjHqazlG2rNYRc3aJ6w3TOMmqs0EnzOi7i3VTX5nWf/BaaBruRLj4Z3gjVtp2Xilh9QRW4v8AwWj8Lxsgl+Hes7T1KzxcfmaFFNXC7i7H6Jww+VtATaT1qw0bOrKwytfnVcf8Fp/BUHX4ea+Sfukzwj/2aoT/AMFrfB8nEPw61xjj+K6hH9arkQ25Nn6NoiwqIwDzU6LtHTFfmyv/AAWr8LGPJ+HGsb8fd+1xfzr6W/Y//bLtP2tLTWri08OzeH001kUpPcJKz7gT/D06UK0WQ4vc+kqWmr3p1DICikJpN1ADqKr3N19nUMRnJxUS3LybSQFDexpXRXK2XaKjjYHODmpK1WxIUU1pApANLTACu7mquoRrJEQV3MRgDvVuq91hVLkdFPPpxSKjufkR/wAFari3tdQ8PadHOGuLmZpBCzZKqOOfxNfd/wCxj4Z0/wCCX7JvhManPb6dbCz+33M7ttVd/wAxJJr8wf8Ago9qUfi79ry20wSPJbolvCBnld7jJHvX6/3vwh0zxj8CbXwJPNNBp8+kRWfncNIg8sDd2BNYRWh0VHeVmeN+Mv8Agp98A/B2qy6dJ4ml1KWI7WfT7Z5UB9N2MV+Uf7d3x68K/H74uJ4g8I/aW09YmjZrqIxkknPT0r7isf8AgiX4RS+eS9+JOrXFqWJEMOmxxsB6bzIc/lXxn+25+y34S/Z0+NHh3wT4T1e+1GO+gRrltRZC0Ts4UfdA4xk9K15btM59dkeufCT/AIKkyfDr9nu1+H0/hCTVtTtLRrOK7afEewggZHXjNfMn7O/xqn+Gv7R2geOB5WnRHUM3SICUWNz8w6+hr9ZvhP8A8Eu/gXpPgLSk1vw9N4j1Oe3jnmvLu8fO5lBIUJtAXnvn618Rf8FQP2WfAX7O994VufBGlS6TDqRkSaHzmkQkDIxnkH8adik2Uf2/fjRD+1v8aPD2geBbZtYNuv2eBIR8zuxH6Vwfh/xR8ev+Ce/iy2Sa0utHtLoiV7O6UvaXI7+wPavbP+COfwgsPFfxQ8Q+M78NI+gxLFbJtyvmP/ET6gCv1a+Knwh8LfGbwpd+H/FWlQalY3CFA0iAvET/ABIexpWYXPwP/an/AGjNJ/aF8TWPim28N/8ACPeJsD7bJE3ySsMEN9eK/bP9ivxtdfEP9lz4ea5fS+fez6aqTSYxlkYr/ICvhj4g/wDBFe6k8TxHwd42ij0GZi0qanCfNgGeFXb97jPWv0V+APwhtvgV8I/Dnga0umvYdIt/J+0MMFySST+ZNUiWz0BadSUtMkKKa5IXjrVOC6mmaTIwV4wRx9aVx2LMkojUs3QU1ds8eRnBrO17xFp3hm0e71O+ttPtEQs811KsaAD3Jr5l8bf8FNPgP4JvLm2bxPLq1zbnY6abbF0LezHGaYz6njTEjpu+X0qRhtwcZwK+avgP/wAFAvhP+0Brk+kaPqcuj6kmDHDqYWLzx/snpXuXi74n+EvAPkDxH4k0zRDMpeIX1ykZdR3GTyKBm/8AavkJ8tt3OFA61+Vn7an/AAUl+LfgL4lXnhHwhaQ+CbawZo3vryyW4e65+8vmIygfQV+g8n7VXwfjbDfEjw4D0x9vT/Gt3S7T4d/E5X1Owi8P+KASC1xEsN1tz0yecUC+R+GHxU/bN+Ov7Q/g0eG/EVy2saOf9YtroyATN2bKRZB+hFeFR/DXxfMpMXhfW5OxMenTH/2Wv3X/AG0f2mE/Yx+Huk6p4a8HWGo3OpXn2YQlPIt4/lJ3MUxzXy98Pf8AgtbbeY0fjv4eGFfMCi48PXiyBR3JSQ5b8DSKPzJPgPxXpDxS3HhjVYMOCvn2Eqhj6crzX77fsEa74w8Q/sy+FbnxraCy1NUaKGPyvKbyF4jyuBjisr4W/wDBQr4D/Gi+tNMsfFEdjqVyQIrHW7c27lz/AAgtlSfoa+moyrRqyEFSMgr0xTE3pYfRSLS0EBTJPu05qjk5HXBqZPoUihcKVkUhsccVQVmS4OG6nmrd35qnLqpAHBzVCHzGZ2KqOeMGuV7nfTty3Z8//wDBRS6Mf7J/jT5vvWyj/wAeFfjH+yPateftIfD2EDLf2vCT9Ac1+yH/AAUqzF+yJ4qYfKzKgOPTcK/LL/gmnodt4h/a88HR3sC3MUJknCv0DKpIP4VpTWjOWUk2rH773EYMLYHvWP4mlnt/DN7LbO0cqwSMGXqCFOK38BuCMis/X4l/sHUEx8pt5P8A0E1bWpmmfz9eD/jL400v9quy1E+JtVeb/hIlidmu3IKGcKVwTjBHFf0KowZQwGMjNfz1fBH4e3PxM/bO0rQ7dd4bxE88vpsjlLHP5V/Qso2qAOgrRbCluLRRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmNIFkVT3p9JQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANZiO1KrZpaSs3uAjKrEEjmlHtTWYetOXpSW4C0UUVfKAUUUVDASjIqKWQH5c9e9RQeYGZWO4djVcxVtC3RTVp1SSNbPam7W3DPNO8xem4Z+tKrBuhzQAtFFFaLYAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUjLuXFLRQAyNSoweaXbtzgZNOopWAQUtFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooqG9QCiiiqQBRRRUtu4BRRRTtcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA5eb4neFYPEC6HJr9gmrs2wWTTqJSfTbXTK2a/Cn4ifGzwhrH7d1h488N6tdaj4dmv4XaRgU2nPIAJ6V+kXxQ/4KYfBv4YQiNtTu9b1VVUvpum2zNKpIzjLFV/WoUlbXc6HS/lPraivPfgX8ZNO+O3w/svFml6dqGlWl19231OJY5R7kKzDH416FVJ31RhKLi7MKKKKYiG4uEt4ZJZDsjjXczHoAK+cfiD/AMFCvgd8MdcfSda8W5vk4aO0tnn2n0JUcfjX0XdWa3lvNDJykiFCPYjFfmz8Wv8AgjmvjbXNa13RfH/2TUb65edLe+tS0ShjkAspyMfSpbdzWPLZ3PqOz/4KCfAXULWKeL4g6cokXdskJVl9mB6GvGPjN/wVr+GngHzbbwrBP4zvhwHtjshX3LGvna0/4In+PJJALz4geHEj/iaGGdm/VBXVW/8AwRPnbyvtXxITYB84is+/tmlZisuh5fqX/BVb4ufFTx1oOkaNa6b4esbi9jhMMMZlaQM4A3E9D9K/U34mfADwh8fPAun6J4+03+1oljSQsrmN0k2jJUjpzX4r/F/4E2XwD/bB8N+B/C15PqkltcWLG4mAzJMzZYgDoOK/fC0My6ZAXXE/lLuX/awM/rU76oqXMtEfNfgf/gm98BPAl2Li28If2nOrb1bVrhrnb7AHtXumi/Cnwb4cjCaZ4X0myUdobOMf0r5H/bi/b41b9mCaw0nR9Hhvtdv1d45LjmKJVIzkd+or5Htf+CyvxZWI7/Dvh+cj+Iq6/pmmmrbDlGUd2fsTJpNla28oisbdF2k4WJQP5V+A3xs0NvHf7bmqaZCqq174hjtwmAwALDnAr648O/8ABat00Mxa/wDDiS71Ergy2F6EjPvhga+df2V5I/2iP29dK15LUWEV3qD6kbfdv8oKM4JwMmgSP3L8L6RHoHh3TdNiRUjtLaOEKowBtUCtSmrxSNJtBq+hluxWYL1oVg3SovtSsDs+dv7oPWpgc0XTCwtFFFMQUU1mCLknA968I8fftxfBn4YeMLrwx4n8Y2+lavbbTJFLG5UBs9wD6VLkluNRb2PeaK53wH8QfDvxO8N23iDwtq1vrWjXOfKvLVso2Ov0/GuiqhBRRRQA1qpalo9lrVu0F9aQ3cLAq0cyBgQe2DV6hV20Arp3R4Tr37DPwI8TX0l3qHw00eW4kJLSIJI8k98KwFYsv/BO39nwj5Ph1YxDHOyWX+rGvpDHOaa1Ry9hrc/HH/gpF+xr4C+Bfh+08ReCLZtLzOIpbPeWX5uh55r0f/gnP+w/8J/i58E18YeLNLfX9Turlo9krlUgC8YAHXOe/pXS/wDBYqP7J8M9HZTzcXiBq9V/4JMNG37JenlWzINQuFcenIxUJu9mdEvhudFqH/BMH9n3UJkkbwjLBt/ggu3VW+or2b4N/s8+AvgHptzZeCNCh0eK5KmZlJZ5CBgEk9etejL3p1a2Rz3YlLRRU8ohrUlOPauO+K3xS0L4OeC7/wAT+IZ2g060Us2xSzMfQAVL93VjSvojrJYvNAB6VEIZYyAp3L/tV+Znib/gtbp1nqUyaH8PJL6wVyqT3N9sZx64C8VVX/gtmrR8/C3a/wD2GFIP/jnFTyqWpfLJaH6ixqVzk5Jp9flh/wAPtLhJl3fCyFou+3WgG/8ARZrSt/8AgtxpYmAu/hXdRRf3odaSQ/8AoritE1FWJ5T9PMA9etLXzV+yP+2dpv7Xq67No/hq90KHR2iSV7i4WQMXDEYwo/umvpSqJFqG5UNDID0KkGpagvD/AKLLnptOaBrc/Br9sy5Vf23JivzCK8tEH0Div3c0HnQ9OP8A07x/+givwl/a5tftn7cM8CRsWlv7MLj/AK6Cv3g0uA2+m2kRGDHCikfRQKxjqjer8RYr8u/28v2Cfip8aP2g08Z+D7S3v7C+giSRmuEiNq0ZAGcnnOc8elfqNto21sYXOW+F+g3/AIV+HfhzR9VnNzqNjYQ29xMW3bnVQDz3rxz9tT9key/ay+H9rpQvY9L1rT5vPs7yRSygkYKkDsa+iwoHSl20wPDP2Pf2Y7D9ln4Tw+GIZ47/AFOaU3F9fIuPOc9B9AOle50dKWgQUUUUAFFFFADGb5gMV5n8fPjt4Y/Z/wDAd34l8TXYgtk+SONeXmkxwgHvXo17cLbwvI7iNEUuzN0AHWvw7/b0+OGt/tHfH4eBdDuGvNHtL1bOytYhnfMxALHHXHvWb3NEtLnNeMfiJ8XP+Cg3xok03QxdTwyMyWumrKYra2gHQyEcZ7819dfDP/gi34ePh62m8deNdWGtEbng0bylhTI5GXRifrxX1v8Ase/sqeHv2Y/hva2NnaK/iK9iSXVL5iWaSXHQE9AMngV79VkuR+AX7aX7Lt7+x78VLGDQ7+/uNFnjWex1Kd1EocHkHaBjBr6g+Jf/AAT5+Jn7U3hHwB410fxtY3Zu9DhaePW5ZEMchAzs2K3B7/Ss7/gtXr7t428A6RFdI0S2U9xLAMFg4ZQpPccE8V+iP7ILPJ+zH8NWlUq50aEkH6Ux8x+Xw/4I2/GXy9j694Qzn7yXNwWHv/qhX2d+wr+wPqf7KepahrmueL5dc1O7gEK2FiWjs489WIb7zehI4r7S2ijgcmgXMZHiLwnofi60Frruj2Gs2wORDqFsk6A/RwRXiXxb/ZN/Z7m8F6zqfiT4ZeF7HTrO1knnu7DTks5Y1VSSQ8IVgfxryD9qn/gqV4N+BOtXPhrwrpv/AAmfie2dormPzDHb27rj5WYck89vSvzu/aU/4KMfFX9ozSZtBu7qz8MeGZxifSNIClZuR9+VvnOP7oIBzyKBHR/8E+Pghovxk/a6e70+zZ/Bnh+5m1GOO4VmBjVz5KFs5yeDye1fugqhUAUYAGAB0FfhR+xx+3zb/sk+C9R0Wy+H9nr2oX9x50+pPqQgdlAwqkYYYHtj8a+wP2fv+Covi/8AaA+NHhvwVpfw1sLW2v5T9rnTVPPeGIfefhQBj3oBu5+i606kpaBEczFYyRVeSQtCAVzmrZAYYNZ+r6lBo9s9zcSLBbQxtLNI5wqIBkkmokupSHTW63UIjyQgHIU81VsdFhty21sgnkZzzX5Tftdf8FIPGHj7xovgf4GXV1a26zGKS/0+ESXN2+cYjyDhevavGtMn/bR8CRz6lbt46tizfaZXljMqnPfDA4+gqVZmqbSsfo9/wVAV4f2RfEoiJChow30zX55f8EidHt9U/anjnmVTJZ6ZPNHns2AOKqfE7/goX8QPH/wP174a/EfRUutVutqR3skBhlXB5LjjJzjpXR/8EcbQSftMarIU/wBTokxBPYllB/nTWhn1P2sHasXxxfDTPB+t3bZ2w2UznHXhDVrXvEOmeF9Ll1HV7+302xhGZLi5kCIv1Jr5h+OX7fHwY0PwD4ltLHxpp+saqbOWGO1tSZNzlSAM4p2vqJbn55/8EyNJuPGH7cE+qxMRFZpeXku7uCSB+pFft5X4CfsQ/tU6D+zH8UPEnjHWdJutS+3WUsFva2hC4LOGA56CvU/i9/wV2+KXjaaWz8H2Vr4QspPljaMebck9vmPT8KobV2ftRRXjn7Ies+MPEX7PHg7U/HVxLdeJLu186eWcYkYEkqW98Yr2OmQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNZwvWgB1Jx0pgkD9O1HfNZvcdhuA0jDGNtSiqkNw0lwV2MAvGSKuU1HqAUUUVYgprNtHQn6CnUVNgGYDKDtxRtx2p9FHKO4i0E4HTNLRRyiGLGOTjk04ADoKRmI6DNKpJ6jFHKAtFFFUAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlGRTZG20inIzQMfS01adQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKarBs47U6gAooorN7gFFFFWtgCiiiiwBRRRTAKKKKACiiigAooooAKKKTNAC0U1pFTqcUzzA/3TmgCWimp3p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH4tXXhX9nfwf+2tZwpcQWfhSzfdNavMPISfIwNxIGPbNfeWtfG79k6bV7GLUbzwNcakHSO3CwQTTAkgDOwEjt1Nc38Hf2Rv2dfjn4P0bxjH4bs9SuSqyT7Lnd8/pIAeenevW9W+DX7Ofw6A13UPCPgbRmtSHF5PaW6spXockZyPzrmppu0rnfNq9ktT2/SIbO30+BbCKKGz2AxJCoVApGRgDtV2uJ+GXxg8FfFqxuLjwZ4gsddtrUiOU2UgYR5zgEduh/Ku2rpOKV09QooooJCiiigApjfdIP3cHJp9NPyrSA/Gv4/Wthaf8FQfDIt5zKhv7EyNIDgEseK/ZJvukHpX40ft93g8G/wDBQjwzrK2rCLfp9wPLGDJtcg49/wDGv2P0+8XUtPtblVKCeJZQrdRuAOP1rOm9NTWpdH5p/wDBYT4W2zeCdD8UofLltLnyyxGSwfAIz9cVwH/BKn9l/wAFfFzw14u1vxx4Rg1yG3uUt7O5vASn3TvCj8q+sP8AgqR4bXxF+y/rzPIENgY7pflz0cVw/wDwRx8QHUP2fdf0w4YWesO4x1AdRgH/AL5NLRaIbvKNz0zx5/wTF+BHjdUeHwy2gTKhUNpczRA57kdCRWT+zT/wTb8Lfs2/Fn/hNdM1y71No4Xigtrgf6vcMZz3r7Ho20zNMK5j4ia1caL4S1K7sUEt3FCzxqRkbgDiumPpWR4k01r7S54o03lkI25xnirfwl07c6ufkJ+yL+0p8RPGv7clhaeJfE98dPku7m3fTWl2wqCCqgL09DX7JrX8+n7Qun6n+zr+1tdalaySQXNvfx6jHKo2YUtll96/dz4S/ECw+J3w58P+J9NuVu7bULSOUyJ/f2jcPqDms49yqm7sdjRSUtbGBBeQ/aIGj/vDr6V+a/7dP/BOTxx8cPicvi/wM2llriNYLuC4l8liB/Hk5z34r9LivOaQKF6VnKF3c0jNxTR4/wDsm/AqT9nP4IaF4Jnv11K6tA0s86JtXzHOWA5PA6Zr2KkpataaEN31CiiimIKKKKACmtTqQrQB+c//AAWOs2m+EWjTsuBDeoQR35AP8677/gkfdWs37LIigbMsOqzrKPThSKq/8FZtHXUP2b7u4deba4iZTj/bA/rWZ/wRxC/8M569g8rrsiH8EX/GsftfM6ZfBfyPvZadSUtbHMFFFFABVDWtD0/xFp8tjqdlBf2cow8FwgdGHuDV4mmNJtIB70rXGfN/ij/gnT8APF2rNqN94Bto7hiWYWc8kCMT6qjAVfs/+Cf/AMArOBIl+G+lSqowDOpkP5k19BZ5NLmp5ew7s8DP7B3wFGAPhnoY/wC2FYPiL/gm5+zv4m2m4+HlrbMoIDWNzPbHn18txn8a+mutLtqrCuzyX4A/stfDv9ma11eDwBpE2lR6q8b3fnXk1xvKBguPMZsfePSvW6TGKWmIQ9qgu2C2spboEOanNRXEYmt5E6blIpPYa3Pwg/ai1Ka5/bpiuIFjSWPUbMR5B2nEgxnmv3gtS7QoZMeYVBbHTOOcV+Bv7Zuj3nhT9se8M1zDJP8Aa7aZDDn5R5gxmv3p0OQy6LYSMcs9vGxPuVFZQTsbVWmy9RRRWxgFFFFABRSE0m6gB1FIDS0AFFFFAHz/APtw/EyT4Wfs8+K9Wt5Whu2s3hgdR0duBX5n/wDBKn4f6d4o+MXiH4ieJ3hk0/wxavdvJMeRM+Tv98AE19W/8Fh/HE+i/A/TNCidQmpXyCRe5UZJH8qs/wDBJv4T+H/+GW7/AFeaBbi58SXU1te7u8aDaFH4MazW7Nr+6eiXX/BUT9n+0m8pvE1277mU7LJjgg4PevLPiZ/wWN+HGh2M0fg7QtS8R6jnbG1xi3hHuTyam8Xf8Ea/hh4h167vtO8UeINDtbhzJ9jtzFIqknJwzqTitz4e/wDBIT4LeD7sXGty6x4wKsGSPULnykUjttiChge+7PStDPQ+Bvh78OfiF/wUq/aH1DXdSZrbS0lVry/Vf3VpCD8sS44yRn8q/cbwX4UsvAvhLR/D2nKUsdMtY7WEMSTtRQBkn6VR8AfDHwr8LdJOmeFNBsdBsmwWisYVjDkdC2Op9zXUUCCmtgqQRnI6U6igR8c/ED/glj8F/iR8TJ/F9/Hrlm11Obm+0y1vytvduxy24kGRc/7DLXq/hb9iH4C+D7CKzsPhR4Znhi+4dUsVv3H/AAO43sfzr26loA8zi/Zh+DkCssXwm8DxK3Xy/Dlmufyjq74D+APw3+F+sXOreEvBGieHdRuF2SXOn2aROV9BgcD6Yrv6KACiiigBGOK+LP8AgqV8fNS+DvwNj0jSPLW/8USNp3mbsNFHtJZh+HH419oyZyCD07etfjd/wVz8VXHjP9o7wp4IRjHHp1mjk5+XdcOFzj22frUy7FRPXf8Agkt+ydb6foB+MHiK1ZtRui0OjwyDCpGPvTY9SeB+NfpnwcgiuM+Cfgc/Df4SeEfC7EM+labDbOQMfMFGf1zXbbR1xU8o29T8rf8Agsp8LYrPT/C/izTNEhhj81ory+gj2nJxtDY9T/KuO/4IraXb3Hxa8c3zqxuLfSFRCeg3Srn+VfTn/BX/AMSadpX7Ly6Xcvi91HU4Ftk7kqdzH8hXiX/BEPSlml+Kmpbfmi+xW+7uA/mtj/xz9Kqwrn2N+3p8CfE/7QnwHuvDPhO7W21UXEdwI3fasyr1Qn3r8wPDf/BLX4tX3hvxDrHihbPwpa6NC8yxzkO1wFUklcdB8vf1r9zcV5r+0pqq6H8AfH963HlaLdEfXyzimCZ+OH/BOn9kXRv2ofiDrr+KnlPh/QYkaaO3faZpCxCgn+6QDmv1n0n9iH4EaJJbS2nwt8OpPblWSZrUM+4dGyepr4o/4Ii5e0+KcmwHLWGW9M+f/h+lfqTTBsitbeK0t44IY1ihjUIiKMBVAwABU1FFBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMu6gBaKRV20tABRRRQAUUUUAFFFFABRRRQAUUUUAFNIywNDUlS5DsIcKx2jHrQBupeO9OVQOlQO4irtp1FFaLYkKKKTNJyAWikoYkdBmlzALRTVbseDTqOYAoooqgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRntTXcL1qssuyRm3ZBqWylFstMPfFNZjHwOe9RRXGd5fgDpTWukkchSWKjkAU7hyu5NDMJQT0p5b0qnZzxMzxrLG0gPKq4JH4Vbpg9ypcK8jACrMUZjQDvTN2yQe9WKBPsItLRRQIKKKKACiiigAooooAKKKKACiiigAoopPwzQAtFJ+GKWgBM0Zoaq9zN5a4z1FJ7DSu7Cy3ISQKOSfShbgbsZrMiyGY5zT4LjyZG8zv0rNSZu6ehrKAuSB1oL47VWhvo5l4z+VTqwbpT5mY2H0itnPGKYxdenIp0bMc5FIkfRRRWi2AKKKKYBRRRQAhOKTd7U2SQJjIJ+gqHzndwFQge9ZylylJFkHNLTUz3p1aEkckwixkE/QVGt15jYRCR3zxU9HFAxjKzdG2/hmk8ndy7bvTtUgpaBDQgHalwB0GKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/JXwf4B8DfsvfEGPwrcfEu98O+IYZDiJi8dvdkjCBlGQSD/6FXKeBf2F/i5+0h8aL7U/GUWpW3w/e/aSS9vbsRCePPHlR7iTkdwPxFfaP7Wn7IM/7Q/hBNV1xIo/FumQltMuNHixLHI2CRIf4xlVx6c18b+Gv26P2i/2SryPw3498OjxRotiTDHJfwNAzL0XEyqf1U1wxpqMtz0ZSbjaJ+nfwO/Zt8B/s8aXNYeCdJ/s2OcL9odpC7zFQQGYnqeT+deodK8C/Y1/aY1L9qT4b3XinUfCp8KGK5NvHB57TLIAOWDFF46dq9+rsjtocEr394KKKKokKKKKACorhtsZzx2/PipCcVDcNiNiFLkD7vrQNbn4vf8ABVhdU8J/Hbwjq8syPcfZ5HgbGceW6Yz+de3/APBOP9q74rftD/GqXTdeuxJ4X0nSm8yONMKrcCPJ9Tg145/wV8i1Fvid4S+12gisYre6jgus8SFihYf8B4/Ovpj/AII6/Cv/AIRX4I654vuIMXfiK9VY5D18mEEAfmxrmULpHXV+Js9z/wCCh0aH9kD4jFomkb+zztKrnadw5r8qv2A/22ov2SdS1yDV9Im1jw3rLRGf7NIBLA6AgMAeoO48e1ft98Svh9pfxW8D6z4U1pWbS9Ut2t5xGcNg9x9K+E9U/wCCKvw2vL1pbPxt4i0+AkkQLHC4GfdhW0Y2OXm0sdzF/wAFfPgC0al5fEkbEAlf7LBAPpnfzW7pP/BVT9n7VIWkfX9QsAMYW7sSpb6YJ/ya8cm/4Im+A/JVYviH4j3fxF4IMH/x2su7/wCCJvh6Nk+w/EbU1X+P7Raxk+2NoHvTa10HG1tT3+4/4Kkfs+Q28ko8UXU2zqkdk24/TJFcjqH/AAV++B8O77JZ+Kb4KfvJpyKp+h8yuI0//giv4E8tRf8Aj3xEXH3vsiQqG+u5DXW+H/8Agjr8F9J8w3+peI9aLY2/aLtY9vXP+rVevv6UK+wtEfAP/BQb9o7wF+01408P694K0nVNPuIIJIr+S/gWPfkrsxtJz0NfWn/BGj4wa1r2i+K/AV9M1zpmkpHd2THJEQZmDp07kg/8Br22D/gkz+z/AB436Lqc2P72pSj+Rr3v4J/s0/Dz9nm0vYPAnh+LRvtwQXUquzvNsztyzEn+I1HLokh8x6eo2iloorUgjmlEKlmOFAyTXgPxc/bn+E3wS8cWPhLxPrVxDrd35ZENtbtKsQc4Uuw+6K931CzN5C6ByhZSufrX5vfHj/glD4q+M3xY1DxYfiTYwQXrjMd1pzs8KKflVSJDu79dtS+a+htGMWtT9JbK8iv7WG5t5FlgmRZI5FOQykZBH1FT1y3ww8Fj4dfD/QPDK3Ul6NKs47U3MhJaQqMFufU11NNX6mT30CiiimIKKKT8KAFopCcUjSBeaVwPjr/gqZcWw/Za1+KZtsu6Mx8dSHXivN/+CMGrG4+CnjKxK48jWhMGz13x4/8AZf1r1L/gphDYy/sueKZtUUKoVVhIPO7euK8T/wCCLek31v8AD/x7qDHOmXGpRRwjPQqjZP47h+VZ3946X8CR+lNFN3dRRurU5h1FN3UbqAEbO4ccUnJxmquqXz2NpJMkLTsiltidTjtX5W/thf8ABQz44eCPiRc6P4Osm8MaNaZXzpdKFw1yTjklwQuMduu6o5lzcvU05Xy8x+rm3DEgdetLX4Y6V/wVK/aP0m+iurvWLXUoMH/R7rRYo0f8VUH9a7K2/wCCzXxjtFxc+FfCsx7NNb3Kf+gyirIP2dWnV+Oem/8ABar4oSvIs/gjwjIduI1hS6BLdusxzX6pfBDx1qXxL+EvhTxTrFgml6nq1hHdXFnGrKsTMPugMScfU0D5Xa53VFJS0EjWpG/1bU6mv8qmkHU/CX/gpFAuh/ti3snlgEW9nNhe58w/4V+4fgm8OoeDdBuiNpnsLeUj03Rqf61+IH7feq23ib9tR4pCs2GtLWbZ93Al7e/Jr9y9HtY9P0ixtYRiGCCOJAf7qqAP0FTHY0qfFcvUUgNI2fwqzMWgHt3r5z/bo+LHxF+Dfwb/AOEk+G9haX2pW95H9r+2QmVUt8NuO0MvOcc5r52+A/8AwV68J+JvDOqJ8RrI+HNcsoPMhkt1LxXZAOQB/Cc7eD1zU8yK5Xa59D/tj/tlaB+yn4TS5mji1TxFdfLZ6WZNrSerH2GRn618YfCX/gsjrmpeOLK08beF7G28P3VwsD3Fi5DwZONxz1x/SvmWDR/Hv/BQ79pS5Nstxc2U93n7TJnydPtCe/YEhf0r2X9ub/gm9H8EfAUHjLwQ0l5pthGseowucsOg8388/nRcasfsRpOpW2s6ba39nKs9pdRLNDIvRkYAg/kat18hf8EvvjVcfF79mXT7bUZxPqvhyb+zJTjnygoMRPvjPPtX17VEhRRRQI/Nr/gs9olxJ8OvB+pJbs9tFqJSefGRGChwPxNex/8ABKe4tJP2PtAS1ZWkjvbrz1DZKuXHUduMVuf8FJvhzrPxN/Zb8Q6dodmLy7tSl+yYy2yI7mC++K+Af+CVP7UWmfB3x5rfg7xfqy6V4f1hVktmuMhYbtW2hfbcGP5VGzZpvGx+0YoIzTVkDqGUhlYZBHQ0uTVGYvSlpu6ue8b/ABF8M/DXRpNV8U65Y6Fp8YJM97MIxx1wDyeo6UwOjorh/hT8bPBXxu0q71LwTr1vr1naS+TNJb7sI3OAcgdcGu4oAKKKKACiiigAooooAa3UV+EH7emuTX/7c2sPdymSK1urSHLY+VFkBAz+NfvBX5Hf8FGP2EPiJqHxR1z4meELV/Emkagonube2H+kWpXB+7/EM88elS1dplJn606fMlxZwzRuJUkRXEgP3sgc1YIyRzivxc/Zu/4KmeOfgqsXh34hWEnibR4nWLe6eVe2qrkEEYAbt/3z719SfEr/AIK9fC6H4cX9z4QXUrzxRNCUtbK4tzH5chGAzE8YHtVCPnX/AILHfG5PE3xP0H4e2bRva6DB9suXX5iZ5OAue2FB/wC+q9E/4If3kQ0v4t2xdVnefTZVjzyVC3Azj2yPzr5g/Z1/ZA8e/t1614x8aX2p/YV3vK9/dgnzrlslUX2GDn04rmLdfjL/AME8fi5HO1u2halIjIS3zWmoQgrnnoe3uM0CP6DK8w/aesU1H9nn4iQOgdTod2dp9omNfM37BX7eXjH9qzx9qvh/WfDFlZWOm6YbubUrJ2K+b5iKienzAsf+AmvsD4paK3iT4beKNKSIzNe6ZcW4jXqxaNhj9aAPzL/4Ii6tIuqfEzTNpMMttZ3BPYFXlUf+hmv1cr+cv4M/GLx5+x/8UZNV0hJtO1C3ZrS802+jZI7mMNna/ryOK+w/FH/BZrxf4g8NrY+F/A1rpviGY7BcvIbhQf8AYj7n60DsfoJ+0h+114C/Zm0eObxFem81a4O210eyIe4mOQOnbqOtemfD/wAWnx34L0jxAdPuNKGo263AtLoYkjDDIDV+av7H/wCxD44+MvxKg+NHx1aadXZb6x029kLyXDkkqZEP3EGBhe9fqLHCkKgRqEAUKAowAB0FAE1FR+YPWmSXKRDJNTcLMnoqv9qG0Ec1XmuJW+4CKXMWoNl8ttpplUEAnGazbeeXcd5Jb+Fc9afMXMiFxt9qOYbp2drmjS1HDnbUlWZsKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUm5fUfnQANUcuPvHIx6U/erdGB+hpjSKMjOamxSuRwmNSWLlt396rIIPSs2ZZbzasJCbGG7I6itAcfSpSu2hyQ6lppIFIHU9CDT5kiB1I2D1oyKa3bFJtAOGF70uajp0fepWrsAPzgDr604UtFacoBRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSU1pFXqf0pAR3RHHNUfNXcRnmluSWlVnB2jjNUL66UwuYYizA43DoKzk9TqhsSX8xSPKk8VmySXt1uSLekcw8pnT7ygg/N68VCr3USmSQFwOcY/wA5qn8QfiloHwf8A6p4w8RXiWWkafAZZm6szfwqo7k+gqbXLk1yn40fH24+Of7H/wC0RrGrLrWtQWsl7Jd2V7LNJNaXMLNkAgnb3AI7V+gn7Gf/AAUe8N/tCSW3hjxLEvhzxj5arH5jDyL5sHcY26AjA+U9d3FeM/BP/goBF+11+0B/wrjxd4G0u88D64rwWVvcx+ZNGVBIZif7wxnGMYFeRf8ABRb9iWD9mm80v4l/DmS4sPD8t4EngiY50+bgxsh67ThvoQB3q07aHNufsqIlLFsc0+vk7/gmv+0Pq37QXwD+0eIbh73xDot0bG7unx+9GMo31x1r6yq0QwooopiCiiigAooooAKKKKACiiigBGbbTTIB2NPpNo4oAaxbGVH51EJ5WJCxbsdcnFWKSgBkTO2d6bPTnNSUlLQAnNNaNZPvAGn0UAQfZI+yinrbovRF/KpKKnlQ7sZ5YHQBfoKXbTqKfKgEFLRRRyoQUUUUwCiiigAooooAQjNJtp1FACAYpaKKAEIzSbadRQAgGKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGdc5rO1jwzo/iGHytU0yz1GPrtuoFkHH+8DWkFPejbSDVFfTdLs9HtVtrC1hsrZfuw28YjQfQAYq1SDilpgFFFFABRRRQA1qNu6lo5oA83+Kv7PfgH41Np58Y+HrfWTYOzwecPulsbunrtH5V2PhXwnpHgnQbTRdC0+DS9KtF2Q2tuu1EHsK1ttLjigpybAY7UtIBiloJCiiigAooooAKKKKACiiigBGptPpKYhFp1FFIYUUUUAFcv44+Jfhr4b6VLqXiTWLXSLOMZMlxIFz9B3rpZORivlb9sr9jK//ap0/T7S18Vf8I+lvIxkWSEyK4bb6EdNv61nLm05TWCTvzFPWP8AgqN8AdJvEgbxNLdZZlL21s7quMckgcdf0r0Hwb+258FPH0QbS/HmmDgZW6k8lhnpw30Nfn7a/wDBFPxnJqdzHcePdFg05TiGWOGUyOPVlxgH8aivP+CJ3jqO5JsfiF4fMQ+600M6v+imq5SEtT0//gqh8bPC/ir4KjTfD/izTdWa4uo1a1s5w5AVgcnH0rC/4I1/FPS9L8L+PfDmpaja6dHHcxX0Yup1jzuUqQuTyAF5+tee3H/BFv4nqVC+OPDtz3PyzcfmtFv/AMEbfivphd7bxhofmOpX900ideuanlNHJbM/VaT42eAIiVfxnoasODuvox/Wom+O3w6Tg+N9BH/b/H/jX5Q/8Oc/jD85bxHoEh6jdK5rndU/4JH/AB6tJwlsNBvE/wCeiX2wfqK0M9D9gofjj8Pbi4igi8aaHJNK21EW/jJYnsOa7dWDqGUhlIyCOhr8WvAP/BKT452PjfQLjVhpFnp8F7FNPPDfb2RFYFuMelftDY2a2NnBbqcrDGsYPsoxQLQlxmszUPC+j6pu+2aXZ3W773nQq2fzFau2jbU2V7i6WObPw18KOm1vDmlsvobRP8Kpz/BvwJdf67wfokn+9Yxn+ldgBilqgOFi+Bfw7t7pLiHwP4fjnT7si6dEGH0O2u1gt0t4kjiRY40AVUUYAA6ACpOtLQO7CimsxFeU/tI/tGaD+zH8OZfGPiOx1DULBJ0txFpsSu5djgZLEAClcLXPWK4n4xfEzTvhH8P9X8Taoyi1sYHkK7wpYgcAZ98V+enjf/gthZLp86eEfhtK90wIhutY1NNi9MFoY1LHvxuFfKHijxZ+0z+3ZrwglsNa1TTpJAqWdjavBp1srkZPPb5AeWP3altbFqLvqcv8HfDfiD9sD9rKyMEe2bUdSF9cSLnEFuj7yec4OBX9CcaCONUHRRgV8NfC/wCC9p/wTq/Zr1XxJaeHm8XfESaLzbgQRtIS2OI0KqSEXPPPPrXyTqn/AAVV/aO1IyGHQdA0lGOEWLRbtmXk8ZaQgn8KcdhS3P2eWqWtTXcOmzvZRrJcqhKBumcV+McX/BVv9ovRo0a70rQLyNTlmm0a5RiPqJAP0rtrf/gtB47bTYYpPh1pEuoDiR1vnAc+ybc/qab2JRy/h39vrx1p/wC1ddWPxO1gXPgiO/n0290doB9nEJYqrbfUADkmvIf2/bH4YzfGK2u/hYsH2K8txJPbWnMYf5du1AO+W/IV0v8AwUA+Fut29n4L+J2peFoPDcviq2N3qENq+5UmkCsgx243fnXsn/BKP9j2bxNrX/C3fF1kkukWitBpFneRhxcS8hpSG7Lxj6+1QosuUk0eZfsE/tsab+yPJe+G/FXhKWOw1i6ie51VUK3EKgHGVI+ZfmPA6c1+lPxF+Lnwy/ah+BHi7w94Y8c6TdNq2lyxqouAsiZUnlTyDxWx+0t+xb8O/wBpTwvJZ6ppNvpeuQxsLHWLGMRywMccHA+ZcgZB/Cvyn+LH/BNH43fBObUNU0S2/wCEg0m1UuL3SZispQdyg5/Cnykqx79/wRj14+G/HvxY8E3VynnMltPHEDw5geVGZfwkBP4V+rFfg1/wTHh8Tx/tleG47FJ43UXH9q+YpyINmXDA9DuA61+8tUhPcKKKKYiK5gjuoXhlRZIpFKsjDIIPUGvyj/bf/wCCYWqWOq6p4/8AhSkuoLcStdXegrw8TZB3Q46/xcewr9YKNoqWtSkz8Lfhh+3Z+0n8C9NXSLr7XqWnwvgReItPeRl28Mqybd2OnevUE/4LFfFxYwg8E+GZXxgt5N3kH6Bq/XWXQtNn/wBZp9rJ/vQqf6VB/wAInonH/EnsRj/p2T/Cmguj8if+Hi/7VHxdxY+CfCcMNxna76Lo0k23d93c0oYL0OOneul8K/sFftCftT+JrLWPjz4vvNO0SNfMW2knEsoz1SOEfJHnaM8enBr9XbXTbSxyLa1ht/8ArlGF/lVmmPm7HBfBf4KeE/gL4KtvDHhDTY9O06L5nYD55pD1dz3JrvaKKCQooooEFFFFABRRRQAUlLRQB4r8XP2NvhB8bZGuPFHgyymvyCBfWmbeYZxk5TAJ4HUGvnHWv+CN/wAIb64SSw1zxFp6b9zRtMkoI9ASoxX3xRQBxXwf+D/hf4GeBbLwn4R09dO0m1y20ElpJD952J7k1t+IvBfh/wAYJEmu6Hp2srFkR/b7VJtmcZxuBxnA6egraooAx/D/AIP0HwkkiaHomn6OsmBILC1SHfjOM7QM4yevrWxTJZBGpZiFUDJJPArmPC/xS8JeNdUvNN0LxFp+rX9pnz7e1nV3jwcHIHvQMzPiB8Cfh78UrfyPFfg/SdbiJyRdWykk+5HNc94L/ZL+Dnw71qPV/Dnw50DStTjGEuobQb1+mc167RxQAxVCKFUBVAwAOgrjNW+Nfw/0HV5dK1LxpoNhqMRAe1udRijkUnsQWrf8QpHe6RdRf2iNPV0eI3G4LsYggHJ6EE1+QnxW/wCCTfxe1TxhqOpaL4h03xXa3sjXI1C7uWjlbcxOD1yce9TcaR+wGl6xpmv24n0y/tdQhI4ltJllX81Jpt5EVjDPztPavwT8D/F34yfsH/FabRpr6fdDIsVxoslyZLa4wTg7c4yMnH+9X7teEdVufE3g/R9Xv7X7Dc31nFcS2qtkIWUNj9almsXZl2O425Kg7cd6ntboTSBEOW789KiWNFRmViy9CDUun24t5JQF5wCfepWrNZtWPkj9qj/gpB4O/Zh8eQ+FJPDOoeKNYiiEt00E6wRwKxGMFgdxPPbjFezfs5/tSeA/2n/Ccer+FtQjS9RR9q0i4dftVqxzwy9xweR6Vxn7T/7Bfw3/AGnLN7rULMaB4oVCsOu6fGolySP9YOPMAxwCeMnHU1+THxv+A/xR/wCCfvxc0zWrLULkQeaX0zxBYs0Ud2E2lo3CtkfeXKnr707dDl3P3p8SeI9K8I6TPqusajbaVp1upaW6upQkafXJxXn/AML/ANqT4XfGbxNqnh/wd4wsNb1TTgpmhhYjeDnmPON4G0525xxXBfCbxd4e/b3/AGS0k1y2j8rW7WSw1KGNQfs90owzJnoQSGH1r8i/GXgnxt/wTr/ag0m4lJul0y4+12F5GCkd/bEjcPc4IDCqTDlP6BqK4v4O/FTRPjV8OdF8YeH7hbjTtSgWQbTkxvj50PupyK7SrJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKlsCOVwuAe9QTKMfL3qeRA2M9qbtHfoKyerLTKsKC3LH+9UUd0lxcOoyu3r71cmUKmQu6q9xcWml2Ut7eTQ2VtEu+WaZwiIo6lmPAH1osy+Zblq1jEanGTn1qQ1keHvF+g+LYpZNC1vTtajhIWR9Pu45whPQEoTj8a1ZFLLgHFWnZWI3dyKQbj1wKhnmEW3YM884qfydygE5IpGtVxknFY8rLTRWutQ8kDJChuMmrMbExrng1Xn0xbpVDHKhgw/Cru3LfSnySBtdATPNSCkWnVrGNtzJhRRRWggooprNjA6mpcgHUUxZB3IHanA55HNLmAWiio5biKHHmSLHnpuYDNHMBJRSBg2MHORkUtUAUUUUwCiiigAooooAKKKKACiiigBKMikakoAXcBTfOTdjPNV7y4WFQSf0qrb7p5Fckgdveg0UdLlnULwQQkqfm+lRWlyzQhnHLdKsModwXX7vT3qNlbzCQny+lZSWpStaxw3xw+JOm/CX4Z614x1jzv7L0mEzzRwEBn5wAM18feDf+CwXwl1a9gtdc8MeI/D9nIcfb7iCOeFeep2OW/Ja+3PiF4B0j4p+DtU8KeIbRbrRdUt2guIyeecYx6HrXxfff8EbvhHcef8AZ9f8R2ivzHGsyMifUFcn86ajoHNbQ+tfhz8bvhz8VrWKXwl4r0nWhIgk8m3uVMqg5+8hO5eh4I7V+XX/AAVg/aVfx78QLL4SeG3WXSNFcSX3kkn7Rdk4WPA67f5tXCftSf8ABP8A+IH7HmlT+PfDXib7b4Ys5AkmoWk32a6tvMdEjVlzl8l/4cgY7Vgf8E4vg/e/Gz9qzS9Qvof7S07w+51jUZbw+YWKsFQMT94l+n0NVYW593/sb/sa/Dv9mf4b+HPiv49drHxsln9vubjUbgJFY71PyKvrtI9818zf8FC/+Ci2lfG7Qb34b+A4TN4aaVTe6xOhU3G1gQqKeQMg89812X7b37I/7THxx+N3iK70qGXVvBE8y/2bZnV4o4FjCgDMZcYORnkV5N4D/wCCP/xq8QXEieIBonhWJcETT3i3O/rwqxE4xjnPqKOUz2PpT/gl58b/AIQ/Db4c6X8Pz4ohPjzxJfyXs9t5TBA7AKkIk+6SFX82r9I6/Pb9mn/glFB8Efil4c8a6v4yTWptHk88WMVpiOSTBAOW5ABNfoTVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopXAKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAI1Np9JQIbRTqKYWBaWiikMKKKKACiiigAooooAKKKKACiiigBOtZfiTwrovjLSZdL17SbLWtNl5ez1C3SeJsdMqwINalGPeoaA860X9m/4U+G9QF9pXw28KadeD/lvbaNbo/wCYSvQoreOCNY4kWONRhVQAAD0Ap9LTsO7GqoUYHSkWGNVCiNQvoAMU+iqEUdQ0PTdWi8u+0+1vY/7lxCsg568EVyH/AAoT4bf2l/aH/CB+Hftmc+d/ZsO4H2+Xiu8JpN1AjnfGHw38LfEDTYtP8SaBp+tWMRDR295AsiIR0wD0xWvo+i2Hh3TYNP0uyg0+xgXbFb20YREHsBVwGloGFIyhlIIyDwQaWigDl9B+GHhLwt4gvdd0jw7p2m6xertuLy2t1SSQZzgke9dRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNJoA+Tf+CmPx61b4E/s5TSeH7g2mveIL1NHt7hThoUdHaSQH1AXH/Aq8B/4JE/s06lo9hqfxo8QS3AuNYje10iF5CBJEWPmzOvfcVXafY1wP/BZH4nyeJviZ4I+GlldEx2Nubu5gUgg3E7osRPuqK3/fZr9S/hz4Xs/BfgLw7oNhax2Vpp1hBbR28QwqBUAwBQW9FY84/bI+Md38Bv2e/FXjGwfZqFrB5FrwOJpGCI34E188f8Eq/j38Tfjx4Z8fXXxB1OTWbTTLmzg067mQBi7CczrkdcDyfzrB/wCCzHxQ/wCEd+DfhfwZHnzPEGpfapQD96K3AJU+26RT+Ar17/gmH8OYPAP7Ivha6UKbvxC0msXEgHLGQ4XP0VVFAaWPkj/gs18QNS0vxl4F8N6Xq15Y2n2W5u7m0t52jR3ZogjMAeTw1fMXgX/gof8AGX4dfCqPwLoviFltIZJDDqEw8y6jQhcIjnlQuDj/AHq9U/4LG3Rb9qrS4my8cXh+2YJnjmSXP54H5V9N/wDBLf8AZz+HfiL9mWPxP4l8K6TrOq6hqFwJLrULdZCI0OEXJ7DJ/Opa1H0Pyfk8eaj4g8dWvinxPd3GuX/26O4uprx/MaUBskHP0r94vgf+3R8H/i7feGPCuheIF/4SLUbYJFprW7Jhkj3MmcYGADj6VB8Vv2N/gHrHgfxDqKeAPDdtdW2n3EiXdhDHE6uIyQdy98gYzX5j/wDBLHT7Ff2y9Omv0jSKzsb14pJmAEb7dqnJ74LDiiwLufo9/wAFHfjxr37Pv7PtxqXhfzrTV9Uvo9Oiv4R/x67kZi+ex44965P/AIJW/tBeJ/jp8MvFcXjDWLrXtb0TUUjF7dHLtDKmUG7vzG/6103/AAUo03w/46/ZS8X2K6xZHVbSOPU7SBZ1ZnMMi7sAHrtcjPvXh/8AwRP0zb4F+JurF8G71K1hEK/dQRpIRgfWQ1OzLcro8H/4KVfHz4q+A/2r9e0nRPH/AIh0HS7W0tpLS00rVp7eKJXjBLBUYAMT1r59/aB/ay+J3xy8K+EvCnja6eO30CAbDIHWa7cqu2ednyXYheG9ye9esftqWS/GD/goxf8Ah20DTG41Wx0d1XknbsDj+dfshrHwJ+HHiOa1m1nwF4b1i4t4Ft4p9Q0mCd1jUAKoZ0JwAOlVvqRsfhH+zj+258V/2c9LTQ/B2q2kuiyXQc6Nd2aS+ZJIRuKEDdk7QMk9xX6oft6fAY/tLfso2/iEadFD4z0PT11q1YwjzVHlB7iAEjIVgM4zjKDPSvfLf9mT4R2erJqdv8MPBsF/GQyXMegWgkQjoVby8it74teJtL8E/C3xVrWsyRw6VY6ZPJOZR8m3yyNp+pIH40uUVz8zv+CMfxxv18U+KfhXePNPYXFmdbsVLEpaukgSZFXOFDeah4HVa/WKvxz/AOCM3hKXWv2gvG/iuLcllpeitat6M1zcKyfpA35V+xlUiXuFFFFMQUUUUAFFFFABRRTG6igB9FFFTcAoqHLbuOnenL92jmHYkopkbbs0+mAUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtRc5NZvcB7MByTXK/Er4leG/hN4RvfE3irUodM0azXdJNKeSewUdz7CulcDaSxCqOWz0xX4jftpfGLxf+2d+0nN4B8CPd6z4fsrg2em6fb/6mR0wss7Y6jcBgngUikj628W/8Fl/hromqSW2k+Fda1q2Tj7VvSEH6Bhmvnj9tL/gpVpX7RnwVj8K+ELLVPDk9xeo2oxzSDM1uFbKBl7Zxkd+K+rf2f/8Aglh8LvA/hSyk8bac3ijxLNApumuJD5UTkcqgHp/Svlr9tj/glzqPw5h1Lxt8LUk1Tw7GGmu9EGWuLZAMlo/76jHTr0qrFaFr/glR+1Z8PPg3a674K8WyHQtU17UVuINWuH/0dlCBVic/wYO7n/ar9F/2ovjhf/Bj4B61498L6fH4luLVFaBIMzRlWOPMymcqOpPSvx8/Zh/YeP7Vnwq8Ta1oms/2J4j8O3HkzW92h8i6BUsG3H7pGCDXsn/BKP4h+M9U+POv/DXWdXm1vwj/AGJdC8026cTwAxSpGCmei/vCOODuFHKBo+D/APgtN4usbV4/EXgfS9UuDtKTWc7Q4HOQwOfbp71s63/wWt1JtLmSw+HVvb37LiKWW93Kh9SMc12H/BVb4L/DX4YfAPT9R8OeC9J0bXtU16C1F3ZW6xkIY5GfOOv3V/OviGfwr4X0P9gmw8QS6dA/i7XvF72qXkg/eC1hjJYL6DcRmnewrX1Pv7/gnD+1Z8Xf2qvin4vu/Ft/af8ACJ6Jpyj7Fa2ixBLmaUeUCwGThIpe/wDOv0Kr4e/4JAeEV0H9lN9TktliutZ1q4uTNtw0sahETJ7gFXx9TX1h4i+MngTwl4li0HXfGGh6LrMoUx2WoalDBM244XCOwY5I445qhbHZLTqRenr70tBIVneIPEWmeFNFvNX1m/t9M0yzjMtxd3UgSONB1JY9KvswGMnGeBX43ftvfFrxx+2N+1OvwV8BXch0TTrt9NjtY7gRw3cygGeWQ5wyrtOM9ADQNK59EfEj/gsx8OPC/iK40/wx4Y1TxdZQMUbUVmS1jcg4+QMCzDrzgV1XwJ/4KzfCv4teIo9F8QWt14BubhlS2uNWlQ2sjHOQ0o4TnaBuxndXo37P3/BP74TfBfwPZaZfeFdL8Va75am91bVbVZ3lk5yFDAhVGTjA+vt41+2h/wAEv/B/xE8NXXiT4Z2dl4O8S2SSTy2cY8u0vFABII6Iw2kgjj5jU2EfVOk/tSfC/XPidP4As/GGnv4piVW+xNJs8zcCQI2OBIcDPyk44z1FerD19RX8y/w38E+LviN4+stC8KW15qPiaRmliNtIRcBkBBKODk4x2r9Bf2RP+CmniH4Z65B8NfjlFMtrYO9o2vXasLq1ZTgLcKRkgdN3X1zRygfqR448X2HgDwbrfiXVJPK07SbOW9nb/YRSx/lX4cfHz9qb4vftkfEm5uPBNtr1vo+mRs1ppWhvIJIosKWlkCHnO0HJ6V9B/wDBQb9uC1+O02i/B74O6sNWtdXuEi1LUbMnZcMxQRwoR1XJbd9BX2p+xH+yTpf7Kfwtj00+XeeJ9S2z6tfBRlnxxGp/urkijlA+B/2JP+CmHiH4f+JLLwP8XLuW+8PyFLWHVbkET2L5IzKTyynIyT0xX6/Wd5DqFpDdW0qz28yLJHIhyrqRkEH0INfmd/wVw/ZLsbzwnZfFjwnpENne6a5i1z7JHt82JigjlIHA2kNk/wC0K9v/AOCV/wAarn4tfsz21hqmotf634bum0+cyNlxD1hyf93I/wCA1QH2RRRRQAUUUUAFFFFABRRRQAUUUUANamPnHFPamswUZPAoGUZlc/Ns3be1TW4Pytsx6j0pbiaQRkwrvbsPWks1m2s83DNj5fSg0cnYmcFqjOBwTU5qCRTuBwT9Kze4kxGVgykfzqfcOPU8U3Zu60qqqn3q1sJn5wf8Fnvi4dH+HXhD4cWk2LjXbptRvEXPEMOBGD/vSMf++K0v+CMPw7GjfBLxV4yntwl1rmqi0hmJBL29uuR9P3ksg/4CK8F/4LEfDrxXefHrw/4lh0y8ufD9zoyWNrPEhdftEcjmRcDkcSx89Dnjoa/Qz9hL4a3Pwp/Za8D6Jex+VfNa/a7iPj5XkJYjj2Iph0Pflpabt3Uowpxnk0EDqKKKACiiigAoopu4bsUAOooooAKKKKACiiigAooooAKKKKACimu+wHgngnj2rwr4sftu/B74I+NI/C3i7xUmnaw2N0SQSTCLP98op29R1/oaAPd6Kz/D+v2HinQ7HWNKuUvNNvoVuLe4j+7IjDII/CtCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCLzGRV8wfOf7vIqWkwD2paACiiioadwCiiiqWwBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnH0oBzz2oZQy4PShVCrgdKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsT2oAdRXI/Ev4reFvg/4VuvEXi7WLfRtKt1y0s7csf7qr1Y+wr4Y8cf8Fovh/o2pNb+GfBmseJrZWwbp5ltVI9QCpNJuw7M/RWivn79l39tb4f8A7VGlt/YN0dN8QQpvutDvGAniBJGQejjg8ivf91F0Fhc0zzk8wx7hvAztzzj1pWztJHWvyn/bV/aQ8Zfs2/tZaP4v0XxG2pWUsHk3XhyVyUSNcZyoI5O44PtRdFKLaufq1mlrx39m/wDae8H/ALSngm01vw9fRR3rRg3WlySDz7ZumGHpkHBr55/4KSfttap+zrodn4V8IvCPFOsI5N0rBmsYxtwSvq244/3TSuibM+6KSvwP8H/tt/tI/C6+sfF2pa9rGo6NcShNusW+61uAOSq8DBwTyDX7Vfs9/GrSv2gPhNoPjbScJFqEIM0G7JglHDofcHNO4+VrU9HooopkhRTWOO+KpaprdhocBn1G+t7GHBPmXEqxjjryTSuBforzqX9or4YwSvHJ480FXU4Km+Tj9a6Xwz8QPDXjRXOg69p+r7ACws7hZCuc4yAfY/lS5kOzOgopOvQ0c+tHMhC0UhqK4uorOCSeeVYYYxueSQgKoHcmjmQyaivkj4nf8FPPgr8L/GB0C81HUNUliYpPc6XbiaKIjsSWGfw9K96+EHxw8G/HXwtHr/g3WodUsWHzopAlhPPDpnKng9fSmFmd7RTVzk06mIKKKKACiiigAooooAKKKKACmSAt0OORStSUDPxA+OOiH4zf8FQ5tEUi6ik8S21uxc5Ajh2ll+mFxX7fKu1QPQYr8K5vGtp8Gf8AgpVe+JPEazWlha+KZ5Lh5FxthkJCt9Buz+FfuPouuaf4j02DUNLvIb+ymUOk1u4dWBGeooKkfkh/wWo8YR6h8VvAvhtE/faZpM10W9fPlVf5Q/rX6SfsneHZPCf7Nfw30qVdr2+iWwK+mUDAfrX5a/8ABYSwkT9qnQ7mRl8mTQrUDn7oWaTOfzr9cfBms6foPwl0TU7ieO30200eGZ5SQFWNYgSfyFAPY/Gv/grnr0GuftbzQWrI7afo9taykdQ43uQfwcV9H/An4K+Ovir/AMExdL8PeCdV/s7XLu/lu49kpjMsXmHMZYdM1+cn7R3xGPxU+OnjXxS0zTpqGpzSxSOc/ugSEA9sACv2V/4JWQ3sP7H3hz7aJAGubhod/wDzzL/Lj2pDeiPy48Yfsc/tG+CtL1abUfDmsR6fZxSS3c8F6XiaNQNxxu5GM9q8k+C3wt8YfGbx7b+GPBMEkuuTI8ilZDHsQfey3Yc1/Q3+0RouoeIvgT480zSld9Ru9HuIYFj+8WKEYHvX5Wf8Ep/hz4x8K/tUNcan4V1Gw0+HSbqC4u7q3ZUSQshXDEdTyOKYuY7T4P8A/BN/xz4E+Hvxd1j4jS2rXMnhi6i0mK3uDMVl2M7McjjGxAMeprG/4JO/G3T/AIT+Bvjfca5crDpukWtpqsSMxAaQLOrKB6sVSv1R+Lkcknwr8YrCcSnRrwLj18h6/mr03xZrPh+x1zSbC7ktrbVAsN5ApP78KzFVI78saloa1Psr/gm34G1j9oL9tC5+IerCa8tdFln1q7up2L5uJNywqSepyxI/3K/bWvkz/gmr+z//AMKP/Z6srjUNOW08R+IGF9eysB5joR+6Vj6AE4H+0a+s6aJe4V+V3/BVD9rWbxdqdr8Dfh9dTX87z+Xry2QLG4lJQw26FTk4O/evQkr6V6d+3F+2d8TtH8cXvwn+Cfhy81DXBAi3uuWls8stu8mcJCMbQcZ+Y5wRxU3/AAT/AP2A734W6tP8Svip5WrePL3bd2lldMZJNNkcuZJZDkhpH+Xnqu085JpiWh6x/wAE7P2Ybr9mn4Hpb67awQ+LtblF5qTxj51UA+VCx/2AzcdizV9UUUUCCiiigAooooAKKKKACkpaKACmtnjFLTWYL1PFTy3Aa77VORikjZWX5Tmqt1drGvHei1mLLwOtQ9Dbl0Ly06mrnvTq0WxkFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRSVLYC0m4DvUEjyMwCcDvUnlBsE81AHzb/AMFDPjhN8C/2ZPEOo6fM0Gt6uRpFg8Z+ZJJQ25x9EDfjivmX/gjV8FdMh8G+KfihdwtPq9xqD6RYTSL9y2RUZ2X/AH3cg/7lcl/wWm+In9peJPh38P7Cd/tVmk2rXEQ6F5WSOH8Rsk/76r9Av2UfhDB8Df2f/B3hGLDTWlkslzIB9+aT55D/AN9MapIdz1ikZA6lWXcrDBBGQakqpq2rWeg6bc6hqFzFZ2NtGZZriZwqIo6kk9KsR4f+1F4l8Nfs9fsz/EDVbK1s9C+0afcW9tHaxrEZruaNkTAGMtk5+gNfFH/BFj4WTrffEL4iXkBXKRaLZy44bJ824578rB+RrzD9tj9obVf26vjd4a+F3w18+88OW915cBVDiecnDTOB/AoHBPQE+tfqX+zP8C9M/Z1+DuheDNOAZ7aPzLyb/ntcMAZH/E/oBQV0Ph//AILYeNHtPC3w08LwFGa5u7vU5gSMqIljVD+Jkf8AKvlr9rjwna+Af2Tf2ZdJtVkjn1HTb7WbxXBGXlEDA4/4E1d7/wAFldWm1H9pbwxpZlP2a38PQIF7Kz3ErE/lt/Km/wDBVbT30HR/gJogRoksfCwiCsMYPyKQf++BUPcpH6N/8E/tJh0f9j34YQwgASaUs7e7OzOf1avg3/gsv4Lfwz8Yvh/47syy3N/YtEDjjzLWVGXHviYflX6L/sh6MPD/AOzL8NbEHd5eiWxyPeMH+tfLX/BZ3wrbal8AfCWuyFUu9O8QLaROTjCzwuW/9Er+VFyd2fZPwH8Y/wDCwPgx4J8RGRZX1LSLa4dlYMCzRqW5Hvmu8r5U/wCCY/jCDxZ+x74LjjmWWfSll06ZVcEoySMVBHb5Cp57EV9V1QnozyX9qr4wJ8DPgP4s8WCQLf29o0OnpnDPdSArEF9SCd2P9k1+ev8AwR8+Clz4t8deLfjPr8c0s1u7WWnXEgOJp5dxuZM9CQNq8f3mrpP+Cznxuhj0Pwt8LtOlaS/klOr6lGhIESqAsH1JLP8Ap619g/sH/Ddfhb+yr4B0hrSWzvJrBb+7iniMUgmm/eMGUgEEbsc+lMLnvy1keMI2m8I63GilnaxnVVAySTG2BWxTXUSKysNysMEHuKBH4k/8EmUjt/2zJ7e6j/fx6NfqgYfNHIJUB/8AHS3519Nf8FcPhP8ACjTfhl/wl13Yxad8RLufbYvZAI92AV81pFH3goK/N7+9fLf7JPxA8JfAX9tL4leLPE2pQ6Xoui2ur/Z/NkCm5n81dkCZ+87APhRzxW94Bk8T/wDBTb9ryO88QLcx+ANFlW4e12ny7W3BykXoGlKn67T6UAfM/wAE/EXjH9nHx14W+KUvhKa70tJt0Et7Zt9nuEGNxjfGMgHr7iv2s/Zz/b0+Fv7RVmkVhrMOh69uCHR9UlWKdjjOUBPzL7ivZfEfwv8ADHivwHN4O1DSbeTw9Jb/AGX7IiBVRMY+Xj5SPUV+Uf7Qn/BI/wAaeAn1TxF8MNVXX9Ohd54dKVmivYk44U/xEdsHtQB+qHxs8DJ8Ufg/4w8LZUjWNKntkbGRuZDtP/fWK/LX/gjjr+o+Ef2g/HvgWdXhiutIee6ikyMXNrcrGAB67bhs/SsT4A/8FT/HvwF0NPBnxA8OzeJf7Nb7NHNcymK8iCnG18j5scDPsa1f+CXOsP8AED9uDxv4vs7CSx0y70u+maEtuELS3EDBSfU7T+R9KAP2HooooAKKKKACiiigAooooAKKKKAGtUNxs2fMcCpiQahkjMmBjjNA0LHEFUY5qQ/L1pVxVW61Kyt28ue7gibH3ZJFU/qalsZHcatBAypvDM3pk0+EPI6OWwM5Az14I/qKzP7Y8OQtJIdS08bfvsblOPrzUGi/Ejwl4i1qXRdJ8TaRqWrQxmWSxs72KWZEBALFFYkDJHOO9QVp0PzA/wCCjn7UXx++Hfx5v/DXhe/1bwx4UWCL+zpLC0U/bMxqZH8wqTkMSMDp+NfOXhPxl+2N4pm/tbQZ/iRrZUgtJb21xOgz0yApAB5+uK/e5kRsblDY6ZGa8w+OX7TXw4/Zx0+xu/H/AIhTRUvmZbaJYJJ5ZMYyRHGrNgZHOMVa2Fc/JDU9W/bl1xVjvdB+IUsakFQdCdhn/gUdbkPj79vtVCjSPHoVVCKv9gDgD/tnX6tfCv8AaT+GfxotYpfB/jLS9XkkQP8AZVmCXCg5xuibDL0PUdq9MDBhkHIqhXZ+K03i/wDb4m+c6X4+G3J50YKP/QK6H9kfUv2pfHH7UHh218Ta14r03T7WYz6qNVgKQC3Xlo8EYy2ABjmv2JpPegkRc85p1FFABRRSFgOpxQAMQBzUEagybs5FNu59q8DNLayLJHwMY60Dtpc+B/2wv+CoF1+zj8bZvAeieE7bW10yOFtTuL6R423SRrIqxbTggIw5Pevsn4I/FSy+Nvwq8N+ONPtpbS01q1W5SCb7yZJBB/EGvxE/4KiMrftsePD0Bisv0s4h/Ov19/YY086X+yT8L7c440aF+P8AaG7+tAHu1FFFAgooooAKKKKACikJx2zTPM3NgAr9aAJK/n0/4KK3Bn/bH+JSzbvkuQq/NgcIuDX9BEZ3DNfz8/8ABSSMD9sj4iEf8/EbH/vhKAP2k/Y2bd+yz8Lz66Da547+WM17LXk37J+mvo/7NXw0tJMF49BtM7enMSmvWaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBryCMZIJ+lJHJ5gzgj60+mKrb2JbK9h6UAPooooAKKKarbiRQA6iiigAooooAKKKKVwCikNJuougHUUmaTdTAdRTGycYbaO9KqkdWzQA6iiigAooooAKKKKACiiigAooooAKKKKACq2oXiWFrJcSnEUY3OfRRViuB+O3iN/Cfwq8S6ouwC3sZWJkzjO3jvUSbS0Gtz8d/wBtz4oeJ/2tv2nLTwB4Zlk1G0tbo2Wm2aMQpdsb2bnHG0Hp2r64+C3/AASF8A6N8P4ZfiE11r3jSeEtKsN2Y7O3fnCoEUMccZJJ6cV8hf8ABNDQW+I37bEOs3Uc7pYx3epGa34VZCQqhsg/Kdze/HWv3J6Uox93U0lufzv/ABt+G/jf9jH41SyaVeyeHryKeQ6ddWFwS4jBHBOemCOvWvT/AIT/ALd/x5+KXxr8E6RP42uY4LzUra0eytYkSORCwDluCSSPev0B/a0/Yl+GP7SHiH+2NS8br4d1yINxFcxbG6Z3q2T27etfnz4X+Gfgb9mr9sDwy83j/TL3SNHvEnW7jcT/ADr2fbjHWs4tpWluNK5+6Sb47MZJd1Tv1JxX4t/8Fbfh1e6T8ZdP8YiMrYaraiEsoPySJyQfru/Q1+gfjP8A4KVfAjwZcWVs3iv+157ptgXS7d5th4xu44zn9DXjv/BVbR9K8cfsz6Z4ts2lRFuIriJmXaHVgMAjHoTVocXZNM/OjRfgb8XPhb8I7b4x+H7640bQ5TH/AKVpt2yS89N4B+vX3qH9nzxfoHxE/aO0HVfjfrt5qejs+bi8vJi7FwB5YYnPy561Npf7SHiLXPgNbfBhPliu9RhjExycoWwo69if1r7W8Gf8EdtL1f4SQy6n4hntfGM6eckiMDbcjKhlxn9e9MR9TftFeGfhp8cP2Z9d0XQL3QbuC3sGn00QyxhYXVcgrjocDFfJP/BGP4nalaeKvHPw2vLndYQ266haW+chZFkKzEfXdH+VfLnxq/Yv+OH7OPns9tqF9oJLr9t0iR3iKDGdyjoOe9er/wDBH3w3q8H7T+pak1ndJZR6DcQzTSQsq7mliIBJ7/IaEtbie1j9p6Kbuo3VoZHLfEbxpZeBPDN7rF9KsdvaRNLJuPBUda/D74+fHP4i/tu/H46F4ZuLy5tZbg2WkaXauY4hGPvO+D7AkntX6Vf8FRPF0Hgz9l/VpRM0V/qMy2NvtPXfyw/IV8tf8Ea/gra6nrnif4m30RL2JGn6eSeFLAmQ47n7oqOpq7ci7mp4B/4IwXV74Xjm8W+PJrHXJF3NBYQrJHGfQs3J/CvIPjN+wj8Yf2O7V/HPhXxTNqOnWcwbzNOd0lRV5BkUHBH/ANev2ulmSCMySuscajLOxwB9TXk/xq+KvgS3+HPiWzvvFOhb5LGZBDLeRtlthwNoPrSJUmfK/wDwT5/4KGa/+0R4qh+HvirR0fXINPkuzrFuwUSKjKp3J6/MvStP/goD+058ef2c72G/8I6ZpC+DpQCNUaDz5Y2BAKurcDORg/Wvkv8A4JOpoOm/tIeMPEer+INN0aOwsHt4Bd3McC3HnS5OzcRnHlDp6iv0k/aI8afBfx18Ntb8O+LfGvh37Ld2rjaNRjkZWAyCArE5zilcrS+p8hfs9f8ABYmxuoZLH4v6U1ncb18nUtIgyhU5yXTPHbpWH/wUI/4KAWPxC8K6B4L+EWtSXK6wT/aF1Cu12VtojiHcEknOOa+Z/wBkn9nHwL8cfiP478PanrrLZ6dA0umXCuUWfG/35wAv514SNH1fwD8ULpPDyS6lfeH7wzwyQW/ngGJ8q7LgggY7jFKLUpOKHY+9/gz/AMEetc8V+C5tX8ceLX0HVb6JZ7WxsY/MKEgnE5fr26dMmvDP2Q/Guv8A7Jv7Zdp4ZvLqeGxn1E6NqMKkhJlZsIzKeODgj619z/su/wDBVrwN8QNNstF+JMqeD/EiIsZvWUmyuWwcncB+7PAyDx83FfM3/BTiDwtoPxy+H/xU8E6tY39vrHl3U8+nzpMhmglDbyBnBKsvX0q7iP2TjYMoYdCM0+ud+HviJPFngbQdajbcl/Yw3AP+8gP9a6KrMgooooAKKKKACiiigAoqnq+qW+i6bc395KIbW2jaWWRuiqBkmvzu8b/8FkfDHh/xxc6ZpPg+91bRrWQxvqHmhC+DjIX0oKUWz9GpM7eOtNBO3JHNfCOlf8Fifg3eW6teWOuWc2BuT7NuAP1FWbr/AIK/fBWGMNFBrU7f3fs23+dAWZvft1fsDWn7TNrb674Yaz0bxlBu864lTAvEIUBHPtt/WvhLwNeftZ/sT3V9pum6Lql3o8c3mSWz25vLRwM/Mh/hznt7elfUevf8Fn/h/bsi6L4O1rU2OQVkZI/m42geuea+6vhj4yPxL+Huh+I59Jm0n+1LRLhrC7ALxbhna1AX7n89X7TXx28XftDfEJvE3jSBLDU0gW1SzWMxiJFJONpHqTRe/tOfGLxB4Ni8KSeONbuNDWE232JJmKNCQBsIA5GBX9DWofC/wfq1z9ovfC2j3U//AD0lsY2b89tWYfAPhi2wIvDmkxY6bLGIf+y0D5j+Ye60m6tiBc28tuOitMjKD9Mivs/4J/8ABUL4h/Bj4d6L4N0zRdAvdO0uEQwtNHIHK5J/h6mv1p+OPxJ+E/wD8O22s+PIdL02xuJTFBusEkaRhgkKAvbI/OvKdD/a2/ZT8XCBhrPhm3eXhFvdPER/H5OPxpBc+StJ/wCC2Gv2sJTV/h7plzJgAG0upE+uQ2a39F/4LW2UbSm6+FWM42m11RI/XOdyHPavtGP4Qfs6/FxYrpPDHgXxN/EjLb28rDd7dRnH6VfT9jD4Dx/d+EXg7/wTwn/2WmSfF15/wWn0HULSa1ufhLdT206NFLG2uxYZWGCCPK5yCa+Cbv4hfDC6+Mx8WH4eXUHh77YLsaFDrMQT72dv+r6e1fufH+x18DFBA+EXg3B4P/Ektz/7LTh+x78CwoH/AAp/wSQOgOg2x/8AZKBp2Phb/h9Zpen2cVrYfCSSFYUEcStrqMoUDAHEIxXvf7En7fGq/tdeNvEOjT+CYfD9lpdml19st777R8zOQEfgYzg4+hr07XP2Cv2fvEkcsV18LfD8KuMEWEH2Ur9DEVI/Cux+CP7M/wANf2c7K/tvh94Xt9AF+VN1Mssk0020kqGkkZmIXc2BnAyaAuj01e9KFC5wMZ5NLRQSFFJRj3qbgBxwT25r8po/+ConxG/4acTwudP0yTwl/wAJANJaNF/eFTJsyGz171+q8i7kKnoRiv5q7y4Om/tBrcNKyeT4kDlgTnIuev14o5hpXP6VY38yNWxjcAadVPSJhcaXaSK25WhRg3rlRVyqEFFFFABRRSd6AEYgdao3U6Hv0qW5LeYAenaq10o2rxT6G9NLcrK0d/MsQUnByWHYV8EfFz/gq5YfDf49P4P07wzHqPhrTb77Df6h5h80tkAmMDjg5r9AbGMGTcONvP8AOv50P2noDbftJeP1xtA164xj/rqKy3Km9bH9G2j6lDrWlWd/b7vIuolmj3DB2sARn86uVy/wuYv8OfDLE5J023/9Fiuoq1scwUUUUwCiiigAooooAKKKKACimtSUDH0UyjIoAfSZqNjQtYSlrYdiSjIHU0i0MobBIzimtST8WP2+LWXx7/wUqsvD0h3QfatFsFA5+R44nb9WNftHaRCC1hjHARFX8hX45/tGCOP/AIK5aL5hCL/bOknLHA/1MeP1xX7JVqtgCvxq/wCCkn7WnxQ8T/EjxP8ACmxs7zSPCVvcm2WOG3dZL8L1bOPmUn04r9lG/TvWXdeF9J1C9W8vdMs7y8UbVnnt0dwvoCRTA/nd+BWv/GD4H+KpPEPgbw5rEWqtAYhN/Yss5VTngZTivoWL4m/th/tWzWXgVk1+wtrhw01y2mPpsQUdTJLtGQPTPNftTFp1pBgx2sMfb5YwKmjjEYwAAPYYoKufzt/tJfDnXPA/7QB8B6v4hufF2qaa1tYLcuWdixRSIlByxIZse5r6n/4LNTRr40+FkEjhXTQ2Z4/4gplx0/A/lX1347/4J26J41/a0074yS63IkEV1Ff3GktECJJ48bCG9MgH8Kz/ANvv9gG//a18ReGvEega/baJrOl2hsJFvY2eKSLzC6Yx0ILv+YqbBzHoP7Nv7Vvwg1j4LeEY18f+HtJmtNMt7eW01TUoLWWNljCkFXYdxXjP/BT74mfDP4mfsp6pYaT4/wDDOsarZ6jbXtrZ6bq9vcTSOpZCAiOSflkbtXjGm/8ABE3W5ohJf/E6xt7lvvrFo/mp+GZBitKP/giTPn978VoNuOieH1HPb/lrRyivrc1/+CJuuao/hf4laJNFMuk293a3cDsD5fmurpIoPTIESEj3HrX6cV86/sYfsixfsjeD9a0VfEX/AAkkup3n2p7j7Ettt4wFwCSfxNfRVMG7u5+H/wC1dND8cP8AgpRFoSSm/s5NcsNHcwnzF8tGUOvGeAAc+mDX7c2VrHY2cFtEoSKFFjVR0AAwBX4kfBGzh1T/AIKqWkd3zH/wlWoSYJ/iSGZlP5gV+31MQUUUUAfit+07/wAE+PiLrH7WWqad4M8L6lf+HNcuReLrbWrmxtvNJMm+XG0EfWv1L/Zp/Zr8L/sz/Duy8O+H7OP7WUVr6/YZluZepJbrjJOB2r16igBF4/nS0UUAeD/Hr9in4WftA6fe/wBt+Hrey1qdCE1qxQR3EbcYbjhunesD9jX9iXQf2RtN177LqT67rWsSKJ9RlTYfJQsUQDtjcc+tfS9FACDpS0UUAFFFFABRUdxcRWsLyzyJDEg3NJIwVVHqSelc1oHxS8HeKtYm0rRvE+k6pqUIzJa2l4kki/gDQB1NFFFABRRXzx+13+2Z4V/ZT8MxvelNU8UXqn7Bo6PgvjGWduiryOuM9qAPe7u3uJWTyZfKAPzcdashTgZ5Nfil4m/4K3fHjXi17odtpmiWEbn5YNLFwCPR3cEDHtXpfwA/4LHeIZvEun6X8UdC0+50q5kSFtW0lGilhJOC7R5IYcjgAUAfcv7bvw5+I3xN+BeoaT8MdUfTvEazJP5cMohkuUXOY1kLAKT79cV+PHwp/ZB+OP7QHinXdOs4Eg1XSbk22qNr2seTLBJnkmPeZGX/AGgpU9jX7/abqEGrafbXtq/m21xGssb4I3KRkHn2rkLf4M+ErH4qXXxFttLWDxZd2a2FxeRyMoliByNy5wWHrilYrm0sfkvff8EfvjtZ2sjwa14PvXC5EcOqXayMfQbogufqa9n/AOCbf7Dfxb+APx21fxd4+0S20bT00mWwhYX8Fy1y8kkbZXypGK7RF/EB94Y71+nFLRYVyJQwOCvHJzn3r52/au/Yd8GftZNpl3rt9f6PrOnRtFb39iwbCE5wyNwefTHWvo6imFz8e/ih/wAEj/ir8O7621H4VeJk8RSK3GLhdNuohxzvLAH/AL67V58Pif8AtefsZ68ZPEa+ILjTIWAddXZr+zkH91ZgWHfqDX7f3VzFZwPNPKkMMYLNJIQFUDqSa/Pf9tj/AIKbeEvAtre+DPAtrYeMddLGK7mvYfNsYBj8nbk9OmKB7nffsf8A/BSfwh+0NPpvhjxDGfDnj26LKlmEZrefaCco+MA8dDzX2fuFfjt/wTX/AGRvFPxB+Klj8ZddtI9G8N2dzJd2kfl7DcyknhF7ID3r9O/j1+0R4L/Zv8JQ+IfGmotZWc84toUhjaWWVyMnai8nA6ntkUBY9Opa4b4P/Gbwl8cvB9t4l8H6oupabcDPIKSRn0dDyp9jXc0EiUjBWxkZpk0yQgFzjNOBzzQAybaUwwwKSHbs+WnsoYYNCqFGAKB9D8Dv+CoikftqeOc947Q/+S0VfsX+xa/mfsr/AAxP/UDth/44K/Hv/gp9Cb79tTxisZxvjtEH1EEa/wA6/aP9mvwjc+A/gJ4D0G8KG6sdIt4pfLbcu4IM4NAM9LooooENdxGpY9BUNtex3W7YG+X+8MVM1eX/ABs/aU+HP7PFnYz+O/EUOi/bmK28PlvJJJjqQqgnAz1oGeo5pa5P4Y/FLwv8YfCdt4l8IatHrOi3BIjuo0ZQSOoIYAgj6V1lAgppB3Zp1fH/AO2V/wAFGPC/7K+rWvh3T9KXxj4rlRnnsorxYI7McbfNbDctk8AcYoA+vo1Krg1/Pt/wUe3f8NjfEcsMf6SoHI6bEr6usP8AguBftcRrefCW3WIsA7Q66SQM9RmDB496+Ff2pvjPZ/tBfG7xN450/TZtIttSKstrcuHdcBRyRx2oA/oA/ZwV4/gF8PVkOWGhWecf9cVr0evOf2cZBN8A/h64OQdDs/8A0UteikkYwM0ALXEfEn42eBvhDZi68YeJ9P0KNvurdThWb6L1NeM/t1ftlWv7JHgfTpbfTzqviXWzJFp0BI8tCgXLyc5x8w6V+Tvwj+Hvjz/gop+0JdDW9bltjMkl3c6hLG8kFuikDy0HQE54HtQB+yfhP9tD4L+N9UtNO0bx/pN3eXT7IYhMAWY9BzXtSsHUMDkHkEd6/Db9sD/gnV4k/ZS0Cy8Y6JrzeINChlUTXccJhms5Mjaxx2J9+1fop/wTU/aEufjp8A4odXvftniDQJvsF1IzZeVQAUk9cEcc+lAH1vRRRQAUUUUAFFIzbVzjNIrblzjFADqKKKACiiigAorO8Q+ItM8J6PdarrF9Bp2nWyF5rm4cIiAepNfK7f8ABVD9nuHUryzl8S30ZtpPLM39nu0cnOMoVzkUAfXNFeT/AA9/at+EXxSW1Xw18QNDvri5IEVo92sM7N/d8t8Nn8K9X9MdKAForG1vxloHhl1TV9c07S3YZVb27jhJHsGIrlNU/aM+FeikC/8AiP4Vs92QPO1i3XOOuMvQB6JRXjGrftmfA3RQhuPip4WbfnAt9TimPHrsJxXn/iv/AIKa/s8+FYyT45j1WUZ/dabayznj3C4/WgD6nor4f8K/8FdPg34s8Z2OgQaf4itUvJ0t4tQubRFh3scDOHLAfUV9uwyrPEkiHcjgMD6g0APooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0ZoAWikzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTVXaSadRQAUUUUAFFJmjt6UALRUaLtZiTnNK0gXrgD3NZvcYSOFxk4zSNzXIfET4seEvhlotxqviPWrLT7a3QyETTqHbHZVzya+JNc/4LN/DXS9auLWz8J6/qllGxVbq3ES78d8Mw4qS1F2ufoMfMKtjCnHFfFX7dX7SPxP8Ag9ov2LwX4W1G7nljMj61FEXitQPUAc55/KvJr7/gtfob3JGmfDm+ltlBLPd3qRsPThQ3X619mfs0fHLT/wBqr4RWni59Dk0uG6Z4JtOusSKcHHcfMKFaTsXF8utj8yvg/wD8FeviX4T1J4PHWn2vimwO1d8KfZ5ocE7jjndnj06V+jP7P37c3wt/aEhgg0bW47LW3QNJpd4fLkU+gz1qD4ufsc/APWNJv9Y8R+DtI0tI43klvIT9mxxySRxn8K/En4oafoXhn4yz2fwrvLyW2S62Wc1vIWbdnGFI5Ip3a0JSUtT+kGORZFDKQynkEHINOrg/gXa39j8IfCUOpvLJqC6bD57Tff37BnNd1uq46ohqzHUUgNLVEhRRRQAUUhbFAYGgBaKKKACiiigBO4r5d/4KPfEm3+Hv7Lfigs6i71BVsoVYE5L9eh7CvqJuBmvz6/4K8akJfgXaWzDa39qQc98ENn+VRLYuKb1PNf8Agif4J+X4i+LpCSZDb6dEOMfLudj0/wBod+1fpZ490G+8TeFdS07T702Vxc20kKuOOWXA57V8X/8ABHPS47f9mvVb0KRNd61MXb12gKP5V957aLKQSep+Inij/gln+0RJr2p3NvZ2N9HJLJIl1/bC+Y654zz1x2xXyH8Sfh/rPws8Zap4U8SWwttZ0+Ux3Cbw204HcDmv6d9tfCn7SH/BLPQv2hPjFdeOT41vNF/tCVXv7IWay7wMAiNsjaeOpDVRNzx79lf/AIJSeBvGXgXwv428T+LtQ1VdQhivktNKCwxq2d21mYNkdAeB0NfRX/BSfwwsf7IGraRpWnyTJbGERrGpby409cfzr6X+Fvw00j4RfD/RfCGhmdtL0q3W3ha4cNIQO7EADP4V0l3Y29/ayW1zDHcW8i7XilUMrD0IPWlZjTPwK/4J4/Aq++L37THhr7Tp8z6JpDf2jdyyxHy/3eNqk+7EflX79JGsaKijaqjAA7Csrw/4P0PwrG6aNpFlpav977JAsefrgVr496VmJsiuLeK5haKaNZonGGjkUMpHoQapaV4d0vQtw07TbSw3fe+zQrHn64FaWKNtUhDaKdtpAKYH51f8Fm/EFpH8IPBmkmQNcTa0ZvLHUBI+f/Q69H/4JM+Hl0j9krTroxbX1C/ubgt/eG8qD+Sivmz/AILSatp/9ueAdNtp9+qR/aZ54M/dV1jVTj3wa+7f2H/Bv/CCfsueAdKKGNv7PWdgTnmT5z/OoWruavRG7+1D8PPE/wAT/g1rnh/whfrp2uXUe2GWRyq+4JFfj18R/wDgmz8a/h74P1jxP4gm0v8AszTYmubiY37OxA9iK/d3vXPfELwHo3xN8Hap4Y8QWxu9H1KEwXESsVYqfQjkGnbqRfofz3/su/sp+Mv2p/Emr6Z4RmsbU6XFHLdTXczIqK5YLjaMnJU19HN/wR1+NEl0Q+t+Gnjz/rGupT+myv03/Zt/ZF8A/stw6yngy0uYpNVZTcTXU7SsVUnaoJPQZP517W3Q4644qvUL22P5n/FGmeI/2f8A4mazo0WqLb6tpkj2s01ixCt2IHsa/Vj/AIJN/s4f8Ir8M9Y+IHiOz83VvFJCRpeR7itupbnn+8WOfXFexfGf/gnT8J/jl8TLTxprNne2l8JPMvbexmMUd4eMb/TGP4cE5r6a0TR7Pw/pNpplhAttZWkSwwxL0VFGAPyoslqhNn50ftj/APBKiDx5q0/iv4SNa6NqExaW80K4YrbzScYaLqEJ5yDx0r8v/it8I/Gvwb1htD8Z6FfaNdJuSJZ1YwvyCTG3Q/ge9f0yVzXjj4Z+FfiVYx2fijQbHW7eNt8a3kIfY2Qcqeo6DpU2K5jk/wBl5J4/2e/h+lwnlyro1spXOekYr1KoLKyg020htbWFLe3hQJHFGMKqgYAA9KnpokKKT0rM8TeI7Hwlod7rGpzpbafZxNNNM5wFUDNFxEmva/p3hjS7jUtWvYNPsLdS8txcOERQO5Jr40+KH/BWr4OfD/XX0vS49U8XSRMVluNKiXyVx6MzDPfp6V8GftsftseJf2rvGkHhLwet5F4Yhna3trC35a+kYgZbAyRwOM96+mP2Vf8AgkX4aj8N6dr3xea6v9WnUSnQLeXyoYlPQSMvzE+wIpjasdLH/wAFpPhs0oB8FeJvL7sFhyPw3179+zn+358Lf2ltYfR9Au7rS9aVN62OqxiJ5fUIckMR7GsfVv8AgmL+zveaTc2tn4Ej024lQql5Fe3DvEexAeQjj3FflH+1p+zlrf7EvxmsBompXosGK3el6uvyPuBBIyO44yKASuf0A3VpDfW7w3EUc8LjDRyKGVh6EHrXhnxC/YZ+CHxMvnvdZ8Bael84w1xY7rZj+CEL+leh/BXxYfHXwl8Ja+0/2h9Q0yCd5T1ZigyfzrtqAPjPU/8Agkx+z/qDhhpmtWg/u22pFR+qmqK/8Eh/2f8AkG38SMf9rVzx/wCOV9s0bRQF2fG3g/8A4JS/A7wb4t0zXrS11a7lsJhOltfXnnROwORuGBnBr7HhhS3hSKJFjjQBVVRgADoBTqWgQUUUUAeIftafsv6P+1V8O4PDWp3r6XNbXIube/ijDvEf4gM+oA/KvhzVv+CJ1xNcSHT/AIoJHC55W60ze2B0wQ4r9UqaxVVLMQABkk9qB3Pxi8cf8Enfjb8PGS88G6/Z+IvLJYfZbh7WZdvIIDEjP0NZ/wADP+Cgnxx/Z98bR+BfGcF34sVLuOxOla0c3cLFtuEl6nr0ORwK+0v23v8Agox4b+BGj3PhvwTf2mueO5t0LGNt8On8D53I4Y8nAB7V8p/sE/s5eO/2kvjtbfGb4k28+o+HbWVrmO81Rc/2hOMhNqt1VTznGOBQPm7n6+aPeS6hpdpdT27Wk00SyPAxBMZIyVJHpV2kVQihVGABgAUtBIUUUUAFFFFADWbFVZJ3WUDHFWXYDAPfpUDRFpie2OKlouNuo+GQyKc1/Nx420c6h+0tqumQ/KJvE7Qpt4xm4xX9I6RjauexzX84vj5W0f8Aas1XDEND4qLAg8j/AEgUrFddD+i7wzZjT/D2m2oYsIbaNMnqcKBWnVHRW36RZN13QRn/AMdFXqoyCikam5pgPpKbk1Wubpo8gCpuUouWiHTyB+B2rK1CQpHnNZ+sa9Jp8RcRl8ntVb+0v7YsyJoGRWHBHrUOp0sdcYcq1N3TbrzliA6hufyNfz3/ALYzhv2qviIQMD+2JOB/viv6D/D0Jjt1V4yjIOM9wa/A79v7Rf7B/bB+IMAGEkvBOv8AwLaaUXcxk7s/eT4WnPw48Mn/AKh1v/6LFdMn3jXIfBtt3wp8In10u3/9FiuyrVbGLGOu5kPpQzHzFA/GmXDOqgqM+tRopuMmQfLjGPrTC3UsrnHPWlr8nP2oP27vi14W/bAvfA/gbxHDZaNBqFvpyWsltG6MxKhySw9zX6raK1y2j2RvJFluzChldBgM2BkgfWgRdooooAKKa1Qt5uTjBHapuOxM1QSSHIwdo71GIJmYktxTms2YYLcHrWb1LVluQ3cnnRFIzuJ6n0pkMLQ5Hm7zjp6VY+wiNcRttb1qG1094yxlbcxNTaXQ0UlYIw37zNWbf7tPCbelOWp5X1Ik7jlp1Qp95qlB4rSPYzZ+Ln7bzfYf+CpmgzDp/a3h9z7f8e/+FftGrblBHQ81+K37edvJcf8ABTK2giO2aa70PYffyoq/aOyVks4Fb7wjUH8q2ET0UUUAFFFFABRRRQAUUUUAFFFFAH4ifBb9z/wVYtM8Y8T34P4wy1+3dfiJ4Ojk8O/8FXoI7hGhP/CVXGRINpG+OTB59civ27oAKKKKACiiigAooooAKKKKACiivz9/4KNftgfFv9m3xl4cj8IaVFa+GXjLy6lcW5lju5eMxE/wbRj67qAP0Ab3OKQFVxz14FfFv7Gv/BSHw7+0heW/hfxBbJ4b8YtGPLQv+5u25yI89+M4969c/bT+PJ/Z3+AGv+JrZ4/7YkQWlgjnGZn4BA74GTQM+Af+Cl37a2u+MPHEnwv+G+r3D6PahoNSfSdxkupjgNEcDOFIxx610H/BI39m3xDo/jrxH4+8ZeGNT0g29pFFo9xfIYvNZy/nEqTknATqO9R/8Ep/2XY/Hmq6l8bPGMEl1P8AamXS1m+7JKSTJMR3GSAPcGv1aVQihVAUDoAKAYtFFISFBJOAKBHlv7Snx90X9m/4Val4w1n94YyILO1X71xcMDsQccdCSenFfkF+z/8ACHxp/wAFC/2jrzxP4wF1e+Gornz9VvBKBHDHk+XbpnGehHy5x3rtP29Pjpqn7YX7Rmi/CXwb5k+i6XqP2CHyT/x8XDECWYg4+VQvGfQ+tfqd+zl8CdE/Z3+FOjeDtFTK2sYNxcMoDzynlmYj3oA2vCPwb8E+BPDceg6L4Z02y0tYxEYFtlIcAfxZHzfjX5af8Fe/gd4Q+G/iTwJ4m8MaXb6PeawbiG6t7ONY4j5RjKuFAABO8/lX6+tX5Cf8FX/EU3jz9qTwD4Ht7hZ7eyjt42hBxslnlGQc8crtoGtT9S/g1I83wn8IPJ99tKty2fXyxXZVkeEdJTQvC+k6dGMJa2sUIH+6oFa9AgooooAK89+P/jzV/hj8H/FHijQdL/tjV9Ns3mt7TkhmHcgdQOtehU2SNZEZHUOjDBVhkEehoA/nv+JX7Wn7QH7RF1Jpt7retT2945jGj6NbNFEc/wAGEGW/GrXh/wD4Jx/tC+IrCO8h8A3cMcuJFF5PHA/PchiDX766T4Y0bQWdtM0mx05nOWNpbJEWPqdoGa06B3Pwab4Dftg+C4YtBtdF+ICWdou2KHR7qYwIPYxnFVx+x3+1R8aby3sdb8NeKphbEvC/im8dYkLcEqZTgHgZx7V+9tNZQ2M0D5mfN37Bf7OE37OXwQsNK1nRoNK8X3JZtWaC5E6ysGO0hgcYwe3rX0nSUtBJHLGsmNyhsetfFP7fv7e9r+zlpp8J+FGF148ukDZ2bo7RD0JP94+lfW3xG8baf8N/A+t+J9VmWCw0u0kupGb/AGVyB9ScD8a/FH9ln4Rah+3F+1bq3iPxB5174ehu31HUJpCSAhYmOIH8OlBSNnRfCv7aPxY0k+MdOu/E8ttcZmi8u6EAdTzlUJ6V1HwH/wCCjHxS/Zv8ZXPhb43WmpanZKFjaO9TF1a4JJYf3sg+vav2F0jTLbRdNtrCyhW3tLaNYookGAqgYAFea/HH9mX4f/tBaLJZeLNBtrqfafKvlQLNGxHUMOTQFz8Nv2pvino/7RH7Umo+J/C0c0enazdW8dt9sXY5OUXLDJxyK/oJ8J2z2fhfSIJMeZHaRI2OmQgr+cvXvh8vw5/aXbwpby+dHpniKK1jYnqomAFf0f6QCuk2QPXyE/8AQRQSWicUbq8x/aWu/G1j8FfE0/w8ilm8XLbk2SQhS5bPO3JAzivxzs/2nP2rvghrk2v+IbnxhDF5wFxDr1pK1lJg8gbl2j/gNA0rn7rySLGpZjtUclicAD1NfiJ+0ZL4n/by/bg1Dwr4RnhWCxd9Psri4ZvIhgiyHlbaG6kn68V9L/Fr/gqR4e8Rfslz3+hh7Tx5rMb6W9lgD7MxXEk33s7cE7T+la//AASD+BEXhv4a6r8TdSt92seIpTDazPyfsysTnkcFmJ6dQBSKWh9W/sm/s/r+zT8GNJ8EnU/7XuLctLPdBNqtI5ywUegNeyU1adTIPPvj38XtM+BXwl8ReNNVcLDptszRRkgGWYjEaDJHJbFfh/8AsyfBfXv24v2k7yXVZTJYvdHVtbupixKxF+IweeTyAPrX2x/wWW+NVrpvgfw38NLWYvfahcjUr6MY+WJOIx1zkkt27V61/wAEu/2d1+EHwIt/EWpWqxeI/E/+lzSc7hBkmJTkDnB/WgD0Txx+wH8E/F/gSTw7H4F0vTHWErb3tnF5UySbcBiw5POOua/B/wCM3w1vvg38S/Eng7URm40u5kt1YA/MoYFWBIHBFf011+I3/BX7QrPTP2o4rm3RInvNIilmCjq/Iyfc4oA/VX9jvUf7U/Zh+G1xz82i2459kAr2SvBP2EZGk/ZL+GxYEEaVGOfYV7tdXCWlrNPIcJEhdj7AZNAH4af8FLvjNJ8cP2mToGmCVbXQnXSYIpMHMxbDuuCeCcflX6wfshfs/wCifAL4NeH9KsbKFNUktElvrxU/eSyMNxyeuMmvwx8VfEyGx/ac1bxm2nDUY4fEEt79nbkuiydPTPFfsD8Jv+Cn/wADPHug276h4hPhLUEjUSWWsRmPB6YVxlW6djQB7d+034DtviX8A/HPh+5jSQXGlzvH5g4WRELqfzWvyx/4I7eOrnwv+0N4g8I/M9trOmu7qD8qPbvgHHqd5r9BfHH7eXwHHhHV41+IelXTzWc0axwSb2YlCAMD61+eX/BJjw3N4j/a217xFZYbTbCwuCzEEcSyDbj/AL5NAH7SUtFFABRSE4r4m/4KPftWeP8A4Aad4e0rwBpd19v1MSPPqYszNGijACrj+LqT9RQB9tUxpEiXLMqD/aOK/Cuz+Pn7YfxVnmi0jUPGF6ZANyWlsYkAPTqBitLT/wBkX9sbx8XuL6PXIC3zbtS1gx7s+gDGgD9sNQ8WaJpChr7WdPslPQ3F0kYP5msTT/jF4G1bWItJsvF2jXepSnEdrDexvIx9AAea/HKb/gmH+0vrkZN41mxHOLnWpG/oa9N/ZQ/4Jp/Fv4efH7wt4n8ZQ6ba6LpM/wBqeS3v2mdmA+UYwO5oA/XCiiigDmfiR8O9F+K3gvVPC3iG3+1aTqMRimQHDY9Qexr4c8Uf8EY/hpeWcy+HvGfijRbpiTF9okhuYIyf9jYrH/vqv0JooA/HL4rf8Eg/H/wz0OTX/Bfja38VahZlrh4xYnTpo1UZDRsJX3N1446V7D/wTB/bS8U+PPEM3wn8d3E2p39ratJp+ozqTNmNiJI5GJ+bAK4PHev0a8RalbaPoV/fXzpHY29vJLO8hwFjVSWP5V+K3/BPfT4fGv7fU2o6VcXNrpkLX9/G0R4dN+Ap6YB3fpQUjt/2qf8Agnf+0j8SvjJrGuWT23jDTdQu5Hguf7WjtxbRE/KrRyupHH93d07V5L8Xv+CZ/wARPgF8GdU+IHirV9FxZ+Xv02xJuJBuYL8zsAo6/wAOa/dvJBr4A/4LKeNpdD+A/hvw/FcPF/beqnzEQ/6xIlBII+rD8qCT5N/Y1/4Jz+HP2tfhw/i3/hY9zpL2t21pdabDoqMY3ADY8zzhnII/hrnf28P2KfC37Ho8F/2b4iv9dOuSzC7+0wCMwxx7MMm1jknc3X0FfbH/AARl0P8As39nDxBe5Y/2hr0kuGHTbGifj92vAP8AgtV4knm+K3gbRHIW0t9HkuU9d7yMD+iigD2/9lP/AIJy/A3xR4M8GfEiy1HxFrNxIsV9Gs92iweapzgoI84B/wBqv0Khj8lAgPyjhRjoPSvnr/gnzAtv+yH8OgqeWGsA236kmvomgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBuKNtfKt5/wUa+Gdv4guNHTTvExurcMZGk0somB6HdzXikn/BZnwV/wmr6XH4I1g6Rv8ldQknjWTfnGTHzgfjWMa0XomdEqFSHxKx+ih+WlVs1+d3j/APbl+OXxOt7i0+EHwd1JLXGV1e7PmFvQquAMfjX1t+zB4s+IHjD4T6Zf/EvQxoPinJSe3A27gOjEdia1jJSV0KdGUFdnrtFJS0zAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBK+UP+CgX7R3j79nzwDpdz4B0Vr/U9Qmkje7FubgWwVVIJQKRzuPX0r6vIpNoPUZqWrjTsz8I779un9rDxxMlvZavrAnzjytJ0bY3PriOrdn4Z/ba+L8jqrfEKcKAxNzcPYx4b03FAelfueI1T7qhfoKdtqeVluVz+ff4ofsa/tCeGtLuNd8eaJfPZQo0r3GoamlxjAycYkPNZH7Gn7Lk/7VPxSHhyS/fS9Ito/OvbmIBnjXsFUnuRX66f8FH7qy/4Zn8SCWULPHESm0884GPxr50/4Is+EdMXwn458Q+Vu1U3kdn5h/hjCbsD8TUpvmsXb3T2jwL/AMEm/gT4NkgnvbLVvElzGVYnUrweUSP9hFHB9CTXV/tQftKeG/2Jfh3Z22i+E3LSL5Vha2MAS3UgD7zDp1FfUeOawvF/gHw94+08WPiLR7TWbRTkRXcQcA+o9KuSfQzT6M/n8/aE/bU+Jv7Q8rLretyWOjrI3k6XZsUQAgcNj73Qdad+xv8AHDwV8AfiBceJfGPg248WSJGoslgdMQPk5chj1xiv2nvP2GPgbfNOZPh1pIMxyxVGGPpzxXKXn/BNH9n28Lk+Cli3dfKuXH9aOXSxV4nz7ff8FpPCCQ7dN+HmtSSgcLNPEqn6YNfV/wCyn+1t4Y/at8KXOp6HBNp9/ZkLeWFxgtETnHI6jg1xUf8AwTE/Z8jheP8A4Q5iG/iN2+R9K9k+C37PXgT9n7RZ9M8EaLHpUE7bpn3FpJD23MetGt9Cbo9GWnU37tDMR0GRVkDqKimuY7eN5JXWKNBlndgAPqa4/VvjV4B0OTy7/wAZ6Dayf3X1CLP5bqVx2O1ory+6/ae+E9ljzviH4eTPT/T0P8jUMP7VXwhuJBHH8RfD7OegF6tLmQWZ6tRVDQ9e0/xLpsOo6VewajYzDdHcW0gdHHsRV+mncQUUUUwGt92vzS/4LLeKLex8D+FdFWBjNeXhlkkHHCL8oH/fVfpa/wB09jX5b/8ABY+BLnQPC0sl0rXMFyQEXjhhj+lZya0RtDZn0F/wSh0MaT+yPo8+STe3lxOQe3zkf0r7Ir43/wCCUWqS6h+yTo8UgULa3c8KFQckbj15r7Iqo7GT3CkpaKoQUUUUAFFFFABRRRQAUg+7RSZ4FID8V/8AgsBpd5aftCaZdTuogfTFMBHXhu9fqv8Asu6l/a37Pfw/ufMEhfRrfLAY52CvzI/4LNa9YzfFnwppUcH+lw6c0ktx/eVmwB+GK/RP9hy4kuP2U/h1JJ97+y4xwMVEXZG0tj3UfeNLSL9406tDETaN2cc0MobrS0UAFFFFABRRRQAUUUUAJ3FfBv8AwVs+OTfD34OWHg6xl8vU/E0hTKtgpCp+Yn2OcV95NX4of8FhPHkHib9o7TdHtpS/9h6UttKp52uzlzgevNQ9yo7nqn/BIH9me01WTU/izrtmlx9mk+yaOrgnY4z5kmOhzwAT6V+rQzn8K/Nf9jH/AIKGfAj4U/Azw54M1nUL/wAP3+mWwE7S2MkiSyEncQ0YOfXmvoGL/gp1+znIpI8egezafcg/rHVIJbn1O1flN/wWy8RWVxffDrRUZWvrZLm5kXPKq+wL/wCgmvpjxT/wVU+AWj6Tcz6f4ln1a9WNjDbw2Mw3sBwCSoA5r8xdSb4mf8FFv2hn1G006S6DSJEGCYhsrTdwCcemetMSP2Q/YrsJ9N/Za+HEFwCJBpEJ59CMivbawvAvheDwV4N0TQbZQkOnWcVsqr0+VQK3aACiiigQUUUUAFFFFAH5z/tYf8FUdX+BPxi1bwT4c8I6fqcelkRz3epSyKWcjnaFI4+tfIfx2/4KlfF34xeHm0Wza18G6dIT57aGZFmmQ/wGRjkD6etfrt4//ZJ+EHxQ8QS654m8AaNq2rzHM15PbgyS+m496p6f+xX8CtMwbf4VeF0YfxHT0J/UUAfz+fDTxP4c0Tx7Zax420m48T6ZHMJprETbTOc5wxIOc1+rvgX/AIK9fBzRdFstJHgzXdAtLSJYo7SzijlSJQMADBXivrfVP2TfgzrSqt/8MfC92q9BNpkTf0rh/Gn/AATv+AXjTT2tZPh7pukAncJNHj+yOD9Uxn8aAOE03/grR8Ab541n1DXNOVuDJdaYdi/UqxP6V9QfDP4p+F/jD4Vt/EfhDVY9Y0efhLiNGQZ7jDAHNfCnjb/gi38PdXuml8N+L9Y0CIn/AFMypdKPoWwf1r7g+C/wssPgv8NNC8H6dJ58GmW6wm48tUMzDq5A7mgDt6KKKACikam5oAZdTQ2sLTTyJFFGCzSSMFCj1Jrx/Wf2xPgp4f1h9Kvvib4bh1BG2NB/aEbFT6HB4r88P+Cj/wC0z4r+Mvxei+B/gG5mfT47hLW5hsSQ97cMcFGI/hX0rrPhb/wRdsLrw3DP488aXVvrEqBzZ6VCpSHPYs3U/Sgq3c/R7w38SvCnjWOKXQfEWm6vGRu3WV5HJge4Br+fr41Ko/a614ADyz4pzwOP9cK+99b/AOCNU2hyLc+Bfitf6bdAk7rmAxMOOMNE2a+BvA/w7uND/ay0Pwbq93Hqt3beJIba5uslxMwlG4nd1zjvSKR/RBofzaHp3Ug28fT/AHRVfVvGOh+H7y3tdT1ezsLm4IWGG4nVGkJOBtBOTWpbwi3gjiUYVFCjHoBivw7/AG+PiFf6x+3hNJ5zyR6HqVnaW6FiVGGXOB260rk2P3IJyARyK8e/ao/aH079mX4UXnjK+s21F43WG3s1bb5rt2z2r1PQZTPoenSN957eNj+Kivz3/wCC1Vxfw/BvwPFbswsJNWm+1KDjJEa7M/iTRzCW59CfsX/tl6T+1v4a1OePTv7E17SpAt3p2/eFRs7HB98H8q+i7lo9pDDJNflr/wAES9Nh874makWLXLLa2x9No3MD9ck1+pN0wVRxyaVr6l6JmfeRwPGi+UWYHjAz+dcZ8Wvix4T+Bfgq48R+Lb23sraJGaKBnCyTsBnagPU816AzJb2rzSsscSqWdm6BQMk1+KX7XHjzWv25P2t7XwL4OmM+l2kxsLI7j5YxxJKR+H6UcpblfRHdfED/AILLeM5PEFwfBvhnS7XRVfbD9vDPK4Hc46V8VfH3476v+0F8RrnxnrVnZ2upXCqHSzUqvy9zX7UfB/8A4J9/DT4S/C290aTQLXXddvbBoby+ukDtJJtP3M/d5Pavw5+JHhG88CfEHXdBvbKTT5LK6kjW3lHKrv4+tOxCP6I/2YdUfWf2f/Ad3Ihjd9Jt8g+yAV6hXnn7P2P+FI+BtoAH9kW/A/3BX5a/8FR/i58SfBH7T2lJa67cadpunW0d5pMMLlUB/iJA6kkd6ZO7P2KkXdiqmralBoulXmoXLbLa1heeRvRVBJ/QV5F+x38a2+PvwB8MeK7l1fU5YPJvdoxiZeG/PrXPft8fGyx+Cf7N/iW6ny+o6xA+l2EQ6tJIME/gCTTF5H5m/sy+FLP9qz/goVqer3Ku2jw6jca42043eVIPLB9s4/Kv29VQqhQMADAr81/+CNPwim0rwT4r+Id/C27VrhbCydh1iiJLH/vtiPwr9J1/XrQDHUUUUCM3xFqDaRol9fpbvdvaQSTrBG2GkKqTtH1xX4/fEH/grv8AGCTxFfQ+H/DWh6HaQzPEI7i1kmnOCR853AZ+gr9kmGevTuMVUXSrOO489LWFZv76oAamxSZ+LGkf8FLv2o/Hdy1j4fs4Lq84Ij03QjMwz7ZOK10/aS/bp1SdzHp3i2Ju62vhSMj/AMejr9mh15xmlo5Quux+M918X/27ryAhrXx4kZ5Zv+EXhjx9D5dfUP8AwTzj/aT17xLq2v8Axc1TVI/DPkNFb2Gr2yxyyyluGUAAqBg/nX3xSHpT2QhvHTPNFI3Sq8kjRyLjoTzWDlqOxYbPamwr8vzcnNRvPHHk5570lreLcSMq/wANEZahy6H41ft2fL/wVE8Ont9v0An8DFX7QV+LH7eTFf8AgppoLZwBf6Gf/Ho6/aeugkKKKKACiiigAooooAKKKKACiiigD8ZPF0KTf8Fcl8ohwPESklTkA+XyK/ZuvxP+LV1L8M/+Cpp1C5z5beI4JfnGCUmAAI9ua/a5WDqGU5DDIoAdRRRQAUUUUAFFFFABRRRQAlcz8Qfhr4a+Knhu60HxTpFvq+l3K7XhuEz+IPY/SunooA/HP9tD/gnVq37PH2z4n/DDUpIvDul7bmSFpStxZndjKkdVBIrwv4uftMePv20bz4aeBZ4WkktzHaJDCebqckK0jepwP0r9uf2jtDs/EfwH8e6ffhTay6Nclt3TKxlh+oFfjX/wS08MaVrv7XuhjUTHItjZXN1bK/I84ABQPflqC1sftX8I/ANh8L/hzoHhjTrZLW30+0jiKIoGWCjcT7k5rsKatOoICvD/ANtH4vR/BP8AZx8YeIRP5F61q1nZsOvnSAquPoMn8K9wr83v+C12tXdn8Lfh5p0MxS1vdVuDPHnh9kSlc/iTQB4F/wAEfvC9r4u/aO8QeIb+IXl3pWmNIkz84klfBfnvwRX7O5Ffzl/AX/hefw61D/hLPhhoPiiP7RGFN1pWmTzRTKCeDtQhhnNfRiftZ/txXOLeLQvFoZjtH/FIOP8Ax8w8UFWP2I8eePND+G/he+8QeIdQi07TLKJpZZpSegHQAZJPsBX48fBfw/qX7dX7el745S0dPDWm36X9xMGG2OJGIhXBOTkr26d6ms/2Wf2uf2sPE1jH8SbjWtJ0Ine11rF0ixRK33gsCvkEgdNtfqh+z7+z34U/Zz8BWfhvwxYRQbEBurvb+9uZO7Mep5oHsenRqsahR0AwKfkVDLII1/2j0p0ZLKCRg1LYrElLTVp1NEhRRRTAKKKKACiiigAooooA+Bv+Cvnxrj8DfA/T/Bdv8194muP3m1sFIY8E5+pOPwrr/wDglj8Hm+Gf7M9jqV1Ei6h4imbUHYD5vLPCKT9K+Mv+CzHnp+0F4ZE0rNaNoqvHGT8qkSEE+1fqj+zo1i3wK8CnTWRrL+yLfyynT7g/rQO56Iq7Sfem3Ewt7eSVvuxqWP0AzUlY3jLVrbQvCes6heTLb2ttaSySSOcBQENAj+fVrwfET9taOeHkaj4uBTzOOBPxn8q/odtIzDawxnqiKv5Cv53P2dox4l/bC8HvanzBJ4k89T2K+azZ/Kv6KaAEIzWN4s8H6T440C90bWrKG/0+8iaGWGZAwIYYJ571tVy3xS8aWfw7+HPiPxJfyNFa6bYy3DMoBbhTjGT1zigD+cj4r+B7bw78afEfhPSXM1tb6vJYWo9MyYX+df0R/ArwPF8Ofg/4Q8OQxxxrp+mwxMI+hbYMn86/B/8AZb0Ob41ftieF2kia7W91ttRuFcdUDF8n9K/objjWONUUYVRgD0FA7igYpaKx/GWqDRPCOtagSVFrZTTZXr8qE/0oEfir8ctUh/aw/wCCjlvormZdJXV49MVXUZEUP3s4J4JB/Ov230nS7fRNLtNPtIxFbWsSwxoowAqjAr8Uv+CY/k+Mv27bnUr6NbmZrTUb5XkGSsgdcH64Y1+3FABX4U/8FYtZfWv2tNVg37hY2MMOD2AGcfrX7qswVSScAckmv51/23fHEfj/APai+IWrQ7mg+2vAjHHRCF4wenFAH7p/sqaGnh39nP4e2CbT5ej2+SvTJQE1oftGa/N4X+A/jzVbdzHPa6PcOjDsdhA/nVX9mHVYNa/Z7+H93bNuik0e3x+CAEVz/wC23dPafsp/EuSMMW/slx8vXBIFAH5Qf8E2P2dfB37TfxK8ZWPjvTrjVLO1sY7mOSC4aIxyO7ZJI6//AFq+vfEn/BGbwLqGoNJoXjrWNDs8nFrNZxXYGfQswxXEf8ETNBt7e3+JWohle5L29s3HIUAsP51+pNAH5V/Fr/gkL4a+Hvwz8S+Jz8StRupNJsZLtYpNLijV2UZAJD9+laf/AART8GiLTfiL4qZG3XM0Ngr4wpCbm4/76rtv+Csn7SzeD/Atn8MPD1yx13XWBvlhILJbngIec5Yn9K95/wCCffwTm+B/7NPh3TL2PytU1AHULtcYIaTkA+4GKAPpEZ70tFFACHP0qveabaakqrd2sN0q8gTRh8fTIqzRQBXtbC2sci3t4bdSMYiQL/KrFFFABRRUf2iITeUZUEuM7Nw3flQBJRRRQAUUV8Y/8FAv26NJ/Z78I33hXw7eJdfEG/i8uOKPDCzRhgu57HHQUAed/wDBUj9tSD4e+F7j4U+FZFudf1mArqN1G4ItYGx8gxnLNyCMgir3/BKH9lO5+F/gm7+I/iK1e21zxFGq2VvKPmgtOoJ92PPT0r51/YL/AGC/Efxn8a2XxT+JEE8XhqKcXkEOofNPqcuchuuVQHB5zmv2Ih8i0WK2j8uIKu2OJSBgDsBQO5KBivye/wCC23jS1n1j4c+F0Ob20iuL9yD0WTCAYx/sZ/Gv1ir8gP8AgpT8CPit8Vv2rrX+zPCuoatot1awW2nXdpAXiVeN5ZhwCDng0CPuD/gm74JTwX+yX4OTyWgnvojeSq3Xcx618D/8FqIy3x68IseFGgce/wC+ev1s+FfhuXwb8N/DOiTRLDNYWENu8a9FZUANfmz/AMFrvBM003w/8VR2ryQrHPYTTImQnIdSx7daAPuj9jOyTT/2X/hzCmAo0iE/L7rXtNfmh/wTx/4KEeD7PwFoPwx8cXJ0TV9PQW9pqFww+zzpngFv4SK/SHS9c0/XLVLnT763vrdxlZbeQOpH1BoAuSSLGjO7BVUZLHoBVTS9asNatzPp97BewgkF4JA4yOvSma9Hb3Gj3tvczJBBPC8TyOwAUFSCf1r8Nv2X/wBqLXv2bP2m7zSYtSm1HwhfazJY3Vm0hdMNKVV164POfegD92aKitp1ureKZPuSIHX6EZFS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGLqHhfTL6ZZJ9Pt5WwQWMSEkHqDkdK/Jr9rj4B+DvDf7cnhRYptP0zR9UmgnuNMtwd7Nu/u4xz9a/XxslcV+OP/BTqO78H/tgeE/EaqMFbd4xvBPyuM5Hasai093c6acm92fr9oOlWel6PZ2tjAkFpHEqxxooUBcccCtHbtrH8G6g2qeFdIu2G0z2kUmPqgNbPNapuxhK93cRadSc0tMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0E0AB7UkjbVJwT9KTJPal59KNhnxL/AMFThHZ/s4avcImyaUqh+bqMjtXln/BFa83eC/iBb4OBfxSfmmP6V3v/AAVU8y4+BuqRIJWbKZ2rlcA/pXJ/8EW7VR8KfGd35TB5NSVTJt4OE6ZrH7VzeT0P0d/ipabz1pc1sc4tFJS0AFFFFABUcu7bhfSnkUjcc5x60AfD37aXw4/aQ+MH2nQPAs9jpPhtIsv9nnMct3njazV8QeG/+CUHx88RXS/2qNL0pWPzTXd4ZT9eBX7fvIkaF3YIgGSzHAFZk3irRLeTZLrFhE/Xa90gP86iW5o5cz2PyVj/AOCLPj+Tbv8AH2hx5+9/ocjY/wDHq2LT/giT4jZozc/FPTohn51h0l8474PmV+p7+MvD8Slm1zTVUdSbuMD+dchrn7R/wv8ADbOmo+O9CtnT7y/bUYj8iaNEtSbsl+AfwftPgR8K9E8F2d5JqEWmxbDdSKFaQ9zivQ65/wAE+PPD/wARtFTV/Deq2+sac52rc2rblJHaugqlZrQQUUUUxCN0r82v+CyPhmK4+HXhrV0ixLBfrG7L0YNnGfyr9I5H2gcE59K+Fv8AgrZpouP2cpZtjsYL+CYMBwACc59uaxnuma0+pqf8Ej2U/spwgNkrqdwCPT5q+2K/Pv8A4I2+Ko9R+BXiDRcYlsdVeU89nGa/QStI7ES3Ciq9/NNb2rvb2/2mUD5YtwXP4nivyN/a28bftW6p8ULu0uNfl8B6CbhhptraarDZq0fZmYMGc49TijmSHGLlqj9eqTd82McetfiY37RH7XP7M2k2Ov6xrMviHw9cHEVxqDJf27AdcshDD6k19qfsnf8ABTzwZ8bfs2g+L1h8I+LHIRFc4trpj3Rj0z6H86OZC5WfcFFMhlWaNXRg6MMhlOQRSMjtIDuHl45XHP51RI+lpAoWloAQ0xiQBTmphPTjPP5UmM/Gb/gsRp3nfGPw5qscUiW8mmmLcw4LK2Tj86/Tb9ja0jsf2YPh1FEMJ/ZEJ5Oeor84v+CzF7P/AMLG8H2JXbCtm8g9Mk4r9DP2GdUbV/2U/h5OzBiNNSPIHpxWK2NZnu6/eNOpgYbjzUGoXi2NnNcOzBIUaRioycAZNaJmRaor5Z+HX/BRz4QfEDxndeFm1O50HV4blrZU1SLy0lYNjhs/zr6ht7iO6hSWJ1licbldDkEeoNO6G4tEtFJzmjn1o5kSLRSUtUAUUUUANavwP/b2tYdc/bi8SW+oxS2lrdX9vC7q4Vgh2ruGRX73TAshA6npk4r8mv8AgsB+zxe2PiTR/inpNnmwmiFrqk8e4tHKD8kh54GOOKl73Lie+xf8Ei/gZr2k2FzBd+KdPaS2jZmtNTjKyMVBLHdE3X2wK47xD/wRT8CXjIdG+IfiDTeSWF3bx3OR6ZBTFd5/wS1/aaf4xfCGTwnrd8LjxL4axFmQ/PLbdEY/TpX2/k00S9z8/fDX/BGT4V2FuE1zxT4j1iUEHfbvHbA88gjD8GvsT4N/AfwR8A/DSaJ4K0ODSbXAEko+aaYju7nk/wAq72lyaYh1FcR4w+NHgvwBr+kaJr/iGz0/VtWlENnZySDzJWPYCu260ALRRRQAUUUUAFFFFABRRRQAUm0ZzjmlooAKKKKACiiigBrVzHxN8YW/gD4e+IfEd0xSDTbGW4ZgcdFOP1xXU18xf8FIPGEXg/8AZB8cs0hjl1CFLCIqcHc7DofoDQNbn57/APBMnwjP8a/2vtd8cXjG4i0jztSlNwPM3vM5CEk55HrX7RV+Yf8AwRN0eBtD+JWriKNZ2ube1LbRu2hN2M+me1fp9QOW5FNIIYnc9FUt+VfzxeFdTlvv2ztMvTK7PJ4w3b2Yk/8AHyR1+lfut+0n8TrT4P8AwT8WeKLqUQi1spFibOP3jAquPfJr8Df2Z7p9c/ak8C3Vz+9Nxr8crCQZyWctk0Dif0dr90fSvwV/aisSn/BQLWoJvnD+JrdiG5zl1NfvXX4g/wDBTSyuPhz+2s3iNbVBHMtpqMSgY8woRn8SRUtBE/bbSVC6XZgDAESAf98ivzP/AOC13jOFfDnw+8LRXC/aZLme9mgB5CbQqkj6g19c/C39sj4ceMPgnp/ji58RWGmQpag3VpPOolikVeU25znI4r8Y/wBt/wDaTf8Aaa+NF34ggg+zaXZL9isU3ZLRqfvfjU9QS1Pur/gibpoXwX8R74YGdRghx34iBr9LpIxJjPavzq/4It6zp8nwl8ZaXFEU1GHU1mmYj7ylMLzX6MN2q1sKT1PFf2zPHj/Df9mfx3rMJKzrp7wRspwQzjbn9a/OT/gjb8Nl8RfFjxb41vrVpX0iyWG0mY8edIx3/jgCvs3/AIKoXL2/7H/iJUJAlureI492rzr/AII16Kln8APEWo7R5t5rDAtjnCqBilfWw+lz2rxZ8SvjPoP7Uem6Dp3hNdV+Gl5BGJdQQYMD9WbP9K/Jj/goxqNjqf7X3jI2LKYYpUiYL/fAG79a/fDWNSi0fSry+mOIraF5nJ9FBJ/lX80vxs8WSeOfi14t8QHLf2jqU7oO+3eQP5UwR/RV8C1Efwa8FKOg0m2/9FivgH/gtV4CFx4c8A+LrezDSW9xNZXVyo+YRkBlB9sk19R/8E+/jNpHxc/Zx8NpYSf6ZolumnXcLH5lZBgH8asf8FB/hxH8S/2UvGlm2BPYQjUoWxyHiOf5E0xbM8p/4I/6t/aH7LssHOLTVJoxn86+Zf8Agq98bI/jN8WPCnwn8KFdTn0m4ZZVj73kuE2fgAKyv+Cfn7bHg/8AZ2+BfxA0DxBdTQ6r5rXmlIqZ852j27fY7uao/wDBMb4I3vx5/aP1j4m+IFkfT9BuGvszDImu5GJVf+Ag5oE9z9Pv2Qfg/N8C/wBn3wl4Su1C6hbWwkuwDnEr/Mwz9TXstFFAgooooAKZJIsYyxxXB/Gj43+D/gJ4TPiPxpqn9maaG2IVRneRvRVHU14Vpn/BUb9nXUpFQ+NZbP3udOuFH5hDU3HY+rPtiM2AcVIJAehzXzTN/wAFHP2d4irH4kWTKegW1nJ/9Aqjdf8ABTf9nGzxu+ICyZ4/c6ddP/KOp36jsfUytmlbpXyPe/8ABUj9naNFaLxzMeeQNIumJ/8AHBXb/Av9t74VftFeKrrw94L1a61DU7aD7Q6z2MsC7c44LgZ+lHSwWPfs7l45qtcMIwWPapooxGo2rsB52ioLiTZJym5e/tXPLQpGcrLPJvI+XPNXrONVuXKcLVO8WE7HWRtgPKrV7TxG37xCxU9mpU3dlP4T8ZP+ChDKv/BSfRCg48/RSx98pmv2mgYeTHz/AAj+Vfi1+3Cya5/wUm02G0dbgrdaXG3knf8AMCMjjuK/aG1Xy7WFT/Cij9K7DEsUU1adTAKKKKACiiigAooooAKKKKAPxS/bzUWf/BSCxkc7FNzpTlm4GMrzX7S2DBrG2IOQY1II+gr8ZP8AgpZAln+31o85YKskWluWJwOGAr9ldDYNomnsDkG3jII/3RQBeooooAKKKKACiiigAooooAKKKKAPKP2rPEUXhX9nP4h6pMwWODR58lunzDaP1Nfjp/wSw0241T9sfQJICf3Fpc3Eij+7tGf5iv1j/b4Xd+x78UxnH/Eob/0Na/PH/giv4fhvvjZ421WSEPLY6PGIZSPu75MNj6gCgdz9jFpaKKBCV+d3/BZ/wZqGufBvwbrltGr2Oj6rILot281Aqn81NfolXzp/wUI8Kjxd+yH8QrZYvNnt7IXcKgZO9GB/lmgDy7/gkp8RR4z/AGYxo7yB7rw7fPZOO4U/MnOPQ19rs6rkk4r8j/8AgjH8XLLQfFnirwHf3CW8mrJHeWStnM0q8Mo9wvrX60Xlu83IYgY+7QVGzepH/akQkK5y3rjAqaK5FwWUcHFZg0UsxJJIP4Vj+PPiJ4T+Evh2XVvFmtWui6dCCxkuH+Z8c4VRlmPsAaDeUYJaHXR7QgzubnGSpqTntX5PeAf2jfjp+1f+15c33wo1uSDwVotwGe2vZjFZ/ZS23c6EAsWx0AJHtX6t2bTtBH9pRUm2jfsOV3d8e31rN7mJYXPOadTVp1WtiWFFFFMQUUUUAFFFFABRRRQB+c//AAWM+CX/AAknw20P4i2S4utDk+x3eBndBIcj8mr1j/gl98YrL4kfsz6RowlH9q+G82FxFnnYOUYeoIr6U+Knw90z4rfD/W/CurwrPZalbPCysOhI4Ye4OK/Dy4s/jF/wTc+ND3UUT21nJKQg3GSzvrfcSFYjjOPxFBSVz97t1fCf/BWD9oaP4a/BVfBenT/8TrxKxikEbfNFAMEk88Z6VzGk/wDBZXwDN4JW6vvDGrReJfKObKEBoTIB/fz0/CvmH4C+B/EX/BRz9qi78V+L0m/4RixP2m5AJEccYP7uFOME560Bbueef8E2vBo8RftieErW4BQ6eJbwqwwSETP581++m6vxH+M2qSfsRf8ABQyXXbC1FvoiTR3KxxLu/wBDlUBlA9QBX6z/AAY/aT+Hvx70eG/8IeIba8eRctZSOqXKf70ec0A12PUc189/t+WtxefsmeP4rZJHlNnnbECTgMCa+g1qtqul2muabc6ff26XVncxmKWGQZV1IwQRQSfiB/wSY0O61T9rTT7uK3MlvY6XcPNIoyseQAu70Oc1+5VeP/BD9lH4c/s96zrmq+C9G/s691g/6TIzlvlyWCrnoMmvYKACuU+K+m3GsfDHxVY2pUXE+mXEce4kDJjb0rq6ZLGssbI67kYFWX1BoA/Dr/glbcNoP7atvBcjEjWOoWjAY4ckeuP7pr9x91fid+2R+xj8VfgB8Xta+JHgWxupPDU1017b6hokheWzLHLLImAy/gCPeuTj/wCCjP7SHjbw9H4N0zWjc3c6i1EtjpoN7LkYK7wuQ3vQVa598ft9f8FBdJ+BekXPg3wfLFqvja7Ro5WXDQ2cZGCWbP3ueBivyjvv2Z/ihqvwyf4q3Hhm9uPDlzcSGW6CNvGfmMhU87CT1r7O/ZH/AOCXPjDxl4tsvG3xoBtdGLC5bRrq4dr66kzkeaMYVe/3sn0r9Yv+Eb0v+wRon9n2/wDZAhFsLLyx5XlgY27emMUCZ+Qv7Kf/AAVVX4J/DjTfB/irwvPrWn6XEIre60plWTbn7rByOa+9fjn8QrX40fsL+MPFOkWN3b2ur6C88VtdIBKg4OGAJHbsa5u6/wCCXvwSuviUfFzaXdRjzhP/AGTHIFtN2c/dx09q+o7rwppk3hWbw8llDFpT2zWgtVQCNYyuNuPSgR+Yv/BE/wAR2P2j4laOWKXzfZ7sBiACnK4HOc5FfoZ8evjp4a/Z9+Hep+K/Ed2sUNtGfJtww8yeTHyoo7kmvxZ+MH7K/wAcv2V/ihf6x4Z03V7Wzku5GstV0He6OhYsqnaOwPcVofCv9m39oD9tbxtBD4v1DXLfSbciWfU/EDSLDGmcERoRgsfYUAdN+zN4F8Sft6/tdT+O/EsE0nhywuhf3UrDEaorZihB6E5AyK/bKCNIYY44xtjRQqj0AHFeffAb4F+Gf2e/h3p/hLwzarDa265mnI/eXEh+87HuSa9EoAWiikOe3WgD5G/b+/bL139lHRvDf/COaJbarqOrSyKz3u7y41UAjGOpr4sP/BYz4uXEeyHwhoPnYwNqysSfYV+vGueFdG8TrEusaTZaosRJjF5brKEJ643A4rOt/hj4PtZA8PhbR43HRlsIgf8A0GgD8iJf+Cin7WXih/tOkeHJIbduQtr4feVcfUrUf/Dcn7Z0n3dC1P8A4D4Wb/4iv2ZttPtbNdtvbQwL02xxhR+lT7R6D8qAPxZuP2y/20NSheBtG11TIMK0Phpo2H0ISrP7JvwZ/aM+Kn7Rmm694ru/FXhq0gk+2XmoakskaSKpyIgpI61+zu0eg/KloAjhV0RVZt2FAz3J9a5H4weObz4a/DTxB4lsNKk1q8021aeKxjzmVgOnHOK7GkZVkUqyhlIwQRkGgD8NvGP/AAU4/aL8cazdxaRef2LHIxRNP03TcyRZ427tpYn3NeQ2v7Mv7QHxu1i81j/hAvFGt3103nS3moRGLzCe++UqD9B0r+g+x8F+H9NunubTRNPtriQ5aWK2RWY+pIFbKqFGFAUewoA/Dq1/Y5/bSttFt7W10/xFb2UMexLVfE1ugVfQKJhge1c3Z/sZ/teadrSaha+EfE1vqsTblvotai35/wB43GMV+9VFAHyB+wTB+01psetaf8ebZl0mG2j/ALKuLq4t5rp5dx3h2ikYkbcfeFfX9FFABXNfED4c+Hfil4Xu/D3inSrfWNHuhiS3nXj6g9QfcV0tIV3daAPyV/aW/wCCQOuL4iuNW+EN3bXWjSkuNFvZvLktz6K5PzfpXz3F+y5+1n8K5G0/R9E8b2sJ/wCgFcytEf8AvhsV+99FAH4QWPwB/bH8ayf2bcWXj/y3GP8Aia3kscXPu7YrufhF/wAEpPjdb/EDRdU8Qw6Xpmn295Fd3Ej3yTO21gxGFJ5r9pqKAILG3NrZwxMQTHGqcdOBip6KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDN0XUm1bTba7MMkInQSLHKAHUHpkAnB/Gvyg/4LAaDaWvxc8A30FoYru4Co9xu4cBwQMdq/Uvx74mm8D+D9S1i20u51me1hZ47CzTLysBwB6V+LP7THx2+Jf7Y3xX8LaFd/DyfQrjTb4Ja2MVrK07ZYAl2K9MfhWU1qrHTDdvoftB8KZPN+G/hlj1OnQf+gCusrnfh9pU+h+CtD0+6UJc21nFFIo7MFGRXRVqYS3YUUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANbHc4qve6jaabaPc3d1Da2yDLTTOERR6kk4FLqFvJdWkscb+W7KQG96/Nr9vT9kr9on41+JtKn8JzRa5oUcBjfToNRitBC2epErqGyPSs5Sadi1FNXufbkn7UnwihvJrVviR4Z+0wnEkY1OIlfr81U9Q/a6+DWlKjXPxJ8Oxhzhf9PQ5P4Gvx70j/glL+0ZqF55Nz4R0/TUP/Le81m1dP/IUjH9K77T/APgjJ8Zrry/tOveDbFWPz/6XcOyj6CEg/nT1YtFue4/8FIv2tvhx4w+D1zong7xjpviHU72RYpbeyO8on97NZH/BLH9pL4d/Cf4M6vo3i/xXpnh+5k1Bpo0vZRGWGMd+tctb/wDBEfxaZl8/4k6Kse35mjs5SQfYccVY1D/giT4kht86f8StKmn9LmwkRfzBb+VLk63KurWPv63/AG1PgZcsQvxQ8Nrgfx36L/M1aj/bC+Ccwby/if4YfaMnGpR/41+Zg/4Iw/F1JXC+LvCGzPDM0+T+Hk0+T/gjL8XPL/5G3wm59FaYf+0hT1Ija+p+qvwz+O3gP4w3OoweDfE2n+IJNPx9p+wyhxHnpkiu+r5i/YT/AGQbj9kzwLqthqmqWusa1qtws881rFtWMAYCBiMsO9fTtUr9Rytf3QooopkhSUtFAHx//wAFCvh38ZfiR4LsNM+GHmNH5jPcC0uTDNjGME55Ffn7pP8AwTe/ab8XKLu8jWynxg/2jq7qzflmv3CoqGi1Kx+J03/BK/8AaRkjAOoaWQeqnWZT/wCy03Sf+CQPxy1K6YalqOgWcZH+sa+kl/QKK/bIjNG2qtoHMeJ/sf8AwBm/Zu+C2meD7y9S/v4WaS4nj+4WJ7e1e20mMUtCViQooopiEr4z/wCCpmsDT/2XdeUY3TSxQfMm4YLdR6GvstmxivjX/gq1a3Fx+yhq7wEBI7qF5RtyWUN0z2rOXYuOh59/wRo8Ow2fwY8T6yqMJ77UtjsXBXCLgADGR+Jr9Da/Nr/gjd4u0Sz+E3imwuNVhtryPUPNe3uJ1QAMOCAa/QuXxp4fhXdJrmnIvq10gH86cdEEtWbDV+XH/BXv4P8AiDxC2meMtO0lprDTU8u5njXPynoSPrX6g2d9balAs9rPHcwt0kicMp/EVx/xo8LweMfhj4i0WeHz0vrSSHZgE5IOCPelLuEW1ofFn/BMjXfD/wAfP2Yb7wJ4n061v/7ImNvJDJEu54m5BJ/Svn7/AIKH/sQ+C/2ftDh8YeBry60yX7SJHsZ5xtUH/njwDkHtk189/AX47eIP2L/j9qBD3P8AZVvdvb6jp6kfvowxxn3r0r4wfETxf/wUu/aG03QPCyT2vh6BQILeYEx2oIw0r479s0irNbnn/gv/AIKNfHXwH4NTw3pnipXtoxiO5u4BNcIvZQ7HoPpWja/tZftT3mljxZH4t8QXmjQvve4SCM249m2p0r6S+LX/AAR/j8H/AAbn1Pw5rVzrnjKzTzpYMfupwByqLjP618Z/CP8AaM8VfAa31jwnfW/2vQ7l2ivdIul+63IPB6Ua9A0P1z/4J5ftkXP7UHgO7svEnkp4y0chbswrsWdD0kC5OPevryvwu/4Jc+Lriz/bGsYbJ2tbHVorlZLdT8pUAsq/hX7oVafciSsMmBKHHWmxR7ecnJp5OcihvlXin5gn0Pxn/wCCyPiBb743eGrEDMdvpxPTnJav0F/4J0xTw/sg+AlnyG+zMRn03HFfnR/wWBsxbfHvQpG5Mmllsf8AA6+2/wBjP9qz4U+F/wBmLwRY65420fR7+0s/JmtbiXa6sCe2KyWxrPsfZqxgMT60skaNGysAVIwQ3TFfNWrf8FG/2ftJkkR/H1rO6dRbxO+fpxXnWo/8Fa/gnJff2fZDWtRMziFJI7UKrFjjjJ96DJJ3PCv24f2ffgt8QPGV23gnxppuh/ExGLtpvnbYp2B+5nojZ9K4L9jL/goN4h/Z+8USfDz4rXEt34dgk8hbqX55bJgefm6steJftjfC1/hL+0VbanK8/wBg8QTxazbmdh5ixu4O3I5GM17t/wAFKtG+Ev8AwrPwJrugC0HjO+giZ2s2BMkewZ8wdOtM1l2PWP2sv+Csdvogt9D+CzQare3UeX1qaHzBC3ZUjIIJ+oNfPXgf/gpl+0L8PfGWl6n4/kudT8PTMPPsrrSIrZZYz/EjiMEEdeDXin7FPxa8A/Br40WXiLx7oX9saei7IXHItZCf9Zs6Nx61+s/7X3wz8M/tW/sq3Wr+G5ba4SG3/tLT7yNeflGSvHtxg0EK3U+kfhr8QdJ+KfgfR/FOiXC3Om6nbrcRMpBxkcqfcHiunr80v+CN/wAZJNS8OeKfhnemRrjS5DqFszNlVjZtrIB2+bmv0srRbEPcWiiimIRq5P4o/DfR/i34D1fwpr1utzpupQmKRWzwezDB6g11lG0UAfg38Wfgj8Xv+Cf/AMWZPEXhd7630qOU/Y9ct4PMhkj6+XKCCMY9RX1l8Cf+CyGg3unwWPxS0K40y/UBTqmlp5sMh9SnVT61+keuaFp3iPTZ9O1Wxt9RsZ1KSW91GHRx6EGvjj4r/wDBJv4OfEC8mvdC+3+CLuZizjTZDJCSf+mbnj6A0FX7nouh/wDBQ/4Aa9p63cfxD0+1U9Y7sNE4PphhXk/x4/4KufC7wV4fuoPA13J4w8QupjgFrGRBG2OGZiOR9K80tf8AgiP4dS6D3HxS1GSEn5oo9HjBI9N3m8flXvfwV/4Jg/Bn4N61BrH2K88UapEBsfWpQ8SMDncsagDP+9kUC0PmT9iH9m/4iftBfGqL46fFsXT6fDJ9p06DUBgzNn5Sq8bVXtxX6q1FbW8NrCkNvGkMMY2rHGoVVA7ADoKloBhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAK8B/bk+Ct/8AHr9nPxH4X0mKObV/ku7RZADmSM5AHua9+prLuFAz8Ev2Qf2svEf7EPxG1fSdb0ieTRryVYtX0yRCkkDoceYg9ccfSv1N8B/8FKPgF47tRInjSLR5woZrfVYXgce2SMH8DXafGr9jf4S/H4SS+KPClqNSc7jqmnxrbXZbGMtKo3N9GyK+G/jB/wAEXbma+N18OfGVt9mY82fiBXDp/uyIDn8QKAbuzkf+Cmv7Z+j/ABvh0X4dfDjVxrOkGcS3s9juK3MnRIvcA818meA9C1P9m39o7wbJ49tH0d7G5tr+dZBkxwtyCR9K/S39k3/glLpHwh8RWPinx/rEPibVrM+Zb6ZBF/okUgP3m3ff+mBXeftif8E49D/ae8S2/ifTddbwv4iWNYJ5DD5sM0ajCgrkYIoGnY7Xwz/wUK+CnjTxzpPhPQvEz6nqupSCKEQW0hQMR0LYrY/ay/ZH8L/tS+DTZajFHZa/aqzWOqRoBIjY4Vmxkr7Vw/7KP/BO3wJ+zPPFrc7DxL4tVdo1G5TEcR9Y0PQ+9fWasGGaBeh+Id1/wSZ+Otlq0mm21vpNzp7S/Lem+ATb2Yrnr+Fep/Gz/gmrZ/Az9kDW9bikXWfHNm0V3e3CrmNIVb51jHtnrX61VDfWNtqVpLa3lvFd2sy7JIZ0Do6+hU8EfWpaHzH53/8ABGn4bX+hfDHxX4uuiyW2s3aw2sbKRlYxy351+i9U9J0bT9BsUstMsbbTrOP7lvaQrFGv0VQAKuU0Jnhv7Z3wLvf2iPgHrnhDTJ47fVJSlxbPIfl3ocgH61+OPw6+N3xr/YG8W6jov2WbTFuJP3unanETbzbT99Pr6iv6AKwfEvgLw34yVRrug6fq+0YBvLZJCPoSM0ra3HfSx+Knxg/4KsfE74ueAdQ8LHTdO0SG9Typ7qzDeaUPUDnjNWfgJ/wTJ8X/ABi+B+seNLppdK1i4USaFZTnb9oHUs3oD2r9aY/2Ufg/DqUeoR/Dnw8t5G25ZvsS5B9a9StbWGxt47e3iSCCNQqRxqFVQOgAHSqC5+Evw/8A2D/2nfD/AIsS10TQtS8O3cMof+0U1BYrdefvfK3zflX7OeBfAurv8G7Hwr471BfEGqS6f9k1G6xxKWXDfX616HSNyMUBc/nV/a7/AGd9S/Zt+MmoeGrtQ+n3DtdaW6tnfCzfKD7gmv2b/wCCfvwYb4K/sz+GtPucHUtSj/tK6OP4pBkD8Bivcda8D+H/ABJqVrf6po1nqF3aHMMtzArtGfVcjit1FVFCqAqgYCgYAFAh1FFFAgpDjqaWigD51/bJ/Y70/wDa+8NaFpV74km8NHSbl7lJ4bNLnzCybcEMy4H0NfJMP/BEfTlwJPivOw/2dAj/APj1fqBRSsVc/NjS/wDgij4Pt3Y3/wASNYu1I4Fvp0UGD/322a11/wCCL/w24z408Qsf9yOv0QopcqDmZ+cevf8ABFrwHc2IXSfG+s2l2DnzLiBJFP4AjFew/sW/sEwfsj+JPEmr/wDCTf8ACRyavbpbBWthF5QV92c5OTX13RRyhzEY7+lV7iFpFI4Aq2aqXiv5LEde1RKK2Y4lJbBYcFD8x61YkuV03TLi6lI2QxtKcnAwoJP8qqWlrPlZJJAqk4Ix2r5K/wCCi37Xmk/Ar4Xah4T0q8hl8aa1btbxW0bbmt4mGGdvTg8VCilsXLsj8+v2fdQn+K//AAUTfXoNOGrv/a15qMNruwH8rdt5/Kvavih4b/bP/ae8ZXlqdJ1TwZ4cjuXFtH532WJF3Fc7lO5uK6j/AII5/s+tawa38V9XgJnmVtP03zFIKjOZHXPr0r6K/wCCif7X2ofst/D7TYfD1usvibXXeK2lf7tuqjJf3Pat0Z7HyZN/wTH/AGirDTRd2fxO87U1XcIP7VuRz7EtivHPE3ib9rb9kfXLHWPEd34iFjaTYE1zKbqwkHcMRnAI7nFfe3/BL3x/8TPi18O/EXjDx9r9xrFre3mywSbGEA+9t46V9c+PvA+j/EfwjqXh3XrSO90u/iaKWGUZHI4P1FMk8B/Yu/bi8OftWaC9oyLpHjGxiD3mmuwxIOnmR+oz2HSvp+vwf0Pw/rv7FP7dWm2CI0VnHqixxBWIElrK+0D3HNfu7HIJY0cdGAI/GgB9FFFABRRRQAUUUUAfi5/wVKjb/ht7Q8KSWtNPxgdfnr9kPC+R4Z0kEYP2SHIP+4K/G3/gpZqSX37fWi2+QyRQaZHwc87zkfXpX7MaKhj0exQgqVgjBB6j5RQBZuLiK1heaeRYYkG5nkYBVHqSa+Ef2qf+Cqnhb4L6+fDvgfT7Xx3q8RIubiK9UWsBx03KG3NnqOMV9WfHv4L2nx6+Hd54SvtZ1LQre6ILXWly7JMDt7ivyE+D83gX4M/tqD4eaN4U0/x9o8+prpD3XiSATTJLu+aSMAY3dR0xQUlc0/FH/BWD4/6/m60my0fRLVTu8u202WXA/wBp3JBH0xX1F+wz/wAFNJ/jh4ysvAXj+xttO8QXi7LDULc4ju5h/wAsyvZsdK+85fCOi3GjnSH0qz/svyzGLMW6CIKRjhcYHFfiT8M/B9r8Pv8AgqNoOiWMP2eztvF2Iox0RGDED9aCT9z6KKKACiiigAooooA82/aQ+Gt58YvgX418F2EscF7rWnvawyS/dDEgjP5V4F/wTd/ZN179mbwT4kl8WRW6eIdZu1P7nqkKDaFz6E819jUUAFFFFABWf4g0Kz8T6Hf6TqEK3FjewtBNGwyGVhgitCigD8Rv2qP2IfiL+yd4+PjX4bDU73w9HObq2v8AT/8AW2LdSrAHJHvirOgf8FcPjhoGh22mXOlabqV5AgRru8tHMzkd2wRzX7WTRJNGUkRZEPVWGQazB4V0YSFxpNiHPVvs6ZP6UDPxp/4bc/a5/aKmj0Pwda3VtPMTj+wNNEDYPHzTPgKPckV1vgj/AIJa/HP4yarBqfxg8YrpVoz+ZLHNqD399z1AHMa8dwx+lfrtb2NtacQW8UI/6ZoF/lUrSBe9A/Q8q/Z3/Zp8F/sy+Dl8P+ELOQK7b7i+uiHuJ29WbA49hXq3TrUckhVQccd6fncARWb3GPWnU1adVR2JYUUUVQgooooAKKKKACiiigBGrm/G3w58N/EjS207xLotnrFoQQEuog+3IwSCehrpaKAPkPUv+CWHwA1K+luf+EdvLZpG3FIL51Qc84FfQvwm+DPhL4I+FofD3g7SIdJ02Pnagy7n1ZupNdvRQO58sftjfsFeG/2sJLHVH1F/D/iWzjMSahGm8SJ2V17gGvlbwX/wR38Z+E/ElrqFr8WLfTVhlV/N06ykjlKg5xnf3r9UKKAuyhoenPpGj2NlJcPdyW8CRNPJ96QqoBY+5xV+iigQUUUUAFMkUtjGCPQ0+igCOSFZo2R0V1YYZWGQfrWPp/gjw9pF615Y6Dpdldty1xb2ccch+rBc1uUUAIBS0UUAFFFFACUBQFAAAHpS0UAIM96WiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM4paZIu7FAD6Kj5xjFKgIoAfRRRQAUUUUAFFFFABRRRQAUUUUAIeagFhbLcm4FvEJyMGXYN/wBM4zU5pMH1oAULilpBmloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqTJp1JQIRadRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGpjSBFLMwVRySTwKc/Svj39sL9kf4p/tJeIrb+wfip/wiXhi3iwNLjgk+eQ8FmKOueKV0XFX3PcPiV+1B8LPhLps134l8c6LZtHn/AEWO8SW4ZgM7RGpLZ/Cvya/bY/b/ANT/AGpJG8D+C7C4t/CckyhU8pjc37g8LgHAHfGM165o/wDwRO1i81JJNe+Ktv8AZ92ZTaaUzyv64Ly4B98Gvsv9nP8AYB+E/wCzeyX2k6XLrniLbhta1hxLN1z8igBE57hc+9TvqPRH5SfDD/gmv+0D8QNLbU7Tw6vh21kAaNdYvfszyDsQo5/MV1c3/BKX9o6ORVFvpUqk43LrowPcg4NfuDjFLRyi5j5i/YG/Zx8X/s3/AAputF8Z6smo6rc3RmEcNy00cK4+6CR/KvpmaNZFG7oDmpKQjNO2lib63Pwf/wCCm3wbu/hz+0XqmrLbyJo2usLmK4ONpcjLKOK+u/8AgjT8H00XwJ4k+IVwjrd6rJ9gh3DgwoQ2R+Nfbnxo/Z48DfH7Rf7L8Z6QupQKP3Tg7ZIT/eRscHFdF8NfhroPwl8G6d4X8N2n2LSbBNkUecsfdjjkn1qVF2Kk00dK33TxX58f8FJP2HtE8ceBdR8f+ENJhsfE2n5uLtbVdv2pMfMSAOT3zX6E4qtqOnxalp9zaTKrRTxtG6sMggjHSnZiWh/Px/wT38TxeDP2t/BFzdRsoe5a1wezONpr+hD0r89fC/8AwSjh8H/tB6d4+07xeg0i11D7eNOe3O8Nu3bQemM1+hdHKwk7jNwDHPFc54s+JXhbwRZ/adf1/T9KgyRuubhVyQM46184ftrfs1/FP42NYXPw78d3HhxoQRLZi4aFH49Vr40X/gkn8avGDxv4o+IFm+58v9ouZbggeoyetV0sGh5R/wAFFvjB4b/aM+PWmHwJNNrX2WEaenlKcTOW6L61o6P/AMElfjLrXg221of2bbXkyCVdNnmIkCkZAJ9a+5v2Wv8Agl34T+AXjCHxTrWtSeLdUt0BtoJIFjgglyDvA6k445r7e2gYwMVPKx8x+THwp/4Iz6trnh5Lnx14wk0PUGPFnp8Sy7fqxFe0/DH/AII9/DzwL4u03WtU8Sar4jhs5PNFlMqRI7jlSSoBwD2r7/20VVtCbu5+aX/BYz4PWMnw38MeOLZVhuNJnXT22r8zRMMKM+gOK+Gf2OP2fdZ/ay+MWk6HqMtxceHNLVZdQuGYnyoAfuA+54r9zP2gPgToH7RXw11DwZ4iaaKxuyria3IEkTqcqwz71wf7In7Gnhj9kXQ9Zs9F1G71m91WZZLi+vQofaowqAKAAOaViuY8O/bS/wCCdPhrxt8I7Nvhp4esdJ8RaDCfJS3j2NdxgcoxH3m9zXxf+x7+2xrX7Luoan8O/iDYXV14VlLWs9pMMPYueGIB6jFfuJtFfk1/wWB/ZpsdBudK+Kmh2zxyajcfY9VSNTsGFJWU+nTFLlDmPOv+CZusQTft8agNDuJBod9BqTqqnarx4Lxgj2r9qsV+H/8AwSD0W7vv2skvYI99vp+k3TXDAcAOuxT+ZFfuDVEsKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACiiigAooooAKT3paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioWkZmKp1pYo3ViWOaAJaKKKAGtSY3cU+svxRbXt54c1O302TydQltpEt5M42yFSFOfripauB5v+01+0Bo/7Nfwr1Lxdqqi5eL93bWgYBppT0UfzNfll+z3+zX4s/4KIfGLWvih41lbT/Ccl3umlUYabaflgj9gO9dUP+Cbf7Q3xU8babF8S9ba48PyXrS3V1PrJujEm7qkWcKSOMj1r9U/hb8MtC+D/gXSvCfhy1W00vT4hGigcse7N6kmjlK5jR8G+ENK8B+G7DQdEs47HTLGJYYYYxgAAY/Ovzs/4LZaC0vgH4d6uiMXj1OW13AcLuiLc/lX6XV5D+1V8A7L9pD4M614PuSkV3Mnm2Vywz5M68qw9PSmtCTyL/glprmlan+yP4etNPlQ3FjNNHdQhgXRy2fmHbIr65YDqTwOtfhv8DfiZ44/4Js/tBXuieN7OZdGu41F9bwjek8Wflmj9W7fjX1T+0H/AMFaPh7rfwl1nTPh2dXl8WahCbe3aa28oQlhgsDk5I9qYHhn/BSTxtovjL9tLwdZaBNHc3mmNa213JCQwMpmUhcjqQK/YnSVZdLsw/3xCgP12ivzV/4Ju/sKXSXMPxh+KFs13q90ftGk2d5lmG7nz5Af4vQH61+mtABRRRQAUUUUAFJmvnP9rT9q7U/2V/7A1i48EXfiPwheSNFf6lZSEPZsBkEjaQBjPJwKwvAP/BTP4C+PNNuLk+K/+Efmt4TK9vrURti2P4UY/K59gaAPzh/4KAX0etf8FBo0sHW9aG80+FhbsJCHDqSpx3HpX7h2v/HtF/uD+Vfhj8F5rT9pr/go7ba1YRvc6Rda42o5kXJ8qPkNj0wBX7pUAJIpZSAcZ71+Dnh3Qbrwj/wUusbfUN0Tp4xMjGUbSFaQkE56ZBr95a/E7/gqJ8IvEXwk/aST4jWCzDTtYkjuLfUI42CQXKDOwtjG7C5x6UDTsftfkLyeBX4uaYr+JP8AgrdYy6ahvUi8TpK5txvCxonzucdh3NUtT/4KofGv4h+BbPwXoWkWkWu3Uf2VtS09GkuZhjb8qdmPrXtn/BNX9iT4g+E/ijH8XfiDbXGkSCGYQ2WooyXkksgwXdWGQMEnNAj9RqKKKACiiigAooooAKKKKACiiigAqPDMxzwKkooAYV96acrknpUjUxl3KQaBjImLsT2pWVg2QuaevHA6U+gdyKRC6EYpyqQoFOJA60jMFxmlYVwUU6kpaBBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAT9aB9MU12O07QC3bdwKbG77f3oUN/sHIoAlopM0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlpDzQAA56dKWkA29OlLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACGkwPWlo20AAxS0mKWgAooooAKKKKACiiigAooooAKKKKAEo4oo20CDNLSYpaBhRRRQAUUUUAFcz8R/h1oHxW8H6j4X8TWK6ho+oRmOaFiVJHqCOQfcV01FAHh37Nf7Hvw/8A2WRrDeDba7NzqjDz7q+n82QIDkRrwMKK9xoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqOV9qj1PFMQlc7mNTcqxPRUC3Cu21WyR1qamLYWiiimIKKKKACiiigAooooAKKKKACiiipbsAUU122j603fhtvtmjmHYkopqtmnUcwgoprsFHNMYnjFHMOxLRTBTXcJjNHMFiWimIwbpT6a1EFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPHvj/APsn/Dn9pS1tk8aaN9qurVWFvewuY5o8jGNw6j2rwz4Tf8Ep/hR8LvHFt4iku9S8RpaP5ttp2pbDBG4OQxwMtj3r7UooAZFEkMaxxqEjUbVVRgADtT6KKACiiigAooooAyfFPhXSPG2g3mi67p8GqaVeIY57W5QMjqexFfF/xG/4JB/BfxdcTXOgy6t4OncHathP5kSHPUI+fyzX3NRQB8x/sn/sD+CP2T9UvNb0rUtR8QeJLyA2suo6jtAWMsGwiAfKeOuelfTSn5iOh/SnUUAIaxvE/g3QfG2nvYa/o9lrNk4IaC+t1lTnjow4PuK2qKAPPfBH7Pfw0+G901z4Y8DaHo1yf+W9tZIJOueGIyK9CoooAKKKKACiiigAooooAKKKKAEo3CgnFNbLY4oAfRSUtACNTBu3HI4qSigBqimqX8w5GF7VJRQA1wWxilpaZIpZcCgBonXcVPFSA56VDHb7W3E5qegAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAjZtq5wT9KRm4HBo38DjBPrT9tA9gWnUgFLQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQ00vigB9FN3UbqAHU1m24o3UjfNilcY+ikWgnFF0IWiolmLOVC/nUlF0AtIx2qTS03lsg/pTAVTlQaWkAwMUtABRRSE45oAWimqwYZFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopGpuTSvYY+kpqt83Jqo8jmQ7G3YPSlzDUbkhmRlIY/Mpp25JEBLcVUkUq5JRTmq8nmS/IgCfSok9TVQLaxpHITGRuxzUqSOOWbj2qtaWSQtlpHZ8c7jxTVmEsjxqCNvOanVsLF4XS5xmpwdwyKz47cs1XVG1QK2Wi1M5LUkoqOMMM7mzUlMgKKKKV7AFFI1M3Hd1qeYCSikWlqlqAUUUVEtwEbpUbLuxUjUxsgcCpGhyjFOqBmbqcjHPAzmuW8T/FLwb4Hu0tdf8UaZo1043iG8ukjcg+xNA9zrJpFjTLVB5yogYHOTiuDl/aG+GAVWfx74fCk8f8TCP/Gmv+0T8LY49zePfDoX/sIR/wCNUlcex6EsysOTioVU/aM/w15F4h/a7+Cnhu1+0X/xI0OKPdt/c3XmHOM9EB9K4W+/4KPfs9abFJKnjyO+MfJjghkY/UZAp8oz6dt4tjM3rU9fDHiT/grp8EtPjM2nr4h1R487Y47MRpKcEYLFq9i/Y9/a+0v9rbw7rmp6ZoF5oiaTcrbv9oYMj5GRgjvgdKpEM+haKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTTQA7IpDIq9TTN3rxSLtf3qWyrEhb5cgZoRiw5XFC06mtSQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBD5J3hsnP6VNTFlVnZQcsvWn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJnrRTVUqzEnOaAH0UUUAFFFFABRRRQAUUUUAFFFFABRSGk3UAK1Q7P3u7PbpSpMJWwPu+tDusasxOcccUrlaj6Oc+1Mmb5cBhk+9U5dQW3KqWDHp1pcyHGDlsXWkVNoJxuOBS7ucd6r28n2pdzLjacimedIt95ZX5CMhql6j5baFhJG3EMoHpip6iReuWzUtFiGFJt5JpajmDNGQpwfajlYgkHmAx5K5H3hTo18tFUktgYyaSLPljPJp9WgCiiimAUUUUAJjHSlopqsGJwwOOuKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADWpu4etObJHFN8lScsM1nLcaKs3mNIcEhaj+WLc2OcVfYBV6VGY0bhlFI1jJGXHIZ5CSx2+lWY7Yrl1OT71P9giwAgCjOeKnEKhQvaqTXUqVRdCpDMJnzyG6Fe1IbdlYsvBJqwwih7qMckk9PesfWfHfhrw3b+dqviHS9MhzjzLu9jiGeuMsw54P5UJXdyObsauyRV461JHGVUbiWPvXl+rftVfB7Q4XlvPiX4YjVeoTU4pGH4KSa820f8A4KMfA7xJ8RtJ8HaT4luNS1PUrpLO3lgtG+ztI52rlzjjJ9Ksl3Z9PLTqatOoICiiipauAjVHt+Yn2p7DIpjNt96h6D3HrTqqC4fzAAufWrWfzqlIBaKKKT1EFFIelNzTTGK3avy+/ah/4JffEn42fGbxJ4ys/FthcWupXPmW9veM26CPHCD0A9q8f/4KBftM/Eiw/ax1TQbHxDfaRougXFskFpaytErggNubBG7O7vX7E+D76TUvCWiXkzb5rixgldvVmjUk/maW7K2PyCs/+CM/xRklIn8S6DDHjhm3Pz6YFa1v/wAEXPHjkCXxroUSnqVtnP8AWv1/WnVdhcx+WnhX/gijHDKza/8AEQvGUxs0+z2HdkdSxPGM12tj/wAEW/hysiG98Za/MqnLLEI13e3K1+i1FMLs+EvEX/BH34M6p4ejstLuda0jUkYN/aC3ZkZhgjBRvl754Havpn9m79nnw9+zN8Nbbwf4dkmubdJGnmurnHmzSN1JwK9UooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGqORSy4HFSN904602NmZcsMGgBkcbKxzzT9vtT6KVh3GqKdRRRsIKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWNVdmAwzdTT6TNLQAUUUm6gBaKQNmloAKKKKACiiigAooooAKKKKACikooAWiiigAopKN1AC0UjNtGaRW3Ur9AHUUUUwCiiigBGphzT2qOVhFGXboOaBieWONuAM5NQ3EMu0iJl5Pf0r4H/a9/4Kbaj+z78QpvCvh/whFq8kcQLXl9O8SKx9AFOenrXyVd/wDBXr473U0v2W28PRI7ZSNLB5GQemd/P5Vn8WqNHGUdGftkttGJPMx85GDTJreDerOFUg5yeK/Edv27P2sPjE39m6C95DMP35Gh6QVk2j5eS24bcsPxxWD4gt/2x9btZ73VJ/Gvkwr5js5MYA6dFA9ar4VqCvfc/dNtSsIAQ13boe+ZVH9axNc+JHhPw3Gs2q+I9LsUJ2hprtBzjOOvtX83+qfEj4g3Wqz2V74l1xtREvlNBJeSby+cbcZ65r334df8E9/2gfjFb2t7Pp9xYWVwcrca1csBj+9gnPeluSftr4R+Mngbxxqb6d4e8VaVrF+qs5trS5V3wOpwDXa5O7pxXwn+wn/wTkuf2ZvGD+NPFGuW+qeIPs8ttDbWSERRhyvzFjyTgEfjX3ZVIlg2e3WkXd3AxTqKYhKWiigAoqC7uVtYTK7BUXliR2r8+/i9/wAFfPDPw/8AHF94f0jwfeaxHptw0F5dyShB8pwdgH49anmsUotq5+hdFeA/B39ub4O/Ge0tRpfjCw07VJow7aZqcwglQ8AjLYVuTjg/hXvFvdR3UKTQyJNE4yskbBlYeoI60cyFZk1QwWqW5crkljkk1KDRzTuhC0UnNLTAKKKQmgAbPGPXmvnz9qr9tLwV+ynoVvPrnm6lrV2+220i1I85htY72z0XK4z/ALQrvvj78XrH4HfCfxD4x1AFotOt2dFXqXIwv64r8Sfgp8O/F/8AwUS/aUvLXXNek3Nbyane3U2W+zWayovlxjsSZVApXsVyu1z6mh/4LeXEmpfN8K4103P+sGrEy4z/AHfLx+tfoH+zz+0d4P8A2lPBEXiLwpeiULhLq0fiW3kxkqw/rXzx4+/4JT/B+++FN9oXhbSJdN8TLEGttZmunaRpQP4wTtwT6Adua/Mn4PeNPFv7Ef7VVrZX17NYJpOqpY6xaRs3lXVuxAclScHjkHsQKLoVrn9CFFVdL1CDVtOtb22cSW1zEk0TjujAEH8iKtUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIaz9a8R6V4chSbVdRtdOikbYj3Uyxhm9ASetX2zjivyL/AOCmereJf2iv2mfDfwq8HWOp6g2kqsDxIjCD7TIwJkzj+FcjJ96VylG5+uUE8d1Ck0MiyxOAyuhyGB7g1JXHfB/wTJ8N/hh4X8MSzNcS6Xp8VtJKxzucKNxz6bs12NAgooopiCiiigAopDUEkxU/Kcn0rOW40rk7dKgk3sQMcetL5jNKinpjNTChK49iBwyL8r4Y9M9K/LX9ur9sH9oTQfiZe+EfCOgaz4O0WEslvfWVoZpr4A4MqyKDtHPSv1RKhsZFQTWFtcOry28UrrwGdASPzp8o+ZdT8KtN+FH7Yf7Q2mgTt4y1TTWbeG1zUGiRj0yA7A9Ce3eqPxH/AOCdvx88A/D/AFLxVrtvDNY2EXmzwQ6g00wQdTt6YH1r96VjWMAKoUDoAK8p/axke3/Zh+K00TmOWLwxqMiOvBVlt3II9wRVIOY/Ab9nH4Ca/wDtLfFCz8F+HjDHdTRNNNcXTEJBCpAaQ45OCw496/Ur4B/8Ek9D+Evjjwv4w1Xxtd6xrGjXcd4LWG0SO2ZkyQOcnrg5z2r45/4JCawmm/tgWds67m1HRb62Q+hCpLn8oz+dfuZQJsRadTVp1MkKKKKV7AI3So3zxjrXmv7Q3x00n9nz4a6t4v1e3muILGPMcMfHnSHO1M9s8/lX51n/AILaax9sl2/DGzNqeYlbVir49SfLx+FZN3ZSR+sCL3wM06vyem/4LZ6z5eY/hjZK2f8AoLl/0EYriPE3/BZz4oak/wDxJvDOgaPEDn98XnYjB46j2/Kr5RM/ZmivBf2I/i140+OH7Pui+MfHNlbWWrahLMYhaoUWSANhH2nOM4P5V71RyiGSjMbUi8KKkpKOUdz8PP8AgqlBHH+2heKiqplsNPZ9oxuPAyffFftR4LXy/B+hKBgCwgH/AJDWvxt/4K3W4t/2xNMlAAMuj2THHfErD+lfsr4YkSHwnpLuwRFsoSWY4AHlijl1uVfQ1NpZsVIBiq9vPDeIk0LrKhB2vG2RXzN+3F+2nbfsheH/AA9JBpMWua5rM8ghs55TGghjX55MjuGaMY/2jVk7n1FRX47+J/8Ags98RLy0VdI8JeH9Kl3Z3s8kzYweMMcen5VyD/8ABUr9o7xJY3F9psFpHZWw3zTWekCREHT5jg4HI5qbj5T9t6K/Ay8/aw/aV/adujoWma7rmpPIdos/D8JiToQS5QcDB7+1ftn8BdB1jwv8FfBGk+ICTrlnpFvFe5cufNEY3ZJ6nPWmJqx6BRXkeuftUfDXwv8AGI/DHWfEMeleKzbx3CQ3a7InEmNiK54LHOcexr1tWDqGUhlIyCOhpiFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopNwJwCCfSgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBn41BeX1tp8fmXVxFbJ/elcKPzNef/AAA0fxdofwj8O2njfXP7f8Si2Vrq9ZApZiM4PTOPevhr/gsNJ40h8O+Dv7Mmu00EOxu5rV2RVlJwu4r2wT+YrNy0uaqld2ufpTb3EV1Ck0EqTRMMq8bAqR6g1LXyD4J8D+OvCf7FXhzT/B/iSabxB9jjnS8kYueRuI3EZwcY+prW/ZN/aU8SeOGvfDfxMgttC8VQSlbSBmCPdRjA34z1yR09ay9suZRa3Nfq8nBziz6opaapzzTq6TlCiiigAooooAKKKKACiiigDz/41fGbRfgd8N9a8Z62skun6WgZoofvyMTgKvua+YPgP/wVb+HHxi8aR+HNW0m88EzXT7LK61C5SWCY88MwA2HjvX1t4/8ABGmeONAk0rVNNttUsJj+9tblNyN15Ir8sP2tv+CW2t6TqFx4k+FsDXVvNKZZdHzt8heSSjeg4GPf2rOUrOx0xjFxu9z9c7e4iu4I5oJEmhkUMkkbBlYHoQR1FS1+PH7G/wC2v40/Za8Tr4E+MkOqN4PlIggu7xWY6a46ENg7kwCNo56HtX68aFrll4l0ey1XTbhbqwvIVngnTo6MMgj8DTjK5hKLRepGIXk8UpNQXE2z5duQerelUxJXdj5C/b7/AG2r/wDZh8KabD4b0Zb/AF3VpHSG8uz+5tgmSW2jlycYxkdc17p+zJ8YJPj18DPCPjqezWwudWtPMnt0bcqSKxRsHHQlc+2cV+R//BTr4sWfxE+Mlh4T0C4/tBNGMluTCc+bPIwGzHbGcV+rf7HPw7vvhX+zP8P/AAzqcfk6hZaavnx91Z2LkH3+asad3qzaolHRHs1FFFbmAUUUUAI1J7Up5o20AcR4q+CvgTxzefavEPhPSdZuOvmXlqshyO/I61R0v9nf4YaLcC4svAPh63mAwGXToj3z3HtXou2k20bbDbbKOnaHp2jriw0+1shjbi3hWPj04FY/xL1KPSPAeuXUrBVjtJCM+u01022vOf2hIxJ8I/ERaTyo1tnLv/dG0jP61E/hsVHdH4FeAbqTxt+1p4dm8hZm1DxVChiA3DaZ1BOO+Bz+Ff0cooRFVQFUDAAGAK/ED/glb8NrXx1+1lLqt3bi8tNAtZr+NmHCTmVVjb8t5r9wdtOOwpaMFp1IBilqiQooooAKKKKAIrq3S6geGRd0bgqw9jXxd8Uv+CUfwi+I+qalqcM2raDqN/cm5lms5wRk5yArAjknP4V9qnmjFGhSk1oj8kPi1/wRp8RaLIlx8OPFqavDwGttXRYpwcHkSJgY4HbvXjE0P7Wv7F908Nnc+ILWwZfLDQp9utWGQcBWVgPudQPXnmv3W20yW3jnUrIiyKeMMAalrsVzH43eDf8Agsb8W/DFxbWnivwzoOsxR4WYtazWl0R65EmzP/AO9fXXwt/4K2/Bbx1BHHr76j4K1A/ei1CHzYRyBxKnHfuBX0Z8Rf2avhn8UtPe08ReDNIv1Y7t7Wqq4bBGdy4OeTX5Of8ABRj9lf4Ufs6tp3/CL30lr4k1BwRokcu6OOLDEyEMCQOAOo+8Kkasz9efBHxw8A/Ejyv+Ea8XaTq7yjKR29yu9vopwe/pXc1+HH/BLv8AZl1T4tfG7TvGt1bTweE/DEv2prpWZBNcrjZGCOo5JPsCK/cVTlRVrYiW+g6mNnIx+NOrN8SaxH4f0S+1OUZhs4Xnde5CqTgflRe2olqfnf8A8FhvjNpWn/DzS/h3Z6iy69qF3Fc3Vsh4W1UOct9W28Vtf8EgfgQnhP4Wan8TNQtGt9Y8TObe2zgKLJCMFRjPzOuev8Ir8wvj98VNS/aH+Omta9eljNqV6La2jJJEab9qgDsK/oQ+CvhG38A/Cbwh4ftY/Kg0/S7e3CccERjP45zSavqaSeh2jV+L3/BYPwCNH+Oem+Jrawkih1K08qe6VMRvMvQZ/vYDflX7RHtX5xf8FmfD15dfC/wrq6XafY7XUVRrVhzvKOA+fTDEfjU7ExPpj9gX4mS/FT9lXwNql1Ms99a2g0+4Zf70PyDPvtC19DV8J/8ABHaORf2XLx2dmjOuXKxqegUBf6k192VS2Je4UUUVQgooooAKKKKACiiigAooooAKKKKACiikbO0460ALRTIt+35/vU+gBKpx6Lp8V898ljbJev8AeuViUSH6tjNXKNoqWrgFLSYpaa0AKKKKYBRRSNntQAN0qLykJzt5qRQe9LUtXHcjWMeZn24qWkpaa0BhRRRTEFcz8TvD9v4s+G/irRbuNZrbUNLurWSNxlWV4mUgj05rpWqnqyiTS7xG5VoXBB/3TQB+If8AwSZ0tYv20reN1V2sdJ1DaxHIb5U3D3wxH41+5Ffit/wSvhSH9uTWkVQAmm6oAAOg86HFftVSGxq06iimIKKKKlq4GJ4z8F6F8QvDd5oPiTS7bWdHvE8uezuk3I4/ofcc14Po/wDwTp/Z20OYywfDWymkznN3d3M4+gV5SAPwr6Sam0KI7nlul/sr/BzSVC2/wu8I4AwPN0aCX/0NTWl/wzr8KOv/AArHwbn/ALAFp/8AG69BWlx702wK2l6VZaHp8Fhp1nb6fY267IbW1iWKKNfRVUAAfSrVJS0LUQUUjU3NMD8Vf+CxTEftWaOV4P8AYVsP/Ijmv0E/bw+B/j34+fBHQdJ+HGptpOr2uoR3kwjumt/Nt/IkUx5UjPzMnHtXwB/wVoP2j9sLSocbv+JRYrz7ymv2W0FSuh6eDyRbxg/98igrZH4Xa9+zL+1Z8HZodVW08SSDT3Eyy2OoyTIMc5KbsEcV7R+z3+0tof7Y3xE0P4W/tF+FLPXNVVmi0rV1jMVwtwMfuXA7MN5J9UFfqJ8YPit4b+C/gPUfFXiq9jstJtFOQ+MzvtYiJR3Y4PHtX5NfsTXF3+0t/wAFFrj4k2ukpYaNZTXmqtFGgVLdDC8MSYAxkmVT/wABNTexW57B/wAFJv2T/hH8Ef2a5Ne8K+F7XRNZm1W2s0uoyS7KUkYpz2OwH8K+e/g/4pm8Pf8ABMv4vSCGNZrjxBBpyzBRv2ShNwz1xkV9Tf8ABa6/8v4KeA7IE5m155doPB2QMP8A2evnTV/BJ8F/8Ej7O8dcTeI/FEV4T6qPNC/+i6ncOh7Z/wAEStCjg8K/FLVHVWnkv7K0DY5URxyE4+u8fkK/Tavgn/gjf4TfSf2c9c1+Thtc1uWUD/ZjVUz+YNffNUtiZbn5x/8ABWT9ku88eaDF8XvDKFtV0K08jV4IzhpLNCzCVf8AaQn8j7Vof8EtP2zLr4paCvwp8VSGTxBoNiJdOvj/AMvVmpRArf7S71H0r9AtU0+DVtNurG6jEttcxNDKjDhlYEEfka/ADwTrjfsl/t0+dMWtrLw/4knsrlVPBti5Qj6YYH8KoLXP6B8nI4xTqrafeQ6jZwXVu4kgnjWSNx0KkZB/KrNBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTBGFYsOtPooAKKTIpaACiiigAopGJHQZpFYnqMUAOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPzP0P9qz4kftAftYalpvwylW78B6Lw16dy24VSqlsgHOd3THNef8A/BRj9qrxdq3hm4+HN74RvdOtRMjvrt3bbYpQMgmMgngkjqAeOlfenwX+Ffw+/ZR+HP8AYOlx2VhIlv8AaL6SSTMk8gA5Jxkivjz9uP4tfED4zfDGXw74Q+GWqX2hSN++8QS2f7sKCTtiJ5wfU46V581G61PT1lG1vmev/sM6j48+MX7KelQ6i/8AZlgim2tZ2ys8qLwGXjBU84JNcb4+/ZA8KWvxs0XxP4x+LNx4e1G1ZJbWGa6jRyFOcH5uM/rXO/sE+Jvi38RP2d9b8Ov4l/4Re00FxZ2dxBbIblF5yvzLgHqc+1Q/D39mH4JfHb47az4Y8U/EbxP8TvFtjZPc3UdzOUhi2uithgvUFwMZ7mnpKSS6BCbimnsfpbo1xBd6XaTWtyt7bPEpjuFYMJFxw2Rwc1drE8F+EtO8B+F9M8PaREYNN06BbeCNmLEKowMk9TW3Xcea9wooopiCiiigAooooAKKKaWC9SBQAtNIDEqRkY5FPpu35s0gOZ8Q/DHwl4qiEeseHNM1OPdu23Vqj89jyPc10FjZwadaw2trClvbQoI44o12qigYAA7DFTtTam2tx9B1RXFsLi2khckB1KkrweRipQaKpiPmbwf/AME8/g/4X+IT+NZNHl1XX2umvPMvpi8ayE53BOnBr6ZACgADAoApaUVZDbb1YUUUVQgooooAKKRiQOBmmq5bquPxpXGPopAaWmIRq8g/aoaab4H+L7QP9nhm02bdcjqhClhx+FeuyvsUcZycV4P+3Jr6eG/2WPiFdyDAbTXhRh1VnwoP60naxcd7nwP/AMEV72Kz+J3xKsHjVrmbTraQP/dVJHHH18wf98iv1y96/JD/AIIp2K3PxA+It+Y8vHp9rCJPqzEj9K/XClEc9woooqjMKKKKACiiigAooooAKKKQnFAHlv7THx00/wDZ1+D+teNb6NbhrVfLtbdjgTTsDsTqPQ/lX4TpN48/bo/aStIL2Uy634gusHy9xisrfqcDJ2qq+vtX1N/wVS/aCl+LvxJ0b4UeHLtbuwsbtPMgTO2S7OUXJB7bzX2h+wT+xLpH7MXgmHVtVt4rzx/qUOb2+4byEbB8mM44HAz15FRvqi/h3PdPgT8GdD+Anwy0bwZoEe20sIgHmYLvmkP3nYgDJJ9vSvQaTGKWqRIjV51+0R4hTwr8E/GeqSBWEGmTHDdOVI/rXorV8sf8FI49a/4ZX8WzaS7Axxp5qp3jJw36Gpl8LKjufh18LLm2n+L3hNrzCWp1mBpWP90zLnmv6ZbPb9lg2Y2bF246YxX8/f7Ff7HuuftYeKtUGmatBodhopglubmZSz8tkBQO52nn2r9+PDelyaHoGnafLP8AaZLW3SFpiMbyqgZ/HFWtgexpN1Ffmf8A8Fn/ABksHgvwj4aVo/8ASLprqRcfPhVfAz6ZIr9L2Y/jX4pf8FaPE7+Lv2ktO8O2Uq3cljbrBHDHyRLIw+U/jUPcI9T7p/4JP6Q+lfsf6GzRGL7Xe3VwMj7wL4z+lfY9eYfsy/D8fC/4C+B/DXleTLZaXCJk9JWUM/8A48TXp9UtiAooopgFFFFABSE4xmlpGUNjPY5oAM8470tJtG7d3xiloAKKKKACiiigAopDWN4u1x/DXhvUtWS3mvGsoHn+zwDLSbVJ20D3NqivyPu/+Cxvjmz+JoN54P02z8J2c/k3WnAt9sZN2C4Zj1HpjHIr6x8J/wDBVL4AeJltEm8SXei3ExAaLUbGRBGT6sAVx+NK43Fo+v6KzfD3iLTfFWkW2qaRew6jp1ygkhuLdwyOp7gitKgkKKKKYBRSV8d/tU/Hb4i/s5/HLwTrEVxHqXwz16WPTryyePBtJiQDIGA7jJ59aTdiox5nY+xaKitZ1ureKZGDJIoYEHIIIzUtMkKRs9uKWigBqg9zmnUUUAFFNf7vUjntXB/GP40+FPgV4TbxH4v1RdM04P5aYG55WwTtVe/AoA71qy/EsjQ+HNVkUkMlpKwI9kNfAXj7/gs18PNItR/wi3hjVtduPM2k3RWCPbg5OeTnOK8c8cf8FoPEGteH72x0bwDp9hLcxtCLi6uml2BlIJ2jHPNBVmcn/wAEj9HuNT/a88Tam5Yi20e8LOepZriGv2g9q/nw/Y//AGurv9lv4p6x4rXQIPEMGq2r289qs/2YRlpFfKsQRxtxj39q+3YP+C2nh8q/nfC7UFcDGYtWjfn6eX096AlufpnRX5Y6p/wW1kUk2HwtPl54N1qJX+SVR8I/8FePid8UviFoXhvwr8NNGaXULuODyTNNPIVLAMflIxgHrigk/Vyio7dne3jaVQkhUFlHQHHIqSgD8xf+Cln7ZHxZ+FfxVs/B3w91G50HTY7WOSa7g08SSTzNn5Vd1Ixg9B6V85+Ff2gf22PEUMb6Vq3jS/ikXcpg0GCYn35izj3r9wJ7SC6KGaGOUocr5iBsH1Galx7UFJn45Qt/wUE8WQjY3iuFG5/0m1tbM/8AoINcj8SvBf7b/g7wrc614k1XxemmRnEr2epB3QYJ3ERNuAAB56V+3eB6VHPbRXUMkM0SSwyKUeORQyspGCCD1BFS0NSXY/ET/gnnrnxj+Kn7Tng+a58V+MNY8L6fcyXGpPeancyWoCxPhHDOVOWK8Gv3ArH8NeDdA8GWstt4f0PTdCtpX8ySHTbSO3R2PViEABPvWxTRLd2UNe1SPRdEv9QmZUitYJJ2ZugCqSc/lX8+OqftlfEyP46SePn8V6nNLb6o1yNNS9kW0MatgJ5W7bjHtX7X/tteKv8AhDP2UPidqgcxsujyW6spwQ0xWEEH6yCvwb+BPwF8T/tFeJNT0XwzB517Y6a+otH3dUKpge5LUNlRPeP2uv2gPDX7S/7Qfwz8SeH7VxdtHYwaghGf3nnKdvvjmvrL9r7/AIKgeJPgj45ufBfhXwkkV1aQoHvNVUgElQcqo6gZr80PhLZyeAf2gPCFv4htpLA6frtqLyC4XDJiUA5Br+inXvhf4N8cNb3mt+GdJ1aYINs11aRyOQQP4iMnpQDP55vi58f/AImftL68JPEurX+vSswMWn2it5KY4BES9xnGcd60vgrpPxq+HPj2wvvA2i+JdP12R1MUcdlKizAEcPkAFfr6V/QXonwr8GeG5RJpXhTRtPlUYElvYxKw/ELmulFrCJFcQxh1+620ZH0pWDmPzD/4LEprV58H/g5e6rZyJIs9x/aTwj93FM0MJ259SQ+P9015Jpvwh+I3iL/gllqL3aOdPsdei1yxt5Dl/sKRyI5A9N0gI+hr9gfF3gvQvHujnS/EOlWusaeXWT7PeRB03DocHvVmPw/pyaKdHFlbjSvKMH2MRAReWRjbt6YxRyi5j8af2Af+CiWn/s2+F7nwN4ysLm+8M+a91ZXVmoaWBnK7kYd16n61996b/wAFPf2etQsUuZPGL2e7rFcWcm8H0wAaxvHf/BKf4E+NL64vINKvtBuJ2LudPumC5PJwpyBzXmE3/BFj4cySME8a+I4rfdkRr5Jx+JSmJnst/wD8FQv2eLOEunjGa7Yf8s7ewlLdCe4A7etflf8At/fHH4dftCfGJPF/gW31CBZrRYr5rqBYvNkUYV8An2zmv0H0P/gjV8HNPkDX2s+I9TXGCj3KRgn1yiA/rXsXw1/4Jz/Ab4Xara6pp3gqK/1G25iuNUnkutrZB3BXJXPHXGaYJ2NH9gOXxLP+yf4Ck8VyM+ptaNs8wfOId7eUG99m2voao4YUt41jjUJGowqqAAo9BUlAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCJgd3SpKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEY4pFYntTqKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD5u8O/sw+CvAa2Op+O/FN94u1e2hWP7drVzsRgMD/AFYOOuK9l1z+ypfD8tnC8cenm1Y7oceWse0+nQYr5Q8HfBGx/Zy+GI1j4z+Nr7xdqiyedN9su5J1MnJCRgjLd8ZxXGaxY/FP9sn+y9K8H2198Mvho0kiXut5MVzeQZAEaJz1Hrgcda8/mSfJY9NxulNzPjW8/ak8a+F/HXiv4a/Di6tLKy1nWDDFft1DEsvX05PPtX6b/sc/st6V+yj8OL/Vta1KLU/FGqj7drOsyfdHGSqsRnaOvua80+IH/BKv4Zr8M0svB8F9Z+MLGPzLfWJLk+bNNjO5+3X0r4T+Nvir9qf4J+CrrwV411fWP+EYvT9mWaX955i84RZB8wBA6H0rblUHYxdqmtz9xPDniKw8VaRBqemzLc2U4zFMvRxnGRWpXyh/wTT+IGp+NP2Z9FtNV0m80650cmyEt1GUE6joy569a+r66VscklyyaCiiimSFFFJQAtFFFACGoPsaFTuyx65zViigBkcYjXAOfrQsmZNu3HvT6SgBG4XNRLMDGXwcDt3qZqguLhbaNmYZCgmga1JY23AHpkd6fX58/tg/8FLdd/Z3+KCeEtI8KWd5EIo5nvLuZslWPOFA4r7i+HHjGD4geBdC8RW7RtHqVpHc/uzlQWUEj8DS5kxyi47nSUUUUyQooooAKKKKAEao3YqOBuNSHmmiP5sk5qGhoVadTGdUPLAH0Jpd1NaAEjBVyTgDvXyT/wAFH9QuP+GZfGlsWT7NLZqVO7gkSJgfXGa+rtRJNlNhN+FJ2k4B4r8OP+ChHxY+KWrfETVdE8Q3klr4RaXFpaQN+7dV6ZNS3qaRR9Z/8EW/A7aX8K/GPieWHYdU1BbeKQjqsS84/FjX6PV8bf8ABKLw7eeH/wBknR2ulZRe3lxdRBhj5GbivsfdVR2IluOopN1Q3V7b2UfmXE0cEecbpWCj8zVEk9FUtN1qw1hZGsL2C8WNtjmCQOFPocGrtABRRRQAUUUlAC14L+2R8fLD4B/CPVdWuLlYb2aB47KMNh5JiCFAGfqfwr3O8vIdPtZbm5lSGCJS8kjnCqoGSSfSvxX/AG1/ixJ+2r+1R4e8A+DJHawt7kaZbzM52SOT88uBkYADVLfQpLqW/wDgmn+zxqP7QHx0vvil4otJbjQdJma5imk+5PfFwVHzA7lUbs++Oa/aMfLgAYGK4L4G/B/RvgT8MND8G6HHstdOgVHkwA00nV3bA5JOTXfUR2CTuwoooqiRG6V4b+2ZpF34j/Z68XaVYsFuZ7N/vdCApyK9yasrxJodt4i0W90+5iWWO4heLDD1Uj+tTJXjYpH4y/8ABJf4oXPw/wD2lNR8JXTRxWfiCzMEgbP+uhOY8c9SGfPWv2tr+fb49fDnxP8Asa/tJR6rYSbZ7e8/tDTp2JCkbidrYx61+kP7P/8AwVc+GfxA0Qw+Opf+EI1y1iBlFxl4JyAMsjD37HmhaLUbR9c/Fr4iaZ8Kfh5rnijV7lba00+1km3McbmAO0D3JxX4Yfs76RrP7VP7aukX1xFJdi41gavesQT5dtG+7rzgfdH419E/8FBv+ChHhX4zeFJPAPgBZNV06dla51JkZQ5BOEQdcng59q+gP+CUX7M9x8L/AIcXnjzX7MQ694jRBbrImHgtl6D23dT9BRuO9lY+9Y0Eaqg6KMCn0m35s5paaMwooopgFFI3SkGaVwHUUxZQzEDtShg2CDilzIdh1FN3ccGm+Z8wXnkZ6UcyCxJRTVNOpiCiiimAhprKGU5GR3Bp1FAHjHxP/Y6+DfxilafxT4C0u8um63NurW0p6/xxFT3rzmD/AIJgfs421zFMngNmMZBCy6reOvHsZq+rdoo2ipauVzGV4Z8NaX4Q0W00jRrGPTtNtIxHDbwjCqo6D3rWpNo3Z7/WlprQQUUUUxCNXhX7a3hq18S/s0eOIp7GW+ngsWntvIj3yRSryrqPavdSM02WGOeJ4pEWSNwVZWGQQeoIqZK5Sdj8rf2N/wDgqpp/hnwzYeDfi0tystiv2eDXETcWUEBVlUdCB39q/UDwv4n0zxloFjrWjXcd9pl7GJYLiI5V1PevkX4rf8Epvg58TNeu9Yh/tLw7e3cplmXT5R5TE8n5COOfSvpL4H/B/S/gR8N9J8GaNdXV5p+nIUjlvH3OcnNUJ6s72iiigQUUUUAI1fM/7av7Gtv+19oOh2cniGbQLnR3lkgZE3xuXCg7lyM/dH619MMoYYIyKKBn5P6f/wAET9WaQC++Jdqsf/THTSTj8Xr1nwF/wRp+FuhsH8T65q/iU7CDGkn2ZN2Rz8nPr371+g9FA+ZnyNo//BK79nXSbpJz4Qurxl6Jdarcun1K78V6FY/sJ/ALTwAnwr8OS8Y/0iyWXP8A31nn3r3eloJPFP8Ahin4D7SP+FSeEef+oRDn89tafw1/ZT+E3wh8TTeIfCPgfS9F1mRGj+2QxkvGjYyqbidgOBwuK9YooAKKKKACiiigAooooAKKKKAPJf2qfgtcftBfA3xJ4GtL5NOutRRPKmlBKblYMAwHbI/lXy1+wN+wT46/Zb+LOteJPEOs6XdaXc6c9ksFmCXdi6MHyRwBtbj3r7/pKlq47nwl+0v/AME4JPjR+0hovxH0nU9O03TRNay6np8kRDTGJgSwI4ywFfdNvCtvbxxLwsahR+AxUtFNaAFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFIWA6nFIxwOarGdZpfLA981LdhpXLVLTV4p1NaiCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXqnhvTdaZDqFnDfLGQyR3EauqkdwCOtX44VhjVI1WNFGFVRgAemKkGaDSHd7DV9Koax4b0rxFFHFqum2mpRxuJES7gWUKw6EBgcHmtEZpaPUWxFb20VpCsUESQxKMKkahVH0AqWiimAUUUUAFRqsnmZJGzHTvUlNZio4GaAHUUlLQAUUUUAFFFFACN0qORdx9umKkpkkZdSFbafWgaPyU/4K7fA3V7jxtovjrS7E3thNb/ZrmO2BZ42XoSB2r7F/wCCZ+rXeo/sl+FYb0XIms/Mt/8ASoyjYDHGM9sV9G6p4M0nXFYajY294Dn/AFiA9evWtLS9Js9Fs47SxtorS2jGFihQKo/AVlFO5rOSlsW6KKK1MQooooAKKKKAI5txT5Tg14v+1B8RPGvw5+FWpap4K0Y6xri4SKNRkoCDl8YOcYH517WwzTDCGXDAMMYORUuNzSMktz8EPEHxO/av+IevyXclz4y+1qSRHYQSRogz2CitrR/G37aNqohs7rx1kDgvalzj/gSmv3ShsoLfPlQxxZ67EA/lUu2lYHJM/EKPxt+3IFJafxs6MNpDWMfOf+AV5v4++FP7TXxMgRPFXhvxRrEaPvUXFkOG554HvX9AwGKWml3J5j8JfCuqftjeBvD1loWgxeMdM0yzXZBbw2i7UHpytbS+KP249Q+UXfjb14hVf/Za/b880m2nYOY/EN4f24rpf3k3jaRfRio/pWJq/wAEf2wviA3l6pp/jC/jHz+XJdbF479R61+7G2jFMfMfHX/BNb9nvxp8C/hprDePPtEGt6rd+cLO4nMpiQDA5z1NfY1N2gHIp1BLdwooooEFFFFAHzv+274J+J/xE+Dt74f+GDRLql9IsVx5k3kkwENvG4n1218wfsDf8E3fFfwW+J9r8QPiHeWi3ljFKlppduwlIkcAeYz9OBnp61+k1G3nNTbW5V9LC0UUVRIUUUUAI1Np1G2gDzH4zfs7+CPjto0tj4p0a3vHZdqXDIDJHx1B7V+dPxM/4Ix6y2uGXwN4ns101mz5OqElk+hC8/lX6ybaNtS0ykz4M/ZZ/wCCVXhb4N69beJvGupp4v16DJitViC2cZOMEqRliMe1feFvbxWsKQwxrDDGAqRxqAqgdAAKfilpoTCiiimIKKQ0m40rjFqN5Ap29PemSM6nLH5PYc1BdPkJsbvk5FQy4xuwjmQP5YOGzmvnv9vDTvH2q/APVV+HV7dWmswss7GyOJXjUEMqkc5ORXvc1wY5lYeWFXl2Y4wvc18/yft4/Cab4vW3w2XUnl1a4m+zCfA8kSZ+6W9SaRs1ytH4/wCh/tEftA/A3X7bU5tb8TWZgkDGLWFkeF/VSGGCDX318Bf+CwXhnxNb2WlfEHQbzTtdlkSBbjS0EsUpJAB25BHJ7V9TftQfEL4T/DX4fX9z8QIdLvUaFjDp8yo0szY4CjqPrX49/sh+DND+MH7Xen6oJNL0DwxZ6g2om01CdYkMSklUGT1yR+VMybTP3y0++i1Kzt7qHd5U8YkTcMHBGRkdqtVnaPrGlarFjTL60vY4wAfssyyBR2+6TitGqjsZhRRRVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTScUAK+GXnmq7Rjd8owafJllwpwaWFiyfN1qWrl7IWPduwalpq06mtCQooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKa8ixrlmCj1NADqKQHPI5FLQAUUUn60ALRRRQAUUhz2pAD3NK4AEw27Jp1FFMAooooAKKKKACiimSP5a5xmgB9FIrblBxiloAKKKKACiiilcAopCcU0SZYjHSlzIB9FIDS073AKKKKYBRRRQAUUUUAFFFFABRRRQAUUhzRnmlcBaKjeZI2Ad1TPTccZp+RRdALRTN5XcSy8fhiuJ1b44fD/Qdch0bUPGmhWmrSnalnJfxiUn025yPxpgdzRUcMyTxq8bK8bDKspyCPUGpKACiiigAooooAKKKKACiiigAoqOaRo0yqFznGBSqxZQSMe1ACTbto2cHNId2Bg0rMd2O1NaRV53AVnLcpCTZ8s4ODis+2t3uELF23dORVld8zM+/930UAVieOPGlh8OfCN/4g1aVktLKMySbRk4+lTc1i3FWRNrmiPNpdyitzJG6MSemVPNfzs6pYapaftK3VlprGfWI/EDLbndjdIJDt5+tfXX7Sf/BWD4ha34g1HSfh9BB4e0H5oBNdWglnnBGCw3D5fwr4P8P+L9fsPHFt4i064d/EC3QuYpVTezTE5HHfmmPmb+I+z/iR+wH+1J8avEk2ueILa1u2mbdELrURtRccALjA4rFs/wDglL8Y9NUTarqPh3Qoxy7vqJ3AevQVrXetftyeO9LivoT4uW2ugrxtZkW5Ax2AIwKyLP8AZl/a5+KWr2eneIh4pFlcTL50+qaiTGi55JG70qrMSstz9HP2BP2T7z9mbwjqz6l4jXxFfa0ySeZC5aJEUcBcmvq+uQ+Evgj/AIVz8O9A8OGZriTT7RIXlZixZgOTk+9dfVLQyk7sKKKKZIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFI1NzQA+imfe4zilXC/LuyfegB1FFJ+NK4C0U1unBpfxpcwC0UnQU3NHMMfRTVp1PcQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqifNStUcjFVyBk0DW5Hg06PIbmnRt5ig4xUTXGbgRAHpnNS3YvcsLTqatOprUzCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJoUuIzG6hlbgg0+igCK3t0tYljTO1em45qWiigApkmfLbGc47U+kbPbr70ARWpPlDdnPvU1FFACMwUZPAoznGORSOodSD0pI08tAvpUNAPoooqlsAUUUUwCiiigApKWigBKWiigAooooAKKKKhoBKNopaKfL3ASlooqgCiiigAooooAKKKKACiiigAoorgvi58b/AAf8E/Ds2seLNat9MgQZWN3HmSH0VepoHud4xxVXULxNNsbi6k/1cKF2x6AZr8ufih/wVW8c+JtUnt/hJ4Ol1DS4n/5CE9rJIxwegC8YNfTX7Of7VGqfHL4W30Xi7RJvC/iGGMxym6TyYZyR/Du7VhOajqzZUnufnh+2T+1f4z+PXxxHhjw1qV9pmnWd19jt4bSV4wz7sbm2nmu90z4zftJ/sHx2MnimU+L/AApcKrmK+dnCbumHzkGvIvAevaT4J/b/AIZLyyt7jT5NWNqyud8YLsAHyD1Br9kfjd4F8P8AibwXf3etQQ3WmwW5eSGZFZDGBnuKorS9mfnd8VP+CxB8XfDK+03w94VudA8R3UflC5kuVkiUHgkcAivjHw5+z78SPir4N1b4lxK1zYRyPI95K7eYzjklf/11jfErw7ZeOPjHqul/DvRZJbaSRhBZ2ozjHUivqz9kP9uK0+DOly/C/wCJ+ht/Yit9n8toyBAehLAmjXoCtex7V/wSn/a+1zxlrVz8KfFtzJeXdvbNNp1zMzGTan3kYk8+2AK/Tevwy8O+LPDPwu/by8N+IvBGqwTaDqF+sY8g8RRyHDKcV+5MUyzRpIp3IwDA+oNXHYymtSSiiiqMwooooAKKQ0m6lcY6imB93QigtilzILDm6VGzhQCTgU7du3LSeWOO+Klt9BjHdQRu6HvUUtnFJGQBwPQ0jWPmXG9mYqOig8VOsQjztz+NTr1KI4QuPKHGwCs/xP4WsfF2j3GmajEJ7OddkkbDIIq/BDIkzMzglj2FfI37Wn/BR7wx+zP4mi8M22kTeJPEIG+4t1kESQL2yT3NXdbMavfQ9h179mD4Z3Gl3Ek/hHS5ZYYH2SPbrlflPOcV+Tn/AAT9+E2meMf23Ly2vrWCbStHlvJ1gYZUsj/Jge1e3eJP+Czz6v4f1Cytfh81tc3EDxJM16CELAjOPxr84tB+IviTwz4tuvEWgavd6Hqk0ryG4s5WRl3HJGRTaDV7n9NF5fWWi2ZmuriCxtYxgyTOI0X8TxS6bqdprFnHd2NzFeWsgyk0Lh1b6EV/Nt4w+PvxP8eWL2et+Ntc1a1cgtby3cjIcd9te8fAv/gpV8VvgT4FsfClha6Xq2lWIKwC+t2LKCc8sME/iaETyn7tr1p1fkn8BP8AgpZ8b/jN8evCXhw2emx6PqF4sVzZ2NhlvL/ibewJAH1r9bKokKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSE4oNNbJpN2GDSKBzTd2e+BSMm4YYjFNaMY+9+tZSbKVgZvJUdXJNG8ZLntUVwfLmiOf1plzIWyFOOR0palWLHnhj8uTS+Ye4xVaSXykGOtQtcOwxyKzbdy1C5Za4ZX2MPfNTLN8tU4JNylpDnHrzT5HVo1dTx0q47A4paFlptnWhZC3bAqvbWzMp3sTnpk1bSFU960SuZuyHLTqSlq1oZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkzQ3SmH8qAHNUcj7V96dzVaThutBSQ5pJNvyLz9KkhjZVBfl/WpI+gp9K1wuNWnUUUbEhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRjgdM0UALRRRQAUUUUAFFFFK4CM20ZoHNDLuGKBwMUwFooooAKKKKACiiigAooooAKKKKACikNJuNAHNfEbxpD4B8I6lrdwVEdpA8pMhwowCea/FHwBpvir/got+1w1l4i1WaLR42ku3xlo4LaM5CKvTLdBmvuj/grT8UP+EP8AgSui22ofZ7/VpVj8hGwzx5+b9K5//gjv8JrPQ/g/q/je4siusavdtbx3Ug58hOgHtms73ZslaNz7U8E/B3wl8P8AwtBoOh6LZ2VlHEIm8uFQz4GMk4618uftG/8ABPnU/jR4ug1DTviBqHh/R1wJLCAEqAOuMHrX21jb70jcU+VSJjN7H4N/tzfs/wCnfss/Efwo/h17xi0S3D3V0+ZJZUIJb26V96/Fz9po61+wDaeLoZY1vNR05bVlZjgyY2kHnNZn/BV74S3PjL4Y2+t6Xow1DU9NlVvOjTMiRZ+cZ9MV+UEfxI8W+JfCGk/DpLq4fSI7nEFmpPMjHABHoDU2exs9Hdn6hf8ABI/9n/Q2+Gd98StVsPtWt6hePFbvOqsscanqvGck+9Vf+Ck37Ct14+uofG3gHSozqaoxv7WBMGUDncMd6+z/ANk/4Wf8Kb/Z/wDB3hdt32i3s1kn3Yz5jjcw4HvXrTRq/UZppXMlKzP5fLX+0vAniyGW4tXtNR024WRreYFWRkbOCPwr+jX9mn4oR/GL4I+FPFKKsb3dmglRM4WRRhgMk+nrXyr/AMFAP+Ces/x0mtfE3w602xtvFSti5jd1gS4XuWOOtex/8E//AII+NfgJ8CIPDHjgwpqUdy8kcEE4lWJD23DirRLtayPpiiiimQFIy7hjOKKaX29aVxjcbWGCSO9OqGbzFU+VgsefmrnPiL8QLD4Y+B9U8TawwistPgaaTkDOBwo9zUNlJC+PviF4c+Ffhu813xHqcGmafbIXeSZwCfYDuTXw/wCJP+CzHwy0/Umg0rw1reqWqttN0VSNevUAnNfC/wAXvjT8Q/8AgoB8c7fw/o0czadcz+XY6ZDuCJGD/rJBnBwOc19w/Dv/AII1/Dmz8Kxr4y1vV9R8QOuZJdNnWGGM+gUqSfzpFW7nrHwd/wCCm3wd+LmsWGjpqFzoOq3jbEh1CLapb03dK+tBNHJCssbq6MNwYHII9a/GH9oz/glV40+FVxca38PrxvEmlw/vUi3bbuHHIx6ke1ep/sH/APBQK4tXtPhF8UvtEF15n2Oy1SUkSIenlyE988A0D5NLnqv7VH/BVDT/AIE/EC88JeGvDUPim8siFup5rkxxxt3XgcmvFbL/AILba20+Lr4aWAjA5EN8+79RX2T40/4J5/B/4i+KT4i1zRDfX0vzS7ZSiTE92A6mq2rf8E0f2f8AU9Pa2j8Fx2MjDHn28zBx9CTTSuRotj5m0/8A4LYaa237V8ObrdjlIbxfzyan+DXi/wCEf/BQr4vahPrnwxljvvI3XF7cS53BegyvSvXtL/4JG/AzS9Zhv/I1i7SNt32We9JjP146V9ZeB/hn4X+G+lQ6f4b0Sy0m3iUIPs0Kox+pAyaHEaklqeGWH/BOr9n/AEnMjeArKdFBOLhmdQPpmvEP+Gsv2QPhH4xm8L2XhGztmspWtpr2DSUaNGBwQSeT9a/QW4gFxbyRE4DqVJHuMV+dHjz/AII56D4t8U61rNv491GxGo3Elz9n+zoyqzEnr171qJan1X8OvG/wH+LVjFJ4Zn8K6iJBkW4ihSUexQjOa9BHwl8E+WUHhTR9h5x9ijx/KvyI+M3/AAS8+JHwP0ebxD4O1xtajskaWQ2rGGYKOcjHtX0p/wAEqv2r/FHxUs9X+Hfi9rjUb7RYvOttSm5fZnBic+o7E0hyjbqfeOjfD/wz4fu0udM0DTbC4XIWW3tURh+IFdFSYpaDMKKKKAGvnbkAk+gxUc1zHa27zXMqQRRrud3YKqj1JNSt71+eH/BYS68U/wDCl9Ol0/UXsNBt9SRL2CJ8G43DCZ9gaVyoxctj9BdM1ax1q1Fzp95b31uTgTW0qyIfxBIq3X5Bf8EZ/iLrkfxO8QeDpNQlfQpNON2lmxBVZQ33hxkce+K/X2mJqwUUUUCCiiigAooooAKKKKACimGQbtvejcc0APopm6kV9wz0oGSUU1W5p1AhrttWm06Tlaj27hjpWctylsI6eZghj+FU7jz0mO1Ny1D4m8Raf4P0G81fU7hbSws42mlkboFAya/PbxR/wWc8MaPr19Z6L8Pb/XLC3kMa3smpJbrJg9RlGwKktNrU/RIJLcYDx7fRqGs3IOG5+tfmhP8A8FtLPafK+E0gPq3iGM/yhrNvv+C3Eqwt9n+FMSv2aTXA4/IRA/rRYOZ9D9PpbOf5CrBiOuagaG73MBGp9K/ILXP+Cz3xT1K6L6R4Y8L6RB2juEnuG/MMKzX/AOCwXxv8sg2HhNc/xLp1wD+r1Ljcrmkfspa2sq/LKODU8luI4z8yoPfpX4jXX/BQH9q/4mTl9Bvb21tuqjQtBjkH5vGx/WuF8VfGj9qvxVqENlqmuePhcTN+7htFmtCzduIgtNK2gXb3P38i2qoI6e9Sbgehr57/AGL9P8eWHwA8My/ELVLy912SBmliv8tOATxvZjuJx6177bYMSsBg+9ax2M5IsUU0dadVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIelNK5p9FAEbL0NNaENyRU1FA7jVGMU6iigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJmgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEo5oakwaBDqKQnFG4UDFopu78KXdQAtFJupaACiiigAooooAKKKKACiiigApMHdnPFLRQAUUUUAFFFFABSZx1oNed/Hb4waT8E/hrrPijVJokFnCTDFI+3zJTwig4PU45xWctNxpN7HbS69pkGpR6fJqNrHfyDKWrTqJWHsucmr9fkF+xP8Odc/be/aG1v4o+ONV1A6JoNyJraGCdkVpScpGpHYd/Wv18VQihQMADAqo7ALRRRVCCiiigAooooAKKKKACikNRGRw5yAE/vZpXGFzcLbRl2yRnHFQTakkMPmtkL9Oak3qzgZ3Z/KqGuW7NaySxuBtU5FYy5r6bGkEm7SPx4/4K4eNZPE3xc8OaOE3W9vAXWTnJLHGMdK/UT9lDwlbeCf2ePAelWsflrHpkUj8AFmYbiT781+PH/BQDUjqX7VFvpzzGW2tfITeep3OM1+3/w7tI7HwH4ct4jmOPTrcKfby1poup2Oi7ihhmilrVaHOc5428FWPjrw3f6LqBkS1vIzHI0Rw2CMcGvnr4Z/8E2/gt8MvFlp4ksdGur7VraQyxyX1y0i7j32fd/Svqfb1oC7aTVyuZ2EChdoAwBwAKdSUtNaEhRRRTAKKKRhuFACMeKY/Ip2z1NDL7ZFQ0MYu7A3EEewr8xf+CvH7SktpYWfwj0aSN2vgl1qLRk+YArZVAQeCT1GOlfob8WPGkHw7+Hut69cHEdjbPNwcdATX4ffsw+FNQ/a8/bOsp9Xne5tpr2XU7iSYlgIYyXVOc8EADHvWd9TVLqfol/wTJ/ZFsfg38NrTxxrFqT4t16ASqZMH7NAw4VRjKkjrzX3DtqK1tYrK2iggQRwxKERFGAqgYAFSbvatFbqZvUrXlnFIvmMMMv8Qr8Ef2xNPtfDf7cGrrpC/Zw2rW8xA6by6kmv3r1a4MOm3MnGEQt+Qr8LPHmgn48f8FDBpdoDdQ32uwoWt2yRChBds+2DS06GsfhP3Q8OM0nh/TGc5drWIk++wVoVDZWq2VnBbpny4UWNc9cAYFT1UdjAKQDFLRVAcj8RPi34O+E+nx33i/xFY6BayHaj3km3cfYdTXi2tf8ABRv9n/RQ+7x5b3TL/Dawu5P04Feb/tzfsIeMP2rvE2l3+m+MbbTLOyQoltdQllXPU/KRmvmew/4Im+MHmQXvxF0pYP4vJsXJ/DLUD0Kv7ZH/AAVUuviFpd74T+F0cmnaNcoYbnVbiMebMp6hAfugjv1rh/2Bf2zfhr+yn4V8S3Gv6Jq2peK9SkG6e1YFJIxyFyTwc96+jfC3/BFHwnazQyeIPHuq6iq/fhtYUiVvbOCRXon/AA57+B4mRhLr3lrgmP7ccN9eKAR6b+xz+29o37Xk3iGLTfD91ocmkbGYXEokDqxwOgHNfTdeT/AD9mLwF+zTol1pngfTJLKO7fzLiaedppJCPVmJ49q9YoB26BRSE4qpLqUSEqG+YcYoBJvYtsM18P8A/BXDTjffstXMiqzNBqFvJhR0Abk19mjUJfOVcF1buBXzp/wUA0b+1v2VvHkRRpTFaGbBGSCCDkVne5so8j1PzU/4JG64un/tbWdrlh9t0u5iHvhC39K/chm2rn+Vfgn/AMEtpWT9svwkV53QXSk+3kNX70zSeXE7+g7VVzORn6z4o0jw3HFJq+qWmmJMwSM3cyx7mPQDJ5NacciTRq6MHRhlWU5BHrX4df8ABTf4ueKvEX7UlzoM99Ouk6IYfsFpwqxscHdwOTn1zX7G/A8XX/Cn/Bhvsm7OlW7SE9dxQEn9aOYVjuqKaDTqe5IUUUUwCiikagBpRc7sc+tNbO4Yryz9pj472f7O/wAI9a8aXUC3hsQix2zNgO7sFUE+mTXwR4Z/4LXFf+Ri+Haqrco2n3mTj3DUFWZ+pEnmbhtAxTdsrcEhR7V8CR/8FmPhU2mCZ/DevC7xzbqqkZ/3q868Zf8ABahRDIPCnw+3tkBZtVuCEAzzkJzSuPU/UZF24HWn18e/sB/tbePP2qrfxJqHibw7p+kaVYuq2tzZrIBKx6qC3BxX19I+089KLk9Rz8LzUCzLJJhajmMkmfLJJ9GPFLHGFHzRbT3K1ne5drGT4u8L2fjbw7eaTqVtDdWVyhjkgnUMjqeoINfgv+3n8FfD/wABvjtceHfD8eLd4VuXgj+VItx4CgdBX9AylcYAx+FfhL/wVSuvP/a610Ic7bO3Vh68cD86B36H29+wP+yN8IfiF+zD4S8QeJfAWka3q915jzXV/apJI5DYGTjkV9LW/wCxj8CbVsp8JPB5P+3o8D/oVNYX7AXhe48I/sl+ALO5G2WWzNyVPUB2JH6V7/NEJuDwem4HBH0NBKPPtJ/Zu+EugyLJp3ww8HWMqjAkg0G1Rh+IjzXQWvww8G2Ugkt/CWhwSDgNFpsKkfiFqj8V/ix4R+CvhCfxL411qLRNHidUNxIWyzk4VVC8kn0H418leI/+Cw3wT0uOYaTY+JtckjbaDFYLFG3OM7mfP6UAfbtroun2aeXb2FtBH12xQqo/ICrbW8TurtEjMv3WKjI+lfmt4i/4LW+FYdPlOifDvWLi8GNn264jii98kZP6V5T4i/4LU+P7y326H4G0HTpG+7LeTS3GPbau3+dUgsz9gWUHqAfwpOnA4FeRfsr/ABE8V/Ff4H+GPFfjSyt7DXdTiaZ4bSF4owhPyEKxJ5HfNeu1XQkVetOpq06hO4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACNxSKxPbFOooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASm+WN4bGDT6KACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSk5qW7AOopBmlpp3AKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFJtpaKAEb6ZrzH9oT456R+z38OL7xjrdjeahp9myiSKyVWk5YDIDMB39a8z8Q/8FJP2ePC+vXejaj4+EV7auY5fK0y7mQMOo3JERXgX7bf7bXwf+IvwC13Q9M1e81GbVrUpZp/Z00YaTOVOZFUAVk6iWxtTg73aPrT9mf8Aae8M/tSeE73xB4XstSsrOznFtIupxxoxYjPGx2GPxr2PcK/NT/gk38cvBehfCLUfBpuJz4lhuHvp4Y7ZyrIQAMNjGRg169+0J/wUq8H/AALuorR/D+razdSqSscKCNQR03OxGB9AarnXUbpuWq2Ps1WDDIORS14P+x/+0w37U3w1k8V/8I/L4eWO5a3EMkokD4/iBx0r3iqunsZNcrsFFFFMkKKKKACiiigAooooARm2jNFDLuGKBwKAFooooAKKKKAIbsyLCTEu5+wNfnj+2Z8Evix+078btA8CQ2dxpHgJtr3mrqd8QUHcTt4544GetfomeaTYM5xWU4czTN6dX2aasec/AT4E+GP2efh/Z+E/CsDR2UPzyTSnMk0hHzOx+v5V6RSKu36UtaGLdwopKTdTEOopN1LQAUUUUAFFFFADW+7TOG4IyKkPNJt96lopCKoGMDFZ2uWpudPuI0Yxs6Fcj3FaWMVBef6hzjJ6AVLTsVF+8j8C/wBvPR9R8P8A7U179viMZZoTC/ZgG6mv3Q+E94dQ+GfhS4JBMml27cdP9Wtfjh/wVa+X416Zc5fzTAd2VwMg9jX6pfsZ+JJfFn7MXw71GbHmvpccbYOfu5X+QpLdGlRWue1UUUVqc4UUUUAFFFFABRRRQAUhz2pabJII13HpQBFMSCAThfWnfeTCtTsLIoPakEYQYFBXQ+F/+Cq3xiX4f/BD+xLaY/2jrcn2ZEDY/d/xn8q/KL4B/EX4i/BXxNH478CWk4ls0MUtx9laWAqeCrY9a+vf+Cy2ovP8XPCenCZmgj055PLzwGLda+//ANif4V+HfD/7K/gqzTSbaVNR05bm686JWMrP1ycciudG89Ldj40+GH/BaK8t7NIPHngN7y4U4a50SQLn/gDn+tenSf8ABZ34XLalh4S8TLc44ikSIAn6h69i8a/8E1/gX421S5v38LnS7q4OWbT5iignqQpyK8+tv+CPnwSt9SW6kuvEVxEG3G1a8RUPtwmcVra5nJx6HyF8ZP8AgpF8XP2kNcfwv8NNKvNB064HlpaafF515L9WHAB7+1fTH/BNP9h/W/hTqN18TviHaGDxTdo6WVpcczW4bId392Br7H+FP7O/w8+CtosXhDwrp+kS4Aa5jiDTP7lzzXo1HKyXLohN1OpNvelqloQFFFFMAooooAKKKKACiiigCG6DtCQhwayJLOSWf7mVx29a2Z0MkTKOD2rw39qz9om2/Zc+DOq+LZ7X+0dRVhBZWrNtEkrkKuf9kE5PtUt9DaEuVEfx8/bC+F/7MEMcPi3WGbVpE3x6VYJ51ww9cZ+UfU18S/Hj/grp4L+Ifwx8ReGNE8Daws+r2cloLrUXiEShgRnCkkmvnv8AZ1/Zf8df8FA/i1rPi7xLfy2Ph5rvzNW1ccn5jkQ224EZAGPQd/f7W/aY/wCCdPwT8Efs5a7qWmaRd2mqeHdMlng1JrpmllZRndIBhSfoAPapSJvrqfn/AP8ABNcTv+2R4EETbCZJQ/OMr5TZH5V+/wBIu+Nhkr7iv5iPhv8AETXfhV4403xR4ZuzZa1p8vm207IGw3TlcEHivraH/gqZ+0fdRlY7vT2GNpYaOC3TrkLj9KdgZc/4Kh+AdQ039rzTryeFmi1qK3MEkfO8hwp6d6/ZrwTAun+CdAgb92IdPt0+bjGI1FfzlfFL49/En4peMLHxJ4y8Q3d/rll81pcSQpD5IByAqqgHX1zXvGk65+2V+0F4PMun3njLWtAcKyyWoW2VgMYw0aoSOOxosB+7EciycowYeqnNSV8T/wDBOL4D/F/4W6Dqmp/E/wAQ6o632Ps2hahdNO0J7uxYkg+2a+2KpEMKKKKYgqMurMVzkjqKe33arrbrGxbJ3NQNHLePvhronxK0mbSdcsodR0ycbZraZdysPpXzz4s/4Je/AnxNFtt/Dj6IT959OlKE/nmvquONoZsqWK+lWgxPtUuKZbkz4aH/AAR9+CIYEza9t7qL0jNeheFv+CavwC8L2SwN4Mi1dh1l1KRpmP1ya+pBS4HpRy9ieY57wL4B8O/DXw/BofhfR7XQ9Jhz5dpZxhEGepwK6BlBHSlpadtBFVmEaneKTzuPlqeaJZUIYVwvxa+L3g74G+FZNf8AF+rRaVYIcJvOXlb+6q9SaztymiaOytrrzm2lGVvpxX4RftqWM3jv9vrV9GaTd9q1S1s18zkAHaMfTmv10/Z5/bG+Gn7Swu4fCeqlNQtn2tYXoEUzjruUZ+YfSvyr+PVk9v8A8FP44rqDaZPE1gyhuQylk5ph1PsL9v8A+N3xn/ZT8F+Fbf4bpZ6P4SgtIbO41WGwimMMqgAKFkUqobHp3r5L+Ev/AAVu+M3g/VjL4rlsvHultkyW89rHazJ7q8Sgce4NftH4m8J6L400mXS9f0qz1rTZcF7S+gWaJsdMqwINeW+Mf2f/AIHeGfAeqf234E8J6Z4ZgiMt0rafDBCAOcnCjnPT3oSuK58W6h+098HP+ClVjpXwy8W2es+AvED3Im0658xJYjLg8A8D5hxyO9eS/Fr/AII6eOvBtlfan4U8T6Vr+nW8TyvDdhobgKozxxtJx715Z+yb4V0H4mft/aCvhfSfs/hS21qS+trVcypHbxFnUknjHyjH1FfuD8TLpbL4eeJbhjtWLT53J9MIaNgPwM/YX+F+jfEn9qbwt4W8SWa3mns9x9qtZUV0JjjZsEHIIyvetjRfh5oOsft/2/hO1sbeHw8nioWws2iUwmNZPubMYwcYxivRv+CV/h9fFn7WtxrU0gMlhp13eITyzF8rnP8AwKvOvA88i/8ABRXS2LMrHxyqk55P+kYoKP34sbC20y0gtbO3itbaBBHFDCgRI1HAVQOAB6Cp6d6UGqWxkfmf8Uv26PFnwj/4KCp4a1jU8/D5Wis5bBUwF8xcCTPqGIP4V+l0UqTRpJGwZHAZWHQg9DX4s/8ABXbwM/hL9ovR/EcAwmr2aSDbx88bfzr9V/2Y/HyfE74A+BvEaSrK13pkQkKnPzoNjA++VqYuyKaPUqKaOtOq07kBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPyI/4JS/s/aR418QeLfFniOwsdSFhN9lt/OVpHWbOWLK3y4Izg5JzX03/wUO+E3gu/+EN7f6ra2emy2VtI9qYowo3KMgbRjvXmH/BNDWI/BvxU+Lnh64JtbV9VY28LDGW3HH9KZ/wUCtfFH7UHxi8PfCH4emZ7uziebVpTn7NACOBI65I6elcOk46PU9HlkpPTQ6H/AIJJ+A/CGi/COfW47uxm8T6q7R3EYkBlEYOQMHnpXq3/AAUM+GHh7Vf2afFl7Npdu11Z2pmjnWMCTcp3Dn8K+b/j9+wDe/BX4L6N4h+H1xdWnjTRYFkv7zTrqUK7ADcUXAyDz1xxXFeAv24PEf7Q3wR8a/Drxtp0lxqdpo08o1G2jwCqRniTJzuyOwo5mo+8iYxu1Z6H1z/wSvt1i/ZR0dx5eXuZchOuQR1r7Dr4n/4JMyCb9mYNGZPJW/kRRJ6gDOPbmvtiuuGxy1FyzaCiiirMgooooAKKKKACiiigAooooAKKSk3UgHUUzzPmIwacDTAWikzS0AFFFFACNSBh6YpT0r4r/wCCiv7Wnjn9nHwzp6+CtPt1nupNs+rXCGQW6noAmMH8TSukUouWx9qcUtfnj/wT5/4KDeN/2hvH0XgLxj4fguLv7FJef29ZHYoVRkB4wMDPTO7rX6HUCtYKKKKYgooooATPalpmz5s5pd3zYpXAVvu1Xum8m3kcc7RVhulQXXzQuuM5FHQa3R+Rv/BYrTLa31rwTLFCq3EwkLy45bivt/8A4JwXct5+x/4EaYAFIpUXH90SNivjL/gs5E39teA1jX90Ff8AeDrnHSvrb/gl7fG9/Y68I5bd5ctzH+Uh/wAayidNU+sqKbu6U6tjlCiik3DdjIz6UALRSGk3UAOopoanUAFIRnqM0tFABTXOFzTqQ80Afjh/wV38B6zH8QND8YTR/wDEplR7ONvRgd3NfoF+wL8UNM+Jn7MvhE2Mqm40u0SxuYl6oy9PzH8q5P8A4KQfBRPix8BL8JC0l/pga9t/J4+dRnB4OQQDXxD/AMEifjhD4L+Ld/4G1W++yWWswt9njnbAFwgLEc+oUjHqax20ZvKSlqj9lRTqKWtI7GIUUjZxwcV8Nf8ABQr9vq//AGa5NP8AC/glbC98XXQWWZrhfNW0TcOGQEZLDIHPencLXPuXnPtS15L+yt4w8X/ED4D+E/EnjkW6+I9UtvtUy20PkoqsxKDZk4O3FetUCCiiimAUUUUAFFFFABRRRQA187TjrX45/wDBYD4wT+JPi7o/gS2uGaw0e382eFD8plk4BP4Gv2JuHMcDsOqgmv56filrs3xa/bUvn8QH7ZDeeJo7KVG/d5hEwXb8uMcDqOah7mkUftv+yH8P9P8Ahp+zj4E0fT7JbENpkN1Oi5+aaRA7scnqSa8v/wCCnHxIT4e/sp+I48B5tYK6aiZwSJDg4+gz0r6n0vTrfR9NtLCzTyrS1hSCFMk7UVQqjJ5PAFflj/wWq+IrvdeB/BcM+ETzNQmiGOSQUXP609hbs8H/AOCUfgDRPHf7UiJr9hbanDp2l3FzHbXaB0MgAQNtPBxu7+lft3a+E9EsVxbaNp9uOmIrVF/kK/Dv/glT4utfC37Wekrdzpbpf2NxZq8jADcRnGT9K/dmmhSPxm/4Kyppkf7TXhTTLS1hhQWkTTxQoFVi0ncD2r9ePh3o9loHgPw/p+nWyWllBYwrFDH0UbAa/Iz/AILDeGX8OftFeGPEiKfLv9LQh8nAkikPH5Yr9RP2afilpvxe+CnhPxBYXEczy6fClxGjAmKVUAZWHY8Z/GmD2PUV606oyM45I57U1pxEN0jqijqW4H50Ek1FNVt2CDkU6gBsjBVJY4HrXxD8e/8AgqV4N+BvxO1bwXN4X1XWbvTJFSee3dEXJXJxu+tfb0kayKVYblPY18z/ABw/4J4/B/47a5d63q+kXGna1eOHub7T52R5SMcnOR2x0oGjyXRf+CxXwb1CENe6Zr+ny94/swkx+Kmum0v/AIKxfAbUJkSbUNXsVbrJPYNtHHfmueT/AII6fBVJCwv/ABDj+79sA/pXMeIv+CLnw+1CYnSvGmuabEf4JFSXH50D0PbrT/gpn+z5dKCvjTYf7sls4Nbnw/8A2/fgv8UPHmn+D/D/AInN1rGoSeVbK0LIrvjOAT3r5Wuv+CJPhoW7m1+I2qfaMfIZrSPZn3xzXQfs1/8ABKF/gz8Y9F8Z654vg1u00e5NxBZRWpRpXCny2Zs8bW2t+FBJ+itFMTOcEc+vbrT6AEbpX5Lf8FsNVvP+Es+HenCeQ2X2W4m+z7js37lG7HTOO9frPnrX5ff8FsNFgbSPhtqQhT7U13Pb+bj5tuwHbn0ziol0LifnF4PvPHvwr/sj4k6EdQ0SOOYxWmrQFlDOBgrkdQRkH617h+z/AOPtU/ac/bq+HeueLxC+o3Gp2zXDW67fMMPzAn67QDX21+yZ8E9C/aQ/4Ju2vhi/s4JLoTXZtp2QM8Vwj7lYHqOw+lfEX7Cfg/xF4R/bm8JaINLku9R0jUZ47uEqQsSrG+5yT0wMnn0osWfuJ8Qvix4P+FOltqHi3xDYaFbAbgbuYKzf7q9T+Ar8iP8AgoN/wUH/AOF/RzeBfAEkyeC4yDfXRyjXxDAgYBzsBAOO9fUP7eX/AAT38f8A7TfxQs/FPhnxTp62K2iWx0vWZpljgIJy0ewNjPGcAZIrxbQf+CJfime1Vta+JWl2s4HENnYyTIvtudh/KqtYjYzv+Cf3xi/Z3/ZZ0tvEfiPx/cX/AI1123EM9tDpUvladGDnZuC8kkDJH5V98/tRfFTS9S/Yw8e+MvDepG60+88PzvY3tsCMl0KqexHJFfJfgH/gizZ6P4t0298TfEAazotu++ewtrDyml4OF3FiAM4zxyM1+jkfgHw5H4Oj8KNoenT+Gktxaf2VNaxvbNEBjYYiNpHtik1cVz8g/wDgjz4G17VvjnrniW3UroFnpclvc3G3arSOV2ov48keleRroj+B/wDgo5Fa6hLtFr45jZpCf784dT+RFfuv4P8Ah94W+HtjJZeFvDWkeGrOR/Me30ewitI2b+8VjUAn3r8kv20P2C/jXq37QXi7x54O0GfWdOv7pb+2udOu8XEbgAAqMhgVI7enFHKPmP2M7ihulfgNL8a/2sPhPavbah4i8fad5DYLajA9wo5xjzJQ2a6Lw/8A8FKP2ltLjWGXWW1JlGA13pKn89iDNFhJXPqj/gtJ4Be98E+CPFtvbSSNZ3r2U8y/dRXUlM+nzAD8a7//AIJCfE4eKv2e73wvMQLvw7fMgXv5b/MP1z+dfnv8cP27PjN8ZPAF94U8Y/YDo93teRV0to3BRgysrN0IIHNfTf8AwRLaZvEHxLG5ntvs1sQx6Ftxz+NLlKbtofq4vWnUlLVJWICiiimIKKKKACkPNLRQA0LjvTqKKACiiigAooooAKKKKACiiigAoqORAzBicCl81d4XPJoAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfi/8AsmaX4+1b9q7xl4Q0PXbddXmEs02rXMRlghC/eJGM5IOBx1Ir9U/g/wDAPw38Hzf32n26z+INUw2p6tJnzLphz0JOBntXzD+yH+xj48+F37SHi34n+LNSsbO0uxNb2+l6exczhjwzkqAFA5GDnNfdO6ualT5Vqddapd2i9CO6tYbq3khmjWSF1KujjKsD1BFfJ/xw+Hvwc8JeAfiF/YL+G/D3iG80ueG5MU6LNuZTgbBk5J4/Gvq28hS4t5I3GVYc5r8wv2m/+CV/jbx78QtY8W+DfGVndtq0/mvaaiZIWjBwMBlVhgde3etJx5laxNKy1bPcf+CUK6fa/s4z2dhqkWpeRqcgm8oH905AODkV9q14R+xr+zRD+y38G7Lws1xHeavNIbvUrmEko87AAhcgHaAABkV7vVQjyqxFWSnNyQUUUVZiFFFFABRRRQAUUUUAFFFFABVW+naG1lZBukCnYucZbsPzqyaY0CSffUMM5waloaep+QvxYtf22vFPxT1ObTh4m0/SmvnFgtlcrHbpGG+XOD0x6jvX3Z+x14P+OugeHJ7r40eK4tWvZuINOSNXeEeryjGT7Yr6Q2DsMUoGKXKaOd1sHNLSYpapKxkFFFFMBG6Vx/xI+FPhf4taLJo/ijSYdUsJPvRyDn867CjbRZPcabTPA/2dP2K/h7+zD4n8Q634NjvEn1hFhaO6m8xYYw27avHrj8q99pAMUtAgooooAKQ9PSlprruXGcUAAXB60u35s0jLllOelOqWrgI3So5ovMjYA4JGKkoz1o6Aflr/AMFhtJew8N+GLuTMrrc7FbHAXrmvVP8Agjv46j139nW+8OkoJ9G1GQ7QfmKyfNk/jXUf8FRvhrH44/Z31W8MeJdLia8SbjIKENt+hxj8a+ev+CJgLX/xOZZT5SxWeIuwLbiT+mKzWx0TfMk/I/VH+JafTKXdVpmIrdKqLHHJP5wzvXirLNxzXlv7RXx00r9nf4Yar4x1WB7mCzVcQxfedmdUX/x5hVXW44xvoehy65ZQ3y2Ml7bJeMAVt2mUOc+ik5q/X4T6h4v+JX7Yni7xh8SvDeqzaJrvh/y57bS7OWQboi2ARyfm/Svdv2P/APgqF4j8M+LJfCXx4vJnsHXZb6tNbBJraQA5EuANynAHTIJqVJN2G49EfrFz2rzn4j/tIfDL4Q3y2XjHxvo+gXrLv+zXVwPNC+pQZIH1FfJ/7aH/AAUv8L/D34fHTvhVrlp4g8XaooWG8tx5kNkm4b2YcfNt3Y9Dg1+dXw5/Zd+Mf7Wsev8Aj1xNewRs0l1rGrE752AzhAfvfh0pSkCj3P3e+G/xe8G/F/S5NR8GeI7HxFZRsFeayk3BSegI6iuwr8Of+CaPxU8Q/B/9rbTvATX6R6JrlxNY39s6nYZFikMZXng7wo71+4o5FOMrikrC0UlLVkGX4l0aPxBol3YShSs8bR/MMjkYr8Fv2vP2Z/F37MfxWm1+1WSKxmvGu7K7tsjyjuyOR2zX7+Mu4YrkfiR8J/C3xb8Oz6H4r0mHVtPmGCko5HIPDDkcis3F3ujSMklZn5y/BP8A4LGWOj+BdKsPiD4a1LVddhXypLvSUUCZQMK2HbrxzzXokn/BZb4bhWCeCPFW/GRvWAD9Hrvov+CWvwTj1SeY+HFNox+SMXEu4c+pbFaKf8Et/wBn0ahFdSeGLqYL1ga9bym47gAH9aeoe6fI/wAXv+CyXiTxJp0mmfDjwgujXsx8v7bqJ8+Rcn+GNTjOPfvVD9kn9gvxz+0L46t/ir8ZJruHTHnF0IL1iLm/IyUBBHyoG2nB6gYr9HfBP7Ifwc+Hc8U+g/D7R7O4jIZZmhMrgjocuTXrojVVCgYUcADpRZiuuhDZWsNjbxW9vEkFtEgSOOMYVVAwAB6YqzSBcUtUtCQooopiCiiigAooooAKKKKAIbtS9vIobYSpG70r+fL9sr4beIPgv+0pr+ovZyWMU2of2jY3W0lGbO4HP1/nX9CLjK4rzr4tfAfwf8atDm0rxRo9tqFvImzdIgLr6EHrkGp5Xe5rFq1j5r/Zd/4KYfDX4ifDiFPG+tW/hHxRpVqqXsN+21LkquN8ZxznH3euTX5m/tZfF65/bI/aekvvDttcPY3LxaZpNts3O0anBcADoTluegr3Px5/wR++J6eOL+LwnNos3htpz9lmvboq8cZPGRyWx719n/sS/wDBOnQv2XruTxJr95b+KfGbx+XDdeSRFYqR8wiz3P8Aexmm0T8J+eXxq/4Jz/Fr4M3Wk6t4Z0W+1yBoI3M2lbnuILg47Kcg5/TNfq5+xT4g+ImvfAfRV+JugXmheI7MfZv9O4luI1+7Iy9QcY6173tFG0ULQTdz5L/4KA/sYz/tYeCtNk0S8js/FWiuWs1uDiGZGIDox7cZI9wK/MLwd4k/aK/4J/8Aiq7ig0++0yy3kz2t5aGfT7oYKgkgZHXIKsOcZzX747RVTUtHsNZtzb6hZW99A3WK5iWRT+BBFMEz8mdJ/wCC03i9bVVv/h/pM9yBhmjvWhBb2UgnGaqeCfiR+0H/AMFGfiJb6Z9tuvBHw8hmSS8Glq6Qoq8n98AGZjjGM4ya/Tcfs4fCn7c14fhx4We6Y7jK+kQMcn6rXb6PoOmeHbMWmlada6Zar0gs4FiQf8BUAUBdDtH02PR9LsrCJneK1hSBGkYsxCqACSep4q7SYpaCQooooAKKKKACiiigBNo9PeloooAaw4r86f8Ags94Y1PWPhH4N1WysmmtNL1VmurgLnyw8ZVfzYiv0YqrqWl2esWrW19aw3luxyYp0DqcexqZK407HwR/wRruryb9nzxJaXBnEFvrbCBZMgKGjUkKD2zX21o/wx8JaB4mvfEWm+HNLsdevjm61K3tES4nP+24GW/E1t6bpFjotuYLCzgsoSdxjgjCLn1wKuVQNiYpaKKBBSUtFABRRRQAyaFLiMpIiyIeqsMg1R/4R3SyCDptoQev7hOf0rRooA5jXvhj4R8T2clrq/hfR9Tt5OGjurGKQHnPdaPBPwy8JfDeCWHwv4d0zQEmOZP7PtUhMmP7xUDP4109FABRSGvm/wDa8/bU0P8AZJj8P/2tot9q76tIQPs2AsaA/MST39qTdh2ufSNFeKfBP9sH4XfHy1gPhfxLbPqEg/5Bt04iuAcEkbT1wAenpXtK9sHPc5oTuA6iiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkyPWhmwKZuDcVLdgH5ozTWYKcYpN/tS5gH0tMVuRxT6pO4BRRRTARjtGcZpqybmxgj8KfTP4xQA+iiigAooooAKKKRmCjJOBQAtFIrBuhzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIzbVzgn6UALRSdaWgAopu8ZA9eB706gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKi88eaEA696AJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAroiW+TtVB0zntTvMGcAFvcUy6tlu4jE+QrEdPY5p0Maw/ulzgetBQy6KC3Yu2xe5qGyZmZtm3ysAKRVxog4wwB+tKsYUYAAHtQO+lh2AOgpaKKCAooooAKKKKACikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiko3AYB6mgBaKQ0hYgZoAdTGbaCaFct2pex4qboNz5g/4KG+HdR8S/s3+LLfTZyky2ErGMHG5QAW/QGvjH/gibq23xz8StPEbDzNOtZd2PlBV2HP1ya+qP+CmHiu98C/s5+JbnT5c3d/CLb74HlK8iIxA6nKsRXyx/wAET7aRfiB8S5R/qV0y1jJ/2i5J/lWaNnsj9UfF3jTQvAWiyat4j1a00bTYyoe6vJRGgJIUDJ9yB+Nef/8ADWnwc3bf+Fj+Hy390XYJrxn9vr9j3xh+1fH4btfD3iaHRrPTg5uLW6DGKZichiAeSMCvjZv+CL/xJ2nZ400EN2/cOD+eaCbH6Oal+2t8DtKjZrj4k6INvVUlZj+QFcj+0Fomm/tSfAfUp/B2p2ms6Vq1nJFbz5yhcfdwMdcjv7V8SeG/+CLfi7+2LNtd8aaadN8wfaRaI4kKdwpPGa/TX4R/Azwx8E/h3Z+DfDdvJFpFsMfvnLs7E5LE+uae60LjJRZ+P3/BNu9vPhv+1pP4L1m323WoBtNlgkPy+YgYgn1HBP5V7d/wV3+Fvgzwn4S8O67p1nDaeIZ79oWaFFVpcpuO8Y5AXJGMcgV5F/wUi0e7+Av7WOi+JvD0Z0e5ls47uG6tTtaSRJDuYn1I4/GvMviH8VviP/wUJ+L3hbw+liTMoS3hhtwxCjHzzSHkZ2gnPFZxi+a5TkeO/AfV/CWg/GLwtfeObRr7wlBdq2oW8ROXQA4/JtpPsK/oK+DPxs+F3xL8M2tv4H1jTDp4j8uLT4ykTKvTATP8q8C8Rf8ABMn4at8AI/COnaVCviS3t1P9tEDzpZsgsScdOuOK/Kr4kfBT4rfsoeI5Lx49Q0uC3fEGqWjMIwN4ALducgfjVS10IsraHqHivS3+Fv8AwUssS9odPhi8VW80CuPldWlUAjHY5r92l+6K/mw0/wCKXiP4kfHDwf4h8SX0mpahFq1iDMxzkCZCMflX9JsbB41YdGGeaqKaJlK6sOXpS0nfFLWpmFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUmzFOooATbS0hIHJ4ooAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKTdgCquqalBo+mXd/dP5drawvPK/91FUsx/IGrNfPv7fHjCbwT+yF8TNRt5DHPJpZskcHBBndYcg+v7ylzDtcZ+zT+3B8P/2pfFHiHQPCiahBqOjoZ3W9iVVmg3hPMQgnjJHHuK+hq/mm+B9z8U7fxRLd/CmbxDBr1valZZvDssiTCDIZlbYRlMrnaeCRX1l8J/8AgqN8a/gvry6b8SNOuPF2nsMNBqcBtbxMA5Kvt5P1BouPlP2mr5F/4KK/teax+yv4B8Ov4V+xzeKdX1DCQ3YDBbWNC8rFfc7Vz7ml+D//AAVA+B/xTh8u812TwfqSoXa01qMqpwCSFkUFWwAfSvzh/am+Imrft9ftiad4f8GBrrTFk/sjSATkeSuXlnIPABCs3/ARUvVhyn7Bfst/FLVvjV8A/B3jbW7WGy1LWbP7RLDACEHzsoxn6V6tXMfDXwPY/DT4f+HvCumosdlo9jFZxhFwDsUAtj1JyfxrpM0J2FYfXzL+0T/wUH+Ff7N+vXHh/Wrm91fxHbqjS6XpcIeRA2DliSFGBz17V9L5r+fX/goUJI/2zPiUHdm3alGPmOflManb9Paq5h2P3H+Afxs0f9ob4W6X440G3ubTTr9nCQ3ahZFKNgg4JHauF/bS/agX9lH4RweKItMGsaleahFptnZu5VWdlZ2JPskbVwf/AASrhaH9i7wjuJO+5vXH0+0P/hXzd/wW11qSOH4Z6X50ghMlxdtDuOwsMKGI6ZAJGfc1L1Gkey/D/wD4KYw+KP2dNf8AiZd+C7rzdBvYbS+srSTeMPIibwfYPnHtXbQ+IPgh/wAFHvhfPYm7EzBFLQSMI7yyYEPkA+6847Zrxv8A4JW/B3SfF37Hnim11eMXFl4n1CeCdcZICKqgj3BwfqK/P39ob4VeMf2Ifjdquj6Vqt1p8E8cv9n6hbOVaW2cFfzwxU/U0itOhwHxW8HwfCX42a94d8JeIJL2HS71rW21S1lMbNzt4ZSOxwfxr+hP4e+LtC8M/DbwfZav4l0+K9j0mzidry+jEjuIVBJ3NkkkGvxS8Hf8E2PjX8RfBdr4t07TrO5tNRhW8t994vmTb2HP15J/Crmof8E3/wBpK6niN5oc12FIRXm1DzNnYEZPGM1SYmrn7wwzx3MKSwyLLE4yrowKsPUEVJXmH7NHgjWfhp8CfBHhbxDKJta0vTkt7lg5f5hnuevUCvT6pO5AUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUmaG6U2gB1LTOe1JuK9SMVLdhjLhtqk1VaYkYDYPapZGEmQp3cdqoybgqEIX/ANkVDZ0QiralhboH5fMUv7EVIrOGBZvlqpp9qOWeHy2J4yasSFjCFIPB9Km4O2yJ7WYyMcjGOlWqoxbscHaakVnWNt7bvp1q1IyktSySFGScCmrKj/ddW+hqm7453kj+6abHIsaNtGT320+YahdF2SQKhOT/AMBGTUcLZyxlYj+6wxWe1m8rH98yqxyasxrGzEIzE+ueDS5tR8i7l7NLVaOBluN+/wCX+7VmtDEKKKKACkOG4PNLScVLdgEGOgFG4ZxnmkU4zUbMqnJOCelLmGlcmo3CmLIOOaa7nPtRzBZkuaWmqwKinVSdxBRRRTAKKKKACiiigAooooAKKKKACiiigApMihulM3AcZoAczccVHJKFhd3fy41UlmPGB60M+Oc4FfOf/BRLxbrHgf8AY5+IesaDfyaZqUMVpGlzEcMqyXkEbgfVHZfxoKscR+29+194u+BvhfR7z4aaNb+I7e53NPqyqbqC22sMq6pyM9Pqa8A+FX/BZ+JY4bT4i+DpUnLgTXukONsak4JMbc5HpWX/AMEZdQ1LxDq/xK03U7qXUtDjtrdls7w+dGJGckn5sjkCtH/gpzpf7PHg3wPqNloui6OnxPurhBGumAiSHa6mQyBeBlcjn1qWx2R+jnwx+Knhj4weF7bxB4U1WHVNNmUMGjPzx5GQrr1U+xrr6/Kn/gkb8R/APwv8G+LG8SeOdN0nVdVu4/K0u6utu1EU4YA9+TX6h+HfE2k+LdMTUdF1G21SxckLcWsgdCR1GRTRL0NOiiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASk2KDnHNOooAKKKKACiiigAooooAKKKKlsAooopoAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQrKjMuGBycCpNvzE0irj060+gYUUUm4ZxnmgQtFFFABRRRQAUh54paZtO4HPFAChQKdSA5paACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEYFlIBwfWk2/dzyVp1NZsHGKAFNMZgBz0pQxPGKUqMUAfDX/AAUe+Mnxk+E8GgXfw2kkt9OzuvGt7fzXY5GBjHSvnSL/AILNeNdI8Lw2d58PrGXxDGgjae4llRWYdWK+vtX6yX2jWepxxrdQR3AT7vmKGxxjvXEar+zv8NtcuDPf+DNHu5i28ySWik5/Ks1FnRzQaWh+JHiG++P37fXjY3H9m6jq8MjeVFHAjQ2VqOuDnjAA71+p37Af7Grfsm+BdR/ta+XUPFGtskl6Yh+7hCg4jQ9T1yc96+m9B8M6V4XsVs9I062021UYEVrEsa/kBWltp2Zk5XEWloxS00iRKGpaSmI+Of27P2Fb39ra48OXen+IIdFvdLRoBJPD5ilGOSWAwSfoRS/sP/8ABPmz/ZM1bVvEGp+IU8T+Ir6IW6TR2vkxQRg5+UFmO49Cc9K+xdtG2oUWXzDDyK87+NHwV0f41+ENQ8Pa3H51hewNBIoVdwz0ZSRwVOGHuBXo+2kCAc96pRXUnmaeh+aPhP8A4Ix6f4X+I2ma+nxJml0jT7yK7i02XSw8z7HDANMJAvbtHz7da/S5eFA/KlxSbcYwTQkDdw/ip1J70tUIKKKaxIUkdaAHU2SRIly7Kg9WOKFzt5r8WP8AgoL+2N4/1b436j4H0HW7nStD0G8CILNzFJMxx99gfmHNK+tilFtXP2pormvhvqF5qvw/8N3mokG+uNPglnI7uYwT+tdLTEFFFFAgooooAKKKKACiiigAopDQTgUr2AWiqy3JkUsPlAPU1jeM/iB4d+Heiy6x4n1qy0LTI+txfTCNeoHGep5HApcyK5WdBIgkQqehpscZjwN3HpXxV4t/4K5fAvwzrMunW0uua35b7Gu7GzUwdeSGLgkY9BX1P8Kfit4a+Mvgux8UeFNTXVNJuxlJeAynurDsR6UcwrM7KiommCtjPNLu5A9auwWZJRTRmnUhBRRRQAUUUUAFFFFABRRRQAUUUUAFFIelNzQA4nFIGBpPrSbvmwBUSHYeelfJH/BUxZT+xZ422cp5tiHX1H2uHH6jP4V9a5rxf9sL4aSfFj9njxnoEKebM+nyTxR5xukjHmJ+O5BUlI+KP+CJ/hG1Gg/EXxN5YM7XMFgrMvIULvIz9SK+7vjP+zd8OPjpYhPG3hyx1IwxsEu5I1EsIx1WQjK49q/Nf/gjf8UpPDfxR8WfDy+umSDVLUXsFu/AW5iO1xg9yv8A6DX3v+3JpHxF8SfADXNF+GUbSeIb8JGywuY5niDqXWNgRglc555GR3oH1Pxh/bM+Hvw3+GPxiu/C3w01KfWbG0KrLI03nRiQjmNSOuDxxXpP/BNP4v8Ag74B/tCTt4+0z7BJfWjW9rq12u3+zH8tnO4EZG8DYMc/MO1fUv7AP/BNW+8C+ILb4g/Fmxt5dRi/eafoVxiURSEEGSZSCrEAkgdjg9q+c/8AgoJ4c8N3X7dltp/hiVZru6ubJdQRcFEnaRFZMew7Uxn1542/4LI/DbQdQ1Cy0Lwl4g8RNau0a3CiKGCTBxncWJA64+WvLNQ/4LZXu2U2vwwEY/5ZtPqBI/HCV9O3H/BL34C69dx6lqfhu5lvJEUyrb3rwQs2Bk7Ex1Nbf/DtX9nceX/xb2E7Bt5vbgZyMc4fmkLQ4H/gn9+2t4z/AGtPGHjeLX9I03S9I0yKJ7NbIsWDMxBBYnnjBz71+XP7ePiKLxF+1n8Rr63O6P8AtJo8+6jaPyr9yvA3wa+Hn7Lfw810+DdBtvD+nQQS3lxIGZ5JNqk/NIxLHpwM1/Pb4rm1T4r/ABI8Q6lYWc+oXV/d3F8Y4gWby9xOfwpgfvH+wmlh4c/Y2+HErGGytItI8+eU4RR8zM7sfzJJr8kv+CjX7SEf7Q3x+ul0y4S58NaADp+nSxtlZRnLyfi2fyrl/CPxO+P/AMUvB+l/CLw9qOuXWi24McemWURiwhb7kjqASnsTivY/jB/wS/8AFXwj/Zzl+IN1qX27X7QJPf6PbxFjFGzBeD3K7sn6UDPvj/glNCsP7HHhwBVBa8u2O3uTKeT714T/AMFrtLsv+EV+H2ofZ0/tA3U8An2jd5YjJ2k+ma+ev+CW8vxOuv2iPDVppl7raeBIDcNq0Jkf7EqmCQp8h+UEybOler/8FqvFUd54o+HvhmCYyXNvazXcsIP3d7BFJ9zg0Afff7F7Fv2VvhiT1/sS3z/3zXtNee/s7eEZvAXwJ8AeHbj/AI+NN0S0tpP95YlBz75r0ShK5Fxq/ep9FFWlYQUUUUN2EFFFFCdwCiiimAUUUUAFFFFABRRRQAUUUUAFFRSSfNtqRfuigBaKKKACiiigAooooARulMboaezBVyelVZ2MnAbavqKluxUVcd5hjC7uneopbgdhmlaYJtXG/wB6qzSvuzsyvdahs3jHUQF4ZlcFfL74r5L/AOCnnxt8T/A/9neyuvC90dP1HWNSj097yJsPAuxpMr9dmPxr6muI0DcMwZv4M18Rf8FmLbzP2bPDbAZMevxn/wAgyiluaTWqON/4JGfHbxz8UPEnjrR/FXiK916zsrWG5gN45fy3ZiCAT7Cv0pdWXBJ4zX5N/wDBE7P/AAnXxH44+w2//obV+sGoQyyY8tttVy3RhF8z1EkmESluuO1RLf8AmHbtIz7VDtmC7Dhx/s81XmZfLYNzjqB1rG1zpjGJZkkdmwgy2alXcjMC6gN71mWYlFwzBQkX95m5rR+ymZchs1SQNJdRrNIZNq/MD6VJFbzQGPaGPPPFSW2InUH/AL6rR7itFHqYzlyuyGx5wM9afRRWhzBRRRQAjfdqvIrMc7toqwxwpJrnvG3jrw/8PfDd7r3iXVLbSNGs9v2i7um2xpkgDJ9yR+dRIuJpIz/OFfeVIyBSTxyHDYJxX5VfFD9uz43fGr41a74a+AjLe+HbBt0V3YWvm74wPvsx6AnivUPg7+3Z8S/g9fQaT+0p4XvNC026fZbeJGtisZO0nBA69qk05mfoJbylxleedv4+lSySNGhZhgCvLfhZ+1F8JvjNrDaf4O8Z6Zq+pqnmGzjcrJj1AOM160yqy4Zdw9KpK4nIjtp/O5AOOlWMivgP9s7/AIKcWHwI17U/BHgixi1rxTbxpv1B3D28EhYZUgfeOMj6kV8jfB//AIKjfFmy+MGg3vjnXln8IzXYF9Y/ZlRFhfKFgQM4UsG4/u1WxDVz9tc0tUdF1a01/SrLU7CZbiyvIVngmXOHRgCpGfUGr1MgKKKKACiiigAooooAKKKKACiiigBG6VDJgfMxwvrUzdKyPFV9eaX4b1O70+yfUL6C3eSC1jIDSOASACTjrQNGkqL1/nXyZ/wVO1MWP7FfjS2P3r2exgX6i7if/wBkr83vEn7fX7SOl/FLUyms3tjci5kRNFuLMMqAZAXbjn8PSvPP2iP2tvjH8bNKttA8f30lrYxnzxZmDyFkI6EjvzUtl2P0H/4Iv+C00n4K+LfEboom1XVhCr5G7ZEgH4csa8a+KX/BKX4o+N/iz4m1l/FWjLY6lqE1zDqF5OS/lsSwDKOR2FfPn7OPwP8A2lPF2gyr8Nl1/StEk/fsUuzaQyEj7y7iAfwruPiB+yv+2BoOk/bdVfxJqsUnHlWOq/aJB9VVsijcZ1N9/wAEafirbx+bY+JfD9+Qu5BG7puPbk1+gf7Av7PGu/szfBpvC/iS8+16xcXsl5OscnmRQ7gBtVvT5RXp/wCzboeteG/gT4H0zxGLhdct9LhS8W6ffIJNo3Bj3Oa9KxVGbFooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSsAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZ5a7w/en03eu7GRn0oAdRRRQAjMFUknA9aM55HSmXEC3MLRvna3XFLHH5aqoPCjFADutJtA6U6igBkalVwTmn0UUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU3b82aU1GZH8zAUY9c0AP3fMBRIu9SM4pshCrvJAC8kk4Arxnxj+2X8HPAOrTaZrfjvS7W+hGZI1l37fbjvSugPaFXauM5p1cN8Lfjb4K+NGlyah4N1+01y2jO1zbv8yn3HUV3HNMewtFFFAgoppfGT0A71yNx8X/BFnqw0ubxdoseoltotmvo9+fTG6lcZ2FFRxzLNGskbK6MMqynII9Qadu7UAOopoanUxBRRRQAUUUUAFFFFABRRRQA1m2qSegr8B/+ChNjbp+2V4lt9Jtwk811BsUdGkbHX8SK/fW5k8u3kb+6pP6V+GP7VNvb+KP+Ci1nbR8xza9p0cn/AH8jz+lZv4jeHwM/b7wzYx6d4d0q1jB8uC2jjXccnAUCtWobWMR28SjoqAfpU1aGAUUUUAFFFFABRRRQAUUUUAI3Sq97FLMqCOTYmfnGOoqxTAwfPHSpaDqcn8R/HFj8Lfh54g8T3uBaaNZS3bB2wGKqSqZ9zgfjX4bT6h8Zf+CjXxo+xRzz6kskrS+Xu8uy0u23HAbAC5A6E8k4r7C/4LAftCPp+gaV8LdJnkS5vpBcaikZ/wBbHwUQ/wDAsGvoP/gmz+zm3wE/Z/s5dSt44/EXiFhqN4653KrD93Gf91f5mkldXLbsfNvxU/4JP+GfA3wbmm0i/wBW1HxJZ27XN3eQBm80gZ2LEG2nn/Zzjmu8/wCCQvgvxn4N+GXiZNe0680zSri/3WsF9A0T5AwWAYdDW1/wUe+Lnxf+ENrZeJfAHiu30LQ9NQG9tHhR2uCzBcEMpyMt2rxD4O/8Fnr6zaz0/wCIvg+GeHhH1PSJtrAY+8YiPXsKiLuzTVI/VGO1fd5jtuYHI9KkeSRtpRcf71eT+Df2sfhd43+HcvjSy8WWEOjwQtNOLmZY5YsDJBUnOfpX5W/Hb/goF8av2iPiRfaV8KbnWtF8OIGFrp+gQCS8ljVv9czqvmAn0UjArTm7E6vc/a+HKjBfe3c1LX4AeFf2uv2iv2dfFFrc65rniQxM5eTTvEaswnGCMEygsOueD2r9lv2S/wBoi0/aY+EOneLYIltrosYLu3U58uVeoo5u5Lj1PaaKT0pae5AUUUUwCiiigAoprZ2nBwagDPDCS53Ee9Juw7Fmiq0Fx5iqW4Zh0qNdTtZGKLdwu+cbVkBP5ZoWoWLh6VFJIItuecnFOzlev5Uzy89TuIOQT2qZXGiNRO0jBtoj7etebfGP9pX4b/s+rZJ448SwaNNeKWt4HVpJJFBwWAUE4z3r04puKkkgj0PFfDX7bX/BPHXv2pvHdt4msPGEGnPb2wt47S7gLoBnPBB4HWoKJvil/wAFcPg74O01z4Y+3eMdRxlIYYzBFnI6uw9M9u1c18BP+Ctfhf4q+KpdG8ZaFZ+C9OkBAv7q/wB0QXB+/le/T8a8Gl/4Is+PVjLJ440R2HRfsz1bs/8Agir4wmUNdePtJic9dlo7VSVw0PFP2vNF0P4N/H6b4i/Bzx1oj6feXIu7NND1E/aLOQ8uu1eik5796+yP2cf+Cu3g7XNNt9I+LFrL4U1O3iCtq0aSXNvPgfeKopcE47A9a8xj/wCCKPiPd8/xK04A9cacx/8AZq3tN/4IlxlV+3/FKZCDnFtpYwPoC9Ow9GfUs3/BTT9m37PIV+JcO8KcD+yb4nOP+uI/mK/Ob4V+MPgR4f8A2un+KHiz4nzeJLD7ZPqMME+g3LhpXVwodpN33dwYEg4KjGOK+nNL/wCCJ/gaNl/tL4jeIrtf4vs1tDCfwzux+RrWj/4Ir/CdSd3jTxi2eT++tR/7Ro5RaI9Puv8Agql+zzZkBfFF5P8A9ctOmP8A7LUS/wDBVz9n1v8AmYL8fXTpf8K8+j/4Iw/CVWBbxh4yYf8AXzbj/wBo1I//AARn+EmMx+K/Fwft5lzAw/ECIfzp2YvdPSpv+Ch37NvxK8P6ho+peNIYLC9haCeK9gli3IRg8leK4X9n/wAX/sX/AAGF9e+EvFvh8XszEvf6nMsk8YbgojOMqpB6DrXw9+3F/wAE99T/AGa5otc8KPeeIfBlx8rzbN0tpJxxJtHQ5614P+zX8D4P2gPiRb+DpfEmn+GLq5jY20+oqxSWQfwDHeizHp0P3j8G/tBfA3UpDceG/GPhFZrjhms7iCN3784wT+Ndkfid4E1uFrRvEuh3sU42NC91E6uD2IJwRX5R6h/wRd+Jlrbs1n4s8M3smSAmZkyM8HJWvP8AUf8Agkz8ftH1BY7XTtNvkJyJrXUURR75JyKXKI/WH4+eCZdS+B/iPRfhlqumeCvEU0cclleaeYbZVZZFYgkYABUMMn1r8tvhb+yL8QPi9+0Fot18U/Gmk3Nta3Mcl5dXWtw3M00aNuESLu6EgDHuarax/wAE5f2pf7PaN47m6hChTCPEHmAj027uR7VxVv8A8E2v2iLXWLXHg6aGXzV23kdyuIjn7xIOeKOUObSx++NvEkEEUcf+rRQq49AOKlrnfhzo9/4d8BeHtL1Wb7RqVnYQwXMuc75FQBjnvyK6KqSsQFFIelMbOOOtMAGefmzTz1Fcz438Waf8P/COq69fuy2thbvcy4POFGcficCviD9m7/gqVH8cfjxpvgC78Ix6TZapNLHYX0U7M2UR3y4PqEP51EiuU/QamR/dpF+Yj0zkVJTjsIa+SpA602GEQRhF6U8nAzSBsnFUIdRRRQAUUUUAFFFFABUUn1x70STbWC45pu8+1BSVx/DKo3U7cAQKprMk0zqhwR1NWU4GM5oBxsS1ArFrg7T8q8NU9FBIUUUUAFFFFACNjacjIqnKSzcABatthlqncxkKcHBqWjSG5A0/7yJAecnPtxUMyv5gIOR7VEpAncH7x6GpbyQwRfIetYOR1ddCs0SNdRMfmKnOAea+O/8Agr7qlpYfsrwQT2/nT3WsQQwSf8822OxP5Lj8a+v4Waa5Qxjac4Oa+Kf+Cyl/Hafs3+H7d1DST69Ht9RiJyT+tVF3FUeqOM/4IqeDBb+BvHfimSJxJeXsdnHIVIBREyQD35av0fv2mM6KnCd6+MP+CQtukH7KCMhBaTVrlmx9RX2rcMzMVAOcdcVr0MIaMqrDJB8wbd6gUKsfKsuWb2plwXghZy+3HcnFJGxkj4yz9iKwubrXVsf9lVWDZwvpVGbXobW9W08xBI3AUsM9PSpLxpFtZWLMAoySozisYyQ3sHnDD3HG0lfm60uZ3skaqN0dPZ5EIB+dmPbnFaY6CsOxkkiAJOOK2o38xAa6I7HHV+IfRRRVGIUUUUANkYLGxY4UDJNfmF/wWY+Nf9n6D4V+G2nXjLNeMdR1CONvvRjiNWH1ya/T2T7pB6V+Inx6jk/ai/4KTf8ACNSSf6EusppSA84igBeTj6I351Ei4n6M/wDBPP8AZ/034J/s9eHrj7HGviDW7ZL6+umQCQ7xuVM9cAEcVyX/AAUi/Zl8UfHj4Y3mo6V4oa20/wAP20upNokkQKTNHGSSG65wDX2Jpenw6TptrZWyLHb28SxRqo4CqMACsb4lQ/aPhz4qi2eZ5mlXS7fXMLDFCVwufzh/CHw7471bxHcX3w9tr99a0eJr5pdNz5sSDhunbBP4Zr6Wm/4KrfGQ/DW48Ju9ompSRfZl1kLi5QAjJ+uARn3rzv8AZc/alb9l29+IDLoialc65ZyWMDt1hbJHPtg1618O/wDgl346+LXwWf4iJqMNlrmpxtfWejSx4MqMcgZ7EjJH4VRR7T+w3/wTht/FFppvxO+Kb/2tLqDC9tdPZxIH3AndKcnIPXH0rif+Cwfwf8PeA/EXw91Hw/pFrotpd2dzbvHaRBFdoyG7ezD86zv2Rf29PEn7Id1J8Lvito14dB06R1XKZu7E5Py4J+Zc46HjNdD/AMFTPjx8Pf2gvhf8O9V8D+IrPWZLW8u/OhUlZoVeOPAZSP8AZP5UC1ufod+x34mfxd+zH8N9Tc5eTRrdG+qIF/pXstfPn7AtmdP/AGR/htCTu/4lqsD7Ekj+dfQdMh7hRRRQIKKKKACiik6UALRSUtABRRRQA1mA6nFNYB1xnj2ptxF5iEHpSIUhQjcAF65PSgZzmofC/wAI6triazeeGtLudVQYW8ktUMv/AH1ivyj/AOCsraZqX7THw+8M2WnWsBS2t0n8qMIXMs3AOPYiv17t9QtbosIbmGYqcERyBsflX47/APBWLwvrfgv9qHQfiBLbLPok8FqbVhKpLSQkFlK5yOnek0VE/XLwHoFv4X8F6LpVrClvDaWkUSxxgYGFA7VvV8qfs8/8FD/hH8XvCtqbzxBa+Ftat4VW5sNUfydrAY+Rjww47Vh+FP8AgpN4N8aftQ23wr0mzNzpdyXgh19ZB5TzKhcjHZcKeaNhan2QvWnVz8njzw3b6pFp0mvaal/L9y3a6Te30Ga3+vIpki0UUUAFFFFACUm4Chjha8X/AGtP2irf9mL4Q33jObTv7WmjkSC2s920SyMejN2AGTn2FS2NI9oVt3bFOr5I/YX/AG6k/a5/t6wvtCTQda0oJMY4Zd8ckT5wQTzkY5r63poGFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtgFFFFNAFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmeWpYNj5hT6KACiiigAooooAKKKKACiiigAooooAYilc5OafRRQAUUUUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAhpjHbT6ztYd47WR0ODt4NTJ2RcVzOx8mf8FHf2jrj4MfBG5g0eeS21zWM2lu68FBkb2/75DD8a+FP2H/APgnrfftIWZ8beNpZoPClxI3l4cie665YN2Gau/8FWvGX9vfFHw/4dtb2S6e3iBe1/hV2OB+dfrP8DfB1p4B+EPhLQbKEQwWenQptAx82wEn8zWUU5K5tO0Hofnd8SP2Y/H/AOxT8WvD2t/AG31PVtL1DAu9PncyoxB5Vh6YzX6MaR46uNL+GEPifxjbLoc8Fl9qv4ByISBkgV2LRK2CQCR046Vx/wAW7GPVvh34j057f7SLrT54xGVyCShA/Wny2Iv7RpHgPw1/4KZfBf4leMm8OwatcaTOWKRXOpR+VDKRngN26d6+prHUrXVLOO7tLmK5tZF3JNE4ZWHqCK/mg034e6pr3xQ/4RC0jEOpyXr26Cb5NpyT17dK9g8TfHb47fs3wal8OrjxXe2Vm0XlhFfd8mR9xuorSPYTikffH/BQj/gohb/DOyvfAPw8vYrrxLIhivdRjbctmpxkLjgt1H41+V8Pgb4ieKI5PEcOg6/qAkYznUYreVgxzktuH9K90/YH/Zks/wBqn4vS3HifVsaZp0guruCSQGe8bJO3nsTjNfudp/g7SfDvhcaNpWm21rYw25hit44wFA24AqWw0R+Nf7E/7e3xO8J/FTwf4G8Qa0+r+F9Qvo9Okhvo8y2+47FCt1HzFa/bFfujnNfzwJpdx4R/bX0+G5tmjlh8YQSLCoyCPtSkV/Q9A3mQo/QsAaqJMth69adTVp1UQFFFFABRSGm7/SgB9FRRu5zvUL6c0/dQA6im7vXijf8AMAAT70ARX3/HrIMbtw24HvxX56+G/wDgnTrvij9qi7+KvirVoYNOt9VW+tbKEHfJs+5k88ZAz64r9D2UOuDyKFQLUta3NYz5Y2EjG0Aegp9Qnd5q4XC5qaqMgooooAKKaW+YCnUAFFFFABRRRQAUxyAjk8DHNONY3jPVl0HwlrOoswQWtpLLuY4AIU4/Wk2HU/C74u6rqH7QX7f9vptz/plvL4kg01UYYxbpMCy5HP3VbnrX7x2FpHYWMFtCoSKGNY1UdgBgCvw4/YA0ofE79vaz1i7/AHv2W7vNUOOhbDKDx/v1+51TG5pM+VP+Ck3w1bx5+y/4puLSMHUdNiW5jbcQdqupbp7A1+cX/BNv9nHwP+0VrfjbTvG1p59nbWSurK5R4jnJdXByOQO/av2o+IPhW28beCNc0G7jMtvqNnLbOinBO5SOtfzk+IpfEnwd+IfizwvoWp32mTGeTT51tJP3k0Yf5U+XnOQOnNLlsVHVFv8AaE8I6N8M/ihrvg/wX4hudf8ADtvOyxPu+83cEL1xX1T/AMEwf2n/AIefALxBqfh7xrYJouoawy7PEdyn3AAcRMTyq/Tqa96/4Jy/8E/rLRdDtviZ8S9Ie48Q3h87T9MvOUgjOcSOp5LNnoSa7j9sz/gmb4f+NjXvirwa8eg+KRHk2qLi3uCMcbc4XjPQCq5RaM6z/gol8P8Awx8W/wBlPxL4q0+LT9S1HT7SO7sNQjVHYr5secP1xtzXg/8AwRT8aJJ4d8eeFZZH8+G5jvY4z0CsuDj8RX55ePm+KvwTkv8AwPr+o6vp1l80MljJKzW8i9Plzxj6V9if8EWbhv8AhbnjZAcI2lx5H0filyg9rH7C9xS00dadVJWMgooopgFFIajZm7HFJuw7EjdKgaNZupOPSnru3DJyKk2j0qfiHscZ8VV1k+A9YtfDoCarPaSxW8h6IxUgGvxA8efsiftJeHfEcwl07X9VkuWMouLK8kKkkk5OG4r98toxjHFG0elLlY+Y/BPSvh7+154Ftz/ZVv43sEXkLb3UjH8BmqXijxT+13rVq2ja/qHxFubecbGtZjNsfHOCRx2r9+cD0pjW8Uhy0SMfdQadmHMfFH/BLn4N+Pvhr8L9X1Lx5PqMNzq9wJLbTL6VmMEYHXaTwSa+2qAAvAGBS1SRLYhrxb4mfthfCX4QeNLbwr4q8WW+na1MVBh2swi3dC5Awtezy7vLOzG7tmvzl/bj/wCCZ2o/FjVNV8feBdTlu/Fd03mXWm383yTjj5Y2P3SP6UxpX3P0O0fWbDxBptvqGmXkN/Y3C74ri2kDo6+oI61d/OvwX+Ef7Unx4/Yh1xfDOo299Fo1vN+80HW4maFlGdwhY/d9cqa/W/8AZh/bI8BftQaBHNoN8tnrsaD7Vo10wWaJu5A/iX3FA3Gx7zSU5ulfO/7dX7REn7OHwB1nXtLv7ez8VXJS20hbhPMDSlgWO3uAm78SKCCL9q79uDwL+yrp0cWqO2s+JLhSbfR7N13/AFkP8A/DmvzV8c/8FI/2ivjc+oWfg2yl0TSbomOOPQrB5bhVzniYAkHHcYrL/ZV/ZH8f/tvfEqXx147ur7/hFZrnztQ1S7djLeDk+XCW6jOPYCv2d+Gvwr8LfCHwzbaF4T0a10ewhQLtt4lVpMfxOQMsfc0F6I+R/wDgmb8M/iPo/wANvFGofFtNYmbVrkPbweIruSdni2/MzJITgGvjI6f4Z8a/8FSNKtfAVpBbaGmvRts02IRQr5KEybQoAAJU59c17r+37/wUm13wT4m8RfDDwFZSaZfWhNpfa1OoLAkfN5S9uM8mvzo+C/x98UfAn4gN4x8OSWsmslXUyX8IlBLDlhnoeTyPWgZ/Smvan18df8E+f22NY/aw03XbPxBo0Gnatoyx7ri0JMU+4HJwehyP1r7FoICiiigQUUUUANY4XJqJkC72BwSKmbpUEkwDYPIoGrnzZ/wUW8VT+Df2R/G19aDFzPHFaq3p5jhSfyzX4yfsWalLp37VnwynjJMo1mKMY/usGVv0Y1+t/wDwVc1a30z9j3XoJpAj3l7bQRL/AHm3Fv5Ka/If9i+Ty/2qvhkx/wCgzF/Wk0VeyP6PV606iihKxIUUh6VFv2yBfWmImopnnLvC55NPoAKKKKACiimS7tp29e1AEN0rctnis/59rhPvdqsTXLop3CoGZpCxT72KzluddNWQWgbdh+tX0bbKVqiu9UyRl6uw3BlyNuCKqOwqnkWqKqfanWZUI4NWPMHfiqOUfRTdwI4NJQA+mthlIzSV8Yf8FNvjd8Rfg18M9Fk8AfarSTUblobnULOMvLBjBGMA4z0z71LdhpXPtBVCjFMkjV+vSvwa8M/GD9rnx9MBpGs+Ob4ydFEToG+hKgfrXR3Hgf8AbW8URtbSW3juYTfKUa6VFP8A48KVy1HzP26bT4WbPSq9wNPt1JnuoY17+ZIo/nX4lWP7Dv7WutTK91Z6xGW5JvNaZMfXa5raj/4Jr/tN6mQbi4gjz1E2uSkVKSHd9z9gNW+IHgvwqvm6r4p0TS0X+K81CGIen8TCvzz/AOCu3xg8D+NvhL4T0vw74u0nXdRi1UzmLSb6K4KLsIyxRjjrXkcf/BIf43a+Y/7X8S6FGrfeMt7POUH0I5rq9I/4In6/JtOqfEGyiH8S2tmT+RJqrJ7A31bNT/gmf+2F8Mfgn8EdR0Dx54wj0a7XUXmhhlt5pPlYDkFFPpX1jP8A8FOv2b7fP/FwlkI7Jpl2f/aVfO+n/wDBFHwqtqBd+P8AU2uMffht0AH51ftf+CK/gqORTN8QvEDx9xHFEpP44NUK6Pa5v+CpX7OMcZK+NZ5mHRE0q5yfzQD9azX/AOCsX7O0bEf8JDqpx3XSZT/SvPY/+CMfwyVfn8a+LGPqJYB/7Tpkv/BGH4ZyAgeOPFi/70kBH/ouotYND2Hwt/wUo/Z38dXQtIvHkOjv1J1qzltY29t7DaPzrutP/am+BV/cRw2nxb8GtIx2pH/btuufbBevkTWP+CJfhCaKQ6Z8Stctp8fJ9qsoplB98FSfzry7xV/wRW8ZaXvfQPiN4fu4/XVreW1xz3ZA+PwpaFqTWzP1b0TxN4c8SWyz6TrmnanBjIls7qOVT+Kk1tw3dszCOOeN27Krgmvw+1//AIJL/G/RfNlsn8La9EqFjJZ6rtBwO3mBDT/+CadhH4G/bTtdJ8V6rHol/Z211BHazTqY5bnKqIlYvgsRuIAyTitEQ9ep+4tLTV606mZhRRRQBDd3C2lrNO/3I0Lt9AM1+NX7BdtB8UP+Ci/iLxJcoM28mo6nCD/eL+Xn8nNfsN4qvrfTfDGr3l3KsFrb2c0ssrnCoioSzE+gANfkd/wSc0OTWP2sPG2u22ZrGzsLhXkj5VTLONmT7hDj6Umi1sfsHj2qG+s01CyuLWQfu5o2jb6EYP8AOrNFCViT8mJ/+CQfim++O0txNrVkvgSa+a6e4X/XiMsW2BfXoPoa/VfQ9Gt/D+jWOmWibLWzhSCNR2VQAP5VoUUwvc8D/aO/Yr+G37S1m7+ItKFrrQQrFq1nhJlPv/e/GvzWvv8Agj38VYfiA2l2eo6a/hhnO3VnmO5Yz/sY+92r9paKAuzjPg78Obf4SfDLw54QtZfPh0mzjtvNxjeVHJ/E12dFFAgooooAKTcKSRgqknpUDXAAzjigpJsn3Comd/MwB8nrUSXSTEMrDYDgkHinZM33QducHII/nUt9h8vcsKRtFLkVEo2dTT6adyWOyKRm4rzX9ob4oaz8G/hTrXi7RPDMniy602MSnTopfLZl3AE5wTxnPAPSvzmk/wCC2XiFXIPwpsU+Yja2stuGPUeTxTCx+sLbmUjFebftEfDvX/ij8HfEvhrwvrj+Hddv4QLe/jJG1gwbbkcjIGM+9fnK3/BbLxEVO34W6cG7Z1lv/jVLZ/8ABa/xD9qi+1fDHT/s+75/J1Vi+PbMfWgdmeNL+xh+1z4L1qa00608RJJK5Et3Ya3mKUZ4O4PgfjU3iD/gnf8AtY/EL7K3iK0l1Yxg+T/aevxyGP8A76c4r9bv2bfj9pv7SPwzs/GGmabeaTFMxje1vUwyuOuD3HvXceMvHHh/4e6HLrPiXWLPQ9KhID3d9KI41JOAMmgd2fiH/wAOmf2iW5bw/pKn1OswHP60W3/BLH9o3SbpJ7bRbGC4jO5JLfV4w4PsQa/bLwb8TPCnxEs/tfhnxFp2uW+ceZY3CyD9DXTUC5mfhPD+wR+0rpPj7RLzU9D1CWVr2ENqUF753krvGWLA8cZr9y9BtH07RdPtJpWmmhgSN3Y5LEKASau9aFj2gAYGDQJu4+iiigQU0uB3pT06ZqrMx7rgVLdioq42ScyTBFPtXw7/AMFhrwW37L9jGRnztahT6fI5/pX27bBBNuJ5zXwV/wAFnLgp+z54bhB/1mtKxH0jb/GhalyXK7I+X/8AgjbHfN+0ZrZgkxZLozG4XJ5O8bP61+09fjn/AMEWYSfjL4ykGNq6UgPry9fsWTiqM2LRVe61C30+3e4upo7W3QZeWZwir9STgVX0bxDpfiK3afStRtdShVtrSWkyyqD6EqTzQI0KKKKACiiigAooooAKKKTNAC0UUUAFFFFACVjeLvGWieA9Dn1nxDqdvpGlwY8y6un2IuegzWy3Svib/grlpd1f/snyXEFw0MVpq9vLOgPEiFXGD+JFAz7A8JeNND8eaPFqvh7VLXWNOl+5c2kgdD+Irar8pf8Agi78RNWm1rxp4Oa4eXQ4YUvYI5Dny3JwcfWv1aoB6BRRRQIKKKKACiiigAooooAKKKKACiiipbAa+dpwcGoVWcTAHBj7nNTkbuDS0LXcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaACigniotr+Zu3/L/dxQBNRTd1LuoAWikzS0AFJu+bFLTSvzA0AOooooAKKKKACiiigAooooAQ0yaZYY2kd1RFGWZjgAepNOdwi5bgV8af8FDv2xtM+BHw/uvDOms1x4t1qCSCBFGVhBGCzfgTxS5knYqMbs958J/tPfDLxx46n8H6H4u0/UvEMLMrWcEm4kr94A98V6mOa/Pn/glz+yQPAfhNvid4psYm8TazmSx86I+ZawtyTncclvoOK/QYcDFMcklsLRRRQQFFFFABRRRQAUitnNLSBdtABVLVpI49PuGk4RY2JP4VdrL8SeX/AGJfCVxHH5LbnboBjrUT+EqO6PwV+MGpXXxU/bgs7KOPz2bXre1Vc53osyk/oDX762EP2ext4sY2RquPoMV+Fn7NelDxt/wUS064tCs8Ftrc917Mqbh/XP4V+7Sqcc0U9I2LqPUcagvIfOt3UDOR09fapzzRim0Zp2dz8Kf24Pgr4+8F/tIav4l0Pw1qFnb3E3n2t1p0LOA3qMV5d4U+APxq/aS8ZW8DaLrWoXEp8ptR1OB444uM/MzDpxX9Dt1pdreMhngjmKHKl0Bx9KmgtYbUEQxJED12KB/Kkk7lykpH4t3n/BMn4+fCax/tzwfqu7VFTc8enXJilz0wpH1NeTeNvHP7U/wySWy8R6141sokGH8yeR48fWv6AdtZ+reHdM163eDUbC3vYXGGSeMMCPxFFmLmP53f2Zb3WfEn7UfgW/u7e48Qan/a8c0qTKzMSCSS306/hX9F1uxaBCRtJAJX0rifDHwM8B+DdXbVNG8LabYaix3faYoFDg+xxxXdBcYqlsDd1YFpaSimQLRXgH7X37X2i/skeC7XWdR0a41++vXMdpYQzCBZGGM7pCrbRjP8Jr41j/4LjWrSL5nwbmWL+Jl8TKzD6D7KM/nU8yK5WfqPJnadvX3pq7tvzYz7V+Y8H/BcDQ5J0WX4S6jHET8zx62jsPophGfzFdjpX/BZn4bXdv5l54M8TWj/ANyJI5f13CndDUWfoM33hxzTZmdYyUALds18RaN/wV7+B9/t/tCLxHo7d/tOnbgPxRmrSuv+Ctn7P0MbNFqusXLjpHHpcuW+mQBRdBytH2eOcZA96dj8K+Epv+Cw3wZjkYR6V4nkQfx/YVA/V6jj/wCCxnwZaRRJpniOKPu5s1OPyai6Fys+8qK+HZf+CwHwKRRsbXJGI+6NPYVSuP8AgsX8Fo42MNh4huZP4Y1tAC34k0roOVn3fRX5v+I/+C0vg21glbRvAWt3rqPlNzJHGuffBJrze+/4LceIo5WNt8L9LMJ+75upybvxwlULY/WiivyLk/4LaeMp12xfDPRYSf8Alo2oSsF/8dqOT/gtF46ZPk8CaEp/vfapCP5Urglc/XfaM5pa/Hab/gst8TpGzD4R0BE/3pD+tMX/AILKfFIuMeE/DrDuuZeaB2P2Mor8aH/4LGfF681KGG18OeHkaRwiwBJGLEnAHJzX63fC/XNZ8TfD/QdV8QWcOn6xeWkc9zbQElI2ZQcDPNCdwasdTRRRTJEb7teG/twas+i/sp/Ee5iuDayjTCqyr1BLqK9yr5r/AOCilvLefsifEC3hRnkezGNvtIhP6A1Eioq7sfC//BF/w3HqHxS8Za88Yd7LTktklJ5BkfLfngV+vtfkf/wRV1byvHXjzTlO1JbSGbb9CRX64VS2HIRuleZaB+zn8O9B8Zah4qh8I6QfEF3cm6bUGtVaVXIxkE9DyelenUmKZNxPYcCl7UbRRigR5B8fP2X/AAR+0R4fm07xLpsbSlCsV3Gu2WNuuQQQT+Neb/sf/sG6D+yXrOu6tY65c63e6moiDTRhBFGDnHB5NfU+0UbRQPmfURetOpMUtAgooooARvumq8uIo2Z3IHrUs5xEeC3sPrXkH7VnxisvgV8EfEfiu5mX7Ta25+yW7MAZpSQAo9eufwqJFIyv2hv2xvh9+zbp8beJdQNzqUv+r06xIaZvw7V8w3X/AAWi8BrMy2ngPXriJf8Alo08S/p1r4M+Dvwh+IP7e3xsnmuZLiW2mm87UdTmyYrWEn7qn17Yr9LbH/gkf8EYfD8FjcxatPeIQz3y3ZVyccgYHApXsNpdzqPgb/wUw+EHxmuoLCXUH8LatNJ5cdpqpC7m/wB7pX1hb3EV1Ck0MiyxSDckiEFWB7g1+P37YH/BLuT4Y2LeIPhpLdXel28bTXEF1IXkQAZJDV65/wAEjf2mdW8YWGrfC/xHez393pUf2mxmuZCzLCDgxjPYGq5rhy6XP0poooqiAoopGoAKNteNftGftXeAf2YdFt77xhfTfabo4ttOsYxJcTY6kKSAB7k18afEX/gtV4Zs9OuI/BfgbUb3UCuIZ9YlWKJT6lEyT+YoK5WfaH7TXw8+F/iz4aazefE6ysP7GtLV2e/uUXzIBjrGxGQ2emO9flX/AMExtFh1L9tq6uPDH2iXw3ZW13LHJcHLeRuCx7/9rnj8a8Q/aH/bQ+KH7TH7rxNrZi0VW3DR9LDxWq+hdc4Y+5zX2P8A8ES4LZ9b+JUpt1NzHb2oWYqMhSWyAe2aB3srH6uN0r8Sf+CsPx6b4mfHNfB9jNnSPCyeS2G+SSc8sfT2r9tJpBDC8jfdUFj+Ffgx8N/C+ifHD/goiNH8SW/23QtV8S3Rns3YqJVUOwU4PTKik2Ee56p8M/8Agrb4g+F/wz0HwrpPwx0+SPTLVYBcm6dEbA+9sVO/1r6b/Y//AOCo2n/HrxxF4P8AGei2nhXWb1gmnyW1w0kVw+CdnI4OB619Xa74C+Ffw38E3D6l4c8N6N4cs4f3oms4Y4goHQ5HOfQ9a/FX4E+H4vi5+3ppU3grSDbeH/8AhI2v44rGLEVtbo5bdwMKvA46c0Jj0Z+ufxS/YP8Agz8ZfHFz4s8U+GHvNZuQBPJDdyQrKQMZZUIyfeuWb/gmD+zqykDwOyZ4yuo3Gf8A0OvqoU6mRdnA/B/4F+B/gToH9jeCdAttFtGO6RoxullPq7n5m/E139JS0CCiiigApKR2CqSeBVR7otjCnDcA0m7FJXJLmbCnFU4ZPNlVT3NSX2ntfW5TzCjMOoqDT7CeFgr8Kvf1pcxvDlUXd6nw5/wWUvEh/Zp0i3ON82txED6I3+NfmF+xDp51T9rL4Y246tq6N/3yrN/SvvX/AILXM6eH/h7Erts82Y7NxweBzivkL/gmh4bk1z9snwIw6afJNet9FiZf/Z6d7mLR/QBSHim0HmmQI0mFPFZ63n+lmE/6/r+FTyptO70qrHIbi7Yr95RxQbRjpcuHH8X3qsp90V83/G/9u74U/s++MLTwt4pvbqXWJsefDp1t5ot1PRn5FfQXh/WLPxFodhqensXsbyFZoWK7cowyOO1BnI0KKKKCQqGdioJHWpqhmXzPlPQ0DW5nzxyS5NV4GeO4YHpV2QMsxEhyvbkj+VeJ/GT9sj4RfAvXk0Dxp4pXTNWKCVreGKWUqp6E7ATUSOlSsrHs0037s0W8pyOxr5f/AOHln7N67X/4T3cPT+zron/0Guv8K/t0fAPxcAbD4j6QjngR3sxgb/vl8GknYOdWtY99TaxBZtzUy5xdJtU8g1zWm/FjwNqluk9n4q0WeJuVeO9jIP61qWPjXw5qd0lvZ65pt1cOcJFDdRs5PsAc1adzG/kadrG0bMD0qVYtrbtxNSjrTqZLYyqeoaTZazAsN7aw3kIbcI5kDLkexq/RSauK5Bb2sNqoSGFIUHAWNQoH5VNn2paKXKIo65rNr4f0e91O+k8mztImmlkPZVGTX5x+IP8Ags54e03xBqVpY+BbrUNOt5WiiuvtSoXwcZII6V+kd9Zw6hZz2tzEs1vMhjkjcZDKRgg/hX5Zf8FKv2L/AIUfCH4T3XjjwzpzaJrVxfIghWZjFIWySAp6etHKVE05P+C2Omo2F+HE5HvfD/4moz/wW0sB/wA02mI/7CA/+Jr5E/4Jz/B3SvjN+0rpGja/o8et+H4rSa5vreeMtEVUAKG9Mk8fSv2CX9gv4Ap0+F+g/wDgMKaGz4P8Vf8ABa7xHcW8ieH/AIf6dZOw+We8unl28+gxXmur/wDBXz45apE8diug6V5nCzQad5rrz2DkqfxFfrx4N+APw5+H6Rr4f8GaNphjOVaGzTcPxxmuzXRdPX7thbD6Qr/hTFc/Fmw/bo/bI8XWofSI9e1CGT7smm+DUkz9CkJ/Srtr8dv29fFMgs7XSfHMLzfKsjeFvsoHf77wgL9Sa/aJbeKNdqxIq+iqBTwNvAAApWDmPxouvhL+378SUji1G68XQwyHB3+ILexUe5CupH5VG3/BMf8Aai8WWcz6/wCILGVpB80GqeI57hz7fLlT+Jr9nKKXKHMfh/q3/BJ39oWx0u4aCz0XUiq5Fvb6vh5PYByq5+pq3+zP/wAE1/jJH8cvCc3jXwvc+GfD2nXaX13frdwscIdwVWjY8kgDHoTX7a0U7BzEcMYiREGcKMDNSUUUyQooooA82/aTkeP9n/4itG/lv/YN4A2cdYWFfm5/wRFYf8Jv8VgTuf8As+xJP/bSWv0B/bS1KbSf2VfiZdQZ81dIkUY9GIU/oTX5/f8ABEm3ePx18UpAh8htOs0EnYsJJDj8jS6lr4WfrZRSdzS0yAooooAKKKKACiiigAooooAjuOYWqqjDYx6hRzVyRdyEHisa6uoNItLy8vJBFZ26NJLI5woVRknP4VnJGkXoeC/tiftcaH+yj4IXUJohqXiG+G3TdK5VWPd39AOa/KLxZ+0N+03+1Pq01zpMnjC702Rz9nsfDNpP9nTn7uYhycfWtj4xeJtU/b7/AGzodJ0oyrpTXX2G2IyyQ28ZO6UjgDIH6iv2q+Ffw30b4T+A9I8M6FaR2ljYwLGBGoXewHLH3JpxiNs/ELS/gf8Atjabbvq8OkfEq2S3XzN0dzMJh2+WIuHY+wFd18C/2/vjZ+zb44sdC+KiaxqGhzzp9rt/E0Esd7BETguhcBuM5xznFfthXwj/AMFZ/gTp/jb4EyeOLXT7Ua34fmjee8IxK1sx2lc98EiqsTc+1PCfijSPiF4V0/XNInj1DR9Tt1mhk2na6MO4I/QiuQv/ANmj4UanJNJc/Dnw1LJMd0kn9mRBmOc5JC5r5p/4JF+NLrxN+zI+n3c7zNo+oyWse8k7U6gD86+4qZOx5Mn7KPwejYFfhv4dB/68Up//AAyr8IfMV/8AhXPh7cpyD9hSvVqKAuzP0fQ9P8PWEdjpdjb6fZxjCQW0axov0AryH9rb9mXT/wBqX4Vy+Frq+bTL2GUXNjeclIpBx8y/xDGa9upGXcMUCPxD1/8A4J0/tK/A3VLi98GPc6haxOWhutA1LZI/v5QIP5itjwj/AMFDf2h/2c9RtdG+Imjy6haxMEeHWrdopyvT5X7mv2dvLqCwt5Li5ljt4I1LNJI21VA6kk1+Wv8AwUu/bR+HPjXwzf8Aw38L2Vp4o1p2WObVlhDC1YMDiKTHJ4xx60i07n3r+zP+0h4a/ac+H0fifw6ZEEb/AGe7t5kKtDMBkrz1HvXrtfEn/BKT4L658KfgLd3uv2kljd69efbIoJDyIdoCnHbNfbdMl7hRRSUCBjtUnGarSyF8gDBxnpU8jLsYscKBkseBXxJ+1r/wU68J/ADUH8P+FrKPxh4mUZk/eYtYOejMpyT7DFJoqJ9m29n+9Dt65xX5xf8ABarUJ4/h74KsgrfZ5Lx5C3bcFxXlWl/8FpPiHHrUJ1LwLoR04uDJFEZll2d9pLdfwqT/AIKLftS/Dn9pn4C+DtR8NamTrkN5uuNLlG2aAFecj0z3qdti9Xqxf+CLNuf+FpeOJOMLp0a/+PGv18Y4U4GfpX5K/wDBFPT5m8aeP7rbmKO2hjZx0ySeK/WvdziqRmz4q/4K367e6D+yZILK6ltvtes2tvP5bYMkRDkqSPcLXk3/AARbvr+48HePbdp9+nwX0exXyWyVycHNb3/BZ/xYlj8FfCvh8FvNvtU+0EY42xqf6mtD/gjj4Ev/AA38BNa129g8mLWtRMluzAgyIqhc8jpmmI/QGiiigAooooASjdQ3SuP+I3xa8H/CPS4tR8X+ILHQLOV/LSS8lCBm9BQB1+6mooUk14L/AMN3fAYuEHxL0TP/AF3p0n7dnwHiUk/ErRDjss4JoHZnve6jdXyd4v8A+CnvwA8JSCP/AISt9Vk7jTrV5QPxAxWz+zf+3p4E/ae8b6j4a8K6fq8U9nB9oNzeQBY3XOPXI/GgLM+mN1LTV606gQjdK+MP+Cs2rWth+yTqFrcZ8y91K2iiIPAYEnJ/Cvs9ulfAv/BZK+jh/Zw0S2YgPPrUZUHvtRs/zoGtzyv/AIIqeBZVj8deLDKohZ47FI9p3HA3E59Oa/U+vkb/AIJf+FNO0H9lPw7fWNp9mm1NmnuGPV2BxmvrmgHuFFFFAgooooAKKKKACiiigAooooAKY8m3tmnHimfeYcVEgHKxYZIxTqKKcdgCiiiqAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCldapaWODPcww5GR5kirx68msO4+KHhC18zzPE2kAx/fH22PK/UbuK8n+P37F/g39pLxLp2qeMNQ1k29knliwsLwwROv+1iuT0j/gm78EPCLi40nQbm1kj+bfPqEsob/eDHmom2tjrpxotpTke9zfGLwRa2Ul3N4q0mO3jXc0jXkeAPzrjl/a8+D01re3EHjvS7qKzBaf7PIZCoHsoJNfm3/wUi8M+DPCz+HfC3hiKO21me5VJWt3IUITjnnP6V9rfslfsW/Df4X/AAz0q7TSbbV9Z1C2WW7vpXMgLEchcjgfhWEJzlo9GVWp0oStFtog8Zf8FQfgP4d025l0/X7zxFfRozJY6fYTb5GH8ILqqj8TXr37NHxwg/aE+Glt4xtdLvdIhu5GC218oDgA+xIx+NF9+y58N7i8a8g8LadZ3hTZ58MC5Hv0616RoGh2nhzSLbTrGGOC2t0CIkaBR+Qrojfqc8uXl0NDBzTqaOtOqzK9xCcc0Ag9KGG4YoVQvApALRRRQAUUUUAFFFFABRRRQBxHxg8aS+A/Auqazb2F1qU9rCzpb2sRkdj2wB1r8yv2Xf2U/FP7WPxv1b4k/Fy01CHw9Z3TPbadqUTIbj5iVXBxhRxX61ModSGGR6GkjjWNcIoUf7IxUuN3cpSsrEOm6fbaTY29lZwrb2tugjiiQYVVAwAKs0m2lqiQooooAKKKKACiiilcAoooougENcP8WvENtpPgrXN4ErLaSZjzj+E13DfdNeSftKXjaX8K9fuI7dZJvskp3+mEJrKo9DSnrI/Jn/gma0F9+23BNJGFLxX0iL1wd1fuDivw6/4JWsNQ/bOsyVztsb+XI7HIP9a/catI7CnqwoooqiAooooAKKKKACiiigAprjcpAOPcU6koA85+M/wL8J/Hfw2dD8YaSmr2Gcqpcxuhz1V1IKn6GvnPUP8AglT+zlp9jdXV5ot5Zwopdp21i5VYwOSTukIr7RZfl461w3xd8CyfELwHq+iSSKq3Vu8Y2kjGRjNZWsaJ30PzV1r4Y/8ABPzw9rR0lvEl3c38bbHeO9ungDZwQWwB+tdXc/Af9gHTY4J7rxFbYlGVVtYust+APFfmP8TPBL+DvidrPhdZPNNpfNbIxALHLYGcAZr9FPB3/BGm38VeCdD1a68e3NlqN5axzzQtah0jLAHAHB/M0XtqO+ti5qHwo/4J8wSFx4p2bedkep3BX9Rn9azr7wb/AME+tAi+1y6vcaiFG4QwXly5b2wOTW+v/BEnTVjbPxKuDLjj/iXLt/8AQq2NF/4Ip+FLe3f+1PHeqXM/8P2WCOJf1DGlcrTueY3Wu/8ABPUfOmk6wWXoIxd8/mapHxb+wA2V/wCEf17Hricf1r2i1/4Iu+BvtaG48X62bbPzIjx7yPY7OPyrfuP+CM/wiGw2+v8AigYHzCW7iOfyiqlqLTufNWseKP2DvsrSWHh3X5LgL8sSeaNx/E1p/sx/BX4A/tZeJ9R0fQPBmqaRDZ/NJcyzM25PY54NfRen/wDBG34NxSIbvVvFE8YOWRL+Nc/+Qq+qvgd+zj4D/Z30A6V4L0gWMbD97cStvml/3mwM/lUuF3cOex43pP8AwTL+Bmj+S0PhnzZ4eVkuJWfJ9SOh/Kty9/4J6fA7VmhbUPBlrctF02lkH4hSK+lNtGPer5URzs8E0H9hX4G+HJUlsvh7pYkQ5VpVaTH4E4rrv+GevhVptpJv8D+H4LdRl2ks4wAPckV32ua5YeG9JudS1O7isbG3QvLPO4VFA7kmvyC/bo/4KBa58btYf4bfC17mHRXn8ia4swfOv3B4VCOdv0o5ewXbPqT4y/tRfsqfBHUm0iTw5pGvagh2y2+j6fHL5ePVsYrxnxR/wUW/Zrt9JnGgfClLu/ZfkWawiiUH3OKq/so/8EmF8QaXb+J/i9e3SC8USjRbWQpIQef3j9QfavtbQ/2BfgNoOmLZQfDzTJlVdvnXCmSU8ddx71VtLBfU+Uf2Of2hvg7+0X8UrTw9P8H9N0jxCFa4ivFiR0BU5B6cGv0vRVjVVUBVUYAHQCvDfg3+xX8JvgL4wuPE3g7w++n6vPG0RkkuGkVVJyQqngV7pSirBKXMwoooqiBK8U/bLU/8M0+P3VA7R6ZKwBGe1e115x+0LaQal8GvFllcxGaC5sJY2UZ7qfSolsXD4kflt/wRh1a2h+OXi20mIW5udJUwLnGdrnd/MV+yNfhV/wAEy7xtA/bS0e1DGHzEu7RkPcHoP0r91apbBLcKKKKZAUUUUAFFFFABRRRQAUUUjdOuKABulfj1/wAFPvi9ffG34/6D8JfDVyZrbT5FgljVvkkuXPf6Cv1h+JHiYeDfAev60W2/YrKacH0KoSP5V/Ofot145+LHxlutT8LLfan4vvL2S/he2G6bcGJDDjsKh7lxP3o/ZF/Z5039m34OaT4atUje/dBPfXSrhpZWGTk+3SvbOPWvxDl8Xft2abD81/45WGMdFiQ4H/fNOh+L37b+h2sstzceM7iIr96a3BK+/C00h8tz9f8A46+ItO8LfB/xhqWpyxx2cOmTl/MIAPyEAc+pIr8q/wDgj/4LuvEn7QnifxakbJpum2ckZZeF3yPlR+Qry7X/AAX+2F+0PYRab4gg8Xazps0nEGoN5cIz3I44r9Sv2Cf2YW/Zl+DMGm6pbW6eKdRf7TqU8I+Yn+FCe+0cUW1uHwqx9L0UUVRmFNanUUAfOH7WH7Evg/8AawjsJNaurnSdUs12RahZhfMCnnHIwfxryPwj/wAEfPgjoluF1mTXPEU3dpr0wg/hGFx+dfdWBRQVzM+V9B/4Jlfs76FG6DwIt/vGC19fTzEfQl8ivZvhD+z/APD74D2NzaeBPC9j4fS6I+0SW6kyzY6B3YliB2BNehUtBJHcR+dbyR5xuUrn6ivwb+MnwI+NHwI/aU1TxV4a8Oa0LuLU5r7S9U0uxacLuJGQoBB4Y8H1r96KSk0UnY/Cpfhr+1T+234qtdK8Tr4judOgdfMn1mD7DZWv+35eFVjj0BNfqt+yX+x74S/ZW8Hx2emxJqXiKdB9u1qaNfOc90U9VTPbNe/0UJWBsRetOpKWmSFFFFABRRSHpQBVab98Yzzu4qlq2oWeg6VeajqNytpY2sbTTTMcBFAyTWjLEdpKhS/vX5F/8FFP2s/Ffj/4qXnwW8JStaaRBdR2VxJbsRJcSMQCpIPI56VEi4nU/FX/AIK4eLF+IGqaT8MfCNrreiWchSK6kjklkmA4LYUdM1y+n/8ABWL47NcMtx8M7W5TvGtlcKf5V+gf7J/7N+h/An4OaBobabZ3GqrCJbq8kt0MrO3JBbGcCvZRoOmKxI060B9fIX/ChK47rsfgR+15+2r4q/asi0i08RaHYaD/AGQzFYLYvvLHruDV6z/wR78LDWP2lr7VZf8AmF6PI6Y9ZGA/pXcf8Fmfh3pfhrxR4K17S7K3s5NQglgnS3iVAxU5zwOtd1/wRV8BtDoPjjxdNHg3E0dlExHYDJFVYnY/TsnAzX5rfHH/AIKy6z8J/jdrXhW38F2N7oGlz+TJPNLIlxKB1K84z+FfpVINykGvlD9qD/gnz4H/AGjPM1HZ/YniRsn+0oBy3puHemOKXU9F/Z1/ak8D/tN+Eo9Q8OXkMeooga40ieQGaBvcdx70n7VXx4tv2c/g3rniqVVa9iiMVojceZMwwoH0zn8K/G740/so/Fr9jHxNba8CxsLWfzrbXNNkIHB4346f/Xqp+1B+2T4o/a0j8IaPd2K2I0+NIPKjcn7ROcKHP1NBSLX7LPwC179uL9oC8udcv5jYiY3+s3zN8+0sSET36V+93h/RbfwzoWn6Valvs1lAlvHuOSVVQBn8q+d/2B/2Zof2cPgpYW93GD4m1dVvdTlzn5yMhR7AV9M0GbCiiigQUyX7pp9Mk+7QNblKSNZpijZ2kc4ODXwP+0V/wS2h+Pnxg1PxfD47bTIr0qZLeS281l46A5FffrKXyvrSws/KntStc2Z+abf8ET/Dxtxj4j332gDr9gQLn/vquX8Q/wDBE/UIraV9E+IltNOB8kd5ZlQx9yCcV+rAc57VIHzS5TPmaPxF8Z/8EhvjP4Zh8zSZNJ8Qr/dtp9rfk2K2v2U/+CcXxs0X41aBrWt2Ung7TdJvI7ie989d7qpyVQDrnp+NftFRTsLmI412qoJ3EDGT3qSiimSFFFFABSZobpTaAHMeK/P3/gstfJF+z34etsjzJtZUqvc4Q9Pzr7/4YY9a/NX/AILXX5h8AfDq0HRtRnc49oxigpbnP/8ABFHwVC0Pj7xVJGTcq8VhG5HRcbiK/U6vjz/gln8NYPAf7LOk6griS51+ZtQmYds8AfkK+wt1AnuLRSbqNwoELSZrC8XePPDXgHTW1DxNr+m+H7Fetxqd3Hbp+bkV5z/w2N8DPNEZ+LPhFW/2tXhA/Pdik3YD2OjNeI6/+238BfDdk91dfFjwrNGoyVsdRjupD9EiLMT7AV5VqH/BV79nezklSHxHql8yHH7jSJwGPsXVR+eKnmHY+w6Wvnf9mX9tjwd+1RrmtWPhPStZt4tLAZ7rUIFjRs9OjHBr6IqlqD0CiiimIKKKKAPF/wBsyyl1D9ln4lwQxtLI2jykKoyeCCf0FfB3/BE2SJdU+JUW9ftHkWreX325Iz+dfon+0cFb4C+Pw/3Tot0P/IZr81/+CJiuPiB8THbhW022UfUStUvctfCz9baWiiqICiiigAooooAKKKKACiiigBG6V+WH/BXj48+NPCXijRvA2jatcaVoF/p5mu0hbaLjJwVJr9T26V+Rv/Bar7A/jzwIsUitqS2Uplj2kHZu4Oen61DLicr/AMErfjF8HPg7rfiC/wDH2uw6H4r1Ara6fc3sUpiEOMkb1UqmT3Yiv2B8L+MtA8baet94f1qw1qzYAiawuUmXn1Kk4r8n/hp/wSRj+KnwF8OeLLDxrLpvibVrUXXlXUIe22t91SV+YVxMv7A/7Vn7Nuqf2v4Eu57sQEuJvCmq4dvc28hXzP8AdwfpTQ2rn7X18V/8FWPjNp/gH9m/UPCjMsmq+KStrFFg5WNWDM/THVQK+KdP/at/bj8M+fZy6N4tvnUGMtfeEWkZT6hhFjP51e+Cv7HXx7/a8+KGm+MPi+dW0/QbeZZZ7rxChhmkVWz5cEBAK9McqBVCtY+3v+CXHwq1L4Y/sw6dJq1m1ld63O2pBJCCxjYfKeDxkdjX2DVTS9Pg0nT7WxtkEdvbxLFGijACqMAfpVugkKKKTrxQI+Sf+CiH7VHi39l/4f6DqPhCwtrm81S8ktpLi8RmSAKoIOB61+d95/wVo+O95ayxRXWj27MMCSKyO5fcZNftb4r8F6D460ltM8Q6TaaxYNybe8iEi/XnpXC2v7K/wismJh+HmgoTyf8ARFP86APwX+IH7WHxf+KDXI1/xvq0kE4Kva28pihIPUFR2rl/hD8Qv+FU+ObPxJP4fsfEv2X5ls9SUmJm7E1/Q4P2b/haOngHQB/24p/hSS/s2/C2aJo38A6CUYYI+xJ/hQO5+Wl1/wAFlviM1vbwaT4O0GwSAAFAXcFR2A4xX6Tfse/tDSftNfBXTvGVzpy6XeySPBcW6HKB1OMqfQ1zPjn/AIJ2/Afx1HN5/gm30yaQYE2muYWX3GK9M+AvwE8M/s6eBx4V8KLcLpgmaf8A0qUyNubrzQI9IpG+6aWmSMEUsxCqBkk9qAPkT/go5+1BZfAf4NahoVleTW3i7xFbNBpzwjiEZG5yc8cZA+tfD/8AwT8/YNvvjhrlr8RvHIJ8NRT+ekEzEyXr88MpH3c85zWB8ZNUuP2zv+Cg1n4Sublm0NNU/syLyiSscMeSzD6kV+0Hgnwfp/gLwrpug6XCsFlYwrCiqAM4GMn3oLfu7HmXxO/Y8+E3xY8NjR9a8H6ekaR+XDcWcQhmi9CrLg1+QP7fP7E1l+yZrmjT6Pq8upaHrLSeTHcAebEV/hJ7j3r9526V+X3/AAWytzJofw6cFeJ51wTzyBSEmeK/8E7f2xvhz+yn4F8Uv4pi1K51XUbqMpDp1ursUA7lnXFfXNv/AMFl/gjJnfonjIEf3NPt2H63Ar5V/wCCcv7C/hP9pLwT4l8Q+OFuHsUnFnafY5zG6sv3j0r6z8Nf8Ef/AIJ6PqElxqM+ua3BuzHbXF5sRR6EoAT+dCG7Hw//AMFEv2zPCn7WF54SXwdp+tW1jpSuZl1S3SGR2Y/w7HcdK91/Zh/4Kp/Dj4P/AAh8PeDtb8FeIoH0mHyWk0sRToQP4v3joc+1fO37Rn7Kvhnwp+29pPwr8NRyWWh6nPaqEeViY1k5IDHJ6A1+j+n/APBK/wDZ7tdNSCbwnc3U+BvuJNTnD5xyRhsfpTDQ4vwB/wAFfvhl48+IemeGx4V8S6Za6jcpbQajcrBtR2OAZFWQ4GcdC3WvvJWDqGU5UjINfGui/wDBKz4M+FfG+j+J9AGsadeaZcpdRW8l350LMpyAVYdPxr7KA2gCgl26C0UUUCEr5i/bS/Yi0r9rbR9Oc6xLoWvabkW1wQXhZT2dP6ivp6igD8n9J/4In66wb+0viVp0Zz8v2XT2fj33Yretf+CJ8G5ftHxPfHcx6Uuf1av1CooKuz80NE/4In+GoZpTq3xE1C6Vvu/Z7FE/Mbq97/ZH/YB0z9k3xxreu6X4ouNbg1C3ECw3NuEdBnPUE19aUUCuxoFOoooEI3SvzY/4LZed/wAKx+HISTbC2q3AdPU+UpFfpO3Svzb/AOC17/8AFsfhwv8A1Frj/wBEigpbn0/+wFbJa/smfD5UGA1iG/Ek19DV88fsAsW/ZK+Hm45P2EfzNfQ9AnuFFFFAgooooAKKKKACiiigAooooAKKKKVgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAh6V4/+078eNF+AXwx1LX9TuY45xEwtYGxmaTHCjJr0Pxl400rwH4Y1LXtbuFsdMsIGuJppWCgKBnHJ61+aq2/iv/gp98SUS6s7rw78G9CuGmhmkgxJfEHG0Nkjn2NZya2N6cU9WfG3jDwb8Rv2iLPXPjDqkP2fSLa6RUMgZCVZhjZxjj61+znwTv5vh58B/DhTT7nVRFYJLIIWDSH5cnGev5181/8ABSaDQPhP+yba+B9Dh/sqGOW3jto7cAGQr/fx9OtfSH7HdxJ4i/Zl8CXM8jeedPVJCDndgYrBXUtDZtWvJDvhL+2b8MPi/rB0bS9djtNcRikmnX37qVXBxtwep+le6rX5D/8ABQT9lHWPAvjRvib4Okuo7yS6ErW9rDsaHHO/K9a+2/8Agn38XvGvxe+B1tf+NrBrW+tJPssU7qVadFGNxB71tTk5LUyqQW8dj6d/ip1N7g06tTmCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtXAKKKKnlYDW+6c15H+1JqkOkfA/xbc3Cs8a6fNgKMnlCK9drwT9tiaeH9njxg9vN5L/AGKRTkZyNtROL5Wa0/iPzS/4I96F9u/ac1PVQW2WejTHp3kYDH6V+1Nfj1/wRfkH/C3vGIYZZtLVg3/A+lfsLWyIYUUUUyQopCQoJPAryXxD+1d8KfCnjUeFNX8a6Zp+t5Cm3nl2hSezN0H40DSb2PW6KyND8WaN4os/tWjapZ6rBjIks51kH6Gvn/8AbA/bU8M/sx+DLlhc2+peK50ZbLT4nDYfsX54FK6Cx9L0V+BN18fP2nv2hNWutf0nVfE1zZwu0qrppaK2hUc7RjAOK+o/2Ff+CjnjG8+IOm/DP4qO1/LdzC0t9RuE23EUp4CyHoR+GaLorlZ+qdFNDZp1MgQ9KhvP+PWUkZGw/wAqmPSqmpvImnzmMAvsOA3Spa0KW5/Pv8XPDMvij9tu90fT4lNze+IYlRe2TICf5V+/9pLB4f8AD1ub6eK1gtLdFlmmcIiBVAySeBX4fagqab/wUs0pm5UeJISce5Nfpb/wUV+Evjf4xfAG40rwK97NqKzq82nWsgUXcP8AEjcZP50k0kkXKPvNM+mNI1rTdetRdaZfW2oW2cedayrImfTKkinaxr2n+HdPkvtUvbfTrKPl7i6lEaL9SeK/AHwR8Xf2hv2L5Xs7H+0/DdgJSz6fqFoJbZm75yOPwIrpNU+NHx3/AOCjHjTRvA093bskYaT7FYRNb2y4HMsvzEk/jj2p3I5baI/YTXP2xPgv4dujbX3xH0CKYHGFvEYfmDWPP+3h8B7fOfiXojH+6k+4/kK/Iv8AaL/4J8eL/wBmv4ZweLtc1G0nV5hFJDFg7SfrXzl4c8E6p4o0XV9Ttos2WlxebcSbQAB6ZxTui1DWx+/Vj+318CdQ1O1sLf4gafJdXMqwxJhvmZjgDOPU19BI6yIrKdysMgjuK/GD/gmr+wvafGnUrf4j+KTNH4e0u8V7OzB/4+pEORu4+6Div2dXZDGB8qIowOwApmb3JKKbu3DKnI7Vn+INct/Dej3epXbhLa2iaV29gM0m7CWp+Z3/AAWG+P1/ZLoXww0O9eP7UPtWoxwHDOM4RCR29q7T/gmt+wpa/DfRbH4meMbZbnxFfwrLp9nMnFkp6Pg/xkd6/Nf9or4ra18c/wBo7XPEllDLe3M98YrCBELEojYUBe/Svqz4ef8ABUn4sfCPUNI0T4geFo5tNgCxTK8BhmCAYG36Ci6NFtY/Yqlrz34J/HLwr8fPBdv4j8KahHe2jgLLGD88L45Vh616FRuQFFFFMQUUUUAJWL4vsE1Lwvqls6CRXgf5T34NbVUdakWHR72R/upEzH6AVMtrDjuj8EfgbrF34Z/b/wBBnsE+wSDxK1uY8A4VmIPB9RX7+1+AfhfVotY/4KGaXd2gAjk8VqE2jjG81+/lEdip/EwoooqiAopOfXj6UtABRRRQAUUUUAFIeRilooA8J/bZ1O80T9mvxpe2PLxWUm5ezKRgj9a/Nf8A4I42NheftAa5cTwxvdwaSzW7MOY8tg4/Cv1t+MPg+Lx98L/E2gSxrKt9YyxBW7nacV+D/wCzL8Vbj9k/9qfT77VxPYabb3z2eqxFMN9n3EcD8qh7lx2P6DWUOu0jINK0Ksu1lDL6EZFYPgfx1ofxE8PWet+H9Rg1HT7pBIkkLhsZGcH0NdBV3uSxFUKAAMAdhTqTNeU/Eb9p74cfCvxRpHh3xB4jhg1nVJ1t7e0h/ePvY4G4D7vPrQI9XopgNPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDH8Y+IIfCfhPWNZuHEcNhaS3LM3QbVJ/pX4xfsBeFx+0N+29qPivVo/tNtZy3GssJPmBYsRHnNfrL+1A88f7PPxBa2jMs40ecqi9T8tfkV/wAEr/jH4b+FHx8vYvEl4unRa3ai0gnmbbGkhbIDE9BUSLjsfuAqhQAOFAwBTqjt7iK8gjmhkWWGRQySIchgehBp0siwxvI52ogLMfQCnHYln5af8FsJofM+G8Yb/SP37bf9nI5r3f8A4JG2Qtv2UIZcAGbVblicdcEV+cP/AAUY/aD/AOF8ftBagbCTdougk6faejFT87fnX33/AMEgPidpGufAO48HpdRjWtKvZZ3tv4vLkIIb86obWh99mk60lcn8TviboHwf8Faj4p8TXn2PSbFN8sgGSfYDuaCTyH9vH4r+GfhX+z14jn1+3tL+7vrd7bT7G6AImmYYHX06/hX4J6PpfiCzeHxfZ6Pdvp1jdrL9sjtmNvG6sGClgMCvp74zfFLxj/wUa/aW0zQvDsE1vpPmmDTLZsgQQ5+ad/w5r9X/AAJ+yP4T8H/s3L8KJIVnsZrRkubhgNzzMOXz9aRpsVP2L/2rNC/ad+GlpdWzpa+JNOiSLU9Nyd0TAYDD/ZNfQ9fhNoN94r/4Js/tcJFdjztImmAnjU8XNkzdvf8Awr9w/CviSz8X+HNN1vT5PNsdQt0uYW9VYAimS0a1FN/ip1BIU1s44606igCpMrLhhz9axfEninQvB9j9u13WbTSLVuk99dCFfzJxXRsAVORkV8Bf8FOf2U/id+0VceE7rwNaLq9np6yLPp7XMcW1j0YbiAaDTmufbWieOPC2tQpNpuvaXfI3SSC6jfP4g10EV1BOAY5o5B/ssDX4NW3/AATL/aLt5kli8Em3kU5WRNVtwy+4IbNdPB+xz+194YgCWMPieOJBxHY+IWXH0w9AWT6n7hZpa/ETTPhj+3J4T3SWq+OiqchWumuj/wCPE5rlNU+OX7W3gXxRa2mrar4wtNRaVVjhu7MlWYnABAXGKBcp+81Fcb8H28RSfDHwy/iyVZvEb2MT3zqu3MhGTxXZUEBRRRQA1/untWB4s8YaL4F0g6hr2sWWjWKnDXF9MsafmTyfpW+yhlIPSvx9/wCCxvxeu9W+KGh+A7a7kTTdNtPtNxCp+VpXPGR9KTZSP1i8H+OfDvj/AE/+0fDet2Wt2anYZrGdZEDehweDX5w/8FspD/YPw5QHBa4n5/4CK+Uf2Ef2oNc/Zh+Lun6dqkd1b+FtbkjivrO5DIqBjxMoP86+jf8Ags54kj12b4ZWdn++tJYZbuO4XlJA2AMHoTzU3Ktqdx8QLj44fC/9h/4Ut8KVvIpI7ESaiNMgZ7oIwyu1QCe/pXy7dfFL9tfwhYpq8934+8ib5/30Mk4H1Tadv4iv2S+Cdqbf4N+CYHXldGtAQw/6ZLXZtEkgwyKw9CKOYLn4zeDf+Co/x/8Ahh9mh8baBDq9sHw39sWElnM/sHwozX33+x/+3h4Y/aw+1abbadNoniSzi86eykO9CvTcrelW/wDgoF4g8IeD/wBmPxdc+IrCzu5ri3NvYQyRqXe4bhdvfjrkV8T/APBF/wAB6nP498Y+L3tGh0mOxWzimZCFdy+cKehwKfMx6G/+3l+x/wDtC/H745XV9oumLrHhDYsdlnU4oYoeOS0bNu/IGvlD9oD/AIJ++Pf2bfhjF4w8Y6jpKiW6S1Sys5XlfJ99uK/f6vzM/wCC03xBjt/CPgrwbHPEZbu5e+liVwXUKMKSOoBqb3DmPg3wr+zVp+q/sz658XtU8XR6bBY3v9n22lramV55j0Ut0XPvUv7NP7FXxH/akM954Ts7aDRLOYQXOqXkqxohPovVjjsK+gPiT4Fj8Af8EsfCbhXE2v65Ffy7hjuQD+lfTP8AwRgtpI/gR4rlZWCPrOFJHBwnOKaVxOR71+xp+xnof7JHhm9hs9Qn1bW9UCNf3UnCblH3UHpW38Pf2uPCnjT4y+I/hdfJLoHi/SZikdreHC3admjbufavdK/Jv/gpxpGq/AP9pTwV8YfCtvPaXM203F0iHymlQ/dY9Mle1VsTufrJS1w3wV+Jmn/GD4X+HfFunTRzQ6lapK/luG2SYG9TjoQc8V3NMkKKKKAPEP23NUl0X9k74oXkDbZYtGl2n6kD+tfDH/BE2O3XUviQTIpu/KtsLn5tmTz9M19tft5RNN+x/wDFZFGWOiS4H0KmvhH/AIIn/L40+IgJ66bbj8fMqJFrY/WmlplPqk7knyX+2H+2J4l/ZT8aeFrifwmuq+Ab4Fb/AFKMnzYmz0UdM49a9s+B/wC0D4K/aE8Jx694P1aO+h6TW5OJoG/uuvatr4p/Cvw58Y/BmoeGPFGnx6hpl5GY2Vh8yZ/iU9iK/GDxdYePP+CZv7Sz3WiSXE3hm5bMLTAmG7tieUPbcPWk2NK5+5mRRkV454J/ao+H/ir4O2XxCm8QWNhpklt5syTTqHjcD5k29Sc+1fml8d/+CqHxP8XfEC8tfhWp07w/auY4tlr50s2D99jg8UuYOU/ZDIpa/L39h3/gpd4l8cfE6LwZ8VtQtdt+y29heJbiJvPJ4R8Dv71+oVUmJqwUUUUxCHpX49/8FnrV1+MHg+YjCNpL4P0fmv2Er8x/+C0Xw5urzw/4L8a28G63s5XsLmXcoC7+UGCc9fSk1cqJ9i/sS6nHq37K/wAOZopPMVdLjjJweoyCOa9y2+1fF/8AwSj+JUHjb9mOz0fz0e+0C5a1ljGdyqeV/wAivtKhCe43aaNpp1FMQ0A06iigAooooAKKKKACiiigAooooAK4f43+IpPCfwg8Y6xCcS2elXEqE9jsOK7evM/2lLE6l8AfH9sP+Wmj3A4/3CaBn5e/8Ef9JtPE37Q3inXdQiWfUINOM8TsN2HdzubPrX7H1+NP/BGzXrWw+PHiDTZZQk95pGIVbgvsbJx+FfsrQOW4HpX5Df8ABZX4nWOu/EHwp4NtmWSbSrd7id88Kznhfriv1Q+KHxI0P4TeB9W8T+Ib6Ow06wgaVpJDyxA4UDuSe1fzi/G74lXnxg+KniPxXeySSDUbt5It45VMnYvtxQET9if+CR+kPp/7KkVyybRd6pcMD64IGa+2K+Z/+CccdlH+yD4GFj9wxOZP+um47q+mKBPc/J344SR6x/wV28FWyDOy8sY2z0yI2NfrHtr8ctS8RJff8FgLOa4DbI/EcVtGOMjEWAevTmv2PoGxuKXdS1WuL61tJYYp7iKGSY7Y0kcKXPoAepoJLG6ik47c0tAB68UzzkH8S/nXk/7VWi+O/EHwK8UWPw3vJLLxZJbH7I0D7JWOeVRv4WI6GvyHX4E/toahfXCvB49eYtiRm1eRQf8Ax7FA0rn7nPeQRqWeaNQOpZgKyLzx14d0+YRXOuafBKeAklygP86/F2D9jP8AbI8SQtFNF4jWOTgpfeJgike4aSrdn/wSr/aN1hfO1Keztp+uLjXBI35qTQOyP2gt/FOjXjKsGq2crN0CXCEn9aupfW8jBVnjZj0CuCa/GW+/4JX/ALRXh+1jvdK120vL1eVgtdaeJ0PszYH61sfCP9jH9rDwZ8VPC2q6rNqK6ZZ6hFNcyDxAJ1EYb5vl3Hdx2oCyP2I3UtRI33fXvUtBIh6V+cX/AAWq0+Wb4R+AbpVzHBrEoc+m6Hiv0dr4G/4LH6tZ2f7OWjWc0Ze6utZj8hgR8u1SW/McUDW57d/wT6kEn7JHw+I7WeP/AB419GV80/8ABOrP/DIfgIE5It2H/jxr6WoB7hRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+VP2k/gr4o/aS+JfhrwhdTXGm/DLT/wDS9bZXKNqLH7sS4zlfXOPoa+jfDPgvSPBfhmy0DQ7OPTNKs4hFDb26hQoA68d61FVnyHB68dKLpmht3IZV44LVCir3ZvKXNZHxF/wVe02xb9nmSVrZJL37VEY7iQfcA9D613P/AATJ8RP4h/ZJ8Ll23yWrSQEn2NdV+138ED8fvhXH4WN00aT3MZaaNcsozyRxXX/s4/AnS/2e/htZeFdFubi4soiZM3QG/cevT3rGMXztlzS5FrqejalotjrEPl31pDdx/wByZAw/I07TdLtNJtUtbK2itLdPuxQoFUfgKt4NLXQko7HNzO1gpaKKYgooooAKKKKACiiigCK5uEtbeWaQ4jjUux9ABk18Y+I/+CsXwX8NeItQ0maHxDdPZSmF5rSxDoWBwcZYV9lahZx6lZT2kwJinQxvg44Iwa+Obv8A4JVfBzUfEl3q11a3kpubgzvCLl1Xk5IwDUu/Q0jy/aNXwb/wVG+BfjTWLXTLbU9Xs7u5dY41vbDYCxOAOGNfWtrcLdW8c6cxyKHU+oIyDXz18Pf2A/gt8M/E9vr2j+Ebf+0LchoXuGMoRh0YBu9fRKqFUADAHAFNX6ilb7ItFFFMgKKKazYXNADqK/PT/gph8SPjV4L1bwovwzu/EWnrJvaZtDUupx2YBTn8a8N/Z0/bb/ai8I+OtPsPGfhTxH4+0S4dYXt7jSzBcJuON6yLHyR6Ggvkkfr7RVezumurWCZongaRFcxSDDJkZ2n3FWKCAooooAKKKSgBa8E/bOtlv/gf4hs3Yp59rINy84whNe87q+Y/+CgnjWLwV+zv4iuXkjE8tu8cKO20sxGMD3qJbGtPc+M/+CKugCbxj4/1ZmKm1tIrdVxw2WPNfrVX5Yf8EeY4/BfgL4neNNUnMOjRhNzsMALGCzNXYeKv+C0HhDS9TuLfSPAuqalbxSGNbl540V8HGQM5pp6ClFn6P0V+aFn/AMFsPDZVvtXw21ZWAyBHeRY/WvR/h3/wV6+D/i+aCDWbPV/C00rBN11EJYwT6svandE8rPszxvqr6L4R1e+jTzZbe1kkRB/EQpIFfzneIdUvfjH+0Bc/25ut7jVtUMEuxctENxAAzX9F0F5Y+OfDlteWkoudM1CEOjYwHjYdfyr8bv8Agod+zbc/AL4lwfETw0n2eynulkKqAUhlzlSPr71nK99DeC921ziPjV8EfiD+yP4d0jxNoPj67h0rVJdsFnBcNHMMDqyg4I/CvmuTxTP4u8YWuqeLr+81OB51N1K7lpGTPIBPGcV6t4g+LPj/APbA8ReB/Bt9El/eRTra262seHO4gMTjjgV+wOjf8E//AIZaT8HoPBkOhWvmtb4udQmhVriWQryS2OOfSkrpakytfTY3v2a/Gnws8b/CPSNI8BXFlaW0Nqii1XYkgfbzkD7xz1r8of21Ph7qHwQ/a2stQEDaZHd3UF9FNGcA/vBuIrJ+P37PHxS/Yz8ZTajpdzqFjov2gyWl9ZSNtUA5G7HFeJ/E343+NfjJd2154w1qfXbq1GIricgui+g9qFvdBeyP6T/Cmoxav4Z0m9hk86K4tYpVkBzuBQHNa9eJ/sY+Jm8W/sx/D+/kOZP7NjiY+pQYz+le11rdGItQXUfnW8iFtoYY3eleP/tafHyH9nX4K654sISS/jiMdlC5wJJiPlFfhNq37W3xW8Q+NP8AhIdS8aa5O32nzzZpqEq24wc7Qm7G3HrRcaWt2fQ+peF20v8A4Kl6VZMWuIl8RwzM8nPydewr9sbi5hs4XlnlSGJBlnkYKqj1JNfgD4Z+Pl/8T/2rfB3ibT7RdL1GS4htRKzEuX6byc9c16v8Vf2bv2wPi14o1mbULPxHrGl3ExMUUmrNHaNGegEZkGRiszSVviR9Qf8ABSj9rz4deHPBV54JsrbT/FvibUImik8tldLRSPvFh1PoAa4v/gjf4G0jRfDXjDx3fz2UFzdTLZW7TTKJI4xyfpmvmWz/AOCVn7Q+qW0l5caBYxOF/wBVdalH5h9utaGi/wDBMn9pXT1FrZ2kem20z5dItVCJn1IBo2Fufan/AAVi8UaJ4g/ZZmXTdUtr+aLVrdNtrKr4JPIOD6V8cfCfSdD03/gn38Q9RgRZtTvN0UrEfMmMfpWV8dPgT4//AGZ/2dtU8N+Pfs0k+ranbz2ckVwZW+U/N82a9gj8J2vhv/gmbqUosI7ZrmIz/aIpA3mN6Gi9zWNos+iv+CQfi6TxB+zVdadJtA0nUnhQKMHDDPNcb/wVy+N3i34caT4R0nwxrl5of26SRrh7N9jOAOBn0qz/AMEYIbpfg34wmcxi0l1VTGo+9nac59qX/gsH8ILvxd8NdD8WWMUs0uiysJFQcCNhyTVJma0Z9G/sFfELUfib+y/4P1jVr46jqXlNBPcMcsxU4598V6Z8bNNn1j4X+I7O1dUuJrKVY2k+6DtPWvh7/gjT8TItV+FfiPwdNcL9s068+0Qwnr5bDn9a/QXxHosXiPRbzTp9wiuYmjYqcHBGKdubYX2rn4kf8E0/DulX37ZCWevtbl7IXJgjmAYSTBjgL719+/8ABRj9mfQfiR8INT16009YfENgvnRTQjbuIHfHavzn/a2+B+vfsgfHiHXvCz3lra+ebu0vMklHzk5b0r660X/grb8PNW+Ca2HizSNQv/FLWPkXFokQEVxJjGd3YGlYLWZ4r/wSH+Lt94U+N194DljY2OuQyOEV+I5YhknFfsxX4q/8ExdLl8eftp3PirS9Ea00S1hu7hwCSlt5inaufXJ6V+1VUiJBRRRTJCiim7qAFrE8ZyCHwjrMhxhbSQnJwMbTWxIzeW2zbu7bulfNH7fX7QmjfBH4A+JYptQSLxDq9o9nptqjAymRxgMV/uj1qWrjjvc/IT9nG3bxF+3B4TNpEcS+Jy6KCW2qJDk5r+hVc7Rnk96/F/8A4JK/A3VPHHxsk+IV1Fs0fw+H2ysv+tuH6YPtX7QU0VLcK+TP+CjPxo8b/BP4M/2x4J8R2Ph2/eURtJNHHJO69xEkisCfwr60r88P+CwnwpvvE3ws0fxVYrJLHo8xNygYkBCPvY6VMrhHc+Xfhf8A8FRP2gvA+m2mr+I4rPxl4Ye5Mck95pwhkOOqrJEFUH6g1+ifwC/4KCfC340+F0vbrXrLw3qsabrqwv5hH5frgnGRXyb/AMEs/D/hX40/Avxj4D8R2Ed19ivftL+bn7ki4GCCMdO1fEX7ZXhjwT4R+Puv6B8O43Gj2LCBtshbzJf4wOTkA1OpWh+p37RX/BVL4a/C3Tb6w8HXK+MvEwjYW4txm0STt5j5HH0r4Rm/4KnftBN4oXXpNUtodFZwRo8OnotuRn7okZC+f+BV4/8AsfwfDi1+OWhw/Fm3YaBJKFKXKssAY9DLgg7a/Yj43fsq/Dr40fAmbTvC1pY2unpaNPpx08DyywXKkEc0aodkdp+yT+09o/7UHwytvEFl5dtqkWIr+xDZaKT1+hr3Gvxr/wCCSOq6h4R/ag8Q+Eby4e1R7GeOSzbgSSxt97Hriv2Uq4mclYKKKKokQ9DXwR+3b/wT7j+NH23xT4NsYIPEqxl9kY2mdvQ/WvvimtGrqVIyDUtFJ2P57Phf8evjT+xl4m1DSrGe5017eXZcaVqELPA5Hfn+le62v/BYz4twrtudG0KeTH8EJXn6V+vPiD4YeEfFc3nax4b0zUpe73Nqjk/UkVhy/s7/AAymJL+BNBYkYJ+wx5/lTK5kfj34i/4KDftM/Gq3ay0KW5sbeRthXw7pxR8Ht5gFe2/sRfsG+M/GHxGh+KHxiF9DLZzrdWlteSbpZ5ByC4Pav088O+AvDfhO0Fro2hafpkAOfLtrdUH6Ct3A9KYuZdBiDaAMk47mpKTFLQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1HT7fVbC4s7uJZ7adDHJG4yGUjBBr8rf2xv8AglXqUmsXfiv4ShZYpiZZtFY7WRuuYz/Sv1bpMUmhp2Pwc+Hn7aXx+/ZJuf8AhF9TkuJILcFF0rxFExCY7qx5IroPiN/wVJ+NHxm0VfCmjWlpotxqA+zOdJjZp5t3G1SeRn2r9n/Enw38K+MLlJ9b8O6Zqky8CS7tUkb6ZIzVTTfg74F0a8iurHwhotpcwsHjlhsY1ZWHQg44NFh8x+X37Hv/AATEuviB4E1/X/ihbT6VqOpxPFp9vdIfNhkPPnMO/PavO/En/BPf9ob9n/4kG++Gy6jqcMJ82DVtCuVt5cdlwSOfrX7aUtMOY+Cf2L/DP7W0PjuO6+KutXEPhGJTvtNXkjnuJvYFeh96+mv2pPgXH+0X8Gdc8FG8GnXF4gNvdMu5Y5AcgkdxXrlFArnyd+xP+wfpP7J8N/ql3qf/AAkHiu+TypL7ZtSOP+6gr6up9JQI/J3/AILUSN/wkfgJG0UJD5MrHVlX5nOf9Xn2619hf8E2f7a/4ZI8H/23nzsSeTu6+Vu+XNfSeqaPY6xGI722iuUH8Mqhh+tWLW3htYEhgjSKJBhUjGAKB30sSfxU6iigQUUUUAJTafRQAynbRS0UANKjFRyQpIylkDFTkH0qaigYzpin0UUCCiiigBK/DD/go5Yt44/bm1DRbb97LM1lZKIzk5YgHp6A1+5zfdNfhz40uY/F3/BUy2AZZ428W29v8h3A4KjtUsuJ9Q/8FF/2MbOP9n7R/FXhuwU634TsoIb1olJe4gRApY46kda/Ny4+L3iD4qXXw68N+IbprnTdDnhtLUSZYhGkUZOa/o717RbTxJot9pV/Es9leQtBNGw4ZWBBFfhx8YP2DPHnwz/ak07w94c8P6hq/h281OK403UILd5IYofMViJXAwhXnqaSQ0z9fviJ8d/h/wDs5+C9Nk8X+ILbTI4bSNYLUMGuJVVQuUjzkgcc186+Jv8Agrz8DtJs7n+zP7d1i+VD5MUdiqI7Y4BYvwPfBrp/22v2FB+1nY+G7i11xNB1vR4TAsskXmRujYyCMj0rxn4c/wDBFvwTo7QT+LvF+pa5IpDSW9mi28Teq92x+NPlJufnz+0l+1F4o/ag+IY1PxXc3NloEco8jS7Vsx28OeoBOC+PWvv/APZ7/wCChv7M3wD+G+l+EvD1t4kto4UV55W0yPdLMQNxYrJzzntXrkf/AASZ+AKDB0fUn/3tQk/xrn/EH/BHb4J6nDL/AGdeeIdHmYfK0N6HUH6Mpz+dHKHMfTHwH/aV8BftIaLdal4H1V7+K1YJcQzwtFLET03Ka/KX/grz4mXxL+05pWiWmJJ9P0+OAqp3He7cDH5cV+qf7Nv7NvhX9l/4exeF/DSyTbn8y5v7gDzrlz3bAr57/aG/4Jt2/wAdv2hrL4jv4q+wWReBr3TDbktKIyDhXB4zj0o5Rpo8m/bs8IzeD/8Agm/8OdIuoWgubB7BXjdSrKxGSCD0616J/wAEc1K/s3audpUNrMhBI4PA6V2X/BTL4Ra/8RP2V7nTPCthNqc+kzw3bWdvG0s0kUfUIqgljj0r8sv2df23vin+yZ5uh6KLaXRhcGW40XVrUj5u4zwyfhR8I7c2x/QdXyd/wU4+GF/8Tv2UPEEWlWv2rUNLmi1FVWPe/lxtmTbjvtr4qtf+C1vxG+2xG58CeGntd37xIZJ1cj0DFiAfqK1dZ/4LMa94i0W/0wfDHTpftcDwlZL5pEwwI5XbyOaaYuVo7f8A4I5/tAQ3Wh6v8KNTuMXtszahpweQfNGfvoo9R1r9Oq/m+/Z58Ya54Y/aN8Ja/olncWd42sxn7LYo3KO+GjA7rg9K/o/jYMoIPB6Uwkuo7NGa+bv277r4paP8HF1z4UXFxHruk3aXk8FtH5jzQL95duDu+lfHvh3/AILOX2i+GxY+J/h5NN4mtk8uSRJ/KjkkHByCMrzSbFY+4v24IJrr9kv4pxwI0kp0OfaqjJPAr4M/4IlwhvE3xHmJyy2luo+m+vIfjV+3H8bf2vIbrQPCWhXunaHLAyXWmaMjTtLGeodsdK8X+Avx4+K/7LGtawvhKylsb/UEFvcwXdg8h+U5GBjrmo3Ktof0UU7NfhZL+3P+1f421CO0sL3VoZZ22JFYaWVYk+mVra+3ftx+MI9qL47ZJRjd5SRj+lCdhWPuP/gqP4+8ffDH4T6H4i8Fa9Jokdvfqt00Jw7Z+7+FRfD9/C//AAUO/Y0im8ZRRtrVrA0VzfhQJLe5jXPmqewOM4r86PiZ8E/2tfF2gsPGnh/xfqWkwDz3ivGDRrt53Ebq4P4aftSeLfg78J/GXgTR55LGLxA675EYhoOocD0Joeo7HlviZLjw7rmq6JaapNc2NldyRRtHK2xgGIyBX7Df8Eq/Bfwt1j4GHU9I0y3u/EqytDqrXih5FbsAD0GK4L9i3/gnj4P+JX7ME2rePtJZvEPibfcWl+T++toz9x19yea+V9Qh+LH/AATL+Oo8l5jok0+5H/5dtTtw3Q+hx+NIZ6X/AMFQfgDp/wAB/ix4b+IHhOJdNi1afc1vFhVE6ENlfTgV+tvwu18+Kvhr4W1hjue+0y2nc5z8zRqW/XNfkt/wUZ/az+Hn7TvwN8AzeG9Vj/4SO21AzXulOjiW2BhIJzt2kbjjg1+kP7EtxLdfsr/DiSW5+1udLQeZ9CRj8KuOxEj3CiiiqJEryv8Aaa+Bmn/tEfBvX/Bd9+7ku4S1rcYBMM68owz716rRQB+EP7PPxy8Zf8E5/jdreieKtCuZ9Omby9Q0zequ6KflkjbO0nHoe9fpH8OP+CpnwE8d29qL/wAQ3nhO/nYL9m1bT59isfWaNGjUe7MBXr3x1/ZT+Gv7RlmkXjXw/He3MYxFfQMYriP6OP65r5M8Vf8ABF/4aak8r6D4v17Qic7ElSO6RT2yDjI/GgvR7n3B4X+MXgXxtbxT6B4w0TV45Pu/Y7+KQn8A2azfiJ8f/h98LdJub/xH4s0uwWCNn8g3KtM+BnCxqSxP0Ffm7e/8ET/EUdxN9i+KGnGHpH5mmyRE/wC8Fb+Vbnhf/gidGt1FL4j+KJmhBBkgsNJ5YdwJHlyv1waAtHue7fsqf8FANT/am+Nmr+G9J8HR6f4RsYHkGqSXBeViDhcgDHzelfaVeZfBH9nnwP8As++HYtH8HaLFYKEVZrsjM1wR1Z27mvTaCXboFFFFAgooooAKKKKACiiigBKy/E2gxeJvDup6ROcQ31tJbufQMpH9a1aKAP585LjxD+wj+10Z1Rp30C+Zo4pFKi7tWJ4z3ypr9L9R/wCCtHwaj+Hv9r2lxqE+uvB8mlfZsETY+6SW+7nvXsP7T/7GfgT9qLSQuvW32HW4UK2+r2qgTR/X1H1r5s8B/wDBGnwBoPiCO98ReKdU8R2ETh0sCqxK2D0YgZIoHc+KvGPxV+Of/BRLx7a6DYW1zJo7zqFs7ZWSztlJxvkbGOB9a+l/2p/+Cab+Fv2YPDi+BrNdR8SeHQ11qqou6a+3L8+zAySD0FfpX4K+Hvhz4d6Pb6X4c0e00mzhQRqltEF4AxyR1roCueCAR6UBc/Br4KftVftB/CHwrH8J/CVtdWUkt0Y7OK500m5hZz0QsvHNftD+z9a+N7b4SeH1+Il3Fe+LTAGvJYhgZPIB4HIHXiu3/sHTPtguv7PtftI6TeSu4fjir9AXPxy/4KifCrV/gj+0boPxc8MxTWsWpSx3BvI8lY7yMjg4HGQK+xv2Zf8Agpd8MPi/4dsLPxVrVt4M8XIix3NvqjiGCV+m5JScYPX5sYr6U+Lnwi8MfG/wPqHhPxbp66hpN4m1lzteM9mRuqsPUV+dXjT/AIIprNrk03hL4jrY6Y7FkttW0wXLxDsu4OMj8KClbqfaXxY/ba+Dnwl8O3Go3/jnR9SuBEz29jpV3HdTXDAcKoRsD8SK+AfgR4k+L/7cH7Uej+PtTbUdK8D+H7z7TbLbK8Vt5atwo7MxGM/zrovA/wDwRWvbXxJZ3Pin4h2N7pUU6vNa2GmsjzIDkqCW+XPrzX6c+EfCOleBfDdhoWi2cNjptlEsUUMKBRgDGTjuaBaLY1Yx8qn+fWnnOOOtFLQSJg4560m2nUUAN20badRQA3bQVzTqKAGbcYp9FFABX5tf8FqLHU7z4b+BXtbOaeyt9RkknmjQsqExkAHHSv0lrO1zw9pnifT3sdWsLfUrN/vQXMYdD+BoGfKf/BLPX7rWv2S9BgurWS3NjcTW6NIMeYucgj2r69rO0Tw/p3huxjsdLsoNPsov9Xb28YRF+gFaNAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAx7q1nhuVlW5IjEeCrHv60yS6+0fu2XzbYjBcdc1cvv8AVn/cNZul/wDHiP8ArpUSOyOqux9hHLpszxmZGtzgQx87h654rcR96g4xVWb/AFkdWk+7Tic83fUdRRRVGYxJN7MMEYp9MX77U+gAooooAKKKKACkPSlooAQdKWiigAooooAKKKKACkIpaKAK0tnHNLHI6KzR/dJAOKl8sbs7Rn1xUlFMd2N206iikIKKKKAGTSCONmJwAK8Y+JH7Xnwo+EHiB9F8W+L7LSdSSLzTA5LNj6DvXsV5/q6/B7/gpl/yc9rv/XGP+tZSfvHRTipJ3P0D+Mn/AAVo+E3gvw7cyeDZpPGWt7CYLdYpIYC3YPJt4H4V+efxA+LXxm/4KBfEK00uDT7qTTpbhfI06xRmtrQE4yzkDIHqa+bdO/482/3a/a7/AIJp/wDJO4/+vdf6U7kv3Hoenfs5/si6L8FvgOPAFxcPqP2+PdqMzIFLsw+ZMA9ByK4KP/glj8EYrye4Gj3DmXJKPKSASc8elfYtMoUUyPaNHxxd/wDBKr4I3t4J/wCyrqAYxsjmI/Gtjwb/AMEwfgP4N1a31GLw9c6jPBIJUTULppY9wOfu9MV9X0+hqwnNyK9rYwWFnFa2sS29vCgjjjjGFRQMAAV85ftlfsw3P7Snwx1Dw3a37WV+zLPbTEDYZU5VX9FPfFfStRj7xpFxm43PhP8AYA/4J6Tfs46tf+LPGj2uoeJ2/c2aQjdHbp3cE87jX3ftpq96fVpGfM2c/wCNvAWg/ETQbnRvEWmW+q6dcIUkhuEDAg9celfDHxM/4I8/DbxRrx1HQ9a1rQo55cy2lu8Pkxqeu0GMn9a/QekpPQak0cN8FvhXYfBX4baH4N0y5nvLPS4fKSe52+Y/fJ2gD9K7n+Gmt94U7+GpFe7Pyc/4LMfF+31DWPDPw8tJmeSzBv7xFPAJGFB/nXnvwD/4Jnt8Zv2Vb7x42pzW/i68DTaTaLt8kxp/Cw25y31riP8AgqR/yd5rn/XpD/6DX6x/sR/8mxeB/wDryWmauKtc/EL9nWxk8E/tNeE9N16wkhmi1aO0uIJ12OhL7Sygj8q/owtdn2WHy/8AV7Rt+mOK/GP9pr/lI34S/wCwvbf+ja/Zuy/484P9xf5UglHliT/40hQNjrx70v8AjS1SRkeCftJfsXeAv2p7rS5/Gd3rkX9nZ8mPS7xIUOeu4NG2f0rhP2nv2ctN8L/sU+JvA3gnT5ZYdPsHa2ikYPM5A7nAyfwr61rM8Rf8gPUP+uDfyNEikz+fL9nv9sL4n/sk/wBsaX4WWxVLyT/SbXVrV5VRxxlQHXBruviT/wAFLPjX8W/BuoeGNaj0FtM1BDHKLXTnEmD2B8w/yrqfj1/yUDUf+vtv510Hw9+9Y/8AXRf51Jocl/wSt1zX/Df7U2mW9vbTix1KCW2vC8LbNuMg56A571+5O2vlD9lP/kaZvrL/ACr6xq4mcjkfiF8KfCvxU0l9N8U6Na6vaOpUrOgJwfQ18rXv/BI/4CXmoy3QtNchSR97QRakQg56DjgV9qt9001elUTqee/Bf4A+B/gDoLaR4K0aPTLeTb5spO6WbAwC79TXo1Mp9AgooooAQnAJr49+OH/BTb4dfAvxxqPhbVdE1u81GzXloYlWN29AWP619gyfdNfjd/wU8/5KFqn+6azlJxaRtTgpbl/4w/8ABY7x34iWSz+Hnh+z8KqW+S+ugt5MV/3CCoP4V8MePvip4j+L3jmTxD491a81q7mlDXDFghC55VFxhRjsABXtX7JX/Hre/jWL+0d/yGo/9+o52ypRUdj7E+Dv/BT74MfAH4c2XhPwf8Odahit49zA3SESzYGWZ2JPJ/Ktfw//AMFoJNa8Uabp7/DIJZ3dykBkh1PzJgrMBkIE5PPSvynj/wCQm/1Netfsjf8AJxngr/sJxf8AoYp3Ykkz+jWzuhfWcFwgZFmjWQBhyMjPNcb8avAKfE74a674dl27L22eM7hnqDXbQ/6uP6Clk7/SjdGezP5w28c/EH9mDxZ4u8JaHrN14eM8xguvJjTfJGCQuGZSw49CK+7f+CV37Itl4mjvfi5450hL+V5iml2+oxM43dWmw3DfjmvlL/goV/yd54h/34v51+3n7Pv/ACRPwX/2DIf5VXRD7nz1+19/wT38EfGjwzqGqeHNEh0jxiqFobi2Z1RjjpsDbf0r8ztT8aftOfsw2U/h+PVtd0XRbEtGrR20csO0d8ujYFfvvXzv+17/AMk38Qf9er/+gmpGj8cv2PfjlqPhf9rzwf4u1zUFdr/U0g1K7eNVzHK21zhQAOvYV/QuGDAEcg1/M78Jv+S4eGv+w3B/6NFf0xVpEmQtFFFUQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMmTzInT+8CK/O3wH/AME0PE/hj9re3+Kc3iaxOi22vHV0tBGTK67twU+h561+itFJq5SdlYQ02n0UJWJG06iimAUUUUAFJS0UAIVB4xXI+I/g/wCBvF4kGt+ENE1USAh/tdhFJuB6g5Xn8a6+ik1cd2eRn9kf4J7w/wDwqjwfuHI/4k0H/wATWxpH7PHwu0C4SfTvhx4Vsp0OVkh0a3VlPqDsyDXolFCVguznYfh/4Ys7hLmDw3pMNzGdyTR2ESupHcELkGt6P5R0PPepKKYDGXdwRkGvP9Y/Z8+Guv3kt3qPgXQb25lbe8s1hGzM3qeK9DopNXC5zHhL4a+FfASSJ4c8O6book+/9itkjLfUgVek8IaHNeC7k0XT3ugciZrVC/54zWzRS5QuUo9IsYWDR2VvGw6MsSg/yq1j8KfRRyhcq31mmoWU9tIoZJY2jO4Z4IxX4Bab+y7r3ib9tKf4bXel3dvaS+IpPNmaIgLaGYsJM9MbTX9A9eBw/wDJ0L/9ev8ASjlHc9n8NeHbPwn4f07RtPiWCxsIEt4Y1GAFUYFcd8bvgH4P/aC8IzeHvF+lx3tswPlTAYlgb+8jdjXo1FHKK5+DP7bn7B2rfst6tFqWlvPrPgi8ciO7ZMtbMeivj271+pH/AATavbi9/Y+8Dtchg6JLGoYYO0OcV3X7V/8AySHUvwrW/Zt/5Ir4X/69/wCpphe56dRRRTEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH//Z"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83-%E6%AF%8F%E5%8D%81%E5%88%86%E9%92%9F%E6%8E%A5%E5%88%B0%E8%AE%A2%E7%A5%A8%E7%94%B5%E8%AF%9D%E7%9A%84%E6%AC%A1%E6%95%B0.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApkAAAFaCAYAAABVO0bVAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAFdnSURBVHhe7b2HtxVllr//+y9m1sys/nbP6plpv/NttZ22bbW7MTQYuhtBmiAoKCBRwhAEYQiSY5MZcs5BMkrOGUGS5CRBco4C7p/P7lN6ZV3lnnteOKeKz7PWXtxbp6pOnaq61HP2++73/f9MCCGEEEKIwEgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRHEmmEEIIIYQIjiRTCCGEEEIER5IphBBCCCGCI8kUQgghhBDBkWQKIYQQQojgSDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMnOIWbNmWc+ePW3gwIEKhUKhUGQlevXqZVOnTk09mYQoPJLMHKJOnTr2wgsvWP369RUKhUKhyEoUK1bMKleunHoyCVF4JJk5xP/8z//Y3/72t9RvQgghxIPnf//3f+2///u/U78JUXgkmTmEJFMIIUS2kWSKUEgycwhJphBCiGwjyRShkGTmEJJMIYQQ2UaSKUIhycwhJJlCCCGyjSRThEKSmUNIMoUQQmQbSaYIhSQzh5BkCiGEyDaSTBEKSWYOIckUQgiRbSSZIhSSzBxCkimEECLbSDJFKCSZOYQkUwghRLaRZIpQPJSS+fXXX9utW7fs7NmzdvPmzdTSv8Pyixcv2tWrV/33O3fu2Pnz5+3MmTN24cIFu3Hjhi+Hy5cv+/Jz587ZtWvXfL/Azywnrly5Yrdv3/bl90KSKYQQIttIMkUoHkrJRCwPHjxoVapUsdWrV6eWmsvg/v377cMPP7Rx48a5NCKWDRs2tFKlSlmTJk1s8eLFvi4y2qdPHytbtqy9++67NmXKFJdO9jFr1iwrX768bzNo0CA7dOiQb3MvJJlCCCGyjSRThOKhk0wEc8uWLdagQQP7/e9/b4sWLUq9Yp51bNOmjZUoUcLl8OTJkzZp0iRr2rSpTZgwwfr372+dO3f2TOcnn3xi7du392WsU7t2bTt8+LCtWbPGevXq5a8hpPXr17cVK1bYV199lXqXH0aSKfJy8tINe2/cJqs8YkPORZ9Fe1NHKYRIGpJMEYqHTjJp7t61a5f17dvX/vjHP36bmUQcyWqStfzzn/9sAwcO9PX4Qxs1apQdOXLE5s2bZx06dHBJRQgRTH7euXOn1atXz9auXWu9e/d2EV26dKldv37dWrZsaTNmzLBTp075++TlxIkTtmTJEn8vArnt1KlT6lXxsHPwzBX7Zet59n+azM65qDpyQ+oohRBJQ5IpQvHQSSYZRfpbfvnll1amTBlbtmyZN3EjlO3atbMxY8ZY5cqVXfo2bdrkTd7r16/3LCf/DhgwwKZPn25vvPGGN5HTr5MMZo8ePVwmkc3u3bvb8ePHPWs6dOhQz4Ky/7uhyZ5mebKdRJEiRVxihQBJphAiG0gyRSgeyj6ZQOaS/pRIJoU9H3/8sVWoUMGOHj1qLVq0cMncuHGjvfbaay6IyOnmzZttyJAhNnLkSCtZsqTNmTPHi3zYhvXHjh3r/TPJZtI/E8kcP368Z0LZ9l6ouVzkRZIphMgGkkwRCknmN5K5cOFCzyDSdI000sSNNCKGrLNt2zZv+t6wYYM3s48YMcIzmbNnz3aZJJPZs2dPl0n6ZrIOFedI5vDhwz2bSVb0XkgyRV4kmUKIbCDJFKGQZH4jmWQmixYtajVr1vQK8meffdbefPNN69evn/9OtThFQAsWLPDKc7KeCCFN63v37rXdu3f7HyTN6F27dnXJRCoRU9ZHSvfs2ZN65x9GkinyIskUQmQDSaYIhSTzG8kkQ0kRD1lHonjx4lanTh2bP3++97ts1KiRZyPps8kfHsMcIZpUoiOFVKK//vrrvh/2R3V5VPAT9d0ks3kvJJnZY8muU9Zjwe6cilYzttu/N5+br+RlOySZQiQXSaYIxUMrmRT/dOnSxZvC74a+lQxRRHM3Y1wime+//75nNRkbk0IhBlqniZyCnebNm1vjxo0928m4mkhlrVq1rFWrVl4IhHxGA7X/GJLM7IHQ5SdTivxDkilEcpFkilA8tJJZUJjx5/Tp07Zy5UrvoxnNBAQUDLFs+fLldunSJV8XqESneZzCIIYpKsgYmSDJzB6SzPRCkilEcpFkilBIMgsA8sj4mshi3owky1nGa3mX8zMzAtEnk6xnQbKYIMnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGQZOYQkszsIclMLySZQiQXSaYIhSQzh5BkZg9JZnohyRQiuUgyRSgkmTmEJDN7SDLTC0mmEMlFkilCIcnMISSZ2UOSmV5IMoVILpJMEQpJZg4hycweksz0QpIpRHKRZIpQSDJzCElm9pBkpheSTCGSiyRThEKSmUNIMrOHJDO9kGQKkVwkmSIUkswcQpKZPSSZ6YUkU4jkIskUoZBk5hCSzOwhyUwvJJlCJBdJpgiFJDOHkGRmD0lmeiHJFCK5SDJFKCSZOYQkM3tIMtMLSaYQyUWSKUIhycwhJJnZQ5KZXkgyhUgukkwRCklmDiHJzB6SzPRCkilEcpFkilBIMnMISWb2kGSmF5JMIZKLJFOEQpKZQ0gys4ckM72QZAqRXCSZIhSSzBxCkpk9JJnphSRTiOQiyRShkGTmEJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4TioZTMW7du2fHjx61Dhw62bds2u3r1qm3YsME++OADa9asmXXt2tVWrVplX3/9tV2+fNl69+7tr/Xr188+/fRT38ft27dt8uTJLoYdO3a0xYsX+37u3LljK1eutFatWvk206dPty+//NK3uReSzOwhyUwvJJlCJBdJpgjFQyeZCOa+ffusZ8+e9uKLL7oc7tq1y8aMGWPdunWzoUOHWr169WzQoEF24MABW7RokTVo0MC6dOlinTt3tv79+38rpe3bt3eZREKbN2/u4vr555/bwIEDrVGjRr4PRHP9+vX+vvdCkpk9JJnphSRTiOQiyRSheOgk8/r167Zp0yZr3Lix/eEPf3DJJJs5e/ZsO3r0qMtg69atrVOnTv4a4kcGc//+/TZr1iyXSiSV1xHCtWvX2vbt261q1aq2efNmGzZsmL/GuteuXbOGDRv6vs+fP586gu+4ePGi7d6925YvX+5RuXJll1nx4JFkpheSTCGSiyRThOKhk8ybN2/apUuXXChLly5ty5YtS71i3jyOhDZp0sSbzJFM1qHpnG0QSjKZc+bMsQoVKtjEiRPt1KlTdujQIc+CspysJz9/8cUX/l5kMydNmmR79uxJvct3kPVk3Zdfftnj0UcftbZt26ZeFQ8SSWZ6IckUIrlIMkUoHjrJRCQJMotly5b9nmQihQsWLLCmTZva+PHjvZm7ePHitnPnTn+NTOWQIUNs9OjRVrJkSc9Q0nSOsA4YMMC3qVatmvXq1cullG3GjRvn63/22Wepd/mOr776ytdDVAmynt27d0+9Kh4kksz0QpIpRHKRZIpQPJSFP0BTdV7JvHHjhjeJ16pVy0aOHOnZSZrVyWTu2LHDX9+4caNnMkeMGOHbIplXrlzxrCX9MpFJtu/Tp49LLJLJvmhCZ1/3Qn0ys4ckM72QZAqRXCSZIhSSzG8kk36Y9I2ksKddu3a2ZcsWX0Zzdt26dW3hwoV29uxZW7JkiVekUzFOs/iECRNcMPfu3esFPlOmTLE2bdpY3759PftJ0zv7HD58uP9+LySZ2UOSmV5IMoVILpJMEQpJ5jeSSVU4Ivjkk096ppImc6SQoHmcQp558+b5Hx5V41u3brWxY8d60zb9MmfMmGFvvPGGrVixwn8mq0mFOZlPCoKQ0RMnTqTe+YeRZGYPSWZ6IckUIrlIMkUoHlrJpC9kjRo1bM2aNV7YU6dOHXviiSe8D2apUqU8A0kTN8Mb8TuV35UqVfKiILKcjH1JhXqZMmV8P6+//rodOXLEzpw543+gf/rTnzzbyf4YBol+oPdCkpk9JJnphSRTiOQiyRSheGglE+k7d+6c95ukvyU/k208ffq0R1S4QyCaDElEtTlZT2Awdvpt0pQ+c+ZMO3jwoBfyMBj7yZMnbfXq1V70Q39OBnQvCJLM7CHJTC8kmUIkF0mmCMVDK5kFBRlFQhFPinmQywikkmW8RnYzylbyM2KJkNIvE/EsCJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGInWQyNiXjUOYH41HyekFm18lFJJnZQ5KZXkgyhUgukkwRilhJJhK5efNm27dvX2rJ97lw4YK/ziw9cUSSmT0kmemFJFOI5CLJFKGIlWSSoWzRooVVrVrVunXrZiNHjrQlS5b4POJffPGFTZ8+3ecWZ4rIOCLJzB6SzPRCkilEcpFkilDEQjLJYDK1I5JZp04dq169uo0dO9bnBh89erT17NnTWrVqZa1bt/bfCzpXeK4hycweksz0QpIpRHKRZIpQxEIyz549a8uXL7dVq1ZZtWrVrHPnzt4sPmPGDOvSpYuVK1fOXnzxRatfv74dPXr0e/OLxwlJZvaQZKYXkkwhkoskU4QiFpK5ZcsWe+edd+z111+3p59+2t58803PWlauXNnefvtt6927t3Xv3t3atGljc+fOtatXr6a2jBeSzOwhyUwvJJlCJBdJpghFLCTz0qVLLpqbNm3yvpgIZ6lSpVwwWUYfzIMHD9qYMWOsfPnyduLEiVhWmEsys4ckM72QZAqRXCSZIhSxkEykcerUqS5giBiFP/Xq1fPmcrKZLVu2tLZt21qHDh2UyRSFQpKZXkgyhUgukkwRilhI5q5du6xp06b21ltvWenSpb3ZvFGjRrZ48WLvi4lwIp61a9d2IVWfTJEuksz0QpIpRHKRZIpQxEIy9+zZ8+3QRc8++6z98Y9/dMkcMWKEvfzyy9asWTN7//33fdn69eu9Ej2OSDKzhyQzvZBkCpFcJJkiFLGQzIsXL9q6dev8xi9atKj3x+zatasPXfTII494NpOK8wkTJtgHH3ygcTJF2kgy0wtJphDJRZIpQhELyTxw4ID16NHDBg4c6P0vaR7v2LGjLViwwEqWLOnCGRUG8Ydx+vRpFf6ItJBkpheSTCGSiyRThCIWknnlyhXbu3evy+aOHTvs008/dak8fPiwF/rQZ5N1mFbys88+U3O5SBtJZnohyRQiuUgyRShiIZlAZvKrr77yYG5yRPL69et2/vx5X4ZkHjt2zEX01q1bqa3ihSQze0gy0wtJphDJRZIpQhEbyUQs165daytXrrTt27d7k3gEArpt2zYf5mjFihUun3FEkpk9JJnphSRTiOQiyRShiI1kMrVk2bJlrXjx4ta8eXMfviiCwdqHDh3qQxhRIKTmcpEuksz0QpIpRHKRZIpQxEoyGSOTbOXWrVvt888/9+V37tyxYcOG+TBGzPhDxjOORT8gycweksz0QpIpRHKRZIpQxEoyy5QpYwsXLrTVq1fboEGDbPjw4T5fea9evWz+/Pl2/Pjx1NrxRJKZPSSZ6YUkU4jkIskUoch5yUQuqSQng/nSSy+5TK5atcrHyGzdurW99tpr3nyOeMY1gxkhycweksz0QpIpRHKRZIpQ5LxkUjE+Z84cF7AXXnjBBgwYYIsWLfKhiz766CNr3769ZzPHjh1ru3fvTm3149DETjX6hg0b7MyZMy6nVKnTn5PCIoZE4negcp1hkZBYmulPnjzpy9mGYZXWrFljGzdutCNHjnhVO8vJqFKkhAzv37+/wHOpSzKzhyQzvZBkCpFcJJkiFDkvmYjb0aNHbfLkyV7YU6lSJevfv78PVYQsAkKHbBII3Y9lNHnt8uXLLoYUES1ZssSr0ZFLBnZnGVNYIpUIJu9drVo1z5gyCPz06dP9fZmFqEOHDlaiRAl7++23bfDgwS6myOv48eN9OXOsd+nSxeX3x44pQpKZPSSZ6YUkU4jkIskUoYhFn8zbt2/btWvXfLrIzZs325QpU7z5nGGMED6Kfch2IodMLYno/RBUnpNhpIjoqaee8qwoMwXR/E5GdN++fdauXTuvVidTidAyyxDbUFjEe3AcZE5Zj2wqwyZVqFDBs5Yff/yxiyV/pGQ3a9So4TMTcYz3QpKZPSSZ6YUkU4jkIskUoYhN4Q+SiVgicEgm2ct+/fq5GCKANHGTfVy6dOmPjpOJZH7xxRc2a9Ys+9Of/uSZzNmzZ/uc52zL+4waNcor1slaksWcNm2anThxwtft1q2bN5GT1URE9+zZ4zJKdfuyZcs8u8kxMisRx9GpUyffnozo3Rw8eNDGjRtn9evX9yhSpIhvLx48ksz0QpIpRHKRZIpQxEIyyVjSBxMBo6KcqSWjZWQamdd85MiRtnz5cvvyyy898/lD8BqieerUKa9WRwzJfjZo0MD7f9I8j3SOGDHC902TN5lO5JM+nMyfjuSyLVlMprJEWnv37u2/v/fee56NZP9kL9kPzecc891E4so+CZrYkVLx4JFkpheSTCGSiyRThCIWkkmzM9lFZC1vRpCmcqRyyJAh3h+TjGFBoU8lg7sjmey3YcOG3qeSfX7yySeepSRrST/NnTt3ujAimwydhDiWKlXKm+jpA8rxIaQ0p1evXt2FkwHi2YZmddanmf9eqLk8e0gy0wtJphDJRZIpQhGb5nIKZwiKcchEInD8TOaRfxG9glaXQ17JJANJc3dUIY6s8kfG+JtvvfWWyyUySRM9y0aPHu0FSDNmzHAxPXTokDeRI5k0e/ft29er0DlGMpQIKxXq90KSmT0kmemFJFOI5CLJFKGIlWTSx5ExMym0YbghfkYsDx8+7MMGRcMOFYS8kkkgiRTtIJNREzyy2apVK5s0aZI3pdM8jwhSLETmNGq6Z/YhCnxoZkcwCfqJ0sROX0+a8ikKuheSzOwhyUwvJJlCJBdJpghFbCSTvpQ0ldMvExljyCCyhPwxIHVdu3b1wdl5vSCymVcyyWCShaSfJVXmFStW9Iwl8soMQwxR9OGHH3qWsm7dup6lRHKbNGnifTkpPqKIaNu2bS6+CGrVqlW9MIkhkSgg+rGK9whJZvaQZKYXkkwhkoskU4QiFpJJFpOmZ4YXQuw6duzo41ouXrzY+2MyhiZZR4pmihUr5tXeNHv/GDS5sx1N3fyMILI9soposn+a4RFKZJFMZ5TdjMbJJMPZuXNn6969uw8Sz9BGyCRV6iynTyeySuW7xsnMbSSZ6YUkU4jkIskUoYiFZJKZpPmZvpONGjWyiRMnenU5WUj6RzKMEEJIcU3lypVd6hDHdGB7KsLpd0nGFKkF5JD3J0PJ++QdHolB3Wmup79l3kHgWYeKc4ZUYlrMewlvhCQze0gy0wtJphDJRZIpQhELyWQ6xypVqnhFN0MKkTWkfyQ/M285s/fQ/xGhQ+zIMv7YMEa5iiQze0gy0wtJphDJRZIpQhELyYyyjOvXr/eCm3fffdf7XpItJMtI1pEsYjT7D//GEUlm9pBkpheSTCGSiyRThCI2hT9IJP0dkbBy5cp5MQ59Iek/Sb9Hok+fPt58TjN2HJFkZg9JZnohyRQiuUgyRShiIZn0cWSIIprEqSCnyptq77/+9a/+x8Bg502bNvWB0Bm7kv6RcUSSmT0kmemFJFOI5CLJFKGIhWTSVD5v3jwv9KGpnOwlY1q++uqrPkYlFeAMY8TwQlR4q7lcpIskM72QZAqRXCSZIhSxkEz6XlLsU6dOHR+Pkmbx+fPn+xiUVJKfOXPGXyfDKckUhUGSmV5IMoVILpJMEYpYSCaV4vSzpMinWrVqVqRIEZfNJ554wivOGVT9xRdftKefftoznQxvFEckmdlDkpleSDKFSC6STBGK2BT+RDCc0fLly33cTAY9Z8iiNWvW+FSTNKcznFG6Y2TmCpLM7CHJTC8kmUIkF0mmCEUsJJPBzMlkUvgTBcU9BK9Rec4sP8wpzlziDHkURySZ2UOSmV5IMoVILpJMEYpYSCaV5VOmTPHMJRlLgmwmUz9S9INUMlMPUzkyNeSFCxdSW8YLSWb2kGSmF5JMIZKLJFOEIhaSSYbyP/7jP6xGjRpe/PPee+95JfkHH3zgzeXHjh2zAwcO2NChQ+3JJ5/03+OIJDN7SDLTC0mmEMlFkilCEQvJpM9liRIlbN++fT7rD/0xmTMcmZw6daq1aNHCx8hkmsmnnnpKkinSRpKZXkgyhUgukkwRilhIJk3hZcqU8arxadOmWbdu3Xy2n44dO/rMP8xrzrI5c+Z41pPB2+OIJDN7SDLTC0mmEMlFkilCEQvJJHNZrFgxW7Jkic/uQ7/Ltm3b+uw/yGbv3r197EyymhcvXtQ4mSJtJJnphSRTiOQiyRShiIVkMiwRY2Fy448aNcrGjBnjc5RPmDDBm9AZ1mjkyJFe+IOIKpMp0kWSmV5IMoVILpJMEYpYSOaJEye8upwbf9KkSf7z+PHjbe7cuXb48GE7dOiQ7d+/33+vXLmyBmMXaSPJTC/eGrrOTly8nnNx41Y8WzGEyCUkmSIUsZBMZvw5evSovfnmmz7gOhnMdu3aecaS17p06eKZzD179tjkyZPt0qVLPnZm3JBkZg9JZnrx783n2m/aL8y5WLzzZOqKCiEKiyRThCIWkgmnTp36dtrI0qVL23PPPWdt2rTxeOWVV6xRo0a2bt06HzeTAdrjiCQze0gykxFzt32ZuqJCiMIiyRShiIVkkpVEHp9//nkv9qlZs6b95S9/sXHjxnnQF7Np06Y2ZMiQ1BbxRJKZPSSZyQhJphCZI8kUoYiNZJ49e9bHw6TI55NPPrEBAwakXv17n00Kgnr27JlaEk8kmdlDkpmMkGQKkTmSTBGK2EjmzZs3vcDnypUr3ufyzJkzqVfNhyyiP+aGDfGueJVkZg9JZjJCkilE5kgyRShi0ycT0aTIh3+Ju8fCpB8mIhpnJJnZQ5KZjJBkCpE5kkwRilhIJvJIdTlDF9EHc+zYsT7wOmNifvjhh9asWTNr2LCh1atXz6vOz58/n9oyXkgys4ckMxkhyRQicySZIhSxkcwjR4740EX0vaRvZvPmzW3Lli0unMwCVKdOHfvrX//q42fSpB5HJJnZQ5KZjJBkCpE5kkwRilhIJs3k9MPcuXOn7dixw6eVrF+/furVv8MMQE2aNEn9Fk8kmdlDkpmMkGQKkTmSTBGKWEgm/S2RzCgGDRpkDRo0+N6ywYMHW+PGjVNbpEdUWEQxEbMFnTt3zgd6531pemfZhQsX7MaNG9+uzxzprM+6165d8+Vw9epVr4QnLl++nNY86pLM7CHJTEZIMoXIHEmmCEUsJJMpI7t27Wrdu3f3KF++vL344osuZES0rEqVKqkt0gN5XLNmje/j1VdfterVq/sUlbt37/Z+niVLlrQPPvjAVqxY4esjle3bt7c33njDateu7f1DI2jOf+edd6xixYrWv3//tPqHSjKzhyQzGSHJFCJzJJkiFLGQzOPHj9vEiRNd5oi6deu6+EW/R8tq1KiR2iI9du3a5c3tyOr8+fOtZcuWPpMQY3FWq1bNhZMm+jFjxrjwUnDE+yGUZFARYPqMrl+/3tq2bev7oUiJbOv27du/l+n8MSSZ2UOSmYyQZAqROZJMEYpYSCZN0MjdwYMHPRAxZv2Jfid69OhR6D+KzZs3+x9Vv379fGYhRPHtt9/2AqPevXt7NhKRHTZsmE2fPt0lkvnSkdPVq1dbnz59bN68eda3b18XTiSUY+rYsaPNnj3bB4vPD5az7sCBAz1KlCjhMisePJLMZIQkU4jMkWSKUMRCMunXSMX44cOHv5VMsoR5yaTwB4Fle/p0Ll++3OdBL1OmjGc0ly1b5pnItWvXeuYSiaQJfebMmS6kNKlT0Y5gUoxEpfvevXt9rvXJkyd7/1F+zw8+C0MysR1RpEgR69ChQ+pV8SCRZCYjJJlCZI4kU4QiFpJJEc6+ffs8k0g/R5qw33vvvW+LbCjAIRNYWMlECGkSp38l86Ajm/SrpB8m01hSFES2c+TIkZ7drFWrli1dutQznAcOHHCZpI8mzfWTJk2yY8eO+XHNmTPHhZiK+IKg5vLsIclMRkgyhcgcSaYIRSwkMxonc8aMGd7XkbExyTwidBTYlCpVyl5++WXPQBYG+mEid7wHVeRII30+X3jhBdu4caMXBq1bt877X7Zq1cqzqAsWLHC5ZTpLjoVB4MlG0neUjCviyrGS+ZRk5j6SzGSEJFOIzJFkilDEprmcbCZ9GL/88ksvBCJbiBQif/SLXLVqVYFl7m6mTZvmWVC2530o+KlcubIP8E6xD0Mk0TxO30sypvTTRDjJYlLs07NnT/89ep1liCZ9N/mdLGxBkGRmD0lmMkKSKUTmSDJFKGIhmfcbRJUinaZNm3pVeaVKlTxjSf9KhkUiI0kTOllJBJJ+mzStI5A0r5PZZDn7YXv6VdK0z5BIFATRdF4QJJnZQ5KZjJBkCpE5kkwRithJJn0kqcimTyTBz4cOHfIMZGFBAmn+pmK9bNmyXthDf0r6YbKMAiD6gFKkQz9QmsmZ1pI+m8yZTkU4ywmyoDTb81pUAc+g7gVBkpk9JJnJCEmmEJkjyRShiJ1kInu/+c1vvL/kc889Z48//rgNHTrUm9FDgxwilPTZZEpLZvABZvyhCZ0B3Dds2PC9AdcRzW3btrkAM1MQU2IWFElm9pBkJiMkmUJkjiRThCJ2komI0feRwhqKbkqXLu1Cl47MpUPUH/Srr75yuYyIpqIk8k4dyXLWpVgonSklQZKZPSSZyQhJphCZI8kUoYidZNJ0TV9JYN5w+j1S9JMEJJnZQ5KZjJBkCpE5kkwRilhIJk3Wixcv9oHRmYmnWbNmXnxDv8miRYv62Jn8zusrV67MqH9mNpFkZg9JZjJCkilE5kgyRShiIZkMAUQVNwL20ksvWYUKFaxXr15eEf7rX//ax6dkGCGGDGJ4oYsXL6a2jBeSzOwhyUxGSDKFyBxJpghFLCSToh6GEWIw9nLlyvnNTxaTgc+ZipGhhZgjnHnFGfOS4ps4IsnMHpLMZIQkU4jMkWSKUMRCMinqYf5wgqGBmA+cJnEGZWfIIZrSo9eJvAU6cUKSmT0kmckISaYQmSPJFKGIXeEP/THzVpczpSTV5elWcucikszsIclMRkgyhcgcSaYIRewks0WLFj7dI4Oe0w+zePHi3lTOuJVxJ+mSufXoBeuxYHdOxmt9V+YrLYp4hSRTiMyRZIpQxE4yx48f71M3tmvXzoOfV6xY8b0B0eNK0iVz7NrD+YqBQhEqJJlCZI4kU4QidpJJ/8y7m8YZ/JzZeeLaFzNCkqlQZBaSTCEyR5IpQhE7yfziiy+8P2Zetm/f7sMcIZtxRpKpUGQWkkwhMkeSKUIRK8kkUzlw4EDvgwlkNJkfvFWrVr487k3mkkyFIrOQZAqROZJMEYrYSSYiNnz4cG8eZ/xMZvupXLmyDRs2LLbjY0ZIMhWKzEKSKUTmSDJFKGLXXN68eXPr1q2bbd682SZPnmy1a9e2mjVr2qxZs1JrxBdJpkKRWUgyhcgcSaYIRSwkk6wlQxQRdevW9Vl/mEqydOnSNnfuXKtevbr169fv23XiOmamJFOhyCwkmUJkjiRThCIWkrl//37r0qWLMTf5448/bj//+c/t9ddf94HZO3ToYMWKFXPxZB3GztTc5bmJJFNxv0OSKUTmSDJFKGIhmUePHrXRo0f7GJlPPvmk/eQnP/HpJIcMGWLjxo3zjGaNGjV8HeYzv3LlSmrLeCHJVCgyC0mmEJkjyRShiIVkIo27d++2vXv32ptvvml//vOfrUmTJj6P+YQJE+ytt97yjCbTTMZ5KCNJpkKRWUgyhcgcSaYIRewKf5hWEqGk0IfmcqSsSpUqNmbMmNQa8UWSqVBkFpJMITJHkilCETvJbNmypY0YMcKLe86cOWOtW7e2hg0bunTeuHEjtVY8kWQqFJmFJFOIzJFkilDESjIRy0gyo98p8mnbtq0PbbR06VJfHlckmQpFZiHJFCJzJJkiFLGSTAZj37Vrl08tmZctW7bY2rVr7fDhw6kl8USSqVBkFpJMITJHkilCERvJJGt57tw5O3v2rF27ds1u3rzpv7N8w4YNPn85y+KMJFOhyCwkmUJkjiRThCIWkok8MoXkp59+ahs3brRjx4550A8T4WTecs34k/tIMhX3OySZQmSOJFOEIhaSeeLECZs2bZoNHjzYx8VkSkn6X5YoUcLH0KQ/5qBBg1xGCZrV44gkU6HILCSZQmSOJFOEIucl8/bt27Zt2zafRvLpp5/2aSUZlJ2B2F944QX7+OOPfQgjBG3NmjW2fv362FaZSzIVisxCkilE5kgyRShyXjLJStL3csWKFV5ZXqtWLZexRo0a2RNPPGEdO3a0V155xQdp79Onjw0dOtTnLy8MyCnjbX7yySdeXEQhUY8ePaxp06b+R0eBUbQeFe4cT7du3WzJkiW+HJDedu3a2YcffmhTp05N61gkmQpFZiHJFCJzJJkiFLGQTIRv+PDhLnQMxI7g9evXz4oUKWLTp0+3ihUr2vvvv+9N6KtWrSpUJvP69eu2c+dOz5SyT36eO3euVa1a1fr27evjcU6ePNn7htJczx9gp06dPHr37m2nT5/2WYk6d+7szfe9evXyGYmYpaigBUmSTIUis5BkCpE5kkwRilhIJtNFIpc9e/b07CAy99lnn/kg7EeOHHGpQ0ILC+9x6NAhz1pWrlzZ5s2b55lTRLFNmzZe0U6Gkyb6hQsX2oABA3zmoa1bt7rYdu3a1eUW+SWLiZwyvSXHxfoMGl8QJJkKRWYhyRQicySZIhSxKPwB5iNH6lauXGn79++348eP2+zZs23Tpk0+GDvyWVjIfC5YsMB+9atfWYMGDVwmyUiSiUQSqWBHIkePHu0iyh8f70dWk4zn2LFjvcId6R02bJiP5Xny5EmfV53fEc784DPRnH7q1CkPtu/evXvq1eQhyVTc75BkCpE5kkwRithIJtlGpIxm61GjRnmTNVlHxI/MJiJYWHbs2OFyV7ZsWVu3bp2L4auvvmrPP/+898NEQnk/3rdVq1beL5R+mPQVPXDggDej0ze0Ro0aNnHiRK94J3s5Z84cz75+/vnnqXf6PiynC8DLL7/s8eijj7owJxVJpuJ+hyRTiMyRZIpQxEIykTEKfWhOfuqpp+yZZ56x1157zaWMgp/GjRv7a2Qead4+f/58asuCQZM329HkTt9KsqMU+5QrV87H5kQyGfCdoiKKfah0X7RokTej0+eSTCbN5PTnRDLpQ8p+PvroI5dIJDY/mBITQV6+fLkH0tylS5fUq8lDkqm43yHJFCJzJJkiFLGQTKSNJuyRI0d6hpFqcoYtItNI0MRNcQ6SiPBduXIltWXBQPAo4JkyZYpvS7N8s2bNrGTJkj4+J8vop0mxEf00EUH6aHJcCCnLeX+a2BFR+ouSzWQ5QZ/SgqA+mQpFZiHJFCJzJJkiFLFpLo9gmCKEkz6SVHWTVYyyh4WFPpQILMVFUWFPvXr1rFKlSl61zvibCCRN6vTdpC8oWdOZM2f6dhT4sBwRRVYRTYYyqlmzpksqg8kXBEmmQpFZSDKFyBxJpghF7CSTpnMKf2jCZtghfqYf5cGDB1NrpA9DDNEsznBFpUqVsuLFi7vMMl5m0aJFXWRpnqd/JYU6FPyUL1/e3n33XatQoYLVrl3blxM0p/Na9erVfVsKg+hLWhAkmQpFZiHJFCJzJJkiFLGTTISNzOPixYtd4Cj4QRJv3bqVWiN9KCpiH/SxpGCH/pSXL1/24D0o7KGqHbm8c+eOvxdSy1BF8+fP959Zzn5YZ9myZT7WJkKMCLO8IEgyFYrMQpIpROZIMkUoYieZCNukSZO8EIjsY0EHOi8MkXzS3E2WMq/I8jNCSoV53kwl02BeuHDBhyQi21pQwQRJpkKRWUgyhcgcSaYIRSybyxkuCMk8duyYS11SkGQqFJmFJFOIzJFkilDERjJpjqYpmqIcxpKkOTppSDIVisxCkilE5kgyRShiIZk0WTPDDzPoUGTDYOk0U0fFNnmDfpQIaRyRZCoUmYUkU4jMkWSKUOS8ZNL3kb6X1apV8yGBEE2C+cIRsigYXojxKxnHkkHO44gkU6HILCSZQmSOJFOEIuclk6IaJBPBZBihcePG+dBCTCc5fvz47wUDsTNmZrqDsecKkkyFIrOQZAqROZJMEYqcl0yavqnuZrggspdM/8hsO8y0w5SOeYOZdfbt21fgcSlzDUmmQpFZSDKFyBxJpghFbAp/aDZn4PX27dv7zDzM+BPXvpc/hCRTocgsJJlCZI4kU4QiNpIZQaYSyWQWnvPnzydKNCWZCkVmIckUInMkmSIUsZNMMppz5szxucOHDx/u1eRJQZKpUGQWkkwhMkeSKUIRO8kEBmHfsGGDbd++Pbb9L/NDkqlQZBaSTCEyR5IpQhE7yaQICMGcPXu2TZkyxWbOnOnzmO/evTu2VeURkkyFIrOQZAqROZJMEYpYFf7s2rXLPv74Yxs5cqT16dPHq82ZYrJbt242ePBgW7JkiV27di2t+cJzCUmmQpFZSDKFyBxJpghFbCSTAdabNGniQxhNnTrVtm7d6tXmNJkzvFHdunXt7bff9mUIaRyRZCoUmYUkU4jMkWSKUMRGMs+ePWslSpSw+fPne7aSvpjIJP9ev37dZsyYYS1atLB58+b563FEkqlQZBaSTCEyR5IpQhGrTCYV5e+//74NHDjQFi5caOvWrbOVK1f6LEANGzb0144ePWq3b99ObRUvJJkKRWYhyRQicySZIhSxkcybN2/a6tWrXTCZp7xfv37eD3PIkCG+bNCgQT7dZFwFEySZCkVmIckUInMkmSIUsZHMCKrIJ02a5DP/IGX00WQec/po3rhxI7VWPJFkKhSZhSRTiMyRZIpQxEYyqRi/dOmSN5EzCPuHH37oTeT8ISCaiCfzlyuTmbtIMhX3OySZQmSOJFOEIjaSycw+nTt3tnbt2tmYMWN87vJPP/3U/504caLVqVPHatWq5QO1q09mbiLJVNzvkGQKkTmSTBGK2EjmuXPnrHz58j4AO8U9Fy5c8MHXKQj68ssvbcSIEV74s3z5cq82jyOSTIUis5BkCpE5kkwRithI5vnz5+29997zAdgZF3Pz5s0+OPuOHTt8EHYGZaf6/PPPP4/tVJOSTIUis5BkCpE5kkwRithIJtnJadOmWcuWLa1169ZeUU6z+ahRo6xHjx7WqlUrrzRn7EzN+JObSDIV9zskmUJkjiRThCI2khlBcQ8z/tA/k4IfMpsfffRR7It+QJKpUGQWkkwhMkeSKUIRO8lkqCL6XzZr1sxq167txT7IJnOanz59OrVWPJFkKhSZhSRTiMyRZIpQxEYyr1696uNhMgg7/86ePdvFcvr06T6kEYLWoUMHF01Vl+cmkkzF/Q5JphCZI8kUoYhV4U/VqlVt2LBhns08fvy4nTlzxivLKfahX2bdunVtw4YNsR2UXZKpUGQWtcd+aj0W7M656Lt4r529cjP1lyBEbiPJFKGIjWQyhFGlSpVs5MiRtm3bNvviiy/sxIkTPi4mswAxxSSSxmDtmUgm01ey/wMHDvjg71SxMxYnYhs1x5MpRWzXrFljmzZtsiNHjvhyOHTokK1fv96PY9++fWlVuksyFYpkxiMtPrF9py6n/hKEyG0kmSIUsZFMxsQcMGCAZzOZ6Wfo0KFeADR+/HgfoL1KlSpedY4kFra6HHk8ePCgVa9e3ZgfHcF8++237bXXXrN69erZvHnzXBrPnj3rY3KWKlXKj4c+olS1UwFPc365cuXsjTfe8Ob7kydPFvh4JJkKRTJDkinihCRThCI2komoMesP4jdhwgSXwC5dulivXr28unzLli0+QHsmwxfR77NFixb2hz/8wQuKaJqvWbOmj8fJ+yC2ZDnpB0rR0cKFC110kVyq2xcsWODb00d07dq1vs7GjRv9uAuCJFOhSGZIMkWckGSKUMRGMiMYfJ3CH8bL5I+gQYMGLpxLly71fpuFJZoXnf0VK1bMZxdigHfG4eQ1BoAnY8l7U83OH+H+/ft9astBgwa5bLJ+7969fT80offt2/fbGYryg6zpuHHjrH79+h5FihTx7GdSkWQqHtaQZIo4IckUoYiNZNLPcvHixS5l9MtE9pA++mLSRN2tWzdfRjbzzp07qa0KBtnPPXv2uDyOHTvWKleubK+//ro3v9PvkmZw+lkinIgk86QjnfTRJINJZrVnz55eeMQx0J+T18iw8sdKn9H8oE8psxUxsDxRokQJ69SpU+rV5CHJVDysIckUcUKSKUIRG8lEHpE7ZA4xo6iGDCFCt3r1ap/xh76U27dv936Z6YAQzpkzx5vIDx8+7GNwlixZ0qWTZngElwIfpJYMKtNbcgwUI5HNnDhxojeZs/2kSZP8uKh8nzVrlmdZyb4WBDWXKxTJDEmmiBOSTBGK2EgmxTZkF8kgIpz0nyTDeO3aNW/OZspJRJN+kSxLB5rakUSymFStN2rUyIt92B+V5bwP/5JtbNu2rTVt2tSP49SpU7Zz506XTzKcFAORaUU8KfjhZySTSvSCIMlUKJIZkkwRJySZIhSxkUxEkv6K77zzjjVv3tyzh1R7ky2kqZzhjag6Z710m8upUKcf5quvvuoZzF/84hf2k5/8xIoWLeoV7UgtfSsp/oma6Pv06eNN7GRRmdqSJnwKg2i6X7Fihfe3RFxZxs8FQZKpUCQzJJkiTkgyRShiI5k0gS9fvtwmT57sGUUGX0f6kDpkjopumsrTFUygSIdMZRSILE3z/fv394wm78NQRvSXpH/lZ599ZhUrVvQ+mxQK0UzOcgIBZrij9u3bu7SuXLnSxbcgSDIVimSGJFPECUmmCEVsJJNxMrnxKcBhCKHGjRt75pIsJn8MSCf9J0NAf0sqxCnqQfpo8u7cubMPWUT/zIsXL9qQIUO+HUaJZnaWEzNnzvRtOC7+ZUaigk5zKclUKJIZkkwRJySZIhSx6pNZpkwZzwzSdF2tWjUfLoi+mAgdQwCRcQwJckhTOcLJTD5RX0+q0ekTypiZ9MnMOw4m/Tfpk0mhEEMqpZNZlWQqFMkMSaaIE5JMEYpYSSYz7MyfP9+bsWmSjgSOWXhYRrN1nJFkKhTJDEmmiBOSTBGK2EgmldzPPPOMD1PEQOlM58gwQYgmFeHREEJxRpKpUCQzJJkiTkgyRShiI5n0d1y2bJkPHUTWkqZxpnukCZsB0JGzRYsWpdaOJ5JMhSKZIckUcUKSKUIRG8kE+kIyADpV3Fu3bvUZc6g6p58m/SbpPxlnJJkKRTJDkinihCRThCJWkpl0JJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzh5BkKhTJDEmmiBOSTBEKSWYOIclUKJIZkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGZJMESckmSIUkswcQpKpUCQzJJkiTkgyRSgkmd/w9ddf282bN+3MmTMeZ8+etatXr9pXX31l58+ft9OnT9uFCxfsxo0b365/8eJFX/fcuXN27do1Xw5sx/bE5cuX7c6dO6lX7o0kU6FIZkgyRZyQZIpQSDK/AcFcu3atlS9f3sqVK2eVKlWyiRMn2o4dO6xevXpWsmRJ++CDD2zFihW+PlLZvn17e+ONN6x27do2depUXw6jRo2yd955xypWrGj9+/d3SS0okkyFIpkhyRRxQpIpQiHJ/IY9e/bYpEmTbPDgwbZs2TJr06aNde3a1UaPHm3VqlWzuXPnWqdOnWzMmDG2f/9+W7JkidWtW9eFkm1Y98iRI7Z+/Xpr27atde/e3aZMmWINGjSw7du3fy/T+WNIMhWKZIYkU8QJSaYIhSTzG44fP26bN2+2gwcP2q1bt6x3795Wo0YNz17yM9lIspXDhg2z6dOnu0R26dLFdu3aZatXr7Y+ffrYvHnzrG/fvi6cSCj76tixo82ePdtOnDiReqfvw3LWHThwoEeJEiVcZpOKJFPxsIYkU8QJSaYIhSQzD/S1pO8lmczixYvbe++955lNMpE0p5O5RCJpQp85c6adPHnSdu/ebePHj3fBrF+/vo0YMcL27t1rp06dssmTJ9ugQYP89/xARMeNG+fbEUWKFLEOHTqkXk0ekkzFwxqSTBEnJJkiFJLMFAgmhT1Lly61hg0bev/M1q1b29atW73PJpnOkSNHWosWLaxWrVq+HhnOAwcOuEzSR5PsJ83ux44d88KfOXPmePM3fTsLgprLFYpkhiRTxAlJpgiFJDMFzeT0q6TwB5kkEMeNGze6fK5bt877X7Zq1cr7Wi5YsMCry+nPSd/Ndu3aeTaSgqHDhw97JpN+mWQ+JZl/R5KpeFhDkinihCRThEKS+Q0MM/T5559bkyZNvs08rlmzxvr16+fFPpcuXfLmcfpe0neSfpoIJ1lMin169uzpv0evswzRpO8mv+/bty/1Tj+OJFOhSGZIMkWckGSKUEgyv4Hm7SFDhthjjz3mWUr6V9K3EuGrUqWKZyQbN27sWUkEcvny5T50EQLZuXNn34blZDvpz0m/SoqEaHKnIIim84IgyVQokhmSTBEnJJkiFJLMbyDTiGQihcgkVeUIJEU5NWvWtJYtW3oREL8z2DrN5M2bN/f16L9JRTjLiQEDBlijRo38NbaNKtYLgiRToUhmSDJFnJBkilBIMn8E5BChnD9/vu3cudNn8AGKhGhCp0l9w4YN3xtwHdHctm2bFwYxU9Dt27dTr9wbSaZCkcyQZIo4IckUoZBk3gP6a16/ft2nmEQuI/iZqnMi79SRLGddioXSmVISJJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzhwglmbfufG2jVh+yHgt251RUHrE+3wewQpH0kGSKOCHJFKGQZOYQoSTzxq07VvRvy/J92CkUigcfkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGb9o8bGtO3DWTly8nlNx6fqt1P8aQnyHJFOEQpKZQ0gyFYpkxk+bzrYn2s6337RfmFPR+eNdqf81hPgOSaYIhSQzh5BkKhSKBxn/M21b6n8NIb5DkilCIcnMISSZCoXiQYYkU+SHJFOEQpKZQ0gyFQrFgwxJpsgPSaYIhSQzh5BkKhSKBxmSTJEfkkwRCklmDiHJVCgUDzIkmSI/JJkiFJLMHEKSqVAoHmRIMkV+SDJFKCSZ94G9e/fa5MmTbdiwYbZw4UI7efJk6pUfR5KpUCgeZEgyRX5IMkUoJJmBOX/+vE2cONGqVatmjRo1sqZNm9q6devs5s2bqTV+GEmmQqF4kPH2sPW28PMTORlHzl1L/Y8mHjSSTBEKSWZgVq1aZV26dLEePXrY9evXrWXLlvbRRx/Zl19+mVrjO7766iu7dOmSnTp1yqNBgwbWpk2bb38vbBw9fsKebzvDflpvnP2s/nhFwOCc6ryGj5/WH2f/p+7YfF9TZB5xvG/7f7wp3//fci1oqcpveZyjW7duVq9evdSTSojCI8kMzOjRo6179+62fPlyl0gEk2Wffvppao3v+Pzzz/2P+eWXX/b4+c9/bo888si3vxc2ir30kv37L5+w//tfT9uvnnlOETD+4/Hf2L89+mS+rykKH//vyWftZ//3cXvst3/I93VFZvHvjz1p//HYb/J9LVfjDy8Uzff/t1yK559/3n7729/aS9/8n5vf63GNxx57zCpWrJh6UglReCSZgRk0aJD17t3bBfLWrVu2ePFiGzx4sC1btiy1xndcvHjRdu/e7UJKzJ8/3xYsWPDt74WNRYsWWbFixTyjmt/risJH3bp1rXLlyvm+pih89O/f35555hmbMWNGvq8rMot3333Xateune9risIHCYUXX3zR/+/O7/W4Bs+QTZs2pZ5UQhQeSWZghgwZYv369XN5jCSTByh/tA8K+n+WLl3aZs2alVoiQkHmmb6zIiwrVqywokWLFrhITqRH69atrVOnTqnfRCg+/vhjK1mypF29ejW1RAiRF0lmYCZNmuSdpteuXevN5VOnTrW+ffv6t8MHhSTz/iHJvD9IMu8vksz7gyRTiB9HkhmYNWvWuGQyfBEdqDt27GgDBw60rVu3pta4/yCZ9KfhP0ARFrpCtG3bNvWbCMXq1avttdde878ZER7+HwoxcoX4PnRvKl++vCRTiB9AkhmYCxcu2IABA+zVV1+15s2b2+9+9zsf0ujy5cupNe4/NNOPGjXKduzYkVoiQrF06VLJ+33gwIED/mXsQf6dPEzMmzfPu+6IsOzcudOGDx9eoCHqhHgYkWQG5vbt2z4YO83kPDRpPj906JDduXMntcb95+uvv7Zjx47ZlStXUktEKM6dO2enT59O/SZCce3aNTty5Ij//YjwnDlzxs6ePZv6TYSC/2P5v/ZB/v8uRJyQZN4HyCQiI1SYMzg7vwshhBBCPExIMoUQQgghRHAkmQmDrCnZU5rH6B9648aN1CsiU2hupDCF5nIy1YweQNcEUThoYmSs2Khogt9172YO9yTnlHMInFd+pnKfe5fzq3s3PThXzODGuYu6HvA7fTGjLjScY/XNFOL7SDITBgUUzDlbqlQpa9KkiS1ZsiT1iigsPGDoK1ilShUfZodzW6NGDduyZYuqSgsJ4sODulWrVjZu3Dg/xzy8mcqO8/vBBx94kZVIH6aqpdiQv39AgPj5ueee83PL8GafffaZJD4NOFcLFy70SvJy5cpZpUqVbM6cObZ+/Xp77733rHjx4j6FcH4zuwnxMCPJTBDHjx/3aSyRoZkzZ/qYjiNGjFChSoaQndi3b581a9bMh6difvqNGzd65kKFKulDtv3EiRPWrl07e+WVV3w0Bub2nzBhgr3//vsuSIwty/1LtkgZt4LDlx6kvUKFCvbOO+/4uVu3bp0PX8Q55d5luCgyxipWKTjbtm3z+5NKcs4h/xf06dPHZ3PjixGV+23atPH/f8lsCiH+jiQzQTANGA9mHiiIJaLJDEQbNmxIrSEKA5mh2bNnW/Xq1f3hwvBQzOBEk6NIH84bkjlmzBgrW7asT8W6fft2a9Cggc/zf/ToUc8SMXg4IzWocK7gcK8ydiPnsmrVqi6SY8eOtcaNG/u9y5dO7l0NFZUeX3zxhbdc8C/ntEOHDlazZk0fpg7R5Iso9y6BkAoh/o4kM0HwbbpFixbeRM7QGsgl/+lNmzYttYYoDGQsyWLw4Gb+Z5rHyLgdPHhQfbAKAdlfMm4EzbhDhw71ZkeEk+ZG7l0mNWAIMISIbKYoGJwrziv3a61atVyIEMumTZtanTp1PFi+a9cufUkqBNy7ZIH5+6eJHHnnXmX5smXLbOTIkS75Qoi/I8lMEPznxpSHfOPmYcMsQ0gmmTdReDiXURaDBzgPlbp16/oYqOqKkBlk15BMpmGlvyDdEpAfZJMsPM2PnHORHpw3ZJLm8s2bN9vhw4f9PiZj/NJLL3lmnj6wouBwLskUz58/379svvnmm9a5c2cfqg6Z54sS9/KMGTNSWwghJJkJgkIJ+gXxnx2DW9NvkP/0+HYtCg8PELJrUUUuDxW6JfTs2dObdkXhiSSTrDv9CJlBhSILpLNfv34+qYEkM30iyQTuXTLu3Ltk38lm8uUT8RQFh3OIpDOb25QpUzzT3r17dy+iIpPJ/Pv0L54+fXpqCyGEJDNB8J8dnftpHqNJh+kP6ZxO30xReMhWdu3a1QsoOK/Lly+3atWqeYGKMpmZEUkm4k6TLn0xGSaKe5c54mmCVHN5+kSSifz06NHDv4CSheP/iBdeeMGzbbp3Cw5fNPkixP3Kl8v9+/d7t6T+/fu7cPIFNCpY0/SdQnyHJDNBUEzBt2iG1+A/PB7adFDnAS4KD0PtkKGgGhrZbN26tffPpF+bBCgzIsnk3qX7AeeVCt4PP/zQGjVqpKkmC0leyUSEEHbuXf4/oOqcrjQawqjgMDUwsv6b3/zGh9finPJlnuZyzvOsWbM8Q4xkIqBCiL8jyUwQVOHu2LHDqx4pAOI/PZrKJUKZQZaCpkWqnSn6YWxHMkGqes4c+gvTl5imSB7OjPFKMRCFFTzIySCJ9GGYIobbool8z549nn1DhuizTbaYQfBFweGLOgL51ltv+f2JaA4bNsy/EPF/Al+KOL+0GknehfgOSWbCQHwYp42BgxFODVUi4gJCSVM5fds00L2IA3wBZYxXxJ3htnTPCvF9JJkJhIc12cuoUEWIuMC9SyZI966IA9yjdEng/1u+4OueFeL7SDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQaUCfQfoLhpxOkn5c7DdX+nNxHEnsW8ZnCjUcUnTNxHd/EzofQoi7kWQKkQYMYE3lczRfcQgodGEszmhWlmxC8QIjElDIkDRp4DwzHufd143PSaRz7jlH3AsF3Yb17rUur3Ns6RxHtuF+OXnypA/yzsgAQgiRF0mmEHlgCj5m9GE8wSpVqvgg1kzTybBQSCDjDzK2I/MX5x0nk3UYKy+qjGZKzwkTJvig+AwynvcBfLdwMF83AzsvWrTIZxSCu4WDoVEYloqBtKNx+qJo3LixD8C/atUqn040Ew4cOODjKzKlI7PtMGh33mAebIZsyY9jx47552WsQGTux+BcMlQR03IyJzxzlbN/zl1eOAeMUcqYhHfPpMKUk/nNwc3MNps2bbLBgwf7eJCcO5YxYwtjGTKwNpLIubpw4YJfKwYpZz56xuls3ry5tWzZ0saMGePHBlwjlrEtx4hUcZ54D4au4fii7bh3GGSe3xnAm2Pks/EeTJBQr149nzGKf999910/Jgah5zWuJ8fJ8d4NU0Eyu8wPwb3CtsyWxPFxLzNGJueWsUjHjh3rM4AxsUDec4Yss28+B+cE4eZzd+zY8XvXkeW8Hg3XA3w5Yr+Mx7t7925fdjesy7XiyxnHP378eJ82lCkuGXOW98r79yCESA6STCHygHQghQ0bNrRXXnnFpY4HJMsQKCSkTJkyLhFDhgzx6fp4EPPgLVGihD/YkRpEFGFAQhjAmTFLgdcZ2JnXEUvmP0ZK2CeD6DPg+6BBg3yQZx7ezCrEgx3p4EH+L//yL/a73/3OihQp8m0888wz9s///M9+nPnJSUHhs3/yySf+mRFmxGPatGnfC84D8zfnB0LD8TNoNQLxQyBpzOSDLCN4iCbnj3n3kZ+8wsFn53O/+eabfj6Rk+h8MAPT3/72N39ffkdICaQJqULcEF+m/xs3bpyv+6c//cmPj3PLlwmkEQni2v71r3+1119/3dq3b+/XB6lduXKlyxNC/PLLL/vc6hw/n4/jevvtt326UUSS68n1ZkYo5LFLly5+zng9klTO7UsvvWS//vWv/d//+q//8utZvHhx3xeD0G/bts0/I/cJ++ReIP7yl79Y6dKlv/2d4P7gMwPnjWPlnuJe4LwiynzZ4b0ROj7n3YOxMwh+5cqV/X35khSNs1uuXDn/UsH55PzypYrXmTmIfSL/fCnh2rA9UsoxcV4QSQSUbRBfzgXLuYbRrE58YeMz8Rk49iiEEMlBkilEHnj48oBmqkOEkoczwsIUh2Sffv/739uTTz5pFSpUsPLly3umiinlunXrZs8//7w/nBEKHsRkpsgG/va3v/UHLSByZBzr169vb7zxhksPMluqVCkPRIZliCmyQoaUrBtyynGxLx7+vH8UCCrT3ZHBYr3CQPM4XQCQgapVq/p7k8XNG0gg0vJDGSs+N+eBmXqQtx+C5tXJkyf7+yCZvDeyzvlEciPRZDkCQqaP4P2RP84f69euXduljPNC9pT9IlbICyKJ/CCJiBrZXjKH3bt39/POlwiyasguGTpEimV8eeA8EIgVssSxclyvvvqqf8Yow8zPCGne6UXJRHMPMN0g2csIMrecF+4Xjrls2bJ+fyCNCCkCyKw8ZJCRM0AIEVHEjODee/HFF/1nBJ37hpmn8vYP5rNwrHPnznX5JmsZnWve4/jx4/65kFgEEFFE+IoVK+biSAaY4+fLAueP881xIORsB9wDkUAj/dz3fAbOHwJZvXp1v5c5P3zh4npFgs015l/OG9lfPh9fXMjik3HVTERCJAtJphB54CHHvM+9evXy5lP+JdMTNYPyAOVBSpYPaeBBywP/8ccft3/4h3/wbCYPfh7SCBcPcR7CPEABOUEaya717t3bsz/sBxEgaM5EpsiIkSVCBBAYsqVIJA9ytkOiokBcOCYybzTL393kXBBoAkdw+HzsDwn685//7MJLlo0s3x//+EfvJoA4IFp8DoQQQSMQaTKgCEiUASNYh3XZJmomR/SQc14Hmkx5f+R63rx5LuMIIJJDtwWkiXWQdjK+SD9ihMxwzJxjhIcvBFyrF154wR599FGXSqQTkSLzyeckY8j1Y/+cK8Sca877kO3k/YsWLfqtdJNZJvsXSSafn+Pj2DnfUSYRfkgyuYY1atTwbB5ZVKZ9Ra5oUuce4/0RWtYh+wpI2Guvvebnj+A+i7K9yCLncPr06f4ZkEuOi9c4Bj4nmVAkHnHkSw1yy88s44sCn4EvU//6r//qGVzOGQIYSSLHwt8AX3w439EXBz4L14V7nGNGetkvks814h5BOlmfY0F6Obf/+I//aE899ZRVrFjRp2JEOJ999lmXZTK6bBNlNYUQyUCSKUQeIslEEqK+ckgAD0mEAylAXJBEhBKBIVPDA/y555779sFKkyWydrdk0txIsyTNhFETfCSZ/I5kIpj03yOThHAgLUgJ4odY8JDOG4gZD2xeQ5LYf7pwXIgJoooc8/noc8hx0NSMXCEdiBxSw+fiuMmilixZ0qWErNQvf/lLF27EhGW8RraO84HUcR4Qa84tohQJGv8i0mRQ2SefA0lDSJEZBI/PT6YR0UY2kRuuDVlMMnWILU29vA+iz9z9nAsydBw725Nh/tWvfuXvzzqIGNeP7DRCjVSRsUZ66OeKdCGZSG4kmUgowsf6fE7EKuKHJJPzy+fmWiHt7AuBRLCQeX7merNO1H+XLCQCyPkg/vM//9Mee+wx/xnp/+lPf+qyzPVAeMkwcq75DFwbhJbrxz55H+45fmYZ9x3XkHudpm62R9C5vzkOvlDxuZBWPj9fAMgSAxKI0HINOP98GeK9EHmyynQd4F+uBX9PiDBiz3Uj887++dvh/HH83Gtcb7bP289ZCBF/JJlC5CGSTB6sNGfSTEyzKg9vsjZIEFkYHq6ICZLJ+ggMAsDDGblAFBHGuyUTIUCCeCgjLAgOD3yyP2R8eA/2yfr8TAYQ+WI95I/j4LiQJgQIWUJwETrejywVGSqkDVlBhvgseQuP8gMh4HMiHGS02D9iQIYLgaW5mX6EvCfHThEHxx9JNoEkc27IeiEZ0XLWIRuMVJLFQ9hZj2PnPcicISBIIcKFJCFMCCLbcG7oIsA2nFf2TzcCrgUihhyR3UQyadLluBBkPgfnEBki88b6yBLSidjQvxKx5hqxnC8RSCxCzz7JUiOyd0smx8Q15jyQ8SyIZCJPSC2CxzXhGuYNlpFpRZijZmmyjOyf80cg0pwbfqb5GknjPHNPIbFRP9G8EklmkOD6IZDR79yDiCKSx3XlGLgWnEe+HHEvRM3r7JMvCVHWGWje5osR+yI7zd8D9ycCzv1KVpPPzPmgCIkvKvxtIJJsx98VoskXNs4ty8kWCyGShSRTiDxEkomUIAo8cHlAkmmieRcZQF4Qr5/97GcuFAgKy+gXST9OBIVMEkJ0t2TSrIkEIjn0FURqkCuaQWlqRiKQBJrG82b6eGjzIH7mmWdcBDkeModkCsm40QyJWEQiwPsgjpEw8POPQZMxzcMcAzJFMzyiSRMm8oO0UWSEqCEYUZNuXhCwH+uTyXvQpI5kIFw04ZKRQzDZhvdBnKJ+nwggx826rMfxsB7niz59fHbEiGtCpo59IzSIJRloMoacM64D74Go0i+T5nQymrwPmVnOLSLFZ+PckskkG0d/Tq7L3ZIZXROkluwgwhaRn2QijYgh78lxIMt8Bv7NG9w7ZBq5f/hSwLGTtYzg+JAyQOz47Egpkglcc+Sba4Ww8bkoTqPZnS8HXEvuOT53dD9wrugGwXshlYgg9wtfVpBAzin3ApIZyS8ZTZaxL84FmU2+6HB92DYv3Cfcy+yba4vAc/65x7mWnGv6ovLlg/cUQiQLSaYQeYgkEzFBeniok+1B6nig8xAm24aM/NM//ZPLCVkcMoks5+GOkCCeZPbulkygTxsyEEkVgkoRC5LBuggV75m3bxrSgfhSiUw2k/UoAmJb3vvpp5/2BzzNm8C2UbN2lFUqCDzoETEkhOPnPCBI7JfPzOs/1GfuXpKZF4STLCTZV84Fv3OOEJVINhAYjoNzimyRyeO8cg0QVLonIH4IFEKE9JE5RapYB9GkQIgMJRlBmsCROzJ3NFvTRIsQcn7IGiL8dDngvfgMSCYZNwQrb5/MvJLJNScjSvaOLw/5SSaFPNw7LONLBOcXKeO4CcST7CzLkXzEj+wogkihT5QRJgPM8fMz2VmOEwGPCn8iyUTaEGOynBQL8Z7sn2B7mvjJLAPbc+9xTRFKrglfphBJZJBlXFOWky3lPiITzJcXMszcyxQYsV/OKdcz77XniwICSUacTD/N5ZxHzivHwDZcV74gsa4QIllIMoXIQySZyCXZJUQkyljx0Eb0yASR9UPykAIyc4gMD32aIHlwIy30J4wkk4c/MhAJASAFbMs+aConq4YY8VDmOPJChpJ1aNYkC0RWiswcTc1k9ZAWhCrKUCENSAGZPcSInwsCUsHnRhTYjs+KZCESCAJZNoQwPwoqmUgaGS6kCaEiY4uIsW+adO/uU8p5QgA5TzQTI3xsT9YP+UHmEHv2w/lF9MgUc07YL0MUcVw0zyNniB3Xhv0SiBJShRzS/zMSIDKUZOz4IvFDmUyyydwXSCRdCDj/yFdeyeRaRE3HXEOOgWPi2JF4tiPYDpnnywHbkClEzPgSQTzyyCPe5xVhi5bxvuyX68tn4R7iHCJvZDrJUiLv7JfgCwNfTPgcQJcArkPUJ5OiMiSTY0Cc2S/iyDVlWfRlg+w+P5Nx5nxFY4by98L6nHeuBZ+De4cvB9yzyCnZYa4755djJUPOPV/QL0JCiPggyRQiD2SjyODRfMj4hmS5EJJf/OIXniFCXigWIdOEXCCRiCUPezKQCBjNt0gm2Udki4wbksID/u4mQR7uSAzZNYSC7BX7RhjygtCQ+SSzhdjQH5TqaZro+R2ZQAQieeCBjTjRZMyDPCrauBdIKeKKwPJ52B7BJpP7k5/8xH/ms+YH4kSTMELxY+Nk8vlYhwIQZB1p4/g4D8ggUhLBeUCiyDCSleMaIIVsE2XYEM5oGVKD4CCMXAd+5lxw7skU/9u//ZtfDzJnSBISxfEg6OybY6JqHdFGbDk+rilfEjjPyGd0bbg/kD4yg3xZ4FoiZhS6IKuRZCJbnA8ylgRfYpBKpJnjpzKb5nnOO19UuAZ8Hu5F7i/2S9CvkmZn7sloGWKIoHH8HBcCzjWjGZpjIntLlpf9EnQxyCuZ3Oc///nPv60uZzskk/MYnU++QCGPXAe+QCGKvB/3dJSZRTY5TxSOkRlFRDl39ClGTjnHSCiZX7LKnB9e57qSnefcs44QIllIMoXIAw92sixkkRhAnYHHyRwiakgehSBkG2l6JFOELFH8gCQgekholJnk4Uq2howTVeBsT2EEwkHmhwwQ/ezIRPIgJ3vK72Tg2D8P4qgwhWwikoDoEPTBpEqabGq0jEwjmVYyesgBYyHStMpn4OeCQAYVAUIAEDO2R0SQS0SEptL8+mMCcsi5Ihv2Q5JJJhJR4jxyrsj8kblEMsiocX4QwwjECXHj/HCuEdmISGjzCjSfky8JZC05x4gecoNw8r50QyCiIhS+MPAlgswjwbFzDpEozgP3AzKJHCK5fC7OLeKKeCJtdFPgOvNefA66M7CP6Lj4DPRn5LORaeQ8kc1EenkfvoxwnXmNLy7IYyR4kdACGULuOe4/jp97kr7BNGtzr7I+ld4INO9FVhqBY59cS4LrR+aQ88j6nCuOl+uM5HMPcu9yHyDq3Iu8B/cf9zPXnnNAdpQsKF0TuH7R/cW1o5sBXwDYJ/ci5497mfucY0F+kVYknowoy8hu8iWJzy6ESA6STCHyQAYJWSBzyMOf7ArZIbJLCAFCgUDwQEZeKGpAMMjkRA/cqJkckAseomQ2EVHW40HN9gRCSzaKhz4Pbx7w7B9BQnR5aJO5iiqkyVoR7I9+d/wbLeN1HvB5JS1TEBGysYgZ54Fz8kOQGUQikSWyXvmBuCEWfE4yX9H+2TdN85wbZCaC1zmHnP+7xRWJQWDydi0ga4hMcS64jlwHMm7IFceGNCJ0XAuyblw7zj1SxnVD1hAjstOR4HFNOc9cb7YHJJBjJWuJKLMu9wr75dohr+wjgtdZj8wpQkZGlM+MQEfNxHxurh37zg8ynpw7rnt0//BenMvouNg/9wvvxb/cQ/wcwfVDrnkfzi1fkDg/wLFE3SvIQHIeEVvua/4e8sK69EWNMqJ54fNxzji3HBfvwd8A0so9QnCPIJuIOMfHtaC7wN3dRIQQ8UaSKURgeHj/GFFTNkL7QyAcPHDvta8HAdKDOIQ4Fj57Xom8H3CckSDyL5HJsXOdEN1cuBYPCq45osk9mLcfcWHIez0i8lsmhEgekkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMoUQQgghRHAkmUIIIYQQIjiSTCGEEEIIERxJphBCCCGECI4kUwghhBBCBEeSKYQQQgghgiPJFEIIIYQQwZFkCiGEEEKI4EgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRGLP/H2S5DyniM30hAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F%E8%A1%A8%E7%A4%BA.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWgAAAByCAYAAAB+30ucAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADDmSURBVHhe7d2HlyZF1Qbw738SEyYUwQyKCRXMGFCMoKKomLMYEbOoKEbELIqYMQdMmHPOOft+59eeZ71b9js7C7NMz859zqnT1dWVurr7qVu3blX/36rRaDQai0QTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3Sj0WgsFE3QjUajsVA0QTcajcZC0QTdaDQaC0UTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3SjsWD8+9//nlzFvs4ravqN4s0haWseQc7r8V//+tfkh5omx2DuvKbdatS6BDXsQJZ9edEE3WgsHCETRDISTZBwx3/+85+TH/aVbh1qmuQR1Lzm/I41HJyP9Rj9Y5qtRMoP6vmBLPfyogm60dgBGAls7jxHBF3Pa7zNQppKqCO5VqSM0QVJO3ctWBd+eVHLXEfQS0YTdKOxYKwjrUo84zk3kk/i7Q/ksb/kOsbhTx5z5zAXtlVI3nNlHojythpN0I3GDsI6YhEWIoIQUnWXBWPaeh5/DasQlvqMcSLlV1cl/61EbReoZS4dTdCNxg5GJZqRdHJewzYLZBmSHyGsEl5FSDakmPSOcUH1HygoY1/1WHcvS0ATdKOxcIRk5ogmmAuPv55vFuKmzKDWIe63v/3t6pe//OXkfvOb3+xVRuL84x//mI5/+MMfVr/4xS9Wv/71ryf3t7/9bU8c7kCg5j+WsS58SWiCbjQWjjkiqef1etzcRGHON4sxDX8IWv7I+eMf//jqnHPOWZ1xxhmrs846a/XjH/94It7EjyQu/C1vecvqWc961uoVr3jF6p3vfOfqpz/96Z56xh0IjB1LcCDL3Co0QTcaCwaJ81e/+tXqL3/5yx4yGUklRJPwv//976uf/OQnE4FWKXV/UOOTgH/+859P+f31r3+dyE4YKfhjH/vY6nGPe9zqqKOOWt3ylrdcffazn1398Y9/3FOmeOrziU98YvWQhzxkddvb3nb1+Mc/fnXeeedNdYx0Dftbx81AfdX797///XRey0gdD0S5W4Um6EZjgUCCf/7zn1fvfe97VxdffPEkbQqDOWKp/j/96U9TGqRIcq3S9P5CWh0EifeLX/ziRHbySl0Q7Pnnn7+65z3vubr97W+/+vCHP7wXGbr+s5/9bEr/wAc+cCLpz33uc1N44lzWum0G6v6FL3xhqruOIvWumAtbCpqgG41twhw5OUcYiPDCCy+cVAKOo353I4RUH/OYx0zkKW0IEdaVOxf2u9/9bvWpT31qdcopp6wuueSSSSLNNfjhD3+4ev3rX786+eSTV3e7291Wr3nNayapH8RB1u973/tW73jHO1b3uc99Vg9+8IMnyTmk6Bi/+PxjPdahpq2o+Ti+7nWvWz396U9fffvb394Tf13apaEJutFYCBAKR0Xw6U9/enWve91rImcSKIIVTqWAdL/5zW9OE3MkZaT4gQ98YJKypUfQ4r///e9fPe1pT1u98pWv3CPVjkiZ3AgqjHe9612rRz3qUauLLrpoIn35htikUU/k+7znPW910kknrV74whdOUrtryPx73/veRODnnnvuJD0jyqhdQpIpPy55j/4a9o1vfGMaXWgP9+b8bW972+qtb33rJC0H4murs88+e/Wwhz1s9a1vfWuPukjZ2mrJaIJuNLYRlXRyvPTSSyfCQ2gIBYmQZL/0pS+t3v72t0+ESbJGRh/96Ecnkn7Sk540kTm1SMgHgZu4e/SjHz0RrHxSBqTsuTD4yEc+snrqU5+6evKTnzzlhZzrdUedhbwR+SMf+chJv4yUgaT8wQ9+cPWZz3xmIu5TTz116ixgJOf4g4THH6Qt5PvSl750aicd1Ic+9KEp7EUvetHqJS95yUTKqS9Cdu1+97vf6rnPfe7q+9///p7yUo+logm60dgGhIBCEgFpkLXDiSeeOJEeVQdQJSDgT37yk5Okeu9733v18pe/fPWDH/xgkkhPOOGE1Qte8IKJFCFkTLI2icfJO+FxFTWctPz85z9/9fCHP3wiN+mCmpZFhk7i85///ETm973vfSdyZFJHknUP/E984hOnjuKCCy6Y0oYg6YVdV17M7+KnmuESbgThXhFsyPi0005bnX766ZNeWzqk/dCHPnS6XidIpdFet7jFLSbLE9J97iF1WSKaoBuNbULII+BHNKRhBIxQQ97UBogFUdHlIkMSNSmRhcXxxx8/hZG45VPTIS3Xv/rVr07SJNQ4MNbFZB+9M+k5UnnAr1wEiKB1GlQMpNPb3e52qy9/+curr3zlKxNJOopngvCZz3zm6mtf+9qecuXjfqRl/SEfzuSmI8mbCoWfHty9qct3v/vdyU9SJrWzCFEfTielLHk4D/nqYL7+9a+vjjjiiEndUvXgS0YTdKOxjUAelSgQHosIZIZgQozisM5AZkzVSI8kRlIlVcQd7nCH1Wtf+9qJwGp+/O95z3sm4qQOiJ46DubOlX//+99/9epXv3o6R3DyShykiyTVV6eC8BDfkUceOZEjSZn0rD7f+c53Vne84x0ndYs6Q8rTuSBiemzqG2ni5/hZgJhoRPapC5UL/bqRBl27tiIlU/886EEPmjqmtEPKMnlp4pQumkpkJ6AJutHYBlSyC5AnAkE61Bkj0SI30uLd7373aUIMSSJGUiNJEhE7N6lYVRkIkD772GOPnaRIYTVvSFzhSF8ngciQf+pa49ADm6RDqKwj1E3517jGNSZJ2uQdkjQKQLJUMG9+85snIq2InTLy5BAvl/MaThUSGA0gY/cdCxdlPuIRj1g94QlPmNJQ/2RCkJMe6d/5znee1B3uAVxbKpqgG41tQEijwlCe+oIESI+bOHHIlxrDZBu9L6IkNZJ0X/ziF09ESCUwSo8IlD750EMP/R/9az1yrpFUkTkJlfSbOAECZ3JH/WGiEhGS7uV99atffZK+5SGvH/3oR6tnPOMZk24aoaecIOdx6QzmrlWn43jsYx+7OvPMM6dz6UjwOjj3SiXC/hkpJ40OTbtS9yBxoxHhS0YTdKOxTQhxBMzRLPYgBZLucj1xELSJNhYRJEjhwkiRVA1veMMbJuLKYpKA9Gni8ZBDDlm98Y1vnKTLoBI5RyfMKuJmN7vZpONNPRLHpB7VBnWKjoGqxQSheMjvrne966SSQNocUjbRSJ+tbIRdSbhCWK7ty8lXO5DgpTFieNOb3jRJ7+pNUkbA0bmDeFQu7LXVnZoj+S0VTdCNxjYBYXABG2FLpkl3MBIHNcLLXvayaSiPdIHkSvJG0EiJxAs1X6TEFO+qV73qNAEZXS7UeMJYi5hkO+yww1avetWrJqkzcVynslAeIoyj2kC8pFV+JK+uJhpdp/vmEKqJQ6h5jvfp3PWEJ07OXdMG8jI6CNy7UYTOw/1WdUrSAvtyOnsSN9Q2WBqaoBuNhYDkfPOb33yycQ5pjESFMOuSZWGkR2HVaqESkmukXARN1UAVUVHjknrpn1k7kHiDWp5y1IOjxki5HH/K5yfBJi6X60Hi7i/kk3JBHvzulYsOfoQwKiQdoXa+LGVfkWiCbjS2CcghDiyDtuEQSbNeqy6o5zV8DoiLSgRB3+Me95jUIElf0/IzYaN/vvGNbzwtQhmxLt14HozXthI1b/eY87nyajiVkI6Qjn3paIJuNLYJlVA41hu3vvWtJ3WF85BOjTuHdeGB6/Sx17rWtVZ3uctdpsUrY345pyawmAOBUZmsi5ew8Ryqf4Rr9b5gTL8ZjPlsJo9ct2jG/TnCvtJtJ5qgG41tBoIw/DfBxsbZ/sqVcKofqr9io3gm9m54wxtOulc2xSOSlk73Bje4wdRRvPvd755IkKuo5cRfw2DuPMc5gh7L2BekqXkENXyMEz/VBoJmpgc1ztLQBN1obDOQE9M1izmoF0xyjcQSAuNfRyjjtUqEiBcp6QAsIqmoaUjabJnVY47IRyTtWHbO59yIdeH7g+ThntNWVQ9dy7BgxiiBdQkkfIlogm40tgkhDQ6ZWMxRrQvmIG6IN/4QUVwwEjTTuSpB51pNw1Tu8MMPnwiaKVvFmD+/skOIQS23QlwuyHnizqVZB3HHcuqkIdR8a7znPOc50/2xaFk6mqAbjW1CJQ5Hi1SoFpjSwUh8iWvlnP0uLBaxVLrmEX+QMMR7netcZy8ddEXi2YnOsnCTlXTQIUHHkRDBOfUMszppOfWri2HA6kYWIq5bXMP0L+Sc/Me8NwJzP7v+WYzCFrzmxaUjqGE5t+Oee3z2s5+9J3ypaIJuNLYRCCLkZDEHKTfEUcmjxmNpYRN68SxAEZ44NQ04R6DM7K5ylatMNsBsiINKjI7Ik6WHelhWnutxc2D/bOc6+3ZYSGO1oxWNScvUjuWIFX4m5thXKyckvlHe64DomQHSJ1ugwrQukFcIGsYy7IB3q1vdqgm60WjMI8TgGCJ7ylOeMulGHUfiqPEs5ba0mz2vpc7CE2eEMNImqfnKV77y1AnYmyPXRsnTghN7cJhQ1AnkesV4brEMaV5dbnOb26yud73rTaaCViyqG2nZ4hbLsO3JbMUjaRpB555gzHcjZJc+bWAxjE4okE/aBHKe/KU55phjpg5j6WiCbuxo7M9HvSRUwggssTZRSDc6SoQ1rrTiklatnBuvQz1HlCTtq13tahP5Uw0EiZc8rFC0+RJLDuZ+pN+RROMqqFps8GTFIOmbTbeVhInnfqwytMkTzOU31ybrIC6iZ9Ps3uif16GWgchtNkUXrwNaOg5qgp572DWMdJCXwjEYz7cSKX8zZYiT+JDzhNVrwRg2F2cpULeN2sA1rt7v6EYJL+FLx1hnsHTZKj4bzltyPd5L/CRWiyzsUEe1kPAav7YrHS3TPSoOpEQfXFHbmLRtL42jjz562mcjO8VBjkHKEM76A2FSv9jn4rjjjpsIPqDS0JnYGjTPFaTlan2DGp54gTag3iANk97nJP0gaXUS7LzVzapN26TOlbskHHQEPT5ISNhceEWNN147EEgZjl6Ueh43Yu7aXBiM59sF9cj9OdZ7DZzH5aOpccb4wZjvTkLuNyCF0o/azIc0OnfP7pFNMxtee3bYGAkpklaZz9nEP0j+SInK4drXvva0VzMpUnhtr8RFYtQPITG6ZOE1TlwNI5WT6qkz7HCnoyHdkshdp4MmPdOFO0/ZSZ8wxzkkTvzu2W52RhE2atIBaAO22ykjceOQOv07U0M77lGTJN5ScVASdI618XM+F56XZXxBqn+rMVePufISvj9xg5zPxb0iUesxuo2uB/wjmTjP86r+nQT1rQ452jDpTne6016LVbgaH8n4hZVJLn8oQUr2N0bYdf+MwN9KbFFKfZL9oDdyCNyqRvt22C0ucC2I31G9kSKJWVrkqX7+CqNupFvStQ6ENJ904zPjr24dXEP4yrCVKemdjt3/Dm2BapQw5sXZxImeXOfD1jw73anHUnHQqjg8kLkXwMvEJIjkwV8/7uqP22rUvOfKqGGOY32qG1HD40/67UIte/TnfKxjveY491yc0zsakrMi2EgHuVTU+4lDZCbSkO14zxzYltREHmsJ+0IjKxYXyCc66QAJIVmrFC3QqH9UgfjrOZhAU48sO69wrm4BNYgNmNQLQZv808GwBiHhCkOe6lktNzwzaZE2adYxzjln0pLzzbqXpGUrThVEX68NTELaO8Q9zum5dRKkbJI9/Xj9o0q9l6XhoNdB5yUHD8kwUm9r8xgfNrieuF4CQyHHDAW3EuoQp4PwwqajSB3iF4c/yHmuSRc3xk0+2w11jUt9HNU3LvcPNV7uMwsQHLncq7azAIP05qMOSUu3E5B2iR9Ig4bf/vqBvNwrJK57JCXadJ4OGvka4tNZU2WYEKx5kmbtj0yapRqpJDdCmHZ1JJkjV2oEkmeNL07qBfKlP0fSeXb8VupZEKJuTPBI8ikjz0850vozuO+SH3lyzumsXWPvTHeetGecccY0IqCDZq+tjghYXaJjV1bqbaUm9Y7VlNpDW+0EHJQEnQeTh+OBeqG8yB48yYChf17WPHQP0QN2zYvDjzy2GjoAujmkQqJxpLurUJ/UH6rfR0py9OJH0jAikAaSlguZbTfSzuD+dY7uwYflgxrbOXX3jDwX8R3FJU1loQM/oiJRjZNfS0Z9vrnXtBFrBxIvSRBJB547AcOKQ3/2ZjKXeNqh5pm2JlEzbyNZpgMLxK11iB/4mbGZ8KM2Ub8RiU9PbXWi9zD5eD7S+UchNQTLEJN5FerInln6OH9C4fgRuok8ZoG+R9+MengXfMPUMNqASsgIIvru1AvEV46FOszxSNCEs4RDjkvEQa3iqA+KNKw3Niw0FIp04uFwruuJbVbOltPDNyxD6lsNH6CPxsvC3MdfNEyo1GFXhfvIS4SI8186q6FMKKmzj8lLXO97bIPtROqizVke+FhIdSRBUpbhcBZQJJ6jSS+6Vm0krvZCSqRI8RE76Yr5GKuDUdrbCUjbBEjr7LPPntoFqblH13VQ2oN0TfWAxEz+aQ8EJJ0RRdqO9IwcLQ4Zdc/gmLgBv3fNUV6kTWRIiPCN5BrE77vSEbie/Bxtmu8Zs6n2fqoPJL0jKdp9VZfOm0tnjvC1gzK8594XdUPinrvvwURlpOhAGTovnZiVmiYwQ+Q7AQftJCHwxyEFUoQXlk6LNFGvO9ezethIgCE7IvRybDW8YCZMDNOuec1rTv9xs8S32mWmXj6C+hF56Q07b3KTm0x2rYbD7EB9rKSrfDTVCdtu1PqQdJGrZ2HIaXMebeD5eDZjXDpGJlW2yyQtmxAz/PXBi0PKRlj0tpvZ4GcpyD1WOEdGiJh06H1EPJ6hzplKw7A+EiudtVVxLBgM4XVW3hfERw/MLlncqtqYc0ENQ4akWZ2hjgBJ55r6yJN6SQeKLBFq3jVxPB8LaiwxV2/1F16R/Ko/bu5d9j26H3pkeRqB+k4JKzoKumhtUPMjgVs+r5Mw6tQ2woPqXxoOaoIG5x4IicSsrz8L58FXOOc8ZLPXZno9aGm3EinHy0y35uOyOTrjfi9R6lVfTh8cRzKgyyMxIzbpdDx54eZc8tpu1Po46hCZkpFqjFaQr+E04k2cOPeOsLSRj9Pop14HQ2EkrvMidS3hnveFWv96P+ru/aCPRX4m15Ch+9aJ2+wHMSI8HZ3JMhIivS+pV1wStQ7PhkckxpSRozLGNqp1SFwjEuXbv4IAg7Rd884hYBOD2lzbj3bFpGES7gMe8IApbYSiYCxr3Xn1G9ESSHQ8Og/nSNkIFFETYLRB4quD94y6JaMLdRzzXSoO6klC8DBIZV7i008/ffofG6x7MBla2rPAhIsHupVIuXpywy12rzawMQz04Y16QhCfVEVKJMmQHuj2DB9JUfWFg5SxVGhT5EKlxNbWUWfDkcQMZfOhuw+Ea4RgGGsYH7iWe0cY9NA6Vp0WktpJGEkj949wdE7aC2nroAgR3mkQRpIUZuJLOyAtpIrAjKqg5p1j/FDPlV3rg+RI6CR5eQv3TEimOgbkh6ipOcb3Vzyqu0jPyRNqGSPm4nK+AyMqLqMt9dMRaQNCTAQWIGHrOPLdV4xlLBE7iqDHBo3f0cML8jBBj29lFF0tvacXZh3kYzhHvUFiAPmsK/eyQnokQhom0dPx2eKRHtULOObvpScFqRMCQ+rIjHqDfm2zqO0Cubc5CE/cjeJdFsiLmsf9M+cipRlJXOlKV5oWYIRUAp0ZIvBs5iYCUz8jEhK5kZLhuPDcAyTeRveSazXeRmmEj+WMaXMcwzaDmg7Gc9hs2OXBRmVUN4d14ZcVc2Xtq/x11yrGeDkfw69I7BiC9gHoGRGVj7Q2GFITTuIdh1EI2fDLMCvqDchHlcbn1yPT79FBk6RrPiQH5SZNkPSbReKTSHQYpCO6aCoLE4eRjGo5CEvddTSGuO4FoVkEsL868pSf/HVgpBskCQnXjvJOm9b68G8WKa/Cufs3CWvC1HM1eUuvru3pVRMPSG70qSRtz2EO4hrq0lHbcIi5Wuoctw7j9Y3iwhi3umA8b+wMeGbr3u/teJ47gqA1jCGr4Z6tCqkCSF6kMMMn0pXhrUknxGoYnA8EySDdk08+ec8G5LlWnWG1IaFhNJ0oacxQ3LARiSAIS1n5DamCpN8sxJWevszsOmI0kWL/XTpYJJM8vSiuG96bGKNDy4Y6iMywDbltFskzR52ayUptqU3ViV6RLhNJ0ombpEKkdJrSJZ/NQtzqEqYs+YZI6VuZjxlJUHtUqI/RgvutqouaJ8jLfZhw1I6JW+MEtS71+hg+dz3n47X6YddrafMaFxLWbhkuWBe+HdgRBI0oEQRyRsIM4K9//etPkrGP3MduT1gqAsSFsE2o+DCoAMzwImhkrsHzIdWHQApHSkzs5E8FgZxJqYbihs300pbMkirH9JuFuKRkHYlVUCRY0nFMzegY80GTXNWDfo9+jaRrcoS0bSgfU8HNQp7JWzp5mkiiMlE2MzadhWWw7lmngKB1COqQyab9gbKqU77O0P0rQwcq3CjBHIH9IpRnPwjx1FOnSPUx3m/yDIxw1JOqxHMTfw6pR/zKMpmlI4gjDHD1vF6vYToOHelYn/jVOe0+Xm+3HFexLvyKxo4gaFIiAibFIjDDfCZmJoSQjI/cx2zCzEw/MmU/iuDYRd7oRjeahr4+Jg1eP844eZBok94Ha7YYefoAkZUdvlhQRA9a89ospLEQxoQfMlRvky2kR9I7MsrHjBBNAJFkDe2RGOlSHS/v73p0DHS67s/kDpL2W342tUYaJp/Eca+ke+UaYVwWpI05z8R9mew06hGWNtQm1BPuD3kjPZ2SDpilANS8RiBk92LfY++ICaIRc+lNOFkmrT108nHULnaNc9Tewpxz9br7YGcMY72cV3Le3/elccWiPqc8t+3EjiBoKgEfKBMs5EaqY5ZFWgpZgo/5pje96UR0hu6GuPSXdJsh7bkGF4YApaPbRVYIgiQpnB7bB08FgUCRV/Jx3N+HaIadtM5EyktgEkzeyIlEG8Q8iLkfYkOQWdyibvuDWl9lIl8SKylQu+ogjjjiiIngIikbVTCPUi8r13SGl/WlTbmOOj8ry1ixCAuEM5c69NBDV0cdddQ0atI5es71R6qOYx2ce/6ezyGHHDJ1aiTjYKN6e77u2cSi0Q1i19nzezac8zGMM5pSrg4exnJyf8L46/02lgXPxmgno7Q8yzy77cCOUXHQv1JXkHYY8DN+Ry75MJAJ8kbQzNZInj48JjYkaBNx0aPmQ4lfB4CIsmgCOegQSEWILFIfadzHWIes+wtpEA6pywfunKRIBUNCpw8Whiyoauhm1Y+kjaypa5Cle98fjPV1ziSJ1GnyzRaMVqi5Z2WBzgkpaz+LQJDlZYFyU7Zy3RcVhxFN4Ho6QuorC3hI8p6j9vLcR0jjWSRv74DJRyMBErF3Jkicilonz9h9c0ZsnnvON3LSxQXyjYO8L+BZmlMgBOhs2y3DUfE5muvwXXj+9Z3hzzO8IrEjCBp8AF50H7dlv3TFdMT5MEgyCMzHTVdM+szHgGAMX0Mw9QPiECQyYFtMOmUlYWKRNMdygpQuXsDvYXH86rUZiEv6NpFFQifhC/My2JiG6RxJ3zlSQo4ktsQxnNYB+bj3d7MXeeSYFw3BIGjSpnxJ1KTH3Jey6fy1H12/Tir57A+kidNWRkCW2+vw6nUwqvD8bC5v603PLROkUONC/WgQtNEJCZqu3odW444Y8wpq+Do/pJ0g1+JcS93iF4781ct8ijq2W4ZjUcVRpTIy8G3U5wk5XpHYMQQNXm4fKwnXdosZigPCokP2PzQTSobLCJBkjPiYsGUJaJDGN3SlEz3ssMMmEkTKzuleWXSwCEAsSLKa8uXD2yxBi4tokE6G7HHKVU+rGHUkVpBZLaYs6Uiz6mJBi9EAor8sSL3jZwnDvhpB6zQQtnD3ZERiwo50rQNTB53ZKF1sBikXiXpOOh8Ss/Dk5Yi0LclFsiZObYRDV5/7lUfS1HSc0ZR8TRLqBLIUPHFyHP3eHRK6+Q0dO8cf595zjJ+jRnNulDZOEjrWdo4T5r3U+SGCdstx3hfPxbuWZ+cY/3ZgRxE06Y5UZRKJrpa6AZAJ8iV50SEjGg0tXBqETkJF2vlQIH7DehIzEy8Tgz506hASNFWKiTTERSVhCI1kQDzkTsLeDEkjWxIi8tUJpHwvAJ0sFYuRgckyEmZUIJG6qEAsosnk2hyEe8F0JAg1L1fKqg4QjU6B6kRHhDTB6IOpoU7LKkxtpw4kVPm6X0Sjk3T/6jj3IqccQOzuSQeKEGs9gJ/kgvB0tEia/tvkcK7nWD+cnFOB0aFLZwSSSULX6/NJPgEdvPfKRKjRCcef8/hZ98z5I+HLd8wb1G0uvLF8jO/ZFY3FEXQaob7s8TM588EgKh9t9M8IA+H50SUVAakQpEFW2S2OzjONDWl8hCBPkiIClc4H5+Nj9oXwEZRJrVhUAPUJUz9DIxIUpK4g75zzIyg6VgRrgUrCwaQhqxRqFhJmTPlA3oiHqoF5HSmxImVwiAixkiBJd1GjBMqLWgi0o3JJ59ozdTbB5l7pc9WZdKGjMnIJ8ZOwqT4MEdkg67hqWRXCdXLqZgTBciVx65FTtg5V56DzINGmnUD96z0kHSsXQ1QErSPJ/SROwF/z282o7QI5z3sQpL0c17XdmFeQNPX6XNx16XczFkHQHkx9OEhm7mEhCEPe6173upPEi8R8lPTSiBsJI1vSX8AvLr0y29iUlRcG2SA/lgMkRaQj3CQdYmYBQpolaZLaERGiJTkjJlK3OCTvqqvOEUhyJEbkQWVgDw1SctWr5j9uJjhJsshOfixPTJRRgZAqLQuXj2G5dHHJhwSMRHU4yM29jRAvHxlp3k56CLF+eJWgdSic+6fnjzRKFUHil96knOdR6xRHyqa2yfOLXbUy6rMKEKv2isljOjNu/Ngd876Q8NUDsUsTEq9xgurfbUgbQm0HYXm24FocuJa2r+kqci151Xhz6RI2hjf+g20n6PHh1Ac2vkjIhArDRB47VNIr0mD5gPCoOXzweYkcER0JlxkZwhWe/IB0ilyRH8sCQ3Dp5IMcWVeQaH34iFG4D59kjvCRICJRh0qaFaRFk20sQ9gZI2gTcux7Ez97c6gDSdPLbftI92VmmVrASIA5HgmUxB1VQ/JQb6oGbaIMjv4WxjpJ5x7US57yq4i0q9PQOVDBGKVoH5AfCxP3gXR1gJnQzPU4nSZJ3TOjhjJjTu8tv7qFZaB9qSt0NKM9c55tTRO/EY120smN+uc5stitcO9xOc9xbN9cA89XR2tuxNyOb8ezqvHi9/yoDj1735FnmNEcp5zEr/7G3lgEQQd5ePF7cHlhEC2VAzUEgqKKsHEQUjOUp9aYS0unSRpDCgg++uMA4XrhSMOkZ9Kb9CEwkrPl1SRRZXghUyfkwkSN5K0u6whaOgSYXb8cObrPxEe20pMC5Q/qw66XdE2KJ8UmvWF/VA0gj9yzdDoTk4mk3Fyv9RIv9+felFuh3YwSSO86MHU1kRLIi2RMlcAqBUGLn3qkPM79e0buwb2ov/bwXHzIiRfwy4Mqhx37qDpJ/IQ5ei7aSqfkWRpZ1XiJC+P5bsL4bGDOX13gWRAqvFd09uZjvIPiyDd5+4Y8O+8FIcq76v3yrSVPcSHnNazxXyxGB10fFFfDkKXhMP2rXemQYn2Y69LF+cCpP0jCo2pAPnPSVVxF4iecH2mRrknTkQaD5JGwes7lHmqeEH8NS9yKMU1N54PQTkgxSJwaL/6NMKaDnFPDIHnSMb96ak8Ocm8cfz3napwgcRNW4wY1TFzqFZN1bLkt6KkjqYqkG8N3CzyX+gxgbGuSLum4SrzgXTfCs6DLhDaizqiJi/CiQ7by0oS2bzYSNOc5zVkBOZ97Xrsd207Q48sCeYk4fsN2vbWPj7Qa87Oahr+GSVvPSWz53VWQMmrauIoa5pg0nCFfXsIqnbs2fgwhrZxXJKzGS/qgxglyD+ImHSBN6gFtVdM41nyTvmIsgzQtjrAa17mhrolCI4hIrUHSjEiZueaoTvUc5u4/4M81R+oY8xDej6iIxKlpaplQ/bsJ2qG2KyTMt0ZSpn4y35I2TNsZUVFrGc3al7xuogXiSSuOURX1IkL2PAgx7L8JSeP3VvNo/BeLkaDBwx0fnOESCwr6W3bCdJgkQz1x4kqXD5I/zjk4sq+lJ/YBk/RiiD7Grajp566T6g3Z6WgjPcK6vBKurqkvjOXPpYeN4vHH0ROT6ql/Yl0SJM6cP/UfUctNPEfDW/dPn0y68iEmjvurSLoxr/hh7nqOwuMfHUmPKofURuVS27ZiDJuLsxuhvbSvUYdvDfGa//DtBXkuSJaKkbBDnYSg89wIKNJTXflezd/oOPM8fLO+XeRtEjcmndDPYh6LmSSMy4cIzpGNXhcJ6JERrEUkhrHjpENeoriAX1xmdojLx8yGeow7ptkIXjqTIPSeXkr5B8lzjihqPYP4Hes9JKy6Me0YX5kkIDpAE486MUjaGr+6mm/C5pBrHJ2zcuio67DVUX7xB0kXjOep34jEqy4Qn1SHNMwVkJ4TXuM1/gvtUtvH0Xvim7Kkn/UO1YWwPA9xzBcgWN+fOFQYsXoS15yE78HEoMlaBB37cPBuGnGaI7BwDEmT2CFxGntjEQTtJciLAHlYjnrdrO4y0WT45OhBI4W8aMknaStyzcfrJWSRgFwz+ZQ08dewYAzzstGpkSCySKPGcawEneO6OoLwuXzq+Ziev4bxI07qhqpygZr36FwLangwF+aDZS1RLTuC+Mc0kLDx2kZh8Qf8SMEIAVlYmYksgqSraRr/gTYZ3yOjQaoqJqnmL/JO570QV4fPpFWHbBLaIi6WU655DvwslghCVCCk6CqFg4lpoxyrRE146wign9M8FqHi8HDiYHx5Rn89H1+i8fro94LQm+rlEbawpIekH9PVsHqtYqx3UNNCzmv4eD5iDK/nc2nW5QO5tq90oz8u2Nd5UMPjr/FG/7rzMdyohWrFPt/50OdQ84DxfDdh7r6p+1jykJ7NJej4xvbybhupZMToyEaeaSPVCIGJ8MSPwK20jIlnhbwIEDoCtvds/hM+V7fdjkXpoBuNxoHHSIbmT5Czvc6RL4KGMR7CZW5JyCEt+3ONka2JaEcT+UaNzOuoOEjbc6RLqqbLtp6BFF2FrMbeaIJuNHYZKiEiUJIxcjbZnQ2sKnJu0RT1BRJm4WHFJr2/9NQWiFtc0jOzS6PUQHjyUbYJZpORJnbFc62qBBv/QRN0o7GLEKKsjkUGU1GT8c4Biea6uR5qCRI0lYQwcw9W9dI1M2HNPuKk8fxBn9qp5hPk3CIWliB1MVVjbzRBNxq7CJUsSazmYZAknTDb+VyPNGui2UQ4k00LvSzvN4HIbNWCFb+So49G4OKx8rA3i0UsSLxa9wQpIz9Apouei9dogm40dh1CkMiX/tiGV3TG9MoQqRdYA1FhIHCrcZEx6x2SMlM5UjdiRtDI2RJw2yog6EwgriNeemjSNlUHi6hWcfwvmqAbjV2EEKAj0zg7DNov3a6BrJsqxCEpI17OoiQqDuSM3JndIXDSL1NLVhwIHKFzTO5MCIbwHbnAdRt1kcQtbkHQjb3RBN1o7DIgS456gxWF7XJN6mX720Ac5Gvyz6QeZxIxC1iQdOyl6Z9dtwAs8cUNITvKL3BuwtH2uXZDROhN0P+LJuhGYxch5AwWgVnV5zdqjiTjXB/dSLAwXk+ceh4Iq3BOArfa0Da6djiMeV/jv2iCbjR2EUKUjvS+Jv6OOOKIafk2lYfwObcvgl7nRtQwVh503/79yZKDFN7YG03QjcYuBKK0PS7dsz/h+0Va/vEZEh1JNuc1vBJ3Da9Yd1159tihA7dXexP0/6IJutHYZQhRkqBZYiBoi1DolIVXawrHqCqSLhj9VaURJM4YlzOxyDIEQVt9eEUSdOpQ6wXO6/1WzI0iYDNhSRu3WTRBNxq7CJUgWGDYBZCKA0HXHRlhM2SSOOviCV9HTuykLXSJisOE47p8Lg/GcqGG1Wv8mays10c/Vwk7YfHnOBe2juhhzLMJutHYRQhBcLYHtbOjfdbpoOvvx0YSid+ud+yb/XLOohUrCFltAGJjGWI/D9cvvvjiaRk3yVx+kPw59tOnnnrq9Bs7i1YOpARdy8152gHiH+Osc7kejNeCdWH1GCQul/o0QTcauwwhAGRqm1YqBgtLkG8liPjjwMSeFYdUEmyY/QSD/bTrrDCQte2AhdMrs5+ma64mdMkPudvf/bjjjpt20zvQVhzKDPGlDvzqZkFNleDn7j+uYl/Xkk9Fwus1xznXBN1o7CLkwwe2yuyPjz766MmaA2FCriduzoGUa/WhvZ79zd4qRCQsPCRsz3V/i7cRkgUoFquMBA027LdC0Z/ubbZ0IAh6rD9/JUeOrbdOJCoeYeo7pst50oOwmlfOOXm4J04Z8jea0Bkoz4ilLnFP+oom6EZjFyFkAhaSINBsekQ1EYRoKmEkzE9h6Yw5JE1NQl0SuG4ZNxWHNHN5AFI+8cQTp6XhSD3hW4lafq2HskLCSJI/hJrORhwuYQknaVd9vetJLy8dkrYVDyEzX2Qx41+MFgPpCLW1rVtdq5BH6qnsJuhGY5chxINM/D2FBEuS9fuyEJrr8YcwAnt2IGULXag5pLXEWxpAPMiZlUiQ/CqoNfxj1D8KxwnKrUK9h7EOzqlk6NIRJfLUaXB+AkEFZFtV7SKOzkyYNvP3npCyPE24GhHoaJCvUYaFP4g5v59DzCZGLZ9H1n42UaX2sc25JuhGYxehfvwIgaRnNzn/+7QvR1DjcQkjRZokZDdNcqRrPuGEE6aj6/Kk1/bTWR1A0o0O/KpMubYxreFbiZonfyVpEi4CNaFJ5UCXzk/PbvMn9fenGMTsnJNGmDZAzvIDRIukka+jEQXpmSmh0YTOTGdAvYHkhWv7EHzqBrWOTdCNxi5CPvyKc845ZyJKUjHSrajx+RENEjv//PMncrF5ks3+7UhHQhTmt1lVvTHmgYCQE7WKzf3rNqcHGiFBQJgsSUjEyLQSbyDMpk6pH0d6JiknXsK1nXyqzj2Tqjo2cVxDzsoUP2njIH55NEE3GrsIlQgCKgtESZKmlhivB8IRliG7NMiO5Mha4/jjj1+dddZZkyTq57OITvxKiAEpFMnZalRaw/51ZW4F5D2XP4KmanBEhiHjStDq6V5yH2mDMYwf4ep4kG+2WUXQ2is6bGoN6o8QdNKnfjkCsm+CbjR2ESoZBM5JvaeccsrqggsumMimEkYlWcN9uuNK5IbwNv1n0UFypo/OznhjWcB6gbRus/+LLrpoD7kdCCh/7l5qOPBfeumlE3nWOMiYTrnGrVI15OgeqDbo4KlOnDvSXyNn0rO0dNU6gZonOE84RxXSBN1o7EKEDAISsV9fnXTSSROZzEEaZHzeeedN5BMioXc988wzV4cffviktqACQS6uQQhPeaRnqpBjjjlmdfbZZ09pIXG3GqnjmL86pV6OrtM5GxFU8ow6o5I2XTWC1gZJm2vSIuK0T4iZX5j8ucTlah6Qc+qkJuhGYxcCAcSBYb4N9+mSkXB2tqtALK6RoHPNUbjN/I888sjVscceO5F9CCpkE78hvlWDpPWsMgyS51ZDuRykLhw7cFYaOoxYcVBdIGSTnDoZBI2Ma3oETarOvUkrD/GqFQfpGckK5+Qdl3PqHeqQCnlCE3SjsQsRgooL0SAL5HnaaadN5EmfCqRAE1sWtfjRq/8TGsonPSAlpOsfg1QFUPPmqEWoPyxicYyUXd1WQ57qUAk25bg/HYb7pjtHsoiZGoJZnE4rBJ00jiHoSNqIXj7Sie+6NkCwVmdqN/m5njgcP8sQ9Uj+Fa3iaDR2IZBBHIRESb0mzexwh0CjZ0YgrDX8dYUKg77aYhQEFTAtu/DCC6cl4Mg8eTsmf5K1DuDcc8/dMzEXJP5WI2XDujLUQyeEUN1zVDziI9EQdFxUHOIlz1yLP9AWlr5T7QSu1w6Dv54H2r0JutHYZVhHCPz0sEjKUB25iCeMOVpdiEFijBojJIOwLM4IwUGuAwnV0D8WDtG/QuIcCNQ6BGMYaVWnQV9sdKBe6kcS1rGIm7pW0obkVfMD8bUhK47onefiBcKlSRzlN0E3GrsII0HEn3AOMSCUELBzEiBHZ8yNOubkITxhjlyuIXp5JCxwTRkHGqknjPWjgiAZGwlQdyBs9eWnY651RtD0xwlzrHnnnKtmdpDwEQnTDvHLpwm60dhlqAQx+qsL6vl4vZ4nrBIU57yS2EbXDgRSRkXK1qEw+/MDWxI+CRohk/RJ1Dojqg/WJqRpkjPCDUHXewn4ES2Cp99mSsi/Lu7ceVwTdKOxyzASQkUlhxE1vF5PeL1Wz0cCrte5SnRbjeTP5TxH5ExCRsbUNlQ7wmKvTBUTtY3rpOxM7kXPHhcoRzqTg/T0l1xyyZR/Rhxjmpq2hsU1QTcauwiVEDaLpJkj2nVwbV/XA/4x761C6pG8Q9RAjYNoLa4hIZOWxSP9xpYZkDhSJklnYjD5jZA/9UjUIPT20tVyYUzvvMZJGU3QjUbjoAbiC/mFGB0RMqmZmVzIeGlogm40Ggc9IpGGoIGkTIoepdsloQm60Wgc9BjJGZwvmZxXq9Xq/wEjtQIr3CFknAAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E7%8B%97%E7%9A%84%E6%95%B0%E9%87%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAsEAAAF5CAYAAAB+wPfxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAGB3SURBVHhe7Z0HmJRllrY3/htm07W7s3nChgmOo6OOedQxATKKiSAgIiAISBpylJxzZoiD5JyRnHPOOUrOUZKg5/c+VjHdPQ3ddDkW71fPfV3n6u6v0lfddHPXqec97x+ZEEIIIYQQKYYkWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIYQQQgiRckiChRBCCCFEyiEJFkIIIYQQKYckWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIcQt+fTTT+38+fN25cqV2JFwuHjxoi1atMj27NnjzyNKXL9+3U6ePGknTpywy5cvx44KIYS4EyTBQohbgkSOGzfONm3aFDvyFTdu3LCrV6/aZ5995kJ2q/r888/tiy++iN3q90Guz507Z6dPn75tXbhwwR8ru/CYe/futZIlS1qbNm1s/fr1fnvO507hNtm5HTKKlB49evTm9TmP48eP24oVK/x7eOnSJT+eKHw/pkyZYv369fOf0dmzZ2OXCCGEyC6SYCHELXn//fft5z//uXXt2jV25CsQU6Ru27ZttmvXLtu9e3emhRAiy7eC68ybN88mTpx421q2bJl3PrMLj7lw4UL71re+Zf/93/9tPXv2tE8++cQOHDhgR44c8fPKTnFdbsNj307mYefOnTZ27Fj76KOPvAuNCPNi4eOPP7aXX37ZSpcu7d+rrO4nO3BO77zzjv3rv/6r/4zWrl0bu0QIIUR2kQQLIW7JBx98YE888YT16tUrduQrhg8fbv/7v/9r//7v/27/8R//ccsqXry4rVu3Lnar3+c3v/mN/fKXv7Rvf/vbt613333Xli5dGrtV1iCJXbp0sT/90z+1WrVqWe/eva18+fJ+Tv/5n/95R8VtKleunGXsYMiQIfbCCy/YI4884p3neNcXyUeCeR7Tpk1LOJqBWG/YsMG+//3ve/HcbvdCQwghROZIgoUQDp1LOpXEHyZPnmxTp061fPny2b333muVKlWySZMm+WV0f5cvX25t27a1Vq1a2VNPPeWy+OKLL1qHDh28ypQpYz/4wQ/szTfftC1btsQe4ffp1q2bPfDAA3b//fe7rLZo0eJmNWzY0Ludf/RHf2RFixa1JUuWxG6VNfPnz/fH5rwQz40bN/q5t27d2jp37mzdu3e3Hj16ZFpVq1b17jcd5Lp16/rzpBt9uzgGXWNE+Z577rESJUp4pxxZhYMHD/r9/vVf/7XHM+hqZwW3j3ejiVjQiT516pTX5s2b/Tlwf6+//rr/XNJeHi+OUcQx4l1txSaEEOJ3SIKFEA6SN378ePvVr35lb7zxhhUoUMD+7//+zzuYDz30kL366quWN29e7wIjdvv27fPc7WuvvebSiLQePnzYDh06ZAMHDvQO8ltvveUxhFtBTIH7Rrbp9HJ/8SJu0b9/f/vjP/5j7wQj3tmBjDEd5h/+8If23HPP2datW70re+zYMT8XhBAxjMtlxkIqef4PP/ywLViwwLvKXPd2MYahQ4fa008/7UUkIm2GmC4tcQXO5ac//ak1b97cF+vdjpEjR9qHH35ov/71r61atWpWvXr1m/Xee+/ZL37xC/uTP/kT/77TbU97ecbi9txP/fr1XeaFEEJ8hSRYCOEgwUgSUluwYEErVKiQi+S//Mu/+Fv8dFYR4VGjRrloXrt2zQWRTjBv9yNucbgOx+nk0pW8FcQskODChQu7WKeFxV90pJFgOqgsLssOXA9R/Md//EcXxKyEMyOIL+fz+OOPe9f1dvA92L9/v3+vfvKTn1iVKlVcpDMK85kzZ+y3v/2tSzAyjKRndr04ZLA5h1y5clnu3LktT548XnTN/+mf/sn+6q/+yiWd+EX8sqyqSJEiNmDAgNgjCCGEkAQLIW6ClKUVM6QOaaMjG7+MotNJR5U8KrEB4hLkVIHLEb7HHnvMZfR2WVpkkG4mwkcHOS1pJbhUqVLZkmBEnvgC8o4sppVgJlEgnnSE0xZdYeIHTLOA7Eowz5PvAY9HNpcOOp30zOC6PD6L44hoPPPMM94xji+gywgvMnjxgDwzoo7r8ZGfA7fl+U2fPv1mXIIXI8QduB6Z48yKn8PtIh1CCJFqSIKFEA6ChKhR5FkRt7gEM4qLy4kVUAgaUw/+53/+x7O/gwYN8rf9uQ235a38++67z+WYY7ciLsF0KYlSpCUnEsx1iDLQKf2v//qvdBLMfSHmHE9bRD5eeukl2759u18vuxKMcM6ePdu++93vuth26tTJpfVW8H0gm0y045//+Z/9+8OLCCQ8I4hx2uK2PA9eVLAgEZnm+8P3mm46cRIiD/Gfwe1KCCHEV0iChRAOmVxyva+88orHHigkF2HjbXhEi9gDEodcMtXhH/7hHzzjumPHDl8Ax0xeFmvRqSQfi+TdDhaMEYdAgulkpuVOJBgZ5PoVK1b0LDKxA+ICaSV4zJgxLp5PPvmkNW3a1B8byed6yHFceLMjwcQgEGCe61/8xV949pbcb2Zd3bTQjWVaBGPNGG/GeSKvc+fO9fPPDMQVueX7/LOf/cyjDdxH/LFYiMhz4nukKRFCCJF9JMFCCIexXixUY8oBExJYUIX40uml+8gxpBFRpsOLJPM1MQi6xyxAIxqApCHK3FdWmVqyrwj222+//Xsd0TuRYKSURW90rRHqcuXKuaRzHnEJZjoEsstjrV692qMRxBd4juSX41MsspJgHgtpZQIG49OQeKZkcK7MJs6q6KDzfaL7zO3pRPN45Kgzk1iiEVyG3DNFo06dOv6cOH8KOeZcixUr5t30+PG0xf1mJehCCJFqSIKFEE48M4tIkZFlnBYxBxbKMRWCr7mcKMSaNWs898tCK0aQzZkzx4WS2bx0Y/nI10jk7bqT7du39+4sC+gyRgnuVILJxdJVZV4v2dmMEsz5MFWB+2L6BCCzLPjjukg8ZCXBTMXgBQEvDujMIqWcP/KNiPJ5VsX3qFGjRv6R+6AaN27s2d208D2fOXOmPf/88/Z3f/d3fj1egNBhjxeL8jgXOu90t9NeFi828lCXWAgh0iMJFkLchK4ju7ghwkjT6NGjLX/+/N4thXiulLf1EUg2yyATy+I4usXxYqEYOVk6shljDmlp0qSJ/fjHP3YxRcLTcicSHIfz536YcpGZBNPxzSjBPL87kWCknxcGdGabNWvm85T5nCkaTKRgfi+zjf/+7//ejxF7iBfRkr/8y7/0ecLMQkZ66YZTGZ8f32MEmMgF98nGH//v//0/v9+09/m3f/u3fpwcdNrH47H+5m/+xr9/gwcP9hc2QgghfockWAhxE7Km8c7iokWLXJ7iEszb6YgxXVfkbdasWfZnf/ZnnqllHjDxgHiRK0aO6YzeToLp3JIfpiOacdFWTiQ4vojsVhKcWSf4TiUYOV21apVnqOPTG+gO8zhEHcghI6wsWCNiQYc6XjwHOs8PPvigLwpkIgW3p9J2ajlOhpkMNkJLdOI73/mOnydd9rT3SQeZc2VDEV7AxI/z82MDkj//8z/32c7aKEMIIdIjCRZC3ASJI1dLR5HcLLN/Gf31b//2b979RIbZrYz8MAKJoLIdMbLK5IN49enT52ZOlRFet4J5xHRFyRlnJCcSHCczCSYTTMc2owTfaRwCeBHAdAiEG/FmYR4fEWNeENCZZeEcLxjSghTzIoPzIOfL7dLC13Sz+R4zA/hHP/qRd4I5J7rY5K2Je6SF63L+LLZL+3gIMd1mzoWOPqIthBDid0iChRA3QR6RLaYWIIV0I5FgYg/IIiKMdCG6iBmCSieS6RBpoUvMNsp0RTN7G55xa0QukMFHH33UF9Fl5OuWYObysrCMkWws+mNCBJtwkLO9k4Vxt4PZvdwXXVu6xRm722z9zAsJXmggyRkXq/E1z5ucMefPIr4pU6b494tcdk4lOD6TWAghxO+QBAshbkLnl2kNCCBSSAeRTiQxAuSQBXCIIQvkeLs9OxKc2excjiHYjGBjygSil5GsJJj4QMZOapzMJJjHo7NKV5sd8FhIRiyB6Add123btvn1cirBZJHZLppMNLIa7yynhU473xeE9lYj1TjG+Xfr1s3zx/HrSIKFEOLrRRIshHDoWjLtga4vskinkq/ZfCK+MC4Oncl4J7hmzZoeA2DEWbyQZ3Y2YxJCxm2TeRwEjS4ni7eYsRvfqCItWUkw98Euc2zekbHjmpkEkwlmni5iPn/+fJ+YwP3TFSbSQa4XcirBnA8dXDK8bBaScRtoGDZsmHeK6aqz3XLG874dOZFgxqdJgoUQInMkwUIIh5wrGy+wkIpNMOj+IsC8dZ9Rgul60u1lCgKjuxBnIgDx+va3v+1TEFislXFhHNlU5JPbMScX0c6YnYWsJJhFddw/+eOMedfMJHjXrl02YsQIl3siGog8i9zoSiPqd7ptckZ4HswhZqHf8uXLf2/cGbBYjjgG583zuxNy587tlV0JprNdr149/3mSh5YECyFEeiTBQgiHSANdUbYSZvQXUx8QWr5m2kNaEEY2p+At+9vVjBkz0skg4hnfaQ25ZZLEypUrY5emJ60EI7OIJdA9JQZBZ5TRbHRfM87AnTBhgndc0+4Yh/AeO3bMpTcuvJmREwnmNiyIY9wbWxsziSGzqAbxBHLJXOdWUY5bwaxgohRZSfCyZcs8Y83WyjwWnWB+Dpm90BBCiFRGEiyEcBBO3qanm0nXtHXr1r5ojY4tMsW4NKZCIHjkVJEqJj/crph0wPUQPmILjGArW7asizWbZNCxvdX82vicXCSY82BXNjK1zOVlEw86rhTnmTFWQPSBRXfEMeISnBWcJ8KOQCObWUkwj0l3lV3g6FTfe++9nm9mcVzGrC9f8/y5HqLMZht3CqKLCGeU4E6dOnn0hBcUvBggt83z5gUCeWcWM7KQMeM5CSFEqiMJFkK4oNGlRIB5qx6OHj3qO7ohWGx+wYI55I3FX3Rz6TgyRm3dunVeLPTi6/gMXXK3dCDpktLVJT7BNAYWjiGMyCuPcSvo1nJ/iC7ZYRaxMTeXaRVEChjjRscW6cwIGVgWv8Vn52YHOs0sniNmQSaaGEhmi9sAuSduwOMwBo7vD9fv169fuq40MQ2ux/eBRYdsscw0inbt2sWukX3o0pO/RnLTQoSF6ArdZR6b50snv0CBAsacYB5bM4KFEOL3kQQLIXyRFt1DJJjOYhw6nUgUsQKmKrBbGZ1hNsKgU8omDkQb6DYiqCzcoluJ7H3ve9/zbDByyAI2usyIK1KLzNF5zWphGIvskDy6uuxAx/2x8IzHZ7oD3enMpk8wg5fuNTN56WpnBySS+/6TP/kTf5y0eeK00FFF8pFlzuNb3/qWfy+GDh36e7lbOrDENbg/dnTjusxGZurDncL3izhJxo4uQs3PjfNFgvme8gLidpEPIYQQkmAhxJcgV0QT+vbt653cOAgXsQQWt3GcnC+yiNjSzWVhG1sFs3UvW/tSbNXL18gykYf69et7HIKFbQghsQbuLysBBm5H15XrswsaOWSKzzmGdGb2Nj9CSscZOWcKRHbo0aOHyzvPB6FfvHhxpovJOCd2YMuVK5fHOipVquTPja5vxnNhAeFHH33kskwnnesSCaHzfqfw/crse8b3k/suUqTIzS70ra4rhBDid0iChRAuTGR46dhmtrMYcofQMfaL7iabPhBvYL4v8kwGlwkEfCRTy7FJkyb5jmzx8WcIJYvv2K3tTheF3SlIMh1sIhuZiWxmEH0gF83ziEttZufJ94rOOflkBJd5ypmNaQOO8T0jsoH8cl2k/uuE7ykRCRYYZvaCQAghROZIgoUQ4kvootL1piueFchtfLyaEEKIMJEECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAcKq9e7du1q/fv3V6lUKpUqKcVoQSbCCBEikuBA6d69u++gVbFiRZVKpVKpklJsMc5OkEKEiCQ4UH7729/aBx98EPtKCCGE+Ob5zW9+47snChEikuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLkRiXr92ws5c+C7IuXLkeexZCJBdJsAgZSXCgSIKFSIwOM3fYU23mBlnv9Fth165/HnsmQiQPSbAIGUlwoEiChUiMBuM32fdqTwmycnVcYFclweIuQBIsQkYSHOPGjRt2+vRpGzt2rB04cMA++eQTmzlzpg0dOtSrf//+Nn78eNu0aZOdOHHCJXTgwIF+2ezZs+3y5cv2xRdf2Jo1a2zMmDFeK1eutKtXr/r979692yZMmGBDhgyxBQsW2KlTp/z4yZMnbcqUKX58xowZ/rjZQRIsRGJIgoVIHEmwCBlJ8Jd8/vnndvz4cZs4caK99NJLLqkbNmyw7t27W/Xq1b3y5MljZcuWdRFevny5vfrqq1ayZEm/rGfPnnb27FmX4w4dOvj1qlatas2bN7cjR464XI8YMcLKlCljVapUsTp16rgsc5tFixZZqVKlrGLFilarVi2bOnXqTXG+HZJgIRJDEixE4kiCRchIgr/kypUrLr6vv/66PfroozZv3rzYJV9Bl7ht27bWt29f27Jliw0fPty6du1qGzdutIsXL7q0UpMnT7b69eu7KG/evNmFF2GeNm2atW7d2jp37uzXR4InTZpk8+fPd4HmDwidYf6Y8BiZdYMRdc7zwoULdv78eb9d+fLlY5cKIe4USbAQiSMJFiEjCf4SBJYu7qpVq+y1116zhQsXxi4xu379um3dutXatWvnneJt27ZZ7dq1LXfu3N41rlChgo0ePdo+/fRTa9mypfXu3dsjE4cOHbIBAwZ4XKJFixbWqVMnF21EduTIkTZ48GA/RreYmAS3nzNnjg0aNMjmzp0be/TfcfToUY9fFC1a1LvQTzzxhL3zzjuxS4UQd4okWIjEkQSLkJEEfwld1s8++8wjEQUKFPCIQhzktGPHjjZs2DDbuXOnxxvoBCPEdHhbtWrl3V9EuUaNGh57IFOMVCO33bp188gE0QoE+tq1a54h7tOnj9+uSZMmLt+I+OrVq12CySVnhMzxrl27vHs8a9Ys7yYTrxBC5AxJsBCJIwkWISMJTsOZM2esYMGCNyU4nhUuXbq0i+elS5dcilnkxkdiEggr8jt9+nSrVq2aL4ijCxyX4Pbt23s+mD8USDQSTMe3R48eLrLNmjWz9evX+3EkmO4xkp0VygQLkRiSYCESRxIsQkYSnIaMEozorlu3zhe6MekBWMxG55ZsL1EJRBeZJQ+M0DLlAdlFhBFVcsB0e/lDEe/4Isp0holJIMnx6RJkkXv16pVpJzgjkmAhEkMSLETiSIJFyEiC05BRgg8ePOgL1RDWPXv2+DFElsgEC964HMllSgRxCOSWr+kas2iuQYMGLsV0dlnIxucsgCNCQRyC6ASj15goQeb3o48+8tuTHc4KSbAQiSEJFiJxJMEiZCTBacgowYgsC9+YF8yYMzh27JjLbL58+SxXrlyeyyUvTIeX6ATRh+LFi1ulSpXs+eef96gDOWJEmkV3DRs2tKefftqFmePkip999lnPB7PgrU2bNjcf63ZIgoVIDEmwEIkjCRYhIwlOA7ncpUuX+gYWEI8+kO9l4RxwncOHD3uEgRzwihUr/GsgHsHtWdxGB3ncuHF27tw5v218tBpxByZG7Nu3z49zW4SYqRJ0gteuXev3kxWSYCESQxIsROJIgkXISIK/ZpBk8sDkgskNs7gOEFuiEMwPpuMcF10W13E94hREIugoZwdJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOFAkwUIkhiRYiMSRBIuQkQQHiiRYiMSQBAuROJJgETKS4ECRBAuRGJJgIRJHEixCRhIcKJJgIRJDEixE4kiCRchIggNFEixEYkiChUgcSbAIGUlwoEiChUgMSbAQiSMJFiEjCQ4USbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjEkAQLkTiSYBEykuBAkQQLkRiSYCESRxIsQkYSHCiSYCESQxIsROJIgkXISIIDRRIsRGJIgoVIHEmwCBlJcKBIgoVIDEmwEIkjCRYhIwkOFEmwEIkhCRYicSTBImQkwYEiCRYiMSTBQiSOJFiEjCQ4UCTBQiSGJFiIxJEEi5CRBAeKJFiIxJAEC5E4kmARMpLgQJEEC5EYkmAhEkcSLEJGEhwokmAhEkMSLETiSIJFyEiCA0USLERiSIKFSBxJsAgZSXCgSIKFSAxJsBCJIwkWISMJDhRJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOMbnn39uly5dsk2bNtm5c+fsxo0bduLECVu2bJmtXbvW1q1bZ4cOHbLr16/7Zbt377YNGzbY1q1b7fjx47F7Mb8O90EdPHjQrw+nTp2yLVu2+P3s3bvXHws+/fRT27Ztmx/fuXOnnT171o9nhSRYiMSQBAuROJJgETKS4BhIKVL76quv2sKFC12ER40aZT/4wQ/sxRdftLx581qvXr38+JkzZ6xGjRr2yiuvWMmSJW3IkCEu0Qhvt27dLH/+/FagQAFr166dXxdpnjhxohUpUsTy5Mlj9erVcyHm+Pr16+3dd9+13LlzW6VKlWz27Nn2xRdfxM7q1kiChUgMSbAQiSMJFiEjCf6Sq1evese3WLFi9vjjj9u8efNs165dNnz4cBdZOrUHDhxwoaXrO2nSJBfQ6dOn29ChQ61169a2Z88emzt3rjVo0MAGDBjgn/OHAbFeunSpdezY0Zo1a+b3VbNmTb/tmjVr7KOPPrLy5cv79bjOwIED7dixY7EzuzWSYCESQxIsROJIgkXISIK/BAnet2+fd35feuklW7BggS1ZssQ7toULF3Zp7d27t23cuNFjEC1atLAePXp4rGH58uV+2fjx461NmzbWpUsXW7Fihd8fn3Oc7nCHDh1sypQpdvnyZevXr58LNh+5DUJ74cIFmzx5sksw95mR06dPuzgj0vXr17c333zTSpQoEbtUCHGnSIKFSBxJsAgZSfCXEGO4cuWKHTlyxGMMixYtstWrV1vXrl1dUtu3b2+VK1e2wYMHuxzzCz9t2jQ7efKkbd++3YW2c+fOHmegM4wA0zEeO3asRyhq1arlIoxEX7t2zWbMmGH9+/e3Ro0aWZMmTbxTzOMjz4MGDfLoREaIYXBePXv2tE6dOlnx4sWtVKlSsUuFEHeKJFiIxJEEi5CRBKeBuEPBggVdNhFiBJfOLdnd5s2be+xhzJgxLsR0i1nERmd45MiRfjmxBi4/fPiwL6ojNoFA8wcCGSZigQQTt0Bma9eubU2bNvUoBMdZgEdXGKnOCsUhhEgMSbAQiSMJFiEjCU5DWgmmM3vx4kVfpEYRXSDSwMc6derYzJkzfeID0yHI9RKRqF69ugvx/v377ejRozZixAjPFCO7RCY2b97s0YupU6d6l5n8MGJNB5jjdIS5niRYiD88kmAhEkcSLEJGEpyGtBJMlpfuLpEHJkcguEQX6AAjqmSCWQy3ePFil2OyvH369PEOL4vsuKxVq1Yee+jbt693gukMc1/du3f3r7mMPyCINZlg4hPIMYKdFZJgIRJDEixE4kiCRchIgtOQVoLpzrZs2dIqVqzoAswv+bhx4zzry2WMNSMvTN63SpUqPvKMYjEdnWIuY/EaksxxxPf999934eU43V6OT5gwwR8TsS5Tpox3jj/55JPYGd0aSbAQiSEJFiJxJMEiZCTBaaBLS7SBqQ9MY0CG6ea2bdvWF6sRc2AeMJcx+YEoA91ihJT4BEUcgtsg0Hxk3BnH58+f75EJ5JgFcWyOwXFGpnEfHKfTzII78sFZIQkWIjEkwUIkjiRYhIwkOAeQEWanN0SWbi5RhjgspNuxY4etWrXKO8tIMyC27CbHRhzkheOiy2QKrsfUCeSb22cHSbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjECFmCf9poulUcttaqDF8XZM3dfjz2UxChIwkWISMJDhRJsBCJEbIEh159Fu6J/RRE6EiCRchEQoJZmHarBWUsPOPy+AK1qCAJFiIxJMHJK0lwdJAEi5AJXoKRWyYrbNy40ScufPbZZy6+THDgMja7YCc2dmSLEpJgIRJDEpy8kgRHB0mwCJlIdIIrVapk+fLls5o1a1rHjh1t8uTJdvDgQdu9e7cNHjzYypUr57N9o4QkWIjEkAQnryTB0UESLEImWAm+ceOGRyDo+FatWtVq167t2w2zNfGgQYOsfv36vkMbO7hxnI0pooQkWIjEkAQnryTB0UESLEImWAk+cuSIjRkzxqto0aK+29qCBQtcgNmRrWTJkvbaa69ZjRo1fBMKIhJRQhIsRGJIgpNXkuDoIAkWIROsBG/dutUFt2zZspYnTx4rXry41a1b10qVKmXVq1d3Ge7bt69vbTx8+HDf4S1KSIKFSAxJcPJKEhwdJMEiZIKV4EuXLnnmd+fOndajRw+X39dff93KlClj27Zts4sXL3oueOjQoVaoUCE7fvy4RyeigiRYiMSQBCevJMHRQRIsQiZYCT58+LAvemvYsKHngUuXLm21atWy+fPnW968eT0PXKVKFWvcuLGtWrVK0yGEEOmQBCevJMHRQRIsQiZYCd6yZYv/4hUpUsReffVVnw5RrVo1mz59uscjWBBHVKJ8+fLeBWYhXZSQBAuRGJLg5JUkODpIgkXIBCvBLHbr0KGDVa5c2X7xi1+4+JIJJgf87LPP+nE6xHSKZ82apekQQoh0SIKTV5Lg6CAJFiETrAQz93fevHnWq1cv7wTTEW7Xrp317NnT7r//fp8Mwefjxo1zOT5z5kzsltFAEixEYkiCk1eS4OggCRYhE6wEsyiuffv21q9fP2vTpo13fdu2betj0hiZxi8m19m0aZNnhZFmLYwTQsSRBCevJMHRQRIsQiZYCWaLZLZEPnXqlC+SIx6xf/9+O3r0qC1fvtyPcR021GBKhOYECyHSIglOXkmCo4MkWIRMsBIMdHYRXQSX+uyzz/xrxqPx9fnz512OGZnGZVFCEixEYkiCk1eS4OggCRYhE7QEs9iNbZJHjx7tMYgDBw7ELvlKkFesWOGyuGjRIo1IE0KkQxKcvJIERwdJsAiZoCWYnC8bYbBbHHlgZDfOoUOHfGFczZo1bcOGDd4hjhKSYCESQxKcvJIERwdJsAiZoCWYPHCBAgVs5syZvgiO2AMxCLq+Xbt29akQ48ePj107WkiChUgMSXDyShIcHSTBImSCl+CCBQva3LlzPQ7RsWNHnxhRoUIF69Kliy1btsxzwVFEEixEYkiCk1eS4OggCRYhE6QEHzt2zBYvXuwbY7zwwgveCUZ4e/ToYc2aNfMZwYxFIx4RpbFoaZEEC5EYkuDklSQ4OkiCRcgEKcFsgzxnzhwX3ty5c3v3d+rUqd4R5jhyTFcYUVy5cmXsVtFCEixEYkiCk1eS4OggCRYhE6QE37hxw+cBT5s2zRo3bmxVq1a1Pn362NatW30UGt3f9evXuxy3aNHCpZnbRAlJsBCJIQlOXkmCo4MkWIRM0JlgYCHczp07fXvkESNG+CYZjE5DemfNmuWSPHDgQPv0009jt7g1yDMS/fnnn/vXfGSqBJX2ONeLH6c4h3jsgsdNezwOt43PMU57/fhjcjztY2SFJFiIxJAEJ68kwdFBEixCJmgJRmwHDBhg9erVs7Fjx9ratWutZcuWVrFiRRfgPXv2+LbJ5IWzmhOMhO7bt88qV65sa9as8Q035s+fbyVKlLCSJUt6xpioBfeDdDOa7a233vLLW7dubWfPnnWBHT58uD8+9dFHH/n9AAv3qlevbu+++64v2mMTD9i1a5efP8ebN2/us42zgyRYiMSQBCevJMHRQRIsQiZYCT5y5IgNGzbM4w50gdky+dy5c75lMh1hxLRTp042Y8YMnyd8uw4rHVhkuUGDBvbMM8+4/DJbmA4yRd4YgeWXffv27b4Qj68R0enTp3vuGCHnNk2bNrU2bdq4ANepU8d27Nhhmzdv9tvy9YQJE1yoeYx4B/v999/3DT94Lpz7mTNnYmd2ayTBQiSGJDh5JQmODpJgETLBSjATIiZPnuwSSuY3DrLL6DTkks0yyA1nBfEJRBVxfu6557xri6AuXLjQTpw44REHBJkNOZYuXeqdXH7pu3fv7oJMFvny5cveleY+5s2b5x1eOrucHyLdrl07l/ZLly65nCO9o0aN8gV8HTp0cIEfOXKk3wcynRE6yuSc6XjHu83vvfde7FIhxJ0iCU5eSYKjgyRYhEzQcQjytEgvgohEMhOYzxFNpPTgwYMeicgKOsF0crl+/vz50+08x/3TmWXnOTbgIHJBt7dUqVIeYShTpowfR8Tr16/vHWA27mDhHpLLpAo27UCcuS1xCsSZTi7TLZo0aeJdYUQcwR40aJBfnhHuH3FmBjLxjBdffNF3yhNC5AxJcPJKEhwdJMEiZIKXYISXHC0RBTq3RBM2btzonVikFoFFcuML0W4H12XzjbQSjEyz6xxRBj4SrWBGMd1mcsRIa/ny5T13XKVKFe/UEtU4efKkyyxdXnLGvXr1ciHnNnSa+ZpYBBJMFIPj69atc4kmEpEVikMIkRiS4OSVJDg6SIJFyAQtwcQUPvnkE++0MiaNeELnzp19NBoL5DhO55Rf0OzkbDNKMN1Zog5FihTxri5ii1CzCC4+4eHjjz+2Dz/80OW3Ro0a3q1FvuncjhkzxiMUHOcPBXliZJeccrdu3fz8OE8W4tEhRubpHBN3yApJsBCJIQlOXkmCo4MkWIRMsBKMgCKORA+YrkAkgY7q6tWrbfDgwS6adIbJBRMdIOOLwN6OtBLMdcng0gFGWLk90s3jkeNFdOkS0wlGRrkNO9YhscQeWKiHkPMHgigEnV8mVnCb/v37+3kh7dw3nV9iHFOmTLmZM84KSbAQiSEJTl5JgqODJFiETLASTKd14sSJLp0sEkMkDxw44B3b3r17eweXritiTCc2HkW4HWklmBFmyOtDDz1krVq1sqFDh/rkCaIQiDGX9evXz7vAzCImAkEkgrwwl3F9csMsjOM2CHLDhg09tsE0COSZ4yyGQ2ZZwEemmPjEli1bYmd0ayTBQiSGJDh5JQmODpJgETLBSjDRAmSUhWlFixZ18WQiRLly5VwkkV/iDEQX6MzSab3dmDS4cOGCiygd4FWrVrncvvrqqy6tCCe70nFfdJjjj4v0Is3xfDJTILgu8QxmCNMRZtEdsss0B7rWhQsX9gkSHCcC8fbbb3s0gusjt5x3VkiChUgMSXDyShIcHSTBImSCzgTHd4tDPJmU0KhRI58QQZSBy+JFjOGbArFFlGfPnu3d6vhjI7ZEKZgTjBjHRZdz5XqMe2NMG7KeHSTBQiSGJDh5JQmODpJgETJBS3A8F0xGl93b6KjSySWiEC+6ueRu6fJ+E9BtJveLzMYXzwEfiWMg6XxMe5zrcRwxzqpbHUcSLERiSIKTV5Lg6CAJFiETrAQTPYhHDdjIonbt2j4V4o033vA8Lh1XjjO+jOhBdiIGISEJFiIxJMHJK0lwdJAEi5AJVoLZMW7SpEkuu2xawVQFJkK88sorPiOYeb5MYCCbS5c1ux3WUJAEC5EYkuDklSQ4OkiCRcgEK8FMY2AbYjabeO2113y7Yhafvfzyy7ZkyRKfsMCMXjrBO3bsyHI8WmhIgoVIDElw8koSHB0kwSJkgs4Ex2FDjCeeeMKee+45H2mWO3due+mll+ypp56yRx991De7YKOLKCEJFiIxJMHJK0lwdJAEi5CJhAQfOnTIIxBMX2BaBDOBKY7xNbvKsfgsSkiChUgMSXDyShIcHSTBImSClWCk9ty5cz6FgcVxFJ8zBYLoA1MXNm7c6LOD2UUuq40yQkMSLERiSIKTV5Lg6CAJFiETrATv27fPd2EbP368L5CL18cff2yHDx926V2zZo1vnMHYNDbNiBKSYCESQxKcvJIERwdJsAiZYCV47ty5dt999/lOa+zCxke2JW7Tpo3v4Ma2yUhw586d7bHHHrOjR4/GbhkNJMFCJIYkOHklCY4OkmARMsFK8LJly6xQoUK+4I2d1tatW+cdYDq+I0aMsCpVqviCOKZFPP300z5SLUpIgoVIDElw8koSHB0kwSJkgpXg5cuX+y5xSDDSy6g0OsE1a9a0/PnzW8mSJX1OMLKMJGtEmhAiLZLg5JUkODpIgkXIBCvBRB5eeOEFzwAPHDjQs7/MBSYOgSAOGDDAOnXqZIMGDfIFdNosQwiRFklw8koSHB0kwSJkgpVg4g9lypTxX8DBgwf7VskUG2YwHo1M8JgxYzwTzIQItlmOEpJgIRJDEpy8kgRHB0mwCJlgJfjEiRM2ZcoU69ixo0vu6NGjves7b948302OCAS7xs2cOdMqV67s2yhHCUmwEIkhCU5eSYKjgyRYhEywEswcYPLA5H+JRgwZMsQzwTdu3PD68MMPrXfv3rZ3716PTDBHmNtEBUmwEIkhCU5eSYKjgyRYhEywEgzHjx+3hx9+2AoWLGh58uTxLZLp+laqVMmeffZZnxCxdOlSO3/+vDLBQoh0SIKTV5Lg6CAJFiETdCeYsWe5cuXy3G+NGjV8WgTxB6pfv37WoEED31AjikiChUgMSXDyShIcHSTBImSClmBmArdv3962b99u8+fPt2HDhsUuNTt16pSNGjXKIxFRRBIsRGJIgpNXkuDoIAkWIRO0BDP799ChQ3b58mW7ePGinTlzJnapefyBrZU3btwYOxItJMFCJIYkOHklCY4OkmARMkFnggEZppDetJ9nrKghCRYiMSTByStJcHSQBIuQCVaCr1696p1eZJBfQnaHY9MMxqZVrFjRSpcubcWKFbPChQtb1apV03WJo4AkWIjEkAQnryTB0UESLEImWAm+du2aHT582GcEs0EGI9Hq1q1ru3btshkzZtjUqVOtTp069s4779isWbPsypUrsVtGA0mwEIkhCU5eSYKjgyRYhEywEkzEgdm/7A63e/dua9eunVWrVi126Vd89NFHLsJRRBIsRGJIgpNXkuDoIAkWIROsBNPZZVFcvBiTRgwi7bEuXbr46LQoIgkWIjEkwckrSXB0kASLkAlWgnfs2OE7xDVp0sTrjTfesKefftqaNm3qxbE333zTSpUqFbtFtJAEC5EYkuDklSQ4OkiCRcgEK8FHjx61CRMm2OTJk30xHIvf2DmOz+NFPKJChQqxW0QLSbAQiSEJTl5JgqODJFiETNBxCBbGHTlyxIvoA9slx7+munbtmu04xPXr130Huu7du9vOnTt91NrevXv9flu3bu3CvX//fj/OTOIBAwZY27ZtbciQIbZ582a/jxs3brh8d+jQwf8wLF++3KdYkF9esWKFderUyTf3mD17tm/mwX0x4SLjY2QHSbAQiSEJTl5JgqODJFiETLASjHCeO3fOtm3bZps2bbIWLVp4Nzgt2V0Yx3198skn1r9/f3vxxRdtwYIF3mkeP368j1rjvhs3bmzTp0+306dP2+LFi124mUjRrFkzF1I27OA8mjdvbjVr1rSWLVv67U6cOOEL99i5jsxymzZt/HYbNmxwic/4GNOmTXMhzwpJsBCJIQlOXkmCo4MkWIRM0J1gJkMwGxjBrFy5snd9T5486Z1c5JiObHYkmPuia1umTBl78sknfQtmRBgx7dOnj3d+mT7Rr18/W7lypeeN6eoit2PHjrVGjRp5R5cuL9dbunSprVu3zvPIW7dudRmn04vwXrhwweUVof74449dmjn/8+fP+/n27ds305nGjISjU83z2rJli0t22bJlY5cKIe4USXDyShIcHSTBImSClWCkkAkQxA+IETAvePTo0S6c+fLls+eee86effZZq1WrVuwWt4bIAhJKFCF//vy2aNEiGzFihEs1C/DYnhnZHTRokMcgihQpYkuWLHGh5WOvXr18LnHRokVt1KhRdvz4cRd0pJjOLh3qjh07ereZjjEbe4wZM8bFuHr16rZ9+3Z/DJ4D579+/frYmf2OgwcPWrdu3ez555+3Rx55xH7yk5/Y22+/HbtUiOTwOTs0Blr1JcFJK0lwdJAEi5AJVoLJ0yKORCLOnj3rRQeVrC0dWrrBCCyinBXcF5EIusgFChRwCSbriwRzf2R6kVm6zsgsUyfoyCLiq1ev9g7x4MGD7fXXX3cZZn4xwoscs5EHHWayxpwrXWdkmvuvV6+eL97jMXh8usM8xsKFC2Nn9jt4rkQr4l1uBFqdYJFMdh67aC93XRRsPdh0ZqaCpvrDlyQ4OkiCRcgEK8F/CJBoJkwgwcOGDbPatWvflGA6zkQViDu89dZb3r1FgolHILt0iBFoZBkJpqtM5xY5Rla5DhJMJ5g8L4UE06mOSzACzWPMnTs3dka3RplgkWw2HDybqeCoVFmVJDg6SIJFyERCgumc0nElisBHiiwuMnonpJVgRq+R/WWxG11YOrc9evRwSWWBG4+J1M6bN8+nRBDF4DgxByZT0LElK8zxBg0auATTob506ZJfn44vcQkeY+PGjS7UQ4cO9cdYtmxZ7IxujSRYJBtJsCqnJQmODpJgETKRkGAmNbzwwgveoSXT+/DDD3vkgPjAnZBWgletWuWdXH7B6fqyAQejzJBeog18zmI6OsAsvuP6CDJj2Yg1zJw500qUKOEL7IYPH+73xUeiDO+//75njukucxxB5jiTJtj5jjxxVkiCRbKRBKtyWpLg6CAJFiETCQlm5BgLyoARZoULF/YFa3dKWgmmy0tX98EHH/Q4Q548ebxLS3eZ8WYsumOBHPlgJJxuMYvXyP++/PLLVrx4ccuVK5dnklkox2g0drRDXJ966imbNWuW55hZDPfAAw+4GPMYCDbxi6yQBItkIwlW5bQkwdFBEixCJhISzPbJcQlGZJFgxpTdKeRy2SCDkWh8jrzOmTPH75uPCC2CiggTWSB2QTc3vrkGIkx8gmkVRDMYk8bkCeb+cr/khbkvzo3zjD8GGWA612yikZ2FfCAJFslGEqzKaUmCo4MkWIRMsBLMzNyJEye6hDKajFFjLCxDTOnSMnOXr7l8xowZPpXhTkFSEWJmANMZ5mtAeFnghrASuUi7uQXSi9iyEQZSzHWBzxFf7ovbxru98cdgIV3ax8gKSbBINpJgVU5LEhwdJMEiZIKVYHKziC4Z3Lx583r8gLgCi87IBCPF8ewuc3mZ6RslJMEi2UiCVTktSXB0kASLkAlWgum20ullAVqxYsV8cRqRBaIIbJSBHBMvYJFaTjvBdzOSYJFsJMGqnJYkODpIgkXIRG5hHJEDFqzlJBMcEpJgkWwkwaqcliQ4OkiCRchEQoLr1q3rnd+jR4/6fGB2bps/f362piyEiiRYJBtJsCqnJQmODpJgETKR6QQzxow8MLN28+XLZ5MmTfKFZlFFEiySjSRYldOSBEcHSbAImUhIMLu7sekEC+MoFsSxeUXUFsOlRRIsko0kWJXTkgRHB0mwCJlISDBbDjOCLC1sT8xiuPiIsqghCRbJRhKsymlJgqODJFiETCQkmNm7zA1OCxtVsN0xghxFJMEi2UiCVTktSXB0kASLkAlegun0durUybcfBhbDIcTMCWaxHNMioogkWCQbSbAqpyUJjg6SYBEykZDgBg0a2MCBAz0SceDAAWvZsqW99957NnTo0MjNB44jCRbJRhKsymlJgqODJFiETCTiEPXq1bNWrVrZwoULbcCAAVarVi0rX768b6scVSTBItlIglU5LUlwdJAEi5AJVoLp8B45csTr/ffft/z581ulSpWsaNGiLr90golJHD582OcH37hxI3bLaCAJFslGEqzKaUmCo4MkWIRMsBK8Y8cOa9iwoTVu3Nh+/OMf23e/+1179dVXbx5j6+Q33njDZwi3aNEicjODJcEi2UiCVTktSXB0kASLkAlWgunwjhgxwsaMGWOPPvqoSzDbJbN98ujRo+2tt96yihUr2siRI238+PE+Mi1KSIJFspEEq3JakuDoIAkWIROsBF++fNn279/vC+FKlixphQoV8gVyVatWtWHDhlmxYsWsXbt29sknn9jBgwcVhxDia0YSrMppSYKjgyRYhEwkFsYReWDL5Dlz5libNm3889KlS3unOKpIgkWykQSrclqS4OggCRYhE7wEMyKNHDAxCGYEMxe4ffv2VrNmTRs7dqydP38+ds1oIQkWyUYSrMppSYKjgyRYhEzwEkzMgU4wEhwHMW7evLmL8MyZM2NHo4UkWCQbSbAqpyUJjg6SYBEykegEHzp0yE6dOhU78hW7du2yzZs3+3i0KCIJFslGEqzKaUmCo4MkWIRM0BJM/OHEiRN2/Phx+/TTT+3q1at28uRJP7548WJbv3697yIXRSTBItlIglU5LUlwdJAEi5AJVoLZLIPJD8uXL/diAgRfDx8+3Meh9ejRQzvGCfEHRBKsymlJgqODJFiETJASTAQiPie4c+fONnDgQFu1apXNmjXLXnvtNR+dVrt2bf/lvHjxoneJuU2UkASLZCMJVuW0JMHRQRIsQiZICWYxHFGH8uXL23333WflypWzwYMH+y8jO8VNnjzZSpQoYfXq1bMFCxbYkiVLPCoRJSTBItlIglU5LUlwdJAEi5AJthN84cIFW7t2rbVu3dplkM5vlSpV7IEHHrBmzZpZ7ty5fQe5jh073uwIRwlJsEg2kmBVTksSHB0kwSJkgpXgvXv3WpcuXVyC2Rxj1KhR1r9/f3vhhRc8FvHee+/5/GBiEnSNr127Frt1NJAEi2QjCVbltCTB0UESLEImaAnu3r27/wKyAI6RaBs3bvSZwWylTBQi7ezgO4UpE2vWrLGpU6d68RjTp093wR45cqRHLjiOYNOVvn79um3atMnnEnOdrVu3xu7JbM+ePTZv3jz7+OOPbeXKlTejGYxvI6oxadIkW7Ro0e+NebsdkmCRbCTBqpyWJDg6SIJFyAQpwXEQT2Rz9uzZtm3bNp8QMXr0aFuxYoXvGod05pQtW7ZYz549vaNM5cmTx9566y0rWbKkPfTQQ/bOO+/4cbrPSDfS3LRpUytVqpRv2dytWzePYDCpguuULVvW3n33XatTp45fn8V606ZNs4oVK9rbb7/tH5ctW5bt7LIkWCQbSbAqpyUJjg6SYBEyQUsw0BUmD4xorl692nPACCJCnMhECG7LvOF49e7d23/ZJ0yYYE2aNLHTp0/7ca537tw5X4CXP39+mz9/vhdRjTlz5ngcg6xyv379bMeOHb6THR1khLddu3ZWq1Yt7yR36tTJp13s3r07dga3RxIsko0kWJXTkgRHB0mwCJlgJZgYAp1YOqg/+9nPvH75y1/aPffcYwULFvTOK5cxQaJGjRp25syZ2C3vDESXmEKrVq2sQYMGvujumWeesWLFilndunVt7ty5PpINSW7ZsqV3pIk/0JGmG81xZJc4BN3iKVOmuCDTZUZ8hw4d6ht6INF9+vSxhQsXxh45PWwIQgyD50NH+fnnn7fixYvHLhXim0cSrMppSYKjgyRYhEywEnzkyBEbO3asZ3XfeOMN78LScSW2wJg0MsGDBg3yzi2d18uXL8dueWewKcf48eP9F50xbGPGjHFZRUjpQCOzZIDbtGnjGWSiDggrUYxq1ap557dv3743s8NkgpHpRo0a+YYeSDQj35BnZh4jyZlBtILMM88Hwa5cubLHLoRIFpJgVU5LEhwdJMEiZIKPQwBSSkeVOAQxASQTQWYHuUQ5f/68yyyyTZyB++QYHeIBAwa4/CK5TKggzsAmHnR8EW+6tnSO2cxj8+bNLrKcI51pzpEuMQvikOCdO3f6fSDc2UFxCJFsJMGqnJYkODpIgkXIREKCEUiytHRaWXC2b98+n+xAVzYRWHhHtrhQoUIuq+SAuU+6w0gwY9mIOtDR5Q8BMsxjxxfo0Znu2rWrH0d+z5496zlhcsDIM/LO4jgeh8sZ95bdrZ4lwSLZSIJVOS1JcHSQBIuQiYQEsziNKRGMMGNMGTOBOUYlAtLLyDMmOmzYsMHGjRvnMQu6uogw49jo6DKdYsaMGS63xB64bq9evVx0OU6emJFqhw4d8gV8yC6dav54INBMhECaO3To4Nnh7CAJFslGEqzKaUmCo4MkWIRMZCSYvG6lSpW8A/x1bYzBAjciCogrMQi+pntLBrlw4cK++A6ZZToEHWImUyDCbOPMZexox6K6+vXr+9fI9Msvv+xijRATp+A2SHLevHn9a45nB0mwSDaSYFVOSxIcHSTBImQiIcHr1q3zBWh0aVmURsb264D4AjOHiVsQs2BxHbng4cOHexFtiEcu6Ayz6QU5X6Y/sICOeAaxCaIUiDTH+YNBbpiJEMwiZjEdxykWvmlOsAgFSbAqpyUJjg6SYBEyQUswskuHFoFkPBnRg2SC2CLMFN3hOPFsMTEKOsNxSecjkQu610y7yK4AgyRYJBtJsCqnJQmODpJgETJBSjDxB3ZioyvLGLSqVav6BAZE89ixY+mKrYm/zu7w3YIkWCQbSbAqpyUJjg6SYBEyQUowndXly5d7npZtilmwxngydnJjJFm82Ma4cePGvhCNsWZRQhIsko0kWJXTkgRHB0mwCJkgJZjYAYvO2BEuX758NmzYMF9sRk6XLG68mLjAphZIMp3jKCEJFslGEqzKaUmCo4MkWIRMkBLMYjM2pGCrYXZsY0wZcQjGo5ERTltsacziNbrHUUISLJKNJFiV05IERwdJsAiZ4BfGIbkdO3b0hXHM60WQUwFJsEg2kmBVTksSHB0kwSJkgpbgOHv37vV5vmxvzEK4qC2CywxJsEg2kmBVTksSHB0kwSJkIiHBTItgtzjmBLNT28WLF2OXRBdJsEg2kmBVTksSHB0kwSJkIiHBwBg05vDu2rUrcvnfzJAEi2QjCVbltCTB0UESLEImEhLMVsOLFy+2UaNG+Q5sTIuYMmWKL5Rj17YoIgkWyUYSrMppSYKjgyRYhEzQEsyoNHZbmzBhgssvWxZ369bNOnXq5NWjRw+XYbY8JjIRJSTBItlIglU5LUlwdJAEi5AJWoLZmrh69erWqlUrl92tW7f6tIjt27f7pAguK126tG9jrBFpQny9SIJVOS1JcHSQBIuQCVqCmRX88ssv2/z58300Gt3eePH1xx9/7DvG8fHy5cuxW0UDSbBINpJgVU5LEhwdJMEiZIKWYLZC/vDDD61y5co+K3jq1Km2aNEimzNnjvXr188qVKhgtWrV8kVzURubJgkWyUYSrMppSYKjgyRYhEzwmWC2Tx48eLB17drVunfv7r+Qffr0sf79+9vQoUNdiqM4N1gSLJKNJFiV05IERwdJsAiZoCU4DhngESNGWPPmzX1WMBEIJHHdunWRi0HEkQSLZCMJVuW0JMHRQRIsQiZoCSb3e+zYMVu4cKFLIQvk6tevb3Xq1LEWLVp4J3jDhg3eMdZ0CCG+XiTBqpyWJDg6SIJFyASfCW7UqJE1bNjQhXfVqlU+IWL16tU2ZswYK1u2rJUsWdIOHjyoTLAQXzOSYFVOSxIcHSTBImSCluBTp05ZwYIFbdKkST4pgnnAxB/4ePr0aRfjunXr2rx58+zKlSuxW0UDSbBINpJgVU5LEhwdJMEiZIKW4LNnz/ovH1lgOr/Lly/3XeJYLMdYNLrESHAUt1KWBItkIwlW5bQkwdFBEixCJmgJpruL7LZu3dozwPwysnPcwIEDfVoEx4cPHx45AQZJsEg2kmBVTksSHB0kwSJkgpbgOOwIN3r0aJdeJkPwcdSoUT41IooCDJJgkWwkwaqcliQ4OkiCRchEQoKZAIEUEn0oX768L4gjCsFWyidOnIhdK1pIgkWykQSrclqS4OggCRYhE7QEswCOjTE6derkG2bMnDnTF8FNmzbNBg0a5LvFMTlCO8YJ8fUjCVbltCTB0UESLEImaAk+c+aMvfvuuy7ARB/o+rJYjo+7d+/2HeSqVavmC+auXr0au1U0kASLZCMJVuW0JMHRQRIsQiZ4CS5VqpR3g1esWOHie+DAAdu/f7+tX7/eunXrZg0aNPBpEdeuXYvdKhpIgkWykQSrclqS4OggCRYhE7QEX7p0yWWwYsWKvktcv379fEEc84FZHMfxtm3b5njHOOIWLLrbu3ev7du3z2cRX7x40Xep4xibcFy4cMGvy+51zC3+5JNPvJhTHOfcuXN+Xe6D28ajGZz/kSNH/L4OHz58R7OMJcEi2UiCVTktSXB0kASLkAl+YRzTH4hCMCe4ffv2vnVy586dfQMNOsMIcE5AaufOnWs/+tGP7LnnnrNcuXK5UM+ePdu7yy+88IIVL17cpk6d6tdHaLt06WJvvPGG5c+f33r16uXHATEvUaKE5c2b1+rVq+cdbFi0aJFVrlzZnnnmGStXrpx3r7OLJFgkG0mwKqclCY4OkmARMsFLMGzevNkXwn344YdWpUoV/4VEWOfMmXNTOO8UurrMIK5QoYItWbLENm7c6JKK0L799ts2f/5869Gjhz/uunXrbM2aNS66w4YN80KI2b6ZbZyR5g4dOviCvSZNmtiCBQv8nBHl6tWre2aZOccTJ060Q4cOxc7g9kiCRbKRBKtyWpLg6CAJFiETtAQTH6ATywYZyOiIESO8+JxfzJYtW3pemMVydHbvhG3btt3s7CKoAwYMcLlFXJFt5Hrx4sX+2P3797chQ4Z4JINxbVu2bPGveWxu06xZMz/Po0eP+uYdHGcxX8eOHf08WbQ3efJkfwyyzZnBc0CeyTm3a9fOihUrZiVLloxdKsQ3jyRYldOSBEcHSbAImaAlGDFkLjAd2aVLl/qCOESTTO6qVatcPunkIqZ3ujAOkY3/ciO9dF2ZNEFHF5ElL7xnzx6X2fr167uYkkmOnwPSW7t2bY9ncD90is+fP2/Lli3zDT04N4SWsW5EOugMs8sd3eLMIGPMdRF7xr4VKFDAO89CJAtJsCqnJQmODpJgETJBSzCRhYIFC9qECRNcPJFiFqohm4xJoyvMphlEF+5k0RkwW3jHjh3+GHSRe/bs6dEFZhIjuJcvX/boAp1gIhjILlEJFrhxG2QWQUd4uQ5SjTgzqaJGjRqeDeaPB1ELFsqRX0akx48fHzuD26M4hEg2kmBVTksSHB0kwSJkgpZghJfsb9GiRb1LSwyCXeLGjh3rndbChQu7cCKsdzodgu4s3eP47Ygr0AWme4uoshCOTnDfvn39DwCL8YhAMAUCIUfMWezWpk0bF1a60cg50su5IsfEIhD0eCcYkR43bpw/XlZIgkWykQSrclqS4OggCRYhE7QEI6nECxBUcrlIKjlbRLV58+YeW2D8WE7Go7HzHPlfbs/jILNEK1jYRkaYrjOZYDbk4HGRXsQWmWUxHOfTtGlTl1qmVsyYMcPlOJ4RJkbBHw9ywNw/8s71Zs2aFTuD2yMJFslGEqzKaT3VZq7l77U0yPpgyBq7ePV67LdASIJFyAQtwczsJZ7AYjK6s3RYq1at6jLJ6DHElWxwTmDiAwvj2HoZ6a1UqZJndplBTIeZrnPNmjW9e8uoMxbSsVCN8yG3y2UILd1iIhnkiolUsLkH49yIRyDKiCyyXqZMGevdu7dHMLKDJFgkG0mwKhULgT97KWejN6OIJFiETCQywUQMyOOWLVvWF6cx2ixthjcnxKMLdevW9SL2sGnTJpdUpJZuLsKNwLIZBkJOR5juLwvi+JzzI+rAdeggMyqNc2IDDjLKTHuge8xt2NiDaAS54ewgCRbJRhKsSsWSBKdHEixCJngJfv311z1KQCaXBWrx3dgYO0YsggjD1wmL5MgiI6x0cxFgIHLBYzIFgmJ3uThs2IE8E59g4Vz8HBFkdoxjAw46xmSXs4skWCQbSbAqFUsSnB5JsAiZoCWYCQ6PPfaYxxDoCJcuXdrlE1FlVBkd1q9bggHhRWR5nIx5Y47d6ji3yXg87X3dCZJgkWwkwapULElweiTBImSClmA6rHRd2d6YuAIRCBal0VElb0sUgkhDFJEEi2QjCValYkmC0yMJFiETtAQDnVQiCcQJtm/f7p1g5JgFcWxzTHQhikiCRbKRBKtSsSTB6ZEEi5AJXoJTFUmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4Fvw2Wef2fr1661WrVpWo0YNq1evns2cOdNWr15tRYoUsUqVKvkv/tChQ+3o0aN25coVGzVqlNWtW9fq169v48ePj92T2dy5c6158+ZWvXp16927t124cMGPb9iwwTp16mQVKlSwdu3a2a5du/x4dpAEi2QjCValYkmC0yMJFiEjCb4F+/bts3HjxlmbNm1s+PDhLsN8jsQWLFjQ+vfvbyNGjLDly5fbsWPHbPv27S7G7du3tw4dOljXrl1dag8cOGCtW7e2hg0bWs+ePf3j2rVrbf/+/TZ48GD/44HQNmjQwGbMmGGnTp2KncHtkQSLZCMJVqViSYLTIwkWISMJvgV79uyxBQsW2NatW70r3K1bN6tatarVrl3bSpcu7YK8aNEil9zjx49757d8+fK2atUqW7NmjfXr18/lecqUKd4ZHj16tF+3T58+NmTIEJs4caLLMh1gush0lAcNGuTd58y4dOmS7dixw+bMmWPTp093KS9TpkzsUiG+eSTBqlQsSXB6JMEiZCTBWfDFF1/Y1atXrUWLFlalShWPReTOndveeOMNe+edd1x0N2/e7ELbq1cv27t3rx0+fNgmT57s3V26xz169LCVK1fauXPnXJyJRrRs2dK7xVOnTrXr16+7/Hbv3t0jF5lB5AJJLlasmL3++uv25JNP+uOLsDl58artO/lpkDVt09FMJUGlinJJgtMjCRYhIwnOArrA69at86hDs2bNPBOM6J4/f97Fl6gDIozUjhw50gWYSAPRBuIKjRo1soEDB9qWLVvs008/9fuii4tM88djyZIlduPGDe88E6WYMGFC7JHT8/nnn9u1a9e8I8z9cFs6zyJs6o/fZPc2nB5k3fPhtEwlQaWKckmC0yMJFiEjCb4NdGgPHTrkMkuMgYVsdHORUTrERBwQVzq6CPGwYcP8+mSEJ02a5JKKHCPBGzdu9AVxZIirVavmcky+mMgFEkzsAqFOu6DudigTHA2qj1qf6X+0KpXq7ixJcHokwSJkJMG3gM4r3dmOHTu6sNIBXrFihccckFwEmYVuxCToBFPke1kgx4I4ogtkgVn8hiTPnz/fTpw44ZLL4jgEmGJxHVJN1rdt27Y2bdq02BncHklwNJAEq1RhlSQ4PZJgETKS4Ftw8uRJF9QnnnjCRRd5RWYZc0ZXmIVtfM6xTZs2+YI4Or/cBvFt2rSpf07Wl8+7dOni+d86derYgAEDPAbRt29fj0UsW7bMGjdu7Jlg4hLZQRIcDSTBKlVYJQlOjyRYhIwk+BYgtixge/TRR61QoUL29ttve5aXLu7LL7/shdAuXrzYr3/27FmX4IoVK/qCtcqVK3s+mEwxHWImOZQrV87y5cvnoku2d+zYsfbuu++6TOfJk8cnThC3yA6S4GggCVapwipJcHokwSJkJMG3gJwuo8tYAHfx4kVfjHb58mUvvqb4nFgEEJ84ffq0xxpmz57ti+c4BtwHnWKiFGR/mTZBphgRJj5Btpixaog0x7ODJDgaSIJVqrBKEpweSbAIGUnw1wjSSyc3vnguDseRZiQZsY6LLh/5mqwwQox4ZxdJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVW3ddohjWZtMVaT9sWbI1dcyj2FyhxJMEiZCTBgSIJjgaSYJVK9U1XmY9Wxf4CJY4kWISMJDhQJMHRQBKsUqm+6ZIEC/EVkuBAkQRHA0mwSqX6pksSLMRXSIKTzL59+6xdu3ZWrVo169atm61fvz52ye2RBEcDSbBKpfqmSxIsxFdIgpPIiRMnbMqUL/8glSljvXv3tiZNmtjo0aPt/PnzsWvcGknwVxw4fcnaTNsWbOXptCDT/6RUKpXqD1WSYCG+QhKcRNauXWudO3e2Fi1a2NmzZ23IkCHWv39/27p1a+wat0YS/BXL957O9I+8SqVSqTIvSbAQXyEJTiIzZszw7u/cuXPt8uXLtmTJEhs8eLB9/PHHsWv8jhs3bniH+OjRo3b48GHr1KmTlShRwo4cOZJwHTp0yCuzy+72mrp8i/1PlSG3rO9XGuSV2WWh1n9XHmLfqzjoy4+DM7089PrqZxat58bP6nsVP4rkzyyqz+2r58XvWeaXh1zFu023gwcP+v8lmf1dvZNq27atVa5cOfY/lRBhIQlOIlOnTnUJ3rhxo127ds3WrVtnH330kY0cOTJ2jd/BH6s+ffrYq6++as8//7z95Cc/se985zv+eaL16KOP2uOPP57pZXd7PfPsc/bQ40/fsn740wftR/c/lOllodaDjz9l/3PPfXbvg49menno9b/33G8/efCRTC8Lte5/5An73g9/Yvc9/Himl4dcP3vkSfv+D++1+34ered270OP2n//+D574LFfZHp5yPXgl/8eH3roIXv22Wcz/bt6J/XTn/7UihUrFvufSoiwkAQnkenTp3sUYs2aNXb16lVbuXKl9evXz4YPHx67xu+4cuWKffLJJ36dpUuX2oIFC2zevHn+eaJVsmRJq1mzZqaXhV6lS5e2qlWrZnpZqLVo0SLLmzevtW/fPtPLQ698+fJZmzZtMr0s1BozZow9+OCDHnnK7PKQa/z48fbII4/4C/jMLg+1unfv7pI3e/bsTC8PuXr16mXPPPOMvxuZ2eV3UgsXLrQNGzbE/qcSIiwkwUlk2bJl1qVLFxs3bpx9+umnNm3aNOvRo4dNnjw5do1vhjp16ljXrl1jX0WLBg0aWIcOHWJfRYPr169b4cKFbdKkSbEj0YKu0tixY2NfRYNdu3b5uy286xM19u/fb08//bS/mI8Ss2bN8nfesrNQOTRooPBC+vTp07EjQqQmkuAkwni0oUOHWo0aNWzx4sXWsmVL69ixo8civkkkwWEhCQ4PSXB4SIKFiD6S4CRCDjj+1jZv2b/55pv+FtylS5di1/hmaNy4sa/wjSLNmzf372mUQIJLlSqV6QLKKPD+++9HTvD37NljL774om3evDl2JDocOHDAXnrppWzPOA8FRLFIkSJ24cKF2JHowP87BQoUsDNnzsSOCJGaSIKTyBdffOHCS5eIzCDxCGYHc/ybBJmiEx1FyLyRWYsSn3/+ub+DsGXLltiRaEEmftOmTbGvosGpU6f8xRjTXaIGItWzZ0+fMBMldu7caQMHDvT1GlGDF2WM4/ymGy5C3G1IgpMMwktHGPm9ePGij0L7puE/6HPnzsW+iha83ccM5ijBv5ljx455jjyKRPG5ffbZZz6Sit/1qME7Ewhw1GSRsZWMAONFZ9SIP7dk/H8jxN2EJFgIkXQQKV6I8a4IL1r4WgghhPhDIgkWkYWuGxnM3bt3x46EDR0p3nomukIxnmjv3r3Bd6roRvE8Jk6c6DOyWRTHW9FREmG69/ExiHSEQ4fnw86WM2fO9HGNFLPMo9Tp5sUYCxl5XqF3ufldYgEj//74Wc2fP983aVq9enUkF/4JkV0kwSkM/5Hxh/748eN28uTJyLwFzfPijz5dxWrVqvkYuijAzwfxLVSokBUtWtQ/MlKPGE3IsPAI+WURUrdu3XyRFXnFKMVYkKjt27f7YqRhw4bFjoYLz6dZs2Y+8YJ/hxRzz6MybYC/H6zRYMEyayZCf15kf0ePHm0VK1b0n9Urr7ziEz0qVaqUrW36hYgqkuAUhlwY/5EVLFjQypUr538kowD/gSH2/IFnIDybSkQBFsKxIQGTE8hgsoNg69at/T/rkKFTT2eK58F/1myUwaYx27Zti10jfPh5VahQwXdnZGv00OFnxr8/fk68WKEQ46jkZ9mYiEVx5cuX93dfQn9eNAbYcImuLz8rtuhH8Onka0KESGUkwSkKfwh5O4w939nFiv/M2AOexRKhvw3N+fOHffny5S4eUZmBTMeUt9JZyEiEgLF2jIBbu3Zt7BphQoebnxeLQ5kKUbZsWZ9+EZWuIs9jzpw5PvqNHchGjRoVuyRcmKHLi8zXX3/dqlev7rO4EUdkK3T43Ro0aJC/28JOmrxAi9LCYV5oMv6NrjB/T0L/ey9EIkiCUxTyYXRIKd6m5W123ormjyMd4pCha0NXimrSpEnk5gQjGozaoovfrl07l8coQPeenxVv17KLIj+/0OHfIrlLtkdnDCKbnERhIxAy6bxw5gUmPzPmVhOH4AVa6PAORKNGjey9997zd8cY/8aoxaiMgOMdJSSfF9EakSZSHUlwisIf+ipVqvhb68jHjh07fD4rWcwoLZSI2mYZ8bc1ydAi+MhiVEDmeYudt6DplpJTDx3eWRkxYoTVr1/ff6/ockdBgtkgAymki8/fD3a9RKqiEGFBfBs2bGh9+/b1Til/E/k7EpV54xMmTLBWrVr5z0pdYJHqSIJTFBZDfPDBB/5WH9EIVufzx59tm/k6KkRNgunS87MrXry4v2iJws8KqSfqEX8HgsV+vXr18g5q6PAiE+Hgd4vufYkSJTxrGvoiVF6gEBFAooh7EIfo1KlT8NEc4N8f74rx749pF0R0atWqZePHj49dI1x4d4UXK/Xq1YtEdEWIRJEEpyhEIMjyke3jLUw6wSzY4T+zKC2UiJIE89Y6I9/YXnvAgAG2b9++SPxHRjadrhuLdICIR+/evSOxaxxxgVy5cvnW6K+99pp9//vf9+kXZJ5DhsWLLNKkI0wWmGww8Qj+TYYOL1j4ufHvkckrxFg+/PBD/1sZOryA5gUmv19CCElwysJ/XnQ7kA+6wCtWrLDOnTt7VkxxiLsTBIP/nBEpcrMsaqRrFXr3jbeceQFGBpO31Vmww1gqusOhw8+MBZrxyp8/v7/bEvqs4EWLFnkch842k2V4V4nOaejrCQCp5+8ii2p//etfe46bsXah/8yA+BR/D+MvOIVIdSTBKQqiy39k/OdFZ4C3bJmpu27dukgsSIrDc1y1alXsq7AhM0vXlMWMdIJ5wTJt2jR/ERMybClMh4opJfERcIhIFOHnFYXcLDEcJl7QUfztb3/rn0clRsW/x/Xr13uWm3+PPD9mjkdhI5ANGzb438OoLPITIlEkwSkKY4DI8rEAhEU7jAJiRBqrhZUVE0IIIUTUkQSnMMgubzmzSQFvZUZpQZwQQgghxO2QBKc4iDBv/1FR2e1JCCGEECIrJMFCCCGEECLlkAQLIYQQQoiUQxIshAgCojsUsR02m1B8RwghRCJIgoUQdy3xHckYT8WmLhSLOZlrzZi/zESYWbVIMhNQAHFm0wMqI9wv98dYQD5yn9yejDwj6fiYER6TDWXYEpktg9PWsWPH/CPnzeMKIYS4e5EECyHuSpDY3bt3W6VKlXxDEGZZU2w68cwzz/gMaEb6ZWT69Ok2cuRI36YYEFK2Kmbea0aYm8rmAdwXm8ewYyKzfJlbXKRIEd9JMaPMsmVw3bp17cknn/Sd0tLWCy+8YK+++qrPOY7CXFkhhIgykmAhxF0J8slQ/6ZNm7qQsnUtG4R06tTJvvvd71rx4sV96+9atWq5HK9Zs8almN2+ENv47mVsNc3l3I5dvyguo/vLxgHMx2bnvfhudb/5zW9s4cKFLrVsL855xAvoTLNb3w9/+EP75S9/ma4eeOABe/rpp23//v2SYCGEuMuRBAsh7kqINDC/+v3337f777/fmjVrZv369bMyZcpYixYt/HN29GrTpo3vdshOc2xJjByXKlXKZXjWrFnWrl07K1++vAszcswGMXSAiTsgu0j0Sy+95B1ctgFu1KiR3+bZZ5+11q1b+3bio0eP9qgDInzu3Dm/vGDBgi7Daevdd9/17Z8PHz6caZRCCCHE3YMkWAhxV0K2lmjCr3/9axdUhJQqWrSoRx4WLFjgndr58+d7jGHcuHHehY3LKULKbekiI8mIa5MmTTxKwe3p1nL/CDMdXKT3nXfecckuVKiQV9myZe3ll192gWbr3AMHDrg40z2mc9yyZct0xe6LderU8ftnO+vM4hpCCCHuDiTBQoi7Ejq169at83wtnV+qffv2vsX3r371Ky+O0fGlGzxlyhQX18GDB9umTZs8A/z22297xIEuMYvqiEJUqFDBli5d6lGLqVOn2gcffODdYT6WK1fOJTpv3rze/V25cqXf/4gRI3xHxTFjxty8zltvvWXFihVzyaZ4LASdcyhcuLANHz7cH0MIIcTdiSRYCHFXwhQGsrsscCOuQKQBIY3HICgWvBFXQIaJPjzxxBNeSCy3qVevns2bN8/lmdvRyaXTS8yCyMLOnTtt9uzZ1qBBA5s4caJ3eYlMvPnmmx6/GD9+vD/OjBkzbp7Pxo0bvaNM7KFx48Z+f6VLl/YOcNWqVf1zJJsJEvEJFUIIIe4+JMFCiLsSBHLPnj0eRShZsqRLJhMckFK6tNSQIUM8CsHiOeIRyCuxh8mTJ1uXLl0838uECW7H4jjklMwwIstxOrzEIR5//HGXV+IQdIXpHPN58+bNvaNLZzkOMQdkl+kQb7zxhv3iF7/wz+lMv/jiiy7f69evVxRCCCHuciTBQoi7EuILc+fO9ZwtEks3l4VvdGqJLtAZJiNMPhdxXbZsmQsuAssMX0SYTi2RhMWLF3s3lw4wMYZt27b5/ROhoKNLTphRbIgvUySIYBB7IN6AKNPVjUOkAqEm9oCc58qVy0ejEYGIZ4q5/ytXrsRuIYQQ4m5EEiyEuCshBrFkyRKfCzxq1Cjr2bOnxyHoBCOuLFpDjun4khNmlnCBAgU8H0y0AZmlE4wEM2mCzTLo/ubLl8/n/wJCy0xhus2INB/JEsc70Iw942tuH4fFeF27dvXFd1WqVLHXXnvN7xP5pUOMtJNlVidYCCHubiTBQoi7FsaMIcNMXmCWL5ta0KWl04vUMuGhf//+3hVmegMTHognMNGBikswM3sZbcZOc3Rt6dQy7oxuLcI7YMAAF2imUJAvpmtMlxe5JV7BrGE23eB8iGEQoUCQn3rqKbv33nvtnnvusccee8wfn4gEos45amtnIYS4e5EECyHuWvbt2+cRA+IPLGCju0pWmEIwiUeQxa1du7YLLTOFhw0b5t1aFrXRFUZGiUGw2QbiyiQHOsIscmMxHdMiWBjHxhlcjy4vnWaiGHSXEWkKWSZLTEwiPp0id+7c9vDDD9vPf/5zF+D48VdeecVjGewuJ4QQ4u5EEiyEuGtBehlThnyS4Y3v2haH7i9Z4HhnlwVsbGrBbnAIKLLL53STuR4j0RDbuExzXXaa4/ZEHigWviHDjETjegg12yhzGd1kFr0R0eC8+Eh3muL+OUa3mc+Rbx5bCCHE3YkkWAgReYgx0PnNuFgNcc4YWeBYRtkWQggRPSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAshhBBCiJRDEiyEEEIIIVIOSbAQQgghhEg5JMFCCCGEECLlkAQLIYQQQoiUQxIshBBCCCFSDkmwEEIIIYRIOSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUgyz/w+pIh3FACiA0gAAAABJRU5ErkJggg=="
- }
- },
+ "attachments": {},
"cell_type": "markdown",
"metadata": {},
"source": [
@@ -49,15 +18,17 @@
"在对数据进行预处理时,经常加入新的操作或改变处理策略,此时如果伴随着随机操作,最好还是指定唯一的随机种子,避免由于随机的差异对结果产生影响。\n",
"\n",
"---\n",
- "# 离散型随机变量\n",
- "## 二项分布\n",
+ "\n",
+ "## 离散型随机变量\n",
+ "\n",
+ "### 二项分布\n",
+ "\n",
"二项分布可以用于只有一次实验只有两种结果,各结果对应的概率相等的多次实验的概率问题。比如处理猜10次拳赢6次的概率等类似的问题。\n",
"\n",
"二项分布概率函数的代码表示:binom.pmf(k) = choose(n, k) p\\*\\*k (1-p)\\*\\*(n-k)\n",
"\n",
"二项分布概率函数的数学表示:\n",
- "\n",
- "\n",
+ "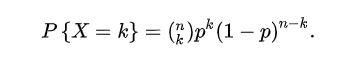\n",
"\n",
"\n",
"- `numpy.random.binomial(n, p, size=None)` Draw samples from a binomial distribution.\n",
@@ -65,6 +36,7 @@
"表示对一个二项分布进行采样,`size`表示采样的次数,`n`表示做了`n`重伯努利试验,`p`表示成功的概率,函数的返回值表示`n`中成功的次数。\n",
"\n",
"【例】野外正在进行9(n=9)口石油勘探井的发掘工作,每一口井能够开发出油的概率是0.1(p=0.1)。请问,最终所有的勘探井都勘探失败的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -90,10 +62,12 @@
"print(np.around(s, 3))\n",
"# [0.387 0.387 0.172 0.045 0.007 0.001 0. 0. 0. 0. ]\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"\n",
"【例】模拟投硬币,投2次,请问两次都为正面的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"from scipy import stats\n",
@@ -112,7 +86,7 @@
"print(np.sum(x == 1) / size) # 0.49874\n",
"print(np.sum(x == 2) / size) # 0.24972\n",
"\n",
- "plt.hist(x, density=True)\n",
+ "plt.hist(x)\n",
"plt.xlabel('随机变量:硬币为正面次数')\n",
"plt.ylabel('50000个样本中出现的次数')\n",
"plt.show()\n",
@@ -121,7 +95,8 @@
"print(np.around(s, 3))\n",
"# [0.25 0.5 0.25]\n",
"```\n",
- "\n",
+ "\n",
+ "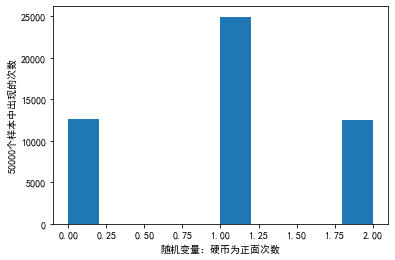\n",
"\n",
"```\n",
"#计算期望和方差\n",
@@ -132,14 +107,16 @@
"moments参数中:m为期望,v为方差\n",
"'''\n",
"```\n",
- "## 泊松分布\n",
+ "\n",
+ "### 泊松分布\n",
+ "\n",
"泊松分布主要用于估计某个时间段某事件发生的概率。\n",
"\n",
"泊松概率函数的代码表示:poisson.pmf(k) = exp(-lam) lam\\*k / k!\n",
"\n",
"泊松概率函数的数学表示:\n",
"\n",
- "\n",
+ "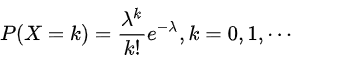\n",
"\n",
"- `numpy.random.poisson(lam=1.0, size=None)` Draw samples from a Poisson distribution.\n",
"\n",
@@ -171,13 +148,14 @@
"print(x) # 0.14900277967433773\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
- "## 超几何分布\n",
+ "### 超几何分布\n",
"\n",
"在超几何分布中,各次实验不是独立的,各次实验成功的概率也不等。\n",
- "超几何分布概率函数的数学表示:\n",
+ "超几何分布概率函数的数学表示:\n",
+ "\n",
"\n",
"\n",
"- `numpy.random.hypergeometric(ngood, nbad, nsample, size=None)` Draw samples from a Hypergeometric distribution.\n",
@@ -219,7 +197,8 @@
"# [0. 0.004 0.048 0.199 0.358 0.286 0.095 0.01 ]\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"```\n",
"'''\n",
"超几何分布的均值与方差\n",
@@ -233,15 +212,17 @@
"```\n",
"\n",
"---\n",
- "# 连续型随机变量\n",
"\n",
- "## 均匀分布\n",
+ "## 连续型随机变量\n",
+ "\n",
+ "### 均匀分布\n",
"\n",
"- `numpy.random.uniform(low=0.0, high=1.0, size=None)` Draw samples from a uniform distribution.\n",
"\n",
"Samples are uniformly distributed over the half-open interval `[low, high)` (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by `uniform`.\n",
"\n",
"【例】在low到high范围内,创建大小为size的均匀分布的随机数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -265,7 +246,8 @@
"print(b - a) # 0.4\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"作为`uniform()`的特列,可以得到`[0,1)`之间的均匀分布的随机数。\n",
"\n",
@@ -315,6 +297,7 @@
"\n",
"\n",
"【例】若`high`不为`None`时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -340,10 +323,10 @@
"```\n",
"\n",
"\n",
- "## 正态分布\n",
+ "### 正态分布\n",
"\n",
"标准正态分布数学表示:\n",
- "\n",
+ "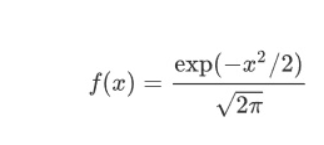\n",
"\n",
"- `numpy.random.randn(d0, d1, ..., dn)` Return a sample (or samples) from the \"standard normal\" distribution.\n",
"\n",
@@ -377,7 +360,7 @@
"print(y3) # 0.9973002039367398\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"还可以指定分布以及所需参数来进行随机,例如高斯分布中的mu和sigma。\n",
@@ -385,13 +368,14 @@
"- `numpy.random.normal(loc=0.0, scale=1.0, size=None)` Draw random samples from a normal (Gaussian) distribution.\n",
"\n",
"`normal()`为创建均值为 loc(mu),标准差为 scale(sigma),大小为 size 的数组。\n",
- "\n",
+ "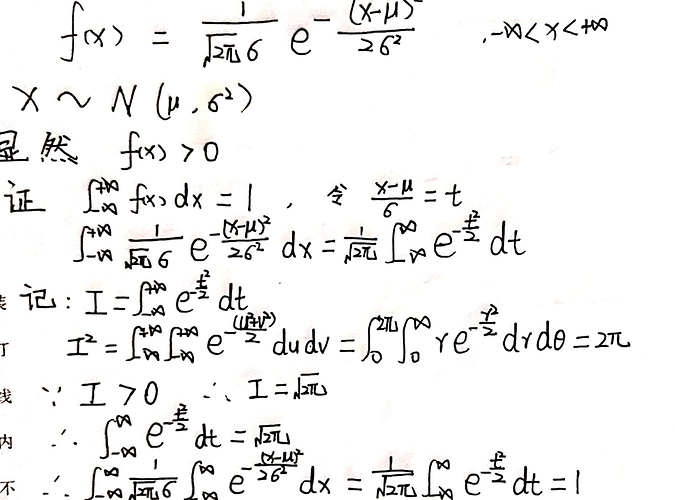\n",
"\n",
"```python\n",
"sigma * np.random.randn(...) + mu\n",
"```\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -424,22 +408,27 @@
"Means Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.\n",
"'''\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
+ "\n",
"```\n",
"plt.hist(x, bins=20)\n",
"plt.show()\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
+ "### 指数分布\n",
"\n",
- "## 指数分布\n",
"指数分布描述时间发生的时间长度间隔。\n",
"\n",
- "指数分布的数学表示:\n",
+ "指数分布的数学表示:\n",
+ "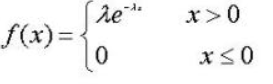\n",
"\n",
"- `numpy.random.exponential(scale=1.0, size=None)` Draw samples from an exponential distribution.\n",
"\n",
"【例】`scale = 1/lambda`\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -470,18 +459,21 @@
"print(y3) # 0.950212931632136\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"---\n",
- "# 其它随机函数\n",
"\n",
- "## 随机从序列中获取元素\n",
+ "## 其它随机函数\n",
+ "\n",
+ "### 随机从序列中获取元素\n",
+ "\n",
"- `numpy.random.choice(a, size=None, replace=True, p=None)` Generates a random sample from a given 1-D array.\n",
"\n",
"从序列中获取元素,若`a`为整数,元素取值从`np.range(a)`中随机获取;若`a`为数组,取值从`a`数组元素中随机获取。该函数还可以控制生成数组中的元素是否重复`replace`,以及选取元素的概率`p`。\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -503,7 +495,8 @@
"x = np.random.randint(0, 10, 3)\n",
"print(x) # [2 0 1]\n",
"```\n",
- "## 对数据集进行洗牌操作\n",
+ "\n",
+ "### 对数据集进行洗牌操作\n",
"\n",
"数据一般都是按照采集顺序排列的,但是在机器学习中很多算法都要求数据之间相互独立,所以需要先对数据集进行洗牌操作。\n",
"\n",
@@ -514,6 +507,7 @@
"对`x`进行重排序,如果`x`为多维数组,只沿第 0 轴洗牌,改变原来的数组,输出为None。\n",
"\n",
"【例】洗牌,改变自身内容,打乱顺序。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -584,71 +578,17 @@
"\n",
"\n",
"---\n",
+ "\n",
"**参考文献**\n",
- "- https://www.jianshu.com/p/63434ad5ea64\n",
- "\n"
+ "\n",
+ "- https://www.jianshu.com/p/63434ad5ea64"
]
},
{
"cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:02.029113Z",
- "start_time": "2020-09-15T01:02:02.026084Z"
- }
- },
+ "execution_count": null,
+ "metadata": {},
"outputs": [],
- "source": [
- "dic={1:('I','V'),2:('X','L'),3:('C','D'),4:'M'}"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:09.390007Z",
- "start_time": "2020-09-15T01:02:09.379035Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'M'"
- ]
- },
- "execution_count": 2,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "dic[4]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:29.206128Z",
- "start_time": "2020-09-15T01:02:29.201134Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'I'"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
"source": []
}
],
diff --git a/LanQiao/readme.md b/LanQiao/readme.md
new file mode 100644
index 0000000..1ba4e99
--- /dev/null
+++ b/LanQiao/readme.md
@@ -0,0 +1,52 @@
+# 编程实践(蓝桥刷题94道)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/LanQiao
+
+## 基本信息
+
+- 学习周期:14天,每天平均花费时间2小时-5小时不等,根据个人学习接受能力强弱有所浮动。
+- 学习形式:练习
+- 人群定位:有一定编程基础,对学习算法有需求的学员。
+- 先修内容:[Python编程语言](https://github.com/datawhalechina/team-learning-program/tree/master/PythonLanguage)、[数据结构与算法](https://github.com/datawhalechina/team-learning-program/tree/master/DataStructureAndAlgorithm)、[编程实践(LeetCode 分类练习)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeClassification)
+- 难度系数:中
+
+## 学习目标
+
+每天刷三道题,利用14天对于蓝桥杯这个比赛有一个初步的了解,掌握基本的蓝桥杯赛题解法。
+
+
+
+## 任务安排
+
+### Task00:熟悉规则(1天)
+- 组队、修改群昵称
+- 熟悉打卡规则
+
+### Task01:热身练习(2天)
+- 完成热身练习文件夹中的7道题目
+- 熟悉基本输入输出及蓝桥杯的练习系统的使用方法。
+
+### Task02:基础练习(3天)
+- 完成基础练习文件夹中的7道题目
+
+### Task03:基础练习2(3天)
+- 完成基础练习2文件夹中的8道题目
+
+### Task04:真题练习(3天)
+- 完成真题练习文件夹中的10道题目
+
+### Task05:真题练习2(3天)
+- 完成真题练习文件夹中的7道题目
+
+
+## 开源贡献者
+
+韩绘锦:华北电力大学
+
+- CSDN:https://blog.csdn.net/weixin_45569785
+
+黄建国:华北电力大学
+
+荆宝加:华北电力大学
+
+吴丹飞:华北电力大学
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/01字串.md b/LanQiao/task1热身练习/01字串.md
new file mode 100644
index 0000000..d1587cf
--- /dev/null
+++ b/LanQiao/task1热身练习/01字串.md
@@ -0,0 +1,79 @@
+## 01字串
+
+**问题描述**
+
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
diff --git a/LanQiao/task1热身练习/1083、Hello,world.md b/LanQiao/task1热身练习/1083、Hello,world.md
new file mode 100644
index 0000000..c031a2d
--- /dev/null
+++ b/LanQiao/task1热身练习/1083、Hello,world.md
@@ -0,0 +1,53 @@
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1083.html
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
diff --git a/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
new file mode 100644
index 0000000..442dd80
--- /dev/null
+++ b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
@@ -0,0 +1,218 @@
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1084.html
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/1095、3n+1问题.md b/LanQiao/task1热身练习/1095、3n+1问题.md
new file mode 100644
index 0000000..2f8c997
--- /dev/null
+++ b/LanQiao/task1热身练习/1095、3n+1问题.md
@@ -0,0 +1,72 @@
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/2080、十六进制转八进制.md b/LanQiao/task1热身练习/2080、十六进制转八进制.md
new file mode 100644
index 0000000..a80f5b6
--- /dev/null
+++ b/LanQiao/task1热身练习/2080、十六进制转八进制.md
@@ -0,0 +1,168 @@
+## 十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2080.html
+
+**题目描述**
+
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+
+**输入**
+
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+
+**输出**
+
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+
+**样例输入**
+
+```
+2
+39
+123ABC
+```
+
+**样例输出**
+
+```
+71
+4435274
+```
+
+
+```
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
diff --git a/LanQiao/task1热身练习/2082、十六进制转十进制.md b/LanQiao/task1热身练习/2082、十六进制转十进制.md
new file mode 100644
index 0000000..9edf75a
--- /dev/null
+++ b/LanQiao/task1热身练习/2082、十六进制转十进制.md
@@ -0,0 +1,47 @@
+## 十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2082.html
+
+**题目描述**
+
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+
+**输入**
+
+```
+一个十六进制数
+
+```
+
+**输出**
+
+```
+对应得十进制
+```
+
+**样例输入**
+
+```
+FFFF
+```
+
+**样例输出**
+
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
diff --git a/LanQiao/task1热身练习/2083、十进制转十六进制.md b/LanQiao/task1热身练习/2083、十进制转十六进制.md
new file mode 100644
index 0000000..c0ba52b
--- /dev/null
+++ b/LanQiao/task1热身练习/2083、十进制转十六进制.md
@@ -0,0 +1,76 @@
+## 十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2083.html
+
+**题目描述**
+
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+
+**输入**
+
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+
+**输出**
+
+```
+输出这个整数的16进制表示
+```
+
+**样例输入**
+
+```
+30
+```
+
+**样例输出**
+
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
diff --git a/LanQiao/task2基础练习/1460、2n皇后问题.md b/LanQiao/task2基础练习/1460、2n皇后问题.md
new file mode 100644
index 0000000..e34c4b2
--- /dev/null
+++ b/LanQiao/task2基础练习/1460、2n皇后问题.md
@@ -0,0 +1,114 @@
+# 2n皇后问题
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1460.html
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
diff --git a/LanQiao/task2基础练习/1462、Huffuman树.md b/LanQiao/task2基础练习/1462、Huffuman树.md
new file mode 100644
index 0000000..0852108
--- /dev/null
+++ b/LanQiao/task2基础练习/1462、Huffuman树.md
@@ -0,0 +1,82 @@
+# Huffuman树
+
+
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1316 解决: 750
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1462.html
+
+**题目描述**
+
+```
+Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
+
+给出一列数{pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
+
+1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
+
+2. 重复步骤1,直到{pi}中只剩下一个数。
+
+在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
+
+本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
+
+
+
+例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
+
+1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
+
+2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
+
+3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
+
+4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
+
+5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。
+
+```
+**输入**
+```
+输入的第一行包含一个正整数n(n< =100)。
+
+接下来是n个正整数,表示p0, p1, …, pn-1,每个数不超过1000。
+
+```
+**输出**
+```
+输出用这些数构造Huffman树的总费用。
+
+```
+**样例输入**
+```
+5
+5 3 8 2 9
+```
+**样例输出**
+```
+59
+```
+
+
+```
+n=int(input())
+list_=list(map(int,input().split()))
+res=[]
+while len(list_)>1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1463、Sine之舞.md b/LanQiao/task2基础练习/1463、Sine之舞.md
new file mode 100644
index 0000000..6a86bd8
--- /dev/null
+++ b/LanQiao/task2基础练习/1463、Sine之舞.md
@@ -0,0 +1,92 @@
+# Sine之舞
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1463.html
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
diff --git a/LanQiao/task2基础练习/1467、完美的代价.md b/LanQiao/task2基础练习/1467、完美的代价.md
new file mode 100644
index 0000000..6bd8b98
--- /dev/null
+++ b/LanQiao/task2基础练习/1467、完美的代价.md
@@ -0,0 +1,143 @@
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1467.html
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1470、时间转换.md b/LanQiao/task2基础练习/1470、时间转换.md
new file mode 100644
index 0000000..91c6951
--- /dev/null
+++ b/LanQiao/task2基础练习/1470、时间转换.md
@@ -0,0 +1,58 @@
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1470.html
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1475、高精度加法.md b/LanQiao/task2基础练习/1475、高精度加法.md
new file mode 100644
index 0000000..f7182a1
--- /dev/null
+++ b/LanQiao/task2基础练习/1475、高精度加法.md
@@ -0,0 +1,92 @@
+## 高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1475.html
+
+**题目描述**
+
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+
+- 输出一行,表示a + b的值。
+
+**样例输入**
+
+```
+20100122201001221234567890
+2010012220100122
+```
+
+**样例输出**
+
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_pointxl and y_up>y_down:
+ cross+=(xr-xl)*(y_up-y_down)
+ count+=1
+ return (count,cross)
+
+
+
+n=int(input())
+for i in range(n):
+ n=int(input())
+ matrixs=[]
+ for j in range(n):
+ matrixs.append(list(map(int,input().strip().split())))
+ for k in range(n):
+ target=matrixs[k]
+ count,cross=Area_cross(target,matrixs,k)
+ print(count,cross)
+
+```
+
+ 1
+ 3
+ 0 0 2 6
+ 1 1 4 4
+ 1 3 3 9
+ 2 6
+ 2 5
+ 2 5
+
+
+
+
+## 试题 基础练习 矩形面积交
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+问题描述
+
+ 平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
+
+输入格式
+
+ 输入仅包含两行,每行描述一个矩形。
+
+ 在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
+
+输出格式
+
+ 输出仅包含一个实数,为交的面积,保留到小数后两位。
+
+样例输入
+
+```
+1 1 3 3
+2 2 4 4
+```
+样例输出
+
+```
+1.00
+```
+
+参考答案
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+x1=[min(x1i[0],x1i[2]),min(x1i[1],x1i[3]),max(x1i[0],x1i[2]),max(x1i[1],x1i[3])]
+x2=[min(x2i[0],x2i[2]),min(x2i[1],x2i[3]),max(x2i[0],x2i[2]),max(x2i[1],x2i[3])]
+xl=max(x1[0],x2[0])
+xr=min(x1[2],x2[2])
+yup=min(x1[3],x2[3])
+ydown=max(x1[1],x2[1])
+x=xr-xl
+y=yup-ydown
+if xr>xl and yup>ydown:
+ print('{:.2f}'.format(x*y))
+else:
+ print('{:.2f}'.format(0))
+```
+
+ 1 1 4 5
+ 1 1 4 5
+ 12.00
diff --git a/LanQiao/task3基础练习2/1097、蛇形矩阵.md b/LanQiao/task3基础练习2/1097、蛇形矩阵.md
new file mode 100644
index 0000000..4a10e0b
--- /dev/null
+++ b/LanQiao/task3基础练习2/1097、蛇形矩阵.md
@@ -0,0 +1,73 @@
+## 题目 1097: 蛇行矩阵
+
+时间限制: 1Sec 内存限制: 64MB 提交: 7484 解决: 5014
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem.php?id=1097
+
+**题目描述**
+蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。
+**输入**
+
+> 本题有多组数据,每组数据由一个正整数N组成。(N不大于100)
+
+**输出**
+
+> 对于每一组数据,输出一个N行的蛇形矩阵。两组输出之间不要额外的空行。矩阵三角中同一行的数字用一个空格分开。行尾不要多余的空格。
+
+**样例输入**
+
+```python
+5
+```
+
+**样例输出**
+
+```python
+1 3 6 10 15
+2 5 9 14
+4 8 13
+7 12
+11
+
+```
+
+参考答案:
+
+
+```
+n=int(input())
+temp=[[] for i in range(n)]
+num=1
+grade=0
+while grade 只有1行,为两个正整数,用一个空格隔开: k w
+
+**输出**
+
+> 1行,是一个正整数,为所求的计算结果,即满足条件的不同的r的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
+> (提示:作为结果的正整数可能很大,但不会超过200位)
+
+**样例输入**
+
+```python
+3 7
+```
+
+**样例输出**
+
+```python
+36
+```
+
+参考答案:
+
+
+```
+k,w=map(int,input().strip().split())
+Digits=w//k # 可以有完整k位的位数
+remainder=w%k # 最高位余下的位数
+def f (count,Digit):
+ if Digit>count:
+ return 0
+ re=1
+ for i in range(1,Digit+1):
+ re*=(count-i+1)/i
+ return re
+s0=sum([f(2**k-1,i) for i in range(2,Digits+1)]) #不考虑最高位或者说是只考虑所有的位数都有完整k位的情况。那么对于每一个位数的可能数就是从2**k-1中选取位数个数字的所有可能性
+
+s1=sum([f(2**k-1-i,Digits) for i in range(1,2**remainder)])# 依次计算最高位取每一个可能的数字时所有的可能性。
+print(int(s0+s1))
+```
+
+ 3 7
+ 36
+
+
+
+
+
+
+
diff --git a/LanQiao/task3基础练习2/1117、K-进制数.md b/LanQiao/task3基础练习2/1117、K-进制数.md
new file mode 100644
index 0000000..1bf2eb1
--- /dev/null
+++ b/LanQiao/task3基础练习2/1117、K-进制数.md
@@ -0,0 +1,75 @@
+## 题目 1117: K-进制数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2458 解决: 959
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1117.html
+
+**题目描述**
+
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+>
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+
+**例:**
+
+1010230 是有效的7位数
+1000198 无效
+0001235 不是7位数, 而是4位数.
+
+给定两个数N和K, 要求计算包含N位数字的有效K-进制数的总数.
+
+假设2 <= K <= 10; 2 <= N; 4 <= N+K <= 18.
+
+**输入**
+
+> 两个十进制整数N和K
+
+**输出**
+
+> 十进制表示的结果
+
+**样例输入**
+
+```python
+2
+10
+```
+
+**样例输出**
+
+```python
+90
+```
+## 提示
+
+> 从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+> 令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+> 前提:n 最小是 2*k-1.
+>
+> 组合 [(h+1)*h*(h-1)*```````(h+1-k)] /[k*(k-1)*(k-2)*``````1]
+>
+> 排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+参考答案:
+
+```
+N=int(input())
+K=int(input())
+re1=(K-1)**N
+def f (n,k):
+ h=n-k
+ re=1
+ for i in range(1,k+1):
+ re*=(h+1-i+1)/i
+ return re*((K-1)**(n-k+1))## n-k+1中+1是加上了首位
+
+
+re2=sum([f(N-1,k) for k in range(1,int(((N-1)+1)/2)+1)])# 因为首位不能为零,所以从其他位置选取为零的点
+print(int(re1+re2))
+```
+
+ 2
+ 10
+ 90
\ No newline at end of file
diff --git a/LanQiao/task3基础练习2/1465、回形取数.md b/LanQiao/task3基础练习2/1465、回形取数.md
new file mode 100644
index 0000000..7c18103
--- /dev/null
+++ b/LanQiao/task3基础练习2/1465、回形取数.md
@@ -0,0 +1,136 @@
+# 回形取数
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1831 解决: 590
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1465.html
+
+**题目描述**
+
+- 回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
+
+**输入**
+
+- 输入第一行是两个不超过200的正整数m, n,表示矩阵的行和列。接下来m行每行n个整数,表示这个矩阵。
+
+**输出**
+
+- 输出只有一行,共mn个数,为输入矩阵回形取数得到的结果。数之间用一个空格分隔,行末不要有多余的空格。
+
+**样例输入**
+```
+3 3
+1 2 3
+4 5 6
+7 8 9
+```
+**样例输出**
+```
+1 4 7 8 9 6 3 2 5
+```
+
+### 思路一
+
+
+```
+m,n=map(int,input().split())
+nn=[]
+for i in range(m):
+ nn.append(input().split())
+dir=[[1,0],[0,1],[-1,0],[0,-1]]
+re=[]
+x=0
+y=0
+state=0
+n_left=0
+m_left=0
+m_right=m-1
+n_right=n-1
+while len(re)m_right):
+ state=(state+1)%4
+ n_left+=1
+ elif((tx+x)n_right):
+ state=(state+1)%4
+ m_right-=1
+ elif ((ty+y) 程序首先读入一个整数N(2< N< 100),表示小朋友的人数。 接着是一行用空格分开的N个偶数(每个偶数不大于1000,不小于2)
+
+**输出**
+
+> 要求程序输出一个整数,表示老师需要补发的糖果数。
+
+**样例输入**
+
+```python
+3
+2 2 4
+```
+
+**样例输出**
+
+```python
+4
+```
+
+参考答案:
+
+
+```
+n=int(input())
+num=list(map(int,input().strip().split()))
+re=0
+def b(num):
+ temp=num[0]
+ for i in num:
+ if i!=temp:
+ return False
+ return True
+while not b(num):
+ temp=num.copy()
+ for i in range(len(temp)):
+ temp[i]=int(temp[i]/2)
+ for i in range(len(num)):
+ num[i]=int(num[i]/2)+temp[(i+1)%len(temp)]
+ if num[i]%2!=0:
+ num[i]+=1
+ re+=1
+print(re)
+
+```
+
+ 3
+ 2 2 4
+ 4
diff --git a/LanQiao/task4真题练习/试题 B 合并检测.md b/LanQiao/task4真题练习/试题 B 合并检测.md
new file mode 100644
index 0000000..6f38276
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 B 合并检测.md
@@ -0,0 +1,143 @@
+## 试题 B: 合并检测
+
+
+本题总分:5 分
+
+**【问题描述】**
+
+新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准备给大量民众进病毒核酸检测。
+然而,用于检测的试剂盒紧缺。
+为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看,如果检测前 k − 1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用了 k + 1 个试剂盒完成了 k 个人的检测。
+A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能最节省试剂盒?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+lis=[]
+for k in range(1,101):
+ temp=100+k*k
+ lis.append([temp/k,k])
+lis.sort(key=lambda x :x[0])
+lis[0][1]
+```
+
+
+
+
+ 10
+
+
+
+
+```
+lis
+```
+
+
+
+
+ [[20.0, 10],
+ [20.09090909090909, 11],
+ [20.11111111111111, 9],
+ [20.333333333333332, 12],
+ [20.5, 8],
+ [20.692307692307693, 13],
+ [21.142857142857142, 14],
+ [21.285714285714285, 7],
+ [21.666666666666668, 15],
+ [22.25, 16],
+ [22.666666666666668, 6],
+ [22.88235294117647, 17],
+ [23.555555555555557, 18],
+ [24.263157894736842, 19],
+ [25.0, 5],
+ [25.0, 20],
+ [25.761904761904763, 21],
+ [26.545454545454547, 22],
+ [27.347826086956523, 23],
+ [28.166666666666668, 24],
+ [29.0, 4],
+ [29.0, 25],
+ [29.846153846153847, 26],
+ [30.703703703703702, 27],
+ [31.571428571428573, 28],
+ [32.44827586206897, 29],
+ [33.333333333333336, 30],
+ [34.225806451612904, 31],
+ [35.125, 32],
+ [36.03030303030303, 33],
+ [36.333333333333336, 3],
+ [36.94117647058823, 34],
+ [37.857142857142854, 35],
+ [38.77777777777778, 36],
+ [39.7027027027027, 37],
+ [40.63157894736842, 38],
+ [41.56410256410256, 39],
+ [42.5, 40],
+ [43.4390243902439, 41],
+ [44.38095238095238, 42],
+ [45.325581395348834, 43],
+ [46.27272727272727, 44],
+ [47.22222222222222, 45],
+ [48.17391304347826, 46],
+ [49.12765957446808, 47],
+ [50.083333333333336, 48],
+ [51.04081632653061, 49],
+ [52.0, 2],
+ [52.0, 50],
+ [52.96078431372549, 51],
+ [53.92307692307692, 52],
+ [54.886792452830186, 53],
+ [55.851851851851855, 54],
+ [56.81818181818182, 55],
+ [57.785714285714285, 56],
+ [58.75438596491228, 57],
+ [59.724137931034484, 58],
+ [60.69491525423729, 59],
+ [61.666666666666664, 60],
+ [62.63934426229508, 61],
+ [63.61290322580645, 62],
+ [64.58730158730158, 63],
+ [65.5625, 64],
+ [66.53846153846153, 65],
+ [67.51515151515152, 66],
+ [68.49253731343283, 67],
+ [69.47058823529412, 68],
+ [70.44927536231884, 69],
+ [71.42857142857143, 70],
+ [72.40845070422536, 71],
+ [73.38888888888889, 72],
+ [74.36986301369863, 73],
+ [75.35135135135135, 74],
+ [76.33333333333333, 75],
+ [77.3157894736842, 76],
+ [78.2987012987013, 77],
+ [79.28205128205128, 78],
+ [80.26582278481013, 79],
+ [81.25, 80],
+ [82.23456790123457, 81],
+ [83.21951219512195, 82],
+ [84.20481927710843, 83],
+ [85.19047619047619, 84],
+ [86.17647058823529, 85],
+ [87.16279069767442, 86],
+ [88.14942528735632, 87],
+ [89.13636363636364, 88],
+ [90.12359550561797, 89],
+ [91.11111111111111, 90],
+ [92.0989010989011, 91],
+ [93.08695652173913, 92],
+ [94.0752688172043, 93],
+ [95.06382978723404, 94],
+ [96.05263157894737, 95],
+ [97.04166666666667, 96],
+ [98.03092783505154, 97],
+ [99.0204081632653, 98],
+ [100.01010101010101, 99],
+ [101.0, 1],
+ [101.0, 100]]
\ No newline at end of file
diff --git a/LanQiao/task4真题练习/试题 C 分配口罩.md b/LanQiao/task4真题练习/试题 C 分配口罩.md
new file mode 100644
index 0000000..72e882d
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 C 分配口罩.md
@@ -0,0 +1,64 @@
+## 试题 C: 分配口罩
+
+本题总分:10 分
+
+**【问题描述】**
+
+某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文
+字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目
+录下有一个文件 mask.txt,内容与下面的文本相同)
+
+```python
+9090400
+8499400
+5926800
+8547000
+4958200
+4422600
+5751200
+4175600
+6309600
+5865200
+6604400
+4635000
+10663400
+8087200
+4554000
+```
+
+
+ 现在市长要把口罩分配给市内的2所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+
+```
+def main():
+ f=open('mask.txt','r')
+ #string=f.readlines()
+ num_lis=[]
+ for i in f:
+ #print(i)
+ num_lis.append(int(i))
+ print(num_lis)
+ re=[abs(num_lis[0]-num_lis[1])]
+ def dfs(num1,num2,num_lis):
+ #global re
+ if not num_lis:
+ re[0]=min(re[0],abs(num1-num2))
+ return
+ dfs(num1+num_lis[0],num2,num_lis[1:])
+ dfs(num1,num2+num_lis[0],num_lis[1:])
+ dfs(0,0,num_lis)
+ print(re[0])
+ return
+main()
+```
+
+ [9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, 6604400, 4635000, 10663400, 8087200, 4554000]
+ 2400
\ No newline at end of file
diff --git a/LanQiao/task4真题练习/试题 F 解码.md b/LanQiao/task4真题练习/试题 F 解码.md
new file mode 100644
index 0000000..dbc5c8c
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 F 解码.md
@@ -0,0 +1,54 @@
+## 试题 F: 解码
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+
+**【问题描述】**
+小明有一串很长的英文字母,可能包含大写和小写。
+在这串字母中,有很多连续的是重复的。小明想了一个办法将这串字母表
+达得更短:将连续的几个相同字母写成字母 + 出现次数的形式。
+例如,连续的 5 个 a,即 aaaaa,小明可以简写成 a5(也可能简写成 a4a、
+aa3a 等)。对于这个例子:HHHellllloo,小明可以简写成 H3el5o2。为了方便表
+达,小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串,请帮助小明还原成原来的串。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出一个字符串,表示还原后的串。
+
+**【样例输入】**
+
+```python
+H3el5o2
+```
+
+**【样例输出】**
+
+```python
+HHHellllloo
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由大小写英文字母和数字组成,长度不超过100。
+请注意原来的串长度可能超过 100。
+
+参考答案:
+
+```
+num_set={'0','1','2','3','4','5','6','7','8','9'}
+string=input()
+re=[]
+for i in string :
+ if i in num_set:
+ for i in range(int(i)-1):
+ re.append(re[-1])
+ else:
+ re.append(i)
+print(''.join(re))
+```
+
+ H3el5o2
+ HHHellllloo
diff --git a/LanQiao/task4真题练习/试题 G 走方格.md b/LanQiao/task4真题练习/试题 G 走方格.md
new file mode 100644
index 0000000..1f61a7f
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 G 走方格.md
@@ -0,0 +1,110 @@
+## 试题 G: 走方格
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+在平面上有一些二维的点阵。
+这些点的编号就像二维数组的编号一样,从上到下依次为第 1 至第 n 行,
+从左到右依次为第 1 至第 m 列,每一个点可以用行号和列号来表示。
+现在有个人站在第 1 行第 1 列,要走到第 n 行第 m 列。只能向右或者向下
+走。
+注意,如果行号和列数都是偶数,不能走入这一格中。
+问有多少种方案。
+
+**【输入格式】**
+
+> 输入一行包含两个整数 n, m。
+
+**【输出格式】**
+
+> 输出一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+3 4
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【样例输入】**
+
+```python
+6 6
+```
+
+参考答案:
+
+
+```
+n,m=map(int,input().strip().split())
+def main():
+ re=[0]
+ def dfs(x,y):
+ if x==n-1 and y==m-1:
+ re[0]+=1
+ if 0<=x+1<=(n-1) and not ((x+1)%2==0 and (y)%2==0):
+ dfs(x+1,y)
+ if 0<=y+1<=(m-1) and not ((x)%2==0 and (y+1)%2==0):
+ dfs(x,y+1)
+ dfs(0,0)
+ print(re[0])
+main()
+```
+
+ 3 4
+ 2
+
+
+### bfs
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ queue=[(0,0)]
+ re=0
+ while queue:
+ x,y=queue.pop(0)
+ if x==n-1 and y==m-1:
+ re+=1
+ if 0<=x+1 第一行包含 2 个整数 n 和 K。
+> 第二行包含 n 个整数 A1, A2, · · · , An。
+
+**【输出格式】**
+
+> 一个整数代表答案。
+
+**【样例输入】**
+
+```python
+4 33
+1 2 3 4
+```
+
+**【样例输出】**
+
+```python
+8
+```
+
+**【评测用例规模与约定】**
+对于 30% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ K ≤ 108, 1 ≤ Ai ≤ 104。
+对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ K ≤ 1010,1 ≤ Ai ≤ 109.
+
+参考答案:
+
+```
+n,K=map(int,input().strip().split())
+num_lis=list(map(int,input().strip().split()))
+re=0
+for i in range(n):
+ for j in range(i+1,n):
+ if (num_lis[i]*10+num_lis[j])<=K:
+# print( num_lis[i]*10+num_lis[j])
+ re+=1
+ if (num_lis[j]*10+num_lis[i])<=K:
+# print(num_lis[j]*10+num_lis[i])
+ re+=1
+print(re)
+
+
+```
+
+ 4 33
+ 1 2 3 4
+ 8
diff --git a/LanQiao/task4真题练习/试题 I BST 插入节点问题.md b/LanQiao/task4真题练习/试题 I BST 插入节点问题.md
new file mode 100644
index 0000000..a0fa6a2
--- /dev/null
+++ b/LanQiao/task4真题练习/试题 I BST 插入节点问题.md
@@ -0,0 +1,102 @@
+## 试题 I: BST 插入节点问题
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分
+
+**【问题描述】**
+
+给定一棵包含 N 个节点的二叉树,节点编号是 1 ∼ N。其中 i 号节点具有
+权值 Wi,并且这些节点的权值恰好形成了一棵排序二叉树 (BST)。
+现在给定一个节点编号 K,小明想知道,在这 N 个权值以外,有多少个整
+数 X (即 X 不等于任何 Wi ) 满足:给编号为 K 的节点增加一个权值为 X 的子
+节点,仍可以得到一棵 BST。
+例如在下图中,括号外的数字表示编号、括号内的数字表示权值。即编号
+1 ∼ 4 的节点权值依次是 0、10、20、30。
+
+如果 K = 1,那么答案为 0。因为 1 号节点已经有左右子节点,不能再增
+加子节点了。
+如果 K = 2,那么答案为无穷多。因为任何一个负数都可以作为 2 的左子
+节点。
+如果 K = 3,那么答案为 9。因为 X = 11, 12, · · · , 19 都可以作为 3 的左子
+节点。
+
+**【输入格式】**
+
+> 第一行包含 2 个整数 N 和 K。
+>
+> 以下 N 行每行包含 2 个整数,其中第 i 行是编号为 i 的节点的父节点编号
+>
+> Pi 和权值 Wi 。注意 Pi = 0 表示 i 是根节点。
+>
+> 输入保证是一棵 BST。
+
+**【输出格式】**
+
+> 一个整数代表答案。如果答案是无穷多,输出 −1。
+
+**【样例输入】**
+
+```python
+4 3
+0 10
+1 0
+1 20
+3 30
+```
+
+**【样例输出】**
+
+```python
+9
+```
+
+**【评测用例规模与约定】**
+
+> 对于 60% 的评测用例,1 ≤ K ≤ N ≤ 100,0 ≤ Wi ≤ 200,且 Wi 各不相同。
+>
+> 对于所有评测用例,1 ≤ K ≤ N ≤ 10000,0 ≤ Wi ≤ 100000000,且 Wi 各不 相同。
+
+参考答案:
+
+```
+class TreeNode:
+ def __init__(self,x):
+ self.val=x
+ self.left=None
+ self.right=None
+ self.parent=None
+N,K=map(int,input().strip().split())
+map_=[]
+map_node=[]
+for i in range(N):
+ p,w=map(int,input().strip().split())
+ map_.append([p,w])
+ map_node.append(TreeNode(w))
+ if p==0:
+ root_index=i
+for i in range(N):
+ if map_node[map_[i][0]-1].val 输入的第一行包含一个整数 n,表示初始时的石子数量。
+>
+> 第二行包含 n 个整数 w1,w2, · · · ,wn,依次表示每颗石子的重量。
+
+**【输出格式】**
+
+> 输出一行包含一个整数,表示最少需要的胶水数。
+
+**【样例输入】**
+
+```python
+3
+3 4 5
+```
+
+**【样例输出】**
+
+```python
+47
+```
+
+**【样例输入】**
+
+```python
+8
+1 5 2 6 3 7 4 8
+```
+
+**【样例输出】**
+
+```python
+546
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 15。
+>
+> 对于 60% 的评测用例,1 ≤ n ≤ 100。
+>
+> 对于 80% 的评测用例,1 ≤ n ≤ 1000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 100000,1 ≤ wi ≤ 1000。
+
+参考答案:
+
+
+```
+n=int(input())
+num_lis=list(map(int,input().strip().split()))
+def f(num_lis):
+ re=num_lis[0]*num_lis[1]
+ re_index=0
+ for i in range(len(num_lis)-1):
+ if num_lis[i]*num_lis[i+1] - 输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从 1 至 n 编号。
+> 接下来 m 行,每行三个整数,表示一个操作。
+> 如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。
+> 如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
+
+**【输出格式】**
+
+> 输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+**【样例输入】**
+
+```python
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+
+**【样例输出】**
+
+```python
+13 13 5 3
+```
+
+**【评测用例规模与约定】**
+
+> 对于 30% 的评测用例,1 ≤ n ≤ 20,1 ≤ m ≤ 100。
+>
+> 对于 50% 的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000。
+>
+> 对于 70% 的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ t ≤ 100。
+
+参考答案:
+
+```
+n,m=map(int,input().strip().split())
+message1=[]
+for i in range(m):
+
+ or1_2,a,b=input().strip().split()
+ message1.append([or1_2,a,b])
+
+
+map_=[[0 for i in range(n)]for i in range(n)]
+for i in range(n):
+ map_[i][i]=1
+
+re=[0 for i in range(n)]
+
+def f(map_,a,b,re,visited):
+ for i in range(n):
+ if map_[a-1][i]==1:
+ if i not in visited:
+ f(map_,i+1,b,re,visited|{i})
+ else:
+ if re[i]==0:
+ re[i]+=b
+
+
+
+for or1_2,a,b in message1:
+ a=int(a)
+ b=int(b)
+ if or1_2=='1':
+ map_[a-1][b-1]=1
+ map_[b-1][a-1]=1
+ else:
+ temp=[0 for i in range(n)]
+ f(map_,a,b,temp,{a-1})
+
+ for i in range(len(re)):
+ re[i]+=temp[i]
+
+for i in re:
+ print(i)
+
+```
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题A解密.md b/LanQiao/task5真题练习2/试题A解密.md
new file mode 100644
index 0000000..b4ef62c
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题A解密.md
@@ -0,0 +1,40 @@
+## 试题 A: 解密
+
+本题总分:5 分
+
+**【问题描述】**
+
+小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的
+字符 Tc。下表给出了字符变换的规则:
+
+
+例如,将字符串 YeRi 加密可得字符串 EaFn。
+小明有一个随机的字符串,加密后为
+EaFnjISplhFviDhwFbEjRjfIBBkRyY
+(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
+(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容
+是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符
+串,后面 52 行依次为表格中的内容。)
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+只包含 30 个大小写英文字母的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
+
+
+
+```
+f=open('str.txt','r')
+strings=f.readlines()
+j=0
+dic_={}
+target=strings[0]
+for string in strings[1:]:
+ a,b=string.strip().split()
+ dic_[b]=a
+for i in target[:-2]:
+ print(dic_[i],end='')
+
+```
+
+ YeRikGSunlRzgDlvRwYkXkrGWWhXa
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题B数列求值.md b/LanQiao/task5真题练习2/试题B数列求值.md
new file mode 100644
index 0000000..8c4264a
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题B数列求值.md
@@ -0,0 +1,29 @@
+## 试题 B: 数列求值
+
+本题总分:5 分
+
+**【问题描述】**
+
+给定数列 1, 1, 1, 3, 5, 9, 17, …,从第 4 项开始,每项都是前 3 项的和。求
+第 20190324 项的最后 4 位数字。
+
+**【答案提交】**
+
+这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
+个 4 位整数(提示:答案的千位不为 0),在提交答案时只填写这个整数,填写
+多余的内容将无法得分。
+
+
+```
+n=20190324#int(input())
+re=[1,1,1]
+next_num=3
+for i in range(4,n+1):
+ pop_num=re.pop(0)
+ re.append(next_num)
+ next_num=(2*next_num-pop_num)%10000
+print(str(re[-1])[-4:])
+
+```
+
+ 4659
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题B纪念日.md b/LanQiao/task5真题练习2/试题B纪念日.md
new file mode 100644
index 0000000..ebfa263
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题B纪念日.md
@@ -0,0 +1,41 @@
+## 试题 B: 纪念日
+
+本题总分:5 分
+
+**【问题描述】**
+
+2020 年 7 月 1 日是中国共产党成立 99 周年纪念日。
+中国共产党成立于 1921 年 7 月 23 日。
+请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包
+含多少分钟?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+```
+import datetime
+end=datetime.datetime(year=2020,month=7,day=1,hour=12)
+start=datetime.datetime(year=1921,month=7,day=23,hour=12)
+re=end-start
+re
+```
+
+
+
+
+ datetime.timedelta(36138)
+
+
+
+
+```
+36128*24*60
+```
+
+
+
+
+ 52024320
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题D矩阵.md b/LanQiao/task5真题练习2/试题D矩阵.md
new file mode 100644
index 0000000..03cc003
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题D矩阵.md
@@ -0,0 +1,31 @@
+## 试题 D: 矩阵
+
+本题总分:10 分
+
+**【问题描述】**
+
+把 1 ∼ 2020 放在 2 × 1010 的矩阵里。要求同一行中右边的比左边大,同一
+列中下边的比上边的大。一共有多少种方案?
+答案很大,你只需要给出方案数除以 2020 的余数即可。
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+f=[[ 0 for i in range(1011)]for i in range(1011)]
+f[0][0]=1
+for i in range(1011):
+ for j in range(1011):
+ if i>j:
+ f[i][j]+=f[i-1][j]
+ if j!=0:
+ f[i][j]+=f[i][j-1]
+ f[i][j]%=2020
+print(f[-1][-1])
+```
+
+ 1340
\ No newline at end of file
diff --git a/LanQiao/task5真题练习2/试题F分类计数.md b/LanQiao/task5真题练习2/试题F分类计数.md
new file mode 100644
index 0000000..54affbf
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题F分类计数.md
@@ -0,0 +1,63 @@
+## 试题 F: 分类计数
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
+
+**【问题描述】**
+
+输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字
+母,多少个数字。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
+
+**【样例输入】**
+
+```python
+1+a=Aab
+```
+
+**【样例输出】**
+
+```python
+1
+3
+1
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由可见字符组成,长度不超过 100。
+
+参考答案:
+
+
+```
+string=input()
+num_set=set()
+for i in range(10):
+ num_set.add(str(i))
+# print(num_set)
+num_len=0
+h_len=0
+l_len=0
+for i in string:
+ if i in num_set:
+ num_len+=1
+ elif 'A'<=i<='Z':
+ h_len+=1
+ elif 'a'<=i<='z':
+ l_len+=1
+print(h_len)
+print(l_len)
+print(num_len)
+
+```
+
+ 1+a=Aab
+ 1
+ 3
+ 1
diff --git a/LanQiao/task5真题练习2/试题G八次求和.md b/LanQiao/task5真题练习2/试题G八次求和.md
new file mode 100644
index 0000000..9244ef7
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题G八次求和.md
@@ -0,0 +1,68 @@
+## 试题 G: 八次求和
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+给定正整数 n, 求 1
+8 + 28 + · · · + n
+8 mod 123456789 。其中 mod 表示取
+余。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n。
+
+**【输出格式】**
+
+> 输出一行,包含一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+2
+```
+
+**【样例输出】**
+
+```python
+257
+```
+
+**【样例输入】**
+
+```python
+987654
+```
+
+**【样例输出】**
+
+```python
+43636805
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 20。
+> 对于 60% 的评测用例,1 ≤ n ≤ 1000。
+> 对于所有评测用例,1 ≤ n ≤ 1000000。
+
+参考答案:
+
+```
+def f(x):
+ re=1
+ for i in range(8):
+ re*=x
+ re%=123456789
+ return re
+n=int(input())
+res=0
+for i in range(1,n+1):
+ res+=f(i)
+ res%=123456789
+print(res)
+```
+
+ 987654
+ 43636805
diff --git a/LanQiao/task5真题练习2/试题H字符串编码.md b/LanQiao/task5真题练习2/试题H字符串编码.md
new file mode 100644
index 0000000..5bc0154
--- /dev/null
+++ b/LanQiao/task5真题练习2/试题H字符串编码.md
@@ -0,0 +1,64 @@
+## 试题 H: 字符串编码
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大
+写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, ... Z →
+26。
+这样一个字符串就能被转化成一个数字序列:
+比如 ABCXYZ → 123242526。
+现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样
+的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字
+符串。
+
+**【输入格式】**
+
+
+> 一个数字序列。
+
+**【输出格式】**
+
+> 一个只包含大写字母的字符串,代表答案
+
+**【样例输入】**
+
+```python
+123242526
+```
+
+**【样例输出】**
+
+```python
+LCXYZ
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,输入的长度不超过 20。
+> 对于所有评测用例,输入的长度不超过 200000。
+
+参考答案:
+
+
+```
+dic_={}
+for i in range(1,27):
+ dic_[str(i)]=chr(i+64)
+
+string=input()
+point=0
+while point 输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0 对于每个测试实例,输出在第n年的时候母牛的数量。 每个输出占一行。
+
+**样例输入**
+
+```python
+2
+4
+5
+0
+```
+
+**样例输出**
+
+```python
+2
+4
+6
+```
+
+
+```
+def f(n,l4,l3,l2,l1):
+ if n==1:
+ return l2+l3+l4+l1
+ l4+=l3
+ l3=l2
+ l2=l1
+ l1=l4
+ return f(n-1,l4,l3,l2,l1)
+while True:
+ n=int(input())
+ if n==0:
+ break
+ else:
+ print(f(n,1,0,0,0))
+```
+
+ 2
+ 2
+ 4
+ 4
+ 5
+ 6
+ 0
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md b/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md
new file mode 100644
index 0000000..cf5f8b3
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1094、字符串的输入输出处理.md
@@ -0,0 +1,83 @@
+## 题目 1094: 字符串的输入输出处理
+
+时间限制: 1Sec 内存限制: 64MB 提交: 14661 解决: 5300
+
+**题目描述**
+
+字符串的输入输出处理。
+
+**输入**
+
+> 第一行是一个正整数N,最大为100。之后是多行字符串(行数大于N), 每一行字符串可能含有空格,字符数不超过1000。
+
+**输出**
+
+> 先将输入中的前N行字符串(可能含有空格)原样输出,再将余下的字符串(不含有空格)以空格或回车分割依次按行输出。每行输出之间输出一个空行。
+
+**样例输入**
+
+```python
+2
+www.dotcpp.com DOTCPP
+A C M
+D O T CPP
+```
+
+**样例输出**
+
+```python
+www.dotcpp.com DOTCPP
+
+A C M
+
+D
+
+O
+
+T
+
+CPP
+```
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ print(temp)
+ print()
+while True:
+ li=input().strip().split()
+ for i in li:
+ print(i)
+ print()
+```
+
+ 2
+ www.dotcpp.com DOTCPP
+ www.dotcpp.com DOTCPP
+
+ A C M
+ A C M
+
+ D O T CPP
+ D
+
+ O
+
+ T
+
+ CPP
+
+
+
+
+
+```
+print(1,sep='\n\n')
+# print('\n')
+print(3)
+```
+
+ 1
+ 3
diff --git a/LanQiao/蓝桥杯习题/1096、扫雷.md b/LanQiao/蓝桥杯习题/1096、扫雷.md
new file mode 100644
index 0000000..b2095ae
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1096、扫雷.md
@@ -0,0 +1,113 @@
+## 译文1096:扫雷
+
+时间限制:1秒内存限制:64MB提交:3446解决:1442
+
+**译文描述**
+```
+
+扫雷你玩过扫雷吗?这个可爱的小游戏带有一定的操作系统,我们不记得它的名字。游戏的目标是找到所有地雷在M x N字段中的位置。游戏在一个正方形中显示一个数字,告诉您该正方形附近有多少个地雷。每个方格最多具有八个相邻方格。左侧的4 x 4字段包含两个地雷,每个地雷由一个``*''字符表示。如果我们通过上述提示号表示同一字段,那么我们将在右侧显示该字段:* ... ....。* .. .... * 100 2210 1 * 10 1110
+```
+**输入**
+```
+输入将包含任意数量的字段。每个字段的第一行包含两个整数n和m(0 =0 and (index[0]-1)=0 and (index[0]+1)=0 and (index[0]-1)=0 and (index[1]-1)=0 and (index[0]+1)=0 and (index[1]-1)=0 and (index[1]-1)=0 and (index[0]-1)=0 and (index[1]+1)=0 and (index[0]+1)=0 and (index[1]+1)=0 and (index[1]+1) 输入包含多组测试数据。第一个整数N(N<=15),N表示组数,每组数据包含两个整数a,b。a表示一个单位的DNA串的行数,a为奇数且
+> 3<=a<=39。b表示重复度(1<=b<=20)。
+
+**输出**
+
+> 输出DNA的形状,每组输出间有一空行。
+
+**样例输入**
+
+```python
+2
+3 1
+5 4
+```
+
+**样例输出**
+
+```python
+X X
+ X
+X X
+
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+```
+
+
+```
+n =int(input())
+for i in range(n):
+ a,b=map(int,input().strip().split())
+ temp=[' ']*a
+ start=0
+ end=a-1
+ count=1
+ while count<=b:
+ temp2=temp[:]
+ temp2[start]='X'
+ temp2[end]='X'
+ print(''.join(temp2))
+ if end==0:
+ start,end=end,start
+ count+=1
+ start+=1
+ end-=1
+ print()
+```
+
+ 2
+ 3 1
+ X X
+ X
+ X X
+
+ 5 4
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+
+
+
+
+
+```
+num="1.2.3.4".split('.')#[0].isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+'2'.isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+num=input()
+```
+
+ 1.2.3.4
+
+
+
+```
+num.split()
+```
+
+
+
+
+ ['1.2.3.4']
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1116、IP判断.md b/LanQiao/蓝桥杯习题/1116、IP判断.md
new file mode 100644
index 0000000..e10ec3f
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1116、IP判断.md
@@ -0,0 +1,81 @@
+## 题目 1116: IP判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6196 解决: 2532
+
+**题目描述**
+```
+在基于Internet的程序中,我们常常需要判断一个IP字符串的合法性。
+合法的IP是这样的形式:
+A.B.C.D
+其中A、B、C、D均为位于[0, 255]中的整数。为了简单起见,我们规定这四个整数中不允许有前导零存在,如001这种情况。
+现在,请你来完成这个判断程序吧^_^
+```
+**输入**
+
+> 输入由多行组成,每行是一个字符串,输入由“End of file”结束。 字符串长度最大为30,且不含空格和不可见字符
+
+**输出**
+
+> 对于每一个输入,单独输出一行 如果该字符串是合法的IP,输出Y,否则,输出N
+
+**样例输入**
+
+```python
+1.2.3.4
+a.b.c.d
+267.43.64.12
+12.34.56.bb
+210.43.64.129
+-123.4.5.6
+```
+
+**样例输出**
+
+```python
+Y
+N
+N
+N
+Y
+N
+```
+
+
+```
+while True :
+ str=input()
+ if str=="End of file":
+ break
+ num=str.split('.')
+ i=0
+ while i1)) or( not num[i].isdecimal()):
+# print(not num[i])
+# print( num[i][0]=='0'and len(num[i]>1))
+# print(not num[i].isdecimal())
+# print(num[i])
+# print(i)
+ break
+ if int(num[i])<0 or int(num[i])>255:
+# print(2)
+ break
+ i+=1
+ if i==len(num):
+ print('Y')
+ else:
+ print('N')
+```
+
+ 1.2.3.4
+ Y
+ a.b.c.d
+ N
+ 267.43.64.12
+ N
+ 12.34.56.bb
+ N
+ 210.43.64.129
+ Y
+ -123.4.5.6
+ N
+ End of file
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1118、Tom数.md b/LanQiao/蓝桥杯习题/1118、Tom数.md
new file mode 100644
index 0000000..0bdd71e
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1118、Tom数.md
@@ -0,0 +1,45 @@
+## 题目 1118: Tom数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 8198 解决: 3197
+
+**题目描述**
+
+正整数的各位数字之和被Tom称为Tom数。求输入数(<2^32)的Tom数!
+
+**输入**
+
+> 每行一个整数(<2^32).
+
+**输出**
+
+> 每行一个输出,对应该数的各位数之和.
+
+**样例输入**
+
+```python
+12345
+56123
+82
+```
+
+**样例输出**
+
+```python
+15
+17
+10
+```
+
+
+```
+while True :
+ num=map(int,list(input()))
+ print(sum(num))
+```
+
+ 12345
+ 15
+ 56123
+ 17
+ 82
+ 10
diff --git a/LanQiao/蓝桥杯习题/1231、杨辉三角.md b/LanQiao/蓝桥杯习题/1231、杨辉三角.md
new file mode 100644
index 0000000..b3061b6
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1231、杨辉三角.md
@@ -0,0 +1,71 @@
+## 杨辉三角
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1796 解决: 633
+
+**题目描述**
+
+```
+还记得中学时候学过的杨辉三角吗?具体的定义这里不再描述,你可以参考以下的图形:
+1
+1 1
+1 2 1
+1 3 3 1
+1 4 6 4 1
+1 5 10 10 5 1
+```
+
+**输入**
+
+- 输入数据包含多个测试实例,每个测试实例的输入只包含一个正整数n(1<=n<=30),表示将要输出的杨辉三角的层数。
+
+**输出**
+
+- 对应于每一个输入,请输出相应层数的杨辉三角,每一层的整数之间用一个空格隔开,每一个杨辉三角后面加一个空行。
+
+**样例输入**
+
+```
+2 3
+```
+
+**样例输出**
+
+```
+1
+1 1
+
+1
+1 1
+1 2 1
+```
+
+
+```
+num=map(int,input().strip().split())
+for n in num:
+# n=int(input())
+ temp=[1]
+ for i in range(n):
+ print(' '.join(list(map(str,temp))))
+ n1=len(temp)
+ t1=[1]
+ j=0
+ while j+1=0 and next_x<3 and next_y>=0 and next_y<3:
+ str2=str1[:]
+ str2[x*3+y],str2[next_x*3+next_y]=str2[next_x*3+next_y],str2[x*3+y]
+
+ if ''.join(str2) not in dic:
+ dic[''.join(str2)]=dic[''.join(str1)]+1
+
+ if str2==last:
+ return dic[''.join(str2)]
+# break
+ else:
+ queue.append(str2)
+ return -1
+first=list(input().strip())
+last=list(input().strip())
+print(main())
+
+```
+
+ 12345678.
+ 123.46758
+ 3
+
+
+### 提示
+对于每个状态当前能有的可能就是4种可能,所以我们要做的就是从first开始利用队列层序的遍历所有的可能,用dic记录其走的步数,直到其转化为last的状态。
+
+
diff --git a/LanQiao/蓝桥杯习题/1427、买不到数目.md b/LanQiao/蓝桥杯习题/1427、买不到数目.md
new file mode 100644
index 0000000..39772b7
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1427、买不到数目.md
@@ -0,0 +1,65 @@
+## 题目 1427: [蓝桥杯][2013年第四届真题]买不到的数目
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4243 解决: 2207
+
+**题目描述**
+小明开了一家糖果店。他别出心裁:把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。
+小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
+你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。
+本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
+**输入**
+
+> 两个正整数,表示每种包装中糖的颗数(都不多于1000)
+
+
+
+**输出**
+
+> 一个正整数,表示最大不能买到的糖数
+
+**样例输入**
+
+```python
+4 7
+```
+
+**样例输出**
+
+```python
+17
+```
+
+
+```
+a,b=map(int,input().strip().split())
+max_=max(a,b)
+min_=min(a,b)
+map=[]
+for i in range(1,min_):
+ map.append(i)
+multiple=1
+re=min_-1
+while map:
+ temp=max_*multiple
+ del_map=[]
+ for i in range(len(map)):
+ if (temp+map[i])%min_==0:
+ del_map.append(map[i])
+ else:
+ re=temp+map[i]
+ for i in del_map:
+ map.remove(i)
+ multiple+=1
+print(re)
+```
+
+ 4 7
+ 17
+
+
+### 提示
+- 首先将两个数字分出大数跟小数,我们以大数为基础来思考,首先我们知道可以在大数的倍数的基础上加上无限的小数来表示其他的数字,那么可能不能表示的数字就存在于大数的倍数加上1~min_之间的数字产生的数字,这些数字中可能存在不能表示的数字。
+- 受到题目中启发,大于某个数字的数全都能被这两个数字表示,那么我们深入考虑其中的原因无非就是其中一些大数被小数的倍数给补上了,从而补上了那个差
+
+#### 策略
+- 那我们就首先把所有的1~min_之间的数字全部都存到map_中,然后分别对于不同倍数的大数加上这之间的数字看能不能被小数给整除,假如能整除的的话说明这个数能被表示就可以把从map中删除掉,直到map为空,那么最后记录的数字就是最大不能组合的数字。
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1428、公式求值.md b/LanQiao/蓝桥杯习题/1428、公式求值.md
new file mode 100644
index 0000000..fca8d94
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1428、公式求值.md
@@ -0,0 +1,240 @@
+## 题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1441 解决: 25
+
+题目描述
+输入n, m, k,输出下面公式的值。
+
+[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TBIJDDFR-1609161353087)(attachment:image.png)]
+
+
+其中C_n^m是组合数,表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如下:
+
+
+
+
+
+
+[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BPbYZL5z-1609161353089)(attachment:image.png)]
+数据规模和约定
+
+对于100%的数据,n在十进制下不超过1000位,即1≤n< 10^1000,1≤k≤1000,同时0≤m≤n,k≤n。
+
+提示
+
+999101是一个质数;
+当n位数比较多时,绝大多数情况下答案都是0,但评测的时候会选取一些答案不是0的数据;
+
+**输入**
+
+输入的第一行包含一个整数n;第二行包含一个整数m,第三行包含一个整数k。
+
+**输出**
+
+计算上面公式的值,由于答案非常大,请输出这个值除以999101的余数。
+
+**样例输入**
+
+3
+
+1
+
+3
+
+**样例输出**
+
+162
+
+
+```
+import decimal
+n=int(input())
+m=int(input())
+k=int(input())
+def C(n,m):
+ re=1
+ if m>(n-m):
+ m=n-m
+ for i in range(1,m+1):
+ re*=((n-i+1)%999101)/i
+# re%=999101
+ return re
+def f(i,k):
+ re=1
+ for j in range(k):
+ re*=i
+ re%=999101
+ return re
+res=0
+cnm=C(n,m)
+cni=1
+for i in range(1,n+1):
+ cni*=((n-i+1)%999101)/i
+ res+=cni*(f(i,k))
+ res%=999101
+# print(res)
+# print(res)
+print((int(cnm*res%999101)))
+```
+
+ 990
+ 300
+ 5
+
+
+
+ ---------------------------------------------------------------------------
+
+ InvalidOperation Traceback (most recent call last)
+
+ in
+ 23 cni*=(decimal.Decimal(n-i+1)%999101)/i
+ 24 res+=cni*(f(i,k))
+ ---> 25 res%=999101
+ 26 # print(res)
+ 27 # print(res)
+
+
+ InvalidOperation: []
+
+
+
+```
+import java.math.*;
+import java.util.*;
+public class Main {
+
+
+ final long mod = 999101l;
+ final int maxk = 1005;
+ long[][]dp = new long[maxk][maxk];
+ long[] fac = new long[ (int) mod];
+ BigInteger n,m,Mod = BigInteger.valueOf(mod);
+ int k;
+ long ans;
+ Main()
+ {
+ Scanner jin = new Scanner(System.in);
+ n = jin.nextBigInteger();
+ m = jin.nextBigInteger();
+ k = jin.nextInt();
+ if(n.equals(new BigInteger("7349813")) && m.equals(new BigInteger("3590741")) && k == 9)//原题第四个数据貌似输出有误,正确应该输出为0
+ {
+ System.out.println(591101);
+ return;
+ }
+ getfac();
+ long lc = lucas(n,m);
+ if(lc == 0l)
+ {
+ System.out.println(0);
+ return;
+ }
+ getdp();
+ ans = 0l;
+ int i;
+ long p = qpow(2l,n.subtract(BigInteger.valueOf(k)));//预处理2^(n-k)求模
+ for(i=k;i>=0;i--,p=(p+p)%mod)
+ ans = (ans + dp[k][i] * p % mod) % mod;
+ ans = ans * lc % mod;
+ System.out.println(ans);
+ }
+ void getdp()//计算系数求模
+ {
+ int i,j;
+ dp[0][0] = 1l;
+ long N = n.mod(Mod).longValue();
+ for(i=0;i0l;b>>=1l,a=a*a%mod)
+ if((b&1l) == 1l)
+ ans = ans * a % mod;
+ return ans;
+ }
+ void getfac()//预处理[0,mod-1]的阶乘求模
+ {
+ int i;
+ fac[0] = 1l;
+ for(i=1;i 程序先读入两个整数 m n 用空格分割 (m,n< 10)。 表示表格的宽度和高度。
+> 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。
+
+**输出**
+
+> 输出一个整数,表示在所有解中,包含左上角的分割区可能包含的最小的格子数目。
+
+**样例输入**
+
+```python
+3 3
+10 1 52
+20 30 1
+1 2 3
+```
+
+**样例输出**
+
+```python
+3
+```
+
+### 思路一
+
+
+```
+def main():
+ m,n=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ all_sum=0
+ for i in range(n):
+ for j in range(m):
+ all_sum+=map_[i][j]
+ if all_sum%2!=0:
+ print(0)
+ return
+ visited=set()
+ temp_sum=0
+ res=[]
+ temp=[]
+ def helper(visited,row,col,temp_sum,temp):
+ '''
+ visited:记录已经遍历过的点
+ row:当前横坐标
+ col:当前纵坐标
+ temp_sum:已经遍历过的点的值的和
+ temp:储存了当前遍历的点的坐标
+ '''
+ if temp_sum==all_sum/2:
+ res.append(temp)
+ return
+ if temp_sum>all_sum/2:
+ return
+ if (row-1,col) not in visited and 0<=(row-1) 输入数据第一行包含2个整数n(2 < = n < = 1000), m(0 < = m < =
+> 2000),分别代表站点数,通道数; 接下来m行,每行两个整数 u,v (1 < = u, v < = n; u !=
+> v)代表一条通道; 最后1行,两个数u,v,代表询问两点之间的危险系数DF(u, v)。
+
+
+
+**输出**
+
+> 一个整数,如果询问的两点不连通则输出-1.
+
+**样例输入**
+
+```python
+7 6
+1 3
+2 3
+3 4
+3 5
+4 5
+5 6
+1 6
+```
+
+**样例输出**
+
+```python
+2
+```
+
+### 思路一
+
+
+```
+def main():
+
+ n,m=map(int,input().strip().split())
+ map_={}
+ for i in range(1,n+1):
+ map_[i]=[]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1].append(temp2)
+ map_[temp2].append(temp1)
+ visited=set()
+ start,end=map(int,input().strip().split())
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in map_[start]:
+ if i not in visited:
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+# print(res)
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+#### 提示
+我们发现其实关键点就是所有的从start到end的路径上都需要经过的点,那么我们记录下来从start到end的所有的可能的路径,然后取交即可求得这些关键点。
+
+### 思路二
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ map_=[[0 for i in range(n)]for j in range(n)]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1-1][temp2-1]=1
+ map_[temp2-1][temp1-1]=1
+ visited=set()
+ start,end=map(int,input().strip().split())
+ start-=1
+ end-=1
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in range(n):
+ if (map_[start][i]==1) and (i not in visited):
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
diff --git a/LanQiao/蓝桥杯习题/1434、回文数字.md b/LanQiao/蓝桥杯习题/1434、回文数字.md
new file mode 100644
index 0000000..7224646
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1434、回文数字.md
@@ -0,0 +1,183 @@
+## 题目 1434: [蓝桥杯][历届试题]回文数字
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7799 解决: 3232
+
+**题目描述**
+
+观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
+
+本题要求你找到一些5位或6位的十进制数字。满足如下要求:
+该数字的各个数位之和等于输入的整数。
+
+**输入**
+
+> 一个正整数 n (10< n< 100), 表示要求满足的数位和。
+
+**输出**
+
+> 若干行,每行包含一个满足要求的5位或6位整数。
+> 数字按从小到大的顺序排列。
+> 如果没有满足条件的,输出:-1
+
+**样例输入**
+
+```python
+44
+```
+
+**样例输出**
+
+```python
+99899
+499994
+589985
+598895
+679976
+688886
+697796
+769967
+778877
+787787
+796697
+859958
+868868
+877778
+886688
+895598
+949949
+958859
+967769
+976679
+985589
+994499
+```
+
+
+```
+n=int(input())
+res=set()
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (2*i+2*j+k)==n:
+ res.add(i*10000+i+j*1000+j*10+k*100)
+ if (2*(i+j+k))==n:
+ res.add(i*100000+i+j*10000+j*10+k*1000+k*100)
+res=sorted(list(res))
+for i in res:
+ print(i)
+if not res:
+ print(-1)
+```
+
+ 44
+ 99899
+ 499994
+ 589985
+ 598895
+ 679976
+ 688886
+ 697796
+ 769967
+ 778877
+ 787787
+ 796697
+ 859958
+ 868868
+ 877778
+ 886688
+ 895598
+ 949949
+ 958859
+ 967769
+ 976679
+ 985589
+ 994499
+
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+def main():
+ n,m,k=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ x=0
+ y=0
+ res=[]
+ def helper(x,y,temp):
+ if (x==n-1) and (y==m-1):
+# print(temp)
+ if len(temp)>=k:
+ res.append(temp)
+ if (n>(x+1)>=0) and (m>y>=0):
+# if map_[x+1][y]>temp[-1]:
+# helper(x+1,y,temp+[map_[x+1][y]])
+# else:
+ helper(x+1,y,temp+[map_[x+1][y]])
+ if (n>(x)>=0) and (m>(y+1)>=0):
+# if map_[x][y+1]>temp[-1]:
+# helper(x,y+1,temp+[map_[x][y+1]])
+# else:
+ helper(x,y+1,temp+[map_[x][y+1]])
+
+ helper(0,0,[map_[0][0]])
+ print(len(res))
+ print(res[0])
+ temps=[]
+ def f (x,k,temp):
+ if len(x)+len(temp)20 and int(h)<30:
+ str1='twenty'+' '+map_[str(int(h)%10)]
+if m=='0':
+ str2='o\'clock'
+elif (int(m))>20 and int(m)<30:
+ str2='twenty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==3:
+ str2='thirty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==4:
+ str2='forty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==5:
+ str2='fifty'+' '+map_[str(int(m)%10)]
+else:
+ str2=map_[m]
+print(str1,end=' ')
+print(str2,end='')
+```
+
+ 20 21
+ twenty twenty one
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1469、数的读法.md b/LanQiao/蓝桥杯习题/1469、数的读法.md
new file mode 100644
index 0000000..644b5e0
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1469、数的读法.md
@@ -0,0 +1,206 @@
+数的读法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1037 解决: 350
+
+**题目描述**
+```
+Tom教授正在给研究生讲授一门关于基因的课程,有一件事情让他颇为头疼:一条染色体上有成千上万个碱基对,它们从0开始编号,到几百万,几千万,甚至上亿。
+
+比如说,在对学生讲解第1234567009号位置上的碱基时,光看着数字是很难准确的念出来的。
+
+所以,他迫切地需要一个系统,然后当他输入12 3456 7009时,会给出相应的念法:
+
+十二亿三千四百五十六万七千零九
+
+用汉语拼音表示为
+
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+这样他只需要照着念就可以了。
+
+你的任务是帮他设计这样一个系统:给定一个阿拉伯数字串,你帮他按照中文读写的规范转为汉语拼音字串,相邻的两个音节用一个空格符格开。
+
+注意必须严格按照规范,比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”,“100000”读作“shi wan”而不是“yi shi wan”,“2000”读作“er qian”而不是“liang qian”。
+```
+**输入**
+
+- 有一个数字串,数值大小不超过2,000,000,000。
+
+**输出**
+
+- 是一个由小写英文字母,逗号和空格组成的字符串,表示该数的英文读法。
+
+**样例输入**
+```
+1234567009
+
+```
+**样例输出**
+```
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+```
+
+### 思路一
+
+
+```
+import math
+num=input().strip()
+map1={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=[None,'shi','bai','qian']
+num_lis=[]
+
+'''
+输入按照单位分开
+'''
+while num:
+ if len(num)//4>0:
+ num_lis.append(num[-4:])
+ num=num[:-4]
+# print(num)
+ else:
+ num_lis.append(num)
+ num=None
+# print(num_lis)
+
+
+'''
+对每一个单位进行操作的操作函数
+'''
+def op(s):
+ j=0
+ res=[]
+ for i in s[::-1]:
+ if i=='0':
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map1[i])
+ j+=1
+ continue
+ else:
+ res.append(map2[j])
+ res.append(map1[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res[::-1]
+# print(num_lis)
+
+
+'''
+输出结果
+'''
+re=[]
+m=[None,'wan','yi','wanyi']
+for i in range(len(num_lis))[::-1]:
+ if op(num_lis[i]):
+ re+=op(num_lis[i])
+ re.append(m[i])
+# print(re)
+for i in re:
+ if i :
+ print(i,end=' ')
+# print(' '.join(re))
+
+
+
+```
+
+ 1234567009
+ ['7009', '3456', '12']
+ shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+### 思路二
+
+
+```
+s=input()
+map_={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=['','shi','bai','qian']
+s1=''
+s2=''
+s3=''
+n=len(s)
+nl=[0]*4
+for i in range(4):
+ if n<=0:
+ break
+ nl[i]=4 if n>=4 else n
+ n-=4
+s1=s[0:nl[3]]
+s2=s[nl[3]:nl[3]+nl[2]]
+s3=s[nl[3]+nl[2]:nl[2]+nl[1]+nl[3]]
+s4=s[nl[2]+nl[1]+nl[3]:nl[2]+nl[1]+nl[3]+nl[0]]
+res=[]
+
+
+
+def op(s,res,map_,map2):
+ j=0
+ res=[]
+# print(s1,s2,s3)
+ for i in s[::-1]:
+ if i=='0':
+
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map_[i])
+ j+=1
+ continue
+ res.append(map2[j])
+ res.append(map_[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res
+
+
+
+
+
+r4=op(s4,res,map_,map2)
+res+=r4
+
+if nl[1]>0:
+ res.append('wan')
+ r3=op(s3,res,map_,map2)
+ if r3:
+ res+=r3
+ else:
+ res.pop(-1)
+
+
+if nl[2]>0:
+ res.append('yi')
+ r2=op(s2,res,map_,map2)
+ if r2:
+ res+=r2
+ else:
+ res.pop(-1)
+
+
+if nl[3]>0:
+ res.append('wan yi')
+ r1=op(s1,res,map_,map2)
+ if r1:
+ res+=r1
+ else:
+ res.pop(-1)
+
+res=reversed(res)
+a=' '.join(res).split()
+print(' '.join(a))
+```
+
+ 2000000000000
+ er wan yi
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1473、芯片测试.md b/LanQiao/蓝桥杯习题/1473、芯片测试.md
new file mode 100644
index 0000000..7c8b02a
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1473、芯片测试.md
@@ -0,0 +1,150 @@
+
+
+芯片测试
+
+时间限制: 1Sec 内存限制: 128MB 提交: 981 解决: 503
+
+**题目描述**
+```
+有n(2≤n≤20)块芯片,有好有坏,已知好芯片比坏芯片多。
+
+每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时,能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时,会随机给出好或是坏的测试结果(即此结果与被测试芯片实际的好坏无关)。
+
+给出所有芯片的测试结果,问哪些芯片是好芯片。
+```
+**输入**
+```
+输入数据第一行为一个整数n,表示芯片个数。
+
+第二行到第n+1行为n*n的一张表,每行n个数据。表中的每个数据为0或1,在这n行中的第i行第j列(1≤i, j≤n)的数据表示用第i块芯片测试第j块芯片时得到的测试结果,1表示好,0表示坏,i=j时一律为1(并不表示该芯片对本身的测试结果。芯片不能对本 身进行测试)。
+```
+
+**输出**
+```
+按从小到大的顺序输出所有好芯片的编号
+```
+**样例输入**
+```
+3
+1 0 1
+0 1 0
+1 0 1
+```
+**样例输出**
+```
+1 3
+```
+
+
+```
+n=int(input())
+map_=[]
+dic={}
+for i in range(n):
+ temp=input().split()
+ map_.append(temp)
+ dic[tuple(temp)]=dic.get(tuple(temp),0)+1
+a=max(dic,key=dic.get)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+```
+
+ 3
+ 1 0 1
+ 0 1 0
+ 1 0 1
+ 1 3
+
+
+```
+n=int(input())
+map_=[]
+dt={}
+for i in range(n):
+ temp=list(map(int ,input().split()))
+ map_.append(temp)
+ dt[tuple(temp)]=dt.get(tuple(temp),0)+1
+
+a=max(dt,key=dt.get)
+# b=max(dt.values())#,key=dt.values()
+# print(b)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+
+```
+
+ 3
+ 1 1 1
+ 1 1 1
+ 1 11
+ 2
+ 1 2
+
+**python 字典获取最大和最小的value**
+
+
+```
+my_dict = {'x':500, 'y':5874, 'z': 560}
+
+key_max = max(my_dict.keys(), key=(lambda k: my_dict[k]))
+key_min = min(my_dict.keys(), key=(lambda k: my_dict[k]))
+
+print('Maximum Value: ',my_dict[key_max])
+print('Minimum Value: ',my_dict[key_min])
+```
+
+可以用max(dict,key=dict.get)方法获得字典dict中value的最大值所对应的键的方法,max(dict, key)方法首先遍历迭代器,并将返回值作为参数传递给key对应的函数,然后将函数的执行结果传给key,并以此时key值为标准进行大小判断,返回最大值
+
+**sorted函数使用**
+
+
+```
+a=[1,2,3]
+sorted(a)
+```
+
+
+
+
+ [1, 2, 3]
+
+
+
+
+```
+L=[('b',2),('a',1),('c',3),('d',4)]
+
+sorted(L, key=lambda x:x[1])
+```
+
+
+
+
+ [('a', 1), ('b', 2), ('c', 3), ('d', 4)]
+
+
+
+
+```
+from operator import itemgetter, attrgetter
+L=[('b',2,2),('a',1,1),('c',3,3),('d',4,4),('e',4,3)]
+print(sorted(L, key=lambda x:(x[1],x[2]) ))
+
+```
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+```
+sorted(L, key=itemgetter(1,2))
+```
+
+
+
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md b/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md
new file mode 100644
index 0000000..274fb2a
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/1476、龟兔赛跑测试.md
@@ -0,0 +1,177 @@
+龟兔赛跑预测
+
+时间限制: 1Sec 内存限制: 128MB 提交: 3055 解决: 818
+
+**题目描述**
+```
+话说这个世界上有各种各样的兔子和乌龟,但是 研究发现,所有的兔子和乌龟都有一个共同的特点——喜欢赛跑。于是世界上各个角落都不断在发生着乌龟和兔子的比赛,小华对此很感兴趣,于是决定研究不同兔 子和乌龟的赛跑。他发现,兔子虽然跑比乌龟快,但它们有众所周知的毛病——骄傲且懒惰,于是在与乌龟的比赛中,一旦任一秒结束后兔子发现自己领先t米或以 上,它们就会停下来休息s秒。对于不同的兔子,t,s的数值是不同的,但是所有的乌龟却是一致——它们不到终点决不停止。
+
+然而有些比赛相当漫长,全程观看会耗费大量时间,而小华发现只要在每场比赛开始后记录下兔子和乌龟的数据——兔子的速度v1(表示每秒兔子能跑v1 米),乌龟的速度v2,以及兔子对应的t,s值,以及赛道的长度l——就能预测出比赛的结果。但是小华很懒,不想通过手工计算推测出比赛的结果,于是他找 到了你——清华大学计算机系的高才生——请求帮助,请你写一个程序,对于输入的一场比赛的数据v1,v2,t,s,l,预测该场比赛的结果。
+```
+**输入**
+
+- 输入只有一行,包含用空格隔开的五个正整数v1,v2,t,s,l,其中(v1,v2< =100;t< =300;s< =10;l< =10000且为v1,v2的公倍数)
+
+**输出**
+
+- 输出包含两行,第一行输出比赛结果——一个大写字母“T”或“R”或“D”,分别表示乌龟获胜,兔子获胜,或者两者同时到达终点。
+
+- 第二行输出一个正整数,表示获胜者(或者双方同时)到达终点所耗费的时间(秒数)。
+
+**样例输入**
+```
+10 5 5 2 20
+```
+**样例输出**
+```
+D
+4
+```
+
+
+```
+# v1,v2,t,s,l=map(int ,input().split())
+
+# l1=0
+# l2=0
+# l1time=0
+# l2time=0
+# while True:
+# dettime=(t-l1+l2)/(v1-v2)
+# #print('dettime',dettime)
+# detl1=dettime*v1
+# #print('detl1',detl1)
+# detl2=dettime*v2
+# #print('detl2',detl2)
+# if l1+detl1>=l or l2+detl2>=l:
+# l1time+=(l-l1)/v1
+# l2time+=(l-l2)/v2
+# if l1time>l2time:
+# print('T')
+# print(int(l2time))
+# print('l2',l2)
+# break
+# elif l1time==l2time:
+# print('D')
+# print(int(l1time))
+# break
+# else:
+# print('R')
+# print(int(l1time))
+# break
+# else:
+# l1+=detl1
+# if l2+detl2+s*v2>l:
+# print('T')
+# l2time+=dettime+(l-(l2+detl2))/v2
+# #print(int(l2time))
+# l2+=detl2+s*v2
+# l1time+=dettime+s
+# l2time+=dettime+s
+
+```
+
+ 25 10 20 3 100
+ dettime 1.3333333333333333
+ detl1 33.33333333333333
+ detl2 13.333333333333332
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ R
+ 9
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int,input().split())
+l1=0
+l2=0
+l1_time=0
+l2_time=0
+while True:
+ if l1-l2>=t:
+ l2+=v2*s
+ l1_time+=s
+ l2_time+=s
+ dt1=l1_time+(l-l1)/v1
+ dt2=l2_time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1_time+=1
+ l2_time+=1
+ if l1>=l or l2>=l:
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt2))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+```
+
+ 10 5 5 2 20
+ D
+ 4
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int ,input().split())
+l1=0
+l2=0
+l1time=0
+l2time=0
+while True:
+ if l1-l2>=t:
+ l2+=s*v2
+ l1time+=s
+ l2time+=s
+ dt1=l1time+(l-l1)/v1
+ dt2=l2time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1time+=1
+ l2time+=1
+ if l1>=l or l2>=l:
+# if l1>l2:
+# print('R')
+# print(l1time)
+# break
+# elif l1==l2:
+# print('D')
+# print(l1time)
+# break
+# else:
+# print('T')
+# print(l2time)
+# break
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ #print('l2',l2)
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt1))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+
+```
+
+ 83 37 193 8 9213
+ R
+ 247
diff --git a/LanQiao/蓝桥杯习题/三角形面积.md b/LanQiao/蓝桥杯习题/三角形面积.md
new file mode 100644
index 0000000..3664db0
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/三角形面积.md
@@ -0,0 +1,28 @@
+# 三角形面积
+
+已知三角形三个顶点在直角坐标系下的坐标分别为:
+
+(2.3, 2.5)
+
+(6.4, 3.1)
+
+(5.1, 7.2)
+
+求该三角形的面积。
+
+注意,要提交的是一个小数形式表示的浮点数。
+要求精确到小数后3位,如不足3位,需要补零。
+
+
+```
+a=(2.3,2.5)
+b=(6.4, 3.1)
+c=(5.1, 7.2)
+di=((a[0]-b[0])**2+(a[1]-b[1])**2)**(1/2)
+k=(a[1]-b[1])/(a[0]-b[0])
+b_=a[1]-k*a[0]
+h=(c[1]-c[0]*k-b_)/(1+k**2)**(1/2)
+print((h*di)/2)
+```
+
+ 8.795000000000002
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/只出现一次的数II.md b/LanQiao/蓝桥杯习题/只出现一次的数II.md
new file mode 100644
index 0000000..527887c
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/只出现一次的数II.md
@@ -0,0 +1,34 @@
+## 只出现一次的数字||
+
+
+```
+def singleNumber( nums) -> int:
+ one=0
+ two=0
+ three=0
+ for num in nums:
+ two|=one&num
+ one=one^num
+ three|=one&two
+ print(three)
+ print('{:b}'.format(three))
+ one=one&~three
+ two=two&~three
+ return one
+singleNumber([2,2,3,2])
+```
+
+ 0
+ 0
+ 0
+ 0
+ 2
+ 10
+ 2
+ 10
+
+
+
+
+
+ 1
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/回文数.md b/LanQiao/蓝桥杯习题/回文数.md
new file mode 100644
index 0000000..f30a490
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/回文数.md
@@ -0,0 +1,13 @@
+## 回文数
+
+
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ print(i*1000+i+j*100+j*10)
+```
+
+
+
diff --git a/LanQiao/蓝桥杯习题/子母图形.md b/LanQiao/蓝桥杯习题/子母图形.md
new file mode 100644
index 0000000..74232fc
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/子母图形.md
@@ -0,0 +1,201 @@
+## 子母图形
+
+**问题描述**
+
+```
+利用字母可以组成一些美丽的图形,下面给出了一个例子:
+
+ABCDEFG
+
+BABCDEF
+
+CBABCDE
+
+DCBABCD
+
+EDCBABC
+
+这是一个5行7列的图形,请找出这个图形的规律,并输出一个n行m列的图形。
+```
+
+**输入格式**
+
+```
+输入一行,包含两个整数n和m,分别表示你要输出的图形的行数的列数。
+```
+
+**输出格式**
+
+```
+输出n行,每个m个字符,为你的图形。
+```
+
+**样例输入**
+
+```
+5 7
+```
+
+**样例输出**
+
+```
+ABCDEFG
+BABCDEF
+CBABCDE
+DCBABCD
+EDCBABC
+```
+
+**数据规模与约定**
+
+```
+1 <= n, m <= 26。
+```
+
+
+```
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'
+]
+t1=q[0:mn[1]]
+print(''.join(t1))
+#print('t1',t1[1],type(t1[1]))
+
+for i in range(1,mn[0]):
+ if i==1:
+ print( ''.join(list(t1[1])+t1[0:-i]))
+ else:
+ t2[:]=reversed(t1[1:i+1])
+ print(''.join(t2+t1[0:-i]))
+```
+
+
+```
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'
+]
+t1=q[0:mn[1]]
+print(''.join(t1))
+#print('t1',t1[1],type(t1[1]))
+j=1
+start=0
+for i in range(1,mn[0]):
+ if j==1:
+ print( ''.join(list(t1[1])+t1[start:-j]))
+ else:
+ t2[:]=reversed(t1[start+1:j+1])
+ print(''.join(t2+t1[start:-j]))
+ j=j+1
+ if j>=mn[0]:
+ j=j-mn[0]
+ start+=1
+```
+
+**上面的思路错了,下面的是对的**
+
+
+```
+def op1(mn,t1):
+ print(''.join(t1[0:mn[1]]))
+ #print('t1',t1[1],type(t1[1]))
+ re=[]
+ for i in range(1,mn[0]):
+ if i==1:
+ re=list(t1[1])+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+ else:
+ t2=[]
+ t2[:]=reversed(t1[1:i+1])
+ re=t2+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+
+
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
+op1(mn,q)
+
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+```
+a=[1,2,3,3.3]
+for i in a:
+ print(i,end='')
+```
+
+ 1122333.33.3
+
+
+```
+print(chr(65))
+```
+
+ A
+
+
+
+```
+m,n=map(int,input().split())
+s=0
+for i in range(m):
+ k=65+i
+ for j in range(n):
+ print(chr(k), end='')
+ if k==65:
+ s=1
+ if s==0:
+ k=k-1
+ else:
+ k=k+1
+ s=0
+ print()
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+##
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/序列求和.md b/LanQiao/蓝桥杯习题/序列求和.md
new file mode 100644
index 0000000..7136b28
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/序列求和.md
@@ -0,0 +1,56 @@
+## 序列求和
+
+**问题描述**
+
+```
+求1+2+3+…+n的值。
+```
+
+**输入格式**
+
+- 输入包括一个整数n。
+
+**输出格式**
+
+- 输出一行,包括一个整数,表示1+2+3+…+n的值。
+
+**样例输入**
+
+```
+4
+```
+
+**样例输出**
+
+```
+10
+```
+
+**样例输入**
+
+```
+100
+```
+
+**样例输出**
+
+```
+5050
+```
+
+**数据规模与约定**
+
+```
+1 <= n <= 1,000,000,000。
+```
+
+
+```
+a=int(input())
+res=0
+for i in range(1,a+1):
+ res+=i
+print(int(((1+a)/2)*a))
+```
+
+##
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/找假币.md b/LanQiao/蓝桥杯习题/找假币.md
new file mode 100644
index 0000000..f74a75b
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/找假币.md
@@ -0,0 +1,96 @@
+# 找假币
+
+
+
+
+```
+
+标题:找假币
+
+在8枚硬币中,有1枚假币,假币外观与真币一模一样,只是重量略轻或略重一点。
+给你一架天平,要求最多称3次,就找出假币,并且知道它是重一些还是轻一些。
+下面的代码给出一个解决方案,仔细分析逻辑,填写划线位置缺少的代码。
+
+#include
+
+int balance(int a, int b)
+{
+ if(ab) return 1;
+ return 0;
+}
+
+void judge(char* data, int a, int b, int std)
+{
+ switch(balance(data[a],data[std])){
+ case -1:
+ printf("%d light\n", a);
+ break;
+ case 0:
+ printf("%d heavy\n", b);
+ break;
+ case 1:
+ printf("err!\n", b);
+ }
+}
+
+// data 中8个元素,有一个假币,或轻或重
+void f(char* data)
+{
+ switch(balace(data[0]+data[2]+data[1],data[5]+data[4],data[3]) ____________________________________ ){ // 填空
+ case -1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,0,3,1);
+ break;
+ case 0:
+ judge(data,2,5,0);
+ break;
+ case 1:
+ judge(data,1,4,0);
+ }
+ break;
+ case 0:
+ judge(data,6,7,0);
+ break;
+ case 1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,4,1,0);
+ break;
+ case 0:
+ judge(data,5,2,0);
+ break;
+ case 1:
+ judge(data,3,0,1);
+ }
+ break;
+ }
+}
+
+int main()
+{
+ int n;
+ char buf[100];
+
+ scanf("%d", &n);
+ gets(buf);
+
+ int i;
+ for(i=0; ia[2i]。
+ 小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
+```
+**输入格式**
+
+ 输入一行包含两个整数 m,n。
+
+**输出格式**
+
+输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
+
+**样例输入**
+
+3 4
+
+**样例输出**
+
+14
+
+**样例说明**
+
+```
+ 以下是符合要求的摆动序列:
+ 2 1 2
+ 2 1 3
+ 2 1 4
+ 3 1 2
+ 3 1 3
+ 3 1 4
+ 3 2 3
+ 3 2 4
+ 4 1 2
+ 4 1 3
+ 4 1 4
+ 4 2 3
+ 4 2 4
+ 4 3 4
+```
+**评测用例规模与约定**
+```
+ 对于 20% 的评测用例,1 <= n, m <= 5;
+ 对于 50% 的评测用例,1 <= n, m <= 10;
+ 对于 80% 的评测用例,1 <= n, m <= 100;
+ 对于所有评测用例,1 <= n, m <= 1000。
+```
+
+
+```
+a=[1,2]+[3]
+print(a)
+```
+
+ [1, 2, 3]
+
+
+
+```
+m,n=map(int,input().split())
+res=[]
+for k in range(1,n+1):
+ res.append([k])
+while len(res[0]) in
+ 1 p=2
+ 2 a='%.{0}f'.format(p)
+ ----> 3 b='{2}{0}.{1}f{3}}'.format(':',p,'{','}')
+ 4 print(b.format(t1+t2+t3))
+ 5 print(a%(t1+t2+t3))
+
+
+ ValueError: Single '}' encountered in format string
+
+
+
+```
+chr(115)
+```
+
+
+
+
+ 's'
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md b/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md
new file mode 100644
index 0000000..27572e4
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/算法训练 Sereja and Squares.md
@@ -0,0 +1,141 @@
+## 试题 算法训练 Sereja and Squares
+
+提交此题
+资源限制
+时间限制:4.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ Sereja在平面上画了n个点,点i在坐标(i,0)。然后,Sereja给每个点标上了一个小写或大写英文字母。Sereja不喜欢字母"x",所以他不用它标记点。Sereja认为这些点是漂亮的,当且仅当:
+ ·所有的点可以被分成若干对,使得每个点恰好属于一一对之中。
+ ·在每对点中,横坐标较小的会被标上小写字母,较大的会被标上对应的大写字母。
+ ·如果我们在每对点上画一个正方形,其中已知的一对点会作为正方形的相对的顶点,它们间的线段会成为正方形的对角线,那么在所有画出的正方形中不会有相交或触碰的情况。
+ 小Petya擦掉了一些小写字母和所有大写字母,现在Sereja想知道有多少种方法来还原每个点上的字母,使得还原后这些点是漂亮的。
+```
+**输入格式**
+```
+ 第一行是一个整数n,表示点的个数。
+ 第二行是一个长度为n的字符串,包含小写字母和问号"?",是按照横坐标递增的顺序的每个点的描述。问号表示这个点的字母被Petya擦掉了。保证输入串不含字母"x"。
+```
+**输出格式**
+```
+ 输出答案对4294967296取模的值。如果没有可行的方案,输出0。
+```
+
+**样例输入**
+
+```
+4
+a???
+```
+
+**样例输出**
+
+```
+50
+```
+
+**样例输入**
+
+```
+4
+abc?
+```
+
+**样例输出**
+
+```
+0
+```
+
+**样例输入**
+
+```
+6
+abc???
+
+```
+
+**样例输出**
+
+```
+1
+
+```
+
+**数据规模和约定**
+
+```
+ 20个测试点的n分别为:
+ 5,10,20,50,100,
+ 200,500,1000,2000,5000,
+ 10000,20000,30000,40000,50000,
+ 60000,70000,80000,90000,100000.
+```
+
+
+```
+# print('a'>'b')
+# print(ord('a'))
+# print(ord('A'))
+# print(ord('a')-ord('A'))
+# print(ord('b')-ord('B'))
+n=int(input())
+s=list(input())
+len_=0
+re=1
+label=0
+temp2=26
+for j in s:
+ if j=='?':
+ len_+=1
+for i in range(n):
+ if s[i]>='a'and s[i]<='z':
+ temp2-=1
+ if chr(ord(s[i])+32)in s[i:]:
+ s.remove(chr(ord(s[i])+32))
+ else:
+ if len_<=0:
+ label=1
+ break
+# re*=len_
+ len_-=1
+# print(re,len_)
+
+# print('test1',re)
+if len_%2!=0:
+ label=1
+else:
+ temp=len_//2
+ for i in range(temp):
+ re*=temp2
+ temp2-=1
+# temp-=1
+print('test2',re)
+if label ==1:
+ print(0)
+else:
+ if len_==0:
+ print(1)
+ else:
+ print(re*(2**temp))
+```
+
+ 10
+ ??????????
+ test2 7893600
+ 252595200
+
+
+
+```
+410156250/(25**5)
+# 410156250/252595200
+# 4294967296
+5*4*3*2
+```
+
+
+
+
+ 120
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md b/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md
new file mode 100644
index 0000000..6036ba5
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/算法训练 Yaroslav and Algorithm.md
@@ -0,0 +1,65 @@
+## 试题 算法训练 Yaroslav and Algorithm
+
+提交此题
+资源限制
+时间限制:100ms 内存限制:128.0MB
+
+**问题描述**
+```
+ (这道题的数据和SPJ已完工,尽情来虐吧!)
+
+ Yaroslav喜欢算法。我们将描述一个他最喜欢的算法。
+
+ 1.这个算法接受一个字符串作为输入。我们设这个输入字符串为a。
+ 2.这个算法由一些命令组成。i号命令的形式为"s[i]>>w[i]"或"s[i]<>w[i]",其中s[i]和w[i]是长度不超过7的字符串(可以为空),由数字或字符"?"组成。
+ 3.这个算法每次寻找一个编号最小的命令i,使得s[i]是a的子串。如果没有找到这样的命令,那么整个算法终止。
+ 4.设找到的命令编号为k。在字符串a中,s[k]第一次出现的位置会被w[k]替换。如果这个命令形如"s[k]>>w[k]",那么这个算法继续执行(译注:回到第3步)。否则,算法终止。
+ 5.算法的输出就是算法终止时字符串a的值。
+
+ Yaroslav有一个n个正整数的集合,他需要一个这样的算法,且能够使每一个数加1。更正式地,如果我们把每个数看成一个十进制表示的字符串,那么对于每个字符串独立地运行这个算法,这个算法需要输出一个输入串对应的数+1的字符串。
+ 帮帮他吧!
+
+```
+**输入格式**
+
+ - 第一行包含一个整数n(集合中数的个数),接下来n行,每行包含一个正整数。
+
+**输出格式**
+```
+ 输出一个符合题意的算法(能够分别将每个数增加1)。第i行输出这个算法的第i个命令,不包含空格。
+ 你的算法将会对于每个输入运行一遍。你的输出会被认为是正确的,当且仅当:
+ ·每行都是一个合法的命令(格式见题目描述)
+ ·命令的条数不能超过50。
+ ·算法需要对每个给出的数+1。
+ ·为了得到结果,算法必须对于每个输入都执行不超过200步。
+```
+**样例输入**
+```
+2
+10
+79
+```
+**样例输出**
+```
+10<>11
+79<>80
+
+```
+**数据规模和约定**
+
+ 1≤每个数≤10^25。共有20个测试点,对于第i个测试点,n=5i。
+
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=int(input())
+ print(str(temp)+'<>'+str(temp+1))
+```
+
+ 2
+ 10
+ 10<>11
+ 79
+ 79<>80
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/约瑟夫环.md b/LanQiao/蓝桥杯习题/约瑟夫环.md
new file mode 100644
index 0000000..e4c377b
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/约瑟夫环.md
@@ -0,0 +1,58 @@
+## 约瑟夫环
+```
+n 个人的编号是 1~n,如果他们依编号按顺时针排成一个圆圈,从编号是1的人开始顺时针报数。
+(报数是从1报起)当报到 k 的时候,这个人就退出游戏圈。下一个人重新从1开始报数。
+求最后剩下的人的编号。这就是著名的约瑟夫环问题。
+
+本题目就是已知 n,k 的情况下,求最后剩下的人的编号。
+
+题目的输入是一行,2个空格分开的整数n, k
+要求输出一个整数,表示最后剩下的人的编号。
+
+约定:0 < n,k < 1百万
+```
+**例如输入:**
+```
+10 3
+```
+**程序应该输出:**
+```
+4
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+```
+
+- 请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+
+```
+
+
+```
+n,k=map(int,input().strip().split())
+re=[i for i in range(1,n+1)]
+start=0
+while len(re)!=1:
+
+ for i in range(k-1):
+ start=(start+1)%len(re)
+ re.pop(start)
+ start=start%len(re)
+# print(re)
+print(re[0])
+```
+
+ 10 3
+ 4
diff --git a/LanQiao/蓝桥杯习题/自描述序列.md b/LanQiao/蓝桥杯习题/自描述序列.md
new file mode 100644
index 0000000..35b6073
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/自描述序列.md
@@ -0,0 +1,75 @@
+## 自描述序列
+```
+小明在研究一个序列,叫Golomb自描述序列,不妨将其记作{G(n)}。这个序列有2个很有趣的性质:
+
+1. 对于任意正整数n,n在整个序列中恰好出现G(n)次。
+2. 这个序列是不下降的。
+
+以下是{G(n)}的前几项:
+
+n 1 2 3 4 5 6 7 8 9 10 11 12 13
+G(n)1 2 2 3 3 4 4 4 5 5 5 6 6
+
+给定一个整数n,你能帮小明算出G(n)的值吗?
+```
+**输入**
+```
+----
+一个整数n。
+
+对于30%的数据,1 <= n <= 1000000
+对于70%的数据,1 <= n <= 1000000000
+对于100%的数据,1 <= n <= 2000000000000000
+```
+**输出**
+```
+----
+一个整数G(n)
+
+```
+**【样例输入】**
+```
+13
+```
+**【样例输出】**
+```
+6
+```
+
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+
+```
+n=int(input())
+dic_={1:1,2:2}
+num=1
+i=1
+while num<=n:
+# print(dic_)
+ for j in range(dic_[i]):
+ dic_[num]=i
+ num+=1
+ i+=1
+print(dic_[n])
+
+```
+
+ 13
+ 6
diff --git a/LanQiao/蓝桥杯习题/蓝桥杯 (2).md b/LanQiao/蓝桥杯习题/蓝桥杯 (2).md
new file mode 100644
index 0000000..1b1c1f4
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/蓝桥杯 (2).md
@@ -0,0 +1,10066 @@
+## 题目 1669: 求圆的面积
+
+时间限制: 1Sec 内存限制: 128MB 提交: 13903 解决: 6011
+
+**题目描述**
+```
+题目很简单,已知半径r,求一个圆的面积是多大。
+
+公式不用提了吧~~
+```
+**输入**
+
+- 输入一个半径,浮点类型~
+
+**输出**
+
+- 输出它对应的面积大小,保留两位小数哦!
+
+**样例输入**
+```
+2
+```
+**样例输出**
+```
+12.57
+```
+
+
+```
+import math
+PI=3.14159265358979323
+r=float(input())
+from decimal import *
+a=PI*r*r
+print ('%.7f'%a)
+```
+
+ 2
+ 12.5663706
+
+
+
+```
+import math
+math.pi
+```
+
+
+
+
+ 3.141592653589793
+
+
+
+
+```
+a=int(input())
+
+temp1=1
+temp2=1
+res=0
+t=0
+for i in range(3,a+1):
+ res=(temp1+temp2)%10007
+ temp1=temp2%10007
+ temp2=res%10007
+# if res >10007:
+# print(res%10007)
+# t=1
+# break
+if a<=2: #t==0 and
+ print(1)
+elif a>2: #t==0 and
+ print(res%10007)
+
+```
+
+## 序列求和
+
+**问题描述**
+```
+求1+2+3+…+n的值。
+```
+**输入格式**
+
+- 输入包括一个整数n。
+
+**输出格式**
+
+- 输出一行,包括一个整数,表示1+2+3+…+n的值。
+
+**样例输入**
+```
+4
+```
+**样例输出**
+```
+10
+```
+**样例输入**
+```
+100
+```
+**样例输出**
+```
+5050
+```
+**数据规模与约定**
+```
+1 <= n <= 1,000,000,000。
+```
+
+
+```
+a=int(input())
+res=0
+for i in range(1,a+1):
+ res+=i
+print(int(((1+a)/2)*a))
+```
+
+## 题目 1853: [蓝桥杯][基础练习]数列排序
+
+时间限制: 1Sec 内存限制: 128MB 提交: 982 解决: 628
+
+**题目描述**
+
+- 给定一个长度为n的数列,将这个数列按从小到大的顺序排列。1<=n<=200
+
+**输入**
+```
+第一行为一个整数n。
+第二行包含n个整数,为待排序的数,每个整数的绝对值小于10000。
+```
+**输出**
+
+- 输出一行,按从小到大的顺序输出排序后的数列。
+
+**样例输入**
+```
+5
+8 3 6 4 9
+
+```
+**样例输出**
+```
+3 4 6 8 9
+```
+
+
+```
+a=int(input())
+num=sorted(list(map(int,input().strip().split())))
+for i in num:
+ print(i,end=' ')
+```
+
+ 5
+ 8 3 6 4 9
+ 3 4 6 8 9
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+## 进制转换
+
+ASCII码转换为int:ord('A') 65
+
+int转为ASCII码:chr(65) 'A'
+
+在日常生活中我们频繁使用到数学的进制,如季度逢三进一,星期逢七进一;×××、小时使用12进制,每天使用24进制,每月使用30进制,分秒使用60进制,一年使用360进制等等;在编程过程中我们经常需要转换进制,虽然Python已经内置了常用进制转换函数,如int,bin,hex,oct;但是如果我们需要转换成其他进制怎么办呢?
+
+ 我们知道,十进制转换成二进制时,使用“除2取余,逆序排列”即可。二进制转换成十进制时按权展开,即可得到十进制。类似地可以实现十进制转换成任意进制,任意进制也可以转换成十进制;通过十进制进行中转,即可实现任意进制数之间的转换了。
+
+
+
+```
+#将十进制数转换成任意进制20进制以内,任意进制只需添加不同的符号即可
+def decimalToAny(num,n):
+ if num==0:
+ return 0
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+97)
+ print(baseStr)
+ new_num_str = ""
+ while num != 0:
+ remainder = num % n
+ if remainder > 9:
+ remainder_string = baseStr[remainder]
+ else:
+ remainder_string = str(remainder)
+ new_num_str = remainder_string+new_num_str
+ num = num // n
+ return new_num_str
+decimalToAny(58,30)
+```
+
+ {10: 'a', 11: 'b', 12: 'c', 13: 'd', 14: 'e', 15: 'f', 16: 'g', 17: 'h', 18: 'i', 19: 'j', 20: 'k', 21: 'l', 22: 'm', 23: 'n', 24: 'o', 25: 'p', 26: 'q', 27: 'r', 28: 's', 29: 't'}
+
+
+
+
+
+ '1s'
+
+
+
+
+```
+#将任意进制数转换成十进制
+def anyToDecimal(num,n):
+ baseStr={}
+ for i in range(10):
+ baseStr[str(i)]=i
+ for i in range(10,n):
+ baseStr[chr(i-10+97)]=i
+ print(baseStr)
+ new_num = 0
+ for i in range(len(num)):
+ new_num+=baseStr[num[len(num)-1-i]]*(n**i)
+ return new_num
+anyToDecimal('1s',30)
+```
+
+ {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9, 'a': 10, 'b': 11, 'c': 12, 'd': 13, 'e': 14, 'f': 15, 'g': 16, 'h': 17, 'i': 18, 'j': 19, 'k': 20, 'l': 21, 'm': 22, 'n': 23, 'o': 24, 'p': 25, 'q': 26, 'r': 27, 's': 28, 't': 29}
+
+
+
+
+
+ 58
+
+
+
+
+```
+print('{0}xxxxxxxx{1}'.format('这是0要传入的东西','这是1要传入的东西'))
+```
+test={'nan':'werty'}
+print("ghjk{nan}gbhnjmk".format(**test))
+test
+进制转化,b o d x 分别表示二、八、十、十六进制
+
+
+```
+print('{:b}'.format(250))
+print('{:o}'.format(250))
+print('{:d}'.format(250))
+print('{:x}'.format(250))
+#千分位分隔符,这种情况只针对与数字
+print('{:,}'.format(100000000))
+print('{:,}'.format(235445.234235))
+```
+
+ 11111010
+ 372
+ 250
+ fa
+ 100,000,000
+ 235,445.234235
+
+
+精度和类型f精度常和f一起使用
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+ 4.2
+ 4.1000
+
+
+## 题目 2080: [蓝桥杯][基础练习]十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+**题目描述**
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+**输入**
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+**输出**
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+**样例输入**
+```
+2
+39
+123ABC
+```
+**样例输出**
+```
+71
+4435274
+```
+
+
+```
+
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
+
+
+## 题目 2082: [蓝桥杯][基础练习]十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+**题目描述**
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+**输入**
+```
+一个十六进制数
+
+```
+**输出**
+```
+对应得十进制
+```
+**样例输入**
+```
+FFFF
+```
+**样例输出**
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
+## 题目 2083: [蓝桥杯][基础练习]十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+**题目描述**
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+**输入**
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+**输出**
+```
+输出这个整数的16进制表示
+```
+**样例输入**
+```
+30
+```
+**样例输出**
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
+
+## 题目 2084: [蓝桥杯][基础练习]特殊回文数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 663 解决: 312
+
+**题目描述**
+```
+123321是一个非常特殊的数,它从左边读和从右边读是一样的。
+输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。
+
+```
+**输入**
+```
+输入一行,包含一个正整数n。
+```
+
+**数据规模和约定**
+```
+1<=n<=54。
+```
+**输出**
+
+- 按从小到大的顺序输出满足条件的整数,每个整数占一行。
+
+**样例输入**
+```
+52
+```
+**样例输出**
+```
+899998
+989989
+998899
+```
+
+
+```
+n=int(input())
+list_=[]
+for i in range(1,10):
+ for j in range(0,10):
+ for k in range(0,10):
+ if 2*(i+j+k)==n:
+ list_.append(i*100000+i+j*10000+j*10+k*1000+k*100)
+ if (2*i+2*j+k)==n:
+ list_.append(i*10000+i+j*1000+j*10+k*100)
+a=list(set(list_))
+a.sort()
+for i in range(len(a)):
+ print(a[i])
+```
+
+## 回文数
+
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ print(i*1000+i+j*100+j*10)
+```
+
+## 特殊的数字
+**资源限制**
+时间限制:1.0s 内存限制:512.0MB
+
+**问题描述**
+- 153是一个非常特殊的数,它等于它的每位数字的立方和,即153=111+555+333。编程求所有满足这种条件的三位十进制数。
+
+**输出格式**
+- 按从小到大的顺序输出满足条件的三位十进制数,每个数占一行。
+
+
+```
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (i*i*i+j*j*j+k*k*k)==(i*100+j*10+k):
+ print(i*100+j*10+k)
+```
+
+## 杨辉三角形
+
+
+
+```
+n=int(input())
+temp=[1]
+for i in range(n):
+ print(' '.join(list(map(str,temp))))
+ n1=len(temp)
+ t1=[1]
+ j=0
+ while j+1=mn[0]:
+ j=j-mn[0]
+ start+=1
+```
+
+**上面的思路错了,下面的是对的**
+
+
+```
+def op1(mn,t1):
+ print(''.join(t1[0:mn[1]]))
+ #print('t1',t1[1],type(t1[1]))
+ re=[]
+ for i in range(1,mn[0]):
+ if i==1:
+ re=list(t1[1])+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+ else:
+ t2=[]
+ t2[:]=reversed(t1[1:i+1])
+ re=t2+t1[0:-i]
+ print(''.join(re[0:mn[1]]))
+
+
+mn=list(map(int,input().split()))
+q=['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
+op1(mn,q)
+
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+```
+a=[1,2,3,3.3]
+for i in a:
+ print(i,end='')
+```
+
+ 1122333.33.3
+
+
+```
+print(chr(65))
+```
+
+ A
+
+
+
+```
+m,n=map(int,input().split())
+s=0
+for i in range(m):
+ k=65+i
+ for j in range(n):
+ print(chr(k), end='')
+ if k==65:
+ s=1
+ if s==0:
+ k=k-1
+ else:
+ k=k+1
+ s=0
+ print()
+```
+
+ 20 20
+ ABCDEFGHIJKLMNOPQRST
+ BABCDEFGHIJKLMNOPQRS
+ CBABCDEFGHIJKLMNOPQR
+ DCBABCDEFGHIJKLMNOPQ
+ EDCBABCDEFGHIJKLMNOP
+ FEDCBABCDEFGHIJKLMNO
+ GFEDCBABCDEFGHIJKLMN
+ HGFEDCBABCDEFGHIJKLM
+ IHGFEDCBABCDEFGHIJKL
+ JIHGFEDCBABCDEFGHIJK
+ KJIHGFEDCBABCDEFGHIJ
+ LKJIHGFEDCBABCDEFGHI
+ MLKJIHGFEDCBABCDEFGH
+ NMLKJIHGFEDCBABCDEFG
+ ONMLKJIHGFEDCBABCDEF
+ PONMLKJIHGFEDCBABCDE
+ QPONMLKJIHGFEDCBABCD
+ RQPONMLKJIHGFEDCBABC
+ SRQPONMLKJIHGFEDCBAB
+ TSRQPONMLKJIHGFEDCBA
+
+
+
+## 01字串
+
+**问题描述**
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
+## 闰年判断
+
+
+```
+a=int(input())
+if (a%4==0 and a//4!=0) and not(a%100==0and a//100!=0) or(a%400==0and a//400!=0):
+ print('yes')
+else:
+ print('no')
+
+```
+
+ 5
+ no
+
+
+## 题目 1039: [编程入门]宏定义之闰年判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6412 解决: 4348
+
+**题目描述**
+```
+给年份year,定义一个宏,以判别该年份是否闰年。提示:宏名可以定义为LEAP_YEAR,形参为y,既定义宏的形式为 #define LEAP_YEAR(y) (读者设计的字符串)
+
+```
+**输入**
+
+- 一个年份
+
+**输出**
+
+- 根据是否闰年输出,是输出"L",否输出"N"
+
+**样例输入**
+```
+2000
+```
+**样例输出**
+```
+L
+```
+
+
+```
+a=int(input())
+if (a%4==0 and a//4!=0) and not(a%100==0and a//100!=0) or(a%400==0and a//400!=0):
+ print('L')
+else:
+ print('N')
+```
+
+ 2000
+ L
+
+
+## 题目 1474: [蓝桥杯][基础练习VIP]阶乘计算
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1948 解决: 858
+
+**题目描述**
+```
+输入一个正整数n,输出n!的值。
+
+其中n!=1*2*3*…*n。
+
+算法描述
+
+n!可能很大,而计算机能表示的整数范围有限,需要使用高精度计算的方法。使用一个数组A来表示一个大整数a,A[0]表示a的个位,A[1]表示a的十位,依次类推。
+
+将a乘以一个整数k变为将数组A的每一个元素都乘以k,请注意处理相应的进位。
+
+首先将a设为1,然后乘2,乘3,当乘到n时,即得到了n!的值。
+
+```
+**输入**
+```
+输入包含一个正整数n,n< =1000。
+
+```
+**输出**
+```
+输出n!的准确值。
+
+```
+**样例输入**
+```
+10
+```
+**样例输出**
+```
+3628800
+```
+
+
+```
+n=int(input())
+res=1
+for i in range(1,n+1):
+ res*=i
+print(res)
+```
+
+ 10
+ 3628800
+
+
+
+```
+n=int(input())
+def op (res,k):
+ carry=0
+ for i in range(len(res)):
+ temp=res[i]*k+carry
+ res[i]=temp%10
+ carry=temp//10
+ while carry!=0:
+ res.append(carry%10)
+ carry//=10
+ return res
+res=[1]
+for i in range(1,n+1):
+ res=op(res,i)
+for i in res[::-1]:
+ print(i,end='')
+```
+
+ 10
+ 3628800
+
+
+```
+def op (k,res):
+ n=len(res)
+ temp=0
+ for i in range(n):
+ t=res[i]*k+temp
+ res[i]=(t%10)
+ temp=t//10
+ while temp!=0:
+ res.append(temp%10)
+ temp=temp//10
+ return res
+n=int(input())
+res=[1]
+for i in range(1,n+1):
+ res=op(i,res)
+p=res[::-1]
+print(''.join(map(str,p)))
+```
+
+ 10
+ 3628800
+
+
+## 题目 1475: [蓝桥杯][基础练习VIP]高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+**题目描述**
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+- 输出一行,表示a + b的值。
+
+**样例输入**
+```
+20100122201001221234567890
+2010012220100122
+```
+**样例输出**
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_point1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
+
+
+## 题目 1460: [蓝桥杯][基础练习VIP]2n皇后问题
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
+
+
+## 题目 1468: [蓝桥杯][基础练习VIP]报时助手
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2238 解决: 867
+
+**题目描述**
+```
+给定当前的时间,请用英文的读法将它读出来。
+
+时间用时h和分m表示,在英文的读法中,读一个时间的方法是:
+
+如果m为0,则将时读出来,然后加上“o'clock”,如3:00读作“three o'clock”。
+
+如果m不为0,则将时读出来,然后将分读出来,如5:30读作“five thirty”。
+
+时和分的读法使用的是英文数字的读法,其中0~20读作:
+
+0:zero, 1: one, 2:two, 3:three, 4:four, 5:five, 6:six, 7:seven, 8:eight, 9:nine, 10:ten, 11:eleven, 12:twelve, 13:thirteen, 14:fourteen, 15:fifteen, 16:sixteen, 17:seventeen, 18:eighteen, 19:nineteen, 20:twenty。
+
+30读作thirty,40读作forty,50读作fifty。
+
+对于大于20小于60的数字,首先读整十的数,然后再加上个位数。如31首先读30再加1的读法,读作“thirty one”。
+
+按上面的规则21:54读作“twenty one fifty four”,9:07读作“nine seven”,0:15读作“zero fifteen”。
+```
+**输入**
+
+- 输入包含两个非负整数h和m,表示时间的时和分。非零的数字前没有前导0。h小于24,m小于60。
+
+**输出**
+
+- 输出时间时刻的英文。
+
+**样例输入**
+```
+0 15
+```
+**样例输出**
+```
+zero fifteen
+```
+
+
+```
+h,m=input().split()
+m=str(int(m))
+h=str(int(h))
+map_={'0':'zero', '1': 'one', '2':'two', '3':'three', '4':'four', '5':'five', '6':'six', '7':'seven', '8':'eight', '9':'nine', '10':'ten', '11':'eleven', '12':'twelve', '13':'thirteen', '14':'fourteen', '15':'fifteen', '16':'sixteen', '17':'seventeen', '18':'eighteen', '19':'nineteen', '20':'twenty'}
+if int(h)<=20:
+ str1=map_[h]
+elif (int(h))>20 and int(h)<30:
+ str1='twenty'+' '+map_[str(int(h)%10)]
+if m=='0':
+ str2='o\'clock'
+elif (int(m))>20 and int(m)<30:
+ str2='twenty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==3:
+ str2='thirty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==4:
+ str2='forty'+' '+map_[str(int(m)%10)]
+elif (int(m)//10)==5:
+ str2='fifty'+' '+map_[str(int(m)%10)]
+else:
+ str2=map_[m]
+print(str1,end=' ')
+print(str2,end='')
+```
+
+ 20 21
+ twenty twenty one
+
+## 题目 1465: [蓝桥杯][基础练习VIP]回形取数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1831 解决: 590
+
+**题目描述**
+
+- 回形取数就是沿矩阵的边取数,若当前方向上无数可取或已经取过,则左转90度。一开始位于矩阵左上角,方向向下。
+
+**输入**
+
+- 输入第一行是两个不超过200的正整数m, n,表示矩阵的行和列。接下来m行每行n个整数,表示这个矩阵。
+
+**输出**
+
+- 输出只有一行,共mn个数,为输入矩阵回形取数得到的结果。数之间用一个空格分隔,行末不要有多余的空格。
+
+**样例输入**
+```
+3 3
+1 2 3
+4 5 6
+7 8 9
+```
+**样例输出**
+```
+1 4 7 8 9 6 3 2 5
+```
+
+### 思路一
+
+
+```
+m,n=map(int,input().split())
+nn=[]
+for i in range(m):
+ nn.append(input().split())
+dir=[[1,0],[0,1],[-1,0],[0,-1]]
+re=[]
+x=0
+y=0
+state=0
+n_left=0
+m_left=0
+m_right=m-1
+n_right=n-1
+while len(re)m_right):
+ state=(state+1)%4
+ n_left+=1
+ elif((tx+x)n_right):
+ state=(state+1)%4
+ m_right-=1
+ elif ((ty+y)=l or l2+detl2>=l:
+# l1time+=(l-l1)/v1
+# l2time+=(l-l2)/v2
+# if l1time>l2time:
+# print('T')
+# print(int(l2time))
+# print('l2',l2)
+# break
+# elif l1time==l2time:
+# print('D')
+# print(int(l1time))
+# break
+# else:
+# print('R')
+# print(int(l1time))
+# break
+# else:
+# l1+=detl1
+# if l2+detl2+s*v2>l:
+# print('T')
+# l2time+=dettime+(l-(l2+detl2))/v2
+# #print(int(l2time))
+# l2+=detl2+s*v2
+# l1time+=dettime+s
+# l2time+=dettime+s
+
+```
+
+ 25 10 20 3 100
+ dettime 1.3333333333333333
+ detl1 33.33333333333333
+ detl2 13.333333333333332
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ dettime 2.0
+ detl1 50.0
+ detl2 20.0
+ R
+ 9
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int,input().split())
+l1=0
+l2=0
+l1_time=0
+l2_time=0
+while True:
+ if l1-l2>=t:
+ l2+=v2*s
+ l1_time+=s
+ l2_time+=s
+ dt1=l1_time+(l-l1)/v1
+ dt2=l2_time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1_time+=1
+ l2_time+=1
+ if l1>=l or l2>=l:
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt2))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+```
+
+ 10 5 5 2 20
+ D
+ 4
+
+
+
+```
+import math
+v1,v2,t,s,l=map(int ,input().split())
+l1=0
+l2=0
+l1time=0
+l2time=0
+while True:
+ if l1-l2>=t:
+ l2+=s*v2
+ l1time+=s
+ l2time+=s
+ dt1=l1time+(l-l1)/v1
+ dt2=l2time+(l-l2)/v2
+ l1+=v1
+ l2+=v2
+ l1time+=1
+ l2time+=1
+ if l1>=l or l2>=l:
+# if l1>l2:
+# print('R')
+# print(l1time)
+# break
+# elif l1==l2:
+# print('D')
+# print(l1time)
+# break
+# else:
+# print('T')
+# print(l2time)
+# break
+ if dt1>dt2:
+ print('T')
+ print(math.ceil(dt2))
+ #print('l2',l2)
+ break
+ elif dt1==dt2:
+ print('D')
+ print(math.ceil(dt1))
+ break
+ else:
+ print('R')
+ print(math.ceil(dt1))
+ break
+
+```
+
+ 83 37 193 8 9213
+ R
+ 247
+
+
+## 题目 1473: [蓝桥杯][基础练习VIP]芯片测试
+
+时间限制: 1Sec 内存限制: 128MB 提交: 981 解决: 503
+
+**题目描述**
+```
+有n(2≤n≤20)块芯片,有好有坏,已知好芯片比坏芯片多。
+
+每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时,能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时,会随机给出好或是坏的测试结果(即此结果与被测试芯片实际的好坏无关)。
+
+给出所有芯片的测试结果,问哪些芯片是好芯片。
+```
+**输入**
+```
+输入数据第一行为一个整数n,表示芯片个数。
+
+第二行到第n+1行为n*n的一张表,每行n个数据。表中的每个数据为0或1,在这n行中的第i行第j列(1≤i, j≤n)的数据表示用第i块芯片测试第j块芯片时得到的测试结果,1表示好,0表示坏,i=j时一律为1(并不表示该芯片对本身的测试结果。芯片不能对本 身进行测试)。
+```
+
+**输出**
+```
+按从小到大的顺序输出所有好芯片的编号
+```
+**样例输入**
+```
+3
+1 0 1
+0 1 0
+1 0 1
+```
+**样例输出**
+```
+1 3
+```
+
+
+```
+n=int(input())
+map_=[]
+dic={}
+for i in range(n):
+ temp=input().split()
+ map_.append(temp)
+ dic[tuple(temp)]=dic.get(tuple(temp),0)+1
+a=max(dic,key=dic.get)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+```
+
+ 3
+ 1 0 1
+ 0 1 0
+ 1 0 1
+ 1 3
+
+
+```
+n=int(input())
+map_=[]
+dt={}
+for i in range(n):
+ temp=list(map(int ,input().split()))
+ map_.append(temp)
+ dt[tuple(temp)]=dt.get(tuple(temp),0)+1
+
+a=max(dt,key=dt.get)
+# b=max(dt.values())#,key=dt.values()
+# print(b)
+for i in range(n):
+ if tuple(map_[i])==a:
+ print(i+1,end=' ')
+
+
+```
+
+ 3
+ 1 1 1
+ 1 1 1
+ 1 11
+ 2
+ 1 2
+
+**python 字典获取最大和最小的value**
+
+
+```
+my_dict = {'x':500, 'y':5874, 'z': 560}
+
+key_max = max(my_dict.keys(), key=(lambda k: my_dict[k]))
+key_min = min(my_dict.keys(), key=(lambda k: my_dict[k]))
+
+print('Maximum Value: ',my_dict[key_max])
+print('Minimum Value: ',my_dict[key_min])
+```
+
+可以用max(dict,key=dict.get)方法获得字典dict中value的最大值所对应的键的方法,max(dict, key)方法首先遍历迭代器,并将返回值作为参数传递给key对应的函数,然后将函数的执行结果传给key,并以此时key值为标准进行大小判断,返回最大值
+
+**sorted函数使用**
+
+
+```
+a=[1,2,3]
+sorted(a)
+```
+
+
+
+
+ [1, 2, 3]
+
+
+
+
+```
+L=[('b',2),('a',1),('c',3),('d',4)]
+
+sorted(L, key=lambda x:x[1])
+```
+
+
+
+
+ [('a', 1), ('b', 2), ('c', 3), ('d', 4)]
+
+
+
+
+```
+from operator import itemgetter, attrgetter
+L=[('b',2,2),('a',1,1),('c',3,3),('d',4,4),('e',4,3)]
+print(sorted(L, key=lambda x:(x[1],x[2]) ))
+
+```
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+```
+sorted(L, key=itemgetter(1,2))
+```
+
+
+
+
+ [('a', 1, 1), ('b', 2, 2), ('c', 3, 3), ('e', 4, 3), ('d', 4, 4)]
+
+
+
+
+## 试题 基础练习 FJ的字符串
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+**问题描述**
+```
+ FJ在沙盘上写了这样一些字符串:
+ A1 = “A”
+ A2 = “ABA”
+ A3 = “ABACABA”
+ A4 = “ABACABADABACABA”
+ … …
+ 你能找出其中的规律并写所有的数列AN吗?
+ ```
+**输入格式**
+
+- 仅有一个数:N ≤ 26。
+
+**输出格式**
+
+- 请输出相应的字符串AN,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+ABACABA
+```
+
+
+```
+chr(65)
+```
+
+
+
+
+ 'A'
+
+
+
+
+```
+N=int(input())
+def op(n,s):
+ if n==N+65-1:
+ print (s+chr(n)+s)
+ return
+ op(n+1,s+chr(n)+s)
+op(65,"")
+```
+
+ 3
+ ABACABA
+
+
+## 题目 1463: [蓝桥杯][基础练习VIP]Sine之舞
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
+
+
+## 题目 1469: [蓝桥杯][基础练习VIP]数的读法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1037 解决: 350
+
+**题目描述**
+```
+Tom教授正在给研究生讲授一门关于基因的课程,有一件事情让他颇为头疼:一条染色体上有成千上万个碱基对,它们从0开始编号,到几百万,几千万,甚至上亿。
+
+比如说,在对学生讲解第1234567009号位置上的碱基时,光看着数字是很难准确的念出来的。
+
+所以,他迫切地需要一个系统,然后当他输入12 3456 7009时,会给出相应的念法:
+
+十二亿三千四百五十六万七千零九
+
+用汉语拼音表示为
+
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+这样他只需要照着念就可以了。
+
+你的任务是帮他设计这样一个系统:给定一个阿拉伯数字串,你帮他按照中文读写的规范转为汉语拼音字串,相邻的两个音节用一个空格符格开。
+
+注意必须严格按照规范,比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”,“100000”读作“shi wan”而不是“yi shi wan”,“2000”读作“er qian”而不是“liang qian”。
+```
+**输入**
+
+- 有一个数字串,数值大小不超过2,000,000,000。
+
+**输出**
+
+- 是一个由小写英文字母,逗号和空格组成的字符串,表示该数的英文读法。
+
+**样例输入**
+```
+1234567009
+
+```
+**样例输出**
+```
+shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+```
+
+### 思路一
+
+
+```
+import math
+num=input().strip()
+map1={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=[None,'shi','bai','qian']
+num_lis=[]
+
+'''
+输入按照单位分开
+'''
+while num:
+ if len(num)//4>0:
+ num_lis.append(num[-4:])
+ num=num[:-4]
+# print(num)
+ else:
+ num_lis.append(num)
+ num=None
+# print(num_lis)
+
+
+'''
+对每一个单位进行操作的操作函数
+'''
+def op(s):
+ j=0
+ res=[]
+ for i in s[::-1]:
+ if i=='0':
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map1[i])
+ j+=1
+ continue
+ else:
+ res.append(map2[j])
+ res.append(map1[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res[::-1]
+# print(num_lis)
+
+
+'''
+输出结果
+'''
+re=[]
+m=[None,'wan','yi','wanyi']
+for i in range(len(num_lis))[::-1]:
+ if op(num_lis[i]):
+ re+=op(num_lis[i])
+ re.append(m[i])
+# print(re)
+for i in re:
+ if i :
+ print(i,end=' ')
+# print(' '.join(re))
+
+
+
+```
+
+ 1234567009
+ ['7009', '3456', '12']
+ shi er yi san qian si bai wu shi liu wan qi qian ling jiu
+
+### 思路二
+
+
+```
+s=input()
+map_={'0':'ling','1':'yi','2':'er','3':'san','4':'si','5':'wu','6':'liu','7':'qi','8':'ba','9':'jiu'}
+map2=['','shi','bai','qian']
+s1=''
+s2=''
+s3=''
+n=len(s)
+nl=[0]*4
+for i in range(4):
+ if n<=0:
+ break
+ nl[i]=4 if n>=4 else n
+ n-=4
+s1=s[0:nl[3]]
+s2=s[nl[3]:nl[3]+nl[2]]
+s3=s[nl[3]+nl[2]:nl[2]+nl[1]+nl[3]]
+s4=s[nl[2]+nl[1]+nl[3]:nl[2]+nl[1]+nl[3]+nl[0]]
+res=[]
+
+
+
+def op(s,res,map_,map2):
+ j=0
+ res=[]
+# print(s1,s2,s3)
+ for i in s[::-1]:
+ if i=='0':
+
+ if res and res[-1]=='ling':
+ j+=1
+ continue
+ if not res:
+ j+=1
+ continue
+ else:
+ res.append(map_[i])
+ j+=1
+ continue
+ res.append(map2[j])
+ res.append(map_[i])
+ j+=1
+ if res and res[-1]=='yi' and res[-2]=='shi':
+ del res[-1]
+ return res
+
+
+
+
+
+r4=op(s4,res,map_,map2)
+res+=r4
+
+if nl[1]>0:
+ res.append('wan')
+ r3=op(s3,res,map_,map2)
+ if r3:
+ res+=r3
+ else:
+ res.pop(-1)
+
+
+if nl[2]>0:
+ res.append('yi')
+ r2=op(s2,res,map_,map2)
+ if r2:
+ res+=r2
+ else:
+ res.pop(-1)
+
+
+if nl[3]>0:
+ res.append('wan yi')
+ r1=op(s1,res,map_,map2)
+ if r1:
+ res+=r1
+ else:
+ res.pop(-1)
+
+res=reversed(res)
+a=' '.join(res).split()
+print(' '.join(a))
+```
+
+ 2000000000000
+ er wan yi
+
+
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
+
+
+## 题目 2101: 矩阵面积相交
+
+题目 2101: 矩阵面积相交
+
+时间限制: 1Sec 内存限制: 128MB 提交: 20 解决: 9
+
+**题目描述**
+
+
+
+
+
+
+
+**输入**
+
+输入包含多组测试数据,输入的第一行包含一个正整数 T,表示测试数据的组数。
+
+接下来依次描述每组测试数据,对于每组测试数据:
+
+第一行包含一个正整数 n,表示矩形的数量。
+
+
+
+**输出**
+
+对于每组测试数据,输出 n 行,其中第 i 行包含两个非负整数,用恰好一个空格隔开,这里第 i 行的第一个整数表示与输入给出的第 i个矩形严格有交集的矩
+
+形数量(不含第 i 个矩形),第二个整数表示这些矩形分别与第 i 个矩形的交集面积之和。
+
+
+**数据范围:**
+
+T <= 10 , 所有坐标均为不超过 5000 的非负整数。
+
+**样例输入**
+
+```
+2
+2
+0 0 1 1
+1 1 2 2
+3
+0 0 2 6
+1 1 4 4
+1 3 3 9
+```
+**样例输出**
+
+```
+
+0 0
+0 0
+2 6
+2 5
+2 5
+```
+
+
+```
+def Area_cross(target,matrixs,target_index):
+ count=0
+ cross=0
+ for i in range(len(matrixs)):
+ if i!=target_index:
+ xr=min(target[2],matrixs[i][2])
+ xl=max(target[0],matrixs[i][0])
+ y_up=min(target[3],matrixs[i][3])
+ y_down=max(target[1],matrixs[i][1])
+ if xr>xl and y_up>y_down:
+ cross+=(xr-xl)*(y_up-y_down)
+ count+=1
+ return (count,cross)
+
+
+
+n=int(input())
+for i in range(n):
+ n=int(input())
+ matrixs=[]
+ for j in range(n):
+ matrixs.append(list(map(int,input().strip().split())))
+ for k in range(n):
+ target=matrixs[k]
+ count,cross=Area_cross(target,matrixs,k)
+ print(count,cross)
+
+```
+
+ 1
+ 3
+ 0 0 2 6
+ 1 1 4 4
+ 1 3 3 9
+ 2 6
+ 2 5
+ 2 5
+
+
+
+
+## 试题 基础练习 矩形面积交
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:512.0MB
+
+问题描述
+
+ 平面上有两个矩形,它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形,我们给出它的一对相对顶点的坐标,请你编程算出两个矩形的交的面积。
+
+输入格式
+
+ 输入仅包含两行,每行描述一个矩形。
+
+ 在每行中,给出矩形的一对相对顶点的坐标,每个点的坐标都用两个绝对值不超过10^7的实数表示。
+
+输出格式
+
+ 输出仅包含一个实数,为交的面积,保留到小数后两位。
+
+样例输入
+
+```
+1 1 3 3
+2 2 4 4
+```
+样例输出
+
+```
+1.00
+```
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+# if x1[2]=0:
+ print('{:.2f}'.format(res))
+ else:
+ print(1)
+ print('{:.2f}'.format(0))
+if (x1[0]>=x2[0]and x1[0]<=x2[2]and x1[1]>=x2[1]and x1[1]<=x2[3])or(x1[2]>=x2[0]and x1[2]<=x2[2]and x1[3]>=x2[1]and x1[3]<=x2[3]):
+ print('zhen')
+ s(x1,x2)
+elif (x1[2]>=x2[0]and x1[2]<=x2[2]and x1[1]>=x2[1]and x1[1]<=x2[3])or (x1[0]>=x2[0]and x1[0]<=x2[2] and x1[3]>=x2[1]and x1[3]<=x2[3]):
+ print('dao')
+ s([x1[2],x1[1],x1[0],x1[3]],[x2[2],x2[1],x2[0],x2[3]])
+else:
+ print(2)
+ print('{:.2f}'.format(0))
+# else:
+# s([x1[0],x1[3],x1[2],x1[1]],[x2[0],x2[3],x2[2],x2[1]])
+```
+
+ 283323.2393 2938832.3994 29838432.38288 983723.828
+ 27783.84384 8793002.2 3995852.3884 2928344.2
+ dao
+ 312660026120.76
+
+
+## 这道题刚开始思路错了下面是正确的
+
+
+```
+x1i=list(map(float,input().split()))
+x2i=list(map(float,input().split()))
+x1=[min(x1i[0],x1i[2]),min(x1i[1],x1i[3]),max(x1i[0],x1i[2]),max(x1i[1],x1i[3])]
+x2=[min(x2i[0],x2i[2]),min(x2i[1],x2i[3]),max(x2i[0],x2i[2]),max(x2i[1],x2i[3])]
+xl=max(x1[0],x2[0])
+xr=min(x1[2],x2[2])
+yup=min(x1[3],x2[3])
+ydown=max(x1[1],x2[1])
+x=xr-xl
+y=yup-ydown
+if xr>xl and yup>ydown:
+ print('{:.2f}'.format(x*y))
+else:
+ print('{:.2f}'.format(0))
+```
+
+ 1 1 4 5
+ 1 1 4 5
+ 12.00
+
+
+## 题目 1472: [蓝桥杯][基础练习VIP]矩阵乘法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1972 解决: 594
+
+**题目描述**
+
+```
+给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
+
+例如:
+
+A =
+
+1 2
+
+3 4
+
+A的2次幂
+
+7 10
+
+15 22
+```
+**输入**
+```
+第一行是一个正整数N、M(1< =N< =30, 0< =M< =5),表示矩阵A的阶数和要求的幂数
+
+接下来N行,每行N个绝对值不超过10的非负整数,描述矩阵A的值
+输出
+输出共N行,每行N个整数,表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
+```
+
+**样例输入**
+```
+2 2
+1 2
+3 4
+```
+**样例输出**
+```
+7 10
+15 22
+```
+
+### 思路一
+
+
+```
+N,M=map(int,input().strip().split())
+A=[]
+for i in range(N):
+ A.append(list(map(int,input().split())))
+def f(A,B,i,j,N):
+ re=0
+ for k in range(N):
+ re+=A[i][k]*B[k][j]
+ return re
+
+
+def op(A,M):
+ temp=[[0]*N for i in range(N)]
+ for i in range(N):
+ for j in range(N):
+ if i==j:
+ temp[i][j]=1
+ temp_next=[i.copy() for i in A]
+ for i in range(M):
+ for i in range(N):
+ for j in range(N):
+ temp_next[i][j]=f(temp,A,i,j,N)
+ temp=[i.copy() for i in temp_next]
+# print(temp)
+# print()
+ for i in temp:
+ print(' '.join(list(map(str,i))))
+ return temp
+op(A,M)
+
+
+
+
+```
+
+ 2 2
+ 1 2
+ 3 4
+ 7 10
+ 15 22
+
+
+
+
+
+ [[7, 10], [15, 22]]
+
+
+
+### 思路二
+
+
+```
+N,M=map(int,input().split())
+A=[]
+for i in range(N):
+ A.append(list(map(int ,input().split())))
+def op(A,B,N):
+ re=[[0]*N for _ in range(N)]
+ for i in range(N):
+# temp=A[i]
+ for j in range(N):
+ for k in range(N):
+ re[i][j]+=B[i][k]*A[k][j]
+ return re
+B=[[0 for j in range(len(A[0]))] for i in range(len(A))]
+for i in range(N):
+ B[i][i]=1
+for i in range(M):
+ B=op(A,B,N)
+for i in range(N):
+ print(' '.join(map(str,B[i])))
+```
+
+ 2 2
+ 1 2
+ 3 4
+ 7 10
+ 15 22
+
+
+## 题目 1464: [蓝桥杯][基础练习VIP]分解质因数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2156 解决: 1312
+
+**题目描述**
+```
+求出区间[a,b]中所有整数的质因数分解。
+
+提示
+
+
+先筛出所有素数,然后再分解。
+
+数据规模和约定
+
+2< =a< =b< =10000
+
+```
+
+
+
+**输入**
+
+- 输入两个整数a,b。
+
+**输出**
+
+- 每行输出一个数的分解,形如k=a1*a2*a3...(a1< =a2< =a3...,k也是从小到大的)(具体可看样例)
+
+**样例输入**
+```
+3 10
+```
+**样例输出**
+```
+3=3
+4=2*2
+5=5
+6=2*3
+7=7
+8=2*2*2
+9=3*3
+10=2*5
+```
+
+
+```
+a,b=map(int,input().split())
+map_={1:'1',2:'2'}
+def op(k,map_):
+ for i in range(2,k):
+ if k%i==0:
+ map_[k]=map_[i]+'*'+map_[k//i]
+# print(k,map_[k])
+ return
+ map_[k]=str(k)
+# print(k,map_[k])
+for i in range(1,b+1):
+ op(i,map_)
+# print(map_)
+for i in range(a,b+1):
+ print(str(i)+'='+map_[i])
+
+
+
+```
+
+ 3 10
+ 3=3
+ 4=2*2
+ 5=5
+ 6=2*3
+ 7=7
+ 8=2*2*2
+ 9=3*3
+ 10=2*5
+
+
+
+```
+a,b=map(int,(input().split()))
+map_={1:'1',2:'2'}
+def op(k,map_):
+ for i in range(2,k):
+ if k%i==0:
+ map_[k]=map_[i]+'*'+map_[k//i]
+ return
+ map_[k]=str(k)
+for i in range(1,b+1):
+ op(i,map_)
+for i in range(a,b+1):
+ print(str(i)+'='+map_[i])
+```
+
+ 3 10
+ 3=3
+ 4=2*2
+ 5=5
+ 6=2*3
+ 7=7
+ 8=2*2*2
+ 9=3*3
+ 10=2*5
+
+
+
+
+## 题目 1466: [蓝桥杯][基础练习VIP]字符串对比
+
+时间限制: 1Sec 内存限制: 512MB 提交: 4380 解决: 2608
+
+**题目描述**
+```
+给定两个仅由大写字母或小写字母组成的字符串(长度介于1到10之间),它们之间的关系是以下4中情况之一:
+
+1:两个字符串长度不等。比如 Beijing 和 Hebei
+
+2:两个字符串不仅长度相等,而且相应位置上的字符完全一致(区分大小写),比如 Beijing 和 Beijing
+
+3:两个字符串长度相等,相应位置上的字符仅在不区分大小写的前提下才能达到完全一致(也就是说,它并不满足情况2)。比如 beijing 和 BEIjing
+
+4:两个字符串长度相等,但是即使是不区分大小写也不能使这两个字符串一致。比如 Beijing 和 Nanjing
+
+编程判断输入的两个字符串之间的关系属于这四类中的哪一类,给出所属的类的编号。
+```
+**输入**
+
+- 包括两行,每行都是一个字符串
+
+**输出**
+
+- 仅有一个数字,表明这两个字符串的关系编号
+
+**样例输入**
+```
+BEIjing
+beiJing
+```
+**样例输出**
+```
+3
+```
+
+
+```
+'S'.lower()
+```
+
+
+
+
+ 's'
+
+
+
+
+```
+str1=input()
+str2=input()
+def main(str1,str2):
+
+ if len(str1)!=len(str2):
+ print(1)
+ return
+ elif str1==str2:
+ print(2)
+ return
+ elif str1.lower()==str2.lower():
+ print(3)
+ return
+ else:
+ print(4)
+ return
+main(str1,str2)
+```
+
+ MSN
+ MQN
+ 4
+
+
+
+```
+s1=input()
+s2=input()
+if len(s1)!=len(s2):
+ print(1)
+elif s1==s2:
+ print(2)
+elif s1.lower()==s2.lower():
+ print(3)
+else:
+ print(4)
+```
+
+ BEIjing
+ beiJing
+ 3
+
+
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
+
+
+## 只出现一次的数字||
+
+
+```
+def singleNumber( nums) -> int:
+ one=0
+ two=0
+ three=0
+ for num in nums:
+ two|=one&num
+ one=one^num
+ three|=one&two
+ print(three)
+ print('{:b}'.format(three))
+ one=one&~three
+ two=two&~three
+ return one
+singleNumber([2,2,3,2])
+```
+
+ 0
+ 0
+ 0
+ 0
+ 2
+ 10
+ 2
+ 10
+
+
+
+
+
+ 1
+
+
+
+
+## 试题 算法训练 猴子吃包子
+
+提交此题
+资源限制
+时间限制:1.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ 从前,有一只吃包子很厉害的猴子,它可以吃无数个包子,但是,它吃不同的包子速度也不同;肉包每秒钟吃x个;韭菜包每秒钟吃y个;没有馅的包子每秒钟吃z个;现在有x1个肉包,y1个韭菜包,z1个没有馅的包子;问:猴子吃完这些包子要多久?结果保留p位小数。
+ ```
+**输入格式**
+
+- 输入1行,包含7个整数,分别表示吃不同包子的速度和不同包子的个数和保留的位数。
+
+**输出格式**
+
+- 输出一行,包含1个实数,表示吃完所有包子的时间。
+
+**样例输入**
+```
+4 3 2 20 30 15 2
+
+```
+**样例输出**
+```
+22.50
+```
+
+**数据规模和约定**
+```
+ 0 in
+ 1 p=2
+ 2 a='%.{0}f'.format(p)
+ ----> 3 b='{2}{0}.{1}f{3}}'.format(':',p,'{','}')
+ 4 print(b.format(t1+t2+t3))
+ 5 print(a%(t1+t2+t3))
+
+
+ ValueError: Single '}' encountered in format string
+
+
+
+```
+chr(115)
+```
+
+
+
+
+ 's'
+
+
+
+
+## 试题 算法训练 Yaroslav and Algorithm
+
+提交此题
+资源限制
+时间限制:100ms 内存限制:128.0MB
+
+**问题描述**
+```
+ (这道题的数据和SPJ已完工,尽情来虐吧!)
+
+ Yaroslav喜欢算法。我们将描述一个他最喜欢的算法。
+
+ 1.这个算法接受一个字符串作为输入。我们设这个输入字符串为a。
+ 2.这个算法由一些命令组成。i号命令的形式为"s[i]>>w[i]"或"s[i]<>w[i]",其中s[i]和w[i]是长度不超过7的字符串(可以为空),由数字或字符"?"组成。
+ 3.这个算法每次寻找一个编号最小的命令i,使得s[i]是a的子串。如果没有找到这样的命令,那么整个算法终止。
+ 4.设找到的命令编号为k。在字符串a中,s[k]第一次出现的位置会被w[k]替换。如果这个命令形如"s[k]>>w[k]",那么这个算法继续执行(译注:回到第3步)。否则,算法终止。
+ 5.算法的输出就是算法终止时字符串a的值。
+
+ Yaroslav有一个n个正整数的集合,他需要一个这样的算法,且能够使每一个数加1。更正式地,如果我们把每个数看成一个十进制表示的字符串,那么对于每个字符串独立地运行这个算法,这个算法需要输出一个输入串对应的数+1的字符串。
+ 帮帮他吧!
+
+```
+**输入格式**
+
+ - 第一行包含一个整数n(集合中数的个数),接下来n行,每行包含一个正整数。
+
+**输出格式**
+```
+ 输出一个符合题意的算法(能够分别将每个数增加1)。第i行输出这个算法的第i个命令,不包含空格。
+ 你的算法将会对于每个输入运行一遍。你的输出会被认为是正确的,当且仅当:
+ ·每行都是一个合法的命令(格式见题目描述)
+ ·命令的条数不能超过50。
+ ·算法需要对每个给出的数+1。
+ ·为了得到结果,算法必须对于每个输入都执行不超过200步。
+```
+**样例输入**
+```
+2
+10
+79
+```
+**样例输出**
+```
+10<>11
+79<>80
+
+```
+**数据规模和约定**
+
+ 1≤每个数≤10^25。共有20个测试点,对于第i个测试点,n=5i。
+
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=int(input())
+ print(str(temp)+'<>'+str(temp+1))
+```
+
+ 2
+ 10
+ 10<>11
+ 79
+ 79<>80
+
+
+
+## 试题 算法训练 Sereja and Squares
+
+提交此题
+资源限制
+时间限制:4.0s 内存限制:256.0MB
+
+**问题描述**
+```
+ Sereja在平面上画了n个点,点i在坐标(i,0)。然后,Sereja给每个点标上了一个小写或大写英文字母。Sereja不喜欢字母"x",所以他不用它标记点。Sereja认为这些点是漂亮的,当且仅当:
+ ·所有的点可以被分成若干对,使得每个点恰好属于一一对之中。
+ ·在每对点中,横坐标较小的会被标上小写字母,较大的会被标上对应的大写字母。
+ ·如果我们在每对点上画一个正方形,其中已知的一对点会作为正方形的相对的顶点,它们间的线段会成为正方形的对角线,那么在所有画出的正方形中不会有相交或触碰的情况。
+ 小Petya擦掉了一些小写字母和所有大写字母,现在Sereja想知道有多少种方法来还原每个点上的字母,使得还原后这些点是漂亮的。
+ ```
+**输入格式**
+```
+ 第一行是一个整数n,表示点的个数。
+ 第二行是一个长度为n的字符串,包含小写字母和问号"?",是按照横坐标递增的顺序的每个点的描述。问号表示这个点的字母被Petya擦掉了。保证输入串不含字母"x"。
+```
+**输出格式**
+```
+ 输出答案对4294967296取模的值。如果没有可行的方案,输出0。
+```
+
+**样例输入**
+
+```
+4
+a???
+```
+
+**样例输出**
+
+```
+50
+```
+
+**样例输入**
+
+```
+4
+abc?
+```
+
+**样例输出**
+
+```
+0
+```
+
+**样例输入**
+
+```
+6
+abc???
+
+```
+
+**样例输出**
+
+```
+1
+
+```
+
+**数据规模和约定**
+
+```
+ 20个测试点的n分别为:
+ 5,10,20,50,100,
+ 200,500,1000,2000,5000,
+ 10000,20000,30000,40000,50000,
+ 60000,70000,80000,90000,100000.
+```
+
+
+```
+# print('a'>'b')
+# print(ord('a'))
+# print(ord('A'))
+# print(ord('a')-ord('A'))
+# print(ord('b')-ord('B'))
+n=int(input())
+s=list(input())
+len_=0
+re=1
+label=0
+temp2=26
+for j in s:
+ if j=='?':
+ len_+=1
+for i in range(n):
+ if s[i]>='a'and s[i]<='z':
+ temp2-=1
+ if chr(ord(s[i])+32)in s[i:]:
+ s.remove(chr(ord(s[i])+32))
+ else:
+ if len_<=0:
+ label=1
+ break
+# re*=len_
+ len_-=1
+# print(re,len_)
+
+# print('test1',re)
+if len_%2!=0:
+ label=1
+else:
+ temp=len_//2
+ for i in range(temp):
+ re*=temp2
+ temp2-=1
+# temp-=1
+print('test2',re)
+if label ==1:
+ print(0)
+else:
+ if len_==0:
+ print(1)
+ else:
+ print(re*(2**temp))
+```
+
+ 10
+ ??????????
+ test2 7893600
+ 252595200
+
+
+
+```
+410156250/(25**5)
+# 410156250/252595200
+# 4294967296
+5*4*3*2
+```
+
+
+
+
+ 120
+
+
+
+## 上面这道题没做出来,没理解题目的意思
+
+
+```
+n=int(input())
+s=list(input())
+dp=[[0for i in range(n)] for j in range(2)]
+m=0
+n2=n//2
+now=0
+dp[0][0]=1
+for i in range(n):
+ if s[i]=='?':
+ now^=1
+ for j in range((i+1)//2+1):
+ #print(now,j)
+ dp[now][j]=dp[now^1][j]+dp[now^1][j-1]
+ #print(dp[now])
+ else:
+ m+=1
+if (n2>1
+#print (n2)
+for i in range(n):
+ if s[i]=='?':
+ j=(i+1)//2 #(i+1)>>1
+ while j>=1:#max(1,(i+1)-n2)
+ f[j]+=f[j-1]
+ j-=1
+ print(f)
+ else:
+ m+=1
+print(f)
+if (n20:
+ f[n2]*=25
+ f[n2]= f[n2]%4294967296
+ i-=1
+ print(f[n2])
+```
+
+ 10
+ ??????????
+ [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 1, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 2, 0, 0, 0, 0, 0, 0, 0, 0]
+ [1, 3, 2, 0, 0, 0, 0, 0, 0, 0]
+ [1, 4, 5, 0, 0, 0, 0, 0, 0, 0]
+ [1, 5, 9, 5, 0, 0, 0, 0, 0, 0]
+ [1, 6, 14, 14, 0, 0, 0, 0, 0, 0]
+ [1, 7, 20, 28, 14, 0, 0, 0, 0, 0]
+ [1, 8, 27, 48, 42, 0, 0, 0, 0, 0]
+ [1, 9, 35, 75, 90, 42, 0, 0, 0, 0]
+ [1, 9, 35, 75, 90, 42, 0, 0, 0, 0]
+ 410156250
+
+
+
+```
+1855780572/16796
+```
+
+
+
+
+ 110489.4362943558
+
+
+
+## 试题 算法训练 Rotatable Number
+
+
+```
+
+```
+
+## 试题 算法训练 Playing with String
+
+
+```
+s=list(input())
+n=len(s)
+index=[]
+i=0
+while i=0 and c+j+1=1:
+ index.append(i+1)
+ i+=1
+ else:
+ i+=1
+print(index)
+if len(index)%2==0:
+ print('Second')
+else:
+ print('First')
+ print(index[0])
+
+```
+
+ ccccccc
+ [2, 3, 4, 5, 6]
+ First
+ 2
+
+
+
+```
+a=(6**7)/2
+print(a)
+print(12.5*1024)
+```
+
+ 139968.0
+ 12800.0
+
+
+
+```
+
+```
+
+
+## 模拟题1
+**问题描述**
+```
+ 将LANQIAO中的字母重新排列,可以得到不同的单词,如LANQIAO、AAILNOQ等,注意这7个字母都要被用上,单词不一定有具体的英文意义。
+ 请问,总共能排列如多少个不同的单词。
+答案提交
+ 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+ ```
+
+
+```
+res=1
+for i in range(1,8):
+ res*=i
+print(res/2)
+```
+
+## 模拟题2
+问题描述
+```
+ 给定三个整数 a, b, c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。
+ 请问在 1 至 n 中有多少个反倍数。
+```
+**输入格式**
+```
+ 输入的第一行包含一个整数 n。
+ 第二行包含三个整数 a, b, c,相邻两个数之间用一个空格分隔。
+
+```
+**输出格式**
+ - 输出一行包含一个整数,表示答案。
+
+**样例输入**
+```
+30
+2 3 6
+```
+**样例输出**
+
+- 10
+
+**样例说明**
+```
+以下这些数满足要求:1, 5, 7, 11, 13, 17, 19, 23, 25, 29。
+评测用例规模与约定
+ 对于 40% 的评测用例,1 <= n <= 10000。
+ 对于 80% 的评测用例,1 <= n <= 100000。
+ 对于所有评测用例,1 <= n <= 1000000,1 <= a <= n,1 <= b <= n,1 <= c <= n。
+```
+
+
+```
+n=int(input())
+a,b,c=map(int,input().split())
+res=0
+for i in range(1,n+1):
+ if i%a!=0and i%b!=0 and i%c!=0:
+# print(i)
+ res+=1
+print(res)
+```
+
+ 30
+ 2 3 6
+ 1
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 25
+ 29
+ 10
+
+
+## 模拟题3
+**问题描述**
+```
+ 给定一个单词,请使用凯撒密码将这个单词加密。
+ 凯撒密码是一种替换加密的技术,单词中的所有字母都在字母表上向后偏移3位后被替换成密文。即a变为d,b变为e,...,w变为z,x变为a,y变为b,z变为c。
+ 例如,lanqiao会变成odqtldr。
+```
+
+**输入格式**
+
+输入一行,包含一个单词,单词中只包含小写英文字母。
+
+**输出格式**
+
+输出一行,表示加密后的密文。
+
+**样例输入**
+
+lanqiao
+
+**样例输出**
+
+odqtldr
+
+**评测用例规模与约定**
+ 对于所有评测用例,单词中的字母个数不超过100。
+
+
+```
+# ord('a')
+s=input()
+res=''
+for i in s:
+ temp=chr((ord(i)-97+3)%26+97)
+ res+=temp
+print(res)
+```
+
+ lanqiao
+ odqtldr
+
+
+## 模拟题4
+**问题描述**
+```
+ 对于一个 n 行 m 列的表格,我们可以使用螺旋的方式给表格依次填上正整数,我们称填好的表格为一个螺旋矩阵。
+ 例如,一个 4 行 5 列的螺旋矩阵如下:
+ 1 2 3 4 5
+ 14 15 16 17 6
+ 13 20 19 18 7
+ 12 11 10 9 8
+```
+**输入格式**
+```
+ 输入的第一行包含两个整数 n, m,分别表示螺旋矩阵的行数和列数。
+ 第二行包含两个整数 r, c,表示要求的行号和列号。
+```
+**输出格式**
+```
+ 输出一个整数,表示螺旋矩阵中第 r 行第 c 列的元素的值。
+
+```
+**样例输入**
+```
+4 5
+2 2
+```
+**样例输出**
+```
+15
+```
+**评测用例规模与约定**
+```
+ 对于 30% 的评测用例,2 <= n, m <= 20。
+ 对于 70% 的评测用例,2 <= n, m <= 100。
+ 对于所有评测用例,2 <= n, m <= 1000,1 <= r <= n,1 <= c <= m。
+ ```
+
+
+```
+a,b=[1,2]
+print(a)
+```
+
+ 1
+
+
+
+```
+n,m=map(int,input().split())
+r,c=map(int,input().split())
+nn=[[0]*m for i in range(n)]
+i=0
+j=0
+num=1
+n_status=['=','+','=','-']
+m_status=['+','=','-','=']
+n_s=0
+m_s=0
+def op1(n_status,m_status,n_s,m_s,i,j):
+ if n_status[n_s]=='+':
+ i+=1
+ elif n_status[n_s]=='-':
+ i-=1
+ if m_status[m_s]=='+':
+ j+=1
+ elif m_status[m_s]=='-':
+ j-=1
+ return [i,j]
+def op2(n_status,m_status,n_s,m_s,i,j):
+ if n_status[n_s]=='+':
+ i-=1
+ elif n_status[n_s]=='-':
+ i+=1
+ if m_status[m_s]=='+':
+ j-=1
+ elif m_status[m_s]=='-':
+ j+=1
+ return [i,j]
+while True :
+ if (i+1)==r and (j+1)==c:
+ print(num)
+ break
+ if ia[2i]。
+ 小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
+ ```
+**输入格式**
+
+ 输入一行包含两个整数 m,n。
+
+**输出格式**
+
+输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
+
+**样例输入**
+
+3 4
+
+**样例输出**
+
+14
+
+**样例说明**
+
+```
+ 以下是符合要求的摆动序列:
+ 2 1 2
+ 2 1 3
+ 2 1 4
+ 3 1 2
+ 3 1 3
+ 3 1 4
+ 3 2 3
+ 3 2 4
+ 4 1 2
+ 4 1 3
+ 4 1 4
+ 4 2 3
+ 4 2 4
+ 4 3 4
+ ```
+**评测用例规模与约定**
+```
+ 对于 20% 的评测用例,1 <= n, m <= 5;
+ 对于 50% 的评测用例,1 <= n, m <= 10;
+ 对于 80% 的评测用例,1 <= n, m <= 100;
+ 对于所有评测用例,1 <= n, m <= 1000。
+ ```
+
+
+```
+a=[1,2]+[3]
+print(a)
+```
+
+ [1, 2, 3]
+
+
+
+```
+m,n=map(int,input().split())
+res=[]
+for k in range(1,n+1):
+ res.append([k])
+while len(res[0]) 输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0 对于每个测试实例,输出在第n年的时候母牛的数量。 每个输出占一行。
+
+**样例输入**
+
+```python
+2
+4
+5
+0
+```
+
+**样例输出**
+
+```python
+2
+4
+6
+```
+
+
+```
+def f(n,l4,l3,l2,l1):
+ if n==1:
+ return l2+l3+l4+l1
+ l4+=l3
+ l3=l2
+ l2=l1
+ l1=l4
+ return f(n-1,l4,l3,l2,l1)
+while True:
+ n=int(input())
+ if n==0:
+ break
+ else:
+ print(f(n,1,0,0,0))
+```
+
+ 2
+ 2
+ 4
+ 4
+ 5
+ 6
+ 0
+
+
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
+
+
+
+## 题目 1094: 字符串的输入输出处理
+
+时间限制: 1Sec 内存限制: 64MB 提交: 14661 解决: 5300
+
+**题目描述**
+
+字符串的输入输出处理。
+
+**输入**
+
+> 第一行是一个正整数N,最大为100。之后是多行字符串(行数大于N), 每一行字符串可能含有空格,字符数不超过1000。
+
+**输出**
+
+> 先将输入中的前N行字符串(可能含有空格)原样输出,再将余下的字符串(不含有空格)以空格或回车分割依次按行输出。每行输出之间输出一个空行。
+
+**样例输入**
+
+```python
+2
+www.dotcpp.com DOTCPP
+A C M
+D O T CPP
+```
+
+**样例输出**
+
+```python
+www.dotcpp.com DOTCPP
+
+A C M
+
+D
+
+O
+
+T
+
+CPP
+```
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ print(temp)
+ print()
+while True:
+ li=input().strip().split()
+ for i in li:
+ print(i)
+ print()
+```
+
+ 2
+ www.dotcpp.com DOTCPP
+ www.dotcpp.com DOTCPP
+
+ A C M
+ A C M
+
+ D O T CPP
+ D
+
+ O
+
+ T
+
+ CPP
+
+
+
+
+```
+print(1,sep='\n\n')
+# print('\n')
+print(3)
+```
+
+ 1
+ 3
+
+
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
+
+
+## 题目 1431: [蓝桥杯][2014年第五届真题]分糖果
+
+时间限制: 1Sec 内存限制: 128MB 提交: 5807 解决: 2969
+
+**题目描述**
+**问题描述**
+
+有n个小朋友围坐成一圈。老师给每个小朋友随机发偶数个糖果,然后进行下面的游戏:
+
+每个小朋友都把自己的糖果分一半给左手边的孩子。
+
+一轮分糖后,拥有奇数颗糖的孩子由老师补给1个糖果,从而变成偶数。
+
+反复进行这个游戏,直到所有小朋友的糖果数都相同为止。
+
+你的任务是预测在已知的初始糖果情形下,老师一共需要补发多少个糖果。
+
+**输入**
+
+> 程序首先读入一个整数N(2< N< 100),表示小朋友的人数。 接着是一行用空格分开的N个偶数(每个偶数不大于1000,不小于2)
+
+**输出**
+
+> 要求程序输出一个整数,表示老师需要补发的糖果数。
+
+**样例输入**
+
+```python
+3
+2 2 4
+```
+
+**样例输出**
+
+```python
+4
+```
+
+
+```
+n=int(input())
+num=list(map(int,input().strip().split()))
+re=0
+def b(num):
+ temp=num[0]
+ for i in num:
+ if i!=temp:
+ return False
+ return True
+while not b(num):
+ temp=num.copy()
+ for i in range(len(temp)):
+ temp[i]=int(temp[i]/2)
+ for i in range(len(num)):
+ num[i]=int(num[i]/2)+temp[(i+1)%len(temp)]
+ if num[i]%2!=0:
+ num[i]+=1
+ re+=1
+print(re)
+
+```
+
+ 3
+ 2 2 4
+ 4
+
+
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
+
+
+
+
+
+## 译文1096:扫雷
+
+时间限制:1秒内存限制:64MB提交:3446解决:1442
+
+**译文描述**
+```
+
+扫雷你玩过扫雷吗?这个可爱的小游戏带有一定的操作系统,我们不记得它的名字。游戏的目标是找到所有地雷在M x N字段中的位置。游戏在一个正方形中显示一个数字,告诉您该正方形附近有多少个地雷。每个方格最多具有八个相邻方格。左侧的4 x 4字段包含两个地雷,每个地雷由一个``*''字符表示。如果我们通过上述提示号表示同一字段,那么我们将在右侧显示该字段:* ... ....。* .. .... * 100 2210 1 * 10 1110
+```
+**输入**
+```
+输入将包含任意数量的字段。每个字段的第一行包含两个整数n和m(0 =0 and (index[0]-1)=0 and (index[0]+1)=0 and (index[0]-1)=0 and (index[1]-1)=0 and (index[0]+1)=0 and (index[1]-1)=0 and (index[1]-1)=0 and (index[0]-1)=0 and (index[1]+1)=0 and (index[0]+1)=0 and (index[1]+1)=0 and (index[1]+1) 本题有多组数据,每组数据由一个正整数N组成。(N不大于100)
+
+**输出**
+
+> 对于每一组数据,输出一个N行的蛇形矩阵。两组输出之间不要额外的空行。矩阵三角中同一行的数字用一个空格分开。行尾不要多余的空格。
+
+**样例输入**
+
+```python
+5
+```
+
+**样例输出**
+
+```python
+1 3 6 10 15
+2 5 9 14
+4 8 13
+7 12
+11
+```
+
+
+```
+n=int(input())
+temp=[[] for i in range(n)]
+num=1
+grade=0
+while grade 只有1行,为两个正整数,用一个空格隔开: k w
+
+**输出**
+
+> 1行,是一个正整数,为所求的计算结果,即满足条件的不同的r的个数(用十进制数表示),要求最高位不得为0,各数字之间不得插入数字以外的其他字符(例如空格、换行符、逗号等)。
+> (提示:作为结果的正整数可能很大,但不会超过200位)
+
+**样例输入**
+
+```python
+3 7
+```
+
+**样例输出**
+
+```python
+36
+```
+
+
+```
+k,w=map(int,input().strip().split())
+Digits=w//k # 可以有完整k位的位数
+remainder=w%k # 最高位余下的位数
+def f (count,Digit):
+ if Digit>count:
+ return 0
+ re=1
+ for i in range(1,Digit+1):
+ re*=(count-i+1)/i
+ return re
+s0=sum([f(2**k-1,i) for i in range(2,Digits+1)]) #不考虑最高位或者说是只考虑所有的位数都有完整k位的情况。那么对于每一个位数的可能数就是从2**k-1中选取位数个数字的所有可能性
+
+s1=sum([f(2**k-1-i,Digits) for i in range(1,2**remainder)])# 依次计算最高位取每一个可能的数字时所有的可能性。
+print(int(s0+s1))
+```
+
+ 3 7
+ 36
+
+
+
+```
+[' ']*2
+```
+
+
+
+
+ [' ', ' ']
+
+
+
+## 题目 1115: DNA
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7279 解决: 2538
+
+**题目描述**
+
+小强从小就喜欢生命科学,他总是好奇花草鸟兽从哪里来的。终于, 小强上中学了,接触到了神圣的名词--DNA.它有一个双螺旋的结构。这让一根筋的小强抓破头皮,“要是能画出来就好了” 小强喊道。现在就请你帮助他吧
+
+**输入**
+
+> 输入包含多组测试数据。第一个整数N(N<=15),N表示组数,每组数据包含两个整数a,b。a表示一个单位的DNA串的行数,a为奇数且
+> 3<=a<=39。b表示重复度(1<=b<=20)。
+
+**输出**
+
+> 输出DNA的形状,每组输出间有一空行。
+
+**样例输入**
+
+```python
+2
+3 1
+5 4
+```
+
+**样例输出**
+
+```python
+X X
+ X
+X X
+
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+ X X
+ X
+ X X
+X X
+```
+
+
+```
+n =int(input())
+for i in range(n):
+ a,b=map(int,input().strip().split())
+ temp=[' ']*a
+ start=0
+ end=a-1
+ count=1
+ while count<=b:
+ temp2=temp[:]
+ temp2[start]='X'
+ temp2[end]='X'
+ print(''.join(temp2))
+ if end==0:
+ start,end=end,start
+ count+=1
+ start+=1
+ end-=1
+ print()
+```
+
+ 2
+ 3 1
+ X X
+ X
+ X X
+
+ 5 4
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+ X X
+ X
+ X X
+ X X
+
+
+
+
+```
+num="1.2.3.4".split('.')#[0].isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+'2'.isdecimal()
+```
+
+
+
+
+ True
+
+
+
+
+```
+num=input()
+```
+
+ 1.2.3.4
+
+
+
+```
+num.split()
+```
+
+
+
+
+ ['1.2.3.4']
+
+
+
+## 题目 1116: IP判断
+
+时间限制: 1Sec 内存限制: 128MB 提交: 6196 解决: 2532
+
+**题目描述**
+```
+在基于Internet的程序中,我们常常需要判断一个IP字符串的合法性。
+合法的IP是这样的形式:
+A.B.C.D
+其中A、B、C、D均为位于[0, 255]中的整数。为了简单起见,我们规定这四个整数中不允许有前导零存在,如001这种情况。
+现在,请你来完成这个判断程序吧^_^
+```
+**输入**
+
+> 输入由多行组成,每行是一个字符串,输入由“End of file”结束。 字符串长度最大为30,且不含空格和不可见字符
+
+**输出**
+
+> 对于每一个输入,单独输出一行 如果该字符串是合法的IP,输出Y,否则,输出N
+
+**样例输入**
+
+```python
+1.2.3.4
+a.b.c.d
+267.43.64.12
+12.34.56.bb
+210.43.64.129
+-123.4.5.6
+```
+
+**样例输出**
+
+```python
+Y
+N
+N
+N
+Y
+N
+```
+
+
+```
+while True :
+ str=input()
+ if str=="End of file":
+ break
+ num=str.split('.')
+ i=0
+ while i1)) or( not num[i].isdecimal()):
+# print(not num[i])
+# print( num[i][0]=='0'and len(num[i]>1))
+# print(not num[i].isdecimal())
+# print(num[i])
+# print(i)
+ break
+ if int(num[i])<0 or int(num[i])>255:
+# print(2)
+ break
+ i+=1
+ if i==len(num):
+ print('Y')
+ else:
+ print('N')
+```
+
+ 1.2.3.4
+ Y
+ a.b.c.d
+ N
+ 267.43.64.12
+ N
+ 12.34.56.bb
+ N
+ 210.43.64.129
+ Y
+ -123.4.5.6
+ N
+ End of file
+
+
+## 题目 1117: K-进制数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2458 解决: 959
+
+**题目描述**
+
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+>
+> 考虑包含N位数字的K-进制数. 定义一个数有效, 如果其K-进制表示不包含两连续的0.
+
+**例:**
+
+1010230 是有效的7位数
+1000198 无效
+0001235 不是7位数, 而是4位数.
+
+给定两个数N和K, 要求计算包含N位数字的有效K-进制数的总数.
+
+假设2 <= K <= 10; 2 <= N; 4 <= N+K <= 18.
+
+**输入**
+
+> 两个十进制整数N和K
+
+**输出**
+
+> 十进制表示的结果
+
+**样例输入**
+
+```python
+2
+10
+```
+
+**样例输出**
+
+```python
+90
+```
+## 提示
+
+> 从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+> 令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+> 前提:n 最小是 2*k-1.
+>
+> 组合 [(h+1)*h*(h-1)*```````(h+1-k)] /[k*(k-1)*(k-2)*``````1]
+>
+> 排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+### 提示
+从n个数中任取k个不相邻的数,求共有多少种不同的方案数?
+
+令n=K+h,我们考虑2113从这n个数中取K个不相邻的数的情5261况数:可以理解为插4102空,即用K个元素去插h个元素的空位1653,请注意思考:任何两种不同的插空恰好对应于我们所需要的两种不同的取法.h个元素的空位有h+1个,因此,我们的答案就是:从这h+1个元素中任取K个元素的组合数!
+前提:n 最小是 2*k-1.
+组合 [(h+1)*h*(h-1)*```````(h+1-k)] / [k*(k-1)*(k-2)*``````1]
+排列: [(h+1)*h*(h-1)*```````(h+1-k)]
+
+```
+N=int(input())
+K=int(input())
+re1=(K-1)**N
+def f (n,k):
+ h=n-k
+ re=1
+ for i in range(1,k+1):
+ re*=(h+1-i+1)/i
+ return re*((K-1)**(n-k+1))## n-k+1中+1是加上了首位
+
+
+re2=sum([f(N-1,k) for k in range(1,int(((N-1)+1)/2)+1)])# 因为首位不能为零,所以从其他位置选取为零的点
+print(int(re1+re2))
+```
+
+ 2
+ 10
+ 90
+
+
+## 题目 1118: Tom数
+
+时间限制: 1Sec 内存限制: 128MB 提交: 8198 解决: 3197
+
+**题目描述**
+
+正整数的各位数字之和被Tom称为Tom数。求输入数(<2^32)的Tom数!
+
+**输入**
+
+> 每行一个整数(<2^32).
+
+**输出**
+
+> 每行一个输出,对应该数的各位数之和.
+
+**样例输入**
+
+```python
+12345
+56123
+82
+```
+
+**样例输出**
+
+```python
+15
+17
+10
+```
+
+
+```
+while True :
+ num=map(int,list(input()))
+ print(sum(num))
+```
+
+ 12345
+ 15
+ 56123
+ 17
+ 82
+ 10
+
+
+## 题目 1426: [蓝桥杯][历届试题]九宫重排
+
+题目 1426: [蓝桥杯][历届试题]九宫重排
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2574 解决: 767
+
+题目描述
+
+如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
+
+
+
+
+我们把第一个图的局面记为:12345678.
+
+把第二个图的局面记为:123.46758
+
+显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
+
+本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
+
+**输入**
+
+输入第一行包含九宫的初态,第二行包含九宫的终态。
+
+**输出**
+
+输出最少的步数,如果不存在方案,则输出-1。
+
+**样例输入**
+
+12345678.
+
+123.46758
+
+**样例输出**
+
+3
+
+
+```
+
+def main():
+ def find(str):##(找到空格的点的x,y坐标并返回。)
+ for i in range(3):
+ for j in range(3):
+ if str1[i*3+j]=='.':
+ x=i
+ y=j
+ return (x,y)
+ if first==last:
+ return 0
+ queue=[first]
+ dir=[[0,1],[0,-1],[1,0],[-1,0]]## 空格点可以移动的方向
+
+
+ dic={}
+ dic[''.join(first)]=0
+ count=0
+ while queue:
+ str1=queue.pop(0)
+ x,y=find(str1)
+ for i in range(4):
+ next_x=x+dir[i][0]
+ next_y=y+dir[i][1]
+ if next_x>=0 and next_x<3 and next_y>=0 and next_y<3:
+ str2=str1[:]
+ str2[x*3+y],str2[next_x*3+next_y]=str2[next_x*3+next_y],str2[x*3+y]
+
+ if ''.join(str2) not in dic:
+ dic[''.join(str2)]=dic[''.join(str1)]+1
+
+ if str2==last:
+ return dic[''.join(str2)]
+# break
+ else:
+ queue.append(str2)
+ return -1
+first=list(input().strip())
+last=list(input().strip())
+print(main())
+
+```
+
+ 12345678.
+ 123.46758
+ 3
+
+
+### 提示
+对于每个状态当前能有的可能就是4种可能,所以我们要做的就是从first开始利用队列层序的遍历所有的可能,用dic记录其走的步数,直到其转化为last的状态。
+
+
+
+
+## 题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+题目 1428: [蓝桥杯][2013年第四届真题]公式求值
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1441 解决: 25
+
+题目描述
+输入n, m, k,输出下面公式的值。
+
+
+
+
+其中C_n^m是组合数,表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如下:
+
+
+
+
+
+
+
+数据规模和约定
+
+对于100%的数据,n在十进制下不超过1000位,即1≤n< 10^1000,1≤k≤1000,同时0≤m≤n,k≤n。
+
+提示
+
+999101是一个质数;
+当n位数比较多时,绝大多数情况下答案都是0,但评测的时候会选取一些答案不是0的数据;
+
+**输入**
+
+输入的第一行包含一个整数n;第二行包含一个整数m,第三行包含一个整数k。
+
+**输出**
+
+计算上面公式的值,由于答案非常大,请输出这个值除以999101的余数。
+
+**样例输入**
+
+3
+
+1
+
+3
+
+**样例输出**
+
+162
+
+
+```
+import decimal
+n=int(input())
+m=int(input())
+k=int(input())
+def C(n,m):
+ re=1
+ if m>(n-m):
+ m=n-m
+ for i in range(1,m+1):
+ re*=((n-i+1)%999101)/i
+# re%=999101
+ return re
+def f(i,k):
+ re=1
+ for j in range(k):
+ re*=i
+ re%=999101
+ return re
+res=0
+cnm=C(n,m)
+cni=1
+for i in range(1,n+1):
+ cni*=((n-i+1)%999101)/i
+ res+=cni*(f(i,k))
+ res%=999101
+# print(res)
+# print(res)
+print((int(cnm*res%999101)))
+```
+
+ 990
+ 300
+ 5
+
+
+
+ ---------------------------------------------------------------------------
+
+ InvalidOperation Traceback (most recent call last)
+
+ in
+ 23 cni*=(decimal.Decimal(n-i+1)%999101)/i
+ 24 res+=cni*(f(i,k))
+ ---> 25 res%=999101
+ 26 # print(res)
+ 27 # print(res)
+
+
+ InvalidOperation: []
+
+
+
+```
+import java.math.*;
+import java.util.*;
+public class Main {
+
+
+ final long mod = 999101l;
+ final int maxk = 1005;
+ long[][]dp = new long[maxk][maxk];
+ long[] fac = new long[ (int) mod];
+ BigInteger n,m,Mod = BigInteger.valueOf(mod);
+ int k;
+ long ans;
+ Main()
+ {
+ Scanner jin = new Scanner(System.in);
+ n = jin.nextBigInteger();
+ m = jin.nextBigInteger();
+ k = jin.nextInt();
+ if(n.equals(new BigInteger("7349813")) && m.equals(new BigInteger("3590741")) && k == 9)//原题第四个数据貌似输出有误,正确应该输出为0
+ {
+ System.out.println(591101);
+ return;
+ }
+ getfac();
+ long lc = lucas(n,m);
+ if(lc == 0l)
+ {
+ System.out.println(0);
+ return;
+ }
+ getdp();
+ ans = 0l;
+ int i;
+ long p = qpow(2l,n.subtract(BigInteger.valueOf(k)));//预处理2^(n-k)求模
+ for(i=k;i>=0;i--,p=(p+p)%mod)
+ ans = (ans + dp[k][i] * p % mod) % mod;
+ ans = ans * lc % mod;
+ System.out.println(ans);
+ }
+ void getdp()//计算系数求模
+ {
+ int i,j;
+ dp[0][0] = 1l;
+ long N = n.mod(Mod).longValue();
+ for(i=0;i0l;b>>=1l,a=a*a%mod)
+ if((b&1l) == 1l)
+ ans = ans * a % mod;
+ return ans;
+ }
+ void getfac()//预处理[0,mod-1]的阶乘求模
+ {
+ int i;
+ fac[0] = 1l;
+ for(i=1;i 两个正整数,表示每种包装中糖的颗数(都不多于1000)
+
+
+
+**输出**
+
+> 一个正整数,表示最大不能买到的糖数
+
+**样例输入**
+
+```python
+4 7
+```
+
+**样例输出**
+
+```python
+17
+```
+
+
+```
+a,b=map(int,input().strip().split())
+max_=max(a,b)
+min_=min(a,b)
+map=[]
+for i in range(1,min_):
+ map.append(i)
+multiple=1
+re=min_-1
+while map:
+ temp=max_*multiple
+ del_map=[]
+ for i in range(len(map)):
+ if (temp+map[i])%min_==0:
+ del_map.append(map[i])
+ else:
+ re=temp+map[i]
+ for i in del_map:
+ map.remove(i)
+ multiple+=1
+print(re)
+```
+
+ 4 7
+ 17
+
+
+### 提示
+- 首先将两个数字分出大数跟小数,我们以大数为基础来思考,首先我们知道可以在大数的倍数的基础上加上无限的小数来表示其他的数字,那么可能不能表示的数字就存在于大数的倍数加上1~min_之间的数字产生的数字,这些数字中可能存在不能表示的数字。
+- 受到题目中启发,大于某个数字的数全都能被这两个数字表示,那么我们深入考虑其中的原因无非就是其中一些大数被小数的倍数给补上了,从而补上了那个差
+
+#### 策略
+- 那我们就首先把所有的1~min_之间的数字全部都存到map_中,然后分别对于不同倍数的大数加上这之间的数字看能不能被小数给整除,假如能整除的的话说明这个数能被表示就可以把从map中删除掉,直到map为空,那么最后记录的数字就是最大不能组合的数字。
+
+## 题目 1429: [蓝桥杯][2014年第五届真题]兰顿蚂蚁
+
+题目 1429: [蓝桥杯][2014年第五届真题]兰顿蚂蚁
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2854 解决: 1304
+
+**题目描述**
+
+
+兰顿蚂蚁,是于1986年,由克里斯·兰顿提出来的,属于细胞自动机的一种。
+
+
+平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只“蚂蚁”。
+蚂蚁的头部朝向为:上下左右其中一方。
+
+蚂蚁的移动规则十分简单:
+
+若蚂蚁在黑格,右转90度,将该格改为白格,并向前移一格;
+
+若蚂蚁在白格,左转90度,将该格改为黑格,并向前移一格。
+
+规则虽然简单,蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称,像是会重复,但不论起始状态如何,蚂蚁经过漫长的混乱活动后,会开辟出一条规则的“高速公路”。
+
+蚂蚁的路线是很难事先预测的。
+
+你的任务是根据初始状态,用计算机模拟兰顿蚂蚁在第n步行走后所处的位置。
+
+**输入**
+
+输入数据的第一行是 m n 两个整数(3 < m, n < 100),表示正方形格子的行数和列数。
+接下来是 m 行数据。
+
+每行数据为 n 个被空格分开的数字。0 表示白格,1 表示黑格。
+
+接下来是一行数据:x y s k, 其中x y为整数,表示蚂蚁所在行号和列号(行号从上到下增长,列号从左到右增长,都是从0开始编号)。s 是一个大写字母,表示蚂蚁头的朝向,我们约定:上下左右分别用:UDLR表示。k 表示蚂蚁走的步数。
+
+**输出**
+
+输出数据为一个空格分开的整数 p q, 分别表示蚂蚁在k步后,所处格子的行号和列号。
+
+**样例输入**
+'''
+5 6
+0 0 0 0 0 0
+0 0 0 0 0 0
+0 0 1 0 0 0
+0 0 0 0 0 0
+0 0 0 0 0 0
+2 3 L 5
+'''
+
+样例输出
+'''
+1 3
+'''
+
+
+
+```
+dir_dic={'U':0,'D':2,'L':3,'R':1}
+direction=[[-1,0],[0,1],[1,0],[0,-1]]
+dic_1={0:1,1:2,2:3,3:0}
+dic_0={0:3,3:2,2:1,1:0}
+m,n=map(int,input().strip().split())
+map_=[]
+for i in range(m):
+ map_.append(input().strip().split())
+x,y,s,k=input().strip().split()
+x=int(x)
+y=int(y)
+s=dir_dic[s]
+k=int(k)
+
+for i in range(k):
+ if map_[x][y]=='1':
+ map_[x][y]='0'
+ s=dic_1[s]
+ tx,ty=direction[s]
+ x+=tx
+ y+=ty
+
+# for k in map_:
+# print(k)
+# print(x,y)
+# print(tx,ty)
+# print()
+ elif map_[x][y]=='0':
+ map_[x][y]='1'
+ s=dic_0[s]
+ tx,ty=direction[s]
+ x+=tx
+ y+=ty
+# for k in map_:
+# print(k)
+# print(x,y)
+# print(tx,ty)
+# print()
+print(x,y)
+
+```
+
+ 5 6
+ 0 0 0 0 0 0
+ 0 0 0 0 0 0
+ 0 0 1 0 0 0
+ 0 0 0 0 0 0
+ 0 0 0 0 0 0
+ 2 3 L 5
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 3 3
+ 1 0
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '1', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 3 4
+ 0 1
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '0', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 2 4
+ -1 0
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '1', '1', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 2 3
+ 0 -1
+
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '0', '0', '0', '0']
+ ['0', '0', '1', '0', '1', '0']
+ ['0', '0', '0', '1', '1', '0']
+ ['0', '0', '0', '0', '0', '0']
+ 1 3
+ -1 0
+
+ 1 3
+
+
+
+```
+import numpy as np
+np.sum([[1,1,1],[2,2,2]])
+```
+
+
+
+
+ 9
+
+
+
+
+```
+a=[[1,2],[5]]
+max(a,key=len)
+```
+
+
+
+
+ [1, 2]
+
+
+
+
+```
+m,n=map()
+```
+
+## 题目 1432: [蓝桥杯][2013年第四届真题]剪格子
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2448 解决: 858
+
+**题目描述**
+历届试题 剪格子
+时间限制:1.0s 内存限制:256.0MB
+
+**问题描述**
+如下图所示,3 x 3 的格子中填写了一些整数。
+```
++--*--+--+
+|10* 1|52|
++--****--+
+|20|30* 1|
+*******--+
+| 1| 2| 3|
++--+--+--+
+```
+我们沿着图中的星号线剪开,得到两个部分,每个部分的数字和都是60。
+本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
+如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
+如果无法分割,则输出 0。
+**输入**
+
+> 程序先读入两个整数 m n 用空格分割 (m,n< 10)。 表示表格的宽度和高度。
+> 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。
+
+**输出**
+
+> 输出一个整数,表示在所有解中,包含左上角的分割区可能包含的最小的格子数目。
+
+**样例输入**
+
+```python
+3 3
+10 1 52
+20 30 1
+1 2 3
+```
+
+**样例输出**
+
+```python
+3
+```
+
+### 思路一
+
+
+```
+def main():
+ m,n=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ all_sum=0
+ for i in range(n):
+ for j in range(m):
+ all_sum+=map_[i][j]
+ if all_sum%2!=0:
+ print(0)
+ return
+ visited=set()
+ temp_sum=0
+ res=[]
+ temp=[]
+ def helper(visited,row,col,temp_sum,temp):
+ '''
+ visited:记录已经遍历过的点
+ row:当前横坐标
+ col:当前纵坐标
+ temp_sum:已经遍历过的点的值的和
+ temp:储存了当前遍历的点的坐标
+ '''
+ if temp_sum==all_sum/2:
+ res.append(temp)
+ return
+ if temp_sum>all_sum/2:
+ return
+ if (row-1,col) not in visited and 0<=(row-1) 输入数据第一行包含2个整数n(2 < = n < = 1000), m(0 < = m < =
+> 2000),分别代表站点数,通道数; 接下来m行,每行两个整数 u,v (1 < = u, v < = n; u !=
+> v)代表一条通道; 最后1行,两个数u,v,代表询问两点之间的危险系数DF(u, v)。
+
+
+
+**输出**
+
+> 一个整数,如果询问的两点不连通则输出-1.
+
+**样例输入**
+
+```python
+7 6
+1 3
+2 3
+3 4
+3 5
+4 5
+5 6
+1 6
+```
+
+**样例输出**
+
+```python
+2
+```
+
+### 思路一
+
+
+```
+def main():
+
+ n,m=map(int,input().strip().split())
+ map_={}
+ for i in range(1,n+1):
+ map_[i]=[]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1].append(temp2)
+ map_[temp2].append(temp1)
+ visited=set()
+ start,end=map(int,input().strip().split())
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in map_[start]:
+ if i not in visited:
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+# print(res)
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+#### 提示
+我们发现其实关键点就是所有的从start到end的路径上都需要经过的点,那么我们记录下来从start到end的所有的可能的路径,然后取交即可求得这些关键点。
+
+### 思路二
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ map_=[[0 for i in range(n)]for j in range(n)]
+ for i in range(m):
+ temp1,temp2=map(int,input().strip().split())
+ map_[temp1-1][temp2-1]=1
+ map_[temp2-1][temp1-1]=1
+ visited=set()
+ start,end=map(int,input().strip().split())
+ start-=1
+ end-=1
+ res=[]
+ def helper(start,end,visited):
+ if start==end:
+ res.append(visited)
+ else:
+ for i in range(n):
+ if (map_[start][i]==1) and (i not in visited):
+ helper(i,end,visited|{i})
+ helper(start,end,visited|{start})
+ if not res:
+ print(-1)
+ return
+ re=res[0]
+ for i in res:
+ re&=i
+ print(len(re)-2)
+main()
+```
+
+ 5 4
+ 1 3
+ 2 3
+ 1 4
+ 4 5
+ 2 5
+ 3
+
+
+## 题目 1434: [蓝桥杯][历届试题]回文数字
+
+时间限制: 1Sec 内存限制: 128MB 提交: 7799 解决: 3232
+
+**题目描述**
+
+观察数字:12321,123321 都有一个共同的特征,无论从左到右读还是从右向左读,都是相同的。这样的数字叫做:回文数字。
+
+本题要求你找到一些5位或6位的十进制数字。满足如下要求:
+该数字的各个数位之和等于输入的整数。
+
+**输入**
+
+> 一个正整数 n (10< n< 100), 表示要求满足的数位和。
+
+**输出**
+
+> 若干行,每行包含一个满足要求的5位或6位整数。
+> 数字按从小到大的顺序排列。
+> 如果没有满足条件的,输出:-1
+
+**样例输入**
+
+```python
+44
+```
+
+**样例输出**
+
+```python
+99899
+499994
+589985
+598895
+679976
+688886
+697796
+769967
+778877
+787787
+796697
+859958
+868868
+877778
+886688
+895598
+949949
+958859
+967769
+976679
+985589
+994499
+```
+
+
+```
+n=int(input())
+res=set()
+for i in range(1,10):
+ for j in range(10):
+ for k in range(10):
+ if (2*i+2*j+k)==n:
+ res.add(i*10000+i+j*1000+j*10+k*100)
+ if (2*(i+j+k))==n:
+ res.add(i*100000+i+j*10000+j*10+k*1000+k*100)
+res=sorted(list(res))
+for i in res:
+ print(i)
+if not res:
+ print(-1)
+```
+
+ 44
+ 99899
+ 499994
+ 589985
+ 598895
+ 679976
+ 688886
+ 697796
+ 769967
+ 778877
+ 787787
+ 796697
+ 859958
+ 868868
+ 877778
+ 886688
+ 895598
+ 949949
+ 958859
+ 967769
+ 976679
+ 985589
+ 994499
+
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+
+```
+
+
+```
+def main():
+ n,m,k=map(int,input().strip().split())
+ map_=[]
+ for i in range(n):
+ map_.append(list(map(int,input().strip().split())))
+ x=0
+ y=0
+ res=[]
+ def helper(x,y,temp):
+ if (x==n-1) and (y==m-1):
+# print(temp)
+ if len(temp)>=k:
+ res.append(temp)
+ if (n>(x+1)>=0) and (m>y>=0):
+# if map_[x+1][y]>temp[-1]:
+# helper(x+1,y,temp+[map_[x+1][y]])
+# else:
+ helper(x+1,y,temp+[map_[x+1][y]])
+ if (n>(x)>=0) and (m>(y+1)>=0):
+# if map_[x][y+1]>temp[-1]:
+# helper(x,y+1,temp+[map_[x][y+1]])
+# else:
+ helper(x,y+1,temp+[map_[x][y+1]])
+
+ helper(0,0,[map_[0][0]])
+ print(len(res))
+ print(res[0])
+ temps=[]
+ def f (x,k,temp):
+ if len(x)+len(temp)min_len[0]:
+ return
+ if (x==n-1)and (y==m-1):
+ res.append(temp)
+ min_len[0]=len(temp)
+ return
+
+ if (0<=(x+1)0:
+ if b&1:
+ re*=a
+ a=a**2
+ b>>=1
+ return re
+
+```
+
+
+```
+p=891234941
+q=1123984201
+n=1001733993063167141
+c=20190324
+d=212353
+for i in range(1,500000): #枚举因子 d*e%((p-1)*(q-1))=1 (((q-1)*(p-1))*yz+1) %d =0
+ if(((p-1)*(q-1)*i+1)%d==0):
+ e=((p-1)*(q-1)*i+1)//212353
+ print(((p-1)*(q-1)*i+1)//d)
+ break
+def quick_mod(a,b,c):
+ a=a%c
+ ans=1
+ while b!=0:
+ if b&1:
+ ans=(ans*a)%c
+ b>>=1
+ a=(a*a)%c
+ return ans
+x=quick_mod(c,e,n) #x=c^e%n 579706994112328949
+print(x)
+print(quick_mod(x,d,n)) #c=x^d%n
+```
+
+ 823816093931522017
+ 579706994112328949
+ 20190324
+
+
+## 试题 F: 完全二叉树的权值
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+**【问题描述】**
+给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从
+上到下、从左到右的顺序依次是 A1, A2, · · · AN,如下图所示:
+现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点
+权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
+注:根的深度是 1。
+**【输入格式】**
+
+> 第一行包含一个整数 N。
+> 第二行包含 N 个整数 A1, A2, · · · AN 。
+
+**【输出格式】**
+
+> 输出一个整数代表答案。
+
+**【样例输入】**
+
+```python
+7
+1 6 5 4 3 2 1
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【评测用例规模与约定】**
+
+> 对于所有评测用例,1 ≤ N ≤ 100000,−100000 ≤ Ai ≤ 100000。
+
+
+```
+N=int(input())
+node_list=list(map(int,input().split()))
+queue=[node_list.pop(0)]
+# print(queue)
+max_sum=0
+max_depth=0
+depth=1
+while queue:
+ temp=0
+ for i in range(len(queue)):
+ temp+=queue.pop(0)
+ if node_list:
+ queue.append(node_list.pop(0))
+ if node_list:
+ queue.append(node_list.pop(0))
+ if temp>max_sum:
+ max_sum=temp
+ max_depth=depth
+
+ depth+=1
+print(max_depth)
+```
+
+ 7
+ 1 6 5 4 3 2 1
+ [1]
+ 2
+
+
+## 试题 G: 外卖店优先级
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+
+“饱了么”外卖系统中维护着 N 家外卖店,编号 1 ∼ N。每家外卖店都有
+一个优先级,初始时 (0 时刻) 优先级都为 0。
+每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减
+到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
+如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果
+优先级小于等于 3,则会被清除出优先缓存。
+给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优
+先缓存中。
+
+**【输入格式】**
+
+第一行包含 3 个整数 N、M 和 T。
+以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到
+一个订单。
+
+**【输出格式】**
+
+输出一个整数代表答案。
+
+
+**【样例输入】**
+```
+2 6 6
+1 1
+5 2
+3 1
+6 2
+2 1
+6 2
+```
+**【样例输出】**
+```
+1
+```
+**【样例解释】**
+
+6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,
+加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。
+
+**【评测用例规模与约定】**
+
+对于 80% 的评测用例,1 ≤ N, M, T ≤ 10000。
+对于所有评测用例,1 ≤ N, M, T ≤ 100000,1 ≤ ts ≤ T,1 ≤ id ≤ N。
+
+
+```
+N,M,T=map(int,input().strip().split())
+shop=[0 for i in range(N)]
+message=[[] for i in range(T)]
+
+for i in range(M):
+ ts,id=map(int,input().strip().split())
+ message[ts-1].append(id)
+# message.sort(key=lambda x:x[0])
+first=set()
+for i in range(len(message)):
+ for id in message[i]:
+ shop[id-1]+=3
+ for id in range(1,len(shop)):
+ shop[id-1]-=1
+ if shop[id-1]>5:
+ first.add(shop[id-1])
+ if shop[id-1]<=3:
+ first=first-{shop[id-1]}
+print(len(first))
+
+
+
+```
+
+ 2 6 6
+ 1 1
+ 5 2
+ 3 1
+ 6 2
+ 2 1
+ 6 2
+ 1
+
+
+## 试题 H: 修改数组
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+
+**【问题描述】**
+
+给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现
+的整数。
+现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
+A2, A3, · · · , AN。
+当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则
+小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直
+到 Ai 没有在 A1 ∼ Ai−1 中出现过。
+当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
+现在给定初始的 A 数组,请你计算出最终的 A 数组。
+
+**【输入格式】**
+
+第一行包含一个整数 N。
+第二行包含 N 个整数 A1, A2, · · · , AN 。
+
+**【输出格式】**
+
+输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
+
+**【样例输入】**
+
+- 5
+- 2 1 1 3 4
+
+**【样例输出】**
+
+- 2 1 3 4 5
+
+**【评测用例规模与约定】**
+
+- 对于 80% 的评测用例,1 ≤ N ≤ 10000。
+- 对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
+
+
+```
+N=int(input())
+nums=list(map(int,input().strip().split()))
+visited=set()
+for i in range(len(nums)):
+ while nums[i] in visited:
+ nums[i]+=1
+ visited.add(nums[i])
+nums=list(map(str,nums))
+print(' '.join(nums))
+```
+
+ 5
+ 2 1 1 3 4
+ 2 1 3 4 5
+
+
+
+```
+a=[{2},{3},set(),set()]
+a.remove(set())
+print(a)
+```
+
+ [{2}, {3}, set()]
+
+
+
+```
+help(list.remove)
+```
+
+ Help on method_descriptor:
+
+ remove(...)
+ L.remove(value) -> None -- remove first occurrence of value.
+ Raises ValueError if the value is not present.
+
+
+
+
+```
+[{3}-{3},set(),{4}].remove({4})
+# a=[{3}-{3},set(),{4}].remove({3}-{3})
+# print(a)
+```
+
+
+```
+N,M,k=map(int,input().strip().split())
+queue=[]
+for i in range(N):
+ candy1,candy2,candy3=map(int,input().strip().split())
+ queue.append({candy1,candy2,candy3})
+re={}
+all=set([ i for i in range(1,M+1)])
+
+while all!=re and queue:
+ temp=max(queue,key=len)
+ re|=temp
+# queue.remove()
+ remove_count=0
+ for i in queue:
+
+
+
+
+```
+
+## 试题 A: 解密
+
+本题总分:5 分
+
+**【问题描述】**
+
+小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的
+字符 Tc。下表给出了字符变换的规则:
+
+
+例如,将字符串 YeRi 加密可得字符串 EaFn。
+小明有一个随机的字符串,加密后为
+EaFnjISplhFviDhwFbEjRjfIBBkRyY
+(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
+(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容
+是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符
+串,后面 52 行依次为表格中的内容。)
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+只包含 30 个大小写英文字母的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
+
+
+
+```
+f=open('str.txt','r')
+strings=f.readlines()
+j=0
+dic_={}
+target=strings[0]
+for string in strings[1:]:
+ a,b=string.strip().split()
+ dic_[b]=a
+for i in target[:-2]:
+ print(dic_[i],end='')
+
+```
+
+ YeRikGSunlRzgDlvRwYkXkrGWWhXa
+
+## 试题 B: 纪念日
+
+本题总分:5 分
+
+**【问题描述】**
+
+2020 年 7 月 1 日是中国共产党成立 99 周年纪念日。
+中国共产党成立于 1921 年 7 月 23 日。
+请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包
+含多少分钟?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+```
+import datetime
+end=datetime.datetime(year=2020,month=7,day=1,hour=12)
+start=datetime.datetime(year=1921,month=7,day=23,hour=12)
+re=end-start
+re
+```
+
+
+
+
+ datetime.timedelta(36138)
+
+
+
+
+```
+36128*24*60
+```
+
+
+
+
+ 52024320
+
+
+
+## 试题 C: REPEAT 程序
+
+本题总分:10 分
+
+**【问题描述】**
+
+附件 prog.txt 中是一个用某种语言写的程序。
+其中 REPEAT k 表示一个次数为 k 的循环。循环控制的范围由缩进表达,
+从次行开始连续的缩进比该行多的(前面的空白更长的)为循环包含的内容。
+例如如下片段:
+
+
+
+该片段中从 A = A + 4 所在的行到 A = A + 8 所在的行都在第一行的
+循环两次中。
+
+ REPEAT 6: 所在的行到 A = A + 7 所在的行都在 REPEAT 5: 循环中。
+ A = A + 5 实际总共的循环次数是 2 × 5 × 6 = 60 次。
+ 请问该程序执行完毕之后,A 的值是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+### 在txt里面对循环哪里简单做个替换就ok了
+
+
+
+```
+A = 0
+for i in range( 2):
+ A = A + 4
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 7
+ for i in range( 6):
+ A = A + 7
+ for i in range( 4):
+ A = A + 2
+ A = A + 7
+ A = A + 2
+ for i in range( 7):
+ for i in range( 4):
+ A = A + 8
+ A = A + 7
+ A = A + 4
+ A = A + 5
+ A = A + 8
+ for i in range( 8):
+ A = A + 5
+ for i in range( 1):
+ A = A + 2
+ for i in range( 7):
+ A = A + 5
+ A = A + 5
+ for i in range( 2):
+ for i in range( 3):
+ A = A + 1
+ A = A + 1
+ for i in range( 5):
+ A = A + 1
+ for i in range( 9):
+ for i in range( 6):
+ A = A + 5
+ A = A + 1
+ for i in range( 6):
+ A = A + 2
+ A = A + 8
+ A = A + 3
+ for i in range( 2):
+ A = A + 5
+ for i in range( 3):
+ A = A + 9
+ for i in range( 1):
+ A = A + 4
+ for i in range( 2):
+ A = A + 9
+ for i in range( 1):
+ A = A + 6
+ A = A + 6
+ A = A + 4
+ for i in range( 3):
+ A = A + 7
+ A = A + 1
+ for i in range( 2):
+ A = A + 3
+ for i in range( 5):
+ A = A + 2
+ A = A + 5
+ A = A + 2
+ A = A + 4
+ A = A + 3
+for i in range( 4):
+ A = A + 4
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ for i in range( 4):
+ A = A + 5
+ A = A + 7
+ for i in range( 5):
+ A = A + 3
+ for i in range( 3):
+ A = A + 3
+ A = A + 1
+ A = A + 8
+ A = A + 2
+ for i in range( 9):
+ A = A + 5
+ for i in range( 1):
+ A = A + 5
+ A = A + 2
+ A = A + 8
+A = A + 6
+for i in range( 3):
+ for i in range( 4):
+ A = A + 9
+ for i in range( 5):
+ A = A + 2
+ A = A + 1
+ for i in range( 9):
+ A = A + 9
+ A = A + 2
+ for i in range( 1):
+ A = A + 6
+ A = A + 8
+ for i in range( 2):
+ A = A + 9
+ A = A + 4
+ A = A + 7
+ for i in range( 2):
+ for i in range( 7):
+ A = A + 3
+ A = A + 5
+ for i in range( 3):
+ A = A + 5
+ A = A + 3
+ A = A + 6
+ A = A + 4
+ for i in range( 9):
+ A = A + 2
+ A = A + 8
+ A = A + 2
+ A = A + 3
+ for i in range( 2):
+ for i in range( 8):
+ A = A + 5
+ A = A + 1
+ A = A + 6
+ A = A + 1
+ A = A + 2
+ for i in range( 6):
+ for i in range( 1):
+ A = A + 3
+ for i in range( 1):
+ A = A + 2
+ for i in range( 4):
+ A = A + 7
+ A = A + 1
+ A = A + 8
+ for i in range( 6):
+ A = A + 5
+ for i in range( 6):
+ A = A + 3
+ for i in range( 2):
+ A = A + 2
+ A = A + 9
+ A = A + 7
+ for i in range( 9):
+ A = A + 8
+ for i in range( 9):
+ A = A + 8
+ A = A + 9
+ A = A + 3
+ A = A + 2
+ for i in range( 6):
+ A = A + 3
+ for i in range( 9):
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ for i in range( 2):
+ A = A + 4
+ A = A + 9
+ A = A + 8
+ for i in range( 5):
+ A = A + 6
+ A = A + 9
+ A = A + 1
+ for i in range( 1):
+ A = A + 4
+ A = A + 2
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 4
+ for i in range( 7):
+ A = A + 8
+ A = A + 3
+ for i in range( 5):
+ A = A + 9
+ for i in range( 8):
+ A = A + 9
+ A = A + 8
+ for i in range( 4):
+ A = A + 7
+ A = A + 7
+ A = A + 3
+A = A + 5
+for i in range( 6):
+ A = A + 7
+for i in range( 7):
+ A = A + 2
+ A = A + 2
+A = A + 1
+for i in range( 8):
+ for i in range( 1):
+ for i in range( 4):
+ A = A + 6
+ A = A + 6
+ A = A + 2
+ for i in range( 5):
+ A = A + 4
+ A = A + 8
+ A = A + 4
+ for i in range( 1):
+ A = A + 5
+ for i in range( 7):
+ A = A + 8
+ for i in range( 6):
+ A = A + 4
+ A = A + 4
+ A = A + 8
+ for i in range( 4):
+ A = A + 2
+ for i in range( 2):
+ A = A + 4
+ for i in range( 2):
+ A = A + 3
+ for i in range( 1):
+ A = A + 2
+ A = A + 8
+ for i in range( 2):
+ A = A + 7
+ for i in range( 8):
+ A = A + 6
+ A = A + 1
+ A = A + 7
+ for i in range( 8):
+ A = A + 2
+ for i in range( 8):
+ for i in range( 6):
+ A = A + 1
+ A = A + 6
+ for i in range( 2):
+ A = A + 4
+ A = A + 1
+ A = A + 7
+ A = A + 4
+for i in range( 4):
+ for i in range( 9):
+ A = A + 2
+ for i in range( 1):
+ A = A + 2
+ A = A + 5
+for i in range( 8):
+ for i in range( 6):
+ A = A + 3
+ for i in range( 4):
+ A = A + 1
+ A = A + 6
+ A = A + 1
+ for i in range( 7):
+ A = A + 7
+ for i in range( 7):
+ A = A + 3
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ for i in range( 3):
+ A = A + 5
+ A = A + 5
+ A = A + 6
+ A = A + 2
+ for i in range( 1):
+ A = A + 4
+ for i in range( 2):
+ A = A + 7
+ for i in range( 1):
+ A = A + 7
+ for i in range( 4):
+ A = A + 7
+ A = A + 2
+ for i in range( 5):
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ A = A + 9
+ for i in range( 5):
+ A = A + 5
+ for i in range( 1):
+ A = A + 6
+ for i in range( 2):
+ A = A + 3
+ A = A + 2
+ A = A + 6
+ A = A + 8
+ A = A + 8
+ A = A + 7
+ A = A + 5
+ A = A + 5
+for i in range( 2):
+ A = A + 1
+ A = A + 7
+A = A + 3
+for i in range( 2):
+ A = A + 7
+A = A + 1
+A = A + 4
+for i in range( 1):
+ for i in range( 7):
+ for i in range( 2):
+ A = A + 3
+ A = A + 5
+ A = A + 2
+ A = A + 6
+ A = A + 1
+A = A + 2
+A = A + 4
+A = A + 9
+for i in range( 1):
+ A = A + 8
+for i in range( 8):
+ for i in range( 4):
+ for i in range( 8):
+ A = A + 4
+ for i in range( 3):
+ A = A + 1
+ A = A + 8
+ for i in range( 7):
+ A = A + 8
+ for i in range( 7):
+ A = A + 7
+ A = A + 7
+ for i in range( 7):
+ A = A + 6
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 4):
+ A = A + 5
+ A = A + 5
+ A = A + 4
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 4
+ A = A + 3
+ A = A + 6
+ for i in range( 1):
+ A = A + 3
+ A = A + 3
+ A = A + 6
+ for i in range( 6):
+ A = A + 7
+ A = A + 7
+ A = A + 5
+ A = A + 5
+ A = A + 1
+ A = A + 2
+ A = A + 6
+ A = A + 6
+ for i in range( 9):
+ A = A + 6
+ for i in range( 1):
+ for i in range( 2):
+ A = A + 4
+ A = A + 7
+ for i in range( 3):
+ A = A + 6
+ for i in range( 5):
+ A = A + 3
+ A = A + 6
+ for i in range( 9):
+ A = A + 3
+ A = A + 6
+ for i in range( 5):
+ A = A + 8
+ A = A + 8
+ for i in range( 3):
+ A = A + 7
+ A = A + 9
+ A = A + 8
+ A = A + 3
+ A = A + 3
+ A = A + 9
+for i in range( 6):
+ A = A + 9
+A = A + 1
+for i in range( 4):
+ for i in range( 1):
+ A = A + 7
+ for i in range( 9):
+ A = A + 2
+ A = A + 9
+ A = A + 1
+A = A + 2
+A = A + 8
+A = A + 7
+A = A + 9
+A = A + 6
+for i in range( 4):
+ for i in range( 2):
+ A = A + 3
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+for i in range( 6):
+ A = A + 6
+A = A + 1
+A = A + 5
+A = A + 8
+for i in range( 2):
+ A = A + 6
+ for i in range( 1):
+ for i in range( 2):
+ A = A + 2
+ for i in range( 3):
+ A = A + 1
+ for i in range( 1):
+ A = A + 8
+ A = A + 7
+ A = A + 4
+ A = A + 2
+ A = A + 8
+ A = A + 4
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 8
+ for i in range( 9):
+ A = A + 5
+ A = A + 5
+ for i in range( 5):
+ A = A + 5
+ for i in range( 3):
+ for i in range( 5):
+ A = A + 4
+ for i in range( 4):
+ A = A + 6
+ A = A + 3
+ for i in range( 7):
+ A = A + 3
+ A = A + 3
+ A = A + 1
+ A = A + 7
+ A = A + 7
+ A = A + 6
+ A = A + 5
+ A = A + 5
+ A = A + 6
+ for i in range( 1):
+ A = A + 9
+ A = A + 3
+ for i in range( 1):
+ for i in range( 1):
+ A = A + 1
+ for i in range( 8):
+ A = A + 5
+ for i in range( 8):
+ A = A + 6
+ for i in range( 4):
+ A = A + 9
+ A = A + 4
+ for i in range( 2):
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ A = A + 7
+ A = A + 5
+ A = A + 8
+ A = A + 7
+ A = A + 8
+ A = A + 5
+ for i in range( 2):
+ A = A + 5
+ A = A + 7
+ A = A + 8
+A = A + 5
+A = A + 9
+for i in range( 2):
+ for i in range( 6):
+ A = A + 9
+ A = A + 1
+ A = A + 8
+ A = A + 7
+ A = A + 1
+ A = A + 5
+ for i in range( 3):
+ A = A + 3
+ A = A + 9
+ A = A + 7
+ for i in range( 3):
+ A = A + 9
+ A = A + 1
+ for i in range( 6):
+ A = A + 1
+ for i in range( 9):
+ for i in range( 7):
+ A = A + 3
+ for i in range( 5):
+ A = A + 5
+ A = A + 8
+ A = A + 8
+ A = A + 1
+ A = A + 2
+ for i in range( 4):
+ A = A + 6
+ for i in range( 3):
+ A = A + 3
+ A = A + 7
+ for i in range( 8):
+ for i in range( 1):
+ A = A + 7
+ A = A + 8
+ A = A + 3
+ A = A + 1
+A = A + 2
+A = A + 4
+A = A + 7
+for i in range( 1):
+ for i in range( 1):
+ for i in range( 1):
+ A = A + 4
+ A = A + 6
+ for i in range( 1):
+ A = A + 3
+ A = A + 9
+ A = A + 6
+ for i in range( 9):
+ A = A + 1
+ A = A + 6
+ for i in range( 5):
+ A = A + 3
+ A = A + 9
+ A = A + 5
+ A = A + 5
+ A = A + 7
+ A = A + 2
+ for i in range( 2):
+ A = A + 7
+ A = A + 7
+ for i in range( 7):
+ for i in range( 4):
+ A = A + 6
+ A = A + 8
+ for i in range( 6):
+ A = A + 6
+ for i in range( 2):
+ A = A + 1
+ A = A + 7
+ A = A + 6
+ A = A + 7
+ for i in range( 4):
+ for i in range( 7):
+ A = A + 1
+ for i in range( 2):
+ A = A + 2
+ A = A + 5
+ A = A + 8
+ A = A + 2
+A = A + 1
+A = A + 4
+for i in range( 8):
+ A = A + 5
+A = A + 6
+for i in range( 7):
+ for i in range( 6):
+ for i in range( 9):
+ A = A + 7
+ A = A + 8
+ for i in range( 4):
+ A = A + 6
+ A = A + 4
+ A = A + 3
+ A = A + 6
+ for i in range( 9):
+ A = A + 3
+ for i in range( 9):
+ A = A + 2
+ A = A + 7
+ A = A + 5
+ A = A + 2
+for i in range( 7):
+ for i in range( 8):
+ for i in range( 6):
+ A = A + 4
+ A = A + 9
+ A = A + 5
+ A = A + 3
+ A = A + 9
+ for i in range( 4):
+ for i in range( 1):
+ A = A + 6
+ A = A + 8
+ for i in range( 1):
+ A = A + 6
+ A = A + 4
+ A = A + 6
+ for i in range( 3):
+ A = A + 7
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+ A = A + 2
+ A = A + 3
+ A = A + 7
+ for i in range( 5):
+ A = A + 6
+ A = A + 5
+ for i in range( 1):
+ for i in range( 8):
+ A = A + 5
+ for i in range( 3):
+ A = A + 6
+ for i in range( 9):
+ A = A + 4
+ A = A + 3
+ for i in range( 6):
+ for i in range( 2):
+ A = A + 1
+ A = A + 5
+ A = A + 2
+A = A + 2
+A = A + 7
+for i in range( 4):
+ A = A + 7
+A = A + 9
+A = A + 2
+for i in range( 8):
+ A = A + 9
+ for i in range( 9):
+ for i in range( 2):
+ A = A + 3
+ A = A + 2
+ A = A + 1
+ A = A + 5
+ for i in range( 9):
+ A = A + 1
+ A = A + 3
+ A = A + 9
+ for i in range( 7):
+ A = A + 2
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 2):
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ for i in range( 5):
+ A = A + 5
+ A = A + 4
+ A = A + 2
+ A = A + 4
+ for i in range( 6):
+ A = A + 2
+ for i in range( 5):
+ A = A + 7
+ A = A + 7
+ A = A + 8
+ A = A + 3
+ for i in range( 8):
+ A = A + 2
+ A = A + 5
+ for i in range( 1):
+ A = A + 8
+ A = A + 5
+ A = A + 1
+ A = A + 1
+ A = A + 5
+ for i in range( 2):
+ A = A + 6
+ for i in range( 6):
+ A = A + 9
+ A = A + 2
+ A = A + 5
+ for i in range( 4):
+ A = A + 7
+ A = A + 1
+ for i in range( 6):
+ A = A + 8
+ A = A + 4
+ for i in range( 3):
+ for i in range( 2):
+ A = A + 1
+ A = A + 5
+ for i in range( 2):
+ A = A + 7
+ for i in range( 9):
+ A = A + 6
+ A = A + 8
+ A = A + 9
+ A = A + 5
+ for i in range( 9):
+ for i in range( 3):
+ A = A + 7
+ A = A + 7
+ A = A + 9
+ A = A + 7
+ for i in range( 5):
+ A = A + 7
+ A = A + 2
+ A = A + 1
+ A = A + 8
+ A = A + 3
+ A = A + 5
+A = A + 1
+for i in range( 8):
+ A = A + 4
+A = A + 2
+A = A + 2
+A = A + 8
+for i in range( 4):
+ for i in range( 4):
+ A = A + 8
+ for i in range( 7):
+ A = A + 5
+ A = A + 2
+ for i in range( 2):
+ A = A + 6
+ for i in range( 4):
+ A = A + 8
+ A = A + 6
+ A = A + 1
+ A = A + 3
+A = A + 2
+A = A + 7
+A = A + 4
+for i in range( 8):
+ A = A + 2
+ A = A + 4
+for i in range( 5):
+ for i in range( 3):
+ for i in range( 6):
+ A = A + 8
+ A = A + 1
+ A = A + 6
+ A = A + 5
+ A = A + 9
+for i in range( 8):
+ A = A + 7
+for i in range( 6):
+ A = A + 4
+A = A + 5
+for i in range( 3):
+ A = A + 1
+ for i in range( 1):
+ for i in range( 5):
+ A = A + 6
+ A = A + 2
+ for i in range( 9):
+ for i in range( 5):
+ A = A + 9
+ A = A + 3
+ for i in range( 9):
+ A = A + 9
+ A = A + 8
+ for i in range( 8):
+ for i in range( 5):
+ A = A + 9
+ A = A + 4
+ for i in range( 9):
+ A = A + 3
+ A = A + 4
+ A = A + 5
+for i in range( 9):
+ for i in range( 7):
+ A = A + 5
+ for i in range( 3):
+ A = A + 7
+ for i in range( 9):
+ for i in range( 6):
+ A = A + 4
+ A = A + 6
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 3
+ A = A + 3
+ A = A + 3
+ A = A + 5
+ for i in range( 7):
+ A = A + 5
+ for i in range( 2):
+ A = A + 5
+ A = A + 6
+ for i in range( 2):
+ A = A + 2
+ A = A + 5
+ A = A + 3
+A = A + 5
+A = A + 5
+for i in range( 4):
+ A = A + 2
+ A = A + 1
+ for i in range( 9):
+ A = A + 9
+ A = A + 5
+ A = A + 6
+ A = A + 2
+ A = A + 2
+ A = A + 5
+ for i in range( 9):
+ A = A + 5
+ A = A + 4
+ for i in range( 4):
+ for i in range( 4):
+ A = A + 1
+ A = A + 2
+ for i in range( 6):
+ A = A + 9
+ A = A + 3
+ for i in range( 2):
+ A = A + 5
+ A = A + 1
+ A = A + 1
+ A = A + 3
+ A = A + 8
+ for i in range( 7):
+ A = A + 4
+ for i in range( 6):
+ A = A + 9
+ for i in range( 5):
+ A = A + 9
+ A = A + 8
+ A = A + 3
+ A = A + 9
+ A = A + 4
+ A = A + 6
+for i in range( 7):
+ A = A + 9
+for i in range( 9):
+ A = A + 4
+ A = A + 9
+ A = A + 1
+ A = A + 3
+ for i in range( 5):
+ for i in range( 1):
+ A = A + 4
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ A = A + 6
+ A = A + 2
+ for i in range( 3):
+ A = A + 4
+ A = A + 4
+ for i in range( 3):
+ A = A + 5
+ A = A + 2
+ A = A + 8
+ A = A + 3
+ A = A + 6
+ A = A + 4
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 5
+ A = A + 3
+ for i in range( 3):
+ A = A + 2
+ A = A + 5
+ A = A + 8
+ A = A + 2
+ A = A + 5
+ for i in range( 8):
+ for i in range( 2):
+ A = A + 6
+ A = A + 7
+ A = A + 6
+ A = A + 9
+ A = A + 2
+for i in range( 2):
+ A = A + 3
+ for i in range( 8):
+ A = A + 7
+ A = A + 2
+ A = A + 1
+ A = A + 4
+ A = A + 1
+ A = A + 5
+ A = A + 2
+ A = A + 1
+ for i in range( 1):
+ A = A + 1
+ for i in range( 6):
+ A = A + 4
+ A = A + 3
+ A = A + 3
+ for i in range( 5):
+ A = A + 3
+ for i in range( 6):
+ for i in range( 1):
+ A = A + 5
+ A = A + 7
+ A = A + 7
+ A = A + 7
+ for i in range( 5):
+ A = A + 9
+ A = A + 7
+ for i in range( 5):
+ A = A + 9
+ A = A + 1
+ A = A + 9
+ A = A + 8
+ for i in range( 1):
+ A = A + 2
+ for i in range( 5):
+ A = A + 8
+ for i in range( 3):
+ A = A + 2
+ A = A + 9
+ A = A + 6
+ A = A + 3
+ for i in range( 5):
+ for i in range( 6):
+ A = A + 5
+ A = A + 5
+ for i in range( 4):
+ A = A + 5
+ A = A + 4
+ for i in range( 8):
+ A = A + 9
+ A = A + 1
+ for i in range( 8):
+ A = A + 8
+ A = A + 1
+ A = A + 4
+ for i in range( 6):
+ A = A + 6
+ for i in range( 2):
+ A = A + 3
+ A = A + 9
+ A = A + 6
+ A = A + 9
+ for i in range( 1):
+ A = A + 4
+ for i in range( 3):
+ A = A + 3
+ A = A + 4
+ A = A + 2
+ A = A + 8
+ for i in range( 2):
+ A = A + 4
+ A = A + 1
+ for i in range( 9):
+ A = A + 2
+ A = A + 9
+ A = A + 7
+for i in range( 7):
+ for i in range( 7):
+ for i in range( 5):
+ A = A + 7
+ for i in range( 5):
+ A = A + 1
+ A = A + 1
+ for i in range( 5):
+ A = A + 6
+ for i in range( 1):
+ A = A + 4
+ for i in range( 9):
+ A = A + 4
+ A = A + 1
+ for i in range( 6):
+ A = A + 8
+ A = A + 5
+ for i in range( 1):
+ A = A + 4
+ for i in range( 5):
+ A = A + 8
+ A = A + 7
+ A = A + 2
+ for i in range( 3):
+ A = A + 3
+ for i in range( 8):
+ for i in range( 8):
+ A = A + 4
+ A = A + 7
+ for i in range( 5):
+ A = A + 1
+ for i in range( 8):
+ A = A + 7
+ A = A + 8
+ A = A + 4
+ A = A + 7
+ A = A + 6
+ A = A + 9
+ A = A + 5
+for i in range( 3):
+ A = A + 5
+ for i in range( 9):
+ A = A + 1
+ A = A + 7
+for i in range( 1):
+ A = A + 8
+A = A + 4
+for i in range( 8):
+ for i in range( 7):
+ A = A + 2
+ for i in range( 4):
+ A = A + 6
+ A = A + 6
+ for i in range( 1):
+ A = A + 7
+ A = A + 1
+for i in range( 9):
+ for i in range( 5):
+ A = A + 6
+ A = A + 5
+ for i in range( 7):
+ A = A + 3
+ A = A + 6
+ A = A + 8
+ for i in range( 2):
+ A = A + 7
+ A = A + 1
+ A = A + 9
+ for i in range( 3):
+ for i in range( 3):
+ A = A + 5
+print(A)
+```
+
+ 241830
+
+
+## 试题 D: 矩阵
+
+本题总分:10 分
+
+**【问题描述】**
+
+把 1 ∼ 2020 放在 2 × 1010 的矩阵里。要求同一行中右边的比左边大,同一
+列中下边的比上边的大。一共有多少种方案?
+答案很大,你只需要给出方案数除以 2020 的余数即可。
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+f=[[ 0 for i in range(1011)]for i in range(1011)]
+f[0][0]=1
+for i in range(1011):
+ for j in range(1011):
+ if i>j:
+ f[i][j]+=f[i-1][j]
+ if j!=0:
+ f[i][j]+=f[i][j-1]
+ f[i][j]%=2020
+print(f[-1][-1])
+```
+
+ 1340
+
+
+## 试题 E: 完美平方数
+本题总分:15 分
+
+**【问题描述】**
+
+如果整个整数 X 本身是完全平方数,同时它的每一位数字也都是完全平方
+数,我们就称 X 是完美平方数。
+前几个完美平方数是 0、1、4、9、49、100、144……
+即第 1 个完美平方数是 0,第 2 个是 1,第 3 个是 4,……
+请你计算第 2020 个完美平方数是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+visited={0}
+def f(string):
+ for i in string:
+ if i not in {'0','1','4','9'}:
+ return False
+ return True
+num=1
+while True :
+ if f(str(num**2)):
+ visited.add(num**2)
+ print(len(visited))
+ if len(visited)==2020:
+ print(num**2)
+ break
+ num+=1
+# 491499994440019919104
+```
+
+
+```
+# def f (x):
+# for i in range(int(x**(0.5))+1):
+# if i**2==x:
+# return True
+# # return False
+
+# import math
+# def is_sqr(n):
+# a = int(math.sqrt(n))
+# return a * a == n
+# # Squares=set()
+# # for i in range(20200000):
+# # Squares.add(i**2)
+# visited={0,1,4,9}
+# #num=50
+# len_=1
+# queue=[1,4,9]
+# while queue:
+# num=queue.pop(0)
+# queue.append(int(str(num)+'0'))
+# queue.append(int(str(num)+'1'))
+# queue.append(int(str(num)+'4'))
+# queue.append(int(str(num)+'9'))
+# # label=1
+# # for i in str(num):
+# # if int(i) not in visited :
+# # label=-1
+# # if label==1:
+# if is_sqr(num) :
+# visited.add(num)
+# len_+=1
+# print(len(visited))
+# if len(visited)==2020:
+# print(num)
+# break
+```
+
+## 试题 F: 分类计数
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
+
+**【问题描述】**
+
+输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字
+母,多少个数字。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
+
+**【样例输入】**
+
+```python
+1+a=Aab
+```
+
+**【样例输出】**
+
+```python
+1
+3
+1
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由可见字符组成,长度不超过 100。
+
+
+```
+string=input()
+num_set=set()
+for i in range(10):
+ num_set.add(str(i))
+# print(num_set)
+num_len=0
+h_len=0
+l_len=0
+for i in string:
+ if i in num_set:
+ num_len+=1
+ elif 'A'<=i<='Z':
+ h_len+=1
+ elif 'a'<=i<='z':
+ l_len+=1
+print(h_len)
+print(l_len)
+print(num_len)
+
+```
+
+ 1+a=Aab
+ 1
+ 3
+ 1
+
+
+
+
+## 试题 G: 八次求和
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+给定正整数 n, 求 1
+8 + 28 + · · · + n
+8 mod 123456789 。其中 mod 表示取
+余。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n。
+
+**【输出格式】**
+
+> 输出一行,包含一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+2
+```
+
+**【样例输出】**
+
+```python
+257
+```
+
+**【样例输入】**
+
+```python
+987654
+```
+
+**【样例输出】**
+
+```python
+43636805
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 20。
+> 对于 60% 的评测用例,1 ≤ n ≤ 1000。
+> 对于所有评测用例,1 ≤ n ≤ 1000000。
+
+
+
+```
+def f(x):
+ re=1
+ for i in range(8):
+ re*=x
+ re%=123456789
+ return re
+n=int(input())
+res=0
+for i in range(1,n+1):
+ res+=f(i)
+ res%=123456789
+print(res)
+```
+
+ 987654
+ 43636805
+
+
+## 试题 H: 字符串编码
+
+时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
+
+**【问题描述】**
+
+小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大
+写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, ... Z →
+26。
+这样一个字符串就能被转化成一个数字序列:
+比如 ABCXYZ → 123242526。
+现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样
+的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字
+符串。
+
+**【输入格式】**
+
+
+> 一个数字序列。
+
+**【输出格式】**
+
+> 一个只包含大写字母的字符串,代表答案
+
+**【样例输入】**
+
+```python
+123242526
+```
+
+**【样例输出】**
+
+```python
+LCXYZ
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,输入的长度不超过 20。
+> 对于所有评测用例,输入的长度不超过 200000。
+
+
+```
+dic_={}
+for i in range(1,27):
+ dic_[str(i)]=chr(i+64)
+
+string=input()
+point=0
+while point 第一行包含 2 个整数 N 和 K。
+>
+> 以下 N 行每行包含 2 个整数,其中第 i 行是编号为 i 的节点的父节点编号
+>
+> Pi 和权值 Wi 。注意 Pi = 0 表示 i 是根节点。
+>
+> 输入保证是一棵 BST。
+
+**【输出格式】**
+
+> 一个整数代表答案。如果答案是无穷多,输出 −1。
+
+**【样例输入】**
+
+```python
+4 3
+0 10
+1 0
+1 20
+3 30
+```
+
+**【样例输出】**
+
+```python
+9
+```
+
+**【评测用例规模与约定】**
+
+> 对于 60% 的评测用例,1 ≤ K ≤ N ≤ 100,0 ≤ Wi ≤ 200,且 Wi 各不相同。
+>
+> 对于所有评测用例,1 ≤ K ≤ N ≤ 10000,0 ≤ Wi ≤ 100000000,且 Wi 各不 相同。
+
+
+
+```
+class TreeNode:
+ def __init__(self,x):
+ self.val=x
+ self.left=None
+ self.right=None
+ self.parent=None
+N,K=map(int,input().strip().split())
+map_=[]
+map_node=[]
+for i in range(N):
+ p,w=map(int,input().strip().split())
+ map_.append([p,w])
+ map_node.append(TreeNode(w))
+ if p==0:
+ root_index=i
+for i in range(N):
+ if map_node[map_[i][0]-1].val - 输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从 1 至 n 编号。
+> 接下来 m 行,每行三个整数,表示一个操作。
+> 如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。
+> 如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
+
+**【输出格式】**
+
+> 输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
+
+**【样例输入】**
+
+```python
+4 8
+1 1 2
+2 1 10
+2 3 5
+1 4 1
+2 2 2
+1 1 2
+1 2 4
+2 2 1
+```
+
+**【样例输出】**
+
+```python
+13 13 5 3
+```
+
+**【评测用例规模与约定】**
+
+> 对于 30% 的评测用例,1 ≤ n ≤ 20,1 ≤ m ≤ 100。
+>
+> 对于 50% 的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000。
+>
+> 对于 70% 的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ t ≤ 100。
+
+
+
+```
+n,m=map(int,input().strip().split())
+message1=[]
+for i in range(m):
+
+ or1_2,a,b=input().strip().split()
+ message1.append([or1_2,a,b])
+
+
+map_=[[0 for i in range(n)]for i in range(n)]
+for i in range(n):
+ map_[i][i]=1
+
+re=[0 for i in range(n)]
+
+def f(map_,a,b,re,visited):
+ for i in range(n):
+ if map_[a-1][i]==1:
+## print(visited)
+ if i not in visited:
+ f(map_,i+1,b,re,visited|{i})
+ else:
+ if re[i]==0:
+ re[i]+=b
+
+
+
+for or1_2,a,b in message1:
+ a=int(a)
+ b=int(b)
+ if or1_2=='1':
+ map_[a-1][b-1]=1
+ map_[b-1][a-1]=1
+## print('a',a,'b',b)
+## print('map',map_)
+ else:
+ temp=[0 for i in range(n)]
+ f(map_,a,b,temp,{a-1})
+
+ for i in range(len(re)):
+ re[i]+=temp[i]
+## print('re',re)
+
+for i in re:
+ print(i)
+
+```
+
+## 试题 B: 合并检测
+
+
+本题总分:5 分
+
+**【问题描述】**
+
+新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准备给大量民众进病毒核酸检测。
+然而,用于检测的试剂盒紧缺。
+为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看,如果检测前 k − 1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用了 k + 1 个试剂盒完成了 k 个人的检测。
+A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能最节省试剂盒?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+lis=[]
+for k in range(1,101):
+ temp=100+k*k
+ lis.append([temp/k,k])
+lis.sort(key=lambda x :x[0])
+lis[0][1]
+```
+
+
+
+
+ 10
+
+
+
+
+```
+lis
+```
+
+
+
+
+ [[20.0, 10],
+ [20.09090909090909, 11],
+ [20.11111111111111, 9],
+ [20.333333333333332, 12],
+ [20.5, 8],
+ [20.692307692307693, 13],
+ [21.142857142857142, 14],
+ [21.285714285714285, 7],
+ [21.666666666666668, 15],
+ [22.25, 16],
+ [22.666666666666668, 6],
+ [22.88235294117647, 17],
+ [23.555555555555557, 18],
+ [24.263157894736842, 19],
+ [25.0, 5],
+ [25.0, 20],
+ [25.761904761904763, 21],
+ [26.545454545454547, 22],
+ [27.347826086956523, 23],
+ [28.166666666666668, 24],
+ [29.0, 4],
+ [29.0, 25],
+ [29.846153846153847, 26],
+ [30.703703703703702, 27],
+ [31.571428571428573, 28],
+ [32.44827586206897, 29],
+ [33.333333333333336, 30],
+ [34.225806451612904, 31],
+ [35.125, 32],
+ [36.03030303030303, 33],
+ [36.333333333333336, 3],
+ [36.94117647058823, 34],
+ [37.857142857142854, 35],
+ [38.77777777777778, 36],
+ [39.7027027027027, 37],
+ [40.63157894736842, 38],
+ [41.56410256410256, 39],
+ [42.5, 40],
+ [43.4390243902439, 41],
+ [44.38095238095238, 42],
+ [45.325581395348834, 43],
+ [46.27272727272727, 44],
+ [47.22222222222222, 45],
+ [48.17391304347826, 46],
+ [49.12765957446808, 47],
+ [50.083333333333336, 48],
+ [51.04081632653061, 49],
+ [52.0, 2],
+ [52.0, 50],
+ [52.96078431372549, 51],
+ [53.92307692307692, 52],
+ [54.886792452830186, 53],
+ [55.851851851851855, 54],
+ [56.81818181818182, 55],
+ [57.785714285714285, 56],
+ [58.75438596491228, 57],
+ [59.724137931034484, 58],
+ [60.69491525423729, 59],
+ [61.666666666666664, 60],
+ [62.63934426229508, 61],
+ [63.61290322580645, 62],
+ [64.58730158730158, 63],
+ [65.5625, 64],
+ [66.53846153846153, 65],
+ [67.51515151515152, 66],
+ [68.49253731343283, 67],
+ [69.47058823529412, 68],
+ [70.44927536231884, 69],
+ [71.42857142857143, 70],
+ [72.40845070422536, 71],
+ [73.38888888888889, 72],
+ [74.36986301369863, 73],
+ [75.35135135135135, 74],
+ [76.33333333333333, 75],
+ [77.3157894736842, 76],
+ [78.2987012987013, 77],
+ [79.28205128205128, 78],
+ [80.26582278481013, 79],
+ [81.25, 80],
+ [82.23456790123457, 81],
+ [83.21951219512195, 82],
+ [84.20481927710843, 83],
+ [85.19047619047619, 84],
+ [86.17647058823529, 85],
+ [87.16279069767442, 86],
+ [88.14942528735632, 87],
+ [89.13636363636364, 88],
+ [90.12359550561797, 89],
+ [91.11111111111111, 90],
+ [92.0989010989011, 91],
+ [93.08695652173913, 92],
+ [94.0752688172043, 93],
+ [95.06382978723404, 94],
+ [96.05263157894737, 95],
+ [97.04166666666667, 96],
+ [98.03092783505154, 97],
+ [99.0204081632653, 98],
+ [100.01010101010101, 99],
+ [101.0, 1],
+ [101.0, 100]]
+
+
+
+## 试题 C: 分配口罩
+
+本题总分:10 分
+
+**【问题描述】**
+
+某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文
+字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目
+录下有一个文件 mask.txt,内容与下面的文本相同)
+
+```python
+9090400
+8499400
+5926800
+8547000
+4958200
+4422600
+5751200
+4175600
+6309600
+5865200
+6604400
+4635000
+10663400
+8087200
+4554000
+```
+
+
+ 现在市长要把口罩分配给市内的2所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+
+```
+def main():
+ f=open('mask.txt','r')
+ #string=f.readlines()
+ num_lis=[]
+ for i in f:
+ #print(i)
+ num_lis.append(int(i))
+ print(num_lis)
+ re=[abs(num_lis[0]-num_lis[1])]
+ def dfs(num1,num2,num_lis):
+ #global re
+ if not num_lis:
+ re[0]=min(re[0],abs(num1-num2))
+ return
+ dfs(num1+num_lis[0],num2,num_lis[1:])
+ dfs(num1,num2+num_lis[0],num_lis[1:])
+ dfs(0,0,num_lis)
+ print(re[0])
+ return
+main()
+```
+
+ [9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, 6604400, 4635000, 10663400, 8087200, 4554000]
+ 2400
+
+
+## 试题 F: 解码
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
+
+**【问题描述】**
+小明有一串很长的英文字母,可能包含大写和小写。
+在这串字母中,有很多连续的是重复的。小明想了一个办法将这串字母表
+达得更短:将连续的几个相同字母写成字母 + 出现次数的形式。
+例如,连续的 5 个 a,即 aaaaa,小明可以简写成 a5(也可能简写成 a4a、
+aa3a 等)。对于这个例子:HHHellllloo,小明可以简写成 H3el5o2。为了方便表
+达,小明不会将连续的超过 9 个相同的字符写成简写的形式。
+现在给出简写后的字符串,请帮助小明还原成原来的串。
+
+**【输入格式】**
+
+> 输入一行包含一个字符串。
+
+**【输出格式】**
+
+> 输出一个字符串,表示还原后的串。
+
+**【样例输入】**
+
+```python
+H3el5o2
+```
+
+**【样例输出】**
+
+```python
+HHHellllloo
+```
+
+**【评测用例规模与约定】**
+对于所有评测用例,字符串由大小写英文字母和数字组成,长度不超过100。
+请注意原来的串长度可能超过 100。
+
+
+
+```
+num_set={'0','1','2','3','4','5','6','7','8','9'}
+string=input()
+re=[]
+for i in string :
+ if i in num_set:
+ for i in range(int(i)-1):
+ re.append(re[-1])
+ else:
+ re.append(i)
+print(''.join(re))
+```
+
+ H3el5o2
+ HHHellllloo
+
+
+## 试题 G: 走方格
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+在平面上有一些二维的点阵。
+这些点的编号就像二维数组的编号一样,从上到下依次为第 1 至第 n 行,
+从左到右依次为第 1 至第 m 列,每一个点可以用行号和列号来表示。
+现在有个人站在第 1 行第 1 列,要走到第 n 行第 m 列。只能向右或者向下
+走。
+注意,如果行号和列数都是偶数,不能走入这一格中。
+问有多少种方案。
+
+**【输入格式】**
+
+> 输入一行包含两个整数 n, m。
+
+**【输出格式】**
+
+> 输出一个整数,表示答案。
+
+**【样例输入】**
+
+```python
+3 4
+```
+
+**【样例输出】**
+
+```python
+2
+```
+
+**【样例输入】**
+
+```python
+6 6
+```
+
+
+
+
+```
+n,m=map(int,input().strip().split())
+def main():
+ re=[0]
+ def dfs(x,y):
+ if x==n-1 and y==m-1:
+ re[0]+=1
+ if 0<=x+1<=(n-1) and not ((x+1)%2==0 and (y)%2==0):
+ dfs(x+1,y)
+ if 0<=y+1<=(m-1) and not ((x)%2==0 and (y+1)%2==0):
+ dfs(x,y+1)
+ dfs(0,0)
+ print(re[0])
+main()
+```
+
+ 3 4
+ 2
+
+
+### bfs
+
+
+```
+def main():
+ n,m=map(int,input().strip().split())
+ queue=[(0,0)]
+ re=0
+ while queue:
+ x,y=queue.pop(0)
+ if x==n-1 and y==m-1:
+ re+=1
+ if 0<=x+1 第一行包含 2 个整数 n 和 K。
+> 第二行包含 n 个整数 A1, A2, · · · , An。
+
+**【输出格式】**
+
+> 一个整数代表答案。
+
+**【样例输入】**
+
+```python
+4 33
+1 2 3 4
+```
+
+**【样例输出】**
+
+```python
+8
+```
+
+**【评测用例规模与约定】**
+对于 30% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ K ≤ 108, 1 ≤ Ai ≤ 104。
+对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ K ≤ 1010,1 ≤ Ai ≤ 109.
+
+
+
+```
+n,K=map(int,input().strip().split())
+num_lis=list(map(int,input().strip().split()))
+re=0
+for i in range(n):
+ for j in range(i+1,n):
+ if (num_lis[i]*10+num_lis[j])<=K:
+# print( num_lis[i]*10+num_lis[j])
+ re+=1
+ if (num_lis[j]*10+num_lis[i])<=K:
+# print(num_lis[j]*10+num_lis[i])
+ re+=1
+print(re)
+
+
+```
+
+ 4 33
+ 1 2 3 4
+ 8
+
+
+## 试题 I: 超级胶水
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:25 分
+
+**【问题描述】**
+
+小明有 n 颗石子,按顺序摆成一排。他准备用胶水将这些石子粘在一起。
+每颗石子有自己的重量,如果将两颗石子粘在一起,将合并成一颗新的石
+子,重量是这两颗石子的重量之和。
+为了保证石子粘贴牢固,粘贴两颗石子所需要的胶水与两颗石子的重量乘
+积成正比,本题不考虑物理单位,认为所需要的胶水在数值上等于两颗石子重
+量的乘积。
+每次合并,小明只能合并位置相邻的两颗石子,并将合并出的新石子放在
+原来的位置。
+现在,小明想用最少的胶水将所有石子粘在一起,请帮助小明计算最少需
+要多少胶水。
+
+**【输入格式】**
+
+> 输入的第一行包含一个整数 n,表示初始时的石子数量。
+>
+> 第二行包含 n 个整数 w1,w2, · · · ,wn,依次表示每颗石子的重量。
+
+**【输出格式】**
+
+> 输出一行包含一个整数,表示最少需要的胶水数。
+
+**【样例输入】**
+
+```python
+3
+3 4 5
+```
+
+**【样例输出】**
+
+```python
+47
+```
+
+**【样例输入】**
+
+```python
+8
+1 5 2 6 3 7 4 8
+```
+
+**【样例输出】**
+
+```python
+546
+```
+
+**【评测用例规模与约定】**
+
+> 对于 20% 的评测用例,1 ≤ n ≤ 15。
+>
+> 对于 60% 的评测用例,1 ≤ n ≤ 100。
+>
+> 对于 80% 的评测用例,1 ≤ n ≤ 1000。
+>
+> 对于所有评测用例,1 ≤ n ≤ 100000,1 ≤ wi ≤ 1000。
+
+
+```
+n=int(input())
+num_lis=list(map(int,input().strip().split()))
+def f(num_lis):
+ re=num_lis[0]*num_lis[1]
+ re_index=0
+ for i in range(len(num_lis)-1):
+ if num_lis[i]*num_lis[i+1]
+
+int balance(int a, int b)
+{
+ if(ab) return 1;
+ return 0;
+}
+
+void judge(char* data, int a, int b, int std)
+{
+ switch(balance(data[a],data[std])){
+ case -1:
+ printf("%d light\n", a);
+ break;
+ case 0:
+ printf("%d heavy\n", b);
+ break;
+ case 1:
+ printf("err!\n", b);
+ }
+}
+
+// data 中8个元素,有一个假币,或轻或重
+void f(char* data)
+{
+ switch(balace(data[0]+data[2]+data[1],data[5]+data[4],data[3]) ____________________________________ ){ // 填空
+ case -1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,0,3,1);
+ break;
+ case 0:
+ judge(data,2,5,0);
+ break;
+ case 1:
+ judge(data,1,4,0);
+ }
+ break;
+ case 0:
+ judge(data,6,7,0);
+ break;
+ case 1:
+ switch(balance(data[0]+data[4],data[3]+data[1])){
+ case -1:
+ judge(data,4,1,0);
+ break;
+ case 0:
+ judge(data,5,2,0);
+ break;
+ case 1:
+ judge(data,3,0,1);
+ }
+ break;
+ }
+}
+
+int main()
+{
+ int n;
+ char buf[100];
+
+ scanf("%d", &n);
+ gets(buf);
+
+ int i;
+ for(i=0; i
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+
+```
+
+
+```
+n,k=map(int,input().strip().split())
+re=[i for i in range(1,n+1)]
+start=0
+while len(re)!=1:
+
+ for i in range(k-1):
+ start=(start+1)%len(re)
+ re.pop(start)
+ start=start%len(re)
+# print(re)
+print(re[0])
+```
+
+ 10 3
+ 4
+
+
+
+## 标题:自描述序列
+```
+小明在研究一个序列,叫Golomb自描述序列,不妨将其记作{G(n)}。这个序列有2个很有趣的性质:
+
+1. 对于任意正整数n,n在整个序列中恰好出现G(n)次。
+2. 这个序列是不下降的。
+
+以下是{G(n)}的前几项:
+
+n 1 2 3 4 5 6 7 8 9 10 11 12 13
+G(n)1 2 2 3 3 4 4 4 5 5 5 6 6
+
+给定一个整数n,你能帮小明算出G(n)的值吗?
+```
+**输入**
+```
+----
+一个整数n。
+
+对于30%的数据,1 <= n <= 1000000
+对于70%的数据,1 <= n <= 1000000000
+对于100%的数据,1 <= n <= 2000000000000000
+```
+**输出**
+```
+----
+一个整数G(n)
+
+```
+**【样例输入】**
+```
+13
+```
+**【样例输出】**
+```
+6
+```
+
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+
+```
+n=int(input())
+dic_={1:1,2:2}
+num=1
+i=1
+while num<=n:
+# print(dic_)
+ for j in range(dic_[i]):
+ dic_[num]=i
+ num+=1
+ i+=1
+print(dic_[n])
+
+```
+
+ 13
+ 6
+
+
+
+## 标题:采油
+```
+LQ公司是世界著名的石油公司,为世界供应优质石油。
+最近,LQ公司又在森林里发现了一大片区域的油田,可以在这个油田中开采n个油井。
+LQ公司在这n个油井之间修建了n-1条道路,每条道路连接两个油井,路径中间不会路过任何油井,而且这些道路将所有油井连通。
+建立油井的时候需要使用一台大型设备,运输起来非常麻烦,LQ公司准备在其中的一个油井位置建立一个空运站,先将设备空运到空运站,之后每次经过他们建立的道路来运输这个大型设备以建立不同的油井,当油井建立完毕后再从空运站将大型设备运走。
+为了减少运输的麻烦,公司要求大型设备在道路上运输的总路程是最短的。
+
+在建立油井和采油的过程中需要花费一些人力,第i个油井需要花费Bi个人,而一旦油井建成,就需要Si个人一直坚守在油井上进行维护。
+当然,如果一个人参与了油井的建设,他可以直接留下来维护油井,或者参与下一个油井的建设,但是在维护油井的人不能再参加后续油井的建设了。
+
+现在LQ公司想知道,大型设备运输的总路径长度最短是多少?在保证总路径长度最短的情况下,LQ公司至少需要花费多少人力才能完成所有油井的建立与维护。
+```
+**【输入格式】**
+```
+ 输入的第一行包含一个整数n,表示油井的数量。油井由1到n依次标号。
+ 第二行包含n个整数,依次表示B1, B2, …, Bn,相邻的整数之间用一个空格分隔。
+ 第三行包含n个整数,依次表示S1, S2, …, Sn,相邻的整数之间用一个空格分隔。
+ 接下来n-1行描述油井之间的道路,其中的第i行包含两个整数a,b,用一个空格分隔,表示一条道路的起点为i+1、终点为a,长度为b,道路是双向的,设备可以从任意一端运送到另一端,每条道路都可以经过任意多次。数据保证任意两个油井之间都可以通过道路连接。
+```
+**【输出格式】**
+```
+ 输出包含两个整数,用一个空格分隔,表示最优情况下大型设备需要运输的总路程,以及在总路程最短的情况下最少需要花费的人力数量。
+```
+**【样例输入】**
+```
+2
+10 20
+15 15
+1 8
+```
+**【样例输出】**
+```
+16 30
+```
+**【样例说明】**
+```
+ 有两种方案达到最优。
+ 方案一:在油井2建立空运站,先建立油井2,再将大型设备运输到油井1建立油井1,最后将大型设备运回油井2。
+ 方案二:在油井1建立空运站,先将大型设备运输到油井2建立油井2,再将大型设备运送到油井1建立油井1。
+```
+**【样例输入】**
+```
+6
+3 10 20 7 15 9
+2 6 10 4 8 7
+1 9
+1 2
+2 5
+3 4
+3 7
+```
+**【样例输出】**
+```
+54 38
+```
+**【数据规模和约定】**
+```
+ 对于20%的数据:n不超过10;
+ 另外20%的数据:每个油井最多和两个油井之间有道路直接连接;
+ 另外10%的数据:有n-1个油井只有一条道路与其他油井连接;
+ 对于100%的数据:n不超过100000,B、S、c均为不超过10000的正整数。
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+```
+n=int(input())
+B_lis=map(int,input().strip().split())
+S_lis=map(int,input().strip().split())
+map_=[[0 for j in range(n)]for j in range(n) ]
+for i in range(1,n):
+ a,b=map(int,input().strip().split())
+ map_[i][a-1]=b
+print(map_)
+```
+
+ 2
+ 10 20
+ 15 15
+ 1 8
+ [[0, 0], [8, 0]]
+
+
+
+```
+int n,l=0,num=0,b,s;
+
+int main(){
+
+ cin>>n;
+
+ for(int i=1;i<=n;i++)
+
+ cin>>b;
+
+ for(int i=1;i<=n;i++){
+
+ cin>>s;
+
+ num+=s;
+
+ }
+
+ for(int i=2;i<=n;i++){
+
+ int a1,a2;
+
+ cin>>a1>>a2;
+
+ l+=a2;
+
+ }
+
+ cout<min_len[0]:
+ return
+ if (x==n-1)and (y==m-1):
+ res.append(temp)
+ min_len[0]=len(temp)
+ return
+
+ if (0<=(x+1)0:
+ if b&1:
+ re*=a
+ a=a**2
+ b>>=1
+ return re
+
+```
+
+
+```
+p=891234941
+q=1123984201
+n=1001733993063167141
+c=20190324
+d=212353
+for i in range(1,500000): #枚举因子 d*e%((p-1)*(q-1))=1 (((q-1)*(p-1))*yz+1) %d =0
+ if(((p-1)*(q-1)*i+1)%d==0):
+ e=((p-1)*(q-1)*i+1)//212353
+ print(((p-1)*(q-1)*i+1)//d)
+ break
+def quick_mod(a,b,c):
+ a=a%c
+ ans=1
+ while b!=0:
+ if b&1:
+ ans=(ans*a)%c
+ b>>=1
+ a=(a*a)%c
+ return ans
+x=quick_mod(c,e,n) #x=c^e%n 579706994112328949
+print(x)
+print(quick_mod(x,d,n)) #c=x^d%n
+```
+
+ 823816093931522017
+ 579706994112328949
+ 20190324
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题E、完美平方数.md b/LanQiao/蓝桥杯习题/试题E、完美平方数.md
new file mode 100644
index 0000000..50514a1
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题E、完美平方数.md
@@ -0,0 +1,75 @@
+## 试题 E: 完美平方数
+本题总分:15 分
+
+**【问题描述】**
+
+如果整个整数 X 本身是完全平方数,同时它的每一位数字也都是完全平方
+数,我们就称 X 是完美平方数。
+前几个完美平方数是 0、1、4、9、49、100、144……
+即第 1 个完美平方数是 0,第 2 个是 1,第 3 个是 4,……
+请你计算第 2020 个完美平方数是多少?
+
+**【答案提交】**
+
+这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
+整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
+
+
+
+```
+visited={0}
+def f(string):
+ for i in string:
+ if i not in {'0','1','4','9'}:
+ return False
+ return True
+num=1
+while True :
+ if f(str(num**2)):
+ visited.add(num**2)
+ print(len(visited))
+ if len(visited)==2020:
+ print(num**2)
+ break
+ num+=1
+# 491499994440019919104
+```
+
+
+```
+# def f (x):
+# for i in range(int(x**(0.5))+1):
+# if i**2==x:
+# return True
+# # return False
+
+# import math
+# def is_sqr(n):
+# a = int(math.sqrt(n))
+# return a * a == n
+# # Squares=set()
+# # for i in range(20200000):
+# # Squares.add(i**2)
+# visited={0,1,4,9}
+# #num=50
+# len_=1
+# queue=[1,4,9]
+# while queue:
+# num=queue.pop(0)
+# queue.append(int(str(num)+'0'))
+# queue.append(int(str(num)+'1'))
+# queue.append(int(str(num)+'4'))
+# queue.append(int(str(num)+'9'))
+# # label=1
+# # for i in str(num):
+# # if int(i) not in visited :
+# # label=-1
+# # if label==1:
+# if is_sqr(num) :
+# visited.add(num)
+# len_+=1
+# print(len(visited))
+# if len(visited)==2020:
+# print(num)
+# break
+```
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md b/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md
new file mode 100644
index 0000000..fdf42c9
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题F完全二叉树的权值.md
@@ -0,0 +1,83 @@
+## 试题 G: 外卖店优先级
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+**【问题描述】**
+
+“饱了么”外卖系统中维护着 N 家外卖店,编号 1 ∼ N。每家外卖店都有
+一个优先级,初始时 (0 时刻) 优先级都为 0。
+每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减
+到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
+如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果
+优先级小于等于 3,则会被清除出优先缓存。
+给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优
+先缓存中。
+
+**【输入格式】**
+
+第一行包含 3 个整数 N、M 和 T。
+以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到
+一个订单。
+
+**【输出格式】**
+
+输出一个整数代表答案。
+
+
+**【样例输入】**
+```
+2 6 6
+1 1
+5 2
+3 1
+6 2
+2 1
+6 2
+```
+**【样例输出】**
+```
+1
+```
+**【样例解释】**
+
+6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,
+加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。
+
+**【评测用例规模与约定】**
+
+对于 80% 的评测用例,1 ≤ N, M, T ≤ 10000。
+对于所有评测用例,1 ≤ N, M, T ≤ 100000,1 ≤ ts ≤ T,1 ≤ id ≤ N。
+
+
+```
+N,M,T=map(int,input().strip().split())
+shop=[0 for i in range(N)]
+message=[[] for i in range(T)]
+
+for i in range(M):
+ ts,id=map(int,input().strip().split())
+ message[ts-1].append(id)
+# message.sort(key=lambda x:x[0])
+first=set()
+for i in range(len(message)):
+ for id in message[i]:
+ shop[id-1]+=3
+ for id in range(1,len(shop)):
+ shop[id-1]-=1
+ if shop[id-1]>5:
+ first.add(shop[id-1])
+ if shop[id-1]<=3:
+ first=first-{shop[id-1]}
+print(len(first))
+
+
+
+```
+
+ 2 6 6
+ 1 1
+ 5 2
+ 3 1
+ 6 2
+ 2 1
+ 6 2
+ 1
diff --git a/LanQiao/蓝桥杯习题/试题G外卖店优先级.md b/LanQiao/蓝桥杯习题/试题G外卖店优先级.md
new file mode 100644
index 0000000..f09ba00
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题G外卖店优先级.md
@@ -0,0 +1,39 @@
+## 题目 1853: [蓝桥杯][基础练习]数列排序
+
+时间限制: 1Sec 内存限制: 128MB 提交: 982 解决: 628
+
+**题目描述**
+
+- 给定一个长度为n的数列,将这个数列按从小到大的顺序排列。1<=n<=200
+
+**输入**
+```
+第一行为一个整数n。
+第二行包含n个整数,为待排序的数,每个整数的绝对值小于10000。
+```
+**输出**
+
+- 输出一行,按从小到大的顺序输出排序后的数列。
+
+**样例输入**
+```
+5
+8 3 6 4 9
+
+```
+**样例输出**
+```
+3 4 6 8 9
+```
+
+
+```
+a=int(input())
+num=sorted(list(map(int,input().strip().split())))
+for i in num:
+ print(i,end=' ')
+```
+
+ 5
+ 8 3 6 4 9
+ 3 4 6 8 9
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/试题H修改数组.md b/LanQiao/蓝桥杯习题/试题H修改数组.md
new file mode 100644
index 0000000..ad384a1
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/试题H修改数组.md
@@ -0,0 +1,107 @@
+## 试题 H: 修改数组
+
+时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
+
+
+**【问题描述】**
+
+给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现
+的整数。
+现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
+A2, A3, · · · , AN。
+当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则
+小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直
+到 Ai 没有在 A1 ∼ Ai−1 中出现过。
+当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
+现在给定初始的 A 数组,请你计算出最终的 A 数组。
+
+**【输入格式】**
+
+第一行包含一个整数 N。
+第二行包含 N 个整数 A1, A2, · · · , AN 。
+
+**【输出格式】**
+
+输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
+
+**【样例输入】**
+
+- 5
+- 2 1 1 3 4
+
+**【样例输出】**
+
+- 2 1 3 4 5
+
+**【评测用例规模与约定】**
+
+- 对于 80% 的评测用例,1 ≤ N ≤ 10000。
+- 对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
+
+
+```
+N=int(input())
+nums=list(map(int,input().strip().split()))
+visited=set()
+for i in range(len(nums)):
+ while nums[i] in visited:
+ nums[i]+=1
+ visited.add(nums[i])
+nums=list(map(str,nums))
+print(' '.join(nums))
+```
+
+ 5
+ 2 1 1 3 4
+ 2 1 3 4 5
+
+
+
+```
+a=[{2},{3},set(),set()]
+a.remove(set())
+print(a)
+```
+
+ [{2}, {3}, set()]
+
+
+
+```
+help(list.remove)
+```
+
+ Help on method_descriptor:
+
+ remove(...)
+ L.remove(value) -> None -- remove first occurrence of value.
+ Raises ValueError if the value is not present.
+
+
+
+
+
+```
+[{3}-{3},set(),{4}].remove({4})
+# a=[{3}-{3},set(),{4}].remove({3}-{3})
+# print(a)
+```
+
+
+```
+N,M,k=map(int,input().strip().split())
+queue=[]
+for i in range(N):
+ candy1,candy2,candy3=map(int,input().strip().split())
+ queue.append({candy1,candy2,candy3})
+re={}
+all=set([ i for i in range(1,M+1)])
+
+while all!=re and queue:
+ temp=max(queue,key=len)
+ re|=temp
+# queue.remove()
+ remove_count=0
+ for i in queue:
+
+```
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/进制转换知识整理.md b/LanQiao/蓝桥杯习题/进制转换知识整理.md
new file mode 100644
index 0000000..59f9e7e
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/进制转换知识整理.md
@@ -0,0 +1,109 @@
+## 进制转换
+
+ASCII码转换为int:ord('A') 65
+
+int转为ASCII码:chr(65) 'A'
+
+在日常生活中我们频繁使用到数学的进制,如季度逢三进一,星期逢七进一;×××、小时使用12进制,每天使用24进制,每月使用30进制,分秒使用60进制,一年使用360进制等等;在编程过程中我们经常需要转换进制,虽然Python已经内置了常用进制转换函数,如int,bin,hex,oct;但是如果我们需要转换成其他进制怎么办呢?
+
+ 我们知道,十进制转换成二进制时,使用“除2取余,逆序排列”即可。二进制转换成十进制时按权展开,即可得到十进制。类似地可以实现十进制转换成任意进制,任意进制也可以转换成十进制;通过十进制进行中转,即可实现任意进制数之间的转换了。
+
+
+
+```
+#将十进制数转换成任意进制20进制以内,任意进制只需添加不同的符号即可
+def decimalToAny(num,n):
+ if num==0:
+ return 0
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+97)
+ print(baseStr)
+ new_num_str = ""
+ while num != 0:
+ remainder = num % n
+ if remainder > 9:
+ remainder_string = baseStr[remainder]
+ else:
+ remainder_string = str(remainder)
+ new_num_str = remainder_string+new_num_str
+ num = num // n
+ return new_num_str
+decimalToAny(58,30)
+```
+
+ {10: 'a', 11: 'b', 12: 'c', 13: 'd', 14: 'e', 15: 'f', 16: 'g', 17: 'h', 18: 'i', 19: 'j', 20: 'k', 21: 'l', 22: 'm', 23: 'n', 24: 'o', 25: 'p', 26: 'q', 27: 'r', 28: 's', 29: 't'}
+
+
+
+
+
+ '1s'
+
+
+
+
+```
+#将任意进制数转换成十进制
+def anyToDecimal(num,n):
+ baseStr={}
+ for i in range(10):
+ baseStr[str(i)]=i
+ for i in range(10,n):
+ baseStr[chr(i-10+97)]=i
+ print(baseStr)
+ new_num = 0
+ for i in range(len(num)):
+ new_num+=baseStr[num[len(num)-1-i]]*(n**i)
+ return new_num
+anyToDecimal('1s',30)
+```
+
+ {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9, 'a': 10, 'b': 11, 'c': 12, 'd': 13, 'e': 14, 'f': 15, 'g': 16, 'h': 17, 'i': 18, 'j': 19, 'k': 20, 'l': 21, 'm': 22, 'n': 23, 'o': 24, 'p': 25, 'q': 26, 'r': 27, 's': 28, 't': 29}
+
+
+
+
+
+ 58
+
+
+
+
+```
+print('{0}xxxxxxxx{1}'.format('这是0要传入的东西','这是1要传入的东西'))
+```
+test={'nan':'werty'}
+print("ghjk{nan}gbhnjmk".format(**test))
+test
+进制转化,b o d x 分别表示二、八、十、十六进制
+
+
+```
+print('{:b}'.format(250))
+print('{:o}'.format(250))
+print('{:d}'.format(250))
+print('{:x}'.format(250))
+#千分位分隔符,这种情况只针对与数字
+print('{:,}'.format(100000000))
+print('{:,}'.format(235445.234235))
+```
+
+ 11111010
+ 372
+ 250
+ fa
+ 100,000,000
+ 235,445.234235
+
+
+精度和类型f精度常和f一起使用
+
+
+```
+print('{:.1f}'.format(4.234324525254))
+print('{:.4f}'.format(4.1))
+```
+
+ 4.2
+ 4.1000
\ No newline at end of file
diff --git a/LanQiao/蓝桥杯习题/采油.md b/LanQiao/蓝桥杯习题/采油.md
new file mode 100644
index 0000000..72022de
--- /dev/null
+++ b/LanQiao/蓝桥杯习题/采油.md
@@ -0,0 +1,138 @@
+## 采油
+```
+LQ公司是世界著名的石油公司,为世界供应优质石油。
+最近,LQ公司又在森林里发现了一大片区域的油田,可以在这个油田中开采n个油井。
+LQ公司在这n个油井之间修建了n-1条道路,每条道路连接两个油井,路径中间不会路过任何油井,而且这些道路将所有油井连通。
+建立油井的时候需要使用一台大型设备,运输起来非常麻烦,LQ公司准备在其中的一个油井位置建立一个空运站,先将设备空运到空运站,之后每次经过他们建立的道路来运输这个大型设备以建立不同的油井,当油井建立完毕后再从空运站将大型设备运走。
+为了减少运输的麻烦,公司要求大型设备在道路上运输的总路程是最短的。
+
+在建立油井和采油的过程中需要花费一些人力,第i个油井需要花费Bi个人,而一旦油井建成,就需要Si个人一直坚守在油井上进行维护。
+当然,如果一个人参与了油井的建设,他可以直接留下来维护油井,或者参与下一个油井的建设,但是在维护油井的人不能再参加后续油井的建设了。
+
+现在LQ公司想知道,大型设备运输的总路径长度最短是多少?在保证总路径长度最短的情况下,LQ公司至少需要花费多少人力才能完成所有油井的建立与维护。
+```
+**【输入格式】**
+```
+ 输入的第一行包含一个整数n,表示油井的数量。油井由1到n依次标号。
+ 第二行包含n个整数,依次表示B1, B2, …, Bn,相邻的整数之间用一个空格分隔。
+ 第三行包含n个整数,依次表示S1, S2, …, Sn,相邻的整数之间用一个空格分隔。
+ 接下来n-1行描述油井之间的道路,其中的第i行包含两个整数a,b,用一个空格分隔,表示一条道路的起点为i+1、终点为a,长度为b,道路是双向的,设备可以从任意一端运送到另一端,每条道路都可以经过任意多次。数据保证任意两个油井之间都可以通过道路连接。
+```
+**【输出格式】**
+```
+ 输出包含两个整数,用一个空格分隔,表示最优情况下大型设备需要运输的总路程,以及在总路程最短的情况下最少需要花费的人力数量。
+```
+**【样例输入】**
+```
+2
+10 20
+15 15
+1 8
+```
+**【样例输出】**
+```
+16 30
+```
+**【样例说明】**
+```
+ 有两种方案达到最优。
+ 方案一:在油井2建立空运站,先建立油井2,再将大型设备运输到油井1建立油井1,最后将大型设备运回油井2。
+ 方案二:在油井1建立空运站,先将大型设备运输到油井2建立油井2,再将大型设备运送到油井1建立油井1。
+```
+**【样例输入】**
+```
+6
+3 10 20 7 15 9
+2 6 10 4 8 7
+1 9
+1 2
+2 5
+3 4
+3 7
+```
+**【样例输出】**
+```
+54 38
+```
+**【数据规模和约定】**
+```
+ 对于20%的数据:n不超过10;
+ 另外20%的数据:每个油井最多和两个油井之间有道路直接连接;
+ 另外10%的数据:有n-1个油井只有一条道路与其他油井连接;
+ 对于100%的数据:n不超过100000,B、S、c均为不超过10000的正整数。
+```
+**资源约定:**
+```
+峰值内存消耗(含虚拟机) < 256M
+CPU消耗 < 1000ms
+
+请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
+```
+**注意:**
+```
+main函数需要返回0;
+只使用ANSI C/ANSI C++ 标准;
+不要调用依赖于编译环境或操作系统的特殊函数。
+所有依赖的函数必须明确地在源文件中 #include
+不能通过工程设置而省略常用头文件。
+
+提交程序时,注意选择所期望的语言类型和编译器类型。
+```
+
+
+```
+n=int(input())
+B_lis=map(int,input().strip().split())
+S_lis=map(int,input().strip().split())
+map_=[[0 for j in range(n)]for j in range(n) ]
+for i in range(1,n):
+ a,b=map(int,input().strip().split())
+ map_[i][a-1]=b
+print(map_)
+```
+
+ 2
+ 10 20
+ 15 15
+ 1 8
+ [[0, 0], [8, 0]]
+
+
+
+```
+int n,l=0,num=0,b,s;
+
+int main(){
+
+ cin>>n;
+
+ for(int i=1;i<=n;i++)
+
+ cin>>b;
+
+ for(int i=1;i<=n;i++){
+
+ cin>>s;
+
+ num+=s;
+
+ }
+
+ for(int i=2;i<=n;i++){
+
+ int a1,a2;
+
+ cin>>a1>>a2;
+
+ l+=a2;
+
+ }
+
+ cout<微信公众号:LSGO软件技术团队|华北电力大学
+马燕鹏|CSDN:https://lsgogroup.blog.csdn.net/
微信公众号:组队学习
韩绘锦|CSDN:https://blog.csdn.net/weixin_45569785|华北电力大学
姚行志|CSDN:https://blog.csdn.net/soulmate______|华北电力大学
徐韬||华北电力大学
diff --git a/Scratch/readme.md b/Scratch/readme.md
index e69de29..64b9d16 100644
--- a/Scratch/readme.md
+++ b/Scratch/readme.md
@@ -0,0 +1,102 @@
+
+
+# 青少年编程(Scratch)电子学会一级
+
+开源学习内容:https://github.com/datawhalechina/team-learning-program/tree/master/Scratch
+
+## 基本信息
+
+- 贡献人员:马燕鹏、王思齐
+- 学习周期:12天,每天平均花费时间1小时,根据个人学习接受能力强弱有所浮动。
+- 学习形式:模拟测试题
+- 人群定位:Scratch初学者
+- 先修内容:无
+- 难度系数:低
+
+## 学习目标
+
+由于测试题目为往年电子学会Scratch一级考试的真题,所以通过做题来掌握Scratch一级考试的知识点,为通过考试做准备。
+
+**一级考试大纲与说明**
+
+(一)考核目标
+
+学生对编程软件的界面认识和基本操作,初步能够导入角色和设置背景,并通过对角色的不同操作以及加入声音,形成一个具有简单顺序结构代码的作品,同时针对参加1级考试的学生将进行简单的逻辑推理能力的考查。
+
+(二)能力目标
+
+通过本级考试的学生,对软件认识良好,会进行软件的基本操作,能完成基本作品。
+
+(三)考试标准
+
+1、初步学会使用编程工具,理解编程工具中的核心概念。
+
+- 1)理解编程环境界面中功能区的分布与作用;
+- 2)能够完成拖拽程序模块到程序区的操作并进行正确的连接;
+- 3)能够通过舞台区按钮完成运行与停止程序的操作;
+- 4)会使用角色的移动、旋转指令模块;
+- 5)能为作品添加背景音乐,并设置声音的播放代码;
+- 6)能够绘制背景并对背景进行切换;
+- 7)能够打开计算机上已保存的项目和保存新制作的项目。
+
+2、按照规定的功能编写出完整的顺序结构程序。
+
+- 1)掌握顺序结构流程图的画法;
+- 2)理解参数的概念,能够调整指令模块中的参数;
+- 3)能够完成一个顺序结构的程序;
+- 4)程序中包含播放一段音频和切换背景;
+- 5)程序中包含切换角色的造型,角色移动和旋转;
+- 6)按指定的要求保存作品。
+
+(四)知识块
+
+- [x] 1. 熟悉编程软件:舞台区,角色区,模块区,脚本区,造型标签,声音标签,背景标签,新建和保存作品,语言的选择,从本地打开软件,程序的运行和停止
+- [x] 2. 角色的导入:库导入,绘制,本地导入等方式,大小设置,顺序结构流程图
+- [x] 3. 背景的认识:选取合适的背景,背景和角色的区别,背景的切换
+- [x] 4. 角色的操作:移动,旋转,造型切换
+- [x] 5. 声音的导入:导入声音并设置为背景音乐,设定声音音效,设定声音音量,设定声音的播放和停止
+- [x] 6. 逻辑推理,编程数学:逻辑推理,形象思维(图形推理)
+
+
+(五)题型配比及分值
+
+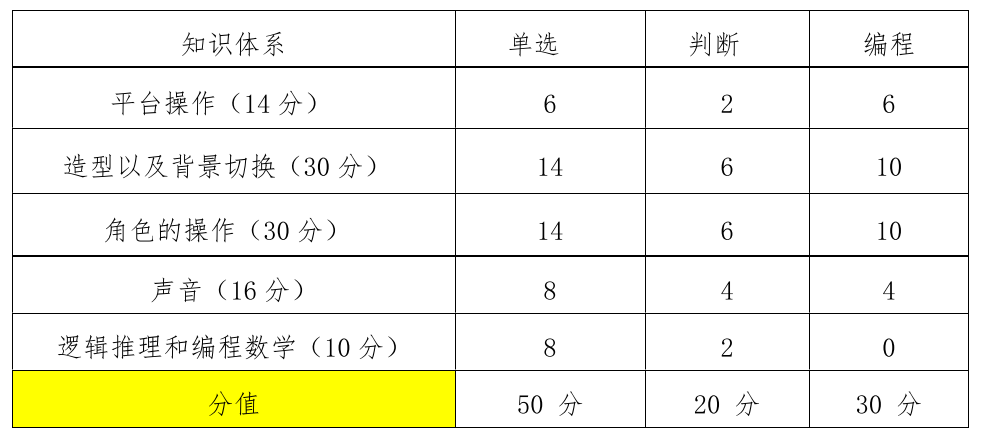
+
+
+
+
+## 任务安排
+
+### Task00:熟悉规则【1天】
+
+- 组队、修改群昵称。
+- 熟悉打卡规则。
+
+### Task01:熟悉Scratch【2天】
+- 熟悉Scratch考级(一级)的考试标准
+- 熟悉Scratch考级(一级)的知识点
+
+
+### Task02:模拟题(一)【2天】
+- 课堂派:判断题15个,单选题20个
+- 写博客:编程题(01 森林的一天、02 舞者凯希)
+
+
+### Task03:模拟题(二)【2天】
+- 课堂派:判断题15个,单选题20个
+- 写博客:编程题(03 小狗散步、04 猫捉老鼠)
+
+
+### Task04:模拟题(三)【2天】
+- 课堂派:判断题15个,单选题20个
+- 写博客:编程题(05 城堡漫步、06 火箭发射)
+
+### Task05:模拟题(四)【2天】
+- 课堂派:判断题15个,单选题20个
+- 写博客:编程题(07 飞向太空、08 小狗长大记)
+
+
+### Task06:模拟题(五)【2天】
+- 课堂派:判断题15个,单选题20个
+- 写博客:编程题(09 运动起来、10 动物园之旅)
+
diff --git a/Scratch/等级考试-01/02. 舞者凯希.md b/Scratch/等级考试-01/02. 舞者凯希.md
index 5326b6c..77f8f2a 100644
--- a/Scratch/等级考试-01/02. 舞者凯希.md
+++ b/Scratch/等级考试-01/02. 舞者凯希.md
@@ -2,7 +2,7 @@
## 1. 准备工作
-(1)从本地上传背景:舞台1、舞台2;
+(1)从本地上传背景:舞台1、舞台2;【背景图像在Img文件夹中】
(2)删除小猫角色,添加Cassy Dance角色,并添加声音dance magic。
diff --git a/Scratch/等级考试-01/Img/舞台1.png b/Scratch/等级考试-01/Img/舞台1.png
new file mode 100644
index 0000000..79be1bf
Binary files /dev/null and b/Scratch/等级考试-01/Img/舞台1.png differ
diff --git a/Scratch/等级考试-01/Img/舞台2.png b/Scratch/等级考试-01/Img/舞台2.png
new file mode 100644
index 0000000..ab5713d
Binary files /dev/null and b/Scratch/等级考试-01/Img/舞台2.png differ
diff --git a/Scratch/等级考试-01/参考答案.md b/Scratch/等级考试-01/参考答案.md
new file mode 100644
index 0000000..cb1fd58
--- /dev/null
+++ b/Scratch/等级考试-01/参考答案.md
@@ -0,0 +1,12 @@
+# 参考答案
+
+- [01 森林的一天](https://mp.weixin.qq.com/s/k-_r7xHGVW335e1FyJKIhg)
+- [02 舞者凯希](https://mp.weixin.qq.com/s/km6rJbI9Ih0heThkWZF27g)
+- [03 小狗散步](https://mp.weixin.qq.com/s/LelNrrmRTIUocde-x0kVzQ)
+- [04 猫捉老鼠](https://mp.weixin.qq.com/s/jPMGhincv_nnk4VOJ1XyzQ)
+- [05 城堡漫步](https://mp.weixin.qq.com/s/S--pZGgJvv5LHU1mX3p15w)
+- [06 火箭发射](https://mp.weixin.qq.com/s/M_agy8qJCmBIZ6ui6sK3Ww)
+- [07 飞向太空](https://mp.weixin.qq.com/s/9eN4MRVCQcV4z7otV7Omfg)
+- [08 小狗长大记](https://mp.weixin.qq.com/s/Gh5jCN2fu6-clPcYevuWlw)
+- [09 运动起来](https://mp.weixin.qq.com/s/amK1Rxi_uqoyJFy-nDB9ug)
+- [10 动物园之旅](https://mp.weixin.qq.com/s/Ff_GB4AnBtrEHwVTCB45qw)
\ No newline at end of file
diff --git a/Turtle/Day1:画几个简单的图形.md b/Turtle/Day1:画几个简单的图形.md
new file mode 100644
index 0000000..49cf62a
--- /dev/null
+++ b/Turtle/Day1:画几个简单的图形.md
@@ -0,0 +1,76 @@
+通过前面的学习,相信你已经能够参考【图图】的说明来进行绘图创造了,那么从现在开始,我们将正式开始各种趣味图形绘画。
+
+
+
+🔑 在【冲鸭】之前,请记住一个【锦囊妙计】,后面的画图过程中会涉及到各种各样的功能,有时我们可能会忘记指令怎么写,所以在每次训练的开头会为大家附上一个【图图】功能查询表,忘了就去看看吧。
+
+|向前走
|t.forward(100)
|
+|:----|:----|:----|:----|
+|向后走
|t.back(100)
|
+|向左转
|t.left(90)
|
+|向右转
|t.right(90)
|
+
+
+万事俱备,只欠冲锋,好啦,正式开始我们图形挑战之旅吧!!!
+
+# 🚀挑战1:
+
+这是一道送分题,别说你不会,赶紧的~
+
+题目描述:请参考下面图片中的内容,从左向右画出一条长度为100的直线吧。
+
+
+
+# 🚀挑战2:
+
+送分题又来了!
+
+题目描述:请参考下面图片中的内容,从左向右画出一个度数为90的角吧。
+
+(边的长度自己决定就好啦,可以也设置成100)
+
+
+
+# 📺示例1:
+
+下面,我们将一起来画几个简单的图形,第一个图形是一个三条边长度都为100的三角形,想一想该怎么画出来,如果想不出来,可以试试在草稿纸上画一画,要注意每次【图图】画完一条线后旋转的角度哦。
+
+
+
+下面是三角形的答案,一定要自己尝试后再来看哦:
+
+**讲解**:三角形一共有三条边,【图图】向前100后,完成第一条边的绘制,然后需要向右旋转120度,接着又向前100,完成第二条边后再向右旋转120度,向前100,完成最后一条边的绘制
+
+```plain
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+#连续画三条边
+t.forward(100)
+t.right(120)
+t.forward(100)
+t.right(120)
+t.forward(100)
+t.right(120)
+t.done()
+```
+# 🚀挑战3:
+
+通过学习后你已经能画出三角形了,那么,再用同样的方式来试试正方形吧
+
+
+
+# 🚀挑战4:
+
+看来你已经能绘制简单图形了,那么现在来尝试一下复杂一点的“十字”图吧,方法和前面的图形差不多哦,但是注意每转动一次后移动的距离:
+
+
+
+真棒,这么快就完成了第一天的打卡内容了,是不是觉得还挺简单,哈哈,别着急,后面会逐渐提高难度,小心哦~
+
+
+
+
+
+
diff --git a/Turtle/Day2:你妈妈叫你回家啦.md b/Turtle/Day2:你妈妈叫你回家啦.md
new file mode 100644
index 0000000..a6dddc0
--- /dev/null
+++ b/Turtle/Day2:你妈妈叫你回家啦.md
@@ -0,0 +1,183 @@
+# 🔑技能包
+
+别忘了昨天学习的技能哦:
+
+
+功能 | 指令
+---|---
+向前走|`t.forward(100)`
+向后走|`t.back(100)`
+向左转|`t.left(90)`
+向右转|`t.right(90)`
+
+---
+今天是第二天,主题是【你妈妈叫你回家啦】
+
+
+
+老师,你在开玩笑?
+
+哈哈,今天的指令确实和回家有关系,叫做【回家指令】,【回家指令】这是个啥?名字起得这么有创意(无聊)吗?难道要让图图回家?
+
+咳咳咳,回答正确,就是一个让图图回家的指令。
+
+# 回家指令介绍
+
+## (1)简介
+
+为什么叫做回家指令呢?这是因为他是通过英文名`home()`翻译过来的,通过这一条指令可以帮助图图回到起点,也就是说,即使你通过指令让图图跑到了千里之外,我也能用这个指令让他回来,是不是一个很6的指令:
+
+
+
+## (2)格式
+
+那么,这么6的指令可以用来做什么呢?我来举个例子🌰吧:
+
+### 📺示例1
+
+题目描述:请参考下面图片中的内容,画出一个直角三角形吧:
+
+
+
+只知道两个直角边分别是80和60,但是另外一条斜边长度不知道,这个时候怎么办呢?
+
+**路人甲:** 不知道哎
+
+**路人乙:** 我是初中生,我学过【勾股定理】可以算
+
+**隔壁小明:** 难道是用`home`指令
+
+是的,隔壁小明真聪明,通过`home`指令就能解决这个问题,最后一条边其实就是图图返回起点走的路:
+
+
+
+程序如下:
+
+```python
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(80)
+t.right(90)
+t.forward(60)
+t.home() # 返回起点
+t.done()
+```
+这样,通过`home`指令,让图图自动返回到起点,于是就画出了最后一条边,是不是非常简单,来试试吧!
+
+# 🚀挑战1
+
+题目描述:请参考下面图片中的内容,画出一个钝角三角形吧。
+
+(备注:钝角三角形就是有一个角度数大于90度的三角形)
+
+
+
+# 🚀挑战2
+
+题目描述:请参考下面图片中的内容,画出对应的图形吧。
+
+
+
+# 🚀挑战3
+
+有点厉害啊,已经解决了两个挑战了,那么咱们增加下难度吧!
+
+题目描述:请参考下面图片中的内容,画出有一条对角线的正方形吧。
+
+备注1:对角线就是两个相对的角顶点的连接线
+
+备注2:图图回到起点后会自动旋转到水平向右
+
+
+
+# 🚀挑战4
+
+能做到这里看来你已经掌握home指令的诀窍了,既然这样,那就来完成最后的挑战吧。
+
+题目描述:请参考下面图片中的内容,画出一个直角梯形。
+
+备注:上底就是较短的一条边,下底就是较长的一条边
+
+提示:上底、下底、高的长度需要你自己设定,只要能画出类似的直角梯形就可以啦
+
+
+
+
+# 参考答案
+
+挑战1:
+
+```
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+
+t.forward(80)
+t.right(60)
+t.forward(60)
+t.home() # 返回起点
+
+t.done()
+```
+
+
+挑战2:
+
+```python
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+
+t.forward(50)
+t.right(90)
+t.forward(100)
+t.left(90)
+t.forward(50)
+t.home() # 返回起点
+
+t.done()
+```
+
+
+挑战3:
+
+```python
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+
+t.forward(100)
+t.right(90)
+t.forward(100)
+t.home()
+t.right(90)
+t.forward(100)
+t.left(90)
+t.forward(100)
+
+t.done()
+```
+
+
+挑战4:
+
+```python
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+
+t.forward(100)
+t.right(90)
+t.forward(100)
+t.right(90)
+t.forward(200)
+t.home()
+
+t.done()
+```
diff --git a/Turtle/Day3:初识循环.md b/Turtle/Day3:初识循环.md
new file mode 100644
index 0000000..14bec66
--- /dev/null
+++ b/Turtle/Day3:初识循环.md
@@ -0,0 +1,129 @@
+今天,正儿八经给大家普及下新知识。
+
+⛽️知识加油站——循环
+
+循环在我们生活中非常普遍,比如我们乘坐旋转木马,旋转木马会一直循环,又比如说月球会一直不停绕着太阳旋转:
+
+
+
+而在编程中循环也是一个非常重要知识,它可以让程序一直重复执行,比如下面这个程序,虽然只输入了一句话,但是通过设置循环次数为5,就能打印5次“我喜欢看海贼王”:
+
+```plain
+for i in range(5):
+ print('我喜欢看海贼王')
+```
+## 循环的格式
+
+想使用循环非常简单,只需要按照下面的格式设置就可以了:
+
+```plain
+# 括号里填写你想循环的次数,写上冒号后,换行,空4个空格后就可以写循环的内容
+for i in range(次数):
+ 循环的内容
+```
+📺练习1:
+
+使用循环画一个正方形。
+
+
+
+一起来分析下,要画一个正方形,需要下面这些步骤:
+
+```plain
+向前100
+旋转90度
+向前100
+旋转90度
+向前100
+旋转90度
+向前100
+旋转90度
+```
+可以看成,我们要让计算机重复执行4次下面的内容:
+
+```plain
+下面的内容要重复执行4次:
+向前100
+向右旋转90度
+```
+这样就就可以写成循环了:
+
+```plain
+for i in range(4):
+ t.forward(100)
+ t.right(90)
+```
+完整代码:
+
+```plain
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+#连续画四条边
+for i in range(4):
+ t.forward(100)
+ t.right(90)
+t.done()
+```
+🚀挑战1:
+
+题目描述:通过循环画出一个边长为100的等边三角形
+
+备注:等边三角形就是三条边的长度相等、三个角角度都为60度的三角形
+
+
+
+🚀挑战2:
+
+题目描述:通过循环画出一个正六边形
+
+备注:正六边形每个角的度数(大小)都一样,6个角总共720度
+
+提示:需要先计算正六边形的每个角大小,再得出图图每次需要转多少度,这是小学三年级除法的难度,你敢说不会?ㄟ(▔︵▔ㄟ)
+
+
+
+🚀挑战3:
+
+能完成上面两道题,说明你还是很厉害的,那么咱们就提高一点难度吧,这道题你还能做对,那可就非常厉害了。
+
+题目描述:使用循环,画出一个五角星:(可以像上面那样,先写出文字步骤来分析一下哦~)
+
+👽拓展:如果画好了,还可以给五角星加上颜色
+
+
+
+🚀挑战4:
+
+光阴似箭,日月如梭,一转眼,你,竟然,做到了最后一道题,你,这么,厉害,爸妈知道吗?如果不知道就赶紧告诉他们吧。
+
+下面是第三天的终极挑战:画一个圆
+
+
+
+提示:画圆其实很简单,虽然你看着是一个圆,但其实,他可以看成是很多短短的边组成的,那么怎么来画圆呢?你可以看一看下面这个视频:
+
+[https://baike.baidu.com/item/%E5%89%B2%E5%9C%86%E6%9C%AF/595781?secondId=25702197](https://baike.baidu.com/item/%E5%89%B2%E5%9C%86%E6%9C%AF/595781?secondId=25702197)
+
+
+
+看完视频是不是发现啦,古代人通过在圆内画多边形来近似测量圆一周的长度,多边形边越多,形状上就越接近圆,那么基于这个方法,我们可以用图图来帮我们画一个圆,怎么来画呢,我们知道圆有360°,也就是说,如果要画圆,【图图】需要围绕中心走360次,每一次走一步,每走一步向右转1度,画出一个有360边的多边形就可以了。
+
+下面就是画圆的关键,如果你不能理解,那就记住这个有趣的画圆公式吧:
+
+```plain
+import turtle as t
+
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+#请删除这一行,然后写上循环360次的程序吧
+ t.forward(1) #向前走一步
+ t.right(1) #向右转一度
+
+t.done()
+```
+如果你已经画好了圆,再试一试修改forward里面的数字,看看会发生什么变化~
+
+#
+
diff --git a/Turtle/Day4:up!up!down!down!.md b/Turtle/Day4:up!up!down!down!.md
new file mode 100644
index 0000000..f329815
--- /dev/null
+++ b/Turtle/Day4:up!up!down!down!.md
@@ -0,0 +1,94 @@
+A:老师,你是在欺负我英语不好吗?整个英文标题
+
+老师:对啊,你怎么知道我在欺负你
+
+A:... ...
+
+# 抬笔与落笔
+
+## (1)简介
+
+今天我们一起来学习一个新的技能【抬笔】与【落笔】。
+
+前面我们画了这么多图形,但是大家有没有发现,我们从来没有抬过笔,这是一件非常不科学的事,就好比,你笔尖从没离开过画纸,但却写下了下面这四个字(不能写连笔):
+
+
+
+
+所以,在常规的绘画和写字中,我们其实是需要【抬笔】和【落笔】这两个动作的,同样的,图图也有这两个指令。
+
+## (2)格式
+
+```python
+t.up() # 抬笔
+t.down() # 落笔
+```
+把这两句放到完整的程序中,先前进100步,然后抬笔,前进50步,然后落笔,然后再前进100步,
+
+想一想可能画出的图形是什么样子,然后再运行一下这段代码看一看吧:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(100)
+t.up() #抬笔
+t.forward(50)
+t.down() #落笔
+t.forward(100)
+t.done()
+```
+
+# 🚀挑战1
+
+题目描述:画出一条虚线
+
+(1)实线每一段长为10
+
+(2)间断距离为5
+
+提示:使用循环会更方便哦
+
+
+
+# 🚀挑战2
+
+题目描述:绘制8条平行线
+
+(1)每条线的长度为100
+
+(2)相邻两条线同一端之间的距离为20
+
+(备注:平行线倾斜程度自己设定就好,可以用文字写出走的步骤,看看循环的部分在哪里)
+
+
+
+# 🚀挑战3
+
+不知不觉,又来到了最后一题,哦不对,是倒数第二题,这一题和上面一题难度差不多,耐心一点就能画出来。
+
+题目描述:请画出四个平行的小旗子
+
+(1)旗子高40
+
+(2)旗面宽50
+
+
+
+# 🚀挑战4
+
+不知不觉,终于来到了最后一题,你还记得之前画过的圆吗?这次有了抬笔功能的配合,我们就可以画出一个很常见的汽车标志啦:
+
+(1)两个圆中心之间的距离是85
+
+(2)想一想每画完一个圆后【图图】要向前移动多少呢?
+
+
+
+画一个圆的关键步骤参考:
+
+```python
+for i in range(360):
+ t.forward(1)
+ t.right(1)
+```
diff --git a/Turtle/Day5:循环升级.md b/Turtle/Day5:循环升级.md
new file mode 100644
index 0000000..ccf3f7c
--- /dev/null
+++ b/Turtle/Day5:循环升级.md
@@ -0,0 +1,138 @@
+**老师**:通过两天的训练,相信大家对于循环已经掌握的非常好了,今天我们要学习的是【循环中的循环】。
+
+**A**:【循环中的循环】?老师,你是在传授武林秘籍吗?
+
+**老师**:你是猴子派来的吗?总想着武林秘籍
+
+**A**:那什么是【循环中的循环】啊?
+
+**老师**:听我细细道来
+
+# 循环中的循环
+
+循环中的循环是编程中常用的一种程序的结构,它也被称为【循环嵌套】,也就是在一个大循环里套着小循环,听起来有点复杂,但其实非常的简单,一起来学习一下吧!
+
+在学习【循环嵌套】前我们先来练习一道题目,这样有助于我们理解【循环嵌套】的含义。
+
+# 🚀挑战1
+
+题目描述:参考下面图示,借助循环,画出四个并排在一起的正方形。
+
+(1)正方形的边长是40
+
+(2)两个正方形之间的距离是20
+
+
+
+⬇️⬇️⬇️ 做完后再看,实在做不出来也可以看,不到万不得已还是别看 ⬇️⬇️⬇️
+
+**解析**:大家说如果要画四个正方形,需要重复画几个一样的正方形?
+
+4个对吧,那如果用图图来画一个正方形需要重复几次【向前走100向右转90度】呢?
+
+也是4次,所以我们来看看,如果要通过图图来画出它需要怎么做:
+
+```python
+#画第一个正方形
+for i in range(4):
+ t.forward(40)
+ t.right(90)
+# 画完后要向前移动到到第二个正方形的顶点,
+# 需要向前移动60步,移动的时候是抬笔的状态
+t.up()
+t.forward(60)
+t.down()
+```
+
+
+如果还要画三次应该怎么办呢?哈哈,对的,继续用同样的语句三遍就行了。
+
+```python
+#画第一个正方形
+for i in range(4):
+ t.forward(40)
+ t.right(90)
+t.up()
+t.forward(60)
+t.down()
+
+#画第二个正方形
+for i in range(4):
+ t.forward(40)
+ t.right(90)
+t.up()
+t.forward(60)
+t.down()
+
+#画第三个正方形
+for i in range(4):
+ t.forward(40)
+ t.right(90)
+t.up()
+t.forward(60)
+t.down()
+
+#画第四个正方形
+for i in range(4):
+ t.forward(40)
+ t.right(90)
+t.up()
+t.forward(60)
+t.down()
+```
+这个时候你发现了什么,是不是下面段落连续出现了4次,我们学习循环时说过,当重复不断出现时可以使用循环,这里仍然可以的,将这个循环的逻辑写成中文就是:
+
+```python
+下面的内容要循环4次:
+ for i in range(4):
+ t.forward(40)
+ t.right(90)
+ t.up()
+ t.forward(60)
+ t.down()
+```
+把中文也变成程序,和之前循环是一样的方式,加上`for i in range()`,但是一定要记得,后面这个整体前面有四个空格,还记得之前讲循环的时候说过吧,加四个空格是为了告诉程序,下面的内容归我管,要循环4次,可不要忘了哦:
+
+
+
+是不是觉得好像听懂了,又好像有一点疑惑,怎么办呢?很简单,再来做两道题自然就懂了。
+
+# 🚀挑战2
+
+题目描述:参考下面的图示,借助循环,画出四个并排在一起的三角形。
+
+提示:
+➡️可以不用循环嵌套,但是呢,使用循环嵌套又会更简单,算了,用不用看你吧!
+
+➡️如果使用嵌套,你可以参考上面画4个正方形的方法哦,先用中文分析循环次数,再写成程序。
+
+(1)等边三角形的边长是40
+
+(2)两个三角形之间的距离是20
+
+
+
+# 🚀挑战3
+
+不得了不得了,已经做到第3题了,少年我看你天赋异禀啊!
+
+题目描述:参考下面的图示,借助循环,画出一个风车
+
+
+
+👽拓展:在风车的基础上进行创作吧,看看你的风车能比下面的好看吗?
+
+
+
+
+
+# 🚀挑战4(选做)
+
+这道题选做哦,如果你觉得前面的已经难不倒你了,那就再来试试这一道题吧!
+
+题目描述:参考下面的图示,借助循环,画出一个飞镖
+
+(1)菱形的两个角分别是60°和120°
+
+
+
diff --git a/Turtle/Day6:乾坤大挪移——坐标.md b/Turtle/Day6:乾坤大挪移——坐标.md
new file mode 100644
index 0000000..74be9dc
--- /dev/null
+++ b/Turtle/Day6:乾坤大挪移——坐标.md
@@ -0,0 +1,93 @@
+# 1、坐标
+
+地瓜:土豆土豆,我是地瓜,我现在已经被敌人包围了,请求支援。
+
+土豆:地瓜地瓜,我是土豆,请立刻告诉我你的坐标。
+
+
+
+什么是坐标呢?
+读完上面这个对话你肯定有点感觉了吧,坐标就是一个物体在空间中的位置,比如上面飞机在天空中的位置,只有告诉友军他的位置,友军才能前去营救。
+
+又比如说下面这个图,就是一个平面空间,我们在上面画了两根轴来帮助大家记录坐标,这两根轴就叫做坐标轴,两根轴交叉的位置记为坐标(0,0),那么怎么来读取坐标呢?其实非常简单,看【图图】对应坐标轴上的数字就可以了。
+
+
+
+就比如这样,图图的位置分别对应横轴的1和纵轴的3,所以它的坐标是(1,3):
+
+
+
+## 🚀挑战1
+
+题目描述:请你写出图图在下图中的位置:
+
+(对应横轴和纵轴来看哦~)
+
+
+
+# 2、goto功能
+
+那么,怎么才能帮图图到指定的坐标呢?
+这就要使用到一个有趣的功能goto,它可以帮助图图去到指定的坐标位置,但是在使用之前需要记住两个重要秘诀:
+
+**秘诀1:如果使用goto功能时没有抬笔,那么图图会向着指定的位置画过去**
+
+这个秘诀说的是什么意思呢?我们一起来看看:
+
+(1)goto语句的用法
+
+```python
+t.goto(x, y) # x,y就是对应的坐标
+```
+如果我使用下面这一段语句,你猜猜会发生什么:
+
+```python
+t.goto(80,80)
+```
+出现了下面的图像,原因是我们让图图去坐标(80,80)的位置,所以图图就直接移动过去了,不过使用goto语句,图图的朝向是不会改变的哦!
+
+
+
+那么,如果我想让图图**瞬间移动**过去要怎么办呢,这时候就要看秘诀2了。
+
+**秘诀2:要让图图瞬间移动到某个坐标,而不留下痕迹,就要使用抬笔和落笔功能**
+
+```python
+t.up()
+t.goto(x,y) # 比如t.goto(80,80)
+t.down()
+```
+## 🚀挑战2
+
+请你将图图**瞬间移动**到坐标为(100,100)的地方,如下图:
+
+(提示:下图中的红色圆圈只是示意图图的初始位置,忽略就可以)
+
+
+
+# 3、乾坤大挪移
+
+有小伙伴儿会问:“乾坤大挪移是什么?”,很简单,就是让图图进行各种移动,各种来考你的题目,hiahiahiahia~
+
+## 🚀挑战3
+
+还记得小时候用过的钉板吗?我们通过钉板制作各种各样的图形,比如下面这种。
+
+那么现在请使用goto语句,参考下面的坐标画出对应的图形:
+
+(备注:如果画出来的图形很小,可以把坐标都放大10倍哦,比如把(1,1)改成(10,10),把(5,1)改成(50,10))
+
+
+
+## 🚀挑战4
+
+看来你已经简单了解了坐标和使用坐标的方式,那么,再来考考你吧。
+
+题目描述:请先将图图移动到坐标为(100,100)的位置,然后画出一个边长为50的五角星
+
+(备注:五角星的每个角都是36°,其它角的参数参考下图2)
+
+
+
+
+
diff --git a/Turtle/Day7:最后的挑战.md b/Turtle/Day7:最后的挑战.md
new file mode 100644
index 0000000..d5d5787
--- /dev/null
+++ b/Turtle/Day7:最后的挑战.md
@@ -0,0 +1,80 @@
+
+恭喜你已经完成了前六天的任务,在前六天中你学习到了编程中的循环,画图模块中的方向功能、抬笔功能、颜色填充功能、回家功能,并且熟悉了常见的三角形、多边形、圆形,能够坚持到第七天,你一定非常厉害,既然这样,那么就请准备好,迎接最后的挑战吧!
+
+# 最后的挑战
+
+世界上有非常多的国家,咱们中国只是其中一个,除了中国,还有很多国家分布在世界各地,他们有的领土大,有的领土小,有的很有名气,有的可能你还没听说过,但是无论哪个国家,他们都有一个象征自己国家的物品,你知道是什么吗?
+
+
+
+对啦,这个物品就是国旗,即使是新成立的国家,也需要设计属于自己的国旗,而每一种国旗都有自己不同的含义,比如咱们中国的国旗,这可不是简单地在上面涂个颜色、画几个星星,星星的角度和数量都是有讲究的。在中国国旗上,红色象征革命,旗上的五颗五角星及其相互关系象征共产党领导下的革命人民大团结。五角星用黄色是为了在红底上显出光明,四颗小五角星各有一尖正对着大星的中心点,表示围绕着一个中心而团结。
+
+
+
+当然啦,其他国家的国旗也有属于自己国家、自己历史的意义。比如冰岛,这可不是一个岛,他也是一个国家,他的国旗是这样的:
+
+
+
+采用了红色、蓝色和白色,象征冰岛是屹立于汪洋大海的一个炽热而又被冰雪覆盖的美丽岛国,十字图案源自丹麦国旗图案,表示冰岛历史上与挪威、丹麦的关系。
+
+国旗上面的图案虽然看起来简单,但是要画出来可不容易,今天我们就为大家准备了下面2种国旗,选择1种你觉得对自己有一定挑战的国旗,并通过图图将它画出来吧。
+
+# ⛽️加油站—图层
+
+在开始画图前我们需要再学习一个重要的知识——图层,认识了图层,你使用图图就能起到事半功倍的作用。
+
+什么是图层呢?
+其实非常简单,你可以理解成一张图是由多层图叠在一起的,比如下面的【瑞士国旗】:
+
+
+
+它可以由两层组合在一起,最下面一层是红色,上面一层是白色的十字。所以,如果要使用图图,就可以先画最下面一层红色背景,再画白色的十字。
+
+## 📺练习1
+
+说说下面的【加拿大国旗】可以由几层组成,分别是哪几层呢?
+
+
+
+答案:
+可以有三层组成,最下面一层是红色长方形,中间层是白色长方形,最上面一层是红色枫叶。
+
+## 🚀挑战1
+
+**任务:绘制冰岛国旗 难度系数🌟🌟🌟**
+
+参考:
+
+- 设置成蓝色:t.color('#0048E0')
+- 设置成红色:t.color('#FF0F00')
+- 设置成白色:t.color('white')
+
+
+
+参考坐标图:
+
+
+
+## 🚀挑战2
+
+**任务:绘制朝鲜国旗 难度系数🌟🌟🌟🌟**
+
+参考:
+
+(1)
+
+- 设置成蓝色:t.color('#0048E0')
+- 设置成红色:t.color('#FF0F00')
+- 设置成白色:t.color('white')
+
+(2)
+
+- 五角星的小边长度为23
+
+
+
+参考坐标图:
+
+
+
+
diff --git a/Turtle/readme.md b/Turtle/readme.md
index 72f7278..58e3e92 100644
--- a/Turtle/readme.md
+++ b/Turtle/readme.md
@@ -1,2 +1,58 @@
-## 简介
+# 6. 青少年编程(Turtle)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/Turtle
+
+## 基本信息
+- 贡献人员:王思齐、马燕鹏、王皓月、杨煜、舒敏、赵可
+- 学习周期:9天
+- 学习形式:练习
+- 人群定位:Turtle初学者
+- 难度系数:低
+
+## 学习目标
+
+通过绘制图形的小例子,由浅入深带着小朋友们熟悉Turtle的使用。
+
+## 任务安排
+
+### Task00:安装软件,熟悉规则(1天)
+
+- 组队、修改群昵称
+- 熟悉打卡规则
+
+### Task01:预备课1、预备课2(2天)
+- 熟悉Turtle基本指令
+- 参与挑战
+
+
+### Task02:画几个简单的图形(1天)
+- 学习示例
+- 参与挑战
+
+### Task03:你妈妈叫你回家啦(1天)
+- 学习示例
+- 参与挑战
+
+### Task04:初识循环(1天)
+- 学习示例
+- 参与挑战
+
+### Task05:up!up!down!down!(1天)
+- 学习示例
+- 参与挑战
+
+
+
+### Task06:循环升级(1天)
+- 学习示例
+- 参与挑战
+
+
+### Task07:乾坤大挪移——坐标(1天)
+- 学习示例
+- 参与挑战
+
+### Task08:最后的挑战(1天)
+- 学习示例
+- 参与挑战
diff --git a/Turtle/参考答案.md b/Turtle/参考答案.md
new file mode 100644
index 0000000..e2f8b2a
--- /dev/null
+++ b/Turtle/参考答案.md
@@ -0,0 +1,21 @@
+
+
+
+
+# 参考答案
+
+- [如何安装和配置Python的开发环境?](https://mp.weixin.qq.com/s/T11-ixtWGrPE_2aXu1lWxQ)
+- [预备课1:认识新伙伴图图](https://mp.weixin.qq.com/s/eJy4-DDIAc65uTvHkAGqxw)
+- [预备课2:图图的其他技能](https://mp.weixin.qq.com/s/o9PqXo9lhGoD00AXF4IK-w)
+- [Day01:画图基础](https://mp.weixin.qq.com/s/46UbQSrA49Vq0lh7xhc1Jw)
+- [Day02:你妈妈叫你回家啦](https://mp.weixin.qq.com/s/Cw8qMk7lojR5nTAKBPJucw)
+- [Day03:初识循环](https://mp.weixin.qq.com/s/eOdqaJbOvIftpSGno0pfvA)
+- [Day04:up!up!down!down!](https://mp.weixin.qq.com/s?__biz=MzIyNDA1NjA1NQ==&mid=2651019390&idx=2&sn=785e6ecba84fec4928f84c7fca42fe16&chksm=f3e33fe6c494b6f034da030099b1d87169e25ae7da401352edda14ac68245d36d21d78735f0a&token=62210453&lang=zh_CN#rd)
+- [Day05:循环提升](https://mp.weixin.qq.com/s?__biz=MzIyNDA1NjA1NQ==&mid=2651019472&idx=2&sn=d5189973afeb64dc61daf6409171e116&chksm=f3e33f48c494b65ed7e7acaa8dc648ad541fd50e156d093766ffff3cdcf124dfd9e13f1a20c4&token=62210453&lang=zh_CN#rd)
+- [Day06:乾坤大挪移——坐标](https://mp.weixin.qq.com/s?__biz=MzIyNDA1NjA1NQ==&mid=2651019719&idx=2&sn=f48b94e7c9bc31adeb84406737e7410a&chksm=f3e33e5fc494b749fd6ba14ce7a3bd8d821db670686e751c91f2b756e718ab716063521b762d&token=1516986273&lang=zh_CN#rd)
+- [Day07:最后的挑战](https://mp.weixin.qq.com/s?__biz=MzIyNDA1NjA1NQ==&mid=2651019754&idx=2&sn=6837db921b69ac68d8829813efaedfb5&chksm=f3e33e72c494b76425bb82d942b2b6567c44386d5e7ab3874cfc69a006383f0a6adf01f9c9a8&token=1516986273&lang=zh_CN#rd)
+
+
+
+
+
diff --git a/Turtle/安装Python与配置.md b/Turtle/安装Python与配置.md
new file mode 100644
index 0000000..49ddaff
--- /dev/null
+++ b/Turtle/安装Python与配置.md
@@ -0,0 +1,234 @@
+本篇主要介绍 Python 的安装与环境配置方法。Python作为一门通用型的编程语言,可以通过很多方法完成安装,同时,也可根据实际需求搭建不同类型的开发环境。由于 Jupyter 是最通用的开发环境,同时,Jupyter 本身也是 Notebook 形式的开发环境,非常适合初学者上手使用。因此,本次内容将主要采用 Jupyter Notebook/Jupyter Lab 来进行演示,本篇也将详细介绍如何通过通用科学计算平台 Anaconda 来进行 Python和Jupyter 的安装。
+
+
+# 1 Anaconda下载与安装
+
+Anaconda 是一个工具包,将 Python 和许多与科学计算相关的库捆绑在一起,形成了一个方便的科学计算环境,你安装了 Ananconda 就相当于安装了 Python 外加这些库,省去了自己下载和安装各种库的麻烦,方便初学者专注于学习 Python。
+
+
+
+此处,我们采用 Anaconda 进行 Python 安装和开发环境搭建。
+
+
+## 1.1 下载Anaconda
+
+访问Anaconda官网(https://www.anaconda.com),在下拉菜单中的 Products 里选择 Individual Edition,个人版,同时也是免费版。此版本中不涉及付费内容,可供个人用户使用。
+
+
+
+进入页面后,点击Download,会自动跳转到操作系统选择的界面。
+
+
+
+此时,可根据自身操作系统进行选择和下载。
+
+
+
+当然,windows 64的用户也可直接通过下述网盘连接进行下载,该版本为 Anaconda3-2020.11-Windows-x86_64。
+
+- 链接:https://pan.baidu.com/s/1IEasB0epWpPRhgYdgSCHaA
+- 提取码:i6zj
+
+## 1.2 安装Anaconda
+
+下载完成后,即可开始安装。双击安装文件,进入欢迎界面,点击 Next。
+
+
+
+点击同意,进入到下一步。
+
+
+
+选择软件使用权限,是指针对当前登录用户还是所有用户,二者都行,无特殊要求。
+
+
+
+选择安装位置,完成安装。
+
+
+
+如果出现此页面,需要勾选配置环境变量选项。
+
+
+
+无需安装VS Code,直接跳过即可。
+
+
+
+安装完成后,在开始菜单栏,或者软件安装位置,找到 Anaconda Navigator 并打开。
+
+
+
+进入到如下界面。
+
+
+
+我们能看到 Anaconda 中集成了非常多数据科学计算相关的功能,并且,在安装过程中,也完成了 Python 的安装和环境变量的设置,以及 Jupyter和PyCharm 的安装。其中 Jupyter 是本次学习将用到的代码编辑工具,而 PyCharm 则是一款集成开发环境(IDE),本次学习并不涉及。
+
+
+## 1.3 启动Jupyter
+
+我们能够看到,在 Anaconda 中有两个 Jupyter 组件,一个是**Notebook**,一个是**JupyterLab**。其中,Lab 是 Notebook 的升级版,用户交互界面更加友好,并且拥有许多额外辅助功能,例如代码框分屏、文件管理系统等,但相比 Notebook,Lab 并不支持第三方插件,因此如果是想使用 Jupyter 丰富的插件,则只能选择 Notebook。不过二者在实际编程的功能使用上没有区别,本次学习推荐使用 JupyterLab。
+
+点击 JupyterLab,启动相关服务,系统会自动打开浏览器并进入到 JupyterLab 界面。
+
+
+
+能够成功弹出浏览器窗口,则说明安装成功。如果浏览器关闭,再次点击 Anaconda 中 Jupyter Lab 组件中的 Launch 即可再次打开 Jupyter 界面。
+
+
+
+或者在浏览器里直接输入 http://localhost:8890/lab。
+
+
+---
+# 2 Jupyter基本操作
+
+接下来,简单介绍 Jupyter 的基本操作。
+
+## 2.1 简单代码编写尝试
+
+在 JupyterLab 主界面中,左边是文件目录,右边是编程界面,首次登陆时,点击 Python3 即可创建一个新的编程文件。
+
+
+
+如下所示:
+
+
+
+同时,在左侧文件目录,也会出现一个新的`ipynb`文件,也就是正在编辑的代码文件。
+
+> ipynb 文件是 ipython Notebook 的简写,Jupyter 脱胎于 ipython 编辑器,因此 Jupyter 文件仍然保留了 ipynb 的文件类型命名方式。
+
+接下来,简单尝试在右侧代码框中输入 Python 代码。点击右侧代码框(cell)中输入`a = 1`。
+
+
+
+
+
+也就是令`a = 1`,然后`shift+enter`执行该代码。执行完成后,会自动新生成一个 cell,接下来的代码就可以在新生成的 cell 中执行。在新生成的 cell 中,输入`a`能够看到,返回结果就是`a`的赋值。
+
+
+
+至此,我们就完成了一次简单的 Python 代码编写和运行。
+
+## 2.2 Notebook式编辑环境
+
+将代码写入一个个**cell**,代码文件由一个个cell组成,书写代码时就像一行一行在记笔记,就是所谓的 Notebook 式的代码编辑环境。Notebook 式代码编辑环境其实也是 REPL(Read Eval Print Loop)环境的一种,即交互式编译。简单来说,交互式编译就是指允许用户逐行输入代码、逐行查看结果,从而逐行进行调试。这无疑是大幅降低了代码编写的难度,这也是建议 Python 初学者使用 Jupyter 的原因。
+
+## 2.3 Jupyter的基本操作
+
+由于后续 Jupyter 将作为主力代码编辑器,因此我们有必要深入了解 Jupyter 的一些常用功能。当然,Jupyter 本身也是一个独立的软件,具体软件的功能介绍可以查看 [Jupyter](https://jupyter.org/) 官网(https://jupyter.org),里面有 Jupyter 所有功能的完整介绍。
+
+
+
+此处先介绍实际学习过程中常用的功能。
+
+### 2.3.1 cell类型选择
+
+在 Jupyter 中,每个 cell 除了代码以外,还可以使用 Markdown 语法输入文本内容,以及尚未确定格式的草稿。
+- 选定一个 cell 后,选择 code 则是代码内容;
+- 选择 Markdown 则是使用 Markdown 语法输入文本内容;
+- 选择 Raw 则是草稿内容,不会输出任何结果。
+
+
+
+例如,使用Markdown语法打印标题:
+
+
+
+同样,是`shift+enter`执行 Markdown 语法。
+
+
+
+可以看出,jupyter 还是个不错的笔记工具,同时,也非常适合编写数据分析报告。
+
+### 2.3.2 cell不同模式及快捷键
+
+cell 有两种不同模式,选中 cell 时是 **command(命令)** 模式,而单击 cell 内,出现光标闪烁时,则是进入了 cell 内容的 **edit(编辑)** 模式,在编辑模式下,可以进行内容输入,而在命令模式下,则可使用一些 cell 快捷键对其进行操作。
+
+
+快捷键 | 操作| 快捷键 | 操作
+:---:|---|:---:|---
+a | 在上方插入一个cell | b | 在下方插入一个cell
+x | 剪切该cell | c | 复制该cell
+v | 在cell下方粘贴复制的cell | m | 转为markdown模式
+y | 转为code模式 | r | 转为raw模式
+z | 撤销操作 | 双击d | 删除该cell
+
+
+### 2.3.3 JupyterLab 文件管理系统
+
+相比 Notebook,JupyterLab 拥有非常便捷的文件管理系统,我们前面已经尝试,当创建一个新的`ipy`文件时,左侧文件栏将出现对应文件。JupyterLab 左侧就是其文件管理界面,在其中,我们可以进行文件创建、文件夹创建、文件上传等操作。
+
+
+
+
+### 2.3.4 JupyterLab 文件系统主目录及修改方式
+
+那么,我们创建的`ipy`文件存在哪呢?
+在 Anaconda 中,一般系统会默认 Jupyter 的主目录就是系统的文档目录。但文档目录在 C 盘下,如果是首次安装 Jupyter,并希望单独设置一个文件夹作为默认主目录,可以按照如下步骤进行操作:
+
+
+**(1)在 Anaconda 中打开 CMD.exe Prompt,进入命令行界面**
+
+
+
+当然,此处也可以`win+r`,然后输入`cmd`进入命令行。
+
+
+
+
+
+
+**(2)生成 Jupyter 配置文件**
+
+在命令行中,输入
+
+```python
+jupyter notebook --generate-config
+```
+
+
+
+注意上述配置文件的保存路径。若已有配置文件,再次输入命令将可选择是否覆盖原配置文件。当然,覆盖原配置文件将导致原配置失效。
+
+
+
+**(3)修改主目录配置**
+
+接下来,按照命令行中提示的配置文件路径,找到配置文件。
+
+
+
+可以用文本编辑器打开,能够看到所有的 Jupyter 可选配置。
+
+
+
+`ctrl+f`进入搜索栏,搜索`c.NotebookApp.notebook_dir`
+
+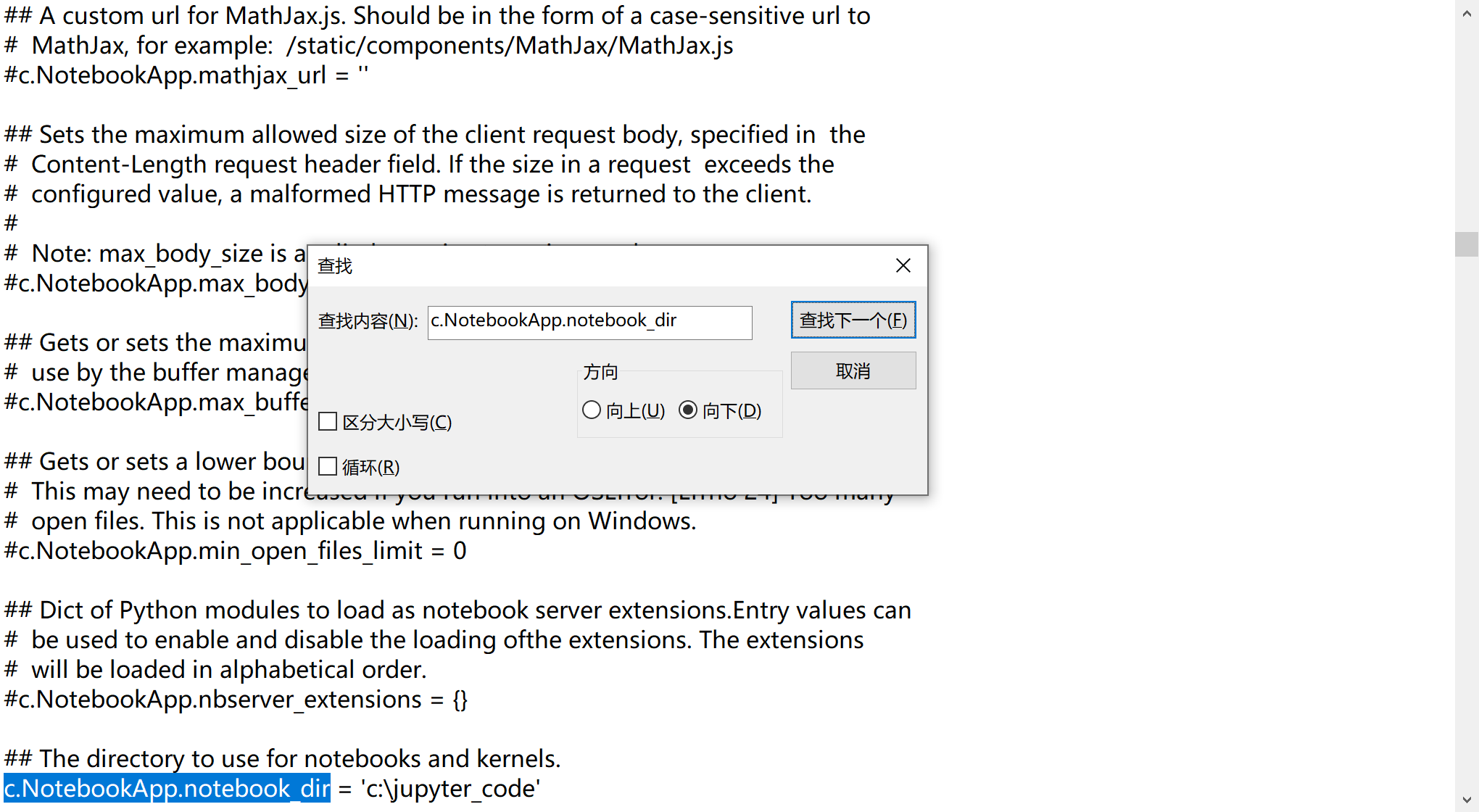
+
+将对应位置的#号删除,使其配置生效,并在等号后面输入新的主目录文件夹位置(自行选择文件位置),保存退出,并在**重启Jupyter后生效**。
+
+
+**(4)查看新的主目录**
+
+进入对应文件夹位置,查看文件夹内文件和 JupyterLab 内显示文件是否一致。
+
+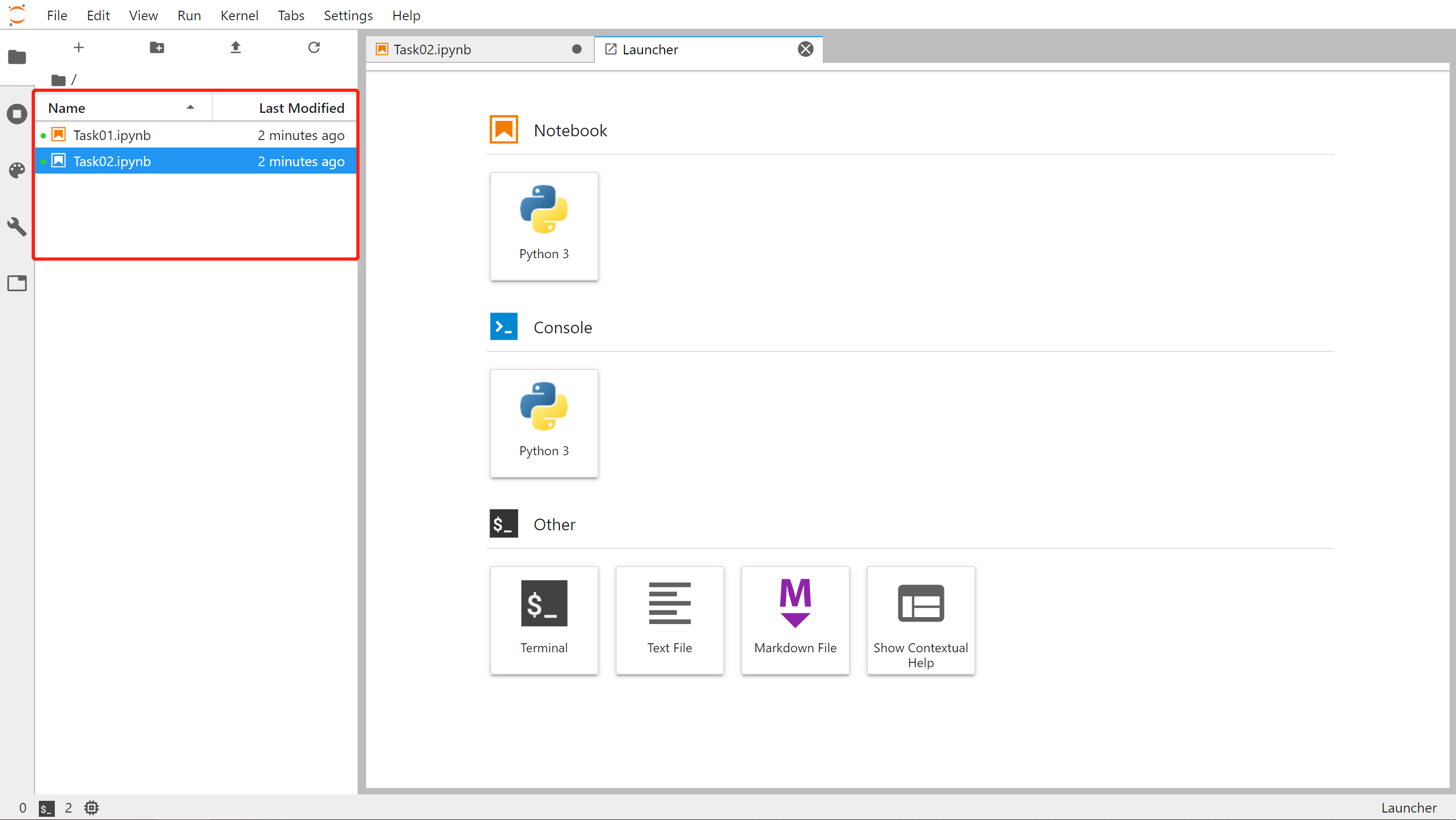
+
+
+
+至此,新的主目录文件设置成功。当然,任何对主目录文件的操作都会同步至 JupyterLab 的文件栏页。
+
+> 不难发现,Jupyter文件系统主目录就类似于其他编程语言的操作空间概念。
+
+### 2.3.5 停止`ipy`进程
+
+由于 Python 代码在运行过程中,对象都存储在内存中,因此,为了合理控制内存,在必要的情况下需要手动终止 Jupyter 进程。此时可以使用左侧栏的 KERNEL SESSIONS 功能,进行操作。
+
+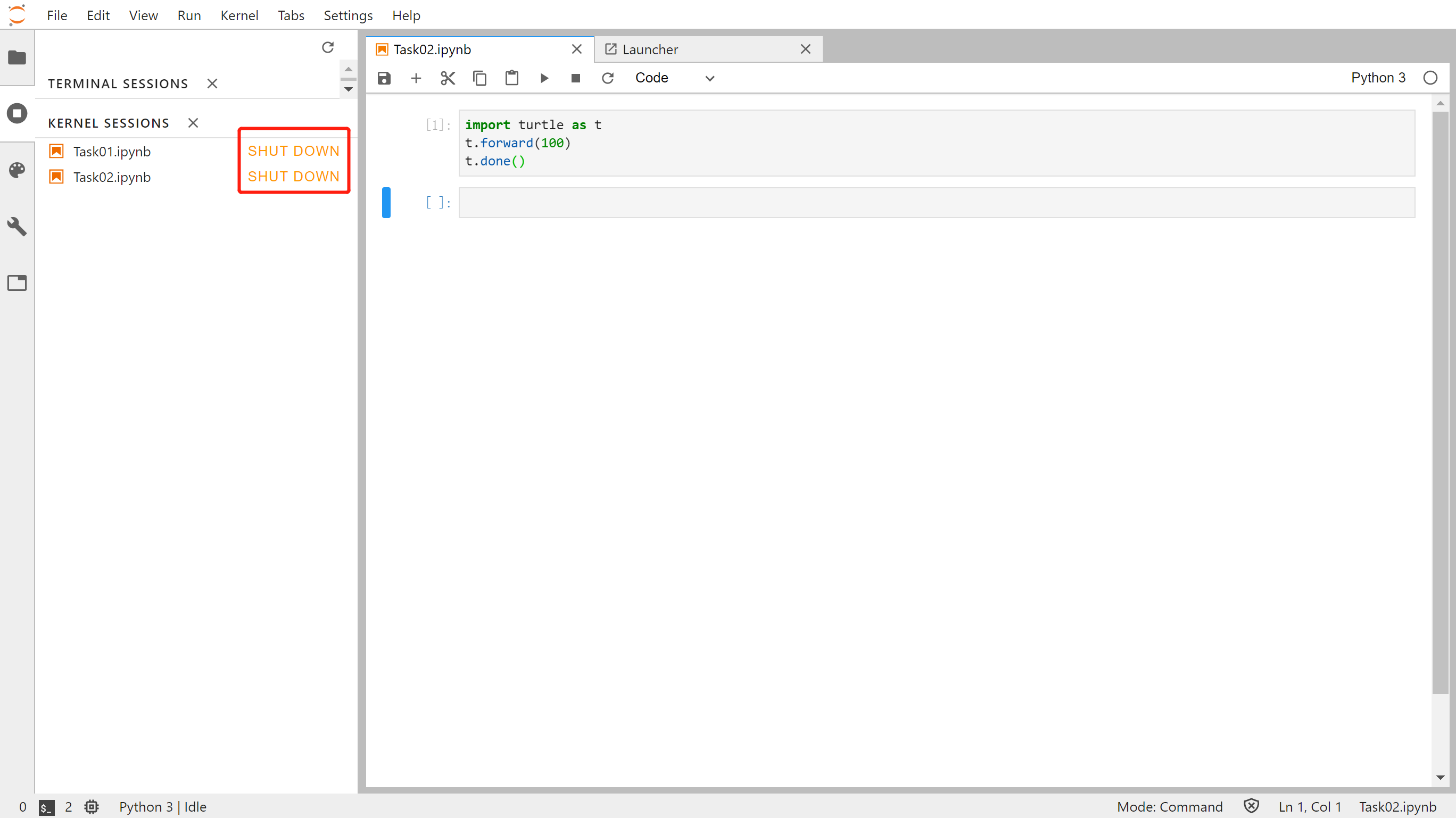
+
+点击 SHUT DOWN 即可关闭对话。
+
diff --git a/Turtle/预备课1:认识新伙伴图图.md b/Turtle/预备课1:认识新伙伴图图.md
new file mode 100644
index 0000000..d5859f2
--- /dev/null
+++ b/Turtle/预备课1:认识新伙伴图图.md
@@ -0,0 +1,149 @@
+# 1、Turtle图图
+
+在开始练习前,先来认识一下接下来会陪伴你好几天的程序小伙伴儿turtle【图图】吧,为什么叫做turtle【图图】呢,是因为它长这样:
+
+
+
+弄错了,是这个:
+
+
+
+虽然有点丑丑的,但确实是一直货真价实的乌龟,乌龟的英文是turtle,你也可以叫它【图图】,当然你要是叫它小乌龟,也......没啥问题......😓
+
+# 2、图图的设置
+
+天啊!乌龟竟然能画图,开玩笑吗?
+
+不过这确实是一只会画图的乌龟,就像乌龟在海滩上爬行能留下痕迹一样,程序中的【图图】也能帮助我们画出各种各样的线条。
+
+
+
+## (1)导入图图库
+
+想要使用图图帮助你画图,需要提前做一些设置,设置很简单,一共就两步:
+
+1、导入图图库
+
+2、设定重要信息
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.done()
+```
+**第一行** 就是导入【图图】库,然后给图图起了个新的名字t(后面会用到)
+
+**第二行** 是固定的设置,咱们每次写上就行
+
+**第三行** 是给图图设置一个形状,这里是turtle(乌龟形状),你也可以改成下面的英文:
+
+```python
+arrow circle square triangle classic
+```
+
+**第四行** 也是一定要有的语句,它的作用是告诉程序,“我画完啦!”
+
+### 练习1:
+
+将第四行的`?`改成其它几个英文单词,看看有什么不一样吧:
+
+(单词:`arrow` `circle` `square` `triangle` `classic`)
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='?')
+t.done()
+```
+# 3、行动吧!图图
+
+## (1)图图走起来
+
+掌握了图图的基本设置,就可以让图图开始行动啦,我们先学习最简单的向前走:
+
+```python
+t.forward(100) # 向前走100步
+```
+想让图图向前走几步,数字就是多少,把这行代码写入到前面的程序中试试:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(100) #向前走100步
+t.done()
+```
+既然有向前走,那么,当然还有向后退,赶紧试试吧:
+
+```plain
+t.back(100) # 向后退100步
+```
+## (2)向左转
+
+既然能走,当然可以转弯啊,图图可是“艾科不来梅西多亚瑟星球”最能转的乌龟
+
+向左转也很简单,就是下面这个口令啦:
+
+```python
+t.left(90) #向左转90度
+```
+再加上向前走我们就能画出一个直角啦:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(100) #向前走100步
+t.left(90) #向左转90度
+t.forward(100) #向前走100步
+t.done()
+```
+
+### 挑战1:
+
+(1)修改`left`中的角度,看看图图能画出下面这些角吗?(钝角和锐角)
+
+(2)除了向左转,也有向右转哦,它的指令是这样的`t.right(100)`,赶紧试试吧!
+
+
+
+
+
+### 练习2:
+
+如果要画出下面这个角度为30度的角应该怎么办呢?
+
+
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(100) #向前走100步
+t.right(30) #向右转30度
+t.forward(100) #向前走100步
+t.done()
+```
+这样写对吗?
+
+哈哈,当然不对,来画一条辅助线看看,图图实际转动的度数是红色箭头指示的角度,我们知道平角等于180度,平角也就是下面这个平平的线啦:
+
+
+
+所以图图实际转动的角度等于180 - 30 = 150,之后我们会画很多这样的角,你也可以做一条辅助线,用180减去标出来的角,就是要转动的角度啦:
+
+
+
+正确的写法:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.forward(100) #向前走100步
+t.right(150) #向右转150度
+t.forward(100) #向前走100步
+t.done()
+```
+
diff --git a/Turtle/预备课2:图图的其他技能.md b/Turtle/预备课2:图图的其他技能.md
new file mode 100644
index 0000000..fdfbe26
--- /dev/null
+++ b/Turtle/预备课2:图图的其他技能.md
@@ -0,0 +1,74 @@
+学完【预备课1】你是不是认为图图只是一个能简单移动的乌龟?
+
+其实图图的能力相当强大,当你学的知识越来越多后甚至可以使用图图去创作这样一幅作品:
+
+
+
+当然,这是很久以后了!!!
+
+
+
+
+不过,千里之行,始于足下,我们再来学习一个基础技能吧:给图画涂色。
+
+给图画涂色其实很简单,和我们用颜料笔画画的步骤是一样的
+
+(1)先用笔在颜料盘中沾一个颜色
+(2)然后开始涂色
+(3)当涂完颜色后结束涂色
+
+用程序写也是这三步:
+
+```python
+t.color('red')
+#color是颜色的英文,括号里写上你想使用的颜色的英文单词
+
+t.begin_fill()
+#开始填充颜色,begin:开始,fill:填充
+
+t.end_fill()
+#结束填充颜色,end:结束
+```
+
+涂色的格式是这样的:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.color('red') #颜色设置成红色
+t.begin_fill() #开始填充
+
+# 这里写要画的图形的指令
+
+t.end_fill() #结束填充
+t.done()
+```
+如果要填充一个直角三角形可以这样写:
+
+```python
+import turtle as t
+t.TurtleScreen._RUNNING = True
+t.shape(name='turtle')
+t.color('red') #颜色设置成红色
+t.begin_fill() #开始填充
+t.forward(60)
+t.right(90)
+t.forward(80)
+t.right(143)
+t.forward(100)
+t.right(127)
+t.end_fill() #结束填充
+t.done()
+```
+将`red`改成其他的颜色试试吧:
+
+- 黄色:yellow
+- 蓝色:blue
+- 绿色:green
+- 紫色:purple
+- 粉丝:pink
+
+
+
+
diff --git a/ValentineDay/readme.md b/ValentineDay/readme.md
deleted file mode 100644
index 72f7278..0000000
--- a/ValentineDay/readme.md
+++ /dev/null
@@ -1,2 +0,0 @@
-## 简介
-
diff --git a/readme.md b/readme.md
index ad3eb96..0966c03 100644
--- a/readme.md
+++ b/readme.md
@@ -4,6 +4,8 @@
主要包括:
+- [Go编程语言](https://github.com/datawhalechina/go-talent)
+- [SQL编程语言](https://github.com/datawhalechina/team-learning-sql)
- [Python编程语言](https://github.com/datawhalechina/team-learning-program/tree/master/PythonLanguage)
- [数据结构与算法](https://github.com/datawhalechina/team-learning-program/tree/master/DataStructureAndAlgorithm)
- [编程实践(Numpy)](https://github.com/datawhalechina/team-learning-program/tree/master/IntroductionToNumpy)
@@ -11,11 +13,12 @@
- [编程实践(LeetCode 分类练习)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeClassification)
- [编程实践(LeetCode 腾讯精选练习50)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeTencent)
- [编程实践(Python 爬虫)](https://github.com/datawhalechina/team-learning-program/tree/master/WebSpider)
-- [编程实践(Python综合)](https://github.com/datawhalechina/team-learning-program/tree/master/ProjectPractice)
+- [编程实践(Python 综合)](https://github.com/datawhalechina/team-learning-program/tree/master/ProjectPractice)
+- [编程实践(区块链)](https://github.com/datawhalechina/team-learning-program/tree/master/Blockchain)
- [编程实践(设计模式)](https://github.com/datawhalechina/team-learning-program/tree/master/DesignPattern)
-- [编程实践(欢欢喜喜情人节)](https://github.com/datawhalechina/team-learning-program/tree/master/ValentineDay)
-- [编程实践(青少年编程Turtle)](https://github.com/datawhalechina/team-learning-program/tree/master/Turtle)
-
+- [编程实践(数据可视化)](https://github.com/datawhalechina/fantastic-matplotlib)
+- [青少年编程(Scratch)](https://github.com/datawhalechina/team-learning-program/tree/master/Scratch)
+- [青少年编程(Turtle)](https://github.com/datawhalechina/team-learning-program/tree/master/Turtle)
## 备注
 +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+### 2.4.2、比特币UTXO
+
+UTXO是 Unspent Transaction Output的缩写,意思是**未花费的输出,**可以简单理解为还没有用掉的收款。比如韩梅梅收到一笔比特币,她没有用掉,这笔比特币对她来说就是一个UTXO。关于UTXO的具体介绍大家可以查看[这篇文章](https://zhuanlan.zhihu.com/p/74050135)。
+
+**UTXO 核心设计思路是:它记录交易事件,而不记录最终状态。**要计算某个用户有多少比特币,就要对其钱包里所有的UTXO求和,得到结果就是他的持币数量。UTXO模型在转账交易时,是以UTXO为单位的,也就是说在支付时,调用的是整数倍UTXO,比如1个UTXO,3个UTXO,没有0.5个UTXO的说法。
+
+* 比特币在基于UTXO的结构中存储有关用户余额的数据,系统的整个状态就是一组UTXO的集合,每个UTXO都有一个所有者和一个面值(就像不同的硬币),而交易会花费若干个输入的UTXO,并根据规则创建若干个新的UTXO
+* 每个引用的输入必须有效并且尚未花费,对于一个交易,必须包含有每个输入的所有者匹配的签名,总输入必须大于等于总输出值。所以系统中用户的余额是用户具有私钥的UTXO的总值
+
+### 2.4.3、以太坊账户
+
+为什么以太坊不用UTXO呢?显然是因为麻烦,以太坊的做法更符合直觉,以太坊中的状态就是系统中所有账户的列表,每个账户都包含了一个余额和以太坊**特殊定义的数据**(代码和内部存储)。如果发送账户有足够多的余额来进行支付,则交易有效,在这种情况下发送账户先扣款,而收款账户将记入这笔收入。**如果接受账户有相关代码,则代码会自动运行,并且它的内部存储也可能被更改,或者代码还可能向其他账户发送额外的消息,这就会导致进一步的借贷资金关系。**
+
+### 2.4.4、优缺点比较
+
+**比特币UTXO的优点**:
+
+* 更高程度的隐私:如果用户为他们收到的每笔交易使用新地址,那么通常很难将账户互相链接。这很大程度上适用于货币,但不太适用于任何dapps,因为dapps通常涉及跟踪和用户绑定的复杂状态,可能不存在像货币那样简单的用户状态划分方案
+* 潜在的可扩展性:UTXO在理论上更符合可扩展性要求,因为我们只需要依赖拥有UTXO的那些人去维护基于Merkle树的所有权证明就够了,即使包括所有者在内的每个人都决定忘记该数据,那么也只有所有者受到对应的UTXO的损失,不影响接下来的交易。而在账户模式中,如果每个人都丢失了与账户相对应的Merkle树的部分,那将会使得和该账户有关的消息完全无法处理,包括发币给它。
+
+**以太坊账户模式的优点**:
+
+* 可以节省大量空间:不将UTXOs分开存储,而是合成一个账户;每个交易只需要一个输入、一个签名并产生一个输出
+* 更好的可替代性:货币本质上都是同质化、可替代的;UTXO的设计使得货币从来源分成了“可花费”和“不可花费”两类,这在实际应用中很难有对应模型
+* 更加简单:更容易编码和理解,特别是设计复杂脚本的时候,UTXO的脚本逻辑复杂时更令人费解
+* 便于维护持久轻节点:只要沿着特定方向扫描状态树,轻节点 可以很容易地随时访问账户相关的所有数据。而UTXO地每个交易都会使得状态引用发生改变,这对应节点来说长时间运行Dapp会有很大压力
+
+### 2.4.5、总结
+
+| | BitCoin | Ethereum |
+| ------------ | ---------------- | ---------------- |
+| **设计定位** | 现金系统 | 去中心化应用平台 |
+| **数据组成** | 交易列表(账本) | 交易和账户状态 |
+| **交易对象** | UTXO | Accounts |
+| **代码控制** | 脚本 | 智能合约 |
+
+## 2.5、以太坊账户类型
+
+以太坊作为智能合约操作平台,将账户划分为两类:外部账户(EOAs)和合约账户(contract account),下面分别做简要介绍:
+
+
+
+### 2.4.2、比特币UTXO
+
+UTXO是 Unspent Transaction Output的缩写,意思是**未花费的输出,**可以简单理解为还没有用掉的收款。比如韩梅梅收到一笔比特币,她没有用掉,这笔比特币对她来说就是一个UTXO。关于UTXO的具体介绍大家可以查看[这篇文章](https://zhuanlan.zhihu.com/p/74050135)。
+
+**UTXO 核心设计思路是:它记录交易事件,而不记录最终状态。**要计算某个用户有多少比特币,就要对其钱包里所有的UTXO求和,得到结果就是他的持币数量。UTXO模型在转账交易时,是以UTXO为单位的,也就是说在支付时,调用的是整数倍UTXO,比如1个UTXO,3个UTXO,没有0.5个UTXO的说法。
+
+* 比特币在基于UTXO的结构中存储有关用户余额的数据,系统的整个状态就是一组UTXO的集合,每个UTXO都有一个所有者和一个面值(就像不同的硬币),而交易会花费若干个输入的UTXO,并根据规则创建若干个新的UTXO
+* 每个引用的输入必须有效并且尚未花费,对于一个交易,必须包含有每个输入的所有者匹配的签名,总输入必须大于等于总输出值。所以系统中用户的余额是用户具有私钥的UTXO的总值
+
+### 2.4.3、以太坊账户
+
+为什么以太坊不用UTXO呢?显然是因为麻烦,以太坊的做法更符合直觉,以太坊中的状态就是系统中所有账户的列表,每个账户都包含了一个余额和以太坊**特殊定义的数据**(代码和内部存储)。如果发送账户有足够多的余额来进行支付,则交易有效,在这种情况下发送账户先扣款,而收款账户将记入这笔收入。**如果接受账户有相关代码,则代码会自动运行,并且它的内部存储也可能被更改,或者代码还可能向其他账户发送额外的消息,这就会导致进一步的借贷资金关系。**
+
+### 2.4.4、优缺点比较
+
+**比特币UTXO的优点**:
+
+* 更高程度的隐私:如果用户为他们收到的每笔交易使用新地址,那么通常很难将账户互相链接。这很大程度上适用于货币,但不太适用于任何dapps,因为dapps通常涉及跟踪和用户绑定的复杂状态,可能不存在像货币那样简单的用户状态划分方案
+* 潜在的可扩展性:UTXO在理论上更符合可扩展性要求,因为我们只需要依赖拥有UTXO的那些人去维护基于Merkle树的所有权证明就够了,即使包括所有者在内的每个人都决定忘记该数据,那么也只有所有者受到对应的UTXO的损失,不影响接下来的交易。而在账户模式中,如果每个人都丢失了与账户相对应的Merkle树的部分,那将会使得和该账户有关的消息完全无法处理,包括发币给它。
+
+**以太坊账户模式的优点**:
+
+* 可以节省大量空间:不将UTXOs分开存储,而是合成一个账户;每个交易只需要一个输入、一个签名并产生一个输出
+* 更好的可替代性:货币本质上都是同质化、可替代的;UTXO的设计使得货币从来源分成了“可花费”和“不可花费”两类,这在实际应用中很难有对应模型
+* 更加简单:更容易编码和理解,特别是设计复杂脚本的时候,UTXO的脚本逻辑复杂时更令人费解
+* 便于维护持久轻节点:只要沿着特定方向扫描状态树,轻节点 可以很容易地随时访问账户相关的所有数据。而UTXO地每个交易都会使得状态引用发生改变,这对应节点来说长时间运行Dapp会有很大压力
+
+### 2.4.5、总结
+
+| | BitCoin | Ethereum |
+| ------------ | ---------------- | ---------------- |
+| **设计定位** | 现金系统 | 去中心化应用平台 |
+| **数据组成** | 交易列表(账本) | 交易和账户状态 |
+| **交易对象** | UTXO | Accounts |
+| **代码控制** | 脚本 | 智能合约 |
+
+## 2.5、以太坊账户类型
+
+以太坊作为智能合约操作平台,将账户划分为两类:外部账户(EOAs)和合约账户(contract account),下面分别做简要介绍:
+
+ +
+ +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+  +
+本次教程将以一个较复杂的投票合约作为结束,我们希望实现的功能是为每个(投票)建议建立一份合约,然后作为合约的创造者-主席,主席将赋予每个成员(地址)投票权,而成员的投票权可以选择委托给其他人也可以自己投票,结束时将返回投票最多的提案。听起来很简单一个功能实现起来却较为复杂,下面我们拆分开进行讲解
+
+注:
+
+1. 代码可直接在Remix编辑器的已有solidity文件中找到,在contract/_Ballot.sol文件里
+2. 若学习者前面部分掌握较牢固,不妨尝试直接自行阅读代码,无需阅读本节内容
+
+
+首先我们定义成员类型,我们为每个投票者定义权重、是否已投票、
+
+```javascript
+struct Voter {
+ uint weight; // weight is accumulated by delegation
+ bool voted; // if true, that person already voted
+ address delegate; // person delegated to
+ uint vote; // index of the voted proposal
+}
+```
+
+然后我们定义提案类型,包含提案名和投票总数:
+
+```javascript
+struct Proposal {
+ bytes32 name; // short name (up to 32 bytes)
+ uint voteCount; // number of accumulated votes
+}
+```
+
+定义三个变量,主席是一个公开的地址,建立投票者与地址的映射,然后定义提案动态数组:
+
+```javascript
+address public chairperson;
+mapping(address => Voter) public voters;
+Proposal[] public proposals;
+```
+
+- `address public chairperson`:投票发起人,类型为 address。
+- `mapping(address => Voter) public voters`:所有投票人,类型为 `address` 到 `Voter` 的映射。
+- `Proposal[] public proposals`:所有提案,类型为动态大小的 `Proposal` 数组。
+
+3 个状态变量都使用了 `public` 关键字,使得变量可以被外部访问(即通过消息调用)。事实上,编译器会自动为 `public `的变量创建同名的 `getter` 函数,供外部直接读取。
+
+我们还需要为每个投票赋予初始权值,并将主席的权重设置为1。我们一般使用`constructor`赋初值,这与C++等语言类似:
+
+```javascript
+constructor(bytes32[] memory proposalNames) {
+ chairperson = msg.sender;
+ voters[chairperson].weight = 1;
+
+ for (uint i = 0; i < proposalNames.length; i++) {
+ proposals.push(Proposal({
+ name: proposalNames[i],
+ voteCount: 0
+ }));
+ }
+}
+```
+
+所有提案的名称通过参数 `bytes32[] proposalNames` 传入,逐个记录到状态变量 `proposals` 中。同时用 `msg.sender` 获取当前调用消息的发送者的地址,记录为投票发起人 `chairperson`,该发起人投票权重设为 1。
+
+接下来我们需要给每个投票者赋予权重:
+
+```javascript
+function giveRightToVote(address voter) public {
+ require(
+ msg.sender == chairperson,
+ "Only chairperson can give right to vote."
+ );
+ require(
+ !voters[voter].voted,
+ "The voter already voted."
+ );
+ require(voters[voter].weight == 0);
+ voters[voter].weight = 1;
+}
+```
+
+该函数给 `address voter` 赋予投票权,即将 `voter` 的投票权重设为 1,存入 `voters` 状态变量。
+
+上面这个函数只有投票发起人 `chairperson` 可以调用。这里用到了 `require((msg.sender == chairperson) && !voters[voter].voted)` 函数。如果` require` 中表达式结果为 `false`,这次调用会中止,且回滚所有状态和以太币余额的改变到调用前。但已消耗的 `Gas` 不会返还。
+
+下面一段是整段代码的重点,其作用是委托其他人代理投票,基本思路是:
+
+1. 使用`require`判断委托人是否已投票(若投过票再委托则重复投票),并判断被委托对象是否是自己
+2. 当判断被委托人不是0地址(主席)时,被委托人代理委托人的票,【绕口警告】由于被委托人也可能委托了别人,因此这里需要一直循环直到找到最后没有委托别人的被委托人为止!
+3. 委托人找到对应的被委托人,委托人已投票(避免重复投票)
+4. 判断被委托人是否已投票,若投了票则将被委托人投的提案票数加上委托人的权重,若未投票则令被委托人的权重加上委托人的权重(以后投票自然相当于投两票)
+
+注:该函数使用了 `while` 循环,这里合约编写者需要十分谨慎,防止调用者消耗过多 `Gas`,甚至出现死循环。
+
+```javascript
+function delegate(address to) public {
+ Voter storage sender = voters[msg.sender];
+ require(!sender.voted, "You already voted.");
+ require(to != msg.sender, "Self-delegation is disallowed.");
+
+ while (voters[to].delegate != address(0)) {
+ to = voters[to].delegate;
+ require(to != msg.sender, "Found loop in delegation.");
+ }
+ sender.voted = true;
+ sender.delegate = to;
+ Voter storage delegate_ = voters[to];
+ if (delegate_.voted) {
+ proposals[delegate_.vote].voteCount += sender.weight;
+ } else {
+ delegate_.weight += sender.weight;
+ }
+}
+```
+
+投票部分仅是几个简单的条件判断:
+
+```javascript
+function vote(uint proposal) public {
+ Voter storage sender = voters[msg.sender];
+ require(sender.weight != 0, "Has no right to vote");
+ require(!sender.voted, "Already voted.");
+ sender.voted = true;
+ sender.vote = proposal;
+ proposals[proposal].voteCount += sender.weight;
+ }
+```
+
+用 `voters[msg.sender]` 获取投票人,即此次调用的发起人。接下来检查是否是重复投票,如果不是,进行投票后相关状态变量的更新。
+
+接下来是计算获胜提案:
+
+```javascript
+function winningProposal() public view
+ returns (uint winningProposal_)
+{
+ uint winningVoteCount = 0;
+ for (uint p = 0; p < proposals.length; p++) {
+ if (proposals[p].voteCount > winningVoteCount) {
+ winningVoteCount = proposals[p].voteCount;
+ winningProposal_ = p;
+ }
+ }
+}
+```
+
+`returns (uint winningProposal)` 指定了函数的返回值类型,`constant` 表示该函数不会改变合约状态变量的值。
+
+最后是查询获胜者名称:
+
+```javascript
+function winnerName() public view
+ returns (bytes32 winnerName_)
+{
+ winnerName_ = proposals[winningProposal()].name;
+}
+```
+
+这里采用内部调用 `winningProposal()` 函数的方式获得获胜提案。如果需要采用外部调用,则需要写为 `this.winningProposal()`。
+
+
+
+**参考自:**
+
+[尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
+[web3.js 1.0中文手册](http://cw.hubwiz.com/card/c/web3.js-1.0/)
+
diff --git a/Blockchain/pic/2021-02-19_110327.png b/Blockchain/pic/2021-02-19_110327.png
new file mode 100644
index 0000000..7b03f57
Binary files /dev/null and b/Blockchain/pic/2021-02-19_110327.png differ
diff --git a/Blockchain/pic/2021-02-19_120756.png b/Blockchain/pic/2021-02-19_120756.png
new file mode 100644
index 0000000..f3e64de
Binary files /dev/null and b/Blockchain/pic/2021-02-19_120756.png differ
diff --git a/Blockchain/pic/2021-02-19_125917.png b/Blockchain/pic/2021-02-19_125917.png
new file mode 100644
index 0000000..2d77359
Binary files /dev/null and b/Blockchain/pic/2021-02-19_125917.png differ
diff --git a/Blockchain/pic/2021-02-19_130053.png b/Blockchain/pic/2021-02-19_130053.png
new file mode 100644
index 0000000..35b98d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_130053.png differ
diff --git a/Blockchain/pic/2021-02-19_133508.png b/Blockchain/pic/2021-02-19_133508.png
new file mode 100644
index 0000000..78c5567
Binary files /dev/null and b/Blockchain/pic/2021-02-19_133508.png differ
diff --git a/Blockchain/pic/2021-02-19_134110.png b/Blockchain/pic/2021-02-19_134110.png
new file mode 100644
index 0000000..c7e7ba5
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134110.png differ
diff --git a/Blockchain/pic/2021-02-19_134257.png b/Blockchain/pic/2021-02-19_134257.png
new file mode 100644
index 0000000..75d426b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134257.png differ
diff --git a/Blockchain/pic/2021-02-19_134634.png b/Blockchain/pic/2021-02-19_134634.png
new file mode 100644
index 0000000..eb63545
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134634.png differ
diff --git a/Blockchain/pic/2021-02-19_135113.png b/Blockchain/pic/2021-02-19_135113.png
new file mode 100644
index 0000000..a8f69cc
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135113.png differ
diff --git a/Blockchain/pic/2021-02-19_135337.png b/Blockchain/pic/2021-02-19_135337.png
new file mode 100644
index 0000000..1b3998b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135337.png differ
diff --git a/Blockchain/pic/2021-02-19_135413.png b/Blockchain/pic/2021-02-19_135413.png
new file mode 100644
index 0000000..b24c373
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135413.png differ
diff --git a/Blockchain/pic/2021-02-19_142407.png b/Blockchain/pic/2021-02-19_142407.png
new file mode 100644
index 0000000..10704d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_142407.png differ
diff --git a/Blockchain/pic/EOA_CA.png b/Blockchain/pic/EOA_CA.png
new file mode 100644
index 0000000..9612e9b
Binary files /dev/null and b/Blockchain/pic/EOA_CA.png differ
diff --git a/Blockchain/pic/aaaaaa b/Blockchain/pic/aaaaaa
new file mode 100644
index 0000000..8b13789
--- /dev/null
+++ b/Blockchain/pic/aaaaaa
@@ -0,0 +1 @@
+
diff --git a/Blockchain/pic/bg2017122703.png b/Blockchain/pic/bg2017122703.png
new file mode 100644
index 0000000..5c91bc5
Binary files /dev/null and b/Blockchain/pic/bg2017122703.png differ
diff --git a/Blockchain/pic/gas.jpg b/Blockchain/pic/gas.jpg
new file mode 100644
index 0000000..13bd71c
Binary files /dev/null and b/Blockchain/pic/gas.jpg differ
diff --git a/Blockchain/pic/image-20210219000835894.png b/Blockchain/pic/image-20210219000835894.png
new file mode 100644
index 0000000..5fea35e
Binary files /dev/null and b/Blockchain/pic/image-20210219000835894.png differ
diff --git a/Blockchain/pic/image-20210219101124978.png b/Blockchain/pic/image-20210219101124978.png
new file mode 100644
index 0000000..28411df
Binary files /dev/null and b/Blockchain/pic/image-20210219101124978.png differ
diff --git a/Blockchain/pic/image-20210219101226095.png b/Blockchain/pic/image-20210219101226095.png
new file mode 100644
index 0000000..8ddead4
Binary files /dev/null and b/Blockchain/pic/image-20210219101226095.png differ
diff --git a/Blockchain/pic/image-20210219101300792.png b/Blockchain/pic/image-20210219101300792.png
new file mode 100644
index 0000000..2dcad74
Binary files /dev/null and b/Blockchain/pic/image-20210219101300792.png differ
diff --git a/Blockchain/pic/image-20210219101332089.png b/Blockchain/pic/image-20210219101332089.png
new file mode 100644
index 0000000..e74b090
Binary files /dev/null and b/Blockchain/pic/image-20210219101332089.png differ
diff --git a/Blockchain/pic/image-20210219102028033.png b/Blockchain/pic/image-20210219102028033.png
new file mode 100644
index 0000000..966feb4
Binary files /dev/null and b/Blockchain/pic/image-20210219102028033.png differ
diff --git a/Blockchain/pic/image-20210219102255927.png b/Blockchain/pic/image-20210219102255927.png
new file mode 100644
index 0000000..8acef84
Binary files /dev/null and b/Blockchain/pic/image-20210219102255927.png differ
diff --git a/Blockchain/pic/image-20210219102322360.png b/Blockchain/pic/image-20210219102322360.png
new file mode 100644
index 0000000..513c9de
Binary files /dev/null and b/Blockchain/pic/image-20210219102322360.png differ
diff --git a/Blockchain/pic/image-20210219102359096.png b/Blockchain/pic/image-20210219102359096.png
new file mode 100644
index 0000000..aa9a394
Binary files /dev/null and b/Blockchain/pic/image-20210219102359096.png differ
diff --git a/Blockchain/pic/image-20210219105522149.png b/Blockchain/pic/image-20210219105522149.png
new file mode 100644
index 0000000..f3e6648
Binary files /dev/null and b/Blockchain/pic/image-20210219105522149.png differ
diff --git a/Blockchain/pic/image-20210219105616335.png b/Blockchain/pic/image-20210219105616335.png
new file mode 100644
index 0000000..a23c2dd
Binary files /dev/null and b/Blockchain/pic/image-20210219105616335.png differ
diff --git a/Blockchain/pic/image-20210219105824087.png b/Blockchain/pic/image-20210219105824087.png
new file mode 100644
index 0000000..c03a2b4
Binary files /dev/null and b/Blockchain/pic/image-20210219105824087.png differ
diff --git a/Blockchain/pic/image-20210219105911910.png b/Blockchain/pic/image-20210219105911910.png
new file mode 100644
index 0000000..eff8c5c
Binary files /dev/null and b/Blockchain/pic/image-20210219105911910.png differ
diff --git a/Blockchain/pic/image1.png b/Blockchain/pic/image1.png
new file mode 100644
index 0000000..8435a7e
Binary files /dev/null and b/Blockchain/pic/image1.png differ
diff --git a/Blockchain/pic/image2.png b/Blockchain/pic/image2.png
new file mode 100644
index 0000000..5688b8c
Binary files /dev/null and b/Blockchain/pic/image2.png differ
diff --git a/Blockchain/pic/image3.png b/Blockchain/pic/image3.png
new file mode 100644
index 0000000..c3bfdca
Binary files /dev/null and b/Blockchain/pic/image3.png differ
diff --git a/Blockchain/pic/image4.png b/Blockchain/pic/image4.png
new file mode 100644
index 0000000..3ce8d94
Binary files /dev/null and b/Blockchain/pic/image4.png differ
diff --git a/Blockchain/pic/image5.png b/Blockchain/pic/image5.png
new file mode 100644
index 0000000..3038f58
Binary files /dev/null and b/Blockchain/pic/image5.png differ
diff --git a/Blockchain/pic/image6.png b/Blockchain/pic/image6.png
new file mode 100644
index 0000000..82f5ecc
Binary files /dev/null and b/Blockchain/pic/image6.png differ
diff --git a/Blockchain/pic/part2-1.png b/Blockchain/pic/part2-1.png
new file mode 100644
index 0000000..8c0da19
Binary files /dev/null and b/Blockchain/pic/part2-1.png differ
diff --git a/Blockchain/pic/part2-10.png b/Blockchain/pic/part2-10.png
new file mode 100644
index 0000000..f0b447e
Binary files /dev/null and b/Blockchain/pic/part2-10.png differ
diff --git a/Blockchain/pic/part2-11.png b/Blockchain/pic/part2-11.png
new file mode 100644
index 0000000..06cca10
Binary files /dev/null and b/Blockchain/pic/part2-11.png differ
diff --git a/Blockchain/pic/part2-12.png b/Blockchain/pic/part2-12.png
new file mode 100644
index 0000000..5eb5b8e
Binary files /dev/null and b/Blockchain/pic/part2-12.png differ
diff --git a/Blockchain/pic/part2-13.png b/Blockchain/pic/part2-13.png
new file mode 100644
index 0000000..e9433fa
Binary files /dev/null and b/Blockchain/pic/part2-13.png differ
diff --git a/Blockchain/pic/part2-14.png b/Blockchain/pic/part2-14.png
new file mode 100644
index 0000000..f87ff72
Binary files /dev/null and b/Blockchain/pic/part2-14.png differ
diff --git a/Blockchain/pic/part2-15.png b/Blockchain/pic/part2-15.png
new file mode 100644
index 0000000..abebc5d
Binary files /dev/null and b/Blockchain/pic/part2-15.png differ
diff --git a/Blockchain/pic/part2-16.png b/Blockchain/pic/part2-16.png
new file mode 100644
index 0000000..7a91692
Binary files /dev/null and b/Blockchain/pic/part2-16.png differ
diff --git a/Blockchain/pic/part2-17.png b/Blockchain/pic/part2-17.png
new file mode 100644
index 0000000..d831f99
Binary files /dev/null and b/Blockchain/pic/part2-17.png differ
diff --git a/Blockchain/pic/part2-18.png b/Blockchain/pic/part2-18.png
new file mode 100644
index 0000000..c42e156
Binary files /dev/null and b/Blockchain/pic/part2-18.png differ
diff --git a/Blockchain/pic/part2-19.png b/Blockchain/pic/part2-19.png
new file mode 100644
index 0000000..cf84b29
Binary files /dev/null and b/Blockchain/pic/part2-19.png differ
diff --git a/Blockchain/pic/part2-2.png b/Blockchain/pic/part2-2.png
new file mode 100644
index 0000000..a8ecb2c
Binary files /dev/null and b/Blockchain/pic/part2-2.png differ
diff --git a/Blockchain/pic/part2-20.png b/Blockchain/pic/part2-20.png
new file mode 100644
index 0000000..cf3cb04
Binary files /dev/null and b/Blockchain/pic/part2-20.png differ
diff --git a/Blockchain/pic/part2-21.png b/Blockchain/pic/part2-21.png
new file mode 100644
index 0000000..84896de
Binary files /dev/null and b/Blockchain/pic/part2-21.png differ
diff --git a/Blockchain/pic/part2-22.png b/Blockchain/pic/part2-22.png
new file mode 100644
index 0000000..db238cf
Binary files /dev/null and b/Blockchain/pic/part2-22.png differ
diff --git a/Blockchain/pic/part2-23.png b/Blockchain/pic/part2-23.png
new file mode 100644
index 0000000..256124b
Binary files /dev/null and b/Blockchain/pic/part2-23.png differ
diff --git a/Blockchain/pic/part2-24.png b/Blockchain/pic/part2-24.png
new file mode 100644
index 0000000..6007692
Binary files /dev/null and b/Blockchain/pic/part2-24.png differ
diff --git a/Blockchain/pic/part2-3.png b/Blockchain/pic/part2-3.png
new file mode 100644
index 0000000..1ff0dda
Binary files /dev/null and b/Blockchain/pic/part2-3.png differ
diff --git a/Blockchain/pic/part2-4.png b/Blockchain/pic/part2-4.png
new file mode 100644
index 0000000..8879b10
Binary files /dev/null and b/Blockchain/pic/part2-4.png differ
diff --git a/Blockchain/pic/part2-5.png b/Blockchain/pic/part2-5.png
new file mode 100644
index 0000000..6308a3d
Binary files /dev/null and b/Blockchain/pic/part2-5.png differ
diff --git a/Blockchain/pic/part2-6.png b/Blockchain/pic/part2-6.png
new file mode 100644
index 0000000..debad8c
Binary files /dev/null and b/Blockchain/pic/part2-6.png differ
diff --git a/Blockchain/pic/part2-7.png b/Blockchain/pic/part2-7.png
new file mode 100644
index 0000000..f9a3ea0
Binary files /dev/null and b/Blockchain/pic/part2-7.png differ
diff --git a/Blockchain/pic/part2-8.png b/Blockchain/pic/part2-8.png
new file mode 100644
index 0000000..ed642a5
Binary files /dev/null and b/Blockchain/pic/part2-8.png differ
diff --git a/Blockchain/pic/part2-9.png b/Blockchain/pic/part2-9.png
new file mode 100644
index 0000000..8c1e817
Binary files /dev/null and b/Blockchain/pic/part2-9.png differ
diff --git a/Blockchain/pic/part3-1.png b/Blockchain/pic/part3-1.png
new file mode 100644
index 0000000..094515c
Binary files /dev/null and b/Blockchain/pic/part3-1.png differ
diff --git a/Blockchain/pic/part3-10.png b/Blockchain/pic/part3-10.png
new file mode 100644
index 0000000..1c2c0c6
Binary files /dev/null and b/Blockchain/pic/part3-10.png differ
diff --git a/Blockchain/pic/part3-11.png b/Blockchain/pic/part3-11.png
new file mode 100644
index 0000000..d6f6474
Binary files /dev/null and b/Blockchain/pic/part3-11.png differ
diff --git a/Blockchain/pic/part3-12.png b/Blockchain/pic/part3-12.png
new file mode 100644
index 0000000..30c4582
Binary files /dev/null and b/Blockchain/pic/part3-12.png differ
diff --git a/Blockchain/pic/part3-13.png b/Blockchain/pic/part3-13.png
new file mode 100644
index 0000000..a1f9783
Binary files /dev/null and b/Blockchain/pic/part3-13.png differ
diff --git a/Blockchain/pic/part3-2.png b/Blockchain/pic/part3-2.png
new file mode 100644
index 0000000..2d74cd1
Binary files /dev/null and b/Blockchain/pic/part3-2.png differ
diff --git a/Blockchain/pic/part3-3.png b/Blockchain/pic/part3-3.png
new file mode 100644
index 0000000..824fd9b
Binary files /dev/null and b/Blockchain/pic/part3-3.png differ
diff --git a/Blockchain/pic/part3-4.png b/Blockchain/pic/part3-4.png
new file mode 100644
index 0000000..152a017
Binary files /dev/null and b/Blockchain/pic/part3-4.png differ
diff --git a/Blockchain/pic/part3-5.png b/Blockchain/pic/part3-5.png
new file mode 100644
index 0000000..9b62fe6
Binary files /dev/null and b/Blockchain/pic/part3-5.png differ
diff --git a/Blockchain/pic/part3-6.png b/Blockchain/pic/part3-6.png
new file mode 100644
index 0000000..00e7473
Binary files /dev/null and b/Blockchain/pic/part3-6.png differ
diff --git a/Blockchain/pic/part3-7.png b/Blockchain/pic/part3-7.png
new file mode 100644
index 0000000..f6dfe7a
Binary files /dev/null and b/Blockchain/pic/part3-7.png differ
diff --git a/Blockchain/pic/part3-8.png b/Blockchain/pic/part3-8.png
new file mode 100644
index 0000000..212eb36
Binary files /dev/null and b/Blockchain/pic/part3-8.png differ
diff --git a/Blockchain/pic/part3-9.png b/Blockchain/pic/part3-9.png
new file mode 100644
index 0000000..567481f
Binary files /dev/null and b/Blockchain/pic/part3-9.png differ
diff --git a/Blockchain/pic/picfile b/Blockchain/pic/picfile
new file mode 100644
index 0000000..ca8de66
--- /dev/null
+++ b/Blockchain/pic/picfile
@@ -0,0 +1 @@
+This folder contains some necessary picture
diff --git a/Blockchain/pic/rating.png b/Blockchain/pic/rating.png
new file mode 100644
index 0000000..204d972
Binary files /dev/null and b/Blockchain/pic/rating.png differ
diff --git a/Blockchain/pic/transaction-struct.png b/Blockchain/pic/transaction-struct.png
new file mode 100644
index 0000000..da26c42
Binary files /dev/null and b/Blockchain/pic/transaction-struct.png differ
diff --git a/Blockchain/pic/utxo_com.jpg b/Blockchain/pic/utxo_com.jpg
new file mode 100644
index 0000000..77c03d0
Binary files /dev/null and b/Blockchain/pic/utxo_com.jpg differ
diff --git a/Blockchain/readme.md b/Blockchain/readme.md
new file mode 100644
index 0000000..6fb3759
--- /dev/null
+++ b/Blockchain/readme.md
@@ -0,0 +1,46 @@
+# 1. 编程实践(区块链)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/Blockchain
+
+## 基本信息
+
+- 贡献人员:陈锴、孙子涵、李岳昆、易远哲
+- 学习周期:12天
+- 学习形式:根据教程主线进行学习
+- 人群定位:具有至少一门编程语言基础,在开展组队学习之前能够熟悉 Linux 基本操作
+- 难度系数:较难
+
+## 学习目标
+
+## 任务安排
+
+### Task00:熟悉规则并先修Linux(2天)
+
+- 组队、修改群昵称
+- 熟悉打卡规则
+- 对Linux不太熟悉的学习者先安装Linux环境(可以是虚拟机或子系统)并掌握基本命令,其他内容可以暂不了解
+
+### Task01:区块链简介与以太坊入门介绍(2天)
+
+* 学习者学习区块链基础与以太坊入门介绍,该部分以了解为主
+* 学习者可以根据教程提供的各个方面内容,对某一部分深入了解并进行打卡
+* 打卡截至时间:3月16日24:00
+
+### Task02:Solidity基础(3天)
+
+* 学习者学习Solidity在线编辑器Remix的使用以及Solidity的基础操作,该部分需要深入掌握,学习者可以根据参考链接提供的资料进一步学习
+* 打卡内容为Task02最后的Solidity练习题部分,其他内容不作硬性要求
+* 打卡截止日期:3月19日24:00
+
+### Task03:web3js基础(3天)
+
+* 学习者学习以太坊客户端的使用以及Geth控制台部署智能合约
+* 打卡内容为学习者完成一个自己编写的合约的部署,并测试函数调用等
+* 打卡截止日期:3月22日24:00
+
+### Task04:合约编写实战实例(2天)
+
+* 学习者学习编写几个Remix官网自带的合约,并回顾 Task01的教程内容重新梳理知识点
+* 打卡内容为学习者自己的学习感悟,内容不限
+* 打卡截止日期:3月23日24:00
+
diff --git a/Docker/00 开篇词.md b/Docker/00 开篇词.md
new file mode 100644
index 0000000..df37501
--- /dev/null
+++ b/Docker/00 开篇词.md
@@ -0,0 +1,24 @@
+# Chapter 0 开篇词
+
+相信大家在开发项目尤其是团队合作项目中一定会遇到下面这些场景:
+
+- 项目在我电脑上明明运行的很好呀!怎么在你这不行了呢?
+- 我这是用python 3.6写的,你电脑是python 2.7应该运行不了。
+- 项目的一些依赖包需要科学上网才能下载,你那没有的话赶紧下载一下才能运行。
+- 论文的代码已经公开到github上了,但是因为自己电脑环境和他的不一样,项目在自己电脑上死活跑不起来。
+
+以上这些问题我相信大家并不陌生,那么通过本次Docker的组队学习,希望大家能够避免卡在科研或者开发的第一步,提高自己的生产力。
+
+---
+
+通过本次docker的组队学习,我们希望你能学到以下几个方面的能力:
+
+- 了解什么是docker
+- docker镜像是怎么构建的
+- 如何运行一个docker容器
+- docker之间的网络通信是怎么样的
+- docker中的数据如何做持久化存储
+- 如何通过docker compose管理自己的项目
+- 如何将自己的个人项目打造成容器化部署的形式
+
+祝你在docker的学习上一切顺利!
\ No newline at end of file
diff --git a/Docker/04 Docker数据管理.md b/Docker/04 Docker数据管理.md
new file mode 100644
index 0000000..4283a12
--- /dev/null
+++ b/Docker/04 Docker数据管理.md
@@ -0,0 +1,176 @@
+# Chapter 4 Docker 数据管理
+
+这一章介绍如何在 Docker 内部以及容器之间管理数据,在容器中管理数据主要有两种方式:
+
+* 数据卷
+* 挂载主机目录
+
+
+## 数据卷
+
+数据卷是一个可供一个或多个容器使用的特殊目录,它绕过 UFS (UNIX File System) ,可以提供很多有用的特性:
+
+* 数据卷可以在容器之间共享和重用
+
+* 对数据卷的修改会立马生效
+
+* 对数据卷的更新,不会影响镜像
+
+* 数据卷默认会一直存在,即使容器被删除
+
+>注意:数据卷的使用,类似于 Linux 下对目录或文件进行 mount,镜像中的被指定为挂载点的目录中的文件会复制到数据卷中(仅数据卷为空时会复制)。
+
+### 创建一个数据卷
+
+```bash
+$ docker volume create datawhale
+```
+
+查看所有的数据卷
+
+```bash
+$ docker volume ls
+
+DRIVER VOLUME NAME
+local datawhale
+```
+
+在主机里使用以下命令可以查看指定数据卷的信息
+
+```bash
+$ docker volume inspect datawhale
+[
+ {
+ "Driver": "local",
+ "Labels": {},
+ "Mountpoint": "/var/lib/docker/volumes/datawhale/_data",
+ "Name": "datawhale",
+ "Options": {},
+ "Scope": "local"
+ }
+]
+```
+
+### 启动一个挂载数据卷的容器
+
+在用 `docker run` 命令的时候,使用 `--mount` 标记来将数据卷挂载到容器里。在一次 `docker run` 中可以挂载多个 `数据卷`。
+
+下面创建一个名为 `web` 的容器,并加载一个数据卷到容器的 `/usr/share/nginx/html` 目录。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount source=datawhale,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+>–-mount参数说明:
+> source :数据卷
+> target :是容器内文件系统挂载点
+
+>注意,可以不需要提前创建好数据卷,直接在运行容器的时候mount 这时如果不存在指定的数据卷,docker会自动创建,自动生成。
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`数据卷` 信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "volume",
+ "Name": "datawhale",
+ "Source": "/var/lib/docker/volumes/datawhale/_data",
+ "Destination": "/usr/share/nginx/html",
+ "Driver": "local",
+ "Mode": "",
+ "RW": true,
+ "Propagation": ""
+ }
+],
+```
+
+### 删除数据卷
+
+```bash
+$ docker volume rm datawhale #datawhale为卷名
+```
+
+数据卷是被设计用来持久化数据的,它的生命周期独立于容器,Docker 不会在容器被删除后自动删除 `数据卷`,并且也不存在垃圾回收这样的机制来处理没有任何容器引用的 `数据卷`。如果需要在删除容器的同时移除数据卷。可以在删除容器的时候使用 `docker rm -v` 这个命令。
+
+无主的数据卷可能会占据很多空间,要清理请使用以下命令
+
+```bash
+$ docker volume prune
+```
+
+## 挂载主机目录
+
+### 挂载一个主机目录作为数据卷
+
+使用 `--mount` 标记可以指定挂载一个本地主机的目录到容器中去。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+
+上面的命令加载主机的 `/src/webapp` 目录到容器的 `/usr/share/nginx/html`目录。这个功能在进行测试的时候十分方便,比如用户可以放置一些程序到本地目录中,来查看容器是否正常工作。本地目录的路径必须是绝对路径,以前使用 `-v` 参数时如果本地目录不存在 Docker 会自动为你创建一个文件夹,现在使用 `--mount` 参数时如果本地目录不存在,Docker 会报错。
+
+Docker 挂载主机目录的默认权限是 `读写`,用户也可以通过增加 `readonly` 指定为 `只读`。
+
+>注意: 如果挂载的目录不存在,创建容器时,docker 不会自动创建,此时会报错
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html,readonly \
+ nginx:alpine
+```
+
+加了 `readonly` 之后,就挂载为 `只读` 了。如果你在容器内 `/usr/share/nginx/html` 目录新建文件,会显示如下错误
+
+```bash
+/usr/share/nginx/html # touch new.txt
+touch: new.txt: Read-only file system
+```
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`挂载主机目录` 的配置信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "bind",
+ "Source": "/src/webapp",
+ "Destination": "/usr/share/nginx/html",
+ "Mode": "",
+ "RW": true,
+ "Propagation": "rprivate"
+ }
+],
+```
+
+### 挂载一个本地主机文件作为数据卷
+
+`--mount` 标记也可以从主机挂载单个文件到容器中
+
+```bash
+$ docker run --rm -it \
+ --mount type=bind,source=$HOME/.bash_history,target=/root/.bash_history \
+ ubuntu:18.04 \
+ bash
+```
diff --git a/Docker/05 Docker网络.md b/Docker/05 Docker网络.md
new file mode 100644
index 0000000..5747442
--- /dev/null
+++ b/Docker/05 Docker网络.md
@@ -0,0 +1,783 @@
+# Chapter 5 Docker 网络
+
+## 内容大纲
+
+### Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+### Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+### Docker高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+
+
+# Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+## 外部访问容器
+
+容器中可以运行一些网络应用,要让外部也可以访问这些应用,可以通过`-P`或`-p`参数来指定端口映射。
+
+当使用`-P`标记时,`Docker`会随机映射一个端口到内部容器开放的网络端口。
+使用`docker container ls`可以看到,本地主机的 32768 被映射到了容器的 80 端口。此时访问本机的 32768 端口即可访问容器内 NGINX 默认页面。
+
+```
+$ docker run -d -P nginx:alpine
+
+$ docker container ls -l
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+fae320d08268 nginx:alpine "/docker-entrypoint.…" 24 seconds ago Up 20 seconds 0.0.0.0:32768->80/tcp bold_mcnulty
+```
+
+同样的,可以通过`docker logs`命令来查看访问记录。
+
+```
+$ docker logs fa
+172.17.0.1 - - [25/Aug/2020:08:34:04 +0000] "GET / HTTP/1.1" 200 612 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:80.0) Gecko/20100101 Firefox/80.0" "-"
+```
+
+`-p`则可以指定要映射的端口,并且,在一个指定端口上只可以绑定一个容器。支持的格式有`ip:hostPort:containerPort | ip::containerPort | hostPort:containerPort`.
+
+### 映射所有接口地址
+
+使用`hostPort:containerPort`格式本地的 80 端口映射到容器的 80 端口,可以执行
+
+```
+$ docker run -d -p 80:80 nginx:alpine
+```
+
+此时默认会绑定本地所有接口上的所有地址。
+
+### 映射到指定地址的指定端口
+
+可以使用`ip:hostPort:containerPort`格式指定映射使用一个特定地址,比如`localhost`地址127.0.0.1
+
+```
+$ docker run -d -p 127.0.0.1:80:80 nginx:alpine
+```
+
+### 映射到指定地址的任意端口
+
+使用`ip::containerPort`绑定`localhost`的任意端口到容器的80端口,本地主机会自动分配一个端口。
+
+```
+$ docker run -d -p 127.0.0.1::80 nginx:alpine
+```
+
+还可以使用`udp`标记来指定`udp`端口
+
+```
+$ docker run -d -p 127.0.0.1:80:80/udp nginx:alpine
+```
+
+### 查看映射端口配置
+
+使用`docker port`来查看当前映射的端口配置,也可以查看到绑定的地址
+
+```
+$ docker port fa 80
+0.0.0.0:32768
+```
+
+**注意:**
+容器有自己的内部网络和 ip 地址(使用`docker inspect`查看,`Docker`还可以有一个可变的网络配置。)
+`-p`标记可以多次使用来绑定多个端口
+
+例如
+
+```
+$ docker run -d \
+ -p 80:80 \
+ -p 443:443 \
+ nginx:alpine
+```
+
+## 容器互联
+
+如果之前有 `Docker`使用经验,可能已经习惯了使用`--link`参数来使容器互联。
+随着 `Docker` 网络的完善,强烈建议大家将容器加入自定义的`Docker`网络来连接多个容器,而不是使用 `--link`参数。
+
+### 新建网络
+
+下面先创建一个新的 `Docker`网络。
+
+```
+$ docker network create -d bridge my-net
+```
+
+`-d`参数指定`Docker`网络类型,有`bridge overlay`,其中`overlay`网络类型用于`Swarm mode`,在本小节中你可以忽略它。
+
+### 连接容器
+
+运行一个容器并连接到新建的`my-net`网络
+
+```
+$ docker run -it --rm --name busybox1 --network my-net busybox sh
+```
+
+打开新的终端,再运行一个容器并加入到 `my-net`网络
+
+```
+$ docker run -it --rm --name busybox2 --network my-net busybox sh
+```
+
+再打开一个新的终端查看容器信息
+
+```
+$ docker container ls
+
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+b47060aca56b busybox "sh" 11 minutes ago Up 11 minutes busybox2
+8720575823ec busybox "sh" 16 minutes ago Up 16 minutes busybox1
+```
+
+下面通过 `ping`来证明`busybox1`容器和`busybox2`容器建立了互联关系。
+在`busybox1`容器输入以下命令
+
+```
+/ # ping busybox2
+PING busybox2 (172.19.0.3): 56 data bytes
+64 bytes from 172.19.0.3: seq=0 ttl=64 time=0.072 ms
+64 bytes from 172.19.0.3: seq=1 ttl=64 time=0.118 ms
+```
+
+用`ping`来测试连接`busybox2`容器,它会解析成 172.19.0.3。
+同理在`busybox2`容器执行`ping busybox1`,也会成功连接到。
+
+```
+/ # ping busybox1
+PING busybox1 (172.19.0.2): 56 data bytes
+64 bytes from 172.19.0.2: seq=0 ttl=64 time=0.064 ms
+64 bytes from 172.19.0.2: seq=1 ttl=64 time=0.143 ms
+```
+
+这样,`busybox1` 容器和 `busybox2` 容器建立了互联关系。
+
+`Docker Compose`
+如果你有多个容器之间需要互相连接,推荐使用`Docker`Compose。
+
+## 配置DNS
+
+如何自定义配置容器的主机名和 DNS 呢?秘诀就是`Docker`利用虚拟文件来挂载容器的 3个相关配置文件。
+
+在容器中使用 `mount`命令可以看到挂载信息:
+
+```
+$ mount
+/dev/disk/by-uuid/1fec...ebdf on /etc/hostname type ext4 ...
+/dev/disk/by-uuid/1fec...ebdf on /etc/hosts type ext4 ...
+tmpfs on /etc/resolv.conf type tmpfs ...
+```
+
+这种机制可以让宿主主机 DNS 信息发生更新后,所有`Docker`容器的 DNS 配置通过 `/etc/resolv.conf`文件立刻得到更新。
+
+配置全部容器的 DNS ,也可以在 `/etc/docker/daemon.json` 文件中增加以下内容来设置。
+
+```
+{
+ "dns" : [
+ "114.114.114.114",
+ "8.8.8.8"
+ ]
+}
+```
+
+这样每次启动的容器 DNS 自动配置为 114.114.114.114 和8.8.8.8。使用以下命令来证明其已经生效。
+
+```
+$ docker run -it --rm ubuntu:18.04 cat etc/resolv.conf
+
+nameserver 114.114.114.114
+nameserver 8.8.8.8
+```
+
+如果用户想要手动指定容器的配置,可以在使用`docker run`命令启动容器时加入如下参数:
+`-h HOSTNAME`或者`--hostname=HOSTNAME`设定容器的主机名,它会被写到容器内的`/etc/hostname 和 /etc/hosts`。但它在容器外部看不到,既不会在`docker container ls`中显示,也不会在其他的容器的`/etc/hosts`看到。
+
+`--dns=IP_ADDRESS`添加 DNS 服务器到容器的`/etc/resolv.conf`中,让容器用这个服务器来解析所有不在 `/etc/hosts `中的主机名。
+
+`--dns-search=DOMAIN`设定容器的搜索域,当设定搜索域为`.example.com`时,在搜索一个名为`host`的主机时,DNS 不仅搜索 `host`,还会搜索`host.example.com`。
+
+**注意:**如果在容器启动时没有指定最后两个参数,`Docker`会默认用主机上的`/etc/resolv.conf`来配置容器。
+
+# Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+可以通过`docker network ls`查看网络,默认创建三种网络。
+
+```
+[root@localhost ~]# docker network ls
+NETWORK ID NAME DRIVER SCOPE
+688d1970f72e bridge bridge local
+885da101da7d host host local
+f4f1b3cf1b7f none null local
+```
+
+常见网络的含义:
+
+| 网络模式 | 简介 |
+| :-------: | :----------------------------------------------------------: |
+| Bridge | 为每一个容器分配、设置 IP 等,并将容器连接到一个 `docker0` 虚拟网桥,默认为该模式。 |
+| Host | 容器将不会虚拟出自己的网卡,配置自己的 IP 等,而是使用宿主机的 IP 和端口。 |
+| None | 容器有独立的 Network namespace,但并没有对其进行任何网络设置,如分配 veth pair 和网桥连接,IP 等。 |
+| Container | 新创建的容器不会创建自己的网卡和配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等。 |
+
+## Bridge模式
+
+当`Docker`进程启动时,会在主机上创建一个名为`docker0`的虚拟网桥,此主机上启动的`Docker`容器会连接到这个虚拟网桥上,附加在其上的任何网卡之间都能自动转发数据包。虚拟网桥的工作方式和物理交换机类似,这样主机上的所有容器就通过交换机连在了一个二层网络中。从`docker0`子网中分配一个 IP 给容器使用,并设置 `docker0 `的 IP 地址为容器的默认网关。在主机上创建一对虚拟网卡`veth pair`设备,`Docker `将 `veth pair` 设备的一端放在新创建的容器中,并命名为`eth0`(容器的网卡),另一端放在主机中,以`vethxxx`这样类似的名字命名,并将这个网络设备加入到 `docker0` 网桥中。可以通过`brctl show`命令查看。
+
+比如运行一个基于 `busybox` 镜像构建的容器 `bbox01`,查看 `ip addr`:
+
+> busybox 被称为嵌入式 Linux 的瑞士军刀,整合了很多小的 unix 下的通用功能到一个小的可执行文件中。
+
+
+
+然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 通过以上的比较可以发现,证实了之前所说的:守护进程会创建一对对等虚拟设备接口 `veth pair`,将其中一个接口设置为容器的 `eth0` 接口(容器的网卡),另一个接口放置在宿主机的命名空间中,以类似 `vethxxx` 这样的名字命名。
+
+ 同时,守护进程还会从网桥 `docker0` 的私有地址空间中分配一个 IP 地址和子网给该容器,并设置 docker0 的 IP 地址为容器的默认网关。也可以安装 `yum install -y bridge-utils` 以后,通过 `brctl show` 命令查看网桥信息。
+
+
+
+ 对于每个容器的 IP 地址和 Gateway 信息,可以通过 `docker inspect 容器名称|ID` 进行查看,在 `NetworkSettings` 节点中可以看到详细信息。
+
+
+
+ 可以通过 `docker network inspect bridge` 查看所有 `bridge` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+> 关于 `bridge` 网络模式的使用,只需要在创建容器时通过参数 `--net bridge` 或者 `--network bridge` 指定即可,当然这也是创建容器默认使用的网络模式,也就是说这个参数是可以省略的。
+
+
+
+
+
+bridge模式是 `docker `的默认网络模式,不写`–net`参数,就是bridge模式。使用`docker run -p`时,`docker `实际是在`iptables`做了`DNAT`规则,实现端口转发功能。可以使用`iptables -t nat -vnL`查看。`bridge`模式如下图所示:
+
+ 演示:
+
+ ```
+$ docker run -tid --net=bridge --name docker_bri1 \
+ ubuntu-base:v3
+ docker run -tid --net=bridge --name docker_bri2 \
+ ubuntu-base:v3
+
+$ brctl show
+$ docker exec -ti docker_bri1 /bin/bash
+$ ifconfig –a
+$ route –n
+ ```
+
+
+
+## Host 模式
+
+- host 网络模式需要在创建容器时通过参数 `--net host` 或者 `--network host` 指定;
+- 采用 host 网络模式的 Docker Container,可以直接使用宿主机的 IP 地址与外界进行通信,若宿主机的 eth0 是一个公有 IP,那么容器也拥有这个公有 IP。同时容器内服务的端口也可以使用宿主机的端口,无需额外进行 NAT 转换;
+- host 网络模式可以让容器共享宿主机网络栈,这样的好处是外部主机与容器直接通信,但是容器的网络缺少隔离性。
+
+
+
+
+
+ 比如基于 `host` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox02`,查看 `ip addr`:
+
+
+
+ 然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 对,你没有看错,返回信息一模一样,也可以肯定没有截错图,不信接着往下看。可以通过 `docker network inspect host` 查看所有 `host` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+如果启动容器的时候使用`host`模式,那么这个容器将不会获得一个独立的`Network Namespace`,而是和宿主机共用一个`Network Namespace`。容器将不会虚拟出自己的网卡,配置自己的`IP`等,而是使用宿主机的`IP`和端口。但是,容器的其他方面,如文件系统、进程列表等还是和宿主机隔离的。 `Host`模式如下图所示:
+
+演示:
+
+```
+$ docker run -tid --net=host --name docker_host1 ubuntu-base:v3
+$ docker run -tid --net=host --name docker_host2 ubuntu-base:v3
+
+$ docker exec -ti docker_host1 /bin/bash
+$ docker exec -ti docker_host1 /bin/bash
+
+$ ifconfig –a
+$ route –n
+```
+
+## None模式
+
+- none 网络模式是指禁用网络功能,只有 lo 接口 local 的简写,代表 127.0.0.1,即 localhost 本地环回接口。在创建容器时通过参数 `--net none` 或者 `--network none` 指定;
+- none 网络模式即不为 Docker Container 创建任何的网络环境,容器内部就只能使用 loopback 网络设备,不会再有其他的网络资源。可以说 none 模式为 Docke Container 做了极少的网络设定,但是俗话说得好“少即是多”,在没有网络配置的情况下,作为 Docker 开发者,才能在这基础做其他无限多可能的网络定制开发。这也恰巧体现了 Docker 设计理念的开放。
+
+
+
+ 比如基于 `none` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox03`,查看 `ip addr`:
+
+
+
+ 可以通过 `docker network inspect none` 查看所有 `none` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+使用`none`模式,`Docker` 容器拥有自己的 `Network Namespace`,但是,并不为`Docker` 容器进行任何网络配置。也就是说,这个 `Docker` 容器没有网卡、IP、路由等信息。需要自己为 `Docker` 容器添加网卡、配置 IP 等。 `None`模式示意图:
+
+ 演示:
+
+```
+$ docker run -tid --net=none --name \
+ docker_non1 ubuntu-base:v3
+
+$ docker exec -ti docker_non1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+## Container 模式
+
+- Container 网络模式是 Docker 中一种较为特别的网络的模式。在创建容器时通过参数 `--net container:已运行的容器名称|ID` 或者 `--network container:已运行的容器名称|ID` 指定;
+- 处于这个模式下的 Docker 容器会共享一个网络栈,这样两个容器之间可以使用 localhost 高效快速通信。
+
+
+
+ **Container 网络模式即新创建的容器不会创建自己的网卡,配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等**。同样两个容器除了网络方面相同之外,其他的如文件系统、进程列表等还是隔离的。
+
+ 比如基于容器 `bbox01` 创建了 `container` 网络模式的容器 `bbox04`,查看 `ip addr`:
+
+
+
+ 容器 `bbox01` 的 `ip addr` 信息如下:
+
+
+
+ 宿主机的 `ip addr` 信息如下:
+
+
+
+ 通过以上测试可以发现,Docker 守护进程只创建了一对对等虚拟设备接口用于连接 bbox01 容器和宿主机,而 bbox04 容器则直接使用了 bbox01 容器的网卡信息。
+
+ 这个时候如果将 bbox01 容器停止,会发现 bbox04 容器就只剩下 lo 接口了。
+
+
+
+ 然后 bbox01 容器重启以后,bbox04 容器也重启一下,就又可以获取到网卡信息了。
+
+
+
+这个模式指定新创建的容器和已经存在的一个容器共享一个`Network Namespace`,而不是和宿主机共享。新创建的容器不会创建自己的网卡,配置自己的`IP`,而是和一个指定的容器共享`IP`、端口范围等。同样,两个容器除了网络方面,其他的如文件系统、进程列表等还是隔离的。两个容器的进程可以通过lo网卡设备通信。 `Container`模式示意图:
+
+演示:
+
+```
+$ docker run -tid --net=container:docker_bri1 \
+ --name docker_con1 ubuntu-base:v3
+
+$ docker exec -ti docker_con1 /bin/bash
+$ docker exec -ti docker_bri1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+
+
+# 高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+## 快速配置指南
+
+下面是一个跟 Docker 网络相关的命令列表。
+
+其中有些命令选项只有在 Docker 服务启动的时候才能配置,而且不能马上生效。
+
+ - `-b BRIDGE` 或 `--bridge=BRIDGE` 指定容器挂载的网桥
+ - `--bip=CIDR`定制 `docker0` 的掩码
+ - `-H SOCKET...` 或 `--host=SOCKET... Docker` 服务端接收命令的通道
+ - `--icc=true|false` 是否支持容器之间进行通信
+ - `--ip-forward=true|false` 请看下文容器之间的通信
+ - `--iptables=true|false` 是否允许 Docker 添加 `iptables` 规则
+ - `--mtu=BYTES` 容器网络中的 `MTU`
+
+下面2个命令选项既可以在启动服务时指定,也可以在启动容器时指定。在 Docker服务启动的时候指定则会成为默认值,后面执行 `docker run` 时可以覆盖设置的默认值。
+
+ - `--dns=IP_ADDRESS...` 使用指定的DNS服务器
+ - `--dns-search=DOMAIN...` 指定DNS搜索域
+
+最后这些选项只有在 `docker run` 执行时使用,因为它是针对容器的特性内容。
+
+ - `-h HOSTNAME` 或 `--hostname=HOSTNAME` 配置容器主机名
+ - `--link=CONTAINER_NAME:ALIAS` 添加到另一个容器的连接
+ - `--net=bridge|none|container:NAME_or_ID|host` 配置容器的桥接模式
+ - `-p SPEC` 或 --publish=SPEC` 映射容器端口到宿主主机
+ - `-P or --publish-all=true|false` 映射容器所有端口到宿主主机
+
+
+
+
+## 容器访问控制
+
+容器的访问控制,主要通过 Linux 上的 `iptables` 防火墙来进行管理和实现。`iptables` 是 Linux 上默认的防火墙软件,在大部分发行版中都自带。
+
+### 容器访问外部网络
+
+容器要想访问外部网络,需要本地系统的转发支持。在Linux 系统中,检查转发是否打开。
+
+
+
+```
+$sysctl net.ipv4.ip_forward
+net.ipv4.ip_forward = 1
+```
+
+如果为 0,说明没有开启转发,则需要手动打开。
+
+
+
+```
+$sysctl -w net.ipv4.ip_forward=1
+```
+
+如果在启动 Docker 服务的时候设定 `--ip-forward=true`, Docker 就会自动设定系统的 `ip_forward` 参数为 1。
+
+### 容器之间访问
+
+容器之间相互访问,需要两方面的支持。
+
+- 容器的网络拓扑是否已经互联。默认情况下,所有容器都会被连接到 `docker0` 网桥上。
+- 本地系统的防火墙软件 `-- iptables` 是否允许通过。
+
+### 访问所有端口
+
+当启动 Docker 服务(即 dockerd)的时候,默认会添加一条转发策略到本地主机 iptables 的 FORWARD 链上。策略为通过(`ACCEPT`)还是禁止(`DROP`)取决于配置`--icc=true`(缺省值)还是 `--icc=false`。当然,如果手动指定 `--iptables=false` 则不会添加 `iptables` 规则。
+
+可见,默认情况下,不同容器之间是允许网络互通的。如果为了安全考虑,可以在 `/etc/docker/daemon.json` 文件中配置 `{"icc": false}` 来禁止它。
+
+### 访问指定端口
+
+在通过 `-icc=false` 关闭网络访问后,还可以通过 `--link=CONTAINER_NAME:ALIAS` 选项来访问容器的开放端口。
+
+例如,在启动 Docker 服务时,可以同时使用 `icc=false --iptables=true` 参数来关闭允许相互的网络访问,并让 Docker 可以修改系统中的 `iptables` 规则。
+
+此时,系统中的 `iptables` 规则可能是类似
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+...
+```
+
+之后,启动容器(`docker run`)时使用 `--link=CONTAINER_NAME:ALIAS` 选项。Docker 会在 `iptable` 中为 两个容器分别添加一条 `ACCEPT` 规则,允许相互访问开放的端口(取决于 `Dockerfile` 中的 `EXPOSE` 指令)。
+
+当添加了 `--link=CONTAINER_NAME:ALIAS` 选项后,添加了 `iptables` 规则。
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+ACCEPT tcp -- 172.17.0.2 172.17.0.3 tcp spt:80
+ACCEPT tcp -- 172.17.0.3 172.17.0.2 tcp dpt:80
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+```
+
+**注意**:`--link=CONTAINER_NAME:ALIAS` 中的 `CONTAINER_NAME` 目前必须是 Docker 分配的名字,或使用 `--name` 参数指定的名字。主机名则不会被识别。
+
+
+
+## 端口映射实现
+
+默认情况下,容器可以主动访问到外部网络的连接,但是外部网络无法访问到容器。
+
+### 容器访问外部实现
+
+容器所有到外部网络的连接,源地址都会被 NAT 成本地系统的 IP 地址。这是使用 `iptables` 的源地址伪装操作实现的。
+
+查看主机的 NAT 规则。
+
+
+
+```
+$ sudo iptables -t nat -nL
+...
+Chain POSTROUTING (policy ACCEPT)
+target prot opt source destination
+MASQUERADE all -- 172.17.0.0/16 !172.17.0.0/16
+...
+```
+
+其中,上述规则将所有源地址在 `172.17.0.0/16` 网段,目标地址为其他网段(外部网络)的流量动态伪装为从系统网卡发出。MASQUERADE 跟传统 SNAT 的好处是它能动态从网卡获取地址。
+
+### 外部访问容器实现
+
+容器允许外部访问,可以在 `docker run` 时候通过 `-p` 或 `-P` 参数来启用。
+
+不管用那种办法,其实也是在本地的 `iptable` 的 nat 表中添加相应的规则。
+
+使用 `-P` 时:
+
+
+
+```
+$ iptables -t nat -nL
+...
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:49153 to:172.17.0.2:80
+```
+
+使用 `-p 80:80` 时:
+
+
+
+```
+$ iptables -t nat -nL
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:80 to:172.17.0.2:80
+```
+
+**注意**:
+
+- 这里的规则映射了 `0.0.0.0`,意味着将接受主机来自所有接口的流量。用户可以通过 `-p IP:host_port:container_port` 或 `-p IP::port` 来指定允许访问容器的主机上的 IP、接口等,以制定更严格的规则。
+- 如果希望永久绑定到某个固定的 IP 地址,可以在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容。
+
+
+
+```
+{
+ "ip": "0.0.0.0"
+}
+```
+
+
+
+## 配置 docker0 网桥
+
+Docker 服务默认会创建一个 `docker0` 网桥(其上有一个 `docker0` 内部接口),它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。
+
+Docker 默认指定了 `docker0` 接口 的 IP 地址和子网掩码,让主机和容器之间可以通过网桥相互通信,它还给出了 MTU(接口允许接收的最大传输单元),通常是 1500 Bytes,或宿主主机网络路由上支持的默认值。这些值都可以在服务启动的时候进行配置。
+
+- `--bip=CIDR` IP 地址加掩码格式,例如 192.168.1.5/24
+- `--mtu=BYTES` 覆盖默认的 Docker mtu 配置
+
+也可以在配置文件中配置 DOCKER_OPTS,然后重启服务。
+
+由于目前 Docker 网桥是 Linux 网桥,用户可以使用 `brctl show` 来查看网桥和端口连接信息。
+
+
+
+```
+$ sudo brctl show
+bridge name bridge id STP enabled interfaces
+docker0 8000.3a1d7362b4ee no veth65f9
+ vethdda6
+```
+
+**注**:`brctl` 命令在 Debian、Ubuntu 中可以使用 `sudo apt-get install bridge-utils` 来安装。
+
+每次创建一个新容器的时候,Docker 从可用的地址段中选择一个空闲的 IP 地址分配给容器的 eth0 端口。使用本地主机上 `docker0` 接口的 IP 作为所有容器的默认网关。
+
+
+
+```
+$ sudo docker run -i -t --rm base /bin/bash
+$ ip addr show eth0
+24: eth0:
+
+本次教程将以一个较复杂的投票合约作为结束,我们希望实现的功能是为每个(投票)建议建立一份合约,然后作为合约的创造者-主席,主席将赋予每个成员(地址)投票权,而成员的投票权可以选择委托给其他人也可以自己投票,结束时将返回投票最多的提案。听起来很简单一个功能实现起来却较为复杂,下面我们拆分开进行讲解
+
+注:
+
+1. 代码可直接在Remix编辑器的已有solidity文件中找到,在contract/_Ballot.sol文件里
+2. 若学习者前面部分掌握较牢固,不妨尝试直接自行阅读代码,无需阅读本节内容
+
+
+首先我们定义成员类型,我们为每个投票者定义权重、是否已投票、
+
+```javascript
+struct Voter {
+ uint weight; // weight is accumulated by delegation
+ bool voted; // if true, that person already voted
+ address delegate; // person delegated to
+ uint vote; // index of the voted proposal
+}
+```
+
+然后我们定义提案类型,包含提案名和投票总数:
+
+```javascript
+struct Proposal {
+ bytes32 name; // short name (up to 32 bytes)
+ uint voteCount; // number of accumulated votes
+}
+```
+
+定义三个变量,主席是一个公开的地址,建立投票者与地址的映射,然后定义提案动态数组:
+
+```javascript
+address public chairperson;
+mapping(address => Voter) public voters;
+Proposal[] public proposals;
+```
+
+- `address public chairperson`:投票发起人,类型为 address。
+- `mapping(address => Voter) public voters`:所有投票人,类型为 `address` 到 `Voter` 的映射。
+- `Proposal[] public proposals`:所有提案,类型为动态大小的 `Proposal` 数组。
+
+3 个状态变量都使用了 `public` 关键字,使得变量可以被外部访问(即通过消息调用)。事实上,编译器会自动为 `public `的变量创建同名的 `getter` 函数,供外部直接读取。
+
+我们还需要为每个投票赋予初始权值,并将主席的权重设置为1。我们一般使用`constructor`赋初值,这与C++等语言类似:
+
+```javascript
+constructor(bytes32[] memory proposalNames) {
+ chairperson = msg.sender;
+ voters[chairperson].weight = 1;
+
+ for (uint i = 0; i < proposalNames.length; i++) {
+ proposals.push(Proposal({
+ name: proposalNames[i],
+ voteCount: 0
+ }));
+ }
+}
+```
+
+所有提案的名称通过参数 `bytes32[] proposalNames` 传入,逐个记录到状态变量 `proposals` 中。同时用 `msg.sender` 获取当前调用消息的发送者的地址,记录为投票发起人 `chairperson`,该发起人投票权重设为 1。
+
+接下来我们需要给每个投票者赋予权重:
+
+```javascript
+function giveRightToVote(address voter) public {
+ require(
+ msg.sender == chairperson,
+ "Only chairperson can give right to vote."
+ );
+ require(
+ !voters[voter].voted,
+ "The voter already voted."
+ );
+ require(voters[voter].weight == 0);
+ voters[voter].weight = 1;
+}
+```
+
+该函数给 `address voter` 赋予投票权,即将 `voter` 的投票权重设为 1,存入 `voters` 状态变量。
+
+上面这个函数只有投票发起人 `chairperson` 可以调用。这里用到了 `require((msg.sender == chairperson) && !voters[voter].voted)` 函数。如果` require` 中表达式结果为 `false`,这次调用会中止,且回滚所有状态和以太币余额的改变到调用前。但已消耗的 `Gas` 不会返还。
+
+下面一段是整段代码的重点,其作用是委托其他人代理投票,基本思路是:
+
+1. 使用`require`判断委托人是否已投票(若投过票再委托则重复投票),并判断被委托对象是否是自己
+2. 当判断被委托人不是0地址(主席)时,被委托人代理委托人的票,【绕口警告】由于被委托人也可能委托了别人,因此这里需要一直循环直到找到最后没有委托别人的被委托人为止!
+3. 委托人找到对应的被委托人,委托人已投票(避免重复投票)
+4. 判断被委托人是否已投票,若投了票则将被委托人投的提案票数加上委托人的权重,若未投票则令被委托人的权重加上委托人的权重(以后投票自然相当于投两票)
+
+注:该函数使用了 `while` 循环,这里合约编写者需要十分谨慎,防止调用者消耗过多 `Gas`,甚至出现死循环。
+
+```javascript
+function delegate(address to) public {
+ Voter storage sender = voters[msg.sender];
+ require(!sender.voted, "You already voted.");
+ require(to != msg.sender, "Self-delegation is disallowed.");
+
+ while (voters[to].delegate != address(0)) {
+ to = voters[to].delegate;
+ require(to != msg.sender, "Found loop in delegation.");
+ }
+ sender.voted = true;
+ sender.delegate = to;
+ Voter storage delegate_ = voters[to];
+ if (delegate_.voted) {
+ proposals[delegate_.vote].voteCount += sender.weight;
+ } else {
+ delegate_.weight += sender.weight;
+ }
+}
+```
+
+投票部分仅是几个简单的条件判断:
+
+```javascript
+function vote(uint proposal) public {
+ Voter storage sender = voters[msg.sender];
+ require(sender.weight != 0, "Has no right to vote");
+ require(!sender.voted, "Already voted.");
+ sender.voted = true;
+ sender.vote = proposal;
+ proposals[proposal].voteCount += sender.weight;
+ }
+```
+
+用 `voters[msg.sender]` 获取投票人,即此次调用的发起人。接下来检查是否是重复投票,如果不是,进行投票后相关状态变量的更新。
+
+接下来是计算获胜提案:
+
+```javascript
+function winningProposal() public view
+ returns (uint winningProposal_)
+{
+ uint winningVoteCount = 0;
+ for (uint p = 0; p < proposals.length; p++) {
+ if (proposals[p].voteCount > winningVoteCount) {
+ winningVoteCount = proposals[p].voteCount;
+ winningProposal_ = p;
+ }
+ }
+}
+```
+
+`returns (uint winningProposal)` 指定了函数的返回值类型,`constant` 表示该函数不会改变合约状态变量的值。
+
+最后是查询获胜者名称:
+
+```javascript
+function winnerName() public view
+ returns (bytes32 winnerName_)
+{
+ winnerName_ = proposals[winningProposal()].name;
+}
+```
+
+这里采用内部调用 `winningProposal()` 函数的方式获得获胜提案。如果需要采用外部调用,则需要写为 `this.winningProposal()`。
+
+
+
+**参考自:**
+
+[尚硅谷区块链全套Go语言→GoWeb→以太坊→项目实战](https://www.bilibili.com/video/BV1sJ411D72u)
+[web3.js 1.0中文手册](http://cw.hubwiz.com/card/c/web3.js-1.0/)
+
diff --git a/Blockchain/pic/2021-02-19_110327.png b/Blockchain/pic/2021-02-19_110327.png
new file mode 100644
index 0000000..7b03f57
Binary files /dev/null and b/Blockchain/pic/2021-02-19_110327.png differ
diff --git a/Blockchain/pic/2021-02-19_120756.png b/Blockchain/pic/2021-02-19_120756.png
new file mode 100644
index 0000000..f3e64de
Binary files /dev/null and b/Blockchain/pic/2021-02-19_120756.png differ
diff --git a/Blockchain/pic/2021-02-19_125917.png b/Blockchain/pic/2021-02-19_125917.png
new file mode 100644
index 0000000..2d77359
Binary files /dev/null and b/Blockchain/pic/2021-02-19_125917.png differ
diff --git a/Blockchain/pic/2021-02-19_130053.png b/Blockchain/pic/2021-02-19_130053.png
new file mode 100644
index 0000000..35b98d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_130053.png differ
diff --git a/Blockchain/pic/2021-02-19_133508.png b/Blockchain/pic/2021-02-19_133508.png
new file mode 100644
index 0000000..78c5567
Binary files /dev/null and b/Blockchain/pic/2021-02-19_133508.png differ
diff --git a/Blockchain/pic/2021-02-19_134110.png b/Blockchain/pic/2021-02-19_134110.png
new file mode 100644
index 0000000..c7e7ba5
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134110.png differ
diff --git a/Blockchain/pic/2021-02-19_134257.png b/Blockchain/pic/2021-02-19_134257.png
new file mode 100644
index 0000000..75d426b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134257.png differ
diff --git a/Blockchain/pic/2021-02-19_134634.png b/Blockchain/pic/2021-02-19_134634.png
new file mode 100644
index 0000000..eb63545
Binary files /dev/null and b/Blockchain/pic/2021-02-19_134634.png differ
diff --git a/Blockchain/pic/2021-02-19_135113.png b/Blockchain/pic/2021-02-19_135113.png
new file mode 100644
index 0000000..a8f69cc
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135113.png differ
diff --git a/Blockchain/pic/2021-02-19_135337.png b/Blockchain/pic/2021-02-19_135337.png
new file mode 100644
index 0000000..1b3998b
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135337.png differ
diff --git a/Blockchain/pic/2021-02-19_135413.png b/Blockchain/pic/2021-02-19_135413.png
new file mode 100644
index 0000000..b24c373
Binary files /dev/null and b/Blockchain/pic/2021-02-19_135413.png differ
diff --git a/Blockchain/pic/2021-02-19_142407.png b/Blockchain/pic/2021-02-19_142407.png
new file mode 100644
index 0000000..10704d3
Binary files /dev/null and b/Blockchain/pic/2021-02-19_142407.png differ
diff --git a/Blockchain/pic/EOA_CA.png b/Blockchain/pic/EOA_CA.png
new file mode 100644
index 0000000..9612e9b
Binary files /dev/null and b/Blockchain/pic/EOA_CA.png differ
diff --git a/Blockchain/pic/aaaaaa b/Blockchain/pic/aaaaaa
new file mode 100644
index 0000000..8b13789
--- /dev/null
+++ b/Blockchain/pic/aaaaaa
@@ -0,0 +1 @@
+
diff --git a/Blockchain/pic/bg2017122703.png b/Blockchain/pic/bg2017122703.png
new file mode 100644
index 0000000..5c91bc5
Binary files /dev/null and b/Blockchain/pic/bg2017122703.png differ
diff --git a/Blockchain/pic/gas.jpg b/Blockchain/pic/gas.jpg
new file mode 100644
index 0000000..13bd71c
Binary files /dev/null and b/Blockchain/pic/gas.jpg differ
diff --git a/Blockchain/pic/image-20210219000835894.png b/Blockchain/pic/image-20210219000835894.png
new file mode 100644
index 0000000..5fea35e
Binary files /dev/null and b/Blockchain/pic/image-20210219000835894.png differ
diff --git a/Blockchain/pic/image-20210219101124978.png b/Blockchain/pic/image-20210219101124978.png
new file mode 100644
index 0000000..28411df
Binary files /dev/null and b/Blockchain/pic/image-20210219101124978.png differ
diff --git a/Blockchain/pic/image-20210219101226095.png b/Blockchain/pic/image-20210219101226095.png
new file mode 100644
index 0000000..8ddead4
Binary files /dev/null and b/Blockchain/pic/image-20210219101226095.png differ
diff --git a/Blockchain/pic/image-20210219101300792.png b/Blockchain/pic/image-20210219101300792.png
new file mode 100644
index 0000000..2dcad74
Binary files /dev/null and b/Blockchain/pic/image-20210219101300792.png differ
diff --git a/Blockchain/pic/image-20210219101332089.png b/Blockchain/pic/image-20210219101332089.png
new file mode 100644
index 0000000..e74b090
Binary files /dev/null and b/Blockchain/pic/image-20210219101332089.png differ
diff --git a/Blockchain/pic/image-20210219102028033.png b/Blockchain/pic/image-20210219102028033.png
new file mode 100644
index 0000000..966feb4
Binary files /dev/null and b/Blockchain/pic/image-20210219102028033.png differ
diff --git a/Blockchain/pic/image-20210219102255927.png b/Blockchain/pic/image-20210219102255927.png
new file mode 100644
index 0000000..8acef84
Binary files /dev/null and b/Blockchain/pic/image-20210219102255927.png differ
diff --git a/Blockchain/pic/image-20210219102322360.png b/Blockchain/pic/image-20210219102322360.png
new file mode 100644
index 0000000..513c9de
Binary files /dev/null and b/Blockchain/pic/image-20210219102322360.png differ
diff --git a/Blockchain/pic/image-20210219102359096.png b/Blockchain/pic/image-20210219102359096.png
new file mode 100644
index 0000000..aa9a394
Binary files /dev/null and b/Blockchain/pic/image-20210219102359096.png differ
diff --git a/Blockchain/pic/image-20210219105522149.png b/Blockchain/pic/image-20210219105522149.png
new file mode 100644
index 0000000..f3e6648
Binary files /dev/null and b/Blockchain/pic/image-20210219105522149.png differ
diff --git a/Blockchain/pic/image-20210219105616335.png b/Blockchain/pic/image-20210219105616335.png
new file mode 100644
index 0000000..a23c2dd
Binary files /dev/null and b/Blockchain/pic/image-20210219105616335.png differ
diff --git a/Blockchain/pic/image-20210219105824087.png b/Blockchain/pic/image-20210219105824087.png
new file mode 100644
index 0000000..c03a2b4
Binary files /dev/null and b/Blockchain/pic/image-20210219105824087.png differ
diff --git a/Blockchain/pic/image-20210219105911910.png b/Blockchain/pic/image-20210219105911910.png
new file mode 100644
index 0000000..eff8c5c
Binary files /dev/null and b/Blockchain/pic/image-20210219105911910.png differ
diff --git a/Blockchain/pic/image1.png b/Blockchain/pic/image1.png
new file mode 100644
index 0000000..8435a7e
Binary files /dev/null and b/Blockchain/pic/image1.png differ
diff --git a/Blockchain/pic/image2.png b/Blockchain/pic/image2.png
new file mode 100644
index 0000000..5688b8c
Binary files /dev/null and b/Blockchain/pic/image2.png differ
diff --git a/Blockchain/pic/image3.png b/Blockchain/pic/image3.png
new file mode 100644
index 0000000..c3bfdca
Binary files /dev/null and b/Blockchain/pic/image3.png differ
diff --git a/Blockchain/pic/image4.png b/Blockchain/pic/image4.png
new file mode 100644
index 0000000..3ce8d94
Binary files /dev/null and b/Blockchain/pic/image4.png differ
diff --git a/Blockchain/pic/image5.png b/Blockchain/pic/image5.png
new file mode 100644
index 0000000..3038f58
Binary files /dev/null and b/Blockchain/pic/image5.png differ
diff --git a/Blockchain/pic/image6.png b/Blockchain/pic/image6.png
new file mode 100644
index 0000000..82f5ecc
Binary files /dev/null and b/Blockchain/pic/image6.png differ
diff --git a/Blockchain/pic/part2-1.png b/Blockchain/pic/part2-1.png
new file mode 100644
index 0000000..8c0da19
Binary files /dev/null and b/Blockchain/pic/part2-1.png differ
diff --git a/Blockchain/pic/part2-10.png b/Blockchain/pic/part2-10.png
new file mode 100644
index 0000000..f0b447e
Binary files /dev/null and b/Blockchain/pic/part2-10.png differ
diff --git a/Blockchain/pic/part2-11.png b/Blockchain/pic/part2-11.png
new file mode 100644
index 0000000..06cca10
Binary files /dev/null and b/Blockchain/pic/part2-11.png differ
diff --git a/Blockchain/pic/part2-12.png b/Blockchain/pic/part2-12.png
new file mode 100644
index 0000000..5eb5b8e
Binary files /dev/null and b/Blockchain/pic/part2-12.png differ
diff --git a/Blockchain/pic/part2-13.png b/Blockchain/pic/part2-13.png
new file mode 100644
index 0000000..e9433fa
Binary files /dev/null and b/Blockchain/pic/part2-13.png differ
diff --git a/Blockchain/pic/part2-14.png b/Blockchain/pic/part2-14.png
new file mode 100644
index 0000000..f87ff72
Binary files /dev/null and b/Blockchain/pic/part2-14.png differ
diff --git a/Blockchain/pic/part2-15.png b/Blockchain/pic/part2-15.png
new file mode 100644
index 0000000..abebc5d
Binary files /dev/null and b/Blockchain/pic/part2-15.png differ
diff --git a/Blockchain/pic/part2-16.png b/Blockchain/pic/part2-16.png
new file mode 100644
index 0000000..7a91692
Binary files /dev/null and b/Blockchain/pic/part2-16.png differ
diff --git a/Blockchain/pic/part2-17.png b/Blockchain/pic/part2-17.png
new file mode 100644
index 0000000..d831f99
Binary files /dev/null and b/Blockchain/pic/part2-17.png differ
diff --git a/Blockchain/pic/part2-18.png b/Blockchain/pic/part2-18.png
new file mode 100644
index 0000000..c42e156
Binary files /dev/null and b/Blockchain/pic/part2-18.png differ
diff --git a/Blockchain/pic/part2-19.png b/Blockchain/pic/part2-19.png
new file mode 100644
index 0000000..cf84b29
Binary files /dev/null and b/Blockchain/pic/part2-19.png differ
diff --git a/Blockchain/pic/part2-2.png b/Blockchain/pic/part2-2.png
new file mode 100644
index 0000000..a8ecb2c
Binary files /dev/null and b/Blockchain/pic/part2-2.png differ
diff --git a/Blockchain/pic/part2-20.png b/Blockchain/pic/part2-20.png
new file mode 100644
index 0000000..cf3cb04
Binary files /dev/null and b/Blockchain/pic/part2-20.png differ
diff --git a/Blockchain/pic/part2-21.png b/Blockchain/pic/part2-21.png
new file mode 100644
index 0000000..84896de
Binary files /dev/null and b/Blockchain/pic/part2-21.png differ
diff --git a/Blockchain/pic/part2-22.png b/Blockchain/pic/part2-22.png
new file mode 100644
index 0000000..db238cf
Binary files /dev/null and b/Blockchain/pic/part2-22.png differ
diff --git a/Blockchain/pic/part2-23.png b/Blockchain/pic/part2-23.png
new file mode 100644
index 0000000..256124b
Binary files /dev/null and b/Blockchain/pic/part2-23.png differ
diff --git a/Blockchain/pic/part2-24.png b/Blockchain/pic/part2-24.png
new file mode 100644
index 0000000..6007692
Binary files /dev/null and b/Blockchain/pic/part2-24.png differ
diff --git a/Blockchain/pic/part2-3.png b/Blockchain/pic/part2-3.png
new file mode 100644
index 0000000..1ff0dda
Binary files /dev/null and b/Blockchain/pic/part2-3.png differ
diff --git a/Blockchain/pic/part2-4.png b/Blockchain/pic/part2-4.png
new file mode 100644
index 0000000..8879b10
Binary files /dev/null and b/Blockchain/pic/part2-4.png differ
diff --git a/Blockchain/pic/part2-5.png b/Blockchain/pic/part2-5.png
new file mode 100644
index 0000000..6308a3d
Binary files /dev/null and b/Blockchain/pic/part2-5.png differ
diff --git a/Blockchain/pic/part2-6.png b/Blockchain/pic/part2-6.png
new file mode 100644
index 0000000..debad8c
Binary files /dev/null and b/Blockchain/pic/part2-6.png differ
diff --git a/Blockchain/pic/part2-7.png b/Blockchain/pic/part2-7.png
new file mode 100644
index 0000000..f9a3ea0
Binary files /dev/null and b/Blockchain/pic/part2-7.png differ
diff --git a/Blockchain/pic/part2-8.png b/Blockchain/pic/part2-8.png
new file mode 100644
index 0000000..ed642a5
Binary files /dev/null and b/Blockchain/pic/part2-8.png differ
diff --git a/Blockchain/pic/part2-9.png b/Blockchain/pic/part2-9.png
new file mode 100644
index 0000000..8c1e817
Binary files /dev/null and b/Blockchain/pic/part2-9.png differ
diff --git a/Blockchain/pic/part3-1.png b/Blockchain/pic/part3-1.png
new file mode 100644
index 0000000..094515c
Binary files /dev/null and b/Blockchain/pic/part3-1.png differ
diff --git a/Blockchain/pic/part3-10.png b/Blockchain/pic/part3-10.png
new file mode 100644
index 0000000..1c2c0c6
Binary files /dev/null and b/Blockchain/pic/part3-10.png differ
diff --git a/Blockchain/pic/part3-11.png b/Blockchain/pic/part3-11.png
new file mode 100644
index 0000000..d6f6474
Binary files /dev/null and b/Blockchain/pic/part3-11.png differ
diff --git a/Blockchain/pic/part3-12.png b/Blockchain/pic/part3-12.png
new file mode 100644
index 0000000..30c4582
Binary files /dev/null and b/Blockchain/pic/part3-12.png differ
diff --git a/Blockchain/pic/part3-13.png b/Blockchain/pic/part3-13.png
new file mode 100644
index 0000000..a1f9783
Binary files /dev/null and b/Blockchain/pic/part3-13.png differ
diff --git a/Blockchain/pic/part3-2.png b/Blockchain/pic/part3-2.png
new file mode 100644
index 0000000..2d74cd1
Binary files /dev/null and b/Blockchain/pic/part3-2.png differ
diff --git a/Blockchain/pic/part3-3.png b/Blockchain/pic/part3-3.png
new file mode 100644
index 0000000..824fd9b
Binary files /dev/null and b/Blockchain/pic/part3-3.png differ
diff --git a/Blockchain/pic/part3-4.png b/Blockchain/pic/part3-4.png
new file mode 100644
index 0000000..152a017
Binary files /dev/null and b/Blockchain/pic/part3-4.png differ
diff --git a/Blockchain/pic/part3-5.png b/Blockchain/pic/part3-5.png
new file mode 100644
index 0000000..9b62fe6
Binary files /dev/null and b/Blockchain/pic/part3-5.png differ
diff --git a/Blockchain/pic/part3-6.png b/Blockchain/pic/part3-6.png
new file mode 100644
index 0000000..00e7473
Binary files /dev/null and b/Blockchain/pic/part3-6.png differ
diff --git a/Blockchain/pic/part3-7.png b/Blockchain/pic/part3-7.png
new file mode 100644
index 0000000..f6dfe7a
Binary files /dev/null and b/Blockchain/pic/part3-7.png differ
diff --git a/Blockchain/pic/part3-8.png b/Blockchain/pic/part3-8.png
new file mode 100644
index 0000000..212eb36
Binary files /dev/null and b/Blockchain/pic/part3-8.png differ
diff --git a/Blockchain/pic/part3-9.png b/Blockchain/pic/part3-9.png
new file mode 100644
index 0000000..567481f
Binary files /dev/null and b/Blockchain/pic/part3-9.png differ
diff --git a/Blockchain/pic/picfile b/Blockchain/pic/picfile
new file mode 100644
index 0000000..ca8de66
--- /dev/null
+++ b/Blockchain/pic/picfile
@@ -0,0 +1 @@
+This folder contains some necessary picture
diff --git a/Blockchain/pic/rating.png b/Blockchain/pic/rating.png
new file mode 100644
index 0000000..204d972
Binary files /dev/null and b/Blockchain/pic/rating.png differ
diff --git a/Blockchain/pic/transaction-struct.png b/Blockchain/pic/transaction-struct.png
new file mode 100644
index 0000000..da26c42
Binary files /dev/null and b/Blockchain/pic/transaction-struct.png differ
diff --git a/Blockchain/pic/utxo_com.jpg b/Blockchain/pic/utxo_com.jpg
new file mode 100644
index 0000000..77c03d0
Binary files /dev/null and b/Blockchain/pic/utxo_com.jpg differ
diff --git a/Blockchain/readme.md b/Blockchain/readme.md
new file mode 100644
index 0000000..6fb3759
--- /dev/null
+++ b/Blockchain/readme.md
@@ -0,0 +1,46 @@
+# 1. 编程实践(区块链)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/Blockchain
+
+## 基本信息
+
+- 贡献人员:陈锴、孙子涵、李岳昆、易远哲
+- 学习周期:12天
+- 学习形式:根据教程主线进行学习
+- 人群定位:具有至少一门编程语言基础,在开展组队学习之前能够熟悉 Linux 基本操作
+- 难度系数:较难
+
+## 学习目标
+
+## 任务安排
+
+### Task00:熟悉规则并先修Linux(2天)
+
+- 组队、修改群昵称
+- 熟悉打卡规则
+- 对Linux不太熟悉的学习者先安装Linux环境(可以是虚拟机或子系统)并掌握基本命令,其他内容可以暂不了解
+
+### Task01:区块链简介与以太坊入门介绍(2天)
+
+* 学习者学习区块链基础与以太坊入门介绍,该部分以了解为主
+* 学习者可以根据教程提供的各个方面内容,对某一部分深入了解并进行打卡
+* 打卡截至时间:3月16日24:00
+
+### Task02:Solidity基础(3天)
+
+* 学习者学习Solidity在线编辑器Remix的使用以及Solidity的基础操作,该部分需要深入掌握,学习者可以根据参考链接提供的资料进一步学习
+* 打卡内容为Task02最后的Solidity练习题部分,其他内容不作硬性要求
+* 打卡截止日期:3月19日24:00
+
+### Task03:web3js基础(3天)
+
+* 学习者学习以太坊客户端的使用以及Geth控制台部署智能合约
+* 打卡内容为学习者完成一个自己编写的合约的部署,并测试函数调用等
+* 打卡截止日期:3月22日24:00
+
+### Task04:合约编写实战实例(2天)
+
+* 学习者学习编写几个Remix官网自带的合约,并回顾 Task01的教程内容重新梳理知识点
+* 打卡内容为学习者自己的学习感悟,内容不限
+* 打卡截止日期:3月23日24:00
+
diff --git a/Docker/00 开篇词.md b/Docker/00 开篇词.md
new file mode 100644
index 0000000..df37501
--- /dev/null
+++ b/Docker/00 开篇词.md
@@ -0,0 +1,24 @@
+# Chapter 0 开篇词
+
+相信大家在开发项目尤其是团队合作项目中一定会遇到下面这些场景:
+
+- 项目在我电脑上明明运行的很好呀!怎么在你这不行了呢?
+- 我这是用python 3.6写的,你电脑是python 2.7应该运行不了。
+- 项目的一些依赖包需要科学上网才能下载,你那没有的话赶紧下载一下才能运行。
+- 论文的代码已经公开到github上了,但是因为自己电脑环境和他的不一样,项目在自己电脑上死活跑不起来。
+
+以上这些问题我相信大家并不陌生,那么通过本次Docker的组队学习,希望大家能够避免卡在科研或者开发的第一步,提高自己的生产力。
+
+---
+
+通过本次docker的组队学习,我们希望你能学到以下几个方面的能力:
+
+- 了解什么是docker
+- docker镜像是怎么构建的
+- 如何运行一个docker容器
+- docker之间的网络通信是怎么样的
+- docker中的数据如何做持久化存储
+- 如何通过docker compose管理自己的项目
+- 如何将自己的个人项目打造成容器化部署的形式
+
+祝你在docker的学习上一切顺利!
\ No newline at end of file
diff --git a/Docker/04 Docker数据管理.md b/Docker/04 Docker数据管理.md
new file mode 100644
index 0000000..4283a12
--- /dev/null
+++ b/Docker/04 Docker数据管理.md
@@ -0,0 +1,176 @@
+# Chapter 4 Docker 数据管理
+
+这一章介绍如何在 Docker 内部以及容器之间管理数据,在容器中管理数据主要有两种方式:
+
+* 数据卷
+* 挂载主机目录
+
+
+## 数据卷
+
+数据卷是一个可供一个或多个容器使用的特殊目录,它绕过 UFS (UNIX File System) ,可以提供很多有用的特性:
+
+* 数据卷可以在容器之间共享和重用
+
+* 对数据卷的修改会立马生效
+
+* 对数据卷的更新,不会影响镜像
+
+* 数据卷默认会一直存在,即使容器被删除
+
+>注意:数据卷的使用,类似于 Linux 下对目录或文件进行 mount,镜像中的被指定为挂载点的目录中的文件会复制到数据卷中(仅数据卷为空时会复制)。
+
+### 创建一个数据卷
+
+```bash
+$ docker volume create datawhale
+```
+
+查看所有的数据卷
+
+```bash
+$ docker volume ls
+
+DRIVER VOLUME NAME
+local datawhale
+```
+
+在主机里使用以下命令可以查看指定数据卷的信息
+
+```bash
+$ docker volume inspect datawhale
+[
+ {
+ "Driver": "local",
+ "Labels": {},
+ "Mountpoint": "/var/lib/docker/volumes/datawhale/_data",
+ "Name": "datawhale",
+ "Options": {},
+ "Scope": "local"
+ }
+]
+```
+
+### 启动一个挂载数据卷的容器
+
+在用 `docker run` 命令的时候,使用 `--mount` 标记来将数据卷挂载到容器里。在一次 `docker run` 中可以挂载多个 `数据卷`。
+
+下面创建一个名为 `web` 的容器,并加载一个数据卷到容器的 `/usr/share/nginx/html` 目录。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount source=datawhale,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+>–-mount参数说明:
+> source :数据卷
+> target :是容器内文件系统挂载点
+
+>注意,可以不需要提前创建好数据卷,直接在运行容器的时候mount 这时如果不存在指定的数据卷,docker会自动创建,自动生成。
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`数据卷` 信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "volume",
+ "Name": "datawhale",
+ "Source": "/var/lib/docker/volumes/datawhale/_data",
+ "Destination": "/usr/share/nginx/html",
+ "Driver": "local",
+ "Mode": "",
+ "RW": true,
+ "Propagation": ""
+ }
+],
+```
+
+### 删除数据卷
+
+```bash
+$ docker volume rm datawhale #datawhale为卷名
+```
+
+数据卷是被设计用来持久化数据的,它的生命周期独立于容器,Docker 不会在容器被删除后自动删除 `数据卷`,并且也不存在垃圾回收这样的机制来处理没有任何容器引用的 `数据卷`。如果需要在删除容器的同时移除数据卷。可以在删除容器的时候使用 `docker rm -v` 这个命令。
+
+无主的数据卷可能会占据很多空间,要清理请使用以下命令
+
+```bash
+$ docker volume prune
+```
+
+## 挂载主机目录
+
+### 挂载一个主机目录作为数据卷
+
+使用 `--mount` 标记可以指定挂载一个本地主机的目录到容器中去。
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html \
+ nginx:alpine
+```
+
+上面的命令加载主机的 `/src/webapp` 目录到容器的 `/usr/share/nginx/html`目录。这个功能在进行测试的时候十分方便,比如用户可以放置一些程序到本地目录中,来查看容器是否正常工作。本地目录的路径必须是绝对路径,以前使用 `-v` 参数时如果本地目录不存在 Docker 会自动为你创建一个文件夹,现在使用 `--mount` 参数时如果本地目录不存在,Docker 会报错。
+
+Docker 挂载主机目录的默认权限是 `读写`,用户也可以通过增加 `readonly` 指定为 `只读`。
+
+>注意: 如果挂载的目录不存在,创建容器时,docker 不会自动创建,此时会报错
+
+```bash
+$ docker run -d -P \
+ --name web \
+ --mount type=bind,source=/src/webapp,target=/usr/share/nginx/html,readonly \
+ nginx:alpine
+```
+
+加了 `readonly` 之后,就挂载为 `只读` 了。如果你在容器内 `/usr/share/nginx/html` 目录新建文件,会显示如下错误
+
+```bash
+/usr/share/nginx/html # touch new.txt
+touch: new.txt: Read-only file system
+```
+
+### 查看数据卷的具体信息
+
+在主机里使用以下命令可以查看 `web` 容器的信息
+
+```bash
+$ docker inspect web
+```
+
+`挂载主机目录` 的配置信息在 "Mounts" Key 下面
+
+```json
+"Mounts": [
+ {
+ "Type": "bind",
+ "Source": "/src/webapp",
+ "Destination": "/usr/share/nginx/html",
+ "Mode": "",
+ "RW": true,
+ "Propagation": "rprivate"
+ }
+],
+```
+
+### 挂载一个本地主机文件作为数据卷
+
+`--mount` 标记也可以从主机挂载单个文件到容器中
+
+```bash
+$ docker run --rm -it \
+ --mount type=bind,source=$HOME/.bash_history,target=/root/.bash_history \
+ ubuntu:18.04 \
+ bash
+```
diff --git a/Docker/05 Docker网络.md b/Docker/05 Docker网络.md
new file mode 100644
index 0000000..5747442
--- /dev/null
+++ b/Docker/05 Docker网络.md
@@ -0,0 +1,783 @@
+# Chapter 5 Docker 网络
+
+## 内容大纲
+
+### Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+### Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+### Docker高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+
+
+# Docker 基础网络介绍
+
+ - [外部访问容器](#外部访问容器)
+ - [容器互联](#容器互联)
+ - [配置DNS](#配置DNS)
+
+## 外部访问容器
+
+容器中可以运行一些网络应用,要让外部也可以访问这些应用,可以通过`-P`或`-p`参数来指定端口映射。
+
+当使用`-P`标记时,`Docker`会随机映射一个端口到内部容器开放的网络端口。
+使用`docker container ls`可以看到,本地主机的 32768 被映射到了容器的 80 端口。此时访问本机的 32768 端口即可访问容器内 NGINX 默认页面。
+
+```
+$ docker run -d -P nginx:alpine
+
+$ docker container ls -l
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+fae320d08268 nginx:alpine "/docker-entrypoint.…" 24 seconds ago Up 20 seconds 0.0.0.0:32768->80/tcp bold_mcnulty
+```
+
+同样的,可以通过`docker logs`命令来查看访问记录。
+
+```
+$ docker logs fa
+172.17.0.1 - - [25/Aug/2020:08:34:04 +0000] "GET / HTTP/1.1" 200 612 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:80.0) Gecko/20100101 Firefox/80.0" "-"
+```
+
+`-p`则可以指定要映射的端口,并且,在一个指定端口上只可以绑定一个容器。支持的格式有`ip:hostPort:containerPort | ip::containerPort | hostPort:containerPort`.
+
+### 映射所有接口地址
+
+使用`hostPort:containerPort`格式本地的 80 端口映射到容器的 80 端口,可以执行
+
+```
+$ docker run -d -p 80:80 nginx:alpine
+```
+
+此时默认会绑定本地所有接口上的所有地址。
+
+### 映射到指定地址的指定端口
+
+可以使用`ip:hostPort:containerPort`格式指定映射使用一个特定地址,比如`localhost`地址127.0.0.1
+
+```
+$ docker run -d -p 127.0.0.1:80:80 nginx:alpine
+```
+
+### 映射到指定地址的任意端口
+
+使用`ip::containerPort`绑定`localhost`的任意端口到容器的80端口,本地主机会自动分配一个端口。
+
+```
+$ docker run -d -p 127.0.0.1::80 nginx:alpine
+```
+
+还可以使用`udp`标记来指定`udp`端口
+
+```
+$ docker run -d -p 127.0.0.1:80:80/udp nginx:alpine
+```
+
+### 查看映射端口配置
+
+使用`docker port`来查看当前映射的端口配置,也可以查看到绑定的地址
+
+```
+$ docker port fa 80
+0.0.0.0:32768
+```
+
+**注意:**
+容器有自己的内部网络和 ip 地址(使用`docker inspect`查看,`Docker`还可以有一个可变的网络配置。)
+`-p`标记可以多次使用来绑定多个端口
+
+例如
+
+```
+$ docker run -d \
+ -p 80:80 \
+ -p 443:443 \
+ nginx:alpine
+```
+
+## 容器互联
+
+如果之前有 `Docker`使用经验,可能已经习惯了使用`--link`参数来使容器互联。
+随着 `Docker` 网络的完善,强烈建议大家将容器加入自定义的`Docker`网络来连接多个容器,而不是使用 `--link`参数。
+
+### 新建网络
+
+下面先创建一个新的 `Docker`网络。
+
+```
+$ docker network create -d bridge my-net
+```
+
+`-d`参数指定`Docker`网络类型,有`bridge overlay`,其中`overlay`网络类型用于`Swarm mode`,在本小节中你可以忽略它。
+
+### 连接容器
+
+运行一个容器并连接到新建的`my-net`网络
+
+```
+$ docker run -it --rm --name busybox1 --network my-net busybox sh
+```
+
+打开新的终端,再运行一个容器并加入到 `my-net`网络
+
+```
+$ docker run -it --rm --name busybox2 --network my-net busybox sh
+```
+
+再打开一个新的终端查看容器信息
+
+```
+$ docker container ls
+
+CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS NAMES
+b47060aca56b busybox "sh" 11 minutes ago Up 11 minutes busybox2
+8720575823ec busybox "sh" 16 minutes ago Up 16 minutes busybox1
+```
+
+下面通过 `ping`来证明`busybox1`容器和`busybox2`容器建立了互联关系。
+在`busybox1`容器输入以下命令
+
+```
+/ # ping busybox2
+PING busybox2 (172.19.0.3): 56 data bytes
+64 bytes from 172.19.0.3: seq=0 ttl=64 time=0.072 ms
+64 bytes from 172.19.0.3: seq=1 ttl=64 time=0.118 ms
+```
+
+用`ping`来测试连接`busybox2`容器,它会解析成 172.19.0.3。
+同理在`busybox2`容器执行`ping busybox1`,也会成功连接到。
+
+```
+/ # ping busybox1
+PING busybox1 (172.19.0.2): 56 data bytes
+64 bytes from 172.19.0.2: seq=0 ttl=64 time=0.064 ms
+64 bytes from 172.19.0.2: seq=1 ttl=64 time=0.143 ms
+```
+
+这样,`busybox1` 容器和 `busybox2` 容器建立了互联关系。
+
+`Docker Compose`
+如果你有多个容器之间需要互相连接,推荐使用`Docker`Compose。
+
+## 配置DNS
+
+如何自定义配置容器的主机名和 DNS 呢?秘诀就是`Docker`利用虚拟文件来挂载容器的 3个相关配置文件。
+
+在容器中使用 `mount`命令可以看到挂载信息:
+
+```
+$ mount
+/dev/disk/by-uuid/1fec...ebdf on /etc/hostname type ext4 ...
+/dev/disk/by-uuid/1fec...ebdf on /etc/hosts type ext4 ...
+tmpfs on /etc/resolv.conf type tmpfs ...
+```
+
+这种机制可以让宿主主机 DNS 信息发生更新后,所有`Docker`容器的 DNS 配置通过 `/etc/resolv.conf`文件立刻得到更新。
+
+配置全部容器的 DNS ,也可以在 `/etc/docker/daemon.json` 文件中增加以下内容来设置。
+
+```
+{
+ "dns" : [
+ "114.114.114.114",
+ "8.8.8.8"
+ ]
+}
+```
+
+这样每次启动的容器 DNS 自动配置为 114.114.114.114 和8.8.8.8。使用以下命令来证明其已经生效。
+
+```
+$ docker run -it --rm ubuntu:18.04 cat etc/resolv.conf
+
+nameserver 114.114.114.114
+nameserver 8.8.8.8
+```
+
+如果用户想要手动指定容器的配置,可以在使用`docker run`命令启动容器时加入如下参数:
+`-h HOSTNAME`或者`--hostname=HOSTNAME`设定容器的主机名,它会被写到容器内的`/etc/hostname 和 /etc/hosts`。但它在容器外部看不到,既不会在`docker container ls`中显示,也不会在其他的容器的`/etc/hosts`看到。
+
+`--dns=IP_ADDRESS`添加 DNS 服务器到容器的`/etc/resolv.conf`中,让容器用这个服务器来解析所有不在 `/etc/hosts `中的主机名。
+
+`--dns-search=DOMAIN`设定容器的搜索域,当设定搜索域为`.example.com`时,在搜索一个名为`host`的主机时,DNS 不仅搜索 `host`,还会搜索`host.example.com`。
+
+**注意:**如果在容器启动时没有指定最后两个参数,`Docker`会默认用主机上的`/etc/resolv.conf`来配置容器。
+
+# Docker的网络模式
+
+- [Bridge 模式](#Bridge模式)
+- [Host 模式](#Host 模式)
+- [None 模式](#None模式)
+- [Container 模式](#Container 模式)
+
+可以通过`docker network ls`查看网络,默认创建三种网络。
+
+```
+[root@localhost ~]# docker network ls
+NETWORK ID NAME DRIVER SCOPE
+688d1970f72e bridge bridge local
+885da101da7d host host local
+f4f1b3cf1b7f none null local
+```
+
+常见网络的含义:
+
+| 网络模式 | 简介 |
+| :-------: | :----------------------------------------------------------: |
+| Bridge | 为每一个容器分配、设置 IP 等,并将容器连接到一个 `docker0` 虚拟网桥,默认为该模式。 |
+| Host | 容器将不会虚拟出自己的网卡,配置自己的 IP 等,而是使用宿主机的 IP 和端口。 |
+| None | 容器有独立的 Network namespace,但并没有对其进行任何网络设置,如分配 veth pair 和网桥连接,IP 等。 |
+| Container | 新创建的容器不会创建自己的网卡和配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等。 |
+
+## Bridge模式
+
+当`Docker`进程启动时,会在主机上创建一个名为`docker0`的虚拟网桥,此主机上启动的`Docker`容器会连接到这个虚拟网桥上,附加在其上的任何网卡之间都能自动转发数据包。虚拟网桥的工作方式和物理交换机类似,这样主机上的所有容器就通过交换机连在了一个二层网络中。从`docker0`子网中分配一个 IP 给容器使用,并设置 `docker0 `的 IP 地址为容器的默认网关。在主机上创建一对虚拟网卡`veth pair`设备,`Docker `将 `veth pair` 设备的一端放在新创建的容器中,并命名为`eth0`(容器的网卡),另一端放在主机中,以`vethxxx`这样类似的名字命名,并将这个网络设备加入到 `docker0` 网桥中。可以通过`brctl show`命令查看。
+
+比如运行一个基于 `busybox` 镜像构建的容器 `bbox01`,查看 `ip addr`:
+
+> busybox 被称为嵌入式 Linux 的瑞士军刀,整合了很多小的 unix 下的通用功能到一个小的可执行文件中。
+
+
+
+然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 通过以上的比较可以发现,证实了之前所说的:守护进程会创建一对对等虚拟设备接口 `veth pair`,将其中一个接口设置为容器的 `eth0` 接口(容器的网卡),另一个接口放置在宿主机的命名空间中,以类似 `vethxxx` 这样的名字命名。
+
+ 同时,守护进程还会从网桥 `docker0` 的私有地址空间中分配一个 IP 地址和子网给该容器,并设置 docker0 的 IP 地址为容器的默认网关。也可以安装 `yum install -y bridge-utils` 以后,通过 `brctl show` 命令查看网桥信息。
+
+
+
+ 对于每个容器的 IP 地址和 Gateway 信息,可以通过 `docker inspect 容器名称|ID` 进行查看,在 `NetworkSettings` 节点中可以看到详细信息。
+
+
+
+ 可以通过 `docker network inspect bridge` 查看所有 `bridge` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+> 关于 `bridge` 网络模式的使用,只需要在创建容器时通过参数 `--net bridge` 或者 `--network bridge` 指定即可,当然这也是创建容器默认使用的网络模式,也就是说这个参数是可以省略的。
+
+
+
+
+
+bridge模式是 `docker `的默认网络模式,不写`–net`参数,就是bridge模式。使用`docker run -p`时,`docker `实际是在`iptables`做了`DNAT`规则,实现端口转发功能。可以使用`iptables -t nat -vnL`查看。`bridge`模式如下图所示:
+
+ 演示:
+
+ ```
+$ docker run -tid --net=bridge --name docker_bri1 \
+ ubuntu-base:v3
+ docker run -tid --net=bridge --name docker_bri2 \
+ ubuntu-base:v3
+
+$ brctl show
+$ docker exec -ti docker_bri1 /bin/bash
+$ ifconfig –a
+$ route –n
+ ```
+
+
+
+## Host 模式
+
+- host 网络模式需要在创建容器时通过参数 `--net host` 或者 `--network host` 指定;
+- 采用 host 网络模式的 Docker Container,可以直接使用宿主机的 IP 地址与外界进行通信,若宿主机的 eth0 是一个公有 IP,那么容器也拥有这个公有 IP。同时容器内服务的端口也可以使用宿主机的端口,无需额外进行 NAT 转换;
+- host 网络模式可以让容器共享宿主机网络栈,这样的好处是外部主机与容器直接通信,但是容器的网络缺少隔离性。
+
+
+
+
+
+ 比如基于 `host` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox02`,查看 `ip addr`:
+
+
+
+ 然后宿主机通过 `ip addr` 查看信息如下:
+
+
+
+ 对,你没有看错,返回信息一模一样,也可以肯定没有截错图,不信接着往下看。可以通过 `docker network inspect host` 查看所有 `host` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+如果启动容器的时候使用`host`模式,那么这个容器将不会获得一个独立的`Network Namespace`,而是和宿主机共用一个`Network Namespace`。容器将不会虚拟出自己的网卡,配置自己的`IP`等,而是使用宿主机的`IP`和端口。但是,容器的其他方面,如文件系统、进程列表等还是和宿主机隔离的。 `Host`模式如下图所示:
+
+演示:
+
+```
+$ docker run -tid --net=host --name docker_host1 ubuntu-base:v3
+$ docker run -tid --net=host --name docker_host2 ubuntu-base:v3
+
+$ docker exec -ti docker_host1 /bin/bash
+$ docker exec -ti docker_host1 /bin/bash
+
+$ ifconfig –a
+$ route –n
+```
+
+## None模式
+
+- none 网络模式是指禁用网络功能,只有 lo 接口 local 的简写,代表 127.0.0.1,即 localhost 本地环回接口。在创建容器时通过参数 `--net none` 或者 `--network none` 指定;
+- none 网络模式即不为 Docker Container 创建任何的网络环境,容器内部就只能使用 loopback 网络设备,不会再有其他的网络资源。可以说 none 模式为 Docke Container 做了极少的网络设定,但是俗话说得好“少即是多”,在没有网络配置的情况下,作为 Docker 开发者,才能在这基础做其他无限多可能的网络定制开发。这也恰巧体现了 Docker 设计理念的开放。
+
+
+
+ 比如基于 `none` 网络模式创建了一个基于 `busybox` 镜像构建的容器 `bbox03`,查看 `ip addr`:
+
+
+
+ 可以通过 `docker network inspect none` 查看所有 `none` 网络模式下的容器,在 `Containers` 节点中可以看到容器名称。
+
+
+
+使用`none`模式,`Docker` 容器拥有自己的 `Network Namespace`,但是,并不为`Docker` 容器进行任何网络配置。也就是说,这个 `Docker` 容器没有网卡、IP、路由等信息。需要自己为 `Docker` 容器添加网卡、配置 IP 等。 `None`模式示意图:
+
+ 演示:
+
+```
+$ docker run -tid --net=none --name \
+ docker_non1 ubuntu-base:v3
+
+$ docker exec -ti docker_non1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+## Container 模式
+
+- Container 网络模式是 Docker 中一种较为特别的网络的模式。在创建容器时通过参数 `--net container:已运行的容器名称|ID` 或者 `--network container:已运行的容器名称|ID` 指定;
+- 处于这个模式下的 Docker 容器会共享一个网络栈,这样两个容器之间可以使用 localhost 高效快速通信。
+
+
+
+ **Container 网络模式即新创建的容器不会创建自己的网卡,配置自己的 IP,而是和一个指定的容器共享 IP、端口范围等**。同样两个容器除了网络方面相同之外,其他的如文件系统、进程列表等还是隔离的。
+
+ 比如基于容器 `bbox01` 创建了 `container` 网络模式的容器 `bbox04`,查看 `ip addr`:
+
+
+
+ 容器 `bbox01` 的 `ip addr` 信息如下:
+
+
+
+ 宿主机的 `ip addr` 信息如下:
+
+
+
+ 通过以上测试可以发现,Docker 守护进程只创建了一对对等虚拟设备接口用于连接 bbox01 容器和宿主机,而 bbox04 容器则直接使用了 bbox01 容器的网卡信息。
+
+ 这个时候如果将 bbox01 容器停止,会发现 bbox04 容器就只剩下 lo 接口了。
+
+
+
+ 然后 bbox01 容器重启以后,bbox04 容器也重启一下,就又可以获取到网卡信息了。
+
+
+
+这个模式指定新创建的容器和已经存在的一个容器共享一个`Network Namespace`,而不是和宿主机共享。新创建的容器不会创建自己的网卡,配置自己的`IP`,而是和一个指定的容器共享`IP`、端口范围等。同样,两个容器除了网络方面,其他的如文件系统、进程列表等还是隔离的。两个容器的进程可以通过lo网卡设备通信。 `Container`模式示意图:
+
+演示:
+
+```
+$ docker run -tid --net=container:docker_bri1 \
+ --name docker_con1 ubuntu-base:v3
+
+$ docker exec -ti docker_con1 /bin/bash
+$ docker exec -ti docker_bri1 /bin/bash
+
+$ ifconfig –a
+$ route -n
+```
+
+
+
+# 高级网络配置
+
+- [快速配置指南](#快速配置指南)
+- [容器访问控制](#容器访问控制)
+- [端口映射实现](#端口映射实现)
+- [配置docker0网桥](#配置 docker0 网桥)
+- [自定义网桥](#自定义网桥)
+- [工具和示例](#工具和示例)
+- [编辑网络配置文件](#编辑网络配置文件)
+- [实例:创建一个点到点连接](#实例:创建一个点到点连接)
+
+## 快速配置指南
+
+下面是一个跟 Docker 网络相关的命令列表。
+
+其中有些命令选项只有在 Docker 服务启动的时候才能配置,而且不能马上生效。
+
+ - `-b BRIDGE` 或 `--bridge=BRIDGE` 指定容器挂载的网桥
+ - `--bip=CIDR`定制 `docker0` 的掩码
+ - `-H SOCKET...` 或 `--host=SOCKET... Docker` 服务端接收命令的通道
+ - `--icc=true|false` 是否支持容器之间进行通信
+ - `--ip-forward=true|false` 请看下文容器之间的通信
+ - `--iptables=true|false` 是否允许 Docker 添加 `iptables` 规则
+ - `--mtu=BYTES` 容器网络中的 `MTU`
+
+下面2个命令选项既可以在启动服务时指定,也可以在启动容器时指定。在 Docker服务启动的时候指定则会成为默认值,后面执行 `docker run` 时可以覆盖设置的默认值。
+
+ - `--dns=IP_ADDRESS...` 使用指定的DNS服务器
+ - `--dns-search=DOMAIN...` 指定DNS搜索域
+
+最后这些选项只有在 `docker run` 执行时使用,因为它是针对容器的特性内容。
+
+ - `-h HOSTNAME` 或 `--hostname=HOSTNAME` 配置容器主机名
+ - `--link=CONTAINER_NAME:ALIAS` 添加到另一个容器的连接
+ - `--net=bridge|none|container:NAME_or_ID|host` 配置容器的桥接模式
+ - `-p SPEC` 或 --publish=SPEC` 映射容器端口到宿主主机
+ - `-P or --publish-all=true|false` 映射容器所有端口到宿主主机
+
+
+
+
+## 容器访问控制
+
+容器的访问控制,主要通过 Linux 上的 `iptables` 防火墙来进行管理和实现。`iptables` 是 Linux 上默认的防火墙软件,在大部分发行版中都自带。
+
+### 容器访问外部网络
+
+容器要想访问外部网络,需要本地系统的转发支持。在Linux 系统中,检查转发是否打开。
+
+
+
+```
+$sysctl net.ipv4.ip_forward
+net.ipv4.ip_forward = 1
+```
+
+如果为 0,说明没有开启转发,则需要手动打开。
+
+
+
+```
+$sysctl -w net.ipv4.ip_forward=1
+```
+
+如果在启动 Docker 服务的时候设定 `--ip-forward=true`, Docker 就会自动设定系统的 `ip_forward` 参数为 1。
+
+### 容器之间访问
+
+容器之间相互访问,需要两方面的支持。
+
+- 容器的网络拓扑是否已经互联。默认情况下,所有容器都会被连接到 `docker0` 网桥上。
+- 本地系统的防火墙软件 `-- iptables` 是否允许通过。
+
+### 访问所有端口
+
+当启动 Docker 服务(即 dockerd)的时候,默认会添加一条转发策略到本地主机 iptables 的 FORWARD 链上。策略为通过(`ACCEPT`)还是禁止(`DROP`)取决于配置`--icc=true`(缺省值)还是 `--icc=false`。当然,如果手动指定 `--iptables=false` 则不会添加 `iptables` 规则。
+
+可见,默认情况下,不同容器之间是允许网络互通的。如果为了安全考虑,可以在 `/etc/docker/daemon.json` 文件中配置 `{"icc": false}` 来禁止它。
+
+### 访问指定端口
+
+在通过 `-icc=false` 关闭网络访问后,还可以通过 `--link=CONTAINER_NAME:ALIAS` 选项来访问容器的开放端口。
+
+例如,在启动 Docker 服务时,可以同时使用 `icc=false --iptables=true` 参数来关闭允许相互的网络访问,并让 Docker 可以修改系统中的 `iptables` 规则。
+
+此时,系统中的 `iptables` 规则可能是类似
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+...
+```
+
+之后,启动容器(`docker run`)时使用 `--link=CONTAINER_NAME:ALIAS` 选项。Docker 会在 `iptable` 中为 两个容器分别添加一条 `ACCEPT` 规则,允许相互访问开放的端口(取决于 `Dockerfile` 中的 `EXPOSE` 指令)。
+
+当添加了 `--link=CONTAINER_NAME:ALIAS` 选项后,添加了 `iptables` 规则。
+
+
+
+```
+$ sudo iptables -nL
+...
+Chain FORWARD (policy ACCEPT)
+target prot opt source destination
+ACCEPT tcp -- 172.17.0.2 172.17.0.3 tcp spt:80
+ACCEPT tcp -- 172.17.0.3 172.17.0.2 tcp dpt:80
+DROP all -- 0.0.0.0/0 0.0.0.0/0
+```
+
+**注意**:`--link=CONTAINER_NAME:ALIAS` 中的 `CONTAINER_NAME` 目前必须是 Docker 分配的名字,或使用 `--name` 参数指定的名字。主机名则不会被识别。
+
+
+
+## 端口映射实现
+
+默认情况下,容器可以主动访问到外部网络的连接,但是外部网络无法访问到容器。
+
+### 容器访问外部实现
+
+容器所有到外部网络的连接,源地址都会被 NAT 成本地系统的 IP 地址。这是使用 `iptables` 的源地址伪装操作实现的。
+
+查看主机的 NAT 规则。
+
+
+
+```
+$ sudo iptables -t nat -nL
+...
+Chain POSTROUTING (policy ACCEPT)
+target prot opt source destination
+MASQUERADE all -- 172.17.0.0/16 !172.17.0.0/16
+...
+```
+
+其中,上述规则将所有源地址在 `172.17.0.0/16` 网段,目标地址为其他网段(外部网络)的流量动态伪装为从系统网卡发出。MASQUERADE 跟传统 SNAT 的好处是它能动态从网卡获取地址。
+
+### 外部访问容器实现
+
+容器允许外部访问,可以在 `docker run` 时候通过 `-p` 或 `-P` 参数来启用。
+
+不管用那种办法,其实也是在本地的 `iptable` 的 nat 表中添加相应的规则。
+
+使用 `-P` 时:
+
+
+
+```
+$ iptables -t nat -nL
+...
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:49153 to:172.17.0.2:80
+```
+
+使用 `-p 80:80` 时:
+
+
+
+```
+$ iptables -t nat -nL
+Chain DOCKER (2 references)
+target prot opt source destination
+DNAT tcp -- 0.0.0.0/0 0.0.0.0/0 tcp dpt:80 to:172.17.0.2:80
+```
+
+**注意**:
+
+- 这里的规则映射了 `0.0.0.0`,意味着将接受主机来自所有接口的流量。用户可以通过 `-p IP:host_port:container_port` 或 `-p IP::port` 来指定允许访问容器的主机上的 IP、接口等,以制定更严格的规则。
+- 如果希望永久绑定到某个固定的 IP 地址,可以在 Docker 配置文件 `/etc/docker/daemon.json` 中添加如下内容。
+
+
+
+```
+{
+ "ip": "0.0.0.0"
+}
+```
+
+
+
+## 配置 docker0 网桥
+
+Docker 服务默认会创建一个 `docker0` 网桥(其上有一个 `docker0` 内部接口),它在内核层连通了其他的物理或虚拟网卡,这就将所有容器和本地主机都放到同一个物理网络。
+
+Docker 默认指定了 `docker0` 接口 的 IP 地址和子网掩码,让主机和容器之间可以通过网桥相互通信,它还给出了 MTU(接口允许接收的最大传输单元),通常是 1500 Bytes,或宿主主机网络路由上支持的默认值。这些值都可以在服务启动的时候进行配置。
+
+- `--bip=CIDR` IP 地址加掩码格式,例如 192.168.1.5/24
+- `--mtu=BYTES` 覆盖默认的 Docker mtu 配置
+
+也可以在配置文件中配置 DOCKER_OPTS,然后重启服务。
+
+由于目前 Docker 网桥是 Linux 网桥,用户可以使用 `brctl show` 来查看网桥和端口连接信息。
+
+
+
+```
+$ sudo brctl show
+bridge name bridge id STP enabled interfaces
+docker0 8000.3a1d7362b4ee no veth65f9
+ vethdda6
+```
+
+**注**:`brctl` 命令在 Debian、Ubuntu 中可以使用 `sudo apt-get install bridge-utils` 来安装。
+
+每次创建一个新容器的时候,Docker 从可用的地址段中选择一个空闲的 IP 地址分配给容器的 eth0 端口。使用本地主机上 `docker0` 接口的 IP 作为所有容器的默认网关。
+
+
+
+```
+$ sudo docker run -i -t --rm base /bin/bash
+$ ip addr show eth0
+24: eth0:  \ No newline at end of file
diff --git a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
index 0e789f1..d48f2af 100644
--- a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
+++ b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
@@ -1,38 +1,7 @@
{
"cells": [
{
- "attachments": {
- "image.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAgAElEQVR4Ae19B3yc1ZX9biBslk02CSH7DyGEABsgoQVMhxgCpkMgYBuDscHgXrCNewM3MO699ypZ7l2y3G1ZVrcs2yq21aVR1/T2zcz5/85939gOS/DIK8xGvPFvLGnmK+877737zj3vvvv+BfqlEdAIaAQ0AhoBjYBGQCPQYAT+pcFn6BM0AhoBjYBGQCOgEdAIaASgSZRuBBoBjYBGQCOgEdAIaAQuAwFNoi4DNH2KRkAjoBHQCGgENAIaAU2idBvQCGgENAIaAY2ARkAjcBkIaBJ1GaDpUzQCGgGNgEZAI6AR0AhoEqXbgEZAI6AR0AhoBDQCGoHLQECTqMsATZ+iEdAIaAQ0AhoBjYBGQJMo3QY0AhoBjYBGQCOgEdAIXAYCmkRdBmj6FI2ARkAjoBHQCGgENAKaROk2oBHQCGgENAIaAY2ARuAyENAk6jJA06doBDQCGgGNgEZAI6AR0CRKtwGNgEZAI6AR0AhoBDQCl4GAJlGXAZo+RSOgEdAIaAQ0AhoBjYAmUboNaAQ0AhoBjYBGQCOgEbgMBDSJugzQ9CkaAY2ARkAjoBHQCGgENInSbUAjoBHQCGgENAIaAY3AZSCgSdRlgKZP0QhoBDQCGgGNgEZAI6BJlG4DGgGNgEZAI6AR0AhoBC4DAU2iLgM0fYpGQCOgEdAIaAQ0AhoBTaJ0G2jCCIQQCpnvJvyU+tE0AhoBjYBG4LtBoEmQqBCxCwGBUBAGDED+DyIUBBCUrxDkASEvgua/EL8MyNcIIoBQiH9wwFWf8ac6OcjLISTn8xp+BENe+NQtG7fWeO/z9w8hwMKzmKEAgixfwLypKqo8E5+DjxkIuREI+eQc/i0XatzSNeBqARB8hSVL44IPfhjnKyOEYDByBHkdVR+qCCRGX30Fg8QhgFDAQCgQgOGtgztnA6b37IoRczZg6zkHCCGrkWVjewiQYJ0HXFV3MBSCX4D+6h303xqBxkFANTlaFNM4mc1SPpe2baj+SxvFRhuiTeNPdoRwG+afvAJtl3IUguxz0nYNsRdsy+x9Hp4i12UHEEso96Y1lD4QYl8wgIDv7zta4zzu+T7HZ2B5wv1XHsd8XrGvjXW/8HWIX5B2iKB5lB2l5Q75lO03bYHUBI8JKntrFtLE3Dhvds9fVkaYgDkmyAOdP9YcPcKHfuNP9fyqPqWIYutpf0IwWDb+x7qV2uIHARnT5Fg2Bw4J/FgMvjzMN95Pf/ntINAkSFSQzS7IBhaEGBL56Ucg/DeH7xCHcP4MIRAMwWDro40KkSOFwK7CY3idAD+hAQqGEAiojsW/eQUam1DQUI23keuEnSJIkhYkEeD9WSYaQvVcNHiq04QU2TI7GMuvzlPHi0ESxtDIBYz4cn74Q0H4xAYQZD8CJDahgBBdPkSIhkxGhEtfVIzGVw5T9RMEyRN/V+8gggF+FkLQcMOoOIUNw15A64790WdFGipMkkyyHSZQbC9+OZ/l5LVkWIq0aF8plf5TI3BpBNiexYkTAqTaHP9WbZjnq7aoRkySHvUOt/XzRIqUiXbv/Lm8MEfiIELSD9iW2e94bdo02kg6Dux6qg+IzQvRntHOKWLA4bgxXzK8y/Vpf8kNWCraKvOZ4Y/YFjSoXHJ9ZTsBtxBOsakBjg3EQxE64seyECfyFhkazhNU5ZbLM9AemxgRLz6SOleeRsYOuWjEhWTdiYeuCJPBa9JGGjD4OcEyyybUV34nlaJ99cEf5IjEsnsRChFDYVMR310f2DgINAkSFYBPlA2SGxoJDqKhkFc6BVUcwCeDthApIVGAQXJEYiUdJySDPjsWgn4E5fggbREM6ShhsqVIgDJEjd9gSQACVMuCPoR4Y1NdCZtRQ8rO+4a9TzXW83sxpOcNJLt845cv4iYXMlgj8CkrJYMD3TnWBY0+rVQw6I3YcHJwCb/4e3gwEfXpvKepHlkIMg1RwBCDV7KzFzq3egdv9lqGBCuNNkkzDY9JooMheIWE8rvwgMRrXbhn+N76p0agURCQEVkpTKrfcvBUJCfM3qk8h0mVKFRso9LW2U7Vm2WRPmA6EdK4aQPopPAtThiVczVYS/smQ6CwRdWFY3TYwaS5YJcwBa9GeU7zImqgZ79XSgodLJIE2mPKKVTPxKlpzJvK49C5JNHks/rFiAuXE0eZipRSpIVqCnGhm63gYanC5RYnVXANIBhQTq6QKJJVwZjnKVX7IlN1yadRbrlf6hOGUtB5PbYFcaT5DMSH44CMaSyRSaLOa/uKRIlzH6FTesmC6QMahEATIVHsLIpIqYGVWoxX1CXxsERZIkEyiZVYD8rXLhii/FBxUsQqFCSjVw1bdUA//B4rKkqtcLh80llIvNjIwwavQYh/w8FUwKgoBYJUbsKeiCJ6SoWil6nKF/TZYLVZUWHzmg4Ly3zB0/wuKYASoM3/w6RHiB6NOQ1REH7Do4zHN+AR/koGj4sUJ6paXyVWPJYGkt6kL+iD3++Cn2S4aDOmtm+Dt/86ALNT3KJCsmSGxwp7bTnKSspQWFCI4qJSFBcXorCsDGV1HoSMb2E0CT+Q/vn9RkAIPAkEB3ZlRmh3qCYo1Yl+hiL6QqCE7IQP5ee0ESQBynGgfaqtLkNRURlKSypR5zXgFYWKBIqqhlJX5dr8nA6aoQiGTBSK4GE6YpSP6Xc24kuRFL+QKLIAOoM+Vy2sVQUoLS5A8bla1HrpeDXui/CQQBkkKIp9KJ4pyh5pj1LpGGgQYF2IjREXVdlUEjDRr2izSEzJ+YII+n1CYYIcK0zlW0iU6XtFSqQIs3LofAiJ26nqXEIM6GgKiVKqIkMUZLYhDBEJr6h6wqoE00autvCd9M9LINAkSJS0bpnrJvEge2f3MafzpOGbipJ8ym/YAKn0eFVL5DEya6em9digRRGiUXOXwpq1FsM/jsHulFLU0cLQg/o2Xuw1LIc4i9LFAX8Q8BlCqhirQ+k2AC+8ebHYuHU9hm45DSdPM3goDRGlZYiyRhS+ixdRVICS1LFENDGUxZU65VeudQOKxmk6A0ESG/OlvHI1jcePzv8t9c87ESe2hULsGfM+Pnz5dTw/IxleepKhEGpOb8COFZ+gd98e6PbSX9Hlg07o+H5rvNN7ELquyYKfA41+aQS+DQSEtPgQDLiUYCxtlv3WgJ/Tbufvyd8uMCh2GzoAKiyBVkx9bT0VheipPfFO657o0XMSNuZUochnwBMyIH2Nxk0MHFUZRic6pT/6Q354wooxnTbDJXaPlqdRX+ZjyIMxZCHgQ3nqKsRM/Qgd23fEuy0WYGd2BaovevJGub+o3iSmyiYygsAfAFRkLEmTKTuJ3Q2qL+lMUyUjoaJ4JmWiPTNZiznT4eZVqHDxMgbnQhh5FhQ7TKgjegkuqhBSrwE6gIpOKT3M5MlyT5bEJ2RJrs9z2SDOh5so7Syi++qDGhWBJkGiJKZFyI1iIJRD6VVUJS3Hmuld0bHDm2j9VAu0ePodtPmwC7r17Y0+vbuhZ5dWeL5le/SYugE7T1rgFO+P88sqtsawn8WZvdGY8PbnmB+bjZwaB/wijZuxSY1aFWanqMtB6rYp+Kx3O7T6aBpWJVaj1KokXZH3g/TrDARcNcg+uAbzJg5Cj0WnUFznFZWFc/b0qkin2DGv/Iuy9hmc3DwL4/r0wd/6Tsas5HJU230S8E0FT3nHNG6Rlu/vpzDUNMcFAsVn5GdCmsQgKoPDekSgHulLPkTPVx7DXa1XIdnwwek8gZ3LNmLBjM2IT9iIVe//F57u1B1vt2yBtu+1wotzklFvKOn8yuOn79jUEVDjsVIWRAFnW7toqs7UQkRdpxMic2w0bRJLyF5DFUmdwy5kS5mNVctGofvSw8g9WYQqhwduIwB7xRmkx67CqD6fYcb08fh01FRMXhaHhFKHDMBUPIxgEH6JHeU1aTck3Lxxq0DijAIgaSNx4U+3vRSVRUdwdNMKjPj559idWobKxr2rqHkkjaGgCwzXBn8PuVFfno4ja0ajR4t30O+zTdibWgE3JyaomosQZ8Zr0XwQc57LYCkhu+o4xiSpqTcGgYfgo62hk9eA+VAxVcKD5Q4qlpP39FTDmReHDRMGY+rUSRg3ZhwmjJ+HefHnUO0LCF3jGMDngd+viG8D7tvIMH/vL9ckSBTjYBhvI7I1GzNdiCBgy09A4rZJGNvtNTx09X/gR7e3x4cjp2NB1GpErV6JlctmYsLobni/9Xto12cGZsTnwR5ymwHmTlSnrMX28f3RuX8sksqssAdIsOilcMCO1N1oQBsjp3BaUJi2Bgs/ewfNf/UYnh+xC7tyauAx5X2ShfD8uLMsGQnRn6NT6wFYlVyKEgcD7DmtSS9JKEUDbt54hwaDFpRkbMCiIR3w0qPP4KHuW3GoyAqHGDSvzPFTJ4qYRCkdXXnTtGXm1B5LrPBQ5oj/S/UL0aQC5kbx4VVYNqY12vzlQTzxwPuYm+ODxVaAjKQcJCadQdGZnVj61A/x0tAZ+GLRcmzfug5RqSVwmwGkjYeKvpJGQCGgnAA6Q1zUQJWcg3dYDqcRkGUuQmpkAYY4heE4JyWK8ChR00NB1B+djtVrJmNwfJmaiqMtLE3BgaUzMbDTcIyesxnbYrdh89JJmDhkGIaMWIrkEsDh4ZhvBktT5RISQSWskW2biDjmohxOLXKKjX00aIElfScmXDUc8ceKURHpPFiEDSkcdkGbKC6WLNjxw1VbhOy9yzDhrT/i8cffwYC58cioJXGisETnSak6LI7Ev5JESYyZwoj4SO2JTVaES0JsaZdkmjUyJS88VIm2KKu+fQj5LShJWYdV/dui16iZWLpuO3ZsWYPF00ei98e9MXpPLvJqqRia078G5yV8ZvuJ1CmNEEB9WEQINAkSRfZPEiUBi6JuKPmakzpGVRoOzfkYD/zHz/Grd5ZiTXoZHBKoF4Qv4IS/fAOmvNQMf7rxGTzZKxrZXh98jDlwZCNhwSiM69QTY5IdqPGI8K1WzIlHGFlHiagWzIOUYaQ8XIozB2ei7y3X4hePDsXEnadR7qcRoiJjKI9UgiWtqDi1E0vbPIa20/Yj7kwtvBIbRq/ru+tQanioQs7OCRjd4jb84DfdMTOxBEVekjxOs3LBceSmmue4HFbUVFehqrISlV95V1RUoKqqApV1Trg8jG/wweMqR1naTqz+oh/GfD4IfT56Cx/d/0e8taQAWVU2uAJ+eDwVKEtagcG//Bm6TI9HfCHTRARgfCXItyF1qI/VCFwaARVEzmllmeSWwZeOH9UFDuBsw1Q4GIBNksOgY6Wuy8BrzvDJii0EYE2chjUmiRJiBTssceMwpl1rPPLiROyrBGx+H4KWeGwb/SHevPtFdN9YhcI6M4BZArzpnJlELmKF+NJPKkeIYWPsjkkWA0FZ2OMLlaMsYzsmXTUMu48VooIP15gv5VGZcVDq/owHCxoh+OqKcW7tm3jmztvxl66TsSizXpxThkyowH0q3eKlSX2Eia8ZGIWQ4RciKPUjTjuJlVLzGPcZyUt4s6QxIBHzyNtfcQjxM3vgpdsfQseNZ3GqmtO+1cg7PBuf/+1m3P7+Mmw5XgoH7ajEl3LdoVrwpAocyZ31MY2JQJMgUWqZqGlZpOWzQXN9WBC+/F3Y8MVruObn1+Pxz/fhUL5d+RGUlEN2hAKJWPvWn/HsVXfggWdHYUcN4AwasGWtxoxPhuDd9guRHAzBHfDKVJ6s1hNb8+2QFEZb+eCFJXcXojv+DL++7nn0mHUAaXXmihzDZ64kFEkGnqpMZK1qhbteG49pO7NhMSjPE4vGD3yPtOEJMiGg+sR6rB54P/7t6lvx0bIMJFs4IFDOl6izyJWogB+lxflIT0tCYmICkpKSkJCQiISEo0hMTMSxY4nyeeKJEpTWOeD1WGDJ2oaorm+i27DliEk+jYw9szH5zdvxwzbLsfNEDsoqLKjIy0Dmhql47d/vxdjV6TheVg+bvRalThXF9e3UcKQo6uOaLgJ0cvwI+b3weypQX2FBbWUd6urqYLVXod5WA1u9DTUOD6x+U2EPeCUQnSu1RCFR47tEFTtTpmBNzAT0iS+CIdNMZ7Dv8zfw9gsv4uEhe1DPLEmS0qAIqSuGott9d+KHXeOQVGJX2dskbUsQgQAXezR+qxcCQsfTCMHgMn7DkBQDvlAZStJ3YcpVIxGfVICKxlbATIzIpZTuTZtIBcdA0FMH49QC9Hj097ivRU98vOY0OOknY4mscjYVf/4u0ZzqJxcDsPyhujLUVFhgqbWh3u1DgIuWJGY1Yn1dykSizPATg6uyA37UJizA7E4v45e39sD8HAfKfKJTwZ6zDQcG3Yf/d20HjNuciTwfSRxjZRnjRZ+ZNr/x667p9sHGe7ImQaIowcrqCPE8VPwQBVxK5FVJ8zG3y+249rob8EFUITKrlLTLph4KuhGqicOklx/Bff/aDI88Pwv7nCG4Qi7krumM/gN6ovXsVLglD5VaEksnjZ6Kwc8a2WNjF6DszFU6vopMnFv1Nm676Zd4ss8CrDpuM3O5hGN/FIkKestQlzsPXf/wBkZP2oNjFZzJ5DHfVUwUezQxCiBQcQzpSzrhjquuwfXdVmJ5epXoT4yJ4iqXiOGjOuR3w+d1wefzwOfznX97vV54PPzMA5+fqQ1qUZq0Fkv6dMBdH0Uj5kQRKr0e2HLjsGvsm/jhT3th0uTe6NSmC1q/2BmffdYd//H/PsCk+NPIPLwCuzfPxbhUK4wGpGBovO6or/R9QEAUi6AfnvoC5CbOw7gBH2Nw33EYM34upi+ZjTmL5mDxnIWI3nIYaWerRLXlQK6GS+Uc0U8yJN45COvRaVgVNRn99pWruJy6g5jz3nNo9lBLPDEjU6iJmuquRfbWsRjx3K245v7ZWJdThRpZEaycG6rX38YwTGvJhTqBAG0SzYMfASOAoFGDyvT9mHLVEOxKKkB5I5MokhqDyp5fQrLVGMESEAy/GzCSsey9P+HJG1/BK502IZMqvp+KkDmhR1Iiij6VQ6VMUSH0eG0wsqMxdUA3DBw1H6sOFaDar0iQpJNoAIokbQw7IDK+UCVORfXGkD/fg1/fOha7qxywcooVIbgKjyB18qu47sd3o/OCwzhWaQaVS4yuUsG+ndr7PvTI/90zNgkSpWKETCZu5kzxSKCxFWc2f4qRLW7Cf/5XS4xPqkChS8yJDOAhjx32xNFo9+TtuOWelmg/8RBKA6RHuYjt9yo+6dQfw2PVwK/yqqh7GK4qVJ3eieWzZmL+pNGYMH0RJq/cjoQDszBj7jR8+dnnWBS9G8cqAgj5vHCfWIUZg3uj+6eLMP9YrepiJBnSQWgJL2TQFSmZHoa3HLacZeh6229wd/N+GByVhXo+G42CLG1lHBg7Uh089Tsw89m70WvkSkSfUoZKlkiLweKy2Yu8V7YXxdak5TSk45n0TXk8okUrwiZdWJL5qcR0TEUjHq23AiWJSzH03h/gV7f3xsioTJTIUl1zVaRYbJbAA4f1DE5sm4G5EydhztSxmDR9NsYtSkChB7JiRQU7XVTwi9q98p5p8CgRemA5l4W9G9Zj/dEClNndEvRpOCpQmrkfUyetxJYVn6Bj+3fxVIu30aHTu2je7GX0H/0lRn05A3NXb0dynRteYiah6hfHqjAwlZ+bGErYmfx1UWn0r//cCLA+TdX3ogfx1ecj79hGzJo4HbMnjcSo2euwdN1WxG9bgNGTJ+PLYeMQFX8c2bXsf+wRYRmElzMHY/YLfhy0oixlK3bNGY3xm/ZiX0IKMjJycDr7LHLP5eF0/jnkn8tDSbkF9Q7GaCq7IylMZPWeWngv7T4UQp2QqEkYtKdUBRvnr8TYvz2KWx9qhccXHFdrkmX6vxa5O8Zi5NO/wjU/64U5SSUo8asFGsqmsHxs7+qz8/3afKKgqxK1J+MRPW0AerzTEm++8z66fDoTy+Kyke8OwiunBhHyOWAvyML+xaMwqN8n6NOnP/qPmIwxy/Yiz08nVYUmBAMVqEqNw7SrRyCWJIo5+gJMJan6l4Rby24NVK/VUn5iEanNEuJD7GUaUZEgPqcYUCqBQRuyFrbD24/8AQ+8+gkW5/jhNRyylo+hIJIeR3w93tGc5pNgcz+C9mLknkhH8v447Fw5HzNGj8Ko9QlIK66F06fiq9Q6S7PgEj9FGkw67Jc8XtJI5HnCxxfg6JyO6HzHHfj1bWOxp8YOq/m07qIEJE97Htf95Gd4/fPNiDvL2FIKBVwEpZ7touaqf72CCDQREqXkTLJ6qjjiaJCkGGdwZHp3dPj9Hbj+wXHYWFCPGuYYYgfx2+EoOYpN/Z7FX556Ga/1n4eY4xZ4ODftOIR5rVqg1wcjMD/NE7Z8KsjQW4nS7MNYPn0JFq1Zh/Vrp2Jc/554++UP0GHYp5g4vidaPtMcLT78FKOOlCPotaN+zyB89Oc/4a7nPsbHm86pdbUBJp5k12QHohysbK10fDEyLnisWYhqcy8e+uOraPPpRmTalXEX7iRBoOw8LnjdqdjU4Ra07jcZ4/dXi41QZIz24yskKixVC4HjcCHmPqImx2PF0yJZkURz7MRmRxZSSJmef5tBjyEP6guOIv7jO/Dfv3wY7b7YhINV4SR7anAJGtUoOxWHzfPGoPvgcZi9YCU2bFiDxbNHYsTQjzHthAMV7gjLKCQqAKfDgfJSC+xen0wfCIkMGvC77SgtPoPC03HYunUdFq5Yi5h1UYhZtBibt25FzK6jOJRZBKeYOU4ByBMrL1SC1V2ywlAET5HhVVxCpEY9IpD1Qd8xAhz02N4uanOeMpw+EoeVsxZiScx6bIr+Av3bd1QpBUZ8igmff4Tn7nsArw5fhhUnatTqXgnLZH81CYmQGNXbnIXx2LduKibOWIrNJyyocbH/q+kjBlxLpn8JcaaCYyaoNa+jSLxoWYrsBIOoT5yCNVGTMHi3BZK76OR89H7tQfz0wTZ4fO4pZW+EyNmQu30cRjW/Dldf8zYm7y1EgStsU0gaeElVZhmcZSWtyj1nhJyozj6KpMVTMWPuTEwY+RkG93oPH7z9Ft56vS+6D1+L/Xm1qLWWI//oFqz+cgRGjZuAz6fNwqx5C7Bw4ULMWbQSM1amIrvaLkQqFCpHZdoOTL5qOGKTilBOB0tIFO0M7aFaAUfopGwMG6PycnHdfFNrIWZmvJniobS17LPm3EUQsKdNw4i3muHuR97EO2sL4DCUEiWLh8zYWZ7LmiM2imCyjqgg+eGqL8aZlL3YvnIplm7ago3RS7BuayziMopR5lIr98Ln8ZlIsVmnTIaqFpRT9VK7N/iRg31j30f7n92B39w6DnE1dtSRRIUAV9FhJMx6Ctf/5Ed4ZuhabDrtUG2DJZMVnA1Q9r8JM/1dgxFoEiRKgjCF4TO/k0dEIwYABuv2YvWAVnj0urtxw8sTsfpAMpJOZOD48TSkpxzEoV0LMazV6+g4aAGWH8xHnRGA33AgVLgeQ194FR07TcTGsyrnkUxBMbt1RRKSd81Hr2G7kV7thM2Vhi2jOuCVm+7HrR2jsG/LF+j17it4ssNwfLL7HIJ+B6yp8zC1b1d0GTwDc47kyx5+TIVO48DOyQgcEenFgNGAsKMF4XPXIGXSU2jxxz/g0Xe/wOKTDpF26SUp75T8jgHSRTj46e/xfJch6Ls2z1RumPdFbQtBw0MXWEx40AVbVSlKC/NxrqAI+QUFKIjgXVhYiKIqF2xeM6M6SYW5UlGMTDgLsUzTkXh6JIjcVZmLM8v/irtv/imadZyI2Ul14o2xPIwFsJfEY9vUzni3+Qt4dNQhpJQ64Ap6cXb/PCwf8CTe31WLfCvRieDFgtDAivGkxxcyg/BpiPg5r6OSlyryF1b2OMGg3qLuCRFU+1eFVTWqAMyqE5CtGXg95pvySM1pEhVB3fzTHCJShZJCzDJ7i3Zj+4oVGDftMIoCXhi2/Zj9ZnM8cfdreG7wEpyMHYY3//wYmg9ahDkpleYKUfoZbGt0k1SQOPtqADbkrJuIpXNmY8axarXlkKn+kLgwhYqEJcvWUmpLIk5JsQOzeV/8Vn0oAFviZERFTcbA3VUw6CRmLECHV5vhB83a4PFZ2aJlcAAPBR3I3T4eo58miWqJiTvzcc5GkmZuNUXeaKoaVLyZ2Jd0jYqHr/40jseuwdIJi7H7rBNWpxv1ObHYMbEL2t57H37+r0/io6kbELN5MRaO6Ya273TEl7tycMbqgY/2x1mCsuTNGNp+GNal56PIQ4fXgsr0HZhw1RDEJpWgXGaoFFZ8YpWeQK20VlONdNC4QloQumSLYr+k3SaxFHXQTOHAJLwq514IKNuBBR++gj/d3By/77UO+TaDafmE5HB3BZ5PkyL4CRqcQWAOLvZ/xskasjND0O+Ep/AY9iweiynTpmL6mh3YdyQVCceLUVLrhMevlCypXWJLZzbAJM/Updwis/mRjT2D26Ptv9yJm26ZgJ21DtTSlhG+osM4PPcp/PI/f4QnB0ch5qRVSJzYK074ioDAtqtfVxqBJkGimCuDHhwD7JibUvRgei+n5mDkR4/g339xE25r8S46dOyBbt17oXunTujeuS96jIzC8kP5yKv3wCtGJoSA145Q5iy0f/oDtO25EgerSD0Y6q1k09rMbUjYMB4LU1ywuX0Ilu/G0oGt8dhdz+CVBTk4m7IFO9etwtrYNGRYlIilNHylCvlZOJHkqdbQuyHBoX/CDsCF/361t5Thg6e2CIfHv4Tn7r4Ov2jeHm+vyJYdoDw0ASQF5AU0cJ56pMy7E8992B2dF6WiRliNJD5RSUPp/4i6RYTKcHr/RmyaNwcLZi/CwtkLMW/uPMydO/cb3/Pmzcey3eeQW1EPQ7QaYsJnIHDkLswK7LkQiRXwI+Rzw27JROrK13H/bT/Fvz3WFe8vSUOlWfZA0IHsmN7o+/y9uPnenpiT60JhnQP2+rNIXj0P097tifknDJ5DSMwAACAASURBVFS5IzMOLIv46KYHSozCxVP4KoVB0u9JmRV+JEdq6oCYSeQ74KfxFOapVkyZdSTnkp4xlQSPiaxoV7pf6/s1IgKWI/MRu3091mXRvvgQLNiI4a89ij+/0BF9ojJgzdqCqMVrselYAXK5AET5L5Ixn0Ok0iyoOjPnUyrW95mABZ9GI9nmhsvlgcfthMfthsdth9tTB6fbDbfTA6/HrwKx2cbYFCWVi0y4iRYTbnpcnbcqahI+iS8TJQdpC9HplQfww4fexGNz0sTesN36Q/XI3vEFRj99Pa65uh0m7MhHnp0OHK0bA6NJmEz+yLABbkgs7kUA7pRliF0/H2MOVAvJCwUVmfFWH0dGVB88f+01+M/bH8ad99+CZ999F51jciWWVNKR8FrBANyWbGTNeBAjtqfiQAmn06pQkRKPiVcNRXxSMcpN+81pQT6vIelaLpAolYCShCMyp0pxQjqrPP7C5uy0EbTDvoAHzrztmPfBy3jwmlvwm//ujugcN6pdzLtpyM4HQk5YGDEkikB5RVVkhbCQLI5y0GhjJGdp/Tmc3TMPc3q+jTe6LcKS/enILq+CzemCJ+REKOAWeyxqn5A0PjBLexb7hnyId35wB264ZRx21DpQx3sEAE9hApJmP4+fX3cNHh+yEutP1qnVnLy/xHBRNw+3iEZs/PpSl0SgSZAoBi2GfFw1wXwZ9KrYsAyU7OyP3q/ehBvvexrto84i55wFxRWVKK0oQyXf1XbUujkPTiavCEHI54I3YwFaPd0RLXutwr5q+pEkNlxdEoThtsPhqEOtRykx/uMLMe7D5/CHh1ph7FEfamxWOG31sNs9cPsY7aNWopDscCUGuzI7JFfQSTnp+XFzXtIPJr7jd/DCVnoMB6e/jlc7tsTLd92CZr97Bn/uHI2TCMIt5k5dh0Yv4HUga+G9eLFzd3RYcgylNBoyzcauqabblPdGg2TA43LAVl+P+vp6WPm28m295Nvm9EnwtlohpJQeWccmnhVNsNfMWcJnDaCu5AjiV/bDk891wEvNr8Nvb2mO13qswjG7SuUVqkvF2q6v47kbbsONj3XA4Nkr8MWoQRjUrxdGfDEfMfGFsHq5+zor9NIvc6xRpoRGT1gmoaAXrwyMOkYlMFRcTpnU8Hwq78RVxyq5HjEW/c4cSjgc+mAEPcpL5jUjK9qlC6+P+I4QMNvJP6xIblFSD5vDBit3DjAcsB0eg7ZPNcPTbUZgUboXPrcD9dZa2F1eeP2ckqLKotQM9ntpZ+LwGEBlLGb26IfO7T7ByKXzsGjpEixbvByLl6zAkiVLsXzxQqxYuAhLlq3E+h3JOHG2VhwTtck6M5wznpAER63qIjmoTZqIVTETMHifRcUFnlqFYa89ghuavYXHZmeIgyblgQPZ28dj5BP/hR//sAtmHipGkZvXCqdWcKkcbKIyc8pK5T1imy9cNx27lszCukL1bNIvqJgHXKg/dxA7+92D3//2Olxz+1/xxuj1SLTT8pmkzNzSJmAvhfdAfzw7dw+WpFUDgUpUZMRi/DWczsuHhTZY0osIMxF7KHZMsqozLYKKA1UO0aWbi1L5leqjVHnlCIva5rMhVHAAczp0RJcXWuDJh+7Fz3/3J7TbXIZTtezn/CfRSyqLvGzRI9YOblGHzOSddBYlRITfMUCf9twPn8uK+vIClGUdxsZJH6JbryHos/AoTjJHlihp5nQelW0iJVhmI3Fie3T+zR349e+/xN5auwSW0zX0FB9GyswXcd1PfoxnPt2GLaeZaNOc56RNkhmNS2Oij2h8BJoEiZINg7lURfZUM/caQh2SZr+F9x6+DXc17415mX44PBzcmadI7XlEPsN93GSeXY2ogM+FQPpcvPnUB3izxwrst4h/oabbhPAoWV28QgRQFDsQfV9/Fn96eiQ2VHthNZRKRNJCYiadkcqTJJdTGx2TPYk8TNXDjC0KBzL6gx7U5e1H3PxhePmdjzEmJhaLx7TDe80fwB+f7YvVxSFYvSRGfCueEPA4kDbvLrz00cfosDgdBeazhP0bqlDKG+P9VHyBOHtCLBrAAsKkgafQWIjDqGRpSdrHyS2JwTJgOxuPjTOH48N2/TBsdSK2TmmJVx++G83eGITZGXYlkxduxJjWf8Y9dz+DF0ZtQOLpPKQmH0PikQSknMhFfi2nBU23NIK2L+W5iDDxXDWNZ9aZKZqJd2l6k6JdES/T2ZQEiBy2ZCCk2seBRE2fqmNpKE1jTyIsS88bgGEEz6EPuZIIfBOJ4neq71JRoUoc8NbhzKrX8XKzZ/F698XYV0dnSMXLCFkX0qTaE/snnSK1jF2RK1h3Y/6AKRg7bCV2nz6F7Jxs5ObkIDsnB6f5Mzsbeaez5fNzRWWosTnFhqjAZjpkKpaS9oekgu1bxURNxOA9phJVEosprZ7GXQ+1xGNzMiU1gpqsrkL2zjEY+Zcb8aPrR2JJRglKDcaOmqqKOSUkA7qUm52CVMSG40u+xIaZ07CzjP2Ryj9DBThd6YffWYaapMnodNdNuPEnv8Of2n6KGSfqZFin2qL6VFCOQ+IIvDp3L5anV4NJeS0Z2/Hlj0ZgV3IxysWRVXjTLpoijIr9EYKl1LiwQ3SpVkILJeu2qSKLz2mSOlcVajK3YNYHb6LjJ5MwZ8kMzBnSBo9dfwtu7r0He87VmCq7ibcZVC42j7izRkTlDsd+ctpPZX+nbeHNgl4rrAWJODSrP4b16otBX0Yh5mgx6oinBLoru6LsKJ+VWBbj+KKu6POnu/Hr2yZid00d6gX/ENxFh5E6pQV+8eNfoNXEeOwtVOerPf9YHq1EXao9fFvfNwkSJUKtNEIGYpIo+AF3FjZ0fwrP3/YwHmk9DwdrQ/CI0WFMD1eBqEBOdlYaOdUpuFmlE6HsJejx7Hvo0G0R4kuUFE1TQK/SY7Wg/NxxnEg/gzKnBQdntEa7Z17EY+3WID3ggSNkoDYvHedys5Fv59QdaRQHXRUDxQBSWY3HXk3SJ14fiQ3NpBvVOfuwae5ofNxrIDpN2Y+0MhcKE2di7AeP49a7X0KrDVUosbLTKhGEndfrqUPqtDvxUpe+6LryBKrF7TQ9YFndQk9HIjOAkB1VBTnITktFemoGMlLTkZaWdul3ejoyCmpQ4+SqEIWFNEp2csYOmPEDQb8b9rP7sHnGUPTvPhB9x+9Aeq0Be9ZcjHzjQTzwcEu8uygLVpqivBUY8tajuK/52+i64axEKvilXpRRYdJTzuRFSlEuJlFiaMXQKWPDuhPohf9x0FPqlPpJTqiIksSw0OiKQedzeuB21KLKUgWrmwPXBWVLYhokGzLvrF//nAj8IxLFz0kYvHBW5iM/+wQyc3NR5jiD2IH34slH2+K9L+KQTSIRcKAqMx45xSUoc6t2RbWI9ENCmNnX5Tiu1j2F7Z9PxdJp65Fsk7kY5YpIWzUdI+E0nGbjP16HA6xa1yVkzmzLzBHEfmc/OgNRq6dgwO4SITYh+wms+/hVPNf8r3ho/FHUcw89Lt9HMU5EDcfg+2/Df/5lObadqUIdY/08DjhqLSiqtMNjiKUzF5AoRTsQcuF09EisnjUGi046Jf6Ge7ypRJMeeOpzcW7LQHzw5D34w49/jFt+/wxeH7YVeTYn3IFw4tAQvHVnUbv+XfSIPoJtZ5iyxYLy9J2YdM0wxCWXwGJO+wUMP7z1pSivtsHKkAnaLklEqtR68f0iaGzKDNKRYn8WFwghRymKj67Fss+6oE3b/pi8JQ2nSk4ha+NI9Ln3Blxz76dYePgcLH61ebNaDX2RvRB7TYsethl8Pr4VwfO5ilGYsQ8HtsRg7cYYrF8+E4tXx2FPShEqrCpNDmc0eF0SJ1k4IIody2lH4c6xGPv6E/jV74ZifUE9qg1+HoDjzC4cGnMfrvuvx9F7VQLS69XnzBUlkxtC5LUdiqBZNPohTYJEcetHtV8cZ7q5S7kHwbJt+PK5B3H3717F00N2IZ95OERVUFN+VH4YJ8DOJVsQSIM24A24ECzbhMkvvol+naZh0zkGOEhEAYIhN0pPbMfW2cMwZOhK7D9zAPM7/wUtnnwDT4/dj8qQDz5nOY6umI2YmC3YX8H4CC/cdTnIOZ6E41nnUFhHs+pWREqkXYhszsBEa0EStk3ugw8/7IGWY7bhjBXgwrSAZS/Wf9YKj9x2H378URySS5wSzCgaWciA01OGlJG349U+AzFg82lZ6SPUQ0J81POKERFJuhLnkuOxJyYK66I3YH3UesSsjcHatWu/+R2zDuuT8pFfSxWJ1zRn4MUYqLDsgNcK+7kE7J7SGR+17oYeYzfhWA0JloGQNx1b+ryGV+98DHd/tBInvEG4irZgyvtP4/kX26LnlkJmQxFZOhjwwF1TgtKzp5FlNeCmhYrgRTwUKVJKHdUlmc40V9mQcPJ7MXhiBC+oCCqIVBmmsDfJKWGvPRdZyVuwbEk0Yo5Vw2Kj2qbUPBJxmeaNoGz6kP+rCHwTiWK/dyF/71IsGz8Wo2etxKGSeIx75mbc9UJfdF2djsqADf7aLGybOgAxBxORSQeHdiZA0uJVCoEow2paKRB0Inf1RKyZMQ3zj5XCIW1JRmBxqMLKKQkKaROjGMXJk/3fmHBTKTV0Cti+qaoLiVozFf13lwjtCoWqcXxBN3T/22t4oEsU0ryAkwkiXSdweNIn+Oimh/HwuGRkVLjggxM1Z5OQELUYM5buQEapDTY/B/nwXnNUOUKoSpyKmMWfYVhULur8QXhkNioAj70YeUdWYMp7j+K1Lu+j5XOPo8WNf8Afb3sPY9cfQ1apDU5vEAGPFTXZ+7F92IuYfPA4Umv5dBWwZMRjytUDEZ9UBAudSvZ9ayFObJiNZSs242BmAWq9ql8GA07BMzJrIBENakU1yRmpqKcKZcdWY/mI9/HGK20wMLYcBbWc2nehKmMl1nS5Ddf+8DH0WpaM5BouUmKd0VCQDtN2KIfRH5ToNgnHoN3w+11w11eg9PQJZGTEYcvSiZgyejQ+Xb4bSdUuWGW3CVUeke/FeSauHK/8olaKIhUAHNkbsGpYa/zxd29h8qFqFNvogNthyViOld1vwA1PDMesI9koZc4t2uDz3rRw8f+rnaxJl6tJkCg2dPHKOGfOAEaXFfaUeWjz5N34j8fb4eXF6fBQtpbO5BUSQMNEBUsNmFRtaPhImHyA9TDmvvYE+rQbiiWZKiaKod8GipG6vA96PXALfnpnfyzePAudWjyK2554By8sTITH64A3fRFGjFmC8etSUcb4LLcTZbHd0f6J3+KRV3tjZHydpFGQJa5mDLM35IJhP459g17H0w+9jL8OXoI9VT5Z+MrQzmCoEtlrh2J4sxtx7U96YXmKBRXmag8qJYb7FGI734G2Q8ZiwqFCNXVnRreqlAPCJqT/Kpmc8/f0b+nERKrzmPH6ooubwfF09dRuFEJJHZY0HJ38HB767RN4b+h67DrHJHISBSZKX250Jwx89re4/d6uWJTvQYX7LPZ8+Ta6tW2JVkuz4GEGZ8MHw1qGU5vmYX7vdpiQWA+Lk4pAhC+ZTqHJJHDKBrKYJH0Gt0oI+GXLCSqP4nNzypUxceLJqfgEWZGjnHCUp8zE+O534d+uvxU/eHMDtp6qBVONETdZ5uxX8QwRlk4f9n8OAQ7JbF9hVShcQLYF9noHDg5viTZ33Y8/vTAAG3bPwxs3/xq/emM4+m3PkYSZ9QlT0KbnGmxILIad7chQ8TE+OCR4OUDjJJyHV3QhWLIHq2bNwtt9ViPJa8Dp96os2FTIZXtZP7wSRG4OjDKQq3KJukVnTRRQ9X190lSsjpqEgbEV8hS0bL7T0VjYpzMee6QfFp8zUEXyf2It1vRpj+ebdcGcbKDaSX6QhyPzB+H9f/sZrr36NvReexLHazgdSZtIddzckN11HAlrlmJM+4XYW+VEtccHj78eZ46swIzur+HGp6YgOrUCRVnrED3wJdx/zQ24+gdvYMiyTGSWOGA/dxRHl4/Fsy8twMZcCyqFllRJTNQXP+qLuKR8lIlVKkNZ5nIM+PdrcOPVN+BvQ5djR5GaEpSFQ6LvRUijZDaedk6toPOd3YDZ3Z5Fi6dfxrsL01BiuOALucWyByqTcWJlW1x/7TW4p180VmfWm3n4FMYynSqqjyJWLAFjobi4xFNVhMK9SzH1vRboMHwG5h/IQYErADdJjhm3RMdLcl2Zhkk0RiFlgE+aBzPGhxD05eL4xhH4+J7b0HLOcaTl18PrOYeUXePQ48mb8cSUY0gscCoCJ43KEMMcqToXbt36Z+Mh0DRIlEzFAMGqkzi+bTo+aNcS7Z+9BTdf/yP84Prf4bePtUav3rOxu8iOar+SoQ16dCJJ8G+aURIDenrMcHsG24a8gF49emLorjK115I4JDaUHF6Ahf1eQbMXPkSH93rh81HD0LdTD7R58X0MG/kpug2Yh/nbM3Cywi4ehihMB0ag28v/jRsfeQsvTTiKKhmAmcFXbcYZdBbDnjIDbzz9OtoOXYGY5FKV44jUhNMAQR+sx2Owvl9z/Oba3+H95ceRUsEAU7IwK3z1uzGj2X3oNmw1VmWHV/qZMQXnpyrFjquAVxIN5ciKhxZpc5KOKh6waD5mAjqqPtxGoRCF+xej101/QKuB0diYXCarF0laxOCEAGf2Wiwf/CIevv8RPLP8DHKr7bDnxGHLrMH48P2O6D9+JT4fPxKffj4dM5bFIiGrCJXcgoX3jOQlHr+S3sMkikOjKrLodueXAkvGdBncLsRgiKepIjlM9hWAvywFKRu/xIAO7fHEL8ZgbSL3+FJL17k4QNpQhMWL5BH0Md8FAqzAryNR3C+zHic3D8Hwbq/jz690Rc8PhmHqF8PwQauP8GGbrhg2bAy6DlmA6KNFKLByvaqaFuaCLZl6E9sUnkpniFFQcsfV5CRg9/Ip6Nr9M6w+mIf8OtlGVrk2QujJYyQaXTVg81fptxIPqWwHO1d94gysjpqCgXvKpD+LQ+CuQ3HSLsSMG4KuHwzBqC+GY3D/fhjEQX5zJqocARgMewjWozRtN9YN7YoOz9+Ldxcdxt5Cl/QZOiEyDc4+EXTBWpqFlI3zMLrTB+jWoQPebvUe2nUejDHzt+HQqXKUOf2yurDuXBISo6ZjaKtX8MJTzfBgs0fxzGsfofekGGxJq4bFQVJDpCyozNiLyVcPxq6kYpSJA+SGozILB8cPxLC3nsL7oxdgbppVCI0E0zeELcjsAtMZUPWqw7Epr6Nj+zZoP34D0qqdss+ohDnQufZaUH5iDT5pfhPubD4Cn63LQikNh0GHjLFPVKADMmvAqUwqZrbcPdg8ayyGDx2DMev34+jpXOSVVqLG7oFP4p7IjpSXKbFhMi1JGmxOS5K7y3EkiWpj9lDAC3fZCWRvnoDR/TpgwKgxGDpkBIb1H4IhM1bhUHE9rB4qUGwWDBWh2qnsuRja76L7fM/v2TRIFKVWegauKlTkJWPrlg3YGr0YK5YuwIKly7Eiegvi4lKRb/PBJY4Ejw/LFOZ4KdoFWzU9MAdOremBvv37oOXMNFSTq3DaKuiHs+oM8tLisTV2P+J3HcKJrEykHz2K/Zt2Yv+hg9h18DTyym1wkZnxakE//OXJSFg/Ej2Gfo53JyTAIX2Hq7yojjHDbz08lmRs3hSHg5nFKLdTBhEBWU2bccrRWozi9J2IWrIMsacrYHGa29A4y+E6Phtt72mN4XP3IrFe7bUlnqR6GkHn78Z5ASvc8v/um/CHX//z787jIUJVlOE2bLAVn8TehdHYn1mOchtJqQq4lYtRDXKUID8jHls2rpcluvVurt2tgSUvDYd2x2LP0SwcOXoIBxNSkZ5TjhrO0zboRWaonkf+VwLcRbaFn6oyy3FCztTxilWGyaE5VcIB0V0NW8FhHIqZi3cfno3YjBLUymoaFczZEJveoEfRB19hBMx2cP6u/JvkxwtrWTrSk/dge9wh7I89htzck0jcux/7d8ThwMGj2HU4B6U2HzwcXE1bFG5avAo/u9DupFsg6KpGbX4q4nbEYk9CEvYdPIi98XHYExeH+Lh47InfgyOpp5FvsYozxsFeBmT+ZI+j42eo6Wlb4gysiZqCQbvLpP1zUCWB89sssGQnYu+OfTicsBfx+w/hcGoO8qsd51fkMT7TU1+BgoQt2DDoQfSPycBhph8gDqrwF57Jb4fNchrHdm5D7LZt2LhhC7bvPoq0M9VwB7iy2HxKww13dQFOHdmFrTHLsHTJUqxcF4u96UUo9zB9AG0s45zKUZkRh4lXj5JkmxbTCTI8dtTlZWHPpLcwZtFSLD3hVNNytKlSsPOVdIlfaEOpGRMzD8pStmDvvv04lG1RK+xoC+QZeV0vPLYSHI+NRszGY0jKq4adnVsOMacDZWuWkGw/Zc/dh4T4OGzdshPb9x5GQl4pqv1++GXBiomdXJwXCLcLVV8sk7I3F477u8/8Lvhq8nDiyE4cSDiC/fsP4/ChJKSctcDB7XIuqhel0YWvcwk49NffCgJNhEQ1Mjb07rKWYtKng9CyxzIk2gAvN80UVccMSJeWHOF9QwZcuVFYvnYZBqw5LV2aRlGmlEiiJAiVoYqRWQh6IBJsyZgdywnkLW2PZ1tOwoLdp1FhGGaMV2TXivAJvpeHyVRowA9/9XGc3j8bbfvtRXJ+DTwyAKhpXtp9/dIINAQBGZulD3Ma2Y7y4mykHzuIA3Qk4nYjfvce7I6Px4HU08irsKkUB8xKze2hqGaYygOFVDoqtsSpWLNmEgbGl8nYTMdMVh2HN7YNk36ZIuSgroKaVXAgvUo7as8cwbper2DeobM4xR2LG/ElK4lFZeLqZLqvSkULBKlE7cT4q0cijjFR55U3H2BYsHtiNyxctwnx5WqvTSpsIsFEaCcb8RHkUuzxsgDI44Q9Zy+S03JwqswGG4lNgNG4SqFm/ejX9wcBTaK+pq7pNwTcp7F39hgMf6c3JiXaUONRy/c5BadWV3zNiV/3ETuUpx6ntk/G/OhFmHW8RrhSWKoXeZ/Tig3peLR7dJKMelRkbsWyLo+j/bzDOJhnkw1IaUAZ1qq78tdVSAM+o+frccKSFYtNiwei85YynKk1t37hChsG6kuG9gZcUx/6vUeA/ZLpAYwApVbzzfxPEtipTAGJEPf/lD1AOSVocPqeU89UcUwBRZAMoD5hElavmYCB+8pEZ2VMFgmSJCDmKlOJa1JTzzI9J84gVxUqRchny0X2geUY2HoM4vPKUd0QBzGC2pTymvdi4ameMAeVL2RBRcYOjL96MGKZbFOmPg0EfDVwFG3A1L5TEL0tBYV+RQolRk0Wx3xXnouprNPx9bvAkBCiSwWOb9YrZx5ENYwAF31I00BAk6j/UY/sCiqMvD5rPaKn98Y9PXcis8YlyfmZQI6z+VSRInoFvAjmrcW4scswOSoNJcJ+eC5X6HFlBme1VaB2pEqUspTMVZeMlJjxeObZaVh3vAaVskzRkKSjfpkOjKiE+qB/gIAEk9YkYPf6JegwYAvyPAacEmehYhIkJk0GwQjbwj+4j/74+4UALQzVGS50UbFYErl3nhnJYCy6NFUnrs5i7JIKPxBCYg7Yyk0KwHZsMqKjJ2LoHk7nMSklV5GpOBm2TIn2kpuSW3HajRue+0QVYkrM/ITt2Dq2P6YcrpNl+CRajf4S+c107OTyfLZiWDK2YNy1w7AjqQTFTNcS8qO2NAd7+7fCnC0ZSC9yIsR0AxIt5lJhGI1euAgvKBWjEKVKHWIMrZBhRYWVH8w61fYgQkSbxGGaRH1NNapgwxB8zhqcSd2M+aPfxpCtZ5FpYRAf80pFTHeU/OyqQnGRBSVVdiFilHslWFGm8igRc61G5AaCfdkwipG5YwUWDhyLGfvLcNbmg/f80lkVC9CAUn4NCvojqoMBnw2VVRacPFcFDzeHlSQa3J+RW3LQXGrFT7eUhiEgY7HYkHCsTDhHWTiGnCEDjMFksLEaqCU2R9Qck2sJCVPxNvWJMzFnfA+8+MksbIjZheRKK+rESKmpOwmjCrgBUUm4LpcrlJkoltwsALe1ElVFeSipN+BlnFXDHueSR0u2LEmLonY5oHPiyE/D8fj5mD9+GN65+jNsSCpCGRdscKNwjwt1+SdRXuWAzcMcV5woY7mUEtfoBbzkE5gHkBsJwVRT+VTU1NSqmqIUa0Cb3pBZhUjvrY/7P4uAJlFfUzWMUZKtFUIhuOpLkH9sJXallKK4zgsmN+MA2pCOzC4nMi/leFGI2PkYF8DYBNXpJPNspBelU+ovR+HJJCTEJiLPZsBtJr/jhpgqv4n2hr6mahv2EQcaM3OzLADg7xKoqjKWs5motBmNPew0rJj66H8yBIRFKRPCAHDScI7NHHvVV7QJtBVqVVh4/k5CgiRImaRLDeA8wVOehrSjOxG14wgy0rJQ5HDAQTvF6THmohOuFU4gqzJqy70Y38xl+rQZ/Be2R40MJ0mTxHEGw6pYEK7qQhTlJCDx4F5smnIUueW1cEpSTAacq1gvgkKSx1VxVNNUDIMijo1cxMguF64jKSD3ORUaJTGtkoVX6lEpgJFdUB/VFBDQJOrralGkc3qCAUkxYDBxntMJnwRt0xtigOfXnfj1n9H3k21XzD2qaEpoVFSCUP6kgWgA6aFiHHDBb7jh4WQ8ryuDPaV6kijK/19fFv1pAxAwVxeqwFjThnMQkylZtdJGCHVDGkMDbq8PbcoIhNuPUjKFPEnAuFKPFN1QDpYIG+EBnLYk3McJj5xohgOQdFCNDjFRpFpgwrgoCT+Q88xEoLQNskSeZeDx5iKX8IKVb6E9k3eo5LR0QpWdoq2S6Ul5DtpURhiRcJkPS+dTysRnlsWSaoXid2jcWDROlSpUSYBVAk4mexJVShSzptxu9bN9FQFNor6KiPAZNVD6ggZcQW7uyMBBbgOgOjNXaDQoEJz3oG0UJ5CyRKkJAgAABb5JREFUtOwhjkDIp4ITeT0SoUiNl9yeZWTWR1oX81TZR5Q+pfht6nP9/+UjIPWsBhlmJpe9yoTA0qCzHjkARr6q8vILos9sWgiwzyomE5764U86bZJXzYyVks84aLO/h/mSkCFz/8/wZST9gVJwmCtYksVS4ZIdEcR6SRpLkhMeKnvlMRhatBQqXiQzarWKrBiO1A5FWil0RmTvUMZrucXJo40S5Ut2LVF9iTaVNpbBDcpghvuYqT7xh6xt/m48RKkDqQvmFhT9UNkAYVbcjFkRqUhh0cc1DQQ0ifpKPbLb+uAx5XKTK4XjP8l1GJjJzLXS0dmtInhxnlyyqfMs3oEyfQiG4UIg4BE+1hAhypwAEOPHZc/iTQpLYyc2t5v4buxMBGD88xwiMRjhJeUckDiQscrDG0fL9F44uek/z3Ppkn63CNAC8N/5l/zK/0yJiL+Z0/zC4+UbBqJfFG9jni7Tgcx0LuqUukQwyNQJJEckHSRn5oAvCqry5mh/ZP83yVlEmYj39siKPlF9zhfuf/+LlEUSe6ryXKzA8znB8tIhkWJwiiw8pacW+JA4sS+KifvfF+eyr0DIVb2xhMoWMMs4A/mViqZmBC77BvrEf0oENIn6mmoTA2ZuuyBp58QRUkZO5GV6eTKafs3J/+AjiQkQYyAXk50mJB5BtnpQBu8fnPo/PhaTaOZdoYGRsEvGNki5eP2LjO3/OFt/EDEC9IxNvYneOqdIZFAyJX0SY+UZmyNaxBfWB36fEVBUScXbCQ4yOl8gUPxTDdLsyxK4JO2MxOciSUocMcY/ihMlU4Gc/iIB8ytVS+IkqT5xet+cPpQ4K49ch7Hn5zdfD4bgY9iCuaqvMetHKWq0mSoo6sLm3jRVXFhDK8u+pY4hWQx7lspBNJ3W83N/jVm6yK+lykeCp7AkqSN/kh0VTFshqWsuJsiRX14f+U+KgCZR/6jiTBmdxky9FIm6IDOHP4/sZ3g4FusVvhRtosjCF+4SydXE5sq5PFq6tniSNFbC7XiA7siRQHnJYwRrwZJ0SpYIqL+Iv7jsAvYlr6MP0AiEEVBtij304rYT/lT1XPUX/w+TK/40X+ahPF/ZlQvkSn1FJ0o5emy1ioipo6UNM2bSvLJkNzcJGOOnGugbhkt0yZ/hksrjCDG8UOawss5nVYTr/AOacUZhDPj5d/cSBMNEziS04ZIJzFI0s+zfXTH1na8wAppEXWHA9e00AhoBjYBGQCOgEWgaCGgS1TTqUT+FRkAjoBHQCGgENAJXGAFNoq4w4Pp2GgGNgEZAI6AR0Ag0DQQ0iWoa9aifQiOgEdAIaAQ0AhqBK4yAJlFXGHB9O42ARkAjoBHQCGgEmgYCmkQ1jXrUT6ER0AhoBDQCGgGNwBVGQJOoKwy4vp1GQCOgEdAIaAQ0Ak0DAU2imkY96qfQCGgENAIaAY2ARuAKI6BJ1BUGXN9OI6AR0AhoBDQCGoGmgYAmUU2jHvVTaAQ0AhoBjYBGQCNwhRHQJOoKA65vpxHQCGgENAIaAY1A00BAk6imUY/6KTQCGgGNgEZAI6ARuMIIaBJ1hQHXt9MIaAQ0AhoBjYBGoGkgoElU06hH/RQaAY2ARkAjoBHQCFxhBDSJusKA69tpBDQCGgGNgEZAI9A0ENAkqmnUo34KjYBGQCOgEdAIaASuMAKaRF1hwPXtNAIaAY2ARkAjoBFoGghoEtU06lE/hUZAI6AR0AhoBDQCVxgBTaKuMOD6dhoBjYBGQCOgEdAINA0ENIlqGvWon0IjoBHQCGgENAIagSuMgCZRVxhwfTuNgEZAI6AR0AhoBJoGAppENY161E+hEdAIaAQ0AhoBjcAVRkCTqCsMuL6dRkAjoBHQCGgENAJNAwFNoppGPeqn0AhoBDQCGgGNgEbgCiOgSdQVBlzfTiOgEdAIaAQ0AhqBpoGAJlFNox71U2gENAIaAY2ARkAjcIUR+P+dZ+PsniJUywAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E6%8A%95%E7%A1%AC%E5%B8%81.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAFdCAYAAADL1o0TAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAEzwSURBVHhe7Z35m1XVmajvP9HdP/a9T/c16Sl2YjtEYxCixJg4RDSKMw4YJ6TDIDhPOIAoKGA7gqCioiDKpEgLBEQBEQcmERwQcQAaUBAkuu591z47lmVVcXTVrn2O532fZz9Vdc6uc/a41ru/tda3/lcQERERqSOUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlJcqWbVqVRgyZEj4r//6r3DXXXe5uLi4uLh0+HLrrbeGefPmVWqmxkV5qZJp06aFH/3oR+H8888PvXv3dnFxcXFx6fBl//33D0OHDq3UTI2L8lIl//3f/x1+97vfhf/5n/+pvCIiItKx/Od//mdsAWh0lJcqUV5ERKRslJcM5aVKlBcRESkb5SVDeakS5UVERMpGeclQXqpEeRERkbJRXjKUlypRXkREpGyUlwzlpUqUFxERKRvlJUN5qRLlRUREykZ5yahrefniiy/Cyy+/HMaNGxeX8ePHh/fffz989dVXlTW+htfefPPNMGzYsHD//feH0aNHh/nz54ctW7ZU1mgb5UVERMpGecmoa3l59913o4iQdXDgwIHhpJNOCjNnzgxbt26trPE1O3bsCFOmTAmdOnUKffr0ietPnDgxfPTRR5U12kZ5ERGRslFeMupaXhCVyZMnhzfeeCNs3rw5Ssl9990XIyzNee+998KECRPCFVdcEd555524/ueff15599sQqdm+fXvYtGlT+Pjjj8OkSZPCEUccobyIiEhpKC8ZdS0vyAcRFZqPNm7cGM4+++zw0EMPhXXr1lXW+JpFixbFaMu+++4bDj/88HDuueeGZ555Jnz55ZeVNb7JZ599FmWnR48ecf2DDjooLkiPiIhIGSgvGT+IDruffvppWLBgQejWrVt4/vnnW4yorF69Ok6u+OSTT4Y5c+aEyy67LIwcOTLOFt0Su3fvjhK0cOHCMHfu3HD77beHrl27GnkR+Z6Mmf92OHPMoppbeo5dHNZt3lHZSpHaRnnJqHt5IeqydOnScNVVV4XbbrstNgm1BB1zN2zYECMqNAnRvHTLLbeEWbNmVdZoG/u8iKTR//FXw99fMqXmln+8dFpYuWFbZStFahvlJaOu5QUJIaJy7733hgsvvDCsWbMm7Nq1q/LuN6HPC31jtm3bFpuK6Og7ePDg8Oyzz1bWaBvlRSQN5UUkHeUlo67lhSjKiBEjwhlnnBGmTp0aPvjggxhhQVDoC9MURhYRnZk3b14cTt23b99w4403hmXLllXWaBvlRSQN5UUkHeUlo67lhdFG3bt3D3vttVcUi2OPPTZcfvnlYciQIeGJJ56orJVB5OWee+4Jv/zlL0Pnzp1Dz549Y4ddmp2qQXkRSUN5EUlHecmoa3khRwujiJ577rmYcI7l9ddfDytXrozRlabs3LkzCszs2bPjQj8ZRihVi/IikobyIpKO8pJR9x12OwrlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJaOu5eWrr74K27dvDxs3bozLpk2bwq5duyrvfpsvvvgiyscnn3wStmzZ0ua6zVFeRNJQXkTSUV4y6lpeEJcHH3wwnHTSSaF79+6hR48eYcmSJeEvf/lLZY1v8tprr4VevXqFo48+OlxxxRXhpZdeqryzZ5QXkTSUF5F0lJeMupaXBQsWRHkZP358mDlzZjj//PPDY489FtatW1dZ42vefffd8NBDD4ULL7wwrnv99deHCRMmxGhNNSgvImkoLyLpKC8ZdS0vq1atCq+//nrYsGFDlJALLrggPPDAA2Ht2rWVNb5m3rx54ZZbboknnYgNwsO6r776amWNb0KT0tKlS+N6d911V+jXr1/o0qVL2Lx5c2UNEfkuKC8i6SgvGT+IDrv0ZXnrrbfCKaecEiZPnhz7vzTnqaeeitGW+fPnx/WRGeRlxowZlTW+yY4dO8KsWbPi//Tu3TuceOKJoVOnTsqLyPdEeRFJR3nJKF1eEIndu3dX/vomX375ZXyfjrmtwXtEXh5//PFw8sknxz4vLTFp0qQwaNCgsGzZsvh9ixcvDvfff3944oknKmu0jc1GImkoLyLpKC8ZpcoLcoJsrFmzpvLKN0EUaNZBYFrj888/D88880w49thjYzRl27aWC6EpU6aEwYMHx+/j84jA0ByE9FSD8iKShvIiko7yklGqvBA1ueyyy8I555wThg4dGptxZs+eHT788MPYwXbixInh0ksvbVVIGFU0ffr0cOWVV4b77rsv9ntpbaQRnXtHjhwZHn300Sg8SMuIESNi591qUF5E0lBeRNJRXjJKkRciLjt37ozyQifb8847L44Eevjhh8O4cePCsGHDopBcc8018XX6n7TEypUrQ//+/cOvfvWrcPXVV4d77703TJs2LYoGw6KbwggkOt+ee+654cknnwwXX3xxGD58eFi9enVljbZRXkTSUF5E0lFeMkqRFzrUzp07NzbdnH322WHIkCHhlVdeiZ1tb7755vCHP/whCknfvn3D+vXrW42mLFq0KNxwww3hzDPPDAMHDowLTUEMnyaC0xSail588cUoS4gOP4nsIFHVoLyIpKG8iKSjvGSUIi+ICgnl6KdywAEHhNNOOy0KBRJyxhlnhDvuuCMOa2akD6OBqhWMPYHA0CRFU9Obb74Zh0xXi/IikobyIpKO8pJRirxs3bo1dsSl8yxRF0SmW7duUV54neHI5GqhDwxiQ1+WtkYcVQufQRSHPi+MOPoun6m8iKShvIiko7xklCIv+dDmW2+9NVx++eXhrLPOiieE4cxEXq666qpw7bXXhhtvvDFGXpCNslFeRNJQXkTSUV4ySpGXFStWhAEDBsSkcscff3xsPqLj7XPPPRcOOeSQeHKIwtCplmYeOviWjfIikobyIpKO8pJRirwwSoiJEYm4HHjggeGwww6L8kLSuK5du8ZoDJ11eY1kcm3leekolBeRNJQXkXSUl4xS5GXLli1x5M+oUaPCoYceGqMvdNClGWmvvfaKr9EXhqHTSE5reV46EuVFJA3lRSQd5SWjFHkho+5tt90WhzUjJzQP3XTTTTFT7lFHHRUlhgkXFy5cGCdERBjao8NuCsqLSBrKi0g6yktGKfLy2WefxeRwjChirqGXX345jjJ65513wtSpU+Ns0ayDKOxpeoCOQnkRSUN5EUlHeckoRV6ASApSwrJr166Yy4VRRcgBryEv77//fnj77bdbTVLXkSgvImkoLyLpKC8ZpckLssJ8Q0ym+MYbb4RPPvmk8k4mNkRcmPGZ95GbslFeRNJQXkTSUV4ySpMXZOW4446LfVwYXdQ0nT8ddOkP06tXr9jvxWYjkfpHeRFJR3nJKFVeyO9CYjomUST3C5DT5Z577omzTTORIlGXsjvrgvIikobyIpKO8pJRqrwwJQBSwASNd999d8zzQmbd22+/PcycOTNm4q0VlBeRNJQXkXSUl4wOlxfmKVq6dGmYMGFCTE5HVl36tQwbNixOC0AzEsOnX3rppZqIuOQoLyJpKC8i6SgvGR0uL4wgmjJlSmwW6ty5c4y4IDDTpk2LHXSZSZroC01GzPxcKygvImkoLyLpKC8ZHS4vzOa8bt268Nhjj4XzzjsvnH766fFEkPMln8PohRdeCNddd124+eabw/bt2+3zIvIDQHkRSUd5ySilzwt5W5CSzZs3h1deeSU2IU2cODFs3LgxCgyddJ966qlw5ZVXRsnZsWNH5T/LQ3kRSUN5EUlHeckorcMu8vL444+HwYMHR3Eh58vIkSNjkxG/M/qICMzcuXPN8yLyA0B5EUlHeckoRV4+/vjjOA3AoEGDwujRo8Py5cvja/R7QWCY92js2LHhz3/+cxxxlDcnlYnyIpKG8iKSjvKSUYq8vPfee1FOHnnkkbB+/frKq1lzErJCJ17EZvLkyZV3ykd5EUlDeRFJR3nJKK3ZiE64LGTPZaoAmob4nQ69/ERwHG0k8sNBeRFJR3nJKFVemIiRnC80D5HXhfmMmFH63XffDR988EHYsmVLZe3yUV5E0lBeRNJRXjJKkxeaiMj5QvMQSemYEoD5jO68884wYsSI2JH36quvjsOlP/3008p/lYfyIpKG8iKSjvKSUYq8EHWhmWj16tWhX79+UVDIsjtr1qwoMYxCYs6jG264IRxxxBExEkNzUpkoLyJpKC8i6SgvGaXIC/ldmM+IIdJ9+vSJssJoI2aWpiMvUkO/l0WLFoWePXuGt956q/Th0sqLSBrKi0g6yktGKfJCP5ezzjorTszIzNKMLmLKAP6+/PLLw5IlS2J/GJLWkfNl27ZtpQ+XVl5E0lBeRNJRXjJKkReiKh999FFYuHBhnMvonHPOCTfddFMcYYQcEGWhaSnPtsvvZaO8iKShvIiko7xklNZhFyH57LPPwi233BJOPPHE0KNHjzB06NA4u/Tw4cPjQsfdhx56yOkBRH4AKC8i6SgvGaXIC01CDIVGSpi/iJPByKLjjz8+jjgaM2ZM6N+/f5y48emnn47rl43yIpKG8iKSjvKSUYq80Dn32WefDXPmzIl9X+64447Y5+XII4+MieloUiIC86c//SnKgtMDiNQ/yotIOspLRinywtBn8rlceOGFcSj0qFGjwvTp08Pvf//7OLKIjro0GfXt2zeOTFJeROof5UUkHeUloxR5IUEdiecQEyIvhxxySPjtb38b9tlnn3DccceFE044IXTp0iUceOCBsemoFjLtKi8iaSgvIukoLxmlddjNYUqAuXPnxrwv5Hl54YUX4vBopgzg9ZdffjmOTiob5UUkDeVFJB3lJaMUeSFbLpEXOuzmy/bt2+PCe4xEou8LwrB8+fLSs+uC8iKShvIiko7yklGKvKxfvz5m1aXDLhGWPMpC9IXOvERa+J3cL0OGDHFuI5EfAMqLSDrKS0Yp8jJz5szw4x//OPZnueiii2LH3V69eoXLLrssvPjii3EY9dq1a+Owafq9fPLJJ5X/LA/lRSQN5UUkHeUloxR5IarCtABvv/12eOmll2I/F5qJmGWaiAwSc+6554ZjjjkmHHzwwcqLyA8A5UUkHeUloxR5QVbIqstoIyZnJMsu2XVvvPHGcPrpp8cRSLfeemuYOnVqeP7550uflBGUF5E0lBeRdJSXjFLkhf4thx9+ePw5evToKC3XXXddzLKLxNx+++0xcd2TTz4Ztm7d6txGIj8AlBeRdJSXjFLkhQkZibxwAsaOHRsefPDBMG7cuPDoo4+GNWvWxOHTSM3gwYNjp14jLyL1j/Iiko7yklGKvGzYsCH2bSGz7oQJE+Lv48ePj1l2161bF955550oMcxr1LNnz5oQBuVFJA3lRSQd5SWjFHkhw+57770XunfvHodJM3P0DTfcECdg5D2akYjGrFy5MjzxxBNx9umym46UF5E0lBeRdJSXjFLkBYi+7LfffjGywpQATAdw7bXXxoX+MJdccklsXmKSRoSmLcgLw3xJ11xzTRSe1qD5ibmTLrjggjjp48CBA2Pz1LZt2/YoR8qLSBrKi0g6yktGKfKCKJDL5Ze//GUUDoZFH3300eHhhx+OC8npBgwYEMViT5B9d9WqVbGjb6dOneJIptZgdBM5Zs4888yY/I7PZ3ZrMvwqLyLForyIpKO8ZJQmL8wcTT6XN954I0ybNi3cfffdlXdD+PDDD8OYMWPiiKM9QVMTERoiKQcddFDMIdMa9KXhpPO99LNZvHhx7GPTEkgR7/HZjIpiBFTXrl2VF5HvifIiko7yklGavNCEg0wwnxHDoZGZnC+//DJGU5iUcU/wOTT70MH3qKOOihl6W4N5kvr37x+OOOKIKCKnnnpquP/++1ucO4l+NnQm7tGjR2zGQoxYiN6IyHdHeRFJR3nJKK3PCwKTT8KIrLA0hfeqGSLN/7MQraHpqS15YR2ajVavXh3nVyKy06dPn/h38341fCZitWnTpjjf0qRJk6L0GHkR+X4oLyLpKC8ZpcgLUkKTDJEN+rgw2ohRRbNmzQpXXXVVuPTSS6NUXHzxxXHkUTUTM9Kxl+kE2pIXmphYj+9HlvjOK664IsyePXuPomSfF5E0lBeRdJSXjFLkZefOnXGoNOJCkrrLL788SsTSpUvjEGn6u5x//vnhD3/4Q0xcR4faPVGNvNBMxXcyVxLb8MADD0RJYn4lRiy1hfIikobyIpKO8pJRirzQREM/lRUrVoRly5bFHC99+/atvJtBXxQ61lZLU3mhuYeh2AhS0+agJUuWxNmrSYjHvElEefgO1m3ebNUc5UUkDeVFJB3lJaMUeaE/C/KSL3feeWfo16/ft14jD0u1EE2hcy2CQs6XGTNmxKgNTUU59F9BWuiA27lz5zhCiaaqalBeRNJQXkTSUV4ySpEXOsiSZ4XcLCzMc3TooYfGmaRZ8tf++Mc/Vv5jzxA5QU7ou0K0BWkhAkPH2xzW4XU64BKpQUSayk1bKC8iaSgvIukoLxmlyAsjfYiK0GGW5cILLwzdunX7698sZMG96KKLKv9RPsqLSBrKi0g6yktGKfJCRIS8LG+//XZciMIgK/nf+WvkZKkVlBeRNJQXkXSUl4zSOuySBI6+Kbmo0OelKd+1w27RKC8iaSgvIukoLxmlyAv9TOj3ct9994VRo0aFc845J+Z0yZPCkW135MiRyovIDwjlRSQd5SWjFHkhxwpJ6p588sk4xxBJ6saNGxf7wZxyyimx/wsjgr7LaKOiUV5E0lBeRNJRXjJKkZd81A/p+smxwgzTdOIlLwsJ45gZmgkWmYuoVlBeRNJQXkTSUV4ySpGXekR5EUlDeRFJR3nJKF1eXnvttfD888/H+YX4yUJH3mrzr3QUyotIGsqLSDrKS0bp8sIcRvvvv3/o0qVL6NSpU9h7773jnEM0KdUSyotIGsqLSDrKS0bp8sIM0ow4IuvtypUrw+9///swb968b8xJVAsoLyJpKC8i6SgvGaXLCzNKM9IImJ+ImaTbmhm6LJQXkTSUF5F0lJeMUuQFSUEG5syZE04//fQoMHPnzg1PP/10bD6666674t+8z8gj5isqG+VFJA3lRSQd5SWjFHkhQd3NN98cJ2Hs2rVrOPXUU8Pw4cPDoEGDwk9/+tM42/OwYcPiBI0kqyMbb9koLyJpKC8i6SgvGaXIC3ldSE43efLkcMIJJ4Q+ffqEqVOnhocffjgcfPDBUWqmTJkSJk2aFNephZFHyotIGsqLSDrKS0Yp8kJn3B07dsTlkksuidMEICjvv/9+OO6442KTUf4+y1dffVX5z/JQXkTSUF5E0lFeMkrvsDtgwIC/jjZasWJFOProo+NoI7Lw1hLKi0gayotIOspLRunywuSLvXr1iifjtttui4Iwffr08Omnn1bWqA2UF5E0lBeRdJSXjNLlhX4u1157bbj++uvjwu/Ma7Rly5bKGrVBe8rL6o8+Dc8t/7Aml83byx/ZJT9MlBeRdJSXjNLlhf4vzZuIvvjii7B79+6a6OuS057yctP0FS0WorWwvPDWxspWirQvyosUya7dX4YPt35ek8unO3dXtjId5SWjdHlhJmn6uzTl9ddfD2vWrIkSUysoLyJpKC9SJC+u3RT2G/RcTS7/NXtNZSvTUV4ySpUXIit33nlnmDZtWvybCAwJ7EhaxwikWupforyIpKG8SJHMffPjFs9vLSy3PLOqspXpKC8ZpcsLcxsxESNRlvXr14cRI0aEHj16hLFjx4bt27dX1iwf5UUkDeVFikR5aSxKbzYaOHBgTEr3yiuvhEcffTTOMn3eeefFEUe1hPIikobyIkWivDQWpcgLnXG3bdsWlwsuuCCcdNJJoXfv3jHb7owZM8I555wT5zfifYZM/9CS1Ckv0ogoL1IkyktjUYq8MLfR4MGD49xFP/nJT8I//uM/hmOPPTY2Id1www3h0EMPjULD/Ed33HHHD25uI+VFGhHlRYpEeWksSpGXdevWhXHjxoXx48eHffbZJ/z93/996N69e+ykS96Xbt26xYgM60yYMOEHN7eR8iKNiPIiRaK8NBalyAtNQatWrYoRGKTlqKOOinMcEXmh38vJJ58cIzNvvvlmHDJNLpiyUV5E0lBepEiUl8ai9A67TA9w0003haeeeirKC1MEMNrokUceqaxRGygvImkoL1IkyktjUbq8kNOF5iFyvJCs7oorrgh9+vSJuV927txZWat8lBeRNJQXKRLlpbEoVV4QFiIvyEv+N3MaXX311VFi5s6dG1+vBZQXkTSUFykS5aWxKFVeGAK9YsWK2IG3KeR8eemll+LUAbWC8iKShvIiRaK8NBalyQtRlk2bNsVlx44dYdeuXWHz5s3x9YULF4bly5fH12oF5UUkDeVFikR5aSxKkRek5IMPPgiLFy8OL7/8cvz9/fffD1OnTo3DokeNGvXX+Y5qBeVFJA3lRYpEeWksSpGXDRs2hEmTJoV77rkn5nVZunRpmDVrVszvwnsMmx49enSUHBYz7HbcorxIUSgvUiTKS2PR4fJCzpZXX301XHzxxeGAAw6IPxkWfffdd4fDDjssPPvss+GMM86InXZfeOGFsGjRojhpY9koLyJpKC9SJMpLY9Hh8kIUhb4tjCRimDQTMebDo8m2y5QAv/71r8Npp50WpwYgAlMLs0srLyJpKC9SJMpLY1GKvLz77rvh/vvvD0OGDAmDBg0KDzzwQBSVzp07x2R1ZNglYd3s2bPDggULaqLjrvIikobyIkWivDQWpcjLypUr4wSMw4cPDxMnTozTANBxt1+/frHz7oABA/6a+6VWUF5E0lBepEiUl8ailA67QD8W+r7MmzcvrF27Nqxfvz5MmTIlLFmyJFxzzTVh8uTJlTVrA+VFJA3lRYpEeWksSpMXIjAIDP1dHnrooRh5Ofvss+PvRGLI/VJLKC8iaSgvUiTKS2NRiry88cYboW/fvrHD7n777Rd+8YtfxJml995773DqqafG5iPeGzhwYOwTwyzUZaO8iKShvEiRKC+NRSnyQofde++9N3bUPfzww8MRRxwRzjzzzNhhl4WRRyNGjIgjjRhGXQtRGOVFJA3lRYpEeWksSms2yqHTLiOP6Pty++23x7wvEyZM+NZ8R23BlALbtm2L8yExDLstyOBLE9X8+fPD66+/Hj755JPKO22jvIikobxIkSgvjUXp8rJs2bKwZs2asHPnzigWb731VnjxxRfDO++8U1mjbeg7g7iQ0I4oDkOrW4M+Nnw+OWSOPvroGOFhGgI+Y08oLyJpKC9SJMpLY1G6vCAUzCyNHPATgSGvC5l4q4H1yQfD1AL77rtvjKi0BqOaRo4cGfvTkLmX6QnoU0MSvD0JjPIikobyIkWivDQWpcsL0jB+/PjQv3//OEz6u04FgLwQpSFfTNeuXduMvNBcdMEFF8Qh2Rs3bgzTp0+PzVY0H+3evbuyVgb9bJhv6frrrw+9e/cOJ554YujUqdMem6WqQXmRRkR5kSJRXhqLmmg2IvrBZIwkqKs24pKDdNDkRB8ZmoJocmoNojInnXRSWL58eZQe/ib6MnPmzG9l8eVvJoxErO666644AqpLly7Ki8j3RHmRIlFeGovS5AVJYQbpUaNGheuuuy5OC5DCRx99FI455pg25YVOwd27d4+RGiI8rIu8kBAPAWoLm41E0lBepEiUl8aiFHkhqkFGXaIaTMw4ZsyYGNGg423zhRwv1XSorUZeGI1EIjyiPURe5syZE0c4IU7KS7YoL1IUyosUifLSWHS4vNDMQ2fZnj17hvPOOy88+uijUWKYpPHWW2/96zJ06NAwePDgmO/ls88+q/x361QjL0jLtddeG5544om4Pv1kmIoAqdlTXxvlRSQN5UWKRHlpLDpcXpCExYsXR3GhjwpJ6GbMmBEnYkRimi5MFUDOF6Ike6KpvNAcxc/nnnvuG31Z6KTL0Gj6vdDPhs679LUh6kOumLZQXkTSUF6kSJSXxqLD5SXv6zJ16tQYWSESgqQw0mj16tXfWJjjiBww1XTiJTqD8Lz//vtRRhh2/corr3wjosLvdOwdNmxY/O7bbrstjjwyz8vXi/IiRaG8SJEoL41FaR12aT4iYRxDkW+88caYZG5P0Y/2gO9AbhCbPDleNSgvImkoL1IkyktjUZq85BBhQWDIdrtly5YOEZjvg/IikobyIkWivDQWpcsLEZinn346ziDNqCOy3dYiyotIGsqLFIny0liULi9APxVGIL3xxhvfynRbKygvImkoL1IkyktjUbq8fPjhh2HhwoUx+vL444/HnCuIAp11qxki3VEoLyJpKC9SJMpLY1GavDDyhxFBzC9EcxHJ4hgBdMMNN4Rbbrkl3HvvvXHCReYYqmY0UNEoLyJpKC9SJMpLY1GavCABzBfEUGmSxTE5IqN/aDpiGDU5WMiGy0zQ33W+oyJQXkTSUF6kSJSXxqI0efn444/DkUceGRPJEV0hEkN/F36SlI4suFdddVV49tlnqx7OXCTKi0gayosUifLSWJQaeenfv39cmLUZiSEr7p///OeYtI4TdOmll8Y5kIy8dNyivEhRKC9SJMpLY1GavBBNmT9/fhQX5jIaOXJknOGZvi68dvfdd8eoSy2ICygvImkoL1IkyktjUZq85KxcuTJOzshcQ5dffnm47rrrwoMPPhj7wNRCc1GO8iKShvIiRaK8NBalyQuZdLdu3RqbikaPHh1ndybLLieGTrwMm2b6ACMvHbsoL1IUyosUifLSWJQmL4gLcxoxNQB9XGhCevnll8O8efPiTNOMNurVq5d9Xjp4UV6kKJQXKRLlpbEoTV4++eSTcMIJJ8Rh0mTYZV6jTz/9NErNBx98EO67774wYMCA2IF3165dlf8qD+VFJA3lRYpEeWksSpMXZnY+77zzYkK6adOmxVme6f9CnhdEIe8DQyK7WpgyQHkRSUN5kSJRXhqL0uSFCRjJ5XLllVfG/i6MMKKj7tixY+PoI16nL0ytzHWkvIikobxIkSgvjUVp8pKzevXq2Dn35ptvjh11hwwZEiZNmlRTnXVBeRFJQ3mRIlFeGovS5eW1116LERYS0tFJ9/zzz4/DpZ955pmwcWPtVKTKi0gayosUifLSWJQmL8wYTRMRyenGjRsXpkyZEidpfPLJJ6PMXHbZZXGiRjr2Mqy6bJQXkTSUFykS5aWxKE1eNm3aFHr06BFFhegLI4yItGzYsCEsX748duTlJC1evDjOd1Q2yotIGsqLFIny0liUJi+IyimnnBKjL2TTfe+998KHH34Y87ow6oiTQ6fdhQsXKi8duCgvUhTKixSJ8tJYlCYv5HQZNWpUOOuss0Lfvn1jXhdGH40fPz72eTnzzDNjAjtyvHz11VeV/yoP5UUkDeVFikR5aSxKkxeEBIFZsmRJFJahQ4fGPi633357HG1ENIbEdbUgLqC8iKShvEiRKC+NRWnykkNSOpqOaCLipPzpT3+KeV7mzp0b5aVWUF5E0lBepEiUl8aiNHn5/PPPw3PPPRcefvjhKC+MOBozZky455574ggk8r0w5xHTBdhs1HGL8iJFobxIkSgvjUVp8sL0AOR1GT58eJg9e3ZMSsccR2vXro2TNDI1AO8vW7bM6QE6cFFepCiUFykS5aWxKE1ePv7443D00UeHGTNmxOYhpgsgGrNjx46wbdu2mHWXaQNmzZoVdu7cWfmv8lBeRNJQXqRIlJfGojR5oTmI0UTkerniiivCo48+GrPqPvXUU7HJ6LTTTguXXHJJFBmbjTpuUV6kKJQXKRLlpbEoTV6IpsyZMydMmDAhTsp42223xSYk+rsgNQ888EBMVlcL2XVBeRFJQ3mRIlFeGovS5IVh0ojKokWLwsSJE0O/fv1Cnz594pDp3r17R5Eh826toLyIpKG8SJEoL41FafLCnEXdunULCxYsCI899lg499xz/5rjhWajiy++OMpNraC8iKShvEiRKC+NRanycswxx8Th0nfccUfM75I3ETEdAJGXXr16xb9rAeVFJA3lRYpEeWksSpMX5jHab7/9wh//+MfQvXv3GHlhskYEhnmOrr76auWlhEV5kaJQXqRIlJfGotQOu+R3mTZtWmweIvrChIwMlyZZHR14n3/++cra5aO8iKShvEiRKC+NRWnyAgyBJtqCtDCXEdEYmoyYGoDZpJ0eoOMX5UWKQnmRIlFeGotS5aWeUF5E0lBepEiUl8ZCeakS5UUkDeVFikR5aSyUlypRXkTSUF6kSJSXxkJ5qRLlRSQN5UWKRHlpLJSXKlFeRNJQXqRIlJfGQnmpEuVFJA3lRYpEeWks6l5eyAuzefPmsHHjxjgD9e7duyvvfBvWZTg22X1ZmF/pL3/5S+XdtlFeRNJQXqRIlJfGou7lZfr06aFnz57huOOOC4MHDw5vv/125Z1vQuZepiI44IAD4rQEzKt05513hnXr1lXWaBvlRSQN5UWKRHlpLOpaXpYvXx4nc7zqqqvCM888E2elJsEdEZjmEJl56qmn4nQEs2bNCvPnzw9vvfVW2LFjR2WNtlFeRNJQXqRIlJfGoq7lZeLEiXEGamai3rp1a5xS4PHHHw9r166trPE1K1asiKLDPEojRoyIM1mT2Zcsvy2xa9eusHTp0jB+/Phw1113hX79+oUuXbrEJqpUlBdpRJQXKRLlpbGoa3lhTiRE5LXXXosRlClTpoT77rsvLF68uLLG17z66qth2LBh4eyzz44n/5xzzgkPPfRQnJ6gJfg8IjTXX3996N27dzjxxBNDp06dlBeR74nyIkWivDQWdS0vyMjdd98dIy10xqVpB6GZN29eZY2v+eCDD2L0hY669H+59dZbw8033xwWLFhQWaNtbDYSSUN5kSJRXhqLupYXOtzec889YdWqVTFSMnXq1DB8+PAW5YVmINZBXIDmJQTm6aefjn/vCeVFJA3lRYpEeWks6lpeJk+eHAWGUUR00h01alT8e8mSJZU1vmbOnDlh7Nix4b333oszV994441h0KBBRl6aLcqLFIXyIkWivDQWdS0vRFyItAwcODA88cQT4ZRTTol9XpAZ+sE05cUXXwxDhw4N11xzTey4e9FFF4UxY8bEvC/VoLyIpKG8SJEoL41FXcvLzp07o7TQofbKK6+MnXFnzpwZZs+eHZemIB1IzYUXXhiXO+6441uC0xbKi0gayosUifLSWNS1vAAddcnXMmPGjLB+/frYt6UIlBeRNJQXKRLlpbGoe3khTwtTAiAxpPpvLW9LKsqLSBrKixSJ8tJY1L28dBTKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0ljUvbysWLEiPPbYY2HMmDFRMDZt2lR559t88MEHYeLEieG+++4L06ZNC++++27lnT2jvIikobxIkSgvjUVdywuiMnbs2HDuueeGvn37hgEDBoRXX301fPHFF5U1vmbbtm3hueeeC2eddVb405/+FC655JLwzDPPhM8//7yyRtsoLyJpKC9SJMpLY1HX8jJ79uxwww03hDvvvDNs3rw59OvXL0ydOjV8/PHHlTW+Bqm54447wsCBA8Onn34afyda895771XW+CZfffVV2L59exQkPo+ITdeuXcNbb70V/05ZrnxkfvjfFz8c/k/v8TW3TF+0qsVtbrp8+OGHLb5eD8tHH30Ul5beq4elno99r9Gza/K636vPI2HBsrUtbnPzpZ6vnXq/9ve07U+/tLLF81sLy7UTFrTbsT/vvPNindfo1LW83HvvvWH48OHhhRdeCJ999ll45JFHwrhx48Lrr79eWeNrpk+fHgYNGhSbi3bu3BlmzpwZozZz5syprPFN+LwJEyaEHj16hMMPPzzst99+4e/+7u/Cr371q/h3yvKz/Q8M//cn/xF+euAhNbd0ObRri9ucL4cddljYf//92+U4lLEcfPDB4Re/+EWL79X6cuihh8brkJ8tvV/ry97/cUDYa+/9Wrzuylx+9v+XQw9r+7pn+fWvfx1+/vOfh86dO7f4fq0vhxxySDjwwANbfK/WFx4cDzjggNClS5cW32fp/P/LrpbOby0s+xxwUDjooINa3O7vuuy1115h8ODBlZqqcalrebn99ttj+GzVqlVhx44d4dlnnw133XVXePHFFytrfM2TTz4Zrr/++rBkyZLYrPTSSy/FyMtTTz1VWeOb7N69O6xbty4sXLgwzJ07NzYbIUDIDn+nLH369AmnnXZai+/V+vL444+HfffdN4pjS+/X+nLRRReFs88+u8X3an15+OGHw9577x2lu6X3a32heff8889v8b16WCgDEBgqjpber/XlqquuCscee2yL79X6QtmLNA4bNqzF92t9IeJ/4okntvjed1148F69enWlpmpc6lpeRowYEe65557YlJPLC81B8+bNq6zxNZMnTw433nhjeO2116KYIDhUwFTGHQ3bSJ+beoROzkQvFi9eXHmlvhgyZEgsxOsRJB1xfOONNyqv1BfXXXddvAfrlV27doU//OEP4emnn668Ul8Qle7Zs2flr/pi69at4aijjooVdz1CPdWrV6/KX9Ie1LW8cDPefffdsSKlmWf8+PFRDFqKvNBZ97bbbotPTxRCiM6oUaNajbwUifJSHspLeSgv5aK8lIfy0v7UtbwQQhs5cmR48MEHYxPP1VdfHS8SmoaIxDSFfjAMkUZgNmzYEJubaHZasGBBZY2Og+++8sorK3/VF3RwJnT+yiuvVF6pL+gjRd+neoRQMf0Wli9fXnmlvrj55pvD0KFDK3/VHzQ3n3766bEJox6hT2C9VqDIywknnBCef/75yiv1BV0UGFAi7UddywvDlm+99dZo5EQy6NA1evTo8Oijj4YnnniislYGkRmajij8L7300lgB0366ZcuWyhodx5///OcwZcqUyl/1BaO6aK5DFusRCr8ZM2ZU/qovGGnANYt81yM8Nc+aNavyV/3xl7/8JfY3WrZsWeWV+uLll1+OgxDqEVJa3H///eHNN9+svFJf0BowadKkyl/SHtS1vFCYkKSOG5KIC/1X1q5dG95///24NOXLL7+MryEwNDXxFMITLJ/R0SBdn3zySeWv+oKnT6Iv1ebHqTUY+r5xY33msqHZgmY7ftYjHPe2kkjWOqRPINElD0L1CNELhtrXI3n5TfqKeoSHZIZKS/tR1/ICdL6lUFy5cmW8QNqSEd4jWR3Cw1NsvVYCIiIijUzdy4uIiIg0FspLO0JTCn1CiAQR4WkrCkTzC+vSfETEKI8CER7lbz6D5qWOap75Lt9L+JwQdN4MwP/xGrDfhEfZLxY+h88uGjpo501Cezr2rNt0G2kGYH22k//lMzg3zTt9FwXfzTHf07Fn+9hW9jPfdhb+hwgk56SMY8+551ixHXuCbWI/2T4yXbPdwM98v9iPjoqKsu0cf843yStbg/XYxvz+ZlvZfuAYs+/5sed97u/8nigSvpumFO7BtmA9trf59ZHvF9vPa3xOW8ehPan22OfXdn7dEDXn9/z6Ydt5jfc4L7xW9LHn8/OygoVtaKvM4Vjn5T3/xzYC10nTY29rQPUoL+0IUxMwFPH444+PQ3Lbmvhx6dKlMWHa0UcfHa644oqwaNGi+Do3wmWXXRaHZPbu3Tt+ZkfAzUNHZr6XuTPIRNwSFILcfIzs6t69ezj55JNjAqb8hmQ0SadOnUK3bt3iwudQoBQNneFIPkciKLZh/fr1lXe+CdtPvycypZKwi22kIyB9GTgGdADnM/isjurcyLYyN9dxxx0Xf7Y2HJTjSIdR5udiu4888sjYWZ1RDO+8804cRUWH9PzY8zkUjEXDuae/GdveFhTupCjgmuG6J1XBmjVr4jmhIyaJG3//+9/H/cjvh6Kh8qAD9AUXXNBmZ2IqFY7xhRdeGM/TmWeeGTuus+1cN+x7fuy5fsgn1RESwLEneSFlRltwHXC8ybCbXx+MmkJ8yJNFWcP9wPxwjOLsCDj2lJHnnHNOi7m5cjjuDLE/6aST4naTZZZzwKhNtp1ylAR2vMc1REqBIiUAcUGcSFaYl4EXX3xx7E/E9dASXPckaeQY33TTTfG6B/pd8r/HHHNMPIdki5fqUF7aCUYgMBKESp3RLEz+yA2ZP501hRuW4d3cdOSfIf8FhT9DYflfLnJGTFE4svC01NpN0R5Q+FKQUYgwQzd5aCjo+N7mTzDsDyOlqPDJkUPuCAo+CjxuRLb3mmuuCfPnz48LFUPRTxMMg7/llltiBmW2jeGgZFBuqWMlT2hICceebWYb6eTNvnK+qHg49hSMdOymL1WRT3F8L3lDmIaC+bO4hvhetrM5eQVKxc5200mdjLVcO8zdRRoAKv782FOYFn3sqfzo/H7KKafEiqMtSGGQXx+MuEO6uP45xg888ECUZs4fhTujBouu/Kk8+e7+/ftH8WgrfwvXMdm7EQWkkP1ge6mE2BeEmXuG4076BZ6ii7xnuSY59tx/VOp7yt9C+cT1wlxw+fXBPtH5nuuHe59jT4WMIPMQVSRclwge2cbJG9VW/hb2k36KjNhhuxlyz/w+HGdGD7LNnBve475H6Io89mw7MsLwZx6aKDO5D9mHlh7UuMa4XnhIZR2ue+blo7zk3mFfKPc5N+Qq64iHvR8Cyks7QQFAtIVpCCi4KMwYrv32229X1vgaKk0qWyopwokPPfRQLDD4DP6Pm5FKiidBJuDipszDjEXAzZV/L2JFhcL38hTQPBTK9jLkkv/haY51eBrl5qPw4+mBG5mcOtzYVMJFVv5AAcCxzyflpPLju1uadBPRYV9PPfXUKCiIDE9vnCcqUKSGColpIfgboSiyIMzFi2NP9AeJ5LqgEG7ruHEemBWdaBmjMDhnpAtg+xFLrkMKwaKPPTLLdUolhIC1BRU/BTTbyjFFNrnmWdgPzgXXFPcCIsA9UCTIEeeaiu83v/lNvH5bg3uaBJekCODYs81EwHjK51qnQuLap0JjvaJHJHFeqaS5BnhypwJsC+5PKk+Ei+uL6wy5Jdkk1x/STLMG9w37wz1eJBx7jh15upi3iGuiGrimqeC5x3noYlu59tg3rhumb+H8FAllMZFzhIrt4cEBeSSi29JDB69zjLlmuC7INcW1TrnP6xwDziUSxPXDZ8ueUV7aiTxaQWXEkwJPcdxYPG02h4qFJ2Qqfp7+eHKjouSGpBCkoOGm4LO4wFmKfAqlAOPpk4KQAownIr6TQoLtaw36OdAsRCHODcxNSuTpj3/8YyxQqcxaiz61J8gIFRBPl7SNUwAz9QP70Zy8sOZJk4Kc5iEKlfzpmXNGNCR/IiWa0VZbdipcAzS7UXiz7ST/IypH4daWeCBcnCO2j/W4Zkh8SCVG5Ilj31r0qT2houB6Z3uJGLYFhTbygmyxzVQ2CA3ixnYTAeOplusQASs6gSSVENuOmHyX5HMIFpEhtpnKiohGLo75QjNYW/dOe5Afe66XPSWfQ8yo4HnQYF22nYqe18k4TSSAz+KaIZrDvVwkHBu+j3uNaGe1yed4kOMe5aGC/UfEKLs45uwbEW+kt+hjn8M2cOyIfhEZaqmsyxOiIiWU4zxkcX0Tgbz22mtj2cPrlAXcE6012cs3UV7aCfpKUGHyBE+lztMooUIuyOZQKdKGS2VLxUgzABczT27cfNwEmDhPJggEUZAinyYosHh64Sc3H1EVvhchaK3ZgcqHJw/2kUKD7aPZiydZKgNC0kRgKNiLnkQM6eOJhagR209Il8KipX4TPDmzf4TF2QcqU6SF40/0hkIRceSplMgZhUuRUS8KLio+nnQpzLkmkBIK6LbkhWsoLxCBa4XKHwHiOCBl7BOvdQRUdnuSlzy6x7XNviE8SDvSxf8iBdwPVAZsO+exI6CiQ/aqkZd8+2i6IFpBBIkHlDz3ERJ/xBFHdFhfL6CZc0/ywvXBQtnEPXLGGWfEY8zC8c/76LD9VKBcgx0B20K/kWrkhWsGWUcGuD+5L3kYQYbZdqKl9KXiQYBrqWjYHso2BIrrh0hQS1BGss2UjZSnXD886PKgSvnCQyrXINcR5RgRGNkzyks7QeiPCocnLiohnmgo3HhSaA4FPRUlT9ncgEQnuLh5MuIpnGYlBIA5bLiYudCLlBcqTsL2VKRUftxMfC/S1Jq8UOiwf3RURGIoxCkYKUT4nYKbJ20Km6JD0HwH20s0gu3n+PIahVlz2D6OZd4UxJM/4sn6bC/SRiGE5PA7kaQi5YXoApUHkssxRUaoUBDh1uSF1xEBBDg/Pxx7fme/eJrlffappehTEVQjL8gWUS+uDfaBJ3z2kydQKt+8QkJauB+IJnUE1coL20zTHg8ZRE7ZXiC6xbHnfa5B9oVoSEvNlkVQjbxwzbOwjfyk0swjAjTfIfq8zj3DOWH7O4Jq5YXtZl2iRGwfEslrHHvOH79TDhFN5b5trcN+e8J35/3OKKtbi/YgNzwI8tBE+cN1xnGnrOcepnzk+qEsYF3Op+wZ5aWdoCmIwoCICxUoMkPl31L7JULD+xg2FzNPoLmd0/zEzcnNh8RQoXIxs15R8ESWfy+FM08GfC/b1/yGpJCggmHfKMAJgVLoAQUeNyaVJ09DVAjsU9EpvTl+fA9hcCIqSBV/tzSBIRUjhRtyQgFIYchTNE1NHGdEgkoHsaQg4biwXlEQaeHcI740QfDUSMFGBIhj3RJUkAgX/5NDMwb7xmcQbSGMzfmspcgLx5friooSySJixjayH1Sm9BWhguKpH/lqST6LoBp54RrgaR6ZZduIjvIa9wLngnuViBIV0WGHHRabjYvu9JpTjbxwzROt46GI/WCEDBUv542yiGgL7/HQxTXfUaMcq5UXzhH3N8c6l1oeErmGqPQ59jwAEPXKm7+LhPPOAxODLbhXeXho7X7lmFJesl1sMyLD3ywcex6gECHqEMoC1pM9o7y0E1g1lSZPZVSmVB48QVMZEcloCpUjBTTtzozYoeChwqKwpjc6IX9uDAp0Po+n5yIrUApZbhiGfxLG50mYpgy2BRlrWhDkT2cMaWWiNCp+CkbCzcgLhQlNMTxhE5qmQqJQLBJ67fN9iAfbwnZRGHPskYOm5J2lObYU0jw1UXhQyVMIMlScY88+UFFRqOZRmiJANqgoGKnD8SP6xjnPjz0i3BwqHAq5ps0qiCZPcSw0zfB5eSStI2gqL4gr10PzzuoIIdvN/uX7zH1Ahc/5Yrgyna9pwuQ6oumxI2gqLxwvZJ5rnAoph2gRlRRpALg/c8FEJIlwEb0gmorQ8z7iXOQDR1NyeeE6Rcp5YKLpsCmIC9c89ysCQAdTrjG2n/1g/7mG6D/COpRnHUFTeaGc4Hu5HpofO84F202Zmj+U8FrTY49IUKbysNRaxLg94HqhiQcBpBykrMjLG8o7moeawvZw3VOm8pDEdU+ZwzXGMaf/HeeALgPsY9EPez8UlJd2Io+gMGyYSpQCjIuZm5InhqZw8fOUQGFNBUkFinVj5YgNoU8KeH5SwbZl9e0BYkRhRydbvpd94OmSip+bLA+PA08IiA7rst2EPik82E8KfSp++sDQnEQ0oOn/FgVCRSXI8br88stjB2KOOce/ebMdlRAVJ9vI8efJh3Azx5eoE4V33rGRKEHeN6YoeIKj3ZxjybZzXKkYEV6aVVp6emf7qWipeHKo6HmSZrvZBwrTjnryByIRHEug8OV6aN5kxdMxsk6Hbq57rjPOD9c9FRbnjeZLrh0kpkhpbArXPw8ebANNhlQq9Flhe3OIJhIhonLkHHHdU9FwnthPKlHOIddO8/8tGiSVKCHHi8qfCrS5tFOucE2w/Rx3hIfoLtcf28/rlFt0fEWi82hq0fA9iAfbgMjT747ICtdEU1iPfcyjq8B5497l/zn2XFOUTU2lswgQI44x9xnXMtcC550HP45d82g7dQPlO9cNkV5khQcl9pE+O2w7r1Me5dF42TPKSzvCDUZFxA1EwdCW/SMwVDgUdBT2+c1KAcTTHxECboKOenLOv5fCoSO/t72gwEKeeJrkuHJ8vytICueQyoCKrKMqfwphnjrzCr8jK76Ohusc6UJikMX8POX3A8LJeeyoylMygUbquXeIYhINkfYFISG6y0MH0bFcUDj2SBt1BuLJw6FUh/LSjlD5cTFS8FIhtfXEznusw7r8T9N1EQkubgr0jnr6hLK+tz34Lse+Lfg/jgHi6bFvf/LzhGw2PU/8bO1+kOLhmuPYc/157Nuf/LpvXj7xMz/2XvffDeVFRERE6grlRUREROoK5UVERETqCuVFpGBo46YPDf0J2ou8rbzWaKnN/ru047Mux6ve+v2wvfRZaM9zLCKto7yIFAx5Txh+y0iO9oIRIYxQosKsFRCP5p0O89eo3KuRGEYjMeqI0S8dQS5LTTtRtkS+Xmv7weg8RlG15zkWkdZRXkQSobIljwP5Gkj2RQZN8n8w5JmKmwRu5Mshp0NTSKhHLhcqQyIzJJ0jvwk5OPg9ryT5mS85TCnBek0/k4q1aeVKJlWyeOa5KJouJDUjpwp5Tb6PALG9DPkk1wm5gUhsSL4NMhuTKI/PZ+F1cljkeTwYhk4COpK58R7/S1I68oyccsopMcEg20vSrhz2h+1EaFiYc4ph5a3lEGJ9jkNb5McKCSRHDbmKBgwYEI8N+YKYLJCkYflr/GRhXYbQkyitaZJA8jZxLlvL0ov4kHWXVAQkHyQfCPvIMeE8krtnT9ssIl+jvIgkQv4GEsSRmJAMrFTIZDQl4RQVE5Uy2YapIJEY0uNTaVKBU7EjD4gOv5MdlwynVJR5ZUaFTeVI0j8SYZEMjmRifC4VLEnt8kn2yBuEVACVLImvfvSjH8XtarrsvffeoXPnzjEq9H2aOthmKl4qYRLjMckc+5bPjk7m0WOOOSYmPiPzKblbkCmS0uVZgJEdEncxozPix36zIH8kK8th+xBAxI7jQDIyfm+eRTaH84HgcLxY8mkeOE75a4gjGX8Zokp+DT6P48d7bO+//uu/xm3M188X1iXKQpIyMqvmn4G0sR+cj3xdjg35gpApIkp5Snj2m0RxSBE5lch8yz6zXr6ISNsoLyKJkAafypAKiCkWqKCoDIk8kDUWUfjVr34V04mTQp9Kkqd2IgwIDxU1wkHmTSSIipBpCnJ5IZkb2ZtJ6X7ccceFX//61+HII48M3bp1i4Jw6KGHxtl0+X++G1EAZIHMn126dInf3XT57W9/G6Mc3zehH1DJ0kzCNhNFIDpCdIHfkSsWjguyxXusj/CQWp0MsCR05H2yOfM/rVXayEEuRWSJJTJCkju2vSWI8hARyqMmHLff/e53oWvXrn+NoiCOCAjwvZxDRAO5IoJy4IEHxm1ClliIcLFOnniSfWCaCUSE4414Hn/88VFKyLyayyXnGtFj/zk3XBOnnnpqfA+xRPh4DckjMSXXxZ4SXIqI8iKSDJUa0xMQNUBGiBLQPEKzDPLAEzlRF57GmYiQpgUqsH/4h3+IURGiDlSc/CRyQsXM+7m8ULkiN3wun8P3UCkiNHwvFSiVH+JAhU4TBU/6RCYQC7aBuVWaLlTeLAgEUR/+57vCdpEyn8gGzTj060EU+FwqZ0SO7f35z3/+V6FCRIgIUZmzsE+IBpV4/hrvN800ytxazBdDcwuig3zRTEcfE9ZHiNhvKvxcgNgf+gTxkxTyecSqJViH6QFo8kPqfvGLX4R///d/j8KDJLJwDpkugu8DhAQBQzzYdvYBEUM8iJTxHnLDa2zXO++8EyNOHIt/+qd/it9DcxnXy29+85somCw//vGP43ksemJBkXpHeRFJBHnhaZ2nbypsmjWowHmyHjVqVHwap4Jj3ieiLVSAzDRL5IMndP6mKYI5fRCb5vJCRU4TFK/R5ESEJ5cXmiaQFyISfBbRCeaxYX2+i+9gklAmg2u6IBe8zqR4+Tw33wUkgUqZSBCV/UEHHRQOOOCAGFk6/PDDwz//8z+Hf/u3fwuHHHJIFLR8rh3SoBMxQgxoWvrlL38Zfvazn8VIx7HHHhtFgc9k/4BjgASw77zH+n/zN38TI1n8P59F5f8v//IvsT9KnnadY4DQITUtyQufmx9fRIRjz3FANpA9ZIvPI1qCnDGhHk1jTaM9RKw4d4gPERPkKo+6ISAIFs1CHCe2hyYlrgkEjz41CNHBBx8c57TK16cJjnXzbRORllFeRBLJm43yvihUYPxOM87s2bNjZYXYMKssTQv0d+Epnuaeww47LEZCqARpzqASbC4vpNKnbwX9aJAcohVUpogAEkTFTF8M/iYCguwQqSGKQ6VMRIGmDMSK32l2IcrD3wgQEQy+g4XoCZJA5KitOW5okmI72Qc+mwqYZhmEiUkKiSjwHewnfWzymXLZXuSJiprOq+w7xwUBo8mGfUP2ctFAkhAJmtZYn8gVUoQM0mk5b+ZBXmguyiNIyBLbRsQGeaF/StNmIz4/7+yMvORNUUgEnYf5m/PGtiGIHFsiJTTh5fA720+zEtEftg9xJRpFRIvJHDmGubzwGRwbFkSJBflCaoig8d0ch46aU0uknlFeRBJBXqiIaBZiBA2VF80I9HfhyZsK6qijjgpHHHFErFCpnKgcaUKg/woV66uvvhoFAPloLi9UrjQBMSIFMUKQiALwXfwPwkBlzEy1NFnkTSd0XGU9voOnfCIi/E60hagFEQ5GzSAtQNSCUVI8/dOnI58stCUQJCITrEvlTlSJ5hyatIg2se/IC7KBDFB5A/tA9AG5InKB3BHZoOIGIkA0NfEZzaFzMRElpIJjTJQKsUHs9t133782TQHHk4gOryEvnA+Oad6ZFolCMKAleaEjMfLZmrwgkcgKx55zw7li34ho0VzYdCQUx5Ht4dwhjESniMzx2ew7HbyJ9nAMkbof8sScIu2F8iKSSB55ocKlEqJCom9GLi958wwCQ9MK0Q0iADR3UMETbaEypU8EQtBcXoCneCIp9LGgiQb5QGKoYOmfQYVOBCAXF6CfBd+DMLE+ssT3I1EsNClRsdMPBfg+IgW8RgXa9PtbgvfpXMzCfvN5VPJUyogSFTUREqI7RGpgT/KCoLQkL2wjM04TwaKCJ6LDKB2iUURg2K9cRgBZ2GeffWLEp6Vmo6Y0lxe2n866CBJNVs3lhf1GmBi9RBQFGUVWkCKOAfJDRAjBgVxeOHdEoRBIRI8mMLaZ7WI0GvuDbBGpEZG2UV5EEkFeqOB4mqbCZpgulSrNI/RRoaJFUKjcEAkqaypKohYMy6Xyox8LT940//AeT/BUYlTaVK6AmNAsQqSG5gr6WFDZ0hTF9+QSkkO0g74jRGfo/4FAUbnSlETzBlESmozyfiJ8NttCRIFmrPx7W4PtIZrAfiIPVMoIE5U0fVqIdhDVaSpBCBj7nQ/RzuWFfeZvKnkiSnQ0zuF1RjUhCnw228XCvtPcgszQJEQTUc73kRcElM9DUmbMmBH/5hixj5zTXF4QPPoYEUGhuYjOtQga+0ukiXPJPiBVrMtxZWE7ibJwPrgmkCQiTUTtODdExzgXTQVURFpGeRFJhOYZKj0qLp6k6dRJBUYnVCosKjHWoUmGSpGoBpU6skMlh0AQlaHJiPfo98FQaf5n5syZUY6agpQQUaFyZtQKssFTfvNKj+8iyoEwMZLlJz/5SVzoJEplT0SIiA+jcoCKlgjD3/7t38btzqMlrcH3kT+FDqqIFxETmpNoquL7qIyp9GnKyvuisI9ET4gkIQ38zbGiAqfPCiKGoDQdxkyUA7lgn5E7XmPhGCJLbCuRqrz5hu8i4tWWvORCwefk8kJ0is7H5HjJh1bTHIWYMSQ9lxea1BBRIjNEkBBQmpk4Duw/x41jQTSMfcubkIjAcD5Zl3NAsx19eRAkIlWcD45BcwkVkW+jvIgkgnzQaZQKjSdxoixUaDSlECUh0sFCpUzUAdEhwkEFx9M7TSm8TpMBFSoCkedt4QmdjqVUcjzZU/EjPDQx0bmTRGo8yfP5eaI4oiZsEx1TqXSJiDA656c//WlcaK7gNSpomrbIL5JPNUBFSxSEiAARjz3BtiFsCBVNJTSXESFBWtgvIj8cC4aCI2bsN/uZRxiIHiEVRKrYBj6DqAnCw/awL0SN+EyOQV6x879ERuhzQtMbx58ICJ9NVISmG5rXOOY0rxHJIrqBALFwrIiWsT18D0LBqCGEj21iO5BO5AqZZBvpSIy8ICfsL1KEOCIoSEneHwaBQpryJjOOD/9DNInzxk+OMUJF9AUBpC8P8sv+sP95PyQRaRnlRSQRKlqe9IkQ8ORN5UMFSIWNyFDJUqEiN/ykQiRSQpMJlTxP26yf95HIIzlUilSOVJR8JiLA/xOloHMugsKoGipI3qOfCOLD51CRMiKJSp3P4ifNMyxESXiNypsKlEqY7f4+5FEkpAt54DsRGo4Jf3MMqJjZ1pYqZJp6kJJ8TiAqfsQE+Ez2hf4nHN+m/886HD/62yAJRGBoZkO6iNpwPDjerS1ETfJIF99JcxZRnZb6mxAxQUDoIMz6OWwPskSn55aiVERl2G8EjOPLdyB0+fEmUsS5pMkP6WVdtivfFxFpHeVFpAbIK+zWoLIjKtLWelSyLFKbNBUz4PeWXhORPaO8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEgdEcL/A7Fjxw5bpmCxAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E9%A2%91%E6%95%B0%E5%9B%BE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApIAAAFYCAYAAADgExwpAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAE6cSURBVHhe7b0Hl1Vltq///wrnA5xxbv9Hn3u6b5/DUdvQ2mZRaRVBERBoRFHJ6ZBDk3NqMk2QLEmQnCTnnKPknHPOzNvP3Hvb6KWpWmXhYr/r94wxR1WtndbeVbvqqRne9/8zIYQQQggh8oBEUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHlCIimEEEIIIfKERFIIIYQQQuQJiaQQQgghhMgTEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIYQQQog8IZEUQgghhBB5QiIphBBCCCHyhERSCCGEEELkCYmkEEIIIYTIExJJIYQQQgiRJySSCWDq1KnWvXt369+/v0KhUCgUsUSPHj3s22+/Tf9lEqEgkUwA1atXt9dff91q1aqlUCgUCkUs8dZbb1n58uXTf5lEKEgkE8Bf/vIX++tf/5r+SgghhPjl+dvf/mb/8z//k/5KhIJEMgFIJIUQQsSNRDJMJJL5wI0bN2zevHnWrFkzjzZt2tjWrVtt1apV1rFjR2vYsKENHz7cDh8+7Nc/ePCgdevWzY/zxtq0aZMf536GDh3q99GlSxdbsGCBH4eZM2f6/bZs2dJ7TC5dupS+JGckkkIIIeJGIhkmEsl8YPv27TZixAjr1KmTDRo0yL788ksbM2aMDRgwwN80NBk3aNDAli5daocOHbIZM2bYF198Yb1797YWLVrYuHHj7Pjx47Zhwwa/focOHTx69uxpp0+ftp07d7qQNmnSxJuVGzVqZLt377abN2+mz+DhSCSFEELEjUQyTCSS+cC6dets0aJFtmfPHrt8+bLVq1fPGjdubM2bN7fBgwfb1atXXQzJJE6ZMsVlsFWrVnb27Fn7+uuv7auvvrK5c+dav379rGnTprZ582ZbuHChde7c2ZYtW+ZZSrKRCCiPgVBy/TNnzqTP4MdcvHjR5XPx4sUeNDcjuUIIIURcSCTDRCKZj9y9e9flsEKFCvbuu++6FK5Zs8Yzh9OmTXMhbNu2rWchEcFr1665KJLNpNTNGwzZJDu5Y8cOGzlypGcz69Sp40L6/fff28mTJz3byddI5YMgQ0ppvFChQh4FChSw1q1bpy8VQgghfnkkkmEikcxHyASSASxevLiVKFHCevXq5SXoW7dueYaRjCMlbkSSvkh6Iiln0z9J9rJKlSreF3nu3Dnbt2+fl7zbt29vlSpVsrFjx9qRI0c8Czl9+nRfFxJhfBA8Hj2Up06d8kBEu3btmr5UCCGE+OWRSIaJRDKfIOu4evVq748cNWqUD8XwpiGLyGVz5szxnkj6GylTUw5HJMlY0lfJgA3rbDG0Q1YTASUjyXVr1KjhIkl/JT2TEyZM8Izjtm3b0o/+cNQjKYQQIm4kkmEikcwHKGmvXbvWZY3M4oEDB1z8eNPQO4kwUr7u06ePl7DpkZw4caJduXLFvvvuOz/OMfoY6ZlEGNevX+/HkU8GbZDNjRs3elaS48SuXbvSZ/BwJJJCCCHiRiIZJhLJfICeRgZj3n//fe9ppDxNryMCyHEkk/LykCFDbPbs2Z5prF+/vq1YscKvQ9mZjCV9lGQsGcgZNmyYD9VwHNlkWAeZZBmgypUru4ieOHEifQYPRyIphBAibiSSYSKRzAcQx4oVK9rTTz9txYoV80AOWSeyaNGiLpFvvPGGT13Tu7hkyRJ78803vZRdpEgR73fkOEJaunRpL4+XKVPGqlat6scJSt9cxuNwW4Zx6IXMDRJJIYQQcSORDBOJZD5A6ZoBGTKE9DASyB8T1vRAjh492nsiL1y4YPfu3fOSNiLIMA1rSyKQlMdv375t+/fvd+Ekc8nnHOc2XIcy+aRJk3zI5vr16348N0gkhRBCxI1EMkwkko8QJBBpPHbsmK8lydeAADKAg3ginAhkBj5nMhsxvT/jeOfOHRdRprAR19xKJOSXSN66c9eaTtpi5Yeueeyi1dTcDR4JIYSIB4lkmEgkE0B+ieSN23ftzb8usn9rMO2xi/d6LkmfpRBCiMcRiWSYSCQTQBJE8uVO823u9hOPXRw6ezX96gkhRLKRSIaJRDIBJEEkH9cYsmx/+tUTQohkI5EME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZD5y7949u337tp09e9Zu3rzpceHCBTt9+rTHqVOn7Ny5c3b16lW/XuYYH7ne3bt3/X6uXLni90Fcvnz5h+M3btzw23P9ixcv+n3kBolkfCGRFEKIFBLJMJFI5iOI4/79++3zzz+35cuX28qVK13iihUr5lGwYEH78ssvbezYsbZ792575513rFChQn5ZkyZNXBzv3Lljw4YNs88++8w++eQT69u3r50/f97vf8GCBVapUiUrWrSotWvXzr7//ns/nhMSyfhCIimEECkkkmEikcwnkMhNmzZZ7dq17aWXXrJ58+a5GG7ZssWWLVvmUatWLWvdurV/PmvWLJdHpJKvuR6ZynXr1lmrVq1c/MaPH+/3t3XrVtu4caO/CRs1amTz58+3hg0b2pw5czwzmRMSyfhCIimEECkkkmEikcwnKDuTIezdu7dnHpG9DJSmT5w4YV26dLGRI0fajh07XOyqVKli7du3d5lcv36938egQYOsc+fOtnDhQs9ucvm0adP8OLcfM2aMX49MJbfbtWtX+lH+AY9F9rJ///4eZDA7dOiQvjTvSCSjh0RSCCFSSCTDRCKZT9y6dcszisePH7cSJUrYokWL0pekspXIYL9+/Wzp0qV24MAB69ixo2coq1evblWrVnVJPHnypGcPKW1T+ubrcePG2YABAzwT2b17dxdOHouM5uDBg72E/lMQ0FGjRvn9E6+88oqXwn8uEsnoIZEUQogUEskwkUjmM5SaS5Ys+SORvHTpktWoUcOmTp3qwzL0PK5YseKHoZzRo0db5cqV/RilbOTx6NGjdubMGZs+fbpnL2vWrGl9+vRxwWTIZvHixS6mlNBzQqXt+EIiKYQQKSSSYSKRzGd+KpJIH1JYtmxZL1dT5maghmlsPjLpTa9js2bNvCeyfv36XrI+ePCgT3RzjFJ3vXr1vJy9fft2v8/Zs2dbr169bO7cuf44D0MiGV9IJIUQIoVEMkwkkvnMT0WSrCKZyJYtW/pADdDX2Lx5c9u3b5+Xw4cPH+7T3GQkM32Nq1evdpns2rWrf002kjfhjBkzPItJzyRiuWrVKr/PhyGRjC8kkkIIkUIiGSYSyXzmpyJJKbpFixY+JHPkyBE/tmfPHhfJtm3buuA1btzY2rRp4z2R9EAinQzZ0ANZunRpzz4ilrwJ69ata1OmTLHy5ct7L+WhQ4f8Ph+GRDK+kEgKIUQKiWSYSCTzGTKMnTp1+iH7yOBLjx49bPPmzb7QOFDWXrNmjZexGbQh68iak5S5r1+//oMwMmDDZDfDOdwv/ZL0WiKmFSpUcFklO5kTEsn4QiIphBApJJJhIpF8DEEaEVF6KtnFhl5KYNkfpBKhpOyNdOYGiWR8IZEUQogUEskwkUg+hpCZZIkfxDGzPSJktmBEIDODOrlBIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJL5yJ07d+zs2bM2ZswY279/v928edO2b9/uEjdo0CAbMmSIrVixwq5fv263bt2yOXPm2PDhw+3bb7+1TZs2pe/FbM2aNTZ69GgbOXKkLVu2zK5du+bHd+/ebePGjbPBgwfb3Llz7eTJk348JySS8YVEUgghUkgkw0QimU/cvXvXjh8/bhMmTLA//elPtmDBAjt16pSLX8GCBf3N06hRI5s8ebKdO3fO9u7da3Xq1LEaNWpY/fr1rX///nb58mU7ceKES1+VKlWsXr161qJFCzt8+LCdPn3axo4daxUqVLC6detaw4YNbdWqVS6rOSGRjC8kkkIIkUIiGSYSyXyCLCPZw+LFi9tzzz1n8+bN82zk0KFDrWfPnrZv3z47f/683bhxw4WTTGStWrVs3bp19t1331nbtm09K0l2smnTpv7x+++/d9HkfmfMmGGdOnWybt26+WM1a9bMpZX7+ilkOy9duuQiSyCsXbt2TV+adySS0UMiKYQQKSSSYSKRzCcQxDNnztiWLVvsww8/tIULF3qQWXzppZfszTff9DcQmcqdO3dagwYNvHR95MgRv82wYcM8Gjdu7NnJzZs327Fjx1xER4wYYW3atHEZXLx4sYsiEslxRPSnILBdunSxQoUKeRQoUMBat26dvjTvSCSjh0RSCCFSSCTDRCKZT1Davn37tvdIlihRwhYtWuRCN378eM84zp8/30vVvXv39s+rVavmPZJcf8+ePfbNN99Y586drWrVqt4fefDgQS9nUwrv1auXZxXJbHKfPA73MXDgQH+cn3Lx4kWXVaSTKF++vGczfy4SyeghkRRCiBQSyTCRSOYzSFzJkiVd8OiFpL+RPkZEk7J0hw4dXBRr1qzpMsh1EEmOkXVEMJHKTF/kpEmTPLtYu3Zt69OnjwtiRiT79u3rJfScUI9kfCGRFEKIFBLJMJFI5jP3iyRZxQ0bNnjZG/nr3r27iyRDMy1btvTyNOVrythkF5E9hmvon9yxY4dfxoR2jx49vDTNm3DlypVe2qaHkuwmGceckEjGFxJJIYRIIZEME4lkPnO/SJJZ5E2zdetWXw6IwRmyjuvXr7dRo0ZZ+/btbe3atTZz5kw/Thmc25C5nD59um3cuNEnveml5DhvQsSSARpum+mlzAmJZHwhkRRCiBQSyTCRSOYz94vkrl27PJv4xz/+0V599VV/A1GSZl1Ilv8pUqSIVapUycqUKeN9jCz9w9qQ9EOWKlXK+yVffPFFz2pyvF+/fvbOO+9YkyZN/DiZTZYMygmJZHwhkRRCiBQSyTCRSOYzlLDJMjLBjTCSiUQemeAmM0lP5L179/wyjjOpTSmbEjW3zdyenkmyj1OmTLELFy74cRYkp6RNJpIM5YEDB7z3MickkvGFRFIIIVJIJMNEIhkTyCS9k4jmoUOHfti9BhjOYX1IhnCuXLnygywik4gok9usScnXuUEiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkmnOnj1rly5dSn/1Y27duuXbFOZmO8LHEYlkfCGRFEKIFBLJMJFI/h22K5wxY4ZNmzbNduzY4XtYI5YIJNsYslXh1KlT7erVq+lbZBcSyfhCIimEECkkkmEikfw7iOTnn39u7777rrVu3doGDhxo8+fPt3379tnWrVvtq6++slKlStmpU6fSt8guJJLxhURSCCFSSCTDJPEiiURCgwYNrFWrVrZ8+XKbPHmyde3a1cqUKWNvvfWW1axZ07Zv3+4ZymxEIhlfSCSFECKFRDJMEi2SO3futObNm1u7du2scOHC1rBhQ5syZYpLJBnKL774wkqXLm116tSx77//XiIpkYwcEkkhhEghkQyTRIvkoUOHvGzdp08fK1++vJUrV86zj9WqVbNBgwbZzJkz7dtvv7XevXtbz5497eLFi+lbZhcSyfhCIimEECkkkmGSaJFkSnvjxo0+aENZu2TJklakSBFr1KiRl7fXrVtny5Yts8GDB3vpmwGcbEQiGV9IJIUQIoVEMkwSLZJMY7dp08YqVapkNWrUsMqVK1uLFi1s4cKF9swzz9inn37q5W2ylFu2bLGbN2+mb5ldSCTjC4mkEEKkkEiGSeJ7JBs3bmwVK1a0999/37ORSBciWaJECe+drFq1qlWoUMGzl1pHUiIZNSSSQgiRQiIZJokWyWPHjtmoUaOsZcuW9vzzz9vbb79tzZo1s06dOtlzzz1nn3zyiYtmhw4dbMyYMXblypX0LbMLiWR8IZEUQogUEskwSbRIHj582IdtOnfu7OtEfvzxxz7FTU/kSy+95GXtkSNH+mLk9evXV4+kRDJySCSFECKFRDJMEi2SR48edVEcN26cDRkyxLp16+YSuWnTJhdHju3atct7Kbt37+7bJGYjEsn4QiIphBApJJJhkmiRBBYkv3btmp05c8ZOnjzpceTIEVu/fr2dP3/e+yKvX79u586dU4+kRDJySCSFECKFRDJMEi+SgEwiiZm4c+eOT2jzOWtHslUigzlakFwiGTUkkkIIkUIiGSaJF0kGaHr16uV9kiw+Thn7fpjg7tKli82ZM8czlw/j9u3bPsDDtDfLBV29etXWrFnj61IytMNjsC4lkkp/Zu3ata1WrVp+ef/+/V1akVfWtWRZIta25JwuX77s98+6lgwCsablsGHD7ODBg348JySS8YVEUgghUkgkwyTxIknJumzZsr5+5OjRo138MiCDPXr08Mt27Njx0IwkEpnppXzjjTds/vz5vq3i119/7SLKTjmsRzlgwADbv3+/LVq0yJcdYiKcXkzkEWGkJ5NjyB+PjWTu3r3bs6JDhw518UQ62c5x8eLFLqs5IZGMLySSQgiRQiIZJokXSSaxixcvbhMmTLAVK1bYvHnzXPTokRw4cKALGJKXE/RRcpt69erZyy+/7CKJiE6bNs17LhFNhBRJ5HEQyqZNm9rYsWNdXskukqlkmSGykWzPiEA2adLE5s6da998841nNDmnGzdueGaSIaEHZSXJbFKKRzQJtn/k+j8XiWT0kEgKIUQKiWSYJFYk6YNEyCgxf/TRR7ZgwQJbu3atixpZxdKlS7voLV++PH2Lh4MEsmg50oiYknHMQA8moklJGhnMlLsLFy5sb731lpUpU8bfYAhgZvkhRPDEiRMulnxNVpGp8tWrV3tmdPr06Z6hXLVqVfpR/sH27ds9C1qoUCGPAgUKWOvWrdOX5h2JZPSQSAohRAqJZJgkViRZ+ofsY+/eve3NN9+0WbNmeRaxbdu2/oP++uuvu/iRPcwNyCLBpDd7dt8vkkgmPZaUoymfnzp1yr777juXRcSTtSyrVatmGzZssDp16nj2keNMkpPRRGwpaXOulL7JbpJppMSNAP8URBOp5XEI7rNr167pS/OORDJ6SCSFECKFRDJMEiuS9EaSbaSMzOLjSOPkyZNt48aNXpJmKAbB69mzp5eZcwtZxftFkqzn3r17rUqVKj4gc+DAAT9GtpGPmeEaMpRTpkzx0jgieejQIZdASu5kF+vWrWt9+/b1Xk1EknJ3nz59XIZzQj2S8YVEUgghUkgkwySxIkmWkAlrprIRRqRsxIgRtnLlSi97AyVi5I0pbAZncrP8z/0iifCRdezYsaMLKwudc4xsI1J5/Phxl0nEsXr16p4RvX9RdMrunBeBTPImJAPJubOQOscR3pyQSMYXEkkhhEghkQyTxA/bII2UudkGkelpltthmR0ykwziLFmyxLOSXJ6bCen7RRJR5T6feeYZF1LK22QUkVUylIgrvY6U0yk/MziDKDKQg0ySCa1cubJNnDjRZs+e7W9CpJShHjKUTIJT6s4JiWR8IZEUQogUEskwSbRIkh2kfEx2kHUe6UdE9JA6luqhj5ElfbZu3epiyMBMTtCbWKlSJe+tJFtIpvGpp56y999/34oVK+YiSEmd0nSRIkXstdde8+vQo0mPJetaMuTDsA/LAzGMQzaU+x0+fLjfhvMrWLCgl8LJaOaERDK+kEgKIUQKiWSYJFokWZuRZXFq1KjhmUBkjfI1ckkGsGrVqv5DT9YQYUP0coLr0H9J+Znb8Dn9kKdPn/bgMbgMKeVrtmTkOhlJ5fZkMhHXSZMmeXk989hcj8nyUaNGedaUwZ7cnJNEMr6QSAohRAqJZJgkWiSROnoRKWNn9tUGPlLWZpkeZI7exV8Syu0XLlxwob1fYDkvyuuIJh8zvZw5IZGMLySSQgiRQiIZJokWScSMDCQf6W0k48dHJI3jBNnE3G5F+LgikYwvJJJCCJFCIhkmiR+2IdtHZpKeRZb/ocTNgA09jiz+zWAMwZJAlKSzEYlkfCGRFEKIFBLJMEm8SDJww0DNF1984TvSsJ4jwyxMS3/55Zf25z//2Y8z+EKpOTc9iY8bEsn4QiIphBApJJJhIpFMi2TLli3t66+/9t5EdpShP5LFw/mcYZsXX3zRJ7pzs5bk44ZEMr6QSAohRAqJZJgkWiQRSBYbZx9qluxhX+tt27ZZq1atfDkg9rG+du2ar9XI9eiVlEhKJKOERFIIIVJIJMMk0SLJQuRkIdmHmtJ28+bNfWmdfv36+UdEk75Ieijpkbx8+fIPk93ZhEQyvpBICiFEColkmCRaJOl3ZP1GlgBiEfBPPvnEPy5dutTXb2R7Q4KM5P79+70Mno1IJOMLiaQQQqSQSIZJ4kUysxbj0KFDfQFyStyUtSllt2/f3lq0aOExcOBAz0xmIxLJ+EIiKYQQKSSSYZJokSQbyeLeyGT9+vU9evTo4dsPjh8/3rdIbNKkiX366ae+HFButiN8HJFIxhcSSSGESCGRDJNEiyTDM/xgM1zzwQcfWM+ePV0e33vvPd/fmoltLmffbaa5s7E/EiSS8YVEUgghUkgkwyTRIokozpkzxwdrihQp8sPAzTPPPGO9e/e24cOHe6m7cOHCNm7cOLty5Ur6ltmFRDK+kEgKIUQKiWSYJFok76dLly5WpUoVX4ycoRsWJkfAqlWr5oLZsWNHz0pmIxLJ+EIiKYQQKSSSYSKRTMPgzYN2rWH5HzKR9Edm4642IJGMLySSQgiRQiIZJhLJHFi3bp2vNclONxq2kUhGDYmkEEKkkEiGSaJFcuPGjfbZZ59Zs2bNfOCGYKvEDh06+ALkV69e9aGbXr16+eT26dOn07fMLiSS8YVEUgghUkgkwyTRIrl48WJ7/vnnrX///r5O5KBBgzz7OHr0aJs3b54HQzYNGjSwp59+2nfCyUYkkvGFRFIIIVJIJMMk0SK5cuVKK1GihGcaKWEvWLDA99dmzUiykAgYGUomuZneZso7G5FIxhcSSSGESCGRDJPEi+RHH33kmcbu3btb2bJlrUyZMlauXDkrVKiQT2uzDNCyZcv8OpldcLINiWR8IZEUQogUEskwSbRIsqf2G2+8YTNnzvT1JKdPn+4xa9YsW79+vY0ZM8a3S6Rn8vLly1qQXCIZOSSSQgiRQiIZJokWya1bt1rt2rX9h/urr776Idh3e/v27XbgwAGXTXon2Trx4sWL6VtmFxLJ+EIiKYQQKSSSYZJokTx79qxviVi3bl375ptvXCARLkreJ06c8MsWLlzoQzlMdHP9bFxLUiIZX0gkhRAihUQyTBItksCgTdGiRX07RPok2dlmw4YNHux007VrV9u2bZvNnj3by9sPE0lK3yxezpqTDOZw3fPnz/sAD5lNlhLia7h165YvP7R8+XLbvHmznTx50o9zm927d/vAz9q1a+3w4cN2+/ZtP37s2DGXXHo29+7d68sT5QaJZHwhkRRCiBQSyTBJvEgicOytzfT222+/7Z/XrFnTatSoYX/605/8I1nJnED0EE3k7/333/cJ8OvXr7tAfvDBB36sadOmLo5I5JEjR6xChQq+xzePN2nSJBdRyuft2rVzuWXtSpYlQj4RVJYl4viHH35onTp1sp07dz5UbDNIJOMLiaQQQqSQSIZJokUSCTt16pRLHutFst92xYoVbf/+/bZv3z5fR7Jt27a+z3ZOsOsNmcLixYvbc88957dlYIcsJ2XxPXv2WJs2bbzfkoxj3759fSF0bsPalUjmuXPnbOTIkX69CRMm2JIlS3yKnOwjA0HII29EspQsR8SAEFs45oREMr6QSAohRAqJZJgkXiTJACJyiB7ZRCa2yRgiaPRETps2zcveOYFIHjp0yKZOnWrvvvuuZyS5baNGjTyjee3aNb+fwYMHe/aRbOTEiRO9F5PrIrGUs8lOIpu7du1y4WRqfNGiRZ6lRCRZ75JMJ5Pk3J7MZk5IJOMLiaQQQqSQSIZJ4kUSaSTDR7/hpUuXfrQNIqVmLtuxY0f6yD+HNSaRSTKclMmRP5YPYiqcNSjpc0QsGeghG0l5mowlgklPJbvrjB8/3m9LNvLChQsupj179vSvq1Wr5jLI/SO53A+lbvo3f0pGTrlPgnI44vlzkUhGD4mkEEKkkEiGSaJFElFE5BA9hBFx4yNfr1692jOEmUD2EMWcIMNZsmRJF0lEj+Edehx5LLKdZBvJPtI3iaAihQjlgAEDXA6LFSvma1kitpwL0knGlJI7UonschtK4FyfoaCfQml+1KhRVqtWLY9XXnnFM5o/F4lk9JBICiFEColkmCRaJBEy5BHhGzZsmGfvWEdy8uTJ9tlnn7kQ0j/J0A273Nyfrfxn3C+SZBIpTSOEZCQpRfNGYk1KdtFBIBFGJrE5NmLECN9Vh8dHPlnHknI2IokQsssOw0GcN+eKlDL5nRMqbccXEkkhhEghkQyTxIskkjd27FiXOCa0q1ev7hPSlJApEfODj8QhkbnZIvF+kSQQQQZlEEayi926dXOhZP9u1q4k+zljxgyXvcxwz5AhQ7xkzaLoDNVQEkciM9s1kkWl9xL5ZRAnJySS8YVEUgghUkgkwyTxpW0GVzKlbbKC9DTSO5kJBmTq16/vn+eG+0WS+ySbSN8j09uffPKJP8bBgwdt7ty5vrxPy5YtXVSRWLKNrDnZoEEDPw+mvRnc2bJli23atMkllMxonz59PFPK0A7SmxMSyfhCIimEECkkkmGSaJFE+ugxpDxMsOwOJe3M1wQZQiapcwt9lCwlRFmaz5FABl06d+7sMsm6kgz4II0IIRnLTJYys44kmUqWHGIx9H79+vmyQAgj098cp8cSIWWB89wIrkQyvpBICiFEColkmCRaJOmPpM+QoRWCJXnIAFIyJjLHiLyCNFImpw+SpXoopwMCSB8kmUaW+iEzmoGFzVlsHJGlJJ6RRa7DObOoOUsT0XeZGySS8YVEUgghUkgkwyTRIklJm+lmeiTJArLEDkvl8HkmOEafYjYjkYwvJJJCCJFCIhkmiRZJhmfI+GWCiW2W6/npsXr16qVvkZ1IJOMLiaQQQqSQSIZJokWS0jAlYpbhYd1IBl8YerkfprkZfslmJJLxhURSCCFSSCTDJNEiyTAMQzHsQENPZIsWLXxZHgZwWPCbZXiqVq3qSwJlMxLJ+EIiKYQQKSSSYZJokWTwJbOOI4uAMznNXtkszUN2krUaWZqHHWWyGYlkfCGRFEKIFBLJMEm0SCYFiWR8IZEUQogUEskwkUgmAIlkfCGRFEKIFBLJMJFIpmG/bcrZrVu39h1l+HzJkiW+1mO2I5GMLySSQgiRQiIZJhLJNE2bNvU1I/lBZ6eZwoULe7/kpUuX0tfIXiSS8YVEUgghUkgkw0QimaZx48Y+VMMuNOwq8+GHH/qWhGxbmO1IJOMLiaQQQqSQSIZJokUysyD5tWvXXCQHDBjgnx87dsxKlixp8+fP968zkZt9rR9HJJLxxeMoknfu3rNTl27YiYvXH7s4f/VW+iyFEKEhkQyTRIskS//QGzl+/HgrUaKErxc5YcIEGz58uL388svWvn17/5rLWRoI6cxGJJLxxeMokofPXbPXuyy0Z9vOfeyi7riN6bMUQoSGRDJMEi2Se/futc6dO1v37t2tUKFCVrZsWevdu7d16tTJnn76aatdu7b16tXLeyYpe1+8eDF9y+xCIhlfPI4iuf/MFfuvFt898Hzjji+GrUmfpRAiNCSSYZJokWR7xEWLFtnSpUvts88+c+Favny5fffdd/bmm29a//79bdmyZT69zXWuX7+evmV2IZGMLySS0UIiKUS4SCTDRMM2aZo1a+ZbIsK5c+esVKlSLpEhIJGMLySS0UIiKUS4SCTDRCKZBtmirM3U9u7du6148eI+tc1ATrYjkYwvJJLRQiIpRLhIJMNEIpmGQZs//OEPVrBgQXvjjTfsySeftMGDB9vx48fT18heJJLxhUQyWkgkhQgXiWSYSCTTbN682TOQ9EwSfH7gwIGs7Yu8H4lkfCGRjBYSSSHCRSIZJhLJNAjjzZs301+lYHvEy5cvp7/KXiSS8YVEMlpIJIUIF4lkmEgk/w4Lja9du9Z27dr1w9e3bt3y6W2muLM9KymRjC8kktFCIilEuEgkw0Qi+XfYBpGdbQYNGuRfI5H79++38uXLW6tWrbK+T1IiGV9IJKOFRFKIcJFIholEMk3Tpk19+Z/bt2/b4cOH7YsvvrBq1arZzJkzs35yWyIZX0gko4VEUohwkUiGiUQyDbLVsmVL3w6xQYMG1rVrV/vyyy9t1KhR6WtkLxLJ+EIiGS0kkkKEi0QyTBItkmx5uH79etuwYYOVLFnSt0msWbOmB/ttly5d2lq0aOHX2bhx4/8zjJMTx44dswULFnimkxgwYICNGDHC9/dm20VK6RxnSpxF0MmGrlixwuWVWLlyZfqezLZt2+b7fg8dOtR7N69cuZK+JGckkvGFRDJaSCSFCBeJZJgkWiQPHjzocofQsW7kv/7rv/pC5H369PFjRYsWtc8//9yvg/BFneDes2ePjRw50ho1auTx0UcfWbly5XzNyhdffNFq1arlx8eOHWtHjhzxXkx22EFkebP16NHDTp8+7dPjbNdYo0YNP07GdOfOnXbjxo30Iz0ciWR8IZGMFhJJIcJFIhkmiRZJeiFZdJzs43PPPWf//u//7llIpGvgwIEukpS3kUiEMEoW8Kcw0IOQsnvOt99+6zLIlDiZyGvXrrkszp8/38qUKWOLFy/2zGSvXr1sxowZvtd3vXr1XG4ZAurUqZNnJ48ePZq+9x/DsNClS5d8lx6iTp06Xqr/uUgko4dEMlpIJIUIF4lkmCRaJBmiQQ4Jfrg//fRTa9iwoX344Yc2efJkH7ghO8nlV69e9WWB8gISidC1a9fOBZKs4+9//3t76623XFSnTJnii58jjkjs999/b4cOHbJJkyZZ27ZtPTNJKZwSOMI5b948F8OtW7emH+HHbN++3bp06eKleqJAgQLWunXr9KV5RyIZPSSS0UIiKUS4SCTDRMM2aZjaRtaQMySyfv36VrVqVZe8nwslaHoeySiOGzfOJ8EnTpzo/ZP0YPK4ZB7bt2/vPZRIJCVteiEpc7ME0VdffeV9mkgtPZuc77p169KP8GPo/aT0TWaTYBkjspg/F4lk9JBIRguJpBDhIpEME4nk3yHTSB8hZW6ylJSbv/nmG6tdu7b/4NNL+XOgzEx/I1JKaZohHPotyVR+/fXX1rFjR++BRPYYxKHkjkgil5UqVfJsIuV1tnFEJBFIRHf16tXpR3g46pGMLySS0UIiKUS4SCTDJPEiiUTSo0j/IuLG10xP02eI4JElZKo7rzDpjTyWLVvWex0ZqkEIkUukld7LDh06eE8mGcu+ffva7t27XV6RWd50vPn69etny5Ytc8mdPXu2L6D+zzKSP0UiGV9IJKOFRFKIcJFIhkmiRRJppOyMtCF79B8ilWQEkUnKz8jlmTNn0reIDredNm2a90UikNOnT7cmTZp4yZkSNpJHeRvJpAeSwRguQxrpjSQogSO0SCf9kz179vRyOJ/nBolkfCGRjBYSSSHCRSIZJokWScrEO3bs8J5Iys4Mqaxatcp7ChFASsrDhg3zEnReYQkg7ofJcMSRjCT3+fLLL9trr73mywvx2Agt5eyPP/7Yy9lMj5PF5PzIXiKiTHRXqVLF/vjHP/rAzYULF9KP8nAkkvGFRDJaSCSFCBeJZJgkViQpKzNYQ69hiRIlvIy9dOlSH4R5//33XeDq1q3rGcGTJ0/61HVetkpEVskcIpDXr1/3UjefL1y40IOyOfcNlNOXL1/umUd6IufMmeMZUkSWc2XZIIZuKHlHOR+JZHwhkYwWEkkhwkUiGSaJFUnkjBI22UGyfExoUz5u3ry5Pfvss74UD+tIsgQQ1xkzZoxL4aOGkjqZS8rtZCIzII0ILf2TlOCjZEklkvGFRDJaSCSFCBeJZJgkurTN4ApZQXoO2WWGNST5IX/iiSesTZs29vbbb3uJmawkwzj3i102IZGMLySS0UIiKUS4SCTDJLEiyaDN2rVr7c9//rMvEk7WMdMjSW8i2T8EjEnqbEciGV9IJKOFRFKIcJFIhkmiM5L0K7K/NcvpsD3h3r17fXqbHkV2miFLyfqO2Y5EMr6QSEYLiaQQ4SKRDJNEiyTQa3j27FkXRgZttm3b5iVueiLnzp3rQpntSCTjC4lktJBIChEuEskwSbRIMtTCFDRl7Y8++sgqVKjg2xG++eabVrlyZe+N5DImqMlS/hLDNo8CiWR8IZGMFhJJIcJFIhkmiRZJeiJZ4gfReuGFF3x9xiJFitjTTz9thQoVsooVK3r/ZKNGjVwwmZbORiSS8YVEMlpIJIUIF4lkmCS+tJ0B2aKkTYm7XLlyvig5u9pQ9s52JJLxhUQyWkgkhQgXiWSYSCTTzJo1yxcDv3z5sg/g0C85fvx427JlS/oa2YtEMr6QSEYLiaQQ4SKRDBOJZBq2RLx48aJ/nhnAOXr06A/HshmJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSCUAiGV9IJKOFRFKIcJFIholE8hFy794927x5s33++edWv359a9SokY0dO9Y2btxow4YNs4YNG1qnTp1sxYoVfv2bN2/a5MmTrVWrVh5Tpkzx47B06VLr2rWrNWnSxAYNGmQXLlxIX5IzEsn4QiIZLSSSQoSLRDJMJJKPkEuXLtns2bOtaNGi1rt3bxsyZIhNnz7dZfGLL76wHj16WMuWLW3kyJG2f/9+27t3r9WuXdvatWtnHTp0sO7du/uxI0eOuAg2btzYjyGT69evt8uXL6cf6eFIJOMLiWS0kEgKES4SyTCRSD5CkMMRI0ZYhQoVXCDXrFljy5Ytc6Hk2MmTJ23WrFk2ePBg+/bbb23q1KlWqVIlz1AiigMGDLBvvvnGZs6c6fI4atQoO3z4sPXt29c/P3jwYPqRfszFixdt586dtnjxYo/y5ct75vPnIpGMHhLJaCGRFCJcJJJhIpF8hGzYsMEzji+//LIVKlTISpcubXXr1rUuXbq4TCJ8u3fv9oxkixYtvHSNJO7Zs8eOHTvm8tm0aVOXQDKaCCa3QUbbt29vmzZtSj/Sj9m+fbs/Bo9JFChQwFq3bp2+NO9IJKOHRDJaSCSFCBeJZJhIJB8hZA9XrVpl27Zts+PHj7vc1ahRw4WR7OOVK1e8bP31119brVq1vKQ9evRoP3b27Fkvi1etWtWaN2/u4rllyxa7evWqCyT9lmQ4H8StW7e8rH7q1CmPOnXq+GP+XCSS0UMiGS0kkkKEi0QyTCSSjxCk79y5c3bjxg0fvBk3bpy1bdvWeyMnTpzoInngwAGXxJo1a7pokp08dOiQCyAZSUrd3IbrIJD0RSKQ9erVs9WrV6cf6eGoRzK+kEhGC4mkEOEikQwTieQjhEwkPZD0Qt6+fdt7Hhs0aOBlaWTy/Pnz3gvZr18/n9Km75HM4Y4dO3zIBqlksnvo0KHWq1cvW7BggZ05c8anuZs1a+al89wgkYwvJJLRQiIpRLhIJMNEIvkIWbRokWcTWeqHMjVZRCave/bs6VPbLOmDRJKJZNhm7dq1Vr16dc9cMmTTpk0bH9bhOPeDTM6dO9fFECndt29f+pEejkQyvpBIRguJpBDhIpEME4nkI4TsISXs119/3YM3EFlFspAsCUQ5+7333vMMJVlL+hq//PJLq1ixopUqVco/p8+S9SUZuClXrpwf477ovaR0nhskkvGFRDJaSCSFCBeJZJhIJB8hd+/etWvXrv0w9EIpm37J69ev+9JAZCHnz5/vy/jcuXPHr89QDtnLGTNmeImb4/RXIqVMbSOm69atc4nkeG6QSMYXEsloIZEUIlwkkmEikYwBBJCeSbKQ7FDDlHUGZJKJbQLhzMDxzCR2FIkEiWR8IZGMFhJJIcJFIhkmEskEIJGMLySS0UIiKUS4SCTDRCKZACSS8YVEMlpIJIUIF4lkmEgkE4BEMr6QSEYLiaQQ4SKRDBOJZAKQSMYXEsloIZEUIlwkkmEikUwAEsn4QiIZLSSSQoSLRDJMJJIJQCIZX0gko4VEUohwkUiGiUQyAUgk4wuJZLSQSAoRLhLJMJFIJgCJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSj5C7d+/a2bNnbeXKlbZixQpbtWqVHTp0yE6fPm1z5861pUuX2rJly2zXrl129epVv/7evXv9esS+ffvS92R27NgxW79+vS1fvty2bdtmN2/eTF+SMxLJ+EIiGS0kkkKEi0QyTCSSj5ArV67YggUL7KOPPrKSJUv6x4EDB9rMmTPtt7/9rRUuXNiKFStm3bt3twMHDtilS5esU6dO9vHHH1upUqWsR48eduPGDbt165aNHDnSypcvbx9++KHVrVvXjhw54uKZGySS8YVEMlpIJIUIF4lkmEgkHyGbNm2yESNG2NSpU138evbsaQ0bNrS2bdtavXr1bPfu3Z6dRCDPnz/vWcgyZcr49WfNmuWCuWTJEtuwYYM1aNDAb09WsmXLln75qVOn0o/0cCSS8YVEMlpIJIUIF4lkmEgkHyEXLlzwUvaZM2fszp07LobVq1e32rVrW8GCBa1q1arWvn17l0VEc/DgwS6JW7ZscckcO3asZyU53qFDB5dHxHPSpEnWp08f27lzZ/qRfsz+/ftt1KhRVqtWLY9XXnnF2rVrl74070gko4dEMlpIJIUIF4lkmEgkfwEoQdPjSGawfv36NmTIEOvYsaP169fP6tSp42+uRYsW+TEuo8x98uRJF0fK2GQw+/fvb+vWrbPLly/bmjVrrEWLFp6dfBAnTpzwkjq3IYoWLeoi+nORSEYPiWS0kEgKES4SyTCRSD5i7t275/JHhrB58+Y2bNgwH6KhlI1gDho0yLOSfET2xowZ49lJspiIZKVKlTxLOXToUM9U0ndJqRshXb16dfpRHo5K2/GFRDJaSCSFCBeJZJhIJB8xTGPTK1m8eHGbMGGCHT161Ce5b9++7ZJJmbpr165ewu7du7dnJClNk8GcOHGil7+5/KuvvrK1a9faxYsXvRSOSJKZzA0SyfhCIhktHleRvHDtlp24eP2xi5OXbtjtu/fSZynE441EMkwkko8Q+iKRv9KlS3smkn7J6dOnW5s2bWzHjh12/fp1L1sjemQfmeZu0qSJZxy3bt1qAwYM8MunTZtmnTt3tilTptjx48f9vshikqHMDRLJ+EIiGS0eV5FsMH6TPdt27mMXr3ReYAf+/v0UIhuQSIaJRPIRwsAMAvjrX//ap7EZsiGTyMBNuXLlrHLlyh4s7cMQzcGDB/14s2bNfKq7SpUqvm4kWUx6ImvUqOFi+cEHH7hUamr78Q+JZLR4XEWy0oi1DzzfuOO3TWfZnlOX02cpxOONRDJMJJKPEMrTZBoZoqE0Tdma8jYZxr59+3pQ2kY4gTUj6aVkupuMI9Pa9FKS2ZwzZ4716tXL15nkMsrfuV2UXCIZX0gko4VEMlpIJEU2IZEME4nkYwaLj2/fvt1L2/RSZqCnkowlk9tMdCOXuUUiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFr9pOtNW7TtrJy5ef6zi0vXb6VdOiH8gkQwTiWQCkEjGFxLJaCGRjBb/q+E0e6r1bHu27dzHKjrO/D79ygnxDySSYSKRTAASyfhCIhktJJJhxF8mbkm/ckL8A4lkmEgks4jdu3fbuHHjbPDgwTZ37lw7efJk+pKHI5GMLySS0UIiGUZIJMWDkEiGiUQySzh//ryNHTvWKlSoYHXr1rWGDRvaqlWr7ObNm+lr/HMkkvGFRDJaSCTDiMdZJL8/fsnmbj/xWMXyPWfszt176TMMF4lkmEgks4Rly5ZZp06drFu3bnb9+nVr1qyZTZgwwY4fP56+xj+4deuWXbp0yU6dOuVRu3Zta9Wq1Q9f5zWOHDthr7WebP+r5ij7Va3RiYx/qzHy7x9z//x7z1j3wNcyzli/86AVaDjugef7sOD7nnr+D748P6Jc37kPPOe447O+cxL/cx/l+dcdseSBr+PjEPX+fm4POueHRdT3fdR49e+/Vw8ePf7A830cgurXg45HjS5duljNmjXTf6lEKEgks4QRI0ZY165dbfHixS6KSCTH1q1bl77GP9i+fbu/YQsVKuTx61//2n7729/+8HVe462337b//V9P2f/5/fP25AuvJi4KPPeS/dtvCth/PfviAy9/ULz8esEHvpZxxptvvW1P/fG1B57vw+J3T79gv/o/T9gTz7/ywMvzI/7w8usPPOe44z+fetZ+8+RzDzzn4OP5V+3//92Tkd73L7z6xgNfx8chOLcHnfM/i9T7/r8jve+jxtMvvmZv//3364PON+54/fXX7Q9/+IO99dZbD7w8Svz3f/+3ffLJJ+m/VCIUJJJZwoABA6xnz54uibdv37b58+fbwIEDbdGiRelr/IOLFy/azp07XTqJ2bNn25w5c374Oq8xb948/2VCZvRBl4ceo0ePtieeeMKGDRv2wMtDjx49etirr75qM2fOfODlIUfZsmW9peRBl4Ue/K5BcpL6vh8zZow9+eSTNnTo0AdeHnrwd+eVV16x6dOnP/DyKMHfkPXr16f/UolQkEhmCV999ZX16dPHBTEjkn379vU35i8F/ZjFixe3qVOnpo8ki127dtlzzz1nmzdvTh9JFgx4FS5c2C5cuJA+khzq1atnvXv3Tn+VLKiAlCxZMrHv+z179tjzzz9vmzZtSh9JFvytee+99+zcuXPpI0L8GIlklvDNN994o/LKlSv9F/u3337rf9j4L++XQiIpkZRIJg+JpERSIikehkQyS1ixYoWLJEv/0LTcvn1769+//y8qNYgk/S2UNpMIf1Bee+0127p1a/pIsliwYIGVKFHCWyeSBisf0F6SRBDJcuXK2YwZM9JHksW+ffvsjTfesC1bkrmkEe1TJBBYOUSIByGRzBLIAvXr18/eeecda9Kkib344ou+HNDly7/cPruU1IcPH27btm1LH0kWp0+f9j7BY8eOpY8kCzKygwYN8lUDkgbZuKVLl6a/ShZ37txJ9Pv+zJkz3ieY1Pc96xfTWnXt2rX0ESF+jEQyS+CXOW9oStpkIil1HzhwwO7evZu+xqPn3r17dvToUbty5Ur6SLIgI3vw4EG7ceNG+kiyuHr1qh05cuQX/Zl7XKAKkNSMDO97JOqX/Kf1cYKMrN73R/xvkBAPQiKZRZARpE+FyW3+qPG1EEIIIURcSCSFEOIhkJHiHzd6Q/XPmxBC/BiJpMgV/AHljyn9QvRrJq3MQ3kPoeD5J0kmeN4IFM+b4GcgSaVtvtf79+/3gQN2lzp06FAiS/s8Z34OklTeZncwdnShN5qgNzhp33ueM68Dv+/5XSDEg5BIilzB5CJ7pBYrVswaNGjgE7xJgl+oGzZs8Of//fffp4+GDX80+SPSunVrK1WqlJUpU8aXwaG9Igl/VJDIw4cP+8Qyz5t97tnejeefNKHgOfNz0KtXr/SRsKEfsGPHjr4QN+954rvvvkvcEjizZs36YUc1esSFeBASSZEjNNqzJePnn39uU6ZM8e0X2eWB/9KTAP+NM7FbtWpVe/bZZxOzjiRN9iz5wpJTkydPtpEjR1qNGjX8n4gkrCVJBm716tU+sbx8+XIbMmSINW7c2NasWZOojDxSxS5arCXYpk2b9NGw4R8IJrWRZzLRxPHjxxMlUwxz8o9Du3bt/Hd9EjPxIndIJEWOsKUV8vjXv/7Vf6EgkywHwR/UJMCyFxs3bvQt4l544YXErCeHLPG9JwNLSRupqly5sm+Vdvbs2fS1woXvO39MkQqmdjMiyetBm0MS4GeA1SKoQhQsWNCzdEmADFyjRo2sWrVq/o/UpEmTvLUjKeVdpJF1U6tUqeJrFrOGrqa2xT9DIilyhJ0NmjZt6pkolv5BIEeMGGETJ05MXyNsyEKQnWMhchYmTuKC5EgVpT3KvMhl0paAWrJkictU7dq1vU8wCdkZpIlqBBshsH4q+4137949fWnY8LPevHlzq1SpkrczfPbZZ74pRBJ+7mnp4B8oKlC0c7B+8ejRo317Xq0lKR6ERFLkyJw5c3xnD7YIo1eQ0i4iSckvSfBfeRJFEqEgC8fe7vxhpW8ySfD8v/76a6tYsaL/Q5WUgSPe62zJWqRIEc/Ct2rVKjEiiTTRF057A2so8r2nCsPvgNDh/U32nWzsqFGjbNWqVd7S0LlzZ39NhPgpEkmRIwsXLvQ/IpQ2+Y907dq1vsPJsGHD0tdIBkkVSTJw7DPNsBVrmCaxxJXpF6XMx0e+Dh2Gy8hE8j6nlYFeuaSIJL/nqETwDwPtPN26dfPgNQkdvtfsnoY4837na6pSZGVp8RHip0gkRY7wywORYMCGbAx7bdOETa9kkkiaSJKJo8zFTkpkJPh+k6VKSp/YiRMnfCcpMvLsbMNHhi8oeyahxEcvLHssf/rpp1a3bl179dVXPTvJrlqhgzzzfeb7Tn/sJ5984j2DSchIMkjHpDYlbapQtDewHW/16tUT2dYjckYiKXKEP6g0m9Mfxy+Uhg0benaC/1aTRNJEkkEL+mE/+ugjF4oOHTp4qYt/LJKwniDDFcgU2RkycW3btvVhE8p7SRi24f3NoAllToKfA7JSDKKEzvjx4/3nnQw0JV1+91GZScJqBfyzyJQ6w4UEQ5b8I8GqDUyuC/FTJJIiR8hKbdu2zSd26RHjP1P+Y+cXTpLglyhSQYYiCZB1IwtHSZvvPVOstDjMmzcvEevpUcInI4VI8Nz552nq1KmJycj+lHHjxvkyUEmA9zoSTZ8ga4jy+46fhSTAzze/2/mnkYGj+vXr+/uexfiTslqBiIZEUuQKZBJ5mDt3rktlkna4EEIIIcSDkUiKXEPjOf+p8l9pUrMyQgghhPgHEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIR45mTUpWVIoP3eF4b5C6tflueTm+XAdpspZNDuk5y+EyD4kkkKIRw57FLPNIvu1sz5jfoBEcl/sMhPCbjs8H8QQ2c4JnjPLsbDLVNKW4RJCPF5IJIUQ+QK7YPTs2dO+/PJLq1q1qs2ePdsOHz7s61Hu3bvX1+VjLUIWuM/ATkkNGjTwvZyRwQMHDtiYMWM82EGFpaYyZLJ1mQwcMsUiydOmTbP9+/f7MeB+MplKxIzLWA+wVq1avh7k/VGhQgXfM549lfMT9mfm+fK8eC5sMZeT8LGkFq8Zt7sfMrlII69H5jx37Njh+3/z/P/ZItksKj1r1ixbvny5P0duv3v3bl9QfODAgfmaGRZCJBeJpBAiXyDbyFaK7IDCDkCIDuLIbkjskPHuu++6zCGb7BiD1LDwM9ddtGiRZ+KQn4oVK/p2nFyXLQoBOURK2aaRy9gHuEuXLlaqVCn7/PPPrVmzZta3b19fOJp94FetWuV7BHOf7ERUoEAB+/3vf2+vvPLKj+LXv/61LzKfX1nSDIgeC7nzmowYMcKFjx2BkDe2nGOhd841I9cI9MmTJ/26f/nLX9L3koLnzv2xMDb3x/Niv2+27eO14nmz8wy3ZbF4YImuCRMm+F7Zffr0sZo1a/ruJJnH5b7uF/OMnAshRFQkkkKIfIFMF5LCLhjsz8yWcmwpyK44hQsXtv/4j/+wEiVKWOnSpX2HJDJk7JTy3HPPuQwhfIjihx9+6CXb8uXL+36/QFZu586dLqRsV8eez2+++aZ98MEHVqxYMZfUQoUK+VaOSBM70CCpZCR37dplb731lr3//vtWpkyZHwX7R7Nzzc/ZqefSpUu2fv16z/ytWLHCVq5c6VnIkiVLusQhvZw3e5aTRWWrTWSY14jzZhs+zpc97Fu2bGlffPGFCzWvJ7soIcNINFvV8XryGIjje++9ZzVq1HAp5DmzfSGvK1JI5hJB5TJeL4SbTPHf/vY3l30eY+nSpZ4B5fXhvIQQIi9IJIUQ+QLigyw1btzYS8mUdymhkmEjO4fQkIEbMGCAjR492nr37m0vv/yy/cu//It/JFPJcYQIsatdu7ZLWAayeRs2bHAJY7tCxAphQ5h4HI4hSVwHuUMiuZ/Nmzf7ObF3Mo95f5CNJHOKqCFsecnMIcBkBxFVRBZR5vMnn3zSRRXpLVq0qGcET58+/UM/JxlEWgB4XLKoPO9nn33Wfve737kgv/jii/560QrAc+e5IJq8xkSvXr38vMmmIoO8Lggrz4HsJveJbP7qV7+y1157zR+rUqVKft9kY5HY3/72t9atWze/HyGEyAsSSSFEvoBIImd16tTxbCJZRgSSLBlZN8RwzZo1/hFBolzLdf7zP//TJk6c6CVbsphky+idvF8kMyLFvr8I4XffffeDSJLZRCR5bDJ1iBsl3HXr1nlpl8zgxx9/bH/+859d+O4PspJk68jcLVmyJE+DK4gkgkZ2jxI1Yoe8InXIHeVozpfL7+9LzIgk4scwEplKni8ZXSSc147XBfkEbkumkTI5z5vXEvlGhMnsks2lRYD74zZdu3b1HlCknkwwIk8Wl2Pjx4/358vryceM3AohRFQkkkKIfAGRROTIClavXt1LtfQ5UjomO4bMIEpkxCj5Ug5Gcn7zm9+4PHJ9pKtKlSoPFEkkit5KSruUuRkgYZgESUOMuIzBGo7Tf5nJRvI1skgZOFMCpq+yYcOGLpNkTOktzGQLGV5BdJEsMnWU1R8GA0GIM/eJGDZv3txLyKNGjfLsK+V5nj9yez8ZkcyAhJKRJdvIgBKvIYNEZFeBDCu3QUgZvuE1YGCI15JWADKXPGdEks8RRO6LTC3iyWtEmwHnyXnxWiPaDAQJIURekUgKIfIFRJJsGSVXZIoMGVKIrCCYzzzzjPcFPvXUU97rh7y98847PghDtiyTWSM7iDTeL5LIESKFfDK8Q4aTnj8eh3IvZWOkChFDIun54zZMQtO7SCYOkSU7+fbbb9uf/vQnlz8Gfbg9EpcBcSMTSEYPIcspW4eIIaetW7f2+0JA27Zt69lVPucyXgPKz/eDFPL6cP9kQhE/BJYhGc6f2yHXPG8uJ4PL/fF8EGsElueErPO6ZOAyHovvBeJMqZ3sKK8P55HJDvPaks2lD1MIIfKKRFIIkS8gkpRymaZmihoZIwOGvJAVpA+SDOQTTzzh4kdvY9myZe2Pf/yjl6WRJq6HZCKA94tkBtaiJJuGHD399NOeyUSWyHIWLFjQRY5sZgZKxkxwI44M/DCQ8/zzz9sLL7zg0+X0DiJ9ZPgyIHb0GCKXSBxC+jCYxqZETvaTzxFEMoGUqimz0zeJsCF43BeiSuaUEj2XMZyDJPIaIOFIIedNOZ5sK+fD+XE5crt9+3bPPJKNZdAIIea15pyBx+GxyUQizfRaIt28/mQ4MxPfZEMZ6sksKSSEEHlBIimEyBcQSUq6ZM3ItO3bt8+FEbGk7MxHBAf5Y9kaMpAI1uuvv+4TxKtXr/ZeR0qwlHYRSaSRpWzIyGWEjo8M1FCqZnkgMnkMjCCR9CciUhkQMta35DKC7B2ChvjxNUM4ZDFZkicDj8e6l0gh5/EwkeQyRJWpcASPHkXK2NwnIoq0kjXlvpBjJJKeSsrdlNtfeuklfy3I2PK6IN2cM+V1JBGR5Llzv8gw90MvKWVphBvR5jUjy0gmEylEPDkvXhdkktcRsaWUz7lynJ5OpuU555wyrkII8TAkkkKIfIFSLsv/kPGi35CBEUrJZL7o62P45dSpU17SRgQRJjJtSBgSSiaP8it9icgNAoR8kunLCFUGbot4clumo5EkSsz3SyQcPXrUxY5sJNcl+0kpnawoGUxK3sgkgpWBc2/RooVPNVMiRiz/GWQsWWz8D3/4g2dYGWQhQ4rc8ZGljBBFBoMoyfMcee7chl5PXiPOkbI4MphZJxL5pexPlhb5Rkx5LcjIIoVINPLM60DwHJFDzpvXlHNmGpzeSe6b8+P5IOn0bpIp5bXge0V2Uwgh8opEUgiRLyCIiCSSRGaMiWJK3GT+yMqRDWQXG2QLuUEe6UFkKRrkiGwmU9yZcjK3IXtIhpN+P4SLDCQlYYSJ+yArh2BRnkZCkU8eA8nk+ogY09pk8yjzkgFEPOnTRCI5RombASGykJn9wOk/JEtKFvGncno/ZPTILvKYCO+kSZP8PHiOlKLJ/nHfLP9DFpQeUErQyCL3jVhTlmayfe7cuZ7FpNzMfdDXiDhyPeQaoczsUkP2kYxvBuSRtSjpseTckUPuFzkly4kwIpBMhHMMqUUqkV0uU3lbCJFXJJJCiHwhUw5GcCgJIyj0/yFGDN4gQATZM0SIEi+ShPwgXMgfmbgMmZ5LJo7J4iFH3CdlYMQSUUKaeFweA1FCSOkz5Diyhtwht1yf4P4olxOU1jlGlpDeQRYwj1rmReAoOyN4lK2RRLKnGaFDinkNOKfu3bv7ud6f4UTguBwJR6p53ZjGpuRPhjUzsQ0ILb2V3C/n+lPIpCKe3A9ZSl4TxJVlgpBjboNYZx6L1weh5LXVguRCiLwikRRCZA3I0j/bWxqQLeTsYeXo/ITHI4t5v4Aig/cLICDMnPsvCed2fzaVLC9f39/zef/nQgiRFySSQgghhBAiT0gkhRBCCCFEnpBICiGEEEKIPCGRFEIIIYQQeUIiKYQQQggh8oREUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHnA7P8CjgKyVQ7kIWEAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E5%9D%87%E5%8C%80%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E8%A1%A8%E7%A4%BA%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAACRCAYAAAC7bsHuAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAACIsSURBVHhe7d2Fsy3Ftcfx9zelQhWSQAgSFyJEiUGUKHF3IS7ElSRECHEXIhB3IO7u7j6vPp35UevN2+fcc849+95zuetb1TUzPT09/tur1+qe/T9T0zRNM2hBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJo18p///Gek5fxeYLNjse5f//rXvLR1bPfvf//78rrNSxXrklDLb4T1KbfdbbdDC2LTrJG8yKG+zLv5Iu8PGx1PPdbtULcx7/w3E65lvuVlXrZf1rUst7+0IDbNGln1cofN1h1IHEOE5g9/+MP0+9//fvr73/9++bqdHGO2yfbbqaeWXW6b4wzJ3y1aEJtmjdSXGVlOXl13sCB+v/zlL6fvfe970xe+8IXpwx/+8Ehf+9rXpr/97W9zqe0R0Vqea03JW0Utp65aPqku7xYtiE1zAPDSerGJD5H55z//eXn+wcT+ieF73vOe6aUvfen0qle9anrYwx423fjGN54e9KAHTT/60Y+27EuMOEnOz3Y5P1PnLy8CJ6VMFT3I/+tf/zqul3z1Zf2q8rtFC2LTHAC8vH/605+mr3zlK0Nk8lIfTByD9OUvf3k688wzp/e+973j2L773e8OYTzhhBOm1772tdNPf/rTeYvNSX1/+ctfRh0//vGPx3zO1bRSl7Nt8ojhxz72senzn//8WK7rTNd17VoQm2bNsHZ+9atfTS984QsvFx0v9MEWxKCZfKMb3Wh6yUteMn3/+98fVtnFF188Xe1qV5se97jHTV//+tfnklvjhz/84XTOOeeMJjdBRMQs570UN9OaXLM3velN0yte8YrxIyIv5WvabVoQm2aNeGlZWG984xunxz/+8dMnPvGJEbhY50u9VbL/n/zkJ9N55503ffzjH59+/etfj+bpJz/5yenqV7/69MQnPnH6xje+MW+xbwjgZz/72emss86avv3tb0//+Mc/xj7SBCZumuevf/3rp/PPP3963/veNyxUgZwcj4RPf/rT40fk+c9//riGqWuZdpMWxKZZI5rJF1100XSve91riOLPfvazec1/2e0XejvYd7XWYJ5P8a1vfet0/etff4jWVpvM0Ey27SMe8Yjp5z//+eX7IHif+cxnhsVHZB/84AdP9773vUd6ylOeMprHv/3tb0cdOZ4//vGP0zvf+c7hyyTYv/nNby5fZ1rTbtGC2DRrwovKunrRi1403fGOdxxNyVg5YTdf5p2wFBSW3Kc+9akhWqw8vsAEgLYCn9/znve8IaSx+tSp+Xyf+9xnevSjHz194AMfmL70pS9N73rXu0beVa961ekBD3jAsJ6JJ3JMmvAve9nLppNOOmn66le/OuoKKbubtCA2e46lSGzlwc82psvtUfNXWUXLad2n+Swvt11S65C89KwhEVwWT912s3pWsSyfZccUoVhV//KYcy6QLyWPALHinvSkJw1rL1HeyqprkGXddZ72tKdd7osEi/Mtb3nLdN3rXnc0kflT/TCwnr/1rW9NN7zhDaerXOUqY5/WVZzXF7/4xWGtvuY1rxnHFHLsu0kLYrPn2eihry9mLZMXZbndRvmrUCb1L1PWr5oPlvnjnvOc5wzr8MILLxw+tKyLAC232xe2WwqS+aSN1oeNypnnS3zDG94wve51rxsWHEFjIfJ5ItvWlHxo0mouO2ddi1Lmm9/85sg75phjpnvc4x7T5z73uZFvn0TxDne4w3TUUUeNdazTkO31j/Sj8tjHPna65JJLLl+3PM/doAWx2dPkpagkL8nLx8912WWXDWvCC1j9TZpu/FMZhWEqeeFZKsmzjXICA142gvaDH/xgvJAiw5aJmjLyBA3M58VcJsfzyEc+cvjJ1LMMCiDTraCsfUlhWZdkP87FMfPjpQ+fc5S3PBbzzu3tb3/79OpXv3r6yEc+Mso5v3e84x2jqV/rr/M179JLLx1NZaIYrHNvCO21rnWt0USOIMK++RtPPvnkIYx8hqjXlIXJh+iHhQUa6nXYLVoQmz1LXoi8PKHmefGJ4Jvf/Obx0px77rmjyefF8uJ7abzYnPaar8ppvr3tbW8b3UkIBgGw7KXV1eOjH/3oaJqxVvTHe+5znzvq5fsSibWeUOijJ1Bi/8RmebzK3Pe+9x3RZXn1Ja9pqyibOupyFQbi953vfGf64Ac/OI5NRJdvji9T1Na5Ez6BHs1TdRAc18uxau46Z0l09wUveMFo1oa676QsE0LNWv7CimNSx1Of+tTp3e9+9/8JLBFE+7ze9a43nXHGGeN41VXP07V1/3QWJ7isyrrv3aQFsdmT5IHPQ79cBsvwQx/60HDUa25p6l1wwQXDCrnZzW42Xug///nPo1uHJtstb3nL0bfuiCOOGF1KXvnKV44+eA996EOHY//4448ffq773//+w9dFYG9/+9uPpp5Oyve85z1H3U9/+tOnF7/4xcP6Uw/LRTeVNImDLiNeckJQcQ4RsvribwU+tQQ5sm2SZc1eVt7DH/7w0cx8whOeMN30pjcd/Qmf/OQnTw95yEOGr+6a17zmEHjb6Apz+umnDwvOeTonyTLRV2f2sQr5zl3fQz9Grnnyk+ynBkQgj3VuZIzjEVhhZcoPts091FeSePohW+Uz3Q1aEJs9SV6ksFwGa41Vc+c733k0pbxcXh6dir34hIB1yKJgZbBS9H8jfkZmsJJ+8YtfDOvwlFNOGdFM4qAZ7AW3jeY3wSUQd7vb3YalwqoUIFHWC2qd47DOMeaFtk4zkIWJ5fFvl1XXIHmSc3/mM585REmz1Hlo7vohuMENbjCOhxVHwI899thhDTsP5VjJrqEfGMm860MMXYtV+83UDxPfnh8AFuCy7BLrJfvVUd2x3eY2txkWLYtxiR8AVuypp546mtcZvbIOWhCbPUlemrBcJjrPeMYzhpCx6Ly48pTx8rD+TjzxxGHhpD8cn6HmZMRS/zfNx2c/+9mjiUj86stvql5N3mtf+9qjK4rmXiw0vkbNZevsi9VIlGO9POYxjxmC+PKXv3zUlbQ/OMdqQQXnRvxYhISMmBMqzdc0R50r64pougb6BRIg5/O73/3u/yXn4npUy65em8zbj65FrqFgTC2TaU2wT8fmh0RT2DXitwy1rKlrzepnTer4nfzc892iBbHZk9QXAvXBNyUAOjtrAnvZ+f/4xySWD/EiVKyi+BIlLxbf4F3ucpfp1re+9WhWepkJpRc79Sd5SUU3iYomYfxXgfje6U53Gt1G1CWQkm01xR0bqzR5y/NgobHIlNlX4j8z5Rowzz0QESEwAiPEkGjbD1GzfI1rXGN61KMeNcTb/jRL+RPjQ6zHUxPq8WLVevtRP+swwaxaBjXPsfJpssj9YLAsCXV+aELdxv0+7bTTxjXWMqjrpN2iBbHZkywf9LrMYiFMxOboo48ewsZH+KxnPWtYe+YJIVEkGprFXlzb5QXXeVj/N34pTUxCGaxPuaUgapbmWCQCoEmt47AmtWBG6jDCwjE6hqDe1G1qe4EIx7qdxA/Iwl0Oq8txqZt1y2pjvRIdPwzWVVK+pn1Ry7EgHQMrWjO9nttGsGQJuh8M1zQfgVAX4atkX/Jve9vbTg984AOHSyT72W1aEJs9SV6EkHlTwsbSYZkJeLBO5K0qv0S+F4/fkICxIo3IYOmtahp6WQUkCCKxrQEDLyXr6Oyzzx4BCE13zdDAmvESC3Ionzqz7WaisYrNRCD1awLnWhCq+93vftNxxx03rGbNaHVYX5vCymZ+uY/Mm9b5lGNl8kv6UeGjzbqw3M5+lSfmxDrHpJ58ISdla3LdNZldU9atvJznbtKCeJBxU/MwbkQePsl8feCw3YdiX+V3+yFbB46RBaapqp9fmn+rqPksDRFLIsqqYd1pUmqGamoqK+UaVwsxgpgyEBhIHfxbfGjZlhXHQjRKZRX1uLZL3db+PEOanAkKWS+CzgrmoxPwUY5bgOUoaLIcV71Vcv4SV4OIto7nflRyXFmf+exbOS4KXZLqPRMoYSkT7lw/WM965G90HvyyAjjZTtnM7wYtiAcRN7Km+ouXvMxnWpOHoT482yX1ZD7U/L0MfyELTNcYfqX4oBw7y82LI4rpxYPrS+BYfESKL1H3GhFOQRZ94IgJcg1iIeo4rJsNyzSwdogr31Y+nxVRkPjIdNVJlBlZJ+3vvQvmHTd/oe5Hgjuar/oWiqjL4zeEa+E8NePT4Xq75PidP2tNlF9AinW6PK+UdXzcCaLEmu+EkQjya+qy5BpxeWgOZ5tAEAm9aDRrfLufI9sOLYgHkXrTzedBygNRU1jm26au3y7ZdlnP/tR5oOAT44MiiKwUIsBf6EVnARE9L5hyXlj97vgXr3Od6wyLkKXkgwEsuyOPPHJYmoIzrDyR6Qgoq0Q3FYEYL6/ghRecBSbSzXJhbRKH+MBcP81y/RZFfoP8ZdoOy23Mu3esPX45TXfHJKIsmmzZcTs2I0ZcD8IjkJMfin1R91nnNXEFefxQuO7I+ppcK/sVUWZpc3Vo+op0s/Jd91vc4hbDN8riXG6vWW179839W+UL3S1aEPcAufF1frkcvHAGzvvVjIjV9dtBYMKDbPtqnWKndR5InD9REkDRsVhTjMXHMtLtxugSliKLgjh54UQ1ddVhIRERLzVRvfnNbz5eSo5+XXVYLyzOCCI/HEuI38tIFdYYwWV9sSBZm17cijrUp8Ox5uKqa7rd6+ycpYplwRnHdPe7331YqvyWrovO2ASHWLIMXReWK1FZBjC2guNNMgKG+Lq21XJGLed5tV9WuI7v/LamPthAIC3HJVGj1Hm+PaN8lDe5yU3GDxmBTZndpgXxIOOmEiMvjBeKj2rZ/QDKaZJ4uDzwrCAPdB6a7WIbnZZ1lWDx1H1at3zp9jKEzctumBnRM0KFRaFJ55oRJs1rI0/4qYgFn5oXjeCxCq2TLxFL623LimThaa4JBBBbwss/SHB0JlbPqnvmR0tTkEjZT5qUO7lfyH3Z6J57hgxPZBlqlhIsefxyjp14OX4/Evtzf23rXN7//vePUTuukfPPuS2PzXo/VCzTJOJXE8uPBR9hrXUZN+6HhbXthyfrs8/dpAXxIOPh4nfy8HqRPdBeHiKZh9ZNN8+P4kHnR9H8yQNj3U4eDPvxQouOphmiruz3UMG18kPiZdKZ2DRRVOfkh8N6FrGpRCisz7bW1fW2dx00nQkii4YlyYJRjqiwVOwr9dTrlntDgI2KEURQZ10nbffeZTvUbU0dAxH2w+q4co7OR15G8uzk/tb9mrounh2Cbx9Zp27LkGeZcDl3x5SU48lyji31BPeOK4R16fpzfezk+LdKC+JBxM1n6fHD8GOxUvh79Nr3q1gfDlE2TUBiKFjgwbe+pu2gvDr4y3Q70UxkfaaudT50u4VjzHnX6XK+LtfzyrplnuXkEUDXnP+KNRRBkbI96nIEQoqfUbM5llnKZrodUm+dr8uZLvNg3j4jWNsh2+aYWWqa4YIjQX5SqHmb7bduV7fJl3JEy1n9hDTlUOd3gxbEg4ibqdkhIMAXxSel+0Y63OZm+6UnmiwVzR/LeTB3+kBkW1YO60WHV81OIomdvKwHmpxDUs0L5uu1yksdki9l2XqWCWvEC6+ppnMzX5yXkuOfVaNstYaSsg/zrq9Itz6PLB0vdNZJ26Vut1EdyV+uS149/61Q68u58eX5Aa8/okl1m2A+511ZLiPbapYTXu4JrhAtmtSR6art94cWxIMIa4O/x2B7N5zvirVG9BLskPj69IXzYGjaIuv254GwreaM4/Cya5Kkc+3+1HugcaxekMyHnId19WWs8yFlkzTxRGK5MQiirjWavvyUiTQrt/QdZvu6D4EbI2N0hxHgqT9o2yX1I5ZoJcspV9cvy26VWpfEZ6up7EfadZJXz6cu15R1dX6jewFiS3Q9+7oN1VbRTq/fvmhBPEi4mYSOEPkaiYfLTdaEZkUEeZqzhFJTGvVByAOyXZbbqVsfMc2T5Uu+V1med10279qFVcsh86aZZyHqY8hCZEH7jqImoimBI2qrqPtJfa6nwILuKazw/NjV49kJts/xos6vIseT+e2gvP05F/0JtWZEtXMOOZa6D9TlZf5yW5gSeknXIe4GAbGsS1oXLYhrYHnDslxvqIdAJJN1KAqpnxg0E+rDZV6EzRAsEUJ5q0h+tst8pS4vy2ma+FiC5rv+aXlYK8mr226XVduqt+5v1fqwP/veDvbhXhA+VhDrhCVtShS2egzKOX7bsKx8qWXpH97rONYcL6HiztERftWHY7dKrssS+a6VZ1DUWRcn171StzW/3X1vRgvimqg3ys1L88bNFqUUWdbFw/hMTTJdQzwE1gdWCovRSArNBg76zR4A5flZWJ7VChER9BImL2Q9lEnXBtsvyyXV5d1iX3WvWrcss5fJsXoGEk3FoXYOSY7fs8qPmnXbJXUFz6GUfD88nteN+hwqu50fpq3SgrgGcgNrys3mkOcj1JdQRFkQxfAz/jtRZNHkvDCazn6J9YHTT4s4VlI3K4bgaVpo8mp+a2bblh9Mvrp1KmahEOS6PVhDvuzMT2aUR/JTppbFqrztkm1rPblOIetqmUOF5XnUF76mQ4V6rM5leT77Q60vy5mv+6gpRsZu0oK4BpY3s8IvpS+hIIrPpvtslBEQIsu6dRAsVoTtOO75rHT5IGjyK8oQMuNtjQQwKoHoKasbj6FS/FYCN5rCt7rVrUakmj+roh7JcTkWowLqOcC8vIp9+xXXP9KY1J0kza9YAcix1OXlsRwqLM/DC5xzqfmHEstj383zSH21XmS5Xru6fjdpQTxA1Bspseruete7jm/56cKQMplKmtXEyXhUVl915KcMK5Iv0tA143I1I1iSgiRXutKVRjNY1x7LhkgpJyhQ8aBJhnT5Ogthrb++pktRMq/JxMdjHC/x3W7SN8+oBcJY66/CsSTHkmT5UEruT87vUDx+yTnUY9/JeeT8k2q+61OvUZ7Fut1yfrdoQVwTuWG5WfXmsayIlt73+qdxHqdMphLLjyVplIRIpwdj+TBqKltn1EC6gug/Jzp35StfeQiqZSNg9HUUKdXZOKQe6OIgyONzVva1ETk+2xFplisrbyvJviXzOipL6qjHESznxciy8+dfIsYZXbKXkx8siRvEMZsm37kfCufhGHMemc9xm+70PHJNVqVcp5QzlV+Pw3O32XO6E1oQ10Be7lUJbqahega36xCtX1tdn3l9DnWF8Wkp3TWSn3LwsIheCooIqlinA7DheL4VyB/owdG0NSpFWYIcUhfR4dvkQ/QlkvqgKVNFKSnL+0OtT4rQmma+rhN8cm7Efa8nvQdMfQLM1I9f8pZl9nKq52G+prp+qynlc11qfUlZV8tnXbaV9IfkdtktWhDXSF7ikBebhUR8NGFZcvnkUS0DEWPRZYKYfzNbplDzBFIEavRvTDO6rk+qWOav9JDxPxLElDFdilOo81tlWc+q+ewvJF/QSTPbhxUEgfZy4hd2nPVY5UnmD4VzkOrxcqfknORbXpbf35RrlP0mr5aRHIOx4ksX0P7QgrhG8mLXecn4TFFjQRX+Q82BUIVAOYKpyeyz67X5mHKmmpz5Yo15zWeRaV+F1uxWjlXIMtVUNS8v+wma0359NdOriIYsJymj+wXLk1W61SRwlCTI5Aciddb91Pkss4Kd66GQXJuanKcp37Dpqm32YqrnoKURt0c9F2nVtjtJqU/dlu0r81lvOfuuvvX9pQVxTdSXGBEwiUWoE7RgCcsv1PLmNW91z9E1Z6OgCjHVZOAjJHasSp9TIrb1C84eHMELTU7NbMcTcYUyItWazLav62B9yLb2rUO3SLbm4L6SIJKpfWTZtwb9D8mq48k+q7V6KJJjd36H8nlUluexk/OyTbbL/Gb1bLZut2hBXDP1Juel1+zLf13kX9pCypr6ZfQdOR/P1K9QMKGiDDExisWfpfsKjj8cF8HlnxRd5vBWjmVG6FhkRl5UAcrUOF1fMxaRTt5mqJfFxkcZq2G7ybbqaP57PV1301XIT1qy0TY7RX1beQauaLQgron64GZe0lzVVMyfIxGqlMk0iUXIPyIaTaQ0F6qIKUNQfUJfJ29jS3Wdud3tbjf8jvwrgi1EU7SZBShCt8qnSJh8+Vk9fJDymgNPrnvuS1guI3l13WaCuhm1jszvpJ5DnRbENeFhysNZE+HxOagjjjhidJjebJic7TVvCR4HMstyWSeLj+Wnq4wvs+iYbeA9p7NO2IYHEkN+RR2o6z4yr07H4T8uWJu66WR9c2BYXu96j7DqfqTMvsptRq1jWY+0U4E9VGlBXBN5oJIIG+uQj4+ldvTRR48hdXx8lboNPJAizf6Mh58weYEfTyRZcMbnpViDrEJCyYdILEW06/cVK/L46FiFugARUr7I5sBS7/nyPmVZUCwBB60Fz44gR4ILmW432W65rR/uPBvL47ki04K4ZoiXpi+B0hlbUIO1p8uNpjN/XvDg5eHLvMQvqP+V7TR3qyBCmeSZSqkn1DKpN8lDTzj1P2RJLutv1s+q+5N598ePKfeKLx75LJYfR8kfPEny9ETQSV+yvK+knPpMU0eScfCH43PQgrgGIkiSoEY+82U8sf5UhqyJMut4XcsuSZ7gg/5eusPkv0+w0XaVff3CE1gWJd+hLj4+YNqCeGDJfaz3yX3LsyHoxF3Cx2uo56mnnjr8yub9U6AvJkn+ObDO7yupQ1n9VdVjWb48fVFZivE3Hy60IK6BPECmmp8CHyLFmqS6mQimiAALcCiTVKn5HkpWor6LgiuhlpGS50WKqNV1oZYhtrr06DpjCKGm/aptmvVRr3emEUNwi/inP/deNy1dnYxuMtrJ1HLyMr+VVMsv69K3NN2zDidaENeMJrGABcHhn/Ng60JTf323kviK8t/CeVjr+qUA1gfZciVliDXrVSDFKBX+zZRdbtMcGOr1l7hb8vxkGGbWV+vfdCfile2Wz0/yTQ8nWhDXSB4mD5Zghz6FvoytibrqQdvoIbQsif4SU5FjddSHOPNLVtUVdOlRn2i0+do8Wm7XHBiW190PIZ8eH2+N/rvfrHtfreafFlhzD1mThHKrqKc+R0l1+XCiBXFNeJA8aJs9XPt62FZtw7IkiIbkbTQEb5m30TLLw0cjat/ErG8OHLkfSwgbsdPLQHM21qF8YqhngHHdPvHGP000/eB6RrYiisv9Lp/X7QjrFYUWxEMMD63msod11Uu0HYhgRq0066GKThUc1HWo8zB0UwRY/1CWYu6TT74RP//C6AeNP9rHhY18MsxTP9T8PWhY1r0VdrLNoU4LYtMcIAiMRNiq9ZX8CFCEk7XH58y/G58xVwlfsi+bc8Hw+7II+ZWNUjr++ONHFJorhOVf66v7qNN6PLXM4UgLYtOsiVXiEgGSsrwsZx0B1M/Q/znrahWXhm5RrEOWoBFICYQJvlin64xhob6jya9o3VIQk2C6PJ66nG0PF1oQm2ZNRFyqoJhPqstLBEv8YZhUywis8Bsec8wxo3cAH2PgY/T5tuOOO2505NdVK9tm+7rMB81lIhHUHKtpLMYWxKZpdo0qLhGWiE5dTpLPGjSsU/9QTWHIlwRT9EXUKZulWMfCG9rnG5isR59XE3SB7YifCLQhf/yREtFVf5JAHb+ldcTVdocbLYhNs0YichGXCF+owTFTwmWIpyAJUUxPgqxXj8/A8SUuewcQMSOiWI/+X1tXL1gvEKNjt//4Pvnkk8c/ORJO85LPxxlO6hudvpRkVEx3zG6aZi0QrvQTrBCrJBA744t9AMS4d/mrAh6ZwnxGRPm6OkHjX2RN2u9ll102rEkfCOFb9GUkI6f8XYQO34aR+sK6dYSQGDsG+21BbJpmV2HJsdZ8nMPwyHTMr+ImER8RY3/rqjO2/89OfsrUlG2JnoCKYaGEzZh0vkXrCKyvHgnO+OqR0S4XXHDB+Fo5/6RlX0k666yzxqilSy+9dARjsu/s53ChBbFp1ojPavlyjEDIiSeeOJqyF1988RC5pfXFB+gLSD6sYGxx/UJ6FcAqVKb+e0fXHM1hokjUNLWhDtZi/jqCGBNCliC/IR+kT8cZVsqiTN05vuzncKEFsWnWiD/y94Ujo01OOOGE6dhjjx19C0V1UYXNf+2cc8454zNeRG4pRpaXeSLEOmfnz/91yI7fcVXSbNck1nnbvP/ZYT36O0/N7qUIHm6i2ILYNGtEoEPkVhOUVSZowZdHiCo+8cUq1F1G1xqCWYUsolTn4evrfIJEN8M5iSRfpWmwjTrt47TTThvbiTiLRItMGw7qWGvddf5woQWxadYE64p/T3CCUGmi+jsIfwDm7x6sD0RQ01XwozZdl6Jk2XbEzvhmlp7t/D1EgiCazPogxo+YJHotWOMPzvgcHdOFF144PgzMSqxfSs9+Mz1caEFsmjVRxYhYsdDOPvvsEQnWgZr/jmBGmIiSr2KnOY0qSKkrQRrBE/5BVp8mNiHlsySQhvEpo3yavcr5CMQZZ5wxfInQp1GfRVYmi7GWPxxpQWyaNUNc0nVGU9VfvZ5yyinTeeedNwIdhuaZF+0lhsouBcmypLzmtua3pq/vY7L6jF3WkdtU4Iaf0Fe2QeA0hzWLTz/99PHnZrEGDQ/0L41EMv7HCOLyGA4HWhCbZk2sEhSWnK/UCK74QAP/ou4w/hNbP0LbpOlbSV06WOtGI0BjzPJRRx01kj8tO/LII8e8KZ8iizFoUotAi0SLemtyq1PQRz/Ek046aUS4CS5yHIcbLYhNcwAhMueff/7wI+qGI0KcoMaqKG+QJ/n3RM1knarPPPPMEYRJkidpjotUV2G1Hb+ljwGzFuPb1Gw/99xzR7NZ1JmFuhTjw4kWxKZZM9XaMs+35xuHrDkdpI0WYR1qrlq/kShC9FhwpI5BFjyp8xLLUx1J+jiyLo1fdizJ10/RF3MuueSSMb/c92bHckWkBbFp1gxBidVlXuBD52jfLtRUNcaY/66WSQqZr+tqquvCMn+5HpbtN/uuZN1ymysyLYhNc4AhMMYXa94KjIj+asLKX6ZQ86pIJS9strxcB8sbieGy7OFAC2LTrInNREXA46KLLhpRYVFmRJzSpF2yrG+z+aQqdsnbjLrt4UgLYtMcBAiVAIaobvyLzcGnBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmYwTf8L0KzWV25D8RQAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAENASURBVHhe7X0HYJ3Fle57CWGzbLJJCNkXQggBNkBCx3SIIWA6BAK2McU2BveCbdwbuIFx771XybLlXiTL3ZZlSZZkWbZVbKv33m7TvVffO9+ZK8ouu8iKwBvvfNLc+5cpZ2bOOfPN/OX+H1hYWFhYWFhYWFw0LImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImyuIxRj/r6QAgcsbCwsLCwaC5cFiRKB0j58NX74ZU/6Kcfsgv50vOyJxtu+TZ/9Tzp09MSfLLPHQ645hi/dYvxJEsdhnmwvk6iueFhHEZpTrBsBm5KWT5uyb9PZPNTPvnXQo2ocorysjaM45Tg0TTc1wiXDCKgyGXaktI4pL3qtE9UfpHN7298C2qzfyUq2+Y/wu9nSdKPPq8EH7zucjhTQjGzd3eMmheKbRdq5LhEZFJtM2lfyaf+iwZnJhStXiRlRAuL7wZf2C4VLqDKqn48rrotDoc79D1U2nr6NH7zWCAyN2Xf+C76AdmmzanuiqWpz9AS4GJ0ptVzjMPkftAbqg1I8LEMn9ikxmtmaIGURD1aQBZTlNkWm9VIzQyWKX7BlOGSOrJ81lGCNAWbmHG0JxhH4qqARkj5MG3PVvuqdNzmUZWZO1+JG0gs4dvBZJq04VuSsj/q5ICX+/yQfZVP85QyJY7GZXESfIF0mokGi+8blwWJ8lPt/FQwGRxpFPotQ2HDvjoVDuH8Foch1uOl9gUUkiZMo2Ac5iNDsBwXxZV4Pp9E0niaizqber/E/g70lUZBuf2Sf70U4BdZjCM09aCBGaOh0fPLGBjlN+lMfP4ZxnCpUIc6kddDMdTqpS9IbEQmEl1Wop6OjHI2AlKl/wTTP9IuErhtguxLf7Hf/F4nvIVnEDriObTtPBD9VsWhUI4zL8rQQKDYrnWBtHJAv+keGymahcVFgzqo+kZNC+icCUY/jcP5MoiWamjQddVNjUdf1pAH0/KcpBEbqFc7oC7T7niePo0+knrPpMYG1OdJULtkXvrXvFBxNX/6X3IDSkVfFZBb/IWJ1czQ/KUdWDac0oJSJn2kj2MD60252G4mDtuJvEWHBraNxGfbkBpROo4NTE+J2V7M1qTV2uh5zbTRMPlr5izYa/LgGOPlcTaW5i+BkXSbqehfZVrK9uSfTOrrxceq3lh877gsSJRPZhdc2SC50YGRjkIUi0bB2QfkPAdtJVKi5ORFXn7oPg1HzJhxJT38QkY0PvdVr2XbBBItYzySvzio5gYJgI+rZawLCyZJMOapgXKSGBrjYx1FLqaTT8r7pYM0Ry8ZpF2ltYVEmYZT566zJmk/OholiG5GNPG/BZo+AG43DCZfJVEKqbISZDoin/StfOfs6oOubd7C631WILKScdmPdDyyIfHZZuKCVA90kNFv5vVlmRYWzQqqFv2S2ImxWwZDcsxJqt+XNk5VlBgBXf8yaDzagMaTSIHInIBpEP3XyZXmZfLncWUFko5F6dSQfpDZMTnFku/mBL2YWUmX8qUc+lqSBJbLdhCvJi5B5A3Eby4wR+PvWVchGSxDNukXOGZwR9tVyydx4TTbNA+lapBbWk7SsE0NAeMkV8cB8demjZmOeUu4iEqYaXmdpBGhvJKDtg8D+4M5UmTuixyaNyWibEKiRH6ztk8Z3Sq/xNB8Lb5fXCYkisZiiJQZWKlOQqLUOKh2omA0WBm4lVhR2bjvc8g+jUIMTWycxKpeSBRXUlRh1QBFYV2VKMytRI3Do8aiMwMSrmZWWpqrWUHjyg3lNXKyPLMKJXURI6Z8fk8VKqtEriohXYwmab4607yU5sTW/+JP5Fbnr9sinwSSxTqvS9u4MdD0DHSCbAc6G/luQMM2s2P/ekQP6uoc6mjqs7Zgeod2ePOvgzA31qkki39e6dPqsnzk5eQhMyMT2Vm5yM7ORGZeHvLKRTbvdzCaWFgQ1Cv6Dx3YuS//ar8SZFDkIdo6/Q9tW+3bRNPzxkeQBMgB0Xn6p7KSPGRl5SE3pwjlbi/cHIzp2wLkgD5P8+ZxTtC8zJvDOMti+bQtOc/lY3K5ZoQhKVJXOlktuh4eRxkqizOQm52B7AtlKBOZuTbdnGDzkEB5SVDoagImLS0o5+jJzSodyYjKpz6G0Uy7q68x0ovPkvZhevFd/jqPUhg/xwruS+QGCmPSsfRvB5tZaZCMXdIiKpcSYmYi5VFk7ROOSyRw7E9NKZAojKaX/SQjnWCbMxbfMy6PG8up3TRBJUpUPGoWHY0opSq+KBmP61ETSExIqlQTGYe7EoPEiwqtK0KitPXOXFQmrcfID0OwJzYX5RqZruc7AC2EctA4RAqSKtTJAY9IJaRKaiTnZNYhBNGdFoZN2zZi+NazqGUyjUpHRJOXbRof87wEUNesDSptKc7ezOXMfWpcnapjBVnXRoP9KKlJbAIws3I6flPLL/YlXxJm3vHB2PX1mdg7riPef/FVPDsrBm7OJCVe6dlQ7Fz1Efr274UeL/wV3d7rgs4d2+KtvkPQfV2SkLyLEtDCovEQlaVd+GUSp3agOku7FRsX3f3SbrnFyOaLZsOhmuse9E0KOVZ5JgjB03vjrba90av3FGxKKUaW+AyX5KW2pkYhQbZJvurEY9Ae6yQPl+SmK8actHkd6veafTiW7L8IkrXf50H+iTUImf4BOnfojLdbLcKu5EKUaIRmBJ2/2Dvro75Ahog62TB3xpI0yUG6cu0D+eBJ+ddVMvoT3aVM9GfyrX5L2l+Ck7loGjkkfsmjd55JvgHX1ygwa41sKBgnlx7Jm3TKCGaisDxzGVEm8QEfZ07Ih6RhdJ2gajqL7xuXBYnSe1qo/QFHweVQ0ToUR6/Eupnd0bnT62j7RCu0evIttHu/G3r074t+fXugd7c2eLZ1B/SaHopdpwtQK+nN9WUO2uKqqs/j3L5gTHrzUywMS0ZKaY2UJcoq5XH21uygUZSn4MT2afikb3u0+WAG1kSVILeSZKSBJHBmJKTKUYrkQ+uwYPIQ9FpyBtnlQhoCxsZZFekUW+X7B2U8h9Nb5mBCv374W/+pmBOTj5JqkYezKekbMzumc2usfKy7CUQDeWJogPYJvxkl4HA0vq8C8cveR++XHsHtbdcgxutBbe0p7FqxCYtmbUFE5Cas6fhveLJLT7zZuhXeebcNnp8XgwohUdYlWXwXoNryMpGuKHHQpq6pfTfouBkQdYWCK04kA3JYV0Oo9zwr8XQQl7yqYudizYox6Ln8CFJPZ6G4xgWnDOzVhecQH7YGY/p9glkzJ+LjMdMxdUU4InNrKIDkLVRK8qiTYFa96DdIMWhJzQiRkZfySdpYD347q3NRlHUUxzavwqhffIo9J/JQFIjeXOBqHkljvd8hIrBs+gQnKvLjcXTdWPRq9RYGfLIZ+04USnsxPtuArc++kb4QWX1sc6blkg+bW+vC2z+YL/2ytKHsexiZkzz2FSM1ApJCQ6AE6U/6b8nfVYLatHCEThqK6dOnYMK4CZg0cQEWRFxAicendE0n2NSNOtEhjlkXUa5F8+LyuJwnykcj1WVrKrNsUzur0iMRtX0Kxvd4BQ9c8S/48S0d8P7omVgUtBZBa1dj9YrZmDS2Bzq2fRft+83CrIg0VIuRcZCv99eiJHY9dkwciK4DwxCdV4lqHwkWZykcsKn+zQzaQG0BMuPWYfEnb6Hlrx/Bs6N2Y3dKqcwqjaOjE2X5dLa1eTGIDP4UXdoOwpqYXOTUCDERw+L9RiRTJsPvH35/AXISQrFkWCe88PBTeKDnNhzOqkSNOjQavFknovNoFNifGti3zJ+DjUlr2oN9Ie3DfUaRfc4NfTJfzD6yBivGtUW7v9yPx+7riPkpHhRUZSAhOgVR0eeQdW4Xlj/xI7wwfBY+W7ISO7ZtQNCJHDjpIC9R+1lc3lAiJIpKH1InKubl4Nmg37LNVQie05VwLp/opFDScECnfksUxtLVdAkVx2Zi7bqpGBqRx9FVjokvzI3FweWzMbjLSIydtwXbw7Zjy/IpmDxsBIaNWo6YHEC4loz5UhJ1nXnSluj7mtu3Sd7mlgTJm99inyRvPvETBfG7MOmHIxFxPBuFFKIZYYgmfbn4HTYMt311cJRlIXnfCkx640949NG3MGh+BBLKSJy4sEQ/YkistgnbnRTni7bnvomj+Utba920K0i8eEWEnfDt0PzY7ZKb3lZCYlYnvjN2A9YMfAd9xszG8g07sHPrOiydORp9P+yLsXtTkVbGFUPqhgQhbnxW3OhP87afReNweVzOEydgZjpc6KYiGefCizre4jgcnvch7vuXX+DXby3Huvg8GcxpXH54fLWoyw/FtBda4J7rnsLjfYKR7PbIrELYfU0yIheNwYQuvTEupgalLl34VodjZoSNM5SLgUouH35vLs4dmo3+N16FXz48HJN3nUV+nRiq1ElJnBo061iJwjNCAto9gndmHED4uTK4xRD1Wr0640sDdTAoRsquSRjb6mb84Lc9MTsqB1lukjxeZuUDx4131UzjqKlEaUkxiouKUPQfQmFhIYqLC1FUXguHi/c3eOBy5CMvbhfWfjYA4z4dgn4fvIEP7v0T3liWgaTiKjjEmbpchciLXoWhv/o5us2MQEQmXxMhAxCdrfbvpWtDi8sZRr/MPUmBS0ec9ChZ4gBOHeYKBwdXiaeDv1ld14FX1JKaKXvy6UNl1AysC5AoJVaoRkH4BIxr3xYPPT8Z+4tkQlknfqEgAtvHvo/X73gePTcVI7OcZVMWyVsy1YmXpm9mvTfCKhHRwZ6r/BI89WKjCTsw5YcjsOd4ppCoxnqERkIbiz7TFM/yeT+Y31sPT3k2Lqx/HU/ddgv+0n0qliRWSP1Jl0gomYY+nnmQNLGNuM/82EYSx1unRFD7h8dkm/1hiK/sNwKaFVe4NA8ZXyTUFR5GxOxeeOGWB9B503mcKZF+85Ug7chcfPq3G3BLxxXYejJXxjCuQEk6yUO8lmxTtmbuN4tG4bIgUQ1OQI1VFYkKLcrHz/TdCP3sFVz5i2vw6Kf7cTi9Wo+TyTvrq0V/o7D+jT/j6R/eivueHoOdpUCtOJaqpLWY9dEwvN1hMWLEuJw+t5A0DrBSBJX/OyIpUhOR3I2C1N0I7vxz/ObqZ9FrzkHEldOwpXCvR8kiV99ouK7iRCStaYPbX5mIGbuSUSACmvsgmNN3I+O3QUuVj5JTG7F28L34pytuwgcrEhBTwAHBXH7lOhHdU6MghCc3Ox3xcdGIiopEdHQ0IiOjJByT/SgcPx6lx6NO5SC3vAZul8xwk7YjqPvr6DFiJUJiziJh71xMff0W/KjdSuw6lYK8wgIUpiUgMXQ6XvnnuzB+bTxO5lWgqroMubVcLG+0dBYWFwlOcmSwrROfIkS+QnSxrKgc5eXlqKwuRkVVKaoqqlBa40JlXWCFXfwPb0TX1Q5RTOqmGTN9qI2dhnUhk9AvIkvicrX3HPZ/+hrefO55PDhsLyokFleyffVZOLFqOHrcfRt+1D0c0TnVIokQKa4QSb4+Hx/2aH6tVwKiBEboiPineq+QRPGxnvo85MTvxrQfjkZEdAYKxS83N7StJFvjbegTSXKkzq5yeM8sQq+H/4C7W/XGh+vOghf9dCwR/0n/riv+DGyjhvS6+iPtVZ6HUum3grIqVDjFm/GhJSlFrxaYor8VSpdFON5+4uU9uOLnyiIXYW6XF/Grm3phYUoN8jycbHpRnbIdB4fcjf93VSdM2JKINA9JnJQoYxGfc2a5WlmL7x2Xxz1RqmaivLQWYTh0CFzA5QyhOHoh5ne7BVddfS3eC8pEYrFZ2qWq1/udqC8Nx5QXH8Ld/7cFHnp2DvbX1sNR70Dquq4YOKg32s49IUyfzovLtMyfusry5Bh3mhHMTWUTQ/UUJuLCmjdx8/W/wuP9FmHNySoz2xCj5jxHSZzU0+/OQ3nqAnT/42sYO2UvjhfKYc2F9bxERsVmkrb3FR5H/LIuuPWHV+KaHquxMr5YJBKZ6bR1/TsQ/9sgeXnrnPC4HfB4XBI8XwS32w2Xi8ckyIDj8wkJil6PZf064fYPghFyKgtFbheqUsOxe/zr+NHP+mDK1L7o0q4b2j7fFZ980hP/8v/ew5SIs0g8sgp7tszHhBOV4qAa/woGC4uLAe2Tq8WuigykRi3AhEEfYmj/CRg3cT5mLpuLeUvmYem8xQjeegRx54t11dYQAOqkmRzR/GUsV19UeWwG1gRNxYD9+XJQvEP5Icx79xm0eKA1HpuVSHPUUO8vQ/K28Rj1zE248t652JBSjFLJTy9JaaTvxmPQW/K+HZ+PPon7dfCJnH5vKYriDwiJGobdQqLyVcrmA0kNX3dSX6e3ZMsf6ycSsBjxJ/DGYMW79+Dx617CS102I5Gr+HVcERJCKfGUmLChmZLkSDa5QuhyV8GbHIzpg3pg8JiFWHM4AyVCiPX1Bxx/WEYjQdLG2w7YMp76IpwJ6othf74Tv7lpPPYU16BSyqO+ODKP4sTUl3H1T+5A10VHcLyIwkhFWJ7Ia0he48u1aD5cFiTK3CMkChQI3HZJ8KES57Z8jNGtrse//ltrTIwuRKaDFsR48u+qRnXUWLR//BbceGdrdJh8GLn6FFwqwga8jI+6DMTIMDPwq5cJ5O91FKP47C6snDMbC6eMxaSZSzB19Q5EHpyDWfNn4PNPPsWS4D1CaETBPW44T63BrKF90fPjJVh4vMyoOkmG5EUH89U36NIgODPxufNRlbIC3W/+Le5oOQBDg5JQIfH1ZkaJx5sZmR6+cnHGOzH76TvQZ/RqBJ8xjoqEizXlJ50Co/I4w5cb/ApsNAIB+ib/DLItXzog8JPESAJdvEw6ZVs+3IXIiVqO4Xf9AL++pS9GByUiRx/VDTwVKf/8kN5CTeU5nNo+C/MnT8G86eMxZeZcTFgSiUwX9IkVQ2CZQBN9DVoWj+vlCBcKLiRhX+hGbDyWgbxqcVCS1ltTiNzEA5g+ZTW2rvoInTu8jSdavYlOXd5GyxYvYuDYzzHmcyl/7Q7ElDvhZptpfZkn+59lSNvqcVOcaQ7ds7hswP6kPtN6voSnIh1pxzdhzuSZmDtlNMbM3YDlG7YhYvsijJ06FZ+PmICgiJNILqP9GdtT3dDs5COg79yt91ciL3Ybds8bi4mb92F/ZCwSElJwNvk8Ui+k4Wz6BaTLd05+ASpqeI8mE9Kv0fZJBcSGJDT4vHIlUVMwZG+ulCO+JH01xv/tYdz0QBs8uuiklMiVL9pPGVJ3jsfoJ3+NK3/eB/Oic5AjBIP5MCu9sqT6bo59Ydfyp37EUYSy0xEInjEIvd5qjdff6ohuH8/GivBkpDv9cGtSSeOpQXVGEg4sHYMhAz5Cv34DMXDUVIxbsQ9pUp5D4qh/8hWi+EQ4ZlwxCmEkUUIseY+WSEtB5F+2pM5sOt47RtHMSg93vh1aLybWy4isE4/pCcmIE+MqJC1ujzcf+iPue/kjLE2pg9tbI8VwJdrIKF9aHtvF+GbJjmSpOhupp+IRcyAcu1YvxKyxYzBmYyTisstQ6zEys+WYusGH8BiffdQJOJ0klYRyyXkTPwPH5nVG11tvxW9uHo+9pdUygvE84MyKRMyMZ3H1T3+OVz/dgvDzvLeU9WI7mrpZXBpcJiQqYFw6kHNdikYnpuA9h6Mze6LTH27FNfdPwKaMCpSKkdIl+OqqUZNzDJsHPI2/PPEiXhm4ACEnC4R8yUyk5jAWtGmFPu+NwsI4GcWpoGpAUoa7CLnJR7By5jIsWbcBG9dPx4SBvfHmi++h04iPMXlib7R+qiVavf8xxhyVuZW7GhV7h+CDP9+D25/5EB9uviCZCdUQOfSGeDUgLgezDrQp1oMG7ICrMglB7e7CA396Ge0+3oTEauPcaTBKwDSuA27nCWzudCPaDpiKiQdK9PwXBi8fXyNRrIMaH1uBdszPxoFxdaZFsiICf5GPlkFSKORPj4mT0OBCRcYxRHx4K/79Vw+i/WebcajYXD5QYRjXW4K8M+HYsmAceg6dgLmLViM0dB2Wzh2NUcM/xIxTNSgUB90oKInyobamBvm5Bah2y/yT90BoW4jrclYjN/scMs+GY9u2DVi8aj1CNgQhZMlSbNm2DSG7j+FwYhZq1c3R9WmNpR5sMw5bDsme9W9oX3Nfgpw15VtcBlDFDIQAXHk4ezQcq+csxrKQjdgc/BkGduhsXikw6mNM+vQDPHP3fXh55AqsOlWquqGcRT6MPYuemwOaa21mBPZvmI7Js5Zjy6kClDpo/4wjA6zE0zf9iwaaFRz6CWUngbwkT+okcwroZUXUNKwTEjV0T4HkIZp7eiH6vnI/fnZ/Ozw6/4yUKPYmeUNIQ+qOCRjT8mpcceWbmLovExkyqTQ+hT6HWRqZ1abFZoy987JTLUqSjyF66XSZKM7GpNGfYGifd/Hem2/gjVf7o+fI9TiQVoayynykH9uKtZ+PwpgJk/DpjDmYs2ARFi9ejHlLVmPW6hNILqlWIlVfn4+iuJ2Y+sORQqKykM8JlpIoKZvi6qVJOSZVVdmURBn/3SgE2qdh4mnuQ6PNmrYVEVAdNwOj3miBOx56HW+tz0CN16xEsS/0FTlMT1nkj22jecq3h75OJHVUZONc7D7sWL0cyzdvxabgZdiwLQzhCdnIc7DdTHymY51IsdVnsELKrehXhPhqj6dg//iO6PDzW/HbmyYgXEhUuRxn+Y6sI4ic8wSu+emP8dTw9dh8Vsie5KM+isSZjSTxLL5/XBYkSm/CFA3StySRBNHGaDDl+7B2UBs8fPUduPbFyVh7MAbRpxJw8mQc4mMP4fDuxRjR5lV0HrIIKw+lo9wrZiEzkfrMjRj+3Mvo3GUyNp3ngE+jptHVw10YjZjdC9FnxB7El9SiyhGHrWM64aXr78VNnYOwf+tn6PP2S3i800h8tOeCTHhqUHliAab3745uQ2dh3tF0yc8tfo3Kb4yT8x6u4BgHxrJoaGKozlLETnkCrf70Rzz89mdYerqGpixxTRwaDU3P5crCoY//gGe7DUP/9WmBlRvJUaaWdMB0PIzLsmQ6iariXORmpuNCRhbSMzKQ0YiQmZmJrGJJ6+aTf3RudLoiiZRFUeh49P0qusRM4umSOOJkilJxbuVfcccNP0OLzpMxN7pcZ2P6L066OicC26d3xdstn8PDYw4jNrcGDr8b5w8swMpBj6Pj7jKkV7J1GgEKwjrKtzp+KcTchN/gyJgPBwbTfgzGwfICgwm6uifxeY4zczOwMD1dpkuIOZ0y9yW21LHhIoHF5QL2ZUMwcGftwY5VqzBhxhFk+dzwVh3A3Ndb4rE7XsEzQ5fhdNgIvP7nR9ByyBLMiy0S/ZDUEnjfj04uJC+990U0yIcqpGyYjOXz5mLW8RK9P5BTKVEoiSs6qPEFXI3WfUlLEiWxZPNrgSJSf6uipiIoaCoG7ymGlyQ/YRE6vdwCP2ghJGpOMlNSpSVujZCoiRj7JElUa0zeJT6giiRNdFnKo8xUeM2fZXLFhaklsafiLE6GrcPySUux53wtKmudqEgJw87J3fDOXXfjF//3cXwwPRQhW5Zi8bgeeOetzvh8dwrOVbqEcEhetTnIi9mC4R1GYEN8OrJcUl59AYrid2LSD4cJicpBvpRLMqn3gFEU9TOyRbloc1oPPiHNs98OE58+irde0ObNKxzM277pF6XAvJ1Y9P5LuOeGlvhDnw1Ir5JRhC5f2sH4TtmR8rX9tDWkveSYS+2f98ny3i45U1cLV+Zx7F06HtNmTMfMdTux/+gJRJ7MRk6ZnKszfkZ7V+sk0rEMvfLhFGnpX5Kxd2gHvPN/bsP1N07CrrIalEne2nxCoo7MfwK/+tcf4/GhMvE7Xakp1F/xgq/IQT9l8f3jsiBRfFcGZ3C8Y4DvphTdUsX3nZmH0R88hH/+5fW4udXb6NS5F3r07IOeXbqgZ9f+6DU6CCsPpyOtwgU3jUQU2+euRn3iHHR48j2803s1DhWTevBWb/kWpS9L3I7I0IlYHCuEwumBP38Plg9ui0dufwovLUrB+dit2LVhDdaHxSGhgIYn4IcEdYoUjgov34Y0iYVwxqWR+OC/1IWO1OuBqywLRya+gGfuuBq/bNkBb65KFnPzi8nQeGjZklRk9rgqELvgNjzzfk90XXICpTQmcYp0iPrSUM5/aMAkb5BZ9YFN2LxgHhbNXYLFcxdjwfwFmD9//n8bFixYiBVCClMLK8QRca2GbcI6SFkUXZ2wOMxATfQldx4nqgsScWL1q7j35p/hnx7pjo7L4lAUkN0nTj05pC/6P3sXbrirN+alOpBZXoPqivOIWbsAM97ujYWnvCh2ao7fCp1BS+mGHLG+bF8jnpFKCpVAlypNo7tsP5IjfirJIgnktYM6Ok/51iR0gKZmmpbESRy8n3GYj8VljYKjCxG2YyM2JNG/SL9nbMLIVx7Gn5/rjH5BCahM2oqgpeux+XgGUvkAiKgFCTgHaw6RZs2CesMVgxPY2G8SFn0cjJgqJxwOF1xOGWSdTgnVcLrKUSvbzlrxSS5JS9JOHaMq0j/JDikE1bJB9fh0Hi/nfcSn84REIW4xurx0H370wOt4ZF6c6jXLr6uvQPLOz4REXYMrr2iPSTvF91VzGkAfwRujaTeSITOmzvMHiSUlh35n7AqEbVyIcQdLtHx9VYn4KXfJSSQE9cOzV12Jf73lQdx27414+u230TUkVe8lbXjykMFZkIykWfdj1I4TOJgjEvmLURgbgck/HI6I6GzkszQpn5cFKYOXba2Eg/JQKGlYJRz8/nYwGX0ACSLXgHTVRo/TjqV3fC7Upu3AgvdexP1X3ojf/ntPBKc4UeIQOYTc8JcPGi5nGkdiCJSbs1/uUyZmLX1kfLr0Dfu+4gLO712Aeb3fxGs9lmDZgXgk5xejqtYh5KtWsnFKcpI6BknAOqpk57F/2Pt46we34tobJ2CnkKhyliGnXZmRiJ77LH5x9ZV4dNhqbDxdLklYmCSTfEjOWC+L7x+XyUqUGLRHjFKIB2cb1HEqdc6ugej78vW47u4n0SHoPFIuFCC7sAi5hXkoYiipRpmT18HJ5CW9GEa9xwG3zOTaPNkZrfuswf4ScQBicLosK8biFUdXU1OOMhcHaXFOJxdjwvvP4I8PtMH4Yx6UVlWitqoC1dUuOD2824eXuDjomhkWTZkGyCfoVE4ZzXmJiKSEAz9nniIRqnKP49DMV/Fy59Z48fYb0eL3T+HPXYNxWkzFKbHVlVImycPnrkHS4rvwfNee6LTsOHJpXHKO9kfDorGa2ZsEOedy1KCqogIVEioZKhkqvzVU1Xr05m1dIpf8jRSsm8mXP7Vj3lnCuvpQnnMUEasH4PFnOuGFllfjdze2xCu91uB4tYhH8ctPYH33V/HMtTfjukc6YejcVfhszBAMGdAHoz5biJCITFS6+evrbKhvB11IQ2D91THJl/ar7jec52DGejCGcalKntgncp4DoH6wXhKJx8xQwuFQBkYhizpLZp48afEPDHY2O/G/6kjRFkcFqmqqUMlfDvCK7RwZh3eeaIEn243CknjReGcNKirLUO0Q/Rf74Nv1qRr6RJrolOqZBK68oigMs3sNQNf2H2H08gVYsnwZVixdiaXLVmHZsuVYuXQxVi2WgXeFDJQ7Y3DqfBk9g0hH0sE3nPN+QhIc0VvmJ2fLoidjTcgkDN0vszbq7Jk1GPHKQ7i2xRt4ZG6CpKb+syYyadkxEaMf+zf85EfdMPtwNrKczEvyYZ5wiJzM10xAeC8hJwvU+cwNM7F72RxsyDR1kxNq5z6fAxUXDmHXgDvxh99djStv+SteG7sRUeL/6BFYd73/SPyrrzoX7oMD8fT8vVgWVyI2V4TChDBMvJKX89JRQB9MP0JioX6Fjca6G1n4o/EkkfxrDJjOrPxIfF2VlyOcPbFfPFWozziIeZ06o9tzrfD4A3fhF7+/B+235OFMGe2cfw3kkzJxkqXeDk7KIJNEfXknJ4tc/dPY0vfsbznmcVSiIj8DeUlHsGnK++jRZxj6LT6G0yIDfSN7Q6LrmKKeVNsyGVGTO6Drb2/Fb/7wOfaVVeuN5WwBV/YRxM5+Hlf/9Cd46uPt2HpWfBgZJ+tDn6R1tbgUuDzuiaKb4aMqVGYaPh0MyoW5v4F3H7wZt7fsiwWJdahxcXAXY+Z9Axw0aV/yrdfZae00eCFRvvj5eP2J9/B6r1U4UEAlpoHQhmggEkRvdVYof1lhg9H/1adxz5OjEVriRqXXrBKRtKjj4B+NkI5J0vD1BPSotGt9Qk2dIc3IOK46GaDL0w4gfOEIvPjWhxgXEoal49rj3Zb34U9P98fa7HohFiRGDFp5+Fw1iFtwO1744EN0WhqPjEBdaFTypXUzszFzUP2IHg9k0FhoxeVbA9tFDvFPMtSX9kktSBQ5u6o6H4FNs0fi/fYDMGJtFLZNa42XH7wDLV4bgrkJ1RoHmZswru2fcecdT+G5MaGIOpuGEzHHEXU0ErGnUpFexsuCKqmEb4fKQ6ej9eJOoF/1mIociPOlg6aDMnF0V9qFwxWdIx2bHJd4jKurWxqXjjLg7CVDvz56zgax+McENYL99019yHNGV0gu9PKJuxzn1ryKF1s8jVd7LsX+ctEB6ojogOoe7UL2mZT6ppfjeE5ICskVKvdg4aBpGD9iNfacPYPklGSkpqTIdwrO8js5GWlnk/X4haw8mZTVSrlmkKbe8hLTF/dPqS9quCdqMobuDaxE5YRhWpsncfsDrfHIvESRhVMAhmIk7xqH0X+5Dj++ZjSWJeQg1yv56YRBAu2CdZCgt0hIoG77UYWTyz5H6OwZ2JVHe+TKv8QRG+Ckta5W5Iyeii63y4T1p7/HPe98jFmnyiWd1FnSG5uSIPEQNQovz9+HlfElUocCFCTswOc/HoXdMdnIl7y+sE31y8ZP6b0/PCeHze0DcqIRkJhSKutEe5Z91o3d7ChGaeJWzHnvdXT+aArmLZuFecPa4ZFrbsQNffdi74VSmQwaWbS9te1ZONPTV1Me9jfjMLCeclz1QPqY+26ZeGZE4fCcgRjRpz+GfB6EkGPZKJd0JHI6sWU9madISX/or8/GySXd0e+eO/CbmydjT2k5KhhfYjizjuDEtFb45U9+iTaTI7Av06Rnu0iG2kaMZ/H947IgUbpQq0oo6k1l5yzBmYTQnk/g2ZsfxENtF+BQWT1c6nR4T4+YNBVZrZQzA0NgaCheby3qk5eh19PvolOPJYjIEQOiA6QhSXxXZQHyL5zEqfhzyKstwKFZbdH+qefxSPt1iPe5UCMylKXF40JqMtKrzexFF/NF4Y1voGOSWQStmqRPDYGOgm7SiZKU/dg8fyw+7DMYXaYdQFyeA5lRszH+vUdx0x0voE1oMXIqWV+xHak7jdftKseJGbfhhW790X31KZTQyQQcBgki20VJnZg/6qtRnCHOOu4E4k8kIOFEPOLi4r49xMcjIaMUpbV8KsS0hUIK0ReQMrAP6pyoPr8fW2YNx8CeQjAn7kS8zOyqk+Zj9Gv3474HW+PtJUmopCtKW4VhbzyMu1u+ie6h56UfxSFrvxinwpee8koe69kYUKKGQUAdbaBP2cZKeHhI4piVuS/jMapZWmccOiRxugHnyEuUzpoyFBcUo1KE4RPkX6QTWXVFyjqvf2CoRgTCV8HjHMLdqC1KR3ryKSSmpiKv5hzCBt+Fxx9+B+9+Fo5kEglfDYoTI5CSnYM80RHqBgc2Dn8kD7ryoPFEnzxnsOPT6Vg+YyNiqjixYTlMY3RSzYrJRf/NH/Ohb+OdhPJNfxHQZfIl2l31sVkIWjsNg/bkyDmx9epT2PDhy3im5V/xwMRjMhB7hcx5JJ9snAoaiaH33ox//ctKbD9XLIO6eCeZhNWUFSCrqBour3o6tQNd6RKZ+JDL2eDRWDtnHJacFv9I2xQBzIsmXXBVpOLC1sF47/E78cef/AQ3/uEpvDpiG9KEADqFODYQMnf5eZRtfBu9go9K2Xxli/jS+F2YcuUIhMfkoED9itifTETdFbnIL6kSm+PKdkAW2hptmW3UCDCemczSnqVObOeaXGQfW48Vn3RDu3cGYurWOJzJOYOkTaPR765rceVdH2PxkQsoqJOek3qqr/uqv1B/TY/OPjJ+ipNk+nCOJx5HNjIT9uPg1hCs3xSCjStnY+nacOyNzUJhJf2+5MXVJ+qHpuP4wHxZTjUyd43H+Fcfw69/PxwbMypQIg6Hdag5txuHx92Nq//tUfRdE4n4CnOc74qimpp2aWTDWDQrLgsS5ZJARs7FV6791PMJi7zt+PyZ+3HH71/Gk8N2I10U1aODqbnkJ+5I4hrD0J8gCBiD2+eQtJsx9fnXMaDLDGy+IEoqRs1LPv56J3JP7cC2uSMwbPhqHDh3EAu7/gWtHn8NT44/gCIxVk9tPo6tmouQkK04UEiDccNZnoKUk9E4mXQBmeV0q07Rel5SooMVEkhjrKuVmUs0tk/th/ff74XW47bjXKVwQfHtvoJ92PhJGzx08934yQfhiMmp1ZsZ+UeZa115iB19C17uNxiDtpw1RE1KkUrqIM/6qhORb9QX4UJMBPaGBGFDcCg2Bm1EyHox+PXr//sQsgEbo2UwKeMqEvOUurHx1RmwTpylV6L6QiT2TOuKD9r2QK/xm3G8VM7TsbvjsbXfK3j5tkdwxwerccrthyNrK6Z1fBLPPv8Oem/NlPwc2i9+IaPOUpklnz+LpEqvOOLGOQdtEbaL1lXSyD+lVFLGEDinDk/iK2miTkhdGm7AN06Xgwc9k+hDdSqSYrZixbJghBwvQYEMfOwzzUM+9DKvKd7iHxLsvf+KRNHuHUjftxwrJo7H2DmrcTgnAhOeugG3PycTlrXxKPJVoa4sCdunD0LIoSgkcoJDnfKRtLhFT6hXkrfol2yIntUide1krJs1AwuP58qki7pEZZI0AV2UDyUopE28i1Enefr7b1z15MDOuJKGaWVCqCRq3XQMFBJF2lVfX4KTi3qg599ewX3dghAnyWr5gkjHKRyZ8hE+uP5BPDghBgmFDpm41KL0fDQig5Zi1vKdSMitQlUd8+cKB8kHJxX1KI6ajpCln2BEUCrK5byLZcufqzobaUdXYdq7D+OVbh3R+plH0eq6P+JPN7+L8RuPI0nyqxVb97kqUZp8ADtGPI+ph07iRBlrV4iChAhMu2IwIqKzUECSSduvzMSp0LlYsWoLDiVmoMxt7NLvq9X2lKIbBTYr20kJivSG11WMvONrsXJUR7z2UjsMDstHRhn9sAPFCauxrtvNuOpHj6DPihjElPIhJfaZZCTtLS0i+dGPCIGSIKl4WP1GXZ0DzopC5J49hYSEcGxdPhnTxo7Fxyv3ILrEgUppL/oLyqPC6+SZ7crxSv60/yV/Ka4mORRrRrTFn37/BqYeLkF2leigv1raaSVW97wW1z42EnOOJiOX79wSeVQPVMZA3hbfOy6PG8upzNR30VQqtdMhg3nsArR7/A78y6Pt8eLSeJlhidLKOToikoCG+5PMgElDE4XkcrtXzKPyCOa/8hj6tR+OZYlMoxd4xD1l48TKfuhz34342W0DsXTLHHRp9TBufuwtPLc4Ci53DdzxSzBq3DJM3HACeSQXzlrkhfVEh8d+h4de7ovREeX6GgWuYlBu3sPslpmet/ok9g95FU8+8CL+OnQZ9hYLIZOqqbEK8UlePxwjW1yHq37aBytjC1AYeNqDKyVe5xmEdb0V7wwbj0mHM8W4WSfWhe0RIBRSltpY4PIlyYrEkBag9TUOZvZFckEyRmctOUomdCYkUTUFcTg29Rk88LvH8O7wjdh9gS+R07vAxGH4kRrcBYOf/h1uuas7lqS7UOg8j72fv4ke77RGm+VJcPENztL+3so8nNm8AAv7tsekqAoU1DKHRkKdJl0mt/Wf3SuHpb4yMPAdL/zJCcojn3JOjvGeOPY/25Mto21n0uXHzsbEnrfjn665CT94PRTbzpSBrxpju+ljznWBdrD4BwX7jvpFa/hqP1IXaPU1ODSyNdrdfi/ueW4QQvcswGs3/Aa/fm0kBuxI0RdmVkROQ7ve6xAalY1q6pH4GtEMSV2jNy/76Jwka9FMOSaTtJy9WDNnDt7stxbRbpkEid7rW7C5Qq5Twjq4RYfpIphOlVgVml9iaZys6QqoQD4qoqdjbdAUIQWFWgt6Ns/ZYCzu1xWPPDQAS2UiWEzyf2o91vXrgGdbdMO8ZKCkVuL603B04RB0/Kef46orbkbf9adxslQKE52mHSmVo604TiJy3XKM67AY+4prUeLyiL1W4JwQqFk9X8F1T0xD8IlCZCVtQPDgF3Dvldfiih+8hmErEpGYUyOTq2M4tnI8nn5hETalFqBIpBRqpvdEffbj/giXCVoebU8+8xJXYtA/X4nrrrgWfxu+EjuzaKmBB4fkmykbBakGCS2JJSednvOhmNvjabR68kW8vTgOOV4hkTIxps37imJwavU7uOaqK3HngGCsTayQ9pdyqBryxZbQ1TAdaEy36A+qi/27irOQKUR7+rut0GnkLCw8mIIMh4xD9CeB+5Y48dJ3XWk/GpnUB8m+R9VD6ijx/J5UnNw0Ch/eeTNazzuJuPQKuF0XELt7Ano9fgMem3YcURm1mo4jk/p5umPmbXFJcHmQKCqjKJG/WBzA9pl4r31rdHj6RtxwzY/xg2t+j9890hZ9+s7FnqxqlIgmc5bHx/ENkTEKrgu0fHpNztXXncP2Yc+hT6/eGL47D/pbS1KM31+FnCOLsHjAS2jx3Pvo9G4ffDpmBPp36YV2z3fEiNEfo8cgGfx3JOB0YbXOMHSF6eAo9Hjx33HdQ2/ghUnHxHVwAOYbfMVwxBr8teJ8Y2fhtSdfxTvDVyEkJte840ji1Ynh8pUClSdDsHFAS/z2qt+j48qTiC0UWWlJdZXwVOzBrBZ3o8eItViTTOdKizJtQkM1lyqlamwqfsuJL/YlXmOhhspMZcP8kYRIDtKWflcmMg8sRZ/r/4g2g4OxKSZPn14kadFy5KM2eT1WDn0eD977EJ5aeQ6pJdWoTpGZ25yheL9jZwycuBqfThyNjz+diVkrwhCZlIUi/gQLy2wMpJ5sE5WJ+/Khg4qK3CCvIT3mfjR6Lw5e3GY6OmjjsDUD0YW6vFjEbvocgzp1wGO/HIf1UfyNLxItzkiZDzNnYRb/uGAHfhOJcslnBU5vGYaRPV7Fn1/qjt7vjcD0z0bgvTYf4P123TFixDh0H7YIwceykFHJO2lod+JTqEKiVzpQ0qcwf6oK7d1djdKUSOxZOQ3de36CtYfSkF6uj2TIn8RTHZa41GfVadkJbJrjtDnjO5hnRdQsIVHTMHhvnuxKWqZ3liM7ejdCJgxD9/eGYcxnIzF04AAM4SC/JRHFNWJXvO3BX4HcuD3YMLw7Oj17F95ecgT7MoXoSb6mTObIshyozE0SW1iAsV3eQ49OnfBmm3fRvutQjFu4HYfP5COvtk6fLiy/EI2ooJkY3uYlPPdEC9zf4mE89coH6DslBFvjSlBQYy7V+yFkKmEfpl4xFLujs5FHe/I7UVOUhEMTB2PEG0+g49hFmB9XKe1obJZ1bzTETnlpng/q8B7Z49NeRecO7dBhYijihEHyd0Z15ZmTa3cB8k+tw0ctr8dtLUfhkw1JyGUjiO/XaxaSF8cNXjXgpUyumFWl7sWWOeMxcvg4jNt4AMfOpiIttwil1S4hRuwj41/Yn9pfWhZbU8plH5GgaTz6HJFRj7nhzDuF5C2TMHZAJwwaMw7Dh43CiIHDMGzWGhzOrkCli31MteBaIFc7RR42y0U0jUXz4fIgUaI9qkMOmdmkxWDb1lBsC16KVcsXYdHylVgVvBXh4SeQXiXzQJ1IMD61UJMGvvhJrZZz/hqcWdcL/Qf2Q+vZcSiRU1zC5b1UtcXnkBYXgW1hBxCx+zBOJSUi/tgxHNi8CwcOH8LuQ2eRll8FB5kZc5M0dfkxiNw4Gr2Gf4q3J0XK/JS2w6e8uDom0ngq4CqIwZbN4TiUmI38ajrcgJT8FgvxVmYjO34XgpatQNjZQhTUCq2jJdXmw3FyLt65sy1Gzt+HqAoSRDlOwzK1Cfx9BeZEAF8789/ja+kIthkPiYzeKlRln8a+xcE4kJiP/CqSUspu4jCdvyYH6QkR2Lppoz6iW+GU9naVoiAtDof3hGHvsSQcPXYYhyJPID4lH6WclF8UpJCAk9VPltmwreBWgzw8yf3AWe5rmwVaS/5JpvzOElRlHMHhkPl4+8G5CEvIQZkMdOYyB0mZSW7xj47/2JHcJ/lxozIvHvExe7Ej/DAOhB1HauppRO07gAM7w3Hw0DHsPpKCXPEtLg6u+velapkvPSJBd9Rs/Y4SlKWfQPhO0fvIaOw/dAj7IsKxNzwcEeER2BuxF0dPnEV6QaVOxqhvOiDryEu/INKJj6FvqBIStU5I1JA9eXKKK1hyXvxKXVUBCpKjsG/nfhyJ3IeIA4dx5EQK0ktqJBsO7sxT5K4oREbkVoQOuR8DQxJwhK8fCMiq8uqfRK+rRlXBWRzftR1h27djU+hW7NhzDHHnSuAUgsOVFq2l1wlnSQbOHN2NbSErsHzZcqzeEIZ98VnIF5vmfY9KXPz5QqLCMfmKMfqyzQJtGKGRrmqUpyVh75Q3MG7Jciw/VStxJQ19KgVpNOhDacVsMxfyYrdi3/4DOJxcYJ6wo7TMT7Y5gXZV5eBkWDBCNh1HdFoJqnlco1APSG9lMi3H+PNT1an7ESn9tW3rLuzYdwSRabkyQRdfL/KbPFk+P7hvWlD/dJvtzjK/jPe1Y3UOeErTcOroLhyMPIoDB47gyOFoxJ4vQI1X6hNIx1Ssm5Rg0llcElwmJKqZIQpZkbQcUz4egta9ViCqCnB7zfKrcVASQTW5kRDn50gNwsr1KzBo3Vk1aTMIyyBNEkWCxpWwRloCZyA6u5V83QWnkLa8A55uPQWL9pxFochp7vGyVvX3Qi+Fymy9ruQkzh4QojpgH2LSS2Ww5ABAx8r7FQKRLSwaCZqmsWFeRq5GfnYy4o8fwkFOJML3IGLPXuyJiMBBIVFphVVctxA/wUkTA+2eg7HopzoSv5Co6Vi3bgoGR+SZ42L/+tSxn6snfAdUgPSLPtPnMA+9ZK0r8ZKJyFB27ig29HkJCw6fxxn+YnEzwtx7KDJL0NV5Dv30UX6uRO3CxCtGI7yBRDGwrt4C7JncA4s3bEZEvsjPVSglKDS4S+PbaPH0qz5XLapTxBfEpeBMnkweSWzET/AirvHLl0Y+i0sDS6K+ATovcJ7FvrnjMPKtvpgiLKrURYckhk9j1qcrApG/DTQoVwXO7JiKhcFLMOdkqfqAhqV6Xd7VS0IXYXj0exLd761AYeI2rOj2KDosOIJDacL21KC5YCx5B6JbNBGc+YrDLEgKw+alg9F1ax7OlQV++oU6wHvDpK1tQ1tcDKgufIrO6+NSayDw/U8N99tIBJIM/v6n/gao+Am/l5fveemZZMTkYdTOh4rIKVi7bhIG789jctFNyUd8ir6AWHSUq2lKvHQFSEiMZMAHUuh3OBnwVKUi+eBKDG47DhFp+Sihc2lGqLyBsrgjpZvLYvUFKEzYKSRqKML4sk2eE7l8nlLUZIViev9pCN4ei8w6+kj6M15+Myvclwa0eSlb2rW+ziHuoeE9UtCgfeLnpT+pp8X/GlgS9Z9AU+Dcz4uKpI0IntkXd/behcRSR+Bdufqcnjq2RsEnM8G09ZgwfgWmBsUhR9kP0/IJPT6ZwavadAwyM9SyGwEml6i8GTI2ZCKeenoGNgg5K6I/5vuNvB7J15KovxcyfKG+NBJ7Ni5Dp0FbkSZEupZOnm3LPtB+ZKM3UhcsLAS0S67O8EEXehQTRId4QkLgSwJXNbjaKf6BusYoDIE4xsJ9qDo+FcHBkzF8Ly/n+fXBCfM+JU2iuXObO9Rd3pguTEW+zcuA0yN3YNv4gZh2pFwfwyfRanaoMAGfpB+sWzYKErZiwlUjsDM6B9kSh6SvLDcF+wa2wbytCYjPqhU3aW4n9/K3K7VGlwiUWw1ffIC2ryG25Kz0AtrGUi/T6hb/W2BJ1DeAMwk6Ek9tKc6d2IKFY9/EsG3nkVjAm/jEmMVY1F4aAxqdoxjZWQXIKa5WIsZZod6sSKci5XBWeDEOgmV7vdlI3LkKiwePx6wDeThf5YGbKyTimHWQV2NutJQW3wTpJ5+nCkXFBTh9oRgu6S/zq1v8fcY66QO6y8DAYGHRSFBfOODKMBz44woMV4hEnxh4ROzYz59W0TeUq6IFVnMa0pOEcaceFVGzMW9iLzz/0RyEhuxGTFElytVJaSL+y9gunkdXSbySFZ9QljLkOMtxVhahOCsNORVeuCUd829O0NeZ16Jwasr8fahJj8PJiIVYOHEE3rriE4RGZyGPskld61wOlKefRn5xDapk4sKJpklnVuKaXcDGgu6Z5ZMAmqm09oPx53pS5Jfek32L/z2wJOoboMvOEmgMjoocpB9fjd2xucgud4MvN+MAejGGTJPTZV4uxwcIDr/Nu4mM0embZxubqdirvy4fmaejERkWhbQqL5xi3Hx6hD9RYN5vQqO2+LtA5yiB74LSBwC4LX1nCDAvh0jfUk8uRhksLKguEvjFQVdJE/cDxzgkm6dIDekRZdMThjNR20i6jH/icVd+HOKO7ULQzqNIiEtCVk0Naqifko7580lB88LJhvyYVr8k0AdRq3nPVMAfUcZmBP2d3gMmcphVMT8cJZnISolE1KF92DztGFLzy1CrMopsdF38kEYhydOnqZkRG8k0Ave+f7DNNFBA/s6p0igRVRqSy1GyTX9xqcSzuDSwJOqbQEOlQ5HAVwx4+eK82lp49KZtzoZ4g2cgbiPAuZ++u6nhiRgeEcdgXhDKbznEMhsLZuFzoM7rhIsX45mvWC7v2TIkisv/JqrF3wFpTzpMnbVTJaSp1UmaDTnH4xdBfi0svkCD/hjSooG6xQGa7EZpA/UvMChL4LekENUL2Dih5zipo2+Rs1yNFjKiq9uSN4NZMzHEyzzIImlUn5k345vVaz3Pfc20ecEyzctpOQk1fkp/k47V1Qj0qULyKKlWVCumsikZ5K7yFNMulwoUi5dKTasG/ujTPWxHttx30XoW/5NhSdQ3oOFJEo8QH4cQJpptnRh4gzHrk29q5BcBOgtyHS7JiwHy9Z36mgN1JsyUpTQyTy2eMkqmysDMMQpKJxqYt1n8vdB+NoMMV6P0t8qUwDKwHzkAWhJlcbGgvpAIGJKkR+Sbg7G+Vy0w0dJjcpqBsUygD6qD/v4nDzAbKiX1VLb5rmB98k58g65CKekwv9CgpEmi6m/lyT8vTPNOI131YplSkJIpzbgZIXnSV3E11+tzShnmSTZd+RLxDG2jg2R9KRFlNvs83nBOv9T4ZOMSgK1CMSgVJ6wNsmkfsu2UwDZz21n8j4clUf8BNBAP73mhU6LB0CaMT1Mr0hszafkNBxoDcR4kT3yQS9yV/HFZXQzR6xDDc2kZEqXRMG6OxisyNCyBy746UtnXn5u4NH7msoL0kGlb6SAOAtrjqg/SuHxaiH2oDyE0Ug8sLATUl6/pjG7yg0ZrDFcvq1Hv5LA5Q/9hjikCXyRK+lug4gt0PiXJ/X6+OoG6a8oyq10SlJFJBJImOUn6zzUqkhw9ztvMmV8g7+aCyqIv9jTyfHUFnvUE5VX5KAYlEpujOPRt6jHp38T6NP2lA8s2/UYJZVs2+ZZx3shvVtHojy+lhBaXApZEfQPUgemsjLM1+aCNqHHQicnsSR3NxRmLLpWrM9DMaIfiWJgXl4WNw2ss1CWKfJSRDoazOpMX5WL+lPPi5LP4BkgbaltLIGHlJRK2uBmLZEsUhO0vEU18C4tGQCzU6FWDjfJLWQOD2TWDNG1ZHYXqmdq0xjWB++aFr+acCZILV825qiU6qr/tqATGnDe/o+nS9FyQ0te20F/IeQ9vW9B4kn8zwpQb8E3KMyiDyMzqSXkkVYYsmTgNN8yLMCYeE2lCHjd5XgoY+Si3aUt2l06MZZ/yGj8hBy6lkBbfOyyJ+q9AG5FAZ2ZAw6CB0JDFWPRY42FMLGBgDVlxU4zODMSNB5PThhm4J6Yt+dHhBBxg4LjF3w/TnPw0/cRt3ZMPOlPbzhYXiwat+boX+VKXvn4+4HM0BBCIYHRRh+6vHGOgL+CAb84aImZiGzLGNSiTo748WP2GUBX1IXqq2cGSVRYWGpCHu+YQz5g6GsIVOMF/2W44ZxJcOmj7NRC5gPwNknHbSKcndcvifwcsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwuGgA/x+dZ+PsC4OU5gAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%A0%B7%E6%9C%AC%E6%A0%87%E5%87%86%E5%B7%AE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcIAAAEbCAYAAABJKYSiAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADmqSURBVHhe7Z0HlBRF/sd9/n2nHmIA9ZAznSRzYM0B04liThgQRRTz7Yo5Zz1B0GEBUQxnVgzorCKKIpwKqBjWwYAonDmgaw6Y69/f31TN9vR0z3RP2O2Z+n7eq7fb1WGqm6U+86uusJgihBBCLIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJCQif/75p9pxxx3VxRdfzGRRIrULRUhIRO6++27Vs2dPteWWWzJZlEjtQhESEpErrrhCXXPNNXqLEFLtUISEROTggw9Wd911l94i1cwff/yRScReKEJCIoD3g7169VJPPfWUzgnHl19+qV577bVMpTtv3jz19ttvy/UqDT5v1KhR6ocfftA5tc/rr7+ujjrqqLyC+/jjjyW633///dVNN92kPv/8c72H2AZFSEgEfvzxR7XYYoupX375RecUZuHCheqCCy5Q3bt3V+eff77aZ5991Pjx49Xee+8tgqokEO3AgQPVlVdeaVXUg/vu3bu3PHe/Lxt4Ftttt52aPXu2fKnZYYcd1CabbKK+//57fQSxCYqQkAjMnDlTbbHFFpEiuT322ENNnTpVnXzyyerAAw/MnHvqqadKNFIp8DmjR4+Wjh6//fabzrUHRHwrr7yyGjt2bM6/15133qk6deqkmpubZbupqUm+4LDJ204oQkIiMG7cOBFYFKZPn65+//13tfbaa6sbbrhB8lAxb7/99urmm2+W7Uowf/58teaaa6oJEybonOoGURyeY6Hk5oEHHlBdu3ZVH3zwgc5J8+ijj0oUiH8bgPMgwpEjR8o2sQuKkJAIHH/88WrixIl6KzwzZsyQinbOnDmy/emnn6qOHTtKs+kbb7wheeUE0jjuuOOkebBWmkRxH4ceeqiM4fRLO+20k/r111/10WlwTrdu3dSFF16YN4rHFxL8+zz++OM6h9gERUhISFCR4r0SOrpE5fTTT1ebb755pjIeM2aMWnfddSUSwbvCcvPuu++q5ZZbTp1xxhk6p/qB1KZNm5Y3eUUITjrpJIkK8X7XD1wX0SFkWStfGkg0KEJCQoJKEu+VvM1vhTDNoKhoDUOGDFH33HOPuvbaa9XTTz+tc8vHLbfcIhHOK6+8onNywf3gXvDTCNq7HTdQLpQRyZTRnefHiy++KM8CPUm94F779+8vTaX4ndgJRUhISN5//315z1dMhYkpuj766CO9la6A8e7O++6qXDQ0NKillloqsKzIP+CAA+QdIqKlQw45RDqOYBvSqK+vDxRLe4EyDx48WG200UZqxRVXlI5HP//8s9wHvmhguMRbb72lj24F5+FZTJ48WeekQT568Q4YMEB+/+yzz6SXKbEPipCQkEyaNEntu+++sY2WDKjUIYYuXbrI716QB6GMGDFCfsf4RshvvfXWU5dddpm6/PLLZfu2227TZ7Q/eOboAQtxLViwQMqNMkKGSLgXbCcSCX1GKzgWz+L666/P+re7+uqrRXxPPvmkDKFAxD5o0CC9l9gERUhISIYPH67OOeccvRVfMFSiT58+MvDfT9pTpkxR2267bWYf3qtBIogKIQ28L8P2Cy+8IPsNLS0tmV6WbQ2i00033VTKB/BzpZVWUmussUZWme+44w7Z7wb3iWeB97TmfDRL43hvijpRAqkNKEJCQoDKFFOr+VW0cQOVPSLCoPGOiJ7cFT4iP0gAERPA+Rj36AWyOfHEE/VWfh5++OGCCTIyCROZ+5XV8Oyzz8q7PAOalFFmNGvivG+++UYiOyM6N9iPZ7Hffvtl9uP+/RI63BD7oAgJCQEq03XWWUeaEQ0YEoHmtEqnqIPhUdmjCTfswP9jjz1WpPLOO+/oHH/Q2eSTTz7RW/lBk+Oll14qM9qgCRLNmhAtpjILSmHKajCdgTCusxBGhPhy4CdKQihCQkKACtTb+QSSQmVsEiImvMOCBPKlM888U+Rz0EEHqV133VVtttlmaq211pLhDu7rmQSZRAFlPO2006RjTyG5oMlxq622kt6w7nvznod97v3tCcp2yimnyLNxD2UJulfk41mgudjGGXZIYShCQkLw6quvqg033DCrsoUYMG+oW1po5sMx+RLOc/80vyOh5yJmn9lrr70y10QnFuwLC66HacXQG9TvvJdfflmkjeZPRHjLLLNM1hhHnIPPNeei2RLXQlQVpRzlBMJGp5hkMim///Of/5Teo6Y8+ImmU7+mTexD+RERmnskxA1FSEgI8B4Ns5p4mTt3bmbIARIW7H3vvff03uJBhY2xbYhkcF3MhRkFHN+hQ4ccceG6prwvvfSSDOzH7xguYcB7QPQqxbGQTo8ePTIdalKplD6q7UA5MO4Sn49eoc8995z87hbbsGHDJLpGeb3gGeBZYEgJIX5QhISEADO04F2XH4iYUDGbdPjhh+cIqFjQlIcmWDSjRrkmxgSiLN5xihAHJgFHRAh5QLQQH3qMIkJEpIWmWiMU9BJFlIVhFTivXPcVFfT4RESKuUCXXnppaYJGlIfxmUceeaTca9DMMRj/if3/+c9/dA4h2VCEhBQA8ujXr1/g0AHsP/vsszMiRPJb8aBYICXMozlr1iydU5ivvvpKygGJesH0a2jChUwQ4UFuZhsz0XijKtwHmoXRLNleQOi4F0SEjz32mJTxwQcflDzMzJPv3R/+bSDNSk1eQKqfWIuwpTmlWvTvrbSoZH2DSi7Um4VoTqiG+kTO8S1NDSrRmFKhGnqca9TVRfjM0OBeEroMKZWoT/rcrz9S/vQKMrksTKqGurrg/SQSEAXGrOVb2BbHQJZGhJ07d5Z3ceUC0Ro62oQF8kJzIt79+UVxUSSNz1522WVFPri3cgk+KsV8Ls7BnK4QZntFsyT+xDsilArdiEIjeQ2qoSncuwoIo84RnpegfF8gQvexWjR1gSm7zC1NuSIW9HUamrT+RLie+81DqtH5LB95Rro3UpAPP/xQenUWqojRoQaRh5Fh0DurtgID4lGOqO8XvVx00UXSEQURMSawriYQNTIaJIWIfdOoVPauSj1vJJRDcPSI62QEVAivCCPjRHuO8DLldiJdXC1XWDguvAj9j48WWZLCoEkQIggTkdx6660ZESKdddZZ7RaJoLxYO3HPPfcsqQw4F/eP+6mmqAoRPGajQTRYTDRJ7CH+7wjRtJkRllPJRxFSHoG1rQidkruit5QjQiPphnoTRaYjQ5Gj3paUJTWc49rnPqZAlBr6XkkOqEgx/2YYIAozxs0kTK7dXhUxyrP77rvLKhc2geeNd54HHnhgVcmbtA8xFWGuJIJSvugQ8knvT0dk5pyMcByBJCEo175W8WSf405FScUI3RFWEmWCXJ1rucsfSc5uIMEsYZJygQoVERWmBAsLhhqYuS+R0Kz69ttv671tDzqSYJHeapgerlzce++98uzbs2maVA+xFmHezimFKv9MhJTb1GiirobGRFpKhShDRGhoaUpKeVKNadFHF2GuoBucZ+Xezk6V6OQTDMSBVdcxnRYiKSR08jC/I1UTiCaKeceEsW7LL798RoaMTAiJLzUrQogm2eRuVjWkr52AiJpSzjGFBZf1njIj2NYEmckxWfl+5ddNu841Ek65WiPWNMVGhN7rtBeo6CE6jPMyAvAmDObOJwREL/gWHzVVCqwhiLXvokoMXwjQHOm+93//+9/t1kRKCAmmNkWoRZNpjnSjozsjncAenRlQFi23gM8LLSLnsxPNzvUa09fJlac3hYnmECHm72DTstD3KZUVI0FU+Hifhg4m1113nQyCRp5Z8w2Dm/PJALO3uOURNuHalQD3gTF8xQgMUj/66KOzyllqD05CSPmJsQhbhZBoyo3CJPmKyRGDyc8RYatgW6MvHaUFYSJAHAOJ+nxmOBHisx1hNSczcosaEfqJM9GYftdYMAV9aSgTd911l1T0V1xxRZY0zBI/8+fP1zn5gVCDEiI/9zY+x6RKAbkPHTpUb0UHc4diMLoR4eqrry6zvpQbDPHAYHim8idS+1RFRJhyKvscVZmoz4sT/WRyvSLU0SBwSyefyEwTa/q8bMmaiM2c71tOnGNk5BFuVBH6ka/s+cBnlUuQixYtkg4hGHTuneYKM4FAAN5FXqsFTKpd6tRciIbdzcUHHHCA3lM+IEJzfabypd12200/YVLLxFSEXtIyyZZEixNdFajCs0TokphDlnQk6guQmIkEsySWjlhzRZr9Ga1kH2/AeVlRm0/ynpNFTrnCkxFhkee7QY9IVBrHH3+8zkmDSG3vvfdWXbp0yTsFlht3xBclVQKU/x//+EfJUQHKh8Vw8Yz69u1bkfJ+/vnnTBVKpPaJoQjRgaVVMJmKWmSV/c5MKvN8EY1LhBLZec51SyYtpWwZZt4feoWDsrg+1x2VBZXJfYzBm+ctU34g3YSTWqUpn2uacjPJT/DlBauHo5L3LpKKVRjQcxKDusN2aMGacebbeJQU9R0h3tUVKtN3330n1w4r8SAgPkzEvcYaa8jitoSQeBE7EUIGRg7ZotDv2MyWnodUxBNU2WsRmuvgZ6sgPCkjFSPMViF7ReiVanY5/aNXRIRu6YHiRZj9LDJ4BN1WoDl0ySWXVPfff7/OSYN3a1FF4n0PGDZFAZEemjw//vhjneMPJnfGzCSlvIPEuViIF8/B+3wIIfEgXiL0RH1eUbhJNZkKPy0e3+NEhEmV8tkXKfpyi9D5PYzQspsc/ctYnAhxrWwRZ4ggQny2fAHIKmdxQF4HH3yw+te//iVRIMR04403yorrWBmgFJFUgv/+978ipkmTJukcfy655BJ1wgkn6K3o4L6xdBM+q7GxUecSQuJGjESYjprczYrBIvREh3qQeg46IvSjKBFCND7iyCnnwpRKZYkqWIQ5kWlOckV+8kUhIPoFEUQossb1yyBCgKV99t13X6n0sfICokH0mIybBBGdHnHEEVJOrG2Xj/3226+kjjJmnUL0PI3bcyCEtBLrzjKZyjogFRRZOUXoFYxIqbUs/sLOT7Do/XBkasqA8rg+O1QKKchSQGVvmjbjWvE/8cQTmYVcjz32WJ2bC8rfrVu3ot/p4Z0lImJKkJD4E2sRlkwlRWjAviKjKv/hFqRSQEg777yzDPSHCLFMUpCkIPOOHTtGfv8IIM+ePXvKkkWldrQhhFSe2hYhIS7uu+8+GcOHdfUgwrXXXjtQdBgSsuOOO0YW4RdffKG23357kWwxEg3ioYceUtOmTdNbhJByQhESa5g7d650kMG7S4hwqaWWChxCgZly0NszSrMmxIdOQ5hJptDQjCjgWhtssIF65JFHdA4hpJxQhMQ6ICwMlIcM582bp3OzOe2009QDDzygtwoDYdbX16u//e1vZZfgMccco9Zff/2qbWbF88Z9mC8V+GlSOaNmQoqFIiTWgQoYM7xAhH5j+7B/vfXWkwnCw4DjL7vsMrneJ598onNLA9fEUk5oZsV1MYdrNfL111+rrbbaStZnRLM0ZI4hJb169ZL7Qs9cTMhASHtCERIrwZhHVMTo1ekFUQqWXgob2Y0fP16u9fzzz4vAghKui+Texk98Dn7HOo4zZ85Ul156qdpss83kmia99dZb+tOqC6xFecMNN6gHH3xQ7gMyRJPzV199JfsxLR/yyhlFExIVipBYyZgxY6RixthHyMjNL7/8orbeemuRUyGwTBPeNSJyi5ownRx+YqmqTp06ZYnPnTDxc5iyxA3I7a9//auU3axCgqnmzPPGT4gQ+exdS9oTipBYydSpU6UCxlhBr2RmzJihBg8enCNIL4jeMH+oEValEqKpagTPD1848HPAgAFyL+4JzPHcTeRbjaIntQNFSKzE9BxFwnssN1g6atiwYXorGIwXxAD9KGnKlCm++ViqyZ0gapOqvdkQkkPEi45EbuHhvvH8DznkkIJfOgipJBQhsRJUyKussopUxM8884zOTXPYYYdJkycpDxA7njOeq5uGhgbJN8+aUSFpLyhCYiWIQPB+DhXx2LFjdW46HwPtq7VzShwZPny4PGfM6GOA9DbaaCNZqxKrl9x0000yEw8jQ9IeUITEWkxHDfeco6igl1hiCUYnZQJiQ9MnnvPs2bN1rlIvv/yy5B166KHyrDH13Z133qn3EtK2UITEWkzPUYxzM5HIhx9+KGMIi41MzjjjDNW/f3+9FY2JEyfKNGpXXXWVRKu1EB3h/eaaa66punfvnvXl4vvvv5f5WAcNGqQGDhyoevfuzS8fpN2gCIm1mHdXyyyzTKYSRg9NRDDFcvHFF6s77rhDb0UDYxpNqhURAtzP/Pnz9VYr6EGKjkm10CGIVDcUIbGWlpYWESGSeSd47rnnyswn7UmtiTAfNtwjiT8UIbEWRIFmHOCECROkUt5ll11kVf2ovPbaa+qggw6SGWtKrdxtEiEhcYAiJNYC0ey1114iQkSCEOOSSy6pFi1apI8IB87D7DCYkQbXwqK8AHLFFGPudP755+fk3XvvvXK8wYiQ78wIaRsoQmI15513nshrjz32kPdU6NIfVUDo4HLRRReppqYmGTj+7bffSj5Ei2u5E6YS8+Z5Iz9GhIS0LRQhsRpEYxAhljmaNWuWOvroo4sSEIS25557ylRi5nz8DJvcUISEtC0UIbEarEcIEXbu3FmNGjVKjR49Wu+JhrkOosKbb75Z8iA05BVKjY2NcryBIiSkbaEIidWgqbJDhw4iJAybQFf+YrjxxhtVjx491K+//irXAhCZtxnULxnh4SeS+x0hZUhI5aEIidVANJtuuqnIa/XVV1effvqp3hONBQsWqK5du0qnmTlz5ujcaECAZmkmlAcrYCCPEFJZKEJiNRDhEUccIeJZaaWVJAorFlyr1PO9yXS8IYRUDoqQWM+IESNEhHwvR4idUITEep599lkRIQbDE0LsgyIk1mM6uIwfP17nEEJsgiIk1oP3eiuuuKJMAk0IsQ+KkFgP3gsWO2yCEFL9UISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkKK4M8//1QnnXSSuvjii5ksS6T2oAgJKYI//vhDrbvuumqLLbZQW265JZNFidQeFCEhRfD777+rDTfcUIRICKluKEJCiuCll15Sm2yyiTSRkuoHX2hMIvZBERJSBGPHjlUXXnih3goHosinnnpKKlv8jjRnzhz1448/6iMqB4R99913W1fRv/7662rw4MF573vGjBnqrLPOUvvvv7+66aab1Oeff673EFugCAmJCKQycOBAddttt+mcwuCcxRZbTPXr10/1799fnX/++dLxYsiQIWqvvfaqqKDw2ZA2Pr9aRfjbb7/lpEWLFqmffvpJfvrtx30j9e7dW+4fv3v54osv1JFHHqneeust+ZKyww47SKT//fff6yOIDVCEhEQEFermm28u0VxYJkyYICKaOHGidLJ57bXXJL+pqUl17ty5ooK67rrrRAaQQ7Vy1113qRNPPDErDRo0SB177LHq8MMPz9k3bty4jPg+/vhjtfLKK0sU7wVfZvDv8v7778s2/j2wjc8j9kAREhIRSGv11VePJK/p06dLU+iAAQPUYYcdpnOVRCqo0P2ilXKAMkKCt99+u86pTnAf3gSx//LLL/LTb7/7mT7wwAOqa9eu6oMPPtA5aSZNmiRRII4HCxYsEBGOHDlStokdUISEROTDDz+UqC6qvFBhd+rUSV177bWyDTHusssu6t5775XtcoPy3XDDDapnz57yWTYD0XXr1i2widQwZswYEeFjjz2mc4gNUISERCSZTGZFdWEx0QZ+gueff16233vvPflZ7qgQ8tt5550lCiVKJkBAVBjUOQlfcNZbbz2RpYkQiR1QhIRE5KKLLlKXXHKJ3grPPffco7bffvuM8O644w7pOHPggQeqCy64QPLKybx580SwiAqDQFkQqUKaplyQALbjLANTRhPpouzIy1fmF198UZ4HepJ6wfn4t3j00Udjfd+kMlCEhEQAFSbENWXKFJ0THogPPRMNqHCnTp2aGVJRbu6//36p+F9++WWdkw0+89BDD5Vjll9+ebkvvHM74IADJO+YY46R3pRxI5VKqW222UatuOKKMqkBhoWYLxnoeBT0pQLSXGqppdTkyZN1Tho8B9wzmqzx+2effVaRLyYkvlCEhEQAFWW1zCiDsXEQWktLi85pBUK/7LLLpML/9ttvpRcrjoUMkRobG2U7kUjoM+IBZLbZZpup++67T+4B5Uc5kSDxbbfdVq222mqZSNEN/s26dOmirr/+ejkX4Oe5554r18EXEiTTgYnYA0VISARQwXbs2DFTkcYVVPoYSI5Iz0/aGPqx1VZbZfbhviCTNdZYQ/LQkxLbiGLdQKroAdse4JkfdNBB6rjjjtM5So0ePVrKefXVV0t0jd8x/6ufCHF+r1691Omnn565b0SSOMeb3JE7qX0oQkIi8Nxzz6k999wz9iJE+XbffXe10UYb+YoQPVUhAQOGFUAApmPN119/rZ588smc+4QgMQA9DA8//HDBhDKYhCbOQs8V7/HM/eDYhoYGKffs2bMlD82mSH7geEhyv/32y1zDRIHeVKgcpLagCAmJAGaDQRd7AypMNKVFSWiG88vPl6JGYSgXoqeNN97YV4RezLABDL7PB64b5noAs+dceuml6sorr5SIDdEbmiUxjVlQiiIglAMR3tprrx2qTLg2RIgvCGHvgdgBRUhISFCR4h2UW0qIHkxzGtKyyy4rQxYQNaIDxiGHHKKOOOII6XiC7vunnHKKvLuDDOvr62VWFBy79dZby3g/dABxX8+kvn37RpIEjsU7wDCz1uBYREn4nDfeeEPnpvPdYDtOApk2bZqUGc/VTdBzQj6kiSbjap5lh5QfipCQkEACK6ywQs48lIh83NLadddd5VhUvEHJ7Hf/NOnXX39VDz74oDRBusVopmULA66Ja+A8dIbx8vbbb0szJ94Bfvrpp3JfiJZwHkA50GkGPwGmiOvevbuqq6vL5LU1+FxMk3bqqafK76ajDGaNMaDJF188/MA5GEd49tlnZ+6TEEAREhISTPC86qqr5ogA25g42wgLqRwrmaOynjt3rkSMuCaaSKNU4Bgvh/O84+ZwjYMPPlj2XXPNNZlm0aFDh+ojlBo2bJgIHcei4wkk+PPPP8txUYRcTt588035fMgMPUQx+B3b6CQD8O+AYRVBq0dgf4cOHWRYCSFuKEJCQoJ5KXfbbTdfGaGSxvyjqJhNeuKJJ/Te0kAFjuECmCLsm2++0bmFQfMfIj13xGRAz0lEgGeccYY0FyKqRW9YDJtAJIrym56XX375pURaw4cPlxXa/XpktgWIxCG/W2+9VcYMnnDCCZmZYPBuc4MNNlBXXHFFzhcVAybWxn3FcWwkaV8oQlIxIAxUSniPNn/+/EwFhXy/2T3iDkRw3nnn6a1csGKBW4QQzQ8//KD3lgaeGVZVgKjCgueNd4/oWenF9ArFIHL0soQ0IUxI5emnn855h4bPx3AL7G9PML0dmj4xiTiEjLLfeOONasSIETK0w+9LigFNoogY20vkJL7EU4TNCdXQmFKtw4BTKtWsf3XjHJfwy89DS1ODc06LalmoM8LgfE5dXYNKRjknFC0qWZ9w7g6kVKI+6brn/KTvQ294WZhUDXV1kZ9NOUFFim/pWNsNnUCWW245WboIkxljkDY6clQb6PyC925BoBI+88wzs2R48skn562co4AKHO/FsDp+WPBvsP766/tW/lHKtXDhQrXMMsuod999V6aYK9c9FUMxn40vBZgo/aqrrgqMGIm9xFaEdR4ppBrrVJ0jRzeSV2dEEg4IJOo5Uh73Z2vRoOOAf8q+fktTwl+i+joNTfpORbjhyyb37yNPuUfPs2pLUOmiN+Qee+wh67uh4kLlgw4XECIEgW/21QTuAe8Hvcv4eMF94t2aW4Z+TZNtBf4t8DdZ6vNGVI8xfOjIE9QZJc7gCwzeLZp1BwlxE18R5lTkTsTklga2I0RQBkii9Roh8S1PFNJlz0RozU6E6/zIFRaOiyJpv+OLey7lAiJA1IKB3H5Te6Fpbemll666FcBxX34dZfxobm6WqbyMCIOeRVuB8Xt4p1bKkAGUHyLEMJAwzyBOoHl60003jdzZiNhDFYkwW2KBUVYB2keEjp5c0VvKEaFTEpWsd8pS3xpJolwiR70tKUtqOMe1z31MgSg18j0XCSKQfLOPPPTQQ1UxM4sX9JTE+6Ww5b7llluyokK8p2svgeBz0ayLLyjVJrFSwb8XOgJhKIhf8zAhIEYiTEdNUmk7gvBW5K0JEVDrsSa5K/ocmZjkyCy9z5FowDGt18n9jNxjIuDIVM5zhJVEZAi5Otdyv8crStIAEmzHKNCN6ZkXtF4fvpW3d4eLYkDnjLBTiwFUwGb6L5PQbb+9vgBAgJijE02cNoHernj2lCDJRywjQpFVYATm1xwYEi2fhiZHRlGEU4aI0NDifDaulGpMR4PRRejzJSDvF4dKdPIJBr34TMWPqbWwBhya5IwAUCG3lwxKAcMNRo4cqbfCsWjRIrXddttlngc6Df3vf//TewkhcSGWIvTrGNNKsSJMNytCGpBNS7O7V2p+ssrj0wQJmaU77riTn4CcsuM6zjUSThlwTjkiQu912hO8jzEDnU3C+zJEgVHeUeEbfDGpEkDcGDA/a9YsnROeGTNmSG9L8yww5ZptzZOExJ0YitAV8ZjmPh3JBacQYsQ1nOuljGy0jArjei8X0PwYWkROGTB0I9mYvk6uPL0pTDRX+ItBy8Iw91k+Xn31Vemc4ZYhEsahoRt+IU477TSZr7NPnz4ygBsdHbAG4DrrrCMznGCpoFVWWUXm0cTcnlhs9f/+7//kHVglgLjw+cWIFueatf1MwqDvaoyKCalV4idCIz0ncpIm0hz5FBMRpmUGWbmjrlRjiOuYCBCRnJapVyvhRIgyOJ/XnMzILWpE6CfOhHMP3jzfFCDxSgEBQIhYUQBL+xgJ3HbbbfqI/OB8v4So0r0NobhTJcCQAZQdn1cMOG/gwIGZZ4CEd46V4JVXXmGqUCK1S+xEiHdnySancpemSEd6ZRChWzBZsgnRySSwPCLsdMRmhOYvVpRXy0iu0UpUEfoRTsK54LPKLcggUSDfTJCMSLHaoqEXXnhBZmgppdyIhDGhgBEhBndXYnYdRMnmM5jKl44++mj9hEktEjMROtIwkZeWRqbCLpgC5OiJ4ryykesHyiC3PGn0+0Z9nVYZuUSZRfbxBr8Iz5vyijGnXOHJPNciz/cC2aGix6oGfmA6L1QomNsyDLhe1FRM02WYdf7GjRsnzbWlYp4BBnZXKsLAhNNMlUmkdomVCE2PyvwVPCKskBGhT8TnFaGRlJ9IM2MVveXxXNcdlQWJ1S9y8+blli0fkG7CSS5x4nNNU24mRYuei+Wrr75Sf/nLXwI7xGCVA0gA0VUhsHKD+SYeJUV9RwhxQk75QBR41FFHlTw7DK6D6b1QTsxJSgiJD/ERoVOBZzqvlEOEuIYjBnSOaZVCQGpMahkimQ4qqdYhFp7ySHOpq89HttBQPm8k1/qO0k3xItTvG/VWhhBNvZVi9uzZUsnjnaAXCAedXzAEAZFbGLzRXtgUBUyKPWXKFL3lD67Zu3dvWbOvFO6++255PpzdhJD4Eb/OMqBEEUIwQefnk01g70p3eZzfwwgt+/PTciyPCHGtbBFniCBCeUbyJSDfkwwPoh00+WHoxPPPPy/yQ4UPkWDVhIMOOqikKb7KDcqFHqiIVPOB4yCwqJJ1g9UcsBzSkCFDKEFCYkgNijBgpQpNtOZHjSkPRONTLq/Q1EKnDFmiChZhVmTqm1z3Ks2eee49gghF1rh+GUSIyr1v377qmWeekSVx1lxzTZlmDR1jVl55ZXXOOefESoIA829CcPvuu29eOWGlB0SExQpswYIFsvoDppUrRaaEkMpRkxFhPnKjtRCgPF7BiJRaheWVXBhyBJoX575NGVAe12eHShVuMkWnE8gC6ccff5QekZjOC7/HTQAoj+nBWWgi7fHjx0skVwxYRR0rUeALASVYOdD6cM8997DZmRQNRRgGPxEa8pY1P6HGMZKy88gjj6hRo0aJCJE+++wzvSeXY489Vtb0iwrEh042vXr1il00XAvg+WIybUwmjgkX8O9IEZJiiacICakQqEC33XZbGSSPaBAV6OOPP673ZoNKFc2iUYc64Dz0YMWsN8UM6Qjiu+++a9eJu+OEEeHUqVPlJ0VISoEiJFaBihIVJipS9GRFBTps2DC9Nxscg/34GRZc//rrr5fzyrkGIcqA6LQaV/avNPj3pAhJKVCExFrQmxUVKJaM8qtAEQni/WqUynXSpElqiSWWUM8995zOKR18/ogRI6Ss6JHblkDASO7mXUS5yDM9g9sbipCUCkVIrGXMmDFSgW6wwQa+FSjGRGJF9rBgZXpMCD5hwoSyVMi4xjvvvCPvGlHO/fffP1J0Wir4fHQUQs9aDItBhxQIHtvoGYzndtJJJ5W1+bcYKEJSKhQhsRb0akUFiuQnGESMY8eO1Vv5+eKLL2Q+0kQiIddChYwU9Ls3Dz8hFLwHhFAxrVu/fv0y5UMKO2F5uZg5c6bMiTpv3rxMGbC+IiZPABAj8jC5entiRIj3sniWhESFIiTW8uWXX6rFF19cKlHIxw0qVCwbhfUECwGB9e/fPzN2stj097//PSMcb+rUqVObR17ohHLrrbeq+fPnSxmwrqK7yffOO++U/KB3rG0FI0JSKhQhsRZEYVjjEJUoKnw32LfkkkvKQsP5wHFDhw6Va1QyITpt60oeYnnxxRczwhs+fLjek+bkk0+WfPTczAfKjWgN14uSwoJjUQ78pAhJMVCExFpQaeK9GypRzIPqZs6cOapnz54iukJgvtInnngidPIej4m/vQlycad3331Xf1rbc8opp8gzmjx5ss5JPzssmoxFkTFpQj7wDClCEmcoQmI1phLFwGx3JXrLLbfI/Ki2V6yQWJ8+feQZffLJJzpXZZpLMXUcmmzDfGGoFBQhKRWKkFgNlldCJbrxxhtnVaL19fXq8ssv11v2Asl17NgxJzpGj1o8t2QyKcfg97Z+h2mgCEmpUITEakxkg1lgTEWPynSbbbaRMYHtSRwq9TfffFOej7vpGOXaZ599MvLDbDdHHnlkm0eFKAeSW4QoQxyeG6kuKEJiNag4sUQSKlIz5yjyll56afXRRx/JdlQwjhDXK6ZCnjZtmpx/xx13qLXXXrvN5eLFRH5YSsoNxIh8vOPEXJ/ogduW4LmgyRa9bdFbF2XBWEfTc7dQBx5C3FCExGpMhYqKFOPmAFbOwFCGYiWE8Yk333yz3ooGKnBENviJMrW3CCHla6+9NqccEN9DDz2kBg0aJGMo2xqUx69TERLy8W9ASFgoQmI1iNowewqkgzlCwe2336723nvvdm1iM4P921uEhNgARUisBwPCIR0zVg/j4y699FK9NzyQ1gknnBA4d2kUENlQhIS0DRQhsZ6JEyeKdNBBBgLDNGKPPfaY3hsevKOaNWuWvKdC8yZ44403ZAydO2HGFm+eOd5gRMi1DAmpPBQhsR68E4R0MIUYekF26NAh8hJKECiu8cEHH0gPVLdIEdW5Ez7Dm4fkhhEhIW0HRUisB1EXpIMEKfbo0aNoASGy6969e9aYOkgyTHJDERLSdlCExHogobXWWkvEgxUeMMtMMQLCdbBEEeYefe2110Sq06dPz0g2Xzr00EP1VdJQhIS0HRQhIQ5mgDg6yuCdnTdCCwPWDsQ1MEh/+eWXVy+99JLkQ2ZhEjDRoREhIstiykIICQ9FSIjDyJEjRTzo6IJ19ooBMttiiy1U165dZfxdMWDYBDrdIKE8e+yxh5SJMiSkclCEhDggeoN4MK9mKpXSudGBDEuVlokKzbUoQUIqC0VIiAM6zGD9QdMcSQixB4qQEAdEX926dVMbbLBB5n0dIcQOKEJCHCA/zDlajllhCCHVBUVIiAZLCY0aNUpvEUJsgSIkRIMem2wWJcQ+KEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJMThzz//lPTkk0+qqVOnSnL//tRTT+kjCSG1BkVIrOePP/5QQ4cOVSuttJJabLHFfNNee+2ljyaE1BoUIbEaSHD77bdXq6++ukokEhL5DRkyRHXq1EltscUW6qabbpLI8PPPP9dnEEJqDYqQWAuaQkeNGiURX1NTk85NM2DAANWlSxf1+++/6xxCSK1CERJrmTJlikhwt912EykaECUOGjRILbvssuq3337TuYSQWoUiJNZy4403iggRFbr54YcfJBrs27cvI0JCLIAiJNZy+eWXiwhTqZTOSfPggw9K/oUXXijRISGktqEIibVMnjxZhPfpp5/qnPR7wz59+qhddtmF0SAhlkAREmvB+7+11lpLjRkzRiI/pDPOOEOtu+66fDdIiEVQhMRqZs+erfbcc0+JDHv06CHNoYwECbELipBYD8SHZGaXIYTYBUVICCHEaihCQgghVhNPETYnVF1dg0ou1Ntlo0Ul6xMq3Vk+pRL1SSenbWlpalCJZr3hZWFSNdTVBe8nhBBSduIrwkbX2C4tiLrAZOSWpqUp4S9RfZ2GJq0/EW72uTk45yS9YnLyEvUNnjKYVFjgqUbnOB8JQ5JZ993GoNekeV+GhJ6T7m1CCKlFqkOEkXGiPUdKmciqOSWyyxUNjisgQgeIKyNPAKH6li9slOn3ue0ToQJ0EJkwYYI65JBDZLJp9KD0S+XqSGI6pURNhBBSCWpUhGl5magr5Ygw3SzaoBrqW6M3yE3kmInmWs/Jwhs5RhYhPtv1Ge7P0lFqzj6dsgRcASCYe+65R0S35pprqmOOOUZWY+jYsaPaYYcd1AUXXCBDCu67776yyQjXLyZRhoSQShAjESJKKqMMHHnJeaZpU2SW/f4NEgx3badsbvGVHBFqcJ0ox1cATC+GKPCAAw7INH9COEcddZRaeuml1a+//ip55cQsdOuXnnnmGfX888+rl19+Wc2dO1d98MEHqqWlRf3000/6bEIIKS81GxEaWpqSEsmlGtPRYHEi9JAvigsUW67oGwLfMyJVorNQNngniOWGEA3OmzdP56ZBFIh8rMVXTQwbNkytscYa7ZogcEJI9RBLEUqzphGhj3QgMzkmK99PHDqSc66RcISHc8KL0NucGaZptEW1RJCXtzxtzSeffCKywzJEXrAMEfZ99dVXOqd8IOIsJoUBC+m2d6IICakuYihCl4ACoqvQAnEiy0Szc73G9HVy5elNAVGYaWYFXjFDiLrZteB1skCEmL+jTsvCIEmXB0wvBtmNHDlS56RBb1G8L9xyyy1zVl/A+8RZs2ZJMyr2nXDCCWrGjBk5x+Xj+OOPV8cdd1xWOvDAAwumKJ9BCCFhiZ8IjWiMYHxkGE6EEKojmuZkRkrRIkIXbhF6QRl9o8NW/AScaPTKMyBV8B3i+++/LyKcNm2azkkzYsQIyX/22Wd1TpqHHnpIygRJoun0/PPPl/d6EOakSZP0UYXBObg23gW+9NJLodKLL76ozyaEkPISOxHiXV6yycjF1flEoq50pGWElnJkkqsg17s4j6AqIcJi3zOGk3ku+LxyCRIR1k477SQ9QwGaHyGc1VZbzXctPsjxiy++UJ07d5ahFjgex/Ts2VNdddVV+ihCCKkuYiZC/U4vJ8pKN5ca4bRKxCXKLLKPN/hFZt7kKzUjQidaTTZlN41KhxenDEnvtfOJKkQUGURGhEWe7yWZTKru3burbt26yRCFrbbaSt15552+zZAQH3pxQogLFiyQPBNVIsojhJBqJFYizMwI4xUFmktdYnFHUyIGH+n4RVzevOgRYev7RoNc05FjzuwzgUDeCSd5pOl99xhioH+5+PHHH9WcOXNEaoXew2HoA8pnjhs3bpxaaaWV1Ndff13w3GoDTcEvvPBCpEQIqT5iJMKUE21pxXhEKM2lrs4n2UJLN4VmCy0dEZZbhN5ytAo6V5D+oFw+gvOIPs6cfvrp0qPU9OREFInOL+h4M3HiRH1U9TNq1Ci1/PLLS7QbNmHoBCGk+ohfZxngFqHzexihZTcVpuVYThEiCsp7PS3LYFCmgN6kEUSIz5SIsUxNo1Ew4nO/D+zfv7+M3cPitosWLdK51Q0i2969e6uZM2eqb7/9NlIihFQf8RYhBOFT4XuFphamVCpLMMEibG16DEq5EVuuaP3zcH1fGUqzZ56mzggilM9FOdtBhADvAr/77ju9pdRnn30mzaXmnWEtgLGA2267rYifEFL7xFeEXjGITFqF5ZVcGHIEWhT+HXHSpPdlCxXvBPW96MgyUqqSJtNaAdFgv379ZKo3QogdVI8IDSZaLAL/4RbhSUdjAc2bLlJNlFe1gskC1l13XUaDhFhEPEVISDsA+WHu1UcffVTnpEGUiGTkiJ/Yxgw8+EkIqW4oQkI0jzzyiAwFccsN70AxtrJr167SWxarcaCXLJap6tChgxo4cKC6//779dGEkGqEIiTEAVEeesRiLlUDhHj44YfLXKpmNY4+ffqou+66S6JBJDSjQoxsSiWkeqEICXHAXKmbbLJJVjSIuVB79eoleWY1juHDh+u9SiYehwghULOWIyGk+qAIifUgmsM0c7feeqvOSXPvvfeqCRMmiAgxn+oKK6yQJTxEhJAjROgWKCGkuqAISU0DQWGZKayUEdR8iWgQQyaCojpMHwfhYfIA9zXwThH5o0eP1jmEkGqEIiQ1CyK2IUOGqC5duoiwXn31Vb2nFYhtnXXWkYnGg8Aq/Th//PjxOid9Hq6NadiwwDG2g0RLCIk3FCGpWTBNGjq5nH322SKyM888U+9pxe/doBvIzZz/5ptv6lylWlpaJG+fffaRYxoaGtRtt92m9xJCqgmKkNQsJkJ766231OKLLy7vAd3Nn5Af1mO8+uqrdU4uOAYz/Ky66qpZssRUcxBhIpGQfPyOJaoIIdUHRUhqHghx8ODBIiusv2iYPHmyWmWVVWRsYBCQKM7DQHt30+fcuXMlH+8JN910UzVmzJjAqJIQEm8oQmIF06dPF3FhlQwjLMgNnWjyAflhBX9vRxrkT5s2TV188cWyqj8lSEj1QhESK0DHGUjQRIXz5s2T3xcuLDBxLCGk5qEIiTXcfffdIj80ZeLd3kknnaT3EEJshiIk1oDmS3R8gQwxZALv/wghhCIkVjFu3DgR4dChQ3UOIcR2KEJiFej0AhG+8sorOocQYjsUIbEO9Ph0D4UghNgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqYizCFpWsr1N1jSm93b60NDWoRLPe8LIwqRrq6oL3x5g2va/mhKqra1DJhXq7bOBvJaHSfykplahPOjnhKNv9B95bumzJhWFLRAhpa2IuwvJWmqj0ShFrqtERs08lW+p1S6Vq7guycF9Pi6YuMBm5pWlpglD0hht9nYYmfQcipexz81GO+8exmc93E1KmUoase08nXFPK4bPPr8x+lP3fkZAaI8YidL7ZVyB6kEohQsSQDcrkrWCjRSCVoiruyyvCyKCcLqk0p6TMuRW93/3ko9T7d0ek2aBsvoIMSannG0r7+yCktom5CH2+BQek0M13+IYeqYLz+TycXyCaKUflFYlquK+SRej8Vbiit5QjwvS9OLJw3Y9vFJX1bMp1/wHXcVL67zH4b9j3OTrPx/t3nCtCfc2ozzHS3wchdhFzEUb5Vm8oUPlIs5n//nQKEYW2S6VSrfcVUQaFcO5TznPKmoQ09H27BVJ0FBX5/tMSznquuIaRlCmrG+zP83ctondJznsvInhfCbbB3wchNUp8RVigwiiG4EokH7kVTINT+bm3s1PbVyhVc1+ojCOX05+WpqT8baQa09FgdBGW4/7zidC5vp9UC/5dp8tl7ifrXnBuEV9Uivv7IMQe4i3CMkcn4SrIwuBbu7cJqz1pr/sK6uCRSZ5/v6xoR4SQfTw+O/eafgJyZIHrONdIOPftLXexzyPq/TufFCjCVGOA7OS+83/Bg9zNNVvvJUCsISjX3wchtUpsRViwknWnkBWE7zWdigwVcviKAt/Y81dkLW3cVb697uvjadeqa6/Lk+5Pqe/0sWlpmLL5/3uFFpETWSaanes1pq9T+G/FT6Zeivl3DRKhUy7J85EX9rvzRIx+ZQ6b8pcZlOfvg5DaJdbvCJMh/pOGrjz9Ki2Q5xu6XwWScL7pe/N8U5Hf3qNTJfdlKnxEcmgi9blOuH9L3K9zX83JzD17zysUAZXv/lEWn2NczZAoS1azpFeEBSg9mov+90GIbcRYhGFIV0ThRBjQtBSxYgpXWeciFWJORVoO2ve+wiLNfU3mHaGrzNKJI11RmzL4NysiYssVDYgqQj+Ku38fyeC5e8XnFk7Ef5fSRVievw9CapkaEKHPt10/nArXt0KJ0oEjyrEeMiIs8vxA2vG+II9MFOSXMhWtUxnj+jmfk/4iY8rfKqOAyttzvKFgOZyUVyZF/7uGEKEI3HVMW4uwHH8fhNQ4MRJhupLzq8R8k/wn9lQygeDa/s1AIqhQFQIq54STXGVAhSbf+F15bdrc1L73FfYdYWZGGG/l65GCOyqT8vsIwy9y8+ZFk0cp/64BIvSUOz3eUYNn4HNfQZQmwlL+Plz/HyOUl5BqpMojQogwhHiCvhU7oBItXNEEVCg+lV6bUhX35XrX6xGhu3ckyBYa/m2995CunMsnwlLvH+cXFmEWbSnCUv4+nHMzz9T9OyE1SHWLMFSFhW/8Qcf4V6zZoEIOiDojCAMVj3y7DhWlhSEe9xUJtwh9Klc/oWU/r7Qcw5xXWB7luP8iRRjhb6B4EZb490EREouoahGKXPJWKqjssr/xZ3eBz1MZAlRq+SLOCMKQSr1sIozPfUXCSADX93kOXqGphSmVyroH3Je/CFubMIOS637Ldv9poeR8Vp5zo4oN9xZdhCX+fQiue6vE3wIhMaK6RCgVmKvCyfefGZWuT2WXEZJJgf/JncrC7JNruc4JkypVeVTzfeHzvOd7/k2LiTxyBJqXct5/uIjQK+oo9xhZhCX/fRBiH9UZEUrlGSxBqXgKRF5yTJVVBlV/X34iNGBfkdFy4CwuFccRoR7UX5h0hFVcM2c4avXvnpBKU+WdZQghhJDSoAgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiNVQhIQQQqyGIiSEEGI1FCEhhBCroQgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiMUo9f+ovebP0qnL/QAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83-%E5%85%AC%E5%BC%8F%E5%B0%8F.jpg": {
- "image/jpeg": "/9j/4AAQSkZJRgABAQEAYABgAAD/4TnWRXhpZgAATU0AKgAAAAgABgALAAIAAAAmAAAIYgESAAMAAAABAAEAAAExAAIAAAAmAAAIiAEyAAIAAAAUAAAIrodpAAQAAAABAAAIwuocAAcAAAgMAAAAVgAAEUYc6gAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdpbmRvd3MgUGhvdG8gRWRpdG9yIDEwLjAuMTAwMTEuMTYzODQAV2luZG93cyBQaG90byBFZGl0b3IgMTAuMC4xMDAxMS4xNjM4NAAyMDIwOjA5OjAzIDE1OjAyOjUxAAAGkAMAAgAAABQAABEckAQAAgAAABQAABEwkpEAAgAAAAMyMgAAkpIAAgAAAAMyMgAAoAEAAwAAAAEAAQAA6hwABwAACAwAAAkQAAAAABzqAAAACAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMjAyMDowOTowMyAxNDo1ODo1NQAyMDIwOjA5OjAzIDE0OjU4OjU1AAAAAAYBAwADAAAAAQAGAAABGgAFAAAAAQAAEZQBGwAFAAAAAQAAEZwBKAADAAAAAQACAAACAQAEAAAAAQAAEaQCAgAEAAAAAQAAKCkAAAAAAAAAYAAAAAEAAABgAAAAAf/Y/9sAQwAIBgYHBgUIBwcHCQkICgwUDQwLCwwZEhMPFB0aHx4dGhwcICQuJyAiLCMcHCg3KSwwMTQ0NB8nOT04MjwuMzQy/9sAQwEJCQkMCwwYDQ0YMiEcITIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIy/8AAEQgAvgEAAwEhAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A9/ooAKw9She91uG3iuZIJYIDPGVPBO7HzDuKARtru2jdjdjnHTNLQAUUAFFACZHrWXKLn/hJLZkEn2XyGDkN8u7PGR60hl+W4ji++4AHqcU9JFdA6kFTyCDmhO4WEklWJC7nCjqSelQQahbXEmyKaN2PICsDmlcdjP1xknu9LsH3AT3G/joQg3EH61iWWqax/wAJHe2w8zUFtQyQAFIlk55Lk45XhflHvimIi1DXNQuNVu9NthcNcrPa5jt1LeUpGZMsB0zWsum2N1r1xaJEJrNR5s0bDKRTZ4Kn+FsckCgDpFUIiqowqjAFLTEFFABketFABTGmiUZaRAN23JYdfT60ARNfWiTxwPcxLLL9xC4y30HerFABRQAUUAIzBVLHoBmuYttW+1eNCEsbxEWwYeZLDtU4cHg+lIZC/iy8Fvav9hQNfv5doQ+QGyQQ/p061r6jeXenXVnKWSS3mkWCSLHIZujKf6UAa9Z93cajFdIltYxzQnG6RrgIV/DBzTBGhWZry2Y0uW5vbR7mK3Bk8uMAtx6ZIoEc3Hcw3MUckHhLWDEyh0bdGuQeRj95W5aaTZX9mst3p00TOMNDdPuYD3wSP1pIZDH4T8Jzzs6aRpk0sTYY+UrFD7+hrSv7i20XR5bgqsNtbRltqgAAeg7UAtzE0nVNRm1O3t9QNnNHeQtKsVuCWtx6OckMCOM4HPHNdDDp9lbSeZb2dvFJj7yRhT+YFCBsw79tRvkMFz4emkQPlXhvUUgjowYMrKfpRZXd7NlLGwsGntv3TC61EvKg9Cyq5/M0IHYy5vEep6dPeL9i02IRsXuJYnuJlDY5ywhAz7ZrprD+1ZWhnnubRrZ03bI4WVuRxyT/AEpgadFAhruscbSOwVVGST0ArJvr29l3QWemyTW80Xy3ayoFGR1xnJ/CgDlNIn8Raff2k2oJeT2zo4jiVc4VV6P/ALWRkH0rpNGnbUtPuZnuybmfkxRtgwccKM9D6n1pWAqWdjr32C9ibUQ98XVVlYHasfoP9vHU+tRah4fvdV0O0sohLpxiuVeVRKHLjPLbvXvTAr6b8PV066tp/wC0pZmiuRM3mKCWCkkAHt15x1rt6ACigAooAa7BEZ26KMmsOzuY9Q8UNc2z74I7Ly2bBHzFwcc+woAv3WjWN3am3kgAj7bOCOc8HtzVmS1hmnimkQM8RyhP8J9aAJqz7nRNMvJzPcWcckp6s2aAL6qERVUYVRgD0FY/irULfTvDl5NclgjoY1CqWJZuAAB70AcjPJrD2DW6DVbeJLNDC7EIqyBR0KHdtxnO41fg1+TUPB14lndJJcQFYnmiczMqMAd5wSSeT+VJDOg8MDboNuvkLEFyo2xlAwB4bB55681Z1vTRq+jXVgXCecmAxGQD15HpTEUdKt7+2n2nRtNsUP8ArZbeTPmfRdo6+54963aAEOcHBAOOCRXO22g6r/wkceq32qWU6xxsiRQWBhPPcuZGJ+nT2oAi0Xw7KtpeWOswpcWrT+bEkhV/mySSCAD6deRXTgAAAdBQAtFACMqupVlDKRggjINCqFUKoAUDAAHSgBajEESzNMIkErDaXC8kemaAJKKACigAooAKKACkwO3egBaKACkZ1XG5gMnAyepoAWq91ZW96IhcRhxFIJUB7MOhoAnwMYwMelMjjhj3LGiL6hQBRcCSigAooAKKACigAooAKKACigAooAKKACigCtfWYvYPL8+aBgcrJE2GBrmLfUL648WQ6Tc3hEdoC5mhG1bl8ZEbehAySB6CkM6XU7m4tdPlmtLZrmcDCRL3P+FZ0Oo6hp93DBrAt/LuDtjnhztV/wC62fXsaOodDTsr6G/jkkg3GNZCgYjhsdSPUf4VgeKLm9W8tI7C5Mb2wN5PGBnzY1wNv4kihgi5okv2/U9T1FXcwl0ghBPylVUNuH13fpSakyXHibTbUu3+jxyXbJ2YAbR+RYGgCTRvElprU7wQRypIkYkYOMcFmX+amtS4mS3geWRgqIpZiewFKT0C2pyL63qut6FPf6RauVV/9GEUg8xyGH31bACkc4znBFaOsx/YrYa9Dm3vY0XzUzxMP7jDueePSiKsgZ0VFUIKKACigAooAKKACigAooAKKACigAooAKzP7CsxbJCvmLtuftO8P8xfdnk+nb6cUAadQ3Vpb31u1vdRLLE3VWoAfDDHbwrFCipGgwqqMACqg0q3GoXV6QWmuIlibccgKM8D0znn6CgCHw9pLaHokOntIJPKZ8MB2LkgfgCB+FVtUsriPW4dVt4Wm/0WS0kRSMgMVYMM9eVA/GgB3h3w5aaFbbo0Ju5UHnyu25mPXGfQEnAq5/Z4aO7iubiW4S5JyrnARcYwuKmQyPRdFh0S3lhhmll8x9xaU5PAAA/ICrdxZxXUsLzDesTb1Q9N3Y/hVCLFFABRQAUUAFFABRQAUUAFFABRQAUUAFFAHA22uNe6hp5ttXvpLiSaENHJAIoZo2ySyqRk/Krcg131JDZ53P8AEU2mqa1CU81LcH7MpGA23CkZ6kljgY9DXaaPfTahZmeWONfnIVo2yrgHqM8j8aEwZoUUxGJpMmoXF5cXUt6r2ZmkjWAxgFNpAGD36Hr61qrd27TGFZ4jKDtKBxkHGcY9cc0DYs1xDbhTNKkYdgil2xlj0H1qrqWp2ul2zXN3IUiUgZ2kkknAAA5JJ7CpkOKH6bqdrqtr9otHLIG2sGQoyt6FWAIPI6+tXKokKKACigAooAKKACigAooAKKACigAooAKKAPHdP8LeJrXxLDeNok5srZWEJW8jE3IUYyzHC/L2Pc16jp9zqF5bzm+05rFgcIhmVywx1yvApDObtvB9rbxgT6QLuSYea0hkCtEyr8q5zySxY5Hc5q3pd14gs9XtdPurNpNPlXK3LsGeP5SSjEcEggDPegDqqrX0P2i0eM3MluDj95G20j8aYjl9M8OxzyJPFf3UsMN1MHSWcujhlIJHbOW6+xqSDwtPpelwWNiyyul6JkupGw6LwWLH+InkfQgdqSG2beu2015pE1vbwxSyyYRfNGVXJxuI746/hVC88PiHw7Y2NmnnvYSwzRCV+XMbhuT74P50AW9Fs54JNQurmMRPeXPmiMNnaoVVGT6/LmtamIKKACigAooAKKACigApCSBxQAisW7U6gbEAxS0CCigAooAqTX3k6hb2rQSlZw22VVyoIGcH04zVoMpJAIJHUZ6UALRQBy2oeMVtJ7xVt18i2mS1M7ygDzmAO3b1IAZST7+1R6B4x0/xfK1kLORFaNiyzEZLLt3Lj23de+DUpjsbVzqWm6IILaTEKspKIkZICjGTwOnI59606oRWv7+30y0a6un2QqQGbGcZOB/OrOaAEzUF7ewafZTXd0/lwQqXdsZwB9KVwLFFMApksscETyyuqRoCzOxwFA7k0AVrDVLLUxL9juFlMTbXAyCM8g4PYjkHoRyM1Ld3K2dpLcukjrEpYrGhdiB6Ack+woAybLxZpd/gwz7leQRwlRnzuQCVA5KgnBOMZB9KZofiu213U7myhgkRoFcsWI/hleLt6lCfpSQ2jey27oMfWmNcwrdR2zOBNIpdU7kDGT+o/Oi4EtFMQUUAFFABRQAUUAcpr16bDXoLa5vGa0v7afEDHaAyKp4YcjjNZ3gDVrZtOuJ5Io7OOdllJku95DGNCV+Y5wCTip6j6HcxyxzRrJE6ujchlOQafVCOOt00Yz+J/wC0vs8lvDqIuWEmDt228Jzj221a8M6r4d1SZhpFqIZIw7gtEEJDNl8f8CPP1FIZV1d9bj8Y20tqlnNElpMPK2sZGj8yHf3xu6Y7VZsLvxHDpKNfW6zagt4kUscajZ5R2gsp46A5J9cjpQBmeNo76+uJLBBdyRu1sVt4Y8rJH5hMxJ6ZCjI57DHWtnS59Tk8V6lHeSSCyRP9CUpgOON5OPQlQPqaAF124kNykK/2vAFGTLZxqyvntzz+lWPFIU+G7pG+64VDnvlgP60AbNQXNytsItySOZJFjURoWwSep9AOpPtTET1jeJtIGs6TJbskky4z9nV1VZD/ALW4EHHXB4PegA8LWM+n+G7K3u2ne5SPEhuFQODk8YQlQB2AJ4xzWhex3MsIS2kiQk4fzFJyuO2CMGgDmITdaTcjR9Gt4BGhVpxBbl0h3HALEyA5OMkDJ7nrWjoPh59Gup5SNO2y7mJt7MxyFmbcSzlyTz2oAfaWF6niGa7ltYUgbO2Rb+Z2Pp+6I2D8KoXekLb+LrK78rUbpXjl5EjbI3MkbDOMALgHg8HGOaAOq3ru27huxnGeaWgAooAKKACigAooArXWnWV88bXdpBO0edhljDbc9cZqAaFpA6aVYj6W6f4UAXYYYreJYoY0jjXhURQAPoBRI6Rxu8hCooJYnsKAOVXWfCOm6Y00YgWCM7ZB5eWUMpbLZ5IKgnJ7Cr3h9dF1Qrr+nWYhmaNrZjt2sFDDKkDjqo/DFLQZqJp9nHqL6gsCC7dPLaXuV44/QflS/b4v7Raxw/mrCJi2PlAJwOfXg/lTDUsg5HFLQIyNd1iXSBZeTbLcNcTtGUMmzCrE8hIJ4zhO/wCYrAg8fW0+jQahc2rRRTXKxFZgYxCrNgFywxuA+Ygfn3pDRLpviLVdcudFltYYIra7t0vXXzc/uWUBlPyn5lZh0K5/AiuwJCjJOAO5piFpM80ABYAVDZ3kF/AZraTfGHeMnBHzIxRh+DKR+FK+oGFc2dl4c1C81qGK4ub7UXEYgVkXewXoCducKhPzE4AOMZINLRfH9pr2qWVtZQEQ3CDJlbZKjmNpMbO6hVHzAkZYYzzhjOwJxUctxFCuXkVeM/McUmwOG0K8uNZ8ZS3kt5CYoJZYoVtGLhl2R4DnaOMhyMnqTXW63qY0jSbi+MZk8lchB/EScAfmaANDeu/ZuG4DJGecUtMQUUAFFABRQAUUAFY3i7I8Ha0QxUixmOR2+Q80Ma3IL7wz4fN1JqF5BGjP5Rcu2FPlFnXj8Tn2q9osWlR2LNo3k/ZZZWkzCcqWPXH5UgMK61u5j1G4iTU7HyYpShX7NK7qeuCV4zzV77BeOH1GXVo7fzIlBkSFQNgyRnf0+8aSQ7k+m6feC4ivH8QS3tuQSsYijCPkcHKjmsqw8Q3uoTRSwtvjnvWhFuLdxthDMu/fjG7jd1xjgDPNMRNrHhed7WBdHuY4LiKbzvOuw85B2shwN3OVZgQfX1rDlttQuLSK6S/0RkivxKIE0yYM9wybQpRpQc4cHnGOD0oA3PDz3dzql2LsxW93auqSpFAF86LZlMk5wAWPAJ5U8mqvxD1KZPDesWFrDHM50yaS4LTeX5MbAqG6HcSd2BxnaeRQwNt9cZfEUGjLZTea4aUyOQq+So5kU87sOUTbwfmz06t1HWbe31W20+PVtKt7l3UPBcyjzXBIACpuByecHnnHBoAp+KXv7Mw3Npe3g3tsMKmJYYwqs7OzGF3HC44zyR05NYGga3qVxq50uxlsVjtpI5roLulGyZt+RJtRSX3EjGfpRYL6HX6uqnU9BJAyL58f+A81Pd9E0OJI2+xWSQo8qLhU2L1ZgO3Xn60xGb4g1Ca60vTX0pZLyG+nCkW0qo0kflu+FYkAZ2AE5zgnHNSaNpKpNJJd2WxAyyWsN1IJ5YCANxDZbAztPU8/hQMTSdC1TT9XmvZtStZI58ebDDaeUDjdz94/MSwye+Kx/F9481vqG67MMVte2lqIMjEm5ondm7/dfj02k0AaFkLhfiDqM891AsZ0+2CoF+8pln24J75xn8K6qgQUUAFFABRQAUUAFZmuaZNrGnTWKXf2eG4ieGb92GLKwwcZ6HGfzoAqa74Xg13TpbOa7uY1kZTlXztA4IHplSyn61Jo+gweGdMu7bTFYxNI00MDdI/lACD2yP1pWHc4KPTPGt3HJqaQT6YlzfR3N1ZQ3GJCAQsgXtyq8fnXQavB4j1Lw9pMywsLqFmkmg2rl5ACsRZTxtz8xHbgjpQgO1RFRFRFCqBgBRgCufbTk0ZQX1ie305rncsARdql33bdwGQpY+vQ46UxG9cQrcW8kLPIiyKVLRuVYZ9COQfcVzb+AtHNr9nia7jX7ULvJuGciUBhvG4nDfMeRzkA9QKAOnwM5xz61k6v4Z0vXJN9/A8m6PypFWVkWVM5CuAQGAJJGc4JOOtAE8ui2M+pWuoSRs11aLthkLtlRgg9+4Y59ePStDFAGLeaE+oavPcXV/dCye1WBLWCZogG3FmfcpDBj8oyCOMg5qmngbSre4jeylurSNTbF4YmUrL9nIMW4urNwFA4YZAoAv6pp2oX15aS293b262kvnRl4DISTG6EEbl4w5PWq114bbUrzTrjUriGf7MHE6JBsSf5laPILHG0qCOTz9aAL8mh2Emnx2PlOsMbmSMrIwdHJJ3Bs5z8x79CR0NSWmmW9nKZU8ySYjb5krl2A44Geg4HTrgUAXaqS6XYTztPNZwySOu1i6A5GCvP4Ej6EigB7WNo8kUjW8ZaIAIdv3QCCB+BAI+lWKACigAooAKKAEyMZzx61kP4gt7WW4F48KRIwEUkcgffnOBtHIPBoAu6bqNtq1hHe2jl4JCQpIx0JB/UVboAyj4i0sX62Rux9oZioj2NkkEA9vUj861aVxmXrmoXNhaw/Y4lluJ5liRW6YwWY47narY98VyVn4z8SXGrQQDw9O9vhBctsxszIYyV56ZBPOSNvuKAO3vdRs9OjWS8uY4FbOC7YzgZP5DmuG12cav4y0UIsl7pLLJBKFCGFnLRsOTkkjbnseOO9MEdnrmoNpOh32oIgdrW2knCHo2xS2P0pNP1UXtw9s0MiTR28Uzkj5fn3cA+o2nP1FLqHQ0aQbstuIIzxgdBTELRQAUUAFFK4CY55NLTAKKACigAooAKKACigDF8L6fcabocdndIyvGSuGlMhI7HcfasXXfDVxLcXaaVYQxwTw2xcxSeSXaOYsUyuDyjMM0ug+pf0e11W1urGBLGOx0u3hkR4fOEhZiVKnPqMN1/vVvW6urTl4ym6QkZfORgc+30pgcze+JNKTxZYsbr5Iba5jkby3wrFocDp/sn8q1NSt7PV47WSS0luoCu+N42K4zjtxSAg1SS0srvQrYSqghut20t9xBDIuSewyQMn1qtJ40tB4hi0u0t2lj80RzXIBCKzDKhTjDHJ55HXvTAZr2nR32uyJfm4WxmsVgDRpuByz+YnAJUkFOR2Fa50fTdRSzuJrHabc7oUcYMZ6ZwO+KBHPeOtIu9XjubZNMkvlnsmgtNrgJBO24GR8ngAFcEAngjvVq0SLStUk1C5sriNJIlaS7ubkGO3XABTG44O4dAMY78UDN+61exsWjW6uFh8xWZWfhSFGTz06c49AT2NXAQyhlIIIyCKBC0UAFISAMmgBAw6Z5p1JAICD0IP0paYENzcx2sDzSsFRBkn0rC0XxZb61rVzY24V4kTzIpkJwyg4Ocj1zjHUUD6HR0UCE5z1paACigAooAKKACigCCGe1u9/lPHJsba4HJU+hqcAAYAwKAOW8Q+JYNHvcy2CT2qPFFczYyULnjgA8AYJ+oqLQte1DUtamtX0IW+nxPIguAvDOjYBHTAx7UhiXvj2DT973FhOIR5pRlyxdY3Cs2AMAdTyenpWr4c18+ILSadrKW0MUgTZLnPKhu4HrjjPTrTCxO/iHSlikkjvY7gROEkFqDOyNzwVTJHT0rzLXdL1nUAjyWUk+kyyqzuqFmJ3zknymTqfMThhgbaARd8LeFL26/e6mhv8W6GyvbxIpAj7EVmABPOFG36HJOa7+yure0v00GNZC9vaJKHboVJZQPr8poAn1TUodJsXu51do0KghACeSB/WrgO5QR3GaAAkDrXP69bJqt4unTRSz24tZJWt45jF5zHCqNwI/2u+OQe1IRzeiaJremagt69jdJMVigVPtQkRY9yFydzHtkDqflFaNzpWo67HHqFpdS2l5/aEis6XDAJAu9BheVJ4VsEYzmmBs+HtKuNGguILmWFleQGNkZvm+UAkhuhJBJAJ5yc81bfWrBdPN6k4lh3mNTEN5dwcFVA6nIPSgCp/aF9fQSTWcCxWrQ+bDdSsPm4B5XqO456YrM8Da3YXmmtYW04/0FREYyPuqvG7dnkH1oGXtO8Rxal4ju7W3uIZLGK0hkWRf+ejSSKRn/AIAKPEPiK2s/C93fW1zmR7aY2zRjdllRjkewx1oEWI9ftlvbSwcSvNKq7pFTKKxUsAT2JAJ/KtGW8tbeRY5rmGN2+6ryAE/QGgCpf69pumT+TeXHlSFN4Gxjke2ByfajSNf03Xo5JNNufPSMgMwRlxkZHUDtQBpUUAZ2jzXNxBNJcyhyJ5EXCbcKrED9BWjQNhXGeKYtPuNVst4uZXS6X7QqM+1Ywjdce+2kwRtaPpFjaXFzqNlJcf6a3mSK7nazYAzg+wAqTSp76aWb7WJQo+6GhCD8DnmgDDbUotL1LxZOVjuZInin+zFwGKrDHnj2wTV/w54vsPEU0ttbxTQzxRrKyyJhWVs8of4hx1oAzYfF2haP4cs3vriN85hZUw7KTngjtnHetq7nbXfCV1JpLFZLm2dYiflYMRjHse1AFLwzaxw3BkCXAla3WJla3ESxBSSAcdW+Y8jI4rc1LTodVsmtLh51if73kzNExHTGVIOPamIZZ2CaPpht7MSyJEp8qOSQseBwoJ7Vw1vJrf8Absl9bw6hcTizgWUSwbNzLIxkjQsAvRhjnHXBoGN1i08TXfhbSoJ7W9mu/ID3KQuod5Q6EKzbgAMbvY/lXTaHDqk+oy3OqRugtw8duJEUMVdt3VSQcKI1+qnrQA9Uc66znRtaA80/6Q2oKYP97y/P+77bPwqC+1ZLLxWgME05FuI9sQBOWLEDkjJwpOBzjtS6gdFbXMV3bRXMD74pVDI3qDXNaTr1np1j5d67o0l9cRx7YmYECfYMkDjll/OmI1fElg+paBd28KbrgxkwENtKyY4IPY1natp80c+jNCLiK2tY5EZbWMMUYhQpxg9AGGQOM0AbWloItNgiFu9usa7FjcgkKOBnFLqVs13pd1bRbQ8sLIuehyMYPtQBy39jajqb6wlxp8dkbywS3t33hhGV3YJ29wW3DHbHeres6FeTwLa2MUO1rB7JZGOBAGwGbHfIA49hQBX0vwteReIW1C+W3J8xJvMiduWWFY9oB7cMcn1FadzpeoXOq/aHg0l4lcbHkjZpAoP5ZoAW60vVLvW4rp7q3FpBnyYgh3AkYLE/3sEgUy30C7025ddNvI4rSV42kR48sNqquFPuF7+tAHQUUAFFABRQAmaXqKAKdvpVhaBhBaRJvzuO3JOeuT1pW0yxYAG1iwI/KGFx8n936UANTSNOjiiiWxtxHEQUXyx8pAI/kTTtO0610qySzs4/LgQkquc4ycmgC3TWbHagEKDkdMUtAGRc+I7G3u2tvKvppFO0m3spZUB7jeqlcjvzxWpDKJ4ElCuocZ2upVh9QelAD6oXOi2F3C8UkJXfL5xeN2R9+MbgykEHBx16cUAWktoY7QWsa+XCqbFVCRgexHSs+Xw5pc62yyWxYW0hkj/eMPmJDEnB+bJAPOeRQBq0UAFFABRQAUUAFFABRQBhaF4hbWLu6t3tjC0ABPzZ65x+nNbtJO6G1ZlIHURZHcLdrreMbSdpXd798frVt13xsu4ruGNw6imI5qzsrmLxjJEdTvpbaKzSTy5JcqXLMDnj0A4revYJ7iDZb3bWsgYHzFUN+GDQMwLfXNSi0TWtSnSGa3s1ka0kUFTOEXJJHQDIwMdqZ4Y+0Q6nPA9zNPG1nDPIZW3YmbO76cbTikB1dQ3N1FaRiSYsFLBRtQtyfYA0xDd0VnFulmIV3zulboWPAyeg7AU3UVtG0+cXwDWu3MgIJGPwoA5nwPNp0Fvd29pbyxebezyR/wCiSIpj3nb8xUDGMY5rUtprm1nubm6GqNAEdyJhDsQLzwEO4k9uvSgDkIpvE+pWd4dGt9RsLeV7idXeOFXLmTKqAzE8gnOQO3Ndhod3qM08sVza3SW6xIUluVVW34wy8Ek9M598dqBm3RQIKKACigAooAKKACigAooAKKAK0Gn2ltMZYYESQjBZepHv61ZoAgktUkvILks4eFWVQGwp3Yzkd+lOuYPtNtJD5kke8Y3xthh9DQBhR+D7WK5kuF1PVfNlADt9qPzY6dql1nxDo+k25t725b5o3DCM7mAGAc46HkD6mge5b0yXTtV0GE2qK9hPDtVCOCpGCCKmsNMs9KiaOzhEasctjknjA/SgRyGu67fSeNrHTbG6toIrcrJM0lwR5m4kFMA4JwO9d3SQ2IyK67XUMPQijAIwRxTEGVXjgUZBFK4C0UwCigBB1paACigAooAKKACigAooAKKAMzTddtNVmkjgEgKMRlkwDjvWnQncbVhrlgjFRuYDgZ6mmQNIIY1uCnnEfMFPGfagQ+QkRsV6gHFctoGj6fqvhzSbq4i8yRAZN56uSTnd6j29qQzegtbTRdOlW1gEcCb5TGg79TgVyWkabdas9vd6jZbTcFnuJTcbllU/dQL6dPpigDXm8KQf2lZXFmYrOO1OQsUQLP6gk9qo+LfEMlhe2EVqlw7Q3iecIsYYFGIQjPPY0wN3QtVfU9Cg1C5ha2Z0LOHAXGO/U8U2x1dNQvnjtr7Tp4kySIJg747ZAPFAHGan4otn12/K3rzW6stvDEt89sBKFyRxyQfXn9a2vC3iJJ9OtEmgliknuZYSsly0zIyngEv83PNIDr6KYgooAKKACigAooAKKACigAooAKKAM+z0a0sZ0lgUqVj8vHHPOcnjJNaFA27kbQxvMkrA70BCnJ70rRRtKkrKC6AhW9M9aBEd5cfZbWSbyJp9o/1cK7mP0FcpYWPiK18HR2dnHFBOkJMYdvnVt2cHt0pDRf8ADNt4hgmuv7emSbeFKMjfLnuAvb+tWbDSdMs9QeG3lmZ4f3gt3lZkiz3UdBQBtVz82g6HeeJPt0jiS+jw/k+dkK2MB9meuOM0xGpY6Xa6crpbB1jbojOSqj0UHoPYVZSKKM5SNFz/AHVAoA5XVdVj8O6g1tZ6RHOJIvNZkPz7ySBxjkADk5GBWXrOv21hqkFwnhtXvGgWVLxrNjtcttOSASqgc5JFK47HTeFb3VdQ0WO51WOBZJCWjMTE7kzxuGBg/StumIKKAKcmoxJqEdmd3mSIXHHGB15qyr7jwOKVyrFa61SxspViubuGGRgCFdwCc8Cn2WoWmowmayuYp4wxQtG2QCOopklmud1TxFPb63b6bp1ul1McNOm/aUUnGeaAOiHTpiigAooAKKACigCsl/aSXBgSdGlHBQHkVZoAgubkwNEqxPI0j7QF7epPtU9AGDdvc3XihbKO4eGOKzM42Hq5YqN3qB6VS0bTfFkOtpc6vqkFxa7WVo4l2j/Z+X19TSGW73xfZWGoSWUtpfmWMZOyHcCPUc9KhtfEVnJJcX0GlaodwAlkaAKAAP8AaYUXCxqaRrMOsxSSQ29zEqEDM8e3d7jnkVysXh2TxJZx3qajPYyNPMZzB1kBPCn24oA6nSreTRfD8MN9dee1rEfMnIxkDJz+VYula/B4p1AxQyvD5cYmRrW8Dhkzj5wPun254pgU9S0e1i124ktvDFvPEIJHeWS0QgyY+XawO45PXg1V8MeDBc3J1XVLGzEU8Hlm0ktRuDZzuB+UAdsbAcdaANXxfqkelaGLDTTJFcGWGGNbdWHlguOMgYXgHgnpW7ba5p13qLWFtcrNcoCZETJ8vBx83pz60AO1DUl09498F3Krf8+9u8uPrtBouftl7Yxvp1ylq7kNuubVmO302FkIP1/KgDk7R/Et9qN5Ii2x+yyNbeaZvJV8ck42SH9a3dITXBfMbyewe02YKwyM8gb67VGPwpWG2Rz6ZY69qOr2Oo2yzQqYeD3G3OPpmtXTNKtdIt3gtFdY2cvhmLYz2Ge1MRh2fia41a6KWItRbvI8MchctIGXqSmPu/jWLrapp/iSylvNVvmuZHVZBA5REUnIwNpGM9cmgDc8X66NO0e5jg883Hkh98SE+WCQNxParHhzxLaa209vbzLK1sFUsM5bjk9PWgRpnUAL0W32S7OTjzRF8g/Go7a5nl1i+gZl8iER7BjnJGTQBoUUAFFAGXZ6RHb3012JpWeR9xy3U4xz7VqUkNkVus6oRcSK7bjgquAB2ohM3lkziPdk48vOMduvemI5X+2mk1yW9tbdSABanzWweuSeAartH4ofXI7l9Wg+xx3wj8hFK7o++eOTSGUZTqviXWdUawmisPskgj8xXffIq9jjp+tQxf2vqGmalocl8XMEYkaWSQlmO7puxnFAzs31I6L4ZjvL8GZool3+SByfbOK4nS/Ft03hH7bpCIk51AxulyvyEuTgcHOKBHUeGtQu/EGj39vqZj85JZLd2hGBjHb860NH0q600bJr4TxKgRFEKocDoSQOTTA1qKBHO3vheW6vHkj1WeCF51uTGsalhIvTDEfd9iD+FXLfQY7bWn1VLmZriYbZ9x4kXHyjA4GPpnnk0AWNQ0uLUfL8ye7hMZyDb3DxZ+u0jP406e1ddKe1hnl3lNgldzvGe+71oA5yDwffKgjn1SGaIuxm32xLXAI4DneAfpg5qr4V8HX/AITm+zWKaetibqSZ5FZlkkVhwCoXHHb5qBk2qWviW3XWbyBNNVbhFIP2mQMgQY4wnU/WrXhObVhdXVrql79qKxxyo3HAYdOg/rSA0tN0y800pAlxC9ohO0tH+8AJJ25/HrWvTEc9q3hubUri68vUGt4LoRmVQm45Tpj0HrVvTtNvLC+uD9pje1mkaYrsw+9sZ/DigCyun7bnz/td0TuzsMny/TGOlSQ2ghvbm5DkmfblcdNoxQBZooAKKAP/2QD/4THoaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdG9yVG9vbD5XaW5kb3dzIFBob3RvIEVkaXRvciAxMC4wLjEwMDExLjE2Mzg0PC94bXA6Q3JlYXRvclRvb2w+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMDktMDNUMTQ6NTg6NTUuMjIxPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICA8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwADAgIDAgIDAwMDBAMDBAUIBQUEBAUKBwcGCAwKDAwLCgsLDQ4SEA0OEQ4LCxAWEBETFBUVFQwPFxgWFBgSFBUU/9sAQwEDBAQFBAUJBQUJFA0LDRQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQU/8AAEQgFWQc6AwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A/VOiiigAooooAKKKKACiiigAooooAKKKKACo/M/e7Mds5qSk2jcD3oAWiiigAooooAKKKKACiiigApKWkoAMcV5N+0r8dtP/AGefhpe+Lb8ecsB2x2+cGVuy5r1gtxX5Y/8ABZb4lXtrD4R8HpLshk3Xc6I/3sdOMVnI1pxTd2ZvgP8A4LTaoPGT/wDCXeCoP+EZmkwrabMTcW656kHhj7ZFfo/8Fvj14L+P3haLXfBusQ6lblQZoAw863Yj7sidVNfGv7JP/BPb4f8Ai79lPSR400dZ9e16E339oxp5dzbBwfLCtk5xwe2a+d/Ffg/x7/wSf+Mlpr2iX3/CV+Bdc/duLgeQLgDkpIAW2uueD3osKy6H7K0Vx/wl+Jem/F74eaH4t0p0a01O3WYKjbtjEcrn1B4rsKtO5GwUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFITgZoAWikznGKWgAooooAKKKKACiiigAooooAKKKKACk60MwWloAaqhelOoooAKKKKACiiigAooooAKKKKACik3D1paACiiigApKWigCGS4EcirtJ3elStypFGKYzLuCbsGsgMjXL5ND0fULtkkZYYmk2wj5jgE4HvXwD8L/8Agqpb698eYvBGq+HprfRrq8GnW14W/eiYuEXcPTJr9E22yRsGAK989K/n7+PVraeGf26r6PQkW3jh8VW8sKRDCq/nqePxotrc1v7rP6CFO9QRTqq6ZI8mn2zSjEjRKW+pAzVqtE7mQUUUUwCiikoAGxgk9qRWDrkVFOxWM80jI2MoQox07VPMVYl5VThs/WlVgehzVKWJHVFZnQ5BPlkjP1xVqMpu2rjIo5g5SWiiiqJCiikPQ0ALRTV+7TqACiiigApsjbEZj0AzTqRvumgCja3YuVdhyAf4uKs+ZgAgZzUaxxsxIXFTRgdqyNHYkoooq+YzCiiiqAKY/UUvme1OoAKKKb5ntU8wDqKKKoAopDyDSIu0VPMA6o5KJI93NRSTCEqDzk4olKxSVwnuIrS2lnkYJFEhd2PQADJNfhb+zjoEv7Q//BQS1vNQDXEC63capNIBkBYmJjz+IWv1N/b7+Kl18Jf2Y/FmpWKh727gNgmeyygox/I18Uf8EW/h/PceKvHPjSYsY4YY9OjYj7xJ3H+lTHUo/WBFEahVGAKiluI4iwz81WWGVI9q+CP2nP8AgpjpXwJ+Ll94Im8H3WppYFDNdbwmSR1UHrilLQI6n3VZyiaNvr0qyFXbxXkn7Ovxr0L45eB7HxJo0ckCXkeXilcEoR2Nem3s5tbVwhw2OD6e9A7GH4k8cWOgtJHdTw20YGDJO4RR9SeKq6Dq41y4tLj7RDdWZ/1clvIHTPbkHFfkT/wUi/a7ufiD49uPBuhTPDpemN5V5JC+BM44I4r7b/4Ja/DfxX4R+Acep+KLuaWPVZPPsLSckmGHt19amzL5kkfZ0c26VlPapqb5a+lLnitznDcPUUtQbA+COKkrPmfYdjE8WeI9M8MaY9/q1/babZpy1xdzLEg7/eYgVb0DXLDxFpNvqGl3kOoWM67ori3kEiOPUMDg18If8Fjtcn034FeHbWG9ktftWqbXWNsb128g/nXXf8EmvEt74g/ZZtory6a5NjfzW0W5slEByB7UjTpY+0ea8i/ae/aA8Pfs3/DC88Ua6yyS8xWVnvCtczY4Ue3TPoK9gr8x/wDgthrEg8K/D7SQf3ctzNOfqABV8pFz6n/Yp/ayg/aw8F6rq6aGugXOnXX2ea2STeCSMg19INnHAzX5x/8ABFqylj+Fnjm7aJ1im1ZQkhU7WxGAcHvX6O0com7n5xf8FD/+CdUfxDhvfiP8NNMK+J0DS6lo9shY3wxktGgBzJ7Ac14B+wh+35r/AMCfEUPw6+KV3dReFIpPs0bahEVn02Qtt2uWwUQHru6c1+zlfE37cn/BOzQP2gtPu/FXhKKHQ/HdvGz/ALtAsV/gE7XAH3j0B96LDuz7D8M+JtJ8X6Pbatomp22q6ZcrviurSVZY3HqGUkGq3jzwrD468F634enuZLSHU7OWzaeLlkEiFNwHtmvxf/Y//bI8V/sY+PJ/h/8AECzuf+EXW6MN5bXIYTWTk43oG/hHX6V+z3gnxtofxE8O2eveHdTt9W0i7UPDdWrh1YemR39qXMFj8xtZ/wCCJd951w+l/Ei2ZWJKLeWLZPoGIJ/SuZvv+CYv7THguMQeGviDFeWUP+qt9P1y4tVA9Ar4Ar9gKKsOZn5EfDT9in9rbT/iXoM+ta3qlpotvfQzXc48TrKPKDqXwNx3cZ4xzX64WsLW9vHEztIY1C+Y5yW46mp6KCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGqu3OO9OoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApglBbb3p9JjnNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAw1+MX7aun3/AMbP+Ciek+Cr1THZx3lrZpk7w0WQzHHHUAiv2db5a/HPR9Ql8ef8FavMkZrkWuvyQqoXG1I4zzUS3RtDZn6/aHpNtoOjWWm2cSwWlpCsEUajAVVGAP0ryr9q/wCAun/tFfBnWvC91bpLfeW0+nyMBmO4VTswe2TgGvZNtG33qzLqflV/wS5+PmrfC/4iat8A/GkctrcCaQ6esxP7qZSd8WMdCBkHNfqtXw3+1h+w9feJPjJ4T+LHw3V7fxRHrFu+qxK4RHgDDe498A8V9wW28QIJPv45qYqw5O5LRRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UANKAkHJGPSnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1kDcmnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA3aPSnUUUAFFFFABRRSUALTSi7t2OfWjdULO29txKqOhFZDsO2gBlI4NfgL+0JajRf29r+OWMBV8V2khU9189DX77SHzoZCrbTjAIr+fb9rbWjH+2Z4h1CWd5GttahcyMeQEdT/Sn1SLXws/oLsZFltYXThGQEfTFWKxvBt9HqfhPRryJt8c9nDIreoKA1sU47EMWiikp8whaQ0xmOetJIxC9cVLnYqwMoYYPI9KOMYHFUpl3fclb8GoZn+WNCS2Ouaz5jXkLTId644FJH99ztw2cD3FU0mmt5VSVt2R3NP8AOlMmBtPbPpVXDlZpUVRXzTMDv+VeCM1O8jR8nkHitOYzcbE9FMBOKM1RA+imZpnDg9etTzDsTUVHg+tAJxRzDsSUhqL69KGJEY2c0uYVgaIPg9KevWomxIpXOKdH8i4PNSUTUVQmvQs3ld6IZvLMgPPNA+Rl7NN8yqEl633dmM8ZpyN8hUvnaKrmH7PuW/MqvHdO1wUMZVB0k7GqtrdB0UJyCTUozkVhzMvkNGm8D5vWq3lyAZ30i3IjUiRxurQy5S7RUCSfuwaZFOH3j0NXzC5S1RUNNk2IN/eouKxO33TVEOJJCCnC80vm7uKIIUEhwOaJPmNEuU/N/wD4LIfFD+y/BHhvwXb4El9P9rfnnC19H/8ABOr4Pr8If2Z/D0T5N5rA/tOcn1k5H6V+bP8AwUO8RSfGf9tSDwnbFmhtbm30ZWXnG+QBj+GTX7W+DvDyeEvCej6LE2+PT7SK1DHvsULn9KqGwpaGvXxh/wAFAv2F7X9o/wAOv4k8M28cPjuxj/d4+UXaD+An19K+0KSqauSnY/B39kf9orxD+xp8Xrjw140tr2y0VrgQ39jLkeQ+7G8DuB1r9Xf2lf2i9C8G/sxa1470XV4Jo7uxK6dcQuCWkdcLj3BNeL/8FOv2P7f4xeAZfHfh+0RPFeixGSfy0+a6twMkHHUgCvyO1D4w+Kdc+Gel/DqWd5NIsboywQnqGJxj86gvc9b/AGFPgPdftOftJWC6zaPe6JZztqesyt91xnIQn1Zu31r9+9O0+20fT7eys4Vt7S3jEcUSDCooGABXy1/wTr/Zvt/gH8C7C5uYseIdeRby9kI5AIyqfgK+htW8baXo7XDX2p2VjDD95rq4SMfqarmIsdJ5gb0oaRI1+8APrXzz4u/bG+Evgoi41L4haU0AJ3xW83mMD6ALmvAPjh/wVQ8AaT4A1CbwLqEOseIGPlw28sTKMHjdk9xS5n2NPZrufoEtxG7FVdWYdQDyKkr4P/4Jqftd6l8fLPX9C8VsG8Rac/2lZEHEkLHgfhX3lT5iJaH5kf8ABa6+k/4RP4f2Kn5ZLmaTb3yAK7T/AIIz3E8n7P3iOKWNljj1ptjEcH5BnH415j/wWu1OH7R8ObFZF+0KJ5iuRuC+uPSvo/8A4JXeED4X/ZP0a5dSkmqXM12wYY6tjNSPofYdflR/wWw1BP7U+HFmGXeI55CuecZ64r9V6/ED/grf8Tj4w/aUTQ4mR7bQLNIAyMGBZjuatTM+2P8Agj9arb/suzSKhUzarMzEjqa+56+Mv+CTVvHF+yTpjoys0l/cMwB6Hd3r7NoAKSlpKAPlz9tr9jfwn+0R8OdYv006Cw8YWNtJc2upW8I82ZkQt5b4HzZxj15r4n/4JD/HHxD4f+J2pfC3U5Jp9IvIpJ7eKZjm3mjOHCg9vWv1l8VajBpHhjV766dY7a2tJZpWcgKFVCTk/QV+O/8AwS50WXxR+2ZrmuWkTDTbGC9n3AZVRJJ8oz2z2qbFrY/Z+iiiqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBrNge9JHu2/N1pWUnFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu4U6k/KloAKKKKACiiigAooooAimcRxszcBRk1+Sv7GNtD4u/4KbeOdaCKY4DfzhcZ2sWC5z68frX6teJpWg0G/lX7yQOw/AGvyb/AOCXN5/aH7ZvxGuJhuuJIbtt3p++IqJG0fhZ+vNFFFWYhSUtFABRRRQAUUUlK6AKWmqu3vmnUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopvPrS9Oc0AB/Km7iu1fvGmxyiRc5FJ/y0+9g1PMOxNRUR3+YCD8vcUk0jLExU8ilzICaiqTTSssbrn5uq1czQpKQNWFopvNHNVcB1JRQ2cGi4iLeWkKlePWnbRt244qFZJEkw+3Zjr3pRcFpMAcVkaWZHfTJpul3M5HyxRtIfwBNfzi/GLV0+Kn7Seu3EW6KLVtfMK/7KtKEr+kC5tku7eWCVd0cilGX1BGDX5q33/BK250z9qbSfFNlcw3vgCTUv7QuLUvsmt2Dbwo9Ruqno7jjZpo/RbwRo6eHfB2iaUn3bKyhtx/wFAv9K2h3oVQqgAYFFUlZGbeotJTMnvxTfMHIzzWdwsEmdpI6jmq7O0kPzjbmms7ru2MWJHTPSq0kjRwhJbgbvcVjKXMbKLJYbdV6HioUm+zSO33xnvTftULL5YlwfY1Vkmht1MDyfe5DE81NzflNL91P+9fHTjNZUc3mXEgWVgM8YNWLcpNAFRtwPFVruG20uNmaTDZ655rRS5h8ps2kiKNhOW75q7uDLgjNYOl3EeoYdGwfat+PpWpz1EFRtMq8ZqSolgCtn731rUxVhHbarbWNETcdanbAU8VTEIZvNVm3f3c8VlLQtalnJ9KZvJxtXimtcKvBpc42fSgBGZ/tGCP3eKZNN8yAHHFSlw2D2xmmbo9y/Lk9qmwD1XbGNx3H1FNWR9zZG5exFEkg4HaobxzbW7bOlUOxXa4G4M8XlYJ5amx3yyDfHJHKD/dNRSXSTAHeCMViXUv9mIJNiCKTkYpXOrlOiMm4Yfg1G2YVYb+SKw7nUo5o4yruZMf6v0qGNrlo5Aaz5kFma8P+oO3/W5p9w88OpJ/d2DNYLSSww9cH1qbTb6VmbLxzHHXNZcyK5GdJGyyOWkfKjkUTTIv7wdT0rIsJpGl8mWTlua2LGKfzH3f6rPFXzomVo6ktp/x7l5OrGriwovQVGv+uNP8yq5jlZJUckYPNLH92nN901e5GzK1Murr+zNPu7yZ90cMbSn6AE/0qaHoc1zXxQmFv8MPFMoHEel3L/lGxpR94tn42fsuL/wuj/go5DrJGbf+27rVD7CPKiv3Cr8Wv+CQdvBqn7UmvX8uPNXS55Ygf9p/8K/aRulaLTQU9xaSlorQzPP/AI6fEjQ/hT8LPEPiHxDcpb6fb2sikOeXYqQFA7k5r+cG5u7mfxXeeIbCxmlsYL83YZYyUQeZuAYgYH41+kH/AAWA+PEHiDVdB+FmkyGWe2mW6u/LOcueFTjv7V9DfsT/ALF2jeFf2WbrQ/Fumw3GoeLoDPfLKnzRKy/IvPQrnNZGm2523wX/AGih+0z+zDqd/wCAXW38XWumtafZCwDRXIjwMexPQ1+dv/Dvv9qX4uapcy+Jma2aZ90k2qaodh57KKg/Z78Ra1+wn+2vJ4R1a6ktfD93qP8AZ95G4+SS3c/uph27jmv22jkWRFdGDowyGU5BHqKvlE3Y/KfwH/wRUv54Vl8X+PUtpc8w6Xb7v/HmrrdS/wCCKfht43+w/EPVIWwdvm20bDPbPFfphRVE3Z8d/sT/ALAf/DJvibWtduPFB8QXeoQC3CrB5aooOc9ea+w6WoL26FlZz3DDKwxtIR9Bmp5Qbufit/wWC8cL4g/aMstDjQ/8SfTUiY+7ndX6r/sq+H4PCv7O3gCxgG2NNJgkP1ZQx/nX4P8A7TPxVl+Ln7SniPxNqh8u2fU/KwozthifaOPoDX6KfET/AIKreAvhx8JdK0X4crNrmvw2MdvG9zCY4YSFAyc9celSWfcvxs+M3h34H/D7UvFHiC+S2tbeImJFYGSaTHyqi9WJOOlfzjfEjxZc/ELxxrfiS5M0s+o38szSTE8BmJVfqB2r6PbTv2kf2+vE2lxanZa1qWkSS7ku5bV7fTYlzyyuVCHA7A19W/tofsI/8IT+yz4W034deFH1rX9HuI31B9NtXmu7piuGYIgLNzWhNj2f/gkiW/4ZQtgQQF1O4AOOvNfa1fL3/BN34c6z8M/2V/D+m+INNu9I1aaea5ms72BoZY9zcBkYAg/UV9Q0EiZozTa8I/an/a08J/s1+Br+/u9Rs7zxDsKWejx3CGd5CPlJjzu2g47UDPM/+CnHx90v4V/s96x4cj1MweJvEkZtLS3t3HmhD99yM5C44z714/8A8Ebfg/daH4H8SfEC+SSNtYkW1tt6EBo0PLA9xmvj/wCE/gL4m/8ABRT4/wAGq+KDqF1oa3Ia/wBRWJ/stlEDnyVbGFJHGOtfuJ4D8C6L8NfCem+G/D1kmn6Rp8QiggTsB3J7k+tBWysdFRRRQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUgCiikZgoJqeZgLRUcUvmrkKy/WpKsAooooAKKKKACiiigAooooAKKjkmEZAxnNSUAFFFJQAtJUbSFVzimu5ZcnjFA7Ml3f5zS/hVNrxV6R7vxqaOTzBnpWd2PlZLuo3U3HvSLllyePatBD91AbNN2j0oAxQBJRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAyPFriPw1qjEZAtpD/wCOmvyP/wCCWF5G37ZXjlWUxyzW96VTr/y2J61+uuu5bRb4MgkPkP8AL0zwa/Kv/glbb2d5+1p8V52t1W6t1ujE2c7VNyVIrOWuxtH4T9Z6KKK0MQooooAKKKKACim7qTcfSo5WA+iiiqugCiiimAUU1mxQrbqBjqKKKBBRRRQAUUUUAFFFFABRRTWbbQAnl/7TU+iigAoopKAFoqIM/qPyqQ1Nxi0VGsm4n2p9UGwtFFFAgooooAKKKKACiiigApKWigCNmCjJNVJNUjJKRhnb6VcaMMvIr4e/bo/ba1n9lXxVpOm6b4KbVhfx+aNRvboxW2c8qpXv9awk3E2pRi9z7YWaJmWMr5b9QrDFLsSbOQc/3s1+SVp/wWi8TwyEz/D3TZj0H/EyI/XbWun/AAWx1WNVU/CyyC99utk/+0qYWP1UkkaGIBCpHqxqKa6niVAId+fvc9K/LMf8FpjcSILr4dsIO8cN+p/pXS6X/wAFoPCu5/tHgHWEXoNtyjAUtexeh+lM2oQwxbwcj/ZpLXUBfJujKj/er84V/wCCyXgSOXevgvVtx6/Ov+NOvP8AgtF4ORSLXwLqbcdTIq0o3QnGPQ/R64upII93y577jgU231RJlLNhB7mvzEk/4LEeF75g03gjWpiPS7QCpv8Ah8X4TdcH4f6swHY3SVNpFcsOp+mkOoGVmwV2Doat+Z5ikA4avzCH/BZ7w78sa/D2+ijzzi6Xj3ruNB/4K7fCmcG41CHWbOT/AJ4pbBh/Oi0iLRPvi4hY7JMcrwTSeY8JyGDe+K+ILH/gr78Iry8eK5tNXtIccO1vkGq+pf8ABYD4T2cMgtrHVL1wDgJBgGq1C7Pu61uhtw8oYtyKtq4bnrX5e3v/AAWc0aOQ/Y/ANxKg+6ZJcEVUX/gtAkLN5XgOR1xxunxVp9wcV0P1QqOTO0kNgV+VNn/wW0uxIftPw5hMXYx3hB/lXJeLv+CzHjnWJJYtB8J6dpcbjA86RpWxVc3kZ8p+vcdxHIOJEf8AGqd9qUVixldlw3yrz3r8Urv/AIKk/GG6t0XT4dItMHJeGGRifxqx/wAPPPjXcRhZtJ0u7UHI/wBDmOPeubkqdja8O5+zLahHuWZphCSOecLUN9uvIo1VgQ/STdz+dfhx4m/4KGfH/wAYXggs9WewiBwtrY6ch/DlCaq6p+1N+1BNaxRS6t4qtEbhGg054z+GFo9mzbnj2P3JbS0s1LGZtuPvyOCa5rVNcskuY7V76KFxxukkQt+TNX4vaa37XvxOwmnn4l6jF6q1zaqP/HgKfN+wn+1H4w1ZLrUfCGvXV2zAfbNS1NSw56lmfNV7Ey9sux+yGoePvDvhm3P9peKLHTo1Gd8t2AfxAbivHfGX7Ynwk8Mwyy3XxC0q/lzzFBfmb8hXwrY/8Eg/jvrV5HJq954dttzASSvqUk7AZ5PTmvoTwn/wRO8KQ2oPiX4g6peXPcabaRwp+BbJq407dQ9sux20f/BUn4LeHUKw6tf3g/6Z2R/wr6c/Z3/aY8EftKeHbjVfBt5NcR2rBLiO4iKPGxHQ5r5U/wCHLPwjUHHi3xdntme3x/6Kr6m/Zj/Zl8M/st+Am8M+HJJb0SztPPf3SKJpmPQMQOg7VpymMpcx67RTqDVmYN9056VUcJGg2AmneZJ5hGOKWVf3YOMt6LWUtTRKwTRrJHnHvSqymMnPFJ5wx04qGaZlQNGoKt7VNwLG5fVaNqVSVH+1HjirHlmmVyjvyqG4/wCPd/Wmc+tRzTfMkdM05R8OnB1WSYAnH3QK8J/bK+MGnfs9/CSXxVcW01wfNWCGGL+8RxXvkJ9TxWZ4y8EaD8RNBn0bxFpdrrOlTj57a6jDoffmnymfPJdT8wPh1/wV00W1iWPxD4ZvYpMf6y2mBFdZD/wV68C2/n7PD2rM2flHH+NfS+uf8E2f2etekLy+ALa1Y/8APnM8P/oJFYY/4JV/s4jr4Ouz/wBxa5/+Lp8kRe0kfP2lf8FevBE9xcPq3hbVE3dNpH+NWrz/AIK4fDprQLb+H9fLLyMFR/WveB/wSr/Zu7+CrtvrrV5/8cp6/wDBK/8AZsX/AJkW4b661e//AB2p9nEr2rPjjxZ/wVwgvdRil0zwZNcICM/brrDY9sd6/Sv9mv4nL8Y/g7oPitdNuNJF9GW+z3Em9hz1z6V5J/w67/Ztx/yT9s+v9rXn/wAdr6J+HvgDRfhf4R07wz4dtTZ6RYR+XBCXL7R9Sc0/ZxIlPmOgpu35s1LRVcqIuMops33fwqrH+64rKTsVGNyWTfuH1qHV9Pj1nSb6wlGYrqF4GB9GUqf505Zv31WlPzGiKSHqfgn8MfFVx+xh+29N9sgaCwsdVks7hfW2kbAP0AIr949L1O21vT7a/s5VntbiNZYpEOQysMg1+af/AAVQ/Y41rxhqEHxQ8Gaabue3h26pDB98gdHA749q479hr/gpBN4Oh034e/Ex2t7GALBZ37oQyjoFbNUD94/Wmo7lnW3lMYy4QlQPXHFc94d8daN4mtkutL1C3vbWRA6yRSqev40XnxH8L6dcm2uvEGm283QxyXUan8ia1J5Wfk38Cf2WfFnxz/bg8Q+JPGOi3lv4d0zV5b24kvIyglKP+7VSRzyB0r9hVRY1VEXCDoKS1nhuYVlt3WSJxlXQ5BHqDU1TyhJ8x+OX/BZSzg0/46eE761CpfS6Uxdh1+V/lNfpP+x98RG+Kn7NvgTxA5Zp5dOjhmZhyXjGwn9K8y/bc/YN079rSTR9Ug1dtD17TgYvP27lkiP8JHrXu3wJ+FVr8E/hP4c8F2konj0m2ELTAY8xsklsfU1Qrne0UUUCCuC+PPihPBXwY8a627+WLLSriQMOoOwgfqa72vAP29rqS0/ZE+JskTbX/smQD8cUAfi/+x7+ze/7XHxkk8N3mpy6VF9nlv7q+jTe+c54B9Sa/Un4Sf8ABKD4N/Dq6jvdZhvPGV9GwcHVHHlBgcg7FAH518p/8EWfC9xcfFfxlrjxSCC000W4lKnbuZxxnpn2r9gqmxXMUdL0iy0OxistOtIbGziG2OC3jCIo9AB0q3T6KokKKKKAPNfj94H8b/EL4d3mj+AfGh8Ca/KRs1QW4lwvdfVfqOa+E9D/AOCQfiHxj4l/tr4sfFu48RTlg0i20Mk8kozyDJMwK59hX6bUUDucZ8KvhF4U+CvhG18N+ENIh0nS7cYCxr88h/vO3Vj7muwp9FAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKTcKG+6aqzS8qPun0oKSuWtw257UAg9KbIW2fKMmlQFRzQSOoopnzUAPpGYKMnpS1Gzbmx2oAkoopKADcOuaNwppjG3FM8pvLAzzWd5ASbxSeYpOM800x+lQw2hSctjj60+YuyLdFFFWQNLgZJNMW5RwCp3A9xXhP7WHjj4rfD3wVFr/wAMdCtvENxZS+ZfWMwy7Q99g7mvGP2dv+Clngf4o6iNF8aQt4H8TxNsljucrBu9Cx6Go5mXyn2/5i4zTFuY3DYPQVnrqMGpW8M9tMs0E67opIzkSD1B7037N5Mg+YnPYVPMyuVDob8GZvn+XtS/2iysoKkZ9apXDR2ymZImkRcltmPlx61Ws/EVhrUoW3lWVl6qjKSPyNHMzX3TpPO+UEZI9qk8we9VrOaKaH9ywcDipRHzT5mYWRNkU1pAqkmnbajeENR7xBFHdGXkDH1pzT4GRlh6inbUUHjbXmHxG/aI+Hfwz8VaD4U8ReIodO1rWpVis7UAsxJ4BbH3QTxzWFmXZHpK3xdioU59abbiVZGZ+V7Cp7e38tBkDd3NPK4rWKb3D3egRyBl+6V+tP3U2mJMkmdjq3+6c1sSS7qN1Rt8qkk8UK27tUczHYlorD8ZeNNE+H/h2713xDqMOlaVarvmuLhgqqP6mvOPgr+1p8Nv2gtY1XTvA+syavLpqB52Fu6Lg+mRzVknsdFFJQAm4UnmYbG3j1qLcXUtjaBXgP7U37ZHg39l/wAMzy6pc/bvEU0ZNlpEDAyyMRwT6AH1rO7Lsdv8cP2ivAv7Pnh86r4x1eGx3AmC2zmWYgdFX+tRfs5ftCaH+0p8OY/GGg2l1Y2TzvB5N1jeCp65HUGvx58C/Cf4wf8ABSb4sXfiLU7h7bRllBmvrkMLS3jzzHEO5x6V+0nwh+FOi/Bf4f6T4R0CLytO0+LYGIw0jd2b3NaCaR2m6jd2703adxOeKj2vvzjigLHzH+2Z+3Fof7JK6Na3ug3XiDUdUVnjt7e4EOxV4ySVNdh+yz8frX9pb4VxeLdNtnsfMlaKSylkDtER6sAM/lXx/wD8FqPDlufCHgLXguLy3u5LZSOpVhn+ld3/AMEcbCWH9nbWbqRiUn1Z/LU9FULQHM0fZfjDxhovwz8I3/iTxLqEen6PZR+ZPcSDhBVH4V/GLwV8YtHGpeDfEVnrtr/F5DEMv1U8iviT/gsl4+8Q+H/hn4Z8PWTCDQNYuWW+kHJYqMquPSvhD9mjRfjT8M/Ctz8YvhzDNdaFp115F/b28pJIHJzGO2PypWQczP6BMV8C/wDBQ7/goSfgT5vgLwHNHN40mjzd32cjT0I7AjlyPcYrR+Dn/BWb4YeMfCdxc+L/ADfC2t2sRaS1IMySEDorADkn2r4R/Z38Br+2/wDtuX2r6pBc3Ph6bUJdUvP9i3Rsxxk++AKZJi+GL79r74qaONd0a7+Ims6S6mQXsFzKkRAGSQ2efwrtv2TP+CiHxF+CvxIt9B+Iep6p4i8MXV0tte2+syPJd2TMQN6ljkYPUV+2em6ZZ6PYw2Vhaw2dnCuyOCBAiIvoAOAK/Hv/AILJfD/SPC/xa8Ja5pVlDZXusWMz3bwx7TI6MuGOO/NA7s/YbT7+DVLG3vLWRZra4jWWORTkMpGQfyqxXjH7GviOfxX+y/8ADnUrmIwzyaVGjKZN5OwlM5wOu3Nez0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKbtPy89KfRQBi+MJJYfC+qPEVWVbaQgscD7p71+T/8AwSmvvs/7YHxMtmYM9xb3R6+lxur9VPiTHdy+BNdSxljhujZyBHkTcAdp7ZFfk9/wSZ0+4X9rbxybgq00FhdGR8clvP2n9ay62NPsn7D0UUVqZhRSbqaXoAfRUUjyD7qqR7morPUIrxpVQ5MZ2t9aV0OxMTjNRqxYb1yQf4aQxbW3F+PepVYMMjpWXMyiSms3YfepGb5c186/tJftmfDn9n24g03xJfXMWqTDckNtHuYD1NHWwlFvY+i13Y+bGfanVwXwR+LPh/41fDvTPFPhq9a/026BUO4w6sOqsPUV3tap3JMDxbrkXhfQr3VbqYpb2sZlbA7AZP8AKuS+Bvx+8H/H/wAKrrnhTUo7qLcUkt2YebGR6rXb+IPDtv4k0u5sLwl7a4jaNkwOhBH9a/Ef4seF/iX/AME6f2gJNU8Pm6h8K3Fz5llMS32W4jJ5R8d8VHvXua3jy2P3Nor5t/ZJ/be8I/tUaS8dqo0bxHbj9/pczjJ9SnqK+kc1adzNqwtFFFMQUUUUAFFFFABSMu6looAKKaWNQySSZQJjJ65qeZDsWKQ9DUFxO0ceRgVSbftkYSGRWGVANO5Si2WofOaQlnTZ2CjmrEjbVqpBGLWHcE5PULUktwvALLzU2G1dhb43MQcg1ZXpWZa3Ijd1I+UdMVoB84weKtajnFpklFFFBkFFFFABRRRQAUUUUAFFFFABXJfEL4TeDvixp8Nj4x8N6b4js4X3xw6hAJAreozXW0lJpPcNeh4Prn7CPwC8RWYtbz4XaIIR0+yrJbt/31Gyn9a5lf8Agmb+zWv/ADTSP8dZ1E/+3FfT9FA7nzCv/BM/9mleR8L7b/waX/8A8fqKb/gmX+zfK2U+HUUI9I9Su/6ymvqL8aRV28DgfSlzCPle6/4Ji/s8XC4TwXLbn1j1G4/q5p0f/BMj9nlLXyf+ELdmxjzWv593/oWP0r6mzRmqsPU+TLb/AIJd/s92y4/4RGeU/wB6S+kz+hFZ+tf8Epf2ftYxs0LU9OH/AE5aiy/zBr7EaozKisFLAMegpcpV2z4oH/BH/wDZ+3EmDxKfb+1v/sKeP+CQf7Py5ItvEm71Orn/AOIr7XGaj87dIVVc46mlzEI+I/8Ahz/8Cv4m8Qt9dRP+FWof+CQ/wBj62evP9dUcf0r7YpKodz5F0f8A4JWfs86O+4eGr+89rzUpJBXT2v8AwTp/Z9tMY+HtjLj/AJ6szfzNfSlFAHgtv+wj8AIeR8KvDch9ZLNWrpfD/wCyn8HvCtwlxpHw28N6fOn3ZIdPjBH6V6rRQBkxeEdDgULHo9gijoFtkH9KmXw/pi/d061H0gX/AAq/RSsBUXRtPjOVsbZT7QqP6VN9jg/54R/98CpqKYhqqq/dUD6CnUUUAFFFFABRRRQAUlLTFXZ1OaAI5F/dkjqKzobyaZH3QlBV2aRFVyT0rNh1RLiQhCyezCsjojG4SaknnJHtNSf2ioV/QVnzQINx2YIfruqnJqItLWZ3ZTxhfepsa2Q++8TQ2d4saM7GTpxUkOssi+WfMMnevCPi58fvB/wx0uS/v/EVhb6hCnyWrSgyflXyZqX/AAVb0W08Q2xgs7q6hTiW4VeD+FLUeh+nUmZLUGMk1Wt4g02zcSR718x/AX9vT4a/Fq+tdPt9eXTL+VseTqBCbj6CvrHZHIEkiVXj/vJVk3LcanywD1p6/dpdnvRH0rU5Lj6KKKBBRRRQAUUUUAFFIvSq80wjqeYaVx00g6VnTTZPlxUkkKTTZ8zJpZIaxkrnXGKRLCXA60q3LRq7t61F89Z0li8s26WTMXasyuVM6GGQTJmvlj9pf/gnb8Of2h7yTWFjfwz4lfltRsFx5h/21719N2syRLgVPFMzdxW1zn5WflXL/wAEi/iz4SSSLwj8Xbe1tGOfLWW5tv0Tiu1+D/8AwSINp4kGv/FPxf8A8JLcK4f7Pbb33kHPzM/Jr9Kd1V3vlXpzV8xPvMbpOl22iabbafZQpbWdrGsUMSDAVVGAKuVD9oHqKbJI2Mg8UcxPKyfNG4Dqaq+dynNK7Pt+Uq31FHMPlLOR60bh61TkuhCUDMAD14p3nqVygwPXFWLlLRYDvXOePPAekfEvwbqvhnXIPtGl6lA1vPHnqp/rWzJ++UMpwBzk09SzdOB7igLHlX7O/wCzH4L/AGY/Dt5pPhCCZIruXzZ5rh98jntk165mm1R+1kyMv8C9W7UCSuX96+oo8xScbhn0rJjvogsmZVH4imWupW8kLs12gjH8RIBoL5V3NrNGR61lTa3p1ja/brjUoYbT/npLIqp+ZrKn+J3hG3k2y+JdLjPo15GP5mgix1WR601pUVcl1A9Sa4y8+M3gCwVjP418PRADJ3apAOP++683k/bc+CcM0yTfErwuFXhR/bFt/wDF1HMPlPe1lRlyHUj1Bp24eteFWP7afwNuJBBD8T/DbsxwMarAf5NXzV+0p/wVS0r4NfFL/hGvD2l2PjDS4Y0aa+tbtWCMeoBUkZAo5h8p+hdFcZ8Hvijonxm+G+h+MPD05uNL1KASIW+8rDhlb3BBBrs6sgKKKKACiiigAooooAKKKKACiiigAooooAQ1WELNNuZcDtVqigadhKWiigQUUUUAFJtHpS0UAFFFFABRRRQAnPpRz6Um4HpzRuqeUB1JS0jMF60uYCGWSOOGR5SFiUEuz9MY5P0r8y/23/2KfC/xq0/UPiN8FZ7HUfEdm5k1TTtNnVxOO7ADowr9APjdoeteJvhF4t0zw3dix1u602aO0nI+65Q4r8gf+CZvxjl+CP7SFx4W8Q/aI49fP9nTxSkjybkHjcD0Ge9SaI77/gn/APt0a34G8R2nwq+JEzppYPkWt1fErLZMOiNntX6t6fqEWoAXUTh9oyy55A9fpXwh/wAFH/2EY/iDo9x8T/ANmLbxRpsZuLyytkCm7VedwA/jGK+R/Bn/AAU48YeE/hfc+G7rT/tGvpbG0g1aSQhgOQSw9RRYnmZ9A/8ABRz9ve+8N6rP8NPhvqKpMUxqWo2nLBm/5ZqR3r4S8G/G740/Au+g1iG/1zTLeY4V9SjlEUvsCwr6t/4Js/sSX/xY8UJ8WfiBFJLodvcedZW10MnUJuu9gRygPfvX3T/wUG+CunfFP9l/xZEljH/aGj2zanZGJACHjBJAwO4zxQK52/7I/wAXI/jh8BvDXiz92Ly6i23aRn7sqnDCvZNtfl7/AMEVfHlzPa+O/B8txJLawRw6lbo3RMnY/wBOSK/USr5UFwpobcKdXF/GD4qaL8Fvh3rPi/XpvK07TYWlZVxukb+FVBIyScDrVCOZ/aU/aA8O/s4/DLU/E+uXqQzrCy2Nsu1pZ5sfKFQkbucZr8l/2Pfh/wCOv21P2rLbx74pluL3S9Ou1v8AUb9VKQoV5WGPjAOQOBXC/ED4ifEX/got+0FpmnQRlFnnENnpuWNvYxZ+ZnODg45ziv2x/Z5+A+gfs5/DDTPBugKJIrVd094yBZLmU9XbHelYd2elUEUtFMR5H+094K8eeO/hLq2l/DvxL/wjPiKSM+XcbfvjHKbgCVJ6ZA71+MU3i39qD9kfVhdardeJtAjLgN/aO6e2k56ZORzX78Vl+JvCuj+MtJm0zXNNttVsJgVe3uow6nIx3oHc+Df2Of8Agp9ZfGzWrbwd44s7fRPEM4xb3qOFt7g+nJ4avvTXde0/wzo11qupXcVpYW0ZllnkYBQoGetfkn+3T/wTdn+D73HxJ+FHmroVm32m40sMWksiDndGf7o+ua+cviF+3j8Uvix8Jbb4datdrNa+YqyXceRNNg8KaVkFz0D9t79sHX/2v/iNbeD/AAUl4/hKCby7KygB36hJn/WEDt6Zr9JP2Af2TYf2afhbFNqK7vFutRpcai2T+7yARH06jvXlf/BOT9gzT/hPoOmfEjxbD9p8XX8HnWtpIo2WKN04/vEV990xC0jEKpLHAxyTRu49K/Nb/gpH/wAFBJ/AtxcfDP4d30cmrSxtFqmoW7Za2J/5ZoR/FQB6D+2l/wAFJfD3wRs7jw34FuLfXvGZYwuykNDZH1f1PsK+QP2Y/wBjv4ifto/EgfEL4pS3kXhqeUXMt5dblkuhniOIfwj+ldf+wT/wTlb4qx23xH+KK3H9jvMLiy0uUnzL05zvlJ52/wA6/W/TdMtNFsILKxto7S0gUJHDCoVUUdgBSsh3MnwV4F0H4deH7bRPDel2+kaXbrtjt7ZAqj39zW2zBVyaUsF6nFBAdcdqYCr8y5r5x/aL/b0+GX7NWvroPiKe8vdcaMSmysYt5VT0yc8V9Hqu1QK/HH9rj9g741fFP9qjxJqGk6b/AGpp2qSC4ttSeXbFFFjHlknuKBHG/wDBQb9ujw3+1ZpXhfTPDGlX9hBpc73Fw18VG/IwAAK9I/Yj/wCCjHw0/Zt+B1v4R1zSdZutUinkmeSziQo5boMlhXjH7SH/AATr179mP4I2fjjxF4htbzUZbxLeXTbWM7YwwOPnJ5PHpXqP7E//AATI8MftIfB218d+KvFGs6b9ruJI4LPTViUbUIBLF1bOfbFAHnf7ZP7bmqftoJp2i6H4PmsdN0uWS6ESN9qldQPvthRtGOa+pv8Agi7q8OpfDvx9oE7LNHFdxymBvmVldSDkfp+NfTPw1/YN+GnwT8G+JtP8IadJHqmr6fLZvqd23nTgMpxgnpz6V+TX7P37Rnin9gX4oeONH/sgalcMHsJbOZ/JxIp+SXkHIHBx+tAHp/8AwVc+Hvwi+HfxC0qy8EWUel+LZkM2qWNhhbdEP3SUxgMfQYrjP2F/2sn/AGNvFl4nibwjcSaV4gjjaS4WIx3CxDo0YI+cd+orT/Y3+COu/tvftLah4x8ZB7/Q7e7/ALQ1e4+6skvVIk9s4GPSv1d/aI/ZB+Hf7R/hFNH1/SIrS7tYvL0/UrJFjmtPQKQPu/7PSgDovgf+0Z4C/aI0OXU/BOtx6kkLbZrdhsmiP+0h5x71+c3/AAWz2/8ACV/Dcggt9hvAw7j5kxXzn8Qvhf8AGP8A4Jx/FhdY0e4lisySLXVreNmtbpP7si54+hNcP8Vvjd49/bX+LHh+XX0hutWlaOws7PS7Zo49rMN+FLH19aAP2Y/4J2/bh+x78PF1CFoJltXCBjklPMYqfxBr6Rrm/h34Uh8BeA/D3hy3RUh0qwhtBsGAdiBScdskE/jXSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJmmiTnGDnGT6UAPoqtNfw26u0jqgXrzzWPqnxA8OaLGz3mtWUKr13Tr/jU8y7lKLeyIfHkc0ng/V/nAH2dyCq84weOtflZ/wSkDL+2F8Sckk/Ybzd9ftYr9DPGf7V3wp0/Rb9ZPGekyt5TIUW4B6ivyV/ZD/an8H/sz/tN+M/E+rrdapoOrLcW8VzYoGKq8wlD4zz6frWSa5rl2ajZn7rnPYUtfMHwN/wCCg/ws+OnjC18LaJqc39t3eTb28lvIocAZPLKMGvpzzPatrkcrQ6vmr9qP9tbwf+zhHDbahdLc6lIwDW0B3SIPXFfSuOMV+CX7cWm/8Jf+3Br2jRebum1G3tArPuA3YyQD061nK5UT638D/tZ/H79rrx4+lfDKzHhXwmu7drlza7wQPc4ANfOviv8Aaa/aG/ZP/aBmi8Z69qWpRQ3Hz290oFvexZ5ZcDHT0r9kvhT8LdA+DfgbTPCnhy1FtpthGEX+857sx7k1wf7Uf7KfhP8Aal8Dy6JriCx1KMZstXhiDTWze2cZHtRyD5/I6D4K/HDwv8fvh7ZeKPD1z51tcJuktmI86Fh1Vlr0JldV+Vs/hX4Y+JvDPxk/4JpfFi2msr2SbR5v9Xcruazu0zyrDopr9Nv2Tf29PA/7T1mbJCPD/iiBV87TLpwA7H/nkx+8Kkk928eeOrLwD4W1HWtRljgtrSMsWkbGTX4JeP7nxZ+2p+1FeWekBtQvtUvGisxn5I4Afve3FfXP/BXL9o2T+3tO+GuhXMsUkKCfUJIZOGDdF4r2L/gl3+x2nwl8HxfEjxBGsniPXLcNZxso/wBGt2GfruIoWruW3ZaH1Z+zj8FdN/Z9+Euh+DtPVC9pEpup14E0xHzv+deo03aKdWkU0YhXE/Fv4O+Fvjd4Nu/DPizTItR02ccblG6JuzKexFdtRVgfh1+0x+yP8RP2FfiEnjT4fXuoTeGA2+21W2G6S16fLNgYx79K+6/2C/8AgoFp37Qmkx+GPGN3a6f48t/lHREvVH8S8/e9q+x/EPhzTfFWi3mk6raRXun3kbRzQTKGVlIwcg1+GH7bn7Lt/wDsY/F7Tda8K3FxH4evpvtGl3O/EkMi8mLIxwPzxUS0Lj725+8Jz/jS15n+zh8SJfi38DfBviy4MRu9T0+OW4WHOxZMYYDJJ4I7mvS81SdyWrC0UUUxBRRRQAUUUUAQqzlmyuB25pJANysc5FSKq8kUmD6VHKyror3GTGwZSR2xXAeIvih4d8N6klre6xa6fcIMNDcSqhH5mvR1XcOa/Nb9rD/gmn8TfjV8XtY8W6B4zso7G+bdHZ3c0iGL2GBionGUtjWM1Hc+2r743eDrO182XxVpVuzcYa7Uiq1r8VvBd1EHXxhpE5UcbL1R/Wvyu8Sf8El/j1Z2m6DU9N1kj/lmuoMG/wDHq5mP/gll+0gqjbp1nCPQauo/rS9m+4/arsfqlrH7WXw08H3Swap4u0u2Mhx+8nUnJ+ma9q8O6pZa9pNrqOn3cV7ZzrvingcOjA+hFfihpf8AwSb+POrahGt7Dp9nFkBppr0Pgd6/XP8AZn+B6fs8fB/R/BK6rPrLWW53u5zyWY5IUdl9BWkU0KdTm2PUqWiirMAooooAKKKKACiiigAooooAKKKSgBm4UyO4jkOFbJrD8beLtP8AA/h+51XVbyGwsrdd0lzcOqIPxNfM11/wUU+D1q2bbxppkv8AwI1nKol0N4w5lc+s5boQ/ebr0p3n/u1b1r5RuP8Agod8GpbVbmfxjpwK8iNWJNcJ4k/4K8fB3RVEdjb6rrMnpbW+F/M1HMHIfcktwY1wp3N71WtdUEzuPMBx/e4r8z/EP/BZrQJdRiNh4G1XyR18yeMZ/CnXf/BZXw7Lny/BF8M/7aii8irKx+mtxcTMR5AVl9Say7uQTMskZxMn3sdK/LXxF/wWOlktVg0LwZNBJ3+03Ix+lYyf8Fi/GUcYSPwPo5Q9WN0xz+OKLyHG0T9dbHU47pAoLbsfxDmp4LVIizKTluTz1r8iof8AgsZ4gk1C3mvPBltFGPvra3WA35iu1m/4LLWQjKx+Er8P7yIKd32IcV0P0+m1C3t5BG8gDn+HvU+6vxU8df8ABWv4ka/q0Vz4e0iw0mGNuftEfnM3sa/Sf9h/4++J/wBo74Mp4q8VaKmj3/2uSBPKQrHOi4w6g/XFaKV+hLirH0RRSUtUZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSHpS0UAZd3CZJ4yvAXr71FNDGuSHAf0FaUzKqnAGfpWTagNITIBn6VkdUGyt9laSHLS7PZh1r5N/bK/ai0r4DWLRyPuvJExDZRuN2fevYf2mvjbp3wZ+HeoeIbm52yQQ/Kn+12r8ZfAvg/x9+35+0MI2aeZbibfd3HLQ2Nvnv6cfrQNy5RPh/8Ffih+3Z8TtU1DSrXEckpaa9uGb7Lbf7Ib+lfaXhT/ginpi6SR4h+IFwdQYdNOtgIgf8AgXJr9CPg58HfDfwN8DWPhbwxZJaWFsuCwUB5W/vMR1NdvWpzczPwF/ap/YV8e/sl3EOtyXA1jw95gEOsWmUMTZ4DDsa+9f8Agmb+2hdfGexk+H3iV/8AieafbeZb3RPMyjr+NfbfxM+HehfFbwTqnhjxFYRajpd9C0ckMoyOnBHoQa/CD4K6XqPwB/bs8OaCbmW2OmeLItPkKNgSQeftwfUEYqLDu2f0E02PpT6KsgKKKKACiiigAooooAQfdrM1zULfSdNuL25ZUhiQsWboBWpXjf7V3wRv/j58EfEng/TdQGn6heRBraRvu715APsazsyk7HKaZ+2R8K3upLUeO/Dz3cb4MMOoR13ej/GXQNftvtcWoWk9senlTV+N+p/8Erv2i7OZgPBNvfgniS11uyA/8eYGr+nf8E7f2qtMt/stn4YvLO3HPlx+IrQD9JKOU29qux+yNx4605Y4n+2wRNL/AMsfOrW03XIbiDlhj61+MM37Bv7WJKyPpWuMw5/5GWMkf+RKlb9mv9tDTbfEcHjJh6R6yW/TfWPKy/aLsfs3ea1Y2bRjzV/OlOq2lrJuLKF9Sa/FAfBj9s64QSf2f42+pnb/ABrZ/wCGef21tYtRDcReKli/uS3u3+tXZi9oux+zM3i2y2h0nXHfkUy38Q6bcTFEuEAH+0K/GX/hjP8Aa9k4Nv4j5/va83/xVWI/2Ef2tW6HWF/3vELf/FVrymftF2P1x8UfFnwr4VlhjuddsojI/O+dBj9aoeKf2jPhx4P0Vr2/8ZaTbxH+IXaN+gNfk9df8Ev/ANpPxM+/U7O0lf8Av3evK5rc0T/gjv8AGHVbqIa1rui2Vrn5mNw0zAfSjlD2nkffurf8FEPgPo+Qvjywmb0jDHP6V5V4i/4K6fCrRzJBbxX2oEcBoIcD9a4G3/4IoaGMfaPiNfyf7lmgrttC/wCCNXwosY1Oo65reoy55O9VFHKRzHnGt/8ABYnwrI/+i+DL1yOR5k2KxNV/4LOSTxeXa+AlQD+9c19kaB/wTh+AWg2qwr4It7wjrJdSM7H862V/YF/Z/Xp8MND/ABg/+vVC5j4Duf8AgtL4nls2gj8B6ap6ZaZiPyrJk/4LMfENUxb+EvD8B/2vMP8AWv0Y/wCGD/gF/wBEv0D/AMBhSf8ADB3wC/6Jd4fP1tRQFz8vvEP/AAVy+MetHEEOi6b/ANc4WP8AWuUT/gpf8ftUWeG11tJDIfuwWu5vwwK/afwf8Dfhx8NbMQeH/B2h6ND0/cWca5/HHNdbF4d0mPmPTLJPdbdB/SgfMfhbbftS/tWXyh7b/hJZ1PRodFmYfpHUt94p/bK+JkbB9O8eNH/saXNAD+OwV+7CWcEa4SCNR6KgFUtd17SPBujXGp6vf2ej6XbjdNdXkqwxRj1ZmIA/Ggk/Dux/ZP8A2uviFELO70XxY8B5K6lrK28f4h3Fdf4V/wCCQ3xy8T5Ovah4f0ADobu/luW/KMEfrX7A+B/ip4Q+JVsbjwv4l0vXox1/s+8jnx9djGuqoHzH5CR/8ETPHUjK03xL0FT322dwx/U1vQ/8ESdVX5n+KdsG/wBnS2P83r9XaKnlDmPykb/giTqWdw+KUDN/2DGX/wBnrG8Rf8EUPFdtp80ukfEHTNQvM5SC4tHjDf8AA8nmv10oo5Q5jzr9nn4TwfA/4M+FPBUJV30uySOeROjzHmRh9WJr0WiiqJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKAFpD0NAIPSloArqnlxnaffmqyrLIm5W3D2Nfn7/wUX/b28TfBPXp/h34Q0x7TU5rVJn1qQHagbsg7mvibRv+Cjn7QGmnbHrq3K9v9EJqOZmqP3lt5GWFRJ9/HNZfibxfo/hHR59T1q/h0ywhyXnuWCLx9a/FJv8Agop+01fKDGlwQf8AnnpT/wCFP1uP9rb9sy207SNQ0TVpdEmYMJXtzawY9WY4qLMVkfsr8N/il4Y+LmhnWfCesWuuaXvMZntX3BW9D6GvyD/4Ke/CqX4H/tPaT460NBaWuuFLtTGcbbhD835gA1+lv7Gv7KNj+yf8OZdCh1OXVdQv5Fub6ZuI/NxjCDsK+Zf+C0fh03fwm8EaukSlrfWPs5kPUb42I/D5a05URc+xP+F2aHpv7Odp8SNZuI4tKk0OO/mZjwxaIEp7ktxX4JaJ8GPHv7R2t+MPE/gjwdcX2nQ3VxfTR2YGyBXcsIxkjOAeg9K9h+IP7VOs/F74D/Dv4EeEIZ7hUjitb5th3yyqfuqO6jOc1+uv7I/7Odl+zX8FdL8I4huNSYGbUriNRiWZuoz3A6CnYR8d/wDBPv8A4KLeG5PDuhfC7xwsOgXmnxLZWF/jZDKq8ASE/dav0d1y0tte8OX1s4S4tbu2dD3VlZSPywa/Kr/gpF+wBF4NXUPiv8PLd1s3m87VtJhX/U5/5axADgZ6j3r0n/gmL+29cfEmA/CzxteRpqen2YGl3czbWuEXhkYk/eApcqA8W/4JXapF4B/bG8beEzJsiubW9sIl9TDPuH6LX7EV+K/7Nenp4Y/4KmXljbOTEPEGpqCDkMjbyOe/Wv2nzVARXl5Bp9rLc3UyW9vEpeSWRgqqo5JJr8Wv24P2kNZ/bK+OemfDX4fXM2o+F4btbOygtztTULknBkPPKDsf0r2H/gqd+2deW+pS/BrwddPDI4X+17y3OXJJ4hTBzn16V6P/AME1/wBgm2+EOi6f8TPGtmX8a30JazsbheNOjPR8EAiQjr6ZoA+iv2T/ANknwp+zD4EsbDT7C2m8SyQr/aWrBdzzSY+baxGQvoK95oooAKKKKACkZgqkk4A5Jpa+Mv2zf2qfEFnqg+Dfwcs5td+J+qr5Vy1vEWTTIGXl2bGA2D+FAHkv/BQD9uZfEDX3wR+FcL+INf1QNZajd2oDrGG4MaEHlvXjHvXzH8QP+CWPxA+F/wABNR+IGsatZJremJ9qm0K1BkaOIcn94OCw9Bke9foT+x1/wT78J/s4JaeJtYP/AAkPxAkjBm1CZi8dtIfveVkAn/eIzX1B4006DVvB+t2V1GJbeeymjdGGQQUPFAHyF/wS3/aVv/jh8G59B1yZrnW/DLLbfaGxmWAjCE98jGK+16/G7/gjH4gms/jp4m0mN2Fre6N5zJ23Iy8/qa/ZGgDI8WWd7qHhnVbbTZFhv5rWSOCRs/K5UgH86/nt8efs5/GP4L+MxrnirwhqN1dw3H2l7yaFrmKZ853ORnINf0U1FcW0N3EYp4kmjbqkihgfwNAH5U/Av/gsV/YMMejfEjwn5UMKhIbnRU2hVHYxn+lfZPwp/wCChHwT+Lt3HZab4pXTL6QcW+rRm2J9gW4Na/xY/YZ+DHxkmFxrvg20gvB/y9aaPs0n/jvH6V8c/tAf8EdbAWMmqfCnXJor+Eb10zVZC4k/2UfsfrQB+mqyR3kYkgdZ0PR0YFfzFWlXHevw/wBJuv2wP2S7gxw23iBtMhOWhkVr232/qa9N8J/8FiPiZqes2WkXPw/0rUbqaQRtDbGYTn6J2oHc/XSlrO8PX1zqeh2N3eWzWVzcQrLJbuctESM7Se5FaNAj80P+C1XjSSz8E+AvCys4h1C7mvJgp6rEoAH5v+lfQ/8AwTHTb+xr4JfG0SG4IGPSVh/Sua/4KIfsW+Iv2soPCNx4Y1WxsL7RXmjljvtwDxy7eQw6bdvTHNfR/wABfhXD8EfhD4X8EQ3CXY0e0Fu1zHHsEr5JZ9uTjJJ70Ad9XxR+2N/wTX8P/tKeIrfxLoeox+FvEDP/AKdP5BlW5XjqAy4OO9fa9IR+dAHn3wL+B/hr9n/4e6f4T8M2qxW1sg824KjzLh+7ue5r0KiigDB8beCdH+IHhu90TW7C31Gxuo2RormMOoJGAee4r4d/Y6/4Jn337PXx21Lxt4k1fS9Z06yEg0K3tRIZI2c/6x9ygKQMjALfWv0AooAbt5yOD3p1FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADG71+b37X3/BRf4kfs6/G6Xw5aeFLKLQfs4e2bUAVe47FwwHA/Ov0jxXE+O/gn4E+J2padqHivwppfiC808k2s2oWyymLPpmolG5cJct9D8cfFf7b37Sn7Snm2PhfQ7yO3k4x4b02V2x/10FXPBH/AATj/ag+KEP2jWbw+GYWOCuv6vIsn/fEYc1+0+i+G9J8N232fSdMtNMt858qzgWJfyUCtHHvS9nEp1JdGfknP/wRN8SpYyyP8UdNkn27jH/ZsmM+m7zP6V53+xL+wv4R+OHxC+I3hnxnqeopN4Zc26CxKwliW27yCDj6V+1lx/q2x6Gvy/8A+CePiqbWv28vjoot/sEVwLovbB9wzDdLGDnA68np3pWWw07q7PqD4B/8E6PhX+z/AOKLbxNpf9qaz4jtWJt7/VLneYgRjAVQBX1HtpefWjn1p2ZldhX4h/td+EU0/wD4KQwWkl55P27VNPne4/557ypxiv28NfiB/wAFJdLvPBX7bq69eO8kVybO7hkI2gCPA2A/gOaqRcD9wKKr2d9DqFnBdW0izW8yLJHIhyGUjII/Cpt1O6Iscn8Svhb4X+L3hmfQPFmkW+r6bN1jmXJU+qnsa/FT9uD9lW9/Yr+JGk6/4N1K8i0S/cvY3AbbJbOuPkyOv41+4HiLxNY+GLT7TfXEdvCD8zSNjAr8m/20vjPqP7b/AMYtC+DPgnSoHGmag7DUt5YuduDkdABUXjsaKL3PHf2Efgncftg/tGPqHjbUjqtlpUa3+ox3MhMlyoICoPbJFfurY2UGm2cFpaxLBbQoI440GFVQMAD8K/C4eEPiH/wTL+PnhjV72WG9F1FidbVz5NzG3DRN9P6V+4PhHxVp/jjwvpWv6TOtzpupW6XNvKpyGRhkVUbITNqiiiqMwoopKACvzS/4LOeL9Lb4e+DtA3RtrTagbqMfxLGFIz9Dmv0kvNQgsLWS5uZkgt4xl5JDgKPU1+IP7cPiOX9qb9ty28JeG5ku4EuINDs3gJZS5OJHH0J/SokaRR+l/wDwTl8N6l4Z/ZA8CQaocz3EMl3GPSKRyUH/AHzj86+l/wCGuc+HPguD4c/D/wAN+FbWWS4ttF0+DT45Zcb3SKMIGbAA3ELk4A5NdJRFaEyd2LRRRVkhRRRQAUUUUANVAvSnUUUAIq7elLVBNSH2gxMMGpvtiO3lq+HPTip5kVyss0VC1wvIVl3e5pyMeSzA+mKOZCsySioI5mZmDLjHepQwNNO4NWHUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAcB8bfg7oXx5+HOqeDfEaTHTb9Cplgcq8TfwsPXHoa/HL9sT/gnBrf7MXhm78YWfiG01/wmlzHEN8flXkYbjlfunn0NfuVtHPAzXxp/wAFYYZG/ZA1cg5KX9qWOO2/B/nUSS3NIt7H5wfsQfsJ6h+1wdY1SfV10HQNLdIHuI4w7yyEZwoPtX3h4b/4I1/CTR9Shub7xB4i1WFPvW7yxxK/1KrmqH/BGGNE+Bfi9lGGOt7T9BGMfzNfoXSVmDbR8or/AMEvf2dFGP8AhCJPqdQn/wDiqcv/AATC/Z6X/mT5j9dQm/8Aiq+rKK0IufMOn/8ABNf9njT5hIvgCCYg52zXUrD/ANCr1Cw/Zj+E+mWotrb4eeH44R/D9hRv1Ir03mjmkFzyPUv2SPg5q0PlXXw50CSP0FqF/liuVX/gn3+z4sm//hV+jH2IkP8A7NX0Lg0bTTA8c0v9jn4KaKoFn8NdBhAOR/o+f5mvWdN0qz0WyistPtYrO0hXbHDAgRFHoAKt0tJKwgooopgFFFFABRTdwHesfUtfh0rz3vZobO3QZ8+aVUX9TQNJs2qK+J/il/wUr+G/hOOay0TxPHr+sZxHHYWzyIx9OBXjvhn/AIKIfGzXviHYJYfDC91zQ58CSCzsZwwz3BI7Vnz+RpGnzdT9OqKp6XfNqOn2tzJbzWjyxq5hmwGQkdDjvVytDIKKKKACiiigAooooArzQrtL5qBrJPMaTJ+lWZNqRNnpjvVe7uAulzzf6sCJm57cVHKaqTR+O/8AwVS/aTfxp45Hw40j9zYaS269deCzdgfWvtX/AIJj/AfTfhT+zzpXiJYs634qiW/upWA3BCTsT6d6/FD4neLj4q+KXiXXpJpL2K81Se4DyMSXQyEgfTGK/c79mn9tP4S/ED4a6JDY6zY+HLi0tY7dtLu5Fh8oqAMDOBjipHJ8x9RUVwtv8ZvBlxbCZfEmmsv+xdI36g1X1T4zeENPUTP4k01YvVrtF/mavmI5TttS1GDSbGa7uZBFDEu5mNfht42uLTxf/wAFLrZ7EiaC88Y6eylfcpmvqv8Abi/4KLeH9I8Har4K8FXw1LxJcELJfQEPBEvfBFcF/wAEu/2P9a8SeNrf41+NbR0sYP32kLc533M5xi457DnFUVZI/WeikpaDIKKKKACiiigAooooAbuo3U6igAooooAZRT6KBjKKfRQAUhOBk8ClrhvjZ4d8VeKvhjrul+C9Wi0TxHcQFbW8mTcqN/8AXoEdwGDDIIIo3A8g5FfiNq37SX7Vv7J+vmz8Xzag1q3JOo2/mxsPUOOK9++Hv/BZHRpmt7XxR4WubIjgvbtvoL5fM/Tykrwb4KftkfDv43ZTRdbgNxnC28jBJD/wE8mvdI5BIu4UE2ZNRRRQIKZNMlvC8kjrHGgLMzHAAHcmnZzyORXwX/wVO/aql+EvgG38DeHdQ+z+JtcGZWgkG+CDPVucrn3oA8m/bo/4KUavpfih/A/wqv4Ha3by73VIQJcydNsRGcn6V4/8Mvhf+2x8UGOu6bqvifSVb/lrq2oNa5+kbYP6V3P/AAS//YhPjnU4Pi546sRNokDn+yLK6j/4+5Af9e4I5UdvU1+uKRrGqqq7EXoBQVzH4OfE74nftafs665Fc+MNd8VaQwfYl1JI0lpIf7ofBQn2r9KT8NdQ/by/Ys8KR+KNUuvD2q6rZpdG4sm+WRlJALr3U46V9PeNvAPh34j6K+k+JtHtNa05juMF3EHUEdxnoazdQ1zwZ8DvAtsLu8sPDPhrTYBFbrLKscaIo4Vcnk+1AXPw++Ln7G/x5/ZAvJ9csItSl0e3ZtuveG5XdFjH8Uyryg/3uK+0f+CVn7WHxJ+M3iDxB4S8ZXMuv6fp9klzDqjIS0LFgAjuOORnAPpXhn7e3/BSJ/jZpt58P/h0rw+ELj91fajImJbzn7ijP3f519g/8Etf2bdR+BnwSn1nxDYSWHiHxNIt09vcRNHPBABhEdWAKnqcGgk+1KKKKACiiigAooooAKKKKACiiigApM460tNkBI4oAarlunNSU1VCinUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMkTd3xT68g/aw+OA/Z5+BXiTxpHEs97ZxBLSFwcPMxwoP8AP8KAPTrHXLC+1C8sILqOW7s9vnwq2Wj3DIz9a0a/ND/glT8VPF3xo+Lnxb8XeIZJJ4tQt7ZmZc+THMDjavpxX6XL0oKkrHM+Jvhl4T8aTLNr3hrStYmUYEl7aRytj0yRmmW/wr8GWePI8IaFD/uabCP/AGWuqoqeVCuVI9JsYhhLO3QeixKP6VaVQqgKAAOABS0VQgr5K/4KffDHVPid+ytrEGjWT39/pdzDqKwxDL7UJ3FR3OCa+taZJGk0bRyKHRgVZWGQQexoA/Hv/gkT+zfd+JPiXefEzWbAro2hwm309pUwJrhuNwBHIUEnNfsPWfofh/TfDOnx2Gk2Fvp1lH92C2jCIPwFaFAEN5Zwahay211Ck9vKpV45FDKwPYg1+Kf/AAUK/Y5179nH4h3PxH8FmWDwlqFybhJLMlZNOnOSV4HCHsc1+2VZHizwnpHjnw/eaJrtjDqWl3aGOa3nUMrCgD8Mv+CaUOoeMf21fC2p3Usl9eYub+5mkJJPyNlj+NfuB8SP+EhbwJrq+E0tX8StZyLp4vJCkPnFTt3MASBn2NeEfs9fsD+BP2bvixrfjXwxNdE31t9mt7GY7ktVJBfaepzivplc45oA/nN1y2+Jn7Ovxug8U+N/Ds7eJLO9F/I2tW3nQ3T5zy3Qg1+qHwY/4K2fCPx5FZWHi1b7wRrbIBO11CJLJW9FkVi2PqtfYvi7wD4d8faXJp3iLRbLWbOQYaK8hWQfqK+I/jp/wSF+GnjbT3m8ATSeCdVUZRCzz27n0IY5H4UAfdHh/wAS6T4s0uLUdF1G11Swl5S4tJRIh/EVoq24n5SB68YNfhk3wh/a2/Yj1eV9Ci1l9NQAvdaCGv7Jh6FNuR+KivqD4C/8FkdE1ZodO+Knh+TR3GEfWtJHmwhvWSIkMo/3QfpQB+l9Fcp8Pfip4S+K2kDU/CWv2Ou2mFLPZyhymRwGHUH611dABWbZ+G9J0/U7rUbXTLS31C6x591FAqyy4/vMBk1pUUAN2n1yaz/Ek8Vt4d1SWeRYoUtZWd3OAo2HJJrSr57/AG8PD/xB8Vfs1+JdK+G8TT67dKqSxREiV7fP7xY8fxEfpmgD89v+CLXhG8vPjR4t19SosrDSPIcnOWaR1wBxjjBzX7G18a/8EwP2c9d+AvwX1KbxTpo0zX9cvftLW7j97FCFAVW9DnJxX2VQAUUUUAFJgccUtFADZI0mQpIqujcFWGQa82s/2bfhppvj1fGln4O0u28SKCBexwAHnvjpmvS6KAEpaKKAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK99Mbe0mlVN5RGbbnGcDpX5N/8E29Rk1b/AIKCfFu8MP2QXEGqTNBu3bc3yDGcDP5V+r2tM0ek3jL94QuR+Rr8kv8Aglncy6h+2r8StTEbNHc2d9k9k8y6WTr+GPxrL7Rol7p+vdFFFamYjdK+I/8Agp1+yjq/x8+GtlrnhGwS98T6JL5rQLxJPBg5VT3I9K+3KQpmgpOzPgP/AIJo/tkaR4v8B6X8KPF2oGx8c6KGtbSO83K13ACSnLD76g7dvXAFffdeQ3P7IfwguvGsXi5vAumx+JIrv7cuoQ+ZG/nf3sKwH4YxXsG2s+Vjuj4l/wCCg2o/E64sbbwr4K8J3Orxa/tto9Tt2/495P8AaHYV0n7Df7Ddh+zRoMus+IXi1jx5ftvuL0jcLcH+BG7/AFr60MatjcA2DkZHSnUo01FtlOo5RSPhr/grl8O9L8Rfs0yeI5o9mqaJewvBMoG4qxKspPpzWL/wR7+Mtz44+COseDdQnM1z4YuwLbexLC2kGQv0VgcfWvSv+CoWm6rqv7I+v22k6XPq0z3dv5sVupZ0i3Es4A9OPzr5V/4Im6PqC+JPiXqnkumlNaWttvYEAyhicfXGaqxNz9YKKKKsgQniq8l0sbAMyqfc1P8Aw15z8cbjxNZ+Cbp/CVp9r1kkCMYHApmtKKnLlZ81/wDBRX9rLR/hZ8K7/wAH6fJJd+LPEVs0FrDH1hDHG84OcjPFeZf8Et/2K73we/8Awt3xrasmq3kTLpVlcrl4gx5nbIyHPIH1Ndp+zz/wT5mvvHl58R/jTcf8JLrksnmWGmSOXhtRycnPccYGa+8I40hjSONQiKMKqjAA9KhJ9R1LR0RJtAzjilooqjEKKKKACiiigAooooAKKKKAPkr9uv8Aa81P9knTdDv9O8OQ67LqsjRI80xjSIqM5bAr4gk/4LEePTcFl8JaSFfrsuGbH04r9cvGfw88NfETTf7P8TaJY65ZA7hDfQrIAfUZ6Vwlt+yP8G7PHlfDjw+mOn+iA1nymvN5n5p3P/BYbx3cLgeBdF+ou5GP/oNUNQ/4Kz/FHULd4YPB+m26+sUspP8AKv1Vh/Z3+GNv/q/AXh9fpYR/4VuW/wAMPB1qCIvCmixg9dunxf8AxNL2aH7Q/G64/wCCqHxpbPl2+moT627f41Hp3/BVT9oS61q1srBtGkWWVI1tV0wO7EnoDmv2VHww8HDp4T0P/wAF0P8A8TUVv8JfBNreR3cPhLRYrqNtyTJYRKyn1BC1UYqIpVLmx4ZutSvPD+nTaxbR2WqyW8b3VvE25IpCPmUHvg5rUpMUtWZBRRRQAUUUUAFFFFABRRRQAUUUUAFfJn/BUK3juf2QPFYkXcEeFx9Q2Qf0r6yr5h/4KSBf+GQfHDPjCwqRke9RL4S4fEeEf8EWbhpPg147i3ZWPW0IHpmL/wCtX6LV+Z//AARHuZH+H/xMgLZiTU7VwvoTE2f5Cv0Z8U+KdM8G6NNqmr3kVjYw/fmmYKB7c0o6BLV2NXcN2O9OrxzwZ+034D8c6glrpniOzu7g/wAMMox+terWOrW+oKfJk3Y5IpqSkOUHEkur6Kyj8yZtif3qqQ+ItPkcRJdI7/WvJf2wPH2ufC/4BeJ/E3h7TRqupWUQdIGBIAzjdgc8V+Nmn/8ABSD41aXP5kWq6e7/AN6SyB/9mqrlKMban76SapDBDvkdc+gNTLeR8BmCsV3Fc9BX4laD/wAFX/ippqM19pGj6gOxZWX+tJ4g/wCCrnxd152/s2w0uxmZdjSRxmTj0ouFodz9u45FkXcjBh6g06vzS/4Je/tHfGH41/EPxHp/ijUV1TwpZ2huZJJotrxSswCRocdOv5V+lWaZk9B9FFFAgpD0NB6Vj+ItYj0XT5Z5ZNgVCc5oGlc8++Kfxm034XaPNf6hcxxpGPlSVwpavxU/aF/ak+JP7WHxCl0vT5bt9OefyrLSdL37HUnALhev1q78bviV42/bi/aK/wCEd8IvdXdhcT/Z9NsUkITy16yv29ya/V/9jf8AYn8M/ss+D0R4rbWPF9z897q7RAsDjGyMkZVf50G8pLocD+wn/wAE/wDRfgH4YTX/ABlp1pq3jm+G+QTRrLHZDPCx5HB9SK+z4bOGEARQxxgcDaoFT0tBhcQKFyQOT1paKKBBRRRQAUUUUAFFFFAERXcMHkVheO5mt/Auvyrw6afO49iIya6GvLv2o/Elx4P/AGc/iRrVp/x8WWg3cyfURNQO5+Lf/BPH9mPRv2oPi1qOk+JYrhtB0/Tmnme3baQ5IC8/U19Z+Pv+CK9mzSSeC/HstvkZEGqQZyf95a53/giNj/hKfidxyLGzx+LNn+VfrJU8pXMfjLJ/wSG+N1jHssPE+mBP7ovXQfkKzLT/AIJP/HvVbs299qGmxW4/5aTXzMPwGa/a2iixB+df7P8A/wAEgfCnhGZNU+JOqt4q1Dr9it8x24Puepr9CdN0210ixgsrKBLW0t1CRwxqFVVHYAcAVcoqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvXvC+j+KrFrPWdLs9VtG6w3kCyr+TA186/Ev8A4Jx/A34lKXfwquhXXafSHMJH4dK+ndwo3D1oA/H345f8EqfHvwikn8TfCjX59ehtjvFkrGK9Re+GHWvRv+CY/wC25r/i7xdc/DH4hahNeapcAvptzdcPuUfNE2ec4/lX3J8cf2jfB/wD8F6jr3iO/hR7dT5dirjz5j2AXrX5HfsN6NefHD9v6z8W6Lpr6dpFvqd34hmUZKwQsTiMt0ySwGPeouaep+5VFFFWZnP+PfG2l/DfwbrHibW7lbPStLtnuZ5n6Kqj+vSvwt+GPh3X/wDgoN+2Qs+rrK9nf3h1C/JYkWunowxGvpwQAPev0R/4K4fFf/hBf2a/+EcgljF54ou1sjGXAbyl+dzj04HNfnT+wL+1hov7Jvi7xPrOtaJNqj6lYLaxSRHDRYcHB9AcCgD95vD/AIf0/wAK6JZaRpNpHY6bZRLDb28K4WNB0AFaNfKv7L3/AAUO+H/7THiL/hHLRJdC19kLw2t66gXGOSsZ7sB2619VUAcl8WfH0fwt+G/iPxZJZzagukWUl39lt1LSS7RkKAOSSa/n1/aP/at8bftKeLr3U9e1K4ttMkf/AEXRbeUiCFRwBjP86/oxnhjuoWiljEsUgwysoIYHsQa51fhf4PViw8LaOG9fsMf/AMTQB/P/APss/Fb4a/B3xUPEnjbwVe+Ndds5lk0+1Nwq2+fV1YEZHuDX70/Af4wWXx4+Feh+OdO0q+0aw1ZGkhtdRVVl2hiobgkEHGQa8/8AjN+wv8HfjlbomueFYLG4Q5W60gC1l/NR/SvVvhf8OdI+Efw/0PwfoKSJpGkW4trcStubaCTknuck0AdTRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8e/wDBSr4G/Ej9oL4ZeGvC3w/s1vYm1QTaojXUUAWIKdrfOw3YJ6DJr7CpOeO9AHh/7H/7Ndj+y/8ABvTvCsJjn1aQ/adTvIxjzpyOfwUcCvcBS0UDbuFFFFAgooooAKKKKACiiigAooooAKKKKACiiigBGUOpDAMD1Br4+/aY/wCCZvw0+Ozvq+hRr4C8WF951HS4h5U3HSSHIU9uRg/WvsKigD8tP+Cdf7Fvxi+CH7RWtX/ic3GgeGNGjkgcxTs1trDtkKYhjDKBySwUjj6V+pdFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1mC4ycU6mSRCTG7tT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMjxZqlpovhnU76+mWC0gt5Hkkc4AGK/J3/gkjeDUv2n/iLdWuY7KTT2lEedwG6UHGfbFfpd+0b4fXxZ8F/FejNcNaveWTokq8lT64yM/nX5x/8EUNHZvGvxL1AplYrK2g83H8TOzEf+O/rWLV5G0dIn6z0UUVsYhRRRQAUUUUAFFFFAEc9vHdQvFNGssTjDI4BBHoRXOeBPhr4Z+Gdjc2fhjRrXRra4l86WO1QKGbGM109FABRRRQA3HFJt3dRmnYo20wEwKDS7aMUC1FooopDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5p/4KLQ2tx+yL49W7JCC03Lj+8OQfzr6VOa+Z/8Ago4W/wCGQPHu04P2YdvespP3S4fEfNv/AARJii/4Vz8TXUfvTq1spbPbymxX2j+01+z/AGX7SXwzuPB9/rN7okMsiy/aLLG7I6Ag9RXx/wD8EVbKCH4O+PZ402zS62iu2TyFiG0fhk/nX6M4oFfW5+MHif8A4JJfG/wLeGfwnrun62i8h7K9a0k/JsVyk3xg/au/Y51C3j8QHVEsbdfLj/ta2+0Wu09PnAyfxav3J21yHxYn8N2PgTVLzxZZ2d9o0ERaWO+iV4/yak0hqb6nz9+xj+254a/a/wDDt5omrWVvp3iyGJmvNHf545oc43LnqOele0yfs2/CqT73w88N/hpsQ/8AZa/I7/gmeba4/b1d/DDPFoPkalIqYOBbYxGpz2BK1+1Ov6tHoWhajqUxCw2dtJcO3oqKWP6CmLU/Kz9sr9qbwB8EPipeeAPA/wAK/CerNZogubqS1U4mPJjAA6isz9gb9pjTviR8d9I8AT/DTwlYadeJcu1xHYqZRtUsoywPpXy78O7VP2hv2wvtieYINS1x74jG4iIMSB+WK9h/4Jv6TG3/AAUFmiWNfLsF1YqoHCgZRcfTdQa8zsfsvaaT4a8AWM89tZaZ4ftGOZZIoo7dCT6kAVrWOoW2qWsd1Z3Ed1bSDKTQuGVh7EV82f8ABSPw7Pr37IfjWS2d45tPjS+DRsVICMM9PrXln/BH34lS+MP2d9W0G9vJbu+0HVnQec5ZkhkVWRRnsCGq+Yytpc+8aKKKokaWFfA//BUv9qab4SeBLTwl4cvPs/iXVuWubeTEttGO4I6Zr7xnkW3tZpZDhUVmLegHNfgf8TtUn/bM/bZttHsrl5LDVNWj0+3kdiwSBT87+2QCaDSOhP8A8E5Pjp4H/Z7+NV/4m8bSyw250yS2gkhj37HJGTj3Ax+Nftt8M/jh4E+MGnRXnhHxPp2tLIu7yYJ185fXdHncPyr5U8T/APBIT4KapoL2mkHWNFvjyt2t602D7q5INfnX8WPgL8YP+CfnxEsNas9Rns7fzsWPiPTWYQSjuki/zU0C0Z+/dFfP37E37UUH7VXwdi8QzW8djr+nznT9WtIz8qzqqneo/usGBH4+lfQNBAUUUUAFFFFABRRRQAUUUUAFc58RvBtp8RPAXiDwxfLutNXsZrOQezoV/rXR0UAfgr/wT7+Ok37LX7TRsfE8jaPo2oB9K1pLgECF1JKMfTDD9a/d/TdStNasIL2yuI7uyuIxJDcQuGSRWGQQR2r86P8AgoV/wTnf4hXWpfEv4cW2/wAQSHz9U0Vel50y8Y7N6jvXjf8AwT3/AOCgEXwNhb4ZfEyS6g0SKfy7G8mBLWHrG+ei5/Kgqx+w1FYvhvxhovi/R4tU0XVbXUtOlGUubeUMh/EVpi6iZNwlUr65oJJ6KzLjXrC2Db7mMY96+Yv2n/2+PA/wR8Paja294mpeIh+7jsYGBbJ70Dsz6nt9Rt7qRkikDMvWrNfk5/wTe8O/GX4zfHKb4sa3r2o2fhWMN5wmZvK1EkYCopOMDqSK/WOgQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNS1G30nTri9u5BDbW8ZllkPACgcmvlyT/AIKc/AOK7kgbxavycb/LODX0Z8RPB0XxC8B+IPDE9xJaQ6vYzWTzwnDoJEKkj86/OqT/AIIo6Sfu/Eu7H105P/iqAPozUf8AgpR8ANL06W5HjeG8k7RW8TsSfQCvkP8AaG/4K5yalHd6X8MNPkttzYTVr/t9FrpIf+CJ9sv+s+JUp/3bBR/WrT/8ETdGP3fiPej/ALck/wAaC+byPhz4Q/CX4lftsfEKJbvVri9tvtObzVNQuMpbIxycAn+Vfsv8FfBPwd/ZM0Wz8HaNqemWOp3Cjzbi4njFzdsTwTzk+wFfGWp/8EgfHfhLTZU8D/FZ45Jf9ZC6vbq31KmuU+G//BLn4yWvxu8Jal4z1G1v9C0+9huLnUY9QaWURRnOxQ3OeKnlFzH6+0UgG0AUtUSfjb/wWo8SXV/8dfCGhlj9i0/QBcqvYvLPIGP1wi193/B//gn98HfBvw107SbzwvbazdT2sZu728G6SViASc9uTXwR/wAFntNmi/aF8LXfkyeVceHkjWTadrMs0uVB7nkce4r9M/2T/jxpP7QHwX8O+ILK6hbUfskcd/aI4LwTBQGDDORkjNA7aH5Eftpfs3av+w78ddH8QeCLm8ttDuj9q0jUEB3W0wyDEW6bvQdxX7Mfs9fGCz+PHwb8MeOLMLGuq2oklhVgTFKCQ6HHQgg8V8+f8FWvA9t4r/ZJ1jUXjzeaHeQX1vIBynzbG/MNXn//AARl8d3OvfATxJ4bnRvK0HVswuRwVmXeRn2Kn86Atpc/QmiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFUNY1RtK0y6vFtpbswoXEEIy747AetfO3wl/wCChnwc+LGuLoMety+GvEG7YdO1+E2rbv7oY/KT+NK6K5WfTFFQwXUV1GJIZEljPRo2DA/iKk3UxHiH7ZsurWP7PXjO/wBFuY7S+ttNmkWaRsAYGa+Uf+CK+hpa/DH4h6pu3Pd6xHDnbj5Y4+x/4Ga90/4KQfEaDwL+zT4nhlmtg2qWr2SQSvh2ZxgEfSud/wCCTfhldB/ZH0m88jypdUvri6ZscuN+0H8lrJO8rov7J9m0UUVqZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFQ3CSyQkRSeU/rgGnxhlQB23NQBFcXC265bgetfOn7eWnz+Jf2VfiBHbODFb6bLNIuRk7eRWR+3N+1dF+zb8PZpofLl1y9Hlabb5BMjd3Ix0FflbqH/AAUR+J3ibwj4t8N+IZ7bVbLX7SW1kdYxE0SsOgAAB/LNc7vJWR0pKK13PuX/AIIu7o/g/wCOgTlTrYwP+2Qr79vvGGi6ZcS291qlpBcRLueGSZVYD6E18Uf8EefD9vYfsy3+qIpE+oazOZGJPIQKq18r/tcfsb/tFa18dPFOs6JYar4h0jUrx5LO40+6f5IeqqQGGMDjnPSrM9Ln6J/FP9uH4V/CWNk1nxTaTznotiwkP6Zr8zf2qf8AgoX41/ams5/AXgbR7mx8NzzYZYUMl1dp/Cr8fKPpXmcv/BO79oiZvNk8C6hM/rIysf1NXfg7/wAL1/ZP1LUdQ074Y3TmbCyyalpLuRg8YOOPwoKsj9Hv+Cdv7Dtv+zv4di8ZeI0MnjvVLXY8Z4FjExDGMY6kkAnPpX0N+1Hrh8N/s4/EvUl+9D4fvcfjCy/1r8u9F/4KpfH7U/EFhpEHhrT7q9ku122CWMgmlQ/wdenvX3x+294qvbX9iPxpqF/b/wBm399pSQzW7HOxpCoZP50ibH50/wDBIbwVD4m/aJ1TW7mMNbaJpbS/MOAzEDNaP/BMqVL39vjxDdJ91rXUmH1Mq816t/wRq8Mx2Xgr4o+LZYlVP3dmGPXCRF3/AFIryD/gkfGLz9rnWriQ75U0q6fceuTKmTVAfq9+094TvPHX7PfxC0DT4ftF/qGiXUNvH6yGMlfxyBX5Vf8ABI74wD4b/H3V/A2rMbeHxLB5KCT5dt1CThSPUjcK/aE/NweRX4RftmeFrz9lP9tqfXdCia3iS+h8Q2JXgYY5cD6ncDTsStrH7wUVxHwV+KWm/Gj4X+HfGWlH/RNWtUnCE5KMR8yn3BzXb1ZBwfxyvtR0n4K+O73SMtqlroV7PagdTIkDsuPfIFfi1/wS00OLXP2y/DzXAD/YLS8uRuH8YUgH82r9z9c0sa3ot/p7sUW6gkgLDsGUr/WvwX+AniST9jH9tyCPxG5gg0nUbjS9QkA/5YPkb/fsaC0fvvXiP7aHgnw147/Zu8b2Xib7LFbxafLNbXV0FP2e4Cny3Uno2cD8a9lt9Stbqzhu4riJ7aZQ6ShxtYEZBBr82f8Agrt+0rb2PhWy+FWi3KS3l8y3OotG2fLjX7qnFBKOZ/4IkLIuq/FNdzGFYrDC543Hzcn6nA/Kv1Yr4O/4JE/B278A/AnU/FGpWgtr3xRdi4jLJhvs6LtjH05Yge5r7xoEFFFFABRRRQAUUUUAFFFFABRRRQAyviH9sX/gmf4a+P8AeT+JfCUsHhfxXKwa42piC69yo6N719wUUDPw5v8A9i/9q34HzPaeHI9budOHT/hH7wvF/wB8E4/Sp7Kw/bZ2+VGvjbH+0FFft/RQPmPxK0/9n39tPx1IRO3iO3jlPzyX16sQH5V9H/AD/gkfaabq8Gv/ABe10+J7teTpkLsYs9tznk1+k9FAcxlaD4e07wno9tpek2MNhp1unlxW9uoREX6CtWkpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPDf2sv2WfD/AO1J8OZ9E1ONLbWbdWfTNT25e2kP9Djmvyhh/Zq/ag/Y18RNrfhfTNRJ3FRc6E5uIZl9HiH+FfuhTHUSfKy7hQVc/GT4vftFftU/Hb4bXfgLWPhtqkFnfKi3VxHosys4BzjO31r7T/4Jg/AXxb8C/gvq8PjDTo9L1DV9SN5Haj/WJHsCgP6cg8V9k49h+VOoC4UUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMAoooo5mAUUUUczAKKKKsAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopu75iMUAOooooAKKKKACiiigAooooAKKKKACiiigBuyvkz9rz/gnp4Q/acaPWbG5Twh4ujwDq1taeb5ijs0YdMn3zX1pz60c+tZ2Y7s/GzUfgr+2l+ylaznw7qWpa/pLHh9Jna9IX1MZG4VyPh//AIKv/H3wTNbWGtDTdVNu/wC+TULIxTSD0LcY+uK/cDbXLeJvhP4K8aSiXX/CWh61L/z0v9Ohmb82Umnylcx+Ff7Tv7bmv/tReH7XTdZ0C2sJobkXAuI75XXaARs2bV/PNfsp+xj4Jvfh3+zD8PNB1GHyL610yMzR4xhm+Y/zrrY/2f8A4YxY2fDnwkuOmNDtf/jdd3HGsaqqgKqjAVRgAelNRsEncfRRRVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANVs06kC7aWgAooooAKKKKACiiigAooooAKKKKACm7Ru3d6Wua+JXih/BXgPXNcjAaSxtXmUMCRkDjgUm7K40rux+KP/BU/x2/jH9p68023u2vItIhSzWNWyqyd8Ad+lfN/xA+BPjn4W6ZpWp+KfD15pNnqi77OadPllHuc8VveG9Wufix+09oN5qbq0mu+KLVZd3PyvcqpB/A4r9/vi78BfB/xu8CP4U8U6TFeWPk+VDIo2yW5xgMh7EYrKN47Gsnc+cf+CSNvdW/7JFj9pt2gV9TuXiLfxoWGGFfadcZ8HfhXpXwU+HGieDdGeSXTtLgEUcs2N7nJJY49Sa7XAq+UzuG0HikaNZFKsoZT1DDINLgUbRRykmDD8P8Awxb6rHqcXh3So9RjGEu0soxKo9mC5ri/2mPgpF+0F8Gdf8EvdfYnv0UxT9ldTlc+1ep0VVhnzl+yH+ylF+zL8FtQ8HXF8upXWoyzT3dxGMBi67cD8ABX5G/sK/HrRP2b/wBpiTXfEDyR6NcxXFhPJGMlMv8AKT+Kiv3+2ivzy+IH/BGrwD4n1q4v9F8W6poS3DmR7cwpKuScnBJpcpXMe7Q/8FFfgNKAT43tl+qGvgL/AIKmfGL4V/HS38IeIPBmuQaprlmr2s/loQxizuAP0JP517B/w5J8Of8ARSdU/wDAKP8Axqyv/BEvwh/F8RdZPfi1iFUK6MD/AIIy/Gq8vF8VfDfUdQlnt7VFv9NglbKxoThwg9yQa/Uuvlr9lX/gn74L/ZX8SXfiDS9Tvtb1i4h+zi4vAo8uPjgAfSvqWgkZX51/8FHv+Cfuq/GTWYviD8OdPhuPETDZqenAiM3QA4kB7t61+i1GB6UDPwP8N/Ej9q3wfoP/AAhNhF40jtbQbIbX+zpZTEB2VscCvdf2bP8Agnb8Rvjd8Qx4z+Oi30GksuWhvrovd3XorZyQv1r9ePs8QbcI03eu0Zp+B6UD5ijoOhaf4Z0e00rSrSGw060jEUFtboESNQMAADpV+iigkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilyoAoooo5UAUUUUWQBRRRTAKKYisvU5p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFN2/MTnrSeZ+8CYP1p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtZWvR6lItqdNdFZZQZQ/dfSgDVopFzgZ60tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5B+1wuuSfs7+Nl8OW013q7WDiGKDlzx2Hf6V7BTWUOpDDIPY1MldWKi7NM/A7/gnP8GZPi5+1NogulY2ugv8A2veBkI2yRvlB1H8ePy71++GB6VzPhn4W+D/Ber6hqugeGdK0bUdQO66ubG0SJ5j/ALRUCuowKXKNyFoooqyAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiio5mAmRRkUzdVZmO/HNTzMpIu0VB5Mn9+pq1JFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqOMSDO8gj2qSigAooooATHfvS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNDgkjI4oAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlN3H0oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUmayAZtqNiPNHGakZgvU0ir82aVix21vWn0UVsQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSZo3U3AoAczbaWmN8wx0pd1Ax1FN3CjdQIdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gBc4yTwKYqJ95QDuokXzI2UnAIxmkhi8iMICWA7mgCWim7jRuoAdRSUmTSbsA6ik5paYBRRRQAUUUUAFFFFABTMsu4nkdqduqNpAG27gDQBIKWq9vO8jMHTYAcAnvU+eKSdxtWFooopiCiiigAooooAKKKKACiiigAoooqeZAFFJRzRcBaKZuOKNxqfaIdh9FNyaMmmpJhYdRTdxo3UcyEOopm73pdxqrodh1FQmRvSjzOm5tv41n7RBYmopu6kzWidwH0UUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADJASKdS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTdgpQ26lrICN4Q1O206igdwooorUQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAReYN2CcH0qhdrNdXAEUrxImVbbjr6185/tlftraR+ynZ2NreaFqmr3+poxgktQqxR4/vOxGK4/4Af8ABTf4RfFaGPTtW1CXwjrBAVo9Y2okrYwSrqSPzIrLmZrGPKrn2PB5iqBIQ2BjIqasnw74p0bxVYR3WjapaapakYWW1mWRT+INafzc9KzXNHzJFVSKNx3Y2n61RutU8mFXCtnftxVqGVnXkc1cZOO5Ti1qycsVxxnNKx20xl37ecYqlq+sQaTZy3E5CxxjczMcAD61pzJamaTk7I0KWvFvDf7Ynwi8U+MP+EWsfGentrYYp9nd9oLDgqGPGc17NHKsiqynIYZBHII+tNNPYGmtx9FFFMQUUUUAFFFJu4JxQAtN3dKA4PGeajZn3KFVSvru/wDrUroBWLeZjb8v97NKrBs45qGWY+ZtCblPU56U1JY7dmUnA65NY85pysuUVVa4ClD1RujCpy+3HFa3RFmPoooqhBRRRQAUUUUAFFFFABRRRQAUVE0xEwTYcEZ3dqczHBx1oAKYju2dyY/Gm7WJDs2Mdh0pJp/LXIx+NJuxSjcfvfuF+nenox289a4Tx3r8mj6XPJFcFZkRpC6D7oAz+dfGXwm/4KRJ44/aCsfAMGm3H2GSV7eW8upBuMikj5QO2RXP7T37G/sWfoPtoZguM0kbeZGrYxkZpTg9a35kYW7j+1Vbi+S3YhzirDHg4Irl/GGpR6Lp82oPHJJ5Y5AHy1E3oXTim9SzY+KLS5uWWS5jhjdtsJdgpc9wM9a39/y8dcV+BH7Un7Q/jP8AaF/aCuNK8P6neW9lFqH9naVZ2Urw/Pu27jg8ndnmv3M+FWi6j4b+G/hjS9Xne51O106CK5eQ7mMgjUNk9+c0oXXxDqKP2TrqKQUtbGIUUUUAJmgsB1qKTKKTgsfQUuQ6jORQOxXu5H5GDtx1r5N/bO/assPgP4Ea6SWZtVuJcWsKttbcPX1FfUet6pDpdncTXEohijUn5v4sCvw+/ac8e6l+13+1hZ+ELAtDp41BdPtlJzt+bDsfXvXJL947M6oe5C/U/RP/AIJ0ftHeP/2hvCOt3njLStllaz5sdTCbBMpP3cd8etfZH8NcZ8Ifhjpnwj+Hei+FdLhWK0063WIbf42A5Y+pJrtOK6Ixsc0nd3Clpu75gMfjTqskKKKKACiiigAooooAKKKKnmQBRTcmjJqADdRuqIyc9KbHIzMcmuf2rL5Sam5psm8r8pwaa0m1RnrUuaAk3UbjVWRhCqszFsn0p32hNwXccms41LFWLG7b1NGarsxbqc1yXiL4teF/CfiCz0fVdYtbC6uU3Is8gXP51XOwsztNv+1QjHnnNRwzRXkEc0MiyROAyuhyCD0IqVVCjFdHKxFZZm891xxXlH7TnxQuvg38LNS8Xw232tdPUO0ePevYBAOTn5j3rA8deBdK+JHhHU/DeuW4utL1CFoJo2GDgjGR7ijlHzLsfJH7HP8AwUg0D9oLUJfDviK3j8PeIFY+QXcCKZc8AE9DivtVZBIoZWDKeQwOQa/FL49f8Exfij8GdcvNb8AiTxFokLmaGSzcrdxLkkDHcgY6V2n7Hf8AwUs134T6wvgn4xPez6RGxiXUbtWa6tmBxhweSo6VrH3RH6/DoKWsHwb400b4geHbPXNA1CLUtLu0DxXELZBBH6Gtv8a0Mx9FJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMBqrtzTqKKdkAUUUVABRRRWoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBzHj34a+GPihocuj+KtEs9c06QYMN3GGx7g9QfpX5/ftGf8EfdB8RO2pfCjUY/D9zjL6XqTtJAx/2WwSPxr9KKaVPQHA+manlRXMz8Ibz4W/tM/sL6lFr8dvqGn6VbyZL2lx9ps3H+0qk4B9xX3n+yn/wVG8FfFqPTfD/AI4x4V8XTFYBJIP9FuX6Aq38JPocV9wapo9nrVhNY39rDe2cy7ZIJ0DIw9CDX5t/tc/8EoINbmuvFPwdddO1J3aafQ5pCI3YkkmFv4Tk9KmzHdH6UKIrmNJEKSxsNyspyD6EU6GLy8kmvxj+E/7aHxt/Y18TWnhH4maZf3vh+CVYZItSQmWOMcfupOhAHvX6z/CL4zeE/jd4Ttte8K6tBqNrMgZ40ceZExHKsvUEdKfNfcbv3O4kkEcbNjoM1+X3/BTv9rHVPDulJ4F0G9e1uL8k3TxMVdEB6Z96/QP44+Oo/hv8N9X12S8itBaws4aU/e46CvxQ+F/w78S/t+ftPyHVLiT+y3uWe6vFU7Y7dWOFHuRis5K87dC4+7Hm6mP+xz+x/wCLP2qPFj3GnXjaToenzBrzV8kSAnnCnu1fvh4P8Pf8In4W0rRvtUt6LG2jthcTHLuEULk+5xXP/CP4M+FPgf4Sg8PeEtMi02xjA3lR88rAY3Me5NdxWkbmUncWiiirJCiiigApu07gc8U6o5JCikgZoArzNH5jDzFDHtmmxL9nj2sFOOc5qldXltbbppdm4ckHqK8m+MH7S/g74L6Pc6nr2u2Fr5aFxZSTD7S47bY+Sc1kdipNq5684mkYOJ1tx2jcA5/HNWGhE0Z3KCCOWzxX40/Gb/grN4y1zxE7eBdMg0axibCS6gPOaRex2YGPzNYfhH/grz8bNB1C1XUoPD+vacjZktfsbQvID2EgY7fyNc9NS1cokfM/bS13lNu0IgGF7/jU+0/Lk8ivln9mL/gob8NP2htPtrO4vrfwl4rI2yaLfTjlv+mchChx+tfUihZAsituUjIIPBrcyJqWmMWCjaAT9aNp7nBrW6Mx9FFFMAopKKAFooooAKKKKAI9v5UdtvTincZ60i8k0DGbtyADnsc1HJGuMkAipjGMYBxis/UlbgrNtx/DXPO5pDV2R82ftsfEq5+EfwX1/X454SqxGGCNupmbge/Ffhn4P+Jmr+EPiRY+M7dxJqdrei8OeAzbskH2NfoX/wAFYPGkupXXhnwNa3Uhu5rozS2qn5WJOFzXinx4/wCCbXiP4R/BXSfH9nqJ1WN7ZLnULZsZgDKG4wO2e9RStZuW501G01Y/YT9m34uD46fBPwr42+z/AGWTVLXfLCBgK4JVsc9MivSua/P3/gkJ8cLfxZ8I73wBcTEah4ffzII27wOSePxNfoLtrZanK9GRnbGpZuPWvnz9sb4qT/Db4L+JNUjby1FrJFH672GBX0Mw3KQeRX5k/wDBYj4gNo/hPRvDFreFZL+4Es8IP8KjoKUk3ZFQt1Pl/wD4Jl/B2b4wftQ2et3aO9hoJbVLqTghpskqM4PUmv3V2/ga+F/+CQvwri8I/s5z+KZrcJqHiO+kkEmOTAnyqOnru/KvuvbV8rIbClooqyAoopGOBQA1qbI21SafjNVL6T92VX/WdvSk3YqKuzyn9pTxhp/gn4U+INUvZQfLtn2c9G28V+XP/BKvwFa/Ez9qjWPFd9C1xHpEMt9GxPAmdyFJ9eDX1Z/wVU8dN4a+Av2NXWO91G6WIcfeXHNcj/wRb8BvY+A/GfiqSPaL65S0ibuVUZP61zQWrZ0TdopH6VelJsFOqFpirbcc10t23Oa1wjjcKwZsg/nUo4AFRR3CyZGckUjTnztgBxjrjii+lws9ieimjNLzTELRRRQAUUUUAFFFNas2rAJRS0zcal2Q7AahiheNiWfcD2xT5pNi5qrJM6jIavPlLl3NYpvYnMxyahWYXGU2sretUGacsT5h/IVahhK4Z3+fHBzU86NnFRJtrbWjY7j2b0pjL5Kb3+dx3qtcal5LbY2V+xLMAK5rVvij4e0BdmsatbacM4LXLLGPwJPNRo9iOU621LyMSTwa/NX/AIK8/BLW7i38P/ELQ/tc8VnugvFt937peobjoK/SPw7rGn+ILRL3TbyG8tWHyvBIHB9+Kf4l8Oaf4u0O90fV7WO90y9haGeCUZVlI5Fd1GC6kczPzv8A+Caf7dQ8XWsfw28eahHFq1rGq6dfzuB56AABCfUDFfpIMNhhyDyCK/DL9vL9je9/ZN8YWHibwrdzf8IxfXDPaSxjD2cuchM+npn0r9Ov2Bf2ih+0R8CNOvbtgNc0cLp98pbLMyKAHP8AvAZrpSvsS+59LUdKKWnymYxucg8ivjD9uD/gn3oH7QGl3nibwvaw6T47hiJV4VCJeY6LJ7+9faNFHKVc/Dz9kv8Aa+8dfsafEI+AfG8E0fhg3nkXVldg/wCifPhpIx6cfiK/avwr4s0nxtoNprOh30Oo6bdIJIp4HDKQRnt39q+Tf29P2DtF/aO8P3HiXRIk03xvYQs6TQoP9NVQSI39/Q18Z/8ABOH9sO/+A/jp/hR43W4TRb29+ywtOTmxud20qQeik8VQ9z9lqWkVgygg5BGQRS0yAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopWQBRRRTAKbvFOpmw1kA+ikpa1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBFbdS01VK5zTqACiiigAooooAKKKKAPOfjh8CfCfx+8F3nhzxTp0VzDMhEVzsHm2744dD2Ir8gPHvw3+L3/AATG+KMOuaFqP27w3dysIrtAxt7pMkiKVT0bGMn16V+4e2vLP2kvDvhPxP8ACvVtP8Y2ttc6XLGVzcKCYyR95T2IrKXu6s0jduyPzM/ak/b80/8AaT/Z7S0sbX+xtYiKpf2EsgJkYgBmTH8Oc4zX0x/wSN+FaeE/2f5vEt1ZrFf61dsySsuH8peB+Br8fPihoekeFfiFrum6HdjUNJtbtktpieWTdwp+g4/Cv3f/AGAfif4W+In7Ovhu38PXUDXWlWyWt9ZoQHhlAAOR6HsamEeVt33He0bH0nS0lLW5kFFFFABRRRQAlRuwC81JXJ/EjxUng3wxf6pMHFvawSTyPGu4hVUk8fhRexcI8zsj5W/bg/bFsv2ePC9zBpNib7xFfhoYPMk2CPsXxtOQPwr83P2d/wBl34jft3ePL3Vb7U7ix0jzS154gu4mmWLJzsjQuufYA8VyXxn+Ll3+1d+0RBdXck0GnX+oRWlnbySZEUTMFz0HJHP41++fwn+HOifCvwFo/hvQLCDT7Kzto4ysKgb2CgM59SSM5rGK7nRUqSkrdD52+Cv/AATD+C3wntoZdR0X/hNdYVQJLzWhvjLY5Kw/dUZ7HNdt8Rf2Cfgb8SdFksLvwFpmkuwwt3osK2kqH1BQY/MV9CKp2jJyaNtVZnNc/Fr9rH/glz4o+B9jP4o8A6jceK/D0G6eVGiEV5YgcjBDHzB74Few/wDBO3/gojHIunfC74k3Uovd4t9M1q6kPz/wrC4K8EcDJNfqFLAk8bRyKskbDDKwyCPQivyR/wCCqf7IaeBdWtfir4G0j+z9MfjVkslCLBLuyJlA+6STzinZjufrgMMMg8HuKdXwP/wS1/a2h+Knw8PgbxNrPn+LNKbFt9qkzLc2+OOT1K4r733VJNhaKTdSMwXGTg1rsIiuLgwx7htPPPNPhk8xQa+Sf21/24/D37NWmixt1j1fxXPExtbFZPlQ9Nz+mK6f9gnxV42+InwNt/GXji9Nxe67cyXVvAY9ggi3EAD1BxWV5OWmxrypRu9z6TopKWtTIKKKKAGNHukDZPHalVduadRQBF8+09M9q5nUbSewE8wZpmJyit057VuX2pLYqAwYljhTjjNcZ8VvF8fhf4beI9XuZltnsLOWYSfw7gpI/WsJ6ux1Um4vm6H5F/Ef7b+0N/wUdstFdVmitdUjtwsJyAkZBbrnuDX7G+MvAth4t+H+o+F7mEPYXNm1rswPu7cDqMZr8nf+CUHh8fFD9qbxh471FGluLOKe9D9V82aQjv6bjiv2LqopIynLmZ+GnwP1rUP2Nf28G8OW8v8AxL59UXTZRdZw9tKRg/LjkZwO3FfuVX4y/wDBVT4e6h4B/aE0z4gWkDR2d0Iisg4xLG24H8a/WT4J+Ov+FlfCPwh4nZ43l1TS7e5m8n7okaMFwMk9GyOacWhSXU62a8igL+Y4UAZr8N/+ClHjGb4mftaT+H7PfMtk8NnCuDzI+P6Gv3B1m8tdH0u8vrx1S2hjaSR26BQMmvxL8B28f7UH/BSgXmkwSS6Q+vC9kdVBCQW4ALdOh2frR1Q1tc/Y34H+Brb4a/CDwf4ZtYjFHpumQQspxnfsBcnAHO4tXcUlLWhkFFFFABSEbqWigBKq3JTcFb5Qe+KtVla1fGzt5TkZ2kqp65qJ7GkE27I/LH/gst4utri48IaBA+97cvLIQfWvsb/gm/4IbwP+yR4Mjltfs1zfxvfSZ6tvY7T/AN8gV+Z37dk194+/a+0zw9PcpfGSW3gWGMcKzuMgj6Gv218FeGbXwb4Q0XQrFDHaabZxWsSk5IVECgfpUQWhdTsbVY99ffZ45mAcKmSWIrXqhrqr/Y95ubaPLbn04q57GcdzkfDvjDSr2+aBtWtI5/M2+RLMqyknoAua7ny8rjJ/Ov5wvip8VvFWi/tBeJ9atdbuvt2na/ctbMZDtTy52CDbnGMAcV+9/wCzD8Tb/wCMnwB8E+MtUiEOo6rYLLcKowDIrMjMB2yVJx70qd7WZpUld6Hpcl3DZxgzzRxL0DSMB/OpVlVlDKQQeQQeDX5g/wDBYb4p+IfC9x4L8PaTezafb3gknla3kKMxBwBkV1H/AASF+NHjL4keH/F+heJdauNYsNHWA2X2o75I92QRvPJHHSruiGlY/RmikFLTMwooooAKa1BakrOTuA12IHFJSyAlTTVB2jmuKbNClM5kYDccKeeO1Vri4IZQo4zWr5fX368VTnjjH8PSsJxN6cl2GLCrRO5XAA9a+Zf2r/2stG/Z20Vbprn7bqJ+7ZqwzXf/ALRX7RGl/A74c6nrVyBNNDGwjhJA3N2r8VtQbx7+3T8dAun2U0k97OqLGoLQ2kZP3mP61rTpxmrmnNyRfMjtfG37e3xt+NHitbLwjdXWjpNIVg03SLdZ5ZsnjO5Tz9Kn8Ufsh/tYfFi1j1LxFoGtakdgdIruRUYgjP3Riv1T/ZH/AGLfCP7LvhSOKC3h1bxPOA93q80QL7scqn90A+lfReBXbGmo/Cjj5mfkJ/wTd0z41/Cf9pCHwf4h03XdO8Py28ov7PUY28hdqna6sfTjGDiv1yuLyC1iMk0qxIBkljip/JjMgcou8DG7HOPrX5g/8FRviz8Zvhr49sYfDNxfaZ4NurMYvLGLeDLnkMcHFVaXQVz1j/gp98YvAS/s+6t4Yu7621DWrza9rbxsGZGB+97Vx/8AwRd8NyWfwj8Z63NEU+3alFFE3qqIc/qRX5J+JNc13xhqT3mr3l1qd2xO53JY5zk8dq+ov2Q/2+fGf7MOlnwwmnWuteH7i7WRorglJIMkBiMD09aqKsF9D94qWsnwpr8XirwxpOswDbFqFpFdKuc4DoGA/WtaqJCiiigBhr8h/wDgrH+zQfh74usPi14YtxZ2eoTBL9bZNgjuBysvHc+tfr0a+Sv+CoNzpsH7IviddRjDtJJCtvxkrJvGCPegqO53n7D/AMaYvjp+zf4T1xpmm1O1tl0+/wDMbc/nxAKSx9WADfjXvVfAn/BGtXH7OuvOwO19achj/F8g5r77oJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKVkAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaAGTTLBG8jkKijcSegFflz/AMFLP2ubmz0FfCOkXMUqX5dWaFwSig4ycV9wftVfGbQ/hP8ACfXrrVL4Ws01pJHAqsAzMVIAFfjL+yb+zX4g/bM+MEi3dxMPD1nIZ7++nLMFTORGD6msWuZ26G8VyrmPof8AYP8A+CcnhT4+fCceO/Hd3qBF/O62lvbP5fyqcFmPfmvN/GS+JP8Agmd+1oR4cuLyXwtPtdVuc+XeWzHlG7Er0z7V+0nw/wDA2k/DXwZpHhjQ7dbbS9Mt0toYwOyjGT7nqfrXzn/wUY/Zttfj58B9RuLa3U+I9BRr6xlVcsQoy6fQiqsRzH0N8M/H2mfFDwHofinSJ47ix1S1juUaNshSyglfqDkfhXT1+Vf/AASF/aR/su/1f4QeI71oWkb7To0NwcbZAT5sPse4HtX6pbq0IHUUUUCCk3D1paTaPSgAB61U1DT4NUt5ILmJJoZUaOSORchlIwRire2k2+9TJXHdp6H58eIP+CQ/hv8A4WXD4r8KeNtQ8PquoC/NnJbJOiHfv2JyuB2Gc4FfoDY27WtrDE8hmeNFQyN1YgYz+NTbe3alC4qbMfM7WFooorQkKwfHXgjSPiP4T1Pw3r1qt7pWoQmGeFu4Pf6it6igD8Ef2mPgn4l/YI/aL0/V/DdxMNM84Xmj3x+RWAOWiOCenSv2N/ZZ/aC0n9pD4Q6P4q0+aP7c0SRajao2TBcBRvGPTOcVxv7dX7Lcf7Unwhl0q0aODxHpzG602eRc/PjlM54DdM1+Wf7Cv7QV/wDsg/tEXnh3xZcTWXh+4uZNL1e36pFMrFBJ9Aw6+lRZmtro/d1jtGa47xp4psPD2j3erarepp1lZRvLJNI2Bhc8D1NXNW+Ifh3R/CLeJbvV7WLRRALgXhlGwoRkEH3Br8df28f2yL79pTxpZ+Afh291JoUNx9nAtyc3szHBxjquaiTvogjE5a40fU/2/v20rkWFu8miNdeXLMn3Us43I357Fl5/Gv3B8IeFNN8C+FtK8PaRALbTNMto7W3iH8KIoA/Hivnj9g/9k3T/ANmf4WWJu4Ffxdq0EdxqEzoBJEWUMYfopJH4V9P7auKsRKVxaKKKskKKKKACiiigChqDK0ZV9uPevib/AIKnfEr/AIQv9m640y1n8q51icWw2nDFCctX2Zq2p2yJKH+ZkOMCvyZ/4K7eMP7d8c+B/BVsc3CRm6dM8DzG2oD+tc3O3I7ErQue7f8ABG/4Snwz8HNc8bTM/m69dm3hU4x5UR69M8t/Kv0MrzX9m34cQfCb4FeCfC8CBHstLg88gAbpmQNIf++ia9KrWzOM+Lv+Co3wtk+IH7PuoX8UG+XR/wDSlcDkY6/hXNf8EfPig/i79n/UfDN1dCW68P3xWKNiSwhcZH4ZyK+yPix4Vi8afDXxNocqqy3+nzQDcOAWQgH86/HD/gnP8X4f2X/2oNX8K+KZV0/StWMmlT3M5KpHLG/yP6YLL19DUxVjW94n6lftg+LIfCfwT8Vz3V01pA2mzKGU43OVwBXw3/wRZ+H6zal488aTW7ErFFp9vcOASCx3vgkdeB+tejf8FWvjZ4R1b4Ax6HpPiW0vNRvLtQkNo+8uqn5gSO1et/8ABMD4ap4A/ZR8PXbFjd668moy9MAFiEA4/ugdc01qO9o2PraiiitTEKKKKACiiigBB3rnvF80Nvptw8jBT5bDce3Fb0hWPknArzP9oDxIvhv4fX955DTqsEjHZ1ACE1nN2izal8aPyT/Z70Oy+Lv/AAUiZtRke8httXnuCc/xQswUfT5RX7d1+Mn/AASkhtfF37YXibWZoz5n2K8v4efus8wHP4Ma/ZynFWRM3diHtUV4qSW0iyDKFSCPapap6w7Lp8204Ow8/hRL4WTHdH85n7Q2mQa9+1R4102wjWKO48RzWyKo4yZip/XNf0G/B7wbB8PfhX4T8N28Qgi0zTLe22D+8EG4/i2T+NfgJqFqPEn7aWoW44Fx43mQsD1H2xhmv6J2ZLe3JY4RF5PsBSjoXI/IP/gtBrKz/EvwNarxJBZTO/f+MYr2f/gi54PSx+EvjHxHJGwuL/UEt0kycGNFzjH1NfEf/BSn4tW3xT/aY1dNPk8zT9HX+z0zz86kiT9RX29/wRl+I39s/CnxR4Rki2yaTeLco4UAFZBzk9zkUAz9GaWkpa0MgooooAa3WmswUUrd6iaMt1rCTsNaj2b5M1H+dG44x2qBJnk4wVw2M1w1DVImLD5lH3scVwXxI+IWnfDvTft+q3sNpZqpMs87BUTFd5GuZCT16Zr4K/4K9WkMP7P8N2L9re4fUY4xCrkCRcZIx3pfFZGtNqL1PhP9vj9rBPjp44l0rw3cufDFkxDMp+WeQHBYd8Zr0v8A4JuftffDX9njSdU07xhEbK8vZsjUEi3ED3PpWF/wTn/Yd8L/ALU1r4k1jxi2r2ulaW8cELafMkazSMMspJQ9B6V7h+1l/wAEnfC/hD4a6n4m+Ftxqzajp8Znl0y/mWdZI1GW2EIDnHau9QjGPKjJu71P008H+LtI8eeGtP13Qr2PUNLvoUngnibIKsoI+hwRxWyOABnNflN/wSB/aE/svV9d+Fmv6k6NOVuNKguGxtkAxJGueR9Pav1ZrVMyasLVPU9HsNatzBqFjb38B/5Z3MSyL+TA1coqhHKQ/CXwPbsWi8G+H42PJZdLgBP47KB8JvBCyNIPB2gb25Lf2ZBk/wDjtdXRQBFbWsNnAkMESQwoNqxxjCqB0AHYVLRRQAUUUUAJX5j/APBZL40W0HhfQPhxZzN9tuZxe3Ko3Gxfug/jX6DfF/4lWHwl+HOveKdQkRItNtXmCu2NzAfKv4mvxG+Hui+N/wDgoh+1Pa32oq9zaees97IQfJsrRWyE9sjA9yanmLj3P1Y/4J4fDGf4W/sp+DrO9tooNQ1CE6lM0a4ZxMd6FvU7CtfSlVNJ0u10PSrPTbGFbeys4Ut4IUGFSNFCqo9gABVuqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAG+tZviLWLfQdFu765uI7aKGMsZZGwo4rTr44/4KdeGfiZ4i+B2PAFvNd20MnmalFZsfP8AKA6qo6j6VEuboVFK+p+ff/BQb9oZvjt8QrDwjoE0l9FYzmI+WcrPMz7dq4681+pH7Ef7O+n/ALPHwP0fTY7TyNc1CCK81WRh8xnKAlfopJFfm/8A8E6/2HfGfjP4taJ8QPF2iTaZ4S0uX7YjagpSS8kxlAqnkjOCSa/aPFEVYucr7BTZoUuIXilQPG4KsrDIIPUU+irMj8W/+Ch3wXH7KP7R3hv4h+D5WsbTWrr7cscIK/Z542UuAfRgen1r9Xv2f/jBp/x4+EPhrxtp21U1O1V5oVYN5MwGJIyR3DZr5R/4LCeA5fEn7OtjrkFt58mi6gsjOo5RH4Y/TiuS/wCCLPiTUtQ+Gfj3RZWlm0XT9Qt5bOR+FV5I281QPqqmgrofpBS0UUEhRRRQAUUUUAFFFFABRRRQAUUUUANK5z6V+bX/AAUc/wCCe178Q7q5+Jvw6svP1tYwNS0S3TDXQH/LVP8AaHcY561+k9FA7s/n60n9m/8Aad8U6LF4atvDPjOTQ5AALW+SRIVXt944Ax2r9J/2Ef8AgnnonwD0my8WeMbaHVPiBMgkVXG6PT1IGEA7uO57V9vUlKyHzMTb706iimSFFFFABRRRQAUUUUAfI37bn7TVp+zX4bk1JIvtep3EqpbW7Z2OepzjmvzZ8M+MLz9uD9tTwNeDSmtXnktVu4Y8tGkUJ8yR+c8Z3fpX1r/wWU8F3118N/DGuxwtPaWd+yzOo4XcDjNef/8ABFv4bxX/AIw8ceOJovMFhaRabaSMB8ryHdJj3wuPxNc0Va7Z0Sk7K2x+tKgKoAGABgAUtJS10nOMlUPGysNytwQa/Fb/AIK3fA4/Dz4xaZ4u021SDR9dg27YRtVLhTzjHcjBr9q25FfDv/BW34ZP42/Ztj1mBZGufDt6t4BHjlSCrZ46YPbuBUWLj2PyD+Geg6j8XPFfhrwTD5lzc32pRxxF3ztRj83X2r+jf4X+B7b4afDvw54Vs+bfSbGK0VjjnaoBPQdTk1+Cn/BO9I5v2xPhrG8auhv2+9/1zYiv6E6cVYJO4UUUVRAUUUUAFFFFAEW3ceQD9a4L46aWt/8ACrxSGBcpp07Iqjv5Zrv9veuZ+JVrcXvgnWIreRY3NrJkuMjbsOaznFyTSNYfErH5Jf8ABGuAt+0h4maUFZY/DszFemD9pjB/nX7LV+Mf/BLbV18P/tt+J9N82NUvLXULRc/xBZt4x+KV+za9KtbESTT1FrE8W6kuleHdTupOEhgkc/QITW1XG/GCTy/hd4qcfeXTbjH/AH7alJXVgjufgd8CdnjP9tLQJ8F477xY9zkcZDTlxX7M/tpftNaR+zz8LtRmmmU6xeQtFaxAgkMRgHFfgZ4G8Zav4C8caZ4i0Jj/AGvptytzbsU3/MvqvevsaPwL8cv+CknjzSNT1nS5NJ8OxCOKfUWh8qFQANzKvc/41Ni2fM2q/B74heMvCd38UR4fvNR0PUruaWbULeMuBKXJbIHQZNfp9/wRp8Dz+HvhT4y1a90+4s7m+1CNI3uIym+NUJBAPbJr7X+Efwe0L4R/CnQvA2n2sMunadaJBJvQETyBQHkYHuzZP412Wn6XZ6TbiCytorWEdI4UCr+Qp2ZPMWaWiirICiimsTSbsrgI3f0rmI/iLoS6hNY3N8tlPFKIR9rIjEjHoFyea4b44ftH+Ffgpo9zdavq9nHNEpJt/MG/ODjivxf8UfGLx3+0l+1Bp93oFzf37vq0MtjZRuxiVRICGK9AMY7e1cbnKb0N4011P3/2j0puBVfTVuv7NtfthUXflJ52zG3fgbgPbOas7huI79aJJMz1I1IVj8tfnB/wWkTy/hj4H2xtifVWEkuTgYjJGR0r9IYyT1ry/wDaP/Z58O/tJ/De78K6+hjbPnWd4n3racAhXA79ehpwje0uxV9T5J/4I2eLtNvPgl4i0FbiL+1LXVWmeLIDsjKMNj04r9CJFDxsrDIIwRX8+cx+LX/BP346XwtFudLurO5MUc0tuDa6nbKxVWyQfldRnjkZr7d8G/8ABaXw/Jp8aeK/BN7a36qBJJp8qyRM2PmK55xnOK3EfJvxVsG+CP8AwUSupdIVlW38Vw3UMUXBIuHEjqPxdhX7y1+FvhPxZa/tf/8ABRjQvEGhWEmnaXfavbXQjnG4xxQqCxbr94qfoTxX7p1cVYUncKKKKogKKKKACiiigAqO4uEtYJJpGCoilixOAAKivryOxt3nlcJGoyWY4FfJf7SPx71rxlDcfDP4aKt94t1M+Q1xCcpbRk4Ziw6YrKdRQ0NYU5T1Wx8o/t0ftBeKP2mvisPgf8O4JLm0a4S3vJYMsGYNhgxH8INfcf7GX7JOj/so/DxtOhdb3X9Q2y6hfbAGLYHyA/3Qc1B+yP8Asb6B+zfor6ldbNa8c6kol1LWZlDSGRhl1Rjzt3E19HYqrEzd9EFLRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJuHrS1GsKhiakoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEVQqhVACgYAHQUtFFABRRRQBieNPBmkfELwxf+H9es0v9KvozFPBIOGU1hfCP4M+Evgf4ZOheD9Ji0qwZ/NkWMcu2MZJ78V3FFABRRRQAUUUUAFFN2+9LQAtFFIWAIBPNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHJfFD4XeHfjB4PvfDPiexS/0u7XDRt1U9mHuK5f9nf8AZw8Kfs0eD7rw74USX7Lc3b3cks+C7E9FJA6KOBXqtFKyHdhRRRTEJXiP7aGqW2j/ALMfj65vLRr22GnOrxIu488A/gcV7fVDXNCsfEmj3ml6lbR3lheRNDPBKuVdWGCCKBp2Z/Oh+yD4+tvhX+0t8PfEt8m6ytNVhWfB6LKNmfw3Z/Cv6PEkEihlIKtyCDkEeor8EP28f2PL79mf4q3F1o9veT+DdTke6sbuKMsbZmdmETEAAbcgD2FfsP8Asa6n4g1n9l34a6h4nl+0axc6PDK0u0gtER+5YgkncYvLY+5PQcAHyvc9pVtygjoaWkXoKWgkKKKKACiiigBrdqg1C3W+s57d1DLIjIQ3QgjGKsYo20BqndH4R+Fb7/hmX/gpKG1EfZ9Pt/FM0cm3/n3uJG2/gN4/Kv3bQhlyDkGvy7/4K/8A7OtjY2Wi/F/Q7aaPVjeJY6p5AyCuC0cowOGBUgn3Few/8E4P23o/jt4TXwV4w1G1TxzpSLHb7V8v7bbKqqrjJ5fAyfXOaDSXvan3JXkf7V3iaXwj+z1441OH/WRabKBxnquP6161uOORiua+JPgvSviL4F1rw1rZZdL1O2a2nZG2sqkdQexFBMdGfj7/AMEhvhTpfxA+NHiPVdY0yDUrLR9PV1S4QOgkc4Bwepr9ndN0uz0e0S1sbWGztk+7FAgRR+Ar48/YP/Zz8Lfst+KvG2hWnjXTvEOqaxIj29vDKPNSCMvgFc9RkZr7P2igG7sKWiigkKKKKACqWrNPHpt09tH5s6xsUjzje204HtzV2kqWrqwH4k+Nv2Jf2jf2jPjFr13rGiy6VZ3WozuLvUJdkCx+Y20qo6jGMYr9Fv2MP2G/Df7Knh1rmRo9b8ZXqL9s1RlOI+ATHEDwFBzzgE19QbaMdKyiraFczIyAUA6j60xVDNuPXpT29KQYXrxUcuow+7nFOU0cHmlxiqhv5Acv8QPhn4X+Knh+60XxVolnrWn3CbHjuo8nGc8MPmX8CK+SvEH/AASF+BetajJdW7+I9HikYt9jstQQwpk5wu+NmAHQZJr7f2ijaK15RXPnn9m39hf4Zfsv6hdan4Xtr2+1e4XZ9v1SVZZUX0XCqB+VfQ9FFWSFFFFABRRRQAUUUUAcX8XvB+o+PfAOq6LpN/8A2Zf3Me2K5/uGuB/Zp/Zn074E6D5126at4quhuvdWdcuzHlgD6bs17lRWbpxcuZ7miqSUeVbCCloorQzCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopN1NeTauQpc+i4oAfRSVE8jbTtXBzj5qAJqKaudoz1xzTqACiiigAooooAKKKKACiiigAooooAKKKKACiiigApCoJBI5paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6lpFlrNube/tIL23JyYriMOv5EVNbWkVnbxW9vEkEEShI4o1CqigYAAHQAVNRQAUUUUAFFFFABRRRQAUUUUAZniDw7pvirSbnS9XsodQsLhSklvcIHVgRjoa/I/wDau/4J1eMP2fNfvPid8IL26udJs5zdLaWzsL2yBOcLj76Lx+FfsFtprRrIpVgGVhgqRkEUDTsfkP8ABn/gsB4m8D6GdH+IPhlvEN9bbYo7qBvImIUY/eKf4jjk+tM8b/8ABRT4uftIarH4d+F3hK6sbi5DQKsKmYFW4yx6KcH8K/TDxH+zH8KfF2pPqGr+AdDvr13LtNJaKGZicknGMnNdZ4V+HfhjwPapbeH9A0/R4UGFWztkjP5gZoKuj43/AGEf2AdR+CevxfEzx/rNxqXji7tiyWIlYx2ZlXMqyf33BOM9Mg191UUUEBRRRQAUUUUAFFFFTzIAopuTTdx9azAUgZpjR7up4pJHKjg1FuB5MmDUcyLSY+NjuK54HFTVX2lYyynnsaWOYrGCx3GsE3F6jtpcs0tIKWvQMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKTcPWgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKYWbP3c/jThQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIx20DkZoYbhQOABQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbvVSQJbzGcK7vJhML2q5tNG2gYbht681DcKzKu045zUMlwVuljRee5NMnVruZQpZPLPJ5plxTuXo5N3BBUj1p9R44BPLCnK3AyOaRA6iiigQUUUUAFFFFABRRRQAUUm6gtRsAtFRNPsx8rH6UfaFDBT8pPIzUcyY7MeW5AxTqjV9yn604NxVgM+0L53lnhu1S0zjduxz60u6gQ6im7qN1ADqKKKACiikY7RQAtFIDkA0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNY4FGTUZZvMwfu4rOSsOwu47Qe+aKbuG7aRwOacrKy5HSoGVLi62kjYTimMyyQjaNkjd6syMvpVZpEJ+dHIB4wKxNktCbzGjt9pGWUYJqKzkLsQYSBnOc/rT45Dcn5TsRTyCOtWFxtGOBUtXaZLfKrE1LVcoc9alXIUCu3mRlYVWJJp1IAOtLVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSloAKbtFOooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIvOTzNn8X+6f51DfanaaXbvcXdzDbQL96SZwqj8TX4O65/wUW/aM+JOsm20vxDNbTXD7orLRbQM3J4UBQT+dXW+FP7Y/wC0FMLW90fxxd20p3F9WVtPt2z3DyFFI+hxWfv9jS0O5+v3jz9rT4SfDeKSTXvHGj2jKu4RrcK7t7AKTzXzR4y/4LGfCHQL5bfSNK13xGM4aS2hSJQfrI65HuK+XvBf/BGv4s699mvPEviPw54eSUBprdp5bu6jJ6g7Y/LYj1DkV774K/4Is+B7BGfxV431jWJ26DToY7RU+hO/P5Cndj902fDv/BZf4T6lqUdrqnhrxLpEbNg3UkcEkae52Slj+Ar6t+F/7UXww+MVvBJ4W8XWF/JMiuLdpPLlGR0KNgg+1fFvxH/4Iu+Er3S5W8GeNdVstRX/AFSa0FmiPsWRQR+Ar88fjt8CfGn7I/xA/sbUtXgh1HZ5kd1pFyRvXPDYOGGfcUubYVrn9GqMHUMpDKRkEHINOrwP9ha/1vUf2Vfh9ea/c3F5fTabHIZrk5coR8uT1PFe91oZi0UUUAFFFFABRRRQBHJlQSOfaq/2hpoWKqUccYbvVrbWfdLNFI8kYWQZ6dxxisJ8xcUie1uBMoUn59oP1qRoVkYFhlhxX4+f8FBfD/xs+B/jq48U2PjnWbjw5qkzzobWRoktdxyI8Z5x0rm/2Of+Cifxi0fxp4f8FXit48sNRulgjhvGJuUBOCVk5wByeRRB6XLa1sftQV6KOMUpcKMsQv41HBI8kCSPHsdlBKZ6H0ql5qTOy3CmPa+VyetOU3F2YuW5p0VSTVEa68kKSuPvAE/h0qaYSSNEUAwGycnHH5VrFqWxHK09SekbODgZNMYtvABUA+vWnIrLnLbufSi6Cw9CWUEjBx0p1JS0yQpv3sjpTqQLgk0AAGABS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAITj6UA55FIF65JIPrSgbQAKAILi8S3wXZY1zg7q4S++PfgfR9Wh03UfEWn2N1J0Wa4VRn0PPFef/tbfFIfCH4b63r80c8qxwMsRQ/KrkYFfjD8I/gL8S/21fiFrE/h5o5ZVka4uLrUrh0hi3HOAcH8qxUm2buCirs/oT0vXNN1uFZdOv7W+iYZD20yyDH1Bq5uG7aDz7ivwh+IP7MP7Rn7FN9b+I9Our6O1VN76l4duXlhjYdRIGz+o/Kvuf/gnT+3xffH5pPAvjdhJ4utIvMgv449i3cajksM/f7nGB7Vpcy5WffA6dMUtFFUSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADKa+ByetSYpjxq3UVE9ikxFAZQcdqrnbDuG/g/w1L5m2NsD7vFVo7pF5ZGJ78VjzIpIi87aWByw/hHtS8tt3ZAI6ZpI7iC4uG2ZLg9DU8rKPvrnFZm4JGxPDYXtVhRtUCqUUxDnj5e1WoZgzENxzxQtTOaZKW2jpmlU5ANJuA+lOGK6VEyHUtFFaEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANX7xp1FJ060ALRTQ6t0INOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDzT4O/s4/Dr4E6PBYeDPCthpJRAr3nlB7mUgY3PKfmJP1r0umhqZNcxW67pZFjHqxxS23AdtG4sBz05py/dHes2+8RaZp1uLi61C2tYOvmTShFP4k07R/EWl+IIWl0vULXUIlOC9rKsgB+oNF0Ow7WNQj0rS7u8mYJFbxtKzH0AJr8BPj346vP2r/ANr1TbR4jvdUTTrRe5iWTGTjPbNfup8YNWh0n4da/POgeNbOUlW7jaa/Gf8A4Jw/D2D4i/tkC/lh22mkSTXwT0O47f1rLeVjZaRP2z8FeHLfwn4R0bRbVNltY2kVsiegVQK26SlrUwCiiimAUUUUAFFFFAEM1wIVJIY844FN84bCV5H86ex3Eg9DXOeINS/4RXStQ1CaVTHFDJKN3GNqkiuebdrmsUnofl7/AMFdv2gZLvVtO+HWnsVSNPtF2pGcE9q6f/gkr+yTZQ6Gnxj11POvrhni0m3kjx5SA4Muc87u3FfBvxe+Iq/tAftFXWreJb9dJ0+7vxA91KC6wwB8E8deK/UK4/4KD/Aj9nf4U6d4Y8FaqNek0mzW3tra1jZVZgvXcR3NEXyqzKlufeHPA6Cqt9ZpdR88MOhr8NvjZ/wVI+LPxNklg0K/bwhphPyx2Lfvtvu4A/PFfo7/AME39a8Z+KP2WtO1nxbq9/qeo393O9vLqTmSTyd5C/MeSD1qk9LyRMVruZn7YX7dH/DJc2h21v4VXxHJqDv5jy3ZgEO046bW3fpT/Cf7bF1+0R8BfEuvfC62WPxxpNiLifSJEMpjfGSqk43dPSuG/wCCp3gPw1qPwWute1bEerWLLHZybsbmPUYrwP8A4It20s3xR8bXWJDAumxIWXhN248EevvWEfej2N5yXNscN8O/+Crvxq+HPi+7h8YwWfiCy+1H7Xp17A0M8HPKoQflx6EGv1L/AGbf2s/An7TnhwX/AIZvxHqEar9p0y5IWaJiORjuPcVy/wC1J+wt8PP2lNFma40+20DxRy0GuWduBJvPP7wKRvBPc81+THjz9lf49/sY+II/F/2C6tLSyn3Ra3pE4nhYA/KZApyoPowrptoYL3tj9+dwHfmm+Y27G3t618nf8E/v2yG/am8Ay2us2skHizR1SO+lVCYbjjiRTgAE/wB3t6mvrWtDMRTuUHGKWiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUw7+2MU+igBu4hcnrTqQrnijnnOPagD4O/4KxeJLjR/gPPYQTYjvp1EgbqMHtVL/gjh4VtrH9n/AFfX1i23mo6nJHJISTlY+Bgdq47/AIK/arDD8PdOtjMftMt4f3eeNor2j/gk3Ypa/sb6BMud89/es/pxMwH6VhE6qjtFI+vNU0uz1zTrmwv7aO7s7hDHLBMoZXU9QRX40ftlfBO//Yh/aK8PeO/h48un6TqFybmLAPlwsZPmgIXHyY7da/aLFYfirwPoHjizjtPEGj2Ws20biRIr2BZVVh0IBHBrTlZjCVnqSeDdabxF4S0fVHAV7y0inYL0yygmtmo4IY7aFIokWONFCqqjAAHQCpKsh7hRRRQIKKKKACiiigAooooAKKKKACiiigAopuTmlzSAWmHNDMRTM7sE9azmykiOZyuQKrxxpKzBmPTpnFWXAY8jNQsWjyUUVzmq12IlVY/ugfXHNSbvMG081V84ozF2yOu3HSo4b5HyVyp9cVldG/Ky+22NVGMdqZNMm7B6KKzLzVltot0pJGfvCqzahJfIJIU2qTwx7ihVFEqNJ9TW+2OR6ir9rIXiUms+zgeaNR9w45q9DG8R2nkDvXXTu9TGpy7ItUtNVgeO9OrW5yhRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJD8pp9NZQwoAq/MoUqpPPpVsdKbGu3Ip9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfk/4L/4LKT+HvhPptrrHhRtc8aQR+S8yT7IZNowHfjIJ9s188/F7/gpX8ZPjLcS2ljcR+HrSZyYrPSVLugPRQ2Mk/WtD9jP/AIJ0a5+1J4Zg8Y3HiOw0nwsLw209upk+1uEPzYHllee3zV+tnwc/ZC+FXwL023g8O+E7E3kSBW1G7iE08hH8RZs4P0xUJKT1Luz8E/GzfFm+0tdV8U/8JadJmOftOpLcLA2fTOFx9K+6f+CL41ubxt4yl3XT+H0s0QF2bylmz0APHSvrL9rz4D+If2tobLwhp2t3HhzQLaXfcSLAHSUj1+YcV6/+zT+zr4f/AGZ/hva+F9EIuJB893fNGEa4k7sR2+maLFPTc5b9uDxvH4D/AGf/ABbfTNkSWTwxqv3tzcZ5r4U/4It+F3v/AB94+8SFgY7e2jt/mzks7EnFep/8FjPH2oeH/h94Y0W0XFpqk0izS5BAx2PetP8A4I06HaWnwJ8QalHsN3daoySMvXaowBSjuVLZH6E0tN3Uu6tDnFooooGFFFFABRRRQAwq27jGK+Sf+CjXxV/4Vf8AAvVJ47xYb+9/cQwq2GIPBNfWVxeR2+3ecbjgV+JP/BVD40P8RfjofDNjctNpukIItkb5V5T2x61hPWyRvTXU84/Zz/YI+JX7T2lxeIdGFnpnh+ado5NRu5CTkHkhO9fYd3/wSB8E+BvAOpa14p+IWsvNY2jzyfYlihhDKucDcrHGfevkv4Q/tjfGz9kfQbfw/a2q2ujn95Bb6nakx885B71L8bP+ClHxX+OHgO88Jaw2mWem3bfvpLCExsw9M56UWk+ojgv2Z/gK/wAfPj/p/hbTba6m8Pi+3XdxJhnS3U87mGByB6DrX9B3hrwrp3gzw1p2h6Rbx2WmafCsMMSDARVFfif/AME6f2pfh3+y7q3iXVvGQ1ie5volitotOsVl4HU7mkXr9K+r/Gn/AAWI+Ht5p8sOj+F/EnmMrBTcLHFk446Fqp7NCW54z/wVk+PlxrWvWfw6g2yW1nIbqWZRjcOgGP8A69fSH/BI/wCD0/gX4J3nie/WNLvX5/MjRR8yRDpmvyM+MHxJvvi58RtU8TXUbeZezmSO3djI0a54XoM19H2n/BQ/43Q/DfRvBnhKzi0Wz0+BbdZ9NsHM7ADAJIBwayjFxikVu3c/djqOtVdU0my1zT57HUbWG+s51KSwXCB0cHsQeDX89msftOftF3F0Rd+M/F8Ezn/Vjzk59htr9SP+CYP/AAtfUPhbqmu/EzVdZ1KPUplfTP7YnZ2EQHVVblQTWyk+pDjbVM+s/BPw38L/AA2sJbLwtoNhoNrK5keKxgEYZj3OK6Skpa0MwooooAKKKKACiiigAooooAKKKKACiiildAFFFFF0AUU0tSbjuxii6HYfSMu5SM4qKSV1wVXcO9LHMZFyV2+1F0Fj8o/+CyOlmF/C9z5shEk7rsJG369OtfT3/BKFSv7GXhwFg3+n32Mdv3x4r5u/4LJagbi18NW/2dlaK4Yq/Zq+gP8Agkjeed+x/pkOAPJ1W9U/jJmsoam1TVo+1KKazbetG6tbmA6io/M+bb1NNWY7vm49Kew7E1FJSM23JPAFK9hC0tfP/wAav2yfh38BdSSLxJrMYLjmK3YSSA+hUdK7D4EftFeDP2jfDMuteC9R+2QQt5c0cilXib0YUuZFuLR6hRXxF+1F/wAFANa/ZT+J+m+Hdd8LQaxpV6ol/tCGVozGhOOmCCQK+o/g38ZPDPxz8D2Xijwtfx31hcKCyqfniburDsRVBKLjud1RRRQQFFFFABRRRQBDJMI+O5PTNPzu9q+Fv+CjHxg+KX7P2k2/ibwobf8AsS5cQ/aHG9reX1Kngg1lfsO/8FKLD4vtbeEPiJJb6R4pVQsF8xCRXh+nRTWMZScndG0oLlTTPvuRsDjk1BFMWkZSOlWI5ElRXjZXRhkMpyD9KTysMWB5PtSkmyE1sU1mkJYtwoJ/EVXkvI0Vmlc5/u+lWrmzMwYhsHGOtRR2oaNvNUM3risrHRFxKceoRtEXU8dBVd75vtCxiMLEw+9U8mmIFOBjJyeaz7qxaJXZW8kAZLHnj8awaZ0xs9ipr2vaTocEr3t3GiIN7FzgAV81fEX/AIKSfBjwDeTae+uTXt9a5V7ext2fDj+EnpXzx/wUp/ai/wCEQuE8EeGbvzNTni3Xd0uCY1PVMYrwr9h//gn3qP7Uyy+KfEWqTaR4QEjRm5s2AuppB127lIx71pTp9WZ1KjWiPoHVf+C0lla6g6aZ4EuLmzRsLNLOqM6+u3tXtHwX/wCCsnwp+IEUdv4nkn8H6m8gRUuVLxHPT5xVQf8ABG34Gtgy6t4yd8ckajbgE/8AgP8A1r57/av/AOCS8ngfw/P4h+F+o3WqWFlGZLjT9SdWnVVGSwZQA34AfSuyMeU5ZSUuh+sPh/WtO8TaVbatpV5Ff6fdoJIZ4WDI6noQRWlX5H/8Eiv2iNU0vx7qfwu1zU7ibT7qIyabb3D7hDKh+ZVzyMjt0r9cBRymTVhaKKKsQUUUUAFFFFADVPzGnVEG/eMBxinZoAfRURkCnBNODZGQaB2H0UgpaBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTWO0E06mt94UAKrblBpaKKACimr9406gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoprMF60KwbpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/PT/AII/ePrBPgHqHh+RZFms9SmlkuG2rCqtyBuJBz+FfQ3xm/bt+DXwVjni1nxbbXupx7gNN0z/AEiZiO3HA/Eivw/8Rn4p/A3VtV+GE97f6NcC4EUtjZ7lE7dPkIALA5rpde/Yp+K/hX4eXXj7xXpCeH9BCrIZNSnBnnVucqAGIJ98VknbcvqfUfjv/gsn4hW8vbfwX4NtLSyZ28m51FiJ2XsWRcgH8a+e/GH/AAUe+OnimaUp4pk0mNst5Vqu0L7Cvs7/AIJ4+D/2XfjJo6afpnw/kn8ZaXao1/N4ixL57/xPGolYY+qj6Vif8Fbv2cfC/g7wB4b8W+FPD2n6IsF2be7Wyi8veGHHAGMVpccmz4C8U+KvH/xo8I3Wta/r+peJIdMuMyLMWkEZfuPQV+uv/BJ3wLJ4R/Zftr6V0dtYu5LtQucqvTBBHHSvmX/gjW+k6xffEPw/q1la38FxFFN5VzErgAHng9q+pfjl+2R8I/2RftGn6RIdRv5kKroOilCkTf3vvALUx0Y+lj7IyKU1+T/7K/8AwUe+IvxQ/aM0jwxJYQ3Hh7Wbloxatlpbdezbvav1g28VoZySWwopaSlpCCiiigApCcUtIw3CgDj/AIjeIrXwn4P8Q63cIzRWFlJOTnHIU8D3r8If2dvDLfGv9p+bWtXhku9ItruXV9QcqX2xKxYZ/Kv0w/4KgfHi3+GHwQvfD1lfbNa1p/I8lT8wjPUn2riP+CRvwG0/T/gzrHjfU7Tzb3xHLJaL5g4NsvHH1JNcyjzXsdPwrU4zx7/wUy+B2vLLo+r/AAik8QQWLm3gaTysFV4BGUzjivjSfw5pH7YX7TNppXw88LL4L0zVJVVre3Uv5KD70pGcA+wr64/4KEfsd/Bb4BfDfUPF+m2F7Fr+pXfl29ql6VjRmOSwXHQeldZ/wRz+A9vp/g/WPiXfwZvryVrOyMkfKxjq4OehrSCsZvud34R/4I8fB7R7eI61qGua7dADezXIiRj34Uf1r5V/4KNfs6/Av9nHw9pmk+DLG6XxleS72U3zyiGP/aUk8n0r9avi9qfirRfAGr3fgvTI9Y8QxwsbazklEe9scYJBGa/JT4HfsZ/Fn9pz9pO/8T/FnT9R0Oxs70Xd/JqVuwW4YMD5MXOCOByOKqzuI+eP2efHz/s4eONJ8WeLfh4+s6BOAF+32xjWQd2R2Uhq/cT9nr42fC343eFrXU/AFxpq7og0umxxpFcW3qrxjkY/Kp/jv+zp4Z+OPwhvfAl7aW9pAYBHY3PkBvscgGFdQCOn1Ffit4++G3xU/wCCevxosNSWaa2e3l3WerWoP2e/iB+645wT3BJxRZiuj9/mtYnYMYkJXoSo4qXaa+c/2Ov20PC/7V3g1J4PK0fxVaoFv9FkuA8gbHLpwCyH1xxX0Zx6VVxai0tN3UbqLoVh1FN3c0oOaYhaKKKACiiigAooooAKKKKACms4UgGnUmAeoqOVgLTWYIuT0p1IRnrUgR+YGUsASKGz5ZxwcUSDbG2Dt+lef/ED4x6B8LrIXviLU4NOsS2zzp2x81TKSjubQi5bHdwRt5IUs27ue9SxoY1wWLe5rwm8/bS+EWm2P2qbx5ohQjK4uBn8q8y1z/gqV8FtBu5YX1pr4RnG6ziZwfoe9LmTK9nI+Zv+CxVnqFxcaNP5ebKGTG4Hua+mP+CUOjxaX+x/ockbszXV/dTOG/hJfpXwf/wUI/bB8C/tD6bZWnhE3sn7wSytcrtAPoBiu9/Yb/4KO+C/2evgTa+DPFGmX1zdWl3I9udPj3Flc5O7Jx19KKacd+4pe89D9dpjlcZxXHfEfxvB8P8Awxf61qUyw2NpE0jMvB4FfnV8Wv8AgszH9mWP4feCjNcD702uF9ifVUKn9a8A+K3/AAVC8b/Gr4V6l4Q8R+GtHgmuyR9u0czQqq+hV3c/rSndr3QjaO57L4R/b4+Lvx4/ac0Hw18PpIIdC+3eXKptdwkgB5Zznpj6V+gn7THjzX/hb8FfEPiTSYDcXVjZPJI0C/OjY4dQewNfBX/BF34bwT3XjPxrPE0k0YSxt5MDYO7YyM5/Gv1K1bSrXW9MutPvoEubO6jaGaGRQVdSMEEGteW6sKUtT4I/Y1/4KiaF8VGt/C3xHmt9C8SYWKC/AKQXZ6c5J2t+lfRf7VX7Rnh34I/C++1a91KNZ5o2S1jhkBaRiOCMdq+A/wBs7/gl3J4L+3eMfhXcyy2MZa6udKuZl82HuTEQo+Uelfn3qPirxN4ym07Rdb1u6uYLdxbQpfTkxw845z6U7c2iElZ3Z6J4R8B+Mv2wfjZcQaNb3F7fapdNNJcTFmjt0J53HtgV+537LP7M/h39mD4cW/h/RkZ76YLLqN27bjNNjkjgYHoK8+/4J4fs8aT8DvgRpksc9pqms6tm7udQtyHX5uiK2OgFfU+2jlIlK54R+1x+yroP7Unw2utGvUjtdchUyadqW35oZB0B9VNflJ+zj8UPG3/BP/8AaUPhfxk1xp3h55/I1G0cExSxk4WaMdPQ5FfultxXyL/wUS/ZM0n4/fCq+8QWln/xWWg27TWVxHwZEHLRsMfMMdKsV31Pqrw94g0/xVollq+lXUd7p95Es0E8TZV1IyCK0a/I3/gl3+2Nf+EfFKfCDxheiLSJmZNMkuvvwTZ5iLHsewr9cVOaAasLRRRQIKKKKAOW+JHw70H4qeENR8M+JbBNS0i+jMcsLcEZ/iU9iPUV+UPx7/4JG+NPBd/c6x8MdUXXNPjLTR2c7+XdQgchUb+LFfsK3WkqXZlxfKfg18Kf25vjp+yr4g/sHW7m9v7C1k8ubQ9fQswA7I7DI/A19+/Cn/grh8JvGy2Fn4jgvvCupzKBO0yBrdH74cHOPrX058YfgH8Nvi9od3D438OadewbCXvJUEcsYx1Egww/OvwK/ae8B+Ffhz8aPEOgeB9YXW/D1tLi3cZcR5/5ZgnO4j1qLA31P6FPh/8AFLwf8TrNrrwp4j03XYQMt9jnDsoPqM5FdRJA5ZdrYHevz2/4JBfAfU/A/wAPdb8a67YTWN3rEojs0nDI3kqOW2nsT61+iNP2cSbmZfL5b56g9q5X4i6jLp/gzUrpd0ccEJbIGTgDJrt5LaOQlmXJ+prO1/Q49e8OahpzAYuoHi59SCBXO6eptGpY/m7/AGhfHEvxA+L3iTVmlMsT3LRxMRztBwK/dD/gn74QvPBP7JvgKyv12XMtmLgpjoHJI/Svw1/aI+Eut/Bf4veIvDmuWzQzQ3UjxyMMCaItkMv51/QT+zRfrqv7P/w/uhG8Yk0a3wsgwwwgHP5V0xtYid3qek1Fd2sd9azW8q7opkaN19VIwR+tT4FG0VZmfglMyfs6/wDBQ+aK1JitNK8U+SFXj9zIw6e3zV+9NrMtxbxyp9yRQ4+hGa/D3/gpVotv4Z/bYe7sFEM929pduV5y+4c8/Sv2v8HyNN4T0WRzl3soGJ9zGtBcuhsUUUUEBRRRQAU1pApAPenU1kViCRkjpQA0r8xpACvAHFSUUDuRsinkqM1FJJGq9QDVnA9KY1vE3VFP4UDuMhYyKP7vY1NQqhFCqMAdqWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmthgRnFOpMe1ADIxt461JSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMaTaQME0NIFGTUF1ciM4H3qgW6M+V2kEdT2rLmZai92TSyF84qWHKoM+lNiUMgz1qXpWonYdS0i9KWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPBJPFH7OnxT8aWWpvrXgfX/E0BH2eY3sDzg9sfNya7H4+fDTRPi18JNe0DV7WO8tJbV3iXj5XC5UivyP+J3/BI344eCdUaTwj/ZXjWyRwYLiwvEsrke7JMVCnPo7fWmR/Br9t/wCH3h+60tLDxRHpaxFJY476G5VExzgrI2ePTNKUUzSxxf7Ffji2/Zz/AGvIl1vU49J0y3mlsruRyQhTPA/lX6hft06XpPx1/Y98S3/h++tdVtYoRe29xC+5W2nJxjvX4Pa+NR/tq/Grec+opKftH2kYk35wcj619KeJP2zPElr+z1oHwv8ACdr/AGNYLb+ZqV3CxaSckkYOenFQM8n+BfxM8f8Aw08S3svgBrv+1by1a2eO1iZ3ZDweBX0v+zd/wTd+Jfx+8TJ4h8fQ3HhvQJpBcz3F+GFzeAnkIMcfjis//glL4otNC/amtbS6hjuv7StJIVlkwfLc85Ge/wBK/cqkB498Hf2R/hX8DZre78KeFbW01OGPyxqEmXnPqdx7mvZKaDS5rRGQtFRNMVbG35f72a8y+Kv7S3gH4L3WkQeLNZj01tUn+z27EbgW98dBT2KUXLY9SoqGzvIdQtIbm3kWWCZBIjqchlIyCPwqagkKQ8AmlpP5UAflb/wU2/Z9+J3xq+L2l6l4X8JXuraPa2flFrfBBbd97Ga+7/hfqHhz4DfAvwrp+ttD4VtNN0uITx3BCiJ9uXBx3zmvQNc8d6B4Zmjj1TVLPTmkcIguJlQsT6A15p+1R+znY/tNfCW98Mpqb6ZPKRPb3kBypcdN2OqmudLSyZ1SkpWUlY/K39tb42RftiftC+HfC3g7UZdQ0V7pbS3wDsZ2bBbHoOa/Yr4K/DSy+EHwv8PeErFESLTbVImMa7Qz4+ZvxOa/Of8AYN/4J5+NPhh+0Jc+J/H9hBBYeHy62GwhluZDwsi+gA5r9Tq0joYz7A360iqqjiikrQzFCjJPeuS+KHwq8NfGHwleeHvFGl2+p2FwhXEyBjGSOGU9QR7V1u6jdQB+G/7QH7DXxd/ZN8eXPirwCupahoFnN59lrWjlkmgTOdsiKxOB06819D/stf8ABXiC9uLfw78ZbJLGUEQx+I7NG2lumJogDt92B/Cv0+mhjuI3jlRZI3G1kcZBHoRXwB+1t/wS18JfE681PxZ4Jv4/CGtzbp7m22j7LO+Oy5UJn64rN+ZotdD7u8N+JtJ8YaNa6tomo22q6bcoJIbq1kEkbqe4IrTr8D/hr+0F8av2DPEs2hIFk0hZszWF1+/tplB58uQEhcj0r9Tv2X/+CgXw7/aO0yOA3kPhvxMqjzdKvpguW/2HONwpBY+nxIGkK4OR7cVItfFnjr9t688BftoaF8MZ20+XwxqMaRzSICZYrh+g3ZwR07d6+1FrRO6FJWFooopkBRRRQAUUUUAFFFFABRRRQAVDcSOsbGJd7jsampixhXZh1brUWYEUjFl2HhmHPtXzD+3V+yxrv7Svwrj0bwzqUFhqttL5yx3PyxzexYAkV9RmMFt3ehY9rEhj+dHLfctScVofixoH/BHH416i0Z1LWvCumQE/MDcyyuB9BFjP419C+Ff+CKvgqPSbZvEXjrXn1Qp+/wD7NW3SEN/s74mOPrX6SdKP1o5RczPx3/bN/wCCZ/gn9nP4O3/jPQPFWuX97byqot9UeDYwJ5+5Epz+Ndj+wT/wT2+EPx2+A+keOPFsWranqlzcTRTW8V8YrddhAAAVQ2ef71e0f8FbNUs7H9nueCSQi5nuolVVPXJ71e/4I/3zT/snGAnKwa3dhc9eQhxU+hq9I3N+b/glD+zpIxI8L6lF6BdYuCB+bH9a+Y/22v8AgmL4B+Evwp1rx74H1bU9ObTUV5NO1CdZYWXOPlIQNn6k1+r2M815D+1p8On+KX7PPjXw9FvM9xYO8Sp1LKNwHT2rSyMrnyT/AMEYPENvdfBzxbpKYE9tqgmP94qy9/xr9E26V+JH/BMP9o7Tv2evjDq3hXxc66bpmvlbZ7y5ygtp0OBuJ4ANftLo+vaV4r037XpWoWuqWMmVE9nMsiH1G5TTB73Py/8A2/P2l/Efjf4uJ8Kvhqszatu+y3FzasWbJ4I46DnnNc34o/4JCa3Z/Bt/EUXiRrnxott9rudP2bkduSVU4zmv0V+G/wCyV8NPhZ421Xxfomhk+ItTlaWe+u5jK4LHJ254Ar2HaKhRsy5STtY/I3/gmb+2FqXw08YR/BbxwJYbK4uWgsJbkEPaT/8APNsn7p7cV+uY6etfiF/wVGsY/hz+2NHrmiQQ6fcm1ttRZofl3zAn5yB3+UV+xfwX8WS+OvhL4Q8QTjE+o6Xb3En+8UGf1zVmR2dMkjWWNkdQyMMMrDIIp9Z+va5Y+G9Hu9T1K4S1sbWMySzSHAVQOaAPxH/4KJfD+3+Bn7YFnr2iWa2VjeNBqsaw8KGVxvxjp0r9qPh9ryeKPA2gaxGSUvrCC4Gf9pAf61+HX7eHxo0/9pP9oaytPCMr6jZwgadbsoz5jO4DEe1ftn8G/Dtz4R+FPhLRrs5ubHTLeCT6qgGKC5O52VFFFBAUUUUANbrUUkwhUs3AqRm68V518aPi1pfwd8C6p4i1u7htrS3RggcgFmI4A/Gsm9bGkVc+Hf8AgqB+2Ung3SX+G/hi9kGt3g3Xl1EwxBGeqY9a8X/4Js/sMD4wahZ/FDxmpl8OWlyWtbGZT/psg6SE5+6DXi3wh+FviD9uz9qLUZpmdtNurxrq+u2UhUt1bhMjpkDtX7sfD3wDo3wx8GaT4Y0G0Wz0nTYBBBCpJwB1OScnJz1qrBKXQ3re3itLeOGCNYoY1CqijAAHQVIBjiloqzMKRVCjA6UtFRygfin/AMFebeOP9prTT5jOJNMQsrLgKQ3TPev1u+Ad1De/BPwPNbhRC2kWwXZ04jA/pX58/wDBaH4cR/2f4P8AG8FqWmR2sLmcAn5DyoPpzX0l/wAEyfixF8TP2VfDtsZHe+0AtplxvABO0koeO20gfhSWho9UfWVIzbVJ9BmiuA+PPjhPh18I/FOvNc/ZZLWwlaKTjIfacYz71XMiFqfjz+1ZqU/7QP8AwUIGjaZbmRo9SttMVV5/1bAu30r9u9Jsxp2m2lov3YIUiH/AVA/pX4wf8Eq/CNx8VP2sdS8ZaoXvTpMM9888h5M0hwrH86/amqKk+gtFFFBAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTXzt+UZNOooAamdo3cGnUUUAFFFFABRRRQAUUUUAFJuFLUTsFUk9KY0SbhRurPfV7eOTZ5gLf3e9TJceYMqRjrU3RXKy1S1m3WpeSmRUVlqktzk7MqKhTTY/Zs1t1G6oI5w6ZPB7im/aM5IPAq7oXKyzS0yKQOop9MgKKKKACiiigAooooAKZIrt90gU+igDMa3aa4IPY1cjthGDU20Ak45panlRo5tqxGsZWnbadRVGYlLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfE2vf8FdPgNpMCPaza9q7t/yztLFAR9S8iiufvP8Agsx8FYbbdHoPi+4mI5hWyt+PbPn4/KtC3/4I6/BKKRWk1zxxcqP+WcurQbf0twf1rUj/AOCRfwEE2+SLxLOveOTVvlP5ID+tZ63Luj8tv2kPjl4F+MfxrtfG+heGLjTbKS5Wa/tLuNF84BuchGYcgV9vWX7dn7Kdn4DFnZ/DjbqMtn5Txf2EjgPtx989RnnrXvo/4JQ/s8rNC48Pal+7/h/tSQhvrWz/AMOw/wBnUyBz4Fyf+whcAfkHp2HdH4j6D4+ufA/xbh8Y6FE9p9l1I3cCW6FF8vfkKAenHGK/Q/U/+C0gGk+TZ+BbpNQVVAlnlQKxwMkgE45r7E03/gnb+zxpaoI/hpp8rL/FPcXDk/XMmK6eD9jP4JW1ukMfw10JY0GAvkE/qTSswuj867r/AILSeMpIIxb+BdLE38Re8bn8NtU2/wCCznxIZsp4I0QL6NPJn+VfpPa/sg/Bizk3w/Dbw+r/AN42gJ/Wt63/AGefhlbRqkfgLw8FXgZ06I/qVrQpzVrfofmBJ/wWZ+IMsJRvAehjcME/a5M/+g18l/tDftJ65+0X4sstV1iyj0v7Ku2G1tZGePcSPm5r99m/Z/8Ahq/XwH4eP/cOi/8Aiax7/wDZT+EepXAnn+HugvKDkEWir+gqZahGfKa37Pc3n/A3wLIWLFtHtiWY5OfLGf1r0Kqul6ba6Np9vY2UCW1pboI4oYxhUUDAAHpVqmtjJu7uFMl/1bfSn0UxH5Tf8FhfCV3px8J+KIZ7m3bzGtf3bkLjqG4PXNfUv/BMPxtf+Nv2UNCk1K+lv7ixuZ7PzZiWfapBAJPX71eg/tVfsp6J+1R4Nh0LVtRuNKaCQSRXFsoJU/Q10f7OfwB0T9m34Z2Xg3Qrm4vLWB2le5useZK7dWOOP/1Vkou50SkpRXc9Nz6V4z+1xr3jzwz8D9d1P4dKzeIrePzE8tQzBR1IBBya9o202SJZoyjAMpGCCODVWMIuzuz8lv2df+Ct+v8Ag+aXQvjFpF9rjxttW+sIVW5j55DxnG4/iK+vvg9/wUk+FHxu8f6f4O0Cx8UQavfEiH7fpipHx3JWRiB+FdL8Qv8Agn/8Dfidr11rWueC4X1O6bfNPazyQFzgDPyMPStL4L/sR/CD4BeIzr3g7wx9i1jYY1u7i6luHVT1C72OPwqipNPU9M+J1x4ltPAGuzeD4refxLHaSNYR3RxG0oHANfj/AKb/AMFWPj98NPGU+k+MbPStQayuil9p93Y+TMuDgqrKRjjpwa/anbXj/wAZv2R/hV8eY5G8XeErK7vn5/tGBPJuQcYz5i4JP1zTEmeYfs//APBSb4SfHjVNO0KO8ufDvia7wi2GpR7UaT+6knQ/jiuH/wCCkn7NHxb+OGj2eo+Atd8zStPhZrrw+s7xSTkc5TaMMf8AZNUfhd/wSN8E/Df4vWvi6TxVe6zo9jP9osdEmtdhhYHK5mEnzAH/AGRX3qqBVAHAFTvuVdLY/nu+GXx5vvhE1z4B+JPhdtV8Oq+2503VISl1a+oTcpI659816F/wxbZ/HVZvF3wE1+GW2IMx0C8n8i9tcD7owSc5Bx9RX6q/tFfsWfDH9pKGSbxLoy22umMpDrFn+7nRscFsffxxwa/KP4z/ALIvxr/Yn8cNr3hS61XUtEQmS313R43YhRj/AF6AnZ+JIxU8r6D5kdL+yn+wn8ZPEHx+8P674s0PUNJ0zRbxLq41DV3LGTYchVJOWzX7ZL0r8rv2OP8Agqp4k8R+LtK8EfErTV1ifUJ47W01fT49kgdiABJHjB+oxX6o04p9SZO4tFFFWQFFFFABRRRQAUUUUroAooopgFFFFABRRRQAUUUUAfBf/BWLwk2ufBG5vY3iAs3jlbd97IPFL/wRyl3/ALMOpLnO3XZz+apXTf8ABUbQhcfs269eB2QLt3bTwea4f/gjHdNN+z94ntyFCQ62SuP9qMZ/lWcd2bSfun6CL0oZQylWAKkYIPQ0UtaGJ8ffHP8A4Jg/CP44eOJvFFw2qeHb64/4+YdHkjihmf8A56FWjb5voce1ex/s2/sz+Ff2XfBc/hrwpc6nd2lxP9olm1SdZZGfGONqqAPoK9d20baB3BelLSUtAj5L/au/4J3eEf2pvHVh4u1HXtQ0XVLeGO2lWCJZYpYlJONpIIPJ5yfpX054O8L2fgjwppHh/TwRZaZax2kO7rtRQoJ9+K2KKAOK+MHxNtvhD4B1XxReWs97DYxl/It13Mxr8e/j5+258Wv2wtUbwR4N0K6sNKvJPLSztUYyyL6Oe1ftndWkF9bvBcwx3ELjDRyqGVh7g1k6P4G8OeHrhrjS9B03Tp2OTLa2kcbn8QM0Afnx+wR/wTRm+GurWfj74mwoddhIkstIUhlgb+9Ie59q/SLpwKWigAooooAKKKKAI5W8uN3J4AzzX4wf8FUP2lJ/HnxFbwBptyp0nSSpvEjHJmxkAnvwRX7RMoYEEZBr42+O3/BMP4d/G74rp45k1C+0W5nlSXUbO2IaK7K4HflcgAfLis3G7uaRkkO/4Jd/Am2+Ff7OeleIJrdo9c8TL9tuDIMFI8kIo9BgZ/GvsiqOh6NaeHdFsdKsIhBZWUCW8EY/hRFCqPyFXq0MwooooAKKKKAPKf2mvgjYftAfB/XvCV4FWeeBntJ2BPlTAfK2B15r8RPgN+0V8QP2G/ixq9jb2xnjhuGtNR0S63JHPtbG4ZBwe4Ir+hDFeS/GL9lH4U/HlYz408G2OqXEZ3LdR7refPvJEVY/iTU2KTPjaH/gtb4JWyiM3gLXPtW0eYqSxbA3cAk5x+FfLP7XX/BR3xN+01aHw14a0+Tw34Zk+WS2fbLPck8bTgHH4V+iK/8ABK39nXzt58I3ZXP+r/tS42/+h5/WvS/hv+xX8E/hNcJc+G/h9plvdpyLi6Ml0+fX96zYP0pcoRdnc8e/4Jf/ALNP/Ck/gnH4j1W0a38UeJ1E9wsgZXhhBOyMjOO27pnmvs+moixqFUBVUYAAwBTqsTCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACMwUZPAoVgygjkUEbuDQqhRgdKAFooooAKKKKACiiigAooooAazBRk1Xl/fx/KeDUsnzZFRbdoAqOY0j3Mh9Dg+0GY7g5OSauLlWVY13ADBzUrQM8zfMQKezR2aFmYDHUtWVjVy7EH9nmZiWGFParVvbpbxhV6VjX3iZA0awnIY4Jq+sjELkkgiqTtsHLN7kzAKzE9D6VBHtYSKCSc1JIwAwTg+9NtbZlm3joetS9WF7Fy1XEantjvU9IvSlrdbHO9wooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu3rnkHsaZcWsN5bSW88STQSKUeORQVZT1BB6ipaKAPniP9gv4O2fxc034i6d4d/snXbGf7SkVjJ5ds8nZjGBj34r6HoooAKKKKACmTSGNNwGafSUACsWUEjFLRSA0rgLRTSaMmoYh1FIKWrQwooopgFFJXlf7RXxwH7P/wAOdV8WzaVJrUdnCWSztyQ8jfXBwKmUlHcqMXJ2R6rSEhRknAr8s7X/AILabpovtfw2WGFvvNFf72/LaKxvGH/BZ7VJNUmPh/wdGtjs/dreTgHdgdQBnrnvS5vIfIz6s/4KTK2vfs1+JdOW8s7AeX5ifaZQHm2noozXmf8AwRhtWh/Z/wDFMxR1WTWyo3d8RLnH518A3Ft8dP2/PiJdXWn6dqOrRXDhjGrNFp1kvC/eY4xxnrnJNfsh+xr+zvL+zH8D9J8HXN1HfamHe6v7iP7jTOeicD5QAo5zznmiKBvSx7pRRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJtGc45paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiip5gCikpadwCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSZGcd6WgAooooAKKKKACiiigAooooAa2c9KjWMiRmPfpU1FTyodxkgbadvJrH1DR7rUCN0oVP7tbdFHKhqTicvJ4Vm3ho3Xg5ANbNrYyLzM2T7VfopcqLdWT0KVzZhyGbPy9MU+BtzYAP5VZowB0FPlRHMwFLRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUroAoooouA1mC9aRT82KR8lgABj1NNjkRnIVgxHUCs29RjpZBGASM84p/FQXTyDb5YBycEnt71HtaSBo/N+f+9T8x8uly5RUKMY9sedxA5NSbqq6FYdRTN9Lup3QWHVXvbG31G3eC5gjuIZBtaORQykHqCDU9FDSYbHgHir9gr4DeNNSnv8AVPhzpbXU7b5Htw0GTjHRCKZov7AXwA0Fomtfhno7PH91rhWlPXPJYnP419BYox70BdmX4b8K6N4O0uLTdD0u00mwiGEt7OFYkUfRR71q0UUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4BRTWbaM4zQrblBpgOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKY4Y4wanmAfRUZB3HBqNmPPzYqeYaVyfcB1Io3D1qrDIs0nDBwvcGpuxz0pXuPlI3ky528j2qVGJUU1VCrlRSZc8jioCxMKKhDherZPoKAu/JywHp0rWMr6BYnopF4UCirJFooooAKKKKACiiigAooooASjNRthmIzzSqu1cZzUcxViSikXpS1ZIUUUUAFFFFABRRRQAUUU103Y5xUcwCBTuJ7U+iirAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKhurpLO3eaTOxBltoJ49a+evDv/BQL4HeJvG8vhO18YpHrKXDW3l3NrNEjSKxUgOyheo9alySdmUouSukfRdFNSRZFDKwZTyCOQaXNUSLRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUySTZ2zTBcKULDnFZPcdmDXARmDYUDuT1psl4kSl2ZRGOrE9KxtfvIYLV5rgME4247Hpivhn9sb9uxPgNfPoEds+o63cWhe3t1OIlyxAZmHNcrqS5uVI6fZLl5mz7/wB/m7XVg0Z/u85qGG3EHmSqmGY/dr8QfB3/AAVi+NPhPVLdrn+y9U0hG5sJLfb8pPQSA5z17V92fs8/8FUfh98ZNes/D+uWE/hHV7gAK91IrQM57Bv8a6NbXZh6H154m1SXQtNuL8OBHAplkXGTtA5rxr4K/tmfDf4469qOgadrUdjrlpK0f2O6YRtJtODtz15Fe7yRxaxbnbJFPZzJglcMGBH8q/Nj/goB+w9JoMsPxN+F1q+marZtvnisflyRzu479al3urbG94uNup+l7yJa7N2fmO0HGakjJwQxBIPavgX9g/8A4KJaZ8UrfTPh74/l/s7xpCrQx3twwEV2VYgLk9HxgfUV96SFLQvK0gRWI+90HFabmVuhY79KQ7u2MV8+/tAftleDP2dbGObXrg3bykhIbRgXznuK8D8I/wDBYr4ZatqVvZaroWr6ZFJMI/tzBWiAJ4JHXioUk9inBx3P0BXO0Z606szw34i03xbodnq+kXkV/pt2nmQ3ELbldfY/XP5Vp1utjFhRRRTEFFFFABRVa6ujBwqFmJwvHWpgxwM9aAH0VFNN5UZbG7HYU2G4Eyg/dPoaV0OxPRSL0paYgooooAKKKKACiiigAooooAKKKKAGtnacdaI920butI2d3Bo5rJ7gPopm40bm+taLYB9FMWQsxUjFPpgFFFFABRRRQAUUnNLQAUUxmPToabJMIsZGc+gqOZDJaKQcilp8wgopjMV6VFNMUhLd81Q7FiioFnyoOKPPGcc5qeYfKyeioBcLu2k4NSMTtPNUKw+ioY5GOeM0sZZuScUCJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKO5qGaTZmp5hpXJs02TJQ4PNUi8r5ZWwv8AKljmLKRvVm9jWdy+UfMzIu7dWbdXk+VRIWfcfmakI82Ykz52nBXPAq2u55Dg446fpUJ3Zulyoms4VtYN2NvqtVmuLm4n+UKluOv95qxta8feE9L1608Oat4k02x1q6AeHT57yOOdwTgYQsGOT04roJ4I4YzIsbEg4wPyq7GSab1J4x8gw2B708g7fvc0yOIbRtOBShTGxZj8tIl2voJFHhyx5NTUxX3HjketO3c4FVH3RDx0pv8Ay0NfEP7VX/BUTwx+zh8RNW8CWnhW98R+I9MMQuW89YLdTJCkqgNgk/LIueODmvev2Tvj9J+018GdM8eSaONBkup7i3ayS4E6AxyFQQ4AzkD04ORVcwrHs9FfnZ+1X/wVbk+B/wAX9Y8DeFvCdrr50VvJvb68ujGpm2qzIgA6qSVIPcGvtj4F/E7/AIXN8IfCvjb7A2mf21ZLdG1dtxjySOvccZHsRVknd0UUUAJmikOM1BPeR23LkKPU0NpAk2Ts6r1OKa8iiMsWAHrXPatqrLIhh+dWPVafJJczWrIqsT6YrP2iOhUtL3NCTUrWKQIZAZD0HrSQapFNMQrj6ZrANtcSSISu0rxk1bsdLlW8ZtodOu/1rLmZq6cIrc6VTuUGnVHEAqhe9SVqpHGFFFFPmEFFFJRzALRRSA5o5gFooop2uAUUUVQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEc0SzRup6MCDjrivxw/b3/wCCe3iHwD4qvfG/w9sr3VtEu5XurmGNi81vIzbiVwOmSTX7JZpjqsilGAIYYKnkEVnKN3c0jNx0Pxp/Y+/4KceI/gn9k8G/E+3vNc8OoVhgu2GLuz553FyN6gk9TkYr9cvAPxJ8NfFDQbfWPDGsWur2MyBw9vIGIGSOR1HIPX0r86v+CsHwZ8L6tB4avdCsIrfxldXIsrSwsIAHvixGThRjjvn0r2z/AIJz/sW6r+zH4cvtd8Rar9p8Qa9bIkmnwlvJtUDFlHOPmxjPHrWUJ3ehdSm0k31PtClpF46nJpC2K6LmA6k3fNik3Un8RNF0MfRSbqWi4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUU3eN2O9G72pXQ7DqKaGz2pjyurYVMj1zRdBYJ28uNmxu9qqr5hjbBVEIyGp9w05mjKsFQcsMZzVGa6+3WcyRrs5Ow+vr+uax+1c2jFtHn/wAXfFU/g3wPq2tThXjtIHk2sflO0Eg1+Fmi6P4v/bS/aOXToZJLrU9YuSpmzlbW2VuWHsq1+mf/AAUq+LWr/Dv4I39naoJotQlFkHLFSoZRlunOCTXk3/BFb4W2048cfEGaFXmilXSLaRhynyrI5H1DAfjUU4py5jas7aH2l4D/AGFPgv4I8EWvh1vA+l6qFhVLi8vYt8s7Y5YtnjnPTpXgv7S3/BKrwP4w8Pvf/C+1Twl4ktz5kcaOfJlwOF5PynivvgkDjPNNVldioYEjqM8it9DkWmp+CXin4yftIfsa+KJvCeqeJNQsZ441ES3DefEykB8qT/vV+oP7BPx38TftPfAG81nxrbWlxdCZ7TdEuFnUblJI7HjtXg3/AAWZt/Dv/Cu/Dcsluh8QC92JMoG8R7c4Nehf8EhbuOb9lkW6qqTQ6jcKxHUgyOQT+dQaM/KL9p3wwfhd+0Z4u03Smntfsd8txbyA7GTeiy5BHozn8q+7f2Q/+Cn2lSeBbXwT8X7ueC6tkZLbxEoMjTLuYr5g7FQQox2Arjf+CunwPg8J+JtC8cWyHztR3Wt48YG0kL8jH3wAK+WvGHwFSH9nnwz8U9MmQW1xI1hqNqGzskV2QMv1Cgn3NK6aswTlGV0dVdeD9e/bW/avvtA8Oas9/ZX1w0kF3Pu8qK3RQC+3t0NfRPx+/wCCScfwt+E934j0PxjeatqVlGJLi1u40WJj327RmvFf+CdX7U3g/wDZh+IWoXvizR2ng1aIWyatF80lqueRt9D371+zV34w8MfG74S3uoeGdQt/Eel31szJ9lcMTgkEEdQQQRj2qnaEROTnK7Pzi/4JD/tJatb+OLz4R65qElzZ3EMk+mRzMT5LRgs6L7H5jj1r9aK/Cr9nfT7f4Z/8FHvCdtF5lrZSay0UbMNmfNhIK/TexFfupu6VcZKSuRJWY6ikpaokKQ8ClpOtK6ApTPJ525Qzbe3YVy/jj4veE/hnpE2p+KNcttIs4SA8twcDn09a6HXb4aZZvIDg9BX4of8ABS/42ar8RPjZ/wAIRYTSzaXpqxQ/ZISf3tw4DAe/3l49c1lzPmsjqULw5nsfqlY/tsfAzUtQSxg+JmgG5cgCN7kJ16dcV7BouuaZ4k0+K/0q+ttSspc7Li1lWSNsHBwwODyCPwr8h/ht/wAEc/F3jD4ef2zrviiz8P61dQeda6V9mMmwkZAkfPGePpXl1l4i/aG/4JsePLG11Hz10ZyTHY3Dm4028jLZbaQRtbk9+CTTMra2R+7S9KWvNf2ffjpoH7Q3wv0nxj4fmDQ3aFZ7cn54JlJV0Yf7wOPUYNek81otjN6PUWikFLTEFFFFABRRRQAUUUUAFI3SlpKAIJN7DIr5+/ak/a80L9lXTrC81+CW6a+3C2t4hzIwHrX0Pt2jivyt/wCC1Vx50/w0ULugVrgM2ON3GB+tYta7msXpsfbn7Iv7V2hftaeAb3xBpNlNpd3p919kvbKY5MbEbkIPcFcGvda/K7/giTeSs3xKg8xvI/0Z/LzxuwQT+lfqjjNaohir92nVGXCYBOKXd70xDi2Kasgboc1UaZvthjY/Ieg/CpoIwp6c1gpOTshtWJ6Wm5xRurW5IyabyyBmpFbdUMkIkbJp6/LgVnd31GRXBfcNhANSJuCjccmo2txJMXYk+2al4UUD6D16UtMVuKXdTFYjkYhjVaZvmAxuLHkelWmx1PFMWFS28dT3paloazCOREOTTjjccLz61MqjAzyaXaOuKvlFcriEbt7KC1PVt7MMcetO3BmZfSgKAMdqsVyDaQ5AkOPTNc/41+IWi/DrTl1DX7+303T94R7q6mCKufrXR+WolXHHtXwF/wAFmNan034A+F7G3meE6hrYjkCHG9FiY7T6jO38qXMXofc/g/x14e8f6X/aPhvWbPW7HdtNxZSiRM+mRW9X5sf8ES7yab4YfESB5XeKLV4NischcwnOPTmv0manuQ1Z2FooooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKQjcCKWigCBVaBcDkCnI7SLnGKhvrpLGCa4lUmOJDIdi7m4BJwPoK+Kfgz/wAFQvBHxZ/aCuPAgsZtH0e72waTql8uyS5ueAUdf4cncB9BnvU3KsfXPjzx34d+G2hSa14o1+x0HS0dY2udSmWOHcegJPetrRdb07xFpsF/pV9b6jYzqHiuLWVZI3X1DA4Irwn9uL9nG5/af+A994U024S21iC5jv7J5PutIgYbD7EMa/Ib9nv4/wDj/wDYL+N15pusWV0LFLkxa54d3AC4+XiRfRgCCD/+qmFj9/aK8q/Z7/aU8EftLeDY9f8AB2pLPt+W6sZsLcWr5I2yJ26ZB7gg16rTJCiiigAooooAKKKKAGf8tBVO8kAZhsZjtPSrjd6iCjcTms3uXHTU8j/ac+Luo/A74G+JfG2j6Q2sXulW6uLXsuSB5jDuBkE18k/sDf8ABRS/+M/jDXPDnxN1HTNNvrjZJpMiKsKHPDR5PfpX6CeI/D2neKtA1HR9Vtku9Nv7d7a5hcZDxsCCPyJr8Zv20v8AgnDrv7PcjeNvh893rfhfz95ht0ZrrTjnKH5eWX37VJVz9kpbWL7Z9pjkUxH5mVTnPvXlv7SX7QGn/s5/B3XvF2pzxLdRo0Wm2shAee4YfIoB5IB5OK+CP2Nf+CoH9lW1p4S+LnmTW8EIit9ZRcuSCdok/DA/CvAv2vf2gNf/AG5Pj/o2geF7O5bS45hp+k2Iywdy+1pmA/E57AUlGzuXzaWOY+BXhH4j/ttftL2N/c6he3OotdLeX+tZbZZQodwUHovTAFfvTpBurexht2EjJDGqb5uWYgYJJ9zXif7H37J+g/sgfDO4tlnF9rl1H9p1fU9uN7KCdq+iqDj3xmvk/wCIn/BZ6z0vWNRs/DXgCS5toJDFBeX13t8wjgkoBwMg9+lUSml0P0vt5Wa28w/KTnj8axNe8VWPh/SrrUdVvLWz0y1UtcXd5IscUI/2mJwOo6+tfkfqX/BZb4oXUkhs/Dfhm0jb7qzxyyMPqQ2DXiPx+/b9+Kn7RXhz/hHdavLXTNF+9PZ6PC0ST+m4E5I+tFiouKd2j9y/hb8TdA+Kmmzar4Z1mx13SlkaH7Tp8qyRh1OCpwTg+x7EHvXc18J/8EefA+peG/2YrvW7uZWs/EOrzXVnCpz5aR4gb83iavuyq5TOT1P50f23vFkPjr9rP4paxbbmgbWpbVdw5IgAgz9P3WfxFfs//wAE6/DFv4U/Y1+GltAjIbmykvpN4IYvNNJISf8AvoD6AV+Ffxyme4+Nnj5xjMmv6gR+M71/QL8BLe2+FX7Lfgo6jOsNro/hq3uLiSVggULAHbJPTHPWnYGfiT/wUPs0sf20vinEieWjagsuMd2tomJ/Ekn8a/Z/9hJpH/Y/+FDSoyOdEiOGGDtJbafoRg/jX4HfGT4k3/xk+LnivxlqJVrvWL2Wc9lVSCqD8FCj8K/oc/Zi0ltC/Zw+FunvF5Mlt4Y02J48YwwtYw3HrnNUQz02iiigQmKz9R08ahtUhgFOfrWjRUyjzFKTRn2+mwoMFOB0B7VY8pYVOBk1KeppOKiyWhXM2Vo4QzcpgVaVBGvApF+9x0qSgmUmyNU3MWPFP9qWm4O8mr5SRaa7bSDn8KVutN9agYyOV2b5l2iia6SHO87VA3FjwoA7k1Ev7ydhu4r4r/4KsfHDXfg38D9JsPDl6bG98R3zWkkyNh1jVMtj06ikOx9oac0dxm4hu1uYn6eW4ZfzFX81+ev/AARw1jxP4k+EfjO/1nWrjVdKg1cWVmtw5cxusayScnkf61T+NfoRTCw+ikXpS1otiQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFQ2AUUUVYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGqu94kd4luwYOy7gccfTNZuTQ7XLPeqOqeetuxthmbBCk9B9auZoyPrRKLkrXHF8rvY860X4S2V5r1j4i8QRQ6jrNi7taMy7lgLcErkdcV6MvyjHpQpArI8VeIofC+i3ep3bJDaW0TSSSSOFC4HeotGjFtmjcqsrGn9oXzgg5NScGvyp+L/8AwVx1zwb4s1DS9B8J2d39nk2i6nuiFlUgEFQoPY14j4u/4KnfHDxZI40b7LpEMwGy3s4zM6cYPOM8nn8aUZuSUkipU1F2uftjr3iTSvC9hJe6vqNtptpGMtNcyBFA+prxjUv27PgPpN/LZ3HxK0UTRHDbZtw/MV+HPxb+K/xg+IVqdQ8c6j4gnspiAPtJkit84xwuMdqtfs1fsq+OP2nvEEul+FLaNLW2/wCPnUbo4hg4yNxA6mrM7W3P6Afhn8aPBPxk06S+8GeI7HxBbRnEjWkgYpyRyOo5FdvXyL+wP+xDdfsmaPrV1rerw6r4h1Zgsn2PcIY41PygZ6n3r66qopozCiiirAKKKKACiiigAooooAKKKKACiiigBjKNxPekNP202SMsjKG2kjGcdKizKuNjztGRg015QrBSevtSoPLVULbmAxnpmnYB6ipGVbjcJI2jGc8HJqq1n9nVpl+/zzngfhWrsVsEimfZxhhnKt2NHKy4zsflZ/wV28Yt/wAI/pegkCQSXazBhxjCDtXq/wDwRctwn7Nfiqb+KTxVPkfS1tqx/wDgrV4B0S1+FsviG4gY6h50aW7L0GcKfpW3/wAEX2/4xp8UJ/c8Uzjg9f8ARbas6el0+5VWSk7o+7tchuptNuFsn8u52Hyzj+LHAr8iv2qP2qP2k/Bvj3V/DFtp95oMCyBUubO1aR5VKgg7wMdD2r9hetVbjSbK8kD3FpBcOOjSxKxH5itrERnyqx/NZ8UvG3xH8Zxwy+OrzWL4I5ZJNTRx8x44JHpXefBf4f8A7Qb+E21T4cWfia20Od2Jl06RkjlYcHAzzyDX3T/wWX36X4Q8J21rYRR2FxMxkmhgVSrDtuA9q7r/AII4+NNW8T/APxBpmoTNJZ6Pq5gs93Xa6LI3/jzGlZil0Z8i6X8JfjN8Rf2ZPibffEN9Ta10WOK5sl1okzeYr5kAJ9q+VdF+IGua34JsvhtHIW0y41NJ44yT/rGbGPpk5r+j3x94NtPG3gnW/D1xEhg1K1kgORxllIBP44r8Kvhv+yX4w8P/ALYnhzwFrWjX1uLXWY5JLxLdmiMCkSK+7GMFcZ+tPlLTufdfjX/gk74I8e/B/R20Jm8MeNEs0lknjO6G4lK9HBBwO3FfAetWPx2/YG8a3dhHeah4bEnyC6tyXs7pSA3y5474+ua/oIgjEUKIOAqhRXK/En4T+E/i74fl0TxbotrrWnSDmO4TJX3U9QfpVW0szJOzPwC8JfGbWviF+0t8PfFetRxDUrfV7JJHt/l83Eq/MR6kGv6J4m3Rxn1ANfDln/wST+FmjfFPTPFmkapq9jZ2N1HdLo+9Hh3IQQMspbBI9a+44YVhjVFGFXgCpjHlHJpoevSlpKWrICims22jdUWu9BnP+Opobbw/c3EzqiwqXO72FfiN8C20/wCKn/BSHR59SgW6tJ/EEx8thlW8mMlOD7oK/af4sLFN4H1mOUcfZJGz3GAa/Eb9h1Um/b88Kkk4/tm+YY/65SVml+8Ol39kkfvTyqgDpXK/E74Z+Hfi54Pv/DviXS7fVdPuomTZcICUYjhlPVSD3FdaOlG2tbHLqndHwd+wf+zH8SP2Zfi5420i/O7wBeAy2h37suGwh9M7eDxzX3ivSjFG2q6Gk5ubuxaKbnFKTQZi0UgpaACiiigAooooAKKazBepwKTcTn07GlfoArfdNfmL/wAFooreDwJ4DCgCYalKxz1I8uv05JO05r8sf+C1c5kt/h7EpPlGSctkfxDioe5pHZnIf8EVfEpsvif440NpBsu9NjuFXA5ZXA6/Qmv1+Ar8WP8AgjbZST/tGa1cRqfKh0dg57csBX7UVUeopdBjKGGCMigKFGAKdSU76EFaa3LSFwPmHQ1MuVAz170x1Ls4DY/Onxx/KAXLEdcjmstd0aS2H5zTWk2nGKeoGKXaKNTNEO0vz0ojDBzk8DpU20UjLxxwaViriVHIewPNNjmPmMjdu9R7is7Hgg9DT+Q46ljYvpSMD0U4oj3bRmmeXJ5pbfhfSgAaPdHgnLetLGwVQvekmkWHDFtpY05GVj8vPuKBky9KWmKTuxT61WxmR7QHZu5oB3c4p9FMZA2POXrmvzh/4LXXTR/DL4ewquAdWmcv6YjFfpJgbs4r8tv+C2F5KX+Gdj5rG2ZL2Zoc/KWCqA2PUc1n1LWrPVv+COvw8l8Lfs23viKU5/4SXVJbiPjnZF+5/LcjV95tXhn7Dei22hfslfC62toUhRtEgnYRjALyLvdvqWYk+5r3WrRMnqFFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAprosilT3prL8x9K+Ef28P+CjWmfAyxvfB3gS5g1Pxw4Mc1wp3R6fnufVsGpuVY639tz9v/wAL/s46be+GdK8jX/HUsflvpZYgWqugKtJgd1YED0NfjJ4B8C+Kfjt8TIbDw7p09zquq324tag7bbe+5jnsBkn8K9i+E37Efxs/a40vUfiHp1tava6hLLImparcrGL2RXZXCcEjDKVyQBxWvp/7B37VHwvkm1TQfCOt6XcwHP2rRNZgMj47qkT+YfypWKP27+FvhW+8D/D3QNB1LVZtbvrC0SCW+uAN8hA749On4V5l+1B+x34D/ai8Nzwa7p8dn4jSLZZa9bpi4gI5AJ/iX2Nflt4P/wCChX7Sv7OuvrpHjiK+1ZISBNpfjGykgucEZ4kYB+QcgnPBHav1u/Zm+NUn7QnwX0Dx3Noknh2XUvOVtPll8wxmOZ487sDIbZuHHQiqJd1qfkT4Z/Zd/aH/AGU/2iNGstAstcjtLjULe3fXNBgea0u4DIpO84xjafmB6HNfuPDv8mPzDl9o3HGOcU5elLTJCiiigAooooAKKKKAGt1pu0HnFJNIU6DNKOlZvcsRlPGOKZc2sV5byW88azQyKUeNxlWB4IIqWvHf2rv2iNM/Zn+D+p+Lb3bNe/8AHvp9qx5nuGB2jHoOp+lID8yP+Cq/wz+DfgPxZpw8GSRad42kkDappVhgwRwleHYDhXz2968T/YZ+PWk/s3/Hiw1fxLosd1ZXKLbSXUkf72zVv+Wq59Qcn616N+xT8EdT/bc/aT1vxt41a4k0fT7salfzKAyz3G4GOAk8YwBkeg969m/4LFeE/Avh208BjR9MtbDxncGbzPsiLHutAqrmTHoeAT6GmUfqNo2saZ4y8O22o6fcQ6lpOowCSKaJg8csbj1HBBBr5juP+CYXwDvPE15rM/haWVrmUytam6cQKT1woPAzXoH7EPgSX4cfsrfDrRZtQk1OQaat150nUCZjMEHsgfaPZRXuVPlIueO+Hf2P/gr4XsYbWy+GfhsrFnbJcafHNJySeXcEnr3Neg6H8P8Awx4ZsUstJ8O6ZptomdsNraRxoMkk4AHqSfxroaKfKSQW9rFZwrFBEkMS9EjUKBnnoKS6uY7K1muJmEcMKNI7McAKBkkn6VYryn9qvxtJ8Ov2cviH4hiIEtnpEwTP95x5Y/V6oD+eL4oanBqXxY8V6hDMDaXGs3MyyRkMCpnYgg9+Oa/SX9tL9tzwbqf7Knh34b+APE6614l1ixsoLw6dJuEEQjUPFIy8B2OBtz2r4s/ZP/ZL1n9rnWvE+laDr1jomu6TbpdomqLIsUoZyGDOisw/KvuH9nz/AII93vh3xpa638UfEmnaja6fKs1vpugtK8UjK2RueVVbH4e3I5oKufmp8Tvg/wCKfg/ren6Z4n09rC/u7SO8gibrsdQ65/A1+yv/AATN/aq8VftHeCdX03XtAt7G08Kw2thDqVsxxcNsOVIPAYKq9PUeterftM/sTfD39qW107/hJkvLC/02Iw2l9prqjovoQVIYV0H7MX7MPhb9lbwHL4Y8LyXF3HcXLXVzeXmPNmcgAZwAOAAB9KCT2CiiigApMjOO9LXPePvFkHgPwbrniO6jeS10qzlvZUj+84RScD8qAN3duY46etVp45ZCApxg5z61+Ul7/wAFqNe/tGf7J8P7U2e8+X5t0Q+3tnAqtN/wWs8VLIwj+HWmlezPevn9FrN7miP1tiOE+bil59cV+M3jb/gsV8U/EWmNDoPh/SPDspBBmDNM/wDwHNfVv/BLX4zfFH43+GfGmueO9VbVtNjvkgtJpY9jLLsDOo9gGX86diWj7uHT1paRelGOvNWSRhgzEg5FNkuEjbDHH41Q1zXNN8K6Peanq15DYadZxtNNcTttVFAySTXg9j/wUC/Z91TUvsUXxG0wzZwC0cir/wB9FayZdj6AtW3zMcEZ9q/Kz/gthrQXxR8NNN8zIhtLm6MRzjLOFU/mh/Kv0Am/a2+DVrbm4f4j6CsSjccXIJx9MZr8if8AgqF8evDHx2+OWkX3g/WYta0bS9IjtluIQwQy+a7MvzAf3hQM/Rn/AIJa/CeX4W/sn6PPO+648TXL6864xtEkcaIP++IkP419dA57Yr8vdI/4Ks+EfhX+zn4L8O+HtLutV8YWOiW1m++LZawSpEqkEnlsY5wMZz1ry74O/wDBRT9o/wCMnxn8NeGtK1XTZhql9GJLC30u32RwAjzDvI3cKCTzV2Qan7LL0paZDu8pN/38fNj1p9UZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUrIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANavL/2jvjppf7OvwzvvGmrWM+o2tq6obe1KiRtx7biB+teokVyXxS+Fvh74xeDb/wx4nslvtKvF2umcMp7Mp7GspJuI476nwtpv/BaH4bTXIW58I+JLaNudzJA2PxEpqzq3/BZ/wCFlqdtv4R8VXfGVkjjtwp/OYH9K6H/AIc8fBn7YZf7X8Uxwk5FtDfRqi+wzGT+tY3xV/4JS/CLw58Odd1Dw9ba1caxbWkkkJur3zCzAZycKB+lZyajq0aKx61+yT+354X/AGtPFer6Bo3h/VtGvdOtRdu2oCLa6FtuF2uxz+FfTOvaDY+JtNm0/U7eO8sZ12y28oyrj0NfjB/wSTkudG/ay1CwAdFOl3EE6k55Vxj+VftfWu+j2E3Z3Wh4z4g/Y3+C/ieQSaj8PNGlmAUeYsJQ4AwBwfQCup8LfAn4ceA7OOLRfBWh6dHCPldbGMuOc/eIJ/WuvvtatNMs7i7vJltbW3UvLNKQqoAM5JrB8J/FDwf8REdNB8Q6fq5wd0dtcK7DnHQGp0WiDXdnxF/wV41yz039n/SbOwtbcJeX4UyRxKNoXPGe1ZH/AARRsPL+FPj67EissmspEI8crthU9ffdXa/8FWPCdrdfs63swgZjaXUc0e3+EHg/rVT/AII2+G4dK/Zr1TVUfdNqetTO6+gRVQf+g1MdByWiPvhcgc0tJuo3Ct7oyFooopgFFIeKFbcM0ALRRRQAUUUUAFFFFABRRRQAUUUUAQtCrSb8fNT6dtpNtQ0yrir0paSlqyT4a/4Kx6fqt5+znqEkFotxZxXMRZ8couQSfzriP+CJ+uxzfBrx9o4IMtv4g+19edslvEo4+sZr6I/4KFXEdl+y34znliW4T7NsELcDJP3s+1fIP/BEZZI2+KEm4mKY2QEfYFfMyfx3fpWC3Zo/hR+qNLSUtbmZ5d+0T8C9E/aF+GuqeEtZjRGuYz9muygZreTswrC/ZD/Zpsf2WfhLB4Rtr3+1LpriS6ur0xhDI7HgYHYDA/CvbNvzZpcYoHfSwEVAbC3a6FyYIjcAYEuwb/z61YooEJS0UUAIeaAMUtFABRRRQBDcK7fcKg/7VEfmfx7fwpWlUSFc5P06VnXfijRdPLC61aytiv3hNcIuPzNY+6nqy9exzPxcQyeDdXVVd5HtHRAvckEV+Kv7DWmyx/t/eGrd1ZXg1a+LA9RiKTNftL4o+JXhCHRbqaXxNowVEZlEl7GwOBzwDmvxn+A/xN8LeBf+ChFp4nl1O1t/DrapdeZfXEgWJPMjZSc9gCeKSfv3Oi94ryP3YXpQzBVLHgAZNfOniz/goJ8BvCETmb4h6XfOv/LPT3M5PsCvH618/Wf/AAVgsvH3xp8P+CvAfhKbVbDUryO2N9dHYZFb7xVe2DkZPpWvMjn5Wz7B8dftHfDn4ZtGvijxbpuiySNtSK4mAf8AFeorv9L1a01rTbbULG4jurO5jWWGaJsq6EZBB9CK/ND/AIKr/shT+IbRPiz4Y06ea+ijWPWLZX3KI1UKrquOMAc1y/7G/wDwU70H4f8Awft/BPjqKW2v9Ht3istQUFhMuSUVh2IGB+FHMkVyqx93ftEftjfD79mN9Oi8ZXF1Hc34LQQW0BkdlBwW+ldn8Efjp4U/aA8FQ+KPCF615pkjtGfMQo6MpIIIPuK/GSHR/iL/AMFLf2imeOaRdHgby3uypNvYW44z/vMBnHqa/Z/4I/Bjw78Cfh/pvhTw5aJbWlpGBJIo+aaQ8s7e5OTVXuKSSR3y0m4buvtivIf2p/DHxC8UfCHU4fhfr02g+L4SsttLDt/eAdU+YHk9q/Mfwr/wUY/aC/Z08UponxW0ybXLWKXbOmqWwiuZPUpKAAR6YFK5CVz9l1O4UteUfs+ftKeCv2kfCa614R1FZnTAurGX5Z7dvRl/r3r1XcaYh1FJnimTTLDGzscAUgPFf2pv2iNI/Z1+H954h1VncrxbwqBiWTbxHn3POa/KY/tJ/tXftTa9c3fgW71610+2LeXDoebeKIZ6FxjceO9dF/wVQ+NV98R/jbpfgO1mc2WmmNZLRT8rTSEYJ99pAr9Uf2ZvhVpHwg+C3hfQNK09LBY7RJJlAy7SONzlj1JyTWEbt3RtJKKsflz8Hf8Agox8Yv2dfG0fhj4y22o65YJII7ldSXF9CCc7w/V+D0Pauy/4KlfF7wP8cvgv4C8T+EdWi1GNr1xjo6Dacqw7HNfb/wC2N+yZ4W/aP+HOqrPpkKeK7W3eXTdTjBSRZAvCsR94HGMGv5//ABJHqnh+9u/Dt8ZIfsFwyPbtkASL8pOPfFaEx2P0m/4Im6Dbyaz8QdZKn7THHDag84Cn5v5iv1jr8+/+CN3hG30v9n/VtfSHbc6rqUiySc/MIyVFfoEveqirCkfKnxh/4KI/D34D/Fj/AIQvxdZ6tbMyJIdQigDwoGAx6E+/pX01o/iKx8QaDa6xptwl3p93AtxBMh4dCMg/lXwT/wAFSv2PtW+LGi2PxC8H2n2vWdGt2ivbFMlp4Mk5UZ6jJ6c18r/sjf8ABQ3VfgT8O9f8D+K57y7jt4JF0gzfes3wcpzycMTwanbQdk7HuH/BQr9v/wAU+APEEXg7wHfR6Tfhd9zeqVkkizyBtYEdPavdP+CYvxo+JPxn+D99qPj62lu4YbpksPEEyLG18uTuG1QFwjZXIHavzL/ZV+D+sftoftNwS+JRdappMlw19rV5IGwYl6RFlxjPAGMV+9nhrwzpfg3QbLRdFsodO0yzjEUFtAuFRR/nr3oUQkzUXpS0i9KWnymYUUUUcoEEkW5iema87+Od34t0f4Z6/f8AgyO3bXLS2aWAXGSGIGTgV6VSMiupDAMCMEHvU8nmaRm4n43Wv/BYL4uaDILPU/DGgzSW58uXzS8chIOCTWv/AMPovG8kWU8EaOD/ALV038sV+l/ij9mX4U+NLqS61rwBoV9cSHLytaKrMfUlcVTsP2Tfg5plsLe2+HHh9IhnhrNWPJz1OTT5RXR+UvxE/wCCunxZ8XWb2uj2OkeHVI5kjQyuOOxP+FfXP/BKv4xfFX4zeHfGGq+OtVm1fRIbhIrC4uIwpEmCXCEAZXkfjX1nZ/s3/CzTxiD4feHUHXnTom/mK7fRPD+l+GbBbHSNOtdLslJK29nCsUYJ6naoAo5RXL4HfvS0UVoSFFFFACdzX5V/8FrstrHwyQbRm3vTn+L+H9K/VP8Air8hf+Czl5O/xl8B2zOwt00hmVc8AtMQx/EACoa6lR3ufpJ+ybbR2f7MvwuiiBCL4csevX/ULmvWK474OWkFh8KfCNtbRrFbxaVbJGiDCqojXAFdjVLYUtwooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+Dv8AgpF+3XN8BdNHgXwPfIvjy8Cm4nTlrCJgGU4P8TAgj2NeB/sef8EztR+LzwfEn40zXK2l/I10miuxE95kkiSZh0U5yAOSD2r9H/FH7Nfwy8Z/EKLxxrngzS9U8UxbNmpXMIeQbAAnXjgAAV6Q0S+SYl/drt2jZxjjtU2KufLmtft6fs4fAmRvBQ8VRWP9hgWf9n6bp88yQbRjYCqEEjoeeteYeLv+CyHwd0W+MGiaR4g8SRcYuIbcW6txzgSENweOnaszxZ/wRx8C+LvHWreIJ/HWvQW+oXL3LWccMRKsxyw8w5J5J7VwH7T37Dv7Pv7I3wG1bxBqNnrPiPX7kG00yS+v2GJm5yFQBQB7imPQT4nf8Fd/h54r0+NY/g5L4kmtzvj/ALeMJjhbscbG/Svon9gP9rzxT+1PZ+IJdS8C2PhjQ9L2R213pshMMjnrGAR1C46V+W37FP7H+oftb/EC9sZLybQ/DOmxrJe3kSluCeI1JPJPPWv3M+CfwS8L/ADwDY+EPCVrJa6ValmDSvveRmYszMfUkk0xPsd8vSlpFz39aWgkKKKKACiiigAooooAY3eojIVJGCcVMc54r5h/ak/b28Efss+JdP0PXbG+1XULqITmOw2ny1z/ABe+Oaze5cddD6ViYyyFlOVr5T/b0/Y48Q/tcWfhW00nxNDolppMksktvcRF1kdgMNweoxj8aqeC/wDgqZ8BPE1upudduNAl6mK+tiMfiK6o/wDBRz9nhevxGsf+/Mv/AMTSGdb+yb+zTpP7Lfwns/CdhIt7fMxnv9QCbTczHvj0AwB7Csr9pD9i34fftPa5oOreLILkX2k4jWS2lKedDu3GNx3Gc/nWfb/8FEv2dZ495+KGlxf7Lwz5/SOhf+Cin7ObMVHxS0vI/wCne5/+NUCPoHQdHs/Dui2OlWESwWVlClvBEv8AAigBR+Qq9mvmLUP+Ck37OmnxyMvxFtbxkGdlvaXBZvYZjA/WvNNS/wCCw3wMs7qSKC28TXqKcCWKwjCt9MyZrRbCsz7ozRmvgpv+CyXwXH3dE8WP9LKH/wCO1nXX/BZz4VRyMLfwj4qnj7M0UKH8t5pisz9Bs15j+0z8KZ/jh8CfGPgi0uEtrzVrPyoJZCQokVldc+2VFfIMP/Bab4VFgsvg7xYp/wCmaW7fzkFTXX/BZ34VR25ktvB3i6c9laGBM/j5hFAWZ2n/AATh/Yv8QfstaT4q1DxmLCTxLq86RxvZyeZst0HALe7EmvtOvzA1b/gt9pMN46aZ8Jry5thjZJea5HC545yghYDn3rHm/wCC4Vwsh2fCFAn+1r+f18igR+q9Ffkd4g/4LbeKri3zovw00uxY8CS+1GSdR+Coma+m/wDgnv8AtteNv2sbrxHbeJvC9jZW2lorLq+lLItuzsT+6KuThgMd6APtaiiigAqtqWm2usafc2N7BHdWdzG0U0MgyrowwVI9CDVmigD5n1T/AIJy/AHVNQmu38CQRPK24pDM6oPoM8VFH/wTd/Z/j/5kaFv96Zz/AFr6doqbDueJeFP2L/gr4NjUad8PNH3qSfNnh81/zavVfDvhTR/CGnmx0TTLXSbMsXMFnEI03HqcDvxWxRVAIucc0tFFAj5q/b0+BHjj9ob4Mp4V8C39vY30l8ktz9qnMSSQhSCuQPUg4r8+tL/4Iy/FS7VZL/xD4f0+QnmOJ3lA/HAr9mqKVirn5D2P/BFvxxIyC78eaNFH32WTM357ua+ZP2vP2R5/2UPHWh+HLnxNb67cahafbS8FuYjChk8vJGT3B6HtX9CdfjF/wVd1BPE37Yui6Pbv501tptjYPGvVZJJRIF/FZAfxpcoczPtv9nn/AIJtfBn4c+GLG8v9Cj8ZapdQJJJd60omT5hn5Yz8qjn07V9A+DfgD8OPh7q41Tw14I0PQ9RA2i6sbGOKQAjBAYDPSuw8OW32Pw/pkH/PO2jT8lFaNUK4gpaKKBBRRRQAUUUUAFMfd/CM0+igBse7aN3WnUUUAFFFFACUA5obkUijatRcB1FFFWAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5t+0B4hg8L/CvxFqNxdtZ+TZytGyn752dCK9JPUV598fLGLUPhB4rjltY7vGnTERyD/YPT3rCv8DLjuflh/wAEjpY9f/ag8X6i8RMp0+WdWA4XdL/9ev2PWvxP/wCCTfiq38MftUavZzyJaxX2m3EREhxysgYD8s1+0Gja9Za7bmeynS4QcHYQcH0pxkloxyu9TzL9qDw7c+J/gx4t020aRJJ9OlRDGcfOV4HHNfgX8IvHHif4QfGTRZtIvbjS9RtdSjtpoxIQrZkCsGHpX9EHxM1RtP8AA+tXZhx5Ns8ib8YLBSRn2r+deCe48XfHy2uAAbq88QI5VRxnzgePahF/Zsfsd/wUa8daLoP7NN3Dr7hrnWLRIbdEH/LXG7PPavzv/ZI/4KGan+y38N9T8K2+hDVllme4tZCwCozcndn39K+t/wDgrXfaddfAXwtbXW6PULe4jMSnqcxjNeB/sA/8E9fC/wC0x8Ob7xh4s1q6itftT2kFnYna6MvVmJ45pKMWN/Cdn4D/AOC1WvWMTJ4t8C2+o4+7Lp0/lt+IbivuP9jz9sfR/wBrrw5q2oadot3oV1pkwint7hw4ORlSGHtXjH/DnP4OeUE/tLW8/wB7zVr3n9mP9jrwh+yqusr4UvNQuE1QoZkvJNygqMAgVXL2MtD3lc7eaWkoz7VoQDfdNNjbtSn6U1V280XQElFJS0wCiiigAooooAKKKKACk5paQru60AC5xzS0iqFGBS0AFFFFAHgX7b2gx+KP2e/E+myyeWkls77sZPygnpXwX/wRZ1qaDx/8Q9GA/wBHNrFPnP8AEHZa/SP9pCOL/hTPiqaSETmKwlIVv901+Xf/AAR11h7b9ovxhp4iUpeaW8jPnGzZLwAP+BfpUaXubP4UfsiKWkWlqzEKSk3HnivAv2tP2hNa/Z28FjxHp3h+bxBEGw0UWcL7nHah6Fxg5uyPf6K+Sf2Z/wDgo18Pvj80Ol3cw8NeJGHzWV22EY5xhWPWvoH4jfFfQPhn4butY1fUrW1ghj8wCWQLv4yMVPMg5Hex2tFfmF4r/wCC0ltpGv3NnpXgJNUsoX2i6a88vePYYr6l/ZT/AG8fAv7UkZsrBZND8SRruk0m6cMxHqjcZp3QuVn0xRRRTJCiiigD5o/bk+G/xN+IXwruovhnrMthrEDiT7NbOYpJ0xyobPWvyhh/Yo/af8a6oY5vCPiWGaRv3l1ql+FjJ7nJbpX76YoxUcqvc39q+VRaPw8n/wCCTP7Q/kRTiPSJpSPnjOsAOPbPSvKfhj+xb4w8dftES/CTUZrTw9rVuhkuppXFwkagbgRt68EV/QTr10LPSbubcybImOV69K/HH9i7xhc6r/wUm1C4ndppLya+hLSHJwucfoKltp2CMbxbN7xh/wAEW/GWk6TNe6T480nVLiFC5t2s3hL454OSK+ef2LdLtPBH7anhHTPEkiobDU5LV2jYBfNUEJ/49X9AToJAVIypGCD0r8N/25PgNr37Mv7TX/Cd2ulyf8Ivd6nHqdlcwNlS4YO6E/wnORg09SYpM/ZL4y/ELwp8Ofh5q+reMLu3t9G8hkkWcjEoIxtAPXNfzffEK4stU8ba9qGixNHo017K9uyqQuwsSo/Kv2blh+Dn/BTfwnoVkPFuowXeixxz32j2DiJwT1DhlORnIyK9v079jH4RaX8PpPCEHg+xbTniaMzSxK0+SPvb8daFzC0W54Z/wSX8Q+CdY/Z6a38O6dHpviC0umj1hc5eR8ko5PcFSMelfca1+Imtr4m/4Jj/ALW0MVjfyXfg+6dZ5I+Slzav1BXI+dOgPtX7N/D/AMcaX8SPBuleJdFnFxpupQLcQuPQjOD7itBSOh7mvKv2iP2d/Cn7RfgO+8P+ItPgluXiYWd+yDzbWQjhlbr1xxXqnRq5Pxp8UvCnw9tZrjxHr1hpMcSGRhc3Cq2B6KTms3uJdz8KfhP8QPFH7Cv7VE9pNJMbbTr77BqUBBC3NuXwHx3+XkGv300TVoNe0ey1K1bdbXcKTxn1VgCP51+E/wDwUA+N3g39oD4+WOpeCLQ3Bj8u2lvIlx9rIYAcD8s1+3nwnt5Lf4ZeFopozFKmmwKyH+E7BxVrYcnc6r+GkmQSJgjOORmnUjAspAODjg0En4F3Fk/ir/goh9j8Rq1yJ/F22RScZRZPkH0wBX75W8axQRoowqqAB7V+E37U9vN8Av2/JNafcyW+q2uoh3XKuG2s+M+mTX7i+GfEFt4m8O6bqtpKJLa8gSaN1ORhgDWcfd3NJvm2NZq/Bz/gqV4e8N6D+1NqjeHYUhF1aQzXaxsSvnkfMcduMV+2Xxa+IFj8Mvh7rXiHUZhDFaW7spPGWwcY/Gv5yPi9441P4sfEDXvFN40lyJ5z++28Ko4UHHTin1Ej9nf+CTcKw/se6FtB+a/vGOfeZq+y1r8zv+CSv7U+m6n4bg+D95aPFqlr5tzaTxqAjx5yQffnrX6YrWnQUhk23y234KbfmDdMV/Pl+39Z+CbX9pbxGnglBFZ5V7pFctF55GX2ZJPXt65r9ef2+P2mov2bvgrf3VpME8R6sjWenKArFWIwXwQRgD1r81P2Ff2H7r9ri81zxl4ukeLw6jSxiQl1e7umBO4MpGArHnFZ9R7K59z/APBJvwr4O0f9m2HVfDsv2nV9RuGbVpXJDiVTjZtJ4UdBjr1r7cavxk/YR+Imv/spftdal8KtfmltdF1a8eykgmAx5wJ8mQZ5GR6Eda/Zv7y1V0TJdQXpS0i9KWqJCiiigAorxT4+ftffDf8AZvurK08Z6tJaXd2u+KCGFpGK+vArzC0/4Kmfs/XSbj4puIefuyWUgP8AKlcrlZ9dUV8q6f8A8FNv2fNQuPK/4TVbf0ee2kVfzIr03wl+1p8IfHFuJdI+IGiXCnjDXSo35GmKzPXaK811v9pH4YeHbczah460OBB63iE/kDXVeC/Heg/ETQIdb8NarbazpMzMqXVq4ZGKnDDPsRQB0FFIvSloEFFFFADT1r8iv+C008EnxS+H0UeBcrprhyOuDMSBX66nrX48f8Fko0l+P3hBd3zHQ1+X0bzzz9cVLfQqKP1U+ChY/CPwcWOW/sq3yT/1zFdrXJ/Ce3Fr8MfC0IOQmm24z/2zFdZTWwnuFFFFMQUUUUAFFFFABRRRQAUUUUAFFNPWvkX9tb9vaL9krxF4d0e38OL4ku9Rhe4nj+0+UYYwcDsck1Nx2PryiuD+BnxWtvjd8K/D/jS0s5dPg1W3Ewt5jlkPcZ7iu8qhBRRRQAUUUUAFFFFABRRRQAUUUUANbrWf4g12y8MaJfatqM3kWFlC088mCdqKMk4rSqC9s4NRs57S5jWa3nRopI26MpGCD+BoA+PfC/8AwVa+A/iLxRPo9xqmpaMiyeXFf39mVgl5xnKkkfiK+Jv22Pi1c/twftUeFPh38PNRj1fw/bstnY3EIIRpJFDXE3PZVBHP92vob42f8EcfDHirUNQ1TwB4ruvDd1dStKbG/XzrYEnOAR8wGfrXxZ8Wv2Lfjn+xnqNl44hjjmttOkEkfiLw45YWzA8GRSAQD7jHvQVc/af4F/A7wz8AfAOneGvDWn29pHDCi3NykYWS6kCgGSRurHjv0r0aPO0Z5PTpX4z/AA//AOCxfxX0ebSIfEui6DrthG6i7khgkju3iGAzcNtB79K/XT4a+PtP+KHgTRPFelLKmn6rbJdRLOhRwGGcEGgk6aiiigAooooAKKKKACiiigBP4q+Nf2uf+Cb3h39pzxa3iuHXrnQfEEiJHNJjzImVFCr8vY4FfZdFTyjTsflTa/8ABE26eUtd/ElCuePLsjyO3etyH/gijo3ljzfiHe7+/l2q4/Wv06oo5R8zPy01b/giejSZ034lSonHy3FkCffkEVCv/BE2Vsb/AImsPXbYD/4qv1Roo5Q5j819B/4Ir+FYLdBq/wAQ9aupcnd9lhjjXGeMZBNdnpf/AARx+Dlrs+3ax4l1LHVXu0QH/vlRX3mxC/MTgAZr4h/az/4KfeE/gLq8nhrwpZw+MfE0Y/f+XcD7LbkjIBdScsO69uhqhXZeH/BJT4BhQv8AZmrH3/tB81Ys/wDgk78ALVstompXHtJqEn9DXwZY/wDBTr9pjx5rc0Xhm7WeSRt0em6T4eivGjB6AfIWNa91/wAFGv2pvhTq+n33jmwuo7CZxustb8NnT/OUdQhMa849CaAuz7Q1n/gkb8AtWnMkVjremjAGy01Ehen+0DUWm/8ABIf4A2aqZbTXr7vum1Ruf++VAr2H9kr9rbwz+1h4Ik1fSojpus2Mnk3+kzMGlt27OPVWHQ/hXvK9O/rzQF2fJ+nf8Et/2cLJV83wLLeuOr3Gq3WT+CyKP0rpbP8A4J3/ALOljbrFH8LdKdR/FNNcSN/300hNfRlFAj5ruv8AgnD+zjdzmV/hfYK3/TO8ukH/AHyJQP0r2L4XfB3wZ8FfD7aJ4J8PWvh7TGkMrQWu5tzHqSzEsfxNdlRQAUUUUAFfKX/BQr9pDxx+zf8ADHTdX8E6St5c3Vz5U99NA0sVquOCwHqa+rapavoun+ILGSy1Oxt9Qs5Bh7e6iWRG+qkYoA/FCP8A4Ky/H26xFA2izyAYJh0uRifw3USf8FLP2m72TdFCAG6CHRJMfyr9idD+C/gHw3I0ml+DNCsZGOS8OnxA/ntrqIdIsbdQsVlbxqOipEoH8qAPw78Qf8FDf2o77TpoXuLrTkI+aaLSGjYD6kV91/8ABLHxd8V/iH8Nde8TfEDWbrVdIu7wx6Y18v7wlCVkIP8Ad3AjHtX2vc6Hp16hS40+1nQ9VkhVgfzFO0vSLHQ7MWunWcFjaqxYQ20YjQEnJOAMcmgC3RRRQAUUUUANZiq5Aya/Gz9pbSIfil/wVe0/TLJ1uov7R02KYL/C8EEZkXnuuw/lX7K1+Htx4t0vwH/wVS1nWdcv49N0u18aXhlu7gkRxqwZQSewyRQB+38aCGNEHRQAPwpl1eQWNvJcXM8dvbxjc8srBVUepJ4ArzDxd+1N8JPBOhPrGq/EPw+tkozm1vo7h246BIyzZ/CvzN/aK/am+IP7fXxGtPhv8FbPVrbwzHlZ3in8lbsEgGWc5AVFGcKTk+mam5SR+vGi6/pniSyF5pOo2mqWhYqLiynWaPI4I3KSMir9eNfstfs56N+zZ8L9M8O6bFu1B4kfU7rzGfz7jHzMMngZ9K9lqiQooprMEUljgVHMA6imrIsgypyKdRzAFFJS1YBRRRQAUUUUAFFNK570o4pWAWmswXANOpjRhjk1N7APoooqwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAa33hXnHx81j+x/hj4hd+IpbCaMsOxKGvSCORXlv7TcKzfAvxiWwPL0+VgfQ4rCt8DNabXMrn862m+JNX8KeNbi+0O9ltdQE8kcc0JwSGYjFfvh+w74B134e/APSJPE2q/wBqarqK/bHkyx2q/KqcgHIBr8A9FvYtN8ZWd3dc28F8sknGflD5P6V+93gH9uH4Df8ACFaPC3xE0WzKWkatbXE4R0wo4INPlV0x8y5bHrvjuYah4R1+31OAJbfY5mXaeoCGvxf/AGC/g+nxV/bELxiNdM0W6lv3WUE5CudoGO+a/QT9pD9v74ON8MddsNB8Y2up6tcWskMAszvG5lIHNfnN+wB+0x4f/Zx+NF/r/iuW4j0XUoGhklhiMjbi2d2B2oFdWPrr/gsxZL/whvheZY2Xbc4z24GBXQ/8EX7ueT4N+L7eRyY4dX+Re3MYJxXl3/BQL9tb4QftB/CkeHvDl5dX2qxzCWKdrVkUD05Fec/8E5f20PDH7MfhnxTpnixpmt7udbmCOCPLEhcEVKLeqP2spNx9K/OzxH/wWc8BabMg03wZrWqRkAl/MSLB78GsS/8A+Czvhry1kt/CV8rn/l3d1J/766VfMjPlP0rknEbKCGwTjNIszGTaUIHrmvy3vP8AgtH5jA2fw9uAPSW7jxXGt/wWb8cQ30zN4P04wEny4zIcgds4NK77MXKu5+vkgZ1YL17URKyqFbk+vavyN0X/AILReL47h21XwPp81ufuraTMrD6k5FesfCL/AILA6X8QfiBovhvVPA02kR6ncJbLefbQyxsxxkjb0pjt5n6PUtMhcSRq6ncrDIPtT60MwooopgFFFFABRSbqTzBnFK6GLRkVGzfNjpTwvvUczb0EOopKWtACiko3DnmgDzf9oyYQfBTxex286fKBuOBnFflB/wAEj782n7WGrwmPcbjS7lSw/hxIDX1X/wAFRP2ptO8E/DGXwZo12JNd1I7JPLkGY0xzkda+UP8AglT8RPA3wn8beL/FHjbXbPRnNqsEE12+CcnLY+tZGtnZH7VrS14HY/t1/AzUIRJB8RNJKE4+aXFOuP25vghbSpG3xA0sljgFZMiruiOVnudzcCFSSM+gHrXxl44/4KGfBvVPH178MvEFhfTSPdHT55HjHlB87TX1h4T8c6B8RtBGr+GtXtdW09sqt1auHUMO31FfiZ/wUs+Hsfwr/ae/tOwwp1CKPUfMjwA0gPP54rOTvoaRSSv1Oy/bk/Yi/wCGe0T4peAtSmbQpbpZY40xm33cggjtmvAbP4gfFv8Aa+17RPAj6y+r3kmI4EkcRrtH976CvavjZ+2Nrf7TPgHwn8JfBGmXEtxLHHFdeYPmlkAAwvtmuF8S/sG/Hz4A+H7fx+umG2+xHzmfSrnfc2wHcgClHbUTlqfb/wAGv+CPvgDTfBKf8LCu77VvEVwmZPss5iitmI6Ljrj3r4g8YeGdQ/YN/bG0w2dw15pum3kUsUzsf3tq5G5WIxkhTj8K+2P2J/8Agp5pnja20/wX8ULlNN8RLiCDVWBWO47ASZ6N715p/wAFjPhrY2t94O8c20oljvhJbOI1ypGMqQw+tUVHzP1T8M+ILXxV4d03WbGQS2l9bpcROvQqwBFadfNf/BO3XTr37IfgOczyXDxW7QM0pyQysQR9BX0nnitEYvQWikFLTEFFQ3V0lnC80rrHEoyWbgCsrRfGmheI7ie30zV7G/uITiWG3nV3T6qDkVLkk7MrlbV7Ffx85j8K6mynDrbuy+mdp61+L37CEkkn/BRCF3VS7XN8XIHAyD0r9lfinerZeBdWkchV+zuC3p8pr8gv+Cbeirrn7c2rXwLstit3MGBHdsc8VL3OmP8ADS9T9qc1heN/Afh/4j+H7jRPEuk2us6VcDEltdIGU+49D7it4L3pafKzki2eM/A/9kn4b/s86xq2qeDNIksr3U+JpJZN+1c5CLwMCvZKdto21Y3qfBf/AAVM/ZT1v45eEdI8VeFbFtQ1zQ1aKS1iHzywsc8DuQa9U/4Jw+F/Fvgv9lzQdI8Y6fPpmo29xcCO1uRiRYjISmfwr6f20uKB30sI1fNf7Tv7Bnw+/agvDqmtS6hpXiARCJNQspuMDpujPDY/CvpXbRtqLMLnxN+z1/wSz+H/AMFPGK+JNU1a88Y39uR9jF5CkUUeO7IMhuehr7XjjWFAijCjgDsB6U6lqyQooooA/Pn/AIKlfsi618YdDsvG3hGw+36xpURS5toh+8ki65A7kV8SfA//AIKIfGD9mjQ/+EQmt7bU7C13LFZa3AyzQMT/AHhhiPav3gZQwIIyD1ridc+CHw/8Tai1/qvg7Rr+9brPPZozH8cVNi+Y/E74jftofHr9rd28GxxR3lrqDCNNJ0jTh39ZMbgPqa/QX9lv/gnH4T8G/AS60Lx/pUeoeI9dQvfyLKwMII+RVweCoxnHU19eeG/hj4S8H3LXGieG9M0qdhgyWtsiNj6gV020UuUOY+CP2TP+Cbup/s1/tAXHjQ+Jba/0KK2lgs7VIyJsOQfnJ44Ar72Wl2iirE3c/MX/AIKu/BTx78VPip8P4vDWi6lrWlT25t5DbQ74reYyYLHHT5cda+8P2d/g1pXwE+EOgeD9HjZIbSLfM0hyzzP80jH/AIETXpLIrHJGaXFRyg3dWPxQ/wCCpng3xF8N/wBrCPxrbboINUit7vTrtVAxNCihvbOVr9Zv2bviI3xX+BfgvxVLJ5txqWmxSzNtC5k24bgcda5P9rj9k3Qf2sfAVvoOqX02kX9jN59lqUC72iYjDAqSNwIrvfgj8K7P4J/Czw74KsLmS9ttItVtxcSgBpCOrY7UcoN6WO4XpS0UVZIUUUUAeEftNfsc+AP2pNNiXxNbS22sWybLXVrZ28yBe4C7tpz7ivkmb/giX4UeZmi+JurQxnon9mRsR+PmD+VfpZgGjaPSpsPmZ+YGrf8ABEvSxCy6b8Srp5Oqm6sAFz7gMa8+1D/gir4+hvnNh490JoONrtHMjfkFr9gMCjaKY+Zn413/APwRr+KqyLEnijQr2LIzNvkBH4EV+kP7Gn7P97+zT8C9K8EalfQ6lf209xPJcwAhT5khcDn0zivc9oo2imK7BelLRRQIKKKKAGN1r8Uf+CrGrSeJP2w7DSY5BJ9ls7S1Cg52l2Bx+Zr9r261/Pv+3BqeqW/7bfjq5/eXN3a65mzikBbcEZfLQD09KmxcT97PAdk2m+CdBtX+9DYwofwQVvVxnwb13VPE3wr8LanrWnvpeqXOnwyXFpIMGNtoyMdq7OqICiiigAooooAKKKKACiiigAooooA8I/as/az8Kfst+D5NQ1mb7RrNxG39n6an35n7Z9Bmvyj+Hvwd+LH/AAUY+Mk/inWvPttBknDXGoTljBBFniKIHgHHGBX66fGj9k/4Z/tA6zpmqeONBOr3enLtgP2h0UDOcEA816L4Q8F6F4B0K30bw7pNpo+mW67Y7aziEaj3OOp9zzU2KuR+A/B9j4A8G6P4d02NY7LTbZLaJVUKMKMZwK3qKKokKKKKACiiigAooooAKKKKACiiigAooooAKYwJ74/Cn0UAfNXx2/YD+F3x48Taf4lvLB9B8RWtzHO9/paiM3GxgQsing9OvWvo+ztVsrSC3T7kKLGufQDFTUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZ+v69Y+F9EvtX1O4S00+yhaeeaQgKiKMk5NAHzr/wUB/aNi/Z7+A+qz2V9Hb+JtUQ2unxBx5gzw0gXOcAd6/P/wDYS/4J63f7QrQfEr4kTSJ4XuLl5UsHBWXUGDHLMTghM9x1FeN/tNfHub9r/wDaaiku9QFl4TS+S0sFuZAkUFqGAaQ57sASa/af4F/ET4b6z4b0/wAL+BfE+j6umjWsdubawuUdlVVAztBzjPfFBVjtfCHw98NeA9KttO8P6JY6VZ26CONLaFVwo98ZNc78dvgj4e+Pvw51Twp4gtYZY7qJlguXjDPbSY+WRM9CDXoa9KWgk+bf2I/2PbT9kXwTq2mHUY9Z1fU7szT36RlN0Y4jTB9B+tfSVFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfnF+27/wS+1j43fEnU/H/gHV9Ps9S1La91pWoKY43kCgNIHAPLHnpX6O0UAfjd8O/wDgjf8AE7Vr+3j8Z6/oujaUr/vRp8rXE7LnnBKAV+kn7NP7I/gb9lvQ7mz8KwTz3t5tN1qN64eaXHQZ6AD0Fe20UrDuIKWiipvYQmaZIqSqUbmklUtnBxVb7VDb+Y0sqosal3djhUUdST0A+tQ2VYsxqsXyrwtP4bnNcj4f+LXgjxZI0ejeLtE1SVZDEY7TUIpG3g4K4DZzmuswCOKYWI+FnJ5JxU0biRcj9aqM3lvnOWzjmrSuNo7U+YbjZCs4RcnpVeO6FxMVjyQOvGKnBJ4xlfWlVQvQYp8zIHUUUUcwCUZFRyBmbg4FCLtXBO6jmKsSZoyKZuxTd3zYqQsTUU1fu06tFsSFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8++P3g/UPH3wb8XaBpTbdRvtPlit8nGXxwPxr0GmlaTipaMa0Z+Dfwn/4Jh/Gb4qa9qVjeWVv4OS0G43euiRY5snomxWzXvPh3/gij4sVlGs/EPRYYu4sbWSU/m6LX62LwKWpswe5+Yo/4Il6VIgMnxRu0fuE0iMj894qwv8AwRF8M9T8U9V6c40iL/45X6ZUU7CPzy0X/gi/8NbG0WPUPGGvahOCSZY0SEEdhtBNdNbf8EfvgrHt8671+Yjri8C5/SvueijlRXMz4tt/+CSfwHhVfMttenYHkvqbc+3Sux8O/wDBNX9n/wAOKNnglL9v79/O0pNfUNFHKg5meC2/7CXwEgXH/CsNCc+rwkn+dWZP2IfgU9u0A+GWgpG3922wfzr3GiqJPkjXv+CXH7PuualJd/8ACLXFjvAHk2V9JFEPcKDWdoP/AASt+Cfhnxpp3iLTbbVYZLCVJ4rWS8aSLcvOTnnrX2PtpNtQ0yrjYYxDCkajCqNqj2HSpKSlqyQooooAKKKKAGt1qKeBJ1AYZxyOcVK3WkrN7lkUMm9SD1XipxUQWPzD2c9alpxRItFFFWI83/aG8ReLPCnwi8Rat4Jsv7Q8SWsBe2t9m4se+B3NfkFr/wC39+0/eW91o01vNbXTEpKU0mRJl9sg9q/cWqraVZNMZTZ25lJyXMS7vzxUcpalY/Ff9nH9gH4l/tba9/wmPxH1K+0XQZJSslzeKftc+04KojdB719reIP+CSfwY1HwcujWDatp16p3f2q04mlJ9wQBivtvGOnAoYZ74pqIuZn5HeKf+CKvixdal/4R3x5o82lYHltqltIs3vkJkfrWTcf8EVfiNsBXxx4bY/3VgmH6kV+w+Pejn1pNMOZngH7Gv7KsX7Kfwzk8ONrk2u3d1N9ouJXG2NGIxtRfT3rl/wBsb9hHw3+1BobXMEx0jxZbRkWd91T/AHWHpX1RRVWFdnxP+xj/AME4NA/Z4mt/EfiiSPXvG8LMVuoWYW8Sk/LtU98d6+0L6xg1KyntLmJZbedDHJGwyGUjBFT0tFkI/Jf9vn/gm3c+Hbj/AITn4S6PLcWe4y6hptu5adG67489R7V8ReKP2i/ibefD8fDbxDqc13otrIWSz1S3DTQNnkBmG4V/SIyhgQRkHqK+Qv2zv+Ce/hz9pjTY7/Q2tfDHiyFs/bUgGycekgHP40rDuzlP+CRPxDi8Vfs1tojyL9u0S/ljeNABhHO5SRX3Q3Svj/8A4J9fsZ+Iv2R9P8WW+v6zZ6s2rTRvF9jVgqhRjnNfYFUJ6gvSlpKWgCrqFjDqVnNbXEaywyrtZG6EGvyv/aw/Y1+K/wAEPidL8TvgZJq91aXT+bc2GlSlriBhyxK4+ZD6YJFfqztpNtTyxbuzRVJRXKj8UfGf/BUD4oal8O73wP418LQJrBRoZNQy9lcDPA3wkNyPXjPoK6D/AII22E9/8ePFmqvFJIg00q0x5AZnzgn1r9VvHfwM+H/xOfzPFfg7Rtem6edeWaPLjsN+N361H8K/gP4D+CUN9D4I8N2nh+G9fzJktQfmP1JJx7UmtdDT2i5bHeilpKWrOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnFNVw3APNJIu4Y3YNRxgQxksfm/vVPMOxPQTjk1TS7VpOH49KladGO0vz6U7j5WSBg3Ir54+Of7C/w1+O3i608Vaja3GkeJbeaOc6npj+XJKyEY3+vTrX0ImBwvSphS5g2INPtRY2NvbK7SLDGsYaQ5Y4GMk+tWKQUtUSFFNJpu/5iO9TzDsLtO7O7j0p9eC/tCftpfDX9mXVdN03xrfXkV7fqZI4bK2MxVAfvNyMCuw+FP7RXw5+NVjDceD/ABbpurSSIH+xrOq3KZ/vRE7h+VHMOx6Qc9iKFBA5OTTPJBk8zc2fTPFS1RIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Zf8FXPidcfD/wDZbu7CzuDb3Wv3kdhlTgmP7zgfhivs2vzZ/wCC1WiatefDrwFqVvC02kWd/MLnbnCMyAKTQB4H+xb/AME0LD9pL4RL441/xFeaPBdzywWVvBF82EO3ec9QT0xXmfxz/Z1+J3/BPv4k6Rr+lanM9gZQ9hrVnuVJSpz5Uo6Zx2PWvs/9hf8A4KCfCDwT8BPDvgzxhrB8J6xolv5Lie2kaKcZJDKUB5PuK8F/b8/bUt/2sdS0j4a/DjS5tW0JbxJFumhInvLj7qiNeoUE9fzoLVz9RP2XfirffGv4D+EfGWpwJb6hqdoJJ1j+7vHBI9jXqteTfso/DvU/hT+zv4E8K6yqx6rpumxxXManIV+SV/DNes0EhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEzRuAqGSHdJu3H6UySTYpGCMVjKWpSjcbeMxAKE+/pXF/Fn4dt8V/hn4g8KwazdaHNqls0S31lJtkQkY5/wBn19q0/HHi5PBPgrXfEElsZ49Ns5Lsop5k2qSBX52fsRft6fFX4+ftQP4f167s5fC99FPLHp8duiG2VT8uHwCT+Jo31LtbQ+ZPiB/wTR/aG+Fes6jfaLoZ1zTrBfOTW9C1OFHcDnPlNIspYd8L+dd1+xT+398S/CPxS0TwP431S88Q6PeXS2DLqCs91bOTgDoSQDX6Gftk/tm+Fv2XfBdwJbqG/wDF93GUsdIjcNJkj77j+FR79a/M/wD4J9+JfAWoftF6z8S/if4p0fQXt2ku7eHUpFjV5pDkkZ44pgftx9l87DnLZ5GeKtIiqAuK4H4X/H74e/Gia9i8EeK9P8SPZKGuPsMu/wAsE4BP413/APFntQQ22KOKWiir5SQoopjMc8VACOwzg01SFGM0yZgrZY9aXYfX9aDRLQf97ocUqrnnNQNlWwc4qxHgDFAPRDhS0i9KWtFsZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQHNLQAUUUmegoAWikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAYxGaar7u1J5Kicy/xEYpWyMkDJ9Kza6ljlRd27HPrT6amSoyMGnVSasSFFITimtKq/eIFO6AfRUH2kOgaPD59DUoY45HNAWHUUlLTEFFNZsHFLu4pXAWikBpaYBRSE0m6gB1FIKWgBKKWigAooooAKKKKACiiigAooooAKKKKACik5o5oAWik5paACikJppY0APopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA055waYtzE0vleahlxkx7hu/Ksrxpfy6X4T1i8hkMUtvaSzI46qVQkH9K/Dn9nL9sLxPoX7XFp4r8aeMr5tIubqSC9kupS0ZhLEAbPugfQVNyrH7wUxpAvWuO+Hnxi8G/FbS01Dwr4isdYtmJA+zzAsCOoK9a6PU5MxNsLB164ockgjFydh1xdM0hVMhf71QSbpo22vuWvk39t39syP8AZt8C+RpZS58S6mrR2cbHJjPdzXzF/wAE5v2ifjp8avj1PFrPiO61nwlFE8l/b3WDDDnpswOuazvzanTy8uh+pUNsIwGao7jE0n7jO/1HSppGZuFXKdt1Nt5PIkxgKD2Fc3tLuxor7k9usscIaRvmz0FaEL+ZGCRivI/j5+0J4b/Zz8Hy+JPE/nNaL8sUMIBaVj2FYH7L/wC2Z4C/amS/i8MPcWuo2Sh5rG8ADhT/ABD1FdMdTmme/ClrmviF40sfh74P1nxHqTMmn6XbNczbepCjOBXwn+zp/wAFVI/i98dY/B2r+HxpujarN5Gk3UZJkzn5d/1rS9jOx99+IPFGj+FrdbjWNTtNLhZtqyXcyxgn0GTV+3niuoUngkSWKRQyyIQQwPQg18Cf8FePhf4m8YfC7w5r/h+2u7+30e7Y3trZhi2xhw5A6gGvPP8AgnT/AMFC9Os9G0v4XfEi+NrdQnytM1m6ckMpOFilYngjpmpGfY/7U37G/gv9qjR7ePXDNpWs2oIttYsVXzkB/hOfvL7Zr8xf2iv+CbPxF/ZdsP8AhNfB3iiTWdOsf3jXtgrWl3a46NlT+oNfsZ40+KXhH4daRHqfiTxFp+j2Mo3RTXM6qJBjPy/3vwr8rP27P+CljfFGxu/h/wDCt7iDRLgmHUNWVGEt0OnlxgHhT+tIZ9Bf8E2/279S+O8UXw88XWk9x4o0608xNXDGT7TEvGZCSTv9SetfftfFP/BMr9k+x+CHwpt/GGpwibxb4khWZ5JI03W0B5WNTyQT1PNfa1aEPcKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQmhhmgBaKRRiloAKKKKACiiigAoopKnmAWkpitimsy5560uYdiWlqHIyuKcCOfrUe0AkoplFaxfMFh9FItLTEFFFFABXK/Er4Y+G/i94TuvDfirTY9V0i5x5kEnqOhB7GuqooA/Ovxh/wRl8A6z4gmu9F8W6voenSNuFiqrKE9QGYZxXvX7Nf7APwy/Zrul1TTLKTW/EYzt1bUsPJGD2QdF+oGa+mqKB3Yi0ZpGprLu7kVPMFhxkVTgsAfrSeanTcM/Wqk1i0hJVzmoLfT5luDIz/AC46UuYvlXc1Nw9aAwboQaqXKtHHlTT7ddowTk9TVk2LGaM18C/8FEv2+9c/Z112z8D+B4rU+Jbi3W6uLu4AkFvG2dvy56nB615n+zz/AMFjIZlttK+LeiC3kJC/23pA3J6AyRZyPqD+FArM/UeisHwR440L4i+G7TXvDmp2+raVdLviubaQOp46cdD7VvUCCiiigAooooAKKKKACiiikAlGRTSwPQ0ZqeZDHZozTc0UcwDtwpPMX1phYHvULSKpwTg1m6juUohcXBWTA6VQmvD5m3eFLcBT97P0qeVt0oIP8PykjvX55/tq/wDBTLXPgD8T9S8DeEPDVrJqVisfnanqaswJYZwq8ZHTmsI+/J3NfhR9nftEyJZ/AHx29w6xKNIuMsf901+XX/BHj4fS+Ivjlrnil42e00SxaNZAQAJJDjGM5PHtXAfE7/gqR8Xfil4H1PwtqcPh+2sdTgMU0trblX2nryWNeT/s6/Fv45eC4dS0T4PT67LJeENcQ6FphupPrwjEV02toRufb37Tf/BLb4pfF748a94q0nxTol3pGrTeYlxq88qz2q4+5tCEEL2wazbX/gibrLaMTcfE3T/7SAOIY9NZos9sylt3/jtfOPiQ/to+Jrx73UNN+Ms0rKFaRdOv7dMD/YRAPxr9Of8AgnD8M/iT4E+D99qHxP1PXrjXtXu/Nj0/XZ2kktYVXCkbjuUtkkg4Ix0q7EXZj/sAfsKaz+yLP4o1DxDrWnazqmrqtvH/AGYZDEkKnIJLqp3HuMfjX2Yq7VAp1FHKSFFFFK9gEzTWmVVzmiQ4BJ9KqSLls54qGy4x5hfNG8uwBpjTIzHa1O/drHyM0kEcbln2nHpSNNELG/nLtVunWrCjy8ZOfeviT9rD/gpd4f8A2Z/iYPBtl4ek8RahAiPfMsvlrFu5AB7nFfVPwh+J1r8Xvh/oniuxtJrSz1S2W4SOcYZc9qol6nbilpq9KdWi2MgopGzjjrTY9235+vtTAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACCgnFNjLFfm605huFAC01lDMD6UtGaAADbS01WDZwc84p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANao5CQwO7AHbHWnshZs7sD0pdoPXmplqhkBuJVuAiw7oz/wAtN39MVZpBxS1PKxDWprKG6gGnNUU0jRrlV3Gk9NykOjUR5UIqoOmKcX7KQW9K86+MXxIT4d+FL7VzFNILaMuwj7ACvy3+KX/BXL4gTahNbeCdJ06wELFDe3imWWTB6eXxge+aSnd2Rq6TSUn1P2Po53e1flL+zn/wWB1OTWLDRfiro9ssE0mx9csmZNuSAMxYwAPXNfqN4f16w8VaRZ6vpV7HeabdxrLDNEcq6kZBzWt+5jY02xmsbX/FWn+GbWS71O5jtLGNSzzyNhUA7k1rSbN3PXFecfFaLwrrfhHVNK8Sz29vp11GY5xdSbEK+hPasJycdUXCKbOn8L/Ejwv4040LX9P1Vtu7ba3CucfQGuhklEaM7YCqM1+Lnxi/Z98Y/sw+Jx8UPg1qV5c+GY387ZCxdUXPK4HVPeu+0X/gsHqGveD7vTPEvhuLTtYWBliurKRikrBcDeDyDn0pqTtcpwsfY3xa/wCCg3w0+DV9La65fC4uY2Km1szulHPcV0v7NX7aHgD9qD7dF4amms9QtW+axvgFkZf7w9RX5Kfsw/sjeJv24PHmu6/qdzc6Poe5ppNQC7gXJ4Rd3UVneNPBviH9gb9rPTNK07WGu2tZbe4W43FVuIJGxtkA9MGtumpFl0P35WlqhoOpJrWiWGoRlSl1BHOCpyPmUHj86v0yAooopXQBRRRRdAFFITSbqYDqKjEnzEHGRTt1K6HYdRSA1HJIV4XGaXMgFeZY2wc5+lORxIuR0qKNpG5bA+lSltq+tHMgFZgOpxWH4u8baL4F0eTVNd1GHTbCM4aedgFrUmX7RtxuXmvgv/grla3Fn+z+t3De3UY+3QxGJZMIytnORiobZpGKZ9UeAf2nPhp8UfFD+H/C/iqz1fVkQyG3gbJ2jqa9SQnvX5H/APBF74f6drHjTxl4tuEk/tDS4I7W3KthMSZ3ZGOTx61+uO3bWl9NRSSVrA1R87uvy0rkdCcVHgIu7fk0yUhk1y0cqqFyvfipI7mOViqsNw7d6QyBuVXdSW9rGGaTy9rk9TSukVZW1LK0tN+70oyaZmOopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAU0tjtQ7beScUtK+tgOL+M94bP4T+L5w2wppdwQf+2Zr+f79mf4AX37TPxig8HWd6th50cs0l0ybhGq5OSK/dv9q3W4PDn7Pfj3UJ22rHpM6g57lSBX5yf8EV/CJ1D4ieO/EkiBlsrOO2RmHIaRs8fgDUPc02R8//ABW/Zy+Nf7EPjCLVLGbUIdNt5M2+uaUWMMg/2l7H1zX098Ef+Cuenw6DFa/EzSruXV41Mf27T/8AVyqMbd6n+Lrmv1J1jRNP8Q6fNY6nZQX1nKCrw3EYdWH0Nfi7/wAFWPhD8N/hR8QPD9r4I0mDRdQvYGnvba1YiIDJw20k4JOfypOKkHPbY8m8Zaj4p/bv/aeNjoSySRahN5NkkmSltbg8sfTiv2p/Zl/Zv8Pfs1/DOx8N6PbxG82772+C4e4lIG4k+melfiz+wn+0hY/st/FeHxBr2jPc6TqEZtpbsxnfEh/ijJ61+i37ZH7dmt+CfhP4e8U/CVrfVbLWzt+3tH5nkccgqOh+tL4dAu2fcX2M7WJOWzWdN5FnL5813GkQ42ysFHvya/D1/wBsT9q/4myKuia74lZ2+QLo1kyq34hcZ5qn4k+F37XfxWto5PEGn+NNXReEF5MVAJ74yKhUtbj52tD7h/4LC6pp8v7P+iJC8VxJJqS+XJGwbC45wRXg/wDwRd8M3V98WPF2ug/6NZ2Ahf3Lniqn7ZHw01H4PfsP/DXQ/FE11J4nuLzzZIrqTe8XGSmfYV63/wAET/DNxb+EPiFr0iAW9zdwWsTf7qksP1FbKNiXK6PrT9vXXk8N/sn/ABBu36GwaIfVjivyO/4Jn+HIvEH7XPg+OeCOdLES3LLIoIyFyp+or75/4K8fGaz8J/A2LwPFJu1TxDMuY1PIiU5JNfOv/BF/4fwa58U/F/i6cLJJpNklvCGGSGkPUenANOwk7H693NvFd28kM0SzRSKVaNxlWB4INflF/wAFBf8AgnFb+EbPWvin8Nljs9OhBu9S0RR8sXdpIvQZ5x2r9YzxWb4m0Gz8T+H9R0m/tobyzvYHglguEDo6sCMMDwRS5QUj8SP2ffg74w/4KEeGo/D2pfEiGxu/BsASyt9QiedpYm6ZO7+Hp3xXY+I/+CMPxX09ZJNI8W+GdXMY+SN3mgkb80Kj8683/Z8vtW/Zu/4KBW+hW9xPBDHrz6Zc28DlElhdvlVgOCuCOPav3ho5R8x+Mn7Pv/BOv9o3wH8bfD17PH/wjWn2V2k93q9nrHyvEDkoAjZbI7Y71+zUalY1UtuIGC3r706irICiiigAooooAKKaxqJrqOOQIzgMe1TzDsyeimqwYZBzTqOYQUUUVQBRRRQAUUUUAFFNfdj5aWp5gKeoXq2qnd0xVXS9QF580ZymcVfurZLpdriiKFIQFQYAqeVvW5tFxUbWJl6U6mUVoYj6KRaWgAoooqeYApDSNTGUZDelQMjaTa2KNxbmmpbr8x7sc0x5WhPB4rJyL9B23bIW74qJZC8m2nLctIoJHGcV5L+1F+0Vpn7Mfw3bxhqek3Gq2yzpAIrc4OW460kuZlN2R6788bhR0qwpJHPWvnr9kH9sPQf2ttH1260fSLzRptGmSKWG6IbIcEqQR9DX0Csm12G3GWrXl5dbkbk60tNU0vWtE7kC0UgpaoAooooAKKKKAGtXxX/wUX/bYvf2a/D9h4e8JS27eMtWUlWbDNax9A+31J6fSvtC6mW2gkmc4SNS7H2Aya/GvwD4af8Ab4/4KDa5fazP53hfRbp5ngLDm2gbZGij0Zu/TmpsWjzaH4t/to6iw1mxT4l3EFwPPW4tdEumhZTzlSIsEY7jitX4X/8ABT747/CnxQU8W6i/im0hcx3eka3CIpo8EZAbaGDe1fuJb29vptnHBCiW9rAgRUUBVRQOB7ACvxP/AOCiPjD4M/Fb9pHT7fwpczWF3HKNP8Qa7aQpJaNhiMxoD87KSdzDr+FFhbn6qfs3ftSeCf2oPBser+HL6OPUE+S90eeRVurZwBkmPO7Zzw2MGu9+I3j/AEX4V+CdV8T6/fQ6fpenQNLJNcSKikgcLliBkngCvxh8ffs0/Gf9grxFpfxC+Hurz+IPDU0Uc8WsabbvsdGG7ZcQjOFxj5icHNcx+1B/wUD8b/tUeBtF8JajplrocEUqtdmxlbZeP0UkE9M9ulMdit4R0XW/28/2zPMvILq/03UL/wA66ba3+jWCHhSw+6uOh96+vv2wP+CUvh+HwjdeJfhBbz2ep2MW+bQ3dpVuUA52E87vavo7/gn9+yloP7PHwj0/U1jW78V69bpdX2oOPmVWAKwr/sj9c19QakvmafdKRkNEw/Q0wvqfjV/wSp+P+q/Dr42p8Otb1CS30LWDJbxWVzJ8sN4DwoB6EkYx7V+0FfhP+yL8OZfGv/BQaO0hYwxaXrt3qD4HQRSMa/digl7hRRRQIKKKKACkpahkYt9w5pN2Q0rhLJt4XlvSo1nKnMg2L6mo/wB4rbjgDpzUrL54AI461hvqVyibd7fK1PVSoweaXaEXijce/FLlGLigsFXk4pNxHbNMfMi8ClzWAbvXrmmGWP61G7CPhjg+lNhjMmDjK5qdDVJW1HNB50oIZlXrwOPcVyPiz4D/AA7+IGoLqHifwRoOvX4AX7TqGnxTSkDoCzAk4o+J/wAcPAfwW00X3jXxRY6BAR8q3DkyN7hFBY/gK850P9v79n/xAq/ZfiXpiFuguYZ4M+/zxiqhHW5m3c+ZP+CrXhX4dfCn9n/S7HQvBfh3SNX1PUUjt5LPSo4nVVBZiGRRjgd69m/4JkfBOD4U/s06NqVxZwxa34iLajPOEXzDG3+rTcCeABnHvXxj/wAFbP2hPBvxcvvBeheEtftPEFrpyy3dxPYOZI1dhhVLYxnrx2719KfB/wD4Kafs/eAfhN4O8P6h4lvlv9P0m2t7iO30q4kVJFjAZd2wZIIPTj3rZi6H3mtLkV8CfEz/AILFfCPw7pDt4PstW8Vamy/u0e1a1iU9ixfBI+gr5a8I/wDBYr4q6b4oub7XNL0XWdEmclNMjiMEkC54Af8AiNWtibM/aClryX9l/wCOk37RXwntPGc3hq88K/aJ5IUsr45ZlULiRTgZVs8fSvWqZIUUU0rnvSsAyZdyketQvGVAHXip2XtVe7uDGpCjJxWT3Li3cgkm8n72NtWLSQTZKjjsapWsLXTF5l+UcVbuGFrpl08IwUjZh9QDQXJn87/7cU0lx+1l8Si0nmY1ZgpJzgBV4r9zf2RYHh/Zn+HCPt3jR4c7enev5+/i3ql34v8Ajh4rvL85urzWpVkOf+mxX+QFf0XfBPw6PCfwh8H6QvS00u3Tj/cB/rWljK7O0Vdox+NOooqhDGkCsFPWn1HJHuwR1p4zjnrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWQYOOcdacp3DNIFxmloAWkpaKAGRxrFkKMZOafSZpN4zQA6ikpaAEoLYBNNcOVbaVBx8ufWmLHL5ahnG/+IgcUAPik8xSdpXnHNPpKWgAooooAKKazbe2aRJN65xigB9FIKWgAooooAKKKKACiiigAooooAQ9KzdVmK25w+wd2B5rRb09aw75GjDh3Hl54YisZnRRinLU+G/8Agph8X9Q8G/Bu6sdGMjf2lIttLdBsFC3QAY54zVv/AIJk/s5+Eb79mnR/E/ibwbpOpatq1zPcRX19brPI8O4KPvDgZVq+T/8AgqH8Qr7xZ8bNH8AadclrGFIpGih/5aTO7KpI9QAfzr9XvgP4BT4S/Anwh4Xs90/9laXGmCuGdyu9hj/eY1FNW1NK07uy2PlL9ur/AIJ86R8WfD8WreAdL0/RtesVJFnYwJCkw9wMc18ueH/iV+0P+xx+z9e2l/b3FvaRX4itmuUMgiUjnB7DjpXQ/tDfty/tH+C/irq1vp/hU+G7G3crFHc6bJdGRASA+/A4Pp2xXzJ8dv2zPjR8bvDZ0fxjdhdIOd8UFgYEY/j3rRxuzLmtofqb/wAE3/2lvEv7Snwt1e48WzwT6pp92YPMhXbmMgFSR69a8v8A+CsGla9pXwbjuLCaaO1a8U3DRMeYx0yRXwN+x9+1p8QP2ctauLfwjpia5p166m509oSxfkDO4civ1v8Ajlp978eP2Qdcn8Q6V/ZV9daZ9sS3UbmjYLkDmsJe67Mq2t0eIf8ABJn4uQfE74L6/wCCNfZNSudGl4W4AbdauPlXB64O786/Pz9vjw54a0P9pTW7PwhbxQ6b5cZMFuBgSlm3AAd+BXC/AH46eIP2c/HTazo1zKgZHt7m3VsLJkEYP0PNfcP/AATl/ZGtPj1rGqfGTx/FJqFo2oSfYbO4GVmfOSxz2GePpXRr0Jew3/gnD+3p4f8Ahvo9l8L/ABpZrpUTTFbXVlGBuJ+7L6fWqP8AwVo+Ff2zXtH+KWjyrd6PKi2stxG4YbuqsPbpXQf8FDv+CdcOj2lz8RPhlp0p2uZtR0u2GSo/vxgV8OXH7S3jWT4V6h8OdauTqehSAeXFdrmW0ZTwAT9KUuYSkftx+wP8Sj8UP2WvBeoy/wDH1a232GfnJLRnGfxGK+ha+C/+CN921x+zPqsbSu4g1uVAjHhcxoeK+9a0jojJ7hRRRUPcQUlBNRO3ze1S9B2Ekm2SYOMY9aiSZmk5Tj1HSory0W6cHuB602EiNdsR4HVc81PObqKsTtIeXVec7TuHapo3Vl44FVLeYMzfMZBnPTv6Ui3ZWZlICp196fMhcrLjybcVD537xuDxUM9wrYwxBpikLIAzn5hRzIpR0Ln2gLjPFRteIG2hsGqn2hJLlkzlVHWp18gyBNpJIzmqDlS6EyTHI53AnsK+Hf8AgrovmfsxysASF1O3z+Zr7jVRG4RWwOtfDn/BWe8W3/Zlvbe5dd8uoW5i9eCaTegR3Z5V/wAESx/xI/iSwHBuLfn8Gr9Nry4MKjg49RX5q/8ABFCzKeDfHtzsYLJdRJv/AIcgHj681+k2oTLCMtk54xjNVfRkR1kiOSbyoRIjBo8/Nmqy3Qt7jDZMZ5XvVXVrTzrUwo0irJgnacUsaLarBG6NIFUANmou+h0qCLE2uvbwyNFbmTaegqex1k3gUmJkJGSDUQkHlsOME/dA5q/DNGkYPl7D0qjOaivslhG3Lk8U6o2VZ0GDSbHzjORWq2OayJ16UtV2m8tguCfepkbcuaVxNWHUUlLTEFFMkkCdTzUSyOZiN2VxUuSWhVrliioZJhG2C2KfCxZSSd3NFxW6j6KaTSM+0Ek8VQh9FVLjVbOzwLi6hgJ6CRwp/Ws/UfHHh7SFDX2t6faKeczXKL/M0rjszXmUMBmnjoK8w8S/tLfC/wAJszar470O2QLu2/a0J+vBq/8AC/4+eAfjQLv/AIQvxPY68bU4mW1k3FPqPSoW9wszwb/gqRr15of7I/iX7JK0RupYbeTbjlGYZFeH/wDBE3w9PafDn4i6xKP3d5qNtBH/AMAjfd/6EK9i/wCCrUE837I+ttDE0oW6gZ8D7q7xzXln/BF7xrZ33wl8Y+GU4vLLU1vG90kQL/NDQy+h+iGoXCWttJI77ECklicYHc1+G/x6jm/a6/b3Ph+wkaexa+TTI2jO4LBGcsw9jlvyr9oPiZ4JvfHWg3FhZavNpLyQSR+ZCOpZSBmviP8AYj/4J4+KfgL8etX8a+Lb61v7aGKRbFojuaV3Y/OfQgfzpDVrHqf7TX7Bngb4j/Ae10DSNOh0nU/DlqX0+6tYwHYqvKt67sV8h/8ABJn4mRW3xG174SeIrOPUbeQTT2iXkayLFJGfnADA4yBX6K/tWfHSz/Z4+DOs+LLy1kuwi/Z4407u/Az+NfkX/wAEy/EE2sft2aJfEFRfLqMzJ6boXb/Cq0EfuTp+h6dpaBbLT7WzUHhbeFUH6Cr1ItLVmZ+Uf/BbHxLLJqfw+0JABGkc90eepOAP61X/AOCdf7Xvw6/Zx/Ze8RR+KdYij1ldVmuINMjUmecFE2/gSD9Oa8a/4KseOp/iB+1bPoNvP5tno9rBYxKw+VJnyWGfxWvS/g1/wRz8U64ul6n4y8VWOnaXcRpObbTVLzFWUEAseO9AHyr+1h+0d4j/AGsPiRL4xudOms9Ms4Vtra1twzxwRhm+cnoGbPP0Fet/8E4/2xvC37KeoeJoPFWnX1xZ64IRHcWQDlGQkcqSP71frj8H/wBlr4e/Bf4byeC9I0K3utLuNzXbXsayvcswAYuSOenSvC5v+CU/wdHxTg8XWsd9aWSSid9BR1azds5xggkL0+XpxQB9e+HdetfFOgadrFl5n2O/t0uYfMXa2x1DDI7HBp/iDWLfw/od/qd1IsNtaQPPJI3RVVSST+VTAWmjacB+6tLK1iwOipGij9AAK/OH9vb/AIKTeDV8B+IPh38Or6TWte1BTZ3OpwAi2gQkhwrZyzYBHAxzQB8wfsu2Z/aQ/wCCikfiGdpLq0bVrjV3ZRkeXF/qyfbgCv3Hr86/+CRf7NmsfD3whq3xD8S6b9hutcjSDTI7iMectuDkuCeVDE9Pav0UoGFFFFAgooooAKKSoJpdr4pXGlclkqr9jSaTzG5PSlM3ydajhIkmw27HbnisHLU0s4q5Rv8AxRomi6pHZ32sWdjcuBst57lEZ88DCk5rdVgygqcqRkEV+CH/AAUn1nW7f9s7xVLd6j589mLYWEkZ/wBRGFDKvsQS351+uP7B/j7VviZ+yr4G17W5PO1Ga3kjklPV9kjKD+QrRK6uZvc9/ooorQQUUUUAFI2e1LRU8wEcbM2cjinrnnNNZsUBqgdhH+9QvSq18y/IGLA5/hqaMBFwMn61XMVbQe2dvHWo2MoYYAK96kDdqXGKsWwbgF5OKWNty5znmk4704Y7VPMSLUb/AHqkoqAIainuBCMlse1SzSbaoyNubNZuSuawjfUR5m25WTrUawrGpLtknnJqCTcbnjpinyMvST5g3G2sm9Tr5SeNlWZVXla+Sf8AgrFEsn7IOtM38F7akf8AfwV9XwK0nloEEaq/AFfJv/BWhQ37IWrZ6rfWpH/fwVpS1ZzVNHY8W/4Ij6fIvg/4oX5BEUt9ZxrkcEhJCf6V+mONrN7mvin/AIJG+ER4d/ZVGoO2ZdV1We4PptCoB/WvsqS4dpsAYWtZyViIq7LnmYbbUiVQZtrZzk1Nb3DMvK96zjJLqOUOpcopqtuHpTq6FqjIKKKKYBRRRQB5r+0h44Hw4+BfjfxHzusdKnkTH97YQP1Nfnx/wRX8Jx6hqnxP8ZXKML4G3skZgcESF5Hwe/KD86+mP+CpHjSbwj+yP4jigxv1WWLT/fDtzj8BXD/8EddBn079mPUtSuLVoDqOtzGOR0KmVEjjUMCeq53DI7g0FdD7m1GzGpafc2pdkWeJoyy9RuBGR+dfzoftafAnXv2efjhr3h/VIphBJO93p97Ip23MDsSHDYwSCcH0r+jla/Nv/gtJ8OItR+G/gzxnDADc6fqDWM8qpz5MiEjcew3KOvrQJOxheG/+Ckfg7Rf2HrLTtSuo9V8fJp7aMdFdfMJCjasr8YClSOp/hr4j/Z3/AGL/AIlftUafret+ELWytbKxkJM95K0Mckh+by4yAQSMj6ZFc9+y1+zZ4g/aa+KFh4W0SJ0sgwk1LUsHyreDqxLAEBsZAB6mv6CfhH8IfDvwR8AaZ4Q8L2gs9KsYwucDzJm/idz3Y+tA+Y/FXR/2iv2nf2JvEEeha5PrSWVudiab4ihkmtJEzjMTuPunHBU19GaT/wAFrUm0Ge21v4dOmptAVWexvwYt5BGdpXOM+9fqBrfhvSfFNm1rrOlWeqWrAgw3tusq4PswNfNnxI/4Jn/AP4j3TXb+FH8PXbdZdBuDbDPPO3BXPPpQFz8+v+CV9xq/jL9su98RCFnhmtb27vJApIi8wnAY9skgDNftZXiH7N37IHgP9ltdWPhH+0bm51IKs93qtwJpti8hAwVcLnnGK9voJCiiigApGOBxS0yQnbgDmk3ZAIrfLzxTDGBkg0yIFVO485pk0nUK3oPzrKU1YtIWGNjkueAaesxbOFxim24Kg72xjnBrx34vfti/CL4Ihk8TeMLFL1eljaN58xPptXofqalJtDZ7FNI20cU/azAEivjvw7/wVa+AfiLUPs0+rappSFtolv8ATysec9dwJr6g8E/FDwj8RtPivPDPiLTtZgkUMv2W4Vmx7rnI/EVVgOl3LGuGPPpXKeIvi74E8H3xsdd8ZaDo96Bk299qUMMgB6EqzA9q6XULEahaTw+a8DSRtGJozh0yMZB9a/K345f8EifHvi74halrHh3xxa6rZXchlEuvyObhSSSVJAOQM8VWnYD9G4/j78LLmQKnxG8JPIei/wBt22fy31esvjJ8P77VoNKs/Gnh+71G45itbfUoZJH+gVjX5Qt/wRk+Kf2Qsnirw4LnP3P3gH/fQWuq+CP/AAST+JnhX4o+HdY8UeJdEtdH026W6lk0m5le5k2kEINyADOPWjQR9J/t6/8ABP68/aq1HT/EnhrXotK8S2kS2zQ6izG0kiXJHCgkNk9cGvm7wv8A8EV9eXR1n8S/FDStHulJMkdppH2uJR6+Y8kZ/DbX6zRrtUAdBxXgX7bHwN8VftAfBa68NeDtYXRtYM6TLI8zxLIo6oSvr71aFc+EvEn/AARd1fUNN+0eEvitoutTg7St3pn2aHI7b4nk5/Cm+Df+CJfia42HxX8R9KsV3fPFo9lJcHHs8mz8sV5Cf2R/2xvgPNJceHrDxJFbwuZFn8Oays6SN3byFkLknA6r6V1/g7/go5+0l+z7qtjafFXQ77VLGQn/AETxHpTafeMo43CRkXI689+aLBzM+qvA/wDwRz+DXh0K+u6p4h8Tyr/DLcpbxH/gKLn/AMersb7/AIJS/s+3Xl+T4f1GxMbBgYNRfqPXdmvX/wBmH9qLwl+1L4DXxB4blNvdQv5V7plwQJreQAE8fxL8www4Nex0xXZmeGfDtl4S8P6fo2nReTYWMK28CE5IRRgVp0UUCCiiigBjMB1qAyLJNsAzx6U+WQbiO/0psfy5OOaye5aXUCCm4KvGKr3Em/SLssMYjf8A9BNSSSS7WwlMuDv0y4XGD5TA/kaBvY/mo8aA3Xxu11YxzJr0gUf9vBr+k7wahh8H6HG/3lsIFP1Ea1/OB4gsX/4aI1O243/8JLImM/8ATwa/pH0KPytD09P7tvGPyUVaethWNDdRuptNEgMhTuBmmtiDz34z/tCeBP2f9IttR8b63HpEF0xSBSpZ5SOu0D0rW+F3xc8K/GbwxF4g8IarHq+lSMU86MEYYdVIPQjI/OvyG/4LH+I9Sn/aa0nR3vJH0u00G2uIbQt8iSvJMGbHqQq/lX35/wAEyPB8fhP9kLwm625gk1N5r+QseXLPt3fkgplW0Pq2lpFpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAE3Ddihm2jOM0m07s0ySRlcKFz70ASK24Zxj60tJS0ARuDnIP+FNRW6tjPtRPJtUgH5yOBRbpIsf7xgze1AyVaWkFLQIKKKKACiiigApAwbODnFJIGZflIB96RIxGuB35NAEclwFYLglvSpKjaFtwZSAfcVLtoGKtLSDiloEFFFFABRRRQAUUUUAFFFFAEbbt3A4+tcp40vv7N0u4uZo3KxI0m1ehwM9a6uZTtyK4D4yWs174PvwkrW6LbSs8gPQBDXPUhfU6KL94/EmHxH/AMLl/bu0O4ltiUk8RQQ+QzbvkSQ8Zx0r99o1CooAwBwBX4M/sD+HIfFf7dWhl5i0dnqFxdhiN3mFCxH0r951HFVFaWInuytPY215kT28U4x/y0QN/Ovjj/gplouh+Hf2frzWH0rTo4428kkWyq5Z+FAIHrX2htrhfjN8FfC3x68E3HhbxdZveaVMwcrG5RlYdGB9RV2ZKep+eH/BGXTfDOtaH49t7rRrefXbSaGT7VNEHIhkBwoyOMFc/jX6V+L/AA7/AMJB4R1TSIgi/arZ4FyOBlcV57+zh+yt4I/Ze0XUtP8ACEFwX1GUS3N1dyb5XwMKuf7o9PevYaFHe4uZn85Pxn+AetfD34+Xvgm8tpWubjUFS22xnDpI+A3H41/QD8G/h5p/wq+GPhzwvpkC29tp9nHEVAwS+0bifcnNa2r/AA/8Na9q1vqmo6FYXuo25BiuprdWkQjphsZrf21SVlYHK5HLEk0bRyIrowwysMgj0r87/wBsj/glhZfFbWLvxd8OLy30PWZFL3GlyJiC4bkllI6MenpX6KbaNtMV7Hxz/wAEyf2e/G37PXwl17TPGkEdnc3+pefDaK+4qoQLuyPX09q+xlORRt6+lCrt4HSgQtFFMZW3bgx6fd7Vm9wG+ZuztHI9arLdLMzoeHX0qwSWz2PtVSQLayB9ud3BJrOb0NIq4jQhU3vKyD2qL7OsjeZGuGx/rB1rz34iftHfDX4W6kll4u8Xabod2yCQW15JhihJAbHoSD+VJ4L/AGoPhD4+mNtoHxE0C9m/55repG34B8VjH3tEbaxWp363SNvBdlZfXFRNHJdbfmBX1FLDfaPqkb/Y761vT1PkTox/Q1UuPEeg6X8s2s2Nvt6ia8RCKrRaM0UotXLEjNCoVueTz/KqrXn7wKwbeFzxXL6z8dPhrot0bTUPHGi20zAPsa8RjjnnIPsapr+0d8I4S0z+PdB54Ja9Qfpmp91vc0U7LY9FtLWNUMy7ju67qleZvLBRQBnGSK8nuv2yPghpbeVP8SfD8TYzt+2J/jWVdft2/AK3cI/xK0Vu/wC7m3D9K6FT03Od1NdUezLI4nU5ZyPSviP/AIKs+BfEHj74KWr6PZXN+1neI8lvbxliR68V6n4g/wCCk/7PvhtlX/hNoL5iN2LKF5P1Ark9S/4Kufs/xxsv9o6heg8lE092B/MUcrtYaqWexT/4JQ/CrW/hr+z3qEmuadPpV9qmpvOkFyu1vLCIFbB9ea+wru4mVioUu2eTjiviO8/4LE/ByzmMVtpeuTRKvystsEGfTBrgdc/4LVeGorl007wDfXMP8LzTqhP4U+V2aIjPld2j9FPt007FTbk4HDGp7a0uGIlkGD2XtX5oXH/Ba2zMeIfhtIzHjD3YA/lXK6z/AMFrvFYkK6Z8PNLii7Nc3cjMPyGKVmXzvofrCtqWk7DueKufZlYfNz9K/FjW/wDgr/8AGPWGl/szT9E01mXCRwwGUqfXnrXIXf8AwUY/ae8QQvHFqtwqyjaTZaNg/gQKqxlKV+p+6awOk+Qw8rH3e+akkmjhQtI6oo6sxAFfzzaj4y/aK8emS6ubzx3eiRsEw21yV9cDaOOvSs6L4b/H/VoWaHRvHl1CxwxaO4UE+mGotIzufuL46/bA+E/w38TW2geIfFdtp+qXBUJCQX6kgElc4GQa9mtbiO7t4p4XEkMqh0dejKRkH8q/nv8Ahn+xz8a/HXjjSEm8Fa1BELuJpbzVI2VUUMCclq/oJ0ey/s3SbKzOCbeBIjt6fKoH9KfKwbXQtjvTdxbO08dKVqpvdC2IAUkMe1VsgUW9iS4aVWG1dw7mqkN1Kt0YjCSOu6n6hq0Gm2sl3dTLb2kQ3SzSsFVB6k18b/Gz/gqt8JvhTqV7pmjx3njHVrc7GWy2pBuyRjeeT+VZS953L+FWZ9nyRmSQFhhfSrK8LX5j6D/wWw0aS8H9ufDPULaxJwJrK9V2H4MoH619FfBT/gph8FPjRqY0yLWLjwvqbHCW+vxrAsnT7sgYqfoSOlMnVo+rjVXU4ribT7lLORYbto2WKRxkKxHBP41PbzR3UKTROssUihkkQ5VgeQQR1FSbRWi2JPyB+OX7Bn7WPjr4k6pq0uvf8JLHdSGSO8t9bFrGqZO1BGSu3Ax0GOa41/8Aglf+0f4gtUOqTaaWDbdl9rPnOB65BIx7V+2FLSsVzs/Gqx/4Iw/FW9tle68WeG7OTvDJJM5H4qhFfZ37Av7Ct5+yX/wkeo+IdWsda13U9kUUmn7xFFCuSR8wGSSfTtX2NRtFLlYcx5x+0N8L4vjJ8G/FPhKVtjahZusTYziQDKn8wK/Fb9iX476l+yL+0TLp2tB7XSLyc6bq0Ew24KsQsn4Hmv3vavh/9tr/AIJu6R+0Tdt4o8IS23h/xfj/AEguCIrzGcbvRuetIaPs7w/4g07xRo9tqek3kV9YXKiSKeBwysD7itBpgnWvyT+Ev7Hf7Y/g4L4Y0nxm3hLw9GWXzheq8QU9Sq4JzX6UfAf4aaz8LPhxZaF4h8U3vi/WFdprnU705ZnYAFV/2Rjj6mi7FZFr41fB/wAPfHr4d6p4P8SQGbTr1PvKcNE45Vx7g818l/sd/wDBNiT9m34z3HjjU/EMOs/ZYpbfTo4oyrKrjbub32kivut4lyX25bGKr/2taR7vOnjtiD0mcKfryaQF5aCcDJqgNc03GRqFrj/ruv8AjTTr2mMCDqNqQf8Apuv+NaLYk/n6/aevk1f9uPxhMW8yJvE0acnIIBRf6V/QbpUaQ6XZxxqFRIUVVHQAKMCvz0+Jn/BMmHxl+1VpPxB0PUrOfwhd6imoavZytucOp3MEIPIbA4r9CG1CystsL3UEJUYCNIAQPpmmBdoryL4iftZfCT4U3xsfE/jrS9OvQgk+z7zI+0kgHCA+hrzu4/4KVfs9wHH/AAnkcvvHayn/ANloCzPpDxBoNn4o0O+0nUI2lsb2FoJo1coWRhgjIORx6V80+GP+CZf7PnhXxBa6zbeC3ubu2lE6LfahcXERcHOTG7lTz2IrN1D/AIKm/s96e20eKLy54zmCwcj6c4rita/4LEfBewujHYab4l1aHGfOhtEQZ9MM+f8A9dAWZ91wwx28KRRIscSKFVEGAoHQAU+vzp17/gtN8ObOzkOmeCvEV3d4/dx3DRQrnsScnivjjxp/wVQ+PfiDxNc6npXiePw/pjSf6NpdvYQPEig5AZ2UsxweeaB8rP3dorxn9jz4ra78bf2dPB/jPxIkS6xqUDtO0ChUkKyMm4KOBnb0r2agkKKKSgCOZsVRlkG7k81NNIzSmLtjOaoXEUbSAFznPrXLL4jppxXUmWdhIqgZTuasWfzSMQflGRj8qzmhNvDIUYnnpmrmlPJImWTaMdfWoWrKnFJXPwL/AOCkFraWP7Y3j1LSZ51lkieQuxO2QxLkD2HFfsj+w3oEHhv9lH4cWtv91tMWZv8AeZiTX4xf8FDGc/tlfEoOMAXkOPp5MVftv+ybj/hmv4cYGB/YsHA/3a647HPJdT1yimZozVED6KgmkWPBY4qk2pw3BKIx4ODU8xSjc0T/AKynHHeq6IFUc+/WjydzZz8tQPlJzg9KY1OjUIuBT6BXsVW/134UyL/XVNNjd9zPFQSTNDxHFlqC76E+8KWHvSNcKrbe9Qqr7sAbd3JqdY9vWq5haEsbblzTqj9KctPlvqQx1IRu4paz9dgvptJvhpckUWpNA62zTA+WJMHaWxzgGjlETNJAjFHmRX9NwBqJYYjMZFnUjGMAivwb+MHwO/arf4qa5c6v4b8ca1rTXDbtV0a3upYJRuO3yni+XZjoB0rLtfhF+17Gg+z6B8WYFB+6BqCfpmpsuxor9z99fscfmF1YHPHWq0+jyMxaJ9pPWvwdb4Y/tlLx/ZXxeH+7LqA/k1dN4Zb9tbwRp7wwQ/E2GLeZCt7bS3ByQBnMoLY46ZxWTp3dzTnl3P3GsbE2y4c5714p+278C9X/AGifgBrHg3QpYIdUuZ7eWJ7jhfklVjz9Aa/KXWvj7+2L4RjW81K+8ZWca/8APxpgA/EbauaR/wAFGP2otJhUNLc6kq87rrRHz9MhRWsYcqMZNyep+tn7L3wVT9n34L6F4GW9F9Lp6MZ5gMAyMdzY9ua9EuIpkmKIeDzX4x6d/wAFfPjfo9/jU9N0S62fK8E1m0T/AInORXoOlf8ABarxJGFOpfD7T527tb3TAH8xWUqbY1Kx+rEVrdLKPlBT+93rQ8p1AwSa/MXT/wDgthatD/pPw3lR8/8ALK8BH61px/8ABazQtv7z4e3wP+zcrQqKsVKdz9L7cFY/m65qWvyZ8ef8FptbnuIf+EQ8EWtvb7f3n9pTF33ZOcbeMYx+tfZf7CP7Wmpftb/D3WNc1Pw+uiXOmXi2hkhJaGfKbjtJ7juO2RXQlZWMj6bopKWmAUUUUAfn/wD8FktQli+BPhKyQgR3XiCPeO5xFIR+tev/APBNPTRp/wCxd8PCH3/aIrifjtm4kXH/AI7Xzr/wWq1qWz8E/DazRSY5NUmuGOOMpHgD/wAer6l/4J92a6f+xz8L4V6f2a7/APfU8jf1oLex9CrWH408C+HviNoM+ieJ9Hs9c0mf/WWl7EJI2x3wa3aKCDmfAnw18K/C/Rf7J8JeH9P8O6bu3m3063WJWbgZOByeByfSulXOORilooAKKKKACiiigAooooAKYzYODTtw9aimYetTLYa1Yu5ccc1BNcQ2sMlxPIsUMal3ZzgKB1JNMVhvzuGBzivhb/grR8fb/wCGvwj0zwjoGoNZax4lkczeS22UWkYBc+wOQKyglc0t0PFP26f+Ckl/4j1O7+HPwfubhV837Pd65ZZaS4PIMcWBnGe9ea/Av/gld8S/jZZW/iDxpfjwjYXR8z/TFMl7MDg7yCeM57+lfQH/AASp/Y2sdM8Lx/F7xfp0dzqWpE/2Nb3SBxDCMf6QM92JYf8AAa/SwDAwBgVuRc/LXxR/wRQj+zr/AMI/8RJA46x6haBlJ/4Ca+Xfjd+yx8Zv2HdW0/xDBq0yacXxHrWiSOqI2chHTPHSv3trn/HfgnSfiH4V1HQdasor6xvIWieOVQ2MgjIz0IpWDmZ8q/8ABPj9uAftPeHZvD3iCIWvjTR7dGmkByt7H0Mo9DnqPevsjaa/nt8H+JNf/Yv/AGvLq0s55LY6LrH2G4hY/wCttmbIzjrlGB/Gv6Eo2LxqxUoSMlT1HtS5RXDaaNpp1FHKguIKWkJCgk8CvAfHX7e3wE+G/iS50HX/AIiWltqttxLDb2V3dBDkjBeGJ1zweM5qhHv1cT8WPg74S+NfhO98P+LNIt9Ts7mJow8kYMkWR95G6givCtY/4Kf/ALOOm2MtxB46n1KVFytra6JfiST2BeFV/Mivz3/ah/4KofEL4rXV1pHgN7nwJ4WJK+fAMX06gnlpP4ARjgUDSuT/ALNfhnxF+zv/AMFFB8PvAuqHUdL/ALRaxu2zuU2gAdhIOxUH8+lftZkV+Z3/AASv+CNj4Rhv/i74x8U6bN4l1xHhtbaXUYZZVibaTK7BiQzfMMHnivsr4yfthfCH4BXGmQeNvGMGmzakrvbR29tNeFlTG4nyUfaPmGN2M84zg0A0ez0tc54B+Ifhz4n+GbPxB4W1a31rR7tQ8V1bHI5AOGHVWwR8pwRmuizQIWkpaKAIwuOornPHnxG8MfDDQ31jxXrdloWmocG4vZQik+gz1NbupX0Gl2NxeXUiw21vG0skjHAVQMkn8K/Ev4lf8J7/AMFJv2r9b0jwpeTf8IrYSeXD58zJa21tGxBlKHjexJPqeKmxSP050f8Ab4+Auu6ilja/EXSftDvsVZH2gn6mvbrXWtP17R5LvTL23v7Z4iVlt5A6nI9RX5veIv8Agivo8mgxjRviBdRav5Y803VopheTuRjkCvmm91r47/8ABNfx0mmXV6l1pWpRnyg0rTWky5K5GT8r4HT6UcpR4bJpNzrf7VU1pEv+k3Pi0xorHHLXJxX9G9lCbezgiPWONVP4DFfzqfs7atL4z/as8D6hcr/pep+KLaeYdvMeck49ua/oxppdRSGtIEHJxVa3vYZ5SEOWHBp1xNaqxWaaNGx0ZwDVOGXTLGR5ftduhPUtKowPzphpY/GD/grRavrf7ZtjZRqWlk0SwgVR3LTTD+tfsL8HvBkHw++FfhTw5bLti03TYIMe4Qbv1Jr8qf2uNV0Txx/wU48ErBd215p0cul2tzIsqlFKzSF8tnHAPrX6K/Gr9tP4R/AbSjd6/wCKLe+myFGn6M6XVye33AwA6dzQS2e5Clry79n79o7wb+0v4Nl8S+DJruSwhuGtpEvYBFKkiqrEFQT2Yd+9eo0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEGe9LRRQA3YN+7HzYxTqKKACiiigAooooAKKKKAEpqyBmwOaSSRVYIwPIpIo1HzLwD2oAkparXFq81xBIshQRkkqP4qs0AFFFFABRRRQAUU0t82ByadQAUUU3b85bPbGKAHUU1V255zk5oZSd3OMjFACnHSvOPjfYXN94D1tY5dsP2GXcg4/gPeu9nm+yqgwXbpmuG+L0c2oeA9bhgcxtJZzKW/u/IecVnN+6b0ou9z8av8AgmaTa/ttaWgXcG+2LnPT73P6V+7C1+Hn/BLPS/O/bVUOQ5t7a+bcepK5Ga/cJacVrciQ6iiirMwooooAKKKKACiiigAooooAKKKKze4DGHNRT2sdwoDjcB0qfbTJNwXCY3f7VDSsNXufBn7fX/BO3Wv2lPE1l4w8Ha3a2ms29mllLp+oDEUiIzsCrgZDZkPXjivz+1X/AIJn/tEabqElungVrryjhbizvYNj+4ORX73m5WJgshG7GeKct1GwB3DkZqVZLQt8zWp+DOl/sE/tRaGxGneEda08sPmNrq8cYP1w/WnSf8E7f2nNSYvceFtQct977Rq8bE+5+ev3oVwwz1FIsyNnBBwcU9BK5+EOn/8ABLH9oXWJ0Evhmzs9zYMl1qcWB7n5ia7iP/gjV8ZZkRv7d8LwEj5o5bqXIP4RkfrX7TeYN2Kdn2qkmFz8Yof+CMvxh2/N4m8JL/21mP8A7Sqdf+CMPxbb7/izwov0ab/41X7LAZpdtWLmPx80v/giz8RpGH27x54at488iKOZ2+v+rArudP8A+CJqyRK2ofE9op88ra6cGX8yw/lX6lbaQKBmgOZn56+Ff+CMfwy0+Ff+Eh8Va9rkwbO6EpbDHHGPm9/zrrV/4JAfAH/lpH4mkP8A2FQP/ZK+3ttG2gV2fFMP/BIj9n6F1Y2fiKUKc7X1YkH6/JXdaZ/wTd/Z+02NFbwHb3pUbd13K7k/XkV9OUtMLs8m8F/so/CL4f25h0P4f6HZLvL5+yh2yQB1bPoK9CtPB+hWEYS20XT4EXoI7VB/SteikIhhs7e3XbFBHEvXaiAD9Kk2KOigfhTqKAEwB0FLRRQA1qrSrtzsYBsZC+9WWryz9oz4sQ/BX4T+JPFsirM2n2byLDu2ktj5efrUTdkXE/O7/gqN+2JqE2pRfDHwnrQtbVkZtaa0IYnBwIt3VTkE8Edq5b9gT/gmvD8aNNXx18VbC8t/C8hH9n6V5jQSagpGTI7KQ4TngggnBrwP9lv4Qal+2T+1FGL5dtlcXTavq0mNypEGyVz6sePxr+gDTdPt9H0+1sbOJYLS2iWGGJeiIoAUD6ACp2Kk+ZaHy1N/wS1/ZnkiZR8O5I2IIDrruo5X3GbjGfqK+Tf2lP8Agj2+g6Xda38ItVu9VMOZToOqujSEDJ2xSKFJ4xgHn3r9X6KCUfi3+xF+3x4w+APjy2+HvxIub6+8KvcGyMF6F83TJ8heHI3lBgDaTgZJHXNftHb3Ed1bxzwuJIpFDo69GUjII/Cvw7/4KseF9M8GftZSzaXFDGNV022vbmOMDPn+Y4LH0JAFftF8NZDJ8OfCrnILaVannr/qVrRCZ01FItLTJCmyN5cbMckKM8U6igD8k/2uv+CoXxR8I/FnUvC/gzTrfwzp2mSmEyanaF5rhgT84yRhTxjjsa8n0/8A4KfftIa1b/6NNZyk8BrfSHf9QSK/ZXxT8H/A3ji+jvfEHhDRNZvI+FuL2wilkA9NxXOOTx71o6T4B8M6DbiDTPDulafCDkR2tlHGufXCqPSpsVdH4mSftWfth/ES/wD+JRqvidWYbPJ0vSxHH1z/ABITnn19K6K10/8Abu1aDzi3juQN3RY1H8hX7Tw2cFrxBBHCP+maBf5VNzRyhzH4i3/wn/bc8UN9nu4PHBVhgmW5WMY+oIqxpf8AwTp/am8UWpuLy+uLRmcgx6jr0gk6DnAJ45/nX7Z49aKXKPmPxYb/AIJf/tL7hH/a1oUxnd/b0uBSyf8ABLX9pCMAf2zYycZ41uXvX7TUVQuY/Ey9/wCCaf7Ttim2G+ScYzth1uUCo9N/4Jk/tL63I015cW1nJuwWutblZj78Z4r9t6KYcx+Ouif8Eb/ijrX7zxB4w0OyYtg7RJcvj13HHvxXayf8EadI8NaDc6n4k+K76dbWqGWe4FkoijQDkksa/Rrxl8dPh58PtQFj4k8Z6Lot60YmFveXiI+wkgNjPTKkfhXG+I/Fnwp/as8G674B03xzp+qLqNuYpk0i/UTqPVcHJoC7Pz3+D/7BH7MnxB8UJp9t8dZfFNzGSDYQslq0hH91mXn8K+p9P/4JLfs+Wu03OjatqBH/AD21aZcj0+Rlr4m/ao/4Jh+I/wBnDwZfePfCvixdb0TSCss8cqC2uoEL4DKwOGIJHPB59q+z/wDglD8XPGXxZ/Z/1KTxZfTaumj6s+nWl/dMWmZBFE+xmPLY8zqfUUA2dSv/AAS5/ZqVQD8PpHx/e1u//pPWzov/AATh/Zz0GdJrf4Z2Uzo24fbby6uRn6SSsMe1fS2KKBXZm+G/DmleEdDs9G0TTrXSNJs08u3srKFYoYl64VVAAGST+NadFFAgoopKAKF5OY5wqoMEfexUC2qzliSCeNo6HP1rQMYkbJGa8p/aa+Nem/s9/CbXPGF7NClxawMtjbyHHnTkHC479q55Ruzbm0shfix+0d8M/gaq/wDCZ+LLHR5mw32dm8yUqeB8gycEg847VzPgX9uz4FePNSGnaP4+04XUmWWO6Jgz0/vgV+SHwc+AnxI/4KH/ABe1rxBf3rWEEjtLc6xco8kEHIIgT0xuztH97PevTPjB/wAEhfiN4B0ObVPDetWni3yfne2hjMcuBkkgGtIxsZ3fU81/4KYTadfftfeIbnTJoLi3ura1dpYHV1ZsAE5Hfge9ftp8DdEj8OfBvwRpsXKW+jWqj/v0p/rX81dzZ3tv4ga21BZEvo7jyZ1lJLB1cAg59On4V/Th4Ai8nwJ4cjx93TbZfyiWtAk7m5UcxYIdtfOv7dH7VF9+yh8LrXxDpmiprOoX10LSJZmKxRHBO5sV88/sy/8ABWzSPiJ4ptPDPxG0iDwzd3cqwwapayFrXeez5+6M96AXc/Qa3aSTcCM0yT7Npdrc3d3JHb26KWkkchVVRzkmrdrNDdQJPbyJNDKA6SRsGVgRwQR2r4N/4KyftKXPwu+GNn4E0S5EeteJVP2nacPHajI3D6kEfhU2K5uh9neCfil4P+ITXMXhnxHpuuSWvEyWU6yNH25A6V1nFfjd/wAEi/gl421T4tH4i200+m+D7GOa3mkbOL5yAPLx3xuBzX7I0uUh7hTWkCyBe9PpKOUQjV83/tl/tiWf7I/hzTNSuPDl5rs+pSGGDy22QIwBPzN619Hn/WCsbxh4H8PfELRpNI8TaJYa/pcnL2eo26zRE+u1gRRyjufjN44/4K//ABp1y9lbQk0fwxbMcJFDZJcso9zJnn8Kxbb9s39rv4paXKdD1bxRqkDZjMmg+HUGDjOBJCmQcEe/Ir9e/Dn7K/wd8I6kuoaL8MfCmm3inK3FtpECOv0IXivT4bWG3ULFFHGo6BFAFPlHzH8/Hh6f9o2H4qeFL/XpPiBZ+IZNShSzu9cS6Vhl/m/1wzt5+nWv6BLGOWK1hSZ/NmWNQ8mMbmxyfzqYopOSoJ+lOqgcrhRRRQSFFFNbC5Yjt1oAjubiO1heaaRIolGWeRgFA9Sa4HU/2gvhnod79jv/AB3oFnddfJm1CMN6Zxn2Nflz+0d+0x8Qf2uP2lL34JeEvEUfhnwvNqUmkQNlk+1OnytvYc4JB4qgv/BGP4qKSD4l8MuM8HzJc/8AoNTqWfrdpfxS8H61D5lh4p0i5j/vx3kZH55q1N438MujI/iDSdp4O69ix+W6vyAvv+CNfxbhXNtr3h6dsfcWZ1H6isKT/gkF8c1m2BdCdMf6xdQUD8jzTFZH65TeHfg/ql5LNPpvgm8u5m3SSSQWbyOfUkgk1jat+zR8D/GFyJbrwN4XvJSuweTDGnHJ6IQO9flha/8ABIX452kqSwXei28g53x6hgj8RWxN/wAE0P2ndFYTWfiBJmUcfZ9fkjI9utMLI/RnUv2A/wBn/VAfM+GWjpkYzErr/wCzVxGuf8Esf2etavBcDwvdafhAnk2N+8cfBJzj15/QV8KSfsT/ALYWksLm01PVBNGchk8RvIf++S1WJ/D/AO3h4bhMJXxnNFHxvt5YnGPqTmgOU+zpv+CS/wCz/JGyx6Tq0RI6/wBpOTX0R8BvgJ4T/Zx8Cnwn4NtprbSmunvHE8pkZpWVVZsn2Rfyr8gY/C/7YfizxvoE2qyeNrGV7uO0F1dSFVjVm5JC8YHPJr9tPD9rPp+h2Fpd3Bu7u3t44pp2HMjhQC34nmgk0KKKKACiiigD8x/+C3CSHwf8MioJH2+6HA7+WuP619dfsEyCT9j/AOFrKcj+ycce0jivlj/gtdCf+FbfDeYcbNalG70zCf8ACvpr/gnju/4Yy+F27r/Z0nX0+0S4/Sgt/Cj6LooooICiiigAooooAKKTNGR60ALSUBg3Q5paAGKvXNNkhDVLRSauNaFJbRUk3Htjk1+Lf7VEmoftff8ABQ628DRXP/EttL2PQ4ZIm3IsSfPM/sfmIP8Au1+tn7RHjx/hh8D/ABx4piBM+l6TcXEW3rvCHb+uK/GX9gv9oz4f/BH4s+JvHvxKa8vdanti1nLbw+a3myNukb64OKlRsWnfU/cfwj4Z0/wV4Y0vQNLhW307TbaO1giUYCoigD+Va+RX5E/tgf8ABU22+KPw/g0X4WT6t4cvpLoi7upY9jvAF42sOhzn8q8M+A//AAUm+LPwT0O50xLyPxPZyTtcbtZdpZVJCjAb0+XOPc1ZPKfvTkUbh61+LF9/wV++NmpSRx6bpOjQvIMKkdmZXJ9hVe7+On7Zn7T1u+k6PpmvQ2cijzP7NsvsKMue8jbR+RoDlOP/AOCjlvpeuftxaovhd49SlumskmW0+bN0BsZPdvlX86/d5WEiqw6MMjjFfmn+xb/wTJ8TfD/4paf8RPipeWdzeWLG5ttNhma4Z52AIklZh94EngZ5FfpdQSFFFFAFbUrFdT065s3do0njaIshwwBGMj3r8vvEX/BFOfU/EV9d2fxRWKyuJnlC3ekiaYbmJ5bzBnrX6lUUAflpD/wRFZFx/wALejT1B8MpJ+puBTp/+CIamENH8XwbkHjd4ZRY8fQXHX3r9SaKB3Z+Smrf8EUfF0KkaZ8T9HuwB8q3WnS2y/QhGb86898Yf8Eevjdodm9zpV34X8SyxYKWljfyRPJk8j9+qKP++q/a2igfMz5l/YH/AGX7z9mP4LW2naxLcp4n1Rvteq2j3KywW82SAsewlfu7ckE5xX0yvSlooJCk3DcB3NLSMNykGgD4s/4KnftDT/Br4EjQdKl8rW/FbPZxsCcpAoBlYe+CB+NQf8Em/g3/AMK7/ZtXxBe2Sx6v4mvHvRcsBva12osan23CQ/jXyB/wUs1af42ftyeGfAWmXBmWxt7LS/srZCi4lldn68co8fPtX7B+EfDdp4O8L6ToVjGsVnptrHaxKowNqKFzj8KB3NTvjvXzT+35+zfY/tEfAnUoHk+zavoaPqdjNxjciHcpPoRX0uVO4GuW+LEbTfC/xai/ebSboD/v01AH4CfsO6PLq37W3wwtfleRfEFvK2Txtibc36Cv6IZlfyn2ffwdufXtX4Af8E6rWS4/bN+Hahcst5LI2e2Fcn9BX9AZGeD0oC9z8Mf2kPh5+1P4r+NmvyajoviW7uGnZbdtJkcW3k728sKVIHQ1R0L9iP8Aat8SW5kXTNasVYAf6dqpQkfTca/dtqSgD+bu2+APj29+PMXwvki2+ODefZnE05KpLgNuLjJIxzX3Pa/8EUvEF+sEmq/E/Tw7KrTLDpbs6tgFgHL8855xWb8LmXXP+CxmvtHErJDqV5uzxjy7XBP13Cv1yoEeW/s5/s9+G/2avhraeEPDUWIlf7Rd3TffubgqqtIfTIRePavUqKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilcAoooougEx8wPaikZtuOKXd7UDFoopkkgj9z6UxD6KYm5m3HgYxilVSu7Jzk5oAdRRRQA0rzkcGnUUUAFFFFABRSE02SQqhIGSO1ACsuea87+NAmh8Ea7PA+1k064YKB1IQ16Gr7lDYx7VyHxS0mbU/BetrEy5+wzrtbvlDWVRe6b0naWp+Of8AwSesDqX7ZD3ckjRywaffSlQfvEnBH61+3i1+DH/BOfxg/gj9t/w5D8uzUbm60uTLYH7wMB+oH51+84rSOxM99B1FJu9qM+1MyFopMn0qGa7SAEsQFGMnPC+59qV7DsT0lcX4/wDF+oeH/Bur6xplob2azheaKOPlZtoyMEV8pfBX/gqd4E8aawNA8cWNx4H1pFYSSXoxBuDEYBPI/Gk5Jbl8jtc+4dwzjPPpQTt618E/tVf8FR9C+ETWun+BLSz8WandRmRbjzswouSBnHPUGvC/g/8A8FlNe/4SaO3+IHh6x/seaUbrrT9++JTgEYJwcdfxpKSauRZn61LnvS1ieDPF2l+PPDGneINFukvdK1CFbi2nToyEfzrbqk7q4PTQKKKKloQxmKsOVA/Wq890Yc5TK5xuzip5I1kIJHI6VSv9NW+ZRI/yD+Dt9azlfY0jbqZ8hl1K4KhRBtHVmyceoFWLPSp7c7DcFowvGBznPrivlr/goT8YvF3wC+C93rXgvVU03UmeKLzTEHZFLEZXPevyR1D9sX4++PdShJ+Jnim51GTEUdrptw8W4DkHZFtB5J7Z4pR1R0Sk7JJn9ESwNkB23LjGc8/yoUQ2cblnVE+8WZgAK/BVfjL+19r2mJp8Wp/Eu4hhbaWhtLiQlsDgyBc9COM1JpvwP/a++MkZElh4+vbVpPKeTVruW2QHAOCJHHGCPatOVnNfufug/jrw1FIUfXtMVxwVN3HkfrV7T9f0zVYzJZaha3canaWhmVwD6cGvxT03/glD+0TqUPn3Mek6fIxyY59Y3Ofc7Sf8isbXP+CfX7UfwxWWewsL+aGNTK0mhazuHfPyhsk4Hp6VaFofuktzF/z1T/voVIGDDIORX84k2s/HPTdX/sifVPHcGrFtiWi3FypJzgHrzzn8q/cP9iPwL4v8A/s7+HrPxzq97q/iG6BvZWv5WklgV1XbES3PG3P/AAKmSe80UUUAFJS1HIx5wdtADlbdmnVAHZXPA2Yz71598Sf2ifh38I4428WeK9O0l5ACsMkoMhBJGdo9wfypXHY9Ior5vt/+ChnwEur9LRPH9kJGOAzKwT88V9C6XqdtrOn299ZTx3VncRrLDNGcq6EZBBphZot0UUUCCiiigBp+9ivhD/grv40j8M/s7ppWxvtGtXiW6ODj5V+Zh+VfdzD5s98V+cv/AAWrVm+Evw92puLa3Iu7+7+6qJLmLi7M5v8A4IyXHhDRfB3jq+vNV0+z8Uz38dqYbidY5GtljQqQCem9m6elfpta6ha3yk21zDcAdTFIG/lX4Wfst/8ABOHx/wDtIfDlfG+j+ItN8OaXczSQ2/2oSGV2jbBI29Fzx+Fd34g/4JnftP8Aw7ZJ/CniFNWdRvL6RrUls+cntIV54HQ9xRyi2P2grgvjD8bPCfwR8K32teJ9XtrBYIGljgkkAklIBwFXryRjNfjxffAf9uOxmETyfEaUqvH2fxM7p1PHEuK3fh//AME3/wBov9oDVIrn4l6rqGg6dCxjN14m1J726wAGASMs3y5Y4Pruo5QujifgH4D1v9vz9si51fXvtF/oRu21HVZnO0RWanEcYxjbu2hRjHev3WsbKDTbG3tLaPyra3jWKKMEnaqgADn0Arx39lf9lLwj+yn4FbRPD0bXWpXhWXU9Vmz5l1IBgHGcIo7KuB1Peva9oqhN3BaWkpaYgooooAKKKKAGs2Gx7Zr51+OH7fHwi+APiSTw94j1qaTW4wrSWVnA0rRhieWI4HSvomRVdSGGQeDXxL+1n/wTF8P/ALSvxCufG1l4on8M6xPaJBLbx2yyQzSKznzWOc5IZV4HRBQPQ+j/AIO/tJ/Dv47aQdQ8H+JbTUFVtjwM4jlRsKcFDz/EK9Nr8SvGX/BLf4/fCu7N54RvINZjhXes+j3bQS9TwVJGTgA/jUHgf9ub9o79lXUP7H8Z2moavbEqFtPEsTfIoJH7uQDodp7+tK47H7e0V4J+xf8AtMTftWfCA+M7jRf7Bmj1CXT3tlcurGNI23qT2PmY/A173TJGtjGScAc9cV+Z3/BQD/goHqMHiC5+EPwhmmufEM0wsNR1CzyzFmAxFblej5OCw+le8/8ABRj9q+b9m34R/Z9FljPijxCWsrIZ+a3Xad834A4HvXzN/wAEp/2OW1qaH45eNFmlnW4kGh2l0p/eNj5rps9eWIX3XNAHYfs//wDBJvQ9V8Ex6r8aLzUNU8Y3jmVore9bZBEyqQjHu4YyZPTkVf0L/glSPhh+0V4N8XeAPFU+m+E9Nmjub22upGa6Z0diUVhgbWXauD71+idDDKnHWgdz4G/4K7/HHS/CfwFb4dQzJL4g8TzQsY1cboLeKVJC7DsG2FfpmvXf+Cb/AMJ0+E/7JnhKIukl3r6nX7howMbrhE2DI64jWMfhX5v/ALWX7Fv7SHjf44eINbv9AvPGCXcjPaX9ncK6Lbb3EcfzEFSB29CK8x8aWv7VPwP8L2una7f/ABF8O+HYYEgihjvbn7DFCo2qm6NyigBcBewAoEf0FA56dKWvyh/4I+/FT4h+JviR4o0XV9X1nXPCH9nvcLJePJNbw3YeIHDt0Ypjj0I9a/V6gAooooAKKKKAI2BLMOi44Ir8af8AgqJ8btU+Nn7Q2mfCjw6GuLLQ5lsBbox/f385AbI6HaNgB7HNfr9448SReDfBuva/PjyNK0+e+fPTbFGzn9Fr8W/+CcOi2nx2/ben8S+JA19Pb/bNeQTfMTMW/d5z/d3Aj6CptqWj9bv2Zfgvp/wD+C/hzwjZW8cNzBbRy6hIigGe6KKJJGI6n5QM+iivUaFqC/u00+xuLqU4jgjaVj7KCTVEn4AftYeH7XT/ANvbxbpcEEcVs/ii2CwogCAP5ZIwOO9f0A2dutnaQQIAqRIqAKMAADFfzpeIfHTfE79sRvFEhMg1PxZDKpY5yonCr+GFFf0Z0COT+Jnwv8M/F7wnd+G/FmlQ6vpF0uHhmHI91PUH3Ffmj+0//wAEi00PR9U8S/CjUp7o26mceHbr5mZRklY37kDGAa/Vmgigdz8eP+Cfv/BQa++E2qWvwy+JVzNLoJnMFtfXTEyac33fLYnqoK/hmvDv2sfF2p/tafto6jY+G7r+14bq+j0TRni5QwDjI/FmNfVX/BVj9jXStH0qT4w+ELKPT284DXreEBUYNgLKqjgHOAa8d/4I7aH4f1L9pfU7vVpUGsWOkSS6VA+DvdmCyEZ7qnNIvzP1q/Z3+D1l8Bfg74a8EWLCRdMt9sswGDLKxLOx9eT+QFej0i0tMzCiiigAorwn9r79qXS/2TfhzF4n1DTpdXuLy4FpaWcbhAz4JJJ9MV8Qw/8ABbO4WPEvwxiMuTnbqe0D81NA7H6qUV+VM3/BbS7/AOWXwxt1/wB/VM/+y1nXX/BbbXNp8j4bacj9g987j8xigfKz9Z6K/Oj9kL/gp54t/aP+PGleB9Q8B2NlY38MrG40+d2a32KW3tu6rxg/hX6L0EhRRRQAVW1K6Sx0+6uJOI4Ymkb6AEmrNcd8Zbw6f8IfG90v3odEvXH4QOaAPxL/AGGLGTx9+314fvhlo11i+1Y4H8OXPP6V+2vxG+LHg74R6TFqfjLxHp/hyxlfZHNqE6xh24yBnr1FfmD/AMESfC1vqnjv4n+J5oA13YWdpaxSH+Hz3lZsf9+RX1z/AMFCP2ONX/ay8J+HJPDurQadr/hxrp7aC6H7q5E6xhkJ/hP7tefc0DPpvw34v0TxjpsF/oerWeq2c6CSOa0mWRWU9+DWvX4Fal8D/wBpT9jea41+007XfDlrBgvfaU/nWrdsNjI525+mK++/+CfH/BRQ/H28j8BePfLtvGpDNY3kS7Yr5FQFlPpJwx9CMUBbS5n/ALR//BV6P4G/GPXvBFn4FbVI9GmFtcXVxdeU7yYBJVcfdwVwe9cof+C1+hCzRv8AhXl99oYfd+0rt/OvsP46/stfCD4lR6z4r8ZeFNOudSjsmM2qPmN9qISCxBAOB3PoK/A/wj4Hj8WXXi6+hjdtJ0jTbnUE25IRQ5WME9s5oKVmfcPjb/gsl8Qde1S2g8HeE9P0dGKKIrzM8krlsYH1BFfq38MtY1nxB8PfDmp+IrWOx1y8sYZ7y3iztjkZQSoz9a/NL/gkB8AfBPjzwT4t8a+JNDt9Z1iz1eOwtDeLvWARwxyblH97Mg59hX6p9OBQJjlpa8h8A/tVfDn4kfFXX/h3omuLP4o0ZnSa1Zdocpw4Q/xbSDn6GvXqCQooooAKKKKAPzi/4LXZPwh8AqOWbW3AHc/uTX0t/wAE+JFl/Y0+FjIwdf7MYZU55E8gI/MGvnP/AILRQs3wj+HEoRiF8R4LAcDMLYBPvj9K93/4JozCb9iD4YEMGxb3inBzjF9cDFA76WPpyiiigQUnWkbODj04pI9wUbuvtQA7Ipa8Q/ab8YfF7wfotncfCPwdpPirUWbF22pXYiMMeCRtXcu7JHrXyj4Z/wCCr2p/DvXh4b+Ofwz1Lwjq0T7J7izUkKOzeU3zEHnlSQe1BVtLn6MydaVcYwa8U+Cn7Y3wn/aFvLiy8G+KoL2+gXe9jdRPbT7cc4SQAsB6gY7djXin/BQD9vG3/Zx0g+F/CNzb3Pj+5hScRyRl0t4GLDeSON3yng/1qbgkfZGoa9peiyQxXuoWtnJMwSNJ5lQux6AAnmr6urKGUhlIyCDwa/nQ1LS/jl+0Na6t48uofE/iez0kNNdanmQw2yg7sIegCg5wOma+/v8Aglf+2vrXjy/k+FHjrUn1DUY4DNol9ckCR40UBoCf4iMFgTz19KYcp+mdFItLTJPDP24rKbUP2SfipFApaT+wrhvl9FGSfyBr8hv2Df2KLf8AbA1DxUb/AMQy6JYeHhaGRbeIO8hmD4HPTiJvyr9lP2somn/Zk+KUaKXd/Dl8qqBkkmFgBX53f8ESvGOm6Z4s+J/hy5uo4tS1a1025s4WPzTLALkSbR32+aM0DuewSf8ABGH4Wm3jSPxNryupyzkp834V2mi/8Ek/gXp+nx295aatqUyHJuJL1kLDjghePX86+1aKAuzxj4U/sf8Awl+DUIHhvwbYxzq/mC6u0E8wOAOGbJA46e5r2GG2jt1CRRrEg6KgAH5CpqKBCLS0mcdaWgAooooAKKKKACiiigAooooAKKKKACiiigD8Y7ZLbxl/wWJmeD/SYIPFRVt/GGt4FV+D6PG1fs3kV+GfiTxFL8B/+Cp+t6vf4VF8ZSzyLnd+5un3oePVJV+mcV+5KsJFVlOVYZBoGO3CvnL/AIKA/GyL4H/syeKNSSYR6pqcf9l2CdS0soIP4BdxzX0Xjg9vevxn/wCCgnxM8R/thftL2fws8B2kmpWXhwzW8Nur/LcXSrummPooXCjPofWgdjgP+CUOljWP2ytBkmO5rWwvLoZ9fL/xav3br8Av+Cfnj60+Av7YXh2bxSX0uAtc6RcmZCDFJIuwBh2wwH51+/UcqTRq8bB0YAqynIYEZBB9KBMcRSbadRQI/Eez8cy/Az/gqtrusa0hjjk8V3cUhXnNvckiIjP+y6/rX7b7hX41f8FgPBx8I/tOeFfFltCtvb6po9vK0sX3muLeebzCffYYcHvg+lfrT8KvFdn45+GfhbxBp9yLy01LTLe5SZT97dGpP45zmgp9zrKWkWue8dfEPw18MtBl1rxVrVnoWlxfeubyTav0Hcn6UEnRUVk+E/Fek+OPDmn69oV9FqWkahEJ7a7hOUlQ9CK1qACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikbOOOtNjDqDvIJz2oAfRRRQAUUUVDTuAUUUhpWYFW6Z4WM2792q8r3NTW8wnhWQdGGaBCSpDEMDT1jCDC8ChRd7lX0HU1lDfWnUVoSIKWiigAooooAKKKKACkY7RS0jDcMUANbmk9utONJt70DG7l5TOCBmqmqfZ73T7m3k2ypJGyMm7G7jpn8amvLUXdu8RYoGGMjqKzL7T00/R51UkmOMsH7kiplsXFRb3P5+rq2f4G/tsQjDRDSfFKSrzjCtKDjP0bFf0N28yXEEcsbbo5FDKw7gjIr+eT9rC+m1D9rjxVdTwNbTPrMJRT6DaM/pX70nXr/w78I7bVLHTZdXvrXS4pUsofvykRjge9JSSWo5LWyO3U0Buufwr8mfGn/BYzx34Z8XXNifhrZ2cNsTE9nqFzIk24Mec7OOMce1Mt/8AgtZ4nnt2LfDLTVkzgbNSkI/9Ap8y3FyM/Wk55x6V8Mf8FLj8RbX4S3Y8IXs9jaRlrm/nt3KyNAozgEdBnNfMesf8Fh/id4iktNP0DwTpen3lxOqptmeeR+RlQpA61+kXirSNQ+Mf7P13DrGnLpt/q2iP9ohPLRu0ecAGolqzSHuX8z4I/wCCQ3x98T+KPFviT4fa/rFzrOktZG9to71zI0TAhWUMecEZ4rtf+CpH7Pvwt0/4a3/jT7Omk+MY9sVqbchRMuSdrL9WPPvXyn+wL4lHwG/ayv8ARNSk+xyXEclgsj9Qd3H516V/wVa8Tah40+MnhL4eWErXl08EDoEbiR5HdQCB9BS5m35By2urnyX+yl8M/CHxZ+LWm6P431waLonDSymXYXH90E9K+v8A9ub9gjwP8O/gnZ+NPhUsl3Zaa4N863Hnl43J+cn24rI+LX/BKPXPh38BY/Fml6tJqXiaxg+1XunqmAq4BYKRySK+Zfhl+1t40+HXhfVvCd7cNq/hzUYJLWexvGY7MqAMc9QRUyUr3iyIW6n6w/8ABKL4lW/jr9lbT9ME3mX3h27k0+4Q/wAIwHT81b+dfZlflj/wRG8RJt+K+jbsFnsb2JM9v36sf0Wv1NFbRtsRLe4tFFFUSNakpxGaTbS0GfI3/BTTwrba9+zL4juJ42P2WNZA69QVJI/Dmvzm/wCCUPi610T9qjTdIvNOtLyHVrSWOOaaHfJDIqFlKHPHPWv1a/bb0mLWv2bvHFnNuEX9myyll6gqMivx5/4J2/ErwR8If2h7LxF40vhp9rDA8UFxIMojOMEmsVu0bPZH7/r0pa5PwD8VPCXxQ09r7wn4hsNetVOGezmDFTgHkdR1HbvXB/tCftZeA/2bdAk1LxVeyGXd5cNnaxl5JZMZ2jsDWtzKzPaKK/Na6/4LZeEo5WWD4ba5KnZmuolz+FYWs/8ABbyzhljGmfCm4nQj5je6uISD7BYmBHTvTuHKz9PX020kuBcPawtcL0laMFh+OM1Zr4t/Y5/4KKS/tYeNL7w8Ph3eaH9li85763uxdQRqeBvOxdpJz619og0xNNC0UUUCErkvih8QtI+FvgnVPEmtXCQWFlGXYu2MnHA+tdXLIsMbOxCqoySe1fjp/wAFP/2mtQ+I3xGX4WeFruWTTLWRI7qOF9wubhmICgD0G386VzSMb6nFfGb9u/4y/tLfEVfD/wAOLnUNNsXcw2tjo4Imm+Y/OzDnBBH5V9D/AAt/4JDv4x0Ky1v4t+ONYuNeukEsunwsHEBYZ2l2JOck5xxX0F+wf+w1on7MvhVNc1Fv7V8aanEsk1zIgAtEZVPkoOxB3ZbvmvrjbU2YOR+ey/8ABGP4XjUIpH8Va/JZq2Xtf3Y3D03dRX3j4N8LWXgjwvpegad5n2HTbdLaHzW3NtUYGT3NbO0UVfQlu4tFFFBIUUUUANavzp/4LURzt8GfAkka/uY9bdpGx9391gH9TX6L4r5z/b3+B9x8dP2d9e0qwCtqNihvoEKbi7IM4HoeKBrc8Q/4I2/Eo+KP2edb8JylTP4Y1ZlQL/zwnXzFP/fYmr78r8Qf+CWPx6b4F/Hi68H6tbCCw8ZPFp07zEIbe5hMhjJz0H71gf8AeHoMft3u96AY+im5NJuoEOJpNx59e1cF8ZvixpnwZ8C6t4o1aZVtLC3eZlZgMlRkKO5LHAr4O/YQ+OPxc/a0/ac1vxvq2r3mmfD3SLaUR6LbkizLycRxdPnYffJOT0GcYFTfWxfK7XP0vBz70tItLVEBRRRQAUUUyRiuWwSAOg70AOxznvQzBVJJwBySa/PP9tj/AIKa6x8BviBc+BvB3hkSatZ/8fGoauhWFuM/ux/EPevhH4n/APBSL46fFTTW0+48UpotlIMSR6ND9nZ19CeT+IoA/X/46fts/Cv4AyLB4h15J74nAs7IiWTv1x06V+U/7XP7VXif9urx5pPhbwd4dmTR4JtlnaxR7prhmJAkcgcDBHHbmvkK8vLvVLo3N3eSXczknzbmYs2T6k19Sfs5ftuH9mvQ4IPD3w68O3Wqrnz9Yumc3EjEAfe7DAH61Nirn7Hfsl/Bo/AX4A+EvB0yr/aFnah711H3p3+Z/wAs4/CvX6/HDVv+CyvxQmA+xeF/D9oO7N5jj36/hX6AfsJ/tGeJv2nfg3c+L/E+ixaLcrqclnbiAMEniWONvMGe25nH/AaYPuflD/wUB+OVp8ZP2uNQ+1yTXHhPw9dR6VHBCdxaKJyZmVemWZn/ACFfo/8AB/8A4KVfs/X0mgeDNKvL3w7AsUVnaC+sxDAmAAFyCQB71+ZX7EvgTwl8av2tLbSPiOwu9PvJLudo7iUoLm45IVj3ySfrX1D/AMFH/wBgfwF8H/hTJ8RfAVrJov2O8hjudNWQvCwkO3cufu4OOKYWP1dtbqG9t457eVJ4JFDJJGwZWB6EEdRUtfEX/BIv4geIfHn7MeoJ4h1GbUn0fX5tNs5Z3LstutvbuqZPYNI+K+3aCQpkkKTLtkRZF9GGRT6KAI4beK3BEUSRj/YUCpKKKACiiigAooooA5L4t6IviX4W+MNJcZW+0e7tyPXdC4/rX42f8EktQj0X9r46fNIEefS7u3XJxuZcHH5Cv26urdLq3lglXdHIhRh6gjBFfgJ8fPAPjb9i39qi91bSvM0hor6TUNHvNpWG4hZ2wuR2OCCtBcex/QAtfPH7efxztPgP+zh4m1Nptmr6nbvpemRg8tNKpBP4Lk/hXyT4I/4LUaQug2ieK/At8NWVNtxJp0qmJmHcBsECvlL44fGT4mf8FD/jHaaXoGlX1xpUUmNL0mIEx2qM2POlI4zyfmPpQLlPlPT7240/UrW9gZxcW8onDA4IZDuyD9a/pb+BHj2L4ofBvwd4qhJK6ppkFwSTn5igDfqDX5a/t0fsJ2vwJ/Zx8Aat4bsJLu+0hjF4iuoE3GQui7pCeu3cCPSvVf8Agjb8etV8SeH/ABJ8L9Q869stDAv9PvHyRFC5CmD2AIJH1NBJ+mNFFFAH56/8Flvii/hz4J+HPBNs5E/iW+aeZVOD5NsFY59izr+Vfm7aeAfiX+y3N8NPi3FEbGHVnW+0q6hbiTGGMbf7ynp6V61/wVR+N3/C0/2mb7Q4ZGj0nwlG2kKAfvzKxaVvxZtv/ARX6lat8BfC37Qn7JvhXwzqWno0P9gWsunPja1vN9nXYw9OcZoKudx+zZ8eNG/aP+EejeNtGxELpTHd2m7LWtwvDxt7jgj2YV6hX4Y/sLfHXWP2R/2ln8GeI5J4NDvr59J1a0YkrFcbiscwHQc7R7gV+5qsGUMOQRkUEi0UUUAeYfHv9nPwR+0l4cs9E8cadJqFlZzfaIBFO8TI5GCcqR2rw/Tf+CVP7O1hMskvhO8vWU5xPqtxtP1AcCvr+igdzwXSf2FfgHo9qkEXwr8OTqvRryzWd/pufJrTT9jX4Fxq6r8JfCA3DBb+x4M/gduRXs9FAXZ4b8F/2Nfhl8AfiFrfjDwXo76Vf6pai0e3WUmCFN5c+Wv8OTt/BR717lRRQIKKKKACvLP2qDj9mv4of9i3f/8Aoh68T/4KXftLeJf2cPg/pNz4PvI9P1/WNQ+yR3TRrIYkVSzMA3HoOlfKXwd/4KNSfFj9n34meA/ixrUVr4nn0a8Gma0sIjS7UxbViKqMb927njINBVj0H/giVpMMPw7+Jmpgfv7jVLO2Y/7McBZf1lav0rr87f8AgitFGPgT45lVCsjeJCpPqBaQY/mfzrwH9uj/AIKAfGXTfix4k8DaJJL4I0fTbhrNTbxEXNxtdv3okPQEEDA9KAsfpb+0x+0h4H/Z7+Heoav4rure6MkbQ2+k7g0l5IVOI9voeck1+VH/AATf8EXvxf8A2z4/HGl6PFpfh/SZrrU7iC3BENt5iusUKn1BIOPSvj7xFdeLvHGpNqmsNq+t3sgwbq7EkznknGTnHUnHvX0n+zR+2R8XPhbZ+Gfhl8PdE0qyku79Q6yWJae8kZgCZDwfu4HsBSKsfqV/wUk8XSeD/wBjfx/LDJ5c19DDp6HOCfNlVWA99u6vzE+EXwtn8Mf8E8/jD8R5w0NzrF/Z6RbKQRugSWPcw+pkYf8AATX2P/wV+1vWY/2ZfBGn3duy3t5rEU979mBaJJI4HyM+m5zj6VgftHaDL4N/4JF+DtOW3+zyPZ6TJNGFwQZCJGJHrk80xLY9A/4I5eHZNJ/Za1W/mQo2reJLq5RsdUEMEfH4xtX3dXyr/wAEw/EGi61+x14Mt9IkVn083FrdoCNyzec7Nn3IZT+NfVtBLPxJ8I3r/AT/AIKw3KzPtgn8WXFvI7cfur3cQfp+9Br9ta/GH/grh8Obz4cftPaH8QbFPIt/EFtDdLcIcMLu1wjAf8AEJ/Gv1u+D3ji1+JPwt8LeJ7OXzoNU06G5DZydxQbgfcHI/CgR2NFFFABRRSUAfA//AAWQh8z9n7we+M7PFNuT+MMor0v/AIJbyCT9h/4eqCCUbUFIz0/0+4P9a88/4LENt/Zx8Pcc/wDCSW3/AKLlruP+CVq+X+xX4Nyc5uL8/wDk3LQVbS59cUnmL/eH51XuJTuAVhjHrUKfKDk55oGo31L3mL/eH50nmIWwGGfTNU1Xc+dwHHrUsMOxiTyc9aBuKXU+S/2+P22NW/ZKXwtBovhmDXrrWDI0kl8zxQRqvQCQDG7OflznFWvhPrfws/4KSfANdS8T+GrKW+DfY9St4yPtNjcKAfklxuCkNkZ45PpXY/twfs7WX7RnwG1vRmiX+27CNr7TLjblklQZKj2YAj8q/O7/AII6+Przwv8AH/xL4MuDKsGs6a0pgJIWOeB+SR6lSw/CgW6NP9sL/gmTL8A/Dd18Q/hn4puE0XSoDJe2+qXghuLf5jhoZF27hyoC9c565r4q+Gvj3RF+Lmka/wDFOz1Dxho0U4a+glnJllII6k8kDA+XPNfe3/BWj47XPxC8feGPgd4Qmnu7qO5jOoxWchYT3UzBIbdlXqV4OD3avqj9nz/gnn8N/BPwF0nwl438K6X4j12QPcajfSJlzM/UI4wQFAUDtxSsK9ix8G/29v2dPGmk2+haR4g07wvb+WLePS9WhFmpGANgDDDccd881+bnjK+8P/ssf8FGItX8J3trc+FYtXhuo5LeUPFHBcqvmpuHGFZ3H4V9W/Gf/gjP4Z126lvfhz4ouPDg2grpuoKZo/MyTkSDkDBAxg9OtfDPxe/YT+Mfwj+IGm6Zf+GbrWlvJ4xb6ho8Tzwznd03f38DJB6ZFAXP6B7WdLq3jmiYPHIodWXoQRkGpazfDdvJZ+HdMglUrLFbRoyt1BCgGtKmSVdV0y21rTLvT72JZ7O6iaCaJhw6MCGB/A1+FPxj8E+IP+CeP7YlrqehGZdKhlGo6dIwIF1ZyEh4vfbhgR7V+8FfNX7b37Hdj+1t4HsbaO+/srxJo7SS6ddkfKxYDKP/ALOQKAPavhf8S9B+LXgnSvE3h7UbbUbC+t0mDW8gfYWUEq3oQeMGurr8FvDOu/tCf8E+fHGoWcGm3lpaNuMqzQvLp90oYgSqQCBnbjseK+ofBv8AwWysLXw/bJ4q+Hl5d6xj95Npl4kcLe+1gSDnP6UAfqRRX5uWv/BbLwRMpMvw61uHnH/H9E3/ALLTLj/gth4O83Za/DfWpywwv+nRg7vTAXmgD9HdS1C10qymu726hsrSJS0lxcSBI0HqWPAH1r8xv2o/21viJ8a/jdafCX9nbUZp7GRFtbzWNPh3F5izCR1kH3YlXHzccg4NefazaftI/wDBSbXgsMVz4N+G63DKFuyYIYwMNyBhpWww7beOtfoT+yf+x/4Q/ZR8JSWGjL/aOt3hD3+sToPMlbaBtX+4nGQo7k+tAHT/ALNfwXl+A/wtsfDd3rl94i1R3N3f6jfztK8tw6qH27jwvygAf416nRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH5H/8FfP2c7zQPiFpPxj0KJ/s2pJHa6m0KEmC5hAEcxx2KBB/wCu1/ZT/AOCtnhjT/Advofxe+2WmrafGsMGq2Nq1wl3GqhQWC5IfIPPTpX6VeIPDumeLNHudK1mwt9T065QxzWtzGHR1IwQQa+MvFH/BIz4KeINcur+1Or6PFM2/7Ja3A8tCeTtyMgUDueGftaf8FU7bxl4ftfDHwQe+a+1FjFc6lNaPFKgPG2NCMknPWvRf+CWf7J/iH4aw6/8AErx5pstn4k1keTZLdnM3kt87TEHlWYttwey17n8A/wDgnr8JP2f9Yl1jS9Lk1rVycxXerESmAcfcGMD6+9fTNAXPzE/4KDf8E2Nf+IHjS7+I/wAK7dbvUL9hLqeiq4jYyjJM0R7k/KNvtmuB/Z/s/wBunwhrmjaDbaRq8Gih44t3iFE8iOFTzuYkkccV+vNJtAYnuetAiO2837PF5+3zto37em7HOPxqWiigD4h/4Ktfs+6j8YPgjp2v+H9PfUNf8M3Zn8mFNzy2zqRKvvjCnH1r4q/YR/4KIT/sz6XdeD/HVtqWs+Ew+bRbcbp9OYHDIFbGRwPlyMV+2LqsisrAMrDBUjIIr5i+In/BN/4F/EzxJPrmpeF3tb64OZf7PuXgR2ySWKqcZ56+woHc8K+J3/BZTwHp+iIPAHhnWdb1qVtqRatbi2jGe/yuzGvJfhT8A/jb+3p8UrTxX8aF1HSfhvby/ak0+4JhSVScrDFH124xliBwa+8PhV+wn8FPg7dC70LwVZy3yvvW71HNzKhwPus+cDjt6mvfEjWNFVFCKowAowBQIy/CfhXSvA/hvTtA0Oyj07SNPhW3trWEYSNB0ArWpkalQQcAZ4xT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBD1qrcapaWsgjmuYYXPRZHAJ/OrLLur4s/bU/YI8T/tM+MLPxP4d+If8Awjl3aWK2aafNHKsT4kd9xdH4Pz4+72qHfoXFRd7s+zGv7aOJpXuIljUZLFxgfjXmHjr9qT4TfD1pIfEHjvRLKZYjKYGu0ZyuSOFB9Qa/Ntf+CWv7S0NnNYJ8TdMFi5yYv7bvNj8YyV8r0FQ+Gf8Agi78RdWvi3inx5oVjBnmWzWa6lP4Oq/zpu7QlZHh/wAZ/FehftQftpaRc+BLO4ubLUdTt4FXysM+yUlnA/u7T19jX70afbrZ2FvAq7VjjVAPQAYr5X/ZR/4J1+Bf2X9XbXkvpvFXiUJsi1G8gEQgB+9sQMcZ9c19YbaSj3CUjzLxr+zJ8LPiPrR1bxL4G0fVtS2eX9pmgwxXJODgjPJP51y91+wr8BLyQPL8MNEZgMDCSLx+DV7tS1XKhXZ4r4a/Yz+Cng3WYNV0f4daPZX8BzFMsbMUPqNzHmvW9Us5LjSbm2tysbvEUXI4GRir1G2iwXZ/Pb+254a1z4W/tMapeSMbC/uHF9btCcbRuKAg/VD+dekfsCrqf7Rn7ZWh6z4slfVZtMtvtLPN8wXyx8g59/51+nH7Vn7C/gf9qWxFxqTS6P4jhj8u31W2UMwALMFYHqNzH865v9h/9guw/ZN/tPVrzWf7d8SainlSSLEFjhjByFQ9TnvmoUWlY0ck22fWVxBHcQvDKiyROpVkYZBB6g1+Tv8AwUk/YCnsbub4i/DvRli0yKAtqen2oACtvZjKo9wQPwr9ZmGar32n2+p2c9pdxLcW0ylJIpBlWU9QRTsyEz8Of+CUnxOHw5/agt9LuGaOz8TWr6cVP/PRTvTPvkH86/c5a+T/AAz/AME4Phx4N/aAtfino17qFjc207XMWixrH9kWRhjcPl3D86+sKEne45NMWiikqyBGz2pPmxWH4q8Uf8I3ptxemFpktk82VVGTs56e/Ffm/wCH/wDgsbcp8WpND8QeErKDwt/aDWovbXzFuIo921Xbc5UnueBWejdjX2cuXmPsT9sXUbhPgh4rsIoleW802aJeD3HPevxS/ZU/ZC8TftZeKvEGiaBqen6TJo8Annl1DeVO5iqqNoJzlTX7WftR67YzfArVPFdtOl3p66dJJG6fMjq6cGvgT/gkX8X/AAT4B1P4lx+I7630a7uTFdLqN7MEjMILDy/rkk/jWcdGyn8KPBvG/wCzL+0P+wrqyeKrE3Vhbx5/4nvhy4aWELn7soxwODwR3619sfsp/EDwr/wUc+Fet+Evif4eW48SaSFeXVIRtLllC+dH12txjBz0ryL9vz/gpFF8QIb/AOHHwzeK50eVvKvNY2nM3YrHk42+5Fe9f8Ep/wBm3W/hL8Or/wAV61cW6v4mVJYbWJw5WLAwWx0Oc960Yr6H5eftdfBGx/Z7+OGt+D9MvJb/AEy2Ie2muHDSlDn7xAAJyD0Aq1+xh8PND+K/7Rfg3wr4ksv7Q0PULl1uLfzHTICE5BUjByBWz+3/AK7P4i/ax8dPMqKILz7OgjyFCqB7n3rrP+CXXh6DXP2xPDC3DSBbOC4uk8sgfOqcZ46c0CP0e+MHgXSv+CfPwb1nxl8FPCdskr3kLara3k0kweEZBIJbIwPfHtXtn7LP7Tfhr9qT4djxJ4fZop7eQWt/ZyDDQT7Fcr7jDDBrd/aE+HcHxT+Dfivw3cKzreWMiqqHB3AEjFfjt/wTz+NWo/s4ftQDwfqVx9m0TWLptNvop87VlBIRxzgHOAT6VSYnqj90aa0gXqefShWDqGHIPIpdoLAkc1RmeG/tc/HG3+C3wQ8T6zIwgvGtZLe0395GXAOPxr8UP2SPjF4N+HPx4g8cfEm0uNegt1kuI8jzGNwfuuQepHavtz/gtb4ovLbTfh/oUUjx2d21xcXGAdrFNoQfq36Vi/sA/wDBPj4U/HT4JaV468WnUNS1O4nmje1trvy4UKyEAFcdcY71NjW9krHrtp/wWW+E/mIs+h65HGTjcsQOPwr6E+AP7cHwr/aO1J9L8L6y8esLkjT76PypXAAJKg9ev6V5z4p/4JU/ATxJbsItF1HTJRHtRrO+ZF3Y4YjBzX5g/s5eHZ/hj+3r4V8O2dy0Y07xM1iZQ3Lxhiu0nvkCmQ9Xof0B0Ui0tMkKKKKACiiigApDyCCMilooA/E//gqL+zhN8E/jZB4+0H/RtC8RSfaQ0Klfsd2pOQMdBwG/Gvaf2Zf+Cu2heH/AOm6F8WbDVLjWbP8Acf23psKSpcRAAK7rlcNnIIAxgDvmv0e+I3ww8L/Frw5PoXizR7fWtLmBDQzg5GRglWGCp9wRXyl40/4JE/ADxRDEml2Wu+EigwW0rVHlLck8/aRL69sUFXVjUh/4Kufs7TQiT/hJdRT1R9KmDD9K5zxV/wAFgPgZocLtpcPiTxFKE3L9k08RJu5+UtI64/I9axov+CLvwbU/vPGHj6QDov2+zAx/4C11vhf/AIJIfs++H1K6hpmveKstu3arrEiEcDj/AEfyhjv0zyeaA0Pg3xz8Svi9/wAFN/irBoHhnTW03w3CxdbTePs9om7madx958YG0kjgYHJNfrZ+zJ8BdN/Zu+D+i+C7CVbqW1TfdXioFNxM3LOf5DPYCuo+Gfwh8GfBzQE0XwV4a0/w5py8mKyiCtIcY3O5yztgDliTxXXYqUtbg3cBS0lLVEhRRRQAUUUUAeXfFz9mf4afHW+srnxv4TsddurMYimnUhguT8u5SCR1qDwT+yj8H/h2ki6B8OtBshIxdt9oJjkgD/lpuxwBXrFFAHKL8JvA69PBvh8fTS4P/iKc/wAK/BckZQ+EdD2HqBpsI/8AZa6migDzPxN+zV8LPF1uLfVvAWg3kGP9W1kgH6AV1/g7wZonw/8ADlloHhzTLfR9Gs12W9laptjjXOcAVuUUDPxt/aq/4Jq/EL4XePtR8a/CuCTWNEa6N5a29hIUvLF2YttVR1APQivNviR8bv2oviF8M5vhh4t0bxBrFjcPHuF3oL/aHKNkAy7ckdOTX7t0xreJ2DNGjN/eKgmgfMfKv/BNb4A69+z3+zqmmeJEEGrazqD6xLa87oN8USBG9wIxn619XUUUEhRRRQAUUUUAFFFFABRRRQA1q5D4jfCXwb8XNJGm+MfDen+IbRc7FvYQ7R57o3VT9CK7CigD5O1P/gl7+zzqUm9fCFxZHuLa/lAPP+0TXtnwf+APgL4EaQ2n+C/DtppCPxJcLGDPJwBhpMbiOBxnFei0UDuUtX0Ww8RaXc6bqdnDf2FyhjmtrhA8cinqCD1rlvhh8FfA3wZ0+4s/Bfhmw8Pw3EhkmNrFh5GPqxySPbOBXb0UCCmk/MBnAx0p1JQB88/Ez9gv4NfFvx83jHX/AAwG1x5VlnktZTGk7g53SKOCT3PfFe/2FjBpdjb2drEsFtbxrFFGgwFUDAA9sVYooA+CviN/wThufGH7aWnfFeHU7X/hFpNQi1XUdPlHzmaIAhVHTBIH6196KAoAHSlooAKKKKACiiigAooooAKKKKACkpaKAPyK/wCC1/jtNQ+IHw78KxfONN0+41F8dN00vl4P/gP+tfJ/xC/Y28ceAfgb4S+KpgF/4Z1y1juHMHMlrvXcN47AjvR+17He3n7YHxCg1r/Wv4mljkx08kzEDH4V+/Wm+EdH1n4Y2nhq5t1u9DuNMSzeB+jwmMLj8qCuY+H/APgixCF/Z28YyGPa7eKZdp7Ffslr0/HNfc3iT4c+E/GdzFceIPC+ja7cQgLHLqWnxXDoASQFLqSBknp61n/CD4P+GPgb4JtvCvhKx+waRbu8ixlixLMxLEnuea7WgVzFtfCGhWMKw22iadbxLwscVpGqj6ACs6H4W+DrfxBDrsPhXR4dZhyY7+OxiWZc8HDhc11dFAjL17w5pXiiwNjrOm2mq2ZYObe8hWVNwOQcMCMivIf2xvgjN8dv2cPFHgzTF2X7wpPYxR4RTLEQyJ9DjGK9yooGfzs+CNa+P37P91qOj+Fh4s8OlblmubbT7KQxNKAFLfcIPCqM+1eiab+0d+1/JEb631bxzPHE20lrB8Z64xs561+8VFAj+eb42eP/AI/ftFwaBB490DxJrCaK8xtn/saZWHm+WHBwncRrX6//APBNzSdZ0P8AY28BWOv2lzY6lELzdb3kTRyohu5jGGVgCPkK9a+mqKACiimSSeXG7Bd7KM7R1PtQA+mH74r4J1f/AIK3eGPBPi/UNB8afDnxJ4dltJ3iEjlWZ1ViA2xgpwcVzfi7/gtV4DsVKeG/BOsavMR8rXk6W6Z9wAxoA7f/AIK+WbXX7M2mOgLGDX7aQ4GcLskBY+wyOa1P+CW/jDQNP/Y38K2t1rmm29zDc3qywy3cavGTcyMAyk5BKkHnsQe9fnT8e/2pvi9+3x4k03wzpmgzDTVkXydB0aGSVNxY/vJnAJ6EDPA4rstJ/wCCSvx7ktY2WTw/YLKA7QyalKvlk9sIpBoKvpY/Ya8+K3gTS8i78Y+Hrbv+/wBUgT+b1h3f7SXwf099l18UvBNs+M7ZvEVmp/WSvyq/4dA/HVlC/wBteE2DcnzNTuxj24jNV5v+COnxyjYBNW8HOCMnbqV0B+sNBOp+rFn+038G9SvorSz+Kvgi7upWVI4bfxFZyMzE4CgCTJJPavTlxtBXkHnIr8afh5/wSd+Lnhz4veDJPEtvot34ajv47i+vtK1B3eJEO7BDqp6qMYGOetfsrDGIYUjXJVFCjPXjigAkVWUq4BVhgg96/n4m+LWqfsk/ti+Ntf8ADtrG91pupahZfZ5h8qq7sMEeoNf0FHAGTwBX8/8A/wAFJPCsPhf9tTx/aWaeZ9ruLe+EarndJcQJKwx/vPQNOx7/AP8ABL34V3H7QPx+8WfGLxxHNqs2jzJJBPNGWil1CRi2VboTEoQ4zxvU1+wNfOP7AnwFj+AH7OPh/SpY9usaov8AauoswwfOlVfl55+VQq/hX0cM4560CFpjRqzAlQSOmRnFPooASloooAKRvbrS0UAZ2s+H9N8R6fNY6rYW9/ZzDa8NxGHVh7g145ffsO/AjUbmSef4ZaE0shyxEGP617pRQB883H/BP/4B3Egf/hXOlxYGNsSlR+Wa3vCn7GvwX8F3C3Gl/D3RY7hW3rNJbh2U+xNe0UUAQWtjb2ESxW0EcEajCpEoUAfQVNS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTWUt3pVGKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooATijigjNJtoELS0g4paBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGJ4ltGktAUCvlgrRuMq454PtzX86n7WmiR+E/wBonx3ptughgXUZG8teANx3Y+mTX9GWvxzSWeIEZ3Vg2F68V+EPx6/Zz+J3xk/as8aW2j+Ctal+1axLGl09m6wLGGwHZyMdOetY/budN700jK+FP7Z2s+Hfgrrvw08QXN1e6PdQslpLvLmHKgBcE9OO3rXC/Bj9lf4n/H6O5m8DeF7rVbBZfKkvZJFhtwwwcEkjPBFdZ+0V+wl8S/2a7Sxv9X059W0qeATTajpsbPFatuI2SHscDP41+gX/AARi1yW++CvizTzbEQ2esEJdZJ37okJHPTGadtbom/u2PjiH/gk3+0RJw3h/SQqcDOrwqfWvav2b/wBhf9q74aeM9Nul1y18P6RYylzBdauZ4X4xjy0J4+mOlfrd1o2iqszO5+BP7Rn7Hfxzh+Luu3uueFpr6e+llvTqNh+8tmjyfmBySOnQ81o/8ExfEmkeBf2stMn8QahBpiG1uLcS3DhEEhGMEn6V+72oWKahY3NrISEnjaJvowIP86/Fv4/f8EsPiv4f+IF4/gnTF8VaLdSPcxXUU6xvFuc/I4OOQMHI45osw5j9m7XXNM1C3E1vf2txCw4dJVZSPrmvwl/4KIeAz8Hf2sb+/wBNaMx6g0etWxhYfLhyOx45U1Zt/wBgf9qXT4vKttD1q3ixjy4dWwPyD1k6x/wT/wD2ktX1W2/tPwbqt/PIBGt1cXQmEa56Ekk4o5Quj9t/2f8A4i2nxY+DfhLxVZv5kWoWEUhOc/PtAYfmDXoVeV/sv/CVvgf8CfCXg2Uk3On2gE+WziRjucZ9Mk16pVEnxt/wU1/Zv1v48/Bu2uPDVtHdavoMzXghI/eSR7fmVT+HSvgL/gn5+2pL+yz4ou/CPjATReD765ZrhWQl7GfhScenAzX7iMocEEZB4I9a+Jv2xP8Agmn4a+P0kmveEntfC/ijGZNsWIbk5J+bHQnPWmNM+mNN+O3gbxF4IuvE+j+J9NvtMitmuPNjuF4wuQCM8H2r8Zv2P/DEnxq/b+tNUjdzb22r3GrySBv4VZivPucVBqX/AATp/aP8MTXelaf4buriykbYz2N7iCUZ4bGeK/QH/gnL+xBqf7NOm6x4k8ZQ2/8AwmGpYiiSCTeILfap2n/a3bs0BdI+4F6U6kXvS0EhRRRQAUUUUAFFFFABRRRQAUlI1GTQA6im5NGTQA6ikWloAKKKKVwCims2KTdRcdh9FNzS0r62ELRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQB8+fGL9hH4PfHLxxF4u8T+H5W11SplubO5aHz9vTeBwTwOevFe96fYw6XY29nbLst7eNYo1JJwoGAMmrFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNb0p1FAHD+NPgl4B+JFz9p8U+D9H1652hPO1CzSV8DtkiszQP2afhR4Wk36T8PPDmnvnO6DTolOfXpXpdFAGfp2gaZo+PsOn2tnxj9xCqfyFX6WigAooooAKKKKAE61w3ib4F/Dzxp4gOu6/4K0LWdaOwG/vrCOWY7AAvzMCeMDFd1RQAyGFLeJIokWONAFVFGAAOgAp9FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIGzkelAC0UUUAFFFFACU0RqrEhVBPU4p2KNtKwGdr+g6f4n0i70rVrSLUNOu4zFPbTqGR1PUEVy3wo+Cvgv4H6Pe6X4I0K30DT7y4N1Nb25O1pCAN3JPYCu620baYAtLSUtABRRRQAUUUUAFFFFABRRRQAUlLRQAijaMZz9aWiigAooooAKKKKACiiigAoprGmTSFIyQQD70rjsPasrVrq9tYZBa7DOUcxeYhZSwGQCBzzVibVI7aN5ZjiNF3Flya8xuv2pvhbY+MLbw7deL7CDWrlxBHaNKCS2eAcdDS5kUovsflb8Tv+ClP7SHh34lXsk9zZ6Dp2n3kkA0v+xQtvMquQAzyKZM47hhX2J+xP8A8FLNM/aE1ODwj4ytLXQfGUrFbf7KW+z3QAzxno3XjNfUvxuXwKnw91i88dWem3ehR2zPIL5EO/AJAUnnP05r8df2H/Aum/Fr9uKzv/Cunf2T4Y0i8l1RIkZjsjXKquSScE+9HMPc/c9aWkWlqjMKSlorN7gQnLd8Uo+Udc05lHpTSo2nis2mV5FaTUBHdJDsZi3O4DgVdpqRqOgp1VHTcTFooorYQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGpKAHZozUbSKvGaa0yqcE4NA7MmyKMiofMywA5qSgLDqWkWloEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJu+bFLSbfmBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARc4GetLRRQAUUUUAFFFFABRRRQAUUhNG6gBaKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopCaTdQA6im7qN1ADqKrtclZthAAxnNTBwwyORSumOw6im7qNxphYbIpZ1+bAp9N7g04Gp5lewhaKKKoAooooAKKa27tj8aVc9/wBKAFooooAKKKKACik5paACio235OCv5U7caAHUVBcXUdrG0ksixxqMlmOAPfNZ+j+KtJ8QSyx6dqdpfSRffS3mVyv1ANK47O1zXopBmlpiCiiigAooooAKKKKACimsaQMTQA+io2UNyaRWCqcA0rjHSNtqlNIJAAx43Y6UXFy7ZVRj3NVft0FrG0l1JHbQqctLMdq/99E4FQ9zbkaVzkvjpqk/h74W+JNSglMMdrp08jFexCHB/Ovw5/Yz8DXPx4/a08PW9/vukXUH1K7nJILKpzgkYxzjpX67/tlfHDwZofwB8ZWI8V6O2oXlhJBHbx3aSOxIxjCk81+cv/BKn4pfDj4R+PvFmveO/FFj4euHtFgsftiNhlLZYhgD7DFOwuZ2PX/+Cm3w5+PnxK+IkGj+GPC+vav4Bt7WP7PFodmbiN2HUyMvzbvY8V8mfCf4W/tQ/ALxBJrvgXwT4w8PanNH5Ek/9g79y5ztKyowx74r9oPA/wC2B8GviR4mt/D3hv4gaTq+s3BKxWcLsHcjrjIFex7RRZkcx5F+yn4s8e+NPgnoWp/EnR5tG8VupW5huIxG74OA5QAbc+mBXr1JS1RIUUUjZwccmoe4hGpjMN3JqFrhuQ67T2pjEsuTzWbkaRjfUthwFznNOByM1mbmVsA4XvV+3bctNSvoKUXElopCaj85d2M81pzW0JJaKQUtWIKKKKACiiigAooooAKKKKACiiigAopGpM0AOopFpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQmmRuW3ZGMGlbO8elIuBnnk0rjFdgtRMwdThsU25kVcDcKrrIA23PWolNI0jHS7HAfvMA7jUzxArubgimmN1TMYy1MW1lkYGV+PSkpN9A0BZhHIBjIIq3GxfJxikjgVccZqWtFtqQ2ItLRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKTIFLSYBqG3cAzS0mMUtUgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJ+FAC0UUUAFFFFABRRSUAMaRVcKQSTTtwb7pyPavlv9vvxV8TfCvwnOo/DW4kgvUfbOsMReUr6rgV+c/7Of/BR/wCJX7P/AImnsvHwvvE+kXk++5h1Albi3PTMZPb2rPmd7G/snyKR+3i06vGPgV+118M/2hLYDwrr8MmorGHl0+Y7Jo8jkYPXHtXsysG5HSqujCzQtFJmjPtVALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4DWqB0VmDsvK+9TtUUi+ZwGxRdFIGkPy7Bu5wfalkZlU4GabH+7BGO+KZNcCNsE5GMk1MpLYpK7siRWVmxgE4phmK4CruFQx3iTbmi5PQ0xWkt4ZHbjniue7K5WWWmbcMJkVJG24Hr+NV7ZpGj8xn4PQCrUbCTkc0o3uQ9NB2KXpRRXQrIgKWkpau6AKKKKLoAooopgFFFFABSUjNggUkjBRzQBm6xrkGixma5cLCEZi3QDAycmvyr/aD/wCCv3jXRfHmoaR8OdH0WPSLOVrc3erW8kzyOpwSpWVRj8K+jf8AgpJ+0TJ8K/hNf6XZFRfasPssMkRO5M9T19K+Tf8AgmD+xboPxubVPiJ49szqmjWc/kWWmzf6u4l6s7+oHp61kpcz0OicFGKvuY/h3/gsJ8adK1S1n17RvDupaYxDSRxWMsEjL3CMZSP0NfpX+yv+2B4N/ao8NyXehu2n6xabVvdJuiBLExGcr/eX3FTfGv8AY/8Aht8YPh3L4cl8MabYSQQGOwubSBYntmxxggdM1+Py6F4g/YF/ag0C5k1Uzw29yGufIY/Pb79rKw78UnJp2MktD9zfH3g5fG3hm+0uWd4vtEbR742K9a/Fv4paP8VP+CfPx1k8UaHczf2ZcTt5bzu0sEyk8pIMjJx0r9ltU+JFufhXL4z0eE6patp/2+3jiP8ArFKbgM1+dfw9/aEsP+CgPiTXvhh4w8OQ6VdTxSGym3btjLkbvZhTWptFvlaPtH9l39rbwn+0d8PbHWbfULXT9Z2AXumyyqrxOByQCeldT4j/AGnPhV4R1NNO1fx9odjescCGS8XdnOK/CP8AaM+AXjL9kD4jNo1zfzwJOhktb+1kZBNHnpkd69J/Z9/4J9+N/wBp34Z3njXSfEumw/vHAs7xmknlYDPLds+9aXtoZ8q6n7o6L4i03xJp8d9pOoW2o2kgBSa3lDqQenIrSVt1fiB+xP8AtJeKP2RfjrN4C8ZtdR6HeXa2N5ZTksLeUHasi56D+lft1b3CXVvHNEweKRQ6sO4IyDTM2rE1FItLQIKKKKAGSNtUnBOPSo4ZDJk7So9GqSTO044NRx7iuCee5oK6Dt7buOneobicx4xxUoUAnB+tQXFsJmC7yD2qbFxtfUpSSC4BVz9McV8l/wDBQH4E/Ef41fC2Cy+H95cvd282ZdNinEInT1JOP519hwWcUPQbm7k1PtA6DFLlZpKotkfzxfED9hv43/Dnwzf+IPEvgq40/R7NPNuLqS9hdV7Z4c12P7H3/BPrxN+1hoeo65b63Z+HNCtZ/s/2m4iaaSRwMnaoIGPrX6G/8FaNc1fRf2abiC1uJBY6jfQ29xGqKV2ZycnGRz3rwT/gl9+178Lfgz8L9S8HeM/EY0DVJtSe5ie5icwMhH95QcfjVGR71+yX/wAEvfD/AOzr4+j8Za14kbxZrFpn7Ci232eKBiOXI3Esfrx7V9yV8nfFb/gpj8EPhtoq3tj4jXxdO52ra6KN7A/7ROMV9FfDPx1bfEzwHofimzt5rS11a1S6jhuBh0VhkA0yWnudPRRRQSFJS0x85wOBjrUSXUCGaMSfMeoqqobcfn+X0qWSUN8vf1qqrBiyjj1rme51QTsK17BCJHeRFjjGXZjgKPUmuF039pX4V6l4ui8L2XjnRrjXZn8pLGG5DSM/oPeuA/bZ1C78K/s3+OdRsbl7KcaeVEsZwwycV+If7L+oXcX7Rfw+njlYzNrMDF+5y3PNVDW7Imtj+klulQxxISSRzRdTGOLI65qJWM2B90HjPfNaPchLQuKQRxTqpxXEKziE3EYlPSPeNx/CrS9xnJFarYgdRRRTEFFFFABRRRQAUUUUAFFFFADWrL8SeJdP8J6Rc6nqc4t7O3QvJIecD6VrVm614dsPEEPk39utxF3jflT9R3qZXtoONr+8Yvw5+J2gfFLR5dS8PXTXVrG/lszRshB/EV1lUdJ0Ww0G1Ftp1nDZQD/lnCgRfyFXqI3S97ccrX93YKKKKokKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKSpcgFoqDzG8wc4HoamVg3SlzALRRRRzAFFFFHMAUUUVQBRRRScgCmtnacdadSUuYCH55OSdgHrVW81D7MuI0aZz0Va0KaI1U5CjNDXMUnY5/ydS1GQGSJLaI++WrXsbBLVMZaQ+rVbpaSgkVKbkrCLS0UVoZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0maWoyytk4zipbAfS01cY4GKdTQBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooorN7gFFFFWtgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbfuG3GO+acM96N1LQAUUUUAFFFFABRSZpFbdQBHPbxXClJY1kQ9VYAivn74/fsM/DD9oFWm1rShYamEKJfWACOueenQ19CmlyKnTqUpOJ+WGrf8ABIvxh4F8UWmqfDb4iLZ+W+RLch45UXPTK9Riv0y8EaXqOi+ENIsNWu1vtTtraOK4uUziRwMFhn1rYmmS3Qu5wvSvFf2kP2sfCn7Mej22oeKLTUZLe6JSF7WHcGfGQpOe9S7GnvVNEj21fl607Ir8m/G3/BajXFv0/wCEY8AWaWQyH/tS5YueeCNnTiuI17/grt8aPFVq0OheGNL05mGPMsoJZ2GenXoaOZk+ztofs3urC1nx14d8Oso1PW9PsCxwBcXKIc/QmvwV1j49ftMfEC+l1F9U8XMznGy1glSIAnpgDArx/WfEnijUfGUVp4t1bVXuUukW4S6lbemWGeCaLsfIf0x29zHdwpNC6ywuAySI2QwPcVLXIfCKOzh+F/hVLCRpbNdNgEcj9WGwcmuvq1sZvcKKKKYgooooAazFVyBmlU7hnGKKKAFooooAKKKKhp3Aa1QrEyyFg2QanavIv2ivjvL8B/B8uuR+HL7xCUUsYbMDjHqazlG2rNYRc3aJ6w3TOMmqs0EnzOi7i3VTX5nWf/BaaBruRLj4Z3gjVtp2Xilh9QRW4v8AwWj8Lxsgl+Hes7T1KzxcfmaFFNXC7i7H6Jww+VtATaT1qw0bOrKwytfnVcf8Fp/BUHX4ea+Sfukzwj/2aoT/AMFrfB8nEPw61xjj+K6hH9arkQ25Nn6NoiwqIwDzU6LtHTFfmyv/AAWr8LGPJ+HGsb8fd+1xfzr6W/Y//bLtP2tLTWri08OzeH001kUpPcJKz7gT/D06UK0WQ4vc+kqWmr3p1DICikJpN1ADqKr3N19nUMRnJxUS3LybSQFDexpXRXK2XaKjjYHODmpK1WxIUU1pApANLTACu7mquoRrJEQV3MRgDvVuq91hVLkdFPPpxSKjufkR/wAFari3tdQ8PadHOGuLmZpBCzZKqOOfxNfd/wCxj4Z0/wCCX7JvhManPb6dbCz+33M7ttVd/wAxJJr8wf8Ago9qUfi79ry20wSPJbolvCBnld7jJHvX6/3vwh0zxj8CbXwJPNNBp8+kRWfncNIg8sDd2BNYRWh0VHeVmeN+Mv8Agp98A/B2qy6dJ4ml1KWI7WfT7Z5UB9N2MV+Uf7d3x68K/H74uJ4g8I/aW09YmjZrqIxkknPT0r7isf8AgiX4RS+eS9+JOrXFqWJEMOmxxsB6bzIc/lXxn+25+y34S/Z0+NHh3wT4T1e+1GO+gRrltRZC0Ts4UfdA4xk9K15btM59dkeufCT/AIKkyfDr9nu1+H0/hCTVtTtLRrOK7afEewggZHXjNfMn7O/xqn+Gv7R2geOB5WnRHUM3SICUWNz8w6+hr9ZvhP8A8Eu/gXpPgLSk1vw9N4j1Oe3jnmvLu8fO5lBIUJtAXnvn618Rf8FQP2WfAX7O994VufBGlS6TDqRkSaHzmkQkDIxnkH8adik2Uf2/fjRD+1v8aPD2geBbZtYNuv2eBIR8zuxH6Vwfh/xR8ev+Ce/iy2Sa0utHtLoiV7O6UvaXI7+wPavbP+COfwgsPFfxQ8Q+M78NI+gxLFbJtyvmP/ET6gCv1a+Knwh8LfGbwpd+H/FWlQalY3CFA0iAvET/ABIexpWYXPwP/an/AGjNJ/aF8TWPim28N/8ACPeJsD7bJE3ySsMEN9eK/bP9ivxtdfEP9lz4ea5fS+fez6aqTSYxlkYr/ICvhj4g/wDBFe6k8TxHwd42ij0GZi0qanCfNgGeFXb97jPWv0V+APwhtvgV8I/Dnga0umvYdIt/J+0MMFySST+ZNUiWz0BadSUtMkKKa5IXjrVOC6mmaTIwV4wRx9aVx2LMkojUs3QU1ds8eRnBrO17xFp3hm0e71O+ttPtEQs811KsaAD3Jr5l8bf8FNPgP4JvLm2bxPLq1zbnY6abbF0LezHGaYz6njTEjpu+X0qRhtwcZwK+avgP/wAFAvhP+0Brk+kaPqcuj6kmDHDqYWLzx/snpXuXi74n+EvAPkDxH4k0zRDMpeIX1ykZdR3GTyKBm/8AavkJ8tt3OFA61+Vn7an/AAUl+LfgL4lXnhHwhaQ+CbawZo3vryyW4e65+8vmIygfQV+g8n7VXwfjbDfEjw4D0x9vT/Gt3S7T4d/E5X1Owi8P+KASC1xEsN1tz0yecUC+R+GHxU/bN+Ov7Q/g0eG/EVy2saOf9YtroyATN2bKRZB+hFeFR/DXxfMpMXhfW5OxMenTH/2Wv3X/AG0f2mE/Yx+Huk6p4a8HWGo3OpXn2YQlPIt4/lJ3MUxzXy98Pf8AgtbbeY0fjv4eGFfMCi48PXiyBR3JSQ5b8DSKPzJPgPxXpDxS3HhjVYMOCvn2Eqhj6crzX77fsEa74w8Q/sy+FbnxraCy1NUaKGPyvKbyF4jyuBjisr4W/wDBQr4D/Gi+tNMsfFEdjqVyQIrHW7c27lz/AAgtlSfoa+moyrRqyEFSMgr0xTE3pYfRSLS0EBTJPu05qjk5HXBqZPoUihcKVkUhsccVQVmS4OG6nmrd35qnLqpAHBzVCHzGZ2KqOeMGuV7nfTty3Z8//wDBRS6Mf7J/jT5vvWyj/wAeFfjH+yPateftIfD2EDLf2vCT9Ac1+yH/AAUqzF+yJ4qYfKzKgOPTcK/LL/gmnodt4h/a88HR3sC3MUJknCv0DKpIP4VpTWjOWUk2rH773EYMLYHvWP4mlnt/DN7LbO0cqwSMGXqCFOK38BuCMis/X4l/sHUEx8pt5P8A0E1bWpmmfz9eD/jL400v9quy1E+JtVeb/hIlidmu3IKGcKVwTjBHFf0KowZQwGMjNfz1fBH4e3PxM/bO0rQ7dd4bxE88vpsjlLHP5V/Qso2qAOgrRbCluLRRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmNIFkVT3p9JQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANZiO1KrZpaSs3uAjKrEEjmlHtTWYetOXpSW4C0UUVfKAUUUVDASjIqKWQH5c9e9RQeYGZWO4djVcxVtC3RTVp1SSNbPam7W3DPNO8xem4Z+tKrBuhzQAtFFFaLYAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUjLuXFLRQAyNSoweaXbtzgZNOopWAQUtFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooqG9QCiiiqQBRRRUtu4BRRRTtcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA5eb4neFYPEC6HJr9gmrs2wWTTqJSfTbXTK2a/Cn4ifGzwhrH7d1h488N6tdaj4dmv4XaRgU2nPIAJ6V+kXxQ/4KYfBv4YQiNtTu9b1VVUvpum2zNKpIzjLFV/WoUlbXc6HS/lPraivPfgX8ZNO+O3w/svFml6dqGlWl19231OJY5R7kKzDH416FVJ31RhKLi7MKKKKYiG4uEt4ZJZDsjjXczHoAK+cfiD/AMFCvgd8MdcfSda8W5vk4aO0tnn2n0JUcfjX0XdWa3lvNDJykiFCPYjFfmz8Wv8AgjmvjbXNa13RfH/2TUb65edLe+tS0ShjkAspyMfSpbdzWPLZ3PqOz/4KCfAXULWKeL4g6cokXdskJVl9mB6GvGPjN/wVr+GngHzbbwrBP4zvhwHtjshX3LGvna0/4In+PJJALz4geHEj/iaGGdm/VBXVW/8AwRPnbyvtXxITYB84is+/tmlZisuh5fqX/BVb4ufFTx1oOkaNa6b4esbi9jhMMMZlaQM4A3E9D9K/U34mfADwh8fPAun6J4+03+1oljSQsrmN0k2jJUjpzX4r/F/4E2XwD/bB8N+B/C15PqkltcWLG4mAzJMzZYgDoOK/fC0My6ZAXXE/lLuX/awM/rU76oqXMtEfNfgf/gm98BPAl2Li28If2nOrb1bVrhrnb7AHtXumi/Cnwb4cjCaZ4X0myUdobOMf0r5H/bi/b41b9mCaw0nR9Hhvtdv1d45LjmKJVIzkd+or5Htf+CyvxZWI7/Dvh+cj+Iq6/pmmmrbDlGUd2fsTJpNla28oisbdF2k4WJQP5V+A3xs0NvHf7bmqaZCqq174hjtwmAwALDnAr648O/8ABat00Mxa/wDDiS71Ergy2F6EjPvhga+df2V5I/2iP29dK15LUWEV3qD6kbfdv8oKM4JwMmgSP3L8L6RHoHh3TdNiRUjtLaOEKowBtUCtSmrxSNJtBq+hluxWYL1oVg3SovtSsDs+dv7oPWpgc0XTCwtFFFMQUU1mCLknA968I8fftxfBn4YeMLrwx4n8Y2+lavbbTJFLG5UBs9wD6VLkluNRb2PeaK53wH8QfDvxO8N23iDwtq1vrWjXOfKvLVso2Ov0/GuiqhBRRRQA1qpalo9lrVu0F9aQ3cLAq0cyBgQe2DV6hV20Arp3R4Tr37DPwI8TX0l3qHw00eW4kJLSIJI8k98KwFYsv/BO39nwj5Ph1YxDHOyWX+rGvpDHOaa1Ry9hrc/HH/gpF+xr4C+Bfh+08ReCLZtLzOIpbPeWX5uh55r0f/gnP+w/8J/i58E18YeLNLfX9Turlo9krlUgC8YAHXOe/pXS/wDBYqP7J8M9HZTzcXiBq9V/4JMNG37JenlWzINQuFcenIxUJu9mdEvhudFqH/BMH9n3UJkkbwjLBt/ggu3VW+or2b4N/s8+AvgHptzZeCNCh0eK5KmZlJZ5CBgEk9etejL3p1a2Rz3YlLRRU8ohrUlOPauO+K3xS0L4OeC7/wAT+IZ2g060Us2xSzMfQAVL93VjSvojrJYvNAB6VEIZYyAp3L/tV+Znib/gtbp1nqUyaH8PJL6wVyqT3N9sZx64C8VVX/gtmrR8/C3a/wD2GFIP/jnFTyqWpfLJaH6ixqVzk5Jp9flh/wAPtLhJl3fCyFou+3WgG/8ARZrSt/8AgtxpYmAu/hXdRRf3odaSQ/8AoritE1FWJ5T9PMA9etLXzV+yP+2dpv7Xq67No/hq90KHR2iSV7i4WQMXDEYwo/umvpSqJFqG5UNDID0KkGpagvD/AKLLnptOaBrc/Br9sy5Vf23JivzCK8tEH0Div3c0HnQ9OP8A07x/+givwl/a5tftn7cM8CRsWlv7MLj/AK6Cv3g0uA2+m2kRGDHCikfRQKxjqjer8RYr8u/28v2Cfip8aP2g08Z+D7S3v7C+giSRmuEiNq0ZAGcnnOc8elfqNto21sYXOW+F+g3/AIV+HfhzR9VnNzqNjYQ29xMW3bnVQDz3rxz9tT9key/ay+H9rpQvY9L1rT5vPs7yRSygkYKkDsa+iwoHSl20wPDP2Pf2Y7D9ln4Tw+GIZ47/AFOaU3F9fIuPOc9B9AOle50dKWgQUUUUAFFFFADGb5gMV5n8fPjt4Y/Z/wDAd34l8TXYgtk+SONeXmkxwgHvXo17cLbwvI7iNEUuzN0AHWvw7/b0+OGt/tHfH4eBdDuGvNHtL1bOytYhnfMxALHHXHvWb3NEtLnNeMfiJ8XP+Cg3xok03QxdTwyMyWumrKYra2gHQyEcZ7819dfDP/gi34ePh62m8deNdWGtEbng0bylhTI5GXRifrxX1v8Ase/sqeHv2Y/hva2NnaK/iK9iSXVL5iWaSXHQE9AMngV79VkuR+AX7aX7Lt7+x78VLGDQ7+/uNFnjWex1Kd1EocHkHaBjBr6g+Jf/AAT5+Jn7U3hHwB410fxtY3Zu9DhaePW5ZEMchAzs2K3B7/Ss7/gtXr7t428A6RFdI0S2U9xLAMFg4ZQpPccE8V+iP7ILPJ+zH8NWlUq50aEkH6Ux8x+Xw/4I2/GXy9j694Qzn7yXNwWHv/qhX2d+wr+wPqf7KepahrmueL5dc1O7gEK2FiWjs489WIb7zehI4r7S2ijgcmgXMZHiLwnofi60Frruj2Gs2wORDqFsk6A/RwRXiXxb/ZN/Z7m8F6zqfiT4ZeF7HTrO1knnu7DTks5Y1VSSQ8IVgfxryD9qn/gqV4N+BOtXPhrwrpv/AAmfie2dormPzDHb27rj5WYck89vSvzu/aU/4KMfFX9ozSZtBu7qz8MeGZxifSNIClZuR9+VvnOP7oIBzyKBHR/8E+Pghovxk/a6e70+zZ/Bnh+5m1GOO4VmBjVz5KFs5yeDye1fugqhUAUYAGAB0FfhR+xx+3zb/sk+C9R0Wy+H9nr2oX9x50+pPqQgdlAwqkYYYHtj8a+wP2fv+Covi/8AaA+NHhvwVpfw1sLW2v5T9rnTVPPeGIfefhQBj3oBu5+i606kpaBEczFYyRVeSQtCAVzmrZAYYNZ+r6lBo9s9zcSLBbQxtLNI5wqIBkkmokupSHTW63UIjyQgHIU81VsdFhty21sgnkZzzX5Tftdf8FIPGHj7xovgf4GXV1a26zGKS/0+ESXN2+cYjyDhevavGtMn/bR8CRz6lbt46tizfaZXljMqnPfDA4+gqVZmqbSsfo9/wVAV4f2RfEoiJChow30zX55f8EidHt9U/anjnmVTJZ6ZPNHns2AOKqfE7/goX8QPH/wP174a/EfRUutVutqR3skBhlXB5LjjJzjpXR/8EcbQSftMarIU/wBTokxBPYllB/nTWhn1P2sHasXxxfDTPB+t3bZ2w2UznHXhDVrXvEOmeF9Ll1HV7+302xhGZLi5kCIv1Jr5h+OX7fHwY0PwD4ltLHxpp+saqbOWGO1tSZNzlSAM4p2vqJbn55/8EyNJuPGH7cE+qxMRFZpeXku7uCSB+pFft5X4CfsQ/tU6D+zH8UPEnjHWdJutS+3WUsFva2hC4LOGA56CvU/i9/wV2+KXjaaWz8H2Vr4QspPljaMebck9vmPT8KobV2ftRRXjn7Ies+MPEX7PHg7U/HVxLdeJLu186eWcYkYEkqW98Yr2OmQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNZwvWgB1Jx0pgkD9O1HfNZvcdhuA0jDGNtSiqkNw0lwV2MAvGSKuU1HqAUUUVYgprNtHQn6CnUVNgGYDKDtxRtx2p9FHKO4i0E4HTNLRRyiGLGOTjk04ADoKRmI6DNKpJ6jFHKAtFFFUAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlGRTZG20inIzQMfS01adQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKarBs47U6gAooorN7gFFFFWtgCiiiiwBRRRTAKKKKACiiigAooooAKKKTNAC0U1pFTqcUzzA/3TmgCWimp3p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH4tXXhX9nfwf+2tZwpcQWfhSzfdNavMPISfIwNxIGPbNfeWtfG79k6bV7GLUbzwNcakHSO3CwQTTAkgDOwEjt1Nc38Hf2Rv2dfjn4P0bxjH4bs9SuSqyT7Lnd8/pIAeenevW9W+DX7Ofw6A13UPCPgbRmtSHF5PaW6spXockZyPzrmppu0rnfNq9ktT2/SIbO30+BbCKKGz2AxJCoVApGRgDtV2uJ+GXxg8FfFqxuLjwZ4gsddtrUiOU2UgYR5zgEduh/Ku2rpOKV09QooooJCiiigApjfdIP3cHJp9NPyrSA/Gv4/Wthaf8FQfDIt5zKhv7EyNIDgEseK/ZJvukHpX40ft93g8G/wDBQjwzrK2rCLfp9wPLGDJtcg49/wDGv2P0+8XUtPtblVKCeJZQrdRuAOP1rOm9NTWpdH5p/wDBYT4W2zeCdD8UofLltLnyyxGSwfAIz9cVwH/BKn9l/wAFfFzw14u1vxx4Rg1yG3uUt7O5vASn3TvCj8q+sP8AgqR4bXxF+y/rzPIENgY7pflz0cVw/wDwRx8QHUP2fdf0w4YWesO4x1AdRgH/AL5NLRaIbvKNz0zx5/wTF+BHjdUeHwy2gTKhUNpczRA57kdCRWT+zT/wTb8Lfs2/Fn/hNdM1y71No4Xigtrgf6vcMZz3r7Ho20zNMK5j4ia1caL4S1K7sUEt3FCzxqRkbgDiumPpWR4k01r7S54o03lkI25xnirfwl07c6ufkJ+yL+0p8RPGv7clhaeJfE98dPku7m3fTWl2wqCCqgL09DX7JrX8+n7Qun6n+zr+1tdalaySQXNvfx6jHKo2YUtll96/dz4S/ECw+J3w58P+J9NuVu7bULSOUyJ/f2jcPqDms49yqm7sdjRSUtbGBBeQ/aIGj/vDr6V+a/7dP/BOTxx8cPicvi/wM2llriNYLuC4l8liB/Hk5z34r9LivOaQKF6VnKF3c0jNxTR4/wDsm/AqT9nP4IaF4Jnv11K6tA0s86JtXzHOWA5PA6Zr2KkpataaEN31CiiimIKKKKACmtTqQrQB+c//AAWOs2m+EWjTsuBDeoQR35AP8677/gkfdWs37LIigbMsOqzrKPThSKq/8FZtHXUP2b7u4deba4iZTj/bA/rWZ/wRxC/8M569g8rrsiH8EX/GsftfM6ZfBfyPvZadSUtbHMFFFFABVDWtD0/xFp8tjqdlBf2cow8FwgdGHuDV4mmNJtIB70rXGfN/ij/gnT8APF2rNqN94Bto7hiWYWc8kCMT6qjAVfs/+Cf/AMArOBIl+G+lSqowDOpkP5k19BZ5NLmp5ew7s8DP7B3wFGAPhnoY/wC2FYPiL/gm5+zv4m2m4+HlrbMoIDWNzPbHn18txn8a+mutLtqrCuzyX4A/stfDv9ma11eDwBpE2lR6q8b3fnXk1xvKBguPMZsfePSvW6TGKWmIQ9qgu2C2spboEOanNRXEYmt5E6blIpPYa3Pwg/ai1Ka5/bpiuIFjSWPUbMR5B2nEgxnmv3gtS7QoZMeYVBbHTOOcV+Bv7Zuj3nhT9se8M1zDJP8Aa7aZDDn5R5gxmv3p0OQy6LYSMcs9vGxPuVFZQTsbVWmy9RRRWxgFFFFABRSE0m6gB1FIDS0AFFFFAHz/APtw/EyT4Wfs8+K9Wt5Whu2s3hgdR0duBX5n/wDBKn4f6d4o+MXiH4ieJ3hk0/wxavdvJMeRM+Tv98AE19W/8Fh/HE+i/A/TNCidQmpXyCRe5UZJH8qs/wDBJv4T+H/+GW7/AFeaBbi58SXU1te7u8aDaFH4MazW7Nr+6eiXX/BUT9n+0m8pvE1277mU7LJjgg4PevLPiZ/wWN+HGh2M0fg7QtS8R6jnbG1xi3hHuTyam8Xf8Ea/hh4h167vtO8UeINDtbhzJ9jtzFIqknJwzqTitz4e/wDBIT4LeD7sXGty6x4wKsGSPULnykUjttiChge+7PStDPQ+Bvh78OfiF/wUq/aH1DXdSZrbS0lVry/Vf3VpCD8sS44yRn8q/cbwX4UsvAvhLR/D2nKUsdMtY7WEMSTtRQBkn6VR8AfDHwr8LdJOmeFNBsdBsmwWisYVjDkdC2Op9zXUUCCmtgqQRnI6U6igR8c/ED/glj8F/iR8TJ/F9/Hrlm11Obm+0y1vytvduxy24kGRc/7DLXq/hb9iH4C+D7CKzsPhR4Znhi+4dUsVv3H/AAO43sfzr26loA8zi/Zh+DkCssXwm8DxK3Xy/Dlmufyjq74D+APw3+F+sXOreEvBGieHdRuF2SXOn2aROV9BgcD6Yrv6KACiiigBGOK+LP8AgqV8fNS+DvwNj0jSPLW/8USNp3mbsNFHtJZh+HH419oyZyCD07etfjd/wVz8VXHjP9o7wp4IRjHHp1mjk5+XdcOFzj22frUy7FRPXf8Agkt+ydb6foB+MHiK1ZtRui0OjwyDCpGPvTY9SeB+NfpnwcgiuM+Cfgc/Df4SeEfC7EM+labDbOQMfMFGf1zXbbR1xU8o29T8rf8Agsp8LYrPT/C/izTNEhhj81ory+gj2nJxtDY9T/KuO/4IraXb3Hxa8c3zqxuLfSFRCeg3Srn+VfTn/BX/AMSadpX7Ly6Xcvi91HU4Ftk7kqdzH8hXiX/BEPSlml+Kmpbfmi+xW+7uA/mtj/xz9Kqwrn2N+3p8CfE/7QnwHuvDPhO7W21UXEdwI3fasyr1Qn3r8wPDf/BLX4tX3hvxDrHihbPwpa6NC8yxzkO1wFUklcdB8vf1r9zcV5r+0pqq6H8AfH963HlaLdEfXyzimCZ+OH/BOn9kXRv2ofiDrr+KnlPh/QYkaaO3faZpCxCgn+6QDmv1n0n9iH4EaJJbS2nwt8OpPblWSZrUM+4dGyepr4o/4Ii5e0+KcmwHLWGW9M+f/h+lfqTTBsitbeK0t44IY1ihjUIiKMBVAwABU1FFBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMu6gBaKRV20tABRRRQAUUUUAFFFFABRRRQAUUUUAFNIywNDUlS5DsIcKx2jHrQBupeO9OVQOlQO4irtp1FFaLYkKKKTNJyAWikoYkdBmlzALRTVbseDTqOYAoooqgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRntTXcL1qssuyRm3ZBqWylFstMPfFNZjHwOe9RRXGd5fgDpTWukkchSWKjkAU7hyu5NDMJQT0p5b0qnZzxMzxrLG0gPKq4JH4Vbpg9ypcK8jACrMUZjQDvTN2yQe9WKBPsItLRRQIKKKKACiiigAooooAKKKKACiiigAoopPwzQAtFJ+GKWgBM0Zoaq9zN5a4z1FJ7DSu7Cy3ISQKOSfShbgbsZrMiyGY5zT4LjyZG8zv0rNSZu6ehrKAuSB1oL47VWhvo5l4z+VTqwbpT5mY2H0itnPGKYxdenIp0bMc5FIkfRRRWi2AKKKKYBRRRQAhOKTd7U2SQJjIJ+gqHzndwFQge9ZylylJFkHNLTUz3p1aEkckwixkE/QVGt15jYRCR3zxU9HFAxjKzdG2/hmk8ndy7bvTtUgpaBDQgHalwB0GKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/JXwf4B8DfsvfEGPwrcfEu98O+IYZDiJi8dvdkjCBlGQSD/6FXKeBf2F/i5+0h8aL7U/GUWpW3w/e/aSS9vbsRCePPHlR7iTkdwPxFfaP7Wn7IM/7Q/hBNV1xIo/FumQltMuNHixLHI2CRIf4xlVx6c18b+Gv26P2i/2SryPw3498OjxRotiTDHJfwNAzL0XEyqf1U1wxpqMtz0ZSbjaJ+nfwO/Zt8B/s8aXNYeCdJ/s2OcL9odpC7zFQQGYnqeT+deodK8C/Y1/aY1L9qT4b3XinUfCp8KGK5NvHB57TLIAOWDFF46dq9+rsjtocEr394KKKKokKKKKACorhtsZzx2/PipCcVDcNiNiFLkD7vrQNbn4vf8ABVhdU8J/Hbwjq8syPcfZ5HgbGceW6Yz+de3/APBOP9q74rftD/GqXTdeuxJ4X0nSm8yONMKrcCPJ9Tg145/wV8i1Fvid4S+12gisYre6jgus8SFihYf8B4/Ovpj/AII6/Cv/AIRX4I654vuIMXfiK9VY5D18mEEAfmxrmULpHXV+Js9z/wCCh0aH9kD4jFomkb+zztKrnadw5r8qv2A/22ov2SdS1yDV9Im1jw3rLRGf7NIBLA6AgMAeoO48e1ft98Svh9pfxW8D6z4U1pWbS9Ut2t5xGcNg9x9K+E9U/wCCKvw2vL1pbPxt4i0+AkkQLHC4GfdhW0Y2OXm0sdzF/wAFfPgC0al5fEkbEAlf7LBAPpnfzW7pP/BVT9n7VIWkfX9QsAMYW7sSpb6YJ/ya8cm/4Im+A/JVYviH4j3fxF4IMH/x2su7/wCCJvh6Nk+w/EbU1X+P7Raxk+2NoHvTa10HG1tT3+4/4Kkfs+Q28ko8UXU2zqkdk24/TJFcjqH/AAV++B8O77JZ+Kb4KfvJpyKp+h8yuI0//giv4E8tRf8Aj3xEXH3vsiQqG+u5DXW+H/8Agjr8F9J8w3+peI9aLY2/aLtY9vXP+rVevv6UK+wtEfAP/BQb9o7wF+01408P694K0nVNPuIIJIr+S/gWPfkrsxtJz0NfWn/BGj4wa1r2i+K/AV9M1zpmkpHd2THJEQZmDp07kg/8Br22D/gkz+z/AB436Lqc2P72pSj+Rr3v4J/s0/Dz9nm0vYPAnh+LRvtwQXUquzvNsztyzEn+I1HLokh8x6eo2iloorUgjmlEKlmOFAyTXgPxc/bn+E3wS8cWPhLxPrVxDrd35ZENtbtKsQc4Uuw+6K931CzN5C6ByhZSufrX5vfHj/glD4q+M3xY1DxYfiTYwQXrjMd1pzs8KKflVSJDu79dtS+a+htGMWtT9JbK8iv7WG5t5FlgmRZI5FOQykZBH1FT1y3ww8Fj4dfD/QPDK3Ul6NKs47U3MhJaQqMFufU11NNX6mT30CiiimIKKKT8KAFopCcUjSBeaVwPjr/gqZcWw/Za1+KZtsu6Mx8dSHXivN/+CMGrG4+CnjKxK48jWhMGz13x4/8AZf1r1L/gphDYy/sueKZtUUKoVVhIPO7euK8T/wCCLek31v8AD/x7qDHOmXGpRRwjPQqjZP47h+VZ3946X8CR+lNFN3dRRurU5h1FN3UbqAEbO4ccUnJxmquqXz2NpJMkLTsiltidTjtX5W/thf8ABQz44eCPiRc6P4Osm8MaNaZXzpdKFw1yTjklwQuMduu6o5lzcvU05Xy8x+rm3DEgdetLX4Y6V/wVK/aP0m+iurvWLXUoMH/R7rRYo0f8VUH9a7K2/wCCzXxjtFxc+FfCsx7NNb3Kf+gyirIP2dWnV+Oem/8ABar4oSvIs/gjwjIduI1hS6BLdusxzX6pfBDx1qXxL+EvhTxTrFgml6nq1hHdXFnGrKsTMPugMScfU0D5Xa53VFJS0EjWpG/1bU6mv8qmkHU/CX/gpFAuh/ti3snlgEW9nNhe58w/4V+4fgm8OoeDdBuiNpnsLeUj03Rqf61+IH7feq23ib9tR4pCs2GtLWbZ93Al7e/Jr9y9HtY9P0ixtYRiGCCOJAf7qqAP0FTHY0qfFcvUUgNI2fwqzMWgHt3r5z/bo+LHxF+Dfwb/AOEk+G9haX2pW95H9r+2QmVUt8NuO0MvOcc5r52+A/8AwV68J+JvDOqJ8RrI+HNcsoPMhkt1LxXZAOQB/Cc7eD1zU8yK5Xa59D/tj/tlaB+yn4TS5mji1TxFdfLZ6WZNrSerH2GRn618YfCX/gsjrmpeOLK08beF7G28P3VwsD3Fi5DwZONxz1x/SvmWDR/Hv/BQ79pS5Nstxc2U93n7TJnydPtCe/YEhf0r2X9ub/gm9H8EfAUHjLwQ0l5pthGseowucsOg8388/nRcasfsRpOpW2s6ba39nKs9pdRLNDIvRkYAg/kat18hf8EvvjVcfF79mXT7bUZxPqvhyb+zJTjnygoMRPvjPPtX17VEhRRRQI/Nr/gs9olxJ8OvB+pJbs9tFqJSefGRGChwPxNex/8ABKe4tJP2PtAS1ZWkjvbrz1DZKuXHUduMVuf8FJvhzrPxN/Zb8Q6dodmLy7tSl+yYy2yI7mC++K+Af+CVP7UWmfB3x5rfg7xfqy6V4f1hVktmuMhYbtW2hfbcGP5VGzZpvGx+0YoIzTVkDqGUhlYZBHQ0uTVGYvSlpu6ue8b/ABF8M/DXRpNV8U65Y6Fp8YJM97MIxx1wDyeo6UwOjorh/hT8bPBXxu0q71LwTr1vr1naS+TNJb7sI3OAcgdcGu4oAKKKKACiiigAooooAa3UV+EH7emuTX/7c2sPdymSK1urSHLY+VFkBAz+NfvBX5Hf8FGP2EPiJqHxR1z4meELV/Emkagonube2H+kWpXB+7/EM88elS1dplJn606fMlxZwzRuJUkRXEgP3sgc1YIyRzivxc/Zu/4KmeOfgqsXh34hWEnibR4nWLe6eVe2qrkEEYAbt/3z719SfEr/AIK9fC6H4cX9z4QXUrzxRNCUtbK4tzH5chGAzE8YHtVCPnX/AILHfG5PE3xP0H4e2bRva6DB9suXX5iZ5OAue2FB/wC+q9E/4If3kQ0v4t2xdVnefTZVjzyVC3Azj2yPzr5g/Z1/ZA8e/t1614x8aX2p/YV3vK9/dgnzrlslUX2GDn04rmLdfjL/AME8fi5HO1u2halIjIS3zWmoQgrnnoe3uM0CP6DK8w/aesU1H9nn4iQOgdTod2dp9omNfM37BX7eXjH9qzx9qvh/WfDFlZWOm6YbubUrJ2K+b5iKienzAsf+AmvsD4paK3iT4beKNKSIzNe6ZcW4jXqxaNhj9aAPzL/4Ii6tIuqfEzTNpMMttZ3BPYFXlUf+hmv1cr+cv4M/GLx5+x/8UZNV0hJtO1C3ZrS802+jZI7mMNna/ryOK+w/FH/BZrxf4g8NrY+F/A1rpviGY7BcvIbhQf8AYj7n60DsfoJ+0h+114C/Zm0eObxFem81a4O210eyIe4mOQOnbqOtemfD/wAWnx34L0jxAdPuNKGo263AtLoYkjDDIDV+av7H/wCxD44+MvxKg+NHx1aadXZb6x029kLyXDkkqZEP3EGBhe9fqLHCkKgRqEAUKAowAB0FAE1FR+YPWmSXKRDJNTcLMnoqv9qG0Ec1XmuJW+4CKXMWoNl8ttpplUEAnGazbeeXcd5Jb+Fc9afMXMiFxt9qOYbp2drmjS1HDnbUlWZsKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUm5fUfnQANUcuPvHIx6U/erdGB+hpjSKMjOamxSuRwmNSWLlt396rIIPSs2ZZbzasJCbGG7I6itAcfSpSu2hyQ6lppIFIHU9CDT5kiB1I2D1oyKa3bFJtAOGF70uajp0fepWrsAPzgDr604UtFacoBRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSU1pFXqf0pAR3RHHNUfNXcRnmluSWlVnB2jjNUL66UwuYYizA43DoKzk9TqhsSX8xSPKk8VmySXt1uSLekcw8pnT7ygg/N68VCr3USmSQFwOcY/wA5qn8QfiloHwf8A6p4w8RXiWWkafAZZm6szfwqo7k+gqbXLk1yn40fH24+Of7H/wC0RrGrLrWtQWsl7Jd2V7LNJNaXMLNkAgnb3AI7V+gn7Gf/AAUe8N/tCSW3hjxLEvhzxj5arH5jDyL5sHcY26AjA+U9d3FeM/BP/goBF+11+0B/wrjxd4G0u88D64rwWVvcx+ZNGVBIZif7wxnGMYFeRf8ABRb9iWD9mm80v4l/DmS4sPD8t4EngiY50+bgxsh67ThvoQB3q07aHNufsqIlLFsc0+vk7/gmv+0Pq37QXwD+0eIbh73xDot0bG7unx+9GMo31x1r6yq0QwooopiCiiigAooooAKKKKACiiigBGbbTTIB2NPpNo4oAaxbGVH51EJ5WJCxbsdcnFWKSgBkTO2d6bPTnNSUlLQAnNNaNZPvAGn0UAQfZI+yinrbovRF/KpKKnlQ7sZ5YHQBfoKXbTqKfKgEFLRRRyoQUUUUwCiiigAooooAQjNJtp1FACAYpaKKAEIzSbadRQAgGKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGdc5rO1jwzo/iGHytU0yz1GPrtuoFkHH+8DWkFPejbSDVFfTdLs9HtVtrC1hsrZfuw28YjQfQAYq1SDilpgFFFFABRRRQA1qNu6lo5oA83+Kv7PfgH41Np58Y+HrfWTYOzwecPulsbunrtH5V2PhXwnpHgnQbTRdC0+DS9KtF2Q2tuu1EHsK1ttLjigpybAY7UtIBiloJCiiigAooooAKKKKACiiigBGptPpKYhFp1FFIYUUUUAFcv44+Jfhr4b6VLqXiTWLXSLOMZMlxIFz9B3rpZORivlb9sr9jK//ap0/T7S18Vf8I+lvIxkWSEyK4bb6EdNv61nLm05TWCTvzFPWP8AgqN8AdJvEgbxNLdZZlL21s7quMckgcdf0r0Hwb+258FPH0QbS/HmmDgZW6k8lhnpw30Nfn7a/wDBFPxnJqdzHcePdFg05TiGWOGUyOPVlxgH8aivP+CJ3jqO5JsfiF4fMQ+600M6v+imq5SEtT0//gqh8bPC/ir4KjTfD/izTdWa4uo1a1s5w5AVgcnH0rC/4I1/FPS9L8L+PfDmpaja6dHHcxX0Yup1jzuUqQuTyAF5+tee3H/BFv4nqVC+OPDtz3PyzcfmtFv/AMEbfivphd7bxhofmOpX900ideuanlNHJbM/VaT42eAIiVfxnoasODuvox/Wom+O3w6Tg+N9BH/b/H/jX5Q/8Oc/jD85bxHoEh6jdK5rndU/4JH/AB6tJwlsNBvE/wCeiX2wfqK0M9D9gofjj8Pbi4igi8aaHJNK21EW/jJYnsOa7dWDqGUhlIyCOhr8WvAP/BKT452PjfQLjVhpFnp8F7FNPPDfb2RFYFuMelftDY2a2NnBbqcrDGsYPsoxQLQlxmszUPC+j6pu+2aXZ3W773nQq2fzFau2jbU2V7i6WObPw18KOm1vDmlsvobRP8Kpz/BvwJdf67wfokn+9Yxn+ldgBilqgOFi+Bfw7t7pLiHwP4fjnT7si6dEGH0O2u1gt0t4kjiRY40AVUUYAA6ACpOtLQO7CimsxFeU/tI/tGaD+zH8OZfGPiOx1DULBJ0txFpsSu5djgZLEAClcLXPWK4n4xfEzTvhH8P9X8Taoyi1sYHkK7wpYgcAZ98V+enjf/gthZLp86eEfhtK90wIhutY1NNi9MFoY1LHvxuFfKHijxZ+0z+3ZrwglsNa1TTpJAqWdjavBp1srkZPPb5AeWP3altbFqLvqcv8HfDfiD9sD9rKyMEe2bUdSF9cSLnEFuj7yec4OBX9CcaCONUHRRgV8NfC/wCC9p/wTq/Zr1XxJaeHm8XfESaLzbgQRtIS2OI0KqSEXPPPPrXyTqn/AAVV/aO1IyGHQdA0lGOEWLRbtmXk8ZaQgn8KcdhS3P2eWqWtTXcOmzvZRrJcqhKBumcV+McX/BVv9ovRo0a70rQLyNTlmm0a5RiPqJAP0rtrf/gtB47bTYYpPh1pEuoDiR1vnAc+ybc/qab2JRy/h39vrx1p/wC1ddWPxO1gXPgiO/n0290doB9nEJYqrbfUADkmvIf2/bH4YzfGK2u/hYsH2K8txJPbWnMYf5du1AO+W/IV0v8AwUA+Fut29n4L+J2peFoPDcviq2N3qENq+5UmkCsgx243fnXsn/BKP9j2bxNrX/C3fF1kkukWitBpFneRhxcS8hpSG7Lxj6+1QosuUk0eZfsE/tsab+yPJe+G/FXhKWOw1i6ie51VUK3EKgHGVI+ZfmPA6c1+lPxF+Lnwy/ah+BHi7w94Y8c6TdNq2lyxqouAsiZUnlTyDxWx+0t+xb8O/wBpTwvJZ6ppNvpeuQxsLHWLGMRywMccHA+ZcgZB/Cvyn+LH/BNH43fBObUNU0S2/wCEg0m1UuL3SZispQdyg5/Cnykqx79/wRj14+G/HvxY8E3VynnMltPHEDw5geVGZfwkBP4V+rFfg1/wTHh8Tx/tleG47FJ43UXH9q+YpyINmXDA9DuA61+8tUhPcKKKKYiK5gjuoXhlRZIpFKsjDIIPUGvyj/bf/wCCYWqWOq6p4/8AhSkuoLcStdXegrw8TZB3Q46/xcewr9YKNoqWtSkz8Lfhh+3Z+0n8C9NXSLr7XqWnwvgReItPeRl28Mqybd2OnevUE/4LFfFxYwg8E+GZXxgt5N3kH6Bq/XWXQtNn/wBZp9rJ/vQqf6VB/wAInonH/EnsRj/p2T/Cmguj8if+Hi/7VHxdxY+CfCcMNxna76Lo0k23d93c0oYL0OOneul8K/sFftCftT+JrLWPjz4vvNO0SNfMW2knEsoz1SOEfJHnaM8enBr9XbXTbSxyLa1ht/8ArlGF/lVmmPm7HBfBf4KeE/gL4KtvDHhDTY9O06L5nYD55pD1dz3JrvaKKCQooooEFFFFABRRRQAUlLRQB4r8XP2NvhB8bZGuPFHgyymvyCBfWmbeYZxk5TAJ4HUGvnHWv+CN/wAIb64SSw1zxFp6b9zRtMkoI9ASoxX3xRQBxXwf+D/hf4GeBbLwn4R09dO0m1y20ElpJD952J7k1t+IvBfh/wAYJEmu6Hp2srFkR/b7VJtmcZxuBxnA6egraooAx/D/AIP0HwkkiaHomn6OsmBILC1SHfjOM7QM4yevrWxTJZBGpZiFUDJJPArmPC/xS8JeNdUvNN0LxFp+rX9pnz7e1nV3jwcHIHvQMzPiB8Cfh78UrfyPFfg/SdbiJyRdWykk+5HNc94L/ZL+Dnw71qPV/Dnw50DStTjGEuobQb1+mc167RxQAxVCKFUBVAwAOgrjNW+Nfw/0HV5dK1LxpoNhqMRAe1udRijkUnsQWrf8QpHe6RdRf2iNPV0eI3G4LsYggHJ6EE1+QnxW/wCCTfxe1TxhqOpaL4h03xXa3sjXI1C7uWjlbcxOD1yce9TcaR+wGl6xpmv24n0y/tdQhI4ltJllX81Jpt5EVjDPztPavwT8D/F34yfsH/FabRpr6fdDIsVxoslyZLa4wTg7c4yMnH+9X7teEdVufE3g/R9Xv7X7Dc31nFcS2qtkIWUNj9almsXZl2O425Kg7cd6ntboTSBEOW789KiWNFRmViy9CDUun24t5JQF5wCfepWrNZtWPkj9qj/gpB4O/Zh8eQ+FJPDOoeKNYiiEt00E6wRwKxGMFgdxPPbjFezfs5/tSeA/2n/Ccer+FtQjS9RR9q0i4dftVqxzwy9xweR6Vxn7T/7Bfw3/AGnLN7rULMaB4oVCsOu6fGolySP9YOPMAxwCeMnHU1+THxv+A/xR/wCCfvxc0zWrLULkQeaX0zxBYs0Ud2E2lo3CtkfeXKnr707dDl3P3p8SeI9K8I6TPqusajbaVp1upaW6upQkafXJxXn/AML/ANqT4XfGbxNqnh/wd4wsNb1TTgpmhhYjeDnmPON4G0525xxXBfCbxd4e/b3/AGS0k1y2j8rW7WSw1KGNQfs90owzJnoQSGH1r8i/GXgnxt/wTr/ag0m4lJul0y4+12F5GCkd/bEjcPc4IDCqTDlP6BqK4v4O/FTRPjV8OdF8YeH7hbjTtSgWQbTkxvj50PupyK7SrJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKlsCOVwuAe9QTKMfL3qeRA2M9qbtHfoKyerLTKsKC3LH+9UUd0lxcOoyu3r71cmUKmQu6q9xcWml2Ut7eTQ2VtEu+WaZwiIo6lmPAH1osy+Zblq1jEanGTn1qQ1keHvF+g+LYpZNC1vTtajhIWR9Pu45whPQEoTj8a1ZFLLgHFWnZWI3dyKQbj1wKhnmEW3YM884qfydygE5IpGtVxknFY8rLTRWutQ8kDJChuMmrMbExrng1Xn0xbpVDHKhgw/Cru3LfSnySBtdATPNSCkWnVrGNtzJhRRRWggooprNjA6mpcgHUUxZB3IHanA55HNLmAWiio5biKHHmSLHnpuYDNHMBJRSBg2MHORkUtUAUUUUwCiiigAooooAKKKKACiiigBKMikakoAXcBTfOTdjPNV7y4WFQSf0qrb7p5Fckgdveg0UdLlnULwQQkqfm+lRWlyzQhnHLdKsModwXX7vT3qNlbzCQny+lZSWpStaxw3xw+JOm/CX4Z614x1jzv7L0mEzzRwEBn5wAM18feDf+CwXwl1a9gtdc8MeI/D9nIcfb7iCOeFeep2OW/Ja+3PiF4B0j4p+DtU8KeIbRbrRdUt2guIyeecYx6HrXxfff8EbvhHcef8AZ9f8R2ivzHGsyMifUFcn86ajoHNbQ+tfhz8bvhz8VrWKXwl4r0nWhIgk8m3uVMqg5+8hO5eh4I7V+XX/AAVg/aVfx78QLL4SeG3WXSNFcSX3kkn7Rdk4WPA67f5tXCftSf8ABP8A+IH7HmlT+PfDXib7b4Ys5AkmoWk32a6tvMdEjVlzl8l/4cgY7Vgf8E4vg/e/Gz9qzS9Qvof7S07w+51jUZbw+YWKsFQMT94l+n0NVYW593/sb/sa/Dv9mf4b+HPiv49drHxsln9vubjUbgJFY71PyKvrtI9818zf8FC/+Ci2lfG7Qb34b+A4TN4aaVTe6xOhU3G1gQqKeQMg89812X7b37I/7THxx+N3iK70qGXVvBE8y/2bZnV4o4FjCgDMZcYORnkV5N4D/wCCP/xq8QXEieIBonhWJcETT3i3O/rwqxE4xjnPqKOUz2PpT/gl58b/AIQ/Db4c6X8Pz4ohPjzxJfyXs9t5TBA7AKkIk+6SFX82r9I6/Pb9mn/glFB8Efil4c8a6v4yTWptHk88WMVpiOSTBAOW5ABNfoTVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopXAKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAI1Np9JQIbRTqKYWBaWiikMKKKKACiiigAooooAKKKKACiiigBOtZfiTwrovjLSZdL17SbLWtNl5ez1C3SeJsdMqwINalGPeoaA860X9m/4U+G9QF9pXw28KadeD/lvbaNbo/wCYSvQoreOCNY4kWONRhVQAAD0Ap9LTsO7GqoUYHSkWGNVCiNQvoAMU+iqEUdQ0PTdWi8u+0+1vY/7lxCsg568EVyH/AAoT4bf2l/aH/CB+Hftmc+d/ZsO4H2+Xiu8JpN1AjnfGHw38LfEDTYtP8SaBp+tWMRDR295AsiIR0wD0xWvo+i2Hh3TYNP0uyg0+xgXbFb20YREHsBVwGloGFIyhlIIyDwQaWigDl9B+GHhLwt4gvdd0jw7p2m6xertuLy2t1SSQZzgke9dRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNJoA+Tf+CmPx61b4E/s5TSeH7g2mveIL1NHt7hThoUdHaSQH1AXH/Aq8B/4JE/s06lo9hqfxo8QS3AuNYje10iF5CBJEWPmzOvfcVXafY1wP/BZH4nyeJviZ4I+GlldEx2Nubu5gUgg3E7osRPuqK3/fZr9S/hz4Xs/BfgLw7oNhax2Vpp1hBbR28QwqBUAwBQW9FY84/bI+Md38Bv2e/FXjGwfZqFrB5FrwOJpGCI34E188f8Eq/j38Tfjx4Z8fXXxB1OTWbTTLmzg067mQBi7CczrkdcDyfzrB/wCCzHxQ/wCEd+DfhfwZHnzPEGpfapQD96K3AJU+26RT+Ar17/gmH8OYPAP7Ivha6UKbvxC0msXEgHLGQ4XP0VVFAaWPkj/gs18QNS0vxl4F8N6Xq15Y2n2W5u7m0t52jR3ZogjMAeTw1fMXgX/gof8AGX4dfCqPwLoviFltIZJDDqEw8y6jQhcIjnlQuDj/AHq9U/4LG3Rb9qrS4my8cXh+2YJnjmSXP54H5V9N/wDBLf8AZz+HfiL9mWPxP4l8K6TrOq6hqFwJLrULdZCI0OEXJ7DJ/Opa1H0Pyfk8eaj4g8dWvinxPd3GuX/26O4uprx/MaUBskHP0r94vgf+3R8H/i7feGPCuheIF/4SLUbYJFprW7Jhkj3MmcYGADj6VB8Vv2N/gHrHgfxDqKeAPDdtdW2n3EiXdhDHE6uIyQdy98gYzX5j/wDBLHT7Ff2y9Omv0jSKzsb14pJmAEb7dqnJ74LDiiwLufo9/wAFHfjxr37Pv7PtxqXhfzrTV9Uvo9Oiv4R/x67kZi+ex44965P/AIJW/tBeJ/jp8MvFcXjDWLrXtb0TUUjF7dHLtDKmUG7vzG/6103/AAUo03w/46/ZS8X2K6xZHVbSOPU7SBZ1ZnMMi7sAHrtcjPvXh/8AwRP0zb4F+JurF8G71K1hEK/dQRpIRgfWQ1OzLcro8H/4KVfHz4q+A/2r9e0nRPH/AIh0HS7W0tpLS00rVp7eKJXjBLBUYAMT1r59/aB/ay+J3xy8K+EvCnja6eO30CAbDIHWa7cqu2ednyXYheG9ye9esftqWS/GD/goxf8Ah20DTG41Wx0d1XknbsDj+dfshrHwJ+HHiOa1m1nwF4b1i4t4Ft4p9Q0mCd1jUAKoZ0JwAOlVvqRsfhH+zj+258V/2c9LTQ/B2q2kuiyXQc6Nd2aS+ZJIRuKEDdk7QMk9xX6oft6fAY/tLfso2/iEadFD4z0PT11q1YwjzVHlB7iAEjIVgM4zjKDPSvfLf9mT4R2erJqdv8MPBsF/GQyXMegWgkQjoVby8it74teJtL8E/C3xVrWsyRw6VY6ZPJOZR8m3yyNp+pIH40uUVz8zv+CMfxxv18U+KfhXePNPYXFmdbsVLEpaukgSZFXOFDeah4HVa/WKvxz/AOCM3hKXWv2gvG/iuLcllpeitat6M1zcKyfpA35V+xlUiXuFFFFMQUUUUAFFFFABRRTG6igB9FFFTcAoqHLbuOnenL92jmHYkopkbbs0+mAUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtRc5NZvcB7MByTXK/Er4leG/hN4RvfE3irUodM0azXdJNKeSewUdz7CulcDaSxCqOWz0xX4jftpfGLxf+2d+0nN4B8CPd6z4fsrg2em6fb/6mR0wss7Y6jcBgngUikj628W/8Fl/hromqSW2k+Fda1q2Tj7VvSEH6Bhmvnj9tL/gpVpX7RnwVj8K+ELLVPDk9xeo2oxzSDM1uFbKBl7Zxkd+K+rf2f/8Aglh8LvA/hSyk8bac3ijxLNApumuJD5UTkcqgHp/Svlr9tj/glzqPw5h1Lxt8LUk1Tw7GGmu9EGWuLZAMlo/76jHTr0qrFaFr/glR+1Z8PPg3a674K8WyHQtU17UVuINWuH/0dlCBVic/wYO7n/ar9F/2ovjhf/Bj4B61498L6fH4luLVFaBIMzRlWOPMymcqOpPSvx8/Zh/YeP7Vnwq8Ta1oms/2J4j8O3HkzW92h8i6BUsG3H7pGCDXsn/BKP4h+M9U+POv/DXWdXm1vwj/AGJdC8026cTwAxSpGCmei/vCOODuFHKBo+D/APgtN4usbV4/EXgfS9UuDtKTWc7Q4HOQwOfbp71s63/wWt1JtLmSw+HVvb37LiKWW93Kh9SMc12H/BVb4L/DX4YfAPT9R8OeC9J0bXtU16C1F3ZW6xkIY5GfOOv3V/OviGfwr4X0P9gmw8QS6dA/i7XvF72qXkg/eC1hjJYL6DcRmnewrX1Pv7/gnD+1Z8Xf2qvin4vu/Ft/af8ACJ6Jpyj7Fa2ixBLmaUeUCwGThIpe/wDOv0Kr4e/4JAeEV0H9lN9TktliutZ1q4uTNtw0sahETJ7gFXx9TX1h4i+MngTwl4li0HXfGGh6LrMoUx2WoalDBM244XCOwY5I445qhbHZLTqRenr70tBIVneIPEWmeFNFvNX1m/t9M0yzjMtxd3UgSONB1JY9KvswGMnGeBX43ftvfFrxx+2N+1OvwV8BXch0TTrt9NjtY7gRw3cygGeWQ5wyrtOM9ADQNK59EfEj/gsx8OPC/iK40/wx4Y1TxdZQMUbUVmS1jcg4+QMCzDrzgV1XwJ/4KzfCv4teIo9F8QWt14BubhlS2uNWlQ2sjHOQ0o4TnaBuxndXo37P3/BP74TfBfwPZaZfeFdL8Va75am91bVbVZ3lk5yFDAhVGTjA+vt41+2h/wAEv/B/xE8NXXiT4Z2dl4O8S2SSTy2cY8u0vFABII6Iw2kgjj5jU2EfVOk/tSfC/XPidP4As/GGnv4piVW+xNJs8zcCQI2OBIcDPyk44z1FerD19RX8y/w38E+LviN4+stC8KW15qPiaRmliNtIRcBkBBKODk4x2r9Bf2RP+CmniH4Z65B8NfjlFMtrYO9o2vXasLq1ZTgLcKRkgdN3X1zRygfqR448X2HgDwbrfiXVJPK07SbOW9nb/YRSx/lX4cfHz9qb4vftkfEm5uPBNtr1vo+mRs1ppWhvIJIosKWlkCHnO0HJ6V9B/wDBQb9uC1+O02i/B74O6sNWtdXuEi1LUbMnZcMxQRwoR1XJbd9BX2p+xH+yTpf7Kfwtj00+XeeJ9S2z6tfBRlnxxGp/urkijlA+B/2JP+CmHiH4f+JLLwP8XLuW+8PyFLWHVbkET2L5IzKTyynIyT0xX6/Wd5DqFpDdW0qz28yLJHIhyrqRkEH0INfmd/wVw/ZLsbzwnZfFjwnpENne6a5i1z7JHt82JigjlIHA2kNk/wC0K9v/AOCV/wAarn4tfsz21hqmotf634bum0+cyNlxD1hyf93I/wCA1QH2RRRRQAUUUUAFFFFABRRRQAUUUUANamPnHFPamswUZPAoGUZlc/Ns3be1TW4Pytsx6j0pbiaQRkwrvbsPWks1m2s83DNj5fSg0cnYmcFqjOBwTU5qCRTuBwT9Kze4kxGVgykfzqfcOPU8U3Zu60qqqn3q1sJn5wf8Fnvi4dH+HXhD4cWk2LjXbptRvEXPEMOBGD/vSMf++K0v+CMPw7GjfBLxV4yntwl1rmqi0hmJBL29uuR9P3ksg/4CK8F/4LEfDrxXefHrw/4lh0y8ufD9zoyWNrPEhdftEcjmRcDkcSx89Dnjoa/Qz9hL4a3Pwp/Za8D6Jex+VfNa/a7iPj5XkJYjj2Iph0Pflpabt3Uowpxnk0EDqKKKACiiigAoopu4bsUAOooooAKKKKACiiigAooooAKKKKACimu+wHgngnj2rwr4sftu/B74I+NI/C3i7xUmnaw2N0SQSTCLP98op29R1/oaAPd6Kz/D+v2HinQ7HWNKuUvNNvoVuLe4j+7IjDII/CtCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCLzGRV8wfOf7vIqWkwD2paACiiioadwCiiiqWwBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnH0oBzz2oZQy4PShVCrgdKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsT2oAdRXI/Ev4reFvg/4VuvEXi7WLfRtKt1y0s7csf7qr1Y+wr4Y8cf8Fovh/o2pNb+GfBmseJrZWwbp5ltVI9QCpNJuw7M/RWivn79l39tb4f8A7VGlt/YN0dN8QQpvutDvGAniBJGQejjg8ivf91F0Fhc0zzk8wx7hvAztzzj1pWztJHWvyn/bV/aQ8Zfs2/tZaP4v0XxG2pWUsHk3XhyVyUSNcZyoI5O44PtRdFKLaufq1mlrx39m/wDae8H/ALSngm01vw9fRR3rRg3WlySDz7ZumGHpkHBr55/4KSfttap+zrodn4V8IvCPFOsI5N0rBmsYxtwSvq244/3TSuibM+6KSvwP8H/tt/tI/C6+sfF2pa9rGo6NcShNusW+61uAOSq8DBwTyDX7Vfs9/GrSv2gPhNoPjbScJFqEIM0G7JglHDofcHNO4+VrU9HooopkhRTWOO+KpaprdhocBn1G+t7GHBPmXEqxjjryTSuBforzqX9or4YwSvHJ480FXU4Km+Tj9a6Xwz8QPDXjRXOg69p+r7ACws7hZCuc4yAfY/lS5kOzOgopOvQ0c+tHMhC0UhqK4uorOCSeeVYYYxueSQgKoHcmjmQyaivkj4nf8FPPgr8L/GB0C81HUNUliYpPc6XbiaKIjsSWGfw9K96+EHxw8G/HXwtHr/g3WodUsWHzopAlhPPDpnKng9fSmFmd7RTVzk06mIKKKKACiiigAooooAKKKKACmSAt0OORStSUDPxA+OOiH4zf8FQ5tEUi6ik8S21uxc5Ajh2ll+mFxX7fKu1QPQYr8K5vGtp8Gf8AgpVe+JPEazWlha+KZ5Lh5FxthkJCt9Buz+FfuPouuaf4j02DUNLvIb+ymUOk1u4dWBGeooKkfkh/wWo8YR6h8VvAvhtE/faZpM10W9fPlVf5Q/rX6SfsneHZPCf7Nfw30qVdr2+iWwK+mUDAfrX5a/8ABYSwkT9qnQ7mRl8mTQrUDn7oWaTOfzr9cfBms6foPwl0TU7ieO30200eGZ5SQFWNYgSfyFAPY/Gv/grnr0GuftbzQWrI7afo9taykdQ43uQfwcV9H/An4K+Ovir/AMExdL8PeCdV/s7XLu/lu49kpjMsXmHMZYdM1+cn7R3xGPxU+OnjXxS0zTpqGpzSxSOc/ugSEA9sACv2V/4JWQ3sP7H3hz7aJAGubhod/wDzzL/Lj2pDeiPy48Yfsc/tG+CtL1abUfDmsR6fZxSS3c8F6XiaNQNxxu5GM9q8k+C3wt8YfGbx7b+GPBMEkuuTI8ilZDHsQfey3Yc1/Q3+0RouoeIvgT480zSld9Ru9HuIYFj+8WKEYHvX5Wf8Ep/hz4x8K/tUNcan4V1Gw0+HSbqC4u7q3ZUSQshXDEdTyOKYuY7T4P8A/BN/xz4E+Hvxd1j4jS2rXMnhi6i0mK3uDMVl2M7McjjGxAMeprG/4JO/G3T/AIT+Bvjfca5crDpukWtpqsSMxAaQLOrKB6sVSv1R+Lkcknwr8YrCcSnRrwLj18h6/mr03xZrPh+x1zSbC7ktrbVAsN5ApP78KzFVI78saloa1Psr/gm34G1j9oL9tC5+IerCa8tdFln1q7up2L5uJNywqSepyxI/3K/bWvkz/gmr+z//AMKP/Z6srjUNOW08R+IGF9eysB5joR+6Vj6AE4H+0a+s6aJe4V+V3/BVD9rWbxdqdr8Dfh9dTX87z+Xry2QLG4lJQw26FTk4O/evQkr6V6d+3F+2d8TtH8cXvwn+Cfhy81DXBAi3uuWls8stu8mcJCMbQcZ+Y5wRxU3/AAT/AP2A734W6tP8Svip5WrePL3bd2lldMZJNNkcuZJZDkhpH+Xnqu085JpiWh6x/wAE7P2Ybr9mn4Hpb67awQ+LtblF5qTxj51UA+VCx/2AzcdizV9UUUUCCiiigAooooAKKKKACkpaKACmtnjFLTWYL1PFTy3Aa77VORikjZWX5Tmqt1drGvHei1mLLwOtQ9Dbl0Ly06mrnvTq0WxkFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRSVLYC0m4DvUEjyMwCcDvUnlBsE81AHzb/AMFDPjhN8C/2ZPEOo6fM0Gt6uRpFg8Z+ZJJQ25x9EDfjivmX/gjV8FdMh8G+KfihdwtPq9xqD6RYTSL9y2RUZ2X/AH3cg/7lcl/wWm+In9peJPh38P7Cd/tVmk2rXEQ6F5WSOH8Rsk/76r9Av2UfhDB8Df2f/B3hGLDTWlkslzIB9+aT55D/AN9MapIdz1ikZA6lWXcrDBBGQakqpq2rWeg6bc6hqFzFZ2NtGZZriZwqIo6kk9KsR4f+1F4l8Nfs9fsz/EDVbK1s9C+0afcW9tHaxrEZruaNkTAGMtk5+gNfFH/BFj4WTrffEL4iXkBXKRaLZy44bJ824578rB+RrzD9tj9obVf26vjd4a+F3w18+88OW915cBVDiecnDTOB/AoHBPQE+tfqX+zP8C9M/Z1+DuheDNOAZ7aPzLyb/ntcMAZH/E/oBQV0Ph//AILYeNHtPC3w08LwFGa5u7vU5gSMqIljVD+Jkf8AKvlr9rjwna+Af2Tf2ZdJtVkjn1HTb7WbxXBGXlEDA4/4E1d7/wAFldWm1H9pbwxpZlP2a38PQIF7Kz3ErE/lt/Km/wDBVbT30HR/gJogRoksfCwiCsMYPyKQf++BUPcpH6N/8E/tJh0f9j34YQwgASaUs7e7OzOf1avg3/gsv4Lfwz8Yvh/47syy3N/YtEDjjzLWVGXHviYflX6L/sh6MPD/AOzL8NbEHd5eiWxyPeMH+tfLX/BZ3wrbal8AfCWuyFUu9O8QLaROTjCzwuW/9Er+VFyd2fZPwH8Y/wDCwPgx4J8RGRZX1LSLa4dlYMCzRqW5Hvmu8r5U/wCCY/jCDxZ+x74LjjmWWfSll06ZVcEoySMVBHb5Cp57EV9V1QnozyX9qr4wJ8DPgP4s8WCQLf29o0OnpnDPdSArEF9SCd2P9k1+ev8AwR8+Clz4t8deLfjPr8c0s1u7WWnXEgOJp5dxuZM9CQNq8f3mrpP+Cznxuhj0Pwt8LtOlaS/klOr6lGhIESqAsH1JLP8Ap619g/sH/Ddfhb+yr4B0hrSWzvJrBb+7iniMUgmm/eMGUgEEbsc+lMLnvy1keMI2m8I63GilnaxnVVAySTG2BWxTXUSKysNysMEHuKBH4k/8EmUjt/2zJ7e6j/fx6NfqgYfNHIJUB/8AHS3519Nf8FcPhP8ACjTfhl/wl13Yxad8RLufbYvZAI92AV81pFH3goK/N7+9fLf7JPxA8JfAX9tL4leLPE2pQ6Xoui2ur/Z/NkCm5n81dkCZ+87APhRzxW94Bk8T/wDBTb9ryO88QLcx+ANFlW4e12ny7W3BykXoGlKn67T6UAfM/wAE/EXjH9nHx14W+KUvhKa70tJt0Et7Zt9nuEGNxjfGMgHr7iv2s/Zz/b0+Fv7RVmkVhrMOh69uCHR9UlWKdjjOUBPzL7ivZfEfwv8ADHivwHN4O1DSbeTw9Jb/AGX7IiBVRMY+Xj5SPUV+Uf7Qn/BI/wAaeAn1TxF8MNVXX9Ohd54dKVmivYk44U/xEdsHtQB+qHxs8DJ8Ufg/4w8LZUjWNKntkbGRuZDtP/fWK/LX/gjjr+o+Ef2g/HvgWdXhiutIee6ikyMXNrcrGAB67bhs/SsT4A/8FT/HvwF0NPBnxA8OzeJf7Nb7NHNcymK8iCnG18j5scDPsa1f+CXOsP8AED9uDxv4vs7CSx0y70u+maEtuELS3EDBSfU7T+R9KAP2HooooAKKKKACiiigAooooAKKKKAGtUNxs2fMcCpiQahkjMmBjjNA0LHEFUY5qQ/L1pVxVW61Kyt28ue7gibH3ZJFU/qalsZHcatBAypvDM3pk0+EPI6OWwM5Az14I/qKzP7Y8OQtJIdS08bfvsblOPrzUGi/Ejwl4i1qXRdJ8TaRqWrQxmWSxs72KWZEBALFFYkDJHOO9QVp0PzA/wCCjn7UXx++Hfx5v/DXhe/1bwx4UWCL+zpLC0U/bMxqZH8wqTkMSMDp+NfOXhPxl+2N4pm/tbQZ/iRrZUgtJb21xOgz0yApAB5+uK/e5kRsblDY6ZGa8w+OX7TXw4/Zx0+xu/H/AIhTRUvmZbaJYJJ5ZMYyRHGrNgZHOMVa2Fc/JDU9W/bl1xVjvdB+IUsakFQdCdhn/gUdbkPj79vtVCjSPHoVVCKv9gDgD/tnX6tfCv8AaT+GfxotYpfB/jLS9XkkQP8AZVmCXCg5xuibDL0PUdq9MDBhkHIqhXZ+K03i/wDb4m+c6X4+G3J50YKP/QK6H9kfUv2pfHH7UHh218Ta14r03T7WYz6qNVgKQC3Xlo8EYy2ABjmv2JpPegkRc85p1FFABRRSFgOpxQAMQBzUEagybs5FNu59q8DNLayLJHwMY60Dtpc+B/2wv+CoF1+zj8bZvAeieE7bW10yOFtTuL6R423SRrIqxbTggIw5Pevsn4I/FSy+Nvwq8N+ONPtpbS01q1W5SCb7yZJBB/EGvxE/4KiMrftsePD0Bisv0s4h/Ov19/YY086X+yT8L7c440aF+P8AaG7+tAHu1FFFAgooooAKKKKACikJx2zTPM3NgAr9aAJK/n0/4KK3Bn/bH+JSzbvkuQq/NgcIuDX9BEZ3DNfz8/8ABSSMD9sj4iEf8/EbH/vhKAP2k/Y2bd+yz8Lz66Da547+WM17LXk37J+mvo/7NXw0tJMF49BtM7enMSmvWaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBryCMZIJ+lJHJ5gzgj60+mKrb2JbK9h6UAPooooAKKKarbiRQA6iiigAooooAKKKKVwCikNJuougHUUmaTdTAdRTGycYbaO9KqkdWzQA6iiigAooooAKKKKACiiigAooooAKKKKACq2oXiWFrJcSnEUY3OfRRViuB+O3iN/Cfwq8S6ouwC3sZWJkzjO3jvUSbS0Gtz8d/wBtz4oeJ/2tv2nLTwB4Zlk1G0tbo2Wm2aMQpdsb2bnHG0Hp2r64+C3/AASF8A6N8P4ZfiE11r3jSeEtKsN2Y7O3fnCoEUMccZJJ6cV8hf8ABNDQW+I37bEOs3Uc7pYx3epGa34VZCQqhsg/Kdze/HWv3J6Uox93U0lufzv/ABt+G/jf9jH41SyaVeyeHryKeQ6ddWFwS4jBHBOemCOvWvT/AIT/ALd/x5+KXxr8E6RP42uY4LzUra0eytYkSORCwDluCSSPev0B/a0/Yl+GP7SHiH+2NS8br4d1yINxFcxbG6Z3q2T27etfnz4X+Gfgb9mr9sDwy83j/TL3SNHvEnW7jcT/ADr2fbjHWs4tpWluNK5+6Sb47MZJd1Tv1JxX4t/8Fbfh1e6T8ZdP8YiMrYaraiEsoPySJyQfru/Q1+gfjP8A4KVfAjwZcWVs3iv+157ptgXS7d5th4xu44zn9DXjv/BVbR9K8cfsz6Z4ts2lRFuIriJmXaHVgMAjHoTVocXZNM/OjRfgb8XPhb8I7b4x+H7640bQ5TH/AKVpt2yS89N4B+vX3qH9nzxfoHxE/aO0HVfjfrt5qejs+bi8vJi7FwB5YYnPy561Npf7SHiLXPgNbfBhPliu9RhjExycoWwo69if1r7W8Gf8EdtL1f4SQy6n4hntfGM6eckiMDbcjKhlxn9e9MR9TftFeGfhp8cP2Z9d0XQL3QbuC3sGn00QyxhYXVcgrjocDFfJP/BGP4nalaeKvHPw2vLndYQ266haW+chZFkKzEfXdH+VfLnxq/Yv+OH7OPns9tqF9oJLr9t0iR3iKDGdyjoOe9er/wDBH3w3q8H7T+pak1ndJZR6DcQzTSQsq7mliIBJ7/IaEtbie1j9p6Kbuo3VoZHLfEbxpZeBPDN7rF9KsdvaRNLJuPBUda/D74+fHP4i/tu/H46F4ZuLy5tZbg2WkaXauY4hGPvO+D7AkntX6Vf8FRPF0Hgz9l/VpRM0V/qMy2NvtPXfyw/IV8tf8Ea/gra6nrnif4m30RL2JGn6eSeFLAmQ47n7oqOpq7ci7mp4B/4IwXV74Xjm8W+PJrHXJF3NBYQrJHGfQs3J/CvIPjN+wj8Yf2O7V/HPhXxTNqOnWcwbzNOd0lRV5BkUHBH/ANev2ulmSCMySuscajLOxwB9TXk/xq+KvgS3+HPiWzvvFOhb5LGZBDLeRtlthwNoPrSJUmfK/wDwT5/4KGa/+0R4qh+HvirR0fXINPkuzrFuwUSKjKp3J6/MvStP/goD+058ef2c72G/8I6ZpC+DpQCNUaDz5Y2BAKurcDORg/Wvkv8A4JOpoOm/tIeMPEer+INN0aOwsHt4Bd3McC3HnS5OzcRnHlDp6iv0k/aI8afBfx18Ntb8O+LfGvh37Ld2rjaNRjkZWAyCArE5zilcrS+p8hfs9f8ABYmxuoZLH4v6U1ncb18nUtIgyhU5yXTPHbpWH/wUI/4KAWPxC8K6B4L+EWtSXK6wT/aF1Cu12VtojiHcEknOOa+Z/wBkn9nHwL8cfiP478PanrrLZ6dA0umXCuUWfG/35wAv514SNH1fwD8ULpPDyS6lfeH7wzwyQW/ngGJ8q7LgggY7jFKLUpOKHY+9/gz/AMEetc8V+C5tX8ceLX0HVb6JZ7WxsY/MKEgnE5fr26dMmvDP2Q/Guv8A7Jv7Zdp4ZvLqeGxn1E6NqMKkhJlZsIzKeODgj619z/su/wDBVrwN8QNNstF+JMqeD/EiIsZvWUmyuWwcncB+7PAyDx83FfM3/BTiDwtoPxy+H/xU8E6tY39vrHl3U8+nzpMhmglDbyBnBKsvX0q7iP2TjYMoYdCM0+ud+HviJPFngbQdajbcl/Yw3AP+8gP9a6KrMgooooAKKKKACiiigAoqnq+qW+i6bc395KIbW2jaWWRuiqBkmvzu8b/8FkfDHh/xxc6ZpPg+91bRrWQxvqHmhC+DjIX0oKUWz9GpM7eOtNBO3JHNfCOlf8Fifg3eW6teWOuWc2BuT7NuAP1FWbr/AIK/fBWGMNFBrU7f3fs23+dAWZvft1fsDWn7TNrb674Yaz0bxlBu864lTAvEIUBHPtt/WvhLwNeftZ/sT3V9pum6Lql3o8c3mSWz25vLRwM/Mh/hznt7elfUevf8Fn/h/bsi6L4O1rU2OQVkZI/m42geuea+6vhj4yPxL+Huh+I59Jm0n+1LRLhrC7ALxbhna1AX7n89X7TXx28XftDfEJvE3jSBLDU0gW1SzWMxiJFJONpHqTRe/tOfGLxB4Ni8KSeONbuNDWE232JJmKNCQBsIA5GBX9DWofC/wfq1z9ovfC2j3U//AD0lsY2b89tWYfAPhi2wIvDmkxY6bLGIf+y0D5j+Ye60m6tiBc28tuOitMjKD9Mivs/4J/8ABUL4h/Bj4d6L4N0zRdAvdO0uEQwtNHIHK5J/h6mv1p+OPxJ+E/wD8O22s+PIdL02xuJTFBusEkaRhgkKAvbI/OvKdD/a2/ZT8XCBhrPhm3eXhFvdPER/H5OPxpBc+StJ/wCC2Gv2sJTV/h7plzJgAG0upE+uQ2a39F/4LW2UbSm6+FWM42m11RI/XOdyHPavtGP4Qfs6/FxYrpPDHgXxN/EjLb28rDd7dRnH6VfT9jD4Dx/d+EXg7/wTwn/2WmSfF15/wWn0HULSa1ufhLdT206NFLG2uxYZWGCCPK5yCa+Cbv4hfDC6+Mx8WH4eXUHh77YLsaFDrMQT72dv+r6e1fufH+x18DFBA+EXg3B4P/Ektz/7LTh+x78CwoH/AAp/wSQOgOg2x/8AZKBp2Phb/h9Zpen2cVrYfCSSFYUEcStrqMoUDAHEIxXvf7En7fGq/tdeNvEOjT+CYfD9lpdml19st777R8zOQEfgYzg4+hr07XP2Cv2fvEkcsV18LfD8KuMEWEH2Ur9DEVI/Cux+CP7M/wANf2c7K/tvh94Xt9AF+VN1Mssk0020kqGkkZmIXc2BnAyaAuj01e9KFC5wMZ5NLRQSFFJRj3qbgBxwT25r8po/+ConxG/4acTwudP0yTwl/wAJANJaNF/eFTJsyGz171+q8i7kKnoRiv5q7y4Om/tBrcNKyeT4kDlgTnIuev14o5hpXP6VY38yNWxjcAadVPSJhcaXaSK25WhRg3rlRVyqEFFFFABRRSd6AEYgdao3U6Hv0qW5LeYAenaq10o2rxT6G9NLcrK0d/MsQUnByWHYV8EfFz/gq5YfDf49P4P07wzHqPhrTb77Df6h5h80tkAmMDjg5r9AbGMGTcONvP8AOv50P2noDbftJeP1xtA164xj/rqKy3Km9bH9G2j6lDrWlWd/b7vIuolmj3DB2sARn86uVy/wuYv8OfDLE5J023/9Fiuoq1scwUUUUwCiiigAooooAKKKKACimtSUDH0UyjIoAfSZqNjQtYSlrYdiSjIHU0i0MobBIzimtST8WP2+LWXx7/wUqsvD0h3QfatFsFA5+R44nb9WNftHaRCC1hjHARFX8hX45/tGCOP/AIK5aL5hCL/bOknLHA/1MeP1xX7JVqtgCvxq/wCCkn7WnxQ8T/EjxP8ACmxs7zSPCVvcm2WOG3dZL8L1bOPmUn04r9lG/TvWXdeF9J1C9W8vdMs7y8UbVnnt0dwvoCRTA/nd+BWv/GD4H+KpPEPgbw5rEWqtAYhN/Yss5VTngZTivoWL4m/th/tWzWXgVk1+wtrhw01y2mPpsQUdTJLtGQPTPNftTFp1pBgx2sMfb5YwKmjjEYwAAPYYoKufzt/tJfDnXPA/7QB8B6v4hufF2qaa1tYLcuWdixRSIlByxIZse5r6n/4LNTRr40+FkEjhXTQ2Z4/4gplx0/A/lX1347/4J26J41/a0074yS63IkEV1Ff3GktECJJ48bCG9MgH8Kz/ANvv9gG//a18ReGvEega/baJrOl2hsJFvY2eKSLzC6Yx0ILv+YqbBzHoP7Nv7Vvwg1j4LeEY18f+HtJmtNMt7eW01TUoLWWNljCkFXYdxXjP/BT74mfDP4mfsp6pYaT4/wDDOsarZ6jbXtrZ6bq9vcTSOpZCAiOSflkbtXjGm/8ABE3W5ohJf/E6xt7lvvrFo/mp+GZBitKP/giTPn978VoNuOieH1HPb/lrRyivrc1/+CJuuao/hf4laJNFMuk293a3cDsD5fmurpIoPTIESEj3HrX6cV86/sYfsixfsjeD9a0VfEX/AAkkup3n2p7j7Ettt4wFwCSfxNfRVMG7u5+H/wC1dND8cP8AgpRFoSSm/s5NcsNHcwnzF8tGUOvGeAAc+mDX7c2VrHY2cFtEoSKFFjVR0AAwBX4kfBGzh1T/AIKqWkd3zH/wlWoSYJ/iSGZlP5gV+31MQUUUUAfit+07/wAE+PiLrH7WWqad4M8L6lf+HNcuReLrbWrmxtvNJMm+XG0EfWv1L/Zp/Zr8L/sz/Duy8O+H7OP7WUVr6/YZluZepJbrjJOB2r16igBF4/nS0UUAeD/Hr9in4WftA6fe/wBt+Hrey1qdCE1qxQR3EbcYbjhunesD9jX9iXQf2RtN177LqT67rWsSKJ9RlTYfJQsUQDtjcc+tfS9FACDpS0UUAFFFFABRUdxcRWsLyzyJDEg3NJIwVVHqSelc1oHxS8HeKtYm0rRvE+k6pqUIzJa2l4kki/gDQB1NFFFABRRXzx+13+2Z4V/ZT8MxvelNU8UXqn7Bo6PgvjGWduiryOuM9qAPe7u3uJWTyZfKAPzcdashTgZ5Nfil4m/4K3fHjXi17odtpmiWEbn5YNLFwCPR3cEDHtXpfwA/4LHeIZvEun6X8UdC0+50q5kSFtW0lGilhJOC7R5IYcjgAUAfcv7bvw5+I3xN+BeoaT8MdUfTvEazJP5cMohkuUXOY1kLAKT79cV+PHwp/ZB+OP7QHinXdOs4Eg1XSbk22qNr2seTLBJnkmPeZGX/AGgpU9jX7/abqEGrafbXtq/m21xGssb4I3KRkHn2rkLf4M+ErH4qXXxFttLWDxZd2a2FxeRyMoliByNy5wWHrilYrm0sfkvff8EfvjtZ2sjwa14PvXC5EcOqXayMfQbogufqa9n/AOCbf7Dfxb+APx21fxd4+0S20bT00mWwhYX8Fy1y8kkbZXypGK7RF/EB94Y71+nFLRYVyJQwOCvHJzn3r52/au/Yd8GftZNpl3rt9f6PrOnRtFb39iwbCE5wyNwefTHWvo6imFz8e/ih/wAEj/ir8O7621H4VeJk8RSK3GLhdNuohxzvLAH/AL67V58Pif8AtefsZ68ZPEa+ILjTIWAddXZr+zkH91ZgWHfqDX7f3VzFZwPNPKkMMYLNJIQFUDqSa/Pf9tj/AIKbeEvAtre+DPAtrYeMddLGK7mvYfNsYBj8nbk9OmKB7nffsf8A/BSfwh+0NPpvhjxDGfDnj26LKlmEZrefaCco+MA8dDzX2fuFfjt/wTX/AGRvFPxB+Klj8ZddtI9G8N2dzJd2kfl7DcyknhF7ID3r9O/j1+0R4L/Zv8JQ+IfGmotZWc84toUhjaWWVyMnai8nA6ntkUBY9Opa4b4P/Gbwl8cvB9t4l8H6oupabcDPIKSRn0dDyp9jXc0EiUjBWxkZpk0yQgFzjNOBzzQAybaUwwwKSHbs+WnsoYYNCqFGAKB9D8Dv+CoikftqeOc947Q/+S0VfsX+xa/mfsr/AAxP/UDth/44K/Hv/gp9Cb79tTxisZxvjtEH1EEa/wA6/aP9mvwjc+A/gJ4D0G8KG6sdIt4pfLbcu4IM4NAM9LooooENdxGpY9BUNtex3W7YG+X+8MVM1eX/ABs/aU+HP7PFnYz+O/EUOi/bmK28PlvJJJjqQqgnAz1oGeo5pa5P4Y/FLwv8YfCdt4l8IatHrOi3BIjuo0ZQSOoIYAgj6V1lAgppB3Zp1fH/AO2V/wAFGPC/7K+rWvh3T9KXxj4rlRnnsorxYI7McbfNbDctk8AcYoA+vo1Krg1/Pt/wUe3f8NjfEcsMf6SoHI6bEr6usP8AguBftcRrefCW3WIsA7Q66SQM9RmDB496+Ff2pvjPZ/tBfG7xN450/TZtIttSKstrcuHdcBRyRx2oA/oA/ZwV4/gF8PVkOWGhWecf9cVr0evOf2cZBN8A/h64OQdDs/8A0UteikkYwM0ALXEfEn42eBvhDZi68YeJ9P0KNvurdThWb6L1NeM/t1ftlWv7JHgfTpbfTzqviXWzJFp0BI8tCgXLyc5x8w6V+Tvwj+Hvjz/gop+0JdDW9bltjMkl3c6hLG8kFuikDy0HQE54HtQB+yfhP9tD4L+N9UtNO0bx/pN3eXT7IYhMAWY9BzXtSsHUMDkHkEd6/Db9sD/gnV4k/ZS0Cy8Y6JrzeINChlUTXccJhms5Mjaxx2J9+1fop/wTU/aEufjp8A4odXvftniDQJvsF1IzZeVQAUk9cEcc+lAH1vRRRQAUUUUAFFIzbVzjNIrblzjFADqKKKACiiigAorO8Q+ItM8J6PdarrF9Bp2nWyF5rm4cIiAepNfK7f8ABVD9nuHUryzl8S30ZtpPLM39nu0cnOMoVzkUAfXNFeT/AA9/at+EXxSW1Xw18QNDvri5IEVo92sM7N/d8t8Nn8K9X9MdKAForG1vxloHhl1TV9c07S3YZVb27jhJHsGIrlNU/aM+FeikC/8AiP4Vs92QPO1i3XOOuMvQB6JRXjGrftmfA3RQhuPip4WbfnAt9TimPHrsJxXn/iv/AIKa/s8+FYyT45j1WUZ/dabayznj3C4/WgD6nor4f8K/8FdPg34s8Z2OgQaf4itUvJ0t4tQubRFh3scDOHLAfUV9uwyrPEkiHcjgMD6g0APooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0ZoAWikzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTVXaSadRQAUUUUAFFJmjt6UALRUaLtZiTnNK0gXrgD3NZvcYSOFxk4zSNzXIfET4seEvhlotxqviPWrLT7a3QyETTqHbHZVzya+JNc/4LN/DXS9auLWz8J6/qllGxVbq3ES78d8Mw4qS1F2ufoMfMKtjCnHFfFX7dX7SPxP8Ag9ov2LwX4W1G7nljMj61FEXitQPUAc55/KvJr7/gtfob3JGmfDm+ltlBLPd3qRsPThQ3X619mfs0fHLT/wBqr4RWni59Dk0uG6Z4JtOusSKcHHcfMKFaTsXF8utj8yvg/wD8FeviX4T1J4PHWn2vimwO1d8KfZ5ocE7jjndnj06V+jP7P37c3wt/aEhgg0bW47LW3QNJpd4fLkU+gz1qD4ufsc/APWNJv9Y8R+DtI0tI43klvIT9mxxySRxn8K/En4oafoXhn4yz2fwrvLyW2S62Wc1vIWbdnGFI5Ip3a0JSUtT+kGORZFDKQynkEHINOrg/gXa39j8IfCUOpvLJqC6bD57Tff37BnNd1uq46ohqzHUUgNLVEhRRRQAUUhbFAYGgBaKKKACiiigBO4r5d/4KPfEm3+Hv7Lfigs6i71BVsoVYE5L9eh7CvqJuBmvz6/4K8akJfgXaWzDa39qQc98ENn+VRLYuKb1PNf8Agif4J+X4i+LpCSZDb6dEOMfLudj0/wBod+1fpZ490G+8TeFdS07T702Vxc20kKuOOWXA57V8X/8ABHPS47f9mvVb0KRNd61MXb12gKP5V957aLKQSep+Inij/gln+0RJr2p3NvZ2N9HJLJIl1/bC+Y654zz1x2xXyH8Sfh/rPws8Zap4U8SWwttZ0+Ux3Cbw204HcDmv6d9tfCn7SH/BLPQv2hPjFdeOT41vNF/tCVXv7IWay7wMAiNsjaeOpDVRNzx79lf/AIJSeBvGXgXwv428T+LtQ1VdQhivktNKCwxq2d21mYNkdAeB0NfRX/BSfwwsf7IGraRpWnyTJbGERrGpby409cfzr6X+Fvw00j4RfD/RfCGhmdtL0q3W3ha4cNIQO7EADP4V0l3Y29/ayW1zDHcW8i7XilUMrD0IPWlZjTPwK/4J4/Aq++L37THhr7Tp8z6JpDf2jdyyxHy/3eNqk+7EflX79JGsaKijaqjAA7Csrw/4P0PwrG6aNpFlpav977JAsefrgVr496VmJsiuLeK5haKaNZonGGjkUMpHoQapaV4d0vQtw07TbSw3fe+zQrHn64FaWKNtUhDaKdtpAKYH51f8Fm/EFpH8IPBmkmQNcTa0ZvLHUBI+f/Q69H/4JM+Hl0j9krTroxbX1C/ubgt/eG8qD+Sivmz/AILSatp/9ueAdNtp9+qR/aZ54M/dV1jVTj3wa+7f2H/Bv/CCfsueAdKKGNv7PWdgTnmT5z/OoWruavRG7+1D8PPE/wAT/g1rnh/whfrp2uXUe2GWRyq+4JFfj18R/wDgmz8a/h74P1jxP4gm0v8AszTYmubiY37OxA9iK/d3vXPfELwHo3xN8Hap4Y8QWxu9H1KEwXESsVYqfQjkGnbqRfofz3/su/sp+Mv2p/Emr6Z4RmsbU6XFHLdTXczIqK5YLjaMnJU19HN/wR1+NEl0Q+t+Gnjz/rGupT+myv03/Zt/ZF8A/stw6yngy0uYpNVZTcTXU7SsVUnaoJPQZP517W3Q4644qvUL22P5n/FGmeI/2f8A4mazo0WqLb6tpkj2s01ixCt2IHsa/Vj/AIJN/s4f8Ir8M9Y+IHiOz83VvFJCRpeR7itupbnn+8WOfXFexfGf/gnT8J/jl8TLTxprNne2l8JPMvbexmMUd4eMb/TGP4cE5r6a0TR7Pw/pNpplhAttZWkSwwxL0VFGAPyoslqhNn50ftj/APBKiDx5q0/iv4SNa6NqExaW80K4YrbzScYaLqEJ5yDx0r8v/it8I/Gvwb1htD8Z6FfaNdJuSJZ1YwvyCTG3Q/ge9f0yVzXjj4Z+FfiVYx2fijQbHW7eNt8a3kIfY2Qcqeo6DpU2K5jk/wBl5J4/2e/h+lwnlyro1spXOekYr1KoLKyg020htbWFLe3hQJHFGMKqgYAA9KnpokKKT0rM8TeI7Hwlod7rGpzpbafZxNNNM5wFUDNFxEmva/p3hjS7jUtWvYNPsLdS8txcOERQO5Jr40+KH/BWr4OfD/XX0vS49U8XSRMVluNKiXyVx6MzDPfp6V8GftsftseJf2rvGkHhLwet5F4Yhna3trC35a+kYgZbAyRwOM96+mP2Vf8AgkX4aj8N6dr3xea6v9WnUSnQLeXyoYlPQSMvzE+wIpjasdLH/wAFpPhs0oB8FeJvL7sFhyPw3179+zn+358Lf2ltYfR9Au7rS9aVN62OqxiJ5fUIckMR7GsfVv8AgmL+zveaTc2tn4Ej024lQql5Fe3DvEexAeQjj3FflH+1p+zlrf7EvxmsBompXosGK3el6uvyPuBBIyO44yKASuf0A3VpDfW7w3EUc8LjDRyKGVh6EHrXhnxC/YZ+CHxMvnvdZ8Bael84w1xY7rZj+CEL+leh/BXxYfHXwl8Ja+0/2h9Q0yCd5T1ZigyfzrtqAPjPU/8Agkx+z/qDhhpmtWg/u22pFR+qmqK/8Eh/2f8AkG38SMf9rVzx/wCOV9s0bRQF2fG3g/8A4JS/A7wb4t0zXrS11a7lsJhOltfXnnROwORuGBnBr7HhhS3hSKJFjjQBVVRgADoBTqWgQUUUUAeIftafsv6P+1V8O4PDWp3r6XNbXIube/ijDvEf4gM+oA/KvhzVv+CJ1xNcSHT/AIoJHC55W60ze2B0wQ4r9UqaxVVLMQABkk9qB3Pxi8cf8Enfjb8PGS88G6/Z+IvLJYfZbh7WZdvIIDEjP0NZ/wADP+Cgnxx/Z98bR+BfGcF34sVLuOxOla0c3cLFtuEl6nr0ORwK+0v23v8Agox4b+BGj3PhvwTf2mueO5t0LGNt8On8D53I4Y8nAB7V8p/sE/s5eO/2kvjtbfGb4k28+o+HbWVrmO81Rc/2hOMhNqt1VTznGOBQPm7n6+aPeS6hpdpdT27Wk00SyPAxBMZIyVJHpV2kVQihVGABgAUtBIUUUUAFFFFADWbFVZJ3WUDHFWXYDAPfpUDRFpie2OKlouNuo+GQyKc1/Nx420c6h+0tqumQ/KJvE7Qpt4xm4xX9I6RjauexzX84vj5W0f8Aas1XDEND4qLAg8j/AEgUrFddD+i7wzZjT/D2m2oYsIbaNMnqcKBWnVHRW36RZN13QRn/AMdFXqoyCikam5pgPpKbk1Wubpo8gCpuUouWiHTyB+B2rK1CQpHnNZ+sa9Jp8RcRl8ntVb+0v7YsyJoGRWHBHrUOp0sdcYcq1N3TbrzliA6hufyNfz3/ALYzhv2qviIQMD+2JOB/viv6D/D0Jjt1V4yjIOM9wa/A79v7Rf7B/bB+IMAGEkvBOv8AwLaaUXcxk7s/eT4WnPw48Mn/AKh1v/6LFdMn3jXIfBtt3wp8In10u3/9FiuyrVbGLGOu5kPpQzHzFA/GmXDOqgqM+tRopuMmQfLjGPrTC3UsrnHPWlr8nP2oP27vi14W/bAvfA/gbxHDZaNBqFvpyWsltG6MxKhySw9zX6raK1y2j2RvJFluzChldBgM2BkgfWgRdooooAKKa1Qt5uTjBHapuOxM1QSSHIwdo71GIJmYktxTms2YYLcHrWb1LVluQ3cnnRFIzuJ6n0pkMLQ5Hm7zjp6VY+wiNcRttb1qG1094yxlbcxNTaXQ0UlYIw37zNWbf7tPCbelOWp5X1Ik7jlp1Qp95qlB4rSPYzZ+Ln7bzfYf+CpmgzDp/a3h9z7f8e/+FftGrblBHQ81+K37edvJcf8ABTK2giO2aa70PYffyoq/aOyVks4Fb7wjUH8q2ET0UUUAFFFFABRRRQAUUUUAFFFFAH4ifBb9z/wVYtM8Y8T34P4wy1+3dfiJ4Ojk8O/8FXoI7hGhP/CVXGRINpG+OTB59civ27oAKKKKACiiigAooooAKKKKACiivz9/4KNftgfFv9m3xl4cj8IaVFa+GXjLy6lcW5lju5eMxE/wbRj67qAP0Ab3OKQFVxz14FfFv7Gv/BSHw7+0heW/hfxBbJ4b8YtGPLQv+5u25yI89+M4969c/bT+PJ/Z3+AGv+JrZ4/7YkQWlgjnGZn4BA74GTQM+Af+Cl37a2u+MPHEnwv+G+r3D6PahoNSfSdxkupjgNEcDOFIxx610H/BI39m3xDo/jrxH4+8ZeGNT0g29pFFo9xfIYvNZy/nEqTknATqO9R/8Ep/2XY/Hmq6l8bPGMEl1P8AamXS1m+7JKSTJMR3GSAPcGv1aVQihVAUDoAKAYtFFISFBJOAKBHlv7Snx90X9m/4Val4w1n94YyILO1X71xcMDsQccdCSenFfkF+z/8ACHxp/wAFC/2jrzxP4wF1e+Gornz9VvBKBHDHk+XbpnGehHy5x3rtP29Pjpqn7YX7Rmi/CXwb5k+i6XqP2CHyT/x8XDECWYg4+VQvGfQ+tfqd+zl8CdE/Z3+FOjeDtFTK2sYNxcMoDzynlmYj3oA2vCPwb8E+BPDceg6L4Z02y0tYxEYFtlIcAfxZHzfjX5af8Fe/gd4Q+G/iTwJ4m8MaXb6PeawbiG6t7ONY4j5RjKuFAABO8/lX6+tX5Cf8FX/EU3jz9qTwD4Ht7hZ7eyjt42hBxslnlGQc8crtoGtT9S/g1I83wn8IPJ99tKty2fXyxXZVkeEdJTQvC+k6dGMJa2sUIH+6oFa9AgooooAK89+P/jzV/hj8H/FHijQdL/tjV9Ns3mt7TkhmHcgdQOtehU2SNZEZHUOjDBVhkEehoA/nv+JX7Wn7QH7RF1Jpt7retT2945jGj6NbNFEc/wAGEGW/GrXh/wD4Jx/tC+IrCO8h8A3cMcuJFF5PHA/PchiDX766T4Y0bQWdtM0mx05nOWNpbJEWPqdoGa06B3Pwab4Dftg+C4YtBtdF+ICWdou2KHR7qYwIPYxnFVx+x3+1R8aby3sdb8NeKphbEvC/im8dYkLcEqZTgHgZx7V+9tNZQ2M0D5mfN37Bf7OE37OXwQsNK1nRoNK8X3JZtWaC5E6ysGO0hgcYwe3rX0nSUtBJHLGsmNyhsetfFP7fv7e9r+zlpp8J+FGF148ukDZ2bo7RD0JP94+lfW3xG8baf8N/A+t+J9VmWCw0u0kupGb/AGVyB9ScD8a/FH9ln4Rah+3F+1bq3iPxB5174ehu31HUJpCSAhYmOIH8OlBSNnRfCv7aPxY0k+MdOu/E8ttcZmi8u6EAdTzlUJ6V1HwH/wCCjHxS/Zv8ZXPhb43WmpanZKFjaO9TF1a4JJYf3sg+vav2F0jTLbRdNtrCyhW3tLaNYookGAqgYAFea/HH9mX4f/tBaLJZeLNBtrqfafKvlQLNGxHUMOTQFz8Nv2pvino/7RH7Umo+J/C0c0enazdW8dt9sXY5OUXLDJxyK/oJ8J2z2fhfSIJMeZHaRI2OmQgr+cvXvh8vw5/aXbwpby+dHpniKK1jYnqomAFf0f6QCuk2QPXyE/8AQRQSWicUbq8x/aWu/G1j8FfE0/w8ilm8XLbk2SQhS5bPO3JAzivxzs/2nP2rvghrk2v+IbnxhDF5wFxDr1pK1lJg8gbl2j/gNA0rn7rySLGpZjtUclicAD1NfiJ+0ZL4n/by/bg1Dwr4RnhWCxd9Psri4ZvIhgiyHlbaG6kn68V9L/Fr/gqR4e8Rfslz3+hh7Tx5rMb6W9lgD7MxXEk33s7cE7T+la//AASD+BEXhv4a6r8TdSt92seIpTDazPyfsysTnkcFmJ6dQBSKWh9W/sm/s/r+zT8GNJ8EnU/7XuLctLPdBNqtI5ywUegNeyU1adTIPPvj38XtM+BXwl8ReNNVcLDptszRRkgGWYjEaDJHJbFfh/8AsyfBfXv24v2k7yXVZTJYvdHVtbupixKxF+IweeTyAPrX2x/wWW+NVrpvgfw38NLWYvfahcjUr6MY+WJOIx1zkkt27V61/wAEu/2d1+EHwIt/EWpWqxeI/E/+lzSc7hBkmJTkDnB/WgD0Txx+wH8E/F/gSTw7H4F0vTHWErb3tnF5UySbcBiw5POOua/B/wCM3w1vvg38S/Eng7URm40u5kt1YA/MoYFWBIHBFf011+I3/BX7QrPTP2o4rm3RInvNIilmCjq/Iyfc4oA/VX9jvUf7U/Zh+G1xz82i2459kAr2SvBP2EZGk/ZL+GxYEEaVGOfYV7tdXCWlrNPIcJEhdj7AZNAH4af8FLvjNJ8cP2mToGmCVbXQnXSYIpMHMxbDuuCeCcflX6wfshfs/wCifAL4NeH9KsbKFNUktElvrxU/eSyMNxyeuMmvwx8VfEyGx/ac1bxm2nDUY4fEEt79nbkuiydPTPFfsD8Jv+Cn/wADPHug276h4hPhLUEjUSWWsRmPB6YVxlW6djQB7d+034DtviX8A/HPh+5jSQXGlzvH5g4WRELqfzWvyx/4I7eOrnwv+0N4g8I/M9trOmu7qD8qPbvgHHqd5r9BfHH7eXwHHhHV41+IelXTzWc0axwSb2YlCAMD61+eX/BJjw3N4j/a217xFZYbTbCwuCzEEcSyDbj/AL5NAH7SUtFFABRSE4r4m/4KPftWeP8A4Aad4e0rwBpd19v1MSPPqYszNGijACrj+LqT9RQB9tUxpEiXLMqD/aOK/Cuz+Pn7YfxVnmi0jUPGF6ZANyWlsYkAPTqBitLT/wBkX9sbx8XuL6PXIC3zbtS1gx7s+gDGgD9sNQ8WaJpChr7WdPslPQ3F0kYP5msTT/jF4G1bWItJsvF2jXepSnEdrDexvIx9AAea/HKb/gmH+0vrkZN41mxHOLnWpG/oa9N/ZQ/4Jp/Fv4efH7wt4n8ZQ6ba6LpM/wBqeS3v2mdmA+UYwO5oA/XCiiigDmfiR8O9F+K3gvVPC3iG3+1aTqMRimQHDY9Qexr4c8Uf8EY/hpeWcy+HvGfijRbpiTF9okhuYIyf9jYrH/vqv0JooA/HL4rf8Eg/H/wz0OTX/Bfja38VahZlrh4xYnTpo1UZDRsJX3N1446V7D/wTB/bS8U+PPEM3wn8d3E2p39ratJp+ozqTNmNiJI5GJ+bAK4PHev0a8RalbaPoV/fXzpHY29vJLO8hwFjVSWP5V+K3/BPfT4fGv7fU2o6VcXNrpkLX9/G0R4dN+Ap6YB3fpQUjt/2qf8Agnf+0j8SvjJrGuWT23jDTdQu5Hguf7WjtxbRE/KrRyupHH93d07V5L8Xv+CZ/wARPgF8GdU+IHirV9FxZ+Xv02xJuJBuYL8zsAo6/wAOa/dvJBr4A/4LKeNpdD+A/hvw/FcPF/beqnzEQ/6xIlBII+rD8qCT5N/Y1/4Jz+HP2tfhw/i3/hY9zpL2t21pdabDoqMY3ADY8zzhnII/hrnf28P2KfC37Ho8F/2b4iv9dOuSzC7+0wCMwxx7MMm1jknc3X0FfbH/AARl0P8As39nDxBe5Y/2hr0kuGHTbGifj92vAP8AgtV4knm+K3gbRHIW0t9HkuU9d7yMD+iigD2/9lP/AIJy/A3xR4M8GfEiy1HxFrNxIsV9Gs92iweapzgoI84B/wBqv0Khj8lAgPyjhRjoPSvnr/gnzAtv+yH8OgqeWGsA236kmvomgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBuKNtfKt5/wUa+Gdv4guNHTTvExurcMZGk0somB6HdzXikn/BZnwV/wmr6XH4I1g6Rv8ldQknjWTfnGTHzgfjWMa0XomdEqFSHxKx+ih+WlVs1+d3j/APbl+OXxOt7i0+EHwd1JLXGV1e7PmFvQquAMfjX1t+zB4s+IHjD4T6Zf/EvQxoPinJSe3A27gOjEdia1jJSV0KdGUFdnrtFJS0zAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBK+UP+CgX7R3j79nzwDpdz4B0Vr/U9Qmkje7FubgWwVVIJQKRzuPX0r6vIpNoPUZqWrjTsz8I779un9rDxxMlvZavrAnzjytJ0bY3PriOrdn4Z/ba+L8jqrfEKcKAxNzcPYx4b03FAelfueI1T7qhfoKdtqeVluVz+ff4ofsa/tCeGtLuNd8eaJfPZQo0r3GoamlxjAycYkPNZH7Gn7Lk/7VPxSHhyS/fS9Ito/OvbmIBnjXsFUnuRX66f8FH7qy/4Zn8SCWULPHESm0884GPxr50/4Is+EdMXwn458Q+Vu1U3kdn5h/hjCbsD8TUpvmsXb3T2jwL/AMEm/gT4NkgnvbLVvElzGVYnUrweUSP9hFHB9CTXV/tQftKeG/2Jfh3Z22i+E3LSL5Vha2MAS3UgD7zDp1FfUeOawvF/gHw94+08WPiLR7TWbRTkRXcQcA+o9KuSfQzT6M/n8/aE/bU+Jv7Q8rLretyWOjrI3k6XZsUQAgcNj73Qdad+xv8AHDwV8AfiBceJfGPg248WSJGoslgdMQPk5chj1xiv2nvP2GPgbfNOZPh1pIMxyxVGGPpzxXKXn/BNH9n28Lk+Cli3dfKuXH9aOXSxV4nz7ff8FpPCCQ7dN+HmtSSgcLNPEqn6YNfV/wCyn+1t4Y/at8KXOp6HBNp9/ZkLeWFxgtETnHI6jg1xUf8AwTE/Z8jheP8A4Q5iG/iN2+R9K9k+C37PXgT9n7RZ9M8EaLHpUE7bpn3FpJD23MetGt9Cbo9GWnU37tDMR0GRVkDqKimuY7eN5JXWKNBlndgAPqa4/VvjV4B0OTy7/wAZ6Dayf3X1CLP5bqVx2O1ory+6/ae+E9ljzviH4eTPT/T0P8jUMP7VXwhuJBHH8RfD7OegF6tLmQWZ6tRVDQ9e0/xLpsOo6VewajYzDdHcW0gdHHsRV+mncQUUUUwGt92vzS/4LLeKLex8D+FdFWBjNeXhlkkHHCL8oH/fVfpa/wB09jX5b/8ABY+BLnQPC0sl0rXMFyQEXjhhj+lZya0RtDZn0F/wSh0MaT+yPo8+STe3lxOQe3zkf0r7Ir43/wCCUWqS6h+yTo8UgULa3c8KFQckbj15r7Iqo7GT3CkpaKoQUUUUAFFFFABRRRQAUg+7RSZ4FID8V/8AgsBpd5aftCaZdTuogfTFMBHXhu9fqv8Asu6l/a37Pfw/ufMEhfRrfLAY52CvzI/4LNa9YzfFnwppUcH+lw6c0ktx/eVmwB+GK/RP9hy4kuP2U/h1JJ97+y4xwMVEXZG0tj3UfeNLSL9406tDETaN2cc0MobrS0UAFFFFABRRRQAUUUUAJ3FfBv8AwVs+OTfD34OWHg6xl8vU/E0hTKtgpCp+Yn2OcV95NX4of8FhPHkHib9o7TdHtpS/9h6UttKp52uzlzgevNQ9yo7nqn/BIH9me01WTU/izrtmlx9mk+yaOrgnY4z5kmOhzwAT6V+rQzn8K/Nf9jH/AIKGfAj4U/Azw54M1nUL/wAP3+mWwE7S2MkiSyEncQ0YOfXmvoGL/gp1+znIpI8egezafcg/rHVIJbn1O1flN/wWy8RWVxffDrRUZWvrZLm5kXPKq+wL/wCgmvpjxT/wVU+AWj6Tcz6f4ln1a9WNjDbw2Mw3sBwCSoA5r8xdSb4mf8FFv2hn1G006S6DSJEGCYhsrTdwCcemetMSP2Q/YrsJ9N/Za+HEFwCJBpEJ59CMivbawvAvheDwV4N0TQbZQkOnWcVsqr0+VQK3aACiiigQUUUUAFFFFAH5z/tYf8FUdX+BPxi1bwT4c8I6fqcelkRz3epSyKWcjnaFI4+tfIfx2/4KlfF34xeHm0Wza18G6dIT57aGZFmmQ/wGRjkD6etfrt4//ZJ+EHxQ8QS654m8AaNq2rzHM15PbgyS+m496p6f+xX8CtMwbf4VeF0YfxHT0J/UUAfz+fDTxP4c0Tx7Zax420m48T6ZHMJprETbTOc5wxIOc1+rvgX/AIK9fBzRdFstJHgzXdAtLSJYo7SzijlSJQMADBXivrfVP2TfgzrSqt/8MfC92q9BNpkTf0rh/Gn/AATv+AXjTT2tZPh7pukAncJNHj+yOD9Uxn8aAOE03/grR8Ab541n1DXNOVuDJdaYdi/UqxP6V9QfDP4p+F/jD4Vt/EfhDVY9Y0efhLiNGQZ7jDAHNfCnjb/gi38PdXuml8N+L9Y0CIn/AFMypdKPoWwf1r7g+C/wssPgv8NNC8H6dJ58GmW6wm48tUMzDq5A7mgDt6KKKACikam5oAZdTQ2sLTTyJFFGCzSSMFCj1Jrx/Wf2xPgp4f1h9Kvvib4bh1BG2NB/aEbFT6HB4r88P+Cj/wC0z4r+Mvxei+B/gG5mfT47hLW5hsSQ97cMcFGI/hX0rrPhb/wRdsLrw3DP488aXVvrEqBzZ6VCpSHPYs3U/Sgq3c/R7w38SvCnjWOKXQfEWm6vGRu3WV5HJge4Br+fr41Ko/a614ADyz4pzwOP9cK+99b/AOCNU2hyLc+Bfitf6bdAk7rmAxMOOMNE2a+BvA/w7uND/ay0Pwbq93Hqt3beJIba5uslxMwlG4nd1zjvSKR/RBofzaHp3Ug28fT/AHRVfVvGOh+H7y3tdT1ezsLm4IWGG4nVGkJOBtBOTWpbwi3gjiUYVFCjHoBivw7/AG+PiFf6x+3hNJ5zyR6HqVnaW6FiVGGXOB260rk2P3IJyARyK8e/ao/aH079mX4UXnjK+s21F43WG3s1bb5rt2z2r1PQZTPoenSN957eNj+Kivz3/wCC1Vxfw/BvwPFbswsJNWm+1KDjJEa7M/iTRzCW59CfsX/tl6T+1v4a1OePTv7E17SpAt3p2/eFRs7HB98H8q+i7lo9pDDJNflr/wAES9Nh874makWLXLLa2x9No3MD9ck1+pN0wVRxyaVr6l6JmfeRwPGi+UWYHjAz+dcZ8Wvix4T+Bfgq48R+Lb23sraJGaKBnCyTsBnagPU816AzJb2rzSsscSqWdm6BQMk1+KX7XHjzWv25P2t7XwL4OmM+l2kxsLI7j5YxxJKR+H6UcpblfRHdfED/AILLeM5PEFwfBvhnS7XRVfbD9vDPK4Hc46V8VfH3476v+0F8RrnxnrVnZ2upXCqHSzUqvy9zX7UfB/8A4J9/DT4S/C290aTQLXXddvbBoby+ukDtJJtP3M/d5Pavw5+JHhG88CfEHXdBvbKTT5LK6kjW3lHKrv4+tOxCP6I/2YdUfWf2f/Ad3Ihjd9Jt8g+yAV6hXnn7P2P+FI+BtoAH9kW/A/3BX5a/8FR/i58SfBH7T2lJa67cadpunW0d5pMMLlUB/iJA6kkd6ZO7P2KkXdiqmralBoulXmoXLbLa1heeRvRVBJ/QV5F+x38a2+PvwB8MeK7l1fU5YPJvdoxiZeG/PrXPft8fGyx+Cf7N/iW6ny+o6xA+l2EQ6tJIME/gCTTF5H5m/sy+FLP9qz/goVqer3Ku2jw6jca42043eVIPLB9s4/Kv29VQqhQMADAr81/+CNPwim0rwT4r+Id/C27VrhbCydh1iiJLH/vtiPwr9J1/XrQDHUUUUCM3xFqDaRol9fpbvdvaQSTrBG2GkKqTtH1xX4/fEH/grv8AGCTxFfQ+H/DWh6HaQzPEI7i1kmnOCR853AZ+gr9kmGevTuMVUXSrOO489LWFZv76oAamxSZ+LGkf8FLv2o/Hdy1j4fs4Lq84Ij03QjMwz7ZOK10/aS/bp1SdzHp3i2Ju62vhSMj/AMejr9mh15xmlo5Quux+M918X/27ryAhrXx4kZ5Zv+EXhjx9D5dfUP8AwTzj/aT17xLq2v8Axc1TVI/DPkNFb2Gr2yxyyyluGUAAqBg/nX3xSHpT2QhvHTPNFI3Sq8kjRyLjoTzWDlqOxYbPamwr8vzcnNRvPHHk5570lreLcSMq/wANEZahy6H41ft2fL/wVE8Ont9v0An8DFX7QV+LH7eTFf8AgppoLZwBf6Gf/Ho6/aeugkKKKKACiiigAooooAKKKKACiiigD8ZPF0KTf8Fcl8ohwPESklTkA+XyK/ZuvxP+LV1L8M/+Cpp1C5z5beI4JfnGCUmAAI9ua/a5WDqGU5DDIoAdRRRQAUUUUAFFFFABRRRQAlcz8Qfhr4a+Knhu60HxTpFvq+l3K7XhuEz+IPY/SunooA/HP9tD/gnVq37PH2z4n/DDUpIvDul7bmSFpStxZndjKkdVBIrwv4uftMePv20bz4aeBZ4WkktzHaJDCebqckK0jepwP0r9uf2jtDs/EfwH8e6ffhTay6Nclt3TKxlh+oFfjX/wS08MaVrv7XuhjUTHItjZXN1bK/I84ABQPflqC1sftX8I/ANh8L/hzoHhjTrZLW30+0jiKIoGWCjcT7k5rsKatOoICvD/ANtH4vR/BP8AZx8YeIRP5F61q1nZsOvnSAquPoMn8K9wr83v+C12tXdn8Lfh5p0MxS1vdVuDPHnh9kSlc/iTQB4F/wAEfvC9r4u/aO8QeIb+IXl3pWmNIkz84klfBfnvwRX7O5Ffzl/AX/hefw61D/hLPhhoPiiP7RGFN1pWmTzRTKCeDtQhhnNfRiftZ/txXOLeLQvFoZjtH/FIOP8Ax8w8UFWP2I8eePND+G/he+8QeIdQi07TLKJpZZpSegHQAZJPsBX48fBfw/qX7dX7el745S0dPDWm36X9xMGG2OJGIhXBOTkr26d6ms/2Wf2uf2sPE1jH8SbjWtJ0Ine11rF0ixRK33gsCvkEgdNtfqh+z7+z34U/Zz8BWfhvwxYRQbEBurvb+9uZO7Mep5oHsenRqsahR0AwKfkVDLII1/2j0p0ZLKCRg1LYrElLTVp1NEhRRRTAKKKKACiiigAooooA+Bv+Cvnxrj8DfA/T/Bdv8194muP3m1sFIY8E5+pOPwrr/wDglj8Hm+Gf7M9jqV1Ei6h4imbUHYD5vLPCKT9K+Mv+CzHnp+0F4ZE0rNaNoqvHGT8qkSEE+1fqj+zo1i3wK8CnTWRrL+yLfyynT7g/rQO56Iq7Sfem3Ewt7eSVvuxqWP0AzUlY3jLVrbQvCes6heTLb2ttaSySSOcBQENAj+fVrwfET9taOeHkaj4uBTzOOBPxn8q/odtIzDawxnqiKv5Cv53P2dox4l/bC8HvanzBJ4k89T2K+azZ/Kv6KaAEIzWN4s8H6T440C90bWrKG/0+8iaGWGZAwIYYJ571tVy3xS8aWfw7+HPiPxJfyNFa6bYy3DMoBbhTjGT1zigD+cj4r+B7bw78afEfhPSXM1tb6vJYWo9MyYX+df0R/ArwPF8Ofg/4Q8OQxxxrp+mwxMI+hbYMn86/B/8AZb0Ob41ftieF2kia7W91ttRuFcdUDF8n9K/objjWONUUYVRgD0FA7igYpaKx/GWqDRPCOtagSVFrZTTZXr8qE/0oEfir8ctUh/aw/wCCjlvormZdJXV49MVXUZEUP3s4J4JB/Ov230nS7fRNLtNPtIxFbWsSwxoowAqjAr8Uv+CY/k+Mv27bnUr6NbmZrTUb5XkGSsgdcH64Y1+3FABX4U/8FYtZfWv2tNVg37hY2MMOD2AGcfrX7qswVSScAckmv51/23fHEfj/APai+IWrQ7mg+2vAjHHRCF4wenFAH7p/sqaGnh39nP4e2CbT5ej2+SvTJQE1oftGa/N4X+A/jzVbdzHPa6PcOjDsdhA/nVX9mHVYNa/Z7+H93bNuik0e3x+CAEVz/wC23dPafsp/EuSMMW/slx8vXBIFAH5Qf8E2P2dfB37TfxK8ZWPjvTrjVLO1sY7mOSC4aIxyO7ZJI6//AFq+vfEn/BGbwLqGoNJoXjrWNDs8nFrNZxXYGfQswxXEf8ETNBt7e3+JWohle5L29s3HIUAsP51+pNAH5V/Fr/gkL4a+Hvwz8S+Jz8StRupNJsZLtYpNLijV2UZAJD9+laf/AART8GiLTfiL4qZG3XM0Ngr4wpCbm4/76rtv+Csn7SzeD/Atn8MPD1yx13XWBvlhILJbngIec5Yn9K95/wCCffwTm+B/7NPh3TL2PytU1AHULtcYIaTkA+4GKAPpEZ70tFFACHP0qveabaakqrd2sN0q8gTRh8fTIqzRQBXtbC2sci3t4bdSMYiQL/KrFFFABRRUf2iITeUZUEuM7Nw3flQBJRRRQAUUV8Y/8FAv26NJ/Z78I33hXw7eJdfEG/i8uOKPDCzRhgu57HHQUAed/wDBUj9tSD4e+F7j4U+FZFudf1mArqN1G4ItYGx8gxnLNyCMgir3/BKH9lO5+F/gm7+I/iK1e21zxFGq2VvKPmgtOoJ92PPT0r51/YL/AGC/Efxn8a2XxT+JEE8XhqKcXkEOofNPqcuchuuVQHB5zmv2Ih8i0WK2j8uIKu2OJSBgDsBQO5KBivye/wCC23jS1n1j4c+F0Ob20iuL9yD0WTCAYx/sZ/Gv1ir8gP8AgpT8CPit8Vv2rrX+zPCuoatot1awW2nXdpAXiVeN5ZhwCDng0CPuD/gm74JTwX+yX4OTyWgnvojeSq3Xcx618D/8FqIy3x68IseFGgce/wC+ev1s+FfhuXwb8N/DOiTRLDNYWENu8a9FZUANfmz/AMFrvBM003w/8VR2ryQrHPYTTImQnIdSx7daAPuj9jOyTT/2X/hzCmAo0iE/L7rXtNfmh/wTx/4KEeD7PwFoPwx8cXJ0TV9PQW9pqFww+zzpngFv4SK/SHS9c0/XLVLnT763vrdxlZbeQOpH1BoAuSSLGjO7BVUZLHoBVTS9asNatzPp97BewgkF4JA4yOvSma9Hb3Gj3tvczJBBPC8TyOwAUFSCf1r8Nv2X/wBqLXv2bP2m7zSYtSm1HwhfazJY3Vm0hdMNKVV164POfegD92aKitp1ureKZPuSIHX6EZFS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGLqHhfTL6ZZJ9Pt5WwQWMSEkHqDkdK/Jr9rj4B+DvDf7cnhRYptP0zR9UmgnuNMtwd7Nu/u4xz9a/XxslcV+OP/BTqO78H/tgeE/EaqMFbd4xvBPyuM5Hasai093c6acm92fr9oOlWel6PZ2tjAkFpHEqxxooUBcccCtHbtrH8G6g2qeFdIu2G0z2kUmPqgNbPNapuxhK93cRadSc0tMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0E0AB7UkjbVJwT9KTJPal59KNhnxL/AMFThHZ/s4avcImyaUqh+bqMjtXln/BFa83eC/iBb4OBfxSfmmP6V3v/AAVU8y4+BuqRIJWbKZ2rlcA/pXJ/8EW7VR8KfGd35TB5NSVTJt4OE6ZrH7VzeT0P0d/ipabz1pc1sc4tFJS0AFFFFABUcu7bhfSnkUjcc5x60AfD37aXw4/aQ+MH2nQPAs9jpPhtIsv9nnMct3njazV8QeG/+CUHx88RXS/2qNL0pWPzTXd4ZT9eBX7fvIkaF3YIgGSzHAFZk3irRLeTZLrFhE/Xa90gP86iW5o5cz2PyVj/AOCLPj+Tbv8AH2hx5+9/ocjY/wDHq2LT/giT4jZozc/FPTohn51h0l8474PmV+p7+MvD8Slm1zTVUdSbuMD+dchrn7R/wv8ADbOmo+O9CtnT7y/bUYj8iaNEtSbsl+AfwftPgR8K9E8F2d5JqEWmxbDdSKFaQ9zivQ65/wAE+PPD/wARtFTV/Deq2+sac52rc2rblJHaugqlZrQQUUUUxCN0r82v+CyPhmK4+HXhrV0ixLBfrG7L0YNnGfyr9I5H2gcE59K+Fv8AgrZpouP2cpZtjsYL+CYMBwACc59uaxnuma0+pqf8Ej2U/spwgNkrqdwCPT5q+2K/Pv8A4I2+Ko9R+BXiDRcYlsdVeU89nGa/QStI7ES3Ciq9/NNb2rvb2/2mUD5YtwXP4nivyN/a28bftW6p8ULu0uNfl8B6CbhhptraarDZq0fZmYMGc49TijmSHGLlqj9eqTd82McetfiY37RH7XP7M2k2Ov6xrMviHw9cHEVxqDJf27AdcshDD6k19qfsnf8ABTzwZ8bfs2g+L1h8I+LHIRFc4trpj3Rj0z6H86OZC5WfcFFMhlWaNXRg6MMhlOQRSMjtIDuHl45XHP51RI+lpAoWloAQ0xiQBTmphPTjPP5UmM/Gb/gsRp3nfGPw5qscUiW8mmmLcw4LK2Tj86/Tb9ja0jsf2YPh1FEMJ/ZEJ5Oeor84v+CzF7P/AMLG8H2JXbCtm8g9Mk4r9DP2GdUbV/2U/h5OzBiNNSPIHpxWK2NZnu6/eNOpgYbjzUGoXi2NnNcOzBIUaRioycAZNaJmRaor5Z+HX/BRz4QfEDxndeFm1O50HV4blrZU1SLy0lYNjhs/zr6ht7iO6hSWJ1licbldDkEeoNO6G4tEtFJzmjn1o5kSLRSUtUAUUUUANavwP/b2tYdc/bi8SW+oxS2lrdX9vC7q4Vgh2ruGRX73TAshA6npk4r8mv8AgsB+zxe2PiTR/inpNnmwmiFrqk8e4tHKD8kh54GOOKl73Lie+xf8Ei/gZr2k2FzBd+KdPaS2jZmtNTjKyMVBLHdE3X2wK47xD/wRT8CXjIdG+IfiDTeSWF3bx3OR6ZBTFd5/wS1/aaf4xfCGTwnrd8LjxL4axFmQ/PLbdEY/TpX2/k00S9z8/fDX/BGT4V2FuE1zxT4j1iUEHfbvHbA88gjD8GvsT4N/AfwR8A/DSaJ4K0ODSbXAEko+aaYju7nk/wAq72lyaYh1FcR4w+NHgvwBr+kaJr/iGz0/VtWlENnZySDzJWPYCu260ALRRRQAUUUUAFFFFABRRRQAUm0ZzjmlooAKKKKACiiigBrVzHxN8YW/gD4e+IfEd0xSDTbGW4ZgcdFOP1xXU18xf8FIPGEXg/8AZB8cs0hjl1CFLCIqcHc7DofoDQNbn57/APBMnwjP8a/2vtd8cXjG4i0jztSlNwPM3vM5CEk55HrX7RV+Yf8AwRN0eBtD+JWriKNZ2ube1LbRu2hN2M+me1fp9QOW5FNIIYnc9FUt+VfzxeFdTlvv2ztMvTK7PJ4w3b2Yk/8AHyR1+lfut+0n8TrT4P8AwT8WeKLqUQi1spFibOP3jAquPfJr8Df2Z7p9c/ak8C3Vz+9Nxr8crCQZyWctk0Dif0dr90fSvwV/aisSn/BQLWoJvnD+JrdiG5zl1NfvXX4g/wDBTSyuPhz+2s3iNbVBHMtpqMSgY8woRn8SRUtBE/bbSVC6XZgDAESAf98ivzP/AOC13jOFfDnw+8LRXC/aZLme9mgB5CbQqkj6g19c/C39sj4ceMPgnp/ji58RWGmQpag3VpPOolikVeU25znI4r8Y/wBt/wDaTf8Aaa+NF34ggg+zaXZL9isU3ZLRqfvfjU9QS1Pur/gibpoXwX8R74YGdRghx34iBr9LpIxJjPavzq/4It6zp8nwl8ZaXFEU1GHU1mmYj7ylMLzX6MN2q1sKT1PFf2zPHj/Df9mfx3rMJKzrp7wRspwQzjbn9a/OT/gjb8Nl8RfFjxb41vrVpX0iyWG0mY8edIx3/jgCvs3/AIKoXL2/7H/iJUJAlureI492rzr/AII16Kln8APEWo7R5t5rDAtjnCqBilfWw+lz2rxZ8SvjPoP7Uem6Dp3hNdV+Gl5BGJdQQYMD9WbP9K/Jj/goxqNjqf7X3jI2LKYYpUiYL/fAG79a/fDWNSi0fSry+mOIraF5nJ9FBJ/lX80vxs8WSeOfi14t8QHLf2jqU7oO+3eQP5UwR/RV8C1Efwa8FKOg0m2/9FivgH/gtV4CFx4c8A+LrezDSW9xNZXVyo+YRkBlB9sk19R/8E+/jNpHxc/Zx8NpYSf6ZolumnXcLH5lZBgH8asf8FB/hxH8S/2UvGlm2BPYQjUoWxyHiOf5E0xbM8p/4I/6t/aH7LssHOLTVJoxn86+Zf8Agq98bI/jN8WPCnwn8KFdTn0m4ZZVj73kuE2fgAKyv+Cfn7bHg/8AZ2+BfxA0DxBdTQ6r5rXmlIqZ852j27fY7uao/wDBMb4I3vx5/aP1j4m+IFkfT9BuGvszDImu5GJVf+Ag5oE9z9Pv2Qfg/N8C/wBn3wl4Su1C6hbWwkuwDnEr/Mwz9TXstFFAgooooAKZJIsYyxxXB/Gj43+D/gJ4TPiPxpqn9maaG2IVRneRvRVHU14Vpn/BUb9nXUpFQ+NZbP3udOuFH5hDU3HY+rPtiM2AcVIJAehzXzTN/wAFHP2d4irH4kWTKegW1nJ/9Aqjdf8ABTf9nGzxu+ICyZ4/c6ddP/KOp36jsfUytmlbpXyPe/8ABUj9naNFaLxzMeeQNIumJ/8AHBXb/Av9t74VftFeKrrw94L1a61DU7aD7Q6z2MsC7c44LgZ+lHSwWPfs7l45qtcMIwWPapooxGo2rsB52ioLiTZJym5e/tXPLQpGcrLPJvI+XPNXrONVuXKcLVO8WE7HWRtgPKrV7TxG37xCxU9mpU3dlP4T8ZP+ChDKv/BSfRCg48/RSx98pmv2mgYeTHz/AAj+Vfi1+3Cya5/wUm02G0dbgrdaXG3knf8AMCMjjuK/aG1Xy7WFT/Cij9K7DEsUU1adTAKKKKACiiigAooooAKKKKAPxS/bzUWf/BSCxkc7FNzpTlm4GMrzX7S2DBrG2IOQY1II+gr8ZP8AgpZAln+31o85YKskWluWJwOGAr9ldDYNomnsDkG3jII/3RQBeooooAKKKKACiiigAooooAKKKKAPKP2rPEUXhX9nP4h6pMwWODR58lunzDaP1Nfjp/wSw0241T9sfQJICf3Fpc3Eij+7tGf5iv1j/b4Xd+x78UxnH/Eob/0Na/PH/giv4fhvvjZ421WSEPLY6PGIZSPu75MNj6gCgdz9jFpaKKBCV+d3/BZ/wZqGufBvwbrltGr2Oj6rILot281Aqn81NfolXzp/wUI8Kjxd+yH8QrZYvNnt7IXcKgZO9GB/lmgDy7/gkp8RR4z/AGYxo7yB7rw7fPZOO4U/MnOPQ19rs6rkk4r8j/8AgjH8XLLQfFnirwHf3CW8mrJHeWStnM0q8Mo9wvrX60Xlu83IYgY+7QVGzepH/akQkK5y3rjAqaK5FwWUcHFZg0UsxJJIP4Vj+PPiJ4T+Evh2XVvFmtWui6dCCxkuH+Z8c4VRlmPsAaDeUYJaHXR7QgzubnGSpqTntX5PeAf2jfjp+1f+15c33wo1uSDwVotwGe2vZjFZ/ZS23c6EAsWx0AJHtX6t2bTtBH9pRUm2jfsOV3d8e31rN7mJYXPOadTVp1WtiWFFFFMQUUUUAFFFFABRRRQB+c//AAWM+CX/AAknw20P4i2S4utDk+x3eBndBIcj8mr1j/gl98YrL4kfsz6RowlH9q+G82FxFnnYOUYeoIr6U+Knw90z4rfD/W/CurwrPZalbPCysOhI4Ye4OK/Dy4s/jF/wTc+ND3UUT21nJKQg3GSzvrfcSFYjjOPxFBSVz97t1fCf/BWD9oaP4a/BVfBenT/8TrxKxikEbfNFAMEk88Z6VzGk/wDBZXwDN4JW6vvDGrReJfKObKEBoTIB/fz0/CvmH4C+B/EX/BRz9qi78V+L0m/4RixP2m5AJEccYP7uFOME560Bbueef8E2vBo8RftieErW4BQ6eJbwqwwSETP581++m6vxH+M2qSfsRf8ABQyXXbC1FvoiTR3KxxLu/wBDlUBlA9QBX6z/AAY/aT+Hvx70eG/8IeIba8eRctZSOqXKf70ec0A12PUc189/t+WtxefsmeP4rZJHlNnnbECTgMCa+g1qtqul2muabc6ff26XVncxmKWGQZV1IwQRQSfiB/wSY0O61T9rTT7uK3MlvY6XcPNIoyseQAu70Oc1+5VeP/BD9lH4c/s96zrmq+C9G/s691g/6TIzlvlyWCrnoMmvYKACuU+K+m3GsfDHxVY2pUXE+mXEce4kDJjb0rq6ZLGssbI67kYFWX1BoA/Dr/glbcNoP7atvBcjEjWOoWjAY4ckeuP7pr9x91fid+2R+xj8VfgB8Xta+JHgWxupPDU1017b6hokheWzLHLLImAy/gCPeuTj/wCCjP7SHjbw9H4N0zWjc3c6i1EtjpoN7LkYK7wuQ3vQVa598ft9f8FBdJ+BekXPg3wfLFqvja7Ro5WXDQ2cZGCWbP3ueBivyjvv2Z/ihqvwyf4q3Hhm9uPDlzcSGW6CNvGfmMhU87CT1r7O/ZH/AOCXPjDxl4tsvG3xoBtdGLC5bRrq4dr66kzkeaMYVe/3sn0r9Yv+Eb0v+wRon9n2/wDZAhFsLLyx5XlgY27emMUCZ+Qv7Kf/AAVVX4J/DjTfB/irwvPrWn6XEIre60plWTbn7rByOa+9fjn8QrX40fsL+MPFOkWN3b2ur6C88VtdIBKg4OGAJHbsa5u6/wCCXvwSuviUfFzaXdRjzhP/AGTHIFtN2c/dx09q+o7rwppk3hWbw8llDFpT2zWgtVQCNYyuNuPSgR+Yv/BE/wAR2P2j4laOWKXzfZ7sBiACnK4HOc5FfoZ8evjp4a/Z9+Hep+K/Ed2sUNtGfJtww8yeTHyoo7kmvxZ+MH7K/wAcv2V/ihf6x4Z03V7Wzku5GstV0He6OhYsqnaOwPcVofCv9m39oD9tbxtBD4v1DXLfSbciWfU/EDSLDGmcERoRgsfYUAdN+zN4F8Sft6/tdT+O/EsE0nhywuhf3UrDEaorZihB6E5AyK/bKCNIYY44xtjRQqj0AHFeffAb4F+Gf2e/h3p/hLwzarDa265mnI/eXEh+87HuSa9EoAWiikOe3WgD5G/b+/bL139lHRvDf/COaJbarqOrSyKz3u7y41UAjGOpr4sP/BYz4uXEeyHwhoPnYwNqysSfYV+vGueFdG8TrEusaTZaosRJjF5brKEJ643A4rOt/hj4PtZA8PhbR43HRlsIgf8A0GgD8iJf+Cin7WXih/tOkeHJIbduQtr4feVcfUrUf/Dcn7Z0n3dC1P8A4D4Wb/4iv2ZttPtbNdtvbQwL02xxhR+lT7R6D8qAPxZuP2y/20NSheBtG11TIMK0Phpo2H0ISrP7JvwZ/aM+Kn7Rmm694ru/FXhq0gk+2XmoakskaSKpyIgpI61+zu0eg/KloAjhV0RVZt2FAz3J9a5H4weObz4a/DTxB4lsNKk1q8021aeKxjzmVgOnHOK7GkZVkUqyhlIwQRkGgD8NvGP/AAU4/aL8cazdxaRef2LHIxRNP03TcyRZ427tpYn3NeQ2v7Mv7QHxu1i81j/hAvFGt3103nS3moRGLzCe++UqD9B0r+g+x8F+H9NunubTRNPtriQ5aWK2RWY+pIFbKqFGFAUewoA/Dq1/Y5/bSttFt7W10/xFb2UMexLVfE1ugVfQKJhge1c3Z/sZ/teadrSaha+EfE1vqsTblvotai35/wB43GMV+9VFAHyB+wTB+01psetaf8ebZl0mG2j/ALKuLq4t5rp5dx3h2ikYkbcfeFfX9FFABXNfED4c+Hfil4Xu/D3inSrfWNHuhiS3nXj6g9QfcV0tIV3daAPyV/aW/wCCQOuL4iuNW+EN3bXWjSkuNFvZvLktz6K5PzfpXz3F+y5+1n8K5G0/R9E8b2sJ/wCgFcytEf8AvhsV+99FAH4QWPwB/bH8ayf2bcWXj/y3GP8Aia3kscXPu7YrufhF/wAEpPjdb/EDRdU8Qw6Xpmn295Fd3Ej3yTO21gxGFJ5r9pqKAILG3NrZwxMQTHGqcdOBip6KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDN0XUm1bTba7MMkInQSLHKAHUHpkAnB/Gvyg/4LAaDaWvxc8A30FoYru4Co9xu4cBwQMdq/Uvx74mm8D+D9S1i20u51me1hZ47CzTLysBwB6V+LP7THx2+Jf7Y3xX8LaFd/DyfQrjTb4Ja2MVrK07ZYAl2K9MfhWU1qrHTDdvoftB8KZPN+G/hlj1OnQf+gCusrnfh9pU+h+CtD0+6UJc21nFFIo7MFGRXRVqYS3YUUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANbHc4qve6jaabaPc3d1Da2yDLTTOERR6kk4FLqFvJdWkscb+W7KQG96/Nr9vT9kr9on41+JtKn8JzRa5oUcBjfToNRitBC2epErqGyPSs5Sadi1FNXufbkn7UnwihvJrVviR4Z+0wnEkY1OIlfr81U9Q/a6+DWlKjXPxJ8Oxhzhf9PQ5P4Gvx70j/glL+0ZqF55Nz4R0/TUP/Le81m1dP/IUjH9K77T/APgjJ8Zrry/tOveDbFWPz/6XcOyj6CEg/nT1YtFue4/8FIv2tvhx4w+D1zong7xjpviHU72RYpbeyO8on97NZH/BLH9pL4d/Cf4M6vo3i/xXpnh+5k1Bpo0vZRGWGMd+tctb/wDBEfxaZl8/4k6Kse35mjs5SQfYccVY1D/giT4kht86f8StKmn9LmwkRfzBb+VLk63KurWPv63/AG1PgZcsQvxQ8Nrgfx36L/M1aj/bC+Ccwby/if4YfaMnGpR/41+Zg/4Iw/F1JXC+LvCGzPDM0+T+Hk0+T/gjL8XPL/5G3wm59FaYf+0hT1Ija+p+qvwz+O3gP4w3OoweDfE2n+IJNPx9p+wyhxHnpkiu+r5i/YT/AGQbj9kzwLqthqmqWusa1qtws881rFtWMAYCBiMsO9fTtUr9Rytf3QooopkhSUtFAHx//wAFCvh38ZfiR4LsNM+GHmNH5jPcC0uTDNjGME55Ffn7pP8AwTe/ab8XKLu8jWynxg/2jq7qzflmv3CoqGi1Kx+J03/BK/8AaRkjAOoaWQeqnWZT/wCy03Sf+CQPxy1K6YalqOgWcZH+sa+kl/QKK/bIjNG2qtoHMeJ/sf8AwBm/Zu+C2meD7y9S/v4WaS4nj+4WJ7e1e20mMUtCViQooopiEr4z/wCCpmsDT/2XdeUY3TSxQfMm4YLdR6GvstmxivjX/gq1a3Fx+yhq7wEBI7qF5RtyWUN0z2rOXYuOh59/wRo8Ow2fwY8T6yqMJ77UtjsXBXCLgADGR+Jr9Da/Nr/gjd4u0Sz+E3imwuNVhtryPUPNe3uJ1QAMOCAa/QuXxp4fhXdJrmnIvq10gH86cdEEtWbDV+XH/BXv4P8AiDxC2meMtO0lprDTU8u5njXPynoSPrX6g2d9balAs9rPHcwt0kicMp/EVx/xo8LweMfhj4i0WeHz0vrSSHZgE5IOCPelLuEW1ofFn/BMjXfD/wAfP2Yb7wJ4n061v/7ImNvJDJEu54m5BJ/Svn7/AIKH/sQ+C/2ftDh8YeBry60yX7SJHsZ5xtUH/njwDkHtk189/AX47eIP2L/j9qBD3P8AZVvdvb6jp6kfvowxxn3r0r4wfETxf/wUu/aG03QPCyT2vh6BQILeYEx2oIw0r479s0irNbnn/gv/AIKNfHXwH4NTw3pnipXtoxiO5u4BNcIvZQ7HoPpWja/tZftT3mljxZH4t8QXmjQvve4SCM249m2p0r6S+LX/AAR/j8H/AAbn1Pw5rVzrnjKzTzpYMfupwByqLjP618Z/CP8AaM8VfAa31jwnfW/2vQ7l2ivdIul+63IPB6Ua9A0P1z/4J5ftkXP7UHgO7svEnkp4y0chbswrsWdD0kC5OPevryvwu/4Jc+Lriz/bGsYbJ2tbHVorlZLdT8pUAsq/hX7oVafciSsMmBKHHWmxR7ecnJp5OcihvlXin5gn0Pxn/wCCyPiBb743eGrEDMdvpxPTnJav0F/4J0xTw/sg+AlnyG+zMRn03HFfnR/wWBsxbfHvQpG5Mmllsf8AA6+2/wBjP9qz4U+F/wBmLwRY65420fR7+0s/JmtbiXa6sCe2KyWxrPsfZqxgMT60skaNGysAVIwQ3TFfNWrf8FG/2ftJkkR/H1rO6dRbxO+fpxXnWo/8Fa/gnJff2fZDWtRMziFJI7UKrFjjjJ96DJJ3PCv24f2ffgt8QPGV23gnxppuh/ExGLtpvnbYp2B+5nojZ9K4L9jL/goN4h/Z+8USfDz4rXEt34dgk8hbqX55bJgefm6steJftjfC1/hL+0VbanK8/wBg8QTxazbmdh5ixu4O3I5GM17t/wAFKtG+Ev8AwrPwJrugC0HjO+giZ2s2BMkewZ8wdOtM1l2PWP2sv+Csdvogt9D+CzQare3UeX1qaHzBC3ZUjIIJ+oNfPXgf/gpl+0L8PfGWl6n4/kudT8PTMPPsrrSIrZZYz/EjiMEEdeDXin7FPxa8A/Br40WXiLx7oX9saei7IXHItZCf9Zs6Nx61+s/7X3wz8M/tW/sq3Wr+G5ba4SG3/tLT7yNeflGSvHtxg0EK3U+kfhr8QdJ+KfgfR/FOiXC3Om6nbrcRMpBxkcqfcHiunr80v+CN/wAZJNS8OeKfhnemRrjS5DqFszNlVjZtrIB2+bmv0srRbEPcWiiimIRq5P4o/DfR/i34D1fwpr1utzpupQmKRWzwezDB6g11lG0UAfg38Wfgj8Xv+Cf/AMWZPEXhd7630qOU/Y9ct4PMhkj6+XKCCMY9RX1l8Cf+CyGg3unwWPxS0K40y/UBTqmlp5sMh9SnVT61+keuaFp3iPTZ9O1Wxt9RsZ1KSW91GHRx6EGvjj4r/wDBJv4OfEC8mvdC+3+CLuZizjTZDJCSf+mbnj6A0FX7nouh/wDBQ/4Aa9p63cfxD0+1U9Y7sNE4PphhXk/x4/4KufC7wV4fuoPA13J4w8QupjgFrGRBG2OGZiOR9K80tf8AgiP4dS6D3HxS1GSEn5oo9HjBI9N3m8flXvfwV/4Jg/Bn4N61BrH2K88UapEBsfWpQ8SMDncsagDP+9kUC0PmT9iH9m/4iftBfGqL46fFsXT6fDJ9p06DUBgzNn5Sq8bVXtxX6q1FbW8NrCkNvGkMMY2rHGoVVA7ADoKloBhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAK8B/bk+Ct/8AHr9nPxH4X0mKObV/ku7RZADmSM5AHua9+prLuFAz8Ev2Qf2svEf7EPxG1fSdb0ieTRryVYtX0yRCkkDoceYg9ccfSv1N8B/8FKPgF47tRInjSLR5woZrfVYXgce2SMH8DXafGr9jf4S/H4SS+KPClqNSc7jqmnxrbXZbGMtKo3N9GyK+G/jB/wAEXbma+N18OfGVt9mY82fiBXDp/uyIDn8QKAbuzkf+Cmv7Z+j/ABvh0X4dfDjVxrOkGcS3s9juK3MnRIvcA818meA9C1P9m39o7wbJ49tH0d7G5tr+dZBkxwtyCR9K/S39k3/glLpHwh8RWPinx/rEPibVrM+Zb6ZBF/okUgP3m3ff+mBXeftif8E49D/ae8S2/ifTddbwv4iWNYJ5DD5sM0ajCgrkYIoGnY7Xwz/wUK+CnjTxzpPhPQvEz6nqupSCKEQW0hQMR0LYrY/ay/ZH8L/tS+DTZajFHZa/aqzWOqRoBIjY4Vmxkr7Vw/7KP/BO3wJ+zPPFrc7DxL4tVdo1G5TEcR9Y0PQ+9fWasGGaBeh+Id1/wSZ+Otlq0mm21vpNzp7S/Lem+ATb2Yrnr+Fep/Gz/gmrZ/Az9kDW9bikXWfHNm0V3e3CrmNIVb51jHtnrX61VDfWNtqVpLa3lvFd2sy7JIZ0Do6+hU8EfWpaHzH53/8ABGn4bX+hfDHxX4uuiyW2s3aw2sbKRlYxy351+i9U9J0bT9BsUstMsbbTrOP7lvaQrFGv0VQAKuU0Jnhv7Z3wLvf2iPgHrnhDTJ47fVJSlxbPIfl3ocgH61+OPw6+N3xr/YG8W6jov2WbTFuJP3unanETbzbT99Pr6iv6AKwfEvgLw34yVRrug6fq+0YBvLZJCPoSM0ra3HfSx+Knxg/4KsfE74ueAdQ8LHTdO0SG9Typ7qzDeaUPUDnjNWfgJ/wTJ8X/ABi+B+seNLppdK1i4USaFZTnb9oHUs3oD2r9aY/2Ufg/DqUeoR/Dnw8t5G25ZvsS5B9a9StbWGxt47e3iSCCNQqRxqFVQOgAHSqC5+Evw/8A2D/2nfD/AIsS10TQtS8O3cMof+0U1BYrdefvfK3zflX7OeBfAurv8G7Hwr471BfEGqS6f9k1G6xxKWXDfX616HSNyMUBc/nV/a7/AGd9S/Zt+MmoeGrtQ+n3DtdaW6tnfCzfKD7gmv2b/wCCfvwYb4K/sz+GtPucHUtSj/tK6OP4pBkD8Bivcda8D+H/ABJqVrf6po1nqF3aHMMtzArtGfVcjit1FVFCqAqgYCgYAFAh1FFFAgpDjqaWigD51/bJ/Y70/wDa+8NaFpV74km8NHSbl7lJ4bNLnzCybcEMy4H0NfJMP/BEfTlwJPivOw/2dAj/APj1fqBRSsVc/NjS/wDgij4Pt3Y3/wASNYu1I4Fvp0UGD/322a11/wCCL/w24z408Qsf9yOv0QopcqDmZ+cevf8ABFrwHc2IXSfG+s2l2DnzLiBJFP4AjFew/sW/sEwfsj+JPEmr/wDCTf8ACRyavbpbBWthF5QV92c5OTX13RRyhzEY7+lV7iFpFI4Aq2aqXiv5LEde1RKK2Y4lJbBYcFD8x61YkuV03TLi6lI2QxtKcnAwoJP8qqWlrPlZJJAqk4Ix2r5K/wCCi37Xmk/Ar4Xah4T0q8hl8aa1btbxW0bbmt4mGGdvTg8VCilsXLsj8+v2fdQn+K//AAUTfXoNOGrv/a15qMNruwH8rdt5/Kvavih4b/bP/ae8ZXlqdJ1TwZ4cjuXFtH532WJF3Fc7lO5uK6j/AII5/s+tawa38V9XgJnmVtP03zFIKjOZHXPr0r6K/wCCif7X2ofst/D7TYfD1usvibXXeK2lf7tuqjJf3Pat0Z7HyZN/wTH/AGirDTRd2fxO87U1XcIP7VuRz7EtivHPE3ib9rb9kfXLHWPEd34iFjaTYE1zKbqwkHcMRnAI7nFfe3/BL3x/8TPi18O/EXjDx9r9xrFre3mywSbGEA+9t46V9c+PvA+j/EfwjqXh3XrSO90u/iaKWGUZHI4P1FMk8B/Yu/bi8OftWaC9oyLpHjGxiD3mmuwxIOnmR+oz2HSvp+vwf0Pw/rv7FP7dWm2CI0VnHqixxBWIElrK+0D3HNfu7HIJY0cdGAI/GgB9FFFABRRRQAUUUUAfi5/wVKjb/ht7Q8KSWtNPxgdfnr9kPC+R4Z0kEYP2SHIP+4K/G3/gpZqSX37fWi2+QyRQaZHwc87zkfXpX7MaKhj0exQgqVgjBB6j5RQBZuLiK1heaeRYYkG5nkYBVHqSa+Ef2qf+Cqnhb4L6+fDvgfT7Xx3q8RIubiK9UWsBx03KG3NnqOMV9WfHv4L2nx6+Hd54SvtZ1LQre6ILXWly7JMDt7ivyE+D83gX4M/tqD4eaN4U0/x9o8+prpD3XiSATTJLu+aSMAY3dR0xQUlc0/FH/BWD4/6/m60my0fRLVTu8u202WXA/wBp3JBH0xX1F+wz/wAFNJ/jh4ysvAXj+xttO8QXi7LDULc4ju5h/wAsyvZsdK+85fCOi3GjnSH0qz/svyzGLMW6CIKRjhcYHFfiT8M/B9r8Pv8AgqNoOiWMP2eztvF2Iox0RGDED9aCT9z6KKKACiiigAooooA82/aQ+Gt58YvgX418F2EscF7rWnvawyS/dDEgjP5V4F/wTd/ZN179mbwT4kl8WRW6eIdZu1P7nqkKDaFz6E819jUUAFFFFABWf4g0Kz8T6Hf6TqEK3FjewtBNGwyGVhgitCigD8Rv2qP2IfiL+yd4+PjX4bDU73w9HObq2v8AT/8AW2LdSrAHJHvirOgf8FcPjhoGh22mXOlabqV5AgRru8tHMzkd2wRzX7WTRJNGUkRZEPVWGQazB4V0YSFxpNiHPVvs6ZP6UDPxp/4bc/a5/aKmj0Pwda3VtPMTj+wNNEDYPHzTPgKPckV1vgj/AIJa/HP4yarBqfxg8YrpVoz+ZLHNqD399z1AHMa8dwx+lfrtb2NtacQW8UI/6ZoF/lUrSBe9A/Q8q/Z3/Zp8F/sy+Dl8P+ELOQK7b7i+uiHuJ29WbA49hXq3TrUckhVQccd6fncARWb3GPWnU1adVR2JYUUUVQgooooAKKKKACiiigBGrm/G3w58N/EjS207xLotnrFoQQEuog+3IwSCehrpaKAPkPUv+CWHwA1K+luf+EdvLZpG3FIL51Qc84FfQvwm+DPhL4I+FofD3g7SIdJ02Pnagy7n1ZupNdvRQO58sftjfsFeG/2sJLHVH1F/D/iWzjMSahGm8SJ2V17gGvlbwX/wR38Z+E/ElrqFr8WLfTVhlV/N06ykjlKg5xnf3r9UKKAuyhoenPpGj2NlJcPdyW8CRNPJ96QqoBY+5xV+iigQUUUUAFMkUtjGCPQ0+igCOSFZo2R0V1YYZWGQfrWPp/gjw9pF615Y6Dpdldty1xb2ccch+rBc1uUUAIBS0UUAFFFFACUBQFAAAHpS0UAIM96WiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM4paZIu7FAD6Kj5xjFKgIoAfRRRQAUUUUAFFFFABRRRQAUUUUAIeagFhbLcm4FvEJyMGXYN/wBM4zU5pMH1oAULilpBmloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqTJp1JQIRadRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGpjSBFLMwVRySTwKc/Svj39sL9kf4p/tJeIrb+wfip/wiXhi3iwNLjgk+eQ8FmKOueKV0XFX3PcPiV+1B8LPhLps134l8c6LZtHn/AEWO8SW4ZgM7RGpLZ/Cvya/bY/b/ANT/AGpJG8D+C7C4t/CckyhU8pjc37g8LgHAHfGM165o/wDwRO1i81JJNe+Ktv8AZ92ZTaaUzyv64Ly4B98Gvsv9nP8AYB+E/wCzeyX2k6XLrniLbhta1hxLN1z8igBE57hc+9TvqPRH5SfDD/gmv+0D8QNLbU7Tw6vh21kAaNdYvfszyDsQo5/MV1c3/BKX9o6ORVFvpUqk43LrowPcg4NfuDjFLRyi5j5i/YG/Zx8X/s3/AAputF8Z6smo6rc3RmEcNy00cK4+6CR/KvpmaNZFG7oDmpKQjNO2lib63Pwf/wCCm3wbu/hz+0XqmrLbyJo2usLmK4ONpcjLKOK+u/8AgjT8H00XwJ4k+IVwjrd6rJ9gh3DgwoQ2R+Nfbnxo/Z48DfH7Rf7L8Z6QupQKP3Tg7ZIT/eRscHFdF8NfhroPwl8G6d4X8N2n2LSbBNkUecsfdjjkn1qVF2Kk00dK33TxX58f8FJP2HtE8ceBdR8f+ENJhsfE2n5uLtbVdv2pMfMSAOT3zX6E4qtqOnxalp9zaTKrRTxtG6sMggjHSnZiWh/Px/wT38TxeDP2t/BFzdRsoe5a1wezONpr+hD0r89fC/8AwSjh8H/tB6d4+07xeg0i11D7eNOe3O8Nu3bQemM1+hdHKwk7jNwDHPFc54s+JXhbwRZ/adf1/T9KgyRuubhVyQM46184ftrfs1/FP42NYXPw78d3HhxoQRLZi4aFH49Vr40X/gkn8avGDxv4o+IFm+58v9ouZbggeoyetV0sGh5R/wAFFvjB4b/aM+PWmHwJNNrX2WEaenlKcTOW6L61o6P/AMElfjLrXg221of2bbXkyCVdNnmIkCkZAJ9a+5v2Wv8Agl34T+AXjCHxTrWtSeLdUt0BtoJIFjgglyDvA6k445r7e2gYwMVPKx8x+THwp/4Iz6trnh5Lnx14wk0PUGPFnp8Sy7fqxFe0/DH/AII9/DzwL4u03WtU8Sar4jhs5PNFlMqRI7jlSSoBwD2r7/20VVtCbu5+aX/BYz4PWMnw38MeOLZVhuNJnXT22r8zRMMKM+gOK+Gf2OP2fdZ/ay+MWk6HqMtxceHNLVZdQuGYnyoAfuA+54r9zP2gPgToH7RXw11DwZ4iaaKxuyria3IEkTqcqwz71wf7In7Gnhj9kXQ9Zs9F1G71m91WZZLi+vQofaowqAKAAOaViuY8O/bS/wCCdPhrxt8I7Nvhp4esdJ8RaDCfJS3j2NdxgcoxH3m9zXxf+x7+2xrX7Luoan8O/iDYXV14VlLWs9pMMPYueGIB6jFfuJtFfk1/wWB/ZpsdBudK+Kmh2zxyajcfY9VSNTsGFJWU+nTFLlDmPOv+CZusQTft8agNDuJBod9BqTqqnarx4Lxgj2r9qsV+H/8AwSD0W7vv2skvYI99vp+k3TXDAcAOuxT+ZFfuDVEsKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACiiigAooooAKT3paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioWkZmKp1pYo3ViWOaAJaKKKAGtSY3cU+svxRbXt54c1O302TydQltpEt5M42yFSFOfripauB5v+01+0Bo/7Nfwr1Lxdqqi5eL93bWgYBppT0UfzNfll+z3+zX4s/4KIfGLWvih41lbT/Ccl3umlUYabaflgj9gO9dUP+Cbf7Q3xU8babF8S9ba48PyXrS3V1PrJujEm7qkWcKSOMj1r9U/hb8MtC+D/gXSvCfhy1W00vT4hGigcse7N6kmjlK5jR8G+ENK8B+G7DQdEs47HTLGJYYYYxgAAY/Ovzs/4LZaC0vgH4d6uiMXj1OW13AcLuiLc/lX6XV5D+1V8A7L9pD4M614PuSkV3Mnm2Vywz5M68qw9PSmtCTyL/glprmlan+yP4etNPlQ3FjNNHdQhgXRy2fmHbIr65YDqTwOtfhv8DfiZ44/4Js/tBXuieN7OZdGu41F9bwjek8Wflmj9W7fjX1T+0H/AMFaPh7rfwl1nTPh2dXl8WahCbe3aa28oQlhgsDk5I9qYHhn/BSTxtovjL9tLwdZaBNHc3mmNa213JCQwMpmUhcjqQK/YnSVZdLsw/3xCgP12ivzV/4Ju/sKXSXMPxh+KFs13q90ftGk2d5lmG7nz5Af4vQH61+mtABRRRQAUUUUAFJmvnP9rT9q7U/2V/7A1i48EXfiPwheSNFf6lZSEPZsBkEjaQBjPJwKwvAP/BTP4C+PNNuLk+K/+Efmt4TK9vrURti2P4UY/K59gaAPzh/4KAX0etf8FBo0sHW9aG80+FhbsJCHDqSpx3HpX7h2v/HtF/uD+Vfhj8F5rT9pr/go7ba1YRvc6Rda42o5kXJ8qPkNj0wBX7pUAJIpZSAcZ71+Dnh3Qbrwj/wUusbfUN0Tp4xMjGUbSFaQkE56ZBr95a/E7/gqJ8IvEXwk/aST4jWCzDTtYkjuLfUI42CQXKDOwtjG7C5x6UDTsftfkLyeBX4uaYr+JP8AgrdYy6ahvUi8TpK5txvCxonzucdh3NUtT/4KofGv4h+BbPwXoWkWkWu3Uf2VtS09GkuZhjb8qdmPrXtn/BNX9iT4g+E/ijH8XfiDbXGkSCGYQ2WooyXkksgwXdWGQMEnNAj9RqKKKACiiigAooooAKKKKACiiigAqPDMxzwKkooAYV96acrknpUjUxl3KQaBjImLsT2pWVg2QuaevHA6U+gdyKRC6EYpyqQoFOJA60jMFxmlYVwUU6kpaBBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAT9aB9MU12O07QC3bdwKbG77f3oUN/sHIoAlopM0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlpDzQAA56dKWkA29OlLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACGkwPWlo20AAxS0mKWgAooooAKKKKACiiigAooooAKKKKAEo4oo20CDNLSYpaBhRRRQAUUUUAFcz8R/h1oHxW8H6j4X8TWK6ho+oRmOaFiVJHqCOQfcV01FAHh37Nf7Hvw/8A2WRrDeDba7NzqjDz7q+n82QIDkRrwMKK9xoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqOV9qj1PFMQlc7mNTcqxPRUC3Cu21WyR1qamLYWiiimIKKKKACiiigAooooAKKKKACiiipbsAUU122j603fhtvtmjmHYkopqtmnUcwgoprsFHNMYnjFHMOxLRTBTXcJjNHMFiWimIwbpT6a1EFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPHvj/APsn/Dn9pS1tk8aaN9qurVWFvewuY5o8jGNw6j2rwz4Tf8Ep/hR8LvHFt4iku9S8RpaP5ttp2pbDBG4OQxwMtj3r7UooAZFEkMaxxqEjUbVVRgADtT6KKACiiigAooooAyfFPhXSPG2g3mi67p8GqaVeIY57W5QMjqexFfF/xG/4JB/BfxdcTXOgy6t4OncHathP5kSHPUI+fyzX3NRQB8x/sn/sD+CP2T9UvNb0rUtR8QeJLyA2suo6jtAWMsGwiAfKeOuelfTSn5iOh/SnUUAIaxvE/g3QfG2nvYa/o9lrNk4IaC+t1lTnjow4PuK2qKAPPfBH7Pfw0+G901z4Y8DaHo1yf+W9tZIJOueGIyK9CoooAKKKKACiiigAooooAKKKKAEo3CgnFNbLY4oAfRSUtACNTBu3HI4qSigBqimqX8w5GF7VJRQA1wWxilpaZIpZcCgBonXcVPFSA56VDHb7W3E5qegAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAjZtq5wT9KRm4HBo38DjBPrT9tA9gWnUgFLQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQ00vigB9FN3UbqAHU1m24o3UjfNilcY+ikWgnFF0IWiolmLOVC/nUlF0AtIx2qTS03lsg/pTAVTlQaWkAwMUtABRRSE45oAWimqwYZFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopGpuTSvYY+kpqt83Jqo8jmQ7G3YPSlzDUbkhmRlIY/Mpp25JEBLcVUkUq5JRTmq8nmS/IgCfSok9TVQLaxpHITGRuxzUqSOOWbj2qtaWSQtlpHZ8c7jxTVmEsjxqCNvOanVsLF4XS5xmpwdwyKz47cs1XVG1QK2Wi1M5LUkoqOMMM7mzUlMgKKKKV7AFFI1M3Hd1qeYCSikWlqlqAUUUVEtwEbpUbLuxUjUxsgcCpGhyjFOqBmbqcjHPAzmuW8T/FLwb4Hu0tdf8UaZo1043iG8ukjcg+xNA9zrJpFjTLVB5yogYHOTiuDl/aG+GAVWfx74fCk8f8TCP/Gmv+0T8LY49zePfDoX/sIR/wCNUlcex6EsysOTioVU/aM/w15F4h/a7+Cnhu1+0X/xI0OKPdt/c3XmHOM9EB9K4W+/4KPfs9abFJKnjyO+MfJjghkY/UZAp8oz6dt4tjM3rU9fDHiT/grp8EtPjM2nr4h1R487Y47MRpKcEYLFq9i/Y9/a+0v9rbw7rmp6ZoF5oiaTcrbv9oYMj5GRgjvgdKpEM+haKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTTQA7IpDIq9TTN3rxSLtf3qWyrEhb5cgZoRiw5XFC06mtSQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBD5J3hsnP6VNTFlVnZQcsvWn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJnrRTVUqzEnOaAH0UUUAFFFFABRRRQAUUUUAFFFFABRSGk3UAK1Q7P3u7PbpSpMJWwPu+tDusasxOcccUrlaj6Oc+1Mmb5cBhk+9U5dQW3KqWDHp1pcyHGDlsXWkVNoJxuOBS7ucd6r28n2pdzLjacimedIt95ZX5CMhql6j5baFhJG3EMoHpip6iReuWzUtFiGFJt5JpajmDNGQpwfajlYgkHmAx5K5H3hTo18tFUktgYyaSLPljPJp9WgCiiimAUUUUAJjHSlopqsGJwwOOuKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADWpu4etObJHFN8lScsM1nLcaKs3mNIcEhaj+WLc2OcVfYBV6VGY0bhlFI1jJGXHIZ5CSx2+lWY7Yrl1OT71P9giwAgCjOeKnEKhQvaqTXUqVRdCpDMJnzyG6Fe1IbdlYsvBJqwwih7qMckk9PesfWfHfhrw3b+dqviHS9MhzjzLu9jiGeuMsw54P5UJXdyObsauyRV461JHGVUbiWPvXl+rftVfB7Q4XlvPiX4YjVeoTU4pGH4KSa820f8A4KMfA7xJ8RtJ8HaT4luNS1PUrpLO3lgtG+ztI52rlzjjJ9Ksl3Z9PLTqatOoICiiipauAjVHt+Yn2p7DIpjNt96h6D3HrTqqC4fzAAufWrWfzqlIBaKKKT1EFFIelNzTTGK3avy+/ah/4JffEn42fGbxJ4ys/FthcWupXPmW9veM26CPHCD0A9q8f/4KBftM/Eiw/ax1TQbHxDfaRougXFskFpaytErggNubBG7O7vX7E+D76TUvCWiXkzb5rixgldvVmjUk/maW7K2PyCs/+CM/xRklIn8S6DDHjhm3Pz6YFa1v/wAEXPHjkCXxroUSnqVtnP8AWv1/WnVdhcx+WnhX/gijHDKza/8AEQvGUxs0+z2HdkdSxPGM12tj/wAEW/hysiG98Za/MqnLLEI13e3K1+i1FMLs+EvEX/BH34M6p4ejstLuda0jUkYN/aC3ZkZhgjBRvl754Havpn9m79nnw9+zN8Nbbwf4dkmubdJGnmurnHmzSN1JwK9UooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGqORSy4HFSN904602NmZcsMGgBkcbKxzzT9vtT6KVh3GqKdRRRsIKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWNVdmAwzdTT6TNLQAUUUm6gBaKQNmloAKKKKACiiigAooooAKKKKACikooAWiiigAopKN1AC0UjNtGaRW3Ur9AHUUUUwCiiigBGphzT2qOVhFGXboOaBieWONuAM5NQ3EMu0iJl5Pf0r4H/a9/4Kbaj+z78QpvCvh/whFq8kcQLXl9O8SKx9AFOenrXyVd/wDBXr473U0v2W28PRI7ZSNLB5GQemd/P5Vn8WqNHGUdGftkttGJPMx85GDTJreDerOFUg5yeK/Edv27P2sPjE39m6C95DMP35Gh6QVk2j5eS24bcsPxxWD4gt/2x9btZ73VJ/Gvkwr5js5MYA6dFA9ar4VqCvfc/dNtSsIAQ13boe+ZVH9axNc+JHhPw3Gs2q+I9LsUJ2hprtBzjOOvtX83+qfEj4g3Wqz2V74l1xtREvlNBJeSby+cbcZ65r334df8E9/2gfjFb2t7Pp9xYWVwcrca1csBj+9gnPeluSftr4R+Mngbxxqb6d4e8VaVrF+qs5trS5V3wOpwDXa5O7pxXwn+wn/wTkuf2ZvGD+NPFGuW+qeIPs8ttDbWSERRhyvzFjyTgEfjX3ZVIlg2e3WkXd3AxTqKYhKWiigAoqC7uVtYTK7BUXliR2r8+/i9/wAFfPDPw/8AHF94f0jwfeaxHptw0F5dyShB8pwdgH49anmsUotq5+hdFeA/B39ub4O/Ge0tRpfjCw07VJow7aZqcwglQ8AjLYVuTjg/hXvFvdR3UKTQyJNE4yskbBlYeoI60cyFZk1QwWqW5crkljkk1KDRzTuhC0UnNLTAKKKQmgAbPGPXmvnz9qr9tLwV+ynoVvPrnm6lrV2+220i1I85htY72z0XK4z/ALQrvvj78XrH4HfCfxD4x1AFotOt2dFXqXIwv64r8Sfgp8O/F/8AwUS/aUvLXXNek3Nbyane3U2W+zWayovlxjsSZVApXsVyu1z6mh/4LeXEmpfN8K4103P+sGrEy4z/AHfLx+tfoH+zz+0d4P8A2lPBEXiLwpeiULhLq0fiW3kxkqw/rXzx4+/4JT/B+++FN9oXhbSJdN8TLEGttZmunaRpQP4wTtwT6Adua/Mn4PeNPFv7Ef7VVrZX17NYJpOqpY6xaRs3lXVuxAclScHjkHsQKLoVrn9CFFVdL1CDVtOtb22cSW1zEk0TjujAEH8iKtUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIaz9a8R6V4chSbVdRtdOikbYj3Uyxhm9ASetX2zjivyL/AOCmereJf2iv2mfDfwq8HWOp6g2kqsDxIjCD7TIwJkzj+FcjJ96VylG5+uUE8d1Ck0MiyxOAyuhyGB7g1JXHfB/wTJ8N/hh4X8MSzNcS6Xp8VtJKxzucKNxz6bs12NAgooopiCiiigAopDUEkxU/Kcn0rOW40rk7dKgk3sQMcetL5jNKinpjNTChK49iBwyL8r4Y9M9K/LX9ur9sH9oTQfiZe+EfCOgaz4O0WEslvfWVoZpr4A4MqyKDtHPSv1RKhsZFQTWFtcOry28UrrwGdASPzp8o+ZdT8KtN+FH7Yf7Q2mgTt4y1TTWbeG1zUGiRj0yA7A9Ce3eqPxH/AOCdvx88A/D/AFLxVrtvDNY2EXmzwQ6g00wQdTt6YH1r96VjWMAKoUDoAK8p/axke3/Zh+K00TmOWLwxqMiOvBVlt3II9wRVIOY/Ab9nH4Ca/wDtLfFCz8F+HjDHdTRNNNcXTEJBCpAaQ45OCw496/Ur4B/8Ek9D+Evjjwv4w1Xxtd6xrGjXcd4LWG0SO2ZkyQOcnrg5z2r45/4JCawmm/tgWds67m1HRb62Q+hCpLn8oz+dfuZQJsRadTVp1MkKKKKV7AI3So3zxjrXmv7Q3x00n9nz4a6t4v1e3muILGPMcMfHnSHO1M9s8/lX51n/AILaax9sl2/DGzNqeYlbVir49SfLx+FZN3ZSR+sCL3wM06vyem/4LZ6z5eY/hjZK2f8AoLl/0EYriPE3/BZz4oak/wDxJvDOgaPEDn98XnYjB46j2/Kr5RM/ZmivBf2I/i140+OH7Pui+MfHNlbWWrahLMYhaoUWSANhH2nOM4P5V71RyiGSjMbUi8KKkpKOUdz8PP8AgqlBHH+2heKiqplsNPZ9oxuPAyffFftR4LXy/B+hKBgCwgH/AJDWvxt/4K3W4t/2xNMlAAMuj2THHfErD+lfsr4YkSHwnpLuwRFsoSWY4AHlijl1uVfQ1NpZsVIBiq9vPDeIk0LrKhB2vG2RXzN+3F+2nbfsheH/AA9JBpMWua5rM8ghs55TGghjX55MjuGaMY/2jVk7n1FRX47+J/8Ags98RLy0VdI8JeH9Kl3Z3s8kzYweMMcen5VyD/8ABUr9o7xJY3F9psFpHZWw3zTWekCREHT5jg4HI5qbj5T9t6K/Ay8/aw/aV/adujoWma7rmpPIdos/D8JiToQS5QcDB7+1ftn8BdB1jwv8FfBGk+ICTrlnpFvFe5cufNEY3ZJ6nPWmJqx6BRXkeuftUfDXwv8AGI/DHWfEMeleKzbx3CQ3a7InEmNiK54LHOcexr1tWDqGUhlIyCOhpiFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopNwJwCCfSgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBn41BeX1tp8fmXVxFbJ/elcKPzNef/AAA0fxdofwj8O2njfXP7f8Si2Vrq9ZApZiM4PTOPevhr/gsNJ40h8O+Dv7Mmu00EOxu5rV2RVlJwu4r2wT+YrNy0uaqld2ufpTb3EV1Ck0EqTRMMq8bAqR6g1LXyD4J8D+OvCf7FXhzT/B/iSabxB9jjnS8kYueRuI3EZwcY+prW/ZN/aU8SeOGvfDfxMgttC8VQSlbSBmCPdRjA34z1yR09ay9suZRa3Nfq8nBziz6opaapzzTq6TlCiiigAooooAKKKKACiiigDz/41fGbRfgd8N9a8Z62skun6WgZoofvyMTgKvua+YPgP/wVb+HHxi8aR+HNW0m88EzXT7LK61C5SWCY88MwA2HjvX1t4/8ABGmeONAk0rVNNttUsJj+9tblNyN15Ir8sP2tv+CW2t6TqFx4k+FsDXVvNKZZdHzt8heSSjeg4GPf2rOUrOx0xjFxu9z9c7e4iu4I5oJEmhkUMkkbBlYHoQR1FS1+PH7G/wC2v40/Za8Tr4E+MkOqN4PlIggu7xWY6a46ENg7kwCNo56HtX68aFrll4l0ey1XTbhbqwvIVngnTo6MMgj8DTjK5hKLRepGIXk8UpNQXE2z5duQerelUxJXdj5C/b7/AG2r/wDZh8KabD4b0Zb/AF3VpHSG8uz+5tgmSW2jlycYxkdc17p+zJ8YJPj18DPCPjqezWwudWtPMnt0bcqSKxRsHHQlc+2cV+R//BTr4sWfxE+Mlh4T0C4/tBNGMluTCc+bPIwGzHbGcV+rf7HPw7vvhX+zP8P/AAzqcfk6hZaavnx91Z2LkH3+asad3qzaolHRHs1FFFbmAUUUUAI1J7Up5o20AcR4q+CvgTxzefavEPhPSdZuOvmXlqshyO/I61R0v9nf4YaLcC4svAPh63mAwGXToj3z3HtXou2k20bbDbbKOnaHp2jriw0+1shjbi3hWPj04FY/xL1KPSPAeuXUrBVjtJCM+u01022vOf2hIxJ8I/ERaTyo1tnLv/dG0jP61E/hsVHdH4FeAbqTxt+1p4dm8hZm1DxVChiA3DaZ1BOO+Bz+Ff0cooRFVQFUDAAGAK/ED/glb8NrXx1+1lLqt3bi8tNAtZr+NmHCTmVVjb8t5r9wdtOOwpaMFp1IBilqiQooooAKKKKAIrq3S6geGRd0bgqw9jXxd8Uv+CUfwi+I+qalqcM2raDqN/cm5lms5wRk5yArAjknP4V9qnmjFGhSk1oj8kPi1/wRp8RaLIlx8OPFqavDwGttXRYpwcHkSJgY4HbvXjE0P7Wv7F908Nnc+ILWwZfLDQp9utWGQcBWVgPudQPXnmv3W20yW3jnUrIiyKeMMAalrsVzH43eDf8Agsb8W/DFxbWnivwzoOsxR4WYtazWl0R65EmzP/AO9fXXwt/4K2/Bbx1BHHr76j4K1A/ei1CHzYRyBxKnHfuBX0Z8Rf2avhn8UtPe08ReDNIv1Y7t7Wqq4bBGdy4OeTX5Of8ABRj9lf4Ufs6tp3/CL30lr4k1BwRokcu6OOLDEyEMCQOAOo+8Kkasz9efBHxw8A/Ejyv+Ea8XaTq7yjKR29yu9vopwe/pXc1+HH/BLv8AZl1T4tfG7TvGt1bTweE/DEv2prpWZBNcrjZGCOo5JPsCK/cVTlRVrYiW+g6mNnIx+NOrN8SaxH4f0S+1OUZhs4Xnde5CqTgflRe2olqfnf8A8FhvjNpWn/DzS/h3Z6iy69qF3Fc3Vsh4W1UOct9W28Vtf8EgfgQnhP4Wan8TNQtGt9Y8TObe2zgKLJCMFRjPzOuev8Ir8wvj98VNS/aH+Omta9eljNqV6La2jJJEab9qgDsK/oQ+CvhG38A/Cbwh4ftY/Kg0/S7e3CccERjP45zSavqaSeh2jV+L3/BYPwCNH+Oem+Jrawkih1K08qe6VMRvMvQZ/vYDflX7RHtX5xf8FmfD15dfC/wrq6XafY7XUVRrVhzvKOA+fTDEfjU7ExPpj9gX4mS/FT9lXwNql1Ms99a2g0+4Zf70PyDPvtC19DV8J/8ABHaORf2XLx2dmjOuXKxqegUBf6k192VS2Je4UUUVQgooooAKKKKACiiigAooooAKKKKACiikbO0460ALRTIt+35/vU+gBKpx6Lp8V898ljbJev8AeuViUSH6tjNXKNoqWrgFLSYpaa0AKKKKYBRRSNntQAN0qLykJzt5qRQe9LUtXHcjWMeZn24qWkpaa0BhRRRTEFcz8TvD9v4s+G/irRbuNZrbUNLurWSNxlWV4mUgj05rpWqnqyiTS7xG5VoXBB/3TQB+If8AwSZ0tYv20reN1V2sdJ1DaxHIb5U3D3wxH41+5Ffit/wSvhSH9uTWkVQAmm6oAAOg86HFftVSGxq06iimIKKKKlq4GJ4z8F6F8QvDd5oPiTS7bWdHvE8uezuk3I4/ofcc14Po/wDwTp/Z20OYywfDWymkznN3d3M4+gV5SAPwr6Sam0KI7nlul/sr/BzSVC2/wu8I4AwPN0aCX/0NTWl/wzr8KOv/AArHwbn/ALAFp/8AG69BWlx702wK2l6VZaHp8Fhp1nb6fY267IbW1iWKKNfRVUAAfSrVJS0LUQUUjU3NMD8Vf+CxTEftWaOV4P8AYVsP/Ijmv0E/bw+B/j34+fBHQdJ+HGptpOr2uoR3kwjumt/Nt/IkUx5UjPzMnHtXwB/wVoP2j9sLSocbv+JRYrz7ymv2W0FSuh6eDyRbxg/98igrZH4Xa9+zL+1Z8HZodVW08SSDT3Eyy2OoyTIMc5KbsEcV7R+z3+0tof7Y3xE0P4W/tF+FLPXNVVmi0rV1jMVwtwMfuXA7MN5J9UFfqJ8YPit4b+C/gPUfFXiq9jstJtFOQ+MzvtYiJR3Y4PHtX5NfsTXF3+0t/wAFFrj4k2ukpYaNZTXmqtFGgVLdDC8MSYAxkmVT/wABNTexW57B/wAFJv2T/hH8Ef2a5Ne8K+F7XRNZm1W2s0uoyS7KUkYpz2OwH8K+e/g/4pm8Pf8ABMv4vSCGNZrjxBBpyzBRv2ShNwz1xkV9Tf8ABa6/8v4KeA7IE5m155doPB2QMP8A2evnTV/BJ8F/8Ej7O8dcTeI/FEV4T6qPNC/+i6ncOh7Z/wAEStCjg8K/FLVHVWnkv7K0DY5URxyE4+u8fkK/Tavgn/gjf4TfSf2c9c1+Thtc1uWUD/ZjVUz+YNffNUtiZbn5x/8ABWT9ku88eaDF8XvDKFtV0K08jV4IzhpLNCzCVf8AaQn8j7Vof8EtP2zLr4paCvwp8VSGTxBoNiJdOvj/AMvVmpRArf7S71H0r9AtU0+DVtNurG6jEttcxNDKjDhlYEEfka/ADwTrjfsl/t0+dMWtrLw/4knsrlVPBti5Qj6YYH8KoLXP6B8nI4xTqrafeQ6jZwXVu4kgnjWSNx0KkZB/KrNBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTBGFYsOtPooAKKTIpaACiiigAopGJHQZpFYnqMUAOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPzP0P9qz4kftAftYalpvwylW78B6Lw16dy24VSqlsgHOd3THNef8A/BRj9qrxdq3hm4+HN74RvdOtRMjvrt3bbYpQMgmMgngkjqAeOlfenwX+Ffw+/ZR+HP8AYOlx2VhIlv8AaL6SSTMk8gA5Jxkivjz9uP4tfED4zfDGXw74Q+GWqX2hSN++8QS2f7sKCTtiJ5wfU46V581G61PT1lG1vmev/sM6j48+MX7KelQ6i/8AZlgim2tZ2ys8qLwGXjBU84JNcb4+/ZA8KWvxs0XxP4x+LNx4e1G1ZJbWGa6jRyFOcH5uM/rXO/sE+Jvi38RP2d9b8Ov4l/4Re00FxZ2dxBbIblF5yvzLgHqc+1Q/D39mH4JfHb47az4Y8U/EbxP8TvFtjZPc3UdzOUhi2uithgvUFwMZ7mnpKSS6BCbimnsfpbo1xBd6XaTWtyt7bPEpjuFYMJFxw2Rwc1drE8F+EtO8B+F9M8PaREYNN06BbeCNmLEKowMk9TW3Xcea9wooopiCiiigAooooAKKKaWC9SBQAtNIDEqRkY5FPpu35s0gOZ8Q/DHwl4qiEeseHNM1OPdu23Vqj89jyPc10FjZwadaw2trClvbQoI44o12qigYAA7DFTtTam2tx9B1RXFsLi2khckB1KkrweRipQaKpiPmbwf/AME8/g/4X+IT+NZNHl1XX2umvPMvpi8ayE53BOnBr6ZACgADAoApaUVZDbb1YUUUVQgooooAKKRiQOBmmq5bquPxpXGPopAaWmIRq8g/aoaab4H+L7QP9nhm02bdcjqhClhx+FeuyvsUcZycV4P+3Jr6eG/2WPiFdyDAbTXhRh1VnwoP60naxcd7nwP/AMEV72Kz+J3xKsHjVrmbTraQP/dVJHHH18wf98iv1y96/JD/AIIp2K3PxA+It+Y8vHp9rCJPqzEj9K/XClEc9woooqjMKKKKACiiigAooooAKKKQnFAHlv7THx00/wDZ1+D+teNb6NbhrVfLtbdjgTTsDsTqPQ/lX4TpN48/bo/aStIL2Uy634gusHy9xisrfqcDJ2qq+vtX1N/wVS/aCl+LvxJ0b4UeHLtbuwsbtPMgTO2S7OUXJB7bzX2h+wT+xLpH7MXgmHVtVt4rzx/qUOb2+4byEbB8mM44HAz15FRvqi/h3PdPgT8GdD+Anwy0bwZoEe20sIgHmYLvmkP3nYgDJJ9vSvQaTGKWqRIjV51+0R4hTwr8E/GeqSBWEGmTHDdOVI/rXorV8sf8FI49a/4ZX8WzaS7Axxp5qp3jJw36Gpl8LKjufh18LLm2n+L3hNrzCWp1mBpWP90zLnmv6ZbPb9lg2Y2bF246YxX8/f7Ff7HuuftYeKtUGmatBodhopglubmZSz8tkBQO52nn2r9+PDelyaHoGnafLP8AaZLW3SFpiMbyqgZ/HFWtgexpN1Ffmf8A8Fn/ABksHgvwj4aVo/8ASLprqRcfPhVfAz6ZIr9L2Y/jX4pf8FaPE7+Lv2ktO8O2Uq3cljbrBHDHyRLIw+U/jUPcI9T7p/4JP6Q+lfsf6GzRGL7Xe3VwMj7wL4z+lfY9eYfsy/D8fC/4C+B/DXleTLZaXCJk9JWUM/8A48TXp9UtiAooopgFFFFABSE4xmlpGUNjPY5oAM8470tJtG7d3xiloAKKKKACiiigAopDWN4u1x/DXhvUtWS3mvGsoHn+zwDLSbVJ20D3NqivyPu/+Cxvjmz+JoN54P02z8J2c/k3WnAt9sZN2C4Zj1HpjHIr6x8J/wDBVL4AeJltEm8SXei3ExAaLUbGRBGT6sAVx+NK43Fo+v6KzfD3iLTfFWkW2qaRew6jp1ygkhuLdwyOp7gitKgkKKKKYBRSV8d/tU/Hb4i/s5/HLwTrEVxHqXwz16WPTryyePBtJiQDIGA7jJ59aTdiox5nY+xaKitZ1ureKZGDJIoYEHIIIzUtMkKRs9uKWigBqg9zmnUUUAFFNf7vUjntXB/GP40+FPgV4TbxH4v1RdM04P5aYG55WwTtVe/AoA71qy/EsjQ+HNVkUkMlpKwI9kNfAXj7/gs18PNItR/wi3hjVtduPM2k3RWCPbg5OeTnOK8c8cf8FoPEGteH72x0bwDp9hLcxtCLi6uml2BlIJ2jHPNBVmcn/wAEj9HuNT/a88Tam5Yi20e8LOepZriGv2g9q/nw/Y//AGurv9lv4p6x4rXQIPEMGq2r289qs/2YRlpFfKsQRxtxj39q+3YP+C2nh8q/nfC7UFcDGYtWjfn6eX096AlufpnRX5Y6p/wW1kUk2HwtPl54N1qJX+SVR8I/8FePid8UviFoXhvwr8NNGaXULuODyTNNPIVLAMflIxgHrigk/Vyio7dne3jaVQkhUFlHQHHIqSgD8xf+Cln7ZHxZ+FfxVs/B3w91G50HTY7WOSa7g08SSTzNn5Vd1Ixg9B6V85+Ff2gf22PEUMb6Vq3jS/ikXcpg0GCYn35izj3r9wJ7SC6KGaGOUocr5iBsH1Galx7UFJn45Qt/wUE8WQjY3iuFG5/0m1tbM/8AoINcj8SvBf7b/g7wrc614k1XxemmRnEr2epB3QYJ3ERNuAAB56V+3eB6VHPbRXUMkM0SSwyKUeORQyspGCCD1BFS0NSXY/ET/gnnrnxj+Kn7Tng+a58V+MNY8L6fcyXGpPeancyWoCxPhHDOVOWK8Gv3ArH8NeDdA8GWstt4f0PTdCtpX8ySHTbSO3R2PViEABPvWxTRLd2UNe1SPRdEv9QmZUitYJJ2ZugCqSc/lX8+OqftlfEyP46SePn8V6nNLb6o1yNNS9kW0MatgJ5W7bjHtX7X/tteKv8AhDP2UPidqgcxsujyW6spwQ0xWEEH6yCvwb+BPwF8T/tFeJNT0XwzB517Y6a+otH3dUKpge5LUNlRPeP2uv2gPDX7S/7Qfwz8SeH7VxdtHYwaghGf3nnKdvvjmvrL9r7/AIKgeJPgj45ufBfhXwkkV1aQoHvNVUgElQcqo6gZr80PhLZyeAf2gPCFv4htpLA6frtqLyC4XDJiUA5Br+inXvhf4N8cNb3mt+GdJ1aYINs11aRyOQQP4iMnpQDP55vi58f/AImftL68JPEurX+vSswMWn2it5KY4BES9xnGcd60vgrpPxq+HPj2wvvA2i+JdP12R1MUcdlKizAEcPkAFfr6V/QXonwr8GeG5RJpXhTRtPlUYElvYxKw/ELmulFrCJFcQxh1+620ZH0pWDmPzD/4LEprV58H/g5e6rZyJIs9x/aTwj93FM0MJ259SQ+P9015Jpvwh+I3iL/gllqL3aOdPsdei1yxt5Dl/sKRyI5A9N0gI+hr9gfF3gvQvHujnS/EOlWusaeXWT7PeRB03DocHvVmPw/pyaKdHFlbjSvKMH2MRAReWRjbt6YxRyi5j8af2Af+CiWn/s2+F7nwN4ysLm+8M+a91ZXVmoaWBnK7kYd16n61996b/wAFPf2etQsUuZPGL2e7rFcWcm8H0wAaxvHf/BKf4E+NL64vINKvtBuJ2LudPumC5PJwpyBzXmE3/BFj4cySME8a+I4rfdkRr5Jx+JSmJnst/wD8FQv2eLOEunjGa7Yf8s7ewlLdCe4A7etflf8At/fHH4dftCfGJPF/gW31CBZrRYr5rqBYvNkUYV8An2zmv0H0P/gjV8HNPkDX2s+I9TXGCj3KRgn1yiA/rXsXw1/4Jz/Ab4Xara6pp3gqK/1G25iuNUnkutrZB3BXJXPHXGaYJ2NH9gOXxLP+yf4Ck8VyM+ptaNs8wfOId7eUG99m2voao4YUt41jjUJGowqqAAo9BUlAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCJgd3SpKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEY4pFYntTqKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD5u8O/sw+CvAa2Op+O/FN94u1e2hWP7drVzsRgMD/AFYOOuK9l1z+ypfD8tnC8cenm1Y7oceWse0+nQYr5Q8HfBGx/Zy+GI1j4z+Nr7xdqiyedN9su5J1MnJCRgjLd8ZxXGaxY/FP9sn+y9K8H2198Mvho0kiXut5MVzeQZAEaJz1Hrgcda8/mSfJY9NxulNzPjW8/ak8a+F/HXiv4a/Di6tLKy1nWDDFft1DEsvX05PPtX6b/sc/st6V+yj8OL/Vta1KLU/FGqj7drOsyfdHGSqsRnaOvua80+IH/BKv4Zr8M0svB8F9Z+MLGPzLfWJLk+bNNjO5+3X0r4T+Nvir9qf4J+CrrwV411fWP+EYvT9mWaX955i84RZB8wBA6H0rblUHYxdqmtz9xPDniKw8VaRBqemzLc2U4zFMvRxnGRWpXyh/wTT+IGp+NP2Z9FtNV0m80650cmyEt1GUE6joy569a+r66VscklyyaCiiimSFFFJQAtFFFACGoPsaFTuyx65zViigBkcYjXAOfrQsmZNu3HvT6SgBG4XNRLMDGXwcDt3qZqguLhbaNmYZCgmga1JY23AHpkd6fX58/tg/8FLdd/Z3+KCeEtI8KWd5EIo5nvLuZslWPOFA4r7i+HHjGD4geBdC8RW7RtHqVpHc/uzlQWUEj8DS5kxyi47nSUUUUyQooooAKKKKAEao3YqOBuNSHmmiP5sk5qGhoVadTGdUPLAH0Jpd1NaAEjBVyTgDvXyT/wAFH9QuP+GZfGlsWT7NLZqVO7gkSJgfXGa+rtRJNlNhN+FJ2k4B4r8OP+ChHxY+KWrfETVdE8Q3klr4RaXFpaQN+7dV6ZNS3qaRR9Z/8EW/A7aX8K/GPieWHYdU1BbeKQjqsS84/FjX6PV8bf8ABKLw7eeH/wBknR2ulZRe3lxdRBhj5GbivsfdVR2IluOopN1Q3V7b2UfmXE0cEecbpWCj8zVEk9FUtN1qw1hZGsL2C8WNtjmCQOFPocGrtABRRRQAUUUlAC14L+2R8fLD4B/CPVdWuLlYb2aB47KMNh5JiCFAGfqfwr3O8vIdPtZbm5lSGCJS8kjnCqoGSSfSvxX/AG1/ixJ+2r+1R4e8A+DJHawt7kaZbzM52SOT88uBkYADVLfQpLqW/wDgmn+zxqP7QHx0vvil4otJbjQdJma5imk+5PfFwVHzA7lUbs++Oa/aMfLgAYGK4L4G/B/RvgT8MND8G6HHstdOgVHkwA00nV3bA5JOTXfUR2CTuwoooqiRG6V4b+2ZpF34j/Z68XaVYsFuZ7N/vdCApyK9yasrxJodt4i0W90+5iWWO4heLDD1Uj+tTJXjYpH4y/8ABJf4oXPw/wD2lNR8JXTRxWfiCzMEgbP+uhOY8c9SGfPWv2tr+fb49fDnxP8Asa/tJR6rYSbZ7e8/tDTp2JCkbidrYx61+kP7P/8AwVc+GfxA0Qw+Opf+EI1y1iBlFxl4JyAMsjD37HmhaLUbR9c/Fr4iaZ8Kfh5rnijV7lba00+1km3McbmAO0D3JxX4Yfs76RrP7VP7aukX1xFJdi41gavesQT5dtG+7rzgfdH419E/8FBv+ChHhX4zeFJPAPgBZNV06dla51JkZQ5BOEQdcng59q+gP+CUX7M9x8L/AIcXnjzX7MQ694jRBbrImHgtl6D23dT9BRuO9lY+9Y0Eaqg6KMCn0m35s5paaMwooopgFFI3SkGaVwHUUxZQzEDtShg2CDilzIdh1FN3ccGm+Z8wXnkZ6UcyCxJRTVNOpiCiiimAhprKGU5GR3Bp1FAHjHxP/Y6+DfxilafxT4C0u8um63NurW0p6/xxFT3rzmD/AIJgfs421zFMngNmMZBCy6reOvHsZq+rdoo2ipauVzGV4Z8NaX4Q0W00jRrGPTtNtIxHDbwjCqo6D3rWpNo3Z7/WlprQQUUUUxCNXhX7a3hq18S/s0eOIp7GW+ngsWntvIj3yRSryrqPavdSM02WGOeJ4pEWSNwVZWGQQeoIqZK5Sdj8rf2N/wDgqpp/hnwzYeDfi0tystiv2eDXETcWUEBVlUdCB39q/UDwv4n0zxloFjrWjXcd9pl7GJYLiI5V1PevkX4rf8Epvg58TNeu9Yh/tLw7e3cplmXT5R5TE8n5COOfSvpL4H/B/S/gR8N9J8GaNdXV5p+nIUjlvH3OcnNUJ6s72iiigQUUUUAI1fM/7av7Gtv+19oOh2cniGbQLnR3lkgZE3xuXCg7lyM/dH619MMoYYIyKKBn5P6f/wAET9WaQC++Jdqsf/THTSTj8Xr1nwF/wRp+FuhsH8T65q/iU7CDGkn2ZN2Rz8nPr371+g9FA+ZnyNo//BK79nXSbpJz4Qurxl6Jdarcun1K78V6FY/sJ/ALTwAnwr8OS8Y/0iyWXP8A31nn3r3eloJPFP8Ahin4D7SP+FSeEef+oRDn89tafw1/ZT+E3wh8TTeIfCPgfS9F1mRGj+2QxkvGjYyqbidgOBwuK9YooAKKKKACiiigAooooAKKKKAPJf2qfgtcftBfA3xJ4GtL5NOutRRPKmlBKblYMAwHbI/lXy1+wN+wT46/Zb+LOteJPEOs6XdaXc6c9ksFmCXdi6MHyRwBtbj3r7/pKlq47nwl+0v/AME4JPjR+0hovxH0nU9O03TRNay6np8kRDTGJgSwI4ywFfdNvCtvbxxLwsahR+AxUtFNaAFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFIWA6nFIxwOarGdZpfLA981LdhpXLVLTV4p1NaiCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXqnhvTdaZDqFnDfLGQyR3EauqkdwCOtX44VhjVI1WNFGFVRgAemKkGaDSHd7DV9Koax4b0rxFFHFqum2mpRxuJES7gWUKw6EBgcHmtEZpaPUWxFb20VpCsUESQxKMKkahVH0AqWiimAUUUUAFRqsnmZJGzHTvUlNZio4GaAHUUlLQAUUUUAFFFFACN0qORdx9umKkpkkZdSFbafWgaPyU/4K7fA3V7jxtovjrS7E3thNb/ZrmO2BZ42XoSB2r7F/wCCZ+rXeo/sl+FYb0XIms/Mt/8ASoyjYDHGM9sV9G6p4M0nXFYajY294Dn/AFiA9evWtLS9Js9Fs47SxtorS2jGFihQKo/AVlFO5rOSlsW6KKK1MQooooAKKKKAI5txT5Tg14v+1B8RPGvw5+FWpap4K0Y6xri4SKNRkoCDl8YOcYH517WwzTDCGXDAMMYORUuNzSMktz8EPEHxO/av+IevyXclz4y+1qSRHYQSRogz2CitrR/G37aNqohs7rx1kDgvalzj/gSmv3ShsoLfPlQxxZ67EA/lUu2lYHJM/EKPxt+3IFJafxs6MNpDWMfOf+AV5v4++FP7TXxMgRPFXhvxRrEaPvUXFkOG554HvX9AwGKWml3J5j8JfCuqftjeBvD1loWgxeMdM0yzXZBbw2i7UHpytbS+KP249Q+UXfjb14hVf/Za/b880m2nYOY/EN4f24rpf3k3jaRfRio/pWJq/wAEf2wviA3l6pp/jC/jHz+XJdbF479R61+7G2jFMfMfHX/BNb9nvxp8C/hprDePPtEGt6rd+cLO4nMpiQDA5z1NfY1N2gHIp1BLdwooooEFFFFAHzv+274J+J/xE+Dt74f+GDRLql9IsVx5k3kkwENvG4n1218wfsDf8E3fFfwW+J9r8QPiHeWi3ljFKlppduwlIkcAeYz9OBnp61+k1G3nNTbW5V9LC0UUVRIUUUUAI1Np1G2gDzH4zfs7+CPjto0tj4p0a3vHZdqXDIDJHx1B7V+dPxM/4Ix6y2uGXwN4ns101mz5OqElk+hC8/lX6ybaNtS0ykz4M/ZZ/wCCVXhb4N69beJvGupp4v16DJitViC2cZOMEqRliMe1feFvbxWsKQwxrDDGAqRxqAqgdAAKfilpoTCiiimIKKQ0m40rjFqN5Ap29PemSM6nLH5PYc1BdPkJsbvk5FQy4xuwjmQP5YOGzmvnv9vDTvH2q/APVV+HV7dWmswss7GyOJXjUEMqkc5ORXvc1wY5lYeWFXl2Y4wvc18/yft4/Cab4vW3w2XUnl1a4m+zCfA8kSZ+6W9SaRs1ytH4/wCh/tEftA/A3X7bU5tb8TWZgkDGLWFkeF/VSGGCDX318Bf+CwXhnxNb2WlfEHQbzTtdlkSBbjS0EsUpJAB25BHJ7V9TftQfEL4T/DX4fX9z8QIdLvUaFjDp8yo0szY4CjqPrX49/sh+DND+MH7Xen6oJNL0DwxZ6g2om01CdYkMSklUGT1yR+VMybTP3y0++i1Kzt7qHd5U8YkTcMHBGRkdqtVnaPrGlarFjTL60vY4wAfssyyBR2+6TitGqjsZhRRRVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTScUAK+GXnmq7Rjd8owafJllwpwaWFiyfN1qWrl7IWPduwalpq06mtCQooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKa8ixrlmCj1NADqKQHPI5FLQAUUUn60ALRRRQAUUhz2pAD3NK4AEw27Jp1FFMAooooAKKKKACiimSP5a5xmgB9FIrblBxiloAKKKKACiiilcAopCcU0SZYjHSlzIB9FIDS073AKKKKYBRRRQAUUUUAFFFFABRRRQAUUhzRnmlcBaKjeZI2Ad1TPTccZp+RRdALRTN5XcSy8fhiuJ1b44fD/Qdch0bUPGmhWmrSnalnJfxiUn025yPxpgdzRUcMyTxq8bK8bDKspyCPUGpKACiiigAooooAKKKKACiiigAoqOaRo0yqFznGBSqxZQSMe1ACTbto2cHNId2Bg0rMd2O1NaRV53AVnLcpCTZ8s4ODis+2t3uELF23dORVld8zM+/930UAVieOPGlh8OfCN/4g1aVktLKMySbRk4+lTc1i3FWRNrmiPNpdyitzJG6MSemVPNfzs6pYapaftK3VlprGfWI/EDLbndjdIJDt5+tfXX7Sf/BWD4ha34g1HSfh9BB4e0H5oBNdWglnnBGCw3D5fwr4P8P+L9fsPHFt4i064d/EC3QuYpVTezTE5HHfmmPmb+I+z/iR+wH+1J8avEk2ueILa1u2mbdELrURtRccALjA4rFs/wDglL8Y9NUTarqPh3Qoxy7vqJ3AevQVrXetftyeO9LivoT4uW2ugrxtZkW5Ax2AIwKyLP8AZl/a5+KWr2eneIh4pFlcTL50+qaiTGi55JG70qrMSstz9HP2BP2T7z9mbwjqz6l4jXxFfa0ySeZC5aJEUcBcmvq+uQ+Evgj/AIVz8O9A8OGZriTT7RIXlZixZgOTk+9dfVLQyk7sKKKKZIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFI1NzQA+imfe4zilXC/LuyfegB1FFJ+NK4C0U1unBpfxpcwC0UnQU3NHMMfRTVp1PcQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqifNStUcjFVyBk0DW5Hg06PIbmnRt5ig4xUTXGbgRAHpnNS3YvcsLTqatOprUzCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJoUuIzG6hlbgg0+igCK3t0tYljTO1em45qWiigApkmfLbGc47U+kbPbr70ARWpPlDdnPvU1FFACMwUZPAoznGORSOodSD0pI08tAvpUNAPoooqlsAUUUUwCiiigApKWigBKWiigAooooAKKKKhoBKNopaKfL3ASlooqgCiiigAooooAKKKKACiiigAoorgvi58b/AAf8E/Ds2seLNat9MgQZWN3HmSH0VepoHud4xxVXULxNNsbi6k/1cKF2x6AZr8ufih/wVW8c+JtUnt/hJ4Ol1DS4n/5CE9rJIxwegC8YNfTX7Of7VGqfHL4W30Xi7RJvC/iGGMxym6TyYZyR/Du7VhOajqzZUnufnh+2T+1f4z+PXxxHhjw1qV9pmnWd19jt4bSV4wz7sbm2nmu90z4zftJ/sHx2MnimU+L/AApcKrmK+dnCbumHzkGvIvAevaT4J/b/AIZLyyt7jT5NWNqyud8YLsAHyD1Br9kfjd4F8P8AibwXf3etQQ3WmwW5eSGZFZDGBnuKorS9mfnd8VP+CxB8XfDK+03w94VudA8R3UflC5kuVkiUHgkcAivjHw5+z78SPir4N1b4lxK1zYRyPI95K7eYzjklf/11jfErw7ZeOPjHqul/DvRZJbaSRhBZ2ozjHUivqz9kP9uK0+DOly/C/wCJ+ht/Yit9n8toyBAehLAmjXoCtex7V/wSn/a+1zxlrVz8KfFtzJeXdvbNNp1zMzGTan3kYk8+2AK/Tevwy8O+LPDPwu/by8N+IvBGqwTaDqF+sY8g8RRyHDKcV+5MUyzRpIp3IwDA+oNXHYymtSSiiiqMwooooAKKQ0m6lcY6imB93QigtilzILDm6VGzhQCTgU7du3LSeWOO+Klt9BjHdQRu6HvUUtnFJGQBwPQ0jWPmXG9mYqOig8VOsQjztz+NTr1KI4QuPKHGwCs/xP4WsfF2j3GmajEJ7OddkkbDIIq/BDIkzMzglj2FfI37Wn/BR7wx+zP4mi8M22kTeJPEIG+4t1kESQL2yT3NXdbMavfQ9h179mD4Z3Gl3Ek/hHS5ZYYH2SPbrlflPOcV+Tn/AAT9+E2meMf23Ly2vrWCbStHlvJ1gYZUsj/Jge1e3eJP+Czz6v4f1Cytfh81tc3EDxJM16CELAjOPxr84tB+IviTwz4tuvEWgavd6Hqk0ryG4s5WRl3HJGRTaDV7n9NF5fWWi2ZmuriCxtYxgyTOI0X8TxS6bqdprFnHd2NzFeWsgyk0Lh1b6EV/Nt4w+PvxP8eWL2et+Ntc1a1cgtby3cjIcd9te8fAv/gpV8VvgT4FsfClha6Xq2lWIKwC+t2LKCc8sME/iaETyn7tr1p1fkn8BP8AgpZ8b/jN8evCXhw2emx6PqF4sVzZ2NhlvL/ibewJAH1r9bKokKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSE4oNNbJpN2GDSKBzTd2e+BSMm4YYjFNaMY+9+tZSbKVgZvJUdXJNG8ZLntUVwfLmiOf1plzIWyFOOR0palWLHnhj8uTS+Ye4xVaSXykGOtQtcOwxyKzbdy1C5Za4ZX2MPfNTLN8tU4JNylpDnHrzT5HVo1dTx0q47A4paFlptnWhZC3bAqvbWzMp3sTnpk1bSFU960SuZuyHLTqSlq1oZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkzQ3SmH8qAHNUcj7V96dzVaThutBSQ5pJNvyLz9KkhjZVBfl/WpI+gp9K1wuNWnUUUbEhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRjgdM0UALRRRQAUUUUAFFFFK4CM20ZoHNDLuGKBwMUwFooooAKKKKACiiigAooooAKKKKACikNJuNAHNfEbxpD4B8I6lrdwVEdpA8pMhwowCea/FHwBpvir/got+1w1l4i1WaLR42ku3xlo4LaM5CKvTLdBmvuj/grT8UP+EP8AgSui22ofZ7/VpVj8hGwzx5+b9K5//gjv8JrPQ/g/q/je4siusavdtbx3Ug58hOgHtms73ZslaNz7U8E/B3wl8P8AwtBoOh6LZ2VlHEIm8uFQz4GMk4618uftG/8ABPnU/jR4ug1DTviBqHh/R1wJLCAEqAOuMHrX21jb70jcU+VSJjN7H4N/tzfs/wCnfss/Efwo/h17xi0S3D3V0+ZJZUIJb26V96/Fz9po61+wDaeLoZY1vNR05bVlZjgyY2kHnNZn/BV74S3PjL4Y2+t6Xow1DU9NlVvOjTMiRZ+cZ9MV+UEfxI8W+JfCGk/DpLq4fSI7nEFmpPMjHABHoDU2exs9Hdn6hf8ABI/9n/Q2+Gd98StVsPtWt6hePFbvOqsscanqvGck+9Vf+Ck37Ct14+uofG3gHSozqaoxv7WBMGUDncMd6+z/ANk/4Wf8Kb/Z/wDB3hdt32i3s1kn3Yz5jjcw4HvXrTRq/UZppXMlKzP5fLX+0vAniyGW4tXtNR024WRreYFWRkbOCPwr+jX9mn4oR/GL4I+FPFKKsb3dmglRM4WRRhgMk+nrXyr/AMFAP+Ces/x0mtfE3w602xtvFSti5jd1gS4XuWOOtex/8E//AII+NfgJ8CIPDHjgwpqUdy8kcEE4lWJD23DirRLtayPpiiiimQFIy7hjOKKaX29aVxjcbWGCSO9OqGbzFU+VgsefmrnPiL8QLD4Y+B9U8TawwistPgaaTkDOBwo9zUNlJC+PviF4c+Ffhu813xHqcGmafbIXeSZwCfYDuTXw/wCJP+CzHwy0/Umg0rw1reqWqttN0VSNevUAnNfC/wAXvjT8Q/8AgoB8c7fw/o0czadcz+XY6ZDuCJGD/rJBnBwOc19w/Dv/AII1/Dmz8Kxr4y1vV9R8QOuZJdNnWGGM+gUqSfzpFW7nrHwd/wCCm3wd+LmsWGjpqFzoOq3jbEh1CLapb03dK+tBNHJCssbq6MNwYHII9a/GH9oz/glV40+FVxca38PrxvEmlw/vUi3bbuHHIx6ke1ep/sH/APBQK4tXtPhF8UvtEF15n2Oy1SUkSIenlyE988A0D5NLnqv7VH/BVDT/AIE/EC88JeGvDUPim8siFup5rkxxxt3XgcmvFbL/AILba20+Lr4aWAjA5EN8+79RX2T40/4J5/B/4i+KT4i1zRDfX0vzS7ZSiTE92A6mq2rf8E0f2f8AU9Pa2j8Fx2MjDHn28zBx9CTTSuRotj5m0/8A4LYaa237V8ObrdjlIbxfzyan+DXi/wCEf/BQr4vahPrnwxljvvI3XF7cS53BegyvSvXtL/4JG/AzS9Zhv/I1i7SNt32We9JjP146V9ZeB/hn4X+G+lQ6f4b0Sy0m3iUIPs0Kox+pAyaHEaklqeGWH/BOr9n/AEnMjeArKdFBOLhmdQPpmvEP+Gsv2QPhH4xm8L2XhGztmspWtpr2DSUaNGBwQSeT9a/QW4gFxbyRE4DqVJHuMV+dHjz/AII56D4t8U61rNv491GxGo3Elz9n+zoyqzEnr171qJan1X8OvG/wH+LVjFJ4Zn8K6iJBkW4ihSUexQjOa9BHwl8E+WUHhTR9h5x9ijx/KvyI+M3/AAS8+JHwP0ebxD4O1xtajskaWQ2rGGYKOcjHtX0p/wAEqv2r/FHxUs9X+Hfi9rjUb7RYvOttSm5fZnBic+o7E0hyjbqfeOjfD/wz4fu0udM0DTbC4XIWW3tURh+IFdFSYpaDMKKKKAGvnbkAk+gxUc1zHa27zXMqQRRrud3YKqj1JNSt71+eH/BYS68U/wDCl9Ol0/UXsNBt9SRL2CJ8G43DCZ9gaVyoxctj9BdM1ax1q1Fzp95b31uTgTW0qyIfxBIq3X5Bf8EZ/iLrkfxO8QeDpNQlfQpNON2lmxBVZQ33hxkce+K/X2mJqwUUUUCCiiigAooooAKKKKACimGQbtvejcc0APopm6kV9wz0oGSUU1W5p1AhrttWm06Tlaj27hjpWctylsI6eZghj+FU7jz0mO1Ny1D4m8Raf4P0G81fU7hbSws42mlkboFAya/PbxR/wWc8MaPr19Z6L8Pb/XLC3kMa3smpJbrJg9RlGwKktNrU/RIJLcYDx7fRqGs3IOG5+tfmhP8A8FtLPafK+E0gPq3iGM/yhrNvv+C3Eqwt9n+FMSv2aTXA4/IRA/rRYOZ9D9PpbOf5CrBiOuagaG73MBGp9K/ILXP+Cz3xT1K6L6R4Y8L6RB2juEnuG/MMKzX/AOCwXxv8sg2HhNc/xLp1wD+r1Ljcrmkfspa2sq/LKODU8luI4z8yoPfpX4jXX/BQH9q/4mTl9Bvb21tuqjQtBjkH5vGx/WuF8VfGj9qvxVqENlqmuePhcTN+7htFmtCzduIgtNK2gXb3P38i2qoI6e9Sbgehr57/AGL9P8eWHwA8My/ELVLy912SBmliv8tOATxvZjuJx6177bYMSsBg+9ax2M5IsUU0dadVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIelNK5p9FAEbL0NNaENyRU1FA7jVGMU6iigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJmgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEo5oakwaBDqKQnFG4UDFopu78KXdQAtFJupaACiiigAooooAKKKKACiiigApMHdnPFLRQAUUUUAFFFFABSZx1oNed/Hb4waT8E/hrrPijVJokFnCTDFI+3zJTwig4PU45xWctNxpN7HbS69pkGpR6fJqNrHfyDKWrTqJWHsucmr9fkF+xP8Odc/be/aG1v4o+ONV1A6JoNyJraGCdkVpScpGpHYd/Wv18VQihQMADAqo7ALRRRVCCiiigAooooAKKKKACikNRGRw5yAE/vZpXGFzcLbRl2yRnHFQTakkMPmtkL9Oak3qzgZ3Z/KqGuW7NaySxuBtU5FYy5r6bGkEm7SPx4/4K4eNZPE3xc8OaOE3W9vAXWTnJLHGMdK/UT9lDwlbeCf2ePAelWsflrHpkUj8AFmYbiT781+PH/BQDUjqX7VFvpzzGW2tfITeep3OM1+3/w7tI7HwH4ct4jmOPTrcKfby1poup2Oi7ihhmilrVaHOc5428FWPjrw3f6LqBkS1vIzHI0Rw2CMcGvnr4Z/8E2/gt8MvFlp4ksdGur7VraQyxyX1y0i7j32fd/Svqfb1oC7aTVyuZ2EChdoAwBwAKdSUtNaEhRRRTAKKKRhuFACMeKY/Ip2z1NDL7ZFQ0MYu7A3EEewr8xf+CvH7SktpYWfwj0aSN2vgl1qLRk+YArZVAQeCT1GOlfob8WPGkHw7+Hut69cHEdjbPNwcdATX4ffsw+FNQ/a8/bOsp9Xne5tpr2XU7iSYlgIYyXVOc8EADHvWd9TVLqfol/wTJ/ZFsfg38NrTxxrFqT4t16ASqZMH7NAw4VRjKkjrzX3DtqK1tYrK2iggQRwxKERFGAqgYAFSbvatFbqZvUrXlnFIvmMMMv8Qr8Ef2xNPtfDf7cGrrpC/Zw2rW8xA6by6kmv3r1a4MOm3MnGEQt+Qr8LPHmgn48f8FDBpdoDdQ32uwoWt2yRChBds+2DS06GsfhP3Q8OM0nh/TGc5drWIk++wVoVDZWq2VnBbpny4UWNc9cAYFT1UdjAKQDFLRVAcj8RPi34O+E+nx33i/xFY6BayHaj3km3cfYdTXi2tf8ABRv9n/RQ+7x5b3TL/Dawu5P04Feb/tzfsIeMP2rvE2l3+m+MbbTLOyQoltdQllXPU/KRmvmew/4Im+MHmQXvxF0pYP4vJsXJ/DLUD0Kv7ZH/AAVUuviFpd74T+F0cmnaNcoYbnVbiMebMp6hAfugjv1rh/2Bf2zfhr+yn4V8S3Gv6Jq2peK9SkG6e1YFJIxyFyTwc96+jfC3/BFHwnazQyeIPHuq6iq/fhtYUiVvbOCRXon/AA57+B4mRhLr3lrgmP7ccN9eKAR6b+xz+29o37Xk3iGLTfD91ocmkbGYXEokDqxwOgHNfTdeT/AD9mLwF+zTol1pngfTJLKO7fzLiaedppJCPVmJ49q9YoB26BRSE4qpLqUSEqG+YcYoBJvYtsM18P8A/BXDTjffstXMiqzNBqFvJhR0Abk19mjUJfOVcF1buBXzp/wUA0b+1v2VvHkRRpTFaGbBGSCCDkVne5so8j1PzU/4JG64un/tbWdrlh9t0u5iHvhC39K/chm2rn+Vfgn/AMEtpWT9svwkV53QXSk+3kNX70zSeXE7+g7VVzORn6z4o0jw3HFJq+qWmmJMwSM3cyx7mPQDJ5NacciTRq6MHRhlWU5BHrX4df8ABTf4ueKvEX7UlzoM99Ouk6IYfsFpwqxscHdwOTn1zX7G/A8XX/Cn/Bhvsm7OlW7SE9dxQEn9aOYVjuqKaDTqe5IUUUUwCiikagBpRc7sc+tNbO4Yryz9pj472f7O/wAI9a8aXUC3hsQix2zNgO7sFUE+mTXwR4Z/4LXFf+Ri+Haqrco2n3mTj3DUFWZ+pEnmbhtAxTdsrcEhR7V8CR/8FmPhU2mCZ/DevC7xzbqqkZ/3q868Zf8ABahRDIPCnw+3tkBZtVuCEAzzkJzSuPU/UZF24HWn18e/sB/tbePP2qrfxJqHibw7p+kaVYuq2tzZrIBKx6qC3BxX19I+089KLk9Rz8LzUCzLJJhajmMkmfLJJ9GPFLHGFHzRbT3K1ne5drGT4u8L2fjbw7eaTqVtDdWVyhjkgnUMjqeoINfgv+3n8FfD/wABvjtceHfD8eLd4VuXgj+VItx4CgdBX9AylcYAx+FfhL/wVSuvP/a610Ic7bO3Vh68cD86B36H29+wP+yN8IfiF+zD4S8QeJfAWka3q915jzXV/apJI5DYGTjkV9LW/wCxj8CbVsp8JPB5P+3o8D/oVNYX7AXhe48I/sl+ALO5G2WWzNyVPUB2JH6V7/NEJuDwem4HBH0NBKPPtJ/Zu+EugyLJp3ww8HWMqjAkg0G1Rh+IjzXQWvww8G2Ugkt/CWhwSDgNFpsKkfiFqj8V/ix4R+CvhCfxL411qLRNHidUNxIWyzk4VVC8kn0H418leI/+Cw3wT0uOYaTY+JtckjbaDFYLFG3OM7mfP6UAfbtroun2aeXb2FtBH12xQqo/ICrbW8TurtEjMv3WKjI+lfmt4i/4LW+FYdPlOifDvWLi8GNn264jii98kZP6V5T4i/4LU+P7y326H4G0HTpG+7LeTS3GPbau3+dUgsz9gWUHqAfwpOnA4FeRfsr/ABE8V/Ff4H+GPFfjSyt7DXdTiaZ4bSF4owhPyEKxJ5HfNeu1XQkVetOpq06hO4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACNxSKxPbFOooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASm+WN4bGDT6KACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSk5qW7AOopBmlpp3AKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFJtpaKAEb6ZrzH9oT456R+z38OL7xjrdjeahp9myiSKyVWk5YDIDMB39a8z8Q/8FJP2ePC+vXejaj4+EV7auY5fK0y7mQMOo3JERXgX7bf7bXwf+IvwC13Q9M1e81GbVrUpZp/Z00YaTOVOZFUAVk6iWxtTg73aPrT9mf8Aae8M/tSeE73xB4XstSsrOznFtIupxxoxYjPGx2GPxr2PcK/NT/gk38cvBehfCLUfBpuJz4lhuHvp4Y7ZyrIQAMNjGRg169+0J/wUq8H/AALuorR/D+razdSqSscKCNQR03OxGB9AarnXUbpuWq2Ps1WDDIORS14P+x/+0w37U3w1k8V/8I/L4eWO5a3EMkokD4/iBx0r3iqunsZNcrsFFFFMkKKKKACiiigAooooARm2jNFDLuGKBwKAFooooAKKKKAIbsyLCTEu5+wNfnj+2Z8Evix+078btA8CQ2dxpHgJtr3mrqd8QUHcTt4544GetfomeaTYM5xWU4czTN6dX2aasec/AT4E+GP2efh/Z+E/CsDR2UPzyTSnMk0hHzOx+v5V6RSKu36UtaGLdwopKTdTEOopN1LQAUUUUAFFFFADW+7TOG4IyKkPNJt96lopCKoGMDFZ2uWpudPuI0Yxs6Fcj3FaWMVBef6hzjJ6AVLTsVF+8j8C/wBvPR9R8P8A7U179viMZZoTC/ZgG6mv3Q+E94dQ+GfhS4JBMml27cdP9Wtfjh/wVa+X416Zc5fzTAd2VwMg9jX6pfsZ+JJfFn7MXw71GbHmvpccbYOfu5X+QpLdGlRWue1UUUVqc4UUUUAFFFFABRRRQAUhz2pabJII13HpQBFMSCAThfWnfeTCtTsLIoPakEYQYFBXQ+F/+Cq3xiX4f/BD+xLaY/2jrcn2ZEDY/d/xn8q/KL4B/EX4i/BXxNH478CWk4ls0MUtx9laWAqeCrY9a+vf+Cy2ovP8XPCenCZmgj055PLzwGLda+//ANif4V+HfD/7K/gqzTSbaVNR05bm686JWMrP1ycciudG89Ldj40+GH/BaK8t7NIPHngN7y4U4a50SQLn/gDn+tenSf8ABZ34XLalh4S8TLc44ikSIAn6h69i8a/8E1/gX421S5v38LnS7q4OWbT5iignqQpyK8+tv+CPnwSt9SW6kuvEVxEG3G1a8RUPtwmcVra5nJx6HyF8ZP8AgpF8XP2kNcfwv8NNKvNB064HlpaafF515L9WHAB7+1fTH/BNP9h/W/hTqN18TviHaGDxTdo6WVpcczW4bId392Br7H+FP7O/w8+CtosXhDwrp+kS4Aa5jiDTP7lzzXo1HKyXLohN1OpNvelqloQFFFFMAooooAKKKKACiiigCG6DtCQhwayJLOSWf7mVx29a2Z0MkTKOD2rw39qz9om2/Zc+DOq+LZ7X+0dRVhBZWrNtEkrkKuf9kE5PtUt9DaEuVEfx8/bC+F/7MEMcPi3WGbVpE3x6VYJ51ww9cZ+UfU18S/Hj/grp4L+Ifwx8ReGNE8Daws+r2cloLrUXiEShgRnCkkmvnv8AZ1/Zf8df8FA/i1rPi7xLfy2Ph5rvzNW1ccn5jkQ224EZAGPQd/f7W/aY/wCCdPwT8Efs5a7qWmaRd2mqeHdMlng1JrpmllZRndIBhSfoAPapSJvrqfn/AP8ABNcTv+2R4EETbCZJQ/OMr5TZH5V+/wBIu+Nhkr7iv5iPhv8AETXfhV4403xR4ZuzZa1p8vm207IGw3TlcEHivraH/gqZ+0fdRlY7vT2GNpYaOC3TrkLj9KdgZc/4Kh+AdQ039rzTryeFmi1qK3MEkfO8hwp6d6/ZrwTAun+CdAgb92IdPt0+bjGI1FfzlfFL49/En4peMLHxJ4y8Q3d/rll81pcSQpD5IByAqqgHX1zXvGk65+2V+0F4PMun3njLWtAcKyyWoW2VgMYw0aoSOOxosB+7EciycowYeqnNSV8T/wDBOL4D/F/4W6Dqmp/E/wAQ6o632Ps2hahdNO0J7uxYkg+2a+2KpEMKKKKYgqMurMVzkjqKe33arrbrGxbJ3NQNHLePvhronxK0mbSdcsodR0ycbZraZdysPpXzz4s/4Je/AnxNFtt/Dj6IT959OlKE/nmvquONoZsqWK+lWgxPtUuKZbkz4aH/AAR9+CIYEza9t7qL0jNeheFv+CavwC8L2SwN4Mi1dh1l1KRpmP1ya+pBS4HpRy9ieY57wL4B8O/DXw/BofhfR7XQ9Jhz5dpZxhEGepwK6BlBHSlpadtBFVmEaneKTzuPlqeaJZUIYVwvxa+L3g74G+FZNf8AF+rRaVYIcJvOXlb+6q9SaztymiaOytrrzm2lGVvpxX4RftqWM3jv9vrV9GaTd9q1S1s18zkAHaMfTmv10/Z5/bG+Gn7Swu4fCeqlNQtn2tYXoEUzjruUZ+YfSvyr+PVk9v8A8FP44rqDaZPE1gyhuQylk5ph1PsL9v8A+N3xn/ZT8F+Fbf4bpZ6P4SgtIbO41WGwimMMqgAKFkUqobHp3r5L+Ev/AAVu+M3g/VjL4rlsvHultkyW89rHazJ7q8Sgce4NftH4m8J6L400mXS9f0qz1rTZcF7S+gWaJsdMqwINeW+Mf2f/AIHeGfAeqf234E8J6Z4ZgiMt0rafDBCAOcnCjnPT3oSuK58W6h+098HP+ClVjpXwy8W2es+AvED3Im0658xJYjLg8A8D5hxyO9eS/Fr/AII6eOvBtlfan4U8T6Vr+nW8TyvDdhobgKozxxtJx715Z+yb4V0H4mft/aCvhfSfs/hS21qS+trVcypHbxFnUknjHyjH1FfuD8TLpbL4eeJbhjtWLT53J9MIaNgPwM/YX+F+jfEn9qbwt4W8SWa3mns9x9qtZUV0JjjZsEHIIyvetjRfh5oOsft/2/hO1sbeHw8nioWws2iUwmNZPubMYwcYxivRv+CV/h9fFn7WtxrU0gMlhp13eITyzF8rnP8AwKvOvA88i/8ABRXS2LMrHxyqk55P+kYoKP34sbC20y0gtbO3itbaBBHFDCgRI1HAVQOAB6Cp6d6UGqWxkfmf8Uv26PFnwj/4KCp4a1jU8/D5Wis5bBUwF8xcCTPqGIP4V+l0UqTRpJGwZHAZWHQg9DX4s/8ABXbwM/hL9ovR/EcAwmr2aSDbx88bfzr9V/2Y/HyfE74A+BvEaSrK13pkQkKnPzoNjA++VqYuyKaPUqKaOtOq07kBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPyI/4JS/s/aR418QeLfFniOwsdSFhN9lt/OVpHWbOWLK3y4Izg5JzX03/wUO+E3gu/+EN7f6ra2emy2VtI9qYowo3KMgbRjvXmH/BNDWI/BvxU+Lnh64JtbV9VY28LDGW3HH9KZ/wUCtfFH7UHxi8PfCH4emZ7uziebVpTn7NACOBI65I6elcOk46PU9HlkpPTQ6H/AIJJ+A/CGi/COfW47uxm8T6q7R3EYkBlEYOQMHnpXq3/AAUM+GHh7Vf2afFl7Npdu11Z2pmjnWMCTcp3Dn8K+b/j9+wDe/BX4L6N4h+H1xdWnjTRYFkv7zTrqUK7ADcUXAyDz1xxXFeAv24PEf7Q3wR8a/Drxtp0lxqdpo08o1G2jwCqRniTJzuyOwo5mo+8iYxu1Z6H1z/wSvt1i/ZR0dx5eXuZchOuQR1r7Dr4n/4JMyCb9mYNGZPJW/kRRJ6gDOPbmvtiuuGxy1FyzaCiiirMgooooAKKKKACiiigAooooAKKSk3UgHUUzzPmIwacDTAWikzS0AFFFFACNSBh6YpT0r4r/wCCiv7Wnjn9nHwzp6+CtPt1nupNs+rXCGQW6noAmMH8TSukUouWx9qcUtfnj/wT5/4KDeN/2hvH0XgLxj4fguLv7FJef29ZHYoVRkB4wMDPTO7rX6HUCtYKKKKYgooooATPalpmz5s5pd3zYpXAVvu1Xum8m3kcc7RVhulQXXzQuuM5FHQa3R+Rv/BYrTLa31rwTLFCq3EwkLy45bivt/8A4JwXct5+x/4EaYAFIpUXH90SNivjL/gs5E39teA1jX90Ff8AeDrnHSvrb/gl7fG9/Y68I5bd5ctzH+Uh/wAayidNU+sqKbu6U6tjlCiik3DdjIz6UALRSGk3UAOopoanUAFIRnqM0tFABTXOFzTqQ80Afjh/wV38B6zH8QND8YTR/wDEplR7ONvRgd3NfoF+wL8UNM+Jn7MvhE2Mqm40u0SxuYl6oy9PzH8q5P8A4KQfBRPix8BL8JC0l/pga9t/J4+dRnB4OQQDXxD/AMEifjhD4L+Ld/4G1W++yWWswt9njnbAFwgLEc+oUjHqax20ZvKSlqj9lRTqKWtI7GIUUjZxwcV8Nf8ABQr9vq//AGa5NP8AC/glbC98XXQWWZrhfNW0TcOGQEZLDIHPencLXPuXnPtS15L+yt4w8X/ED4D+E/EnjkW6+I9UtvtUy20PkoqsxKDZk4O3FetUCCiiimAUUUUAFFFFABRRRQA187TjrX45/wDBYD4wT+JPi7o/gS2uGaw0e382eFD8plk4BP4Gv2JuHMcDsOqgmv56filrs3xa/bUvn8QH7ZDeeJo7KVG/d5hEwXb8uMcDqOah7mkUftv+yH8P9P8Ahp+zj4E0fT7JbENpkN1Oi5+aaRA7scnqSa8v/wCCnHxIT4e/sp+I48B5tYK6aiZwSJDg4+gz0r6n0vTrfR9NtLCzTyrS1hSCFMk7UVQqjJ5PAFflj/wWq+IrvdeB/BcM+ETzNQmiGOSQUXP609hbs8H/AOCUfgDRPHf7UiJr9hbanDp2l3FzHbXaB0MgAQNtPBxu7+lft3a+E9EsVxbaNp9uOmIrVF/kK/Dv/glT4utfC37Wekrdzpbpf2NxZq8jADcRnGT9K/dmmhSPxm/4Kyppkf7TXhTTLS1hhQWkTTxQoFVi0ncD2r9ePh3o9loHgPw/p+nWyWllBYwrFDH0UbAa/Iz/AILDeGX8OftFeGPEiKfLv9LQh8nAkikPH5Yr9RP2afilpvxe+CnhPxBYXEczy6fClxGjAmKVUAZWHY8Z/GmD2PUV606oyM45I57U1pxEN0jqijqW4H50Ek1FNVt2CDkU6gBsjBVJY4HrXxD8e/8AgqV4N+BvxO1bwXN4X1XWbvTJFSee3dEXJXJxu+tfb0kayKVYblPY18z/ABw/4J4/B/47a5d63q+kXGna1eOHub7T52R5SMcnOR2x0oGjyXRf+CxXwb1CENe6Zr+ny94/swkx+Kmum0v/AIKxfAbUJkSbUNXsVbrJPYNtHHfmueT/AII6fBVJCwv/ABDj+79sA/pXMeIv+CLnw+1CYnSvGmuabEf4JFSXH50D0PbrT/gpn+z5dKCvjTYf7sls4Nbnw/8A2/fgv8UPHmn+D/D/AInN1rGoSeVbK0LIrvjOAT3r5Wuv+CJPhoW7m1+I2qfaMfIZrSPZn3xzXQfs1/8ABKF/gz8Y9F8Z654vg1u00e5NxBZRWpRpXCny2Zs8bW2t+FBJ+itFMTOcEc+vbrT6AEbpX5Lf8FsNVvP+Es+HenCeQ2X2W4m+z7js37lG7HTOO9frPnrX5ff8FsNFgbSPhtqQhT7U13Pb+bj5tuwHbn0ziol0LifnF4PvPHvwr/sj4k6EdQ0SOOYxWmrQFlDOBgrkdQRkH617h+z/AOPtU/ac/bq+HeueLxC+o3Gp2zXDW67fMMPzAn67QDX21+yZ8E9C/aQ/4Ju2vhi/s4JLoTXZtp2QM8Vwj7lYHqOw+lfEX7Cfg/xF4R/bm8JaINLku9R0jUZ47uEqQsSrG+5yT0wMnn0osWfuJ8Qvix4P+FOltqHi3xDYaFbAbgbuYKzf7q9T+Ar8iP8AgoN/wUH/AOF/RzeBfAEkyeC4yDfXRyjXxDAgYBzsBAOO9fUP7eX/AAT38f8A7TfxQs/FPhnxTp62K2iWx0vWZpljgIJy0ewNjPGcAZIrxbQf+CJfime1Vta+JWl2s4HENnYyTIvtudh/KqtYjYzv+Cf3xi/Z3/ZZ0tvEfiPx/cX/AI1123EM9tDpUvladGDnZuC8kkDJH5V98/tRfFTS9S/Yw8e+MvDepG60+88PzvY3tsCMl0KqexHJFfJfgH/gizZ6P4t0298TfEAazotu++ewtrDyml4OF3FiAM4zxyM1+jkfgHw5H4Oj8KNoenT+Gktxaf2VNaxvbNEBjYYiNpHtik1cVz8g/wDgjz4G17VvjnrniW3UroFnpclvc3G3arSOV2ov48keleRroj+B/wDgo5Fa6hLtFr45jZpCf784dT+RFfuv4P8Ah94W+HtjJZeFvDWkeGrOR/Me30ewitI2b+8VjUAn3r8kv20P2C/jXq37QXi7x54O0GfWdOv7pb+2udOu8XEbgAAqMhgVI7enFHKPmP2M7ihulfgNL8a/2sPhPavbah4i8fad5DYLajA9wo5xjzJQ2a6Lw/8A8FKP2ltLjWGXWW1JlGA13pKn89iDNFhJXPqj/gtJ4Be98E+CPFtvbSSNZ3r2U8y/dRXUlM+nzAD8a7//AIJCfE4eKv2e73wvMQLvw7fMgXv5b/MP1z+dfnv8cP27PjN8ZPAF94U8Y/YDo93teRV0to3BRgysrN0IIHNfTf8AwRLaZvEHxLG5ntvs1sQx6Ftxz+NLlKbtofq4vWnUlLVJWICiiimIKKKKACkPNLRQA0LjvTqKKACiiigAooooAKKKKACiiigAoqORAzBicCl81d4XPJoAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfi/8AsmaX4+1b9q7xl4Q0PXbddXmEs02rXMRlghC/eJGM5IOBx1Ir9U/g/wDAPw38Hzf32n26z+INUw2p6tJnzLphz0JOBntXzD+yH+xj48+F37SHi34n+LNSsbO0uxNb2+l6exczhjwzkqAFA5GDnNfdO6ualT5Vqddapd2i9CO6tYbq3khmjWSF1KujjKsD1BFfJ/xw+Hvwc8JeAfiF/YL+G/D3iG80ueG5MU6LNuZTgbBk5J4/Gvq28hS4t5I3GVYc5r8wv2m/+CV/jbx78QtY8W+DfGVndtq0/mvaaiZIWjBwMBlVhgde3etJx5laxNKy1bPcf+CUK6fa/s4z2dhqkWpeRqcgm8oH905AODkV9q14R+xr+zRD+y38G7Lws1xHeavNIbvUrmEko87AAhcgHaAABkV7vVQjyqxFWSnNyQUUUVZiFFFFABRRRQAUUUUAFFFFABVW+naG1lZBukCnYucZbsPzqyaY0CSffUMM5waloaep+QvxYtf22vFPxT1ObTh4m0/SmvnFgtlcrHbpGG+XOD0x6jvX3Z+x14P+OugeHJ7r40eK4tWvZuINOSNXeEeryjGT7Yr6Q2DsMUoGKXKaOd1sHNLSYpapKxkFFFFMBG6Vx/xI+FPhf4taLJo/ijSYdUsJPvRyDn867CjbRZPcabTPA/2dP2K/h7+zD4n8Q634NjvEn1hFhaO6m8xYYw27avHrj8q99pAMUtAgooooAKQ9PSlprruXGcUAAXB60u35s0jLllOelOqWrgI3So5ovMjYA4JGKkoz1o6Aflr/AMFhtJew8N+GLuTMrrc7FbHAXrmvVP8Agjv46j139nW+8OkoJ9G1GQ7QfmKyfNk/jXUf8FRvhrH44/Z31W8MeJdLia8SbjIKENt+hxj8a+ev+CJgLX/xOZZT5SxWeIuwLbiT+mKzWx0TfMk/I/VH+JafTKXdVpmIrdKqLHHJP5wzvXirLNxzXlv7RXx00r9nf4Yar4x1WB7mCzVcQxfedmdUX/x5hVXW44xvoehy65ZQ3y2Ml7bJeMAVt2mUOc+ik5q/X4T6h4v+JX7Yni7xh8SvDeqzaJrvh/y57bS7OWQboi2ARyfm/Svdv2P/APgqF4j8M+LJfCXx4vJnsHXZb6tNbBJraQA5EuANynAHTIJqVJN2G49EfrFz2rzn4j/tIfDL4Q3y2XjHxvo+gXrLv+zXVwPNC+pQZIH1FfJ/7aH/AAUv8L/D34fHTvhVrlp4g8XaooWG8tx5kNkm4b2YcfNt3Y9Dg1+dXw5/Zd+Mf7Wsev8Aj1xNewRs0l1rGrE752AzhAfvfh0pSkCj3P3e+G/xe8G/F/S5NR8GeI7HxFZRsFeayk3BSegI6iuwr8Of+CaPxU8Q/B/9rbTvATX6R6JrlxNY39s6nYZFikMZXng7wo71+4o5FOMrikrC0UlLVkGX4l0aPxBol3YShSs8bR/MMjkYr8Fv2vP2Z/F37MfxWm1+1WSKxmvGu7K7tsjyjuyOR2zX7+Mu4YrkfiR8J/C3xb8Oz6H4r0mHVtPmGCko5HIPDDkcis3F3ujSMklZn5y/BP8A4LGWOj+BdKsPiD4a1LVddhXypLvSUUCZQMK2HbrxzzXokn/BZb4bhWCeCPFW/GRvWAD9Hrvov+CWvwTj1SeY+HFNox+SMXEu4c+pbFaKf8Et/wBn0ahFdSeGLqYL1ga9bym47gAH9aeoe6fI/wAXv+CyXiTxJp0mmfDjwgujXsx8v7bqJ8+Rcn+GNTjOPfvVD9kn9gvxz+0L46t/ir8ZJruHTHnF0IL1iLm/IyUBBHyoG2nB6gYr9HfBP7Ifwc+Hc8U+g/D7R7O4jIZZmhMrgjocuTXrojVVCgYUcADpRZiuuhDZWsNjbxW9vEkFtEgSOOMYVVAwAB6YqzSBcUtUtCQooopiCiiigAooooAKKKKAIbtS9vIobYSpG70r+fL9sr4beIPgv+0pr+ovZyWMU2of2jY3W0lGbO4HP1/nX9CLjK4rzr4tfAfwf8atDm0rxRo9tqFvImzdIgLr6EHrkGp5Xe5rFq1j5r/Zd/4KYfDX4ifDiFPG+tW/hHxRpVqqXsN+21LkquN8ZxznH3euTX5m/tZfF65/bI/aekvvDttcPY3LxaZpNts3O0anBcADoTluegr3Px5/wR++J6eOL+LwnNos3htpz9lmvboq8cZPGRyWx719n/sS/wDBOnQv2XruTxJr95b+KfGbx+XDdeSRFYqR8wiz3P8Aexmm0T8J+eXxq/4Jz/Fr4M3Wk6t4Z0W+1yBoI3M2lbnuILg47Kcg5/TNfq5+xT4g+ImvfAfRV+JugXmheI7MfZv9O4luI1+7Iy9QcY6173tFG0ULQTdz5L/4KA/sYz/tYeCtNk0S8js/FWiuWs1uDiGZGIDox7cZI9wK/MLwd4k/aK/4J/8Aiq7ig0++0yy3kz2t5aGfT7oYKgkgZHXIKsOcZzX747RVTUtHsNZtzb6hZW99A3WK5iWRT+BBFMEz8mdJ/wCC03i9bVVv/h/pM9yBhmjvWhBb2UgnGaqeCfiR+0H/AMFGfiJb6Z9tuvBHw8hmSS8Glq6Qoq8n98AGZjjGM4ya/Tcfs4fCn7c14fhx4We6Y7jK+kQMcn6rXb6PoOmeHbMWmlada6Zar0gs4FiQf8BUAUBdDtH02PR9LsrCJneK1hSBGkYsxCqACSep4q7SYpaCQooooAKKKKACiiigBNo9PeloooAaw4r86f8Ags94Y1PWPhH4N1WysmmtNL1VmurgLnyw8ZVfzYiv0YqrqWl2esWrW19aw3luxyYp0DqcexqZK407HwR/wRruryb9nzxJaXBnEFvrbCBZMgKGjUkKD2zX21o/wx8JaB4mvfEWm+HNLsdevjm61K3tES4nP+24GW/E1t6bpFjotuYLCzgsoSdxjgjCLn1wKuVQNiYpaKKBBSUtFABRRRQAyaFLiMpIiyIeqsMg1R/4R3SyCDptoQev7hOf0rRooA5jXvhj4R8T2clrq/hfR9Tt5OGjurGKQHnPdaPBPwy8JfDeCWHwv4d0zQEmOZP7PtUhMmP7xUDP4109FABRSGvm/wDa8/bU0P8AZJj8P/2tot9q76tIQPs2AsaA/MST39qTdh2ufSNFeKfBP9sH4XfHy1gPhfxLbPqEg/5Bt04iuAcEkbT1wAenpXtK9sHPc5oTuA6iiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkyPWhmwKZuDcVLdgH5ozTWYKcYpN/tS5gH0tMVuRxT6pO4BRRRTARjtGcZpqybmxgj8KfTP4xQA+iiigAooooAKKKRmCjJOBQAtFIrBuhzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIzbVzgn6UALRSdaWgAopu8ZA9eB706gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKi88eaEA696AJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAroiW+TtVB0zntTvMGcAFvcUy6tlu4jE+QrEdPY5p0Maw/ulzgetBQy6KC3Yu2xe5qGyZmZtm3ysAKRVxog4wwB+tKsYUYAAHtQO+lh2AOgpaKKCAooooAKKKKACikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiko3AYB6mgBaKQ0hYgZoAdTGbaCaFct2pex4qboNz5g/4KG+HdR8S/s3+LLfTZyky2ErGMHG5QAW/QGvjH/gibq23xz8StPEbDzNOtZd2PlBV2HP1ya+qP+CmHiu98C/s5+JbnT5c3d/CLb74HlK8iIxA6nKsRXyx/wAET7aRfiB8S5R/qV0y1jJ/2i5J/lWaNnsj9UfF3jTQvAWiyat4j1a00bTYyoe6vJRGgJIUDJ9yB+Nef/8ADWnwc3bf+Fj+Hy390XYJrxn9vr9j3xh+1fH4btfD3iaHRrPTg5uLW6DGKZichiAeSMCvjZv+CL/xJ2nZ400EN2/cOD+eaCbH6Oal+2t8DtKjZrj4k6INvVUlZj+QFcj+0Fomm/tSfAfUp/B2p2ms6Vq1nJFbz5yhcfdwMdcjv7V8SeG/+CLfi7+2LNtd8aaadN8wfaRaI4kKdwpPGa/TX4R/Azwx8E/h3Z+DfDdvJFpFsMfvnLs7E5LE+uae60LjJRZ+P3/BNu9vPhv+1pP4L1m323WoBtNlgkPy+YgYgn1HBP5V7d/wV3+Fvgzwn4S8O67p1nDaeIZ79oWaFFVpcpuO8Y5AXJGMcgV5F/wUi0e7+Av7WOi+JvD0Z0e5ls47uG6tTtaSRJDuYn1I4/GvMviH8VviP/wUJ+L3hbw+liTMoS3hhtwxCjHzzSHkZ2gnPFZxi+a5TkeO/AfV/CWg/GLwtfeObRr7wlBdq2oW8ROXQA4/JtpPsK/oK+DPxs+F3xL8M2tv4H1jTDp4j8uLT4ykTKvTATP8q8C8Rf8ABMn4at8AI/COnaVCviS3t1P9tEDzpZsgsScdOuOK/Kr4kfBT4rfsoeI5Lx49Q0uC3fEGqWjMIwN4ALducgfjVS10IsraHqHivS3+Fv8AwUssS9odPhi8VW80CuPldWlUAjHY5r92l+6K/mw0/wCKXiP4kfHDwf4h8SX0mpahFq1iDMxzkCZCMflX9JsbB41YdGGeaqKaJlK6sOXpS0nfFLWpmFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUmzFOooATbS0hIHJ4ooAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKTdgCquqalBo+mXd/dP5drawvPK/91FUsx/IGrNfPv7fHjCbwT+yF8TNRt5DHPJpZskcHBBndYcg+v7ylzDtcZ+zT+3B8P/2pfFHiHQPCiahBqOjoZ3W9iVVmg3hPMQgnjJHHuK+hq/mm+B9z8U7fxRLd/CmbxDBr1valZZvDssiTCDIZlbYRlMrnaeCRX1l8J/8AgqN8a/gvry6b8SNOuPF2nsMNBqcBtbxMA5Kvt5P1BouPlP2mr5F/4KK/teax+yv4B8Ov4V+xzeKdX1DCQ3YDBbWNC8rFfc7Vz7ml+D//AAVA+B/xTh8u812TwfqSoXa01qMqpwCSFkUFWwAfSvzh/am+Imrft9ftiad4f8GBrrTFk/sjSATkeSuXlnIPABCs3/ARUvVhyn7Bfst/FLVvjV8A/B3jbW7WGy1LWbP7RLDACEHzsoxn6V6tXMfDXwPY/DT4f+HvCumosdlo9jFZxhFwDsUAtj1JyfxrpM0J2FYfXzL+0T/wUH+Ff7N+vXHh/Wrm91fxHbqjS6XpcIeRA2DliSFGBz17V9L5r+fX/goUJI/2zPiUHdm3alGPmOflManb9Paq5h2P3H+Afxs0f9ob4W6X440G3ubTTr9nCQ3ahZFKNgg4JHauF/bS/agX9lH4RweKItMGsaleahFptnZu5VWdlZ2JPskbVwf/AASrhaH9i7wjuJO+5vXH0+0P/hXzd/wW11qSOH4Z6X50ghMlxdtDuOwsMKGI6ZAJGfc1L1Gkey/D/wD4KYw+KP2dNf8AiZd+C7rzdBvYbS+srSTeMPIibwfYPnHtXbQ+IPgh/wAFHvhfPYm7EzBFLQSMI7yyYEPkA+6847Zrxv8A4JW/B3SfF37Hnim11eMXFl4n1CeCdcZICKqgj3BwfqK/P39ob4VeMf2Ifjdquj6Vqt1p8E8cv9n6hbOVaW2cFfzwxU/U0itOhwHxW8HwfCX42a94d8JeIJL2HS71rW21S1lMbNzt4ZSOxwfxr+hP4e+LtC8M/DbwfZav4l0+K9j0mzidry+jEjuIVBJ3NkkkGvxS8Hf8E2PjX8RfBdr4t07TrO5tNRhW8t994vmTb2HP15J/Crmof8E3/wBpK6niN5oc12FIRXm1DzNnYEZPGM1SYmrn7wwzx3MKSwyLLE4yrowKsPUEVJXmH7NHgjWfhp8CfBHhbxDKJta0vTkt7lg5f5hnuevUCvT6pO5AUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUmaG6U2gB1LTOe1JuK9SMVLdhjLhtqk1VaYkYDYPapZGEmQp3cdqoybgqEIX/ANkVDZ0QiralhboH5fMUv7EVIrOGBZvlqpp9qOWeHy2J4yasSFjCFIPB9Km4O2yJ7WYyMcjGOlWqoxbscHaakVnWNt7bvp1q1IyktSySFGScCmrKj/ddW+hqm7453kj+6abHIsaNtGT320+YahdF2SQKhOT/AMBGTUcLZyxlYj+6wxWe1m8rH98yqxyasxrGzEIzE+ueDS5tR8i7l7NLVaOBluN+/wCX+7VmtDEKKKKACkOG4PNLScVLdgEGOgFG4ZxnmkU4zUbMqnJOCelLmGlcmo3CmLIOOaa7nPtRzBZkuaWmqwKinVSdxBRRRTAKKKKACiiigAooooAKKKKACiiigApMihulM3AcZoAczccVHJKFhd3fy41UlmPGB60M+Oc4FfOf/BRLxbrHgf8AY5+IesaDfyaZqUMVpGlzEcMqyXkEbgfVHZfxoKscR+29+194u+BvhfR7z4aaNb+I7e53NPqyqbqC22sMq6pyM9Pqa8A+FX/BZ+JY4bT4i+DpUnLgTXukONsak4JMbc5HpWX/AMEZdQ1LxDq/xK03U7qXUtDjtrdls7w+dGJGckn5sjkCtH/gpzpf7PHg3wPqNloui6OnxPurhBGumAiSHa6mQyBeBlcjn1qWx2R+jnwx+Knhj4weF7bxB4U1WHVNNmUMGjPzx5GQrr1U+xrr6/Kn/gkb8R/APwv8G+LG8SeOdN0nVdVu4/K0u6utu1EU4YA9+TX6h+HfE2k+LdMTUdF1G21SxckLcWsgdCR1GRTRL0NOiiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASk2KDnHNOooAKKKKACiiigAooooAKKKKlsAooopoAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQrKjMuGBycCpNvzE0irj060+gYUUUm4ZxnmgQtFFFABRRRQAUh54paZtO4HPFAChQKdSA5paACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEYFlIBwfWk2/dzyVp1NZsHGKAFNMZgBz0pQxPGKUqMUAfDX/AAUe+Mnxk+E8GgXfw2kkt9OzuvGt7fzXY5GBjHSvnSL/AILNeNdI8Lw2d58PrGXxDGgjae4llRWYdWK+vtX6yX2jWepxxrdQR3AT7vmKGxxjvXEar+zv8NtcuDPf+DNHu5i28ySWik5/Ks1FnRzQaWh+JHiG++P37fXjY3H9m6jq8MjeVFHAjQ2VqOuDnjAA71+p37Af7Grfsm+BdR/ta+XUPFGtskl6Yh+7hCg4jQ9T1yc96+m9B8M6V4XsVs9I062021UYEVrEsa/kBWltp2Zk5XEWloxS00iRKGpaSmI+Of27P2Fb39ra48OXen+IIdFvdLRoBJPD5ilGOSWAwSfoRS/sP/8ABPmz/ZM1bVvEGp+IU8T+Ir6IW6TR2vkxQRg5+UFmO49Cc9K+xdtG2oUWXzDDyK87+NHwV0f41+ENQ8Pa3H51hewNBIoVdwz0ZSRwVOGHuBXo+2kCAc96pRXUnmaeh+aPhP8A4Ix6f4X+I2ma+nxJml0jT7yK7i02XSw8z7HDANMJAvbtHz7da/S5eFA/KlxSbcYwTQkDdw/ip1J70tUIKKKaxIUkdaAHU2SRIly7Kg9WOKFzt5r8WP8AgoL+2N4/1b436j4H0HW7nStD0G8CILNzFJMxx99gfmHNK+tilFtXP2pormvhvqF5qvw/8N3mokG+uNPglnI7uYwT+tdLTEFFFFAgooooAKKKKACiiigAopDQTgUr2AWiqy3JkUsPlAPU1jeM/iB4d+Heiy6x4n1qy0LTI+txfTCNeoHGep5HApcyK5WdBIgkQqehpscZjwN3HpXxV4t/4K5fAvwzrMunW0uua35b7Gu7GzUwdeSGLgkY9BX1P8Kfit4a+Mvgux8UeFNTXVNJuxlJeAynurDsR6UcwrM7KiommCtjPNLu5A9auwWZJRTRmnUhBRRRQAUUUUAFFFFABRRRQAUUUUAFFIelNzQA4nFIGBpPrSbvmwBUSHYeelfJH/BUxZT+xZ422cp5tiHX1H2uHH6jP4V9a5rxf9sL4aSfFj9njxnoEKebM+nyTxR5xukjHmJ+O5BUlI+KP+CJ/hG1Gg/EXxN5YM7XMFgrMvIULvIz9SK+7vjP+zd8OPjpYhPG3hyx1IwxsEu5I1EsIx1WQjK49q/Nf/gjf8UpPDfxR8WfDy+umSDVLUXsFu/AW5iO1xg9yv8A6DX3v+3JpHxF8SfADXNF+GUbSeIb8JGywuY5niDqXWNgRglc555GR3oH1Pxh/bM+Hvw3+GPxiu/C3w01KfWbG0KrLI03nRiQjmNSOuDxxXpP/BNP4v8Ag74B/tCTt4+0z7BJfWjW9rq12u3+zH8tnO4EZG8DYMc/MO1fUv7AP/BNW+8C+ILb4g/Fmxt5dRi/eafoVxiURSEEGSZSCrEAkgdjg9q+c/8AgoJ4c8N3X7dltp/hiVZru6ubJdQRcFEnaRFZMew7Uxn1542/4LI/DbQdQ1Cy0Lwl4g8RNau0a3CiKGCTBxncWJA64+WvLNQ/4LZXu2U2vwwEY/5ZtPqBI/HCV9O3H/BL34C69dx6lqfhu5lvJEUyrb3rwQs2Bk7Ex1Nbf/DtX9nceX/xb2E7Bt5vbgZyMc4fmkLQ4H/gn9+2t4z/AGtPGHjeLX9I03S9I0yKJ7NbIsWDMxBBYnnjBz71+XP7ePiKLxF+1n8Rr63O6P8AtJo8+6jaPyr9yvA3wa+Hn7Lfw810+DdBtvD+nQQS3lxIGZ5JNqk/NIxLHpwM1/Pb4rm1T4r/ABI8Q6lYWc+oXV/d3F8Y4gWby9xOfwpgfvH+wmlh4c/Y2+HErGGytItI8+eU4RR8zM7sfzJJr8kv+CjX7SEf7Q3x+ul0y4S58NaADp+nSxtlZRnLyfi2fyrl/CPxO+P/AMUvB+l/CLw9qOuXWi24McemWURiwhb7kjqASnsTivY/jB/wS/8AFXwj/Zzl+IN1qX27X7QJPf6PbxFjFGzBeD3K7sn6UDPvj/glNCsP7HHhwBVBa8u2O3uTKeT714T/AMFrtLsv+EV+H2ofZ0/tA3U8An2jd5YjJ2k+ma+ev+CW8vxOuv2iPDVppl7raeBIDcNq0Jkf7EqmCQp8h+UEybOler/8FqvFUd54o+HvhmCYyXNvazXcsIP3d7BFJ9zg0Afff7F7Fv2VvhiT1/sS3z/3zXtNee/s7eEZvAXwJ8AeHbj/AI+NN0S0tpP95YlBz75r0ShK5Fxq/ep9FFWlYQUUUUN2EFFFFCdwCiiimAUUUUAFFFFABRRRQAUUUUAFFRSSfNtqRfuigBaKKKACiiigAooooARulMboaezBVyelVZ2MnAbavqKluxUVcd5hjC7uneopbgdhmlaYJtXG/wB6qzSvuzsyvdahs3jHUQF4ZlcFfL74r5L/AOCnnxt8T/A/9neyuvC90dP1HWNSj097yJsPAuxpMr9dmPxr6muI0DcMwZv4M18Rf8FmLbzP2bPDbAZMevxn/wAgyiluaTWqON/4JGfHbxz8UPEnjrR/FXiK916zsrWG5gN45fy3ZiCAT7Cv0pdWXBJ4zX5N/wDBE7P/AAnXxH44+w2//obV+sGoQyyY8tttVy3RhF8z1EkmESluuO1RLf8AmHbtIz7VDtmC7Dhx/s81XmZfLYNzjqB1rG1zpjGJZkkdmwgy2alXcjMC6gN71mWYlFwzBQkX95m5rR+ymZchs1SQNJdRrNIZNq/MD6VJFbzQGPaGPPPFSW2InUH/AL6rR7itFHqYzlyuyGx5wM9afRRWhzBRRRQAjfdqvIrMc7toqwxwpJrnvG3jrw/8PfDd7r3iXVLbSNGs9v2i7um2xpkgDJ9yR+dRIuJpIz/OFfeVIyBSTxyHDYJxX5VfFD9uz43fGr41a74a+AjLe+HbBt0V3YWvm74wPvsx6AnivUPg7+3Z8S/g9fQaT+0p4XvNC026fZbeJGtisZO0nBA69qk05mfoJbylxleedv4+lSySNGhZhgCvLfhZ+1F8JvjNrDaf4O8Z6Zq+pqnmGzjcrJj1AOM160yqy4Zdw9KpK4nIjtp/O5AOOlWMivgP9s7/AIKcWHwI17U/BHgixi1rxTbxpv1B3D28EhYZUgfeOMj6kV8jfB//AIKjfFmy+MGg3vjnXln8IzXYF9Y/ZlRFhfKFgQM4UsG4/u1WxDVz9tc0tUdF1a01/SrLU7CZbiyvIVngmXOHRgCpGfUGr1MgKKKKACiiigAooooAKKKKACiiigBG6VDJgfMxwvrUzdKyPFV9eaX4b1O70+yfUL6C3eSC1jIDSOASACTjrQNGkqL1/nXyZ/wVO1MWP7FfjS2P3r2exgX6i7if/wBkr83vEn7fX7SOl/FLUyms3tjci5kRNFuLMMqAZAXbjn8PSvPP2iP2tvjH8bNKttA8f30lrYxnzxZmDyFkI6EjvzUtl2P0H/4Iv+C00n4K+LfEboom1XVhCr5G7ZEgH4csa8a+KX/BKX4o+N/iz4m1l/FWjLY6lqE1zDqF5OS/lsSwDKOR2FfPn7OPwP8A2lPF2gyr8Nl1/StEk/fsUuzaQyEj7y7iAfwruPiB+yv+2BoOk/bdVfxJqsUnHlWOq/aJB9VVsijcZ1N9/wAEafirbx+bY+JfD9+Qu5BG7puPbk1+gf7Av7PGu/szfBpvC/iS8+16xcXsl5OscnmRQ7gBtVvT5RXp/wCzboeteG/gT4H0zxGLhdct9LhS8W6ffIJNo3Bj3Oa9KxVGbFooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSsAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZ5a7w/en03eu7GRn0oAdRRRQAjMFUknA9aM55HSmXEC3MLRvna3XFLHH5aqoPCjFADutJtA6U6igBkalVwTmn0UUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU3b82aU1GZH8zAUY9c0AP3fMBRIu9SM4pshCrvJAC8kk4Arxnxj+2X8HPAOrTaZrfjvS7W+hGZI1l37fbjvSugPaFXauM5p1cN8Lfjb4K+NGlyah4N1+01y2jO1zbv8yn3HUV3HNMewtFFFAgoppfGT0A71yNx8X/BFnqw0ubxdoseoltotmvo9+fTG6lcZ2FFRxzLNGskbK6MMqynII9Qadu7UAOopoanUxBRRRQAUUUUAFFFFABRRRQA1m2qSegr8B/+ChNjbp+2V4lt9Jtwk811BsUdGkbHX8SK/fW5k8u3kb+6pP6V+GP7VNvb+KP+Ci1nbR8xza9p0cn/AH8jz+lZv4jeHwM/b7wzYx6d4d0q1jB8uC2jjXccnAUCtWobWMR28SjoqAfpU1aGAUUUUAFFFFABRRRQAUUUUAI3Sq97FLMqCOTYmfnGOoqxTAwfPHSpaDqcn8R/HFj8Lfh54g8T3uBaaNZS3bB2wGKqSqZ9zgfjX4bT6h8Zf+CjXxo+xRzz6kskrS+Xu8uy0u23HAbAC5A6E8k4r7C/4LAftCPp+gaV8LdJnkS5vpBcaikZ/wBbHwUQ/wDAsGvoP/gmz+zm3wE/Z/s5dSt44/EXiFhqN4653KrD93Gf91f5mkldXLbsfNvxU/4JP+GfA3wbmm0i/wBW1HxJZ27XN3eQBm80gZ2LEG2nn/Zzjmu8/wCCQvgvxn4N+GXiZNe0680zSri/3WsF9A0T5AwWAYdDW1/wUe+Lnxf+ENrZeJfAHiu30LQ9NQG9tHhR2uCzBcEMpyMt2rxD4O/8Fnr6zaz0/wCIvg+GeHhH1PSJtrAY+8YiPXsKiLuzTVI/VGO1fd5jtuYHI9KkeSRtpRcf71eT+Df2sfhd43+HcvjSy8WWEOjwQtNOLmZY5YsDJBUnOfpX5W/Hb/goF8av2iPiRfaV8KbnWtF8OIGFrp+gQCS8ljVv9czqvmAn0UjArTm7E6vc/a+HKjBfe3c1LX4AeFf2uv2iv2dfFFrc65rniQxM5eTTvEaswnGCMEygsOueD2r9lv2S/wBoi0/aY+EOneLYIltrosYLu3U58uVeoo5u5Lj1PaaKT0pae5AUUUUwCiiigAoprZ2nBwagDPDCS53Ee9Juw7Fmiq0Fx5iqW4Zh0qNdTtZGKLdwu+cbVkBP5ZoWoWLh6VFJIItuecnFOzlev5Uzy89TuIOQT2qZXGiNRO0jBtoj7etebfGP9pX4b/s+rZJ448SwaNNeKWt4HVpJJFBwWAUE4z3r04puKkkgj0PFfDX7bX/BPHXv2pvHdt4msPGEGnPb2wt47S7gLoBnPBB4HWoKJvil/wAFcPg74O01z4Y+3eMdRxlIYYzBFnI6uw9M9u1c18BP+Ctfhf4q+KpdG8ZaFZ+C9OkBAv7q/wB0QXB+/le/T8a8Gl/4Is+PVjLJ440R2HRfsz1bs/8Agir4wmUNdePtJic9dlo7VSVw0PFP2vNF0P4N/H6b4i/Bzx1oj6feXIu7NND1E/aLOQ8uu1eik5796+yP2cf+Cu3g7XNNt9I+LFrL4U1O3iCtq0aSXNvPgfeKopcE47A9a8xj/wCCKPiPd8/xK04A9cacx/8AZq3tN/4IlxlV+3/FKZCDnFtpYwPoC9Ow9GfUs3/BTT9m37PIV+JcO8KcD+yb4nOP+uI/mK/Ob4V+MPgR4f8A2un+KHiz4nzeJLD7ZPqMME+g3LhpXVwodpN33dwYEg4KjGOK+nNL/wCCJ/gaNl/tL4jeIrtf4vs1tDCfwzux+RrWj/4Ir/CdSd3jTxi2eT++tR/7Ro5RaI9Puv8Agql+zzZkBfFF5P8A9ctOmP8A7LUS/wDBVz9n1v8AmYL8fXTpf8K8+j/4Iw/CVWBbxh4yYf8AXzbj/wBo1I//AARn+EmMx+K/Fwft5lzAw/ECIfzp2YvdPSpv+Ch37NvxK8P6ho+peNIYLC9haCeK9gli3IRg8leK4X9n/wAX/sX/AAGF9e+EvFvh8XszEvf6nMsk8YbgojOMqpB6DrXw9+3F/wAE99T/AGa5otc8KPeeIfBlx8rzbN0tpJxxJtHQ5614P+zX8D4P2gPiRb+DpfEmn+GLq5jY20+oqxSWQfwDHeizHp0P3j8G/tBfA3UpDceG/GPhFZrjhms7iCN3784wT+Ndkfid4E1uFrRvEuh3sU42NC91E6uD2IJwRX5R6h/wRd+Jlrbs1n4s8M3smSAmZkyM8HJWvP8AUf8Agkz8ftH1BY7XTtNvkJyJrXUURR75JyKXKI/WH4+eCZdS+B/iPRfhlqumeCvEU0cclleaeYbZVZZFYgkYABUMMn1r8tvhb+yL8QPi9+0Fot18U/Gmk3Nta3Mcl5dXWtw3M00aNuESLu6EgDHuarax/wAE5f2pf7PaN47m6hChTCPEHmAj027uR7VxVv8A8E2v2iLXWLXHg6aGXzV23kdyuIjn7xIOeKOUObSx++NvEkEEUcf+rRQq49AOKlrnfhzo9/4d8BeHtL1Wb7RqVnYQwXMuc75FQBjnvyK6KqSsQFFIelMbOOOtMAGefmzTz1Fcz438Waf8P/COq69fuy2thbvcy4POFGcficCviD9m7/gqVH8cfjxpvgC78Ix6TZapNLHYX0U7M2UR3y4PqEP51EiuU/QamR/dpF+Yj0zkVJTjsIa+SpA602GEQRhF6U8nAzSBsnFUIdRRRQAUUUUAFFFFABUUn1x70STbWC45pu8+1BSVx/DKo3U7cAQKprMk0zqhwR1NWU4GM5oBxsS1ArFrg7T8q8NU9FBIUUUUAFFFFACNjacjIqnKSzcABatthlqncxkKcHBqWjSG5A0/7yJAecnPtxUMyv5gIOR7VEpAncH7x6GpbyQwRfIetYOR1ddCs0SNdRMfmKnOAea+O/8Agr7qlpYfsrwQT2/nT3WsQQwSf8822OxP5Lj8a+v4Waa5Qxjac4Oa+Kf+Cyl/Hafs3+H7d1DST69Ht9RiJyT+tVF3FUeqOM/4IqeDBb+BvHfimSJxJeXsdnHIVIBREyQD35av0fv2mM6KnCd6+MP+CQtukH7KCMhBaTVrlmx9RX2rcMzMVAOcdcVr0MIaMqrDJB8wbd6gUKsfKsuWb2plwXghZy+3HcnFJGxkj4yz9iKwubrXVsf9lVWDZwvpVGbXobW9W08xBI3AUsM9PSpLxpFtZWLMAoySozisYyQ3sHnDD3HG0lfm60uZ3skaqN0dPZ5EIB+dmPbnFaY6CsOxkkiAJOOK2o38xAa6I7HHV+IfRRRVGIUUUUANkYLGxY4UDJNfmF/wWY+Nf9n6D4V+G2nXjLNeMdR1CONvvRjiNWH1ya/T2T7pB6V+Inx6jk/ai/4KTf8ACNSSf6EusppSA84igBeTj6I351Ei4n6M/wDBPP8AZ/034J/s9eHrj7HGviDW7ZL6+umQCQ7xuVM9cAEcVyX/AAUi/Zl8UfHj4Y3mo6V4oa20/wAP20upNokkQKTNHGSSG65wDX2Jpenw6TptrZWyLHb28SxRqo4CqMACsb4lQ/aPhz4qi2eZ5mlXS7fXMLDFCVwufzh/CHw7471bxHcX3w9tr99a0eJr5pdNz5sSDhunbBP4Zr6Wm/4KrfGQ/DW48Ju9ompSRfZl1kLi5QAjJ+uARn3rzv8AZc/alb9l29+IDLoialc65ZyWMDt1hbJHPtg1618O/wDgl346+LXwWf4iJqMNlrmpxtfWejSx4MqMcgZ7EjJH4VRR7T+w3/wTht/FFppvxO+Kb/2tLqDC9tdPZxIH3AndKcnIPXH0rif+Cwfwf8PeA/EXw91Hw/pFrotpd2dzbvHaRBFdoyG7ezD86zv2Rf29PEn7Id1J8Lvito14dB06R1XKZu7E5Py4J+Zc46HjNdD/AMFTPjx8Pf2gvhf8O9V8D+IrPWZLW8u/OhUlZoVeOPAZSP8AZP5UC1ufod+x34mfxd+zH8N9Tc5eTRrdG+qIF/pXstfPn7AtmdP/AGR/htCTu/4lqsD7Ekj+dfQdMh7hRRRQIKKKKACiik6UALRSUtABRRRQA1mA6nFNYB1xnj2ptxF5iEHpSIUhQjcAF65PSgZzmofC/wAI6triazeeGtLudVQYW8ktUMv/AH1ivyj/AOCsraZqX7THw+8M2WnWsBS2t0n8qMIXMs3AOPYiv17t9QtbosIbmGYqcERyBsflX47/APBWLwvrfgv9qHQfiBLbLPok8FqbVhKpLSQkFlK5yOnek0VE/XLwHoFv4X8F6LpVrClvDaWkUSxxgYGFA7VvV8qfs8/8FD/hH8XvCtqbzxBa+Ftat4VW5sNUfydrAY+Rjww47Vh+FP8AgpN4N8aftQ23wr0mzNzpdyXgh19ZB5TzKhcjHZcKeaNhan2QvWnVz8njzw3b6pFp0mvaal/L9y3a6Te30Ga3+vIpki0UUUAFFFFACUm4Chjha8X/AGtP2irf9mL4Q33jObTv7WmjkSC2s920SyMejN2AGTn2FS2NI9oVt3bFOr5I/YX/AG6k/a5/t6wvtCTQda0oJMY4Zd8ckT5wQTzkY5r63poGFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtgFFFFNAFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmeWpYNj5hT6KACiiigAooooAKKKKACiiigAooooAYilc5OafRRQAUUUUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAhpjHbT6ztYd47WR0ODt4NTJ2RcVzOx8mf8FHf2jrj4MfBG5g0eeS21zWM2lu68FBkb2/75DD8a+FP2H/APgnrfftIWZ8beNpZoPClxI3l4cie665YN2Gau/8FWvGX9vfFHw/4dtb2S6e3iBe1/hV2OB+dfrP8DfB1p4B+EPhLQbKEQwWenQptAx82wEn8zWUU5K5tO0Hofnd8SP2Y/H/AOxT8WvD2t/AG31PVtL1DAu9PncyoxB5Vh6YzX6MaR46uNL+GEPifxjbLoc8Fl9qv4ByISBkgV2LRK2CQCR046Vx/wAW7GPVvh34j057f7SLrT54xGVyCShA/Wny2Iv7RpHgPw1/4KZfBf4leMm8OwatcaTOWKRXOpR+VDKRngN26d6+prHUrXVLOO7tLmK5tZF3JNE4ZWHqCK/mg034e6pr3xQ/4RC0jEOpyXr26Cb5NpyT17dK9g8TfHb47fs3wal8OrjxXe2Vm0XlhFfd8mR9xuorSPYTikffH/BQj/gohb/DOyvfAPw8vYrrxLIhivdRjbctmpxkLjgt1H41+V8Pgb4ieKI5PEcOg6/qAkYznUYreVgxzktuH9K90/YH/Zks/wBqn4vS3HifVsaZp0guruCSQGe8bJO3nsTjNfudp/g7SfDvhcaNpWm21rYw25hit44wFA24AqWw0R+Nf7E/7e3xO8J/FTwf4G8Qa0+r+F9Qvo9Okhvo8y2+47FCt1HzFa/bFfujnNfzwJpdx4R/bX0+G5tmjlh8YQSLCoyCPtSkV/Q9A3mQo/QsAaqJMth69adTVp1UQFFFFABRSGm7/SgB9FRRu5zvUL6c0/dQA6im7vXijf8AMAAT70ARX3/HrIMbtw24HvxX56+G/wDgnTrvij9qi7+KvirVoYNOt9VW+tbKEHfJs+5k88ZAz64r9D2UOuDyKFQLUta3NYz5Y2EjG0Aegp9Qnd5q4XC5qaqMgooooAKKaW+YCnUAFFFFABRRRQAUxyAjk8DHNONY3jPVl0HwlrOoswQWtpLLuY4AIU4/Wk2HU/C74u6rqH7QX7f9vptz/plvL4kg01UYYxbpMCy5HP3VbnrX7x2FpHYWMFtCoSKGNY1UdgBgCvw4/YA0ofE79vaz1i7/AHv2W7vNUOOhbDKDx/v1+51TG5pM+VP+Ck3w1bx5+y/4puLSMHUdNiW5jbcQdqupbp7A1+cX/BNv9nHwP+0VrfjbTvG1p59nbWSurK5R4jnJdXByOQO/av2o+IPhW28beCNc0G7jMtvqNnLbOinBO5SOtfzk+IpfEnwd+IfizwvoWp32mTGeTT51tJP3k0Yf5U+XnOQOnNLlsVHVFv8AaE8I6N8M/ihrvg/wX4hudf8ADtvOyxPu+83cEL1xX1T/AMEwf2n/AIefALxBqfh7xrYJouoawy7PEdyn3AAcRMTyq/Tqa96/4Jy/8E/rLRdDtviZ8S9Ie48Q3h87T9MvOUgjOcSOp5LNnoSa7j9sz/gmb4f+NjXvirwa8eg+KRHk2qLi3uCMcbc4XjPQCq5RaM6z/gol8P8Awx8W/wBlPxL4q0+LT9S1HT7SO7sNQjVHYr5secP1xtzXg/8AwRT8aJJ4d8eeFZZH8+G5jvY4z0CsuDj8RX55ePm+KvwTkv8AwPr+o6vp1l80MljJKzW8i9Plzxj6V9if8EWbhv8AhbnjZAcI2lx5H0filyg9rH7C9xS00dadVJWMgooopgFFIajZm7HFJuw7EjdKgaNZupOPSnru3DJyKk2j0qfiHscZ8VV1k+A9YtfDoCarPaSxW8h6IxUgGvxA8efsiftJeHfEcwl07X9VkuWMouLK8kKkkk5OG4r98toxjHFG0elLlY+Y/BPSvh7+154Ftz/ZVv43sEXkLb3UjH8BmqXijxT+13rVq2ja/qHxFubecbGtZjNsfHOCRx2r9+cD0pjW8Uhy0SMfdQadmHMfFH/BLn4N+Pvhr8L9X1Lx5PqMNzq9wJLbTL6VmMEYHXaTwSa+2qAAvAGBS1SRLYhrxb4mfthfCX4QeNLbwr4q8WW+na1MVBh2swi3dC5Awtezy7vLOzG7tmvzl/bj/wCCZ2o/FjVNV8feBdTlu/Fd03mXWm383yTjj5Y2P3SP6UxpX3P0O0fWbDxBptvqGmXkN/Y3C74ri2kDo6+oI61d/OvwX+Ef7Unx4/Yh1xfDOo299Fo1vN+80HW4maFlGdwhY/d9cqa/W/8AZh/bI8BftQaBHNoN8tnrsaD7Vo10wWaJu5A/iX3FA3Gx7zSU5ulfO/7dX7REn7OHwB1nXtLv7ez8VXJS20hbhPMDSlgWO3uAm78SKCCL9q79uDwL+yrp0cWqO2s+JLhSbfR7N13/AFkP8A/DmvzV8c/8FI/2ivjc+oWfg2yl0TSbomOOPQrB5bhVzniYAkHHcYrL/ZV/ZH8f/tvfEqXx147ur7/hFZrnztQ1S7djLeDk+XCW6jOPYCv2d+Gvwr8LfCHwzbaF4T0a10ewhQLtt4lVpMfxOQMsfc0F6I+R/wDgmb8M/iPo/wANvFGofFtNYmbVrkPbweIruSdni2/MzJITgGvjI6f4Z8a/8FSNKtfAVpBbaGmvRts02IRQr5KEybQoAAJU59c17r+37/wUm13wT4m8RfDDwFZSaZfWhNpfa1OoLAkfN5S9uM8mvzo+C/x98UfAn4gN4x8OSWsmslXUyX8IlBLDlhnoeTyPWgZ/Smvan18df8E+f22NY/aw03XbPxBo0Gnatoyx7ri0JMU+4HJwehyP1r7FoICiiigQUUUUANY4XJqJkC72BwSKmbpUEkwDYPIoGrnzZ/wUW8VT+Df2R/G19aDFzPHFaq3p5jhSfyzX4yfsWalLp37VnwynjJMo1mKMY/usGVv0Y1+t/wDwVc1a30z9j3XoJpAj3l7bQRL/AHm3Fv5Ka/If9i+Ty/2qvhkx/wCgzF/Wk0VeyP6PV606iihKxIUUh6VFv2yBfWmImopnnLvC55NPoAKKKKACiimS7tp29e1AEN0rctnis/59rhPvdqsTXLop3CoGZpCxT72KzluddNWQWgbdh+tX0bbKVqiu9UyRl6uw3BlyNuCKqOwqnkWqKqfanWZUI4NWPMHfiqOUfRTdwI4NJQA+mthlIzSV8Yf8FNvjd8Rfg18M9Fk8AfarSTUblobnULOMvLBjBGMA4z0z71LdhpXPtBVCjFMkjV+vSvwa8M/GD9rnx9MBpGs+Ob4ydFEToG+hKgfrXR3Hgf8AbW8URtbSW3juYTfKUa6VFP8A48KVy1HzP26bT4WbPSq9wNPt1JnuoY17+ZIo/nX4lWP7Dv7WutTK91Z6xGW5JvNaZMfXa5raj/4Jr/tN6mQbi4gjz1E2uSkVKSHd9z9gNW+IHgvwqvm6r4p0TS0X+K81CGIen8TCvzz/AOCu3xg8D+NvhL4T0vw74u0nXdRi1UzmLSb6K4KLsIyxRjjrXkcf/BIf43a+Y/7X8S6FGrfeMt7POUH0I5rq9I/4In6/JtOqfEGyiH8S2tmT+RJqrJ7A31bNT/gmf+2F8Mfgn8EdR0Dx54wj0a7XUXmhhlt5pPlYDkFFPpX1jP8A8FOv2b7fP/FwlkI7Jpl2f/aVfO+n/wDBFHwqtqBd+P8AU2uMffht0AH51ftf+CK/gqORTN8QvEDx9xHFEpP44NUK6Pa5v+CpX7OMcZK+NZ5mHRE0q5yfzQD9azX/AOCsX7O0bEf8JDqpx3XSZT/SvPY/+CMfwyVfn8a+LGPqJYB/7Tpkv/BGH4ZyAgeOPFi/70kBH/ouotYND2Hwt/wUo/Z38dXQtIvHkOjv1J1qzltY29t7DaPzrutP/am+BV/cRw2nxb8GtIx2pH/btuufbBevkTWP+CJfhCaKQ6Z8Stctp8fJ9qsoplB98FSfzry7xV/wRW8ZaXvfQPiN4fu4/XVreW1xz3ZA+PwpaFqTWzP1b0TxN4c8SWyz6TrmnanBjIls7qOVT+Kk1tw3dszCOOeN27Krgmvw+1//AIJL/G/RfNlsn8La9EqFjJZ6rtBwO3mBDT/+CadhH4G/bTtdJ8V6rHol/Z211BHazTqY5bnKqIlYvgsRuIAyTitEQ9ep+4tLTV606mZhRRRQBDd3C2lrNO/3I0Lt9AM1+NX7BdtB8UP+Ci/iLxJcoM28mo6nCD/eL+Xn8nNfsN4qvrfTfDGr3l3KsFrb2c0ssrnCoioSzE+gANfkd/wSc0OTWP2sPG2u22ZrGzsLhXkj5VTLONmT7hDj6Umi1sfsHj2qG+s01CyuLWQfu5o2jb6EYP8AOrNFCViT8mJ/+CQfim++O0txNrVkvgSa+a6e4X/XiMsW2BfXoPoa/VfQ9Gt/D+jWOmWibLWzhSCNR2VQAP5VoUUwvc8D/aO/Yr+G37S1m7+ItKFrrQQrFq1nhJlPv/e/GvzWvv8Agj38VYfiA2l2eo6a/hhnO3VnmO5Yz/sY+92r9paKAuzjPg78Obf4SfDLw54QtZfPh0mzjtvNxjeVHJ/E12dFFAgooooAKTcKSRgqknpUDXAAzjigpJsn3Comd/MwB8nrUSXSTEMrDYDgkHinZM33QducHII/nUt9h8vcsKRtFLkVEo2dTT6adyWOyKRm4rzX9ob4oaz8G/hTrXi7RPDMniy602MSnTopfLZl3AE5wTxnPAPSvzmk/wCC2XiFXIPwpsU+Yja2stuGPUeTxTCx+sLbmUjFebftEfDvX/ij8HfEvhrwvrj+Hddv4QLe/jJG1gwbbkcjIGM+9fnK3/BbLxEVO34W6cG7Z1lv/jVLZ/8ABa/xD9qi+1fDHT/s+75/J1Vi+PbMfWgdmeNL+xh+1z4L1qa00608RJJK5Et3Ya3mKUZ4O4PgfjU3iD/gnf8AtY/EL7K3iK0l1Yxg+T/aevxyGP8A76c4r9bv2bfj9pv7SPwzs/GGmabeaTFMxje1vUwyuOuD3HvXceMvHHh/4e6HLrPiXWLPQ9KhID3d9KI41JOAMmgd2fiH/wAOmf2iW5bw/pKn1OswHP60W3/BLH9o3SbpJ7bRbGC4jO5JLfV4w4PsQa/bLwb8TPCnxEs/tfhnxFp2uW+ceZY3CyD9DXTUC5mfhPD+wR+0rpPj7RLzU9D1CWVr2ENqUF753krvGWLA8cZr9y9BtH07RdPtJpWmmhgSN3Y5LEKASau9aFj2gAYGDQJu4+iiigQU0uB3pT06ZqrMx7rgVLdioq42ScyTBFPtXw7/AMFhrwW37L9jGRnztahT6fI5/pX27bBBNuJ5zXwV/wAFnLgp+z54bhB/1mtKxH0jb/GhalyXK7I+X/8AgjbHfN+0ZrZgkxZLozG4XJ5O8bP61+09fjn/AMEWYSfjL4ykGNq6UgPry9fsWTiqM2LRVe61C30+3e4upo7W3QZeWZwir9STgVX0bxDpfiK3afStRtdShVtrSWkyyqD6EqTzQI0KKKKACiiigAooooAKKKTNAC0UUUAFFFFACVjeLvGWieA9Dn1nxDqdvpGlwY8y6un2IuegzWy3Svib/grlpd1f/snyXEFw0MVpq9vLOgPEiFXGD+JFAz7A8JeNND8eaPFqvh7VLXWNOl+5c2kgdD+Irar8pf8Agi78RNWm1rxp4Oa4eXQ4YUvYI5Dny3JwcfWv1aoB6BRRRQIKKKKACiiigAooooAKKKKACiiipbAa+dpwcGoVWcTAHBj7nNTkbuDS0LXcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaACigniotr+Zu3/L/dxQBNRTd1LuoAWikzS0AFJu+bFLTSvzA0AOooooAKKKKACiiigAooooAQ0yaZYY2kd1RFGWZjgAepNOdwi5bgV8af8FDv2xtM+BHw/uvDOms1x4t1qCSCBFGVhBGCzfgTxS5knYqMbs958J/tPfDLxx46n8H6H4u0/UvEMLMrWcEm4kr94A98V6mOa/Pn/glz+yQPAfhNvid4psYm8TazmSx86I+ZawtyTncclvoOK/QYcDFMcklsLRRRQQFFFFABRRRQAUitnNLSBdtABVLVpI49PuGk4RY2JP4VdrL8SeX/AGJfCVxHH5LbnboBjrUT+EqO6PwV+MGpXXxU/bgs7KOPz2bXre1Vc53osyk/oDX762EP2ext4sY2RquPoMV+Fn7NelDxt/wUS064tCs8Ftrc917Mqbh/XP4V+7Sqcc0U9I2LqPUcagvIfOt3UDOR09fapzzRim0Zp2dz8Kf24Pgr4+8F/tIav4l0Pw1qFnb3E3n2t1p0LOA3qMV5d4U+APxq/aS8ZW8DaLrWoXEp8ptR1OB444uM/MzDpxX9Dt1pdreMhngjmKHKl0Bx9KmgtYbUEQxJED12KB/Kkk7lykpH4t3n/BMn4+fCax/tzwfqu7VFTc8enXJilz0wpH1NeTeNvHP7U/wySWy8R6141sokGH8yeR48fWv6AdtZ+reHdM163eDUbC3vYXGGSeMMCPxFFmLmP53f2Zb3WfEn7UfgW/u7e48Qan/a8c0qTKzMSCSS306/hX9F1uxaBCRtJAJX0rifDHwM8B+DdXbVNG8LabYaix3faYoFDg+xxxXdBcYqlsDd1YFpaSimQLRXgH7X37X2i/skeC7XWdR0a41++vXMdpYQzCBZGGM7pCrbRjP8Jr41j/4LjWrSL5nwbmWL+Jl8TKzD6D7KM/nU8yK5WfqPJnadvX3pq7tvzYz7V+Y8H/BcDQ5J0WX4S6jHET8zx62jsPophGfzFdjpX/BZn4bXdv5l54M8TWj/ANyJI5f13CndDUWfoM33hxzTZmdYyUALds18RaN/wV7+B9/t/tCLxHo7d/tOnbgPxRmrSuv+Ctn7P0MbNFqusXLjpHHpcuW+mQBRdBytH2eOcZA96dj8K+Epv+Cw3wZjkYR6V4nkQfx/YVA/V6jj/wCCxnwZaRRJpniOKPu5s1OPyai6Fys+8qK+HZf+CwHwKRRsbXJGI+6NPYVSuP8AgsX8Fo42MNh4huZP4Y1tAC34k0roOVn3fRX5v+I/+C0vg21glbRvAWt3rqPlNzJHGuffBJrze+/4LceIo5WNt8L9LMJ+75upybvxwlULY/WiivyLk/4LaeMp12xfDPRYSf8Alo2oSsF/8dqOT/gtF46ZPk8CaEp/vfapCP5Urglc/XfaM5pa/Hab/gst8TpGzD4R0BE/3pD+tMX/AILKfFIuMeE/DrDuuZeaB2P2Mor8aH/4LGfF681KGG18OeHkaRwiwBJGLEnAHJzX63fC/XNZ8TfD/QdV8QWcOn6xeWkc9zbQElI2ZQcDPNCdwasdTRRRTJEb7teG/twas+i/sp/Ee5iuDayjTCqyr1BLqK9yr5r/AOCilvLefsifEC3hRnkezGNvtIhP6A1Eioq7sfC//BF/w3HqHxS8Za88Yd7LTktklJ5BkfLfngV+vtfkf/wRV1byvHXjzTlO1JbSGbb9CRX64VS2HIRuleZaB+zn8O9B8Zah4qh8I6QfEF3cm6bUGtVaVXIxkE9DyelenUmKZNxPYcCl7UbRRigR5B8fP2X/AAR+0R4fm07xLpsbSlCsV3Gu2WNuuQQQT+Neb/sf/sG6D+yXrOu6tY65c63e6moiDTRhBFGDnHB5NfU+0UbRQPmfURetOpMUtAgooooARvumq8uIo2Z3IHrUs5xEeC3sPrXkH7VnxisvgV8EfEfiu5mX7Ta25+yW7MAZpSQAo9eufwqJFIyv2hv2xvh9+zbp8beJdQNzqUv+r06xIaZvw7V8w3X/AAWi8BrMy2ngPXriJf8Alo08S/p1r4M+Dvwh+IP7e3xsnmuZLiW2mm87UdTmyYrWEn7qn17Yr9LbH/gkf8EYfD8FjcxatPeIQz3y3ZVyccgYHApXsNpdzqPgb/wUw+EHxmuoLCXUH8LatNJ5cdpqpC7m/wB7pX1hb3EV1Ck0MiyxSDckiEFWB7g1+P37YH/BLuT4Y2LeIPhpLdXel28bTXEF1IXkQAZJDV65/wAEjf2mdW8YWGrfC/xHez393pUf2mxmuZCzLCDgxjPYGq5rhy6XP0poooqiAoopGoAKNteNftGftXeAf2YdFt77xhfTfabo4ttOsYxJcTY6kKSAB7k18afEX/gtV4Zs9OuI/BfgbUb3UCuIZ9YlWKJT6lEyT+YoK5WfaH7TXw8+F/iz4aazefE6ysP7GtLV2e/uUXzIBjrGxGQ2emO9flX/AMExtFh1L9tq6uPDH2iXw3ZW13LHJcHLeRuCx7/9rnj8a8Q/aH/bQ+KH7TH7rxNrZi0VW3DR9LDxWq+hdc4Y+5zX2P8A8ES4LZ9b+JUpt1NzHb2oWYqMhSWyAe2aB3srH6uN0r8Sf+CsPx6b4mfHNfB9jNnSPCyeS2G+SSc8sfT2r9tJpBDC8jfdUFj+Ffgx8N/C+ifHD/goiNH8SW/23QtV8S3Rns3YqJVUOwU4PTKik2Ee56p8M/8Agrb4g+F/wz0HwrpPwx0+SPTLVYBcm6dEbA+9sVO/1r6b/Y//AOCo2n/HrxxF4P8AGei2nhXWb1gmnyW1w0kVw+CdnI4OB619Xa74C+Ffw38E3D6l4c8N6N4cs4f3oms4Y4goHQ5HOfQ9a/FX4E+H4vi5+3ppU3grSDbeH/8AhI2v44rGLEVtbo5bdwMKvA46c0Jj0Z+ufxS/YP8Agz8ZfHFz4s8U+GHvNZuQBPJDdyQrKQMZZUIyfeuWb/gmD+zqykDwOyZ4yuo3Gf8A0OvqoU6mRdnA/B/4F+B/gToH9jeCdAttFtGO6RoxullPq7n5m/E139JS0CCiiigApKR2CqSeBVR7otjCnDcA0m7FJXJLmbCnFU4ZPNlVT3NSX2ntfW5TzCjMOoqDT7CeFgr8Kvf1pcxvDlUXd6nw5/wWUvEh/Zp0i3ON82txED6I3+NfmF+xDp51T9rL4Y246tq6N/3yrN/SvvX/AILXM6eH/h7Erts82Y7NxweBzivkL/gmh4bk1z9snwIw6afJNet9FiZf/Z6d7mLR/QBSHim0HmmQI0mFPFZ63n+lmE/6/r+FTyptO70qrHIbi7Yr95RxQbRjpcuHH8X3qsp90V83/G/9u74U/s++MLTwt4pvbqXWJsefDp1t5ot1PRn5FfQXh/WLPxFodhqensXsbyFZoWK7cowyOO1BnI0KKKKCQqGdioJHWpqhmXzPlPQ0DW5nzxyS5NV4GeO4YHpV2QMsxEhyvbkj+VeJ/GT9sj4RfAvXk0Dxp4pXTNWKCVreGKWUqp6E7ATUSOlSsrHs0037s0W8pyOxr5f/AOHln7N67X/4T3cPT+zron/0Guv8K/t0fAPxcAbD4j6QjngR3sxgb/vl8GknYOdWtY99TaxBZtzUy5xdJtU8g1zWm/FjwNqluk9n4q0WeJuVeO9jIP61qWPjXw5qd0lvZ65pt1cOcJFDdRs5PsAc1adzG/kadrG0bMD0qVYtrbtxNSjrTqZLYyqeoaTZazAsN7aw3kIbcI5kDLkexq/RSauK5Bb2sNqoSGFIUHAWNQoH5VNn2paKXKIo65rNr4f0e91O+k8mztImmlkPZVGTX5x+IP8Ags54e03xBqVpY+BbrUNOt5WiiuvtSoXwcZII6V+kd9Zw6hZz2tzEs1vMhjkjcZDKRgg/hX5Zf8FKv2L/AIUfCH4T3XjjwzpzaJrVxfIghWZjFIWySAp6etHKVE05P+C2Omo2F+HE5HvfD/4moz/wW0sB/wA02mI/7CA/+Jr5E/4Jz/B3SvjN+0rpGja/o8et+H4rSa5vreeMtEVUAKG9Mk8fSv2CX9gv4Ap0+F+g/wDgMKaGz4P8Vf8ABa7xHcW8ieH/AIf6dZOw+We8unl28+gxXmur/wDBXz45apE8diug6V5nCzQad5rrz2DkqfxFfrx4N+APw5+H6Rr4f8GaNphjOVaGzTcPxxmuzXRdPX7thbD6Qr/hTFc/Fmw/bo/bI8XWofSI9e1CGT7smm+DUkz9CkJ/Srtr8dv29fFMgs7XSfHMLzfKsjeFvsoHf77wgL9Sa/aJbeKNdqxIq+iqBTwNvAAApWDmPxouvhL+378SUji1G68XQwyHB3+ILexUe5CupH5VG3/BMf8Aai8WWcz6/wCILGVpB80GqeI57hz7fLlT+Jr9nKKXKHMfh/q3/BJ39oWx0u4aCz0XUiq5Fvb6vh5PYByq5+pq3+zP/wAE1/jJH8cvCc3jXwvc+GfD2nXaX13frdwscIdwVWjY8kgDHoTX7a0U7BzEcMYiREGcKMDNSUUUyQooooA82/aTkeP9n/4itG/lv/YN4A2cdYWFfm5/wRFYf8Jv8VgTuf8As+xJP/bSWv0B/bS1KbSf2VfiZdQZ81dIkUY9GIU/oTX5/f8ABEm3ePx18UpAh8htOs0EnYsJJDj8jS6lr4WfrZRSdzS0yAooooAKKKKACiiigAooooAjuOYWqqjDYx6hRzVyRdyEHisa6uoNItLy8vJBFZ26NJLI5woVRknP4VnJGkXoeC/tiftcaH+yj4IXUJohqXiG+G3TdK5VWPd39AOa/KLxZ+0N+03+1Pq01zpMnjC702Rz9nsfDNpP9nTn7uYhycfWtj4xeJtU/b7/AGzodJ0oyrpTXX2G2IyyQ28ZO6UjgDIH6iv2q+Ffw30b4T+A9I8M6FaR2ljYwLGBGoXewHLH3JpxiNs/ELS/gf8Atjabbvq8OkfEq2S3XzN0dzMJh2+WIuHY+wFd18C/2/vjZ+zb44sdC+KiaxqGhzzp9rt/E0Esd7BETguhcBuM5xznFfthXwj/AMFZ/gTp/jb4EyeOLXT7Ua34fmjee8IxK1sx2lc98EiqsTc+1PCfijSPiF4V0/XNInj1DR9Tt1mhk2na6MO4I/QiuQv/ANmj4UanJNJc/Dnw1LJMd0kn9mRBmOc5JC5r5p/4JF+NLrxN+zI+n3c7zNo+oyWse8k7U6gD86+4qZOx5Mn7KPwejYFfhv4dB/68Up//AAyr8IfMV/8AhXPh7cpyD9hSvVqKAuzP0fQ9P8PWEdjpdjb6fZxjCQW0axov0AryH9rb9mXT/wBqX4Vy+Frq+bTL2GUXNjeclIpBx8y/xDGa9upGXcMUCPxD1/8A4J0/tK/A3VLi98GPc6haxOWhutA1LZI/v5QIP5itjwj/AMFDf2h/2c9RtdG+Imjy6haxMEeHWrdopyvT5X7mv2dvLqCwt5Li5ljt4I1LNJI21VA6kk1+Wv8AwUu/bR+HPjXwzf8Aw38L2Vp4o1p2WObVlhDC1YMDiKTHJ4xx60i07n3r+zP+0h4a/ac+H0fifw6ZEEb/AGe7t5kKtDMBkrz1HvXrtfEn/BKT4L658KfgLd3uv2kljd69efbIoJDyIdoCnHbNfbdMl7hRRSUCBjtUnGarSyF8gDBxnpU8jLsYscKBkseBXxJ+1r/wU68J/ADUH8P+FrKPxh4mUZk/eYtYOejMpyT7DFJoqJ9m29n+9Dt65xX5xf8ABarUJ4/h74KsgrfZ5Lx5C3bcFxXlWl/8FpPiHHrUJ1LwLoR04uDJFEZll2d9pLdfwqT/AIKLftS/Dn9pn4C+DtR8NamTrkN5uuNLlG2aAFecj0z3qdti9Xqxf+CLNuf+FpeOJOMLp0a/+PGv18Y4U4GfpX5K/wDBFPT5m8aeP7rbmKO2hjZx0ySeK/WvdziqRmz4q/4K367e6D+yZILK6ltvtes2tvP5bYMkRDkqSPcLXk3/AARbvr+48HePbdp9+nwX0exXyWyVycHNb3/BZ/xYlj8FfCvh8FvNvtU+0EY42xqf6mtD/gjj4Ev/AA38BNa129g8mLWtRMluzAgyIqhc8jpmmI/QGiiigAooooASjdQ3SuP+I3xa8H/CPS4tR8X+ILHQLOV/LSS8lCBm9BQB1+6mooUk14L/AMN3fAYuEHxL0TP/AF3p0n7dnwHiUk/ErRDjss4JoHZnve6jdXyd4v8A+CnvwA8JSCP/AISt9Vk7jTrV5QPxAxWz+zf+3p4E/ae8b6j4a8K6fq8U9nB9oNzeQBY3XOPXI/GgLM+mN1LTV606gQjdK+MP+Cs2rWth+yTqFrcZ8y91K2iiIPAYEnJ/Cvs9ulfAv/BZK+jh/Zw0S2YgPPrUZUHvtRs/zoGtzyv/AIIqeBZVj8deLDKohZ47FI9p3HA3E59Oa/U+vkb/AIJf+FNO0H9lPw7fWNp9mm1NmnuGPV2BxmvrmgHuFFFFAgooooAKKKKACiiigAooooAKY8m3tmnHimfeYcVEgHKxYZIxTqKKcdgCiiiqAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCldapaWODPcww5GR5kirx68msO4+KHhC18zzPE2kAx/fH22PK/UbuK8n+P37F/g39pLxLp2qeMNQ1k29knliwsLwwROv+1iuT0j/gm78EPCLi40nQbm1kj+bfPqEsob/eDHmom2tjrpxotpTke9zfGLwRa2Ul3N4q0mO3jXc0jXkeAPzrjl/a8+D01re3EHjvS7qKzBaf7PIZCoHsoJNfm3/wUi8M+DPCz+HfC3hiKO21me5VJWt3IUITjnnP6V9rfslfsW/Df4X/AAz0q7TSbbV9Z1C2WW7vpXMgLEchcjgfhWEJzlo9GVWp0oStFtog8Zf8FQfgP4d025l0/X7zxFfRozJY6fYTb5GH8ILqqj8TXr37NHxwg/aE+Glt4xtdLvdIhu5GC218oDgA+xIx+NF9+y58N7i8a8g8LadZ3hTZ58MC5Hv0616RoGh2nhzSLbTrGGOC2t0CIkaBR+Qrojfqc8uXl0NDBzTqaOtOqzK9xCcc0Ag9KGG4YoVQvApALRRRQAUUUUAFFFFABRRRQBxHxg8aS+A/Auqazb2F1qU9rCzpb2sRkdj2wB1r8yv2Xf2U/FP7WPxv1b4k/Fy01CHw9Z3TPbadqUTIbj5iVXBxhRxX61ModSGGR6GkjjWNcIoUf7IxUuN3cpSsrEOm6fbaTY29lZwrb2tugjiiQYVVAwAKs0m2lqiQooooAKKKKACiiilcAoooougENcP8WvENtpPgrXN4ErLaSZjzj+E13DfdNeSftKXjaX8K9fuI7dZJvskp3+mEJrKo9DSnrI/Jn/gma0F9+23BNJGFLxX0iL1wd1fuDivw6/4JWsNQ/bOsyVztsb+XI7HIP9a/catI7CnqwoooqiAooooAKKKKACiiigAprjcpAOPcU6koA85+M/wL8J/Hfw2dD8YaSmr2Gcqpcxuhz1V1IKn6GvnPUP8AglT+zlp9jdXV5ot5Zwopdp21i5VYwOSTukIr7RZfl461w3xd8CyfELwHq+iSSKq3Vu8Y2kjGRjNZWsaJ30PzV1r4Y/8ABPzw9rR0lvEl3c38bbHeO9ungDZwQWwB+tdXc/Af9gHTY4J7rxFbYlGVVtYust+APFfmP8TPBL+DvidrPhdZPNNpfNbIxALHLYGcAZr9FPB3/BGm38VeCdD1a68e3NlqN5axzzQtah0jLAHAHB/M0XtqO+ti5qHwo/4J8wSFx4p2bedkep3BX9Rn9azr7wb/AME+tAi+1y6vcaiFG4QwXly5b2wOTW+v/BEnTVjbPxKuDLjj/iXLt/8AQq2NF/4Ip+FLe3f+1PHeqXM/8P2WCOJf1DGlcrTueY3Wu/8ABPUfOmk6wWXoIxd8/mapHxb+wA2V/wCEf17Hricf1r2i1/4Iu+BvtaG48X62bbPzIjx7yPY7OPyrfuP+CM/wiGw2+v8AigYHzCW7iOfyiqlqLTufNWseKP2DvsrSWHh3X5LgL8sSeaNx/E1p/sx/BX4A/tZeJ9R0fQPBmqaRDZ/NJcyzM25PY54NfRen/wDBG34NxSIbvVvFE8YOWRL+Nc/+Qq+qvgd+zj4D/Z30A6V4L0gWMbD97cStvml/3mwM/lUuF3cOex43pP8AwTL+Bmj+S0PhnzZ4eVkuJWfJ9SOh/Kty9/4J6fA7VmhbUPBlrctF02lkH4hSK+lNtGPer5URzs8E0H9hX4G+HJUlsvh7pYkQ5VpVaTH4E4rrv+GevhVptpJv8D+H4LdRl2ks4wAPckV32ua5YeG9JudS1O7isbG3QvLPO4VFA7kmvyC/bo/4KBa58btYf4bfC17mHRXn8ia4swfOv3B4VCOdv0o5ewXbPqT4y/tRfsqfBHUm0iTw5pGvagh2y2+j6fHL5ePVsYrxnxR/wUW/Zrt9JnGgfClLu/ZfkWawiiUH3OKq/so/8EmF8QaXb+J/i9e3SC8USjRbWQpIQef3j9QfavtbQ/2BfgNoOmLZQfDzTJlVdvnXCmSU8ddx71VtLBfU+Uf2Of2hvg7+0X8UrTw9P8H9N0jxCFa4ivFiR0BU5B6cGv0vRVjVVUBVUYAHQCvDfg3+xX8JvgL4wuPE3g7w++n6vPG0RkkuGkVVJyQqngV7pSirBKXMwoooqiBK8U/bLU/8M0+P3VA7R6ZKwBGe1e115x+0LaQal8GvFllcxGaC5sJY2UZ7qfSolsXD4kflt/wRh1a2h+OXi20mIW5udJUwLnGdrnd/MV+yNfhV/wAEy7xtA/bS0e1DGHzEu7RkPcHoP0r91apbBLcKKKKZAUUUUAFFFFABRRRQAUUUjdOuKABulfj1/wAFPvi9ffG34/6D8JfDVyZrbT5FgljVvkkuXPf6Cv1h+JHiYeDfAev60W2/YrKacH0KoSP5V/Ofot145+LHxlutT8LLfan4vvL2S/he2G6bcGJDDjsKh7lxP3o/ZF/Z5039m34OaT4atUje/dBPfXSrhpZWGTk+3SvbOPWvxDl8Xft2abD81/45WGMdFiQ4H/fNOh+L37b+h2sstzceM7iIr96a3BK+/C00h8tz9f8A46+ItO8LfB/xhqWpyxx2cOmTl/MIAPyEAc+pIr8q/wDgj/4LuvEn7QnifxakbJpum2ckZZeF3yPlR+Qry7X/AAX+2F+0PYRab4gg8Xazps0nEGoN5cIz3I44r9Sv2Cf2YW/Zl+DMGm6pbW6eKdRf7TqU8I+Yn+FCe+0cUW1uHwqx9L0UUVRmFNanUUAfOH7WH7Evg/8AawjsJNaurnSdUs12RahZhfMCnnHIwfxryPwj/wAEfPgjoluF1mTXPEU3dpr0wg/hGFx+dfdWBRQVzM+V9B/4Jlfs76FG6DwIt/vGC19fTzEfQl8ivZvhD+z/APD74D2NzaeBPC9j4fS6I+0SW6kyzY6B3YliB2BNehUtBJHcR+dbyR5xuUrn6ivwb+MnwI+NHwI/aU1TxV4a8Oa0LuLU5r7S9U0uxacLuJGQoBB4Y8H1r96KSk0UnY/Cpfhr+1T+234qtdK8Tr4judOgdfMn1mD7DZWv+35eFVjj0BNfqt+yX+x74S/ZW8Hx2emxJqXiKdB9u1qaNfOc90U9VTPbNe/0UJWBsRetOpKWmSFFFFABRRSHpQBVab98Yzzu4qlq2oWeg6VeajqNytpY2sbTTTMcBFAyTWjLEdpKhS/vX5F/8FFP2s/Ffj/4qXnwW8JStaaRBdR2VxJbsRJcSMQCpIPI56VEi4nU/FX/AIK4eLF+IGqaT8MfCNrreiWchSK6kjklkmA4LYUdM1y+n/8ABWL47NcMtx8M7W5TvGtlcKf5V+gf7J/7N+h/An4OaBobabZ3GqrCJbq8kt0MrO3JBbGcCvZRoOmKxI060B9fIX/ChK47rsfgR+15+2r4q/asi0i08RaHYaD/AGQzFYLYvvLHruDV6z/wR78LDWP2lr7VZf8AmF6PI6Y9ZGA/pXcf8Fmfh3pfhrxR4K17S7K3s5NQglgnS3iVAxU5zwOtd1/wRV8BtDoPjjxdNHg3E0dlExHYDJFVYnY/TsnAzX5rfHH/AIKy6z8J/jdrXhW38F2N7oGlz+TJPNLIlxKB1K84z+FfpVINykGvlD9qD/gnz4H/AGjPM1HZ/YniRsn+0oBy3puHemOKXU9F/Z1/ak8D/tN+Eo9Q8OXkMeooga40ieQGaBvcdx70n7VXx4tv2c/g3rniqVVa9iiMVojceZMwwoH0zn8K/G740/so/Fr9jHxNba8CxsLWfzrbXNNkIHB4346f/Xqp+1B+2T4o/a0j8IaPd2K2I0+NIPKjcn7ROcKHP1NBSLX7LPwC179uL9oC8udcv5jYiY3+s3zN8+0sSET36V+93h/RbfwzoWn6Valvs1lAlvHuOSVVQBn8q+d/2B/2Zof2cPgpYW93GD4m1dVvdTlzn5yMhR7AV9M0GbCiiigQUyX7pp9Mk+7QNblKSNZpijZ2kc4ODXwP+0V/wS2h+Pnxg1PxfD47bTIr0qZLeS281l46A5FffrKXyvrSws/KntStc2Z+abf8ET/Dxtxj4j332gDr9gQLn/vquX8Q/wDBE/UIraV9E+IltNOB8kd5ZlQx9yCcV+rAc57VIHzS5TPmaPxF8Z/8EhvjP4Zh8zSZNJ8Qr/dtp9rfk2K2v2U/+CcXxs0X41aBrWt2Ung7TdJvI7ie989d7qpyVQDrnp+NftFRTsLmI412qoJ3EDGT3qSiimSFFFFABSZobpTaAHMeK/P3/gstfJF+z34etsjzJtZUqvc4Q9Pzr7/4YY9a/NX/AILXX5h8AfDq0HRtRnc49oxigpbnP/8ABFHwVC0Pj7xVJGTcq8VhG5HRcbiK/U6vjz/gln8NYPAf7LOk6griS51+ZtQmYds8AfkK+wt1AnuLRSbqNwoELSZrC8XePPDXgHTW1DxNr+m+H7Fetxqd3Hbp+bkV5z/w2N8DPNEZ+LPhFW/2tXhA/Pdik3YD2OjNeI6/+238BfDdk91dfFjwrNGoyVsdRjupD9EiLMT7AV5VqH/BV79nezklSHxHql8yHH7jSJwGPsXVR+eKnmHY+w6Wvnf9mX9tjwd+1RrmtWPhPStZt4tLAZ7rUIFjRs9OjHBr6IqlqD0CiiimIKKKKAPF/wBsyyl1D9ln4lwQxtLI2jykKoyeCCf0FfB3/BE2SJdU+JUW9ftHkWreX325Iz+dfon+0cFb4C+Pw/3Tot0P/IZr81/+CJiuPiB8THbhW022UfUStUvctfCz9baWiiqICiiigAooooAKKKKACiiigBG6V+WH/BXj48+NPCXijRvA2jatcaVoF/p5mu0hbaLjJwVJr9T26V+Rv/Bar7A/jzwIsUitqS2Uplj2kHZu4Oen61DLicr/AMErfjF8HPg7rfiC/wDH2uw6H4r1Ara6fc3sUpiEOMkb1UqmT3Yiv2B8L+MtA8baet94f1qw1qzYAiawuUmXn1Kk4r8n/hp/wSRj+KnwF8OeLLDxrLpvibVrUXXlXUIe22t91SV+YVxMv7A/7Vn7Nuqf2v4Eu57sQEuJvCmq4dvc28hXzP8AdwfpTQ2rn7X18V/8FWPjNp/gH9m/UPCjMsmq+KStrFFg5WNWDM/THVQK+KdP/at/bj8M+fZy6N4tvnUGMtfeEWkZT6hhFjP51e+Cv7HXx7/a8+KGm+MPi+dW0/QbeZZZ7rxChhmkVWz5cEBAK9McqBVCtY+3v+CXHwq1L4Y/sw6dJq1m1ld63O2pBJCCxjYfKeDxkdjX2DVTS9Pg0nT7WxtkEdvbxLFGijACqMAfpVugkKKKTrxQI+Sf+CiH7VHi39l/4f6DqPhCwtrm81S8ktpLi8RmSAKoIOB61+d95/wVo+O95ayxRXWj27MMCSKyO5fcZNftb4r8F6D460ltM8Q6TaaxYNybe8iEi/XnpXC2v7K/wismJh+HmgoTyf8ARFP86APwX+IH7WHxf+KDXI1/xvq0kE4Kva28pihIPUFR2rl/hD8Qv+FU+ObPxJP4fsfEv2X5ls9SUmJm7E1/Q4P2b/haOngHQB/24p/hSS/s2/C2aJo38A6CUYYI+xJ/hQO5+Wl1/wAFlviM1vbwaT4O0GwSAAFAXcFR2A4xX6Tfse/tDSftNfBXTvGVzpy6XeySPBcW6HKB1OMqfQ1zPjn/AIJ2/Afx1HN5/gm30yaQYE2muYWX3GK9M+AvwE8M/s6eBx4V8KLcLpgmaf8A0qUyNubrzQI9IpG+6aWmSMEUsxCqBkk9qAPkT/go5+1BZfAf4NahoVleTW3i7xFbNBpzwjiEZG5yc8cZA+tfD/8AwT8/YNvvjhrlr8RvHIJ8NRT+ekEzEyXr88MpH3c85zWB8ZNUuP2zv+Cg1n4Sublm0NNU/syLyiSscMeSzD6kV+0Hgnwfp/gLwrpug6XCsFlYwrCiqAM4GMn3oLfu7HmXxO/Y8+E3xY8NjR9a8H6ekaR+XDcWcQhmi9CrLg1+QP7fP7E1l+yZrmjT6Pq8upaHrLSeTHcAebEV/hJ7j3r9526V+X3/AAWytzJofw6cFeJ51wTzyBSEmeK/8E7f2xvhz+yn4F8Uv4pi1K51XUbqMpDp1ursUA7lnXFfXNv/AMFl/gjJnfonjIEf3NPt2H63Ar5V/wCCcv7C/hP9pLwT4l8Q+OFuHsUnFnafY5zG6sv3j0r6z8Nf8Ef/AIJ6PqElxqM+ua3BuzHbXF5sRR6EoAT+dCG7Hw//AMFEv2zPCn7WF54SXwdp+tW1jpSuZl1S3SGR2Y/w7HcdK91/Zh/4Kp/Dj4P/AAh8PeDtb8FeIoH0mHyWk0sRToQP4v3joc+1fO37Rn7Kvhnwp+29pPwr8NRyWWh6nPaqEeViY1k5IDHJ6A1+j+n/APBK/wDZ7tdNSCbwnc3U+BvuJNTnD5xyRhsfpTDQ4vwB/wAFfvhl48+IemeGx4V8S6Za6jcpbQajcrBtR2OAZFWQ4GcdC3WvvJWDqGU5UjINfGui/wDBKz4M+FfG+j+J9AGsadeaZcpdRW8l350LMpyAVYdPxr7KA2gCgl26C0UUUCEr5i/bS/Yi0r9rbR9Oc6xLoWvabkW1wQXhZT2dP6ivp6igD8n9J/4In66wb+0viVp0Zz8v2XT2fj33Yretf+CJ8G5ftHxPfHcx6Uuf1av1CooKuz80NE/4In+GoZpTq3xE1C6Vvu/Z7FE/Mbq97/ZH/YB0z9k3xxreu6X4ouNbg1C3ECw3NuEdBnPUE19aUUCuxoFOoooEI3SvzY/4LZed/wAKx+HISTbC2q3AdPU+UpFfpO3Svzb/AOC17/8AFsfhwv8A1Frj/wBEigpbn0/+wFbJa/smfD5UGA1iG/Ek19DV88fsAsW/ZK+Hm45P2EfzNfQ9AnuFFFFAgooooAKKKKACiiigAooooAKKKKVgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAh6V4/+078eNF+AXwx1LX9TuY45xEwtYGxmaTHCjJr0Pxl400rwH4Y1LXtbuFsdMsIGuJppWCgKBnHJ61+aq2/iv/gp98SUS6s7rw78G9CuGmhmkgxJfEHG0Nkjn2NZya2N6cU9WfG3jDwb8Rv2iLPXPjDqkP2fSLa6RUMgZCVZhjZxjj61+znwTv5vh58B/DhTT7nVRFYJLIIWDSH5cnGev5181/8ABSaDQPhP+yba+B9Dh/sqGOW3jto7cAGQr/fx9OtfSH7HdxJ4i/Zl8CXM8jeedPVJCDndgYrBXUtDZtWvJDvhL+2b8MPi/rB0bS9djtNcRikmnX37qVXBxtwep+le6rX5D/8ABQT9lHWPAvjRvib4Okuo7yS6ErW9rDsaHHO/K9a+2/8Agn38XvGvxe+B1tf+NrBrW+tJPssU7qVadFGNxB71tTk5LUyqQW8dj6d/ip1N7g06tTmCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtXAKKKKnlYDW+6c15H+1JqkOkfA/xbc3Cs8a6fNgKMnlCK9drwT9tiaeH9njxg9vN5L/AGKRTkZyNtROL5Wa0/iPzS/4I96F9u/ac1PVQW2WejTHp3kYDH6V+1Nfj1/wRfkH/C3vGIYZZtLVg3/A+lfsLWyIYUUUUyQopCQoJPAryXxD+1d8KfCnjUeFNX8a6Zp+t5Cm3nl2hSezN0H40DSb2PW6KyND8WaN4os/tWjapZ6rBjIks51kH6Gvn/8AbA/bU8M/sx+DLlhc2+peK50ZbLT4nDYfsX54FK6Cx9L0V+BN18fP2nv2hNWutf0nVfE1zZwu0qrppaK2hUc7RjAOK+o/2Ff+CjnjG8+IOm/DP4qO1/LdzC0t9RuE23EUp4CyHoR+GaLorlZ+qdFNDZp1MgQ9KhvP+PWUkZGw/wAqmPSqmpvImnzmMAvsOA3Spa0KW5/Pv8XPDMvij9tu90fT4lNze+IYlRe2TICf5V+/9pLB4f8AD1ub6eK1gtLdFlmmcIiBVAySeBX4fagqab/wUs0pm5UeJISce5Nfpb/wUV+Evjf4xfAG40rwK97NqKzq82nWsgUXcP8AEjcZP50k0kkXKPvNM+mNI1rTdetRdaZfW2oW2cedayrImfTKkinaxr2n+HdPkvtUvbfTrKPl7i6lEaL9SeK/AHwR8Xf2hv2L5Xs7H+0/DdgJSz6fqFoJbZm75yOPwIrpNU+NHx3/AOCjHjTRvA093bskYaT7FYRNb2y4HMsvzEk/jj2p3I5baI/YTXP2xPgv4dujbX3xH0CKYHGFvEYfmDWPP+3h8B7fOfiXojH+6k+4/kK/Iv8AaL/4J8eL/wBmv4ZweLtc1G0nV5hFJDFg7SfrXzl4c8E6p4o0XV9Ttos2WlxebcSbQAB6ZxTui1DWx+/Vj+318CdQ1O1sLf4gafJdXMqwxJhvmZjgDOPU19BI6yIrKdysMgjuK/GD/gmr+wvafGnUrf4j+KTNH4e0u8V7OzB/4+pEORu4+6Div2dXZDGB8qIowOwApmb3JKKbu3DKnI7Vn+INct/Dej3epXbhLa2iaV29gM0m7CWp+Z3/AAWG+P1/ZLoXww0O9eP7UPtWoxwHDOM4RCR29q7T/gmt+wpa/DfRbH4meMbZbnxFfwrLp9nMnFkp6Pg/xkd6/Nf9or4ra18c/wBo7XPEllDLe3M98YrCBELEojYUBe/Svqz4ef8ABUn4sfCPUNI0T4geFo5tNgCxTK8BhmCAYG36Ci6NFtY/Yqlrz34J/HLwr8fPBdv4j8KahHe2jgLLGD88L45Vh616FRuQFFFFMQUUUUAJWL4vsE1Lwvqls6CRXgf5T34NbVUdakWHR72R/upEzH6AVMtrDjuj8EfgbrF34Z/b/wBBnsE+wSDxK1uY8A4VmIPB9RX7+1+AfhfVotY/4KGaXd2gAjk8VqE2jjG81+/lEdip/EwoooqiAopOfXj6UtABRRRQAUUUUAFIeRilooA8J/bZ1O80T9mvxpe2PLxWUm5ezKRgj9a/Nf8A4I42NheftAa5cTwxvdwaSzW7MOY8tg4/Cv1t+MPg+Lx98L/E2gSxrKt9YyxBW7nacV+D/wCzL8Vbj9k/9qfT77VxPYabb3z2eqxFMN9n3EcD8qh7lx2P6DWUOu0jINK0Ksu1lDL6EZFYPgfx1ofxE8PWet+H9Rg1HT7pBIkkLhsZGcH0NdBV3uSxFUKAAMAdhTqTNeU/Eb9p74cfCvxRpHh3xB4jhg1nVJ1t7e0h/ePvY4G4D7vPrQI9XopgNPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDH8Y+IIfCfhPWNZuHEcNhaS3LM3QbVJ/pX4xfsBeFx+0N+29qPivVo/tNtZy3GssJPmBYsRHnNfrL+1A88f7PPxBa2jMs40ecqi9T8tfkV/wAEr/jH4b+FHx8vYvEl4unRa3ai0gnmbbGkhbIDE9BUSLjsfuAqhQAOFAwBTqjt7iK8gjmhkWWGRQySIchgehBp0siwxvI52ogLMfQCnHYln5af8FsJofM+G8Yb/SP37bf9nI5r3f8A4JG2Qtv2UIZcAGbVblicdcEV+cP/AAUY/aD/AOF8ftBagbCTdougk6faejFT87fnX33/AMEgPidpGufAO48HpdRjWtKvZZ3tv4vLkIIb86obWh99mk60lcn8TviboHwf8Faj4p8TXn2PSbFN8sgGSfYDuaCTyH9vH4r+GfhX+z14jn1+3tL+7vrd7bT7G6AImmYYHX06/hX4J6PpfiCzeHxfZ6Pdvp1jdrL9sjtmNvG6sGClgMCvp74zfFLxj/wUa/aW0zQvDsE1vpPmmDTLZsgQQ5+ad/w5r9X/AAJ+yP4T8H/s3L8KJIVnsZrRkubhgNzzMOXz9aRpsVP2L/2rNC/ad+GlpdWzpa+JNOiSLU9Nyd0TAYDD/ZNfQ9fhNoN94r/4Js/tcJFdjztImmAnjU8XNkzdvf8Awr9w/CviSz8X+HNN1vT5PNsdQt0uYW9VYAimS0a1FN/ip1BIU1s44606igCpMrLhhz9axfEninQvB9j9u13WbTSLVuk99dCFfzJxXRsAVORkV8Bf8FOf2U/id+0VceE7rwNaLq9np6yLPp7XMcW1j0YbiAaDTmufbWieOPC2tQpNpuvaXfI3SSC6jfP4g10EV1BOAY5o5B/ssDX4NW3/AATL/aLt5kli8Em3kU5WRNVtwy+4IbNdPB+xz+194YgCWMPieOJBxHY+IWXH0w9AWT6n7hZpa/ETTPhj+3J4T3SWq+OiqchWumuj/wCPE5rlNU+OX7W3gXxRa2mrar4wtNRaVVjhu7MlWYnABAXGKBcp+81Fcb8H28RSfDHwy/iyVZvEb2MT3zqu3MhGTxXZUEBRRRQA1/untWB4s8YaL4F0g6hr2sWWjWKnDXF9MsafmTyfpW+yhlIPSvx9/wCCxvxeu9W+KGh+A7a7kTTdNtPtNxCp+VpXPGR9KTZSP1i8H+OfDvj/AE/+0fDet2Wt2anYZrGdZEDehweDX5w/8FspD/YPw5QHBa4n5/4CK+Uf2Ef2oNc/Zh+Lun6dqkd1b+FtbkjivrO5DIqBjxMoP86+jf8Ags54kj12b4ZWdn++tJYZbuO4XlJA2AMHoTzU3Ktqdx8QLj44fC/9h/4Ut8KVvIpI7ESaiNMgZ7oIwyu1QCe/pXy7dfFL9tfwhYpq8934+8ib5/30Mk4H1Tadv4iv2S+Cdqbf4N+CYHXldGtAQw/6ZLXZtEkgwyKw9CKOYLn4zeDf+Co/x/8Ahh9mh8baBDq9sHw39sWElnM/sHwozX33+x/+3h4Y/aw+1abbadNoniSzi86eykO9CvTcrelW/wDgoF4g8IeD/wBmPxdc+IrCzu5ri3NvYQyRqXe4bhdvfjrkV8T/APBF/wAB6nP498Y+L3tGh0mOxWzimZCFdy+cKehwKfMx6G/+3l+x/wDtC/H745XV9oumLrHhDYsdlnU4oYoeOS0bNu/IGvlD9oD/AIJ++Pf2bfhjF4w8Y6jpKiW6S1Sys5XlfJ99uK/f6vzM/wCC03xBjt/CPgrwbHPEZbu5e+liVwXUKMKSOoBqb3DmPg3wr+zVp+q/sz658XtU8XR6bBY3v9n22lramV55j0Ut0XPvUv7NP7FXxH/akM954Ts7aDRLOYQXOqXkqxohPovVjjsK+gPiT4Fj8Af8EsfCbhXE2v65Ffy7hjuQD+lfTP8AwRgtpI/gR4rlZWCPrOFJHBwnOKaVxOR71+xp+xnof7JHhm9hs9Qn1bW9UCNf3UnCblH3UHpW38Pf2uPCnjT4y+I/hdfJLoHi/SZikdreHC3admjbufavdK/Jv/gpxpGq/AP9pTwV8YfCtvPaXM203F0iHymlQ/dY9Mle1VsTufrJS1w3wV+Jmn/GD4X+HfFunTRzQ6lapK/luG2SYG9TjoQc8V3NMkKKKKAPEP23NUl0X9k74oXkDbZYtGl2n6kD+tfDH/BE2O3XUviQTIpu/KtsLn5tmTz9M19tft5RNN+x/wDFZFGWOiS4H0KmvhH/AIIn/L40+IgJ66bbj8fMqJFrY/WmlplPqk7knyX+2H+2J4l/ZT8aeFrifwmuq+Ab4Fb/AFKMnzYmz0UdM49a9s+B/wC0D4K/aE8Jx694P1aO+h6TW5OJoG/uuvatr4p/Cvw58Y/BmoeGPFGnx6hpl5GY2Vh8yZ/iU9iK/GDxdYePP+CZv7Sz3WiSXE3hm5bMLTAmG7tieUPbcPWk2NK5+5mRRkV454J/ao+H/ir4O2XxCm8QWNhpklt5syTTqHjcD5k29Sc+1fml8d/+CqHxP8XfEC8tfhWp07w/auY4tlr50s2D99jg8UuYOU/ZDIpa/L39h3/gpd4l8cfE6LwZ8VtQtdt+y29heJbiJvPJ4R8Dv71+oVUmJqwUUUUxCHpX49/8FnrV1+MHg+YjCNpL4P0fmv2Er8x/+C0Xw5urzw/4L8a28G63s5XsLmXcoC7+UGCc9fSk1cqJ9i/sS6nHq37K/wAOZopPMVdLjjJweoyCOa9y2+1fF/8AwSj+JUHjb9mOz0fz0e+0C5a1ljGdyqeV/wAivtKhCe43aaNpp1FMQ0A06iigAooooAKKKKACiiigAooooAK4f43+IpPCfwg8Y6xCcS2elXEqE9jsOK7evM/2lLE6l8AfH9sP+Wmj3A4/3CaBn5e/8Ef9JtPE37Q3inXdQiWfUINOM8TsN2HdzubPrX7H1+NP/BGzXrWw+PHiDTZZQk95pGIVbgvsbJx+FfsrQOW4HpX5Df8ABZX4nWOu/EHwp4NtmWSbSrd7id88Kznhfriv1Q+KHxI0P4TeB9W8T+Ib6Ow06wgaVpJDyxA4UDuSe1fzi/G74lXnxg+KniPxXeySSDUbt5It45VMnYvtxQET9if+CR+kPp/7KkVyybRd6pcMD64IGa+2K+Z/+CccdlH+yD4GFj9wxOZP+um47q+mKBPc/J344SR6x/wV28FWyDOy8sY2z0yI2NfrHtr8ctS8RJff8FgLOa4DbI/EcVtGOMjEWAevTmv2PoGxuKXdS1WuL61tJYYp7iKGSY7Y0kcKXPoAepoJLG6ik47c0tAB68UzzkH8S/nXk/7VWi+O/EHwK8UWPw3vJLLxZJbH7I0D7JWOeVRv4WI6GvyHX4E/toahfXCvB49eYtiRm1eRQf8Ax7FA0rn7nPeQRqWeaNQOpZgKyLzx14d0+YRXOuafBKeAklygP86/F2D9jP8AbI8SQtFNF4jWOTgpfeJgike4aSrdn/wSr/aN1hfO1Keztp+uLjXBI35qTQOyP2gt/FOjXjKsGq2crN0CXCEn9aupfW8jBVnjZj0CuCa/GW+/4JX/ALRXh+1jvdK120vL1eVgtdaeJ0PszYH61sfCP9jH9rDwZ8VPC2q6rNqK6ZZ6hFNcyDxAJ1EYb5vl3Hdx2oCyP2I3UtRI33fXvUtBIh6V+cX/AAWq0+Wb4R+AbpVzHBrEoc+m6Hiv0dr4G/4LH6tZ2f7OWjWc0Ze6utZj8hgR8u1SW/McUDW57d/wT6kEn7JHw+I7WeP/AB419GV80/8ABOrP/DIfgIE5It2H/jxr6WoB7hRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+VP2k/gr4o/aS+JfhrwhdTXGm/DLT/wDS9bZXKNqLH7sS4zlfXOPoa+jfDPgvSPBfhmy0DQ7OPTNKs4hFDb26hQoA68d61FVnyHB68dKLpmht3IZV44LVCir3ZvKXNZHxF/wVe02xb9nmSVrZJL37VEY7iQfcA9D613P/AATJ8RP4h/ZJ8Ll23yWrSQEn2NdV+138ED8fvhXH4WN00aT3MZaaNcsozyRxXX/s4/AnS/2e/htZeFdFubi4soiZM3QG/cevT3rGMXztlzS5FrqejalotjrEPl31pDdx/wByZAw/I07TdLtNJtUtbK2itLdPuxQoFUfgKt4NLXQko7HNzO1gpaKKYgooooAKKKKACiiigCK5uEtbeWaQ4jjUux9ABk18Y+I/+CsXwX8NeItQ0maHxDdPZSmF5rSxDoWBwcZYV9lahZx6lZT2kwJinQxvg44Iwa+Obv8A4JVfBzUfEl3q11a3kpubgzvCLl1Xk5IwDUu/Q0jy/aNXwb/wVG+BfjTWLXTLbU9Xs7u5dY41vbDYCxOAOGNfWtrcLdW8c6cxyKHU+oIyDXz18Pf2A/gt8M/E9vr2j+Ebf+0LchoXuGMoRh0YBu9fRKqFUADAHAFNX6ilb7ItFFFMgKKKazYXNADqK/PT/gph8SPjV4L1bwovwzu/EWnrJvaZtDUupx2YBTn8a8N/Z0/bb/ai8I+OtPsPGfhTxH4+0S4dYXt7jSzBcJuON6yLHyR6Ggvkkfr7RVezumurWCZongaRFcxSDDJkZ2n3FWKCAooooAKKKSgBa8E/bOtlv/gf4hs3Yp59rINy84whNe87q+Y/+CgnjWLwV+zv4iuXkjE8tu8cKO20sxGMD3qJbGtPc+M/+CKugCbxj4/1ZmKm1tIrdVxw2WPNfrVX5Yf8EeY4/BfgL4neNNUnMOjRhNzsMALGCzNXYeKv+C0HhDS9TuLfSPAuqalbxSGNbl540V8HGQM5pp6ClFn6P0V+aFn/AMFsPDZVvtXw21ZWAyBHeRY/WvR/h3/wV6+D/i+aCDWbPV/C00rBN11EJYwT6svandE8rPszxvqr6L4R1e+jTzZbe1kkRB/EQpIFfzneIdUvfjH+0Bc/25ut7jVtUMEuxctENxAAzX9F0F5Y+OfDlteWkoudM1CEOjYwHjYdfyr8bv8Agod+zbc/AL4lwfETw0n2eynulkKqAUhlzlSPr71nK99DeC921ziPjV8EfiD+yP4d0jxNoPj67h0rVJdsFnBcNHMMDqyg4I/CvmuTxTP4u8YWuqeLr+81OB51N1K7lpGTPIBPGcV6t4g+LPj/APbA8ReB/Bt9El/eRTra262seHO4gMTjjgV+wOjf8E//AIZaT8HoPBkOhWvmtb4udQmhVriWQryS2OOfSkrpakytfTY3v2a/Gnws8b/CPSNI8BXFlaW0Nqii1XYkgfbzkD7xz1r8of21Ph7qHwQ/a2stQEDaZHd3UF9FNGcA/vBuIrJ+P37PHxS/Yz8ZTajpdzqFjov2gyWl9ZSNtUA5G7HFeJ/E343+NfjJd2154w1qfXbq1GIricgui+g9qFvdBeyP6T/Cmoxav4Z0m9hk86K4tYpVkBzuBQHNa9eJ/sY+Jm8W/sx/D+/kOZP7NjiY+pQYz+le11rdGItQXUfnW8iFtoYY3eleP/tafHyH9nX4K654sISS/jiMdlC5wJJiPlFfhNq37W3xW8Q+NP8AhIdS8aa5O32nzzZpqEq24wc7Qm7G3HrRcaWt2fQ+peF20v8A4Kl6VZMWuIl8RwzM8nPydewr9sbi5hs4XlnlSGJBlnkYKqj1JNfgD4Z+Pl/8T/2rfB3ibT7RdL1GS4htRKzEuX6byc9c16v8Vf2bv2wPi14o1mbULPxHrGl3ExMUUmrNHaNGegEZkGRiszSVviR9Qf8ABSj9rz4deHPBV54JsrbT/FvibUImik8tldLRSPvFh1PoAa4v/gjf4G0jRfDXjDx3fz2UFzdTLZW7TTKJI4xyfpmvmWz/AOCVn7Q+qW0l5caBYxOF/wBVdalH5h9utaGi/wDBMn9pXT1FrZ2kem20z5dItVCJn1IBo2Fufan/AAVi8UaJ4g/ZZmXTdUtr+aLVrdNtrKr4JPIOD6V8cfCfSdD03/gn38Q9RgRZtTvN0UrEfMmMfpWV8dPgT4//AGZ/2dtU8N+Pfs0k+ranbz2ckVwZW+U/N82a9gj8J2vhv/gmbqUosI7ZrmIz/aIpA3mN6Gi9zWNos+iv+CQfi6TxB+zVdadJtA0nUnhQKMHDDPNcb/wVy+N3i34caT4R0nwxrl5of26SRrh7N9jOAOBn0qz/AMEYIbpfg34wmcxi0l1VTGo+9nac59qX/gsH8ILvxd8NdD8WWMUs0uiysJFQcCNhyTVJma0Z9G/sFfELUfib+y/4P1jVr46jqXlNBPcMcsxU4598V6Z8bNNn1j4X+I7O1dUuJrKVY2k+6DtPWvh7/gjT8TItV+FfiPwdNcL9s068+0Qwnr5bDn9a/QXxHosXiPRbzTp9wiuYmjYqcHBGKdubYX2rn4kf8E0/DulX37ZCWevtbl7IXJgjmAYSTBjgL719+/8ABRj9mfQfiR8INT16009YfENgvnRTQjbuIHfHavzn/a2+B+vfsgfHiHXvCz3lra+ebu0vMklHzk5b0r660X/grb8PNW+Ca2HizSNQv/FLWPkXFokQEVxJjGd3YGlYLWZ4r/wSH+Lt94U+N194DljY2OuQyOEV+I5YhknFfsxX4q/8ExdLl8eftp3PirS9Ea00S1hu7hwCSlt5inaufXJ6V+1VUiJBRRRTJCiim7qAFrE8ZyCHwjrMhxhbSQnJwMbTWxIzeW2zbu7bulfNH7fX7QmjfBH4A+JYptQSLxDq9o9nptqjAymRxgMV/uj1qWrjjvc/IT9nG3bxF+3B4TNpEcS+Jy6KCW2qJDk5r+hVc7Rnk96/F/8A4JK/A3VPHHxsk+IV1Fs0fw+H2ysv+tuH6YPtX7QU0VLcK+TP+CjPxo8b/BP4M/2x4J8R2Ph2/eURtJNHHJO69xEkisCfwr60r88P+CwnwpvvE3ws0fxVYrJLHo8xNygYkBCPvY6VMrhHc+Xfhf8A8FRP2gvA+m2mr+I4rPxl4Ye5Mck95pwhkOOqrJEFUH6g1+ifwC/4KCfC340+F0vbrXrLw3qsabrqwv5hH5frgnGRXyb/AMEs/D/hX40/Avxj4D8R2Ed19ivftL+bn7ki4GCCMdO1fEX7ZXhjwT4R+Puv6B8O43Gj2LCBtshbzJf4wOTkA1OpWh+p37RX/BVL4a/C3Tb6w8HXK+MvEwjYW4txm0STt5j5HH0r4Rm/4KnftBN4oXXpNUtodFZwRo8OnotuRn7okZC+f+BV4/8AsfwfDi1+OWhw/Fm3YaBJKFKXKssAY9DLgg7a/Yj43fsq/Dr40fAmbTvC1pY2unpaNPpx08DyywXKkEc0aodkdp+yT+09o/7UHwytvEFl5dtqkWIr+xDZaKT1+hr3Gvxr/wCCSOq6h4R/ag8Q+Eby4e1R7GeOSzbgSSxt97Hriv2Uq4mclYKKKKokQ9DXwR+3b/wT7j+NH23xT4NsYIPEqxl9kY2mdvQ/WvvimtGrqVIyDUtFJ2P57Phf8evjT+xl4m1DSrGe5017eXZcaVqELPA5Hfn+le62v/BYz4twrtudG0KeTH8EJXn6V+vPiD4YeEfFc3nax4b0zUpe73Nqjk/UkVhy/s7/AAymJL+BNBYkYJ+wx5/lTK5kfj34i/4KDftM/Gq3ay0KW5sbeRthXw7pxR8Ht5gFe2/sRfsG+M/GHxGh+KHxiF9DLZzrdWlteSbpZ5ByC4Pav088O+AvDfhO0Fro2hafpkAOfLtrdUH6Ct3A9KYuZdBiDaAMk47mpKTFLQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1HT7fVbC4s7uJZ7adDHJG4yGUjBBr8rf2xv8AglXqUmsXfiv4ShZYpiZZtFY7WRuuYz/Sv1bpMUmhp2Pwc+Hn7aXx+/ZJuf8AhF9TkuJILcFF0rxFExCY7qx5IroPiN/wVJ+NHxm0VfCmjWlpotxqA+zOdJjZp5t3G1SeRn2r9n/Enw38K+MLlJ9b8O6Zqky8CS7tUkb6ZIzVTTfg74F0a8iurHwhotpcwsHjlhsY1ZWHQg44NFh8x+X37Hv/AATEuviB4E1/X/ihbT6VqOpxPFp9vdIfNhkPPnMO/PavO/En/BPf9ob9n/4kG++Gy6jqcMJ82DVtCuVt5cdlwSOfrX7aUtMOY+Cf2L/DP7W0PjuO6+KutXEPhGJTvtNXkjnuJvYFeh96+mv2pPgXH+0X8Gdc8FG8GnXF4gNvdMu5Y5AcgkdxXrlFArnyd+xP+wfpP7J8N/ql3qf/AAkHiu+TypL7ZtSOP+6gr6up9JQI/J3/AILUSN/wkfgJG0UJD5MrHVlX5nOf9Xn2619hf8E2f7a/4ZI8H/23nzsSeTu6+Vu+XNfSeqaPY6xGI722iuUH8Mqhh+tWLW3htYEhgjSKJBhUjGAKB30sSfxU6iigQUUUUAJTafRQAynbRS0UANKjFRyQpIylkDFTkH0qaigYzpin0UUCCiiigBK/DD/go5Yt44/bm1DRbb97LM1lZKIzk5YgHp6A1+5zfdNfhz40uY/F3/BUy2AZZ428W29v8h3A4KjtUsuJ9Q/8FF/2MbOP9n7R/FXhuwU634TsoIb1olJe4gRApY46kda/Ny4+L3iD4qXXw68N+IbprnTdDnhtLUSZYhGkUZOa/o717RbTxJot9pV/Es9leQtBNGw4ZWBBFfhx8YP2DPHnwz/ak07w94c8P6hq/h281OK403UILd5IYofMViJXAwhXnqaSQ0z9fviJ8d/h/wDs5+C9Nk8X+ILbTI4bSNYLUMGuJVVQuUjzkgcc186+Jv8Agrz8DtJs7n+zP7d1i+VD5MUdiqI7Y4BYvwPfBrp/22v2FB+1nY+G7i11xNB1vR4TAsskXmRujYyCMj0rxn4c/wDBFvwTo7QT+LvF+pa5IpDSW9mi28Teq92x+NPlJufnz+0l+1F4o/ag+IY1PxXc3NloEco8jS7Vsx28OeoBOC+PWvv/APZ7/wCChv7M3wD+G+l+EvD1t4kto4UV55W0yPdLMQNxYrJzzntXrkf/AASZ+AKDB0fUn/3tQk/xrn/EH/BHb4J6nDL/AGdeeIdHmYfK0N6HUH6Mpz+dHKHMfTHwH/aV8BftIaLdal4H1V7+K1YJcQzwtFLET03Ka/KX/grz4mXxL+05pWiWmJJ9P0+OAqp3He7cDH5cV+qf7Nv7NvhX9l/4exeF/DSyTbn8y5v7gDzrlz3bAr57/aG/4Jt2/wAdv2hrL4jv4q+wWReBr3TDbktKIyDhXB4zj0o5Rpo8m/bs8IzeD/8Agm/8OdIuoWgubB7BXjdSrKxGSCD0616J/wAEc1K/s3audpUNrMhBI4PA6V2X/BTL4Ra/8RP2V7nTPCthNqc+kzw3bWdvG0s0kUfUIqgljj0r8sv2df23vin+yZ5uh6KLaXRhcGW40XVrUj5u4zwyfhR8I7c2x/QdXyd/wU4+GF/8Tv2UPEEWlWv2rUNLmi1FVWPe/lxtmTbjvtr4qtf+C1vxG+2xG58CeGntd37xIZJ1cj0DFiAfqK1dZ/4LMa94i0W/0wfDHTpftcDwlZL5pEwwI5XbyOaaYuVo7f8A4I5/tAQ3Wh6v8KNTuMXtszahpweQfNGfvoo9R1r9Oq/m+/Z58Ya54Y/aN8Ja/olncWd42sxn7LYo3KO+GjA7rg9K/o/jYMoIPB6Uwkuo7NGa+bv277r4paP8HF1z4UXFxHruk3aXk8FtH5jzQL95duDu+lfHvh3/AILOX2i+GxY+J/h5NN4mtk8uSRJ/KjkkHByCMrzSbFY+4v24IJrr9kv4pxwI0kp0OfaqjJPAr4M/4IlwhvE3xHmJyy2luo+m+vIfjV+3H8bf2vIbrQPCWhXunaHLAyXWmaMjTtLGeodsdK8X+Avx4+K/7LGtawvhKylsb/UEFvcwXdg8h+U5GBjrmo3Ktof0UU7NfhZL+3P+1f421CO0sL3VoZZ22JFYaWVYk+mVra+3ftx+MI9qL47ZJRjd5SRj+lCdhWPuP/gqP4+8ffDH4T6H4i8Fa9Jokdvfqt00Jw7Z+7+FRfD9/C//AAUO/Y0im8ZRRtrVrA0VzfhQJLe5jXPmqewOM4r86PiZ8E/2tfF2gsPGnh/xfqWkwDz3ivGDRrt53Ebq4P4aftSeLfg78J/GXgTR55LGLxA675EYhoOocD0Joeo7HlviZLjw7rmq6JaapNc2NldyRRtHK2xgGIyBX7Df8Eq/Bfwt1j4GHU9I0y3u/EqytDqrXih5FbsAD0GK4L9i3/gnj4P+JX7ME2rePtJZvEPibfcWl+T++toz9x19yea+V9Qh+LH/AATL+Oo8l5jok0+5H/5dtTtw3Q+hx+NIZ6X/AMFQfgDp/wAB/ix4b+IHhOJdNi1afc1vFhVE6ENlfTgV+tvwu18+Kvhr4W1hjue+0y2nc5z8zRqW/XNfkt/wUZ/az+Hn7TvwN8AzeG9Vj/4SO21AzXulOjiW2BhIJzt2kbjjg1+kP7EtxLdfsr/DiSW5+1udLQeZ9CRj8KuOxEj3CiiiqJEryv8Aaa+Bmn/tEfBvX/Bd9+7ku4S1rcYBMM68owz716rRQB+EP7PPxy8Zf8E5/jdreieKtCuZ9Omby9Q0zequ6KflkjbO0nHoe9fpH8OP+CpnwE8d29qL/wAQ3nhO/nYL9m1bT59isfWaNGjUe7MBXr3x1/ZT+Gv7RlmkXjXw/He3MYxFfQMYriP6OP65r5M8Vf8ABF/4aak8r6D4v17Qic7ElSO6RT2yDjI/GgvR7n3B4X+MXgXxtbxT6B4w0TV45Pu/Y7+KQn8A2azfiJ8f/h98LdJub/xH4s0uwWCNn8g3KtM+BnCxqSxP0Ffm7e/8ET/EUdxN9i+KGnGHpH5mmyRE/wC8Fb+Vbnhf/gidGt1FL4j+KJmhBBkgsNJ5YdwJHlyv1waAtHue7fsqf8FANT/am+Nmr+G9J8HR6f4RsYHkGqSXBeViDhcgDHzelfaVeZfBH9nnwP8As++HYtH8HaLFYKEVZrsjM1wR1Z27mvTaCXboFFFFAgooooAKKKKACiiigBKy/E2gxeJvDup6ROcQ31tJbufQMpH9a1aKAP585LjxD+wj+10Z1Rp30C+Zo4pFKi7tWJ4z3ypr9L9R/wCCtHwaj+Hv9r2lxqE+uvB8mlfZsETY+6SW+7nvXsP7T/7GfgT9qLSQuvW32HW4UK2+r2qgTR/X1H1r5s8B/wDBGnwBoPiCO98ReKdU8R2ETh0sCqxK2D0YgZIoHc+KvGPxV+Of/BRLx7a6DYW1zJo7zqFs7ZWSztlJxvkbGOB9a+l/2p/+Cab+Fv2YPDi+BrNdR8SeHQ11qqou6a+3L8+zAySD0FfpX4K+Hvhz4d6Pb6X4c0e00mzhQRqltEF4AxyR1roCueCAR6UBc/Br4KftVftB/CHwrH8J/CVtdWUkt0Y7OK500m5hZz0QsvHNftD+z9a+N7b4SeH1+Il3Fe+LTAGvJYhgZPIB4HIHXiu3/sHTPtguv7PtftI6TeSu4fjir9AXPxy/4KifCrV/gj+0boPxc8MxTWsWpSx3BvI8lY7yMjg4HGQK+xv2Zf8Agpd8MPi/4dsLPxVrVt4M8XIix3NvqjiGCV+m5JScYPX5sYr6U+Lnwi8MfG/wPqHhPxbp66hpN4m1lzteM9mRuqsPUV+dXjT/AIIprNrk03hL4jrY6Y7FkttW0wXLxDsu4OMj8KClbqfaXxY/ba+Dnwl8O3Go3/jnR9SuBEz29jpV3HdTXDAcKoRsD8SK+AfgR4k+L/7cH7Uej+PtTbUdK8D+H7z7TbLbK8Vt5atwo7MxGM/zrovA/wDwRWvbXxJZ3Pin4h2N7pUU6vNa2GmsjzIDkqCW+XPrzX6c+EfCOleBfDdhoWi2cNjptlEsUUMKBRgDGTjuaBaLY1Yx8qn+fWnnOOOtFLQSJg4560m2nUUAN20badRQA3bQVzTqKAGbcYp9FFABX5tf8FqLHU7z4b+BXtbOaeyt9RkknmjQsqExkAHHSv0lrO1zw9pnifT3sdWsLfUrN/vQXMYdD+BoGfKf/BLPX7rWv2S9BgurWS3NjcTW6NIMeYucgj2r69rO0Tw/p3huxjsdLsoNPsov9Xb28YRF+gFaNAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAx7q1nhuVlW5IjEeCrHv60yS6+0fu2XzbYjBcdc1cvv8AVn/cNZul/wDHiP8ArpUSOyOqux9hHLpszxmZGtzgQx87h654rcR96g4xVWb/AFkdWk+7Tic83fUdRRRVGYxJN7MMEYp9MX77U+gAooooAKKKKACkPSlooAQdKWiigAooooAKKKKACkIpaKAK0tnHNLHI6KzR/dJAOKl8sbs7Rn1xUlFMd2N206iikIKKKKAGTSCONmJwAK8Y+JH7Xnwo+EHiB9F8W+L7LSdSSLzTA5LNj6DvXsV5/q6/B7/gpl/yc9rv/XGP+tZSfvHRTipJ3P0D+Mn/AAVo+E3gvw7cyeDZpPGWt7CYLdYpIYC3YPJt4H4V+efxA+LXxm/4KBfEK00uDT7qTTpbhfI06xRmtrQE4yzkDIHqa+bdO/482/3a/a7/AIJp/wDJO4/+vdf6U7kv3Hoenfs5/si6L8FvgOPAFxcPqP2+PdqMzIFLsw+ZMA9ByK4KP/glj8EYrye4Gj3DmXJKPKSASc8elfYtMoUUyPaNHxxd/wDBKr4I3t4J/wCyrqAYxsjmI/Gtjwb/AMEwfgP4N1a31GLw9c6jPBIJUTULppY9wOfu9MV9X0+hqwnNyK9rYwWFnFa2sS29vCgjjjjGFRQMAAV85ftlfsw3P7Snwx1Dw3a37WV+zLPbTEDYZU5VX9FPfFfStRj7xpFxm43PhP8AYA/4J6Tfs46tf+LPGj2uoeJ2/c2aQjdHbp3cE87jX3ftpq96fVpGfM2c/wCNvAWg/ETQbnRvEWmW+q6dcIUkhuEDAg9celfDHxM/4I8/DbxRrx1HQ9a1rQo55cy2lu8Pkxqeu0GMn9a/QekpPQak0cN8FvhXYfBX4baH4N0y5nvLPS4fKSe52+Y/fJ2gD9K7n+Gmt94U7+GpFe7Pyc/4LMfF+31DWPDPw8tJmeSzBv7xFPAJGFB/nXnvwD/4Jnt8Zv2Vb7x42pzW/i68DTaTaLt8kxp/Cw25y31riP8AgqR/yd5rn/XpD/6DX6x/sR/8mxeB/wDryWmauKtc/EL9nWxk8E/tNeE9N16wkhmi1aO0uIJ12OhL7Sygj8q/owtdn2WHy/8AV7Rt+mOK/GP9pr/lI34S/wCwvbf+ja/Zuy/484P9xf5UglHliT/40hQNjrx70v8AjS1SRkeCftJfsXeAv2p7rS5/Gd3rkX9nZ8mPS7xIUOeu4NG2f0rhP2nv2ctN8L/sU+JvA3gnT5ZYdPsHa2ikYPM5A7nAyfwr61rM8Rf8gPUP+uDfyNEikz+fL9nv9sL4n/sk/wBsaX4WWxVLyT/SbXVrV5VRxxlQHXBruviT/wAFLPjX8W/BuoeGNaj0FtM1BDHKLXTnEmD2B8w/yrqfj1/yUDUf+vtv510Hw9+9Y/8AXRf51Jocl/wSt1zX/Df7U2mW9vbTix1KCW2vC8LbNuMg56A571+5O2vlD9lP/kaZvrL/ACr6xq4mcjkfiF8KfCvxU0l9N8U6Na6vaOpUrOgJwfQ18rXv/BI/4CXmoy3QtNchSR97QRakQg56DjgV9qt9001elUTqee/Bf4A+B/gDoLaR4K0aPTLeTb5spO6WbAwC79TXo1Mp9AgooooAQnAJr49+OH/BTb4dfAvxxqPhbVdE1u81GzXloYlWN29AWP619gyfdNfjd/wU8/5KFqn+6azlJxaRtTgpbl/4w/8ABY7x34iWSz+Hnh+z8KqW+S+ugt5MV/3CCoP4V8MePvip4j+L3jmTxD491a81q7mlDXDFghC55VFxhRjsABXtX7JX/Hre/jWL+0d/yGo/9+o52ypRUdj7E+Dv/BT74MfAH4c2XhPwf8Odahit49zA3SESzYGWZ2JPJ/Ktfw//AMFoJNa8Uabp7/DIJZ3dykBkh1PzJgrMBkIE5PPSvynj/wCQm/1Netfsjf8AJxngr/sJxf8AoYp3Ykkz+jWzuhfWcFwgZFmjWQBhyMjPNcb8avAKfE74a674dl27L22eM7hnqDXbQ/6uP6Clk7/SjdGezP5w28c/EH9mDxZ4u8JaHrN14eM8xguvJjTfJGCQuGZSw49CK+7f+CV37Itl4mjvfi5450hL+V5iml2+oxM43dWmw3DfjmvlL/goV/yd54h/34v51+3n7Pv/ACRPwX/2DIf5VXRD7nz1+19/wT38EfGjwzqGqeHNEh0jxiqFobi2Z1RjjpsDbf0r8ztT8aftOfsw2U/h+PVtd0XRbEtGrR20csO0d8ujYFfvvXzv+17/AMk38Qf9er/+gmpGj8cv2PfjlqPhf9rzwf4u1zUFdr/U0g1K7eNVzHK21zhQAOvYV/QuGDAEcg1/M78Jv+S4eGv+w3B/6NFf0xVpEmQtFFFUQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMmTzInT+8CK/O3wH/AME0PE/hj9re3+Kc3iaxOi22vHV0tBGTK67twU+h561+itFJq5SdlYQ02n0UJWJG06iimAUUUUAFJS0UAIVB4xXI+I/g/wCBvF4kGt+ENE1USAh/tdhFJuB6g5Xn8a6+ik1cd2eRn9kf4J7w/wDwqjwfuHI/4k0H/wATWxpH7PHwu0C4SfTvhx4Vsp0OVkh0a3VlPqDsyDXolFCVguznYfh/4Ys7hLmDw3pMNzGdyTR2ESupHcELkGt6P5R0PPepKKYDGXdwRkGvP9Y/Z8+Guv3kt3qPgXQb25lbe8s1hGzM3qeK9DopNXC5zHhL4a+FfASSJ4c8O6book+/9itkjLfUgVek8IaHNeC7k0XT3ugciZrVC/54zWzRS5QuUo9IsYWDR2VvGw6MsSg/yq1j8KfRRyhcq31mmoWU9tIoZJY2jO4Z4IxX4Bab+y7r3ib9tKf4bXel3dvaS+IpPNmaIgLaGYsJM9MbTX9A9eBw/wDJ0L/9ev8ASjlHc9n8NeHbPwn4f07RtPiWCxsIEt4Y1GAFUYFcd8bvgH4P/aC8IzeHvF+lx3tswPlTAYlgb+8jdjXo1FHKK5+DP7bn7B2rfst6tFqWlvPrPgi8ciO7ZMtbMeivj271+pH/AATavbi9/Y+8Dtchg6JLGoYYO0OcV3X7V/8AySHUvwrW/Zt/5Ir4X/69/wCpphe56dRRRTEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH//Z"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83-%E6%AF%8F%E5%8D%81%E5%88%86%E9%92%9F%E6%8E%A5%E5%88%B0%E8%AE%A2%E7%A5%A8%E7%94%B5%E8%AF%9D%E7%9A%84%E6%AC%A1%E6%95%B0.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApkAAAFaCAYAAABVO0bVAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAFdnSURBVHhe7b2HtxVllr//+y9m1sys/nbP6plpv/NttZ22bbW7MTQYuhtBmiAoKCBRwhAEYQiSY5MZcs5BMkrOGUGS5CRBco4C7p/P7lN6ZV3lnnteOKeKz7PWXtxbp6pOnaq61HP2++73/f9MCCGEEEKIwEgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRHEmmEEIIIYQIjiRTCCGEEEIER5IphBBCCCGCI8kUQgghhBDBkWQKIYQQQojgSDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMnOIWbNmWc+ePW3gwIEKhUKhUGQlevXqZVOnTk09mYQoPJLMHKJOnTr2wgsvWP369RUKhUKhyEoUK1bMKleunHoyCVF4JJk5xP/8z//Y3/72t9RvQgghxIPnf//3f+2///u/U78JUXgkmTmEJFMIIUS2kWSKUEgycwhJphBCiGwjyRShkGTmEJJMIYQQ2UaSKUIhycwhJJlCCCGyjSRThEKSmUNIMoUQQmQbSaYIhSQzh5BkCiGEyDaSTBEKSWYOIckUQgiRbSSZIhSSzBxCkimEECLbSDJFKCSZOYQkUwghRLaRZIpQPJSS+fXXX9utW7fs7NmzdvPmzdTSv8Pyixcv2tWrV/33O3fu2Pnz5+3MmTN24cIFu3Hjhi+Hy5cv+/Jz587ZtWvXfL/Azywnrly5Yrdv3/bl90KSKYQQIttIMkUoHkrJRCwPHjxoVapUsdWrV6eWmsvg/v377cMPP7Rx48a5NCKWDRs2tFKlSlmTJk1s8eLFvi4y2qdPHytbtqy9++67NmXKFJdO9jFr1iwrX768bzNo0CA7dOiQb3MvJJlCCCGyjSRThOKhk0wEc8uWLdagQQP7/e9/b4sWLUq9Yp51bNOmjZUoUcLl8OTJkzZp0iRr2rSpTZgwwfr372+dO3f2TOcnn3xi7du392WsU7t2bTt8+LCtWbPGevXq5a8hpPXr17cVK1bYV199lXqXH0aSKfJy8tINe2/cJqs8YkPORZ9Fe1NHKYRIGpJMEYqHTjJp7t61a5f17dvX/vjHP36bmUQcyWqStfzzn/9sAwcO9PX4Qxs1apQdOXLE5s2bZx06dHBJRQgRTH7euXOn1atXz9auXWu9e/d2EV26dKldv37dWrZsaTNmzLBTp075++TlxIkTtmTJEn8vArnt1KlT6lXxsHPwzBX7Zet59n+azM65qDpyQ+oohRBJQ5IpQvHQSSYZRfpbfvnll1amTBlbtmyZN3EjlO3atbMxY8ZY5cqVXfo2bdrkTd7r16/3LCf/DhgwwKZPn25vvPGGN5HTr5MMZo8ePVwmkc3u3bvb8ePHPWs6dOhQz4Ky/7uhyZ5mebKdRJEiRVxihQBJphAiG0gyRSgeyj6ZQOaS/pRIJoU9H3/8sVWoUMGOHj1qLVq0cMncuHGjvfbaay6IyOnmzZttyJAhNnLkSCtZsqTNmTPHi3zYhvXHjh3r/TPJZtI/E8kcP368Z0LZ9l6ouVzkRZIphMgGkkwRCknmN5K5cOFCzyDSdI000sSNNCKGrLNt2zZv+t6wYYM3s48YMcIzmbNnz3aZJJPZs2dPl0n6ZrIOFedI5vDhwz2bSVb0XkgyRV4kmUKIbCDJFKGQZH4jmWQmixYtajVr1vQK8meffdbefPNN69evn/9OtThFQAsWLPDKc7KeCCFN63v37rXdu3f7HyTN6F27dnXJRCoRU9ZHSvfs2ZN65x9GkinyIskUQmQDSaYIhSTzG8kkQ0kRD1lHonjx4lanTh2bP3++97ts1KiRZyPps8kfHsMcIZpUoiOFVKK//vrrvh/2R3V5VPAT9d0ks3kvJJnZY8muU9Zjwe6cilYzttu/N5+br+RlOySZQiQXSaYIxUMrmRT/dOnSxZvC74a+lQxRRHM3Y1wime+//75nNRkbk0IhBlqniZyCnebNm1vjxo0928m4mkhlrVq1rFWrVl4IhHxGA7X/GJLM7IHQ5SdTivxDkilEcpFkilA8tJJZUJjx5/Tp07Zy5UrvoxnNBAQUDLFs+fLldunSJV8XqESneZzCIIYpKsgYmSDJzB6SzPRCkilEcpFkilBIMgsA8sj4mshi3owky1nGa3mX8zMzAtEnk6xnQbKYIMnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGQZOYQkszsIclMLySZQiQXSaYIhSQzh5BkZg9JZnohyRQiuUgyRSgkmTmEJDN7SDLTC0mmEMlFkilCIcnMISSZ2UOSmV5IMoVILpJMEQpJZg4hycweksz0QpIpRHKRZIpQSDJzCElm9pBkpheSTCGSiyRThEKSmUNIMrOHJDO9kGQKkVwkmSIUkswcQpKZPSSZ6YUkU4jkIskUoZBk5hCSzOwhyUwvJJlCJBdJpgiFJDOHkGRmD0lmeiHJFCK5SDJFKCSZOYQkM3tIMtMLSaYQyUWSKUIhycwhJJnZQ5KZXkgyhUgukkwRCklmDiHJzB6SzPRCkilEcpFkilBIMnMISWb2kGSmF5JMIZKLJFOEQpKZQ0gys4ckM72QZAqRXCSZIhSSzBxCkpk9JJnphSRTiOQiyRShkGTmEJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4TioZTMW7du2fHjx61Dhw62bds2u3r1qm3YsME++OADa9asmXXt2tVWrVplX3/9tV2+fNl69+7tr/Xr188+/fRT38ft27dt8uTJLoYdO3a0xYsX+37u3LljK1eutFatWvk206dPty+//NK3uReSzOwhyUwvJJlCJBdJpgjFQyeZCOa+ffusZ8+e9uKLL7oc7tq1y8aMGWPdunWzoUOHWr169WzQoEF24MABW7RokTVo0MC6dOlinTt3tv79+38rpe3bt3eZREKbN2/u4vr555/bwIEDrVGjRr4PRHP9+vX+vvdCkpk9JJnphSRTiOQiyRSheOgk8/r167Zp0yZr3Lix/eEPf3DJJJs5e/ZsO3r0qMtg69atrVOnTv4a4kcGc//+/TZr1iyXSiSV1xHCtWvX2vbt261q1aq2efNmGzZsmL/GuteuXbOGDRv6vs+fP586gu+4ePGi7d6925YvX+5RuXJll1nx4JFkpheSTCGSiyRThOKhk8ybN2/apUuXXChLly5ty5YtS71i3jyOhDZp0sSbzJFM1qHpnG0QSjKZc+bMsQoVKtjEiRPt1KlTdujQIc+CspysJz9/8cUX/l5kMydNmmR79uxJvct3kPVk3Zdfftnj0UcftbZt26ZeFQ8SSWZ6IckUIrlIMkUoHjrJRCQJMotly5b9nmQihQsWLLCmTZva+PHjvZm7ePHitnPnTn+NTOWQIUNs9OjRVrJkSc9Q0nSOsA4YMMC3qVatmvXq1cullG3GjRvn63/22Wepd/mOr776ytdDVAmynt27d0+9Kh4kksz0QpIpRHKRZIpQPJSFP0BTdV7JvHHjhjeJ16pVy0aOHOnZSZrVyWTu2LHDX9+4caNnMkeMGOHbIplXrlzxrCX9MpFJtu/Tp49LLJLJvmhCZ1/3Qn0ys4ckM72QZAqRXCSZIhSSzG8kk36Y9I2ksKddu3a2ZcsWX0Zzdt26dW3hwoV29uxZW7JkiVekUzFOs/iECRNcMPfu3esFPlOmTLE2bdpY3759PftJ0zv7HD58uP9+LySZ2UOSmV5IMoVILpJMEQpJ5jeSSVU4Ivjkk096ppImc6SQoHmcQp558+b5Hx5V41u3brWxY8d60zb9MmfMmGFvvPGGrVixwn8mq0mFOZlPCoKQ0RMnTqTe+YeRZGYPSWZ6IckUIrlIMkUoHlrJpC9kjRo1bM2aNV7YU6dOHXviiSe8D2apUqU8A0kTN8Mb8TuV35UqVfKiILKcjH1JhXqZMmV8P6+//rodOXLEzpw543+gf/rTnzzbyf4YBol+oPdCkpk9JJnphSRTiOQiyRSheGglE+k7d+6c95ukvyU/k208ffq0R1S4QyCaDElEtTlZT2Awdvpt0pQ+c+ZMO3jwoBfyMBj7yZMnbfXq1V70Q39OBnQvCJLM7CHJTC8kmUIkF0mmCMVDK5kFBRlFQhFPinmQywikkmW8RnYzylbyM2KJkNIvE/EsCJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGInWQyNiXjUOYH41HyekFm18lFJJnZQ5KZXkgyhUgukkwRilhJJhK5efNm27dvX2rJ97lw4YK/ziw9cUSSmT0kmemFJFOI5CLJFKGIlWSSoWzRooVVrVrVunXrZiNHjrQlS5b4POJffPGFTZ8+3ecWZ4rIOCLJzB6SzPRCkilEcpFkilDEQjLJYDK1I5JZp04dq169uo0dO9bnBh89erT17NnTWrVqZa1bt/bfCzpXeK4hycweksz0QpIpRHKRZIpQxEIyz549a8uXL7dVq1ZZtWrVrHPnzt4sPmPGDOvSpYuVK1fOXnzxRatfv74dPXr0e/OLxwlJZvaQZKYXkkwhkoskU4QiFpK5ZcsWe+edd+z111+3p59+2t58803PWlauXNnefvtt6927t3Xv3t3atGljc+fOtatXr6a2jBeSzOwhyUwvJJlCJBdJpghFLCTz0qVLLpqbNm3yvpgIZ6lSpVwwWUYfzIMHD9qYMWOsfPnyduLEiVhWmEsys4ckM72QZAqRXCSZIhSxkEykcerUqS5giBiFP/Xq1fPmcrKZLVu2tLZt21qHDh2UyRSFQpKZXkgyhUgukkwRilhI5q5du6xp06b21ltvWenSpb3ZvFGjRrZ48WLvi4lwIp61a9d2IVWfTJEuksz0QpIpRHKRZIpQxEIy9+zZ8+3QRc8++6z98Y9/dMkcMWKEvfzyy9asWTN7//33fdn69eu9Ej2OSDKzhyQzvZBkCpFcJJkiFLGQzIsXL9q6dev8xi9atKj3x+zatasPXfTII494NpOK8wkTJtgHH3ygcTJF2kgy0wtJphDJRZIpQhELyTxw4ID16NHDBg4c6P0vaR7v2LGjLViwwEqWLOnCGRUG8Ydx+vRpFf6ItJBkpheSTCGSiyRThCIWknnlyhXbu3evy+aOHTvs008/dak8fPiwF/rQZ5N1mFbys88+U3O5SBtJZnohyRQiuUgyRShiIZlAZvKrr77yYG5yRPL69et2/vx5X4ZkHjt2zEX01q1bqa3ihSQze0gy0wtJphDJRZIpQhEbyUQs165daytXrrTt27d7k3gEArpt2zYf5mjFihUun3FEkpk9JJnphSRTiOQiyRShiI1kMrVk2bJlrXjx4ta8eXMfviiCwdqHDh3qQxhRIKTmcpEuksz0QpIpRHKRZIpQxEoyGSOTbOXWrVvt888/9+V37tyxYcOG+TBGzPhDxjOORT8gycweksz0QpIpRHKRZIpQxEoyy5QpYwsXLrTVq1fboEGDbPjw4T5fea9evWz+/Pl2/Pjx1NrxRJKZPSSZ6YUkU4jkIskUoch5yUQuqSQng/nSSy+5TK5atcrHyGzdurW99tpr3nyOeMY1gxkhycweksz0QpIpRHKRZIpQ5LxkUjE+Z84cF7AXXnjBBgwYYIsWLfKhiz766CNr3769ZzPHjh1ru3fvTm3149DETjX6hg0b7MyZMy6nVKnTn5PCIoZE4negcp1hkZBYmulPnjzpy9mGYZXWrFljGzdutCNHjnhVO8vJqFKkhAzv37+/wHOpSzKzhyQzvZBkCpFcJJkiFDkvmYjb0aNHbfLkyV7YU6lSJevfv78PVYQsAkKHbBII3Y9lNHnt8uXLLoYUES1ZssSr0ZFLBnZnGVNYIpUIJu9drVo1z5gyCPz06dP9fZmFqEOHDlaiRAl7++23bfDgwS6myOv48eN9OXOsd+nSxeX3x44pQpKZPSSZ6YUkU4jkIskUoYhFn8zbt2/btWvXfLrIzZs325QpU7z5nGGMED6Kfch2IodMLYno/RBUnpNhpIjoqaee8qwoMwXR/E5GdN++fdauXTuvVidTidAyyxDbUFjEe3AcZE5Zj2wqwyZVqFDBs5Yff/yxiyV/pGQ3a9So4TMTcYz3QpKZPSSZ6YUkU4jkIskUoYhN4Q+SiVgicEgm2ct+/fq5GCKANHGTfVy6dOmPjpOJZH7xxRc2a9Ys+9Of/uSZzNmzZ/uc52zL+4waNcor1slaksWcNm2anThxwtft1q2bN5GT1URE9+zZ4zJKdfuyZcs8u8kxMisRx9GpUyffnozo3Rw8eNDGjRtn9evX9yhSpIhvLx48ksz0QpIpRHKRZIpQxEIyyVjSBxMBo6KcqSWjZWQamdd85MiRtnz5cvvyyy898/lD8BqieerUKa9WRwzJfjZo0MD7f9I8j3SOGDHC902TN5lO5JM+nMyfjuSyLVlMprJEWnv37u2/v/fee56NZP9kL9kPzecc891E4so+CZrYkVLx4JFkpheSTCGSiyRThCIWkkmzM9lFZC1vRpCmcqRyyJAh3h+TjGFBoU8lg7sjmey3YcOG3qeSfX7yySeepSRrST/NnTt3ujAimwydhDiWKlXKm+jpA8rxIaQ0p1evXt2FkwHi2YZmddanmf9eqLk8e0gy0wtJphDJRZIpQhGb5nIKZwiKcchEInD8TOaRfxG9glaXQ17JJANJc3dUIY6s8kfG+JtvvfWWyyUySRM9y0aPHu0FSDNmzHAxPXTokDeRI5k0e/ft29er0DlGMpQIKxXq90KSmT0kmemFJFOI5CLJFKGIlWTSx5ExMym0YbghfkYsDx8+7MMGRcMOFYS8kkkgiRTtIJNREzyy2apVK5s0aZI3pdM8jwhSLETmNGq6Z/YhCnxoZkcwCfqJ0sROX0+a8ikKuheSzOwhyUwvJJlCJBdJpghFbCSTvpQ0ldMvExljyCCyhPwxIHVdu3b1wdl5vSCymVcyyWCShaSfJVXmFStW9Iwl8soMQwxR9OGHH3qWsm7dup6lRHKbNGnifTkpPqKIaNu2bS6+CGrVqlW9MIkhkSgg+rGK9whJZvaQZKYXkkwhkoskU4QiFpJJFpOmZ4YXQuw6duzo41ouXrzY+2MyhiZZR4pmihUr5tXeNHv/GDS5sx1N3fyMILI9soposn+a4RFKZJFMZ5TdjMbJJMPZuXNn6969uw8Sz9BGyCRV6iynTyeySuW7xsnMbSSZ6YUkU4jkIskUoYiFZJKZpPmZvpONGjWyiRMnenU5WUj6RzKMEEJIcU3lypVd6hDHdGB7KsLpd0nGFKkF5JD3J0PJ++QdHolB3Wmup79l3kHgWYeKc4ZUYlrMewlvhCQze0gy0wtJphDJRZIpQhELyWQ6xypVqnhFN0MKkTWkfyQ/M285s/fQ/xGhQ+zIMv7YMEa5iiQze0gy0wtJphDJRZIpQhELyYyyjOvXr/eCm3fffdf7XpItJMtI1pEsYjT7D//GEUlm9pBkpheSTCGSiyRThCI2hT9IJP0dkbBy5cp5MQ59Iek/Sb9Hok+fPt58TjN2HJFkZg9JZnohyRQiuUgyRShiIZn0cWSIIprEqSCnyptq77/+9a/+x8Bg502bNvWB0Bm7kv6RcUSSmT0kmemFJFOI5CLJFKGIhWTSVD5v3jwv9KGpnOwlY1q++uqrPkYlFeAMY8TwQlR4q7lcpIskM72QZAqRXCSZIhSxkEz6XlLsU6dOHR+Pkmbx+fPn+xiUVJKfOXPGXyfDKckUhUGSmV5IMoVILpJMEYpYSCaV4vSzpMinWrVqVqRIEZfNJ554wivOGVT9xRdftKefftoznQxvFEckmdlDkpleSDKFSC6STBGK2BT+RDCc0fLly33cTAY9Z8iiNWvW+FSTNKcznFG6Y2TmCpLM7CHJTC8kmUIkF0mmCEUsJJPBzMlkUvgTBcU9BK9Rec4sP8wpzlziDHkURySZ2UOSmV5IMoVILpJMEYpYSCaV5VOmTPHMJRlLgmwmUz9S9INUMlMPUzkyNeSFCxdSW8YLSWb2kGSmF5JMIZKLJFOEIhaSSYbyP/7jP6xGjRpe/PPee+95JfkHH3zgzeXHjh2zAwcO2NChQ+3JJ5/03+OIJDN7SDLTC0mmEMlFkilCEQvJpM9liRIlbN++fT7rD/0xmTMcmZw6daq1aNHCx8hkmsmnnnpKkinSRpKZXkgyhUgukkwRilhIJk3hZcqU8arxadOmWbdu3Xy2n44dO/rMP8xrzrI5c+Z41pPB2+OIJDN7SDLTC0mmEMlFkilCEQvJJHNZrFgxW7Jkic/uQ7/Ltm3b+uw/yGbv3r197EyymhcvXtQ4mSJtJJnphSRTiOQiyRShiIVkMiwRY2Fy448aNcrGjBnjc5RPmDDBm9AZ1mjkyJFe+IOIKpMp0kWSmV5IMoVILpJMEYpYSOaJEye8upwbf9KkSf7z+PHjbe7cuXb48GE7dOiQ7d+/33+vXLmyBmMXaSPJTC/eGrrOTly8nnNx41Y8WzGEyCUkmSIUsZBMZvw5evSovfnmmz7gOhnMdu3aecaS17p06eKZzD179tjkyZPt0qVLPnZm3JBkZg9JZnrx783n2m/aL8y5WLzzZOqKCiEKiyRThCIWkgmnTp36dtrI0qVL23PPPWdt2rTxeOWVV6xRo0a2bt06HzeTAdrjiCQze0gykxFzt32ZuqJCiMIiyRShiIVkkpVEHp9//nkv9qlZs6b95S9/sXHjxnnQF7Np06Y2ZMiQ1BbxRJKZPSSZyQhJphCZI8kUoYiNZJ49e9bHw6TI55NPPrEBAwakXv17n00Kgnr27JlaEk8kmdlDkpmMkGQKkTmSTBGK2EjmzZs3vcDnypUr3ufyzJkzqVfNhyyiP+aGDfGueJVkZg9JZjJCkilE5kgyRShi0ycT0aTIh3+Ju8fCpB8mIhpnJJnZQ5KZjJBkCpE5kkwRilhIJvJIdTlDF9EHc+zYsT7wOmNifvjhh9asWTNr2LCh1atXz6vOz58/n9oyXkgys4ckMxkhyRQicySZIhSxkcwjR4740EX0vaRvZvPmzW3Lli0unMwCVKdOHfvrX//q42fSpB5HJJnZQ5KZjJBkCpE5kkwRilhIJs3k9MPcuXOn7dixw6eVrF+/furVv8MMQE2aNEn9Fk8kmdlDkpmMkGQKkTmSTBGKWEgm/S2RzCgGDRpkDRo0+N6ywYMHW+PGjVNbpEdUWEQxEbMFnTt3zgd6531pemfZhQsX7MaNG9+uzxzprM+6165d8+Vw9epVr4QnLl++nNY86pLM7CHJTEZIMoXIHEmmCEUsJJMpI7t27Wrdu3f3KF++vL344osuZES0rEqVKqkt0gN5XLNmje/j1VdfterVq/sUlbt37/Z+niVLlrQPPvjAVqxY4esjle3bt7c33njDateu7f1DI2jOf+edd6xixYrWv3//tPqHSjKzhyQzGSHJFCJzJJkiFLGQzOPHj9vEiRNd5oi6deu6+EW/R8tq1KiR2iI9du3a5c3tyOr8+fOtZcuWPpMQY3FWq1bNhZMm+jFjxrjwUnDE+yGUZFARYPqMrl+/3tq2bev7oUiJbOv27du/l+n8MSSZ2UOSmYyQZAqROZJMEYpYSCZN0MjdwYMHPRAxZv2Jfid69OhR6D+KzZs3+x9Vv379fGYhRPHtt9/2AqPevXt7NhKRHTZsmE2fPt0lkvnSkdPVq1dbnz59bN68eda3b18XTiSUY+rYsaPNnj3bB4vPD5az7sCBAz1KlCjhMisePJLMZIQkU4jMkWSKUMRCMunXSMX44cOHv5VMsoR5yaTwB4Fle/p0Ll++3OdBL1OmjGc0ly1b5pnItWvXeuYSiaQJfebMmS6kNKlT0Y5gUoxEpfvevXt9rvXJkyd7/1F+zw8+C0MysR1RpEgR69ChQ+pV8SCRZCYjJJlCZI4kU4QiFpJJEc6+ffs8k0g/R5qw33vvvW+LbCjAIRNYWMlECGkSp38l86Ajm/SrpB8m01hSFES2c+TIkZ7drFWrli1dutQznAcOHHCZpI8mzfWTJk2yY8eO+XHNmTPHhZiK+IKg5vLsIclMRkgyhcgcSaYIRSwkMxonc8aMGd7XkbExyTwidBTYlCpVyl5++WXPQBYG+mEid7wHVeRII30+X3jhBdu4caMXBq1bt877X7Zq1cqzqAsWLHC5ZTpLjoVB4MlG0neUjCviyrGS+ZRk5j6SzGSEJFOIzJFkilDEprmcbCZ9GL/88ksvBCJbiBQif/SLXLVqVYFl7m6mTZvmWVC2530o+KlcubIP8E6xD0Mk0TxO30sypvTTRDjJYlLs07NnT/89ep1liCZ9N/mdLGxBkGRmD0lmMkKSKUTmSDJFKGIhmfcbRJUinaZNm3pVeaVKlTxjSf9KhkUiI0kTOllJBJJ+mzStI5A0r5PZZDn7YXv6VdK0z5BIFATRdF4QJJnZQ5KZjJBkCpE5kkwRithJJn0kqcimTyTBz4cOHfIMZGFBAmn+pmK9bNmyXthDf0r6YbKMAiD6gFKkQz9QmsmZ1pI+m8yZTkU4ywmyoDTb81pUAc+g7gVBkpk9JJnJCEmmEJkjyRShiJ1kInu/+c1vvL/kc889Z48//rgNHTrUm9FDgxwilPTZZEpLZvABZvyhCZ0B3Dds2PC9AdcRzW3btrkAM1MQU2IWFElm9pBkJiMkmUJkjiRThCJ2komI0feRwhqKbkqXLu1Cl47MpUPUH/Srr75yuYyIpqIk8k4dyXLWpVgonSklQZKZPSSZyQhJphCZI8kUoYidZNJ0TV9JYN5w+j1S9JMEJJnZQ5KZjJBkCpE5kkwRilhIJk3Wixcv9oHRmYmnWbNmXnxDv8miRYv62Jn8zusrV67MqH9mNpFkZg9JZjJCkilE5kgyRShiIZkMAUQVNwL20ksvWYUKFaxXr15eEf7rX//ax6dkGCGGDGJ4oYsXL6a2jBeSzOwhyUxGSDKFyBxJpghFLCSToh6GEWIw9nLlyvnNTxaTgc+ZipGhhZgjnHnFGfOS4ps4IsnMHpLMZIQkU4jMkWSKUMRCMinqYf5wgqGBmA+cJnEGZWfIIZrSo9eJvAU6cUKSmT0kmckISaYQmSPJFKGIXeEP/THzVpczpSTV5elWcucikszsIclMRkgyhcgcSaYIRewks0WLFj7dI4Oe0w+zePHi3lTOuJVxJ+mSufXoBeuxYHdOxmt9V+YrLYp4hSRTiMyRZIpQxE4yx48f71M3tmvXzoOfV6xY8b0B0eNK0iVz7NrD+YqBQhEqJJlCZI4kU4QidpJJ/8y7m8YZ/JzZeeLaFzNCkqlQZBaSTCEyR5IpQhE7yfziiy+8P2Zetm/f7sMcIZtxRpKpUGQWkkwhMkeSKUIRK8kkUzlw4EDvgwlkNJkfvFWrVr487k3mkkyFIrOQZAqROZJMEYrYSSYiNnz4cG8eZ/xMZvupXLmyDRs2LLbjY0ZIMhWKzEKSKUTmSDJFKGLXXN68eXPr1q2bbd682SZPnmy1a9e2mjVr2qxZs1JrxBdJpkKRWUgyhcgcSaYIRSwkk6wlQxQRdevW9Vl/mEqydOnSNnfuXKtevbr169fv23XiOmamJFOhyCwkmUJkjiRThCIWkrl//37r0qWLMTf5448/bj//+c/t9ddf94HZO3ToYMWKFXPxZB3GztTc5bmJJFNxv0OSKUTmSDJFKGIhmUePHrXRo0f7GJlPPvmk/eQnP/HpJIcMGWLjxo3zjGaNGjV8HeYzv3LlSmrLeCHJVCgyC0mmEJkjyRShiIVkIo27d++2vXv32ptvvml//vOfrUmTJj6P+YQJE+ytt97yjCbTTMZ5KCNJpkKRWUgyhcgcSaYIRewKf5hWEqGk0IfmcqSsSpUqNmbMmNQa8UWSqVBkFpJMITJHkilCETvJbNmypY0YMcKLe86cOWOtW7e2hg0bunTeuHEjtVY8kWQqFJmFJFOIzJFkilDESjIRy0gyo98p8mnbtq0PbbR06VJfHlckmQpFZiHJFCJzJJkiFLGSTAZj37Vrl08tmZctW7bY2rVr7fDhw6kl8USSqVBkFpJMITJHkilCERvJJGt57tw5O3v2rF27ds1u3rzpv7N8w4YNPn85y+KMJFOhyCwkmUJkjiRThCIWkok8MoXkp59+ahs3brRjx4550A8T4WTecs34k/tIMhX3OySZQmSOJFOEIhaSeeLECZs2bZoNHjzYx8VkSkn6X5YoUcLH0KQ/5qBBg1xGCZrV44gkU6HILCSZQmSOJFOEIucl8/bt27Zt2zafRvLpp5/2aSUZlJ2B2F944QX7+OOPfQgjBG3NmjW2fv362FaZSzIVisxCkilE5kgyRShyXjLJStL3csWKFV5ZXqtWLZexRo0a2RNPPGEdO3a0V155xQdp79Onjw0dOtTnLy8MyCnjbX7yySdeXEQhUY8ePaxp06b+R0eBUbQeFe4cT7du3WzJkiW+HJDedu3a2YcffmhTp05N61gkmQpFZiHJFCJzJJkiFLGQTIRv+PDhLnQMxI7g9evXz4oUKWLTp0+3ihUr2vvvv+9N6KtWrSpUJvP69eu2c+dOz5SyT36eO3euVa1a1fr27evjcU6ePNn7htJczx9gp06dPHr37m2nT5/2WYk6d+7szfe9evXyGYmYpaigBUmSTIUis5BkCpE5kkwRilhIJtNFIpc9e/b07CAy99lnn/kg7EeOHHGpQ0ILC+9x6NAhz1pWrlzZ5s2b55lTRLFNmzZe0U6Gkyb6hQsX2oABA3zmoa1bt7rYdu3a1eUW+SWLiZwyvSXHxfoMGl8QJJkKRWYhyRQicySZIhSxKPwB5iNH6lauXGn79++348eP2+zZs23Tpk0+GDvyWVjIfC5YsMB+9atfWYMGDVwmyUiSiUQSqWBHIkePHu0iyh8f70dWk4zn2LFjvcId6R02bJiP5Xny5EmfV53fEc784DPRnH7q1CkPtu/evXvq1eQhyVTc75BkCpE5kkwRithIJtlGpIxm61GjRnmTNVlHxI/MJiJYWHbs2OFyV7ZsWVu3bp2L4auvvmrPP/+898NEQnk/3rdVq1beL5R+mPQVPXDggDej0ze0Ro0aNnHiRK94J3s5Z84cz75+/vnnqXf6PiynC8DLL7/s8eijj7owJxVJpuJ+hyRTiMyRZIpQxEIykTEKfWhOfuqpp+yZZ56x1157zaWMgp/GjRv7a2Qead4+f/58asuCQZM329HkTt9KsqMU+5QrV87H5kQyGfCdoiKKfah0X7RokTej0+eSTCbN5PTnRDLpQ8p+PvroI5dIJDY/mBITQV6+fLkH0tylS5fUq8lDkqm43yHJFCJzJJkiFLGQTKSNJuyRI0d6hpFqcoYtItNI0MRNcQ6SiPBduXIltWXBQPAo4JkyZYpvS7N8s2bNrGTJkj4+J8vop0mxEf00EUH6aHJcCCnLeX+a2BFR+ouSzWQ5QZ/SgqA+mQpFZiHJFCJzJJkiFLFpLo9gmCKEkz6SVHWTVYyyh4WFPpQILMVFUWFPvXr1rFKlSl61zvibCCRN6vTdpC8oWdOZM2f6dhT4sBwRRVYRTYYyqlmzpksqg8kXBEmmQpFZSDKFyBxJpghF7CSTpnMKf2jCZtghfqYf5cGDB1NrpA9DDNEsznBFpUqVsuLFi7vMMl5m0aJFXWRpnqd/JYU6FPyUL1/e3n33XatQoYLVrl3blxM0p/Na9erVfVsKg+hLWhAkmQpFZiHJFCJzJJkiFLGTTISNzOPixYtd4Cj4QRJv3bqVWiN9KCpiH/SxpGCH/pSXL1/24D0o7KGqHbm8c+eOvxdSy1BF8+fP959Zzn5YZ9myZT7WJkKMCLO8IEgyFYrMQpIpROZIMkUoYieZCNukSZO8EIjsY0EHOi8MkXzS3E2WMq/I8jNCSoV53kwl02BeuHDBhyQi21pQwQRJpkKRWUgyhcgcSaYIRSybyxkuCMk8duyYS11SkGQqFJmFJFOIzJFkilDERjJpjqYpmqIcxpKkOTppSDIVisxCkilE5kgyRShiIZk0WTPDDzPoUGTDYOk0U0fFNnmDfpQIaRyRZCoUmYUkU4jMkWSKUOS8ZNL3kb6X1apV8yGBEE2C+cIRsigYXojxKxnHkkHO44gkU6HILCSZQmSOJFOEIuclk6IaJBPBZBihcePG+dBCTCc5fvz47wUDsTNmZrqDsecKkkyFIrOQZAqROZJMEYqcl0yavqnuZrggspdM/8hsO8y0w5SOeYOZdfbt21fgcSlzDUmmQpFZSDKFyBxJpghFbAp/aDZn4PX27dv7zDzM+BPXvpc/hCRTocgsJJlCZI4kU4QiNpIZQaYSyWQWnvPnzydKNCWZCkVmIckUInMkmSIUsZNMMppz5szxucOHDx/u1eRJQZKpUGQWkkwhMkeSKUIRO8kEBmHfsGGDbd++Pbb9L/NDkqlQZBaSTCEyR5IpQhE7yaQICMGcPXu2TZkyxWbOnOnzmO/evTu2VeURkkyFIrOQZAqROZJMEYpYFf7s2rXLPv74Yxs5cqT16dPHq82ZYrJbt242ePBgW7JkiV27di2t+cJzCUmmQpFZSDKFyBxJpghFbCSTAdabNGniQxhNnTrVtm7d6tXmNJkzvFHdunXt7bff9mUIaRyRZCoUmYUkU4jMkWSKUMRGMs+ePWslSpSw+fPne7aSvpjIJP9ev37dZsyYYS1atLB58+b563FEkqlQZBaSTCEyR5IpQhGrTCYV5e+//74NHDjQFi5caOvWrbOVK1f6LEANGzb0144ePWq3b99ObRUvJJkKRWYhyRQicySZIhSxkcybN2/a6tWrXTCZp7xfv37eD3PIkCG+bNCgQT7dZFwFEySZCkVmIckUInMkmSIUsZHMCKrIJ02a5DP/IGX00WQec/po3rhxI7VWPJFkKhSZhSRTiMyRZIpQxEYyqRi/dOmSN5EzCPuHH37oTeT8ISCaiCfzlyuTmbtIMhX3OySZQmSOJFOEIjaSycw+nTt3tnbt2tmYMWN87vJPP/3U/504caLVqVPHatWq5QO1q09mbiLJVNzvkGQKkTmSTBGK2EjmuXPnrHz58j4AO8U9Fy5c8MHXKQj68ssvbcSIEV74s3z5cq82jyOSTIUis5BkCpE5kkwRithI5vnz5+29997zAdgZF3Pz5s0+OPuOHTt8EHYGZaf6/PPPP4/tVJOSTIUis5BkCpE5kkwRithIJtnJadOmWcuWLa1169ZeUU6z+ahRo6xHjx7WqlUrrzRn7EzN+JObSDIV9zskmUJkjiRThCI2khlBcQ8z/tA/k4IfMpsfffRR7It+QJKpUGQWkkwhMkeSKUIRO8lkqCL6XzZr1sxq167txT7IJnOanz59OrVWPJFkKhSZhSRTiMyRZIpQxEYyr1696uNhMgg7/86ePdvFcvr06T6kEYLWoUMHF01Vl+cmkkzF/Q5JphCZI8kUoYhV4U/VqlVt2LBhns08fvy4nTlzxivLKfahX2bdunVtw4YNsR2UXZKpUGQWtcd+aj0W7M656Lt4r529cjP1lyBEbiPJFKGIjWQyhFGlSpVs5MiRtm3bNvviiy/sxIkTPi4mswAxxSSSxmDtmUgm01ey/wMHDvjg71SxMxYnYhs1x5MpRWzXrFljmzZtsiNHjvhyOHTokK1fv96PY9++fWlVuksyFYpkxiMtPrF9py6n/hKEyG0kmSIUsZFMxsQcMGCAZzOZ6Wfo0KFeADR+/HgfoL1KlSpedY4kFra6HHk8ePCgVa9e3ZgfHcF8++237bXXXrN69erZvHnzXBrPnj3rY3KWKlXKj4c+olS1UwFPc365cuXsjTfe8Ob7kydPFvh4JJkKRTJDkinihCRThCI2komoMesP4jdhwgSXwC5dulivXr28unzLli0+QHsmwxfR77NFixb2hz/8wQuKaJqvWbOmj8fJ+yC2ZDnpB0rR0cKFC110kVyq2xcsWODb00d07dq1vs7GjRv9uAuCJFOhSGZIMkWckGSKUMRGMiMYfJ3CH8bL5I+gQYMGLpxLly71fpuFJZoXnf0VK1bMZxdigHfG4eQ1BoAnY8l7U83OH+H+/ft9astBgwa5bLJ+7969fT80offt2/fbGYryg6zpuHHjrH79+h5FihTx7GdSkWQqHtaQZIo4IckUoYiNZNLPcvHixS5l9MtE9pA++mLSRN2tWzdfRjbzzp07qa0KBtnPPXv2uDyOHTvWKleubK+//ro3v9PvkmZw+lkinIgk86QjnfTRJINJZrVnz55eeMQx0J+T18iw8sdKn9H8oE8psxUxsDxRokQJ69SpU+rV5CHJVDysIckUcUKSKUIRG8lEHpE7ZA4xo6iGDCFCt3r1ap/xh76U27dv936Z6YAQzpkzx5vIDx8+7GNwlixZ0qWTZngElwIfpJYMKtNbcgwUI5HNnDhxojeZs/2kSZP8uKh8nzVrlmdZyb4WBDWXKxTJDEmmiBOSTBGK2EgmxTZkF8kgIpz0nyTDeO3aNW/OZspJRJN+kSxLB5rakUSymFStN2rUyIt92B+V5bwP/5JtbNu2rTVt2tSP49SpU7Zz506XTzKcFAORaUU8KfjhZySTSvSCIMlUKJIZkkwRJySZIhSxkUxEkv6K77zzjjVv3tyzh1R7ky2kqZzhjag6Z710m8upUKcf5quvvuoZzF/84hf2k5/8xIoWLeoV7UgtfSsp/oma6Pv06eNN7GRRmdqSJnwKg2i6X7Fihfe3RFxZxs8FQZKpUCQzJJkiTkgyRShiI5k0gS9fvtwmT57sGUUGX0f6kDpkjopumsrTFUygSIdMZRSILE3z/fv394wm78NQRvSXpH/lZ599ZhUrVvQ+mxQK0UzOcgIBZrij9u3bu7SuXLnSxbcgSDIVimSGJFPECUmmCEVsJJNxMrnxKcBhCKHGjRt75pIsJn8MSCf9J0NAf0sqxCnqQfpo8u7cubMPWUT/zIsXL9qQIUO+HUaJZnaWEzNnzvRtOC7+ZUaigk5zKclUKJIZkkwRJySZIhSx6pNZpkwZzwzSdF2tWjUfLoi+mAgdQwCRcQwJckhTOcLJTD5RX0+q0ekTypiZ9MnMOw4m/Tfpk0mhEEMqpZNZlWQqFMkMSaaIE5JMEYpYSSYz7MyfP9+bsWmSjgSOWXhYRrN1nJFkKhTJDEmmiBOSTBGK2EgmldzPPPOMD1PEQOlM58gwQYgmFeHREEJxRpKpUCQzJJkiTkgyRShiI5n0d1y2bJkPHUTWkqZxpnukCZsB0JGzRYsWpdaOJ5JMhSKZIckUcUKSKUIRG8kE+kIyADpV3Fu3bvUZc6g6p58m/SbpPxlnJJkKRTJDkinihCRThCJWkpl0JJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzh5BkKhTJDEmmiBOSTBEKSWYOIclUKJIZkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGZJMESckmSIUkswcQpKpUCQzJJkiTkgyRSgkmd/w9ddf282bN+3MmTMeZ8+etatXr9pXX31l58+ft9OnT9uFCxfsxo0b365/8eJFX/fcuXN27do1Xw5sx/bE5cuX7c6dO6lX7o0kU6FIZkgyRZyQZIpQSDK/AcFcu3atlS9f3sqVK2eVKlWyiRMn2o4dO6xevXpWsmRJ++CDD2zFihW+PlLZvn17e+ONN6x27do2depUXw6jRo2yd955xypWrGj9+/d3SS0okkyFIpkhyRRxQpIpQiHJ/IY9e/bYpEmTbPDgwbZs2TJr06aNde3a1UaPHm3VqlWzuXPnWqdOnWzMmDG2f/9+W7JkidWtW9eFkm1Y98iRI7Z+/Xpr27atde/e3aZMmWINGjSw7du3fy/T+WNIMhWKZIYkU8QJSaYIhSTzG44fP26bN2+2gwcP2q1bt6x3795Wo0YNz17yM9lIspXDhg2z6dOnu0R26dLFdu3aZatXr7Y+ffrYvHnzrG/fvi6cSCj76tixo82ePdtOnDiReqfvw3LWHThwoEeJEiVcZpOKJFPxsIYkU8QJSaYIhSQzD/S1pO8lmczixYvbe++955lNMpE0p5O5RCJpQp85c6adPHnSdu/ebePHj3fBrF+/vo0YMcL27t1rp06dssmTJ9ugQYP89/xARMeNG+fbEUWKFLEOHTqkXk0ekkzFwxqSTBEnJJkiFJLMFAgmhT1Lly61hg0bev/M1q1b29atW73PJpnOkSNHWosWLaxWrVq+HhnOAwcOuEzSR5PsJ83ux44d88KfOXPmePM3fTsLgprLFYpkhiRTxAlJpgiFJDMFzeT0q6TwB5kkEMeNGze6fK5bt877X7Zq1cr7Wi5YsMCry+nPSd/Ndu3aeTaSgqHDhw97JpN+mWQ+JZl/R5KpeFhDkinihCRThEKS+Q0MM/T5559bkyZNvs08rlmzxvr16+fFPpcuXfLmcfpe0neSfpoIJ1lMin169uzpv0evswzRpO8mv+/bty/1Tj+OJFOhSGZIMkWckGSKUEgyv4Hm7SFDhthjjz3mWUr6V9K3EuGrUqWKZyQbN27sWUkEcvny5T50EQLZuXNn34blZDvpz0m/SoqEaHKnIIim84IgyVQokhmSTBEnJJkiFJLMbyDTiGQihcgkVeUIJEU5NWvWtJYtW3oREL8z2DrN5M2bN/f16L9JRTjLiQEDBlijRo38NbaNKtYLgiRToUhmSDJFnJBkilBIMn8E5BChnD9/vu3cudNn8AGKhGhCp0l9w4YN3xtwHdHctm2bFwYxU9Dt27dTr9wbSaZCkcyQZIo4IckUoZBk3gP6a16/ft2nmEQuI/iZqnMi79SRLGddioXSmVISJJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzhwglmbfufG2jVh+yHgt251RUHrE+3wewQpH0kGSKOCHJFKGQZOYQoSTzxq07VvRvy/J92CkUigcfkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGb9o8bGtO3DWTly8nlNx6fqt1P8aQnyHJFOEQpKZQ0gyFYpkxk+bzrYn2s6337RfmFPR+eNdqf81hPgOSaYIhSQzh5BkKhSKBxn/M21b6n8NIb5DkilCIcnMISSZCoXiQYYkU+SHJFOEQpKZQ0gyFQrFgwxJpsgPSaYIhSQzh5BkKhSKBxmSTJEfkkwRCklmDiHJVCgUDzIkmSI/JJkiFJLMHEKSqVAoHmRIMkV+SDJFKCSZ94G9e/fa5MmTbdiwYbZw4UI7efJk6pUfR5KpUCgeZEgyRX5IMkUoJJmBOX/+vE2cONGqVatmjRo1sqZNm9q6devs5s2bqTV+GEmmQqF4kPH2sPW28PMTORlHzl1L/Y8mHjSSTBEKSWZgVq1aZV26dLEePXrY9evXrWXLlvbRRx/Zl19+mVrjO7766iu7dOmSnTp1yqNBgwbWpk2bb38vbBw9fsKebzvDflpvnP2s/nhFwOCc6ryGj5/WH2f/p+7YfF9TZB5xvG/7f7wp3//fci1oqcpveZyjW7duVq9evdSTSojCI8kMzOjRo6179+62fPlyl0gEk2Wffvppao3v+Pzzz/2P+eWXX/b4+c9/bo888si3vxc2ir30kv37L5+w//tfT9uvnnlOETD+4/Hf2L89+mS+rykKH//vyWftZ//3cXvst3/I93VFZvHvjz1p//HYb/J9LVfjDy8Uzff/t1yK559/3n7729/aS9/8n5vf63GNxx57zCpWrJh6UglReCSZgRk0aJD17t3bBfLWrVu2ePFiGzx4sC1btiy1xndcvHjRdu/e7UJKzJ8/3xYsWPDt74WNRYsWWbFixTyjmt/risJH3bp1rXLlyvm+pih89O/f35555hmbMWNGvq8rMot3333Xateune9risIHCYUXX3zR/+/O7/W4Bs+QTZs2pZ5UQhQeSWZghgwZYv369XN5jCSTByh/tA8K+n+WLl3aZs2alVoiQkHmmb6zIiwrVqywokWLFrhITqRH69atrVOnTqnfRCg+/vhjK1mypF29ejW1RAiRF0lmYCZNmuSdpteuXevN5VOnTrW+ffv6t8MHhSTz/iHJvD9IMu8vksz7gyRTiB9HkhmYNWvWuGQyfBEdqDt27GgDBw60rVu3pta4/yCZ9KfhP0ARFrpCtG3bNvWbCMXq1avttdde878ZER7+HwoxcoX4PnRvKl++vCRTiB9AkhmYCxcu2IABA+zVV1+15s2b2+9+9zsf0ujy5cupNe4/NNOPGjXKduzYkVoiQrF06VLJ+33gwIED/mXsQf6dPEzMmzfPu+6IsOzcudOGDx9eoCHqhHgYkWQG5vbt2z4YO83kPDRpPj906JDduXMntcb95+uvv7Zjx47ZlStXUktEKM6dO2enT59O/SZCce3aNTty5Ij//YjwnDlzxs6ePZv6TYSC/2P5v/ZB/v8uRJyQZN4HyCQiI1SYMzg7vwshhBBCPExIMoUQQgghRHAkmQmDrCnZU5rH6B9648aN1CsiU2hupDCF5nIy1YweQNcEUThoYmSs2Khogt9172YO9yTnlHMInFd+pnKfe5fzq3s3PThXzODGuYu6HvA7fTGjLjScY/XNFOL7SDITBgUUzDlbqlQpa9KkiS1ZsiT1iigsPGDoK1ilShUfZodzW6NGDduyZYuqSgsJ4sODulWrVjZu3Dg/xzy8mcqO8/vBBx94kZVIH6aqpdiQv39AgPj5ueee83PL8GafffaZJD4NOFcLFy70SvJy5cpZpUqVbM6cObZ+/Xp77733rHjx4j6FcH4zuwnxMCPJTBDHjx/3aSyRoZkzZ/qYjiNGjFChSoaQndi3b581a9bMh6difvqNGzd65kKFKulDtv3EiRPWrl07e+WVV3w0Bub2nzBhgr3//vsuSIwty/1LtkgZt4LDlx6kvUKFCvbOO+/4uVu3bp0PX8Q55d5luCgyxipWKTjbtm3z+5NKcs4h/xf06dPHZ3PjixGV+23atPH/f8lsCiH+jiQzQTANGA9mHiiIJaLJDEQbNmxIrSEKA5mh2bNnW/Xq1f3hwvBQzOBEk6NIH84bkjlmzBgrW7asT8W6fft2a9Cggc/zf/ToUc8SMXg4IzWocK7gcK8ydiPnsmrVqi6SY8eOtcaNG/u9y5dO7l0NFZUeX3zxhbdc8C/ntEOHDlazZk0fpg7R5Iso9y6BkAoh/o4kM0HwbbpFixbeRM7QGsgl/+lNmzYttYYoDGQsyWLw4Gb+Z5rHyLgdPHhQfbAKAdlfMm4EzbhDhw71ZkeEk+ZG7l0mNWAIMISIbKYoGJwrziv3a61atVyIEMumTZtanTp1PFi+a9cufUkqBNy7ZIH5+6eJHHnnXmX5smXLbOTIkS75Qoi/I8lMEPznxpSHfOPmYcMsQ0gmmTdReDiXURaDBzgPlbp16/oYqOqKkBlk15BMpmGlvyDdEpAfZJMsPM2PnHORHpw3ZJLm8s2bN9vhw4f9PiZj/NJLL3lmnj6wouBwLskUz58/379svvnmm9a5c2cfqg6Z54sS9/KMGTNSWwghJJkJgkIJ+gXxnx2DW9NvkP/0+HYtCg8PELJrUUUuDxW6JfTs2dObdkXhiSSTrDv9CJlBhSILpLNfv34+qYEkM30iyQTuXTLu3Ltk38lm8uUT8RQFh3OIpDOb25QpUzzT3r17dy+iIpPJ/Pv0L54+fXpqCyGEJDNB8J8dnftpHqNJh+kP6ZxO30xReMhWdu3a1QsoOK/Lly+3atWqeYGKMpmZEUkm4k6TLn0xGSaKe5c54mmCVHN5+kSSifz06NHDv4CSheP/iBdeeMGzbbp3Cw5fNPkixP3Kl8v9+/d7t6T+/fu7cPIFNCpY0/SdQnyHJDNBUEzBt2iG1+A/PB7adFDnAS4KD0PtkKGgGhrZbN26tffPpF+bBCgzIsnk3qX7AeeVCt4PP/zQGjVqpKkmC0leyUSEEHbuXf4/oOqcrjQawqjgMDUwsv6b3/zGh9finPJlnuZyzvOsWbM8Q4xkIqBCiL8jyUwQVOHu2LHDqx4pAOI/PZrKJUKZQZaCpkWqnSn6YWxHMkGqes4c+gvTl5imSB7OjPFKMRCFFTzIySCJ9GGYIobbool8z549nn1DhuizTbaYQfBFweGLOgL51ltv+f2JaA4bNsy/EPF/Al+KOL+0GknehfgOSWbCQHwYp42BgxFODVUi4gJCSVM5fds00L2IA3wBZYxXxJ3htnTPCvF9JJkJhIc12cuoUEWIuMC9SyZI966IA9yjdEng/1u+4OueFeL7SDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQaUCfQfoLhpxOkn5c7DdX+nNxHEnsW8ZnCjUcUnTNxHd/EzofQoi7kWQKkQYMYE3lczRfcQgodGEszmhWlmxC8QIjElDIkDRp4DwzHufd143PSaRz7jlH3AsF3Yb17rUur3Ns6RxHtuF+OXnypA/yzsgAQgiRF0mmEHlgCj5m9GE8wSpVqvgg1kzTybBQSCDjDzK2I/MX5x0nk3UYKy+qjGZKzwkTJvig+AwynvcBfLdwMF83AzsvWrTIZxSCu4WDoVEYloqBtKNx+qJo3LixD8C/atUqn040Ew4cOODjKzKlI7PtMGh33mAebIZsyY9jx47552WsQGTux+BcMlQR03IyJzxzlbN/zl1eOAeMUcqYhHfPpMKUk/nNwc3MNps2bbLBgwf7eJCcO5YxYwtjGTKwNpLIubpw4YJfKwYpZz56xuls3ry5tWzZ0saMGePHBlwjlrEtx4hUcZ54D4au4fii7bh3GGSe3xnAm2Pks/EeTJBQr149nzGKf999910/Jgah5zWuJ8fJ8d4NU0Eyu8wPwb3CtsyWxPFxLzNGJueWsUjHjh3rM4AxsUDec4Yss28+B+cE4eZzd+zY8XvXkeW8Hg3XA3w5Yr+Mx7t7925fdjesy7XiyxnHP378eJ82lCkuGXOW98r79yCESA6STCHygHQghQ0bNrRXXnnFpY4HJMsQKCSkTJkyLhFDhgzx6fp4EPPgLVGihD/YkRpEFGFAQhjAmTFLgdcZ2JnXEUvmP0ZK2CeD6DPg+6BBg3yQZx7ezCrEgx3p4EH+L//yL/a73/3OihQp8m0888wz9s///M9+nPnJSUHhs3/yySf+mRFmxGPatGnfC84D8zfnB0LD8TNoNQLxQyBpzOSDLCN4iCbnj3n3kZ+8wsFn53O/+eabfj6Rk+h8MAPT3/72N39ffkdICaQJqULcEF+m/xs3bpyv+6c//cmPj3PLlwmkEQni2v71r3+1119/3dq3b+/XB6lduXKlyxNC/PLLL/vc6hw/n4/jevvtt326UUSS68n1ZkYo5LFLly5+zng9klTO7UsvvWS//vWv/d//+q//8utZvHhx3xeD0G/bts0/I/cJ++ReIP7yl79Y6dKlv/2d4P7gMwPnjWPlnuJe4LwiynzZ4b0ROj7n3YOxMwh+5cqV/X35khSNs1uuXDn/UsH55PzypYrXmTmIfSL/fCnh2rA9UsoxcV4QSQSUbRBfzgXLuYbRrE58YeMz8Rk49iiEEMlBkilEHnj48oBmqkOEkoczwsIUh2Sffv/739uTTz5pFSpUsPLly3umiinlunXrZs8//7w/nBEKHsRkpsgG/va3v/UHLSByZBzr169vb7zxhksPMluqVCkPRIZliCmyQoaUrBtyynGxLx7+vH8UCCrT3ZHBYr3CQPM4XQCQgapVq/p7k8XNG0gg0vJDGSs+N+eBmXqQtx+C5tXJkyf7+yCZvDeyzvlEciPRZDkCQqaP4P2RP84f69euXduljPNC9pT9IlbICyKJ/CCJiBrZXjKH3bt39/POlwiyasguGTpEimV8eeA8EIgVssSxclyvvvqqf8Yow8zPCGne6UXJRHMPMN0g2csIMrecF+4Xjrls2bJ+fyCNCCkCyKw8ZJCRM0AIEVHEjODee/HFF/1nBJ37hpmn8vYP5rNwrHPnznX5JmsZnWve4/jx4/65kFgEEFFE+IoVK+biSAaY4+fLAueP881xIORsB9wDkUAj/dz3fAbOHwJZvXp1v5c5P3zh4npFgs015l/OG9lfPh9fXMjik3HVTERCJAtJphB54CHHvM+9evXy5lP+JdMTNYPyAOVBSpYPaeBBywP/8ccft3/4h3/wbCYPfh7SCBcPcR7CPEABOUEaya717t3bsz/sBxEgaM5EpsiIkSVCBBAYsqVIJA9ytkOiokBcOCYybzTL393kXBBoAkdw+HzsDwn685//7MJLlo0s3x//+EfvJoA4IFp8DoQQQSMQaTKgCEiUASNYh3XZJmomR/SQc14Hmkx5f+R63rx5LuMIIJJDtwWkiXWQdjK+SD9ihMxwzJxjhIcvBFyrF154wR599FGXSqQTkSLzyeckY8j1Y/+cK8Sca877kO3k/YsWLfqtdJNZJvsXSSafn+Pj2DnfUSYRfkgyuYY1atTwbB5ZVKZ9Ra5oUuce4/0RWtYh+wpI2Guvvebnj+A+i7K9yCLncPr06f4ZkEuOi9c4Bj4nmVAkHnHkSw1yy88s44sCn4EvU//6r//qGVzOGQIYSSLHwt8AX3w439EXBz4L14V7nGNGetkvks814h5BOlmfY0F6Obf/+I//aE899ZRVrFjRp2JEOJ999lmXZTK6bBNlNYUQyUCSKUQeIslEEqK+ckgAD0mEAylAXJBEhBKBIVPDA/y555779sFKkyWydrdk0txIsyTNhFETfCSZ/I5kIpj03yOThHAgLUgJ4odY8JDOG4gZD2xeQ5LYf7pwXIgJoooc8/noc8hx0NSMXCEdiBxSw+fiuMmilixZ0qWErNQvf/lLF27EhGW8RraO84HUcR4Qa84tohQJGv8i0mRQ2SefA0lDSJEZBI/PT6YR0UY2kRuuDVlMMnWILU29vA+iz9z9nAsydBw725Nh/tWvfuXvzzqIGNeP7DRCjVSRsUZ66OeKdCGZSG4kmUgowsf6fE7EKuKHJJPzy+fmWiHt7AuBRLCQeX7merNO1H+XLCQCyPkg/vM//9Mee+wx/xnp/+lPf+qyzPVAeMkwcq75DFwbhJbrxz55H+45fmYZ9x3XkHudpm62R9C5vzkOvlDxuZBWPj9fAMgSAxKI0HINOP98GeK9EHmyynQd4F+uBX9PiDBiz3Uj887++dvh/HH83Gtcb7bP289ZCBF/JJlC5CGSTB6sNGfSTEyzKg9vsjZIEFkYHq6ICZLJ+ggMAsDDGblAFBHGuyUTIUCCeCgjLAgOD3yyP2R8eA/2yfr8TAYQ+WI95I/j4LiQJgQIWUJwETrejywVGSqkDVlBhvgseQuP8gMh4HMiHGS02D9iQIYLgaW5mX6EvCfHThEHxx9JNoEkc27IeiEZ0XLWIRuMVJLFQ9hZj2PnPcicISBIIcKFJCFMCCLbcG7oIsA2nFf2TzcCrgUihhyR3UQyadLluBBkPgfnEBki88b6yBLSidjQvxKx5hqxnC8RSCxCzz7JUiOyd0smx8Q15jyQ8SyIZCJPSC2CxzXhGuYNlpFpRZijZmmyjOyf80cg0pwbfqb5GknjPHNPIbFRP9G8EklmkOD6IZDR79yDiCKSx3XlGLgWnEe+HHEvRM3r7JMvCVHWGWje5osR+yI7zd8D9ycCzv1KVpPPzPmgCIkvKvxtIJJsx98VoskXNs4ty8kWCyGShSRTiDxEkomUIAo8cHlAkmmieRcZQF4Qr5/97GcuFAgKy+gXST9OBIVMEkJ0t2TSrIkEIjn0FURqkCuaQWlqRiKQBJrG82b6eGjzIH7mmWdcBDkeModkCsm40QyJWEQiwPsgjpEw8POPQZMxzcMcAzJFMzyiSRMm8oO0UWSEqCEYUZNuXhCwH+uTyXvQpI5kIFw04ZKRQzDZhvdBnKJ+nwggx826rMfxsB7niz59fHbEiGtCpo59IzSIJRloMoacM64D74Go0i+T5nQymrwPmVnOLSLFZ+PckskkG0d/Tq7L3ZIZXROkluwgwhaRn2QijYgh78lxIMt8Bv7NG9w7ZBq5f/hSwLGTtYzg+JAyQOz47Egpkglcc+Sba4Ww8bkoTqPZnS8HXEvuOT53dD9wrugGwXshlYgg9wtfVpBAzin3ApIZyS8ZTZaxL84FmU2+6HB92DYv3Cfcy+yba4vAc/65x7mWnGv6ovLlg/cUQiQLSaYQeYgkEzFBeniok+1B6nig8xAm24aM/NM//ZPLCVkcMoks5+GOkCCeZPbulkygTxsyEEkVgkoRC5LBuggV75m3bxrSgfhSiUw2k/UoAmJb3vvpp5/2BzzNm8C2UbN2lFUqCDzoETEkhOPnPCBI7JfPzOs/1GfuXpKZF4STLCTZV84Fv3OOEJVINhAYjoNzimyRyeO8cg0QVLonIH4IFEKE9JE5RapYB9GkQIgMJRlBmsCROzJ3NFvTRIsQcn7IGiL8dDngvfgMSCYZNwQrb5/MvJLJNScjSvaOLw/5SSaFPNw7LONLBOcXKeO4CcST7CzLkXzEj+wogkihT5QRJgPM8fMz2VmOEwGPCn8iyUTaEGOynBQL8Z7sn2B7mvjJLAPbc+9xTRFKrglfphBJZJBlXFOWky3lPiITzJcXMszcyxQYsV/OKdcz77XniwICSUacTD/N5ZxHzivHwDZcV74gsa4QIllIMoXIQySZyCXZJUQkyljx0Eb0yASR9UPykAIyc4gMD32aIHlwIy30J4wkk4c/MhAJASAFbMs+aConq4YY8VDmOPJChpJ1aNYkC0RWiswcTc1k9ZAWhCrKUCENSAGZPcSInwsCUsHnRhTYjs+KZCESCAJZNoQwPwoqmUgaGS6kCaEiY4uIsW+adO/uU8p5QgA5TzQTI3xsT9YP+UHmEHv2w/lF9MgUc07YL0MUcVw0zyNniB3Xhv0SiBJShRzS/zMSIDKUZOz4IvFDmUyyydwXSCRdCDj/yFdeyeRaRE3HXEOOgWPi2JF4tiPYDpnnywHbkClEzPgSQTzyyCPe5xVhi5bxvuyX68tn4R7iHCJvZDrJUiLv7JfgCwNfTPgcQJcArkPUJ5OiMiSTY0Cc2S/iyDVlWfRlg+w+P5Nx5nxFY4by98L6nHeuBZ+De4cvB9yzyCnZYa4755djJUPOPV/QL0JCiPggyRQiD2SjyODRfMj4hmS5EJJf/OIXniFCXigWIdOEXCCRiCUPezKQCBjNt0gm2Udki4wbksID/u4mQR7uSAzZNYSC7BX7RhjygtCQ+SSzhdjQH5TqaZro+R2ZQAQieeCBjTjRZMyDPCrauBdIKeKKwPJ52B7BJpP7k5/8xH/ms+YH4kSTMELxY+Nk8vlYhwIQZB1p4/g4D8ggUhLBeUCiyDCSleMaIIVsE2XYEM5oGVKD4CCMXAd+5lxw7skU/9u//ZtfDzJnSBISxfEg6OybY6JqHdFGbDk+rilfEjjPyGd0bbg/kD4yg3xZ4FoiZhS6IKuRZCJbnA8ylgRfYpBKpJnjpzKb5nnOO19UuAZ8Hu5F7i/2S9CvkmZn7sloGWKIoHH8HBcCzjWjGZpjIntLlpf9EnQxyCuZ3Oc///nPv60uZzskk/MYnU++QCGPXAe+QCGKvB/3dJSZRTY5TxSOkRlFRDl39ClGTjnHSCiZX7LKnB9e57qSnefcs44QIllIMoXIAw92sixkkRhAnYHHyRwiakgehSBkG2l6JFOELFH8gCQgekholJnk4Uq2howTVeBsT2EEwkHmhwwQ/ezIRPIgJ3vK72Tg2D8P4qgwhWwikoDoEPTBpEqabGq0jEwjmVYyesgBYyHStMpn4OeCQAYVAUIAEDO2R0SQS0SEptL8+mMCcsi5Ihv2Q5JJJhJR4jxyrsj8kblEMsiocX4QwwjECXHj/HCuEdmISGjzCjSfky8JZC05x4gecoNw8r50QyCiIhS+MPAlgswjwbFzDpEozgP3AzKJHCK5fC7OLeKKeCJtdFPgOvNefA66M7CP6Lj4DPRn5LORaeQ8kc1EenkfvoxwnXmNLy7IYyR4kdACGULuOe4/jp97kr7BNGtzr7I+ld4INO9FVhqBY59cS4LrR+aQ88j6nCuOl+uM5HMPcu9yHyDq3Iu8B/cf9zPXnnNAdpQsKF0TuH7R/cW1o5sBXwDYJ/ci5497mfucY0F+kVYknowoy8hu8iWJzy6ESA6STCHyQAYJWSBzyMOf7ArZIbJLCAFCgUDwQEZeKGpAMMjkRA/cqJkckAseomQ2EVHW40HN9gRCSzaKhz4Pbx7w7B9BQnR5aJO5iiqkyVoR7I9+d/wbLeN1HvB5JS1TEBGysYgZ54Fz8kOQGUQikSWyXvmBuCEWfE4yX9H+2TdN85wbZCaC1zmHnP+7xRWJQWDydi0ga4hMcS64jlwHMm7IFceGNCJ0XAuyblw7zj1SxnVD1hAjstOR4HFNOc9cb7YHJJBjJWuJKLMu9wr75dohr+wjgtdZj8wpQkZGlM+MQEfNxHxurh37zg8ynpw7rnt0//BenMvouNg/9wvvxb/cQ/wcwfVDrnkfzi1fkDg/wLFE3SvIQHIeEVvua/4e8sK69EWNMqJ54fNxzji3HBfvwd8A0so9QnCPIJuIOMfHtaC7wN3dRIQQ8UaSKURgeHj/GFFTNkL7QyAcPHDvta8HAdKDOIQ4Fj57Xom8H3CckSDyL5HJsXOdEN1cuBYPCq45osk9mLcfcWHIez0i8lsmhEgekkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMoUQQgghRHAkmUIIIYQQIjiSTCGEEEIIERxJphBCCCGECI4kUwghhBBCBEeSKYQQQgghgiPJFEIIIYQQwZFkCiGEEEKI4EgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRGLP/H2S5DyniM30hAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F%E8%A1%A8%E7%A4%BA.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWgAAAByCAYAAAB+30ucAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADDmSURBVHhe7d2HlyZF1Qbw738SEyYUwQyKCRXMGFCMoKKomLMYEbOoKEbELIqYMQdMmHPOOft+59eeZ71b9js7C7NMz859zqnT1dWVurr7qVu3blX/36rRaDQai0QTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3Sj0WgsFE3QjUajsVA0QTcajcZC0QTdaDQaC0UTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3SjsWD8+9//nlzFvs4ravqN4s0haWseQc7r8V//+tfkh5omx2DuvKbdatS6BDXsQJZ9edEE3WgsHCETRDISTZBwx3/+85+TH/aVbh1qmuQR1Lzm/I41HJyP9Rj9Y5qtRMoP6vmBLPfyogm60dgBGAls7jxHBF3Pa7zNQppKqCO5VqSM0QVJO3ctWBd+eVHLXEfQS0YTdKOxYKwjrUo84zk3kk/i7Q/ksb/kOsbhTx5z5zAXtlVI3nNlHojythpN0I3GDsI6YhEWIoIQUnWXBWPaeh5/DasQlvqMcSLlV1cl/61EbReoZS4dTdCNxg5GJZqRdHJewzYLZBmSHyGsEl5FSDakmPSOcUH1HygoY1/1WHcvS0ATdKOxcIRk5ogmmAuPv55vFuKmzKDWIe63v/3t6pe//OXkfvOb3+xVRuL84x//mI5/+MMfVr/4xS9Wv/71ryf3t7/9bU8c7kCg5j+WsS58SWiCbjQWjjkiqef1etzcRGHON4sxDX8IWv7I+eMf//jqnHPOWZ1xxhmrs846a/XjH/94It7EjyQu/C1vecvqWc961uoVr3jF6p3vfOfqpz/96Z56xh0IjB1LcCDL3Co0QTcaCwaJ81e/+tXqL3/5yx4yGUklRJPwv//976uf/OQnE4FWKXV/UOOTgH/+859P+f31r3+dyE4YKfhjH/vY6nGPe9zqqKOOWt3ylrdcffazn1398Y9/3FOmeOrziU98YvWQhzxkddvb3nb1+Mc/fnXeeedNdYx0Dftbx81AfdX797///XRey0gdD0S5W4Um6EZjgUCCf/7zn1fvfe97VxdffPEkbQqDOWKp/j/96U9TGqRIcq3S9P5CWh0EifeLX/ziRHbySl0Q7Pnnn7+65z3vubr97W+/+vCHP7wXGbr+s5/9bEr/wAc+cCLpz33uc1N44lzWum0G6v6FL3xhqruOIvWumAtbCpqgG41twhw5OUcYiPDCCy+cVAKOo353I4RUH/OYx0zkKW0IEdaVOxf2u9/9bvWpT31qdcopp6wuueSSSSLNNfjhD3+4ev3rX786+eSTV3e7291Wr3nNayapH8RB1u973/tW73jHO1b3uc99Vg9+8IMnyTmk6Bi/+PxjPdahpq2o+Ti+7nWvWz396U9fffvb394Tf13apaEJutFYCBAKR0Xw6U9/enWve91rImcSKIIVTqWAdL/5zW9OE3MkZaT4gQ98YJKypUfQ4r///e9fPe1pT1u98pWv3CPVjkiZ3AgqjHe9612rRz3qUauLLrpoIn35htikUU/k+7znPW910kknrV74whdOUrtryPx73/veRODnnnvuJD0jyqhdQpIpPy55j/4a9o1vfGMaXWgP9+b8bW972+qtb33rJC0H4murs88+e/Wwhz1s9a1vfWuPukjZ2mrJaIJuNLYRlXRyvPTSSyfCQ2gIBYmQZL/0pS+t3v72t0+ESbJGRh/96Ecnkn7Sk540kTm1SMgHgZu4e/SjHz0RrHxSBqTsuTD4yEc+snrqU5+6evKTnzzlhZzrdUedhbwR+SMf+chJv4yUgaT8wQ9+cPWZz3xmIu5TTz116ixgJOf4g4THH6Qt5PvSl750aicd1Ic+9KEp7EUvetHqJS95yUTKqS9Cdu1+97vf6rnPfe7q+9///p7yUo+logm60dgGhIBCEgFpkLXDiSeeOJEeVQdQJSDgT37yk5Okeu9733v18pe/fPWDH/xgkkhPOOGE1Qte8IKJFCFkTLI2icfJO+FxFTWctPz85z9/9fCHP3wiN+mCmpZFhk7i85///ETm973vfSdyZFJHknUP/E984hOnjuKCCy6Y0oYg6YVdV17M7+KnmuESbgThXhFsyPi0005bnX766ZNeWzqk/dCHPnS6XidIpdFet7jFLSbLE9J97iF1WSKaoBuNbULII+BHNKRhBIxQQ97UBogFUdHlIkMSNSmRhcXxxx8/hZG45VPTIS3Xv/rVr07SJNQ4MNbFZB+9M+k5UnnAr1wEiKB1GlQMpNPb3e52qy9/+curr3zlKxNJOopngvCZz3zm6mtf+9qecuXjfqRl/SEfzuSmI8mbCoWfHty9qct3v/vdyU9SJrWzCFEfTielLHk4D/nqYL7+9a+vjjjiiEndUvXgS0YTdKOxjUAelSgQHosIZIZgQozisM5AZkzVSI8kRlIlVcQd7nCH1Wtf+9qJwGp+/O95z3sm4qQOiJ46DubOlX//+99/9epXv3o6R3DyShykiyTVV6eC8BDfkUceOZEjSZn0rD7f+c53Vne84x0ndYs6Q8rTuSBiemzqG2ni5/hZgJhoRPapC5UL/bqRBl27tiIlU/886EEPmjqmtEPKMnlp4pQumkpkJ6AJutHYBlSyC5AnAkE61Bkj0SI30uLd7373aUIMSSJGUiNJEhE7N6lYVRkIkD772GOPnaRIYTVvSFzhSF8ngciQf+pa49ADm6RDqKwj1E3517jGNSZJ2uQdkjQKQLJUMG9+85snIq2InTLy5BAvl/MaThUSGA0gY/cdCxdlPuIRj1g94QlPmNJQ/2RCkJMe6d/5znee1B3uAVxbKpqgG41tQEijwlCe+oIESI+bOHHIlxrDZBu9L6IkNZJ0X/ziF09ESCUwSo8IlD750EMP/R/9az1yrpFUkTkJlfSbOAECZ3JH/WGiEhGS7uV99atffZK+5SGvH/3oR6tnPOMZk24aoaecIOdx6QzmrlWn43jsYx+7OvPMM6dz6UjwOjj3SiXC/hkpJ40OTbtS9yBxoxHhS0YTdKOxTQhxBMzRLPYgBZLucj1xELSJNhYRJEjhwkiRVA1veMMbJuLKYpKA9Gni8ZBDDlm98Y1vnKTLoBI5RyfMKuJmN7vZpONNPRLHpB7VBnWKjoGqxQSheMjvrne966SSQNocUjbRSJ+tbIRdSbhCWK7ty8lXO5DgpTFieNOb3jRJ7+pNUkbA0bmDeFQu7LXVnZoj+S0VTdCNxjYBYXABG2FLpkl3MBIHNcLLXvayaSiPdIHkSvJG0EiJxAs1X6TEFO+qV73qNAEZXS7UeMJYi5hkO+yww1avetWrJqkzcVynslAeIoyj2kC8pFV+JK+uJhpdp/vmEKqJQ6h5jvfp3PWEJ07OXdMG8jI6CNy7UYTOw/1WdUrSAvtyOnsSN9Q2WBqaoBuNhYDkfPOb33yycQ5pjESFMOuSZWGkR2HVaqESkmukXARN1UAVUVHjknrpn1k7kHiDWp5y1IOjxki5HH/K5yfBJi6X60Hi7i/kk3JBHvzulYsOfoQwKiQdoXa+LGVfkWiCbjS2CcghDiyDtuEQSbNeqy6o5zV8DoiLSgRB3+Me95jUIElf0/IzYaN/vvGNbzwtQhmxLt14HozXthI1b/eY87nyajiVkI6Qjn3paIJuNLYJlVA41hu3vvWtJ3WF85BOjTuHdeGB6/Sx17rWtVZ3uctdpsUrY345pyawmAOBUZmsi5ew8Ryqf4Rr9b5gTL8ZjPlsJo9ct2jG/TnCvtJtJ5qgG41tBoIw/DfBxsbZ/sqVcKofqr9io3gm9m54wxtOulc2xSOSlk73Bje4wdRRvPvd755IkKuo5cRfw2DuPMc5gh7L2BekqXkENXyMEz/VBoJmpgc1ztLQBN1obDOQE9M1izmoF0xyjcQSAuNfRyjjtUqEiBcp6QAsIqmoaUjabJnVY47IRyTtWHbO59yIdeH7g+ThntNWVQ9dy7BgxiiBdQkkfIlogm40tgkhDQ6ZWMxRrQvmIG6IN/4QUVwwEjTTuSpB51pNw1Tu8MMPnwiaKVvFmD+/skOIQS23QlwuyHnizqVZB3HHcuqkIdR8a7znPOc50/2xaFk6mqAbjW1CJQ5Hi1SoFpjSwUh8iWvlnP0uLBaxVLrmEX+QMMR7netcZy8ddEXi2YnOsnCTlXTQIUHHkRDBOfUMszppOfWri2HA6kYWIq5bXMP0L+Sc/Me8NwJzP7v+WYzCFrzmxaUjqGE5t+Oee3z2s5+9J3ypaIJuNLYRCCLkZDEHKTfEUcmjxmNpYRN68SxAEZ44NQ04R6DM7K5ylatMNsBsiINKjI7Ik6WHelhWnutxc2D/bOc6+3ZYSGO1oxWNScvUjuWIFX4m5thXKyckvlHe64DomQHSJ1ugwrQukFcIGsYy7IB3q1vdqgm60WjMI8TgGCJ7ylOeMulGHUfiqPEs5ba0mz2vpc7CE2eEMNImqfnKV77y1AnYmyPXRsnTghN7cJhQ1AnkesV4brEMaV5dbnOb26yud73rTaaCViyqG2nZ4hbLsO3JbMUjaRpB555gzHcjZJc+bWAxjE4okE/aBHKe/KU55phjpg5j6WiCbuxo7M9HvSRUwggssTZRSDc6SoQ1rrTiklatnBuvQz1HlCTtq13tahP5Uw0EiZc8rFC0+RJLDuZ+pN+RROMqqFps8GTFIOmbTbeVhInnfqwytMkTzOU31ybrIC6iZ9Ps3uif16GWgchtNkUXrwNaOg5qgp572DWMdJCXwjEYz7cSKX8zZYiT+JDzhNVrwRg2F2cpULeN2sA1rt7v6EYJL+FLx1hnsHTZKj4bzltyPd5L/CRWiyzsUEe1kPAav7YrHS3TPSoOpEQfXFHbmLRtL42jjz562mcjO8VBjkHKEM76A2FSv9jn4rjjjpsIPqDS0JnYGjTPFaTlan2DGp54gTag3iANk97nJP0gaXUS7LzVzapN26TOlbskHHQEPT5ISNhceEWNN147EEgZjl6Ueh43Yu7aXBiM59sF9cj9OdZ7DZzH5aOpccb4wZjvTkLuNyCF0o/azIc0OnfP7pFNMxtee3bYGAkpklaZz9nEP0j+SInK4drXvva0VzMpUnhtr8RFYtQPITG6ZOE1TlwNI5WT6qkz7HCnoyHdkshdp4MmPdOFO0/ZSZ8wxzkkTvzu2W52RhE2atIBaAO22ykjceOQOv07U0M77lGTJN5ScVASdI618XM+F56XZXxBqn+rMVePufISvj9xg5zPxb0iUesxuo2uB/wjmTjP86r+nQT1rQ452jDpTne6016LVbgaH8n4hZVJLn8oQUr2N0bYdf+MwN9KbFFKfZL9oDdyCNyqRvt22C0ucC2I31G9kSKJWVrkqX7+CqNupFvStQ6ENJ904zPjr24dXEP4yrCVKemdjt3/Dm2BapQw5sXZxImeXOfD1jw73anHUnHQqjg8kLkXwMvEJIjkwV8/7uqP22rUvOfKqGGOY32qG1HD40/67UIte/TnfKxjveY491yc0zsakrMi2EgHuVTU+4lDZCbSkO14zxzYltREHmsJ+0IjKxYXyCc66QAJIVmrFC3QqH9UgfjrOZhAU48sO69wrm4BNYgNmNQLQZv808GwBiHhCkOe6lktNzwzaZE2adYxzjln0pLzzbqXpGUrThVEX68NTELaO8Q9zum5dRKkbJI9/Xj9o0q9l6XhoNdB5yUHD8kwUm9r8xgfNrieuF4CQyHHDAW3EuoQp4PwwqajSB3iF4c/yHmuSRc3xk0+2w11jUt9HNU3LvcPNV7uMwsQHLncq7azAIP05qMOSUu3E5B2iR9Ig4bf/vqBvNwrJK57JCXadJ4OGvka4tNZU2WYEKx5kmbtj0yapRqpJDdCmHZ1JJkjV2oEkmeNL07qBfKlP0fSeXb8VupZEKJuTPBI8ikjz0850vozuO+SH3lyzumsXWPvTHeetGecccY0IqCDZq+tjghYXaJjV1bqbaUm9Y7VlNpDW+0EHJQEnQeTh+OBeqG8yB48yYChf17WPHQP0QN2zYvDjzy2GjoAujmkQqJxpLurUJ/UH6rfR0py9OJH0jAikAaSlguZbTfSzuD+dY7uwYflgxrbOXX3jDwX8R3FJU1loQM/oiJRjZNfS0Z9vrnXtBFrBxIvSRBJB547AcOKQ3/2ZjKXeNqh5pm2JlEzbyNZpgMLxK11iB/4mbGZ8KM2Ub8RiU9PbXWi9zD5eD7S+UchNQTLEJN5FerInln6OH9C4fgRuok8ZoG+R9+MengXfMPUMNqASsgIIvru1AvEV46FOszxSNCEs4RDjkvEQa3iqA+KNKw3Niw0FIp04uFwruuJbVbOltPDNyxD6lsNH6CPxsvC3MdfNEyo1GFXhfvIS4SI8186q6FMKKmzj8lLXO97bIPtROqizVke+FhIdSRBUpbhcBZQJJ6jSS+6Vm0krvZCSqRI8RE76Yr5GKuDUdrbCUjbBEjr7LPPntoFqblH13VQ2oN0TfWAxEz+aQ8EJJ0RRdqO9IwcLQ4Zdc/gmLgBv3fNUV6kTWRIiPCN5BrE77vSEbie/Bxtmu8Zs6n2fqoPJL0jKdp9VZfOm0tnjvC1gzK8594XdUPinrvvwURlpOhAGTovnZiVmiYwQ+Q7AQftJCHwxyEFUoQXlk6LNFGvO9ezethIgCE7IvRybDW8YCZMDNOuec1rTv9xs8S32mWmXj6C+hF56Q07b3KTm0x2rYbD7EB9rKSrfDTVCdtu1PqQdJGrZ2HIaXMebeD5eDZjXDpGJlW2yyQtmxAz/PXBi0PKRlj0tpvZ4GcpyD1WOEdGiJh06H1EPJ6hzplKw7A+EiudtVVxLBgM4XVW3hfERw/MLlncqtqYc0ENQ4akWZ2hjgBJ55r6yJN6SQeKLBFq3jVxPB8LaiwxV2/1F16R/Ko/bu5d9j26H3pkeRqB+k4JKzoKumhtUPMjgVs+r5Mw6tQ2woPqXxoOaoIG5x4IicSsrz8L58FXOOc8ZLPXZno9aGm3EinHy0y35uOyOTrjfi9R6lVfTh8cRzKgyyMxIzbpdDx54eZc8tpu1Po46hCZkpFqjFaQr+E04k2cOPeOsLSRj9Pop14HQ2EkrvMidS3hnveFWv96P+ru/aCPRX4m15Ch+9aJ2+wHMSI8HZ3JMhIivS+pV1wStQ7PhkckxpSRozLGNqp1SFwjEuXbv4IAg7Rd884hYBOD2lzbj3bFpGES7gMe8IApbYSiYCxr3Xn1G9ESSHQ8Og/nSNkIFFETYLRB4quD94y6JaMLdRzzXSoO6klC8DBIZV7i008/ffofG6x7MBla2rPAhIsHupVIuXpywy12rzawMQz04Y16QhCfVEVKJMmQHuj2DB9JUfWFg5SxVGhT5EKlxNbWUWfDkcQMZfOhuw+Ea4RgGGsYH7iWe0cY9NA6Vp0WktpJGEkj949wdE7aC2nroAgR3mkQRpIUZuJLOyAtpIrAjKqg5p1j/FDPlV3rg+RI6CR5eQv3TEimOgbkh6ipOcb3Vzyqu0jPyRNqGSPm4nK+AyMqLqMt9dMRaQNCTAQWIGHrOPLdV4xlLBE7iqDHBo3f0cML8jBBj29lFF0tvacXZh3kYzhHvUFiAPmsK/eyQnokQhom0dPx2eKRHtULOObvpScFqRMCQ+rIjHqDfm2zqO0Cubc5CE/cjeJdFsiLmsf9M+cipRlJXOlKV5oWYIRUAp0ZIvBs5iYCUz8jEhK5kZLhuPDcAyTeRveSazXeRmmEj+WMaXMcwzaDmg7Gc9hs2OXBRmVUN4d14ZcVc2Xtq/x11yrGeDkfw69I7BiC9gHoGRGVj7Q2GFITTuIdh1EI2fDLMCvqDchHlcbn1yPT79FBk6RrPiQH5SZNkPSbReKTSHQYpCO6aCoLE4eRjGo5CEvddTSGuO4FoVkEsL868pSf/HVgpBskCQnXjvJOm9b68G8WKa/Cufs3CWvC1HM1eUuvru3pVRMPSG70qSRtz2EO4hrq0lHbcIi5Wuoctw7j9Y3iwhi3umA8b+wMeGbr3u/teJ47gqA1jCGr4Z6tCqkCSF6kMMMn0pXhrUknxGoYnA8EySDdk08+ec8G5LlWnWG1IaFhNJ0oacxQ3LARiSAIS1n5DamCpN8sxJWevszsOmI0kWL/XTpYJJM8vSiuG96bGKNDy4Y6iMywDbltFskzR52ayUptqU3ViV6RLhNJ0ombpEKkdJrSJZ/NQtzqEqYs+YZI6VuZjxlJUHtUqI/RgvutqouaJ8jLfZhw1I6JW+MEtS71+hg+dz3n47X6YddrafMaFxLWbhkuWBe+HdgRBI0oEQRyRsIM4K9//etPkrGP3MduT1gqAsSFsE2o+DCoAMzwImhkrsHzIdWHQApHSkzs5E8FgZxJqYbihs300pbMkirH9JuFuKRkHYlVUCRY0nFMzegY80GTXNWDfo9+jaRrcoS0bSgfU8HNQp7JWzp5mkiiMlE2MzadhWWw7lmngKB1COqQyab9gbKqU77O0P0rQwcq3CjBHIH9IpRnPwjx1FOnSPUx3m/yDIxw1JOqxHMTfw6pR/zKMpmlI4gjDHD1vF6vYToOHelYn/jVOe0+Xm+3HFexLvyKxo4gaFIiAibFIjDDfCZmJoSQjI/cx2zCzEw/MmU/iuDYRd7oRjeahr4+Jg1eP844eZBok94Ha7YYefoAkZUdvlhQRA9a89ospLEQxoQfMlRvky2kR9I7MsrHjBBNAJFkDe2RGOlSHS/v73p0DHS67s/kDpL2W342tUYaJp/Eca+ke+UaYVwWpI05z8R9mew06hGWNtQm1BPuD3kjPZ2SDpilANS8RiBk92LfY++ICaIRc+lNOFkmrT108nHULnaNc9Tewpxz9br7YGcMY72cV3Le3/elccWiPqc8t+3EjiBoKgEfKBMs5EaqY5ZFWgpZgo/5pje96UR0hu6GuPSXdJsh7bkGF4YApaPbRVYIgiQpnB7bB08FgUCRV/Jx3N+HaIadtM5EyktgEkzeyIlEG8Q8iLkfYkOQWdyibvuDWl9lIl8SKylQu+ogjjjiiIngIikbVTCPUi8r13SGl/WlTbmOOj8ry1ixCAuEM5c69NBDV0cdddQ0atI5es71R6qOYx2ce/6ezyGHHDJ1aiTjYKN6e77u2cSi0Q1i19nzezac8zGMM5pSrg4exnJyf8L46/02lgXPxmgno7Q8yzy77cCOUXHQv1JXkHYY8DN+Ry75MJAJ8kbQzNZInj48JjYkaBNx0aPmQ4lfB4CIsmgCOegQSEWILFIfadzHWIes+wtpEA6pywfunKRIBUNCpw8Whiyoauhm1Y+kjaypa5Cle98fjPV1ziSJ1GnyzRaMVqi5Z2WBzgkpaz+LQJDlZYFyU7Zy3RcVhxFN4Ho6QuorC3hI8p6j9vLcR0jjWSRv74DJRyMBErF3Jkicilonz9h9c0ZsnnvON3LSxQXyjYO8L+BZmlMgBOhs2y3DUfE5muvwXXj+9Z3hzzO8IrEjCBp8AF50H7dlv3TFdMT5MEgyCMzHTVdM+szHgGAMX0Mw9QPiECQyYFtMOmUlYWKRNMdygpQuXsDvYXH86rUZiEv6NpFFQifhC/My2JiG6RxJ3zlSQo4ktsQxnNYB+bj3d7MXeeSYFw3BIGjSpnxJ1KTH3Jey6fy1H12/Tir57A+kidNWRkCW2+vw6nUwqvD8bC5v603PLROkUONC/WgQtNEJCZqu3odW444Y8wpq+Do/pJ0g1+JcS93iF4781ct8ijq2W4ZjUcVRpTIy8G3U5wk5XpHYMQQNXm4fKwnXdosZigPCokP2PzQTSobLCJBkjPiYsGUJaJDGN3SlEz3ssMMmEkTKzuleWXSwCEAsSLKa8uXD2yxBi4tokE6G7HHKVU+rGHUkVpBZLaYs6Uiz6mJBi9EAor8sSL3jZwnDvhpB6zQQtnD3ZERiwo50rQNTB53ZKF1sBikXiXpOOh8Ss/Dk5Yi0LclFsiZObYRDV5/7lUfS1HSc0ZR8TRLqBLIUPHFyHP3eHRK6+Q0dO8cf595zjJ+jRnNulDZOEjrWdo4T5r3U+SGCdstx3hfPxbuWZ+cY/3ZgRxE06Y5UZRKJrpa6AZAJ8iV50SEjGg0tXBqETkJF2vlQIH7DehIzEy8Tgz506hASNFWKiTTERSVhCI1kQDzkTsLeDEkjWxIi8tUJpHwvAJ0sFYuRgckyEmZUIJG6qEAsosnk2hyEe8F0JAg1L1fKqg4QjU6B6kRHhDTB6IOpoU7LKkxtpw4kVPm6X0Sjk3T/6jj3IqccQOzuSQeKEGs9gJ/kgvB0tEia/tvkcK7nWD+cnFOB0aFLZwSSSULX6/NJPgEdvPfKRKjRCcef8/hZ98z5I+HLd8wb1G0uvLF8jO/ZFY3FEXQaob7s8TM588EgKh9t9M8IA+H50SUVAakQpEFW2S2OzjONDWl8hCBPkiIClc4H5+Nj9oXwEZRJrVhUAPUJUz9DIxIUpK4g75zzIyg6VgRrgUrCwaQhqxRqFhJmTPlA3oiHqoF5HSmxImVwiAixkiBJd1GjBMqLWgi0o3JJ59ozdTbB5l7pc9WZdKGjMnIJ8ZOwqT4MEdkg67hqWRXCdXLqZgTBciVx65FTtg5V56DzINGmnUD96z0kHSsXQ1QErSPJ/SROwF/z282o7QI5z3sQpL0c17XdmFeQNPX6XNx16XczFkHQHkx9OEhm7mEhCEPe6173upPEi8R8lPTSiBsJI1vSX8AvLr0y29iUlRcG2SA/lgMkRaQj3CQdYmYBQpolaZLaERGiJTkjJlK3OCTvqqvOEUhyJEbkQWVgDw1SctWr5j9uJjhJsshOfixPTJRRgZAqLQuXj2G5dHHJhwSMRHU4yM29jRAvHxlp3k56CLF+eJWgdSic+6fnjzRKFUHil96knOdR6xRHyqa2yfOLXbUy6rMKEKv2isljOjNu/Ngd876Q8NUDsUsTEq9xgurfbUgbQm0HYXm24FocuJa2r+kqci151Xhz6RI2hjf+g20n6PHh1Ac2vkjIhArDRB47VNIr0mD5gPCoOXzweYkcER0JlxkZwhWe/IB0ilyRH8sCQ3Dp5IMcWVeQaH34iFG4D59kjvCRICJRh0qaFaRFk20sQ9gZI2gTcux7Ez97c6gDSdPLbftI92VmmVrASIA5HgmUxB1VQ/JQb6oGbaIMjv4WxjpJ5x7US57yq4i0q9PQOVDBGKVoH5AfCxP3gXR1gJnQzPU4nSZJ3TOjhjJjTu8tv7qFZaB9qSt0NKM9c55tTRO/EY120smN+uc5stitcO9xOc9xbN9cA89XR2tuxNyOb8ezqvHi9/yoDj1735FnmNEcp5zEr/7G3lgEQQd5ePF7cHlhEC2VAzUEgqKKsHEQUjOUp9aYS0unSRpDCgg++uMA4XrhSMOkZ9Kb9CEwkrPl1SRRZXghUyfkwkSN5K0u6whaOgSYXb8cObrPxEe20pMC5Q/qw66XdE2KJ8UmvWF/VA0gj9yzdDoTk4mk3Fyv9RIv9+felFuh3YwSSO86MHU1kRLIi2RMlcAqBUGLn3qkPM79e0buwb2ov/bwXHzIiRfwy4Mqhx37qDpJ/IQ5ei7aSqfkWRpZ1XiJC+P5bsL4bGDOX13gWRAqvFd09uZjvIPiyDd5+4Y8O+8FIcq76v3yrSVPcSHnNazxXyxGB10fFFfDkKXhMP2rXemQYn2Y69LF+cCpP0jCo2pAPnPSVVxF4iecH2mRrknTkQaD5JGwes7lHmqeEH8NS9yKMU1N54PQTkgxSJwaL/6NMKaDnFPDIHnSMb96ak8Ocm8cfz3napwgcRNW4wY1TFzqFZN1bLkt6KkjqYqkG8N3CzyX+gxgbGuSLum4SrzgXTfCs6DLhDaizqiJi/CiQ7by0oS2bzYSNOc5zVkBOZ97Xrsd207Q48sCeYk4fsN2vbWPj7Qa87Oahr+GSVvPSWz53VWQMmrauIoa5pg0nCFfXsIqnbs2fgwhrZxXJKzGS/qgxglyD+ImHSBN6gFtVdM41nyTvmIsgzQtjrAa17mhrolCI4hIrUHSjEiZueaoTvUc5u4/4M81R+oY8xDej6iIxKlpaplQ/bsJ2qG2KyTMt0ZSpn4y35I2TNsZUVFrGc3al7xuogXiSSuOURX1IkL2PAgx7L8JSeP3VvNo/BeLkaDBwx0fnOESCwr6W3bCdJgkQz1x4kqXD5I/zjk4sq+lJ/YBk/RiiD7Grajp566T6g3Z6WgjPcK6vBKurqkvjOXPpYeN4vHH0ROT6ql/Yl0SJM6cP/UfUctNPEfDW/dPn0y68iEmjvurSLoxr/hh7nqOwuMfHUmPKofURuVS27ZiDJuLsxuhvbSvUYdvDfGa//DtBXkuSJaKkbBDnYSg89wIKNJTXflezd/oOPM8fLO+XeRtEjcmndDPYh6LmSSMy4cIzpGNXhcJ6JERrEUkhrHjpENeoriAX1xmdojLx8yGeow7ptkIXjqTIPSeXkr5B8lzjihqPYP4Hes9JKy6Me0YX5kkIDpAE486MUjaGr+6mm/C5pBrHJ2zcuio67DVUX7xB0kXjOep34jEqy4Qn1SHNMwVkJ4TXuM1/gvtUtvH0Xvim7Kkn/UO1YWwPA9xzBcgWN+fOFQYsXoS15yE78HEoMlaBB37cPBuGnGaI7BwDEmT2CFxGntjEQTtJciLAHlYjnrdrO4y0WT45OhBI4W8aMknaStyzcfrJWSRgFwz+ZQ08dewYAzzstGpkSCySKPGcawEneO6OoLwuXzq+Ziev4bxI07qhqpygZr36FwLangwF+aDZS1RLTuC+Mc0kLDx2kZh8Qf8SMEIAVlYmYksgqSraRr/gTYZ3yOjQaoqJqnmL/JO570QV4fPpFWHbBLaIi6WU655DvwslghCVCCk6CqFg4lpoxyrRE146wign9M8FqHi8HDiYHx5Rn89H1+i8fro94LQm+rlEbawpIekH9PVsHqtYqx3UNNCzmv4eD5iDK/nc2nW5QO5tq90oz8u2Nd5UMPjr/FG/7rzMdyohWrFPt/50OdQ84DxfDdh7r6p+1jykJ7NJej4xvbybhupZMToyEaeaSPVCIGJ8MSPwK20jIlnhbwIEDoCtvds/hM+V7fdjkXpoBuNxoHHSIbmT5Czvc6RL4KGMR7CZW5JyCEt+3ONka2JaEcT+UaNzOuoOEjbc6RLqqbLtp6BFF2FrMbeaIJuNHYZKiEiUJIxcjbZnQ2sKnJu0RT1BRJm4WHFJr2/9NQWiFtc0jOzS6PUQHjyUbYJZpORJnbFc62qBBv/QRN0o7GLEKKsjkUGU1GT8c4Biea6uR5qCRI0lYQwcw9W9dI1M2HNPuKk8fxBn9qp5hPk3CIWliB1MVVjbzRBNxq7CJUsSazmYZAknTDb+VyPNGui2UQ4k00LvSzvN4HIbNWCFb+So49G4OKx8rA3i0UsSLxa9wQpIz9Apouei9dogm40dh1CkMiX/tiGV3TG9MoQqRdYA1FhIHCrcZEx6x2SMlM5UjdiRtDI2RJw2yog6EwgriNeemjSNlUHi6hWcfwvmqAbjV2EEKAj0zg7DNov3a6BrJsqxCEpI17OoiQqDuSM3JndIXDSL1NLVhwIHKFzTO5MCIbwHbnAdRt1kcQtbkHQjb3RBN1o7DIgS456gxWF7XJN6mX720Ac5Gvyz6QeZxIxC1iQdOyl6Z9dtwAs8cUNITvKL3BuwtH2uXZDROhN0P+LJuhGYxch5AwWgVnV5zdqjiTjXB/dSLAwXk+ceh4Iq3BOArfa0Da6djiMeV/jv2iCbjR2EUKUjvS+Jv6OOOKIafk2lYfwObcvgl7nRtQwVh503/79yZKDFN7YG03QjcYuBKK0PS7dsz/h+0Va/vEZEh1JNuc1vBJ3Da9Yd1159tihA7dXexP0/6IJutHYZQhRkqBZYiBoi1DolIVXawrHqCqSLhj9VaURJM4YlzOxyDIEQVt9eEUSdOpQ6wXO6/1WzI0iYDNhSRu3WTRBNxq7CJUgWGDYBZCKA0HXHRlhM2SSOOviCV9HTuykLXSJisOE47p8Lg/GcqGG1Wv8mays10c/Vwk7YfHnOBe2juhhzLMJutHYRQhBcLYHtbOjfdbpoOvvx0YSid+ud+yb/XLOohUrCFltAGJjGWI/D9cvvvjiaRk3yVx+kPw59tOnnnrq9Bs7i1YOpARdy8152gHiH+Osc7kejNeCdWH1GCQul/o0QTcauwwhAGRqm1YqBgtLkG8liPjjwMSeFYdUEmyY/QSD/bTrrDCQte2AhdMrs5+ma64mdMkPudvf/bjjjpt20zvQVhzKDPGlDvzqZkFNleDn7j+uYl/Xkk9Fwus1xznXBN1o7CLkwwe2yuyPjz766MmaA2FCriduzoGUa/WhvZ79zd4qRCQsPCRsz3V/i7cRkgUoFquMBA027LdC0Z/ubbZ0IAh6rD9/JUeOrbdOJCoeYeo7pst50oOwmlfOOXm4J04Z8jea0Bkoz4ilLnFP+oom6EZjFyFkAhaSINBsekQ1EYRoKmEkzE9h6Yw5JE1NQl0SuG4ZNxWHNHN5AFI+8cQTp6XhSD3hW4lafq2HskLCSJI/hJrORhwuYQknaVd9vetJLy8dkrYVDyEzX2Qx41+MFgPpCLW1rVtdq5BH6qnsJuhGY5chxINM/D2FBEuS9fuyEJrr8YcwAnt2IGULXag5pLXEWxpAPMiZlUiQ/CqoNfxj1D8KxwnKrUK9h7EOzqlk6NIRJfLUaXB+AkEFZFtV7SKOzkyYNvP3npCyPE24GhHoaJCvUYaFP4g5v59DzCZGLZ9H1n42UaX2sc25JuhGYxehfvwIgaRnNzn/+7QvR1DjcQkjRZokZDdNcqRrPuGEE6aj6/Kk1/bTWR1A0o0O/KpMubYxreFbiZonfyVpEi4CNaFJ5UCXzk/PbvMn9fenGMTsnJNGmDZAzvIDRIukka+jEQXpmSmh0YTOTGdAvYHkhWv7EHzqBrWOTdCNxi5CPvyKc845ZyJKUjHSrajx+RENEjv//PMncrF5ks3+7UhHQhTmt1lVvTHmgYCQE7WKzf3rNqcHGiFBQJgsSUjEyLQSbyDMpk6pH0d6JiknXsK1nXyqzj2Tqjo2cVxDzsoUP2njIH55NEE3GrsIlQgCKgtESZKmlhivB8IRliG7NMiO5Mha4/jjj1+dddZZkyTq57OITvxKiAEpFMnZalRaw/51ZW4F5D2XP4KmanBEhiHjStDq6V5yH2mDMYwf4ep4kG+2WUXQ2is6bGoN6o8QdNKnfjkCsm+CbjR2ESoZBM5JvaeccsrqggsumMimEkYlWcN9uuNK5IbwNv1n0UFypo/OznhjWcB6gbRus/+LLrpoD7kdCCh/7l5qOPBfeumlE3nWOMiYTrnGrVI15OgeqDbo4KlOnDvSXyNn0rO0dNU6gZonOE84RxXSBN1o7EKEDAISsV9fnXTSSROZzEEaZHzeeedN5BMioXc988wzV4cffviktqACQS6uQQhPeaRnqpBjjjlmdfbZZ09pIXG3GqnjmL86pV6OrtM5GxFU8ow6o5I2XTWC1gZJm2vSIuK0T4iZX5j8ucTlah6Qc+qkJuhGYxcCAcSBYb4N9+mSkXB2tqtALK6RoHPNUbjN/I888sjVscceO5F9CCpkE78hvlWDpPWsMgyS51ZDuRykLhw7cFYaOoxYcVBdIGSTnDoZBI2Ma3oETarOvUkrD/GqFQfpGckK5+Qdl3PqHeqQCnlCE3SjsQsRgooL0SAL5HnaaadN5EmfCqRAE1sWtfjRq/8TGsonPSAlpOsfg1QFUPPmqEWoPyxicYyUXd1WQ57qUAk25bg/HYb7pjtHsoiZGoJZnE4rBJ00jiHoSNqIXj7Sie+6NkCwVmdqN/m5njgcP8sQ9Uj+Fa3iaDR2IZBBHIRESb0mzexwh0CjZ0YgrDX8dYUKg77aYhQEFTAtu/DCC6cl4Mg8eTsmf5K1DuDcc8/dMzEXJP5WI2XDujLUQyeEUN1zVDziI9EQdFxUHOIlz1yLP9AWlr5T7QSu1w6Dv54H2r0JutHYZVhHCPz0sEjKUB25iCeMOVpdiEFijBojJIOwLM4IwUGuAwnV0D8WDtG/QuIcCNQ6BGMYaVWnQV9sdKBe6kcS1rGIm7pW0obkVfMD8bUhK47onefiBcKlSRzlN0E3GrsII0HEn3AOMSCUELBzEiBHZ8yNOubkITxhjlyuIXp5JCxwTRkHGqknjPWjgiAZGwlQdyBs9eWnY651RtD0xwlzrHnnnKtmdpDwEQnTDvHLpwm60dhlqAQx+qsL6vl4vZ4nrBIU57yS2EbXDgRSRkXK1qEw+/MDWxI+CRohk/RJ1Dojqg/WJqRpkjPCDUHXewn4ES2Cp99mSsi/Lu7ceVwTdKOxyzASQkUlhxE1vF5PeL1Wz0cCrte5SnRbjeTP5TxH5ExCRsbUNlQ7wmKvTBUTtY3rpOxM7kXPHhcoRzqTg/T0l1xyyZR/Rhxjmpq2hsU1QTcauwiVEDaLpJkj2nVwbV/XA/4x761C6pG8Q9RAjYNoLa4hIZOWxSP9xpYZkDhSJklnYjD5jZA/9UjUIPT20tVyYUzvvMZJGU3QjUbjoAbiC/mFGB0RMqmZmVzIeGlogm40Ggc9IpGGoIGkTIoepdsloQm60Wgc9BjJGZwvmZxXq9Xq/wEjtQIr3CFknAAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E7%8B%97%E7%9A%84%E6%95%B0%E9%87%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAsEAAAF5CAYAAAB+wPfxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAGB3SURBVHhe7Z0HmJRllrY3/htm07W7s3nChgmOo6OOedQxATKKiSAgIiAISBpylJxzZoiD5JyRnHPOOUrOUZKg5/c+VjHdPQ3ddDkW71fPfV3n6u6v0lfddHPXqec97x+ZEEIIIYQQKYYkWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIYQQQgiRckiChRBCCCFEyiEJFkIIIYQQKYckWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIcQt+fTTT+38+fN25cqV2JFwuHjxoi1atMj27NnjzyNKXL9+3U6ePGknTpywy5cvx44KIYS4EyTBQohbgkSOGzfONm3aFDvyFTdu3LCrV6/aZ5995kJ2q/r888/tiy++iN3q90Guz507Z6dPn75tXbhwwR8ru/CYe/futZIlS1qbNm1s/fr1fnvO507hNtm5HTKKlB49evTm9TmP48eP24oVK/x7eOnSJT+eKHw/pkyZYv369fOf0dmzZ2OXCCGEyC6SYCHELXn//fft5z//uXXt2jV25CsQU6Ru27ZttmvXLtu9e3emhRAiy7eC68ybN88mTpx421q2bJl3PrMLj7lw4UL71re+Zf/93/9tPXv2tE8++cQOHDhgR44c8fPKTnFdbsNj307mYefOnTZ27Fj76KOPvAuNCPNi4eOPP7aXX37ZSpcu7d+rrO4nO3BO77zzjv3rv/6r/4zWrl0bu0QIIUR2kQQLIW7JBx98YE888YT16tUrduQrhg8fbv/7v/9r//7v/27/8R//ccsqXry4rVu3Lnar3+c3v/mN/fKXv7Rvf/vbt613333Xli5dGrtV1iCJXbp0sT/90z+1WrVqWe/eva18+fJ+Tv/5n/95R8VtKleunGXsYMiQIfbCCy/YI4884p3neNcXyUeCeR7Tpk1LOJqBWG/YsMG+//3ve/HcbvdCQwghROZIgoUQDp1LOpXEHyZPnmxTp061fPny2b333muVKlWySZMm+WV0f5cvX25t27a1Vq1a2VNPPeWy+OKLL1qHDh28ypQpYz/4wQ/szTfftC1btsQe4ffp1q2bPfDAA3b//fe7rLZo0eJmNWzY0Ludf/RHf2RFixa1JUuWxG6VNfPnz/fH5rwQz40bN/q5t27d2jp37mzdu3e3Hj16ZFpVq1b17jcd5Lp16/rzpBt9uzgGXWNE+Z577rESJUp4pxxZhYMHD/r9/vVf/7XHM+hqZwW3j3ejiVjQiT516pTX5s2b/Tlwf6+//rr/XNJeHi+OUcQx4l1txSaEEOJ3SIKFEA6SN378ePvVr35lb7zxhhUoUMD+7//+zzuYDz30kL366quWN29e7wIjdvv27fPc7WuvvebSiLQePnzYDh06ZAMHDvQO8ltvveUxhFtBTIH7Rrbp9HJ/8SJu0b9/f/vjP/5j7wQj3tmBjDEd5h/+8If23HPP2datW70re+zYMT8XhBAxjMtlxkIqef4PP/ywLViwwLvKXPd2MYahQ4fa008/7UUkIm2GmC4tcQXO5ac//ak1b97cF+vdjpEjR9qHH35ov/71r61atWpWvXr1m/Xee+/ZL37xC/uTP/kT/77TbU97ecbi9txP/fr1XeaFEEJ8hSRYCOEgwUgSUluwYEErVKiQi+S//Mu/+Fv8dFYR4VGjRrloXrt2zQWRTjBv9yNucbgOx+nk0pW8FcQskODChQu7WKeFxV90pJFgOqgsLssOXA9R/Md//EcXxKyEMyOIL+fz+OOPe9f1dvA92L9/v3+vfvKTn1iVKlVcpDMK85kzZ+y3v/2tSzAyjKRndr04ZLA5h1y5clnu3LktT548XnTN/+mf/sn+6q/+yiWd+EX8sqyqSJEiNmDAgNgjCCGEkAQLIW6ClKUVM6QOaaMjG7+MotNJR5U8KrEB4hLkVIHLEb7HHnvMZfR2WVpkkG4mwkcHOS1pJbhUqVLZkmBEnvgC8o4sppVgJlEgnnSE0xZdYeIHTLOA7Eowz5PvAY9HNpcOOp30zOC6PD6L44hoPPPMM94xji+gywgvMnjxgDwzoo7r8ZGfA7fl+U2fPv1mXIIXI8QduB6Z48yKn8PtIh1CCJFqSIKFEA6ChKhR5FkRt7gEM4qLy4kVUAgaUw/+53/+x7O/gwYN8rf9uQ235a38++67z+WYY7ciLsF0KYlSpCUnEsx1iDLQKf2v//qvdBLMfSHmHE9bRD5eeukl2759u18vuxKMcM6ePdu++93vuth26tTJpfVW8H0gm0y045//+Z/9+8OLCCQ8I4hx2uK2PA9eVLAgEZnm+8P3mm46cRIiD/Gfwe1KCCHEV0iChRAOmVxyva+88orHHigkF2HjbXhEi9gDEodcMtXhH/7hHzzjumPHDl8Ax0xeFmvRqSQfi+TdDhaMEYdAgulkpuVOJBgZ5PoVK1b0LDKxA+ICaSV4zJgxLp5PPvmkNW3a1B8byed6yHFceLMjwcQgEGCe61/8xV949pbcb2Zd3bTQjWVaBGPNGG/GeSKvc+fO9fPPDMQVueX7/LOf/cyjDdxH/LFYiMhz4nukKRFCCJF9JMFCCIexXixUY8oBExJYUIX40uml+8gxpBFRpsOLJPM1MQi6xyxAIxqApCHK3FdWmVqyrwj222+//Xsd0TuRYKSURW90rRHqcuXKuaRzHnEJZjoEsstjrV692qMRxBd4juSX41MsspJgHgtpZQIG49OQeKZkcK7MJs6q6KDzfaL7zO3pRPN45Kgzk1iiEVyG3DNFo06dOv6cOH8KOeZcixUr5t30+PG0xf1mJehCCJFqSIKFEE48M4tIkZFlnBYxBxbKMRWCr7mcKMSaNWs898tCK0aQzZkzx4WS2bx0Y/nI10jk7bqT7du39+4sC+gyRgnuVILJxdJVZV4v2dmMEsz5MFWB+2L6BCCzLPjjukg8ZCXBTMXgBQEvDujMIqWcP/KNiPJ5VsX3qFGjRv6R+6AaN27s2d208D2fOXOmPf/88/Z3f/d3fj1egNBhjxeL8jgXOu90t9NeFi828lCXWAgh0iMJFkLchK4ju7ghwkjT6NGjLX/+/N4thXiulLf1EUg2yyATy+I4usXxYqEYOVk6shljDmlp0qSJ/fjHP3YxRcLTcicSHIfz536YcpGZBNPxzSjBPL87kWCknxcGdGabNWvm85T5nCkaTKRgfi+zjf/+7//ejxF7iBfRkr/8y7/0ecLMQkZ66YZTGZ8f32MEmMgF98nGH//v//0/v9+09/m3f/u3fpwcdNrH47H+5m/+xr9/gwcP9hc2QgghfockWAhxE7Km8c7iokWLXJ7iEszb6YgxXVfkbdasWfZnf/ZnnqllHjDxgHiRK0aO6YzeToLp3JIfpiOacdFWTiQ4vojsVhKcWSf4TiUYOV21apVnqOPTG+gO8zhEHcghI6wsWCNiQYc6XjwHOs8PPvigLwpkIgW3p9J2ajlOhpkMNkJLdOI73/mOnydd9rT3SQeZc2VDEV7AxI/z82MDkj//8z/32c7aKEMIIdIjCRZC3ASJI1dLR5HcLLN/Gf31b//2b979RIbZrYz8MAKJoLIdMbLK5IN49enT52ZOlRFet4J5xHRFyRlnJCcSHCczCSYTTMc2owTfaRwCeBHAdAiEG/FmYR4fEWNeENCZZeEcLxjSghTzIoPzIOfL7dLC13Sz+R4zA/hHP/qRd4I5J7rY5K2Je6SF63L+LLZL+3gIMd1mzoWOPqIthBDid0iChRA3QR6RLaYWIIV0I5FgYg/IIiKMdCG6iBmCSieS6RBpoUvMNsp0RTN7G55xa0QukMFHH33UF9Fl5OuWYObysrCMkWws+mNCBJtwkLO9k4Vxt4PZvdwXXVu6xRm722z9zAsJXmggyRkXq/E1z5ucMefPIr4pU6b494tcdk4lOD6TWAghxO+QBAshbkLnl2kNCCBSSAeRTiQxAuSQBXCIIQvkeLs9OxKc2excjiHYjGBjygSil5GsJJj4QMZOapzMJJjHo7NKV5sd8FhIRiyB6Add123btvn1cirBZJHZLppMNLIa7yynhU473xeE9lYj1TjG+Xfr1s3zx/HrSIKFEOLrRRIshHDoWjLtga4vskinkq/ZfCK+MC4Oncl4J7hmzZoeA2DEWbyQZ3Y2YxJCxm2TeRwEjS4ni7eYsRvfqCItWUkw98Euc2zekbHjmpkEkwlmni5iPn/+fJ+YwP3TFSbSQa4XcirBnA8dXDK8bBaScRtoGDZsmHeK6aqz3XLG874dOZFgxqdJgoUQInMkwUIIh5wrGy+wkIpNMOj+IsC8dZ9Rgul60u1lCgKjuxBnIgDx+va3v+1TEFislXFhHNlU5JPbMScX0c6YnYWsJJhFddw/+eOMedfMJHjXrl02YsQIl3siGog8i9zoSiPqd7ptckZ4HswhZqHf8uXLf2/cGbBYjjgG583zuxNy587tlV0JprNdr149/3mSh5YECyFEeiTBQgiHSANdUbYSZvQXUx8QWr5m2kNaEEY2p+At+9vVjBkz0skg4hnfaQ25ZZLEypUrY5emJ60EI7OIJdA9JQZBZ5TRbHRfM87AnTBhgndc0+4Yh/AeO3bMpTcuvJmREwnmNiyIY9wbWxsziSGzqAbxBHLJXOdWUY5bwaxgohRZSfCyZcs8Y83WyjwWnWB+Dpm90BBCiFRGEiyEcBBO3qanm0nXtHXr1r5ojY4tMsW4NKZCIHjkVJEqJj/crph0wPUQPmILjGArW7asizWbZNCxvdX82vicXCSY82BXNjK1zOVlEw86rhTnmTFWQPSBRXfEMeISnBWcJ8KOQCObWUkwj0l3lV3g6FTfe++9nm9mcVzGrC9f8/y5HqLMZht3CqKLCGeU4E6dOnn0hBcUvBggt83z5gUCeWcWM7KQMeM5CSFEqiMJFkK4oNGlRIB5qx6OHj3qO7ohWGx+wYI55I3FX3Rz6TgyRm3dunVeLPTi6/gMXXK3dCDpktLVJT7BNAYWjiGMyCuPcSvo1nJ/iC7ZYRaxMTeXaRVEChjjRscW6cwIGVgWv8Vn52YHOs0sniNmQSaaGEhmi9sAuSduwOMwBo7vD9fv169fuq40MQ2ux/eBRYdsscw0inbt2sWukX3o0pO/RnLTQoSF6ArdZR6b50snv0CBAsacYB5bM4KFEOL3kQQLIXyRFt1DJJjOYhw6nUgUsQKmKrBbGZ1hNsKgU8omDkQb6DYiqCzcoluJ7H3ve9/zbDByyAI2usyIK1KLzNF5zWphGIvskDy6uuxAx/2x8IzHZ7oD3enMpk8wg5fuNTN56WpnBySS+/6TP/kTf5y0eeK00FFF8pFlzuNb3/qWfy+GDh36e7lbOrDENbg/dnTjusxGZurDncL3izhJxo4uQs3PjfNFgvme8gLidpEPIYQQkmAhxJcgV0QT+vbt653cOAgXsQQWt3GcnC+yiNjSzWVhG1sFs3UvW/tSbNXL18gykYf69et7HIKFbQghsQbuLysBBm5H15XrswsaOWSKzzmGdGb2Nj9CSscZOWcKRHbo0aOHyzvPB6FfvHhxpovJOCd2YMuVK5fHOipVquTPja5vxnNhAeFHH33kskwnnesSCaHzfqfw/crse8b3k/suUqTIzS70ra4rhBDid0iChRAuTGR46dhmtrMYcofQMfaL7iabPhBvYL4v8kwGlwkEfCRTy7FJkyb5jmzx8WcIJYvv2K3tTheF3SlIMh1sIhuZiWxmEH0gF83ziEttZufJ94rOOflkBJd5ypmNaQOO8T0jsoH8cl2k/uuE7ykRCRYYZvaCQAghROZIgoUQ4kvootL1piueFchtfLyaEEKIMJEECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAcKq9e7du1q/fv3V6lUKpUqKcVoQSbCCBEikuBA6d69u++gVbFiRZVKpVKpklJsMc5OkEKEiCQ4UH7729/aBx98EPtKCCGE+Ob5zW9+47snChEikuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLkRiXr92ws5c+C7IuXLkeexZCJBdJsAgZSXCgSIKFSIwOM3fYU23mBlnv9Fth165/HnsmQiQPSbAIGUlwoEiChUiMBuM32fdqTwmycnVcYFclweIuQBIsQkYSHOPGjRt2+vRpGzt2rB04cMA++eQTmzlzpg0dOtSrf//+Nn78eNu0aZOdOHHCJXTgwIF+2ezZs+3y5cv2xRdf2Jo1a2zMmDFeK1eutKtXr/r979692yZMmGBDhgyxBQsW2KlTp/z4yZMnbcqUKX58xowZ/rjZQRIsRGJIgoVIHEmwCBlJ8Jd8/vnndvz4cZs4caK99NJLLqkbNmyw7t27W/Xq1b3y5MljZcuWdRFevny5vfrqq1ayZEm/rGfPnnb27FmX4w4dOvj1qlatas2bN7cjR464XI8YMcLKlCljVapUsTp16rgsc5tFixZZqVKlrGLFilarVi2bOnXqTXG+HZJgIRJDEixE4kiCRchIgr/kypUrLr6vv/66PfroozZv3rzYJV9Bl7ht27bWt29f27Jliw0fPty6du1qGzdutIsXL7q0UpMnT7b69eu7KG/evNmFF2GeNm2atW7d2jp37uzXR4InTZpk8+fPd4HmDwidYf6Y8BiZdYMRdc7zwoULdv78eb9d+fLlY5cKIe4USbAQiSMJFiEjCf4SBJYu7qpVq+y1116zhQsXxi4xu379um3dutXatWvnneJt27ZZ7dq1LXfu3N41rlChgo0ePdo+/fRTa9mypfXu3dsjE4cOHbIBAwZ4XKJFixbWqVMnF21EduTIkTZ48GA/RreYmAS3nzNnjg0aNMjmzp0be/TfcfToUY9fFC1a1LvQTzzxhL3zzjuxS4UQd4okWIjEkQSLkJEEfwld1s8++8wjEQUKFPCIQhzktGPHjjZs2DDbuXOnxxvoBCPEdHhbtWrl3V9EuUaNGh57IFOMVCO33bp188gE0QoE+tq1a54h7tOnj9+uSZMmLt+I+OrVq12CySVnhMzxrl27vHs8a9Ys7yYTrxBC5AxJsBCJIwkWISMJTsOZM2esYMGCNyU4nhUuXbq0i+elS5dcilnkxkdiEggr8jt9+nSrVq2aL4ijCxyX4Pbt23s+mD8USDQSTMe3R48eLrLNmjWz9evX+3EkmO4xkp0VygQLkRiSYCESRxIsQkYSnIaMEozorlu3zhe6MekBWMxG55ZsL1EJRBeZJQ+M0DLlAdlFhBFVcsB0e/lDEe/4Isp0holJIMnx6RJkkXv16pVpJzgjkmAhEkMSLETiSIJFyEiC05BRgg8ePOgL1RDWPXv2+DFElsgEC964HMllSgRxCOSWr+kas2iuQYMGLsV0dlnIxucsgCNCQRyC6ASj15goQeb3o48+8tuTHc4KSbAQiSEJFiJxJMEiZCTBacgowYgsC9+YF8yYMzh27JjLbL58+SxXrlyeyyUvTIeX6ATRh+LFi1ulSpXs+eef96gDOWJEmkV3DRs2tKefftqFmePkip999lnPB7PgrU2bNjcf63ZIgoVIDEmwEIkjCRYhIwlOA7ncpUuX+gYWEI8+kO9l4RxwncOHD3uEgRzwihUr/GsgHsHtWdxGB3ncuHF27tw5v218tBpxByZG7Nu3z49zW4SYqRJ0gteuXev3kxWSYCESQxIsROJIgkXISIK/ZpBk8sDkgskNs7gOEFuiEMwPpuMcF10W13E94hREIugoZwdJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOFAkwUIkhiRYiMSRBIuQkQQHiiRYiMSQBAuROJJgETKS4ECRBAuRGJJgIRJHEixCRhIcKJJgIRJDEixE4kiCRchIggNFEixEYkiChUgcSbAIGUlwoEiChUgMSbAQiSMJFiEjCQ4USbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjEkAQLkTiSYBEykuBAkQQLkRiSYCESRxIsQkYSHCiSYCESQxIsROJIgkXISIIDRRIsRGJIgoVIHEmwCBlJcKBIgoVIDEmwEIkjCRYhIwkOFEmwEIkhCRYicSTBImQkwYEiCRYiMSTBQiSOJFiEjCQ4UCTBQiSGJFiIxJEEi5CRBAeKJFiIxJAEC5E4kmARMpLgQJEEC5EYkmAhEkcSLEJGEhwokmAhEkMSLETiSIJFyEiCA0USLERiSIKFSBxJsAgZSXCgSIKFSAxJsBCJIwkWISMJDhRJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOMbnn39uly5dsk2bNtm5c+fsxo0bduLECVu2bJmtXbvW1q1bZ4cOHbLr16/7Zbt377YNGzbY1q1b7fjx47F7Mb8O90EdPHjQrw+nTp2yLVu2+P3s3bvXHws+/fRT27Ztmx/fuXOnnT171o9nhSRYiMSQBAuROJJgETKS4BhIKVL76quv2sKFC12ER40aZT/4wQ/sxRdftLx581qvXr38+JkzZ6xGjRr2yiuvWMmSJW3IkCEu0Qhvt27dLH/+/FagQAFr166dXxdpnjhxohUpUsTy5Mlj9erVcyHm+Pr16+3dd9+13LlzW6VKlWz27Nn2xRdfxM7q1kiChUgMSbAQiSMJFiEjCf6Sq1evese3WLFi9vjjj9u8efNs165dNnz4cBdZOrUHDhxwoaXrO2nSJBfQ6dOn29ChQ61169a2Z88emzt3rjVo0MAGDBjgn/OHAbFeunSpdezY0Zo1a+b3VbNmTb/tmjVr7KOPPrLy5cv79bjOwIED7dixY7EzuzWSYCESQxIsROJIgkXISIK/BAnet2+fd35feuklW7BggS1ZssQ7toULF3Zp7d27t23cuNFjEC1atLAePXp4rGH58uV+2fjx461NmzbWpUsXW7Fihd8fn3Oc7nCHDh1sypQpdvnyZevXr58LNh+5DUJ74cIFmzx5sksw95mR06dPuzgj0vXr17c333zTSpQoEbtUCHGnSIKFSBxJsAgZSfCXEGO4cuWKHTlyxGMMixYtstWrV1vXrl1dUtu3b2+VK1e2wYMHuxzzCz9t2jQ7efKkbd++3YW2c+fOHmegM4wA0zEeO3asRyhq1arlIoxEX7t2zWbMmGH9+/e3Ro0aWZMmTbxTzOMjz4MGDfLoREaIYXBePXv2tE6dOlnx4sWtVKlSsUuFEHeKJFiIxJEEi5CRBKeBuEPBggVdNhFiBJfOLdnd5s2be+xhzJgxLsR0i1nERmd45MiRfjmxBi4/fPiwL6ojNoFA8wcCGSZigQQTt0Bma9eubU2bNvUoBMdZgEdXGKnOCsUhhEgMSbAQiSMJFiEjCU5DWgmmM3vx4kVfpEYRXSDSwMc6derYzJkzfeID0yHI9RKRqF69ugvx/v377ejRozZixAjPFCO7RCY2b97s0YupU6d6l5n8MGJNB5jjdIS5niRYiD88kmAhEkcSLEJGEpyGtBJMlpfuLpEHJkcguEQX6AAjqmSCWQy3ePFil2OyvH369PEOL4vsuKxVq1Yee+jbt693gukMc1/du3f3r7mMPyCINZlg4hPIMYKdFZJgIRJDEixE4kiCRchIgtOQVoLpzrZs2dIqVqzoAswv+bhx4zzry2WMNSMvTN63SpUqPvKMYjEdnWIuY/EaksxxxPf999934eU43V6OT5gwwR8TsS5Tpox3jj/55JPYGd0aSbAQiSEJFiJxJMEiZCTBaaBLS7SBqQ9MY0CG6ea2bdvWF6sRc2AeMJcx+YEoA91ihJT4BEUcgtsg0Hxk3BnH58+f75EJ5JgFcWyOwXFGpnEfHKfTzII78sFZIQkWIjEkwUIkjiRYhIwkOAeQEWanN0SWbi5RhjgspNuxY4etWrXKO8tIMyC27CbHRhzkheOiy2QKrsfUCeSb22cHSbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjECFmCf9poulUcttaqDF8XZM3dfjz2UxChIwkWISMJDhRJsBCJEbIEh159Fu6J/RRE6EiCRchEQoJZmHarBWUsPOPy+AK1qCAJFiIxJMHJK0lwdJAEi5AJXoKRWyYrbNy40ScufPbZZy6+THDgMja7YCc2dmSLEpJgIRJDEpy8kgRHB0mwCJlIdIIrVapk+fLls5o1a1rHjh1t8uTJdvDgQdu9e7cNHjzYypUr57N9o4QkWIjEkAQnryTB0UESLEImWAm+ceOGRyDo+FatWtVq167t2w2zNfGgQYOsfv36vkMbO7hxnI0pooQkWIjEkAQnryTB0UESLEImWAk+cuSIjRkzxqto0aK+29qCBQtcgNmRrWTJkvbaa69ZjRo1fBMKIhJRQhIsRGJIgpNXkuDoIAkWIROsBG/dutUFt2zZspYnTx4rXry41a1b10qVKmXVq1d3Ge7bt69vbTx8+HDf4S1KSIKFSAxJcPJKEhwdJMEiZIKV4EuXLnnmd+fOndajRw+X39dff93KlClj27Zts4sXL3oueOjQoVaoUCE7fvy4RyeigiRYiMSQBCevJMHRQRIsQiZYCT58+LAvemvYsKHngUuXLm21atWy+fPnW968eT0PXKVKFWvcuLGtWrVK0yGEEOmQBCevJMHRQRIsQiZYCd6yZYv/4hUpUsReffVVnw5RrVo1mz59uscjWBBHVKJ8+fLeBWYhXZSQBAuRGJLg5JUkODpIgkXIBCvBLHbr0KGDVa5c2X7xi1+4+JIJJgf87LPP+nE6xHSKZ82apekQQoh0SIKTV5Lg6CAJFiETrAQz93fevHnWq1cv7wTTEW7Xrp317NnT7r//fp8Mwefjxo1zOT5z5kzsltFAEixEYkiCk1eS4OggCRYhE6wEsyiuffv21q9fP2vTpo13fdu2betj0hiZxi8m19m0aZNnhZFmLYwTQsSRBCevJMHRQRIsQiZYCWaLZLZEPnXqlC+SIx6xf/9+O3r0qC1fvtyPcR021GBKhOYECyHSIglOXkmCo4MkWIRMsBIMdHYRXQSX+uyzz/xrxqPx9fnz512OGZnGZVFCEixEYkiCk1eS4OggCRYhE7QEs9iNbZJHjx7tMYgDBw7ELvlKkFesWOGyuGjRIo1IE0KkQxKcvJIERwdJsAiZoCWYnC8bYbBbHHlgZDfOoUOHfGFczZo1bcOGDd4hjhKSYCESQxKcvJIERwdJsAiZoCWYPHCBAgVs5syZvgiO2AMxCLq+Xbt29akQ48ePj107WkiChUgMSXDyShIcHSTBImSCl+CCBQva3LlzPQ7RsWNHnxhRoUIF69Kliy1btsxzwVFEEixEYkiCk1eS4OggCRYhE6QEHzt2zBYvXuwbY7zwwgveCUZ4e/ToYc2aNfMZwYxFIx4RpbFoaZEEC5EYkuDklSQ4OkiCRcgEKcFsgzxnzhwX3ty5c3v3d+rUqd4R5jhyTFcYUVy5cmXsVtFCEixEYkiCk1eS4OggCRYhE6QE37hxw+cBT5s2zRo3bmxVq1a1Pn362NatW30UGt3f9evXuxy3aNHCpZnbRAlJsBCJIQlOXkmCo4MkWIRM0JlgYCHczp07fXvkESNG+CYZjE5DemfNmuWSPHDgQPv0009jt7g1yDMS/fnnn/vXfGSqBJX2ONeLH6c4h3jsgsdNezwOt43PMU57/fhjcjztY2SFJFiIxJAEJ68kwdFBEixCJmgJRmwHDBhg9erVs7Fjx9ratWutZcuWVrFiRRfgPXv2+LbJ5IWzmhOMhO7bt88qV65sa9as8Q035s+fbyVKlLCSJUt6xpioBfeDdDOa7a233vLLW7dubWfPnnWBHT58uD8+9dFHH/n9AAv3qlevbu+++64v2mMTD9i1a5efP8ebN2/us42zgyRYiMSQBCevJMHRQRIsQiZYCT5y5IgNGzbM4w50gdky+dy5c75lMh1hxLRTp042Y8YMnyd8uw4rHVhkuUGDBvbMM8+4/DJbmA4yRd4YgeWXffv27b4Qj68R0enTp3vuGCHnNk2bNrU2bdq4ANepU8d27Nhhmzdv9tvy9YQJE1yoeYx4B/v999/3DT94Lpz7mTNnYmd2ayTBQiSGJDh5JQmODpJgETLBSjATIiZPnuwSSuY3DrLL6DTkks0yyA1nBfEJRBVxfu6557xri6AuXLjQTpw44REHBJkNOZYuXeqdXH7pu3fv7oJMFvny5cveleY+5s2b5x1eOrucHyLdrl07l/ZLly65nCO9o0aN8gV8HTp0cIEfOXKk3wcynRE6yuSc6XjHu83vvfde7FIhxJ0iCU5eSYKjgyRYhEzQcQjytEgvgohEMhOYzxFNpPTgwYMeicgKOsF0crl+/vz50+08x/3TmWXnOTbgIHJBt7dUqVIeYShTpowfR8Tr16/vHWA27mDhHpLLpAo27UCcuS1xCsSZTi7TLZo0aeJdYUQcwR40aJBfnhHuH3FmBjLxjBdffNF3yhNC5AxJcPJKEhwdJMEiZIKXYISXHC0RBTq3RBM2btzonVikFoFFcuML0W4H12XzjbQSjEyz6xxRBj4SrWBGMd1mcsRIa/ny5T13XKVKFe/UEtU4efKkyyxdXnLGvXr1ciHnNnSa+ZpYBBJMFIPj69atc4kmEpEVikMIkRiS4OSVJDg6SIJFyAQtwcQUPvnkE++0MiaNeELnzp19NBoL5DhO55Rf0OzkbDNKMN1Zog5FihTxri5ii1CzCC4+4eHjjz+2Dz/80OW3Ro0a3q1FvuncjhkzxiMUHOcPBXliZJeccrdu3fz8OE8W4tEhRubpHBN3yApJsBCJIQlOXkmCo4MkWIRMsBKMgCKORA+YrkAkgY7q6tWrbfDgwS6adIbJBRMdIOOLwN6OtBLMdcng0gFGWLk90s3jkeNFdOkS0wlGRrkNO9YhscQeWKiHkPMHgigEnV8mVnCb/v37+3kh7dw3nV9iHFOmTLmZM84KSbAQiSEJTl5JgqODJFiETLASTKd14sSJLp0sEkMkDxw44B3b3r17eweXritiTCc2HkW4HWklmBFmyOtDDz1krVq1sqFDh/rkCaIQiDGX9evXz7vAzCImAkEkgrwwl3F9csMsjOM2CHLDhg09tsE0COSZ4yyGQ2ZZwEemmPjEli1bYmd0ayTBQiSGJDh5JQmODpJgETLBSjDRAmSUhWlFixZ18WQiRLly5VwkkV/iDEQX6MzSab3dmDS4cOGCiygd4FWrVrncvvrqqy6tCCe70nFfdJjjj4v0Is3xfDJTILgu8QxmCNMRZtEdsss0B7rWhQsX9gkSHCcC8fbbb3s0gusjt5x3VkiChUgMSXDyShIcHSTBImSCzgTHd4tDPJmU0KhRI58QQZSBy+JFjOGbArFFlGfPnu3d6vhjI7ZEKZgTjBjHRZdz5XqMe2NMG7KeHSTBQiSGJDh5JQmODpJgETJBS3A8F0xGl93b6KjSySWiEC+6ueRu6fJ+E9BtJveLzMYXzwEfiWMg6XxMe5zrcRwxzqpbHUcSLERiSIKTV5Lg6CAJFiETrAQTPYhHDdjIonbt2j4V4o033vA8Lh1XjjO+jOhBdiIGISEJFiIxJMHJK0lwdJAEi5AJVoLZMW7SpEkuu2xawVQFJkK88sorPiOYeb5MYCCbS5c1ux3WUJAEC5EYkuDklSQ4OkiCRcgEK8FMY2AbYjabeO2113y7Yhafvfzyy7ZkyRKfsMCMXjrBO3bsyHI8WmhIgoVIDElw8koSHB0kwSJkgs4Ex2FDjCeeeMKee+45H2mWO3due+mll+ypp56yRx991De7YKOLKCEJFiIxJMHJK0lwdJAEi5CJhAQfOnTIIxBMX2BaBDOBKY7xNbvKsfgsSkiChUgMSXDyShIcHSTBImSClWCk9ty5cz6FgcVxFJ8zBYLoA1MXNm7c6LOD2UUuq40yQkMSLERiSIKTV5Lg6CAJFiETrATv27fPd2EbP368L5CL18cff2yHDx926V2zZo1vnMHYNDbNiBKSYCESQxKcvJIERwdJsAiZYCV47ty5dt999/lOa+zCxke2JW7Tpo3v4Ma2yUhw586d7bHHHrOjR4/GbhkNJMFCJIYkOHklCY4OkmARMsFK8LJly6xQoUK+4I2d1tatW+cdYDq+I0aMsCpVqviCOKZFPP300z5SLUpIgoVIDElw8koSHB0kwSJkgpXg5cuX+y5xSDDSy6g0OsE1a9a0/PnzW8mSJX1OMLKMJGtEmhAiLZLg5JUkODpIgkXIBCvBRB5eeOEFzwAPHDjQs7/MBSYOgSAOGDDAOnXqZIMGDfIFdNosQwiRFklw8koSHB0kwSJkgpVg4g9lypTxX8DBgwf7VskUG2YwHo1M8JgxYzwTzIQItlmOEpJgIRJDEpy8kgRHB0mwCJlgJfjEiRM2ZcoU69ixo0vu6NGjves7b948302OCAS7xs2cOdMqV67s2yhHCUmwEIkhCU5eSYKjgyRYhEywEswcYPLA5H+JRgwZMsQzwTdu3PD68MMPrXfv3rZ3716PTDBHmNtEBUmwEIkhCU5eSYKjgyRYhEywEgzHjx+3hx9+2AoWLGh58uTxLZLp+laqVMmeffZZnxCxdOlSO3/+vDLBQoh0SIKTV5Lg6CAJFiETdCeYsWe5cuXy3G+NGjV8WgTxB6pfv37WoEED31AjikiChUgMSXDyShIcHSTBImSClmBmArdv3962b99u8+fPt2HDhsUuNTt16pSNGjXKIxFRRBIsRGJIgpNXkuDoIAkWIRO0BDP799ChQ3b58mW7ePGinTlzJnapefyBrZU3btwYOxItJMFCJIYkOHklCY4OkmARMkFnggEZppDetJ9nrKghCRYiMSTByStJcHSQBIuQCVaCr1696p1eZJBfQnaHY9MMxqZVrFjRSpcubcWKFbPChQtb1apV03WJo4AkWIjEkAQnryTB0UESLEImWAm+du2aHT582GcEs0EGI9Hq1q1ru3btshkzZtjUqVOtTp069s4779isWbPsypUrsVtGA0mwEIkhCU5eSYKjgyRYhEywEkzEgdm/7A63e/dua9eunVWrVi126Vd89NFHLsJRRBIsRGJIgpNXkuDoIAkWIROsBNPZZVFcvBiTRgwi7bEuXbr46LQoIgkWIjEkwckrSXB0kASLkAlWgnfs2OE7xDVp0sTrjTfesKefftqaNm3qxbE333zTSpUqFbtFtJAEC5EYkuDklSQ4OkiCRcgEK8FHjx61CRMm2OTJk30xHIvf2DmOz+NFPKJChQqxW0QLSbAQiSEJTl5JgqODJFiETNBxCBbGHTlyxIvoA9slx7+munbtmu04xPXr130Huu7du9vOnTt91NrevXv9flu3bu3CvX//fj/OTOIBAwZY27ZtbciQIbZ582a/jxs3brh8d+jQwf8wLF++3KdYkF9esWKFderUyTf3mD17tm/mwX0x4SLjY2QHSbAQiSEJTl5JgqODJFiETLASjHCeO3fOtm3bZps2bbIWLVp4Nzgt2V0Yx3198skn1r9/f3vxxRdtwYIF3mkeP368j1rjvhs3bmzTp0+306dP2+LFi124mUjRrFkzF1I27OA8mjdvbjVr1rSWLVv67U6cOOEL99i5jsxymzZt/HYbNmxwic/4GNOmTXMhzwpJsBCJIQlOXkmCo4MkWIRM0J1gJkMwGxjBrFy5snd9T5486Z1c5JiObHYkmPuia1umTBl78sknfQtmRBgx7dOnj3d+mT7Rr18/W7lypeeN6eoit2PHjrVGjRp5R5cuL9dbunSprVu3zvPIW7dudRmn04vwXrhwweUVof74449dmjn/8+fP+/n27ds305nGjISjU83z2rJli0t22bJlY5cKIe4USXDyShIcHSTBImSClWCkkAkQxA+IETAvePTo0S6c+fLls+eee86effZZq1WrVuwWt4bIAhJKFCF//vy2aNEiGzFihEs1C/DYnhnZHTRokMcgihQpYkuWLHGh5WOvXr18LnHRokVt1KhRdvz4cRd0pJjOLh3qjh07ereZjjEbe4wZM8bFuHr16rZ9+3Z/DJ4D579+/frYmf2OgwcPWrdu3ez555+3Rx55xH7yk5/Y22+/HbtUiOTwOTs0Blr1JcFJK0lwdJAEi5AJVoLJ0yKORCLOnj3rRQeVrC0dWrrBCCyinBXcF5EIusgFChRwCSbriwRzf2R6kVm6zsgsUyfoyCLiq1ev9g7x4MGD7fXXX3cZZn4xwoscs5EHHWayxpwrXWdkmvuvV6+eL97jMXh8usM8xsKFC2Nn9jt4rkQr4l1uBFqdYJFMdh67aC93XRRsPdh0ZqaCpvrDlyQ4OkiCRcgEK8F/CJBoJkwgwcOGDbPatWvflGA6zkQViDu89dZb3r1FgolHILt0iBFoZBkJpqtM5xY5Rla5DhJMJ5g8L4UE06mOSzACzWPMnTs3dka3RplgkWw2HDybqeCoVFmVJDg6SIJFyERCgumc0nElisBHiiwuMnonpJVgRq+R/WWxG11YOrc9evRwSWWBG4+J1M6bN8+nRBDF4DgxByZT0LElK8zxBg0auATTob506ZJfn44vcQkeY+PGjS7UQ4cO9cdYtmxZ7IxujSRYJBtJsCqnJQmODpJgETKRkGAmNbzwwgveoSXT+/DDD3vkgPjAnZBWgletWuWdXH7B6fqyAQejzJBeog18zmI6OsAsvuP6CDJj2Yg1zJw500qUKOEL7IYPH+73xUeiDO+//75njukucxxB5jiTJtj5jjxxVkiCRbKRBKtyWpLg6CAJFiETCQlm5BgLyoARZoULF/YFa3dKWgmmy0tX98EHH/Q4Q548ebxLS3eZ8WYsumOBHPlgJJxuMYvXyP++/PLLVrx4ccuVK5dnklkox2g0drRDXJ966imbNWuW55hZDPfAAw+4GPMYCDbxi6yQBItkIwlW5bQkwdFBEixCJhISzPbJcQlGZJFgxpTdKeRy2SCDkWh8jrzOmTPH75uPCC2CiggTWSB2QTc3vrkGIkx8gmkVRDMYk8bkCeb+cr/khbkvzo3zjD8GGWA612yikZ2FfCAJFslGEqzKaUmCo4MkWIRMsBLMzNyJEye6hDKajFFjLCxDTOnSMnOXr7l8xowZPpXhTkFSEWJmANMZ5mtAeFnghrASuUi7uQXSi9iyEQZSzHWBzxFf7ovbxru98cdgIV3ax8gKSbBINpJgVU5LEhwdJMEiZIKVYHKziC4Z3Lx583r8gLgCi87IBCPF8ewuc3mZ6RslJMEi2UiCVTktSXB0kASLkAlWgum20ullAVqxYsV8cRqRBaIIbJSBHBMvYJFaTjvBdzOSYJFsJMGqnJYkODpIgkXIRG5hHJEDFqzlJBMcEpJgkWwkwaqcliQ4OkiCRchEQoLr1q3rnd+jR4/6fGB2bps/f362piyEiiRYJBtJsCqnJQmODpJgETKR6QQzxow8MLN28+XLZ5MmTfKFZlFFEiySjSRYldOSBEcHSbAImUhIMLu7sekEC+MoFsSxeUXUFsOlRRIsko0kWJXTkgRHB0mwCJlISDBbDjOCLC1sT8xiuPiIsqghCRbJRhKsymlJgqODJFiETCQkmNm7zA1OCxtVsN0xghxFJMEi2UiCVTktSXB0kASLkAlegun0durUybcfBhbDIcTMCWaxHNMioogkWCQbSbAqpyUJjg6SYBEykZDgBg0a2MCBAz0SceDAAWvZsqW99957NnTo0MjNB44jCRbJRhKsymlJgqODJFiETCTiEPXq1bNWrVrZwoULbcCAAVarVi0rX768b6scVSTBItlIglU5LUlwdJAEi5AJVoLp8B45csTr/ffft/z581ulSpWsaNGiLr90golJHD582OcH37hxI3bLaCAJFslGEqzKaUmCo4MkWIRMsBK8Y8cOa9iwoTVu3Nh+/OMf23e/+1179dVXbx5j6+Q33njDZwi3aNEicjODJcEi2UiCVTktSXB0kASLkAlWgunwjhgxwsaMGWOPPvqoSzDbJbN98ujRo+2tt96yihUr2siRI238+PE+Mi1KSIJFspEEq3JakuDoIAkWIROsBF++fNn279/vC+FKlixphQoV8gVyVatWtWHDhlmxYsWsXbt29sknn9jBgwcVhxDia0YSrMppSYKjgyRYhEwkFsYReWDL5Dlz5libNm3889KlS3unOKpIgkWykQSrclqS4OggCRYhE7wEMyKNHDAxCGYEMxe4ffv2VrNmTRs7dqydP38+ds1oIQkWyUYSrMppSYKjgyRYhEzwEkzMgU4wEhwHMW7evLmL8MyZM2NHo4UkWCQbSbAqpyUJjg6SYBEykegEHzp0yE6dOhU78hW7du2yzZs3+3i0KCIJFslGEqzKaUmCo4MkWIRM0BJM/OHEiRN2/Phx+/TTT+3q1at28uRJP7548WJbv3697yIXRSTBItlIglU5LUlwdJAEi5AJVoLZLIPJD8uXL/diAgRfDx8+3Meh9ejRQzvGCfEHRBKsymlJgqODJFiETJASTAQiPie4c+fONnDgQFu1apXNmjXLXnvtNR+dVrt2bf/lvHjxoneJuU2UkASLZCMJVuW0JMHRQRIsQiZICWYxHFGH8uXL23333WflypWzwYMH+y8jO8VNnjzZSpQoYfXq1bMFCxbYkiVLPCoRJSTBItlIglU5LUlwdJAEi5AJthN84cIFW7t2rbVu3dplkM5vlSpV7IEHHrBmzZpZ7ty5fQe5jh073uwIRwlJsEg2kmBVTksSHB0kwSJkgpXgvXv3WpcuXVyC2Rxj1KhR1r9/f3vhhRc8FvHee+/5/GBiEnSNr127Frt1NJAEi2QjCVbltCTB0UESLEImaAnu3r27/wKyAI6RaBs3bvSZwWylTBQi7ezgO4UpE2vWrLGpU6d68RjTp093wR45cqRHLjiOYNOVvn79um3atMnnEnOdrVu3xu7JbM+ePTZv3jz7+OOPbeXKlTejGYxvI6oxadIkW7Ro0e+NebsdkmCRbCTBqpyWJDg6SIJFyAQpwXEQT2Rz9uzZtm3bNp8QMXr0aFuxYoXvGod05pQtW7ZYz549vaNM5cmTx9566y0rWbKkPfTQQ/bOO+/4cbrPSDfS3LRpUytVqpRv2dytWzePYDCpguuULVvW3n33XatTp45fn8V606ZNs4oVK9rbb7/tH5ctW5bt7LIkWCQbSbAqpyUJjg6SYBEyQUsw0BUmD4xorl692nPACCJCnMhECG7LvOF49e7d23/ZJ0yYYE2aNLHTp0/7ca537tw5X4CXP39+mz9/vhdRjTlz5ngcg6xyv379bMeOHb6THR1khLddu3ZWq1Yt7yR36tTJp13s3r07dga3RxIsko0kWJXTkgRHB0mwCJlgJZgYAp1YOqg/+9nPvH75y1/aPffcYwULFvTOK5cxQaJGjRp25syZ2C3vDESXmEKrVq2sQYMGvujumWeesWLFilndunVt7ty5PpINSW7ZsqV3pIk/0JGmG81xZJc4BN3iKVOmuCDTZUZ8hw4d6ht6INF9+vSxhQsXxh45PWwIQgyD50NH+fnnn7fixYvHLhXim0cSrMppSYKjgyRYhEywEnzkyBEbO3asZ3XfeOMN78LScSW2wJg0MsGDBg3yzi2d18uXL8dueWewKcf48eP9F50xbGPGjHFZRUjpQCOzZIDbtGnjGWSiDggrUYxq1ap557dv3743s8NkgpHpRo0a+YYeSDQj35BnZh4jyZlBtILMM88Hwa5cubLHLoRIFpJgVU5LEhwdJMEiZIKPQwBSSkeVOAQxASQTQWYHuUQ5f/68yyyyTZyB++QYHeIBAwa4/CK5TKggzsAmHnR8EW+6tnSO2cxj8+bNLrKcI51pzpEuMQvikOCdO3f6fSDc2UFxCJFsJMGqnJYkODpIgkXIREKCEUiytHRaWXC2b98+n+xAVzYRWHhHtrhQoUIuq+SAuU+6w0gwY9mIOtDR5Q8BMsxjxxfo0Znu2rWrH0d+z5496zlhcsDIM/LO4jgeh8sZ95bdrZ4lwSLZSIJVOS1JcHSQBIuQiYQEsziNKRGMMGNMGTOBOUYlAtLLyDMmOmzYsMHGjRvnMQu6uogw49jo6DKdYsaMGS63xB64bq9evVx0OU6emJFqhw4d8gV8yC6dav54INBMhECaO3To4Nnh7CAJFslGEqzKaUmCo4MkWIRMZCSYvG6lSpW8A/x1bYzBAjciCogrMQi+pntLBrlw4cK++A6ZZToEHWImUyDCbOPMZexox6K6+vXr+9fI9Msvv+xijRATp+A2SHLevHn9a45nB0mwSDaSYFVOSxIcHSTBImQiIcHr1q3zBWh0aVmURsb264D4AjOHiVsQs2BxHbng4cOHexFtiEcu6Ayz6QU5X6Y/sICOeAaxCaIUiDTH+YNBbpiJEMwiZjEdxykWvmlOsAgFSbAqpyUJjg6SYBEyQUswskuHFoFkPBnRg2SC2CLMFN3hOPFsMTEKOsNxSecjkQu610y7yK4AgyRYJBtJsCqnJQmODpJgETJBSjDxB3ZioyvLGLSqVav6BAZE89ixY+mKrYm/zu7w3YIkWCQbSbAqpyUJjg6SYBEyQUowndXly5d7npZtilmwxngydnJjJFm82Ma4cePGvhCNsWZRQhIsko0kWJXTkgRHB0mwCJkgJZjYAYvO2BEuX758NmzYMF9sRk6XLG68mLjAphZIMp3jKCEJFslGEqzKaUmCo4MkWIRMkBLMYjM2pGCrYXZsY0wZcQjGo5ERTltsacziNbrHUUISLJKNJFiV05IERwdJsAiZ4BfGIbkdO3b0hXHM60WQUwFJsEg2kmBVTksSHB0kwSJkgpbgOHv37vV5vmxvzEK4qC2CywxJsEg2kmBVTksSHB0kwSJkIiHBTItgtzjmBLNT28WLF2OXRBdJsEg2kmBVTksSHB0kwSJkIiHBwBg05vDu2rUrcvnfzJAEi2QjCVbltCTB0UESLEImEhLMVsOLFy+2UaNG+Q5sTIuYMmWKL5Rj17YoIgkWyUYSrMppSYKjgyRYhEzQEsyoNHZbmzBhgssvWxZ369bNOnXq5NWjRw+XYbY8JjIRJSTBItlIglU5LUlwdJAEi5AJWoLZmrh69erWqlUrl92tW7f6tIjt27f7pAguK126tG9jrBFpQny9SIJVOS1JcHSQBIuQCVqCmRX88ssv2/z58300Gt3eePH1xx9/7DvG8fHy5cuxW0UDSbBINpJgVU5LEhwdJMEiZIKWYLZC/vDDD61y5co+K3jq1Km2aNEimzNnjvXr188qVKhgtWrV8kVzURubJgkWyUYSrMppSYKjgyRYhEzwmWC2Tx48eLB17drVunfv7r+Qffr0sf79+9vQoUNdiqM4N1gSLJKNJFiV05IERwdJsAiZoCU4DhngESNGWPPmzX1WMBEIJHHdunWRi0HEkQSLZCMJVuW0JMHRQRIsQiZoCSb3e+zYMVu4cKFLIQvk6tevb3Xq1LEWLVp4J3jDhg3eMdZ0CCG+XiTBqpyWJDg6SIJFyASfCW7UqJE1bNjQhXfVqlU+IWL16tU2ZswYK1u2rJUsWdIOHjyoTLAQXzOSYFVOSxIcHSTBImSCluBTp05ZwYIFbdKkST4pgnnAxB/4ePr0aRfjunXr2rx58+zKlSuxW0UDSbBINpJgVU5LEhwdJMEiZIKW4LNnz/ovH1lgOr/Lly/3XeJYLMdYNLrESHAUt1KWBItkIwlW5bQkwdFBEixCJmgJpruL7LZu3dozwPwysnPcwIEDfVoEx4cPHx45AQZJsEg2kmBVTksSHB0kwSJkgpbgOOwIN3r0aJdeJkPwcdSoUT41IooCDJJgkWwkwaqcliQ4OkiCRchEQoKZAIEUEn0oX768L4gjCsFWyidOnIhdK1pIgkWykQSrclqS4OggCRYhE7QEswCOjTE6derkG2bMnDnTF8FNmzbNBg0a5LvFMTlCO8YJ8fUjCVbltCTB0UESLEImaAk+c+aMvfvuuy7ARB/o+rJYjo+7d+/2HeSqVavmC+auXr0au1U0kASLZCMJVuW0JMHRQRIsQiZ4CS5VqpR3g1esWOHie+DAAdu/f7+tX7/eunXrZg0aNPBpEdeuXYvdKhpIgkWykQSrclqS4OggCRYhE7QEX7p0yWWwYsWKvktcv379fEEc84FZHMfxtm3b5njHOOIWLLrbu3ev7du3z2cRX7x40Xep4xibcFy4cMGvy+51zC3+5JNPvJhTHOfcuXN+Xe6D28ajGZz/kSNH/L4OHz58R7OMJcEi2UiCVTktSXB0kASLkAl+YRzTH4hCMCe4ffv2vnVy586dfQMNOsMIcE5AaufOnWs/+tGP7LnnnrNcuXK5UM+ePdu7yy+88IIVL17cpk6d6tdHaLt06WJvvPGG5c+f33r16uXHATEvUaKE5c2b1+rVq+cdbFi0aJFVrlzZnnnmGStXrpx3r7OLJFgkG0mwKqclCY4OkmARMsFLMGzevNkXwn344YdWpUoV/4VEWOfMmXNTOO8UurrMIK5QoYItWbLENm7c6JKK0L799ts2f/5869Gjhz/uunXrbM2aNS66w4YN80KI2b6ZbZyR5g4dOviCvSZNmtiCBQv8nBHl6tWre2aZOccTJ060Q4cOxc7g9kiCRbKRBKtyWpLg6CAJFiETtAQTH6ATywYZyOiIESO8+JxfzJYtW3pemMVydHbvhG3btt3s7CKoAwYMcLlFXJFt5Hrx4sX+2P3797chQ4Z4JINxbVu2bPGveWxu06xZMz/Po0eP+uYdHGcxX8eOHf08WbQ3efJkfwyyzZnBc0CeyTm3a9fOihUrZiVLloxdKsQ3jyRYldOSBEcHSbAImaAlGDFkLjAd2aVLl/qCOESTTO6qVatcPunkIqZ3ujAOkY3/ciO9dF2ZNEFHF5ElL7xnzx6X2fr167uYkkmOnwPSW7t2bY9ncD90is+fP2/Lli3zDT04N4SWsW5EOugMs8sd3eLMIGPMdRF7xr4VKFDAO89CJAtJsCqnJQmODpJgETJBSzCRhYIFC9qECRNcPJFiFqohm4xJoyvMphlEF+5k0RkwW3jHjh3+GHSRe/bs6dEFZhIjuJcvX/boAp1gIhjILlEJFrhxG2QWQUd4uQ5SjTgzqaJGjRqeDeaPB1ELFsqRX0akx48fHzuD26M4hEg2kmBVTksSHB0kwSJkgpZghJfsb9GiRb1LSwyCXeLGjh3rndbChQu7cCKsdzodgu4s3eP47Ygr0AWme4uoshCOTnDfvn39DwCL8YhAMAUCIUfMWezWpk0bF1a60cg50su5IsfEIhD0eCcYkR43bpw/XlZIgkWykQSrclqS4OggCRYhE7QEI6nECxBUcrlIKjlbRLV58+YeW2D8WE7Go7HzHPlfbs/jILNEK1jYRkaYrjOZYDbk4HGRXsQWmWUxHOfTtGlTl1qmVsyYMcPlOJ4RJkbBHw9ywNw/8s71Zs2aFTuD2yMJFslGEqzKaT3VZq7l77U0yPpgyBq7ePV67LdASIJFyAQtwczsJZ7AYjK6s3RYq1at6jLJ6DHElWxwTmDiAwvj2HoZ6a1UqZJndplBTIeZrnPNmjW9e8uoMxbSsVCN8yG3y2UILd1iIhnkiolUsLkH49yIRyDKiCyyXqZMGevdu7dHMLKDJFgkG0mwKhULgT97KWejN6OIJFiETCQywUQMyOOWLVvWF6cx2ixthjcnxKMLdevW9SL2sGnTJpdUpJZuLsKNwLIZBkJOR5juLwvi+JzzI+rAdeggMyqNc2IDDjLKTHuge8xt2NiDaAS54ewgCRbJRhKsSsWSBKdHEixCJngJfv311z1KQCaXBWrx3dgYO0YsggjD1wmL5MgiI6x0cxFgIHLBYzIFgmJ3uThs2IE8E59g4Vz8HBFkdoxjAw46xmSXs4skWCQbSbAqFUsSnB5JsAiZoCWYCQ6PPfaYxxDoCJcuXdrlE1FlVBkd1q9bggHhRWR5nIx5Y47d6ji3yXg87X3dCZJgkWwkwapULElweiTBImSClmA6rHRd2d6YuAIRCBal0VElb0sUgkhDFJEEi2QjCValYkmC0yMJFiETtAQDnVQiCcQJtm/f7p1g5JgFcWxzTHQhikiCRbKRBKtSsSTB6ZEEi5AJXoJTFUmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4Fvw2Wef2fr1661WrVpWo0YNq1evns2cOdNWr15tRYoUsUqVKvkv/tChQ+3o0aN25coVGzVqlNWtW9fq169v48ePj92T2dy5c6158+ZWvXp16927t124cMGPb9iwwTp16mQVKlSwdu3a2a5du/x4dpAEi2QjCValYkmC0yMJFiEjCb4F+/bts3HjxlmbNm1s+PDhLsN8jsQWLFjQ+vfvbyNGjLDly5fbsWPHbPv27S7G7du3tw4dOljXrl1dag8cOGCtW7e2hg0bWs+ePf3j2rVrbf/+/TZ48GD/44HQNmjQwGbMmGGnTp2KncHtkQSLZCMJVqViSYLTIwkWISMJvgV79uyxBQsW2NatW70r3K1bN6tatarVrl3bSpcu7YK8aNEil9zjx49757d8+fK2atUqW7NmjfXr18/lecqUKd4ZHj16tF+3T58+NmTIEJs4caLLMh1gush0lAcNGuTd58y4dOmS7dixw+bMmWPTp093KS9TpkzsUiG+eSTBqlQsSXB6JMEiZCTBWfDFF1/Y1atXrUWLFlalShWPReTOndveeOMNe+edd1x0N2/e7ELbq1cv27t3rx0+fNgmT57s3V26xz169LCVK1fauXPnXJyJRrRs2dK7xVOnTrXr16+7/Hbv3t0jF5lB5AJJLlasmL3++uv25JNP+uOLsDl58artO/lpkDVt09FMJUGlinJJgtMjCRYhIwnOArrA69at86hDs2bNPBOM6J4/f97Fl6gDIozUjhw50gWYSAPRBuIKjRo1soEDB9qWLVvs008/9fuii4tM88djyZIlduPGDe88E6WYMGFC7JHT8/nnn9u1a9e8I8z9cFs6zyJs6o/fZPc2nB5k3fPhtEwlQaWKckmC0yMJFiEjCb4NdGgPHTrkMkuMgYVsdHORUTrERBwQVzq6CPGwYcP8+mSEJ02a5JKKHCPBGzdu9AVxZIirVavmcky+mMgFEkzsAqFOu6DudigTHA2qj1qf6X+0KpXq7ixJcHokwSJkJMG3gM4r3dmOHTu6sNIBXrFihccckFwEmYVuxCToBFPke1kgx4I4ogtkgVn8hiTPnz/fTpw44ZLL4jgEmGJxHVJN1rdt27Y2bdq02BncHklwNJAEq1RhlSQ4PZJgETKS4Ftw8uRJF9QnnnjCRRd5RWYZc0ZXmIVtfM6xTZs2+YI4Or/cBvFt2rSpf07Wl8+7dOni+d86derYgAEDPAbRt29fj0UsW7bMGjdu7Jlg4hLZQRIcDSTBKlVYJQlOjyRYhIwk+BYgtixge/TRR61QoUL29ttve5aXLu7LL7/shdAuXrzYr3/27FmX4IoVK/qCtcqVK3s+mEwxHWImOZQrV87y5cvnoku2d+zYsfbuu++6TOfJk8cnThC3yA6S4GggCVapwipJcHokwSJkJMG3gJwuo8tYAHfx4kVfjHb58mUvvqb4nFgEEJ84ffq0xxpmz57ti+c4BtwHnWKiFGR/mTZBphgRJj5Btpixaog0x7ODJDgaSIJVqrBKEpweSbAIGUnw1wjSSyc3vnguDseRZiQZsY6LLh/5mqwwQox4ZxdJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVW3ddohjWZtMVaT9sWbI1dcyj2FyhxJMEiZCTBgSIJjgaSYJVK9U1XmY9Wxf4CJY4kWISMJDhQJMHRQBKsUqm+6ZIEC/EVkuBAkQRHA0mwSqX6pksSLMRXSIKTzL59+6xdu3ZWrVo169atm61fvz52ye2RBEcDSbBKpfqmSxIsxFdIgpPIiRMnbMqUL/8glSljvXv3tiZNmtjo0aPt/PnzsWvcGknwVxw4fcnaTNsWbOXptCDT/6RUKpXqD1WSYCG+QhKcRNauXWudO3e2Fi1a2NmzZ23IkCHWv39/27p1a+wat0YS/BXL957O9I+8SqVSqTIvSbAQXyEJTiIzZszw7u/cuXPt8uXLtmTJEhs8eLB9/PHHsWv8jhs3bniH+OjRo3b48GHr1KmTlShRwo4cOZJwHTp0yCuzy+72mrp8i/1PlSG3rO9XGuSV2WWh1n9XHmLfqzjoy4+DM7089PrqZxat58bP6nsVP4rkzyyqz+2r58XvWeaXh1zFu023gwcP+v8lmf1dvZNq27atVa5cOfY/lRBhIQlOIlOnTnUJ3rhxo127ds3WrVtnH330kY0cOTJ2jd/BH6s+ffrYq6++as8//7z95Cc/se985zv+eaL16KOP2uOPP57pZXd7PfPsc/bQ40/fsn740wftR/c/lOllodaDjz9l/3PPfXbvg49menno9b/33G8/efCRTC8Lte5/5An73g9/Yvc9/Himl4dcP3vkSfv+D++1+34ered270OP2n//+D574LFfZHp5yPXgl/8eH3roIXv22Wcz/bt6J/XTn/7UihUrFvufSoiwkAQnkenTp3sUYs2aNXb16lVbuXKl9evXz4YPHx67xu+4cuWKffLJJ36dpUuX2oIFC2zevHn+eaJVsmRJq1mzZqaXhV6lS5e2qlWrZnpZqLVo0SLLmzevtW/fPtPLQ698+fJZmzZtMr0s1BozZow9+OCDHnnK7PKQa/z48fbII4/4C/jMLg+1unfv7pI3e/bsTC8PuXr16mXPPPOMvxuZ2eV3UgsXLrQNGzbE/qcSIiwkwUlk2bJl1qVLFxs3bpx9+umnNm3aNOvRo4dNnjw5do1vhjp16ljXrl1jX0WLBg0aWIcOHWJfRYPr169b4cKFbdKkSbEj0YKu0tixY2NfRYNdu3b5uy286xM19u/fb08//bS/mI8Ss2bN8nfesrNQOTRooPBC+vTp07EjQqQmkuAkwni0oUOHWo0aNWzx4sXWsmVL69ixo8civkkkwWEhCQ4PSXB4SIKFiD6S4CRCDjj+1jZv2b/55pv+FtylS5di1/hmaNy4sa/wjSLNmzf372mUQIJLlSqV6QLKKPD+++9HTvD37NljL774om3evDl2JDocOHDAXnrppWzPOA8FRLFIkSJ24cKF2JHowP87BQoUsDNnzsSOCJGaSIKTyBdffOHCS5eIzCDxCGYHc/ybBJmiEx1FyLyRWYsSn3/+ub+DsGXLltiRaEEmftOmTbGvosGpU6f8xRjTXaIGItWzZ0+fMBMldu7caQMHDvT1GlGDF2WM4/ymGy5C3G1IgpMMwktHGPm9ePGij0L7puE/6HPnzsW+iha83ccM5ijBv5ljx455jjyKRPG5ffbZZz6Sit/1qME7Ewhw1GSRsZWMAONFZ9SIP7dk/H8jxN2EJFgIkXQQKV6I8a4IL1r4WgghhPhDIgkWkYWuGxnM3bt3x46EDR0p3nomukIxnmjv3r3Bd6roRvE8Jk6c6DOyWRTHW9FREmG69/ExiHSEQ4fnw86WM2fO9HGNFLPMo9Tp5sUYCxl5XqF3ufldYgEj//74Wc2fP983aVq9enUkF/4JkV0kwSkM/5Hxh/748eN28uTJyLwFzfPijz5dxWrVqvkYuijAzwfxLVSokBUtWtQ/MlKPGE3IsPAI+WURUrdu3XyRFXnFKMVYkKjt27f7YqRhw4bFjoYLz6dZs2Y+8YJ/hxRzz6MybYC/H6zRYMEyayZCf15kf0ePHm0VK1b0n9Urr7ziEz0qVaqUrW36hYgqkuAUhlwY/5EVLFjQypUr538kowD/gSH2/IFnIDybSkQBFsKxIQGTE8hgsoNg69at/T/rkKFTT2eK58F/1myUwaYx27Zti10jfPh5VahQwXdnZGv00OFnxr8/fk68WKEQ46jkZ9mYiEVx5cuX93dfQn9eNAbYcImuLz8rtuhH8Onka0KESGUkwSkKfwh5O4w939nFiv/M2AOexRKhvw3N+fOHffny5S4eUZmBTMeUt9JZyEiEgLF2jIBbu3Zt7BphQoebnxeLQ5kKUbZsWZ9+EZWuIs9jzpw5PvqNHchGjRoVuyRcmKHLi8zXX3/dqlev7rO4EUdkK3T43Ro0aJC/28JOmrxAi9LCYV5oMv6NrjB/T0L/ey9EIkiCUxTyYXRIKd6m5W123ormjyMd4pCha0NXimrSpEnk5gQjGozaoovfrl07l8coQPeenxVv17KLIj+/0OHfIrlLtkdnDCKbnERhIxAy6bxw5gUmPzPmVhOH4AVa6PAORKNGjey9997zd8cY/8aoxaiMgOMdJSSfF9EakSZSHUlwisIf+ipVqvhb68jHjh07fD4rWcwoLZSI2mYZ8bc1ydAi+MhiVEDmeYudt6DplpJTDx3eWRkxYoTVr1/ff6/ockdBgtkgAymki8/fD3a9RKqiEGFBfBs2bGh9+/b1Til/E/k7EpV54xMmTLBWrVr5z0pdYJHqSIJTFBZDfPDBB/5WH9EIVufzx59tm/k6KkRNgunS87MrXry4v2iJws8KqSfqEX8HgsV+vXr18g5q6PAiE+Hgd4vufYkSJTxrGvoiVF6gEBFAooh7EIfo1KlT8NEc4N8f74rx749pF0R0atWqZePHj49dI1x4d4UXK/Xq1YtEdEWIRJEEpyhEIMjyke3jLUw6wSzY4T+zKC2UiJIE89Y6I9/YXnvAgAG2b9++SPxHRjadrhuLdICIR+/evSOxaxxxgVy5cvnW6K+99pp9//vf9+kXZJ5DhsWLLNKkI0wWmGww8Qj+TYYOL1j4ufHvkckrxFg+/PBD/1sZOryA5gUmv19CCElwysJ/XnQ7kA+6wCtWrLDOnTt7VkxxiLsTBIP/nBEpcrMsaqRrFXr3jbeceQFGBpO31Vmww1gqusOhw8+MBZrxyp8/v7/bEvqs4EWLFnkch842k2V4V4nOaejrCQCp5+8ii2p//etfe46bsXah/8yA+BR/D+MvOIVIdSTBKQqiy39k/OdFZ4C3bJmpu27dukgsSIrDc1y1alXsq7AhM0vXlMWMdIJ5wTJt2jR/ERMybClMh4opJfERcIhIFOHnFYXcLDEcJl7QUfztb3/rn0clRsW/x/Xr13uWm3+PPD9mjkdhI5ANGzb438OoLPITIlEkwSkKY4DI8rEAhEU7jAJiRBqrhZUVE0IIIUTUkQSnMMgubzmzSQFvZUZpQZwQQgghxO2QBKc4iDBv/1FR2e1JCCGEECIrJMFCCCGEECLlkAQLIYQQQoiUQxIshAgCojsUsR02m1B8RwghRCJIgoUQdy3xHckYT8WmLhSLOZlrzZi/zESYWbVIMhNQAHFm0wMqI9wv98dYQD5yn9yejDwj6fiYER6TDWXYEpktg9PWsWPH/CPnzeMKIYS4e5EECyHuSpDY3bt3W6VKlXxDEGZZU2w68cwzz/gMaEb6ZWT69Ok2cuRI36YYEFK2Kmbea0aYm8rmAdwXm8ewYyKzfJlbXKRIEd9JMaPMsmVw3bp17cknn/Sd0tLWCy+8YK+++qrPOY7CXFkhhIgykmAhxF0J8slQ/6ZNm7qQsnUtG4R06tTJvvvd71rx4sV96+9atWq5HK9Zs8almN2+ENv47mVsNc3l3I5dvyguo/vLxgHMx2bnvfhudb/5zW9s4cKFLrVsL855xAvoTLNb3w9/+EP75S9/ma4eeOABe/rpp23//v2SYCGEuMuRBAsh7kqINDC/+v3337f777/fmjVrZv369bMyZcpYixYt/HN29GrTpo3vdshOc2xJjByXKlXKZXjWrFnWrl07K1++vAszcswGMXSAiTsgu0j0Sy+95B1ctgFu1KiR3+bZZ5+11q1b+3bio0eP9qgDInzu3Dm/vGDBgi7Daevdd9/17Z8PHz6caZRCCCHE3YMkWAhxV0K2lmjCr3/9axdUhJQqWrSoRx4WLFjgndr58+d7jGHcuHHehY3LKULKbekiI8mIa5MmTTxKwe3p1nL/CDMdXKT3nXfecckuVKiQV9myZe3ll192gWbr3AMHDrg40z2mc9yyZct0xe6LderU8ftnO+vM4hpCCCHuDiTBQoi7Ejq169at83wtnV+qffv2vsX3r371Ky+O0fGlGzxlyhQX18GDB9umTZs8A/z22297xIEuMYvqiEJUqFDBli5d6lGLqVOn2gcffODdYT6WK1fOJTpv3rze/V25cqXf/4gRI3xHxTFjxty8zltvvWXFihVzyaZ4LASdcyhcuLANHz7cH0MIIcTdiSRYCHFXwhQGsrsscCOuQKQBIY3HICgWvBFXQIaJPjzxxBNeSCy3qVevns2bN8/lmdvRyaXTS8yCyMLOnTtt9uzZ1qBBA5s4caJ3eYlMvPnmmx6/GD9+vD/OjBkzbp7Pxo0bvaNM7KFx48Z+f6VLl/YOcNWqVf1zJJsJEvEJFUIIIe4+JMFCiLsSBHLPnj0eRShZsqRLJhMckFK6tNSQIUM8CsHiOeIRyCuxh8mTJ1uXLl0838uECW7H4jjklMwwIstxOrzEIR5//HGXV+IQdIXpHPN58+bNvaNLZzkOMQdkl+kQb7zxhv3iF7/wz+lMv/jiiy7f69evVxRCCCHuciTBQoi7EuILc+fO9ZwtEks3l4VvdGqJLtAZJiNMPhdxXbZsmQsuAssMX0SYTi2RhMWLF3s3lw4wMYZt27b5/ROhoKNLTphRbIgvUySIYBB7IN6AKNPVjUOkAqEm9oCc58qVy0ejEYGIZ4q5/ytXrsRuIYQQ4m5EEiyEuCshBrFkyRKfCzxq1Cjr2bOnxyHoBCOuLFpDjun4khNmlnCBAgU8H0y0AZmlE4wEM2mCzTLo/ubLl8/n/wJCy0xhus2INB/JEsc70Iw942tuH4fFeF27dvXFd1WqVLHXXnvN7xP5pUOMtJNlVidYCCHubiTBQoi7FsaMIcNMXmCWL5ta0KWl04vUMuGhf//+3hVmegMTHognMNGBikswM3sZbcZOc3Rt6dQy7oxuLcI7YMAAF2imUJAvpmtMlxe5JV7BrGE23eB8iGEQoUCQn3rqKbv33nvtnnvusccee8wfn4gEos45amtnIYS4e5EECyHuWvbt2+cRA+IPLGCju0pWmEIwiUeQxa1du7YLLTOFhw0b5t1aFrXRFUZGiUGw2QbiyiQHOsIscmMxHdMiWBjHxhlcjy4vnWaiGHSXEWkKWSZLTEwiPp0id+7c9vDDD9vPf/5zF+D48VdeecVjGewuJ4QQ4u5EEiyEuGtBehlThnyS4Y3v2haH7i9Z4HhnlwVsbGrBbnAIKLLL53STuR4j0RDbuExzXXaa4/ZEHigWviHDjETjegg12yhzGd1kFr0R0eC8+Eh3muL+OUa3mc+Rbx5bCCHE3YkkWAgReYgx0PnNuFgNcc4YWeBYRtkWQggRPSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAshhBBCiJRDEiyEEEIIIVIOSbAQQgghhEg5JMFCCCGEECLlkAQLIYQQQoiUQxIshBBCCCFSDkmwEEIIIYRIOSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUgyz/w+pIh3FACiA0gAAAABJRU5ErkJggg=="
- }
- },
+ "attachments": {},
"cell_type": "markdown",
"metadata": {},
"source": [
@@ -49,15 +18,17 @@
"在对数据进行预处理时,经常加入新的操作或改变处理策略,此时如果伴随着随机操作,最好还是指定唯一的随机种子,避免由于随机的差异对结果产生影响。\n",
"\n",
"---\n",
- "# 离散型随机变量\n",
- "## 二项分布\n",
+ "\n",
+ "## 离散型随机变量\n",
+ "\n",
+ "### 二项分布\n",
+ "\n",
"二项分布可以用于只有一次实验只有两种结果,各结果对应的概率相等的多次实验的概率问题。比如处理猜10次拳赢6次的概率等类似的问题。\n",
"\n",
"二项分布概率函数的代码表示:binom.pmf(k) = choose(n, k) p\\*\\*k (1-p)\\*\\*(n-k)\n",
"\n",
"二项分布概率函数的数学表示:\n",
- "\n",
- "\n",
+ "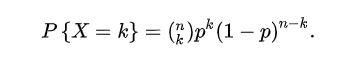\n",
"\n",
"\n",
"- `numpy.random.binomial(n, p, size=None)` Draw samples from a binomial distribution.\n",
@@ -65,6 +36,7 @@
"表示对一个二项分布进行采样,`size`表示采样的次数,`n`表示做了`n`重伯努利试验,`p`表示成功的概率,函数的返回值表示`n`中成功的次数。\n",
"\n",
"【例】野外正在进行9(n=9)口石油勘探井的发掘工作,每一口井能够开发出油的概率是0.1(p=0.1)。请问,最终所有的勘探井都勘探失败的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -90,10 +62,12 @@
"print(np.around(s, 3))\n",
"# [0.387 0.387 0.172 0.045 0.007 0.001 0. 0. 0. 0. ]\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"\n",
"【例】模拟投硬币,投2次,请问两次都为正面的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"from scipy import stats\n",
@@ -112,7 +86,7 @@
"print(np.sum(x == 1) / size) # 0.49874\n",
"print(np.sum(x == 2) / size) # 0.24972\n",
"\n",
- "plt.hist(x, density=True)\n",
+ "plt.hist(x)\n",
"plt.xlabel('随机变量:硬币为正面次数')\n",
"plt.ylabel('50000个样本中出现的次数')\n",
"plt.show()\n",
@@ -121,7 +95,8 @@
"print(np.around(s, 3))\n",
"# [0.25 0.5 0.25]\n",
"```\n",
- "\n",
+ "\n",
+ "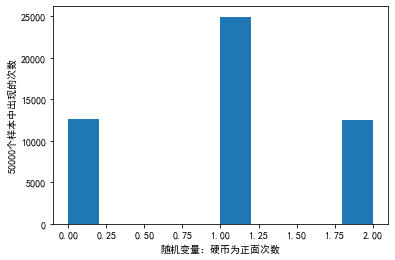\n",
"\n",
"```\n",
"#计算期望和方差\n",
@@ -132,14 +107,16 @@
"moments参数中:m为期望,v为方差\n",
"'''\n",
"```\n",
- "## 泊松分布\n",
+ "\n",
+ "### 泊松分布\n",
+ "\n",
"泊松分布主要用于估计某个时间段某事件发生的概率。\n",
"\n",
"泊松概率函数的代码表示:poisson.pmf(k) = exp(-lam) lam\\*k / k!\n",
"\n",
"泊松概率函数的数学表示:\n",
"\n",
- "\n",
+ "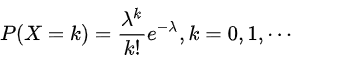\n",
"\n",
"- `numpy.random.poisson(lam=1.0, size=None)` Draw samples from a Poisson distribution.\n",
"\n",
@@ -171,13 +148,14 @@
"print(x) # 0.14900277967433773\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
- "## 超几何分布\n",
+ "### 超几何分布\n",
"\n",
"在超几何分布中,各次实验不是独立的,各次实验成功的概率也不等。\n",
- "超几何分布概率函数的数学表示:\n",
+ "超几何分布概率函数的数学表示:\n",
+ "\n",
"\n",
"\n",
"- `numpy.random.hypergeometric(ngood, nbad, nsample, size=None)` Draw samples from a Hypergeometric distribution.\n",
@@ -219,7 +197,8 @@
"# [0. 0.004 0.048 0.199 0.358 0.286 0.095 0.01 ]\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"```\n",
"'''\n",
"超几何分布的均值与方差\n",
@@ -233,15 +212,17 @@
"```\n",
"\n",
"---\n",
- "# 连续型随机变量\n",
"\n",
- "## 均匀分布\n",
+ "## 连续型随机变量\n",
+ "\n",
+ "### 均匀分布\n",
"\n",
"- `numpy.random.uniform(low=0.0, high=1.0, size=None)` Draw samples from a uniform distribution.\n",
"\n",
"Samples are uniformly distributed over the half-open interval `[low, high)` (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by `uniform`.\n",
"\n",
"【例】在low到high范围内,创建大小为size的均匀分布的随机数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -265,7 +246,8 @@
"print(b - a) # 0.4\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"作为`uniform()`的特列,可以得到`[0,1)`之间的均匀分布的随机数。\n",
"\n",
@@ -315,6 +297,7 @@
"\n",
"\n",
"【例】若`high`不为`None`时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -340,10 +323,10 @@
"```\n",
"\n",
"\n",
- "## 正态分布\n",
+ "### 正态分布\n",
"\n",
"标准正态分布数学表示:\n",
- "\n",
+ "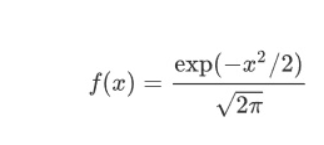\n",
"\n",
"- `numpy.random.randn(d0, d1, ..., dn)` Return a sample (or samples) from the \"standard normal\" distribution.\n",
"\n",
@@ -377,7 +360,7 @@
"print(y3) # 0.9973002039367398\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"还可以指定分布以及所需参数来进行随机,例如高斯分布中的mu和sigma。\n",
@@ -385,13 +368,14 @@
"- `numpy.random.normal(loc=0.0, scale=1.0, size=None)` Draw random samples from a normal (Gaussian) distribution.\n",
"\n",
"`normal()`为创建均值为 loc(mu),标准差为 scale(sigma),大小为 size 的数组。\n",
- "\n",
+ "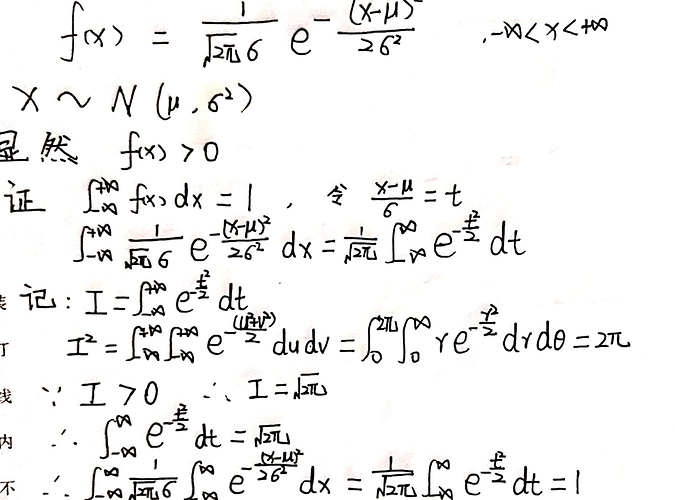\n",
"\n",
"```python\n",
"sigma * np.random.randn(...) + mu\n",
"```\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -424,22 +408,27 @@
"Means Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.\n",
"'''\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
+ "\n",
"```\n",
"plt.hist(x, bins=20)\n",
"plt.show()\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
+ "### 指数分布\n",
"\n",
- "## 指数分布\n",
"指数分布描述时间发生的时间长度间隔。\n",
"\n",
- "指数分布的数学表示:\n",
+ "指数分布的数学表示:\n",
+ "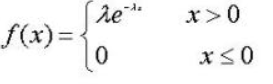\n",
"\n",
"- `numpy.random.exponential(scale=1.0, size=None)` Draw samples from an exponential distribution.\n",
"\n",
"【例】`scale = 1/lambda`\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -470,18 +459,21 @@
"print(y3) # 0.950212931632136\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"---\n",
- "# 其它随机函数\n",
"\n",
- "## 随机从序列中获取元素\n",
+ "## 其它随机函数\n",
+ "\n",
+ "### 随机从序列中获取元素\n",
+ "\n",
"- `numpy.random.choice(a, size=None, replace=True, p=None)` Generates a random sample from a given 1-D array.\n",
"\n",
"从序列中获取元素,若`a`为整数,元素取值从`np.range(a)`中随机获取;若`a`为数组,取值从`a`数组元素中随机获取。该函数还可以控制生成数组中的元素是否重复`replace`,以及选取元素的概率`p`。\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -503,7 +495,8 @@
"x = np.random.randint(0, 10, 3)\n",
"print(x) # [2 0 1]\n",
"```\n",
- "## 对数据集进行洗牌操作\n",
+ "\n",
+ "### 对数据集进行洗牌操作\n",
"\n",
"数据一般都是按照采集顺序排列的,但是在机器学习中很多算法都要求数据之间相互独立,所以需要先对数据集进行洗牌操作。\n",
"\n",
@@ -514,6 +507,7 @@
"对`x`进行重排序,如果`x`为多维数组,只沿第 0 轴洗牌,改变原来的数组,输出为None。\n",
"\n",
"【例】洗牌,改变自身内容,打乱顺序。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -584,71 +578,17 @@
"\n",
"\n",
"---\n",
+ "\n",
"**参考文献**\n",
- "- https://www.jianshu.com/p/63434ad5ea64\n",
- "\n"
+ "\n",
+ "- https://www.jianshu.com/p/63434ad5ea64"
]
},
{
"cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:02.029113Z",
- "start_time": "2020-09-15T01:02:02.026084Z"
- }
- },
+ "execution_count": null,
+ "metadata": {},
"outputs": [],
- "source": [
- "dic={1:('I','V'),2:('X','L'),3:('C','D'),4:'M'}"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:09.390007Z",
- "start_time": "2020-09-15T01:02:09.379035Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'M'"
- ]
- },
- "execution_count": 2,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "dic[4]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:29.206128Z",
- "start_time": "2020-09-15T01:02:29.201134Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'I'"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
"source": []
}
],
diff --git a/LanQiao/readme.md b/LanQiao/readme.md
new file mode 100644
index 0000000..1ba4e99
--- /dev/null
+++ b/LanQiao/readme.md
@@ -0,0 +1,52 @@
+# 编程实践(蓝桥刷题94道)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/LanQiao
+
+## 基本信息
+
+- 学习周期:14天,每天平均花费时间2小时-5小时不等,根据个人学习接受能力强弱有所浮动。
+- 学习形式:练习
+- 人群定位:有一定编程基础,对学习算法有需求的学员。
+- 先修内容:[Python编程语言](https://github.com/datawhalechina/team-learning-program/tree/master/PythonLanguage)、[数据结构与算法](https://github.com/datawhalechina/team-learning-program/tree/master/DataStructureAndAlgorithm)、[编程实践(LeetCode 分类练习)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeClassification)
+- 难度系数:中
+
+## 学习目标
+
+每天刷三道题,利用14天对于蓝桥杯这个比赛有一个初步的了解,掌握基本的蓝桥杯赛题解法。
+
+
+
+## 任务安排
+
+### Task00:熟悉规则(1天)
+- 组队、修改群昵称
+- 熟悉打卡规则
+
+### Task01:热身练习(2天)
+- 完成热身练习文件夹中的7道题目
+- 熟悉基本输入输出及蓝桥杯的练习系统的使用方法。
+
+### Task02:基础练习(3天)
+- 完成基础练习文件夹中的7道题目
+
+### Task03:基础练习2(3天)
+- 完成基础练习2文件夹中的8道题目
+
+### Task04:真题练习(3天)
+- 完成真题练习文件夹中的10道题目
+
+### Task05:真题练习2(3天)
+- 完成真题练习文件夹中的7道题目
+
+
+## 开源贡献者
+
+韩绘锦:华北电力大学
+
+- CSDN:https://blog.csdn.net/weixin_45569785
+
+黄建国:华北电力大学
+
+荆宝加:华北电力大学
+
+吴丹飞:华北电力大学
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/01字串.md b/LanQiao/task1热身练习/01字串.md
new file mode 100644
index 0000000..d1587cf
--- /dev/null
+++ b/LanQiao/task1热身练习/01字串.md
@@ -0,0 +1,79 @@
+## 01字串
+
+**问题描述**
+
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
diff --git a/LanQiao/task1热身练习/1083、Hello,world.md b/LanQiao/task1热身练习/1083、Hello,world.md
new file mode 100644
index 0000000..c031a2d
--- /dev/null
+++ b/LanQiao/task1热身练习/1083、Hello,world.md
@@ -0,0 +1,53 @@
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1083.html
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
diff --git a/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
new file mode 100644
index 0000000..442dd80
--- /dev/null
+++ b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
@@ -0,0 +1,218 @@
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1084.html
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/1095、3n+1问题.md b/LanQiao/task1热身练习/1095、3n+1问题.md
new file mode 100644
index 0000000..2f8c997
--- /dev/null
+++ b/LanQiao/task1热身练习/1095、3n+1问题.md
@@ -0,0 +1,72 @@
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/2080、十六进制转八进制.md b/LanQiao/task1热身练习/2080、十六进制转八进制.md
new file mode 100644
index 0000000..a80f5b6
--- /dev/null
+++ b/LanQiao/task1热身练习/2080、十六进制转八进制.md
@@ -0,0 +1,168 @@
+## 十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2080.html
+
+**题目描述**
+
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+
+**输入**
+
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+
+**输出**
+
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+
+**样例输入**
+
+```
+2
+39
+123ABC
+```
+
+**样例输出**
+
+```
+71
+4435274
+```
+
+
+```
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
diff --git a/LanQiao/task1热身练习/2082、十六进制转十进制.md b/LanQiao/task1热身练习/2082、十六进制转十进制.md
new file mode 100644
index 0000000..9edf75a
--- /dev/null
+++ b/LanQiao/task1热身练习/2082、十六进制转十进制.md
@@ -0,0 +1,47 @@
+## 十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2082.html
+
+**题目描述**
+
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+
+**输入**
+
+```
+一个十六进制数
+
+```
+
+**输出**
+
+```
+对应得十进制
+```
+
+**样例输入**
+
+```
+FFFF
+```
+
+**样例输出**
+
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
diff --git a/LanQiao/task1热身练习/2083、十进制转十六进制.md b/LanQiao/task1热身练习/2083、十进制转十六进制.md
new file mode 100644
index 0000000..c0ba52b
--- /dev/null
+++ b/LanQiao/task1热身练习/2083、十进制转十六进制.md
@@ -0,0 +1,76 @@
+## 十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2083.html
+
+**题目描述**
+
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+
+**输入**
+
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+
+**输出**
+
+```
+输出这个整数的16进制表示
+```
+
+**样例输入**
+
+```
+30
+```
+
+**样例输出**
+
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
diff --git a/LanQiao/task2基础练习/1460、2n皇后问题.md b/LanQiao/task2基础练习/1460、2n皇后问题.md
new file mode 100644
index 0000000..e34c4b2
--- /dev/null
+++ b/LanQiao/task2基础练习/1460、2n皇后问题.md
@@ -0,0 +1,114 @@
+# 2n皇后问题
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1460.html
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
diff --git a/LanQiao/task2基础练习/1462、Huffuman树.md b/LanQiao/task2基础练习/1462、Huffuman树.md
new file mode 100644
index 0000000..0852108
--- /dev/null
+++ b/LanQiao/task2基础练习/1462、Huffuman树.md
@@ -0,0 +1,82 @@
+# Huffuman树
+
+
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1316 解决: 750
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1462.html
+
+**题目描述**
+
+```
+Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
+
+给出一列数{pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
+
+1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
+
+2. 重复步骤1,直到{pi}中只剩下一个数。
+
+在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
+
+本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
+
+
+
+例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
+
+1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
+
+2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
+
+3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
+
+4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
+
+5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。
+
+```
+**输入**
+```
+输入的第一行包含一个正整数n(n< =100)。
+
+接下来是n个正整数,表示p0, p1, …, pn-1,每个数不超过1000。
+
+```
+**输出**
+```
+输出用这些数构造Huffman树的总费用。
+
+```
+**样例输入**
+```
+5
+5 3 8 2 9
+```
+**样例输出**
+```
+59
+```
+
+
+```
+n=int(input())
+list_=list(map(int,input().split()))
+res=[]
+while len(list_)>1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1463、Sine之舞.md b/LanQiao/task2基础练习/1463、Sine之舞.md
new file mode 100644
index 0000000..6a86bd8
--- /dev/null
+++ b/LanQiao/task2基础练习/1463、Sine之舞.md
@@ -0,0 +1,92 @@
+# Sine之舞
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1463.html
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
diff --git a/LanQiao/task2基础练习/1467、完美的代价.md b/LanQiao/task2基础练习/1467、完美的代价.md
new file mode 100644
index 0000000..6bd8b98
--- /dev/null
+++ b/LanQiao/task2基础练习/1467、完美的代价.md
@@ -0,0 +1,143 @@
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1467.html
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1470、时间转换.md b/LanQiao/task2基础练习/1470、时间转换.md
new file mode 100644
index 0000000..91c6951
--- /dev/null
+++ b/LanQiao/task2基础练习/1470、时间转换.md
@@ -0,0 +1,58 @@
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1470.html
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1475、高精度加法.md b/LanQiao/task2基础练习/1475、高精度加法.md
new file mode 100644
index 0000000..f7182a1
--- /dev/null
+++ b/LanQiao/task2基础练习/1475、高精度加法.md
@@ -0,0 +1,92 @@
+## 高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1475.html
+
+**题目描述**
+
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+
+- 输出一行,表示a + b的值。
+
+**样例输入**
+
+```
+20100122201001221234567890
+2010012220100122
+```
+
+**样例输出**
+
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_point
\ No newline at end of file
diff --git a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
index 0e789f1..d48f2af 100644
--- a/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
+++ b/IntroductionToNumpy/task07 随机抽样/11. 随机抽样.ipynb
@@ -1,38 +1,7 @@
{
"cells": [
{
- "attachments": {
- "image.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAgAElEQVR4Ae19B3yc1ZX9biBslk02CSH7DyGEABsgoQVMhxgCpkMgYBuDscHgXrCNewM3MO699ypZ7l2y3G1ZVrcs2yq21aVR1/T2zcz5/85939gOS/DIK8xGvPFvLGnmK+877737zj3vvvv+BfqlEdAIaAQ0AhoBjYBGQCPQYAT+pcFn6BM0AhoBjYBGQCOgEdAIaASgSZRuBBoBjYBGQCOgEdAIaAQuAwFNoi4DNH2KRkAjoBHQCGgENAIaAU2idBvQCGgENAIaAY2ARkAjcBkIaBJ1GaDpUzQCGgGNgEZAI6AR0AhoEqXbgEZAI6AR0AhoBDQCGoHLQECTqMsATZ+iEdAIaAQ0AhoBjYBGQJMo3QY0AhoBjYBGQCOgEdAIXAYCmkRdBmj6FI2ARkAjoBHQCGgENAKaROk2oBHQCGgENAIaAY2ARuAyENAk6jJA06doBDQCGgGNgEZAI6AR0CRKtwGNgEZAI6AR0AhoBDQCl4GAJlGXAZo+RSOgEdAIaAQ0AhoBjYAmUboNaAQ0AhoBjYBGQCOgEbgMBDSJugzQ9CkaAY2ARkAjoBHQCGgENInSbUAjoBHQCGgENAIaAY3AZSCgSdRlgKZP0QhoBDQCGgGNgEZAI6BJlG4DGgGNgEZAI6AR0AhoBC4DAU2iLgM0fYpGQCOgEdAIaAQ0AhoBTaJ0G2jCCIQQCpnvJvyU+tE0AhoBjYBG4LtBoEmQqBCxCwGBUBAGDED+DyIUBBCUrxDkASEvgua/EL8MyNcIIoBQiH9wwFWf8ac6OcjLISTn8xp+BENe+NQtG7fWeO/z9w8hwMKzmKEAgixfwLypKqo8E5+DjxkIuREI+eQc/i0XatzSNeBqARB8hSVL44IPfhjnKyOEYDByBHkdVR+qCCRGX30Fg8QhgFDAQCgQgOGtgztnA6b37IoRczZg6zkHCCGrkWVjewiQYJ0HXFV3MBSCX4D+6h303xqBxkFANTlaFNM4mc1SPpe2baj+SxvFRhuiTeNPdoRwG+afvAJtl3IUguxz0nYNsRdsy+x9Hp4i12UHEEso96Y1lD4QYl8wgIDv7zta4zzu+T7HZ2B5wv1XHsd8XrGvjXW/8HWIX5B2iKB5lB2l5Q75lO03bYHUBI8JKntrFtLE3Dhvds9fVkaYgDkmyAOdP9YcPcKHfuNP9fyqPqWIYutpf0IwWDb+x7qV2uIHARnT5Fg2Bw4J/FgMvjzMN95Pf/ntINAkSFSQzS7IBhaEGBL56Ucg/DeH7xCHcP4MIRAMwWDro40KkSOFwK7CY3idAD+hAQqGEAiojsW/eQUam1DQUI23keuEnSJIkhYkEeD9WSYaQvVcNHiq04QU2TI7GMuvzlPHi0ESxtDIBYz4cn74Q0H4xAYQZD8CJDahgBBdPkSIhkxGhEtfVIzGVw5T9RMEyRN/V+8gggF+FkLQcMOoOIUNw15A64790WdFGipMkkyyHSZQbC9+OZ/l5LVkWIq0aF8plf5TI3BpBNiexYkTAqTaHP9WbZjnq7aoRkySHvUOt/XzRIqUiXbv/Lm8MEfiIELSD9iW2e94bdo02kg6Dux6qg+IzQvRntHOKWLA4bgxXzK8y/Vpf8kNWCraKvOZ4Y/YFjSoXHJ9ZTsBtxBOsakBjg3EQxE64seyECfyFhkazhNU5ZbLM9AemxgRLz6SOleeRsYOuWjEhWTdiYeuCJPBa9JGGjD4OcEyyybUV34nlaJ99cEf5IjEsnsRChFDYVMR310f2DgINAkSFYBPlA2SGxoJDqKhkFc6BVUcwCeDthApIVGAQXJEYiUdJySDPjsWgn4E5fggbREM6ShhsqVIgDJEjd9gSQACVMuCPoR4Y1NdCZtRQ8rO+4a9TzXW83sxpOcNJLt845cv4iYXMlgj8CkrJYMD3TnWBY0+rVQw6I3YcHJwCb/4e3gwEfXpvKepHlkIMg1RwBCDV7KzFzq3egdv9lqGBCuNNkkzDY9JooMheIWE8rvwgMRrXbhn+N76p0agURCQEVkpTKrfcvBUJCfM3qk8h0mVKFRso9LW2U7Vm2WRPmA6EdK4aQPopPAtThiVczVYS/smQ6CwRdWFY3TYwaS5YJcwBa9GeU7zImqgZ79XSgodLJIE2mPKKVTPxKlpzJvK49C5JNHks/rFiAuXE0eZipRSpIVqCnGhm63gYanC5RYnVXANIBhQTq6QKJJVwZjnKVX7IlN1yadRbrlf6hOGUtB5PbYFcaT5DMSH44CMaSyRSaLOa/uKRIlzH6FTesmC6QMahEATIVHsLIpIqYGVWoxX1CXxsERZIkEyiZVYD8rXLhii/FBxUsQqFCSjVw1bdUA//B4rKkqtcLh80llIvNjIwwavQYh/w8FUwKgoBYJUbsKeiCJ6SoWil6nKF/TZYLVZUWHzmg4Ly3zB0/wuKYASoM3/w6RHiB6NOQ1REH7Do4zHN+AR/koGj4sUJ6paXyVWPJYGkt6kL+iD3++Cn2S4aDOmtm+Dt/86ALNT3KJCsmSGxwp7bTnKSspQWFCI4qJSFBcXorCsDGV1HoSMb2E0CT+Q/vn9RkAIPAkEB3ZlRmh3qCYo1Yl+hiL6QqCE7IQP5ee0ESQBynGgfaqtLkNRURlKSypR5zXgFYWKBIqqhlJX5dr8nA6aoQiGTBSK4GE6YpSP6Xc24kuRFL+QKLIAOoM+Vy2sVQUoLS5A8bla1HrpeDXui/CQQBkkKIp9KJ4pyh5pj1LpGGgQYF2IjREXVdlUEjDRr2izSEzJ+YII+n1CYYIcK0zlW0iU6XtFSqQIs3LofAiJ26nqXEIM6GgKiVKqIkMUZLYhDBEJr6h6wqoE00autvCd9M9LINAkSJS0bpnrJvEge2f3MafzpOGbipJ8ym/YAKn0eFVL5DEya6em9digRRGiUXOXwpq1FsM/jsHulFLU0cLQg/o2Xuw1LIc4i9LFAX8Q8BlCqhirQ+k2AC+8ebHYuHU9hm45DSdPM3goDRGlZYiyRhS+ixdRVICS1LFENDGUxZU65VeudQOKxmk6A0ESG/OlvHI1jcePzv8t9c87ESe2hULsGfM+Pnz5dTw/IxleepKhEGpOb8COFZ+gd98e6PbSX9Hlg07o+H5rvNN7ELquyYKfA41+aQS+DQSEtPgQDLiUYCxtlv3WgJ/Tbufvyd8uMCh2GzoAKiyBVkx9bT0VheipPfFO657o0XMSNuZUochnwBMyIH2Nxk0MHFUZRic6pT/6Q354wooxnTbDJXaPlqdRX+ZjyIMxZCHgQ3nqKsRM/Qgd23fEuy0WYGd2BaovevJGub+o3iSmyiYygsAfAFRkLEmTKTuJ3Q2qL+lMUyUjoaJ4JmWiPTNZiznT4eZVqHDxMgbnQhh5FhQ7TKgjegkuqhBSrwE6gIpOKT3M5MlyT5bEJ2RJrs9z2SDOh5so7Syi++qDGhWBJkGiJKZFyI1iIJRD6VVUJS3Hmuld0bHDm2j9VAu0ePodtPmwC7r17Y0+vbuhZ5dWeL5le/SYugE7T1rgFO+P88sqtsawn8WZvdGY8PbnmB+bjZwaB/wijZuxSY1aFWanqMtB6rYp+Kx3O7T6aBpWJVaj1KokXZH3g/TrDARcNcg+uAbzJg5Cj0WnUFznFZWFc/b0qkin2DGv/Iuy9hmc3DwL4/r0wd/6Tsas5HJU230S8E0FT3nHNG6Rlu/vpzDUNMcFAsVn5GdCmsQgKoPDekSgHulLPkTPVx7DXa1XIdnwwek8gZ3LNmLBjM2IT9iIVe//F57u1B1vt2yBtu+1wotzklFvKOn8yuOn79jUEVDjsVIWRAFnW7toqs7UQkRdpxMic2w0bRJLyF5DFUmdwy5kS5mNVctGofvSw8g9WYQqhwduIwB7xRmkx67CqD6fYcb08fh01FRMXhaHhFKHDMBUPIxgEH6JHeU1aTck3Lxxq0DijAIgaSNx4U+3vRSVRUdwdNMKjPj559idWobKxr2rqHkkjaGgCwzXBn8PuVFfno4ja0ajR4t30O+zTdibWgE3JyaomosQZ8Zr0XwQc57LYCkhu+o4xiSpqTcGgYfgo62hk9eA+VAxVcKD5Q4qlpP39FTDmReHDRMGY+rUSRg3ZhwmjJ+HefHnUO0LCF3jGMDngd+viG8D7tvIMH/vL9ckSBTjYBhvI7I1GzNdiCBgy09A4rZJGNvtNTx09X/gR7e3x4cjp2NB1GpErV6JlctmYsLobni/9Xto12cGZsTnwR5ymwHmTlSnrMX28f3RuX8sksqssAdIsOilcMCO1N1oQBsjp3BaUJi2Bgs/ewfNf/UYnh+xC7tyauAx5X2ShfD8uLMsGQnRn6NT6wFYlVyKEgcD7DmtSS9JKEUDbt54hwaDFpRkbMCiIR3w0qPP4KHuW3GoyAqHGDSvzPFTJ4qYRCkdXXnTtGXm1B5LrPBQ5oj/S/UL0aQC5kbx4VVYNqY12vzlQTzxwPuYm+ODxVaAjKQcJCadQdGZnVj61A/x0tAZ+GLRcmzfug5RqSVwmwGkjYeKvpJGQCGgnAA6Q1zUQJWcg3dYDqcRkGUuQmpkAYY4heE4JyWK8ChR00NB1B+djtVrJmNwfJmaiqMtLE3BgaUzMbDTcIyesxnbYrdh89JJmDhkGIaMWIrkEsDh4ZhvBktT5RISQSWskW2biDjmohxOLXKKjX00aIElfScmXDUc8ceKURHpPFiEDSkcdkGbKC6WLNjxw1VbhOy9yzDhrT/i8cffwYC58cioJXGisETnSak6LI7Ev5JESYyZwoj4SO2JTVaES0JsaZdkmjUyJS88VIm2KKu+fQj5LShJWYdV/dui16iZWLpuO3ZsWYPF00ei98e9MXpPLvJqqRia078G5yV8ZvuJ1CmNEEB9WEQINAkSRfZPEiUBi6JuKPmakzpGVRoOzfkYD/zHz/Grd5ZiTXoZHBKoF4Qv4IS/fAOmvNQMf7rxGTzZKxrZXh98jDlwZCNhwSiM69QTY5IdqPGI8K1WzIlHGFlHiagWzIOUYaQ8XIozB2ei7y3X4hePDsXEnadR7qcRoiJjKI9UgiWtqDi1E0vbPIa20/Yj7kwtvBIbRq/ru+tQanioQs7OCRjd4jb84DfdMTOxBEVekjxOs3LBceSmmue4HFbUVFehqrISlV95V1RUoKqqApV1Trg8jG/wweMqR1naTqz+oh/GfD4IfT56Cx/d/0e8taQAWVU2uAJ+eDwVKEtagcG//Bm6TI9HfCHTRARgfCXItyF1qI/VCFwaARVEzmllmeSWwZeOH9UFDuBsw1Q4GIBNksOgY6Wuy8BrzvDJii0EYE2chjUmiRJiBTssceMwpl1rPPLiROyrBGx+H4KWeGwb/SHevPtFdN9YhcI6M4BZArzpnJlELmKF+NJPKkeIYWPsjkkWA0FZ2OMLlaMsYzsmXTUMu48VooIP15gv5VGZcVDq/owHCxoh+OqKcW7tm3jmztvxl66TsSizXpxThkyowH0q3eKlSX2Eia8ZGIWQ4RciKPUjTjuJlVLzGPcZyUt4s6QxIBHzyNtfcQjxM3vgpdsfQseNZ3GqmtO+1cg7PBuf/+1m3P7+Mmw5XgoH7ajEl3LdoVrwpAocyZ31MY2JQJMgUWqZqGlZpOWzQXN9WBC+/F3Y8MVruObn1+Pxz/fhUL5d+RGUlEN2hAKJWPvWn/HsVXfggWdHYUcN4AwasGWtxoxPhuDd9guRHAzBHfDKVJ6s1hNb8+2QFEZb+eCFJXcXojv+DL++7nn0mHUAaXXmihzDZ64kFEkGnqpMZK1qhbteG49pO7NhMSjPE4vGD3yPtOEJMiGg+sR6rB54P/7t6lvx0bIMJFs4IFDOl6izyJWogB+lxflIT0tCYmICkpKSkJCQiISEo0hMTMSxY4nyeeKJEpTWOeD1WGDJ2oaorm+i27DliEk+jYw9szH5zdvxwzbLsfNEDsoqLKjIy0Dmhql47d/vxdjV6TheVg+bvRalThXF9e3UcKQo6uOaLgJ0cvwI+b3weypQX2FBbWUd6urqYLVXod5WA1u9DTUOD6x+U2EPeCUQnSu1RCFR47tEFTtTpmBNzAT0iS+CIdNMZ7Dv8zfw9gsv4uEhe1DPLEmS0qAIqSuGott9d+KHXeOQVGJX2dskbUsQgQAXezR+qxcCQsfTCMHgMn7DkBQDvlAZStJ3YcpVIxGfVICKxlbATIzIpZTuTZtIBcdA0FMH49QC9Hj097ivRU98vOY0OOknY4mscjYVf/4u0ZzqJxcDsPyhujLUVFhgqbWh3u1DgIuWJGY1Yn1dykSizPATg6uyA37UJizA7E4v45e39sD8HAfKfKJTwZ6zDQcG3Yf/d20HjNuciTwfSRxjZRnjRZ+ZNr/x667p9sHGe7ImQaIowcrqCPE8VPwQBVxK5FVJ8zG3y+249rob8EFUITKrlLTLph4KuhGqicOklx/Bff/aDI88Pwv7nCG4Qi7krumM/gN6ovXsVLglD5VaEksnjZ6Kwc8a2WNjF6DszFU6vopMnFv1Nm676Zd4ss8CrDpuM3O5hGN/FIkKestQlzsPXf/wBkZP2oNjFZzJ5DHfVUwUezQxCiBQcQzpSzrhjquuwfXdVmJ5epXoT4yJ4iqXiOGjOuR3w+d1wefzwOfznX97vV54PPzMA5+fqQ1qUZq0Fkv6dMBdH0Uj5kQRKr0e2HLjsGvsm/jhT3th0uTe6NSmC1q/2BmffdYd//H/PsCk+NPIPLwCuzfPxbhUK4wGpGBovO6or/R9QEAUi6AfnvoC5CbOw7gBH2Nw33EYM34upi+ZjTmL5mDxnIWI3nIYaWerRLXlQK6GS+Uc0U8yJN45COvRaVgVNRn99pWruJy6g5jz3nNo9lBLPDEjU6iJmuquRfbWsRjx3K245v7ZWJdThRpZEaycG6rX38YwTGvJhTqBAG0SzYMfASOAoFGDyvT9mHLVEOxKKkB5I5MokhqDyp5fQrLVGMESEAy/GzCSsey9P+HJG1/BK502IZMqvp+KkDmhR1Iiij6VQ6VMUSH0eG0wsqMxdUA3DBw1H6sOFaDar0iQpJNoAIokbQw7IDK+UCVORfXGkD/fg1/fOha7qxywcooVIbgKjyB18qu47sd3o/OCwzhWaQaVS4yuUsG+ndr7PvTI/90zNgkSpWKETCZu5kzxSKCxFWc2f4qRLW7Cf/5XS4xPqkChS8yJDOAhjx32xNFo9+TtuOWelmg/8RBKA6RHuYjt9yo+6dQfw2PVwK/yqqh7GK4qVJ3eieWzZmL+pNGYMH0RJq/cjoQDszBj7jR8+dnnWBS9G8cqAgj5vHCfWIUZg3uj+6eLMP9YrepiJBnSQWgJL2TQFSmZHoa3HLacZeh6229wd/N+GByVhXo+G42CLG1lHBg7Uh089Tsw89m70WvkSkSfUoZKlkiLweKy2Yu8V7YXxdak5TSk45n0TXk8okUrwiZdWJL5qcR0TEUjHq23AiWJSzH03h/gV7f3xsioTJTIUl1zVaRYbJbAA4f1DE5sm4G5EydhztSxmDR9NsYtSkChB7JiRQU7XVTwi9q98p5p8CgRemA5l4W9G9Zj/dEClNndEvRpOCpQmrkfUyetxJYVn6Bj+3fxVIu30aHTu2je7GX0H/0lRn05A3NXb0dynRteYiah6hfHqjAwlZ+bGErYmfx1UWn0r//cCLA+TdX3ogfx1ecj79hGzJo4HbMnjcSo2euwdN1WxG9bgNGTJ+PLYeMQFX8c2bXsf+wRYRmElzMHY/YLfhy0oixlK3bNGY3xm/ZiX0IKMjJycDr7LHLP5eF0/jnkn8tDSbkF9Q7GaCq7IylMZPWeWngv7T4UQp2QqEkYtKdUBRvnr8TYvz2KWx9qhccXHFdrkmX6vxa5O8Zi5NO/wjU/64U5SSUo8asFGsqmsHxs7+qz8/3afKKgqxK1J+MRPW0AerzTEm++8z66fDoTy+Kyke8OwiunBhHyOWAvyML+xaMwqN8n6NOnP/qPmIwxy/Yiz08nVYUmBAMVqEqNw7SrRyCWJIo5+gJMJan6l4Rby24NVK/VUn5iEanNEuJD7GUaUZEgPqcYUCqBQRuyFrbD24/8AQ+8+gkW5/jhNRyylo+hIJIeR3w93tGc5pNgcz+C9mLknkhH8v447Fw5HzNGj8Ko9QlIK66F06fiq9Q6S7PgEj9FGkw67Jc8XtJI5HnCxxfg6JyO6HzHHfj1bWOxp8YOq/m07qIEJE97Htf95Gd4/fPNiDvL2FIKBVwEpZ7touaqf72CCDQREqXkTLJ6qjjiaJCkGGdwZHp3dPj9Hbj+wXHYWFCPGuYYYgfx2+EoOYpN/Z7FX556Ga/1n4eY4xZ4ODftOIR5rVqg1wcjMD/NE7Z8KsjQW4nS7MNYPn0JFq1Zh/Vrp2Jc/554++UP0GHYp5g4vidaPtMcLT78FKOOlCPotaN+zyB89Oc/4a7nPsbHm86pdbUBJp5k12QHohysbK10fDEyLnisWYhqcy8e+uOraPPpRmTalXEX7iRBoOw8LnjdqdjU4Ra07jcZ4/dXi41QZIz24yskKixVC4HjcCHmPqImx2PF0yJZkURz7MRmRxZSSJmef5tBjyEP6guOIv7jO/Dfv3wY7b7YhINV4SR7anAJGtUoOxWHzfPGoPvgcZi9YCU2bFiDxbNHYsTQjzHthAMV7gjLKCQqAKfDgfJSC+xen0wfCIkMGvC77SgtPoPC03HYunUdFq5Yi5h1UYhZtBibt25FzK6jOJRZBKeYOU4ByBMrL1SC1V2ywlAET5HhVVxCpEY9IpD1Qd8xAhz02N4uanOeMpw+EoeVsxZiScx6bIr+Av3bd1QpBUZ8igmff4Tn7nsArw5fhhUnatTqXgnLZH81CYmQGNXbnIXx2LduKibOWIrNJyyocbH/q+kjBlxLpn8JcaaCYyaoNa+jSLxoWYrsBIOoT5yCNVGTMHi3BZK76OR89H7tQfz0wTZ4fO4pZW+EyNmQu30cRjW/Dldf8zYm7y1EgStsU0gaeElVZhmcZSWtyj1nhJyozj6KpMVTMWPuTEwY+RkG93oPH7z9Ft56vS+6D1+L/Xm1qLWWI//oFqz+cgRGjZuAz6fNwqx5C7Bw4ULMWbQSM1amIrvaLkQqFCpHZdoOTL5qOGKTilBOB0tIFO0M7aFaAUfopGwMG6PycnHdfFNrIWZmvJniobS17LPm3EUQsKdNw4i3muHuR97EO2sL4DCUEiWLh8zYWZ7LmiM2imCyjqgg+eGqL8aZlL3YvnIplm7ago3RS7BuayziMopR5lIr98Ln8ZlIsVmnTIaqFpRT9VK7N/iRg31j30f7n92B39w6DnE1dtSRRIUAV9FhJMx6Ctf/5Ed4ZuhabDrtUG2DJZMVnA1Q9r8JM/1dgxFoEiRKgjCF4TO/k0dEIwYABuv2YvWAVnj0urtxw8sTsfpAMpJOZOD48TSkpxzEoV0LMazV6+g4aAGWH8xHnRGA33AgVLgeQ194FR07TcTGsyrnkUxBMbt1RRKSd81Hr2G7kV7thM2Vhi2jOuCVm+7HrR2jsG/LF+j17it4ssNwfLL7HIJ+B6yp8zC1b1d0GTwDc47kyx5+TIVO48DOyQgcEenFgNGAsKMF4XPXIGXSU2jxxz/g0Xe/wOKTDpF26SUp75T8jgHSRTj46e/xfJch6Ls2z1RumPdFbQtBw0MXWEx40AVbVSlKC/NxrqAI+QUFKIjgXVhYiKIqF2xeM6M6SYW5UlGMTDgLsUzTkXh6JIjcVZmLM8v/irtv/imadZyI2Ul14o2xPIwFsJfEY9vUzni3+Qt4dNQhpJQ64Ap6cXb/PCwf8CTe31WLfCvRieDFgtDAivGkxxcyg/BpiPg5r6OSlyryF1b2OMGg3qLuCRFU+1eFVTWqAMyqE5CtGXg95pvySM1pEhVB3fzTHCJShZJCzDJ7i3Zj+4oVGDftMIoCXhi2/Zj9ZnM8cfdreG7wEpyMHYY3//wYmg9ahDkpleYKUfoZbGt0k1SQOPtqADbkrJuIpXNmY8axarXlkKn+kLgwhYqEJcvWUmpLIk5JsQOzeV/8Vn0oAFviZERFTcbA3VUw6CRmLECHV5vhB83a4PFZ2aJlcAAPBR3I3T4eo58miWqJiTvzcc5GkmZuNUXeaKoaVLyZ2Jd0jYqHr/40jseuwdIJi7H7rBNWpxv1ObHYMbEL2t57H37+r0/io6kbELN5MRaO6Ya273TEl7tycMbqgY/2x1mCsuTNGNp+GNal56PIQ4fXgsr0HZhw1RDEJpWgXGaoFFZ8YpWeQK20VlONdNC4QloQumSLYr+k3SaxFHXQTOHAJLwq514IKNuBBR++gj/d3By/77UO+TaDafmE5HB3BZ5PkyL4CRqcQWAOLvZ/xskasjND0O+Ep/AY9iweiynTpmL6mh3YdyQVCceLUVLrhMevlCypXWJLZzbAJM/Updwis/mRjT2D26Ptv9yJm26ZgJ21DtTSlhG+osM4PPcp/PI/f4QnB0ch5qRVSJzYK074ioDAtqtfVxqBJkGimCuDHhwD7JibUvRgei+n5mDkR4/g339xE25r8S46dOyBbt17oXunTujeuS96jIzC8kP5yKv3wCtGJoSA145Q5iy0f/oDtO25EgerSD0Y6q1k09rMbUjYMB4LU1ywuX0Ilu/G0oGt8dhdz+CVBTk4m7IFO9etwtrYNGRYlIilNHylCvlZOJHkqdbQuyHBoX/CDsCF/361t5Thg6e2CIfHv4Tn7r4Ov2jeHm+vyJYdoDw0ASQF5AU0cJ56pMy7E8992B2dF6WiRliNJD5RSUPp/4i6RYTKcHr/RmyaNwcLZi/CwtkLMW/uPMydO/cb3/Pmzcey3eeQW1EPQ7QaYsJnIHDkLswK7LkQiRXwI+Rzw27JROrK13H/bT/Fvz3WFe8vSUOlWfZA0IHsmN7o+/y9uPnenpiT60JhnQP2+rNIXj0P097tifknDJ5DSMwAACAASURBVFS5IzMOLIv46KYHSozCxVP4KoVB0u9JmRV+JEdq6oCYSeQ74KfxFOapVkyZdSTnkp4xlQSPiaxoV7pf6/s1IgKWI/MRu3091mXRvvgQLNiI4a89ij+/0BF9ojJgzdqCqMVrselYAXK5AET5L5Ixn0Ok0iyoOjPnUyrW95mABZ9GI9nmhsvlgcfthMfthsdth9tTB6fbDbfTA6/HrwKx2cbYFCWVi0y4iRYTbnpcnbcqahI+iS8TJQdpC9HplQfww4fexGNz0sTesN36Q/XI3vEFRj99Pa65uh0m7MhHnp0OHK0bA6NJmEz+yLABbkgs7kUA7pRliF0/H2MOVAvJCwUVmfFWH0dGVB88f+01+M/bH8ad99+CZ999F51jciWWVNKR8FrBANyWbGTNeBAjtqfiQAmn06pQkRKPiVcNRXxSMcpN+81pQT6vIelaLpAolYCShCMyp0pxQjqrPP7C5uy0EbTDvoAHzrztmPfBy3jwmlvwm//ujugcN6pdzLtpyM4HQk5YGDEkikB5RVVkhbCQLI5y0GhjJGdp/Tmc3TMPc3q+jTe6LcKS/enILq+CzemCJ+REKOAWeyxqn5A0PjBLexb7hnyId35wB264ZRx21DpQx3sEAE9hApJmP4+fX3cNHh+yEutP1qnVnLy/xHBRNw+3iEZs/PpSl0SgSZAoBi2GfFw1wXwZ9KrYsAyU7OyP3q/ehBvvexrto84i55wFxRWVKK0oQyXf1XbUujkPTiavCEHI54I3YwFaPd0RLXutwr5q+pEkNlxdEoThtsPhqEOtRykx/uMLMe7D5/CHh1ph7FEfamxWOG31sNs9cPsY7aNWopDscCUGuzI7JFfQSTnp+XFzXtIPJr7jd/DCVnoMB6e/jlc7tsTLd92CZr97Bn/uHI2TCMIt5k5dh0Yv4HUga+G9eLFzd3RYcgylNBoyzcauqabblPdGg2TA43LAVl+P+vp6WPm28m295Nvm9EnwtlohpJQeWccmnhVNsNfMWcJnDaCu5AjiV/bDk891wEvNr8Nvb2mO13qswjG7SuUVqkvF2q6v47kbbsONj3XA4Nkr8MWoQRjUrxdGfDEfMfGFsHq5+zor9NIvc6xRpoRGT1gmoaAXrwyMOkYlMFRcTpnU8Hwq78RVxyq5HjEW/c4cSjgc+mAEPcpL5jUjK9qlC6+P+I4QMNvJP6xIblFSD5vDBit3DjAcsB0eg7ZPNcPTbUZgUboXPrcD9dZa2F1eeP2ckqLKotQM9ntpZ+LwGEBlLGb26IfO7T7ByKXzsGjpEixbvByLl6zAkiVLsXzxQqxYuAhLlq3E+h3JOHG2VhwTtck6M5wznpAER63qIjmoTZqIVTETMHifRcUFnlqFYa89ghuavYXHZmeIgyblgQPZ28dj5BP/hR//sAtmHipGkZvXCqdWcKkcbKIyc8pK5T1imy9cNx27lszCukL1bNIvqJgHXKg/dxA7+92D3//2Olxz+1/xxuj1SLTT8pmkzNzSJmAvhfdAfzw7dw+WpFUDgUpUZMRi/DWczsuHhTZY0osIMxF7KHZMsqozLYKKA1UO0aWbi1L5leqjVHnlCIva5rMhVHAAczp0RJcXWuDJh+7Fz3/3J7TbXIZTtezn/CfRSyqLvGzRI9YOblGHzOSddBYlRITfMUCf9twPn8uK+vIClGUdxsZJH6JbryHos/AoTjJHlihp5nQelW0iJVhmI3Fie3T+zR349e+/xN5auwSW0zX0FB9GyswXcd1PfoxnPt2GLaeZaNOc56RNkhmNS2Oij2h8BJoEiZINg7lURfZUM/caQh2SZr+F9x6+DXc17415mX44PBzcmadI7XlEPsN93GSeXY2ogM+FQPpcvPnUB3izxwrst4h/oabbhPAoWV28QgRQFDsQfV9/Fn96eiQ2VHthNZRKRNJCYiadkcqTJJdTGx2TPYk8TNXDjC0KBzL6gx7U5e1H3PxhePmdjzEmJhaLx7TDe80fwB+f7YvVxSFYvSRGfCueEPA4kDbvLrz00cfosDgdBeazhP0bqlDKG+P9VHyBOHtCLBrAAsKkgafQWIjDqGRpSdrHyS2JwTJgOxuPjTOH48N2/TBsdSK2TmmJVx++G83eGITZGXYlkxduxJjWf8Y9dz+DF0ZtQOLpPKQmH0PikQSknMhFfi2nBU23NIK2L+W5iDDxXDWNZ9aZKZqJd2l6k6JdES/T2ZQEiBy2ZCCk2seBRE2fqmNpKE1jTyIsS88bgGEEz6EPuZIIfBOJ4neq71JRoUoc8NbhzKrX8XKzZ/F698XYV0dnSMXLCFkX0qTaE/snnSK1jF2RK1h3Y/6AKRg7bCV2nz6F7Jxs5ObkIDsnB6f5Mzsbeaez5fNzRWWosTnFhqjAZjpkKpaS9oekgu1bxURNxOA9phJVEosprZ7GXQ+1xGNzMiU1gpqsrkL2zjEY+Zcb8aPrR2JJRglKDcaOmqqKOSUkA7qUm52CVMSG40u+xIaZ07CzjP2Ryj9DBThd6YffWYaapMnodNdNuPEnv8Of2n6KGSfqZFin2qL6VFCOQ+IIvDp3L5anV4NJeS0Z2/Hlj0ZgV3IxysWRVXjTLpoijIr9EYKl1LiwQ3SpVkILJeu2qSKLz2mSOlcVajK3YNYHb6LjJ5MwZ8kMzBnSBo9dfwtu7r0He87VmCq7ibcZVC42j7izRkTlDsd+ctpPZX+nbeHNgl4rrAWJODSrP4b16otBX0Yh5mgx6oinBLoru6LsKJ+VWBbj+KKu6POnu/Hr2yZid00d6gX/ENxFh5E6pQV+8eNfoNXEeOwtVOerPf9YHq1EXao9fFvfNwkSJUKtNEIGYpIo+AF3FjZ0fwrP3/YwHmk9DwdrQ/CI0WFMD1eBqEBOdlYaOdUpuFmlE6HsJejx7Hvo0G0R4kuUFE1TQK/SY7Wg/NxxnEg/gzKnBQdntEa7Z17EY+3WID3ggSNkoDYvHedys5Fv59QdaRQHXRUDxQBSWY3HXk3SJ14fiQ3NpBvVOfuwae5ofNxrIDpN2Y+0MhcKE2di7AeP49a7X0KrDVUosbLTKhGEndfrqUPqtDvxUpe+6LryBKrF7TQ9YFndQk9HIjOAkB1VBTnITktFemoGMlLTkZaWdul3ejoyCmpQ4+SqEIWFNEp2csYOmPEDQb8b9rP7sHnGUPTvPhB9x+9Aeq0Be9ZcjHzjQTzwcEu8uygLVpqivBUY8tajuK/52+i64axEKvilXpRRYdJTzuRFSlEuJlFiaMXQKWPDuhPohf9x0FPqlPpJTqiIksSw0OiKQedzeuB21KLKUgWrmwPXBWVLYhokGzLvrF//nAj8IxLFz0kYvHBW5iM/+wQyc3NR5jiD2IH34slH2+K9L+KQTSIRcKAqMx45xSUoc6t2RbWI9ENCmNnX5Tiu1j2F7Z9PxdJp65Fsk7kY5YpIWzUdI+E0nGbjP16HA6xa1yVkzmzLzBHEfmc/OgNRq6dgwO4SITYh+wms+/hVPNf8r3ho/FHUcw89Lt9HMU5EDcfg+2/Df/5lObadqUIdY/08DjhqLSiqtMNjiKUzF5AoRTsQcuF09EisnjUGi046Jf6Ge7ypRJMeeOpzcW7LQHzw5D34w49/jFt+/wxeH7YVeTYn3IFw4tAQvHVnUbv+XfSIPoJtZ5iyxYLy9J2YdM0wxCWXwGJO+wUMP7z1pSivtsHKkAnaLklEqtR68f0iaGzKDNKRYn8WFwghRymKj67Fss+6oE3b/pi8JQ2nSk4ha+NI9Ln3Blxz76dYePgcLH61ebNaDX2RvRB7TYsethl8Pr4VwfO5ilGYsQ8HtsRg7cYYrF8+E4tXx2FPShEqrCpNDmc0eF0SJ1k4IIody2lH4c6xGPv6E/jV74ZifUE9qg1+HoDjzC4cGnMfrvuvx9F7VQLS69XnzBUlkxtC5LUdiqBZNPohTYJEcetHtV8cZ7q5S7kHwbJt+PK5B3H3717F00N2IZ95OERVUFN+VH4YJ8DOJVsQSIM24A24ECzbhMkvvol+naZh0zkGOEhEAYIhN0pPbMfW2cMwZOhK7D9zAPM7/wUtnnwDT4/dj8qQDz5nOY6umI2YmC3YX8H4CC/cdTnIOZ6E41nnUFhHs+pWREqkXYhszsBEa0EStk3ugw8/7IGWY7bhjBXgwrSAZS/Wf9YKj9x2H378URySS5wSzCgaWciA01OGlJG349U+AzFg82lZ6SPUQ0J81POKERFJuhLnkuOxJyYK66I3YH3UesSsjcHatWu/+R2zDuuT8pFfSxWJ1zRn4MUYqLDsgNcK+7kE7J7SGR+17oYeYzfhWA0JloGQNx1b+ryGV+98DHd/tBInvEG4irZgyvtP4/kX26LnlkJmQxFZOhjwwF1TgtKzp5FlNeCmhYrgRTwUKVJKHdUlmc40V9mQcPJ7MXhiBC+oCCqIVBmmsDfJKWGvPRdZyVuwbEk0Yo5Vw2Kj2qbUPBJxmeaNoGz6kP+rCHwTiWK/dyF/71IsGz8Wo2etxKGSeIx75mbc9UJfdF2djsqADf7aLGybOgAxBxORSQeHdiZA0uJVCoEow2paKRB0Inf1RKyZMQ3zj5XCIW1JRmBxqMLKKQkKaROjGMXJk/3fmHBTKTV0Cti+qaoLiVozFf13lwjtCoWqcXxBN3T/22t4oEsU0ryAkwkiXSdweNIn+Oimh/HwuGRkVLjggxM1Z5OQELUYM5buQEapDTY/B/nwXnNUOUKoSpyKmMWfYVhULur8QXhkNioAj70YeUdWYMp7j+K1Lu+j5XOPo8WNf8Afb3sPY9cfQ1apDU5vEAGPFTXZ+7F92IuYfPA4Umv5dBWwZMRjytUDEZ9UBAudSvZ9ayFObJiNZSs242BmAWq9ql8GA07BMzJrIBENakU1yRmpqKcKZcdWY/mI9/HGK20wMLYcBbWc2nehKmMl1nS5Ddf+8DH0WpaM5BouUmKd0VCQDtN2KIfRH5ToNgnHoN3w+11w11eg9PQJZGTEYcvSiZgyejQ+Xb4bSdUuWGW3CVUeke/FeSauHK/8olaKIhUAHNkbsGpYa/zxd29h8qFqFNvogNthyViOld1vwA1PDMesI9koZc4t2uDz3rRw8f+rnaxJl6tJkCg2dPHKOGfOAEaXFfaUeWjz5N34j8fb4eXF6fBQtpbO5BUSQMNEBUsNmFRtaPhImHyA9TDmvvYE+rQbiiWZKiaKod8GipG6vA96PXALfnpnfyzePAudWjyK2554By8sTITH64A3fRFGjFmC8etSUcb4LLcTZbHd0f6J3+KRV3tjZHydpFGQJa5mDLM35IJhP459g17H0w+9jL8OXoI9VT5Z+MrQzmCoEtlrh2J4sxtx7U96YXmKBRXmag8qJYb7FGI734G2Q8ZiwqFCNXVnRreqlAPCJqT/Kpmc8/f0b+nERKrzmPH6ooubwfF09dRuFEJJHZY0HJ38HB767RN4b+h67DrHJHISBSZKX250Jwx89re4/d6uWJTvQYX7LPZ8+Ta6tW2JVkuz4GEGZ8MHw1qGU5vmYX7vdpiQWA+Lk4pAhC+ZTqHJJHDKBrKYJH0Gt0oI+GXLCSqP4nNzypUxceLJqfgEWZGjnHCUp8zE+O534d+uvxU/eHMDtp6qBVONETdZ5uxX8QwRlk4f9n8OAQ7JbF9hVShcQLYF9noHDg5viTZ33Y8/vTAAG3bPwxs3/xq/emM4+m3PkYSZ9QlT0KbnGmxILIad7chQ8TE+OCR4OUDjJJyHV3QhWLIHq2bNwtt9ViPJa8Dp96os2FTIZXtZP7wSRG4OjDKQq3KJukVnTRRQ9X190lSsjpqEgbEV8hS0bL7T0VjYpzMee6QfFp8zUEXyf2It1vRpj+ebdcGcbKDaSX6QhyPzB+H9f/sZrr36NvReexLHazgdSZtIddzckN11HAlrlmJM+4XYW+VEtccHj78eZ46swIzur+HGp6YgOrUCRVnrED3wJdx/zQ24+gdvYMiyTGSWOGA/dxRHl4/Fsy8twMZcCyqFllRJTNQXP+qLuKR8lIlVKkNZ5nIM+PdrcOPVN+BvQ5djR5GaEpSFQ6LvRUijZDaedk6toPOd3YDZ3Z5Fi6dfxrsL01BiuOALucWyByqTcWJlW1x/7TW4p180VmfWm3n4FMYynSqqjyJWLAFjobi4xFNVhMK9SzH1vRboMHwG5h/IQYErADdJjhm3RMdLcl2Zhkk0RiFlgE+aBzPGhxD05eL4xhH4+J7b0HLOcaTl18PrOYeUXePQ48mb8cSUY0gscCoCJ43KEMMcqToXbt36Z+Mh0DRIlEzFAMGqkzi+bTo+aNcS7Z+9BTdf/yP84Prf4bePtUav3rOxu8iOar+SoQ16dCJJ8G+aURIDenrMcHsG24a8gF49emLorjK115I4JDaUHF6Ahf1eQbMXPkSH93rh81HD0LdTD7R58X0MG/kpug2Yh/nbM3Cywi4ehihMB0ag28v/jRsfeQsvTTiKKhmAmcFXbcYZdBbDnjIDbzz9OtoOXYGY5FKV44jUhNMAQR+sx2Owvl9z/Oba3+H95ceRUsEAU7IwK3z1uzGj2X3oNmw1VmWHV/qZMQXnpyrFjquAVxIN5ciKhxZpc5KOKh6waD5mAjqqPtxGoRCF+xej101/QKuB0diYXCarF0laxOCEAGf2Wiwf/CIevv8RPLP8DHKr7bDnxGHLrMH48P2O6D9+JT4fPxKffj4dM5bFIiGrCJXcgoX3jOQlHr+S3sMkikOjKrLodueXAkvGdBncLsRgiKepIjlM9hWAvywFKRu/xIAO7fHEL8ZgbSL3+FJL17k4QNpQhMWL5BH0Md8FAqzAryNR3C+zHic3D8Hwbq/jz690Rc8PhmHqF8PwQauP8GGbrhg2bAy6DlmA6KNFKLByvaqaFuaCLZl6E9sUnkpniFFQcsfV5CRg9/Ip6Nr9M6w+mIf8OtlGVrk2QujJYyQaXTVg81fptxIPqWwHO1d94gysjpqCgXvKpD+LQ+CuQ3HSLsSMG4KuHwzBqC+GY3D/fhjEQX5zJqocARgMewjWozRtN9YN7YoOz9+Ldxcdxt5Cl/QZOiEyDc4+EXTBWpqFlI3zMLrTB+jWoQPebvUe2nUejDHzt+HQqXKUOf2yurDuXBISo6ZjaKtX8MJTzfBgs0fxzGsfofekGGxJq4bFQVJDpCyozNiLyVcPxq6kYpSJA+SGozILB8cPxLC3nsL7oxdgbppVCI0E0zeELcjsAtMZUPWqw7Epr6Nj+zZoP34D0qqdss+ohDnQufZaUH5iDT5pfhPubD4Cn63LQikNh0GHjLFPVKADMmvAqUwqZrbcPdg8ayyGDx2DMev34+jpXOSVVqLG7oFP4p7IjpSXKbFhMi1JGmxOS5K7y3EkiWpj9lDAC3fZCWRvnoDR/TpgwKgxGDpkBIb1H4IhM1bhUHE9rB4qUGwWDBWh2qnsuRja76L7fM/v2TRIFKVWegauKlTkJWPrlg3YGr0YK5YuwIKly7Eiegvi4lKRb/PBJY4Ejw/LFOZ4KdoFWzU9MAdOremBvv37oOXMNFSTq3DaKuiHs+oM8tLisTV2P+J3HcKJrEykHz2K/Zt2Yv+hg9h18DTyym1wkZnxakE//OXJSFg/Ej2Gfo53JyTAIX2Hq7yojjHDbz08lmRs3hSHg5nFKLdTBhEBWU2bccrRWozi9J2IWrIMsacrYHGa29A4y+E6Phtt72mN4XP3IrFe7bUlnqR6GkHn78Z5ASvc8v/um/CHX//z787jIUJVlOE2bLAVn8TehdHYn1mOchtJqQq4lYtRDXKUID8jHls2rpcluvVurt2tgSUvDYd2x2LP0SwcOXoIBxNSkZ5TjhrO0zboRWaonkf+VwLcRbaFn6oyy3FCztTxilWGyaE5VcIB0V0NW8FhHIqZi3cfno3YjBLUymoaFczZEJveoEfRB19hBMx2cP6u/JvkxwtrWTrSk/dge9wh7I89htzck0jcux/7d8ThwMGj2HU4B6U2HzwcXE1bFG5avAo/u9DupFsg6KpGbX4q4nbEYk9CEvYdPIi98XHYExeH+Lh47InfgyOpp5FvsYozxsFeBmT+ZI+j42eo6Wlb4gysiZqCQbvLpP1zUCWB89sssGQnYu+OfTicsBfx+w/hcGoO8qsd51fkMT7TU1+BgoQt2DDoQfSPycBhph8gDqrwF57Jb4fNchrHdm5D7LZt2LhhC7bvPoq0M9VwB7iy2HxKww13dQFOHdmFrTHLsHTJUqxcF4u96UUo9zB9AG0s45zKUZkRh4lXj5JkmxbTCTI8dtTlZWHPpLcwZtFSLD3hVNNytKlSsPOVdIlfaEOpGRMzD8pStmDvvv04lG1RK+xoC+QZeV0vPLYSHI+NRszGY0jKq4adnVsOMacDZWuWkGw/Zc/dh4T4OGzdshPb9x5GQl4pqv1++GXBiomdXJwXCLcLVV8sk7I3F477u8/8Lvhq8nDiyE4cSDiC/fsP4/ChJKSctcDB7XIuqhel0YWvcwk49NffCgJNhEQ1Mjb07rKWYtKng9CyxzIk2gAvN80UVccMSJeWHOF9QwZcuVFYvnYZBqw5LV2aRlGmlEiiJAiVoYqRWQh6IBJsyZgdywnkLW2PZ1tOwoLdp1FhGGaMV2TXivAJvpeHyVRowA9/9XGc3j8bbfvtRXJ+DTwyAKhpXtp9/dIINAQBGZulD3Ma2Y7y4mykHzuIA3Qk4nYjfvce7I6Px4HU08irsKkUB8xKze2hqGaYygOFVDoqtsSpWLNmEgbGl8nYTMdMVh2HN7YNk36ZIuSgroKaVXAgvUo7as8cwbper2DeobM4xR2LG/ElK4lFZeLqZLqvSkULBKlE7cT4q0cijjFR55U3H2BYsHtiNyxctwnx5WqvTSpsIsFEaCcb8RHkUuzxsgDI44Q9Zy+S03JwqswGG4lNgNG4SqFm/ejX9wcBTaK+pq7pNwTcp7F39hgMf6c3JiXaUONRy/c5BadWV3zNiV/3ETuUpx6ntk/G/OhFmHW8RrhSWKoXeZ/Tig3peLR7dJKMelRkbsWyLo+j/bzDOJhnkw1IaUAZ1qq78tdVSAM+o+frccKSFYtNiwei85YynKk1t37hChsG6kuG9gZcUx/6vUeA/ZLpAYwApVbzzfxPEtipTAGJEPf/lD1AOSVocPqeU89UcUwBRZAMoD5hElavmYCB+8pEZ2VMFgmSJCDmKlOJa1JTzzI9J84gVxUqRchny0X2geUY2HoM4vPKUd0QBzGC2pTymvdi4ameMAeVL2RBRcYOjL96MGKZbFOmPg0EfDVwFG3A1L5TEL0tBYV+RQolRk0Wx3xXnouprNPx9bvAkBCiSwWOb9YrZx5ENYwAF31I00BAk6j/UY/sCiqMvD5rPaKn98Y9PXcis8YlyfmZQI6z+VSRInoFvAjmrcW4scswOSoNJcJ+eC5X6HFlBme1VaB2pEqUspTMVZeMlJjxeObZaVh3vAaVskzRkKSjfpkOjKiE+qB/gIAEk9YkYPf6JegwYAvyPAacEmehYhIkJk0GwQjbwj+4j/74+4UALQzVGS50UbFYErl3nhnJYCy6NFUnrs5i7JIKPxBCYg7Yyk0KwHZsMqKjJ2LoHk7nMSklV5GpOBm2TIn2kpuSW3HajRue+0QVYkrM/ITt2Dq2P6YcrpNl+CRajf4S+c107OTyfLZiWDK2YNy1w7AjqQTFTNcS8qO2NAd7+7fCnC0ZSC9yIsR0AxIt5lJhGI1euAgvKBWjEKVKHWIMrZBhRYWVH8w61fYgQkSbxGGaRH1NNapgwxB8zhqcSd2M+aPfxpCtZ5FpYRAf80pFTHeU/OyqQnGRBSVVdiFilHslWFGm8igRc61G5AaCfdkwipG5YwUWDhyLGfvLcNbmg/f80lkVC9CAUn4NCvojqoMBnw2VVRacPFcFDzeHlSQa3J+RW3LQXGrFT7eUhiEgY7HYkHCsTDhHWTiGnCEDjMFksLEaqCU2R9Qck2sJCVPxNvWJMzFnfA+8+MksbIjZheRKK+rESKmpOwmjCrgBUUm4LpcrlJkoltwsALe1ElVFeSipN+BlnFXDHueSR0u2LEmLonY5oHPiyE/D8fj5mD9+GN65+jNsSCpCGRdscKNwjwt1+SdRXuWAzcMcV5woY7mUEtfoBbzkE5gHkBsJwVRT+VTU1NSqmqIUa0Cb3pBZhUjvrY/7P4uAJlFfUzWMUZKtFUIhuOpLkH9sJXallKK4zgsmN+MA2pCOzC4nMi/leFGI2PkYF8DYBNXpJPNspBelU+ovR+HJJCTEJiLPZsBtJr/jhpgqv4n2hr6mahv2EQcaM3OzLADg7xKoqjKWs5motBmNPew0rJj66H8yBIRFKRPCAHDScI7NHHvVV7QJtBVqVVh4/k5CgiRImaRLDeA8wVOehrSjOxG14wgy0rJQ5HDAQTvF6THmohOuFU4gqzJqy70Y38xl+rQZ/Be2R40MJ0mTxHEGw6pYEK7qQhTlJCDx4F5smnIUueW1cEpSTAacq1gvgkKSx1VxVNNUDIMijo1cxMguF64jKSD3ORUaJTGtkoVX6lEpgJFdUB/VFBDQJOrralGkc3qCAUkxYDBxntMJnwRt0xtigOfXnfj1n9H3k21XzD2qaEpoVFSCUP6kgWgA6aFiHHDBb7jh4WQ8ryuDPaV6kijK/19fFv1pAxAwVxeqwFjThnMQkylZtdJGCHVDGkMDbq8PbcoIhNuPUjKFPEnAuFKPFN1QDpYIG+EBnLYk3McJj5xohgOQdFCNDjFRpFpgwrgoCT+Q88xEoLQNskSeZeDx5iKX8IKVb6E9k3eo5LR0QpWdoq2S6Ul5DtpURhiRcJkPS+dTysRnlsWSaoXid2jcWDROlSpUSYBVAk4mexJVShSzptxu9bN9FQFNor6KiPAZNVD6ggZcQW7uyMBBbgOgOjNXaDQoEJz3oG0UJ5CyRKkJAgAABb5JREFUtOwhjkDIp4ITeT0SoUiNl9yeZWTWR1oX81TZR5Q+pfht6nP9/+UjIPWsBhlmJpe9yoTA0qCzHjkARr6q8vILos9sWgiwzyomE5764U86bZJXzYyVks84aLO/h/mSkCFz/8/wZST9gVJwmCtYksVS4ZIdEcR6SRpLkhMeKnvlMRhatBQqXiQzarWKrBiO1A5FWil0RmTvUMZrucXJo40S5Ut2LVF9iTaVNpbBDcpghvuYqT7xh6xt/m48RKkDqQvmFhT9UNkAYVbcjFkRqUhh0cc1DQQ0ifpKPbLb+uAx5XKTK4XjP8l1GJjJzLXS0dmtInhxnlyyqfMs3oEyfQiG4UIg4BE+1hAhypwAEOPHZc/iTQpLYyc2t5v4buxMBGD88xwiMRjhJeUckDiQscrDG0fL9F44uek/z3Ppkn63CNAC8N/5l/zK/0yJiL+Z0/zC4+UbBqJfFG9jni7Tgcx0LuqUukQwyNQJJEckHSRn5oAvCqry5mh/ZP83yVlEmYj39siKPlF9zhfuf/+LlEUSe6ryXKzA8znB8tIhkWJwiiw8pacW+JA4sS+KifvfF+eyr0DIVb2xhMoWMMs4A/mViqZmBC77BvrEf0oENIn6mmoTA2ZuuyBp58QRUkZO5GV6eTKafs3J/+AjiQkQYyAXk50mJB5BtnpQBu8fnPo/PhaTaOZdoYGRsEvGNki5eP2LjO3/OFt/EDEC9IxNvYneOqdIZFAyJX0SY+UZmyNaxBfWB36fEVBUScXbCQ4yOl8gUPxTDdLsyxK4JO2MxOciSUocMcY/ihMlU4Gc/iIB8ytVS+IkqT5xet+cPpQ4K49ch7Hn5zdfD4bgY9iCuaqvMetHKWq0mSoo6sLm3jRVXFhDK8u+pY4hWQx7lspBNJ3W83N/jVm6yK+lykeCp7AkqSN/kh0VTFshqWsuJsiRX14f+U+KgCZR/6jiTBmdxky9FIm6IDOHP4/sZ3g4FusVvhRtosjCF+4SydXE5sq5PFq6tniSNFbC7XiA7siRQHnJYwRrwZJ0SpYIqL+Iv7jsAvYlr6MP0AiEEVBtij304rYT/lT1XPUX/w+TK/40X+ahPF/ZlQvkSn1FJ0o5emy1ioipo6UNM2bSvLJkNzcJGOOnGugbhkt0yZ/hksrjCDG8UOawss5nVYTr/AOacUZhDPj5d/cSBMNEziS04ZIJzFI0s+zfXTH1na8wAppEXWHA9e00AhoBjYBGQCOgEWgaCGgS1TTqUT+FRkAjoBHQCGgENAJXGAFNoq4w4Pp2GgGNgEZAI6AR0Ag0DQQ0iWoa9aifQiOgEdAIaAQ0AhqBK4yAJlFXGHB9O42ARkAjoBHQCGgEmgYCmkQ1jXrUT6ER0AhoBDQCGgGNwBVGQJOoKwy4vp1GQCOgEdAIaAQ0Ak0DAU2imkY96qfQCGgENAIaAY2ARuAKI6BJ1BUGXN9OI6AR0AhoBDQCGoGmgYAmUU2jHvVTaAQ0AhoBjYBGQCNwhRHQJOoKA65vpxHQCGgENAIaAY1A00BAk6imUY/6KTQCGgGNgEZAI6ARuMIIaBJ1hQHXt9MIaAQ0AhoBjYBGoGkgoElU06hH/RQaAY2ARkAjoBHQCFxhBDSJusKA69tpBDQCGgGNgEZAI9A0ENAkqmnUo34KjYBGQCOgEdAIaASuMAKaRF1hwPXtNAIaAY2ARkAjoBFoGghoEtU06lE/hUZAI6AR0AhoBDQCVxgBTaKuMOD6dhoBjYBGQCOgEdAINA0ENIlqGvWon0IjoBHQCGgENAIagSuMgCZRVxhwfTuNgEZAI6AR0AhoBJoGAppENY161E+hEdAIaAQ0AhoBjcAVRkCTqCsMuL6dRkAjoBHQCGgENAJNAwFNoppGPeqn0AhoBDQCGgGNgEbgCiOgSdQVBlzfTiOgEdAIaAQ0AhqBpoGAJlFNox71U2gENAIaAY2ARkAjcIUR+P+dZ+PsniJUywAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E6%8A%95%E7%A1%AC%E5%B8%81.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAFdCAYAAADL1o0TAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAEzwSURBVHhe7Z35m1XVmajvP9HdP/a9T/c16Sl2YjtEYxCixJg4RDSKMw4YJ6TDIDhPOIAoKGA7gqCioiDKpEgLBEQBEQcmERwQcQAaUBAkuu591z47lmVVcXTVrn2O532fZz9Vdc6uc/a41ru/tda3/lcQERERqSOUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlBcRERGpK5QXERERqSuUFxEREakrlJcqWbVqVRgyZEj4r//6r3DXXXe5uLi4uLh0+HLrrbeGefPmVWqmxkV5qZJp06aFH/3oR+H8888PvXv3dnFxcXFx6fBl//33D0OHDq3UTI2L8lIl//3f/x1+97vfhf/5n/+pvCIiItKx/Od//mdsAWh0lJcqUV5ERKRslJcM5aVKlBcRESkb5SVDeakS5UVERMpGeclQXqpEeRERkbJRXjKUlypRXkREpGyUlwzlpUqUFxERKRvlJUN5qRLlRUREykZ5yahrefniiy/Cyy+/HMaNGxeX8ePHh/fffz989dVXlTW+htfefPPNMGzYsHD//feH0aNHh/nz54ctW7ZU1mgb5UVERMpGecmoa3l59913o4iQdXDgwIHhpJNOCjNnzgxbt26trPE1O3bsCFOmTAmdOnUKffr0ietPnDgxfPTRR5U12kZ5ERGRslFeMupaXhCVyZMnhzfeeCNs3rw5Ssl9990XIyzNee+998KECRPCFVdcEd555524/ueff15599sQqdm+fXvYtGlT+Pjjj8OkSZPCEUccobyIiEhpKC8ZdS0vyAcRFZqPNm7cGM4+++zw0EMPhXXr1lXW+JpFixbFaMu+++4bDj/88HDuueeGZ555Jnz55ZeVNb7JZ599FmWnR48ecf2DDjooLkiPiIhIGSgvGT+IDruffvppWLBgQejWrVt4/vnnW4yorF69Ok6u+OSTT4Y5c+aEyy67LIwcOTLOFt0Su3fvjhK0cOHCMHfu3HD77beHrl27GnkR+Z6Mmf92OHPMoppbeo5dHNZt3lHZSpHaRnnJqHt5IeqydOnScNVVV4XbbrstNgm1BB1zN2zYECMqNAnRvHTLLbeEWbNmVdZoG/u8iKTR//FXw99fMqXmln+8dFpYuWFbZStFahvlJaOu5QUJIaJy7733hgsvvDCsWbMm7Nq1q/LuN6HPC31jtm3bFpuK6Og7ePDg8Oyzz1bWaBvlRSQN5UUkHeUlo67lhSjKiBEjwhlnnBGmTp0aPvjggxhhQVDoC9MURhYRnZk3b14cTt23b99w4403hmXLllXWaBvlRSQN5UUkHeUlo67lhdFG3bt3D3vttVcUi2OPPTZcfvnlYciQIeGJJ56orJVB5OWee+4Jv/zlL0Pnzp1Dz549Y4ddmp2qQXkRSUN5EUlHecmoa3khRwujiJ577rmYcI7l9ddfDytXrozRlabs3LkzCszs2bPjQj8ZRihVi/IikobyIpKO8pJR9x12OwrlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJUN5qRLlRSQN5UUkHeUlQ3mpEuVFJA3lRSQd5SVDeakS5UUkDeVFJB3lJaOu5eWrr74K27dvDxs3bozLpk2bwq5duyrvfpsvvvgiyscnn3wStmzZ0ua6zVFeRNJQXkTSUV4y6lpeEJcHH3wwnHTSSaF79+6hR48eYcmSJeEvf/lLZY1v8tprr4VevXqFo48+OlxxxRXhpZdeqryzZ5QXkTSUF5F0lJeMupaXBQsWRHkZP358mDlzZjj//PPDY489FtatW1dZ42vefffd8NBDD4ULL7wwrnv99deHCRMmxGhNNSgvImkoLyLpKC8ZdS0vq1atCq+//nrYsGFDlJALLrggPPDAA2Ht2rWVNb5m3rx54ZZbboknnYgNwsO6r776amWNb0KT0tKlS+N6d911V+jXr1/o0qVL2Lx5c2UNEfkuKC8i6SgvGT+IDrv0ZXnrrbfCKaecEiZPnhz7vzTnqaeeitGW+fPnx/WRGeRlxowZlTW+yY4dO8KsWbPi//Tu3TuceOKJoVOnTsqLyPdEeRFJR3nJKF1eEIndu3dX/vomX375ZXyfjrmtwXtEXh5//PFw8sknxz4vLTFp0qQwaNCgsGzZsvh9ixcvDvfff3944oknKmu0jc1GImkoLyLpKC8ZpcoLcoJsrFmzpvLKN0EUaNZBYFrj888/D88880w49thjYzRl27aWC6EpU6aEwYMHx+/j84jA0ByE9FSD8iKShvIiko7yklGqvBA1ueyyy8I555wThg4dGptxZs+eHT788MPYwXbixInh0ksvbVVIGFU0ffr0cOWVV4b77rsv9ntpbaQRnXtHjhwZHn300Sg8SMuIESNi591qUF5E0lBeRNJRXjJKkRciLjt37ozyQifb8847L44Eevjhh8O4cePCsGHDopBcc8018XX6n7TEypUrQ//+/cOvfvWrcPXVV4d77703TJs2LYoGw6KbwggkOt+ee+654cknnwwXX3xxGD58eFi9enVljbZRXkTSUF5E0lFeMkqRFzrUzp07NzbdnH322WHIkCHhlVdeiZ1tb7755vCHP/whCknfvn3D+vXrW42mLFq0KNxwww3hzDPPDAMHDowLTUEMnyaC0xSail588cUoS4gOP4nsIFHVoLyIpKG8iKSjvGSUIi+ICgnl6KdywAEHhNNOOy0KBRJyxhlnhDvuuCMOa2akD6OBqhWMPYHA0CRFU9Obb74Zh0xXi/IikobyIpKO8pJRirxs3bo1dsSl8yxRF0SmW7duUV54neHI5GqhDwxiQ1+WtkYcVQufQRSHPi+MOPoun6m8iKShvIiko7xklCIv+dDmW2+9NVx++eXhrLPOiieE4cxEXq666qpw7bXXhhtvvDFGXpCNslFeRNJQXkTSUV4ySpGXFStWhAEDBsSkcscff3xsPqLj7XPPPRcOOeSQeHKIwtCplmYeOviWjfIikobyIpKO8pJRirwwSoiJEYm4HHjggeGwww6L8kLSuK5du8ZoDJ11eY1kcm3leekolBeRNJQXkXSUl4xS5GXLli1x5M+oUaPCoYceGqMvdNClGWmvvfaKr9EXhqHTSE5reV46EuVFJA3lRSQd5SWjFHkho+5tt90WhzUjJzQP3XTTTTFT7lFHHRUlhgkXFy5cGCdERBjao8NuCsqLSBrKi0g6yktGKfLy2WefxeRwjChirqGXX345jjJ65513wtSpU+Ns0ayDKOxpeoCOQnkRSUN5EUlHeckoRV6ASApSwrJr166Yy4VRRcgBryEv77//fnj77bdbTVLXkSgvImkoLyLpKC8ZpckLssJ8Q0ym+MYbb4RPPvmk8k4mNkRcmPGZ95GbslFeRNJQXkTSUV4ySpMXZOW4446LfVwYXdQ0nT8ddOkP06tXr9jvxWYjkfpHeRFJR3nJKFVeyO9CYjomUST3C5DT5Z577omzTTORIlGXsjvrgvIikobyIpKO8pJRqrwwJQBSwASNd999d8zzQmbd22+/PcycOTNm4q0VlBeRNJQXkXSUl4wOlxfmKVq6dGmYMGFCTE5HVl36tQwbNixOC0AzEsOnX3rppZqIuOQoLyJpKC8i6SgvGR0uL4wgmjJlSmwW6ty5c4y4IDDTpk2LHXSZSZroC01GzPxcKygvImkoLyLpKC8ZHS4vzOa8bt268Nhjj4XzzjsvnH766fFEkPMln8PohRdeCNddd124+eabw/bt2+3zIvIDQHkRSUd5ySilzwt5W5CSzZs3h1deeSU2IU2cODFs3LgxCgyddJ966qlw5ZVXRsnZsWNH5T/LQ3kRSUN5EUlHeckorcMu8vL444+HwYMHR3Eh58vIkSNjkxG/M/qICMzcuXPN8yLyA0B5EUlHeckoRV4+/vjjOA3AoEGDwujRo8Py5cvja/R7QWCY92js2LHhz3/+cxxxlDcnlYnyIpKG8iKSjvKSUYq8vPfee1FOHnnkkbB+/frKq1lzErJCJ17EZvLkyZV3ykd5EUlDeRFJR3nJKK3ZiE64LGTPZaoAmob4nQ69/ERwHG0k8sNBeRFJR3nJKFVemIiRnC80D5HXhfmMmFH63XffDR988EHYsmVLZe3yUV5E0lBeRNJRXjJKkxeaiMj5QvMQSemYEoD5jO68884wYsSI2JH36quvjsOlP/3008p/lYfyIpKG8iKSjvKSUYq8EHWhmWj16tWhX79+UVDIsjtr1qwoMYxCYs6jG264IRxxxBExEkNzUpkoLyJpKC8i6SgvGaXIC/ldmM+IIdJ9+vSJssJoI2aWpiMvUkO/l0WLFoWePXuGt956q/Th0sqLSBrKi0g6yktGKfJCP5ezzjorTszIzNKMLmLKAP6+/PLLw5IlS2J/GJLWkfNl27ZtpQ+XVl5E0lBeRNJRXjJKkReiKh999FFYuHBhnMvonHPOCTfddFMcYYQcEGWhaSnPtsvvZaO8iKShvIiko7xklNZhFyH57LPPwi233BJOPPHE0KNHjzB06NA4u/Tw4cPjQsfdhx56yOkBRH4AKC8i6SgvGaXIC01CDIVGSpi/iJPByKLjjz8+jjgaM2ZM6N+/f5y48emnn47rl43yIpKG8iKSjvKSUYq80Dn32WefDXPmzIl9X+64447Y5+XII4+MieloUiIC86c//SnKgtMDiNQ/yotIOspLRinywtBn8rlceOGFcSj0qFGjwvTp08Pvf//7OLKIjro0GfXt2zeOTFJeROof5UUkHeUloxR5IUEdiecQEyIvhxxySPjtb38b9tlnn3DccceFE044IXTp0iUceOCBsemoFjLtKi8iaSgvIukoLxmlddjNYUqAuXPnxrwv5Hl54YUX4vBopgzg9ZdffjmOTiob5UUkDeVFJB3lJaMUeSFbLpEXOuzmy/bt2+PCe4xEou8LwrB8+fLSs+uC8iKShvIiko7yklGKvKxfvz5m1aXDLhGWPMpC9IXOvERa+J3cL0OGDHFuI5EfAMqLSDrKS0Yp8jJz5szw4x//OPZnueiii2LH3V69eoXLLrssvPjii3EY9dq1a+Owafq9fPLJJ5X/LA/lRSQN5UUkHeUloxR5IarCtABvv/12eOmll2I/F5qJmGWaiAwSc+6554ZjjjkmHHzwwcqLyA8A5UUkHeUloxR5QVbIqstoIyZnJMsu2XVvvPHGcPrpp8cRSLfeemuYOnVqeP7550uflBGUF5E0lBeRdJSXjFLkhf4thx9+ePw5evToKC3XXXddzLKLxNx+++0xcd2TTz4Ztm7d6txGIj8AlBeRdJSXjFLkhQkZibxwAsaOHRsefPDBMG7cuPDoo4+GNWvWxOHTSM3gwYNjp14jLyL1j/Iiko7yklGKvGzYsCH2bSGz7oQJE+Lv48ePj1l2161bF955550oMcxr1LNnz5oQBuVFJA3lRSQd5SWjFHkhw+57770XunfvHodJM3P0DTfcECdg5D2akYjGrFy5MjzxxBNx9umym46UF5E0lBeRdJSXjFLkBYi+7LfffjGywpQATAdw7bXXxoX+MJdccklsXmKSRoSmLcgLw3xJ11xzTRSe1qD5ibmTLrjggjjp48CBA2Pz1LZt2/YoR8qLSBrKi0g6yktGKfKCKJDL5Ze//GUUDoZFH3300eHhhx+OC8npBgwYEMViT5B9d9WqVbGjb6dOneJIptZgdBM5Zs4888yY/I7PZ3ZrMvwqLyLForyIpKO8ZJQmL8wcTT6XN954I0ybNi3cfffdlXdD+PDDD8OYMWPiiKM9QVMTERoiKQcddFDMIdMa9KXhpPO99LNZvHhx7GPTEkgR7/HZjIpiBFTXrl2VF5HvifIiko7yklGavNCEg0wwnxHDoZGZnC+//DJGU5iUcU/wOTT70MH3qKOOihl6W4N5kvr37x+OOOKIKCKnnnpquP/++1ucO4l+NnQm7tGjR2zGQoxYiN6IyHdHeRFJR3nJKK3PCwKTT8KIrLA0hfeqGSLN/7MQraHpqS15YR2ajVavXh3nVyKy06dPn/h38341fCZitWnTpjjf0qRJk6L0GHkR+X4oLyLpKC8ZpcgLUkKTDJEN+rgw2ohRRbNmzQpXXXVVuPTSS6NUXHzxxXHkUTUTM9Kxl+kE2pIXmphYj+9HlvjOK664IsyePXuPomSfF5E0lBeRdJSXjFLkZefOnXGoNOJCkrrLL788SsTSpUvjEGn6u5x//vnhD3/4Q0xcR4faPVGNvNBMxXcyVxLb8MADD0RJYn4lRiy1hfIikobyIpKO8pJRirzQREM/lRUrVoRly5bFHC99+/atvJtBXxQ61lZLU3mhuYeh2AhS0+agJUuWxNmrSYjHvElEefgO1m3ebNUc5UUkDeVFJB3lJaMUeaE/C/KSL3feeWfo16/ft14jD0u1EE2hcy2CQs6XGTNmxKgNTUU59F9BWuiA27lz5zhCiaaqalBeRNJQXkTSUV4ySpEXOsiSZ4XcLCzMc3TooYfGmaRZ8tf++Mc/Vv5jzxA5QU7ou0K0BWkhAkPH2xzW4XU64BKpQUSayk1bKC8iaSgvIukoLxmlyAsjfYiK0GGW5cILLwzdunX7698sZMG96KKLKv9RPsqLSBrKi0g6yktGKfJCRIS8LG+//XZciMIgK/nf+WvkZKkVlBeRNJQXkXSUl4zSOuySBI6+Kbmo0OelKd+1w27RKC8iaSgvIukoLxmlyAv9TOj3ct9994VRo0aFc845J+Z0yZPCkW135MiRyovIDwjlRSQd5SWjFHkhxwpJ6p588sk4xxBJ6saNGxf7wZxyyimx/wsjgr7LaKOiUV5E0lBeRNJRXjJKkZd81A/p+smxwgzTdOIlLwsJ45gZmgkWmYuoVlBeRNJQXkTSUV4ySpGXekR5EUlDeRFJR3nJKF1eXnvttfD888/H+YX4yUJH3mrzr3QUyotIGsqLSDrKS0bp8sIcRvvvv3/o0qVL6NSpU9h7773jnEM0KdUSyotIGsqLSDrKS0bp8sIM0ow4IuvtypUrw+9///swb968b8xJVAsoLyJpKC8i6SgvGaXLCzNKM9IImJ+ImaTbmhm6LJQXkTSUF5F0lJeMUuQFSUEG5syZE04//fQoMHPnzg1PP/10bD6666674t+8z8gj5isqG+VFJA3lRSQd5SWjFHkhQd3NN98cJ2Hs2rVrOPXUU8Pw4cPDoEGDwk9/+tM42/OwYcPiBI0kqyMbb9koLyJpKC8i6SgvGaXIC3ldSE43efLkcMIJJ4Q+ffqEqVOnhocffjgcfPDBUWqmTJkSJk2aFNephZFHyotIGsqLSDrKS0Yp8kJn3B07dsTlkksuidMEICjvv/9+OO6442KTUf4+y1dffVX5z/JQXkTSUF5E0lFeMkrvsDtgwIC/jjZasWJFOProo+NoI7Lw1hLKi0gayotIOspLRunywuSLvXr1iifjtttui4Iwffr08Omnn1bWqA2UF5E0lBeRdJSXjNLlhX4u1157bbj++uvjwu/Ma7Rly5bKGrVBe8rL6o8+Dc8t/7Aml83byx/ZJT9MlBeRdJSXjNLlhf4vzZuIvvjii7B79+6a6OuS057yctP0FS0WorWwvPDWxspWirQvyosUya7dX4YPt35ek8unO3dXtjId5SWjdHlhJmn6uzTl9ddfD2vWrIkSUysoLyJpKC9SJC+u3RT2G/RcTS7/NXtNZSvTUV4ySpUXIit33nlnmDZtWvybCAwJ7EhaxwikWupforyIpKG8SJHMffPjFs9vLSy3PLOqspXpKC8ZpcsLcxsxESNRlvXr14cRI0aEHj16hLFjx4bt27dX1iwf5UUkDeVFikR5aSxKbzYaOHBgTEr3yiuvhEcffTTOMn3eeefFEUe1hPIikobyIkWivDQWpcgLnXG3bdsWlwsuuCCcdNJJoXfv3jHb7owZM8I555wT5zfifYZM/9CS1Ckv0ogoL1IkyktjUYq8MLfR4MGD49xFP/nJT8I//uM/hmOPPTY2Id1www3h0EMPjULD/Ed33HHHD25uI+VFGhHlRYpEeWksSpGXdevWhXHjxoXx48eHffbZJ/z93/996N69e+ykS96Xbt26xYgM60yYMOEHN7eR8iKNiPIiRaK8NBalyAtNQatWrYoRGKTlqKOOinMcEXmh38vJJ58cIzNvvvlmHDJNLpiyUV5E0lBepEiUl8ai9A67TA9w0003haeeeirKC1MEMNrokUceqaxRGygvImkoL1IkyktjUbq8kNOF5iFyvJCs7oorrgh9+vSJuV927txZWat8lBeRNJQXKRLlpbEoVV4QFiIvyEv+N3MaXX311VFi5s6dG1+vBZQXkTSUFykS5aWxKFVeGAK9YsWK2IG3KeR8eemll+LUAbWC8iKShvIiRaK8NBalyQtRlk2bNsVlx44dYdeuXWHz5s3x9YULF4bly5fH12oF5UUkDeVFikR5aSxKkRek5IMPPgiLFy8OL7/8cvz9/fffD1OnTo3DokeNGvXX+Y5qBeVFJA3lRYpEeWksSpGXDRs2hEmTJoV77rkn5nVZunRpmDVrVszvwnsMmx49enSUHBYz7HbcorxIUSgvUiTKS2PR4fJCzpZXX301XHzxxeGAAw6IPxkWfffdd4fDDjssPPvss+GMM86InXZfeOGFsGjRojhpY9koLyJpKC9SJMpLY9Hh8kIUhb4tjCRimDQTMebDo8m2y5QAv/71r8Npp50WpwYgAlMLs0srLyJpKC9SJMpLY1GKvLz77rvh/vvvD0OGDAmDBg0KDzzwQBSVzp07x2R1ZNglYd3s2bPDggULaqLjrvIikobyIkWivDQWpcjLypUr4wSMw4cPDxMnTozTANBxt1+/frHz7oABA/6a+6VWUF5E0lBepEiUl8ailA67QD8W+r7MmzcvrF27Nqxfvz5MmTIlLFmyJFxzzTVh8uTJlTVrA+VFJA3lRYpEeWksSpMXIjAIDP1dHnrooRh5Ofvss+PvRGLI/VJLKC8iaSgvUiTKS2NRiry88cYboW/fvrHD7n777Rd+8YtfxJml995773DqqafG5iPeGzhwYOwTwyzUZaO8iKShvEiRKC+NRSnyQofde++9N3bUPfzww8MRRxwRzjzzzNhhl4WRRyNGjIgjjRhGXQtRGOVFJA3lRYpEeWksSms2yqHTLiOP6Pty++23x7wvEyZM+NZ8R23BlALbtm2L8yExDLstyOBLE9X8+fPD66+/Hj755JPKO22jvIikobxIkSgvjUXp8rJs2bKwZs2asHPnzigWb731VnjxxRfDO++8U1mjbeg7g7iQ0I4oDkOrW4M+Nnw+OWSOPvroGOFhGgI+Y08oLyJpKC9SJMpLY1G6vCAUzCyNHPATgSGvC5l4q4H1yQfD1AL77rtvjKi0BqOaRo4cGfvTkLmX6QnoU0MSvD0JjPIikobyIkWivDQWpcsL0jB+/PjQv3//OEz6u04FgLwQpSFfTNeuXduMvNBcdMEFF8Qh2Rs3bgzTp0+PzVY0H+3evbuyVgb9bJhv6frrrw+9e/cOJ554YujUqdMem6WqQXmRRkR5kSJRXhqLmmg2IvrBZIwkqKs24pKDdNDkRB8ZmoJocmoNojInnXRSWL58eZQe/ib6MnPmzG9l8eVvJoxErO666644AqpLly7Ki8j3RHmRIlFeGovS5AVJYQbpUaNGheuuuy5OC5DCRx99FI455pg25YVOwd27d4+RGiI8rIu8kBAPAWoLm41E0lBepEiUl8aiFHkhqkFGXaIaTMw4ZsyYGNGg423zhRwv1XSorUZeGI1EIjyiPURe5syZE0c4IU7KS7YoL1IUyosUifLSWHS4vNDMQ2fZnj17hvPOOy88+uijUWKYpPHWW2/96zJ06NAwePDgmO/ls88+q/x361QjL0jLtddeG5544om4Pv1kmIoAqdlTXxvlRSQN5UWKRHlpLDpcXpCExYsXR3GhjwpJ6GbMmBEnYkRimi5MFUDOF6Ike6KpvNAcxc/nnnvuG31Z6KTL0Gj6vdDPhs679LUh6kOumLZQXkTSUF6kSJSXxqLD5SXv6zJ16tQYWSESgqQw0mj16tXfWJjjiBww1XTiJTqD8Lz//vtRRhh2/corr3wjosLvdOwdNmxY/O7bbrstjjwyz8vXi/IiRaG8SJEoL41FaR12aT4iYRxDkW+88caYZG5P0Y/2gO9AbhCbPDleNSgvImkoL1IkyktjUZq85BBhQWDIdrtly5YOEZjvg/IikobyIkWivDQWpcsLEZinn346ziDNqCOy3dYiyotIGsqLFIny0liULi9APxVGIL3xxhvfynRbKygvImkoL1IkyktjUbq8fPjhh2HhwoUx+vL444/HnCuIAp11qxki3VEoLyJpKC9SJMpLY1GavDDyhxFBzC9EcxHJ4hgBdMMNN4Rbbrkl3HvvvXHCReYYqmY0UNEoLyJpKC9SJMpLY1GavCABzBfEUGmSxTE5IqN/aDpiGDU5WMiGy0zQ33W+oyJQXkTSUF6kSJSXxqI0efn444/DkUceGRPJEV0hEkN/F36SlI4suFdddVV49tlnqx7OXCTKi0gayosUifLSWJQaeenfv39cmLUZiSEr7p///OeYtI4TdOmll8Y5kIy8dNyivEhRKC9SJMpLY1GavBBNmT9/fhQX5jIaOXJknOGZvi68dvfdd8eoSy2ICygvImkoL1IkyktjUZq85KxcuTJOzshcQ5dffnm47rrrwoMPPhj7wNRCc1GO8iKShvIiRaK8NBalyQuZdLdu3RqbikaPHh1ndybLLieGTrwMm2b6ACMvHbsoL1IUyosUifLSWJQmL4gLcxoxNQB9XGhCevnll8O8efPiTNOMNurVq5d9Xjp4UV6kKJQXKRLlpbEoTV4++eSTcMIJJ8Rh0mTYZV6jTz/9NErNBx98EO67774wYMCA2IF3165dlf8qD+VFJA3lRYpEeWksSpMXZnY+77zzYkK6adOmxVme6f9CnhdEIe8DQyK7WpgyQHkRSUN5kSJRXhqL0uSFCRjJ5XLllVfG/i6MMKKj7tixY+PoI16nL0ytzHWkvIikobxIkSgvjUVp8pKzevXq2Dn35ptvjh11hwwZEiZNmlRTnXVBeRFJQ3mRIlFeGovS5eW1116LERYS0tFJ9/zzz4/DpZ955pmwcWPtVKTKi0gayosUifLSWJQmL8wYTRMRyenGjRsXpkyZEidpfPLJJ6PMXHbZZXGiRjr2Mqy6bJQXkTSUFykS5aWxKE1eNm3aFHr06BFFhegLI4yItGzYsCEsX748duTlJC1evDjOd1Q2yotIGsqLFIny0liUJi+IyimnnBKjL2TTfe+998KHH34Y87ow6oiTQ6fdhQsXKi8duCgvUhTKixSJ8tJYlCYv5HQZNWpUOOuss0Lfvn1jXhdGH40fPz72eTnzzDNjAjtyvHz11VeV/yoP5UUkDeVFikR5aSxKkxeEBIFZsmRJFJahQ4fGPi633357HG1ENIbEdbUgLqC8iKShvEiRKC+NRWnykkNSOpqOaCLipPzpT3+KeV7mzp0b5aVWUF5E0lBepEiUl8aiNHn5/PPPw3PPPRcefvjhKC+MOBozZky455574ggk8r0w5xHTBdhs1HGL8iJFobxIkSgvjUVp8sL0AOR1GT58eJg9e3ZMSsccR2vXro2TNDI1AO8vW7bM6QE6cFFepCiUFykS5aWxKE1ePv7443D00UeHGTNmxOYhpgsgGrNjx46wbdu2mHWXaQNmzZoVdu7cWfmv8lBeRNJQXqRIlJfGojR5oTmI0UTkerniiivCo48+GrPqPvXUU7HJ6LTTTguXXHJJFBmbjTpuUV6kKJQXKRLlpbEoTV6IpsyZMydMmDAhTsp42223xSYk+rsgNQ888EBMVlcL2XVBeRFJQ3mRIlFeGovS5IVh0ojKokWLwsSJE0O/fv1Cnz594pDp3r17R5Eh826toLyIpKG8SJEoL41FafLCnEXdunULCxYsCI899lg499xz/5rjhWajiy++OMpNraC8iKShvEiRKC+NRanycswxx8Th0nfccUfM75I3ETEdAJGXXr16xb9rAeVFJA3lRYpEeWksSpMX5jHab7/9wh//+MfQvXv3GHlhskYEhnmOrr76auWlhEV5kaJQXqRIlJfGotQOu+R3mTZtWmweIvrChIwMlyZZHR14n3/++cra5aO8iKShvEiRKC+NRWnyAgyBJtqCtDCXEdEYmoyYGoDZpJ0eoOMX5UWKQnmRIlFeGotS5aWeUF5E0lBepEiUl8ZCeakS5UUkDeVFikR5aSyUlypRXkTSUF6kSJSXxkJ5qRLlRSQN5UWKRHlpLJSXKlFeRNJQXqRIlJfGQnmpEuVFJA3lRYpEeWks6l5eyAuzefPmsHHjxjgD9e7duyvvfBvWZTg22X1ZmF/pL3/5S+XdtlFeRNJQXqRIlJfGou7lZfr06aFnz57huOOOC4MHDw5vv/125Z1vQuZepiI44IAD4rQEzKt05513hnXr1lXWaBvlRSQN5UWKRHlpLOpaXpYvXx4nc7zqqqvCM888E2elJsEdEZjmEJl56qmn4nQEs2bNCvPnzw9vvfVW2LFjR2WNtlFeRNJQXqRIlJfGoq7lZeLEiXEGamai3rp1a5xS4PHHHw9r166trPE1K1asiKLDPEojRoyIM1mT2Zcsvy2xa9eusHTp0jB+/Phw1113hX79+oUuXbrEJqpUlBdpRJQXKRLlpbGoa3lhTiRE5LXXXosRlClTpoT77rsvLF68uLLG17z66qth2LBh4eyzz44n/5xzzgkPPfRQnJ6gJfg8IjTXX3996N27dzjxxBNDp06dlBeR74nyIkWivDQWdS0vyMjdd98dIy10xqVpB6GZN29eZY2v+eCDD2L0hY669H+59dZbw8033xwWLFhQWaNtbDYSSUN5kSJRXhqLupYXOtzec889YdWqVTFSMnXq1DB8+PAW5YVmINZBXIDmJQTm6aefjn/vCeVFJA3lRYpEeWks6lpeJk+eHAWGUUR00h01alT8e8mSJZU1vmbOnDlh7Nix4b333oszV994441h0KBBRl6aLcqLFIXyIkWivDQWdS0vRFyItAwcODA88cQT4ZRTTol9XpAZ+sE05cUXXwxDhw4N11xzTey4e9FFF4UxY8bEvC/VoLyIpKG8SJEoL41FXcvLzp07o7TQofbKK6+MnXFnzpwZZs+eHZemIB1IzYUXXhiXO+6441uC0xbKi0gayosUifLSWNS1vAAddcnXMmPGjLB+/frYt6UIlBeRNJQXKRLlpbGoe3khTwtTAiAxpPpvLW9LKsqLSBrKixSJ8tJY1L28dBTKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0lgoL1WivIikobxIkSgvjYXyUiXKi0gayosUifLSWCgvVaK8iKShvEiRKC+NhfJSJcqLSBrKixSJ8tJYKC9VoryIpKG8SJEoL42F8lIlyotIGsqLFIny0ljUvbysWLEiPPbYY2HMmDFRMDZt2lR559t88MEHYeLEieG+++4L06ZNC++++27lnT2jvIikobxIkSgvjUVdywuiMnbs2HDuueeGvn37hgEDBoRXX301fPHFF5U1vmbbtm3hueeeC2eddVb405/+FC655JLwzDPPhM8//7yyRtsoLyJpKC9SJMpLY1HX8jJ79uxwww03hDvvvDNs3rw59OvXL0ydOjV8/PHHlTW+Bqm54447wsCBA8Onn34afyda895771XW+CZfffVV2L59exQkPo+ITdeuXcNbb70V/05ZrnxkfvjfFz8c/k/v8TW3TF+0qsVtbrp8+OGHLb5eD8tHH30Ul5beq4elno99r9Gza/K636vPI2HBsrUtbnPzpZ6vnXq/9ve07U+/tLLF81sLy7UTFrTbsT/vvPNindfo1LW83HvvvWH48OHhhRdeCJ999ll45JFHwrhx48Lrr79eWeNrpk+fHgYNGhSbi3bu3BlmzpwZozZz5syprPFN+LwJEyaEHj16hMMPPzzst99+4e/+7u/Cr371q/h3yvKz/Q8M//cn/xF+euAhNbd0ObRri9ucL4cddljYf//92+U4lLEcfPDB4Re/+EWL79X6cuihh8brkJ8tvV/ry97/cUDYa+/9Wrzuylx+9v+XQw9r+7pn+fWvfx1+/vOfh86dO7f4fq0vhxxySDjwwANbfK/WFx4cDzjggNClS5cW32fp/P/LrpbOby0s+xxwUDjooINa3O7vuuy1115h8ODBlZqqcalrebn99ttj+GzVqlVhx44d4dlnnw133XVXePHFFytrfM2TTz4Zrr/++rBkyZLYrPTSSy/FyMtTTz1VWeOb7N69O6xbty4sXLgwzJ07NzYbIUDIDn+nLH369AmnnXZai+/V+vL444+HfffdN4pjS+/X+nLRRReFs88+u8X3an15+OGHw9577x2lu6X3a32heff8889v8b16WCgDEBgqjpber/XlqquuCscee2yL79X6QtmLNA4bNqzF92t9IeJ/4okntvjed1148F69enWlpmpc6lpeRowYEe65557YlJPLC81B8+bNq6zxNZMnTw433nhjeO2116KYIDhUwFTGHQ3bSJ+beoROzkQvFi9eXHmlvhgyZEgsxOsRJB1xfOONNyqv1BfXXXddvAfrlV27doU//OEP4emnn668Ul8Qle7Zs2flr/pi69at4aijjooVdz1CPdWrV6/KX9Ie1LW8cDPefffdsSKlmWf8+PFRDFqKvNBZ97bbbotPTxRCiM6oUaNajbwUifJSHspLeSgv5aK8lIfy0v7UtbwQQhs5cmR48MEHYxPP1VdfHS8SmoaIxDSFfjAMkUZgNmzYEJubaHZasGBBZY2Og+++8sorK3/VF3RwJnT+yiuvVF6pL+gjRd+neoRQMf0Wli9fXnmlvrj55pvD0KFDK3/VHzQ3n3766bEJox6hT2C9VqDIywknnBCef/75yiv1BV0UGFAi7UddywvDlm+99dZo5EQy6NA1evTo8Oijj4YnnniislYGkRmajij8L7300lgB0366ZcuWyhodx5///OcwZcqUyl/1BaO6aK5DFusRCr8ZM2ZU/qovGGnANYt81yM8Nc+aNavyV/3xl7/8JfY3WrZsWeWV+uLll1+OgxDqEVJa3H///eHNN9+svFJf0BowadKkyl/SHtS1vFCYkKSOG5KIC/1X1q5dG95///24NOXLL7+MryEwNDXxFMITLJ/R0SBdn3zySeWv+oKnT6Iv1ebHqTUY+r5xY33msqHZgmY7ftYjHPe2kkjWOqRPINElD0L1CNELhtrXI3n5TfqKeoSHZIZKS/tR1/ICdL6lUFy5cmW8QNqSEd4jWR3Cw1NsvVYCIiIijUzdy4uIiIg0FspLO0JTCn1CiAQR4WkrCkTzC+vSfETEKI8CER7lbz6D5qWOap75Lt9L+JwQdN4MwP/xGrDfhEfZLxY+h88uGjpo501Cezr2rNt0G2kGYH22k//lMzg3zTt9FwXfzTHf07Fn+9hW9jPfdhb+hwgk56SMY8+551ixHXuCbWI/2T4yXbPdwM98v9iPjoqKsu0cf843yStbg/XYxvz+ZlvZfuAYs+/5sed97u/8nigSvpumFO7BtmA9trf59ZHvF9vPa3xOW8ehPan22OfXdn7dEDXn9/z6Ydt5jfc4L7xW9LHn8/OygoVtaKvM4Vjn5T3/xzYC10nTY29rQPUoL+0IUxMwFPH444+PQ3Lbmvhx6dKlMWHa0UcfHa644oqwaNGi+Do3wmWXXRaHZPbu3Tt+ZkfAzUNHZr6XuTPIRNwSFILcfIzs6t69ezj55JNjAqb8hmQ0SadOnUK3bt3iwudQoBQNneFIPkciKLZh/fr1lXe+CdtPvycypZKwi22kIyB9GTgGdADnM/isjurcyLYyN9dxxx0Xf7Y2HJTjSIdR5udiu4888sjYWZ1RDO+8804cRUWH9PzY8zkUjEXDuae/GdveFhTupCjgmuG6J1XBmjVr4jmhIyaJG3//+9/H/cjvh6Kh8qAD9AUXXNBmZ2IqFY7xhRdeGM/TmWeeGTuus+1cN+x7fuy5fsgn1RESwLEneSFlRltwHXC8ybCbXx+MmkJ8yJNFWcP9wPxwjOLsCDj2lJHnnHNOi7m5cjjuDLE/6aST4naTZZZzwKhNtp1ylAR2vMc1REqBIiUAcUGcSFaYl4EXX3xx7E/E9dASXPckaeQY33TTTfG6B/pd8r/HHHNMPIdki5fqUF7aCUYgMBKESp3RLEz+yA2ZP501hRuW4d3cdOSfIf8FhT9DYflfLnJGTFE4svC01NpN0R5Q+FKQUYgwQzd5aCjo+N7mTzDsDyOlqPDJkUPuCAo+CjxuRLb3mmuuCfPnz48LFUPRTxMMg7/llltiBmW2jeGgZFBuqWMlT2hICceebWYb6eTNvnK+qHg49hSMdOymL1WRT3F8L3lDmIaC+bO4hvhetrM5eQVKxc5200mdjLVcO8zdRRoAKv782FOYFn3sqfzo/H7KKafEiqMtSGGQXx+MuEO6uP45xg888ECUZs4fhTujBouu/Kk8+e7+/ftH8WgrfwvXMdm7EQWkkP1ge6mE2BeEmXuG4076BZ6ii7xnuSY59tx/VOp7yt9C+cT1wlxw+fXBPtH5nuuHe59jT4WMIPMQVSRclwge2cbJG9VW/hb2k36KjNhhuxlyz/w+HGdGD7LNnBve475H6Io89mw7MsLwZx6aKDO5D9mHlh7UuMa4XnhIZR2ue+blo7zk3mFfKPc5N+Qq64iHvR8Cyks7QQFAtIVpCCi4KMwYrv32229X1vgaKk0qWyopwokPPfRQLDD4DP6Pm5FKiidBJuDipszDjEXAzZV/L2JFhcL38hTQPBTK9jLkkv/haY51eBrl5qPw4+mBG5mcOtzYVMJFVv5AAcCxzyflpPLju1uadBPRYV9PPfXUKCiIDE9vnCcqUKSGColpIfgboSiyIMzFi2NP9AeJ5LqgEG7ruHEemBWdaBmjMDhnpAtg+xFLrkMKwaKPPTLLdUolhIC1BRU/BTTbyjFFNrnmWdgPzgXXFPcCIsA9UCTIEeeaiu83v/lNvH5bg3uaBJekCODYs81EwHjK51qnQuLap0JjvaJHJHFeqaS5BnhypwJsC+5PKk+Ei+uL6wy5Jdkk1x/STLMG9w37wz1eJBx7jh15upi3iGuiGrimqeC5x3noYlu59tg3rhumb+H8FAllMZFzhIrt4cEBeSSi29JDB69zjLlmuC7INcW1TrnP6xwDziUSxPXDZ8ueUV7aiTxaQWXEkwJPcdxYPG02h4qFJ2Qqfp7+eHKjouSGpBCkoOGm4LO4wFmKfAqlAOPpk4KQAownIr6TQoLtaw36OdAsRCHODcxNSuTpj3/8YyxQqcxaiz61J8gIFRBPl7SNUwAz9QP70Zy8sOZJk4Kc5iEKlfzpmXNGNCR/IiWa0VZbdipcAzS7UXiz7ST/IypH4daWeCBcnCO2j/W4Zkh8SCVG5Ilj31r0qT2houB6Z3uJGLYFhTbygmyxzVQ2CA3ixnYTAeOplusQASs6gSSVENuOmHyX5HMIFpEhtpnKiohGLo75QjNYW/dOe5Afe66XPSWfQ8yo4HnQYF22nYqe18k4TSSAz+KaIZrDvVwkHBu+j3uNaGe1yed4kOMe5aGC/UfEKLs45uwbEW+kt+hjn8M2cOyIfhEZaqmsyxOiIiWU4zxkcX0Tgbz22mtj2cPrlAXcE6012cs3UV7aCfpKUGHyBE+lztMooUIuyOZQKdKGS2VLxUgzABczT27cfNwEmDhPJggEUZAinyYosHh64Sc3H1EVvhchaK3ZgcqHJw/2kUKD7aPZiydZKgNC0kRgKNiLnkQM6eOJhagR209Il8KipX4TPDmzf4TF2QcqU6SF40/0hkIRceSplMgZhUuRUS8KLio+nnQpzLkmkBIK6LbkhWsoLxCBa4XKHwHiOCBl7BOvdQRUdnuSlzy6x7XNviE8SDvSxf8iBdwPVAZsO+exI6CiQ/aqkZd8+2i6IFpBBIkHlDz3ERJ/xBFHdFhfL6CZc0/ywvXBQtnEPXLGGWfEY8zC8c/76LD9VKBcgx0B20K/kWrkhWsGWUcGuD+5L3kYQYbZdqKl9KXiQYBrqWjYHso2BIrrh0hQS1BGss2UjZSnXD886PKgSvnCQyrXINcR5RgRGNkzyks7QeiPCocnLiohnmgo3HhSaA4FPRUlT9ncgEQnuLh5MuIpnGYlBIA5bLiYudCLlBcqTsL2VKRUftxMfC/S1Jq8UOiwf3RURGIoxCkYKUT4nYKbJ20Km6JD0HwH20s0gu3n+PIahVlz2D6OZd4UxJM/4sn6bC/SRiGE5PA7kaQi5YXoApUHkssxRUaoUBDh1uSF1xEBBDg/Pxx7fme/eJrlffappehTEVQjL8gWUS+uDfaBJ3z2kydQKt+8QkJauB+IJnUE1coL20zTHg8ZRE7ZXiC6xbHnfa5B9oVoSEvNlkVQjbxwzbOwjfyk0swjAjTfIfq8zj3DOWH7O4Jq5YXtZl2iRGwfEslrHHvOH79TDhFN5b5trcN+e8J35/3OKKtbi/YgNzwI8tBE+cN1xnGnrOcepnzk+qEsYF3Op+wZ5aWdoCmIwoCICxUoMkPl31L7JULD+xg2FzNPoLmd0/zEzcnNh8RQoXIxs15R8ESWfy+FM08GfC/b1/yGpJCggmHfKMAJgVLoAQUeNyaVJ09DVAjsU9EpvTl+fA9hcCIqSBV/tzSBIRUjhRtyQgFIYchTNE1NHGdEgkoHsaQg4biwXlEQaeHcI740QfDUSMFGBIhj3RJUkAgX/5NDMwb7xmcQbSGMzfmspcgLx5friooSySJixjayH1Sm9BWhguKpH/lqST6LoBp54RrgaR6ZZduIjvIa9wLngnuViBIV0WGHHRabjYvu9JpTjbxwzROt46GI/WCEDBUv542yiGgL7/HQxTXfUaMcq5UXzhH3N8c6l1oeErmGqPQ59jwAEPXKm7+LhPPOAxODLbhXeXho7X7lmFJesl1sMyLD3ywcex6gECHqEMoC1pM9o7y0E1g1lSZPZVSmVB48QVMZEcloCpUjBTTtzozYoeChwqKwpjc6IX9uDAp0Po+n5yIrUApZbhiGfxLG50mYpgy2BRlrWhDkT2cMaWWiNCp+CkbCzcgLhQlNMTxhE5qmQqJQLBJ67fN9iAfbwnZRGHPskYOm5J2lObYU0jw1UXhQyVMIMlScY88+UFFRqOZRmiJANqgoGKnD8SP6xjnPjz0i3BwqHAq5ps0qiCZPcSw0zfB5eSStI2gqL4gr10PzzuoIIdvN/uX7zH1Ahc/5Yrgyna9pwuQ6oumxI2gqLxwvZJ5rnAoph2gRlRRpALg/c8FEJIlwEb0gmorQ8z7iXOQDR1NyeeE6Rcp5YKLpsCmIC9c89ysCQAdTrjG2n/1g/7mG6D/COpRnHUFTeaGc4Hu5HpofO84F202Zmj+U8FrTY49IUKbysNRaxLg94HqhiQcBpBykrMjLG8o7moeawvZw3VOm8pDEdU+ZwzXGMaf/HeeALgPsY9EPez8UlJd2Io+gMGyYSpQCjIuZm5InhqZw8fOUQGFNBUkFinVj5YgNoU8KeH5SwbZl9e0BYkRhRydbvpd94OmSip+bLA+PA08IiA7rst2EPik82E8KfSp++sDQnEQ0oOn/FgVCRSXI8br88stjB2KOOce/ebMdlRAVJ9vI8efJh3Azx5eoE4V33rGRKEHeN6YoeIKj3ZxjybZzXKkYEV6aVVp6emf7qWipeHKo6HmSZrvZBwrTjnryByIRHEug8OV6aN5kxdMxsk6Hbq57rjPOD9c9FRbnjeZLrh0kpkhpbArXPw8ebANNhlQq9Flhe3OIJhIhonLkHHHdU9FwnthPKlHOIddO8/8tGiSVKCHHi8qfCrS5tFOucE2w/Rx3hIfoLtcf28/rlFt0fEWi82hq0fA9iAfbgMjT747ICtdEU1iPfcyjq8B5497l/zn2XFOUTU2lswgQI44x9xnXMtcC550HP45d82g7dQPlO9cNkV5khQcl9pE+O2w7r1Me5dF42TPKSzvCDUZFxA1EwdCW/SMwVDgUdBT2+c1KAcTTHxECboKOenLOv5fCoSO/t72gwEKeeJrkuHJ8vytICueQyoCKrKMqfwphnjrzCr8jK76Ohusc6UJikMX8POX3A8LJeeyoylMygUbquXeIYhINkfYFISG6y0MH0bFcUDj2SBt1BuLJw6FUh/LSjlD5cTFS8FIhtfXEznusw7r8T9N1EQkubgr0jnr6hLK+tz34Lse+Lfg/jgHi6bFvf/LzhGw2PU/8bO1+kOLhmuPYc/157Nuf/LpvXj7xMz/2XvffDeVFRERE6grlRUREROoK5UVERETqCuVFpGBo46YPDf0J2ou8rbzWaKnN/ru047Mux6ve+v2wvfRZaM9zLCKto7yIFAx5Txh+y0iO9oIRIYxQosKsFRCP5p0O89eo3KuRGEYjMeqI0S8dQS5LTTtRtkS+Xmv7weg8RlG15zkWkdZRXkQSobIljwP5Gkj2RQZN8n8w5JmKmwRu5Mshp0NTSKhHLhcqQyIzJJ0jvwk5OPg9ryT5mS85TCnBek0/k4q1aeVKJlWyeOa5KJouJDUjpwp5Tb6PALG9DPkk1wm5gUhsSL4NMhuTKI/PZ+F1cljkeTwYhk4COpK58R7/S1I68oyccsopMcEg20vSrhz2h+1EaFiYc4ph5a3lEGJ9jkNb5McKCSRHDbmKBgwYEI8N+YKYLJCkYflr/GRhXYbQkyitaZJA8jZxLlvL0ov4kHWXVAQkHyQfCPvIMeE8krtnT9ssIl+jvIgkQv4GEsSRmJAMrFTIZDQl4RQVE5Uy2YapIJEY0uNTaVKBU7EjD4gOv5MdlwynVJR5ZUaFTeVI0j8SYZEMjmRifC4VLEnt8kn2yBuEVACVLImvfvSjH8XtarrsvffeoXPnzjEq9H2aOthmKl4qYRLjMckc+5bPjk7m0WOOOSYmPiPzKblbkCmS0uVZgJEdEncxozPix36zIH8kK8th+xBAxI7jQDIyfm+eRTaH84HgcLxY8mkeOE75a4gjGX8Zokp+DT6P48d7bO+//uu/xm3M188X1iXKQpIyMqvmn4G0sR+cj3xdjg35gpApIkp5Snj2m0RxSBE5lch8yz6zXr6ISNsoLyKJkAafypAKiCkWqKCoDIk8kDUWUfjVr34V04mTQp9Kkqd2IgwIDxU1wkHmTSSIipBpCnJ5IZkb2ZtJ6X7ccceFX//61+HII48M3bp1i4Jw6KGHxtl0+X++G1EAZIHMn126dInf3XT57W9/G6Mc3zehH1DJ0kzCNhNFIDpCdIHfkSsWjguyxXusj/CQWp0MsCR05H2yOfM/rVXayEEuRWSJJTJCkju2vSWI8hARyqMmHLff/e53oWvXrn+NoiCOCAjwvZxDRAO5IoJy4IEHxm1ClliIcLFOnniSfWCaCUSE4414Hn/88VFKyLyayyXnGtFj/zk3XBOnnnpqfA+xRPh4DckjMSXXxZ4SXIqI8iKSDJUa0xMQNUBGiBLQPEKzDPLAEzlRF57GmYiQpgUqsH/4h3+IURGiDlSc/CRyQsXM+7m8ULkiN3wun8P3UCkiNHwvFSiVH+JAhU4TBU/6RCYQC7aBuVWaLlTeLAgEUR/+57vCdpEyn8gGzTj060EU+FwqZ0SO7f35z3/+V6FCRIgIUZmzsE+IBpV4/hrvN800ytxazBdDcwuig3zRTEcfE9ZHiNhvKvxcgNgf+gTxkxTyecSqJViH6QFo8kPqfvGLX4R///d/j8KDJLJwDpkugu8DhAQBQzzYdvYBEUM8iJTxHnLDa2zXO++8EyNOHIt/+qd/it9DcxnXy29+85somCw//vGP43ksemJBkXpHeRFJBHnhaZ2nbypsmjWowHmyHjVqVHwap4Jj3ieiLVSAzDRL5IMndP6mKYI5fRCb5vJCRU4TFK/R5ESEJ5cXmiaQFyISfBbRCeaxYX2+i+9gklAmg2u6IBe8zqR4+Tw33wUkgUqZSBCV/UEHHRQOOOCAGFk6/PDDwz//8z+Hf/u3fwuHHHJIFLR8rh3SoBMxQgxoWvrlL38Zfvazn8VIx7HHHhtFgc9k/4BjgASw77zH+n/zN38TI1n8P59F5f8v//IvsT9KnnadY4DQITUtyQufmx9fRIRjz3FANpA9ZIvPI1qCnDGhHk1jTaM9RKw4d4gPERPkKo+6ISAIFs1CHCe2hyYlrgkEjz41CNHBBx8c57TK16cJjnXzbRORllFeRBLJm43yvihUYPxOM87s2bNjZYXYMKssTQv0d+Epnuaeww47LEZCqARpzqASbC4vpNKnbwX9aJAcohVUpogAEkTFTF8M/iYCguwQqSGKQ6VMRIGmDMSK32l2IcrD3wgQEQy+g4XoCZJA5KitOW5okmI72Qc+mwqYZhmEiUkKiSjwHewnfWzymXLZXuSJiprOq+w7xwUBo8mGfUP2ctFAkhAJmtZYn8gVUoQM0mk5b+ZBXmguyiNIyBLbRsQGeaF/StNmIz4/7+yMvORNUUgEnYf5m/PGtiGIHFsiJTTh5fA720+zEtEftg9xJRpFRIvJHDmGubzwGRwbFkSJBflCaoig8d0ch46aU0uknlFeRBJBXqiIaBZiBA2VF80I9HfhyZsK6qijjgpHHHFErFCpnKgcaUKg/woV66uvvhoFAPloLi9UrjQBMSIFMUKQiALwXfwPwkBlzEy1NFnkTSd0XGU9voOnfCIi/E60hagFEQ5GzSAtQNSCUVI8/dOnI58stCUQJCITrEvlTlSJ5hyatIg2se/IC7KBDFB5A/tA9AG5InKB3BHZoOIGIkA0NfEZzaFzMRElpIJjTJQKsUHs9t133782TQHHk4gOryEvnA+Oad6ZFolCMKAleaEjMfLZmrwgkcgKx55zw7li34ho0VzYdCQUx5Ht4dwhjESniMzx2ew7HbyJ9nAMkbof8sScIu2F8iKSSB55ocKlEqJCom9GLi958wwCQ9MK0Q0iADR3UMETbaEypU8EQtBcXoCneCIp9LGgiQb5QGKoYOmfQYVOBCAXF6CfBd+DMLE+ssT3I1EsNClRsdMPBfg+IgW8RgXa9PtbgvfpXMzCfvN5VPJUyogSFTUREqI7RGpgT/KCoLQkL2wjM04TwaKCJ6LDKB2iUURg2K9cRgBZ2GeffWLEp6Vmo6Y0lxe2n866CBJNVs3lhf1GmBi9RBQFGUVWkCKOAfJDRAjBgVxeOHdEoRBIRI8mMLaZ7WI0GvuDbBGpEZG2UV5EEkFeqOB4mqbCZpgulSrNI/RRoaJFUKjcEAkqaypKohYMy6Xyox8LT940//AeT/BUYlTaVK6AmNAsQqSG5gr6WFDZ0hTF9+QSkkO0g74jRGfo/4FAUbnSlETzBlESmozyfiJ8NttCRIFmrPx7W4PtIZrAfiIPVMoIE5U0fVqIdhDVaSpBCBj7nQ/RzuWFfeZvKnkiSnQ0zuF1RjUhCnw228XCvtPcgszQJEQTUc73kRcElM9DUmbMmBH/5hixj5zTXF4QPPoYEUGhuYjOtQga+0ukiXPJPiBVrMtxZWE7ibJwPrgmkCQiTUTtODdExzgXTQVURFpGeRFJhOYZKj0qLp6k6dRJBUYnVCosKjHWoUmGSpGoBpU6skMlh0AQlaHJiPfo98FQaf5n5syZUY6agpQQUaFyZtQKssFTfvNKj+8iyoEwMZLlJz/5SVzoJEplT0SIiA+jcoCKlgjD3/7t38btzqMlrcH3kT+FDqqIFxETmpNoquL7qIyp9GnKyvuisI9ET4gkIQ38zbGiAqfPCiKGoDQdxkyUA7lgn5E7XmPhGCJLbCuRqrz5hu8i4tWWvORCwefk8kJ0is7H5HjJh1bTHIWYMSQ9lxea1BBRIjNEkBBQmpk4Duw/x41jQTSMfcubkIjAcD5Zl3NAsx19eRAkIlWcD45BcwkVkW+jvIgkgnzQaZQKjSdxoixUaDSlECUh0sFCpUzUAdEhwkEFx9M7TSm8TpMBFSoCkedt4QmdjqVUcjzZU/EjPDQx0bmTRGo8yfP5eaI4oiZsEx1TqXSJiDA656c//WlcaK7gNSpomrbIL5JPNUBFSxSEiAARjz3BtiFsCBVNJTSXESFBWtgvIj8cC4aCI2bsN/uZRxiIHiEVRKrYBj6DqAnCw/awL0SN+EyOQV6x879ERuhzQtMbx58ICJ9NVISmG5rXOOY0rxHJIrqBALFwrIiWsT18D0LBqCGEj21iO5BO5AqZZBvpSIy8ICfsL1KEOCIoSEneHwaBQpryJjOOD/9DNInzxk+OMUJF9AUBpC8P8sv+sP95PyQRaRnlRSQRKlqe9IkQ8ORN5UMFSIWNyFDJUqEiN/ykQiRSQpMJlTxP26yf95HIIzlUilSOVJR8JiLA/xOloHMugsKoGipI3qOfCOLD51CRMiKJSp3P4ifNMyxESXiNypsKlEqY7f4+5FEkpAt54DsRGo4Jf3MMqJjZ1pYqZJp6kJJ8TiAqfsQE+Ez2hf4nHN+m/886HD/62yAJRGBoZkO6iNpwPDjerS1ETfJIF99JcxZRnZb6mxAxQUDoIMz6OWwPskSn55aiVERl2G8EjOPLdyB0+fEmUsS5pMkP6WVdtivfFxFpHeVFpAbIK+zWoLIjKtLWelSyLFKbNBUz4PeWXhORPaO8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEhdobyIiIhIXaG8iIiISF2hvIiIiEgdEcL/A7Fjxw5bpmCxAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83-%E9%A2%91%E6%95%B0%E5%9B%BE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApIAAAFYCAYAAADgExwpAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAE6cSURBVHhe7b0Hl1Vltq///wrnA5xxbv9Hn3u6b5/DUdvQ2mZRaRVBERBoRFHJ6ZBDk3NqMk2QLEmQnCTnnKPknHPOzNvP3Hvb6KWpWmXhYr/r94wxR1WtndbeVbvqqRne9/8zIYQQQggh8oBEUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHlCIimEEEIIIfKERFIIIYQQQuQJiaQQQgghhMgTEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIYQQQog8IZEUQgghhBB5QiIphBBCCCHyhERSCCGEEELkCYmkEEIIIYTIExJJIYQQQgiRJySSCWDq1KnWvXt369+/v0KhUCgUsUSPHj3s22+/Tf9lEqEgkUwA1atXt9dff91q1aqlUCgUCkUs8dZbb1n58uXTf5lEKEgkE8Bf/vIX++tf/5r+SgghhPjl+dvf/mb/8z//k/5KhIJEMgFIJIUQQsSNRDJMJJL5wI0bN2zevHnWrFkzjzZt2tjWrVtt1apV1rFjR2vYsKENHz7cDh8+7Nc/ePCgdevWzY/zxtq0aZMf536GDh3q99GlSxdbsGCBH4eZM2f6/bZs2dJ7TC5dupS+JGckkkIIIeJGIhkmEsl8YPv27TZixAjr1KmTDRo0yL788ksbM2aMDRgwwN80NBk3aNDAli5daocOHbIZM2bYF198Yb1797YWLVrYuHHj7Pjx47Zhwwa/focOHTx69uxpp0+ftp07d7qQNmnSxJuVGzVqZLt377abN2+mz+DhSCSFEELEjUQyTCSS+cC6dets0aJFtmfPHrt8+bLVq1fPGjdubM2bN7fBgwfb1atXXQzJJE6ZMsVlsFWrVnb27Fn7+uuv7auvvrK5c+dav379rGnTprZ582ZbuHChde7c2ZYtW+ZZSrKRCCiPgVBy/TNnzqTP4MdcvHjR5XPx4sUeNDcjuUIIIURcSCTDRCKZj9y9e9flsEKFCvbuu++6FK5Zs8Yzh9OmTXMhbNu2rWchEcFr1665KJLNpNTNGwzZJDu5Y8cOGzlypGcz69Sp40L6/fff28mTJz3byddI5YMgQ0ppvFChQh4FChSw1q1bpy8VQgghfnkkkmEikcxHyASSASxevLiVKFHCevXq5SXoW7dueYaRjCMlbkSSvkh6Iiln0z9J9rJKlSreF3nu3Dnbt2+fl7zbt29vlSpVsrFjx9qRI0c8Czl9+nRfFxJhfBA8Hj2Up06d8kBEu3btmr5UCCGE+OWRSIaJRDKfIOu4evVq748cNWqUD8XwpiGLyGVz5szxnkj6GylTUw5HJMlY0lfJgA3rbDG0Q1YTASUjyXVr1KjhIkl/JT2TEyZM8Izjtm3b0o/+cNQjKYQQIm4kkmEikcwHKGmvXbvWZY3M4oEDB1z8eNPQO4kwUr7u06ePl7DpkZw4caJduXLFvvvuOz/OMfoY6ZlEGNevX+/HkU8GbZDNjRs3elaS48SuXbvSZ/BwJJJCCCHiRiIZJhLJfICeRgZj3n//fe9ppDxNryMCyHEkk/LykCFDbPbs2Z5prF+/vq1YscKvQ9mZjCV9lGQsGcgZNmyYD9VwHNlkWAeZZBmgypUru4ieOHEifQYPRyIphBAibiSSYSKRzAcQx4oVK9rTTz9txYoV80AOWSeyaNGiLpFvvPGGT13Tu7hkyRJ78803vZRdpEgR73fkOEJaunRpL4+XKVPGqlat6scJSt9cxuNwW4Zx6IXMDRJJIYQQcSORDBOJZD5A6ZoBGTKE9DASyB8T1vRAjh492nsiL1y4YPfu3fOSNiLIMA1rSyKQlMdv375t+/fvd+Ekc8nnHOc2XIcy+aRJk3zI5vr16348N0gkhRBCxI1EMkwkko8QJBBpPHbsmK8lydeAADKAg3ginAhkBj5nMhsxvT/jeOfOHRdRprAR19xKJOSXSN66c9eaTtpi5Yeueeyi1dTcDR4JIYSIB4lkmEgkE0B+ieSN23ftzb8usn9rMO2xi/d6LkmfpRBCiMcRiWSYSCQTQBJE8uVO823u9hOPXRw6ezX96gkhRLKRSIaJRDIBJEEkH9cYsmx/+tUTQohkI5EME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZAKQSMYXEkkhhEghkQwTiWQCkEjGFxJJIYRIIZEME4lkApBIxhcSSSGESCGRDBOJZD5y7949u337tp09e9Zu3rzpceHCBTt9+rTHqVOn7Ny5c3b16lW/XuYYH7ne3bt3/X6uXLni90Fcvnz5h+M3btzw23P9ixcv+n3kBolkfCGRFEKIFBLJMJFI5iOI4/79++3zzz+35cuX28qVK13iihUr5lGwYEH78ssvbezYsbZ792575513rFChQn5ZkyZNXBzv3Lljw4YNs88++8w++eQT69u3r50/f97vf8GCBVapUiUrWrSotWvXzr7//ns/nhMSyfhCIimEECkkkmEikcwnkMhNmzZZ7dq17aWXXrJ58+a5GG7ZssWWLVvmUatWLWvdurV/PmvWLJdHpJKvuR6ZynXr1lmrVq1c/MaPH+/3t3XrVtu4caO/CRs1amTz58+3hg0b2pw5czwzmRMSyfhCIimEECkkkmEikcwnKDuTIezdu7dnHpG9DJSmT5w4YV26dLGRI0fajh07XOyqVKli7du3d5lcv36938egQYOsc+fOtnDhQs9ucvm0adP8OLcfM2aMX49MJbfbtWtX+lH+AY9F9rJ///4eZDA7dOiQvjTvSCSjh0RSCCFSSCTDRCKZT9y6dcszisePH7cSJUrYokWL0pekspXIYL9+/Wzp0qV24MAB69ixo2coq1evblWrVnVJPHnypGcPKW1T+ubrcePG2YABAzwT2b17dxdOHouM5uDBg72E/lMQ0FGjRvn9E6+88oqXwn8uEsnoIZEUQogUEskwkUjmM5SaS5Ys+SORvHTpktWoUcOmTp3qwzL0PK5YseKHoZzRo0db5cqV/RilbOTx6NGjdubMGZs+fbpnL2vWrGl9+vRxwWTIZvHixS6mlNBzQqXt+EIiKYQQKSSSYSKRzGd+KpJIH1JYtmxZL1dT5maghmlsPjLpTa9js2bNvCeyfv36XrI+ePCgT3RzjFJ3vXr1vJy9fft2v8/Zs2dbr169bO7cuf44D0MiGV9IJIUQIoVEMkwkkvnMT0WSrCKZyJYtW/pADdDX2Lx5c9u3b5+Xw4cPH+7T3GQkM32Nq1evdpns2rWrf002kjfhjBkzPItJzyRiuWrVKr/PhyGRjC8kkkIIkUIiGSYSyXzmpyJJKbpFixY+JHPkyBE/tmfPHhfJtm3buuA1btzY2rRp4z2R9EAinQzZ0ANZunRpzz4ilrwJ69ata1OmTLHy5ct7L+WhQ4f8Ph+GRDK+kEgKIUQKiWSYSCTzGTKMnTp1+iH7yOBLjx49bPPmzb7QOFDWXrNmjZexGbQh68iak5S5r1+//oMwMmDDZDfDOdwv/ZL0WiKmFSpUcFklO5kTEsn4QiIphBApJJJhIpF8DEEaEVF6KtnFhl5KYNkfpBKhpOyNdOYGiWR8IZEUQogUEskwkUg+hpCZZIkfxDGzPSJktmBEIDODOrlBIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJL5yJ07d+zs2bM2ZswY279/v928edO2b9/uEjdo0CAbMmSIrVixwq5fv263bt2yOXPm2PDhw+3bb7+1TZs2pe/FbM2aNTZ69GgbOXKkLVu2zK5du+bHd+/ebePGjbPBgwfb3Llz7eTJk348JySS8YVEUgghUkgkw0QimU/cvXvXjh8/bhMmTLA//elPtmDBAjt16pSLX8GCBf3N06hRI5s8ebKdO3fO9u7da3Xq1LEaNWpY/fr1rX///nb58mU7ceKES1+VKlWsXr161qJFCzt8+LCdPn3axo4daxUqVLC6detaw4YNbdWqVS6rOSGRjC8kkkIIkUIiGSYSyXyCLCPZw+LFi9tzzz1n8+bN82zk0KFDrWfPnrZv3z47f/683bhxw4WTTGStWrVs3bp19t1331nbtm09K0l2smnTpv7x+++/d9HkfmfMmGGdOnWybt26+WM1a9bMpZX7+ilkOy9duuQiSyCsXbt2TV+adySS0UMiKYQQKSSSYSKRzCcQxDNnztiWLVvsww8/tIULF3qQWXzppZfszTff9DcQmcqdO3dagwYNvHR95MgRv82wYcM8Gjdu7NnJzZs327Fjx1xER4wYYW3atHEZXLx4sYsiEslxRPSnILBdunSxQoUKeRQoUMBat26dvjTvSCSjh0RSCCFSSCTDRCKZT1Davn37tvdIlihRwhYtWuRCN378eM84zp8/30vVvXv39s+rVavmPZJcf8+ePfbNN99Y586drWrVqt4fefDgQS9nUwrv1auXZxXJbHKfPA73MXDgQH+cn3Lx4kWXVaSTKF++vGczfy4SyeghkRRCiBQSyTCRSOYzSFzJkiVd8OiFpL+RPkZEk7J0hw4dXBRr1qzpMsh1EEmOkXVEMJHKTF/kpEmTPLtYu3Zt69OnjwtiRiT79u3rJfScUI9kfCGRFEKIFBLJMJFI5jP3iyRZxQ0bNnjZG/nr3r27iyRDMy1btvTyNOVrythkF5E9hmvon9yxY4dfxoR2jx49vDTNm3DlypVe2qaHkuwmGceckEjGFxJJIYRIIZEME4lkPnO/SJJZ5E2zdetWXw6IwRmyjuvXr7dRo0ZZ+/btbe3atTZz5kw/Thmc25C5nD59um3cuNEnveml5DhvQsSSARpum+mlzAmJZHwhkRRCiBQSyTCRSOYz94vkrl27PJv4xz/+0V599VV/A1GSZl1Ilv8pUqSIVapUycqUKeN9jCz9w9qQ9EOWKlXK+yVffPFFz2pyvF+/fvbOO+9YkyZN/DiZTZYMygmJZHwhkRRCiBQSyTCRSOYzlLDJMjLBjTCSiUQemeAmM0lP5L179/wyjjOpTSmbEjW3zdyenkmyj1OmTLELFy74cRYkp6RNJpIM5YEDB7z3MickkvGFRFIIIVJIJMNEIhkTyCS9k4jmoUOHfti9BhjOYX1IhnCuXLnygywik4gok9usScnXuUEiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkglAIhlfSCSFECKFRDJMJJIJQCIZX0gkhRAihUQyTCSSCUAiGV9IJIUQIoVEMkwkkmnOnj1rly5dSn/1Y27duuXbFOZmO8LHEYlkfCGRFEKIFBLJMJFI/h22K5wxY4ZNmzbNduzY4XtYI5YIJNsYslXh1KlT7erVq+lbZBcSyfhCIimEECkkkmEikfw7iOTnn39u7777rrVu3doGDhxo8+fPt3379tnWrVvtq6++slKlStmpU6fSt8guJJLxhURSCCFSSCTDJPEiiURCgwYNrFWrVrZ8+XKbPHmyde3a1cqUKWNvvfWW1axZ07Zv3+4ZymxEIhlfSCSFECKFRDJMEi2SO3futObNm1u7du2scOHC1rBhQ5syZYpLJBnKL774wkqXLm116tSx77//XiIpkYwcEkkhhEghkQyTRIvkoUOHvGzdp08fK1++vJUrV86zj9WqVbNBgwbZzJkz7dtvv7XevXtbz5497eLFi+lbZhcSyfhCIimEECkkkmGSaJFkSnvjxo0+aENZu2TJklakSBFr1KiRl7fXrVtny5Yts8GDB3vpmwGcbEQiGV9IJIUQIoVEMkwSLZJMY7dp08YqVapkNWrUsMqVK1uLFi1s4cKF9swzz9inn37q5W2ylFu2bLGbN2+mb5ldSCTjC4mkEEKkkEiGSeJ7JBs3bmwVK1a0999/37ORSBciWaJECe+drFq1qlWoUMGzl1pHUiIZNSSSQgiRQiIZJokWyWPHjtmoUaOsZcuW9vzzz9vbb79tzZo1s06dOtlzzz1nn3zyiYtmhw4dbMyYMXblypX0LbMLiWR8IZEUQogUEskwSbRIHj582IdtOnfu7OtEfvzxxz7FTU/kSy+95GXtkSNH+mLk9evXV4+kRDJySCSFECKFRDJMEi2SR48edVEcN26cDRkyxLp16+YSuWnTJhdHju3atct7Kbt37+7bJGYjEsn4QiIphBApJJJhkmiRBBYkv3btmp05c8ZOnjzpceTIEVu/fr2dP3/e+yKvX79u586dU4+kRDJySCSFECKFRDJMEi+SgEwiiZm4c+eOT2jzOWtHslUigzlakFwiGTUkkkIIkUIiGSaJF0kGaHr16uV9kiw+Thn7fpjg7tKli82ZM8czlw/j9u3bPsDDtDfLBV29etXWrFnj61IytMNjsC4lkkp/Zu3ata1WrVp+ef/+/V1akVfWtWRZIta25JwuX77s98+6lgwCsablsGHD7ODBg348JySS8YVEUgghUkgkwyTxIknJumzZsr5+5OjRo138MiCDPXr08Mt27Njx0IwkEpnppXzjjTds/vz5vq3i119/7SLKTjmsRzlgwADbv3+/LVq0yJcdYiKcXkzkEWGkJ5NjyB+PjWTu3r3bs6JDhw518UQ62c5x8eLFLqs5IZGMLySSQgiRQiIZJokXSSaxixcvbhMmTLAVK1bYvHnzXPTokRw4cKALGJKXE/RRcpt69erZyy+/7CKJiE6bNs17LhFNhBRJ5HEQyqZNm9rYsWNdXskukqlkmSGykWzPiEA2adLE5s6da998841nNDmnGzdueGaSIaEHZSXJbFKKRzQJtn/k+j8XiWT0kEgKIUQKiWSYJFYk6YNEyCgxf/TRR7ZgwQJbu3atixpZxdKlS7voLV++PH2Lh4MEsmg50oiYknHMQA8moklJGhnMlLsLFy5sb731lpUpU8bfYAhgZvkhRPDEiRMulnxNVpGp8tWrV3tmdPr06Z6hXLVqVfpR/sH27ds9C1qoUCGPAgUKWOvWrdOX5h2JZPSQSAohRAqJZJgkViRZ+ofsY+/eve3NN9+0WbNmeRaxbdu2/oP++uuvu/iRPcwNyCLBpDd7dt8vkkgmPZaUoymfnzp1yr777juXRcSTtSyrVatmGzZssDp16nj2keNMkpPRRGwpaXOulL7JbpJppMSNAP8URBOp5XEI7rNr167pS/OORDJ6SCSFECKFRDJMEiuS9EaSbaSMzOLjSOPkyZNt48aNXpJmKAbB69mzp5eZcwtZxftFkqzn3r17rUqVKj4gc+DAAT9GtpGPmeEaMpRTpkzx0jgieejQIZdASu5kF+vWrWt9+/b1Xk1EknJ3nz59XIZzQj2S8YVEUgghUkgkwySxIkmWkAlrprIRRqRsxIgRtnLlSi97AyVi5I0pbAZncrP8z/0iifCRdezYsaMLKwudc4xsI1J5/Phxl0nEsXr16p4RvX9RdMrunBeBTPImJAPJubOQOscR3pyQSMYXEkkhhEghkQyTxA/bII2UudkGkelpltthmR0ykwziLFmyxLOSXJ6bCen7RRJR5T6feeYZF1LK22QUkVUylIgrvY6U0yk/MziDKDKQg0ySCa1cubJNnDjRZs+e7W9CpJShHjKUTIJT6s4JiWR8IZEUQogUEskwSbRIkh2kfEx2kHUe6UdE9JA6luqhj5ElfbZu3epiyMBMTtCbWKlSJe+tJFtIpvGpp56y999/34oVK+YiSEmd0nSRIkXstdde8+vQo0mPJetaMuTDsA/LAzGMQzaU+x0+fLjfhvMrWLCgl8LJaOaERDK+kEgKIUQKiWSYJFokWZuRZXFq1KjhmUBkjfI1ckkGsGrVqv5DT9YQYUP0coLr0H9J+Znb8Dn9kKdPn/bgMbgMKeVrtmTkOhlJ5fZkMhHXSZMmeXk989hcj8nyUaNGedaUwZ7cnJNEMr6QSAohRAqJZJgkWiSROnoRKWNn9tUGPlLWZpkeZI7exV8Syu0XLlxwob1fYDkvyuuIJh8zvZw5IZGMLySSQgiRQiIZJokWScSMDCQf6W0k48dHJI3jBNnE3G5F+LgikYwvJJJCCJFCIhkmiR+2IdtHZpKeRZb/ocTNgA09jiz+zWAMwZJAlKSzEYlkfCGRFEKIFBLJMEm8SDJww0DNF1984TvSsJ4jwyxMS3/55Zf25z//2Y8z+EKpOTc9iY8bEsn4QiIphBApJJJhIpFMi2TLli3t66+/9t5EdpShP5LFw/mcYZsXX3zRJ7pzs5bk44ZEMr6QSAohRAqJZJgkWiQRSBYbZx9qluxhX+tt27ZZq1atfDkg9rG+du2ar9XI9eiVlEhKJKOERFIIIVJIJMMk0SLJQuRkIdmHmtJ28+bNfWmdfv36+UdEk75Ieijpkbx8+fIPk93ZhEQyvpBICiFEColkmCRaJOl3ZP1GlgBiEfBPPvnEPy5dutTXb2R7Q4KM5P79+70Mno1IJOMLiaQQQqSQSIZJ4kUysxbj0KFDfQFyStyUtSllt2/f3lq0aOExcOBAz0xmIxLJ+EIiKYQQKSSSYZJokSQbyeLeyGT9+vU9evTo4dsPjh8/3rdIbNKkiX366ae+HFButiN8HJFIxhcSSSGESCGRDJNEiyTDM/xgM1zzwQcfWM+ePV0e33vvPd/fmoltLmffbaa5s7E/EiSS8YVEUgghUkgkwyTRIokozpkzxwdrihQp8sPAzTPPPGO9e/e24cOHe6m7cOHCNm7cOLty5Ur6ltmFRDK+kEgKIUQKiWSYJFok76dLly5WpUoVX4ycoRsWJkfAqlWr5oLZsWNHz0pmIxLJ+EIiKYQQKSSSYSKRTMPgzYN2rWH5HzKR9Edm4642IJGMLySSQgiRQiIZJhLJHFi3bp2vNclONxq2kUhGDYmkEEKkkEiGSaJFcuPGjfbZZ59Zs2bNfOCGYKvEDh06+ALkV69e9aGbXr16+eT26dOn07fMLiSS8YVEUgghUkgkwyTRIrl48WJ7/vnnrX///r5O5KBBgzz7OHr0aJs3b54HQzYNGjSwp59+2nfCyUYkkvGFRFIIIVJIJMMk0SK5cuVKK1GihGcaKWEvWLDA99dmzUiykAgYGUomuZneZso7G5FIxhcSSSGESCGRDJPEi+RHH33kmcbu3btb2bJlrUyZMlauXDkrVKiQT2uzDNCyZcv8OpldcLINiWR8IZEUQogUEskwSbRIsqf2G2+8YTNnzvT1JKdPn+4xa9YsW79+vY0ZM8a3S6Rn8vLly1qQXCIZOSSSQgiRQiIZJokWya1bt1rt2rX9h/urr776Idh3e/v27XbgwAGXTXon2Trx4sWL6VtmFxLJ+EIiKYQQKSSSYZJokTx79qxviVi3bl375ptvXCARLkreJ06c8MsWLlzoQzlMdHP9bFxLUiIZX0gkhRAihUQyTBItksCgTdGiRX07RPok2dlmw4YNHux007VrV9u2bZvNnj3by9sPE0lK3yxezpqTDOZw3fPnz/sAD5lNlhLia7h165YvP7R8+XLbvHmznTx50o9zm927d/vAz9q1a+3w4cN2+/ZtP37s2DGXXHo29+7d68sT5QaJZHwhkRRCiBQSyTBJvEgicOytzfT222+/7Z/XrFnTatSoYX/605/8I1nJnED0EE3k7/333/cJ8OvXr7tAfvDBB36sadOmLo5I5JEjR6xChQq+xzePN2nSJBdRyuft2rVzuWXtSpYlQj4RVJYl4viHH35onTp1sp07dz5UbDNIJOMLiaQQQqSQSIZJokUSCTt16pRLHutFst92xYoVbf/+/bZv3z5fR7Jt27a+z3ZOsOsNmcLixYvbc88957dlYIcsJ2XxPXv2WJs2bbzfkoxj3759fSF0bsPalUjmuXPnbOTIkX69CRMm2JIlS3yKnOwjA0HII29EspQsR8SAEFs45oREMr6QSAohRAqJZJgkXiTJACJyiB7ZRCa2yRgiaPRETps2zcveOYFIHjp0yKZOnWrvvvuuZyS5baNGjTyjee3aNb+fwYMHe/aRbOTEiRO9F5PrIrGUs8lOIpu7du1y4WRqfNGiRZ6lRCRZ75JMJ5Pk3J7MZk5IJOMLiaQQQqSQSIZJ4kUSaSTDR7/hpUuXfrQNIqVmLtuxY0f6yD+HNSaRSTKclMmRP5YPYiqcNSjpc0QsGeghG0l5mowlgklPJbvrjB8/3m9LNvLChQsupj179vSvq1Wr5jLI/SO53A+lbvo3f0pGTrlPgnI44vlzkUhGD4mkEEKkkEiGSaJFElFE5BA9hBFx4yNfr1692jOEmUD2EMWcIMNZsmRJF0lEj+Edehx5LLKdZBvJPtI3iaAihQjlgAEDXA6LFSvma1kitpwL0knGlJI7UonschtK4FyfoaCfQml+1KhRVqtWLY9XXnnFM5o/F4lk9JBICiFEColkmCRaJBEy5BHhGzZsmGfvWEdy8uTJ9tlnn7kQ0j/J0A273Nyfrfxn3C+SZBIpTSOEZCQpRfNGYk1KdtFBIBFGJrE5NmLECN9Vh8dHPlnHknI2IokQsssOw0GcN+eKlDL5nRMqbccXEkkhhEghkQyTxIskkjd27FiXOCa0q1ev7hPSlJApEfODj8QhkbnZIvF+kSQQQQZlEEayi926dXOhZP9u1q4k+zljxgyXvcxwz5AhQ7xkzaLoDNVQEkciM9s1kkWl9xL5ZRAnJySS8YVEUgghUkgkwyTxpW0GVzKlbbKC9DTSO5kJBmTq16/vn+eG+0WS+ySbSN8j09uffPKJP8bBgwdt7ty5vrxPy5YtXVSRWLKNrDnZoEEDPw+mvRnc2bJli23atMkllMxonz59PFPK0A7SmxMSyfhCIimEECkkkmGSaJFE+ugxpDxMsOwOJe3M1wQZQiapcwt9lCwlRFmaz5FABl06d+7sMsm6kgz4II0IIRnLTJYys44kmUqWHGIx9H79+vmyQAgj098cp8cSIWWB89wIrkQyvpBICiFEColkmCRaJOmPpM+QoRWCJXnIAFIyJjLHiLyCNFImpw+SpXoopwMCSB8kmUaW+iEzmoGFzVlsHJGlJJ6RRa7DObOoOUsT0XeZGySS8YVEUgghUkgkwyTRIklJm+lmeiTJArLEDkvl8HkmOEafYjYjkYwvJJJCCJFCIhkmiRZJhmfI+GWCiW2W6/npsXr16qVvkZ1IJOMLiaQQQqSQSIZJokWS0jAlYpbhYd1IBl8YerkfprkZfslmJJLxhURSCCFSSCTDJNEiyTAMQzHsQENPZIsWLXxZHgZwWPCbZXiqVq3qSwJlMxLJ+EIiKYQQKSSSYZJokWTwJbOOI4uAMznNXtkszUN2krUaWZqHHWWyGYlkfCGRFEKIFBLJMEm0SCYFiWR8IZEUQogUEskwkUgmAIlkfCGRFEKIFBLJMJFIpmG/bcrZrVu39h1l+HzJkiW+1mO2I5GMLySSQgiRQiIZJhLJNE2bNvU1I/lBZ6eZwoULe7/kpUuX0tfIXiSS8YVEUgghUkgkw0QimaZx48Y+VMMuNOwq8+GHH/qWhGxbmO1IJOMLiaQQQqSQSIZJokUysyD5tWvXXCQHDBjgnx87dsxKlixp8+fP968zkZt9rR9HJJLxxeMoknfu3rNTl27YiYvXH7s4f/VW+iyFEKEhkQyTRIskS//QGzl+/HgrUaKErxc5YcIEGz58uL388svWvn17/5rLWRoI6cxGJJLxxeMokofPXbPXuyy0Z9vOfeyi7riN6bMUQoSGRDJMEi2Se/futc6dO1v37t2tUKFCVrZsWevdu7d16tTJnn76aatdu7b16tXLeyYpe1+8eDF9y+xCIhlfPI4iuf/MFfuvFt898Hzjji+GrUmfpRAiNCSSYZJokWR7xEWLFtnSpUvts88+c+Favny5fffdd/bmm29a//79bdmyZT69zXWuX7+evmV2IZGMLySS0UIiKUS4SCTDRMM2aZo1a+ZbIsK5c+esVKlSLpEhIJGMLySS0UIiKUS4SCTDRCKZBtmirM3U9u7du6148eI+tc1ATrYjkYwvJJLRQiIpRLhIJMNEIpmGQZs//OEPVrBgQXvjjTfsySeftMGDB9vx48fT18heJJLxhUQyWkgkhQgXiWSYSCTTbN682TOQ9EwSfH7gwIGs7Yu8H4lkfCGRjBYSSSHCRSIZJhLJNAjjzZs301+lYHvEy5cvp7/KXiSS8YVEMlpIJIUIF4lkmEgk/w4Lja9du9Z27dr1w9e3bt3y6W2muLM9KymRjC8kktFCIilEuEgkw0Qi+XfYBpGdbQYNGuRfI5H79++38uXLW6tWrbK+T1IiGV9IJKOFRFKIcJFIholEMk3Tpk19+Z/bt2/b4cOH7YsvvrBq1arZzJkzs35yWyIZX0gko4VEUohwkUiGiUQyDbLVsmVL3w6xQYMG1rVrV/vyyy9t1KhR6WtkLxLJ+EIiGS0kkkKEi0QyTBItkmx5uH79etuwYYOVLFnSt0msWbOmB/ttly5d2lq0aOHX2bhx4/8zjJMTx44dswULFnimkxgwYICNGDHC9/dm20VK6RxnSpxF0MmGrlixwuWVWLlyZfqezLZt2+b7fg8dOtR7N69cuZK+JGckkvGFRDJaSCSFCBeJZJgkWiQPHjzocofQsW7kv/7rv/pC5H369PFjRYsWtc8//9yvg/BFneDes2ePjRw50ho1auTx0UcfWbly5XzNyhdffNFq1arlx8eOHWtHjhzxXkx22EFkebP16NHDTp8+7dPjbNdYo0YNP07GdOfOnXbjxo30Iz0ciWR8IZGMFhJJIcJFIhkmiRZJeiFZdJzs43PPPWf//u//7llIpGvgwIEukpS3kUiEMEoW8Kcw0IOQsnvOt99+6zLIlDiZyGvXrrkszp8/38qUKWOLFy/2zGSvXr1sxowZvtd3vXr1XG4ZAurUqZNnJ48ePZq+9x/DsNClS5d8lx6iTp06Xqr/uUgko4dEMlpIJIUIF4lkmCRaJBmiQQ4Jfrg//fRTa9iwoX344Yc2efJkH7ghO8nlV69e9WWB8gISidC1a9fOBZKs4+9//3t76623XFSnTJnii58jjkjs999/b4cOHbJJkyZZ27ZtPTNJKZwSOMI5b948F8OtW7emH+HHbN++3bp06eKleqJAgQLWunXr9KV5RyIZPSSS0UIiKUS4SCTDRMM2aZjaRtaQMySyfv36VrVqVZe8nwslaHoeySiOGzfOJ8EnTpzo/ZP0YPK4ZB7bt2/vPZRIJCVteiEpc7ME0VdffeV9mkgtPZuc77p169KP8GPo/aT0TWaTYBkjspg/F4lk9JBIRguJpBDhIpEME4nk3yHTSB8hZW6ylJSbv/nmG6tdu7b/4NNL+XOgzEx/I1JKaZohHPotyVR+/fXX1rFjR++BRPYYxKHkjkgil5UqVfJsIuV1tnFEJBFIRHf16tXpR3g46pGMLySS0UIiKUS4SCTDJPEiiUTSo0j/IuLG10xP02eI4JElZKo7rzDpjTyWLVvWex0ZqkEIkUukld7LDh06eE8mGcu+ffva7t27XV6RWd50vPn69etny5Ytc8mdPXu2L6D+zzKSP0UiGV9IJKOFRFKIcJFIhkmiRRJppOyMtCF79B8ilWQEkUnKz8jlmTNn0reIDredNm2a90UikNOnT7cmTZp4yZkSNpJHeRvJpAeSwRguQxrpjSQogSO0SCf9kz179vRyOJ/nBolkfCGRjBYSSSHCRSIZJokWScrEO3bs8J5Iys4Mqaxatcp7ChFASsrDhg3zEnReYQkg7ofJcMSRjCT3+fLLL9trr73mywvx2Agt5eyPP/7Yy9lMj5PF5PzIXiKiTHRXqVLF/vjHP/rAzYULF9KP8nAkkvGFRDJaSCSFCBeJZJgkViQpKzNYQ69hiRIlvIy9dOlSH4R5//33XeDq1q3rGcGTJ0/61HVetkpEVskcIpDXr1/3UjefL1y40IOyOfcNlNOXL1/umUd6IufMmeMZUkSWc2XZIIZuKHlHOR+JZHwhkYwWEkkhwkUiGSaJFUnkjBI22UGyfExoUz5u3ry5Pfvss74UD+tIsgQQ1xkzZoxL4aOGkjqZS8rtZCIzII0ILf2TlOCjZEklkvGFRDJaSCSFCBeJZJgkurTN4ApZQXoO2WWGNST5IX/iiSesTZs29vbbb3uJmawkwzj3i102IZGMLySS0UIiKUS4SCTDJLEiyaDN2rVr7c9//rMvEk7WMdMjSW8i2T8EjEnqbEciGV9IJKOFRFKIcJFIhkmiM5L0K7K/NcvpsD3h3r17fXqbHkV2miFLyfqO2Y5EMr6QSEYLiaQQ4SKRDJNEiyTQa3j27FkXRgZttm3b5iVueiLnzp3rQpntSCTjC4lktJBIChEuEskwSbRIMtTCFDRl7Y8++sgqVKjg2xG++eabVrlyZe+N5DImqMlS/hLDNo8CiWR8IZGMFhJJIcJFIhkmiRZJeiJZ4gfReuGFF3x9xiJFitjTTz9thQoVsooVK3r/ZKNGjVwwmZbORiSS8YVEMlpIJIUIF4lkmCS+tJ0B2aKkTYm7XLlyvig5u9pQ9s52JJLxhUQyWkgkhQgXiWSYSCTTzJo1yxcDv3z5sg/g0C85fvx427JlS/oa2YtEMr6QSEYLiaQQ4SKRDBOJZBq2RLx48aJ/nhnAOXr06A/HshmJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSCUAiGV9IJKOFRFKIcJFIholE8hFy794927x5s33++edWv359a9SokY0dO9Y2btxow4YNs4YNG1qnTp1sxYoVfv2bN2/a5MmTrVWrVh5Tpkzx47B06VLr2rWrNWnSxAYNGmQXLlxIX5IzEsn4QiIZLSSSQoSLRDJMJJKPkEuXLtns2bOtaNGi1rt3bxsyZIhNnz7dZfGLL76wHj16WMuWLW3kyJG2f/9+27t3r9WuXdvatWtnHTp0sO7du/uxI0eOuAg2btzYjyGT69evt8uXL6cf6eFIJOMLiWS0kEgKES4SyTCRSD5CkMMRI0ZYhQoVXCDXrFljy5Ytc6Hk2MmTJ23WrFk2ePBg+/bbb23q1KlWqVIlz1AiigMGDLBvvvnGZs6c6fI4atQoO3z4sPXt29c/P3jwYPqRfszFixdt586dtnjxYo/y5ct75vPnIpGMHhLJaCGRFCJcJJJhIpF8hGzYsMEzji+//LIVKlTISpcubXXr1rUuXbq4TCJ8u3fv9oxkixYtvHSNJO7Zs8eOHTvm8tm0aVOXQDKaCCa3QUbbt29vmzZtSj/Sj9m+fbs/Bo9JFChQwFq3bp2+NO9IJKOHRDJaSCSFCBeJZJhIJB8hZA9XrVpl27Zts+PHj7vc1ahRw4WR7OOVK1e8bP31119brVq1vKQ9evRoP3b27Fkvi1etWtWaN2/u4rllyxa7evWqCyT9lmQ4H8StW7e8rH7q1CmPOnXq+GP+XCSS0UMiGS0kkkKEi0QyTCSSjxCk79y5c3bjxg0fvBk3bpy1bdvWeyMnTpzoInngwAGXxJo1a7pokp08dOiQCyAZSUrd3IbrIJD0RSKQ9erVs9WrV6cf6eGoRzK+kEhGC4mkEOEikQwTieQjhEwkPZD0Qt6+fdt7Hhs0aOBlaWTy/Pnz3gvZr18/n9Km75HM4Y4dO3zIBqlksnvo0KHWq1cvW7BggZ05c8anuZs1a+al89wgkYwvJJLRQiIpRLhIJMNEIvkIWbRokWcTWeqHMjVZRCave/bs6VPbLOmDRJKJZNhm7dq1Vr16dc9cMmTTpk0bH9bhOPeDTM6dO9fFECndt29f+pEejkQyvpBIRguJpBDhIpEME4nkI4TsISXs119/3YM3EFlFspAsCUQ5+7333vMMJVlL+hq//PJLq1ixopUqVco/p8+S9SUZuClXrpwf477ovaR0nhskkvGFRDJaSCSFCBeJZJhIJB8hd+/etWvXrv0w9EIpm37J69ev+9JAZCHnz5/vy/jcuXPHr89QDtnLGTNmeImb4/RXIqVMbSOm69atc4nkeG6QSMYXEsloIZEUIlwkkmEikYwBBJCeSbKQ7FDDlHUGZJKJbQLhzMDxzCR2FIkEiWR8IZGMFhJJIcJFIhkmEskEIJGMLySS0UIiKUS4SCTDRCKZACSS8YVEMlpIJIUIF4lkmEgkE4BEMr6QSEYLiaQQ4SKRDBOJZAKQSMYXEsloIZEUIlwkkmEikUwAEsn4QiIZLSSSQoSLRDJMJJIJQCIZX0gko4VEUohwkUiGiUQyAUgk4wuJZLSQSAoRLhLJMJFIJgCJZHwhkYwWEkkhwkUiGSYSyQQgkYwvJJLRQiIpRLhIJMNEIpkAJJLxhUQyWkgkhQgXiWSYSCQTgEQyvpBIRguJpBDhIpEME4lkApBIxhcSyWghkRQiXCSSYSKRTAASyfhCIhktJJJChItEMkwkkglAIhlfSCSjhURSiHCRSIaJRDIBSCTjC4lktJBIChEuEskwkUgmAIlkfCGRjBYSSSHCRSIZJhLJBCCRjC8kktFCIilEuEgkw0QimQAkkvGFRDJaSCSFCBeJZJhIJBOARDK+kEhGC4mkEOEikQwTiWQCkEjGFxLJaCGRFCJcJJJhIpFMABLJ+EIiGS0kkkKEi0QyTCSSj5C7d+/a2bNnbeXKlbZixQpbtWqVHTp0yE6fPm1z5861pUuX2rJly2zXrl129epVv/7evXv9esS+ffvS92R27NgxW79+vS1fvty2bdtmN2/eTF+SMxLJ+EIiGS0kkkKEi0QyTCSSj5ArV67YggUL7KOPPrKSJUv6x4EDB9rMmTPtt7/9rRUuXNiKFStm3bt3twMHDtilS5esU6dO9vHHH1upUqWsR48eduPGDbt165aNHDnSypcvbx9++KHVrVvXjhw54uKZGySS8YVEMlpIJIUIF4lkmEgkHyGbNm2yESNG2NSpU138evbsaQ0bNrS2bdtavXr1bPfu3Z6dRCDPnz/vWcgyZcr49WfNmuWCuWTJEtuwYYM1aNDAb09WsmXLln75qVOn0o/0cCSS8YVEMlpIJIUIF4lkmEgkHyEXLlzwUvaZM2fszp07LobVq1e32rVrW8GCBa1q1arWvn17l0VEc/DgwS6JW7ZscckcO3asZyU53qFDB5dHxHPSpEnWp08f27lzZ/qRfsz+/ftt1KhRVqtWLY9XXnnF2rVrl74070gko4dEMlpIJIUIF4lkmEgkfwEoQdPjSGawfv36NmTIEOvYsaP169fP6tSp42+uRYsW+TEuo8x98uRJF0fK2GQw+/fvb+vWrbPLly/bmjVrrEWLFp6dfBAnTpzwkjq3IYoWLeoi+nORSEYPiWS0kEgKES4SyTCRSD5i7t275/JHhrB58+Y2bNgwH6KhlI1gDho0yLOSfET2xowZ49lJspiIZKVKlTxLOXToUM9U0ndJqRshXb16dfpRHo5K2/GFRDJaSCSFCBeJZJhIJB8xTGPTK1m8eHGbMGGCHT161Ce5b9++7ZJJmbpr165ewu7du7dnJClNk8GcOHGil7+5/KuvvrK1a9faxYsXvRSOSJKZzA0SyfhCIhktHleRvHDtlp24eP2xi5OXbtjtu/fSZynE441EMkwkko8Q+iKRv9KlS3smkn7J6dOnW5s2bWzHjh12/fp1L1sjemQfmeZu0qSJZxy3bt1qAwYM8MunTZtmnTt3tilTptjx48f9vshikqHMDRLJ+EIiGS0eV5FsMH6TPdt27mMXr3ReYAf+/v0UIhuQSIaJRPIRwsAMAvjrX//ap7EZsiGTyMBNuXLlrHLlyh4s7cMQzcGDB/14s2bNfKq7SpUqvm4kWUx6ImvUqOFi+cEHH7hUamr78Q+JZLR4XEWy0oi1DzzfuOO3TWfZnlOX02cpxOONRDJMJJKPEMrTZBoZoqE0Tdma8jYZxr59+3pQ2kY4gTUj6aVkupuMI9Pa9FKS2ZwzZ4716tXL15nkMsrfuV2UXCIZX0gko4VEMlpIJEU2IZEME4nkYwaLj2/fvt1L2/RSZqCnkowlk9tMdCOXuUUiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFhJJkU1IJMNEIpkAJJLxhUQyWkgko4VEUmQTEskwkUgmAIlkfCGRjBYSyWghkRTZhEQyTCSSCUAiGV9IJKOFRDJaSCRFNiGRDBOJZAKQSMYXEsloIZGMFr9pOtNW7TtrJy5ef6zi0vXb6VdOiH8gkQwTiWQCkEjGFxLJaCGRjBb/q+E0e6r1bHu27dzHKjrO/D79ygnxDySSYSKRTAASyfhCIhktJJJhxF8mbkm/ckL8A4lkmEgks4jdu3fbuHHjbPDgwTZ37lw7efJk+pKHI5GMLySS0UIiGUZIJMWDkEiGiUQySzh//ryNHTvWKlSoYHXr1rWGDRvaqlWr7ObNm+lr/HMkkvGFRDJaSCTDiMdZJL8/fsnmbj/xWMXyPWfszt176TMMF4lkmEgks4Rly5ZZp06drFu3bnb9+nVr1qyZTZgwwY4fP56+xj+4deuWXbp0yU6dOuVRu3Zta9Wq1Q9f5zWOHDthr7WebP+r5ij7Va3RiYx/qzHy7x9z//x7z1j3wNcyzli/86AVaDjugef7sOD7nnr+D748P6Jc37kPPOe447O+cxL/cx/l+dcdseSBr+PjEPX+fm4POueHRdT3fdR49e+/Vw8ePf7A830cgurXg45HjS5duljNmjXTf6lEKEgks4QRI0ZY165dbfHixS6KSCTH1q1bl77GP9i+fbu/YQsVKuTx61//2n7729/+8HVe462337b//V9P2f/5/fP25AuvJi4KPPeS/dtvCth/PfviAy9/ULz8esEHvpZxxptvvW1P/fG1B57vw+J3T79gv/o/T9gTz7/ywMvzI/7w8usPPOe44z+fetZ+8+RzDzzn4OP5V+3//92Tkd73L7z6xgNfx8chOLcHnfM/i9T7/r8jve+jxtMvvmZv//3364PON+54/fXX7Q9/+IO99dZbD7w8Svz3f/+3ffLJJ+m/VCIUJJJZwoABA6xnz54uibdv37b58+fbwIEDbdGiRelr/IOLFy/azp07XTqJ2bNn25w5c374Oq8xb948/2VCZvRBl4ceo0ePtieeeMKGDRv2wMtDjx49etirr75qM2fOfODlIUfZsmW9peRBl4Ue/K5BcpL6vh8zZow9+eSTNnTo0AdeHnrwd+eVV16x6dOnP/DyKMHfkPXr16f/UolQkEhmCV999ZX16dPHBTEjkn379vU35i8F/ZjFixe3qVOnpo8ki127dtlzzz1nmzdvTh9JFgx4FS5c2C5cuJA+khzq1atnvXv3Tn+VLKiAlCxZMrHv+z179tjzzz9vmzZtSh9JFvytee+99+zcuXPpI0L8GIlklvDNN994o/LKlSv9F/u3337rf9j4L++XQiIpkZRIJg+JpERSIikehkQyS1ixYoWLJEv/0LTcvn1769+//y8qNYgk/S2UNpMIf1Bee+0127p1a/pIsliwYIGVKFHCWyeSBisf0F6SRBDJcuXK2YwZM9JHksW+ffvsjTfesC1bkrmkEe1TJBBYOUSIByGRzBLIAvXr18/eeecda9Kkib344ou+HNDly7/cPruU1IcPH27btm1LH0kWp0+f9j7BY8eOpY8kCzKygwYN8lUDkgbZuKVLl6a/ShZ37txJ9Pv+zJkz3ieY1Pc96xfTWnXt2rX0ESF+jEQyS+CXOW9oStpkIil1HzhwwO7evZu+xqPn3r17dvToUbty5Ur6SLIgI3vw4EG7ceNG+kiyuHr1qh05cuQX/Zl7XKAKkNSMDO97JOqX/Kf1cYKMrN73R/xvkBAPQiKZRZARpE+FyW3+qPG1EEIIIURcSCSFEOIhkJHiHzd6Q/XPmxBC/BiJpMgV/AHljyn9QvRrJq3MQ3kPoeD5J0kmeN4IFM+b4GcgSaVtvtf79+/3gQN2lzp06FAiS/s8Z34OklTeZncwdnShN5qgNzhp33ueM68Dv+/5XSDEg5BIilzB5CJ7pBYrVswaNGjgE7xJgl+oGzZs8Of//fffp4+GDX80+SPSunVrK1WqlJUpU8aXwaG9Igl/VJDIw4cP+8Qyz5t97tnejeefNKHgOfNz0KtXr/SRsKEfsGPHjr4QN+954rvvvkvcEjizZs36YUc1esSFeBASSZEjNNqzJePnn39uU6ZM8e0X2eWB/9KTAP+NM7FbtWpVe/bZZxOzjiRN9iz5wpJTkydPtpEjR1qNGjX8n4gkrCVJBm716tU+sbx8+XIbMmSINW7c2NasWZOojDxSxS5arCXYpk2b9NGw4R8IJrWRZzLRxPHjxxMlUwxz8o9Du3bt/Hd9EjPxIndIJEWOsKUV8vjXv/7Vf6EgkywHwR/UJMCyFxs3bvQt4l544YXErCeHLPG9JwNLSRupqly5sm+Vdvbs2fS1woXvO39MkQqmdjMiyetBm0MS4GeA1SKoQhQsWNCzdEmADFyjRo2sWrVq/o/UpEmTvLUjKeVdpJF1U6tUqeJrFrOGrqa2xT9DIilyhJ0NmjZt6pkolv5BIEeMGGETJ05MXyNsyEKQnWMhchYmTuKC5EgVpT3KvMhl0paAWrJkictU7dq1vU8wCdkZpIlqBBshsH4q+4137949fWnY8LPevHlzq1SpkrczfPbZZ74pRBJ+7mnp4B8oKlC0c7B+8ejRo317Xq0lKR6ERFLkyJw5c3xnD7YIo1eQ0i4iSckvSfBfeRJFEqEgC8fe7vxhpW8ySfD8v/76a6tYsaL/Q5WUgSPe62zJWqRIEc/Ct2rVKjEiiTTRF057A2so8r2nCsPvgNDh/U32nWzsqFGjbNWqVd7S0LlzZ39NhPgpEkmRIwsXLvQ/IpQ2+Y907dq1vsPJsGHD0tdIBkkVSTJw7DPNsBVrmCaxxJXpF6XMx0e+Dh2Gy8hE8j6nlYFeuaSIJL/nqETwDwPtPN26dfPgNQkdvtfsnoY4837na6pSZGVp8RHip0gkRY7wywORYMCGbAx7bdOETa9kkkiaSJKJo8zFTkpkJPh+k6VKSp/YiRMnfCcpMvLsbMNHhi8oeyahxEcvLHssf/rpp1a3bl179dVXPTvJrlqhgzzzfeb7Tn/sJ5984j2DSchIMkjHpDYlbapQtDewHW/16tUT2dYjckYiKXKEP6g0m9Mfxy+Uhg0benaC/1aTRNJEkkEL+mE/+ugjF4oOHTp4qYt/LJKwniDDFcgU2RkycW3btvVhE8p7SRi24f3NoAllToKfA7JSDKKEzvjx4/3nnQw0JV1+91GZScJqBfyzyJQ6w4UEQ5b8I8GqDUyuC/FTJJIiR8hKbdu2zSd26RHjP1P+Y+cXTpLglyhSQYYiCZB1IwtHSZvvPVOstDjMmzcvEevpUcInI4VI8Nz552nq1KmJycj+lHHjxvkyUEmA9zoSTZ8ga4jy+46fhSTAzze/2/mnkYGj+vXr+/uexfiTslqBiIZEUuQKZBJ5mDt3rktlkna4EEIIIcSDkUiKXEPjOf+p8l9pUrMyQgghhPgHEkkhhBBCCJEnJJJCCCGEECJPSCSFEEIIIUSekEgKIR45mTUpWVIoP3eF4b5C6tflueTm+XAdpspZNDuk5y+EyD4kkkKIRw57FLPNIvu1sz5jfoBEcl/sMhPCbjs8H8QQ2c4JnjPLsbDLVNKW4RJCPF5IJIUQ+QK7YPTs2dO+/PJLq1q1qs2ePdsOHz7s61Hu3bvX1+VjLUIWuM/ATkkNGjTwvZyRwQMHDtiYMWM82EGFpaYyZLJ1mQwcMsUiydOmTbP9+/f7MeB+MplKxIzLWA+wVq1avh7k/VGhQgXfM549lfMT9mfm+fK8eC5sMZeT8LGkFq8Zt7sfMrlII69H5jx37Njh+3/z/P/ZItksKj1r1ixbvny5P0duv3v3bl9QfODAgfmaGRZCJBeJpBAiXyDbyFaK7IDCDkCIDuLIbkjskPHuu++6zCGb7BiD1LDwM9ddtGiRZ+KQn4oVK/p2nFyXLQoBOURK2aaRy9gHuEuXLlaqVCn7/PPPrVmzZta3b19fOJp94FetWuV7BHOf7ERUoEAB+/3vf2+vvPLKj+LXv/61LzKfX1nSDIgeC7nzmowYMcKFjx2BkDe2nGOhd841I9cI9MmTJ/26f/nLX9L3koLnzv2xMDb3x/Niv2+27eO14nmz8wy3ZbF4YImuCRMm+F7Zffr0sZo1a/ruJJnH5b7uF/OMnAshRFQkkkKIfIFMF5LCLhjsz8yWcmwpyK44hQsXtv/4j/+wEiVKWOnSpX2HJDJk7JTy3HPPuQwhfIjihx9+6CXb8uXL+36/QFZu586dLqRsV8eez2+++aZ98MEHVqxYMZfUQoUK+VaOSBM70CCpZCR37dplb731lr3//vtWpkyZHwX7R7Nzzc/ZqefSpUu2fv16z/ytWLHCVq5c6VnIkiVLusQhvZw3e5aTRWWrTWSY14jzZhs+zpc97Fu2bGlffPGFCzWvJ7soIcNINFvV8XryGIjje++9ZzVq1HAp5DmzfSGvK1JI5hJB5TJeL4SbTPHf/vY3l30eY+nSpZ4B5fXhvIQQIi9IJIUQ+QLigyw1btzYS8mUdymhkmEjO4fQkIEbMGCAjR492nr37m0vv/yy/cu//It/JFPJcYQIsatdu7ZLWAayeRs2bHAJY7tCxAphQ5h4HI4hSVwHuUMiuZ/Nmzf7ObF3Mo95f5CNJHOKqCFsecnMIcBkBxFVRBZR5vMnn3zSRRXpLVq0qGcET58+/UM/JxlEWgB4XLKoPO9nn33Wfve737kgv/jii/560QrAc+e5IJq8xkSvXr38vMmmIoO8Lggrz4HsJveJbP7qV7+y1157zR+rUqVKft9kY5HY3/72t9atWze/HyGEyAsSSSFEvoBIImd16tTxbCJZRgSSLBlZN8RwzZo1/hFBolzLdf7zP//TJk6c6CVbsphky+idvF8kMyLFvr8I4XffffeDSJLZRCR5bDJ1iBsl3HXr1nlpl8zgxx9/bH/+859d+O4PspJk68jcLVmyJE+DK4gkgkZ2jxI1Yoe8InXIHeVozpfL7+9LzIgk4scwEplKni8ZXSSc147XBfkEbkumkTI5z5vXEvlGhMnsks2lRYD74zZdu3b1HlCknkwwIk8Wl2Pjx4/358vryceM3AohRFQkkkKIfAGRROTIClavXt1LtfQ5UjomO4bMIEpkxCj5Ug5Gcn7zm9+4PHJ9pKtKlSoPFEkkit5KSruUuRkgYZgESUOMuIzBGo7Tf5nJRvI1skgZOFMCpq+yYcOGLpNkTOktzGQLGV5BdJEsMnWU1R8GA0GIM/eJGDZv3txLyKNGjfLsK+V5nj9yez8ZkcyAhJKRJdvIgBKvIYNEZFeBDCu3QUgZvuE1YGCI15JWADKXPGdEks8RRO6LTC3iyWtEmwHnyXnxWiPaDAQJIURekUgKIfIFRJJsGSVXZIoMGVKIrCCYzzzzjPcFPvXUU97rh7y98847PghDtiyTWSM7iDTeL5LIESKFfDK8Q4aTnj8eh3IvZWOkChFDIun54zZMQtO7SCYOkSU7+fbbb9uf/vQnlz8Gfbg9EpcBcSMTSEYPIcspW4eIIaetW7f2+0JA27Zt69lVPucyXgPKz/eDFPL6cP9kQhE/BJYhGc6f2yHXPG8uJ4PL/fF8EGsElueErPO6ZOAyHovvBeJMqZ3sKK8P55HJDvPaks2lD1MIIfKKRFIIkS8gkpRymaZmihoZIwOGvJAVpA+SDOQTTzzh4kdvY9myZe2Pf/yjl6WRJq6HZCKA94tkBtaiJJuGHD399NOeyUSWyHIWLFjQRY5sZgZKxkxwI44M/DCQ8/zzz9sLL7zg0+X0DiJ9ZPgyIHb0GCKXSBxC+jCYxqZETvaTzxFEMoGUqimz0zeJsCF43BeiSuaUEj2XMZyDJPIaIOFIIedNOZ5sK+fD+XE5crt9+3bPPJKNZdAIIea15pyBx+GxyUQizfRaIt28/mQ4MxPfZEMZ6sksKSSEEHlBIimEyBcQSUq6ZM3ItO3bt8+FEbGk7MxHBAf5Y9kaMpAI1uuvv+4TxKtXr/ZeR0qwlHYRSaSRpWzIyGWEjo8M1FCqZnkgMnkMjCCR9CciUhkQMta35DKC7B2ChvjxNUM4ZDFZkicDj8e6l0gh5/EwkeQyRJWpcASPHkXK2NwnIoq0kjXlvpBjJJKeSsrdlNtfeuklfy3I2PK6IN2cM+V1JBGR5Llzv8gw90MvKWVphBvR5jUjy0gmEylEPDkvXhdkktcRsaWUz7lynJ5OpuU555wyrkII8TAkkkKIfIFSLsv/kPGi35CBEUrJZL7o62P45dSpU17SRgQRJjJtSBgSSiaP8it9icgNAoR8kunLCFUGbot4clumo5EkSsz3SyQcPXrUxY5sJNcl+0kpnawoGUxK3sgkgpWBc2/RooVPNVMiRiz/GWQsWWz8D3/4g2dYGWQhQ4rc8ZGljBBFBoMoyfMcee7chl5PXiPOkbI4MphZJxL5pexPlhb5Rkx5LcjIIoVINPLM60DwHJFDzpvXlHNmGpzeSe6b8+P5IOn0bpIp5bXge0V2Uwgh8opEUgiRLyCIiCSSRGaMiWJK3GT+yMqRDWQXG2QLuUEe6UFkKRrkiGwmU9yZcjK3IXtIhpN+P4SLDCQlYYSJ+yArh2BRnkZCkU8eA8nk+ogY09pk8yjzkgFEPOnTRCI5RombASGykJn9wOk/JEtKFvGncno/ZPTILvKYCO+kSZP8PHiOlKLJ/nHfLP9DFpQeUErQyCL3jVhTlmayfe7cuZ7FpNzMfdDXiDhyPeQaoczsUkP2kYxvBuSRtSjpseTckUPuFzkly4kwIpBMhHMMqUUqkV0uU3lbCJFXJJJCiHwhUw5GcCgJIyj0/yFGDN4gQATZM0SIEi+ShPwgXMgfmbgMmZ5LJo7J4iFH3CdlYMQSUUKaeFweA1FCSOkz5Diyhtwht1yf4P4olxOU1jlGlpDeQRYwj1rmReAoOyN4lK2RRLKnGaFDinkNOKfu3bv7ud6f4UTguBwJR6p53ZjGpuRPhjUzsQ0ILb2V3C/n+lPIpCKe3A9ZSl4TxJVlgpBjboNYZx6L1weh5LXVguRCiLwikRRCZA3I0j/bWxqQLeTsYeXo/ITHI4t5v4Aig/cLICDMnPsvCed2fzaVLC9f39/zef/nQgiRFySSQgghhBAiT0gkhRBCCCFEnpBICiGEEEKIPCGRFEIIIYQQeUIiKYQQQggh8oREUgghhBBC5AmJpBBCCCGEyBMSSSGEEEIIkSckkkIIIYQQIk9IJIUQQgghRJ6QSAohhBBCiDwhkRRCCCGEEHnA7P8CjgKyVQ7kIWEAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E5%9D%87%E5%8C%80%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E8%A1%A8%E7%A4%BA%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAACRCAYAAAC7bsHuAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAACIsSURBVHhe7d2Fsy3Ftcfx9zelQhWSQAgSFyJEiUGUKHF3IS7ElSRECHEXIhB3IO7u7j6vPp35UevN2+fcc849+95zuetb1TUzPT09/tur1+qe/T9T0zRNM2hBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJqmmWlBbJo18p///Gek5fxeYLNjse5f//rXvLR1bPfvf//78rrNSxXrklDLb4T1KbfdbbdDC2LTrJG8yKG+zLv5Iu8PGx1PPdbtULcx7/w3E65lvuVlXrZf1rUst7+0IDbNGln1cofN1h1IHEOE5g9/+MP0+9//fvr73/9++bqdHGO2yfbbqaeWXW6b4wzJ3y1aEJtmjdSXGVlOXl13sCB+v/zlL6fvfe970xe+8IXpwx/+8Ehf+9rXpr/97W9zqe0R0Vqea03JW0Utp65aPqku7xYtiE1zAPDSerGJD5H55z//eXn+wcT+ieF73vOe6aUvfen0qle9anrYwx423fjGN54e9KAHTT/60Y+27EuMOEnOz3Y5P1PnLy8CJ6VMFT3I/+tf/zqul3z1Zf2q8rtFC2LTHAC8vH/605+mr3zlK0Nk8lIfTByD9OUvf3k688wzp/e+973j2L773e8OYTzhhBOm1772tdNPf/rTeYvNSX1/+ctfRh0//vGPx3zO1bRSl7Nt8ojhxz72senzn//8WK7rTNd17VoQm2bNsHZ+9atfTS984QsvFx0v9MEWxKCZfKMb3Wh6yUteMn3/+98fVtnFF188Xe1qV5se97jHTV//+tfnklvjhz/84XTOOeeMJjdBRMQs570UN9OaXLM3velN0yte8YrxIyIv5WvabVoQm2aNeGlZWG984xunxz/+8dMnPvGJEbhY50u9VbL/n/zkJ9N55503ffzjH59+/etfj+bpJz/5yenqV7/69MQnPnH6xje+MW+xbwjgZz/72emss86avv3tb0//+Mc/xj7SBCZumuevf/3rp/PPP3963/veNyxUgZwcj4RPf/rT40fk+c9//riGqWuZdpMWxKZZI5rJF1100XSve91riOLPfvazec1/2e0XejvYd7XWYJ5P8a1vfet0/etff4jWVpvM0Ey27SMe8Yjp5z//+eX7IHif+cxnhsVHZB/84AdP9773vUd6ylOeMprHv/3tb0cdOZ4//vGP0zvf+c7hyyTYv/nNby5fZ1rTbtGC2DRrwovKunrRi1403fGOdxxNyVg5YTdf5p2wFBSW3Kc+9akhWqw8vsAEgLYCn9/znve8IaSx+tSp+Xyf+9xnevSjHz194AMfmL70pS9N73rXu0beVa961ekBD3jAsJ6JJ3JMmvAve9nLppNOOmn66le/OuoKKbubtCA2e46lSGzlwc82psvtUfNXWUXLad2n+Swvt11S65C89KwhEVwWT912s3pWsSyfZccUoVhV//KYcy6QLyWPALHinvSkJw1rL1HeyqprkGXddZ72tKdd7osEi/Mtb3nLdN3rXnc0kflT/TCwnr/1rW9NN7zhDaerXOUqY5/WVZzXF7/4xWGtvuY1rxnHFHLsu0kLYrPn2eihry9mLZMXZbndRvmrUCb1L1PWr5oPlvnjnvOc5wzr8MILLxw+tKyLAC232xe2WwqS+aSN1oeNypnnS3zDG94wve51rxsWHEFjIfJ5ItvWlHxo0mouO2ddi1Lmm9/85sg75phjpnvc4x7T5z73uZFvn0TxDne4w3TUUUeNdazTkO31j/Sj8tjHPna65JJLLl+3PM/doAWx2dPkpagkL8nLx8912WWXDWvCC1j9TZpu/FMZhWEqeeFZKsmzjXICA142gvaDH/xgvJAiw5aJmjLyBA3M58VcJsfzyEc+cvjJ1LMMCiDTraCsfUlhWZdkP87FMfPjpQ+fc5S3PBbzzu3tb3/79OpXv3r6yEc+Mso5v3e84x2jqV/rr/M179JLLx1NZaIYrHNvCO21rnWt0USOIMK++RtPPvnkIYx8hqjXlIXJh+iHhQUa6nXYLVoQmz1LXoi8PKHmefGJ4Jvf/Obx0px77rmjyefF8uJ7abzYnPaar8ppvr3tbW8b3UkIBgGw7KXV1eOjH/3oaJqxVvTHe+5znzvq5fsSibWeUOijJ1Bi/8RmebzK3Pe+9x3RZXn1Ja9pqyibOupyFQbi953vfGf64Ac/OI5NRJdvji9T1Na5Ez6BHs1TdRAc18uxau46Z0l09wUveMFo1oa676QsE0LNWv7CimNSx1Of+tTp3e9+9/8JLBFE+7ze9a43nXHGGeN41VXP07V1/3QWJ7isyrrv3aQFsdmT5IHPQ79cBsvwQx/60HDUa25p6l1wwQXDCrnZzW42Xug///nPo1uHJtstb3nL0bfuiCOOGF1KXvnKV44+eA996EOHY//4448ffq773//+w9dFYG9/+9uPpp5Oyve85z1H3U9/+tOnF7/4xcP6Uw/LRTeVNImDLiNeckJQcQ4RsvribwU+tQQ5sm2SZc1eVt7DH/7w0cx8whOeMN30pjcd/Qmf/OQnTw95yEOGr+6a17zmEHjb6Apz+umnDwvOeTonyTLRV2f2sQr5zl3fQz9Grnnyk+ynBkQgj3VuZIzjEVhhZcoPts091FeSePohW+Uz3Q1aEJs9SV6ksFwGa41Vc+c733k0pbxcXh6dir34hIB1yKJgZbBS9H8jfkZmsJJ+8YtfDOvwlFNOGdFM4qAZ7AW3jeY3wSUQd7vb3YalwqoUIFHWC2qd47DOMeaFtk4zkIWJ5fFvl1XXIHmSc3/mM585REmz1Hlo7vohuMENbjCOhxVHwI899thhDTsP5VjJrqEfGMm860MMXYtV+83UDxPfnh8AFuCy7BLrJfvVUd2x3eY2txkWLYtxiR8AVuypp546mtcZvbIOWhCbPUlemrBcJjrPeMYzhpCx6Ly48pTx8rD+TjzxxGHhpD8cn6HmZMRS/zfNx2c/+9mjiUj86stvql5N3mtf+9qjK4rmXiw0vkbNZevsi9VIlGO9POYxjxmC+PKXv3zUlbQ/OMdqQQXnRvxYhISMmBMqzdc0R50r64pougb6BRIg5/O73/3u/yXn4npUy65em8zbj65FrqFgTC2TaU2wT8fmh0RT2DXitwy1rKlrzepnTer4nfzc892iBbHZk9QXAvXBNyUAOjtrAnvZ+f/4xySWD/EiVKyi+BIlLxbf4F3ucpfp1re+9WhWepkJpRc79Sd5SUU3iYomYfxXgfje6U53Gt1G1CWQkm01xR0bqzR5y/NgobHIlNlX4j8z5Rowzz0QESEwAiPEkGjbD1GzfI1rXGN61KMeNcTb/jRL+RPjQ6zHUxPq8WLVevtRP+swwaxaBjXPsfJpssj9YLAsCXV+aELdxv0+7bTTxjXWMqjrpN2iBbHZkywf9LrMYiFMxOboo48ewsZH+KxnPWtYe+YJIVEkGprFXlzb5QXXeVj/N34pTUxCGaxPuaUgapbmWCQCoEmt47AmtWBG6jDCwjE6hqDe1G1qe4EIx7qdxA/Iwl0Oq8txqZt1y2pjvRIdPwzWVVK+pn1Ry7EgHQMrWjO9nttGsGQJuh8M1zQfgVAX4atkX/Jve9vbTg984AOHSyT72W1aEJs9SV6EkHlTwsbSYZkJeLBO5K0qv0S+F4/fkICxIo3IYOmtahp6WQUkCCKxrQEDLyXr6Oyzzx4BCE13zdDAmvESC3Ionzqz7WaisYrNRCD1awLnWhCq+93vftNxxx03rGbNaHVYX5vCymZ+uY/Mm9b5lGNl8kv6UeGjzbqw3M5+lSfmxDrHpJ58ISdla3LdNZldU9atvJznbtKCeJBxU/MwbkQePsl8feCw3YdiX+V3+yFbB46RBaapqp9fmn+rqPksDRFLIsqqYd1pUmqGamoqK+UaVwsxgpgyEBhIHfxbfGjZlhXHQjRKZRX1uLZL3db+PEOanAkKWS+CzgrmoxPwUY5bgOUoaLIcV71Vcv4SV4OIto7nflRyXFmf+exbOS4KXZLqPRMoYSkT7lw/WM965G90HvyyAjjZTtnM7wYtiAcRN7Km+ouXvMxnWpOHoT482yX1ZD7U/L0MfyELTNcYfqX4oBw7y82LI4rpxYPrS+BYfESKL1H3GhFOQRZ94IgJcg1iIeo4rJsNyzSwdogr31Y+nxVRkPjIdNVJlBlZJ+3vvQvmHTd/oe5Hgjuar/oWiqjL4zeEa+E8NePT4Xq75PidP2tNlF9AinW6PK+UdXzcCaLEmu+EkQjya+qy5BpxeWgOZ5tAEAm9aDRrfLufI9sOLYgHkXrTzedBygNRU1jm26au3y7ZdlnP/tR5oOAT44MiiKwUIsBf6EVnARE9L5hyXlj97vgXr3Od6wyLkKXkgwEsuyOPPHJYmoIzrDyR6Qgoq0Q3FYEYL6/ghRecBSbSzXJhbRKH+MBcP81y/RZFfoP8ZdoOy23Mu3esPX45TXfHJKIsmmzZcTs2I0ZcD8IjkJMfin1R91nnNXEFefxQuO7I+ppcK/sVUWZpc3Vo+op0s/Jd91vc4hbDN8riXG6vWW179839W+UL3S1aEPcAufF1frkcvHAGzvvVjIjV9dtBYMKDbPtqnWKndR5InD9REkDRsVhTjMXHMtLtxugSliKLgjh54UQ1ddVhIRERLzVRvfnNbz5eSo5+XXVYLyzOCCI/HEuI38tIFdYYwWV9sSBZm17cijrUp8Ox5uKqa7rd6+ycpYplwRnHdPe7331YqvyWrovO2ASHWLIMXReWK1FZBjC2guNNMgKG+Lq21XJGLed5tV9WuI7v/LamPthAIC3HJVGj1Hm+PaN8lDe5yU3GDxmBTZndpgXxIOOmEiMvjBeKj2rZ/QDKaZJ4uDzwrCAPdB6a7WIbnZZ1lWDx1H1at3zp9jKEzctumBnRM0KFRaFJ55oRJs1rI0/4qYgFn5oXjeCxCq2TLxFL623LimThaa4JBBBbwss/SHB0JlbPqnvmR0tTkEjZT5qUO7lfyH3Z6J57hgxPZBlqlhIsefxyjp14OX4/Evtzf23rXN7//vePUTuukfPPuS2PzXo/VCzTJOJXE8uPBR9hrXUZN+6HhbXthyfrs8/dpAXxIOPh4nfy8HqRPdBeHiKZh9ZNN8+P4kHnR9H8yQNj3U4eDPvxQouOphmiruz3UMG18kPiZdKZ2DRRVOfkh8N6FrGpRCisz7bW1fW2dx00nQkii4YlyYJRjqiwVOwr9dTrlntDgI2KEURQZ10nbffeZTvUbU0dAxH2w+q4co7OR15G8uzk/tb9mrounh2Cbx9Zp27LkGeZcDl3x5SU48lyji31BPeOK4R16fpzfezk+LdKC+JBxM1n6fHD8GOxUvh79Nr3q1gfDlE2TUBiKFjgwbe+pu2gvDr4y3Q70UxkfaaudT50u4VjzHnX6XK+LtfzyrplnuXkEUDXnP+KNRRBkbI96nIEQoqfUbM5llnKZrodUm+dr8uZLvNg3j4jWNsh2+aYWWqa4YIjQX5SqHmb7bduV7fJl3JEy1n9hDTlUOd3gxbEg4ibqdkhIMAXxSel+0Y63OZm+6UnmiwVzR/LeTB3+kBkW1YO60WHV81OIomdvKwHmpxDUs0L5uu1yksdki9l2XqWCWvEC6+ppnMzX5yXkuOfVaNstYaSsg/zrq9Itz6PLB0vdNZJ26Vut1EdyV+uS149/61Q68u58eX5Aa8/okl1m2A+511ZLiPbapYTXu4JrhAtmtSR6art94cWxIMIa4O/x2B7N5zvirVG9BLskPj69IXzYGjaIuv254GwreaM4/Cya5Kkc+3+1HugcaxekMyHnId19WWs8yFlkzTxRGK5MQiirjWavvyUiTQrt/QdZvu6D4EbI2N0hxHgqT9o2yX1I5ZoJcspV9cvy26VWpfEZ6up7EfadZJXz6cu15R1dX6jewFiS3Q9+7oN1VbRTq/fvmhBPEi4mYSOEPkaiYfLTdaEZkUEeZqzhFJTGvVByAOyXZbbqVsfMc2T5Uu+V1med10279qFVcsh86aZZyHqY8hCZEH7jqImoimBI2qrqPtJfa6nwILuKazw/NjV49kJts/xos6vIseT+e2gvP05F/0JtWZEtXMOOZa6D9TlZf5yW5gSeknXIe4GAbGsS1oXLYhrYHnDslxvqIdAJJN1KAqpnxg0E+rDZV6EzRAsEUJ5q0h+tst8pS4vy2ma+FiC5rv+aXlYK8mr226XVduqt+5v1fqwP/veDvbhXhA+VhDrhCVtShS2egzKOX7bsKx8qWXpH97rONYcL6HiztERftWHY7dKrssS+a6VZ1DUWRcn171StzW/3X1vRgvimqg3ys1L88bNFqUUWdbFw/hMTTJdQzwE1gdWCovRSArNBg76zR4A5flZWJ7VChER9BImL2Q9lEnXBtsvyyXV5d1iX3WvWrcss5fJsXoGEk3FoXYOSY7fs8qPmnXbJXUFz6GUfD88nteN+hwqu50fpq3SgrgGcgNrys3mkOcj1JdQRFkQxfAz/jtRZNHkvDCazn6J9YHTT4s4VlI3K4bgaVpo8mp+a2bblh9Mvrp1KmahEOS6PVhDvuzMT2aUR/JTppbFqrztkm1rPblOIetqmUOF5XnUF76mQ4V6rM5leT77Q60vy5mv+6gpRsZu0oK4BpY3s8IvpS+hIIrPpvtslBEQIsu6dRAsVoTtOO75rHT5IGjyK8oQMuNtjQQwKoHoKasbj6FS/FYCN5rCt7rVrUakmj+roh7JcTkWowLqOcC8vIp9+xXXP9KY1J0kza9YAcix1OXlsRwqLM/DC5xzqfmHEstj383zSH21XmS5Xru6fjdpQTxA1Bspseruete7jm/56cKQMplKmtXEyXhUVl915KcMK5Iv0tA143I1I1iSgiRXutKVRjNY1x7LhkgpJyhQ8aBJhnT5Ogthrb++pktRMq/JxMdjHC/x3W7SN8+oBcJY66/CsSTHkmT5UEruT87vUDx+yTnUY9/JeeT8k2q+61OvUZ7Fut1yfrdoQVwTuWG5WfXmsayIlt73+qdxHqdMphLLjyVplIRIpwdj+TBqKltn1EC6gug/Jzp35StfeQiqZSNg9HUUKdXZOKQe6OIgyONzVva1ETk+2xFplisrbyvJviXzOipL6qjHESznxciy8+dfIsYZXbKXkx8siRvEMZsm37kfCufhGHMemc9xm+70PHJNVqVcp5QzlV+Pw3O32XO6E1oQ10Be7lUJbqahega36xCtX1tdn3l9DnWF8Wkp3TWSn3LwsIheCooIqlinA7DheL4VyB/owdG0NSpFWYIcUhfR4dvkQ/QlkvqgKVNFKSnL+0OtT4rQmma+rhN8cm7Efa8nvQdMfQLM1I9f8pZl9nKq52G+prp+qynlc11qfUlZV8tnXbaV9IfkdtktWhDXSF7ikBebhUR8NGFZcvnkUS0DEWPRZYKYfzNbplDzBFIEavRvTDO6rk+qWOav9JDxPxLElDFdilOo81tlWc+q+ewvJF/QSTPbhxUEgfZy4hd2nPVY5UnmD4VzkOrxcqfknORbXpbf35RrlP0mr5aRHIOx4ksX0P7QgrhG8mLXecn4TFFjQRX+Q82BUIVAOYKpyeyz67X5mHKmmpz5Yo15zWeRaV+F1uxWjlXIMtVUNS8v+wma0359NdOriIYsJymj+wXLk1W61SRwlCTI5Aciddb91Pkss4Kd66GQXJuanKcp37Dpqm32YqrnoKURt0c9F2nVtjtJqU/dlu0r81lvOfuuvvX9pQVxTdSXGBEwiUWoE7RgCcsv1PLmNW91z9E1Z6OgCjHVZOAjJHasSp9TIrb1C84eHMELTU7NbMcTcYUyItWazLav62B9yLb2rUO3SLbm4L6SIJKpfWTZtwb9D8mq48k+q7V6KJJjd36H8nlUluexk/OyTbbL/Gb1bLZut2hBXDP1Juel1+zLf13kX9pCypr6ZfQdOR/P1K9QMKGiDDExisWfpfsKjj8cF8HlnxRd5vBWjmVG6FhkRl5UAcrUOF1fMxaRTt5mqJfFxkcZq2G7ybbqaP57PV1301XIT1qy0TY7RX1beQauaLQgron64GZe0lzVVMyfIxGqlMk0iUXIPyIaTaQ0F6qIKUNQfUJfJ29jS3Wdud3tbjf8jvwrgi1EU7SZBShCt8qnSJh8+Vk9fJDymgNPrnvuS1guI3l13WaCuhm1jszvpJ5DnRbENeFhysNZE+HxOagjjjhidJjebJic7TVvCR4HMstyWSeLj+Wnq4wvs+iYbeA9p7NO2IYHEkN+RR2o6z4yr07H4T8uWJu66WR9c2BYXu96j7DqfqTMvsptRq1jWY+0U4E9VGlBXBN5oJIIG+uQj4+ldvTRR48hdXx8lboNPJAizf6Mh58weYEfTyRZcMbnpViDrEJCyYdILEW06/cVK/L46FiFugARUr7I5sBS7/nyPmVZUCwBB60Fz44gR4ILmW432W65rR/uPBvL47ki04K4ZoiXpi+B0hlbUIO1p8uNpjN/XvDg5eHLvMQvqP+V7TR3qyBCmeSZSqkn1DKpN8lDTzj1P2RJLutv1s+q+5N598ePKfeKLx75LJYfR8kfPEny9ETQSV+yvK+knPpMU0eScfCH43PQgrgGIkiSoEY+82U8sf5UhqyJMut4XcsuSZ7gg/5eusPkv0+w0XaVff3CE1gWJd+hLj4+YNqCeGDJfaz3yX3LsyHoxF3Cx2uo56mnnjr8yub9U6AvJkn+ObDO7yupQ1n9VdVjWb48fVFZivE3Hy60IK6BPECmmp8CHyLFmqS6mQimiAALcCiTVKn5HkpWor6LgiuhlpGS50WKqNV1oZYhtrr06DpjCKGm/aptmvVRr3emEUNwi/inP/deNy1dnYxuMtrJ1HLyMr+VVMsv69K3NN2zDidaENeMJrGABcHhn/Ng60JTf323kviK8t/CeVjr+qUA1gfZciVliDXrVSDFKBX+zZRdbtMcGOr1l7hb8vxkGGbWV+vfdCfile2Wz0/yTQ8nWhDXSB4mD5Zghz6FvoytibrqQdvoIbQsif4SU5FjddSHOPNLVtUVdOlRn2i0+do8Wm7XHBiW190PIZ8eH2+N/rvfrHtfreafFlhzD1mThHKrqKc+R0l1+XCiBXFNeJA8aJs9XPt62FZtw7IkiIbkbTQEb5m30TLLw0cjat/ErG8OHLkfSwgbsdPLQHM21qF8YqhngHHdPvHGP000/eB6RrYiisv9Lp/X7QjrFYUWxEMMD63msod11Uu0HYhgRq0066GKThUc1HWo8zB0UwRY/1CWYu6TT74RP//C6AeNP9rHhY18MsxTP9T8PWhY1r0VdrLNoU4LYtMcIAiMRNiq9ZX8CFCEk7XH58y/G58xVwlfsi+bc8Hw+7II+ZWNUjr++ONHFJorhOVf66v7qNN6PLXM4UgLYtOsiVXiEgGSsrwsZx0B1M/Q/znrahWXhm5RrEOWoBFICYQJvlin64xhob6jya9o3VIQk2C6PJ66nG0PF1oQm2ZNRFyqoJhPqstLBEv8YZhUywis8Bsec8wxo3cAH2PgY/T5tuOOO2505NdVK9tm+7rMB81lIhHUHKtpLMYWxKZpdo0qLhGWiE5dTpLPGjSsU/9QTWHIlwRT9EXUKZulWMfCG9rnG5isR59XE3SB7YifCLQhf/yREtFVf5JAHb+ldcTVdocbLYhNs0YichGXCF+owTFTwmWIpyAJUUxPgqxXj8/A8SUuewcQMSOiWI/+X1tXL1gvEKNjt//4Pvnkk8c/ORJO85LPxxlO6hudvpRkVEx3zG6aZi0QrvQTrBCrJBA744t9AMS4d/mrAh6ZwnxGRPm6OkHjX2RN2u9ll102rEkfCOFb9GUkI6f8XYQO34aR+sK6dYSQGDsG+21BbJpmV2HJsdZ8nMPwyHTMr+ImER8RY3/rqjO2/89OfsrUlG2JnoCKYaGEzZh0vkXrCKyvHgnO+OqR0S4XXHDB+Fo5/6RlX0k666yzxqilSy+9dARjsu/s53ChBbFp1ojPavlyjEDIiSeeOJqyF1988RC5pfXFB+gLSD6sYGxx/UJ6FcAqVKb+e0fXHM1hokjUNLWhDtZi/jqCGBNCliC/IR+kT8cZVsqiTN05vuzncKEFsWnWiD/y94Ujo01OOOGE6dhjjx19C0V1UYXNf+2cc8454zNeRG4pRpaXeSLEOmfnz/91yI7fcVXSbNck1nnbvP/ZYT36O0/N7qUIHm6i2ILYNGtEoEPkVhOUVSZowZdHiCo+8cUq1F1G1xqCWYUsolTn4evrfIJEN8M5iSRfpWmwjTrt47TTThvbiTiLRItMGw7qWGvddf5woQWxadYE64p/T3CCUGmi+jsIfwDm7x6sD0RQ01XwozZdl6Jk2XbEzvhmlp7t/D1EgiCazPogxo+YJHotWOMPzvgcHdOFF144PgzMSqxfSs9+Mz1caEFsmjVRxYhYsdDOPvvsEQnWgZr/jmBGmIiSr2KnOY0qSKkrQRrBE/5BVp8mNiHlsySQhvEpo3yavcr5CMQZZ5wxfInQp1GfRVYmi7GWPxxpQWyaNUNc0nVGU9VfvZ5yyinTeeedNwIdhuaZF+0lhsouBcmypLzmtua3pq/vY7L6jF3WkdtU4Iaf0Fe2QeA0hzWLTz/99PHnZrEGDQ/0L41EMv7HCOLyGA4HWhCbZk2sEhSWnK/UCK74QAP/ou4w/hNbP0LbpOlbSV06WOtGI0BjzPJRRx01kj8tO/LII8e8KZ8iizFoUotAi0SLemtyq1PQRz/Ek046aUS4CS5yHIcbLYhNcwAhMueff/7wI+qGI0KcoMaqKG+QJ/n3RM1knarPPPPMEYRJkidpjotUV2G1Hb+ljwGzFuPb1Gw/99xzR7NZ1JmFuhTjw4kWxKZZM9XaMs+35xuHrDkdpI0WYR1qrlq/kShC9FhwpI5BFjyp8xLLUx1J+jiyLo1fdizJ10/RF3MuueSSMb/c92bHckWkBbFp1gxBidVlXuBD52jfLtRUNcaY/66WSQqZr+tqquvCMn+5HpbtN/uuZN1ymysyLYhNc4AhMMYXa94KjIj+asLKX6ZQ86pIJS9strxcB8sbieGy7OFAC2LTrInNREXA46KLLhpRYVFmRJzSpF2yrG+z+aQqdsnbjLrt4UgLYtMcBAiVAIaobvyLzcGnBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmamBbFpmmYwTf8L0KzWV25D8RQAAAAASUVORK5CYII="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAABOCAYAAAAAY0O5AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAENASURBVHhe7X0HYJ3Fle57CWGzbLJJCNkXQggBNkBCx3SIIWA6BAK2McU2BveCbdwbuIFx771XybLlXiTL3ZZlSZZkWbZVbKv33m7TvVffO9+ZK8ouu8iKwBvvfNLc+5cpZ2bOOfPN/OX+H1hYWFhYWFhYWFw0LImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImysLCwsLCwsGgCLImyuIxRj/r6QAgcsbCwsLCwaC5cFiRKB0j58NX74ZU/6Kcfsgv50vOyJxtu+TZ/9Tzp09MSfLLPHQ645hi/dYvxJEsdhnmwvk6iueFhHEZpTrBsBm5KWT5uyb9PZPNTPvnXQo2ocorysjaM45Tg0TTc1wiXDCKgyGXaktI4pL3qtE9UfpHN7298C2qzfyUq2+Y/wu9nSdKPPq8EH7zucjhTQjGzd3eMmheKbRdq5LhEZFJtM2lfyaf+iwZnJhStXiRlRAuL7wZf2C4VLqDKqn48rrotDoc79D1U2nr6NH7zWCAyN2Xf+C76AdmmzanuiqWpz9AS4GJ0ptVzjMPkftAbqg1I8LEMn9ikxmtmaIGURD1aQBZTlNkWm9VIzQyWKX7BlOGSOrJ81lGCNAWbmHG0JxhH4qqARkj5MG3PVvuqdNzmUZWZO1+JG0gs4dvBZJq04VuSsj/q5ICX+/yQfZVP85QyJY7GZXESfIF0mokGi+8blwWJ8lPt/FQwGRxpFPotQ2HDvjoVDuH8Foch1uOl9gUUkiZMo2Ac5iNDsBwXxZV4Pp9E0niaizqber/E/g70lUZBuf2Sf70U4BdZjCM09aCBGaOh0fPLGBjlN+lMfP4ZxnCpUIc6kddDMdTqpS9IbEQmEl1Wop6OjHI2AlKl/wTTP9IuErhtguxLf7Hf/F4nvIVnEDriObTtPBD9VsWhUI4zL8rQQKDYrnWBtHJAv+keGymahcVFgzqo+kZNC+icCUY/jcP5MoiWamjQddVNjUdf1pAH0/KcpBEbqFc7oC7T7niePo0+knrPpMYG1OdJULtkXvrXvFBxNX/6X3IDSkVfFZBb/IWJ1czQ/KUdWDac0oJSJn2kj2MD60252G4mDtuJvEWHBraNxGfbkBpROo4NTE+J2V7M1qTV2uh5zbTRMPlr5izYa/LgGOPlcTaW5i+BkXSbqehfZVrK9uSfTOrrxceq3lh877gsSJRPZhdc2SC50YGRjkIUi0bB2QfkPAdtJVKi5ORFXn7oPg1HzJhxJT38QkY0PvdVr2XbBBItYzySvzio5gYJgI+rZawLCyZJMOapgXKSGBrjYx1FLqaTT8r7pYM0Ry8ZpF2ltYVEmYZT566zJmk/OholiG5GNPG/BZo+AG43DCZfJVEKqbISZDoin/StfOfs6oOubd7C631WILKScdmPdDyyIfHZZuKCVA90kNFv5vVlmRYWzQqqFv2S2ImxWwZDcsxJqt+XNk5VlBgBXf8yaDzagMaTSIHInIBpEP3XyZXmZfLncWUFko5F6dSQfpDZMTnFku/mBL2YWUmX8qUc+lqSBJbLdhCvJi5B5A3Eby4wR+PvWVchGSxDNukXOGZwR9tVyydx4TTbNA+lapBbWk7SsE0NAeMkV8cB8demjZmOeUu4iEqYaXmdpBGhvJKDtg8D+4M5UmTuixyaNyWibEKiRH6ztk8Z3Sq/xNB8Lb5fXCYkisZiiJQZWKlOQqLUOKh2omA0WBm4lVhR2bjvc8g+jUIMTWycxKpeSBRXUlRh1QBFYV2VKMytRI3Do8aiMwMSrmZWWpqrWUHjyg3lNXKyPLMKJXURI6Z8fk8VKqtEriohXYwmab4607yU5sTW/+JP5Fbnr9sinwSSxTqvS9u4MdD0DHSCbAc6G/luQMM2s2P/ekQP6uoc6mjqs7Zgeod2ePOvgzA31qkki39e6dPqsnzk5eQhMyMT2Vm5yM7ORGZeHvLKRTbvdzCaWFgQ1Cv6Dx3YuS//ar8SZFDkIdo6/Q9tW+3bRNPzxkeQBMgB0Xn6p7KSPGRl5SE3pwjlbi/cHIzp2wLkgD5P8+ZxTtC8zJvDOMti+bQtOc/lY3K5ZoQhKVJXOlktuh4eRxkqizOQm52B7AtlKBOZuTbdnGDzkEB5SVDoagImLS0o5+jJzSodyYjKpz6G0Uy7q68x0ovPkvZhevFd/jqPUhg/xwruS+QGCmPSsfRvB5tZaZCMXdIiKpcSYmYi5VFk7ROOSyRw7E9NKZAojKaX/SQjnWCbMxbfMy6PG8up3TRBJUpUPGoWHY0opSq+KBmP61ETSExIqlQTGYe7EoPEiwqtK0KitPXOXFQmrcfID0OwJzYX5RqZruc7AC2EctA4RAqSKtTJAY9IJaRKaiTnZNYhBNGdFoZN2zZi+NazqGUyjUpHRJOXbRof87wEUNesDSptKc7ezOXMfWpcnapjBVnXRoP9KKlJbAIws3I6flPLL/YlXxJm3vHB2PX1mdg7riPef/FVPDsrBm7OJCVe6dlQ7Fz1Efr274UeL/wV3d7rgs4d2+KtvkPQfV2SkLyLEtDCovEQlaVd+GUSp3agOku7FRsX3f3SbrnFyOaLZsOhmuse9E0KOVZ5JgjB03vjrba90av3FGxKKUaW+AyX5KW2pkYhQbZJvurEY9Ae6yQPl+SmK8actHkd6veafTiW7L8IkrXf50H+iTUImf4BOnfojLdbLcKu5EKUaIRmBJ2/2Dvro75Ahog62TB3xpI0yUG6cu0D+eBJ+ddVMvoT3aVM9GfyrX5L2l+Ck7loGjkkfsmjd55JvgHX1ygwa41sKBgnlx7Jm3TKCGaisDxzGVEm8QEfZ07Ih6RhdJ2gajqL7xuXBYnSe1qo/QFHweVQ0ToUR6/Eupnd0bnT62j7RCu0evIttHu/G3r074t+fXugd7c2eLZ1B/SaHopdpwtQK+nN9WUO2uKqqs/j3L5gTHrzUywMS0ZKaY2UJcoq5XH21uygUZSn4MT2afikb3u0+WAG1kSVILeSZKSBJHBmJKTKUYrkQ+uwYPIQ9FpyBtnlQhoCxsZZFekUW+X7B2U8h9Nb5mBCv374W/+pmBOTj5JqkYezKekbMzumc2usfKy7CUQDeWJogPYJvxkl4HA0vq8C8cveR++XHsHtbdcgxutBbe0p7FqxCYtmbUFE5Cas6fhveLJLT7zZuhXeebcNnp8XgwohUdYlWXwXoNryMpGuKHHQpq6pfTfouBkQdYWCK04kA3JYV0Oo9zwr8XQQl7yqYudizYox6Ln8CFJPZ6G4xgWnDOzVhecQH7YGY/p9glkzJ+LjMdMxdUU4InNrKIDkLVRK8qiTYFa96DdIMWhJzQiRkZfySdpYD347q3NRlHUUxzavwqhffIo9J/JQFIjeXOBqHkljvd8hIrBs+gQnKvLjcXTdWPRq9RYGfLIZ+04USnsxPtuArc++kb4QWX1sc6blkg+bW+vC2z+YL/2ytKHsexiZkzz2FSM1ApJCQ6AE6U/6b8nfVYLatHCEThqK6dOnYMK4CZg0cQEWRFxAicendE0n2NSNOtEhjlkXUa5F8+LyuJwnykcj1WVrKrNsUzur0iMRtX0Kxvd4BQ9c8S/48S0d8P7omVgUtBZBa1dj9YrZmDS2Bzq2fRft+83CrIg0VIuRcZCv99eiJHY9dkwciK4DwxCdV4lqHwkWZykcsKn+zQzaQG0BMuPWYfEnb6Hlrx/Bs6N2Y3dKqcwqjaOjE2X5dLa1eTGIDP4UXdoOwpqYXOTUCDERw+L9RiRTJsPvH35/AXISQrFkWCe88PBTeKDnNhzOqkSNOjQavFknovNoFNifGti3zJ+DjUlr2oN9Ie3DfUaRfc4NfTJfzD6yBivGtUW7v9yPx+7riPkpHhRUZSAhOgVR0eeQdW4Xlj/xI7wwfBY+W7ISO7ZtQNCJHDjpIC9R+1lc3lAiJIpKH1InKubl4Nmg37LNVQie05VwLp/opFDScECnfksUxtLVdAkVx2Zi7bqpGBqRx9FVjokvzI3FweWzMbjLSIydtwXbw7Zjy/IpmDxsBIaNWo6YHEC4loz5UhJ1nXnSluj7mtu3Sd7mlgTJm99inyRvPvETBfG7MOmHIxFxPBuFFKIZYYgmfbn4HTYMt311cJRlIXnfCkx640949NG3MGh+BBLKSJy4sEQ/YkistgnbnRTni7bnvomj+Utba920K0i8eEWEnfDt0PzY7ZKb3lZCYlYnvjN2A9YMfAd9xszG8g07sHPrOiydORp9P+yLsXtTkVbGFUPqhgQhbnxW3OhP87afReNweVzOEydgZjpc6KYiGefCizre4jgcnvch7vuXX+DXby3Huvg8GcxpXH54fLWoyw/FtBda4J7rnsLjfYKR7PbIrELYfU0yIheNwYQuvTEupgalLl34VodjZoSNM5SLgUouH35vLs4dmo3+N16FXz48HJN3nUV+nRiq1ElJnBo061iJwjNCAto9gndmHED4uTK4xRD1Wr0640sDdTAoRsquSRjb6mb84Lc9MTsqB1lukjxeZuUDx4131UzjqKlEaUkxiouKUPQfQmFhIYqLC1FUXguHi/c3eOBy5CMvbhfWfjYA4z4dgn4fvIEP7v0T3liWgaTiKjjEmbpchciLXoWhv/o5us2MQEQmXxMhAxCdrfbvpWtDi8sZRr/MPUmBS0ec9ChZ4gBOHeYKBwdXiaeDv1ld14FX1JKaKXvy6UNl1AysC5AoJVaoRkH4BIxr3xYPPT8Z+4tkQlknfqEgAtvHvo/X73gePTcVI7OcZVMWyVsy1YmXpm9mvTfCKhHRwZ6r/BI89WKjCTsw5YcjsOd4ppCoxnqERkIbiz7TFM/yeT+Y31sPT3k2Lqx/HU/ddgv+0n0qliRWSP1Jl0gomYY+nnmQNLGNuM/82EYSx1unRFD7h8dkm/1hiK/sNwKaFVe4NA8ZXyTUFR5GxOxeeOGWB9B503mcKZF+85Ug7chcfPq3G3BLxxXYejJXxjCuQEk6yUO8lmxTtmbuN4tG4bIgUQ1OQI1VFYkKLcrHz/TdCP3sFVz5i2vw6Kf7cTi9Wo+TyTvrq0V/o7D+jT/j6R/eivueHoOdpUCtOJaqpLWY9dEwvN1hMWLEuJw+t5A0DrBSBJX/OyIpUhOR3I2C1N0I7vxz/ObqZ9FrzkHEldOwpXCvR8kiV99ouK7iRCStaYPbX5mIGbuSUSACmvsgmNN3I+O3QUuVj5JTG7F28L34pytuwgcrEhBTwAHBXH7lOhHdU6MghCc3Ox3xcdGIiopEdHQ0IiOjJByT/SgcPx6lx6NO5SC3vAZul8xwk7YjqPvr6DFiJUJiziJh71xMff0W/KjdSuw6lYK8wgIUpiUgMXQ6XvnnuzB+bTxO5lWgqroMubVcLG+0dBYWFwlOcmSwrROfIkS+QnSxrKgc5eXlqKwuRkVVKaoqqlBa40JlXWCFXfwPb0TX1Q5RTOqmGTN9qI2dhnUhk9AvIkvicrX3HPZ/+hrefO55PDhsLyokFleyffVZOLFqOHrcfRt+1D0c0TnVIokQKa4QSb4+Hx/2aH6tVwKiBEboiPineq+QRPGxnvo85MTvxrQfjkZEdAYKxS83N7StJFvjbegTSXKkzq5yeM8sQq+H/4C7W/XGh+vOghf9dCwR/0n/riv+DGyjhvS6+iPtVZ6HUum3grIqVDjFm/GhJSlFrxaYor8VSpdFON5+4uU9uOLnyiIXYW6XF/Grm3phYUoN8jycbHpRnbIdB4fcjf93VSdM2JKINA9JnJQoYxGfc2a5WlmL7x2Xxz1RqmaivLQWYTh0CFzA5QyhOHoh5ne7BVddfS3eC8pEYrFZ2qWq1/udqC8Nx5QXH8Ld/7cFHnp2DvbX1sNR70Dquq4YOKg32s49IUyfzovLtMyfusry5Bh3mhHMTWUTQ/UUJuLCmjdx8/W/wuP9FmHNySoz2xCj5jxHSZzU0+/OQ3nqAnT/42sYO2UvjhfKYc2F9bxERsVmkrb3FR5H/LIuuPWHV+KaHquxMr5YJBKZ6bR1/TsQ/9sgeXnrnPC4HfB4XBI8XwS32w2Xi8ckyIDj8wkJil6PZf064fYPghFyKgtFbheqUsOxe/zr+NHP+mDK1L7o0q4b2j7fFZ980hP/8v/ew5SIs0g8sgp7tszHhBOV4qAa/woGC4uLAe2Tq8WuigykRi3AhEEfYmj/CRg3cT5mLpuLeUvmYem8xQjeegRx54t11dYQAOqkmRzR/GUsV19UeWwG1gRNxYD9+XJQvEP5Icx79xm0eKA1HpuVSHPUUO8vQ/K28Rj1zE248t652JBSjFLJTy9JaaTvxmPQW/K+HZ+PPon7dfCJnH5vKYriDwiJGobdQqLyVcrmA0kNX3dSX6e3ZMsf6ycSsBjxJ/DGYMW79+Dx617CS102I5Gr+HVcERJCKfGUmLChmZLkSDa5QuhyV8GbHIzpg3pg8JiFWHM4AyVCiPX1Bxx/WEYjQdLG2w7YMp76IpwJ6othf74Tv7lpPPYU16BSyqO+ODKP4sTUl3H1T+5A10VHcLyIwkhFWJ7Ia0he48u1aD5cFiTK3CMkChQI3HZJ8KES57Z8jNGtrse//ltrTIwuRKaDFsR48u+qRnXUWLR//BbceGdrdJh8GLn6FFwqwga8jI+6DMTIMDPwq5cJ5O91FKP47C6snDMbC6eMxaSZSzB19Q5EHpyDWfNn4PNPPsWS4D1CaETBPW44T63BrKF90fPjJVh4vMyoOkmG5EUH89U36NIgODPxufNRlbIC3W/+Le5oOQBDg5JQIfH1ZkaJx5sZmR6+cnHGOzH76TvQZ/RqBJ8xjoqEizXlJ50Co/I4w5cb/ApsNAIB+ib/DLItXzog8JPESAJdvEw6ZVs+3IXIiVqO4Xf9AL++pS9GByUiRx/VDTwVKf/8kN5CTeU5nNo+C/MnT8G86eMxZeZcTFgSiUwX9IkVQ2CZQBN9DVoWj+vlCBcKLiRhX+hGbDyWgbxqcVCS1ltTiNzEA5g+ZTW2rvoInTu8jSdavYlOXd5GyxYvYuDYzzHmcyl/7Q7ElDvhZptpfZkn+59lSNvqcVOcaQ7ds7hswP6kPtN6voSnIh1pxzdhzuSZmDtlNMbM3YDlG7YhYvsijJ06FZ+PmICgiJNILqP9GdtT3dDs5COg79yt91ciL3Ybds8bi4mb92F/ZCwSElJwNvk8Ui+k4Wz6BaTLd05+ASpqeI8mE9Kv0fZJBcSGJDT4vHIlUVMwZG+ulCO+JH01xv/tYdz0QBs8uuiklMiVL9pPGVJ3jsfoJ3+NK3/eB/Oic5AjBIP5MCu9sqT6bo59Ydfyp37EUYSy0xEInjEIvd5qjdff6ohuH8/GivBkpDv9cGtSSeOpQXVGEg4sHYMhAz5Cv34DMXDUVIxbsQ9pUp5D4qh/8hWi+EQ4ZlwxCmEkUUIseY+WSEtB5F+2pM5sOt47RtHMSg93vh1aLybWy4isE4/pCcmIE+MqJC1ujzcf+iPue/kjLE2pg9tbI8VwJdrIKF9aHtvF+GbJjmSpOhupp+IRcyAcu1YvxKyxYzBmYyTisstQ6zEys+WYusGH8BiffdQJOJ0klYRyyXkTPwPH5nVG11tvxW9uHo+9pdUygvE84MyKRMyMZ3H1T3+OVz/dgvDzvLeU9WI7mrpZXBpcJiQqYFw6kHNdikYnpuA9h6Mze6LTH27FNfdPwKaMCpSKkdIl+OqqUZNzDJsHPI2/PPEiXhm4ACEnC4R8yUyk5jAWtGmFPu+NwsI4GcWpoGpAUoa7CLnJR7By5jIsWbcBG9dPx4SBvfHmi++h04iPMXlib7R+qiVavf8xxhyVuZW7GhV7h+CDP9+D25/5EB9uviCZCdUQOfSGeDUgLgezDrQp1oMG7ICrMglB7e7CA396Ge0+3oTEauPcaTBKwDSuA27nCWzudCPaDpiKiQdK9PwXBi8fXyNRrIMaH1uBdszPxoFxdaZFsiICf5GPlkFSKORPj4mT0OBCRcYxRHx4K/79Vw+i/WebcajYXD5QYRjXW4K8M+HYsmAceg6dgLmLViM0dB2Wzh2NUcM/xIxTNSgUB90oKInyobamBvm5Bah2y/yT90BoW4jrclYjN/scMs+GY9u2DVi8aj1CNgQhZMlSbNm2DSG7j+FwYhZq1c3R9WmNpR5sMw5bDsme9W9oX3Nfgpw15VtcBlDFDIQAXHk4ezQcq+csxrKQjdgc/BkGduhsXikw6mNM+vQDPHP3fXh55AqsOlWquqGcRT6MPYuemwOaa21mBPZvmI7Js5Zjy6kClDpo/4wjA6zE0zf9iwaaFRz6CWUngbwkT+okcwroZUXUNKwTEjV0T4HkIZp7eiH6vnI/fnZ/Ozw6/4yUKPYmeUNIQ+qOCRjT8mpcceWbmLovExkyqTQ+hT6HWRqZ1abFZoy987JTLUqSjyF66XSZKM7GpNGfYGifd/Hem2/gjVf7o+fI9TiQVoayynykH9uKtZ+PwpgJk/DpjDmYs2ARFi9ejHlLVmPW6hNILqlWIlVfn4+iuJ2Y+sORQqKykM8JlpIoKZvi6qVJOSZVVdmURBn/3SgE2qdh4mnuQ6PNmrYVEVAdNwOj3miBOx56HW+tz0CN16xEsS/0FTlMT1nkj22jecq3h75OJHVUZONc7D7sWL0cyzdvxabgZdiwLQzhCdnIc7DdTHymY51IsdVnsELKrehXhPhqj6dg//iO6PDzW/HbmyYgXEhUuRxn+Y6sI4ic8wSu+emP8dTw9dh8Vsie5KM+isSZjSTxLL5/XBYkSm/CFA3StySRBNHGaDDl+7B2UBs8fPUduPbFyVh7MAbRpxJw8mQc4mMP4fDuxRjR5lV0HrIIKw+lo9wrZiEzkfrMjRj+3Mvo3GUyNp3ngE+jptHVw10YjZjdC9FnxB7El9SiyhGHrWM64aXr78VNnYOwf+tn6PP2S3i800h8tOeCTHhqUHliAab3745uQ2dh3tF0yc8tfo3Kb4yT8x6u4BgHxrJoaGKozlLETnkCrf70Rzz89mdYerqGpixxTRwaDU3P5crCoY//gGe7DUP/9WmBlRvJUaaWdMB0PIzLsmQ6iariXORmpuNCRhbSMzKQ0YiQmZmJrGJJ6+aTf3RudLoiiZRFUeh49P0qusRM4umSOOJkilJxbuVfcccNP0OLzpMxN7pcZ2P6L066OicC26d3xdstn8PDYw4jNrcGDr8b5w8swMpBj6Pj7jKkV7J1GgEKwjrKtzp+KcTchN/gyJgPBwbTfgzGwfICgwm6uifxeY4zczOwMD1dpkuIOZ0y9yW21LHhIoHF5QL2ZUMwcGftwY5VqzBhxhFk+dzwVh3A3Ndb4rE7XsEzQ5fhdNgIvP7nR9ByyBLMiy0S/ZDUEnjfj04uJC+990U0yIcqpGyYjOXz5mLW8RK9P5BTKVEoiSs6qPEFXI3WfUlLEiWxZPNrgSJSf6uipiIoaCoG7ymGlyQ/YRE6vdwCP2ghJGpOMlNSpSVujZCoiRj7JElUa0zeJT6giiRNdFnKo8xUeM2fZXLFhaklsafiLE6GrcPySUux53wtKmudqEgJw87J3fDOXXfjF//3cXwwPRQhW5Zi8bgeeOetzvh8dwrOVbqEcEhetTnIi9mC4R1GYEN8OrJcUl59AYrid2LSD4cJicpBvpRLMqn3gFEU9TOyRbloc1oPPiHNs98OE58+irde0ObNKxzM277pF6XAvJ1Y9P5LuOeGlvhDnw1Ir5JRhC5f2sH4TtmR8rX9tDWkveSYS+2f98ny3i45U1cLV+Zx7F06HtNmTMfMdTux/+gJRJ7MRk6ZnKszfkZ7V+sk0rEMvfLhFGnpX5Kxd2gHvPN/bsP1N07CrrIalEne2nxCoo7MfwK/+tcf4/GhMvE7Xakp1F/xgq/IQT9l8f3jsiBRfFcGZ3C8Y4DvphTdUsX3nZmH0R88hH/+5fW4udXb6NS5F3r07IOeXbqgZ9f+6DU6CCsPpyOtwgU3jUQU2+euRn3iHHR48j2803s1DhWTevBWb/kWpS9L3I7I0IlYHCuEwumBP38Plg9ui0dufwovLUrB+dit2LVhDdaHxSGhgIYn4IcEdYoUjgov34Y0iYVwxqWR+OC/1IWO1OuBqywLRya+gGfuuBq/bNkBb65KFnPzi8nQeGjZklRk9rgqELvgNjzzfk90XXICpTQmcYp0iPrSUM5/aMAkb5BZ9YFN2LxgHhbNXYLFcxdjwfwFmD9//n8bFixYiBVCClMLK8QRca2GbcI6SFkUXZ2wOMxATfQldx4nqgsScWL1q7j35p/hnx7pjo7L4lAUkN0nTj05pC/6P3sXbrirN+alOpBZXoPqivOIWbsAM97ujYWnvCh2ao7fCp1BS+mGHLG+bF8jnpFKCpVAlypNo7tsP5IjfirJIgnktYM6Ok/51iR0gKZmmpbESRy8n3GYj8VljYKjCxG2YyM2JNG/SL9nbMLIVx7Gn5/rjH5BCahM2oqgpeux+XgGUvkAiKgFCTgHaw6RZs2CesMVgxPY2G8SFn0cjJgqJxwOF1xOGWSdTgnVcLrKUSvbzlrxSS5JS9JOHaMq0j/JDikE1bJB9fh0Hi/nfcSn84REIW4xurx0H370wOt4ZF6c6jXLr6uvQPLOz4REXYMrr2iPSTvF91VzGkAfwRujaTeSITOmzvMHiSUlh35n7AqEbVyIcQdLtHx9VYn4KXfJSSQE9cOzV12Jf73lQdx27414+u230TUkVe8lbXjykMFZkIykWfdj1I4TOJgjEvmLURgbgck/HI6I6GzkszQpn5cFKYOXba2Eg/JQKGlYJRz8/nYwGX0ACSLXgHTVRo/TjqV3fC7Upu3AgvdexP1X3ojf/ntPBKc4UeIQOYTc8JcPGi5nGkdiCJSbs1/uUyZmLX1kfLr0Dfu+4gLO712Aeb3fxGs9lmDZgXgk5xejqtYh5KtWsnFKcpI6BknAOqpk57F/2Pt46we34tobJ2CnkKhyliGnXZmRiJ77LH5x9ZV4dNhqbDxdLklYmCSTfEjOWC+L7x+XyUqUGLRHjFKIB2cb1HEqdc6ugej78vW47u4n0SHoPFIuFCC7sAi5hXkoYiipRpmT18HJ5CW9GEa9xwG3zOTaPNkZrfuswf4ScQBicLosK8biFUdXU1OOMhcHaXFOJxdjwvvP4I8PtMH4Yx6UVlWitqoC1dUuOD2824eXuDjomhkWTZkGyCfoVE4ZzXmJiKSEAz9nniIRqnKP49DMV/Fy59Z48fYb0eL3T+HPXYNxWkzFKbHVlVImycPnrkHS4rvwfNee6LTsOHJpXHKO9kfDorGa2ZsEOedy1KCqogIVEioZKhkqvzVU1Xr05m1dIpf8jRSsm8mXP7Vj3lnCuvpQnnMUEasH4PFnOuGFllfjdze2xCu91uB4tYhH8ctPYH33V/HMtTfjukc6YejcVfhszBAMGdAHoz5biJCITFS6+evrbKhvB11IQ2D91THJl/ar7jec52DGejCGcalKntgncp4DoH6wXhKJx8xQwuFQBkYhizpLZp48afEPDHY2O/G/6kjRFkcFqmqqUMlfDvCK7RwZh3eeaIEn243CknjReGcNKirLUO0Q/Rf74Nv1qRr6RJrolOqZBK68oigMs3sNQNf2H2H08gVYsnwZVixdiaXLVmHZsuVYuXQxVi2WgXeFDJQ7Y3DqfBk9g0hH0sE3nPN+QhIc0VvmJ2fLoidjTcgkDN0vszbq7Jk1GPHKQ7i2xRt4ZG6CpKb+syYyadkxEaMf+zf85EfdMPtwNrKczEvyYZ5wiJzM10xAeC8hJwvU+cwNM7F72RxsyDR1kxNq5z6fAxUXDmHXgDvxh99djStv+SteG7sRUeL/6BFYd73/SPyrrzoX7oMD8fT8vVgWVyI2V4TChDBMvJKX89JRQB9MP0JioX6Fjca6G1n4o/EkkfxrDJjOrPxIfF2VlyOcPbFfPFWozziIeZ06o9tzrfD4A3fhF7+/B+235OFMGe2cfw3kkzJxkqXeDk7KIJNEfXknJ4tc/dPY0vfsbznmcVSiIj8DeUlHsGnK++jRZxj6LT6G0yIDfSN7Q6LrmKKeVNsyGVGTO6Drb2/Fb/7wOfaVVeuN5WwBV/YRxM5+Hlf/9Cd46uPt2HpWfBgZJ+tDn6R1tbgUuDzuiaKb4aMqVGYaPh0MyoW5v4F3H7wZt7fsiwWJdahxcXAXY+Z9Axw0aV/yrdfZae00eCFRvvj5eP2J9/B6r1U4UEAlpoHQhmggEkRvdVYof1lhg9H/1adxz5OjEVriRqXXrBKRtKjj4B+NkI5J0vD1BPSotGt9Qk2dIc3IOK46GaDL0w4gfOEIvPjWhxgXEoal49rj3Zb34U9P98fa7HohFiRGDFp5+Fw1iFtwO1744EN0WhqPjEBdaFTypXUzszFzUP2IHg9k0FhoxeVbA9tFDvFPMtSX9kktSBQ5u6o6H4FNs0fi/fYDMGJtFLZNa42XH7wDLV4bgrkJ1RoHmZswru2fcecdT+G5MaGIOpuGEzHHEXU0ErGnUpFexsuCKqmEb4fKQ6ej9eJOoF/1mIociPOlg6aDMnF0V9qFwxWdIx2bHJd4jKurWxqXjjLg7CVDvz56zgax+McENYL99019yHNGV0gu9PKJuxzn1ryKF1s8jVd7LsX+ctEB6ojogOoe7UL2mZT6ppfjeE5ICskVKvdg4aBpGD9iNfacPYPklGSkpqTIdwrO8js5GWlnk/X4haw8mZTVSrlmkKbe8hLTF/dPqS9quCdqMobuDaxE5YRhWpsncfsDrfHIvESRhVMAhmIk7xqH0X+5Dj++ZjSWJeQg1yv56YRBAu2CdZCgt0hIoG77UYWTyz5H6OwZ2JVHe+TKv8QRG+Ckta5W5Iyeii63y4T1p7/HPe98jFmnyiWd1FnSG5uSIPEQNQovz9+HlfElUocCFCTswOc/HoXdMdnIl7y+sE31y8ZP6b0/PCeHze0DcqIRkJhSKutEe5Z91o3d7ChGaeJWzHnvdXT+aArmLZuFecPa4ZFrbsQNffdi74VSmQwaWbS9te1ZONPTV1Me9jfjMLCeclz1QPqY+26ZeGZE4fCcgRjRpz+GfB6EkGPZKJd0JHI6sWU9madISX/or8/GySXd0e+eO/CbmydjT2k5KhhfYjizjuDEtFb45U9+iTaTI7Av06Rnu0iG2kaMZ/H947IgUbpQq0oo6k1l5yzBmYTQnk/g2ZsfxENtF+BQWT1c6nR4T4+YNBVZrZQzA0NgaCheby3qk5eh19PvolOPJYjIEQOiA6QhSXxXZQHyL5zEqfhzyKstwKFZbdH+qefxSPt1iPe5UCMylKXF40JqMtKrzexFF/NF4Y1voGOSWQStmqRPDYGOgm7SiZKU/dg8fyw+7DMYXaYdQFyeA5lRszH+vUdx0x0voE1oMXIqWV+xHak7jdftKseJGbfhhW790X31KZTQyQQcBgki20VJnZg/6qtRnCHOOu4E4k8kIOFEPOLi4r49xMcjIaMUpbV8KsS0hUIK0ReQMrAP6pyoPr8fW2YNx8CeQjAn7kS8zOyqk+Zj9Gv3474HW+PtJUmopCtKW4VhbzyMu1u+ie6h56UfxSFrvxinwpee8koe69kYUKKGQUAdbaBP2cZKeHhI4piVuS/jMapZWmccOiRxugHnyEuUzpoyFBcUo1KE4RPkX6QTWXVFyjqvf2CoRgTCV8HjHMLdqC1KR3ryKSSmpiKv5hzCBt+Fxx9+B+9+Fo5kEglfDYoTI5CSnYM80RHqBgc2Dn8kD7ryoPFEnzxnsOPT6Vg+YyNiqjixYTlMY3RSzYrJRf/NH/Ohb+OdhPJNfxHQZfIl2l31sVkIWjsNg/bkyDmx9epT2PDhy3im5V/xwMRjMhB7hcx5JJ9snAoaiaH33ox//ctKbD9XLIO6eCeZhNWUFSCrqBour3o6tQNd6RKZ+JDL2eDRWDtnHJacFv9I2xQBzIsmXXBVpOLC1sF47/E78cef/AQ3/uEpvDpiG9KEADqFODYQMnf5eZRtfBu9go9K2Xxli/jS+F2YcuUIhMfkoED9itifTETdFbnIL6kSm+PKdkAW2hptmW3UCDCemczSnqVObOeaXGQfW48Vn3RDu3cGYurWOJzJOYOkTaPR765rceVdH2PxkQsoqJOek3qqr/uqv1B/TY/OPjJ+ipNk+nCOJx5HNjIT9uPg1hCs3xSCjStnY+nacOyNzUJhJf2+5MXVJ+qHpuP4wHxZTjUyd43H+Fcfw69/PxwbMypQIg6Hdag5txuHx92Nq//tUfRdE4n4CnOc74qimpp2aWTDWDQrLgsS5ZJARs7FV6791PMJi7zt+PyZ+3HH71/Gk8N2I10U1aODqbnkJ+5I4hrD0J8gCBiD2+eQtJsx9fnXMaDLDGy+IEoqRs1LPv56J3JP7cC2uSMwbPhqHDh3EAu7/gWtHn8NT44/gCIxVk9tPo6tmouQkK04UEiDccNZnoKUk9E4mXQBmeV0q07Rel5SooMVEkhjrKuVmUs0tk/th/ff74XW47bjXKVwQfHtvoJ92PhJGzx08934yQfhiMmp1ZsZ+UeZa115iB19C17uNxiDtpw1RE1KkUrqIM/6qhORb9QX4UJMBPaGBGFDcCg2Bm1EyHox+PXr//sQsgEbo2UwKeMqEvOUurHx1RmwTpylV6L6QiT2TOuKD9r2QK/xm3G8VM7TsbvjsbXfK3j5tkdwxwerccrthyNrK6Z1fBLPPv8Oem/NlPwc2i9+IaPOUpklnz+LpEqvOOLGOQdtEbaL1lXSyD+lVFLGEDinDk/iK2miTkhdGm7AN06Xgwc9k+hDdSqSYrZixbJghBwvQYEMfOwzzUM+9DKvKd7iHxLsvf+KRNHuHUjftxwrJo7H2DmrcTgnAhOeugG3PycTlrXxKPJVoa4sCdunD0LIoSgkcoJDnfKRtLhFT6hXkrfol2yIntUide1krJs1AwuP58qki7pEZZI0AV2UDyUopE28i1Enefr7b1z15MDOuJKGaWVCqCRq3XQMFBJF2lVfX4KTi3qg599ewX3dghAnyWr5gkjHKRyZ8hE+uP5BPDghBgmFDpm41KL0fDQig5Zi1vKdSMitQlUd8+cKB8kHJxX1KI6ajpCln2BEUCrK5byLZcufqzobaUdXYdq7D+OVbh3R+plH0eq6P+JPN7+L8RuPI0nyqxVb97kqUZp8ADtGPI+ph07iRBlrV4iChAhMu2IwIqKzUECSSduvzMSp0LlYsWoLDiVmoMxt7NLvq9X2lKIbBTYr20kJivSG11WMvONrsXJUR7z2UjsMDstHRhn9sAPFCauxrtvNuOpHj6DPihjElPIhJfaZZCTtLS0i+dGPCIGSIKl4WP1GXZ0DzopC5J49hYSEcGxdPhnTxo7Fxyv3ILrEgUppL/oLyqPC6+SZ7crxSv60/yV/Ka4mORRrRrTFn37/BqYeLkF2leigv1raaSVW97wW1z42EnOOJiOX79wSeVQPVMZA3hbfOy6PG8upzNR30VQqtdMhg3nsArR7/A78y6Pt8eLSeJlhidLKOToikoCG+5PMgElDE4XkcrtXzKPyCOa/8hj6tR+OZYlMoxd4xD1l48TKfuhz34342W0DsXTLHHRp9TBufuwtPLc4Ci53DdzxSzBq3DJM3HACeSQXzlrkhfVEh8d+h4de7ovREeX6GgWuYlBu3sPslpmet/ok9g95FU8+8CL+OnQZ9hYLIZOqqbEK8UlePxwjW1yHq37aBytjC1AYeNqDKyVe5xmEdb0V7wwbj0mHM8W4WSfWhe0RIBRSltpY4PIlyYrEkBag9TUOZvZFckEyRmctOUomdCYkUTUFcTg29Rk88LvH8O7wjdh9gS+R07vAxGH4kRrcBYOf/h1uuas7lqS7UOg8j72fv4ke77RGm+VJcPENztL+3so8nNm8AAv7tsekqAoU1DKHRkKdJl0mt/Wf3SuHpb4yMPAdL/zJCcojn3JOjvGeOPY/25Mto21n0uXHzsbEnrfjn665CT94PRTbzpSBrxpju+ljznWBdrD4BwX7jvpFa/hqP1IXaPU1ODSyNdrdfi/ueW4QQvcswGs3/Aa/fm0kBuxI0RdmVkROQ7ve6xAalY1q6pH4GtEMSV2jNy/76Jwka9FMOSaTtJy9WDNnDt7stxbRbpkEid7rW7C5Qq5Twjq4RYfpIphOlVgVml9iaZys6QqoQD4qoqdjbdAUIQWFWgt6Ns/ZYCzu1xWPPDQAS2UiWEzyf2o91vXrgGdbdMO8ZKCkVuL603B04RB0/Kef46orbkbf9adxslQKE52mHSmVo604TiJy3XKM67AY+4prUeLyiL1W4JwQqFk9X8F1T0xD8IlCZCVtQPDgF3Dvldfiih+8hmErEpGYUyOTq2M4tnI8nn5hETalFqBIpBRqpvdEffbj/giXCVoebU8+8xJXYtA/X4nrrrgWfxu+EjuzaKmBB4fkmykbBakGCS2JJSednvOhmNvjabR68kW8vTgOOV4hkTIxps37imJwavU7uOaqK3HngGCsTayQ9pdyqBryxZbQ1TAdaEy36A+qi/27irOQKUR7+rut0GnkLCw8mIIMh4xD9CeB+5Y48dJ3XWk/GpnUB8m+R9VD6ijx/J5UnNw0Ch/eeTNazzuJuPQKuF0XELt7Ano9fgMem3YcURm1mo4jk/p5umPmbXFJcHmQKCqjKJG/WBzA9pl4r31rdHj6RtxwzY/xg2t+j9890hZ9+s7FnqxqlIgmc5bHx/ENkTEKrgu0fHpNztXXncP2Yc+hT6/eGL47D/pbS1KM31+FnCOLsHjAS2jx3Pvo9G4ffDpmBPp36YV2z3fEiNEfo8cgGfx3JOB0YbXOMHSF6eAo9Hjx33HdQ2/ghUnHxHVwAOYbfMVwxBr8teJ8Y2fhtSdfxTvDVyEkJte840ji1Ynh8pUClSdDsHFAS/z2qt+j48qTiC0UWWlJdZXwVOzBrBZ3o8eItViTTOdKizJtQkM1lyqlamwqfsuJL/YlXmOhhspMZcP8kYRIDtKWflcmMg8sRZ/r/4g2g4OxKSZPn14kadFy5KM2eT1WDn0eD977EJ5aeQ6pJdWoTpGZ25yheL9jZwycuBqfThyNjz+diVkrwhCZlIUi/gQLy2wMpJ5sE5WJ+/Khg4qK3CCvIT3mfjR6Lw5e3GY6OmjjsDUD0YW6vFjEbvocgzp1wGO/HIf1UfyNLxItzkiZDzNnYRb/uGAHfhOJcslnBU5vGYaRPV7Fn1/qjt7vjcD0z0bgvTYf4P123TFixDh0H7YIwceykFHJO2lod+JTqEKiVzpQ0qcwf6oK7d1djdKUSOxZOQ3de36CtYfSkF6uj2TIn8RTHZa41GfVadkJbJrjtDnjO5hnRdQsIVHTMHhvnuxKWqZ3liM7ejdCJgxD9/eGYcxnIzF04AAM4SC/JRHFNWJXvO3BX4HcuD3YMLw7Oj17F95ecgT7MoXoSb6mTObIshyozE0SW1iAsV3eQ49OnfBmm3fRvutQjFu4HYfP5COvtk6fLiy/EI2ooJkY3uYlPPdEC9zf4mE89coH6DslBFvjSlBQYy7V+yFkKmEfpl4xFLujs5FHe/I7UVOUhEMTB2PEG0+g49hFmB9XKe1obJZ1bzTETnlpng/q8B7Z49NeRecO7dBhYijihEHyd0Z15ZmTa3cB8k+tw0ctr8dtLUfhkw1JyGUjiO/XaxaSF8cNXjXgpUyumFWl7sWWOeMxcvg4jNt4AMfOpiIttwil1S4hRuwj41/Yn9pfWhZbU8plH5GgaTz6HJFRj7nhzDuF5C2TMHZAJwwaMw7Dh43CiIHDMGzWGhzOrkCli31MteBaIFc7RR42y0U0jUXz4fIgUaI9qkMOmdmkxWDb1lBsC16KVcsXYdHylVgVvBXh4SeQXiXzQJ1IMD61UJMGvvhJrZZz/hqcWdcL/Qf2Q+vZcSiRU1zC5b1UtcXnkBYXgW1hBxCx+zBOJSUi/tgxHNi8CwcOH8LuQ2eRll8FB5kZc5M0dfkxiNw4Gr2Gf4q3J0XK/JS2w6e8uDom0ngq4CqIwZbN4TiUmI38ajrcgJT8FgvxVmYjO34XgpatQNjZQhTUCq2jJdXmw3FyLt65sy1Gzt+HqAoSRDlOwzK1Cfx9BeZEAF8789/ja+kIthkPiYzeKlRln8a+xcE4kJiP/CqSUspu4jCdvyYH6QkR2Lppoz6iW+GU9naVoiAtDof3hGHvsSQcPXYYhyJPID4lH6WclF8UpJCAk9VPltmwreBWgzw8yf3AWe5rmwVaS/5JpvzOElRlHMHhkPl4+8G5CEvIQZkMdOYyB0mZSW7xj47/2JHcJ/lxozIvHvExe7Ej/DAOhB1HauppRO07gAM7w3Hw0DHsPpKCXPEtLg6u+velapkvPSJBd9Rs/Y4SlKWfQPhO0fvIaOw/dAj7IsKxNzwcEeER2BuxF0dPnEV6QaVOxqhvOiDryEu/INKJj6FvqBIStU5I1JA9eXKKK1hyXvxKXVUBCpKjsG/nfhyJ3IeIA4dx5EQK0ktqJBsO7sxT5K4oREbkVoQOuR8DQxJwhK8fCMiq8uqfRK+rRlXBWRzftR1h27djU+hW7NhzDHHnSuAUgsOVFq2l1wlnSQbOHN2NbSErsHzZcqzeEIZ98VnIF5vmfY9KXPz5QqLCMfmKMfqyzQJtGKGRrmqUpyVh75Q3MG7Jciw/VStxJQ19KgVpNOhDacVsMxfyYrdi3/4DOJxcYJ6wo7TMT7Y5gXZV5eBkWDBCNh1HdFoJqnlco1APSG9lMi3H+PNT1an7ESn9tW3rLuzYdwSRabkyQRdfL/KbPFk+P7hvWlD/dJvtzjK/jPe1Y3UOeErTcOroLhyMPIoDB47gyOFoxJ4vQI1X6hNIx1Ssm5Rg0llcElwmJKqZIQpZkbQcUz4egta9ViCqCnB7zfKrcVASQTW5kRDn50gNwsr1KzBo3Vk1aTMIyyBNEkWCxpWwRloCZyA6u5V83QWnkLa8A55uPQWL9pxFochp7vGyVvX3Qi+Fymy9ruQkzh4QojpgH2LSS2Ww5ABAx8r7FQKRLSwaCZqmsWFeRq5GfnYy4o8fwkFOJML3IGLPXuyJiMBBIVFphVVctxA/wUkTA+2eg7HopzoSv5Co6Vi3bgoGR+SZ42L/+tSxn6snfAdUgPSLPtPnMA+9ZK0r8ZKJyFB27ig29HkJCw6fxxn+YnEzwtx7KDJL0NV5Dv30UX6uRO3CxCtGI7yBRDGwrt4C7JncA4s3bEZEvsjPVSglKDS4S+PbaPH0qz5XLapTxBfEpeBMnkweSWzET/AirvHLl0Y+i0sDS6K+ATovcJ7FvrnjMPKtvpgiLKrURYckhk9j1qcrApG/DTQoVwXO7JiKhcFLMOdkqfqAhqV6Xd7VS0IXYXj0exLd761AYeI2rOj2KDosOIJDacL21KC5YCx5B6JbNBGc+YrDLEgKw+alg9F1ax7OlQV++oU6wHvDpK1tQ1tcDKgufIrO6+NSayDw/U8N99tIBJIM/v6n/gao+Am/l5fveemZZMTkYdTOh4rIKVi7bhIG789jctFNyUd8ir6AWHSUq2lKvHQFSEiMZMAHUuh3OBnwVKUi+eBKDG47DhFp+Sihc2lGqLyBsrgjpZvLYvUFKEzYKSRqKML4sk2eE7l8nlLUZIViev9pCN4ei8w6+kj6M15+Myvclwa0eSlb2rW+ziHuoeE9UtCgfeLnpT+pp8X/GlgS9Z9AU+Dcz4uKpI0IntkXd/behcRSR+Bdufqcnjq2RsEnM8G09ZgwfgWmBsUhR9kP0/IJPT6ZwavadAwyM9SyGwEml6i8GTI2ZCKeenoGNgg5K6I/5vuNvB7J15KovxcyfKG+NBJ7Ni5Dp0FbkSZEupZOnm3LPtB+ZKM3UhcsLAS0S67O8EEXehQTRId4QkLgSwJXNbjaKf6BusYoDIE4xsJ9qDo+FcHBkzF8Ly/n+fXBCfM+JU2iuXObO9Rd3pguTEW+zcuA0yN3YNv4gZh2pFwfwyfRanaoMAGfpB+sWzYKErZiwlUjsDM6B9kSh6SvLDcF+wa2wbytCYjPqhU3aW4n9/K3K7VGlwiUWw1ffIC2ryG25Kz0AtrGUi/T6hb/W2BJ1DeAMwk6Ek9tKc6d2IKFY9/EsG3nkVjAm/jEmMVY1F4aAxqdoxjZWQXIKa5WIsZZod6sSKci5XBWeDEOgmV7vdlI3LkKiwePx6wDeThf5YGbKyTimHWQV2NutJQW3wTpJ5+nCkXFBTh9oRgu6S/zq1v8fcY66QO6y8DAYGHRSFBfOODKMBz44woMV4hEnxh4ROzYz59W0TeUq6IFVnMa0pOEcaceFVGzMW9iLzz/0RyEhuxGTFElytVJaSL+y9gunkdXSbySFZ9QljLkOMtxVhahOCsNORVeuCUd829O0NeZ16Jwasr8fahJj8PJiIVYOHEE3rriE4RGZyGPskld61wOlKefRn5xDapk4sKJpklnVuKaXcDGgu6Z5ZMAmqm09oPx53pS5Jfek32L/z2wJOoboMvOEmgMjoocpB9fjd2xucgud4MvN+MAejGGTJPTZV4uxwcIDr/Nu4mM0embZxubqdirvy4fmaejERkWhbQqL5xi3Hx6hD9RYN5vQqO2+LtA5yiB74LSBwC4LX1nCDAvh0jfUk8uRhksLKguEvjFQVdJE/cDxzgkm6dIDekRZdMThjNR20i6jH/icVd+HOKO7ULQzqNIiEtCVk0Naqifko7580lB88LJhvyYVr8k0AdRq3nPVMAfUcZmBP2d3gMmcphVMT8cJZnISolE1KF92DztGFLzy1CrMopsdF38kEYhydOnqZkRG8k0Ave+f7DNNFBA/s6p0igRVRqSy1GyTX9xqcSzuDSwJOqbQEOlQ5HAVwx4+eK82lp49KZtzoZ4g2cgbiPAuZ++u6nhiRgeEcdgXhDKbznEMhsLZuFzoM7rhIsX45mvWC7v2TIkisv/JqrF3wFpTzpMnbVTJaSp1UmaDTnH4xdBfi0svkCD/hjSooG6xQGa7EZpA/UvMChL4LekENUL2Dih5zipo2+Rs1yNFjKiq9uSN4NZMzHEyzzIImlUn5k345vVaz3Pfc20ecEyzctpOQk1fkp/k47V1Qj0qULyKKlWVCumsikZ5K7yFNMulwoUi5dKTasG/ujTPWxHttx30XoW/5NhSdQ3oOFJEo8QH4cQJpptnRh4gzHrk29q5BcBOgtyHS7JiwHy9Z36mgN1JsyUpTQyTy2eMkqmysDMMQpKJxqYt1n8vdB+NoMMV6P0t8qUwDKwHzkAWhJlcbGgvpAIGJKkR+Sbg7G+Vy0w0dJjcpqBsUygD6qD/v4nDzAbKiX1VLb5rmB98k58g65CKekwv9CgpEmi6m/lyT8vTPNOI131YplSkJIpzbgZIXnSV3E11+tzShnmSTZd+RLxDG2jg2R9KRFlNvs83nBOv9T4ZOMSgK1CMSgVJ6wNsmkfsu2UwDZz21n8j4clUf8BNBAP73mhU6LB0CaMT1Mr0hszafkNBxoDcR4kT3yQS9yV/HFZXQzR6xDDc2kZEqXRMG6OxisyNCyBy746UtnXn5u4NH7msoL0kGlb6SAOAtrjqg/SuHxaiH2oDyE0Ug8sLATUl6/pjG7yg0ZrDFcvq1Hv5LA5Q/9hjikCXyRK+lug4gt0PiXJ/X6+OoG6a8oyq10SlJFJBJImOUn6zzUqkhw9ztvMmV8g7+aCyqIv9jTyfHUFnvUE5VX5KAYlEpujOPRt6jHp38T6NP2lA8s2/UYJZVs2+ZZx3shvVtHojy+lhBaXApZEfQPUgemsjLM1+aCNqHHQicnsSR3NxRmLLpWrM9DMaIfiWJgXl4WNw2ss1CWKfJSRDoazOpMX5WL+lPPi5LP4BkgbaltLIGHlJRK2uBmLZEsUhO0vEU18C4tGQCzU6FWDjfJLWQOD2TWDNG1ZHYXqmdq0xjWB++aFr+acCZILV825qiU6qr/tqATGnDe/o+nS9FyQ0te20F/IeQ9vW9B4kn8zwpQb8E3KMyiDyMzqSXkkVYYsmTgNN8yLMCYeE2lCHjd5XgoY+Si3aUt2l06MZZ/yGj8hBy6lkBbfOyyJ+q9AG5FAZ2ZAw6CB0JDFWPRY42FMLGBgDVlxU4zODMSNB5PThhm4J6Yt+dHhBBxg4LjF3w/TnPw0/cRt3ZMPOlPbzhYXiwat+boX+VKXvn4+4HM0BBCIYHRRh+6vHGOgL+CAb84aImZiGzLGNSiTo748WP2GUBX1IXqq2cGSVRYWGpCHu+YQz5g6GsIVOMF/2W44ZxJcOmj7NRC5gPwNknHbSKcndcvifwcsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwaAIsibKwsLCwsLCwuGgA/x+dZ+PsC4OU5gAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%A0%B7%E6%9C%AC%E6%A0%87%E5%87%86%E5%B7%AE.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcIAAAEbCAYAAABJKYSiAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADmqSURBVHhe7Z0HlBRF/sd9/n2nHmIA9ZAznSRzYM0B04liThgQRRTz7Yo5Zz1B0GEBUQxnVgzorCKKIpwKqBjWwYAonDmgaw6Y69/f31TN9vR0z3RP2O2Z+n7eq7fb1WGqm6U+86uusJgihBBCLIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJCQif/75p9pxxx3VxRdfzGRRIrULRUhIRO6++27Vs2dPteWWWzJZlEjtQhESEpErrrhCXXPNNXqLEFLtUISEROTggw9Wd911l94i1cwff/yRScReKEJCIoD3g7169VJPPfWUzgnHl19+qV577bVMpTtv3jz19ttvy/UqDT5v1KhR6ocfftA5tc/rr7+ujjrqqLyC+/jjjyW633///dVNN92kPv/8c72H2AZFSEgEfvzxR7XYYoupX375RecUZuHCheqCCy5Q3bt3V+eff77aZ5991Pjx49Xee+8tgqokEO3AgQPVlVdeaVXUg/vu3bu3PHe/Lxt4Ftttt52aPXu2fKnZYYcd1CabbKK+//57fQSxCYqQkAjMnDlTbbHFFpEiuT322ENNnTpVnXzyyerAAw/MnHvqqadKNFIp8DmjR4+Wjh6//fabzrUHRHwrr7yyGjt2bM6/15133qk6deqkmpubZbupqUm+4LDJ204oQkIiMG7cOBFYFKZPn65+//13tfbaa6sbbrhB8lAxb7/99urmm2+W7Uowf/58teaaa6oJEybonOoGURyeY6Hk5oEHHlBdu3ZVH3zwgc5J8+ijj0oUiH8bgPMgwpEjR8o2sQuKkJAIHH/88WrixIl6KzwzZsyQinbOnDmy/emnn6qOHTtKs+kbb7wheeUE0jjuuOOkebBWmkRxH4ceeqiM4fRLO+20k/r111/10WlwTrdu3dSFF16YN4rHFxL8+zz++OM6h9gERUhISFCR4r0SOrpE5fTTT1ebb755pjIeM2aMWnfddSUSwbvCcvPuu++q5ZZbTp1xxhk6p/qB1KZNm5Y3eUUITjrpJIkK8X7XD1wX0SFkWStfGkg0KEJCQoJKEu+VvM1vhTDNoKhoDUOGDFH33HOPuvbaa9XTTz+tc8vHLbfcIhHOK6+8onNywf3gXvDTCNq7HTdQLpQRyZTRnefHiy++KM8CPUm94F779+8vTaX4ndgJRUhISN5//315z1dMhYkpuj766CO9la6A8e7O++6qXDQ0NKillloqsKzIP+CAA+QdIqKlQw45RDqOYBvSqK+vDxRLe4EyDx48WG200UZqxRVXlI5HP//8s9wHvmhguMRbb72lj24F5+FZTJ48WeekQT568Q4YMEB+/+yzz6SXKbEPipCQkEyaNEntu+++sY2WDKjUIYYuXbrI716QB6GMGDFCfsf4RshvvfXWU5dddpm6/PLLZfu2227TZ7Q/eOboAQtxLViwQMqNMkKGSLgXbCcSCX1GKzgWz+L666/P+re7+uqrRXxPPvmkDKFAxD5o0CC9l9gERUhISIYPH67OOeccvRVfMFSiT58+MvDfT9pTpkxR2267bWYf3qtBIogKIQ28L8P2Cy+8IPsNLS0tmV6WbQ2i00033VTKB/BzpZVWUmussUZWme+44w7Z7wb3iWeB97TmfDRL43hvijpRAqkNKEJCQoDKFFOr+VW0cQOVPSLCoPGOiJ7cFT4iP0gAERPA+Rj36AWyOfHEE/VWfh5++OGCCTIyCROZ+5XV8Oyzz8q7PAOalFFmNGvivG+++UYiOyM6N9iPZ7Hffvtl9uP+/RI63BD7oAgJCQEq03XWWUeaEQ0YEoHmtEqnqIPhUdmjCTfswP9jjz1WpPLOO+/oHH/Q2eSTTz7RW/lBk+Oll14qM9qgCRLNmhAtpjILSmHKajCdgTCusxBGhPhy4CdKQihCQkKACtTb+QSSQmVsEiImvMOCBPKlM888U+Rz0EEHqV133VVtttlmaq211pLhDu7rmQSZRAFlPO2006RjTyG5oMlxq622kt6w7nvznod97v3tCcp2yimnyLNxD2UJulfk41mgudjGGXZIYShCQkLw6quvqg033DCrsoUYMG+oW1po5sMx+RLOc/80vyOh5yJmn9lrr70y10QnFuwLC66HacXQG9TvvJdfflmkjeZPRHjLLLNM1hhHnIPPNeei2RLXQlQVpRzlBMJGp5hkMim///Of/5Teo6Y8+ImmU7+mTexD+RERmnskxA1FSEgI8B4Ns5p4mTt3bmbIARIW7H3vvff03uJBhY2xbYhkcF3MhRkFHN+hQ4ccceG6prwvvfSSDOzH7xguYcB7QPQqxbGQTo8ePTIdalKplD6q7UA5MO4Sn49eoc8995z87hbbsGHDJLpGeb3gGeBZYEgJIX5QhISEADO04F2XH4iYUDGbdPjhh+cIqFjQlIcmWDSjRrkmxgSiLN5xihAHJgFHRAh5QLQQH3qMIkJEpIWmWiMU9BJFlIVhFTivXPcVFfT4RESKuUCXXnppaYJGlIfxmUceeaTca9DMMRj/if3/+c9/dA4h2VCEhBQA8ujXr1/g0AHsP/vsszMiRPJb8aBYICXMozlr1iydU5ivvvpKygGJesH0a2jChUwQ4UFuZhsz0XijKtwHmoXRLNleQOi4F0SEjz32mJTxwQcflDzMzJPv3R/+bSDNSk1eQKqfWIuwpTmlWvTvrbSoZH2DSi7Um4VoTqiG+kTO8S1NDSrRmFKhGnqca9TVRfjM0OBeEroMKZWoT/rcrz9S/vQKMrksTKqGurrg/SQSEAXGrOVb2BbHQJZGhJ07d5Z3ceUC0Ro62oQF8kJzIt79+UVxUSSNz1522WVFPri3cgk+KsV8Ls7BnK4QZntFsyT+xDsilArdiEIjeQ2qoSncuwoIo84RnpegfF8gQvexWjR1gSm7zC1NuSIW9HUamrT+RLie+81DqtH5LB95Rro3UpAPP/xQenUWqojRoQaRh5Fh0DurtgID4lGOqO8XvVx00UXSEQURMSawriYQNTIaJIWIfdOoVPauSj1vJJRDcPSI62QEVAivCCPjRHuO8DLldiJdXC1XWDguvAj9j48WWZLCoEkQIggTkdx6660ZESKdddZZ7RaJoLxYO3HPPfcsqQw4F/eP+6mmqAoRPGajQTRYTDRJ7CH+7wjRtJkRllPJRxFSHoG1rQidkruit5QjQiPphnoTRaYjQ5Gj3paUJTWc49rnPqZAlBr6XkkOqEgx/2YYIAozxs0kTK7dXhUxyrP77rvLKhc2geeNd54HHnhgVcmbtA8xFWGuJIJSvugQ8knvT0dk5pyMcByBJCEo175W8WSf405FScUI3RFWEmWCXJ1rucsfSc5uIMEsYZJygQoVERWmBAsLhhqYuS+R0Kz69ttv671tDzqSYJHeapgerlzce++98uzbs2maVA+xFmHezimFKv9MhJTb1GiirobGRFpKhShDRGhoaUpKeVKNadFHF2GuoBucZ+Xezk6V6OQTDMSBVdcxnRYiKSR08jC/I1UTiCaKeceEsW7LL798RoaMTAiJLzUrQogm2eRuVjWkr52AiJpSzjGFBZf1njIj2NYEmckxWfl+5ddNu841Ek65WiPWNMVGhN7rtBeo6CE6jPMyAvAmDObOJwREL/gWHzVVCqwhiLXvokoMXwjQHOm+93//+9/t1kRKCAmmNkWoRZNpjnSjozsjncAenRlQFi23gM8LLSLnsxPNzvUa09fJlac3hYnmECHm72DTstD3KZUVI0FU+Hifhg4m1113nQyCRp5Z8w2Dm/PJALO3uOURNuHalQD3gTF8xQgMUj/66KOzyllqD05CSPmJsQhbhZBoyo3CJPmKyRGDyc8RYatgW6MvHaUFYSJAHAOJ+nxmOBHisx1hNSczcosaEfqJM9GYftdYMAV9aSgTd911l1T0V1xxRZY0zBI/8+fP1zn5gVCDEiI/9zY+x6RKAbkPHTpUb0UHc4diMLoR4eqrry6zvpQbDPHAYHim8idS+1RFRJhyKvscVZmoz4sT/WRyvSLU0SBwSyefyEwTa/q8bMmaiM2c71tOnGNk5BFuVBH6ka/s+cBnlUuQixYtkg4hGHTuneYKM4FAAN5FXqsFTKpd6tRciIbdzcUHHHCA3lM+IEJzfabypd12200/YVLLxFSEXtIyyZZEixNdFajCs0TokphDlnQk6guQmIkEsySWjlhzRZr9Ga1kH2/AeVlRm0/ynpNFTrnCkxFhkee7QY9IVBrHH3+8zkmDSG3vvfdWXbp0yTsFlht3xBclVQKU/x//+EfJUQHKh8Vw8Yz69u1bkfJ+/vnnTBVKpPaJoQjRgaVVMJmKWmSV/c5MKvN8EY1LhBLZec51SyYtpWwZZt4feoWDsrg+1x2VBZXJfYzBm+ctU34g3YSTWqUpn2uacjPJT/DlBauHo5L3LpKKVRjQcxKDusN2aMGacebbeJQU9R0h3tUVKtN3330n1w4r8SAgPkzEvcYaa8jitoSQeBE7EUIGRg7ZotDv2MyWnodUxBNU2WsRmuvgZ6sgPCkjFSPMViF7ReiVanY5/aNXRIRu6YHiRZj9LDJ4BN1WoDl0ySWXVPfff7/OSYN3a1FF4n0PGDZFAZEemjw//vhjneMPJnfGzCSlvIPEuViIF8/B+3wIIfEgXiL0RH1eUbhJNZkKPy0e3+NEhEmV8tkXKfpyi9D5PYzQspsc/ctYnAhxrWwRZ4ggQny2fAHIKmdxQF4HH3yw+te//iVRIMR04403yorrWBmgFJFUgv/+978ipkmTJukcfy655BJ1wgkn6K3o4L6xdBM+q7GxUecSQuJGjESYjprczYrBIvREh3qQeg46IvSjKBFCND7iyCnnwpRKZYkqWIQ5kWlOckV+8kUhIPoFEUQossb1yyBCgKV99t13X6n0sfICokH0mIybBBGdHnHEEVJOrG2Xj/3226+kjjJmnUL0PI3bcyCEtBLrzjKZyjogFRRZOUXoFYxIqbUs/sLOT7Do/XBkasqA8rg+O1QKKchSQGVvmjbjWvE/8cQTmYVcjz32WJ2bC8rfrVu3ot/p4Z0lImJKkJD4E2sRlkwlRWjAviKjKv/hFqRSQEg777yzDPSHCLFMUpCkIPOOHTtGfv8IIM+ePXvKkkWldrQhhFSe2hYhIS7uu+8+GcOHdfUgwrXXXjtQdBgSsuOOO0YW4RdffKG23357kWwxEg3ioYceUtOmTdNbhJByQhESa5g7d650kMG7S4hwqaWWChxCgZly0NszSrMmxIdOQ5hJptDQjCjgWhtssIF65JFHdA4hpJxQhMQ6ICwMlIcM582bp3OzOe2009QDDzygtwoDYdbX16u//e1vZZfgMccco9Zff/2qbWbF88Z9mC8V+GlSOaNmQoqFIiTWgQoYM7xAhH5j+7B/vfXWkwnCw4DjL7vsMrneJ598onNLA9fEUk5oZsV1MYdrNfL111+rrbbaStZnRLM0ZI4hJb169ZL7Qs9cTMhASHtCERIrwZhHVMTo1ekFUQqWXgob2Y0fP16u9fzzz4vAghKui+Texk98Dn7HOo4zZ85Ul156qdpss83kmia99dZb+tOqC6xFecMNN6gHH3xQ7gMyRJPzV199JfsxLR/yyhlFExIVipBYyZgxY6RixthHyMjNL7/8orbeemuRUyGwTBPeNSJyi5ownRx+YqmqTp06ZYnPnTDxc5iyxA3I7a9//auU3axCgqnmzPPGT4gQ+exdS9oTipBYydSpU6UCxlhBr2RmzJihBg8enCNIL4jeMH+oEValEqKpagTPD1848HPAgAFyL+4JzPHcTeRbjaIntQNFSKzE9BxFwnssN1g6atiwYXorGIwXxAD9KGnKlCm++ViqyZ0gapOqvdkQkkPEi45EbuHhvvH8DznkkIJfOgipJBQhsRJUyKussopUxM8884zOTXPYYYdJkycpDxA7njOeq5uGhgbJN8+aUSFpLyhCYiWIQPB+DhXx2LFjdW46HwPtq7VzShwZPny4PGfM6GOA9DbaaCNZqxKrl9x0000yEw8jQ9IeUITEWkxHDfeco6igl1hiCUYnZQJiQ9MnnvPs2bN1rlIvv/yy5B166KHyrDH13Z133qn3EtK2UITEWkzPUYxzM5HIhx9+KGMIi41MzjjjDNW/f3+9FY2JEyfKNGpXXXWVRKu1EB3h/eaaa66punfvnvXl4vvvv5f5WAcNGqQGDhyoevfuzS8fpN2gCIm1mHdXyyyzTKYSRg9NRDDFcvHFF6s77rhDb0UDYxpNqhURAtzP/Pnz9VYr6EGKjkm10CGIVDcUIbGWlpYWESGSeSd47rnnyswn7UmtiTAfNtwjiT8UIbEWRIFmHOCECROkUt5ll11kVf2ovPbaa+qggw6SGWtKrdxtEiEhcYAiJNYC0ey1114iQkSCEOOSSy6pFi1apI8IB87D7DCYkQbXwqK8AHLFFGPudP755+fk3XvvvXK8wYiQ78wIaRsoQmI15513nshrjz32kPdU6NIfVUDo4HLRRReppqYmGTj+7bffSj5Ei2u5E6YS8+Z5Iz9GhIS0LRQhsRpEYxAhljmaNWuWOvroo4sSEIS25557ylRi5nz8DJvcUISEtC0UIbEarEcIEXbu3FmNGjVKjR49Wu+JhrkOosKbb75Z8iA05BVKjY2NcryBIiSkbaEIidWgqbJDhw4iJAybQFf+YrjxxhtVjx491K+//irXAhCZtxnULxnh4SeS+x0hZUhI5aEIidVANJtuuqnIa/XVV1effvqp3hONBQsWqK5du0qnmTlz5ujcaECAZmkmlAcrYCCPEFJZKEJiNRDhEUccIeJZaaWVJAorFlyr1PO9yXS8IYRUDoqQWM+IESNEhHwvR4idUITEep599lkRIQbDE0LsgyIk1mM6uIwfP17nEEJsgiIk1oP3eiuuuKJMAk0IsQ+KkFgP3gsWO2yCEFL9UISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkIIIVZDERJCCLEaipAQQojVUISEEEKshiIkhBBiNRQhIYQQq6EICSGEWA1FSAghxGooQkKK4M8//1QnnXSSuvjii5ksS6T2oAgJKYI//vhDrbvuumqLLbZQW265JZNFidQeFCEhRfD777+rDTfcUIRICKluKEJCiuCll15Sm2yyiTSRkuoHX2hMIvZBERJSBGPHjlUXXnih3goHosinnnpKKlv8jjRnzhz1448/6iMqB4R99913W1fRv/7662rw4MF573vGjBnqrLPOUvvvv7+66aab1Oeff673EFugCAmJCKQycOBAddttt+mcwuCcxRZbTPXr10/1799fnX/++dLxYsiQIWqvvfaqqKDw2ZA2Pr9aRfjbb7/lpEWLFqmffvpJfvrtx30j9e7dW+4fv3v54osv1JFHHqneeust+ZKyww47SKT//fff6yOIDVCEhEQEFermm28u0VxYJkyYICKaOHGidLJ57bXXJL+pqUl17ty5ooK67rrrRAaQQ7Vy1113qRNPPDErDRo0SB177LHq8MMPz9k3bty4jPg+/vhjtfLKK0sU7wVfZvDv8v7778s2/j2wjc8j9kAREhIRSGv11VePJK/p06dLU+iAAQPUYYcdpnOVRCqo0P2ilXKAMkKCt99+u86pTnAf3gSx//LLL/LTb7/7mT7wwAOqa9eu6oMPPtA5aSZNmiRRII4HCxYsEBGOHDlStokdUISEROTDDz+UqC6qvFBhd+rUSV177bWyDTHusssu6t5775XtcoPy3XDDDapnz57yWTYD0XXr1i2widQwZswYEeFjjz2mc4gNUISERCSZTGZFdWEx0QZ+gueff16233vvPflZ7qgQ8tt5550lCiVKJkBAVBjUOQlfcNZbbz2RpYkQiR1QhIRE5KKLLlKXXHKJ3grPPffco7bffvuM8O644w7pOHPggQeqCy64QPLKybx580SwiAqDQFkQqUKaplyQALbjLANTRhPpouzIy1fmF198UZ4HepJ6wfn4t3j00Udjfd+kMlCEhEQAFSbENWXKFJ0THogPPRMNqHCnTp2aGVJRbu6//36p+F9++WWdkw0+89BDD5Vjll9+ebkvvHM74IADJO+YY46R3pRxI5VKqW222UatuOKKMqkBhoWYLxnoeBT0pQLSXGqppdTkyZN1Tho8B9wzmqzx+2effVaRLyYkvlCEhEQAFWW1zCiDsXEQWktLi85pBUK/7LLLpML/9ttvpRcrjoUMkRobG2U7kUjoM+IBZLbZZpup++67T+4B5Uc5kSDxbbfdVq222mqZSNEN/s26dOmirr/+ejkX4Oe5554r18EXEiTTgYnYA0VISARQwXbs2DFTkcYVVPoYSI5Iz0/aGPqx1VZbZfbhviCTNdZYQ/LQkxLbiGLdQKroAdse4JkfdNBB6rjjjtM5So0ePVrKefXVV0t0jd8x/6ufCHF+r1691Omnn565b0SSOMeb3JE7qX0oQkIi8Nxzz6k999wz9iJE+XbffXe10UYb+YoQPVUhAQOGFUAApmPN119/rZ588smc+4QgMQA9DA8//HDBhDKYhCbOQs8V7/HM/eDYhoYGKffs2bMlD82mSH7geEhyv/32y1zDRIHeVKgcpLagCAmJAGaDQRd7AypMNKVFSWiG88vPl6JGYSgXoqeNN97YV4RezLABDL7PB64b5noAs+dceuml6sorr5SIDdEbmiUxjVlQiiIglAMR3tprrx2qTLg2RIgvCGHvgdgBRUhISFCR4h2UW0qIHkxzGtKyyy4rQxYQNaIDxiGHHKKOOOII6XiC7vunnHKKvLuDDOvr62VWFBy79dZby3g/dABxX8+kvn37RpIEjsU7wDCz1uBYREn4nDfeeEPnpvPdYDtOApk2bZqUGc/VTdBzQj6kiSbjap5lh5QfipCQkEACK6ywQs48lIh83NLadddd5VhUvEHJ7Hf/NOnXX39VDz74oDRBusVopmULA66Ja+A8dIbx8vbbb0szJ94Bfvrpp3JfiJZwHkA50GkGPwGmiOvevbuqq6vL5LU1+FxMk3bqqafK76ajDGaNMaDJF188/MA5GEd49tlnZ+6TEEAREhISTPC86qqr5ogA25g42wgLqRwrmaOynjt3rkSMuCaaSKNU4Bgvh/O84+ZwjYMPPlj2XXPNNZlm0aFDh+ojlBo2bJgIHcei4wkk+PPPP8txUYRcTt588035fMgMPUQx+B3b6CQD8O+AYRVBq0dgf4cOHWRYCSFuKEJCQoJ5KXfbbTdfGaGSxvyjqJhNeuKJJ/Te0kAFjuECmCLsm2++0bmFQfMfIj13xGRAz0lEgGeccYY0FyKqRW9YDJtAJIrym56XX375pURaw4cPlxXa/XpktgWIxCG/W2+9VcYMnnDCCZmZYPBuc4MNNlBXXHFFzhcVAybWxn3FcWwkaV8oQlIxIAxUSniPNn/+/EwFhXy/2T3iDkRw3nnn6a1csGKBW4QQzQ8//KD3lgaeGVZVgKjCgueNd4/oWenF9ArFIHL0soQ0IUxI5emnn855h4bPx3AL7G9PML0dmj4xiTiEjLLfeOONasSIETK0w+9LigFNoogY20vkJL7EU4TNCdXQmFKtw4BTKtWsf3XjHJfwy89DS1ODc06LalmoM8LgfE5dXYNKRjknFC0qWZ9w7g6kVKI+6brn/KTvQ294WZhUDXV1kZ9NOUFFim/pWNsNnUCWW245WboIkxljkDY6clQb6PyC925BoBI+88wzs2R48skn562co4AKHO/FsDp+WPBvsP766/tW/lHKtXDhQrXMMsuod999V6aYK9c9FUMxn40vBZgo/aqrrgqMGIm9xFaEdR4ppBrrVJ0jRzeSV2dEEg4IJOo5Uh73Z2vRoOOAf8q+fktTwl+i+joNTfpORbjhyyb37yNPuUfPs2pLUOmiN+Qee+wh67uh4kLlgw4XECIEgW/21QTuAe8Hvcv4eMF94t2aW4Z+TZNtBf4t8DdZ6vNGVI8xfOjIE9QZJc7gCwzeLZp1BwlxE18R5lTkTsTklga2I0RQBkii9Roh8S1PFNJlz0RozU6E6/zIFRaOiyJpv+OLey7lAiJA1IKB3H5Te6Fpbemll666FcBxX34dZfxobm6WqbyMCIOeRVuB8Xt4p1bKkAGUHyLEMJAwzyBOoHl60003jdzZiNhDFYkwW2KBUVYB2keEjp5c0VvKEaFTEpWsd8pS3xpJolwiR70tKUtqOMe1z31MgSg18j0XCSKQfLOPPPTQQ1UxM4sX9JTE+6Ww5b7llluyokK8p2svgeBz0ayLLyjVJrFSwb8XOgJhKIhf8zAhIEYiTEdNUmk7gvBW5K0JEVDrsSa5K/ocmZjkyCy9z5FowDGt18n9jNxjIuDIVM5zhJVEZAi5Otdyv8crStIAEmzHKNCN6ZkXtF4fvpW3d4eLYkDnjLBTiwFUwGb6L5PQbb+9vgBAgJijE02cNoHernj2lCDJRywjQpFVYATm1xwYEi2fhiZHRlGEU4aI0NDifDaulGpMR4PRRejzJSDvF4dKdPIJBr34TMWPqbWwBhya5IwAUCG3lwxKAcMNRo4cqbfCsWjRIrXddttlngc6Df3vf//TewkhcSGWIvTrGNNKsSJMNytCGpBNS7O7V2p+ssrj0wQJmaU77riTn4CcsuM6zjUSThlwTjkiQu912hO8jzEDnU3C+zJEgVHeUeEbfDGpEkDcGDA/a9YsnROeGTNmSG9L8yww5ZptzZOExJ0YitAV8ZjmPh3JBacQYsQ1nOuljGy0jArjei8X0PwYWkROGTB0I9mYvk6uPL0pTDRX+ItBy8Iw91k+Xn31Vemc4ZYhEsahoRt+IU477TSZr7NPnz4ygBsdHbAG4DrrrCMznGCpoFVWWUXm0cTcnlhs9f/+7//kHVglgLjw+cWIFueatf1MwqDvaoyKCalV4idCIz0ncpIm0hz5FBMRpmUGWbmjrlRjiOuYCBCRnJapVyvhRIgyOJ/XnMzILWpE6CfOhHMP3jzfFCDxSgEBQIhYUQBL+xgJ3HbbbfqI/OB8v4So0r0NobhTJcCQAZQdn1cMOG/gwIGZZ4CEd46V4JVXXmGqUCK1S+xEiHdnySancpemSEd6ZRChWzBZsgnRySSwPCLsdMRmhOYvVpRXy0iu0UpUEfoRTsK54LPKLcggUSDfTJCMSLHaoqEXXnhBZmgppdyIhDGhgBEhBndXYnYdRMnmM5jKl44++mj9hEktEjMROtIwkZeWRqbCLpgC5OiJ4ryykesHyiC3PGn0+0Z9nVYZuUSZRfbxBr8Iz5vyijGnXOHJPNciz/cC2aGix6oGfmA6L1QomNsyDLhe1FRM02WYdf7GjRsnzbWlYp4BBnZXKsLAhNNMlUmkdomVCE2PyvwVPCKskBGhT8TnFaGRlJ9IM2MVveXxXNcdlQWJ1S9y8+blli0fkG7CSS5x4nNNU24mRYuei+Wrr75Sf/nLXwI7xGCVA0gA0VUhsHKD+SYeJUV9RwhxQk75QBR41FFHlTw7DK6D6b1QTsxJSgiJD/ERoVOBZzqvlEOEuIYjBnSOaZVCQGpMahkimQ4qqdYhFp7ySHOpq89HttBQPm8k1/qO0k3xItTvG/VWhhBNvZVi9uzZUsnjnaAXCAedXzAEAZFbGLzRXtgUBUyKPWXKFL3lD67Zu3dvWbOvFO6++255PpzdhJD4Eb/OMqBEEUIwQefnk01g70p3eZzfwwgt+/PTciyPCHGtbBFniCBCeUbyJSDfkwwPoh00+WHoxPPPPy/yQ4UPkWDVhIMOOqikKb7KDcqFHqiIVPOB4yCwqJJ1g9UcsBzSkCFDKEFCYkgNijBgpQpNtOZHjSkPRONTLq/Q1EKnDFmiChZhVmTqm1z3Ks2eee49gghF1rh+GUSIyr1v377qmWeekSVx1lxzTZlmDR1jVl55ZXXOOefESoIA829CcPvuu29eOWGlB0SExQpswYIFsvoDppUrRaaEkMpRkxFhPnKjtRCgPF7BiJRaheWVXBhyBJoX575NGVAe12eHShVuMkWnE8gC6ccff5QekZjOC7/HTQAoj+nBWWgi7fHjx0skVwxYRR0rUeALASVYOdD6cM8997DZmRQNRRgGPxEa8pY1P6HGMZKy88gjj6hRo0aJCJE+++wzvSeXY489Vtb0iwrEh042vXr1il00XAvg+WIybUwmjgkX8O9IEZJiiacICakQqEC33XZbGSSPaBAV6OOPP673ZoNKFc2iUYc64Dz0YMWsN8UM6Qjiu+++a9eJu+OEEeHUqVPlJ0VISoEiJFaBihIVJipS9GRFBTps2DC9Nxscg/34GRZc//rrr5fzyrkGIcqA6LQaV/avNPj3pAhJKVCExFrQmxUVKJaM8qtAEQni/WqUynXSpElqiSWWUM8995zOKR18/ogRI6Ss6JHblkDASO7mXUS5yDM9g9sbipCUCkVIrGXMmDFSgW6wwQa+FSjGRGJF9rBgZXpMCD5hwoSyVMi4xjvvvCPvGlHO/fffP1J0Wir4fHQUQs9aDItBhxQIHtvoGYzndtJJJ5W1+bcYKEJSKhQhsRb0akUFiuQnGESMY8eO1Vv5+eKLL2Q+0kQiIddChYwU9Ls3Dz8hFLwHhFAxrVu/fv0y5UMKO2F5uZg5c6bMiTpv3rxMGbC+IiZPABAj8jC5entiRIj3sniWhESFIiTW8uWXX6rFF19cKlHIxw0qVCwbhfUECwGB9e/fPzN2stj097//PSMcb+rUqVObR17ohHLrrbeq+fPnSxmwrqK7yffOO++U/KB3rG0FI0JSKhQhsRZEYVjjEJUoKnw32LfkkkvKQsP5wHFDhw6Va1QyITpt60oeYnnxxRczwhs+fLjek+bkk0+WfPTczAfKjWgN14uSwoJjUQ78pAhJMVCExFpQaeK9GypRzIPqZs6cOapnz54iukJgvtInnngidPIej4m/vQlycad3331Xf1rbc8opp8gzmjx5ss5JPzssmoxFkTFpQj7wDClCEmcoQmI1phLFwGx3JXrLLbfI/Ki2V6yQWJ8+feQZffLJJzpXZZpLMXUcmmzDfGGoFBQhKRWKkFgNlldCJbrxxhtnVaL19fXq8ssv11v2Asl17NgxJzpGj1o8t2QyKcfg97Z+h2mgCEmpUITEakxkg1lgTEWPynSbbbaRMYHtSRwq9TfffFOej7vpGOXaZ599MvLDbDdHHnlkm0eFKAeSW4QoQxyeG6kuKEJiNag4sUQSKlIz5yjyll56afXRRx/JdlQwjhDXK6ZCnjZtmpx/xx13qLXXXrvN5eLFRH5YSsoNxIh8vOPEXJ/ogduW4LmgyRa9bdFbF2XBWEfTc7dQBx5C3FCExGpMhYqKFOPmAFbOwFCGYiWE8Yk333yz3ooGKnBENviJMrW3CCHla6+9NqccEN9DDz2kBg0aJGMo2xqUx69TERLy8W9ASFgoQmI1iNowewqkgzlCwe2336723nvvdm1iM4P921uEhNgARUisBwPCIR0zVg/j4y699FK9NzyQ1gknnBA4d2kUENlQhIS0DRQhsZ6JEyeKdNBBBgLDNGKPPfaY3hsevKOaNWuWvKdC8yZ44403ZAydO2HGFm+eOd5gRMi1DAmpPBQhsR68E4R0MIUYekF26NAh8hJKECiu8cEHH0gPVLdIEdW5Ez7Dm4fkhhEhIW0HRUisB1EXpIMEKfbo0aNoASGy6969e9aYOkgyTHJDERLSdlCExHogobXWWkvEgxUeMMtMMQLCdbBEEeYefe2110Sq06dPz0g2Xzr00EP1VdJQhIS0HRQhIQ5mgDg6yuCdnTdCCwPWDsQ1MEh/+eWXVy+99JLkQ2ZhEjDRoREhIstiykIICQ9FSIjDyJEjRTzo6IJ19ooBMttiiy1U165dZfxdMWDYBDrdIKE8e+yxh5SJMiSkclCEhDggeoN4MK9mKpXSudGBDEuVlokKzbUoQUIqC0VIiAM6zGD9QdMcSQixB4qQEAdEX926dVMbbLBB5n0dIcQOKEJCHCA/zDlajllhCCHVBUVIiAZLCY0aNUpvEUJsgSIkRIMem2wWJcQ+KEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJMThzz//lPTkk0+qqVOnSnL//tRTT+kjCSG1BkVIrOePP/5QQ4cOVSuttJJabLHFfNNee+2ljyaE1BoUIbEaSHD77bdXq6++ukokEhL5DRkyRHXq1EltscUW6qabbpLI8PPPP9dnEEJqDYqQWAuaQkeNGiURX1NTk85NM2DAANWlSxf1+++/6xxCSK1CERJrmTJlikhwt912EykaECUOGjRILbvssuq3337TuYSQWoUiJNZy4403iggRFbr54YcfJBrs27cvI0JCLIAiJNZy+eWXiwhTqZTOSfPggw9K/oUXXijRISGktqEIibVMnjxZhPfpp5/qnPR7wz59+qhddtmF0SAhlkAREmvB+7+11lpLjRkzRiI/pDPOOEOtu+66fDdIiEVQhMRqZs+erfbcc0+JDHv06CHNoYwECbELipBYD8SHZGaXIYTYBUVICCHEaihCQgghVhNPETYnVF1dg0ou1Ntlo0Ul6xMq3Vk+pRL1SSenbWlpalCJZr3hZWFSNdTVBe8nhBBSduIrwkbX2C4tiLrAZOSWpqUp4S9RfZ2GJq0/EW72uTk45yS9YnLyEvUNnjKYVFjgqUbnOB8JQ5JZ993GoNekeV+GhJ6T7m1CCKlFqkOEkXGiPUdKmciqOSWyyxUNjisgQgeIKyNPAKH6li9slOn3ue0ToQJ0EJkwYYI65JBDZLJp9KD0S+XqSGI6pURNhBBSCWpUhGl5magr5Ygw3SzaoBrqW6M3yE3kmInmWs/Jwhs5RhYhPtv1Ge7P0lFqzj6dsgRcASCYe+65R0S35pprqmOOOUZWY+jYsaPaYYcd1AUXXCBDCu67776yyQjXLyZRhoSQShAjESJKKqMMHHnJeaZpU2SW/f4NEgx3badsbvGVHBFqcJ0ox1cATC+GKPCAAw7INH9COEcddZRaeuml1a+//ip55cQsdOuXnnnmGfX888+rl19+Wc2dO1d98MEHqqWlRf3000/6bEIIKS81GxEaWpqSEsmlGtPRYHEi9JAvigsUW67oGwLfMyJVorNQNngniOWGEA3OmzdP56ZBFIh8rMVXTQwbNkytscYa7ZogcEJI9RBLEUqzphGhj3QgMzkmK99PHDqSc66RcISHc8KL0NucGaZptEW1RJCXtzxtzSeffCKywzJEXrAMEfZ99dVXOqd8IOIsJoUBC+m2d6IICakuYihCl4ACoqvQAnEiy0Szc73G9HVy5elNAVGYaWYFXjFDiLrZteB1skCEmL+jTsvCIEmXB0wvBtmNHDlS56RBb1G8L9xyyy1zVl/A+8RZs2ZJMyr2nXDCCWrGjBk5x+Xj+OOPV8cdd1xWOvDAAwumKJ9BCCFhiZ8IjWiMYHxkGE6EEKojmuZkRkrRIkIXbhF6QRl9o8NW/AScaPTKMyBV8B3i+++/LyKcNm2azkkzYsQIyX/22Wd1TpqHHnpIygRJoun0/PPPl/d6EOakSZP0UYXBObg23gW+9NJLodKLL76ozyaEkPISOxHiXV6yycjF1flEoq50pGWElnJkkqsg17s4j6AqIcJi3zOGk3ku+LxyCRIR1k477SQ9QwGaHyGc1VZbzXctPsjxiy++UJ07d5ahFjgex/Ts2VNdddVV+ihCCKkuYiZC/U4vJ8pKN5ca4bRKxCXKLLKPN/hFZt7kKzUjQidaTTZlN41KhxenDEnvtfOJKkQUGURGhEWe7yWZTKru3burbt26yRCFrbbaSt15552+zZAQH3pxQogLFiyQPBNVIsojhJBqJFYizMwI4xUFmktdYnFHUyIGH+n4RVzevOgRYev7RoNc05FjzuwzgUDeCSd5pOl99xhioH+5+PHHH9WcOXNEaoXew2HoA8pnjhs3bpxaaaWV1Ndff13w3GoDTcEvvPBCpEQIqT5iJMKUE21pxXhEKM2lrs4n2UJLN4VmCy0dEZZbhN5ytAo6V5D+oFw+gvOIPs6cfvrp0qPU9OREFInOL+h4M3HiRH1U9TNq1Ci1/PLLS7QbNmHoBCGk+ohfZxngFqHzexihZTcVpuVYThEiCsp7PS3LYFCmgN6kEUSIz5SIsUxNo1Ew4nO/D+zfv7+M3cPitosWLdK51Q0i2969e6uZM2eqb7/9NlIihFQf8RYhBOFT4XuFphamVCpLMMEibG16DEq5EVuuaP3zcH1fGUqzZ56mzggilM9FOdtBhADvAr/77ju9pdRnn30mzaXmnWEtgLGA2267rYifEFL7xFeEXjGITFqF5ZVcGHIEWhT+HXHSpPdlCxXvBPW96MgyUqqSJtNaAdFgv379ZKo3QogdVI8IDSZaLAL/4RbhSUdjAc2bLlJNlFe1gskC1l13XUaDhFhEPEVISDsA+WHu1UcffVTnpEGUiGTkiJ/Yxgw8+EkIqW4oQkI0jzzyiAwFccsN70AxtrJr167SWxarcaCXLJap6tChgxo4cKC6//779dGEkGqEIiTEAVEeesRiLlUDhHj44YfLXKpmNY4+ffqou+66S6JBJDSjQoxsSiWkeqEICXHAXKmbbLJJVjSIuVB79eoleWY1juHDh+u9SiYehwghULOWIyGk+qAIifUgmsM0c7feeqvOSXPvvfeqCRMmiAgxn+oKK6yQJTxEhJAjROgWKCGkuqAISU0DQWGZKayUEdR8iWgQQyaCojpMHwfhYfIA9zXwThH5o0eP1jmEkGqEIiQ1CyK2IUOGqC5duoiwXn31Vb2nFYhtnXXWkYnGg8Aq/Th//PjxOid9Hq6NadiwwDG2g0RLCIk3FCGpWTBNGjq5nH322SKyM888U+9pxe/doBvIzZz/5ptv6lylWlpaJG+fffaRYxoaGtRtt92m9xJCqgmKkNQsJkJ766231OKLLy7vAd3Nn5Af1mO8+uqrdU4uOAYz/Ky66qpZssRUcxBhIpGQfPyOJaoIIdUHRUhqHghx8ODBIiusv2iYPHmyWmWVVWRsYBCQKM7DQHt30+fcuXMlH+8JN910UzVmzJjAqJIQEm8oQmIF06dPF3FhlQwjLMgNnWjyAflhBX9vRxrkT5s2TV188cWyqj8lSEj1QhESK0DHGUjQRIXz5s2T3xcuLDBxLCGk5qEIiTXcfffdIj80ZeLd3kknnaT3EEJshiIk1oDmS3R8gQwxZALv/wghhCIkVjFu3DgR4dChQ3UOIcR2KEJiFej0AhG+8sorOocQYjsUIbEO9Ph0D4UghNgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqKEJCCCFWQxESQgixGoqQEEKI1VCEhBBCrIYiJIQQYjUUISGEEKuhCAkhhFgNRUgIIcRqYizCFpWsr1N1jSm93b60NDWoRLPe8LIwqRrq6oL3x5g2va/mhKqra1DJhXq7bOBvJaHSfykplahPOjnhKNv9B95bumzJhWFLRAhpa2IuwvJWmqj0ShFrqtERs08lW+p1S6Vq7guycF9Pi6YuMBm5pWlpglD0hht9nYYmfQcipexz81GO+8exmc93E1KmUoase08nXFPK4bPPr8x+lP3fkZAaI8YidL7ZVyB6kEohQsSQDcrkrWCjRSCVoiruyyvCyKCcLqk0p6TMuRW93/3ko9T7d0ek2aBsvoIMSannG0r7+yCktom5CH2+BQek0M13+IYeqYLz+TycXyCaKUflFYlquK+SRej8Vbiit5QjwvS9OLJw3Y9vFJX1bMp1/wHXcVL67zH4b9j3OTrPx/t3nCtCfc2ozzHS3wchdhFzEUb5Vm8oUPlIs5n//nQKEYW2S6VSrfcVUQaFcO5TznPKmoQ09H27BVJ0FBX5/tMSznquuIaRlCmrG+zP83ctondJznsvInhfCbbB3wchNUp8RVigwiiG4EokH7kVTINT+bm3s1PbVyhVc1+ojCOX05+WpqT8baQa09FgdBGW4/7zidC5vp9UC/5dp8tl7ifrXnBuEV9Uivv7IMQe4i3CMkcn4SrIwuBbu7cJqz1pr/sK6uCRSZ5/v6xoR4SQfTw+O/eafgJyZIHrONdIOPftLXexzyPq/TufFCjCVGOA7OS+83/Bg9zNNVvvJUCsISjX3wchtUpsRViwknWnkBWE7zWdigwVcviKAt/Y81dkLW3cVb697uvjadeqa6/Lk+5Pqe/0sWlpmLL5/3uFFpETWSaanes1pq9T+G/FT6Zeivl3DRKhUy7J85EX9rvzRIx+ZQ6b8pcZlOfvg5DaJdbvCJMh/pOGrjz9Ki2Q5xu6XwWScL7pe/N8U5Hf3qNTJfdlKnxEcmgi9blOuH9L3K9zX83JzD17zysUAZXv/lEWn2NczZAoS1azpFeEBSg9mov+90GIbcRYhGFIV0ThRBjQtBSxYgpXWeciFWJORVoO2ve+wiLNfU3mHaGrzNKJI11RmzL4NysiYssVDYgqQj+Ku38fyeC5e8XnFk7Ef5fSRVievw9CapkaEKHPt10/nArXt0KJ0oEjyrEeMiIs8vxA2vG+II9MFOSXMhWtUxnj+jmfk/4iY8rfKqOAyttzvKFgOZyUVyZF/7uGEKEI3HVMW4uwHH8fhNQ4MRJhupLzq8R8k/wn9lQygeDa/s1AIqhQFQIq54STXGVAhSbf+F15bdrc1L73FfYdYWZGGG/l65GCOyqT8vsIwy9y8+ZFk0cp/64BIvSUOz3eUYNn4HNfQZQmwlL+Plz/HyOUl5BqpMojQogwhHiCvhU7oBItXNEEVCg+lV6bUhX35XrX6xGhu3ckyBYa/m2995CunMsnwlLvH+cXFmEWbSnCUv4+nHMzz9T9OyE1SHWLMFSFhW/8Qcf4V6zZoEIOiDojCAMVj3y7DhWlhSEe9xUJtwh9Klc/oWU/r7Qcw5xXWB7luP8iRRjhb6B4EZb490EREouoahGKXPJWKqjssr/xZ3eBz1MZAlRq+SLOCMKQSr1sIozPfUXCSADX93kOXqGphSmVyroH3Je/CFubMIOS637Ldv9poeR8Vp5zo4oN9xZdhCX+fQiue6vE3wIhMaK6RCgVmKvCyfefGZWuT2WXEZJJgf/JncrC7JNruc4JkypVeVTzfeHzvOd7/k2LiTxyBJqXct5/uIjQK+oo9xhZhCX/fRBiH9UZEUrlGSxBqXgKRF5yTJVVBlV/X34iNGBfkdFy4CwuFccRoR7UX5h0hFVcM2c4avXvnpBKU+WdZQghhJDSoAgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiNVQhIQQQqyGIiSEEGI1FCEhhBCroQgJIYRYDUVICCHEaihCQgghVkMREkIIsRqKkBBCiMUo9f+ovebP0qnL/QAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83-%E5%85%AC%E5%BC%8F%E5%B0%8F.jpg": {
- "image/jpeg": "/9j/4AAQSkZJRgABAQEAYABgAAD/4TnWRXhpZgAATU0AKgAAAAgABgALAAIAAAAmAAAIYgESAAMAAAABAAEAAAExAAIAAAAmAAAIiAEyAAIAAAAUAAAIrodpAAQAAAABAAAIwuocAAcAAAgMAAAAVgAAEUYc6gAAAAgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdpbmRvd3MgUGhvdG8gRWRpdG9yIDEwLjAuMTAwMTEuMTYzODQAV2luZG93cyBQaG90byBFZGl0b3IgMTAuMC4xMDAxMS4xNjM4NAAyMDIwOjA5OjAzIDE1OjAyOjUxAAAGkAMAAgAAABQAABEckAQAAgAAABQAABEwkpEAAgAAAAMyMgAAkpIAAgAAAAMyMgAAoAEAAwAAAAEAAQAA6hwABwAACAwAAAkQAAAAABzqAAAACAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMjAyMDowOTowMyAxNDo1ODo1NQAyMDIwOjA5OjAzIDE0OjU4OjU1AAAAAAYBAwADAAAAAQAGAAABGgAFAAAAAQAAEZQBGwAFAAAAAQAAEZwBKAADAAAAAQACAAACAQAEAAAAAQAAEaQCAgAEAAAAAQAAKCkAAAAAAAAAYAAAAAEAAABgAAAAAf/Y/9sAQwAIBgYHBgUIBwcHCQkICgwUDQwLCwwZEhMPFB0aHx4dGhwcICQuJyAiLCMcHCg3KSwwMTQ0NB8nOT04MjwuMzQy/9sAQwEJCQkMCwwYDQ0YMiEcITIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIy/8AAEQgAvgEAAwEhAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A9/ooAKw9She91uG3iuZIJYIDPGVPBO7HzDuKARtru2jdjdjnHTNLQAUUAFFACZHrWXKLn/hJLZkEn2XyGDkN8u7PGR60hl+W4ji++4AHqcU9JFdA6kFTyCDmhO4WEklWJC7nCjqSelQQahbXEmyKaN2PICsDmlcdjP1xknu9LsH3AT3G/joQg3EH61iWWqax/wAJHe2w8zUFtQyQAFIlk55Lk45XhflHvimIi1DXNQuNVu9NthcNcrPa5jt1LeUpGZMsB0zWsum2N1r1xaJEJrNR5s0bDKRTZ4Kn+FsckCgDpFUIiqowqjAFLTEFFABketFABTGmiUZaRAN23JYdfT60ARNfWiTxwPcxLLL9xC4y30HerFABRQAUUAIzBVLHoBmuYttW+1eNCEsbxEWwYeZLDtU4cHg+lIZC/iy8Fvav9hQNfv5doQ+QGyQQ/p061r6jeXenXVnKWSS3mkWCSLHIZujKf6UAa9Z93cajFdIltYxzQnG6RrgIV/DBzTBGhWZry2Y0uW5vbR7mK3Bk8uMAtx6ZIoEc3Hcw3MUckHhLWDEyh0bdGuQeRj95W5aaTZX9mst3p00TOMNDdPuYD3wSP1pIZDH4T8Jzzs6aRpk0sTYY+UrFD7+hrSv7i20XR5bgqsNtbRltqgAAeg7UAtzE0nVNRm1O3t9QNnNHeQtKsVuCWtx6OckMCOM4HPHNdDDp9lbSeZb2dvFJj7yRhT+YFCBsw79tRvkMFz4emkQPlXhvUUgjowYMrKfpRZXd7NlLGwsGntv3TC61EvKg9Cyq5/M0IHYy5vEep6dPeL9i02IRsXuJYnuJlDY5ywhAz7ZrprD+1ZWhnnubRrZ03bI4WVuRxyT/AEpgadFAhruscbSOwVVGST0ArJvr29l3QWemyTW80Xy3ayoFGR1xnJ/CgDlNIn8Raff2k2oJeT2zo4jiVc4VV6P/ALWRkH0rpNGnbUtPuZnuybmfkxRtgwccKM9D6n1pWAqWdjr32C9ibUQ98XVVlYHasfoP9vHU+tRah4fvdV0O0sohLpxiuVeVRKHLjPLbvXvTAr6b8PV066tp/wC0pZmiuRM3mKCWCkkAHt15x1rt6ACigAooAa7BEZ26KMmsOzuY9Q8UNc2z74I7Ly2bBHzFwcc+woAv3WjWN3am3kgAj7bOCOc8HtzVmS1hmnimkQM8RyhP8J9aAJqz7nRNMvJzPcWcckp6s2aAL6qERVUYVRgD0FY/irULfTvDl5NclgjoY1CqWJZuAAB70AcjPJrD2DW6DVbeJLNDC7EIqyBR0KHdtxnO41fg1+TUPB14lndJJcQFYnmiczMqMAd5wSSeT+VJDOg8MDboNuvkLEFyo2xlAwB4bB55681Z1vTRq+jXVgXCecmAxGQD15HpTEUdKt7+2n2nRtNsUP8ArZbeTPmfRdo6+54963aAEOcHBAOOCRXO22g6r/wkceq32qWU6xxsiRQWBhPPcuZGJ+nT2oAi0Xw7KtpeWOswpcWrT+bEkhV/mySSCAD6deRXTgAAAdBQAtFACMqupVlDKRggjINCqFUKoAUDAAHSgBajEESzNMIkErDaXC8kemaAJKKACigAooAKKACkwO3egBaKACkZ1XG5gMnAyepoAWq91ZW96IhcRhxFIJUB7MOhoAnwMYwMelMjjhj3LGiL6hQBRcCSigAooAKKACigAooAKKACigAooAKKACigCtfWYvYPL8+aBgcrJE2GBrmLfUL648WQ6Tc3hEdoC5mhG1bl8ZEbehAySB6CkM6XU7m4tdPlmtLZrmcDCRL3P+FZ0Oo6hp93DBrAt/LuDtjnhztV/wC62fXsaOodDTsr6G/jkkg3GNZCgYjhsdSPUf4VgeKLm9W8tI7C5Mb2wN5PGBnzY1wNv4kihgi5okv2/U9T1FXcwl0ghBPylVUNuH13fpSakyXHibTbUu3+jxyXbJ2YAbR+RYGgCTRvElprU7wQRypIkYkYOMcFmX+amtS4mS3geWRgqIpZiewFKT0C2pyL63qut6FPf6RauVV/9GEUg8xyGH31bACkc4znBFaOsx/YrYa9Dm3vY0XzUzxMP7jDueePSiKsgZ0VFUIKKACigAooAKKACigAooAKKACigAooAKzP7CsxbJCvmLtuftO8P8xfdnk+nb6cUAadQ3Vpb31u1vdRLLE3VWoAfDDHbwrFCipGgwqqMACqg0q3GoXV6QWmuIlibccgKM8D0znn6CgCHw9pLaHokOntIJPKZ8MB2LkgfgCB+FVtUsriPW4dVt4Wm/0WS0kRSMgMVYMM9eVA/GgB3h3w5aaFbbo0Ju5UHnyu25mPXGfQEnAq5/Z4aO7iubiW4S5JyrnARcYwuKmQyPRdFh0S3lhhmll8x9xaU5PAAA/ICrdxZxXUsLzDesTb1Q9N3Y/hVCLFFABRQAUUAFFABRQAUUAFFABRQAUUAFFAHA22uNe6hp5ttXvpLiSaENHJAIoZo2ySyqRk/Krcg131JDZ53P8AEU2mqa1CU81LcH7MpGA23CkZ6kljgY9DXaaPfTahZmeWONfnIVo2yrgHqM8j8aEwZoUUxGJpMmoXF5cXUt6r2ZmkjWAxgFNpAGD36Hr61qrd27TGFZ4jKDtKBxkHGcY9cc0DYs1xDbhTNKkYdgil2xlj0H1qrqWp2ul2zXN3IUiUgZ2kkknAAA5JJ7CpkOKH6bqdrqtr9otHLIG2sGQoyt6FWAIPI6+tXKokKKACigAooAKKACigAooAKKACigAooAKKAPHdP8LeJrXxLDeNok5srZWEJW8jE3IUYyzHC/L2Pc16jp9zqF5bzm+05rFgcIhmVywx1yvApDObtvB9rbxgT6QLuSYea0hkCtEyr8q5zySxY5Hc5q3pd14gs9XtdPurNpNPlXK3LsGeP5SSjEcEggDPegDqqrX0P2i0eM3MluDj95G20j8aYjl9M8OxzyJPFf3UsMN1MHSWcujhlIJHbOW6+xqSDwtPpelwWNiyyul6JkupGw6LwWLH+InkfQgdqSG2beu2015pE1vbwxSyyYRfNGVXJxuI746/hVC88PiHw7Y2NmnnvYSwzRCV+XMbhuT74P50AW9Fs54JNQurmMRPeXPmiMNnaoVVGT6/LmtamIKKACigAooAKKACigApCSBxQAisW7U6gbEAxS0CCigAooAqTX3k6hb2rQSlZw22VVyoIGcH04zVoMpJAIJHUZ6UALRQBy2oeMVtJ7xVt18i2mS1M7ygDzmAO3b1IAZST7+1R6B4x0/xfK1kLORFaNiyzEZLLt3Lj23de+DUpjsbVzqWm6IILaTEKspKIkZICjGTwOnI59606oRWv7+30y0a6un2QqQGbGcZOB/OrOaAEzUF7ewafZTXd0/lwQqXdsZwB9KVwLFFMApksscETyyuqRoCzOxwFA7k0AVrDVLLUxL9juFlMTbXAyCM8g4PYjkHoRyM1Ld3K2dpLcukjrEpYrGhdiB6Ack+woAybLxZpd/gwz7leQRwlRnzuQCVA5KgnBOMZB9KZofiu213U7myhgkRoFcsWI/hleLt6lCfpSQ2jey27oMfWmNcwrdR2zOBNIpdU7kDGT+o/Oi4EtFMQUUAFFABRQAUUAcpr16bDXoLa5vGa0v7afEDHaAyKp4YcjjNZ3gDVrZtOuJ5Io7OOdllJku95DGNCV+Y5wCTip6j6HcxyxzRrJE6ujchlOQafVCOOt00Yz+J/wC0vs8lvDqIuWEmDt228Jzj221a8M6r4d1SZhpFqIZIw7gtEEJDNl8f8CPP1FIZV1d9bj8Y20tqlnNElpMPK2sZGj8yHf3xu6Y7VZsLvxHDpKNfW6zagt4kUscajZ5R2gsp46A5J9cjpQBmeNo76+uJLBBdyRu1sVt4Y8rJH5hMxJ6ZCjI57DHWtnS59Tk8V6lHeSSCyRP9CUpgOON5OPQlQPqaAF124kNykK/2vAFGTLZxqyvntzz+lWPFIU+G7pG+64VDnvlgP60AbNQXNytsItySOZJFjURoWwSep9AOpPtTET1jeJtIGs6TJbskky4z9nV1VZD/ALW4EHHXB4PegA8LWM+n+G7K3u2ne5SPEhuFQODk8YQlQB2AJ4xzWhex3MsIS2kiQk4fzFJyuO2CMGgDmITdaTcjR9Gt4BGhVpxBbl0h3HALEyA5OMkDJ7nrWjoPh59Gup5SNO2y7mJt7MxyFmbcSzlyTz2oAfaWF6niGa7ltYUgbO2Rb+Z2Pp+6I2D8KoXekLb+LrK78rUbpXjl5EjbI3MkbDOMALgHg8HGOaAOq3ru27huxnGeaWgAooAKKACigAooArXWnWV88bXdpBO0edhljDbc9cZqAaFpA6aVYj6W6f4UAXYYYreJYoY0jjXhURQAPoBRI6Rxu8hCooJYnsKAOVXWfCOm6Y00YgWCM7ZB5eWUMpbLZ5IKgnJ7Cr3h9dF1Qrr+nWYhmaNrZjt2sFDDKkDjqo/DFLQZqJp9nHqL6gsCC7dPLaXuV44/QflS/b4v7Raxw/mrCJi2PlAJwOfXg/lTDUsg5HFLQIyNd1iXSBZeTbLcNcTtGUMmzCrE8hIJ4zhO/wCYrAg8fW0+jQahc2rRRTXKxFZgYxCrNgFywxuA+Ygfn3pDRLpviLVdcudFltYYIra7t0vXXzc/uWUBlPyn5lZh0K5/AiuwJCjJOAO5piFpM80ABYAVDZ3kF/AZraTfGHeMnBHzIxRh+DKR+FK+oGFc2dl4c1C81qGK4ub7UXEYgVkXewXoCducKhPzE4AOMZINLRfH9pr2qWVtZQEQ3CDJlbZKjmNpMbO6hVHzAkZYYzzhjOwJxUctxFCuXkVeM/McUmwOG0K8uNZ8ZS3kt5CYoJZYoVtGLhl2R4DnaOMhyMnqTXW63qY0jSbi+MZk8lchB/EScAfmaANDeu/ZuG4DJGecUtMQUUAFFABRQAUUAFY3i7I8Ha0QxUixmOR2+Q80Ma3IL7wz4fN1JqF5BGjP5Rcu2FPlFnXj8Tn2q9osWlR2LNo3k/ZZZWkzCcqWPXH5UgMK61u5j1G4iTU7HyYpShX7NK7qeuCV4zzV77BeOH1GXVo7fzIlBkSFQNgyRnf0+8aSQ7k+m6feC4ivH8QS3tuQSsYijCPkcHKjmsqw8Q3uoTRSwtvjnvWhFuLdxthDMu/fjG7jd1xjgDPNMRNrHhed7WBdHuY4LiKbzvOuw85B2shwN3OVZgQfX1rDlttQuLSK6S/0RkivxKIE0yYM9wybQpRpQc4cHnGOD0oA3PDz3dzql2LsxW93auqSpFAF86LZlMk5wAWPAJ5U8mqvxD1KZPDesWFrDHM50yaS4LTeX5MbAqG6HcSd2BxnaeRQwNt9cZfEUGjLZTea4aUyOQq+So5kU87sOUTbwfmz06t1HWbe31W20+PVtKt7l3UPBcyjzXBIACpuByecHnnHBoAp+KXv7Mw3Npe3g3tsMKmJYYwqs7OzGF3HC44zyR05NYGga3qVxq50uxlsVjtpI5roLulGyZt+RJtRSX3EjGfpRYL6HX6uqnU9BJAyL58f+A81Pd9E0OJI2+xWSQo8qLhU2L1ZgO3Xn60xGb4g1Ca60vTX0pZLyG+nCkW0qo0kflu+FYkAZ2AE5zgnHNSaNpKpNJJd2WxAyyWsN1IJ5YCANxDZbAztPU8/hQMTSdC1TT9XmvZtStZI58ebDDaeUDjdz94/MSwye+Kx/F9481vqG67MMVte2lqIMjEm5ondm7/dfj02k0AaFkLhfiDqM891AsZ0+2CoF+8pln24J75xn8K6qgQUUAFFABRQAUUAFZmuaZNrGnTWKXf2eG4ieGb92GLKwwcZ6HGfzoAqa74Xg13TpbOa7uY1kZTlXztA4IHplSyn61Jo+gweGdMu7bTFYxNI00MDdI/lACD2yP1pWHc4KPTPGt3HJqaQT6YlzfR3N1ZQ3GJCAQsgXtyq8fnXQavB4j1Lw9pMywsLqFmkmg2rl5ACsRZTxtz8xHbgjpQgO1RFRFRFCqBgBRgCufbTk0ZQX1ie305rncsARdql33bdwGQpY+vQ46UxG9cQrcW8kLPIiyKVLRuVYZ9COQfcVzb+AtHNr9nia7jX7ULvJuGciUBhvG4nDfMeRzkA9QKAOnwM5xz61k6v4Z0vXJN9/A8m6PypFWVkWVM5CuAQGAJJGc4JOOtAE8ui2M+pWuoSRs11aLthkLtlRgg9+4Y59ePStDFAGLeaE+oavPcXV/dCye1WBLWCZogG3FmfcpDBj8oyCOMg5qmngbSre4jeylurSNTbF4YmUrL9nIMW4urNwFA4YZAoAv6pp2oX15aS293b262kvnRl4DISTG6EEbl4w5PWq114bbUrzTrjUriGf7MHE6JBsSf5laPILHG0qCOTz9aAL8mh2Emnx2PlOsMbmSMrIwdHJJ3Bs5z8x79CR0NSWmmW9nKZU8ySYjb5krl2A44Geg4HTrgUAXaqS6XYTztPNZwySOu1i6A5GCvP4Ej6EigB7WNo8kUjW8ZaIAIdv3QCCB+BAI+lWKACigAooAKKAEyMZzx61kP4gt7WW4F48KRIwEUkcgffnOBtHIPBoAu6bqNtq1hHe2jl4JCQpIx0JB/UVboAyj4i0sX62Rux9oZioj2NkkEA9vUj861aVxmXrmoXNhaw/Y4lluJ5liRW6YwWY47narY98VyVn4z8SXGrQQDw9O9vhBctsxszIYyV56ZBPOSNvuKAO3vdRs9OjWS8uY4FbOC7YzgZP5DmuG12cav4y0UIsl7pLLJBKFCGFnLRsOTkkjbnseOO9MEdnrmoNpOh32oIgdrW2knCHo2xS2P0pNP1UXtw9s0MiTR28Uzkj5fn3cA+o2nP1FLqHQ0aQbstuIIzxgdBTELRQAUUAFFK4CY55NLTAKKACigAooAKKACigDF8L6fcabocdndIyvGSuGlMhI7HcfasXXfDVxLcXaaVYQxwTw2xcxSeSXaOYsUyuDyjMM0ug+pf0e11W1urGBLGOx0u3hkR4fOEhZiVKnPqMN1/vVvW6urTl4ym6QkZfORgc+30pgcze+JNKTxZYsbr5Iba5jkby3wrFocDp/sn8q1NSt7PV47WSS0luoCu+N42K4zjtxSAg1SS0srvQrYSqghut20t9xBDIuSewyQMn1qtJ40tB4hi0u0t2lj80RzXIBCKzDKhTjDHJ55HXvTAZr2nR32uyJfm4WxmsVgDRpuByz+YnAJUkFOR2Fa50fTdRSzuJrHabc7oUcYMZ6ZwO+KBHPeOtIu9XjubZNMkvlnsmgtNrgJBO24GR8ngAFcEAngjvVq0SLStUk1C5sriNJIlaS7ubkGO3XABTG44O4dAMY78UDN+61exsWjW6uFh8xWZWfhSFGTz06c49AT2NXAQyhlIIIyCKBC0UAFISAMmgBAw6Z5p1JAICD0IP0paYENzcx2sDzSsFRBkn0rC0XxZb61rVzY24V4kTzIpkJwyg4Ocj1zjHUUD6HR0UCE5z1paACigAooAKKACigCCGe1u9/lPHJsba4HJU+hqcAAYAwKAOW8Q+JYNHvcy2CT2qPFFczYyULnjgA8AYJ+oqLQte1DUtamtX0IW+nxPIguAvDOjYBHTAx7UhiXvj2DT973FhOIR5pRlyxdY3Cs2AMAdTyenpWr4c18+ILSadrKW0MUgTZLnPKhu4HrjjPTrTCxO/iHSlikkjvY7gROEkFqDOyNzwVTJHT0rzLXdL1nUAjyWUk+kyyqzuqFmJ3zknymTqfMThhgbaARd8LeFL26/e6mhv8W6GyvbxIpAj7EVmABPOFG36HJOa7+yure0v00GNZC9vaJKHboVJZQPr8poAn1TUodJsXu51do0KghACeSB/WrgO5QR3GaAAkDrXP69bJqt4unTRSz24tZJWt45jF5zHCqNwI/2u+OQe1IRzeiaJremagt69jdJMVigVPtQkRY9yFydzHtkDqflFaNzpWo67HHqFpdS2l5/aEis6XDAJAu9BheVJ4VsEYzmmBs+HtKuNGguILmWFleQGNkZvm+UAkhuhJBJAJ5yc81bfWrBdPN6k4lh3mNTEN5dwcFVA6nIPSgCp/aF9fQSTWcCxWrQ+bDdSsPm4B5XqO456YrM8Da3YXmmtYW04/0FREYyPuqvG7dnkH1oGXtO8Rxal4ju7W3uIZLGK0hkWRf+ejSSKRn/AIAKPEPiK2s/C93fW1zmR7aY2zRjdllRjkewx1oEWI9ftlvbSwcSvNKq7pFTKKxUsAT2JAJ/KtGW8tbeRY5rmGN2+6ryAE/QGgCpf69pumT+TeXHlSFN4Gxjke2ByfajSNf03Xo5JNNufPSMgMwRlxkZHUDtQBpUUAZ2jzXNxBNJcyhyJ5EXCbcKrED9BWjQNhXGeKYtPuNVst4uZXS6X7QqM+1Ywjdce+2kwRtaPpFjaXFzqNlJcf6a3mSK7nazYAzg+wAqTSp76aWb7WJQo+6GhCD8DnmgDDbUotL1LxZOVjuZInin+zFwGKrDHnj2wTV/w54vsPEU0ttbxTQzxRrKyyJhWVs8of4hx1oAzYfF2haP4cs3vriN85hZUw7KTngjtnHetq7nbXfCV1JpLFZLm2dYiflYMRjHse1AFLwzaxw3BkCXAla3WJla3ESxBSSAcdW+Y8jI4rc1LTodVsmtLh51if73kzNExHTGVIOPamIZZ2CaPpht7MSyJEp8qOSQseBwoJ7Vw1vJrf8Absl9bw6hcTizgWUSwbNzLIxkjQsAvRhjnHXBoGN1i08TXfhbSoJ7W9mu/ID3KQuod5Q6EKzbgAMbvY/lXTaHDqk+oy3OqRugtw8duJEUMVdt3VSQcKI1+qnrQA9Uc66znRtaA80/6Q2oKYP97y/P+77bPwqC+1ZLLxWgME05FuI9sQBOWLEDkjJwpOBzjtS6gdFbXMV3bRXMD74pVDI3qDXNaTr1np1j5d67o0l9cRx7YmYECfYMkDjll/OmI1fElg+paBd28KbrgxkwENtKyY4IPY1natp80c+jNCLiK2tY5EZbWMMUYhQpxg9AGGQOM0AbWloItNgiFu9usa7FjcgkKOBnFLqVs13pd1bRbQ8sLIuehyMYPtQBy39jajqb6wlxp8dkbywS3t33hhGV3YJ29wW3DHbHeres6FeTwLa2MUO1rB7JZGOBAGwGbHfIA49hQBX0vwteReIW1C+W3J8xJvMiduWWFY9oB7cMcn1FadzpeoXOq/aHg0l4lcbHkjZpAoP5ZoAW60vVLvW4rp7q3FpBnyYgh3AkYLE/3sEgUy30C7025ddNvI4rSV42kR48sNqquFPuF7+tAHQUUAFFABRQAmaXqKAKdvpVhaBhBaRJvzuO3JOeuT1pW0yxYAG1iwI/KGFx8n936UANTSNOjiiiWxtxHEQUXyx8pAI/kTTtO0610qySzs4/LgQkquc4ycmgC3TWbHagEKDkdMUtAGRc+I7G3u2tvKvppFO0m3spZUB7jeqlcjvzxWpDKJ4ElCuocZ2upVh9QelAD6oXOi2F3C8UkJXfL5xeN2R9+MbgykEHBx16cUAWktoY7QWsa+XCqbFVCRgexHSs+Xw5pc62yyWxYW0hkj/eMPmJDEnB+bJAPOeRQBq0UAFFABRQAUUAFFABRQBhaF4hbWLu6t3tjC0ABPzZ65x+nNbtJO6G1ZlIHURZHcLdrreMbSdpXd798frVt13xsu4ruGNw6imI5qzsrmLxjJEdTvpbaKzSTy5JcqXLMDnj0A4revYJ7iDZb3bWsgYHzFUN+GDQMwLfXNSi0TWtSnSGa3s1ka0kUFTOEXJJHQDIwMdqZ4Y+0Q6nPA9zNPG1nDPIZW3YmbO76cbTikB1dQ3N1FaRiSYsFLBRtQtyfYA0xDd0VnFulmIV3zulboWPAyeg7AU3UVtG0+cXwDWu3MgIJGPwoA5nwPNp0Fvd29pbyxebezyR/wCiSIpj3nb8xUDGMY5rUtprm1nubm6GqNAEdyJhDsQLzwEO4k9uvSgDkIpvE+pWd4dGt9RsLeV7idXeOFXLmTKqAzE8gnOQO3Ndhod3qM08sVza3SW6xIUluVVW34wy8Ek9M598dqBm3RQIKKACigAooAKKACigAooAKKAK0Gn2ltMZYYESQjBZepHv61ZoAgktUkvILks4eFWVQGwp3Yzkd+lOuYPtNtJD5kke8Y3xthh9DQBhR+D7WK5kuF1PVfNlADt9qPzY6dql1nxDo+k25t725b5o3DCM7mAGAc46HkD6mge5b0yXTtV0GE2qK9hPDtVCOCpGCCKmsNMs9KiaOzhEasctjknjA/SgRyGu67fSeNrHTbG6toIrcrJM0lwR5m4kFMA4JwO9d3SQ2IyK67XUMPQijAIwRxTEGVXjgUZBFK4C0UwCigBB1paACigAooAKKACigAooAKKAMzTddtNVmkjgEgKMRlkwDjvWnQncbVhrlgjFRuYDgZ6mmQNIIY1uCnnEfMFPGfagQ+QkRsV6gHFctoGj6fqvhzSbq4i8yRAZN56uSTnd6j29qQzegtbTRdOlW1gEcCb5TGg79TgVyWkabdas9vd6jZbTcFnuJTcbllU/dQL6dPpigDXm8KQf2lZXFmYrOO1OQsUQLP6gk9qo+LfEMlhe2EVqlw7Q3iecIsYYFGIQjPPY0wN3QtVfU9Cg1C5ha2Z0LOHAXGO/U8U2x1dNQvnjtr7Tp4kySIJg747ZAPFAHGan4otn12/K3rzW6stvDEt89sBKFyRxyQfXn9a2vC3iJJ9OtEmgliknuZYSsly0zIyngEv83PNIDr6KYgooAKKACigAooAKKACigAooAKKAM+z0a0sZ0lgUqVj8vHHPOcnjJNaFA27kbQxvMkrA70BCnJ70rRRtKkrKC6AhW9M9aBEd5cfZbWSbyJp9o/1cK7mP0FcpYWPiK18HR2dnHFBOkJMYdvnVt2cHt0pDRf8ADNt4hgmuv7emSbeFKMjfLnuAvb+tWbDSdMs9QeG3lmZ4f3gt3lZkiz3UdBQBtVz82g6HeeJPt0jiS+jw/k+dkK2MB9meuOM0xGpY6Xa6crpbB1jbojOSqj0UHoPYVZSKKM5SNFz/AHVAoA5XVdVj8O6g1tZ6RHOJIvNZkPz7ySBxjkADk5GBWXrOv21hqkFwnhtXvGgWVLxrNjtcttOSASqgc5JFK47HTeFb3VdQ0WO51WOBZJCWjMTE7kzxuGBg/StumIKKAKcmoxJqEdmd3mSIXHHGB15qyr7jwOKVyrFa61SxspViubuGGRgCFdwCc8Cn2WoWmowmayuYp4wxQtG2QCOopklmud1TxFPb63b6bp1ul1McNOm/aUUnGeaAOiHTpiigAooAKKACigCsl/aSXBgSdGlHBQHkVZoAgubkwNEqxPI0j7QF7epPtU9AGDdvc3XihbKO4eGOKzM42Hq5YqN3qB6VS0bTfFkOtpc6vqkFxa7WVo4l2j/Z+X19TSGW73xfZWGoSWUtpfmWMZOyHcCPUc9KhtfEVnJJcX0GlaodwAlkaAKAAP8AaYUXCxqaRrMOsxSSQ29zEqEDM8e3d7jnkVysXh2TxJZx3qajPYyNPMZzB1kBPCn24oA6nSreTRfD8MN9dee1rEfMnIxkDJz+VYula/B4p1AxQyvD5cYmRrW8Dhkzj5wPun254pgU9S0e1i124ktvDFvPEIJHeWS0QgyY+XawO45PXg1V8MeDBc3J1XVLGzEU8Hlm0ktRuDZzuB+UAdsbAcdaANXxfqkelaGLDTTJFcGWGGNbdWHlguOMgYXgHgnpW7ba5p13qLWFtcrNcoCZETJ8vBx83pz60AO1DUl09498F3Krf8+9u8uPrtBouftl7Yxvp1ylq7kNuubVmO302FkIP1/KgDk7R/Et9qN5Ii2x+yyNbeaZvJV8ck42SH9a3dITXBfMbyewe02YKwyM8gb67VGPwpWG2Rz6ZY69qOr2Oo2yzQqYeD3G3OPpmtXTNKtdIt3gtFdY2cvhmLYz2Ge1MRh2fia41a6KWItRbvI8MchctIGXqSmPu/jWLrapp/iSylvNVvmuZHVZBA5REUnIwNpGM9cmgDc8X66NO0e5jg883Hkh98SE+WCQNxParHhzxLaa209vbzLK1sFUsM5bjk9PWgRpnUAL0W32S7OTjzRF8g/Go7a5nl1i+gZl8iER7BjnJGTQBoUUAFFAGXZ6RHb3012JpWeR9xy3U4xz7VqUkNkVus6oRcSK7bjgquAB2ohM3lkziPdk48vOMduvemI5X+2mk1yW9tbdSABanzWweuSeAartH4ofXI7l9Wg+xx3wj8hFK7o++eOTSGUZTqviXWdUawmisPskgj8xXffIq9jjp+tQxf2vqGmalocl8XMEYkaWSQlmO7puxnFAzs31I6L4ZjvL8GZool3+SByfbOK4nS/Ft03hH7bpCIk51AxulyvyEuTgcHOKBHUeGtQu/EGj39vqZj85JZLd2hGBjHb860NH0q600bJr4TxKgRFEKocDoSQOTTA1qKBHO3vheW6vHkj1WeCF51uTGsalhIvTDEfd9iD+FXLfQY7bWn1VLmZriYbZ9x4kXHyjA4GPpnnk0AWNQ0uLUfL8ye7hMZyDb3DxZ+u0jP406e1ddKe1hnl3lNgldzvGe+71oA5yDwffKgjn1SGaIuxm32xLXAI4DneAfpg5qr4V8HX/AITm+zWKaetibqSZ5FZlkkVhwCoXHHb5qBk2qWviW3XWbyBNNVbhFIP2mQMgQY4wnU/WrXhObVhdXVrql79qKxxyo3HAYdOg/rSA0tN0y800pAlxC9ohO0tH+8AJJ25/HrWvTEc9q3hubUri68vUGt4LoRmVQm45Tpj0HrVvTtNvLC+uD9pje1mkaYrsw+9sZ/DigCyun7bnz/td0TuzsMny/TGOlSQ2ghvbm5DkmfblcdNoxQBZooAKKAP/2QD/4THoaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLwA8P3hwYWNrZXQgYmVnaW49J++7vycgaWQ9J1c1TTBNcENlaGlIenJlU3pOVGN6a2M5ZCc/Pg0KPHg6eG1wbWV0YSB4bWxuczp4PSJhZG9iZTpuczptZXRhLyI+PHJkZjpSREYgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj48cmRmOkRlc2NyaXB0aW9uIHJkZjphYm91dD0idXVpZDpmYWY1YmRkNS1iYTNkLTExZGEtYWQzMS1kMzNkNzUxODJmMWIiIHhtbG5zOnhtcD0iaHR0cDovL25zLmFkb2JlLmNvbS94YXAvMS4wLyI+PHhtcDpDcmVhdG9yVG9vbD5XaW5kb3dzIFBob3RvIEVkaXRvciAxMC4wLjEwMDExLjE2Mzg0PC94bXA6Q3JlYXRvclRvb2w+PHhtcDpDcmVhdGVEYXRlPjIwMjAtMDktMDNUMTQ6NTg6NTUuMjIxPC94bXA6Q3JlYXRlRGF0ZT48L3JkZjpEZXNjcmlwdGlvbj48L3JkZjpSREY+PC94OnhtcG1ldGE+DQogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICA8P3hwYWNrZXQgZW5kPSd3Jz8+/9sAQwADAgIDAgIDAwMDBAMDBAUIBQUEBAUKBwcGCAwKDAwLCgsLDQ4SEA0OEQ4LCxAWEBETFBUVFQwPFxgWFBgSFBUU/9sAQwEDBAQFBAUJBQUJFA0LDRQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQU/8AAEQgFWQc6AwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A/VOiiigAooooAKKKKACiiigAooooAKKKKACo/M/e7Mds5qSk2jcD3oAWiiigAooooAKKKKACiiigApKWkoAMcV5N+0r8dtP/AGefhpe+Lb8ecsB2x2+cGVuy5r1gtxX5Y/8ABZb4lXtrD4R8HpLshk3Xc6I/3sdOMVnI1pxTd2ZvgP8A4LTaoPGT/wDCXeCoP+EZmkwrabMTcW656kHhj7ZFfo/8Fvj14L+P3haLXfBusQ6lblQZoAw863Yj7sidVNfGv7JP/BPb4f8Ai79lPSR400dZ9e16E339oxp5dzbBwfLCtk5xwe2a+d/Ffg/x7/wSf+Mlpr2iX3/CV+Bdc/duLgeQLgDkpIAW2uueD3osKy6H7K0Vx/wl+Jem/F74eaH4t0p0a01O3WYKjbtjEcrn1B4rsKtO5GwUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFITgZoAWikznGKWgAooooAKKKKACiiigAooooAKKKKACk60MwWloAaqhelOoooAKKKKACiiigAooooAKKKKACik3D1paACiiigApKWigCGS4EcirtJ3elStypFGKYzLuCbsGsgMjXL5ND0fULtkkZYYmk2wj5jgE4HvXwD8L/8Agqpb698eYvBGq+HprfRrq8GnW14W/eiYuEXcPTJr9E22yRsGAK989K/n7+PVraeGf26r6PQkW3jh8VW8sKRDCq/nqePxotrc1v7rP6CFO9QRTqq6ZI8mn2zSjEjRKW+pAzVqtE7mQUUUUwCiikoAGxgk9qRWDrkVFOxWM80jI2MoQox07VPMVYl5VThs/WlVgehzVKWJHVFZnQ5BPlkjP1xVqMpu2rjIo5g5SWiiiqJCiikPQ0ALRTV+7TqACiiigApsjbEZj0AzTqRvumgCja3YuVdhyAf4uKs+ZgAgZzUaxxsxIXFTRgdqyNHYkoooq+YzCiiiqAKY/UUvme1OoAKKKb5ntU8wDqKKKoAopDyDSIu0VPMA6o5KJI93NRSTCEqDzk4olKxSVwnuIrS2lnkYJFEhd2PQADJNfhb+zjoEv7Q//BQS1vNQDXEC63capNIBkBYmJjz+IWv1N/b7+Kl18Jf2Y/FmpWKh727gNgmeyygox/I18Uf8EW/h/PceKvHPjSYsY4YY9OjYj7xJ3H+lTHUo/WBFEahVGAKiluI4iwz81WWGVI9q+CP2nP8AgpjpXwJ+Ll94Im8H3WppYFDNdbwmSR1UHrilLQI6n3VZyiaNvr0qyFXbxXkn7Ovxr0L45eB7HxJo0ckCXkeXilcEoR2Nem3s5tbVwhw2OD6e9A7GH4k8cWOgtJHdTw20YGDJO4RR9SeKq6Dq41y4tLj7RDdWZ/1clvIHTPbkHFfkT/wUi/a7ufiD49uPBuhTPDpemN5V5JC+BM44I4r7b/4Ja/DfxX4R+Acep+KLuaWPVZPPsLSckmGHt19amzL5kkfZ0c26VlPapqb5a+lLnitznDcPUUtQbA+COKkrPmfYdjE8WeI9M8MaY9/q1/babZpy1xdzLEg7/eYgVb0DXLDxFpNvqGl3kOoWM67ori3kEiOPUMDg18If8Fjtcn034FeHbWG9ktftWqbXWNsb128g/nXXf8EmvEt74g/ZZtory6a5NjfzW0W5slEByB7UjTpY+0ea8i/ae/aA8Pfs3/DC88Ua6yyS8xWVnvCtczY4Ue3TPoK9gr8x/wDgthrEg8K/D7SQf3ctzNOfqABV8pFz6n/Yp/ayg/aw8F6rq6aGugXOnXX2ea2STeCSMg19INnHAzX5x/8ABFqylj+Fnjm7aJ1im1ZQkhU7WxGAcHvX6O0com7n5xf8FD/+CdUfxDhvfiP8NNMK+J0DS6lo9shY3wxktGgBzJ7Ac14B+wh+35r/AMCfEUPw6+KV3dReFIpPs0bahEVn02Qtt2uWwUQHru6c1+zlfE37cn/BOzQP2gtPu/FXhKKHQ/HdvGz/ALtAsV/gE7XAH3j0B96LDuz7D8M+JtJ8X6Pbatomp22q6ZcrviurSVZY3HqGUkGq3jzwrD468F634enuZLSHU7OWzaeLlkEiFNwHtmvxf/Y//bI8V/sY+PJ/h/8AECzuf+EXW6MN5bXIYTWTk43oG/hHX6V+z3gnxtofxE8O2eveHdTt9W0i7UPDdWrh1YemR39qXMFj8xtZ/wCCJd951w+l/Ei2ZWJKLeWLZPoGIJ/SuZvv+CYv7THguMQeGviDFeWUP+qt9P1y4tVA9Ar4Ar9gKKsOZn5EfDT9in9rbT/iXoM+ta3qlpotvfQzXc48TrKPKDqXwNx3cZ4xzX64WsLW9vHEztIY1C+Y5yW46mp6KCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGqu3OO9OoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApglBbb3p9JjnNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAw1+MX7aun3/AMbP+Ciek+Cr1THZx3lrZpk7w0WQzHHHUAiv2db5a/HPR9Ql8ef8FavMkZrkWuvyQqoXG1I4zzUS3RtDZn6/aHpNtoOjWWm2cSwWlpCsEUajAVVGAP0ryr9q/wCAun/tFfBnWvC91bpLfeW0+nyMBmO4VTswe2TgGvZNtG33qzLqflV/wS5+PmrfC/4iat8A/GkctrcCaQ6esxP7qZSd8WMdCBkHNfqtXw3+1h+w9feJPjJ4T+LHw3V7fxRHrFu+qxK4RHgDDe498A8V9wW28QIJPv45qYqw5O5LRRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UANKAkHJGPSnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1kDcmnUUUAFFFFABRRRQAUUUUAFFFFABRRRQA3aPSnUUUAFFFFABRRSUALTSi7t2OfWjdULO29txKqOhFZDsO2gBlI4NfgL+0JajRf29r+OWMBV8V2khU9189DX77SHzoZCrbTjAIr+fb9rbWjH+2Z4h1CWd5GttahcyMeQEdT/Sn1SLXws/oLsZFltYXThGQEfTFWKxvBt9HqfhPRryJt8c9nDIreoKA1sU47EMWiikp8whaQ0xmOetJIxC9cVLnYqwMoYYPI9KOMYHFUpl3fclb8GoZn+WNCS2Ouaz5jXkLTId644FJH99ztw2cD3FU0mmt5VSVt2R3NP8AOlMmBtPbPpVXDlZpUVRXzTMDv+VeCM1O8jR8nkHitOYzcbE9FMBOKM1RA+imZpnDg9etTzDsTUVHg+tAJxRzDsSUhqL69KGJEY2c0uYVgaIPg9KevWomxIpXOKdH8i4PNSUTUVQmvQs3ld6IZvLMgPPNA+Rl7NN8yqEl633dmM8ZpyN8hUvnaKrmH7PuW/MqvHdO1wUMZVB0k7GqtrdB0UJyCTUozkVhzMvkNGm8D5vWq3lyAZ30i3IjUiRxurQy5S7RUCSfuwaZFOH3j0NXzC5S1RUNNk2IN/eouKxO33TVEOJJCCnC80vm7uKIIUEhwOaJPmNEuU/N/wD4LIfFD+y/BHhvwXb4El9P9rfnnC19H/8ABOr4Pr8If2Z/D0T5N5rA/tOcn1k5H6V+bP8AwUO8RSfGf9tSDwnbFmhtbm30ZWXnG+QBj+GTX7W+DvDyeEvCej6LE2+PT7SK1DHvsULn9KqGwpaGvXxh/wAFAv2F7X9o/wAOv4k8M28cPjuxj/d4+UXaD+An19K+0KSqauSnY/B39kf9orxD+xp8Xrjw140tr2y0VrgQ39jLkeQ+7G8DuB1r9Xf2lf2i9C8G/sxa1470XV4Jo7uxK6dcQuCWkdcLj3BNeL/8FOv2P7f4xeAZfHfh+0RPFeixGSfy0+a6twMkHHUgCvyO1D4w+Kdc+Gel/DqWd5NIsboywQnqGJxj86gvc9b/AGFPgPdftOftJWC6zaPe6JZztqesyt91xnIQn1Zu31r9+9O0+20fT7eys4Vt7S3jEcUSDCooGABXy1/wTr/Zvt/gH8C7C5uYseIdeRby9kI5AIyqfgK+htW8baXo7XDX2p2VjDD95rq4SMfqarmIsdJ5gb0oaRI1+8APrXzz4u/bG+Evgoi41L4haU0AJ3xW83mMD6ALmvAPjh/wVQ8AaT4A1CbwLqEOseIGPlw28sTKMHjdk9xS5n2NPZrufoEtxG7FVdWYdQDyKkr4P/4Jqftd6l8fLPX9C8VsG8Rac/2lZEHEkLHgfhX3lT5iJaH5kf8ABa6+k/4RP4f2Kn5ZLmaTb3yAK7T/AIIz3E8n7P3iOKWNljj1ptjEcH5BnH415j/wWu1OH7R8ObFZF+0KJ5iuRuC+uPSvo/8A4JXeED4X/ZP0a5dSkmqXM12wYY6tjNSPofYdflR/wWw1BP7U+HFmGXeI55CuecZ64r9V6/ED/grf8Tj4w/aUTQ4mR7bQLNIAyMGBZjuatTM+2P8Agj9arb/suzSKhUzarMzEjqa+56+Mv+CTVvHF+yTpjoys0l/cMwB6Hd3r7NoAKSlpKAPlz9tr9jfwn+0R8OdYv006Cw8YWNtJc2upW8I82ZkQt5b4HzZxj15r4n/4JD/HHxD4f+J2pfC3U5Jp9IvIpJ7eKZjm3mjOHCg9vWv1l8VajBpHhjV766dY7a2tJZpWcgKFVCTk/QV+O/8AwS50WXxR+2ZrmuWkTDTbGC9n3AZVRJJ8oz2z2qbFrY/Z+iiiqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBrNge9JHu2/N1pWUnFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu4U6k/KloAKKKKACiiigAooooAimcRxszcBRk1+Sv7GNtD4u/4KbeOdaCKY4DfzhcZ2sWC5z68frX6teJpWg0G/lX7yQOw/AGvyb/AOCXN5/aH7ZvxGuJhuuJIbtt3p++IqJG0fhZ+vNFFFWYhSUtFABRRRQAUUUlK6AKWmqu3vmnUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopvPrS9Oc0AB/Km7iu1fvGmxyiRc5FJ/y0+9g1PMOxNRUR3+YCD8vcUk0jLExU8ilzICaiqTTSssbrn5uq1czQpKQNWFopvNHNVcB1JRQ2cGi4iLeWkKlePWnbRt244qFZJEkw+3Zjr3pRcFpMAcVkaWZHfTJpul3M5HyxRtIfwBNfzi/GLV0+Kn7Seu3EW6KLVtfMK/7KtKEr+kC5tku7eWCVd0cilGX1BGDX5q33/BK250z9qbSfFNlcw3vgCTUv7QuLUvsmt2Dbwo9Ruqno7jjZpo/RbwRo6eHfB2iaUn3bKyhtx/wFAv9K2h3oVQqgAYFFUlZGbeotJTMnvxTfMHIzzWdwsEmdpI6jmq7O0kPzjbmms7ru2MWJHTPSq0kjRwhJbgbvcVjKXMbKLJYbdV6HioUm+zSO33xnvTftULL5YlwfY1Vkmht1MDyfe5DE81NzflNL91P+9fHTjNZUc3mXEgWVgM8YNWLcpNAFRtwPFVruG20uNmaTDZ655rRS5h8ps2kiKNhOW75q7uDLgjNYOl3EeoYdGwfat+PpWpz1EFRtMq8ZqSolgCtn731rUxVhHbarbWNETcdanbAU8VTEIZvNVm3f3c8VlLQtalnJ9KZvJxtXimtcKvBpc42fSgBGZ/tGCP3eKZNN8yAHHFSlw2D2xmmbo9y/Lk9qmwD1XbGNx3H1FNWR9zZG5exFEkg4HaobxzbW7bOlUOxXa4G4M8XlYJ5amx3yyDfHJHKD/dNRSXSTAHeCMViXUv9mIJNiCKTkYpXOrlOiMm4Yfg1G2YVYb+SKw7nUo5o4yruZMf6v0qGNrlo5Aaz5kFma8P+oO3/W5p9w88OpJ/d2DNYLSSww9cH1qbTb6VmbLxzHHXNZcyK5GdJGyyOWkfKjkUTTIv7wdT0rIsJpGl8mWTlua2LGKfzH3f6rPFXzomVo6ktp/x7l5OrGriwovQVGv+uNP8yq5jlZJUckYPNLH92nN901e5GzK1Murr+zNPu7yZ90cMbSn6AE/0qaHoc1zXxQmFv8MPFMoHEel3L/lGxpR94tn42fsuL/wuj/go5DrJGbf+27rVD7CPKiv3Cr8Wv+CQdvBqn7UmvX8uPNXS55Ygf9p/8K/aRulaLTQU9xaSlorQzPP/AI6fEjQ/hT8LPEPiHxDcpb6fb2sikOeXYqQFA7k5r+cG5u7mfxXeeIbCxmlsYL83YZYyUQeZuAYgYH41+kH/AAWA+PEHiDVdB+FmkyGWe2mW6u/LOcueFTjv7V9DfsT/ALF2jeFf2WbrQ/Fumw3GoeLoDPfLKnzRKy/IvPQrnNZGm2523wX/AGih+0z+zDqd/wCAXW38XWumtafZCwDRXIjwMexPQ1+dv/Dvv9qX4uapcy+Jma2aZ90k2qaodh57KKg/Z78Ra1+wn+2vJ4R1a6ktfD93qP8AZ95G4+SS3c/uph27jmv22jkWRFdGDowyGU5BHqKvlE3Y/KfwH/wRUv54Vl8X+PUtpc8w6Xb7v/HmrrdS/wCCKfht43+w/EPVIWwdvm20bDPbPFfphRVE3Z8d/sT/ALAf/DJvibWtduPFB8QXeoQC3CrB5aooOc9ea+w6WoL26FlZz3DDKwxtIR9Bmp5Qbufit/wWC8cL4g/aMstDjQ/8SfTUiY+7ndX6r/sq+H4PCv7O3gCxgG2NNJgkP1ZQx/nX4P8A7TPxVl+Ln7SniPxNqh8u2fU/KwozthifaOPoDX6KfET/AIKreAvhx8JdK0X4crNrmvw2MdvG9zCY4YSFAyc9celSWfcvxs+M3h34H/D7UvFHiC+S2tbeImJFYGSaTHyqi9WJOOlfzjfEjxZc/ELxxrfiS5M0s+o38szSTE8BmJVfqB2r6PbTv2kf2+vE2lxanZa1qWkSS7ku5bV7fTYlzyyuVCHA7A19W/tofsI/8IT+yz4W034deFH1rX9HuI31B9NtXmu7piuGYIgLNzWhNj2f/gkiW/4ZQtgQQF1O4AOOvNfa1fL3/BN34c6z8M/2V/D+m+INNu9I1aaea5ms72BoZY9zcBkYAg/UV9Q0EiZozTa8I/an/a08J/s1+Br+/u9Rs7zxDsKWejx3CGd5CPlJjzu2g47UDPM/+CnHx90v4V/s96x4cj1MweJvEkZtLS3t3HmhD99yM5C44z714/8A8Ebfg/daH4H8SfEC+SSNtYkW1tt6EBo0PLA9xmvj/wCE/gL4m/8ABRT4/wAGq+KDqF1oa3Ia/wBRWJ/stlEDnyVbGFJHGOtfuJ4D8C6L8NfCem+G/D1kmn6Rp8QiggTsB3J7k+tBWysdFRRRQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUgCiikZgoJqeZgLRUcUvmrkKy/WpKsAooooAKKKKACiiigAooooAKKjkmEZAxnNSUAFFFJQAtJUbSFVzimu5ZcnjFA7Ml3f5zS/hVNrxV6R7vxqaOTzBnpWd2PlZLuo3U3HvSLllyePatBD91AbNN2j0oAxQBJRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAyPFriPw1qjEZAtpD/wCOmvyP/wCCWF5G37ZXjlWUxyzW96VTr/y2J61+uuu5bRb4MgkPkP8AL0zwa/Kv/glbb2d5+1p8V52t1W6t1ujE2c7VNyVIrOWuxtH4T9Z6KKK0MQooooAKKKKACim7qTcfSo5WA+iiiqugCiiimAUU1mxQrbqBjqKKKBBRRRQAUUUUAFFFFABRRTWbbQAnl/7TU+iigAoopKAFoqIM/qPyqQ1Nxi0VGsm4n2p9UGwtFFFAgooooAKKKKACiiigApKWigCNmCjJNVJNUjJKRhnb6VcaMMvIr4e/bo/ba1n9lXxVpOm6b4KbVhfx+aNRvboxW2c8qpXv9awk3E2pRi9z7YWaJmWMr5b9QrDFLsSbOQc/3s1+SVp/wWi8TwyEz/D3TZj0H/EyI/XbWun/AAWx1WNVU/CyyC99utk/+0qYWP1UkkaGIBCpHqxqKa6niVAId+fvc9K/LMf8FpjcSILr4dsIO8cN+p/pXS6X/wAFoPCu5/tHgHWEXoNtyjAUtexeh+lM2oQwxbwcj/ZpLXUBfJujKj/er84V/wCCyXgSOXevgvVtx6/Ov+NOvP8AgtF4ORSLXwLqbcdTIq0o3QnGPQ/R64upII93y577jgU231RJlLNhB7mvzEk/4LEeF75g03gjWpiPS7QCpv8Ah8X4TdcH4f6swHY3SVNpFcsOp+mkOoGVmwV2Doat+Z5ikA4avzCH/BZ7w78sa/D2+ijzzi6Xj3ruNB/4K7fCmcG41CHWbOT/AJ4pbBh/Oi0iLRPvi4hY7JMcrwTSeY8JyGDe+K+ILH/gr78Iry8eK5tNXtIccO1vkGq+pf8ABYD4T2cMgtrHVL1wDgJBgGq1C7Pu61uhtw8oYtyKtq4bnrX5e3v/AAWc0aOQ/Y/ANxKg+6ZJcEVUX/gtAkLN5XgOR1xxunxVp9wcV0P1QqOTO0kNgV+VNn/wW0uxIftPw5hMXYx3hB/lXJeLv+CzHjnWJJYtB8J6dpcbjA86RpWxVc3kZ8p+vcdxHIOJEf8AGqd9qUVixldlw3yrz3r8Urv/AIKk/GG6t0XT4dItMHJeGGRifxqx/wAPPPjXcRhZtJ0u7UHI/wBDmOPeubkqdja8O5+zLahHuWZphCSOecLUN9uvIo1VgQ/STdz+dfhx4m/4KGfH/wAYXggs9WewiBwtrY6ch/DlCaq6p+1N+1BNaxRS6t4qtEbhGg054z+GFo9mzbnj2P3JbS0s1LGZtuPvyOCa5rVNcskuY7V76KFxxukkQt+TNX4vaa37XvxOwmnn4l6jF6q1zaqP/HgKfN+wn+1H4w1ZLrUfCGvXV2zAfbNS1NSw56lmfNV7Ey9sux+yGoePvDvhm3P9peKLHTo1Gd8t2AfxAbivHfGX7Ynwk8Mwyy3XxC0q/lzzFBfmb8hXwrY/8Eg/jvrV5HJq954dttzASSvqUk7AZ5PTmvoTwn/wRO8KQ2oPiX4g6peXPcabaRwp+BbJq407dQ9sux20f/BUn4LeHUKw6tf3g/6Z2R/wr6c/Z3/aY8EftKeHbjVfBt5NcR2rBLiO4iKPGxHQ5r5U/wCHLPwjUHHi3xdntme3x/6Kr6m/Zj/Zl8M/st+Am8M+HJJb0SztPPf3SKJpmPQMQOg7VpymMpcx67RTqDVmYN9056VUcJGg2AmneZJ5hGOKWVf3YOMt6LWUtTRKwTRrJHnHvSqymMnPFJ5wx04qGaZlQNGoKt7VNwLG5fVaNqVSVH+1HjirHlmmVyjvyqG4/wCPd/Wmc+tRzTfMkdM05R8OnB1WSYAnH3QK8J/bK+MGnfs9/CSXxVcW01wfNWCGGL+8RxXvkJ9TxWZ4y8EaD8RNBn0bxFpdrrOlTj57a6jDoffmnymfPJdT8wPh1/wV00W1iWPxD4ZvYpMf6y2mBFdZD/wV68C2/n7PD2rM2flHH+NfS+uf8E2f2etekLy+ALa1Y/8APnM8P/oJFYY/4JV/s4jr4Ouz/wBxa5/+Lp8kRe0kfP2lf8FevBE9xcPq3hbVE3dNpH+NWrz/AIK4fDprQLb+H9fLLyMFR/WveB/wSr/Zu7+CrtvrrV5/8cp6/wDBK/8AZsX/AJkW4b661e//AB2p9nEr2rPjjxZ/wVwgvdRil0zwZNcICM/brrDY9sd6/Sv9mv4nL8Y/g7oPitdNuNJF9GW+z3Em9hz1z6V5J/w67/Ztx/yT9s+v9rXn/wAdr6J+HvgDRfhf4R07wz4dtTZ6RYR+XBCXL7R9Sc0/ZxIlPmOgpu35s1LRVcqIuMops33fwqrH+64rKTsVGNyWTfuH1qHV9Pj1nSb6wlGYrqF4GB9GUqf505Zv31WlPzGiKSHqfgn8MfFVx+xh+29N9sgaCwsdVks7hfW2kbAP0AIr949L1O21vT7a/s5VntbiNZYpEOQysMg1+af/AAVQ/Y41rxhqEHxQ8Gaabue3h26pDB98gdHA749q479hr/gpBN4Oh034e/Ex2t7GALBZ37oQyjoFbNUD94/Wmo7lnW3lMYy4QlQPXHFc94d8daN4mtkutL1C3vbWRA6yRSqev40XnxH8L6dcm2uvEGm283QxyXUan8ia1J5Wfk38Cf2WfFnxz/bg8Q+JPGOi3lv4d0zV5b24kvIyglKP+7VSRzyB0r9hVRY1VEXCDoKS1nhuYVlt3WSJxlXQ5BHqDU1TyhJ8x+OX/BZSzg0/46eE761CpfS6Uxdh1+V/lNfpP+x98RG+Kn7NvgTxA5Zp5dOjhmZhyXjGwn9K8y/bc/YN079rSTR9Ug1dtD17TgYvP27lkiP8JHrXu3wJ+FVr8E/hP4c8F2konj0m2ELTAY8xsklsfU1Qrne0UUUCCuC+PPihPBXwY8a627+WLLSriQMOoOwgfqa72vAP29rqS0/ZE+JskTbX/smQD8cUAfi/+x7+ze/7XHxkk8N3mpy6VF9nlv7q+jTe+c54B9Sa/Un4Sf8ABKD4N/Dq6jvdZhvPGV9GwcHVHHlBgcg7FAH518p/8EWfC9xcfFfxlrjxSCC000W4lKnbuZxxnpn2r9gqmxXMUdL0iy0OxistOtIbGziG2OC3jCIo9AB0q3T6KokKKKKAPNfj94H8b/EL4d3mj+AfGh8Ca/KRs1QW4lwvdfVfqOa+E9D/AOCQfiHxj4l/tr4sfFu48RTlg0i20Mk8kozyDJMwK59hX6bUUDucZ8KvhF4U+CvhG18N+ENIh0nS7cYCxr88h/vO3Vj7muwp9FAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKTcKG+6aqzS8qPun0oKSuWtw257UAg9KbIW2fKMmlQFRzQSOoopnzUAPpGYKMnpS1Gzbmx2oAkoopKADcOuaNwppjG3FM8pvLAzzWd5ASbxSeYpOM800x+lQw2hSctjj60+YuyLdFFFWQNLgZJNMW5RwCp3A9xXhP7WHjj4rfD3wVFr/wAMdCtvENxZS+ZfWMwy7Q99g7mvGP2dv+Clngf4o6iNF8aQt4H8TxNsljucrBu9Cx6Go5mXyn2/5i4zTFuY3DYPQVnrqMGpW8M9tMs0E67opIzkSD1B7037N5Mg+YnPYVPMyuVDob8GZvn+XtS/2iysoKkZ9apXDR2ymZImkRcltmPlx61Ws/EVhrUoW3lWVl6qjKSPyNHMzX3TpPO+UEZI9qk8we9VrOaKaH9ywcDipRHzT5mYWRNkU1pAqkmnbajeENR7xBFHdGXkDH1pzT4GRlh6inbUUHjbXmHxG/aI+Hfwz8VaD4U8ReIodO1rWpVis7UAsxJ4BbH3QTxzWFmXZHpK3xdioU59abbiVZGZ+V7Cp7e38tBkDd3NPK4rWKb3D3egRyBl+6V+tP3U2mJMkmdjq3+6c1sSS7qN1Rt8qkk8UK27tUczHYlorD8ZeNNE+H/h2713xDqMOlaVarvmuLhgqqP6mvOPgr+1p8Nv2gtY1XTvA+syavLpqB52Fu6Lg+mRzVknsdFFJQAm4UnmYbG3j1qLcXUtjaBXgP7U37ZHg39l/wAMzy6pc/bvEU0ZNlpEDAyyMRwT6AH1rO7Lsdv8cP2ivAv7Pnh86r4x1eGx3AmC2zmWYgdFX+tRfs5ftCaH+0p8OY/GGg2l1Y2TzvB5N1jeCp65HUGvx58C/Cf4wf8ABSb4sXfiLU7h7bRllBmvrkMLS3jzzHEO5x6V+0nwh+FOi/Bf4f6T4R0CLytO0+LYGIw0jd2b3NaCaR2m6jd2703adxOeKj2vvzjigLHzH+2Z+3Fof7JK6Na3ug3XiDUdUVnjt7e4EOxV4ySVNdh+yz8frX9pb4VxeLdNtnsfMlaKSylkDtER6sAM/lXx/wD8FqPDlufCHgLXguLy3u5LZSOpVhn+ld3/AMEcbCWH9nbWbqRiUn1Z/LU9FULQHM0fZfjDxhovwz8I3/iTxLqEen6PZR+ZPcSDhBVH4V/GLwV8YtHGpeDfEVnrtr/F5DEMv1U8iviT/gsl4+8Q+H/hn4Z8PWTCDQNYuWW+kHJYqMquPSvhD9mjRfjT8M/Ctz8YvhzDNdaFp115F/b28pJIHJzGO2PypWQczP6BMV8C/wDBQ7/goSfgT5vgLwHNHN40mjzd32cjT0I7AjlyPcYrR+Dn/BWb4YeMfCdxc+L/ADfC2t2sRaS1IMySEDorADkn2r4R/Z38Br+2/wDtuX2r6pBc3Ph6bUJdUvP9i3Rsxxk++AKZJi+GL79r74qaONd0a7+Ims6S6mQXsFzKkRAGSQ2efwrtv2TP+CiHxF+CvxIt9B+Iep6p4i8MXV0tte2+syPJd2TMQN6ljkYPUV+2em6ZZ6PYw2Vhaw2dnCuyOCBAiIvoAOAK/Hv/AILJfD/SPC/xa8Ja5pVlDZXusWMz3bwx7TI6MuGOO/NA7s/YbT7+DVLG3vLWRZra4jWWORTkMpGQfyqxXjH7GviOfxX+y/8ADnUrmIwzyaVGjKZN5OwlM5wOu3Nez0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKbtPy89KfRQBi+MJJYfC+qPEVWVbaQgscD7p71+T/8AwSmvvs/7YHxMtmYM9xb3R6+lxur9VPiTHdy+BNdSxljhujZyBHkTcAdp7ZFfk9/wSZ0+4X9rbxybgq00FhdGR8clvP2n9ay62NPsn7D0UUVqZhRSbqaXoAfRUUjyD7qqR7morPUIrxpVQ5MZ2t9aV0OxMTjNRqxYb1yQf4aQxbW3F+PepVYMMjpWXMyiSms3YfepGb5c186/tJftmfDn9n24g03xJfXMWqTDckNtHuYD1NHWwlFvY+i13Y+bGfanVwXwR+LPh/41fDvTPFPhq9a/026BUO4w6sOqsPUV3tap3JMDxbrkXhfQr3VbqYpb2sZlbA7AZP8AKuS+Bvx+8H/H/wAKrrnhTUo7qLcUkt2YebGR6rXb+IPDtv4k0u5sLwl7a4jaNkwOhBH9a/Ef4seF/iX/AME6f2gJNU8Pm6h8K3Fz5llMS32W4jJ5R8d8VHvXua3jy2P3Nor5t/ZJ/be8I/tUaS8dqo0bxHbj9/pczjJ9SnqK+kc1adzNqwtFFFMQUUUUAFFFFABSMu6looAKKaWNQySSZQJjJ65qeZDsWKQ9DUFxO0ceRgVSbftkYSGRWGVANO5Si2WofOaQlnTZ2CjmrEjbVqpBGLWHcE5PULUktwvALLzU2G1dhb43MQcg1ZXpWZa3Ijd1I+UdMVoB84weKtajnFpklFFFBkFFFFABRRRQAUUUUAFFFFABXJfEL4TeDvixp8Nj4x8N6b4js4X3xw6hAJAreozXW0lJpPcNeh4Prn7CPwC8RWYtbz4XaIIR0+yrJbt/31Gyn9a5lf8Agmb+zWv/ADTSP8dZ1E/+3FfT9FA7nzCv/BM/9mleR8L7b/waX/8A8fqKb/gmX+zfK2U+HUUI9I9Su/6ymvqL8aRV28DgfSlzCPle6/4Ji/s8XC4TwXLbn1j1G4/q5p0f/BMj9nlLXyf+ELdmxjzWv593/oWP0r6mzRmqsPU+TLb/AIJd/s92y4/4RGeU/wB6S+kz+hFZ+tf8Epf2ftYxs0LU9OH/AE5aiy/zBr7EaozKisFLAMegpcpV2z4oH/BH/wDZ+3EmDxKfb+1v/sKeP+CQf7Py5ItvEm71Orn/AOIr7XGaj87dIVVc46mlzEI+I/8Ahz/8Cv4m8Qt9dRP+FWof+CQ/wBj62evP9dUcf0r7YpKodz5F0f8A4JWfs86O+4eGr+89rzUpJBXT2v8AwTp/Z9tMY+HtjLj/AJ6szfzNfSlFAHgtv+wj8AIeR8KvDch9ZLNWrpfD/wCyn8HvCtwlxpHw28N6fOn3ZIdPjBH6V6rRQBkxeEdDgULHo9gijoFtkH9KmXw/pi/d061H0gX/AAq/RSsBUXRtPjOVsbZT7QqP6VN9jg/54R/98CpqKYhqqq/dUD6CnUUUAFFFFABRRRQAUlLTFXZ1OaAI5F/dkjqKzobyaZH3QlBV2aRFVyT0rNh1RLiQhCyezCsjojG4SaknnJHtNSf2ioV/QVnzQINx2YIfruqnJqItLWZ3ZTxhfepsa2Q++8TQ2d4saM7GTpxUkOssi+WfMMnevCPi58fvB/wx0uS/v/EVhb6hCnyWrSgyflXyZqX/AAVb0W08Q2xgs7q6hTiW4VeD+FLUeh+nUmZLUGMk1Wt4g02zcSR718x/AX9vT4a/Fq+tdPt9eXTL+VseTqBCbj6CvrHZHIEkiVXj/vJVk3LcanywD1p6/dpdnvRH0rU5Lj6KKKBBRRRQAUUUUAFFIvSq80wjqeYaVx00g6VnTTZPlxUkkKTTZ8zJpZIaxkrnXGKRLCXA60q3LRq7t61F89Z0li8s26WTMXasyuVM6GGQTJmvlj9pf/gnb8Of2h7yTWFjfwz4lfltRsFx5h/21719N2syRLgVPFMzdxW1zn5WflXL/wAEi/iz4SSSLwj8Xbe1tGOfLWW5tv0Tiu1+D/8AwSINp4kGv/FPxf8A8JLcK4f7Pbb33kHPzM/Jr9Kd1V3vlXpzV8xPvMbpOl22iabbafZQpbWdrGsUMSDAVVGAKuVD9oHqKbJI2Mg8UcxPKyfNG4Dqaq+dynNK7Pt+Uq31FHMPlLOR60bh61TkuhCUDMAD14p3nqVygwPXFWLlLRYDvXOePPAekfEvwbqvhnXIPtGl6lA1vPHnqp/rWzJ++UMpwBzk09SzdOB7igLHlX7O/wCzH4L/AGY/Dt5pPhCCZIruXzZ5rh98jntk165mm1R+1kyMv8C9W7UCSuX96+oo8xScbhn0rJjvogsmZVH4imWupW8kLs12gjH8RIBoL5V3NrNGR61lTa3p1ja/brjUoYbT/npLIqp+ZrKn+J3hG3k2y+JdLjPo15GP5mgix1WR601pUVcl1A9Sa4y8+M3gCwVjP418PRADJ3apAOP++683k/bc+CcM0yTfErwuFXhR/bFt/wDF1HMPlPe1lRlyHUj1Bp24eteFWP7afwNuJBBD8T/DbsxwMarAf5NXzV+0p/wVS0r4NfFL/hGvD2l2PjDS4Y0aa+tbtWCMeoBUkZAo5h8p+hdFcZ8Hvijonxm+G+h+MPD05uNL1KASIW+8rDhlb3BBBrs6sgKKKKACiiigAooooAKKKKACiiigAooooAQ1WELNNuZcDtVqigadhKWiigQUUUUAFJtHpS0UAFFFFABRRRQAnPpRz6Um4HpzRuqeUB1JS0jMF60uYCGWSOOGR5SFiUEuz9MY5P0r8y/23/2KfC/xq0/UPiN8FZ7HUfEdm5k1TTtNnVxOO7ADowr9APjdoeteJvhF4t0zw3dix1u602aO0nI+65Q4r8gf+CZvxjl+CP7SFx4W8Q/aI49fP9nTxSkjybkHjcD0Ge9SaI77/gn/APt0a34G8R2nwq+JEzppYPkWt1fErLZMOiNntX6t6fqEWoAXUTh9oyy55A9fpXwh/wAFH/2EY/iDo9x8T/ANmLbxRpsZuLyytkCm7VedwA/jGK+R/Bn/AAU48YeE/hfc+G7rT/tGvpbG0g1aSQhgOQSw9RRYnmZ9A/8ABRz9ve+8N6rP8NPhvqKpMUxqWo2nLBm/5ZqR3r4S8G/G740/Au+g1iG/1zTLeY4V9SjlEUvsCwr6t/4Js/sSX/xY8UJ8WfiBFJLodvcedZW10MnUJuu9gRygPfvX3T/wUG+CunfFP9l/xZEljH/aGj2zanZGJACHjBJAwO4zxQK52/7I/wAXI/jh8BvDXiz92Ly6i23aRn7sqnDCvZNtfl7/AMEVfHlzPa+O/B8txJLawRw6lbo3RMnY/wBOSK/USr5UFwpobcKdXF/GD4qaL8Fvh3rPi/XpvK07TYWlZVxukb+FVBIyScDrVCOZ/aU/aA8O/s4/DLU/E+uXqQzrCy2Nsu1pZ5sfKFQkbucZr8l/2Pfh/wCOv21P2rLbx74pluL3S9Ou1v8AUb9VKQoV5WGPjAOQOBXC/ED4ifEX/got+0FpmnQRlFnnENnpuWNvYxZ+ZnODg45ziv2x/Z5+A+gfs5/DDTPBugKJIrVd094yBZLmU9XbHelYd2elUEUtFMR5H+094K8eeO/hLq2l/DvxL/wjPiKSM+XcbfvjHKbgCVJ6ZA71+MU3i39qD9kfVhdardeJtAjLgN/aO6e2k56ZORzX78Vl+JvCuj+MtJm0zXNNttVsJgVe3uow6nIx3oHc+Df2Of8Agp9ZfGzWrbwd44s7fRPEM4xb3qOFt7g+nJ4avvTXde0/wzo11qupXcVpYW0ZllnkYBQoGetfkn+3T/wTdn+D73HxJ+FHmroVm32m40sMWksiDndGf7o+ua+cviF+3j8Uvix8Jbb4datdrNa+YqyXceRNNg8KaVkFz0D9t79sHX/2v/iNbeD/AAUl4/hKCby7KygB36hJn/WEDt6Zr9JP2Af2TYf2afhbFNqK7vFutRpcai2T+7yARH06jvXlf/BOT9gzT/hPoOmfEjxbD9p8XX8HnWtpIo2WKN04/vEV990xC0jEKpLHAxyTRu49K/Nb/gpH/wAFBJ/AtxcfDP4d30cmrSxtFqmoW7Za2J/5ZoR/FQB6D+2l/wAFJfD3wRs7jw34FuLfXvGZYwuykNDZH1f1PsK+QP2Y/wBjv4ifto/EgfEL4pS3kXhqeUXMt5dblkuhniOIfwj+ldf+wT/wTlb4qx23xH+KK3H9jvMLiy0uUnzL05zvlJ52/wA6/W/TdMtNFsILKxto7S0gUJHDCoVUUdgBSsh3MnwV4F0H4deH7bRPDel2+kaXbrtjt7ZAqj39zW2zBVyaUsF6nFBAdcdqYCr8y5r5x/aL/b0+GX7NWvroPiKe8vdcaMSmysYt5VT0yc8V9Hqu1QK/HH9rj9g741fFP9qjxJqGk6b/AGpp2qSC4ttSeXbFFFjHlknuKBHG/wDBQb9ujw3+1ZpXhfTPDGlX9hBpc73Fw18VG/IwAAK9I/Yj/wCCjHw0/Zt+B1v4R1zSdZutUinkmeSziQo5boMlhXjH7SH/AATr179mP4I2fjjxF4htbzUZbxLeXTbWM7YwwOPnJ5PHpXqP7E//AATI8MftIfB218d+KvFGs6b9ruJI4LPTViUbUIBLF1bOfbFAHnf7ZP7bmqftoJp2i6H4PmsdN0uWS6ESN9qldQPvthRtGOa+pv8Agi7q8OpfDvx9oE7LNHFdxymBvmVldSDkfp+NfTPw1/YN+GnwT8G+JtP8IadJHqmr6fLZvqd23nTgMpxgnpz6V+TX7P37Rnin9gX4oeONH/sgalcMHsJbOZ/JxIp+SXkHIHBx+tAHp/8AwVc+Hvwi+HfxC0qy8EWUel+LZkM2qWNhhbdEP3SUxgMfQYrjP2F/2sn/AGNvFl4nibwjcSaV4gjjaS4WIx3CxDo0YI+cd+orT/Y3+COu/tvftLah4x8ZB7/Q7e7/ALQ1e4+6skvVIk9s4GPSv1d/aI/ZB+Hf7R/hFNH1/SIrS7tYvL0/UrJFjmtPQKQPu/7PSgDovgf+0Z4C/aI0OXU/BOtx6kkLbZrdhsmiP+0h5x71+c3/AAWz2/8ACV/Dcggt9hvAw7j5kxXzn8Qvhf8AGP8A4Jx/FhdY0e4lisySLXVreNmtbpP7si54+hNcP8Vvjd49/bX+LHh+XX0hutWlaOws7PS7Zo49rMN+FLH19aAP2Y/4J2/bh+x78PF1CFoJltXCBjklPMYqfxBr6Rrm/h34Uh8BeA/D3hy3RUh0qwhtBsGAdiBScdskE/jXSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJmmiTnGDnGT6UAPoqtNfw26u0jqgXrzzWPqnxA8OaLGz3mtWUKr13Tr/jU8y7lKLeyIfHkc0ng/V/nAH2dyCq84weOtflZ/wSkDL+2F8Sckk/Ybzd9ftYr9DPGf7V3wp0/Rb9ZPGekyt5TIUW4B6ivyV/ZD/an8H/sz/tN+M/E+rrdapoOrLcW8VzYoGKq8wlD4zz6frWSa5rl2ajZn7rnPYUtfMHwN/wCCg/ws+OnjC18LaJqc39t3eTb28lvIocAZPLKMGvpzzPatrkcrQ6vmr9qP9tbwf+zhHDbahdLc6lIwDW0B3SIPXFfSuOMV+CX7cWm/8Jf+3Br2jRebum1G3tArPuA3YyQD061nK5UT638D/tZ/H79rrx4+lfDKzHhXwmu7drlza7wQPc4ANfOviv8Aaa/aG/ZP/aBmi8Z69qWpRQ3Hz290oFvexZ5ZcDHT0r9kvhT8LdA+DfgbTPCnhy1FtpthGEX+857sx7k1wf7Uf7KfhP8Aal8Dy6JriCx1KMZstXhiDTWze2cZHtRyD5/I6D4K/HDwv8fvh7ZeKPD1z51tcJuktmI86Fh1Vlr0JldV+Vs/hX4Y+JvDPxk/4JpfFi2msr2SbR5v9Xcruazu0zyrDopr9Nv2Tf29PA/7T1mbJCPD/iiBV87TLpwA7H/nkx+8Kkk928eeOrLwD4W1HWtRljgtrSMsWkbGTX4JeP7nxZ+2p+1FeWekBtQvtUvGisxn5I4Afve3FfXP/BXL9o2T+3tO+GuhXMsUkKCfUJIZOGDdF4r2L/gl3+x2nwl8HxfEjxBGsniPXLcNZxso/wBGt2GfruIoWruW3ZaH1Z+zj8FdN/Z9+Euh+DtPVC9pEpup14E0xHzv+deo03aKdWkU0YhXE/Fv4O+Fvjd4Nu/DPizTItR02ccblG6JuzKexFdtRVgfh1+0x+yP8RP2FfiEnjT4fXuoTeGA2+21W2G6S16fLNgYx79K+6/2C/8AgoFp37Qmkx+GPGN3a6f48t/lHREvVH8S8/e9q+x/EPhzTfFWi3mk6raRXun3kbRzQTKGVlIwcg1+GH7bn7Lt/wDsY/F7Tda8K3FxH4evpvtGl3O/EkMi8mLIxwPzxUS0Lj725+8Jz/jS15n+zh8SJfi38DfBviy4MRu9T0+OW4WHOxZMYYDJJ4I7mvS81SdyWrC0UUUxBRRRQAUUUUAQqzlmyuB25pJANysc5FSKq8kUmD6VHKyror3GTGwZSR2xXAeIvih4d8N6klre6xa6fcIMNDcSqhH5mvR1XcOa/Nb9rD/gmn8TfjV8XtY8W6B4zso7G+bdHZ3c0iGL2GBionGUtjWM1Hc+2r743eDrO182XxVpVuzcYa7Uiq1r8VvBd1EHXxhpE5UcbL1R/Wvyu8Sf8El/j1Z2m6DU9N1kj/lmuoMG/wDHq5mP/gll+0gqjbp1nCPQauo/rS9m+4/arsfqlrH7WXw08H3Swap4u0u2Mhx+8nUnJ+ma9q8O6pZa9pNrqOn3cV7ZzrvingcOjA+hFfihpf8AwSb+POrahGt7Dp9nFkBppr0Pgd6/XP8AZn+B6fs8fB/R/BK6rPrLWW53u5zyWY5IUdl9BWkU0KdTm2PUqWiirMAooooAKKKKACiiigAooooAKKKSgBm4UyO4jkOFbJrD8beLtP8AA/h+51XVbyGwsrdd0lzcOqIPxNfM11/wUU+D1q2bbxppkv8AwI1nKol0N4w5lc+s5boQ/ebr0p3n/u1b1r5RuP8Agod8GpbVbmfxjpwK8iNWJNcJ4k/4K8fB3RVEdjb6rrMnpbW+F/M1HMHIfcktwY1wp3N71WtdUEzuPMBx/e4r8z/EP/BZrQJdRiNh4G1XyR18yeMZ/CnXf/BZXw7Lny/BF8M/7aii8irKx+mtxcTMR5AVl9Say7uQTMskZxMn3sdK/LXxF/wWOlktVg0LwZNBJ3+03Ix+lYyf8Fi/GUcYSPwPo5Q9WN0xz+OKLyHG0T9dbHU47pAoLbsfxDmp4LVIizKTluTz1r8iof8AgsZ4gk1C3mvPBltFGPvra3WA35iu1m/4LLWQjKx+Er8P7yIKd32IcV0P0+m1C3t5BG8gDn+HvU+6vxU8df8ABWv4ka/q0Vz4e0iw0mGNuftEfnM3sa/Sf9h/4++J/wBo74Mp4q8VaKmj3/2uSBPKQrHOi4w6g/XFaKV+hLirH0RRSUtUZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSHpS0UAZd3CZJ4yvAXr71FNDGuSHAf0FaUzKqnAGfpWTagNITIBn6VkdUGyt9laSHLS7PZh1r5N/bK/ai0r4DWLRyPuvJExDZRuN2fevYf2mvjbp3wZ+HeoeIbm52yQQ/Kn+12r8ZfAvg/x9+35+0MI2aeZbibfd3HLQ2Nvnv6cfrQNy5RPh/8Ffih+3Z8TtU1DSrXEckpaa9uGb7Lbf7Ib+lfaXhT/ginpi6SR4h+IFwdQYdNOtgIgf8AgXJr9CPg58HfDfwN8DWPhbwxZJaWFsuCwUB5W/vMR1NdvWpzczPwF/ap/YV8e/sl3EOtyXA1jw95gEOsWmUMTZ4DDsa+9f8Agmb+2hdfGexk+H3iV/8AieafbeZb3RPMyjr+NfbfxM+HehfFbwTqnhjxFYRajpd9C0ckMoyOnBHoQa/CD4K6XqPwB/bs8OaCbmW2OmeLItPkKNgSQeftwfUEYqLDu2f0E02PpT6KsgKKKKACiiigAooooAQfdrM1zULfSdNuL25ZUhiQsWboBWpXjf7V3wRv/j58EfEng/TdQGn6heRBraRvu715APsazsyk7HKaZ+2R8K3upLUeO/Dz3cb4MMOoR13ej/GXQNftvtcWoWk9senlTV+N+p/8Erv2i7OZgPBNvfgniS11uyA/8eYGr+nf8E7f2qtMt/stn4YvLO3HPlx+IrQD9JKOU29qux+yNx4605Y4n+2wRNL/AMsfOrW03XIbiDlhj61+MM37Bv7WJKyPpWuMw5/5GWMkf+RKlb9mv9tDTbfEcHjJh6R6yW/TfWPKy/aLsfs3ea1Y2bRjzV/OlOq2lrJuLKF9Sa/FAfBj9s64QSf2f42+pnb/ABrZ/wCGef21tYtRDcReKli/uS3u3+tXZi9oux+zM3i2y2h0nXHfkUy38Q6bcTFEuEAH+0K/GX/hjP8Aa9k4Nv4j5/va83/xVWI/2Ef2tW6HWF/3vELf/FVrymftF2P1x8UfFnwr4VlhjuddsojI/O+dBj9aoeKf2jPhx4P0Vr2/8ZaTbxH+IXaN+gNfk9df8Ev/ANpPxM+/U7O0lf8Av3evK5rc0T/gjv8AGHVbqIa1rui2Vrn5mNw0zAfSjlD2nkffurf8FEPgPo+Qvjywmb0jDHP6V5V4i/4K6fCrRzJBbxX2oEcBoIcD9a4G3/4IoaGMfaPiNfyf7lmgrttC/wCCNXwosY1Oo65reoy55O9VFHKRzHnGt/8ABYnwrI/+i+DL1yOR5k2KxNV/4LOSTxeXa+AlQD+9c19kaB/wTh+AWg2qwr4It7wjrJdSM7H862V/YF/Z/Xp8MND/ABg/+vVC5j4Duf8AgtL4nls2gj8B6ap6ZaZiPyrJk/4LMfENUxb+EvD8B/2vMP8AWv0Y/wCGD/gF/wBEv0D/AMBhSf8ADB3wC/6Jd4fP1tRQFz8vvEP/AAVy+MetHEEOi6b/ANc4WP8AWuUT/gpf8ftUWeG11tJDIfuwWu5vwwK/afwf8Dfhx8NbMQeH/B2h6ND0/cWca5/HHNdbF4d0mPmPTLJPdbdB/SgfMfhbbftS/tWXyh7b/hJZ1PRodFmYfpHUt94p/bK+JkbB9O8eNH/saXNAD+OwV+7CWcEa4SCNR6KgFUtd17SPBujXGp6vf2ej6XbjdNdXkqwxRj1ZmIA/Ggk/Dux/ZP8A2uviFELO70XxY8B5K6lrK28f4h3Fdf4V/wCCQ3xy8T5Ovah4f0ADobu/luW/KMEfrX7A+B/ip4Q+JVsbjwv4l0vXox1/s+8jnx9djGuqoHzH5CR/8ETPHUjK03xL0FT322dwx/U1vQ/8ESdVX5n+KdsG/wBnS2P83r9XaKnlDmPykb/giTqWdw+KUDN/2DGX/wBnrG8Rf8EUPFdtp80ukfEHTNQvM5SC4tHjDf8AA8nmv10oo5Q5jzr9nn4TwfA/4M+FPBUJV30uySOeROjzHmRh9WJr0WiiqJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKAFpD0NAIPSloArqnlxnaffmqyrLIm5W3D2Nfn7/wUX/b28TfBPXp/h34Q0x7TU5rVJn1qQHagbsg7mvibRv+Cjn7QGmnbHrq3K9v9EJqOZmqP3lt5GWFRJ9/HNZfibxfo/hHR59T1q/h0ywhyXnuWCLx9a/FJv8Agop+01fKDGlwQf8AnnpT/wCFP1uP9rb9sy207SNQ0TVpdEmYMJXtzawY9WY4qLMVkfsr8N/il4Y+LmhnWfCesWuuaXvMZntX3BW9D6GvyD/4Ke/CqX4H/tPaT460NBaWuuFLtTGcbbhD835gA1+lv7Gv7KNj+yf8OZdCh1OXVdQv5Fub6ZuI/NxjCDsK+Zf+C0fh03fwm8EaukSlrfWPs5kPUb42I/D5a05URc+xP+F2aHpv7Odp8SNZuI4tKk0OO/mZjwxaIEp7ktxX4JaJ8GPHv7R2t+MPE/gjwdcX2nQ3VxfTR2YGyBXcsIxkjOAeg9K9h+IP7VOs/F74D/Dv4EeEIZ7hUjitb5th3yyqfuqO6jOc1+uv7I/7Odl+zX8FdL8I4huNSYGbUriNRiWZuoz3A6CnYR8d/wDBPv8A4KLeG5PDuhfC7xwsOgXmnxLZWF/jZDKq8ASE/dav0d1y0tte8OX1s4S4tbu2dD3VlZSPywa/Kr/gpF+wBF4NXUPiv8PLd1s3m87VtJhX/U5/5axADgZ6j3r0n/gmL+29cfEmA/CzxteRpqen2YGl3czbWuEXhkYk/eApcqA8W/4JXapF4B/bG8beEzJsiubW9sIl9TDPuH6LX7EV+K/7Nenp4Y/4KmXljbOTEPEGpqCDkMjbyOe/Wv2nzVARXl5Bp9rLc3UyW9vEpeSWRgqqo5JJr8Wv24P2kNZ/bK+OemfDX4fXM2o+F4btbOygtztTULknBkPPKDsf0r2H/gqd+2deW+pS/BrwddPDI4X+17y3OXJJ4hTBzn16V6P/AME1/wBgm2+EOi6f8TPGtmX8a30JazsbheNOjPR8EAiQjr6ZoA+iv2T/ANknwp+zD4EsbDT7C2m8SyQr/aWrBdzzSY+baxGQvoK95oooAKKKKACkZgqkk4A5Jpa+Mv2zf2qfEFnqg+Dfwcs5td+J+qr5Vy1vEWTTIGXl2bGA2D+FAHkv/BQD9uZfEDX3wR+FcL+INf1QNZajd2oDrGG4MaEHlvXjHvXzH8QP+CWPxA+F/wABNR+IGsatZJremJ9qm0K1BkaOIcn94OCw9Bke9foT+x1/wT78J/s4JaeJtYP/AAkPxAkjBm1CZi8dtIfveVkAn/eIzX1B4006DVvB+t2V1GJbeeymjdGGQQUPFAHyF/wS3/aVv/jh8G59B1yZrnW/DLLbfaGxmWAjCE98jGK+16/G7/gjH4gms/jp4m0mN2Fre6N5zJ23Iy8/qa/ZGgDI8WWd7qHhnVbbTZFhv5rWSOCRs/K5UgH86/nt8efs5/GP4L+MxrnirwhqN1dw3H2l7yaFrmKZ853ORnINf0U1FcW0N3EYp4kmjbqkihgfwNAH5U/Av/gsV/YMMejfEjwn5UMKhIbnRU2hVHYxn+lfZPwp/wCChHwT+Lt3HZab4pXTL6QcW+rRm2J9gW4Na/xY/YZ+DHxkmFxrvg20gvB/y9aaPs0n/jvH6V8c/tAf8EdbAWMmqfCnXJor+Eb10zVZC4k/2UfsfrQB+mqyR3kYkgdZ0PR0YFfzFWlXHevw/wBJuv2wP2S7gxw23iBtMhOWhkVr232/qa9N8J/8FiPiZqes2WkXPw/0rUbqaQRtDbGYTn6J2oHc/XSlrO8PX1zqeh2N3eWzWVzcQrLJbuctESM7Se5FaNAj80P+C1XjSSz8E+AvCys4h1C7mvJgp6rEoAH5v+lfQ/8AwTHTb+xr4JfG0SG4IGPSVh/Sua/4KIfsW+Iv2soPCNx4Y1WxsL7RXmjljvtwDxy7eQw6bdvTHNfR/wABfhXD8EfhD4X8EQ3CXY0e0Fu1zHHsEr5JZ9uTjJJ70Ad9XxR+2N/wTX8P/tKeIrfxLoeox+FvEDP/AKdP5BlW5XjqAy4OO9fa9IR+dAHn3wL+B/hr9n/4e6f4T8M2qxW1sg824KjzLh+7ue5r0KiigDB8beCdH+IHhu90TW7C31Gxuo2RormMOoJGAee4r4d/Y6/4Jn337PXx21Lxt4k1fS9Z06yEg0K3tRIZI2c/6x9ygKQMjALfWv0AooAbt5yOD3p1FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADG71+b37X3/BRf4kfs6/G6Xw5aeFLKLQfs4e2bUAVe47FwwHA/Ov0jxXE+O/gn4E+J2padqHivwppfiC808k2s2oWyymLPpmolG5cJct9D8cfFf7b37Sn7Snm2PhfQ7yO3k4x4b02V2x/10FXPBH/AATj/ag+KEP2jWbw+GYWOCuv6vIsn/fEYc1+0+i+G9J8N232fSdMtNMt858qzgWJfyUCtHHvS9nEp1JdGfknP/wRN8SpYyyP8UdNkn27jH/ZsmM+m7zP6V53+xL+wv4R+OHxC+I3hnxnqeopN4Zc26CxKwliW27yCDj6V+1lx/q2x6Gvy/8A+CePiqbWv28vjoot/sEVwLovbB9wzDdLGDnA68np3pWWw07q7PqD4B/8E6PhX+z/AOKLbxNpf9qaz4jtWJt7/VLneYgRjAVQBX1HtpefWjn1p2ZldhX4h/td+EU0/wD4KQwWkl55P27VNPne4/557ypxiv28NfiB/wAFJdLvPBX7bq69eO8kVybO7hkI2gCPA2A/gOaqRcD9wKKr2d9DqFnBdW0izW8yLJHIhyGUjII/Cpt1O6Iscn8Svhb4X+L3hmfQPFmkW+r6bN1jmXJU+qnsa/FT9uD9lW9/Yr+JGk6/4N1K8i0S/cvY3AbbJbOuPkyOv41+4HiLxNY+GLT7TfXEdvCD8zSNjAr8m/20vjPqP7b/AMYtC+DPgnSoHGmag7DUt5YuduDkdABUXjsaKL3PHf2Efgncftg/tGPqHjbUjqtlpUa3+ox3MhMlyoICoPbJFfurY2UGm2cFpaxLBbQoI440GFVQMAD8K/C4eEPiH/wTL+PnhjV72WG9F1FidbVz5NzG3DRN9P6V+4PhHxVp/jjwvpWv6TOtzpupW6XNvKpyGRhkVUbITNqiiiqMwoopKACvzS/4LOeL9Lb4e+DtA3RtrTagbqMfxLGFIz9Dmv0kvNQgsLWS5uZkgt4xl5JDgKPU1+IP7cPiOX9qb9ty28JeG5ku4EuINDs3gJZS5OJHH0J/SokaRR+l/wDwTl8N6l4Z/ZA8CQaocz3EMl3GPSKRyUH/AHzj86+l/wCGuc+HPguD4c/D/wAN+FbWWS4ttF0+DT45Zcb3SKMIGbAA3ELk4A5NdJRFaEyd2LRRRVkhRRRQAUUUUANVAvSnUUUAIq7elLVBNSH2gxMMGpvtiO3lq+HPTip5kVyss0VC1wvIVl3e5pyMeSzA+mKOZCsySioI5mZmDLjHepQwNNO4NWHUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAcB8bfg7oXx5+HOqeDfEaTHTb9Cplgcq8TfwsPXHoa/HL9sT/gnBrf7MXhm78YWfiG01/wmlzHEN8flXkYbjlfunn0NfuVtHPAzXxp/wAFYYZG/ZA1cg5KX9qWOO2/B/nUSS3NIt7H5wfsQfsJ6h+1wdY1SfV10HQNLdIHuI4w7yyEZwoPtX3h4b/4I1/CTR9Shub7xB4i1WFPvW7yxxK/1KrmqH/BGGNE+Bfi9lGGOt7T9BGMfzNfoXSVmDbR8or/AMEvf2dFGP8AhCJPqdQn/wDiqcv/AATC/Z6X/mT5j9dQm/8Aiq+rKK0IufMOn/8ABNf9njT5hIvgCCYg52zXUrD/ANCr1Cw/Zj+E+mWotrb4eeH44R/D9hRv1Ir03mjmkFzyPUv2SPg5q0PlXXw50CSP0FqF/liuVX/gn3+z4sm//hV+jH2IkP8A7NX0Lg0bTTA8c0v9jn4KaKoFn8NdBhAOR/o+f5mvWdN0qz0WyistPtYrO0hXbHDAgRFHoAKt0tJKwgooopgFFFFABRTdwHesfUtfh0rz3vZobO3QZ8+aVUX9TQNJs2qK+J/il/wUr+G/hOOay0TxPHr+sZxHHYWzyIx9OBXjvhn/AIKIfGzXviHYJYfDC91zQ58CSCzsZwwz3BI7Vnz+RpGnzdT9OqKp6XfNqOn2tzJbzWjyxq5hmwGQkdDjvVytDIKKKKACiiigAooooArzQrtL5qBrJPMaTJ+lWZNqRNnpjvVe7uAulzzf6sCJm57cVHKaqTR+O/8AwVS/aTfxp45Hw40j9zYaS269deCzdgfWvtX/AIJj/AfTfhT+zzpXiJYs634qiW/upWA3BCTsT6d6/FD4neLj4q+KXiXXpJpL2K81Se4DyMSXQyEgfTGK/c79mn9tP4S/ED4a6JDY6zY+HLi0tY7dtLu5Fh8oqAMDOBjipHJ8x9RUVwtv8ZvBlxbCZfEmmsv+xdI36g1X1T4zeENPUTP4k01YvVrtF/mavmI5TttS1GDSbGa7uZBFDEu5mNfht42uLTxf/wAFLrZ7EiaC88Y6eylfcpmvqv8Abi/4KLeH9I8Har4K8FXw1LxJcELJfQEPBEvfBFcF/wAEu/2P9a8SeNrf41+NbR0sYP32kLc533M5xi457DnFUVZI/WeikpaDIKKKKACiiigAooooAbuo3U6igAooooAZRT6KBjKKfRQAUhOBk8ClrhvjZ4d8VeKvhjrul+C9Wi0TxHcQFbW8mTcqN/8AXoEdwGDDIIIo3A8g5FfiNq37SX7Vv7J+vmz8Xzag1q3JOo2/mxsPUOOK9++Hv/BZHRpmt7XxR4WubIjgvbtvoL5fM/Tykrwb4KftkfDv43ZTRdbgNxnC28jBJD/wE8mvdI5BIu4UE2ZNRRRQIKZNMlvC8kjrHGgLMzHAAHcmnZzyORXwX/wVO/aql+EvgG38DeHdQ+z+JtcGZWgkG+CDPVucrn3oA8m/bo/4KUavpfih/A/wqv4Ha3by73VIQJcydNsRGcn6V4/8Mvhf+2x8UGOu6bqvifSVb/lrq2oNa5+kbYP6V3P/AAS//YhPjnU4Pi546sRNokDn+yLK6j/4+5Af9e4I5UdvU1+uKRrGqqq7EXoBQVzH4OfE74nftafs665Fc+MNd8VaQwfYl1JI0lpIf7ofBQn2r9KT8NdQ/by/Ys8KR+KNUuvD2q6rZpdG4sm+WRlJALr3U46V9PeNvAPh34j6K+k+JtHtNa05juMF3EHUEdxnoazdQ1zwZ8DvAtsLu8sPDPhrTYBFbrLKscaIo4Vcnk+1AXPw++Ln7G/x5/ZAvJ9csItSl0e3ZtuveG5XdFjH8Uyryg/3uK+0f+CVn7WHxJ+M3iDxB4S8ZXMuv6fp9klzDqjIS0LFgAjuOORnAPpXhn7e3/BSJ/jZpt58P/h0rw+ELj91fajImJbzn7ijP3f519g/8Etf2bdR+BnwSn1nxDYSWHiHxNIt09vcRNHPBABhEdWAKnqcGgk+1KKKKACiiigAooooAKKKKACiiigApM460tNkBI4oAarlunNSU1VCinUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMkTd3xT68g/aw+OA/Z5+BXiTxpHEs97ZxBLSFwcPMxwoP8AP8KAPTrHXLC+1C8sILqOW7s9vnwq2Wj3DIz9a0a/ND/glT8VPF3xo+Lnxb8XeIZJJ4tQt7ZmZc+THMDjavpxX6XL0oKkrHM+Jvhl4T8aTLNr3hrStYmUYEl7aRytj0yRmmW/wr8GWePI8IaFD/uabCP/AGWuqoqeVCuVI9JsYhhLO3QeixKP6VaVQqgKAAOABS0VQgr5K/4KffDHVPid+ytrEGjWT39/pdzDqKwxDL7UJ3FR3OCa+taZJGk0bRyKHRgVZWGQQexoA/Hv/gkT+zfd+JPiXefEzWbAro2hwm309pUwJrhuNwBHIUEnNfsPWfofh/TfDOnx2Gk2Fvp1lH92C2jCIPwFaFAEN5Zwahay211Ck9vKpV45FDKwPYg1+Kf/AAUK/Y5179nH4h3PxH8FmWDwlqFybhJLMlZNOnOSV4HCHsc1+2VZHizwnpHjnw/eaJrtjDqWl3aGOa3nUMrCgD8Mv+CaUOoeMf21fC2p3Usl9eYub+5mkJJPyNlj+NfuB8SP+EhbwJrq+E0tX8StZyLp4vJCkPnFTt3MASBn2NeEfs9fsD+BP2bvixrfjXwxNdE31t9mt7GY7ktVJBfaepzivplc45oA/nN1y2+Jn7Ovxug8U+N/Ds7eJLO9F/I2tW3nQ3T5zy3Qg1+qHwY/4K2fCPx5FZWHi1b7wRrbIBO11CJLJW9FkVi2PqtfYvi7wD4d8faXJp3iLRbLWbOQYaK8hWQfqK+I/jp/wSF+GnjbT3m8ATSeCdVUZRCzz27n0IY5H4UAfdHh/wAS6T4s0uLUdF1G11Swl5S4tJRIh/EVoq24n5SB68YNfhk3wh/a2/Yj1eV9Ci1l9NQAvdaCGv7Jh6FNuR+KivqD4C/8FkdE1ZodO+Knh+TR3GEfWtJHmwhvWSIkMo/3QfpQB+l9Fcp8Pfip4S+K2kDU/CWv2Ou2mFLPZyhymRwGHUH611dABWbZ+G9J0/U7rUbXTLS31C6x591FAqyy4/vMBk1pUUAN2n1yaz/Ek8Vt4d1SWeRYoUtZWd3OAo2HJJrSr57/AG8PD/xB8Vfs1+JdK+G8TT67dKqSxREiV7fP7xY8fxEfpmgD89v+CLXhG8vPjR4t19SosrDSPIcnOWaR1wBxjjBzX7G18a/8EwP2c9d+AvwX1KbxTpo0zX9cvftLW7j97FCFAVW9DnJxX2VQAUUUUAFJgccUtFADZI0mQpIqujcFWGQa82s/2bfhppvj1fGln4O0u28SKCBexwAHnvjpmvS6KAEpaKKAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK99Mbe0mlVN5RGbbnGcDpX5N/8E29Rk1b/AIKCfFu8MP2QXEGqTNBu3bc3yDGcDP5V+r2tM0ek3jL94QuR+Rr8kv8Aglncy6h+2r8StTEbNHc2d9k9k8y6WTr+GPxrL7Rol7p+vdFFFamYjdK+I/8Agp1+yjq/x8+GtlrnhGwS98T6JL5rQLxJPBg5VT3I9K+3KQpmgpOzPgP/AIJo/tkaR4v8B6X8KPF2oGx8c6KGtbSO83K13ACSnLD76g7dvXAFffdeQ3P7IfwguvGsXi5vAumx+JIrv7cuoQ+ZG/nf3sKwH4YxXsG2s+Vjuj4l/wCCg2o/E64sbbwr4K8J3Orxa/tto9Tt2/495P8AaHYV0n7Df7Ddh+zRoMus+IXi1jx5ftvuL0jcLcH+BG7/AFr60MatjcA2DkZHSnUo01FtlOo5RSPhr/grl8O9L8Rfs0yeI5o9mqaJewvBMoG4qxKspPpzWL/wR7+Mtz44+COseDdQnM1z4YuwLbexLC2kGQv0VgcfWvSv+CoWm6rqv7I+v22k6XPq0z3dv5sVupZ0i3Es4A9OPzr5V/4Im6PqC+JPiXqnkumlNaWttvYEAyhicfXGaqxNz9YKKKKsgQniq8l0sbAMyqfc1P8Aw15z8cbjxNZ+Cbp/CVp9r1kkCMYHApmtKKnLlZ81/wDBRX9rLR/hZ8K7/wAH6fJJd+LPEVs0FrDH1hDHG84OcjPFeZf8Et/2K73we/8Awt3xrasmq3kTLpVlcrl4gx5nbIyHPIH1Ndp+zz/wT5mvvHl58R/jTcf8JLrksnmWGmSOXhtRycnPccYGa+8I40hjSONQiKMKqjAA9KhJ9R1LR0RJtAzjilooqjEKKKKACiiigAooooAKKKKAPkr9uv8Aa81P9knTdDv9O8OQ67LqsjRI80xjSIqM5bAr4gk/4LEePTcFl8JaSFfrsuGbH04r9cvGfw88NfETTf7P8TaJY65ZA7hDfQrIAfUZ6Vwlt+yP8G7PHlfDjw+mOn+iA1nymvN5n5p3P/BYbx3cLgeBdF+ou5GP/oNUNQ/4Kz/FHULd4YPB+m26+sUspP8AKv1Vh/Z3+GNv/q/AXh9fpYR/4VuW/wAMPB1qCIvCmixg9dunxf8AxNL2aH7Q/G64/wCCqHxpbPl2+moT627f41Hp3/BVT9oS61q1srBtGkWWVI1tV0wO7EnoDmv2VHww8HDp4T0P/wAF0P8A8TUVv8JfBNreR3cPhLRYrqNtyTJYRKyn1BC1UYqIpVLmx4ZutSvPD+nTaxbR2WqyW8b3VvE25IpCPmUHvg5rUpMUtWZBRRRQAUUUUAFFFFABRRRQAUUUUAFfJn/BUK3juf2QPFYkXcEeFx9Q2Qf0r6yr5h/4KSBf+GQfHDPjCwqRke9RL4S4fEeEf8EWbhpPg147i3ZWPW0IHpmL/wCtX6LV+Z//AARHuZH+H/xMgLZiTU7VwvoTE2f5Cv0Z8U+KdM8G6NNqmr3kVjYw/fmmYKB7c0o6BLV2NXcN2O9OrxzwZ+034D8c6glrpniOzu7g/wAMMox+terWOrW+oKfJk3Y5IpqSkOUHEkur6Kyj8yZtif3qqQ+ItPkcRJdI7/WvJf2wPH2ufC/4BeJ/E3h7TRqupWUQdIGBIAzjdgc8V+Nmn/8ABSD41aXP5kWq6e7/AN6SyB/9mqrlKMban76SapDBDvkdc+gNTLeR8BmCsV3Fc9BX4laD/wAFX/ippqM19pGj6gOxZWX+tJ4g/wCCrnxd152/s2w0uxmZdjSRxmTj0ouFodz9u45FkXcjBh6g06vzS/4Je/tHfGH41/EPxHp/ijUV1TwpZ2huZJJotrxSswCRocdOv5V+lWaZk9B9FFFAgpD0NB6Vj+ItYj0XT5Z5ZNgVCc5oGlc8++Kfxm034XaPNf6hcxxpGPlSVwpavxU/aF/ak+JP7WHxCl0vT5bt9OefyrLSdL37HUnALhev1q78bviV42/bi/aK/wCEd8IvdXdhcT/Z9NsUkITy16yv29ya/V/9jf8AYn8M/ss+D0R4rbWPF9z897q7RAsDjGyMkZVf50G8pLocD+wn/wAE/wDRfgH4YTX/ABlp1pq3jm+G+QTRrLHZDPCx5HB9SK+z4bOGEARQxxgcDaoFT0tBhcQKFyQOT1paKKBBRRRQAUUUUAFFFFAERXcMHkVheO5mt/Auvyrw6afO49iIya6GvLv2o/Elx4P/AGc/iRrVp/x8WWg3cyfURNQO5+Lf/BPH9mPRv2oPi1qOk+JYrhtB0/Tmnme3baQ5IC8/U19Z+Pv+CK9mzSSeC/HstvkZEGqQZyf95a53/giNj/hKfidxyLGzx+LNn+VfrJU8pXMfjLJ/wSG+N1jHssPE+mBP7ovXQfkKzLT/AIJP/HvVbs299qGmxW4/5aTXzMPwGa/a2iixB+df7P8A/wAEgfCnhGZNU+JOqt4q1Dr9it8x24Puepr9CdN0210ixgsrKBLW0t1CRwxqFVVHYAcAVcoqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvXvC+j+KrFrPWdLs9VtG6w3kCyr+TA186/Ev8A4Jx/A34lKXfwquhXXafSHMJH4dK+ndwo3D1oA/H345f8EqfHvwikn8TfCjX59ehtjvFkrGK9Re+GHWvRv+CY/wC25r/i7xdc/DH4hahNeapcAvptzdcPuUfNE2ec4/lX3J8cf2jfB/wD8F6jr3iO/hR7dT5dirjz5j2AXrX5HfsN6NefHD9v6z8W6Lpr6dpFvqd34hmUZKwQsTiMt0ySwGPeouaep+5VFFFWZnP+PfG2l/DfwbrHibW7lbPStLtnuZ5n6Kqj+vSvwt+GPh3X/wDgoN+2Qs+rrK9nf3h1C/JYkWunowxGvpwQAPev0R/4K4fFf/hBf2a/+EcgljF54ou1sjGXAbyl+dzj04HNfnT+wL+1hov7Jvi7xPrOtaJNqj6lYLaxSRHDRYcHB9AcCgD95vD/AIf0/wAK6JZaRpNpHY6bZRLDb28K4WNB0AFaNfKv7L3/AAUO+H/7THiL/hHLRJdC19kLw2t66gXGOSsZ7sB2619VUAcl8WfH0fwt+G/iPxZJZzagukWUl39lt1LSS7RkKAOSSa/n1/aP/at8bftKeLr3U9e1K4ttMkf/AEXRbeUiCFRwBjP86/oxnhjuoWiljEsUgwysoIYHsQa51fhf4PViw8LaOG9fsMf/AMTQB/P/APss/Fb4a/B3xUPEnjbwVe+Ndds5lk0+1Nwq2+fV1YEZHuDX70/Af4wWXx4+Feh+OdO0q+0aw1ZGkhtdRVVl2hiobgkEHGQa8/8AjN+wv8HfjlbomueFYLG4Q5W60gC1l/NR/SvVvhf8OdI+Efw/0PwfoKSJpGkW4trcStubaCTknuck0AdTRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8e/wDBSr4G/Ej9oL4ZeGvC3w/s1vYm1QTaojXUUAWIKdrfOw3YJ6DJr7CpOeO9AHh/7H/7Ndj+y/8ABvTvCsJjn1aQ/adTvIxjzpyOfwUcCvcBS0UDbuFFFFAgooooAKKKKACiiigAooooAKKKKACiiigBGUOpDAMD1Br4+/aY/wCCZvw0+Ozvq+hRr4C8WF951HS4h5U3HSSHIU9uRg/WvsKigD8tP+Cdf7Fvxi+CH7RWtX/ic3GgeGNGjkgcxTs1trDtkKYhjDKBySwUjj6V+pdFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1mC4ycU6mSRCTG7tT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMjxZqlpovhnU76+mWC0gt5Hkkc4AGK/J3/gkjeDUv2n/iLdWuY7KTT2lEedwG6UHGfbFfpd+0b4fXxZ8F/FejNcNaveWTokq8lT64yM/nX5x/8EUNHZvGvxL1AplYrK2g83H8TOzEf+O/rWLV5G0dIn6z0UUVsYhRRRQAUUUUAFFFFAEc9vHdQvFNGssTjDI4BBHoRXOeBPhr4Z+Gdjc2fhjRrXRra4l86WO1QKGbGM109FABRRRQA3HFJt3dRmnYo20wEwKDS7aMUC1FooopDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5p/4KLQ2tx+yL49W7JCC03Lj+8OQfzr6VOa+Z/8Ago4W/wCGQPHu04P2YdvespP3S4fEfNv/AARJii/4Vz8TXUfvTq1spbPbymxX2j+01+z/AGX7SXwzuPB9/rN7okMsiy/aLLG7I6Ag9RXx/wD8EVbKCH4O+PZ402zS62iu2TyFiG0fhk/nX6M4oFfW5+MHif8A4JJfG/wLeGfwnrun62i8h7K9a0k/JsVyk3xg/au/Y51C3j8QHVEsbdfLj/ta2+0Wu09PnAyfxav3J21yHxYn8N2PgTVLzxZZ2d9o0ERaWO+iV4/yak0hqb6nz9+xj+254a/a/wDDt5omrWVvp3iyGJmvNHf545oc43LnqOele0yfs2/CqT73w88N/hpsQ/8AZa/I7/gmeba4/b1d/DDPFoPkalIqYOBbYxGpz2BK1+1Ov6tHoWhajqUxCw2dtJcO3oqKWP6CmLU/Kz9sr9qbwB8EPipeeAPA/wAK/CerNZogubqS1U4mPJjAA6isz9gb9pjTviR8d9I8AT/DTwlYadeJcu1xHYqZRtUsoywPpXy78O7VP2hv2wvtieYINS1x74jG4iIMSB+WK9h/4Jv6TG3/AAUFmiWNfLsF1YqoHCgZRcfTdQa8zsfsvaaT4a8AWM89tZaZ4ftGOZZIoo7dCT6kAVrWOoW2qWsd1Z3Ed1bSDKTQuGVh7EV82f8ABSPw7Pr37IfjWS2d45tPjS+DRsVICMM9PrXln/BH34lS+MP2d9W0G9vJbu+0HVnQec5ZkhkVWRRnsCGq+Yytpc+8aKKKokaWFfA//BUv9qab4SeBLTwl4cvPs/iXVuWubeTEttGO4I6Zr7xnkW3tZpZDhUVmLegHNfgf8TtUn/bM/bZttHsrl5LDVNWj0+3kdiwSBT87+2QCaDSOhP8A8E5Pjp4H/Z7+NV/4m8bSyw250yS2gkhj37HJGTj3Ax+Nftt8M/jh4E+MGnRXnhHxPp2tLIu7yYJ185fXdHncPyr5U8T/APBIT4KapoL2mkHWNFvjyt2t602D7q5INfnX8WPgL8YP+CfnxEsNas9Rns7fzsWPiPTWYQSjuki/zU0C0Z+/dFfP37E37UUH7VXwdi8QzW8djr+nznT9WtIz8qzqqneo/usGBH4+lfQNBAUUUUAFFFFABRRRQAUUUUAFc58RvBtp8RPAXiDwxfLutNXsZrOQezoV/rXR0UAfgr/wT7+Ok37LX7TRsfE8jaPo2oB9K1pLgECF1JKMfTDD9a/d/TdStNasIL2yuI7uyuIxJDcQuGSRWGQQR2r86P8AgoV/wTnf4hXWpfEv4cW2/wAQSHz9U0Vel50y8Y7N6jvXjf8AwT3/AOCgEXwNhb4ZfEyS6g0SKfy7G8mBLWHrG+ei5/Kgqx+w1FYvhvxhovi/R4tU0XVbXUtOlGUubeUMh/EVpi6iZNwlUr65oJJ6KzLjXrC2Db7mMY96+Yv2n/2+PA/wR8Paja294mpeIh+7jsYGBbJ70Dsz6nt9Rt7qRkikDMvWrNfk5/wTe8O/GX4zfHKb4sa3r2o2fhWMN5wmZvK1EkYCopOMDqSK/WOgQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNS1G30nTri9u5BDbW8ZllkPACgcmvlyT/AIKc/AOK7kgbxavycb/LODX0Z8RPB0XxC8B+IPDE9xJaQ6vYzWTzwnDoJEKkj86/OqT/AIIo6Sfu/Eu7H105P/iqAPozUf8AgpR8ANL06W5HjeG8k7RW8TsSfQCvkP8AaG/4K5yalHd6X8MNPkttzYTVr/t9FrpIf+CJ9sv+s+JUp/3bBR/WrT/8ETdGP3fiPej/ALck/wAaC+byPhz4Q/CX4lftsfEKJbvVri9tvtObzVNQuMpbIxycAn+Vfsv8FfBPwd/ZM0Wz8HaNqemWOp3Cjzbi4njFzdsTwTzk+wFfGWp/8EgfHfhLTZU8D/FZ45Jf9ZC6vbq31KmuU+G//BLn4yWvxu8Jal4z1G1v9C0+9huLnUY9QaWURRnOxQ3OeKnlFzH6+0UgG0AUtUSfjb/wWo8SXV/8dfCGhlj9i0/QBcqvYvLPIGP1wi193/B//gn98HfBvw107SbzwvbazdT2sZu728G6SViASc9uTXwR/wAFntNmi/aF8LXfkyeVceHkjWTadrMs0uVB7nkce4r9M/2T/jxpP7QHwX8O+ILK6hbUfskcd/aI4LwTBQGDDORkjNA7aH5Eftpfs3av+w78ddH8QeCLm8ttDuj9q0jUEB3W0wyDEW6bvQdxX7Mfs9fGCz+PHwb8MeOLMLGuq2oklhVgTFKCQ6HHQgg8V8+f8FWvA9t4r/ZJ1jUXjzeaHeQX1vIBynzbG/MNXn//AARl8d3OvfATxJ4bnRvK0HVswuRwVmXeRn2Kn86Atpc/QmiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFUNY1RtK0y6vFtpbswoXEEIy747AetfO3wl/wCChnwc+LGuLoMety+GvEG7YdO1+E2rbv7oY/KT+NK6K5WfTFFQwXUV1GJIZEljPRo2DA/iKk3UxHiH7ZsurWP7PXjO/wBFuY7S+ttNmkWaRsAYGa+Uf+CK+hpa/DH4h6pu3Pd6xHDnbj5Y4+x/4Ga90/4KQfEaDwL+zT4nhlmtg2qWr2SQSvh2ZxgEfSud/wCCTfhldB/ZH0m88jypdUvri6ZscuN+0H8lrJO8rov7J9m0UUVqZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFQ3CSyQkRSeU/rgGnxhlQB23NQBFcXC265bgetfOn7eWnz+Jf2VfiBHbODFb6bLNIuRk7eRWR+3N+1dF+zb8PZpofLl1y9Hlabb5BMjd3Ix0FflbqH/AAUR+J3ibwj4t8N+IZ7bVbLX7SW1kdYxE0SsOgAAB/LNc7vJWR0pKK13PuX/AIIu7o/g/wCOgTlTrYwP+2Qr79vvGGi6ZcS291qlpBcRLueGSZVYD6E18Uf8EefD9vYfsy3+qIpE+oazOZGJPIQKq18r/tcfsb/tFa18dPFOs6JYar4h0jUrx5LO40+6f5IeqqQGGMDjnPSrM9Ln6J/FP9uH4V/CWNk1nxTaTznotiwkP6Zr8zf2qf8AgoX41/ams5/AXgbR7mx8NzzYZYUMl1dp/Cr8fKPpXmcv/BO79oiZvNk8C6hM/rIysf1NXfg7/wAL1/ZP1LUdQ074Y3TmbCyyalpLuRg8YOOPwoKsj9Hv+Cdv7Dtv+zv4di8ZeI0MnjvVLXY8Z4FjExDGMY6kkAnPpX0N+1Hrh8N/s4/EvUl+9D4fvcfjCy/1r8u9F/4KpfH7U/EFhpEHhrT7q9ku122CWMgmlQ/wdenvX3x+294qvbX9iPxpqF/b/wBm399pSQzW7HOxpCoZP50ibH50/wDBIbwVD4m/aJ1TW7mMNbaJpbS/MOAzEDNaP/BMqVL39vjxDdJ91rXUmH1Mq816t/wRq8Mx2Xgr4o+LZYlVP3dmGPXCRF3/AFIryD/gkfGLz9rnWriQ75U0q6fceuTKmTVAfq9+094TvPHX7PfxC0DT4ftF/qGiXUNvH6yGMlfxyBX5Vf8ABI74wD4b/H3V/A2rMbeHxLB5KCT5dt1CThSPUjcK/aE/NweRX4RftmeFrz9lP9tqfXdCia3iS+h8Q2JXgYY5cD6ncDTsStrH7wUVxHwV+KWm/Gj4X+HfGWlH/RNWtUnCE5KMR8yn3BzXb1ZBwfxyvtR0n4K+O73SMtqlroV7PagdTIkDsuPfIFfi1/wS00OLXP2y/DzXAD/YLS8uRuH8YUgH82r9z9c0sa3ot/p7sUW6gkgLDsGUr/WvwX+AniST9jH9tyCPxG5gg0nUbjS9QkA/5YPkb/fsaC0fvvXiP7aHgnw147/Zu8b2Xib7LFbxafLNbXV0FP2e4Cny3Uno2cD8a9lt9Stbqzhu4riJ7aZQ6ShxtYEZBBr82f8Agrt+0rb2PhWy+FWi3KS3l8y3OotG2fLjX7qnFBKOZ/4IkLIuq/FNdzGFYrDC543Hzcn6nA/Kv1Yr4O/4JE/B278A/AnU/FGpWgtr3xRdi4jLJhvs6LtjH05Yge5r7xoEFFFFABRRRQAUUUUAFFFFABRRRQAyviH9sX/gmf4a+P8AeT+JfCUsHhfxXKwa42piC69yo6N719wUUDPw5v8A9i/9q34HzPaeHI9budOHT/hH7wvF/wB8E4/Sp7Kw/bZ2+VGvjbH+0FFft/RQPmPxK0/9n39tPx1IRO3iO3jlPzyX16sQH5V9H/AD/gkfaabq8Gv/ABe10+J7teTpkLsYs9tznk1+k9FAcxlaD4e07wno9tpek2MNhp1unlxW9uoREX6CtWkpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPDf2sv2WfD/AO1J8OZ9E1ONLbWbdWfTNT25e2kP9Djmvyhh/Zq/ag/Y18RNrfhfTNRJ3FRc6E5uIZl9HiH+FfuhTHUSfKy7hQVc/GT4vftFftU/Hb4bXfgLWPhtqkFnfKi3VxHosys4BzjO31r7T/4Jg/AXxb8C/gvq8PjDTo9L1DV9SN5Haj/WJHsCgP6cg8V9k49h+VOoC4UUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMAoooo5mAUUUUczAKKKKsAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopu75iMUAOooooAKKKKACiiigAooooAKKKKACiiigBuyvkz9rz/gnp4Q/acaPWbG5Twh4ujwDq1taeb5ijs0YdMn3zX1pz60c+tZ2Y7s/GzUfgr+2l+ylaznw7qWpa/pLHh9Jna9IX1MZG4VyPh//AIKv/H3wTNbWGtDTdVNu/wC+TULIxTSD0LcY+uK/cDbXLeJvhP4K8aSiXX/CWh61L/z0v9Ohmb82Umnylcx+Ff7Tv7bmv/tReH7XTdZ0C2sJobkXAuI75XXaARs2bV/PNfsp+xj4Jvfh3+zD8PNB1GHyL610yMzR4xhm+Y/zrrY/2f8A4YxY2fDnwkuOmNDtf/jdd3HGsaqqgKqjAVRgAelNRsEncfRRRVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANVs06kC7aWgAooooAKKKKACiiigAooooAKKKKACm7Ru3d6Wua+JXih/BXgPXNcjAaSxtXmUMCRkDjgUm7K40rux+KP/BU/x2/jH9p68023u2vItIhSzWNWyqyd8Ad+lfN/xA+BPjn4W6ZpWp+KfD15pNnqi77OadPllHuc8VveG9Wufix+09oN5qbq0mu+KLVZd3PyvcqpB/A4r9/vi78BfB/xu8CP4U8U6TFeWPk+VDIo2yW5xgMh7EYrKN47Gsnc+cf+CSNvdW/7JFj9pt2gV9TuXiLfxoWGGFfadcZ8HfhXpXwU+HGieDdGeSXTtLgEUcs2N7nJJY49Sa7XAq+UzuG0HikaNZFKsoZT1DDINLgUbRRykmDD8P8Awxb6rHqcXh3So9RjGEu0soxKo9mC5ri/2mPgpF+0F8Gdf8EvdfYnv0UxT9ldTlc+1ep0VVhnzl+yH+ylF+zL8FtQ8HXF8upXWoyzT3dxGMBi67cD8ABX5G/sK/HrRP2b/wBpiTXfEDyR6NcxXFhPJGMlMv8AKT+Kiv3+2ivzy+IH/BGrwD4n1q4v9F8W6poS3DmR7cwpKuScnBJpcpXMe7Q/8FFfgNKAT43tl+qGvgL/AIKmfGL4V/HS38IeIPBmuQaprlmr2s/loQxizuAP0JP517B/w5J8Of8ARSdU/wDAKP8Axqyv/BEvwh/F8RdZPfi1iFUK6MD/AIIy/Gq8vF8VfDfUdQlnt7VFv9NglbKxoThwg9yQa/Uuvlr9lX/gn74L/ZX8SXfiDS9Tvtb1i4h+zi4vAo8uPjgAfSvqWgkZX51/8FHv+Cfuq/GTWYviD8OdPhuPETDZqenAiM3QA4kB7t61+i1GB6UDPwP8N/Ej9q3wfoP/AAhNhF40jtbQbIbX+zpZTEB2VscCvdf2bP8Agnb8Rvjd8Qx4z+Oi30GksuWhvrovd3XorZyQv1r9ePs8QbcI03eu0Zp+B6UD5ijoOhaf4Z0e00rSrSGw060jEUFtboESNQMAADpV+iigkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilyoAoooo5UAUUUUWQBRRRTAKKYisvU5p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFN2/MTnrSeZ+8CYP1p9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtZWvR6lItqdNdFZZQZQ/dfSgDVopFzgZ60tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5B+1wuuSfs7+Nl8OW013q7WDiGKDlzx2Hf6V7BTWUOpDDIPY1MldWKi7NM/A7/gnP8GZPi5+1NogulY2ugv8A2veBkI2yRvlB1H8ePy71++GB6VzPhn4W+D/Ber6hqugeGdK0bUdQO66ubG0SJ5j/ALRUCuowKXKNyFoooqyAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiio5mAmRRkUzdVZmO/HNTzMpIu0VB5Mn9+pq1JFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqOMSDO8gj2qSigAooooATHfvS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNDgkjI4oAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlN3H0oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUmayAZtqNiPNHGakZgvU0ir82aVix21vWn0UVsQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSZo3U3AoAczbaWmN8wx0pd1Ax1FN3CjdQIdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTd1G6gBc4yTwKYqJ95QDuokXzI2UnAIxmkhi8iMICWA7mgCWim7jRuoAdRSUmTSbsA6ik5paYBRRRQAUUUUAFFFFABTMsu4nkdqduqNpAG27gDQBIKWq9vO8jMHTYAcAnvU+eKSdxtWFooopiCiiigAooooAKKKKACiiigAoooqeZAFFJRzRcBaKZuOKNxqfaIdh9FNyaMmmpJhYdRTdxo3UcyEOopm73pdxqrodh1FQmRvSjzOm5tv41n7RBYmopu6kzWidwH0UUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADJASKdS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTdgpQ26lrICN4Q1O206igdwooorUQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAReYN2CcH0qhdrNdXAEUrxImVbbjr6185/tlftraR+ynZ2NreaFqmr3+poxgktQqxR4/vOxGK4/4Af8ABTf4RfFaGPTtW1CXwjrBAVo9Y2okrYwSrqSPzIrLmZrGPKrn2PB5iqBIQ2BjIqasnw74p0bxVYR3WjapaapakYWW1mWRT+INafzc9KzXNHzJFVSKNx3Y2n61RutU8mFXCtnftxVqGVnXkc1cZOO5Ti1qycsVxxnNKx20xl37ecYqlq+sQaTZy3E5CxxjczMcAD61pzJamaTk7I0KWvFvDf7Ynwi8U+MP+EWsfGentrYYp9nd9oLDgqGPGc17NHKsiqynIYZBHII+tNNPYGmtx9FFFMQUUUUAFFFJu4JxQAtN3dKA4PGeajZn3KFVSvru/wDrUroBWLeZjb8v97NKrBs45qGWY+ZtCblPU56U1JY7dmUnA65NY85pysuUVVa4ClD1RujCpy+3HFa3RFmPoooqhBRRRQAUUUUAFFFFABRRRQAUVE0xEwTYcEZ3dqczHBx1oAKYju2dyY/Gm7WJDs2Mdh0pJp/LXIx+NJuxSjcfvfuF+nenox289a4Tx3r8mj6XPJFcFZkRpC6D7oAz+dfGXwm/4KRJ44/aCsfAMGm3H2GSV7eW8upBuMikj5QO2RXP7T37G/sWfoPtoZguM0kbeZGrYxkZpTg9a35kYW7j+1Vbi+S3YhzirDHg4Irl/GGpR6Lp82oPHJJ5Y5AHy1E3oXTim9SzY+KLS5uWWS5jhjdtsJdgpc9wM9a39/y8dcV+BH7Un7Q/jP8AaF/aCuNK8P6neW9lFqH9naVZ2Urw/Pu27jg8ndnmv3M+FWi6j4b+G/hjS9Xne51O106CK5eQ7mMgjUNk9+c0oXXxDqKP2TrqKQUtbGIUUUUAJmgsB1qKTKKTgsfQUuQ6jORQOxXu5H5GDtx1r5N/bO/assPgP4Ea6SWZtVuJcWsKttbcPX1FfUet6pDpdncTXEohijUn5v4sCvw+/ac8e6l+13+1hZ+ELAtDp41BdPtlJzt+bDsfXvXJL947M6oe5C/U/RP/AIJ0ftHeP/2hvCOt3njLStllaz5sdTCbBMpP3cd8etfZH8NcZ8Ifhjpnwj+Hei+FdLhWK0063WIbf42A5Y+pJrtOK6Ixsc0nd3Clpu75gMfjTqskKKKKACiiigAooooAKKKKnmQBRTcmjJqADdRuqIyc9KbHIzMcmuf2rL5Sam5psm8r8pwaa0m1RnrUuaAk3UbjVWRhCqszFsn0p32hNwXccms41LFWLG7b1NGarsxbqc1yXiL4teF/CfiCz0fVdYtbC6uU3Is8gXP51XOwsztNv+1QjHnnNRwzRXkEc0MiyROAyuhyCD0IqVVCjFdHKxFZZm891xxXlH7TnxQuvg38LNS8Xw232tdPUO0ePevYBAOTn5j3rA8deBdK+JHhHU/DeuW4utL1CFoJo2GDgjGR7ijlHzLsfJH7HP8AwUg0D9oLUJfDviK3j8PeIFY+QXcCKZc8AE9DivtVZBIoZWDKeQwOQa/FL49f8Exfij8GdcvNb8AiTxFokLmaGSzcrdxLkkDHcgY6V2n7Hf8AwUs134T6wvgn4xPez6RGxiXUbtWa6tmBxhweSo6VrH3RH6/DoKWsHwb400b4geHbPXNA1CLUtLu0DxXELZBBH6Gtv8a0Mx9FJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFRzMBqrtzTqKKdkAUUUVABRRRWoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBzHj34a+GPihocuj+KtEs9c06QYMN3GGx7g9QfpX5/ftGf8EfdB8RO2pfCjUY/D9zjL6XqTtJAx/2WwSPxr9KKaVPQHA+manlRXMz8Ibz4W/tM/sL6lFr8dvqGn6VbyZL2lx9ps3H+0qk4B9xX3n+yn/wVG8FfFqPTfD/AI4x4V8XTFYBJIP9FuX6Aq38JPocV9wapo9nrVhNY39rDe2cy7ZIJ0DIw9CDX5t/tc/8EoINbmuvFPwdddO1J3aafQ5pCI3YkkmFv4Tk9KmzHdH6UKIrmNJEKSxsNyspyD6EU6GLy8kmvxj+E/7aHxt/Y18TWnhH4maZf3vh+CVYZItSQmWOMcfupOhAHvX6z/CL4zeE/jd4Ttte8K6tBqNrMgZ40ceZExHKsvUEdKfNfcbv3O4kkEcbNjoM1+X3/BTv9rHVPDulJ4F0G9e1uL8k3TxMVdEB6Z96/QP44+Oo/hv8N9X12S8itBaws4aU/e46CvxQ+F/w78S/t+ftPyHVLiT+y3uWe6vFU7Y7dWOFHuRis5K87dC4+7Hm6mP+xz+x/wCLP2qPFj3GnXjaToenzBrzV8kSAnnCnu1fvh4P8Pf8In4W0rRvtUt6LG2jthcTHLuEULk+5xXP/CP4M+FPgf4Sg8PeEtMi02xjA3lR88rAY3Me5NdxWkbmUncWiiirJCiiigApu07gc8U6o5JCikgZoArzNH5jDzFDHtmmxL9nj2sFOOc5qldXltbbppdm4ckHqK8m+MH7S/g74L6Pc6nr2u2Fr5aFxZSTD7S47bY+Sc1kdipNq5684mkYOJ1tx2jcA5/HNWGhE0Z3KCCOWzxX40/Gb/grN4y1zxE7eBdMg0axibCS6gPOaRex2YGPzNYfhH/grz8bNB1C1XUoPD+vacjZktfsbQvID2EgY7fyNc9NS1cokfM/bS13lNu0IgGF7/jU+0/Lk8ivln9mL/gob8NP2htPtrO4vrfwl4rI2yaLfTjlv+mchChx+tfUihZAsituUjIIPBrcyJqWmMWCjaAT9aNp7nBrW6Mx9FFFMAopKKAFooooAKKKKAI9v5UdtvTincZ60i8k0DGbtyADnsc1HJGuMkAipjGMYBxis/UlbgrNtx/DXPO5pDV2R82ftsfEq5+EfwX1/X454SqxGGCNupmbge/Ffhn4P+Jmr+EPiRY+M7dxJqdrei8OeAzbskH2NfoX/wAFYPGkupXXhnwNa3Uhu5rozS2qn5WJOFzXinx4/wCCbXiP4R/BXSfH9nqJ1WN7ZLnULZsZgDKG4wO2e9RStZuW501G01Y/YT9m34uD46fBPwr42+z/AGWTVLXfLCBgK4JVsc9MivSua/P3/gkJ8cLfxZ8I73wBcTEah4ffzII27wOSePxNfoLtrZanK9GRnbGpZuPWvnz9sb4qT/Db4L+JNUjby1FrJFH672GBX0Mw3KQeRX5k/wDBYj4gNo/hPRvDFreFZL+4Es8IP8KjoKUk3ZFQt1Pl/wD4Jl/B2b4wftQ2et3aO9hoJbVLqTghpskqM4PUmv3V2/ga+F/+CQvwri8I/s5z+KZrcJqHiO+kkEmOTAnyqOnru/KvuvbV8rIbClooqyAoopGOBQA1qbI21SafjNVL6T92VX/WdvSk3YqKuzyn9pTxhp/gn4U+INUvZQfLtn2c9G28V+XP/BKvwFa/Ez9qjWPFd9C1xHpEMt9GxPAmdyFJ9eDX1Z/wVU8dN4a+Av2NXWO91G6WIcfeXHNcj/wRb8BvY+A/GfiqSPaL65S0ibuVUZP61zQWrZ0TdopH6VelJsFOqFpirbcc10t23Oa1wjjcKwZsg/nUo4AFRR3CyZGckUjTnztgBxjrjii+lws9ieimjNLzTELRRRQAUUUUAFFFNas2rAJRS0zcal2Q7AahiheNiWfcD2xT5pNi5qrJM6jIavPlLl3NYpvYnMxyahWYXGU2sretUGacsT5h/IVahhK4Z3+fHBzU86NnFRJtrbWjY7j2b0pjL5Kb3+dx3qtcal5LbY2V+xLMAK5rVvij4e0BdmsatbacM4LXLLGPwJPNRo9iOU621LyMSTwa/NX/AIK8/BLW7i38P/ELQ/tc8VnugvFt937peobjoK/SPw7rGn+ILRL3TbyG8tWHyvBIHB9+Kf4l8Oaf4u0O90fV7WO90y9haGeCUZVlI5Fd1GC6kczPzv8A+Caf7dQ8XWsfw28eahHFq1rGq6dfzuB56AABCfUDFfpIMNhhyDyCK/DL9vL9je9/ZN8YWHibwrdzf8IxfXDPaSxjD2cuchM+npn0r9Ov2Bf2ih+0R8CNOvbtgNc0cLp98pbLMyKAHP8AvAZrpSvsS+59LUdKKWnymYxucg8ivjD9uD/gn3oH7QGl3nibwvaw6T47hiJV4VCJeY6LJ7+9faNFHKVc/Dz9kv8Aa+8dfsafEI+AfG8E0fhg3nkXVldg/wCifPhpIx6cfiK/avwr4s0nxtoNprOh30Oo6bdIJIp4HDKQRnt39q+Tf29P2DtF/aO8P3HiXRIk03xvYQs6TQoP9NVQSI39/Q18Z/8ABOH9sO/+A/jp/hR43W4TRb29+ywtOTmxud20qQeik8VQ9z9lqWkVgygg5BGQRS0yAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopWQBRRRTAKbvFOpmw1kA+ikpa1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBFbdS01VK5zTqACiiigAooooAKKKKAPOfjh8CfCfx+8F3nhzxTp0VzDMhEVzsHm2744dD2Ir8gPHvw3+L3/AATG+KMOuaFqP27w3dysIrtAxt7pMkiKVT0bGMn16V+4e2vLP2kvDvhPxP8ACvVtP8Y2ttc6XLGVzcKCYyR95T2IrKXu6s0jduyPzM/ak/b80/8AaT/Z7S0sbX+xtYiKpf2EsgJkYgBmTH8Oc4zX0x/wSN+FaeE/2f5vEt1ZrFf61dsySsuH8peB+Br8fPihoekeFfiFrum6HdjUNJtbtktpieWTdwp+g4/Cv3f/AGAfif4W+In7Ovhu38PXUDXWlWyWt9ZoQHhlAAOR6HsamEeVt33He0bH0nS0lLW5kFFFFABRRRQAlRuwC81JXJ/EjxUng3wxf6pMHFvawSTyPGu4hVUk8fhRexcI8zsj5W/bg/bFsv2ePC9zBpNib7xFfhoYPMk2CPsXxtOQPwr83P2d/wBl34jft3ePL3Vb7U7ix0jzS154gu4mmWLJzsjQuufYA8VyXxn+Ll3+1d+0RBdXck0GnX+oRWlnbySZEUTMFz0HJHP41++fwn+HOifCvwFo/hvQLCDT7Kzto4ysKgb2CgM59SSM5rGK7nRUqSkrdD52+Cv/AATD+C3wntoZdR0X/hNdYVQJLzWhvjLY5Kw/dUZ7HNdt8Rf2Cfgb8SdFksLvwFpmkuwwt3osK2kqH1BQY/MV9CKp2jJyaNtVZnNc/Fr9rH/glz4o+B9jP4o8A6jceK/D0G6eVGiEV5YgcjBDHzB74Few/wDBO3/gojHIunfC74k3Uovd4t9M1q6kPz/wrC4K8EcDJNfqFLAk8bRyKskbDDKwyCPQivyR/wCCqf7IaeBdWtfir4G0j+z9MfjVkslCLBLuyJlA+6STzinZjufrgMMMg8HuKdXwP/wS1/a2h+Knw8PgbxNrPn+LNKbFt9qkzLc2+OOT1K4r733VJNhaKTdSMwXGTg1rsIiuLgwx7htPPPNPhk8xQa+Sf21/24/D37NWmixt1j1fxXPExtbFZPlQ9Nz+mK6f9gnxV42+InwNt/GXji9Nxe67cyXVvAY9ggi3EAD1BxWV5OWmxrypRu9z6TopKWtTIKKKKAGNHukDZPHalVduadRQBF8+09M9q5nUbSewE8wZpmJyit057VuX2pLYqAwYljhTjjNcZ8VvF8fhf4beI9XuZltnsLOWYSfw7gpI/WsJ6ux1Um4vm6H5F/Ef7b+0N/wUdstFdVmitdUjtwsJyAkZBbrnuDX7G+MvAth4t+H+o+F7mEPYXNm1rswPu7cDqMZr8nf+CUHh8fFD9qbxh471FGluLOKe9D9V82aQjv6bjiv2LqopIynLmZ+GnwP1rUP2Nf28G8OW8v8AxL59UXTZRdZw9tKRg/LjkZwO3FfuVX4y/wDBVT4e6h4B/aE0z4gWkDR2d0Iisg4xLG24H8a/WT4J+Ov+FlfCPwh4nZ43l1TS7e5m8n7okaMFwMk9GyOacWhSXU62a8igL+Y4UAZr8N/+ClHjGb4mftaT+H7PfMtk8NnCuDzI+P6Gv3B1m8tdH0u8vrx1S2hjaSR26BQMmvxL8B28f7UH/BSgXmkwSS6Q+vC9kdVBCQW4ALdOh2frR1Q1tc/Y34H+Brb4a/CDwf4ZtYjFHpumQQspxnfsBcnAHO4tXcUlLWhkFFFFABSEbqWigBKq3JTcFb5Qe+KtVla1fGzt5TkZ2kqp65qJ7GkE27I/LH/gst4utri48IaBA+97cvLIQfWvsb/gm/4IbwP+yR4Mjltfs1zfxvfSZ6tvY7T/AN8gV+Z37dk194+/a+0zw9PcpfGSW3gWGMcKzuMgj6Gv218FeGbXwb4Q0XQrFDHaabZxWsSk5IVECgfpUQWhdTsbVY99ffZ45mAcKmSWIrXqhrqr/Y95ubaPLbn04q57GcdzkfDvjDSr2+aBtWtI5/M2+RLMqyknoAua7ny8rjJ/Ov5wvip8VvFWi/tBeJ9atdbuvt2na/ctbMZDtTy52CDbnGMAcV+9/wCzD8Tb/wCMnwB8E+MtUiEOo6rYLLcKowDIrMjMB2yVJx70qd7WZpUld6Hpcl3DZxgzzRxL0DSMB/OpVlVlDKQQeQQeDX5g/wDBYb4p+IfC9x4L8PaTezafb3gknla3kKMxBwBkV1H/AASF+NHjL4keH/F+heJdauNYsNHWA2X2o75I92QRvPJHHSruiGlY/RmikFLTMwooooAKa1BakrOTuA12IHFJSyAlTTVB2jmuKbNClM5kYDccKeeO1Vri4IZQo4zWr5fX368VTnjjH8PSsJxN6cl2GLCrRO5XAA9a+Zf2r/2stG/Z20Vbprn7bqJ+7ZqwzXf/ALRX7RGl/A74c6nrVyBNNDGwjhJA3N2r8VtQbx7+3T8dAun2U0k97OqLGoLQ2kZP3mP61rTpxmrmnNyRfMjtfG37e3xt+NHitbLwjdXWjpNIVg03SLdZ5ZsnjO5Tz9Kn8Ufsh/tYfFi1j1LxFoGtakdgdIruRUYgjP3Riv1T/ZH/AGLfCP7LvhSOKC3h1bxPOA93q80QL7scqn90A+lfReBXbGmo/Cjj5mfkJ/wTd0z41/Cf9pCHwf4h03XdO8Py28ov7PUY28hdqna6sfTjGDiv1yuLyC1iMk0qxIBkljip/JjMgcou8DG7HOPrX5g/8FRviz8Zvhr49sYfDNxfaZ4NurMYvLGLeDLnkMcHFVaXQVz1j/gp98YvAS/s+6t4Yu7621DWrza9rbxsGZGB+97Vx/8AwRd8NyWfwj8Z63NEU+3alFFE3qqIc/qRX5J+JNc13xhqT3mr3l1qd2xO53JY5zk8dq+ov2Q/2+fGf7MOlnwwmnWuteH7i7WRorglJIMkBiMD09aqKsF9D94qWsnwpr8XirwxpOswDbFqFpFdKuc4DoGA/WtaqJCiiigBhr8h/wDgrH+zQfh74usPi14YtxZ2eoTBL9bZNgjuBysvHc+tfr0a+Sv+CoNzpsH7IviddRjDtJJCtvxkrJvGCPegqO53n7D/AMaYvjp+zf4T1xpmm1O1tl0+/wDMbc/nxAKSx9WADfjXvVfAn/BGtXH7OuvOwO19achj/F8g5r77oJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKVkAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaAGTTLBG8jkKijcSegFflz/AMFLP2ubmz0FfCOkXMUqX5dWaFwSig4ycV9wftVfGbQ/hP8ACfXrrVL4Ws01pJHAqsAzMVIAFfjL+yb+zX4g/bM+MEi3dxMPD1nIZ7++nLMFTORGD6msWuZ26G8VyrmPof8AYP8A+CcnhT4+fCceO/Hd3qBF/O62lvbP5fyqcFmPfmvN/GS+JP8Agmd+1oR4cuLyXwtPtdVuc+XeWzHlG7Er0z7V+0nw/wDA2k/DXwZpHhjQ7dbbS9Mt0toYwOyjGT7nqfrXzn/wUY/Zttfj58B9RuLa3U+I9BRr6xlVcsQoy6fQiqsRzH0N8M/H2mfFDwHofinSJ47ix1S1juUaNshSyglfqDkfhXT1+Vf/AASF/aR/su/1f4QeI71oWkb7To0NwcbZAT5sPse4HtX6pbq0IHUUUUCCk3D1paTaPSgAB61U1DT4NUt5ILmJJoZUaOSORchlIwRire2k2+9TJXHdp6H58eIP+CQ/hv8A4WXD4r8KeNtQ8PquoC/NnJbJOiHfv2JyuB2Gc4FfoDY27WtrDE8hmeNFQyN1YgYz+NTbe3alC4qbMfM7WFooorQkKwfHXgjSPiP4T1Pw3r1qt7pWoQmGeFu4Pf6it6igD8Ef2mPgn4l/YI/aL0/V/DdxMNM84Xmj3x+RWAOWiOCenSv2N/ZZ/aC0n9pD4Q6P4q0+aP7c0SRajao2TBcBRvGPTOcVxv7dX7Lcf7Unwhl0q0aODxHpzG602eRc/PjlM54DdM1+Wf7Cv7QV/wDsg/tEXnh3xZcTWXh+4uZNL1e36pFMrFBJ9Aw6+lRZmtro/d1jtGa47xp4psPD2j3erarepp1lZRvLJNI2Bhc8D1NXNW+Ifh3R/CLeJbvV7WLRRALgXhlGwoRkEH3Br8df28f2yL79pTxpZ+Afh291JoUNx9nAtyc3szHBxjquaiTvogjE5a40fU/2/v20rkWFu8miNdeXLMn3Us43I357Fl5/Gv3B8IeFNN8C+FtK8PaRALbTNMto7W3iH8KIoA/Hivnj9g/9k3T/ANmf4WWJu4Ffxdq0EdxqEzoBJEWUMYfopJH4V9P7auKsRKVxaKKKskKKKKACiiigChqDK0ZV9uPevib/AIKnfEr/AIQv9m640y1n8q51icWw2nDFCctX2Zq2p2yJKH+ZkOMCvyZ/4K7eMP7d8c+B/BVsc3CRm6dM8DzG2oD+tc3O3I7ErQue7f8ABG/4Snwz8HNc8bTM/m69dm3hU4x5UR69M8t/Kv0MrzX9m34cQfCb4FeCfC8CBHstLg88gAbpmQNIf++ia9KrWzOM+Lv+Co3wtk+IH7PuoX8UG+XR/wDSlcDkY6/hXNf8EfPig/i79n/UfDN1dCW68P3xWKNiSwhcZH4ZyK+yPix4Vi8afDXxNocqqy3+nzQDcOAWQgH86/HD/gnP8X4f2X/2oNX8K+KZV0/StWMmlT3M5KpHLG/yP6YLL19DUxVjW94n6lftg+LIfCfwT8Vz3V01pA2mzKGU43OVwBXw3/wRZ+H6zal488aTW7ErFFp9vcOASCx3vgkdeB+tejf8FWvjZ4R1b4Ax6HpPiW0vNRvLtQkNo+8uqn5gSO1et/8ABMD4ap4A/ZR8PXbFjd668moy9MAFiEA4/ugdc01qO9o2PraiiitTEKKKKACiiigBB3rnvF80Nvptw8jBT5bDce3Fb0hWPknArzP9oDxIvhv4fX955DTqsEjHZ1ACE1nN2izal8aPyT/Z70Oy+Lv/AAUiZtRke8httXnuCc/xQswUfT5RX7d1+Mn/AASkhtfF37YXibWZoz5n2K8v4efus8wHP4Ma/ZynFWRM3diHtUV4qSW0iyDKFSCPapap6w7Lp8204Ow8/hRL4WTHdH85n7Q2mQa9+1R4102wjWKO48RzWyKo4yZip/XNf0G/B7wbB8PfhX4T8N28Qgi0zTLe22D+8EG4/i2T+NfgJqFqPEn7aWoW44Fx43mQsD1H2xhmv6J2ZLe3JY4RF5PsBSjoXI/IP/gtBrKz/EvwNarxJBZTO/f+MYr2f/gi54PSx+EvjHxHJGwuL/UEt0kycGNFzjH1NfEf/BSn4tW3xT/aY1dNPk8zT9HX+z0zz86kiT9RX29/wRl+I39s/CnxR4Rki2yaTeLco4UAFZBzk9zkUAz9GaWkpa0MgooooAa3WmswUUrd6iaMt1rCTsNaj2b5M1H+dG44x2qBJnk4wVw2M1w1DVImLD5lH3scVwXxI+IWnfDvTft+q3sNpZqpMs87BUTFd5GuZCT16Zr4K/4K9WkMP7P8N2L9re4fUY4xCrkCRcZIx3pfFZGtNqL1PhP9vj9rBPjp44l0rw3cufDFkxDMp+WeQHBYd8Zr0v8A4JuftffDX9njSdU07xhEbK8vZsjUEi3ED3PpWF/wTn/Yd8L/ALU1r4k1jxi2r2ulaW8cELafMkazSMMspJQ9B6V7h+1l/wAEnfC/hD4a6n4m+Ftxqzajp8Znl0y/mWdZI1GW2EIDnHau9QjGPKjJu71P008H+LtI8eeGtP13Qr2PUNLvoUngnibIKsoI+hwRxWyOABnNflN/wSB/aE/svV9d+Fmv6k6NOVuNKguGxtkAxJGueR9Pav1ZrVMyasLVPU9HsNatzBqFjb38B/5Z3MSyL+TA1coqhHKQ/CXwPbsWi8G+H42PJZdLgBP47KB8JvBCyNIPB2gb25Lf2ZBk/wDjtdXRQBFbWsNnAkMESQwoNqxxjCqB0AHYVLRRQAUUUUAJX5j/APBZL40W0HhfQPhxZzN9tuZxe3Ko3Gxfug/jX6DfF/4lWHwl+HOveKdQkRItNtXmCu2NzAfKv4mvxG+Hui+N/wDgoh+1Pa32oq9zaees97IQfJsrRWyE9sjA9yanmLj3P1Y/4J4fDGf4W/sp+DrO9tooNQ1CE6lM0a4ZxMd6FvU7CtfSlVNJ0u10PSrPTbGFbeys4Ut4IUGFSNFCqo9gABVuqICiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAG+tZviLWLfQdFu765uI7aKGMsZZGwo4rTr44/4KdeGfiZ4i+B2PAFvNd20MnmalFZsfP8AKA6qo6j6VEuboVFK+p+ff/BQb9oZvjt8QrDwjoE0l9FYzmI+WcrPMz7dq4681+pH7Ef7O+n/ALPHwP0fTY7TyNc1CCK81WRh8xnKAlfopJFfm/8A8E6/2HfGfjP4taJ8QPF2iTaZ4S0uX7YjagpSS8kxlAqnkjOCSa/aPFEVYucr7BTZoUuIXilQPG4KsrDIIPUU+irMj8W/+Ch3wXH7KP7R3hv4h+D5WsbTWrr7cscIK/Z542UuAfRgen1r9Xv2f/jBp/x4+EPhrxtp21U1O1V5oVYN5MwGJIyR3DZr5R/4LCeA5fEn7OtjrkFt58mi6gsjOo5RH4Y/TiuS/wCCLPiTUtQ+Gfj3RZWlm0XT9Qt5bOR+FV5I281QPqqmgrofpBS0UUEhRRRQAUUUUAFFFFABRRRQAUUUUANK5z6V+bX/AAUc/wCCe178Q7q5+Jvw6svP1tYwNS0S3TDXQH/LVP8AaHcY561+k9FA7s/n60n9m/8Aad8U6LF4atvDPjOTQ5AALW+SRIVXt944Ax2r9J/2Ef8AgnnonwD0my8WeMbaHVPiBMgkVXG6PT1IGEA7uO57V9vUlKyHzMTb706iimSFFFFABRRRQAUUUUAfI37bn7TVp+zX4bk1JIvtep3EqpbW7Z2OepzjmvzZ8M+MLz9uD9tTwNeDSmtXnktVu4Y8tGkUJ8yR+c8Z3fpX1r/wWU8F3118N/DGuxwtPaWd+yzOo4XcDjNef/8ABFv4bxX/AIw8ceOJovMFhaRabaSMB8ryHdJj3wuPxNc0Va7Z0Sk7K2x+tKgKoAGABgAUtJS10nOMlUPGysNytwQa/Fb/AIK3fA4/Dz4xaZ4u021SDR9dg27YRtVLhTzjHcjBr9q25FfDv/BW34ZP42/Ztj1mBZGufDt6t4BHjlSCrZ46YPbuBUWLj2PyD+Geg6j8XPFfhrwTD5lzc32pRxxF3ztRj83X2r+jf4X+B7b4afDvw54Vs+bfSbGK0VjjnaoBPQdTk1+Cn/BO9I5v2xPhrG8auhv2+9/1zYiv6E6cVYJO4UUUVRAUUUUAFFFFAEW3ceQD9a4L46aWt/8ACrxSGBcpp07Iqjv5Zrv9veuZ+JVrcXvgnWIreRY3NrJkuMjbsOaznFyTSNYfErH5Jf8ABGuAt+0h4maUFZY/DszFemD9pjB/nX7LV+Mf/BLbV18P/tt+J9N82NUvLXULRc/xBZt4x+KV+za9KtbESTT1FrE8W6kuleHdTupOEhgkc/QITW1XG/GCTy/hd4qcfeXTbjH/AH7alJXVgjufgd8CdnjP9tLQJ8F477xY9zkcZDTlxX7M/tpftNaR+zz8LtRmmmU6xeQtFaxAgkMRgHFfgZ4G8Zav4C8caZ4i0Jj/AGvptytzbsU3/MvqvevsaPwL8cv+CknjzSNT1nS5NJ8OxCOKfUWh8qFQANzKvc/41Ni2fM2q/B74heMvCd38UR4fvNR0PUruaWbULeMuBKXJbIHQZNfp9/wRp8Dz+HvhT4y1a90+4s7m+1CNI3uIym+NUJBAPbJr7X+Efwe0L4R/CnQvA2n2sMunadaJBJvQETyBQHkYHuzZP412Wn6XZ6TbiCytorWEdI4UCr+Qp2ZPMWaWiirICiimsTSbsrgI3f0rmI/iLoS6hNY3N8tlPFKIR9rIjEjHoFyea4b44ftH+Ffgpo9zdavq9nHNEpJt/MG/ODjivxf8UfGLx3+0l+1Bp93oFzf37vq0MtjZRuxiVRICGK9AMY7e1cbnKb0N4011P3/2j0puBVfTVuv7NtfthUXflJ52zG3fgbgPbOas7huI79aJJMz1I1IVj8tfnB/wWkTy/hj4H2xtifVWEkuTgYjJGR0r9IYyT1ry/wDaP/Z58O/tJ/De78K6+hjbPnWd4n3racAhXA79ehpwje0uxV9T5J/4I2eLtNvPgl4i0FbiL+1LXVWmeLIDsjKMNj04r9CJFDxsrDIIwRX8+cx+LX/BP346XwtFudLurO5MUc0tuDa6nbKxVWyQfldRnjkZr7d8G/8ABaXw/Jp8aeK/BN7a36qBJJp8qyRM2PmK55xnOK3EfJvxVsG+CP8AwUSupdIVlW38Vw3UMUXBIuHEjqPxdhX7y1+FvhPxZa/tf/8ABRjQvEGhWEmnaXfavbXQjnG4xxQqCxbr94qfoTxX7p1cVYUncKKKKogKKKKACiiigAqO4uEtYJJpGCoilixOAAKivryOxt3nlcJGoyWY4FfJf7SPx71rxlDcfDP4aKt94t1M+Q1xCcpbRk4Ziw6YrKdRQ0NYU5T1Wx8o/t0ftBeKP2mvisPgf8O4JLm0a4S3vJYMsGYNhgxH8INfcf7GX7JOj/so/DxtOhdb3X9Q2y6hfbAGLYHyA/3Qc1B+yP8Asb6B+zfor6ldbNa8c6kol1LWZlDSGRhl1Rjzt3E19HYqrEzd9EFLRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJuHrS1GsKhiakoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEVQqhVACgYAHQUtFFABRRRQBieNPBmkfELwxf+H9es0v9KvozFPBIOGU1hfCP4M+Evgf4ZOheD9Ji0qwZ/NkWMcu2MZJ78V3FFABRRRQAUUUUAFFN2+9LQAtFFIWAIBPNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHJfFD4XeHfjB4PvfDPiexS/0u7XDRt1U9mHuK5f9nf8AZw8Kfs0eD7rw74USX7Lc3b3cks+C7E9FJA6KOBXqtFKyHdhRRRTEJXiP7aGqW2j/ALMfj65vLRr22GnOrxIu488A/gcV7fVDXNCsfEmj3ml6lbR3lheRNDPBKuVdWGCCKBp2Z/Oh+yD4+tvhX+0t8PfEt8m6ytNVhWfB6LKNmfw3Z/Cv6PEkEihlIKtyCDkEeor8EP28f2PL79mf4q3F1o9veT+DdTke6sbuKMsbZmdmETEAAbcgD2FfsP8Asa6n4g1n9l34a6h4nl+0axc6PDK0u0gtER+5YgkncYvLY+5PQcAHyvc9pVtygjoaWkXoKWgkKKKKACiiigBrdqg1C3W+s57d1DLIjIQ3QgjGKsYo20BqndH4R+Fb7/hmX/gpKG1EfZ9Pt/FM0cm3/n3uJG2/gN4/Kv3bQhlyDkGvy7/4K/8A7OtjY2Wi/F/Q7aaPVjeJY6p5AyCuC0cowOGBUgn3Few/8E4P23o/jt4TXwV4w1G1TxzpSLHb7V8v7bbKqqrjJ5fAyfXOaDSXvan3JXkf7V3iaXwj+z1441OH/WRabKBxnquP6161uOORiua+JPgvSviL4F1rw1rZZdL1O2a2nZG2sqkdQexFBMdGfj7/AMEhvhTpfxA+NHiPVdY0yDUrLR9PV1S4QOgkc4Bwepr9ndN0uz0e0S1sbWGztk+7FAgRR+Ar48/YP/Zz8Lfst+KvG2hWnjXTvEOqaxIj29vDKPNSCMvgFc9RkZr7P2igG7sKWiigkKKKKACqWrNPHpt09tH5s6xsUjzje204HtzV2kqWrqwH4k+Nv2Jf2jf2jPjFr13rGiy6VZ3WozuLvUJdkCx+Y20qo6jGMYr9Fv2MP2G/Df7Knh1rmRo9b8ZXqL9s1RlOI+ATHEDwFBzzgE19QbaMdKyiraFczIyAUA6j60xVDNuPXpT29KQYXrxUcuow+7nFOU0cHmlxiqhv5Acv8QPhn4X+Knh+60XxVolnrWn3CbHjuo8nGc8MPmX8CK+SvEH/AASF+BetajJdW7+I9HikYt9jstQQwpk5wu+NmAHQZJr7f2ijaK15RXPnn9m39hf4Zfsv6hdan4Xtr2+1e4XZ9v1SVZZUX0XCqB+VfQ9FFWSFFFFABRRRQAUUUUAcX8XvB+o+PfAOq6LpN/8A2Zf3Me2K5/uGuB/Zp/Zn074E6D5126at4quhuvdWdcuzHlgD6bs17lRWbpxcuZ7miqSUeVbCCloorQzCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopN1NeTauQpc+i4oAfRSVE8jbTtXBzj5qAJqKaudoz1xzTqACiiigAooooAKKKKACiiigAooooAKKKKACiiigApCoJBI5paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6lpFlrNube/tIL23JyYriMOv5EVNbWkVnbxW9vEkEEShI4o1CqigYAAHQAVNRQAUUUUAFFFFABRRRQAUUUUAZniDw7pvirSbnS9XsodQsLhSklvcIHVgRjoa/I/wDau/4J1eMP2fNfvPid8IL26udJs5zdLaWzsL2yBOcLj76Lx+FfsFtprRrIpVgGVhgqRkEUDTsfkP8ABn/gsB4m8D6GdH+IPhlvEN9bbYo7qBvImIUY/eKf4jjk+tM8b/8ABRT4uftIarH4d+F3hK6sbi5DQKsKmYFW4yx6KcH8K/TDxH+zH8KfF2pPqGr+AdDvr13LtNJaKGZicknGMnNdZ4V+HfhjwPapbeH9A0/R4UGFWztkjP5gZoKuj43/AGEf2AdR+CevxfEzx/rNxqXji7tiyWIlYx2ZlXMqyf33BOM9Mg191UUUEBRRRQAUUUUAFFFFTzIAopuTTdx9azAUgZpjR7up4pJHKjg1FuB5MmDUcyLSY+NjuK54HFTVX2lYyynnsaWOYrGCx3GsE3F6jtpcs0tIKWvQMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKTcPWgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKYWbP3c/jThQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIx20DkZoYbhQOABQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbvVSQJbzGcK7vJhML2q5tNG2gYbht681DcKzKu045zUMlwVuljRee5NMnVruZQpZPLPJ5plxTuXo5N3BBUj1p9R44BPLCnK3AyOaRA6iiigQUUUUAFFFFABRRRQAUUm6gtRsAtFRNPsx8rH6UfaFDBT8pPIzUcyY7MeW5AxTqjV9yn604NxVgM+0L53lnhu1S0zjduxz60u6gQ6im7qN1ADqKKKACiikY7RQAtFIDkA0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNY4FGTUZZvMwfu4rOSsOwu47Qe+aKbuG7aRwOacrKy5HSoGVLi62kjYTimMyyQjaNkjd6syMvpVZpEJ+dHIB4wKxNktCbzGjt9pGWUYJqKzkLsQYSBnOc/rT45Dcn5TsRTyCOtWFxtGOBUtXaZLfKrE1LVcoc9alXIUCu3mRlYVWJJp1IAOtLVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSloAKbtFOooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIvOTzNn8X+6f51DfanaaXbvcXdzDbQL96SZwqj8TX4O65/wUW/aM+JOsm20vxDNbTXD7orLRbQM3J4UBQT+dXW+FP7Y/wC0FMLW90fxxd20p3F9WVtPt2z3DyFFI+hxWfv9jS0O5+v3jz9rT4SfDeKSTXvHGj2jKu4RrcK7t7AKTzXzR4y/4LGfCHQL5bfSNK13xGM4aS2hSJQfrI65HuK+XvBf/BGv4s699mvPEviPw54eSUBprdp5bu6jJ6g7Y/LYj1DkV774K/4Is+B7BGfxV431jWJ26DToY7RU+hO/P5Cndj902fDv/BZf4T6lqUdrqnhrxLpEbNg3UkcEkae52Slj+Ar6t+F/7UXww+MVvBJ4W8XWF/JMiuLdpPLlGR0KNgg+1fFvxH/4Iu+Er3S5W8GeNdVstRX/AFSa0FmiPsWRQR+Ar88fjt8CfGn7I/xA/sbUtXgh1HZ5kd1pFyRvXPDYOGGfcUubYVrn9GqMHUMpDKRkEHINOrwP9ha/1vUf2Vfh9ea/c3F5fTabHIZrk5coR8uT1PFe91oZi0UUUAFFFFABRRRQBHJlQSOfaq/2hpoWKqUccYbvVrbWfdLNFI8kYWQZ6dxxisJ8xcUie1uBMoUn59oP1qRoVkYFhlhxX4+f8FBfD/xs+B/jq48U2PjnWbjw5qkzzobWRoktdxyI8Z5x0rm/2Of+Cifxi0fxp4f8FXit48sNRulgjhvGJuUBOCVk5wByeRRB6XLa1sftQV6KOMUpcKMsQv41HBI8kCSPHsdlBKZ6H0ql5qTOy3CmPa+VyetOU3F2YuW5p0VSTVEa68kKSuPvAE/h0qaYSSNEUAwGycnHH5VrFqWxHK09SekbODgZNMYtvABUA+vWnIrLnLbufSi6Cw9CWUEjBx0p1JS0yQpv3sjpTqQLgk0AAGABS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAITj6UA55FIF65JIPrSgbQAKAILi8S3wXZY1zg7q4S++PfgfR9Wh03UfEWn2N1J0Wa4VRn0PPFef/tbfFIfCH4b63r80c8qxwMsRQ/KrkYFfjD8I/gL8S/21fiFrE/h5o5ZVka4uLrUrh0hi3HOAcH8qxUm2buCirs/oT0vXNN1uFZdOv7W+iYZD20yyDH1Bq5uG7aDz7ivwh+IP7MP7Rn7FN9b+I9Our6O1VN76l4duXlhjYdRIGz+o/Kvuf/gnT+3xffH5pPAvjdhJ4utIvMgv449i3cajksM/f7nGB7Vpcy5WffA6dMUtFFUSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADKa+ByetSYpjxq3UVE9ikxFAZQcdqrnbDuG/g/w1L5m2NsD7vFVo7pF5ZGJ78VjzIpIi87aWByw/hHtS8tt3ZAI6ZpI7iC4uG2ZLg9DU8rKPvrnFZm4JGxPDYXtVhRtUCqUUxDnj5e1WoZgzENxzxQtTOaZKW2jpmlU5ANJuA+lOGK6VEyHUtFFaEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANX7xp1FJ060ALRTQ6t0INOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDzT4O/s4/Dr4E6PBYeDPCthpJRAr3nlB7mUgY3PKfmJP1r0umhqZNcxW67pZFjHqxxS23AdtG4sBz05py/dHes2+8RaZp1uLi61C2tYOvmTShFP4k07R/EWl+IIWl0vULXUIlOC9rKsgB+oNF0Ow7WNQj0rS7u8mYJFbxtKzH0AJr8BPj346vP2r/ANr1TbR4jvdUTTrRe5iWTGTjPbNfup8YNWh0n4da/POgeNbOUlW7jaa/Gf8A4Jw/D2D4i/tkC/lh22mkSTXwT0O47f1rLeVjZaRP2z8FeHLfwn4R0bRbVNltY2kVsiegVQK26SlrUwCiiimAUUUUAFFFFAEM1wIVJIY844FN84bCV5H86ex3Eg9DXOeINS/4RXStQ1CaVTHFDJKN3GNqkiuebdrmsUnofl7/AMFdv2gZLvVtO+HWnsVSNPtF2pGcE9q6f/gkr+yTZQ6Gnxj11POvrhni0m3kjx5SA4Muc87u3FfBvxe+Iq/tAftFXWreJb9dJ0+7vxA91KC6wwB8E8deK/UK4/4KD/Aj9nf4U6d4Y8FaqNek0mzW3tra1jZVZgvXcR3NEXyqzKlufeHPA6Cqt9ZpdR88MOhr8NvjZ/wVI+LPxNklg0K/bwhphPyx2Lfvtvu4A/PFfo7/AME39a8Z+KP2WtO1nxbq9/qeo393O9vLqTmSTyd5C/MeSD1qk9LyRMVruZn7YX7dH/DJc2h21v4VXxHJqDv5jy3ZgEO046bW3fpT/Cf7bF1+0R8BfEuvfC62WPxxpNiLifSJEMpjfGSqk43dPSuG/wCCp3gPw1qPwWute1bEerWLLHZybsbmPUYrwP8A4It20s3xR8bXWJDAumxIWXhN248EevvWEfej2N5yXNscN8O/+Crvxq+HPi+7h8YwWfiCy+1H7Xp17A0M8HPKoQflx6EGv1L/AGbf2s/An7TnhwX/AIZvxHqEar9p0y5IWaJiORjuPcVy/wC1J+wt8PP2lNFma40+20DxRy0GuWduBJvPP7wKRvBPc81+THjz9lf49/sY+II/F/2C6tLSyn3Ra3pE4nhYA/KZApyoPowrptoYL3tj9+dwHfmm+Y27G3t618nf8E/v2yG/am8Ay2us2skHizR1SO+lVCYbjjiRTgAE/wB3t6mvrWtDMRTuUHGKWiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUw7+2MU+igBu4hcnrTqQrnijnnOPagD4O/4KxeJLjR/gPPYQTYjvp1EgbqMHtVL/gjh4VtrH9n/AFfX1i23mo6nJHJISTlY+Bgdq47/AIK/arDD8PdOtjMftMt4f3eeNor2j/gk3Ypa/sb6BMud89/es/pxMwH6VhE6qjtFI+vNU0uz1zTrmwv7aO7s7hDHLBMoZXU9QRX40ftlfBO//Yh/aK8PeO/h48un6TqFybmLAPlwsZPmgIXHyY7da/aLFYfirwPoHjizjtPEGj2Ws20biRIr2BZVVh0IBHBrTlZjCVnqSeDdabxF4S0fVHAV7y0inYL0yygmtmo4IY7aFIokWONFCqqjAAHQCpKsh7hRRRQIKKKKACiiigAooooAKKKKACiiigAopuTmlzSAWmHNDMRTM7sE9azmykiOZyuQKrxxpKzBmPTpnFWXAY8jNQsWjyUUVzmq12IlVY/ugfXHNSbvMG081V84ozF2yOu3HSo4b5HyVyp9cVldG/Ky+22NVGMdqZNMm7B6KKzLzVltot0pJGfvCqzahJfIJIU2qTwx7ihVFEqNJ9TW+2OR6ir9rIXiUms+zgeaNR9w45q9DG8R2nkDvXXTu9TGpy7ItUtNVgeO9OrW5yhRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJD8pp9NZQwoAq/MoUqpPPpVsdKbGu3Ip9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfk/4L/4LKT+HvhPptrrHhRtc8aQR+S8yT7IZNowHfjIJ9s188/F7/gpX8ZPjLcS2ljcR+HrSZyYrPSVLugPRQ2Mk/WtD9jP/AIJ0a5+1J4Zg8Y3HiOw0nwsLw209upk+1uEPzYHllee3zV+tnwc/ZC+FXwL023g8O+E7E3kSBW1G7iE08hH8RZs4P0xUJKT1Luz8E/GzfFm+0tdV8U/8JadJmOftOpLcLA2fTOFx9K+6f+CL41ubxt4yl3XT+H0s0QF2bylmz0APHSvrL9rz4D+If2tobLwhp2t3HhzQLaXfcSLAHSUj1+YcV6/+zT+zr4f/AGZ/hva+F9EIuJB893fNGEa4k7sR2+maLFPTc5b9uDxvH4D/AGf/ABbfTNkSWTwxqv3tzcZ5r4U/4It+F3v/AB94+8SFgY7e2jt/mzks7EnFep/8FjPH2oeH/h94Y0W0XFpqk0izS5BAx2PetP8A4I06HaWnwJ8QalHsN3daoySMvXaowBSjuVLZH6E0tN3Uu6tDnFooooGFFFFABRRRQAwq27jGK+Sf+CjXxV/4Vf8AAvVJ47xYb+9/cQwq2GIPBNfWVxeR2+3ecbjgV+JP/BVD40P8RfjofDNjctNpukIItkb5V5T2x61hPWyRvTXU84/Zz/YI+JX7T2lxeIdGFnpnh+ado5NRu5CTkHkhO9fYd3/wSB8E+BvAOpa14p+IWsvNY2jzyfYlihhDKucDcrHGfevkv4Q/tjfGz9kfQbfw/a2q2ujn95Bb6nakx885B71L8bP+ClHxX+OHgO88Jaw2mWem3bfvpLCExsw9M56UWk+ojgv2Z/gK/wAfPj/p/hbTba6m8Pi+3XdxJhnS3U87mGByB6DrX9B3hrwrp3gzw1p2h6Rbx2WmafCsMMSDARVFfif/AME6f2pfh3+y7q3iXVvGQ1ie5volitotOsVl4HU7mkXr9K+r/Gn/AAWI+Ht5p8sOj+F/EnmMrBTcLHFk446Fqp7NCW54z/wVk+PlxrWvWfw6g2yW1nIbqWZRjcOgGP8A69fSH/BI/wCD0/gX4J3nie/WNLvX5/MjRR8yRDpmvyM+MHxJvvi58RtU8TXUbeZezmSO3djI0a54XoM19H2n/BQ/43Q/DfRvBnhKzi0Wz0+BbdZ9NsHM7ADAJIBwayjFxikVu3c/djqOtVdU0my1zT57HUbWG+s51KSwXCB0cHsQeDX89msftOftF3F0Rd+M/F8Ezn/Vjzk59htr9SP+CYP/AAtfUPhbqmu/EzVdZ1KPUplfTP7YnZ2EQHVVblQTWyk+pDjbVM+s/BPw38L/AA2sJbLwtoNhoNrK5keKxgEYZj3OK6Skpa0MwooooAKKKKACiiigAooooAKKKKACiiildAFFFFF0AUU0tSbjuxii6HYfSMu5SM4qKSV1wVXcO9LHMZFyV2+1F0Fj8o/+CyOlmF/C9z5shEk7rsJG369OtfT3/BKFSv7GXhwFg3+n32Mdv3x4r5u/4LJagbi18NW/2dlaK4Yq/Zq+gP8Agkjeed+x/pkOAPJ1W9U/jJmsoam1TVo+1KKazbetG6tbmA6io/M+bb1NNWY7vm49Kew7E1FJSM23JPAFK9hC0tfP/wAav2yfh38BdSSLxJrMYLjmK3YSSA+hUdK7D4EftFeDP2jfDMuteC9R+2QQt5c0cilXib0YUuZFuLR6hRXxF+1F/wAFANa/ZT+J+m+Hdd8LQaxpV6ol/tCGVozGhOOmCCQK+o/g38ZPDPxz8D2Xijwtfx31hcKCyqfniburDsRVBKLjud1RRRQQFFFFABRRRQBDJMI+O5PTNPzu9q+Fv+CjHxg+KX7P2k2/ibwobf8AsS5cQ/aHG9reX1Kngg1lfsO/8FKLD4vtbeEPiJJb6R4pVQsF8xCRXh+nRTWMZScndG0oLlTTPvuRsDjk1BFMWkZSOlWI5ElRXjZXRhkMpyD9KTysMWB5PtSkmyE1sU1mkJYtwoJ/EVXkvI0Vmlc5/u+lWrmzMwYhsHGOtRR2oaNvNUM3risrHRFxKceoRtEXU8dBVd75vtCxiMLEw+9U8mmIFOBjJyeaz7qxaJXZW8kAZLHnj8awaZ0xs9ipr2vaTocEr3t3GiIN7FzgAV81fEX/AIKSfBjwDeTae+uTXt9a5V7ext2fDj+EnpXzx/wUp/ai/wCEQuE8EeGbvzNTni3Xd0uCY1PVMYrwr9h//gn3qP7Uyy+KfEWqTaR4QEjRm5s2AuppB127lIx71pTp9WZ1KjWiPoHVf+C0lla6g6aZ4EuLmzRsLNLOqM6+u3tXtHwX/wCCsnwp+IEUdv4nkn8H6m8gRUuVLxHPT5xVQf8ABG34Gtgy6t4yd8ckajbgE/8AgP8A1r57/av/AOCS8ngfw/P4h+F+o3WqWFlGZLjT9SdWnVVGSwZQA34AfSuyMeU5ZSUuh+sPh/WtO8TaVbatpV5Ff6fdoJIZ4WDI6noQRWlX5H/8Eiv2iNU0vx7qfwu1zU7ibT7qIyabb3D7hDKh+ZVzyMjt0r9cBRymTVhaKKKsQUUUUAFFFFADVPzGnVEG/eMBxinZoAfRURkCnBNODZGQaB2H0UgpaBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTWO0E06mt94UAKrblBpaKKACimr9406gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoprMF60KwbpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/PT/AII/ePrBPgHqHh+RZFms9SmlkuG2rCqtyBuJBz+FfQ3xm/bt+DXwVjni1nxbbXupx7gNN0z/AEiZiO3HA/Eivw/8Rn4p/A3VtV+GE97f6NcC4EUtjZ7lE7dPkIALA5rpde/Yp+K/hX4eXXj7xXpCeH9BCrIZNSnBnnVucqAGIJ98VknbcvqfUfjv/gsn4hW8vbfwX4NtLSyZ28m51FiJ2XsWRcgH8a+e/GH/AAUe+OnimaUp4pk0mNst5Vqu0L7Cvs7/AIJ4+D/2XfjJo6afpnw/kn8ZaXao1/N4ixL57/xPGolYY+qj6Vif8Fbv2cfC/g7wB4b8W+FPD2n6IsF2be7Wyi8veGHHAGMVpccmz4C8U+KvH/xo8I3Wta/r+peJIdMuMyLMWkEZfuPQV+uv/BJ3wLJ4R/Zftr6V0dtYu5LtQucqvTBBHHSvmX/gjW+k6xffEPw/q1la38FxFFN5VzErgAHng9q+pfjl+2R8I/2RftGn6RIdRv5kKroOilCkTf3vvALUx0Y+lj7IyKU1+T/7K/8AwUe+IvxQ/aM0jwxJYQ3Hh7Wbloxatlpbdezbvav1g28VoZySWwopaSlpCCiiigApCcUtIw3CgDj/AIjeIrXwn4P8Q63cIzRWFlJOTnHIU8D3r8If2dvDLfGv9p+bWtXhku9ItruXV9QcqX2xKxYZ/Kv0w/4KgfHi3+GHwQvfD1lfbNa1p/I8lT8wjPUn2riP+CRvwG0/T/gzrHjfU7Tzb3xHLJaL5g4NsvHH1JNcyjzXsdPwrU4zx7/wUy+B2vLLo+r/AAik8QQWLm3gaTysFV4BGUzjivjSfw5pH7YX7TNppXw88LL4L0zVJVVre3Uv5KD70pGcA+wr64/4KEfsd/Bb4BfDfUPF+m2F7Fr+pXfl29ql6VjRmOSwXHQeldZ/wRz+A9vp/g/WPiXfwZvryVrOyMkfKxjq4OehrSCsZvud34R/4I8fB7R7eI61qGua7dADezXIiRj34Uf1r5V/4KNfs6/Av9nHw9pmk+DLG6XxleS72U3zyiGP/aUk8n0r9avi9qfirRfAGr3fgvTI9Y8QxwsbazklEe9scYJBGa/JT4HfsZ/Fn9pz9pO/8T/FnT9R0Oxs70Xd/JqVuwW4YMD5MXOCOByOKqzuI+eP2efHz/s4eONJ8WeLfh4+s6BOAF+32xjWQd2R2Uhq/cT9nr42fC343eFrXU/AFxpq7og0umxxpFcW3qrxjkY/Kp/jv+zp4Z+OPwhvfAl7aW9pAYBHY3PkBvscgGFdQCOn1Ffit4++G3xU/wCCevxosNSWaa2e3l3WerWoP2e/iB+645wT3BJxRZiuj9/mtYnYMYkJXoSo4qXaa+c/2Ov20PC/7V3g1J4PK0fxVaoFv9FkuA8gbHLpwCyH1xxX0Zx6VVxai0tN3UbqLoVh1FN3c0oOaYhaKKKACiiigAooooAKKKKACms4UgGnUmAeoqOVgLTWYIuT0p1IRnrUgR+YGUsASKGz5ZxwcUSDbG2Dt+lef/ED4x6B8LrIXviLU4NOsS2zzp2x81TKSjubQi5bHdwRt5IUs27ue9SxoY1wWLe5rwm8/bS+EWm2P2qbx5ohQjK4uBn8q8y1z/gqV8FtBu5YX1pr4RnG6ziZwfoe9LmTK9nI+Zv+CxVnqFxcaNP5ebKGTG4Hua+mP+CUOjxaX+x/ockbszXV/dTOG/hJfpXwf/wUI/bB8C/tD6bZWnhE3sn7wSytcrtAPoBiu9/Yb/4KO+C/2evgTa+DPFGmX1zdWl3I9udPj3Flc5O7Jx19KKacd+4pe89D9dpjlcZxXHfEfxvB8P8Awxf61qUyw2NpE0jMvB4FfnV8Wv8AgszH9mWP4feCjNcD702uF9ifVUKn9a8A+K3/AAVC8b/Gr4V6l4Q8R+GtHgmuyR9u0czQqq+hV3c/rSndr3QjaO57L4R/b4+Lvx4/ac0Hw18PpIIdC+3eXKptdwkgB5Zznpj6V+gn7THjzX/hb8FfEPiTSYDcXVjZPJI0C/OjY4dQewNfBX/BF34bwT3XjPxrPE0k0YSxt5MDYO7YyM5/Gv1K1bSrXW9MutPvoEubO6jaGaGRQVdSMEEGteW6sKUtT4I/Y1/4KiaF8VGt/C3xHmt9C8SYWKC/AKQXZ6c5J2t+lfRf7VX7Rnh34I/C++1a91KNZ5o2S1jhkBaRiOCMdq+A/wBs7/gl3J4L+3eMfhXcyy2MZa6udKuZl82HuTEQo+Uelfn3qPirxN4ym07Rdb1u6uYLdxbQpfTkxw845z6U7c2iElZ3Z6J4R8B+Mv2wfjZcQaNb3F7fapdNNJcTFmjt0J53HtgV+537LP7M/h39mD4cW/h/RkZ76YLLqN27bjNNjkjgYHoK8+/4J4fs8aT8DvgRpksc9pqms6tm7udQtyHX5uiK2OgFfU+2jlIlK54R+1x+yroP7Unw2utGvUjtdchUyadqW35oZB0B9VNflJ+zj8UPG3/BP/8AaUPhfxk1xp3h55/I1G0cExSxk4WaMdPQ5FfultxXyL/wUS/ZM0n4/fCq+8QWln/xWWg27TWVxHwZEHLRsMfMMdKsV31Pqrw94g0/xVollq+lXUd7p95Es0E8TZV1IyCK0a/I3/gl3+2Nf+EfFKfCDxheiLSJmZNMkuvvwTZ5iLHsewr9cVOaAasLRRRQIKKKKAOW+JHw70H4qeENR8M+JbBNS0i+jMcsLcEZ/iU9iPUV+UPx7/4JG+NPBd/c6x8MdUXXNPjLTR2c7+XdQgchUb+LFfsK3WkqXZlxfKfg18Kf25vjp+yr4g/sHW7m9v7C1k8ubQ9fQswA7I7DI/A19+/Cn/grh8JvGy2Fn4jgvvCupzKBO0yBrdH74cHOPrX058YfgH8Nvi9od3D438OadewbCXvJUEcsYx1Egww/OvwK/ae8B+Ffhz8aPEOgeB9YXW/D1tLi3cZcR5/5ZgnO4j1qLA31P6FPh/8AFLwf8TrNrrwp4j03XYQMt9jnDsoPqM5FdRJA5ZdrYHevz2/4JBfAfU/A/wAPdb8a67YTWN3rEojs0nDI3kqOW2nsT61+iNP2cSbmZfL5b56g9q5X4i6jLp/gzUrpd0ccEJbIGTgDJrt5LaOQlmXJ+prO1/Q49e8OahpzAYuoHi59SCBXO6eptGpY/m7/AGhfHEvxA+L3iTVmlMsT3LRxMRztBwK/dD/gn74QvPBP7JvgKyv12XMtmLgpjoHJI/Svw1/aI+Eut/Bf4veIvDmuWzQzQ3UjxyMMCaItkMv51/QT+zRfrqv7P/w/uhG8Yk0a3wsgwwwgHP5V0xtYid3qek1Fd2sd9azW8q7opkaN19VIwR+tT4FG0VZmfglMyfs6/wDBQ+aK1JitNK8U+SFXj9zIw6e3zV+9NrMtxbxyp9yRQ4+hGa/D3/gpVotv4Z/bYe7sFEM929pduV5y+4c8/Sv2v8HyNN4T0WRzl3soGJ9zGtBcuhsUUUUEBRRRQAU1pApAPenU1kViCRkjpQA0r8xpACvAHFSUUDuRsinkqM1FJJGq9QDVnA9KY1vE3VFP4UDuMhYyKP7vY1NQqhFCqMAdqWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmthgRnFOpMe1ADIxt461JSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMaTaQME0NIFGTUF1ciM4H3qgW6M+V2kEdT2rLmZai92TSyF84qWHKoM+lNiUMgz1qXpWonYdS0i9KWgkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPBJPFH7OnxT8aWWpvrXgfX/E0BH2eY3sDzg9sfNya7H4+fDTRPi18JNe0DV7WO8tJbV3iXj5XC5UivyP+J3/BI344eCdUaTwj/ZXjWyRwYLiwvEsrke7JMVCnPo7fWmR/Br9t/wCH3h+60tLDxRHpaxFJY476G5VExzgrI2ePTNKUUzSxxf7Ffji2/Zz/AGvIl1vU49J0y3mlsruRyQhTPA/lX6hft06XpPx1/Y98S3/h++tdVtYoRe29xC+5W2nJxjvX4Pa+NR/tq/Grec+opKftH2kYk35wcj619KeJP2zPElr+z1oHwv8ACdr/AGNYLb+ZqV3CxaSckkYOenFQM8n+BfxM8f8Aw08S3svgBrv+1by1a2eO1iZ3ZDweBX0v+zd/wTd+Jfx+8TJ4h8fQ3HhvQJpBcz3F+GFzeAnkIMcfjis//glL4otNC/amtbS6hjuv7StJIVlkwfLc85Ge/wBK/cqkB498Hf2R/hX8DZre78KeFbW01OGPyxqEmXnPqdx7mvZKaDS5rRGQtFRNMVbG35f72a8y+Kv7S3gH4L3WkQeLNZj01tUn+z27EbgW98dBT2KUXLY9SoqGzvIdQtIbm3kWWCZBIjqchlIyCPwqagkKQ8AmlpP5UAflb/wU2/Z9+J3xq+L2l6l4X8JXuraPa2flFrfBBbd97Ga+7/hfqHhz4DfAvwrp+ttD4VtNN0uITx3BCiJ9uXBx3zmvQNc8d6B4Zmjj1TVLPTmkcIguJlQsT6A15p+1R+znY/tNfCW98Mpqb6ZPKRPb3kBypcdN2OqmudLSyZ1SkpWUlY/K39tb42RftiftC+HfC3g7UZdQ0V7pbS3wDsZ2bBbHoOa/Yr4K/DSy+EHwv8PeErFESLTbVImMa7Qz4+ZvxOa/Of8AYN/4J5+NPhh+0Jc+J/H9hBBYeHy62GwhluZDwsi+gA5r9Tq0joYz7A360iqqjiikrQzFCjJPeuS+KHwq8NfGHwleeHvFGl2+p2FwhXEyBjGSOGU9QR7V1u6jdQB+G/7QH7DXxd/ZN8eXPirwCupahoFnN59lrWjlkmgTOdsiKxOB06819D/stf8ABXiC9uLfw78ZbJLGUEQx+I7NG2lumJogDt92B/Cv0+mhjuI3jlRZI3G1kcZBHoRXwB+1t/wS18JfE681PxZ4Jv4/CGtzbp7m22j7LO+Oy5UJn64rN+ZotdD7u8N+JtJ8YaNa6tomo22q6bcoJIbq1kEkbqe4IrTr8D/hr+0F8av2DPEs2hIFk0hZszWF1+/tplB58uQEhcj0r9Tv2X/+CgXw7/aO0yOA3kPhvxMqjzdKvpguW/2HONwpBY+nxIGkK4OR7cVItfFnjr9t688BftoaF8MZ20+XwxqMaRzSICZYrh+g3ZwR07d6+1FrRO6FJWFooopkBRRRQAUUUUAFFFFABRRRQAVDcSOsbGJd7jsampixhXZh1brUWYEUjFl2HhmHPtXzD+3V+yxrv7Svwrj0bwzqUFhqttL5yx3PyxzexYAkV9RmMFt3ehY9rEhj+dHLfctScVofixoH/BHH416i0Z1LWvCumQE/MDcyyuB9BFjP419C+Ff+CKvgqPSbZvEXjrXn1Qp+/wD7NW3SEN/s74mOPrX6SdKP1o5RczPx3/bN/wCCZ/gn9nP4O3/jPQPFWuX97byqot9UeDYwJ5+5Epz+Ndj+wT/wT2+EPx2+A+keOPFsWranqlzcTRTW8V8YrddhAAAVQ2ef71e0f8FbNUs7H9nueCSQi5nuolVVPXJ71e/4I/3zT/snGAnKwa3dhc9eQhxU+hq9I3N+b/glD+zpIxI8L6lF6BdYuCB+bH9a+Y/22v8AgmL4B+Evwp1rx74H1bU9ObTUV5NO1CdZYWXOPlIQNn6k1+r2M815D+1p8On+KX7PPjXw9FvM9xYO8Sp1LKNwHT2rSyMrnyT/AMEYPENvdfBzxbpKYE9tqgmP94qy9/xr9E26V+JH/BMP9o7Tv2evjDq3hXxc66bpmvlbZ7y5ygtp0OBuJ4ANftLo+vaV4r037XpWoWuqWMmVE9nMsiH1G5TTB73Py/8A2/P2l/Efjf4uJ8Kvhqszatu+y3FzasWbJ4I46DnnNc34o/4JCa3Z/Bt/EUXiRrnxott9rudP2bkduSVU4zmv0V+G/wCyV8NPhZ421Xxfomhk+ItTlaWe+u5jK4LHJ254Ar2HaKhRsy5STtY/I3/gmb+2FqXw08YR/BbxwJYbK4uWgsJbkEPaT/8APNsn7p7cV+uY6etfiF/wVGsY/hz+2NHrmiQQ6fcm1ttRZofl3zAn5yB3+UV+xfwX8WS+OvhL4Q8QTjE+o6Xb3En+8UGf1zVmR2dMkjWWNkdQyMMMrDIIp9Z+va5Y+G9Hu9T1K4S1sbWMySzSHAVQOaAPxH/4KJfD+3+Bn7YFnr2iWa2VjeNBqsaw8KGVxvxjp0r9qPh9ryeKPA2gaxGSUvrCC4Gf9pAf61+HX7eHxo0/9pP9oaytPCMr6jZwgadbsoz5jO4DEe1ftn8G/Dtz4R+FPhLRrs5ubHTLeCT6qgGKC5O52VFFFBAUUUUANbrUUkwhUs3AqRm68V518aPi1pfwd8C6p4i1u7htrS3RggcgFmI4A/Gsm9bGkVc+Hf8AgqB+2Ung3SX+G/hi9kGt3g3Xl1EwxBGeqY9a8X/4Js/sMD4wahZ/FDxmpl8OWlyWtbGZT/psg6SE5+6DXi3wh+FviD9uz9qLUZpmdtNurxrq+u2UhUt1bhMjpkDtX7sfD3wDo3wx8GaT4Y0G0Wz0nTYBBBCpJwB1OScnJz1qrBKXQ3re3itLeOGCNYoY1CqijAAHQVIBjiloqzMKRVCjA6UtFRygfin/AMFebeOP9prTT5jOJNMQsrLgKQ3TPev1u+Ad1De/BPwPNbhRC2kWwXZ04jA/pX58/wDBaH4cR/2f4P8AG8FqWmR2sLmcAn5DyoPpzX0l/wAEyfixF8TP2VfDtsZHe+0AtplxvABO0koeO20gfhSWho9UfWVIzbVJ9BmiuA+PPjhPh18I/FOvNc/ZZLWwlaKTjIfacYz71XMiFqfjz+1ZqU/7QP8AwUIGjaZbmRo9SttMVV5/1bAu30r9u9Jsxp2m2lov3YIUiH/AVA/pX4wf8Eq/CNx8VP2sdS8ZaoXvTpMM9888h5M0hwrH86/amqKk+gtFFFBAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTXzt+UZNOooAamdo3cGnUUUAFFFFABRRRQAUUUUAFJuFLUTsFUk9KY0SbhRurPfV7eOTZ5gLf3e9TJceYMqRjrU3RXKy1S1m3WpeSmRUVlqktzk7MqKhTTY/Zs1t1G6oI5w6ZPB7im/aM5IPAq7oXKyzS0yKQOop9MgKKKKACiiigAooooAKZIrt90gU+igDMa3aa4IPY1cjthGDU20Ak45panlRo5tqxGsZWnbadRVGYlLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfE2vf8FdPgNpMCPaza9q7t/yztLFAR9S8iiufvP8Agsx8FYbbdHoPi+4mI5hWyt+PbPn4/KtC3/4I6/BKKRWk1zxxcqP+WcurQbf0twf1rUj/AOCRfwEE2+SLxLOveOTVvlP5ID+tZ63Luj8tv2kPjl4F+MfxrtfG+heGLjTbKS5Wa/tLuNF84BuchGYcgV9vWX7dn7Kdn4DFnZ/DjbqMtn5Txf2EjgPtx989RnnrXvo/4JQ/s8rNC48Pal+7/h/tSQhvrWz/AMOw/wBnUyBz4Fyf+whcAfkHp2HdH4j6D4+ufA/xbh8Y6FE9p9l1I3cCW6FF8vfkKAenHGK/Q/U/+C0gGk+TZ+BbpNQVVAlnlQKxwMkgE45r7E03/gnb+zxpaoI/hpp8rL/FPcXDk/XMmK6eD9jP4JW1ukMfw10JY0GAvkE/qTSswuj867r/AILSeMpIIxb+BdLE38Re8bn8NtU2/wCCznxIZsp4I0QL6NPJn+VfpPa/sg/Bizk3w/Dbw+r/AN42gJ/Wt63/AGefhlbRqkfgLw8FXgZ06I/qVrQpzVrfofmBJ/wWZ+IMsJRvAehjcME/a5M/+g18l/tDftJ65+0X4sstV1iyj0v7Ku2G1tZGePcSPm5r99m/Z/8Ahq/XwH4eP/cOi/8Aiax7/wDZT+EepXAnn+HugvKDkEWir+gqZahGfKa37Pc3n/A3wLIWLFtHtiWY5OfLGf1r0Kqul6ba6Np9vY2UCW1pboI4oYxhUUDAAHpVqmtjJu7uFMl/1bfSn0UxH5Tf8FhfCV3px8J+KIZ7m3bzGtf3bkLjqG4PXNfUv/BMPxtf+Nv2UNCk1K+lv7ixuZ7PzZiWfapBAJPX71eg/tVfsp6J+1R4Nh0LVtRuNKaCQSRXFsoJU/Q10f7OfwB0T9m34Z2Xg3Qrm4vLWB2le5useZK7dWOOP/1Vkou50SkpRXc9Nz6V4z+1xr3jzwz8D9d1P4dKzeIrePzE8tQzBR1IBBya9o202SJZoyjAMpGCCODVWMIuzuz8lv2df+Ct+v8Ag+aXQvjFpF9rjxttW+sIVW5j55DxnG4/iK+vvg9/wUk+FHxu8f6f4O0Cx8UQavfEiH7fpipHx3JWRiB+FdL8Qv8Agn/8Dfidr11rWueC4X1O6bfNPazyQFzgDPyMPStL4L/sR/CD4BeIzr3g7wx9i1jYY1u7i6luHVT1C72OPwqipNPU9M+J1x4ltPAGuzeD4refxLHaSNYR3RxG0oHANfj/AKb/AMFWPj98NPGU+k+MbPStQayuil9p93Y+TMuDgqrKRjjpwa/anbXj/wAZv2R/hV8eY5G8XeErK7vn5/tGBPJuQcYz5i4JP1zTEmeYfs//APBSb4SfHjVNO0KO8ufDvia7wi2GpR7UaT+6knQ/jiuH/wCCkn7NHxb+OGj2eo+Atd8zStPhZrrw+s7xSTkc5TaMMf8AZNUfhd/wSN8E/Df4vWvi6TxVe6zo9jP9osdEmtdhhYHK5mEnzAH/AGRX3qqBVAHAFTvuVdLY/nu+GXx5vvhE1z4B+JPhdtV8Oq+2503VISl1a+oTcpI659816F/wxbZ/HVZvF3wE1+GW2IMx0C8n8i9tcD7owSc5Bx9RX6q/tFfsWfDH9pKGSbxLoy22umMpDrFn+7nRscFsffxxwa/KP4z/ALIvxr/Yn8cNr3hS61XUtEQmS313R43YhRj/AF6AnZ+JIxU8r6D5kdL+yn+wn8ZPEHx+8P674s0PUNJ0zRbxLq41DV3LGTYchVJOWzX7ZL0r8rv2OP8Agqp4k8R+LtK8EfErTV1ifUJ47W01fT49kgdiABJHjB+oxX6o04p9SZO4tFFFWQFFFFABRRRQAUUUUroAooopgFFFFABRRRQAUUUUAfBf/BWLwk2ufBG5vY3iAs3jlbd97IPFL/wRyl3/ALMOpLnO3XZz+apXTf8ABUbQhcfs269eB2QLt3bTwea4f/gjHdNN+z94ntyFCQ62SuP9qMZ/lWcd2bSfun6CL0oZQylWAKkYIPQ0UtaGJ8ffHP8A4Jg/CP44eOJvFFw2qeHb64/4+YdHkjihmf8A56FWjb5voce1ex/s2/sz+Ff2XfBc/hrwpc6nd2lxP9olm1SdZZGfGONqqAPoK9d20baB3BelLSUtAj5L/au/4J3eEf2pvHVh4u1HXtQ0XVLeGO2lWCJZYpYlJONpIIPJ5yfpX054O8L2fgjwppHh/TwRZaZax2kO7rtRQoJ9+K2KKAOK+MHxNtvhD4B1XxReWs97DYxl/It13Mxr8e/j5+258Wv2wtUbwR4N0K6sNKvJPLSztUYyyL6Oe1ftndWkF9bvBcwx3ELjDRyqGVh7g1k6P4G8OeHrhrjS9B03Tp2OTLa2kcbn8QM0Afnx+wR/wTRm+GurWfj74mwoddhIkstIUhlgb+9Ie59q/SLpwKWigAooooAKKKKAI5W8uN3J4AzzX4wf8FUP2lJ/HnxFbwBptyp0nSSpvEjHJmxkAnvwRX7RMoYEEZBr42+O3/BMP4d/G74rp45k1C+0W5nlSXUbO2IaK7K4HflcgAfLis3G7uaRkkO/4Jd/Am2+Ff7OeleIJrdo9c8TL9tuDIMFI8kIo9BgZ/GvsiqOh6NaeHdFsdKsIhBZWUCW8EY/hRFCqPyFXq0MwooooAKKKKAPKf2mvgjYftAfB/XvCV4FWeeBntJ2BPlTAfK2B15r8RPgN+0V8QP2G/ixq9jb2xnjhuGtNR0S63JHPtbG4ZBwe4Ir+hDFeS/GL9lH4U/HlYz408G2OqXEZ3LdR7refPvJEVY/iTU2KTPjaH/gtb4JWyiM3gLXPtW0eYqSxbA3cAk5x+FfLP7XX/BR3xN+01aHw14a0+Tw34Zk+WS2fbLPck8bTgHH4V+iK/8ABK39nXzt58I3ZXP+r/tS42/+h5/WvS/hv+xX8E/hNcJc+G/h9plvdpyLi6Ml0+fX96zYP0pcoRdnc8e/4Jf/ALNP/Ck/gnH4j1W0a38UeJ1E9wsgZXhhBOyMjOO27pnmvs+moixqFUBVUYAAwBTqsTCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACMwUZPAoVgygjkUEbuDQqhRgdKAFooooAKKKKACiiigAooooAazBRk1Xl/fx/KeDUsnzZFRbdoAqOY0j3Mh9Dg+0GY7g5OSauLlWVY13ADBzUrQM8zfMQKezR2aFmYDHUtWVjVy7EH9nmZiWGFParVvbpbxhV6VjX3iZA0awnIY4Jq+sjELkkgiqTtsHLN7kzAKzE9D6VBHtYSKCSc1JIwAwTg+9NtbZlm3joetS9WF7Fy1XEantjvU9IvSlrdbHO9wooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBu3rnkHsaZcWsN5bSW88STQSKUeORQVZT1BB6ipaKAPniP9gv4O2fxc034i6d4d/snXbGf7SkVjJ5ds8nZjGBj34r6HoooAKKKKACmTSGNNwGafSUACsWUEjFLRSA0rgLRTSaMmoYh1FIKWrQwooopgFFJXlf7RXxwH7P/wAOdV8WzaVJrUdnCWSztyQ8jfXBwKmUlHcqMXJ2R6rSEhRknAr8s7X/AILabpovtfw2WGFvvNFf72/LaKxvGH/BZ7VJNUmPh/wdGtjs/dreTgHdgdQBnrnvS5vIfIz6s/4KTK2vfs1+JdOW8s7AeX5ifaZQHm2noozXmf8AwRhtWh/Z/wDFMxR1WTWyo3d8RLnH518A3Ft8dP2/PiJdXWn6dqOrRXDhjGrNFp1kvC/eY4xxnrnJNfsh+xr+zvL+zH8D9J8HXN1HfamHe6v7iP7jTOeicD5QAo5zznmiKBvSx7pRRRVkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJtGc45paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiip5gCikpadwCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSZGcd6WgAooooAKKKKACiiigAooooAa2c9KjWMiRmPfpU1FTyodxkgbadvJrH1DR7rUCN0oVP7tbdFHKhqTicvJ4Vm3ho3Xg5ANbNrYyLzM2T7VfopcqLdWT0KVzZhyGbPy9MU+BtzYAP5VZowB0FPlRHMwFLRRVEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUroAoooouA1mC9aRT82KR8lgABj1NNjkRnIVgxHUCs29RjpZBGASM84p/FQXTyDb5YBycEnt71HtaSBo/N+f+9T8x8uly5RUKMY9sedxA5NSbqq6FYdRTN9Lup3QWHVXvbG31G3eC5gjuIZBtaORQykHqCDU9FDSYbHgHir9gr4DeNNSnv8AVPhzpbXU7b5Htw0GTjHRCKZov7AXwA0Fomtfhno7PH91rhWlPXPJYnP419BYox70BdmX4b8K6N4O0uLTdD0u00mwiGEt7OFYkUfRR71q0UUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4BRTWbaM4zQrblBpgOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKY4Y4wanmAfRUZB3HBqNmPPzYqeYaVyfcB1Io3D1qrDIs0nDBwvcGpuxz0pXuPlI3ky528j2qVGJUU1VCrlRSZc8jioCxMKKhDherZPoKAu/JywHp0rWMr6BYnopF4UCirJFooooAKKKKACiiigAooooASjNRthmIzzSqu1cZzUcxViSikXpS1ZIUUUUAFFFFABRRRQAUUU103Y5xUcwCBTuJ7U+iirAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKhurpLO3eaTOxBltoJ49a+evDv/BQL4HeJvG8vhO18YpHrKXDW3l3NrNEjSKxUgOyheo9alySdmUouSukfRdFNSRZFDKwZTyCOQaXNUSLRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUySTZ2zTBcKULDnFZPcdmDXARmDYUDuT1psl4kSl2ZRGOrE9KxtfvIYLV5rgME4247Hpivhn9sb9uxPgNfPoEds+o63cWhe3t1OIlyxAZmHNcrqS5uVI6fZLl5mz7/wB/m7XVg0Z/u85qGG3EHmSqmGY/dr8QfB3/AAVi+NPhPVLdrn+y9U0hG5sJLfb8pPQSA5z17V92fs8/8FUfh98ZNes/D+uWE/hHV7gAK91IrQM57Bv8a6NbXZh6H154m1SXQtNuL8OBHAplkXGTtA5rxr4K/tmfDf4469qOgadrUdjrlpK0f2O6YRtJtODtz15Fe7yRxaxbnbJFPZzJglcMGBH8q/Nj/goB+w9JoMsPxN+F1q+marZtvnisflyRzu479al3urbG94uNup+l7yJa7N2fmO0HGakjJwQxBIPavgX9g/8A4KJaZ8UrfTPh74/l/s7xpCrQx3twwEV2VYgLk9HxgfUV96SFLQvK0gRWI+90HFabmVuhY79KQ7u2MV8+/tAftleDP2dbGObXrg3bykhIbRgXznuK8D8I/wDBYr4ZatqVvZaroWr6ZFJMI/tzBWiAJ4JHXioUk9inBx3P0BXO0Z606szw34i03xbodnq+kXkV/pt2nmQ3ELbldfY/XP5Vp1utjFhRRRTEFFFFABRVa6ujBwqFmJwvHWpgxwM9aAH0VFNN5UZbG7HYU2G4Eyg/dPoaV0OxPRSL0paYgooooAKKKKACiiigAooooAKKKKAGtnacdaI920butI2d3Bo5rJ7gPopm40bm+taLYB9FMWQsxUjFPpgFFFFABRRRQAUUnNLQAUUxmPToabJMIsZGc+gqOZDJaKQcilp8wgopjMV6VFNMUhLd81Q7FiioFnyoOKPPGcc5qeYfKyeioBcLu2k4NSMTtPNUKw+ioY5GOeM0sZZuScUCJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKO5qGaTZmp5hpXJs02TJQ4PNUi8r5ZWwv8AKljmLKRvVm9jWdy+UfMzIu7dWbdXk+VRIWfcfmakI82Ykz52nBXPAq2u55Dg446fpUJ3Zulyoms4VtYN2NvqtVmuLm4n+UKluOv95qxta8feE9L1608Oat4k02x1q6AeHT57yOOdwTgYQsGOT04roJ4I4YzIsbEg4wPyq7GSab1J4x8gw2B708g7fvc0yOIbRtOBShTGxZj8tIl2voJFHhyx5NTUxX3HjketO3c4FVH3RDx0pv8Ay0NfEP7VX/BUTwx+zh8RNW8CWnhW98R+I9MMQuW89YLdTJCkqgNgk/LIueODmvev2Tvj9J+018GdM8eSaONBkup7i3ayS4E6AxyFQQ4AzkD04ORVcwrHs9FfnZ+1X/wVbk+B/wAX9Y8DeFvCdrr50VvJvb68ujGpm2qzIgA6qSVIPcGvtj4F/E7/AIXN8IfCvjb7A2mf21ZLdG1dtxjySOvccZHsRVknd0UUUAJmikOM1BPeR23LkKPU0NpAk2Ts6r1OKa8iiMsWAHrXPatqrLIhh+dWPVafJJczWrIqsT6YrP2iOhUtL3NCTUrWKQIZAZD0HrSQapFNMQrj6ZrANtcSSISu0rxk1bsdLlW8ZtodOu/1rLmZq6cIrc6VTuUGnVHEAqhe9SVqpHGFFFFPmEFFFJRzALRRSA5o5gFooop2uAUUUVQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEc0SzRup6MCDjrivxw/b3/wCCe3iHwD4qvfG/w9sr3VtEu5XurmGNi81vIzbiVwOmSTX7JZpjqsilGAIYYKnkEVnKN3c0jNx0Pxp/Y+/4KceI/gn9k8G/E+3vNc8OoVhgu2GLuz553FyN6gk9TkYr9cvAPxJ8NfFDQbfWPDGsWur2MyBw9vIGIGSOR1HIPX0r86v+CsHwZ8L6tB4avdCsIrfxldXIsrSwsIAHvixGThRjjvn0r2z/AIJz/sW6r+zH4cvtd8Rar9p8Qa9bIkmnwlvJtUDFlHOPmxjPHrWUJ3ehdSm0k31PtClpF46nJpC2K6LmA6k3fNik3Un8RNF0MfRSbqWi4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUU3eN2O9G72pXQ7DqKaGz2pjyurYVMj1zRdBYJ28uNmxu9qqr5hjbBVEIyGp9w05mjKsFQcsMZzVGa6+3WcyRrs5Ow+vr+uax+1c2jFtHn/wAXfFU/g3wPq2tThXjtIHk2sflO0Eg1+Fmi6P4v/bS/aOXToZJLrU9YuSpmzlbW2VuWHsq1+mf/AAUq+LWr/Dv4I39naoJotQlFkHLFSoZRlunOCTXk3/BFb4W2048cfEGaFXmilXSLaRhynyrI5H1DAfjUU4py5jas7aH2l4D/AGFPgv4I8EWvh1vA+l6qFhVLi8vYt8s7Y5YtnjnPTpXgv7S3/BKrwP4w8Pvf/C+1Twl4ktz5kcaOfJlwOF5PynivvgkDjPNNVldioYEjqM8it9DkWmp+CXin4yftIfsa+KJvCeqeJNQsZ441ES3DefEykB8qT/vV+oP7BPx38TftPfAG81nxrbWlxdCZ7TdEuFnUblJI7HjtXg3/AAWZt/Dv/Cu/Dcsluh8QC92JMoG8R7c4Nehf8EhbuOb9lkW6qqTQ6jcKxHUgyOQT+dQaM/KL9p3wwfhd+0Z4u03Smntfsd8txbyA7GTeiy5BHozn8q+7f2Q/+Cn2lSeBbXwT8X7ueC6tkZLbxEoMjTLuYr5g7FQQox2Arjf+CunwPg8J+JtC8cWyHztR3Wt48YG0kL8jH3wAK+WvGHwFSH9nnwz8U9MmQW1xI1hqNqGzskV2QMv1Cgn3NK6aswTlGV0dVdeD9e/bW/avvtA8Oas9/ZX1w0kF3Pu8qK3RQC+3t0NfRPx+/wCCScfwt+E934j0PxjeatqVlGJLi1u40WJj327RmvFf+CdX7U3g/wDZh+IWoXvizR2ng1aIWyatF80lqueRt9D371+zV34w8MfG74S3uoeGdQt/Eel31szJ9lcMTgkEEdQQQRj2qnaEROTnK7Pzi/4JD/tJatb+OLz4R65qElzZ3EMk+mRzMT5LRgs6L7H5jj1r9aK/Cr9nfT7f4Z/8FHvCdtF5lrZSay0UbMNmfNhIK/TexFfupu6VcZKSuRJWY6ikpaokKQ8ClpOtK6ApTPJ525Qzbe3YVy/jj4veE/hnpE2p+KNcttIs4SA8twcDn09a6HXb4aZZvIDg9BX4of8ABS/42ar8RPjZ/wAIRYTSzaXpqxQ/ZISf3tw4DAe/3l49c1lzPmsjqULw5nsfqlY/tsfAzUtQSxg+JmgG5cgCN7kJ16dcV7BouuaZ4k0+K/0q+ttSspc7Li1lWSNsHBwwODyCPwr8h/ht/wAEc/F3jD4ef2zrviiz8P61dQeda6V9mMmwkZAkfPGePpXl1l4i/aG/4JsePLG11Hz10ZyTHY3Dm4028jLZbaQRtbk9+CTTMra2R+7S9KWvNf2ffjpoH7Q3wv0nxj4fmDQ3aFZ7cn54JlJV0Yf7wOPUYNek81otjN6PUWikFLTEFFFFABRRRQAUUUUAFI3SlpKAIJN7DIr5+/ak/a80L9lXTrC81+CW6a+3C2t4hzIwHrX0Pt2jivyt/wCC1Vx50/w0ULugVrgM2ON3GB+tYta7msXpsfbn7Iv7V2hftaeAb3xBpNlNpd3p919kvbKY5MbEbkIPcFcGvda/K7/giTeSs3xKg8xvI/0Z/LzxuwQT+lfqjjNaohir92nVGXCYBOKXd70xDi2Kasgboc1UaZvthjY/Ieg/CpoIwp6c1gpOTshtWJ6Wm5xRurW5IyabyyBmpFbdUMkIkbJp6/LgVnd31GRXBfcNhANSJuCjccmo2txJMXYk+2al4UUD6D16UtMVuKXdTFYjkYhjVaZvmAxuLHkelWmx1PFMWFS28dT3paloazCOREOTTjjccLz61MqjAzyaXaOuKvlFcriEbt7KC1PVt7MMcetO3BmZfSgKAMdqsVyDaQ5AkOPTNc/41+IWi/DrTl1DX7+303T94R7q6mCKufrXR+WolXHHtXwF/wAFmNan034A+F7G3meE6hrYjkCHG9FiY7T6jO38qXMXofc/g/x14e8f6X/aPhvWbPW7HdtNxZSiRM+mRW9X5sf8ES7yab4YfESB5XeKLV4NischcwnOPTmv0manuQ1Z2FooooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKQjcCKWigCBVaBcDkCnI7SLnGKhvrpLGCa4lUmOJDIdi7m4BJwPoK+Kfgz/wAFQvBHxZ/aCuPAgsZtH0e72waTql8uyS5ueAUdf4cncB9BnvU3KsfXPjzx34d+G2hSa14o1+x0HS0dY2udSmWOHcegJPetrRdb07xFpsF/pV9b6jYzqHiuLWVZI3X1DA4Irwn9uL9nG5/af+A994U024S21iC5jv7J5PutIgYbD7EMa/Ib9nv4/wDj/wDYL+N15pusWV0LFLkxa54d3AC4+XiRfRgCCD/+qmFj9/aK8q/Z7/aU8EftLeDY9f8AB2pLPt+W6sZsLcWr5I2yJ26ZB7gg16rTJCiiigAooooAKKKKAGf8tBVO8kAZhsZjtPSrjd6iCjcTms3uXHTU8j/ac+Luo/A74G+JfG2j6Q2sXulW6uLXsuSB5jDuBkE18k/sDf8ABRS/+M/jDXPDnxN1HTNNvrjZJpMiKsKHPDR5PfpX6CeI/D2neKtA1HR9Vtku9Nv7d7a5hcZDxsCCPyJr8Zv20v8AgnDrv7PcjeNvh893rfhfz95ht0ZrrTjnKH5eWX37VJVz9kpbWL7Z9pjkUxH5mVTnPvXlv7SX7QGn/s5/B3XvF2pzxLdRo0Wm2shAee4YfIoB5IB5OK+CP2Nf+CoH9lW1p4S+LnmTW8EIit9ZRcuSCdok/DA/CvAv2vf2gNf/AG5Pj/o2geF7O5bS45hp+k2Iywdy+1pmA/E57AUlGzuXzaWOY+BXhH4j/ttftL2N/c6he3OotdLeX+tZbZZQodwUHovTAFfvTpBurexht2EjJDGqb5uWYgYJJ9zXif7H37J+g/sgfDO4tlnF9rl1H9p1fU9uN7KCdq+iqDj3xmvk/wCIn/BZ6z0vWNRs/DXgCS5toJDFBeX13t8wjgkoBwMg9+lUSml0P0vt5Wa28w/KTnj8axNe8VWPh/SrrUdVvLWz0y1UtcXd5IscUI/2mJwOo6+tfkfqX/BZb4oXUkhs/Dfhm0jb7qzxyyMPqQ2DXiPx+/b9+Kn7RXhz/hHdavLXTNF+9PZ6PC0ST+m4E5I+tFiouKd2j9y/hb8TdA+Kmmzar4Z1mx13SlkaH7Tp8qyRh1OCpwTg+x7EHvXc18J/8EefA+peG/2YrvW7uZWs/EOrzXVnCpz5aR4gb83iavuyq5TOT1P50f23vFkPjr9rP4paxbbmgbWpbVdw5IgAgz9P3WfxFfs//wAE6/DFv4U/Y1+GltAjIbmykvpN4IYvNNJISf8AvoD6AV+Ffxyme4+Nnj5xjMmv6gR+M71/QL8BLe2+FX7Lfgo6jOsNro/hq3uLiSVggULAHbJPTHPWnYGfiT/wUPs0sf20vinEieWjagsuMd2tomJ/Ekn8a/Z/9hJpH/Y/+FDSoyOdEiOGGDtJbafoRg/jX4HfGT4k3/xk+LnivxlqJVrvWL2Wc9lVSCqD8FCj8K/oc/Zi0ltC/Zw+FunvF5Mlt4Y02J48YwwtYw3HrnNUQz02iiigQmKz9R08ahtUhgFOfrWjRUyjzFKTRn2+mwoMFOB0B7VY8pYVOBk1KeppOKiyWhXM2Vo4QzcpgVaVBGvApF+9x0qSgmUmyNU3MWPFP9qWm4O8mr5SRaa7bSDn8KVutN9agYyOV2b5l2iia6SHO87VA3FjwoA7k1Ev7ydhu4r4r/4KsfHDXfg38D9JsPDl6bG98R3zWkkyNh1jVMtj06ikOx9oac0dxm4hu1uYn6eW4ZfzFX81+ev/AARw1jxP4k+EfjO/1nWrjVdKg1cWVmtw5cxusayScnkf61T+NfoRTCw+ikXpS1otiQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFQ2AUUUVYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGqu94kd4luwYOy7gccfTNZuTQ7XLPeqOqeetuxthmbBCk9B9auZoyPrRKLkrXHF8rvY860X4S2V5r1j4i8QRQ6jrNi7taMy7lgLcErkdcV6MvyjHpQpArI8VeIofC+i3ep3bJDaW0TSSSSOFC4HeotGjFtmjcqsrGn9oXzgg5NScGvyp+L/8AwVx1zwb4s1DS9B8J2d39nk2i6nuiFlUgEFQoPY14j4u/4KnfHDxZI40b7LpEMwGy3s4zM6cYPOM8nn8aUZuSUkipU1F2uftjr3iTSvC9hJe6vqNtptpGMtNcyBFA+prxjUv27PgPpN/LZ3HxK0UTRHDbZtw/MV+HPxb+K/xg+IVqdQ8c6j4gnspiAPtJkit84xwuMdqtfs1fsq+OP2nvEEul+FLaNLW2/wCPnUbo4hg4yNxA6mrM7W3P6Afhn8aPBPxk06S+8GeI7HxBbRnEjWkgYpyRyOo5FdvXyL+wP+xDdfsmaPrV1rerw6r4h1Zgsn2PcIY41PygZ6n3r66qopozCiiirAKKKKACiiigAooooAKKKKACiiigBjKNxPekNP202SMsjKG2kjGcdKizKuNjztGRg015QrBSevtSoPLVULbmAxnpmnYB6ipGVbjcJI2jGc8HJqq1n9nVpl+/zzngfhWrsVsEimfZxhhnKt2NHKy4zsflZ/wV28Yt/wAI/pegkCQSXazBhxjCDtXq/wDwRctwn7Nfiqb+KTxVPkfS1tqx/wDgrV4B0S1+FsviG4gY6h50aW7L0GcKfpW3/wAEX2/4xp8UJ/c8Uzjg9f8ARbas6el0+5VWSk7o+7tchuptNuFsn8u52Hyzj+LHAr8iv2qP2qP2k/Bvj3V/DFtp95oMCyBUubO1aR5VKgg7wMdD2r9hetVbjSbK8kD3FpBcOOjSxKxH5itrERnyqx/NZ8UvG3xH8Zxwy+OrzWL4I5ZJNTRx8x44JHpXefBf4f8A7Qb+E21T4cWfia20Od2Jl06RkjlYcHAzzyDX3T/wWX36X4Q8J21rYRR2FxMxkmhgVSrDtuA9q7r/AII4+NNW8T/APxBpmoTNJZ6Pq5gs93Xa6LI3/jzGlZil0Z8i6X8JfjN8Rf2ZPibffEN9Ta10WOK5sl1okzeYr5kAJ9q+VdF+IGua34JsvhtHIW0y41NJ44yT/rGbGPpk5r+j3x94NtPG3gnW/D1xEhg1K1kgORxllIBP44r8Kvhv+yX4w8P/ALYnhzwFrWjX1uLXWY5JLxLdmiMCkSK+7GMFcZ+tPlLTufdfjX/gk74I8e/B/R20Jm8MeNEs0lknjO6G4lK9HBBwO3FfAetWPx2/YG8a3dhHeah4bEnyC6tyXs7pSA3y5474+ua/oIgjEUKIOAqhRXK/En4T+E/i74fl0TxbotrrWnSDmO4TJX3U9QfpVW0szJOzPwC8JfGbWviF+0t8PfFetRxDUrfV7JJHt/l83Eq/MR6kGv6J4m3Rxn1ANfDln/wST+FmjfFPTPFmkapq9jZ2N1HdLo+9Hh3IQQMspbBI9a+44YVhjVFGFXgCpjHlHJpoevSlpKWrICims22jdUWu9BnP+Opobbw/c3EzqiwqXO72FfiN8C20/wCKn/BSHR59SgW6tJ/EEx8thlW8mMlOD7oK/af4sLFN4H1mOUcfZJGz3GAa/Eb9h1Um/b88Kkk4/tm+YY/65SVml+8Ol39kkfvTyqgDpXK/E74Z+Hfi54Pv/DviXS7fVdPuomTZcICUYjhlPVSD3FdaOlG2tbHLqndHwd+wf+zH8SP2Zfi5420i/O7wBeAy2h37suGwh9M7eDxzX3ivSjFG2q6Gk5ubuxaKbnFKTQZi0UgpaACiiigAooooAKKazBepwKTcTn07GlfoArfdNfmL/wAFooreDwJ4DCgCYalKxz1I8uv05JO05r8sf+C1c5kt/h7EpPlGSctkfxDioe5pHZnIf8EVfEpsvif440NpBsu9NjuFXA5ZXA6/Qmv1+Ar8WP8AgjbZST/tGa1cRqfKh0dg57csBX7UVUeopdBjKGGCMigKFGAKdSU76EFaa3LSFwPmHQ1MuVAz170x1Ls4DY/Onxx/KAXLEdcjmstd0aS2H5zTWk2nGKeoGKXaKNTNEO0vz0ojDBzk8DpU20UjLxxwaViriVHIewPNNjmPmMjdu9R7is7Hgg9DT+Q46ljYvpSMD0U4oj3bRmmeXJ5pbfhfSgAaPdHgnLetLGwVQvekmkWHDFtpY05GVj8vPuKBky9KWmKTuxT61WxmR7QHZu5oB3c4p9FMZA2POXrmvzh/4LXXTR/DL4ewquAdWmcv6YjFfpJgbs4r8tv+C2F5KX+Gdj5rG2ZL2Zoc/KWCqA2PUc1n1LWrPVv+COvw8l8Lfs23viKU5/4SXVJbiPjnZF+5/LcjV95tXhn7Dei22hfslfC62toUhRtEgnYRjALyLvdvqWYk+5r3WrRMnqFFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAprosilT3prL8x9K+Ef28P+CjWmfAyxvfB3gS5g1Pxw4Mc1wp3R6fnufVsGpuVY639tz9v/wAL/s46be+GdK8jX/HUsflvpZYgWqugKtJgd1YED0NfjJ4B8C+Kfjt8TIbDw7p09zquq324tag7bbe+5jnsBkn8K9i+E37Efxs/a40vUfiHp1tava6hLLImparcrGL2RXZXCcEjDKVyQBxWvp/7B37VHwvkm1TQfCOt6XcwHP2rRNZgMj47qkT+YfypWKP27+FvhW+8D/D3QNB1LVZtbvrC0SCW+uAN8hA749On4V5l+1B+x34D/ai8Nzwa7p8dn4jSLZZa9bpi4gI5AJ/iX2Nflt4P/wCChX7Sv7OuvrpHjiK+1ZISBNpfjGykgucEZ4kYB+QcgnPBHav1u/Zm+NUn7QnwX0Dx3Noknh2XUvOVtPll8wxmOZ487sDIbZuHHQiqJd1qfkT4Z/Zd/aH/AGU/2iNGstAstcjtLjULe3fXNBgea0u4DIpO84xjafmB6HNfuPDv8mPzDl9o3HGOcU5elLTJCiiigAooooAKKKKAGt1pu0HnFJNIU6DNKOlZvcsRlPGOKZc2sV5byW88azQyKUeNxlWB4IIqWvHf2rv2iNM/Zn+D+p+Lb3bNe/8AHvp9qx5nuGB2jHoOp+lID8yP+Cq/wz+DfgPxZpw8GSRad42kkDappVhgwRwleHYDhXz2968T/YZ+PWk/s3/Hiw1fxLosd1ZXKLbSXUkf72zVv+Wq59Qcn616N+xT8EdT/bc/aT1vxt41a4k0fT7salfzKAyz3G4GOAk8YwBkeg969m/4LFeE/Avh208BjR9MtbDxncGbzPsiLHutAqrmTHoeAT6GmUfqNo2saZ4y8O22o6fcQ6lpOowCSKaJg8csbj1HBBBr5juP+CYXwDvPE15rM/haWVrmUytam6cQKT1woPAzXoH7EPgSX4cfsrfDrRZtQk1OQaat150nUCZjMEHsgfaPZRXuVPlIueO+Hf2P/gr4XsYbWy+GfhsrFnbJcafHNJySeXcEnr3Neg6H8P8Awx4ZsUstJ8O6ZptomdsNraRxoMkk4AHqSfxroaKfKSQW9rFZwrFBEkMS9EjUKBnnoKS6uY7K1muJmEcMKNI7McAKBkkn6VYryn9qvxtJ8Ov2cviH4hiIEtnpEwTP95x5Y/V6oD+eL4oanBqXxY8V6hDMDaXGs3MyyRkMCpnYgg9+Oa/SX9tL9tzwbqf7Knh34b+APE6614l1ixsoLw6dJuEEQjUPFIy8B2OBtz2r4s/ZP/ZL1n9rnWvE+laDr1jomu6TbpdomqLIsUoZyGDOisw/KvuH9nz/AII93vh3xpa638UfEmnaja6fKs1vpugtK8UjK2RueVVbH4e3I5oKufmp8Tvg/wCKfg/ren6Z4n09rC/u7SO8gibrsdQ65/A1+yv/AATN/aq8VftHeCdX03XtAt7G08Kw2thDqVsxxcNsOVIPAYKq9PUeterftM/sTfD39qW107/hJkvLC/02Iw2l9prqjovoQVIYV0H7MX7MPhb9lbwHL4Y8LyXF3HcXLXVzeXmPNmcgAZwAOAAB9KCT2CiiigApMjOO9LXPePvFkHgPwbrniO6jeS10qzlvZUj+84RScD8qAN3duY46etVp45ZCApxg5z61+Ul7/wAFqNe/tGf7J8P7U2e8+X5t0Q+3tnAqtN/wWs8VLIwj+HWmlezPevn9FrN7miP1tiOE+bil59cV+M3jb/gsV8U/EWmNDoPh/SPDspBBmDNM/wDwHNfVv/BLX4zfFH43+GfGmueO9VbVtNjvkgtJpY9jLLsDOo9gGX86diWj7uHT1paRelGOvNWSRhgzEg5FNkuEjbDHH41Q1zXNN8K6Peanq15DYadZxtNNcTttVFAySTXg9j/wUC/Z91TUvsUXxG0wzZwC0cir/wB9FayZdj6AtW3zMcEZ9q/Kz/gthrQXxR8NNN8zIhtLm6MRzjLOFU/mh/Kv0Am/a2+DVrbm4f4j6CsSjccXIJx9MZr8if8AgqF8evDHx2+OWkX3g/WYta0bS9IjtluIQwQy+a7MvzAf3hQM/Rn/AIJa/CeX4W/sn6PPO+648TXL6864xtEkcaIP++IkP419dA57Yr8vdI/4Ks+EfhX+zn4L8O+HtLutV8YWOiW1m++LZawSpEqkEnlsY5wMZz1ry74O/wDBRT9o/wCMnxn8NeGtK1XTZhql9GJLC30u32RwAjzDvI3cKCTzV2Qan7LL0paZDu8pN/38fNj1p9UZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUrIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANavL/2jvjppf7OvwzvvGmrWM+o2tq6obe1KiRtx7biB+teokVyXxS+Fvh74xeDb/wx4nslvtKvF2umcMp7Mp7GspJuI476nwtpv/BaH4bTXIW58I+JLaNudzJA2PxEpqzq3/BZ/wCFlqdtv4R8VXfGVkjjtwp/OYH9K6H/AIc8fBn7YZf7X8Uxwk5FtDfRqi+wzGT+tY3xV/4JS/CLw58Odd1Dw9ba1caxbWkkkJur3zCzAZycKB+lZyajq0aKx61+yT+354X/AGtPFer6Bo3h/VtGvdOtRdu2oCLa6FtuF2uxz+FfTOvaDY+JtNm0/U7eO8sZ12y28oyrj0NfjB/wSTkudG/ay1CwAdFOl3EE6k55Vxj+VftfWu+j2E3Z3Wh4z4g/Y3+C/ieQSaj8PNGlmAUeYsJQ4AwBwfQCup8LfAn4ceA7OOLRfBWh6dHCPldbGMuOc/eIJ/WuvvtatNMs7i7vJltbW3UvLNKQqoAM5JrB8J/FDwf8REdNB8Q6fq5wd0dtcK7DnHQGp0WiDXdnxF/wV41yz039n/SbOwtbcJeX4UyRxKNoXPGe1ZH/AARRsPL+FPj67EissmspEI8crthU9ffdXa/8FWPCdrdfs63swgZjaXUc0e3+EHg/rVT/AII2+G4dK/Zr1TVUfdNqetTO6+gRVQf+g1MdByWiPvhcgc0tJuo3Ct7oyFooopgFFIeKFbcM0ALRRRQAUUUUAFFFFABRRRQAUUUUAQtCrSb8fNT6dtpNtQ0yrir0paSlqyT4a/4Kx6fqt5+znqEkFotxZxXMRZ8couQSfzriP+CJ+uxzfBrx9o4IMtv4g+19edslvEo4+sZr6I/4KFXEdl+y34znliW4T7NsELcDJP3s+1fIP/BEZZI2+KEm4mKY2QEfYFfMyfx3fpWC3Zo/hR+qNLSUtbmZ5d+0T8C9E/aF+GuqeEtZjRGuYz9muygZreTswrC/ZD/Zpsf2WfhLB4Rtr3+1LpriS6ur0xhDI7HgYHYDA/CvbNvzZpcYoHfSwEVAbC3a6FyYIjcAYEuwb/z61YooEJS0UUAIeaAMUtFABRRRQBDcK7fcKg/7VEfmfx7fwpWlUSFc5P06VnXfijRdPLC61aytiv3hNcIuPzNY+6nqy9exzPxcQyeDdXVVd5HtHRAvckEV+Kv7DWmyx/t/eGrd1ZXg1a+LA9RiKTNftL4o+JXhCHRbqaXxNowVEZlEl7GwOBzwDmvxn+A/xN8LeBf+ChFp4nl1O1t/DrapdeZfXEgWJPMjZSc9gCeKSfv3Oi94ryP3YXpQzBVLHgAZNfOniz/goJ8BvCETmb4h6XfOv/LPT3M5PsCvH618/Wf/AAVgsvH3xp8P+CvAfhKbVbDUryO2N9dHYZFb7xVe2DkZPpWvMjn5Wz7B8dftHfDn4ZtGvijxbpuiySNtSK4mAf8AFeorv9L1a01rTbbULG4jurO5jWWGaJsq6EZBB9CK/ND/AIKr/shT+IbRPiz4Y06ea+ijWPWLZX3KI1UKrquOMAc1y/7G/wDwU70H4f8Awft/BPjqKW2v9Ht3istQUFhMuSUVh2IGB+FHMkVyqx93ftEftjfD79mN9Oi8ZXF1Hc34LQQW0BkdlBwW+ldn8Efjp4U/aA8FQ+KPCF615pkjtGfMQo6MpIIIPuK/GSHR/iL/AMFLf2imeOaRdHgby3uypNvYW44z/vMBnHqa/Z/4I/Bjw78Cfh/pvhTw5aJbWlpGBJIo+aaQ8s7e5OTVXuKSSR3y0m4buvtivIf2p/DHxC8UfCHU4fhfr02g+L4SsttLDt/eAdU+YHk9q/Mfwr/wUY/aC/Z08UponxW0ybXLWKXbOmqWwiuZPUpKAAR6YFK5CVz9l1O4UteUfs+ftKeCv2kfCa614R1FZnTAurGX5Z7dvRl/r3r1XcaYh1FJnimTTLDGzscAUgPFf2pv2iNI/Z1+H954h1VncrxbwqBiWTbxHn3POa/KY/tJ/tXftTa9c3fgW71610+2LeXDoebeKIZ6FxjceO9dF/wVQ+NV98R/jbpfgO1mc2WmmNZLRT8rTSEYJ99pAr9Uf2ZvhVpHwg+C3hfQNK09LBY7RJJlAy7SONzlj1JyTWEbt3RtJKKsflz8Hf8Agox8Yv2dfG0fhj4y22o65YJII7ldSXF9CCc7w/V+D0Pauy/4KlfF7wP8cvgv4C8T+EdWi1GNr1xjo6Dacqw7HNfb/wC2N+yZ4W/aP+HOqrPpkKeK7W3eXTdTjBSRZAvCsR94HGMGv5//ABJHqnh+9u/Dt8ZIfsFwyPbtkASL8pOPfFaEx2P0m/4Im6Dbyaz8QdZKn7THHDag84Cn5v5iv1jr8+/+CN3hG30v9n/VtfSHbc6rqUiySc/MIyVFfoEveqirCkfKnxh/4KI/D34D/Fj/AIQvxdZ6tbMyJIdQigDwoGAx6E+/pX01o/iKx8QaDa6xptwl3p93AtxBMh4dCMg/lXwT/wAFSv2PtW+LGi2PxC8H2n2vWdGt2ivbFMlp4Mk5UZ6jJ6c18r/sjf8ABQ3VfgT8O9f8D+K57y7jt4JF0gzfes3wcpzycMTwanbQdk7HuH/BQr9v/wAU+APEEXg7wHfR6Tfhd9zeqVkkizyBtYEdPavdP+CYvxo+JPxn+D99qPj62lu4YbpksPEEyLG18uTuG1QFwjZXIHavzL/ZV+D+sftoftNwS+JRdappMlw19rV5IGwYl6RFlxjPAGMV+9nhrwzpfg3QbLRdFsodO0yzjEUFtAuFRR/nr3oUQkzUXpS0i9KWnymYUUUUcoEEkW5iema87+Od34t0f4Z6/f8AgyO3bXLS2aWAXGSGIGTgV6VSMiupDAMCMEHvU8nmaRm4n43Wv/BYL4uaDILPU/DGgzSW58uXzS8chIOCTWv/AMPovG8kWU8EaOD/ALV038sV+l/ij9mX4U+NLqS61rwBoV9cSHLytaKrMfUlcVTsP2Tfg5plsLe2+HHh9IhnhrNWPJz1OTT5RXR+UvxE/wCCunxZ8XWb2uj2OkeHVI5kjQyuOOxP+FfXP/BKv4xfFX4zeHfGGq+OtVm1fRIbhIrC4uIwpEmCXCEAZXkfjX1nZ/s3/CzTxiD4feHUHXnTom/mK7fRPD+l+GbBbHSNOtdLslJK29nCsUYJ6naoAo5RXL4HfvS0UVoSFFFFACdzX5V/8FrstrHwyQbRm3vTn+L+H9K/VP8Air8hf+Czl5O/xl8B2zOwt00hmVc8AtMQx/EACoa6lR3ufpJ+ybbR2f7MvwuiiBCL4csevX/ULmvWK474OWkFh8KfCNtbRrFbxaVbJGiDCqojXAFdjVLYUtwooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+Dv8AgpF+3XN8BdNHgXwPfIvjy8Cm4nTlrCJgGU4P8TAgj2NeB/sef8EztR+LzwfEn40zXK2l/I10miuxE95kkiSZh0U5yAOSD2r9H/FH7Nfwy8Z/EKLxxrngzS9U8UxbNmpXMIeQbAAnXjgAAV6Q0S+SYl/drt2jZxjjtU2KufLmtft6fs4fAmRvBQ8VRWP9hgWf9n6bp88yQbRjYCqEEjoeeteYeLv+CyHwd0W+MGiaR4g8SRcYuIbcW6txzgSENweOnaszxZ/wRx8C+LvHWreIJ/HWvQW+oXL3LWccMRKsxyw8w5J5J7VwH7T37Dv7Pv7I3wG1bxBqNnrPiPX7kG00yS+v2GJm5yFQBQB7imPQT4nf8Fd/h54r0+NY/g5L4kmtzvj/ALeMJjhbscbG/Svon9gP9rzxT+1PZ+IJdS8C2PhjQ9L2R213pshMMjnrGAR1C46V+W37FP7H+oftb/EC9sZLybQ/DOmxrJe3kSluCeI1JPJPPWv3M+CfwS8L/ADwDY+EPCVrJa6ValmDSvveRmYszMfUkk0xPsd8vSlpFz39aWgkKKKKACiiigAooooAY3eojIVJGCcVMc54r5h/ak/b28Efss+JdP0PXbG+1XULqITmOw2ny1z/ABe+Oaze5cddD6ViYyyFlOVr5T/b0/Y48Q/tcWfhW00nxNDolppMksktvcRF1kdgMNweoxj8aqeC/wDgqZ8BPE1upudduNAl6mK+tiMfiK6o/wDBRz9nhevxGsf+/Mv/AMTSGdb+yb+zTpP7Lfwns/CdhIt7fMxnv9QCbTczHvj0AwB7Csr9pD9i34fftPa5oOreLILkX2k4jWS2lKedDu3GNx3Gc/nWfb/8FEv2dZ495+KGlxf7Lwz5/SOhf+Cin7ObMVHxS0vI/wCne5/+NUCPoHQdHs/Dui2OlWESwWVlClvBEv8AAigBR+Qq9mvmLUP+Ck37OmnxyMvxFtbxkGdlvaXBZvYZjA/WvNNS/wCCw3wMs7qSKC28TXqKcCWKwjCt9MyZrRbCsz7ozRmvgpv+CyXwXH3dE8WP9LKH/wCO1nXX/BZz4VRyMLfwj4qnj7M0UKH8t5pisz9Bs15j+0z8KZ/jh8CfGPgi0uEtrzVrPyoJZCQokVldc+2VFfIMP/Bab4VFgsvg7xYp/wCmaW7fzkFTXX/BZ34VR25ktvB3i6c9laGBM/j5hFAWZ2n/AATh/Yv8QfstaT4q1DxmLCTxLq86RxvZyeZst0HALe7EmvtOvzA1b/gt9pMN46aZ8Jry5thjZJea5HC545yghYDn3rHm/wCC4Vwsh2fCFAn+1r+f18igR+q9Ffkd4g/4LbeKri3zovw00uxY8CS+1GSdR+Coma+m/wDgnv8AtteNv2sbrxHbeJvC9jZW2lorLq+lLItuzsT+6KuThgMd6APtaiiigAqtqWm2usafc2N7BHdWdzG0U0MgyrowwVI9CDVmigD5n1T/AIJy/AHVNQmu38CQRPK24pDM6oPoM8VFH/wTd/Z/j/5kaFv96Zz/AFr6doqbDueJeFP2L/gr4NjUad8PNH3qSfNnh81/zavVfDvhTR/CGnmx0TTLXSbMsXMFnEI03HqcDvxWxRVAIucc0tFFAj5q/b0+BHjj9ob4Mp4V8C39vY30l8ktz9qnMSSQhSCuQPUg4r8+tL/4Iy/FS7VZL/xD4f0+QnmOJ3lA/HAr9mqKVirn5D2P/BFvxxIyC78eaNFH32WTM357ua+ZP2vP2R5/2UPHWh+HLnxNb67cahafbS8FuYjChk8vJGT3B6HtX9CdfjF/wVd1BPE37Yui6Pbv501tptjYPGvVZJJRIF/FZAfxpcoczPtv9nn/AIJtfBn4c+GLG8v9Cj8ZapdQJJJd60omT5hn5Yz8qjn07V9A+DfgD8OPh7q41Tw14I0PQ9RA2i6sbGOKQAjBAYDPSuw8OW32Pw/pkH/PO2jT8lFaNUK4gpaKKBBRRRQAUUUUAFMfd/CM0+igBse7aN3WnUUUAFFFFACUA5obkUijatRcB1FFFWAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAncV5t+0B4hg8L/CvxFqNxdtZ+TZytGyn752dCK9JPUV598fLGLUPhB4rjltY7vGnTERyD/YPT3rCv8DLjuflh/wAEjpY9f/ag8X6i8RMp0+WdWA4XdL/9ev2PWvxP/wCCTfiq38MftUavZzyJaxX2m3EREhxysgYD8s1+0Gja9Za7bmeynS4QcHYQcH0pxkloxyu9TzL9qDw7c+J/gx4t020aRJJ9OlRDGcfOV4HHNfgX8IvHHif4QfGTRZtIvbjS9RtdSjtpoxIQrZkCsGHpX9EHxM1RtP8AA+tXZhx5Ns8ib8YLBSRn2r+deCe48XfHy2uAAbq88QI5VRxnzgePahF/Zsfsd/wUa8daLoP7NN3Dr7hrnWLRIbdEH/LXG7PPavzv/ZI/4KGan+y38N9T8K2+hDVllme4tZCwCozcndn39K+t/wDgrXfaddfAXwtbXW6PULe4jMSnqcxjNeB/sA/8E9fC/wC0x8Ob7xh4s1q6itftT2kFnYna6MvVmJ45pKMWN/Cdn4D/AOC1WvWMTJ4t8C2+o4+7Lp0/lt+IbivuP9jz9sfR/wBrrw5q2oadot3oV1pkwint7hw4ORlSGHtXjH/DnP4OeUE/tLW8/wB7zVr3n9mP9jrwh+yqusr4UvNQuE1QoZkvJNygqMAgVXL2MtD3lc7eaWkoz7VoQDfdNNjbtSn6U1V280XQElFJS0wCiiigAooooAKKKKACk5paQru60AC5xzS0iqFGBS0AFFFFAHgX7b2gx+KP2e/E+myyeWkls77sZPygnpXwX/wRZ1qaDx/8Q9GA/wBHNrFPnP8AEHZa/SP9pCOL/hTPiqaSETmKwlIVv901+Xf/AAR11h7b9ovxhp4iUpeaW8jPnGzZLwAP+BfpUaXubP4UfsiKWkWlqzEKSk3HnivAv2tP2hNa/Z28FjxHp3h+bxBEGw0UWcL7nHah6Fxg5uyPf6K+Sf2Z/wDgo18Pvj80Ol3cw8NeJGHzWV22EY5xhWPWvoH4jfFfQPhn4butY1fUrW1ghj8wCWQLv4yMVPMg5Hex2tFfmF4r/wCC0ltpGv3NnpXgJNUsoX2i6a88vePYYr6l/ZT/AG8fAv7UkZsrBZND8SRruk0m6cMxHqjcZp3QuVn0xRRRTJCiiigD5o/bk+G/xN+IXwruovhnrMthrEDiT7NbOYpJ0xyobPWvyhh/Yo/af8a6oY5vCPiWGaRv3l1ql+FjJ7nJbpX76YoxUcqvc39q+VRaPw8n/wCCTP7Q/kRTiPSJpSPnjOsAOPbPSvKfhj+xb4w8dftES/CTUZrTw9rVuhkuppXFwkagbgRt68EV/QTr10LPSbubcybImOV69K/HH9i7xhc6r/wUm1C4ndppLya+hLSHJwucfoKltp2CMbxbN7xh/wAEW/GWk6TNe6T480nVLiFC5t2s3hL454OSK+ef2LdLtPBH7anhHTPEkiobDU5LV2jYBfNUEJ/49X9AToJAVIypGCD0r8N/25PgNr37Mv7TX/Cd2ulyf8Ivd6nHqdlcwNlS4YO6E/wnORg09SYpM/ZL4y/ELwp8Ofh5q+reMLu3t9G8hkkWcjEoIxtAPXNfzffEK4stU8ba9qGixNHo017K9uyqQuwsSo/Kv2blh+Dn/BTfwnoVkPFuowXeixxz32j2DiJwT1DhlORnIyK9v079jH4RaX8PpPCEHg+xbTniaMzSxK0+SPvb8daFzC0W54Z/wSX8Q+CdY/Z6a38O6dHpviC0umj1hc5eR8ko5PcFSMelfca1+Imtr4m/4Jj/ALW0MVjfyXfg+6dZ5I+Slzav1BXI+dOgPtX7N/D/AMcaX8SPBuleJdFnFxpupQLcQuPQjOD7itBSOh7mvKv2iP2d/Cn7RfgO+8P+ItPgluXiYWd+yDzbWQjhlbr1xxXqnRq5Pxp8UvCnw9tZrjxHr1hpMcSGRhc3Cq2B6KTms3uJdz8KfhP8QPFH7Cv7VE9pNJMbbTr77BqUBBC3NuXwHx3+XkGv300TVoNe0ey1K1bdbXcKTxn1VgCP51+E/wDwUA+N3g39oD4+WOpeCLQ3Bj8u2lvIlx9rIYAcD8s1+3nwnt5Lf4ZeFopozFKmmwKyH+E7BxVrYcnc6r+GkmQSJgjOORmnUjAspAODjg0En4F3Fk/ir/goh9j8Rq1yJ/F22RScZRZPkH0wBX75W8axQRoowqqAB7V+E37U9vN8Av2/JNafcyW+q2uoh3XKuG2s+M+mTX7i+GfEFt4m8O6bqtpKJLa8gSaN1ORhgDWcfd3NJvm2NZq/Bz/gqV4e8N6D+1NqjeHYUhF1aQzXaxsSvnkfMcduMV+2Xxa+IFj8Mvh7rXiHUZhDFaW7spPGWwcY/Gv5yPi9441P4sfEDXvFN40lyJ5z++28Ko4UHHTin1Ej9nf+CTcKw/se6FtB+a/vGOfeZq+y1r8zv+CSv7U+m6n4bg+D95aPFqlr5tzaTxqAjx5yQffnrX6YrWnQUhk23y234KbfmDdMV/Pl+39Z+CbX9pbxGnglBFZ5V7pFctF55GX2ZJPXt65r9ef2+P2mov2bvgrf3VpME8R6sjWenKArFWIwXwQRgD1r81P2Ff2H7r9ri81zxl4ukeLw6jSxiQl1e7umBO4MpGArHnFZ9R7K59z/APBJvwr4O0f9m2HVfDsv2nV9RuGbVpXJDiVTjZtJ4UdBjr1r7cavxk/YR+Imv/spftdal8KtfmltdF1a8eykgmAx5wJ8mQZ5GR6Eda/Zv7y1V0TJdQXpS0i9KWqJCiiigAorxT4+ftffDf8AZvurK08Z6tJaXd2u+KCGFpGK+vArzC0/4Kmfs/XSbj4puIefuyWUgP8AKlcrlZ9dUV8q6f8A8FNv2fNQuPK/4TVbf0ee2kVfzIr03wl+1p8IfHFuJdI+IGiXCnjDXSo35GmKzPXaK811v9pH4YeHbczah460OBB63iE/kDXVeC/Heg/ETQIdb8NarbazpMzMqXVq4ZGKnDDPsRQB0FFIvSloEFFFFADT1r8iv+C008EnxS+H0UeBcrprhyOuDMSBX66nrX48f8Fko0l+P3hBd3zHQ1+X0bzzz9cVLfQqKP1U+ChY/CPwcWOW/sq3yT/1zFdrXJ/Ce3Fr8MfC0IOQmm24z/2zFdZTWwnuFFFFMQUUUUAFFFFABRRRQAUUUUAFFNPWvkX9tb9vaL9krxF4d0e38OL4ku9Rhe4nj+0+UYYwcDsck1Nx2PryiuD+BnxWtvjd8K/D/jS0s5dPg1W3Ewt5jlkPcZ7iu8qhBRRRQAUUUUAFFFFABRRRQAUUUUANbrWf4g12y8MaJfatqM3kWFlC088mCdqKMk4rSqC9s4NRs57S5jWa3nRopI26MpGCD+BoA+PfC/8AwVa+A/iLxRPo9xqmpaMiyeXFf39mVgl5xnKkkfiK+Jv22Pi1c/twftUeFPh38PNRj1fw/bstnY3EIIRpJFDXE3PZVBHP92vob42f8EcfDHirUNQ1TwB4ruvDd1dStKbG/XzrYEnOAR8wGfrXxZ8Wv2Lfjn+xnqNl44hjjmttOkEkfiLw45YWzA8GRSAQD7jHvQVc/af4F/A7wz8AfAOneGvDWn29pHDCi3NykYWS6kCgGSRurHjv0r0aPO0Z5PTpX4z/AA//AOCxfxX0ebSIfEui6DrthG6i7khgkju3iGAzcNtB79K/XT4a+PtP+KHgTRPFelLKmn6rbJdRLOhRwGGcEGgk6aiiigAooooAKKKKACiiigBP4q+Nf2uf+Cb3h39pzxa3iuHXrnQfEEiJHNJjzImVFCr8vY4FfZdFTyjTsflTa/8ABE26eUtd/ElCuePLsjyO3etyH/gijo3ljzfiHe7+/l2q4/Wv06oo5R8zPy01b/giejSZ034lSonHy3FkCffkEVCv/BE2Vsb/AImsPXbYD/4qv1Roo5Q5j819B/4Ir+FYLdBq/wAQ9aupcnd9lhjjXGeMZBNdnpf/AARx+Dlrs+3ax4l1LHVXu0QH/vlRX3mxC/MTgAZr4h/az/4KfeE/gLq8nhrwpZw+MfE0Y/f+XcD7LbkjIBdScsO69uhqhXZeH/BJT4BhQv8AZmrH3/tB81Ys/wDgk78ALVstompXHtJqEn9DXwZY/wDBTr9pjx5rc0Xhm7WeSRt0em6T4eivGjB6AfIWNa91/wAFGv2pvhTq+n33jmwuo7CZxustb8NnT/OUdQhMa849CaAuz7Q1n/gkb8AtWnMkVjremjAGy01Ehen+0DUWm/8ABIf4A2aqZbTXr7vum1Ruf++VAr2H9kr9rbwz+1h4Ik1fSojpus2Mnk3+kzMGlt27OPVWHQ/hXvK9O/rzQF2fJ+nf8Et/2cLJV83wLLeuOr3Gq3WT+CyKP0rpbP8A4J3/ALOljbrFH8LdKdR/FNNcSN/300hNfRlFAj5ruv8AgnD+zjdzmV/hfYK3/TO8ukH/AHyJQP0r2L4XfB3wZ8FfD7aJ4J8PWvh7TGkMrQWu5tzHqSzEsfxNdlRQAUUUUAFfKX/BQr9pDxx+zf8ADHTdX8E6St5c3Vz5U99NA0sVquOCwHqa+rapavoun+ILGSy1Oxt9Qs5Bh7e6iWRG+qkYoA/FCP8A4Ky/H26xFA2izyAYJh0uRifw3USf8FLP2m72TdFCAG6CHRJMfyr9idD+C/gHw3I0ml+DNCsZGOS8OnxA/ntrqIdIsbdQsVlbxqOipEoH8qAPw78Qf8FDf2o77TpoXuLrTkI+aaLSGjYD6kV91/8ABLHxd8V/iH8Nde8TfEDWbrVdIu7wx6Y18v7wlCVkIP8Ad3AjHtX2vc6Hp16hS40+1nQ9VkhVgfzFO0vSLHQ7MWunWcFjaqxYQ20YjQEnJOAMcmgC3RRRQAUUUUANZiq5Aya/Gz9pbSIfil/wVe0/TLJ1uov7R02KYL/C8EEZkXnuuw/lX7K1+Htx4t0vwH/wVS1nWdcv49N0u18aXhlu7gkRxqwZQSewyRQB+38aCGNEHRQAPwpl1eQWNvJcXM8dvbxjc8srBVUepJ4ArzDxd+1N8JPBOhPrGq/EPw+tkozm1vo7h246BIyzZ/CvzN/aK/am+IP7fXxGtPhv8FbPVrbwzHlZ3in8lbsEgGWc5AVFGcKTk+mam5SR+vGi6/pniSyF5pOo2mqWhYqLiynWaPI4I3KSMir9eNfstfs56N+zZ8L9M8O6bFu1B4kfU7rzGfz7jHzMMngZ9K9lqiQooprMEUljgVHMA6imrIsgypyKdRzAFFJS1YBRRRQAUUUUAFFNK570o4pWAWmswXANOpjRhjk1N7APoooqwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAa33hXnHx81j+x/hj4hd+IpbCaMsOxKGvSCORXlv7TcKzfAvxiWwPL0+VgfQ4rCt8DNabXMrn862m+JNX8KeNbi+0O9ltdQE8kcc0JwSGYjFfvh+w74B134e/APSJPE2q/wBqarqK/bHkyx2q/KqcgHIBr8A9FvYtN8ZWd3dc28F8sknGflD5P6V+93gH9uH4Df8ACFaPC3xE0WzKWkatbXE4R0wo4INPlV0x8y5bHrvjuYah4R1+31OAJbfY5mXaeoCGvxf/AGC/g+nxV/bELxiNdM0W6lv3WUE5CudoGO+a/QT9pD9v74ON8MddsNB8Y2up6tcWskMAszvG5lIHNfnN+wB+0x4f/Zx+NF/r/iuW4j0XUoGhklhiMjbi2d2B2oFdWPrr/gsxZL/whvheZY2Xbc4z24GBXQ/8EX7ueT4N+L7eRyY4dX+Re3MYJxXl3/BQL9tb4QftB/CkeHvDl5dX2qxzCWKdrVkUD05Fec/8E5f20PDH7MfhnxTpnixpmt7udbmCOCPLEhcEVKLeqP2spNx9K/OzxH/wWc8BabMg03wZrWqRkAl/MSLB78GsS/8A+Czvhry1kt/CV8rn/l3d1J/766VfMjPlP0rknEbKCGwTjNIszGTaUIHrmvy3vP8AgtH5jA2fw9uAPSW7jxXGt/wWb8cQ30zN4P04wEny4zIcgds4NK77MXKu5+vkgZ1YL17URKyqFbk+vavyN0X/AILReL47h21XwPp81ufuraTMrD6k5FesfCL/AILA6X8QfiBovhvVPA02kR6ncJbLefbQyxsxxkjb0pjt5n6PUtMhcSRq6ncrDIPtT60MwooopgFFFFABRSbqTzBnFK6GLRkVGzfNjpTwvvUczb0EOopKWtACiko3DnmgDzf9oyYQfBTxex286fKBuOBnFflB/wAEj782n7WGrwmPcbjS7lSw/hxIDX1X/wAFRP2ptO8E/DGXwZo12JNd1I7JPLkGY0xzkda+UP8AglT8RPA3wn8beL/FHjbXbPRnNqsEE12+CcnLY+tZGtnZH7VrS14HY/t1/AzUIRJB8RNJKE4+aXFOuP25vghbSpG3xA0sljgFZMiruiOVnudzcCFSSM+gHrXxl44/4KGfBvVPH178MvEFhfTSPdHT55HjHlB87TX1h4T8c6B8RtBGr+GtXtdW09sqt1auHUMO31FfiZ/wUs+Hsfwr/ae/tOwwp1CKPUfMjwA0gPP54rOTvoaRSSv1Oy/bk/Yi/wCGe0T4peAtSmbQpbpZY40xm33cggjtmvAbP4gfFv8Aa+17RPAj6y+r3kmI4EkcRrtH976CvavjZ+2Nrf7TPgHwn8JfBGmXEtxLHHFdeYPmlkAAwvtmuF8S/sG/Hz4A+H7fx+umG2+xHzmfSrnfc2wHcgClHbUTlqfb/wAGv+CPvgDTfBKf8LCu77VvEVwmZPss5iitmI6Ljrj3r4g8YeGdQ/YN/bG0w2dw15pum3kUsUzsf3tq5G5WIxkhTj8K+2P2J/8Agp5pnja20/wX8ULlNN8RLiCDVWBWO47ASZ6N715p/wAFjPhrY2t94O8c20oljvhJbOI1ypGMqQw+tUVHzP1T8M+ILXxV4d03WbGQS2l9bpcROvQqwBFadfNf/BO3XTr37IfgOczyXDxW7QM0pyQysQR9BX0nnitEYvQWikFLTEFFQ3V0lnC80rrHEoyWbgCsrRfGmheI7ie30zV7G/uITiWG3nV3T6qDkVLkk7MrlbV7Ffx85j8K6mynDrbuy+mdp61+L37CEkkn/BRCF3VS7XN8XIHAyD0r9lfinerZeBdWkchV+zuC3p8pr8gv+Cbeirrn7c2rXwLstit3MGBHdsc8VL3OmP8ADS9T9qc1heN/Afh/4j+H7jRPEuk2us6VcDEltdIGU+49D7it4L3pafKzki2eM/A/9kn4b/s86xq2qeDNIksr3U+JpJZN+1c5CLwMCvZKdto21Y3qfBf/AAVM/ZT1v45eEdI8VeFbFtQ1zQ1aKS1iHzywsc8DuQa9U/4Jw+F/Fvgv9lzQdI8Y6fPpmo29xcCO1uRiRYjISmfwr6f20uKB30sI1fNf7Tv7Bnw+/agvDqmtS6hpXiARCJNQspuMDpujPDY/CvpXbRtqLMLnxN+z1/wSz+H/AMFPGK+JNU1a88Y39uR9jF5CkUUeO7IMhuehr7XjjWFAijCjgDsB6U6lqyQooooA/Pn/AIKlfsi618YdDsvG3hGw+36xpURS5toh+8ki65A7kV8SfA//AIKIfGD9mjQ/+EQmt7bU7C13LFZa3AyzQMT/AHhhiPav3gZQwIIyD1ridc+CHw/8Tai1/qvg7Rr+9brPPZozH8cVNi+Y/E74jftofHr9rd28GxxR3lrqDCNNJ0jTh39ZMbgPqa/QX9lv/gnH4T8G/AS60Lx/pUeoeI9dQvfyLKwMII+RVweCoxnHU19eeG/hj4S8H3LXGieG9M0qdhgyWtsiNj6gV020UuUOY+CP2TP+Cbup/s1/tAXHjQ+Jba/0KK2lgs7VIyJsOQfnJ44Ar72Wl2iirE3c/MX/AIKu/BTx78VPip8P4vDWi6lrWlT25t5DbQ74reYyYLHHT5cda+8P2d/g1pXwE+EOgeD9HjZIbSLfM0hyzzP80jH/AIETXpLIrHJGaXFRyg3dWPxQ/wCCpng3xF8N/wBrCPxrbboINUit7vTrtVAxNCihvbOVr9Zv2bviI3xX+BfgvxVLJ5txqWmxSzNtC5k24bgcda5P9rj9k3Qf2sfAVvoOqX02kX9jN59lqUC72iYjDAqSNwIrvfgj8K7P4J/Czw74KsLmS9ttItVtxcSgBpCOrY7UcoN6WO4XpS0UVZIUUUUAeEftNfsc+AP2pNNiXxNbS22sWybLXVrZ28yBe4C7tpz7ivkmb/giX4UeZmi+JurQxnon9mRsR+PmD+VfpZgGjaPSpsPmZ+YGrf8ABEvSxCy6b8Srp5Oqm6sAFz7gMa8+1D/gir4+hvnNh490JoONrtHMjfkFr9gMCjaKY+Zn413/APwRr+KqyLEnijQr2LIzNvkBH4EV+kP7Gn7P97+zT8C9K8EalfQ6lf209xPJcwAhT5khcDn0zivc9oo2imK7BelLRRQIKKKKAGN1r8Uf+CrGrSeJP2w7DSY5BJ9ls7S1Cg52l2Bx+Zr9r261/Pv+3BqeqW/7bfjq5/eXN3a65mzikBbcEZfLQD09KmxcT97PAdk2m+CdBtX+9DYwofwQVvVxnwb13VPE3wr8LanrWnvpeqXOnwyXFpIMGNtoyMdq7OqICiiigAooooAKKKKACiiigAooooA8I/as/az8Kfst+D5NQ1mb7RrNxG39n6an35n7Z9Bmvyj+Hvwd+LH/AAUY+Mk/inWvPttBknDXGoTljBBFniKIHgHHGBX66fGj9k/4Z/tA6zpmqeONBOr3enLtgP2h0UDOcEA816L4Q8F6F4B0K30bw7pNpo+mW67Y7aziEaj3OOp9zzU2KuR+A/B9j4A8G6P4d02NY7LTbZLaJVUKMKMZwK3qKKokKKKKACiiigAooooAKKKKACiiigAooooAKYwJ74/Cn0UAfNXx2/YD+F3x48Taf4lvLB9B8RWtzHO9/paiM3GxgQsing9OvWvo+ztVsrSC3T7kKLGufQDFTUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZ+v69Y+F9EvtX1O4S00+yhaeeaQgKiKMk5NAHzr/wUB/aNi/Z7+A+qz2V9Hb+JtUQ2unxBx5gzw0gXOcAd6/P/wDYS/4J63f7QrQfEr4kTSJ4XuLl5UsHBWXUGDHLMTghM9x1FeN/tNfHub9r/wDaaiku9QFl4TS+S0sFuZAkUFqGAaQ57sASa/af4F/ET4b6z4b0/wAL+BfE+j6umjWsdubawuUdlVVAztBzjPfFBVjtfCHw98NeA9KttO8P6JY6VZ26CONLaFVwo98ZNc78dvgj4e+Pvw51Twp4gtYZY7qJlguXjDPbSY+WRM9CDXoa9KWgk+bf2I/2PbT9kXwTq2mHUY9Z1fU7szT36RlN0Y4jTB9B+tfSVFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfnF+27/wS+1j43fEnU/H/gHV9Ps9S1La91pWoKY43kCgNIHAPLHnpX6O0UAfjd8O/wDgjf8AE7Vr+3j8Z6/oujaUr/vRp8rXE7LnnBKAV+kn7NP7I/gb9lvQ7mz8KwTz3t5tN1qN64eaXHQZ6AD0Fe20UrDuIKWiipvYQmaZIqSqUbmklUtnBxVb7VDb+Y0sqosal3djhUUdST0A+tQ2VYsxqsXyrwtP4bnNcj4f+LXgjxZI0ejeLtE1SVZDEY7TUIpG3g4K4DZzmuswCOKYWI+FnJ5JxU0biRcj9aqM3lvnOWzjmrSuNo7U+YbjZCs4RcnpVeO6FxMVjyQOvGKnBJ4xlfWlVQvQYp8zIHUUUUcwCUZFRyBmbg4FCLtXBO6jmKsSZoyKZuxTd3zYqQsTUU1fu06tFsSFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8++P3g/UPH3wb8XaBpTbdRvtPlit8nGXxwPxr0GmlaTipaMa0Z+Dfwn/4Jh/Gb4qa9qVjeWVv4OS0G43euiRY5snomxWzXvPh3/gij4sVlGs/EPRYYu4sbWSU/m6LX62LwKWpswe5+Yo/4Il6VIgMnxRu0fuE0iMj894qwv8AwRF8M9T8U9V6c40iL/45X6ZUU7CPzy0X/gi/8NbG0WPUPGGvahOCSZY0SEEdhtBNdNbf8EfvgrHt8671+Yjri8C5/SvueijlRXMz4tt/+CSfwHhVfMttenYHkvqbc+3Sux8O/wDBNX9n/wAOKNnglL9v79/O0pNfUNFHKg5meC2/7CXwEgXH/CsNCc+rwkn+dWZP2IfgU9u0A+GWgpG3922wfzr3GiqJPkjXv+CXH7PuualJd/8ACLXFjvAHk2V9JFEPcKDWdoP/AASt+Cfhnxpp3iLTbbVYZLCVJ4rWS8aSLcvOTnnrX2PtpNtQ0yrjYYxDCkajCqNqj2HSpKSlqyQooooAKKKKAGt1qKeBJ1AYZxyOcVK3WkrN7lkUMm9SD1XipxUQWPzD2c9alpxRItFFFWI83/aG8ReLPCnwi8Rat4Jsv7Q8SWsBe2t9m4se+B3NfkFr/wC39+0/eW91o01vNbXTEpKU0mRJl9sg9q/cWqraVZNMZTZ25lJyXMS7vzxUcpalY/Ff9nH9gH4l/tba9/wmPxH1K+0XQZJSslzeKftc+04KojdB719reIP+CSfwY1HwcujWDatp16p3f2q04mlJ9wQBivtvGOnAoYZ74pqIuZn5HeKf+CKvixdal/4R3x5o82lYHltqltIs3vkJkfrWTcf8EVfiNsBXxx4bY/3VgmH6kV+w+Pejn1pNMOZngH7Gv7KsX7Kfwzk8ONrk2u3d1N9ouJXG2NGIxtRfT3rl/wBsb9hHw3+1BobXMEx0jxZbRkWd91T/AHWHpX1RRVWFdnxP+xj/AME4NA/Z4mt/EfiiSPXvG8LMVuoWYW8Sk/LtU98d6+0L6xg1KyntLmJZbedDHJGwyGUjBFT0tFkI/Jf9vn/gm3c+Hbj/AITn4S6PLcWe4y6hptu5adG67489R7V8ReKP2i/ibefD8fDbxDqc13otrIWSz1S3DTQNnkBmG4V/SIyhgQRkHqK+Qv2zv+Ce/hz9pjTY7/Q2tfDHiyFs/bUgGycekgHP40rDuzlP+CRPxDi8Vfs1tojyL9u0S/ljeNABhHO5SRX3Q3Svj/8A4J9fsZ+Iv2R9P8WW+v6zZ6s2rTRvF9jVgqhRjnNfYFUJ6gvSlpKWgCrqFjDqVnNbXEaywyrtZG6EGvyv/aw/Y1+K/wAEPidL8TvgZJq91aXT+bc2GlSlriBhyxK4+ZD6YJFfqztpNtTyxbuzRVJRXKj8UfGf/BUD4oal8O73wP418LQJrBRoZNQy9lcDPA3wkNyPXjPoK6D/AII22E9/8ePFmqvFJIg00q0x5AZnzgn1r9VvHfwM+H/xOfzPFfg7Rtem6edeWaPLjsN+N361H8K/gP4D+CUN9D4I8N2nh+G9fzJktQfmP1JJx7UmtdDT2i5bHeilpKWrOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnFNVw3APNJIu4Y3YNRxgQxksfm/vVPMOxPQTjk1TS7VpOH49KladGO0vz6U7j5WSBg3Ir54+Of7C/w1+O3i608Vaja3GkeJbeaOc6npj+XJKyEY3+vTrX0ImBwvSphS5g2INPtRY2NvbK7SLDGsYaQ5Y4GMk+tWKQUtUSFFNJpu/5iO9TzDsLtO7O7j0p9eC/tCftpfDX9mXVdN03xrfXkV7fqZI4bK2MxVAfvNyMCuw+FP7RXw5+NVjDceD/ABbpurSSIH+xrOq3KZ/vRE7h+VHMOx6Qc9iKFBA5OTTPJBk8zc2fTPFS1RIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8Zf8FXPidcfD/wDZbu7CzuDb3Wv3kdhlTgmP7zgfhivs2vzZ/wCC1WiatefDrwFqVvC02kWd/MLnbnCMyAKTQB4H+xb/AME0LD9pL4RL441/xFeaPBdzywWVvBF82EO3ec9QT0xXmfxz/Z1+J3/BPv4k6Rr+lanM9gZQ9hrVnuVJSpz5Uo6Zx2PWvs/9hf8A4KCfCDwT8BPDvgzxhrB8J6xolv5Lie2kaKcZJDKUB5PuK8F/b8/bUt/2sdS0j4a/DjS5tW0JbxJFumhInvLj7qiNeoUE9fzoLVz9RP2XfirffGv4D+EfGWpwJb6hqdoJJ1j+7vHBI9jXqteTfso/DvU/hT+zv4E8K6yqx6rpumxxXManIV+SV/DNes0EhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEzRuAqGSHdJu3H6UySTYpGCMVjKWpSjcbeMxAKE+/pXF/Fn4dt8V/hn4g8KwazdaHNqls0S31lJtkQkY5/wBn19q0/HHi5PBPgrXfEElsZ49Ns5Lsop5k2qSBX52fsRft6fFX4+ftQP4f167s5fC99FPLHp8duiG2VT8uHwCT+Jo31LtbQ+ZPiB/wTR/aG+Fes6jfaLoZ1zTrBfOTW9C1OFHcDnPlNIspYd8L+dd1+xT+398S/CPxS0TwP431S88Q6PeXS2DLqCs91bOTgDoSQDX6Gftk/tm+Fv2XfBdwJbqG/wDF93GUsdIjcNJkj77j+FR79a/M/wD4J9+JfAWoftF6z8S/if4p0fQXt2ku7eHUpFjV5pDkkZ44pgftx9l87DnLZ5GeKtIiqAuK4H4X/H74e/Gia9i8EeK9P8SPZKGuPsMu/wAsE4BP413/APFntQQ22KOKWiir5SQoopjMc8VACOwzg01SFGM0yZgrZY9aXYfX9aDRLQf97ocUqrnnNQNlWwc4qxHgDFAPRDhS0i9KWtFsZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQHNLQAUUUmegoAWikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAYxGaar7u1J5Kicy/xEYpWyMkDJ9Kza6ljlRd27HPrT6amSoyMGnVSasSFFITimtKq/eIFO6AfRUH2kOgaPD59DUoY45HNAWHUUlLTEFFNZsHFLu4pXAWikBpaYBRSE0m6gB1FIKWgBKKWigAooooAKKKKACiiigAooooAKKKKACik5o5oAWik5paACikJppY0APopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA055waYtzE0vleahlxkx7hu/Ksrxpfy6X4T1i8hkMUtvaSzI46qVQkH9K/Dn9nL9sLxPoX7XFp4r8aeMr5tIubqSC9kupS0ZhLEAbPugfQVNyrH7wUxpAvWuO+Hnxi8G/FbS01Dwr4isdYtmJA+zzAsCOoK9a6PU5MxNsLB164ockgjFydh1xdM0hVMhf71QSbpo22vuWvk39t39syP8AZt8C+RpZS58S6mrR2cbHJjPdzXzF/wAE5v2ifjp8avj1PFrPiO61nwlFE8l/b3WDDDnpswOuazvzanTy8uh+pUNsIwGao7jE0n7jO/1HSppGZuFXKdt1Nt5PIkxgKD2Fc3tLuxor7k9usscIaRvmz0FaEL+ZGCRivI/j5+0J4b/Zz8Hy+JPE/nNaL8sUMIBaVj2FYH7L/wC2Z4C/amS/i8MPcWuo2Sh5rG8ADhT/ABD1FdMdTmme/ClrmviF40sfh74P1nxHqTMmn6XbNczbepCjOBXwn+zp/wAFVI/i98dY/B2r+HxpujarN5Gk3UZJkzn5d/1rS9jOx99+IPFGj+FrdbjWNTtNLhZtqyXcyxgn0GTV+3niuoUngkSWKRQyyIQQwPQg18Cf8FePhf4m8YfC7w5r/h+2u7+30e7Y3trZhi2xhw5A6gGvPP8AgnT/AMFC9Os9G0v4XfEi+NrdQnytM1m6ckMpOFilYngjpmpGfY/7U37G/gv9qjR7ePXDNpWs2oIttYsVXzkB/hOfvL7Zr8xf2iv+CbPxF/ZdsP8AhNfB3iiTWdOsf3jXtgrWl3a46NlT+oNfsZ40+KXhH4daRHqfiTxFp+j2Mo3RTXM6qJBjPy/3vwr8rP27P+CljfFGxu/h/wDCt7iDRLgmHUNWVGEt0OnlxgHhT+tIZ9Bf8E2/279S+O8UXw88XWk9x4o0608xNXDGT7TEvGZCSTv9SetfftfFP/BMr9k+x+CHwpt/GGpwibxb4khWZ5JI03W0B5WNTyQT1PNfa1aEPcKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQmhhmgBaKRRiloAKKKKACiiigAoopKnmAWkpitimsy5560uYdiWlqHIyuKcCOfrUe0AkoplFaxfMFh9FItLTEFFFFABXK/Er4Y+G/i94TuvDfirTY9V0i5x5kEnqOhB7GuqooA/Ovxh/wRl8A6z4gmu9F8W6voenSNuFiqrKE9QGYZxXvX7Nf7APwy/Zrul1TTLKTW/EYzt1bUsPJGD2QdF+oGa+mqKB3Yi0ZpGprLu7kVPMFhxkVTgsAfrSeanTcM/Wqk1i0hJVzmoLfT5luDIz/AC46UuYvlXc1Nw9aAwboQaqXKtHHlTT7ddowTk9TVk2LGaM18C/8FEv2+9c/Z112z8D+B4rU+Jbi3W6uLu4AkFvG2dvy56nB615n+zz/AMFjIZlttK+LeiC3kJC/23pA3J6AyRZyPqD+FArM/UeisHwR440L4i+G7TXvDmp2+raVdLviubaQOp46cdD7VvUCCiiigAooooAKKKKACiiikAlGRTSwPQ0ZqeZDHZozTc0UcwDtwpPMX1phYHvULSKpwTg1m6juUohcXBWTA6VQmvD5m3eFLcBT97P0qeVt0oIP8PykjvX55/tq/wDBTLXPgD8T9S8DeEPDVrJqVisfnanqaswJYZwq8ZHTmsI+/J3NfhR9nftEyJZ/AHx29w6xKNIuMsf901+XX/BHj4fS+Ivjlrnil42e00SxaNZAQAJJDjGM5PHtXAfE7/gqR8Xfil4H1PwtqcPh+2sdTgMU0trblX2nryWNeT/s6/Fv45eC4dS0T4PT67LJeENcQ6FphupPrwjEV02toRufb37Tf/BLb4pfF748a94q0nxTol3pGrTeYlxq88qz2q4+5tCEEL2wazbX/gibrLaMTcfE3T/7SAOIY9NZos9sylt3/jtfOPiQ/to+Jrx73UNN+Ms0rKFaRdOv7dMD/YRAPxr9Of8AgnD8M/iT4E+D99qHxP1PXrjXtXu/Nj0/XZ2kktYVXCkbjuUtkkg4Ix0q7EXZj/sAfsKaz+yLP4o1DxDrWnazqmrqtvH/AGYZDEkKnIJLqp3HuMfjX2Yq7VAp1FHKSFFFFK9gEzTWmVVzmiQ4BJ9KqSLls54qGy4x5hfNG8uwBpjTIzHa1O/drHyM0kEcbln2nHpSNNELG/nLtVunWrCjy8ZOfeviT9rD/gpd4f8A2Z/iYPBtl4ek8RahAiPfMsvlrFu5AB7nFfVPwh+J1r8Xvh/oniuxtJrSz1S2W4SOcYZc9qol6nbilpq9KdWi2MgopGzjjrTY9235+vtTAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACCgnFNjLFfm605huFAC01lDMD6UtGaAADbS01WDZwc84p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANao5CQwO7AHbHWnshZs7sD0pdoPXmplqhkBuJVuAiw7oz/wAtN39MVZpBxS1PKxDWprKG6gGnNUU0jRrlV3Gk9NykOjUR5UIqoOmKcX7KQW9K86+MXxIT4d+FL7VzFNILaMuwj7ACvy3+KX/BXL4gTahNbeCdJ06wELFDe3imWWTB6eXxge+aSnd2Rq6TSUn1P2Po53e1flL+zn/wWB1OTWLDRfiro9ssE0mx9csmZNuSAMxYwAPXNfqN4f16w8VaRZ6vpV7HeabdxrLDNEcq6kZBzWt+5jY02xmsbX/FWn+GbWS71O5jtLGNSzzyNhUA7k1rSbN3PXFecfFaLwrrfhHVNK8Sz29vp11GY5xdSbEK+hPasJycdUXCKbOn8L/Ejwv4040LX9P1Vtu7ba3CucfQGuhklEaM7YCqM1+Lnxi/Z98Y/sw+Jx8UPg1qV5c+GY387ZCxdUXPK4HVPeu+0X/gsHqGveD7vTPEvhuLTtYWBliurKRikrBcDeDyDn0pqTtcpwsfY3xa/wCCg3w0+DV9La65fC4uY2Km1szulHPcV0v7NX7aHgD9qD7dF4amms9QtW+axvgFkZf7w9RX5Kfsw/sjeJv24PHmu6/qdzc6Poe5ppNQC7gXJ4Rd3UVneNPBviH9gb9rPTNK07WGu2tZbe4W43FVuIJGxtkA9MGtumpFl0P35WlqhoOpJrWiWGoRlSl1BHOCpyPmUHj86v0yAooopXQBRRRRdAFFITSbqYDqKjEnzEHGRTt1K6HYdRSA1HJIV4XGaXMgFeZY2wc5+lORxIuR0qKNpG5bA+lSltq+tHMgFZgOpxWH4u8baL4F0eTVNd1GHTbCM4aedgFrUmX7RtxuXmvgv/grla3Fn+z+t3De3UY+3QxGJZMIytnORiobZpGKZ9UeAf2nPhp8UfFD+H/C/iqz1fVkQyG3gbJ2jqa9SQnvX5H/APBF74f6drHjTxl4tuEk/tDS4I7W3KthMSZ3ZGOTx61+uO3bWl9NRSSVrA1R87uvy0rkdCcVHgIu7fk0yUhk1y0cqqFyvfipI7mOViqsNw7d6QyBuVXdSW9rGGaTy9rk9TSukVZW1LK0tN+70oyaZmOopBS0AFFFFABRRRQAUUUUAFFFFABRRRQAU0tjtQ7beScUtK+tgOL+M94bP4T+L5w2wppdwQf+2Zr+f79mf4AX37TPxig8HWd6th50cs0l0ybhGq5OSK/dv9q3W4PDn7Pfj3UJ22rHpM6g57lSBX5yf8EV/CJ1D4ieO/EkiBlsrOO2RmHIaRs8fgDUPc02R8//ABW/Zy+Nf7EPjCLVLGbUIdNt5M2+uaUWMMg/2l7H1zX098Ef+Cuenw6DFa/EzSruXV41Mf27T/8AVyqMbd6n+Lrmv1J1jRNP8Q6fNY6nZQX1nKCrw3EYdWH0Nfi7/wAFWPhD8N/hR8QPD9r4I0mDRdQvYGnvba1YiIDJw20k4JOfypOKkHPbY8m8Zaj4p/bv/aeNjoSySRahN5NkkmSltbg8sfTiv2p/Zl/Zv8Pfs1/DOx8N6PbxG82772+C4e4lIG4k+melfiz+wn+0hY/st/FeHxBr2jPc6TqEZtpbsxnfEh/ijJ61+i37ZH7dmt+CfhP4e8U/CVrfVbLWzt+3tH5nkccgqOh+tL4dAu2fcX2M7WJOWzWdN5FnL5813GkQ42ysFHvya/D1/wBsT9q/4myKuia74lZ2+QLo1kyq34hcZ5qn4k+F37XfxWto5PEGn+NNXReEF5MVAJ74yKhUtbj52tD7h/4LC6pp8v7P+iJC8VxJJqS+XJGwbC45wRXg/wDwRd8M3V98WPF2ug/6NZ2Ahf3Lniqn7ZHw01H4PfsP/DXQ/FE11J4nuLzzZIrqTe8XGSmfYV63/wAET/DNxb+EPiFr0iAW9zdwWsTf7qksP1FbKNiXK6PrT9vXXk8N/sn/ABBu36GwaIfVjivyO/4Jn+HIvEH7XPg+OeCOdLES3LLIoIyFyp+or75/4K8fGaz8J/A2LwPFJu1TxDMuY1PIiU5JNfOv/BF/4fwa58U/F/i6cLJJpNklvCGGSGkPUenANOwk7H693NvFd28kM0SzRSKVaNxlWB4INflF/wAFBf8AgnFb+EbPWvin8Nljs9OhBu9S0RR8sXdpIvQZ5x2r9YzxWb4m0Gz8T+H9R0m/tobyzvYHglguEDo6sCMMDwRS5QUj8SP2ffg74w/4KEeGo/D2pfEiGxu/BsASyt9QiedpYm6ZO7+Hp3xXY+I/+CMPxX09ZJNI8W+GdXMY+SN3mgkb80Kj8683/Z8vtW/Zu/4KBW+hW9xPBDHrz6Zc28DlElhdvlVgOCuCOPav3ho5R8x+Mn7Pv/BOv9o3wH8bfD17PH/wjWn2V2k93q9nrHyvEDkoAjZbI7Y71+zUalY1UtuIGC3r706irICiiigAooooAKKaxqJrqOOQIzgMe1TzDsyeimqwYZBzTqOYQUUUVQBRRRQAUUUUAFFNfdj5aWp5gKeoXq2qnd0xVXS9QF580ZymcVfurZLpdriiKFIQFQYAqeVvW5tFxUbWJl6U6mUVoYj6KRaWgAoooqeYApDSNTGUZDelQMjaTa2KNxbmmpbr8x7sc0x5WhPB4rJyL9B23bIW74qJZC8m2nLctIoJHGcV5L+1F+0Vpn7Mfw3bxhqek3Gq2yzpAIrc4OW460kuZlN2R6788bhR0qwpJHPWvnr9kH9sPQf2ttH1260fSLzRptGmSKWG6IbIcEqQR9DX0Csm12G3GWrXl5dbkbk60tNU0vWtE7kC0UgpaoAooooAKKKKAGtXxX/wUX/bYvf2a/D9h4e8JS27eMtWUlWbDNax9A+31J6fSvtC6mW2gkmc4SNS7H2Aya/GvwD4af8Ab4/4KDa5fazP53hfRbp5ngLDm2gbZGij0Zu/TmpsWjzaH4t/to6iw1mxT4l3EFwPPW4tdEumhZTzlSIsEY7jitX4X/8ABT747/CnxQU8W6i/im0hcx3eka3CIpo8EZAbaGDe1fuJb29vptnHBCiW9rAgRUUBVRQOB7ACvxP/AOCiPjD4M/Fb9pHT7fwpczWF3HKNP8Qa7aQpJaNhiMxoD87KSdzDr+FFhbn6qfs3ftSeCf2oPBser+HL6OPUE+S90eeRVurZwBkmPO7Zzw2MGu9+I3j/AEX4V+CdV8T6/fQ6fpenQNLJNcSKikgcLliBkngCvxh8ffs0/Gf9grxFpfxC+Hurz+IPDU0Uc8WsabbvsdGG7ZcQjOFxj5icHNcx+1B/wUD8b/tUeBtF8JajplrocEUqtdmxlbZeP0UkE9M9ulMdit4R0XW/28/2zPMvILq/03UL/wA66ba3+jWCHhSw+6uOh96+vv2wP+CUvh+HwjdeJfhBbz2ep2MW+bQ3dpVuUA52E87vavo7/gn9+yloP7PHwj0/U1jW78V69bpdX2oOPmVWAKwr/sj9c19QakvmafdKRkNEw/Q0wvqfjV/wSp+P+q/Dr42p8Otb1CS30LWDJbxWVzJ8sN4DwoB6EkYx7V+0FfhP+yL8OZfGv/BQaO0hYwxaXrt3qD4HQRSMa/digl7hRRRQIKKKKACkpahkYt9w5pN2Q0rhLJt4XlvSo1nKnMg2L6mo/wB4rbjgDpzUrL54AI461hvqVyibd7fK1PVSoweaXaEXijce/FLlGLigsFXk4pNxHbNMfMi8ClzWAbvXrmmGWP61G7CPhjg+lNhjMmDjK5qdDVJW1HNB50oIZlXrwOPcVyPiz4D/AA7+IGoLqHifwRoOvX4AX7TqGnxTSkDoCzAk4o+J/wAcPAfwW00X3jXxRY6BAR8q3DkyN7hFBY/gK850P9v79n/xAq/ZfiXpiFuguYZ4M+/zxiqhHW5m3c+ZP+CrXhX4dfCn9n/S7HQvBfh3SNX1PUUjt5LPSo4nVVBZiGRRjgd69m/4JkfBOD4U/s06NqVxZwxa34iLajPOEXzDG3+rTcCeABnHvXxj/wAFbP2hPBvxcvvBeheEtftPEFrpyy3dxPYOZI1dhhVLYxnrx2719KfB/wD4Kafs/eAfhN4O8P6h4lvlv9P0m2t7iO30q4kVJFjAZd2wZIIPTj3rZi6H3mtLkV8CfEz/AILFfCPw7pDt4PstW8Vamy/u0e1a1iU9ixfBI+gr5a8I/wDBYr4q6b4oub7XNL0XWdEmclNMjiMEkC54Af8AiNWtibM/aClryX9l/wCOk37RXwntPGc3hq88K/aJ5IUsr45ZlULiRTgZVs8fSvWqZIUUU0rnvSsAyZdyketQvGVAHXip2XtVe7uDGpCjJxWT3Li3cgkm8n72NtWLSQTZKjjsapWsLXTF5l+UcVbuGFrpl08IwUjZh9QDQXJn87/7cU0lx+1l8Si0nmY1ZgpJzgBV4r9zf2RYHh/Zn+HCPt3jR4c7enev5+/i3ql34v8Ajh4rvL85urzWpVkOf+mxX+QFf0XfBPw6PCfwh8H6QvS00u3Tj/cB/rWljK7O0Vdox+NOooqhDGkCsFPWn1HJHuwR1p4zjnrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWQYOOcdacp3DNIFxmloAWkpaKAGRxrFkKMZOafSZpN4zQA6ikpaAEoLYBNNcOVbaVBx8ufWmLHL5ahnG/+IgcUAPik8xSdpXnHNPpKWgAooooAKKazbe2aRJN65xigB9FIKWgAooooAKKKKACiiigAooooAQ9KzdVmK25w+wd2B5rRb09aw75GjDh3Hl54YisZnRRinLU+G/8Agph8X9Q8G/Bu6sdGMjf2lIttLdBsFC3QAY54zVv/AIJk/s5+Eb79mnR/E/ibwbpOpatq1zPcRX19brPI8O4KPvDgZVq+T/8AgqH8Qr7xZ8bNH8AadclrGFIpGih/5aTO7KpI9QAfzr9XvgP4BT4S/Anwh4Xs90/9laXGmCuGdyu9hj/eY1FNW1NK07uy2PlL9ur/AIJ86R8WfD8WreAdL0/RtesVJFnYwJCkw9wMc18ueH/iV+0P+xx+z9e2l/b3FvaRX4itmuUMgiUjnB7DjpXQ/tDfty/tH+C/irq1vp/hU+G7G3crFHc6bJdGRASA+/A4Pp2xXzJ8dv2zPjR8bvDZ0fxjdhdIOd8UFgYEY/j3rRxuzLmtofqb/wAE3/2lvEv7Snwt1e48WzwT6pp92YPMhXbmMgFSR69a8v8A+CsGla9pXwbjuLCaaO1a8U3DRMeYx0yRXwN+x9+1p8QP2ctauLfwjpia5p166m509oSxfkDO4civ1v8Ajlp978eP2Qdcn8Q6V/ZV9daZ9sS3UbmjYLkDmsJe67Mq2t0eIf8ABJn4uQfE74L6/wCCNfZNSudGl4W4AbdauPlXB64O786/Pz9vjw54a0P9pTW7PwhbxQ6b5cZMFuBgSlm3AAd+BXC/AH46eIP2c/HTazo1zKgZHt7m3VsLJkEYP0PNfcP/AATl/ZGtPj1rGqfGTx/FJqFo2oSfYbO4GVmfOSxz2GePpXRr0Jew3/gnD+3p4f8Ahvo9l8L/ABpZrpUTTFbXVlGBuJ+7L6fWqP8AwVo+Ff2zXtH+KWjyrd6PKi2stxG4YbuqsPbpXQf8FDv+CdcOj2lz8RPhlp0p2uZtR0u2GSo/vxgV8OXH7S3jWT4V6h8OdauTqehSAeXFdrmW0ZTwAT9KUuYSkftx+wP8Sj8UP2WvBeoy/wDH1a232GfnJLRnGfxGK+ha+C/+CN921x+zPqsbSu4g1uVAjHhcxoeK+9a0jojJ7hRRRUPcQUlBNRO3ze1S9B2Ekm2SYOMY9aiSZmk5Tj1HSory0W6cHuB602EiNdsR4HVc81PObqKsTtIeXVec7TuHapo3Vl44FVLeYMzfMZBnPTv6Ui3ZWZlICp196fMhcrLjybcVD537xuDxUM9wrYwxBpikLIAzn5hRzIpR0Ln2gLjPFRteIG2hsGqn2hJLlkzlVHWp18gyBNpJIzmqDlS6EyTHI53AnsK+Hf8AgrovmfsxysASF1O3z+Zr7jVRG4RWwOtfDn/BWe8W3/Zlvbe5dd8uoW5i9eCaTegR3Z5V/wAESx/xI/iSwHBuLfn8Gr9Nry4MKjg49RX5q/8ABFCzKeDfHtzsYLJdRJv/AIcgHj681+k2oTLCMtk54xjNVfRkR1kiOSbyoRIjBo8/Nmqy3Qt7jDZMZ5XvVXVrTzrUwo0irJgnacUsaLarBG6NIFUANmou+h0qCLE2uvbwyNFbmTaegqex1k3gUmJkJGSDUQkHlsOME/dA5q/DNGkYPl7D0qjOaivslhG3Lk8U6o2VZ0GDSbHzjORWq2OayJ16UtV2m8tguCfepkbcuaVxNWHUUlLTEFFMkkCdTzUSyOZiN2VxUuSWhVrliioZJhG2C2KfCxZSSd3NFxW6j6KaTSM+0Ek8VQh9FVLjVbOzwLi6hgJ6CRwp/Ws/UfHHh7SFDX2t6faKeczXKL/M0rjszXmUMBmnjoK8w8S/tLfC/wAJszar470O2QLu2/a0J+vBq/8AC/4+eAfjQLv/AIQvxPY68bU4mW1k3FPqPSoW9wszwb/gqRr15of7I/iX7JK0RupYbeTbjlGYZFeH/wDBE3w9PafDn4i6xKP3d5qNtBH/AMAjfd/6EK9i/wCCrUE837I+ttDE0oW6gZ8D7q7xzXln/BF7xrZ33wl8Y+GU4vLLU1vG90kQL/NDQy+h+iGoXCWttJI77ECklicYHc1+G/x6jm/a6/b3Ph+wkaexa+TTI2jO4LBGcsw9jlvyr9oPiZ4JvfHWg3FhZavNpLyQSR+ZCOpZSBmviP8AYj/4J4+KfgL8etX8a+Lb61v7aGKRbFojuaV3Y/OfQgfzpDVrHqf7TX7Bngb4j/Ae10DSNOh0nU/DlqX0+6tYwHYqvKt67sV8h/8ABJn4mRW3xG174SeIrOPUbeQTT2iXkayLFJGfnADA4yBX6K/tWfHSz/Z4+DOs+LLy1kuwi/Z4407u/Az+NfkX/wAEy/EE2sft2aJfEFRfLqMzJ6boXb/Cq0EfuTp+h6dpaBbLT7WzUHhbeFUH6Cr1ItLVmZ+Uf/BbHxLLJqfw+0JABGkc90eepOAP61X/AOCdf7Xvw6/Zx/Ze8RR+KdYij1ldVmuINMjUmecFE2/gSD9Oa8a/4KseOp/iB+1bPoNvP5tno9rBYxKw+VJnyWGfxWvS/g1/wRz8U64ul6n4y8VWOnaXcRpObbTVLzFWUEAseO9AHyr+1h+0d4j/AGsPiRL4xudOms9Ms4Vtra1twzxwRhm+cnoGbPP0Fet/8E4/2xvC37KeoeJoPFWnX1xZ64IRHcWQDlGQkcqSP71frj8H/wBlr4e/Bf4byeC9I0K3utLuNzXbXsayvcswAYuSOenSvC5v+CU/wdHxTg8XWsd9aWSSid9BR1azds5xggkL0+XpxQB9e+HdetfFOgadrFl5n2O/t0uYfMXa2x1DDI7HBp/iDWLfw/od/qd1IsNtaQPPJI3RVVSST+VTAWmjacB+6tLK1iwOipGij9AAK/OH9vb/AIKTeDV8B+IPh38Or6TWte1BTZ3OpwAi2gQkhwrZyzYBHAxzQB8wfsu2Z/aQ/wCCikfiGdpLq0bVrjV3ZRkeXF/qyfbgCv3Hr86/+CRf7NmsfD3whq3xD8S6b9hutcjSDTI7iMectuDkuCeVDE9Pav0UoGFFFFAgooooAKKSoJpdr4pXGlclkqr9jSaTzG5PSlM3ydajhIkmw27HbnisHLU0s4q5Rv8AxRomi6pHZ32sWdjcuBst57lEZ88DCk5rdVgygqcqRkEV+CH/AAUn1nW7f9s7xVLd6j589mLYWEkZ/wBRGFDKvsQS351+uP7B/j7VviZ+yr4G17W5PO1Ga3kjklPV9kjKD+QrRK6uZvc9/ooorQQUUUUAFI2e1LRU8wEcbM2cjinrnnNNZsUBqgdhH+9QvSq18y/IGLA5/hqaMBFwMn61XMVbQe2dvHWo2MoYYAK96kDdqXGKsWwbgF5OKWNty5znmk4704Y7VPMSLUb/AHqkoqAIainuBCMlse1SzSbaoyNubNZuSuawjfUR5m25WTrUawrGpLtknnJqCTcbnjpinyMvST5g3G2sm9Tr5SeNlWZVXla+Sf8AgrFEsn7IOtM38F7akf8AfwV9XwK0nloEEaq/AFfJv/BWhQ37IWrZ6rfWpH/fwVpS1ZzVNHY8W/4Ij6fIvg/4oX5BEUt9ZxrkcEhJCf6V+mONrN7mvin/AIJG+ER4d/ZVGoO2ZdV1We4PptCoB/WvsqS4dpsAYWtZyViIq7LnmYbbUiVQZtrZzk1Nb3DMvK96zjJLqOUOpcopqtuHpTq6FqjIKKKKYBRRRQB5r+0h44Hw4+BfjfxHzusdKnkTH97YQP1Nfnx/wRX8Jx6hqnxP8ZXKML4G3skZgcESF5Hwe/KD86+mP+CpHjSbwj+yP4jigxv1WWLT/fDtzj8BXD/8EddBn079mPUtSuLVoDqOtzGOR0KmVEjjUMCeq53DI7g0FdD7m1GzGpafc2pdkWeJoyy9RuBGR+dfzoftafAnXv2efjhr3h/VIphBJO93p97Ip23MDsSHDYwSCcH0r+jla/Nv/gtJ8OItR+G/gzxnDADc6fqDWM8qpz5MiEjcew3KOvrQJOxheG/+Ckfg7Rf2HrLTtSuo9V8fJp7aMdFdfMJCjasr8YClSOp/hr4j/Z3/AGL/AIlftUafret+ELWytbKxkJM95K0Mckh+by4yAQSMj6ZFc9+y1+zZ4g/aa+KFh4W0SJ0sgwk1LUsHyreDqxLAEBsZAB6mv6CfhH8IfDvwR8AaZ4Q8L2gs9KsYwucDzJm/idz3Y+tA+Y/FXR/2iv2nf2JvEEeha5PrSWVudiab4ihkmtJEzjMTuPunHBU19GaT/wAFrUm0Ge21v4dOmptAVWexvwYt5BGdpXOM+9fqBrfhvSfFNm1rrOlWeqWrAgw3tusq4PswNfNnxI/4Jn/AP4j3TXb+FH8PXbdZdBuDbDPPO3BXPPpQFz8+v+CV9xq/jL9su98RCFnhmtb27vJApIi8wnAY9skgDNftZXiH7N37IHgP9ltdWPhH+0bm51IKs93qtwJpti8hAwVcLnnGK9voJCiiigApGOBxS0yQnbgDmk3ZAIrfLzxTDGBkg0yIFVO485pk0nUK3oPzrKU1YtIWGNjkueAaesxbOFxim24Kg72xjnBrx34vfti/CL4Ihk8TeMLFL1eljaN58xPptXofqalJtDZ7FNI20cU/azAEivjvw7/wVa+AfiLUPs0+rappSFtolv8ATysec9dwJr6g8E/FDwj8RtPivPDPiLTtZgkUMv2W4Vmx7rnI/EVVgOl3LGuGPPpXKeIvi74E8H3xsdd8ZaDo96Bk299qUMMgB6EqzA9q6XULEahaTw+a8DSRtGJozh0yMZB9a/K345f8EifHvi74halrHh3xxa6rZXchlEuvyObhSSSVJAOQM8VWnYD9G4/j78LLmQKnxG8JPIei/wBt22fy31esvjJ8P77VoNKs/Gnh+71G45itbfUoZJH+gVjX5Qt/wRk+Kf2Qsnirw4LnP3P3gH/fQWuq+CP/AAST+JnhX4o+HdY8UeJdEtdH026W6lk0m5le5k2kEINyADOPWjQR9J/t6/8ABP68/aq1HT/EnhrXotK8S2kS2zQ6izG0kiXJHCgkNk9cGvm7wv8A8EV9eXR1n8S/FDStHulJMkdppH2uJR6+Y8kZ/DbX6zRrtUAdBxXgX7bHwN8VftAfBa68NeDtYXRtYM6TLI8zxLIo6oSvr71aFc+EvEn/AARd1fUNN+0eEvitoutTg7St3pn2aHI7b4nk5/Cm+Df+CJfia42HxX8R9KsV3fPFo9lJcHHs8mz8sV5Cf2R/2xvgPNJceHrDxJFbwuZFn8Oays6SN3byFkLknA6r6V1/g7/go5+0l+z7qtjafFXQ77VLGQn/AETxHpTafeMo43CRkXI689+aLBzM+qvA/wDwRz+DXh0K+u6p4h8Tyr/DLcpbxH/gKLn/AMersb7/AIJS/s+3Xl+T4f1GxMbBgYNRfqPXdmvX/wBmH9qLwl+1L4DXxB4blNvdQv5V7plwQJreQAE8fxL8www4Nex0xXZmeGfDtl4S8P6fo2nReTYWMK28CE5IRRgVp0UUCCiiigBjMB1qAyLJNsAzx6U+WQbiO/0psfy5OOaye5aXUCCm4KvGKr3Em/SLssMYjf8A9BNSSSS7WwlMuDv0y4XGD5TA/kaBvY/mo8aA3Xxu11YxzJr0gUf9vBr+k7wahh8H6HG/3lsIFP1Ea1/OB4gsX/4aI1O243/8JLImM/8ATwa/pH0KPytD09P7tvGPyUVaethWNDdRuptNEgMhTuBmmtiDz34z/tCeBP2f9IttR8b63HpEF0xSBSpZ5SOu0D0rW+F3xc8K/GbwxF4g8IarHq+lSMU86MEYYdVIPQjI/OvyG/4LH+I9Sn/aa0nR3vJH0u00G2uIbQt8iSvJMGbHqQq/lX35/wAEyPB8fhP9kLwm625gk1N5r+QseXLPt3fkgplW0Pq2lpFpaCQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAE3Ddihm2jOM0m07s0ySRlcKFz70ASK24Zxj60tJS0ARuDnIP+FNRW6tjPtRPJtUgH5yOBRbpIsf7xgze1AyVaWkFLQIKKKKACiiigApAwbODnFJIGZflIB96RIxGuB35NAEclwFYLglvSpKjaFtwZSAfcVLtoGKtLSDiloEFFFFABRRRQAUUUUAFFFFAEbbt3A4+tcp40vv7N0u4uZo3KxI0m1ehwM9a6uZTtyK4D4yWs174PvwkrW6LbSs8gPQBDXPUhfU6KL94/EmHxH/AMLl/bu0O4ltiUk8RQQ+QzbvkSQ8Zx0r99o1CooAwBwBX4M/sD+HIfFf7dWhl5i0dnqFxdhiN3mFCxH0r951HFVFaWInuytPY215kT28U4x/y0QN/Ovjj/gplouh+Hf2frzWH0rTo4428kkWyq5Z+FAIHrX2htrhfjN8FfC3x68E3HhbxdZveaVMwcrG5RlYdGB9RV2ZKep+eH/BGXTfDOtaH49t7rRrefXbSaGT7VNEHIhkBwoyOMFc/jX6V+L/AA7/AMJB4R1TSIgi/arZ4FyOBlcV57+zh+yt4I/Ze0XUtP8ACEFwX1GUS3N1dyb5XwMKuf7o9PevYaFHe4uZn85Pxn+AetfD34+Xvgm8tpWubjUFS22xnDpI+A3H41/QD8G/h5p/wq+GPhzwvpkC29tp9nHEVAwS+0bifcnNa2r/AA/8Na9q1vqmo6FYXuo25BiuprdWkQjphsZrf21SVlYHK5HLEk0bRyIrowwysMgj0r87/wBsj/glhZfFbWLvxd8OLy30PWZFL3GlyJiC4bkllI6MenpX6KbaNtMV7Hxz/wAEyf2e/G37PXwl17TPGkEdnc3+pefDaK+4qoQLuyPX09q+xlORRt6+lCrt4HSgQtFFMZW3bgx6fd7Vm9wG+ZuztHI9arLdLMzoeHX0qwSWz2PtVSQLayB9ud3BJrOb0NIq4jQhU3vKyD2qL7OsjeZGuGx/rB1rz34iftHfDX4W6kll4u8Xabod2yCQW15JhihJAbHoSD+VJ4L/AGoPhD4+mNtoHxE0C9m/55repG34B8VjH3tEbaxWp363SNvBdlZfXFRNHJdbfmBX1FLDfaPqkb/Y761vT1PkTox/Q1UuPEeg6X8s2s2Nvt6ia8RCKrRaM0UotXLEjNCoVueTz/KqrXn7wKwbeFzxXL6z8dPhrot0bTUPHGi20zAPsa8RjjnnIPsapr+0d8I4S0z+PdB54Ja9Qfpmp91vc0U7LY9FtLWNUMy7ju67qleZvLBRQBnGSK8nuv2yPghpbeVP8SfD8TYzt+2J/jWVdft2/AK3cI/xK0Vu/wC7m3D9K6FT03Od1NdUezLI4nU5ZyPSviP/AIKs+BfEHj74KWr6PZXN+1neI8lvbxliR68V6n4g/wCCk/7PvhtlX/hNoL5iN2LKF5P1Ark9S/4Kufs/xxsv9o6heg8lE092B/MUcrtYaqWexT/4JQ/CrW/hr+z3qEmuadPpV9qmpvOkFyu1vLCIFbB9ea+wru4mVioUu2eTjiviO8/4LE/ByzmMVtpeuTRKvystsEGfTBrgdc/4LVeGorl007wDfXMP8LzTqhP4U+V2aIjPld2j9FPt007FTbk4HDGp7a0uGIlkGD2XtX5oXH/Ba2zMeIfhtIzHjD3YA/lXK6z/AMFrvFYkK6Z8PNLii7Nc3cjMPyGKVmXzvofrCtqWk7DueKufZlYfNz9K/FjW/wDgr/8AGPWGl/szT9E01mXCRwwGUqfXnrXIXf8AwUY/ae8QQvHFqtwqyjaTZaNg/gQKqxlKV+p+6awOk+Qw8rH3e+akkmjhQtI6oo6sxAFfzzaj4y/aK8emS6ubzx3eiRsEw21yV9cDaOOvSs6L4b/H/VoWaHRvHl1CxwxaO4UE+mGotIzufuL46/bA+E/w38TW2geIfFdtp+qXBUJCQX6kgElc4GQa9mtbiO7t4p4XEkMqh0dejKRkH8q/nv8Ahn+xz8a/HXjjSEm8Fa1BELuJpbzVI2VUUMCclq/oJ0ey/s3SbKzOCbeBIjt6fKoH9KfKwbXQtjvTdxbO08dKVqpvdC2IAUkMe1VsgUW9iS4aVWG1dw7mqkN1Kt0YjCSOu6n6hq0Gm2sl3dTLb2kQ3SzSsFVB6k18b/Gz/gqt8JvhTqV7pmjx3njHVrc7GWy2pBuyRjeeT+VZS953L+FWZ9nyRmSQFhhfSrK8LX5j6D/wWw0aS8H9ufDPULaxJwJrK9V2H4MoH619FfBT/gph8FPjRqY0yLWLjwvqbHCW+vxrAsnT7sgYqfoSOlMnVo+rjVXU4ribT7lLORYbto2WKRxkKxHBP41PbzR3UKTROssUihkkQ5VgeQQR1FSbRWi2JPyB+OX7Bn7WPjr4k6pq0uvf8JLHdSGSO8t9bFrGqZO1BGSu3Ax0GOa41/8Aglf+0f4gtUOqTaaWDbdl9rPnOB65BIx7V+2FLSsVzs/Gqx/4Iw/FW9tle68WeG7OTvDJJM5H4qhFfZ37Av7Ct5+yX/wkeo+IdWsda13U9kUUmn7xFFCuSR8wGSSfTtX2NRtFLlYcx5x+0N8L4vjJ8G/FPhKVtjahZusTYziQDKn8wK/Fb9iX476l+yL+0TLp2tB7XSLyc6bq0Ew24KsQsn4Hmv3vavh/9tr/AIJu6R+0Tdt4o8IS23h/xfj/AEguCIrzGcbvRuetIaPs7w/4g07xRo9tqek3kV9YXKiSKeBwysD7itBpgnWvyT+Ev7Hf7Y/g4L4Y0nxm3hLw9GWXzheq8QU9Sq4JzX6UfAf4aaz8LPhxZaF4h8U3vi/WFdprnU705ZnYAFV/2Rjj6mi7FZFr41fB/wAPfHr4d6p4P8SQGbTr1PvKcNE45Vx7g818l/sd/wDBNiT9m34z3HjjU/EMOs/ZYpbfTo4oyrKrjbub32kivut4lyX25bGKr/2taR7vOnjtiD0mcKfryaQF5aCcDJqgNc03GRqFrj/ruv8AjTTr2mMCDqNqQf8Apuv+NaLYk/n6/aevk1f9uPxhMW8yJvE0acnIIBRf6V/QbpUaQ6XZxxqFRIUVVHQAKMCvz0+Jn/BMmHxl+1VpPxB0PUrOfwhd6imoavZytucOp3MEIPIbA4r9CG1CystsL3UEJUYCNIAQPpmmBdoryL4iftZfCT4U3xsfE/jrS9OvQgk+z7zI+0kgHCA+hrzu4/4KVfs9wHH/AAnkcvvHayn/ANloCzPpDxBoNn4o0O+0nUI2lsb2FoJo1coWRhgjIORx6V80+GP+CZf7PnhXxBa6zbeC3ubu2lE6LfahcXERcHOTG7lTz2IrN1D/AIKm/s96e20eKLy54zmCwcj6c4rita/4LEfBewujHYab4l1aHGfOhtEQZ9MM+f8A9dAWZ91wwx28KRRIscSKFVEGAoHQAU+vzp17/gtN8ObOzkOmeCvEV3d4/dx3DRQrnsScnivjjxp/wVQ+PfiDxNc6npXiePw/pjSf6NpdvYQPEig5AZ2UsxweeaB8rP3dorxn9jz4ra78bf2dPB/jPxIkS6xqUDtO0ChUkKyMm4KOBnb0r2agkKKKSgCOZsVRlkG7k81NNIzSmLtjOaoXEUbSAFznPrXLL4jppxXUmWdhIqgZTuasWfzSMQflGRj8qzmhNvDIUYnnpmrmlPJImWTaMdfWoWrKnFJXPwL/AOCkFraWP7Y3j1LSZ51lkieQuxO2QxLkD2HFfsj+w3oEHhv9lH4cWtv91tMWZv8AeZiTX4xf8FDGc/tlfEoOMAXkOPp5MVftv+ybj/hmv4cYGB/YsHA/3a647HPJdT1yimZozVED6KgmkWPBY4qk2pw3BKIx4ODU8xSjc0T/AKynHHeq6IFUc+/WjydzZz8tQPlJzg9KY1OjUIuBT6BXsVW/134UyL/XVNNjd9zPFQSTNDxHFlqC76E+8KWHvSNcKrbe9Qqr7sAbd3JqdY9vWq5haEsbblzTqj9KctPlvqQx1IRu4paz9dgvptJvhpckUWpNA62zTA+WJMHaWxzgGjlETNJAjFHmRX9NwBqJYYjMZFnUjGMAivwb+MHwO/arf4qa5c6v4b8ca1rTXDbtV0a3upYJRuO3yni+XZjoB0rLtfhF+17Gg+z6B8WYFB+6BqCfpmpsuxor9z99fscfmF1YHPHWq0+jyMxaJ9pPWvwdb4Y/tlLx/ZXxeH+7LqA/k1dN4Zb9tbwRp7wwQ/E2GLeZCt7bS3ByQBnMoLY46ZxWTp3dzTnl3P3GsbE2y4c5714p+278C9X/AGifgBrHg3QpYIdUuZ7eWJ7jhfklVjz9Aa/KXWvj7+2L4RjW81K+8ZWca/8APxpgA/EbauaR/wAFGP2otJhUNLc6kq87rrRHz9MhRWsYcqMZNyep+tn7L3wVT9n34L6F4GW9F9Lp6MZ5gMAyMdzY9ua9EuIpkmKIeDzX4x6d/wAFfPjfo9/jU9N0S62fK8E1m0T/AInORXoOlf8ABarxJGFOpfD7T527tb3TAH8xWUqbY1Kx+rEVrdLKPlBT+93rQ8p1AwSa/MXT/wDgthatD/pPw3lR8/8ALK8BH61px/8ABazQtv7z4e3wP+zcrQqKsVKdz9L7cFY/m65qWvyZ8ef8FptbnuIf+EQ8EWtvb7f3n9pTF33ZOcbeMYx+tfZf7CP7Wmpftb/D3WNc1Pw+uiXOmXi2hkhJaGfKbjtJ7juO2RXQlZWMj6bopKWmAUUUUAfn/wD8FktQli+BPhKyQgR3XiCPeO5xFIR+tev/APBNPTRp/wCxd8PCH3/aIrifjtm4kXH/AI7Xzr/wWq1qWz8E/DazRSY5NUmuGOOMpHgD/wAer6l/4J92a6f+xz8L4V6f2a7/APfU8jf1oLex9CrWH408C+HviNoM+ieJ9Hs9c0mf/WWl7EJI2x3wa3aKCDmfAnw18K/C/Rf7J8JeH9P8O6bu3m3063WJWbgZOByeByfSulXOORilooAKKKKACiiigAooooAKYzYODTtw9aimYetTLYa1Yu5ccc1BNcQ2sMlxPIsUMal3ZzgKB1JNMVhvzuGBzivhb/grR8fb/wCGvwj0zwjoGoNZax4lkczeS22UWkYBc+wOQKyglc0t0PFP26f+Ckl/4j1O7+HPwfubhV837Pd65ZZaS4PIMcWBnGe9ea/Av/gld8S/jZZW/iDxpfjwjYXR8z/TFMl7MDg7yCeM57+lfQH/AASp/Y2sdM8Lx/F7xfp0dzqWpE/2Nb3SBxDCMf6QM92JYf8AAa/SwDAwBgVuRc/LXxR/wRQj+zr/AMI/8RJA46x6haBlJ/4Ca+Xfjd+yx8Zv2HdW0/xDBq0yacXxHrWiSOqI2chHTPHSv3trn/HfgnSfiH4V1HQdasor6xvIWieOVQ2MgjIz0IpWDmZ8q/8ABPj9uAftPeHZvD3iCIWvjTR7dGmkByt7H0Mo9DnqPevsjaa/nt8H+JNf/Yv/AGvLq0s55LY6LrH2G4hY/wCttmbIzjrlGB/Gv6Eo2LxqxUoSMlT1HtS5RXDaaNpp1FHKguIKWkJCgk8CvAfHX7e3wE+G/iS50HX/AIiWltqttxLDb2V3dBDkjBeGJ1zweM5qhHv1cT8WPg74S+NfhO98P+LNIt9Ts7mJow8kYMkWR95G6givCtY/4Kf/ALOOm2MtxB46n1KVFytra6JfiST2BeFV/Mivz3/ah/4KofEL4rXV1pHgN7nwJ4WJK+fAMX06gnlpP4ARjgUDSuT/ALNfhnxF+zv/AMFFB8PvAuqHUdL/ALRaxu2zuU2gAdhIOxUH8+lftZkV+Z3/AASv+CNj4Rhv/i74x8U6bN4l1xHhtbaXUYZZVibaTK7BiQzfMMHnivsr4yfthfCH4BXGmQeNvGMGmzakrvbR29tNeFlTG4nyUfaPmGN2M84zg0A0ez0tc54B+Ifhz4n+GbPxB4W1a31rR7tQ8V1bHI5AOGHVWwR8pwRmuizQIWkpaKAIwuOornPHnxG8MfDDQ31jxXrdloWmocG4vZQik+gz1NbupX0Gl2NxeXUiw21vG0skjHAVQMkn8K/Ev4lf8J7/AMFJv2r9b0jwpeTf8IrYSeXD58zJa21tGxBlKHjexJPqeKmxSP050f8Ab4+Auu6ilja/EXSftDvsVZH2gn6mvbrXWtP17R5LvTL23v7Z4iVlt5A6nI9RX5veIv8Agivo8mgxjRviBdRav5Y803VopheTuRjkCvmm91r47/8ABNfx0mmXV6l1pWpRnyg0rTWky5K5GT8r4HT6UcpR4bJpNzrf7VU1pEv+k3Pi0xorHHLXJxX9G9lCbezgiPWONVP4DFfzqfs7atL4z/as8D6hcr/pep+KLaeYdvMeck49ua/oxppdRSGtIEHJxVa3vYZ5SEOWHBp1xNaqxWaaNGx0ZwDVOGXTLGR5ftduhPUtKowPzphpY/GD/grRavrf7ZtjZRqWlk0SwgVR3LTTD+tfsL8HvBkHw++FfhTw5bLti03TYIMe4Qbv1Jr8qf2uNV0Txx/wU48ErBd215p0cul2tzIsqlFKzSF8tnHAPrX6K/Gr9tP4R/AbSjd6/wCKLe+myFGn6M6XVye33AwA6dzQS2e5Clry79n79o7wb+0v4Nl8S+DJruSwhuGtpEvYBFKkiqrEFQT2Yd+9eo0CCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEGe9LRRQA3YN+7HzYxTqKKACiiigAooooAKKKKAEpqyBmwOaSSRVYIwPIpIo1HzLwD2oAkparXFq81xBIshQRkkqP4qs0AFFFFABRRRQAUU0t82ByadQAUUU3b85bPbGKAHUU1V255zk5oZSd3OMjFACnHSvOPjfYXN94D1tY5dsP2GXcg4/gPeu9nm+yqgwXbpmuG+L0c2oeA9bhgcxtJZzKW/u/IecVnN+6b0ou9z8av8AgmaTa/ttaWgXcG+2LnPT73P6V+7C1+Hn/BLPS/O/bVUOQ5t7a+bcepK5Ga/cJacVrciQ6iiirMwooooAKKKKACiiigAooooAKKKKze4DGHNRT2sdwoDjcB0qfbTJNwXCY3f7VDSsNXufBn7fX/BO3Wv2lPE1l4w8Ha3a2ms29mllLp+oDEUiIzsCrgZDZkPXjivz+1X/AIJn/tEabqElungVrryjhbizvYNj+4ORX73m5WJgshG7GeKct1GwB3DkZqVZLQt8zWp+DOl/sE/tRaGxGneEda08sPmNrq8cYP1w/WnSf8E7f2nNSYvceFtQct977Rq8bE+5+ev3oVwwz1FIsyNnBBwcU9BK5+EOn/8ABLH9oXWJ0Evhmzs9zYMl1qcWB7n5ia7iP/gjV8ZZkRv7d8LwEj5o5bqXIP4RkfrX7TeYN2Kdn2qkmFz8Yof+CMvxh2/N4m8JL/21mP8A7Sqdf+CMPxbb7/izwov0ab/41X7LAZpdtWLmPx80v/giz8RpGH27x54at488iKOZ2+v+rArudP8A+CJqyRK2ofE9op88ra6cGX8yw/lX6lbaQKBmgOZn56+Ff+CMfwy0+Ff+Eh8Va9rkwbO6EpbDHHGPm9/zrrV/4JAfAH/lpH4mkP8A2FQP/ZK+3ttG2gV2fFMP/BIj9n6F1Y2fiKUKc7X1YkH6/JXdaZ/wTd/Z+02NFbwHb3pUbd13K7k/XkV9OUtMLs8m8F/so/CL4f25h0P4f6HZLvL5+yh2yQB1bPoK9CtPB+hWEYS20XT4EXoI7VB/SteikIhhs7e3XbFBHEvXaiAD9Kk2KOigfhTqKAEwB0FLRRQA1qrSrtzsYBsZC+9WWryz9oz4sQ/BX4T+JPFsirM2n2byLDu2ktj5efrUTdkXE/O7/gqN+2JqE2pRfDHwnrQtbVkZtaa0IYnBwIt3VTkE8Edq5b9gT/gmvD8aNNXx18VbC8t/C8hH9n6V5jQSagpGTI7KQ4TngggnBrwP9lv4Qal+2T+1FGL5dtlcXTavq0mNypEGyVz6sePxr+gDTdPt9H0+1sbOJYLS2iWGGJeiIoAUD6ACp2Kk+ZaHy1N/wS1/ZnkiZR8O5I2IIDrruo5X3GbjGfqK+Tf2lP8Agj2+g6Xda38ItVu9VMOZToOqujSEDJ2xSKFJ4xgHn3r9X6KCUfi3+xF+3x4w+APjy2+HvxIub6+8KvcGyMF6F83TJ8heHI3lBgDaTgZJHXNftHb3Ed1bxzwuJIpFDo69GUjII/Cvw7/4KseF9M8GftZSzaXFDGNV022vbmOMDPn+Y4LH0JAFftF8NZDJ8OfCrnILaVannr/qVrRCZ01FItLTJCmyN5cbMckKM8U6igD8k/2uv+CoXxR8I/FnUvC/gzTrfwzp2mSmEyanaF5rhgT84yRhTxjjsa8n0/8A4KfftIa1b/6NNZyk8BrfSHf9QSK/ZXxT8H/A3ji+jvfEHhDRNZvI+FuL2wilkA9NxXOOTx71o6T4B8M6DbiDTPDulafCDkR2tlHGufXCqPSpsVdH4mSftWfth/ES/wD+JRqvidWYbPJ0vSxHH1z/ABITnn19K6K10/8Abu1aDzi3juQN3RY1H8hX7Tw2cFrxBBHCP+maBf5VNzRyhzH4i3/wn/bc8UN9nu4PHBVhgmW5WMY+oIqxpf8AwTp/am8UWpuLy+uLRmcgx6jr0gk6DnAJ45/nX7Z49aKXKPmPxYb/AIJf/tL7hH/a1oUxnd/b0uBSyf8ABLX9pCMAf2zYycZ41uXvX7TUVQuY/Ey9/wCCaf7Ttim2G+ScYzth1uUCo9N/4Jk/tL63I015cW1nJuwWutblZj78Z4r9t6KYcx+Ouif8Eb/ijrX7zxB4w0OyYtg7RJcvj13HHvxXayf8EadI8NaDc6n4k+K76dbWqGWe4FkoijQDkksa/Rrxl8dPh58PtQFj4k8Z6Lot60YmFveXiI+wkgNjPTKkfhXG+I/Fnwp/as8G674B03xzp+qLqNuYpk0i/UTqPVcHJoC7Pz3+D/7BH7MnxB8UJp9t8dZfFNzGSDYQslq0hH91mXn8K+p9P/4JLfs+Wu03OjatqBH/AD21aZcj0+Rlr4m/ao/4Jh+I/wBnDwZfePfCvixdb0TSCss8cqC2uoEL4DKwOGIJHPB59q+z/wDglD8XPGXxZ/Z/1KTxZfTaumj6s+nWl/dMWmZBFE+xmPLY8zqfUUA2dSv/AAS5/ZqVQD8PpHx/e1u//pPWzov/AATh/Zz0GdJrf4Z2Uzo24fbby6uRn6SSsMe1fS2KKBXZm+G/DmleEdDs9G0TTrXSNJs08u3srKFYoYl64VVAAGST+NadFFAgoopKAKF5OY5wqoMEfexUC2qzliSCeNo6HP1rQMYkbJGa8p/aa+Nem/s9/CbXPGF7NClxawMtjbyHHnTkHC479q55Ruzbm0shfix+0d8M/gaq/wDCZ+LLHR5mw32dm8yUqeB8gycEg847VzPgX9uz4FePNSGnaP4+04XUmWWO6Jgz0/vgV+SHwc+AnxI/4KH/ABe1rxBf3rWEEjtLc6xco8kEHIIgT0xuztH97PevTPjB/wAEhfiN4B0ObVPDetWni3yfne2hjMcuBkkgGtIxsZ3fU81/4KYTadfftfeIbnTJoLi3ura1dpYHV1ZsAE5Hfge9ftp8DdEj8OfBvwRpsXKW+jWqj/v0p/rX81dzZ3tv4ga21BZEvo7jyZ1lJLB1cAg59On4V/Th4Ai8nwJ4cjx93TbZfyiWtAk7m5UcxYIdtfOv7dH7VF9+yh8LrXxDpmiprOoX10LSJZmKxRHBO5sV88/sy/8ABWzSPiJ4ptPDPxG0iDwzd3cqwwapayFrXeez5+6M96AXc/Qa3aSTcCM0yT7Npdrc3d3JHb26KWkkchVVRzkmrdrNDdQJPbyJNDKA6SRsGVgRwQR2r4N/4KyftKXPwu+GNn4E0S5EeteJVP2nacPHajI3D6kEfhU2K5uh9neCfil4P+ITXMXhnxHpuuSWvEyWU6yNH25A6V1nFfjd/wAEi/gl421T4tH4i200+m+D7GOa3mkbOL5yAPLx3xuBzX7I0uUh7hTWkCyBe9PpKOUQjV83/tl/tiWf7I/hzTNSuPDl5rs+pSGGDy22QIwBPzN619Hn/WCsbxh4H8PfELRpNI8TaJYa/pcnL2eo26zRE+u1gRRyjufjN44/4K//ABp1y9lbQk0fwxbMcJFDZJcso9zJnn8Kxbb9s39rv4paXKdD1bxRqkDZjMmg+HUGDjOBJCmQcEe/Ir9e/Dn7K/wd8I6kuoaL8MfCmm3inK3FtpECOv0IXivT4bWG3ULFFHGo6BFAFPlHzH8/Hh6f9o2H4qeFL/XpPiBZ+IZNShSzu9cS6Vhl/m/1wzt5+nWv6BLGOWK1hSZ/NmWNQ8mMbmxyfzqYopOSoJ+lOqgcrhRRRQSFFFNbC5Yjt1oAjubiO1heaaRIolGWeRgFA9Sa4HU/2gvhnod79jv/AB3oFnddfJm1CMN6Zxn2Nflz+0d+0x8Qf2uP2lL34JeEvEUfhnwvNqUmkQNlk+1OnytvYc4JB4qgv/BGP4qKSD4l8MuM8HzJc/8AoNTqWfrdpfxS8H61D5lh4p0i5j/vx3kZH55q1N438MujI/iDSdp4O69ix+W6vyAvv+CNfxbhXNtr3h6dsfcWZ1H6isKT/gkF8c1m2BdCdMf6xdQUD8jzTFZH65TeHfg/ql5LNPpvgm8u5m3SSSQWbyOfUkgk1jat+zR8D/GFyJbrwN4XvJSuweTDGnHJ6IQO9flha/8ABIX452kqSwXei28g53x6hgj8RWxN/wAE0P2ndFYTWfiBJmUcfZ9fkjI9utMLI/RnUv2A/wBn/VAfM+GWjpkYzErr/wCzVxGuf8Esf2etavBcDwvdafhAnk2N+8cfBJzj15/QV8KSfsT/ALYWksLm01PVBNGchk8RvIf++S1WJ/D/AO3h4bhMJXxnNFHxvt5YnGPqTmgOU+zpv+CS/wCz/JGyx6Tq0RI6/wBpOTX0R8BvgJ4T/Zx8Cnwn4NtprbSmunvHE8pkZpWVVZsn2Rfyr8gY/C/7YfizxvoE2qyeNrGV7uO0F1dSFVjVm5JC8YHPJr9tPD9rPp+h2Fpd3Bu7u3t44pp2HMjhQC34nmgk0KKKKACiiigD8x/+C3CSHwf8MioJH2+6HA7+WuP619dfsEyCT9j/AOFrKcj+ycce0jivlj/gtdCf+FbfDeYcbNalG70zCf8ACvpr/gnju/4Yy+F27r/Z0nX0+0S4/Sgt/Cj6LooooICiiigAooooAKKTNGR60ALSUBg3Q5paAGKvXNNkhDVLRSauNaFJbRUk3Htjk1+Lf7VEmoftff8ABQ628DRXP/EttL2PQ4ZIm3IsSfPM/sfmIP8Au1+tn7RHjx/hh8D/ABx4piBM+l6TcXEW3rvCHb+uK/GX9gv9oz4f/BH4s+JvHvxKa8vdanti1nLbw+a3myNukb64OKlRsWnfU/cfwj4Z0/wV4Y0vQNLhW307TbaO1giUYCoigD+Va+RX5E/tgf8ABU22+KPw/g0X4WT6t4cvpLoi7upY9jvAF42sOhzn8q8M+A//AAUm+LPwT0O50xLyPxPZyTtcbtZdpZVJCjAb0+XOPc1ZPKfvTkUbh61+LF9/wV++NmpSRx6bpOjQvIMKkdmZXJ9hVe7+On7Zn7T1u+k6PpmvQ2cijzP7NsvsKMue8jbR+RoDlOP/AOCjlvpeuftxaovhd49SlumskmW0+bN0BsZPdvlX86/d5WEiqw6MMjjFfmn+xb/wTJ8TfD/4paf8RPipeWdzeWLG5ttNhma4Z52AIklZh94EngZ5FfpdQSFFFFAFbUrFdT065s3do0njaIshwwBGMj3r8vvEX/BFOfU/EV9d2fxRWKyuJnlC3ekiaYbmJ5bzBnrX6lUUAflpD/wRFZFx/wALejT1B8MpJ+puBTp/+CIamENH8XwbkHjd4ZRY8fQXHX3r9SaKB3Z+Smrf8EUfF0KkaZ8T9HuwB8q3WnS2y/QhGb86898Yf8Eevjdodm9zpV34X8SyxYKWljfyRPJk8j9+qKP++q/a2igfMz5l/YH/AGX7z9mP4LW2naxLcp4n1Rvteq2j3KywW82SAsewlfu7ckE5xX0yvSlooJCk3DcB3NLSMNykGgD4s/4KnftDT/Br4EjQdKl8rW/FbPZxsCcpAoBlYe+CB+NQf8Em/g3/AMK7/ZtXxBe2Sx6v4mvHvRcsBva12osan23CQ/jXyB/wUs1af42ftyeGfAWmXBmWxt7LS/srZCi4lldn68co8fPtX7B+EfDdp4O8L6ToVjGsVnptrHaxKowNqKFzj8KB3NTvjvXzT+35+zfY/tEfAnUoHk+zavoaPqdjNxjciHcpPoRX0uVO4GuW+LEbTfC/xai/ebSboD/v01AH4CfsO6PLq37W3wwtfleRfEFvK2Txtibc36Cv6IZlfyn2ffwdufXtX4Af8E6rWS4/bN+Hahcst5LI2e2Fcn9BX9AZGeD0oC9z8Mf2kPh5+1P4r+NmvyajoviW7uGnZbdtJkcW3k728sKVIHQ1R0L9iP8Aat8SW5kXTNasVYAf6dqpQkfTca/dtqSgD+bu2+APj29+PMXwvki2+ODefZnE05KpLgNuLjJIxzX3Pa/8EUvEF+sEmq/E/Tw7KrTLDpbs6tgFgHL8855xWb8LmXXP+CxmvtHErJDqV5uzxjy7XBP13Cv1yoEeW/s5/s9+G/2avhraeEPDUWIlf7Rd3TffubgqqtIfTIRePavUqKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiilcAoooougEx8wPaikZtuOKXd7UDFoopkkgj9z6UxD6KYm5m3HgYxilVSu7Jzk5oAdRRRQA0rzkcGnUUUAFFFFABRSE02SQqhIGSO1ACsuea87+NAmh8Ea7PA+1k064YKB1IQ16Gr7lDYx7VyHxS0mbU/BetrEy5+wzrtbvlDWVRe6b0naWp+Of8AwSesDqX7ZD3ckjRywaffSlQfvEnBH61+3i1+DH/BOfxg/gj9t/w5D8uzUbm60uTLYH7wMB+oH51+84rSOxM99B1FJu9qM+1MyFopMn0qGa7SAEsQFGMnPC+59qV7DsT0lcX4/wDF+oeH/Bur6xplob2azheaKOPlZtoyMEV8pfBX/gqd4E8aawNA8cWNx4H1pFYSSXoxBuDEYBPI/Gk5Jbl8jtc+4dwzjPPpQTt618E/tVf8FR9C+ETWun+BLSz8WandRmRbjzswouSBnHPUGvC/g/8A8FlNe/4SaO3+IHh6x/seaUbrrT9++JTgEYJwcdfxpKSauRZn61LnvS1ieDPF2l+PPDGneINFukvdK1CFbi2nToyEfzrbqk7q4PTQKKKKloQxmKsOVA/Wq890Yc5TK5xuzip5I1kIJHI6VSv9NW+ZRI/yD+Dt9azlfY0jbqZ8hl1K4KhRBtHVmyceoFWLPSp7c7DcFowvGBznPrivlr/goT8YvF3wC+C93rXgvVU03UmeKLzTEHZFLEZXPevyR1D9sX4++PdShJ+Jnim51GTEUdrptw8W4DkHZFtB5J7Z4pR1R0Sk7JJn9ESwNkB23LjGc8/yoUQ2cblnVE+8WZgAK/BVfjL+19r2mJp8Wp/Eu4hhbaWhtLiQlsDgyBc9COM1JpvwP/a++MkZElh4+vbVpPKeTVruW2QHAOCJHHGCPatOVnNfufug/jrw1FIUfXtMVxwVN3HkfrV7T9f0zVYzJZaha3canaWhmVwD6cGvxT03/glD+0TqUPn3Mek6fIxyY59Y3Ofc7Sf8isbXP+CfX7UfwxWWewsL+aGNTK0mhazuHfPyhsk4Hp6VaFofuktzF/z1T/voVIGDDIORX84k2s/HPTdX/sifVPHcGrFtiWi3FypJzgHrzzn8q/cP9iPwL4v8A/s7+HrPxzq97q/iG6BvZWv5WklgV1XbES3PG3P/AAKmSe80UUUAFJS1HIx5wdtADlbdmnVAHZXPA2Yz71598Sf2ifh38I4428WeK9O0l5ACsMkoMhBJGdo9wfypXHY9Ior5vt/+ChnwEur9LRPH9kJGOAzKwT88V9C6XqdtrOn299ZTx3VncRrLDNGcq6EZBBphZot0UUUCCiiigBp+9ivhD/grv40j8M/s7ppWxvtGtXiW6ODj5V+Zh+VfdzD5s98V+cv/AAWrVm+Evw92puLa3Iu7+7+6qJLmLi7M5v8A4IyXHhDRfB3jq+vNV0+z8Uz38dqYbidY5GtljQqQCem9m6elfpta6ha3yk21zDcAdTFIG/lX4Wfst/8ABOHx/wDtIfDlfG+j+ItN8OaXczSQ2/2oSGV2jbBI29Fzx+Fd34g/4JnftP8Aw7ZJ/CniFNWdRvL6RrUls+cntIV54HQ9xRyi2P2grgvjD8bPCfwR8K32teJ9XtrBYIGljgkkAklIBwFXryRjNfjxffAf9uOxmETyfEaUqvH2fxM7p1PHEuK3fh//AME3/wBov9oDVIrn4l6rqGg6dCxjN14m1J726wAGASMs3y5Y4Pruo5QujifgH4D1v9vz9si51fXvtF/oRu21HVZnO0RWanEcYxjbu2hRjHev3WsbKDTbG3tLaPyra3jWKKMEnaqgADn0Arx39lf9lLwj+yn4FbRPD0bXWpXhWXU9Vmz5l1IBgHGcIo7KuB1Peva9oqhN3BaWkpaYgooooAKKKKAGs2Gx7Zr51+OH7fHwi+APiSTw94j1qaTW4wrSWVnA0rRhieWI4HSvomRVdSGGQeDXxL+1n/wTF8P/ALSvxCufG1l4on8M6xPaJBLbx2yyQzSKznzWOc5IZV4HRBQPQ+j/AIO/tJ/Dv47aQdQ8H+JbTUFVtjwM4jlRsKcFDz/EK9Nr8SvGX/BLf4/fCu7N54RvINZjhXes+j3bQS9TwVJGTgA/jUHgf9ub9o79lXUP7H8Z2moavbEqFtPEsTfIoJH7uQDodp7+tK47H7e0V4J+xf8AtMTftWfCA+M7jRf7Bmj1CXT3tlcurGNI23qT2PmY/A173TJGtjGScAc9cV+Z3/BQD/goHqMHiC5+EPwhmmufEM0wsNR1CzyzFmAxFblej5OCw+le8/8ABRj9q+b9m34R/Z9FljPijxCWsrIZ+a3Xad834A4HvXzN/wAEp/2OW1qaH45eNFmlnW4kGh2l0p/eNj5rps9eWIX3XNAHYfs//wDBJvQ9V8Ex6r8aLzUNU8Y3jmVore9bZBEyqQjHu4YyZPTkVf0L/glSPhh+0V4N8XeAPFU+m+E9Nmjub22upGa6Z0diUVhgbWXauD71+idDDKnHWgdz4G/4K7/HHS/CfwFb4dQzJL4g8TzQsY1cboLeKVJC7DsG2FfpmvXf+Cb/AMJ0+E/7JnhKIukl3r6nX7howMbrhE2DI64jWMfhX5v/ALWX7Fv7SHjf44eINbv9AvPGCXcjPaX9ncK6Lbb3EcfzEFSB29CK8x8aWv7VPwP8L2una7f/ABF8O+HYYEgihjvbn7DFCo2qm6NyigBcBewAoEf0FA56dKWvyh/4I+/FT4h+JviR4o0XV9X1nXPCH9nvcLJePJNbw3YeIHDt0Ypjj0I9a/V6gAooooAKKKKAI2BLMOi44Ir8af8AgqJ8btU+Nn7Q2mfCjw6GuLLQ5lsBbox/f385AbI6HaNgB7HNfr9448SReDfBuva/PjyNK0+e+fPTbFGzn9Fr8W/+CcOi2nx2/ben8S+JA19Pb/bNeQTfMTMW/d5z/d3Aj6CptqWj9bv2Zfgvp/wD+C/hzwjZW8cNzBbRy6hIigGe6KKJJGI6n5QM+iivUaFqC/u00+xuLqU4jgjaVj7KCTVEn4AftYeH7XT/ANvbxbpcEEcVs/ii2CwogCAP5ZIwOO9f0A2dutnaQQIAqRIqAKMAADFfzpeIfHTfE79sRvFEhMg1PxZDKpY5yonCr+GFFf0Z0COT+Jnwv8M/F7wnd+G/FmlQ6vpF0uHhmHI91PUH3Ffmj+0//wAEi00PR9U8S/CjUp7o26mceHbr5mZRklY37kDGAa/Vmgigdz8eP+Cfv/BQa++E2qWvwy+JVzNLoJnMFtfXTEyac33fLYnqoK/hmvDv2sfF2p/tafto6jY+G7r+14bq+j0TRni5QwDjI/FmNfVX/BVj9jXStH0qT4w+ELKPT284DXreEBUYNgLKqjgHOAa8d/4I7aH4f1L9pfU7vVpUGsWOkSS6VA+DvdmCyEZ7qnNIvzP1q/Z3+D1l8Bfg74a8EWLCRdMt9sswGDLKxLOx9eT+QFej0i0tMzCiiigAorwn9r79qXS/2TfhzF4n1DTpdXuLy4FpaWcbhAz4JJJ9MV8Qw/8ABbO4WPEvwxiMuTnbqe0D81NA7H6qUV+VM3/BbS7/AOWXwxt1/wB/VM/+y1nXX/BbbXNp8j4bacj9g987j8xigfKz9Z6K/Oj9kL/gp54t/aP+PGleB9Q8B2NlY38MrG40+d2a32KW3tu6rxg/hX6L0EhRRRQAVW1K6Sx0+6uJOI4Ymkb6AEmrNcd8Zbw6f8IfG90v3odEvXH4QOaAPxL/AGGLGTx9+314fvhlo11i+1Y4H8OXPP6V+2vxG+LHg74R6TFqfjLxHp/hyxlfZHNqE6xh24yBnr1FfmD/AMESfC1vqnjv4n+J5oA13YWdpaxSH+Hz3lZsf9+RX1z/AMFCP2ONX/ay8J+HJPDurQadr/hxrp7aC6H7q5E6xhkJ/hP7tefc0DPpvw34v0TxjpsF/oerWeq2c6CSOa0mWRWU9+DWvX4Fal8D/wBpT9jea41+007XfDlrBgvfaU/nWrdsNjI525+mK++/+CfH/BRQ/H28j8BePfLtvGpDNY3kS7Yr5FQFlPpJwx9CMUBbS5n/ALR//BV6P4G/GPXvBFn4FbVI9GmFtcXVxdeU7yYBJVcfdwVwe9cof+C1+hCzRv8AhXl99oYfd+0rt/OvsP46/stfCD4lR6z4r8ZeFNOudSjsmM2qPmN9qISCxBAOB3PoK/A/wj4Hj8WXXi6+hjdtJ0jTbnUE25IRQ5WME9s5oKVmfcPjb/gsl8Qde1S2g8HeE9P0dGKKIrzM8krlsYH1BFfq38MtY1nxB8PfDmp+IrWOx1y8sYZ7y3iztjkZQSoz9a/NL/gkB8AfBPjzwT4t8a+JNDt9Z1iz1eOwtDeLvWARwxyblH97Mg59hX6p9OBQJjlpa8h8A/tVfDn4kfFXX/h3omuLP4o0ZnSa1Zdocpw4Q/xbSDn6GvXqCQooooAKKKKAPzi/4LXZPwh8AqOWbW3AHc/uTX0t/wAE+JFl/Y0+FjIwdf7MYZU55E8gI/MGvnP/AILRQs3wj+HEoRiF8R4LAcDMLYBPvj9K93/4JozCb9iD4YEMGxb3inBzjF9cDFA76WPpyiiigQUnWkbODj04pI9wUbuvtQA7Ipa8Q/ab8YfF7wfotncfCPwdpPirUWbF22pXYiMMeCRtXcu7JHrXyj4Z/wCCr2p/DvXh4b+Ofwz1Lwjq0T7J7izUkKOzeU3zEHnlSQe1BVtLn6MydaVcYwa8U+Cn7Y3wn/aFvLiy8G+KoL2+gXe9jdRPbT7cc4SQAsB6gY7djXin/BQD9vG3/Zx0g+F/CNzb3Pj+5hScRyRl0t4GLDeSON3yng/1qbgkfZGoa9peiyQxXuoWtnJMwSNJ5lQux6AAnmr6urKGUhlIyCDwa/nQ1LS/jl+0Na6t48uofE/iez0kNNdanmQw2yg7sIegCg5wOma+/v8Aglf+2vrXjy/k+FHjrUn1DUY4DNol9ckCR40UBoCf4iMFgTz19KYcp+mdFItLTJPDP24rKbUP2SfipFApaT+wrhvl9FGSfyBr8hv2Df2KLf8AbA1DxUb/AMQy6JYeHhaGRbeIO8hmD4HPTiJvyr9lP2somn/Zk+KUaKXd/Dl8qqBkkmFgBX53f8ESvGOm6Z4s+J/hy5uo4tS1a1025s4WPzTLALkSbR32+aM0DuewSf8ABGH4Wm3jSPxNryupyzkp834V2mi/8Ek/gXp+nx295aatqUyHJuJL1kLDjghePX86+1aKAuzxj4U/sf8Awl+DUIHhvwbYxzq/mC6u0E8wOAOGbJA46e5r2GG2jt1CRRrEg6KgAH5CpqKBCLS0mcdaWgAooooAKKKKACiiigAooooAKKKKACiiigD8Y7ZLbxl/wWJmeD/SYIPFRVt/GGt4FV+D6PG1fs3kV+GfiTxFL8B/+Cp+t6vf4VF8ZSzyLnd+5un3oePVJV+mcV+5KsJFVlOVYZBoGO3CvnL/AIKA/GyL4H/syeKNSSYR6pqcf9l2CdS0soIP4BdxzX0Xjg9vevxn/wCCgnxM8R/thftL2fws8B2kmpWXhwzW8Nur/LcXSrummPooXCjPofWgdjgP+CUOljWP2ytBkmO5rWwvLoZ9fL/xav3br8Av+Cfnj60+Av7YXh2bxSX0uAtc6RcmZCDFJIuwBh2wwH51+/UcqTRq8bB0YAqynIYEZBB9KBMcRSbadRQI/Eez8cy/Az/gqtrusa0hjjk8V3cUhXnNvckiIjP+y6/rX7b7hX41f8FgPBx8I/tOeFfFltCtvb6po9vK0sX3muLeebzCffYYcHvg+lfrT8KvFdn45+GfhbxBp9yLy01LTLe5SZT97dGpP45zmgp9zrKWkWue8dfEPw18MtBl1rxVrVnoWlxfeubyTav0Hcn6UEnRUVk+E/Fek+OPDmn69oV9FqWkahEJ7a7hOUlQ9CK1qACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikbOOOtNjDqDvIJz2oAfRRRQAUUUVDTuAUUUhpWYFW6Z4WM2792q8r3NTW8wnhWQdGGaBCSpDEMDT1jCDC8ChRd7lX0HU1lDfWnUVoSIKWiigAooooAKKKKACkY7RS0jDcMUANbmk9utONJt70DG7l5TOCBmqmqfZ73T7m3k2ypJGyMm7G7jpn8amvLUXdu8RYoGGMjqKzL7T00/R51UkmOMsH7kiplsXFRb3P5+rq2f4G/tsQjDRDSfFKSrzjCtKDjP0bFf0N28yXEEcsbbo5FDKw7gjIr+eT9rC+m1D9rjxVdTwNbTPrMJRT6DaM/pX70nXr/w78I7bVLHTZdXvrXS4pUsofvykRjge9JSSWo5LWyO3U0Buufwr8mfGn/BYzx34Z8XXNifhrZ2cNsTE9nqFzIk24Mec7OOMce1Mt/8AgtZ4nnt2LfDLTVkzgbNSkI/9Ap8y3FyM/Wk55x6V8Mf8FLj8RbX4S3Y8IXs9jaRlrm/nt3KyNAozgEdBnNfMesf8Fh/id4iktNP0DwTpen3lxOqptmeeR+RlQpA61+kXirSNQ+Mf7P13DrGnLpt/q2iP9ohPLRu0ecAGolqzSHuX8z4I/wCCQ3x98T+KPFviT4fa/rFzrOktZG9to71zI0TAhWUMecEZ4rtf+CpH7Pvwt0/4a3/jT7Omk+MY9sVqbchRMuSdrL9WPPvXyn+wL4lHwG/ayv8ARNSk+xyXEclgsj9Qd3H516V/wVa8Tah40+MnhL4eWErXl08EDoEbiR5HdQCB9BS5m35By2urnyX+yl8M/CHxZ+LWm6P431waLonDSymXYXH90E9K+v8A9ub9gjwP8O/gnZ+NPhUsl3Zaa4N863Hnl43J+cn24rI+LX/BKPXPh38BY/Fml6tJqXiaxg+1XunqmAq4BYKRySK+Zfhl+1t40+HXhfVvCd7cNq/hzUYJLWexvGY7MqAMc9QRUyUr3iyIW6n6w/8ABKL4lW/jr9lbT9ME3mX3h27k0+4Q/wAIwHT81b+dfZlflj/wRG8RJt+K+jbsFnsb2JM9v36sf0Wv1NFbRtsRLe4tFFFUSNakpxGaTbS0GfI3/BTTwrba9+zL4juJ42P2WNZA69QVJI/Dmvzm/wCCUPi610T9qjTdIvNOtLyHVrSWOOaaHfJDIqFlKHPHPWv1a/bb0mLWv2bvHFnNuEX9myyll6gqMivx5/4J2/ErwR8If2h7LxF40vhp9rDA8UFxIMojOMEmsVu0bPZH7/r0pa5PwD8VPCXxQ09r7wn4hsNetVOGezmDFTgHkdR1HbvXB/tCftZeA/2bdAk1LxVeyGXd5cNnaxl5JZMZ2jsDWtzKzPaKK/Na6/4LZeEo5WWD4ba5KnZmuolz+FYWs/8ABbyzhljGmfCm4nQj5je6uISD7BYmBHTvTuHKz9PX020kuBcPawtcL0laMFh+OM1Zr4t/Y5/4KKS/tYeNL7w8Ph3eaH9li85763uxdQRqeBvOxdpJz619og0xNNC0UUUCErkvih8QtI+FvgnVPEmtXCQWFlGXYu2MnHA+tdXLIsMbOxCqoySe1fjp/wAFP/2mtQ+I3xGX4WeFruWTTLWRI7qOF9wubhmICgD0G386VzSMb6nFfGb9u/4y/tLfEVfD/wAOLnUNNsXcw2tjo4Imm+Y/OzDnBBH5V9D/AAt/4JDv4x0Ky1v4t+ONYuNeukEsunwsHEBYZ2l2JOck5xxX0F+wf+w1on7MvhVNc1Fv7V8aanEsk1zIgAtEZVPkoOxB3ZbvmvrjbU2YOR+ey/8ABGP4XjUIpH8Va/JZq2Xtf3Y3D03dRX3j4N8LWXgjwvpegad5n2HTbdLaHzW3NtUYGT3NbO0UVfQlu4tFFFBIUUUUANavzp/4LURzt8GfAkka/uY9bdpGx9391gH9TX6L4r5z/b3+B9x8dP2d9e0qwCtqNihvoEKbi7IM4HoeKBrc8Q/4I2/Eo+KP2edb8JylTP4Y1ZlQL/zwnXzFP/fYmr78r8Qf+CWPx6b4F/Hi68H6tbCCw8ZPFp07zEIbe5hMhjJz0H71gf8AeHoMft3u96AY+im5NJuoEOJpNx59e1cF8ZvixpnwZ8C6t4o1aZVtLC3eZlZgMlRkKO5LHAr4O/YQ+OPxc/a0/ac1vxvq2r3mmfD3SLaUR6LbkizLycRxdPnYffJOT0GcYFTfWxfK7XP0vBz70tItLVEBRRRQAUUUyRiuWwSAOg70AOxznvQzBVJJwBySa/PP9tj/AIKa6x8BviBc+BvB3hkSatZ/8fGoauhWFuM/ux/EPevhH4n/APBSL46fFTTW0+48UpotlIMSR6ND9nZ19CeT+IoA/X/46fts/Cv4AyLB4h15J74nAs7IiWTv1x06V+U/7XP7VXif9urx5pPhbwd4dmTR4JtlnaxR7prhmJAkcgcDBHHbmvkK8vLvVLo3N3eSXczknzbmYs2T6k19Sfs5ftuH9mvQ4IPD3w68O3Wqrnz9Yumc3EjEAfe7DAH61Nirn7Hfsl/Bo/AX4A+EvB0yr/aFnah711H3p3+Z/wAs4/CvX6/HDVv+CyvxQmA+xeF/D9oO7N5jj36/hX6AfsJ/tGeJv2nfg3c+L/E+ixaLcrqclnbiAMEniWONvMGe25nH/AaYPuflD/wUB+OVp8ZP2uNQ+1yTXHhPw9dR6VHBCdxaKJyZmVemWZn/ACFfo/8AB/8A4KVfs/X0mgeDNKvL3w7AsUVnaC+sxDAmAAFyCQB71+ZX7EvgTwl8av2tLbSPiOwu9PvJLudo7iUoLm45IVj3ySfrX1D/AMFH/wBgfwF8H/hTJ8RfAVrJov2O8hjudNWQvCwkO3cufu4OOKYWP1dtbqG9t457eVJ4JFDJJGwZWB6EEdRUtfEX/BIv4geIfHn7MeoJ4h1GbUn0fX5tNs5Z3LstutvbuqZPYNI+K+3aCQpkkKTLtkRZF9GGRT6KAI4beK3BEUSRj/YUCpKKKACiiigAooooA5L4t6IviX4W+MNJcZW+0e7tyPXdC4/rX42f8EktQj0X9r46fNIEefS7u3XJxuZcHH5Cv26urdLq3lglXdHIhRh6gjBFfgJ8fPAPjb9i39qi91bSvM0hor6TUNHvNpWG4hZ2wuR2OCCtBcex/QAtfPH7efxztPgP+zh4m1Nptmr6nbvpemRg8tNKpBP4Lk/hXyT4I/4LUaQug2ieK/At8NWVNtxJp0qmJmHcBsECvlL44fGT4mf8FD/jHaaXoGlX1xpUUmNL0mIEx2qM2POlI4zyfmPpQLlPlPT7240/UrW9gZxcW8onDA4IZDuyD9a/pb+BHj2L4ofBvwd4qhJK6ppkFwSTn5igDfqDX5a/t0fsJ2vwJ/Zx8Aat4bsJLu+0hjF4iuoE3GQui7pCeu3cCPSvVf8Agjb8etV8SeH/ABJ8L9Q869stDAv9PvHyRFC5CmD2AIJH1NBJ+mNFFFAH56/8Flvii/hz4J+HPBNs5E/iW+aeZVOD5NsFY59izr+Vfm7aeAfiX+y3N8NPi3FEbGHVnW+0q6hbiTGGMbf7ynp6V61/wVR+N3/C0/2mb7Q4ZGj0nwlG2kKAfvzKxaVvxZtv/ARX6lat8BfC37Qn7JvhXwzqWno0P9gWsunPja1vN9nXYw9OcZoKudx+zZ8eNG/aP+EejeNtGxELpTHd2m7LWtwvDxt7jgj2YV6hX4Y/sLfHXWP2R/2ln8GeI5J4NDvr59J1a0YkrFcbiscwHQc7R7gV+5qsGUMOQRkUEi0UUUAeYfHv9nPwR+0l4cs9E8cadJqFlZzfaIBFO8TI5GCcqR2rw/Tf+CVP7O1hMskvhO8vWU5xPqtxtP1AcCvr+igdzwXSf2FfgHo9qkEXwr8OTqvRryzWd/pufJrTT9jX4Fxq6r8JfCA3DBb+x4M/gduRXs9FAXZ4b8F/2Nfhl8AfiFrfjDwXo76Vf6pai0e3WUmCFN5c+Wv8OTt/BR717lRRQIKKKKACvLP2qDj9mv4of9i3f/8Aoh68T/4KXftLeJf2cPg/pNz4PvI9P1/WNQ+yR3TRrIYkVSzMA3HoOlfKXwd/4KNSfFj9n34meA/ixrUVr4nn0a8Gma0sIjS7UxbViKqMb927njINBVj0H/giVpMMPw7+Jmpgfv7jVLO2Y/7McBZf1lav0rr87f8AgitFGPgT45lVCsjeJCpPqBaQY/mfzrwH9uj/AIKAfGXTfix4k8DaJJL4I0fTbhrNTbxEXNxtdv3okPQEEDA9KAsfpb+0x+0h4H/Z7+Heoav4rure6MkbQ2+k7g0l5IVOI9voeck1+VH/AATf8EXvxf8A2z4/HGl6PFpfh/SZrrU7iC3BENt5iusUKn1BIOPSvj7xFdeLvHGpNqmsNq+t3sgwbq7EkznknGTnHUnHvX0n+zR+2R8XPhbZ+Gfhl8PdE0qyku79Q6yWJae8kZgCZDwfu4HsBSKsfqV/wUk8XSeD/wBjfx/LDJ5c19DDp6HOCfNlVWA99u6vzE+EXwtn8Mf8E8/jD8R5w0NzrF/Z6RbKQRugSWPcw+pkYf8AATX2P/wV+1vWY/2ZfBGn3duy3t5rEU979mBaJJI4HyM+m5zj6VgftHaDL4N/4JF+DtOW3+zyPZ6TJNGFwQZCJGJHrk80xLY9A/4I5eHZNJ/Za1W/mQo2reJLq5RsdUEMEfH4xtX3dXyr/wAEw/EGi61+x14Mt9IkVn083FrdoCNyzec7Nn3IZT+NfVtBLPxJ8I3r/AT/AIKw3KzPtgn8WXFvI7cfur3cQfp+9Br9ta/GH/grh8Obz4cftPaH8QbFPIt/EFtDdLcIcMLu1wjAf8AEJ/Gv1u+D3ji1+JPwt8LeJ7OXzoNU06G5DZydxQbgfcHI/CgR2NFFFABRRSUAfA//AAWQh8z9n7we+M7PFNuT+MMor0v/AIJbyCT9h/4eqCCUbUFIz0/0+4P9a88/4LENt/Zx8Pcc/wDCSW3/AKLlruP+CVq+X+xX4Nyc5uL8/wDk3LQVbS59cUnmL/eH51XuJTuAVhjHrUKfKDk55oGo31L3mL/eH50nmIWwGGfTNU1Xc+dwHHrUsMOxiTyc9aBuKXU+S/2+P22NW/ZKXwtBovhmDXrrWDI0kl8zxQRqvQCQDG7OflznFWvhPrfws/4KSfANdS8T+GrKW+DfY9St4yPtNjcKAfklxuCkNkZ45PpXY/twfs7WX7RnwG1vRmiX+27CNr7TLjblklQZKj2YAj8q/O7/AII6+Przwv8AH/xL4MuDKsGs6a0pgJIWOeB+SR6lSw/CgW6NP9sL/gmTL8A/Dd18Q/hn4puE0XSoDJe2+qXghuLf5jhoZF27hyoC9c565r4q+Gvj3RF+Lmka/wDFOz1Dxho0U4a+glnJllII6k8kDA+XPNfe3/BWj47XPxC8feGPgd4Qmnu7qO5jOoxWchYT3UzBIbdlXqV4OD3avqj9nz/gnn8N/BPwF0nwl438K6X4j12QPcajfSJlzM/UI4wQFAUDtxSsK9ix8G/29v2dPGmk2+haR4g07wvb+WLePS9WhFmpGANgDDDccd881+bnjK+8P/ssf8FGItX8J3trc+FYtXhuo5LeUPFHBcqvmpuHGFZ3H4V9W/Gf/gjP4Z126lvfhz4ouPDg2grpuoKZo/MyTkSDkDBAxg9OtfDPxe/YT+Mfwj+IGm6Zf+GbrWlvJ4xb6ho8Tzwznd03f38DJB6ZFAXP6B7WdLq3jmiYPHIodWXoQRkGpazfDdvJZ+HdMglUrLFbRoyt1BCgGtKmSVdV0y21rTLvT72JZ7O6iaCaJhw6MCGB/A1+FPxj8E+IP+CeP7YlrqehGZdKhlGo6dIwIF1ZyEh4vfbhgR7V+8FfNX7b37Hdj+1t4HsbaO+/srxJo7SS6ddkfKxYDKP/ALOQKAPavhf8S9B+LXgnSvE3h7UbbUbC+t0mDW8gfYWUEq3oQeMGurr8FvDOu/tCf8E+fHGoWcGm3lpaNuMqzQvLp90oYgSqQCBnbjseK+ofBv8AwWysLXw/bJ4q+Hl5d6xj95Npl4kcLe+1gSDnP6UAfqRRX5uWv/BbLwRMpMvw61uHnH/H9E3/ALLTLj/gth4O83Za/DfWpywwv+nRg7vTAXmgD9HdS1C10qymu726hsrSJS0lxcSBI0HqWPAH1r8xv2o/21viJ8a/jdafCX9nbUZp7GRFtbzWNPh3F5izCR1kH3YlXHzccg4NefazaftI/wDBSbXgsMVz4N+G63DKFuyYIYwMNyBhpWww7beOtfoT+yf+x/4Q/ZR8JSWGjL/aOt3hD3+sToPMlbaBtX+4nGQo7k+tAHT/ALNfwXl+A/wtsfDd3rl94i1R3N3f6jfztK8tw6qH27jwvygAf416nRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH5H/8FfP2c7zQPiFpPxj0KJ/s2pJHa6m0KEmC5hAEcxx2KBB/wCu1/ZT/AOCtnhjT/Advofxe+2WmrafGsMGq2Nq1wl3GqhQWC5IfIPPTpX6VeIPDumeLNHudK1mwt9T065QxzWtzGHR1IwQQa+MvFH/BIz4KeINcur+1Or6PFM2/7Ja3A8tCeTtyMgUDueGftaf8FU7bxl4ftfDHwQe+a+1FjFc6lNaPFKgPG2NCMknPWvRf+CWf7J/iH4aw6/8AErx5pstn4k1keTZLdnM3kt87TEHlWYttwey17n8A/wDgnr8JP2f9Yl1jS9Lk1rVycxXerESmAcfcGMD6+9fTNAXPzE/4KDf8E2Nf+IHjS7+I/wAK7dbvUL9hLqeiq4jYyjJM0R7k/KNvtmuB/Z/s/wBunwhrmjaDbaRq8Gih44t3iFE8iOFTzuYkkccV+vNJtAYnuetAiO2837PF5+3zto37em7HOPxqWiigD4h/4Ktfs+6j8YPgjp2v+H9PfUNf8M3Zn8mFNzy2zqRKvvjCnH1r4q/YR/4KIT/sz6XdeD/HVtqWs+Ew+bRbcbp9OYHDIFbGRwPlyMV+2LqsisrAMrDBUjIIr5i+In/BN/4F/EzxJPrmpeF3tb64OZf7PuXgR2ySWKqcZ56+woHc8K+J3/BZTwHp+iIPAHhnWdb1qVtqRatbi2jGe/yuzGvJfhT8A/jb+3p8UrTxX8aF1HSfhvby/ak0+4JhSVScrDFH124xliBwa+8PhV+wn8FPg7dC70LwVZy3yvvW71HNzKhwPus+cDjt6mvfEjWNFVFCKowAowBQIy/CfhXSvA/hvTtA0Oyj07SNPhW3trWEYSNB0ArWpkalQQcAZ4xT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBD1qrcapaWsgjmuYYXPRZHAJ/OrLLur4s/bU/YI8T/tM+MLPxP4d+If8Awjl3aWK2aafNHKsT4kd9xdH4Pz4+72qHfoXFRd7s+zGv7aOJpXuIljUZLFxgfjXmHjr9qT4TfD1pIfEHjvRLKZYjKYGu0ZyuSOFB9Qa/Ntf+CWv7S0NnNYJ8TdMFi5yYv7bvNj8YyV8r0FQ+Gf8Agi78RdWvi3inx5oVjBnmWzWa6lP4Oq/zpu7QlZHh/wAZ/FehftQftpaRc+BLO4ubLUdTt4FXysM+yUlnA/u7T19jX70afbrZ2FvAq7VjjVAPQAYr5X/ZR/4J1+Bf2X9XbXkvpvFXiUJsi1G8gEQgB+9sQMcZ9c19YbaSj3CUjzLxr+zJ8LPiPrR1bxL4G0fVtS2eX9pmgwxXJODgjPJP51y91+wr8BLyQPL8MNEZgMDCSLx+DV7tS1XKhXZ4r4a/Yz+Cng3WYNV0f4daPZX8BzFMsbMUPqNzHmvW9Us5LjSbm2tysbvEUXI4GRir1G2iwXZ/Pb+254a1z4W/tMapeSMbC/uHF9btCcbRuKAg/VD+dekfsCrqf7Rn7ZWh6z4slfVZtMtvtLPN8wXyx8g59/51+nH7Vn7C/gf9qWxFxqTS6P4jhj8u31W2UMwALMFYHqNzH865v9h/9guw/ZN/tPVrzWf7d8SainlSSLEFjhjByFQ9TnvmoUWlY0ck22fWVxBHcQvDKiyROpVkYZBB6g1+Tv8AwUk/YCnsbub4i/DvRli0yKAtqen2oACtvZjKo9wQPwr9ZmGar32n2+p2c9pdxLcW0ylJIpBlWU9QRTsyEz8Of+CUnxOHw5/agt9LuGaOz8TWr6cVP/PRTvTPvkH86/c5a+T/AAz/AME4Phx4N/aAtfino17qFjc207XMWixrH9kWRhjcPl3D86+sKEne45NMWiikqyBGz2pPmxWH4q8Uf8I3ptxemFpktk82VVGTs56e/Ffm/wCH/wDgsbcp8WpND8QeErKDwt/aDWovbXzFuIo921Xbc5UnueBWejdjX2cuXmPsT9sXUbhPgh4rsIoleW802aJeD3HPevxS/ZU/ZC8TftZeKvEGiaBqen6TJo8Annl1DeVO5iqqNoJzlTX7WftR67YzfArVPFdtOl3p66dJJG6fMjq6cGvgT/gkX8X/AAT4B1P4lx+I7630a7uTFdLqN7MEjMILDy/rkk/jWcdGyn8KPBvG/wCzL+0P+wrqyeKrE3Vhbx5/4nvhy4aWELn7soxwODwR3619sfsp/EDwr/wUc+Fet+Evif4eW48SaSFeXVIRtLllC+dH12txjBz0ryL9vz/gpFF8QIb/AOHHwzeK50eVvKvNY2nM3YrHk42+5Fe9f8Ep/wBm3W/hL8Or/wAV61cW6v4mVJYbWJw5WLAwWx0Oc960Yr6H5eftdfBGx/Z7+OGt+D9MvJb/AEy2Ie2muHDSlDn7xAAJyD0Aq1+xh8PND+K/7Rfg3wr4ksv7Q0PULl1uLfzHTICE5BUjByBWz+3/AK7P4i/ax8dPMqKILz7OgjyFCqB7n3rrP+CXXh6DXP2xPDC3DSBbOC4uk8sgfOqcZ46c0CP0e+MHgXSv+CfPwb1nxl8FPCdskr3kLara3k0kweEZBIJbIwPfHtXtn7LP7Tfhr9qT4djxJ4fZop7eQWt/ZyDDQT7Fcr7jDDBrd/aE+HcHxT+Dfivw3cKzreWMiqqHB3AEjFfjt/wTz+NWo/s4ftQDwfqVx9m0TWLptNvop87VlBIRxzgHOAT6VSYnqj90aa0gXqefShWDqGHIPIpdoLAkc1RmeG/tc/HG3+C3wQ8T6zIwgvGtZLe0395GXAOPxr8UP2SPjF4N+HPx4g8cfEm0uNegt1kuI8jzGNwfuuQepHavtz/gtb4ovLbTfh/oUUjx2d21xcXGAdrFNoQfq36Vi/sA/wDBPj4U/HT4JaV468WnUNS1O4nmje1trvy4UKyEAFcdcY71NjW9krHrtp/wWW+E/mIs+h65HGTjcsQOPwr6E+AP7cHwr/aO1J9L8L6y8esLkjT76PypXAAJKg9ev6V5z4p/4JU/ATxJbsItF1HTJRHtRrO+ZF3Y4YjBzX5g/s5eHZ/hj+3r4V8O2dy0Y07xM1iZQ3Lxhiu0nvkCmQ9Xof0B0Ui0tMkKKKKACiiigApDyCCMilooA/E//gqL+zhN8E/jZB4+0H/RtC8RSfaQ0Klfsd2pOQMdBwG/Gvaf2Zf+Cu2heH/AOm6F8WbDVLjWbP8Acf23psKSpcRAAK7rlcNnIIAxgDvmv0e+I3ww8L/Frw5PoXizR7fWtLmBDQzg5GRglWGCp9wRXyl40/4JE/ADxRDEml2Wu+EigwW0rVHlLck8/aRL69sUFXVjUh/4Kufs7TQiT/hJdRT1R9KmDD9K5zxV/wAFgPgZocLtpcPiTxFKE3L9k08RJu5+UtI64/I9axov+CLvwbU/vPGHj6QDov2+zAx/4C11vhf/AIJIfs++H1K6hpmveKstu3arrEiEcDj/AEfyhjv0zyeaA0Pg3xz8Svi9/wAFN/irBoHhnTW03w3CxdbTePs9om7madx958YG0kjgYHJNfrZ+zJ8BdN/Zu+D+i+C7CVbqW1TfdXioFNxM3LOf5DPYCuo+Gfwh8GfBzQE0XwV4a0/w5py8mKyiCtIcY3O5yztgDliTxXXYqUtbg3cBS0lLVEhRRRQAUUUUAeXfFz9mf4afHW+srnxv4TsddurMYimnUhguT8u5SCR1qDwT+yj8H/h2ki6B8OtBshIxdt9oJjkgD/lpuxwBXrFFAHKL8JvA69PBvh8fTS4P/iKc/wAK/BckZQ+EdD2HqBpsI/8AZa6migDzPxN+zV8LPF1uLfVvAWg3kGP9W1kgH6AV1/g7wZonw/8ADlloHhzTLfR9Gs12W9laptjjXOcAVuUUDPxt/aq/4Jq/EL4XePtR8a/CuCTWNEa6N5a29hIUvLF2YttVR1APQivNviR8bv2oviF8M5vhh4t0bxBrFjcPHuF3oL/aHKNkAy7ckdOTX7t0xreJ2DNGjN/eKgmgfMfKv/BNb4A69+z3+zqmmeJEEGrazqD6xLa87oN8USBG9wIxn619XUUUEhRRRQAUUUUAFFFFABRRRQA1q5D4jfCXwb8XNJGm+MfDen+IbRc7FvYQ7R57o3VT9CK7CigD5O1P/gl7+zzqUm9fCFxZHuLa/lAPP+0TXtnwf+APgL4EaQ2n+C/DtppCPxJcLGDPJwBhpMbiOBxnFei0UDuUtX0Ww8RaXc6bqdnDf2FyhjmtrhA8cinqCD1rlvhh8FfA3wZ0+4s/Bfhmw8Pw3EhkmNrFh5GPqxySPbOBXb0UCCmk/MBnAx0p1JQB88/Ez9gv4NfFvx83jHX/AAwG1x5VlnktZTGk7g53SKOCT3PfFe/2FjBpdjb2drEsFtbxrFFGgwFUDAA9sVYooA+CviN/wThufGH7aWnfFeHU7X/hFpNQi1XUdPlHzmaIAhVHTBIH6196KAoAHSlooAKKKKACiiigAooooAKKKKACkpaKAPyK/wCC1/jtNQ+IHw78KxfONN0+41F8dN00vl4P/gP+tfJ/xC/Y28ceAfgb4S+KpgF/4Z1y1juHMHMlrvXcN47AjvR+17He3n7YHxCg1r/Wv4mljkx08kzEDH4V+/Wm+EdH1n4Y2nhq5t1u9DuNMSzeB+jwmMLj8qCuY+H/APgixCF/Z28YyGPa7eKZdp7Ffslr0/HNfc3iT4c+E/GdzFceIPC+ja7cQgLHLqWnxXDoASQFLqSBknp61n/CD4P+GPgb4JtvCvhKx+waRbu8ixlixLMxLEnuea7WgVzFtfCGhWMKw22iadbxLwscVpGqj6ACs6H4W+DrfxBDrsPhXR4dZhyY7+OxiWZc8HDhc11dFAjL17w5pXiiwNjrOm2mq2ZYObe8hWVNwOQcMCMivIf2xvgjN8dv2cPFHgzTF2X7wpPYxR4RTLEQyJ9DjGK9yooGfzs+CNa+P37P91qOj+Fh4s8OlblmubbT7KQxNKAFLfcIPCqM+1eiab+0d+1/JEb631bxzPHE20lrB8Z64xs561+8VFAj+eb42eP/AI/ftFwaBB490DxJrCaK8xtn/saZWHm+WHBwncRrX6//APBNzSdZ0P8AY28BWOv2lzY6lELzdb3kTRyohu5jGGVgCPkK9a+mqKACiimSSeXG7Bd7KM7R1PtQA+mH74r4J1f/AIK3eGPBPi/UNB8afDnxJ4dltJ3iEjlWZ1ViA2xgpwcVzfi7/gtV4DsVKeG/BOsavMR8rXk6W6Z9wAxoA7f/AIK+WbXX7M2mOgLGDX7aQ4GcLskBY+wyOa1P+CW/jDQNP/Y38K2t1rmm29zDc3qywy3cavGTcyMAyk5BKkHnsQe9fnT8e/2pvi9+3x4k03wzpmgzDTVkXydB0aGSVNxY/vJnAJ6EDPA4rstJ/wCCSvx7ktY2WTw/YLKA7QyalKvlk9sIpBoKvpY/Ya8+K3gTS8i78Y+Hrbv+/wBUgT+b1h3f7SXwf099l18UvBNs+M7ZvEVmp/WSvyq/4dA/HVlC/wBteE2DcnzNTuxj24jNV5v+COnxyjYBNW8HOCMnbqV0B+sNBOp+rFn+038G9SvorSz+Kvgi7upWVI4bfxFZyMzE4CgCTJJPavTlxtBXkHnIr8afh5/wSd+Lnhz4veDJPEtvot34ajv47i+vtK1B3eJEO7BDqp6qMYGOetfsrDGIYUjXJVFCjPXjigAkVWUq4BVhgg96/n4m+LWqfsk/ti+Ntf8ADtrG91pupahZfZ5h8qq7sMEeoNf0FHAGTwBX8/8A/wAFJPCsPhf9tTx/aWaeZ9ruLe+EarndJcQJKwx/vPQNOx7/AP8ABL34V3H7QPx+8WfGLxxHNqs2jzJJBPNGWil1CRi2VboTEoQ4zxvU1+wNfOP7AnwFj+AH7OPh/SpY9usaov8AauoswwfOlVfl55+VQq/hX0cM4560CFpjRqzAlQSOmRnFPooASloooAKRvbrS0UAZ2s+H9N8R6fNY6rYW9/ZzDa8NxGHVh7g145ffsO/AjUbmSef4ZaE0shyxEGP617pRQB883H/BP/4B3Egf/hXOlxYGNsSlR+Wa3vCn7GvwX8F3C3Gl/D3RY7hW3rNJbh2U+xNe0UUAQWtjb2ESxW0EcEajCpEoUAfQVNS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRTWUt3pVGKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooATijigjNJtoELS0g4paBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGJ4ltGktAUCvlgrRuMq454PtzX86n7WmiR+E/wBonx3ptughgXUZG8teANx3Y+mTX9GWvxzSWeIEZ3Vg2F68V+EPx6/Zz+J3xk/as8aW2j+Ctal+1axLGl09m6wLGGwHZyMdOetY/budN700jK+FP7Z2s+Hfgrrvw08QXN1e6PdQslpLvLmHKgBcE9OO3rXC/Bj9lf4n/H6O5m8DeF7rVbBZfKkvZJFhtwwwcEkjPBFdZ+0V+wl8S/2a7Sxv9X059W0qeATTajpsbPFatuI2SHscDP41+gX/AARi1yW++CvizTzbEQ2esEJdZJ37okJHPTGadtbom/u2PjiH/gk3+0RJw3h/SQqcDOrwqfWvav2b/wBhf9q74aeM9Nul1y18P6RYylzBdauZ4X4xjy0J4+mOlfrd1o2iqszO5+BP7Rn7Hfxzh+Luu3uueFpr6e+llvTqNh+8tmjyfmBySOnQ81o/8ExfEmkeBf2stMn8QahBpiG1uLcS3DhEEhGMEn6V+72oWKahY3NrISEnjaJvowIP86/Fv4/f8EsPiv4f+IF4/gnTF8VaLdSPcxXUU6xvFuc/I4OOQMHI45osw5j9m7XXNM1C3E1vf2txCw4dJVZSPrmvwl/4KIeAz8Hf2sb+/wBNaMx6g0etWxhYfLhyOx45U1Zt/wBgf9qXT4vKttD1q3ixjy4dWwPyD1k6x/wT/wD2ktX1W2/tPwbqt/PIBGt1cXQmEa56Ekk4o5Quj9t/2f8A4i2nxY+DfhLxVZv5kWoWEUhOc/PtAYfmDXoVeV/sv/CVvgf8CfCXg2Uk3On2gE+WziRjucZ9Mk16pVEnxt/wU1/Zv1v48/Bu2uPDVtHdavoMzXghI/eSR7fmVT+HSvgL/gn5+2pL+yz4ou/CPjATReD765ZrhWQl7GfhScenAzX7iMocEEZB4I9a+Jv2xP8Agmn4a+P0kmveEntfC/ijGZNsWIbk5J+bHQnPWmNM+mNN+O3gbxF4IuvE+j+J9NvtMitmuPNjuF4wuQCM8H2r8Zv2P/DEnxq/b+tNUjdzb22r3GrySBv4VZivPucVBqX/AATp/aP8MTXelaf4buriykbYz2N7iCUZ4bGeK/QH/gnL+xBqf7NOm6x4k8ZQ2/8AwmGpYiiSCTeILfap2n/a3bs0BdI+4F6U6kXvS0EhRRRQAUUUUAFFFFABRRRQAUlI1GTQA6im5NGTQA6ikWloAKKKKVwCims2KTdRcdh9FNzS0r62ELRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQB8+fGL9hH4PfHLxxF4u8T+H5W11SplubO5aHz9vTeBwTwOevFe96fYw6XY29nbLst7eNYo1JJwoGAMmrFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNb0p1FAHD+NPgl4B+JFz9p8U+D9H1652hPO1CzSV8DtkiszQP2afhR4Wk36T8PPDmnvnO6DTolOfXpXpdFAGfp2gaZo+PsOn2tnxj9xCqfyFX6WigAooooAKKKKAE61w3ib4F/Dzxp4gOu6/4K0LWdaOwG/vrCOWY7AAvzMCeMDFd1RQAyGFLeJIokWONAFVFGAAOgAp9FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIGzkelAC0UUUAFFFFACU0RqrEhVBPU4p2KNtKwGdr+g6f4n0i70rVrSLUNOu4zFPbTqGR1PUEVy3wo+Cvgv4H6Pe6X4I0K30DT7y4N1Nb25O1pCAN3JPYCu620baYAtLSUtABRRRQAUUUUAFFFFABRRRQAUlLRQAijaMZz9aWiigAooooAKKKKACiiigAoprGmTSFIyQQD70rjsPasrVrq9tYZBa7DOUcxeYhZSwGQCBzzVibVI7aN5ZjiNF3Flya8xuv2pvhbY+MLbw7deL7CDWrlxBHaNKCS2eAcdDS5kUovsflb8Tv+ClP7SHh34lXsk9zZ6Dp2n3kkA0v+xQtvMquQAzyKZM47hhX2J+xP8A8FLNM/aE1ODwj4ytLXQfGUrFbf7KW+z3QAzxno3XjNfUvxuXwKnw91i88dWem3ehR2zPIL5EO/AJAUnnP05r8df2H/Aum/Fr9uKzv/Cunf2T4Y0i8l1RIkZjsjXKquSScE+9HMPc/c9aWkWlqjMKSlorN7gQnLd8Uo+Udc05lHpTSo2nis2mV5FaTUBHdJDsZi3O4DgVdpqRqOgp1VHTcTFooorYQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUZpGpKAHZozUbSKvGaa0yqcE4NA7MmyKMiofMywA5qSgLDqWkWloEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJu+bFLSbfmBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARc4GetLRRQAUUUUAFFFFABRRRQAUUhNG6gBaKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopCaTdQA6im7qN1ADqKrtclZthAAxnNTBwwyORSumOw6im7qNxphYbIpZ1+bAp9N7g04Gp5lewhaKKKoAooooAKKa27tj8aVc9/wBKAFooooAKKKKACik5paACio235OCv5U7caAHUVBcXUdrG0ksixxqMlmOAPfNZ+j+KtJ8QSyx6dqdpfSRffS3mVyv1ANK47O1zXopBmlpiCiiigAooooAKKKKACimsaQMTQA+io2UNyaRWCqcA0rjHSNtqlNIJAAx43Y6UXFy7ZVRj3NVft0FrG0l1JHbQqctLMdq/99E4FQ9zbkaVzkvjpqk/h74W+JNSglMMdrp08jFexCHB/Ovw5/Yz8DXPx4/a08PW9/vukXUH1K7nJILKpzgkYxzjpX67/tlfHDwZofwB8ZWI8V6O2oXlhJBHbx3aSOxIxjCk81+cv/BKn4pfDj4R+PvFmveO/FFj4euHtFgsftiNhlLZYhgD7DFOwuZ2PX/+Cm3w5+PnxK+IkGj+GPC+vav4Bt7WP7PFodmbiN2HUyMvzbvY8V8mfCf4W/tQ/ALxBJrvgXwT4w8PanNH5Ek/9g79y5ztKyowx74r9oPA/wC2B8GviR4mt/D3hv4gaTq+s3BKxWcLsHcjrjIFex7RRZkcx5F+yn4s8e+NPgnoWp/EnR5tG8VupW5huIxG74OA5QAbc+mBXr1JS1RIUUUjZwccmoe4hGpjMN3JqFrhuQ67T2pjEsuTzWbkaRjfUthwFznNOByM1mbmVsA4XvV+3bctNSvoKUXElopCaj85d2M81pzW0JJaKQUtWIKKKKACiiigAooooAKKKKACiiigAopGpM0AOopFpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQmmRuW3ZGMGlbO8elIuBnnk0rjFdgtRMwdThsU25kVcDcKrrIA23PWolNI0jHS7HAfvMA7jUzxArubgimmN1TMYy1MW1lkYGV+PSkpN9A0BZhHIBjIIq3GxfJxikjgVccZqWtFtqQ2ItLRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKTIFLSYBqG3cAzS0mMUtUgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJ+FAC0UUUAFFFFABRRSUAMaRVcKQSTTtwb7pyPavlv9vvxV8TfCvwnOo/DW4kgvUfbOsMReUr6rgV+c/7Of/BR/wCJX7P/AImnsvHwvvE+kXk++5h1Albi3PTMZPb2rPmd7G/snyKR+3i06vGPgV+118M/2hLYDwrr8MmorGHl0+Y7Jo8jkYPXHtXsysG5HSqujCzQtFJmjPtVALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFK4DWqB0VmDsvK+9TtUUi+ZwGxRdFIGkPy7Bu5wfalkZlU4GabH+7BGO+KZNcCNsE5GMk1MpLYpK7siRWVmxgE4phmK4CruFQx3iTbmi5PQ0xWkt4ZHbjniue7K5WWWmbcMJkVJG24Hr+NV7ZpGj8xn4PQCrUbCTkc0o3uQ9NB2KXpRRXQrIgKWkpau6AKKKKLoAooopgFFFFABSUjNggUkjBRzQBm6xrkGixma5cLCEZi3QDAycmvyr/aD/wCCv3jXRfHmoaR8OdH0WPSLOVrc3erW8kzyOpwSpWVRj8K+jf8AgpJ+0TJ8K/hNf6XZFRfasPssMkRO5M9T19K+Tf8AgmD+xboPxubVPiJ49szqmjWc/kWWmzf6u4l6s7+oHp61kpcz0OicFGKvuY/h3/gsJ8adK1S1n17RvDupaYxDSRxWMsEjL3CMZSP0NfpX+yv+2B4N/ao8NyXehu2n6xabVvdJuiBLExGcr/eX3FTfGv8AY/8Aht8YPh3L4cl8MabYSQQGOwubSBYntmxxggdM1+Py6F4g/YF/ag0C5k1Uzw29yGufIY/Pb79rKw78UnJp2MktD9zfH3g5fG3hm+0uWd4vtEbR742K9a/Fv4paP8VP+CfPx1k8UaHczf2ZcTt5bzu0sEyk8pIMjJx0r9ltU+JFufhXL4z0eE6patp/2+3jiP8ArFKbgM1+dfw9/aEsP+CgPiTXvhh4w8OQ6VdTxSGym3btjLkbvZhTWptFvlaPtH9l39rbwn+0d8PbHWbfULXT9Z2AXumyyqrxOByQCeldT4j/AGnPhV4R1NNO1fx9odjescCGS8XdnOK/CP8AaM+AXjL9kD4jNo1zfzwJOhktb+1kZBNHnpkd69J/Z9/4J9+N/wBp34Z3njXSfEumw/vHAs7xmknlYDPLds+9aXtoZ8q6n7o6L4i03xJp8d9pOoW2o2kgBSa3lDqQenIrSVt1fiB+xP8AtJeKP2RfjrN4C8ZtdR6HeXa2N5ZTksLeUHasi56D+lft1b3CXVvHNEweKRQ6sO4IyDTM2rE1FItLQIKKKKAGSNtUnBOPSo4ZDJk7So9GqSTO044NRx7iuCee5oK6Dt7buOneobicx4xxUoUAnB+tQXFsJmC7yD2qbFxtfUpSSC4BVz9McV8l/wDBQH4E/Ef41fC2Cy+H95cvd282ZdNinEInT1JOP519hwWcUPQbm7k1PtA6DFLlZpKotkfzxfED9hv43/Dnwzf+IPEvgq40/R7NPNuLqS9hdV7Z4c12P7H3/BPrxN+1hoeo65b63Z+HNCtZ/s/2m4iaaSRwMnaoIGPrX6G/8FaNc1fRf2abiC1uJBY6jfQ29xGqKV2ZycnGRz3rwT/gl9+178Lfgz8L9S8HeM/EY0DVJtSe5ie5icwMhH95QcfjVGR71+yX/wAEvfD/AOzr4+j8Za14kbxZrFpn7Ci232eKBiOXI3Esfrx7V9yV8nfFb/gpj8EPhtoq3tj4jXxdO52ra6KN7A/7ROMV9FfDPx1bfEzwHofimzt5rS11a1S6jhuBh0VhkA0yWnudPRRRQSFJS0x85wOBjrUSXUCGaMSfMeoqqobcfn+X0qWSUN8vf1qqrBiyjj1rme51QTsK17BCJHeRFjjGXZjgKPUmuF039pX4V6l4ui8L2XjnRrjXZn8pLGG5DSM/oPeuA/bZ1C78K/s3+OdRsbl7KcaeVEsZwwycV+If7L+oXcX7Rfw+njlYzNrMDF+5y3PNVDW7Imtj+klulQxxISSRzRdTGOLI65qJWM2B90HjPfNaPchLQuKQRxTqpxXEKziE3EYlPSPeNx/CrS9xnJFarYgdRRRTEFFFFABRRRQAUUUUAFFFFADWrL8SeJdP8J6Rc6nqc4t7O3QvJIecD6VrVm614dsPEEPk39utxF3jflT9R3qZXtoONr+8Yvw5+J2gfFLR5dS8PXTXVrG/lszRshB/EV1lUdJ0Ww0G1Ftp1nDZQD/lnCgRfyFXqI3S97ccrX93YKKKKokKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKSpcgFoqDzG8wc4HoamVg3SlzALRRRRzAFFFFHMAUUUVQBRRRScgCmtnacdadSUuYCH55OSdgHrVW81D7MuI0aZz0Va0KaI1U5CjNDXMUnY5/ydS1GQGSJLaI++WrXsbBLVMZaQ+rVbpaSgkVKbkrCLS0UVoZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0maWoyytk4zipbAfS01cY4GKdTQBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooorN7gFFFFWtgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMbfuG3GO+acM96N1LQAUUUUAFFFFABRSZpFbdQBHPbxXClJY1kQ9VYAivn74/fsM/DD9oFWm1rShYamEKJfWACOueenQ19CmlyKnTqUpOJ+WGrf8ABIvxh4F8UWmqfDb4iLZ+W+RLch45UXPTK9Riv0y8EaXqOi+ENIsNWu1vtTtraOK4uUziRwMFhn1rYmmS3Qu5wvSvFf2kP2sfCn7Mej22oeKLTUZLe6JSF7WHcGfGQpOe9S7GnvVNEj21fl607Ir8m/G3/BajXFv0/wCEY8AWaWQyH/tS5YueeCNnTiuI17/grt8aPFVq0OheGNL05mGPMsoJZ2GenXoaOZk+ztofs3urC1nx14d8Oso1PW9PsCxwBcXKIc/QmvwV1j49ftMfEC+l1F9U8XMznGy1glSIAnpgDArx/WfEnijUfGUVp4t1bVXuUukW4S6lbemWGeCaLsfIf0x29zHdwpNC6ywuAySI2QwPcVLXIfCKOzh+F/hVLCRpbNdNgEcj9WGwcmuvq1sZvcKKKKYgooooAazFVyBmlU7hnGKKKAFooooAKKKKhp3Aa1QrEyyFg2QanavIv2ivjvL8B/B8uuR+HL7xCUUsYbMDjHqazlG2rNYRc3aJ6w3TOMmqs0EnzOi7i3VTX5nWf/BaaBruRLj4Z3gjVtp2Xilh9QRW4v8AwWj8Lxsgl+Hes7T1KzxcfmaFFNXC7i7H6Jww+VtATaT1qw0bOrKwytfnVcf8Fp/BUHX4ea+Sfukzwj/2aoT/AMFrfB8nEPw61xjj+K6hH9arkQ25Nn6NoiwqIwDzU6LtHTFfmyv/AAWr8LGPJ+HGsb8fd+1xfzr6W/Y//bLtP2tLTWri08OzeH001kUpPcJKz7gT/D06UK0WQ4vc+kqWmr3p1DICikJpN1ADqKr3N19nUMRnJxUS3LybSQFDexpXRXK2XaKjjYHODmpK1WxIUU1pApANLTACu7mquoRrJEQV3MRgDvVuq91hVLkdFPPpxSKjufkR/wAFari3tdQ8PadHOGuLmZpBCzZKqOOfxNfd/wCxj4Z0/wCCX7JvhManPb6dbCz+33M7ttVd/wAxJJr8wf8Ago9qUfi79ry20wSPJbolvCBnld7jJHvX6/3vwh0zxj8CbXwJPNNBp8+kRWfncNIg8sDd2BNYRWh0VHeVmeN+Mv8Agp98A/B2qy6dJ4ml1KWI7WfT7Z5UB9N2MV+Uf7d3x68K/H74uJ4g8I/aW09YmjZrqIxkknPT0r7isf8AgiX4RS+eS9+JOrXFqWJEMOmxxsB6bzIc/lXxn+25+y34S/Z0+NHh3wT4T1e+1GO+gRrltRZC0Ts4UfdA4xk9K15btM59dkeufCT/AIKkyfDr9nu1+H0/hCTVtTtLRrOK7afEewggZHXjNfMn7O/xqn+Gv7R2geOB5WnRHUM3SICUWNz8w6+hr9ZvhP8A8Eu/gXpPgLSk1vw9N4j1Oe3jnmvLu8fO5lBIUJtAXnvn618Rf8FQP2WfAX7O994VufBGlS6TDqRkSaHzmkQkDIxnkH8adik2Uf2/fjRD+1v8aPD2geBbZtYNuv2eBIR8zuxH6Vwfh/xR8ev+Ce/iy2Sa0utHtLoiV7O6UvaXI7+wPavbP+COfwgsPFfxQ8Q+M78NI+gxLFbJtyvmP/ET6gCv1a+Knwh8LfGbwpd+H/FWlQalY3CFA0iAvET/ABIexpWYXPwP/an/AGjNJ/aF8TWPim28N/8ACPeJsD7bJE3ySsMEN9eK/bP9ivxtdfEP9lz4ea5fS+fez6aqTSYxlkYr/ICvhj4g/wDBFe6k8TxHwd42ij0GZi0qanCfNgGeFXb97jPWv0V+APwhtvgV8I/Dnga0umvYdIt/J+0MMFySST+ZNUiWz0BadSUtMkKKa5IXjrVOC6mmaTIwV4wRx9aVx2LMkojUs3QU1ds8eRnBrO17xFp3hm0e71O+ttPtEQs811KsaAD3Jr5l8bf8FNPgP4JvLm2bxPLq1zbnY6abbF0LezHGaYz6njTEjpu+X0qRhtwcZwK+avgP/wAFAvhP+0Brk+kaPqcuj6kmDHDqYWLzx/snpXuXi74n+EvAPkDxH4k0zRDMpeIX1ykZdR3GTyKBm/8AavkJ8tt3OFA61+Vn7an/AAUl+LfgL4lXnhHwhaQ+CbawZo3vryyW4e65+8vmIygfQV+g8n7VXwfjbDfEjw4D0x9vT/Gt3S7T4d/E5X1Owi8P+KASC1xEsN1tz0yecUC+R+GHxU/bN+Ov7Q/g0eG/EVy2saOf9YtroyATN2bKRZB+hFeFR/DXxfMpMXhfW5OxMenTH/2Wv3X/AG0f2mE/Yx+Huk6p4a8HWGo3OpXn2YQlPIt4/lJ3MUxzXy98Pf8AgtbbeY0fjv4eGFfMCi48PXiyBR3JSQ5b8DSKPzJPgPxXpDxS3HhjVYMOCvn2Eqhj6crzX77fsEa74w8Q/sy+FbnxraCy1NUaKGPyvKbyF4jyuBjisr4W/wDBQr4D/Gi+tNMsfFEdjqVyQIrHW7c27lz/AAgtlSfoa+moyrRqyEFSMgr0xTE3pYfRSLS0EBTJPu05qjk5HXBqZPoUihcKVkUhsccVQVmS4OG6nmrd35qnLqpAHBzVCHzGZ2KqOeMGuV7nfTty3Z8//wDBRS6Mf7J/jT5vvWyj/wAeFfjH+yPateftIfD2EDLf2vCT9Ac1+yH/AAUqzF+yJ4qYfKzKgOPTcK/LL/gmnodt4h/a88HR3sC3MUJknCv0DKpIP4VpTWjOWUk2rH773EYMLYHvWP4mlnt/DN7LbO0cqwSMGXqCFOK38BuCMis/X4l/sHUEx8pt5P8A0E1bWpmmfz9eD/jL400v9quy1E+JtVeb/hIlidmu3IKGcKVwTjBHFf0KowZQwGMjNfz1fBH4e3PxM/bO0rQ7dd4bxE88vpsjlLHP5V/Qso2qAOgrRbCluLRRRTJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmNIFkVT3p9JQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANZiO1KrZpaSs3uAjKrEEjmlHtTWYetOXpSW4C0UUVfKAUUUVDASjIqKWQH5c9e9RQeYGZWO4djVcxVtC3RTVp1SSNbPam7W3DPNO8xem4Z+tKrBuhzQAtFFFaLYAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUjLuXFLRQAyNSoweaXbtzgZNOopWAQUtFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooqG9QCiiiqQBRRRUtu4BRRRTtcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA5eb4neFYPEC6HJr9gmrs2wWTTqJSfTbXTK2a/Cn4ifGzwhrH7d1h488N6tdaj4dmv4XaRgU2nPIAJ6V+kXxQ/4KYfBv4YQiNtTu9b1VVUvpum2zNKpIzjLFV/WoUlbXc6HS/lPraivPfgX8ZNO+O3w/svFml6dqGlWl19231OJY5R7kKzDH416FVJ31RhKLi7MKKKKYiG4uEt4ZJZDsjjXczHoAK+cfiD/AMFCvgd8MdcfSda8W5vk4aO0tnn2n0JUcfjX0XdWa3lvNDJykiFCPYjFfmz8Wv8AgjmvjbXNa13RfH/2TUb65edLe+tS0ShjkAspyMfSpbdzWPLZ3PqOz/4KCfAXULWKeL4g6cokXdskJVl9mB6GvGPjN/wVr+GngHzbbwrBP4zvhwHtjshX3LGvna0/4In+PJJALz4geHEj/iaGGdm/VBXVW/8AwRPnbyvtXxITYB84is+/tmlZisuh5fqX/BVb4ufFTx1oOkaNa6b4esbi9jhMMMZlaQM4A3E9D9K/U34mfADwh8fPAun6J4+03+1oljSQsrmN0k2jJUjpzX4r/F/4E2XwD/bB8N+B/C15PqkltcWLG4mAzJMzZYgDoOK/fC0My6ZAXXE/lLuX/awM/rU76oqXMtEfNfgf/gm98BPAl2Li28If2nOrb1bVrhrnb7AHtXumi/Cnwb4cjCaZ4X0myUdobOMf0r5H/bi/b41b9mCaw0nR9Hhvtdv1d45LjmKJVIzkd+or5Htf+CyvxZWI7/Dvh+cj+Iq6/pmmmrbDlGUd2fsTJpNla28oisbdF2k4WJQP5V+A3xs0NvHf7bmqaZCqq174hjtwmAwALDnAr648O/8ABat00Mxa/wDDiS71Ergy2F6EjPvhga+df2V5I/2iP29dK15LUWEV3qD6kbfdv8oKM4JwMmgSP3L8L6RHoHh3TdNiRUjtLaOEKowBtUCtSmrxSNJtBq+hluxWYL1oVg3SovtSsDs+dv7oPWpgc0XTCwtFFFMQUU1mCLknA968I8fftxfBn4YeMLrwx4n8Y2+lavbbTJFLG5UBs9wD6VLkluNRb2PeaK53wH8QfDvxO8N23iDwtq1vrWjXOfKvLVso2Ov0/GuiqhBRRRQA1qpalo9lrVu0F9aQ3cLAq0cyBgQe2DV6hV20Arp3R4Tr37DPwI8TX0l3qHw00eW4kJLSIJI8k98KwFYsv/BO39nwj5Ph1YxDHOyWX+rGvpDHOaa1Ry9hrc/HH/gpF+xr4C+Bfh+08ReCLZtLzOIpbPeWX5uh55r0f/gnP+w/8J/i58E18YeLNLfX9Turlo9krlUgC8YAHXOe/pXS/wDBYqP7J8M9HZTzcXiBq9V/4JMNG37JenlWzINQuFcenIxUJu9mdEvhudFqH/BMH9n3UJkkbwjLBt/ggu3VW+or2b4N/s8+AvgHptzZeCNCh0eK5KmZlJZ5CBgEk9etejL3p1a2Rz3YlLRRU8ohrUlOPauO+K3xS0L4OeC7/wAT+IZ2g060Us2xSzMfQAVL93VjSvojrJYvNAB6VEIZYyAp3L/tV+Znib/gtbp1nqUyaH8PJL6wVyqT3N9sZx64C8VVX/gtmrR8/C3a/wD2GFIP/jnFTyqWpfLJaH6ixqVzk5Jp9flh/wAPtLhJl3fCyFou+3WgG/8ARZrSt/8AgtxpYmAu/hXdRRf3odaSQ/8AoritE1FWJ5T9PMA9etLXzV+yP+2dpv7Xq67No/hq90KHR2iSV7i4WQMXDEYwo/umvpSqJFqG5UNDID0KkGpagvD/AKLLnptOaBrc/Br9sy5Vf23JivzCK8tEH0Div3c0HnQ9OP8A07x/+givwl/a5tftn7cM8CRsWlv7MLj/AK6Cv3g0uA2+m2kRGDHCikfRQKxjqjer8RYr8u/28v2Cfip8aP2g08Z+D7S3v7C+giSRmuEiNq0ZAGcnnOc8elfqNto21sYXOW+F+g3/AIV+HfhzR9VnNzqNjYQ29xMW3bnVQDz3rxz9tT9key/ay+H9rpQvY9L1rT5vPs7yRSygkYKkDsa+iwoHSl20wPDP2Pf2Y7D9ln4Tw+GIZ47/AFOaU3F9fIuPOc9B9AOle50dKWgQUUUUAFFFFADGb5gMV5n8fPjt4Y/Z/wDAd34l8TXYgtk+SONeXmkxwgHvXo17cLbwvI7iNEUuzN0AHWvw7/b0+OGt/tHfH4eBdDuGvNHtL1bOytYhnfMxALHHXHvWb3NEtLnNeMfiJ8XP+Cg3xok03QxdTwyMyWumrKYra2gHQyEcZ7819dfDP/gi34ePh62m8deNdWGtEbng0bylhTI5GXRifrxX1v8Ase/sqeHv2Y/hva2NnaK/iK9iSXVL5iWaSXHQE9AMngV79VkuR+AX7aX7Lt7+x78VLGDQ7+/uNFnjWex1Kd1EocHkHaBjBr6g+Jf/AAT5+Jn7U3hHwB410fxtY3Zu9DhaePW5ZEMchAzs2K3B7/Ss7/gtXr7t428A6RFdI0S2U9xLAMFg4ZQpPccE8V+iP7ILPJ+zH8NWlUq50aEkH6Ux8x+Xw/4I2/GXy9j694Qzn7yXNwWHv/qhX2d+wr+wPqf7KepahrmueL5dc1O7gEK2FiWjs489WIb7zehI4r7S2ijgcmgXMZHiLwnofi60Frruj2Gs2wORDqFsk6A/RwRXiXxb/ZN/Z7m8F6zqfiT4ZeF7HTrO1knnu7DTks5Y1VSSQ8IVgfxryD9qn/gqV4N+BOtXPhrwrpv/AAmfie2dormPzDHb27rj5WYck89vSvzu/aU/4KMfFX9ozSZtBu7qz8MeGZxifSNIClZuR9+VvnOP7oIBzyKBHR/8E+Pghovxk/a6e70+zZ/Bnh+5m1GOO4VmBjVz5KFs5yeDye1fugqhUAUYAGAB0FfhR+xx+3zb/sk+C9R0Wy+H9nr2oX9x50+pPqQgdlAwqkYYYHtj8a+wP2fv+Covi/8AaA+NHhvwVpfw1sLW2v5T9rnTVPPeGIfefhQBj3oBu5+i606kpaBEczFYyRVeSQtCAVzmrZAYYNZ+r6lBo9s9zcSLBbQxtLNI5wqIBkkmokupSHTW63UIjyQgHIU81VsdFhty21sgnkZzzX5Tftdf8FIPGHj7xovgf4GXV1a26zGKS/0+ESXN2+cYjyDhevavGtMn/bR8CRz6lbt46tizfaZXljMqnPfDA4+gqVZmqbSsfo9/wVAV4f2RfEoiJChow30zX55f8EidHt9U/anjnmVTJZ6ZPNHns2AOKqfE7/goX8QPH/wP174a/EfRUutVutqR3skBhlXB5LjjJzjpXR/8EcbQSftMarIU/wBTokxBPYllB/nTWhn1P2sHasXxxfDTPB+t3bZ2w2UznHXhDVrXvEOmeF9Ll1HV7+302xhGZLi5kCIv1Jr5h+OX7fHwY0PwD4ltLHxpp+saqbOWGO1tSZNzlSAM4p2vqJbn55/8EyNJuPGH7cE+qxMRFZpeXku7uCSB+pFft5X4CfsQ/tU6D+zH8UPEnjHWdJutS+3WUsFva2hC4LOGA56CvU/i9/wV2+KXjaaWz8H2Vr4QspPljaMebck9vmPT8KobV2ftRRXjn7Ies+MPEX7PHg7U/HVxLdeJLu186eWcYkYEkqW98Yr2OmQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNZwvWgB1Jx0pgkD9O1HfNZvcdhuA0jDGNtSiqkNw0lwV2MAvGSKuU1HqAUUUVYgprNtHQn6CnUVNgGYDKDtxRtx2p9FHKO4i0E4HTNLRRyiGLGOTjk04ADoKRmI6DNKpJ6jFHKAtFFFUAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlGRTZG20inIzQMfS01adQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKarBs47U6gAooorN7gFFFFWtgCiiiiwBRRRTAKKKKACiiigAooooAKKKTNAC0U1pFTqcUzzA/3TmgCWimp3p1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH4tXXhX9nfwf+2tZwpcQWfhSzfdNavMPISfIwNxIGPbNfeWtfG79k6bV7GLUbzwNcakHSO3CwQTTAkgDOwEjt1Nc38Hf2Rv2dfjn4P0bxjH4bs9SuSqyT7Lnd8/pIAeenevW9W+DX7Ofw6A13UPCPgbRmtSHF5PaW6spXockZyPzrmppu0rnfNq9ktT2/SIbO30+BbCKKGz2AxJCoVApGRgDtV2uJ+GXxg8FfFqxuLjwZ4gsddtrUiOU2UgYR5zgEduh/Ku2rpOKV09QooooJCiiigApjfdIP3cHJp9NPyrSA/Gv4/Wthaf8FQfDIt5zKhv7EyNIDgEseK/ZJvukHpX40ft93g8G/wDBQjwzrK2rCLfp9wPLGDJtcg49/wDGv2P0+8XUtPtblVKCeJZQrdRuAOP1rOm9NTWpdH5p/wDBYT4W2zeCdD8UofLltLnyyxGSwfAIz9cVwH/BKn9l/wAFfFzw14u1vxx4Rg1yG3uUt7O5vASn3TvCj8q+sP8AgqR4bXxF+y/rzPIENgY7pflz0cVw/wDwRx8QHUP2fdf0w4YWesO4x1AdRgH/AL5NLRaIbvKNz0zx5/wTF+BHjdUeHwy2gTKhUNpczRA57kdCRWT+zT/wTb8Lfs2/Fn/hNdM1y71No4Xigtrgf6vcMZz3r7Ho20zNMK5j4ia1caL4S1K7sUEt3FCzxqRkbgDiumPpWR4k01r7S54o03lkI25xnirfwl07c6ufkJ+yL+0p8RPGv7clhaeJfE98dPku7m3fTWl2wqCCqgL09DX7JrX8+n7Qun6n+zr+1tdalaySQXNvfx6jHKo2YUtll96/dz4S/ECw+J3w58P+J9NuVu7bULSOUyJ/f2jcPqDms49yqm7sdjRSUtbGBBeQ/aIGj/vDr6V+a/7dP/BOTxx8cPicvi/wM2llriNYLuC4l8liB/Hk5z34r9LivOaQKF6VnKF3c0jNxTR4/wDsm/AqT9nP4IaF4Jnv11K6tA0s86JtXzHOWA5PA6Zr2KkpataaEN31CiiimIKKKKACmtTqQrQB+c//AAWOs2m+EWjTsuBDeoQR35AP8677/gkfdWs37LIigbMsOqzrKPThSKq/8FZtHXUP2b7u4deba4iZTj/bA/rWZ/wRxC/8M569g8rrsiH8EX/GsftfM6ZfBfyPvZadSUtbHMFFFFABVDWtD0/xFp8tjqdlBf2cow8FwgdGHuDV4mmNJtIB70rXGfN/ij/gnT8APF2rNqN94Bto7hiWYWc8kCMT6qjAVfs/+Cf/AMArOBIl+G+lSqowDOpkP5k19BZ5NLmp5ew7s8DP7B3wFGAPhnoY/wC2FYPiL/gm5+zv4m2m4+HlrbMoIDWNzPbHn18txn8a+mutLtqrCuzyX4A/stfDv9ma11eDwBpE2lR6q8b3fnXk1xvKBguPMZsfePSvW6TGKWmIQ9qgu2C2spboEOanNRXEYmt5E6blIpPYa3Pwg/ai1Ka5/bpiuIFjSWPUbMR5B2nEgxnmv3gtS7QoZMeYVBbHTOOcV+Bv7Zuj3nhT9se8M1zDJP8Aa7aZDDn5R5gxmv3p0OQy6LYSMcs9vGxPuVFZQTsbVWmy9RRRWxgFFFFABRSE0m6gB1FIDS0AFFFFAHz/APtw/EyT4Wfs8+K9Wt5Whu2s3hgdR0duBX5n/wDBKn4f6d4o+MXiH4ieJ3hk0/wxavdvJMeRM+Tv98AE19W/8Fh/HE+i/A/TNCidQmpXyCRe5UZJH8qs/wDBJv4T+H/+GW7/AFeaBbi58SXU1te7u8aDaFH4MazW7Nr+6eiXX/BUT9n+0m8pvE1277mU7LJjgg4PevLPiZ/wWN+HGh2M0fg7QtS8R6jnbG1xi3hHuTyam8Xf8Ea/hh4h167vtO8UeINDtbhzJ9jtzFIqknJwzqTitz4e/wDBIT4LeD7sXGty6x4wKsGSPULnykUjttiChge+7PStDPQ+Bvh78OfiF/wUq/aH1DXdSZrbS0lVry/Vf3VpCD8sS44yRn8q/cbwX4UsvAvhLR/D2nKUsdMtY7WEMSTtRQBkn6VR8AfDHwr8LdJOmeFNBsdBsmwWisYVjDkdC2Op9zXUUCCmtgqQRnI6U6igR8c/ED/glj8F/iR8TJ/F9/Hrlm11Obm+0y1vytvduxy24kGRc/7DLXq/hb9iH4C+D7CKzsPhR4Znhi+4dUsVv3H/AAO43sfzr26loA8zi/Zh+DkCssXwm8DxK3Xy/Dlmufyjq74D+APw3+F+sXOreEvBGieHdRuF2SXOn2aROV9BgcD6Yrv6KACiiigBGOK+LP8AgqV8fNS+DvwNj0jSPLW/8USNp3mbsNFHtJZh+HH419oyZyCD07etfjd/wVz8VXHjP9o7wp4IRjHHp1mjk5+XdcOFzj22frUy7FRPXf8Agkt+ydb6foB+MHiK1ZtRui0OjwyDCpGPvTY9SeB+NfpnwcgiuM+Cfgc/Df4SeEfC7EM+labDbOQMfMFGf1zXbbR1xU8o29T8rf8Agsp8LYrPT/C/izTNEhhj81ory+gj2nJxtDY9T/KuO/4IraXb3Hxa8c3zqxuLfSFRCeg3Srn+VfTn/BX/AMSadpX7Ly6Xcvi91HU4Ftk7kqdzH8hXiX/BEPSlml+Kmpbfmi+xW+7uA/mtj/xz9Kqwrn2N+3p8CfE/7QnwHuvDPhO7W21UXEdwI3fasyr1Qn3r8wPDf/BLX4tX3hvxDrHihbPwpa6NC8yxzkO1wFUklcdB8vf1r9zcV5r+0pqq6H8AfH963HlaLdEfXyzimCZ+OH/BOn9kXRv2ofiDrr+KnlPh/QYkaaO3faZpCxCgn+6QDmv1n0n9iH4EaJJbS2nwt8OpPblWSZrUM+4dGyepr4o/4Ii5e0+KcmwHLWGW9M+f/h+lfqTTBsitbeK0t44IY1ihjUIiKMBVAwABU1FFBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMu6gBaKRV20tABRRRQAUUUUAFFFFABRRRQAUUUUAFNIywNDUlS5DsIcKx2jHrQBupeO9OVQOlQO4irtp1FFaLYkKKKTNJyAWikoYkdBmlzALRTVbseDTqOYAoooqgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRntTXcL1qssuyRm3ZBqWylFstMPfFNZjHwOe9RRXGd5fgDpTWukkchSWKjkAU7hyu5NDMJQT0p5b0qnZzxMzxrLG0gPKq4JH4Vbpg9ypcK8jACrMUZjQDvTN2yQe9WKBPsItLRRQIKKKKACiiigAooooAKKKKACiiigAoopPwzQAtFJ+GKWgBM0Zoaq9zN5a4z1FJ7DSu7Cy3ISQKOSfShbgbsZrMiyGY5zT4LjyZG8zv0rNSZu6ehrKAuSB1oL47VWhvo5l4z+VTqwbpT5mY2H0itnPGKYxdenIp0bMc5FIkfRRRWi2AKKKKYBRRRQAhOKTd7U2SQJjIJ+gqHzndwFQge9ZylylJFkHNLTUz3p1aEkckwixkE/QVGt15jYRCR3zxU9HFAxjKzdG2/hmk8ndy7bvTtUgpaBDQgHalwB0GKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA/JXwf4B8DfsvfEGPwrcfEu98O+IYZDiJi8dvdkjCBlGQSD/6FXKeBf2F/i5+0h8aL7U/GUWpW3w/e/aSS9vbsRCePPHlR7iTkdwPxFfaP7Wn7IM/7Q/hBNV1xIo/FumQltMuNHixLHI2CRIf4xlVx6c18b+Gv26P2i/2SryPw3498OjxRotiTDHJfwNAzL0XEyqf1U1wxpqMtz0ZSbjaJ+nfwO/Zt8B/s8aXNYeCdJ/s2OcL9odpC7zFQQGYnqeT+deodK8C/Y1/aY1L9qT4b3XinUfCp8KGK5NvHB57TLIAOWDFF46dq9+rsjtocEr394KKKKokKKKKACorhtsZzx2/PipCcVDcNiNiFLkD7vrQNbn4vf8ABVhdU8J/Hbwjq8syPcfZ5HgbGceW6Yz+de3/APBOP9q74rftD/GqXTdeuxJ4X0nSm8yONMKrcCPJ9Tg145/wV8i1Fvid4S+12gisYre6jgus8SFihYf8B4/Ovpj/AII6/Cv/AIRX4I654vuIMXfiK9VY5D18mEEAfmxrmULpHXV+Js9z/wCCh0aH9kD4jFomkb+zztKrnadw5r8qv2A/22ov2SdS1yDV9Im1jw3rLRGf7NIBLA6AgMAeoO48e1ft98Svh9pfxW8D6z4U1pWbS9Ut2t5xGcNg9x9K+E9U/wCCKvw2vL1pbPxt4i0+AkkQLHC4GfdhW0Y2OXm0sdzF/wAFfPgC0al5fEkbEAlf7LBAPpnfzW7pP/BVT9n7VIWkfX9QsAMYW7sSpb6YJ/ya8cm/4Im+A/JVYviH4j3fxF4IMH/x2su7/wCCJvh6Nk+w/EbU1X+P7Raxk+2NoHvTa10HG1tT3+4/4Kkfs+Q28ko8UXU2zqkdk24/TJFcjqH/AAV++B8O77JZ+Kb4KfvJpyKp+h8yuI0//giv4E8tRf8Aj3xEXH3vsiQqG+u5DXW+H/8Agjr8F9J8w3+peI9aLY2/aLtY9vXP+rVevv6UK+wtEfAP/BQb9o7wF+01408P694K0nVNPuIIJIr+S/gWPfkrsxtJz0NfWn/BGj4wa1r2i+K/AV9M1zpmkpHd2THJEQZmDp07kg/8Br22D/gkz+z/AB436Lqc2P72pSj+Rr3v4J/s0/Dz9nm0vYPAnh+LRvtwQXUquzvNsztyzEn+I1HLokh8x6eo2iloorUgjmlEKlmOFAyTXgPxc/bn+E3wS8cWPhLxPrVxDrd35ZENtbtKsQc4Uuw+6K931CzN5C6ByhZSufrX5vfHj/glD4q+M3xY1DxYfiTYwQXrjMd1pzs8KKflVSJDu79dtS+a+htGMWtT9JbK8iv7WG5t5FlgmRZI5FOQykZBH1FT1y3ww8Fj4dfD/QPDK3Ul6NKs47U3MhJaQqMFufU11NNX6mT30CiiimIKKKT8KAFopCcUjSBeaVwPjr/gqZcWw/Za1+KZtsu6Mx8dSHXivN/+CMGrG4+CnjKxK48jWhMGz13x4/8AZf1r1L/gphDYy/sueKZtUUKoVVhIPO7euK8T/wCCLek31v8AD/x7qDHOmXGpRRwjPQqjZP47h+VZ3946X8CR+lNFN3dRRurU5h1FN3UbqAEbO4ccUnJxmquqXz2NpJMkLTsiltidTjtX5W/thf8ABQz44eCPiRc6P4Osm8MaNaZXzpdKFw1yTjklwQuMduu6o5lzcvU05Xy8x+rm3DEgdetLX4Y6V/wVK/aP0m+iurvWLXUoMH/R7rRYo0f8VUH9a7K2/wCCzXxjtFxc+FfCsx7NNb3Kf+gyirIP2dWnV+Oem/8ABar4oSvIs/gjwjIduI1hS6BLdusxzX6pfBDx1qXxL+EvhTxTrFgml6nq1hHdXFnGrKsTMPugMScfU0D5Xa53VFJS0EjWpG/1bU6mv8qmkHU/CX/gpFAuh/ti3snlgEW9nNhe58w/4V+4fgm8OoeDdBuiNpnsLeUj03Rqf61+IH7feq23ib9tR4pCs2GtLWbZ93Al7e/Jr9y9HtY9P0ixtYRiGCCOJAf7qqAP0FTHY0qfFcvUUgNI2fwqzMWgHt3r5z/bo+LHxF+Dfwb/AOEk+G9haX2pW95H9r+2QmVUt8NuO0MvOcc5r52+A/8AwV68J+JvDOqJ8RrI+HNcsoPMhkt1LxXZAOQB/Cc7eD1zU8yK5Xa59D/tj/tlaB+yn4TS5mji1TxFdfLZ6WZNrSerH2GRn618YfCX/gsjrmpeOLK08beF7G28P3VwsD3Fi5DwZONxz1x/SvmWDR/Hv/BQ79pS5Nstxc2U93n7TJnydPtCe/YEhf0r2X9ub/gm9H8EfAUHjLwQ0l5pthGseowucsOg8388/nRcasfsRpOpW2s6ba39nKs9pdRLNDIvRkYAg/kat18hf8EvvjVcfF79mXT7bUZxPqvhyb+zJTjnygoMRPvjPPtX17VEhRRRQI/Nr/gs9olxJ8OvB+pJbs9tFqJSefGRGChwPxNex/8ABKe4tJP2PtAS1ZWkjvbrz1DZKuXHUduMVuf8FJvhzrPxN/Zb8Q6dodmLy7tSl+yYy2yI7mC++K+Af+CVP7UWmfB3x5rfg7xfqy6V4f1hVktmuMhYbtW2hfbcGP5VGzZpvGx+0YoIzTVkDqGUhlYZBHQ0uTVGYvSlpu6ue8b/ABF8M/DXRpNV8U65Y6Fp8YJM97MIxx1wDyeo6UwOjorh/hT8bPBXxu0q71LwTr1vr1naS+TNJb7sI3OAcgdcGu4oAKKKKACiiigAooooAa3UV+EH7emuTX/7c2sPdymSK1urSHLY+VFkBAz+NfvBX5Hf8FGP2EPiJqHxR1z4meELV/Emkagonube2H+kWpXB+7/EM88elS1dplJn606fMlxZwzRuJUkRXEgP3sgc1YIyRzivxc/Zu/4KmeOfgqsXh34hWEnibR4nWLe6eVe2qrkEEYAbt/3z719SfEr/AIK9fC6H4cX9z4QXUrzxRNCUtbK4tzH5chGAzE8YHtVCPnX/AILHfG5PE3xP0H4e2bRva6DB9suXX5iZ5OAue2FB/wC+q9E/4If3kQ0v4t2xdVnefTZVjzyVC3Azj2yPzr5g/Z1/ZA8e/t1614x8aX2p/YV3vK9/dgnzrlslUX2GDn04rmLdfjL/AME8fi5HO1u2halIjIS3zWmoQgrnnoe3uM0CP6DK8w/aesU1H9nn4iQOgdTod2dp9omNfM37BX7eXjH9qzx9qvh/WfDFlZWOm6YbubUrJ2K+b5iKienzAsf+AmvsD4paK3iT4beKNKSIzNe6ZcW4jXqxaNhj9aAPzL/4Ii6tIuqfEzTNpMMttZ3BPYFXlUf+hmv1cr+cv4M/GLx5+x/8UZNV0hJtO1C3ZrS802+jZI7mMNna/ryOK+w/FH/BZrxf4g8NrY+F/A1rpviGY7BcvIbhQf8AYj7n60DsfoJ+0h+114C/Zm0eObxFem81a4O210eyIe4mOQOnbqOtemfD/wAWnx34L0jxAdPuNKGo263AtLoYkjDDIDV+av7H/wCxD44+MvxKg+NHx1aadXZb6x029kLyXDkkqZEP3EGBhe9fqLHCkKgRqEAUKAowAB0FAE1FR+YPWmSXKRDJNTcLMnoqv9qG0Ec1XmuJW+4CKXMWoNl8ttpplUEAnGazbeeXcd5Jb+Fc9afMXMiFxt9qOYbp2drmjS1HDnbUlWZsKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUm5fUfnQANUcuPvHIx6U/erdGB+hpjSKMjOamxSuRwmNSWLlt396rIIPSs2ZZbzasJCbGG7I6itAcfSpSu2hyQ6lppIFIHU9CDT5kiB1I2D1oyKa3bFJtAOGF70uajp0fepWrsAPzgDr604UtFacoBRRRVAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSU1pFXqf0pAR3RHHNUfNXcRnmluSWlVnB2jjNUL66UwuYYizA43DoKzk9TqhsSX8xSPKk8VmySXt1uSLekcw8pnT7ygg/N68VCr3USmSQFwOcY/wA5qn8QfiloHwf8A6p4w8RXiWWkafAZZm6szfwqo7k+gqbXLk1yn40fH24+Of7H/wC0RrGrLrWtQWsl7Jd2V7LNJNaXMLNkAgnb3AI7V+gn7Gf/AAUe8N/tCSW3hjxLEvhzxj5arH5jDyL5sHcY26AjA+U9d3FeM/BP/goBF+11+0B/wrjxd4G0u88D64rwWVvcx+ZNGVBIZif7wxnGMYFeRf8ABRb9iWD9mm80v4l/DmS4sPD8t4EngiY50+bgxsh67ThvoQB3q07aHNufsqIlLFsc0+vk7/gmv+0Pq37QXwD+0eIbh73xDot0bG7unx+9GMo31x1r6yq0QwooopiCiiigAooooAKKKKACiiigBGbbTTIB2NPpNo4oAaxbGVH51EJ5WJCxbsdcnFWKSgBkTO2d6bPTnNSUlLQAnNNaNZPvAGn0UAQfZI+yinrbovRF/KpKKnlQ7sZ5YHQBfoKXbTqKfKgEFLRRRyoQUUUUwCiiigAooooAQjNJtp1FACAYpaKKAEIzSbadRQAgGKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGdc5rO1jwzo/iGHytU0yz1GPrtuoFkHH+8DWkFPejbSDVFfTdLs9HtVtrC1hsrZfuw28YjQfQAYq1SDilpgFFFFABRRRQA1qNu6lo5oA83+Kv7PfgH41Np58Y+HrfWTYOzwecPulsbunrtH5V2PhXwnpHgnQbTRdC0+DS9KtF2Q2tuu1EHsK1ttLjigpybAY7UtIBiloJCiiigAooooAKKKKACiiigBGptPpKYhFp1FFIYUUUUAFcv44+Jfhr4b6VLqXiTWLXSLOMZMlxIFz9B3rpZORivlb9sr9jK//ap0/T7S18Vf8I+lvIxkWSEyK4bb6EdNv61nLm05TWCTvzFPWP8AgqN8AdJvEgbxNLdZZlL21s7quMckgcdf0r0Hwb+258FPH0QbS/HmmDgZW6k8lhnpw30Nfn7a/wDBFPxnJqdzHcePdFg05TiGWOGUyOPVlxgH8aivP+CJ3jqO5JsfiF4fMQ+600M6v+imq5SEtT0//gqh8bPC/ir4KjTfD/izTdWa4uo1a1s5w5AVgcnH0rC/4I1/FPS9L8L+PfDmpaja6dHHcxX0Yup1jzuUqQuTyAF5+tee3H/BFv4nqVC+OPDtz3PyzcfmtFv/AMEbfivphd7bxhofmOpX900ideuanlNHJbM/VaT42eAIiVfxnoasODuvox/Wom+O3w6Tg+N9BH/b/H/jX5Q/8Oc/jD85bxHoEh6jdK5rndU/4JH/AB6tJwlsNBvE/wCeiX2wfqK0M9D9gofjj8Pbi4igi8aaHJNK21EW/jJYnsOa7dWDqGUhlIyCOhr8WvAP/BKT452PjfQLjVhpFnp8F7FNPPDfb2RFYFuMelftDY2a2NnBbqcrDGsYPsoxQLQlxmszUPC+j6pu+2aXZ3W773nQq2fzFau2jbU2V7i6WObPw18KOm1vDmlsvobRP8Kpz/BvwJdf67wfokn+9Yxn+ldgBilqgOFi+Bfw7t7pLiHwP4fjnT7si6dEGH0O2u1gt0t4kjiRY40AVUUYAA6ACpOtLQO7CimsxFeU/tI/tGaD+zH8OZfGPiOx1DULBJ0txFpsSu5djgZLEAClcLXPWK4n4xfEzTvhH8P9X8Taoyi1sYHkK7wpYgcAZ98V+enjf/gthZLp86eEfhtK90wIhutY1NNi9MFoY1LHvxuFfKHijxZ+0z+3ZrwglsNa1TTpJAqWdjavBp1srkZPPb5AeWP3altbFqLvqcv8HfDfiD9sD9rKyMEe2bUdSF9cSLnEFuj7yec4OBX9CcaCONUHRRgV8NfC/wCC9p/wTq/Zr1XxJaeHm8XfESaLzbgQRtIS2OI0KqSEXPPPPrXyTqn/AAVV/aO1IyGHQdA0lGOEWLRbtmXk8ZaQgn8KcdhS3P2eWqWtTXcOmzvZRrJcqhKBumcV+McX/BVv9ovRo0a70rQLyNTlmm0a5RiPqJAP0rtrf/gtB47bTYYpPh1pEuoDiR1vnAc+ybc/qab2JRy/h39vrx1p/wC1ddWPxO1gXPgiO/n0290doB9nEJYqrbfUADkmvIf2/bH4YzfGK2u/hYsH2K8txJPbWnMYf5du1AO+W/IV0v8AwUA+Fut29n4L+J2peFoPDcviq2N3qENq+5UmkCsgx243fnXsn/BKP9j2bxNrX/C3fF1kkukWitBpFneRhxcS8hpSG7Lxj6+1QosuUk0eZfsE/tsab+yPJe+G/FXhKWOw1i6ie51VUK3EKgHGVI+ZfmPA6c1+lPxF+Lnwy/ah+BHi7w94Y8c6TdNq2lyxqouAsiZUnlTyDxWx+0t+xb8O/wBpTwvJZ6ppNvpeuQxsLHWLGMRywMccHA+ZcgZB/Cvyn+LH/BNH43fBObUNU0S2/wCEg0m1UuL3SZispQdyg5/Cnykqx79/wRj14+G/HvxY8E3VynnMltPHEDw5geVGZfwkBP4V+rFfg1/wTHh8Tx/tleG47FJ43UXH9q+YpyINmXDA9DuA61+8tUhPcKKKKYiK5gjuoXhlRZIpFKsjDIIPUGvyj/bf/wCCYWqWOq6p4/8AhSkuoLcStdXegrw8TZB3Q46/xcewr9YKNoqWtSkz8Lfhh+3Z+0n8C9NXSLr7XqWnwvgReItPeRl28Mqybd2OnevUE/4LFfFxYwg8E+GZXxgt5N3kH6Bq/XWXQtNn/wBZp9rJ/vQqf6VB/wAInonH/EnsRj/p2T/Cmguj8if+Hi/7VHxdxY+CfCcMNxna76Lo0k23d93c0oYL0OOneul8K/sFftCftT+JrLWPjz4vvNO0SNfMW2knEsoz1SOEfJHnaM8enBr9XbXTbSxyLa1ht/8ArlGF/lVmmPm7HBfBf4KeE/gL4KtvDHhDTY9O06L5nYD55pD1dz3JrvaKKCQooooEFFFFABRRRQAUlLRQB4r8XP2NvhB8bZGuPFHgyymvyCBfWmbeYZxk5TAJ4HUGvnHWv+CN/wAIb64SSw1zxFp6b9zRtMkoI9ASoxX3xRQBxXwf+D/hf4GeBbLwn4R09dO0m1y20ElpJD952J7k1t+IvBfh/wAYJEmu6Hp2srFkR/b7VJtmcZxuBxnA6egraooAx/D/AIP0HwkkiaHomn6OsmBILC1SHfjOM7QM4yevrWxTJZBGpZiFUDJJPArmPC/xS8JeNdUvNN0LxFp+rX9pnz7e1nV3jwcHIHvQMzPiB8Cfh78UrfyPFfg/SdbiJyRdWykk+5HNc94L/ZL+Dnw71qPV/Dnw50DStTjGEuobQb1+mc167RxQAxVCKFUBVAwAOgrjNW+Nfw/0HV5dK1LxpoNhqMRAe1udRijkUnsQWrf8QpHe6RdRf2iNPV0eI3G4LsYggHJ6EE1+QnxW/wCCTfxe1TxhqOpaL4h03xXa3sjXI1C7uWjlbcxOD1yce9TcaR+wGl6xpmv24n0y/tdQhI4ltJllX81Jpt5EVjDPztPavwT8D/F34yfsH/FabRpr6fdDIsVxoslyZLa4wTg7c4yMnH+9X7teEdVufE3g/R9Xv7X7Dc31nFcS2qtkIWUNj9almsXZl2O425Kg7cd6ntboTSBEOW789KiWNFRmViy9CDUun24t5JQF5wCfepWrNZtWPkj9qj/gpB4O/Zh8eQ+FJPDOoeKNYiiEt00E6wRwKxGMFgdxPPbjFezfs5/tSeA/2n/Ccer+FtQjS9RR9q0i4dftVqxzwy9xweR6Vxn7T/7Bfw3/AGnLN7rULMaB4oVCsOu6fGolySP9YOPMAxwCeMnHU1+THxv+A/xR/wCCfvxc0zWrLULkQeaX0zxBYs0Ud2E2lo3CtkfeXKnr707dDl3P3p8SeI9K8I6TPqusajbaVp1upaW6upQkafXJxXn/AML/ANqT4XfGbxNqnh/wd4wsNb1TTgpmhhYjeDnmPON4G0525xxXBfCbxd4e/b3/AGS0k1y2j8rW7WSw1KGNQfs90owzJnoQSGH1r8i/GXgnxt/wTr/ag0m4lJul0y4+12F5GCkd/bEjcPc4IDCqTDlP6BqK4v4O/FTRPjV8OdF8YeH7hbjTtSgWQbTkxvj50PupyK7SrJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKlsCOVwuAe9QTKMfL3qeRA2M9qbtHfoKyerLTKsKC3LH+9UUd0lxcOoyu3r71cmUKmQu6q9xcWml2Ut7eTQ2VtEu+WaZwiIo6lmPAH1osy+Zblq1jEanGTn1qQ1keHvF+g+LYpZNC1vTtajhIWR9Pu45whPQEoTj8a1ZFLLgHFWnZWI3dyKQbj1wKhnmEW3YM884qfydygE5IpGtVxknFY8rLTRWutQ8kDJChuMmrMbExrng1Xn0xbpVDHKhgw/Cru3LfSnySBtdATPNSCkWnVrGNtzJhRRRWggooprNjA6mpcgHUUxZB3IHanA55HNLmAWiio5biKHHmSLHnpuYDNHMBJRSBg2MHORkUtUAUUUUwCiiigAooooAKKKKACiiigBKMikakoAXcBTfOTdjPNV7y4WFQSf0qrb7p5Fckgdveg0UdLlnULwQQkqfm+lRWlyzQhnHLdKsModwXX7vT3qNlbzCQny+lZSWpStaxw3xw+JOm/CX4Z614x1jzv7L0mEzzRwEBn5wAM18feDf+CwXwl1a9gtdc8MeI/D9nIcfb7iCOeFeep2OW/Ja+3PiF4B0j4p+DtU8KeIbRbrRdUt2guIyeecYx6HrXxfff8EbvhHcef8AZ9f8R2ivzHGsyMifUFcn86ajoHNbQ+tfhz8bvhz8VrWKXwl4r0nWhIgk8m3uVMqg5+8hO5eh4I7V+XX/AAVg/aVfx78QLL4SeG3WXSNFcSX3kkn7Rdk4WPA67f5tXCftSf8ABP8A+IH7HmlT+PfDXib7b4Ys5AkmoWk32a6tvMdEjVlzl8l/4cgY7Vgf8E4vg/e/Gz9qzS9Qvof7S07w+51jUZbw+YWKsFQMT94l+n0NVYW593/sb/sa/Dv9mf4b+HPiv49drHxsln9vubjUbgJFY71PyKvrtI9818zf8FC/+Ci2lfG7Qb34b+A4TN4aaVTe6xOhU3G1gQqKeQMg89812X7b37I/7THxx+N3iK70qGXVvBE8y/2bZnV4o4FjCgDMZcYORnkV5N4D/wCCP/xq8QXEieIBonhWJcETT3i3O/rwqxE4xjnPqKOUz2PpT/gl58b/AIQ/Db4c6X8Pz4ohPjzxJfyXs9t5TBA7AKkIk+6SFX82r9I6/Pb9mn/glFB8Efil4c8a6v4yTWptHk88WMVpiOSTBAOW5ABNfoTVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooopXAKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAI1Np9JQIbRTqKYWBaWiikMKKKKACiiigAooooAKKKKACiiigBOtZfiTwrovjLSZdL17SbLWtNl5ez1C3SeJsdMqwINalGPeoaA860X9m/4U+G9QF9pXw28KadeD/lvbaNbo/wCYSvQoreOCNY4kWONRhVQAAD0Ap9LTsO7GqoUYHSkWGNVCiNQvoAMU+iqEUdQ0PTdWi8u+0+1vY/7lxCsg568EVyH/AAoT4bf2l/aH/CB+Hftmc+d/ZsO4H2+Xiu8JpN1AjnfGHw38LfEDTYtP8SaBp+tWMRDR295AsiIR0wD0xWvo+i2Hh3TYNP0uyg0+xgXbFb20YREHsBVwGloGFIyhlIIyDwQaWigDl9B+GHhLwt4gvdd0jw7p2m6xertuLy2t1SSQZzgke9dRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNJoA+Tf+CmPx61b4E/s5TSeH7g2mveIL1NHt7hThoUdHaSQH1AXH/Aq8B/4JE/s06lo9hqfxo8QS3AuNYje10iF5CBJEWPmzOvfcVXafY1wP/BZH4nyeJviZ4I+GlldEx2Nubu5gUgg3E7osRPuqK3/fZr9S/hz4Xs/BfgLw7oNhax2Vpp1hBbR28QwqBUAwBQW9FY84/bI+Md38Bv2e/FXjGwfZqFrB5FrwOJpGCI34E188f8Eq/j38Tfjx4Z8fXXxB1OTWbTTLmzg067mQBi7CczrkdcDyfzrB/wCCzHxQ/wCEd+DfhfwZHnzPEGpfapQD96K3AJU+26RT+Ar17/gmH8OYPAP7Ivha6UKbvxC0msXEgHLGQ4XP0VVFAaWPkj/gs18QNS0vxl4F8N6Xq15Y2n2W5u7m0t52jR3ZogjMAeTw1fMXgX/gof8AGX4dfCqPwLoviFltIZJDDqEw8y6jQhcIjnlQuDj/AHq9U/4LG3Rb9qrS4my8cXh+2YJnjmSXP54H5V9N/wDBLf8AZz+HfiL9mWPxP4l8K6TrOq6hqFwJLrULdZCI0OEXJ7DJ/Opa1H0Pyfk8eaj4g8dWvinxPd3GuX/26O4uprx/MaUBskHP0r94vgf+3R8H/i7feGPCuheIF/4SLUbYJFprW7Jhkj3MmcYGADj6VB8Vv2N/gHrHgfxDqKeAPDdtdW2n3EiXdhDHE6uIyQdy98gYzX5j/wDBLHT7Ff2y9Omv0jSKzsb14pJmAEb7dqnJ74LDiiwLufo9/wAFHfjxr37Pv7PtxqXhfzrTV9Uvo9Oiv4R/x67kZi+ex44965P/AIJW/tBeJ/jp8MvFcXjDWLrXtb0TUUjF7dHLtDKmUG7vzG/6103/AAUo03w/46/ZS8X2K6xZHVbSOPU7SBZ1ZnMMi7sAHrtcjPvXh/8AwRP0zb4F+JurF8G71K1hEK/dQRpIRgfWQ1OzLcro8H/4KVfHz4q+A/2r9e0nRPH/AIh0HS7W0tpLS00rVp7eKJXjBLBUYAMT1r59/aB/ay+J3xy8K+EvCnja6eO30CAbDIHWa7cqu2ednyXYheG9ye9esftqWS/GD/goxf8Ah20DTG41Wx0d1XknbsDj+dfshrHwJ+HHiOa1m1nwF4b1i4t4Ft4p9Q0mCd1jUAKoZ0JwAOlVvqRsfhH+zj+258V/2c9LTQ/B2q2kuiyXQc6Nd2aS+ZJIRuKEDdk7QMk9xX6oft6fAY/tLfso2/iEadFD4z0PT11q1YwjzVHlB7iAEjIVgM4zjKDPSvfLf9mT4R2erJqdv8MPBsF/GQyXMegWgkQjoVby8it74teJtL8E/C3xVrWsyRw6VY6ZPJOZR8m3yyNp+pIH40uUVz8zv+CMfxxv18U+KfhXePNPYXFmdbsVLEpaukgSZFXOFDeah4HVa/WKvxz/AOCM3hKXWv2gvG/iuLcllpeitat6M1zcKyfpA35V+xlUiXuFFFFMQUUUUAFFFFABRRTG6igB9FFFTcAoqHLbuOnenL92jmHYkopkbbs0+mAUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtRc5NZvcB7MByTXK/Er4leG/hN4RvfE3irUodM0azXdJNKeSewUdz7CulcDaSxCqOWz0xX4jftpfGLxf+2d+0nN4B8CPd6z4fsrg2em6fb/6mR0wss7Y6jcBgngUikj628W/8Fl/hromqSW2k+Fda1q2Tj7VvSEH6Bhmvnj9tL/gpVpX7RnwVj8K+ELLVPDk9xeo2oxzSDM1uFbKBl7Zxkd+K+rf2f/8Aglh8LvA/hSyk8bac3ijxLNApumuJD5UTkcqgHp/Svlr9tj/glzqPw5h1Lxt8LUk1Tw7GGmu9EGWuLZAMlo/76jHTr0qrFaFr/glR+1Z8PPg3a674K8WyHQtU17UVuINWuH/0dlCBVic/wYO7n/ar9F/2ovjhf/Bj4B61498L6fH4luLVFaBIMzRlWOPMymcqOpPSvx8/Zh/YeP7Vnwq8Ta1oms/2J4j8O3HkzW92h8i6BUsG3H7pGCDXsn/BKP4h+M9U+POv/DXWdXm1vwj/AGJdC8026cTwAxSpGCmei/vCOODuFHKBo+D/APgtN4usbV4/EXgfS9UuDtKTWc7Q4HOQwOfbp71s63/wWt1JtLmSw+HVvb37LiKWW93Kh9SMc12H/BVb4L/DX4YfAPT9R8OeC9J0bXtU16C1F3ZW6xkIY5GfOOv3V/OviGfwr4X0P9gmw8QS6dA/i7XvF72qXkg/eC1hjJYL6DcRmnewrX1Pv7/gnD+1Z8Xf2qvin4vu/Ft/af8ACJ6Jpyj7Fa2ixBLmaUeUCwGThIpe/wDOv0Kr4e/4JAeEV0H9lN9TktliutZ1q4uTNtw0sahETJ7gFXx9TX1h4i+MngTwl4li0HXfGGh6LrMoUx2WoalDBM244XCOwY5I445qhbHZLTqRenr70tBIVneIPEWmeFNFvNX1m/t9M0yzjMtxd3UgSONB1JY9KvswGMnGeBX43ftvfFrxx+2N+1OvwV8BXch0TTrt9NjtY7gRw3cygGeWQ5wyrtOM9ADQNK59EfEj/gsx8OPC/iK40/wx4Y1TxdZQMUbUVmS1jcg4+QMCzDrzgV1XwJ/4KzfCv4teIo9F8QWt14BubhlS2uNWlQ2sjHOQ0o4TnaBuxndXo37P3/BP74TfBfwPZaZfeFdL8Va75am91bVbVZ3lk5yFDAhVGTjA+vt41+2h/wAEv/B/xE8NXXiT4Z2dl4O8S2SSTy2cY8u0vFABII6Iw2kgjj5jU2EfVOk/tSfC/XPidP4As/GGnv4piVW+xNJs8zcCQI2OBIcDPyk44z1FerD19RX8y/w38E+LviN4+stC8KW15qPiaRmliNtIRcBkBBKODk4x2r9Bf2RP+CmniH4Z65B8NfjlFMtrYO9o2vXasLq1ZTgLcKRkgdN3X1zRygfqR448X2HgDwbrfiXVJPK07SbOW9nb/YRSx/lX4cfHz9qb4vftkfEm5uPBNtr1vo+mRs1ppWhvIJIosKWlkCHnO0HJ6V9B/wDBQb9uC1+O02i/B74O6sNWtdXuEi1LUbMnZcMxQRwoR1XJbd9BX2p+xH+yTpf7Kfwtj00+XeeJ9S2z6tfBRlnxxGp/urkijlA+B/2JP+CmHiH4f+JLLwP8XLuW+8PyFLWHVbkET2L5IzKTyynIyT0xX6/Wd5DqFpDdW0qz28yLJHIhyrqRkEH0INfmd/wVw/ZLsbzwnZfFjwnpENne6a5i1z7JHt82JigjlIHA2kNk/wC0K9v/AOCV/wAarn4tfsz21hqmotf634bum0+cyNlxD1hyf93I/wCA1QH2RRRRQAUUUUAFFFFABRRRQAUUUUANamPnHFPamswUZPAoGUZlc/Ns3be1TW4Pytsx6j0pbiaQRkwrvbsPWks1m2s83DNj5fSg0cnYmcFqjOBwTU5qCRTuBwT9Kze4kxGVgykfzqfcOPU8U3Zu60qqqn3q1sJn5wf8Fnvi4dH+HXhD4cWk2LjXbptRvEXPEMOBGD/vSMf++K0v+CMPw7GjfBLxV4yntwl1rmqi0hmJBL29uuR9P3ksg/4CK8F/4LEfDrxXefHrw/4lh0y8ufD9zoyWNrPEhdftEcjmRcDkcSx89Dnjoa/Qz9hL4a3Pwp/Za8D6Jex+VfNa/a7iPj5XkJYjj2Iph0Pflpabt3Uowpxnk0EDqKKKACiiigAoopu4bsUAOooooAKKKKACiiigAooooAKKKKACimu+wHgngnj2rwr4sftu/B74I+NI/C3i7xUmnaw2N0SQSTCLP98op29R1/oaAPd6Kz/D+v2HinQ7HWNKuUvNNvoVuLe4j+7IjDII/CtCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCLzGRV8wfOf7vIqWkwD2paACiiioadwCiiiqWwBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAQnH0oBzz2oZQy4PShVCrgdKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsT2oAdRXI/Ev4reFvg/4VuvEXi7WLfRtKt1y0s7csf7qr1Y+wr4Y8cf8Fovh/o2pNb+GfBmseJrZWwbp5ltVI9QCpNJuw7M/RWivn79l39tb4f8A7VGlt/YN0dN8QQpvutDvGAniBJGQejjg8ivf91F0Fhc0zzk8wx7hvAztzzj1pWztJHWvyn/bV/aQ8Zfs2/tZaP4v0XxG2pWUsHk3XhyVyUSNcZyoI5O44PtRdFKLaufq1mlrx39m/wDae8H/ALSngm01vw9fRR3rRg3WlySDz7ZumGHpkHBr55/4KSfttap+zrodn4V8IvCPFOsI5N0rBmsYxtwSvq244/3TSuibM+6KSvwP8H/tt/tI/C6+sfF2pa9rGo6NcShNusW+61uAOSq8DBwTyDX7Vfs9/GrSv2gPhNoPjbScJFqEIM0G7JglHDofcHNO4+VrU9HooopkhRTWOO+KpaprdhocBn1G+t7GHBPmXEqxjjryTSuBforzqX9or4YwSvHJ480FXU4Km+Tj9a6Xwz8QPDXjRXOg69p+r7ACws7hZCuc4yAfY/lS5kOzOgopOvQ0c+tHMhC0UhqK4uorOCSeeVYYYxueSQgKoHcmjmQyaivkj4nf8FPPgr8L/GB0C81HUNUliYpPc6XbiaKIjsSWGfw9K96+EHxw8G/HXwtHr/g3WodUsWHzopAlhPPDpnKng9fSmFmd7RTVzk06mIKKKKACiiigAooooAKKKKACmSAt0OORStSUDPxA+OOiH4zf8FQ5tEUi6ik8S21uxc5Ajh2ll+mFxX7fKu1QPQYr8K5vGtp8Gf8AgpVe+JPEazWlha+KZ5Lh5FxthkJCt9Buz+FfuPouuaf4j02DUNLvIb+ymUOk1u4dWBGeooKkfkh/wWo8YR6h8VvAvhtE/faZpM10W9fPlVf5Q/rX6SfsneHZPCf7Nfw30qVdr2+iWwK+mUDAfrX5a/8ABYSwkT9qnQ7mRl8mTQrUDn7oWaTOfzr9cfBms6foPwl0TU7ieO30200eGZ5SQFWNYgSfyFAPY/Gv/grnr0GuftbzQWrI7afo9taykdQ43uQfwcV9H/An4K+Ovir/AMExdL8PeCdV/s7XLu/lu49kpjMsXmHMZYdM1+cn7R3xGPxU+OnjXxS0zTpqGpzSxSOc/ugSEA9sACv2V/4JWQ3sP7H3hz7aJAGubhod/wDzzL/Lj2pDeiPy48Yfsc/tG+CtL1abUfDmsR6fZxSS3c8F6XiaNQNxxu5GM9q8k+C3wt8YfGbx7b+GPBMEkuuTI8ilZDHsQfey3Yc1/Q3+0RouoeIvgT480zSld9Ru9HuIYFj+8WKEYHvX5Wf8Ep/hz4x8K/tUNcan4V1Gw0+HSbqC4u7q3ZUSQshXDEdTyOKYuY7T4P8A/BN/xz4E+Hvxd1j4jS2rXMnhi6i0mK3uDMVl2M7McjjGxAMeprG/4JO/G3T/AIT+Bvjfca5crDpukWtpqsSMxAaQLOrKB6sVSv1R+Lkcknwr8YrCcSnRrwLj18h6/mr03xZrPh+x1zSbC7ktrbVAsN5ApP78KzFVI78saloa1Psr/gm34G1j9oL9tC5+IerCa8tdFln1q7up2L5uJNywqSepyxI/3K/bWvkz/gmr+z//AMKP/Z6srjUNOW08R+IGF9eysB5joR+6Vj6AE4H+0a+s6aJe4V+V3/BVD9rWbxdqdr8Dfh9dTX87z+Xry2QLG4lJQw26FTk4O/evQkr6V6d+3F+2d8TtH8cXvwn+Cfhy81DXBAi3uuWls8stu8mcJCMbQcZ+Y5wRxU3/AAT/AP2A734W6tP8Svip5WrePL3bd2lldMZJNNkcuZJZDkhpH+Xnqu085JpiWh6x/wAE7P2Ybr9mn4Hpb67awQ+LtblF5qTxj51UA+VCx/2AzcdizV9UUUUCCiiigAooooAKKKKACkpaKACmtnjFLTWYL1PFTy3Aa77VORikjZWX5Tmqt1drGvHei1mLLwOtQ9Dbl0Ly06mrnvTq0WxkFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRSVLYC0m4DvUEjyMwCcDvUnlBsE81AHzb/AMFDPjhN8C/2ZPEOo6fM0Gt6uRpFg8Z+ZJJQ25x9EDfjivmX/gjV8FdMh8G+KfihdwtPq9xqD6RYTSL9y2RUZ2X/AH3cg/7lcl/wWm+In9peJPh38P7Cd/tVmk2rXEQ6F5WSOH8Rsk/76r9Av2UfhDB8Df2f/B3hGLDTWlkslzIB9+aT55D/AN9MapIdz1ikZA6lWXcrDBBGQakqpq2rWeg6bc6hqFzFZ2NtGZZriZwqIo6kk9KsR4f+1F4l8Nfs9fsz/EDVbK1s9C+0afcW9tHaxrEZruaNkTAGMtk5+gNfFH/BFj4WTrffEL4iXkBXKRaLZy44bJ824578rB+RrzD9tj9obVf26vjd4a+F3w18+88OW915cBVDiecnDTOB/AoHBPQE+tfqX+zP8C9M/Z1+DuheDNOAZ7aPzLyb/ntcMAZH/E/oBQV0Ph//AILYeNHtPC3w08LwFGa5u7vU5gSMqIljVD+Jkf8AKvlr9rjwna+Af2Tf2ZdJtVkjn1HTb7WbxXBGXlEDA4/4E1d7/wAFldWm1H9pbwxpZlP2a38PQIF7Kz3ErE/lt/Km/wDBVbT30HR/gJogRoksfCwiCsMYPyKQf++BUPcpH6N/8E/tJh0f9j34YQwgASaUs7e7OzOf1avg3/gsv4Lfwz8Yvh/47syy3N/YtEDjjzLWVGXHviYflX6L/sh6MPD/AOzL8NbEHd5eiWxyPeMH+tfLX/BZ3wrbal8AfCWuyFUu9O8QLaROTjCzwuW/9Er+VFyd2fZPwH8Y/wDCwPgx4J8RGRZX1LSLa4dlYMCzRqW5Hvmu8r5U/wCCY/jCDxZ+x74LjjmWWfSll06ZVcEoySMVBHb5Cp57EV9V1QnozyX9qr4wJ8DPgP4s8WCQLf29o0OnpnDPdSArEF9SCd2P9k1+ev8AwR8+Clz4t8deLfjPr8c0s1u7WWnXEgOJp5dxuZM9CQNq8f3mrpP+Cznxuhj0Pwt8LtOlaS/klOr6lGhIESqAsH1JLP8Ap619g/sH/Ddfhb+yr4B0hrSWzvJrBb+7iniMUgmm/eMGUgEEbsc+lMLnvy1keMI2m8I63GilnaxnVVAySTG2BWxTXUSKysNysMEHuKBH4k/8EmUjt/2zJ7e6j/fx6NfqgYfNHIJUB/8AHS3519Nf8FcPhP8ACjTfhl/wl13Yxad8RLufbYvZAI92AV81pFH3goK/N7+9fLf7JPxA8JfAX9tL4leLPE2pQ6Xoui2ur/Z/NkCm5n81dkCZ+87APhRzxW94Bk8T/wDBTb9ryO88QLcx+ANFlW4e12ny7W3BykXoGlKn67T6UAfM/wAE/EXjH9nHx14W+KUvhKa70tJt0Et7Zt9nuEGNxjfGMgHr7iv2s/Zz/b0+Fv7RVmkVhrMOh69uCHR9UlWKdjjOUBPzL7ivZfEfwv8ADHivwHN4O1DSbeTw9Jb/AGX7IiBVRMY+Xj5SPUV+Uf7Qn/BI/wAaeAn1TxF8MNVXX9Ohd54dKVmivYk44U/xEdsHtQB+qHxs8DJ8Ufg/4w8LZUjWNKntkbGRuZDtP/fWK/LX/gjjr+o+Ef2g/HvgWdXhiutIee6ikyMXNrcrGAB67bhs/SsT4A/8FT/HvwF0NPBnxA8OzeJf7Nb7NHNcymK8iCnG18j5scDPsa1f+CXOsP8AED9uDxv4vs7CSx0y70u+maEtuELS3EDBSfU7T+R9KAP2HooooAKKKKACiiigAooooAKKKKAGtUNxs2fMcCpiQahkjMmBjjNA0LHEFUY5qQ/L1pVxVW61Kyt28ue7gibH3ZJFU/qalsZHcatBAypvDM3pk0+EPI6OWwM5Az14I/qKzP7Y8OQtJIdS08bfvsblOPrzUGi/Ejwl4i1qXRdJ8TaRqWrQxmWSxs72KWZEBALFFYkDJHOO9QVp0PzA/wCCjn7UXx++Hfx5v/DXhe/1bwx4UWCL+zpLC0U/bMxqZH8wqTkMSMDp+NfOXhPxl+2N4pm/tbQZ/iRrZUgtJb21xOgz0yApAB5+uK/e5kRsblDY6ZGa8w+OX7TXw4/Zx0+xu/H/AIhTRUvmZbaJYJJ5ZMYyRHGrNgZHOMVa2Fc/JDU9W/bl1xVjvdB+IUsakFQdCdhn/gUdbkPj79vtVCjSPHoVVCKv9gDgD/tnX6tfCv8AaT+GfxotYpfB/jLS9XkkQP8AZVmCXCg5xuibDL0PUdq9MDBhkHIqhXZ+K03i/wDb4m+c6X4+G3J50YKP/QK6H9kfUv2pfHH7UHh218Ta14r03T7WYz6qNVgKQC3Xlo8EYy2ABjmv2JpPegkRc85p1FFABRRSFgOpxQAMQBzUEagybs5FNu59q8DNLayLJHwMY60Dtpc+B/2wv+CoF1+zj8bZvAeieE7bW10yOFtTuL6R423SRrIqxbTggIw5Pevsn4I/FSy+Nvwq8N+ONPtpbS01q1W5SCb7yZJBB/EGvxE/4KiMrftsePD0Bisv0s4h/Ov19/YY086X+yT8L7c440aF+P8AaG7+tAHu1FFFAgooooAKKKKACikJx2zTPM3NgAr9aAJK/n0/4KK3Bn/bH+JSzbvkuQq/NgcIuDX9BEZ3DNfz8/8ABSSMD9sj4iEf8/EbH/vhKAP2k/Y2bd+yz8Lz66Da547+WM17LXk37J+mvo/7NXw0tJMF49BtM7enMSmvWaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBryCMZIJ+lJHJ5gzgj60+mKrb2JbK9h6UAPooooAKKKarbiRQA6iiigAooooAKKKKVwCikNJuougHUUmaTdTAdRTGycYbaO9KqkdWzQA6iiigAooooAKKKKACiiigAooooAKKKKACq2oXiWFrJcSnEUY3OfRRViuB+O3iN/Cfwq8S6ouwC3sZWJkzjO3jvUSbS0Gtz8d/wBtz4oeJ/2tv2nLTwB4Zlk1G0tbo2Wm2aMQpdsb2bnHG0Hp2r64+C3/AASF8A6N8P4ZfiE11r3jSeEtKsN2Y7O3fnCoEUMccZJJ6cV8hf8ABNDQW+I37bEOs3Uc7pYx3epGa34VZCQqhsg/Kdze/HWv3J6Uox93U0lufzv/ABt+G/jf9jH41SyaVeyeHryKeQ6ddWFwS4jBHBOemCOvWvT/AIT/ALd/x5+KXxr8E6RP42uY4LzUra0eytYkSORCwDluCSSPev0B/a0/Yl+GP7SHiH+2NS8br4d1yINxFcxbG6Z3q2T27etfnz4X+Gfgb9mr9sDwy83j/TL3SNHvEnW7jcT/ADr2fbjHWs4tpWluNK5+6Sb47MZJd1Tv1JxX4t/8Fbfh1e6T8ZdP8YiMrYaraiEsoPySJyQfru/Q1+gfjP8A4KVfAjwZcWVs3iv+157ptgXS7d5th4xu44zn9DXjv/BVbR9K8cfsz6Z4ts2lRFuIriJmXaHVgMAjHoTVocXZNM/OjRfgb8XPhb8I7b4x+H7640bQ5TH/AKVpt2yS89N4B+vX3qH9nzxfoHxE/aO0HVfjfrt5qejs+bi8vJi7FwB5YYnPy561Npf7SHiLXPgNbfBhPliu9RhjExycoWwo69if1r7W8Gf8EdtL1f4SQy6n4hntfGM6eckiMDbcjKhlxn9e9MR9TftFeGfhp8cP2Z9d0XQL3QbuC3sGn00QyxhYXVcgrjocDFfJP/BGP4nalaeKvHPw2vLndYQ266haW+chZFkKzEfXdH+VfLnxq/Yv+OH7OPns9tqF9oJLr9t0iR3iKDGdyjoOe9er/wDBH3w3q8H7T+pak1ndJZR6DcQzTSQsq7mliIBJ7/IaEtbie1j9p6Kbuo3VoZHLfEbxpZeBPDN7rF9KsdvaRNLJuPBUda/D74+fHP4i/tu/H46F4ZuLy5tZbg2WkaXauY4hGPvO+D7AkntX6Vf8FRPF0Hgz9l/VpRM0V/qMy2NvtPXfyw/IV8tf8Ea/gra6nrnif4m30RL2JGn6eSeFLAmQ47n7oqOpq7ci7mp4B/4IwXV74Xjm8W+PJrHXJF3NBYQrJHGfQs3J/CvIPjN+wj8Yf2O7V/HPhXxTNqOnWcwbzNOd0lRV5BkUHBH/ANev2ulmSCMySuscajLOxwB9TXk/xq+KvgS3+HPiWzvvFOhb5LGZBDLeRtlthwNoPrSJUmfK/wDwT5/4KGa/+0R4qh+HvirR0fXINPkuzrFuwUSKjKp3J6/MvStP/goD+058ef2c72G/8I6ZpC+DpQCNUaDz5Y2BAKurcDORg/Wvkv8A4JOpoOm/tIeMPEer+INN0aOwsHt4Bd3McC3HnS5OzcRnHlDp6iv0k/aI8afBfx18Ntb8O+LfGvh37Ld2rjaNRjkZWAyCArE5zilcrS+p8hfs9f8ABYmxuoZLH4v6U1ncb18nUtIgyhU5yXTPHbpWH/wUI/4KAWPxC8K6B4L+EWtSXK6wT/aF1Cu12VtojiHcEknOOa+Z/wBkn9nHwL8cfiP478PanrrLZ6dA0umXCuUWfG/35wAv514SNH1fwD8ULpPDyS6lfeH7wzwyQW/ngGJ8q7LgggY7jFKLUpOKHY+9/gz/AMEetc8V+C5tX8ceLX0HVb6JZ7WxsY/MKEgnE5fr26dMmvDP2Q/Guv8A7Jv7Zdp4ZvLqeGxn1E6NqMKkhJlZsIzKeODgj619z/su/wDBVrwN8QNNstF+JMqeD/EiIsZvWUmyuWwcncB+7PAyDx83FfM3/BTiDwtoPxy+H/xU8E6tY39vrHl3U8+nzpMhmglDbyBnBKsvX0q7iP2TjYMoYdCM0+ud+HviJPFngbQdajbcl/Yw3AP+8gP9a6KrMgooooAKKKKACiiigAoqnq+qW+i6bc395KIbW2jaWWRuiqBkmvzu8b/8FkfDHh/xxc6ZpPg+91bRrWQxvqHmhC+DjIX0oKUWz9GpM7eOtNBO3JHNfCOlf8Fifg3eW6teWOuWc2BuT7NuAP1FWbr/AIK/fBWGMNFBrU7f3fs23+dAWZvft1fsDWn7TNrb674Yaz0bxlBu864lTAvEIUBHPtt/WvhLwNeftZ/sT3V9pum6Lql3o8c3mSWz25vLRwM/Mh/hznt7elfUevf8Fn/h/bsi6L4O1rU2OQVkZI/m42geuea+6vhj4yPxL+Huh+I59Jm0n+1LRLhrC7ALxbhna1AX7n89X7TXx28XftDfEJvE3jSBLDU0gW1SzWMxiJFJONpHqTRe/tOfGLxB4Ni8KSeONbuNDWE232JJmKNCQBsIA5GBX9DWofC/wfq1z9ovfC2j3U//AD0lsY2b89tWYfAPhi2wIvDmkxY6bLGIf+y0D5j+Ye60m6tiBc28tuOitMjKD9Mivs/4J/8ABUL4h/Bj4d6L4N0zRdAvdO0uEQwtNHIHK5J/h6mv1p+OPxJ+E/wD8O22s+PIdL02xuJTFBusEkaRhgkKAvbI/OvKdD/a2/ZT8XCBhrPhm3eXhFvdPER/H5OPxpBc+StJ/wCC2Gv2sJTV/h7plzJgAG0upE+uQ2a39F/4LW2UbSm6+FWM42m11RI/XOdyHPavtGP4Qfs6/FxYrpPDHgXxN/EjLb28rDd7dRnH6VfT9jD4Dx/d+EXg7/wTwn/2WmSfF15/wWn0HULSa1ufhLdT206NFLG2uxYZWGCCPK5yCa+Cbv4hfDC6+Mx8WH4eXUHh77YLsaFDrMQT72dv+r6e1fufH+x18DFBA+EXg3B4P/Ektz/7LTh+x78CwoH/AAp/wSQOgOg2x/8AZKBp2Phb/h9Zpen2cVrYfCSSFYUEcStrqMoUDAHEIxXvf7En7fGq/tdeNvEOjT+CYfD9lpdml19st777R8zOQEfgYzg4+hr07XP2Cv2fvEkcsV18LfD8KuMEWEH2Ur9DEVI/Cux+CP7M/wANf2c7K/tvh94Xt9AF+VN1Mssk0020kqGkkZmIXc2BnAyaAuj01e9KFC5wMZ5NLRQSFFJRj3qbgBxwT25r8po/+ConxG/4acTwudP0yTwl/wAJANJaNF/eFTJsyGz171+q8i7kKnoRiv5q7y4Om/tBrcNKyeT4kDlgTnIuev14o5hpXP6VY38yNWxjcAadVPSJhcaXaSK25WhRg3rlRVyqEFFFFABRRSd6AEYgdao3U6Hv0qW5LeYAenaq10o2rxT6G9NLcrK0d/MsQUnByWHYV8EfFz/gq5YfDf49P4P07wzHqPhrTb77Df6h5h80tkAmMDjg5r9AbGMGTcONvP8AOv50P2noDbftJeP1xtA164xj/rqKy3Km9bH9G2j6lDrWlWd/b7vIuolmj3DB2sARn86uVy/wuYv8OfDLE5J023/9Fiuoq1scwUUUUwCiiigAooooAKKKKACimtSUDH0UyjIoAfSZqNjQtYSlrYdiSjIHU0i0MobBIzimtST8WP2+LWXx7/wUqsvD0h3QfatFsFA5+R44nb9WNftHaRCC1hjHARFX8hX45/tGCOP/AIK5aL5hCL/bOknLHA/1MeP1xX7JVqtgCvxq/wCCkn7WnxQ8T/EjxP8ACmxs7zSPCVvcm2WOG3dZL8L1bOPmUn04r9lG/TvWXdeF9J1C9W8vdMs7y8UbVnnt0dwvoCRTA/nd+BWv/GD4H+KpPEPgbw5rEWqtAYhN/Yss5VTngZTivoWL4m/th/tWzWXgVk1+wtrhw01y2mPpsQUdTJLtGQPTPNftTFp1pBgx2sMfb5YwKmjjEYwAAPYYoKufzt/tJfDnXPA/7QB8B6v4hufF2qaa1tYLcuWdixRSIlByxIZse5r6n/4LNTRr40+FkEjhXTQ2Z4/4gplx0/A/lX1347/4J26J41/a0074yS63IkEV1Ff3GktECJJ48bCG9MgH8Kz/ANvv9gG//a18ReGvEega/baJrOl2hsJFvY2eKSLzC6Yx0ILv+YqbBzHoP7Nv7Vvwg1j4LeEY18f+HtJmtNMt7eW01TUoLWWNljCkFXYdxXjP/BT74mfDP4mfsp6pYaT4/wDDOsarZ6jbXtrZ6bq9vcTSOpZCAiOSflkbtXjGm/8ABE3W5ohJf/E6xt7lvvrFo/mp+GZBitKP/giTPn978VoNuOieH1HPb/lrRyivrc1/+CJuuao/hf4laJNFMuk293a3cDsD5fmurpIoPTIESEj3HrX6cV86/sYfsixfsjeD9a0VfEX/AAkkup3n2p7j7Ettt4wFwCSfxNfRVMG7u5+H/wC1dND8cP8AgpRFoSSm/s5NcsNHcwnzF8tGUOvGeAAc+mDX7c2VrHY2cFtEoSKFFjVR0AAwBX4kfBGzh1T/AIKqWkd3zH/wlWoSYJ/iSGZlP5gV+31MQUUUUAfit+07/wAE+PiLrH7WWqad4M8L6lf+HNcuReLrbWrmxtvNJMm+XG0EfWv1L/Zp/Zr8L/sz/Duy8O+H7OP7WUVr6/YZluZepJbrjJOB2r16igBF4/nS0UUAeD/Hr9in4WftA6fe/wBt+Hrey1qdCE1qxQR3EbcYbjhunesD9jX9iXQf2RtN177LqT67rWsSKJ9RlTYfJQsUQDtjcc+tfS9FACDpS0UUAFFFFABRUdxcRWsLyzyJDEg3NJIwVVHqSelc1oHxS8HeKtYm0rRvE+k6pqUIzJa2l4kki/gDQB1NFFFABRRXzx+13+2Z4V/ZT8MxvelNU8UXqn7Bo6PgvjGWduiryOuM9qAPe7u3uJWTyZfKAPzcdashTgZ5Nfil4m/4K3fHjXi17odtpmiWEbn5YNLFwCPR3cEDHtXpfwA/4LHeIZvEun6X8UdC0+50q5kSFtW0lGilhJOC7R5IYcjgAUAfcv7bvw5+I3xN+BeoaT8MdUfTvEazJP5cMohkuUXOY1kLAKT79cV+PHwp/ZB+OP7QHinXdOs4Eg1XSbk22qNr2seTLBJnkmPeZGX/AGgpU9jX7/abqEGrafbXtq/m21xGssb4I3KRkHn2rkLf4M+ErH4qXXxFttLWDxZd2a2FxeRyMoliByNy5wWHrilYrm0sfkvff8EfvjtZ2sjwa14PvXC5EcOqXayMfQbogufqa9n/AOCbf7Dfxb+APx21fxd4+0S20bT00mWwhYX8Fy1y8kkbZXypGK7RF/EB94Y71+nFLRYVyJQwOCvHJzn3r52/au/Yd8GftZNpl3rt9f6PrOnRtFb39iwbCE5wyNwefTHWvo6imFz8e/ih/wAEj/ir8O7621H4VeJk8RSK3GLhdNuohxzvLAH/AL67V58Pif8AtefsZ68ZPEa+ILjTIWAddXZr+zkH91ZgWHfqDX7f3VzFZwPNPKkMMYLNJIQFUDqSa/Pf9tj/AIKbeEvAtre+DPAtrYeMddLGK7mvYfNsYBj8nbk9OmKB7nffsf8A/BSfwh+0NPpvhjxDGfDnj26LKlmEZrefaCco+MA8dDzX2fuFfjt/wTX/AGRvFPxB+Klj8ZddtI9G8N2dzJd2kfl7DcyknhF7ID3r9O/j1+0R4L/Zv8JQ+IfGmotZWc84toUhjaWWVyMnai8nA6ntkUBY9Opa4b4P/Gbwl8cvB9t4l8H6oupabcDPIKSRn0dDyp9jXc0EiUjBWxkZpk0yQgFzjNOBzzQAybaUwwwKSHbs+WnsoYYNCqFGAKB9D8Dv+CoikftqeOc947Q/+S0VfsX+xa/mfsr/AAxP/UDth/44K/Hv/gp9Cb79tTxisZxvjtEH1EEa/wA6/aP9mvwjc+A/gJ4D0G8KG6sdIt4pfLbcu4IM4NAM9LooooENdxGpY9BUNtex3W7YG+X+8MVM1eX/ABs/aU+HP7PFnYz+O/EUOi/bmK28PlvJJJjqQqgnAz1oGeo5pa5P4Y/FLwv8YfCdt4l8IatHrOi3BIjuo0ZQSOoIYAgj6V1lAgppB3Zp1fH/AO2V/wAFGPC/7K+rWvh3T9KXxj4rlRnnsorxYI7McbfNbDctk8AcYoA+vo1Krg1/Pt/wUe3f8NjfEcsMf6SoHI6bEr6usP8AguBftcRrefCW3WIsA7Q66SQM9RmDB496+Ff2pvjPZ/tBfG7xN450/TZtIttSKstrcuHdcBRyRx2oA/oA/ZwV4/gF8PVkOWGhWecf9cVr0evOf2cZBN8A/h64OQdDs/8A0UteikkYwM0ALXEfEn42eBvhDZi68YeJ9P0KNvurdThWb6L1NeM/t1ftlWv7JHgfTpbfTzqviXWzJFp0BI8tCgXLyc5x8w6V+Tvwj+Hvjz/gop+0JdDW9bltjMkl3c6hLG8kFuikDy0HQE54HtQB+yfhP9tD4L+N9UtNO0bx/pN3eXT7IYhMAWY9BzXtSsHUMDkHkEd6/Db9sD/gnV4k/ZS0Cy8Y6JrzeINChlUTXccJhms5Mjaxx2J9+1fop/wTU/aEufjp8A4odXvftniDQJvsF1IzZeVQAUk9cEcc+lAH1vRRRQAUUUUAFFIzbVzjNIrblzjFADqKKKACiiigAorO8Q+ItM8J6PdarrF9Bp2nWyF5rm4cIiAepNfK7f8ABVD9nuHUryzl8S30ZtpPLM39nu0cnOMoVzkUAfXNFeT/AA9/at+EXxSW1Xw18QNDvri5IEVo92sM7N/d8t8Nn8K9X9MdKAForG1vxloHhl1TV9c07S3YZVb27jhJHsGIrlNU/aM+FeikC/8AiP4Vs92QPO1i3XOOuMvQB6JRXjGrftmfA3RQhuPip4WbfnAt9TimPHrsJxXn/iv/AIKa/s8+FYyT45j1WUZ/dabayznj3C4/WgD6nor4f8K/8FdPg34s8Z2OgQaf4itUvJ0t4tQubRFh3scDOHLAfUV9uwyrPEkiHcjgMD6g0APooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0ZoAWikzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTVXaSadRQAUUUUAFFJmjt6UALRUaLtZiTnNK0gXrgD3NZvcYSOFxk4zSNzXIfET4seEvhlotxqviPWrLT7a3QyETTqHbHZVzya+JNc/4LN/DXS9auLWz8J6/qllGxVbq3ES78d8Mw4qS1F2ufoMfMKtjCnHFfFX7dX7SPxP8Ag9ov2LwX4W1G7nljMj61FEXitQPUAc55/KvJr7/gtfob3JGmfDm+ltlBLPd3qRsPThQ3X619mfs0fHLT/wBqr4RWni59Dk0uG6Z4JtOusSKcHHcfMKFaTsXF8utj8yvg/wD8FeviX4T1J4PHWn2vimwO1d8KfZ5ocE7jjndnj06V+jP7P37c3wt/aEhgg0bW47LW3QNJpd4fLkU+gz1qD4ufsc/APWNJv9Y8R+DtI0tI43klvIT9mxxySRxn8K/En4oafoXhn4yz2fwrvLyW2S62Wc1vIWbdnGFI5Ip3a0JSUtT+kGORZFDKQynkEHINOrg/gXa39j8IfCUOpvLJqC6bD57Tff37BnNd1uq46ohqzHUUgNLVEhRRRQAUUhbFAYGgBaKKKACiiigBO4r5d/4KPfEm3+Hv7Lfigs6i71BVsoVYE5L9eh7CvqJuBmvz6/4K8akJfgXaWzDa39qQc98ENn+VRLYuKb1PNf8Agif4J+X4i+LpCSZDb6dEOMfLudj0/wBod+1fpZ490G+8TeFdS07T702Vxc20kKuOOWXA57V8X/8ABHPS47f9mvVb0KRNd61MXb12gKP5V957aLKQSep+Inij/gln+0RJr2p3NvZ2N9HJLJIl1/bC+Y654zz1x2xXyH8Sfh/rPws8Zap4U8SWwttZ0+Ux3Cbw204HcDmv6d9tfCn7SH/BLPQv2hPjFdeOT41vNF/tCVXv7IWay7wMAiNsjaeOpDVRNzx79lf/AIJSeBvGXgXwv428T+LtQ1VdQhivktNKCwxq2d21mYNkdAeB0NfRX/BSfwwsf7IGraRpWnyTJbGERrGpby409cfzr6X+Fvw00j4RfD/RfCGhmdtL0q3W3ha4cNIQO7EADP4V0l3Y29/ayW1zDHcW8i7XilUMrD0IPWlZjTPwK/4J4/Aq++L37THhr7Tp8z6JpDf2jdyyxHy/3eNqk+7EflX79JGsaKijaqjAA7Csrw/4P0PwrG6aNpFlpav977JAsefrgVr496VmJsiuLeK5haKaNZonGGjkUMpHoQapaV4d0vQtw07TbSw3fe+zQrHn64FaWKNtUhDaKdtpAKYH51f8Fm/EFpH8IPBmkmQNcTa0ZvLHUBI+f/Q69H/4JM+Hl0j9krTroxbX1C/ubgt/eG8qD+Sivmz/AILSatp/9ueAdNtp9+qR/aZ54M/dV1jVTj3wa+7f2H/Bv/CCfsueAdKKGNv7PWdgTnmT5z/OoWruavRG7+1D8PPE/wAT/g1rnh/whfrp2uXUe2GWRyq+4JFfj18R/wDgmz8a/h74P1jxP4gm0v8AszTYmubiY37OxA9iK/d3vXPfELwHo3xN8Hap4Y8QWxu9H1KEwXESsVYqfQjkGnbqRfofz3/su/sp+Mv2p/Emr6Z4RmsbU6XFHLdTXczIqK5YLjaMnJU19HN/wR1+NEl0Q+t+Gnjz/rGupT+myv03/Zt/ZF8A/stw6yngy0uYpNVZTcTXU7SsVUnaoJPQZP517W3Q4644qvUL22P5n/FGmeI/2f8A4mazo0WqLb6tpkj2s01ixCt2IHsa/Vj/AIJN/s4f8Ir8M9Y+IHiOz83VvFJCRpeR7itupbnn+8WOfXFexfGf/gnT8J/jl8TLTxprNne2l8JPMvbexmMUd4eMb/TGP4cE5r6a0TR7Pw/pNpplhAttZWkSwwxL0VFGAPyoslqhNn50ftj/APBKiDx5q0/iv4SNa6NqExaW80K4YrbzScYaLqEJ5yDx0r8v/it8I/Gvwb1htD8Z6FfaNdJuSJZ1YwvyCTG3Q/ge9f0yVzXjj4Z+FfiVYx2fijQbHW7eNt8a3kIfY2Qcqeo6DpU2K5jk/wBl5J4/2e/h+lwnlyro1spXOekYr1KoLKyg020htbWFLe3hQJHFGMKqgYAA9KnpokKKT0rM8TeI7Hwlod7rGpzpbafZxNNNM5wFUDNFxEmva/p3hjS7jUtWvYNPsLdS8txcOERQO5Jr40+KH/BWr4OfD/XX0vS49U8XSRMVluNKiXyVx6MzDPfp6V8GftsftseJf2rvGkHhLwet5F4Yhna3trC35a+kYgZbAyRwOM96+mP2Vf8AgkX4aj8N6dr3xea6v9WnUSnQLeXyoYlPQSMvzE+wIpjasdLH/wAFpPhs0oB8FeJvL7sFhyPw3179+zn+358Lf2ltYfR9Au7rS9aVN62OqxiJ5fUIckMR7GsfVv8AgmL+zveaTc2tn4Ej024lQql5Fe3DvEexAeQjj3FflH+1p+zlrf7EvxmsBompXosGK3el6uvyPuBBIyO44yKASuf0A3VpDfW7w3EUc8LjDRyKGVh6EHrXhnxC/YZ+CHxMvnvdZ8Bael84w1xY7rZj+CEL+leh/BXxYfHXwl8Ja+0/2h9Q0yCd5T1ZigyfzrtqAPjPU/8Agkx+z/qDhhpmtWg/u22pFR+qmqK/8Eh/2f8AkG38SMf9rVzx/wCOV9s0bRQF2fG3g/8A4JS/A7wb4t0zXrS11a7lsJhOltfXnnROwORuGBnBr7HhhS3hSKJFjjQBVVRgADoBTqWgQUUUUAeIftafsv6P+1V8O4PDWp3r6XNbXIube/ijDvEf4gM+oA/KvhzVv+CJ1xNcSHT/AIoJHC55W60ze2B0wQ4r9UqaxVVLMQABkk9qB3Pxi8cf8Enfjb8PGS88G6/Z+IvLJYfZbh7WZdvIIDEjP0NZ/wADP+Cgnxx/Z98bR+BfGcF34sVLuOxOla0c3cLFtuEl6nr0ORwK+0v23v8Agox4b+BGj3PhvwTf2mueO5t0LGNt8On8D53I4Y8nAB7V8p/sE/s5eO/2kvjtbfGb4k28+o+HbWVrmO81Rc/2hOMhNqt1VTznGOBQPm7n6+aPeS6hpdpdT27Wk00SyPAxBMZIyVJHpV2kVQihVGABgAUtBIUUUUAFFFFADWbFVZJ3WUDHFWXYDAPfpUDRFpie2OKlouNuo+GQyKc1/Nx420c6h+0tqumQ/KJvE7Qpt4xm4xX9I6RjauexzX84vj5W0f8Aas1XDEND4qLAg8j/AEgUrFddD+i7wzZjT/D2m2oYsIbaNMnqcKBWnVHRW36RZN13QRn/AMdFXqoyCikam5pgPpKbk1Wubpo8gCpuUouWiHTyB+B2rK1CQpHnNZ+sa9Jp8RcRl8ntVb+0v7YsyJoGRWHBHrUOp0sdcYcq1N3TbrzliA6hufyNfz3/ALYzhv2qviIQMD+2JOB/viv6D/D0Jjt1V4yjIOM9wa/A79v7Rf7B/bB+IMAGEkvBOv8AwLaaUXcxk7s/eT4WnPw48Mn/AKh1v/6LFdMn3jXIfBtt3wp8In10u3/9FiuyrVbGLGOu5kPpQzHzFA/GmXDOqgqM+tRopuMmQfLjGPrTC3UsrnHPWlr8nP2oP27vi14W/bAvfA/gbxHDZaNBqFvpyWsltG6MxKhySw9zX6raK1y2j2RvJFluzChldBgM2BkgfWgRdooooAKKa1Qt5uTjBHapuOxM1QSSHIwdo71GIJmYktxTms2YYLcHrWb1LVluQ3cnnRFIzuJ6n0pkMLQ5Hm7zjp6VY+wiNcRttb1qG1094yxlbcxNTaXQ0UlYIw37zNWbf7tPCbelOWp5X1Ik7jlp1Qp95qlB4rSPYzZ+Ln7bzfYf+CpmgzDp/a3h9z7f8e/+FftGrblBHQ81+K37edvJcf8ABTK2giO2aa70PYffyoq/aOyVks4Fb7wjUH8q2ET0UUUAFFFFABRRRQAUUUUAFFFFAH4ifBb9z/wVYtM8Y8T34P4wy1+3dfiJ4Ojk8O/8FXoI7hGhP/CVXGRINpG+OTB59civ27oAKKKKACiiigAooooAKKKKACiivz9/4KNftgfFv9m3xl4cj8IaVFa+GXjLy6lcW5lju5eMxE/wbRj67qAP0Ab3OKQFVxz14FfFv7Gv/BSHw7+0heW/hfxBbJ4b8YtGPLQv+5u25yI89+M4969c/bT+PJ/Z3+AGv+JrZ4/7YkQWlgjnGZn4BA74GTQM+Af+Cl37a2u+MPHEnwv+G+r3D6PahoNSfSdxkupjgNEcDOFIxx610H/BI39m3xDo/jrxH4+8ZeGNT0g29pFFo9xfIYvNZy/nEqTknATqO9R/8Ep/2XY/Hmq6l8bPGMEl1P8AamXS1m+7JKSTJMR3GSAPcGv1aVQihVAUDoAKAYtFFISFBJOAKBHlv7Snx90X9m/4Val4w1n94YyILO1X71xcMDsQccdCSenFfkF+z/8ACHxp/wAFC/2jrzxP4wF1e+Gornz9VvBKBHDHk+XbpnGehHy5x3rtP29Pjpqn7YX7Rmi/CXwb5k+i6XqP2CHyT/x8XDECWYg4+VQvGfQ+tfqd+zl8CdE/Z3+FOjeDtFTK2sYNxcMoDzynlmYj3oA2vCPwb8E+BPDceg6L4Z02y0tYxEYFtlIcAfxZHzfjX5af8Fe/gd4Q+G/iTwJ4m8MaXb6PeawbiG6t7ONY4j5RjKuFAABO8/lX6+tX5Cf8FX/EU3jz9qTwD4Ht7hZ7eyjt42hBxslnlGQc8crtoGtT9S/g1I83wn8IPJ99tKty2fXyxXZVkeEdJTQvC+k6dGMJa2sUIH+6oFa9AgooooAK89+P/jzV/hj8H/FHijQdL/tjV9Ns3mt7TkhmHcgdQOtehU2SNZEZHUOjDBVhkEehoA/nv+JX7Wn7QH7RF1Jpt7retT2945jGj6NbNFEc/wAGEGW/GrXh/wD4Jx/tC+IrCO8h8A3cMcuJFF5PHA/PchiDX766T4Y0bQWdtM0mx05nOWNpbJEWPqdoGa06B3Pwab4Dftg+C4YtBtdF+ICWdou2KHR7qYwIPYxnFVx+x3+1R8aby3sdb8NeKphbEvC/im8dYkLcEqZTgHgZx7V+9tNZQ2M0D5mfN37Bf7OE37OXwQsNK1nRoNK8X3JZtWaC5E6ysGO0hgcYwe3rX0nSUtBJHLGsmNyhsetfFP7fv7e9r+zlpp8J+FGF148ukDZ2bo7RD0JP94+lfW3xG8baf8N/A+t+J9VmWCw0u0kupGb/AGVyB9ScD8a/FH9ln4Rah+3F+1bq3iPxB5174ehu31HUJpCSAhYmOIH8OlBSNnRfCv7aPxY0k+MdOu/E8ttcZmi8u6EAdTzlUJ6V1HwH/wCCjHxS/Zv8ZXPhb43WmpanZKFjaO9TF1a4JJYf3sg+vav2F0jTLbRdNtrCyhW3tLaNYookGAqgYAFea/HH9mX4f/tBaLJZeLNBtrqfafKvlQLNGxHUMOTQFz8Nv2pvino/7RH7Umo+J/C0c0enazdW8dt9sXY5OUXLDJxyK/oJ8J2z2fhfSIJMeZHaRI2OmQgr+cvXvh8vw5/aXbwpby+dHpniKK1jYnqomAFf0f6QCuk2QPXyE/8AQRQSWicUbq8x/aWu/G1j8FfE0/w8ilm8XLbk2SQhS5bPO3JAzivxzs/2nP2rvghrk2v+IbnxhDF5wFxDr1pK1lJg8gbl2j/gNA0rn7rySLGpZjtUclicAD1NfiJ+0ZL4n/by/bg1Dwr4RnhWCxd9Psri4ZvIhgiyHlbaG6kn68V9L/Fr/gqR4e8Rfslz3+hh7Tx5rMb6W9lgD7MxXEk33s7cE7T+la//AASD+BEXhv4a6r8TdSt92seIpTDazPyfsysTnkcFmJ6dQBSKWh9W/sm/s/r+zT8GNJ8EnU/7XuLctLPdBNqtI5ywUegNeyU1adTIPPvj38XtM+BXwl8ReNNVcLDptszRRkgGWYjEaDJHJbFfh/8AsyfBfXv24v2k7yXVZTJYvdHVtbupixKxF+IweeTyAPrX2x/wWW+NVrpvgfw38NLWYvfahcjUr6MY+WJOIx1zkkt27V61/wAEu/2d1+EHwIt/EWpWqxeI/E/+lzSc7hBkmJTkDnB/WgD0Txx+wH8E/F/gSTw7H4F0vTHWErb3tnF5UySbcBiw5POOua/B/wCM3w1vvg38S/Eng7URm40u5kt1YA/MoYFWBIHBFf011+I3/BX7QrPTP2o4rm3RInvNIilmCjq/Iyfc4oA/VX9jvUf7U/Zh+G1xz82i2459kAr2SvBP2EZGk/ZL+GxYEEaVGOfYV7tdXCWlrNPIcJEhdj7AZNAH4af8FLvjNJ8cP2mToGmCVbXQnXSYIpMHMxbDuuCeCcflX6wfshfs/wCifAL4NeH9KsbKFNUktElvrxU/eSyMNxyeuMmvwx8VfEyGx/ac1bxm2nDUY4fEEt79nbkuiydPTPFfsD8Jv+Cn/wADPHug276h4hPhLUEjUSWWsRmPB6YVxlW6djQB7d+034DtviX8A/HPh+5jSQXGlzvH5g4WRELqfzWvyx/4I7eOrnwv+0N4g8I/M9trOmu7qD8qPbvgHHqd5r9BfHH7eXwHHhHV41+IelXTzWc0axwSb2YlCAMD61+eX/BJjw3N4j/a217xFZYbTbCwuCzEEcSyDbj/AL5NAH7SUtFFABRSE4r4m/4KPftWeP8A4Aad4e0rwBpd19v1MSPPqYszNGijACrj+LqT9RQB9tUxpEiXLMqD/aOK/Cuz+Pn7YfxVnmi0jUPGF6ZANyWlsYkAPTqBitLT/wBkX9sbx8XuL6PXIC3zbtS1gx7s+gDGgD9sNQ8WaJpChr7WdPslPQ3F0kYP5msTT/jF4G1bWItJsvF2jXepSnEdrDexvIx9AAea/HKb/gmH+0vrkZN41mxHOLnWpG/oa9N/ZQ/4Jp/Fv4efH7wt4n8ZQ6ba6LpM/wBqeS3v2mdmA+UYwO5oA/XCiiigDmfiR8O9F+K3gvVPC3iG3+1aTqMRimQHDY9Qexr4c8Uf8EY/hpeWcy+HvGfijRbpiTF9okhuYIyf9jYrH/vqv0JooA/HL4rf8Eg/H/wz0OTX/Bfja38VahZlrh4xYnTpo1UZDRsJX3N1446V7D/wTB/bS8U+PPEM3wn8d3E2p39ratJp+ozqTNmNiJI5GJ+bAK4PHev0a8RalbaPoV/fXzpHY29vJLO8hwFjVSWP5V+K3/BPfT4fGv7fU2o6VcXNrpkLX9/G0R4dN+Ap6YB3fpQUjt/2qf8Agnf+0j8SvjJrGuWT23jDTdQu5Hguf7WjtxbRE/KrRyupHH93d07V5L8Xv+CZ/wARPgF8GdU+IHirV9FxZ+Xv02xJuJBuYL8zsAo6/wAOa/dvJBr4A/4LKeNpdD+A/hvw/FcPF/beqnzEQ/6xIlBII+rD8qCT5N/Y1/4Jz+HP2tfhw/i3/hY9zpL2t21pdabDoqMY3ADY8zzhnII/hrnf28P2KfC37Ho8F/2b4iv9dOuSzC7+0wCMwxx7MMm1jknc3X0FfbH/AARl0P8As39nDxBe5Y/2hr0kuGHTbGifj92vAP8AgtV4knm+K3gbRHIW0t9HkuU9d7yMD+iigD2/9lP/AIJy/A3xR4M8GfEiy1HxFrNxIsV9Gs92iweapzgoI84B/wBqv0Khj8lAgPyjhRjoPSvnr/gnzAtv+yH8OgqeWGsA236kmvomgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBuKNtfKt5/wUa+Gdv4guNHTTvExurcMZGk0somB6HdzXikn/BZnwV/wmr6XH4I1g6Rv8ldQknjWTfnGTHzgfjWMa0XomdEqFSHxKx+ih+WlVs1+d3j/APbl+OXxOt7i0+EHwd1JLXGV1e7PmFvQquAMfjX1t+zB4s+IHjD4T6Zf/EvQxoPinJSe3A27gOjEdia1jJSV0KdGUFdnrtFJS0zAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBK+UP+CgX7R3j79nzwDpdz4B0Vr/U9Qmkje7FubgWwVVIJQKRzuPX0r6vIpNoPUZqWrjTsz8I779un9rDxxMlvZavrAnzjytJ0bY3PriOrdn4Z/ba+L8jqrfEKcKAxNzcPYx4b03FAelfueI1T7qhfoKdtqeVluVz+ff4ofsa/tCeGtLuNd8eaJfPZQo0r3GoamlxjAycYkPNZH7Gn7Lk/7VPxSHhyS/fS9Ito/OvbmIBnjXsFUnuRX66f8FH7qy/4Zn8SCWULPHESm0884GPxr50/4Is+EdMXwn458Q+Vu1U3kdn5h/hjCbsD8TUpvmsXb3T2jwL/AMEm/gT4NkgnvbLVvElzGVYnUrweUSP9hFHB9CTXV/tQftKeG/2Jfh3Z22i+E3LSL5Vha2MAS3UgD7zDp1FfUeOawvF/gHw94+08WPiLR7TWbRTkRXcQcA+o9KuSfQzT6M/n8/aE/bU+Jv7Q8rLretyWOjrI3k6XZsUQAgcNj73Qdad+xv8AHDwV8AfiBceJfGPg248WSJGoslgdMQPk5chj1xiv2nvP2GPgbfNOZPh1pIMxyxVGGPpzxXKXn/BNH9n28Lk+Cli3dfKuXH9aOXSxV4nz7ff8FpPCCQ7dN+HmtSSgcLNPEqn6YNfV/wCyn+1t4Y/at8KXOp6HBNp9/ZkLeWFxgtETnHI6jg1xUf8AwTE/Z8jheP8A4Q5iG/iN2+R9K9k+C37PXgT9n7RZ9M8EaLHpUE7bpn3FpJD23MetGt9Cbo9GWnU37tDMR0GRVkDqKimuY7eN5JXWKNBlndgAPqa4/VvjV4B0OTy7/wAZ6Dayf3X1CLP5bqVx2O1ory+6/ae+E9ljzviH4eTPT/T0P8jUMP7VXwhuJBHH8RfD7OegF6tLmQWZ6tRVDQ9e0/xLpsOo6VewajYzDdHcW0gdHHsRV+mncQUUUUwGt92vzS/4LLeKLex8D+FdFWBjNeXhlkkHHCL8oH/fVfpa/wB09jX5b/8ABY+BLnQPC0sl0rXMFyQEXjhhj+lZya0RtDZn0F/wSh0MaT+yPo8+STe3lxOQe3zkf0r7Ir43/wCCUWqS6h+yTo8UgULa3c8KFQckbj15r7Iqo7GT3CkpaKoQUUUUAFFFFABRRRQAUg+7RSZ4FID8V/8AgsBpd5aftCaZdTuogfTFMBHXhu9fqv8Asu6l/a37Pfw/ufMEhfRrfLAY52CvzI/4LNa9YzfFnwppUcH+lw6c0ktx/eVmwB+GK/RP9hy4kuP2U/h1JJ97+y4xwMVEXZG0tj3UfeNLSL9406tDETaN2cc0MobrS0UAFFFFABRRRQAUUUUAJ3FfBv8AwVs+OTfD34OWHg6xl8vU/E0hTKtgpCp+Yn2OcV95NX4of8FhPHkHib9o7TdHtpS/9h6UttKp52uzlzgevNQ9yo7nqn/BIH9me01WTU/izrtmlx9mk+yaOrgnY4z5kmOhzwAT6V+rQzn8K/Nf9jH/AIKGfAj4U/Azw54M1nUL/wAP3+mWwE7S2MkiSyEncQ0YOfXmvoGL/gp1+znIpI8egezafcg/rHVIJbn1O1flN/wWy8RWVxffDrRUZWvrZLm5kXPKq+wL/wCgmvpjxT/wVU+AWj6Tcz6f4ln1a9WNjDbw2Mw3sBwCSoA5r8xdSb4mf8FFv2hn1G006S6DSJEGCYhsrTdwCcemetMSP2Q/YrsJ9N/Za+HEFwCJBpEJ59CMivbawvAvheDwV4N0TQbZQkOnWcVsqr0+VQK3aACiiigQUUUUAFFFFAH5z/tYf8FUdX+BPxi1bwT4c8I6fqcelkRz3epSyKWcjnaFI4+tfIfx2/4KlfF34xeHm0Wza18G6dIT57aGZFmmQ/wGRjkD6etfrt4//ZJ+EHxQ8QS654m8AaNq2rzHM15PbgyS+m496p6f+xX8CtMwbf4VeF0YfxHT0J/UUAfz+fDTxP4c0Tx7Zax420m48T6ZHMJprETbTOc5wxIOc1+rvgX/AIK9fBzRdFstJHgzXdAtLSJYo7SzijlSJQMADBXivrfVP2TfgzrSqt/8MfC92q9BNpkTf0rh/Gn/AATv+AXjTT2tZPh7pukAncJNHj+yOD9Uxn8aAOE03/grR8Ab541n1DXNOVuDJdaYdi/UqxP6V9QfDP4p+F/jD4Vt/EfhDVY9Y0efhLiNGQZ7jDAHNfCnjb/gi38PdXuml8N+L9Y0CIn/AFMypdKPoWwf1r7g+C/wssPgv8NNC8H6dJ58GmW6wm48tUMzDq5A7mgDt6KKKACikam5oAZdTQ2sLTTyJFFGCzSSMFCj1Jrx/Wf2xPgp4f1h9Kvvib4bh1BG2NB/aEbFT6HB4r88P+Cj/wC0z4r+Mvxei+B/gG5mfT47hLW5hsSQ97cMcFGI/hX0rrPhb/wRdsLrw3DP488aXVvrEqBzZ6VCpSHPYs3U/Sgq3c/R7w38SvCnjWOKXQfEWm6vGRu3WV5HJge4Br+fr41Ko/a614ADyz4pzwOP9cK+99b/AOCNU2hyLc+Bfitf6bdAk7rmAxMOOMNE2a+BvA/w7uND/ay0Pwbq93Hqt3beJIba5uslxMwlG4nd1zjvSKR/RBofzaHp3Ug28fT/AHRVfVvGOh+H7y3tdT1ezsLm4IWGG4nVGkJOBtBOTWpbwi3gjiUYVFCjHoBivw7/AG+PiFf6x+3hNJ5zyR6HqVnaW6FiVGGXOB260rk2P3IJyARyK8e/ao/aH079mX4UXnjK+s21F43WG3s1bb5rt2z2r1PQZTPoenSN957eNj+Kivz3/wCC1Vxfw/BvwPFbswsJNWm+1KDjJEa7M/iTRzCW59CfsX/tl6T+1v4a1OePTv7E17SpAt3p2/eFRs7HB98H8q+i7lo9pDDJNflr/wAES9Nh874makWLXLLa2x9No3MD9ck1+pN0wVRxyaVr6l6JmfeRwPGi+UWYHjAz+dcZ8Wvix4T+Bfgq48R+Lb23sraJGaKBnCyTsBnagPU816AzJb2rzSsscSqWdm6BQMk1+KX7XHjzWv25P2t7XwL4OmM+l2kxsLI7j5YxxJKR+H6UcpblfRHdfED/AILLeM5PEFwfBvhnS7XRVfbD9vDPK4Hc46V8VfH3476v+0F8RrnxnrVnZ2upXCqHSzUqvy9zX7UfB/8A4J9/DT4S/C290aTQLXXddvbBoby+ukDtJJtP3M/d5Pavw5+JHhG88CfEHXdBvbKTT5LK6kjW3lHKrv4+tOxCP6I/2YdUfWf2f/Ad3Ihjd9Jt8g+yAV6hXnn7P2P+FI+BtoAH9kW/A/3BX5a/8FR/i58SfBH7T2lJa67cadpunW0d5pMMLlUB/iJA6kkd6ZO7P2KkXdiqmralBoulXmoXLbLa1heeRvRVBJ/QV5F+x38a2+PvwB8MeK7l1fU5YPJvdoxiZeG/PrXPft8fGyx+Cf7N/iW6ny+o6xA+l2EQ6tJIME/gCTTF5H5m/sy+FLP9qz/goVqer3Ku2jw6jca42043eVIPLB9s4/Kv29VQqhQMADAr81/+CNPwim0rwT4r+Id/C27VrhbCydh1iiJLH/vtiPwr9J1/XrQDHUUUUCM3xFqDaRol9fpbvdvaQSTrBG2GkKqTtH1xX4/fEH/grv8AGCTxFfQ+H/DWh6HaQzPEI7i1kmnOCR853AZ+gr9kmGevTuMVUXSrOO489LWFZv76oAamxSZ+LGkf8FLv2o/Hdy1j4fs4Lq84Ij03QjMwz7ZOK10/aS/bp1SdzHp3i2Ju62vhSMj/AMejr9mh15xmlo5Quux+M918X/27ryAhrXx4kZ5Zv+EXhjx9D5dfUP8AwTzj/aT17xLq2v8Axc1TVI/DPkNFb2Gr2yxyyyluGUAAqBg/nX3xSHpT2QhvHTPNFI3Sq8kjRyLjoTzWDlqOxYbPamwr8vzcnNRvPHHk5570lreLcSMq/wANEZahy6H41ft2fL/wVE8Ont9v0An8DFX7QV+LH7eTFf8AgppoLZwBf6Gf/Ho6/aeugkKKKKACiiigAooooAKKKKACiiigD8ZPF0KTf8Fcl8ohwPESklTkA+XyK/ZuvxP+LV1L8M/+Cpp1C5z5beI4JfnGCUmAAI9ua/a5WDqGU5DDIoAdRRRQAUUUUAFFFFABRRRQAlcz8Qfhr4a+Knhu60HxTpFvq+l3K7XhuEz+IPY/SunooA/HP9tD/gnVq37PH2z4n/DDUpIvDul7bmSFpStxZndjKkdVBIrwv4uftMePv20bz4aeBZ4WkktzHaJDCebqckK0jepwP0r9uf2jtDs/EfwH8e6ffhTay6Nclt3TKxlh+oFfjX/wS08MaVrv7XuhjUTHItjZXN1bK/I84ABQPflqC1sftX8I/ANh8L/hzoHhjTrZLW30+0jiKIoGWCjcT7k5rsKatOoICvD/ANtH4vR/BP8AZx8YeIRP5F61q1nZsOvnSAquPoMn8K9wr83v+C12tXdn8Lfh5p0MxS1vdVuDPHnh9kSlc/iTQB4F/wAEfvC9r4u/aO8QeIb+IXl3pWmNIkz84klfBfnvwRX7O5Ffzl/AX/hefw61D/hLPhhoPiiP7RGFN1pWmTzRTKCeDtQhhnNfRiftZ/txXOLeLQvFoZjtH/FIOP8Ax8w8UFWP2I8eePND+G/he+8QeIdQi07TLKJpZZpSegHQAZJPsBX48fBfw/qX7dX7el745S0dPDWm36X9xMGG2OJGIhXBOTkr26d6ms/2Wf2uf2sPE1jH8SbjWtJ0Ine11rF0ixRK33gsCvkEgdNtfqh+z7+z34U/Zz8BWfhvwxYRQbEBurvb+9uZO7Mep5oHsenRqsahR0AwKfkVDLII1/2j0p0ZLKCRg1LYrElLTVp1NEhRRRTAKKKKACiiigAooooA+Bv+Cvnxrj8DfA/T/Bdv8194muP3m1sFIY8E5+pOPwrr/wDglj8Hm+Gf7M9jqV1Ei6h4imbUHYD5vLPCKT9K+Mv+CzHnp+0F4ZE0rNaNoqvHGT8qkSEE+1fqj+zo1i3wK8CnTWRrL+yLfyynT7g/rQO56Iq7Sfem3Ewt7eSVvuxqWP0AzUlY3jLVrbQvCes6heTLb2ttaSySSOcBQENAj+fVrwfET9taOeHkaj4uBTzOOBPxn8q/odtIzDawxnqiKv5Cv53P2dox4l/bC8HvanzBJ4k89T2K+azZ/Kv6KaAEIzWN4s8H6T440C90bWrKG/0+8iaGWGZAwIYYJ571tVy3xS8aWfw7+HPiPxJfyNFa6bYy3DMoBbhTjGT1zigD+cj4r+B7bw78afEfhPSXM1tb6vJYWo9MyYX+df0R/ArwPF8Ofg/4Q8OQxxxrp+mwxMI+hbYMn86/B/8AZb0Ob41ftieF2kia7W91ttRuFcdUDF8n9K/objjWONUUYVRgD0FA7igYpaKx/GWqDRPCOtagSVFrZTTZXr8qE/0oEfir8ctUh/aw/wCCjlvormZdJXV49MVXUZEUP3s4J4JB/Ov230nS7fRNLtNPtIxFbWsSwxoowAqjAr8Uv+CY/k+Mv27bnUr6NbmZrTUb5XkGSsgdcH64Y1+3FABX4U/8FYtZfWv2tNVg37hY2MMOD2AGcfrX7qswVSScAckmv51/23fHEfj/APai+IWrQ7mg+2vAjHHRCF4wenFAH7p/sqaGnh39nP4e2CbT5ej2+SvTJQE1oftGa/N4X+A/jzVbdzHPa6PcOjDsdhA/nVX9mHVYNa/Z7+H93bNuik0e3x+CAEVz/wC23dPafsp/EuSMMW/slx8vXBIFAH5Qf8E2P2dfB37TfxK8ZWPjvTrjVLO1sY7mOSC4aIxyO7ZJI6//AFq+vfEn/BGbwLqGoNJoXjrWNDs8nFrNZxXYGfQswxXEf8ETNBt7e3+JWohle5L29s3HIUAsP51+pNAH5V/Fr/gkL4a+Hvwz8S+Jz8StRupNJsZLtYpNLijV2UZAJD9+laf/AART8GiLTfiL4qZG3XM0Ngr4wpCbm4/76rtv+Csn7SzeD/Atn8MPD1yx13XWBvlhILJbngIec5Yn9K95/wCCffwTm+B/7NPh3TL2PytU1AHULtcYIaTkA+4GKAPpEZ70tFFACHP0qveabaakqrd2sN0q8gTRh8fTIqzRQBXtbC2sci3t4bdSMYiQL/KrFFFABRRUf2iITeUZUEuM7Nw3flQBJRRRQAUUV8Y/8FAv26NJ/Z78I33hXw7eJdfEG/i8uOKPDCzRhgu57HHQUAed/wDBUj9tSD4e+F7j4U+FZFudf1mArqN1G4ItYGx8gxnLNyCMgir3/BKH9lO5+F/gm7+I/iK1e21zxFGq2VvKPmgtOoJ92PPT0r51/YL/AGC/Efxn8a2XxT+JEE8XhqKcXkEOofNPqcuchuuVQHB5zmv2Ih8i0WK2j8uIKu2OJSBgDsBQO5KBivye/wCC23jS1n1j4c+F0Ob20iuL9yD0WTCAYx/sZ/Gv1ir8gP8AgpT8CPit8Vv2rrX+zPCuoatot1awW2nXdpAXiVeN5ZhwCDng0CPuD/gm74JTwX+yX4OTyWgnvojeSq3Xcx618D/8FqIy3x68IseFGgce/wC+ev1s+FfhuXwb8N/DOiTRLDNYWENu8a9FZUANfmz/AMFrvBM003w/8VR2ryQrHPYTTImQnIdSx7daAPuj9jOyTT/2X/hzCmAo0iE/L7rXtNfmh/wTx/4KEeD7PwFoPwx8cXJ0TV9PQW9pqFww+zzpngFv4SK/SHS9c0/XLVLnT763vrdxlZbeQOpH1BoAuSSLGjO7BVUZLHoBVTS9asNatzPp97BewgkF4JA4yOvSma9Hb3Gj3tvczJBBPC8TyOwAUFSCf1r8Nv2X/wBqLXv2bP2m7zSYtSm1HwhfazJY3Vm0hdMNKVV164POfegD92aKitp1ureKZPuSIHX6EZFS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGLqHhfTL6ZZJ9Pt5WwQWMSEkHqDkdK/Jr9rj4B+DvDf7cnhRYptP0zR9UmgnuNMtwd7Nu/u4xz9a/XxslcV+OP/BTqO78H/tgeE/EaqMFbd4xvBPyuM5Hasai093c6acm92fr9oOlWel6PZ2tjAkFpHEqxxooUBcccCtHbtrH8G6g2qeFdIu2G0z2kUmPqgNbPNapuxhK93cRadSc0tMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0E0AB7UkjbVJwT9KTJPal59KNhnxL/AMFThHZ/s4avcImyaUqh+bqMjtXln/BFa83eC/iBb4OBfxSfmmP6V3v/AAVU8y4+BuqRIJWbKZ2rlcA/pXJ/8EW7VR8KfGd35TB5NSVTJt4OE6ZrH7VzeT0P0d/ipabz1pc1sc4tFJS0AFFFFABUcu7bhfSnkUjcc5x60AfD37aXw4/aQ+MH2nQPAs9jpPhtIsv9nnMct3njazV8QeG/+CUHx88RXS/2qNL0pWPzTXd4ZT9eBX7fvIkaF3YIgGSzHAFZk3irRLeTZLrFhE/Xa90gP86iW5o5cz2PyVj/AOCLPj+Tbv8AH2hx5+9/ocjY/wDHq2LT/giT4jZozc/FPTohn51h0l8474PmV+p7+MvD8Slm1zTVUdSbuMD+dchrn7R/wv8ADbOmo+O9CtnT7y/bUYj8iaNEtSbsl+AfwftPgR8K9E8F2d5JqEWmxbDdSKFaQ9zivQ65/wAE+PPD/wARtFTV/Deq2+sac52rc2rblJHaugqlZrQQUUUUxCN0r82v+CyPhmK4+HXhrV0ixLBfrG7L0YNnGfyr9I5H2gcE59K+Fv8AgrZpouP2cpZtjsYL+CYMBwACc59uaxnuma0+pqf8Ej2U/spwgNkrqdwCPT5q+2K/Pv8A4I2+Ko9R+BXiDRcYlsdVeU89nGa/QStI7ES3Ciq9/NNb2rvb2/2mUD5YtwXP4nivyN/a28bftW6p8ULu0uNfl8B6CbhhptraarDZq0fZmYMGc49TijmSHGLlqj9eqTd82McetfiY37RH7XP7M2k2Ov6xrMviHw9cHEVxqDJf27AdcshDD6k19qfsnf8ABTzwZ8bfs2g+L1h8I+LHIRFc4trpj3Rj0z6H86OZC5WfcFFMhlWaNXRg6MMhlOQRSMjtIDuHl45XHP51RI+lpAoWloAQ0xiQBTmphPTjPP5UmM/Gb/gsRp3nfGPw5qscUiW8mmmLcw4LK2Tj86/Tb9ja0jsf2YPh1FEMJ/ZEJ5Oeor84v+CzF7P/AMLG8H2JXbCtm8g9Mk4r9DP2GdUbV/2U/h5OzBiNNSPIHpxWK2NZnu6/eNOpgYbjzUGoXi2NnNcOzBIUaRioycAZNaJmRaor5Z+HX/BRz4QfEDxndeFm1O50HV4blrZU1SLy0lYNjhs/zr6ht7iO6hSWJ1licbldDkEeoNO6G4tEtFJzmjn1o5kSLRSUtUAUUUUANavwP/b2tYdc/bi8SW+oxS2lrdX9vC7q4Vgh2ruGRX73TAshA6npk4r8mv8AgsB+zxe2PiTR/inpNnmwmiFrqk8e4tHKD8kh54GOOKl73Lie+xf8Ei/gZr2k2FzBd+KdPaS2jZmtNTjKyMVBLHdE3X2wK47xD/wRT8CXjIdG+IfiDTeSWF3bx3OR6ZBTFd5/wS1/aaf4xfCGTwnrd8LjxL4axFmQ/PLbdEY/TpX2/k00S9z8/fDX/BGT4V2FuE1zxT4j1iUEHfbvHbA88gjD8GvsT4N/AfwR8A/DSaJ4K0ODSbXAEko+aaYju7nk/wAq72lyaYh1FcR4w+NHgvwBr+kaJr/iGz0/VtWlENnZySDzJWPYCu260ALRRRQAUUUUAFFFFABRRRQAUm0ZzjmlooAKKKKACiiigBrVzHxN8YW/gD4e+IfEd0xSDTbGW4ZgcdFOP1xXU18xf8FIPGEXg/8AZB8cs0hjl1CFLCIqcHc7DofoDQNbn57/APBMnwjP8a/2vtd8cXjG4i0jztSlNwPM3vM5CEk55HrX7RV+Yf8AwRN0eBtD+JWriKNZ2ube1LbRu2hN2M+me1fp9QOW5FNIIYnc9FUt+VfzxeFdTlvv2ztMvTK7PJ4w3b2Yk/8AHyR1+lfut+0n8TrT4P8AwT8WeKLqUQi1spFibOP3jAquPfJr8Df2Z7p9c/ak8C3Vz+9Nxr8crCQZyWctk0Dif0dr90fSvwV/aisSn/BQLWoJvnD+JrdiG5zl1NfvXX4g/wDBTSyuPhz+2s3iNbVBHMtpqMSgY8woRn8SRUtBE/bbSVC6XZgDAESAf98ivzP/AOC13jOFfDnw+8LRXC/aZLme9mgB5CbQqkj6g19c/C39sj4ceMPgnp/ji58RWGmQpag3VpPOolikVeU25znI4r8Y/wBt/wDaTf8Aaa+NF34ggg+zaXZL9isU3ZLRqfvfjU9QS1Pur/gibpoXwX8R74YGdRghx34iBr9LpIxJjPavzq/4It6zp8nwl8ZaXFEU1GHU1mmYj7ylMLzX6MN2q1sKT1PFf2zPHj/Df9mfx3rMJKzrp7wRspwQzjbn9a/OT/gjb8Nl8RfFjxb41vrVpX0iyWG0mY8edIx3/jgCvs3/AIKoXL2/7H/iJUJAlureI492rzr/AII16Kln8APEWo7R5t5rDAtjnCqBilfWw+lz2rxZ8SvjPoP7Uem6Dp3hNdV+Gl5BGJdQQYMD9WbP9K/Jj/goxqNjqf7X3jI2LKYYpUiYL/fAG79a/fDWNSi0fSry+mOIraF5nJ9FBJ/lX80vxs8WSeOfi14t8QHLf2jqU7oO+3eQP5UwR/RV8C1Efwa8FKOg0m2/9FivgH/gtV4CFx4c8A+LrezDSW9xNZXVyo+YRkBlB9sk19R/8E+/jNpHxc/Zx8NpYSf6ZolumnXcLH5lZBgH8asf8FB/hxH8S/2UvGlm2BPYQjUoWxyHiOf5E0xbM8p/4I/6t/aH7LssHOLTVJoxn86+Zf8Agq98bI/jN8WPCnwn8KFdTn0m4ZZVj73kuE2fgAKyv+Cfn7bHg/8AZ2+BfxA0DxBdTQ6r5rXmlIqZ852j27fY7uao/wDBMb4I3vx5/aP1j4m+IFkfT9BuGvszDImu5GJVf+Ag5oE9z9Pv2Qfg/N8C/wBn3wl4Su1C6hbWwkuwDnEr/Mwz9TXstFFAgooooAKZJIsYyxxXB/Gj43+D/gJ4TPiPxpqn9maaG2IVRneRvRVHU14Vpn/BUb9nXUpFQ+NZbP3udOuFH5hDU3HY+rPtiM2AcVIJAehzXzTN/wAFHP2d4irH4kWTKegW1nJ/9Aqjdf8ABTf9nGzxu+ICyZ4/c6ddP/KOp36jsfUytmlbpXyPe/8ABUj9naNFaLxzMeeQNIumJ/8AHBXb/Av9t74VftFeKrrw94L1a61DU7aD7Q6z2MsC7c44LgZ+lHSwWPfs7l45qtcMIwWPapooxGo2rsB52ioLiTZJym5e/tXPLQpGcrLPJvI+XPNXrONVuXKcLVO8WE7HWRtgPKrV7TxG37xCxU9mpU3dlP4T8ZP+ChDKv/BSfRCg48/RSx98pmv2mgYeTHz/AAj+Vfi1+3Cya5/wUm02G0dbgrdaXG3knf8AMCMjjuK/aG1Xy7WFT/Cij9K7DEsUU1adTAKKKKACiiigAooooAKKKKAPxS/bzUWf/BSCxkc7FNzpTlm4GMrzX7S2DBrG2IOQY1II+gr8ZP8AgpZAln+31o85YKskWluWJwOGAr9ldDYNomnsDkG3jII/3RQBeooooAKKKKACiiigAooooAKKKKAPKP2rPEUXhX9nP4h6pMwWODR58lunzDaP1Nfjp/wSw0241T9sfQJICf3Fpc3Eij+7tGf5iv1j/b4Xd+x78UxnH/Eob/0Na/PH/giv4fhvvjZ421WSEPLY6PGIZSPu75MNj6gCgdz9jFpaKKBCV+d3/BZ/wZqGufBvwbrltGr2Oj6rILot281Aqn81NfolXzp/wUI8Kjxd+yH8QrZYvNnt7IXcKgZO9GB/lmgDy7/gkp8RR4z/AGYxo7yB7rw7fPZOO4U/MnOPQ19rs6rkk4r8j/8AgjH8XLLQfFnirwHf3CW8mrJHeWStnM0q8Mo9wvrX60Xlu83IYgY+7QVGzepH/akQkK5y3rjAqaK5FwWUcHFZg0UsxJJIP4Vj+PPiJ4T+Evh2XVvFmtWui6dCCxkuH+Z8c4VRlmPsAaDeUYJaHXR7QgzubnGSpqTntX5PeAf2jfjp+1f+15c33wo1uSDwVotwGe2vZjFZ/ZS23c6EAsWx0AJHtX6t2bTtBH9pRUm2jfsOV3d8e31rN7mJYXPOadTVp1WtiWFFFFMQUUUUAFFFFABRRRQB+c//AAWM+CX/AAknw20P4i2S4utDk+x3eBndBIcj8mr1j/gl98YrL4kfsz6RowlH9q+G82FxFnnYOUYeoIr6U+Knw90z4rfD/W/CurwrPZalbPCysOhI4Ye4OK/Dy4s/jF/wTc+ND3UUT21nJKQg3GSzvrfcSFYjjOPxFBSVz97t1fCf/BWD9oaP4a/BVfBenT/8TrxKxikEbfNFAMEk88Z6VzGk/wDBZXwDN4JW6vvDGrReJfKObKEBoTIB/fz0/CvmH4C+B/EX/BRz9qi78V+L0m/4RixP2m5AJEccYP7uFOME560Bbueef8E2vBo8RftieErW4BQ6eJbwqwwSETP581++m6vxH+M2qSfsRf8ABQyXXbC1FvoiTR3KxxLu/wBDlUBlA9QBX6z/AAY/aT+Hvx70eG/8IeIba8eRctZSOqXKf70ec0A12PUc189/t+WtxefsmeP4rZJHlNnnbECTgMCa+g1qtqul2muabc6ff26XVncxmKWGQZV1IwQRQSfiB/wSY0O61T9rTT7uK3MlvY6XcPNIoyseQAu70Oc1+5VeP/BD9lH4c/s96zrmq+C9G/s691g/6TIzlvlyWCrnoMmvYKACuU+K+m3GsfDHxVY2pUXE+mXEce4kDJjb0rq6ZLGssbI67kYFWX1BoA/Dr/glbcNoP7atvBcjEjWOoWjAY4ckeuP7pr9x91fid+2R+xj8VfgB8Xta+JHgWxupPDU1017b6hokheWzLHLLImAy/gCPeuTj/wCCjP7SHjbw9H4N0zWjc3c6i1EtjpoN7LkYK7wuQ3vQVa598ft9f8FBdJ+BekXPg3wfLFqvja7Ro5WXDQ2cZGCWbP3ueBivyjvv2Z/ihqvwyf4q3Hhm9uPDlzcSGW6CNvGfmMhU87CT1r7O/ZH/AOCXPjDxl4tsvG3xoBtdGLC5bRrq4dr66kzkeaMYVe/3sn0r9Yv+Eb0v+wRon9n2/wDZAhFsLLyx5XlgY27emMUCZ+Qv7Kf/AAVVX4J/DjTfB/irwvPrWn6XEIre60plWTbn7rByOa+9fjn8QrX40fsL+MPFOkWN3b2ur6C88VtdIBKg4OGAJHbsa5u6/wCCXvwSuviUfFzaXdRjzhP/AGTHIFtN2c/dx09q+o7rwppk3hWbw8llDFpT2zWgtVQCNYyuNuPSgR+Yv/BE/wAR2P2j4laOWKXzfZ7sBiACnK4HOc5FfoZ8evjp4a/Z9+Hep+K/Ed2sUNtGfJtww8yeTHyoo7kmvxZ+MH7K/wAcv2V/ihf6x4Z03V7Wzku5GstV0He6OhYsqnaOwPcVofCv9m39oD9tbxtBD4v1DXLfSbciWfU/EDSLDGmcERoRgsfYUAdN+zN4F8Sft6/tdT+O/EsE0nhywuhf3UrDEaorZihB6E5AyK/bKCNIYY44xtjRQqj0AHFeffAb4F+Gf2e/h3p/hLwzarDa265mnI/eXEh+87HuSa9EoAWiikOe3WgD5G/b+/bL139lHRvDf/COaJbarqOrSyKz3u7y41UAjGOpr4sP/BYz4uXEeyHwhoPnYwNqysSfYV+vGueFdG8TrEusaTZaosRJjF5brKEJ643A4rOt/hj4PtZA8PhbR43HRlsIgf8A0GgD8iJf+Cin7WXih/tOkeHJIbduQtr4feVcfUrUf/Dcn7Z0n3dC1P8A4D4Wb/4iv2ZttPtbNdtvbQwL02xxhR+lT7R6D8qAPxZuP2y/20NSheBtG11TIMK0Phpo2H0ISrP7JvwZ/aM+Kn7Rmm694ru/FXhq0gk+2XmoakskaSKpyIgpI61+zu0eg/KloAjhV0RVZt2FAz3J9a5H4weObz4a/DTxB4lsNKk1q8021aeKxjzmVgOnHOK7GkZVkUqyhlIwQRkGgD8NvGP/AAU4/aL8cazdxaRef2LHIxRNP03TcyRZ427tpYn3NeQ2v7Mv7QHxu1i81j/hAvFGt3103nS3moRGLzCe++UqD9B0r+g+x8F+H9NunubTRNPtriQ5aWK2RWY+pIFbKqFGFAUewoA/Dq1/Y5/bSttFt7W10/xFb2UMexLVfE1ugVfQKJhge1c3Z/sZ/teadrSaha+EfE1vqsTblvotai35/wB43GMV+9VFAHyB+wTB+01psetaf8ebZl0mG2j/ALKuLq4t5rp5dx3h2ikYkbcfeFfX9FFABXNfED4c+Hfil4Xu/D3inSrfWNHuhiS3nXj6g9QfcV0tIV3daAPyV/aW/wCCQOuL4iuNW+EN3bXWjSkuNFvZvLktz6K5PzfpXz3F+y5+1n8K5G0/R9E8b2sJ/wCgFcytEf8AvhsV+99FAH4QWPwB/bH8ayf2bcWXj/y3GP8Aia3kscXPu7YrufhF/wAEpPjdb/EDRdU8Qw6Xpmn295Fd3Ej3yTO21gxGFJ5r9pqKAILG3NrZwxMQTHGqcdOBip6KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDN0XUm1bTba7MMkInQSLHKAHUHpkAnB/Gvyg/4LAaDaWvxc8A30FoYru4Co9xu4cBwQMdq/Uvx74mm8D+D9S1i20u51me1hZ47CzTLysBwB6V+LP7THx2+Jf7Y3xX8LaFd/DyfQrjTb4Ja2MVrK07ZYAl2K9MfhWU1qrHTDdvoftB8KZPN+G/hlj1OnQf+gCusrnfh9pU+h+CtD0+6UJc21nFFIo7MFGRXRVqYS3YUUUUEhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANbHc4qve6jaabaPc3d1Da2yDLTTOERR6kk4FLqFvJdWkscb+W7KQG96/Nr9vT9kr9on41+JtKn8JzRa5oUcBjfToNRitBC2epErqGyPSs5Sadi1FNXufbkn7UnwihvJrVviR4Z+0wnEkY1OIlfr81U9Q/a6+DWlKjXPxJ8Oxhzhf9PQ5P4Gvx70j/glL+0ZqF55Nz4R0/TUP/Le81m1dP/IUjH9K77T/APgjJ8Zrry/tOveDbFWPz/6XcOyj6CEg/nT1YtFue4/8FIv2tvhx4w+D1zong7xjpviHU72RYpbeyO8on97NZH/BLH9pL4d/Cf4M6vo3i/xXpnh+5k1Bpo0vZRGWGMd+tctb/wDBEfxaZl8/4k6Kse35mjs5SQfYccVY1D/giT4kht86f8StKmn9LmwkRfzBb+VLk63KurWPv63/AG1PgZcsQvxQ8Nrgfx36L/M1aj/bC+Ccwby/if4YfaMnGpR/41+Zg/4Iw/F1JXC+LvCGzPDM0+T+Hk0+T/gjL8XPL/5G3wm59FaYf+0hT1Ija+p+qvwz+O3gP4w3OoweDfE2n+IJNPx9p+wyhxHnpkiu+r5i/YT/AGQbj9kzwLqthqmqWusa1qtws881rFtWMAYCBiMsO9fTtUr9Rytf3QooopkhSUtFAHx//wAFCvh38ZfiR4LsNM+GHmNH5jPcC0uTDNjGME55Ffn7pP8AwTe/ab8XKLu8jWynxg/2jq7qzflmv3CoqGi1Kx+J03/BK/8AaRkjAOoaWQeqnWZT/wCy03Sf+CQPxy1K6YalqOgWcZH+sa+kl/QKK/bIjNG2qtoHMeJ/sf8AwBm/Zu+C2meD7y9S/v4WaS4nj+4WJ7e1e20mMUtCViQooopiEr4z/wCCpmsDT/2XdeUY3TSxQfMm4YLdR6GvstmxivjX/gq1a3Fx+yhq7wEBI7qF5RtyWUN0z2rOXYuOh59/wRo8Ow2fwY8T6yqMJ77UtjsXBXCLgADGR+Jr9Da/Nr/gjd4u0Sz+E3imwuNVhtryPUPNe3uJ1QAMOCAa/QuXxp4fhXdJrmnIvq10gH86cdEEtWbDV+XH/BXv4P8AiDxC2meMtO0lprDTU8u5njXPynoSPrX6g2d9balAs9rPHcwt0kicMp/EVx/xo8LweMfhj4i0WeHz0vrSSHZgE5IOCPelLuEW1ofFn/BMjXfD/wAfP2Yb7wJ4n061v/7ImNvJDJEu54m5BJ/Svn7/AIKH/sQ+C/2ftDh8YeBry60yX7SJHsZ5xtUH/njwDkHtk189/AX47eIP2L/j9qBD3P8AZVvdvb6jp6kfvowxxn3r0r4wfETxf/wUu/aG03QPCyT2vh6BQILeYEx2oIw0r479s0irNbnn/gv/AIKNfHXwH4NTw3pnipXtoxiO5u4BNcIvZQ7HoPpWja/tZftT3mljxZH4t8QXmjQvve4SCM249m2p0r6S+LX/AAR/j8H/AAbn1Pw5rVzrnjKzTzpYMfupwByqLjP618Z/CP8AaM8VfAa31jwnfW/2vQ7l2ivdIul+63IPB6Ua9A0P1z/4J5ftkXP7UHgO7svEnkp4y0chbswrsWdD0kC5OPevryvwu/4Jc+Lriz/bGsYbJ2tbHVorlZLdT8pUAsq/hX7oVafciSsMmBKHHWmxR7ecnJp5OcihvlXin5gn0Pxn/wCCyPiBb743eGrEDMdvpxPTnJav0F/4J0xTw/sg+AlnyG+zMRn03HFfnR/wWBsxbfHvQpG5Mmllsf8AA6+2/wBjP9qz4U+F/wBmLwRY65420fR7+0s/JmtbiXa6sCe2KyWxrPsfZqxgMT60skaNGysAVIwQ3TFfNWrf8FG/2ftJkkR/H1rO6dRbxO+fpxXnWo/8Fa/gnJff2fZDWtRMziFJI7UKrFjjjJ96DJJ3PCv24f2ffgt8QPGV23gnxppuh/ExGLtpvnbYp2B+5nojZ9K4L9jL/goN4h/Z+8USfDz4rXEt34dgk8hbqX55bJgefm6steJftjfC1/hL+0VbanK8/wBg8QTxazbmdh5ixu4O3I5GM17t/wAFKtG+Ev8AwrPwJrugC0HjO+giZ2s2BMkewZ8wdOtM1l2PWP2sv+Csdvogt9D+CzQare3UeX1qaHzBC3ZUjIIJ+oNfPXgf/gpl+0L8PfGWl6n4/kudT8PTMPPsrrSIrZZYz/EjiMEEdeDXin7FPxa8A/Br40WXiLx7oX9saei7IXHItZCf9Zs6Nx61+s/7X3wz8M/tW/sq3Wr+G5ba4SG3/tLT7yNeflGSvHtxg0EK3U+kfhr8QdJ+KfgfR/FOiXC3Om6nbrcRMpBxkcqfcHiunr80v+CN/wAZJNS8OeKfhnemRrjS5DqFszNlVjZtrIB2+bmv0srRbEPcWiiimIRq5P4o/DfR/i34D1fwpr1utzpupQmKRWzwezDB6g11lG0UAfg38Wfgj8Xv+Cf/AMWZPEXhd7630qOU/Y9ct4PMhkj6+XKCCMY9RX1l8Cf+CyGg3unwWPxS0K40y/UBTqmlp5sMh9SnVT61+keuaFp3iPTZ9O1Wxt9RsZ1KSW91GHRx6EGvjj4r/wDBJv4OfEC8mvdC+3+CLuZizjTZDJCSf+mbnj6A0FX7nouh/wDBQ/4Aa9p63cfxD0+1U9Y7sNE4PphhXk/x4/4KufC7wV4fuoPA13J4w8QupjgFrGRBG2OGZiOR9K80tf8AgiP4dS6D3HxS1GSEn5oo9HjBI9N3m8flXvfwV/4Jg/Bn4N61BrH2K88UapEBsfWpQ8SMDncsagDP+9kUC0PmT9iH9m/4iftBfGqL46fFsXT6fDJ9p06DUBgzNn5Sq8bVXtxX6q1FbW8NrCkNvGkMMY2rHGoVVA7ADoKloBhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAK8B/bk+Ct/8AHr9nPxH4X0mKObV/ku7RZADmSM5AHua9+prLuFAz8Ev2Qf2svEf7EPxG1fSdb0ieTRryVYtX0yRCkkDoceYg9ccfSv1N8B/8FKPgF47tRInjSLR5woZrfVYXgce2SMH8DXafGr9jf4S/H4SS+KPClqNSc7jqmnxrbXZbGMtKo3N9GyK+G/jB/wAEXbma+N18OfGVt9mY82fiBXDp/uyIDn8QKAbuzkf+Cmv7Z+j/ABvh0X4dfDjVxrOkGcS3s9juK3MnRIvcA818meA9C1P9m39o7wbJ49tH0d7G5tr+dZBkxwtyCR9K/S39k3/glLpHwh8RWPinx/rEPibVrM+Zb6ZBF/okUgP3m3ff+mBXeftif8E49D/ae8S2/ifTddbwv4iWNYJ5DD5sM0ajCgrkYIoGnY7Xwz/wUK+CnjTxzpPhPQvEz6nqupSCKEQW0hQMR0LYrY/ay/ZH8L/tS+DTZajFHZa/aqzWOqRoBIjY4Vmxkr7Vw/7KP/BO3wJ+zPPFrc7DxL4tVdo1G5TEcR9Y0PQ+9fWasGGaBeh+Id1/wSZ+Otlq0mm21vpNzp7S/Lem+ATb2Yrnr+Fep/Gz/gmrZ/Az9kDW9bikXWfHNm0V3e3CrmNIVb51jHtnrX61VDfWNtqVpLa3lvFd2sy7JIZ0Do6+hU8EfWpaHzH53/8ABGn4bX+hfDHxX4uuiyW2s3aw2sbKRlYxy351+i9U9J0bT9BsUstMsbbTrOP7lvaQrFGv0VQAKuU0Jnhv7Z3wLvf2iPgHrnhDTJ47fVJSlxbPIfl3ocgH61+OPw6+N3xr/YG8W6jov2WbTFuJP3unanETbzbT99Pr6iv6AKwfEvgLw34yVRrug6fq+0YBvLZJCPoSM0ra3HfSx+Knxg/4KsfE74ueAdQ8LHTdO0SG9Typ7qzDeaUPUDnjNWfgJ/wTJ8X/ABi+B+seNLppdK1i4USaFZTnb9oHUs3oD2r9aY/2Ufg/DqUeoR/Dnw8t5G25ZvsS5B9a9StbWGxt47e3iSCCNQqRxqFVQOgAHSqC5+Evw/8A2D/2nfD/AIsS10TQtS8O3cMof+0U1BYrdefvfK3zflX7OeBfAurv8G7Hwr471BfEGqS6f9k1G6xxKWXDfX616HSNyMUBc/nV/a7/AGd9S/Zt+MmoeGrtQ+n3DtdaW6tnfCzfKD7gmv2b/wCCfvwYb4K/sz+GtPucHUtSj/tK6OP4pBkD8Bivcda8D+H/ABJqVrf6po1nqF3aHMMtzArtGfVcjit1FVFCqAqgYCgYAFAh1FFFAgpDjqaWigD51/bJ/Y70/wDa+8NaFpV74km8NHSbl7lJ4bNLnzCybcEMy4H0NfJMP/BEfTlwJPivOw/2dAj/APj1fqBRSsVc/NjS/wDgij4Pt3Y3/wASNYu1I4Fvp0UGD/322a11/wCCL/w24z408Qsf9yOv0QopcqDmZ+cevf8ABFrwHc2IXSfG+s2l2DnzLiBJFP4AjFew/sW/sEwfsj+JPEmr/wDCTf8ACRyavbpbBWthF5QV92c5OTX13RRyhzEY7+lV7iFpFI4Aq2aqXiv5LEde1RKK2Y4lJbBYcFD8x61YkuV03TLi6lI2QxtKcnAwoJP8qqWlrPlZJJAqk4Ix2r5K/wCCi37Xmk/Ar4Xah4T0q8hl8aa1btbxW0bbmt4mGGdvTg8VCilsXLsj8+v2fdQn+K//AAUTfXoNOGrv/a15qMNruwH8rdt5/Kvavih4b/bP/ae8ZXlqdJ1TwZ4cjuXFtH532WJF3Fc7lO5uK6j/AII5/s+tawa38V9XgJnmVtP03zFIKjOZHXPr0r6K/wCCif7X2ofst/D7TYfD1usvibXXeK2lf7tuqjJf3Pat0Z7HyZN/wTH/AGirDTRd2fxO87U1XcIP7VuRz7EtivHPE3ib9rb9kfXLHWPEd34iFjaTYE1zKbqwkHcMRnAI7nFfe3/BL3x/8TPi18O/EXjDx9r9xrFre3mywSbGEA+9t46V9c+PvA+j/EfwjqXh3XrSO90u/iaKWGUZHI4P1FMk8B/Yu/bi8OftWaC9oyLpHjGxiD3mmuwxIOnmR+oz2HSvp+vwf0Pw/rv7FP7dWm2CI0VnHqixxBWIElrK+0D3HNfu7HIJY0cdGAI/GgB9FFFABRRRQAUUUUAfi5/wVKjb/ht7Q8KSWtNPxgdfnr9kPC+R4Z0kEYP2SHIP+4K/G3/gpZqSX37fWi2+QyRQaZHwc87zkfXpX7MaKhj0exQgqVgjBB6j5RQBZuLiK1heaeRYYkG5nkYBVHqSa+Ef2qf+Cqnhb4L6+fDvgfT7Xx3q8RIubiK9UWsBx03KG3NnqOMV9WfHv4L2nx6+Hd54SvtZ1LQre6ILXWly7JMDt7ivyE+D83gX4M/tqD4eaN4U0/x9o8+prpD3XiSATTJLu+aSMAY3dR0xQUlc0/FH/BWD4/6/m60my0fRLVTu8u202WXA/wBp3JBH0xX1F+wz/wAFNJ/jh4ysvAXj+xttO8QXi7LDULc4ju5h/wAsyvZsdK+85fCOi3GjnSH0qz/svyzGLMW6CIKRjhcYHFfiT8M/B9r8Pv8AgqNoOiWMP2eztvF2Iox0RGDED9aCT9z6KKKACiiigAooooA82/aQ+Gt58YvgX418F2EscF7rWnvawyS/dDEgjP5V4F/wTd/ZN179mbwT4kl8WRW6eIdZu1P7nqkKDaFz6E819jUUAFFFFABWf4g0Kz8T6Hf6TqEK3FjewtBNGwyGVhgitCigD8Rv2qP2IfiL+yd4+PjX4bDU73w9HObq2v8AT/8AW2LdSrAHJHvirOgf8FcPjhoGh22mXOlabqV5AgRru8tHMzkd2wRzX7WTRJNGUkRZEPVWGQazB4V0YSFxpNiHPVvs6ZP6UDPxp/4bc/a5/aKmj0Pwda3VtPMTj+wNNEDYPHzTPgKPckV1vgj/AIJa/HP4yarBqfxg8YrpVoz+ZLHNqD399z1AHMa8dwx+lfrtb2NtacQW8UI/6ZoF/lUrSBe9A/Q8q/Z3/Zp8F/sy+Dl8P+ELOQK7b7i+uiHuJ29WbA49hXq3TrUckhVQccd6fncARWb3GPWnU1adVR2JYUUUVQgooooAKKKKACiiigBGrm/G3w58N/EjS207xLotnrFoQQEuog+3IwSCehrpaKAPkPUv+CWHwA1K+luf+EdvLZpG3FIL51Qc84FfQvwm+DPhL4I+FofD3g7SIdJ02Pnagy7n1ZupNdvRQO58sftjfsFeG/2sJLHVH1F/D/iWzjMSahGm8SJ2V17gGvlbwX/wR38Z+E/ElrqFr8WLfTVhlV/N06ykjlKg5xnf3r9UKKAuyhoenPpGj2NlJcPdyW8CRNPJ96QqoBY+5xV+iigQUUUUAFMkUtjGCPQ0+igCOSFZo2R0V1YYZWGQfrWPp/gjw9pF615Y6Dpdldty1xb2ccch+rBc1uUUAIBS0UUAFFFFACUBQFAAAHpS0UAIM96WiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM4paZIu7FAD6Kj5xjFKgIoAfRRRQAUUUUAFFFFABRRRQAUUUUAIeagFhbLcm4FvEJyMGXYN/wBM4zU5pMH1oAULilpBmloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqTJp1JQIRadRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGpjSBFLMwVRySTwKc/Svj39sL9kf4p/tJeIrb+wfip/wiXhi3iwNLjgk+eQ8FmKOueKV0XFX3PcPiV+1B8LPhLps134l8c6LZtHn/AEWO8SW4ZgM7RGpLZ/Cvya/bY/b/ANT/AGpJG8D+C7C4t/CckyhU8pjc37g8LgHAHfGM165o/wDwRO1i81JJNe+Ktv8AZ92ZTaaUzyv64Ly4B98Gvsv9nP8AYB+E/wCzeyX2k6XLrniLbhta1hxLN1z8igBE57hc+9TvqPRH5SfDD/gmv+0D8QNLbU7Tw6vh21kAaNdYvfszyDsQo5/MV1c3/BKX9o6ORVFvpUqk43LrowPcg4NfuDjFLRyi5j5i/YG/Zx8X/s3/AAputF8Z6smo6rc3RmEcNy00cK4+6CR/KvpmaNZFG7oDmpKQjNO2lib63Pwf/wCCm3wbu/hz+0XqmrLbyJo2usLmK4ONpcjLKOK+u/8AgjT8H00XwJ4k+IVwjrd6rJ9gh3DgwoQ2R+Nfbnxo/Z48DfH7Rf7L8Z6QupQKP3Tg7ZIT/eRscHFdF8NfhroPwl8G6d4X8N2n2LSbBNkUecsfdjjkn1qVF2Kk00dK33TxX58f8FJP2HtE8ceBdR8f+ENJhsfE2n5uLtbVdv2pMfMSAOT3zX6E4qtqOnxalp9zaTKrRTxtG6sMggjHSnZiWh/Px/wT38TxeDP2t/BFzdRsoe5a1wezONpr+hD0r89fC/8AwSjh8H/tB6d4+07xeg0i11D7eNOe3O8Nu3bQemM1+hdHKwk7jNwDHPFc54s+JXhbwRZ/adf1/T9KgyRuubhVyQM46184ftrfs1/FP42NYXPw78d3HhxoQRLZi4aFH49Vr40X/gkn8avGDxv4o+IFm+58v9ouZbggeoyetV0sGh5R/wAFFvjB4b/aM+PWmHwJNNrX2WEaenlKcTOW6L61o6P/AMElfjLrXg221of2bbXkyCVdNnmIkCkZAJ9a+5v2Wv8Agl34T+AXjCHxTrWtSeLdUt0BtoJIFjgglyDvA6k445r7e2gYwMVPKx8x+THwp/4Iz6trnh5Lnx14wk0PUGPFnp8Sy7fqxFe0/DH/AII9/DzwL4u03WtU8Sar4jhs5PNFlMqRI7jlSSoBwD2r7/20VVtCbu5+aX/BYz4PWMnw38MeOLZVhuNJnXT22r8zRMMKM+gOK+Gf2OP2fdZ/ay+MWk6HqMtxceHNLVZdQuGYnyoAfuA+54r9zP2gPgToH7RXw11DwZ4iaaKxuyria3IEkTqcqwz71wf7In7Gnhj9kXQ9Zs9F1G71m91WZZLi+vQofaowqAKAAOaViuY8O/bS/wCCdPhrxt8I7Nvhp4esdJ8RaDCfJS3j2NdxgcoxH3m9zXxf+x7+2xrX7Luoan8O/iDYXV14VlLWs9pMMPYueGIB6jFfuJtFfk1/wWB/ZpsdBudK+Kmh2zxyajcfY9VSNTsGFJWU+nTFLlDmPOv+CZusQTft8agNDuJBod9BqTqqnarx4Lxgj2r9qsV+H/8AwSD0W7vv2skvYI99vp+k3TXDAcAOuxT+ZFfuDVEsKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACiiigAooooAKT3paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioWkZmKp1pYo3ViWOaAJaKKKAGtSY3cU+svxRbXt54c1O302TydQltpEt5M42yFSFOfripauB5v+01+0Bo/7Nfwr1Lxdqqi5eL93bWgYBppT0UfzNfll+z3+zX4s/4KIfGLWvih41lbT/Ccl3umlUYabaflgj9gO9dUP+Cbf7Q3xU8babF8S9ba48PyXrS3V1PrJujEm7qkWcKSOMj1r9U/hb8MtC+D/gXSvCfhy1W00vT4hGigcse7N6kmjlK5jR8G+ENK8B+G7DQdEs47HTLGJYYYYxgAAY/Ovzs/4LZaC0vgH4d6uiMXj1OW13AcLuiLc/lX6XV5D+1V8A7L9pD4M614PuSkV3Mnm2Vywz5M68qw9PSmtCTyL/glprmlan+yP4etNPlQ3FjNNHdQhgXRy2fmHbIr65YDqTwOtfhv8DfiZ44/4Js/tBXuieN7OZdGu41F9bwjek8Wflmj9W7fjX1T+0H/AMFaPh7rfwl1nTPh2dXl8WahCbe3aa28oQlhgsDk5I9qYHhn/BSTxtovjL9tLwdZaBNHc3mmNa213JCQwMpmUhcjqQK/YnSVZdLsw/3xCgP12ivzV/4Ju/sKXSXMPxh+KFs13q90ftGk2d5lmG7nz5Af4vQH61+mtABRRRQAUUUUAFJmvnP9rT9q7U/2V/7A1i48EXfiPwheSNFf6lZSEPZsBkEjaQBjPJwKwvAP/BTP4C+PNNuLk+K/+Efmt4TK9vrURti2P4UY/K59gaAPzh/4KAX0etf8FBo0sHW9aG80+FhbsJCHDqSpx3HpX7h2v/HtF/uD+Vfhj8F5rT9pr/go7ba1YRvc6Rda42o5kXJ8qPkNj0wBX7pUAJIpZSAcZ71+Dnh3Qbrwj/wUusbfUN0Tp4xMjGUbSFaQkE56ZBr95a/E7/gqJ8IvEXwk/aST4jWCzDTtYkjuLfUI42CQXKDOwtjG7C5x6UDTsftfkLyeBX4uaYr+JP8AgrdYy6ahvUi8TpK5txvCxonzucdh3NUtT/4KofGv4h+BbPwXoWkWkWu3Uf2VtS09GkuZhjb8qdmPrXtn/BNX9iT4g+E/ijH8XfiDbXGkSCGYQ2WooyXkksgwXdWGQMEnNAj9RqKKKACiiigAooooAKKKKACiiigAqPDMxzwKkooAYV96acrknpUjUxl3KQaBjImLsT2pWVg2QuaevHA6U+gdyKRC6EYpyqQoFOJA60jMFxmlYVwUU6kpaBBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAT9aB9MU12O07QC3bdwKbG77f3oUN/sHIoAlopM0tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlpDzQAA56dKWkA29OlLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACGkwPWlo20AAxS0mKWgAooooAKKKKACiiigAooooAKKKKAEo4oo20CDNLSYpaBhRRRQAUUUUAFcz8R/h1oHxW8H6j4X8TWK6ho+oRmOaFiVJHqCOQfcV01FAHh37Nf7Hvw/8A2WRrDeDba7NzqjDz7q+n82QIDkRrwMKK9xoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqOV9qj1PFMQlc7mNTcqxPRUC3Cu21WyR1qamLYWiiimIKKKKACiiigAooooAKKKKACiiipbsAUU122j603fhtvtmjmHYkopqtmnUcwgoprsFHNMYnjFHMOxLRTBTXcJjNHMFiWimIwbpT6a1EFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPHvj/APsn/Dn9pS1tk8aaN9qurVWFvewuY5o8jGNw6j2rwz4Tf8Ep/hR8LvHFt4iku9S8RpaP5ttp2pbDBG4OQxwMtj3r7UooAZFEkMaxxqEjUbVVRgADtT6KKACiiigAooooAyfFPhXSPG2g3mi67p8GqaVeIY57W5QMjqexFfF/xG/4JB/BfxdcTXOgy6t4OncHathP5kSHPUI+fyzX3NRQB8x/sn/sD+CP2T9UvNb0rUtR8QeJLyA2suo6jtAWMsGwiAfKeOuelfTSn5iOh/SnUUAIaxvE/g3QfG2nvYa/o9lrNk4IaC+t1lTnjow4PuK2qKAPPfBH7Pfw0+G901z4Y8DaHo1yf+W9tZIJOueGIyK9CoooAKKKKACiiigAooooAKKKKAEo3CgnFNbLY4oAfRSUtACNTBu3HI4qSigBqimqX8w5GF7VJRQA1wWxilpaZIpZcCgBonXcVPFSA56VDHb7W3E5qegAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAjZtq5wT9KRm4HBo38DjBPrT9tA9gWnUgFLQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKQ00vigB9FN3UbqAHU1m24o3UjfNilcY+ikWgnFF0IWiolmLOVC/nUlF0AtIx2qTS03lsg/pTAVTlQaWkAwMUtABRRSE45oAWimqwYZFOoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopGpuTSvYY+kpqt83Jqo8jmQ7G3YPSlzDUbkhmRlIY/Mpp25JEBLcVUkUq5JRTmq8nmS/IgCfSok9TVQLaxpHITGRuxzUqSOOWbj2qtaWSQtlpHZ8c7jxTVmEsjxqCNvOanVsLF4XS5xmpwdwyKz47cs1XVG1QK2Wi1M5LUkoqOMMM7mzUlMgKKKKV7AFFI1M3Hd1qeYCSikWlqlqAUUUVEtwEbpUbLuxUjUxsgcCpGhyjFOqBmbqcjHPAzmuW8T/FLwb4Hu0tdf8UaZo1043iG8ukjcg+xNA9zrJpFjTLVB5yogYHOTiuDl/aG+GAVWfx74fCk8f8TCP/Gmv+0T8LY49zePfDoX/sIR/wCNUlcex6EsysOTioVU/aM/w15F4h/a7+Cnhu1+0X/xI0OKPdt/c3XmHOM9EB9K4W+/4KPfs9abFJKnjyO+MfJjghkY/UZAp8oz6dt4tjM3rU9fDHiT/grp8EtPjM2nr4h1R487Y47MRpKcEYLFq9i/Y9/a+0v9rbw7rmp6ZoF5oiaTcrbv9oYMj5GRgjvgdKpEM+haKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTTQA7IpDIq9TTN3rxSLtf3qWyrEhb5cgZoRiw5XFC06mtSQooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBD5J3hsnP6VNTFlVnZQcsvWn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJnrRTVUqzEnOaAH0UUUAFFFFABRRRQAUUUUAFFFFABRSGk3UAK1Q7P3u7PbpSpMJWwPu+tDusasxOcccUrlaj6Oc+1Mmb5cBhk+9U5dQW3KqWDHp1pcyHGDlsXWkVNoJxuOBS7ucd6r28n2pdzLjacimedIt95ZX5CMhql6j5baFhJG3EMoHpip6iReuWzUtFiGFJt5JpajmDNGQpwfajlYgkHmAx5K5H3hTo18tFUktgYyaSLPljPJp9WgCiiimAUUUUAJjHSlopqsGJwwOOuKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADWpu4etObJHFN8lScsM1nLcaKs3mNIcEhaj+WLc2OcVfYBV6VGY0bhlFI1jJGXHIZ5CSx2+lWY7Yrl1OT71P9giwAgCjOeKnEKhQvaqTXUqVRdCpDMJnzyG6Fe1IbdlYsvBJqwwih7qMckk9PesfWfHfhrw3b+dqviHS9MhzjzLu9jiGeuMsw54P5UJXdyObsauyRV461JHGVUbiWPvXl+rftVfB7Q4XlvPiX4YjVeoTU4pGH4KSa820f8A4KMfA7xJ8RtJ8HaT4luNS1PUrpLO3lgtG+ztI52rlzjjJ9Ksl3Z9PLTqatOoICiiipauAjVHt+Yn2p7DIpjNt96h6D3HrTqqC4fzAAufWrWfzqlIBaKKKT1EFFIelNzTTGK3avy+/ah/4JffEn42fGbxJ4ys/FthcWupXPmW9veM26CPHCD0A9q8f/4KBftM/Eiw/ax1TQbHxDfaRougXFskFpaytErggNubBG7O7vX7E+D76TUvCWiXkzb5rixgldvVmjUk/maW7K2PyCs/+CM/xRklIn8S6DDHjhm3Pz6YFa1v/wAEXPHjkCXxroUSnqVtnP8AWv1/WnVdhcx+WnhX/gijHDKza/8AEQvGUxs0+z2HdkdSxPGM12tj/wAEW/hysiG98Za/MqnLLEI13e3K1+i1FMLs+EvEX/BH34M6p4ejstLuda0jUkYN/aC3ZkZhgjBRvl754Havpn9m79nnw9+zN8Nbbwf4dkmubdJGnmurnHmzSN1JwK9UooJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBGqORSy4HFSN904602NmZcsMGgBkcbKxzzT9vtT6KVh3GqKdRRRsIKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMWNVdmAwzdTT6TNLQAUUUm6gBaKQNmloAKKKKACiiigAooooAKKKKACikooAWiiigAopKN1AC0UjNtGaRW3Ur9AHUUUUwCiiigBGphzT2qOVhFGXboOaBieWONuAM5NQ3EMu0iJl5Pf0r4H/a9/4Kbaj+z78QpvCvh/whFq8kcQLXl9O8SKx9AFOenrXyVd/wDBXr473U0v2W28PRI7ZSNLB5GQemd/P5Vn8WqNHGUdGftkttGJPMx85GDTJreDerOFUg5yeK/Edv27P2sPjE39m6C95DMP35Gh6QVk2j5eS24bcsPxxWD4gt/2x9btZ73VJ/Gvkwr5js5MYA6dFA9ar4VqCvfc/dNtSsIAQ13boe+ZVH9axNc+JHhPw3Gs2q+I9LsUJ2hprtBzjOOvtX83+qfEj4g3Wqz2V74l1xtREvlNBJeSby+cbcZ65r334df8E9/2gfjFb2t7Pp9xYWVwcrca1csBj+9gnPeluSftr4R+Mngbxxqb6d4e8VaVrF+qs5trS5V3wOpwDXa5O7pxXwn+wn/wTkuf2ZvGD+NPFGuW+qeIPs8ttDbWSERRhyvzFjyTgEfjX3ZVIlg2e3WkXd3AxTqKYhKWiigAoqC7uVtYTK7BUXliR2r8+/i9/wAFfPDPw/8AHF94f0jwfeaxHptw0F5dyShB8pwdgH49anmsUotq5+hdFeA/B39ub4O/Ge0tRpfjCw07VJow7aZqcwglQ8AjLYVuTjg/hXvFvdR3UKTQyJNE4yskbBlYeoI60cyFZk1QwWqW5crkljkk1KDRzTuhC0UnNLTAKKKQmgAbPGPXmvnz9qr9tLwV+ynoVvPrnm6lrV2+220i1I85htY72z0XK4z/ALQrvvj78XrH4HfCfxD4x1AFotOt2dFXqXIwv64r8Sfgp8O/F/8AwUS/aUvLXXNek3Nbyane3U2W+zWayovlxjsSZVApXsVyu1z6mh/4LeXEmpfN8K4103P+sGrEy4z/AHfLx+tfoH+zz+0d4P8A2lPBEXiLwpeiULhLq0fiW3kxkqw/rXzx4+/4JT/B+++FN9oXhbSJdN8TLEGttZmunaRpQP4wTtwT6Adua/Mn4PeNPFv7Ef7VVrZX17NYJpOqpY6xaRs3lXVuxAclScHjkHsQKLoVrn9CFFVdL1CDVtOtb22cSW1zEk0TjujAEH8iKtUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIaz9a8R6V4chSbVdRtdOikbYj3Uyxhm9ASetX2zjivyL/AOCmereJf2iv2mfDfwq8HWOp6g2kqsDxIjCD7TIwJkzj+FcjJ96VylG5+uUE8d1Ck0MiyxOAyuhyGB7g1JXHfB/wTJ8N/hh4X8MSzNcS6Xp8VtJKxzucKNxz6bs12NAgooopiCiiigAopDUEkxU/Kcn0rOW40rk7dKgk3sQMcetL5jNKinpjNTChK49iBwyL8r4Y9M9K/LX9ur9sH9oTQfiZe+EfCOgaz4O0WEslvfWVoZpr4A4MqyKDtHPSv1RKhsZFQTWFtcOry28UrrwGdASPzp8o+ZdT8KtN+FH7Yf7Q2mgTt4y1TTWbeG1zUGiRj0yA7A9Ce3eqPxH/AOCdvx88A/D/AFLxVrtvDNY2EXmzwQ6g00wQdTt6YH1r96VjWMAKoUDoAK8p/axke3/Zh+K00TmOWLwxqMiOvBVlt3II9wRVIOY/Ab9nH4Ca/wDtLfFCz8F+HjDHdTRNNNcXTEJBCpAaQ45OCw496/Ur4B/8Ek9D+Evjjwv4w1Xxtd6xrGjXcd4LWG0SO2ZkyQOcnrg5z2r45/4JCawmm/tgWds67m1HRb62Q+hCpLn8oz+dfuZQJsRadTVp1MkKKKKV7AI3So3zxjrXmv7Q3x00n9nz4a6t4v1e3muILGPMcMfHnSHO1M9s8/lX51n/AILaax9sl2/DGzNqeYlbVir49SfLx+FZN3ZSR+sCL3wM06vyem/4LZ6z5eY/hjZK2f8AoLl/0EYriPE3/BZz4oak/wDxJvDOgaPEDn98XnYjB46j2/Kr5RM/ZmivBf2I/i140+OH7Pui+MfHNlbWWrahLMYhaoUWSANhH2nOM4P5V71RyiGSjMbUi8KKkpKOUdz8PP8AgqlBHH+2heKiqplsNPZ9oxuPAyffFftR4LXy/B+hKBgCwgH/AJDWvxt/4K3W4t/2xNMlAAMuj2THHfErD+lfsr4YkSHwnpLuwRFsoSWY4AHlijl1uVfQ1NpZsVIBiq9vPDeIk0LrKhB2vG2RXzN+3F+2nbfsheH/AA9JBpMWua5rM8ghs55TGghjX55MjuGaMY/2jVk7n1FRX47+J/8Ags98RLy0VdI8JeH9Kl3Z3s8kzYweMMcen5VyD/8ABUr9o7xJY3F9psFpHZWw3zTWekCREHT5jg4HI5qbj5T9t6K/Ay8/aw/aV/adujoWma7rmpPIdos/D8JiToQS5QcDB7+1ftn8BdB1jwv8FfBGk+ICTrlnpFvFe5cufNEY3ZJ6nPWmJqx6BRXkeuftUfDXwv8AGI/DHWfEMeleKzbx3CQ3a7InEmNiK54LHOcexr1tWDqGUhlIyCOhpiFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopNwJwCCfSgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBn41BeX1tp8fmXVxFbJ/elcKPzNef/AAA0fxdofwj8O2njfXP7f8Si2Vrq9ZApZiM4PTOPevhr/gsNJ40h8O+Dv7Mmu00EOxu5rV2RVlJwu4r2wT+YrNy0uaqld2ufpTb3EV1Ck0EqTRMMq8bAqR6g1LXyD4J8D+OvCf7FXhzT/B/iSabxB9jjnS8kYueRuI3EZwcY+prW/ZN/aU8SeOGvfDfxMgttC8VQSlbSBmCPdRjA34z1yR09ay9suZRa3Nfq8nBziz6opaapzzTq6TlCiiigAooooAKKKKACiiigDz/41fGbRfgd8N9a8Z62skun6WgZoofvyMTgKvua+YPgP/wVb+HHxi8aR+HNW0m88EzXT7LK61C5SWCY88MwA2HjvX1t4/8ABGmeONAk0rVNNttUsJj+9tblNyN15Ir8sP2tv+CW2t6TqFx4k+FsDXVvNKZZdHzt8heSSjeg4GPf2rOUrOx0xjFxu9z9c7e4iu4I5oJEmhkUMkkbBlYHoQR1FS1+PH7G/wC2v40/Za8Tr4E+MkOqN4PlIggu7xWY6a46ENg7kwCNo56HtX68aFrll4l0ey1XTbhbqwvIVngnTo6MMgj8DTjK5hKLRepGIXk8UpNQXE2z5duQerelUxJXdj5C/b7/AG2r/wDZh8KabD4b0Zb/AF3VpHSG8uz+5tgmSW2jlycYxkdc17p+zJ8YJPj18DPCPjqezWwudWtPMnt0bcqSKxRsHHQlc+2cV+R//BTr4sWfxE+Mlh4T0C4/tBNGMluTCc+bPIwGzHbGcV+rf7HPw7vvhX+zP8P/AAzqcfk6hZaavnx91Z2LkH3+asad3qzaolHRHs1FFFbmAUUUUAI1J7Up5o20AcR4q+CvgTxzefavEPhPSdZuOvmXlqshyO/I61R0v9nf4YaLcC4svAPh63mAwGXToj3z3HtXou2k20bbDbbKOnaHp2jriw0+1shjbi3hWPj04FY/xL1KPSPAeuXUrBVjtJCM+u01022vOf2hIxJ8I/ERaTyo1tnLv/dG0jP61E/hsVHdH4FeAbqTxt+1p4dm8hZm1DxVChiA3DaZ1BOO+Bz+Ff0cooRFVQFUDAAGAK/ED/glb8NrXx1+1lLqt3bi8tNAtZr+NmHCTmVVjb8t5r9wdtOOwpaMFp1IBilqiQooooAKKKKAIrq3S6geGRd0bgqw9jXxd8Uv+CUfwi+I+qalqcM2raDqN/cm5lms5wRk5yArAjknP4V9qnmjFGhSk1oj8kPi1/wRp8RaLIlx8OPFqavDwGttXRYpwcHkSJgY4HbvXjE0P7Wv7F908Nnc+ILWwZfLDQp9utWGQcBWVgPudQPXnmv3W20yW3jnUrIiyKeMMAalrsVzH43eDf8Agsb8W/DFxbWnivwzoOsxR4WYtazWl0R65EmzP/AO9fXXwt/4K2/Bbx1BHHr76j4K1A/ei1CHzYRyBxKnHfuBX0Z8Rf2avhn8UtPe08ReDNIv1Y7t7Wqq4bBGdy4OeTX5Of8ABRj9lf4Ufs6tp3/CL30lr4k1BwRokcu6OOLDEyEMCQOAOo+8Kkasz9efBHxw8A/Ejyv+Ea8XaTq7yjKR29yu9vopwe/pXc1+HH/BLv8AZl1T4tfG7TvGt1bTweE/DEv2prpWZBNcrjZGCOo5JPsCK/cVTlRVrYiW+g6mNnIx+NOrN8SaxH4f0S+1OUZhs4Xnde5CqTgflRe2olqfnf8A8FhvjNpWn/DzS/h3Z6iy69qF3Fc3Vsh4W1UOct9W28Vtf8EgfgQnhP4Wan8TNQtGt9Y8TObe2zgKLJCMFRjPzOuev8Ir8wvj98VNS/aH+Omta9eljNqV6La2jJJEab9qgDsK/oQ+CvhG38A/Cbwh4ftY/Kg0/S7e3CccERjP45zSavqaSeh2jV+L3/BYPwCNH+Oem+Jrawkih1K08qe6VMRvMvQZ/vYDflX7RHtX5xf8FmfD15dfC/wrq6XafY7XUVRrVhzvKOA+fTDEfjU7ExPpj9gX4mS/FT9lXwNql1Ms99a2g0+4Zf70PyDPvtC19DV8J/8ABHaORf2XLx2dmjOuXKxqegUBf6k192VS2Je4UUUVQgooooAKKKKACiiigAooooAKKKKACiikbO0460ALRTIt+35/vU+gBKpx6Lp8V898ljbJev8AeuViUSH6tjNXKNoqWrgFLSYpaa0AKKKKYBRRSNntQAN0qLykJzt5qRQe9LUtXHcjWMeZn24qWkpaa0BhRRRTEFcz8TvD9v4s+G/irRbuNZrbUNLurWSNxlWV4mUgj05rpWqnqyiTS7xG5VoXBB/3TQB+If8AwSZ0tYv20reN1V2sdJ1DaxHIb5U3D3wxH41+5Ffit/wSvhSH9uTWkVQAmm6oAAOg86HFftVSGxq06iimIKKKKlq4GJ4z8F6F8QvDd5oPiTS7bWdHvE8uezuk3I4/ofcc14Po/wDwTp/Z20OYywfDWymkznN3d3M4+gV5SAPwr6Sam0KI7nlul/sr/BzSVC2/wu8I4AwPN0aCX/0NTWl/wzr8KOv/AArHwbn/ALAFp/8AG69BWlx702wK2l6VZaHp8Fhp1nb6fY267IbW1iWKKNfRVUAAfSrVJS0LUQUUjU3NMD8Vf+CxTEftWaOV4P8AYVsP/Ijmv0E/bw+B/j34+fBHQdJ+HGptpOr2uoR3kwjumt/Nt/IkUx5UjPzMnHtXwB/wVoP2j9sLSocbv+JRYrz7ymv2W0FSuh6eDyRbxg/98igrZH4Xa9+zL+1Z8HZodVW08SSDT3Eyy2OoyTIMc5KbsEcV7R+z3+0tof7Y3xE0P4W/tF+FLPXNVVmi0rV1jMVwtwMfuXA7MN5J9UFfqJ8YPit4b+C/gPUfFXiq9jstJtFOQ+MzvtYiJR3Y4PHtX5NfsTXF3+0t/wAFFrj4k2ukpYaNZTXmqtFGgVLdDC8MSYAxkmVT/wABNTexW57B/wAFJv2T/hH8Ef2a5Ne8K+F7XRNZm1W2s0uoyS7KUkYpz2OwH8K+e/g/4pm8Pf8ABMv4vSCGNZrjxBBpyzBRv2ShNwz1xkV9Tf8ABa6/8v4KeA7IE5m155doPB2QMP8A2evnTV/BJ8F/8Ej7O8dcTeI/FEV4T6qPNC/+i6ncOh7Z/wAEStCjg8K/FLVHVWnkv7K0DY5URxyE4+u8fkK/Tavgn/gjf4TfSf2c9c1+Thtc1uWUD/ZjVUz+YNffNUtiZbn5x/8ABWT9ku88eaDF8XvDKFtV0K08jV4IzhpLNCzCVf8AaQn8j7Vof8EtP2zLr4paCvwp8VSGTxBoNiJdOvj/AMvVmpRArf7S71H0r9AtU0+DVtNurG6jEttcxNDKjDhlYEEfka/ADwTrjfsl/t0+dMWtrLw/4knsrlVPBti5Qj6YYH8KoLXP6B8nI4xTqrafeQ6jZwXVu4kgnjWSNx0KkZB/KrNBIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTBGFYsOtPooAKKTIpaACiiigAopGJHQZpFYnqMUAOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPzP0P9qz4kftAftYalpvwylW78B6Lw16dy24VSqlsgHOd3THNef8A/BRj9qrxdq3hm4+HN74RvdOtRMjvrt3bbYpQMgmMgngkjqAeOlfenwX+Ffw+/ZR+HP8AYOlx2VhIlv8AaL6SSTMk8gA5Jxkivjz9uP4tfED4zfDGXw74Q+GWqX2hSN++8QS2f7sKCTtiJ5wfU46V581G61PT1lG1vmev/sM6j48+MX7KelQ6i/8AZlgim2tZ2ys8qLwGXjBU84JNcb4+/ZA8KWvxs0XxP4x+LNx4e1G1ZJbWGa6jRyFOcH5uM/rXO/sE+Jvi38RP2d9b8Ov4l/4Re00FxZ2dxBbIblF5yvzLgHqc+1Q/D39mH4JfHb47az4Y8U/EbxP8TvFtjZPc3UdzOUhi2uithgvUFwMZ7mnpKSS6BCbimnsfpbo1xBd6XaTWtyt7bPEpjuFYMJFxw2Rwc1drE8F+EtO8B+F9M8PaREYNN06BbeCNmLEKowMk9TW3Xcea9wooopiCiiigAooooAKKKaWC9SBQAtNIDEqRkY5FPpu35s0gOZ8Q/DHwl4qiEeseHNM1OPdu23Vqj89jyPc10FjZwadaw2trClvbQoI44o12qigYAA7DFTtTam2tx9B1RXFsLi2khckB1KkrweRipQaKpiPmbwf/AME8/g/4X+IT+NZNHl1XX2umvPMvpi8ayE53BOnBr6ZACgADAoApaUVZDbb1YUUUVQgooooAKKRiQOBmmq5bquPxpXGPopAaWmIRq8g/aoaab4H+L7QP9nhm02bdcjqhClhx+FeuyvsUcZycV4P+3Jr6eG/2WPiFdyDAbTXhRh1VnwoP60naxcd7nwP/AMEV72Kz+J3xKsHjVrmbTraQP/dVJHHH18wf98iv1y96/JD/AIIp2K3PxA+It+Y8vHp9rCJPqzEj9K/XClEc9woooqjMKKKKACiiigAooooAKKKQnFAHlv7THx00/wDZ1+D+teNb6NbhrVfLtbdjgTTsDsTqPQ/lX4TpN48/bo/aStIL2Uy634gusHy9xisrfqcDJ2qq+vtX1N/wVS/aCl+LvxJ0b4UeHLtbuwsbtPMgTO2S7OUXJB7bzX2h+wT+xLpH7MXgmHVtVt4rzx/qUOb2+4byEbB8mM44HAz15FRvqi/h3PdPgT8GdD+Anwy0bwZoEe20sIgHmYLvmkP3nYgDJJ9vSvQaTGKWqRIjV51+0R4hTwr8E/GeqSBWEGmTHDdOVI/rXorV8sf8FI49a/4ZX8WzaS7Axxp5qp3jJw36Gpl8LKjufh18LLm2n+L3hNrzCWp1mBpWP90zLnmv6ZbPb9lg2Y2bF246YxX8/f7Ff7HuuftYeKtUGmatBodhopglubmZSz8tkBQO52nn2r9+PDelyaHoGnafLP8AaZLW3SFpiMbyqgZ/HFWtgexpN1Ffmf8A8Fn/ABksHgvwj4aVo/8ASLprqRcfPhVfAz6ZIr9L2Y/jX4pf8FaPE7+Lv2ktO8O2Uq3cljbrBHDHyRLIw+U/jUPcI9T7p/4JP6Q+lfsf6GzRGL7Xe3VwMj7wL4z+lfY9eYfsy/D8fC/4C+B/DXleTLZaXCJk9JWUM/8A48TXp9UtiAooopgFFFFABSE4xmlpGUNjPY5oAM8470tJtG7d3xiloAKKKKACiiigAopDWN4u1x/DXhvUtWS3mvGsoHn+zwDLSbVJ20D3NqivyPu/+Cxvjmz+JoN54P02z8J2c/k3WnAt9sZN2C4Zj1HpjHIr6x8J/wDBVL4AeJltEm8SXei3ExAaLUbGRBGT6sAVx+NK43Fo+v6KzfD3iLTfFWkW2qaRew6jp1ygkhuLdwyOp7gitKgkKKKKYBRSV8d/tU/Hb4i/s5/HLwTrEVxHqXwz16WPTryyePBtJiQDIGA7jJ59aTdiox5nY+xaKitZ1ureKZGDJIoYEHIIIzUtMkKRs9uKWigBqg9zmnUUUAFFNf7vUjntXB/GP40+FPgV4TbxH4v1RdM04P5aYG55WwTtVe/AoA71qy/EsjQ+HNVkUkMlpKwI9kNfAXj7/gs18PNItR/wi3hjVtduPM2k3RWCPbg5OeTnOK8c8cf8FoPEGteH72x0bwDp9hLcxtCLi6uml2BlIJ2jHPNBVmcn/wAEj9HuNT/a88Tam5Yi20e8LOepZriGv2g9q/nw/Y//AGurv9lv4p6x4rXQIPEMGq2r289qs/2YRlpFfKsQRxtxj39q+3YP+C2nh8q/nfC7UFcDGYtWjfn6eX096AlufpnRX5Y6p/wW1kUk2HwtPl54N1qJX+SVR8I/8FePid8UviFoXhvwr8NNGaXULuODyTNNPIVLAMflIxgHrigk/Vyio7dne3jaVQkhUFlHQHHIqSgD8xf+Cln7ZHxZ+FfxVs/B3w91G50HTY7WOSa7g08SSTzNn5Vd1Ixg9B6V85+Ff2gf22PEUMb6Vq3jS/ikXcpg0GCYn35izj3r9wJ7SC6KGaGOUocr5iBsH1Galx7UFJn45Qt/wUE8WQjY3iuFG5/0m1tbM/8AoINcj8SvBf7b/g7wrc614k1XxemmRnEr2epB3QYJ3ERNuAAB56V+3eB6VHPbRXUMkM0SSwyKUeORQyspGCCD1BFS0NSXY/ET/gnnrnxj+Kn7Tng+a58V+MNY8L6fcyXGpPeancyWoCxPhHDOVOWK8Gv3ArH8NeDdA8GWstt4f0PTdCtpX8ySHTbSO3R2PViEABPvWxTRLd2UNe1SPRdEv9QmZUitYJJ2ZugCqSc/lX8+OqftlfEyP46SePn8V6nNLb6o1yNNS9kW0MatgJ5W7bjHtX7X/tteKv8AhDP2UPidqgcxsujyW6spwQ0xWEEH6yCvwb+BPwF8T/tFeJNT0XwzB517Y6a+otH3dUKpge5LUNlRPeP2uv2gPDX7S/7Qfwz8SeH7VxdtHYwaghGf3nnKdvvjmvrL9r7/AIKgeJPgj45ufBfhXwkkV1aQoHvNVUgElQcqo6gZr80PhLZyeAf2gPCFv4htpLA6frtqLyC4XDJiUA5Br+inXvhf4N8cNb3mt+GdJ1aYINs11aRyOQQP4iMnpQDP55vi58f/AImftL68JPEurX+vSswMWn2it5KY4BES9xnGcd60vgrpPxq+HPj2wvvA2i+JdP12R1MUcdlKizAEcPkAFfr6V/QXonwr8GeG5RJpXhTRtPlUYElvYxKw/ELmulFrCJFcQxh1+620ZH0pWDmPzD/4LEprV58H/g5e6rZyJIs9x/aTwj93FM0MJ259SQ+P9015Jpvwh+I3iL/gllqL3aOdPsdei1yxt5Dl/sKRyI5A9N0gI+hr9gfF3gvQvHujnS/EOlWusaeXWT7PeRB03DocHvVmPw/pyaKdHFlbjSvKMH2MRAReWRjbt6YxRyi5j8af2Af+CiWn/s2+F7nwN4ysLm+8M+a91ZXVmoaWBnK7kYd16n61996b/wAFPf2etQsUuZPGL2e7rFcWcm8H0wAaxvHf/BKf4E+NL64vINKvtBuJ2LudPumC5PJwpyBzXmE3/BFj4cySME8a+I4rfdkRr5Jx+JSmJnst/wD8FQv2eLOEunjGa7Yf8s7ewlLdCe4A7etflf8At/fHH4dftCfGJPF/gW31CBZrRYr5rqBYvNkUYV8An2zmv0H0P/gjV8HNPkDX2s+I9TXGCj3KRgn1yiA/rXsXw1/4Jz/Ab4Xara6pp3gqK/1G25iuNUnkutrZB3BXJXPHXGaYJ2NH9gOXxLP+yf4Ck8VyM+ptaNs8wfOId7eUG99m2voao4YUt41jjUJGowqqAAo9BUlAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCJgd3SpKWigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEY4pFYntTqKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD5u8O/sw+CvAa2Op+O/FN94u1e2hWP7drVzsRgMD/AFYOOuK9l1z+ypfD8tnC8cenm1Y7oceWse0+nQYr5Q8HfBGx/Zy+GI1j4z+Nr7xdqiyedN9su5J1MnJCRgjLd8ZxXGaxY/FP9sn+y9K8H2198Mvho0kiXut5MVzeQZAEaJz1Hrgcda8/mSfJY9NxulNzPjW8/ak8a+F/HXiv4a/Di6tLKy1nWDDFft1DEsvX05PPtX6b/sc/st6V+yj8OL/Vta1KLU/FGqj7drOsyfdHGSqsRnaOvua80+IH/BKv4Zr8M0svB8F9Z+MLGPzLfWJLk+bNNjO5+3X0r4T+Nvir9qf4J+CrrwV411fWP+EYvT9mWaX955i84RZB8wBA6H0rblUHYxdqmtz9xPDniKw8VaRBqemzLc2U4zFMvRxnGRWpXyh/wTT+IGp+NP2Z9FtNV0m80650cmyEt1GUE6joy569a+r66VscklyyaCiiimSFFFJQAtFFFACGoPsaFTuyx65zViigBkcYjXAOfrQsmZNu3HvT6SgBG4XNRLMDGXwcDt3qZqguLhbaNmYZCgmga1JY23AHpkd6fX58/tg/8FLdd/Z3+KCeEtI8KWd5EIo5nvLuZslWPOFA4r7i+HHjGD4geBdC8RW7RtHqVpHc/uzlQWUEj8DS5kxyi47nSUUUUyQooooAKKKKAEao3YqOBuNSHmmiP5sk5qGhoVadTGdUPLAH0Jpd1NaAEjBVyTgDvXyT/wAFH9QuP+GZfGlsWT7NLZqVO7gkSJgfXGa+rtRJNlNhN+FJ2k4B4r8OP+ChHxY+KWrfETVdE8Q3klr4RaXFpaQN+7dV6ZNS3qaRR9Z/8EW/A7aX8K/GPieWHYdU1BbeKQjqsS84/FjX6PV8bf8ABKLw7eeH/wBknR2ulZRe3lxdRBhj5GbivsfdVR2IluOopN1Q3V7b2UfmXE0cEecbpWCj8zVEk9FUtN1qw1hZGsL2C8WNtjmCQOFPocGrtABRRRQAUUUlAC14L+2R8fLD4B/CPVdWuLlYb2aB47KMNh5JiCFAGfqfwr3O8vIdPtZbm5lSGCJS8kjnCqoGSSfSvxX/AG1/ixJ+2r+1R4e8A+DJHawt7kaZbzM52SOT88uBkYADVLfQpLqW/wDgmn+zxqP7QHx0vvil4otJbjQdJma5imk+5PfFwVHzA7lUbs++Oa/aMfLgAYGK4L4G/B/RvgT8MND8G6HHstdOgVHkwA00nV3bA5JOTXfUR2CTuwoooqiRG6V4b+2ZpF34j/Z68XaVYsFuZ7N/vdCApyK9yasrxJodt4i0W90+5iWWO4heLDD1Uj+tTJXjYpH4y/8ABJf4oXPw/wD2lNR8JXTRxWfiCzMEgbP+uhOY8c9SGfPWv2tr+fb49fDnxP8Asa/tJR6rYSbZ7e8/tDTp2JCkbidrYx61+kP7P/8AwVc+GfxA0Qw+Opf+EI1y1iBlFxl4JyAMsjD37HmhaLUbR9c/Fr4iaZ8Kfh5rnijV7lba00+1km3McbmAO0D3JxX4Yfs76RrP7VP7aukX1xFJdi41gavesQT5dtG+7rzgfdH419E/8FBv+ChHhX4zeFJPAPgBZNV06dla51JkZQ5BOEQdcng59q+gP+CUX7M9x8L/AIcXnjzX7MQ694jRBbrImHgtl6D23dT9BRuO9lY+9Y0Eaqg6KMCn0m35s5paaMwooopgFFI3SkGaVwHUUxZQzEDtShg2CDilzIdh1FN3ccGm+Z8wXnkZ6UcyCxJRTVNOpiCiiimAhprKGU5GR3Bp1FAHjHxP/Y6+DfxilafxT4C0u8um63NurW0p6/xxFT3rzmD/AIJgfs421zFMngNmMZBCy6reOvHsZq+rdoo2ipauVzGV4Z8NaX4Q0W00jRrGPTtNtIxHDbwjCqo6D3rWpNo3Z7/WlprQQUUUUxCNXhX7a3hq18S/s0eOIp7GW+ngsWntvIj3yRSryrqPavdSM02WGOeJ4pEWSNwVZWGQQeoIqZK5Sdj8rf2N/wDgqpp/hnwzYeDfi0tystiv2eDXETcWUEBVlUdCB39q/UDwv4n0zxloFjrWjXcd9pl7GJYLiI5V1PevkX4rf8Epvg58TNeu9Yh/tLw7e3cplmXT5R5TE8n5COOfSvpL4H/B/S/gR8N9J8GaNdXV5p+nIUjlvH3OcnNUJ6s72iiigQUUUUAI1fM/7av7Gtv+19oOh2cniGbQLnR3lkgZE3xuXCg7lyM/dH619MMoYYIyKKBn5P6f/wAET9WaQC++Jdqsf/THTSTj8Xr1nwF/wRp+FuhsH8T65q/iU7CDGkn2ZN2Rz8nPr371+g9FA+ZnyNo//BK79nXSbpJz4Qurxl6Jdarcun1K78V6FY/sJ/ALTwAnwr8OS8Y/0iyWXP8A31nn3r3eloJPFP8Ahin4D7SP+FSeEef+oRDn89tafw1/ZT+E3wh8TTeIfCPgfS9F1mRGj+2QxkvGjYyqbidgOBwuK9YooAKKKKACiiigAooooAKKKKAPJf2qfgtcftBfA3xJ4GtL5NOutRRPKmlBKblYMAwHbI/lXy1+wN+wT46/Zb+LOteJPEOs6XdaXc6c9ksFmCXdi6MHyRwBtbj3r7/pKlq47nwl+0v/AME4JPjR+0hovxH0nU9O03TRNay6np8kRDTGJgSwI4ywFfdNvCtvbxxLwsahR+AxUtFNaAFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFIWA6nFIxwOarGdZpfLA981LdhpXLVLTV4p1NaiCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXqnhvTdaZDqFnDfLGQyR3EauqkdwCOtX44VhjVI1WNFGFVRgAemKkGaDSHd7DV9Koax4b0rxFFHFqum2mpRxuJES7gWUKw6EBgcHmtEZpaPUWxFb20VpCsUESQxKMKkahVH0AqWiimAUUUUAFRqsnmZJGzHTvUlNZio4GaAHUUlLQAUUUUAFFFFACN0qORdx9umKkpkkZdSFbafWgaPyU/4K7fA3V7jxtovjrS7E3thNb/ZrmO2BZ42XoSB2r7F/wCCZ+rXeo/sl+FYb0XIms/Mt/8ASoyjYDHGM9sV9G6p4M0nXFYajY294Dn/AFiA9evWtLS9Js9Fs47SxtorS2jGFihQKo/AVlFO5rOSlsW6KKK1MQooooAKKKKAI5txT5Tg14v+1B8RPGvw5+FWpap4K0Y6xri4SKNRkoCDl8YOcYH517WwzTDCGXDAMMYORUuNzSMktz8EPEHxO/av+IevyXclz4y+1qSRHYQSRogz2CitrR/G37aNqohs7rx1kDgvalzj/gSmv3ShsoLfPlQxxZ67EA/lUu2lYHJM/EKPxt+3IFJafxs6MNpDWMfOf+AV5v4++FP7TXxMgRPFXhvxRrEaPvUXFkOG554HvX9AwGKWml3J5j8JfCuqftjeBvD1loWgxeMdM0yzXZBbw2i7UHpytbS+KP249Q+UXfjb14hVf/Za/b880m2nYOY/EN4f24rpf3k3jaRfRio/pWJq/wAEf2wviA3l6pp/jC/jHz+XJdbF479R61+7G2jFMfMfHX/BNb9nvxp8C/hprDePPtEGt6rd+cLO4nMpiQDA5z1NfY1N2gHIp1BLdwooooEFFFFAHzv+274J+J/xE+Dt74f+GDRLql9IsVx5k3kkwENvG4n1218wfsDf8E3fFfwW+J9r8QPiHeWi3ljFKlppduwlIkcAeYz9OBnp61+k1G3nNTbW5V9LC0UUVRIUUUUAI1Np1G2gDzH4zfs7+CPjto0tj4p0a3vHZdqXDIDJHx1B7V+dPxM/4Ix6y2uGXwN4ns101mz5OqElk+hC8/lX6ybaNtS0ykz4M/ZZ/wCCVXhb4N69beJvGupp4v16DJitViC2cZOMEqRliMe1feFvbxWsKQwxrDDGAqRxqAqgdAAKfilpoTCiiimIKKQ0m40rjFqN5Ap29PemSM6nLH5PYc1BdPkJsbvk5FQy4xuwjmQP5YOGzmvnv9vDTvH2q/APVV+HV7dWmswss7GyOJXjUEMqkc5ORXvc1wY5lYeWFXl2Y4wvc18/yft4/Cab4vW3w2XUnl1a4m+zCfA8kSZ+6W9SaRs1ytH4/wCh/tEftA/A3X7bU5tb8TWZgkDGLWFkeF/VSGGCDX318Bf+CwXhnxNb2WlfEHQbzTtdlkSBbjS0EsUpJAB25BHJ7V9TftQfEL4T/DX4fX9z8QIdLvUaFjDp8yo0szY4CjqPrX49/sh+DND+MH7Xen6oJNL0DwxZ6g2om01CdYkMSklUGT1yR+VMybTP3y0++i1Kzt7qHd5U8YkTcMHBGRkdqtVnaPrGlarFjTL60vY4wAfssyyBR2+6TitGqjsZhRRRVCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApM0NTScUAK+GXnmq7Rjd8owafJllwpwaWFiyfN1qWrl7IWPduwalpq06mtCQooopiCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKa8ixrlmCj1NADqKQHPI5FLQAUUUn60ALRRRQAUUhz2pAD3NK4AEw27Jp1FFMAooooAKKKKACiimSP5a5xmgB9FIrblBxiloAKKKKACiiilcAopCcU0SZYjHSlzIB9FIDS073AKKKKYBRRRQAUUUUAFFFFABRRRQAUUhzRnmlcBaKjeZI2Ad1TPTccZp+RRdALRTN5XcSy8fhiuJ1b44fD/Qdch0bUPGmhWmrSnalnJfxiUn025yPxpgdzRUcMyTxq8bK8bDKspyCPUGpKACiiigAooooAKKKKACiiigAoqOaRo0yqFznGBSqxZQSMe1ACTbto2cHNId2Bg0rMd2O1NaRV53AVnLcpCTZ8s4ODis+2t3uELF23dORVld8zM+/930UAVieOPGlh8OfCN/4g1aVktLKMySbRk4+lTc1i3FWRNrmiPNpdyitzJG6MSemVPNfzs6pYapaftK3VlprGfWI/EDLbndjdIJDt5+tfXX7Sf/BWD4ha34g1HSfh9BB4e0H5oBNdWglnnBGCw3D5fwr4P8P+L9fsPHFt4i064d/EC3QuYpVTezTE5HHfmmPmb+I+z/iR+wH+1J8avEk2ueILa1u2mbdELrURtRccALjA4rFs/wDglL8Y9NUTarqPh3Qoxy7vqJ3AevQVrXetftyeO9LivoT4uW2ugrxtZkW5Ax2AIwKyLP8AZl/a5+KWr2eneIh4pFlcTL50+qaiTGi55JG70qrMSstz9HP2BP2T7z9mbwjqz6l4jXxFfa0ySeZC5aJEUcBcmvq+uQ+Evgj/AIVz8O9A8OGZriTT7RIXlZixZgOTk+9dfVLQyk7sKKKKZIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFI1NzQA+imfe4zilXC/LuyfegB1FFJ+NK4C0U1unBpfxpcwC0UnQU3NHMMfRTVp1PcQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooARqifNStUcjFVyBk0DW5Hg06PIbmnRt5ig4xUTXGbgRAHpnNS3YvcsLTqatOprUzCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABTJoUuIzG6hlbgg0+igCK3t0tYljTO1em45qWiigApkmfLbGc47U+kbPbr70ARWpPlDdnPvU1FFACMwUZPAoznGORSOodSD0pI08tAvpUNAPoooqlsAUUUUwCiiigApKWigBKWiigAooooAKKKKhoBKNopaKfL3ASlooqgCiiigAooooAKKKKACiiigAoorgvi58b/AAf8E/Ds2seLNat9MgQZWN3HmSH0VepoHud4xxVXULxNNsbi6k/1cKF2x6AZr8ufih/wVW8c+JtUnt/hJ4Ol1DS4n/5CE9rJIxwegC8YNfTX7Of7VGqfHL4W30Xi7RJvC/iGGMxym6TyYZyR/Du7VhOajqzZUnufnh+2T+1f4z+PXxxHhjw1qV9pmnWd19jt4bSV4wz7sbm2nmu90z4zftJ/sHx2MnimU+L/AApcKrmK+dnCbumHzkGvIvAevaT4J/b/AIZLyyt7jT5NWNqyud8YLsAHyD1Br9kfjd4F8P8AibwXf3etQQ3WmwW5eSGZFZDGBnuKorS9mfnd8VP+CxB8XfDK+03w94VudA8R3UflC5kuVkiUHgkcAivjHw5+z78SPir4N1b4lxK1zYRyPI95K7eYzjklf/11jfErw7ZeOPjHqul/DvRZJbaSRhBZ2ozjHUivqz9kP9uK0+DOly/C/wCJ+ht/Yit9n8toyBAehLAmjXoCtex7V/wSn/a+1zxlrVz8KfFtzJeXdvbNNp1zMzGTan3kYk8+2AK/Tevwy8O+LPDPwu/by8N+IvBGqwTaDqF+sY8g8RRyHDKcV+5MUyzRpIp3IwDA+oNXHYymtSSiiiqMwooooAKKQ0m6lcY6imB93QigtilzILDm6VGzhQCTgU7du3LSeWOO+Klt9BjHdQRu6HvUUtnFJGQBwPQ0jWPmXG9mYqOig8VOsQjztz+NTr1KI4QuPKHGwCs/xP4WsfF2j3GmajEJ7OddkkbDIIq/BDIkzMzglj2FfI37Wn/BR7wx+zP4mi8M22kTeJPEIG+4t1kESQL2yT3NXdbMavfQ9h179mD4Z3Gl3Ek/hHS5ZYYH2SPbrlflPOcV+Tn/AAT9+E2meMf23Ly2vrWCbStHlvJ1gYZUsj/Jge1e3eJP+Czz6v4f1Cytfh81tc3EDxJM16CELAjOPxr84tB+IviTwz4tuvEWgavd6Hqk0ryG4s5WRl3HJGRTaDV7n9NF5fWWi2ZmuriCxtYxgyTOI0X8TxS6bqdprFnHd2NzFeWsgyk0Lh1b6EV/Nt4w+PvxP8eWL2et+Ntc1a1cgtby3cjIcd9te8fAv/gpV8VvgT4FsfClha6Xq2lWIKwC+t2LKCc8sME/iaETyn7tr1p1fkn8BP8AgpZ8b/jN8evCXhw2emx6PqF4sVzZ2NhlvL/ibewJAH1r9bKokKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSE4oNNbJpN2GDSKBzTd2e+BSMm4YYjFNaMY+9+tZSbKVgZvJUdXJNG8ZLntUVwfLmiOf1plzIWyFOOR0palWLHnhj8uTS+Ye4xVaSXykGOtQtcOwxyKzbdy1C5Za4ZX2MPfNTLN8tU4JNylpDnHrzT5HVo1dTx0q47A4paFlptnWhZC3bAqvbWzMp3sTnpk1bSFU960SuZuyHLTqSlq1oZhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkzQ3SmH8qAHNUcj7V96dzVaThutBSQ5pJNvyLz9KkhjZVBfl/WpI+gp9K1wuNWnUUUbEhRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRjgdM0UALRRRQAUUUUAFFFFK4CM20ZoHNDLuGKBwMUwFooooAKKKKACiiigAooooAKKKKACikNJuNAHNfEbxpD4B8I6lrdwVEdpA8pMhwowCea/FHwBpvir/got+1w1l4i1WaLR42ku3xlo4LaM5CKvTLdBmvuj/grT8UP+EP8AgSui22ofZ7/VpVj8hGwzx5+b9K5//gjv8JrPQ/g/q/je4siusavdtbx3Ug58hOgHtms73ZslaNz7U8E/B3wl8P8AwtBoOh6LZ2VlHEIm8uFQz4GMk4618uftG/8ABPnU/jR4ug1DTviBqHh/R1wJLCAEqAOuMHrX21jb70jcU+VSJjN7H4N/tzfs/wCnfss/Efwo/h17xi0S3D3V0+ZJZUIJb26V96/Fz9po61+wDaeLoZY1vNR05bVlZjgyY2kHnNZn/BV74S3PjL4Y2+t6Xow1DU9NlVvOjTMiRZ+cZ9MV+UEfxI8W+JfCGk/DpLq4fSI7nEFmpPMjHABHoDU2exs9Hdn6hf8ABI/9n/Q2+Gd98StVsPtWt6hePFbvOqsscanqvGck+9Vf+Ck37Ct14+uofG3gHSozqaoxv7WBMGUDncMd6+z/ANk/4Wf8Kb/Z/wDB3hdt32i3s1kn3Yz5jjcw4HvXrTRq/UZppXMlKzP5fLX+0vAniyGW4tXtNR024WRreYFWRkbOCPwr+jX9mn4oR/GL4I+FPFKKsb3dmglRM4WRRhgMk+nrXyr/AMFAP+Ces/x0mtfE3w602xtvFSti5jd1gS4XuWOOtex/8E//AII+NfgJ8CIPDHjgwpqUdy8kcEE4lWJD23DirRLtayPpiiiimQFIy7hjOKKaX29aVxjcbWGCSO9OqGbzFU+VgsefmrnPiL8QLD4Y+B9U8TawwistPgaaTkDOBwo9zUNlJC+PviF4c+Ffhu813xHqcGmafbIXeSZwCfYDuTXw/wCJP+CzHwy0/Umg0rw1reqWqttN0VSNevUAnNfC/wAXvjT8Q/8AgoB8c7fw/o0czadcz+XY6ZDuCJGD/rJBnBwOc19w/Dv/AII1/Dmz8Kxr4y1vV9R8QOuZJdNnWGGM+gUqSfzpFW7nrHwd/wCCm3wd+LmsWGjpqFzoOq3jbEh1CLapb03dK+tBNHJCssbq6MNwYHII9a/GH9oz/glV40+FVxca38PrxvEmlw/vUi3bbuHHIx6ke1ep/sH/APBQK4tXtPhF8UvtEF15n2Oy1SUkSIenlyE988A0D5NLnqv7VH/BVDT/AIE/EC88JeGvDUPim8siFup5rkxxxt3XgcmvFbL/AILba20+Lr4aWAjA5EN8+79RX2T40/4J5/B/4i+KT4i1zRDfX0vzS7ZSiTE92A6mq2rf8E0f2f8AU9Pa2j8Fx2MjDHn28zBx9CTTSuRotj5m0/8A4LYaa237V8ObrdjlIbxfzyan+DXi/wCEf/BQr4vahPrnwxljvvI3XF7cS53BegyvSvXtL/4JG/AzS9Zhv/I1i7SNt32We9JjP146V9ZeB/hn4X+G+lQ6f4b0Sy0m3iUIPs0Kox+pAyaHEaklqeGWH/BOr9n/AEnMjeArKdFBOLhmdQPpmvEP+Gsv2QPhH4xm8L2XhGztmspWtpr2DSUaNGBwQSeT9a/QW4gFxbyRE4DqVJHuMV+dHjz/AII56D4t8U61rNv491GxGo3Elz9n+zoyqzEnr171qJan1X8OvG/wH+LVjFJ4Zn8K6iJBkW4ihSUexQjOa9BHwl8E+WUHhTR9h5x9ijx/KvyI+M3/AAS8+JHwP0ebxD4O1xtajskaWQ2rGGYKOcjHtX0p/wAEqv2r/FHxUs9X+Hfi9rjUb7RYvOttSm5fZnBic+o7E0hyjbqfeOjfD/wz4fu0udM0DTbC4XIWW3tURh+IFdFSYpaDMKKKKAGvnbkAk+gxUc1zHa27zXMqQRRrud3YKqj1JNSt71+eH/BYS68U/wDCl9Ol0/UXsNBt9SRL2CJ8G43DCZ9gaVyoxctj9BdM1ax1q1Fzp95b31uTgTW0qyIfxBIq3X5Bf8EZ/iLrkfxO8QeDpNQlfQpNON2lmxBVZQ33hxkce+K/X2mJqwUUUUCCiiigAooooAKKKKACimGQbtvejcc0APopm6kV9wz0oGSUU1W5p1AhrttWm06Tlaj27hjpWctylsI6eZghj+FU7jz0mO1Ny1D4m8Raf4P0G81fU7hbSws42mlkboFAya/PbxR/wWc8MaPr19Z6L8Pb/XLC3kMa3smpJbrJg9RlGwKktNrU/RIJLcYDx7fRqGs3IOG5+tfmhP8A8FtLPafK+E0gPq3iGM/yhrNvv+C3Eqwt9n+FMSv2aTXA4/IRA/rRYOZ9D9PpbOf5CrBiOuagaG73MBGp9K/ILXP+Cz3xT1K6L6R4Y8L6RB2juEnuG/MMKzX/AOCwXxv8sg2HhNc/xLp1wD+r1Ljcrmkfspa2sq/LKODU8luI4z8yoPfpX4jXX/BQH9q/4mTl9Bvb21tuqjQtBjkH5vGx/WuF8VfGj9qvxVqENlqmuePhcTN+7htFmtCzduIgtNK2gXb3P38i2qoI6e9Sbgehr57/AGL9P8eWHwA8My/ELVLy912SBmliv8tOATxvZjuJx6177bYMSsBg+9ax2M5IsUU0dadVEBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIelNK5p9FAEbL0NNaENyRU1FA7jVGMU6iigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFJmgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEo5oakwaBDqKQnFG4UDFopu78KXdQAtFJupaACiiigAooooAKKKKACiiigApMHdnPFLRQAUUUUAFFFFABSZx1oNed/Hb4waT8E/hrrPijVJokFnCTDFI+3zJTwig4PU45xWctNxpN7HbS69pkGpR6fJqNrHfyDKWrTqJWHsucmr9fkF+xP8Odc/be/aG1v4o+ONV1A6JoNyJraGCdkVpScpGpHYd/Wv18VQihQMADAqo7ALRRRVCCiiigAooooAKKKKACikNRGRw5yAE/vZpXGFzcLbRl2yRnHFQTakkMPmtkL9Oak3qzgZ3Z/KqGuW7NaySxuBtU5FYy5r6bGkEm7SPx4/4K4eNZPE3xc8OaOE3W9vAXWTnJLHGMdK/UT9lDwlbeCf2ePAelWsflrHpkUj8AFmYbiT781+PH/BQDUjqX7VFvpzzGW2tfITeep3OM1+3/w7tI7HwH4ct4jmOPTrcKfby1poup2Oi7ihhmilrVaHOc5428FWPjrw3f6LqBkS1vIzHI0Rw2CMcGvnr4Z/8E2/gt8MvFlp4ksdGur7VraQyxyX1y0i7j32fd/Svqfb1oC7aTVyuZ2EChdoAwBwAKdSUtNaEhRRRTAKKKRhuFACMeKY/Ip2z1NDL7ZFQ0MYu7A3EEewr8xf+CvH7SktpYWfwj0aSN2vgl1qLRk+YArZVAQeCT1GOlfob8WPGkHw7+Hut69cHEdjbPNwcdATX4ffsw+FNQ/a8/bOsp9Xne5tpr2XU7iSYlgIYyXVOc8EADHvWd9TVLqfol/wTJ/ZFsfg38NrTxxrFqT4t16ASqZMH7NAw4VRjKkjrzX3DtqK1tYrK2iggQRwxKERFGAqgYAFSbvatFbqZvUrXlnFIvmMMMv8Qr8Ef2xNPtfDf7cGrrpC/Zw2rW8xA6by6kmv3r1a4MOm3MnGEQt+Qr8LPHmgn48f8FDBpdoDdQ32uwoWt2yRChBds+2DS06GsfhP3Q8OM0nh/TGc5drWIk++wVoVDZWq2VnBbpny4UWNc9cAYFT1UdjAKQDFLRVAcj8RPi34O+E+nx33i/xFY6BayHaj3km3cfYdTXi2tf8ABRv9n/RQ+7x5b3TL/Dawu5P04Feb/tzfsIeMP2rvE2l3+m+MbbTLOyQoltdQllXPU/KRmvmew/4Im+MHmQXvxF0pYP4vJsXJ/DLUD0Kv7ZH/AAVUuviFpd74T+F0cmnaNcoYbnVbiMebMp6hAfugjv1rh/2Bf2zfhr+yn4V8S3Gv6Jq2peK9SkG6e1YFJIxyFyTwc96+jfC3/BFHwnazQyeIPHuq6iq/fhtYUiVvbOCRXon/AA57+B4mRhLr3lrgmP7ccN9eKAR6b+xz+29o37Xk3iGLTfD91ocmkbGYXEokDqxwOgHNfTdeT/AD9mLwF+zTol1pngfTJLKO7fzLiaedppJCPVmJ49q9YoB26BRSE4qpLqUSEqG+YcYoBJvYtsM18P8A/BXDTjffstXMiqzNBqFvJhR0Abk19mjUJfOVcF1buBXzp/wUA0b+1v2VvHkRRpTFaGbBGSCCDkVne5so8j1PzU/4JG64un/tbWdrlh9t0u5iHvhC39K/chm2rn+Vfgn/AMEtpWT9svwkV53QXSk+3kNX70zSeXE7+g7VVzORn6z4o0jw3HFJq+qWmmJMwSM3cyx7mPQDJ5NacciTRq6MHRhlWU5BHrX4df8ABTf4ueKvEX7UlzoM99Ouk6IYfsFpwqxscHdwOTn1zX7G/A8XX/Cn/Bhvsm7OlW7SE9dxQEn9aOYVjuqKaDTqe5IUUUUwCiikagBpRc7sc+tNbO4Yryz9pj472f7O/wAI9a8aXUC3hsQix2zNgO7sFUE+mTXwR4Z/4LXFf+Ri+Haqrco2n3mTj3DUFWZ+pEnmbhtAxTdsrcEhR7V8CR/8FmPhU2mCZ/DevC7xzbqqkZ/3q868Zf8ABahRDIPCnw+3tkBZtVuCEAzzkJzSuPU/UZF24HWn18e/sB/tbePP2qrfxJqHibw7p+kaVYuq2tzZrIBKx6qC3BxX19I+089KLk9Rz8LzUCzLJJhajmMkmfLJJ9GPFLHGFHzRbT3K1ne5drGT4u8L2fjbw7eaTqVtDdWVyhjkgnUMjqeoINfgv+3n8FfD/wABvjtceHfD8eLd4VuXgj+VItx4CgdBX9AylcYAx+FfhL/wVSuvP/a610Ic7bO3Vh68cD86B36H29+wP+yN8IfiF+zD4S8QeJfAWka3q915jzXV/apJI5DYGTjkV9LW/wCxj8CbVsp8JPB5P+3o8D/oVNYX7AXhe48I/sl+ALO5G2WWzNyVPUB2JH6V7/NEJuDwem4HBH0NBKPPtJ/Zu+EugyLJp3ww8HWMqjAkg0G1Rh+IjzXQWvww8G2Ugkt/CWhwSDgNFpsKkfiFqj8V/ix4R+CvhCfxL411qLRNHidUNxIWyzk4VVC8kn0H418leI/+Cw3wT0uOYaTY+JtckjbaDFYLFG3OM7mfP6UAfbtroun2aeXb2FtBH12xQqo/ICrbW8TurtEjMv3WKjI+lfmt4i/4LW+FYdPlOifDvWLi8GNn264jii98kZP6V5T4i/4LU+P7y326H4G0HTpG+7LeTS3GPbau3+dUgsz9gWUHqAfwpOnA4FeRfsr/ABE8V/Ff4H+GPFfjSyt7DXdTiaZ4bSF4owhPyEKxJ5HfNeu1XQkVetOpq06hO4gooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACNxSKxPbFOooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASm+WN4bGDT6KACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSk5qW7AOopBmlpp3AKKKKYBRRRQAUUUUAFFFFABRRRQAUUUUAFJtpaKAEb6ZrzH9oT456R+z38OL7xjrdjeahp9myiSKyVWk5YDIDMB39a8z8Q/8FJP2ePC+vXejaj4+EV7auY5fK0y7mQMOo3JERXgX7bf7bXwf+IvwC13Q9M1e81GbVrUpZp/Z00YaTOVOZFUAVk6iWxtTg73aPrT9mf8Aae8M/tSeE73xB4XstSsrOznFtIupxxoxYjPGx2GPxr2PcK/NT/gk38cvBehfCLUfBpuJz4lhuHvp4Y7ZyrIQAMNjGRg169+0J/wUq8H/AALuorR/D+razdSqSscKCNQR03OxGB9AarnXUbpuWq2Ps1WDDIORS14P+x/+0w37U3w1k8V/8I/L4eWO5a3EMkokD4/iBx0r3iqunsZNcrsFFFFMkKKKKACiiigAooooARm2jNFDLuGKBwKAFooooAKKKKAIbsyLCTEu5+wNfnj+2Z8Evix+078btA8CQ2dxpHgJtr3mrqd8QUHcTt4544GetfomeaTYM5xWU4czTN6dX2aasec/AT4E+GP2efh/Z+E/CsDR2UPzyTSnMk0hHzOx+v5V6RSKu36UtaGLdwopKTdTEOopN1LQAUUUUAFFFFADW+7TOG4IyKkPNJt96lopCKoGMDFZ2uWpudPuI0Yxs6Fcj3FaWMVBef6hzjJ6AVLTsVF+8j8C/wBvPR9R8P8A7U179viMZZoTC/ZgG6mv3Q+E94dQ+GfhS4JBMml27cdP9Wtfjh/wVa+X416Zc5fzTAd2VwMg9jX6pfsZ+JJfFn7MXw71GbHmvpccbYOfu5X+QpLdGlRWue1UUUVqc4UUUUAFFFFABRRRQAUhz2pabJII13HpQBFMSCAThfWnfeTCtTsLIoPakEYQYFBXQ+F/+Cq3xiX4f/BD+xLaY/2jrcn2ZEDY/d/xn8q/KL4B/EX4i/BXxNH478CWk4ls0MUtx9laWAqeCrY9a+vf+Cy2ovP8XPCenCZmgj055PLzwGLda+//ANif4V+HfD/7K/gqzTSbaVNR05bm686JWMrP1ycciudG89Ldj40+GH/BaK8t7NIPHngN7y4U4a50SQLn/gDn+tenSf8ABZ34XLalh4S8TLc44ikSIAn6h69i8a/8E1/gX421S5v38LnS7q4OWbT5iignqQpyK8+tv+CPnwSt9SW6kuvEVxEG3G1a8RUPtwmcVra5nJx6HyF8ZP8AgpF8XP2kNcfwv8NNKvNB064HlpaafF515L9WHAB7+1fTH/BNP9h/W/hTqN18TviHaGDxTdo6WVpcczW4bId392Br7H+FP7O/w8+CtosXhDwrp+kS4Aa5jiDTP7lzzXo1HKyXLohN1OpNvelqloQFFFFMAooooAKKKKACiiigCG6DtCQhwayJLOSWf7mVx29a2Z0MkTKOD2rw39qz9om2/Zc+DOq+LZ7X+0dRVhBZWrNtEkrkKuf9kE5PtUt9DaEuVEfx8/bC+F/7MEMcPi3WGbVpE3x6VYJ51ww9cZ+UfU18S/Hj/grp4L+Ifwx8ReGNE8Daws+r2cloLrUXiEShgRnCkkmvnv8AZ1/Zf8df8FA/i1rPi7xLfy2Ph5rvzNW1ccn5jkQ224EZAGPQd/f7W/aY/wCCdPwT8Efs5a7qWmaRd2mqeHdMlng1JrpmllZRndIBhSfoAPapSJvrqfn/AP8ABNcTv+2R4EETbCZJQ/OMr5TZH5V+/wBIu+Nhkr7iv5iPhv8AETXfhV4403xR4ZuzZa1p8vm207IGw3TlcEHivraH/gqZ+0fdRlY7vT2GNpYaOC3TrkLj9KdgZc/4Kh+AdQ039rzTryeFmi1qK3MEkfO8hwp6d6/ZrwTAun+CdAgb92IdPt0+bjGI1FfzlfFL49/En4peMLHxJ4y8Q3d/rll81pcSQpD5IByAqqgHX1zXvGk65+2V+0F4PMun3njLWtAcKyyWoW2VgMYw0aoSOOxosB+7EciycowYeqnNSV8T/wDBOL4D/F/4W6Dqmp/E/wAQ6o632Ps2hahdNO0J7uxYkg+2a+2KpEMKKKKYgqMurMVzkjqKe33arrbrGxbJ3NQNHLePvhronxK0mbSdcsodR0ycbZraZdysPpXzz4s/4Je/AnxNFtt/Dj6IT959OlKE/nmvquONoZsqWK+lWgxPtUuKZbkz4aH/AAR9+CIYEza9t7qL0jNeheFv+CavwC8L2SwN4Mi1dh1l1KRpmP1ya+pBS4HpRy9ieY57wL4B8O/DXw/BofhfR7XQ9Jhz5dpZxhEGepwK6BlBHSlpadtBFVmEaneKTzuPlqeaJZUIYVwvxa+L3g74G+FZNf8AF+rRaVYIcJvOXlb+6q9SaztymiaOytrrzm2lGVvpxX4RftqWM3jv9vrV9GaTd9q1S1s18zkAHaMfTmv10/Z5/bG+Gn7Swu4fCeqlNQtn2tYXoEUzjruUZ+YfSvyr+PVk9v8A8FP44rqDaZPE1gyhuQylk5ph1PsL9v8A+N3xn/ZT8F+Fbf4bpZ6P4SgtIbO41WGwimMMqgAKFkUqobHp3r5L+Ev/AAVu+M3g/VjL4rlsvHultkyW89rHazJ7q8Sgce4NftH4m8J6L400mXS9f0qz1rTZcF7S+gWaJsdMqwINeW+Mf2f/AIHeGfAeqf234E8J6Z4ZgiMt0rafDBCAOcnCjnPT3oSuK58W6h+098HP+ClVjpXwy8W2es+AvED3Im0658xJYjLg8A8D5hxyO9eS/Fr/AII6eOvBtlfan4U8T6Vr+nW8TyvDdhobgKozxxtJx715Z+yb4V0H4mft/aCvhfSfs/hS21qS+trVcypHbxFnUknjHyjH1FfuD8TLpbL4eeJbhjtWLT53J9MIaNgPwM/YX+F+jfEn9qbwt4W8SWa3mns9x9qtZUV0JjjZsEHIIyvetjRfh5oOsft/2/hO1sbeHw8nioWws2iUwmNZPubMYwcYxivRv+CV/h9fFn7WtxrU0gMlhp13eITyzF8rnP8AwKvOvA88i/8ABRXS2LMrHxyqk55P+kYoKP34sbC20y0gtbO3itbaBBHFDCgRI1HAVQOAB6Cp6d6UGqWxkfmf8Uv26PFnwj/4KCp4a1jU8/D5Wis5bBUwF8xcCTPqGIP4V+l0UqTRpJGwZHAZWHQg9DX4s/8ABXbwM/hL9ovR/EcAwmr2aSDbx88bfzr9V/2Y/HyfE74A+BvEaSrK13pkQkKnPzoNjA++VqYuyKaPUqKaOtOq07kBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPyI/4JS/s/aR418QeLfFniOwsdSFhN9lt/OVpHWbOWLK3y4Izg5JzX03/wUO+E3gu/+EN7f6ra2emy2VtI9qYowo3KMgbRjvXmH/BNDWI/BvxU+Lnh64JtbV9VY28LDGW3HH9KZ/wUCtfFH7UHxi8PfCH4emZ7uziebVpTn7NACOBI65I6elcOk46PU9HlkpPTQ6H/AIJJ+A/CGi/COfW47uxm8T6q7R3EYkBlEYOQMHnpXq3/AAUM+GHh7Vf2afFl7Npdu11Z2pmjnWMCTcp3Dn8K+b/j9+wDe/BX4L6N4h+H1xdWnjTRYFkv7zTrqUK7ADcUXAyDz1xxXFeAv24PEf7Q3wR8a/Drxtp0lxqdpo08o1G2jwCqRniTJzuyOwo5mo+8iYxu1Z6H1z/wSvt1i/ZR0dx5eXuZchOuQR1r7Dr4n/4JMyCb9mYNGZPJW/kRRJ6gDOPbmvtiuuGxy1FyzaCiiirMgooooAKKKKACiiigAooooAKKSk3UgHUUzzPmIwacDTAWikzS0AFFFFACNSBh6YpT0r4r/wCCiv7Wnjn9nHwzp6+CtPt1nupNs+rXCGQW6noAmMH8TSukUouWx9qcUtfnj/wT5/4KDeN/2hvH0XgLxj4fguLv7FJef29ZHYoVRkB4wMDPTO7rX6HUCtYKKKKYgooooATPalpmz5s5pd3zYpXAVvu1Xum8m3kcc7RVhulQXXzQuuM5FHQa3R+Rv/BYrTLa31rwTLFCq3EwkLy45bivt/8A4JwXct5+x/4EaYAFIpUXH90SNivjL/gs5E39teA1jX90Ff8AeDrnHSvrb/gl7fG9/Y68I5bd5ctzH+Uh/wAayidNU+sqKbu6U6tjlCiik3DdjIz6UALRSGk3UAOopoanUAFIRnqM0tFABTXOFzTqQ80Afjh/wV38B6zH8QND8YTR/wDEplR7ONvRgd3NfoF+wL8UNM+Jn7MvhE2Mqm40u0SxuYl6oy9PzH8q5P8A4KQfBRPix8BL8JC0l/pga9t/J4+dRnB4OQQDXxD/AMEifjhD4L+Ld/4G1W++yWWswt9njnbAFwgLEc+oUjHqax20ZvKSlqj9lRTqKWtI7GIUUjZxwcV8Nf8ABQr9vq//AGa5NP8AC/glbC98XXQWWZrhfNW0TcOGQEZLDIHPencLXPuXnPtS15L+yt4w8X/ED4D+E/EnjkW6+I9UtvtUy20PkoqsxKDZk4O3FetUCCiiimAUUUUAFFFFABRRRQA187TjrX45/wDBYD4wT+JPi7o/gS2uGaw0e382eFD8plk4BP4Gv2JuHMcDsOqgmv56filrs3xa/bUvn8QH7ZDeeJo7KVG/d5hEwXb8uMcDqOah7mkUftv+yH8P9P8Ahp+zj4E0fT7JbENpkN1Oi5+aaRA7scnqSa8v/wCCnHxIT4e/sp+I48B5tYK6aiZwSJDg4+gz0r6n0vTrfR9NtLCzTyrS1hSCFMk7UVQqjJ5PAFflj/wWq+IrvdeB/BcM+ETzNQmiGOSQUXP609hbs8H/AOCUfgDRPHf7UiJr9hbanDp2l3FzHbXaB0MgAQNtPBxu7+lft3a+E9EsVxbaNp9uOmIrVF/kK/Dv/glT4utfC37Wekrdzpbpf2NxZq8jADcRnGT9K/dmmhSPxm/4Kyppkf7TXhTTLS1hhQWkTTxQoFVi0ncD2r9ePh3o9loHgPw/p+nWyWllBYwrFDH0UbAa/Iz/AILDeGX8OftFeGPEiKfLv9LQh8nAkikPH5Yr9RP2afilpvxe+CnhPxBYXEczy6fClxGjAmKVUAZWHY8Z/GmD2PUV606oyM45I57U1pxEN0jqijqW4H50Ek1FNVt2CDkU6gBsjBVJY4HrXxD8e/8AgqV4N+BvxO1bwXN4X1XWbvTJFSee3dEXJXJxu+tfb0kayKVYblPY18z/ABw/4J4/B/47a5d63q+kXGna1eOHub7T52R5SMcnOR2x0oGjyXRf+CxXwb1CENe6Zr+ny94/swkx+Kmum0v/AIKxfAbUJkSbUNXsVbrJPYNtHHfmueT/AII6fBVJCwv/ABDj+79sA/pXMeIv+CLnw+1CYnSvGmuabEf4JFSXH50D0PbrT/gpn+z5dKCvjTYf7sls4Nbnw/8A2/fgv8UPHmn+D/D/AInN1rGoSeVbK0LIrvjOAT3r5Wuv+CJPhoW7m1+I2qfaMfIZrSPZn3xzXQfs1/8ABKF/gz8Y9F8Z654vg1u00e5NxBZRWpRpXCny2Zs8bW2t+FBJ+itFMTOcEc+vbrT6AEbpX5Lf8FsNVvP+Es+HenCeQ2X2W4m+z7js37lG7HTOO9frPnrX5ff8FsNFgbSPhtqQhT7U13Pb+bj5tuwHbn0ziol0LifnF4PvPHvwr/sj4k6EdQ0SOOYxWmrQFlDOBgrkdQRkH617h+z/AOPtU/ac/bq+HeueLxC+o3Gp2zXDW67fMMPzAn67QDX21+yZ8E9C/aQ/4Ju2vhi/s4JLoTXZtp2QM8Vwj7lYHqOw+lfEX7Cfg/xF4R/bm8JaINLku9R0jUZ47uEqQsSrG+5yT0wMnn0osWfuJ8Qvix4P+FOltqHi3xDYaFbAbgbuYKzf7q9T+Ar8iP8AgoN/wUH/AOF/RzeBfAEkyeC4yDfXRyjXxDAgYBzsBAOO9fUP7eX/AAT38f8A7TfxQs/FPhnxTp62K2iWx0vWZpljgIJy0ewNjPGcAZIrxbQf+CJfime1Vta+JWl2s4HENnYyTIvtudh/KqtYjYzv+Cf3xi/Z3/ZZ0tvEfiPx/cX/AI1123EM9tDpUvladGDnZuC8kkDJH5V98/tRfFTS9S/Yw8e+MvDepG60+88PzvY3tsCMl0KqexHJFfJfgH/gizZ6P4t0298TfEAazotu++ewtrDyml4OF3FiAM4zxyM1+jkfgHw5H4Oj8KNoenT+Gktxaf2VNaxvbNEBjYYiNpHtik1cVz8g/wDgjz4G17VvjnrniW3UroFnpclvc3G3arSOV2ov48keleRroj+B/wDgo5Fa6hLtFr45jZpCf784dT+RFfuv4P8Ah94W+HtjJZeFvDWkeGrOR/Me30ewitI2b+8VjUAn3r8kv20P2C/jXq37QXi7x54O0GfWdOv7pb+2udOu8XEbgAAqMhgVI7enFHKPmP2M7ihulfgNL8a/2sPhPavbah4i8fad5DYLajA9wo5xjzJQ2a6Lw/8A8FKP2ltLjWGXWW1JlGA13pKn89iDNFhJXPqj/gtJ4Be98E+CPFtvbSSNZ3r2U8y/dRXUlM+nzAD8a7//AIJCfE4eKv2e73wvMQLvw7fMgXv5b/MP1z+dfnv8cP27PjN8ZPAF94U8Y/YDo93teRV0to3BRgysrN0IIHNfTf8AwRLaZvEHxLG5ntvs1sQx6Ftxz+NLlKbtofq4vWnUlLVJWICiiimIKKKKACkPNLRQA0LjvTqKKACiiigAooooAKKKKACiiigAoqORAzBicCl81d4XPJoAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfi/8AsmaX4+1b9q7xl4Q0PXbddXmEs02rXMRlghC/eJGM5IOBx1Ir9U/g/wDAPw38Hzf32n26z+INUw2p6tJnzLphz0JOBntXzD+yH+xj48+F37SHi34n+LNSsbO0uxNb2+l6exczhjwzkqAFA5GDnNfdO6ualT5Vqddapd2i9CO6tYbq3khmjWSF1KujjKsD1BFfJ/xw+Hvwc8JeAfiF/YL+G/D3iG80ueG5MU6LNuZTgbBk5J4/Gvq28hS4t5I3GVYc5r8wv2m/+CV/jbx78QtY8W+DfGVndtq0/mvaaiZIWjBwMBlVhgde3etJx5laxNKy1bPcf+CUK6fa/s4z2dhqkWpeRqcgm8oH905AODkV9q14R+xr+zRD+y38G7Lws1xHeavNIbvUrmEko87AAhcgHaAABkV7vVQjyqxFWSnNyQUUUVZiFFFFABRRRQAUUUUAFFFFABVW+naG1lZBukCnYucZbsPzqyaY0CSffUMM5waloaep+QvxYtf22vFPxT1ObTh4m0/SmvnFgtlcrHbpGG+XOD0x6jvX3Z+x14P+OugeHJ7r40eK4tWvZuINOSNXeEeryjGT7Yr6Q2DsMUoGKXKaOd1sHNLSYpapKxkFFFFMBG6Vx/xI+FPhf4taLJo/ijSYdUsJPvRyDn867CjbRZPcabTPA/2dP2K/h7+zD4n8Q634NjvEn1hFhaO6m8xYYw27avHrj8q99pAMUtAgooooAKQ9PSlprruXGcUAAXB60u35s0jLllOelOqWrgI3So5ovMjYA4JGKkoz1o6Aflr/AMFhtJew8N+GLuTMrrc7FbHAXrmvVP8Agjv46j139nW+8OkoJ9G1GQ7QfmKyfNk/jXUf8FRvhrH44/Z31W8MeJdLia8SbjIKENt+hxj8a+ev+CJgLX/xOZZT5SxWeIuwLbiT+mKzWx0TfMk/I/VH+JafTKXdVpmIrdKqLHHJP5wzvXirLNxzXlv7RXx00r9nf4Yar4x1WB7mCzVcQxfedmdUX/x5hVXW44xvoehy65ZQ3y2Ml7bJeMAVt2mUOc+ik5q/X4T6h4v+JX7Yni7xh8SvDeqzaJrvh/y57bS7OWQboi2ARyfm/Svdv2P/APgqF4j8M+LJfCXx4vJnsHXZb6tNbBJraQA5EuANynAHTIJqVJN2G49EfrFz2rzn4j/tIfDL4Q3y2XjHxvo+gXrLv+zXVwPNC+pQZIH1FfJ/7aH/AAUv8L/D34fHTvhVrlp4g8XaooWG8tx5kNkm4b2YcfNt3Y9Dg1+dXw5/Zd+Mf7Wsev8Aj1xNewRs0l1rGrE752AzhAfvfh0pSkCj3P3e+G/xe8G/F/S5NR8GeI7HxFZRsFeayk3BSegI6iuwr8Of+CaPxU8Q/B/9rbTvATX6R6JrlxNY39s6nYZFikMZXng7wo71+4o5FOMrikrC0UlLVkGX4l0aPxBol3YShSs8bR/MMjkYr8Fv2vP2Z/F37MfxWm1+1WSKxmvGu7K7tsjyjuyOR2zX7+Mu4YrkfiR8J/C3xb8Oz6H4r0mHVtPmGCko5HIPDDkcis3F3ujSMklZn5y/BP8A4LGWOj+BdKsPiD4a1LVddhXypLvSUUCZQMK2HbrxzzXokn/BZb4bhWCeCPFW/GRvWAD9Hrvov+CWvwTj1SeY+HFNox+SMXEu4c+pbFaKf8Et/wBn0ahFdSeGLqYL1ga9bym47gAH9aeoe6fI/wAXv+CyXiTxJp0mmfDjwgujXsx8v7bqJ8+Rcn+GNTjOPfvVD9kn9gvxz+0L46t/ir8ZJruHTHnF0IL1iLm/IyUBBHyoG2nB6gYr9HfBP7Ifwc+Hc8U+g/D7R7O4jIZZmhMrgjocuTXrojVVCgYUcADpRZiuuhDZWsNjbxW9vEkFtEgSOOMYVVAwAB6YqzSBcUtUtCQooopiCiiigAooooAKKKKAIbtS9vIobYSpG70r+fL9sr4beIPgv+0pr+ovZyWMU2of2jY3W0lGbO4HP1/nX9CLjK4rzr4tfAfwf8atDm0rxRo9tqFvImzdIgLr6EHrkGp5Xe5rFq1j5r/Zd/4KYfDX4ifDiFPG+tW/hHxRpVqqXsN+21LkquN8ZxznH3euTX5m/tZfF65/bI/aekvvDttcPY3LxaZpNts3O0anBcADoTluegr3Px5/wR++J6eOL+LwnNos3htpz9lmvboq8cZPGRyWx719n/sS/wDBOnQv2XruTxJr95b+KfGbx+XDdeSRFYqR8wiz3P8Aexmm0T8J+eXxq/4Jz/Fr4M3Wk6t4Z0W+1yBoI3M2lbnuILg47Kcg5/TNfq5+xT4g+ImvfAfRV+JugXmheI7MfZv9O4luI1+7Iy9QcY6173tFG0ULQTdz5L/4KA/sYz/tYeCtNk0S8js/FWiuWs1uDiGZGIDox7cZI9wK/MLwd4k/aK/4J/8Aiq7ig0++0yy3kz2t5aGfT7oYKgkgZHXIKsOcZzX747RVTUtHsNZtzb6hZW99A3WK5iWRT+BBFMEz8mdJ/wCC03i9bVVv/h/pM9yBhmjvWhBb2UgnGaqeCfiR+0H/AMFGfiJb6Z9tuvBHw8hmSS8Glq6Qoq8n98AGZjjGM4ya/Tcfs4fCn7c14fhx4We6Y7jK+kQMcn6rXb6PoOmeHbMWmlada6Zar0gs4FiQf8BUAUBdDtH02PR9LsrCJneK1hSBGkYsxCqACSep4q7SYpaCQooooAKKKKACiiigBNo9PeloooAaw4r86f8Ags94Y1PWPhH4N1WysmmtNL1VmurgLnyw8ZVfzYiv0YqrqWl2esWrW19aw3luxyYp0DqcexqZK407HwR/wRruryb9nzxJaXBnEFvrbCBZMgKGjUkKD2zX21o/wx8JaB4mvfEWm+HNLsdevjm61K3tES4nP+24GW/E1t6bpFjotuYLCzgsoSdxjgjCLn1wKuVQNiYpaKKBBSUtFABRRRQAyaFLiMpIiyIeqsMg1R/4R3SyCDptoQev7hOf0rRooA5jXvhj4R8T2clrq/hfR9Tt5OGjurGKQHnPdaPBPwy8JfDeCWHwv4d0zQEmOZP7PtUhMmP7xUDP4109FABRSGvm/wDa8/bU0P8AZJj8P/2tot9q76tIQPs2AsaA/MST39qTdh2ufSNFeKfBP9sH4XfHy1gPhfxLbPqEg/5Bt04iuAcEkbT1wAenpXtK9sHPc5oTuA6iiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkyPWhmwKZuDcVLdgH5ozTWYKcYpN/tS5gH0tMVuRxT6pO4BRRRTARjtGcZpqybmxgj8KfTP4xQA+iiigAooooAKKKRmCjJOBQAtFIrBuhzS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFIzbVzgn6UALRSdaWgAopu8ZA9eB706gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKi88eaEA696AJaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAroiW+TtVB0zntTvMGcAFvcUy6tlu4jE+QrEdPY5p0Maw/ulzgetBQy6KC3Yu2xe5qGyZmZtm3ysAKRVxog4wwB+tKsYUYAAHtQO+lh2AOgpaKKCAooooAKKKKACikpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiko3AYB6mgBaKQ0hYgZoAdTGbaCaFct2pex4qboNz5g/4KG+HdR8S/s3+LLfTZyky2ErGMHG5QAW/QGvjH/gibq23xz8StPEbDzNOtZd2PlBV2HP1ya+qP+CmHiu98C/s5+JbnT5c3d/CLb74HlK8iIxA6nKsRXyx/wAET7aRfiB8S5R/qV0y1jJ/2i5J/lWaNnsj9UfF3jTQvAWiyat4j1a00bTYyoe6vJRGgJIUDJ9yB+Nef/8ADWnwc3bf+Fj+Hy390XYJrxn9vr9j3xh+1fH4btfD3iaHRrPTg5uLW6DGKZichiAeSMCvjZv+CL/xJ2nZ400EN2/cOD+eaCbH6Oal+2t8DtKjZrj4k6INvVUlZj+QFcj+0Fomm/tSfAfUp/B2p2ms6Vq1nJFbz5yhcfdwMdcjv7V8SeG/+CLfi7+2LNtd8aaadN8wfaRaI4kKdwpPGa/TX4R/Azwx8E/h3Z+DfDdvJFpFsMfvnLs7E5LE+uae60LjJRZ+P3/BNu9vPhv+1pP4L1m323WoBtNlgkPy+YgYgn1HBP5V7d/wV3+Fvgzwn4S8O67p1nDaeIZ79oWaFFVpcpuO8Y5AXJGMcgV5F/wUi0e7+Av7WOi+JvD0Z0e5ls47uG6tTtaSRJDuYn1I4/GvMviH8VviP/wUJ+L3hbw+liTMoS3hhtwxCjHzzSHkZ2gnPFZxi+a5TkeO/AfV/CWg/GLwtfeObRr7wlBdq2oW8ROXQA4/JtpPsK/oK+DPxs+F3xL8M2tv4H1jTDp4j8uLT4ykTKvTATP8q8C8Rf8ABMn4at8AI/COnaVCviS3t1P9tEDzpZsgsScdOuOK/Kr4kfBT4rfsoeI5Lx49Q0uC3fEGqWjMIwN4ALducgfjVS10IsraHqHivS3+Fv8AwUssS9odPhi8VW80CuPldWlUAjHY5r92l+6K/mw0/wCKXiP4kfHDwf4h8SX0mpahFq1iDMxzkCZCMflX9JsbB41YdGGeaqKaJlK6sOXpS0nfFLWpmFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUmzFOooATbS0hIHJ4ooAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKTdgCquqalBo+mXd/dP5drawvPK/91FUsx/IGrNfPv7fHjCbwT+yF8TNRt5DHPJpZskcHBBndYcg+v7ylzDtcZ+zT+3B8P/2pfFHiHQPCiahBqOjoZ3W9iVVmg3hPMQgnjJHHuK+hq/mm+B9z8U7fxRLd/CmbxDBr1valZZvDssiTCDIZlbYRlMrnaeCRX1l8J/8AgqN8a/gvry6b8SNOuPF2nsMNBqcBtbxMA5Kvt5P1BouPlP2mr5F/4KK/teax+yv4B8Ov4V+xzeKdX1DCQ3YDBbWNC8rFfc7Vz7ml+D//AAVA+B/xTh8u812TwfqSoXa01qMqpwCSFkUFWwAfSvzh/am+Imrft9ftiad4f8GBrrTFk/sjSATkeSuXlnIPABCs3/ARUvVhyn7Bfst/FLVvjV8A/B3jbW7WGy1LWbP7RLDACEHzsoxn6V6tXMfDXwPY/DT4f+HvCumosdlo9jFZxhFwDsUAtj1JyfxrpM0J2FYfXzL+0T/wUH+Ff7N+vXHh/Wrm91fxHbqjS6XpcIeRA2DliSFGBz17V9L5r+fX/goUJI/2zPiUHdm3alGPmOflManb9Paq5h2P3H+Afxs0f9ob4W6X440G3ubTTr9nCQ3ahZFKNgg4JHauF/bS/agX9lH4RweKItMGsaleahFptnZu5VWdlZ2JPskbVwf/AASrhaH9i7wjuJO+5vXH0+0P/hXzd/wW11qSOH4Z6X50ghMlxdtDuOwsMKGI6ZAJGfc1L1Gkey/D/wD4KYw+KP2dNf8AiZd+C7rzdBvYbS+srSTeMPIibwfYPnHtXbQ+IPgh/wAFHvhfPYm7EzBFLQSMI7yyYEPkA+6847Zrxv8A4JW/B3SfF37Hnim11eMXFl4n1CeCdcZICKqgj3BwfqK/P39ob4VeMf2Ifjdquj6Vqt1p8E8cv9n6hbOVaW2cFfzwxU/U0itOhwHxW8HwfCX42a94d8JeIJL2HS71rW21S1lMbNzt4ZSOxwfxr+hP4e+LtC8M/DbwfZav4l0+K9j0mzidry+jEjuIVBJ3NkkkGvxS8Hf8E2PjX8RfBdr4t07TrO5tNRhW8t994vmTb2HP15J/Crmof8E3/wBpK6niN5oc12FIRXm1DzNnYEZPGM1SYmrn7wwzx3MKSwyLLE4yrowKsPUEVJXmH7NHgjWfhp8CfBHhbxDKJta0vTkt7lg5f5hnuevUCvT6pO5AUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUmaG6U2gB1LTOe1JuK9SMVLdhjLhtqk1VaYkYDYPapZGEmQp3cdqoybgqEIX/ANkVDZ0QiralhboH5fMUv7EVIrOGBZvlqpp9qOWeHy2J4yasSFjCFIPB9Km4O2yJ7WYyMcjGOlWqoxbscHaakVnWNt7bvp1q1IyktSySFGScCmrKj/ddW+hqm7453kj+6abHIsaNtGT320+YahdF2SQKhOT/AMBGTUcLZyxlYj+6wxWe1m8rH98yqxyasxrGzEIzE+ueDS5tR8i7l7NLVaOBluN+/wCX+7VmtDEKKKKACkOG4PNLScVLdgEGOgFG4ZxnmkU4zUbMqnJOCelLmGlcmo3CmLIOOaa7nPtRzBZkuaWmqwKinVSdxBRRRTAKKKKACiiigAooooAKKKKACiiigApMihulM3AcZoAczccVHJKFhd3fy41UlmPGB60M+Oc4FfOf/BRLxbrHgf8AY5+IesaDfyaZqUMVpGlzEcMqyXkEbgfVHZfxoKscR+29+194u+BvhfR7z4aaNb+I7e53NPqyqbqC22sMq6pyM9Pqa8A+FX/BZ+JY4bT4i+DpUnLgTXukONsak4JMbc5HpWX/AMEZdQ1LxDq/xK03U7qXUtDjtrdls7w+dGJGckn5sjkCtH/gpzpf7PHg3wPqNloui6OnxPurhBGumAiSHa6mQyBeBlcjn1qWx2R+jnwx+Knhj4weF7bxB4U1WHVNNmUMGjPzx5GQrr1U+xrr6/Kn/gkb8R/APwv8G+LG8SeOdN0nVdVu4/K0u6utu1EU4YA9+TX6h+HfE2k+LdMTUdF1G21SxckLcWsgdCR1GRTRL0NOiiimIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASk2KDnHNOooAKKKKACiiigAooooAKKKKlsAooopoAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQrKjMuGBycCpNvzE0irj060+gYUUUm4ZxnmgQtFFFABRRRQAUh54paZtO4HPFAChQKdSA5paACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEYFlIBwfWk2/dzyVp1NZsHGKAFNMZgBz0pQxPGKUqMUAfDX/AAUe+Mnxk+E8GgXfw2kkt9OzuvGt7fzXY5GBjHSvnSL/AILNeNdI8Lw2d58PrGXxDGgjae4llRWYdWK+vtX6yX2jWepxxrdQR3AT7vmKGxxjvXEar+zv8NtcuDPf+DNHu5i28ySWik5/Ks1FnRzQaWh+JHiG++P37fXjY3H9m6jq8MjeVFHAjQ2VqOuDnjAA71+p37Af7Grfsm+BdR/ta+XUPFGtskl6Yh+7hCg4jQ9T1yc96+m9B8M6V4XsVs9I062021UYEVrEsa/kBWltp2Zk5XEWloxS00iRKGpaSmI+Of27P2Fb39ra48OXen+IIdFvdLRoBJPD5ilGOSWAwSfoRS/sP/8ABPmz/ZM1bVvEGp+IU8T+Ir6IW6TR2vkxQRg5+UFmO49Cc9K+xdtG2oUWXzDDyK87+NHwV0f41+ENQ8Pa3H51hewNBIoVdwz0ZSRwVOGHuBXo+2kCAc96pRXUnmaeh+aPhP8A4Ix6f4X+I2ma+nxJml0jT7yK7i02XSw8z7HDANMJAvbtHz7da/S5eFA/KlxSbcYwTQkDdw/ip1J70tUIKKKaxIUkdaAHU2SRIly7Kg9WOKFzt5r8WP8AgoL+2N4/1b436j4H0HW7nStD0G8CILNzFJMxx99gfmHNK+tilFtXP2pormvhvqF5qvw/8N3mokG+uNPglnI7uYwT+tdLTEFFFFAgooooAKKKKACiiigAopDQTgUr2AWiqy3JkUsPlAPU1jeM/iB4d+Heiy6x4n1qy0LTI+txfTCNeoHGep5HApcyK5WdBIgkQqehpscZjwN3HpXxV4t/4K5fAvwzrMunW0uua35b7Gu7GzUwdeSGLgkY9BX1P8Kfit4a+Mvgux8UeFNTXVNJuxlJeAynurDsR6UcwrM7KiommCtjPNLu5A9auwWZJRTRmnUhBRRRQAUUUUAFFFFABRRRQAUUUUAFFIelNzQA4nFIGBpPrSbvmwBUSHYeelfJH/BUxZT+xZ422cp5tiHX1H2uHH6jP4V9a5rxf9sL4aSfFj9njxnoEKebM+nyTxR5xukjHmJ+O5BUlI+KP+CJ/hG1Gg/EXxN5YM7XMFgrMvIULvIz9SK+7vjP+zd8OPjpYhPG3hyx1IwxsEu5I1EsIx1WQjK49q/Nf/gjf8UpPDfxR8WfDy+umSDVLUXsFu/AW5iO1xg9yv8A6DX3v+3JpHxF8SfADXNF+GUbSeIb8JGywuY5niDqXWNgRglc555GR3oH1Pxh/bM+Hvw3+GPxiu/C3w01KfWbG0KrLI03nRiQjmNSOuDxxXpP/BNP4v8Ag74B/tCTt4+0z7BJfWjW9rq12u3+zH8tnO4EZG8DYMc/MO1fUv7AP/BNW+8C+ILb4g/Fmxt5dRi/eafoVxiURSEEGSZSCrEAkgdjg9q+c/8AgoJ4c8N3X7dltp/hiVZru6ubJdQRcFEnaRFZMew7Uxn1542/4LI/DbQdQ1Cy0Lwl4g8RNau0a3CiKGCTBxncWJA64+WvLNQ/4LZXu2U2vwwEY/5ZtPqBI/HCV9O3H/BL34C69dx6lqfhu5lvJEUyrb3rwQs2Bk7Ex1Nbf/DtX9nceX/xb2E7Bt5vbgZyMc4fmkLQ4H/gn9+2t4z/AGtPGHjeLX9I03S9I0yKJ7NbIsWDMxBBYnnjBz71+XP7ePiKLxF+1n8Rr63O6P8AtJo8+6jaPyr9yvA3wa+Hn7Lfw810+DdBtvD+nQQS3lxIGZ5JNqk/NIxLHpwM1/Pb4rm1T4r/ABI8Q6lYWc+oXV/d3F8Y4gWby9xOfwpgfvH+wmlh4c/Y2+HErGGytItI8+eU4RR8zM7sfzJJr8kv+CjX7SEf7Q3x+ul0y4S58NaADp+nSxtlZRnLyfi2fyrl/CPxO+P/AMUvB+l/CLw9qOuXWi24McemWURiwhb7kjqASnsTivY/jB/wS/8AFXwj/Zzl+IN1qX27X7QJPf6PbxFjFGzBeD3K7sn6UDPvj/glNCsP7HHhwBVBa8u2O3uTKeT714T/AMFrtLsv+EV+H2ofZ0/tA3U8An2jd5YjJ2k+ma+ev+CW8vxOuv2iPDVppl7raeBIDcNq0Jkf7EqmCQp8h+UEybOler/8FqvFUd54o+HvhmCYyXNvazXcsIP3d7BFJ9zg0Afff7F7Fv2VvhiT1/sS3z/3zXtNee/s7eEZvAXwJ8AeHbj/AI+NN0S0tpP95YlBz75r0ShK5Fxq/ep9FFWlYQUUUUN2EFFFFCdwCiiimAUUUUAFFFFABRRRQAUUUUAFFRSSfNtqRfuigBaKKKACiiigAooooARulMboaezBVyelVZ2MnAbavqKluxUVcd5hjC7uneopbgdhmlaYJtXG/wB6qzSvuzsyvdahs3jHUQF4ZlcFfL74r5L/AOCnnxt8T/A/9neyuvC90dP1HWNSj097yJsPAuxpMr9dmPxr6muI0DcMwZv4M18Rf8FmLbzP2bPDbAZMevxn/wAgyiluaTWqON/4JGfHbxz8UPEnjrR/FXiK916zsrWG5gN45fy3ZiCAT7Cv0pdWXBJ4zX5N/wDBE7P/AAnXxH44+w2//obV+sGoQyyY8tttVy3RhF8z1EkmESluuO1RLf8AmHbtIz7VDtmC7Dhx/s81XmZfLYNzjqB1rG1zpjGJZkkdmwgy2alXcjMC6gN71mWYlFwzBQkX95m5rR+ymZchs1SQNJdRrNIZNq/MD6VJFbzQGPaGPPPFSW2InUH/AL6rR7itFHqYzlyuyGx5wM9afRRWhzBRRRQAjfdqvIrMc7toqwxwpJrnvG3jrw/8PfDd7r3iXVLbSNGs9v2i7um2xpkgDJ9yR+dRIuJpIz/OFfeVIyBSTxyHDYJxX5VfFD9uz43fGr41a74a+AjLe+HbBt0V3YWvm74wPvsx6AnivUPg7+3Z8S/g9fQaT+0p4XvNC026fZbeJGtisZO0nBA69qk05mfoJbylxleedv4+lSySNGhZhgCvLfhZ+1F8JvjNrDaf4O8Z6Zq+pqnmGzjcrJj1AOM160yqy4Zdw9KpK4nIjtp/O5AOOlWMivgP9s7/AIKcWHwI17U/BHgixi1rxTbxpv1B3D28EhYZUgfeOMj6kV8jfB//AIKjfFmy+MGg3vjnXln8IzXYF9Y/ZlRFhfKFgQM4UsG4/u1WxDVz9tc0tUdF1a01/SrLU7CZbiyvIVngmXOHRgCpGfUGr1MgKKKKACiiigAooooAKKKKACiiigBG6VDJgfMxwvrUzdKyPFV9eaX4b1O70+yfUL6C3eSC1jIDSOASACTjrQNGkqL1/nXyZ/wVO1MWP7FfjS2P3r2exgX6i7if/wBkr83vEn7fX7SOl/FLUyms3tjci5kRNFuLMMqAZAXbjn8PSvPP2iP2tvjH8bNKttA8f30lrYxnzxZmDyFkI6EjvzUtl2P0H/4Iv+C00n4K+LfEboom1XVhCr5G7ZEgH4csa8a+KX/BKX4o+N/iz4m1l/FWjLY6lqE1zDqF5OS/lsSwDKOR2FfPn7OPwP8A2lPF2gyr8Nl1/StEk/fsUuzaQyEj7y7iAfwruPiB+yv+2BoOk/bdVfxJqsUnHlWOq/aJB9VVsijcZ1N9/wAEafirbx+bY+JfD9+Qu5BG7puPbk1+gf7Av7PGu/szfBpvC/iS8+16xcXsl5OscnmRQ7gBtVvT5RXp/wCzboeteG/gT4H0zxGLhdct9LhS8W6ffIJNo3Bj3Oa9KxVGbFooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSsAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZ5a7w/en03eu7GRn0oAdRRRQAjMFUknA9aM55HSmXEC3MLRvna3XFLHH5aqoPCjFADutJtA6U6igBkalVwTmn0UUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU3b82aU1GZH8zAUY9c0AP3fMBRIu9SM4pshCrvJAC8kk4Arxnxj+2X8HPAOrTaZrfjvS7W+hGZI1l37fbjvSugPaFXauM5p1cN8Lfjb4K+NGlyah4N1+01y2jO1zbv8yn3HUV3HNMewtFFFAgoppfGT0A71yNx8X/BFnqw0ubxdoseoltotmvo9+fTG6lcZ2FFRxzLNGskbK6MMqynII9Qadu7UAOopoanUxBRRRQAUUUUAFFFFABRRRQA1m2qSegr8B/+ChNjbp+2V4lt9Jtwk811BsUdGkbHX8SK/fW5k8u3kb+6pP6V+GP7VNvb+KP+Ci1nbR8xza9p0cn/AH8jz+lZv4jeHwM/b7wzYx6d4d0q1jB8uC2jjXccnAUCtWobWMR28SjoqAfpU1aGAUUUUAFFFFABRRRQAUUUUAI3Sq97FLMqCOTYmfnGOoqxTAwfPHSpaDqcn8R/HFj8Lfh54g8T3uBaaNZS3bB2wGKqSqZ9zgfjX4bT6h8Zf+CjXxo+xRzz6kskrS+Xu8uy0u23HAbAC5A6E8k4r7C/4LAftCPp+gaV8LdJnkS5vpBcaikZ/wBbHwUQ/wDAsGvoP/gmz+zm3wE/Z/s5dSt44/EXiFhqN4653KrD93Gf91f5mkldXLbsfNvxU/4JP+GfA3wbmm0i/wBW1HxJZ27XN3eQBm80gZ2LEG2nn/Zzjmu8/wCCQvgvxn4N+GXiZNe0680zSri/3WsF9A0T5AwWAYdDW1/wUe+Lnxf+ENrZeJfAHiu30LQ9NQG9tHhR2uCzBcEMpyMt2rxD4O/8Fnr6zaz0/wCIvg+GeHhH1PSJtrAY+8YiPXsKiLuzTVI/VGO1fd5jtuYHI9KkeSRtpRcf71eT+Df2sfhd43+HcvjSy8WWEOjwQtNOLmZY5YsDJBUnOfpX5W/Hb/goF8av2iPiRfaV8KbnWtF8OIGFrp+gQCS8ljVv9czqvmAn0UjArTm7E6vc/a+HKjBfe3c1LX4AeFf2uv2iv2dfFFrc65rniQxM5eTTvEaswnGCMEygsOueD2r9lv2S/wBoi0/aY+EOneLYIltrosYLu3U58uVeoo5u5Lj1PaaKT0pae5AUUUUwCiiigAoprZ2nBwagDPDCS53Ee9Juw7Fmiq0Fx5iqW4Zh0qNdTtZGKLdwu+cbVkBP5ZoWoWLh6VFJIItuecnFOzlev5Uzy89TuIOQT2qZXGiNRO0jBtoj7etebfGP9pX4b/s+rZJ448SwaNNeKWt4HVpJJFBwWAUE4z3r04puKkkgj0PFfDX7bX/BPHXv2pvHdt4msPGEGnPb2wt47S7gLoBnPBB4HWoKJvil/wAFcPg74O01z4Y+3eMdRxlIYYzBFnI6uw9M9u1c18BP+Ctfhf4q+KpdG8ZaFZ+C9OkBAv7q/wB0QXB+/le/T8a8Gl/4Is+PVjLJ440R2HRfsz1bs/8Agir4wmUNdePtJic9dlo7VSVw0PFP2vNF0P4N/H6b4i/Bzx1oj6feXIu7NND1E/aLOQ8uu1eik5796+yP2cf+Cu3g7XNNt9I+LFrL4U1O3iCtq0aSXNvPgfeKopcE47A9a8xj/wCCKPiPd8/xK04A9cacx/8AZq3tN/4IlxlV+3/FKZCDnFtpYwPoC9Ow9GfUs3/BTT9m37PIV+JcO8KcD+yb4nOP+uI/mK/Ob4V+MPgR4f8A2un+KHiz4nzeJLD7ZPqMME+g3LhpXVwodpN33dwYEg4KjGOK+nNL/wCCJ/gaNl/tL4jeIrtf4vs1tDCfwzux+RrWj/4Ir/CdSd3jTxi2eT++tR/7Ro5RaI9Puv8Agql+zzZkBfFF5P8A9ctOmP8A7LUS/wDBVz9n1v8AmYL8fXTpf8K8+j/4Iw/CVWBbxh4yYf8AXzbj/wBo1I//AARn+EmMx+K/Fwft5lzAw/ECIfzp2YvdPSpv+Ch37NvxK8P6ho+peNIYLC9haCeK9gli3IRg8leK4X9n/wAX/sX/AAGF9e+EvFvh8XszEvf6nMsk8YbgojOMqpB6DrXw9+3F/wAE99T/AGa5otc8KPeeIfBlx8rzbN0tpJxxJtHQ5614P+zX8D4P2gPiRb+DpfEmn+GLq5jY20+oqxSWQfwDHeizHp0P3j8G/tBfA3UpDceG/GPhFZrjhms7iCN3784wT+Ndkfid4E1uFrRvEuh3sU42NC91E6uD2IJwRX5R6h/wRd+Jlrbs1n4s8M3smSAmZkyM8HJWvP8AUf8Agkz8ftH1BY7XTtNvkJyJrXUURR75JyKXKI/WH4+eCZdS+B/iPRfhlqumeCvEU0cclleaeYbZVZZFYgkYABUMMn1r8tvhb+yL8QPi9+0Fot18U/Gmk3Nta3Mcl5dXWtw3M00aNuESLu6EgDHuarax/wAE5f2pf7PaN47m6hChTCPEHmAj027uR7VxVv8A8E2v2iLXWLXHg6aGXzV23kdyuIjn7xIOeKOUObSx++NvEkEEUcf+rRQq49AOKlrnfhzo9/4d8BeHtL1Wb7RqVnYQwXMuc75FQBjnvyK6KqSsQFFIelMbOOOtMAGefmzTz1Fcz438Waf8P/COq69fuy2thbvcy4POFGcficCviD9m7/gqVH8cfjxpvgC78Ix6TZapNLHYX0U7M2UR3y4PqEP51EiuU/QamR/dpF+Yj0zkVJTjsIa+SpA602GEQRhF6U8nAzSBsnFUIdRRRQAUUUUAFFFFABUUn1x70STbWC45pu8+1BSVx/DKo3U7cAQKprMk0zqhwR1NWU4GM5oBxsS1ArFrg7T8q8NU9FBIUUUUAFFFFACNjacjIqnKSzcABatthlqncxkKcHBqWjSG5A0/7yJAecnPtxUMyv5gIOR7VEpAncH7x6GpbyQwRfIetYOR1ddCs0SNdRMfmKnOAea+O/8Agr7qlpYfsrwQT2/nT3WsQQwSf8822OxP5Lj8a+v4Waa5Qxjac4Oa+Kf+Cyl/Hafs3+H7d1DST69Ht9RiJyT+tVF3FUeqOM/4IqeDBb+BvHfimSJxJeXsdnHIVIBREyQD35av0fv2mM6KnCd6+MP+CQtukH7KCMhBaTVrlmx9RX2rcMzMVAOcdcVr0MIaMqrDJB8wbd6gUKsfKsuWb2plwXghZy+3HcnFJGxkj4yz9iKwubrXVsf9lVWDZwvpVGbXobW9W08xBI3AUsM9PSpLxpFtZWLMAoySozisYyQ3sHnDD3HG0lfm60uZ3skaqN0dPZ5EIB+dmPbnFaY6CsOxkkiAJOOK2o38xAa6I7HHV+IfRRRVGIUUUUANkYLGxY4UDJNfmF/wWY+Nf9n6D4V+G2nXjLNeMdR1CONvvRjiNWH1ya/T2T7pB6V+Inx6jk/ai/4KTf8ACNSSf6EusppSA84igBeTj6I351Ei4n6M/wDBPP8AZ/034J/s9eHrj7HGviDW7ZL6+umQCQ7xuVM9cAEcVyX/AAUi/Zl8UfHj4Y3mo6V4oa20/wAP20upNokkQKTNHGSSG65wDX2Jpenw6TptrZWyLHb28SxRqo4CqMACsb4lQ/aPhz4qi2eZ5mlXS7fXMLDFCVwufzh/CHw7471bxHcX3w9tr99a0eJr5pdNz5sSDhunbBP4Zr6Wm/4KrfGQ/DW48Ju9ompSRfZl1kLi5QAjJ+uARn3rzv8AZc/alb9l29+IDLoialc65ZyWMDt1hbJHPtg1618O/wDgl346+LXwWf4iJqMNlrmpxtfWejSx4MqMcgZ7EjJH4VRR7T+w3/wTht/FFppvxO+Kb/2tLqDC9tdPZxIH3AndKcnIPXH0rif+Cwfwf8PeA/EXw91Hw/pFrotpd2dzbvHaRBFdoyG7ezD86zv2Rf29PEn7Id1J8Lvito14dB06R1XKZu7E5Py4J+Zc46HjNdD/AMFTPjx8Pf2gvhf8O9V8D+IrPWZLW8u/OhUlZoVeOPAZSP8AZP5UC1ufod+x34mfxd+zH8N9Tc5eTRrdG+qIF/pXstfPn7AtmdP/AGR/htCTu/4lqsD7Ekj+dfQdMh7hRRRQIKKKKACiik6UALRSUtABRRRQA1mA6nFNYB1xnj2ptxF5iEHpSIUhQjcAF65PSgZzmofC/wAI6triazeeGtLudVQYW8ktUMv/AH1ivyj/AOCsraZqX7THw+8M2WnWsBS2t0n8qMIXMs3AOPYiv17t9QtbosIbmGYqcERyBsflX47/APBWLwvrfgv9qHQfiBLbLPok8FqbVhKpLSQkFlK5yOnek0VE/XLwHoFv4X8F6LpVrClvDaWkUSxxgYGFA7VvV8qfs8/8FD/hH8XvCtqbzxBa+Ftat4VW5sNUfydrAY+Rjww47Vh+FP8AgpN4N8aftQ23wr0mzNzpdyXgh19ZB5TzKhcjHZcKeaNhan2QvWnVz8njzw3b6pFp0mvaal/L9y3a6Te30Ga3+vIpki0UUUAFFFFACUm4Chjha8X/AGtP2irf9mL4Q33jObTv7WmjkSC2s920SyMejN2AGTn2FS2NI9oVt3bFOr5I/YX/AG6k/a5/t6wvtCTQda0oJMY4Zd8ckT5wQTzkY5r63poGFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtgFFFFNAFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACmeWpYNj5hT6KACiiigAooooAKKKKACiiigAooooAYilc5OafRRQAUUUUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAhpjHbT6ztYd47WR0ODt4NTJ2RcVzOx8mf8FHf2jrj4MfBG5g0eeS21zWM2lu68FBkb2/75DD8a+FP2H/APgnrfftIWZ8beNpZoPClxI3l4cie665YN2Gau/8FWvGX9vfFHw/4dtb2S6e3iBe1/hV2OB+dfrP8DfB1p4B+EPhLQbKEQwWenQptAx82wEn8zWUU5K5tO0Hofnd8SP2Y/H/AOxT8WvD2t/AG31PVtL1DAu9PncyoxB5Vh6YzX6MaR46uNL+GEPifxjbLoc8Fl9qv4ByISBkgV2LRK2CQCR046Vx/wAW7GPVvh34j057f7SLrT54xGVyCShA/Wny2Iv7RpHgPw1/4KZfBf4leMm8OwatcaTOWKRXOpR+VDKRngN26d6+prHUrXVLOO7tLmK5tZF3JNE4ZWHqCK/mg034e6pr3xQ/4RC0jEOpyXr26Cb5NpyT17dK9g8TfHb47fs3wal8OrjxXe2Vm0XlhFfd8mR9xuorSPYTikffH/BQj/gohb/DOyvfAPw8vYrrxLIhivdRjbctmpxkLjgt1H41+V8Pgb4ieKI5PEcOg6/qAkYznUYreVgxzktuH9K90/YH/Zks/wBqn4vS3HifVsaZp0guruCSQGe8bJO3nsTjNfudp/g7SfDvhcaNpWm21rYw25hit44wFA24AqWw0R+Nf7E/7e3xO8J/FTwf4G8Qa0+r+F9Qvo9Okhvo8y2+47FCt1HzFa/bFfujnNfzwJpdx4R/bX0+G5tmjlh8YQSLCoyCPtSkV/Q9A3mQo/QsAaqJMth69adTVp1UQFFFFABRSGm7/SgB9FRRu5zvUL6c0/dQA6im7vXijf8AMAAT70ARX3/HrIMbtw24HvxX56+G/wDgnTrvij9qi7+KvirVoYNOt9VW+tbKEHfJs+5k88ZAz64r9D2UOuDyKFQLUta3NYz5Y2EjG0Aegp9Qnd5q4XC5qaqMgooooAKKaW+YCnUAFFFFABRRRQAUxyAjk8DHNONY3jPVl0HwlrOoswQWtpLLuY4AIU4/Wk2HU/C74u6rqH7QX7f9vptz/plvL4kg01UYYxbpMCy5HP3VbnrX7x2FpHYWMFtCoSKGNY1UdgBgCvw4/YA0ofE79vaz1i7/AHv2W7vNUOOhbDKDx/v1+51TG5pM+VP+Ck3w1bx5+y/4puLSMHUdNiW5jbcQdqupbp7A1+cX/BNv9nHwP+0VrfjbTvG1p59nbWSurK5R4jnJdXByOQO/av2o+IPhW28beCNc0G7jMtvqNnLbOinBO5SOtfzk+IpfEnwd+IfizwvoWp32mTGeTT51tJP3k0Yf5U+XnOQOnNLlsVHVFv8AaE8I6N8M/ihrvg/wX4hudf8ADtvOyxPu+83cEL1xX1T/AMEwf2n/AIefALxBqfh7xrYJouoawy7PEdyn3AAcRMTyq/Tqa96/4Jy/8E/rLRdDtviZ8S9Ie48Q3h87T9MvOUgjOcSOp5LNnoSa7j9sz/gmb4f+NjXvirwa8eg+KRHk2qLi3uCMcbc4XjPQCq5RaM6z/gol8P8Awx8W/wBlPxL4q0+LT9S1HT7SO7sNQjVHYr5secP1xtzXg/8AwRT8aJJ4d8eeFZZH8+G5jvY4z0CsuDj8RX55ePm+KvwTkv8AwPr+o6vp1l80MljJKzW8i9Plzxj6V9if8EWbhv8AhbnjZAcI2lx5H0filyg9rH7C9xS00dadVJWMgooopgFFIajZm7HFJuw7EjdKgaNZupOPSnru3DJyKk2j0qfiHscZ8VV1k+A9YtfDoCarPaSxW8h6IxUgGvxA8efsiftJeHfEcwl07X9VkuWMouLK8kKkkk5OG4r98toxjHFG0elLlY+Y/BPSvh7+154Ftz/ZVv43sEXkLb3UjH8BmqXijxT+13rVq2ja/qHxFubecbGtZjNsfHOCRx2r9+cD0pjW8Uhy0SMfdQadmHMfFH/BLn4N+Pvhr8L9X1Lx5PqMNzq9wJLbTL6VmMEYHXaTwSa+2qAAvAGBS1SRLYhrxb4mfthfCX4QeNLbwr4q8WW+na1MVBh2swi3dC5Awtezy7vLOzG7tmvzl/bj/wCCZ2o/FjVNV8feBdTlu/Fd03mXWm383yTjj5Y2P3SP6UxpX3P0O0fWbDxBptvqGmXkN/Y3C74ri2kDo6+oI61d/OvwX+Ef7Unx4/Yh1xfDOo299Fo1vN+80HW4maFlGdwhY/d9cqa/W/8AZh/bI8BftQaBHNoN8tnrsaD7Vo10wWaJu5A/iX3FA3Gx7zSU5ulfO/7dX7REn7OHwB1nXtLv7ez8VXJS20hbhPMDSlgWO3uAm78SKCCL9q79uDwL+yrp0cWqO2s+JLhSbfR7N13/AFkP8A/DmvzV8c/8FI/2ivjc+oWfg2yl0TSbomOOPQrB5bhVzniYAkHHcYrL/ZV/ZH8f/tvfEqXx147ur7/hFZrnztQ1S7djLeDk+XCW6jOPYCv2d+Gvwr8LfCHwzbaF4T0a10ewhQLtt4lVpMfxOQMsfc0F6I+R/wDgmb8M/iPo/wANvFGofFtNYmbVrkPbweIruSdni2/MzJITgGvjI6f4Z8a/8FSNKtfAVpBbaGmvRts02IRQr5KEybQoAAJU59c17r+37/wUm13wT4m8RfDDwFZSaZfWhNpfa1OoLAkfN5S9uM8mvzo+C/x98UfAn4gN4x8OSWsmslXUyX8IlBLDlhnoeTyPWgZ/Smvan18df8E+f22NY/aw03XbPxBo0Gnatoyx7ri0JMU+4HJwehyP1r7FoICiiigQUUUUANY4XJqJkC72BwSKmbpUEkwDYPIoGrnzZ/wUW8VT+Df2R/G19aDFzPHFaq3p5jhSfyzX4yfsWalLp37VnwynjJMo1mKMY/usGVv0Y1+t/wDwVc1a30z9j3XoJpAj3l7bQRL/AHm3Fv5Ka/If9i+Ty/2qvhkx/wCgzF/Wk0VeyP6PV606iihKxIUUh6VFv2yBfWmImopnnLvC55NPoAKKKKACiimS7tp29e1AEN0rctnis/59rhPvdqsTXLop3CoGZpCxT72KzluddNWQWgbdh+tX0bbKVqiu9UyRl6uw3BlyNuCKqOwqnkWqKqfanWZUI4NWPMHfiqOUfRTdwI4NJQA+mthlIzSV8Yf8FNvjd8Rfg18M9Fk8AfarSTUblobnULOMvLBjBGMA4z0z71LdhpXPtBVCjFMkjV+vSvwa8M/GD9rnx9MBpGs+Ob4ydFEToG+hKgfrXR3Hgf8AbW8URtbSW3juYTfKUa6VFP8A48KVy1HzP26bT4WbPSq9wNPt1JnuoY17+ZIo/nX4lWP7Dv7WutTK91Z6xGW5JvNaZMfXa5raj/4Jr/tN6mQbi4gjz1E2uSkVKSHd9z9gNW+IHgvwqvm6r4p0TS0X+K81CGIen8TCvzz/AOCu3xg8D+NvhL4T0vw74u0nXdRi1UzmLSb6K4KLsIyxRjjrXkcf/BIf43a+Y/7X8S6FGrfeMt7POUH0I5rq9I/4In6/JtOqfEGyiH8S2tmT+RJqrJ7A31bNT/gmf+2F8Mfgn8EdR0Dx54wj0a7XUXmhhlt5pPlYDkFFPpX1jP8A8FOv2b7fP/FwlkI7Jpl2f/aVfO+n/wDBFHwqtqBd+P8AU2uMffht0AH51ftf+CK/gqORTN8QvEDx9xHFEpP44NUK6Pa5v+CpX7OMcZK+NZ5mHRE0q5yfzQD9azX/AOCsX7O0bEf8JDqpx3XSZT/SvPY/+CMfwyVfn8a+LGPqJYB/7Tpkv/BGH4ZyAgeOPFi/70kBH/ouotYND2Hwt/wUo/Z38dXQtIvHkOjv1J1qzltY29t7DaPzrutP/am+BV/cRw2nxb8GtIx2pH/btuufbBevkTWP+CJfhCaKQ6Z8Stctp8fJ9qsoplB98FSfzry7xV/wRW8ZaXvfQPiN4fu4/XVreW1xz3ZA+PwpaFqTWzP1b0TxN4c8SWyz6TrmnanBjIls7qOVT+Kk1tw3dszCOOeN27Krgmvw+1//AIJL/G/RfNlsn8La9EqFjJZ6rtBwO3mBDT/+CadhH4G/bTtdJ8V6rHol/Z211BHazTqY5bnKqIlYvgsRuIAyTitEQ9ep+4tLTV606mZhRRRQBDd3C2lrNO/3I0Lt9AM1+NX7BdtB8UP+Ci/iLxJcoM28mo6nCD/eL+Xn8nNfsN4qvrfTfDGr3l3KsFrb2c0ssrnCoioSzE+gANfkd/wSc0OTWP2sPG2u22ZrGzsLhXkj5VTLONmT7hDj6Umi1sfsHj2qG+s01CyuLWQfu5o2jb6EYP8AOrNFCViT8mJ/+CQfim++O0txNrVkvgSa+a6e4X/XiMsW2BfXoPoa/VfQ9Gt/D+jWOmWibLWzhSCNR2VQAP5VoUUwvc8D/aO/Yr+G37S1m7+ItKFrrQQrFq1nhJlPv/e/GvzWvv8Agj38VYfiA2l2eo6a/hhnO3VnmO5Yz/sY+92r9paKAuzjPg78Obf4SfDLw54QtZfPh0mzjtvNxjeVHJ/E12dFFAgooooAKTcKSRgqknpUDXAAzjigpJsn3Comd/MwB8nrUSXSTEMrDYDgkHinZM33QducHII/nUt9h8vcsKRtFLkVEo2dTT6adyWOyKRm4rzX9ob4oaz8G/hTrXi7RPDMniy602MSnTopfLZl3AE5wTxnPAPSvzmk/wCC2XiFXIPwpsU+Yja2stuGPUeTxTCx+sLbmUjFebftEfDvX/ij8HfEvhrwvrj+Hddv4QLe/jJG1gwbbkcjIGM+9fnK3/BbLxEVO34W6cG7Z1lv/jVLZ/8ABa/xD9qi+1fDHT/s+75/J1Vi+PbMfWgdmeNL+xh+1z4L1qa00608RJJK5Et3Ya3mKUZ4O4PgfjU3iD/gnf8AtY/EL7K3iK0l1Yxg+T/aevxyGP8A76c4r9bv2bfj9pv7SPwzs/GGmabeaTFMxje1vUwyuOuD3HvXceMvHHh/4e6HLrPiXWLPQ9KhID3d9KI41JOAMmgd2fiH/wAOmf2iW5bw/pKn1OswHP60W3/BLH9o3SbpJ7bRbGC4jO5JLfV4w4PsQa/bLwb8TPCnxEs/tfhnxFp2uW+ceZY3CyD9DXTUC5mfhPD+wR+0rpPj7RLzU9D1CWVr2ENqUF753krvGWLA8cZr9y9BtH07RdPtJpWmmhgSN3Y5LEKASau9aFj2gAYGDQJu4+iiigQU0uB3pT06ZqrMx7rgVLdioq42ScyTBFPtXw7/AMFhrwW37L9jGRnztahT6fI5/pX27bBBNuJ5zXwV/wAFnLgp+z54bhB/1mtKxH0jb/GhalyXK7I+X/8AgjbHfN+0ZrZgkxZLozG4XJ5O8bP61+09fjn/AMEWYSfjL4ykGNq6UgPry9fsWTiqM2LRVe61C30+3e4upo7W3QZeWZwir9STgVX0bxDpfiK3afStRtdShVtrSWkyyqD6EqTzQI0KKKKACiiigAooooAKKKTNAC0UUUAFFFFACVjeLvGWieA9Dn1nxDqdvpGlwY8y6un2IuegzWy3Svib/grlpd1f/snyXEFw0MVpq9vLOgPEiFXGD+JFAz7A8JeNND8eaPFqvh7VLXWNOl+5c2kgdD+Irar8pf8Agi78RNWm1rxp4Oa4eXQ4YUvYI5Dny3JwcfWv1aoB6BRRRQIKKKKACiiigAooooAKKKKACiiipbAa+dpwcGoVWcTAHBj7nNTkbuDS0LXcAoooqgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKTNGaACigniotr+Zu3/L/dxQBNRTd1LuoAWikzS0AFJu+bFLTSvzA0AOooooAKKKKACiiigAooooAQ0yaZYY2kd1RFGWZjgAepNOdwi5bgV8af8FDv2xtM+BHw/uvDOms1x4t1qCSCBFGVhBGCzfgTxS5knYqMbs958J/tPfDLxx46n8H6H4u0/UvEMLMrWcEm4kr94A98V6mOa/Pn/glz+yQPAfhNvid4psYm8TazmSx86I+ZawtyTncclvoOK/QYcDFMcklsLRRRQQFFFFABRRRQAUitnNLSBdtABVLVpI49PuGk4RY2JP4VdrL8SeX/AGJfCVxHH5LbnboBjrUT+EqO6PwV+MGpXXxU/bgs7KOPz2bXre1Vc53osyk/oDX762EP2ext4sY2RquPoMV+Fn7NelDxt/wUS064tCs8Ftrc917Mqbh/XP4V+7Sqcc0U9I2LqPUcagvIfOt3UDOR09fapzzRim0Zp2dz8Kf24Pgr4+8F/tIav4l0Pw1qFnb3E3n2t1p0LOA3qMV5d4U+APxq/aS8ZW8DaLrWoXEp8ptR1OB444uM/MzDpxX9Dt1pdreMhngjmKHKl0Bx9KmgtYbUEQxJED12KB/Kkk7lykpH4t3n/BMn4+fCax/tzwfqu7VFTc8enXJilz0wpH1NeTeNvHP7U/wySWy8R6141sokGH8yeR48fWv6AdtZ+reHdM163eDUbC3vYXGGSeMMCPxFFmLmP53f2Zb3WfEn7UfgW/u7e48Qan/a8c0qTKzMSCSS306/hX9F1uxaBCRtJAJX0rifDHwM8B+DdXbVNG8LabYaix3faYoFDg+xxxXdBcYqlsDd1YFpaSimQLRXgH7X37X2i/skeC7XWdR0a41++vXMdpYQzCBZGGM7pCrbRjP8Jr41j/4LjWrSL5nwbmWL+Jl8TKzD6D7KM/nU8yK5WfqPJnadvX3pq7tvzYz7V+Y8H/BcDQ5J0WX4S6jHET8zx62jsPophGfzFdjpX/BZn4bXdv5l54M8TWj/ANyJI5f13CndDUWfoM33hxzTZmdYyUALds18RaN/wV7+B9/t/tCLxHo7d/tOnbgPxRmrSuv+Ctn7P0MbNFqusXLjpHHpcuW+mQBRdBytH2eOcZA96dj8K+Epv+Cw3wZjkYR6V4nkQfx/YVA/V6jj/wCCxnwZaRRJpniOKPu5s1OPyai6Fys+8qK+HZf+CwHwKRRsbXJGI+6NPYVSuP8AgsX8Fo42MNh4huZP4Y1tAC34k0roOVn3fRX5v+I/+C0vg21glbRvAWt3rqPlNzJHGuffBJrze+/4LceIo5WNt8L9LMJ+75upybvxwlULY/WiivyLk/4LaeMp12xfDPRYSf8Alo2oSsF/8dqOT/gtF46ZPk8CaEp/vfapCP5Urglc/XfaM5pa/Hab/gst8TpGzD4R0BE/3pD+tMX/AILKfFIuMeE/DrDuuZeaB2P2Mor8aH/4LGfF681KGG18OeHkaRwiwBJGLEnAHJzX63fC/XNZ8TfD/QdV8QWcOn6xeWkc9zbQElI2ZQcDPNCdwasdTRRRTJEb7teG/twas+i/sp/Ee5iuDayjTCqyr1BLqK9yr5r/AOCilvLefsifEC3hRnkezGNvtIhP6A1Eioq7sfC//BF/w3HqHxS8Za88Yd7LTktklJ5BkfLfngV+vtfkf/wRV1byvHXjzTlO1JbSGbb9CRX64VS2HIRuleZaB+zn8O9B8Zah4qh8I6QfEF3cm6bUGtVaVXIxkE9DyelenUmKZNxPYcCl7UbRRigR5B8fP2X/AAR+0R4fm07xLpsbSlCsV3Gu2WNuuQQQT+Neb/sf/sG6D+yXrOu6tY65c63e6moiDTRhBFGDnHB5NfU+0UbRQPmfURetOpMUtAgooooARvumq8uIo2Z3IHrUs5xEeC3sPrXkH7VnxisvgV8EfEfiu5mX7Ta25+yW7MAZpSQAo9eufwqJFIyv2hv2xvh9+zbp8beJdQNzqUv+r06xIaZvw7V8w3X/AAWi8BrMy2ngPXriJf8Alo08S/p1r4M+Dvwh+IP7e3xsnmuZLiW2mm87UdTmyYrWEn7qn17Yr9LbH/gkf8EYfD8FjcxatPeIQz3y3ZVyccgYHApXsNpdzqPgb/wUw+EHxmuoLCXUH8LatNJ5cdpqpC7m/wB7pX1hb3EV1Ck0MiyxSDckiEFWB7g1+P37YH/BLuT4Y2LeIPhpLdXel28bTXEF1IXkQAZJDV65/wAEjf2mdW8YWGrfC/xHez393pUf2mxmuZCzLCDgxjPYGq5rhy6XP0poooqiAoopGoAKNteNftGftXeAf2YdFt77xhfTfabo4ttOsYxJcTY6kKSAB7k18afEX/gtV4Zs9OuI/BfgbUb3UCuIZ9YlWKJT6lEyT+YoK5WfaH7TXw8+F/iz4aazefE6ysP7GtLV2e/uUXzIBjrGxGQ2emO9flX/AMExtFh1L9tq6uPDH2iXw3ZW13LHJcHLeRuCx7/9rnj8a8Q/aH/bQ+KH7TH7rxNrZi0VW3DR9LDxWq+hdc4Y+5zX2P8A8ES4LZ9b+JUpt1NzHb2oWYqMhSWyAe2aB3srH6uN0r8Sf+CsPx6b4mfHNfB9jNnSPCyeS2G+SSc8sfT2r9tJpBDC8jfdUFj+Ffgx8N/C+ifHD/goiNH8SW/23QtV8S3Rns3YqJVUOwU4PTKik2Ee56p8M/8Agrb4g+F/wz0HwrpPwx0+SPTLVYBcm6dEbA+9sVO/1r6b/Y//AOCo2n/HrxxF4P8AGei2nhXWb1gmnyW1w0kVw+CdnI4OB619Xa74C+Ffw38E3D6l4c8N6N4cs4f3oms4Y4goHQ5HOfQ9a/FX4E+H4vi5+3ppU3grSDbeH/8AhI2v44rGLEVtbo5bdwMKvA46c0Jj0Z+ufxS/YP8Agz8ZfHFz4s8U+GHvNZuQBPJDdyQrKQMZZUIyfeuWb/gmD+zqykDwOyZ4yuo3Gf8A0OvqoU6mRdnA/B/4F+B/gToH9jeCdAttFtGO6RoxullPq7n5m/E139JS0CCiiigApKR2CqSeBVR7otjCnDcA0m7FJXJLmbCnFU4ZPNlVT3NSX2ntfW5TzCjMOoqDT7CeFgr8Kvf1pcxvDlUXd6nw5/wWUvEh/Zp0i3ON82txED6I3+NfmF+xDp51T9rL4Y246tq6N/3yrN/SvvX/AILXM6eH/h7Erts82Y7NxweBzivkL/gmh4bk1z9snwIw6afJNet9FiZf/Z6d7mLR/QBSHim0HmmQI0mFPFZ63n+lmE/6/r+FTyptO70qrHIbi7Yr95RxQbRjpcuHH8X3qsp90V83/G/9u74U/s++MLTwt4pvbqXWJsefDp1t5ot1PRn5FfQXh/WLPxFodhqensXsbyFZoWK7cowyOO1BnI0KKKKCQqGdioJHWpqhmXzPlPQ0DW5nzxyS5NV4GeO4YHpV2QMsxEhyvbkj+VeJ/GT9sj4RfAvXk0Dxp4pXTNWKCVreGKWUqp6E7ATUSOlSsrHs0037s0W8pyOxr5f/AOHln7N67X/4T3cPT+zron/0Guv8K/t0fAPxcAbD4j6QjngR3sxgb/vl8GknYOdWtY99TaxBZtzUy5xdJtU8g1zWm/FjwNqluk9n4q0WeJuVeO9jIP61qWPjXw5qd0lvZ65pt1cOcJFDdRs5PsAc1adzG/kadrG0bMD0qVYtrbtxNSjrTqZLYyqeoaTZazAsN7aw3kIbcI5kDLkexq/RSauK5Bb2sNqoSGFIUHAWNQoH5VNn2paKXKIo65rNr4f0e91O+k8mztImmlkPZVGTX5x+IP8Ags54e03xBqVpY+BbrUNOt5WiiuvtSoXwcZII6V+kd9Zw6hZz2tzEs1vMhjkjcZDKRgg/hX5Zf8FKv2L/AIUfCH4T3XjjwzpzaJrVxfIghWZjFIWySAp6etHKVE05P+C2Omo2F+HE5HvfD/4moz/wW0sB/wA02mI/7CA/+Jr5E/4Jz/B3SvjN+0rpGja/o8et+H4rSa5vreeMtEVUAKG9Mk8fSv2CX9gv4Ap0+F+g/wDgMKaGz4P8Vf8ABa7xHcW8ieH/AIf6dZOw+We8unl28+gxXmur/wDBXz45apE8diug6V5nCzQad5rrz2DkqfxFfrx4N+APw5+H6Rr4f8GaNphjOVaGzTcPxxmuzXRdPX7thbD6Qr/hTFc/Fmw/bo/bI8XWofSI9e1CGT7smm+DUkz9CkJ/Srtr8dv29fFMgs7XSfHMLzfKsjeFvsoHf77wgL9Sa/aJbeKNdqxIq+iqBTwNvAAApWDmPxouvhL+378SUji1G68XQwyHB3+ILexUe5CupH5VG3/BMf8Aai8WWcz6/wCILGVpB80GqeI57hz7fLlT+Jr9nKKXKHMfh/q3/BJ39oWx0u4aCz0XUiq5Fvb6vh5PYByq5+pq3+zP/wAE1/jJH8cvCc3jXwvc+GfD2nXaX13frdwscIdwVWjY8kgDHoTX7a0U7BzEcMYiREGcKMDNSUUUyQooooA82/aTkeP9n/4itG/lv/YN4A2cdYWFfm5/wRFYf8Jv8VgTuf8As+xJP/bSWv0B/bS1KbSf2VfiZdQZ81dIkUY9GIU/oTX5/f8ABEm3ePx18UpAh8htOs0EnYsJJDj8jS6lr4WfrZRSdzS0yAooooAKKKKACiiigAooooAjuOYWqqjDYx6hRzVyRdyEHisa6uoNItLy8vJBFZ26NJLI5woVRknP4VnJGkXoeC/tiftcaH+yj4IXUJohqXiG+G3TdK5VWPd39AOa/KLxZ+0N+03+1Pq01zpMnjC702Rz9nsfDNpP9nTn7uYhycfWtj4xeJtU/b7/AGzodJ0oyrpTXX2G2IyyQ28ZO6UjgDIH6iv2q+Ffw30b4T+A9I8M6FaR2ljYwLGBGoXewHLH3JpxiNs/ELS/gf8Atjabbvq8OkfEq2S3XzN0dzMJh2+WIuHY+wFd18C/2/vjZ+zb44sdC+KiaxqGhzzp9rt/E0Esd7BETguhcBuM5xznFfthXwj/AMFZ/gTp/jb4EyeOLXT7Ua34fmjee8IxK1sx2lc98EiqsTc+1PCfijSPiF4V0/XNInj1DR9Tt1mhk2na6MO4I/QiuQv/ANmj4UanJNJc/Dnw1LJMd0kn9mRBmOc5JC5r5p/4JF+NLrxN+zI+n3c7zNo+oyWse8k7U6gD86+4qZOx5Mn7KPwejYFfhv4dB/68Up//AAyr8IfMV/8AhXPh7cpyD9hSvVqKAuzP0fQ9P8PWEdjpdjb6fZxjCQW0axov0AryH9rb9mXT/wBqX4Vy+Frq+bTL2GUXNjeclIpBx8y/xDGa9upGXcMUCPxD1/8A4J0/tK/A3VLi98GPc6haxOWhutA1LZI/v5QIP5itjwj/AMFDf2h/2c9RtdG+Imjy6haxMEeHWrdopyvT5X7mv2dvLqCwt5Li5ljt4I1LNJI21VA6kk1+Wv8AwUu/bR+HPjXwzf8Aw38L2Vp4o1p2WObVlhDC1YMDiKTHJ4xx60i07n3r+zP+0h4a/ac+H0fifw6ZEEb/AGe7t5kKtDMBkrz1HvXrtfEn/BKT4L658KfgLd3uv2kljd69efbIoJDyIdoCnHbNfbdMl7hRRSUCBjtUnGarSyF8gDBxnpU8jLsYscKBkseBXxJ+1r/wU68J/ADUH8P+FrKPxh4mUZk/eYtYOejMpyT7DFJoqJ9m29n+9Dt65xX5xf8ABarUJ4/h74KsgrfZ5Lx5C3bcFxXlWl/8FpPiHHrUJ1LwLoR04uDJFEZll2d9pLdfwqT/AIKLftS/Dn9pn4C+DtR8NamTrkN5uuNLlG2aAFecj0z3qdti9Xqxf+CLNuf+FpeOJOMLp0a/+PGv18Y4U4GfpX5K/wDBFPT5m8aeP7rbmKO2hjZx0ySeK/WvdziqRmz4q/4K367e6D+yZILK6ltvtes2tvP5bYMkRDkqSPcLXk3/AARbvr+48HePbdp9+nwX0exXyWyVycHNb3/BZ/xYlj8FfCvh8FvNvtU+0EY42xqf6mtD/gjj4Ev/AA38BNa129g8mLWtRMluzAgyIqhc8jpmmI/QGiiigAooooASjdQ3SuP+I3xa8H/CPS4tR8X+ILHQLOV/LSS8lCBm9BQB1+6mooUk14L/AMN3fAYuEHxL0TP/AF3p0n7dnwHiUk/ErRDjss4JoHZnve6jdXyd4v8A+CnvwA8JSCP/AISt9Vk7jTrV5QPxAxWz+zf+3p4E/ae8b6j4a8K6fq8U9nB9oNzeQBY3XOPXI/GgLM+mN1LTV606gQjdK+MP+Cs2rWth+yTqFrcZ8y91K2iiIPAYEnJ/Cvs9ulfAv/BZK+jh/Zw0S2YgPPrUZUHvtRs/zoGtzyv/AIIqeBZVj8deLDKohZ47FI9p3HA3E59Oa/U+vkb/AIJf+FNO0H9lPw7fWNp9mm1NmnuGPV2BxmvrmgHuFFFFAgooooAKKKKACiiigAooooAKY8m3tmnHimfeYcVEgHKxYZIxTqKKcdgCiiiqAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCldapaWODPcww5GR5kirx68msO4+KHhC18zzPE2kAx/fH22PK/UbuK8n+P37F/g39pLxLp2qeMNQ1k29knliwsLwwROv+1iuT0j/gm78EPCLi40nQbm1kj+bfPqEsob/eDHmom2tjrpxotpTke9zfGLwRa2Ul3N4q0mO3jXc0jXkeAPzrjl/a8+D01re3EHjvS7qKzBaf7PIZCoHsoJNfm3/wUi8M+DPCz+HfC3hiKO21me5VJWt3IUITjnnP6V9rfslfsW/Df4X/AAz0q7TSbbV9Z1C2WW7vpXMgLEchcjgfhWEJzlo9GVWp0oStFtog8Zf8FQfgP4d025l0/X7zxFfRozJY6fYTb5GH8ILqqj8TXr37NHxwg/aE+Glt4xtdLvdIhu5GC218oDgA+xIx+NF9+y58N7i8a8g8LadZ3hTZ58MC5Hv0616RoGh2nhzSLbTrGGOC2t0CIkaBR+Qrojfqc8uXl0NDBzTqaOtOqzK9xCcc0Ag9KGG4YoVQvApALRRRQAUUUUAFFFFABRRRQBxHxg8aS+A/Auqazb2F1qU9rCzpb2sRkdj2wB1r8yv2Xf2U/FP7WPxv1b4k/Fy01CHw9Z3TPbadqUTIbj5iVXBxhRxX61ModSGGR6GkjjWNcIoUf7IxUuN3cpSsrEOm6fbaTY29lZwrb2tugjiiQYVVAwAKs0m2lqiQooooAKKKKACiiilcAoooougENcP8WvENtpPgrXN4ErLaSZjzj+E13DfdNeSftKXjaX8K9fuI7dZJvskp3+mEJrKo9DSnrI/Jn/gma0F9+23BNJGFLxX0iL1wd1fuDivw6/4JWsNQ/bOsyVztsb+XI7HIP9a/catI7CnqwoooqiAooooAKKKKACiiigAprjcpAOPcU6koA85+M/wL8J/Hfw2dD8YaSmr2Gcqpcxuhz1V1IKn6GvnPUP8AglT+zlp9jdXV5ot5Zwopdp21i5VYwOSTukIr7RZfl461w3xd8CyfELwHq+iSSKq3Vu8Y2kjGRjNZWsaJ30PzV1r4Y/8ABPzw9rR0lvEl3c38bbHeO9ungDZwQWwB+tdXc/Af9gHTY4J7rxFbYlGVVtYust+APFfmP8TPBL+DvidrPhdZPNNpfNbIxALHLYGcAZr9FPB3/BGm38VeCdD1a68e3NlqN5axzzQtah0jLAHAHB/M0XtqO+ti5qHwo/4J8wSFx4p2bedkep3BX9Rn9azr7wb/AME+tAi+1y6vcaiFG4QwXly5b2wOTW+v/BEnTVjbPxKuDLjj/iXLt/8AQq2NF/4Ip+FLe3f+1PHeqXM/8P2WCOJf1DGlcrTueY3Wu/8ABPUfOmk6wWXoIxd8/mapHxb+wA2V/wCEf17Hricf1r2i1/4Iu+BvtaG48X62bbPzIjx7yPY7OPyrfuP+CM/wiGw2+v8AigYHzCW7iOfyiqlqLTufNWseKP2DvsrSWHh3X5LgL8sSeaNx/E1p/sx/BX4A/tZeJ9R0fQPBmqaRDZ/NJcyzM25PY54NfRen/wDBG34NxSIbvVvFE8YOWRL+Nc/+Qq+qvgd+zj4D/Z30A6V4L0gWMbD97cStvml/3mwM/lUuF3cOex43pP8AwTL+Bmj+S0PhnzZ4eVkuJWfJ9SOh/Kty9/4J6fA7VmhbUPBlrctF02lkH4hSK+lNtGPer5URzs8E0H9hX4G+HJUlsvh7pYkQ5VpVaTH4E4rrv+GevhVptpJv8D+H4LdRl2ks4wAPckV32ua5YeG9JudS1O7isbG3QvLPO4VFA7kmvyC/bo/4KBa58btYf4bfC17mHRXn8ia4swfOv3B4VCOdv0o5ewXbPqT4y/tRfsqfBHUm0iTw5pGvagh2y2+j6fHL5ePVsYrxnxR/wUW/Zrt9JnGgfClLu/ZfkWawiiUH3OKq/so/8EmF8QaXb+J/i9e3SC8USjRbWQpIQef3j9QfavtbQ/2BfgNoOmLZQfDzTJlVdvnXCmSU8ddx71VtLBfU+Uf2Of2hvg7+0X8UrTw9P8H9N0jxCFa4ivFiR0BU5B6cGv0vRVjVVUBVUYAHQCvDfg3+xX8JvgL4wuPE3g7w++n6vPG0RkkuGkVVJyQqngV7pSirBKXMwoooqiBK8U/bLU/8M0+P3VA7R6ZKwBGe1e115x+0LaQal8GvFllcxGaC5sJY2UZ7qfSolsXD4kflt/wRh1a2h+OXi20mIW5udJUwLnGdrnd/MV+yNfhV/wAEy7xtA/bS0e1DGHzEu7RkPcHoP0r91apbBLcKKKKZAUUUUAFFFFABRRRQAUUUjdOuKABulfj1/wAFPvi9ffG34/6D8JfDVyZrbT5FgljVvkkuXPf6Cv1h+JHiYeDfAev60W2/YrKacH0KoSP5V/Ofot145+LHxlutT8LLfan4vvL2S/he2G6bcGJDDjsKh7lxP3o/ZF/Z5039m34OaT4atUje/dBPfXSrhpZWGTk+3SvbOPWvxDl8Xft2abD81/45WGMdFiQ4H/fNOh+L37b+h2sstzceM7iIr96a3BK+/C00h8tz9f8A46+ItO8LfB/xhqWpyxx2cOmTl/MIAPyEAc+pIr8q/wDgj/4LuvEn7QnifxakbJpum2ckZZeF3yPlR+Qry7X/AAX+2F+0PYRab4gg8Xazps0nEGoN5cIz3I44r9Sv2Cf2YW/Zl+DMGm6pbW6eKdRf7TqU8I+Yn+FCe+0cUW1uHwqx9L0UUVRmFNanUUAfOH7WH7Evg/8AawjsJNaurnSdUs12RahZhfMCnnHIwfxryPwj/wAEfPgjoluF1mTXPEU3dpr0wg/hGFx+dfdWBRQVzM+V9B/4Jlfs76FG6DwIt/vGC19fTzEfQl8ivZvhD+z/APD74D2NzaeBPC9j4fS6I+0SW6kyzY6B3YliB2BNehUtBJHcR+dbyR5xuUrn6ivwb+MnwI+NHwI/aU1TxV4a8Oa0LuLU5r7S9U0uxacLuJGQoBB4Y8H1r96KSk0UnY/Cpfhr+1T+234qtdK8Tr4judOgdfMn1mD7DZWv+35eFVjj0BNfqt+yX+x74S/ZW8Hx2emxJqXiKdB9u1qaNfOc90U9VTPbNe/0UJWBsRetOpKWmSFFFFABRRSHpQBVab98Yzzu4qlq2oWeg6VeajqNytpY2sbTTTMcBFAyTWjLEdpKhS/vX5F/8FFP2s/Ffj/4qXnwW8JStaaRBdR2VxJbsRJcSMQCpIPI56VEi4nU/FX/AIK4eLF+IGqaT8MfCNrreiWchSK6kjklkmA4LYUdM1y+n/8ABWL47NcMtx8M7W5TvGtlcKf5V+gf7J/7N+h/An4OaBobabZ3GqrCJbq8kt0MrO3JBbGcCvZRoOmKxI060B9fIX/ChK47rsfgR+15+2r4q/asi0i08RaHYaD/AGQzFYLYvvLHruDV6z/wR78LDWP2lr7VZf8AmF6PI6Y9ZGA/pXcf8Fmfh3pfhrxR4K17S7K3s5NQglgnS3iVAxU5zwOtd1/wRV8BtDoPjjxdNHg3E0dlExHYDJFVYnY/TsnAzX5rfHH/AIKy6z8J/jdrXhW38F2N7oGlz+TJPNLIlxKB1K84z+FfpVINykGvlD9qD/gnz4H/AGjPM1HZ/YniRsn+0oBy3puHemOKXU9F/Z1/ak8D/tN+Eo9Q8OXkMeooga40ieQGaBvcdx70n7VXx4tv2c/g3rniqVVa9iiMVojceZMwwoH0zn8K/G740/so/Fr9jHxNba8CxsLWfzrbXNNkIHB4346f/Xqp+1B+2T4o/a0j8IaPd2K2I0+NIPKjcn7ROcKHP1NBSLX7LPwC179uL9oC8udcv5jYiY3+s3zN8+0sSET36V+93h/RbfwzoWn6Valvs1lAlvHuOSVVQBn8q+d/2B/2Zof2cPgpYW93GD4m1dVvdTlzn5yMhR7AV9M0GbCiiigQUyX7pp9Mk+7QNblKSNZpijZ2kc4ODXwP+0V/wS2h+Pnxg1PxfD47bTIr0qZLeS281l46A5FffrKXyvrSws/KntStc2Z+abf8ET/Dxtxj4j332gDr9gQLn/vquX8Q/wDBE/UIraV9E+IltNOB8kd5ZlQx9yCcV+rAc57VIHzS5TPmaPxF8Z/8EhvjP4Zh8zSZNJ8Qr/dtp9rfk2K2v2U/+CcXxs0X41aBrWt2Ung7TdJvI7ie989d7qpyVQDrnp+NftFRTsLmI412qoJ3EDGT3qSiimSFFFFABSZobpTaAHMeK/P3/gstfJF+z34etsjzJtZUqvc4Q9Pzr7/4YY9a/NX/AILXX5h8AfDq0HRtRnc49oxigpbnP/8ABFHwVC0Pj7xVJGTcq8VhG5HRcbiK/U6vjz/gln8NYPAf7LOk6griS51+ZtQmYds8AfkK+wt1AnuLRSbqNwoELSZrC8XePPDXgHTW1DxNr+m+H7Fetxqd3Hbp+bkV5z/w2N8DPNEZ+LPhFW/2tXhA/Pdik3YD2OjNeI6/+238BfDdk91dfFjwrNGoyVsdRjupD9EiLMT7AV5VqH/BV79nezklSHxHql8yHH7jSJwGPsXVR+eKnmHY+w6Wvnf9mX9tjwd+1RrmtWPhPStZt4tLAZ7rUIFjRs9OjHBr6IqlqD0CiiimIKKKKAPF/wBsyyl1D9ln4lwQxtLI2jykKoyeCCf0FfB3/BE2SJdU+JUW9ftHkWreX325Iz+dfon+0cFb4C+Pw/3Tot0P/IZr81/+CJiuPiB8THbhW022UfUStUvctfCz9baWiiqICiiigAooooAKKKKACiiigBG6V+WH/BXj48+NPCXijRvA2jatcaVoF/p5mu0hbaLjJwVJr9T26V+Rv/Bar7A/jzwIsUitqS2Uplj2kHZu4Oen61DLicr/AMErfjF8HPg7rfiC/wDH2uw6H4r1Ara6fc3sUpiEOMkb1UqmT3Yiv2B8L+MtA8baet94f1qw1qzYAiawuUmXn1Kk4r8n/hp/wSRj+KnwF8OeLLDxrLpvibVrUXXlXUIe22t91SV+YVxMv7A/7Vn7Nuqf2v4Eu57sQEuJvCmq4dvc28hXzP8AdwfpTQ2rn7X18V/8FWPjNp/gH9m/UPCjMsmq+KStrFFg5WNWDM/THVQK+KdP/at/bj8M+fZy6N4tvnUGMtfeEWkZT6hhFjP51e+Cv7HXx7/a8+KGm+MPi+dW0/QbeZZZ7rxChhmkVWz5cEBAK9McqBVCtY+3v+CXHwq1L4Y/sw6dJq1m1ld63O2pBJCCxjYfKeDxkdjX2DVTS9Pg0nT7WxtkEdvbxLFGijACqMAfpVugkKKKTrxQI+Sf+CiH7VHi39l/4f6DqPhCwtrm81S8ktpLi8RmSAKoIOB61+d95/wVo+O95ayxRXWj27MMCSKyO5fcZNftb4r8F6D460ltM8Q6TaaxYNybe8iEi/XnpXC2v7K/wismJh+HmgoTyf8ARFP86APwX+IH7WHxf+KDXI1/xvq0kE4Kva28pihIPUFR2rl/hD8Qv+FU+ObPxJP4fsfEv2X5ls9SUmJm7E1/Q4P2b/haOngHQB/24p/hSS/s2/C2aJo38A6CUYYI+xJ/hQO5+Wl1/wAFlviM1vbwaT4O0GwSAAFAXcFR2A4xX6Tfse/tDSftNfBXTvGVzpy6XeySPBcW6HKB1OMqfQ1zPjn/AIJ2/Afx1HN5/gm30yaQYE2muYWX3GK9M+AvwE8M/s6eBx4V8KLcLpgmaf8A0qUyNubrzQI9IpG+6aWmSMEUsxCqBkk9qAPkT/go5+1BZfAf4NahoVleTW3i7xFbNBpzwjiEZG5yc8cZA+tfD/8AwT8/YNvvjhrlr8RvHIJ8NRT+ekEzEyXr88MpH3c85zWB8ZNUuP2zv+Cg1n4Sublm0NNU/syLyiSscMeSzD6kV+0Hgnwfp/gLwrpug6XCsFlYwrCiqAM4GMn3oLfu7HmXxO/Y8+E3xY8NjR9a8H6ekaR+XDcWcQhmi9CrLg1+QP7fP7E1l+yZrmjT6Pq8upaHrLSeTHcAebEV/hJ7j3r9526V+X3/AAWytzJofw6cFeJ51wTzyBSEmeK/8E7f2xvhz+yn4F8Uv4pi1K51XUbqMpDp1ursUA7lnXFfXNv/AMFl/gjJnfonjIEf3NPt2H63Ar5V/wCCcv7C/hP9pLwT4l8Q+OFuHsUnFnafY5zG6sv3j0r6z8Nf8Ef/AIJ6PqElxqM+ua3BuzHbXF5sRR6EoAT+dCG7Hw//AMFEv2zPCn7WF54SXwdp+tW1jpSuZl1S3SGR2Y/w7HcdK91/Zh/4Kp/Dj4P/AAh8PeDtb8FeIoH0mHyWk0sRToQP4v3joc+1fO37Rn7Kvhnwp+29pPwr8NRyWWh6nPaqEeViY1k5IDHJ6A1+j+n/APBK/wDZ7tdNSCbwnc3U+BvuJNTnD5xyRhsfpTDQ4vwB/wAFfvhl48+IemeGx4V8S6Za6jcpbQajcrBtR2OAZFWQ4GcdC3WvvJWDqGU5UjINfGui/wDBKz4M+FfG+j+J9AGsadeaZcpdRW8l350LMpyAVYdPxr7KA2gCgl26C0UUUCEr5i/bS/Yi0r9rbR9Oc6xLoWvabkW1wQXhZT2dP6ivp6igD8n9J/4In66wb+0viVp0Zz8v2XT2fj33Yretf+CJ8G5ftHxPfHcx6Uuf1av1CooKuz80NE/4In+GoZpTq3xE1C6Vvu/Z7FE/Mbq97/ZH/YB0z9k3xxreu6X4ouNbg1C3ECw3NuEdBnPUE19aUUCuxoFOoooEI3SvzY/4LZed/wAKx+HISTbC2q3AdPU+UpFfpO3Svzb/AOC17/8AFsfhwv8A1Frj/wBEigpbn0/+wFbJa/smfD5UGA1iG/Ek19DV88fsAsW/ZK+Hm45P2EfzNfQ9AnuFFFFAgooooAKKKKACiiigAooooAKKKKVgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAh6V4/+078eNF+AXwx1LX9TuY45xEwtYGxmaTHCjJr0Pxl400rwH4Y1LXtbuFsdMsIGuJppWCgKBnHJ61+aq2/iv/gp98SUS6s7rw78G9CuGmhmkgxJfEHG0Nkjn2NZya2N6cU9WfG3jDwb8Rv2iLPXPjDqkP2fSLa6RUMgZCVZhjZxjj61+znwTv5vh58B/DhTT7nVRFYJLIIWDSH5cnGev5181/8ABSaDQPhP+yba+B9Dh/sqGOW3jto7cAGQr/fx9OtfSH7HdxJ4i/Zl8CXM8jeedPVJCDndgYrBXUtDZtWvJDvhL+2b8MPi/rB0bS9djtNcRikmnX37qVXBxtwep+le6rX5D/8ABQT9lHWPAvjRvib4Okuo7yS6ErW9rDsaHHO/K9a+2/8Agn38XvGvxe+B1tf+NrBrW+tJPssU7qVadFGNxB71tTk5LUyqQW8dj6d/ip1N7g06tTmCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRUtXAKKKKnlYDW+6c15H+1JqkOkfA/xbc3Cs8a6fNgKMnlCK9drwT9tiaeH9njxg9vN5L/AGKRTkZyNtROL5Wa0/iPzS/4I96F9u/ac1PVQW2WejTHp3kYDH6V+1Nfj1/wRfkH/C3vGIYZZtLVg3/A+lfsLWyIYUUUUyQopCQoJPAryXxD+1d8KfCnjUeFNX8a6Zp+t5Cm3nl2hSezN0H40DSb2PW6KyND8WaN4os/tWjapZ6rBjIks51kH6Gvn/8AbA/bU8M/sx+DLlhc2+peK50ZbLT4nDYfsX54FK6Cx9L0V+BN18fP2nv2hNWutf0nVfE1zZwu0qrppaK2hUc7RjAOK+o/2Ff+CjnjG8+IOm/DP4qO1/LdzC0t9RuE23EUp4CyHoR+GaLorlZ+qdFNDZp1MgQ9KhvP+PWUkZGw/wAqmPSqmpvImnzmMAvsOA3Spa0KW5/Pv8XPDMvij9tu90fT4lNze+IYlRe2TICf5V+/9pLB4f8AD1ub6eK1gtLdFlmmcIiBVAySeBX4fagqab/wUs0pm5UeJISce5Nfpb/wUV+Evjf4xfAG40rwK97NqKzq82nWsgUXcP8AEjcZP50k0kkXKPvNM+mNI1rTdetRdaZfW2oW2cedayrImfTKkinaxr2n+HdPkvtUvbfTrKPl7i6lEaL9SeK/AHwR8Xf2hv2L5Xs7H+0/DdgJSz6fqFoJbZm75yOPwIrpNU+NHx3/AOCjHjTRvA093bskYaT7FYRNb2y4HMsvzEk/jj2p3I5baI/YTXP2xPgv4dujbX3xH0CKYHGFvEYfmDWPP+3h8B7fOfiXojH+6k+4/kK/Iv8AaL/4J8eL/wBmv4ZweLtc1G0nV5hFJDFg7SfrXzl4c8E6p4o0XV9Ttos2WlxebcSbQAB6ZxTui1DWx+/Vj+318CdQ1O1sLf4gafJdXMqwxJhvmZjgDOPU19BI6yIrKdysMgjuK/GD/gmr+wvafGnUrf4j+KTNH4e0u8V7OzB/4+pEORu4+6Div2dXZDGB8qIowOwApmb3JKKbu3DKnI7Vn+INct/Dej3epXbhLa2iaV29gM0m7CWp+Z3/AAWG+P1/ZLoXww0O9eP7UPtWoxwHDOM4RCR29q7T/gmt+wpa/DfRbH4meMbZbnxFfwrLp9nMnFkp6Pg/xkd6/Nf9or4ra18c/wBo7XPEllDLe3M98YrCBELEojYUBe/Svqz4ef8ABUn4sfCPUNI0T4geFo5tNgCxTK8BhmCAYG36Ci6NFtY/Yqlrz34J/HLwr8fPBdv4j8KahHe2jgLLGD88L45Vh616FRuQFFFFMQUUUUAJWL4vsE1Lwvqls6CRXgf5T34NbVUdakWHR72R/upEzH6AVMtrDjuj8EfgbrF34Z/b/wBBnsE+wSDxK1uY8A4VmIPB9RX7+1+AfhfVotY/4KGaXd2gAjk8VqE2jjG81+/lEdip/EwoooqiAopOfXj6UtABRRRQAUUUUAFIeRilooA8J/bZ1O80T9mvxpe2PLxWUm5ezKRgj9a/Nf8A4I42NheftAa5cTwxvdwaSzW7MOY8tg4/Cv1t+MPg+Lx98L/E2gSxrKt9YyxBW7nacV+D/wCzL8Vbj9k/9qfT77VxPYabb3z2eqxFMN9n3EcD8qh7lx2P6DWUOu0jINK0Ksu1lDL6EZFYPgfx1ofxE8PWet+H9Rg1HT7pBIkkLhsZGcH0NdBV3uSxFUKAAMAdhTqTNeU/Eb9p74cfCvxRpHh3xB4jhg1nVJ1t7e0h/ePvY4G4D7vPrQI9XopgNPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDH8Y+IIfCfhPWNZuHEcNhaS3LM3QbVJ/pX4xfsBeFx+0N+29qPivVo/tNtZy3GssJPmBYsRHnNfrL+1A88f7PPxBa2jMs40ecqi9T8tfkV/wAEr/jH4b+FHx8vYvEl4unRa3ai0gnmbbGkhbIDE9BUSLjsfuAqhQAOFAwBTqjt7iK8gjmhkWWGRQySIchgehBp0siwxvI52ogLMfQCnHYln5af8FsJofM+G8Yb/SP37bf9nI5r3f8A4JG2Qtv2UIZcAGbVblicdcEV+cP/AAUY/aD/AOF8ftBagbCTdougk6faejFT87fnX33/AMEgPidpGufAO48HpdRjWtKvZZ3tv4vLkIIb86obWh99mk60lcn8TviboHwf8Faj4p8TXn2PSbFN8sgGSfYDuaCTyH9vH4r+GfhX+z14jn1+3tL+7vrd7bT7G6AImmYYHX06/hX4J6PpfiCzeHxfZ6Pdvp1jdrL9sjtmNvG6sGClgMCvp74zfFLxj/wUa/aW0zQvDsE1vpPmmDTLZsgQQ5+ad/w5r9X/AAJ+yP4T8H/s3L8KJIVnsZrRkubhgNzzMOXz9aRpsVP2L/2rNC/ad+GlpdWzpa+JNOiSLU9Nyd0TAYDD/ZNfQ9fhNoN94r/4Js/tcJFdjztImmAnjU8XNkzdvf8Awr9w/CviSz8X+HNN1vT5PNsdQt0uYW9VYAimS0a1FN/ip1BIU1s44606igCpMrLhhz9axfEninQvB9j9u13WbTSLVuk99dCFfzJxXRsAVORkV8Bf8FOf2U/id+0VceE7rwNaLq9np6yLPp7XMcW1j0YbiAaDTmufbWieOPC2tQpNpuvaXfI3SSC6jfP4g10EV1BOAY5o5B/ssDX4NW3/AATL/aLt5kli8Em3kU5WRNVtwy+4IbNdPB+xz+194YgCWMPieOJBxHY+IWXH0w9AWT6n7hZpa/ETTPhj+3J4T3SWq+OiqchWumuj/wCPE5rlNU+OX7W3gXxRa2mrar4wtNRaVVjhu7MlWYnABAXGKBcp+81Fcb8H28RSfDHwy/iyVZvEb2MT3zqu3MhGTxXZUEBRRRQA1/untWB4s8YaL4F0g6hr2sWWjWKnDXF9MsafmTyfpW+yhlIPSvx9/wCCxvxeu9W+KGh+A7a7kTTdNtPtNxCp+VpXPGR9KTZSP1i8H+OfDvj/AE/+0fDet2Wt2anYZrGdZEDehweDX5w/8FspD/YPw5QHBa4n5/4CK+Uf2Ef2oNc/Zh+Lun6dqkd1b+FtbkjivrO5DIqBjxMoP86+jf8Ags54kj12b4ZWdn++tJYZbuO4XlJA2AMHoTzU3Ktqdx8QLj44fC/9h/4Ut8KVvIpI7ESaiNMgZ7oIwyu1QCe/pXy7dfFL9tfwhYpq8934+8ib5/30Mk4H1Tadv4iv2S+Cdqbf4N+CYHXldGtAQw/6ZLXZtEkgwyKw9CKOYLn4zeDf+Co/x/8Ahh9mh8baBDq9sHw39sWElnM/sHwozX33+x/+3h4Y/aw+1abbadNoniSzi86eykO9CvTcrelW/wDgoF4g8IeD/wBmPxdc+IrCzu5ri3NvYQyRqXe4bhdvfjrkV8T/APBF/wAB6nP498Y+L3tGh0mOxWzimZCFdy+cKehwKfMx6G/+3l+x/wDtC/H745XV9oumLrHhDYsdlnU4oYoeOS0bNu/IGvlD9oD/AIJ++Pf2bfhjF4w8Y6jpKiW6S1Sys5XlfJ99uK/f6vzM/wCC03xBjt/CPgrwbHPEZbu5e+liVwXUKMKSOoBqb3DmPg3wr+zVp+q/sz658XtU8XR6bBY3v9n22lramV55j0Ut0XPvUv7NP7FXxH/akM954Ts7aDRLOYQXOqXkqxohPovVjjsK+gPiT4Fj8Af8EsfCbhXE2v65Ffy7hjuQD+lfTP8AwRgtpI/gR4rlZWCPrOFJHBwnOKaVxOR71+xp+xnof7JHhm9hs9Qn1bW9UCNf3UnCblH3UHpW38Pf2uPCnjT4y+I/hdfJLoHi/SZikdreHC3admjbufavdK/Jv/gpxpGq/AP9pTwV8YfCtvPaXM203F0iHymlQ/dY9Mle1VsTufrJS1w3wV+Jmn/GD4X+HfFunTRzQ6lapK/luG2SYG9TjoQc8V3NMkKKKKAPEP23NUl0X9k74oXkDbZYtGl2n6kD+tfDH/BE2O3XUviQTIpu/KtsLn5tmTz9M19tft5RNN+x/wDFZFGWOiS4H0KmvhH/AIIn/L40+IgJ66bbj8fMqJFrY/WmlplPqk7knyX+2H+2J4l/ZT8aeFrifwmuq+Ab4Fb/AFKMnzYmz0UdM49a9s+B/wC0D4K/aE8Jx694P1aO+h6TW5OJoG/uuvatr4p/Cvw58Y/BmoeGPFGnx6hpl5GY2Vh8yZ/iU9iK/GDxdYePP+CZv7Sz3WiSXE3hm5bMLTAmG7tieUPbcPWk2NK5+5mRRkV454J/ao+H/ir4O2XxCm8QWNhpklt5syTTqHjcD5k29Sc+1fml8d/+CqHxP8XfEC8tfhWp07w/auY4tlr50s2D99jg8UuYOU/ZDIpa/L39h3/gpd4l8cfE6LwZ8VtQtdt+y29heJbiJvPJ4R8Dv71+oVUmJqwUUUUxCHpX49/8FnrV1+MHg+YjCNpL4P0fmv2Er8x/+C0Xw5urzw/4L8a28G63s5XsLmXcoC7+UGCc9fSk1cqJ9i/sS6nHq37K/wAOZopPMVdLjjJweoyCOa9y2+1fF/8AwSj+JUHjb9mOz0fz0e+0C5a1ljGdyqeV/wAivtKhCe43aaNpp1FMQ0A06iigAooooAKKKKACiiigAooooAK4f43+IpPCfwg8Y6xCcS2elXEqE9jsOK7evM/2lLE6l8AfH9sP+Wmj3A4/3CaBn5e/8Ef9JtPE37Q3inXdQiWfUINOM8TsN2HdzubPrX7H1+NP/BGzXrWw+PHiDTZZQk95pGIVbgvsbJx+FfsrQOW4HpX5Df8ABZX4nWOu/EHwp4NtmWSbSrd7id88Kznhfriv1Q+KHxI0P4TeB9W8T+Ib6Ow06wgaVpJDyxA4UDuSe1fzi/G74lXnxg+KniPxXeySSDUbt5It45VMnYvtxQET9if+CR+kPp/7KkVyybRd6pcMD64IGa+2K+Z/+CccdlH+yD4GFj9wxOZP+um47q+mKBPc/J344SR6x/wV28FWyDOy8sY2z0yI2NfrHtr8ctS8RJff8FgLOa4DbI/EcVtGOMjEWAevTmv2PoGxuKXdS1WuL61tJYYp7iKGSY7Y0kcKXPoAepoJLG6ik47c0tAB68UzzkH8S/nXk/7VWi+O/EHwK8UWPw3vJLLxZJbH7I0D7JWOeVRv4WI6GvyHX4E/toahfXCvB49eYtiRm1eRQf8Ax7FA0rn7nPeQRqWeaNQOpZgKyLzx14d0+YRXOuafBKeAklygP86/F2D9jP8AbI8SQtFNF4jWOTgpfeJgike4aSrdn/wSr/aN1hfO1Keztp+uLjXBI35qTQOyP2gt/FOjXjKsGq2crN0CXCEn9aupfW8jBVnjZj0CuCa/GW+/4JX/ALRXh+1jvdK120vL1eVgtdaeJ0PszYH61sfCP9jH9rDwZ8VPC2q6rNqK6ZZ6hFNcyDxAJ1EYb5vl3Hdx2oCyP2I3UtRI33fXvUtBIh6V+cX/AAWq0+Wb4R+AbpVzHBrEoc+m6Hiv0dr4G/4LH6tZ2f7OWjWc0Ze6utZj8hgR8u1SW/McUDW57d/wT6kEn7JHw+I7WeP/AB419GV80/8ABOrP/DIfgIE5It2H/jxr6WoB7hRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+VP2k/gr4o/aS+JfhrwhdTXGm/DLT/wDS9bZXKNqLH7sS4zlfXOPoa+jfDPgvSPBfhmy0DQ7OPTNKs4hFDb26hQoA68d61FVnyHB68dKLpmht3IZV44LVCir3ZvKXNZHxF/wVe02xb9nmSVrZJL37VEY7iQfcA9D613P/AATJ8RP4h/ZJ8Ll23yWrSQEn2NdV+138ED8fvhXH4WN00aT3MZaaNcsozyRxXX/s4/AnS/2e/htZeFdFubi4soiZM3QG/cevT3rGMXztlzS5FrqejalotjrEPl31pDdx/wByZAw/I07TdLtNJtUtbK2itLdPuxQoFUfgKt4NLXQko7HNzO1gpaKKYgooooAKKKKACiiigCK5uEtbeWaQ4jjUux9ABk18Y+I/+CsXwX8NeItQ0maHxDdPZSmF5rSxDoWBwcZYV9lahZx6lZT2kwJinQxvg44Iwa+Obv8A4JVfBzUfEl3q11a3kpubgzvCLl1Xk5IwDUu/Q0jy/aNXwb/wVG+BfjTWLXTLbU9Xs7u5dY41vbDYCxOAOGNfWtrcLdW8c6cxyKHU+oIyDXz18Pf2A/gt8M/E9vr2j+Ebf+0LchoXuGMoRh0YBu9fRKqFUADAHAFNX6ilb7ItFFFMgKKKazYXNADqK/PT/gph8SPjV4L1bwovwzu/EWnrJvaZtDUupx2YBTn8a8N/Z0/bb/ai8I+OtPsPGfhTxH4+0S4dYXt7jSzBcJuON6yLHyR6Ggvkkfr7RVezumurWCZongaRFcxSDDJkZ2n3FWKCAooooAKKKSgBa8E/bOtlv/gf4hs3Yp59rINy84whNe87q+Y/+CgnjWLwV+zv4iuXkjE8tu8cKO20sxGMD3qJbGtPc+M/+CKugCbxj4/1ZmKm1tIrdVxw2WPNfrVX5Yf8EeY4/BfgL4neNNUnMOjRhNzsMALGCzNXYeKv+C0HhDS9TuLfSPAuqalbxSGNbl540V8HGQM5pp6ClFn6P0V+aFn/AMFsPDZVvtXw21ZWAyBHeRY/WvR/h3/wV6+D/i+aCDWbPV/C00rBN11EJYwT6svandE8rPszxvqr6L4R1e+jTzZbe1kkRB/EQpIFfzneIdUvfjH+0Bc/25ut7jVtUMEuxctENxAAzX9F0F5Y+OfDlteWkoudM1CEOjYwHjYdfyr8bv8Agod+zbc/AL4lwfETw0n2eynulkKqAUhlzlSPr71nK99DeC921ziPjV8EfiD+yP4d0jxNoPj67h0rVJdsFnBcNHMMDqyg4I/CvmuTxTP4u8YWuqeLr+81OB51N1K7lpGTPIBPGcV6t4g+LPj/APbA8ReB/Bt9El/eRTra262seHO4gMTjjgV+wOjf8E//AIZaT8HoPBkOhWvmtb4udQmhVriWQryS2OOfSkrpakytfTY3v2a/Gnws8b/CPSNI8BXFlaW0Nqii1XYkgfbzkD7xz1r8of21Ph7qHwQ/a2stQEDaZHd3UF9FNGcA/vBuIrJ+P37PHxS/Yz8ZTajpdzqFjov2gyWl9ZSNtUA5G7HFeJ/E343+NfjJd2154w1qfXbq1GIricgui+g9qFvdBeyP6T/Cmoxav4Z0m9hk86K4tYpVkBzuBQHNa9eJ/sY+Jm8W/sx/D+/kOZP7NjiY+pQYz+le11rdGItQXUfnW8iFtoYY3eleP/tafHyH9nX4K654sISS/jiMdlC5wJJiPlFfhNq37W3xW8Q+NP8AhIdS8aa5O32nzzZpqEq24wc7Qm7G3HrRcaWt2fQ+peF20v8A4Kl6VZMWuIl8RwzM8nPydewr9sbi5hs4XlnlSGJBlnkYKqj1JNfgD4Z+Pl/8T/2rfB3ibT7RdL1GS4htRKzEuX6byc9c16v8Vf2bv2wPi14o1mbULPxHrGl3ExMUUmrNHaNGegEZkGRiszSVviR9Qf8ABSj9rz4deHPBV54JsrbT/FvibUImik8tldLRSPvFh1PoAa4v/gjf4G0jRfDXjDx3fz2UFzdTLZW7TTKJI4xyfpmvmWz/AOCVn7Q+qW0l5caBYxOF/wBVdalH5h9utaGi/wDBMn9pXT1FrZ2kem20z5dItVCJn1IBo2Fufan/AAVi8UaJ4g/ZZmXTdUtr+aLVrdNtrKr4JPIOD6V8cfCfSdD03/gn38Q9RgRZtTvN0UrEfMmMfpWV8dPgT4//AGZ/2dtU8N+Pfs0k+ranbz2ckVwZW+U/N82a9gj8J2vhv/gmbqUosI7ZrmIz/aIpA3mN6Gi9zWNos+iv+CQfi6TxB+zVdadJtA0nUnhQKMHDDPNcb/wVy+N3i34caT4R0nwxrl5of26SRrh7N9jOAOBn0qz/AMEYIbpfg34wmcxi0l1VTGo+9nac59qX/gsH8ILvxd8NdD8WWMUs0uiysJFQcCNhyTVJma0Z9G/sFfELUfib+y/4P1jVr46jqXlNBPcMcsxU4598V6Z8bNNn1j4X+I7O1dUuJrKVY2k+6DtPWvh7/gjT8TItV+FfiPwdNcL9s068+0Qwnr5bDn9a/QXxHosXiPRbzTp9wiuYmjYqcHBGKdubYX2rn4kf8E0/DulX37ZCWevtbl7IXJgjmAYSTBjgL719+/8ABRj9mfQfiR8INT16009YfENgvnRTQjbuIHfHavzn/a2+B+vfsgfHiHXvCz3lra+ebu0vMklHzk5b0r660X/grb8PNW+Ca2HizSNQv/FLWPkXFokQEVxJjGd3YGlYLWZ4r/wSH+Lt94U+N194DljY2OuQyOEV+I5YhknFfsxX4q/8ExdLl8eftp3PirS9Ea00S1hu7hwCSlt5inaufXJ6V+1VUiJBRRRTJCiim7qAFrE8ZyCHwjrMhxhbSQnJwMbTWxIzeW2zbu7bulfNH7fX7QmjfBH4A+JYptQSLxDq9o9nptqjAymRxgMV/uj1qWrjjvc/IT9nG3bxF+3B4TNpEcS+Jy6KCW2qJDk5r+hVc7Rnk96/F/8A4JK/A3VPHHxsk+IV1Fs0fw+H2ysv+tuH6YPtX7QU0VLcK+TP+CjPxo8b/BP4M/2x4J8R2Ph2/eURtJNHHJO69xEkisCfwr60r88P+CwnwpvvE3ws0fxVYrJLHo8xNygYkBCPvY6VMrhHc+Xfhf8A8FRP2gvA+m2mr+I4rPxl4Ye5Mck95pwhkOOqrJEFUH6g1+ifwC/4KCfC340+F0vbrXrLw3qsabrqwv5hH5frgnGRXyb/AMEs/D/hX40/Avxj4D8R2Ed19ivftL+bn7ki4GCCMdO1fEX7ZXhjwT4R+Puv6B8O43Gj2LCBtshbzJf4wOTkA1OpWh+p37RX/BVL4a/C3Tb6w8HXK+MvEwjYW4txm0STt5j5HH0r4Rm/4KnftBN4oXXpNUtodFZwRo8OnotuRn7okZC+f+BV4/8AsfwfDi1+OWhw/Fm3YaBJKFKXKssAY9DLgg7a/Yj43fsq/Dr40fAmbTvC1pY2unpaNPpx08DyywXKkEc0aodkdp+yT+09o/7UHwytvEFl5dtqkWIr+xDZaKT1+hr3Gvxr/wCCSOq6h4R/ag8Q+Eby4e1R7GeOSzbgSSxt97Hriv2Uq4mclYKKKKokQ9DXwR+3b/wT7j+NH23xT4NsYIPEqxl9kY2mdvQ/WvvimtGrqVIyDUtFJ2P57Phf8evjT+xl4m1DSrGe5017eXZcaVqELPA5Hfn+le62v/BYz4twrtudG0KeTH8EJXn6V+vPiD4YeEfFc3nax4b0zUpe73Nqjk/UkVhy/s7/AAymJL+BNBYkYJ+wx5/lTK5kfj34i/4KDftM/Gq3ay0KW5sbeRthXw7pxR8Ht5gFe2/sRfsG+M/GHxGh+KHxiF9DLZzrdWlteSbpZ5ByC4Pav088O+AvDfhO0Fro2hafpkAOfLtrdUH6Ct3A9KYuZdBiDaAMk47mpKTFLQQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1HT7fVbC4s7uJZ7adDHJG4yGUjBBr8rf2xv8AglXqUmsXfiv4ShZYpiZZtFY7WRuuYz/Sv1bpMUmhp2Pwc+Hn7aXx+/ZJuf8AhF9TkuJILcFF0rxFExCY7qx5IroPiN/wVJ+NHxm0VfCmjWlpotxqA+zOdJjZp5t3G1SeRn2r9n/Enw38K+MLlJ9b8O6Zqky8CS7tUkb6ZIzVTTfg74F0a8iurHwhotpcwsHjlhsY1ZWHQg44NFh8x+X37Hv/AATEuviB4E1/X/ihbT6VqOpxPFp9vdIfNhkPPnMO/PavO/En/BPf9ob9n/4kG++Gy6jqcMJ82DVtCuVt5cdlwSOfrX7aUtMOY+Cf2L/DP7W0PjuO6+KutXEPhGJTvtNXkjnuJvYFeh96+mv2pPgXH+0X8Gdc8FG8GnXF4gNvdMu5Y5AcgkdxXrlFArnyd+xP+wfpP7J8N/ql3qf/AAkHiu+TypL7ZtSOP+6gr6up9JQI/J3/AILUSN/wkfgJG0UJD5MrHVlX5nOf9Xn2619hf8E2f7a/4ZI8H/23nzsSeTu6+Vu+XNfSeqaPY6xGI722iuUH8Mqhh+tWLW3htYEhgjSKJBhUjGAKB30sSfxU6iigQUUUUAJTafRQAynbRS0UANKjFRyQpIylkDFTkH0qaigYzpin0UUCCiiigBK/DD/go5Yt44/bm1DRbb97LM1lZKIzk5YgHp6A1+5zfdNfhz40uY/F3/BUy2AZZ428W29v8h3A4KjtUsuJ9Q/8FF/2MbOP9n7R/FXhuwU634TsoIb1olJe4gRApY46kda/Ny4+L3iD4qXXw68N+IbprnTdDnhtLUSZYhGkUZOa/o717RbTxJot9pV/Es9leQtBNGw4ZWBBFfhx8YP2DPHnwz/ak07w94c8P6hq/h281OK403UILd5IYofMViJXAwhXnqaSQ0z9fviJ8d/h/wDs5+C9Nk8X+ILbTI4bSNYLUMGuJVVQuUjzkgcc186+Jv8Agrz8DtJs7n+zP7d1i+VD5MUdiqI7Y4BYvwPfBrp/22v2FB+1nY+G7i11xNB1vR4TAsskXmRujYyCMj0rxn4c/wDBFvwTo7QT+LvF+pa5IpDSW9mi28Teq92x+NPlJufnz+0l+1F4o/ag+IY1PxXc3NloEco8jS7Vsx28OeoBOC+PWvv/APZ7/wCChv7M3wD+G+l+EvD1t4kto4UV55W0yPdLMQNxYrJzzntXrkf/AASZ+AKDB0fUn/3tQk/xrn/EH/BHb4J6nDL/AGdeeIdHmYfK0N6HUH6Mpz+dHKHMfTHwH/aV8BftIaLdal4H1V7+K1YJcQzwtFLET03Ka/KX/grz4mXxL+05pWiWmJJ9P0+OAqp3He7cDH5cV+qf7Nv7NvhX9l/4exeF/DSyTbn8y5v7gDzrlz3bAr57/aG/4Jt2/wAdv2hrL4jv4q+wWReBr3TDbktKIyDhXB4zj0o5Rpo8m/bs8IzeD/8Agm/8OdIuoWgubB7BXjdSrKxGSCD0616J/wAEc1K/s3audpUNrMhBI4PA6V2X/BTL4Ra/8RP2V7nTPCthNqc+kzw3bWdvG0s0kUfUIqgljj0r8sv2df23vin+yZ5uh6KLaXRhcGW40XVrUj5u4zwyfhR8I7c2x/QdXyd/wU4+GF/8Tv2UPEEWlWv2rUNLmi1FVWPe/lxtmTbjvtr4qtf+C1vxG+2xG58CeGntd37xIZJ1cj0DFiAfqK1dZ/4LMa94i0W/0wfDHTpftcDwlZL5pEwwI5XbyOaaYuVo7f8A4I5/tAQ3Wh6v8KNTuMXtszahpweQfNGfvoo9R1r9Oq/m+/Z58Ya54Y/aN8Ja/olncWd42sxn7LYo3KO+GjA7rg9K/o/jYMoIPB6Uwkuo7NGa+bv277r4paP8HF1z4UXFxHruk3aXk8FtH5jzQL95duDu+lfHvh3/AILOX2i+GxY+J/h5NN4mtk8uSRJ/KjkkHByCMrzSbFY+4v24IJrr9kv4pxwI0kp0OfaqjJPAr4M/4IlwhvE3xHmJyy2luo+m+vIfjV+3H8bf2vIbrQPCWhXunaHLAyXWmaMjTtLGeodsdK8X+Avx4+K/7LGtawvhKylsb/UEFvcwXdg8h+U5GBjrmo3Ktof0UU7NfhZL+3P+1f421CO0sL3VoZZ22JFYaWVYk+mVra+3ftx+MI9qL47ZJRjd5SRj+lCdhWPuP/gqP4+8ffDH4T6H4i8Fa9Jokdvfqt00Jw7Z+7+FRfD9/C//AAUO/Y0im8ZRRtrVrA0VzfhQJLe5jXPmqewOM4r86PiZ8E/2tfF2gsPGnh/xfqWkwDz3ivGDRrt53Ebq4P4aftSeLfg78J/GXgTR55LGLxA675EYhoOocD0Joeo7HlviZLjw7rmq6JaapNc2NldyRRtHK2xgGIyBX7Df8Eq/Bfwt1j4GHU9I0y3u/EqytDqrXih5FbsAD0GK4L9i3/gnj4P+JX7ME2rePtJZvEPibfcWl+T++toz9x19yea+V9Qh+LH/AATL+Oo8l5jok0+5H/5dtTtw3Q+hx+NIZ6X/AMFQfgDp/wAB/ix4b+IHhOJdNi1afc1vFhVE6ENlfTgV+tvwu18+Kvhr4W1hjue+0y2nc5z8zRqW/XNfkt/wUZ/az+Hn7TvwN8AzeG9Vj/4SO21AzXulOjiW2BhIJzt2kbjjg1+kP7EtxLdfsr/DiSW5+1udLQeZ9CRj8KuOxEj3CiiiqJEryv8Aaa+Bmn/tEfBvX/Bd9+7ku4S1rcYBMM68owz716rRQB+EP7PPxy8Zf8E5/jdreieKtCuZ9Omby9Q0zequ6KflkjbO0nHoe9fpH8OP+CpnwE8d29qL/wAQ3nhO/nYL9m1bT59isfWaNGjUe7MBXr3x1/ZT+Gv7RlmkXjXw/He3MYxFfQMYriP6OP65r5M8Vf8ABF/4aak8r6D4v17Qic7ElSO6RT2yDjI/GgvR7n3B4X+MXgXxtbxT6B4w0TV45Pu/Y7+KQn8A2azfiJ8f/h98LdJub/xH4s0uwWCNn8g3KtM+BnCxqSxP0Ffm7e/8ET/EUdxN9i+KGnGHpH5mmyRE/wC8Fb+Vbnhf/gidGt1FL4j+KJmhBBkgsNJ5YdwJHlyv1waAtHue7fsqf8FANT/am+Nmr+G9J8HR6f4RsYHkGqSXBeViDhcgDHzelfaVeZfBH9nnwP8As++HYtH8HaLFYKEVZrsjM1wR1Z27mvTaCXboFFFFAgooooAKKKKACiiigBKy/E2gxeJvDup6ROcQ31tJbufQMpH9a1aKAP585LjxD+wj+10Z1Rp30C+Zo4pFKi7tWJ4z3ypr9L9R/wCCtHwaj+Hv9r2lxqE+uvB8mlfZsETY+6SW+7nvXsP7T/7GfgT9qLSQuvW32HW4UK2+r2qgTR/X1H1r5s8B/wDBGnwBoPiCO98ReKdU8R2ETh0sCqxK2D0YgZIoHc+KvGPxV+Of/BRLx7a6DYW1zJo7zqFs7ZWSztlJxvkbGOB9a+l/2p/+Cab+Fv2YPDi+BrNdR8SeHQ11qqou6a+3L8+zAySD0FfpX4K+Hvhz4d6Pb6X4c0e00mzhQRqltEF4AxyR1roCueCAR6UBc/Br4KftVftB/CHwrH8J/CVtdWUkt0Y7OK500m5hZz0QsvHNftD+z9a+N7b4SeH1+Il3Fe+LTAGvJYhgZPIB4HIHXiu3/sHTPtguv7PtftI6TeSu4fjir9AXPxy/4KifCrV/gj+0boPxc8MxTWsWpSx3BvI8lY7yMjg4HGQK+xv2Zf8Agpd8MPi/4dsLPxVrVt4M8XIix3NvqjiGCV+m5JScYPX5sYr6U+Lnwi8MfG/wPqHhPxbp66hpN4m1lzteM9mRuqsPUV+dXjT/AIIprNrk03hL4jrY6Y7FkttW0wXLxDsu4OMj8KClbqfaXxY/ba+Dnwl8O3Go3/jnR9SuBEz29jpV3HdTXDAcKoRsD8SK+AfgR4k+L/7cH7Uej+PtTbUdK8D+H7z7TbLbK8Vt5atwo7MxGM/zrovA/wDwRWvbXxJZ3Pin4h2N7pUU6vNa2GmsjzIDkqCW+XPrzX6c+EfCOleBfDdhoWi2cNjptlEsUUMKBRgDGTjuaBaLY1Yx8qn+fWnnOOOtFLQSJg4560m2nUUAN20badRQA3bQVzTqKAGbcYp9FFABX5tf8FqLHU7z4b+BXtbOaeyt9RkknmjQsqExkAHHSv0lrO1zw9pnifT3sdWsLfUrN/vQXMYdD+BoGfKf/BLPX7rWv2S9BgurWS3NjcTW6NIMeYucgj2r69rO0Tw/p3huxjsdLsoNPsov9Xb28YRF+gFaNAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAx7q1nhuVlW5IjEeCrHv60yS6+0fu2XzbYjBcdc1cvv8AVn/cNZul/wDHiP8ArpUSOyOqux9hHLpszxmZGtzgQx87h654rcR96g4xVWb/AFkdWk+7Tic83fUdRRRVGYxJN7MMEYp9MX77U+gAooooAKKKKACkPSlooAQdKWiigAooooAKKKKACkIpaKAK0tnHNLHI6KzR/dJAOKl8sbs7Rn1xUlFMd2N206iikIKKKKAGTSCONmJwAK8Y+JH7Xnwo+EHiB9F8W+L7LSdSSLzTA5LNj6DvXsV5/q6/B7/gpl/yc9rv/XGP+tZSfvHRTipJ3P0D+Mn/AAVo+E3gvw7cyeDZpPGWt7CYLdYpIYC3YPJt4H4V+efxA+LXxm/4KBfEK00uDT7qTTpbhfI06xRmtrQE4yzkDIHqa+bdO/482/3a/a7/AIJp/wDJO4/+vdf6U7kv3Hoenfs5/si6L8FvgOPAFxcPqP2+PdqMzIFLsw+ZMA9ByK4KP/glj8EYrye4Gj3DmXJKPKSASc8elfYtMoUUyPaNHxxd/wDBKr4I3t4J/wCyrqAYxsjmI/Gtjwb/AMEwfgP4N1a31GLw9c6jPBIJUTULppY9wOfu9MV9X0+hqwnNyK9rYwWFnFa2sS29vCgjjjjGFRQMAAV85ftlfsw3P7Snwx1Dw3a37WV+zLPbTEDYZU5VX9FPfFfStRj7xpFxm43PhP8AYA/4J6Tfs46tf+LPGj2uoeJ2/c2aQjdHbp3cE87jX3ftpq96fVpGfM2c/wCNvAWg/ETQbnRvEWmW+q6dcIUkhuEDAg9celfDHxM/4I8/DbxRrx1HQ9a1rQo55cy2lu8Pkxqeu0GMn9a/QekpPQak0cN8FvhXYfBX4baH4N0y5nvLPS4fKSe52+Y/fJ2gD9K7n+Gmt94U7+GpFe7Pyc/4LMfF+31DWPDPw8tJmeSzBv7xFPAJGFB/nXnvwD/4Jnt8Zv2Vb7x42pzW/i68DTaTaLt8kxp/Cw25y31riP8AgqR/yd5rn/XpD/6DX6x/sR/8mxeB/wDryWmauKtc/EL9nWxk8E/tNeE9N16wkhmi1aO0uIJ12OhL7Sygj8q/owtdn2WHy/8AV7Rt+mOK/GP9pr/lI34S/wCwvbf+ja/Zuy/484P9xf5UglHliT/40hQNjrx70v8AjS1SRkeCftJfsXeAv2p7rS5/Gd3rkX9nZ8mPS7xIUOeu4NG2f0rhP2nv2ctN8L/sU+JvA3gnT5ZYdPsHa2ikYPM5A7nAyfwr61rM8Rf8gPUP+uDfyNEikz+fL9nv9sL4n/sk/wBsaX4WWxVLyT/SbXVrV5VRxxlQHXBruviT/wAFLPjX8W/BuoeGNaj0FtM1BDHKLXTnEmD2B8w/yrqfj1/yUDUf+vtv510Hw9+9Y/8AXRf51Jocl/wSt1zX/Df7U2mW9vbTix1KCW2vC8LbNuMg56A571+5O2vlD9lP/kaZvrL/ACr6xq4mcjkfiF8KfCvxU0l9N8U6Na6vaOpUrOgJwfQ18rXv/BI/4CXmoy3QtNchSR97QRakQg56DjgV9qt9001elUTqee/Bf4A+B/gDoLaR4K0aPTLeTb5spO6WbAwC79TXo1Mp9AgooooAQnAJr49+OH/BTb4dfAvxxqPhbVdE1u81GzXloYlWN29AWP619gyfdNfjd/wU8/5KFqn+6azlJxaRtTgpbl/4w/8ABY7x34iWSz+Hnh+z8KqW+S+ugt5MV/3CCoP4V8MePvip4j+L3jmTxD491a81q7mlDXDFghC55VFxhRjsABXtX7JX/Hre/jWL+0d/yGo/9+o52ypRUdj7E+Dv/BT74MfAH4c2XhPwf8Odahit49zA3SESzYGWZ2JPJ/Ktfw//AMFoJNa8Uabp7/DIJZ3dykBkh1PzJgrMBkIE5PPSvynj/wCQm/1Netfsjf8AJxngr/sJxf8AoYp3Ykkz+jWzuhfWcFwgZFmjWQBhyMjPNcb8avAKfE74a674dl27L22eM7hnqDXbQ/6uP6Clk7/SjdGezP5w28c/EH9mDxZ4u8JaHrN14eM8xguvJjTfJGCQuGZSw49CK+7f+CV37Itl4mjvfi5450hL+V5iml2+oxM43dWmw3DfjmvlL/goV/yd54h/34v51+3n7Pv/ACRPwX/2DIf5VXRD7nz1+19/wT38EfGjwzqGqeHNEh0jxiqFobi2Z1RjjpsDbf0r8ztT8aftOfsw2U/h+PVtd0XRbEtGrR20csO0d8ujYFfvvXzv+17/AMk38Qf9er/+gmpGj8cv2PfjlqPhf9rzwf4u1zUFdr/U0g1K7eNVzHK21zhQAOvYV/QuGDAEcg1/M78Jv+S4eGv+w3B/6NFf0xVpEmQtFFFUQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAMmTzInT+8CK/O3wH/AME0PE/hj9re3+Kc3iaxOi22vHV0tBGTK67twU+h561+itFJq5SdlYQ02n0UJWJG06iimAUUUUAFJS0UAIVB4xXI+I/g/wCBvF4kGt+ENE1USAh/tdhFJuB6g5Xn8a6+ik1cd2eRn9kf4J7w/wDwqjwfuHI/4k0H/wATWxpH7PHwu0C4SfTvhx4Vsp0OVkh0a3VlPqDsyDXolFCVguznYfh/4Ys7hLmDw3pMNzGdyTR2ESupHcELkGt6P5R0PPepKKYDGXdwRkGvP9Y/Z8+Guv3kt3qPgXQb25lbe8s1hGzM3qeK9DopNXC5zHhL4a+FfASSJ4c8O6book+/9itkjLfUgVek8IaHNeC7k0XT3ugciZrVC/54zWzRS5QuUo9IsYWDR2VvGw6MsSg/yq1j8KfRRyhcq31mmoWU9tIoZJY2jO4Z4IxX4Bab+y7r3ib9tKf4bXel3dvaS+IpPNmaIgLaGYsJM9MbTX9A9eBw/wDJ0L/9ev8ASjlHc9n8NeHbPwn4f07RtPiWCxsIEt4Y1GAFUYFcd8bvgH4P/aC8IzeHvF+lx3tswPlTAYlgb+8jdjXo1FHKK5+DP7bn7B2rfst6tFqWlvPrPgi8ciO7ZMtbMeivj271+pH/AATavbi9/Y+8Dtchg6JLGoYYO0OcV3X7V/8AySHUvwrW/Zt/5Ir4X/69/wCpphe56dRRRTEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH//Z"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83-%E6%AF%8F%E5%8D%81%E5%88%86%E9%92%9F%E6%8E%A5%E5%88%B0%E8%AE%A2%E7%A5%A8%E7%94%B5%E8%AF%9D%E7%9A%84%E6%AC%A1%E6%95%B0.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAApkAAAFaCAYAAABVO0bVAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAFdnSURBVHhe7b2HtxVllr//+y9m1sys/nbP6plpv/NttZ22bbW7MTQYuhtBmiAoKCBRwhAEYQiSY5MZcs5BMkrOGUGS5CRBco4C7p/P7lN6ZV3lnnteOKeKz7PWXtxbp6pOnaq61HP2++73/f9MCCGEEEKIwEgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRHEmmEEIIIYQIjiRTCCGEEEIER5IphBBCCCGCI8kUQgghhBDBkWQKIYQQQojgSDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMnOIWbNmWc+ePW3gwIEKhUKhUGQlevXqZVOnTk09mYQoPJLMHKJOnTr2wgsvWP369RUKhUKhyEoUK1bMKleunHoyCVF4JJk5xP/8z//Y3/72t9RvQgghxIPnf//3f+2///u/U78JUXgkmTmEJFMIIUS2kWSKUEgycwhJphBCiGwjyRShkGTmEJJMIYQQ2UaSKUIhycwhJJlCCCGyjSRThEKSmUNIMoUQQmQbSaYIhSQzh5BkCiGEyDaSTBEKSWYOIckUQgiRbSSZIhSSzBxCkimEECLbSDJFKCSZOYQkUwghRLaRZIpQPJSS+fXXX9utW7fs7NmzdvPmzdTSv8Pyixcv2tWrV/33O3fu2Pnz5+3MmTN24cIFu3Hjhi+Hy5cv+/Jz587ZtWvXfL/Azywnrly5Yrdv3/bl90KSKYQQIttIMkUoHkrJRCwPHjxoVapUsdWrV6eWmsvg/v377cMPP7Rx48a5NCKWDRs2tFKlSlmTJk1s8eLFvi4y2qdPHytbtqy9++67NmXKFJdO9jFr1iwrX768bzNo0CA7dOiQb3MvJJlCCCGyjSRThOKhk0wEc8uWLdagQQP7/e9/b4sWLUq9Yp51bNOmjZUoUcLl8OTJkzZp0iRr2rSpTZgwwfr372+dO3f2TOcnn3xi7du392WsU7t2bTt8+LCtWbPGevXq5a8hpPXr17cVK1bYV199lXqXH0aSKfJy8tINe2/cJqs8YkPORZ9Fe1NHKYRIGpJMEYqHTjJp7t61a5f17dvX/vjHP36bmUQcyWqStfzzn/9sAwcO9PX4Qxs1apQdOXLE5s2bZx06dHBJRQgRTH7euXOn1atXz9auXWu9e/d2EV26dKldv37dWrZsaTNmzLBTp075++TlxIkTtmTJEn8vArnt1KlT6lXxsHPwzBX7Zet59n+azM65qDpyQ+oohRBJQ5IpQvHQSSYZRfpbfvnll1amTBlbtmyZN3EjlO3atbMxY8ZY5cqVXfo2bdrkTd7r16/3LCf/DhgwwKZPn25vvPGGN5HTr5MMZo8ePVwmkc3u3bvb8ePHPWs6dOhQz4Ky/7uhyZ5mebKdRJEiRVxihQBJphAiG0gyRSgeyj6ZQOaS/pRIJoU9H3/8sVWoUMGOHj1qLVq0cMncuHGjvfbaay6IyOnmzZttyJAhNnLkSCtZsqTNmTPHi3zYhvXHjh3r/TPJZtI/E8kcP368Z0LZ9l6ouVzkRZIphMgGkkwRCknmN5K5cOFCzyDSdI000sSNNCKGrLNt2zZv+t6wYYM3s48YMcIzmbNnz3aZJJPZs2dPl0n6ZrIOFedI5vDhwz2bSVb0XkgyRV4kmUKIbCDJFKGQZH4jmWQmixYtajVr1vQK8meffdbefPNN69evn/9OtThFQAsWLPDKc7KeCCFN63v37rXdu3f7HyTN6F27dnXJRCoRU9ZHSvfs2ZN65x9GkinyIskUQmQDSaYIhSTzG8kkQ0kRD1lHonjx4lanTh2bP3++97ts1KiRZyPps8kfHsMcIZpUoiOFVKK//vrrvh/2R3V5VPAT9d0ks3kvJJnZY8muU9Zjwe6cilYzttu/N5+br+RlOySZQiQXSaYIxUMrmRT/dOnSxZvC74a+lQxRRHM3Y1wime+//75nNRkbk0IhBlqniZyCnebNm1vjxo0928m4mkhlrVq1rFWrVl4IhHxGA7X/GJLM7IHQ5SdTivxDkilEcpFkilA8tJJZUJjx5/Tp07Zy5UrvoxnNBAQUDLFs+fLldunSJV8XqESneZzCIIYpKsgYmSDJzB6SzPRCkilEcpFkilBIMgsA8sj4mshi3owky1nGa3mX8zMzAtEnk6xnQbKYIMnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGQZOYQkszsIclMLySZQiQXSaYIhSQzh5BkZg9JZnohyRQiuUgyRSgkmTmEJDN7SDLTC0mmEMlFkilCIcnMISSZ2UOSmV5IMoVILpJMEQpJZg4hycweksz0QpIpRHKRZIpQSDJzCElm9pBkpheSTCGSiyRThEKSmUNIMrOHJDO9kGQKkVwkmSIUkswcQpKZPSSZ6YUkU4jkIskUoZBk5hCSzOwhyUwvJJlCJBdJpgiFJDOHkGRmD0lmeiHJFCK5SDJFKCSZOYQkM3tIMtMLSaYQyUWSKUIhycwhJJnZQ5KZXkgyhUgukkwRCklmDiHJzB6SzPRCkilEcpFkilBIMnMISWb2kGSmF5JMIZKLJFOEQpKZQ0gys4ckM72QZAqRXCSZIhSSzBxCkpk9JJnphSRTiOQiyRShkGTmEJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4TioZTMW7du2fHjx61Dhw62bds2u3r1qm3YsME++OADa9asmXXt2tVWrVplX3/9tV2+fNl69+7tr/Xr188+/fRT38ft27dt8uTJLoYdO3a0xYsX+37u3LljK1eutFatWvk206dPty+//NK3uReSzOwhyUwvJJlCJBdJpgjFQyeZCOa+ffusZ8+e9uKLL7oc7tq1y8aMGWPdunWzoUOHWr169WzQoEF24MABW7RokTVo0MC6dOlinTt3tv79+38rpe3bt3eZREKbN2/u4vr555/bwIEDrVGjRr4PRHP9+vX+vvdCkpk9JJnphSRTiOQiyRSheOgk8/r167Zp0yZr3Lix/eEPf3DJJJs5e/ZsO3r0qMtg69atrVOnTv4a4kcGc//+/TZr1iyXSiSV1xHCtWvX2vbt261q1aq2efNmGzZsmL/GuteuXbOGDRv6vs+fP586gu+4ePGi7d6925YvX+5RuXJll1nx4JFkpheSTCGSiyRThOKhk8ybN2/apUuXXChLly5ty5YtS71i3jyOhDZp0sSbzJFM1qHpnG0QSjKZc+bMsQoVKtjEiRPt1KlTdujQIc+CspysJz9/8cUX/l5kMydNmmR79uxJvct3kPVk3Zdfftnj0UcftbZt26ZeFQ8SSWZ6IckUIrlIMkUoHjrJRCQJMotly5b9nmQihQsWLLCmTZva+PHjvZm7ePHitnPnTn+NTOWQIUNs9OjRVrJkSc9Q0nSOsA4YMMC3qVatmvXq1cullG3GjRvn63/22Wepd/mOr776ytdDVAmynt27d0+9Kh4kksz0QpIpRHKRZIpQPJSFP0BTdV7JvHHjhjeJ16pVy0aOHOnZSZrVyWTu2LHDX9+4caNnMkeMGOHbIplXrlzxrCX9MpFJtu/Tp49LLJLJvmhCZ1/3Qn0ys4ckM72QZAqRXCSZIhSSzG8kk36Y9I2ksKddu3a2ZcsWX0Zzdt26dW3hwoV29uxZW7JkiVekUzFOs/iECRNcMPfu3esFPlOmTLE2bdpY3759PftJ0zv7HD58uP9+LySZ2UOSmV5IMoVILpJMEQpJ5jeSSVU4Ivjkk096ppImc6SQoHmcQp558+b5Hx5V41u3brWxY8d60zb9MmfMmGFvvPGGrVixwn8mq0mFOZlPCoKQ0RMnTqTe+YeRZGYPSWZ6IckUIrlIMkUoHlrJpC9kjRo1bM2aNV7YU6dOHXviiSe8D2apUqU8A0kTN8Mb8TuV35UqVfKiILKcjH1JhXqZMmV8P6+//rodOXLEzpw543+gf/rTnzzbyf4YBol+oPdCkpk9JJnphSRTiOQiyRSheGglE+k7d+6c95ukvyU/k208ffq0R1S4QyCaDElEtTlZT2Awdvpt0pQ+c+ZMO3jwoBfyMBj7yZMnbfXq1V70Q39OBnQvCJLM7CHJTC8kmUIkF0mmCMVDK5kFBRlFQhFPinmQywikkmW8RnYzylbyM2KJkNIvE/EsCJLM7CHJTC8kmUIkF0mmCIUkM4eQZGYPSWZ6IckUIrlIMkUoJJk5hCQze0gy0wtJphDJRZIpQiHJzCEkmdlDkpleSDKFSC6STBEKSWYOIcnMHpLM9EKSKURykWSKUEgycwhJZvaQZKYXkkwhkoskU4RCkplDSDKzhyQzvZBkCpFcJJkiFJLMHEKSmT0kmemFJFOI5CLJFKGInWQyNiXjUOYH41HyekFm18lFJJnZQ5KZXkgyhUgukkwRilhJJhK5efNm27dvX2rJ97lw4YK/ziw9cUSSmT0kmemFJFOI5CLJFKGIlWSSoWzRooVVrVrVunXrZiNHjrQlS5b4POJffPGFTZ8+3ecWZ4rIOCLJzB6SzPRCkilEcpFkilDEQjLJYDK1I5JZp04dq169uo0dO9bnBh89erT17NnTWrVqZa1bt/bfCzpXeK4hycweksz0QpIpRHKRZIpQxEIyz549a8uXL7dVq1ZZtWrVrHPnzt4sPmPGDOvSpYuVK1fOXnzxRatfv74dPXr0e/OLxwlJZvaQZKYXkkwhkoskU4QiFpK5ZcsWe+edd+z111+3p59+2t58803PWlauXNnefvtt6927t3Xv3t3atGljc+fOtatXr6a2jBeSzOwhyUwvJJlCJBdJpghFLCTz0qVLLpqbNm3yvpgIZ6lSpVwwWUYfzIMHD9qYMWOsfPnyduLEiVhWmEsys4ckM72QZAqRXCSZIhSxkEykcerUqS5giBiFP/Xq1fPmcrKZLVu2tLZt21qHDh2UyRSFQpKZXkgyhUgukkwRilhI5q5du6xp06b21ltvWenSpb3ZvFGjRrZ48WLvi4lwIp61a9d2IVWfTJEuksz0QpIpRHKRZIpQxEIy9+zZ8+3QRc8++6z98Y9/dMkcMWKEvfzyy9asWTN7//33fdn69eu9Ej2OSDKzhyQzvZBkCpFcJJkiFLGQzIsXL9q6dev8xi9atKj3x+zatasPXfTII494NpOK8wkTJtgHH3ygcTJF2kgy0wtJphDJRZIpQhELyTxw4ID16NHDBg4c6P0vaR7v2LGjLViwwEqWLOnCGRUG8Ydx+vRpFf6ItJBkpheSTCGSiyRThCIWknnlyhXbu3evy+aOHTvs008/dak8fPiwF/rQZ5N1mFbys88+U3O5SBtJZnohyRQiuUgyRShiIZlAZvKrr77yYG5yRPL69et2/vx5X4ZkHjt2zEX01q1bqa3ihSQze0gy0wtJphDJRZIpQhEbyUQs165daytXrrTt27d7k3gEArpt2zYf5mjFihUun3FEkpk9JJnphSRTiOQiyRShiI1kMrVk2bJlrXjx4ta8eXMfviiCwdqHDh3qQxhRIKTmcpEuksz0QpIpRHKRZIpQxEoyGSOTbOXWrVvt888/9+V37tyxYcOG+TBGzPhDxjOORT8gycweksz0QpIpRHKRZIpQxEoyy5QpYwsXLrTVq1fboEGDbPjw4T5fea9evWz+/Pl2/Pjx1NrxRJKZPSSZ6YUkU4jkIskUoch5yUQuqSQng/nSSy+5TK5atcrHyGzdurW99tpr3nyOeMY1gxkhycweksz0QpIpRHKRZIpQ5LxkUjE+Z84cF7AXXnjBBgwYYIsWLfKhiz766CNr3769ZzPHjh1ru3fvTm3149DETjX6hg0b7MyZMy6nVKnTn5PCIoZE4negcp1hkZBYmulPnjzpy9mGYZXWrFljGzdutCNHjnhVO8vJqFKkhAzv37+/wHOpSzKzhyQzvZBkCpFcJJkiFDkvmYjb0aNHbfLkyV7YU6lSJevfv78PVYQsAkKHbBII3Y9lNHnt8uXLLoYUES1ZssSr0ZFLBnZnGVNYIpUIJu9drVo1z5gyCPz06dP9fZmFqEOHDlaiRAl7++23bfDgwS6myOv48eN9OXOsd+nSxeX3x44pQpKZPSSZ6YUkU4jkIskUoYhFn8zbt2/btWvXfLrIzZs325QpU7z5nGGMED6Kfch2IodMLYno/RBUnpNhpIjoqaee8qwoMwXR/E5GdN++fdauXTuvVidTidAyyxDbUFjEe3AcZE5Zj2wqwyZVqFDBs5Yff/yxiyV/pGQ3a9So4TMTcYz3QpKZPSSZ6YUkU4jkIskUoYhN4Q+SiVgicEgm2ct+/fq5GCKANHGTfVy6dOmPjpOJZH7xxRc2a9Ys+9Of/uSZzNmzZ/uc52zL+4waNcor1slaksWcNm2anThxwtft1q2bN5GT1URE9+zZ4zJKdfuyZcs8u8kxMisRx9GpUyffnozo3Rw8eNDGjRtn9evX9yhSpIhvLx48ksz0QpIpRHKRZIpQxEIyyVjSBxMBo6KcqSWjZWQamdd85MiRtnz5cvvyyy898/lD8BqieerUKa9WRwzJfjZo0MD7f9I8j3SOGDHC902TN5lO5JM+nMyfjuSyLVlMprJEWnv37u2/v/fee56NZP9kL9kPzecc891E4so+CZrYkVLx4JFkpheSTCGSiyRThCIWkkmzM9lFZC1vRpCmcqRyyJAh3h+TjGFBoU8lg7sjmey3YcOG3qeSfX7yySeepSRrST/NnTt3ujAimwydhDiWKlXKm+jpA8rxIaQ0p1evXt2FkwHi2YZmddanmf9eqLk8e0gy0wtJphDJRZIpQhGb5nIKZwiKcchEInD8TOaRfxG9glaXQ17JJANJc3dUIY6s8kfG+JtvvfWWyyUySRM9y0aPHu0FSDNmzHAxPXTokDeRI5k0e/ft29er0DlGMpQIKxXq90KSmT0kmemFJFOI5CLJFKGIlWTSx5ExMym0YbghfkYsDx8+7MMGRcMOFYS8kkkgiRTtIJNREzyy2apVK5s0aZI3pdM8jwhSLETmNGq6Z/YhCnxoZkcwCfqJ0sROX0+a8ikKuheSzOwhyUwvJJlCJBdJpghFbCSTvpQ0ldMvExljyCCyhPwxIHVdu3b1wdl5vSCymVcyyWCShaSfJVXmFStW9Iwl8soMQwxR9OGHH3qWsm7dup6lRHKbNGnifTkpPqKIaNu2bS6+CGrVqlW9MIkhkSgg+rGK9whJZvaQZKYXkkwhkoskU4QiFpJJFpOmZ4YXQuw6duzo41ouXrzY+2MyhiZZR4pmihUr5tXeNHv/GDS5sx1N3fyMILI9soposn+a4RFKZJFMZ5TdjMbJJMPZuXNn6969uw8Sz9BGyCRV6iynTyeySuW7xsnMbSSZ6YUkU4jkIskUoYiFZJKZpPmZvpONGjWyiRMnenU5WUj6RzKMEEJIcU3lypVd6hDHdGB7KsLpd0nGFKkF5JD3J0PJ++QdHolB3Wmup79l3kHgWYeKc4ZUYlrMewlvhCQze0gy0wtJphDJRZIpQhELyWQ6xypVqnhFN0MKkTWkfyQ/M285s/fQ/xGhQ+zIMv7YMEa5iiQze0gy0wtJphDJRZIpQhELyYyyjOvXr/eCm3fffdf7XpItJMtI1pEsYjT7D//GEUlm9pBkpheSTCGSiyRThCI2hT9IJP0dkbBy5cp5MQ59Iek/Sb9Hok+fPt58TjN2HJFkZg9JZnohyRQiuUgyRShiIZn0cWSIIprEqSCnyptq77/+9a/+x8Bg502bNvWB0Bm7kv6RcUSSmT0kmemFJFOI5CLJFKGIhWTSVD5v3jwv9KGpnOwlY1q++uqrPkYlFeAMY8TwQlR4q7lcpIskM72QZAqRXCSZIhSxkEz6XlLsU6dOHR+Pkmbx+fPn+xiUVJKfOXPGXyfDKckUhUGSmV5IMoVILpJMEYpYSCaV4vSzpMinWrVqVqRIEZfNJ554wivOGVT9xRdftKefftoznQxvFEckmdlDkpleSDKFSC6STBGK2BT+RDCc0fLly33cTAY9Z8iiNWvW+FSTNKcznFG6Y2TmCpLM7CHJTC8kmUIkF0mmCEUsJJPBzMlkUvgTBcU9BK9Rec4sP8wpzlziDHkURySZ2UOSmV5IMoVILpJMEYpYSCaV5VOmTPHMJRlLgmwmUz9S9INUMlMPUzkyNeSFCxdSW8YLSWb2kGSmF5JMIZKLJFOEIhaSSYbyP/7jP6xGjRpe/PPee+95JfkHH3zgzeXHjh2zAwcO2NChQ+3JJ5/03+OIJDN7SDLTC0mmEMlFkilCEQvJpM9liRIlbN++fT7rD/0xmTMcmZw6daq1aNHCx8hkmsmnnnpKkinSRpKZXkgyhUgukkwRilhIJk3hZcqU8arxadOmWbdu3Xy2n44dO/rMP8xrzrI5c+Z41pPB2+OIJDN7SDLTC0mmEMlFkilCEQvJJHNZrFgxW7Jkic/uQ7/Ltm3b+uw/yGbv3r197EyymhcvXtQ4mSJtJJnphSRTiOQiyRShiIVkMiwRY2Fy448aNcrGjBnjc5RPmDDBm9AZ1mjkyJFe+IOIKpMp0kWSmV5IMoVILpJMEYpYSOaJEye8upwbf9KkSf7z+PHjbe7cuXb48GE7dOiQ7d+/33+vXLmyBmMXaSPJTC/eGrrOTly8nnNx41Y8WzGEyCUkmSIUsZBMZvw5evSovfnmmz7gOhnMdu3aecaS17p06eKZzD179tjkyZPt0qVLPnZm3JBkZg9JZnrx783n2m/aL8y5WLzzZOqKCiEKiyRThCIWkgmnTp36dtrI0qVL23PPPWdt2rTxeOWVV6xRo0a2bt06HzeTAdrjiCQze0gykxFzt32ZuqJCiMIiyRShiIVkkpVEHp9//nkv9qlZs6b95S9/sXHjxnnQF7Np06Y2ZMiQ1BbxRJKZPSSZyQhJphCZI8kUoYiNZJ49e9bHw6TI55NPPrEBAwakXv17n00Kgnr27JlaEk8kmdlDkpmMkGQKkTmSTBGK2EjmzZs3vcDnypUr3ufyzJkzqVfNhyyiP+aGDfGueJVkZg9JZjJCkilE5kgyRShi0ycT0aTIh3+Ju8fCpB8mIhpnJJnZQ5KZjJBkCpE5kkwRilhIJvJIdTlDF9EHc+zYsT7wOmNifvjhh9asWTNr2LCh1atXz6vOz58/n9oyXkgys4ckMxkhyRQicySZIhSxkcwjR4740EX0vaRvZvPmzW3Lli0unMwCVKdOHfvrX//q42fSpB5HJJnZQ5KZjJBkCpE5kkwRilhIJs3k9MPcuXOn7dixw6eVrF+/furVv8MMQE2aNEn9Fk8kmdlDkpmMkGQKkTmSTBGKWEgm/S2RzCgGDRpkDRo0+N6ywYMHW+PGjVNbpEdUWEQxEbMFnTt3zgd6531pemfZhQsX7MaNG9+uzxzprM+6165d8+Vw9epVr4QnLl++nNY86pLM7CHJTEZIMoXIHEmmCEUsJJMpI7t27Wrdu3f3KF++vL344osuZES0rEqVKqkt0gN5XLNmje/j1VdfterVq/sUlbt37/Z+niVLlrQPPvjAVqxY4esjle3bt7c33njDateu7f1DI2jOf+edd6xixYrWv3//tPqHSjKzhyQzGSHJFCJzJJkiFLGQzOPHj9vEiRNd5oi6deu6+EW/R8tq1KiR2iI9du3a5c3tyOr8+fOtZcuWPpMQY3FWq1bNhZMm+jFjxrjwUnDE+yGUZFARYPqMrl+/3tq2bev7oUiJbOv27du/l+n8MSSZ2UOSmYyQZAqROZJMEYpYSCZN0MjdwYMHPRAxZv2Jfid69OhR6D+KzZs3+x9Vv379fGYhRPHtt9/2AqPevXt7NhKRHTZsmE2fPt0lkvnSkdPVq1dbnz59bN68eda3b18XTiSUY+rYsaPNnj3bB4vPD5az7sCBAz1KlCjhMisePJLMZIQkU4jMkWSKUMRCMunXSMX44cOHv5VMsoR5yaTwB4Fle/p0Ll++3OdBL1OmjGc0ly1b5pnItWvXeuYSiaQJfebMmS6kNKlT0Y5gUoxEpfvevXt9rvXJkyd7/1F+zw8+C0MysR1RpEgR69ChQ+pV8SCRZCYjJJlCZI4kU4QiFpJJEc6+ffs8k0g/R5qw33vvvW+LbCjAIRNYWMlECGkSp38l86Ajm/SrpB8m01hSFES2c+TIkZ7drFWrli1dutQznAcOHHCZpI8mzfWTJk2yY8eO+XHNmTPHhZiK+IKg5vLsIclMRkgyhcgcSaYIRSwkMxonc8aMGd7XkbExyTwidBTYlCpVyl5++WXPQBYG+mEid7wHVeRII30+X3jhBdu4caMXBq1bt877X7Zq1cqzqAsWLHC5ZTpLjoVB4MlG0neUjCviyrGS+ZRk5j6SzGSEJFOIzJFkilDEprmcbCZ9GL/88ksvBCJbiBQif/SLXLVqVYFl7m6mTZvmWVC2530o+KlcubIP8E6xD0Mk0TxO30sypvTTRDjJYlLs07NnT/89ep1liCZ9N/mdLGxBkGRmD0lmMkKSKUTmSDJFKGIhmfcbRJUinaZNm3pVeaVKlTxjSf9KhkUiI0kTOllJBJJ+mzStI5A0r5PZZDn7YXv6VdK0z5BIFATRdF4QJJnZQ5KZjJBkCpE5kkwRithJJn0kqcimTyTBz4cOHfIMZGFBAmn+pmK9bNmyXthDf0r6YbKMAiD6gFKkQz9QmsmZ1pI+m8yZTkU4ywmyoDTb81pUAc+g7gVBkpk9JJnJCEmmEJkjyRShiJ1kInu/+c1vvL/kc889Z48//rgNHTrUm9FDgxwilPTZZEpLZvABZvyhCZ0B3Dds2PC9AdcRzW3btrkAM1MQU2IWFElm9pBkJiMkmUJkjiRThCJ2komI0feRwhqKbkqXLu1Cl47MpUPUH/Srr75yuYyIpqIk8k4dyXLWpVgonSklQZKZPSSZyQhJphCZI8kUoYidZNJ0TV9JYN5w+j1S9JMEJJnZQ5KZjJBkCpE5kkwRilhIJk3Wixcv9oHRmYmnWbNmXnxDv8miRYv62Jn8zusrV67MqH9mNpFkZg9JZjJCkilE5kgyRShiIZkMAUQVNwL20ksvWYUKFaxXr15eEf7rX//ax6dkGCGGDGJ4oYsXL6a2jBeSzOwhyUxGSDKFyBxJpghFLCSToh6GEWIw9nLlyvnNTxaTgc+ZipGhhZgjnHnFGfOS4ps4IsnMHpLMZIQkU4jMkWSKUMRCMinqYf5wgqGBmA+cJnEGZWfIIZrSo9eJvAU6cUKSmT0kmckISaYQmSPJFKGIXeEP/THzVpczpSTV5elWcucikszsIclMRkgyhcgcSaYIRewks0WLFj7dI4Oe0w+zePHi3lTOuJVxJ+mSufXoBeuxYHdOxmt9V+YrLYp4hSRTiMyRZIpQxE4yx48f71M3tmvXzoOfV6xY8b0B0eNK0iVz7NrD+YqBQhEqJJlCZI4kU4QidpJJ/8y7m8YZ/JzZeeLaFzNCkqlQZBaSTCEyR5IpQhE7yfziiy+8P2Zetm/f7sMcIZtxRpKpUGQWkkwhMkeSKUIRK8kkUzlw4EDvgwlkNJkfvFWrVr487k3mkkyFIrOQZAqROZJMEYrYSSYiNnz4cG8eZ/xMZvupXLmyDRs2LLbjY0ZIMhWKzEKSKUTmSDJFKGLXXN68eXPr1q2bbd682SZPnmy1a9e2mjVr2qxZs1JrxBdJpkKRWUgyhcgcSaYIRSwkk6wlQxQRdevW9Vl/mEqydOnSNnfuXKtevbr169fv23XiOmamJFOhyCwkmUJkjiRThCIWkrl//37r0qWLMTf5448/bj//+c/t9ddf94HZO3ToYMWKFXPxZB3GztTc5bmJJFNxv0OSKUTmSDJFKGIhmUePHrXRo0f7GJlPPvmk/eQnP/HpJIcMGWLjxo3zjGaNGjV8HeYzv3LlSmrLeCHJVCgyC0mmEJkjyRShiIVkIo27d++2vXv32ptvvml//vOfrUmTJj6P+YQJE+ytt97yjCbTTMZ5KCNJpkKRWUgyhcgcSaYIRewKf5hWEqGk0IfmcqSsSpUqNmbMmNQa8UWSqVBkFpJMITJHkilCETvJbNmypY0YMcKLe86cOWOtW7e2hg0bunTeuHEjtVY8kWQqFJmFJFOIzJFkilDESjIRy0gyo98p8mnbtq0PbbR06VJfHlckmQpFZiHJFCJzJJkiFLGSTAZj37Vrl08tmZctW7bY2rVr7fDhw6kl8USSqVBkFpJMITJHkilCERvJJGt57tw5O3v2rF27ds1u3rzpv7N8w4YNPn85y+KMJFOhyCwkmUJkjiRThCIWkok8MoXkp59+ahs3brRjx4550A8T4WTecs34k/tIMhX3OySZQmSOJFOEIhaSeeLECZs2bZoNHjzYx8VkSkn6X5YoUcLH0KQ/5qBBg1xGCZrV44gkU6HILCSZQmSOJFOEIucl8/bt27Zt2zafRvLpp5/2aSUZlJ2B2F944QX7+OOPfQgjBG3NmjW2fv362FaZSzIVisxCkilE5kgyRShyXjLJStL3csWKFV5ZXqtWLZexRo0a2RNPPGEdO3a0V155xQdp79Onjw0dOtTnLy8MyCnjbX7yySdeXEQhUY8ePaxp06b+R0eBUbQeFe4cT7du3WzJkiW+HJDedu3a2YcffmhTp05N61gkmQpFZiHJFCJzJJkiFLGQTIRv+PDhLnQMxI7g9evXz4oUKWLTp0+3ihUr2vvvv+9N6KtWrSpUJvP69eu2c+dOz5SyT36eO3euVa1a1fr27evjcU6ePNn7htJczx9gp06dPHr37m2nT5/2WYk6d+7szfe9evXyGYmYpaigBUmSTIUis5BkCpE5kkwRilhIJtNFIpc9e/b07CAy99lnn/kg7EeOHHGpQ0ILC+9x6NAhz1pWrlzZ5s2b55lTRLFNmzZe0U6Gkyb6hQsX2oABA3zmoa1bt7rYdu3a1eUW+SWLiZwyvSXHxfoMGl8QJJkKRWYhyRQicySZIhSxKPwB5iNH6lauXGn79++348eP2+zZs23Tpk0+GDvyWVjIfC5YsMB+9atfWYMGDVwmyUiSiUQSqWBHIkePHu0iyh8f70dWk4zn2LFjvcId6R02bJiP5Xny5EmfV53fEc784DPRnH7q1CkPtu/evXvq1eQhyVTc75BkCpE5kkwRithIJtlGpIxm61GjRnmTNVlHxI/MJiJYWHbs2OFyV7ZsWVu3bp2L4auvvmrPP/+898NEQnk/3rdVq1beL5R+mPQVPXDggDej0ze0Ro0aNnHiRK94J3s5Z84cz75+/vnnqXf6PiynC8DLL7/s8eijj7owJxVJpuJ+hyRTiMyRZIpQxEIykTEKfWhOfuqpp+yZZ56x1157zaWMgp/GjRv7a2Qead4+f/58asuCQZM329HkTt9KsqMU+5QrV87H5kQyGfCdoiKKfah0X7RokTej0+eSTCbN5PTnRDLpQ8p+PvroI5dIJDY/mBITQV6+fLkH0tylS5fUq8lDkqm43yHJFCJzJJkiFLGQTKSNJuyRI0d6hpFqcoYtItNI0MRNcQ6SiPBduXIltWXBQPAo4JkyZYpvS7N8s2bNrGTJkj4+J8vop0mxEf00EUH6aHJcCCnLeX+a2BFR+ouSzWQ5QZ/SgqA+mQpFZiHJFCJzJJkiFLFpLo9gmCKEkz6SVHWTVYyyh4WFPpQILMVFUWFPvXr1rFKlSl61zvibCCRN6vTdpC8oWdOZM2f6dhT4sBwRRVYRTYYyqlmzpksqg8kXBEmmQpFZSDKFyBxJpghF7CSTpnMKf2jCZtghfqYf5cGDB1NrpA9DDNEsznBFpUqVsuLFi7vMMl5m0aJFXWRpnqd/JYU6FPyUL1/e3n33XatQoYLVrl3blxM0p/Na9erVfVsKg+hLWhAkmQpFZiHJFCJzJJkiFLGTTISNzOPixYtd4Cj4QRJv3bqVWiN9KCpiH/SxpGCH/pSXL1/24D0o7KGqHbm8c+eOvxdSy1BF8+fP959Zzn5YZ9myZT7WJkKMCLO8IEgyFYrMQpIpROZIMkUoYieZCNukSZO8EIjsY0EHOi8MkXzS3E2WMq/I8jNCSoV53kwl02BeuHDBhyQi21pQwQRJpkKRWUgyhcgcSaYIRSybyxkuCMk8duyYS11SkGQqFJmFJFOIzJFkilDERjJpjqYpmqIcxpKkOTppSDIVisxCkilE5kgyRShiIZk0WTPDDzPoUGTDYOk0U0fFNnmDfpQIaRyRZCoUmYUkU4jMkWSKUOS8ZNL3kb6X1apV8yGBEE2C+cIRsigYXojxKxnHkkHO44gkU6HILCSZQmSOJFOEIuclk6IaJBPBZBihcePG+dBCTCc5fvz47wUDsTNmZrqDsecKkkyFIrOQZAqROZJMEYqcl0yavqnuZrggspdM/8hsO8y0w5SOeYOZdfbt21fgcSlzDUmmQpFZSDKFyBxJpghFbAp/aDZn4PX27dv7zDzM+BPXvpc/hCRTocgsJJlCZI4kU4QiNpIZQaYSyWQWnvPnzydKNCWZCkVmIckUInMkmSIUsZNMMppz5szxucOHDx/u1eRJQZKpUGQWkkwhMkeSKUIRO8kEBmHfsGGDbd++Pbb9L/NDkqlQZBaSTCEyR5IpQhE7yaQICMGcPXu2TZkyxWbOnOnzmO/evTu2VeURkkyFIrOQZAqROZJMEYpYFf7s2rXLPv74Yxs5cqT16dPHq82ZYrJbt242ePBgW7JkiV27di2t+cJzCUmmQpFZSDKFyBxJpghFbCSTAdabNGniQxhNnTrVtm7d6tXmNJkzvFHdunXt7bff9mUIaRyRZCoUmYUkU4jMkWSKUMRGMs+ePWslSpSw+fPne7aSvpjIJP9ev37dZsyYYS1atLB58+b563FEkqlQZBaSTCEyR5IpQhGrTCYV5e+//74NHDjQFi5caOvWrbOVK1f6LEANGzb0144ePWq3b99ObRUvJJkKRWYhyRQicySZIhSxkcybN2/a6tWrXTCZp7xfv37eD3PIkCG+bNCgQT7dZFwFEySZCkVmIckUInMkmSIUsZHMCKrIJ02a5DP/IGX00WQec/po3rhxI7VWPJFkKhSZhSRTiMyRZIpQxEYyqRi/dOmSN5EzCPuHH37oTeT8ISCaiCfzlyuTmbtIMhX3OySZQmSOJFOEIjaSycw+nTt3tnbt2tmYMWN87vJPP/3U/504caLVqVPHatWq5QO1q09mbiLJVNzvkGQKkTmSTBGK2EjmuXPnrHz58j4AO8U9Fy5c8MHXKQj68ssvbcSIEV74s3z5cq82jyOSTIUis5BkCpE5kkwRithI5vnz5+29997zAdgZF3Pz5s0+OPuOHTt8EHYGZaf6/PPPP4/tVJOSTIUis5BkCpE5kkwRithIJtnJadOmWcuWLa1169ZeUU6z+ahRo6xHjx7WqlUrrzRn7EzN+JObSDIV9zskmUJkjiRThCI2khlBcQ8z/tA/k4IfMpsfffRR7It+QJKpUGQWkkwhMkeSKUIRO8lkqCL6XzZr1sxq167txT7IJnOanz59OrVWPJFkKhSZhSRTiMyRZIpQxEYyr1696uNhMgg7/86ePdvFcvr06T6kEYLWoUMHF01Vl+cmkkzF/Q5JphCZI8kUoYhV4U/VqlVt2LBhns08fvy4nTlzxivLKfahX2bdunVtw4YNsR2UXZKpUGQWtcd+aj0W7M656Lt4r529cjP1lyBEbiPJFKGIjWQyhFGlSpVs5MiRtm3bNvviiy/sxIkTPi4mswAxxSSSxmDtmUgm01ey/wMHDvjg71SxMxYnYhs1x5MpRWzXrFljmzZtsiNHjvhyOHTokK1fv96PY9++fWlVuksyFYpkxiMtPrF9py6n/hKEyG0kmSIUsZFMxsQcMGCAZzOZ6Wfo0KFeADR+/HgfoL1KlSpedY4kFra6HHk8ePCgVa9e3ZgfHcF8++237bXXXrN69erZvHnzXBrPnj3rY3KWKlXKj4c+olS1UwFPc365cuXsjTfe8Ob7kydPFvh4JJkKRTJDkinihCRThCI2komoMesP4jdhwgSXwC5dulivXr28unzLli0+QHsmwxfR77NFixb2hz/8wQuKaJqvWbOmj8fJ+yC2ZDnpB0rR0cKFC110kVyq2xcsWODb00d07dq1vs7GjRv9uAuCJFOhSGZIMkWckGSKUMRGMiMYfJ3CH8bL5I+gQYMGLpxLly71fpuFJZoXnf0VK1bMZxdigHfG4eQ1BoAnY8l7U83OH+H+/ft9astBgwa5bLJ+7969fT80offt2/fbGYryg6zpuHHjrH79+h5FihTx7GdSkWQqHtaQZIo4IckUoYiNZNLPcvHixS5l9MtE9pA++mLSRN2tWzdfRjbzzp07qa0KBtnPPXv2uDyOHTvWKleubK+//ro3v9PvkmZw+lkinIgk86QjnfTRJINJZrVnz55eeMQx0J+T18iw8sdKn9H8oE8psxUxsDxRokQJ69SpU+rV5CHJVDysIckUcUKSKUIRG8lEHpE7ZA4xo6iGDCFCt3r1ap/xh76U27dv936Z6YAQzpkzx5vIDx8+7GNwlixZ0qWTZngElwIfpJYMKtNbcgwUI5HNnDhxojeZs/2kSZP8uKh8nzVrlmdZyb4WBDWXKxTJDEmmiBOSTBGK2EgmxTZkF8kgIpz0nyTDeO3aNW/OZspJRJN+kSxLB5rakUSymFStN2rUyIt92B+V5bwP/5JtbNu2rTVt2tSP49SpU7Zz506XTzKcFAORaUU8KfjhZySTSvSCIMlUKJIZkkwRJySZIhSxkUxEkv6K77zzjjVv3tyzh1R7ky2kqZzhjag6Z710m8upUKcf5quvvuoZzF/84hf2k5/8xIoWLeoV7UgtfSsp/oma6Pv06eNN7GRRmdqSJnwKg2i6X7Fihfe3RFxZxs8FQZKpUCQzJJkiTkgyRShiI5k0gS9fvtwmT57sGUUGX0f6kDpkjopumsrTFUygSIdMZRSILE3z/fv394wm78NQRvSXpH/lZ599ZhUrVvQ+mxQK0UzOcgIBZrij9u3bu7SuXLnSxbcgSDIVimSGJFPECUmmCEVsJJNxMrnxKcBhCKHGjRt75pIsJn8MSCf9J0NAf0sqxCnqQfpo8u7cubMPWUT/zIsXL9qQIUO+HUaJZnaWEzNnzvRtOC7+ZUaigk5zKclUKJIZkkwRJySZIhSx6pNZpkwZzwzSdF2tWjUfLoi+mAgdQwCRcQwJckhTOcLJTD5RX0+q0ekTypiZ9MnMOw4m/Tfpk0mhEEMqpZNZlWQqFMkMSaaIE5JMEYpYSSYz7MyfP9+bsWmSjgSOWXhYRrN1nJFkKhTJDEmmiBOSTBGK2EgmldzPPPOMD1PEQOlM58gwQYgmFeHREEJxRpKpUCQzJJkiTkgyRShiI5n0d1y2bJkPHUTWkqZxpnukCZsB0JGzRYsWpdaOJ5JMhSKZIckUcUKSKUIRG8kE+kIyADpV3Fu3bvUZc6g6p58m/SbpPxlnJJkKRTJDkinihCRThCJWkpl0JJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzh5BkKhTJDEmmiBOSTBEKSWYOIclUKJIZkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGZJMESckmSIUkswcQpKpUCQzJJkiTkgyRSgkmd/w9ddf282bN+3MmTMeZ8+etatXr9pXX31l58+ft9OnT9uFCxfsxo0b365/8eJFX/fcuXN27do1Xw5sx/bE5cuX7c6dO6lX7o0kU6FIZkgyRZyQZIpQSDK/AcFcu3atlS9f3sqVK2eVKlWyiRMn2o4dO6xevXpWsmRJ++CDD2zFihW+PlLZvn17e+ONN6x27do2depUXw6jRo2yd955xypWrGj9+/d3SS0okkyFIpkhyRRxQpIpQiHJ/IY9e/bYpEmTbPDgwbZs2TJr06aNde3a1UaPHm3VqlWzuXPnWqdOnWzMmDG2f/9+W7JkidWtW9eFkm1Y98iRI7Z+/Xpr27atde/e3aZMmWINGjSw7du3fy/T+WNIMhWKZIYkU8QJSaYIhSTzG44fP26bN2+2gwcP2q1bt6x3795Wo0YNz17yM9lIspXDhg2z6dOnu0R26dLFdu3aZatXr7Y+ffrYvHnzrG/fvi6cSCj76tixo82ePdtOnDiReqfvw3LWHThwoEeJEiVcZpOKJFPxsIYkU8QJSaYIhSQzD/S1pO8lmczixYvbe++955lNMpE0p5O5RCJpQp85c6adPHnSdu/ebePHj3fBrF+/vo0YMcL27t1rp06dssmTJ9ugQYP89/xARMeNG+fbEUWKFLEOHTqkXk0ekkzFwxqSTBEnJJkiFJLMFAgmhT1Lly61hg0bev/M1q1b29atW73PJpnOkSNHWosWLaxWrVq+HhnOAwcOuEzSR5PsJ83ux44d88KfOXPmePM3fTsLgprLFYpkhiRTxAlJpgiFJDMFzeT0q6TwB5kkEMeNGze6fK5bt877X7Zq1cr7Wi5YsMCry+nPSd/Ndu3aeTaSgqHDhw97JpN+mWQ+JZl/R5KpeFhDkinihCRThEKS+Q0MM/T5559bkyZNvs08rlmzxvr16+fFPpcuXfLmcfpe0neSfpoIJ1lMin169uzpv0evswzRpO8mv+/bty/1Tj+OJFOhSGZIMkWckGSKUEgyv4Hm7SFDhthjjz3mWUr6V9K3EuGrUqWKZyQbN27sWUkEcvny5T50EQLZuXNn34blZDvpz0m/SoqEaHKnIIim84IgyVQokhmSTBEnJJkiFJLMbyDTiGQihcgkVeUIJEU5NWvWtJYtW3oREL8z2DrN5M2bN/f16L9JRTjLiQEDBlijRo38NbaNKtYLgiRToUhmSDJFnJBkilBIMn8E5BChnD9/vu3cudNn8AGKhGhCp0l9w4YN3xtwHdHctm2bFwYxU9Dt27dTr9wbSaZCkcyQZIo4IckUoZBk3gP6a16/ft2nmEQuI/iZqnMi79SRLGddioXSmVISJJkKRTJDkinihCRThEKSmUNIMhWKZIYkU8QJSaYIhSQzhwglmbfufG2jVh+yHgt251RUHrE+3wewQpH0kGSKOCHJFKGQZOYQoSTzxq07VvRvy/J92CkUigcfkkwRJySZIhSSzBxCkqlQJDMkmSJOSDJFKCSZOYQkU6FIZkgyRZyQZIpQSDJzCEmmQpHMkGSKOCHJFKGQZOYQkkyFIpkhyRRxQpIpQiHJzCEkmQpFMkOSKeKEJFOEQpKZQ0gyFYpkhiRTxAlJpgiFJDOHkGQqFMkMSaaIE5JMEQpJZg4hyVQokhmSTBEnJJkiFJLMHEKSqVAkMySZIk5IMkUoJJk5hCRToUhmSDJFnJBkilBIMnMISaZCkcyQZIo4IckUoZBk5hCSTIUimSHJFHFCkilCIcnMISSZCkUyQ5Ip4oQkU4RCkplDSDIVimSGJFPECUmmCIUkM4eQZCoUyQxJpogTkkwRCklmDiHJVCiSGb9o8bGtO3DWTly8nlNx6fqt1P8aQnyHJFOEQpKZQ0gyFYpkxk+bzrYn2s6337RfmFPR+eNdqf81hPgOSaYIhSQzh5BkKhSKBxn/M21b6n8NIb5DkilCIcnMISSZCoXiQYYkU+SHJFOEQpKZQ0gyFQrFgwxJpsgPSaYIhSQzh5BkKhSKBxmSTJEfkkwRCklmDiHJVCgUDzIkmSI/JJkiFJLMHEKSqVAoHmRIMkV+SDJFKCSZ94G9e/fa5MmTbdiwYbZw4UI7efJk6pUfR5KpUCgeZEgyRX5IMkUoJJmBOX/+vE2cONGqVatmjRo1sqZNm9q6devs5s2bqTV+GEmmQqF4kPH2sPW28PMTORlHzl1L/Y8mHjSSTBEKSWZgVq1aZV26dLEePXrY9evXrWXLlvbRRx/Zl19+mVrjO7766iu7dOmSnTp1yqNBgwbWpk2bb38vbBw9fsKebzvDflpvnP2s/nhFwOCc6ryGj5/WH2f/p+7YfF9TZB5xvG/7f7wp3//fci1oqcpveZyjW7duVq9evdSTSojCI8kMzOjRo6179+62fPlyl0gEk2Wffvppao3v+Pzzz/2P+eWXX/b4+c9/bo888si3vxc2ir30kv37L5+w//tfT9uvnnlOETD+4/Hf2L89+mS+rykKH//vyWftZ//3cXvst3/I93VFZvHvjz1p//HYb/J9LVfjDy8Uzff/t1yK559/3n7729/aS9/8n5vf63GNxx57zCpWrJh6UglReCSZgRk0aJD17t3bBfLWrVu2ePFiGzx4sC1btiy1xndcvHjRdu/e7UJKzJ8/3xYsWPDt74WNRYsWWbFixTyjmt/risJH3bp1rXLlyvm+pih89O/f35555hmbMWNGvq8rMot3333Xateune9risIHCYUXX3zR/+/O7/W4Bs+QTZs2pZ5UQhQeSWZghgwZYv369XN5jCSTByh/tA8K+n+WLl3aZs2alVoiQkHmmb6zIiwrVqywokWLFrhITqRH69atrVOnTqnfRCg+/vhjK1mypF29ejW1RAiRF0lmYCZNmuSdpteuXevN5VOnTrW+ffv6t8MHhSTz/iHJvD9IMu8vksz7gyRTiB9HkhmYNWvWuGQyfBEdqDt27GgDBw60rVu3pta4/yCZ9KfhP0ARFrpCtG3bNvWbCMXq1avttdde878ZER7+HwoxcoX4PnRvKl++vCRTiB9AkhmYCxcu2IABA+zVV1+15s2b2+9+9zsf0ujy5cupNe4/NNOPGjXKduzYkVoiQrF06VLJ+33gwIED/mXsQf6dPEzMmzfPu+6IsOzcudOGDx9eoCHqhHgYkWQG5vbt2z4YO83kPDRpPj906JDduXMntcb95+uvv7Zjx47ZlStXUktEKM6dO2enT59O/SZCce3aNTty5Ij//YjwnDlzxs6ePZv6TYSC/2P5v/ZB/v8uRJyQZN4HyCQiI1SYMzg7vwshhBBCPExIMoUQQgghRHAkmQmDrCnZU5rH6B9648aN1CsiU2hupDCF5nIy1YweQNcEUThoYmSs2Khogt9172YO9yTnlHMInFd+pnKfe5fzq3s3PThXzODGuYu6HvA7fTGjLjScY/XNFOL7SDITBgUUzDlbqlQpa9KkiS1ZsiT1iigsPGDoK1ilShUfZodzW6NGDduyZYuqSgsJ4sODulWrVjZu3Dg/xzy8mcqO8/vBBx94kZVIH6aqpdiQv39AgPj5ueee83PL8GafffaZJD4NOFcLFy70SvJy5cpZpUqVbM6cObZ+/Xp77733rHjx4j6FcH4zuwnxMCPJTBDHjx/3aSyRoZkzZ/qYjiNGjFChSoaQndi3b581a9bMh6difvqNGzd65kKFKulDtv3EiRPWrl07e+WVV3w0Bub2nzBhgr3//vsuSIwty/1LtkgZt4LDlx6kvUKFCvbOO+/4uVu3bp0PX8Q55d5luCgyxipWKTjbtm3z+5NKcs4h/xf06dPHZ3PjixGV+23atPH/f8lsCiH+jiQzQTANGA9mHiiIJaLJDEQbNmxIrSEKA5mh2bNnW/Xq1f3hwvBQzOBEk6NIH84bkjlmzBgrW7asT8W6fft2a9Cggc/zf/ToUc8SMXg4IzWocK7gcK8ydiPnsmrVqi6SY8eOtcaNG/u9y5dO7l0NFZUeX3zxhbdc8C/ntEOHDlazZk0fpg7R5Iso9y6BkAoh/o4kM0HwbbpFixbeRM7QGsgl/+lNmzYttYYoDGQsyWLw4Gb+Z5rHyLgdPHhQfbAKAdlfMm4EzbhDhw71ZkeEk+ZG7l0mNWAIMISIbKYoGJwrziv3a61atVyIEMumTZtanTp1PFi+a9cufUkqBNy7ZIH5+6eJHHnnXmX5smXLbOTIkS75Qoi/I8lMEPznxpSHfOPmYcMsQ0gmmTdReDiXURaDBzgPlbp16/oYqOqKkBlk15BMpmGlvyDdEpAfZJMsPM2PnHORHpw3ZJLm8s2bN9vhw4f9PiZj/NJLL3lmnj6wouBwLskUz58/379svvnmm9a5c2cfqg6Z54sS9/KMGTNSWwghJJkJgkIJ+gXxnx2DW9NvkP/0+HYtCg8PELJrUUUuDxW6JfTs2dObdkXhiSSTrDv9CJlBhSILpLNfv34+qYEkM30iyQTuXTLu3Ltk38lm8uUT8RQFh3OIpDOb25QpUzzT3r17dy+iIpPJ/Pv0L54+fXpqCyGEJDNB8J8dnftpHqNJh+kP6ZxO30xReMhWdu3a1QsoOK/Lly+3atWqeYGKMpmZEUkm4k6TLn0xGSaKe5c54mmCVHN5+kSSifz06NHDv4CSheP/iBdeeMGzbbp3Cw5fNPkixP3Kl8v9+/d7t6T+/fu7cPIFNCpY0/SdQnyHJDNBUEzBt2iG1+A/PB7adFDnAS4KD0PtkKGgGhrZbN26tffPpF+bBCgzIsnk3qX7AeeVCt4PP/zQGjVqpKkmC0leyUSEEHbuXf4/oOqcrjQawqjgMDUwsv6b3/zGh9finPJlnuZyzvOsWbM8Q4xkIqBCiL8jyUwQVOHu2LHDqx4pAOI/PZrKJUKZQZaCpkWqnSn6YWxHMkGqes4c+gvTl5imSB7OjPFKMRCFFTzIySCJ9GGYIobbool8z549nn1DhuizTbaYQfBFweGLOgL51ltv+f2JaA4bNsy/EPF/Al+KOL+0GknehfgOSWbCQHwYp42BgxFODVUi4gJCSVM5fds00L2IA3wBZYxXxJ3htnTPCvF9JJkJhIc12cuoUEWIuMC9SyZI966IA9yjdEng/1u+4OueFeL7SDKFEEIIIURwJJlCCCGEECI4kkwhhBBCCBEcSaYQaUCfQfoLhpxOkn5c7DdX+nNxHEnsW8ZnCjUcUnTNxHd/EzofQoi7kWQKkQYMYE3lczRfcQgodGEszmhWlmxC8QIjElDIkDRp4DwzHufd143PSaRz7jlH3AsF3Yb17rUur3Ns6RxHtuF+OXnypA/yzsgAQgiRF0mmEHlgCj5m9GE8wSpVqvgg1kzTybBQSCDjDzK2I/MX5x0nk3UYKy+qjGZKzwkTJvig+AwynvcBfLdwMF83AzsvWrTIZxSCu4WDoVEYloqBtKNx+qJo3LixD8C/atUqn040Ew4cOODjKzKlI7PtMGh33mAebIZsyY9jx47552WsQGTux+BcMlQR03IyJzxzlbN/zl1eOAeMUcqYhHfPpMKUk/nNwc3MNps2bbLBgwf7eJCcO5YxYwtjGTKwNpLIubpw4YJfKwYpZz56xuls3ry5tWzZ0saMGePHBlwjlrEtx4hUcZ54D4au4fii7bh3GGSe3xnAm2Pks/EeTJBQr149nzGKf999910/Jgah5zWuJ8fJ8d4NU0Eyu8wPwb3CtsyWxPFxLzNGJueWsUjHjh3rM4AxsUDec4Yss28+B+cE4eZzd+zY8XvXkeW8Hg3XA3w5Yr+Mx7t7925fdjesy7XiyxnHP378eJ82lCkuGXOW98r79yCESA6STCHygHQghQ0bNrRXXnnFpY4HJMsQKCSkTJkyLhFDhgzx6fp4EPPgLVGihD/YkRpEFGFAQhjAmTFLgdcZ2JnXEUvmP0ZK2CeD6DPg+6BBg3yQZx7ezCrEgx3p4EH+L//yL/a73/3OihQp8m0888wz9s///M9+nPnJSUHhs3/yySf+mRFmxGPatGnfC84D8zfnB0LD8TNoNQLxQyBpzOSDLCN4iCbnj3n3kZ+8wsFn53O/+eabfj6Rk+h8MAPT3/72N39ffkdICaQJqULcEF+m/xs3bpyv+6c//cmPj3PLlwmkEQni2v71r3+1119/3dq3b+/XB6lduXKlyxNC/PLLL/vc6hw/n4/jevvtt326UUSS68n1ZkYo5LFLly5+zng9klTO7UsvvWS//vWv/d//+q//8utZvHhx3xeD0G/bts0/I/cJ++ReIP7yl79Y6dKlv/2d4P7gMwPnjWPlnuJe4LwiynzZ4b0ROj7n3YOxMwh+5cqV/X35khSNs1uuXDn/UsH55PzypYrXmTmIfSL/fCnh2rA9UsoxcV4QSQSUbRBfzgXLuYbRrE58YeMz8Rk49iiEEMlBkilEHnj48oBmqkOEkoczwsIUh2Sffv/739uTTz5pFSpUsPLly3umiinlunXrZs8//7w/nBEKHsRkpsgG/va3v/UHLSByZBzr169vb7zxhksPMluqVCkPRIZliCmyQoaUrBtyynGxLx7+vH8UCCrT3ZHBYr3CQPM4XQCQgapVq/p7k8XNG0gg0vJDGSs+N+eBmXqQtx+C5tXJkyf7+yCZvDeyzvlEciPRZDkCQqaP4P2RP84f69euXduljPNC9pT9IlbICyKJ/CCJiBrZXjKH3bt39/POlwiyasguGTpEimV8eeA8EIgVssSxclyvvvqqf8Yow8zPCGne6UXJRHMPMN0g2csIMrecF+4Xjrls2bJ+fyCNCCkCyKw8ZJCRM0AIEVHEjODee/HFF/1nBJ37hpmn8vYP5rNwrHPnznX5JmsZnWve4/jx4/65kFgEEFFE+IoVK+biSAaY4+fLAueP881xIORsB9wDkUAj/dz3fAbOHwJZvXp1v5c5P3zh4npFgs015l/OG9lfPh9fXMjik3HVTERCJAtJphB54CHHvM+9evXy5lP+JdMTNYPyAOVBSpYPaeBBywP/8ccft3/4h3/wbCYPfh7SCBcPcR7CPEABOUEaya717t3bsz/sBxEgaM5EpsiIkSVCBBAYsqVIJA9ytkOiokBcOCYybzTL393kXBBoAkdw+HzsDwn685//7MJLlo0s3x//+EfvJoA4IFp8DoQQQSMQaTKgCEiUASNYh3XZJmomR/SQc14Hmkx5f+R63rx5LuMIIJJDtwWkiXWQdjK+SD9ihMxwzJxjhIcvBFyrF154wR599FGXSqQTkSLzyeckY8j1Y/+cK8Sca877kO3k/YsWLfqtdJNZJvsXSSafn+Pj2DnfUSYRfkgyuYY1atTwbB5ZVKZ9Ra5oUuce4/0RWtYh+wpI2Guvvebnj+A+i7K9yCLncPr06f4ZkEuOi9c4Bj4nmVAkHnHkSw1yy88s44sCn4EvU//6r//qGVzOGQIYSSLHwt8AX3w439EXBz4L14V7nGNGetkvks814h5BOlmfY0F6Obf/+I//aE899ZRVrFjRp2JEOJ999lmXZTK6bBNlNYUQyUCSKUQeIslEEqK+ckgAD0mEAylAXJBEhBKBIVPDA/y555779sFKkyWydrdk0txIsyTNhFETfCSZ/I5kIpj03yOThHAgLUgJ4odY8JDOG4gZD2xeQ5LYf7pwXIgJoooc8/noc8hx0NSMXCEdiBxSw+fiuMmilixZ0qWErNQvf/lLF27EhGW8RraO84HUcR4Qa84tohQJGv8i0mRQ2SefA0lDSJEZBI/PT6YR0UY2kRuuDVlMMnWILU29vA+iz9z9nAsydBw725Nh/tWvfuXvzzqIGNeP7DRCjVSRsUZ66OeKdCGZSG4kmUgowsf6fE7EKuKHJJPzy+fmWiHt7AuBRLCQeX7merNO1H+XLCQCyPkg/vM//9Mee+wx/xnp/+lPf+qyzPVAeMkwcq75DFwbhJbrxz55H+45fmYZ9x3XkHudpm62R9C5vzkOvlDxuZBWPj9fAMgSAxKI0HINOP98GeK9EHmyynQd4F+uBX9PiDBiz3Uj887++dvh/HH83Gtcb7bP289ZCBF/JJlC5CGSTB6sNGfSTEyzKg9vsjZIEFkYHq6ICZLJ+ggMAsDDGblAFBHGuyUTIUCCeCgjLAgOD3yyP2R8eA/2yfr8TAYQ+WI95I/j4LiQJgQIWUJwETrejywVGSqkDVlBhvgseQuP8gMh4HMiHGS02D9iQIYLgaW5mX6EvCfHThEHxx9JNoEkc27IeiEZ0XLWIRuMVJLFQ9hZj2PnPcicISBIIcKFJCFMCCLbcG7oIsA2nFf2TzcCrgUihhyR3UQyadLluBBkPgfnEBki88b6yBLSidjQvxKx5hqxnC8RSCxCzz7JUiOyd0smx8Q15jyQ8SyIZCJPSC2CxzXhGuYNlpFpRZijZmmyjOyf80cg0pwbfqb5GknjPHNPIbFRP9G8EklmkOD6IZDR79yDiCKSx3XlGLgWnEe+HHEvRM3r7JMvCVHWGWje5osR+yI7zd8D9ycCzv1KVpPPzPmgCIkvKvxtIJJsx98VoskXNs4ty8kWCyGShSRTiDxEkomUIAo8cHlAkmmieRcZQF4Qr5/97GcuFAgKy+gXST9OBIVMEkJ0t2TSrIkEIjn0FURqkCuaQWlqRiKQBJrG82b6eGjzIH7mmWdcBDkeModkCsm40QyJWEQiwPsgjpEw8POPQZMxzcMcAzJFMzyiSRMm8oO0UWSEqCEYUZNuXhCwH+uTyXvQpI5kIFw04ZKRQzDZhvdBnKJ+nwggx826rMfxsB7niz59fHbEiGtCpo59IzSIJRloMoacM64D74Go0i+T5nQymrwPmVnOLSLFZ+PckskkG0d/Tq7L3ZIZXROkluwgwhaRn2QijYgh78lxIMt8Bv7NG9w7ZBq5f/hSwLGTtYzg+JAyQOz47Egpkglcc+Sba4Ww8bkoTqPZnS8HXEvuOT53dD9wrugGwXshlYgg9wtfVpBAzin3ApIZyS8ZTZaxL84FmU2+6HB92DYv3Cfcy+yba4vAc/65x7mWnGv6ovLlg/cUQiQLSaYQeYgkEzFBeniok+1B6nig8xAm24aM/NM//ZPLCVkcMoks5+GOkCCeZPbulkygTxsyEEkVgkoRC5LBuggV75m3bxrSgfhSiUw2k/UoAmJb3vvpp5/2BzzNm8C2UbN2lFUqCDzoETEkhOPnPCBI7JfPzOs/1GfuXpKZF4STLCTZV84Fv3OOEJVINhAYjoNzimyRyeO8cg0QVLonIH4IFEKE9JE5RapYB9GkQIgMJRlBmsCROzJ3NFvTRIsQcn7IGiL8dDngvfgMSCYZNwQrb5/MvJLJNScjSvaOLw/5SSaFPNw7LONLBOcXKeO4CcST7CzLkXzEj+wogkihT5QRJgPM8fMz2VmOEwGPCn8iyUTaEGOynBQL8Z7sn2B7mvjJLAPbc+9xTRFKrglfphBJZJBlXFOWky3lPiITzJcXMszcyxQYsV/OKdcz77XniwICSUacTD/N5ZxHzivHwDZcV74gsa4QIllIMoXIQySZyCXZJUQkyljx0Eb0yASR9UPykAIyc4gMD32aIHlwIy30J4wkk4c/MhAJASAFbMs+aConq4YY8VDmOPJChpJ1aNYkC0RWiswcTc1k9ZAWhCrKUCENSAGZPcSInwsCUsHnRhTYjs+KZCESCAJZNoQwPwoqmUgaGS6kCaEiY4uIsW+adO/uU8p5QgA5TzQTI3xsT9YP+UHmEHv2w/lF9MgUc07YL0MUcVw0zyNniB3Xhv0SiBJShRzS/zMSIDKUZOz4IvFDmUyyydwXSCRdCDj/yFdeyeRaRE3HXEOOgWPi2JF4tiPYDpnnywHbkClEzPgSQTzyyCPe5xVhi5bxvuyX68tn4R7iHCJvZDrJUiLv7JfgCwNfTPgcQJcArkPUJ5OiMiSTY0Cc2S/iyDVlWfRlg+w+P5Nx5nxFY4by98L6nHeuBZ+De4cvB9yzyCnZYa4755djJUPOPV/QL0JCiPggyRQiD2SjyODRfMj4hmS5EJJf/OIXniFCXigWIdOEXCCRiCUPezKQCBjNt0gm2Udki4wbksID/u4mQR7uSAzZNYSC7BX7RhjygtCQ+SSzhdjQH5TqaZro+R2ZQAQieeCBjTjRZMyDPCrauBdIKeKKwPJ52B7BJpP7k5/8xH/ms+YH4kSTMELxY+Nk8vlYhwIQZB1p4/g4D8ggUhLBeUCiyDCSleMaIIVsE2XYEM5oGVKD4CCMXAd+5lxw7skU/9u//ZtfDzJnSBISxfEg6OybY6JqHdFGbDk+rilfEjjPyGd0bbg/kD4yg3xZ4FoiZhS6IKuRZCJbnA8ylgRfYpBKpJnjpzKb5nnOO19UuAZ8Hu5F7i/2S9CvkmZn7sloGWKIoHH8HBcCzjWjGZpjIntLlpf9EnQxyCuZ3Oc///nPv60uZzskk/MYnU++QCGPXAe+QCGKvB/3dJSZRTY5TxSOkRlFRDl39ClGTjnHSCiZX7LKnB9e57qSnefcs44QIllIMoXIAw92sixkkRhAnYHHyRwiakgehSBkG2l6JFOELFH8gCQgekholJnk4Uq2howTVeBsT2EEwkHmhwwQ/ezIRPIgJ3vK72Tg2D8P4qgwhWwikoDoEPTBpEqabGq0jEwjmVYyesgBYyHStMpn4OeCQAYVAUIAEDO2R0SQS0SEptL8+mMCcsi5Ihv2Q5JJJhJR4jxyrsj8kblEMsiocX4QwwjECXHj/HCuEdmISGjzCjSfky8JZC05x4gecoNw8r50QyCiIhS+MPAlgswjwbFzDpEozgP3AzKJHCK5fC7OLeKKeCJtdFPgOvNefA66M7CP6Lj4DPRn5LORaeQ8kc1EenkfvoxwnXmNLy7IYyR4kdACGULuOe4/jp97kr7BNGtzr7I+ld4INO9FVhqBY59cS4LrR+aQ88j6nCuOl+uM5HMPcu9yHyDq3Iu8B/cf9zPXnnNAdpQsKF0TuH7R/cW1o5sBXwDYJ/ci5497mfucY0F+kVYknowoy8hu8iWJzy6ESA6STCHyQAYJWSBzyMOf7ArZIbJLCAFCgUDwQEZeKGpAMMjkRA/cqJkckAseomQ2EVHW40HN9gRCSzaKhz4Pbx7w7B9BQnR5aJO5iiqkyVoR7I9+d/wbLeN1HvB5JS1TEBGysYgZ54Fz8kOQGUQikSWyXvmBuCEWfE4yX9H+2TdN85wbZCaC1zmHnP+7xRWJQWDydi0ga4hMcS64jlwHMm7IFceGNCJ0XAuyblw7zj1SxnVD1hAjstOR4HFNOc9cb7YHJJBjJWuJKLMu9wr75dohr+wjgtdZj8wpQkZGlM+MQEfNxHxurh37zg8ynpw7rnt0//BenMvouNg/9wvvxb/cQ/wcwfVDrnkfzi1fkDg/wLFE3SvIQHIeEVvua/4e8sK69EWNMqJ54fNxzji3HBfvwd8A0so9QnCPIJuIOMfHtaC7wN3dRIQQ8UaSKURgeHj/GFFTNkL7QyAcPHDvta8HAdKDOIQ4Fj57Xom8H3CckSDyL5HJsXOdEN1cuBYPCq45osk9mLcfcWHIez0i8lsmhEgekkwhhBBCCBEcSaYQQgghhAiOJFMIIYQQQgRHkimEEEIIIYIjyRRCCCGEEMGRZAohhBBCiOBIMoUQQgghRHAkmUIIIYQQIjiSTCGEEEIIERxJphBCCCGECI4kUwghhBBCBEeSKYQQQgghgiPJFEIIIYQQwZFkCiGEEEKI4EgyhRBCCCFEcCSZQgghhBAiOJJMIYQQQggRGLP/H2S5DyniM30hAAAAAElFTkSuQmCC"
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E6%95%B0%E5%AD%A6%E5%85%AC%E5%BC%8F%E8%A1%A8%E7%A4%BA.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAWgAAAByCAYAAAB+30ucAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAADDmSURBVHhe7d2HlyZF1Qbw738SEyYUwQyKCRXMGFCMoKKomLMYEbOoKEbELIqYMQdMmHPOOft+59eeZ71b9js7C7NMz859zqnT1dWVurr7qVu3blX/36rRaDQai0QTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3Sj0WgsFE3QjUajsVA0QTcajcZC0QTdaDQaC0UTdKPRaCwUTdCNRqOxUDRBNxqNxkLRBN1oNBoLRRN0o9FoLBRN0I1Go7FQNEE3Go3GQtEE3Wg0GgtFE3SjsWD8+9//nlzFvs4ravqN4s0haWseQc7r8V//+tfkh5omx2DuvKbdatS6BDXsQJZ9edEE3WgsHCETRDISTZBwx3/+85+TH/aVbh1qmuQR1Lzm/I41HJyP9Rj9Y5qtRMoP6vmBLPfyogm60dgBGAls7jxHBF3Pa7zNQppKqCO5VqSM0QVJO3ctWBd+eVHLXEfQS0YTdKOxYKwjrUo84zk3kk/i7Q/ksb/kOsbhTx5z5zAXtlVI3nNlHojythpN0I3GDsI6YhEWIoIQUnWXBWPaeh5/DasQlvqMcSLlV1cl/61EbReoZS4dTdCNxg5GJZqRdHJewzYLZBmSHyGsEl5FSDakmPSOcUH1HygoY1/1WHcvS0ATdKOxcIRk5ogmmAuPv55vFuKmzKDWIe63v/3t6pe//OXkfvOb3+xVRuL84x//mI5/+MMfVr/4xS9Wv/71ryf3t7/9bU8c7kCg5j+WsS58SWiCbjQWjjkiqef1etzcRGHON4sxDX8IWv7I+eMf//jqnHPOWZ1xxhmrs846a/XjH/94It7EjyQu/C1vecvqWc961uoVr3jF6p3vfOfqpz/96Z56xh0IjB1LcCDL3Co0QTcaCwaJ81e/+tXqL3/5yx4yGUklRJPwv//976uf/OQnE4FWKXV/UOOTgH/+859P+f31r3+dyE4YKfhjH/vY6nGPe9zqqKOOWt3ylrdcffazn1398Y9/3FOmeOrziU98YvWQhzxkddvb3nb1+Mc/fnXeeedNdYx0Dftbx81AfdX797///XRey0gdD0S5W4Um6EZjgUCCf/7zn1fvfe97VxdffPEkbQqDOWKp/j/96U9TGqRIcq3S9P5CWh0EifeLX/ziRHbySl0Q7Pnnn7+65z3vubr97W+/+vCHP7wXGbr+s5/9bEr/wAc+cCLpz33uc1N44lzWum0G6v6FL3xhqruOIvWumAtbCpqgG41twhw5OUcYiPDCCy+cVAKOo353I4RUH/OYx0zkKW0IEdaVOxf2u9/9bvWpT31qdcopp6wuueSSSSLNNfjhD3+4ev3rX786+eSTV3e7291Wr3nNayapH8RB1u973/tW73jHO1b3uc99Vg9+8IMnyTmk6Bi/+PxjPdahpq2o+Ti+7nWvWz396U9fffvb394Tf13apaEJutFYCBAKR0Xw6U9/enWve91rImcSKIIVTqWAdL/5zW9OE3MkZaT4gQ98YJKypUfQ4r///e9fPe1pT1u98pWv3CPVjkiZ3AgqjHe9612rRz3qUauLLrpoIn35htikUU/k+7znPW910kknrV74whdOUrtryPx73/veRODnnnvuJD0jyqhdQpIpPy55j/4a9o1vfGMaXWgP9+b8bW972+qtb33rJC0H4murs88+e/Wwhz1s9a1vfWuPukjZ2mrJaIJuNLYRlXRyvPTSSyfCQ2gIBYmQZL/0pS+t3v72t0+ESbJGRh/96Ecnkn7Sk540kTm1SMgHgZu4e/SjHz0RrHxSBqTsuTD4yEc+snrqU5+6evKTnzzlhZzrdUedhbwR+SMf+chJv4yUgaT8wQ9+cPWZz3xmIu5TTz116ixgJOf4g4THH6Qt5PvSl750aicd1Ic+9KEp7EUvetHqJS95yUTKqS9Cdu1+97vf6rnPfe7q+9///p7yUo+logm60dgGhIBCEgFpkLXDiSeeOJEeVQdQJSDgT37yk5Okeu9733v18pe/fPWDH/xgkkhPOOGE1Qte8IKJFCFkTLI2icfJO+FxFTWctPz85z9/9fCHP3wiN+mCmpZFhk7i85///ETm973vfSdyZFJHknUP/E984hOnjuKCCy6Y0oYg6YVdV17M7+KnmuESbgThXhFsyPi0005bnX766ZNeWzqk/dCHPnS6XidIpdFet7jFLSbLE9J97iF1WSKaoBuNbULII+BHNKRhBIxQQ97UBogFUdHlIkMSNSmRhcXxxx8/hZG45VPTIS3Xv/rVr07SJNQ4MNbFZB+9M+k5UnnAr1wEiKB1GlQMpNPb3e52qy9/+curr3zlKxNJOopngvCZz3zm6mtf+9qecuXjfqRl/SEfzuSmI8mbCoWfHty9qct3v/vdyU9SJrWzCFEfTielLHk4D/nqYL7+9a+vjjjiiEndUvXgS0YTdKOxjUAelSgQHosIZIZgQozisM5AZkzVSI8kRlIlVcQd7nCH1Wtf+9qJwGp+/O95z3sm4qQOiJ46DubOlX//+99/9epXv3o6R3DyShykiyTVV6eC8BDfkUceOZEjSZn0rD7f+c53Vne84x0ndYs6Q8rTuSBiemzqG2ni5/hZgJhoRPapC5UL/bqRBl27tiIlU/886EEPmjqmtEPKMnlp4pQumkpkJ6AJutHYBlSyC5AnAkE61Bkj0SI30uLd7373aUIMSSJGUiNJEhE7N6lYVRkIkD772GOPnaRIYTVvSFzhSF8ngciQf+pa49ADm6RDqKwj1E3517jGNSZJ2uQdkjQKQLJUMG9+85snIq2InTLy5BAvl/MaThUSGA0gY/cdCxdlPuIRj1g94QlPmNJQ/2RCkJMe6d/5znee1B3uAVxbKpqgG41tQEijwlCe+oIESI+bOHHIlxrDZBu9L6IkNZJ0X/ziF09ESCUwSo8IlD750EMP/R/9az1yrpFUkTkJlfSbOAECZ3JH/WGiEhGS7uV99atffZK+5SGvH/3oR6tnPOMZk24aoaecIOdx6QzmrlWn43jsYx+7OvPMM6dz6UjwOjj3SiXC/hkpJ40OTbtS9yBxoxHhS0YTdKOxTQhxBMzRLPYgBZLucj1xELSJNhYRJEjhwkiRVA1veMMbJuLKYpKA9Gni8ZBDDlm98Y1vnKTLoBI5RyfMKuJmN7vZpONNPRLHpB7VBnWKjoGqxQSheMjvrne966SSQNocUjbRSJ+tbIRdSbhCWK7ty8lXO5DgpTFieNOb3jRJ7+pNUkbA0bmDeFQu7LXVnZoj+S0VTdCNxjYBYXABG2FLpkl3MBIHNcLLXvayaSiPdIHkSvJG0EiJxAs1X6TEFO+qV73qNAEZXS7UeMJYi5hkO+yww1avetWrJqkzcVynslAeIoyj2kC8pFV+JK+uJhpdp/vmEKqJQ6h5jvfp3PWEJ07OXdMG8jI6CNy7UYTOw/1WdUrSAvtyOnsSN9Q2WBqaoBuNhYDkfPOb33yycQ5pjESFMOuSZWGkR2HVaqESkmukXARN1UAVUVHjknrpn1k7kHiDWp5y1IOjxki5HH/K5yfBJi6X60Hi7i/kk3JBHvzulYsOfoQwKiQdoXa+LGVfkWiCbjS2CcghDiyDtuEQSbNeqy6o5zV8DoiLSgRB3+Me95jUIElf0/IzYaN/vvGNbzwtQhmxLt14HozXthI1b/eY87nyajiVkI6Qjn3paIJuNLYJlVA41hu3vvWtJ3WF85BOjTuHdeGB6/Sx17rWtVZ3uctdpsUrY345pyawmAOBUZmsi5ew8Ryqf4Rr9b5gTL8ZjPlsJo9ct2jG/TnCvtJtJ5qgG41tBoIw/DfBxsbZ/sqVcKofqr9io3gm9m54wxtOulc2xSOSlk73Bje4wdRRvPvd755IkKuo5cRfw2DuPMc5gh7L2BekqXkENXyMEz/VBoJmpgc1ztLQBN1obDOQE9M1izmoF0xyjcQSAuNfRyjjtUqEiBcp6QAsIqmoaUjabJnVY47IRyTtWHbO59yIdeH7g+ThntNWVQ9dy7BgxiiBdQkkfIlogm40tgkhDQ6ZWMxRrQvmIG6IN/4QUVwwEjTTuSpB51pNw1Tu8MMPnwiaKVvFmD+/skOIQS23QlwuyHnizqVZB3HHcuqkIdR8a7znPOc50/2xaFk6mqAbjW1CJQ5Hi1SoFpjSwUh8iWvlnP0uLBaxVLrmEX+QMMR7netcZy8ddEXi2YnOsnCTlXTQIUHHkRDBOfUMszppOfWri2HA6kYWIq5bXMP0L+Sc/Me8NwJzP7v+WYzCFrzmxaUjqGE5t+Oee3z2s5+9J3ypaIJuNLYRCCLkZDEHKTfEUcmjxmNpYRN68SxAEZ44NQ04R6DM7K5ylatMNsBsiINKjI7Ik6WHelhWnutxc2D/bOc6+3ZYSGO1oxWNScvUjuWIFX4m5thXKyckvlHe64DomQHSJ1ugwrQukFcIGsYy7IB3q1vdqgm60WjMI8TgGCJ7ylOeMulGHUfiqPEs5ba0mz2vpc7CE2eEMNImqfnKV77y1AnYmyPXRsnTghN7cJhQ1AnkesV4brEMaV5dbnOb26yud73rTaaCViyqG2nZ4hbLsO3JbMUjaRpB555gzHcjZJc+bWAxjE4okE/aBHKe/KU55phjpg5j6WiCbuxo7M9HvSRUwggssTZRSDc6SoQ1rrTiklatnBuvQz1HlCTtq13tahP5Uw0EiZc8rFC0+RJLDuZ+pN+RROMqqFps8GTFIOmbTbeVhInnfqwytMkTzOU31ybrIC6iZ9Ps3uif16GWgchtNkUXrwNaOg5qgp572DWMdJCXwjEYz7cSKX8zZYiT+JDzhNVrwRg2F2cpULeN2sA1rt7v6EYJL+FLx1hnsHTZKj4bzltyPd5L/CRWiyzsUEe1kPAav7YrHS3TPSoOpEQfXFHbmLRtL42jjz562mcjO8VBjkHKEM76A2FSv9jn4rjjjpsIPqDS0JnYGjTPFaTlan2DGp54gTag3iANk97nJP0gaXUS7LzVzapN26TOlbskHHQEPT5ISNhceEWNN147EEgZjl6Ueh43Yu7aXBiM59sF9cj9OdZ7DZzH5aOpccb4wZjvTkLuNyCF0o/azIc0OnfP7pFNMxtee3bYGAkpklaZz9nEP0j+SInK4drXvva0VzMpUnhtr8RFYtQPITG6ZOE1TlwNI5WT6qkz7HCnoyHdkshdp4MmPdOFO0/ZSZ8wxzkkTvzu2W52RhE2atIBaAO22ykjceOQOv07U0M77lGTJN5ScVASdI618XM+F56XZXxBqn+rMVePufISvj9xg5zPxb0iUesxuo2uB/wjmTjP86r+nQT1rQ452jDpTne6016LVbgaH8n4hZVJLn8oQUr2N0bYdf+MwN9KbFFKfZL9oDdyCNyqRvt22C0ucC2I31G9kSKJWVrkqX7+CqNupFvStQ6ENJ904zPjr24dXEP4yrCVKemdjt3/Dm2BapQw5sXZxImeXOfD1jw73anHUnHQqjg8kLkXwMvEJIjkwV8/7uqP22rUvOfKqGGOY32qG1HD40/67UIte/TnfKxjveY491yc0zsakrMi2EgHuVTU+4lDZCbSkO14zxzYltREHmsJ+0IjKxYXyCc66QAJIVmrFC3QqH9UgfjrOZhAU48sO69wrm4BNYgNmNQLQZv808GwBiHhCkOe6lktNzwzaZE2adYxzjln0pLzzbqXpGUrThVEX68NTELaO8Q9zum5dRKkbJI9/Xj9o0q9l6XhoNdB5yUHD8kwUm9r8xgfNrieuF4CQyHHDAW3EuoQp4PwwqajSB3iF4c/yHmuSRc3xk0+2w11jUt9HNU3LvcPNV7uMwsQHLncq7azAIP05qMOSUu3E5B2iR9Ig4bf/vqBvNwrJK57JCXadJ4OGvka4tNZU2WYEKx5kmbtj0yapRqpJDdCmHZ1JJkjV2oEkmeNL07qBfKlP0fSeXb8VupZEKJuTPBI8ikjz0850vozuO+SH3lyzumsXWPvTHeetGecccY0IqCDZq+tjghYXaJjV1bqbaUm9Y7VlNpDW+0EHJQEnQeTh+OBeqG8yB48yYChf17WPHQP0QN2zYvDjzy2GjoAujmkQqJxpLurUJ/UH6rfR0py9OJH0jAikAaSlguZbTfSzuD+dY7uwYflgxrbOXX3jDwX8R3FJU1loQM/oiJRjZNfS0Z9vrnXtBFrBxIvSRBJB547AcOKQ3/2ZjKXeNqh5pm2JlEzbyNZpgMLxK11iB/4mbGZ8KM2Ub8RiU9PbXWi9zD5eD7S+UchNQTLEJN5FerInln6OH9C4fgRuok8ZoG+R9+MengXfMPUMNqASsgIIvru1AvEV46FOszxSNCEs4RDjkvEQa3iqA+KNKw3Niw0FIp04uFwruuJbVbOltPDNyxD6lsNH6CPxsvC3MdfNEyo1GFXhfvIS4SI8186q6FMKKmzj8lLXO97bIPtROqizVke+FhIdSRBUpbhcBZQJJ6jSS+6Vm0krvZCSqRI8RE76Yr5GKuDUdrbCUjbBEjr7LPPntoFqblH13VQ2oN0TfWAxEz+aQ8EJJ0RRdqO9IwcLQ4Zdc/gmLgBv3fNUV6kTWRIiPCN5BrE77vSEbie/Bxtmu8Zs6n2fqoPJL0jKdp9VZfOm0tnjvC1gzK8594XdUPinrvvwURlpOhAGTovnZiVmiYwQ+Q7AQftJCHwxyEFUoQXlk6LNFGvO9ezethIgCE7IvRybDW8YCZMDNOuec1rTv9xs8S32mWmXj6C+hF56Q07b3KTm0x2rYbD7EB9rKSrfDTVCdtu1PqQdJGrZ2HIaXMebeD5eDZjXDpGJlW2yyQtmxAz/PXBi0PKRlj0tpvZ4GcpyD1WOEdGiJh06H1EPJ6hzplKw7A+EiudtVVxLBgM4XVW3hfERw/MLlncqtqYc0ENQ4akWZ2hjgBJ55r6yJN6SQeKLBFq3jVxPB8LaiwxV2/1F16R/Ko/bu5d9j26H3pkeRqB+k4JKzoKumhtUPMjgVs+r5Mw6tQ2woPqXxoOaoIG5x4IicSsrz8L58FXOOc8ZLPXZno9aGm3EinHy0y35uOyOTrjfi9R6lVfTh8cRzKgyyMxIzbpdDx54eZc8tpu1Po46hCZkpFqjFaQr+E04k2cOPeOsLSRj9Pop14HQ2EkrvMidS3hnveFWv96P+ru/aCPRX4m15Ch+9aJ2+wHMSI8HZ3JMhIivS+pV1wStQ7PhkckxpSRozLGNqp1SFwjEuXbv4IAg7Rd884hYBOD2lzbj3bFpGES7gMe8IApbYSiYCxr3Xn1G9ESSHQ8Og/nSNkIFFETYLRB4quD94y6JaMLdRzzXSoO6klC8DBIZV7i008/ffofG6x7MBla2rPAhIsHupVIuXpywy12rzawMQz04Y16QhCfVEVKJMmQHuj2DB9JUfWFg5SxVGhT5EKlxNbWUWfDkcQMZfOhuw+Ea4RgGGsYH7iWe0cY9NA6Vp0WktpJGEkj949wdE7aC2nroAgR3mkQRpIUZuJLOyAtpIrAjKqg5p1j/FDPlV3rg+RI6CR5eQv3TEimOgbkh6ipOcb3Vzyqu0jPyRNqGSPm4nK+AyMqLqMt9dMRaQNCTAQWIGHrOPLdV4xlLBE7iqDHBo3f0cML8jBBj29lFF0tvacXZh3kYzhHvUFiAPmsK/eyQnokQhom0dPx2eKRHtULOObvpScFqRMCQ+rIjHqDfm2zqO0Cubc5CE/cjeJdFsiLmsf9M+cipRlJXOlKV5oWYIRUAp0ZIvBs5iYCUz8jEhK5kZLhuPDcAyTeRveSazXeRmmEj+WMaXMcwzaDmg7Gc9hs2OXBRmVUN4d14ZcVc2Xtq/x11yrGeDkfw69I7BiC9gHoGRGVj7Q2GFITTuIdh1EI2fDLMCvqDchHlcbn1yPT79FBk6RrPiQH5SZNkPSbReKTSHQYpCO6aCoLE4eRjGo5CEvddTSGuO4FoVkEsL868pSf/HVgpBskCQnXjvJOm9b68G8WKa/Cufs3CWvC1HM1eUuvru3pVRMPSG70qSRtz2EO4hrq0lHbcIi5Wuoctw7j9Y3iwhi3umA8b+wMeGbr3u/teJ47gqA1jCGr4Z6tCqkCSF6kMMMn0pXhrUknxGoYnA8EySDdk08+ec8G5LlWnWG1IaFhNJ0oacxQ3LARiSAIS1n5DamCpN8sxJWevszsOmI0kWL/XTpYJJM8vSiuG96bGKNDy4Y6iMywDbltFskzR52ayUptqU3ViV6RLhNJ0ombpEKkdJrSJZ/NQtzqEqYs+YZI6VuZjxlJUHtUqI/RgvutqouaJ8jLfZhw1I6JW+MEtS71+hg+dz3n47X6YddrafMaFxLWbhkuWBe+HdgRBI0oEQRyRsIM4K9//etPkrGP3MduT1gqAsSFsE2o+DCoAMzwImhkrsHzIdWHQApHSkzs5E8FgZxJqYbihs300pbMkirH9JuFuKRkHYlVUCRY0nFMzegY80GTXNWDfo9+jaRrcoS0bSgfU8HNQp7JWzp5mkiiMlE2MzadhWWw7lmngKB1COqQyab9gbKqU77O0P0rQwcq3CjBHIH9IpRnPwjx1FOnSPUx3m/yDIxw1JOqxHMTfw6pR/zKMpmlI4gjDHD1vF6vYToOHelYn/jVOe0+Xm+3HFexLvyKxo4gaFIiAibFIjDDfCZmJoSQjI/cx2zCzEw/MmU/iuDYRd7oRjeahr4+Jg1eP844eZBok94Ha7YYefoAkZUdvlhQRA9a89ospLEQxoQfMlRvky2kR9I7MsrHjBBNAJFkDe2RGOlSHS/v73p0DHS67s/kDpL2W342tUYaJp/Eca+ke+UaYVwWpI05z8R9mew06hGWNtQm1BPuD3kjPZ2SDpilANS8RiBk92LfY++ICaIRc+lNOFkmrT108nHULnaNc9Tewpxz9br7YGcMY72cV3Le3/elccWiPqc8t+3EjiBoKgEfKBMs5EaqY5ZFWgpZgo/5pje96UR0hu6GuPSXdJsh7bkGF4YApaPbRVYIgiQpnB7bB08FgUCRV/Jx3N+HaIadtM5EyktgEkzeyIlEG8Q8iLkfYkOQWdyibvuDWl9lIl8SKylQu+ogjjjiiIngIikbVTCPUi8r13SGl/WlTbmOOj8ry1ixCAuEM5c69NBDV0cdddQ0atI5es71R6qOYx2ce/6ezyGHHDJ1aiTjYKN6e77u2cSi0Q1i19nzezac8zGMM5pSrg4exnJyf8L46/02lgXPxmgno7Q8yzy77cCOUXHQv1JXkHYY8DN+Ry75MJAJ8kbQzNZInj48JjYkaBNx0aPmQ4lfB4CIsmgCOegQSEWILFIfadzHWIes+wtpEA6pywfunKRIBUNCpw8Whiyoauhm1Y+kjaypa5Cle98fjPV1ziSJ1GnyzRaMVqi5Z2WBzgkpaz+LQJDlZYFyU7Zy3RcVhxFN4Ho6QuorC3hI8p6j9vLcR0jjWSRv74DJRyMBErF3Jkicilonz9h9c0ZsnnvON3LSxQXyjYO8L+BZmlMgBOhs2y3DUfE5muvwXXj+9Z3hzzO8IrEjCBp8AF50H7dlv3TFdMT5MEgyCMzHTVdM+szHgGAMX0Mw9QPiECQyYFtMOmUlYWKRNMdygpQuXsDvYXH86rUZiEv6NpFFQifhC/My2JiG6RxJ3zlSQo4ktsQxnNYB+bj3d7MXeeSYFw3BIGjSpnxJ1KTH3Jey6fy1H12/Tir57A+kidNWRkCW2+vw6nUwqvD8bC5v603PLROkUONC/WgQtNEJCZqu3odW444Y8wpq+Do/pJ0g1+JcS93iF4781ct8ijq2W4ZjUcVRpTIy8G3U5wk5XpHYMQQNXm4fKwnXdosZigPCokP2PzQTSobLCJBkjPiYsGUJaJDGN3SlEz3ssMMmEkTKzuleWXSwCEAsSLKa8uXD2yxBi4tokE6G7HHKVU+rGHUkVpBZLaYs6Uiz6mJBi9EAor8sSL3jZwnDvhpB6zQQtnD3ZERiwo50rQNTB53ZKF1sBikXiXpOOh8Ss/Dk5Yi0LclFsiZObYRDV5/7lUfS1HSc0ZR8TRLqBLIUPHFyHP3eHRK6+Q0dO8cf595zjJ+jRnNulDZOEjrWdo4T5r3U+SGCdstx3hfPxbuWZ+cY/3ZgRxE06Y5UZRKJrpa6AZAJ8iV50SEjGg0tXBqETkJF2vlQIH7DehIzEy8Tgz506hASNFWKiTTERSVhCI1kQDzkTsLeDEkjWxIi8tUJpHwvAJ0sFYuRgckyEmZUIJG6qEAsosnk2hyEe8F0JAg1L1fKqg4QjU6B6kRHhDTB6IOpoU7LKkxtpw4kVPm6X0Sjk3T/6jj3IqccQOzuSQeKEGs9gJ/kgvB0tEia/tvkcK7nWD+cnFOB0aFLZwSSSULX6/NJPgEdvPfKRKjRCcef8/hZ98z5I+HLd8wb1G0uvLF8jO/ZFY3FEXQaob7s8TM588EgKh9t9M8IA+H50SUVAakQpEFW2S2OzjONDWl8hCBPkiIClc4H5+Nj9oXwEZRJrVhUAPUJUz9DIxIUpK4g75zzIyg6VgRrgUrCwaQhqxRqFhJmTPlA3oiHqoF5HSmxImVwiAixkiBJd1GjBMqLWgi0o3JJ59ozdTbB5l7pc9WZdKGjMnIJ8ZOwqT4MEdkg67hqWRXCdXLqZgTBciVx65FTtg5V56DzINGmnUD96z0kHSsXQ1QErSPJ/SROwF/z282o7QI5z3sQpL0c17XdmFeQNPX6XNx16XczFkHQHkx9OEhm7mEhCEPe6173upPEi8R8lPTSiBsJI1vSX8AvLr0y29iUlRcG2SA/lgMkRaQj3CQdYmYBQpolaZLaERGiJTkjJlK3OCTvqqvOEUhyJEbkQWVgDw1SctWr5j9uJjhJsshOfixPTJRRgZAqLQuXj2G5dHHJhwSMRHU4yM29jRAvHxlp3k56CLF+eJWgdSic+6fnjzRKFUHil96knOdR6xRHyqa2yfOLXbUy6rMKEKv2isljOjNu/Ngd876Q8NUDsUsTEq9xgurfbUgbQm0HYXm24FocuJa2r+kqci151Xhz6RI2hjf+g20n6PHh1Ac2vkjIhArDRB47VNIr0mD5gPCoOXzweYkcER0JlxkZwhWe/IB0ilyRH8sCQ3Dp5IMcWVeQaH34iFG4D59kjvCRICJRh0qaFaRFk20sQ9gZI2gTcux7Ez97c6gDSdPLbftI92VmmVrASIA5HgmUxB1VQ/JQb6oGbaIMjv4WxjpJ5x7US57yq4i0q9PQOVDBGKVoH5AfCxP3gXR1gJnQzPU4nSZJ3TOjhjJjTu8tv7qFZaB9qSt0NKM9c55tTRO/EY120smN+uc5stitcO9xOc9xbN9cA89XR2tuxNyOb8ezqvHi9/yoDj1735FnmNEcp5zEr/7G3lgEQQd5ePF7cHlhEC2VAzUEgqKKsHEQUjOUp9aYS0unSRpDCgg++uMA4XrhSMOkZ9Kb9CEwkrPl1SRRZXghUyfkwkSN5K0u6whaOgSYXb8cObrPxEe20pMC5Q/qw66XdE2KJ8UmvWF/VA0gj9yzdDoTk4mk3Fyv9RIv9+felFuh3YwSSO86MHU1kRLIi2RMlcAqBUGLn3qkPM79e0buwb2ov/bwXHzIiRfwy4Mqhx37qDpJ/IQ5ei7aSqfkWRpZ1XiJC+P5bsL4bGDOX13gWRAqvFd09uZjvIPiyDd5+4Y8O+8FIcq76v3yrSVPcSHnNazxXyxGB10fFFfDkKXhMP2rXemQYn2Y69LF+cCpP0jCo2pAPnPSVVxF4iecH2mRrknTkQaD5JGwes7lHmqeEH8NS9yKMU1N54PQTkgxSJwaL/6NMKaDnFPDIHnSMb96ak8Ocm8cfz3napwgcRNW4wY1TFzqFZN1bLkt6KkjqYqkG8N3CzyX+gxgbGuSLum4SrzgXTfCs6DLhDaizqiJi/CiQ7by0oS2bzYSNOc5zVkBOZ97Xrsd207Q48sCeYk4fsN2vbWPj7Qa87Oahr+GSVvPSWz53VWQMmrauIoa5pg0nCFfXsIqnbs2fgwhrZxXJKzGS/qgxglyD+ImHSBN6gFtVdM41nyTvmIsgzQtjrAa17mhrolCI4hIrUHSjEiZueaoTvUc5u4/4M81R+oY8xDej6iIxKlpaplQ/bsJ2qG2KyTMt0ZSpn4y35I2TNsZUVFrGc3al7xuogXiSSuOURX1IkL2PAgx7L8JSeP3VvNo/BeLkaDBwx0fnOESCwr6W3bCdJgkQz1x4kqXD5I/zjk4sq+lJ/YBk/RiiD7Grajp566T6g3Z6WgjPcK6vBKurqkvjOXPpYeN4vHH0ROT6ql/Yl0SJM6cP/UfUctNPEfDW/dPn0y68iEmjvurSLoxr/hh7nqOwuMfHUmPKofURuVS27ZiDJuLsxuhvbSvUYdvDfGa//DtBXkuSJaKkbBDnYSg89wIKNJTXflezd/oOPM8fLO+XeRtEjcmndDPYh6LmSSMy4cIzpGNXhcJ6JERrEUkhrHjpENeoriAX1xmdojLx8yGeow7ptkIXjqTIPSeXkr5B8lzjihqPYP4Hes9JKy6Me0YX5kkIDpAE486MUjaGr+6mm/C5pBrHJ2zcuio67DVUX7xB0kXjOep34jEqy4Qn1SHNMwVkJ4TXuM1/gvtUtvH0Xvim7Kkn/UO1YWwPA9xzBcgWN+fOFQYsXoS15yE78HEoMlaBB37cPBuGnGaI7BwDEmT2CFxGntjEQTtJciLAHlYjnrdrO4y0WT45OhBI4W8aMknaStyzcfrJWSRgFwz+ZQ08dewYAzzstGpkSCySKPGcawEneO6OoLwuXzq+Ziev4bxI07qhqpygZr36FwLangwF+aDZS1RLTuC+Mc0kLDx2kZh8Qf8SMEIAVlYmYksgqSraRr/gTYZ3yOjQaoqJqnmL/JO570QV4fPpFWHbBLaIi6WU655DvwslghCVCCk6CqFg4lpoxyrRE146wign9M8FqHi8HDiYHx5Rn89H1+i8fro94LQm+rlEbawpIekH9PVsHqtYqx3UNNCzmv4eD5iDK/nc2nW5QO5tq90oz8u2Nd5UMPjr/FG/7rzMdyohWrFPt/50OdQ84DxfDdh7r6p+1jykJ7NJej4xvbybhupZMToyEaeaSPVCIGJ8MSPwK20jIlnhbwIEDoCtvds/hM+V7fdjkXpoBuNxoHHSIbmT5Czvc6RL4KGMR7CZW5JyCEt+3ONka2JaEcT+UaNzOuoOEjbc6RLqqbLtp6BFF2FrMbeaIJuNHYZKiEiUJIxcjbZnQ2sKnJu0RT1BRJm4WHFJr2/9NQWiFtc0jOzS6PUQHjyUbYJZpORJnbFc62qBBv/QRN0o7GLEKKsjkUGU1GT8c4Biea6uR5qCRI0lYQwcw9W9dI1M2HNPuKk8fxBn9qp5hPk3CIWliB1MVVjbzRBNxq7CJUsSazmYZAknTDb+VyPNGui2UQ4k00LvSzvN4HIbNWCFb+So49G4OKx8rA3i0UsSLxa9wQpIz9Apouei9dogm40dh1CkMiX/tiGV3TG9MoQqRdYA1FhIHCrcZEx6x2SMlM5UjdiRtDI2RJw2yog6EwgriNeemjSNlUHi6hWcfwvmqAbjV2EEKAj0zg7DNov3a6BrJsqxCEpI17OoiQqDuSM3JndIXDSL1NLVhwIHKFzTO5MCIbwHbnAdRt1kcQtbkHQjb3RBN1o7DIgS456gxWF7XJN6mX720Ac5Gvyz6QeZxIxC1iQdOyl6Z9dtwAs8cUNITvKL3BuwtH2uXZDROhN0P+LJuhGYxch5AwWgVnV5zdqjiTjXB/dSLAwXk+ceh4Iq3BOArfa0Da6djiMeV/jv2iCbjR2EUKUjvS+Jv6OOOKIafk2lYfwObcvgl7nRtQwVh503/79yZKDFN7YG03QjcYuBKK0PS7dsz/h+0Va/vEZEh1JNuc1vBJ3Da9Yd1159tihA7dXexP0/6IJutHYZQhRkqBZYiBoi1DolIVXawrHqCqSLhj9VaURJM4YlzOxyDIEQVt9eEUSdOpQ6wXO6/1WzI0iYDNhSRu3WTRBNxq7CJUgWGDYBZCKA0HXHRlhM2SSOOviCV9HTuykLXSJisOE47p8Lg/GcqGG1Wv8mays10c/Vwk7YfHnOBe2juhhzLMJutHYRQhBcLYHtbOjfdbpoOvvx0YSid+ud+yb/XLOohUrCFltAGJjGWI/D9cvvvjiaRk3yVx+kPw59tOnnnrq9Bs7i1YOpARdy8152gHiH+Osc7kejNeCdWH1GCQul/o0QTcauwwhAGRqm1YqBgtLkG8liPjjwMSeFYdUEmyY/QSD/bTrrDCQte2AhdMrs5+ma64mdMkPudvf/bjjjpt20zvQVhzKDPGlDvzqZkFNleDn7j+uYl/Xkk9Fwus1xznXBN1o7CLkwwe2yuyPjz766MmaA2FCriduzoGUa/WhvZ79zd4qRCQsPCRsz3V/i7cRkgUoFquMBA027LdC0Z/ubbZ0IAh6rD9/JUeOrbdOJCoeYeo7pst50oOwmlfOOXm4J04Z8jea0Bkoz4ilLnFP+oom6EZjFyFkAhaSINBsekQ1EYRoKmEkzE9h6Yw5JE1NQl0SuG4ZNxWHNHN5AFI+8cQTp6XhSD3hW4lafq2HskLCSJI/hJrORhwuYQknaVd9vetJLy8dkrYVDyEzX2Qx41+MFgPpCLW1rVtdq5BH6qnsJuhGY5chxINM/D2FBEuS9fuyEJrr8YcwAnt2IGULXag5pLXEWxpAPMiZlUiQ/CqoNfxj1D8KxwnKrUK9h7EOzqlk6NIRJfLUaXB+AkEFZFtV7SKOzkyYNvP3npCyPE24GhHoaJCvUYaFP4g5v59DzCZGLZ9H1n42UaX2sc25JuhGYxehfvwIgaRnNzn/+7QvR1DjcQkjRZokZDdNcqRrPuGEE6aj6/Kk1/bTWR1A0o0O/KpMubYxreFbiZonfyVpEi4CNaFJ5UCXzk/PbvMn9fenGMTsnJNGmDZAzvIDRIukka+jEQXpmSmh0YTOTGdAvYHkhWv7EHzqBrWOTdCNxi5CPvyKc845ZyJKUjHSrajx+RENEjv//PMncrF5ks3+7UhHQhTmt1lVvTHmgYCQE7WKzf3rNqcHGiFBQJgsSUjEyLQSbyDMpk6pH0d6JiknXsK1nXyqzj2Tqjo2cVxDzsoUP2njIH55NEE3GrsIlQgCKgtESZKmlhivB8IRliG7NMiO5Mha4/jjj1+dddZZkyTq57OITvxKiAEpFMnZalRaw/51ZW4F5D2XP4KmanBEhiHjStDq6V5yH2mDMYwf4ep4kG+2WUXQ2is6bGoN6o8QdNKnfjkCsm+CbjR2ESoZBM5JvaeccsrqggsumMimEkYlWcN9uuNK5IbwNv1n0UFypo/OznhjWcB6gbRus/+LLrpoD7kdCCh/7l5qOPBfeumlE3nWOMiYTrnGrVI15OgeqDbo4KlOnDvSXyNn0rO0dNU6gZonOE84RxXSBN1o7EKEDAISsV9fnXTSSROZzEEaZHzeeedN5BMioXc988wzV4cffviktqACQS6uQQhPeaRnqpBjjjlmdfbZZ09pIXG3GqnjmL86pV6OrtM5GxFU8ow6o5I2XTWC1gZJm2vSIuK0T4iZX5j8ucTlah6Qc+qkJuhGYxcCAcSBYb4N9+mSkXB2tqtALK6RoHPNUbjN/I888sjVscceO5F9CCpkE78hvlWDpPWsMgyS51ZDuRykLhw7cFYaOoxYcVBdIGSTnDoZBI2Ma3oETarOvUkrD/GqFQfpGckK5+Qdl3PqHeqQCnlCE3SjsQsRgooL0SAL5HnaaadN5EmfCqRAE1sWtfjRq/8TGsonPSAlpOsfg1QFUPPmqEWoPyxicYyUXd1WQ57qUAk25bg/HYb7pjtHsoiZGoJZnE4rBJ00jiHoSNqIXj7Sie+6NkCwVmdqN/m5njgcP8sQ9Uj+Fa3iaDR2IZBBHIRESb0mzexwh0CjZ0YgrDX8dYUKg77aYhQEFTAtu/DCC6cl4Mg8eTsmf5K1DuDcc8/dMzEXJP5WI2XDujLUQyeEUN1zVDziI9EQdFxUHOIlz1yLP9AWlr5T7QSu1w6Dv54H2r0JutHYZVhHCPz0sEjKUB25iCeMOVpdiEFijBojJIOwLM4IwUGuAwnV0D8WDtG/QuIcCNQ6BGMYaVWnQV9sdKBe6kcS1rGIm7pW0obkVfMD8bUhK47onefiBcKlSRzlN0E3GrsII0HEn3AOMSCUELBzEiBHZ8yNOubkITxhjlyuIXp5JCxwTRkHGqknjPWjgiAZGwlQdyBs9eWnY651RtD0xwlzrHnnnKtmdpDwEQnTDvHLpwm60dhlqAQx+qsL6vl4vZ4nrBIU57yS2EbXDgRSRkXK1qEw+/MDWxI+CRohk/RJ1Dojqg/WJqRpkjPCDUHXewn4ES2Cp99mSsi/Lu7ceVwTdKOxyzASQkUlhxE1vF5PeL1Wz0cCrte5SnRbjeTP5TxH5ExCRsbUNlQ7wmKvTBUTtY3rpOxM7kXPHhcoRzqTg/T0l1xyyZR/Rhxjmpq2hsU1QTcauwiVEDaLpJkj2nVwbV/XA/4x761C6pG8Q9RAjYNoLa4hIZOWxSP9xpYZkDhSJklnYjD5jZA/9UjUIPT20tVyYUzvvMZJGU3QjUbjoAbiC/mFGB0RMqmZmVzIeGlogm40Ggc9IpGGoIGkTIoepdsloQm60Wgc9BjJGZwvmZxXq9Xq/wEjtQIr3CFknAAAAABJRU5ErkJggg=="
- },
- "task11%E9%9A%8F%E6%9C%BA%E6%8A%BD%E6%A0%B7-%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83-%E7%8B%97%E7%9A%84%E6%95%B0%E9%87%8F.png": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAsEAAAF5CAYAAAB+wPfxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAGB3SURBVHhe7Z0HmJRllrY3/htm07W7s3nChgmOo6OOedQxATKKiSAgIiAISBpylJxzZoiD5JyRnHPOOUrOUZKg5/c+VjHdPQ3ddDkW71fPfV3n6u6v0lfddHPXqec97x+ZEEIIIYQQKYYkWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIYQQQgiRckiChRBCCCFEyiEJFkIIIYQQKYckWAghhBBCpBySYCGEEEIIkXJIgoUQQgghRMohCRZCCCGEECmHJFgIIYQQQqQckmAhhBBCCJFySIKFEEIIIUTKIQkWQgghhBAphyRYCCGEEEKkHJJgIcQt+fTTT+38+fN25cqV2JFwuHjxoi1atMj27NnjzyNKXL9+3U6ePGknTpywy5cvx44KIYS4EyTBQohbgkSOGzfONm3aFDvyFTdu3LCrV6/aZ5995kJ2q/r888/tiy++iN3q90Guz507Z6dPn75tXbhwwR8ru/CYe/futZIlS1qbNm1s/fr1fnvO507hNtm5HTKKlB49evTm9TmP48eP24oVK/x7eOnSJT+eKHw/pkyZYv369fOf0dmzZ2OXCCGEyC6SYCHELXn//fft5z//uXXt2jV25CsQU6Ru27ZttmvXLtu9e3emhRAiy7eC68ybN88mTpx421q2bJl3PrMLj7lw4UL71re+Zf/93/9tPXv2tE8++cQOHDhgR44c8fPKTnFdbsNj307mYefOnTZ27Fj76KOPvAuNCPNi4eOPP7aXX37ZSpcu7d+rrO4nO3BO77zzjv3rv/6r/4zWrl0bu0QIIUR2kQQLIW7JBx98YE888YT16tUrduQrhg8fbv/7v/9r//7v/27/8R//ccsqXry4rVu3Lnar3+c3v/mN/fKXv7Rvf/vbt613333Xli5dGrtV1iCJXbp0sT/90z+1WrVqWe/eva18+fJ+Tv/5n/95R8VtKleunGXsYMiQIfbCCy/YI4884p3neNcXyUeCeR7Tpk1LOJqBWG/YsMG+//3ve/HcbvdCQwghROZIgoUQDp1LOpXEHyZPnmxTp061fPny2b333muVKlWySZMm+WV0f5cvX25t27a1Vq1a2VNPPeWy+OKLL1qHDh28ypQpYz/4wQ/szTfftC1btsQe4ffp1q2bPfDAA3b//fe7rLZo0eJmNWzY0Ludf/RHf2RFixa1JUuWxG6VNfPnz/fH5rwQz40bN/q5t27d2jp37mzdu3e3Hj16ZFpVq1b17jcd5Lp16/rzpBt9uzgGXWNE+Z577rESJUp4pxxZhYMHD/r9/vVf/7XHM+hqZwW3j3ejiVjQiT516pTX5s2b/Tlwf6+//rr/XNJeHi+OUcQx4l1txSaEEOJ3SIKFEA6SN378ePvVr35lb7zxhhUoUMD+7//+zzuYDz30kL366quWN29e7wIjdvv27fPc7WuvvebSiLQePnzYDh06ZAMHDvQO8ltvveUxhFtBTIH7Rrbp9HJ/8SJu0b9/f/vjP/5j7wQj3tmBjDEd5h/+8If23HPP2datW70re+zYMT8XhBAxjMtlxkIqef4PP/ywLViwwLvKXPd2MYahQ4fa008/7UUkIm2GmC4tcQXO5ac//ak1b97cF+vdjpEjR9qHH35ov/71r61atWpWvXr1m/Xee+/ZL37xC/uTP/kT/77TbU97ecbi9txP/fr1XeaFEEJ8hSRYCOEgwUgSUluwYEErVKiQi+S//Mu/+Fv8dFYR4VGjRrloXrt2zQWRTjBv9yNucbgOx+nk0pW8FcQskODChQu7WKeFxV90pJFgOqgsLssOXA9R/Md//EcXxKyEMyOIL+fz+OOPe9f1dvA92L9/v3+vfvKTn1iVKlVcpDMK85kzZ+y3v/2tSzAyjKRndr04ZLA5h1y5clnu3LktT548XnTN/+mf/sn+6q/+yiWd+EX8sqyqSJEiNmDAgNgjCCGEkAQLIW6ClKUVM6QOaaMjG7+MotNJR5U8KrEB4hLkVIHLEb7HHnvMZfR2WVpkkG4mwkcHOS1pJbhUqVLZkmBEnvgC8o4sppVgJlEgnnSE0xZdYeIHTLOA7Eowz5PvAY9HNpcOOp30zOC6PD6L44hoPPPMM94xji+gywgvMnjxgDwzoo7r8ZGfA7fl+U2fPv1mXIIXI8QduB6Z48yKn8PtIh1CCJFqSIKFEA6ChKhR5FkRt7gEM4qLy4kVUAgaUw/+53/+x7O/gwYN8rf9uQ235a38++67z+WYY7ciLsF0KYlSpCUnEsx1iDLQKf2v//qvdBLMfSHmHE9bRD5eeukl2759u18vuxKMcM6ePdu++93vuth26tTJpfVW8H0gm0y045//+Z/9+8OLCCQ8I4hx2uK2PA9eVLAgEZnm+8P3mm46cRIiD/Gfwe1KCCHEV0iChRAOmVxyva+88orHHigkF2HjbXhEi9gDEodcMtXhH/7hHzzjumPHDl8Ax0xeFmvRqSQfi+TdDhaMEYdAgulkpuVOJBgZ5PoVK1b0LDKxA+ICaSV4zJgxLp5PPvmkNW3a1B8byed6yHFceLMjwcQgEGCe61/8xV949pbcb2Zd3bTQjWVaBGPNGG/GeSKvc+fO9fPPDMQVueX7/LOf/cyjDdxH/LFYiMhz4nukKRFCCJF9JMFCCIexXixUY8oBExJYUIX40uml+8gxpBFRpsOLJPM1MQi6xyxAIxqApCHK3FdWmVqyrwj222+//Xsd0TuRYKSURW90rRHqcuXKuaRzHnEJZjoEsstjrV692qMRxBd4juSX41MsspJgHgtpZQIG49OQeKZkcK7MJs6q6KDzfaL7zO3pRPN45Kgzk1iiEVyG3DNFo06dOv6cOH8KOeZcixUr5t30+PG0xf1mJehCCJFqSIKFEE48M4tIkZFlnBYxBxbKMRWCr7mcKMSaNWs898tCK0aQzZkzx4WS2bx0Y/nI10jk7bqT7du39+4sC+gyRgnuVILJxdJVZV4v2dmMEsz5MFWB+2L6BCCzLPjjukg8ZCXBTMXgBQEvDujMIqWcP/KNiPJ5VsX3qFGjRv6R+6AaN27s2d208D2fOXOmPf/88/Z3f/d3fj1egNBhjxeL8jgXOu90t9NeFi828lCXWAgh0iMJFkLchK4ju7ghwkjT6NGjLX/+/N4thXiulLf1EUg2yyATy+I4usXxYqEYOVk6shljDmlp0qSJ/fjHP3YxRcLTcicSHIfz536YcpGZBNPxzSjBPL87kWCknxcGdGabNWvm85T5nCkaTKRgfi+zjf/+7//ejxF7iBfRkr/8y7/0ecLMQkZ66YZTGZ8f32MEmMgF98nGH//v//0/v9+09/m3f/u3fpwcdNrH47H+5m/+xr9/gwcP9hc2QgghfockWAhxE7Km8c7iokWLXJ7iEszb6YgxXVfkbdasWfZnf/ZnnqllHjDxgHiRK0aO6YzeToLp3JIfpiOacdFWTiQ4vojsVhKcWSf4TiUYOV21apVnqOPTG+gO8zhEHcghI6wsWCNiQYc6XjwHOs8PPvigLwpkIgW3p9J2ajlOhpkMNkJLdOI73/mOnydd9rT3SQeZc2VDEV7AxI/z82MDkj//8z/32c7aKEMIIdIjCRZC3ASJI1dLR5HcLLN/Gf31b//2b979RIbZrYz8MAKJoLIdMbLK5IN49enT52ZOlRFet4J5xHRFyRlnJCcSHCczCSYTTMc2owTfaRwCeBHAdAiEG/FmYR4fEWNeENCZZeEcLxjSghTzIoPzIOfL7dLC13Sz+R4zA/hHP/qRd4I5J7rY5K2Je6SF63L+LLZL+3gIMd1mzoWOPqIthBDid0iChRA3QR6RLaYWIIV0I5FgYg/IIiKMdCG6iBmCSieS6RBpoUvMNsp0RTN7G55xa0QukMFHH33UF9Fl5OuWYObysrCMkWws+mNCBJtwkLO9k4Vxt4PZvdwXXVu6xRm722z9zAsJXmggyRkXq/E1z5ucMefPIr4pU6b494tcdk4lOD6TWAghxO+QBAshbkLnl2kNCCBSSAeRTiQxAuSQBXCIIQvkeLs9OxKc2excjiHYjGBjygSil5GsJJj4QMZOapzMJJjHo7NKV5sd8FhIRiyB6Add123btvn1cirBZJHZLppMNLIa7yynhU473xeE9lYj1TjG+Xfr1s3zx/HrSIKFEOLrRRIshHDoWjLtga4vskinkq/ZfCK+MC4Oncl4J7hmzZoeA2DEWbyQZ3Y2YxJCxm2TeRwEjS4ni7eYsRvfqCItWUkw98Euc2zekbHjmpkEkwlmni5iPn/+fJ+YwP3TFSbSQa4XcirBnA8dXDK8bBaScRtoGDZsmHeK6aqz3XLG874dOZFgxqdJgoUQInMkwUIIh5wrGy+wkIpNMOj+IsC8dZ9Rgul60u1lCgKjuxBnIgDx+va3v+1TEFislXFhHNlU5JPbMScX0c6YnYWsJJhFddw/+eOMedfMJHjXrl02YsQIl3siGog8i9zoSiPqd7ptckZ4HswhZqHf8uXLf2/cGbBYjjgG583zuxNy587tlV0JprNdr149/3mSh5YECyFEeiTBQgiHSANdUbYSZvQXUx8QWr5m2kNaEEY2p+At+9vVjBkz0skg4hnfaQ25ZZLEypUrY5emJ60EI7OIJdA9JQZBZ5TRbHRfM87AnTBhgndc0+4Yh/AeO3bMpTcuvJmREwnmNiyIY9wbWxsziSGzqAbxBHLJXOdWUY5bwaxgohRZSfCyZcs8Y83WyjwWnWB+Dpm90BBCiFRGEiyEcBBO3qanm0nXtHXr1r5ojY4tMsW4NKZCIHjkVJEqJj/crph0wPUQPmILjGArW7asizWbZNCxvdX82vicXCSY82BXNjK1zOVlEw86rhTnmTFWQPSBRXfEMeISnBWcJ8KOQCObWUkwj0l3lV3g6FTfe++9nm9mcVzGrC9f8/y5HqLMZht3CqKLCGeU4E6dOnn0hBcUvBggt83z5gUCeWcWM7KQMeM5CSFEqiMJFkK4oNGlRIB5qx6OHj3qO7ohWGx+wYI55I3FX3Rz6TgyRm3dunVeLPTi6/gMXXK3dCDpktLVJT7BNAYWjiGMyCuPcSvo1nJ/iC7ZYRaxMTeXaRVEChjjRscW6cwIGVgWv8Vn52YHOs0sniNmQSaaGEhmi9sAuSduwOMwBo7vD9fv169fuq40MQ2ux/eBRYdsscw0inbt2sWukX3o0pO/RnLTQoSF6ArdZR6b50snv0CBAsacYB5bM4KFEOL3kQQLIXyRFt1DJJjOYhw6nUgUsQKmKrBbGZ1hNsKgU8omDkQb6DYiqCzcoluJ7H3ve9/zbDByyAI2usyIK1KLzNF5zWphGIvskDy6uuxAx/2x8IzHZ7oD3enMpk8wg5fuNTN56WpnBySS+/6TP/kTf5y0eeK00FFF8pFlzuNb3/qWfy+GDh36e7lbOrDENbg/dnTjusxGZurDncL3izhJxo4uQs3PjfNFgvme8gLidpEPIYQQkmAhxJcgV0QT+vbt653cOAgXsQQWt3GcnC+yiNjSzWVhG1sFs3UvW/tSbNXL18gykYf69et7HIKFbQghsQbuLysBBm5H15XrswsaOWSKzzmGdGb2Nj9CSscZOWcKRHbo0aOHyzvPB6FfvHhxpovJOCd2YMuVK5fHOipVquTPja5vxnNhAeFHH33kskwnnesSCaHzfqfw/crse8b3k/suUqTIzS70ra4rhBDid0iChRAuTGR46dhmtrMYcofQMfaL7iabPhBvYL4v8kwGlwkEfCRTy7FJkyb5jmzx8WcIJYvv2K3tTheF3SlIMh1sIhuZiWxmEH0gF83ziEttZufJ94rOOflkBJd5ypmNaQOO8T0jsoH8cl2k/uuE7ykRCRYYZvaCQAghROZIgoUQ4kvootL1piueFchtfLyaEEKIMJEECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAcKq9e7du1q/fv3V6lUKpUqKcVoQSbCCBEikuBA6d69u++gVbFiRZVKpVKpklJsMc5OkEKEiCQ4UH7729/aBx98EPtKCCGE+Ob5zW9+47snChEikuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLIYRINpJgETKS4ECRBAshhEg2kmARMpLgQJEECyGESDaSYBEykuBAkQQLkRiXr92ws5c+C7IuXLkeexZCJBdJsAgZSXCgSIKFSIwOM3fYU23mBlnv9Fth165/HnsmQiQPSbAIGUlwoEiChUiMBuM32fdqTwmycnVcYFclweIuQBIsQkYSHOPGjRt2+vRpGzt2rB04cMA++eQTmzlzpg0dOtSrf//+Nn78eNu0aZOdOHHCJXTgwIF+2ezZs+3y5cv2xRdf2Jo1a2zMmDFeK1eutKtXr/r979692yZMmGBDhgyxBQsW2KlTp/z4yZMnbcqUKX58xowZ/rjZQRIsRGJIgoVIHEmwCBlJ8Jd8/vnndvz4cZs4caK99NJLLqkbNmyw7t27W/Xq1b3y5MljZcuWdRFevny5vfrqq1ayZEm/rGfPnnb27FmX4w4dOvj1qlatas2bN7cjR464XI8YMcLKlCljVapUsTp16rgsc5tFixZZqVKlrGLFilarVi2bOnXqTXG+HZJgIRJDEixE4kiCRchIgr/kypUrLr6vv/66PfroozZv3rzYJV9Bl7ht27bWt29f27Jliw0fPty6du1qGzdutIsXL7q0UpMnT7b69eu7KG/evNmFF2GeNm2atW7d2jp37uzXR4InTZpk8+fPd4HmDwidYf6Y8BiZdYMRdc7zwoULdv78eb9d+fLlY5cKIe4USbAQiSMJFiEjCf4SBJYu7qpVq+y1116zhQsXxi4xu379um3dutXatWvnneJt27ZZ7dq1LXfu3N41rlChgo0ePdo+/fRTa9mypfXu3dsjE4cOHbIBAwZ4XKJFixbWqVMnF21EduTIkTZ48GA/RreYmAS3nzNnjg0aNMjmzp0be/TfcfToUY9fFC1a1LvQTzzxhL3zzjuxS4UQd4okWIjEkQSLkJEEfwld1s8++8wjEQUKFPCIQhzktGPHjjZs2DDbuXOnxxvoBCPEdHhbtWrl3V9EuUaNGh57IFOMVCO33bp188gE0QoE+tq1a54h7tOnj9+uSZMmLt+I+OrVq12CySVnhMzxrl27vHs8a9Ys7yYTrxBC5AxJsBCJIwkWISMJTsOZM2esYMGCNyU4nhUuXbq0i+elS5dcilnkxkdiEggr8jt9+nSrVq2aL4ijCxyX4Pbt23s+mD8USDQSTMe3R48eLrLNmjWz9evX+3EkmO4xkp0VygQLkRiSYCESRxIsQkYSnIaMEozorlu3zhe6MekBWMxG55ZsL1EJRBeZJQ+M0DLlAdlFhBFVcsB0e/lDEe/4Isp0holJIMnx6RJkkXv16pVpJzgjkmAhEkMSLETiSIJFyEiC05BRgg8ePOgL1RDWPXv2+DFElsgEC964HMllSgRxCOSWr+kas2iuQYMGLsV0dlnIxucsgCNCQRyC6ASj15goQeb3o48+8tuTHc4KSbAQiSEJFiJxJMEiZCTBacgowYgsC9+YF8yYMzh27JjLbL58+SxXrlyeyyUvTIeX6ATRh+LFi1ulSpXs+eef96gDOWJEmkV3DRs2tKefftqFmePkip999lnPB7PgrU2bNjcf63ZIgoVIDEmwEIkjCRYhIwlOA7ncpUuX+gYWEI8+kO9l4RxwncOHD3uEgRzwihUr/GsgHsHtWdxGB3ncuHF27tw5v218tBpxByZG7Nu3z49zW4SYqRJ0gteuXev3kxWSYCESQxIsROJIgkXISIK/ZpBk8sDkgskNs7gOEFuiEMwPpuMcF10W13E94hREIugoZwdJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOFAkwUIkhiRYiMSRBIuQkQQHiiRYiMSQBAuROJJgETKS4ECRBAuRGJJgIRJHEixCRhIcKJJgIRJDEixE4kiCRchIggNFEixEYkiChUgcSbAIGUlwoEiChUgMSbAQiSMJFiEjCQ4USbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjEkAQLkTiSYBEykuBAkQQLkRiSYCESRxIsQkYSHCiSYCESQxIsROJIgkXISIIDRRIsRGJIgoVIHEmwCBlJcKBIgoVIDEmwEIkjCRYhIwkOFEmwEIkhCRYicSTBImQkwYEiCRYiMSTBQiSOJFiEjCQ4UCTBQiSGJFiIxJEEi5CRBAeKJFiIxJAEC5E4kmARMpLgQJEEC5EYkmAhEkcSLEJGEhwokmAhEkMSLETiSIJFyEiCA0USLERiSIKFSBxJsAgZSXCgSIKFSAxJsBCJIwkWISMJDhRJsBCJIQkWInEkwSJkJMGBIgkWIjEkwUIkjiRYhIwkOMbnn39uly5dsk2bNtm5c+fsxo0bduLECVu2bJmtXbvW1q1bZ4cOHbLr16/7Zbt377YNGzbY1q1b7fjx47F7Mb8O90EdPHjQrw+nTp2yLVu2+P3s3bvXHws+/fRT27Ztmx/fuXOnnT171o9nhSRYiMSQBAuROJJgETKS4BhIKVL76quv2sKFC12ER40aZT/4wQ/sxRdftLx581qvXr38+JkzZ6xGjRr2yiuvWMmSJW3IkCEu0Qhvt27dLH/+/FagQAFr166dXxdpnjhxohUpUsTy5Mlj9erVcyHm+Pr16+3dd9+13LlzW6VKlWz27Nn2xRdfxM7q1kiChUgMSbAQiSMJFiEjCf6Sq1evese3WLFi9vjjj9u8efNs165dNnz4cBdZOrUHDhxwoaXrO2nSJBfQ6dOn29ChQ61169a2Z88emzt3rjVo0MAGDBjgn/OHAbFeunSpdezY0Zo1a+b3VbNmTb/tmjVr7KOPPrLy5cv79bjOwIED7dixY7EzuzWSYCESQxIsROJIgkXISIK/BAnet2+fd35feuklW7BggS1ZssQ7toULF3Zp7d27t23cuNFjEC1atLAePXp4rGH58uV+2fjx461NmzbWpUsXW7Fihd8fn3Oc7nCHDh1sypQpdvnyZevXr58LNh+5DUJ74cIFmzx5sksw95mR06dPuzgj0vXr17c333zTSpQoEbtUCHGnSIKFSBxJsAgZSfCXEGO4cuWKHTlyxGMMixYtstWrV1vXrl1dUtu3b2+VK1e2wYMHuxzzCz9t2jQ7efKkbd++3YW2c+fOHmegM4wA0zEeO3asRyhq1arlIoxEX7t2zWbMmGH9+/e3Ro0aWZMmTbxTzOMjz4MGDfLoREaIYXBePXv2tE6dOlnx4sWtVKlSsUuFEHeKJFiIxJEEi5CRBKeBuEPBggVdNhFiBJfOLdnd5s2be+xhzJgxLsR0i1nERmd45MiRfjmxBi4/fPiwL6ojNoFA8wcCGSZigQQTt0Bma9eubU2bNvUoBMdZgEdXGKnOCsUhhEgMSbAQiSMJFiEjCU5DWgmmM3vx4kVfpEYRXSDSwMc6derYzJkzfeID0yHI9RKRqF69ugvx/v377ejRozZixAjPFCO7RCY2b97s0YupU6d6l5n8MGJNB5jjdIS5niRYiD88kmAhEkcSLEJGEpyGtBJMlpfuLpEHJkcguEQX6AAjqmSCWQy3ePFil2OyvH369PEOL4vsuKxVq1Yee+jbt693gukMc1/du3f3r7mMPyCINZlg4hPIMYKdFZJgIRJDEixE4kiCRchIgtOQVoLpzrZs2dIqVqzoAswv+bhx4zzry2WMNSMvTN63SpUqPvKMYjEdnWIuY/EaksxxxPf999934eU43V6OT5gwwR8TsS5Tpox3jj/55JPYGd0aSbAQiSEJFiJxJMEiZCTBaaBLS7SBqQ9MY0CG6ea2bdvWF6sRc2AeMJcx+YEoA91ihJT4BEUcgtsg0Hxk3BnH58+f75EJ5JgFcWyOwXFGpnEfHKfTzII78sFZIQkWIjEkwUIkjiRYhIwkOAeQEWanN0SWbi5RhjgspNuxY4etWrXKO8tIMyC27CbHRhzkheOiy2QKrsfUCeSb22cHSbAQiSEJFiJxJMEiZCTBgSIJFiIxJMFCJI4kWISMJDhQJMFCJIYkWIjEkQSLkJEEB4okWIjECFmCf9poulUcttaqDF8XZM3dfjz2UxChIwkWISMJDhRJsBCJEbIEh159Fu6J/RRE6EiCRchEQoJZmHarBWUsPOPy+AK1qCAJFiIxJMHJK0lwdJAEi5AJXoKRWyYrbNy40ScufPbZZy6+THDgMja7YCc2dmSLEpJgIRJDEpy8kgRHB0mwCJlIdIIrVapk+fLls5o1a1rHjh1t8uTJdvDgQdu9e7cNHjzYypUr57N9o4QkWIjEkAQnryTB0UESLEImWAm+ceOGRyDo+FatWtVq167t2w2zNfGgQYOsfv36vkMbO7hxnI0pooQkWIjEkAQnryTB0UESLEImWAk+cuSIjRkzxqto0aK+29qCBQtcgNmRrWTJkvbaa69ZjRo1fBMKIhJRQhIsRGJIgpNXkuDoIAkWIROsBG/dutUFt2zZspYnTx4rXry41a1b10qVKmXVq1d3Ge7bt69vbTx8+HDf4S1KSIKFSAxJcPJKEhwdJMEiZIKV4EuXLnnmd+fOndajRw+X39dff93KlClj27Zts4sXL3oueOjQoVaoUCE7fvy4RyeigiRYiMSQBCevJMHRQRIsQiZYCT58+LAvemvYsKHngUuXLm21atWy+fPnW968eT0PXKVKFWvcuLGtWrVK0yGEEOmQBCevJMHRQRIsQiZYCd6yZYv/4hUpUsReffVVnw5RrVo1mz59uscjWBBHVKJ8+fLeBWYhXZSQBAuRGJLg5JUkODpIgkXIBCvBLHbr0KGDVa5c2X7xi1+4+JIJJgf87LPP+nE6xHSKZ82apekQQoh0SIKTV5Lg6CAJFiETrAQz93fevHnWq1cv7wTTEW7Xrp317NnT7r//fp8Mwefjxo1zOT5z5kzsltFAEixEYkiCk1eS4OggCRYhE6wEsyiuffv21q9fP2vTpo13fdu2betj0hiZxi8m19m0aZNnhZFmLYwTQsSRBCevJMHRQRIsQiZYCWaLZLZEPnXqlC+SIx6xf/9+O3r0qC1fvtyPcR021GBKhOYECyHSIglOXkmCo4MkWIRMsBIMdHYRXQSX+uyzz/xrxqPx9fnz512OGZnGZVFCEixEYkiCk1eS4OggCRYhE7QEs9iNbZJHjx7tMYgDBw7ELvlKkFesWOGyuGjRIo1IE0KkQxKcvJIERwdJsAiZoCWYnC8bYbBbHHlgZDfOoUOHfGFczZo1bcOGDd4hjhKSYCESQxKcvJIERwdJsAiZoCWYPHCBAgVs5syZvgiO2AMxCLq+Xbt29akQ48ePj107WkiChUgMSXDyShIcHSTBImSCl+CCBQva3LlzPQ7RsWNHnxhRoUIF69Kliy1btsxzwVFEEixEYkiCk1eS4OggCRYhE6QEHzt2zBYvXuwbY7zwwgveCUZ4e/ToYc2aNfMZwYxFIx4RpbFoaZEEC5EYkuDklSQ4OkiCRcgEKcFsgzxnzhwX3ty5c3v3d+rUqd4R5jhyTFcYUVy5cmXsVtFCEixEYkiCk1eS4OggCRYhE6QE37hxw+cBT5s2zRo3bmxVq1a1Pn362NatW30UGt3f9evXuxy3aNHCpZnbRAlJsBCJIQlOXkmCo4MkWIRM0JlgYCHczp07fXvkESNG+CYZjE5DemfNmuWSPHDgQPv0009jt7g1yDMS/fnnn/vXfGSqBJX2ONeLH6c4h3jsgsdNezwOt43PMU57/fhjcjztY2SFJFiIxJAEJ68kwdFBEixCJmgJRmwHDBhg9erVs7Fjx9ratWutZcuWVrFiRRfgPXv2+LbJ5IWzmhOMhO7bt88qV65sa9as8Q035s+fbyVKlLCSJUt6xpioBfeDdDOa7a233vLLW7dubWfPnnWBHT58uD8+9dFHH/n9AAv3qlevbu+++64v2mMTD9i1a5efP8ebN2/us42zgyRYiMSQBCevJMHRQRIsQiZYCT5y5IgNGzbM4w50gdky+dy5c75lMh1hxLRTp042Y8YMnyd8uw4rHVhkuUGDBvbMM8+4/DJbmA4yRd4YgeWXffv27b4Qj68R0enTp3vuGCHnNk2bNrU2bdq4ANepU8d27Nhhmzdv9tvy9YQJE1yoeYx4B/v999/3DT94Lpz7mTNnYmd2ayTBQiSGJDh5JQmODpJgETLBSjATIiZPnuwSSuY3DrLL6DTkks0yyA1nBfEJRBVxfu6557xri6AuXLjQTpw44REHBJkNOZYuXeqdXH7pu3fv7oJMFvny5cveleY+5s2b5x1eOrucHyLdrl07l/ZLly65nCO9o0aN8gV8HTp0cIEfOXKk3wcynRE6yuSc6XjHu83vvfde7FIhxJ0iCU5eSYKjgyRYhEzQcQjytEgvgohEMhOYzxFNpPTgwYMeicgKOsF0crl+/vz50+08x/3TmWXnOTbgIHJBt7dUqVIeYShTpowfR8Tr16/vHWA27mDhHpLLpAo27UCcuS1xCsSZTi7TLZo0aeJdYUQcwR40aJBfnhHuH3FmBjLxjBdffNF3yhNC5AxJcPJKEhwdJMEiZIKXYISXHC0RBTq3RBM2btzonVikFoFFcuML0W4H12XzjbQSjEyz6xxRBj4SrWBGMd1mcsRIa/ny5T13XKVKFe/UEtU4efKkyyxdXnLGvXr1ciHnNnSa+ZpYBBJMFIPj69atc4kmEpEVikMIkRiS4OSVJDg6SIJFyAQtwcQUPvnkE++0MiaNeELnzp19NBoL5DhO55Rf0OzkbDNKMN1Zog5FihTxri5ii1CzCC4+4eHjjz+2Dz/80OW3Ro0a3q1FvuncjhkzxiMUHOcPBXliZJeccrdu3fz8OE8W4tEhRubpHBN3yApJsBCJIQlOXkmCo4MkWIRMsBKMgCKORA+YrkAkgY7q6tWrbfDgwS6adIbJBRMdIOOLwN6OtBLMdcng0gFGWLk90s3jkeNFdOkS0wlGRrkNO9YhscQeWKiHkPMHgigEnV8mVnCb/v37+3kh7dw3nV9iHFOmTLmZM84KSbAQiSEJTl5JgqODJFiETLASTKd14sSJLp0sEkMkDxw44B3b3r17eweXritiTCc2HkW4HWklmBFmyOtDDz1krVq1sqFDh/rkCaIQiDGX9evXz7vAzCImAkEkgrwwl3F9csMsjOM2CHLDhg09tsE0COSZ4yyGQ2ZZwEemmPjEli1bYmd0ayTBQiSGJDh5JQmODpJgETLBSjDRAmSUhWlFixZ18WQiRLly5VwkkV/iDEQX6MzSab3dmDS4cOGCiygd4FWrVrncvvrqqy6tCCe70nFfdJjjj4v0Is3xfDJTILgu8QxmCNMRZtEdsss0B7rWhQsX9gkSHCcC8fbbb3s0gusjt5x3VkiChUgMSXDyShIcHSTBImSCzgTHd4tDPJmU0KhRI58QQZSBy+JFjOGbArFFlGfPnu3d6vhjI7ZEKZgTjBjHRZdz5XqMe2NMG7KeHSTBQiSGJDh5JQmODpJgETJBS3A8F0xGl93b6KjSySWiEC+6ueRu6fJ+E9BtJveLzMYXzwEfiWMg6XxMe5zrcRwxzqpbHUcSLERiSIKTV5Lg6CAJFiETrAQTPYhHDdjIonbt2j4V4o033vA8Lh1XjjO+jOhBdiIGISEJFiIxJMHJK0lwdJAEi5AJVoLZMW7SpEkuu2xawVQFJkK88sorPiOYeb5MYCCbS5c1ux3WUJAEC5EYkuDklSQ4OkiCRcgEK8FMY2AbYjabeO2113y7Yhafvfzyy7ZkyRKfsMCMXjrBO3bsyHI8WmhIgoVIDElw8koSHB0kwSJkgs4Ex2FDjCeeeMKee+45H2mWO3due+mll+ypp56yRx991De7YKOLKCEJFiIxJMHJK0lwdJAEi5CJhAQfOnTIIxBMX2BaBDOBKY7xNbvKsfgsSkiChUgMSXDyShIcHSTBImSClWCk9ty5cz6FgcVxFJ8zBYLoA1MXNm7c6LOD2UUuq40yQkMSLERiSIKTV5Lg6CAJFiETrATv27fPd2EbP368L5CL18cff2yHDx926V2zZo1vnMHYNDbNiBKSYCESQxKcvJIERwdJsAiZYCV47ty5dt999/lOa+zCxke2JW7Tpo3v4Ma2yUhw586d7bHHHrOjR4/GbhkNJMFCJIYkOHklCY4OkmARMsFK8LJly6xQoUK+4I2d1tatW+cdYDq+I0aMsCpVqviCOKZFPP300z5SLUpIgoVIDElw8koSHB0kwSJkgpXg5cuX+y5xSDDSy6g0OsE1a9a0/PnzW8mSJX1OMLKMJGtEmhAiLZLg5JUkODpIgkXIBCvBRB5eeOEFzwAPHDjQs7/MBSYOgSAOGDDAOnXqZIMGDfIFdNosQwiRFklw8koSHB0kwSJkgpVg4g9lypTxX8DBgwf7VskUG2YwHo1M8JgxYzwTzIQItlmOEpJgIRJDEpy8kgRHB0mwCJlgJfjEiRM2ZcoU69ixo0vu6NGjves7b948302OCAS7xs2cOdMqV67s2yhHCUmwEIkhCU5eSYKjgyRYhEywEswcYPLA5H+JRgwZMsQzwTdu3PD68MMPrXfv3rZ3716PTDBHmNtEBUmwEIkhCU5eSYKjgyRYhEywEgzHjx+3hx9+2AoWLGh58uTxLZLp+laqVMmeffZZnxCxdOlSO3/+vDLBQoh0SIKTV5Lg6CAJFiETdCeYsWe5cuXy3G+NGjV8WgTxB6pfv37WoEED31AjikiChUgMSXDyShIcHSTBImSClmBmArdv3962b99u8+fPt2HDhsUuNTt16pSNGjXKIxFRRBIsRGJIgpNXkuDoIAkWIRO0BDP799ChQ3b58mW7ePGinTlzJnapefyBrZU3btwYOxItJMFCJIYkOHklCY4OkmARMkFnggEZppDetJ9nrKghCRYiMSTByStJcHSQBIuQCVaCr1696p1eZJBfQnaHY9MMxqZVrFjRSpcubcWKFbPChQtb1apV03WJo4AkWIjEkAQnryTB0UESLEImWAm+du2aHT582GcEs0EGI9Hq1q1ru3btshkzZtjUqVOtTp069s4779isWbPsypUrsVtGA0mwEIkhCU5eSYKjgyRYhEywEkzEgdm/7A63e/dua9eunVWrVi126Vd89NFHLsJRRBIsRGJIgpNXkuDoIAkWIROsBNPZZVFcvBiTRgwi7bEuXbr46LQoIgkWIjEkwckrSXB0kASLkAlWgnfs2OE7xDVp0sTrjTfesKefftqaNm3qxbE333zTSpUqFbtFtJAEC5EYkuDklSQ4OkiCRcgEK8FHjx61CRMm2OTJk30xHIvf2DmOz+NFPKJChQqxW0QLSbAQiSEJTl5JgqODJFiETNBxCBbGHTlyxIvoA9slx7+munbtmu04xPXr130Huu7du9vOnTt91NrevXv9flu3bu3CvX//fj/OTOIBAwZY27ZtbciQIbZ582a/jxs3brh8d+jQwf8wLF++3KdYkF9esWKFderUyTf3mD17tm/mwX0x4SLjY2QHSbAQiSEJTl5JgqODJFiETLASjHCeO3fOtm3bZps2bbIWLVp4Nzgt2V0Yx3198skn1r9/f3vxxRdtwYIF3mkeP368j1rjvhs3bmzTp0+306dP2+LFi124mUjRrFkzF1I27OA8mjdvbjVr1rSWLVv67U6cOOEL99i5jsxymzZt/HYbNmxwic/4GNOmTXMhzwpJsBCJIQlOXkmCo4MkWIRM0J1gJkMwGxjBrFy5snd9T5486Z1c5JiObHYkmPuia1umTBl78sknfQtmRBgx7dOnj3d+mT7Rr18/W7lypeeN6eoit2PHjrVGjRp5R5cuL9dbunSprVu3zvPIW7dudRmn04vwXrhwweUVof74449dmjn/8+fP+/n27ds305nGjISjU83z2rJli0t22bJlY5cKIe4USXDyShIcHSTBImSClWCkkAkQxA+IETAvePTo0S6c+fLls+eee86effZZq1WrVuwWt4bIAhJKFCF//vy2aNEiGzFihEs1C/DYnhnZHTRokMcgihQpYkuWLHGh5WOvXr18LnHRokVt1KhRdvz4cRd0pJjOLh3qjh07ereZjjEbe4wZM8bFuHr16rZ9+3Z/DJ4D579+/frYmf2OgwcPWrdu3ez555+3Rx55xH7yk5/Y22+/HbtUiOTwOTs0Blr1JcFJK0lwdJAEi5AJVoLJ0yKORCLOnj3rRQeVrC0dWrrBCCyinBXcF5EIusgFChRwCSbriwRzf2R6kVm6zsgsUyfoyCLiq1ev9g7x4MGD7fXXX3cZZn4xwoscs5EHHWayxpwrXWdkmvuvV6+eL97jMXh8usM8xsKFC2Nn9jt4rkQr4l1uBFqdYJFMdh67aC93XRRsPdh0ZqaCpvrDlyQ4OkiCRcgEK8F/CJBoJkwgwcOGDbPatWvflGA6zkQViDu89dZb3r1FgolHILt0iBFoZBkJpqtM5xY5Rla5DhJMJ5g8L4UE06mOSzACzWPMnTs3dka3RplgkWw2HDybqeCoVFmVJDg6SIJFyERCgumc0nElisBHiiwuMnonpJVgRq+R/WWxG11YOrc9evRwSWWBG4+J1M6bN8+nRBDF4DgxByZT0LElK8zxBg0auATTob506ZJfn44vcQkeY+PGjS7UQ4cO9cdYtmxZ7IxujSRYJBtJsCqnJQmODpJgETKRkGAmNbzwwgveoSXT+/DDD3vkgPjAnZBWgletWuWdXH7B6fqyAQejzJBeog18zmI6OsAsvuP6CDJj2Yg1zJw500qUKOEL7IYPH+73xUeiDO+//75njukucxxB5jiTJtj5jjxxVkiCRbKRBKtyWpLg6CAJFiETCQlm5BgLyoARZoULF/YFa3dKWgmmy0tX98EHH/Q4Q548ebxLS3eZ8WYsumOBHPlgJJxuMYvXyP++/PLLVrx4ccuVK5dnklkox2g0drRDXJ966imbNWuW55hZDPfAAw+4GPMYCDbxi6yQBItkIwlW5bQkwdFBEixCJhISzPbJcQlGZJFgxpTdKeRy2SCDkWh8jrzOmTPH75uPCC2CiggTWSB2QTc3vrkGIkx8gmkVRDMYk8bkCeb+cr/khbkvzo3zjD8GGWA612yikZ2FfCAJFslGEqzKaUmCo4MkWIRMsBLMzNyJEye6hDKajFFjLCxDTOnSMnOXr7l8xowZPpXhTkFSEWJmANMZ5mtAeFnghrASuUi7uQXSi9iyEQZSzHWBzxFf7ovbxru98cdgIV3ax8gKSbBINpJgVU5LEhwdJMEiZIKVYHKziC4Z3Lx583r8gLgCi87IBCPF8ewuc3mZ6RslJMEi2UiCVTktSXB0kASLkAlWgum20ullAVqxYsV8cRqRBaIIbJSBHBMvYJFaTjvBdzOSYJFsJMGqnJYkODpIgkXIRG5hHJEDFqzlJBMcEpJgkWwkwaqcliQ4OkiCRchEQoLr1q3rnd+jR4/6fGB2bps/f362piyEiiRYJBtJsCqnJQmODpJgETKR6QQzxow8MLN28+XLZ5MmTfKFZlFFEiySjSRYldOSBEcHSbAImUhIMLu7sekEC+MoFsSxeUXUFsOlRRIsko0kWJXTkgRHB0mwCJlISDBbDjOCLC1sT8xiuPiIsqghCRbJRhKsymlJgqODJFiETCQkmNm7zA1OCxtVsN0xghxFJMEi2UiCVTktSXB0kASLkAlegun0durUybcfBhbDIcTMCWaxHNMioogkWCQbSbAqpyUJjg6SYBEykZDgBg0a2MCBAz0SceDAAWvZsqW99957NnTo0MjNB44jCRbJRhKsymlJgqODJFiETCTiEPXq1bNWrVrZwoULbcCAAVarVi0rX768b6scVSTBItlIglU5LUlwdJAEi5AJVoLp8B45csTr/ffft/z581ulSpWsaNGiLr90golJHD582OcH37hxI3bLaCAJFslGEqzKaUmCo4MkWIRMsBK8Y8cOa9iwoTVu3Nh+/OMf23e/+1179dVXbx5j6+Q33njDZwi3aNEicjODJcEi2UiCVTktSXB0kASLkAlWgunwjhgxwsaMGWOPPvqoSzDbJbN98ujRo+2tt96yihUr2siRI238+PE+Mi1KSIJFspEEq3JakuDoIAkWIROsBF++fNn279/vC+FKlixphQoV8gVyVatWtWHDhlmxYsWsXbt29sknn9jBgwcVhxDia0YSrMppSYKjgyRYhEwkFsYReWDL5Dlz5libNm3889KlS3unOKpIgkWykQSrclqS4OggCRYhE7wEMyKNHDAxCGYEMxe4ffv2VrNmTRs7dqydP38+ds1oIQkWyUYSrMppSYKjgyRYhEzwEkzMgU4wEhwHMW7evLmL8MyZM2NHo4UkWCQbSbAqpyUJjg6SYBEykegEHzp0yE6dOhU78hW7du2yzZs3+3i0KCIJFslGEqzKaUmCo4MkWIRM0BJM/OHEiRN2/Phx+/TTT+3q1at28uRJP7548WJbv3697yIXRSTBItlIglU5LUlwdJAEi5AJVoLZLIPJD8uXL/diAgRfDx8+3Meh9ejRQzvGCfEHRBKsymlJgqODJFiETJASTAQiPie4c+fONnDgQFu1apXNmjXLXnvtNR+dVrt2bf/lvHjxoneJuU2UkASLZCMJVuW0JMHRQRIsQiZICWYxHFGH8uXL23333WflypWzwYMH+y8jO8VNnjzZSpQoYfXq1bMFCxbYkiVLPCoRJSTBItlIglU5LUlwdJAEi5AJthN84cIFW7t2rbVu3dplkM5vlSpV7IEHHrBmzZpZ7ty5fQe5jh073uwIRwlJsEg2kmBVTksSHB0kwSJkgpXgvXv3WpcuXVyC2Rxj1KhR1r9/f3vhhRc8FvHee+/5/GBiEnSNr127Frt1NJAEi2QjCVbltCTB0UESLEImaAnu3r27/wKyAI6RaBs3bvSZwWylTBQi7ezgO4UpE2vWrLGpU6d68RjTp093wR45cqRHLjiOYNOVvn79um3atMnnEnOdrVu3xu7JbM+ePTZv3jz7+OOPbeXKlTejGYxvI6oxadIkW7Ro0e+NebsdkmCRbCTBqpyWJDg6SIJFyAQpwXEQT2Rz9uzZtm3bNp8QMXr0aFuxYoXvGod05pQtW7ZYz549vaNM5cmTx9566y0rWbKkPfTQQ/bOO+/4cbrPSDfS3LRpUytVqpRv2dytWzePYDCpguuULVvW3n33XatTp45fn8V606ZNs4oVK9rbb7/tH5ctW5bt7LIkWCQbSbAqpyUJjg6SYBEyQUsw0BUmD4xorl692nPACCJCnMhECG7LvOF49e7d23/ZJ0yYYE2aNLHTp0/7ca537tw5X4CXP39+mz9/vhdRjTlz5ngcg6xyv379bMeOHb6THR1khLddu3ZWq1Yt7yR36tTJp13s3r07dga3RxIsko0kWJXTkgRHB0mwCJlgJZgYAp1YOqg/+9nPvH75y1/aPffcYwULFvTOK5cxQaJGjRp25syZ2C3vDESXmEKrVq2sQYMGvujumWeesWLFilndunVt7ty5PpINSW7ZsqV3pIk/0JGmG81xZJc4BN3iKVOmuCDTZUZ8hw4d6ht6INF9+vSxhQsXxh45PWwIQgyD50NH+fnnn7fixYvHLhXim0cSrMppSYKjgyRYhEywEnzkyBEbO3asZ3XfeOMN78LScSW2wJg0MsGDBg3yzi2d18uXL8dueWewKcf48eP9F50xbGPGjHFZRUjpQCOzZIDbtGnjGWSiDggrUYxq1ap557dv3743s8NkgpHpRo0a+YYeSDQj35BnZh4jyZlBtILMM88Hwa5cubLHLoRIFpJgVU5LEhwdJMEiZIKPQwBSSkeVOAQxASQTQWYHuUQ5f/68yyyyTZyB++QYHeIBAwa4/CK5TKggzsAmHnR8EW+6tnSO2cxj8+bNLrKcI51pzpEuMQvikOCdO3f6fSDc2UFxCJFsJMGqnJYkODpIgkXIREKCEUiytHRaWXC2b98+n+xAVzYRWHhHtrhQoUIuq+SAuU+6w0gwY9mIOtDR5Q8BMsxjxxfo0Znu2rWrH0d+z5496zlhcsDIM/LO4jgeh8sZ95bdrZ4lwSLZSIJVOS1JcHSQBIuQiYQEsziNKRGMMGNMGTOBOUYlAtLLyDMmOmzYsMHGjRvnMQu6uogw49jo6DKdYsaMGS63xB64bq9evVx0OU6emJFqhw4d8gV8yC6dav54INBMhECaO3To4Nnh7CAJFslGEqzKaUmCo4MkWIRMZCSYvG6lSpW8A/x1bYzBAjciCogrMQi+pntLBrlw4cK++A6ZZToEHWImUyDCbOPMZexox6K6+vXr+9fI9Msvv+xijRATp+A2SHLevHn9a45nB0mwSDaSYFVOSxIcHSTBImQiIcHr1q3zBWh0aVmURsb264D4AjOHiVsQs2BxHbng4cOHexFtiEcu6Ayz6QU5X6Y/sICOeAaxCaIUiDTH+YNBbpiJEMwiZjEdxykWvmlOsAgFSbAqpyUJjg6SYBEyQUswskuHFoFkPBnRg2SC2CLMFN3hOPFsMTEKOsNxSecjkQu610y7yK4AgyRYJBtJsCqnJQmODpJgETJBSjDxB3ZioyvLGLSqVav6BAZE89ixY+mKrYm/zu7w3YIkWCQbSbAqpyUJjg6SYBEyQUowndXly5d7npZtilmwxngydnJjJFm82Ma4cePGvhCNsWZRQhIsko0kWJXTkgRHB0mwCJkgJZjYAYvO2BEuX758NmzYMF9sRk6XLG68mLjAphZIMp3jKCEJFslGEqzKaUmCo4MkWIRMkBLMYjM2pGCrYXZsY0wZcQjGo5ERTltsacziNbrHUUISLJKNJFiV05IERwdJsAiZ4BfGIbkdO3b0hXHM60WQUwFJsEg2kmBVTksSHB0kwSJkgpbgOHv37vV5vmxvzEK4qC2CywxJsEg2kmBVTksSHB0kwSJkIiHBTItgtzjmBLNT28WLF2OXRBdJsEg2kmBVTksSHB0kwSJkIiHBwBg05vDu2rUrcvnfzJAEi2QjCVbltCTB0UESLEImEhLMVsOLFy+2UaNG+Q5sTIuYMmWKL5Rj17YoIgkWyUYSrMppSYKjgyRYhEzQEsyoNHZbmzBhgssvWxZ369bNOnXq5NWjRw+XYbY8JjIRJSTBItlIglU5LUlwdJAEi5AJWoLZmrh69erWqlUrl92tW7f6tIjt27f7pAguK126tG9jrBFpQny9SIJVOS1JcHSQBIuQCVqCmRX88ssv2/z58300Gt3eePH1xx9/7DvG8fHy5cuxW0UDSbBINpJgVU5LEhwdJMEiZIKWYLZC/vDDD61y5co+K3jq1Km2aNEimzNnjvXr188qVKhgtWrV8kVzURubJgkWyUYSrMppSYKjgyRYhEzwmWC2Tx48eLB17drVunfv7r+Qffr0sf79+9vQoUNdiqM4N1gSLJKNJFiV05IERwdJsAiZoCU4DhngESNGWPPmzX1WMBEIJHHdunWRi0HEkQSLZCMJVuW0JMHRQRIsQiZoCSb3e+zYMVu4cKFLIQvk6tevb3Xq1LEWLVp4J3jDhg3eMdZ0CCG+XiTBqpyWJDg6SIJFyASfCW7UqJE1bNjQhXfVqlU+IWL16tU2ZswYK1u2rJUsWdIOHjyoTLAQXzOSYFVOSxIcHSTBImSCluBTp05ZwYIFbdKkST4pgnnAxB/4ePr0aRfjunXr2rx58+zKlSuxW0UDSbBINpJgVU5LEhwdJMEiZIKW4LNnz/ovH1lgOr/Lly/3XeJYLMdYNLrESHAUt1KWBItkIwlW5bQkwdFBEixCJmgJpruL7LZu3dozwPwysnPcwIEDfVoEx4cPHx45AQZJsEg2kmBVTksSHB0kwSJkgpbgOOwIN3r0aJdeJkPwcdSoUT41IooCDJJgkWwkwaqcliQ4OkiCRchEQoKZAIEUEn0oX768L4gjCsFWyidOnIhdK1pIgkWykQSrclqS4OggCRYhE7QEswCOjTE6derkG2bMnDnTF8FNmzbNBg0a5LvFMTlCO8YJ8fUjCVbltCTB0UESLEImaAk+c+aMvfvuuy7ARB/o+rJYjo+7d+/2HeSqVavmC+auXr0au1U0kASLZCMJVuW0JMHRQRIsQiZ4CS5VqpR3g1esWOHie+DAAdu/f7+tX7/eunXrZg0aNPBpEdeuXYvdKhpIgkWykQSrclqS4OggCRYhE7QEX7p0yWWwYsWKvktcv379fEEc84FZHMfxtm3b5njHOOIWLLrbu3ev7du3z2cRX7x40Xep4xibcFy4cMGvy+51zC3+5JNPvJhTHOfcuXN+Xe6D28ajGZz/kSNH/L4OHz58R7OMJcEi2UiCVTktSXB0kASLkAl+YRzTH4hCMCe4ffv2vnVy586dfQMNOsMIcE5AaufOnWs/+tGP7LnnnrNcuXK5UM+ePdu7yy+88IIVL17cpk6d6tdHaLt06WJvvPGG5c+f33r16uXHATEvUaKE5c2b1+rVq+cdbFi0aJFVrlzZnnnmGStXrpx3r7OLJFgkG0mwKqclCY4OkmARMsFLMGzevNkXwn344YdWpUoV/4VEWOfMmXNTOO8UurrMIK5QoYItWbLENm7c6JKK0L799ts2f/5869Gjhz/uunXrbM2aNS66w4YN80KI2b6ZbZyR5g4dOviCvSZNmtiCBQv8nBHl6tWre2aZOccTJ060Q4cOxc7g9kiCRbKRBKtyWpLg6CAJFiETtAQTH6ATywYZyOiIESO8+JxfzJYtW3pemMVydHbvhG3btt3s7CKoAwYMcLlFXJFt5Hrx4sX+2P3797chQ4Z4JINxbVu2bPGveWxu06xZMz/Po0eP+uYdHGcxX8eOHf08WbQ3efJkfwyyzZnBc0CeyTm3a9fOihUrZiVLloxdKsQ3jyRYldOSBEcHSbAImaAlGDFkLjAd2aVLl/qCOESTTO6qVatcPunkIqZ3ujAOkY3/ciO9dF2ZNEFHF5ElL7xnzx6X2fr167uYkkmOnwPSW7t2bY9ncD90is+fP2/Lli3zDT04N4SWsW5EOugMs8sd3eLMIGPMdRF7xr4VKFDAO89CJAtJsCqnJQmODpJgETJBSzCRhYIFC9qECRNcPJFiFqohm4xJoyvMphlEF+5k0RkwW3jHjh3+GHSRe/bs6dEFZhIjuJcvX/boAp1gIhjILlEJFrhxG2QWQUd4uQ5SjTgzqaJGjRqeDeaPB1ELFsqRX0akx48fHzuD26M4hEg2kmBVTksSHB0kwSJkgpZghJfsb9GiRb1LSwyCXeLGjh3rndbChQu7cCKsdzodgu4s3eP47Ygr0AWme4uoshCOTnDfvn39DwCL8YhAMAUCIUfMWezWpk0bF1a60cg50su5IsfEIhD0eCcYkR43bpw/XlZIgkWykQSrclqS4OggCRYhE7QEI6nECxBUcrlIKjlbRLV58+YeW2D8WE7Go7HzHPlfbs/jILNEK1jYRkaYrjOZYDbk4HGRXsQWmWUxHOfTtGlTl1qmVsyYMcPlOJ4RJkbBHw9ywNw/8s71Zs2aFTuD2yMJFslGEqzKaT3VZq7l77U0yPpgyBq7ePV67LdASIJFyAQtwczsJZ7AYjK6s3RYq1at6jLJ6DHElWxwTmDiAwvj2HoZ6a1UqZJndplBTIeZrnPNmjW9e8uoMxbSsVCN8yG3y2UILd1iIhnkiolUsLkH49yIRyDKiCyyXqZMGevdu7dHMLKDJFgkG0mwKhULgT97KWejN6OIJFiETCQywUQMyOOWLVvWF6cx2ixthjcnxKMLdevW9SL2sGnTJpdUpJZuLsKNwLIZBkJOR5juLwvi+JzzI+rAdeggMyqNc2IDDjLKTHuge8xt2NiDaAS54ewgCRbJRhKsSsWSBKdHEixCJngJfv311z1KQCaXBWrx3dgYO0YsggjD1wmL5MgiI6x0cxFgIHLBYzIFgmJ3uThs2IE8E59g4Vz8HBFkdoxjAw46xmSXs4skWCQbSbAqFUsSnB5JsAiZoCWYCQ6PPfaYxxDoCJcuXdrlE1FlVBkd1q9bggHhRWR5nIx5Y47d6ji3yXg87X3dCZJgkWwkwapULElweiTBImSClmA6rHRd2d6YuAIRCBal0VElb0sUgkhDFJEEi2QjCValYkmC0yMJFiETtAQDnVQiCcQJtm/f7p1g5JgFcWxzTHQhikiCRbKRBKtSsSTB6ZEEi5AJXoJTFUmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4ECRBItkIwlWpWJJgtMjCRYhIwkOFEmwSDaSYFUqliQ4PZJgETKS4Fvw2Wef2fr1661WrVpWo0YNq1evns2cOdNWr15tRYoUsUqVKvkv/tChQ+3o0aN25coVGzVqlNWtW9fq169v48ePj92T2dy5c6158+ZWvXp16927t124cMGPb9iwwTp16mQVKlSwdu3a2a5du/x4dpAEi2QjCValYkmC0yMJFiEjCb4F+/bts3HjxlmbNm1s+PDhLsN8jsQWLFjQ+vfvbyNGjLDly5fbsWPHbPv27S7G7du3tw4dOljXrl1dag8cOGCtW7e2hg0bWs+ePf3j2rVrbf/+/TZ48GD/44HQNmjQwGbMmGGnTp2KncHtkQSLZCMJVqViSYLTIwkWISMJvgV79uyxBQsW2NatW70r3K1bN6tatarVrl3bSpcu7YK8aNEil9zjx49757d8+fK2atUqW7NmjfXr18/lecqUKd4ZHj16tF+3T58+NmTIEJs4caLLMh1gush0lAcNGuTd58y4dOmS7dixw+bMmWPTp093KS9TpkzsUiG+eSTBqlQsSXB6JMEiZCTBWfDFF1/Y1atXrUWLFlalShWPReTOndveeOMNe+edd1x0N2/e7ELbq1cv27t3rx0+fNgmT57s3V26xz169LCVK1fauXPnXJyJRrRs2dK7xVOnTrXr16+7/Hbv3t0jF5lB5AJJLlasmL3++uv25JNP+uOLsDl58artO/lpkDVt09FMJUGlinJJgtMjCRYhIwnOArrA69at86hDs2bNPBOM6J4/f97Fl6gDIozUjhw50gWYSAPRBuIKjRo1soEDB9qWLVvs008/9fuii4tM88djyZIlduPGDe88E6WYMGFC7JHT8/nnn9u1a9e8I8z9cFs6zyJs6o/fZPc2nB5k3fPhtEwlQaWKckmC0yMJFiEjCb4NdGgPHTrkMkuMgYVsdHORUTrERBwQVzq6CPGwYcP8+mSEJ02a5JKKHCPBGzdu9AVxZIirVavmcky+mMgFEkzsAqFOu6DudigTHA2qj1qf6X+0KpXq7ixJcHokwSJkJMG3gM4r3dmOHTu6sNIBXrFihccckFwEmYVuxCToBFPke1kgx4I4ogtkgVn8hiTPnz/fTpw44ZLL4jgEmGJxHVJN1rdt27Y2bdq02BncHklwNJAEq1RhlSQ4PZJgETKS4Ftw8uRJF9QnnnjCRRd5RWYZc0ZXmIVtfM6xTZs2+YI4Or/cBvFt2rSpf07Wl8+7dOni+d86derYgAEDPAbRt29fj0UsW7bMGjdu7Jlg4hLZQRIcDSTBKlVYJQlOjyRYhIwk+BYgtixge/TRR61QoUL29ttve5aXLu7LL7/shdAuXrzYr3/27FmX4IoVK/qCtcqVK3s+mEwxHWImOZQrV87y5cvnoku2d+zYsfbuu++6TOfJk8cnThC3yA6S4GggCVapwipJcHokwSJkJMG3gJwuo8tYAHfx4kVfjHb58mUvvqb4nFgEEJ84ffq0xxpmz57ti+c4BtwHnWKiFGR/mTZBphgRJj5Btpixaog0x7ODJDgaSIJVqrBKEpweSbAIGUnw1wjSSyc3vnguDseRZiQZsY6LLh/5mqwwQox4ZxdJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVWSYLTIwkWISMJDhRJcDSQBKtUYZUkOD2SYBEykuBAkQRHA0mwShVW3ddohjWZtMVaT9sWbI1dcyj2FyhxJMEiZCTBgSIJjgaSYJVK9U1XmY9Wxf4CJY4kWISMJDhQJMHRQBKsUqm+6ZIEC/EVkuBAkQRHA0mwSqX6pksSLMRXSIKTzL59+6xdu3ZWrVo169atm61fvz52ye2RBEcDSbBKpfqmSxIsxFdIgpPIiRMnbMqUL/8glSljvXv3tiZNmtjo0aPt/PnzsWvcGknwVxw4fcnaTNsWbOXptCDT/6RUKpXqD1WSYCG+QhKcRNauXWudO3e2Fi1a2NmzZ23IkCHWv39/27p1a+wat0YS/BXL957O9I+8SqVSqTIvSbAQXyEJTiIzZszw7u/cuXPt8uXLtmTJEhs8eLB9/PHHsWv8jhs3bniH+OjRo3b48GHr1KmTlShRwo4cOZJwHTp0yCuzy+72mrp8i/1PlSG3rO9XGuSV2WWh1n9XHmLfqzjoy4+DM7089PrqZxat58bP6nsVP4rkzyyqz+2r58XvWeaXh1zFu023gwcP+v8lmf1dvZNq27atVa5cOfY/lRBhIQlOIlOnTnUJ3rhxo127ds3WrVtnH330kY0cOTJ2jd/BH6s+ffrYq6++as8//7z95Cc/se985zv+eaL16KOP2uOPP57pZXd7PfPsc/bQ40/fsn740wftR/c/lOllodaDjz9l/3PPfXbvg49menno9b/33G8/efCRTC8Lte5/5An73g9/Yvc9/Himl4dcP3vkSfv+D++1+34ered270OP2n//+D574LFfZHp5yPXgl/8eH3roIXv22Wcz/bt6J/XTn/7UihUrFvufSoiwkAQnkenTp3sUYs2aNXb16lVbuXKl9evXz4YPHx67xu+4cuWKffLJJ36dpUuX2oIFC2zevHn+eaJVsmRJq1mzZqaXhV6lS5e2qlWrZnpZqLVo0SLLmzevtW/fPtPLQ698+fJZmzZtMr0s1BozZow9+OCDHnnK7PKQa/z48fbII4/4C/jMLg+1unfv7pI3e/bsTC8PuXr16mXPPPOMvxuZ2eV3UgsXLrQNGzbE/qcSIiwkwUlk2bJl1qVLFxs3bpx9+umnNm3aNOvRo4dNnjw5do1vhjp16ljXrl1jX0WLBg0aWIcOHWJfRYPr169b4cKFbdKkSbEj0YKu0tixY2NfRYNdu3b5uy286xM19u/fb08//bS/mI8Ss2bN8nfesrNQOTRooPBC+vTp07EjQqQmkuAkwni0oUOHWo0aNWzx4sXWsmVL69ixo8civkkkwWEhCQ4PSXB4SIKFiD6S4CRCDjj+1jZv2b/55pv+FtylS5di1/hmaNy4sa/wjSLNmzf372mUQIJLlSqV6QLKKPD+++9HTvD37NljL774om3evDl2JDocOHDAXnrppWzPOA8FRLFIkSJ24cKF2JHowP87BQoUsDNnzsSOCJGaSIKTyBdffOHCS5eIzCDxCGYHc/ybBJmiEx1FyLyRWYsSn3/+ub+DsGXLltiRaEEmftOmTbGvosGpU6f8xRjTXaIGItWzZ0+fMBMldu7caQMHDvT1GlGDF2WM4/ymGy5C3G1IgpMMwktHGPm9ePGij0L7puE/6HPnzsW+iha83ccM5ijBv5ljx455jjyKRPG5ffbZZz6Sit/1qME7Ewhw1GSRsZWMAONFZ9SIP7dk/H8jxN2EJFgIkXQQKV6I8a4IL1r4WgghhPhDIgkWkYWuGxnM3bt3x46EDR0p3nomukIxnmjv3r3Bd6roRvE8Jk6c6DOyWRTHW9FREmG69/ExiHSEQ4fnw86WM2fO9HGNFLPMo9Tp5sUYCxl5XqF3ufldYgEj//74Wc2fP983aVq9enUkF/4JkV0kwSkM/5Hxh/748eN28uTJyLwFzfPijz5dxWrVqvkYuijAzwfxLVSokBUtWtQ/MlKPGE3IsPAI+WURUrdu3XyRFXnFKMVYkKjt27f7YqRhw4bFjoYLz6dZs2Y+8YJ/hxRzz6MybYC/H6zRYMEyayZCf15kf0ePHm0VK1b0n9Urr7ziEz0qVaqUrW36hYgqkuAUhlwY/5EVLFjQypUr538kowD/gSH2/IFnIDybSkQBFsKxIQGTE8hgsoNg69at/T/rkKFTT2eK58F/1myUwaYx27Zti10jfPh5VahQwXdnZGv00OFnxr8/fk68WKEQ46jkZ9mYiEVx5cuX93dfQn9eNAbYcImuLz8rtuhH8Onka0KESGUkwSkKfwh5O4w939nFiv/M2AOexRKhvw3N+fOHffny5S4eUZmBTMeUt9JZyEiEgLF2jIBbu3Zt7BphQoebnxeLQ5kKUbZsWZ9+EZWuIs9jzpw5PvqNHchGjRoVuyRcmKHLi8zXX3/dqlev7rO4EUdkK3T43Ro0aJC/28JOmrxAi9LCYV5oMv6NrjB/T0L/ey9EIkiCUxTyYXRIKd6m5W123ormjyMd4pCha0NXimrSpEnk5gQjGozaoovfrl07l8coQPeenxVv17KLIj+/0OHfIrlLtkdnDCKbnERhIxAy6bxw5gUmPzPmVhOH4AVa6PAORKNGjey9997zd8cY/8aoxaiMgOMdJSSfF9EakSZSHUlwisIf+ipVqvhb68jHjh07fD4rWcwoLZSI2mYZ8bc1ydAi+MhiVEDmeYudt6DplpJTDx3eWRkxYoTVr1/ff6/ockdBgtkgAymki8/fD3a9RKqiEGFBfBs2bGh9+/b1Til/E/k7EpV54xMmTLBWrVr5z0pdYJHqSIJTFBZDfPDBB/5WH9EIVufzx59tm/k6KkRNgunS87MrXry4v2iJws8KqSfqEX8HgsV+vXr18g5q6PAiE+Hgd4vufYkSJTxrGvoiVF6gEBFAooh7EIfo1KlT8NEc4N8f74rx749pF0R0atWqZePHj49dI1x4d4UXK/Xq1YtEdEWIRJEEpyhEIMjyke3jLUw6wSzY4T+zKC2UiJIE89Y6I9/YXnvAgAG2b9++SPxHRjadrhuLdICIR+/evSOxaxxxgVy5cvnW6K+99pp9//vf9+kXZJ5DhsWLLNKkI0wWmGww8Qj+TYYOL1j4ufHvkckrxFg+/PBD/1sZOryA5gUmv19CCElwysJ/XnQ7kA+6wCtWrLDOnTt7VkxxiLsTBIP/nBEpcrMsaqRrFXr3jbeceQFGBpO31Vmww1gqusOhw8+MBZrxyp8/v7/bEvqs4EWLFnkch842k2V4V4nOaejrCQCp5+8ii2p//etfe46bsXah/8yA+BR/D+MvOIVIdSTBKQqiy39k/OdFZ4C3bJmpu27dukgsSIrDc1y1alXsq7AhM0vXlMWMdIJ5wTJt2jR/ERMybClMh4opJfERcIhIFOHnFYXcLDEcJl7QUfztb3/rn0clRsW/x/Xr13uWm3+PPD9mjkdhI5ANGzb438OoLPITIlEkwSkKY4DI8rEAhEU7jAJiRBqrhZUVE0IIIUTUkQSnMMgubzmzSQFvZUZpQZwQQgghxO2QBKc4iDBv/1FR2e1JCCGEECIrJMFCCCGEECLlkAQLIYQQQoiUQxIshAgCojsUsR02m1B8RwghRCJIgoUQdy3xHckYT8WmLhSLOZlrzZi/zESYWbVIMhNQAHFm0wMqI9wv98dYQD5yn9yejDwj6fiYER6TDWXYEpktg9PWsWPH/CPnzeMKIYS4e5EECyHuSpDY3bt3W6VKlXxDEGZZU2w68cwzz/gMaEb6ZWT69Ok2cuRI36YYEFK2Kmbea0aYm8rmAdwXm8ewYyKzfJlbXKRIEd9JMaPMsmVw3bp17cknn/Sd0tLWCy+8YK+++qrPOY7CXFkhhIgykmAhxF0J8slQ/6ZNm7qQsnUtG4R06tTJvvvd71rx4sV96+9atWq5HK9Zs8almN2+ENv47mVsNc3l3I5dvyguo/vLxgHMx2bnvfhudb/5zW9s4cKFLrVsL855xAvoTLNb3w9/+EP75S9/ma4eeOABe/rpp23//v2SYCGEuMuRBAsh7kqINDC/+v3337f777/fmjVrZv369bMyZcpYixYt/HN29GrTpo3vdshOc2xJjByXKlXKZXjWrFnWrl07K1++vAszcswGMXSAiTsgu0j0Sy+95B1ctgFu1KiR3+bZZ5+11q1b+3bio0eP9qgDInzu3Dm/vGDBgi7Daevdd9/17Z8PHz6caZRCCCHE3YMkWAhxV0K2lmjCr3/9axdUhJQqWrSoRx4WLFjgndr58+d7jGHcuHHehY3LKULKbekiI8mIa5MmTTxKwe3p1nL/CDMdXKT3nXfecckuVKiQV9myZe3ll192gWbr3AMHDrg40z2mc9yyZct0xe6LderU8ftnO+vM4hpCCCHuDiTBQoi7Ejq169at83wtnV+qffv2vsX3r371Ky+O0fGlGzxlyhQX18GDB9umTZs8A/z22297xIEuMYvqiEJUqFDBli5d6lGLqVOn2gcffODdYT6WK1fOJTpv3rze/V25cqXf/4gRI3xHxTFjxty8zltvvWXFihVzyaZ4LASdcyhcuLANHz7cH0MIIcTdiSRYCHFXwhQGsrsscCOuQKQBIY3HICgWvBFXQIaJPjzxxBNeSCy3qVevns2bN8/lmdvRyaXTS8yCyMLOnTtt9uzZ1qBBA5s4caJ3eYlMvPnmmx6/GD9+vD/OjBkzbp7Pxo0bvaNM7KFx48Z+f6VLl/YOcNWqVf1zJJsJEvEJFUIIIe4+JMFCiLsSBHLPnj0eRShZsqRLJhMckFK6tNSQIUM8CsHiOeIRyCuxh8mTJ1uXLl0838uECW7H4jjklMwwIstxOrzEIR5//HGXV+IQdIXpHPN58+bNvaNLZzkOMQdkl+kQb7zxhv3iF7/wz+lMv/jiiy7f69evVxRCCCHuciTBQoi7EuILc+fO9ZwtEks3l4VvdGqJLtAZJiNMPhdxXbZsmQsuAssMX0SYTi2RhMWLF3s3lw4wMYZt27b5/ROhoKNLTphRbIgvUySIYBB7IN6AKNPVjUOkAqEm9oCc58qVy0ejEYGIZ4q5/ytXrsRuIYQQ4m5EEiyEuCshBrFkyRKfCzxq1Cjr2bOnxyHoBCOuLFpDjun4khNmlnCBAgU8H0y0AZmlE4wEM2mCzTLo/ubLl8/n/wJCy0xhus2INB/JEsc70Iw942tuH4fFeF27dvXFd1WqVLHXXnvN7xP5pUOMtJNlVidYCCHubiTBQoi7FsaMIcNMXmCWL5ta0KWl04vUMuGhf//+3hVmegMTHognMNGBikswM3sZbcZOc3Rt6dQy7oxuLcI7YMAAF2imUJAvpmtMlxe5JV7BrGE23eB8iGEQoUCQn3rqKbv33nvtnnvusccee8wfn4gEos45amtnIYS4e5EECyHuWvbt2+cRA+IPLGCju0pWmEIwiUeQxa1du7YLLTOFhw0b5t1aFrXRFUZGiUGw2QbiyiQHOsIscmMxHdMiWBjHxhlcjy4vnWaiGHSXEWkKWSZLTEwiPp0id+7c9vDDD9vPf/5zF+D48VdeecVjGewuJ4QQ4u5EEiyEuGtBehlThnyS4Y3v2haH7i9Z4HhnlwVsbGrBbnAIKLLL53STuR4j0RDbuExzXXaa4/ZEHigWviHDjETjegg12yhzGd1kFr0R0eC8+Eh3muL+OUa3mc+Rbx5bCCHE3YkkWAgReYgx0PnNuFgNcc4YWeBYRtkWQggRPSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUg5JsBBCCCGESDkkwUIIIYQQIuWQBAshhBBCiJRDEiyEEEIIIVIOSbAQQgghhEg5JMFCCCGEECLlkAQLIYQQQoiUQxIshBBCCCFSDkmwEEIIIYRIOSTBQgghhBAi5ZAECyGEEEKIlEMSLIQQQgghUgyz/w+pIh3FACiA0gAAAABJRU5ErkJggg=="
- }
- },
+ "attachments": {},
"cell_type": "markdown",
"metadata": {},
"source": [
@@ -49,15 +18,17 @@
"在对数据进行预处理时,经常加入新的操作或改变处理策略,此时如果伴随着随机操作,最好还是指定唯一的随机种子,避免由于随机的差异对结果产生影响。\n",
"\n",
"---\n",
- "# 离散型随机变量\n",
- "## 二项分布\n",
+ "\n",
+ "## 离散型随机变量\n",
+ "\n",
+ "### 二项分布\n",
+ "\n",
"二项分布可以用于只有一次实验只有两种结果,各结果对应的概率相等的多次实验的概率问题。比如处理猜10次拳赢6次的概率等类似的问题。\n",
"\n",
"二项分布概率函数的代码表示:binom.pmf(k) = choose(n, k) p\\*\\*k (1-p)\\*\\*(n-k)\n",
"\n",
"二项分布概率函数的数学表示:\n",
- "\n",
- "\n",
+ "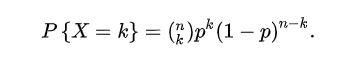\n",
"\n",
"\n",
"- `numpy.random.binomial(n, p, size=None)` Draw samples from a binomial distribution.\n",
@@ -65,6 +36,7 @@
"表示对一个二项分布进行采样,`size`表示采样的次数,`n`表示做了`n`重伯努利试验,`p`表示成功的概率,函数的返回值表示`n`中成功的次数。\n",
"\n",
"【例】野外正在进行9(n=9)口石油勘探井的发掘工作,每一口井能够开发出油的概率是0.1(p=0.1)。请问,最终所有的勘探井都勘探失败的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -90,10 +62,12 @@
"print(np.around(s, 3))\n",
"# [0.387 0.387 0.172 0.045 0.007 0.001 0. 0. 0. 0. ]\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"\n",
"【例】模拟投硬币,投2次,请问两次都为正面的概率?\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"from scipy import stats\n",
@@ -112,7 +86,7 @@
"print(np.sum(x == 1) / size) # 0.49874\n",
"print(np.sum(x == 2) / size) # 0.24972\n",
"\n",
- "plt.hist(x, density=True)\n",
+ "plt.hist(x)\n",
"plt.xlabel('随机变量:硬币为正面次数')\n",
"plt.ylabel('50000个样本中出现的次数')\n",
"plt.show()\n",
@@ -121,7 +95,8 @@
"print(np.around(s, 3))\n",
"# [0.25 0.5 0.25]\n",
"```\n",
- "\n",
+ "\n",
+ "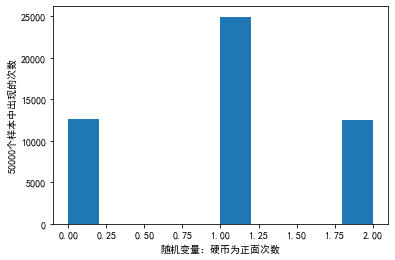\n",
"\n",
"```\n",
"#计算期望和方差\n",
@@ -132,14 +107,16 @@
"moments参数中:m为期望,v为方差\n",
"'''\n",
"```\n",
- "## 泊松分布\n",
+ "\n",
+ "### 泊松分布\n",
+ "\n",
"泊松分布主要用于估计某个时间段某事件发生的概率。\n",
"\n",
"泊松概率函数的代码表示:poisson.pmf(k) = exp(-lam) lam\\*k / k!\n",
"\n",
"泊松概率函数的数学表示:\n",
"\n",
- "\n",
+ "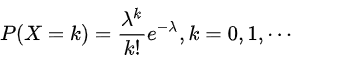\n",
"\n",
"- `numpy.random.poisson(lam=1.0, size=None)` Draw samples from a Poisson distribution.\n",
"\n",
@@ -171,13 +148,14 @@
"print(x) # 0.14900277967433773\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
- "## 超几何分布\n",
+ "### 超几何分布\n",
"\n",
"在超几何分布中,各次实验不是独立的,各次实验成功的概率也不等。\n",
- "超几何分布概率函数的数学表示:\n",
+ "超几何分布概率函数的数学表示:\n",
+ "\n",
"\n",
"\n",
"- `numpy.random.hypergeometric(ngood, nbad, nsample, size=None)` Draw samples from a Hypergeometric distribution.\n",
@@ -219,7 +197,8 @@
"# [0. 0.004 0.048 0.199 0.358 0.286 0.095 0.01 ]\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"```\n",
"'''\n",
"超几何分布的均值与方差\n",
@@ -233,15 +212,17 @@
"```\n",
"\n",
"---\n",
- "# 连续型随机变量\n",
"\n",
- "## 均匀分布\n",
+ "## 连续型随机变量\n",
+ "\n",
+ "### 均匀分布\n",
"\n",
"- `numpy.random.uniform(low=0.0, high=1.0, size=None)` Draw samples from a uniform distribution.\n",
"\n",
"Samples are uniformly distributed over the half-open interval `[low, high)` (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by `uniform`.\n",
"\n",
"【例】在low到high范围内,创建大小为size的均匀分布的随机数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -265,7 +246,8 @@
"print(b - a) # 0.4\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
"\n",
"作为`uniform()`的特列,可以得到`[0,1)`之间的均匀分布的随机数。\n",
"\n",
@@ -315,6 +297,7 @@
"\n",
"\n",
"【例】若`high`不为`None`时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -340,10 +323,10 @@
"```\n",
"\n",
"\n",
- "## 正态分布\n",
+ "### 正态分布\n",
"\n",
"标准正态分布数学表示:\n",
- "\n",
+ "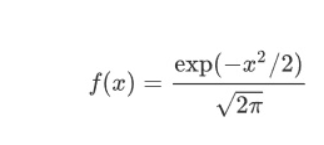\n",
"\n",
"- `numpy.random.randn(d0, d1, ..., dn)` Return a sample (or samples) from the \"standard normal\" distribution.\n",
"\n",
@@ -377,7 +360,7 @@
"print(y3) # 0.9973002039367398\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"还可以指定分布以及所需参数来进行随机,例如高斯分布中的mu和sigma。\n",
@@ -385,13 +368,14 @@
"- `numpy.random.normal(loc=0.0, scale=1.0, size=None)` Draw random samples from a normal (Gaussian) distribution.\n",
"\n",
"`normal()`为创建均值为 loc(mu),标准差为 scale(sigma),大小为 size 的数组。\n",
- "\n",
+ "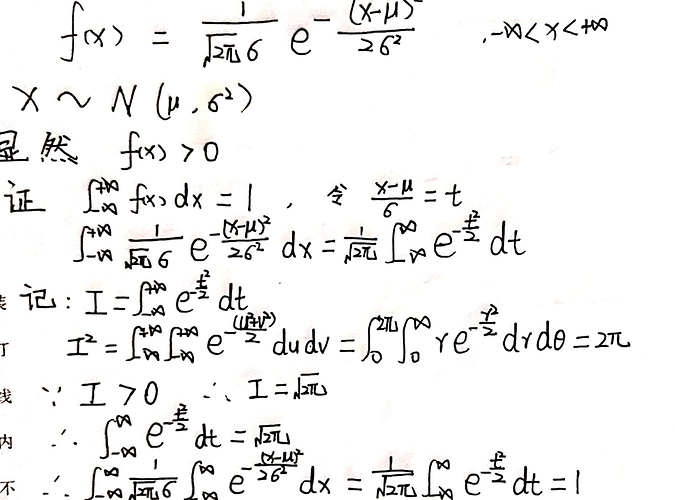\n",
"\n",
"```python\n",
"sigma * np.random.randn(...) + mu\n",
"```\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -424,22 +408,27 @@
"Means Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.\n",
"'''\n",
"```\n",
- "\n",
+ "\n",
+ "\n",
+ "\n",
"```\n",
"plt.hist(x, bins=20)\n",
"plt.show()\n",
"```\n",
"\n",
- "\n",
+ "\n",
+ "\n",
+ "### 指数分布\n",
"\n",
- "## 指数分布\n",
"指数分布描述时间发生的时间长度间隔。\n",
"\n",
- "指数分布的数学表示:\n",
+ "指数分布的数学表示:\n",
+ "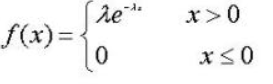\n",
"\n",
"- `numpy.random.exponential(scale=1.0, size=None)` Draw samples from an exponential distribution.\n",
"\n",
"【例】`scale = 1/lambda`\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
@@ -470,18 +459,21 @@
"print(y3) # 0.950212931632136\n",
"```\n",
"\n",
- "\n",
+ "\n",
"\n",
"\n",
"---\n",
- "# 其它随机函数\n",
"\n",
- "## 随机从序列中获取元素\n",
+ "## 其它随机函数\n",
+ "\n",
+ "### 随机从序列中获取元素\n",
+ "\n",
"- `numpy.random.choice(a, size=None, replace=True, p=None)` Generates a random sample from a given 1-D array.\n",
"\n",
"从序列中获取元素,若`a`为整数,元素取值从`np.range(a)`中随机获取;若`a`为数组,取值从`a`数组元素中随机获取。该函数还可以控制生成数组中的元素是否重复`replace`,以及选取元素的概率`p`。\n",
"\n",
"【例】\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -503,7 +495,8 @@
"x = np.random.randint(0, 10, 3)\n",
"print(x) # [2 0 1]\n",
"```\n",
- "## 对数据集进行洗牌操作\n",
+ "\n",
+ "### 对数据集进行洗牌操作\n",
"\n",
"数据一般都是按照采集顺序排列的,但是在机器学习中很多算法都要求数据之间相互独立,所以需要先对数据集进行洗牌操作。\n",
"\n",
@@ -514,6 +507,7 @@
"对`x`进行重排序,如果`x`为多维数组,只沿第 0 轴洗牌,改变原来的数组,输出为None。\n",
"\n",
"【例】洗牌,改变自身内容,打乱顺序。\n",
+ "\n",
"```python\n",
"import numpy as np\n",
"\n",
@@ -584,71 +578,17 @@
"\n",
"\n",
"---\n",
+ "\n",
"**参考文献**\n",
- "- https://www.jianshu.com/p/63434ad5ea64\n",
- "\n"
+ "\n",
+ "- https://www.jianshu.com/p/63434ad5ea64"
]
},
{
"cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:02.029113Z",
- "start_time": "2020-09-15T01:02:02.026084Z"
- }
- },
+ "execution_count": null,
+ "metadata": {},
"outputs": [],
- "source": [
- "dic={1:('I','V'),2:('X','L'),3:('C','D'),4:'M'}"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:09.390007Z",
- "start_time": "2020-09-15T01:02:09.379035Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'M'"
- ]
- },
- "execution_count": 2,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "dic[4]"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "ExecuteTime": {
- "end_time": "2020-09-15T01:02:29.206128Z",
- "start_time": "2020-09-15T01:02:29.201134Z"
- }
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "'I'"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
"source": []
}
],
diff --git a/LanQiao/readme.md b/LanQiao/readme.md
new file mode 100644
index 0000000..1ba4e99
--- /dev/null
+++ b/LanQiao/readme.md
@@ -0,0 +1,52 @@
+# 编程实践(蓝桥刷题94道)
+
+开源内容:https://github.com/datawhalechina/team-learning-program/tree/master/LanQiao
+
+## 基本信息
+
+- 学习周期:14天,每天平均花费时间2小时-5小时不等,根据个人学习接受能力强弱有所浮动。
+- 学习形式:练习
+- 人群定位:有一定编程基础,对学习算法有需求的学员。
+- 先修内容:[Python编程语言](https://github.com/datawhalechina/team-learning-program/tree/master/PythonLanguage)、[数据结构与算法](https://github.com/datawhalechina/team-learning-program/tree/master/DataStructureAndAlgorithm)、[编程实践(LeetCode 分类练习)](https://github.com/datawhalechina/team-learning-program/tree/master/LeetCodeClassification)
+- 难度系数:中
+
+## 学习目标
+
+每天刷三道题,利用14天对于蓝桥杯这个比赛有一个初步的了解,掌握基本的蓝桥杯赛题解法。
+
+
+
+## 任务安排
+
+### Task00:熟悉规则(1天)
+- 组队、修改群昵称
+- 熟悉打卡规则
+
+### Task01:热身练习(2天)
+- 完成热身练习文件夹中的7道题目
+- 熟悉基本输入输出及蓝桥杯的练习系统的使用方法。
+
+### Task02:基础练习(3天)
+- 完成基础练习文件夹中的7道题目
+
+### Task03:基础练习2(3天)
+- 完成基础练习2文件夹中的8道题目
+
+### Task04:真题练习(3天)
+- 完成真题练习文件夹中的10道题目
+
+### Task05:真题练习2(3天)
+- 完成真题练习文件夹中的7道题目
+
+
+## 开源贡献者
+
+韩绘锦:华北电力大学
+
+- CSDN:https://blog.csdn.net/weixin_45569785
+
+黄建国:华北电力大学
+
+荆宝加:华北电力大学
+
+吴丹飞:华北电力大学
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/01字串.md b/LanQiao/task1热身练习/01字串.md
new file mode 100644
index 0000000..d1587cf
--- /dev/null
+++ b/LanQiao/task1热身练习/01字串.md
@@ -0,0 +1,79 @@
+## 01字串
+
+**问题描述**
+
+```
+对于长度为5位的一个01串,每一位都可能是0或1,一共有32种可能。它们的前几个是:
+00000
+00001
+00010
+00011
+00100
+请按从小到大的顺序输出这32种01串。
+```
+
+**输入格式**
+
+- 本试题没有输入。
+
+**输出格式**
+
+- 输出32行,按从小到大的顺序每行一个长度为5的01串。
+
+**样例输出**
+
+```
+00000
+00001
+00010
+00011
+<以下部分省略>
+```
+
+
+```
+for i in range(32):
+ t1=i
+ temp=[0]*5
+ for j in range(5)[::-1]:
+ if 2**j<=t1:
+ temp[j]=1
+ t1=t1-2**j
+ print(''.join(map(str,reversed(temp))))
+
+```
+
+ 00000
+ 00001
+ 00010
+ 00011
+ 00100
+ 00101
+ 00110
+ 00111
+ 01000
+ 01001
+ 01010
+ 01011
+ 01100
+ 01101
+ 01110
+ 01111
+ 10000
+ 10001
+ 10010
+ 10011
+ 10100
+ 10101
+ 10110
+ 10111
+ 11000
+ 11001
+ 11010
+ 11011
+ 11100
+ 11101
+ 11110
+ 11111
+
+
diff --git a/LanQiao/task1热身练习/1083、Hello,world.md b/LanQiao/task1热身练习/1083、Hello,world.md
new file mode 100644
index 0000000..c031a2d
--- /dev/null
+++ b/LanQiao/task1热身练习/1083、Hello,world.md
@@ -0,0 +1,53 @@
+## 题目 1083: Hello, world!
+
+时间限制: 1Sec 内存限制: 64MB 提交: 10817 解决: 5250
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1083.html
+
+**题目描述**
+
+这是要测试的第一个问题。 由于我们都知道ASCII码,因此您的工作很简单:输入数字并输出相应的消息。
+**输入**
+
+> 输入将包含一个由空格(空格,换行符,TAB)分隔的正整数列表。 请处理到文件末尾(EOF)。 整数将不少于32。
+
+**输出**
+
+> 输出相应的消息。 请注意,输出末尾没有换行符。
+
+**样例输入**
+
+```python
+72 101 108 108 111 44
+32 119 111 114 108 100 33
+```
+
+**样例输出**
+
+```python
+Hello, world!
+```
+
+
+```
+while True:
+ num=list(map(int,input().strip().split()))
+ for i in num:
+ print(chr(i),end='')
+```
+
+ 72 101 108 108 111 44 32 119 111 114 108 100 33
+ Hello, world!
+
+
+```
+num2=[2,2,2]
+num=num2.copy()
+for i in range(len(num)):
+ num[i]=int(num[i]/2)
+print(num2)
+```
+
+ [2, 2, 2]
diff --git a/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
new file mode 100644
index 0000000..442dd80
--- /dev/null
+++ b/LanQiao/task1热身练习/1084、用筛法求N之内的素数.md
@@ -0,0 +1,218 @@
+## 题目 1084: 用筛法求之N内的素数。
+
+时间限制: 1Sec 内存限制: 64MB 提交: 11990 解决: 7204
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1084.html
+
+**题目描述**
+
+用筛法求之N内的素数。
+
+**输入**
+
+> N
+
+**输出**
+
+> 0~N的素数
+
+**样例输入**
+
+```python
+100
+```
+
+**样例输出**
+
+```python
+2
+3
+5
+7
+11
+13
+17
+19
+23
+29
+31
+37
+41
+43
+47
+53
+59
+61
+67
+71
+73
+79
+83
+89
+97
+```
+
+
+
+```
+import math
+```
+
+
+```
+math.sqrt(9)
+```
+
+
+
+
+ 3.0
+
+
+
+
+```
+def f(num):
+ for i in range(2,num):
+ if num%i==0:
+ return False
+ return True
+n=int(input())
+for i in range(2,n):
+ if f(i):
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+
+```
+
+
+```
+N = eval(input())
+for i in range(2,N):
+ for j in range(2,i):
+ if i % j == 0:
+ break
+ else:
+ print(i)
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+import math
+def f (num):
+ if num<=3:
+ return num>1
+ if num%6!=1 and num%6!=5:
+ return False
+ i=5
+ while i<=math.sqrt(num):
+ if (num%i==0) or (num%(i+2)==0):
+ return False
+ i+=6
+ return True
+
+n=int(input())
+for i in range(n):
+ if f(i):
+ print(i)
+
+```
+
+ 100
+ 2
+ 3
+ 5
+ 7
+ 11
+ 13
+ 17
+ 19
+ 23
+ 29
+ 31
+ 37
+ 41
+ 43
+ 47
+ 53
+ 59
+ 61
+ 67
+ 71
+ 73
+ 79
+ 83
+ 89
+ 97
+
+
+
+```
+int(0x02)
+```
+
+
+
+
+ 2
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/1095、3n+1问题.md b/LanQiao/task1热身练习/1095、3n+1问题.md
new file mode 100644
index 0000000..2f8c997
--- /dev/null
+++ b/LanQiao/task1热身练习/1095、3n+1问题.md
@@ -0,0 +1,72 @@
+## 译文1095:3n +1问题
+
+时间限制:1秒内存限制:64MB提交:9228解决:2551
+
+**译文描述**
+
+考虑以下算法来生成数字序列。以整数n开头。如果n为偶数,则除以2。如果n为奇数,则乘以3并加1。以新的n值重复此过程,在n = 1时终止。例如,将为n生成以下数字序列= 22:22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1据推测(但尚未证明),对于每个整数n,该算法都将在n = 1处终止。尽管如此,猜想仍然适用于所有至少为1,000,000的整数。对于输入n,n的循环长度是生成的数字的数量,直到1(包括1)。在上面的示例中,循环长度22中的16是16。给定两个数字i和j,您将确定i和j之间所有数字(包括两个端点)的最大循环长度。
+
+**输入**
+
+> 输入将包含一系列成对的整数i和j,每行一对整数。所有整数将小于1,000,000并大于0。
+
+**输出**
+
+> 对于每对输入整数i和j,按照它们在输入中出现的顺序输出i,j,然后输出介于i和j之间(包括i和j)的整数的最大循环长度。这三个数字应以一个空格分隔,所有三个数字在一行上,每行输入对应一个输出行。
+
+**样例输入**
+
+```python
+1 10
+100 200
+201 210
+900 1000
+```
+
+**样例输出**
+
+```python
+1 10 20
+100 200 125
+201 210 89
+900 1000 174
+```
+
+
+```
+def f(n):
+ re=1
+ while n!=1:
+ if n%2==0:
+ n=n//2
+ else:
+ n=n*3+1
+ re+=1
+ return re
+while True :
+ i,j=map(int,input().strip().split())
+ temp=[]
+ for k in range(min(i,j),max(i,j)+1):
+ temp.append(f(k))
+ print(i,j,max(temp))
+```
+
+ 1 10
+ 1 10 20
+ 100 200
+ 100 200 125
+ 201 210
+ 201 210 89
+ 900 1000
+ 900 1000 174
+
+
+
+```
+list('....')
+```
+
+
+
+
+ ['.', '.', '.', '.']
\ No newline at end of file
diff --git a/LanQiao/task1热身练习/2080、十六进制转八进制.md b/LanQiao/task1热身练习/2080、十六进制转八进制.md
new file mode 100644
index 0000000..a80f5b6
--- /dev/null
+++ b/LanQiao/task1热身练习/2080、十六进制转八进制.md
@@ -0,0 +1,168 @@
+## 十六进制转八进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 489 解决: 362
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2080.html
+
+**题目描述**
+
+```
+给定n个十六进制正整数,输出它们对应的八进制数。
+```
+
+**输入**
+
+```
+输入的第一行为一个正整数n (1<=n<=10)。
+接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
+```
+
+**输出**
+
+```
+输出n行,每行为输入对应的八进制正整数。
+```
+
+
+**【注意】**
+
+```
+输入的十六进制数不会有前导0,比如012A。
+输出的八进制数也不能有前导0。
+```
+
+**样例输入**
+
+```
+2
+39
+123ABC
+```
+
+**样例输出**
+
+```
+71
+4435274
+```
+
+
+```
+ord('A')
+```
+
+
+
+
+ 65
+
+
+
+### 方法1
+
+
+```
+n=int(input())
+def f(num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=char(i-10+65)
+ re=''
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+for i in range(n):
+ num=int(input(),16)
+ print(f(num,8))
+```
+
+ 1
+ 39
+ 71
+
+
+### 方法2
+
+
+```
+n=int(input())
+for i in range(n):
+ temp=input()
+ mid=int(temp,16)
+ print('{:o}'.format(mid))
+```
+
+### 方法3
+
+
+```
+mapping= \
+{
+'0':"0000",
+'1':"0001",
+'2':"0010",
+'3':"0011",
+'4':"0100",
+'5':"0101",
+'6':"0110",
+'7':"0111",
+'8':"1000",
+'9':"1001",
+'A':"1010",
+'B':"1011",
+'C':"1100",
+'D':"1101",
+'E':"1110",
+'F':"1111"
+}
+
+n=int(input())
+
+for _ in range(n):
+ n16=input()
+ n2=''
+ n8=''
+ for i in n16:
+ n2+=mapping[i]
+
+ temp=len(n16)*4%3
+ if temp==1:
+ n2='00'+n2
+ elif temp==2:
+ n2='0'+n2
+
+ flag=0
+ for i in range(0,len(n2),3):
+ num=4*int(n2[i])+2*int(n2[i+1])+int(n2[i+2])
+ if num!=0:
+ flag=1
+ if flag:
+ print(num,end='')
+
+ print('')
+```
+
+ 1
+ 39
+ 71
+
+进行协议解析时,总是会遇到各种各样的数据转换的问题,从二进制到十进制,从字节串到整数等等
+整数之间的进制转换:
+10进制转16进制: hex(16) ==> 0x10
+16进制转10进制: int('0x10', 16) ==> 16
+类似的还有oct(), bin()
+
+
+
+字符串转整数:
+10进制字符串: int('10') ==> 10
+16进制字符串: int('10', 16) ==> 16
+16进制字符串: int('0x10', 16) ==> 16
+
diff --git a/LanQiao/task1热身练习/2082、十六进制转十进制.md b/LanQiao/task1热身练习/2082、十六进制转十进制.md
new file mode 100644
index 0000000..9edf75a
--- /dev/null
+++ b/LanQiao/task1热身练习/2082、十六进制转十进制.md
@@ -0,0 +1,47 @@
+## 十六进制转十进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 415 解决: 298
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2082.html
+
+**题目描述**
+
+```
+从键盘输入一个不超过8位的正的十六进制数字符串,将它转换为正的十进制数后输出。
+注:十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
+
+```
+
+**输入**
+
+```
+一个十六进制数
+
+```
+
+**输出**
+
+```
+对应得十进制
+```
+
+**样例输入**
+
+```
+FFFF
+```
+
+**样例输出**
+
+```
+65535
+```
+
+
+```
+a=input()
+print(int(a,16))
+```
+
diff --git a/LanQiao/task1热身练习/2083、十进制转十六进制.md b/LanQiao/task1热身练习/2083、十进制转十六进制.md
new file mode 100644
index 0000000..c0ba52b
--- /dev/null
+++ b/LanQiao/task1热身练习/2083、十进制转十六进制.md
@@ -0,0 +1,76 @@
+## 十进制转十六进制
+
+时间限制: 1Sec 内存限制: 128MB 提交: 511 解决: 235
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem2083.html
+
+**题目描述**
+
+```
+十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号,分别表示十进制数的0至15。十六进制的计数方法是满16进1,所以十进制数16在十六进制中是10,而十进制的17在十六进制中是11,以此类推,十进制的30在十六进制中是1E。
+给出一个非负整数,将它表示成十六进制的形式。
+```
+
+**输入**
+
+```
+输入包含一个非负整数a,表示要转换的数。0<=a<=2147483647
+```
+
+**输出**
+
+```
+输出这个整数的16进制表示
+```
+
+**样例输入**
+
+```
+30
+```
+
+**样例输出**
+
+```
+1E
+```
+
+### 法一
+
+
+```
+def f (num,n):
+ baseStr={}
+ for i in range(10,n):
+ baseStr[i]=chr(i-10+65)
+ re=''
+ if num==0:
+ return 0
+ while num!=0:
+ temp=num%n
+ if temp>9:
+ re=baseStr[temp]+re
+ else:
+ re=str(temp)+re
+ num//=n
+ return re
+print(f(int(input()),16))
+```
+
+ 30
+ 1E
+
+
+### 法二
+
+
+```
+a=int(input())
+print ('{:x}'.format(a).upper())
+```
+
+ 30
+ 1E
+
diff --git a/LanQiao/task2基础练习/1460、2n皇后问题.md b/LanQiao/task2基础练习/1460、2n皇后问题.md
new file mode 100644
index 0000000..e34c4b2
--- /dev/null
+++ b/LanQiao/task2基础练习/1460、2n皇后问题.md
@@ -0,0 +1,114 @@
+# 2n皇后问题
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1133 解决: 557
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1460.html
+
+**题目描述**
+```
+给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
+输入
+输入的第一行为一个整数n,表示棋盘的大小。
+
+接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
+```
+**输出**
+
+- 输出一个整数,表示总共有多少种放法。
+
+**样例输入**
+```
+4
+1 1 1 1
+1 1 1 1
+1 1 1 1
+1 1 1 1
+```
+**样例输出**
+```
+2
+```
+
+
+```
+
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(input().strip().split())
+ res=[]
+ def helper(row,temp,nn,cols,z,f):
+ if row==n:
+ res.append(temp)
+ return
+ for col in range(n):
+ if (col not in cols )and( (row+col)not in z) and ((row-col) not in f) and nn[row][col]=='1':
+ helper(row+1,temp+[nn[row][:col]+['2']+nn[row][col+1:]],nn,cols|{col},z|{row+col},f|{row-col})
+ helper(0,[],nn,set(),set(),set())
+ re_=len(res)
+ for i in range(len(res)):
+ helper(0,[],res[i],set(),set(),set())
+ return len(res)-re_
+print(m())
+```
+
+ 4
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 2
+
+
+### 小提示
+- 对于n皇后问题,因为同一行、同一列或同一条对角线上都不能放置皇后,所以我们的思路是使用递归来遍历行,然后用for循环遍历列,同时建立列跟对角线的集合,只有不在集合中的位置才能放置皇后。
+- 那么对于2n皇后问题我们就先对nn进行一次n皇后问题,接下来就在这个所有的放置完黑皇后的可能下来放置白皇后,等于是跑了两遍n皇后的算法来解决这个问题。
+
+
+
+```
+# n=int(input())
+# nn=[]
+# nn.append(list(map(int,input().split())))
+def m():
+ n=int(input())
+ nn=[]
+ for i in range(n):
+ nn.append(list(input().split()))
+ res=[[]]
+
+ r=0
+ def helper(i,temp,nn,col,z,f,l):
+ if i==n:
+# print('t',temp)
+# print('r',l,res[l])
+ res[l].append(temp)
+ return
+
+ for j in range(n):
+ if (j not in col)and ((i+j) not in z)and ((i-j) not in f )and nn[i][j]=='1':
+ helper(i+1,temp+[list(''.join(nn[i][:j])+'2'+''.join(nn[i][j+1:]))],nn,col|{j},z|{i+j},f|{i-j},l)
+ helper(0,[],nn,set(),set(),set(),0)
+ #print('res',res)
+ for k in range(len(res[0])):
+ res.append([])
+ helper(0,[],res[0][k],set(),set(),set(),k+1)
+ #print(len(res[k+1]))
+ r+=len(res[k+1])
+ return r
+print(m())
+
+
+```
+
+ 4
+ 1 0 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 1 1 1 1
+ 0
diff --git a/LanQiao/task2基础练习/1462、Huffuman树.md b/LanQiao/task2基础练习/1462、Huffuman树.md
new file mode 100644
index 0000000..0852108
--- /dev/null
+++ b/LanQiao/task2基础练习/1462、Huffuman树.md
@@ -0,0 +1,82 @@
+# Huffuman树
+
+
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1316 解决: 750
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1462.html
+
+**题目描述**
+
+```
+Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
+
+给出一列数{pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
+
+1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
+
+2. 重复步骤1,直到{pi}中只剩下一个数。
+
+在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
+
+本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
+
+
+
+例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
+
+1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
+
+2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
+
+3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
+
+4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
+
+5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。
+
+```
+**输入**
+```
+输入的第一行包含一个正整数n(n< =100)。
+
+接下来是n个正整数,表示p0, p1, …, pn-1,每个数不超过1000。
+
+```
+**输出**
+```
+输出用这些数构造Huffman树的总费用。
+
+```
+**样例输入**
+```
+5
+5 3 8 2 9
+```
+**样例输出**
+```
+59
+```
+
+
+```
+n=int(input())
+list_=list(map(int,input().split()))
+res=[]
+while len(list_)>1:
+ a1=min(list_)
+ list_.remove(a1)
+ a2=min(list_)
+ list_.remove(a2)
+ list_.append(a1+a2)
+ res.append(a1+a2)
+print(sum(res))
+```
+
+ 5
+ 5 3 8 2 9
+ 59
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1463、Sine之舞.md b/LanQiao/task2基础练习/1463、Sine之舞.md
new file mode 100644
index 0000000..6a86bd8
--- /dev/null
+++ b/LanQiao/task2基础练习/1463、Sine之舞.md
@@ -0,0 +1,92 @@
+# Sine之舞
+
+
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1605 解决: 964
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1463.html
+
+**题目描述**
+```
+最近FJ为他的奶牛们开设了数学分析课,FJ知道若要学好这门课,必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏,寓教于乐,提高奶牛们的计算能力。
+不妨设
+An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)
+Sn=(...(A1+n)A2+n-1)A3+...+2)An+1
+FJ想让奶牛们计算Sn的值,请你帮助FJ打印出Sn的完整表达式,以方便奶牛们做题。
+```
+**输入**
+
+- 仅有一个数:N<201。
+
+**输出**
+
+- 请输出相应的表达式Sn,以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
+
+**样例输入**
+```
+3
+```
+**样例输出**
+```
+((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+```
+
+### 思路一
+
+
+```
+N=int(input())
+An=['']*N
+An[0]='sin(1)'
+sin='sin()'
+for i in range(1,N):
+ if i%2==0:
+ An[i]=An[i-1][:-i]+'+'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+ else:
+ An[i]=An[i-1][:-i]+'-'+sin[:-1]+str(i+1)+sin[-1:]+An[i-1][-i:]
+n=N
+temp=An[0]+'+'+str(n)
+n-=1
+for i in range(1,N):
+ temp="("+temp+")"+An[i]+'+'+str(n)
+ n-=1
+print(temp)
+```
+
+ 3
+ ((sin(1)+3)sin(1-sin(2))+2)sin(1-sin(2+sin(3)))+1
+
+
+### 思路二
+
+
+```
+N=int(input())
+sin='sin()'
+An=['']*N
+def op(N,s):
+ if N==1:
+ return sin[0:-1]+'1-'+s+sin[-1]
+ if N%2==0:
+ return op(N-1,sin[0:-1]+str(N)+'+'+s+sin[-1])
+ else:
+ return op(N-1,sin[0:-1]+str(N)+'-'+s+sin[-1])
+# a=op(N-1,sin[0:-1]+str(N)+sin[-1])
+#print(a)
+An[0]='sin(1)'
+for i in range(1,N):
+ An[i]=op(i,sin[0:-1]+str(i+1)+sin[-1])
+ #print(i+1,An[i])
+n2=N
+def op2(n,s,n2):
+ if n==N-1:
+ print(s+str(An[n])+'+'+str(n2))#+'+'+'str(1)
+ return
+ op2(n+1,'('+s+An[n]+'+'+str(n2)+')',n2-1)
+op2(0,'',n2)
+```
+
+ 1
+ sin(1)+1
diff --git a/LanQiao/task2基础练习/1467、完美的代价.md b/LanQiao/task2基础练习/1467、完美的代价.md
new file mode 100644
index 0000000..6bd8b98
--- /dev/null
+++ b/LanQiao/task2基础练习/1467、完美的代价.md
@@ -0,0 +1,143 @@
+## 题目 1467: [蓝桥杯][基础练习VIP]完美的代价
+
+时间限制: 1Sec 内存限制: 128MB 提交: 1659 解决: 536
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1467.html
+
+**题目描述**
+```
+回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
+
+交换的定义是:交换两个相邻的字符
+
+例如mamad
+
+第一次交换 ad : mamda
+
+第二次交换 md : madma
+
+第三次交换 ma : madam (回文!完美!)
+```
+**输入**
+```
+第一行是一个整数N,表示接下来的字符串的长度(N < = 8000)
+
+第二行是一个字符串,长度为N.只包含小写字母
+输出
+如果可能,输出最少的交换次数。
+
+否则输出Impossible
+
+```
+**样例输入**
+```
+5
+mamad
+```
+**样例输出**
+```
+3
+```
+
+### 思路一
+
+
+```
+n=int(input())
+l=list(input())
+
+def find(target,l,n):
+ i=n-1
+ while i>=0:
+ if target==l[i]:
+ return i
+ i-=1
+def swap(i,j,l):
+ if i<=j:
+ temp=l[i]
+ t=j-i
+ for k in range(t):
+ l[i+k]=l[i+k+1]
+ l[j]=temp
+ return l
+k=0
+res=0
+label=0
+while k<=(n//2-1):
+ j=n-1-k
+ if l[k]==l[j]:
+ k+=1
+ else:
+ i=find(l[k],l[k:j+1],n-2*k)+k
+ if i==k:
+ if n%2==0:
+ print('Impossible')
+ label=1
+ break
+ else:
+ l=swap(i,i+1,l)
+ res+=1
+ else:
+ l=swap(i,j,l)
+ res+=j-i
+ k+=1
+
+if label==0:
+ print(res)
+
+
+```
+
+ 7847
+ fdkzklcfzyuhivkbxnocsizsvkppdyuxaznbcxjmihvtrdpbepgjcffpkjwybhslljvwwvpzmvxxjozykikfwbrddjtbdebxvvttbnqaarmkvdvanbdhdchyilcmodoiiunqtikddvpmrkpiztampaagfukaslozztwsyteiiyksmwntlrxczldclgarwkaypxujkhtacmlnprmvkdvdbxsysoglpdrbmuhfceutkrxjhqrxfoaecdgdsalqrpxplvnctwamwaajfapqmezxikcyeegyocyiqiltmcdxpdfhjdbhnlivdwkygctihktsutwjplqhepzkrtolgtqmcmwvpbzlhvrwkztgtonhelqutjomhalxbrwzjqpsodzmjsalxvgxgdnutaseseqoysqzrgyetikmvzklphyfrrihugwnhuzidyaqpbodphhyjiecmryvtgyfsgnaxuvvtoamfuwrlzqkpevigdngbckrwvjvytebhmcvrovixxxtqalwliiapmwifezoperwwypwwghtuswkjvnotxegtqzpvfsauydgpklzotupvnhjcjyldjdgtbipzmnszkqpquvusvgdvfwptpzkisxkvhzposvvnxuhayphfplrdmouyvqmtvmrqxnwykrwxhnnnefmkituyttxeqhrjikemwqylveegrwlvlqdzdwuzjcmpveuscpbcnidfsxbluxxxaepjaqzsaiigzgpxiuyiognquvveszucyiuwpqesmhyfjorspusfvuqyenqlryragxnihdegqllgqoyfgwxaxegenleinvxkiftnkjiipdeqxlakjqufihkjxsupuvontntlsqiswrmovsipyulyqcsxnvjnaqttcblnkejdhjcibayfewgbiuekjlvdysnvolskbptfshwabpysqereamxtoydkrbswowuiyfwfvbfakkgtxnuqwmxwmatbnfchjaampuwmzcmoddmahtavzokckryrizzfxbobwnnzxvghcypcamxuhzbjynlzlkhzjdtgwbdajhxhajdxbedxkpqmbsfcaxtwsegabxvvadlerkbeqpyccrjewzkilrgyzdyiojjrsukewvtenrxzsdlpmbznmkbuotctowchgcwrwbqvfywdsebrjinhahgkasxbirdvilfdazgxlezknwjuhxkafntttljzzkubhgmtwqwokiatoqflpckkmkhfgrohhmalstdmyxuwnanhfbdgtrrsqxxqyctvnaykbzkirloozmhuvrvztdrvapcyubiwxnetdyzdbyihbhjqynumfdkwpzvcpupzouklvwsccgewnmorfiuqatnwmnaozdvzycpvxmrilgsykximfcitsnzsprzduxhwixagyfuecquctgzkopgaxmyvsfxyijfjjgzwhcdivrfmvtkubegkfbrynqxfvsvnzafclkfszwxlvcvikovwasqnixexilkpubsdsozccuoyxtpszkmsmuzmgttkkfhgsuaicsbhzpxzrneomnejqhkfmltwhkvmpefqzdtmadxgtscbdftrkjayulvhlpcprnxgryadrkwoarjgzuatkheuvtdtxiknsfqyuqhowbmnuysnamxenzauxgmlpaltffnaiadgqnpswecimeroavjdlryjtzgznhceqlengueuwdwegjxbjdspirxwegzzpuvujlugrlbfqmlifgsnedlsjrthcfedqpfzayviuigrgqjtqbcimxewmxnidjgjnqshubkwjilnhlaeeyysgxihknkdjoqtibhlfnkfsshgskxyptlnwyokvnruqrtkfliuaknhcmsqmaabvpskppbcwjtblwvfhyyquwkqnidonifgdtivsmcijpdxnsjytxtnmyxvzxrkkdqcusfgsrxwervarycsscpogymccfrjpctwdpcfkkfchiflzitbwazwurzryrmbyvsgnibmmldvrtjeywdydahixdntvfxxyqvhdsofxxbwqkggynybaaoqkyfafjipuqvexmshifjxjgznhpzwiytxkvofxidnfgvgnvpodpzvspntrrsdwhyhsucwjoenayigtmqiaxmlmamohmnrxjiomjvphxslfwrdmltvzrxnrvjlxuyubcwjulunfegfypwxcwpoduekwbjfhhwdijmymzhecummckwegggsjauahmocdwqzyzooylyutivttzebksukgmavbtsmlzujzdyeikabrqrixkismlxthotgkgaoxelhzqknmguwhuqzswalhprdbarubzsbsathyxpqrzihlkepgnnumbozxmbmagwjnvpiqhusbmemaivopofekcervnecptgqsyygxdaiqygvymbhralfqpyzbokmsmknxpibhekqmihvpgqxpmbktqiifcsugzldchfygpdysxmnhilvaaoarcwyxumrwotahailehxbyqgkkutflczojbzttwlgqbobizvsuzxiigzablwqxvvjvxenvuzfwlzijarcoywnuzejoihkerjoivvnaywpgvgmgcqfhexkonshgmgaemudywivlqghwswpjyvktdhnhigizzhiencsrehqvaznmvbvgzdesaeuetfykpmupvxcpbflhnipnhawxiikrrztznzewixwipfsmozbxyswsmymcpwckizzpbbyzamudnoxxhhfitrvzariqiltmhbpiostorafdxodmqseoiefzrmlxgbrniuuzexvhsbnybwrseygkogzghwoicblwsbdgcasydgxcxvptmtkixpwbdzfjhkeeevlqygdudcqxrivhejrctainfzjazvmfmelwulnaxbczealkqfiqwsfjhwprafxwmdrhbbourjpslwrjlhdsptzakqqcwsusgiozuuocftlsupxnetqhealgamhowyoabvacgjhezhrjpssmeyvhvslwzakahkeiloriihntexdphiurvcerwcwkftqwszmtmdwadjbcpxljduejbpazsgluoqnrcouomavbkxryzlvrhxmpstgdxbpsawipusnatocxsoqulkbxevqjbzwecymtydtjjypewmhhhmjpaihybuxiryuqgbjnyspammyzaefvlzmgvtqrvlvzhbxsesqbaghccfdtirwauvweymioyznrgpooqorcmwmzpkyfzgickjqtjwghwtpchudyscinfgjfkkzwlriopfhmjupnpktiakbkttwubfzrdfjdrqibfykggaraoqyswobpngmjjuywxrqpobckbpbtdzqdcgdyafkoflmjxhdljqvtvmdbiyoafmigwxhevfpxucnncwydaiqcnwjrgjxmckkuiaokysatipfylmvflaeqfhrgbhqdvinpbrfwyofmyggbicafcutzucqzxxlsoycvaklcubhbbxwzrhpodloejherwttletirwbsqvbexbvmoeucjogjamnczfaxatywoccklrlkiylgviqhnpqorhylkirlsuvdyqtbcgyqrxoiheicokbavpuwsahlankcggcrahqhvrilyphmtwlpwydfxzvahbbmmkmeigwrxcjomiabkacbxremziklosvbzivmqghrlvvnoarjyxgqsktjpqfvrgpelscokehfjqkrppiwjvygnohkzaqewkkicmplyxpboacgqzdlmtzkgslfcbfdjcrsgokqprdrvquyjpyubienziuldnkxcjciihyszzswkjojeegzgamuuzatubkvdjgurflccyxletmnpbwadsakhickjmvqovwrhmmkwrslbgxydazcpffysbavvieuqetcxipnksjahfzzkmnvahzxovgrcnbvtrdkppmevuscrwlkivmrckwmfsugpizyooqjmbnscraygtujpjjkisytxvqnqyuvqmbvsxdtlriwbrkcdjphgmfqbdisgckrvkxsjnaqeslahrjblequaukjqsbrpiziiqzpkuhjgerhdrirksbhhrvtklrnyykiomxqkpcelkphroqsuvkmivabfxpuahnpqzekwsnrkxqtzhyxfcqlkhudnqoplpcbcyfycmjrmrrbknmsgxckeedhwmmvyugkuqflmtdbhflaujjpnkteeuehxcduiknevguakcfdxubvbppygvanmjnjtmznxirgozwmatnebkseccjnnhoqqdezyygoncmbahbphczsdohgivbtcxdiiljcknizdrsicgrbsefpurbpxjtqnesuojdyvjujbxroxlsxszugihenfpsqlycnoworgrnyjzrknxwldsluuelfqdqsholeoocmvdauugrkdyawfugtmdtmmukvppjlonqidldwxbaeccoehzfyjdlwwzkucephrbahldykixpsskoayumirbxvfzouupznxkvcwdhmqqrfkjmjbyfhykrbirkhekuzlmimapqintpzvgnplovkkqkmzbtlcjiwtgqwvqhdsprxcsgawtovdrltjmyztxrtggcmrubdtltkvmgubsnrhaunvnawexaqytxxalpdconpjcmmeqrhdvwmviwjjizaqrvaftjvbskmtszgycqflgymeipkdsfguftmcbxspeorpnizxzrwszbatgyyygriwpjrpaqwcrykytihsmwaexuqqihxidqtyzalhkcwovezzjknnvhxeazehwoubvpivltgzphqisdlgkkqmegmuisyvjieakiproivnaeuynmjlxoypahxirmzvinpcxklhzhulktsnuhfinjnqozamcxgggjizvlimhupyywinbnockxtaxfmeukildeyqvfumnpdduujaaaxbdsatifqbqqtviimsmbyegsstkhcdtjtabdttbjvqynxzhnfelongxmofcenpnotfvnbmqyeeavqlmzqxnmgdikibxuwbuugtdikkxmcbhtgnlrzxmpskllrytywfveqbbbaauxyvljdyctkvngmkkvzzpnihsymwdlotwvxujmqaqskhabyjcdosdjgalqiplkvhxnazezjbwhymoincwnplbpsdadibmcyovihrpcmbhtwvceyxcousqikemnpioecwzbmmjdbxyaljsmkulvsvoozmujsloxlwsippcwlaoxdgjtyaiolkyniniiakpksqqziutheuqqblfiifccuxcqsxzqahfwyocvwlflwwiesqpkhleyfhjqsbmvwecuwdurnitvmrpohnmqbvmgcuutvdhqzcyibdzlzifxcxvgqtnevvtfktmmqpvvypliyesejxpivylunocnwufizulnwpqnmfavzgkufoxaierswyiiyzbolmqedcuihsywgcqkxaenaqljvrwnmuojckyifjwljzdzbzlgrjevgksaymfaaeahcrmibbszzoxgnwqfyfijrfurliizjtbijwgdskicqnmuhdzypxuvovzqchxrwihstgbviakungphxerhijjrhmhbdmsgwfyxjdhiaxkthgkatvlqegcovxilthhniboaqnwvizabxwlmhyaatqddfwdxfrsrzylimkaimqbikonagevxwiawjwywxziftbzxlxdezrldikqhyjdpyzqdlrrudcefjaswaohhvfasnkurcaxwoiurrgqzrxtrcfiuvitzoqpglmgbpmeekjbywcgzbrpglgujjhfrixloodpupuywaddmkrjkylxdanfjlpsuetrddqndqpfumfffxlzhttdklwktuwzktrmwtsfemhycbhhltyoiwlbroutrvtwktwghemivakwyzwgixvwhoqxuovxslkkhziievwwxafimdhtzccentfyyqbalinpxsryegitavfkgwvykhzcmtopovpzfezmllljqbwwgrvkjgywsisowhcgvsxwtgfvectfpodpptgsgvqwptprpmzdykyuzjxlnibmzzpjeawmgiamrvfqrgybvtlqxcwjmlcoaiflyllvluzzxtslaaxqexzdxdnvrcluspopxvxkycecmjlyfnvrwdwnkxnfmaqrlckuwzwgxkxsakqgfmgvhlwrtkustuwokizjksuogdqqwhyonkcwuquhidvaiepiravjjihbvlsujevpsawagecqvcollazzvthgxnrrozxorzjgjrqzblrfxzqndfavhjvaiftozcldlcxddtatatxndoboxlqcysmotxhxmcdtztgcvybdiusuebvuefozwzehnxzjbxjutwaabqxfuiomqznfysimtprihmbtajodsrntqvjgyubexnrhfgelhbrmexgwiuuuomxvamgadrrszdqghsntsfhsfgliuaqvemewxbsfcvmvviqejevkloomdbdjysawqpiorvzrhrgsnqoeamqnkttzynsrsfhkamdswmnfuytykrzkngcynlowepabfbfuptbyysafaeivimsksbwthkbfrxkhmvwspwyltjwmrsmdfmocsnszlacqheorueucwtwwthymjegpynwdumrztwpxhhsonodwszfzhqundwqdmqspfwwhgoodmgcwidgyzmjwjlostsxtrmukxcfsiudrmkmqigzpyiswiyveufyvvqufjxhalgdejwpmhswzchfbspkcoyrpttrxuwcebcjxogsqgesheujpcmeqfwpmrntkutsvpuwdsqpsxtwkzrwppmyatibvpgcvnjfyzlszyldesviqhetixjqisoclwrdmfxtwoddjegabhwnaexvpvpahvtkezjhxihnusccujsffzsansuiobrrezbtzpnhmzjwuszkpckejshhvyncwznklgklsmakmbkqwwcuejswasvtptlgnqzvyuftzvrldutawjyyhduwpliabwwpyxvqtrwuxvzgfubvpadpzppvnlzmqqtdekmzknmjglhgnpvifuvwrsbiudivzolvtqidhrklyyxcjhlsqcnxrbtikctwxmniknmlpttoormkwxmslrdpmucjxixnyfbaznzwtkhxhsiojwkdvgkmeeaoqatxtxtpbwllrwwgxnufvtjhmtkeaurmtqisniaiglxaerpxlkdwnqowkcpzycimnhxosoyfdadluuopqgwwmzshjfuiqwhtjaxeayhtlugvrclkfymjubuhsanfpwscyexyaxvxoxrurbsfrwxrliamdcwqqmivhafpxbvsvsopbprxfkrwaeatepgnvcxhmxbvjadmmnflmhmhypaznzptoewprirvxxciheutbttrxbhtcoyjlceidlylvrpzeitzkgnhopdgkdztjovsyntcxyjjcolcdpipoxnnbxdwppoyulptnblrarzvjosnximcsoobaioeitxxjlbnqsqvcxblwmuzynunoisylhaezvikfudtfdzilbmvrcwniphvauywdhytpvfbiqndwjowxfapauryferyixvvpnqnrclyxbwsljjeyszcnoaucyhunxkieghvmwhlhyhxowtmsfpuctpphkgxhsikqmehzivuqgzxsdysedxzkltdfqjdaadrvynpyhwaudezwvquinmpnkjvkwtlhkfkxiqllvtrxmjbrfbgvsuqihpwhwopmagizhuknlushnzgiknyublzpnajxcdchfkkodrgqfjlnjjeccdbbhfvalpwrckqntrankglwikiekqzfgweuukfriugiluwoeiwwjzgifmyuwzvyeqvovdynpfsmejzsttuvbtklzxynvauxsgbewrhrvipn
+ 460825
+
+
+### 思路二
+
+
+```
+
+
+
+def main():
+ def swap(point_left,point_right):
+ temp=s[point_left]
+ for i in range(point_left,point_right):
+ s[i]=s[i+1]
+ s[point_right]=temp
+ return point_right-point_left
+
+
+ n=int(input())
+ s=list(input().strip())
+# print(s)
+ i=0
+ res=0
+ while i<=(n//2-1):
+ point_right=n-1-i
+ if s[i]==s[point_right]:
+ i+=1
+ else:
+ point_left=''.join(s[i:point_right+1]).rfind(s[i])+i
+ if point_left==i:
+ if n%2==0:
+ print('Impossible')
+ return
+ else:
+ res+=swap(point_left,point_left+1)
+ else:
+ res+=swap(point_left,point_right)
+ i+=1
+ print(res)
+ return
+main()
+
+
+```
+
+ 5
+ mamad
+ 3
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1470、时间转换.md b/LanQiao/task2基础练习/1470、时间转换.md
new file mode 100644
index 0000000..91c6951
--- /dev/null
+++ b/LanQiao/task2基础练习/1470、时间转换.md
@@ -0,0 +1,58 @@
+## 题目 1470: [蓝桥杯][基础练习VIP]时间转换
+
+时间限制: 1Sec 内存限制: 128MB 提交: 4205 解决: 2804
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1470.html
+
+**题目描述**
+```
+给定一个以秒为单位的时间t,要求用 “< H> :< M> :< S> ”的格式来表示这个时间。< H> 表示时间,< M> 表示分钟, 而< S> 表示秒,它们都是整数且没有前导的“0”。例如,若t=0,则应输出是“0:0:0”;若t=3661,则输出“1:1:1”。
+```
+**输入**
+
+- 输入只有一行,是一个整数t(0< =t< =86399)。
+
+**输出**
+
+- 输出只有一行,是以“< H> :< M> :< S> ”的格式所表示的时间,不包括引号。
+
+**样例输入**
+```
+5436
+```
+**样例输出**
+```
+1:30:36
+```
+
+
+```
+H,M,S=0,0,0
+time=int(input())
+S=time%60
+time=time//60
+M=time%60
+time=time//60
+H=time%60
+print(str(H)+':'+str(M)+':'+str(S))
+```
+
+ 5436
+ 1:30:36
+
+
+
+```
+t=int(input())
+s=t%60
+t=t//60
+m=t%60
+t=t//60
+h=t
+print(str(h)+':'+str(m)+':'+str(s))
+```
+
+ 5436
+ 1:30:36
\ No newline at end of file
diff --git a/LanQiao/task2基础练习/1475、高精度加法.md b/LanQiao/task2基础练习/1475、高精度加法.md
new file mode 100644
index 0000000..f7182a1
--- /dev/null
+++ b/LanQiao/task2基础练习/1475、高精度加法.md
@@ -0,0 +1,92 @@
+## 高精度加法
+
+时间限制: 1Sec 内存限制: 128MB 提交: 2264 解决: 899
+
+提交地址:
+
+https://www.dotcpp.com/oj/problem1475.html
+
+**题目描述**
+
+```
+输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
+
+算法描述
+
+由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。
+
+定义一个数组A,A[0]用于存储a的个位,A[1]用于存储a的十位,依此类推。同样可以用一个数组B来存储b。
+
+计算c = a + b的时候,首先将A[0]与B[0]相加,如果有进位产生,则把进位(即和的十位数)存入r,把和的个位数存入C[0],即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加,这时还应将低位进上来的值r也加起来,即C[1]应该是A[1]、B[1]和r三个数的和.如果又有进位产生,则仍可将新的进位存入到r中,和的个位存到C[1]中。依此类推,即可求出C的所有位。
+
+最后将C输出即可。
+```
+
+**输入**
+
+- 输入包括两行,第一行为一个非负整数a,第二行为一个非负整数b。两个整数都不超过100位,两数的最高位都不是0。
+
+**输出**
+
+- 输出一行,表示a + b的值。
+
+**样例输入**
+
+```
+20100122201001221234567890
+2010012220100122
+```
+
+**样例输出**
+
+```
+20100122203011233454668012
+```
+
+
+```
+a=int(input())
+b=int(input())
+print(a+b)
+```
+
+ 20100122201001221234567890
+ 2010012220100122
+ 20100122203011233454668012
+
+
+
+```
+a=list(map(int,list(input())))
+b=list(map(int,list(input())))
+a=a[::-1]
+b=b[::-1]
+a_point=0
+b_point=0
+carry=0
+re=[]
+while a_point